等值线等值面生成
matlab做隐函数的等值(高)线等值面

matlab做隐函数的等值(⾼)线等值⾯2维及3维空间上隐函数的等值⾯(线)图2维,3维的⽬的都⼀样,就是做出隐函数表⽰的结构图,将函数值为0的点视为表⾯并显⽰出来,然后计算等值线(⾯)所围之外的⾯积(体积)占整个空间的⾯积(体积)的百分⽐。
⼀.2维平⾯隐函数等值线2维平⾯上的等值线图使⽤contourf函数就可以实现。
应该也有许多其他⽅法。
使⽤函数z=\cos(x)*\cos(y)+0.51. 做出带填充的等值(⾼)线图clear all;clc;% 给出定义域,⽣成⽹格。
x = 0:0.01:2*pi;y = 0:0.01:2*pi;[X, Y] = meshgrid(x, y);% 给出隐函数表达式Z = cos(X).*cos(Y)+0.5;% 做等值线图ax = figure;[M, C] = contourf(X, Y, Z);axis off;C.LineWidth = 1;C.ShowText = 'on';⽣成的图像为:根据⼆元函数求极值的⽅法,\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}都等于0,且\frac{\partial^2 f}{\partial x^2}\frac{\partial^2 f}{\partial y^2} - (\frac{\partial^2 f}{\partial x \partial y})^2 > 0,则x,y为函数极值点,若\frac{\partial^2 f}{\partial x^2}和\frac{\partial^2 f}{\partial y^2}都⼤于0,则为极⼩值,都⼩于0,则为极⼤值。
求出函数的极⼤值点分别为(0, 0)、\left(\pi,\pi\right),函数值为1.5。
极⼩值点分别为(0, \pi)、(\pi, 0),函数值为-0.5。
一种基于IDW的等值线、等值面前端生成方法

目前,各GIS 平台及类库均已实现各类插值算法生成等值线、等值面[1-3]。
本文针对水环境治理工程中各类监测数据生成等值线、等值面问题,对等值线、等值面生成的方法和流程进行了设计,提出一种结合反距离加权插值算法[4]、等值线追踪算法、三次样条平滑算法[5]直接在前端计算并渲染等值线、等值面的方法。
并以10个测站某一时段的临时降雨量数据为例,对所提出的等值线、等值面生成方法进行验证,结果表明所提出的方法可以快捷地在前端生成各类监测数据的等值线、等值面。
1等值线、等值面生成方法等值线是在表示连续现象(如高程、温度、降雨量、污染程度或大气压力)的栅格数据集中连接等值位置的线。
这些线要素会将输入中具有同一常量值的像元连接在一起。
等值线的集合常被称为等值线图。
等值线、等值面的生成一般有2种思路:①一种是先进行插值生成等值面栅格图,然后将等值面提取成等值线;②进行插值后,根据等值线追踪算法进行插值点连接生成一条尽量闭合且平滑的曲线。
本文拟采用根据插值点直接连接成一条闭合曲线的思路生成等值线、等值面。
生成等值线、等值面的关键是离散点的插值。
离散点插值的算法非常多,如克里金插值[6]、反距离加权插值(IDW)等。
根据地理学第一定律[7]:地物之间的相关性与距离有关,一般而言,距离越近,地物间相关性越大;距离越远,地物间相异性越大。
所以本文拟采用反距离加权插值(IDW )算法实现根据已知点算出未知点的检测值。
等值线、等值面的生成一般有2种解决方案:一种是后台算法计算结果,前端展示;另一种是前端直接计算结果并展示。
本文拟采取前端直接生成等值线、等值面的解决方案。
收稿日期:2020-04-30。
一种基于IDW 的等值线、等值面前端生成方法殷甲伟1,2,房晓亮1,2,余豪1(1.中国电建集团中南勘测设计研究院有限公司,湖南长沙410014;2.GIS 技术应用研究中心,湖南长沙410014)摘要:在对等值线、等值面生成算法进行分析的基础上,针对流域治理一体化管控平台的降雨量等监测数据,设计了降雨量等监测数据的等值线、等值面生成算法流程。
surfer与ArcGIS生成等值线和等值面

surfer
与 Arcgis 生成等值线和等直面的步骤如下: 准备 surfer 用的 book1.dat 文件,格式如下: Y 40.8 40.72 Z 1 116.24 … …
2、在 surfer 中,选择 Grid->data 菜单,打开 book1.dat 文件,单击 OK,生成 book1.grd 文件 3、在 surfer 中,选择 file->open 菜单,打开 book1.grd 文件,然后选 择 File->Save as ,保存为 book1.dem 4、在 Arcgis 中打开 book1.dem 文件,用 spatial analyst->surface analysis->contour 工具,在弹出的对话框中,等高线间隔根据需要设 置,确定,生成 contour.shp 5、用准备好的区域的边界去剪切等高线,生成 contour_clip.shp 6、用 feature to point 工具,生成 contour_clip_FeatureToPoint.shp 7、用 feature to polygon 工具,选择区域图层和 contour_clip.shp,lable layer 选 contour_clip_FeatureToPoint.shp 生成等值面, 注意如果区域图 层和 contour_clip.shp 没有相交,要用 buffer 工具向内(-0.005)生成 新的区域,然后再用 feature to ploygon 工具处理
等值线等值面的生成

• 如图所示,(x0, y0) 为“-”,(x0, y1) 为“+”,则交点为
xt x0 Ft F00 yt y0 F F ( y1 y0 ) 01 00 y0 ( F01 Ft ) y1 ( Ft F00 ) F01 F00
网格序列法
• 如何从中选择一种正确的连接方式呢?这可从单元内的双线性插 值函数分析入手。由于在单元边上采用了线性插值,由此单元面 上函数值的变化是双线性的,
F ( x , y ) a a x a y a xy 0 1 2 3
• 即等值线在单元内不是直线段而是双曲线。二义性连接可通过求 该双曲线两条渐近线交点处的函数值来判定,这是因为渐近线的 交点总是与其中一对顶点落入同一区域内 ,如渐近线交点为 “+”,则取图5a的连接方式;如为“-”,则取图5b的连接方 式。即在图5a中,表示单元中部为“+”,在图5b中,表示单元 中部为“-”。在实际计算中,为简化计算,往往采用单元对角 线交点代替渐近线交点的计算。
一 Cuberille方法(立方体方法)
网格序列法
• (1) 将网格点分为“IN”和“OUT”两种状态,表示该点在等值线 内,或在等值线外。如果 Fij≤Ft ,则顶点 (xi, yj) 为“ IN” ,记为 “-”;如果Fij﹥Ft,则顶点(xi, yj)为“OUT”,记为“+”。 • (2) 如果单元四个顶点全为“+”,或全为“-”,则网格单元 与值为Ft的等值线无交点,否则 • (3) 对于两个顶点分别为“+”、“-”的单元边,可用线性插 值计算等值线在这条边上的交点。
第 3章
二维标量场等值线的生成
二维标量场可看成是定义于某一个面上的二维标量函 数F=F(x, y),所谓等值线是由所有点(xi, yi)构成,其中F(xi, yi) =Ft(为一给定值),将这些点按一定顺序连接起来就 组成了函数值为Ft的等值线。对于二维标量场,其数据往 往是分布在规则网格点上的,常用的等值线抽取方法有网 格序列法和单元剖分法。
使用sufer制作等值线图(等厚图等)及从sufer中转mapgis
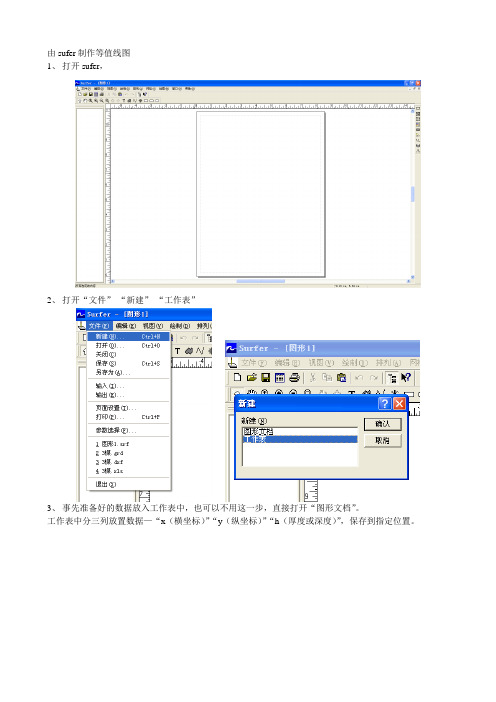
1、打开sufer,
2、打开“文件”-“新建”-“工作表”
3、事先准备好的数据放入工作表中,也可以不用这一步,直接打开“图形文档”。
工作表中分三列放置数据—“x(横坐标)”“y(纵坐标)”“h(厚度或深度)”,保存到指定位置。
4、打开“网格”-“数据”,打开你存数据的excel表格,x对应“x”所在列,y对应“y”所在列,z对应“h”所在列。
5、出来的sufer报告不用管,不用保存。打开“地图”-“等值线图”-பைடு நூலகம்新建等值线图
”,成功生成等值线图。
5、打开“文件”-“输出”-“类型选择cad-dxf”,接下来就可以用mapgis打开dxf生成点、线、面即可。
6、sufer中等值线图出来后可以改变其等值线间距和起始值。
右击图片位置,选择“属性”—“等级”,在里面修改起始值,间距和是否显示标注。
marching cubes 5个三角形的等值面

marching cubes 5个三角形的等值面全文共四篇示例,供读者参考第一篇示例:Marching Cubes算法是一种用于生成等值面的计算机图形学算法。
它可以将三维数据集中的体素(立方体像素)转换为多边形网格,从而形成真实感观的三维模型。
在这篇文章中,我们将讨论Marching Cubes算法生成的五个三角形等值面。
Marching Cubes算法的原理是将体素网格中的每个体素转换为一个八位二进制数,其中每一位代表该体素内是否包含等值面。
然后根据这些二进制数生成对应的多边形网格。
在我们的示例中,我们假设三维数据集是一个立方体,其中包含五个三角形等值面。
让我们考虑一个简单的等值面案例,具有以下的三维数据集:```0 1 01 1 10 1 0```这个数据集代表一个平面等值面,其中只有中间的体素为1,其他体素为0。
根据Marching Cubes算法,我们可以将这个数据集转换为一个包含五个三角形的等值面网格。
接下来,我们将对每个体素应用Marching Cubes算法,并逐步生成五个三角形等值面。
我们将立方体分为八个体素,对每个体素应用Marching Cubes算法,得到以下结果:```0 11 1```第一个体素包含三角形等值面的一个角点和对应的边,接着我们将体素分隔成更小的体素,重复这个过程。
在第四步,我们得到了一个三角形等值面的完整定义,包括所有的角点和法线。
```A/ | \D--B--C\ | /E```在以上示意图中,A、B、C、D、E代表三角形等值面的角点,通过连接这些点可以得到等值面的完整形状。
我们还可以计算出三角形等值面的法线,以便在渲染过程中增加真实感。
通过这个简单的示例,我们可以看出Marching Cubes算法是一种有效的方法来生成真实感触等值面的多边形网格。
在实际应用中,我们可以通过调整阈值来生成不同形状的等值面,从而实现更加复杂的三维模型。
Marching Cubes算法是一个非常有用的算法,可以帮助我们将三维数据集转换为可视化的三维模型。
绘制等值线(等高线)方法

如何根据离散点自动绘制等值线(等高线)之三角形法自动绘制等值线的方法从技术方向上看可以分为两大类,插值和曲线拟合.其中曲线拟合总的来说效果不如插值算法经典和应用广泛,效果也较逊色.这里着重介绍插值算法.其中插值算法中,按照方式不同分为离散点客观化和三角网方式.两者区别在于三角网计算主要在生成三角网过程,省去了插值到格点的过程.而客观分析过程则是将离散点分析到格点后再内插到细网格,然后大多利用追踪法生成等值线,也有在这里再使用曲线拟合.1、三角形算法a、首先生成delaunay三角形,这一点在我的帖子"delaunay triangulation之丰衣足食“内有源程序,大家可以参考。
b、随后需要在三角形的边上插补等值点。
要确定某个三角形的边上是否有等值点,需要进行判断和处理。
注意:如果某原始数据点和等值线值相同,将该点改变一个微量。
如果一个三角形三顶点的值相同则各边无等值点。
如果一个三角形的任意边两端点(A、B〕的Z值(Za、Zb)满足满足(Zd-Za)*(Zd-Zb)<0,其中Zd代表等值线的值,则该边必有等值点,其平面位置是Xd=Xa+(Xb-Xa)*(Zd-Za)/(Zd-Za) , Yd=Ya+(Yb-Ya)*(Zd-Za)/(Zb-Za)。
每个三角形上不可能三边都有同值的等值点,另一边上必定有同值的等值点。
c、等值点的追踪。
为了能将内插的等值点顺序追踪排列,绘出等值线,还必须找出相互重叠的环形网内所计算的等值点间的平面位置关系。
因每个环形网都是由多个三角形组成的,我们先简单分析一下单个三角形中存在等值点的情况。
由于不必考虑等值线穿过端点,如果一个三角形的边上存在等值点的话,只可能在某两条边上存在等值点,而不可能三条边上同时都有。
也就是说,只要三角形一边上存在等值点,则其余的两条边中必有一边存在等值点。
根据上面的约定,我们再研究等值线穿过任一环形网中两条及两条以上相邻的径边时,可能出现的几种情形:① 等值线不通过环形网的界边。
利用ARCENGINE生成等值线

我想利用ARCENGINE生成等值线,在生成等值线前需要先生成表面(surface),利用IInterpolationOp.IDW 方法生成表面,可是在这个地方怎么设置Z字段和网格单位大小啊,请教!已成功,谢谢'--------------------生成等值线--------------------------Public Sub Contour()Dim pInterpolationOp As IInterpolationOpSet pInterpolationOp = New RasterInterpolationOp' Create the input point objectDim pInputDataset As IGeoDatasetDim pFeatLayer As IFeatureLayer' Calls function to open the point dataset from diskSet pFeatLayer = basSub.FindLayerName(frmMain.MapControl1, "水准测量点")Set pInputDataset = pFeatLayer' Define the search radiusDim pRadius As IRasterRadiusSet pRadius = New RasterRadiuspRadius.SetVariable 12'Create FeatureClassDescriptor using a value fieldDim pFCDescriptor As IFeatureClassDescriptorSet pFCDescriptor = New FeatureClassDescriptorpFCDescriptor.Create pFeatLayer.FeatureClass, Nothing, "沉降量"'Set cellsize for output raster in the environmentDim dCellSize As DoubledCellSize = 200Dim pEnv As IRasterAnalysisEnvironmentSet pEnv = pInterpolationOppEnv.SetCellSize esriRasterEnvValue, dCellSize'Perform the interpolationDim pOutRaster As IRasterSet pOutRaster = pInterpolationOp.IDW(pFCDescriptor, 2, pRadius)'Add output into ArcMap as a raster layerDim pOutRasLayer As IRasterLayerSet pOutRasLayer = New RasterLayerpOutRasLayer.CreateFromRaster pOutRasterfrmMain.MapControl1.AddLayer pOutRasLayerEnd Sub本文介绍c#写的利用ArcGIS Engine生成等值线的方法。
等值线绘制算法

1.等值线绘制的过程分为三个步骤,离散数据网格化、等值线生成
以及等值线图的填充。
项目中的数学模型将离散数据进行了网格化,本模块需要提供等值线的生成和等值线几何体的绘制。
2.等值线的生成方法。
规则化的网格数据提供了每一个网格点上的
坐标和浓度值,基本思路是从区域边界开始,利用线性插值逐网格跟踪等值线得到等值线在其所穿过的网格边上等值点的坐标,保存这些坐标并根据一定的方位判别法对这些等值点进行排序,为下一步绘制几何体做准备。
3.等值线几何体的绘制。
一个网格内的等值线确定为直线,不需要
进行平滑处理。
首先对上一步骤中得到的各条等值线按照其起点的位置进行排序,排序的顺序与等值线追踪的顺序一致,即区域左、上、右、下、内部等值线,内部等值线按照横坐标递增排序,这样排好序的等值线按照起点坐标左、上、右、下、内部的顺序保存起来。
整个算法的基本描述如下:
1) 按起点纵坐标从下至上的顺序对起点在左边界上的等值线排序;
2) 按起点横坐标从左至右的顺序对起点在上边界上的等值线排序;
3) 按起点纵坐标从上至下的顺序对起点在右边界上的等值线排序;
4) 按起点横坐标从右至左的顺序对起点在下边界上的等值线排序;
5) 按起点横坐标从左至右的顺序对内部封闭的等值线排序;
6) 填充第三种等值线与网格下边界或左边界以及起点和终点所在的边界所围的区域。
对最后一条等值线, 则还需填充与网格上边界或右边界所围的区域;
7) 填充第二种等值线与起点和终点所在的边界以及这二边界相交的顶点所围的区域;
8) 填充第一种等值线与起点和终点所在的边界的顶点所围的区域;
9) 填充内部封闭等值线所围的区域.。
一种快速的等值线生成算法

一种快速的等值线生成算法作者:董肇伟卢海达倪广元王剑秦来源:《科技资讯》2014年第10期摘要:本文提出了一种新的等值点位于网格点时,对等值点的调整方法;在分析已有等值线追踪算法的基础上,提出了一种基于TIN网格的快速等值线追踪算法,实验表明该算法具有较高的执行效率。
关键词:等值线等值点 TIN网格中图分类号:TP391.41 文献标识码:A 文章编号:1672-3791(2014)04(a)-0033-02等值线图能直观地展示数据的变化趋势,是众多领域展示成果的重要图件之一,被广泛应用于石油勘探、矿物开采、气象预报等众多领域。
等值线的绘制是指从大量采样数据中提取出具有相同值的点的信息,并生成形态完整、位置精确的等值线的过程,包括等值线网格化、等值线追踪、等值线光滑、等值线填充与标注几个处理步骤[1]。
其中等值线网格化是对网格边进行线性插值,进而求出等值点的过程。
等值线的追踪则是利用等值线网格化产生的等值点数据,将其中相同等值点进行连接的过程。
等值线追踪的传统方法是,在网格单元边上选取一个等值点,寻找邻近的等值点,顺次连接成线,直到等值点回到起始点或位于工区边界,完成单条等值线的追踪,并以此为基础遍历所有的等值点。
在追踪过程中,等值线分为闭合与非闭合两种情形,需要先追踪开曲线,再追踪闭曲线,否则不能确保结果正确。
特定的搜索顺序提高了处理过程的复杂性,增加了网格单元的重复搜索次数,致使效率低下。
针对此类问题,很多学者提出了在不规则三角网(TIN网格)下的改进方法,成建梅[2]等提出为三角形三边分别赋予不同的权值,以方便确定三角形单元内等值点的位置。
但是这只是对局部的改进,未涉及等值线追踪过程的优化。
黄维科[3]等基于三角形单元内等值线段容易确定的事实,提出了使用“焊接法”将相同的等值点连接从而生成整条等值线的方法。
但是在搜索等值线段间的共同等值点时,需要对已确定的等值线段进行遍历,执行效率提高幅度有限;并且使用的是简单的坐标值判别法,容易因机器误差引起错误结果。
高中地理等值线知识点

高中地理等值线知识点等值线也叫等高线或等位线,是地理学中用于表示地形或其他物理现象的方式之一。
在地图上,等值线是连接具有相同数值的点的曲线。
以下是高中地理中关于等值线的一些知识点:1. 定义:等值线是连接相同数值的点的曲线,可以用来表示地形高度、温度、降雨量等一些物理现象或属性的变化情况。
2. 等值线的特点:- 等值线一定是一条闭合的曲线。
- 等值线上的每一个点都具有相同的数值,通常是等距离的。
- 相邻等值线之间的间距代表了变化的大小。
间距越小表示变化越剧烈,间距越大表示变化越平缓。
- 等值线上的每一点都表示了该点所对应的数值。
3. 绘制等值线:- 绘制等值线需要有一系列的数值点的数据。
- 根据数据,给定等值线的间距,一般可以在图上标出等值线的值,并连接各点绘制出等值线。
- 在等值线的绘制中,也可以使用等值面,即在相邻的等值线之间填充颜色,用来表示不同的数值范围。
4. 应用:- 通过等值线可以表示地形高度的变化,可以用于绘制地形图和高程图,帮助人们了解地形和地势。
- 等值线也可以表示其他地理现象,比如气温、降雨量、海洋水深等,利用等值线可以观察和分析这些地理现象在不同地区的分布情况。
5. 等值线图的读取:- 等值线图可以通过观察等值线的间距来了解变化的幅度。
- 等值线的稀密程度可以表示某一现象在不同地区的变化情况。
- 等值线的形态可以表示地势的变化情况,比如陡峭的山脉、平坦的平原等。
总之,等值线是地理学中一种常用的表示地形或其他物理现象的方式,通过绘制和读取等值线图可以更好地了解地理现象在空间分布上的变化。
等值线原理

等值线原理
等值线原理是地图上用来表示地形高度或其他属性分布的一种方法。
它通过连接等值线上等值点的方式来显示地形或属性的分布。
等值线上的每个点都具有相同的值,这些值可以表示高度、温度、气压、降水量等。
这些等值点相互连接形成等值线,而等值线的密度和形状可以反映出地形或属性的变化情况。
在制作等值线图时,需要先确定一系列等值点,并用线段将它们连接起来。
这些线段的形状和走向可以显示出地形特征,例如山脉、河流、山谷等。
在实际应用中,等值线图可以帮助我们分析地形地貌、气候分布、水文系统等。
例如,在地理学和地质学研究中,等值线图可以帮助研究者更好地理解地球表面的变化;在气象学中,等值线图可以用来预测天气变化和风险评估等。
总之,等值线原理是一种常用的表达地形或其他属性分布的方法,它通过连接等值点来显示出分布的变化情况,帮助我们更好地理解地理环境。
等值线图生成
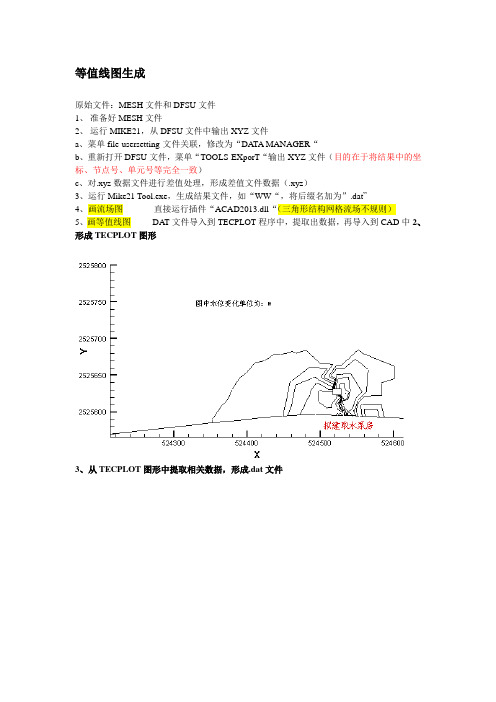
等值线图生成
原始文件:MESH文件和DFSU文件
1、准备好MESH文件
2、运行MIKE21,从DFSU文件中输出XYZ文件
a、菜单file-usersetting-文件关联,修改为“DA TA MANAGER“
b、重新打开DFSU文件,菜单“TOOLS-EXporT“输出XYZ文件(目的在于将结果中的坐标、节点号、单元号等完全一致)
c、对.xyz数据文件进行差值处理,形成差值文件数据(.xyz)
3、运行Mike21 Tool.exe,生成结果文件,如“WW“,将后缀名加为”.dat”
4、画流场图直接运行插件“ACAD2013.dll“(三角形结构网格流场不规则)
5、画等值线图DA T文件导入到TECPLOT程序中,提取出数据,再导入到CAD中2、形成TECPLOT图形
3、从TECPLOT图形中提取相关数据,形成.dat文件
Mesh show 变为no
Data-extract
Zone style
4、启动CAD ,引入插件(.dll 文件),直接打开TECPLOT 数据格式即可进行等值线图绘制;
流场图生成
1、 新建DFS2文件
坐标很重要,要记下来
需要修改完成后另存为.dfs2文件
新建文件
双击
选择已生成的DFS2文件
勾选要输出的变量
选中起始、结束的时段,TIME修改,点击SELECT,如下:
输出TXT文件
点击,成功后出
现以上界面
对TXT文件进行处理(加上中心修正坐标值),形成数据文件,另存为CSV文件,再运行姜工流场处理程序(CAD-流场后处理)。
举例详细说明等值面的计算原理

举例详细说明等值面的计算原理等值面是地球科学中常用的一种数学表示方法,用于展示地球上某个特定属性在空间上的分布情况。
等值面通过连接具有相同数值的点,在三维空间中形成一个平面或曲面,以显示地球某一属性的分布情况。
等值面的计算原理主要基于插值方法。
插值是一种通过已知数据点之间的推断来估计未知点数值的方法。
在等值面的计算过程中,首先收集地球表面上具有特定属性数值的离散数据点。
这些数据点可以来自于地理测量或者遥感技术获取的数据。
接下来,使用插值方法通过已知数据点推断未知点的数值,从而得到连续的数值表面。
常用的插值算法包括反距离权重法、Kriging法和三角剖分法等。
其中,反距离权重法是一种简单且常用的插值方法。
它基于已知点与未知点之间的距离和属性值之间的关系,通过加权平均的方式计算未知点的属性值。
在计算等值面时,反距离权重法会根据离未知点较近的已知点的权重进行插值,并且随着距离增加而逐渐减小权重,以反映距离远的点对未知点的影响较小。
另一个常用的插值方法是Kriging法,它是一种基于空间自相关性的插值方法。
Kriging法利用已知点之间的空间相关性来推断未知点的属性值。
通过计算已知点之间的差异程度和空间相关性,Kriging法可以准确地估计未知点的属性值,并生成连续的等值面。
三角剖分法是一种基于三角形的插值方法。
它通过将地球表面上的点连接起来,形成不规则的三角形网格。
每个三角形的顶点都具有已知的属性值,通过插值计算三角形内部的点的属性值。
通过连接相同属性值的点,可以得到连续的等值面。
在等值面的计算中,选择合适的插值方法是十分重要的,它会直接影响到结果的准确性和可靠性。
不同的插值方法适用于不同类型的数据和空间分布情况。
因此,在实际应用中,需要根据数据的特点和分析目的选择合适的插值方法,以获得准确可靠的等值面结果。
多元函数的等值线

多元函数的等值线多元函数的等值线是指在多元函数的定义域中,取定一个特定的函数值,将函数的定义域中相应的点连接起来形成的曲线或曲面。
等值线的形状和分布可以反映出函数在定义域内的变化规律,具有重要的物理和几何意义。
对于二元函数,即定义在二维平面上的函数,其等值线可以形成一条曲线或多条曲线。
例如,对于方程f(x,y)=c,其中c为常数,可以将f(x,y)视为z轴上的高度,等值线就是该曲面与xoy平面的交线。
等值线的高度等于常数c,因此等值线可以看作是在平面上表示函数f(x,y)取常数值c的点的集合。
这些点可以是连续的曲线,也可以是孤立的点。
不同的常数c对应不同的等值线,通过改变c的值,可以得到函数在二维平面上的等值线分布情况。
对于三元函数,即定义在三维空间中的函数,其等值线可以形成一条曲线、多条曲线或曲面。
例如,对于方程f(x,y,z)=c,其中c为常数,可以将f(x,y,z)视为空间中的等值面,等值线就是该等值面在xoy平面、yoz平面或xoz平面上的交线。
等值线的高度等于常数c,因此等值线可以看作是在空间中表示函数f(x,y,z)取常数值c的点的集合。
这些点可以是连续的二维曲线或三维曲面,也可以是孤立的点。
不同的常数c对应不同的等值线,通过改变c的值,可以得到函数在三维空间中的等值线分布情况。
等值线的形状和特征反映了函数在定义域内的变化规律。
对于二元函数,等值线的密集程度和曲线的陡峭程度表示了函数在该区域内的变化速率和梯度大小。
等值线的密集表示函数变化较快,而等值线的稀疏表示函数变化较慢。
曲线的陡峭程度表示函数的斜率和变化方向。
在物理学中,等值线可以用来表示电场、温度场、地形图等,从而揭示出这些量在空间中的分布情况。
对于三元函数,等值线的形状和分布更加复杂。
等值线的特征可以用来表示函数的梯度和曲率。
梯度表示函数在某一点处的变化率和变化方向,等值线在梯度方向上的投影越长,表示函数的变化越剧烈;而曲率表示函数曲线的弯曲程度,等值线的曲率越大,表示函数的变化越快。
面绘制方法

嵌套树Nesting tree
• 嵌套树:描述每一断 层上轮廓线的嵌套关 系。树中每一结点对 应于一条轮廓线,其 根结点对应于一虚拟 的包围所有轮廓线的 外轮廓线,树中每一 结点的后续结点对应 于被该结点的轮廓线 所直接包围的所有轮 廓线。
合,将该集合称为一个“水平集”。 • 分析“水平集”中双曲线拓扑性质的变化,可以简单直观
地确定体素内部曲面的拓扑和几何形状。
临界点与临界线
• 4种存在二义性的体素 中的等值面都存在临 界点(右图中两条点划 线的交点),“水平集” 中过临界点的等值线 (图中点划线),称 之为临界曲线。
确定临界点与临界线
• 连通分叉:在一个层面上有嵌套的两条等 值线,在另一个层面上是一条等值线。
马鞍面三角片的处理
马鞍面三角片的处理: • 在层面间引入附加点来重构等值面。 • 当层面间距离较小时,也可直接将附加点加在某一层面上,
不会产生太大的视觉误差。如上页图所示,两条轮廓线被 归类到单条轮廓线。 另外一种三角面片——极值点三角片:建立平面三角片网。
• 计算法向量:采用中心差 分计算出体素顶点处的梯 度,再用线性插值计算等 值点处的梯度值作为该点 的法向量。
二义性
• 在14种模式中,某 3A
3B
些模式存在二义性,
如右图示。
• 下节将着重讨论4
7B
7C
种存在二义性的体
素中等值面的重构
方法。
12A
12B
6A
6B
7D
10A
13A
13B
13E
(a)
(b)
一种快速的等值线生成算法

信 息 技 术33科技资讯 S CI EN CE & T EC HNO LO GY I NF OR MA TI ON 等值线图能直观地展示数据的变化趋势,是众多领域展示成果的重要图件之一,被广泛应用于石油勘探、矿物开采、气象预报等众多领域。
等值线的绘制是指从大量采样数据中提取出具有相同值的点的信息,并生成形态完整、位置精确的等值线的过程,包括等值线网格化、等值线追踪、等值线光滑、等值线填充与标注几个处理步骤[1]。
其中等值线网格化是对网格边进行线性插值,进而求出等值点的过程。
等值线的追踪则是利用等值线网格化产生的等值点数据,将其中相同等值点进行连接的过程。
等值线追踪的传统方法是,在网格单元边上选取一个等值点,寻找邻近的等值点,顺次连接成线,直到等值点回到起始点或位于工区边界,完成单条等值线的追踪,并以此为基础遍历所有的等值点。
在追踪过程中,等值线分为闭合与非闭合两种情形,需要先追踪开曲线,再追踪闭曲线,否则不能确保结果正确。
特定的搜索顺序提高了处理过程的复杂性,增加了网格单元的重复搜索次数,致使效率低下。
针对此类问题,很多学者提出了在不规则三角网(TIN网格)下的改进方法,成建梅[2]等提出为三角形三边分别赋予不同的权值,以方便确定三角形单元内等值点的位置。
但是这只是对局部的改进,未涉及等值线追踪过程的优化。
黄维科[3]等基于三角形单元内等值线段容易确定的事实,提出了使用“焊接法”将相同的等值点连接从而生成整条等值线的方法。
但是在搜索等值线段间的共同等值点时,需要对已确定的等值线段进行遍历,执行效率提高幅度有限;并且使用的是简单的坐标值判别法,容易因机器误差引起错误结果。
1 改进的等值线生成算法现在常用的用于生成等值线的网格有矩形网格、TIN网格等。
综合考虑,本文选用TIN网格。
生成等值线的主要步骤中,等值线的网格化处理与等值线的追踪是基础与关键,直接影响等值线的准确度和生成速度。
接下来将针对TIN网格,介绍对这两个过程的改进。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元剖分法
• 中心点函数值Fmid的计算可采用两种方式: • 如有显式函数F(x, y),则Fmid = F(xmid, ymid); • 如只有四个点的函数值,无法求显式函数形式,则可用
四点的平均值代替Fmid。 • 图7列出了几种可能的情况,可以看出,通过利用矩形
单元中点的函数值,等值线的精度提高了,其抽取过程 也相对简单些。
第1页/共60页
网格序列法
• (1) 将网格点分为“IN”和“OUT”两种状态,表示该点在等值线 内,或在等值线外。如果Fij≤Ft,则顶点(xi, yj)为“IN”,记为 “-”;如果Fij﹥Ft,则顶点(xi, yj)为“OUT”,记为“+”。
• (2) 如果单元四个顶点全为“+”,或全为“-”,则网格单元 与值为Ft的等值线无交点,否则
第5页/共60页
第6页/共60页
第7页/共60页
网格序列法
• 如何从中选择一种正确的连接方式呢?这可从单元内的双线性插 值函数分析入手。由于在单元边上采用了线性插值,由此单元面 上函数值的变化是双线性的,
F(x, y) a0 a1x a2 y a3 xy
• 即等值线在单元内不是直线段而是双曲线。二义性连接可通过求 该双曲线两条渐近线交点处的函数值来判定,这是因为渐近线的 交点总是与其中一对顶点落入同一区域内,如渐近线交点为 “+”,则取图5a的连接方式;如为“-”,则取图5b的连接方 式。即在图5a中,表示单元中部为“+”,在图5b中,表示单元 中部为“-”。在实际计算中,为简化计算,往往采用单元对角 线交点代替渐近线交点的计算。
第10页/共60页
第11页/共60页
第12页/共60页
第4章 等值面的生成
所谓等值面是指空间中的一个曲面,在该曲面上函数 F(x, y, z)的值等于某一给定值Ft,即等值面是由所有点 SFt = {(x, y, z):F(x, y, z) = Ft}组成的一个曲面。
等值面技术在可视化中应用很广,许多标量场的可视 化问题都可归纳为等值面的抽取和绘制,如各种等势面、 等位面、等压面、等温面等。等值面技术除生成等值面的 几何表示外,还包括显示技术,如要考虑合适的光照模型、 解决等值面的相互遮挡等。等值面的生成和显示也是可视 化研究中的一个重要领域。
网格序列法
• 网格序列法(grid sequence)的基本思想是按网格单元的排列次序,
逐个处理每一单元,寻找每一单元内相应的等值线段,在处理完
所有单元后,就自然生成了该网格中的等值线分布。 • 规则网格数据等值线的生成 • 设一规则网格数据如图所示,网格线是相互正交的,每一网格单
元是一矩形,其中四个顶点分别为(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1),对应的值分别为F00、F01、F10、F11。要在该单元内生成值 为Ft的等值线,其主要计算步骤为: • 逐个计算每一网格单元与等值线的交点; • 连接该单元内等值线的交点,生成在该单元中的等值线线段; • 由一系列单元内的等值线线段构成该网格中的等值线。 • 网格单元与等值线的交点计算主要是求各单元的边线与等值线的 交点。假设函数在单元内呈线性变化,可以采用顶点判定,边上 插值的方法计算交点,具体步骤为:
• (3) 对于两个顶点分别为“+”、“-”的单元边,可用线性插 值计算等值线在这条边上的交点。
• 如图所示,(x0, y0) 为“-”,(x0, y1) 为“+”,则交点为
xt x0
yt
y0
Ft F00 F01 F00
( y1
y0 )
y0
• (F01 Ft )
y1 (Ft
F00 )
第13页/共60页
一 Cuberille方法(立方体方法)
• Cuberrille等值面方法又称Opaque Cube算法,最初由Herman等 人提出,后来又多次改进。算法主要分为两个步骤。
• (1) 确定边界单元 • 对于规则网格数据,其网格单元可看成是正六面体单元,整个三
维数据就是由这种正六面体组成的,这种组成三维图象的基本正 六面体单元称为体元。对于给定的阈值Ft,遍历体数据中的各个 单元,将组成体元8个顶点上的值与Ft进行比较,找出顶点值跨 越Ft的所有体元,即体元中有的顶点值大于阈值,有的顶点值小 于阈值,因此体元内包含等值面片,这就是边界单元。 • (2) 绘制各边界单元的6个多边形面,即将等值面看成是由各单元 的六个外表面拼合而成。
• ② 有4个交点,即“+”、“-”顶点的分布相互交叉,这时的 连接在规定了函数的走向后,可确定P,R为入点,S,Q为出点, 连接情况如图4b所示。
• 在上述②的情况下,如果不规定等值线的走向,其实存在两种连 接方式,见图5。在实际情况中,这两种方式都是可能的,这种 二义性的主要原因是在该单元内存在一马鞍点。
F01 F00 第2页/共60页
网格序列法
• 在每一单元内计算出等值线与该网格单元边的交点后,利用这些 交点,就能构成在该单元内的等值线段。为了正确地连接交点生 成等值线段,必须规定等值线的方向。等值线的方向定义如下:
• 沿等值线走,大于等值线值的点在等值线的左边,小于等值线值 的点在等值线的右边。也就是“-”点在等值线的右边,“+” 矩形单元可分如下四种情况进行:
• (1) 顶点全为“+”,或全为“-”,无等值线段; • (2) 有一个顶点为“+”或“-”,共可求出两个交点,有一条
等值线段,如图3。
第3页/共60页
第4页/共60页
网格序列法
• (3) 有两个“+”,两个“-”顶点的情况,根据顶点的分布又 可分成下面两种情况:
• ① 有两个交点,即两个“+”或两个“-”的顶点位于同一条单 元边上,等值线段的连接如图4a所示。
第8页/共60页
单元剖分法
• 在网格序列法中,提出了解决矩形单元内等值线的生成 算法,其中马鞍点二义性的解决是算法的一个主要复杂 点,除此之外人们还提出了单元剖分法,该方法与矩形 单元法相比,其主要特点是采用三角片简化单元内等值 线的抽取,无需再进行马鞍点的判定,但处理的单元数 是原来的四倍。
• 算法的基本思想是利用对角线将矩形单元分成四个三角 形单元,见图6,求出中心点的函数值,等值线的抽取 直接在每个三角片中进行。由于每一个三角片至多只包 含一条等值线,因而在由三角片的三个点决定的平面内, 可直接用直线段连接等值线。
