微积分曹定华版课后题答案习题详解

合集下载

微积分(曹定华)(修订版)课后题答案第九章习题详解

第9章习题9-1．判定下列级数的收敛性：115n n a ∞=⋅∑（＞）； ∑∞=-+1)1(n n n∑∞=+131n n ∑∞=-+12)1(2n nn ∑∞=+11ln n n n∑∞=-12)1(n n∑∞=+11n n n 0(1)21n n n n ∞=-⋅+∑．解：（）该级数为等比级数，公比为1a 且0a > 故当1||1a < 即1a >时，级数收敛，当1||1a≥即01a <≤时，级数发散（）(1n S n =++++1=lim n n S →∞=∞∴1n ∞=∑发散（）113n n ∞=+∑是调和级数11n n ∞=∑去掉前项得到的级数，而调和级数11n n ∞=∑发散，故原级数113n n ∞=+∑发散（）1112(1)1(1)222n n nn n n n ∞∞-==⎛⎫+--=+ ⎪⎝⎭∑∑ 而1112n n ∞-=∑ 1(1)2m n n ∞=-∑是公比分别为12的收敛的等比级数，所以由数项级数的基本性质知111(1)22n n n n ∞-=⎛⎫-+ ⎪⎝⎭∑收敛，即原级数收敛（）lnln ln(1)1nn n n =-++ 于是(ln1ln 2)(ln 2ln 3)[ln ln(1)]n S n n =-+-+-+ln1ln(1)ln(1)n n =-+=-+故lim n n S →∞=-∞ 所以级数1ln1n nn ∞=+∑发散（）2210,2n n S S +==-∴lim n n S →∞不存在，从而级数1(1)2n n ∞=-∑发散（）1lim lim10n n n n U n→∞→∞+==≠ ∴ 级数11n n n ∞=+∑发散（） (1)(1)1, lim 21212n n n n n n U n n →∞--==++ ∴ lim 0n x U →∞≠，故级数1(1)21n n nn ∞=-+∑发散．判别下列级数的收敛性，若收敛则求其和：∑∞=⎪⎭⎫ ⎝⎛+13121n n n ；∑∞=++1)2)(1(1n n n n∑∞=⋅12sin n n n π0πcos 2n n ∞=∑．解：（）1111, 23n n n n ∞∞==∑∑都收敛，且其和分别为和12，则11123n n n ∞=⎛⎫+ ⎪⎝⎭∑收敛，且其和为 12 32（）11121(1)(2)212n n n n n n ⎛⎫=-+ ⎪++++⎝⎭∴121112111211121122322342345212n S n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-++-++-+++-+ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭11112212n n ⎛⎫=-+ ⎪++⎝⎭1lim 4n n S →∞=故级数收敛，且其和为14（）πsin 2n U n n = 而πsinππ2lim lim 0π222n n n U n→∞→∞=⋅=≠，故级数1πsin2n n n ∞=⋅∑发散（）πcos2n n U = 而4lim limcos2π1k k k U k →∞→∞== 42lim limcos(21)π1k k k U k +→∞→∞=+=-故lim n n U →∞不存在，所以级数0πcos2n n ∞=∑发散 ※．设1n n U ∞=∑ ＞加括号后收敛，证明1n n U ∞=∑亦收敛．证：设1(0)n n n U U ∞=>∑加括号后级数1n n A ∞=∑收敛，其和为考虑原级数1n n U ∞=∑的部分和1n k k S U ∞==∑，并注意到0(1,2,)k U k >=，故存在0n 使11n n k t k t S U A s ∞===<<∑∑又显然1n n S S +<对一切n 成立，于是，{}n S 是单调递增且有上界的数列，因此，极限lim nn S →∞存在，即原级数1n n U ∞=∑亦收敛习题．判定下列正项级数的收敛性：∑∞=++1n n n )2)(1(1 ∑∞=+1n n n1∑∞=++1n n n n )2(2 ∑∞=+1n n n )5(12；111nn a ∞=+∑ ＞ ∑∞=+1n n b a 1＞ ()∑∞=--+1n a n a n 22＞ ∑∞=-+1n n n 1214； ∑∞=⋅1n nn n 23； ※∑∞=1n n n n !∑∞=+⋅⋅⋅⋅+⋅⋅⋅⋅1n n n )13(1074)12(753 ∑∞=1n n n3；※∑∞=1n n n 22)!(2； ∑∞=⎪⎭⎫⎝⎛+1n nn n 12∑∞=1πn n n3sin2 ∑∞=1πn n n n 2cos 32．解：（）因为211(1)(2)n n n <++而211n n ∞=∑收敛，由比较判别法知级数11(1)(2)n n n ∞=++∑收敛（）因为limlim 10n n n U →∞→∞==≠，故原级数发散（）因为21(1)(1)1n n n n n n n +>=+++，而111n n ∞=+∑发散，由比较判别法知，级数12(1)n n n n ∞=++∑发散（）321n<=而n ∞=是收敛的p -级数3(1)2p => 由比较判别法知级数1n ∞=收敛（）因为111lim lim lim(1)111n n n n n n n n a a a a a→∞→∞→∞+==-++ 11112001a a a >⎧⎪⎪==⎨⎪<<⎪⎩而当1a >时，11n n a ∞=∑收敛，故111nn a ∞=+∑收敛当1a =时，11n n a ∞=∑ 11n ∞=∑发散，故111nn a∞=+∑发散当01a <<时1lim101nn a →∞=≠+，故1lim 1n n a →∞+发散综上所述，当01a <≤时，级数1lim1nn a →∞+发散，当1a >时，1lim 1n n a →∞+收敛（）因为1lim lim lim(1)1n n n nn n n nb a a b a b a b b →∞→∞→∞+==-++1111101b b a b >⎧⎪⎪==⎨+⎪<<⎪⎩ 而当1b >时 11n n b ∞=∑收敛，故11nn a b ∞=+∑收敛当1b =时，1111n n n b ∞∞===∑∑发散，故而由0a > 101a <<+∞+ 故11nn a b ∞=+∑也发散当01b <<时，11lim 0n n a b a →∞=≠+故11n n a b ∞=+∑发散综上所述知，当01b <≤时，级数11n n a b ∞=+∑发散当时，级数11nn a b ∞=+∑收敛（）因为lim n n n→∞=0n a ==>而11n n ∞=∑发散，故级数10)n a ∞=>∑发散（）因为434431121lim lim 1212n n n n n n n n →∞→∞++-==-而311n n∞=∑收敛，故级数21121n n n ∞=+-∑收敛（）因为1113233lim lim lim 1(1)232(1)2n n n n n n n n nU n n U n n +++→∞→∞→∞⋅⋅==>+⋅+由达朗贝尔比值判别法知，级数132nnn n ∞=⋅∑发散（）因为11(1)!1lim lim lim(1)1(1)!n n n n n n n nU n n e U n n n ++→∞→∞→∞+=⋅=+=>+，由达朗贝尔比值判别法知，级数1!nn n n ∞=∑发散（）因为1357(21)(23)4710(31)limlim 4710(31)(34)357(21)n n n n U n n n U n n n +→∞→∞⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+=⋅⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+ 232lim1343n n n →∞+==<+由达朗贝尔比值判别法知原级数收敛（）因为111311lim lim lim 1333n n n n n n nU n n U n n ++→∞→∞→∞++=⋅==<，由达朗贝尔比值判别法知，级数13n n n ∞=∑收敛（）因为22221221(1)[(1)!]2(1)lim lim lim (!)22n n n n n n n nU n n U n +++→∞→∞→∞++=⋅= 由2212121(1)2(1)1lim lim lim 222ln 22ln 2x x x x x x x x x +++→∞→+∞→+∞+++==⋅⋅2121lim 022(ln 2)x x +→+∞==⋅知2121(1)lim lim 012n n n n nU n U ++→∞→∞+==<由达朗贝尔比值判别法知，级数221(!)2nn n ∞=∑收敛（）因为1lim 1212n n n n →∞==<+，由柯西根值判别法知级数121nn n n ∞=⎛⎫ ⎪+⎝⎭∑收敛（）因为ππ2sinsin 33lim lim 1π2π33n n nn n n n n→∞→∞==⋅而112233nn n n n ∞∞==⎛⎫= ⎪⎝⎭∑∑是收敛的等比级数，它的每项乘以常数π后新得级数12π3n n n ∞=⋅∑仍收敛，由比较判别法的极限形式知，级数1π2sin3n n n ∞=∑收敛（）因为2πcos 322n nn n n ≤而与（）题类似地可证级数12n n n ∞=∑收敛，由比较判别法知级数1πcos 32nn n n ∞=∑收敛．试在，内讨论在什么区间取值时，下列级数收敛：∑∞=1n n n x nn x n ∑∞=⎪⎭⎫⎝⎛123．解：（）因为11lim lim lim 11n n n n n n nU x n nxx U n x n ++→∞→∞→∞=⋅==++由达朗贝尔比值判别法知，当1x >时，原级数发散当01x <<时，原级数收敛而当1x =时，原级数变为调11n n∞=∑，它是发散的综上所述，当01x <<时，级数1nn x n∞=∑收敛（）因为1313(1)2limlim 22n n n n n nx n U xU x n ++→∞→∞⎛⎫+⋅ ⎪⎝⎭==⎛⎫⋅ ⎪⎝⎭由达朗贝尔比值判别法知，当12x >即2x >时，原级数发散当012x<<即02x <<时，原级收敛而当12x =即 2x =时，原级数变为31n n ∞=∑，而由3lim n n →∞=+∞知31n n ∞=∑发散，综上所述，当02x <<时，级数31()2n n xn ∞=∑收敛习题．判定下列级数是否收敛，如果是收敛级数，指出其是绝对收敛还是条件收敛：∑∞=--1121)1(n nn 11(1)2(1)2n n nn ∞-=-+-⋅∑ ∑∞=12sin n n nx４ 111π(1)sin πn n n n ∞+=-∑∑∞=-⎪⎭⎫ ⎝⎛-11210121n n n ； ∑∞=+-1)1(n n x n∑∞=⋅1!)2sin(n n n x ．解：（）这是一个交错级数121n U n =- 1lim lim 021n n n U n →∞→∞==- 1112121n n U U n n +=>=-+ 由莱布尼茨判别法知11(1)21nn n ∞=--∑ 又1111(1)2121n n n n n ∞∞==-=--∑∑，由1121lim 12n n n→∞-= 及11n n ∞=∑发散，知级数1121n n ∞=-∑发散，所以级数11(1)21nn n ∞=--∑条件收敛（）因为2111(1)211(1)22(1)2n n n n n ----+-=+-⋅-⋅ 故11111(1)21111(1)22(1)22(1)2n n n n n n n n n ------+--=+≤+-⋅-⋅-⋅ 1113222n n n-=+= 而112n n ∞=∑收敛，故132n n ∞=∑亦收敛，由比较判别法知11(1)2(1)2n n nn ∞-=-+-⋅∑收敛，所以级数11(1)2(1)2n n n n ∞-=-+-⋅∑绝对收敛（）因为22sin 1,nx n n ≤而级数211n n∞=∑收敛，由比较判别法知21sin n nxn ∞=∑收敛，因此，级数21sin n nxn ∞=∑绝对收敛（）因为121ππ|(1)sin |sin πlimlim 11πn n n n n n n n+→∞→∞-==而211n n∞=∑收敛，由比较判别法的极限形式知，级数111π|(1)sin |πn n n n ∞+=-∑收敛，从而级数11π(1)sin πn n n+-绝对收敛（）因为212121111111210210210n n n n n n ----≤+=+ 而级数112n n ∞=∑收敛的等比级数1()2q = 由比值判别法，易知级数211110n n ∞-=∑收敛，因而21111210n n n ∞-=⎛⎫+ ⎪⎝⎭∑收敛，由比较判别法知级数21111210n n n ∞-=-∑收敛，所以原级数21111210n n n ∞-=-∑绝对收敛（）当为负整数时，级数显然无意义；当不为负整数时，此交错级数满足莱布尼茨判别法的条件，故它是收敛的，但因11n x n∞=+∑发散，故原级数当不为负整数时仅为条件收敛（）因为sin(2)1!!n x n n ⋅≤ 由比值判别法知11!n n ∞=∑收敛 1(1)!lim 01!n n n →∞+= ，从而由比较判别法知1sin(2)!n n x n ∞=⋅∑收敛，所以级数1sin(2)!n n x n ∞=⋅∑，绝对收敛．讨论级数∑∞=--111)1(n p n n的收敛性＞．解：当1p >时，由于11111(1)n p p n n n n ∞∞-==-=∑∑收敛，故级数111(1)n p n n ∞-=-∑绝对收敛当01p <≤时，由于111,(1)n n p p u u n n +=>=+ lim 0n n u →∞= 由莱布尼茨判别法知交错级数111(1)n p n n ∞-=-∑收敛，然而，当01p <≤时，11111(1)n p p n n n n ∞∞-==-=∑∑发散，故此时，级数111(1)n p n n ∞-=-∑条件收敛综上所述，当01p <≤时，原级数条件收敛当时，原级数绝对收敛 ※．设级数∑∞=12n n a 及∑∞=12n n b 都收敛，证明级数∑∞=1n n n b a 及()∑∞=+12n n n b a 也都收敛．证：因为2222||||110||222n n n n n n a b a b a b +≤≤=+ 而由已知1nn a ∞=∑及21n n b ∞=∑都收敛，故221111,22n n n n a b ∞∞==∑∑收敛，从而2211122n n n a b ∞=⎛⎫+ ⎪⎝⎭∑收敛，由正项级数的比较判别法知1n n n a b ∞=∑也收敛，从而级数1n n n a b ∞=∑绝对收敛又由222()2,n n n n n n a b a a b b +=++及2211,n n n n a b ∞∞==∑∑ 以及1n n n a b ∞=∑收敛，利用数项级数的基本性质知，221(2)nn n n n aa b b ∞=++∑收剑，亦即21()n n n a b ∞=+∑收敛习题．指出下列幂级数的收敛区间：∑∞=0!n n n x ； ∑∞=0!n n n x nn ；∑∞=⋅022n n n n x ； ∑∞=++-01212)1(n n n n x ． ∑∞=⋅+02)2(n n n n x ； ∑∞=-0)1(2n n nx n．解：（）因为111(1)!limlim lim 011!n n n n na n p a n n +→∞→∞→∞+====+，所以收敛半径r =+∞，幂级数1!n n x n ∞=∑的收敛区间为(,)-∞+∞（）因为-111lim lim lim 1e 11nnn n n n na n p a n n +→∞→∞→∞⎛⎫===-= ⎪++⎝⎭，所以收敛半径1e r p == 当时，级数01!!e n n n n n n n n x n n ∞∞===∑∑，此时11(1)n n n u e u n+=+，因为1(1)n n +是单调递增数列，且1(1)n n+ 所以1n nu u + 从而lim 0n n u →∞≠，于是级数当时，原级数发散类似地，可证当时，原级数也发散可证lim ||0n n u →∞≠ 综上所述，级数0!nn n n x n ∞=∑的收敛区间为（）因为2111limlim ()212n n n n a n p a n +→∞→∞===+ 所以收敛半径为当2x =时，级数221012n n n n x n n∞∞===⋅∑∑是收敛的一级数（）当时，级数22011(1)2n n n n n x n n ∞∞===-⋅⋅∑∑是交错级数，它满足莱布尼茨判别法的条件，故它收敛综上所述，级数202nn n x n∞=⋅∑的收敛区间为（）此级数缺少偶次幂的项，不能直接运用定理求收敛半径，改用达朗贝尔比值判别法求收敛区间令21(1)21n nn x u n +=-+，则22121lim lim 23n n n nu n x x u n +→∞→∞+=⋅=+当21x <时，即||1x <时，原级数绝对收敛当21x >时，即||1x >时，级数0||n n u ∞=∑发散，从而210(1)21n nn x n +∞=-+∑发散，当1x =时，级数变为01(1)21nn n ∞=-+∑ 当1x =-时，级数变为101(1)21n n n ∞+=-+∑ 它们都是交错级数，且满足莱布尼茨判别法的条件，故它们都收敛综上所述，级数21(1)21n nn x n +∞=-+∑的收敛区间为（）此级数为（）的幂级数因为11limlim 2(1)2n n n n a n p a n +→∞→∞===+ 所以收敛半径12r p==，即|2|2x +<时，也即40x -<<时级数绝对收敛当|2|2x +>即4x <-或0x >时，原级数发散当4x =-时，级数变为01(1)n n n∞=-∑是收敛的交错级数，当时，级数变为调和级数11n n∞=∑ 它是发散的综上所述，原级数的收敛区间为（）此级数（）的幂级数12limlim 21n n n n a np a n +→∞→∞===+ 故收敛半径12r =于是当1|1|2x -<即1322x <<时，原级数绝对收敛当1|1|2x ->即12x <或32x >时，原级数发散当32x =时，原级数变为01n n∞=∑是调和级数，发散当12x =时，原级数变为11(1)n n n ∞=-∑，是收敛的交错级数综上所述，原级数的收敛区间为13,22⎡⎫⎪⎢⎣⎭．求下列幂级数的和函数：∑∞=-1)1(n nnn x ； ∑∞=-1122n n nx ；nn x n n ∑∞=+1)1(1； ∑∞=+0)12(n n x n ．解：（）可求得所给幂级数的收敛半径设1()(1)nnn x S x n ∞==-∑ 则1111()(1)(1)1n n n n n n x S x x n x ∞∞-=='⎡⎤'=-=-=-⎢⎥+⎣⎦∑∑∴001()()d d ln(1) (||1)1xxS x S x x x x x x-'===-+<+⎰⎰ 又当时，原级数收敛，且()S x 在处连续∴1(1)ln(1) (11)nnn x x x n ∞=-=-+-<≤∑ （）所给级数的收敛半经，设211()2n n S x nx ∞-==∑ 当||1x <时，有2121011()d 2d 2d xx xn n n n S x x nxx nx x ∞∞--====∑∑⎰⎰⎰22211nn x xx∞===-∑ 于是22222()1(1)x xs x x x '⎛⎫== ⎪--⎝⎭又当1x =±时，原级数发散故 2122122 (||1)(1)n n xnx x x ∞-==<-∑（）可求所给级数的收敛半径为令1111()(0)(1)(1)n n n n x x s x x n n x n n +∞∞====≠++∑∑ 令11()(1)n n x g x n n +∞==+∑ 则111()1n n g x x x ∞-=''==-∑01()d ()(0)d 1xxg x x g x g x x''''=-=-⎰⎰(0)0,()ln(1)g g x x ''==--()d ()(0)ln(1)d ,(0)0xxg x x g x g x x g '=-=--=⎰⎰所以0()ln(1)d ln(1)ln(1)xg x x x x x x x =--=+---⎰所以1()11ln(1),||1,S x x x x⎛⎫=+--< ⎪⎝⎭且0x ≠当1x ±时，级数为11(1)n n n ∞=+∑和11(1)(1)n n n n ∞=-+∑ 它们都收敛且显然有(0)0S =故111ln(1)(1,0)(0,1)()00,1x x S x x x x ⎧⎛⎫+--∈-⋃⎪ ⎪=⎝⎭⎨⎪=±⎩（）可求得所给级数的收敛半径为且1x ±时，级数发散，设10()n n S x nx ∞-==∑则001()d .1xn n s x x x x∞===-∑⎰ 于是211()()1(1)S x x x '==-- 即1211(1)n n nx x ∞-==-∑ 所以111(21)2nn n n n n n x x nxx ∞∞∞-===+=+∑∑∑221112(1)1(1)xx x x x +=⋅+=--- (||1)x < ．求下列级数的和：∑∞=125n n n ； ∑∞=-12)12(1n nn ；∑∞=--112212n n n ； 1(1)2n n n n ∞=+∑．解：（）考察幂级数21n n n x ∞=∑，可求得其收敛半径1r = ，且当1x ±时，级数的通项2n n u n x =，2lim ||lim n n n u n →∞→∞==+∞，因而lim 0n n u →∞≠，故当1x ±时，级数21nn n x ∞=∑发散，故幂级数21n n n x ∞=∑的收敛区间为（，）设21() (||1)nn S x n x x ∞==<∑，则211()n n S x x n x ∞-==∑令2111()n n S x n x ∞-==∑ 则11011()d xnn n n S x x nx x nx ∞∞-====∑∑⎰再令121()n n S x nx∞-==∑ 则201()d 1xn n xS x x x x∞===-∑⎰ 故221()(||1)1(1)x S x x x x '⎛⎫==< ⎪--⎝⎭，从而有120()d (1)x x S x x x =-⎰ 1231() (||1)(1)(1)x xS x x x x '⎛⎫+==< ⎪--⎝⎭于是 213()() (||1)(1)x x S x xS x x x +==<- 取15x =，则223111()11555()5532115n n n S ∞=+===⎛⎫- ⎪⎝⎭∑ （）考察幂级数21121n n x n ∞=-∑，可求得收敛半径，设2211111() (||1)2121nn n n S x x x x x n n ∞∞-====<--∑∑令21111()21n n S x x n ∞-==-∑ 则221211()1n n S x x x ∞-='==-∑ 1200d 11()d ln 1-21xxx x S x x x x +'==-⎰⎰即 1111()(0)ln (,(0)0)21xS x S s x+-==- 于是 111()ln,(||<1)21xS x x x+=-，从而 11()()ln (||1)21x xS x xS x x x+==<-取x =则11(21)21n n S n ∞===-∑=（）考察幂级数211(21)n n n x ∞-=-∑，可求得其级数半经为因为212121111(21)2n n n n n n n xnxx ∞∞∞---===-=-∑∑∑令2111()2n n S x nx∞-==∑，则221201()d 1xnn x S x x xx ∞===-∑⎰ 所以212222() (||1)1(1)x xS x x x x '⎛⎫==< ⎪--⎝⎭ 于是212121111(21)2n n n n n n n xnxx ∞∞∞---===-=-∑∑∑3222222 (||1)(1)1(1)x x x x x x x x +=-=<--- 取12x =，得3212111()121102212291()2n n n S ∞-=+-⎛⎫=== ⎪⎛⎫⎝⎭-⎪⎝⎭∑（）考察幂级数1(1)n n n n x ∞=+∑，可求得其收敛半径设1()(1) (||1)n n S x n n x x ∞==+<∑则121011()d xn n n n S x x nxxnx∞∞+-====∑∑⎰又设111()n n S x nx ∞-==∑则101()d 1xn n x S x x x x∞===-∑⎰ 从而121()1(1)x S x x x '⎛⎫== ⎪--⎝⎭2212()d ()(1)xx S x x x S x x ==-⎰2232() ||1(1)(1)x x S x x x x '⎛⎫==< ⎪--⎝⎭取12x =，则31121(1)2822112nn n n S ∞=⨯+⎛⎫=== ⎪⎝⎭⎛⎫- ⎪⎝⎭∑习题．将下列函数展开成的幂级数： 2cos 2x 2sin x ； 2x x -e211x -； πcos()4x -．解：（）2201cos 11cos (1)2222(2)!n n n x x x n ∞=+==+-∑ 211(1) (-)2(2)!nnn x x n ∞==+-∞<<+∞∑ （）2101sin (1) ()2(21)!2n n n x x x n +∞=⎛⎫=--∞<<+∞ ⎪+⎝⎭∑（）22210011e ()(1) ()!!x n n n n n x x x x x n n ∞∞-+===-=--∞<+∞∑∑ （）211111211x x x ⎡⎤=+⎢⎥--+⎣⎦002011(1)221[(1)]2 ||1n n nn n n n n n n n x x x x x x ∞∞==∞=∞==+-=+-=<∑∑∑∑（）πππcos cos cos sin sin 444x x x ⎛⎫-=+ ⎪⎝⎭2210sin )(1) ()2(2)!(21)!n n n n x x x x x n n +∞==+⎡⎤=-+-∞<<+∞⎢⎥+⎣⎦∑ ．将下列函数在指定点处展开成幂级数，并求其收敛区间：x -31 在＝１；在 3π 3412++x x 在 21x 在＝３．解：（）因为11113212x x =⋅--- 而 0111 (||112212n n x x x ∞=--⎛⎫=< ⎪-⎝⎭-∑即13x -<< 所以100111(1) (13)3222nn n n n x x x x ∞∞+==--⎛⎫=⋅=-<< ⎪-⎝⎭∑∑ 收敛区间为：（，）（）πππ2π2cos cos ()cos cos()sin sin()333333x x x x ⎡⎤=+-=---⎢⎥⎣⎦22100()()133(1)(1)2(2)!2(21)!n n n n n n x x n n ππ+∞∞==--=-+-+∑∑221011(1)()[)2(2)!3(21)!3n n n n x x n n ππ∞+=⎡⎤=--+-⎢⎥+⎣⎦∑ ()x -∞<<+∞ 收敛区间为(,)-∞+∞（）211111111()1143213481124x x x x x x =-=⋅-⋅--++++++ 001111(1)(1)4284n nn n n n x x ∞∞==--⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭∑∑ 223011(1)(1)22n n n n n x ∞++=⎛⎫=--- ⎪⎝⎭∑由112x -<且114x -<得13x -<<，故收敛区间为（，）（）因为011113(1)()333313n n n x x x ∞=-=⋅=-⋅-+∑ 10(3)(1)3nnn n x ∞+=-=-∑ 而21011(3)(1)3n n n n x x x ∞+=''⎡⎤-⎛⎫=-=-- ⎪⎢⎥⎝⎭⎣⎦∑ 111(1)(3)3nn n n n x ∞-+=-=-⋅-∑1111(1)(3)3n n n n n x +∞-+=-=-∑ 20(1)(1)(3)3n n n n n x ∞+=-+=-∑ 由313x -<得06x << 故收敛区间为（，）。

微积分曹定华修订版课后题答案第九章习题详解

Q Q、c.n -、、n ）发散•n =1ACO A CO A °° 1是调和级数7 1去掉前3项得到的级数，而调和级数、-发散，故原级数—n 仝n n 三n1 +(-1)nQ n4 Q n2 2丿“ 1a （「1）m1而肯，7 （亠是公比分别为1的收敛的等比级数，所以由数项级数的基本性质知 n 壬2 n 经 2 2(5) T In—In n -ln(n 1) n +1 是 S n =(ln1 -In 2) (In 2-In 3) |"[ln n -ln(n 1)]QO故ng —,所以级数j 亠发散•判定下列级数的收敛性:习题9-1CO __________⑵ ' (、n 1 - n)；n 42 (—1)nn42nCOr'Tn 丄n 1 n 1 「(一1)n2;n T(8)na (-1) nnzo 2n 1解: （1）该级数为等比级数, 1 11公比为一，且a 0,故当|一卜：1,即a 1时，级数收敛，当|一 |亠1即0 ：：： a 乞1a a a时, 级数发散• (2) T S n=（迈- .1）（七- 一 2）川（百-」n ）发散• (3) oOzn 吕n 3(4)cOn -丄n 4j<2 2 收敛，即原级数收敛.Q Q. limS 不存在，从而级数「(-1)n2发散• n—门 n 丄 n +1 (7) T lim U = lim 1 - 0n Y n Y n00n +1.级数D 发散•n 二 n2 .判别下列级数的收敛性，若收敛则求其和:oOn n故lim U n 不存在，所以级数 7 cos 一发散.n‘：n£2QOoa3 *.设7 U n (U n > 0)加括号后收敛，证明、• U n 亦收敛.n 理 n 』(6) TS2n =0, S2n 1--2U n(-1)n 2n 1i ium丰nA(")nn 2n 1发散.1n(n 1)(n2)cd_n(3) ' n sin - n 仝 2nCO(4) 7 COSn=0解:(1)■ -都收敛，且其和分别为n 吕3n1和1，则二丄•丄收敛，且其和为2 n 吕 2n 3n(2)1_1『12 丄 1]n(n 1)(n 2)2 n n 1 n 2lim S n故级数收敛，且其和为丄.n —*4 4.n sin — (3) U n 二 nsin —，而 limU n =lim - 2= 0 ,2n f re ? n 200冗故级数' n sin 发散.心2 n2n-n =cos 一 2 ，而 k i m U 4k =k i mcos2kn 1，k i m U4k 2 limcos(2 k 1) n -1k —5 -1 2□a,故级数、Zn 4od QO ao QO 证：设7 U n(U n 0)加括号后级数7 A n收敛，其和为S.考虑原级数V U n的部分和S n八，U k,并注n=i n・nd k -1意到U k o(k =1,2,丨1()，故存在n。

《微积分》课后答案(复旦大学出版社(曹定华_李建平_毛志强_著))第2章

而 , 使当n N时，有
xn a xn a
由数列极限的定义得考察数列
即
xn a
lim xn a
n
n n
xn (1) n ，知 lim xn 不存在，而 xn 1 ， lim xn 1 ，
n
xn 0
由数列极限的定义可得 4. 利用夹逼定理证明：
即 xn
即 xn 0
lim xn 0
n
1
本文档由天天learn提供，查看其他章节请点击/html/69/n-69.html
微积分复旦大学出版社曹定华主编课后答案
微积分复旦大学出版社曹定华主编课后答案
又所以
xn 1 xn xn ( 2 xn ) ，而 xn 0 , xn 2 ， xn 1 xn 0
即
xn 1 xn ，
即数列是单调递增数列。综上所述，数列 xn 是单调递增有上界的数列，故其极限存在。（3）由数列 xn 单调递增， yn 单调递减得 xn x1 ， yn y1 。又由 lim( xn yn ) 0 知数列 xn yn 有界，于是存在 M >0，使 xn yn M ,
即xn 1 xn
所以 xn 为单调递减有下界的数列，故 xn 有极限。（2）因为 x1
2 2 ，不妨设 xk 2 ，则
xk 1 2 xk 22 2
故有对于任意正整数 n，有 xn 2 ，即数列 xn 有上界，
2
本文档由天天learn提供，查看其他章节请点击/html/69/n-69.html
lim
2n 0 n n !

《微积分》课后答案(复旦大学出版社(曹定华_李建平_毛志强_著))第7章

故 a b b c c a
3 . 2
4．在 xＯy 坐标面上求向量 a，使其垂直于向量 b=4i-3j+5k,且｜a｜=2｜b｜．解：设向量 a ( x, y, 0) ,由 a b 得 a b 0 即 4x 3y 0 , 由 | a | 2 | b | 得解方程组
(6,10, 2) (6, 6, 6) (16, 4, 12) (16, 0, 20)
5．已知两点 M1(0，1，2)和 M2(1，-1，0)，求向量 M 1M 2 ，并求 M 1M 2 及与 M 1M 2 平行的单位向量．解： M 1M 2 (1 0)i (1 1) j (0 2)k i 2 j 2k (1, 2, 2)

2．试用向量证明：如果平面上一个四边形的对角线互相平分，则该四边形是平行四边形．证：（如上题图），依题意有 AM MC , DM MB. 于是 AB AM MB MC DM DC. 故 ABCD 是平行四边形. 3．已知向量 a=i-2j+3k 的始点为(1，3，-2)，求向量 a 的终点坐标．解：设 a 的终点坐标为( x, y, z ),则
即与 M 1M 2 平行的单位向量为 ,

1 3
2 2 1 2 2 , 或 , , . 3 3 3 3 3
习题 7-3
) 1．已知 a =2, b =1, (a,b
解：（1） a a | a | 4
2
，求(1) a·a,(2) a·b,(3) (2a+3b)·(3a-b)． 3 ) 2 1 cos π 1 （2） a a | a | | b | cos(a,b 3

微积分曹定华课后题答案第二章习题详解

第二章习题2-11、试利用本节定义5后面的注(3)证明:若lim n →∞x n =a ,则对任何自然数k ,有lim n →∞x n +k =a 、证:由lim n n x a →∞=,知0ε∀>,1N ∃,当1n N >时,有n x a ε-<取1N N k =-,有0ε∀>,N ∃,设n N >时(此时1n k N +>)有n k x a ε+-<由数列极限的定义得 lim n k x x a +→∞=、2、试利用不等式A B A B -≤-说明:若lim n →∞x n =a ,则lim n →∞∣x n ∣=|a|、考察数列x n =(-1)n ,说明上述结论反之不成立、证:lim 0,,.使当时，有n x n x aN n N x a εε→∞=∴∀>∃>-<Q而 n n x a x a -≤- 于就是0ε∀>,,使当时，有N n N ∃>n n x a x a ε-≤-< 即 n x a ε-<由数列极限的定义得 lim n n x a →∞=考察数列 (1)nn x =-,知lim n n x →∞不存在,而1n x =,lim 1n n x →∞=,所以前面所证结论反之不成立。

3、利用夹逼定理证明:(1) lim n →∞222111(1)(2)n n n ⎛⎫+++ ⎪+⎝⎭L =0; (2) lim n →∞2!n n =0、证:(1)因为222222111112(1)(2)n n n n n n n n n n++≤+++≤≤=+L 而且 21lim0n n →∞=,2lim 0n n→∞=, 所以由夹逼定理,得222111lim 0(1)(2)n n n n →∞⎛⎫+++= ⎪+⎝⎭L 、 (2)因为22222240!1231n n n n n<=<-g g g L g g ,而且4lim 0n n →∞=, 所以,由夹逼定理得2lim 0!nn n →∞= 4、利用单调有界数列收敛准则证明下列数列的极限存在、 (1) x n =11ne +,n =1,2,…;(2) x 1,x n +1n =1,2,…、证:(1)略。

微积分曹定华修订版课后题答案第九章习题详解.doc

第9章习题9-11．判定下列级数的收敛性：(1) 115n n a ∞=⋅∑（a ＞0）； (2)∑∞=-+1)1(n n n ;(3) ∑∞=+131n n ; (4)∑∞=-+12)1(2n nn; (5) ∑∞=+11ln n n n; (6)∑∞=-12)1(n n;(7) ∑∞=+11n nn ; (8)0(1)21n n nn ∞=-⋅+∑．解：（1）该级数为等比级数，公比为1a ,且0a >,故当1||1a <,即1a >时，级数收敛，当1||1a≥即01a <≤时，级数发散. （2）(1n S n =++++1=lim n n S →∞=∞∴1n ∞=∑发散.（3）113n n ∞=+∑是调和级数11n n ∞=∑去掉前3项得到的级数，而调和级数11n n∞=∑发散，故原级数113n n ∞=+∑发散. （4）1112(1)1(1)222n n nn n n n ∞∞-==⎛⎫+--=+ ⎪⎝⎭∑∑ 而1112n n ∞-=∑,1(1)2m nn ∞=-∑是公比分别为12的收敛的等比级数，所以由数项级数的基本性质知111(1)22n n n n ∞-=⎛⎫-+ ⎪⎝⎭∑收敛，即原级数收敛.（5）lnln ln(1)1nn n n =-++ 于是(ln1ln 2)(ln 2ln 3)[ln ln(1)]n S n n =-+-+-+ln1ln(1)ln(1)n n =-+=-+ 故lim n n S →∞=-∞,所以级数1ln1n nn ∞=+∑发散. （6）2210,2n n S S +==-∴lim n n S →∞不存在，从而级数1(1)2n n ∞=-∑发散.（7）1lim lim10n n n n U n→∞→∞+==≠∴ 级数11n n n ∞=+∑发散. （8） (1)(1)1, lim 21212n n n n n n U n n →∞--==++∴ lim 0n x U →∞≠，故级数1(1)21n n nn ∞=-+∑发散.2．判别下列级数的收敛性，若收敛则求其和：(1) ∑∞=⎪⎭⎫ ⎝⎛+13121n n n ； (2) ※∑∞=++1)2)(1(1n n n n ; (3) ∑∞=⋅12sin n n n π; (4)πcos2n n ∞=∑．解：（1）1111, 23n n n n ∞∞==∑∑都收敛，且其和分别为1和12，则11123n n n ∞=⎛⎫+ ⎪⎝⎭∑收敛，且其和为1+12=32. （2）11121(1)(2)212n n n n n n ⎛⎫=-+ ⎪++++⎝⎭∴121112111211121122322342345212n S n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-++-++-+++-+ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭11112212n n ⎛⎫=-+ ⎪++⎝⎭1lim 4n n S →∞=故级数收敛，且其和为14. （3）πsin 2n U n n =,而πsinππ2lim lim 0π222n n n U n→∞→∞=⋅=≠，故级数1πsin2n n n ∞=⋅∑发散. （4）πcos 2n n U =,而4lim limcos2π1k k k U k →∞→∞==,42lim limcos(21)π1k k k U k +→∞→∞=+=-故lim n n U →∞不存在，所以级数πcos2n n ∞=∑发散. 3※．设1nn U∞=∑ (U n ＞0)加括号后收敛，证明1nn U∞=∑亦收敛．证：设1(0)nn n UU ∞=>∑加括号后级数1n n A ∞=∑收敛，其和为S .考虑原级数1n n U ∞=∑的部分和1n k k S U ∞==∑，并注意到0(1,2,)k U k >=，故存在0n ,使11n n k t k t S U A s ∞===<<∑∑又显然1n n S S +<对一切n 成立，于是，{}n S 是单调递增且有上界的数列，因此，极限lim nn S →∞存在，即原级数1nn U∞=∑亦收敛.习题9-21．判定下列正项级数的收敛性：(1) ∑∞=++1n n n )2)(1(1; (2)∑∞=+1n n n 1; (3) ∑∞=++1n n n n )2(2; (4)∑∞=+1n n n )5(12；(5) 111nn a∞=+∑ (a ＞0); (6) ∑∞=+1n nba 1(a , b ＞0);(7)()∑∞=--+1n a n a n 22 (a ＞0); (8)∑∞=-+1n nn 1214； (9) ∑∞=⋅1n nn n 23； (10) ※∑∞=1n nn n !; (11) ∑∞=+⋅⋅⋅⋅+⋅⋅⋅⋅1n n n )13(1074)12(753 ; (12)∑∞=1n n n3； (13) ※∑∞=1n n n 22)!(2； (14)∑∞=⎪⎭⎫ ⎝⎛+1n nn n 12; (15)∑∞=1πn nn3sin2; (16) ∑∞=1πn n n n 2cos 32．解：（1）因为211(1)(2)n n n <++而211n n∞=∑收敛，由比较判别法知级数11(1)(2)n n n ∞=++∑收敛.（2）因为lim lim10n n n U →∞→∞==≠，故原级数发散. （3）因为21(1)(1)1n n n n n n n +>=+++，而111n n ∞=+∑发散，由比较判别法知，级数12(1)n n n n ∞=++∑发散. （4）321n<=,而1n ∞=是收敛的p -级数3(1)2p =>,由比较判别法知,级数1n ∞=收敛.（5）因为111lim lim lim(1)111n n n n n n n n a a a aa→∞→∞→∞+==-++ 11112001a a a >⎧⎪⎪==⎨⎪<<⎪⎩而当1a >时，11n n a ∞=∑收敛，故111nn a∞=+∑收敛; 当1a =时，11n n a∞=∑=11n ∞=∑发散，故111nn a ∞=+∑发散; 当01a <<时1lim101n n a →∞=≠+，故1lim1nn a →∞+发散; 综上所述，当01a <≤时，级数1lim 1n n a →∞+发散，当1a >时，1lim 1nn a →∞+收敛. （6）因为1lim lim lim(1)1n n n nn n n nb a a b a b a b b →∞→∞→∞+==-++1111101b b a b >⎧⎪⎪==⎨+⎪<<⎪⎩ 而当1b >时, 11n n b ∞=∑收敛，故11nn a b ∞=+∑收敛; 当1b =时，1111n n n b ∞∞===∑∑发散，故而由0a >, 101a <<+∞+,故11nn a b ∞=+∑也发散; 当01b <<时，11lim 0n n a b a →∞=≠+故11n n a b ∞=+∑发散; 综上所述知，当01b <≤时，级数11n n a b ∞=+∑发散;当b >1时，级数11nn a b∞=+∑收敛. （7）因为n n n→∞=0n a ==>而11n n∞=∑发散，故级数10)n a ∞=>∑发散.（8）因为434431121lim lim 1212n n n n n n n n →∞→∞++-==-而311n n ∞=∑收敛，故级数21121n n n ∞=+-∑收敛.（9）因为1113233lim lim lim 1(1)232(1)2n n n n n n n n nU n n U n n +++→∞→∞→∞⋅⋅==>+⋅+由达朗贝尔比值判别法知，级数132nnn n ∞=⋅∑发散. （10）因为11(1)!1lim lim lim(1)1(1)!n n n n n n n nU n n e U n n n ++→∞→∞→∞+=⋅=+=>+，由达朗贝尔比值判别法知，级数1!nn n n ∞=∑发散.（11）因为1357(21)(23)4710(31)limlim 4710(31)(34)357(21)n n n nU n n n U n n n +→∞→∞⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+=⋅⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+232lim1343n n n →∞+==<+,由达朗贝尔比值判别法知原级数收敛.（12）因为111311lim lim lim 1333n n n n n n nU n n U n n ++→∞→∞→∞++=⋅==<，由达朗贝尔比值判别法知，级数13nn n∞=∑收敛. （13）因为22221221(1)[(1)!]2(1)lim lim lim (!)22n n n n n n n nU n n U n +++→∞→∞→∞++=⋅= 由2212121(1)2(1)1lim lim lim 222ln 22ln 2x x x x x x x x x +++→∞→+∞→+∞+++==⋅⋅2121lim 022(ln 2)x x +→+∞==⋅知2121(1)lim lim 012n n n n nU n U ++→∞→∞+==<由达朗贝尔比值判别法知，级数221(!)2n n n ∞=∑收敛.（14）因为1lim 1212n n n n →∞==<+，由柯西根值判别法知级数121nn n n ∞=⎛⎫⎪+⎝⎭∑收敛.（15）因为ππ2sinsin 33lim lim 1π2π33n n nn n n n n→∞→∞==⋅而112233nn n n n ∞∞==⎛⎫= ⎪⎝⎭∑∑是收敛的等比级数，它的每项乘以常数π后新得级数12π3n n n ∞=⋅∑仍收敛，由比较判别法的极限形式知，级数1π2sin3n nn ∞=∑收敛. （16）因为2πcos 322n n n n n ≤而与（12）题类似地可证级数12n n n ∞=∑收敛，由比较判别法知级数1πcos 32nn n n ∞=∑收敛.2．试在(0，+∞)内讨论x 在什么区间取值时，下列级数收敛：(1) ∑∞=1n nn x ; (2)nn x n ∑∞=⎪⎭⎫ ⎝⎛123．解：（1）因为11lim lim lim 11n n n n n n nU x n nxx U n x n ++→∞→∞→∞=⋅==++由达朗贝尔比值判别法知，当1x >时，原级数发散;当01x <<时，原级数收敛; 而当1x =时，原级数变为调11n n ∞=∑，它是发散的. 综上所述，当01x <<时，级数1nn x n ∞=∑收敛.（2）因为1313(1)2limlim 22n n n n n nx n U xU x n ++→∞→∞⎛⎫+⋅ ⎪⎝⎭==⎛⎫⋅ ⎪⎝⎭,由达朗贝尔比值判别法知，当12x >即2x >时，原级数发散;。

微积分(曹定华)(修订版)课后题答案第一章习题详解

第一章习题1-11.用区间表示下列不等式的解2(1)9;(2)1;1(3)(1)(2)0;(4)00.011 x x x x x ≤>--+<<<+ 解 (1)原不等式可化为(3)(3)0x x -+≤,其解为33x -≤≤,用区间表示是[-3,3].(2)原不等式可化为11x ->或11x -<-,其解为2x >或0x <,用区间表示是(-∞,0)∪(2,+ ∞).(3)原不等式的解为21x -<<,用区间表示是(-2,1).(4)原不等式可化为0.0110.0110x x -<+<⎧⎨+≠⎩即 1.010.991x x -<<-⎧⎨≠⎩ 用区间表示是(-1.01,-1)∪(-1,-0.99).2.用区间表示下列函数的定义域:1(1)(2)arcsin(1)lg(lg );1(3).ln(2) y y x x x y x ==-+=- 解 (1)要使函数有意义,必须2010x x ≠⎧⎨-≥⎩即011x x ≠⎧⎨-≤≤⎩所以函数的定义域为[-1,0)∪(0,1].(2)要使函数有意义,必须111lg 00x x x -≤-≤⎧⎪>⎨⎪>⎩即0210x x x ≤≤⎧⎪>⎨⎪>⎩所以函数的定义域是12x <≤,用区间表示就是(1,2].(3)要使函数有意义,必须2650ln(2)020x x x x ⎧--≥⎪-≠⎨⎪->⎩即6112x x x -≤≤⎧⎪≠⎨⎪<⎩所以函数的定义域是-6≤x <1,用区间表示就是[-6,1).3.确定下列函数的定义域及求函数值f (0),ff (a )(a 为实数),并作出图形(1)1,0,2,011,12x x y x x x ⎧<⎪⎪=⎨≤<⎪⎪<≤⎩； (2)y＝211,12x x x ⎧≤⎪⎨-<<⎪⎩解 (1)函数的定义域(){|0}{|01}{|12}{|112}(,1)(1,2]或D f x x x x x x x x x =<≤<<≤=<<≤=-∞1(0)200,1,()201112a af f f a a a a ⎧<⎪⎪=⨯===⎨≤<⎪⎪<≤⎩,图1-1 图1-2(2)函数的定义域(){|1}{|12}{|2}(2,2)D f x x x x x x =≤<<=<=-221(0)1,11,()112a f f f a a a ≤===-==-<<⎪⎩4※.设1,1()1,1x f x x ⎧≤⎪=⎨->⎪⎩,求f (f (x )).解当|x |≤1时, f (x )=1, f (f (x ))= f (1)=1;当|x |>1时, f (x )=-1, f (f (x ))= f (-1)=1,综上所述f (f (x ))=1(x ∈R ).5.判定下列函数的奇偶性：(1) f (x )＝21cos x x -； (2)f (x )＝(x 2＋x )sin x ；(3) ※ f (x )＝1e ,0e 1,0x x x x -⎧-≤⎨->⎩解 (1) ∵221()1()()cos()cos x x f x f x x x----===- ∴f (x )是偶函数.(2)∵222()[()()]sin()()(sin )()sin ()f x x x x x x x x x x f x -=-+--=--=--≠ 且()()f x f x -≠-,∴f (x )是非奇非偶函数.(3) ※当x <0时,-x >0, ()1(1)()e e x x f x f x ---=-=--=-; 当x ≥0时,-x ≤0, ()()11(1)()e e e x x x f x f x ---=-=-=--=-,综上所述, x ∀∈R ,有f (-x )=-f (x ),所以f (x )是奇函数.6.设f (x )在区间(-l ,l )内有定义,试证明：(1) f (-x )+f (x )为偶函数； (2) f (-x ) -f (x )为奇函数.证 (1)令()()()F x f x f x =-+(,)x l l ∀∈-有()[()]()()()()F x f x f x f x f x F x -=--+-=+-=所以()()()F x f x f x =-+是偶函数;(2)令()()()F x f x f x =--,(,)x l l ∀∈-有()[()]()()()[()()]()F x f x f x f x f x f x f x F x -=----=--=---=-所以()()()F x f x f x =--是奇函数.7. 试证：(1) 两个偶函数的代数和仍为偶函数； (2) 奇函数与偶函数的积是奇函数. 证 (1)设f (x ),g (x )均为偶函数,令()()()F x f x g x =±则 ()()()()()()F x f x g x f x g x F x -=-±-=±=,所以()()f x g x ±是偶函数,即两个偶函数的代数和仍为偶函数.(2)设f (x )为奇函数,g (x )为偶函数,令()()()F x f x g x =⋅,则 ()()()()()()F x f x g x f x g x F x -=-⋅-=-=-,所以()()f x g x ⋅是奇函数,即奇函数与偶函数之积是奇函数.8. 求下列函数的反函数:22(1)2sin 3,,;(2);66212101,(3)()2(2)1 2.xx y x x y x x f x x x ππ⎡⎤=∈-=⎢⎥+⎣⎦-≤≤⎧=⎨--<≤⎩解 (1)由2sin3y x =得1arcsin 32yx =所以函数2sin3y x =的反函数为1arcsin (22)32xy x =-≤≤.(2)由221xx y =+得21x y y =-,即2log 1yx y =-. 所以函数221x x y =+的反函数为2log (01)1xy x x =<<-.(3) ※当01x ≤≤时,由21y x =-得1,112yx y +=-≤≤;当12x <≤时,由22(2)y x =--得22x y =<≤;于是有1112212yy x y +⎧-≤≤⎪=⎨⎪<≤⎩,所以函数22101()2(2)12x x f x x x -≤≤⎧=⎨--<≤⎩的反函数是1112()212x x f x x +⎧-≤≤⎪=⎨⎪<≤⎩.9. 将y 表示成x 的函数,并求定义域:222(1)10,1;(2)ln ,2,sin ;(3)arctan ,(). 为实数u v y u x y u u v x y u u v a x a ==+======+解 (1)211010u x y +==,定义域为(-∞,+∞);(2) sin ln ln 2ln 2sin ln 2v x y u x ====⋅定义域为(-∞,+∞);(3) arctan y u ===(a 为实数),定义域为(-∞,+∞).习题1-21.下列初等函数是由哪些基本初等函数复合而成的?(1) y= ； (2) y =sin 3ln x ;(3) y = tan 2x a ； (4) y =ln ［ln 2(ln 3x )］.解 (1)令arcsin x u a =,则y ,再令xv a =,则arcsin u v =,因此y =是由基本初等函数arcsin ,x y u v v a ===复合而成的.(2)令sin ln u x =,则3y u =,再令ln v x =,则sin u v =.因此3sin ln y x =是由基本初等函数3,sin ,ln y u u v v x ===复合而成.(3)令2tan u x =,则u y a =,再令2v x =,则tan u v =,因此2tan x y a =是由基本初等函数2,tan ,u y a u v v x ===复合而成.(4)令23ln (ln )u x =,则ln y u =,再令3ln(ln )v x =则2u v =,再令3ln w x =,则ln v w =,再令ln t x =,则3w t =,因此23ln[ln (ln )]y x =是由基本初等函数2ln ,,ln ,y u u v v w === 3,ln w t t x ==复合而成.2.设f (x )的定义域为［0,1］,分别求下列函数的定义域：(1) f (x 2)； (2) f (sin x );(3) f (x +a ),(a ＞0)； (4) f (e x +1).解 (1)由f (x )的定义域为[0,1]得0≤x 2≤1,于是-1≤x ≤1,所以f (x 2)的定义域为[-1,1].(2)由f (x )的定义域为[0,1]得0≤sin x ≤1,于是2k π≤x ≤(2k +1)π,k ∈z ,所以f (sin x )的定义域为[2k π,(2k +1) π], k ∈Z .(3)由f (x )的定义域为[0,1]得0≤x+a ≤1即-a ≤x ≤1-a 所以f (x+a )的定义域为[-a ,1-a ].(4)由f (x )的定义域为[0,1]得0≤e x +1≤1,解此不等式得x ≤-1,所以f (e x +1)的定义域为(-∞,-1].3. 求下列函数的表达式：(1) 设ϕ(sin x )=cos 2x +sin x +5,求ϕ(x );(2) 设g (x -1)=x 2+x +1,求g (x );(3) 设1()f x x +=x 2+21x,求f (x ). 解 (1)法一:令sin t x =,则222cos 1sin 1x x t =-=-,代入函数式,得:22()156t t t t t ϕ=-++=+-,即 2()6x x x ϕ=++.法二:将函数的表达式变形得:22(sin )(1sin )sin 56sin sin x x x x x ϕ=-++=+-令sin t x =,得 2()6t t t ϕ=+-,即 2()6x x x ϕ=+-.(2)法一:令1t x =-,则1x t =+,将其代入函数式,得22()(1)(1)133g t t t t t =++++=++即 2()33g x x x =++.法二:将函数表达式变形,得22(1)(21)(33)3(1)3(1)3g x x x x x x -=-++-+=-+-+令1x t -=,得 2()33g t t t =++,即 2()33g x x x =++.(3)法一:令1x t x +=,两边平方得22212x t x ++= 即22212x t x+=-,将其代入函数式,得2()2f t t =-,即2()2f x x =-. 法二:将函数表达式变形,得222111222f x x x x x x ⎛⎫⎛⎫⎛⎫=-=-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 令1x t x+=,得2()2f t t =-,即2()2f x x =-.习题1-31.设销售商品的总收入是销售量x 的二次函数,已知x =0,2,4时,总收入分别是0,6,8,试确定总收入函数TR(x ).解设2()TR x ax bx c =++,由已知(0)0,(2)6,(4)8TR TR TR === 即 04261648c a b c a b c =⎧⎪++=⎨⎪++=⎩ 解得 1240a b c ⎧=-⎪⎪⎨=⎪⎪=⎩ 所以总收入函数21()42TR x x x =-+. 2.设某厂生产某种产品1000吨,定价为130元/吨,当一次售出700吨以内时,按原价出售；若一次成交超过700吨时,超过700吨的部分按原价的9折出售,试将总收入表示成销售量的函数.解设销售量为x ,实际每吨售价为P 元,由题设可得P 与x 间函数关系为1307001177001000x P x ≤⎧=⎨<≤⎩,总收入 130700()130700(700)1177001000TR x x x x x ≤⎧=⎨⨯+-⨯<≤⎩,即 130700()91001177001000TR x x x x x ≤⎧=⎨+<≤⎩.3. 已知需求函数为105Q P =-,成本函数为C =50+2Q ,P 、Q 分别表示价格和销售量.写出利润L 与销售量Q 的关系,并求平均利润.解由题设知总收入2()105Q R Q PQ Q ==- ,则总利润 ()221()()()8505021055Q L Q R Q C Q Q Q Q Q ⎛⎫=-=-=--+- ⎪⎝⎭, 平均利润 ()150()85L Q AL Q Q Q Q==--. 4. 已知需求函数Q d 和供给函数Q s ,分别为Q d =100233P -,Q s =-20+10P ,求相应的市场均衡价格.解当d s Q Q =时供需平衡,由d s Q Q =得1002201033P P -=-+,解得5P = 所以市场均衡价格5P =.。

《微积分》课后答案(复旦大学出版社(曹定华_李建平_毛志强_著))第11章

(3) a 1 , f (t ) 2 于是由非齐次方程的特解公式 (11 2 5) 有：
t t 1 t 1 1 1 yt (1)i 2t i 1 2t 1 ( )i 2t 2 3 i 0 i 0
由 (11 2 4) 式，得所给方程的通解
1 yt A(1)t 2t 3
(A 为任意常数)
*
(4)对应齐次差分方程为 yt 1 yt 0 ，其通解为 yt A ，设原方程特解为
yt 2t ( B1 cos πt B2 sin πt ) 代入原方程得：
2t 1[ B1 cos π(t 1) B2 sin π(t 1)] 2t ( B1 cos πt B2 sin πt ) 2t cos πt
yt 1
1 4 yt ，其中 3 3
1 4 a ， b ，由通解公式 (11 2 7) 得原方程的通解为： 3 3
1 yt y A (t ) yt A( )t 1 (A 为任意常数) 3 1 3 t 1 3 1 (2)方程可化为 yt 1 yt ，其中 a ， b0 ， b1 ，故由通解公式 2 2 2 2 2 2 (11 2 9) 得方程的通解为： 3 1 1 1 t 1 7 t yt A( ) 2 2 2 t 即 yt A( )t . 1 1 1 2 9 3 2 1 (1 ) 2 1 2 2 2
t
(4) a 4 ， π ， b1 0 ， b2 3 ， D (4 cos π) sin π=9 0 ，且
2 2
由公式 (11 2 14) 得 = [0 (4 cos π) 3 sin π]=0 ， = [3(4 cos π) 0 sin π]=1 ，方程通解为 yt A(4) sin πt ，以 t 0 时 y0 1 代入上式，得 A 1 ，故原方程特解为：

《微积分》课后答案(复旦大学出版社(曹定华_李建平_毛志强_著))第四章

f (0) 0 ,依题意知 f ( x0 ) 0 .即有 f (0) f ( x0 ) .由罗尓定理,至少存在一点 (0, x0 ) ,使
得 f ( ) 0 成立,即
a0 n n 1 a1 (n 1) n 2 … an 1 0
成立,这就说明是方程 a0 nx n 1 a1 (n 1) x n 2 an 1 0 的一个小于 x0 的正根. 7. 设 f(a) = f(c) = f(b),且 a＜c＜b, f ″(x)在［a,b］上存在，证明在(a,b)内至少存在一点ξ，使 f ″(ξ) = 0. 证: 显然 f ( x ) 分别在 a , c 和 c, b 上满足罗尓定理的条件 , 从而至少存在
x x x
由 e 在 , 上连续,可导, f ( x) 在 a, b 上连续,在 a, b 内可导,知 F ( x) 在 a, b 上连
x
续,在 a, b 内可导,而且 F ( a ) e f ( a ) 0, F (b) e f (b) 0, 即F ( a ) F (b) ,
(4) lim
(a x) x a x ,(a＞0)； x 0 x2
(6) lim sin x ln x ;
x 0
1 ln(1 ) x ; (7) lim x arc cot x
(9) lim(1 sin x) x ;
x 0
1
(8) lim(
x 0
ex 1 ); x ex 1
x 0

f ( x) 在 0,π 上不连续,
显然 f ( x) 在
0, π

微积分曹定华版课后题答案习题详解

第二章习题2-11. 试利用本节定义5后面的注3证明：若lim n →∞x n =a ,则对任何自然数k ,有lim n →∞x n +k =a .证：由lim n n x a →∞=,知0ε∀>,1N ∃,当1n N >时,有取1N N k =-,有0ε∀>,N ∃,设n N >时此时1n k N +>有由数列极限的定义得 lim n k x x a +→∞=.2. 试利用不等式A B A B -≤-说明：若lim n →∞x n =a ,则lim n →∞∣x n ∣=|a|.考察数列x n =-1n ,说明上述结论反之不成立.证：而 n n x a x a -≤- 于是0ε∀>,,使当时，有N n N ∃>n n x a x a ε-≤-< 即 n x a ε-<由数列极限的定义得 lim n n x a →∞=考察数列 (1)nn x =-,知lim n n x →∞不存在,而1n x =,lim 1n n x →∞=,所以前面所证结论反之不成立;3. 利用夹逼定理证明：1 lim n →∞222111(1)(2)n n n ⎛⎫+++ ⎪+⎝⎭=0； 2 lim n →∞2!n n =0. 证：1因为222222111112(1)(2)n n n n n n n n n n++≤+++≤≤=+ 而且 21lim0n n →∞=,2lim 0n n→∞=, 所以由夹逼定理,得222111lim 0(1)(2)n n n n →∞⎛⎫+++= ⎪+⎝⎭. 2因为22222240!1231n n n n n<=<-,而且4lim 0n n →∞=,所以,由夹逼定理得4. 利用单调有界数列收敛准则证明下列数列的极限存在. 1 x n =11n e +,n =1,2,…；2 x 1x n +1n =1,2,…. 证：1略;2因为12x <,不妨设2k x <,则故有对于任意正整数n ,有2n x <,即数列{}n x 有上界,又 1n n x x +-=,而0n x >,2n x <,所以 10n n x x +-> 即 1n n x x +>, 即数列是单调递增数列;综上所述,数列{}n x 是单调递增有上界的数列,故其极限存在;习题2-21※. 证明：0lim x x →fx =a 的充要条件是fx 在x 0处的左、右极限均存在且都等于a .证：先证充分性：即证若0lim ()lim ()x x x x f x f x a -+→→==,则0lim ()x x f x a →=. 由0lim ()x x f x a -→=及0lim ()x x f x a +→=知： 10,0εδ∀>∃>,当010x x δ<-<时,有()f x a ε-<,20δ∃>当020x x δ<-<时,有()f x a ε-<;取{}12min ,δδδ=,则当00x x δ<-<或00x x δ<-<时,有()f x a ε-<, 而00x x δ<-<或00x x δ<-<就是00x x δ<-<, 于是0,0εδ∀>∃>,当00x x δ<-<时,有()f x a ε-<, 所以 0lim ()x x f x a →=.再证必要性：即若0lim ()x x f x a →=,则0lim ()lim ()x x x x f x f x a -+→→==, 由0lim ()x x f x a →=知,0,0εδ∀>∃>,当00x x δ<-<时,有()f x a ε-<,由00x x δ<-<就是 00x x δ<-<或00x x δ<-<,于是0,0εδ∀>∃>,当00x x δ<-<或00x x δ<-<时,有()f x a ε-<.所以 0lim ()lim ()x x x x f x f x a -+→→== 综上所述,0lim x x →fx =a 的充要条件是fx 在x 0处的左、右极限均存在且都等于a .2. 1 利用极限的几何意义确定0lim x → x 2+a ,和0lim x -→1e x； 2 设fx = 12e ,0,,0,xx x a x ⎧⎪<⎨⎪+≥⎩,问常数a 为何值时,0lim x →fx 存在.解：1因为x 无限接近于0时,2x a +的值无限接近于a ,故2lim()x x a a →+=.当x 从小于0的方向无限接近于0时,1e x 的值无限接近于0,故10lim e 0xx -→=. 2若0lim ()x f x →存在,则00lim ()lim ()x x f x f x +-→→=, 由1知 22lim ()lim()lim()x x x f x x a x a a +--→→→=+=+=, 所以,当0a =时,0lim ()x f x →存在;3. 利用极限的几何意义说明lim x →+∞sin x 不存在.解：因为当x →+∞时,sin x 的值在-1与1之间来回振摆动,即sin x 不无限接近某一定直线y A =,亦即()y f x =不以直线y A =为渐近线,所以lim sin x x →+∞不存在;习题2-31. 举例说明：在某极限过程中,两个无穷小量之商、两个无穷大量之商、无穷小量与无穷大量之积都不一定是无穷小量,也不一定是无穷大量.解：例1：当0x →时,tan ,sin x x 都是无穷小量,但由sin cos tan xx x=当0x →时,cos 1x →不是无穷大量,也不是无穷小量;例2：当x →∞时,2x 与x 都是无穷大量,但22xx=不是无穷大量,也不是无穷小量; 例3：当0x +→时,tan x 是无穷小量,而cot x 是无穷大量,但tan cot 1x x =不是无穷大量,也不是无穷小量;2. 判断下列命题是否正确：1 无穷小量与无穷小量的商一定是无穷小量；2 有界函数与无穷小量之积为无穷小量；3 有界函数与无穷大量之积为无穷大量；4 有限个无穷小量之和为无穷小量；5 有限个无穷大量之和为无穷大量；6 y =x sin x 在-∞,+∞内无界,但lim x →∞x sin x ≠∞；7 无穷大量的倒数都是无穷小量；8 无穷小量的倒数都是无穷大量. 解：1错误,如第1题例1； 2正确,见教材§定理3；3错误,例当0x →时,cot x 为无穷大量,sin x 是有界函数,cot sin cos x x x =不是无穷大量；4正确,见教材§定理2；5错误,例如当0x →时,1x 与1x -都是无穷大量,但它们之和11()0x x+-=不是无穷大量；6正确,因为0M ∀>,∃正整数k ,使π2π+2k M >,从而ππππ(2π+)(2π+)sin(2π+)2π+2222f k k k k M ==>,即sin y x x =在(,)-∞+∞内无界,又0M ∀>,无论X 多么大,总存在正整数k ,使π>k X ,使(2π)πsin(π)0f k k k M ==<,即x →+∞时,sin x x 不无限增大,即lim sin x x x →+∞≠∞；7正确,见教材§定理5；8错误,只有非零的无穷小量的倒数才是无穷大量;零是无穷小量,但其倒数无意义; 3. 指出下列函数哪些是该极限过程中的无穷小量,哪些是该极限过程中的无穷大量. 1 fx =234x -,x →2; 2 fx =ln x ,x →0+,x →1,x →+∞； 3 fx = 1e x,x →0+,x →0-； 4 fx =2π-arctan x ,x →+∞;5 fx =1x sin x ,x →∞; 6 fx = 21xx →∞. 解：122lim(4)0x x →-=因为,即2x →时,24x -是无穷小量,所以214x -是无穷小量,因而234x -也是无穷大量; 2从()ln f x x =的图像可以看出,1lim ln ,limln 0,lim ln x x x x x x +→→+∞→=-∞==+∞,所以,当0x +→时,x →+∞时,()ln f x x =是无穷大量；当1x →时,()ln f x x =是无穷小量;3从1()e x f x =的图可以看出,110lim e ,lim e 0x xx x +-→→=+∞=, 所以,当0x +→时,1()e xf x =是无穷大量；当0x -→时,1()e xf x =是无穷小量;4πlim(arctan)02xx→+∞-=,∴当x→+∞时,π()arctan2f x x=-是无穷小量;5当x→∞时,1x是无穷小量,sin x 是有界函数,∴1sin xx是无穷小量;6当x→∞时,21x是无穷小量,∴;习题2-41.若limx x→fx存在,limx x→gx不存在,问limx x→fx±gx,limx x→fx·gx是否存在,为什么解：若limx x→fx存在,limx x→gx不存在,则1limx x→fx±gx不存在;因为若limx x→fx±gx存在,则由()()[()()]g x f x f x g x=--或()[()()]()g x f x g x f x=+-以及极限的运算法则可得limx x→gx,与题设矛盾;2limx x→fx·gx可能存在,也可能不存在,如：()sinf x x=,1()g xx=,则limsin0xx→=,1limx x→不存在,但limx x→fx·gx=1lim sin0xxx→=存在;又如：()sinf x x=,1()cosg xx=,则π2limsin1xx→=,π21limcosx x→不存在,而0limx x→fx·gxπ2lim tanxx→=不存在;2. 若limx x→fx和limx x→gx均存在,且fx≥gx,证明limx x→fx≥limx x→gx.证：设limx x→fx=A,limx x→gx=B,则0ε∀>,分别存在1δ>,2δ>,使得当010x xδ<-<时,有()A f xε-<,当020x xδ<-<时,有()g x Bε<+令{}12min,δδδ=,则当0x xδ<-<时,有从而2A Bε<+,由ε的任意性推出A B≤即00lim()lim()x x x xf xg x→→≤.3. 利用夹逼定理证明：若a1,a2,…,a m为m个正常数,则limn →∞nma ++=A , 其中A =max{a 1,a2,…,a m }.n n n m a m A ≤++≤,即而lim n A A →∞=,1lim nn mA A →∞=,由夹逼定理得nm n a A ++=.4※. 利用单调有界数列必存在极限这一收敛准则证明：若x1＝,x 2x n +1=1,2,…,则lim n →∞x n 存在,并求该极限.证：因为12x x ==有21x x >今设1k k x x ->,则1k k x x -=>=,由数学归纳法知,对于任意正整数n有1n n x x +>,即数列{}n x 单调递增;又因为12x =<,今设2k x <,则12k x -=<=,由数学归纳法知,对于任意的正整数 n 有2n x <,即数列{}n x 有上界,由极限收敛准则知lim n n x →∞存在;设lim n n x b →∞=,对等式1n x +=两边取极限得b =即22b b =+,解得2b =,1b =-由极限的保号性,舍去,所以lim 2n n x →∞=.5. 求下列极限：1 lim n →∞33232451n n n n n +++-+；2 lim n →∞1cos n ⎡⎤⎛⎢⎥⎝⎣⎦； 3 lim n →∞4 limn →∞11(2)3(2)3n nn n ++-+-+； 5 lim n →∞1112211133n n ++++++. 解：1原式=23232433lim 11155nn n n n n→∞++=+-+；2因为lim(10n →∞=,即当n →∞时,1是无穷小量,而cos n 是有界变量,由无穷小量与有界变量的乘积是无穷小量得：lim (10n n →∞⎡⎤=⎢⎥⎣⎦；322lim(n n n→∞=而lim 0nn→∞→∞==, 2n n →∞∴==∞；41111121(1)()(2)31333limlim2(2)33(1)()13nn n n n n n n n n ++→∞→∞++-+-+==-+-+； 5111111()21111114[1()]42222lim lim lim 1111311()3[1()]3333113n n n n n n n n n ++→∞→∞→∞++-+++--===+++---.6. 求下列极限： 1 3limx →239x x --； 2 1limx →22354x x x --+； 3 lim x →∞3426423x x x ++;4 2limx π→sin cos cos 2x xx -; 5 0lim h →33()x h x h+-; 6 3lim x→7 1lim x →21n x x x n x +++--; 8 lim x →∞sin sin x x x x +-；9 lim x →+∞ 10 1lim x →313()11x x---； 11 0lim x →21(sin )x x.解：23333311(1)limlim lim 9(3)(3)36x x x x x x x x x →→→--===--++2211lim(54)0,lim(23)1x x x x x →→-+=-=-3344226464lim lim 03232x x x x x x x x→∞→∞++==++； 4π2ππsincos sin cos 22lim1cos 2cos πx x xx →--==-； 5[]223300()()()()lim limh h x h x x h x h x x x h x h h→→⎡⎤+-+++++-⎣⎦= 222lim ()()3h x h x h x x x →⎡⎤=++++=⎣⎦；633(23)92)x x x →→+-=343x x →→===；72211(1)(1)(1)limlim 11n n x x x x x n x x x x x →→+++--+-++-=--1123(1)2n n n =++++=+； 8sin lim0x x x →∞=无穷小量1x与有界函数sin x之积为无穷小量sin 1sin lim lim 1sin sin 1xx x x x x xx x x→∞→∞++∴==--； 922limlimx x→+∞=limlim1x x ===；101lim x →313()11x x---231(1)3lim 1x x x x →++-=- 11当0x →时,2x 是无穷小量,1sinx是有界函数,∴它们之积21sinx x 是无穷小量,即201lim sin 0x x x →⎛⎫= ⎪⎝⎭;习题2-5求下列极限其中a ＞0,a ≠1为常数： 1. 0limx →sin 53x x; 2. 0lim x →tan 2sin 5xx ; 3. 0lim x →x cot x ;4. 0lim x→; 5. 0lim x →2cos5cos 2x x x -; 6. lim x →∞1xx x ⎛⎫⎪+⎝⎭; 7. 0lim x →()cot 13sin xx +; 8. 0lim x →1x a x-; 9. 0lim x →x x a a x --;10. lim x →+∞ln(1)ln x x x +-; 11. lim x →∞3222xx x -⎛⎫⎪-⎝⎭; 12.lim x →∞211xx ⎛⎫+ ⎪⎝⎭; 13. 0limx →arcsin x x ; 14. 0lim x →arctan xx; .解：1. 000sin 55sin 55sin 55lim lim lim 335353x x x x x x x x x →→→===；2. 000tan 2sin 221sin 25lim lim lim sin 5cos 2sin 55cos 22sin 5x x x x x x x x x x x x x→→→== 0205021sin 252lim lim lim 5cos 22sin 55x x x x x x x x →→→==； 3. 0000lim cotlim cos lim limcos 1cos01sin sin x x xx x xx x x x x x →→→→=⋅==⨯=；4. 0000sin22limlim22x x x x x x x→→→→=== 0sin2221222xx →===； 5. 2200073732sin sin sin sin cos5cos 2732222lim lim lim (2)732222x x x x x x x x x x x x x →→→⎡⎤-⎢⎥-==-⋅⋅⋅⋅⎢⎥⎢⎥⎣⎦0073sin sin 212122limlim 732222x x x x x x →→=-⋅=-；6. 111lim lim lim 111e (1)xxx x x x x x x x x →∞→∞→∞⎛⎫ ⎪⎛⎫=== ⎪ ⎪++⎝⎭ ⎪+⎝⎭； 7. 3cos cos 1cot sin 3sin 0lim(13sin )lim(13sin )lim (13sin )xx xxx x x x x x x →→→⎡⎤+=+=+⎢⎥⎣⎦8.令1xu a =-,则log (1)a x u =+,当0x →时,0u →,111ln log elimlog (1)a ua u a u →===+. 9. 000(1)(1)11lim lim lim x x x x x x x x x a a a a a a x x xx ---→→→⎛⎫------==+ ⎪-⎝⎭ 利用了第8题结论01limln x x a a x→-=； 10. ln(1)ln 11limlim lnx x x x xx x x→+∞→+∞+-+=⋅ 1111lim ln(1)lim lim ln(1)0x x x x x x x→+∞→+∞→+∞=+=+=； 11. 22223211lim lim 1lim 1222222x xxxxx x x x x x x --→∞→∞→∞⎡⎤-⎛⎫⎛⎫⎛⎫=+=+⎢⎥ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦1232lim e 22xx x x -→∞-⎛⎫∴= ⎪-⎝⎭； 12. 1221222111ln (1)lim ln(1)2211lim(1)lim (1)lim eex x xxx xx x x xx x x x x →∞⎡⎤++⎢⎥⎣⎦→∞→∞→∞⎡⎤+=+==⎢⎥⎣⎦2121lim lim ln(1)0lne 0e e e 1xx x x x→∞→∞+⋅====；13.令arcsin x u =,则sin x u =,当0x →,0u →,000arcsin 1limlim 1sin sin limx u u x u u x u u→→→===；14.令arctan x u =,则tan x u =,当0x →,0u →,00000arctan 1lim lim lim cos lim limcos 1sin tan sin x u u u u x u u u u u xu u u→→→→→====. 习题2-61. 证明：若当x →x 0时,αx →0,βx →0,且αx ≠0,则当x →x ０时,αx ～βx 的充要条件是0lim x x →()()()x x x αβα-＝０. 证：先证充分性.若0lim x x →()()()x x x αβα-＝０,则0lim x x →()(1)()x x βα-＝0, 即0()1lim 0()x x x x βα→-=,即0()lim 1()x x x x βα→=. 也即0()lim 1()x x x x αβ→=,所以当0x x →时,()()x x αβ. 再证必要性：若当0x x →时,()()x x αβ,则0()lim 1()x x x x αβ→=, 所以0lim x x →()()()x x x αβα-＝0lim x x →()(1)()x x βα-＝0()1lim ()x x x x βα→-=011110()lim ()x x x x αβ→-=-=. 综上所述,当x →x 0时,αx ～βx 的充要条件是0lim x x →()()()x x x αβα-＝０. 2. 若βx ≠0,0lim x x →βx =0且0lim x x →()()x x αβ存在,证明0lim x x →αx =0. 证：0000()()lim ()lim ()lim lim ()()()x x x x x x x x x x x x x x x αααββββ→→→→==0()lim 00()x x x x αβ→== 即 0lim ()0x x x α→=. 3. 证明：若当x →0时,fx =ox a ,gx =ox b ,则fx ·gx ＝o a b x+,其中a ,b 都大于0,并由此判断当x →0时,tan x －sin x 是x 的几阶无穷小量.证: ∵当x →0时, fx =ox a ,gx =ox b ∴00()()lim(0),lim (0)a bx x f x g x A A B B x x →→=≠=≠ 于是: 0000()()()()()()lim lim lim lim 0a b a b a b x x x x f x g x f x g x f x g x AB x x x x x +→→→→⋅=⋅=⋅=≠ ∴当x →0时, ()()()a b f x g x O x +⋅=,∵tan sin tan (1cos )x x x x -=-而当x →0时, 2tan (),1cos ()x O x x O x =-=,由前面所证的结论知, 3tan (1cos )()x x O x -=,所以,当x →0时,tan sin x x -是x 的3阶无穷小量.4. 利用等价无穷小量求下列极限：1 0lim x →sin tan ax bx b ≠0；2 0lim x →21cos kx x-； 3 0lim x→； 4 0lim x→5 0lim x →arctan arcsin x x ；6 0lim x →sin sin e e ax bx ax bx-- a ≠b ； 7 0limx →ln cos 2ln cos3x x ； 8 设0lim x →2()3f x x-＝100,求0lim x →fx . 解 00sin (1)lim lim .tan x x ax ax a bx bx b→→== 8由20()3lim 100x f x x →-=,及20lim 0x x →=知必有0lim[()3]0x f x →-=, 即 00lim[()3]lim ()30x x f x f x →→-=-=, 所以 0lim ()3x f x →=. 习题2-7１.研究下列函数的连续性,并画出函数的图形：1 fx = 31,01,3,12;x x x x ⎧+≤<⎨-≤≤⎩ 2 fx ＝,111,1 1.x x x x -≤<⎧⎨<-≥⎩，或解: 1300lim ()lim(1)1(0)x x f x x f ++→→=+== ∴ fx 在x =0处右连续,又11lim ()lim(3)2x x f x x ++→→=-= ∴ fx 在x =1处连续.又 22lim ()lim(3)1(2)x x f x x f --→→=-== ∴ fx 在x =2处连续.又fx 在0,1,1,2显然连续,综上所述, fx 在0,2上连续.图形如下:图2-12 11lim ()lim 1x x f x x --→→==∴ fx 在x =1处连续.又11lim ()lim 11x x f x -+→-→-== 故11lim ()lim ()x x f x f x -+→-→-≠ ∴ fx 在x =-1处间断, x =-1是跳跃间断点.又fx 在(,1),(1,1),(1,)-∞--+∞显然连续.综上所述函数fx 在x =-1处间断,在(,1),(1,)-∞--+∞上连续.图形如下:图2-22. 说明函数fx 在点x 0处有定义、有极限、连续这三个概念有什么不同又有什么联系略.3.函数在其第二类间断点处的左、右极限是否一定均不存在试举例说明.解:函数在其第二类间断点处的左、右极限不一定均不存在. 例如0(),010x x f x x x x ≤⎧⎪==⎨>⎪⎩是其的一个第二类间断点,但00lim ()lim 0x x f x x --→→==即在0x =处左极限存在,而001lim ()lim x x f x x++→→==+∞,即在0x =处右极限不存在. 4.求下列函数的间断点,并说明间断点的类型：1 fx = 22132x x x -++；2 fx ＝sin sin x x x+； 3 fx = ()11x x+； 4 fx = 224x x +-； 5 fx = 1sinx x . 解: 1由2320x x ++=得x =-1, x =-2∴ x =-1是可去间断点,x =-2是无穷间断点.2由sin x =0得πx k =,k 为整数.∴ x =0是跳跃间断点.4由x 2-4=0得x =2,x =-2.∴ x =2是无穷间断点,x =-2是可去间断点. 5 001lim ()lim sin 0,()x x f x x f x x→→==在x =0无定义故x =0是fx 的可去间断点.5.适当选择a 值,使函数fx = ,0,,0x e x a x x ⎧<⎨+≥⎩在点x =0处连续.解: ∵f 0=a ,要fx 在x =0处连续,必须00lim ()lim ()(0)x x f x f x f +-→→==. 即a =1.6※.设fx = lim x →+∞x xx x a a a a ---+,讨论fx 的连续性. 解: 22101()lim lim sgn()10100x x xx x x a a x a aa f x x x a a a x --→+∞→+∞-<⎧--⎪====>⎨++⎪=⎩ 所以, fx 在(,0)(0,)-∞+∞上连续,x =0为跳跃间断点. 7. 求下列极限：1 2lim x →222x x x +-； 2 0lim x→； 3 2lim x →ln x -1; 4 12lim x →5 lim x e→ln x x . 解: 222222(1)lim 1;2222x x x x →⨯==+-+- 习题2-81. 证明方程x 5-x 4-x 2-3x =1至少有一个介于1和2之间的根.证: 令542()31f x x x x x =----,则()f x 在1,2上连续,且 (1)50f =-<, (2)50f =>由零点存在定理知至少存在一点0(1,2),x ∈使得0()0f x =.即 542000031x x x x ---=, 即方程54231x x x x ---=至少有一个介于1和2之间的根.2. 证明方程ln １＋e x -2x =0至少有一个小于1的正根.证: 令()ln(1)2e x f x x =+-,则()f x 在(,)-∞+∞上连续,因而在0,1上连续, 且 0(0)ln(1)20ln 20e f =+-⨯=>由零点存在定理知至少存在一点0(0,1)x ∈使得0()0f x =.即方程ln(1)20e xx +-=至少有一个小于1的正根.3※. 设fx ∈C -∞,+∞,且lim x →-∞fx =A , lim x →+∞fx =B , A ·B ＜0,试由极限及零点存在定理的几何意义说明至少存在一点x 0∈－∞,＋∞,使得fx 0＝０.证: 由A ·B <0知A 与B 异号,不防设A >0,B <0由lim ()0,lim ()0x x f x A f x B →-∞→+∞=>=<,及函数极限的保号性知,10X ∃>,使当1x X <-,有()0,f x >20X ∃<,使当2x X >时,有()0f x <.现取1x a X =<-,则()0f a >,2x b X =>,则()0f b <,且a b <,由题设知()f x 在[,]a b 上连续,由零点存在定理,至少存在一点0(,)x a b ∈使0()0f x =, 即至少存在一点0(,)x ∈-∞+∞使0()0f x =.4.设多项式P n x ＝x n +a 11n x-+…+a n .,利用第3题证明：当n 为奇数时,方程P n x =0至少有一实根.证: 122()1n n n n a a a P x x x x x ⎛⎫=++++ ⎪⎝⎭()lim 10n nx P x x →∞∴=>,由极限的保号性知. 0X ∃>,使当X x >时有()0nn P x x>,此时()n P x 与n x 同号,因为n 为奇数,所以2X n 与-2X n 异号,于是(2)n P X -与(2)n P X 异号,以()n P x 在[2,2]X X -上连续,由零点存在定理,至少存在一点0(2,2)X X X ∈-,使0()0n P x =,即()0n P x =至少有一实根.。

微积分(曹定华)(修订版)课后题答案第六章习题详解

第六章习题6-11. 利用定积分定义计算由直线y =x +1,直线x =a ，x =b （a<b ）及x 轴所围成的图形的面积. 解因y =x 2+1在[a,b ]上连续,所以x 2+1在[a,b ]上可积,从而可特殊地将[a,b ]n 等分,并取2,,()()1Δi i i b a b a b a a i x f a i n n nξξ---=+==++, 于是21122221222()[()1]1()[()2()1]111(1)1()[()(1)(21)2()]62Δ nni i i i ni b a b a f x a i n ni i b a a b a a b a n n n n n b a na b a n n n b a a n n n nξ===--=++=-+-+-++=-+-⋅⋅+++-⋅⋅+⋅∑∑∑ 故面积 22211(1)l i m ()()[()()1]3d Δnbi i a n i S x x f x b a a b a a b a ξ→∞==+==-+-+-+∑⎰ 331()()3b a b a =-+- 2. 利用定积分的几何意义求定积分： (1)12d x x ⎰;(2)x ⎰（a ＞0）.解 (1)根据定积分的几何意义知, 102d x x ⎰表示由直线y =2x ,x =0,x =1及x 轴所围的三角形的面积,而此三角形面积为1,所以12d x x ⎰=1.(2)根据定积分的几何意义知,0x ⎰表示由曲线0,y x x a ===及x轴所围成的14圆的面积,而此14圆面积为214πa ,所以2014πx a =⎰.3. 根据定积分的性质，比较积分值的大小： (1)12d x x ⎰与13d x x ⎰； (2)1e d xx ⎰与1(1)d x x +⎰.解 (1)∵当[0,1]x ∈时,232(1)0x x x x -=-≥,即23x x ≥,又2x3x ,所以11230d d x x x x >⎰⎰.(2)令()1,()1e e x xf x x f x '=--=-,因01x ≤≤,所以()0f x '>,从而()(0)0f x f ≥=,说明1e xx ≥+,又ex1+x .所以11(1)e d d xx x x >+⎰⎰.4. 估计下列各积分值的范围：(1)421(1)d x x +⎰；(2) arctan d x x ;(3)2e d ax ax --⎰（a ＞0)； (4)22e d x x x -⎰.解 (1)在区间[1,4]上,函数2()1f x x =+是增函数,故在[1,4]上的最大值(4)17M f ==,最小值(1)2m f ==,所以4212(41)(1)17(41)d x x -≤+≤-⎰, 即 4216(1)51d x x ≤+≤⎰.(2)令()arctan f x x x =,则2()arctan 1x f x x x '=++,当x ∈时,()0f x '>,从而()f x在上是增函数,从而f (x )在上的最大值M f ==,最小值m f ==,所以2arctan 93ππd x x =≤≤=即2arctan 93ππd x x ≤≤. (3)令2()e x f x -=,则2()2e x f x x -'=-,令()0f x '=得驻点x =0,又(0)1f =，2()()e a f a f a -=-=,a >0时, 21e a -<,故()f x 在[-a,a ]上的最大值M =1,最小值 2e a m -=,所以2222e e d aa x aa x a ---≤≤⎰.(4)令2()ex xf x -=,则2()(21)e xxf x x -'=-,令()0f x '=得驻点12x =,又(0)1,f = 1241(),(2)2e ef f -==,从而()f x 在[0,2]上的最大值2e M =,最小值14e m -=,所以 212242ee d e x x x --≤≤⎰,而2222ed e d x xx x x x --=-⎰⎰,故 21024222e ed ex xx ---≤≤-⎰.习题6-21. 求下列导数：(1)20d d x t x ⎰; (2) 53ln 2d e d d x t t t x -⎰； (3) cos 2sin cos()d xxt t '⎡⎤π⎢⎥⎣⎦⎰; (4) 22dsin d d x t t x tπ⎰ (x ＞0). 解220(1)()d d x t x x'⋅=⎰5353ln 2(2)d e d e d x tx t t x x --=⎰cos cos sin 222sin 00cos sin 220022222(3)cos()cos()cos()cos()cos()cos(cos )(cos )cos(sin )(sin )cos(cos )sin cos(sin )cos cos(sin )sin πd πd πd πd πd πππππx x xx xx t t t t t t t t t tx x x x x x x x x x ''⎡⎤⎡⎤=-⎣⎦⎣⎦''⎡⎤⎡⎤=-⎣⎦⎣⎦''=⋅-⋅=--=-⎰⎰⎰⎰⎰22cos(sin )cos (sin cos )cos(sin )ππx x x x x =-2222sin sin sin (4)cos sin sin cos .ππd d d d d d d d d d xx t t x t t xt x x x t x x x x x x x x x⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭--=-=⎰⎰ 2. 求下列极限：(1) 02arctan d limxx t t x →⎰; (2) 2020sin 3d lim e d x xx tt t t t→-⎰⎰; (3)()22220e d lime d xt xx t t t t→⎰⎰.解 ()022000021a r c t a n a r c t a n a r c t a n11(1)l i m l i ml i m l i m 222d d x xx x xxt t t t x x x xx →→→→'⎡⎤--⎣⎦+====-'⎰⎰ 2220030003300222200sin 3sin 3sin 32(2)lim lim lim 2sin 3sin 3lim lim 663d d e e d e d e e x x x x x x x t x t x xx x t t t t x x x t t t t x x x x-→→→--→→'⎡⎤⋅⎢⎥⎣⎦=='⎡⎤⎣⎦=⋅=⋅⋅=⎰⎰⎰⎰()()[]222222222222222200002000022000200022(3)lim lim lim lim 222lim lim lim 2122e d e d e d e e d e e e d e d e d e e e e xxx x t t t x tx x x x x x x t x t x t x x x x x x x t t t t x x t tt t t x x x x →→→→→→→'⎡⎤⋅⎢⎥⎣⎦==='⎡⎤⎣⎦'⎡⎤⎣⎦====+'+⋅⎰⎰⎰⎰⎰⎰⎰ 3. 求由方程e d cos d 0yxtt t t +=⎰⎰所确定的隐函数y =y (x )的导数.解方程两边对x 求导数得:cos 0e y y x '⋅+=, cos e yxy '∴=-. 又由已知方程有000sin e y xtt +=,即1sin sin 00e y x -+-=即1sin e yx =-,于是有cos cos sin 1e yx xy x '=-=-. 4. 当x 为何值时，I (x )=2e d xt t t -⎰有极值?解 2()e x I x x -'=,令()0I x '=得驻点0x =,又22()(12),(0)10e x I x x I -''''=-=>, 所以当x =0时,I (x )有极小值,且极小值为I (0)=0.5. 计算下列定积分：(1)3x ⎰; (2)221d x x x --⎰;(3)()d f x x π⎰,其中,0,2()sin ,2x x f x x x π⎧≤≤⎪⎪=⎨π⎪≤≤π;⎪⎩ (4) {}222max 1,d x x -⎰.解433322233222(1)(43)(8333x x ⎛⎫==-=- ⎪⎝⎭⎰201222221101(2)()()()d d d d x x x x x x x x x x x x --=-+-+--⎰⎰⎰⎰012322332101111111116322332x x x x x x -⎛⎫⎛⎫⎛⎫=++=--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()22220022(3)()sin 1cos 82ππππππππd d d xf x x x x x x x =+=+=+-⎰⎰⎰(4)由于22221()max{1,}11112x x f x x x x x ⎧-≤<-⎪==-≤<⎨⎪≤≤⎩,于是 21121212223312122111120max{1,}333d d 1d d x x x x x x x x x x -------=++=++=⎰⎰⎰⎰ 6. 已知f (x )连续，且f (2)=3,求2222()d d lim(2)xt x f u u tx →⎡⎤⎢⎥⎣⎦-⎰⎰.解 []222222222222()()()()limlim lim lim (2)2(2)2(2)(2)d d d d d d x xx x t t x x x x t f u u t f u u f u u f u u x x x x →→→→''⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦===--''-⎡⎤-⎣⎦⎰⎰⎰⎰⎰⎰ 22()113lim lim ()(2)2222x x f x f x f →→-==-=-=-.习题6-31. 计算下列积分： (1)3sin()d x x πππ+3⎰; (2) 32d (115)xx 1-+⎰;(3)1x -⎰; (4) 320sin cos d ϕϕϕπ⎰;(5)22cos d u u ππ6⎰;(6)2e 1⎰;(7)1;(8)x ;(9)ln 3ln 2d e ex xx--⎰; (10) 322d 2xx x +-⎰;(11)21x ⎰;(12) 22x ππ-⎰.解 333(1)sin()d sin()d()[cos()]x x x x x ππππππππππ+=++=-+3333⎰⎰42coscos 033ππ=-+= 12332221d 1d(511)151(2)(511)(115)5(511)10512x x x x x 11---+==-=+++⎰⎰1111(3)4)14x x--=-==⎰⎰2334220011(4)sin cos d cos dcos cos44ϕϕϕϕϕϕπππ=-==-⎰⎰22222π2π61cos211(5)cos d d d cos2d22241πππ1sin226264uu u u u u uuππππππππ6666+==+⎛⎫=+=-⎪⎝⎭⎰⎰⎰⎰222e e11(6)1)===⎰⎰(7)令x=tan t,则d x=sec2t d t,当x=1时,π4t=;当x=,π3t=,于是ππ33π21π44cos1dsin sinttt t==-=⎰(8)令x t,则d dx t t=,当x=0时,t=0;当x=,π2t=,于是πππ222200π12cos d(1cos2)d(sin2)22x t t t t t t==+==+⎰⎰.(9)令e x t=,则1ln,d dx t x tt==,当ln2x=时,2t=;当ln3x=时,3t=,于是3ln3332ln2222d d1113111d ln lne e12222111x xx t ttt t t t--⎛⎫====-⎪---++⎝⎭⎰⎰⎰.3 333222222d d11111(10)()d ln19231232()241211(ln ln)ln2ln53543x x xxx x x x xx-==-=+--+++-=-=-⎰⎰⎰(11)t=,则65,d6dx t x t t==,当x=1时,t=1;当x=2,t于是2111611d6()d1x t tt t t t==-++⎰6(ln ln(7ln26ln(1t t=-+=-220202(12)d sin )d sin d x x x x x x x x xπ-π-π-==-+=-⎰⎰⎰33022202224cos cos 333x x ππ-=-= 2. 利用被积函数的奇偶性计算下列积分值：(1)ln(aa x x -+⎰(a 为正常数)；(2) 325425sin d 21x xx x x -++⎰; (3) 4224cos d θθππ-⎰.解((1)()l n f x x =+是奇函数.(ln 0d aax x -∴=+⎰.3242sin (2)()21x xf x x x =++ 是奇函数.325425sin 021d x x x x x -∴=++⎰4(3)()cos f θθ= 是偶函数.4422222022202020222004cos 24cos 2(1cos )2(12cos 2cos 2)312(2cos 2cos 4)22(34cos 2cos 4)1332sin 2sin 442ππππππππππd d d d d d θθθθθθθθθθθθθθθθθθ-∴==+=++=++=++=++=⎰⎰⎰⎰⎰⎰π3. 证明下列等式： (1)2321()d ()d 2aa x f x x xf x x =⎰⎰ (a 为正整数)；(2)证明：11221d d 11xx x x x x =++⎰⎰ (x ＞0)；(3) 设f (x )是定义在(-∞，+∞)上的周期为T 的连续函数，则对任意a ∈［－∞，＋∞），有()d ()d a TTaf x x f x x +=⎰⎰.证 (1)令x 2=t ,则d x x t ==,当x =0时,t =0;当x =a 时,t =a 2, 于是2223200011()()()()22d d d aa a a x f x x t t tf t t xf x x ===⎰⎰⎰⎰即2321()()2d d aa x f x x xf x x =⎰⎰.(2)令1x t=则21d d x t t -=,1111111222231111111111111d d d d d t xx t tx t t t x x t t x t t⎛⎫=⋅=-⋅==- ⎪++++⎝⎭+⎰⎰⎰⎰⎰ 即 1122111d d xx x x x x =++⎰⎰. 4. 若f (t )是连续函数且为奇函数，证明0()d xf t t ⎰是偶函数；若f (t )是连续函数且为偶函数，证明()d xf t t ⎰是奇函数.证令0()()d xF x f t t =⎰.若f (t )为奇函数,则f (-t )=- f (t ),从而()()()()()d d d xxxF x f t tt u f u u f u u F x -==---==⎰⎰⎰,所以0()()d xF x f t t =⎰是偶函数.若f (t )为偶函数,则f (-t )=f (t ),从而()()()()()d d d xxxF x f t tt u f u u f u u F x --==---=-=-⎰⎰⎰,所以0()()d xF x f t t =⎰是奇函数.5※. 设f (x )在(-∞，+∞)内连续，且F (x )= 0(2)()d xx -t f t t ⎰,试证：若f (x )单调不减，则F (x )单调不增.证 00()()()2()()2()d d d x xxF x f t t xf x xf x xf t t tf t x '⎡⎤'==+--⎣⎦⎰⎰⎰()()()()[()()]d xf t t xf x f x xf x x f f x ξξ=-=-=-⎰,其中ξ在x 与0之间.当x >0时,x >ξ,由f (x )单调不减有()()0f f x ξ-≤,即()0F x '≤;当x <0时,ξ> x ,由f (x )单调不减有()()0f f x ξ-≥,即()0F x '≤;综上所述知F (x )单调不增.习题6-41. 计算下列定积分： (1)10e d xx x -⎰; (2)e1ln d x x x ⎰;(3)41x ⎰; (4) 324d sin xx x ππ⎰; (5) 220e cos d x x x π⎰; (6)221log d x x x ⎰;(7)π20(sin )d x x x ⎰; (8)e1sin(ln )d x x ⎰；(9)230e d x x ; (10)1201lnd 1xx x x+-⎰. 解 (1)1111000e d de e e d x x x xx x x x x ----=-=-+⎰⎰⎰ 111012e e e e e 1ex----=--=--+=-.e e e 22222ee 11111111111(2)ln d ln d ln d e (e 1)222244x x x x x x x x x x ==-=-=+⎰⎰⎰444441111(3)2ln 28ln 28ln 24x x x x ==-=-=-⎰⎰⎰33332444434(4)d dcot cot cot d sin π131πln πlnsin 492249xx x x x x x xx x ππππππππππ=-=-+⎛=-+=+- ⎝⎭⎰⎰⎰22222222000π2π222220π220(5)e cos d e dsin e sin 2e sin d e 2e dcos e 2e cos 4e cos d e 24e cos d xxxx xxx x x x x xx xx x x x x xππππππππ==-=+=+-=--⎰⎰⎰⎰⎰⎰故2π201e cos d (e 2)5x x x π=-⎰.()2222222111111(6)log d ln d ln d 2ln 22ln 2133(4ln 2)22ln 224ln 2x x x x x x x x x ==-=-=-⎰⎰⎰πππ2232π000033ππ2π0003ππ0033π01111(7)(sin )d (1cos 2)d (dsin2)2232π1π1(sin 22sin2d )dcos26464π1(cos 2cos d )64ππ1ππsin 264864x x x x x x x x x x x x x x x xx x x x x =-=-=--=-=--=-+=-⎰⎰⎰⎰⎰⎰ee e111ee11e1(8)sin(ln )d sin(ln )cos(ln )d esin1cos(ln )sin(ln )d esin1ecos11sin(ln )d x x x x x x x x x x x x=-=--=-+-⎰⎰⎰⎰故e11sin(ln )d (esin1ecos11)2x x =-+⎰. 222222322000011(9)e d de e e d 22111ln 2ln 2e ln 2222x x x x x x x x x x==-=-=-=-1112122222220000111222200012011111(10)ln d ln d ln d 121211111111ln 3(1)d ln 3()d 818211111131ln 3ln ln 3822281x x x x x x x x x x x x x x x x x x x x x +++==+----=++=++---+-=++=-+⎰⎰⎰⎰⎰2. 已知f (2)= 12,f ′(2)=0, 2()d 1f x x =⎰,求220()d x f x x ''⎰.解222222200()d d ()()2()d x f x x x f x x f x xf x x '''''==-⎰⎰⎰222004(2)2d ()2()2()d 14(2)21420.2f x f x xf x f x xf '=-=-+=-+⨯=-⨯+=⎰⎰3※. 利用分部积分公式证明：()()()d ()d d xxuf u x u u f x x u -=⎰⎰⎰.证令0()()d uF u f x x =⎰则()()F u F u '=,则(())()()()d d d d xu x xx f x x u f u u uF u uF u u '==-⎰⎰⎰⎰()()()()()()()()()()d d d d d d d d x x xx x x xxxF x uf u u x f x x uf u ux f u u uf u u xf u u uf u u x u f u u=-=-=-=-=-⎰⎰⎰⎰⎰⎰⎰⎰即等式成立.习题6-51. 求由下列曲线所围成的平面图形的面积：(1) y =e x 与直线x =0及y =e; (2) y =x 3与y =2x ;(3) y =x 2,4y =x 3; (4) y =x 2与直线y =x 及y =2x ; (5) y =1x,x 轴与直线y =x 及x =2; (6) y =(x -1)(x -2)与x 轴； (7) y =e x ,y =e -x 与直线x =1; (8) y =ln x ,y 轴与直线y =ln a ,y =ln b , (0)a b <<. 解 (1)可求得y =e x 与y =e 的交点坐标(1,e), y =e x 与x =0的交点为(0,1),它们所围成的图形如图6-1中阴影部分,其面积eee111d ln d (ln )1S x y y y y y y ===-=⎰⎰图6-1 图6-2(2)解方程组32y x y x ⎧=⎨=⎩得0,0x x x y y y ⎧⎧===⎧⎪⎪⎨⎨⎨==-=⎩⎪⎪⎩⎩即三次抛物线3y x =和直线2y x =的交点坐标分别为(0,0),(-,它们所围成的图形的面积3342240112)d )d ()(244S x x x x x x x x x x =-+-=-+-=⎰.(3)解方程234y xy x⎧=⎪⎨=⎪⎩得两曲线的交点为(0,0),(4,16),所求面积为 4233440011116()d ()43163S x x x x x =-=-=⎰.图6-3 图6-4(4)可求得2y x =与y x =的交点为(0,0),(1,1);2y x =与2y x =的交点为(0,0),(2,4); y =x 与y =2x 的交点为(0,0),它们所围图形如图6-4中阴影所示,其面积为:121122012231201(2)d (2)d d (2)d 117()236S x x x x x x x x x x xx x x =-+-=+-=+-=⎰⎰⎰⎰(5) 1y x =与y x =的交点为(1,1),1y x=,x 轴与直线x =1,及x =2所围成的图形如图6-5阴影所示,其面积:2121201111d d ln ln 222x S x x x xx =+=+=+⎰⎰.图6-5 图6-6(6) 231(1)(2)()24y x x x =--=--,顶点坐标为31(,)24-,与x 轴所围成的图形如图6-6中阴影所示,由231()24y x =--得32x =所求面积0143021433d 2222112364S y y y --⎡⎤⎛⎛=-=⎢⎥ ⎝⎝⎣⎦⎛⎫=⋅=+ ⎪⎝⎭⎰⎰(7)可求得曲线e x y =与e x y -=的交点(0,1),曲线e x y =,e x y -=与x =1所围成的图形如图6-7阴影所示,其面积:10)() 2.101(e e d e e e ex x x x S x --=-=+=+-⎰图6-7 图6-8(8)曲线ln ,y x y =轴与直线ln ,ln y a y b ==所围成的图形如图6-8阴影所示,其面积:ln ln ln ln ln ln .d e d e bby yb aaaS x y y b a ====-⎰⎰2. 求由下列曲线围成的平面图形绕指定轴旋转而成的旋转体的体积：(1) y =e x ,x =0,y =0,x =1,绕y 轴； (2) y =x 3,x =2,x 轴，分别绕x 轴与y 轴； (3) y =x 2,x =y 2，绕y 轴； (4) y 2=2px ,y =0,x =a (p ＞0,a ＞0),绕x 轴； (5) (x -2)2+y 2≤1,绕y 轴.解 (1)如图6-9所求旋转体的体积为矩形OABD ,与曲边梯形CBD 绕y 轴旋转所成的几何体体积之差,可求得y =e x 与x =1的交点为(1,e), y =e x 与y 轴的交点为(0,1),所以,所求旋转体的体积.222111(ln )(ln )2(ln )22(1)2(ln )eee11ee1πe πd πe πd πe πe ππe e π.d y V y y y y y y y y y ⎡⎤=⋅⋅-=--⎣⎦⎡⎤=-+=-+=-⎣⎦⎰⎰⎰722262000128(2)7ππd πd π7x x V y x x x ===⋅=⎰⎰25882283336428323255πππd ππd ππy V x y y y y =⨯⨯-=-=-⋅⋅=⎰⎰.图6-9 图6-10(3)解方程组22y xx y⎧=⎪⎨=⎪⎩得交点(0,0),(1,1),所求旋转体的体积2511410031025πdπdππxx xV x x x x⎛⎫=-=⋅=-⎪⎝⎭⎰⎰.图6-11 图6-1222300(4)2πdπdππa aaxV y x px x p x pa===⋅=⎰⎰.(5)所求旋转体的体积是由右半圆2x=2x=x轴旋转生成的旋转体的体积之差,即((122122281641dπππyV yy yπ-⎡⎤=-+-⎢⎥⎣⎦===⎰⎰⎰图6-133. 已知曲线y=(a＞0)与y(x0,y0)处有公共切线，求：(1) 常数a及切点(x0,y0);(2) 两曲线与x轴围成的平面图形的面积S.解(1)由题意有点00(,)x y在已知曲线上,且在点00(,)x y处两函数的导数相等.即有00x xyy==⎧=⎪⎪==即12yyx⎧=⎪⎪=⎨=解得211eexya⎧=⎪⎪=⎨⎪=⎪⎩.(2)由(1)知两曲线的交点为2(,1)e,又在区间(0,1)上,曲线y=y=方,它们与x轴所围成的平面图形的面积122231221111()6223d ee ee e yyS y yy⎛⎫===-⎡⎤-- ⎪⎣⎦⎝⎭⎰.(由ey==得2()x ey=,由y=得2e yx=).4※. 设2()lim1e nxnxf xx→+∞=+-,试求曲线y=f(x),直线y=12x及x=1所围图形的面积.解2200()lim101nxnxxf x xx e xx→∞≥⎧⎪==⎨+-<⎪+⎩解方程2121y xxyx⎧=⎪⎪⎨⎪=⎪+⎩得交点为11,2⎛⎫--⎪⎝⎭,且易知当(1,0)x∈-时,12y x=位于21xyx=+的上方.所围图形如阴影部分所示,其面积2221111111111ln2ln(1)22422142dxS xx x xx--⎛⎫⎡⎤=+⨯⨯=+=--+⎪⎢⎥+⎣⎦⎝⎭⎰.5. 一抛物线y=ax2+bx+c通过点(0，0)、(1，2)两点，且a＜0，试确定a,b,c的值，使抛物线与x轴所围图形的面积最小.解由抛物线过(0,0),(1,2)点,有c=0,a+b=2,又由抛物线方程2y ax bx=+得与x轴的两交点为(0,0), ,0ba⎛⎫-⎪⎝⎭,抛物线与x轴所围图形的面积.2220()6d b ab S ax bx x a-=+=⎰,由2a b +=得2b a =-,代入上式有32(2)6a S a -=, 23(2)(4)6a a S a--+'=,令0S '=得2a =或4a =-, 由已知0a <得4a =-,从而26b a =-=, 所以4,6,0a b c =-==.6. 已知某产品产量的变化率是时间t (单位：月)的函数f (t )=2t +5,t ≥0,问：第一个5月和第二个5月的总产量各是多少?解设产品产量为()Q t ,则()()Q t f t '=,第一个5月的总产量552510()(25)(5)50.d d Q f t t t t t t ==+=+=⎰⎰ 第2个5月的总产量为10252055()(25)(5)100.d d tQ f t t t t t t ==+=+=⎰⎰ 7. 某厂生产某产品Q (百台)的总成本C (万元)的变化率为C ′(Q )=2(设固定成本为零)，总收入R (万元)的变化率为产量Q (百台)的函数R ′(Q )=7-2Q .问： (1) 生产量为多少时，总利润最大?最大利润为多少?(2) 在利润最大的基础上又生产了50台，总利润减少了多少? 解 (1)总利润()()()L Q R Q C Q =-当()0L Q '=即()()0R Q C Q ''-=即7220Q --=, Q =2.5百台时,总利润最大,此时的总成本2.5 2.52.50()225d d C C Q Q Q Q'====⎰⎰总利润11.255 6.25L R C =-=-=(万元).即当产量为2.5百台时,总利润最大,最大利润是6.25万元.(2)在利润最大的基础上又生产了50台,此时产量为3百台,总成本3300()26d d C C Q Q Q '===⎰⎰,总收入3323000()(72)(7)12d d R R Q Q Q Q Q Q '==-=-=⎰⎰, 总利润为1266L R C =-=-=(万元).减少了6.25-6=0.25万元.即在利润最大的基础上又生产了50台时,总利润减少了0.25万元.8. 某项目的投资成本为100万元，在10年中每年可获收益25万元，年利率为5％，试求这10年中该投资的纯收入的现值. 解投资后T 年中总收入的现值(1)e rt ay r-=-,由题意知 25,5%0.05,10.a r T ====所以0.051025(1)196.730.05e y -⨯=-= 纯收入的现值为196.73-100=96.73.即这10年中该投资的纯收入的现值为96.73万元.习题6-61. 判断下列广义积分的敛散性，若收敛，则求其值： (1)41d xx +∞⎰; (2)1+∞⎰; (3)0e d axx +∞-⎰ (a ＞0); (4)0cos d x x +∞⎰;(5)0e sin d x x x +∞⎰; (6)2d 22xx x +∞-∞++⎰; (7)21⎰; (8)10ln d x x ⎰;(9)e1⎰(10)22d (1)xx -⎰;(11)1⎰解 (1)1431d 1133x x x +∞+∞=-=⎰,此广义积分收敛.(2)1+∞==+∞⎰,此广义积分发散. (3)111e d e ax axx aa+∞--+∞=-=⎰,此广义积分收敛. (4)1cos d sin lim sin sin 0lim sin x x x x xx x +∞+∞→+∞→+∞==-=⎰不存在,所以,此广义积分发散.00(5)e sin d e d cos e cos e cos d e cos e dsin e cos e sin e sin d 11e sin d (e sin e cos )e (sin cos )22e sin d lim e sin d lim x x x x x x x x x x x x x b x x b b x x x x x x x x x x x xx x x x x x x x x x +∞→+∞→=-=-+=-+=-+-∴=-=-∴==⎰⎰⎰⎰⎰⎰⎰⎰ 01e (sin cos )211 lim e (sin cos )22x b b b x x b b +∞→+∞⎧⎫⎡⎤-⎨⎬⎢⎥⎣⎦⎩⎭⎡⎤=-+⎢⎥⎣⎦不存在,此广义积分发散.22d d(1)(6)arctan(1)π22(1)1xx x x x x +∞+∞+∞-∞-∞-∞+==+=++++⎰⎰,收敛.23222110013202(7)lim lim (1)3222lim 2,.2333收敛x x εεεεεε++++→→+→⎡==-+⎢⎣⎛==-- ⎝⎰⎰111011eee1111222220100(8)ln d ln d ln 1 ln d lim ln d lim (ln 1)1,.π(9)arcsin(ln ),.211d d d (10)lim (1)(1)(1)收敛收敛x x x x x x x x x x x x x x x x εεσεεεεεεεεεεεε+++→→-+→=-=--∴==--=-===⎛⎫+= ⎪---⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰120100112 lim lim ,211xxεεεεε++-+→→⎛⎫⎛⎫===+∞+- ⎪ ⎪--⎝⎭⎝⎭此广义积分发散.)211-00001(11)lim lim 2lim 1,1εεεεε+++-→→→==-=-=⎰⎰此广义积分收敛. 2. 当k 为何值时，广义积分+2d (ln )kxx x ∞⎰收敛?当k 为何值时，这广义积分发散?又当k 为何值时，这广义积分取得最小值? 解当k =1时,++222d dln ln(ln )ln ln x x x x x x∞∞+∞===+∞⎰⎰,发散.当1k ≠时,1++122211d (ln )(1)(ln 2)(ln )dln (ln)11kk kk k x x k x x x kk -∞∞--+∞⎧>⎪-==⎨-⎪+∞<⎩⎰⎰所以,当k >1时,此广义积分收敛,当k ≤1时,此广义积分发散.记1()(1)(ln 2),k f k k -=-11()(ln 2)(1)(ln 2)lnln 2k k f k k --'=+-.令()0f k '=得11ln ln 2k =-. 又 1()(ln 2)lnln 2[2(1)lnln 2]k f k k -''=+-,且 1ln ln 21(1)(ln 2)ln ln 20ln ln 2f -''-=<, 故()f k 在11ln ln 2k =-有极大值,而()f k 只有一个驻点,所以当11ln ln 2k =-时()f k 取得最大值,因而11ln ln 2k =-时,这个广义积分取得最小值.3. 利用递推公式计算反常积分+0e d n x n I x x ∞-=⎰.解 ++110de e e d n x n xn x n n I x x n x x nI ∞∞----+∞-=-=-+=⎰⎰又 +10de e e 1x x xI x x ∞---+∞+∞=-=--=⎰故 121(1)(1)2!n n n I nI n n I n n I n --==-=-= 4. 求120(1)d n n I x x =-⎰(n 0,1,2,…).解设x =sin t ,则d x =cosd t ,π2120cos d n n I t t +=⎰而 ππ2200(21)!!π2(2)!!2sin d cos d (2)!!21(21)!!n n k n kk x x x x k n k k -⎧⋅=⎪⎪==⎨⎪=+⎪+⎩⎰⎰所以 π221220(2)!!(!)cosd 2 (0,1,2,)(21)!!(21)!n nn n n I t t n n n +====++⎰.6. 用Γ函数表示下列积分：(1)e d nx x +∞-⎰ (n ＞0)； (2)101(ln )d x x α⎰ (α＞-1)； (3) 0e d n m x x x +∞-⎰1(>0)m n +; (4)220e d n x x x +∞-⎰ （12n >-）.解 (1)令nx t =,则1111,d d nn x t x t t n-==,于是1111+++001111ed e d e d ()nx tt n n x t t t t n n n n --∞∞∞---=⋅==Γ⎰⎰⎰.(2)令1lnt x =,则e ,d e d .t t x x t --==- 于是 10+(1)1001(ln )d e d e d (1).a a t a tx t t tt a x∞-+--+∞=-==Γ+⎰⎰⎰ (3)令nx t =,则1111,d d nn x t x t t n-==,于是1111+++001111ed ()e d e d ()nm m x m tt n n n m x x t t t t t n n n n+-∞∞∞---+=⋅⋅=⋅=Γ⎰⎰⎰.(4)令2x t =,则x x t ==,于是21+++2220011+201ed e e d 2111e d ()222n n x ntt n t x x t t tt t n ∞∞∞----⎛⎫-+∞ ⎪-⎝⎭=⋅===Γ+⎰⎰⎰⎰。

微积分(曹定华)(修订版)课后题答案第三章习题详解

第三章习题3-11．设s =12gt ２，求2d d t s t=．解：22221214()(2)2lim lim 22t t t g g dss t s dt t t t →→=-⨯-==-- 21lim(2)22t g t g →=+= 2．设f (x )=1x，求f '(x 0) (x 0≠0)．解：1211()()()f x x x x--'''===00201()(0)f x x x '=-≠ 3．（1）求曲线2y x =上点（2，4）处的切线方程和法线方程；（2）求过点（3，8）且与曲线2y x =相切的直线方程；（3）求xy e =上点（2，2e ）处的切线方程和法线方程；（4）求过点（2，0）且与xy e =相切的直线方程。

解：略。

4．下列各题中均假定f ′(x 0)存在，按照导数定义观察下列极限，指出A 表示什么：(1) 0limx ∆→00()()f x x f x x-∆-∆=A ;(2) f (x 0)=0, 0limx x →0()f x x x-＝A ； (3) 0limh →00()()f x h f x h h+--=A ．解：(1)0000000()()[()]()limlim ()x x f x x f x f x x f x f x x x→-→--+--'=-=-- 0()A f x '∴=- (2)00000()()()limlim ()x x x x f x f x f x f x x x x x →→-'=-=---0()A f x '∴=-(3)000()()limh f x h f x h h→+--00000[()()][()()]lim h f x h f x f x h f x h→+----=000000()()[()]()lim limh h f x h f x f x h f x h h→-→+-+--=+- 000()()2()f x f x f x '''=+= 02()A f x '∴=5．求下列函数的导数：(1) y ；(2) y；(3) y 3225x x．解：(1)12y x x ==11221()2y x x -''∴=== (2)23y x-=225133322()33y x x x ----''∴==-=-=(3)2152362y x x xx -==15661()6y x x -''∴===6．讨论函数y x =0点处的连续性和可导性．解：30lim 0(0)x x f →==000()(0)0lim lim 0x x x f x f x x →→→--===∞-∴函数y =0x =点处连续但不可导。

微积分曹定华版课后题答案习题详解

第9章习题9-11．判定下列级数的收敛性：(1) 115n n a ∞=⋅∑（a ＞0）； (2)∑∞=-+1)1(n n n ;(3) ∑∞=+131n n ; (4)∑∞=-+12)1(2n nn; (5) ∑∞=+11ln n n n ; (6)∑∞=-12)1(n n;(7) ∑∞=+11n n n ; (8)(1)21n n nn ∞=-⋅+∑．解：（1）该级数为等比级数，公比为1a ,且0a >,故当1||1a <,即1a >时，级数收敛，当1||1a≥即01a <≤时，级数发散.（2）Q n S =+++L∴1n ∞=∑发散.（3）113n n ∞=+∑是调和级数11n n ∞=∑去掉前3项得到的级数，而调和级数11n n∞=∑发散，故原级数113n n ∞=+∑发散. （4）Q 1112(1)1(1)222n n nn n n n ∞∞-==⎛⎫+--=+ ⎪⎝⎭∑∑ 而1112n n ∞-=∑,1(1)2m nn ∞=-∑是公比分别为12的收敛的等比级数，所以由数项级数的基本性质知111(1)22n n n n ∞-=⎛⎫-+ ⎪⎝⎭∑收敛，即原级数收敛.（5）Q lnln ln(1)1nn n n =-++ 于是(ln1ln 2)(ln 2ln 3)[ln ln(1)]n S n n =-+-+-+L故lim n n S →∞=-∞,所以级数1ln1n nn ∞=+∑发散. （6）Q 2210,2n n S S +==-∴lim n n S →∞不存在，从而级数1(1)2n n ∞=-∑发散.（7）Q 1lim lim10n n n n U n→∞→∞+==≠∴ 级数11n n n ∞=+∑发散. （8）Q (1)(1)1, lim 21212n n n n n n U n n →∞--==++∴ lim 0n x U →∞≠，故级数1(1)21n n nn ∞=-+∑发散.2．判别下列级数的收敛性，若收敛则求其和：(1) ∑∞=⎪⎭⎫ ⎝⎛+13121n n n ； (2) ※∑∞=++1)2)(1(1n n n n ; (3) ∑∞=⋅12sin n n n π; (4)πcos2n n ∞=∑．解：Q （1）1111, 23n n n n ∞∞==∑∑都收敛，且其和分别为1和12，则11123n n n ∞=⎛⎫+ ⎪⎝⎭∑收敛，且其和为1+12=32.（2）Q11121(1)(2)212n n n n n n ⎛⎫=-+ ⎪++++⎝⎭1lim 4n n S →∞=故级数收敛，且其和为14. （3）πsin 2n U n n =,而πsinππ2lim lim 0π222n n n U n→∞→∞=⋅=≠，故级数1πsin2n n n ∞=⋅∑发散. （4）πcos 2n n U =,而4lim limcos2π1k k k U k →∞→∞==,42lim limcos(21)π1k k k U k +→∞→∞=+=-故lim n n U →∞不存在，所以级数πcos2n n ∞=∑发散.3※．设1nn U∞=∑ (U n ＞0)加括号后收敛，证明1nn U∞=∑亦收敛．证：设1(0)nn n UU ∞=>∑加括号后级数1n n A ∞=∑收敛，其和为S .考虑原级数1n n U ∞=∑的部分和1n k k S U ∞==∑，并注意到0(1,2,)k U k >=L ，故存在0n ,使又显然1n n S S +<对一切n 成立，于是，{}n S 是单调递增且有上界的数列，因此，极限lim n n S →∞存在，即原级数1nn U∞=∑亦收敛.习题9-21．判定下列正项级数的收敛性：(1) ∑∞=++1n n n )2)(1(1; (2)∑∞=+1n n n1; (3) ∑∞=++1n n n n )2(2; (4)∑∞=+1n n n )5(12；(5) 111nn a ∞=+∑ (a ＞0); (6) ∑∞=+1n nb a 1(a , b ＞0); (7)()∑∞=--+1n a n a n22(a ＞0); (8)∑∞=-+1n n n 1214； (9) ∑∞=⋅1n nn n 23； (10) ※∑∞=1n nn n !; (11) ∑∞=+⋅⋅⋅⋅+⋅⋅⋅⋅1n n n )13(1074)12(753ΛΛ; (12)∑∞=1n nn3；(13) ※∑∞=1n n n 22)!(2； (14)∑∞=⎪⎭⎫ ⎝⎛+1n nn n 12; (15)∑∞=1πn nn3sin2; (16) ∑∞=1πn n n n 2cos 32．解：（1）因为211(1)(2)n n n <++而211n n ∞=∑收敛，由比较判别法知级数11(1)(2)n n n ∞=++∑收敛.（2）因为lim 10n n n U →∞==≠，故原级数发散.（3）因为21(1)(1)1n n n n n n n +>=+++，而111n n ∞=+∑发散，由比较判别法知，级数12(1)n n n n ∞=++∑发散.（4321n<=,而1n ∞=是收敛的p -级数3(1)2p =>,由比较判别法知,级数n ∞=.（5）因为111lim lim lim(1)111n n n n n n n na a a a a →∞→∞→∞+==-++ 而当1a >时，11n n a ∞=∑收敛，故111nn a ∞=+∑收敛; 当1a =时，11n n a∞=∑=11n ∞=∑发散，故111nn a∞=+∑发散;当01a <<时1lim101n n a →∞=≠+，故1lim1nn a →∞+发散; 综上所述，当01a <≤时，级数1lim 1n n a →∞+发散，当1a >时，1lim 1nn a →∞+收敛. （6）因为1lim lim lim(1)1n n n n n n n n b aa b a b a bb→∞→∞→∞+==-++ 而当1b >时, 11n n b ∞=∑收敛，故11nn a b ∞=+∑收敛; 当1b =时，1111n n n b ∞∞===∑∑发散，故而由0a >, 101a <<+∞+,故11nn a b ∞=+∑也发散; 当01b <<时，11lim 0n n a b a →∞=≠+故11n n a b ∞=+∑发散; 综上所述知，当01b <≤时，级数11n n a b ∞=+∑发散;当b >1时，级数11nn a b∞=+∑收敛. （7）因为lim lim 1n n n→∞→∞=而11n n ∞=∑发散，故级数10)n a ∞=>∑发散. （8）因为434431121lim lim 1212n n n n n n n n→∞→∞++-==-而311n n ∞=∑收敛，故级数21121n n n ∞=+-∑收敛.（9）因为1113233lim lim lim 1(1)232(1)2n n n n n n n n nU n n U n n +++→∞→∞→∞⋅⋅==>+⋅+由达朗贝尔比值判别法知，级数132nnn n ∞=⋅∑发散. （10）因为11(1)!1lim lim lim(1)1(1)!n n n n n n n nU n n e U n n n ++→∞→∞→∞+=⋅=+=>+，由达朗贝尔比值判别法知，级数1!nn n n ∞=∑发散. （11）因为1357(21)(23)4710(31)limlim 4710(31)(34)357(21)n n n nU n n n U n n n +→∞→∞⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+=⋅⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+L L L L232lim1343n n n →∞+==<+,由达朗贝尔比值判别法知原级数收敛.（12）因为111311lim lim lim 1333n n n n n n nU n n U n n ++→∞→∞→∞++=⋅==<，由达朗贝尔比值判别法知，级数13n n n ∞=∑收敛.（13）因为22221221(1)[(1)!]2(1)lim lim lim (!)22n n n n n n n nU n n U n +++→∞→∞→∞++=⋅= 由2212121(1)2(1)1lim lim lim 222ln 22ln 2x x x x x x x x x +++→∞→+∞→+∞+++==⋅⋅2121lim 022(ln 2)x x +→+∞==⋅知2121(1)lim lim 012n n n n n U n U ++→∞→∞+==< 由达朗贝尔比值判别法知，级数221(!)2n n n ∞=∑收敛.（14）因为1lim 1212n n n n →∞==<+，由柯西根值判别法知级数121nn n n ∞=⎛⎫ ⎪+⎝⎭∑收敛. （15）因为ππ2sinsin 33lim lim 1π2π33n n nn n n n n→∞→∞==⋅ 而112233nn n n n ∞∞==⎛⎫= ⎪⎝⎭∑∑是收敛的等比级数，它的每项乘以常数π后新得级数12π3n n n ∞=⋅∑仍收敛，由比较判别法的极限形式知，级数1π2sin3n n n ∞=∑收敛. （16）因为2πcos 322n nn n n ≤而与（12）题类似地可证级数12n n n ∞=∑收敛，由比较判别法知级数1πcos 32nn n n ∞=∑收敛.2．试在(0，+∞)内讨论x 在什么区间取值时，下列级数收敛：(1) ∑∞=1n nn x ; (2)nn x n ∑∞=⎪⎭⎫⎝⎛123．解：（1）因为11lim lim lim 11n n n n n n nU x n nxx U n x n ++→∞→∞→∞=⋅==++由达朗贝尔比值判别法知，当1x >时，原级数发散;当01x <<时，原级数收敛; 而当1x =时，原级数变为调11n n∞=∑，它是发散的. 综上所述，当01x <<时，级数1nn x n ∞=∑收敛.（2）因为1313(1)2limlim 22n n n n n nx n U xU x n ++→∞→∞⎛⎫+⋅ ⎪⎝⎭==⎛⎫⋅ ⎪⎝⎭,由达朗贝尔比值判别法知，当12x >即2x >时，原级数发散;当012x<<即02x <<时，原级收敛.而当12x =即 2x =时，原级数变为31n n ∞=∑，而由3lim n n →∞=+∞知31n n ∞=∑发散，综上所述，当02x <<时，级数31()2n n xn ∞=∑收敛.习题9-31．判定下列级数是否收敛，如果是收敛级数，指出其是绝对收敛还是条件收敛：(1) ∑∞=--1121)1(n nn ; (2)11(1)2(1)2n n nn ∞-=-+-⋅∑; (3) ∑∞=12sin n n nx; (４) 111π(1)sin πn n n n∞+=-∑; (5) ∑∞=-⎪⎭⎫ ⎝⎛-11210121n n n ； (6)∑∞=+-1)1(n n x n ; (7) ∑∞=⋅1!)2sin(n n n x ．解：（1）这是一个交错级数121n U n =-, 1lim lim 021n n n U n →∞→∞==-, 1112121n n U U n n +=>=-+ 由莱布尼茨判别法知11(1)21nn n ∞=--∑. 又1111(1)2121n n n n n ∞∞==-=--∑∑，由1121lim 12n n n→∞-=,及11n n ∞=∑发散，知级数1121n n ∞=-∑发散，所以级数11(1)21nn n ∞=--∑条件收敛. （2）因为2111(1)211(1)22(1)2n n n n n ----+-=+-⋅-⋅,故而112n n ∞=∑收敛，故132n n ∞=∑亦收敛，由比较判别法知11(1)2(1)2n n nn ∞-=-+-⋅∑收敛，所以级数11(1)2(1)2n n n n ∞-=-+-⋅∑绝对收敛.（3）因为22sin 1,nx n n ≤而级数211n n ∞=∑收敛，由比较判别法知21sin n nxn ∞=∑收敛，因此，级数21sin n nxn ∞=∑绝对收敛.（4）因为121ππ|(1)sin |sin πlimlim 11πn n n n n n n n+→∞→∞-==而211n n∞=∑收敛，由比较判别法的极限形式知，级数111π|(1)sin |πn n n n∞+=-∑收敛，从而级数11π(1)sin πn n n+-绝对收敛. （5）因为212121111111210210210n n n n n n ----≤+=+,而级数112nn ∞=∑收敛的等比级数1()2q =;由比值判别法，易知级数211110n n ∞-=∑收敛，因而21111210n n n ∞-=⎛⎫+ ⎪⎝⎭∑收敛，由比较判别法知级数21111210n n n ∞-=-∑收敛，所以原级数21111210n n n ∞-=-∑绝对收敛. （6）当x 为负整数时，级数显然无意义；当x 不为负整数时，此交错级数满足莱布尼茨判别法的条件，故它是收敛的，但因11n x n ∞=+∑发散，故原级数当x 不为负整数时仅为条件收敛. （7）因为sin(2)1!!n x n n ⋅≤由比值判别法知11!n n ∞=∑收敛(Q 1(1)!lim 01!n n n →∞+=)，从而由比较判别法知1sin(2)!n n x n ∞=⋅∑收敛，所以级数1sin(2)!n n x n ∞=⋅∑，绝对收敛.2．讨论级数∑∞=--111)1(n pn n 的收敛性(p ＞0)．解：当1p >时，由于11111(1)n p p n n n n ∞∞-==-=∑∑收敛，故级数111(1)n p n n ∞-=-∑绝对收敛. 当01p <≤时，由于111,(1)n n p pu u n n +=>=+ lim 0n n u →∞=,由莱布尼茨判别法知交错级数111(1)n p n n ∞-=-∑收敛，然而，当01p <≤时，11111(1)n p p n n n n ∞∞-==-=∑∑发散，故此时，级数111(1)n p n n ∞-=-∑条件收敛.综上所述，当01p <≤时，原级数条件收敛;当p >1时，原级数绝对收敛.3※．设级数∑∞=12n na及∑∞=12n nb都收敛，证明级数∑∞=1n n n b a 及()∑∞=+12n n n b a 也都收敛．证：因为2222||||110||222n n n n n n a b a b a b +≤≤=+ 而由已知1nn a ∞=∑及21n n b ∞=∑都收敛，故221111,22n n n n a b ∞∞==∑∑收敛，从而2211122n n n a b ∞=⎛⎫+ ⎪⎝⎭∑收敛，由正项级数的比较判别法知1n nn a b∞=∑也收敛，从而级数1n nn a b∞=∑绝对收敛.又由222()2,n n n n n n a b a a b b +=++及2211,n n n n a b ∞∞==∑∑,以及1n n n a b ∞=∑收敛，利用数项级数的基本性质知，221(2)nn n n n aa b b ∞=++∑收剑，亦即21()n n n a b ∞=+∑收敛.习题9-41．指出下列幂级数的收敛区间：(1) ∑∞=0!n nn x (0!=1)； (2)∑∞=0!n nn x n n ； (3) ∑∞=⋅022n n nnx ； (4)∑∞=++-01212)1(n n nn x ． (5) ∑∞=⋅+02)2(n n nn x ； (6)∑∞=-0)1(2n n nx n．解：（1）因为111(1)!limlim lim 011!n n n n na n p a n n +→∞→∞→∞+====+，所以收敛半径r =+∞，幂级数1!n n x n ∞=∑的收敛区间为(,)-∞+∞.（2）因为-111lim lim lim 1e 11n nn n n n na n p a n n +→∞→∞→∞⎛⎫===-= ⎪++⎝⎭，所以收敛半径1e r p ==. 当x =e 时，级数01!!e n n n n n n n n x n n ∞∞===∑∑，此时11(1)n n n u e u n+=+，因为1(1)nn +是单调递增数列，且1(1)n n+<e 所以1n n u u +>1,从而lim 0n n u →∞≠，于是级数当x =e 时，原级数发散.类似地，可证当x =-e 时，原级数也发散(可证lim ||0n n u →∞≠),综上所述，级数!nnn n x n∞=∑的收敛区间为(-e,e).（3）因为2111limlim ()212n n n n a n p a n +→∞→∞===+,所以收敛半径为r =2. 当2x =时，级数221012n n n n x n n∞∞===⋅∑∑是收敛的p 一级数（p =2>1）;当x =-2时，级数22011(1)2n nn n n x n n ∞∞===-⋅⋅∑∑是交错级数，它满足莱布尼茨判别法的条件，故它收敛.综上所述，级数202nn n x n∞=⋅∑的收敛区间为[-2,2].（4）此级数缺少偶次幂的项，不能直接运用定理2求收敛半径，改用达朗贝尔比值判别法求收敛区间.令21(1)21n nn x u n +=-+，则22121lim lim 23n n n nu n x x u n +→∞→∞+=⋅=+.当21x <时，即||1x <时，原级数绝对收敛.当21x >时，即||1x >时，级数0||n n u ∞=∑发散，从而210(1)21n nn x n +∞=-+∑发散，当1x =时，级数变为01(1)21nn n ∞=-+∑;当1x =-时，级数变为11(1)21n n n ∞+=-+∑;它们都是交错级数，且满足莱布尼茨判别法的条件，故它们都收敛.综上所述，级数210(1)21n nn x n +∞=-+∑的收敛区间为[-1,1].（5）此级数为（x +2）的幂级数. 因为11limlim 2(1)2n n n n a n p a n +→∞→∞===+. 所以收敛半径12r p==，即|2|2x +<时，也即40x -<<时级数绝对收敛.当|2|2x +>即4x <-或0x >时，原级数发散.当4x =-时，级数变为01(1)nn n ∞=-∑是收敛的交错级数，当x =0时，级数变为调和级数11n n ∞=∑,它是发散的.综上所述，原级数的收敛区间为[-4,0).（6）此级数（x -1）的幂级数故收敛半径12r =. 于是当1|1|2x -<即1322x <<时，原级数绝对收敛. 当1|1|2x ->即12x <或32x >时，原级数发散. 当32x =时，原级数变为01n n∞=∑是调和级数，发散. 当12x =时，原级数变为11(1)n n n ∞=-∑，是收敛的交错级数. 综上所述，原级数的收敛区间为13,22⎡⎫⎪⎢⎣⎭. 2．求下列幂级数的和函数： (1) ∑∞=-1)1(n nn n x ； (2) ∑∞=-1122n n nx ； (3) n n x n n ∑∞=+1)1(1； (4) ∑∞=+0)12(n n xn ．解：（1）可求得所给幂级数的收敛半径r =1. 设1()(1)nnn x S x n ∞==-∑,则 1111()(1)(1)1n n n n n n x S x x n x ∞∞-=='⎡⎤'=-=-=-⎢⎥+⎣⎦∑∑ 又当x =1时，原级数收敛，且()S x 在x =1处连续.（2）所给级数的收敛半经r =1，设211()2n n S x nx∞-==∑,当||1x <时，有于是22222()1(1)x x s x x x '⎛⎫== ⎪--⎝⎭又当1x =±时，原级数发散.故 2122122 (||1)(1)n n x nx x x ∞-==<-∑ （3）可求所给级数的收敛半径为1.令1111()(0)(1)(1)n n n n x x s x x n n x n n +∞∞====≠++∑∑ 令11()(1)n n x g x n n +∞==+∑,则111()1n n g x x x ∞-=''==-∑ 所以0()ln(1)d ln(1)ln(1)xg x x x x x x x =--=+---⎰; 所以1()11ln(1),||1,S x x x x ⎛⎫=+--< ⎪⎝⎭且0x ≠. 当1x ±时，级数为11(1)n n n ∞=+∑和11(1)(1)n n n n ∞=-+∑,它们都收敛.且显然有(0)0S =. 故111ln(1)(1,0)(0,1)()00,1x x S x x x x ⎧⎛⎫+--∈-⋃⎪ ⎪=⎝⎭⎨⎪=±⎩. （4）可求得所给级数的收敛半径为r =1且1x ±时，级数发散，设10()n n S x nx ∞-==∑,则001()d .1xn n s x x x x∞===-∑⎰ 于是211()()1(1)S x x x '==--,即1211(1)n n nx x ∞-==-∑. 所以1101(21)2n n n n n n n xx nx x ∞∞∞-===+=+∑∑∑ 3．求下列级数的和： (1) ∑∞=125n n n ； (2)∑∞=-12)12(1n n n ； (3) ∑∞=--112212n n n ； (4) 1(1)2n n n n ∞=+∑．解：（1）考察幂级数21n n n x ∞=∑，可求得其收敛半径1r = ，且当1x ±时，级数的通项2n n u n x =，2lim ||lim n n n u n →∞→∞==+∞，因而lim 0n n u →∞≠，故当1x ±时，级数21n n n x ∞=∑发散，故幂级数21n n n x ∞=∑的收敛区间为（-1，1）.设21() (||1)n n S x n x x ∞==<∑，则211()n n S x x n x ∞-==∑ 令2111()n n S x n x∞-==∑,则11011()d x n n n n S x x nx x nx ∞∞-====∑∑⎰. 再令121()n n S x nx∞-==∑,则201()d 1x n n x S x x x x∞===-∑⎰. 故221()(||1)1(1)x S x x x x '⎛⎫==< ⎪--⎝⎭，从而有120()d (1)x x S x x x =-⎰. 于是 213()() (||1)(1)x x S x xS x x x +==<- 取15x =，则223111()11555()5532115n n n S ∞=+===⎛⎫- ⎪⎝⎭∑. （2）考察幂级数21121n n x n ∞=-∑，可求得收敛半径r =1，设令21111()21n n S x x n ∞-==-∑,则221211()1n n S x x x ∞-='==-∑. 即 1111()(0)ln (,(0)0)21x S x S s x+-==-. 于是 111()ln ,(||<1)21x S x x x +=-，从而取x =则11(21)21n n S n ∞===--∑（3）考察幂级数211(21)n n n x∞-=-∑，可求得其级数半经为r =1,因为令2111()2n n S x nx∞-==∑，则221201()d 1x n n x S x x xx ∞===-∑⎰.所以212222() (||1)1(1)x x S x x x x '⎛⎫==< ⎪--⎝⎭,于是取12x =，得 3212111()121102212291()2n n n S ∞-=+-⎛⎫=== ⎪⎛⎫⎝⎭- ⎪⎝⎭∑. （4）考察幂级数1(1)n n n n x∞=+∑，可求得其收敛半径r =1. 设1()(1) (||1)n n S x n n xx ∞==+<∑ 则121011()d xn n n n S x x nx x nx ∞∞+-====∑∑⎰. 又设111()n n S x nx∞-==∑则101()d 1x n n x S x x x x∞===-∑⎰. 从而121()1(1)x S x x x '⎛⎫== ⎪--⎝⎭, 取12x =，则习题9-51．将下列函数展开成x 的幂级数：(1) 2cos 2x ; (2) 2sin x ； (3) 2x x -e ; (4) 211x -； (5)πcos()4x -．解：（1）2201cos 11cos (1)2222(2)!n n n x x x n ∞=+==+-∑ （2）2101sin (1) ()2(21)!2n n n x x x n +∞=⎛⎫=--∞<<+∞ ⎪+⎝⎭∑ （3）22210011e ()(1) ()!!x n n n n n x x x x x n n ∞∞-+===-=--∞<+∞∑∑ （4）211111211x x x ⎡⎤=+⎢⎥--+⎣⎦（5）πππcos cos cos sin sin 444x x x ⎛⎫-=+ ⎪⎝⎭ 2．将下列函数在指定点处展开成幂级数，并求其收敛区间： (1)x -31,在x 0＝１； (2) cos x,在x 0=3π; (3) 3412++x x ,在x 0=1; (4) 21x, 在x 0＝３．解：（1）因为11113212x x =⋅---,而 0111 (||112212nn x x x ∞=--⎛⎫=< ⎪-⎝⎭-∑即13x -<<). 所以100111(1) (13)3222nnn n n x x x x ∞∞+==--⎛⎫=⋅=-<< ⎪-⎝⎭∑∑. 收敛区间为：（-1，3）.（2）πππ2π2cos cos ()cos cos()sin sin()333333x x x x ⎡⎤=+-=---⎢⎥⎣⎦ 收敛区间为(,)-∞+∞.（3）211111111()1143213481124x x x x x x =-=⋅-⋅--++++++ 由112x -<且114x -<得13x -<<，故收敛区间为（-1，3）（4）因为011113(1)()333313n n n x x x ∞=-=⋅=-⋅-+∑ 而21011(3)(1)3n n n n x x x ∞+=''⎡⎤-⎛⎫=-=-- ⎪⎢⎥⎝⎭⎣⎦∑ 由313x -<得06x <<. 故收敛区间为（0，6）.。

微积分(曹定华)(修订版)课后题答案第二章习题详解

第二章习题2-11. 试利用本节定义5后面的注（3）证明：若lim n →∞x n =a ,则对任何自然数k ，有lim n →∞x n +k =a .证：由lim n n x a →∞=，知0ε∀>，1N ∃，当1n N >时，有n x a ε-<取1N N k =-，有0ε∀>，N ∃，设n N >时（此时1n k N +>）有n k x a ε+-<由数列极限的定义得 lim n k x x a +→∞=.2. 试利用不等式A B A B -≤-说明：若li m n →∞x n =a ,则lim n →∞∣x n ∣=|a|.考察数列x n =(-1)n ，说明上述结论反之不成立.证：lim 0,,.使当时，有n x n x aN n N x a εε→∞=∴∀>∃>-<而 n n x a x a -≤- 于是0ε∀>，,使当时，有N n N ∃>n n x a x a ε-≤-< 即 n x a ε-<由数列极限的定义得 lim n n x a →∞=考察数列 (1)nn x =-，知lim n n x →∞不存在，而1n x =，lim 1n n x →∞=，所以前面所证结论反之不成立。

3. 利用夹逼定理证明：(1) lim n →∞222111(1)(2)n n n ⎛⎫+++ ⎪+⎝⎭=0； (2) lim n →∞2!nn =0.证：（1）因为222222111112(1)(2)n n nn n n n n nn++≤+++≤≤=+而且 21lim0n n →∞=，2lim 0n n→∞=，所以由夹逼定理，得222111lim 0(1)(2)n n n n →∞⎛⎫+++= ⎪+⎝⎭. （2）因为22222240!1231n n n n n<=<-，而且4lim 0n n →∞=，所以，由夹逼定理得2lim 0!nn n →∞= 4. 利用单调有界数列收敛准则证明下列数列的极限存在. (1) x n =11ne +，n =1,2,…；(2) x 1,x n +1n =1,2,…. 证：（1）略。

微积分(曹定华)(修订版)课后题答案第八章习题详解

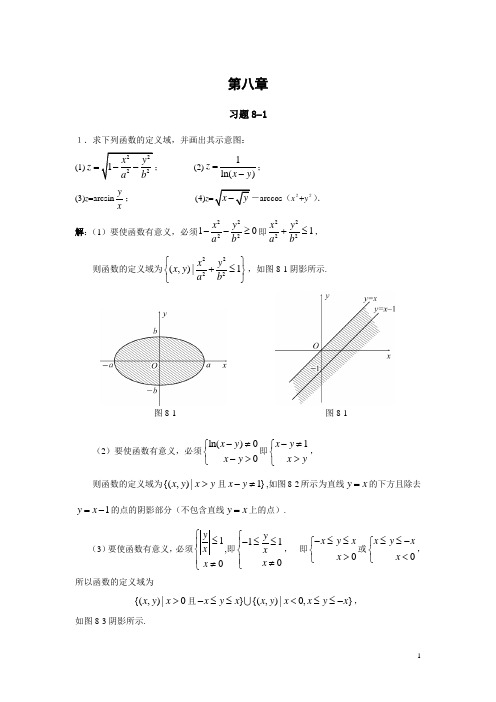
第八章习题8-1１．求下列函数的定义域，并画出其示意图：(1)22221x y z a b=--； (2)1ln()z x y =-；(3)z =arcsiny x； (4)z =x y -－arccos （x ２+y ２）．解：（1）要使函数有意义，必须222210x y a b --≥即22221x y a b+≤，则函数的定义域为2222(,)|1x y x y a b ⎧⎫+≤⎨⎬⎩⎭，如图8-1阴影所示.图8-1 图8-1（2）要使函数有意义，必须ln()00x y x y -≠⎧⎨->⎩即1x y x y -≠⎧⎨>⎩，则函数的定义域为{(,)|x y x y >且1}x y -≠,如图8-2所示为直线y x =的下方且除去1y x =-的点的阴影部分（不包含直线y x =上的点）.（3）要使函数有意义，必须10y x x ⎧≤⎪⎨⎪≠⎩,即110y xx ⎧-≤≤⎪⎨⎪≠⎩，即0x y x x -≤≤⎧⎨>⎩或0x y x x ≤≤-⎧⎨<⎩，所以函数的定义域为{(,)|0x y x >且}{(,)|0,}x y x x y x x y x -≤≤<≤≤-，如图8-3阴影所示.图8-3 图8-4（4）要使函数有意义，必须2200||1x y y x y ⎧⎪≥⎨⎪+≤⎩即222001x y x y x y ≥⎧⎪≥⎪⎨≥⎪⎪+≤⎩, 所以函数的定义域为222{(,)|0,0,,1}x y x y x y x y ≥≥≥+≤,如图8-4阴影所示.２．设函数f (x ,y )=x 3-2xy +3y 2，求 (1) f (-2,3); (2) f 12,x y ⎛⎫⎪⎝⎭； (3)f (x +y ,x -y ). 解：（1）32(2,3)(2)2(2)33331f -=--⨯-⨯+⨯=;（2）23321211221412,23f x y x x y y x xy y ⎛⎫⎛⎫⎛⎫=-⋅⋅+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; （3）32(,)()2()()3()f x y x y x y x y x y x y +-=+-+-+- 3222()2()3()x y x y x y =+--+-. ３．设F (x ,y )y f x －１），若当y =1时，F (x ,1)=x ，求f (x )及F (x ,y )的表达式．解：由(,1)F x x =得(1)x y f x =即 1)1f x x =-1x t =则2(1)x t =+代入上式有2()(1)1(2)f t t t t =+-=+所以 ()(2)f x x x =+于是(,)1)1)1F x y f x ===-４．指出下列集合A 的内点、边界点和聚点：(1){(,)01,0}A x y x y x =≤≤≤≤；(2){(,)31}A x y x y =+=； (3)A ＝｛（x ,y ）｜x ２＋y ２＞０｝； (4)(0,2]A =．解：（1）内点{(,)|01,0}x y x y x <<<<边界点{(,)|01,0}{(,)|01,1}x y x y x y y x ≤≤=≤≤= {(,)|,01}x y y x x =≤≤聚点A （2）内点∅ 边界点A 聚点A （3）内点A边界点（0，0）聚点A（4）内点∅ 边界点[0,2] 聚点[0,2]习题8-2１．讨论下列函数在点(0，0)处的极限是否存在：(1) z =224xy x y +； (2) z =x yx y+-．解：(1)当(,)P x y 沿曲线2x ky =趋于（0，0）时，有24244200lim (,)lim 1y y y kxky kf x y k y y k →→===++这个值随k 的不同而不同，所以函数224Z=xy x y+在(0,0)处的极限不存在. (2)当(,)P x y 沿直线(1)y kx k =≠趋于(0,0)时，有001lim (,)lim(1)1y x y kxx kx kf x y k x kx k→→=++==≠--，这个极限值随k 的不同而不同，所以函数Z=x yx y+-在(0,0)处的极限不存在. ２．求下列极限：(1) 00sin limx y xy x →→； (2)22011lim x y xyx y→→-+；(3)00x y →→ (4)22sin lim x y xy x y →∞→∞+．解：（1）0000sin sin()limlim 0x x y y xy xy y x xy →→→→=⋅=（2）2222011101lim101x y xy x y →→--⨯==++（3）0000001)2x x x y y y →→→→→→=== （4）当,x y →∞→∞时，221x y+是无穷小量，而sin xy 是有界函数，所以它们的积为无穷小量,即22sin lim0x y xyx y →∞→∞=+.３．求函数z =2222y xy x+-的间断点．解:由于220y x -=时函数无定义，故在抛物线22y x =处函数间断，函数的间断点是2{(,)|2,R}x y y x x =∈.习题8-3１．求下列各函数的偏导数：(1) z =(１+x )y ; (2) z =lntany x； (3) z =arctan yx； (4) u =zx y ．解：（1）1(1)y zy x x-∂=+∂(1)ln(1)y zx x y∂=++∂; （2）22221sec cot sec ;tan z y y y y y yx x x x x x x∂-=⋅⋅=-∂ 22111sec cot sec ;tan z y y y yy x x x x xx∂=⋅⋅=∂ （3）22221;1zy yxx x yy x ∂--=⋅=∂+⎛⎫+ ⎪⎝⎭22211;1zx yx x y y x ∂=⋅=∂+⎛⎫+ ⎪⎝⎭（4）22ln ln ;z zx x u z z yy y y x x x∂-=⋅⋅=-⋅∂1;1ln ln .zxzz x xu z y y xu y y y y z x x-∂=∂∂=⋅⋅=⋅∂２．已知f (x ,y )=e -sin x (x +2y )，求x f '(0，1)，y f '(0，1)．解：sin sin sin (,)e(cos )(2)e e [cos (2)1]xx x x f x y x x y x x y ---'=⋅-++=-⋅++ sin sin (,)e22e xx y f x y --'=⋅=所以sin0(0,1)e(cos 0(021)1)1x f -'=-⋅+⨯+=- sin0(0,1)2e2y f -'==３．设z =x +y +(y -112811,x x y y zz xy====∂∂∂∂．解：1122112d (,1)d(1)1d d x x y x z f x x xxx====∂==+=∂又23211(3z x x y y y y-⎛⎫∂-=+-⋅ ⎪∂⎝⎭所以1811π11arcsin 126x y z y==∂=+=+=+∂. ４．验证z =11+ex y ⎛⎫- ⎪⎝⎭满足222z zxy z x y∂∂+=∂∂．解：1111()()2211e e x y x y z x x x-+-+∂-=⋅-=∂ 1111()()2211e ex yx y z y y y-+-+∂-=⋅-=∂ 所以1111()()22222211e ex yx y z z x y x y x y x y-+-+∂∂+=⋅+⋅∂∂ 11()2e 2x yz --+==５．设函数z =2222422,00,0xy x y x y x y ⎧+≠⎪+⎨⎪+=⎩,试判断它在点(0，0)处的偏导数是否存在?解：00(0,0)(0,0)00(0,0)lim lim 0y y y f y f z y y∆→∆→+∆--'===∆∆ 00(0,0)(0,0)00(0,0)limlim 0x x x f x f z x x∆→∆→+∆--'===∆∆ 所以函数在（0，0）处的偏导数存在且(0,0)(0,0)0x y z z ''==.６．求曲线22(),4z x y y ⎧=+⎪⎨⎪=⎩14在点(2,4,5)处的切线与x 轴正向所成的倾角．解：因为 242z x x x ∂==∂，故曲线221()44z x y y ⎧=+⎪⎨⎪=⎩在点（2，4，5）的切线斜率是(2,4,5)1z x ∂=∂,所以切线与x 轴正向所成的倾角πarctan14α==.７．求函数z =xy 在(2,3)处，当Δx ＝0.1与Δy =－0.2时的全增量Δz 与全微分d z ．解：,z zy x x y ∂∂==∂∂ ∴ d d d z zz x y x y∂∂=+∂∂ 而()()z x x y y xy x y y x x y ∆=+∆+∆-=∆+∆+∆∆ 当0.1,0.2,2,3x y x y ∆=∆=-==时，d 30.12(0.2)0.1z =⨯+⨯-=-2(0.2)30.10.1(0.2)0.12z ∆=⨯-+⨯+⨯-=-. ８．求下列函数的全微分：(1) 设u =()zx y，求d u｜(1,1,1)．(2) 设z ，求d z ．解：（1）1121(),()z z u x u x x z z x y y y y y --∂∂-=⋅⋅=⋅⋅∂∂;()ln ,z u x xz y y ∂=∂ (1,1,1)(1,1,1)1,1,u uxy∂∂∴==-∂∂(1,1,1)0u z∂=∂,于是(1,1,1)(1,1,1)(1,1,1)(1,1,1)d d d d d d z z z ux y z x y xyz∂∂∂=++=-∂∂∂（2）y z x-∂==∂2zy∂==∂ ∴ 2d d d z z z x y x y x y ∂∂=+=+∂∂习题8-4１．求下列各函数的导数：(1) z =e 2x +3y , x =cos t , y =t 2; (2)z =tan(3t +2x 2+y 3), x =1t，y ．解：（1）d d d d d d z z x z yt x t y t∂∂=+⋅∂∂ 22323232cos 3e 2(sin )e 32=2e (3sin )2e (3sin )x y x y x y t t t tt t t t ++++=⋅⋅-+⋅⋅-=-（2）d d d d d d z f f x f y t t x t y t∂∂∂=+⋅+⋅∂∂∂223223222321sec (32)3sec (32)4 sec (32)3t x y t x y xt t x y y -=++⋅+++⋅+++⋅3223242(3(3)t t t t=-+++. ２．求下列各函数的偏导数：(1) z =x 2y -xy 2, x =u cos v , y =u sin v ; (2) z =e uv , u =v =arctan yx．解：（1）z z x z y u x u y u∂∂∂∂∂=⋅+⋅∂∂∂∂∂ 22222222222(2)cos (2)sin 2sin cos sin cos sin cos 2sin cos 3sin cos (cos sin )xy y v x xy vu v v u v v u v v u v v u v v v v =-+-=-+-=-z z x z y v x v y v∂∂∂∂∂=⋅+⋅∂∂∂∂∂ 22323333323333(2)sin (2)cos 2sin cos sin cos 2sin cos 2sin cos (sin cos )(sin cos )xy y u v x xy u vu v v u v u v u v v u v v v v u v v =--+-=-++-=-+++（2）221e e 1()uv uv z z u z v y v u y x u x v x x x∂∂∂∂∂-=⋅+⋅=⋅⋅∂∂∂∂∂+arctan2222e e()(arctanyuvxyxv yu x y x y x y x=-=-++211e e 1()uv uv z z u z vv u yy u y v yxx∂∂∂∂∂=⋅+⋅=+⋅⋅∂∂∂∂∂+2222e e()(arctany uvxyyv xu x x x y x y x=+=+++ ３．求下列函数的一阶偏导数，其中f 可微： (1) u =f (,x yy z)； (2) z =f (x 2+y 2)； (3) u =f (x , xy , xyz )．解：（1）121110u f f f x y y ∂'''=⋅+⋅=∂12212211u x x f f f f y y z z y∂-''''=⋅+⋅=-∂122220u y y f f f z z z∂-'''=⋅+⋅=∂ （2）令22,u x y =+则()z f u =22d ()22()d z f u f u x xf x y x u x∂∂''=⋅=⋅=+∂∂22d ()22()d z f u f u y yf x y y u y∂∂''=⋅=⋅=+∂∂ （3）令,,t x v xy w xyz ===,则(,,)u f t v w =.123123d 1d u f t f v f w f f y f yz f yf yzf x t x v x w x∂∂∂∂∂∂''''''=⋅+⋅+⋅=⋅+⋅+⋅=++∂∂∂∂∂∂ 12323d 0d u f t f v f w f f x f xz xf xzf y t y v y w y∂∂∂∂∂∂'''''=⋅+⋅+⋅=⋅+⋅+⋅=+∂∂∂∂∂∂1233d 00d u f t f v f w f f f xy xyf z t z v z w z∂∂∂∂∂∂''''=⋅+⋅+⋅=⋅+⋅+⋅=∂∂∂∂∂∂ ４．设z =xy +x 2Ｆ(u ),u =yx，Ｆ（u ）可导．证明：2z zxy z x y∂∂+=∂∂．证：222()()2()()z yy xF u x F u y xF u yF u x x∂-''=++⋅=+-∂ 21()()z x x F u x xF u y x∂''=+⋅=+∂22()()()z z xy xy x F u xyF u xy xyF u x y∂∂''∴==+-++∂∂ 22[()]xy x F u z =+=∂ ５．利用全微分形式不变性求全微分：(1) z =(x 2+y 2)sin(2x +y )； (2) u =222()yf x y z --，f 可微．解：（1）令22,sin(2)u x y v x y =+=+，则vz u =122d d d d()ln dsin(2)v v z zz u v vu x y u u x y u v-∂∂=+=++⋅+∂∂122sin(2)2222(2d 2d )ln cos(2)d(2)[2(d d )ln cos(2)(2d d )]2sin(2)()(d d )cos(2)ln()(2d d )v v v x y vu x x y y u u x y x y vu x x y y u x y x y ux y x y x x y y x y x y x y x y -+=++⋅++=⋅++⋅++⎡⎤+=++++++⎢⎥+⎣⎦（2）22222222111d d d d ()d()yu y y f y f x y z x y z f f f f-'=+⋅=-----222222222222221()d (2d 2d 2d )12()d (d d d )()()yf x y z y x x y y z z f fyf x y z y x x y y z z f x y z f x y z '--=---'--=-------６．求下列隐函数的导数：(1) 设e x +y +xyz =e x ，求x z ',y z '； (2)设xz=ln z y ，求,z z x y ∂∂∂∂．解：（1）设(,,)e e 0x yx F x y z xyz +=+-=，则ee ,e ,x yx x y x y z F yz F xz F xy ++'''=+-=+=故e e e ,x x y x yy x y z F Fx yz xzz z Fz xy F xy++'--+''=-==-=-（2）设(,,)ln 0x zF x y z z y=-=,则 2221111,,x y z y z x y x F F F z z y y z z y z z--'''==-⋅==-⋅=--故211x z F z z z x xF x z z z '∂=-=-='∂+--2211()y z F z z yx yF y x z z z'∂=-=-='∂+-- ７．设x +z =yf (x 2-z 2)，其中f 可微，证明：z zzy x x y∂∂+=∂∂．证：设22(,,)()F x y z x z yf x z =+--则2212()x F xyf x z ''=--2222()12()y z F f x z F yzf x z '=--''=+-故22222()112()x z F zxyf x z x F yzf x z ''∂--=-=''∂+- 2222()12()y zF z f x y y yzf x z F '∂-=-='∂+-' 从而22222222()()12()12()z z xyzf x z z yf x y z y x y yzf x z yzf x z '∂∂∂---+=+''∂∂+-+- 222222222222222()()12()2()12()[2()1]12()xyzf x z z yf x y yzf x z xyzf x z z x zyzf x z x yzf x z x yzf x z '--+-='+-'--++='+-'-+=='+-８．设x =e u cos v , y =e u sin v , z =uv ,求z x ∂∂及z y∂∂．解法一：由e cos ,e sin u ux v y v ==得221ln(),arctan ,2yu x y v z uv x=+==故22(cos sin )e uz z u z v xv yu v v u v x u x v x x y-∂∂∂∂∂-=+==-∂∂∂∂∂+22(sin cos )e uz z u z v yv xu v v u v y u y v y x y-∂∂∂∂∂+=+==-∂∂∂∂∂+ 解法二：设方程组e cos e sin uux vy v⎧=⎪⎨=⎪⎩确定了函数(,),(,)u u x y v v x y ==,对方程组的两个方程关于x 求偏导得1e cos e sin 0e sin e cos uu u u u v v v x xu v v v x x ∂∂⎧=-⎪⎪∂∂⎨∂∂⎪=+⎪∂∂⎩解方程组得e cos e sin u u uv xv v x --∂⎧=⎪⎪∂⎨∂⎪=-⎪∂⎩又方程组的两个方程关于y 求偏导得0e cos e sin 1e sin e cos uu u u u v v v y y u v v vy y ∂∂⎧=-⎪∂∂⎪⎨∂∂⎪=+⎪∂∂⎩解方程组得：e sin e cos uu u v y v v y--∂⎧=⎪∂⎪⎨∂⎪=⎪∂⎩ 从而e (cos sin )u z z u z vv v u v x u x v x-∂∂∂∂∂=⋅+=-∂∂∂∂∂e (sin cos )u z z u z v v v u v y u y v y-∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂ ９．设u =f (x ,y ,z )有连续偏导数，y =y (x )和z =z (x )分别由方程0xye y -=和e z -xz =0确定，求d d ux．解：方程e 0xyy -=两边对x 求导得d de ()0d d xyy yy x x x+-=，解得2d e d 1e 1xy xy y y y x x xy ==--方程e 0zxz -=两边对x 求导得d de 0d d zz z z x x x--= 解得d de z z z zx x xz x==-- 从而2d d d d d d 1y z x y z x y f zf u y zf f f f x x x xy xz x''''''=++=++--习题8-5１．求下列函数的二阶偏导数： (1) z =x 4+y 4-4x 2y 2； (2) z =arctany x； (3) z =y x ； (4) z =x ln(xy )．解：（1）23222248, 128;z z x xy x y x x∂∂=-=-∂∂232222248, 128;1622z z y x y y x y y zxy x y∂∂=-=-∂∂∂=-（2）22221,1()z y y y x x x y x∂-=⋅=-∂++ 22222222222222222222222222222211,1()2(2),()()22()()()2()()z x y y x x y xz y xyx x x y x y z x xyy y x y x y z x y y y y x x y x y x y ∂=⋅=∂++∂-=-⋅=∂++∂--=⋅=∂++∂+-⋅-=-=∂∂++（3）1ln , ,x x z zy y xy x y-∂∂==∂∂222222211ln , (1),1ln (1ln )x x x x x z z y y x x y x y z xy y y y x y x y y---∂∂==-∂∂∂=+⋅=+∂∂（4）1ln()1ln(),z xy x y xy x xy∂=+⋅⋅=+∂22222211,1,11.z y x xy x z x x x y xy y z xy y z x x y xy y∂=⋅=∂∂=⋅⋅=∂∂=-∂∂=⋅=∂∂２．求下列函数的二阶偏导数，其中f (u ,v )可微： (1) z =f (x 2+y 2)； (2) z =f (xy ,x +2y )．解：（1）2222, 22224z zxf f xf x f x f x x ∂∂'''''''==+⋅=+∂∂ 2222, 22224z zyf f yf y f y f y y ∂∂'''''''==+⋅=+∂∂2224zxf y xyf x y∂''''=⋅=∂∂ （2）1212, =+2 z zyf f xf f x y∂∂''''=+∂∂ 22111221221112222(1)12zy f y f f y f y f yf f x ∂''''''''''''''=⋅+⋅+⋅+⋅=++∂ 22111221221112222(2)2(2)44zx f x f f x f x f xf f y∂''''''''''''''=⋅+⋅+⋅+⋅=++∂ 21111221221111222(2)2 (2)2zf y f x f f x f x y f xyf x y f f ∂'''''''''=++⋅+⋅+⋅∂∂'''''''=++++３．求由e z -xyz =0所确定的z =f (x ,y )的所有二阶偏导数．解：设(,,)e 0zF x y z xyz =-=，则,,e z x y z F yz F xz F xy '''=-=-=-于是,e x z z F z yz zx F xy xz x∂=-==∂--e z z xz z y xy yz y∂==∂-- 从而222()(1)()z z xz x z z x zx x xxz x ∂∂--+-∂∂∂=∂-232223(1)221.(1)(1)z z z z z z z z x z x z --+---==-- 223222223()(1)(1)221.()(1)(1)z zz yz y z z y z z z zz z z y y z yyz y y z y z ∂∂--+---+∂--∂∂-===∂--- 2222233()()(1)(1).()(1)(1)(1)z z z z xz x z x z z z z z y y y y z x y xz x x z xy z xy z ∂∂---∂---∂∂-====∂∂----习题8-6１．求下列函数的极值： (1) z=x ３-4x 2+2xy -y 2+3； (2) z =e 2x (x +2y +y 2)； (3) z =xy (a -x -y )， a ≠0．解：（1）由方程组：23820220xy z x x y z x y ⎧'=-+=⎪⎨'=-=⎪⎩ 得驻点（0，0），（2，2）又68,2,2,xx xy yy z x z z ''''=-==-在点（0，0）处，2120B AC -=-<,又80A =-<，所以函数取得极大值(0,0)3;f = 在点（2，2）处，2120,B AC -=>该点不是极值点.（2）由方程组222e (2241)0e (22)0x xx y z x y y z y ⎧'=+++=⎪⎨'=+=⎪⎩ 得驻点1(,1)2-.又2222e (4484),e (44),2e xxxxx xy yy z x y y z y z ''''''=+++=+=，在点1(,1)2-处22202e 2e 4e 0,B AC -=-⋅=-<且2e 0A =>,所以函数取得极小值11(,1) e.22f -=- （3）由方程组(2)0(2)0xy z y a x y z x a y x ⎧'=--=⎪⎨'=--=⎪⎩ 得四个驻点（0，0），(0,),(,0),,.33a a a a ⎛⎫⎪⎝⎭又2,22,2xx xy yy z y z a x y z x ''''''=-=--=-.在点（0，0）处，220,B AC a -=>该点不是极值点. 在点(0,)a 处，220B AC a -=>,该点不是极值点. 在点(,0)a 处，220B AC a -=>,该点不是极值点.在点,33a a ⎛⎫ ⎪⎝⎭处,2203a B AC -=-<，所以函数在该点有极值，且极值为3,3327a a af ⎛⎫= ⎪⎝⎭,由于23xx A z a ''==-故当0a >时，(0)A <，函数有极大值327a ,当0a <时，(0)A >，函数有极小值327a .２．求函数z =x 3-4x 2+2xy -y 2在闭区域D ：-1≤x ≤4,-1≤y ≤1上的最大值和最小值． [分析]由(,)f x y 在D 上连续，所以必有最大最小值，又由于(,)f x y 在D 内可导，所以(,)f x y 的最值在D 的内部驻点或在D 的边界上，由(,)f x y 在D 内部驻点上值与边界上函数比较可求出(,)f x y 的最大和最小值.解：由方程23820220xy z x x y z x y ⎧'=-+=⎪⎨'=-=⎪⎩得驻点（0，0），（2，2）（2，2）D ∈应该舍去，(0,0)0f =（可由充分条件判别知是极大值）.D 的边界可分为四部分：12:1,11; :1,14;L x y L y x =--≤≤=--≤≤ 34:4,11; :1,1 4.L x y L y x =-≤≤=-≤≤在1L 上，2(1,)52(),1 1.f y y y y y ϕ-=---=-≤≤因为()2(1)0,y y ϕ'=-+≤所以()y ϕ单调递减，因而(1)4ϕ-=-最大，(1)8ϕ=-最小. 在2L 上，32(,1)421(),14f x x x x g x x -=---=-≤≤令()0g x '=得1244,33x x +==.而122227min{(1),(),(),(4)}()27g g x g x g g x --==,121227max{(1),(),(),(4)}()27g g x g x g g x -==分别是(,)f x y 在2L 上的最小值与最大值.类似讨论可得：在3L 上(4,1)7,(4,1)9f f =-=-，分别是(,)f x y 的最大值与最小值;在4L 上(4,1)7,(1,1)f f =-=-8分别是(,)f x y 的最大值与最小值.比较(,)f x y 在内部驻点（0，0）与整个边界上函数值的情况得到(4,1)7f =是函数(,)f x y 在D 上的最大值，116.1f ⎫-=≈-⎪⎪⎝⎭. ３．求函数z =x +y 在条件111x y+= (x ＞０,y ＞０)下的条件极值．解：构造拉格朗日函数11(,)1F x y x y x y λ⎛⎫=+++- ⎪⎝⎭解方程组221010111x y F x F y x yλλ⎧'=-=⎪⎪⎪'=-=⎨⎪⎪+=⎪⎩ 得2,2,4x y λ===,故得驻点(2,2)。

微积分(曹定华)(修订版)课后题答案第二章习题详解

微积分(曹定华)(修订版)课后题答案第二章习题详解本文将详细解答曹定华《微积分》修订版第二章的课后习题。

第二章主要涉及导数的基本概念和基本公式，包括导数定义、可导性、导数计算公式等。

本章共计43道习题，以下将一一解答。

2.1 导数的定义及其物理隐含义习题2.11. 求函数f(x)=3x2+2的导数。

根据导数公式，对于幂函数y=xn，其导数为y’=nxn-1。

因此，对于本题中的函数f(x)=3x2+2，其导数为f’(x)=6x。

2. 求函数f(x)=x3-5x+1在x=2处的导数。

同样地，根据导数公式，对于幂函数y=xn，其导数为y’=nxn-1。

因此，对于本题中的函数f(x)=x3-5x+1，其导数为f’(x)=3x2-5。

将x=2代入，则得到f’(2)=3*(22)-5=7。

习题2.21. 用导数的定义证明函数f(x)=2x在任意一点处的导数为2。

根据导数的定义，对于函数f(x)在x=a处的导数，有f’(a)=lim(h->0) [(f(a+h)-f(a))/h]。

因此，代入本题中的函数f(x)=2x，得到f’(a)=lim(h->0) [(2(a+h)-2a)/h]，化简可得f’(a)=2。

因此，函数f(x)=2x在任意一点处的导数均为2。

2. 求f(x)=x2+3x的可导性，并说明理由。

对于函数f(x)=x2+3x，在任意一点x处的导数为f’(x)=2x+3。

因此，对于任意值x，均存在导数f’(x)。

因此，函数f(x)在定义域内可导。

2.2 基本导数公式习题2.31. 求函数f(x)=sin(x)在x=π/6处的导数。

根据导数公式，对于正弦函数y=sin(x)，其导数为y’=cos(x)。

因此，对于本题中的函数f(x)=sin(x)，其导数为f’(x)=cos(x)。

将x=π/6代入，则得到f’(π/6)=cos(π/6)=√3/2。

2. 求函数f(x)=2x在x=0处的导数。

微积分(曹定华)(修订版)课后题答案第四章习题详解

习题 4-11.验证函数f (x )=lnsin x 在[π5π,66]上满足罗尔定理的条件，并求出相应的ξ，使f ′(ξ)=0.解: 显然()ln sin f x x =在5π,66x ⎡⎤⎢⎥⎣⎦上连续,在π5π,66⎛⎫⎪⎝⎭内可导,且π5π()()ln 266f f ==-,满足罗尓定理的条件. 令cos ()cot 0sin xf x x x '===,则π2x =即存在ππ5π(,)66ξα=∈,使()0f ξ'=成立.2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的ξ ?[][][]2(1)()1,;(2)(),;1,10,21sin ,0π(3)()0,π1,exf x f x x x x f x x =-=--<≤⎧=⎨=⎩解: (1) 2()1e x f x =-在[]1,1-上连续,在()1,1-内可导,且(1)1,(1)1,e e f f -=-=- 即 (1)(1)f f-= () f x ∴在[]1,1-上满足罗尓定理的三个条件. 令 2()20e x f x x '==得 0x =, 即存在0(1,1)ξ=∈-,使()0f ξ'=.(2) 101()1112xx f x x x x -≤<⎧==-⎨-≤≤⎩显然()f x 在(0,1),(1,2)内连续,又1111(10)lim ()lim (1)0,(10)lim ()lim (1)0,(10)(10)(1)0,即x x x x f f x x f f x x f f f --++→→→→-==-=+==-=-=+==所以()f x 在1x =处连续,而且22(00)lim ()lim (1)1(0),(20)lim ()lim (1)1(2),x x x x f f x x f f f x x f ++--→→→→+==-==-==-==即()f x 在0x =处右连续,在2x =处左连续,所以()f x 在[]0,2 上连续.又1111()(1)1(1)lim lim 1,11()(1)1(1)lim lim 111x x x x f x f x f x x f x f x f x x --++-→→+→→--'===-----'===--(1)(1)(f f f x -+''∴≠∴在1x =处不可导,从而()f x 在(0,2)内不可导. 又 (0)(2)1f f ==又由 101()112x f x x -<<⎧'=⎨<<⎩ 知 ()0f x '≠综上所述,函数()f x 满足罗尓定理的条件(1),(3)不满足条件(2),没有满足定理结论的ξ. (3) 由0(00)lim sin 0(0)1x f x f +→+==≠=知()f x 在0x =不右连续,() f x ∴在[]0,π上不连续,显然()f x 在()0,π上可导,又(0)1,(π)0f f ==,即(0)(π)f f ≠,且()cos (0,π) f x x x '=∈,取π(0,π)2ξ=∈,有π()cos cos02f ξξ'===.综上所述,函数()f x 满足罗尓定理的条件(2),不满足条件(1),(3),有满足定理结论的ξ,ξ=π2.3. 不用求出函数()(1)(2)(3)f x x x x =---的导数，说明方程()0f x '=有几个实根，并指出它们所在的区间.解: 显然()f x 在[]1,2上连续,在()1,2内可导,且(1)(2)0f f ==,由罗尓定理知,在()1,2内至少存在一点1ξ,使1()0f ξ'=,即()0f x '=在()1,2内至少有一个实根.同理 ()0f x '=在()2,3内也至少有一个实根2ξ.又()0f x '=是二次方程,最多有两个实根,故()0f x '=有两个实根,分别在区间()1,2和()2,3内.4. 验证拉格朗日中值定理对函数3()2f x x x =+在区间［0，1］上的正确性.解: 显然3()2f x x x =+在［0，1］上连续,在()0,1内可导,满足拉格朗日中值定理的条件.若令2(1)(0)()32310f f f x x-'=+==-则3x =±,取3ξ=,即存在(0,1)3ξ=,使得(1)(0)()10f f f ξ-=-成立.从而拉格朗日中值定理对函数3()2f x x x =+在［0，1］上成立.5※. 设()f x '在［a ,b ］上连续，在［a ,b ］内可导，f ′(a ) = 0，f ′′(x ) > 0，证明：f ′(a )> f (b )。

微积分(曹定华)(修订版)课后题答案第九章习题详解

AHA12GAGGAGAGGAFFFFAFAF第9章习题9-11．判定下列级数的收敛性： (1) 115nn a ∞=⋅∑（a ＞0）； (2) ∑∞=-+1)1(n n n ;(3) ∑∞=+131n n ; (4) ∑∞=-+12)1(2n n n ;(5) ∑∞=+11ln n n n; (6) ∑∞=-12)1(n n ;(7) ∑∞=+11n nn ; (8) 0(1)21n n n n ∞=-⋅+∑．解：（1）该级数为等比级数，公比为1a,且0a >,故当1||1a<,即1a >时，级数收敛，当1||1a≥即01a <≤时，级数发散. （2）(1n S n =++++1=lim n n S →∞=∞∴ 1n ∞=∑发散.（3）113n n ∞=+∑是调和级数11n n∞=∑去掉前3项得到的级数，而调和级数11n n ∞=∑发散，故原级数113n n ∞=+∑发散.AHA12GAGGAGAGGAFFFFAFAF（4）1112(1)1(1)222n n nn n n n ∞∞-==⎛⎫+--=+ ⎪⎝⎭∑∑ 而1112n n ∞-=∑,1(1)2mnn ∞=-∑是公比分别为12的收敛的等比级数，所以由数项级数的基本性质知AHA12GAGGAGAGGAFFFFAFAF111(1)22n n n n ∞-=⎛⎫-+ ⎪⎝⎭∑收敛，即原级数收敛.（5）lnln ln(1)1nn n n =-++ 于是(ln1ln 2)(ln 2ln 3)[ln ln(1)]n S n n =-+-+-+ln1ln(1)ln(1)n n =-+=-+故lim n n S →∞=-∞,所以级数1ln1n nn ∞=+∑发散. （6）2210,2n n S S +==-∴ lim n n S →∞不存在，从而级数1(1)2n n ∞=-∑发散.（7）1lim lim10n n n n U n→∞→∞+==≠∴ 级数11n n n∞=+∑发散.（8）(1)(1)1, lim 21212n n n n n n U n n →∞--==++ ∴ lim 0n x U →∞≠，故级数1(1)21n n nn ∞=-+∑发散. 2．判别下列级数的收敛性，若收敛则求其和：(1) ∑∞=⎪⎭⎫ ⎝⎛+13121n n n ； (2) ※ ∑∞=++1)2)(1(1n n n n ;(3) ∑∞=⋅12sin n n n π; (4) 0πcos 2n n ∞=∑．解：（1）1111, 23n nn n ∞∞==∑∑都收敛，且其和分别为1和12，则AHA12GAGGAGAGGAFFFFAFAF11123n n n ∞=⎛⎫+ ⎪⎝⎭∑收敛，且其和为1+12=32.（2）11121(1)(2)212n n n n n n ⎛⎫=-+ ⎪++++⎝⎭AHA12GAGGAGAGGAFFFFAFAF∴121112111211121122322342345212n S n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-++-++-+++-+ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭11112212n n ⎛⎫=-+ ⎪++⎝⎭1lim 4n n S →∞=故级数收敛，且其和为14. （3）πsin 2n U n n =,而πsinππ2lim lim 0π222n n n U n→∞→∞=⋅=≠，故级数1πsin2n n n ∞=⋅∑发散.（4）πcos2n n U =,而4lim limcos2π1k k k U k →∞→∞==,42lim limcos(21)π1k k k U k +→∞→∞=+=-故lim n n U →∞不存在，所以级数0πcos2n n ∞=∑发散. 3※．设1n n U ∞=∑ (U n ＞0)加括号后收敛，证明1n n U ∞=∑亦收敛．证：设1(0)n n n U U ∞=>∑加括号后级数1n n A ∞=∑收敛，其和为S .考虑原级数1n n U ∞=∑的部分和1n k k S U ∞==∑，并注意到0(1,2,)k U k >=，故存在0n ,使11n n k t k t S U A s ∞===<<∑∑又显然1n n S S +<对一切n 成立，于是，{}n S 是单调递增且有上界的数列，因此，极限lim n n S →∞存在，即原级数1n n U ∞=∑亦收敛.习题9-2 1．判定下列正项级数的收敛性：(1) ∑∞=++1nnn)2)(1(1; (2) ∑∞=+1nnn1;(3) ∑∞=++ 1nnnn)2(2; (4) ∑∞=+1n nn)5(12；AHA12GAGGAGAGGAFFFFAFAFAHA12GAGGAGAGGAFFFFAFAF(5) 111nn a ∞=+∑ (a ＞0); (6) ∑∞=+1n nba 1 (a ,b ＞0); (7) ()∑∞=--+1n an a n 22 (a ＞0); (8) ∑∞=-+1n n n 1214；(9) ∑∞=⋅1n nnn 23； (10)※∑∞=1n nn n !; (11) ∑∞=+⋅⋅⋅⋅+⋅⋅⋅⋅1n n n )13(1074)12(753 ; (12) ∑∞=1n nn 3；(13)※∑∞=1n n n 22)!(2； (14) ∑∞=⎪⎭⎫⎝⎛+1n nn n 12;(15) ∑∞=1πn nn3sin2; (16) ∑∞=1πn nn n 2cos 32．解：（1）因为211(1)(2)n n n<++而211n n∞=∑收敛，由比较判别法知级数11(1)(2)n n n ∞=++∑收敛.（2）因为lim 10n n n U →∞==≠，故原级数发散. （3）因为21(1)(1)1n n n n n n n +>=+++，而111n n ∞=+∑发散，由比较判别法知，级数12(1)n n n n ∞=++∑发散.（4321n<=,而1n ∞=是收敛的p -级数3(1)2p =>,由比较判别法知,级数1n ∞=收敛.（5）因为111lim lim lim(1) 111nnn nn n nnaaa aa→∞→∞→∞+==-++AHA12GAGGAGAGGAFFFFAFAFAHA12GAGGAGAGGAFFFFAFAF11112001a a a >⎧⎪⎪==⎨⎪<<⎪⎩而当1a >时，11nn a ∞=∑收敛，故111nn a∞=+∑收敛;当1a =时，11nn a ∞=∑= 11n ∞=∑发散，故111nn a∞=+∑发散;当01a <<时1lim101nn a →∞=≠+，故1lim1n n a →∞+发散;综上所述，当01a <≤时，级数1lim1nn a →∞+发散，当1a >时，1lim1nn a →∞+收敛.（6）因为1lim lim lim(1)1n n n nn n n nb a a b a b a b b →∞→∞→∞+==-++1111101b b a b >⎧⎪⎪==⎨+⎪<<⎪⎩ 而当1b >时, 11nn b ∞=∑收敛，故11nn a b∞=+∑收敛;当1b =时，1111nn n b ∞∞===∑∑发散，故而由0a >, 101a <<+∞+,故11n n a b∞=+∑也发散;当01b <<时，11lim 0n n a b a →∞=≠+故11n n a b∞=+∑发散;综上所述知，当01b <≤时，级数11nn a b∞=+∑发散;当b >1时，级数11nn a b∞=+∑收敛.（7）因为lim1n nn→∞=na==>AHA12GAGGAGAGGAFFFFAFAFAHA12GAGGAGAGGAFFFFAFAF而11n n ∞=∑发散，故级数10)n a ∞=>∑发散.（8）因为434431121lim lim 1212n n n n n n n n→∞→∞++-==-而311n n∞=∑收敛，故级数21121n n n ∞=+-∑收敛. （9）因为1113233lim lim lim 1(1)232(1)2n n n n n n n n nU n n U n n +++→∞→∞→∞⋅⋅==>+⋅+由达朗贝尔比值判别法知，级数132nnn n ∞=⋅∑发散.（10）因为11(1)!1lim lim lim(1)1(1)!n n n n n n n nU n n e U n n n ++→∞→∞→∞+=⋅=+=>+，由达朗贝尔比值判别法知，级数1!nn n n ∞=∑发散.（11）因为1357(21)(23)4710(31)limlim 4710(31)(34)357(21)n n n nU n n n U n n n +→∞→∞⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+=⋅⋅⋅⋅⋅+⋅+⋅⋅⋅⋅+232lim 1343n n n →∞+==<+,由达朗贝尔比值判别法知原级数收敛.（12）因为111311lim lim lim 1333n n n n n n nU n n U n n ++→∞→∞→∞++=⋅==<，由达朗贝尔比值判别法知，级数13n n n ∞=∑收敛.（13）因为22221221(1)[(1)!]2(1)lim lim lim (!)22n n n n n n n nU n n U n +++→∞→∞→∞++=⋅= 由2212121(1)2(1)1lim lim lim 222ln 22ln 2x x x x x x x x x +++→∞→+∞→+∞+++==⋅⋅AHA12GAGGAGAGGAFFFFAFAF2121lim 022(ln 2)x x +→+∞==⋅知2121(1)lim lim 012n n n n nU n U ++→∞→∞+==<AHA12GAGGAGAGGAFFFFAFAF由达朗贝尔比值判别法知，级数221(!)2n n n ∞=∑收敛.（14）因为1lim1212n n n n →∞==<+，由柯西根值判别法知级数121nn n n ∞=⎛⎫⎪+⎝⎭∑收敛.（15）因为ππ2sinsin 33lim lim 1π2π33n n nn n n n n→∞→∞==⋅ 而112233nn n n n ∞∞==⎛⎫= ⎪⎝⎭∑∑是收敛的等比级数，它的每项乘以常数π后新得级数12π3n nn ∞=⋅∑仍收敛，由比较判别法的极限形式知，级数1π2sin3n nn ∞=∑收敛.（16）因为2πcos 322n nn n n ≤而与（12）题类似地可证级数12n n n∞=∑收敛，由比较判别法知级数1πcos 32nn n n ∞=∑收敛.2．试在(0，+∞)内讨论x 在什么区间取值时，下列级数收敛：(1) ∑∞=1n nnx ; (2) nn x n ∑∞=⎪⎭⎫⎝⎛123．解：（1）因为11lim lim lim 11n n n n n n nU x n nxx U n x n ++→∞→∞→∞=⋅==++由达朗贝尔比值判别法知，当1x >时，原级数发散;AHA12GAGGAGAGGAFFFFAFAF当01x <<时，原级数收敛;而当1x =时，原级数变为调11n n∞=∑，它是发散的.综上所述，当01x <<时，级数1nn x n∞=∑收敛.（2）因为1313(1)2limlim 22n n n n n nx n U xU x n ++→∞→∞⎛⎫+⋅ ⎪⎝⎭==⎛⎫⋅ ⎪⎝⎭,由达朗贝尔比值判别法知，当12x >即AHA12GAGGAGAGGAFFFFAFAF2x >时，原级数发散;当012x <<即02x <<时，原级收敛.而当12x =即 2x =时，原级数变为31n n ∞=∑，而由3lim n n →∞=+∞知31n n ∞=∑发散，综上所述，当02x <<时，级数31()2n n x n ∞=∑收敛.习题9-31．判定下列级数是否收敛，如果是收敛级数，指出其是绝对收敛还是条件收敛：(1) ∑∞=--1121)1(n nn ; (2) 11(1)2(1)2n n nn ∞-=-+-⋅∑;(3) ∑∞=12sin n n nx; (４) 111π(1)sin πn n n n ∞+=-∑;(5) ∑∞=-⎪⎭⎫ ⎝⎛-11210121n n n ； (6) ∑∞=+-1)1(n n x n ;(7) ∑∞=⋅1!)2sin(n n n x ．解：（1）这是一个交错级数121n U n =-, 1lim lim 021n n n U n →∞→∞==-,1112121n n U U n n +=>=-+ 由莱布尼茨判别法知11(1)21n n n ∞=--∑.又1111(1)2121n n n n n ∞∞==-=--∑∑，由1121lim12n n n→∞-=,及11n n∞=∑发散，知级数AHA12GAGGAGAGGAFFFFAFAF1121n n ∞=-∑发散，所以级数11(1)21nn n ∞=--∑条件收敛. （2）因为2111(1)211(1)22(1)2n n n n n ----+-=+-⋅-⋅,故11111(1)21111(1)22(1)22(1)2n n n n n n n n n ------+--=+≤+-⋅-⋅-⋅AHA12GAGGAGAGGAFFFFAFAF1113222n n n-=+=而112nn ∞=∑收敛，故132nn ∞=∑亦收敛，由比较判别法知11(1)2(1)2n n nn ∞-=-+-⋅∑收敛，所以级数11(1)2(1)2n n nn ∞-=-+-⋅∑绝对收敛.（3）因为22sin 1,nx n n ≤而级数211n n∞=∑收敛，由比较判别法知21sin n nxn ∞=∑收敛，因此，级数21sin n nx n∞=∑绝对收敛.（4）因为121ππ|(1)sin |sin πlimlim 11πn n n n n n n n+→∞→∞-==而211n n∞=∑收敛，由比较判别法的极限形式知，级数111π|(1)sin |πn n n n ∞+=-∑收敛，从而级数11π(1)sin πn n n+-绝对收敛. （5）因为212121111111210210210n n n n n n ----≤+=+,而级数112n n ∞=∑收敛的等比级数1()2q =;由比值判别法，易知级数211110n n ∞-=∑收敛，因而21111210n n n ∞-=⎛⎫+ ⎪⎝⎭∑收敛，由比较判别法知级数21111210n n n ∞-=-∑收敛，所以原级数21111210n n n ∞-=-∑绝对收敛.（6）当x 为负整数时，级数显然无意义；当x 不为负整数时，此交错级数满足莱布尼茨判别法的条件，故它是收AHA12GAGGAGAGGAFFFFAFAF敛的，但因11n x n∞=+∑发散，故原级数当x 不为负整数时仅为条件收敛.（7）因为sin(2)1!!n x n n ⋅≤由比值判别法知11!n n ∞=∑收敛(1(1)!lim 01!n n n →∞+=)，从而由比较判别法知1sin(2)!n n x n ∞=⋅∑收敛，所以级数AHA12GAGGAGAGGAFFFFAFAF1sin(2)!n n x n ∞=⋅∑，绝对收敛. 2．讨论级数∑∞=--111)1(n pn n 的收敛性(p ＞0)．解：当1p >时，由于11111(1)n p pn n n n ∞∞-==-=∑∑收敛，故级数111(1)n pn n ∞-=-∑绝对收敛.当01p <≤时，由于111,(1)n n p pu u n n +=>=+ lim 0n n u →∞=,由莱布尼茨判别法知交错级数111(1)n pn n ∞-=-∑收敛，然而，当01p <≤时，11111(1)n p pn n n n ∞∞-==-=∑∑发散，故此时，级数111(1)n pn n ∞-=-∑条件收敛.综上所述，当01p <≤时，原级数条件收敛;当p >1时，原级数绝对收敛.3※．设级数∑∞=12n n a 及∑∞=12n n b 都收敛，证明级数∑∞=1n n n b a 及()∑∞=+12n n n b a 也都收敛．证：因为2222||||110||222n n n n n n a b a b a b +≤≤=+ 而由已知1nn a ∞=∑及21n n b ∞=∑都收敛，故221111,22n nn n a b ∞∞==∑∑收敛，从而2211122n n n a b ∞=⎛⎫+ ⎪⎝⎭∑收敛，由正项级数的比较判别法知1n nn a b ∞=∑也收AHA12GAGGAGAGGAFFFFAFAF敛，从而级数1n n n a b ∞=∑绝对收敛.又由222()2,n n n n n n a b a a b b +=++及2211,n nn n a b ∞∞==∑∑,以及1n n n a b ∞=∑收敛，利用数项级数的基本性质知，221(2)nn n n n a a b b ∞=++∑收剑，亦即21()n n n a b ∞=+∑收敛.习题9-41．指出下列幂级数的收敛区间：(1) ∑∞=0!n nn x (0!=1)； (2) ∑∞=0!n n n x nn ；AHA12GAGGAGAGGAFFFFAFAF(3) ∑∞=⋅022n n nnx ； (4) ∑∞=++-01212)1(n n nn x ．(5) ∑∞=⋅+02)2(n nnn x ； (6) ∑∞=-0)1(2n n nx n．解：（1）因为111(1)!limlim lim 011!n n n n na n p a n n +→∞→∞→∞+====+，所以收敛半径r =+∞，幂级数1!nn x n ∞=∑的收敛区间为(,)-∞+∞.（2）因为-111lim lim lim 1e 11n nn n n n na n p a n n +→∞→∞→∞⎛⎫===-= ⎪++⎝⎭，所以收敛半径1e r p==.当x =e时，级数01!!en nn n n n n n x n n∞∞===∑∑，此时11(1)n nnu eu n+=+，因为1(1)nn+是单调递增数列，且1(1)n n+<e 所以1n nu u +>1,从而lim 0n n u →∞≠，于是级数当x =e 时，原级数发散.类似地，可证当x =-e 时，原级数也发散(可证lim ||0n n u →∞≠),综上所述，级数0!n n n n x n∞=∑的收敛区间为(-e,e).（3）因为2111limlim ()212n n n na n p a n +→∞→∞===+,所以收敛半径为r =2.当2x =时，级数221012nn n n x n n∞∞===⋅∑∑是收敛的p 一级数（p =2>1）;AHA12GAGGAGAGGAFFFFAFAF当x =-2时，级数22011(1)2nn n n n x n n ∞∞===-⋅⋅∑∑是交错级数，它满足莱布尼茨判别法的条件，故它收敛.综上所述，级数202nn n x n∞=⋅∑的收敛区间为[-2,2].AHA12GAGGAGAGGAFFFFAFAF（4）此级数缺少偶次幂的项，不能直接运用定理2求收敛半径，改用达朗贝尔比值判别法求收敛区间.令21(1)21n nn x u n +=-+，则22121lim lim 23n n n nu n x x u n +→∞→∞+=⋅=+.当21x <时，即||1x <时，原级数绝对收敛.当21x >时，即||1x >时，级数0||n n u ∞=∑发散，从而210(1)21n nn x n +∞=-+∑发散，当1x =时，级数变为01(1)21nn n ∞=-+∑;当1x =-时，级数变为11(1)21n n n ∞+=-+∑;它们都是交错级数，且满足莱布尼茨判别法的条件，故它们都收敛.综上所述，级数21(1)21n nn x n +∞=-+∑的收敛区间为[-1,1].（5）此级数为（x +2）的幂级数.因为11limlim2(1)2n n n na n p a n +→∞→∞===+.所以收敛半径12r p==，即|2|2x +<时，也即40x -<<时级数绝对收敛.当|2|2x +>即4x <-或0x >时，原级数发散.当4x =-时，级数变为01(1)n n n∞=-∑是收敛的交错级数，当x =0时，级数变为调和级数11n n∞=∑,它是发散的.AHA12GAGGAGAGGAFFFFAFAF综上所述，原级数的收敛区间为[-4,0). （6）此级数（x -1）的幂级数12limlim 21n n n na np a n +→∞→∞===+ 故收敛半径12r =.于是当1|1|2x -<即1322x <<时，原级数绝对收敛.当1|1|2x ->即12x <或32x >时，原级数发散.AHA12GAGGAGAGGAFFFFAFAF当32x =时，原级数变为01n n ∞=∑是调和级数，发散.当12x =时，原级数变为11(1)n n n ∞=-∑，是收敛的交错级数.综上所述，原级数的收敛区间为13,22⎡⎫⎪⎢⎣⎭.2．求下列幂级数的和函数：(1) ∑∞=-1)1(n n nn x ； (2) ∑∞=-1122n n nx ；(3) nn x n n ∑∞=+1)1(1； (4) ∑∞=+0)12(n n x n ．解：（1）可求得所给幂级数的收敛半径r =1.设1()(1)n nn x S x n ∞==-∑,则1111()(1)(1)1n n n n n n x S x x n x ∞∞-=='⎡⎤'=-=-=-⎢⎥+⎣⎦∑∑∴001()()d d ln(1) (||1)1x x S x S x x x x x x-'===-+<+⎰⎰又当x =1时，原级数收敛，且()S x 在x =1处连续.∴1(1)ln(1) (11)nnn x x x n ∞=-=-+-<≤∑ （2）所给级数的收敛半经r =1，设211()2n n S x nx ∞-==∑,当||1x <时，有2121011()d 2d 2d xx xn n n n S x x nxx nx x ∞∞--====∑∑⎰⎰⎰AHA12GAGGAGAGGAFFFFAFAF22211nn x xx ∞===-∑ 于是22222()1(1)x x s x x x '⎛⎫== ⎪--⎝⎭又当1x =±时，原级数发散.AHA12GAGGAGAGGAFFFFAFAF故 2122122 (||1)(1)n n xnx x x ∞-==<-∑（3）可求所给级数的收敛半径为1.令1111()(0)(1)(1)n n n n x x s x x n n x n n +∞∞====≠++∑∑ 令11()(1)n n x g x n n +∞==+∑,则111()1n n g x x x ∞-=''==-∑01()d ()(0)d 1xxg x x g x g x x''''=-=-⎰⎰(0)0,()ln(1)g g x x ''==--()d ()(0)ln(1)d ,(0)0xxg x x g x g x x g '=-=--=⎰⎰所以0()ln(1)d ln(1)ln(1)xg x x x x x x x =--=+---⎰;所以1()11ln(1),||1,S x x x x⎛⎫=+--< ⎪⎝⎭且0x ≠.当1x ±时，级数为11(1)n n n ∞=+∑和11(1)(1)n n n n ∞=-+∑,它们都收敛.且显然有(0)0S =.故111ln(1)(1,0)(0,1)()00,1x x S x x x x ⎧⎛⎫+--∈-⋃⎪ ⎪=⎝⎭⎨⎪=±⎩. （4）可求得所给级数的收敛半径为r =1且1x ±时，级数发散，设1()n n S x nx ∞-==∑,则001()d .1xn n s x x x x∞===-∑⎰ 于是211()()1(1)S x x x '==--,即1211(1)n n nx x ∞-==-∑.AHA12GAGGAGAGGAFFFFAFAF所以111(21)2nn n n n n n xx nxx ∞∞∞-===+=+∑∑∑221112(1)1(1)xx x x x +=⋅+=--- (||1)x <3．求下列级数的和：AHA12GAGGAGAGGAFFFFAFAF(1) ∑∞=125n nn ； (2) ∑∞=-12)12(1n nn ；(3) ∑∞=--112212n n n ； (4) 1(1)2n n n n ∞=+∑．解：（1）考察幂级数21n n n x ∞=∑，可求得其收敛半径1r = ，且当1x ±时，级数的通项2n n u n x =，2lim||lim n n n u n →∞→∞==+∞，因而lim 0n n u →∞≠，故当1x ±时，级数21nn nx∞=∑发散，故幂级数21n n n x ∞=∑的收敛区间为（-1，1）. 设21() (||1)nn S x nx x ∞==<∑，则211()n n S x x n x ∞-==∑令2111()n n S x nx∞-==∑,则11011()d xnn n n S x x nxx nx ∞∞-====∑∑⎰.再令121()n n S x nx ∞-==∑,则201()d 1xn n xS x x x x∞===-∑⎰. 故221()(||1)1(1)x S x x x x '⎛⎫==< ⎪--⎝⎭，从而有120()d (1)x x S x x x =-⎰. 1231() (||1)(1)(1)x xS x x x x '⎛⎫+==< ⎪--⎝⎭ 于是 213()() (||1)(1)x x S x xS x x x +==<- 取15x =，则223111()11555()5532115n n n S ∞=+===⎛⎫- ⎪⎝⎭∑.AHA12GAGGAGAGGAFFFFAFAF（2）考察幂级数21121n n x n ∞=-∑，可求得收敛半径r =1，设2211111() (||1)2121nn n n S x x x x x n n ∞∞-====<--∑∑AHA12GAGGAGAGGAFFFFAFAF令21111()21n n S x x n ∞-==-∑,则221211()1n n S x x x ∞-='==-∑.1200d 11()d ln1-21xxx xS x x x x+'==-⎰⎰即 1111()(0)ln (,(0)0)21x S x S s x+-==-.于是 111()ln ,(||<1)21x S x x x+=-，从而11()()ln (||1)21x xS x xS x x x+==<-取x =则11(21)21n n S n ∞===--∑=（3）考察幂级数211(21)n n n x ∞-=-∑，可求得其级数半经为r =1,因为212121111(21)2n n n n n n n xnxx ∞∞∞---===-=-∑∑∑令2111()2n n S x nx∞-==∑，则221201()d 1xnn x S x x xx ∞===-∑⎰.所以212222() (||1)1(1)x x S x x x x '⎛⎫==< ⎪--⎝⎭,于是212121111(21)2n n n n n n n xnxx ∞∞∞---===-=-∑∑∑3222222 (||1)(1)1(1)x x x x x x x x +=-=<---AHA12GAGGAGAGGAFFFFAFAF取12x =，得3212111()121102212291()2n n n S ∞-=+-⎛⎫=== ⎪⎛⎫⎝⎭-⎪⎝⎭∑.AHA12GAGGAGAGGAFFFFAFAF（4）考察幂级数1(1)n n n n x ∞=+∑，可求得其收敛半径r =1.设1()(1) (||1)n n S x n n x x ∞==+<∑则121011()d xn n n n S x x nxxnx ∞∞+-====∑∑⎰.又设111()n n S x nx ∞-==∑则101()d 1xn n x S x x x x ∞===-∑⎰.从而121()1(1)x S x x x '⎛⎫== ⎪--⎝⎭,2212()d ()(1)xx S x x x S x x ==-⎰2232() ||1(1)(1)x x S x x x x '⎛⎫==< ⎪--⎝⎭ 取12x =，则31121(1)2822112nn n n S ∞=⨯+⎛⎫=== ⎪⎝⎭⎛⎫- ⎪⎝⎭∑ 习题9-51．将下列函数展开成x 的幂级数：(1) 2cos 2x ; (2) 2sin x ； (3) 2x x -e ; (4)211x -；(5)πcos()4x -．解：（1）2201cos 11cos (1)2222(2)!nn n x x x n ∞=+==+-∑AHA12GAGGAGAGGAFFFFAFAF211(1)(-)2(2)!nnn x x n ∞==+-∞<<+∞∑ （2）2101sin (1) ()2(21)!2n n n x x x n +∞=⎛⎫=--∞<<+∞ ⎪+⎝⎭∑（3）22210011e()(1) ()!!x nn n n n x x x x x n n ∞∞-+===-=--∞<+∞∑∑AHA12GAGGAGAGGAFFFFAFAF（4）211111211x x x ⎡⎤=+⎢⎥--+⎣⎦0002011(1)221[(1)]2 ||1n n nn n n n nn n n x x x x x x ∞∞==∞=∞==+-=+-=<∑∑∑∑（5）πππcos cos cos sin sin 444x x x ⎛⎫-=+ ⎪⎝⎭2210(cos sin )2(1) ()2(2)!(21)!n n n n x x x xx n n +∞==+⎡⎤=-+-∞<<+∞⎢⎥+⎣⎦∑ 2．将下列函数在指定点处展开成幂级数，并求其收敛区间： (1) x-31,在x 0＝１； (2) cos x,在x 0=3π;(3)3412++x x ,在x 0=1; (4) 21x , 在x 0＝３．解：（1）因为11113212x x =⋅---,而0111 (||112212nn x x x ∞=--⎛⎫=< ⎪-⎝⎭-∑即13x -<<). 所以100111(1) (13)3222nnn n n x x x x ∞∞+==--⎛⎫=⋅=-<< ⎪-⎝⎭∑∑.收敛区间为：（-1，3）.（2）πππ2π2cos cos ()cos cos()sin sin()333333x x x x ⎡⎤=+-=---⎢⎥⎣⎦AHA12GAGGAGAGGAFFFFAFAF22100()()133(1)(1)2(2)!2(21)!n n n n n n x x n n ππ+∞∞==--=-+-+∑∑221011(1)())2(2)!33nn n n x x n ππ∞+=⎡⎤=--+-⎢⎥⎣⎦∑ ()x -∞<<+∞AHA12GAGGAGAGGAFFFFAFAF收敛区间为(,)-∞+∞. （3）211111111()1143213481124x x x x x x =-=⋅-⋅--++++++ 001111(1)(1)4284n nn n n n x x ∞∞==--⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭∑∑223011(1)(1)22n n n n n x ∞++=⎛⎫=--- ⎪⎝⎭∑由112x -<且114x -<得13x -<<，故收敛区间为（-1，3）（4）因为011113(1)()333313n n n x x x ∞=-=⋅=-⋅-+∑1(3)(1)3nnn n x ∞+=-=-∑ 而21011(3)(1)3n n n n x x x ∞+=''⎡⎤-⎛⎫=-=-- ⎪⎢⎥⎝⎭⎣⎦∑111(1)(3)3n n n n n x ∞-+=-=-⋅-∑1111(1)(3)3n n n n n x +∞-+=-=-∑ 2(1)(1)(3)3n n n n n x ∞+=-+=-∑ 由313x -<得06x <<. 故收敛区间为（0，6）.如有侵权请联系告知删除，感谢你们的配合！33387 826B 艫Hn32578 7F42 罂 y#• 33471 82BF 芿24819 60F3 想27944 6D28 洨。

《微积分》课后答案(复旦大学出版社(曹定华_李建平_毛志强_著))第7章

M 3 (0, 0,5) ，则点 M (4, 3,5) 到 x 轴，y 轴，z 轴的距离分别为：
d x | MM 1 | (4 4) 2 (3 0) 2 (5 0) 2 34. d y | MM 2 | (4 0) 2 (3 3) 2 (5 0) 2 41. d z | MM 3 | (4 0) 2 (3 0) 2 (5 5) 2 5.
5．在 yＯz 面上，求与三个已知点 A(3，1，2)，B(4，-2，2)和 C(0，5，1)等距离的点．解：设所求点 P (0, b, c) ,则 | PA || PB || PC | 即 9 (b 1) (c 2) 16 (b 2) (c 2)
2 2 2 2
| AB || AC | ,且 | AB |2 | AC |2 | BC |2
所以 ABC 是等腰直角三角形. 习题 7-2 1．在平行四边形 ABCD 内，设 AB a , AD b ，M 为对角线的交点，试用向量 a 和 b 表示向量 MA, MB, MC 和 MD ．解：（如图） DC AB a, BC AD b,

2．试用向量证明：如果平面上一个四边形的对角线互相平分，则该四边形是平行四边形．证：（如上题图），依题意有 AM MC , DM MB. 于是 AB AM MB MC DM DC. 故 ABCD 是平行四边形. 3．已知向量 a=i-2j+3k 的始点为(1，3，-2)，求向量 a 的终点坐标．解：设 a 的终点坐标为( x, y, z ),则源自
a ( x 1)i ( y 3) j ( z 2)k ,
而 a i 2 j 3k , 从而有