多重共线性处理方法
多元回归分析中的多重共线性及其解决方法

多元回归分析中的多重共线性及其解决方法在多元回归分析中,多重共线性是一个常见的问题,特别是在自变量之间存在高度相关性的情况下。
多重共线性指的是自变量之间存在线性相关性,这会造成回归模型的稳定性和可靠性下降,使得解释变量的效果难以准确估计。
本文将介绍多重共线性的原因及其解决方法。
一、多重共线性的原因多重共线性常常发生在自变量之间存在高度相关性的情况下,其主要原因有以下几点:1. 样本数据的问题:样本数据中可能存在过多的冗余信息,或者样本数据的分布不均匀,导致变量之间的相关性增加。
2. 选择自变量的问题:在构建回归模型时,选择了过多具有相似解释作用的自变量,这会增加自变量之间的相关性。
3. 数据采集的问题:数据采集过程中可能存在误差或者不完整数据,导致变量之间的相关性增加。
二、多重共线性的影响多重共线性会对多元回归模型的解释变量产生不良影响,主要表现在以下几个方面:1. 回归系数的不稳定性:多重共线性使得回归系数的估计不稳定,难以准确反映各个自变量对因变量的影响。
2. 系数估计值的无效性:多重共线性会导致回归系数估计偏离其真实值,使得对因变量的解释变得不可靠。
3. 预测的不准确性:多重共线性使得模型的解释能力下降,导致对未知数据的预测不准确。
三、多重共线性的解决方法针对多重共线性问题,我们可以采取以下几种方法来解决:1. 剔除相关变量:通过计算自变量之间的相关系数,发现高度相关的变量,选择其中一个作为代表,将其他相关变量剔除。
2. 主成分分析:主成分分析是一种降维技术,可以通过线性变换将原始自变量转化为一组互不相关的主成分,从而降低多重共线性造成的影响。
3. 岭回归:岭回归是一种改良的最小二乘法估计方法,通过在回归模型中加入一个惩罚项,使得回归系数的估计更加稳定。
4. 方差膨胀因子(VIF):VIF可以用来检测自变量之间的相关性程度,若某个自变量的VIF值大于10,则表明该自变量存在较高的共线性,需要进行处理。
多重共线性修正

新模型可以有效地消除存在于原模型中的多重共 线性。 一般讲,增量之间的线性关系远比总量之间的线 性关系弱得多。
△
588 587 1088 1628 1441 1651 2920 1762 1854 2960 4584 8637 12610 12294 9093
△ C(-1)
333 329 383 673 1079 769 909 1909 1196 806 1784 2806 4230 7034 7313
4、检验简单相关系数
列 出 X, K, X X 1 K 0.9883 P 1 0.9804 P 0 0.9878 P1, P0 K 0.9883 1 0.9700 0.9695 的相关系数矩阵: P1 P0 0.9804 0.9878 0.9700 0.9695 1 0.9918 0.9918 1
第一类: 第一类:删除引起共线性解释变量
找出引起多重共线性的解释变量,将 它排除出去,是最为有效的克服多重共线 性问题的方法。 这类方法以逐步回归法为代表,得到 了最广泛的应用。
逐步回归法:
具体步骤 1)先用被解释变量对每一个所考虑的解 释变量做简单回归; 2)以对被解释变量贡献最大的解释变量 所对应的回归方程为基础; 3)逐个引入其余的解释变量。 好处 将统计上不显著的解释变量剔除,最后 保留在模型中的解释变量之间多重共线性不明 显,而且对被解释变量有较好的解释贡献。
减少参数估计量的方法多重共线性的主要后果是参数估计量具有较大的方差所以采取适当方法减小参数估计量的方差虽然没有消除模型中的多重共线性但确能消除多重共线性造成的后果
回归分析中的多重共线性问题及解决方法(七)

回归分析是统计学中常用的一种方法,它用于研究自变量和因变量之间的关系。
然而,在实际应用中,经常会遇到多重共线性的问题,这给回归分析带来了一定的困难。
本文将讨论回归分析中的多重共线性问题及解决方法。
多重共线性是指独立自变量之间存在高度相关性的情况。
在回归分析中,当自变量之间存在多重共线性时,会导致回归系数估计不准确,标准误差增大,对因变量的预测能力降低,模型的解释能力受到影响。
因此,多重共线性是回归分析中需要重点关注和解决的问题之一。
解决多重共线性问题的方法有很多种,下面将介绍几种常用的方法。
一、增加样本量增加样本量是解决多重共线性问题的一种方法。
当样本量足够大时,即使自变量之间存在一定的相关性,也能够得到较为稳健的回归系数估计。
因此,可以通过增加样本量来减轻多重共线性对回归分析的影响。
二、使用主成分回归分析主成分回归分析是一种常用的处理多重共线性问题的方法。
主成分回归分析通过将原始自变量进行线性变换,得到一组新的主成分变量,这些主成分变量之间不存在相关性,从而避免了多重共线性问题。
然后,利用这些主成分变量进行回归分析,可以得到更为准确稳健的回归系数估计。
三、岭回归岭回归是一种经典的解决多重共线性问题的方法。
岭回归通过对回归系数施加惩罚项,从而减小回归系数的估计值,进而降低多重共线性对回归分析的影响。
岭回归的思想是在最小二乘估计的基础上加上一个惩罚项,通过调节惩罚项的系数来平衡拟合优度和模型的复杂度,从而得到更为稳健的回归系数估计。
四、逐步回归逐步回归是一种逐步选择自变量的方法,可以用来解决多重共线性问题。
逐步回归可以通过逐步引入或剔除自变量的方式,来得到一组最优的自变量组合,从而避免了多重共线性对回归系数估计的影响。
以上所述的方法都可以用来解决回归分析中的多重共线性问题。
在实际应用中,应该根据具体的情况选择合适的方法来处理多重共线性问题,从而得到准确可靠的回归分析结果。
总之,多重共线性是回归分析中需要重点关注的问题,通过合适的方法来处理多重共线性问题,可以得到更为准确稳健的回归系数估计,从而提高回归分析的预测能力和解释能力。
多重共线性(统计累赘)的概念、特征及其测量方式和处理方式

试述多重共线性(统计累赘)的概念、特征及其测量方式和处理方式。
1、概念多重共线性是指自变量之间存在线性相关关。
倘若其中两个自变项的关系特别强,则在相互控制后就会使每者的效果减弱,而其他的变相的效果就会因此而增大。
2、特征3、产生原因产生多重相关性的原因主要包括四方面。
一是没有足够多的样本数据; 二是选取的自变量之间客观上就有共线性的关系; 还可能由其它因素导致, 如数据采集所用的方法, 模型设定, 一个过度决定的模型等。
但多数研究者认为共线性本质上是由于样本数据不足引起的。
4、测量方式(1)经验式的诊断方法通过观察,得到一些多重相关性严重存在的迹象。
①在自变量的简单相关系数矩阵中,有某些自变量的相关系数值较大。
②回归系数的代数符号与专业知识或一般经验相反;或者该自变量与因变量的简单相关系数符号相反。
③对重要自变量的回归系数进行t 检验,其结果不显著。
特别是当F 检验能在高精度下通过,测定系数R 2的值也很大,但自变量的t 检验却全都不显著,这时多重相关性的可能将会很大。
④如果增加或删除一个变量,或者增加或删除一个观测值,回归系数发生了明显的变化。
⑤重要自变量的回归系数置信区别明显过大。
⑥在自变量中,某一个自变量是另一部分自变量的完全或近似完全的线性组合。
⑦对于一般的观测数据,如果样本点的个数过少,比如接近于变量的个数或者少于变量的个数,样本数据中的多重相关性就会经常存在。
(2)统计检验方法共线性的诊断方法是基于对自变量的观测数据构成的矩阵X ’X 进行分析,使用各种反映自变量间相关性的指标。
共线性诊断常用的统计量有方差膨胀因子VIF 或容限TOL 、条件指数和方差比例等。
方差膨胀因子VIF 是指回归系数的估计量由于自变量的共线性使其方差增加的一个相对度量。
对于第i 个回归系数,它的方差膨胀因子定义为:VIF=1/1-R 2=1/TOL i 其中R2i 是自变量Xi 对模型中其余自变量线性回归模型的R 平方。
多重共线性处理方法

多重共线性处理方法
处理多重共线性的方法主要有以下几种:
1. 去除变量:根据变量之间的相关性,剔除其中一个或多个高度相关的变量。
通过领域知识或经验来选择保留哪些变量。
2. 合并变量:将高度相关的变量合并为一个新的变量。
例如,如果变量A和变量B高度相关,可以计算出变量C=A+B,并用C代替A和B。
3. 使用主成分分析(PCA):通过将一组高度相关的变量转换为一组线性无关的主成分,来减少多重共线性的影响。
4. 正则化方法:通过加入正则化项,如岭回归(Ridge Regression)或Lasso 回归(Lasso Regression),来减少多重共线性的影响。
5. 数据采样:如果数据集中某些特定的值导致多重共线性问题,可以考虑采样或调整这些数据点,以减少多重共线性的影响。
需要根据具体的情况选择适当的方法来处理多重共线性。
如果多重共线性问题比较严重,可能需要综合使用多种方法来解决。
如何进行多重共线性的剔除变量和合并变量处理

如何进行多重共线性的剔除变量和合并变量处理在进行统计分析时,研究人员常常会面临多重共线性的问题。
多重共线性是指自变量之间存在高度相关性,这可能会导致回归模型的不准确性和不可靠性。
为了解决多重共线性问题,研究人员可以采取剔除变量和合并变量的处理方法。
1. 多重共线性的检测在进行多重共线性的处理之前,首先需要进行多重共线性的检测。
常用的方法包括计算变量间的相关系数矩阵、方差膨胀因子和特征值等。
当相关系数矩阵中存在高度相关的变量对,方差膨胀因子大于10或特征值接近于0时,便可以判断存在多重共线性的问题。
2. 剔除变量剔除变量是指在多重共线性问题较为严重的情况下,研究人员可以选择将相关性较高的变量从模型中剔除。
剔除变量的方法包括:(1)选择与因变量关系较弱的变量;(2)选择与其他自变量之间相关性较弱的变量;(3)通过逐步回归、岭回归等方法进行变量选择。
3. 合并变量合并变量是指将多个具有相关性的变量合并成一个新的变量。
合并变量的方法包括:(1)计算多个变量的平均值、加权平均值或标准化值作为新的变量;(2)进行主成分分析,提取主成分作为新的变量;(3)进行因子分析,提取公因子作为新的变量。
4. 多重共线性处理的注意事项在进行多重共线性处理时,还需要注意以下几点:(1)根据研究目的和背景知识选择要剔除或合并的变量;(2)确保剔除或合并后的变量仍能保持原有变量的信息;(3)在剔除或合并变量后重新评估回归模型的拟合程度和解释能力。
总结起来,解决多重共线性问题的方法包括剔除变量和合并变量。
通过合理选择要剔除或合并的变量,并进行适当的处理,可以提高回归模型的准确性和可靠性。
在实际应用中,根据研究目的和数据特点来选择合适的方法进行多重共线性处理,从而得到更可靠的统计分析结果。
自变量存在多重共线性,如何通过变量筛选来解决?

⾃变量存在多重共线性,如何通过变量筛选来解决?多重线性回归要求各个⾃变量之间相互独⽴,不存在多重共线性。
所谓多重共线性,是指⾃变量之间存在某种相关或者⾼度相关的关系,其中某个⾃变量可以被其他⾃变量组成的线性组合来解释。
医学研究中常见的⽣理资料,如收缩压和舒张压、总胆固醇和低密度脂蛋⽩胆固醇等,这些变量之间本⾝在⼈体中就存在⼀定的关联性。
如果在构建多重线性回归模型时,把具有多重共线性的变量⼀同放在模型中进⾏拟合,就会出现⽅程估计的偏回归系数明显与常识不相符,甚⾄出现符号⽅向相反的情况,对模型的拟合带来严重的影响。
今天我们就来讨论⼀下,如果⾃变量之间存在多重共线性,如何通过有效的变量筛选来加以解决?⼀、多重共线性判断回顾⼀下前期讲解多重线性回归时,介绍的判断⾃变量多重共线性的⽅法。
1. 计算⾃变量两两之间的相关系数及其对应的P值,⼀般认为相关系数>0.7,且P<0.05时可考虑⾃变量之间存在共线性,可以作为初步判断多重共线性的⼀种⽅法。
2. 共线性诊断统计量,即Tolerance(容忍度)和VIF(⽅差膨胀因⼦)。
⼀般认为如果Tolerance<0.2或VIF>5(Tolerance和VIF呈倒数关系), 则提⽰要考虑⾃变量之间存在多重共线性的问题。
⼆、多重共线性解决⽅法:变量剔除顾名思义,当⾃变量之间存在多重共线性时,最简单的⽅法就是对共线的⾃变量进⾏⼀定的筛选,保留更为重要的变量,删除次要或可替代的变量,从⽽减少变量之间的重复信息,避免在模型拟合时出现多重共线性的问题。
对于如何去把握应该删除哪⼀个变量,保留哪⼀个变量,近期也有⼩伙伴在微信平台中问到这个问题,下⾯举个例⼦进⾏⼀个简单的说明。
表1. ⾃变量相关性如表1所⽰, X3和X4、X5之间相关系数>0.7,变量X4与X1、X3、X5之间相关系数>0.7,X5与X3、X4之间相关系数>0.7,说明X3、X4、X5之间存在⼀定的共线性,由于X4与X1的相关性也较⾼,故此时建议可以先将X4删除再进⾏模型拟合,当然也需要结合容忍度和VIF值及专业知识来进⾏判断。
ridge方法

ridge方法Ridge方法是一种常用的统计分析方法,用于处理线性回归模型中的多重共线性问题。
本文将详细介绍Ridge方法的原理、应用和优缺点。
一、Ridge方法的原理Ridge方法是一种正则化方法,通过引入L2正则化项来惩罚模型中的参数,从而减小多重共线性对模型的影响。
在线性回归模型中,多重共线性指的是自变量之间存在高度相关性,这会导致模型参数估计不稳定。
Ridge方法通过在目标函数中添加一个L2正则化项,使得模型的参数估计更加稳定。
具体而言,Ridge方法的目标函数可以表示为:$$\min _{w}\left\|X w-y\right\|_{2}^{2}+\alpha\left\|w\right\|_{2}^{2}$$其中,X是自变量矩阵,y是因变量向量,w是待估计的参数向量,α是正则化参数。
Ridge方法通过调整α的值,可以控制正则化的强度。
当α=0时,Ridge方法退化为普通的线性回归方法;当α趋近于无穷大时,Ridge方法的参数估计趋近于0。
二、Ridge方法的应用Ridge方法在实际应用中有着广泛的应用。
首先,Ridge方法能够有效地解决多重共线性问题,提高模型的稳定性和准确性。
在金融领域,Ridge方法常常用于预测股票价格、利率变动等问题。
其次,Ridge方法还可以用于特征选择,通过调整正则化参数α的值,可以筛选出对模型预测性能影响较大的特征变量。
此外,Ridge方法还可以应用于图像处理、信号处理等领域。
三、Ridge方法的优缺点Ridge方法具有以下几个优点:首先,Ridge方法能够有效地减小多重共线性对模型的影响,提高模型的稳定性和准确性;其次,Ridge方法具有良好的数学性质,可通过解析方法或优化算法求解;此外,Ridge方法不会使得参数估计值偏向于0,而是通过调整参数的权重,保留了所有的自变量。
然而,Ridge方法也存在一些缺点:首先,Ridge方法需要预先设定正则化参数α的值,对于不同的数据集,需要通过交叉验证等方法来选择最优的α值;其次,当自变量之间存在较强的相关性时,Ridge方法可能会将相关变量的系数压缩到接近于0的程度,导致模型的解释性不强。
如何解决多重共线性问题

如何解决多重共线性问题多重共线性是统计学中常见的问题,特别是在回归分析中。
它指的是自变量之间存在高度相关性,导致回归模型的稳定性和解释能力下降。
在实际应用中,解决多重共线性问题是非常重要的,下面将探讨一些常用的方法。
1. 数据收集和预处理在解决多重共线性问题之前,首先需要对数据进行收集和预处理。
数据的收集应该尽可能地多样化和全面,以避免自变量之间的相关性。
此外,还需要对数据进行清洗和转换,以确保数据的准确性和一致性。
2. 相关性分析在回归分析中,可以通过计算自变量之间的相关系数来评估它们之间的相关性。
常用的相关系数包括皮尔逊相关系数和斯皮尔曼相关系数。
如果发现自变量之间存在高度相关性,就需要考虑解决多重共线性问题。
3. 方差膨胀因子(VIF)方差膨胀因子是用来评估自变量之间共线性程度的指标。
它的计算方法是将每个自变量作为因变量,其他自变量作为自变量进行回归分析,然后计算回归系数的标准误差。
VIF越大,表示自变量之间的共线性越强。
一般来说,VIF大于10就表明存在严重的多重共线性问题。
4. 特征选择特征选择是解决多重共线性问题的一种常用方法。
通过选择与因变量相关性较高,但与其他自变量相关性较低的自变量,可以减少共线性的影响。
常用的特征选择方法包括逐步回归、岭回归和Lasso回归等。
5. 主成分分析(PCA)主成分分析是一种降维技术,可以将多个相关自变量转化为一组无关的主成分。
通过保留主成分的前几个,可以减少自变量之间的相关性,从而解决多重共线性问题。
但需要注意的是,主成分分析会损失部分信息,可能会影响模型的解释能力。
6. 岭回归和Lasso回归岭回归和Lasso回归是一种通过引入惩罚项来解决多重共线性问题的方法。
岭回归通过在最小二乘估计中添加一个L2正则化项,可以减小回归系数的估计值,从而减少共线性的影响。
Lasso回归则通过在最小二乘估计中添加一个L1正则化项,可以使得一些回归系数变为零,从而实现变量选择的效果。
7.4多重共线性的修正方法

• 增大样本容量 • 剔除变量法 • 利用附加信息 • 变换变量形式 • 横截面数据与时序数据并用 • 逐步回归法
1. 增大样本容量
如果样本容量增加,会减小回归参数的方差, 标准误差也同样会减小。因此尽可能地收集 足够多的样本数据可以改进模型参数的估计。
问题:增加样本数据在实际计量分析中常面 临许多困难。
Y பைடு நூலகம் AL K
劳动投入量L和资金投入量K之间通常是高度相关 的,如果已知附加信息:
+=1 (规模报酬不变)
则
Y AL1 K AL( K )
L
即
Y A( K )
LL
记
Y* Y , L
K* K L
则C-D生产函数可表示成:
Y* AK*
4. 变换变量形式 对原设定模型中的变量进行适当的变换,可以 消除或削弱原模型中解释变量之间的相关关系, 如引入差分变量、相对数变量等。
(2)在基本回归方程中分别引入第二个解释变 量,重新进行线性回归。
若新变量的引入改进了R2和F检验,且回归参数 的t检验在统计上也是显著的,则在模型中保留 该变量。
若新变量的引入未能改进R2和F检验,且对 其他回归参数估计值的t检验也未带来什么 影响,则认为该变量是多余变量。
若新变量的引入未能改进R2和F检验,且显 著地影响了其他回归参数估计值的数值或符 号,同时本身的回归参数也通不过t检验,说 明出现了严重的多重共线性。
2. 剔除变量法
把引起多重共线性的解释变量首先剔除,再 重 新建立回归方程,直至回归方程中不再存在 严 重 注的 意多: 若重剔共除线了性重。要变量,可能引起模型的 设 定误差。
3. 利用附加信息
多重共线性问题的几种解决方法

多重共线性问题的几种解决方法在多元线性回归模型经典假设中,其重要假定之一是回归模型的解释变量之间不存在线性关系,也就是说,解释变量X1,X2,……,Xk中的任何一个都不能是其他解释变量的线性组合。
如果违背这一假定,即线性回归模型中某一个解释变量与其他解释变量间存在线性关系,就称线性回归模型中存在多重共线性。
多重共线性违背了解释变量间不相关的古典假设,将给普通最小二乘法带来严重后果。
这里,我们总结了8个处理多重共线性问题的可用方法,大家在遇到多重共线性问题时可作参考:1、保留重要解释变量,去掉次要或可替代解释变量2、用相对数变量替代绝对数变量3、差分法4、逐步回归分析5、主成份分析6、偏最小二乘回归7、岭回归8、增加样本容量这次我们主要研究逐步回归分析方法是如何处理多重共线性问题的。
逐步回归分析方法的基本思想是通过相关系数r、拟合优度R2和标准误差三个方面综合判断一系列回归方程的优劣,从而得到最优回归方程。
具体方法分为两步:第一步,先将被解释变量y对每个解释变量作简单回归:对每一个回归方程进行统计检验分析(相关系数r、拟合优度R2和标准误差),并结合经济理论分析选出最优回归方程,也称为基本回归方程。
第二步,将其他解释变量逐一引入到基本回归方程中,建立一系列回归方程,根据每个新加的解释变量的标准差和复相关系数来考察其对每个回归系数的影响,一般根据如下标准进行分类判别:1.如果新引进的解释变量使R2得到提高,而其他参数回归系数在统计上和经济理论上仍然合理,则认为这个新引入的变量对回归模型是有利的,可以作为解释变量予以保留。
2.如果新引进的解释变量对R2改进不明显,对其他回归系数也没有多大影响,则不必保留在回归模型中。
3.如果新引进的解释变量不仅改变了R2,而且对其他回归系数的数值或符号具有明显影响,则认为该解释变量为不利变量,引进后会使回归模型出现多重共线性问题。
不利变量未必是多余的,如果它可能对被解释变量是不可缺少的,则不能简单舍弃,而是应研究改善模型的形式,寻找更符合实际的模型,重新进行估计。
如何处理逻辑回归模型中的多重共线性(五)

逻辑回归模型是一种非常常用的统计分析方法,用于预测二元变量的结果。
然而,在逻辑回归模型中,多重共线性是一个常见的问题,它会导致模型参数的不稳定性和预测结果的不准确性。
因此,如何处理逻辑回归模型中的多重共线性是一个非常重要的问题。
首先,我们需要了解多重共线性是什么以及它是如何影响逻辑回归模型的。
多重共线性是指自变量之间存在高度相关性的情况,这会导致模型参数估计的不准确性。
在逻辑回归模型中,多重共线性会导致模型参数的标准误差增大,使得参数的显著性检验结果失效。
此外,多重共线性还会导致模型的解释性下降,使得我们无法准确地解释自变量对因变量的影响。
针对逻辑回归模型中的多重共线性问题,我们可以采取一些方法来处理。
首先,我们可以通过降维的方法来减少自变量之间的相关性。
例如,可以使用主成分分析或者因子分析来对自变量进行降维处理,从而减少多重共线性的影响。
另外,我们还可以通过删除高度相关的自变量来解决多重共线性问题,从而减少模型参数的不稳定性。
除了降维和删除自变量之外,我们还可以使用岭回归或者套索回归等正则化方法来处理多重共线性。
这些方法可以通过对模型参数添加惩罚项来减少参数的估计误差,从而提高模型的稳定性和准确性。
此外,我们还可以使用方差膨胀因子(VIF)来检测自变量之间的多重共线性,并剔除VIF较高的自变量,从而减少模型参数的不稳定性。
此外,我们还可以使用交互项来处理多重共线性。
通过引入自变量之间的交互项,可以减少自变量之间的相关性,从而降低多重共线性的影响。
然而,需要注意的是,引入交互项会增加模型的复杂性,需要谨慎使用。
总的来说,处理逻辑回归模型中的多重共线性是一个非常重要的问题。
我们可以通过降维、删除自变量、正则化或者引入交互项等方法来处理多重共线性,从而提高模型的稳定性和准确性。
不同的方法适用于不同的情况,需要根据具体的数据和模型来选择合适的方法。
希望本文对处理逻辑回归模型中的多重共线性问题有所帮助。
第5章多重共线性的情形及其处理

记
C=(cij)=(X*′X*)-1 称其主对角线元素VIFj=cjj为自变量xj的方差扩大因子(Variance Inflation Factor,简记为VIF)。根据OLS性质3可知,
var(ˆ j ) cjj 2 / Ljj , j 1,, p
外,除非我们修改容忍度的默认值。
§5.2 多重共线性的诊断
以下用SPSS软件诊断例3.2中国民航客运量一例中的多重共线性问题。
Coeffi ci entsa
Unst andardized Coef f icients
Std.
B
Error
(C onstant ) 450. 909 178. 078
X1
每个数值平方后再除以特征值,然后再把每列数据 除以列数据之和,使得每列数据之和为1,这样就 得到了输出结果6.2的方差比。
再次强调的是线性回归分析共线性诊断中设计 阵X包含代表常数项的一列1,而因子分析模块中 给出的特征向量是对标准化的设计阵给出的,两者 之间有一些差异。
三、 等级相关系数法 (Spearman Rank Correlation )
根据矩阵行列式的性质,矩阵的行列式等于其 特征根的连乘积。因而,当行列式|X′X|≈0时, 矩 阵X′X至少有一个特征根近似为零。反之可以证明, 当矩阵X′X至少有一个特征根近似为零时,X 的列 向量间必存在复共线性,证明如下:
记X =(X0 ,X1,…,Xp),其中 Xi为X 的列向量, X0 =(1,1,…,1)′是元素全为1的n维列向量。 λ是矩阵X′X的一个近似为零的特征根,λ≈0 c=(c0,c1, …,cp)′是对应于特征根λ的单位特征向量,则
(完整版)多重共线性检验与修正
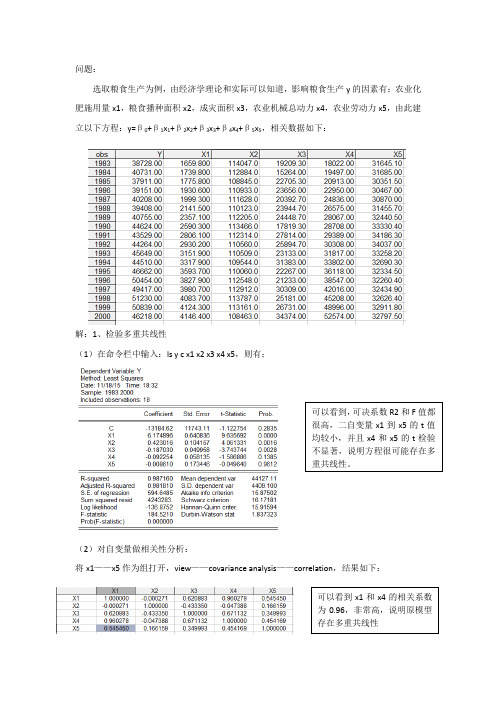
问题:选取粮食生产为例,由经济学理论和实际可以知道,影响粮食生产y的因素有:农业化肥施用量x1,粮食播种面积x2,成灾面积x3,农业机械总动力x4,农业劳动力x5,由此建立以下方程:y=β0+β1x1+β2x2+β3x3+β4x4+β5x5,相关数据如下:解:1、检验多重共线性(1)在命令栏中输入:ls y c x1 x2 x3 x4 x5,则有;可以看到,可决系数R2和F值都很高,二自变量x1到x5的t值均较小,并且x4和x5的t检验不显著,说明方程很可能存在多重共线性。
(2)对自变量做相关性分析:将x1——x5作为组打开,view——covariance analysis——correlation,结果如下:可以看到x1和x4的相关系数为0.96,非常高,说明原模型存在多重共线性2、多重共线性的修正 (1)逐步回归法第一步:首先确定一个基准的解释变量,即从x1,x2,x3,x4,x5中选择解释y 的最好的一个建立基准模型。
分别用x1,x2,x3,x4,x5对y 求回归,结果如下:在基准模型的基础上,逐步将x2,x3等加入到模型中, 加入x2,结果:从上面5个输出结果可以知道,y 对x1的可决系数R2=0.89(最高),因此选择第一个方程作为基准回归模型。
即: Y = 30867.31062 + 4.576114592* x1再加入x3,结果:再加入x4,结果:拟合优度R2=0.961395,显著提高;并且参数符号符合经济常识,且均显著。
所以将模型修改为:Y= -44174.52+ 4.576460*x1+ 0.672680*x2拟合优度R2=0.984174,显著提高;并且参数符号符合经济常识(成灾面积越大,粮食产量越低),且均显著。
所以将模型修改为:Y=-12559.35+5.271306*x1+0.417257*x2-0.212103*x3拟合优度R2=0.987158,虽然比上一次拟合提高了;但是变量x4的系数为-0.091271,符号不符合经济常识(农业机械总动力越高,粮食产量越高),并且x4的t检验不显著。
多重共线性和非线性回归及解决方法

多重共线性和非线性回归的问题(1)多重共线性问题我们都知道在进行多元回归的时候,特别是进行经济上指标回归的时候,很多变量存在共同趋势相关性,让我们得不到希望的回归模型。
这里经常用到的有三种方法,而不同的方法有不同的目的,我们分别来看看:第一个,是最熟悉也是最方便的——逐步回归法。
逐步回归法是根据自变量与因变量相关性的大小,将自变量一个一个选入方法中,并且每选入一个自变量都进行一次检验。
最终留在模型里的自变量是对因变量有最大显著性的,而剔除的自变量是与因变量无显著线性相关性的,以及与其他自变量存在共线性的。
用逐步回归法做的多元回归分析,通常自变量不宜太多,一般十几个以下,而且你的数据量要是变量个数3倍以上才可以,不然做出来的回归模型误差较大。
比如说你有10个变量,数据只有15组,然后做拟合回归,得到9个自变量的系数,虽然可以得到,但是精度不高。
这个方法我们不仅可以找到对因变量影响显著的几个自变量,还可以得到一个精确的预测模型,进行预测,这个非常重要的。
而往往通过逐步回归只能得到几个自变量进入方程中,有时甚至只有一两个,令我们非常失望,这是因为自变量很多都存在共线性,被剔除了,这时可以通过第二个方法来做回归。
第二个,通过因子分析(或主成分分析)再进行回归。
这种方法用的也很多,而且可以很好的解决自变量间的多重共线性。
首先通过因子分析将几个存在共线性的自变量合为一个因子,再用因子分析得到的几个因子和因变量做回归分析,这里的因子之间没有显著的线性相关性,根本谈不上共线性的问题。
通过这种方法可以得到哪个因子对因变量存在显著的相关性,哪个因子没有显著的相关性,再从因子中的变量对因子的载荷来看,得知哪个变量对因变量的影响大小关系。
而这个方法只能得到这些信息,第一它不是得到一个精确的,可以预测的回归模型;第二这种方法不知道有显著影响的因子中每个变量是不是都对因变量有显著的影响,比如说因子分析得到三个因子,用这三个因子和因变量做回归分析,得到第一和第二个因子对因变量有显著的影响,而在第一个因子中有4个变量组成,第二个因子有3个变量组成,这里就不知道这7个变量是否都对因变量存在显著的影响;第三它不能得到每个变量对因变量准确的影响大小关系,而我们可以通过逐步回归法直观的看到自变量前面的系数大小,从而判断自变量对因变量影响的大小。
如何解决支持向量机算法中的多重共线性问题

如何解决支持向量机算法中的多重共线性问题支持向量机(Support Vector Machine,简称SVM)是一种常用的机器学习算法,被广泛应用于分类和回归问题。
然而,在实际应用中,我们常常会遇到多重共线性问题,这会导致SVM的性能下降甚至失效。
本文将探讨如何解决SVM中的多重共线性问题。
1. 引言多重共线性是指在数据集中存在多个自变量之间高度相关的情况。
在SVM中,多重共线性会导致模型的不稳定性和预测精度的下降。
因此,解决多重共线性问题对于提高SVM的性能至关重要。
2. 特征选择特征选择是解决多重共线性问题的一种常用方法。
通过选择与目标变量相关性较高的特征,可以减少冗余信息和共线性带来的干扰。
特征选择的方法包括过滤法、包装法和嵌入法等。
其中,嵌入法是一种基于模型的特征选择方法,可以通过正则化项来约束模型的复杂度,从而减少共线性的影响。
3. 数据标准化数据标准化是解决多重共线性问题的另一种常用方法。
通过将数据进行标准化处理,可以将不同特征的取值范围统一,避免由于尺度不同而引起的共线性问题。
常用的数据标准化方法包括Z-Score标准化和MinMax标准化等。
4. 正则化正则化是一种常用的解决多重共线性问题的方法。
在SVM中,正则化可以通过引入惩罚项来约束模型的复杂度,从而减少共线性的影响。
常用的正则化方法包括L1正则化和L2正则化等。
这些方法可以在优化目标函数中加入正则化项,从而通过调整正则化参数来平衡模型的复杂度和拟合精度。
5. 核函数选择核函数选择也是解决多重共线性问题的一种重要方法。
在SVM中,核函数可以将数据从原始空间映射到高维特征空间,从而解决非线性问题。
通过选择适当的核函数,可以将数据在特征空间中进行有效的分离,减少共线性的影响。
常用的核函数包括线性核函数、多项式核函数和高斯核函数等。
6. 交叉验证交叉验证是一种常用的评估模型性能和选择超参数的方法。
在解决多重共线性问题时,可以通过交叉验证来选择最优的正则化参数和核函数参数,从而提高模型的鲁棒性和泛化能力。
多重共线性(Multi-Collinearity)

i 0 1 1i 2 2i
k ki i
(i=1,2,…,n)
其基本假设之一是解释变量
X,
1
X2,,
X
k
互相独立 。
如果某两个或多个解释变量之间出现了相关性, 则称为多重共线性。
如果存在
c1X1i+c2X2i+…+ckXki=0
i=1,2,…,n
其中: ci不全为0,即某一个解释变量可以用其它解释 变量的线性组合表示,则称为解释变量间存在完全
2
1
x12i 1 r 2
2
x12i
所以,多重共线性使参数估计量的方差增大。
方差扩大因子(Variance Inflation Factor)为1/(1-r2), 其增大趋势见下表:
相关系 0 0.5 0.8 0.9 0.95 0.96 0.97 0.98 0.99 0.999 数平方 方差扩 1 2 5 10 20 25 33 50 100 1000 大因子
多重共线性(Multi-Collinearity)
§2.8 多重共线性
Multi-Collinearity
一、多重共线性的概念 二、多重共线性的后果 三、多重共线性的检验 四、克服多重共线性的方法 五、案例
一、多重共线性的概念
1、多重共线性
• 对于模型
Y X X X
以二元回归模型中的参数估计量ˆ 为例,ˆ 的方差为
1
1
Var(ˆ )
1
ˆ 2
(X X
)1
22
(
ˆ
2
(
x2
2i
)
x2 )( x2 ) ( x
多重共线性的情形及其处理

多重共线性的情形及其处理多重共线性的情形及其处理⼀、多重共线性对回归模型的影响设回归模型εββββ++++=p p x x x y 22110存在完全的多重共线性,即对设计矩阵X 的列向量存在不全为零的⼀组数p c c c c ,,,,210 ,使得:22110=++++ip p i i x c x c x c c (n i ,,2,1 =),此时设计矩阵X 的秩Rank(X)在实际问题研究当中,022110≈++++ip p i i x c x c x c c ,虽然Rank(X)=p+1成⽴,但是|X X '|≈0,1)(-'X X 的对⾓线元素很⼤,β的⽅差阵12)()?(-'=X X D σβ的对⾓线元素很⼤,⽽)?(βD 的对⾓线元素即为)?var(0β,)?var(1β,…, )?var(p β,因⽽p βββ,,,10的估计精度很低,这样,虽然OLSE 能得到β的⽆偏估计,但估计量β?的⽅差很⼤,不能正确判断解释变量对被解释变量的影响程度。
例如在⼆元回归中,假定y 与1x ,2x 都已经中⼼化,此时回归常数项为零,回归⽅程为2211x x y ββ+=,由此可以得到 1121221)1()?var(L r -=σβ,2221222)1()?var(L r -=σβ,其中∑==n i i x L 12111,∑==ni i i x x L 12112,∑==ni i x L 12222则1x ,2x 之间的相关系数22111212L L L r =。
随着⾃变量1x 与2x 的相关性增强,1?β和2β的⽅差将逐渐增⼤。
当1x 与2x 完全相关时,r=1,⽅差将变为⽆穷⼤。
当给定不同的12r 值时,从下表可以看出⽅差增⼤的速度。
表6.1为了⽅便,假设1112=L σ,相关系数从0.5变为0.9时,回归系数的⽅差增加了295%,相关系数从0.5变为0.95时,回归系数的⽅差增加了670%、当回归⾃变量1x 与2x 相关程度越⾼,多重共线性越严重,那么回归系数的估计值⽅差就越⼤,回归系数的置信区间就变得很宽,估计的精确性就⼤幅度降低,使估计值稳定性变得很差,进⼀步致使在回归⽅程整体⾼度显著时,⼀些回归系数则通不过显著性检验,回归系数的正负号也可能出现倒置,使得⽆法对回归⽅程得到合理的经济解释,直接影响到最⼩⼆乘法的应⽤效果,降低回归⽅程的价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、岭回归:
1962年,A.E.Hoerl针对多重共线性的问题, 提出了一种叫岭回归的回归估计方法。对线 性模型
Y 0 1 X 1 2 X 2 m X m
定义偏回归系数β的岭估计为
1 T T ˆ k X X kI X Y
其中k称为岭参数。
2、主成分回归
1965年,W.F.Massy提出了主成分回归 (PrincipalComponent Regression,简称PCR) 方法,首先提取自变量的主成分, 由于各主 成分之间相互正交,相关系数为0,此时即 可用最小二乘法估计偏回归系数,建立因变 量与相互独立的前几个主成分的回归模型, 然后再还原为原自变量的回归方程式。
可见,主成分回归分析解决多重共线性问题 是通过降维的处理而克服多重共线性的影响, 正确表征变量间的关系。 然而,由于PCR提取X的主成分是独立于因变 量Y而进行的,没有考虑到X对Y的解释作用, 这就增加了所建模型的不可靠性。
3、偏最小二乘回归
针对多重共线性干扰问题,S.Wold和C.Alban 在1983年提出了偏最小二乘回归(Partia Least Squares Regression,简称PLSR)方法。 PLSR方法吸取了主成分回归分析从自变量中 提取信息的思想,同时还考虑了自变量对因 变量的解释问题。
小结
以上介绍了三种解决多重共线性问题的方法, 它们各自都有其特点及适用范围:偏最小二 乘法在解决多因变量与自变量方面及预测方 面有着比其它两种方法更优越的地方,但在t 的实际意义解释方面与主成分一样比较欠缺。
岭回归由于在其K值的确定上有很大的人为 因素,使之缺乏一定的科学性,但也正因为如 此,使它能够很好地把定性分析与定量分析 两者有机地结合起来。由于这三种方法估计 出的参数值都是有偏的,所以在未出现多重 线性相关问题时最好还是用普通最小二乘法 来估计参数。从实际运用来看最小二乘法与 岭回归的模拟效果相对来说好一些。
岭回归的核心思想是当出现多重共线性 时, | X T X | 0 , X X 的特征根 j 至少有 一个非常接近于0,从而使参数β的最小二 1 T ˆ 乘估计 X X X T Y 很不稳定。给X T X T | X X kI 等 | 加上一个正常数矩阵kI(k>0),则 T | X X | 的可能性要小得 于零的可能性就比 多,X T X kI 的特征根 j k 接近于0 的 程度就会得到改善。
T
ˆ k 且从理论上可以证明,存在k>0,使得的 ˆ 的均方误差小。因此,用岭 均方误差比 回归来估计偏回归系数比用普通最小二乘法 估计要稳定得多。这样就消除了多重共线性 对参数估计的危害。
在实际应用中,通常确定k值的方法有以下几平方和法
多重共线性的处理
为了避免共线性的影响,目前多采用回归系 数有偏估计的方法,即为了减小偏回归系数 估计的方差而放弃对估计的无偏性要求。换 言之,允许估计有不大的偏度,以换取估计方 差可显著减小的结果,并在使其总均方差为 最小的原则下估计回归系数。
解决多重共线性问题的方法
1、岭回归 2、主成分回归 3、偏最小二乘回归 4、其它:神经网络、通径分析
基本思路
首先在自变量集中提取第一潜因子t1(t1是 x1,x2,…,xm的线性组合,且尽可能多地提取原自变 量集中的变异信息);同时在因变量集中也提取第一 潜因子u1,并要求t1与u1相关程度达最大。 然后建立因变量Y与t1的回归,如果回归方程已达到 满意的精度,则算法终止。否则继续第二轮潜在因 子的提取,直到能达到满意的精度为止。 若最终对自变量集提取m个潜因子t1,t2,…,tm,偏 最小二乘回归将建立Y与t1,t2,…,tm的回归式,然 后再表示为Y与原自变量的回归方程式。
