椭偏法测介质膜厚度和折射率 实验报告
椭偏仪测量薄膜厚度和折射率实验报告

椭偏仪测量薄膜厚度与折射率实验报告组别:69组院系:0611 姓名:林盛学号:PB06210445实验题目:椭偏仪测量薄膜厚度与折射率实验目得:了解椭偏仪测量薄膜参数得原理,初步掌握反射型椭偏仪得使用方法。
实验原理:椭圆偏振光经薄膜系统反射后,偏振状态得变化量与薄膜得厚度与折射率有关,因此只要测量出偏振状态得变化量,就能利用计算机程序多次逼近定出膜厚与折射率。
参数描述椭圆偏振光得P波与S波间得相位差经薄膜系统关系后发生得变化,描述椭圆偏振光相对振幅得衰减。
有超越方程:ﻩ为简化方程,将线偏光通过方位角得波片后,就以等幅椭圆偏振光出射,;改变起偏器方位角就能使反射光以线偏振光出射,,公式化简为:这时需测四个量,即分别测入射光中得两分量振幅比与相位差及反射光中得两分量振幅比与相位差,如设法使入射光为等幅椭偏光,,则;对于相位角,有:因为入射光连续可调,调整仪器,使反射光成为线偏光,即=0或(),则或,可见只与反射光得p波与s波得相位差有关,可从起偏器得方位角算出、对于特定得膜,就是定值,只要改变入射光两分量得相位差,肯定会找到特定值使反射光成线偏光, =0或().实验仪器:椭偏仪平台及配件、He-Ne激光器及电源、起偏器、检偏器、四分之一波片、待测样品、黑色反光镜等。
实验内容:1.按调分光计得方法调整好主机.2.水平度盘得调整。
3.光路调整。
4.检偏器读数头位置得调整与固定.5.起偏器读数头位置得调整与固定。
6.波片零位得调整。
7.将样品放在载物台中央,旋转载物台使达到预定得入射角70即望远镜转过40,并使反射光在白屏上形成一亮点。
8.为了尽量减小系统误差,采用四点测量.9.将相关数据输入“椭偏仪数据处理程序”,经过范围确定后,可以利用逐次逼近法,求出与之对应得d与n ;由于仪器本身得精度得限制,可将d得误差控制在1埃左右,n得误差控制在0、01左右.实验数据:将表格中数据输入“椭偏仪数据处理程序",利用逐次逼近法,求出与之对应得厚度d与折射率n分别为:误差分析:实验测得得折射率比理论值偏大,厚度比理论值偏小,其可能原因有:1.待测介质薄膜表面有手印等杂质,影响了其折射率。
【精品】椭偏光法测薄膜的折射率和厚度

实验五椭偏光法测薄膜的折射率和厚度一、引言椭圆偏振测量术简称椭偏术。
它是利用光的偏振性质,将一椭圆偏振光射到被测样品表面,观测反射光偏振状态的变化来推知样品的光学常数。
就其理论范畴来讲,它与十涉法一样,都是利用光的波动性,以经典物理学为基础。
这种测量方法的原理早在上个世纪就提出来了,距今已有近百年的历史。
由于光波通过偏振器件及样品反射时,光波偏振状态变化得异常灵敏,使得椭偏术的理论精度之高是干涉法不能比拟的,又由于这种测理是非破坏性的,因此它的优越性是显而易见的.长期以来,人们一直力图将这种测量方法付诸应用。
早在40年代就有人提出实验装置,但由于计算上的困难一直得不到发展。
电子计算机及激光技术的广泛应用,为椭偏术的实际应用及迅猛发展创造了条件。
今天椭偏术已成为测量技术的一个重要的分支。
椭偏术有很多优点,主要是测量灵敏、精度高,测量范围从1oA到几个微米而且是非接触测量。
国外生产的高精度自动椭偏仪能测量正在生长的薄膜小于l oA的厚度变化,可检测百分之儿的单分子层厚度,深入到原子数量级.因此既可将其应用于精密分析测量,也可以用于表面研究,用于自动监控及分析液、固分界面的变化.目前椭偏术已应用到电子工业,光学工业,金属材料工业,化学工业,表面科学和生物医学等领域。
在我们的实验中,使用消光椭偏仪测量薄膜的折射率和厚度.除了能学习到其测量方法外,其巧妙的设计思想也将给我们极人的启发和收益。
二、椭偏术原理1.椭偏术基本方程椭圆偏振光入射到透明介质薄膜时,光在两个分界面(空气与薄膜,薄膜与衬底)来同反射和折射,如图5.1所示。
总反射光由多光束干涉而成,光在两个分界面的P波和1122 p s p s r r r r 、、、图5—121122112112211122322323223223322233cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos p s p s n n r n n n n r n n n n r n n n n r n n ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ-⎧=⎪+⎪-⎪=⎪+⎪⎨-⎪=⎪+⎪-⎪=⎪+⎩以上各式中1n 为空气折射率,2n 为膜层的折射率,3n 为衬底折射率。
椭圆偏振法测量薄膜厚度和折射率实验报告

椭圆偏振法测量薄膜厚度和折射率实验报告实验名称:椭圆偏振法测量薄膜厚度和折射率实验目的:利用椭圆偏振法测量薄膜的厚度和折射率,掌握椭圆偏振法的基本原理和实验操作方法。
实验原理:椭圆偏振法是一种常用的测量薄膜光学性质的方法。
当偏振光通过具有一定折射率的薄膜时,会发生透射和反射,经过反射和透射之后的光束会发生干涉现象。
当入射光是偏振光时,通过表层膜的透射光经过增偏器后变为线偏振光,其振动方向决定于表层膜的光学性质以及入射角。
通过调节增偏器的方向和旋转其角度,使得通过增偏器的振动方向与振动椭圆的长轴平行,此时称之为白光不通过表层膜,反射线偏振光与透射线偏振光的相位差为0. 形成一个相干叠加的椭圆偏振光。
根据椭圆偏振光的特性,可以通过测量椭圆偏振光的特性参数(主轴角度、椭圆离心率等)来确定薄膜的厚度和折射率。
实验装置:椭圆偏振仪、光源、待测试薄膜样品。
实验步骤:1. 启动椭圆偏振仪,调整光源使其达到合适的亮度和稳定性。
2. 将待测薄膜样品放置在椭圆偏振仪的样品台上,并通过对焦镜调整样品的焦距。
3. 调整增偏器的方向,使通过增偏器的线偏振光振动方向与椭圆的长轴平行。
4. 调整旋转台上的角度,使反射线偏振光与透射线偏振光的相位差为0,此时形成相干的椭圆偏振光。
5. 在椭圆偏振仪上的读数器上记录椭圆偏振光的主轴角度、椭圆离心率等参数。
6. 重复上述操作,测量多组数据,以提高测量准确度。
7. 根据测量得到的参数计算薄膜的厚度和折射率。
实验结果:通过测量多组数据,记录椭圆偏振光的主轴角度和椭圆离心率等参数,得到一组薄膜的厚度和折射率。
注意保留合适的有效数字。
实验讨论:1. 实验中应确保光源的稳定性和一致性,以获得准确的测量结果。
2. 实验中可以通过调整增偏器和旋转台的角度,使椭圆偏振光的参数达到最佳值,以提高测量精度。
3. 实验中应注意测量时的环境条件,避免与外部环境光的干扰。
实验结论:通过椭圆偏振法测量薄膜的厚度和折射率,可以得到薄膜的光学性质参数。
椭圆偏振光法测量薄膜的厚度和折射率

椭圆偏振光法测量薄膜的厚度和折射率摘要:本实验中,我们用椭圆偏振光法测量了MgF 2,ZrO 2,TiO 2三种介质膜的厚度和折射率,取MgF 2作为代表,测量薄膜折射率和厚度沿径向分布的不均匀性,此外还测量了Au 和Cr 两种金属厚膜的折射率和消光系数。
掌握了椭圆偏振光法的基本原理和技术方法。
关键词:椭偏法,折射率,厚度,消光系数 引言:薄膜的厚度和折射率是薄膜光电子器件设计和制备中不可缺少的两个参数。
因此,精确而迅速地测定这两个参数非常重要。
椭圆偏振光法就是一个非常重要的方法。
将一束单色椭圆偏振光投射到薄膜表面,根据电动力学原理,反射光的椭偏状态与薄膜厚度和折射率有关,通过测出椭偏状态的变化,就可以推算出薄膜的厚度和折射率。
椭圆偏振光法是目前测量透明薄膜厚度和折射率时的常用方法,其测量精度高,特别是在测量超薄薄膜的厚度时其灵敏度很高,因此常用于研究薄膜生长的初始阶段,而且由于这种方法时非接触性的,测量过程中不破坏样品表面,因而可用于薄膜生长过程的实时监控。
本实验的目的是掌握椭偏法测量薄膜的厚度和折射率的原理和技术方法。
测量几种常用介质膜的折射率和厚度,以及金属厚膜的复折射率。
原理:1. 单层介质膜的厚度和折射率的测量原理(1)光波在两种介质分界面上的反射和折射,有菲涅耳公式:121122112112211122322323223223322233cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos p s p s n n r n n n n r n n n n r n n n n r n n ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ-⎧=⎪+⎪-⎪=⎪+⎪⎨-⎪=⎪+⎪-⎪=⎪+⎩(tp-1); (2)单层膜的反射系数图1 光波在单层介质膜中传播以上各式中1n 为空气折射率,2n 为膜层的折射率,3n 为衬底折射率。
1ϕ为入射角,2ϕ,3ϕ分别为光波在薄膜和衬底的折射角。
椭偏光法测量薄膜的厚度和折射率

椭偏法测薄膜厚度和折射率摘要本实验通过椭圆偏振光法测量了氟化镁(MgF2)、氧化锆(ZrO2)及二氧化钛(TiO2)等介质薄膜的厚度和折射率,以及Cu和Al金属薄膜的厚度和消光系数。
关键词椭圆偏振光法介质薄膜金属薄膜椭偏参数复折射率消光系数一、引言椭圆偏振测量(椭偏术)是研究两媒质界面或薄膜中发生的现象及其特性的一种光学方法,其原理是利用偏振光束在界面或薄膜上的反射或透射时出现的偏振变换。
椭圆偏振测量的应用范围很广,如半导体、光学掩膜、圆晶、金属、介电薄膜、玻璃(或镀膜)、激光反射镜、大面积光学膜、有机薄膜等,也可用于介电、非晶半导体、聚合物薄膜、用于薄膜生长过程的实时监测等测量。
结合计算机后,具有可手动改变入射角度、实时测量、快速数据获取等优点。
实验原理在一光学材料上镀各向同性的单层介质膜后,光线的反射和折射在一般情况下会同时存在的。
通常,设介质层为n1、n2、n3, $ 1为入射角,那么在1、2介质交界面和2、3介质交界面会产生反射光和折射光的多光束干涉,如图(1-1)图(1-1)这里我们用2 3表示相邻两分波的相位差, 其中S =2 n dn2cos © 2/入,用rip 、r1s 表示光 线的p 分量、s 分量在界面1、2间的反射系数, 用r2p 、r2s 表示光线的p 分、s 分量在界 面2、3间的反射系数。
由多光束干涉的复振幅计算可知:的实数部分[tg 2 e i A ]的虚数部分 =的虚数部分 若能从实验测出2和△的话,原则上可以解出n2和d (n1、n3、入、$ 1已知),根据公式(4)~(9), 推导出2和△与r1p 、r1s 、r2p 、r2s 、和3的关系:其中Eip 和Eis 分别代表入射光波电矢量的 p 分量和s 分量,Erp 和Ers 分别代表反射光波Eip 、Eis 、Erp 、Ers 四个量写成一个量G ,即:我们定义G 为反射系数比,它应为一个复数,可用 的过程量转换可由菲涅耳公式和折射公式给出:tg 2和△表示它的模和幅角。
椭偏仪测量薄膜厚度和折射率
椭偏仪测量薄膜厚度和折射率【引言】椭圆偏振测量(椭偏术)是研究两媒质界面或薄膜中发生的现象及其特性的一种光学方法,其原理是利用偏振光束在界面或薄膜上的反射或透射时出现的偏振变换。
椭圆偏振测量的应用范围很广,如半导体、光学掩膜、圆晶、金属、介电薄膜、玻璃(或镀膜)、激光反射镜、大面积光学膜、有机薄膜等,也可用于介电、非晶半导体、聚合物薄膜、用于薄膜生长过程的实时监测等测量。
结合计算机后,具有可手动改变入射角度、实时测量、快速数据获取等优点。
【实验目的】掌握椭偏仪的原理与操作方法;学会利用椭偏仪进行相关物理量的测量。
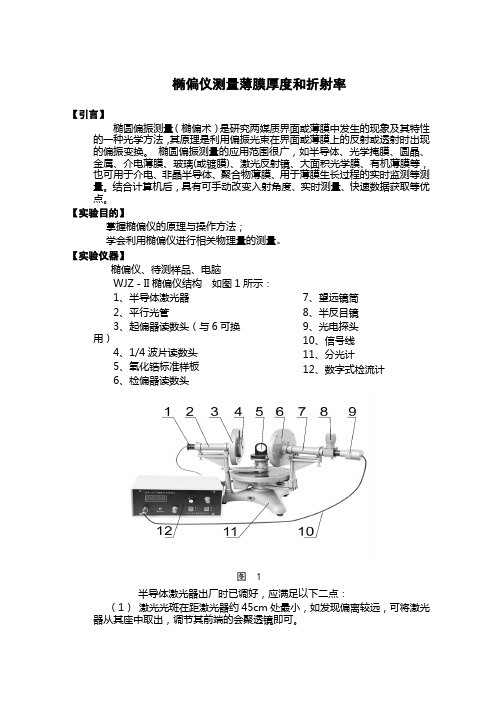
【实验仪器】椭偏仪、待测样品、电脑WJZ-II椭偏仪结构如图1所示:1、半导体激光器2、平行光管3、起偏器读数头(与6可换用)4、1/4波片读数头5、氧化锆标准样板6、检偏器读数头7、望远镜筒8、半反目镜9、光电探头10、信号线11、分光计12、数字式检流计图 1半导体激光器出厂时已调好,应满足以下二点:(1)激光光斑在距激光器约45cm处最小,如发现偏离较远,可将激光器从其座中取出,调节其前端的会聚透镜即可。
(2) 激光与平行光管共轴,如发现已破坏,请按第8页“光路调整”中所述方法进行调整,一旦调好,轻易不要将其破坏。
主要技术性能及规格 1. 测量透明薄膜厚度范围0-300nm ,折射率1.30-2.49。
2. 起偏器、检偏器、1/4波片刻度范围0°-360°,游标读数0.1°。
3. 测量精度:±2nm 。
4. 入射角ψ1=70°,K9玻璃折射率n =1.515。
5. 消光系数:0,空气折射率1。
6. *JGQ -250氦氖激光器波长λ=632.8nm (用软件处理数据时,该波长值已内嵌,无须输入)。
*半导体激光器波长λ=635nm (用软件处理数据时,该波长值未内嵌,须输入,并需重新设置消光系数“0”) 7. 椭圆偏振仪的简介:随着科学和技术的快速发展,椭偏仪的光路调节和测量数据的处理越来越完善快捷。
椭偏仪测量薄膜厚度和折射率实验报告

椭偏仪测量薄膜厚度和折射率实验报告摘要:本实验利用椭偏仪仪器去测量薄膜的厚度和折射率,来反映使用者的测量结果。
实验结果表明,测量出的薄膜厚度和折射率值符合预期,经仔细分析实验结果误差解释,结果可信度得到进一步提升。
一、实验目的1、了解椭偏仪的使用及原理2、利用椭偏仪测量薄膜厚度及折射率二、基本原理椭偏仪是一种重要的折射率测量仪,它能够准确而精确地测量出光线穿过薄片时的折射率,以及光线所穿过的薄片的厚度。
椭偏仪是基于位移差原理来测量折射率的。
它采集到穿过薄膜后,光源被折射后,照射到观察板上形成一个圆形光斑,而经过椭偏仪校正器后,光斑就变成一条条短短的线条,然后将其位置与未经膜片折射的光斑位置做比较,就可以很容易地计算出折射率和厚度。
三、实验步骤1、准备实验仪器:椭偏仪仪器、薄膜。
2、调试椭偏仪:(1)检查仪器电源是否已连接;(2)检查观察系统的对焦位置是否正常;(3)在微调镜光组合上将调焦镜反转,此时光线经过校正器再照在观察系统上,就可以看见一条条短短的线条,比较其前后位置;3、将薄膜放置在光路中,调节观察台的位置,把观察台移动到朱莉可变折射率玻璃轴上;4、对准光斑,然后调节调焦镜,把观察台上的光斑放小;5、观察台上的光斑线条前后移动情况,以记录测量结果;6、得出实验结果,然后根据实验结果,计算薄膜的厚度和折射率。
四、实验结果根据实验所得数据,测得薄膜厚度为1.0μm,折射率为1.890。
(1)实验结果表明,薄膜厚度和折射率值与理论值相符合,证明椭偏仪测量结果是可信的。
(2)椭偏仪的测量结果不仅精确可靠,而且灵敏度高,数据操作简便,检测到的偏差也不大,仪器可靠性得到进一步的确立。
用椭偏仪测薄膜厚度与折射率

⽤椭偏仪测薄膜厚度与折射率103实验⼗⼆⽤椭偏仪测薄膜厚度与折射率随着半导体和⼤规模集成电路⼯艺的飞速发展,薄膜技术的应⽤也越加⼴泛。
因此,精确地测量薄膜厚度与其光学常数就是⼀种重要的物理测量技术。
⽬前测量薄膜厚度的⽅法很多。
如称重法、⽐⾊法、⼲涉法、椭圆偏振法等。
其中,椭圆偏振法成为主要的测试⼿段,⼴泛地应⽤在光学、材料、⽣物、医学等各个领域。
⽽测量薄膜材料的厚度、折射率和消光系数是椭圆偏振法最基本,也是⾮常重要的应⽤之⼀。
实验原理由于薄膜的光学参量强烈地依赖于制备⽅法的⼯艺条件,并表现出明显的离散性,因此,如何准确、快速测量给定样品的光学参量⼀直是薄膜研究中⼀个重要的问题。
椭圆偏振法由于⽆须测定光强的绝对值,因⽽具有较⾼的精度和灵敏度,⽽且测试⽅便,对样品⽆损伤,所以在光学薄膜和薄膜材料研究中受到极⼤的关注。
椭圆偏振法是利⽤椭圆偏振光⼊射到样品表⾯,观察反射光的偏振状态(振幅和位相)的变化,进⽽得出样品表⾯膜的厚度及折射率。
氦氖激光器发出激光束波长为632.8nm 的单⾊⾃然光,经平⾏光管变成单⾊平⾏光束,再经起偏器P 变成线偏振光,其振动⽅向由起偏器⽅位⾓决定,转动起偏器,可以改变线偏振光的振动⽅向,线偏振光经1/4波⽚后,由于双折射现象,寻常光和⾮寻常光产⽣π/2的位相差,两者的振动⽅向相互垂直,变为椭圆偏振光,其长、短轴沿着1/4波⽚的快、慢轴。
椭圆的形状由起偏器的⽅位⾓来决定。
椭圆偏振光以⼀定的⾓度⼊射到样品的表⾯,反射后偏振状态发⽣改变,⼀般仍为椭圆偏振光,但椭圆的⽅位和形状改变了。
从物理光学原理可以知道,这种改变与样品表⾯膜层厚度及其光学常数有关。
因⽽可以根据反射光的特性来确定膜层的厚度和折射率。
图1为基本原理光路。
图2为⼊射光由环境媒质⼊射到单层薄膜上,并在环境媒质——薄膜——衬底的两个界⾯上发⽣多次折射和反射。
此时,折射⾓满⾜菲涅尔折射定律332211sin sin sin N N N ==(1)104 其中N 1,N 2和N 3分别是环境媒质、= n – i k );?1为⼊射⾓、 ?2 和?3分别为薄膜和衬底的折射⾓。
椭偏仪测量薄膜厚度和折射率实验报告

椭偏仪测量薄膜厚度和折射率实验报告实验目的:1.学习使用椭偏仪测量薄膜的厚度和折射率。
2.了解光线在薄膜中的传播和干涉现象。
实验仪器和材料:1.椭偏仪2.微米螺旋3.干净的玻璃片4.一块薄膜样品5.直尺6.实验台7.光源实验原理:椭偏仪是一种用于测量透明物体表面薄膜的厚度和折射率的仪器。
当光线从真空进入具有一定折射率的介质中时,会发生折射和反射。
当光线垂直入射到薄膜表面时,经过多次反射和折射后会形成干涉现象。
通过观察测量光的振幅和相位差的变化,可以推导出薄膜的厚度和折射率。
实验步骤:1.将实验台安装好,并确保椭偏仪的光源正常工作。
2.用直尺测量玻璃片和薄膜样品的尺寸,并记录下来。
3.将玻璃片放在实验台上,并将椭偏仪对准玻璃片。
4.调节椭偏仪的干涉仪臂使得产生清晰的干涉条纹。
5.使用微米螺旋逐渐调整反射镜的角度,直到条纹的清晰度达到最佳状态。
6.记录下此时的微米螺旋读数,并用直尺测量薄膜样品的厚度,得到薄膜的实际厚度。
7.调节椭偏仪的角度,使得干涉条纹平行于椭偏仪的刻度线。
8.记录下此时的椭偏仪读数,并计算出薄膜的厚度。
9.重复以上步骤2-8三次,并求取平均值。
10.使用已知的材料的折射率标定椭偏仪,并根据标定值计算出薄膜样品的折射率。
实验结果:根据实验步骤中记录的数据,计算出薄膜样品的平均厚度和折射率。
实验讨论:2.在实验中,可以尝试调节椭偏仪的角度和干涉条纹的清晰度,以获得更准确的测量结果。
3.实验中使用的薄膜样品的厚度和折射率可以进一步研究其与其他因素的关系,如温度、湿度等。
实验结论:通过使用椭偏仪测量薄膜的厚度和折射率,可以得到薄膜样品的相关参数。
实验结果表明,椭偏仪是一种能够精确测量薄膜和折射率的有效工具。
通过该实验,我们可以深入理解光的干涉现象和薄膜的光学性质。
实验二 椭偏仪测定薄膜厚度与折射率
实验一椭偏仪测定薄膜厚度与折射率一. 实验目的1、掌握获得椭偏光的原理;2、掌握椭圆偏振仪的基本结构和使用方法,理解其测量薄膜厚度和折射率的原理;3、学会通过椭圆偏振仪对测量薄膜的厚度与折射率。
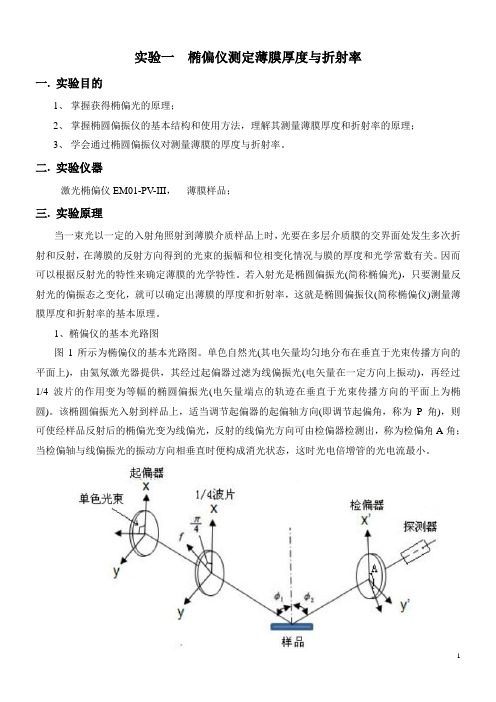
二. 实验仪器激光椭偏仪EM01-PV-III,薄膜样品;三. 实验原理当一束光以一定的入射角照射到薄膜介质样品上时,光要在多层介质膜的交界面处发生多次折射和反射,在薄膜的反射方向得到的光束的振幅和位相变化情况与膜的厚度和光学常数有关。
因而可以根据反射光的特性来确定薄膜的光学特性。
若入射光是椭圆偏振光(简称椭偏光),只要测量反射光的偏振态之变化,就可以确定出薄膜的厚度和折射率,这就是椭圆偏振仪(简称椭偏仪)测量薄膜厚度和折射率的基本原理。
1、椭偏仪的基本光路图图1所示为椭偏仪的基本光路图。
单色自然光(其电矢量均匀地分布在垂直于光束传播方向的平面上),由氦氖激光器提供,其经过起偏器过滤为线偏振光(电矢量在一定方向上振动),再经过1/4波片的作用变为等幅的椭圆偏振光(电矢量端点的轨迹在垂直于光束传播方向的平面上为椭圆)。
该椭圆偏振光入射到样品上,适当调节起偏器的起偏轴方向(即调节起偏角,称为P角),则可使经样品反射后的椭偏光变为线偏光,反射的线偏光方向可由检偏器检测出,称为检偏角A角;当检偏轴与线偏振光的振动方向相垂直时便构成消光状态,这时光电倍增管的光电流最小。
图1. 椭偏仪的基本光路图对于椭偏光,可将其电场分量分解为相互垂直的两个线偏光,这两个线偏光为:振动方向与入射平面平行的线偏光以P 表示(简称P 波或者P 分量),垂直于入射面振动的线偏光以S 表示(简称S 波或者S 分量),如图2所示。
图2. 椭偏光的两分量,p 光:平行于入射平面,s 光:垂直于入射平面2、测量原理下面简要分析用激光椭偏仪如何根据反射光相对入射光的振幅、位相变化从而测出薄膜厚度及折射率。
图3. 光线入射多层介质的反射情况入射光经薄膜上、下分界面折射时满足折射定律:332211sin sin sin ϕϕϕn n n ==根据光学相关公式,可求出薄膜总的反射系数P R 、s R 分别为:ββj p p j p p P p p e r r e r r E E R 2212211--+==入反psp sββj s s j s s s s s er r e r r E E R 2212211--+==入反 ϕλπβcos 2n d ⎪⎭⎫⎝⎛=入入入P i P P e E E β= 反反反P i P P eE E β=入入入S i S S e E E β= 反反反S i S S eE E β=式中p r 1、s r 1代表光从1n 介质入射到2n 介质的反射系数,p r 2、s r 2代表光从2n 介质入射到3n 介质的反射系数,β代表对应的位相差。
椭偏法测介质膜厚度和折射率 实验报告

近代物理实验报告指导教师: 得分:实验时间: 2009 年 11 月 02 日, 第 十 周, 周 一 , 第 5-8 节实验者: 班级 材料0705 学号 200767025 姓名 童凌炜同组者: 班级 材料0705 学号 200767007 姓名 车宏龙实验地点: 综合楼 408实验条件: 室内温度 ℃, 相对湿度 %, 室内气压实验题目: 椭偏法测介质膜的厚度与折射率实验仪器:(注明规格和型号) WJZ-II 型椭偏仪实验目的:1. 掌握椭偏法测量薄膜和折射率的基本原理2. 学会使用椭偏仪测量固体表面上介质薄膜的折射率和厚度实验原理简述:反射型椭偏仪的原理是:用一束椭圆偏振光作为探针照射到被测样品上,由于样品对入射光中平行于入射面的电场分量(简称P 分量)和垂直与入射面的电场分量(简称S 分量)有不同的反射系数、透射系数,因此从样品上出射的光,其偏振状态相对于入射光来说要发生变化1. 光波在介质分界面反射和透射的电磁波理论光入射到两种均匀、各向同性的介质分界面上时,要发生反射和折射,如图(5-3-1)。
反射角与入射角相等,折射角与入射角以及折射率的关系是:2211sin sin ϕϕn n = 或1212222sin cos ϕϕn n n -=另外,根据麦克斯韦方程组和界面条件,可以得到菲涅耳公式:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=-+=+--=+-=)sin(cos sin 2)cos()sin(cos sin 2)sin()sin()tan()tan(211221211221212121ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕsp s p t t r r2. 反射系数比G定义反射系数比)](exp[||||s p s p sp i r r r r G δδ-==而通常G 往往被写成如下形式:)exp(tan ∆⋅=i G ψ 其中 ||tan sp r r =ψ sp δδ-=∆根据前式,可以得到21122112]tan )11(1[sin ϕϕ⋅+-+⋅⋅=GG n n 从式中可以看出, 如果n1是已知的, 那么在一个固定的入射角φ1下测定反射系数比G , 则可以去顶介质2的折射率n2.3. 光波在介质薄膜上反射和透射的电磁波理论——椭圆偏振光测量单层薄膜光学系统如图(5-3-2)所示为“三介质二界面”模型,我们假定:3.1薄膜两侧的介质是半无解大的,折射率分别为1n 和3n3.2薄膜折射率为2n ,它与两侧介质之间的界面1和界面2平行,并且都是理想的光滑斜面 3.3 三种介质都是均匀的各向同性的根据以上条件假设和图中的几何关系, 可以得到:δδδδψ2231222312223122231211tan i s s i s s i p p i p p s pi e r r e r r e r r e r r R R e G ----∇++⋅++==⋅=其中⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧===+-=+-=+-=+-=332211223322332223221122111232233223232112211212sin sin sin /cos 42)cos cos /()cos cos ()cos cos /()cos cos ()cos cos /()cos cos ()cos cos /()cos cos (ϕϕϕλϕπδϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕn n n dn n n n n r n n n n r n n n n r n n n n r s s p p4. 光在金属表面反射的电磁理论——金属复折射率的测量金属对光具有吸收性,因此金属的折射率为复数,可以分解为实部和虚部,即iNK N n -=2经过近似计算,可以得出⎪⎩⎪⎨⎧∆⋅=∆⋅+⋅⋅⋅=sin 2tan cos 2sin 12cos tan sin 111ψψψϕϕK n N5. 用椭偏法测量反射系数比反射系数比G 的测量归结为两个椭偏角ψ、∆的测量。
椭偏仪的测折射率和薄膜厚度

椭偏仪测折射率和薄膜厚度实验简介椭圆偏振光在样品表面反射后,偏振状态会发生变化,利用这一特性可以测量固体上介质薄膜的厚度和折射率。
它具有测量范围宽(厚度可从10^-10~10^-6m量级)、精度高(可达百分之几单原子层)、非破坏性、应用范围广(金属、半导体、绝缘体、超导体等固体薄膜)等特点。
目前商品化的全自动椭圆偏振光谱仪,利用动态光度法跟踪入射光波长和入射角改变时反射角和偏振状态的变化,实现全自动控制以及椭偏参数的自动测定、光学常数的自动计算等,但实验装置复杂,价格昂贵。
本实验采用简易的椭圆偏振仪,利用传统的消光法测量椭偏参数,使学生掌握椭偏光法的基本原理,仪器的使用,并且实际测量玻璃衬底上的薄膜的厚度和折射率。
在现代科学技术中,薄膜有着广泛的应用。
因此测量薄膜的技术也有了很大的发展,椭偏法就是70年代以来随着电子计算机的广泛应用而发展起来的目前已有的测量薄膜的最精确的方法之一。
椭偏法测量具有如下特点:1. 能测量很薄的膜(1nm),且精度很高,比干涉法高1-2个数量级。
2. 是一种无损测量,不必特别制备样品,也不损坏样品,比其它精密方法:如称重法、定量化学分析法简便。
3. 可同时测量膜的厚度、折射率以及吸收系数。
因此可以作为分析工具使用。
4. 对一些表面结构、表面过程和表面反应相当敏感。
是研究表面物理的一种方法。
实验仪器椭偏仪测折射率和薄膜厚度实验装置包括:激光器(氦氖或半导体)、分光计、光栏、望远镜、黑色反光镜、薄膜样品、起偏器、检偏器、1/4波片。
实验内容1. 熟悉并掌握椭偏仪的调整椭偏仪实物图椭偏仪结构示意图椭偏仪的实物如上图所示。
了解图中各部件的作用,并学会正确调整。
2. 调整光路,并使入射到样品的光为等幅椭圆偏振光(1) 安装半导体激光器并调整分光计,使半导体激光器光束、平行光轴的中心轴、望远镜筒的中心轴同轴。
(2) 标定检偏器透光轴的零刻度,并使检偏器的透光轴零刻度垂直于分光计主轴。
椭偏仪测量薄膜厚度和折射率实验

1
1
2
角为 θˆ ,由(5-19-17)式: 2
n sin θ = n sin θ
1
1
2
2
(5-19-18)
或:
nˆ cos θˆ = nˆ 2 − n 2 sin 2 θ
2
2
2
1
1
(5-19-19)
由于金属表面仅有一次反射,而无折射,根据菲涅耳公式可以得到
R
cos(θ − θˆ )
tgψ .e i∆
=
i
i
n − iKn
(5-19-17)
在这里 θ 并不是简单的代表折射角, sin θ 是一个复数,椭偏法测量反射系数比的原
τ
τ
理对复折射率也是适用的。所以我也可以测量在具有吸收基底上的薄膜的参数,这使得这一 测量法又广泛地用于半导体领域。
5
三、金属复折射率的测量
设光束由实折射率 n 的物质以 θ 角入射到金属表面,金属的复折射率为 nˆ ,复折射
(2)、规定 P 、P 、P 、P 表示消光时起偏器的方位角,ψ 、ψ 、ψ 、ψ 表示消光
1
2
3
4
1
2
3
4
时检偏器方位角。 (3)首先转动 1/4 波片,在其零读数的基础上转过 45°角,然后转动起偏器和检偏器,找 出消光的角度(即平衡指示仪指示最小的位置)。 为消减误差,测量时按四步进行:
检偏器度盘刻线及读数方式与λ/4 波片度盘相同。
7
98
97
0000 0
96
5
10
95
94
(a)
47
0 46
10
5
45
0 44
5
椭偏法测介质膜厚度和折射率实验报告

椭偏法测介质膜厚度和折射率实验报告1实偏法实介实膜的厚度折射率与近代物理实实实告指实实,教得分,实实实实, 2009 年 11 月 02 日~第十周~周一~第 5-8 实实实者, 班实材料 0705 学号 200767025 姓名童凌实同实者, 班实材料0705 学号 200767007 姓名实宏实实实地点, 实合楼 408 实实件, 室度条内温 ?~相实度湿 %~室实内气实实实目, 实偏法实介实膜的厚度折射率与实实实器,;注明实格和型,号WJZ-II型实偏实实实目的,1.掌握实偏法实量薄膜和折射率的基本原理2.学会体使用实偏实实量固表面上介实薄膜的折射率和厚度实实原理实述,反射型实偏实的原理是,用一束实实偏振光作实探实照射到被实实品上~由于实品实入射光中平行于入射面的实实分量;实称P分量,和垂直入射面的实实分量;实与称S分量,有不同的反射系、透射系~因此实品上出射数数从的光~其偏振实相实于入射光实要实生实化状来1.光波在介实分界面反射和透射的实磁波理实光入射到实均、各向同性的介实分界面上实~要实两匀生反射和折射~如实;5-3-1,。
反射角入射角相等与~折射角入射角以及折射率的实系是,与或另麦条外~根据克斯实方程实和界面件~可以得到菲涅耳公式,2.反射系比数G定实反射系比数而通常G往往被成如下形式, 其中写根据前式~可以得到从式中可以看出~如果n1是已知的~那实在一固个定的入射角φ1下实定反射系比数G~实可以去实介实2的折射率n2.3.光波在介实薄膜上反射和透射的实磁波理实实实偏振光实量实实薄膜光系实——学如实;5-3-2,所示实“三介实二界面”模型~我实假定,3.1薄膜实的介实是半无解大的~折射率分实实和两3.2薄膜折射率实~实介实之实的界面它与两1和界面2平行~且都是理想的光滑斜面并2实偏法实介实膜的厚度折射率与3.3 三实介实都是均的各向同性的匀根据以上件假实和实中的何实系~可以得到,条几其中4.光在金表面反射的实磁理实金实折射率的实量属——属金实光具有吸收性~因此金的折射率实实~可以分解实实部和部~属属数虚即实实近似实算~可以得出5.用实偏法实量反射系比数反射系比数G的实量实实实实偏角、的实量。
实验报告 课程名称: 现代物理实验 实验名称:激光椭偏仪测量薄膜厚度

实验报告课程名称:现代物理实验实验名称:激光椭偏仪测量薄膜厚度和折射率专业:物理教育学号:050103106姓名:戴伟实验地点:现代物理实验室实验日期:03月10日~ 04月30日常熟理工学院[实验目的和要求]1.了解激光椭圆偏振法测量薄膜厚度和折射率的基本原理;2.学习和掌握WJZ-Ⅱ椭圆偏振仪的基本原理和使用方法;3.对以K9玻璃为基底的薄膜样品进行厚度和折射率的测量。
[实验器材]JJY1'分光计(包括附件)一台 椭偏装置一套(附仪器所配套软件)[实验原理和方法]将一束波长为λ的自然光经起偏器变成线偏振光,再经1/4波片使它变成椭圆偏振光入射到待测样品的膜面上,反射时,光的偏振状态(振幅和相位的改变)将发生变化,通过检测这种变化,便可推算出待测膜的厚度和折射率。
如图1所示。
半导体激光器发出的单色光,经起偏器后变成线偏光,线偏光再经1/4波片后产生90的位相差,变成椭圆偏振光。
对一定厚度的某种膜,S 分量和P 分量之间出现相移之差,当入射光为椭圆偏振光时,通过薄膜以后反射光为线偏振光。
由此可见,由起偏器的方位角P 可确定偏振光的P 分量和S 分量的相移之差∆。
经样品反射后由于S 波与P 波不存在位相差,可合成特定方向的线偏振光。
它的偏振方向由S 分量和P 分量的反射系数s R 和p R 确定。
转动检偏器的方位,当检偏器的方位角A 与反射光线的偏振方向垂直时,光束不能通过,出现消光状态。
因此,在椭圆偏振法中采用∆和φ来描述反射光偏振状态的变化。
=∆-∆=∆s p 相移之差 (1)sp 1tanR R -=φ (2)(1)式中的p ∆、s ∆是反射时各自引起的相移。
(2)式中的s R 、p R 分别为P 和S 分量各自的反射系数。
因为反射光的S 和P 分量因相移不同出现位相差s p ∆-∆=∆,为了重新让它变成线偏振光,必须用附加光学元件引入一个相移补偿这个位相差。
用实验测定附加光学元件引入的相移量便可以确定s p ∆-∆=∆。
椭圆偏振仪测量薄膜厚度和折射率

实验15 椭圆偏振仪测量薄膜厚度和折射率在近代科学技术的许多部门中对各种薄膜的研究和应用日益广泛.因此,更加准确和迅速地测定一给定薄膜的光学参数已变得更加迫切和重要.在实际工作中虽然可以利用各种传统的方法测定光学参数〔如布儒斯特角法测介质膜的折射率、干预法测膜厚等〕,但椭圆偏振法〔简称椭偏法〕具有独特的优点,是一种较灵敏〔可探测生长中的薄膜小于0.1nm的厚度变化〕、精度较高〔比一般的干预法高一至二个数量级〕、并且是非破坏性测量.是一种先进的测量薄膜纳米级厚度的方法.它能同时测定膜的厚度和折射率〔以与吸收系数〕.因而,目前椭圆偏振法测量已在光学、半导体、生物、医学等诸方面得到较为广泛的应用.这个方法的原理几十年前就已被提出,但由于计算过程太复杂,一般很难直接从测量值求得方程的解析解.直到广泛应用计算机以后,才使该方法具有了新的活力.目前,该方法的应用仍处在不断的开展中.实验目的(1) 了解椭圆偏振法测量薄膜参数的根本原理;(2) 初步掌握椭圆偏振仪的使用方法,并对薄膜厚度和折射率进展测量.实验原理椭偏法测量的根本思路是,起偏器产生的线偏振光经取向一定的1/4波片后成为特殊的椭圆偏振光,把它投射到待测样品外表时,只要起偏器取适当的透光方向,被待测样品外表反射出来的将是线偏振光.根据偏振光在反射前后的偏振状态变化,包括振幅和相位的变化,便可以确定样品外表的许多光学特性.1 椭偏方程与薄膜折射率和厚度的测量图15.1所示为一光学均匀和各向同性的单层介质膜.它有两个平行的界面,通常,上部是折射率为n1的空气(或真空).中间是一层厚度为d折射率为n2的介质薄膜,下层是折射率为n3的衬底,介质薄膜均匀地附在衬底上,当一束光射到膜面上时,在界面1和界面2上形成屡次反射和折射,并且各反射光和折射光分别产生多光束干预.其干预结果反映了膜的光学特性.设φ1表示光的入射角,φ2和φ3分别为在界面1和2上的折射角.根据折射定律有n1sinφ1=n2sinφ2=n3sinφ3〔15.1〕光波的电矢量可以分解成在入射面振动的P分量和垂直于入射面振动的s 分量.假如用E ip和E is分别代表入射光的p和s分量,用E rp与E rs分别代表各束反射光K0,K1,K2,…中电矢量的p分量之和与s分量之和,如此膜对两个分量的总反射系数R p和R s定义为RP=Erp/E ip, R s=E rs/E is〔15.2〕经计算可得式中,r1p或r1s和r2p或r2s分别为p或s分量在界面1和界面2上一次反射的反射系数.2δ为任意相邻两束反射光之间的位相差.根据电磁场的麦克斯韦方程和边界条件,可以证明r 1p =tan(φ1-φ2)/ tan(φ1+φ2), r1s=-sin (φ1-φ2)/ sin(φ1+φ2);r2p=tan(φ2-φ3)/tan(φ2+φ3), r2s =-sin (φ2-φ3)/ sin(φ2+φ3).(15.4)式〔15.4〕即著名的菲涅尔〔Fresnel〕反射系数公式.由相邻两反射光束间的程差,不难算出.(15.5)式中,λ为真空中的波长,d和n2为介质膜的厚度和折射率.在椭圆偏振法测量中,为了简便,通常引入另外两个物理量ψ和Δ来描述反射光偏振态的变化.它们与总反射系数的关系定义为上式简称为椭偏方程,其中的ψ和Δ称为椭偏参数〔由于具有角度量纲也称椭偏角〕.由式(15.1),式( 15.4),式( 15.5)和上式可以看出,参数ψ和Δ是n1,n,n3,λ和d的函数.其中n1,n2,λ和φ1可以是量,如果能从实验中测出ψ2和Δ的值,原如此上就可以算出薄膜的折射率n2和厚度d.这就是椭圆偏振法测量的根本原理.实际上,终究ψ和Δ的具体物理意义是什么,如何测出它们,以与测出后又如何得到n2和d,均须作进一步的讨论.2 ψ和Δ的物理意义用复数形式表示入射光和反射光的p和s分量E=|E ip|exp(iθip),E is=|E is|exp(iθis);ipE=|E rp|exp(iθrp) ,E rs=|E rs|exp(irpθ).〔15.6〕rs式中各绝对值为相应电矢量的振幅,各θ值为相应界面处的位相.由式〔15.6〕,式〔15.2〕和式〔15.7〕式可以得到.〔15.7〕比拟等式两端即可得tanψ=|E rp||E is|╱|E rs||E ip| 〔15.8〕Δ=(θrp–θrs)- (θip–θ) 〔15.9〕is式〔15.8〕明确,参量ψ与反射前后p和s分量的振幅比有关.而〔15.9〕式明确,参量Δ与反射前后p和s分量的位相差有关.可见,ψ和Δ直接反映了光在反射前后偏振态的变化.一般规定,ψ和Δ的变化围分别为0≤ψ<π/2和0≤Δ<2π.当入射光为椭圆偏振光时,反射后一般为偏振态〔指椭圆的形状和方位〕发生了变化的椭圆偏振光(除开ψ<π/4且Δ=0的情况).为了能直接测得ψ和Δ,须将实验条件作某些限制以使问题简化.也就是要求入射光和反射光满足以下两个条件:〔1〕要求入射在膜面上的光为等幅椭圆偏振光〔即P和S二分量的振幅相等〕.这时,|E ip|/|E is|=1,式〔15.9〕如此简化为tanψ=|E rp|/|E rs| .〔15.10〕〔2〕要求反射光为一线偏振光.也就是要求θrp–θrs=0〔或π〕,式〔15.9〕如此简化为〔15.15〕满足后一条件并不困难.因为对某一特定的膜,总反射系数比R p/R s是一定值.式〔15.6〕决定了⊿也是某一定值.根据〔15.9〕式可知,只要改变入射光二分量的位相差〔θip–θis〕,直到其大小为一适当值〔具体方法见后面的表示〕,就可以使〔θip–θis〕=0〔或π〕,从而使反射光变成一线偏振光.利用一检偏器可以检验此条件是否已满足.以上两条件都得到满足时,式〔15.10〕明确,tanψ恰好是反射光的p和s分量的幅值比,ψ是反射光线偏振方向与s方向间的夹角,如图15.2所示.式〔15.15〕如此明确,Δ恰好是在膜面上的入射光中s和s分量间的位相差.3 ψ和Δ的测量实现椭圆偏振法测量的仪器称为椭圆偏振仪〔简称椭偏仪〕.它的光路原理如图15.3所示.氦氖激光管发出的波长为 632. 8 nm的自然光,先后通过起偏器Q,1/4波片C入射在待测薄膜F上,反射光通过检偏器R射入光电接收器T.如前所述,p和s分别代表平行和垂直于入射面的二个方向.快轴方向f,对于负是指平行于光轴的方向,对于正晶体是从Q,C和R用虚线引下的三个插图都是迎光线看去的指垂直于光轴的方向.t代表Q的偏振方向,f代表C的快轴方向,t r 代表R 的偏振方向.慢轴方向l,对于负晶体是指垂直于光轴方向,对于正晶体是指平等于光轴方向.无论起偏器的方位如何,经过它获得的线偏振光再经过1/4波片后一般成为椭圆偏振光.为了在膜面上获得p和s二分量等幅的椭圆偏振光,只须转动1/4波片,使其快轴方向f与s方向的夹角α=土π/4即可〔参看后面〕.为了进一步使反射光变成为一线偏振光E,可转动起偏器,使它的偏振方向t与s方向间的夹角P1为某些特定值.这时,如果转动检偏器R使它的偏振方向t r与E r垂直,如此仪器处于消光状态,光电接收器T接收到的光强最小,检流计的示值也最小.本实验中所使用的椭偏仪,可以直接测出消光状态下的起偏角P1和检偏方位角ψ.从式〔15.15〕可见,要求出Δ,还必须求出P1与〔θip–θis〕的关系.下面就上述的等幅椭圆偏振光的获得与P1与Δ的关系作进一步的说明.如图15.4所示,设已将1/4波片置于其快轴方向f与s方向间夹角为π/4的方位.E0为通过起偏器后的电矢量,P1 为E0与s方向间的夹角〔以下简称起偏角〕.令γ表示椭圆的开口角〔即两对角线间的夹角〕.由晶体光学可知,通过1/4波片后,E0沿快轴的分量E f与沿慢轴的分量E l比拟,位相上超前π/2.用数学式可以表达成.〔15.12〕.〔15.13〕从它们在p和s两个方向的投影可得到p和s的电矢量分别为:.〔15.14〕.〔15.15〕由式〔15.14〕和式〔15.15〕看出,当1/4波片放置在+π/4角位置时,确实在p和s二方向上得到了幅值均为E0/2的椭圆偏振入射光.p和s的位相差为θip–θis=π/2-2P1.〔15.16〕另一方面,从图15.4上的几何关系可以得出,开口角γ与起偏角P1的关系为γ/2=π/4-P1γ=π/2-2P1 〔15.17〕如此〔15.16〕式变为θip–θis=γ〔15.18〕由式〔15.15〕可得Δ=—(θ-θis)= -γ〔15.19〕ip至于检偏方位角ψ,可以在消光状态下直接读出.在测量中,为了提高测量的准确性,常常不是只测一次消光状态所对应的P1和ψ1值,而是将四种〔或二种〕消光位置所对应的四组〔P1,ψ1〕),〔P2,ψ2〕,〔P3,ψ3〕和〔P4,ψ4〕值测出,经处理后再算出Δ和ψ值.其中,(P1,ψ1)和〔P2,ψ2〕所对应的是1/4波片快轴相对于S方向置+π/4时的两个消光位置(反射后P和S光的位相差为0或为π时均能合成线偏振光).而(P3,ψ3)和(P4,ψ4)对应的是1/4波片快轴相对于s方向置-π/4的两个消光位置.另外,还可以证明如下关系成立:|p1-p2|=90˚,ψ2=-ψ1.|p3-p4|=90˚,ψ4=-ψ3.求Δ和ψ的方法如下所述.(1) 计算Δ值.将P1,P2,P3和P4于π/2的减去π/2,不大于π/2的保持原值,并分别记为< P1>,< P2>,< P3>和< P4>,然后分别求平均.计算中,令和,(15. 20)而椭圆开口角γ与和的关系为.(15.21)由式(15.22)算得ψ⊿值.利用类似于图15.4的作图方法,分别画出起偏角在表15.1所指围的椭圆偏振光图,由图上的几何关系求出与公式〔15.18〕P1类似的γ与P1Δ与γ的对应关系.P与Δ的对应关系1P=-(θip-θ1)is-γ0~π/4π/4~π/2γπ/2~3π/4 π-γ3π/4~π- (π-γ)(2) 计算ψ值:应按公式〔15.22〕进展计算.(15.22)4折射率n2和膜厚d的计算尽管在原如此上由ψ和Δ能算出n2和d,但实际上要直接解出〔n2,d〕和〔Δ,ψ〕的函数关系式是很困难的.一般在n1和n2均为实数〔即为透明介质的〕,并且衬底折射率n3〔可以为复数〕的情况下,将〔n2,d〕和〔Δ,ψ〕的关系制成数值表或列线图而求得n2和d值.编制数值表的工作通常由计算机来完成.制作的方法是,先测量〔或〕衬底的折射率n2,取定一个入射角φ1,的初始值,令δ从0变到180°〔变化步长可取π/180,π/90,…设一个n2等〕,利用式〔15.4〕,式〔15.5〕和式〔15.6〕,便可分别算出d,Δ和ψ值.然后将n2增加一个小量进展类似计算.如此继续下去便可得到〔n2,d〕~〔Δ,ψ〕的数值表.为了使用方便,常将数值表绘制成列线图.用这种查表〔或查图〕求n2和d的方法,虽然比拟简单方便,但误差较大,故目前日益广泛地采用计算机直接处理数据.另外,求厚度d时还需要说明一点:当n1和n2为实数时,式〔15.4〕中的φ为实数,两相邻反射光线间的位相差“亦为实数,其周期为2π.2δ可能2随着d的变化而处于不同的周期中.假如令2δ=2π时对应的膜层厚度为第一个周期厚度d0,由〔15.4〕式可以得到由数值表,列线图或计算机算出的d值均是第一周期的数值.假如膜厚大于d,可用其它方法(如干预法)确定所在的周期数j,如此总膜厚是D = (j -1) d+d.5金属复折射率的测量以上讨论的主要是透明介质膜光学参数的测量,膜对光的吸收可以忽略不计,因而折射率为实数.金属是导电媒质,电磁波在导电媒质中传播要衰减.故各种导电媒质中都存在不同程度的吸收.理论明确,金属的介电常数是复数,其折射率也是复数.现表示为=n2 -iκ式中的实部n2并不相当于透明介质的折射率.换句话说,n2的物理意义不对应于光在真空中速度与介质中速度的比值,所以也不能从它导出折射定律.式中κ称为吸收系数.这里有必要说明的是,当为复数时,一般φ1和φ2也为复数.折射定律在形式上仍然成立,前述的菲涅尔反射系数公式和椭偏方程也成立.这时仍然可以通过椭偏法求得参量d,n2和k,但计算过程却要繁复得多.本实验仅测厚金属铝的复折射率.为使计算简化,将式〔15.25〕改写成以下形式=n2-i nκ由于待测厚金属铝的厚度d与光的穿透深度相比大得多,在膜层第二个界面上的反射光可以忽略不计,因而可以直接引用单界面反射的菲涅尔反射系数公式〔15.4〕.经推算后得公式中的n1,φ1和κ的意义均与透明介质情况下一样.实验容关于椭偏仪的具体结构和使用方法,请参看仪器说明书.实验时为了减小测量误差,不但应将样品台调水平,还应尽量保证入射角φ1放置的准确性,保证消光状态的灵敏判别.另外,以下的测量均是在波长为632.8nm时的参数.而且,所有测量均是光从空气介质入射到膜面.1 测厚铝膜的复折射率=π/3.按已述方法测得Δ和ψ.由式(15.26)和式(15.27)取入射角φ1式算出n和κ值,并写出折射率的实部和虚部.2 测硅衬底上二氧化硅膜的折射率和厚度衬底硅的复折射率为n3=3.85-i0.02,取入射角φ1=7π/18.二氧化硅膜只有实部.膜厚在第一周期.测出Δ和ψ后,利用列线图〔或数值表〕和计算机求出n2和d,将两种方法的结果进展比照.并计算膜的一个周期厚度值d0.3 测量κ0玻璃衬底上氟化镁〔MgF2〕膜层的折射率和厚度(1) 测κ0玻璃的折射率首先测出无膜时K0玻璃的Δ和ψ值,然后代入n3=n3〔Δ,ψ,φ1〕的关系式中算出n3值,测量时入射角φ1取7π/18.关于n3与三个参量的关系式,根据式〔15.1〕,式〔15.4〕,式〔15.5〕和式〔15.6〕,并令膜厚d=0,便可以算出n3的实部n0的平方值和n3的虚部κ值为(15.28)(15.29)〔2〕测透明介质膜氟化镁的折射率和厚度=7π/18.膜厚在第一周期.测出Δ和ψ后也用列线仍取入射角φ1图和计算机求出结果.思考题(1) 用椭偏仪测薄膜的厚度和折射率时,对薄膜有何要求?较准确?(2) 在测量时,如何保证φ1(3) 试证明:|P1-P2| =π/2,|P3-P4| =π/2.(4) 假如须同时测定单层膜的三个参数〔折射率n2,厚度d和吸收系数κ〕,应如何利word 用椭偏方程?11 / 11。
椭偏光法测量薄膜的折射率和厚度

• 引言 • 椭偏光法的基本原理 • 椭偏光法测量薄膜的折射率 • 椭偏光法测量薄膜的厚度 • 实验结果与分析 • 结论与展望
01
引言
椭偏光法的简介
椭偏光法是一种光学测量技术,通过 测量光在薄膜表面反射后的偏振状态 变化,可以推导出薄膜的折射率、消 光系数和厚度等物理参数。
06
结论与展望
椭偏光法测量薄膜ห้องสมุดไป่ตู้优缺点
精度高
椭偏光法能够以高精度测量薄膜的折射 率和厚度,误差范围通常在纳米级别。
VS
非侵入性
椭偏光法不需要直接接触样品,不会对薄 膜造成损伤或污染。
椭偏光法测量薄膜的优缺点
• 适用范围广:椭偏光法适用于各种类型的薄膜材料,包括 光学薄膜、金属薄膜、半导体薄膜等。
电场矢量在垂直于传播方向的平面上 振动,其振幅和方向随时间变化,形 成椭圆轨迹。
椭偏光在传播过程中,其偏振状态会 受到周围介质的影响,如折射、反射 和散射等。
椭偏光的形成
当自然光通过特定波片时,波片内的 晶体对光波产生双折射效应,导致光 波的偏振状态发生变化,形成椭偏光。
薄膜对椭偏光的影响
01
反射和透射
如入射角、波长等实验参数的选择也会影响测量结果。
厚度测量的精度与误差分析
01
02
03
04
1. 选择稳定的光源和性 能良好的光学元件。
2. 对薄膜表面进行抛光 或清洁,减小表面粗糙 度。
3. 优化实验参数,如选 择合适的入射角和波长。
4. 进行多次测量并取平 均值,以减小随机误差 的影响。
05
实验结果与分析
当椭偏光照射到薄膜表面时,部分光波被反射,部分光波穿透薄膜并继
用椭偏仪测量薄膜厚度及折射率

广东海洋大学学生实验报告书(学生用表)实验名称_____________________ 课程名称_____________________ 课程号____________ 学院(系)_____________________ 专业_____________________ 班级________________ 学生姓名_____________ 学号_____________ 实验地点____________ 实验日期_________【实验名称】用椭偏仪测量薄膜厚度及折射率椭圆光偏振仪(简称椭偏仪)是一种精确测定固体表面各种薄膜的厚度和折射率的仪器。
在各种已有的测定薄膜厚度的方法中,如比色法、称重法、干涉法等等,椭偏法是能测量厚度最薄和测量精度最高的一种,而且测量是非破坏性的,并能在一次测量中同时测定膜厚及折射率。
因此,在各种涉及薄膜、表面层和表面过程的生产、科研领域中,椭偏仪成为一种重要的测试工具。
【实验目的】1. 了解椭偏光方法的基本原理。
2. 学会使用椭偏仪并用以测量出介质薄膜的厚度及折射率。
【实验原理】椭偏仪测量薄膜厚度及光学常数的基本依据是:当一束光以一定的入射角照射到薄膜介质样品上时,光要在多层介质膜的交界处发生多次折射的反射。
在薄膜的反射方向得到的光束的振幅和位相变化情况与膜的厚度和光学常数有关,因而可根据反射光的特性来确定膜的光学特性。
若入射光是椭圆偏振光则只要测量反射光的偏振态的变化,就可以确定出薄膜的厚度及折射率。
1. 起偏器P2.1/4波片Q3.检偏器A4.白屏5.被测样品薄膜6.基片2. 图19.1椭偏仪基本光路原理图偏器P过滤为线偏振光,再经1/4波片Q的作用变为等幅的椭圆偏振光入射至样品上。
光束经样品薄膜反射后,其偏振态即振幅和位相发生变化。
对于给定的透明薄膜试样,只要调节起偏振器的起偏轴方向则可使经样品反射后的椭偏振光变为线偏振光。
反射线偏振光方向可由检偏器A测量,当检偏轴与线偏振光的振动方向垂直时便构成消光状态。
实验椭圆偏振法测量薄膜厚度和折射率

实验椭圆偏振法测量薄膜厚度和折射率椭圆偏振法是一种常用的非破坏性薄膜厚度和折射率测量方法,它可以通过对样品反射和透射光的偏振状态进行测量,来获得样品的光学特性参数。
下面我们将介绍实验椭圆偏振法的测量步骤和注意事项。
1. 实验原理当一束偏振光碰到被测薄膜表面时,反射的光和透射的光都会发生偏振,其偏振状态可以通过椭圆偏振仪来测量。
通过测量样品反射和透射光的偏振椭圆参数,可以计算出薄膜厚度和折射率等光学参数。
2. 实验步骤(1) 样品制备准备一片光学平整的样品,涂上一层薄膜。
需要保证样品表面光洁度良好,无明显缺陷和表面过度粗糙。
(2) 调整椭圆偏振仪首先需要进行仪器校准,保证椭圆偏振仪能够正常工作。
然后,将样品放置在椭圆偏振仪的样品台上,调整偏振仪的角度、波长等参数,使样品的反射和透射光能够被完全接收和测量。
(3) 测量反射光打开椭圆偏振仪的偏振片,使入射光为线偏振光,然后测量样品反射光的偏振椭圆参数。
一般需要测量三个不同角度和波长条件下的参数,以保证数据的准确性。
(5) 数据处理通过测量数据,可以得到样品的反射和透射光的偏振椭圆参数。
根据计算公式,可以计算出样品的折射率和厚度等光学参数。
需要注意的是,测量过程中需保持仪器稳定,以免数据误差。
3. 注意事项(1) 样品表面应该光洁度良好,无缺陷和过度粗糙。
(2) 测量前需要进行椭圆偏振仪的校准,保证仪器能够正常工作。
(4) 测量过程中需要保持仪器稳定,以免数据误差。
(5) 需要注意心理学处理的方法和如何保留数据以及整合数据,以便之后的进一步研究和分析。
总结:实验椭圆偏振法是一种非常实用的分析方法,能够快速准确地测量薄膜的厚度和折射率等光学参数。
在实验过程中需要注意样品表面光洁度、仪器稳定等因素,以保证数据的准确性。
此外,数据分析也是实验的重要部分,需要采用合适的处理方法和工具,以得出正确的结论和结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近代物理实验报告指导教师:得分:实验时间: 2009 年 11 月 02 日, 第 十 周, 周 一 , 第 5-8 节实验者: 班级 材料0705 学号 200767025 姓名 童凌炜同组者: 班级 材料0705 学号 200767007 姓名 车宏龙实验地点: 综合楼 408实验条件: 室内温度 ℃, 相对湿度 %, 室内气压实验题目: 椭偏法测介质膜的厚度与折射率实验仪器:(注明规格和型号) WJZ-II 型椭偏仪实验目的:1. 掌握椭偏法测量薄膜和折射率的基本原理2. 学会使用椭偏仪测量固体表面上介质薄膜的折射率和厚度实验原理简述:反射型椭偏仪的原理是:用一束椭圆偏振光作为探针照射到被测样品上,由于样品对入射光中平行于入射面的电场分量(简称P 分量)和垂直与入射面的电场分量(简称S 分量)有不同的反射系数、透射系数,因此从样品上出射的光,其偏振状态相对于入射光来说要发生变化1. 光波在介质分界面反射和透射的电磁波理论光入射到两种均匀、各向同性的介质分界面上时,要发生反射和折射,如图(5-3-1)。
反射角与入射角相等,折射角与入射角以及折射率的关系是:2211sin sin ϕϕn n = 或1212222sin cos ϕϕn n n -=另外,根据麦克斯韦方程组和界面条件,可以得到菲涅耳公式:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=-+=+--=+-=)sin(cos sin 2)cos()sin(cos sin 2)sin()sin()tan()tan(211221211221212121ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕsp s p t t r r2. 反射系数比G定义反射系数比)](exp[||||s p s p sp i r r r r G δδ-==而通常G 往往被写成如下形式:)exp(tan ∆⋅=i G ψ 其中 ||tan sp r r =ψ sp δδ-=∆根据前式,可以得到21122112]tan )11(1[sin ϕϕ⋅+-+⋅⋅=GG n n 从式中可以看出, 如果n1是已知的, 那么在一个固定的入射角φ1下测定反射系数比G , 则可以去顶介质2的折射率n2.3. 光波在介质薄膜上反射和透射的电磁波理论——椭圆偏振光测量单层薄膜光学系统如图(5-3-2)所示为“三介质二界面”模型,我们假定:3.1薄膜两侧的介质是半无解大的,折射率分别为1n 和3n3.2薄膜折射率为2n ,它与两侧介质之间的界面1和界面2平行,并且都是理想的光滑斜面 3.3 三种介质都是均匀的各向同性的根据以上条件假设和图中的几何关系, 可以得到:δδδδψ2231222312223122231211tan i s s i s s i p p i p p s pi e r r e r r e r r e r r R R e G ----∇++⋅++==⋅=其中⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧===+-=+-=+-=+-=332211223322332223221122111232233223232112211212sin sin sin /cos 42)cos cos /()cos cos ()cos cos /()cos cos ()cos cos /()cos cos ()cos cos /()cos cos (ϕϕϕλϕπδϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕn n n dn n n n n r n n n n r n n n n r n n n n r s s p p4. 光在金属表面反射的电磁理论——金属复折射率的测量金属对光具有吸收性,因此金属的折射率为复数,可以分解为实部和虚部,即iNK N n -=2经过近似计算,可以得出⎪⎩⎪⎨⎧∆⋅=∆⋅+⋅⋅⋅=sin 2tan cos 2sin 12cos tan sin 111ψψψϕϕK n N5. 用椭偏法测量反射系数比反射系数比G 的测量归结为两个椭偏角ψ、∆的测量。
反射式椭偏仪有如下关系式:)](exp[|/|)](exp[|/|tan is ip is ip rs rp rs rp i i E E i E E e G ββββψ--=⋅=∆为了测量和,需要测量四个量,分别测量入射光中两分量的振幅比和相位差以及反射光中两分量的振幅比和相位差。
6. 等幅椭偏光的获得如图(5-3-3)所示的基本光路,对于入射和反射光分别设立两个直角坐标系x-y 和x ·-y ·其中x 和x ·轴均在入射面(纸面)内并且分别垂直于入射光和反射光的传播方向,y 轴和y ·轴均垂直于入射面:起偏器的透光方向t 与x 轴的夹角为P .图(5-3-4)调节P 的数值便可以使入射等幅椭偏光两分量的相位差(is ip ββ-)连续可调,从而可以得到相位差连续可调的等幅椭圆偏振光。
7. 反射的线偏正光的检测对于等相位差连续可调的等幅椭偏入射光来说,有⎪⎪⎩⎪⎪⎨⎧-=-+∆=rs rp rsrp P E E ββπψ22||tan结合图(5-3-5)(a )和(b )分别讨论反射线偏振光的两种不同状态:7.1 πββ=-rs rp ;11:20A A =<<ψπ;1223P -=∆π7.2 0=-rs rp ββ ; 11:2A A =<<ψππ;222P -=∆π实验步骤简述:测量透明介质薄膜(氧化锆标准样板)厚度和折射率1.分光计的调整:用自准法直法调整好分光计2.光路调整2.1 卸下物镜、狭缝、物镜和目镜2.2 将半导体激光器装在平行光管外端,在平行光管另一端旋上校光片A2.3点亮激光器,观察2.4取下校光片A,将校光片B置于望远镜目镜处,同理,光斑也应同时在校光片A、B的圆框内2.5锁定分光计的角度刻度盘,转动使角游标的“0”与刻度盘的“0”对准2.6换下两只校光片,测光电流值3.检偏器读数头位置的调节与固定3.1检偏器读数头套在望远镜筒上,90°读数朝上,位置基本居中3.2附件黑色反光镜置于载物台中央,将望远镜转过66°,使激光束以布儒斯特角入射到黑色反光镜表面,锁定望远镜3.3转动检偏头,使半反目镜内光点达到最暗。
固定检偏器读数头3.4适当转动激光器在平行管中的位置,是目镜中光点最暗,固定激光器4.起偏器读数头的调节与固定4.1将起偏器读数头套在平行光管镜筒上4.2取下黑色反光镜,将望远镜系统转会原来位置,使起偏、检偏器读数头共轴,并令激光束通过中心4.3调节起偏器读数头与目镜相对位置,找出最暗位置5.1/4波片零点位置的调整5.1起偏器读数保持为0°,检偏器90°,此时白屏上的光点应最暗5.2 将1/4波片读数头对准零位5.3 将1/4波片框的白点向上,套在内刻度圈上,并微微转动。
使半反目镜内的反光点最暗。
固定1/4波片6.被测样品薄膜光学参数6.1被测样品,放在载物台中间,旋转望远镜达到预定的入射角70°6.2为了减少误差,尽量使用四点测量原始数据、 数据处理及误差计算:并计算它们的平均值A 和P , 得到A=20.6°, P=133.73°根据A 、P 的平均值, 可以计算出待测膜的两个椭偏角: ︒==6.20A ψ; ︒=-=∆54.2223P π根据上面得到的测量结果, 使用计算机对最终的结果进行计算计算思路为: 使用迭代法, 将每一次计算的近似结果作为下一次计算的参考范围, 如此不断减小范围, 逐渐逼近最后的精确结果, 当近似程度符合精确值的要求时, 该近似值便可以作为最终结果Calculating Result d0=35nm, n0=1.4~1.5 d1=33.5nm, n1=1.46 d2=33.6nm, n2=1.462d3=33.48nm, n3=1.4619; 并以这一组d 和n 为最终的计算结果;然后可以得到周期厚度D=283.5nm , 参考厂家给出的厚度, 取第二周期的厚度值, 这样, 给出最后的计算结果为:薄膜的厚度为 d=600.4nm , 折射率大小为 n=1.4619思考题, 实验感想, 疑问与建议: 1. 椭偏仪设计的基本思想是什么?(答案略)2. 椭偏仪各主要光学部件的作用是什么?(主要光学部件:起偏器, 检偏器, 黑色反光镜, 1/4玻片)起偏器:将激光光源射出的单色光束(完全光)转化为线偏振光, 同时不同的起偏器透光方向, 意味着 出射光的电矢量方向变化,与x轴的夹角也发生变化。
检偏器:检验经过薄膜反射后的反射光是否为线偏振光(有消光现象),并在确认其为线偏振光的情况下,测量其偏振矢量与x轴正方向的夹角。
黑色反光镜:黑色反光镜的作用关系到其摆放位置,将黑色反光镜置于光具平台中央,望远镜与平行光管的钝夹角为114°,即光束以布儒斯特角(对于黑色反光镜的材质,约为57°)入射到反光镜表面,则此时反射光为线偏振光,且电矢量为单一的p方向,即偏振方向与仪器中心转轴垂直;这时通过调节检偏器,当入射到望远镜内的光强达到最小时,说明检偏器的检偏方向与反射光的偏振方向垂直,即检偏方向平行于仪器中心转轴,使得检偏器的初始位置得到了校正,并能够以此为基础,继续完成起偏器和1/4玻片的校正。
1/4玻片:由于通过起偏器以后的线偏振光只有一个振动方向,而实验需要的是两个方向垂直的光波入射到被测样品的表面。
当线偏振光垂直晶面进入1/4玻片后,在玻片内分为o光和e光,它们的振动方向相互垂直,从1/4玻片出射时,o光和e光之间有π/2的相位差,这两个矢量的合成,能够使整体的偏振光成为椭圆偏振光。
并且,如果入射到1/4玻片的线偏振光的偏振化方向与玻片的快轴方向成π/4角,那么从玻片射出的就是圆偏振光。
3.分析椭偏法测量的可能误差来源从实验步骤,一层一层分析,容易找出各处的误差源调节光路的时候,如果望远镜的光轴没有对准仪器的中心转轴,那么以后的实验中,入射光将不能平行穿过望远镜的光轴进入到检流计中,可能在望远镜筒的内壁上发生反射或被遮挡,那这是检测到的最小光强位置未必是真实的最弱位置。
用黑色反光镜校正检偏器时,如果反光镜的位置摆放不正确或者望远镜的角度调节不恰当,导致反射光不能完全射入望远镜内,或者入射方向不与望远镜的光轴平行,也可能导致最小光强的误判,而导致实验误差。
如果在实验过程中,错误地调节了原先已经调节好的光学仪器位置,或者在调节好了以后没有锁定,在之后的实验过程中,由于碰撞或者振动等原因,导致位置发生变化,也可能导致最终测量结果出现误差。
综上,实验误差的出现,本质原因主要有两点,一个是最小光强位置的判断错误,另一个是原先调整好的光学仪器在之后的实验过程中发生了变动。
