八年级期末考试2
人教部编版八年级语文上册 期末测试卷 (2)

第一学期期末测试卷八年级·语文上(R版) 时间:100分钟满分:120分一、积累与运用(30分)1.下列加点字读音无误的一项是( )(2分)A.琐屑.(xiè)栅.栏(zhà)池沼.(zhǎo)惟妙惟肖.(xiāo)B.颓.唐(tuí) 妥帖.(tiē) 着.眼(zháo) 触.目伤怀(chù) C.轩榭.(xiè) 气氛.(fēn) 纤.细(xiān) 迥.然不同(jiǒng) D.河堤.(tí) 踌躇.(chú) 脂.粉(zhǐ) 情郁.于中(yù) 2.下列词语中没有错别字的一项是( )(2分)A.和谐暮年藏污纳垢诚慌诚恐B.漫延酒肆不可遏制交头结耳C.蔷薇滞留刀剑入鞘春寒料峭D.宛然臼齿潜滋暗长坦荡如坻3.下列句子中加点词语的解释有误的一项是( )(2分)A.由于人民解放军英勇善战,锐不可当....(形容来势凶猛,不可阻挡),敌人节节败退。
B.不宜笼统地提问,不能笼统地答复,艺术形式处理中,往往是失之..毫厘,谬以千里.......(开始相差得很小,结果会造成很大的错误。
强调不能有一点儿差错)。
C.全在乎设计者和匠师们生平多阅历,胸中有丘壑.....(设计者和匠师的脑中有关于山水风景的高明构思),才能使游览者攀登的时候忘却苏州城市,只觉得身在山间。
D.他触目伤怀....(触碰到自己的眼睛,心里不高兴),自然情不能自已。
4.下列句子中没有语病的一项是( )(2分)A.为庆祝中华人民共和国成立七十周年,我市开展的“我和我的祖国”快闪录制活动,极大地激发了广大市民的爱国热情。
B.中华优秀传统文化蕴含着高度的民族认同感,发扬鲜明的民族性特征。
C.为了防止安全事故不再发生,我校开展了“安全伴我行”知识讲座活动。
D.《标准汉语》的主要读者是为英语国家的中国留学生子女及汉语爱好者编写的一套汉语教材。
5.下列句子中标点符号使用正确的一项是( )(2分)A.一艘准备驶过拱桥的巨大漕船的细节描绘,一直为人们所称道。
浙江省台州市玉环市2024年八年级英语第二学期期末考试试题含答案

浙江省台州市玉环市2024年八年级英语第二学期期末考试试题满分120分,时间90分钟一、单项选择(共10小题,满分20分)1、—Tom has changed quite a lot. He used to be very shy, but now he’s outgoing.—That’s for sure. People ________ always stay the same.A. can’tB. won’tC. mustn’tD. needn’t2、—Jane, would you like to help your brother ________ the toys on the floor?—OK, mom. I will.A. eat upB. cut upC. pick up3、Boys and girls, believe in yourself. If you ________ hard, your dream will come true.A. will studyB. studiedC. studyD. are studying4、—Sir, could you please put out your cigarette? This is a smoke-free (无烟的) school.—______A. I'm sorry about this.B. No problem.C. Sure, I'd love to.D. Never mind.5、How careless Tina was! She cut ________ again.A. herB. herselfC. sheD. hers6、Children in poor areas need not only food and clothes, but also ________.A. educationB. conversationC. situationD. condition7、From the notice, we know that Ms Smith ________.A. never uses the handbagB. paid 80 dollars for the handbagC. keeps her handbag in good conditionsD. would like to get a new handbag8、I feel ________ about the coming school trip this Saturday, so I hope this day will come soon.A. excitedB. tiredC. nervousD. careful9、— As a student, we ________ study too hard because hard work leads to success.— I agree.A. mustn’tB. needn’tC. shouldn’tD. can’t10、Stay away from junk food, please. It’s bad for us, ________ for children.A. recentlyB. especiallyC. probablyD. suddenly二、完成句子(共5小题,满分10分)11、在餐馆用餐后,你想结账,可以这样对服务员说:May I __________________________________?12、对亚洲产生巨大影响____________________13、by, we, are, connected, the, Internet_______________________________________________________________________________.14、Just make yourself at home, and have w________ you want.15、Why is he keeping ________ /’saɪlənt / all the time?三、补全对话(10分)16、根据下面的对话情景,在每个空白处填上一个适当的句子, 使对话的意思连贯、完整。
初中数学八年级下期末经典题(含答案解析)(2)
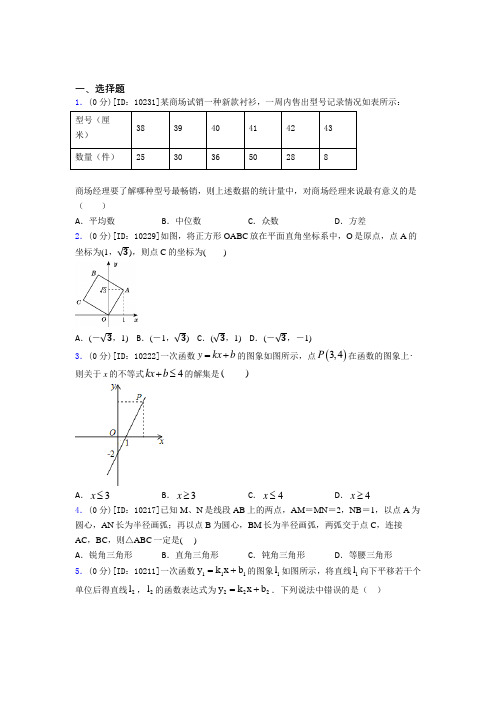
一、选择题1.(0分)[ID :10231]某商场试销一种新款衬衫,一周内售出型号记录情况如表所示: 型号(厘米) 38 39 40 41 42 43 数量(件)25303650288商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是( ) A .平均数B .中位数C .众数D .方差2.(0分)[ID :10229]如图,将正方形OABC 放在平面直角坐标系中,O 是原点,点A 的坐标为(1,√3),则点C 的坐标为( )A .(-√3,1)B .(-1,√3)C .(√3,1)D .(-√3,-1)3.(0分)[ID :10222]一次函数y kx b =+的图象如图所示,点()3,4P 在函数的图象上.则关于x 的不等式4kx b +≤的解集是( )A .3x ≤B .3x ≥C .4x ≤D .4x ≥4.(0分)[ID :10217]已知M 、N 是线段AB 上的两点,AM =MN =2,NB =1,以点A 为圆心,AN 长为半径画弧;再以点B 为圆心,BM 长为半径画弧,两弧交于点C ,连接AC ,BC ,则△ABC 一定是( ) A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形5.(0分)[ID :10211]一次函数111y k x b =+的图象1l 如图所示,将直线1l 向下平移若干个单位后得直线2l ,2l 的函数表达式为222y k x b =+.下列说法中错误的是( )A .12k k =B .12b b <C .12b b >D .当5x =时,12y y >6.(0分)[ID :10205]以下命题,正确的是( ). A .对角线相等的菱形是正方形 B .对角线相等的平行四边形是正方形 C .对角线互相垂直的平行四边形是正方形 D .对角线互相垂直平分的四边形是正方形7.(0分)[ID :10199]将一张长方形纸片按如图所示的方式折叠,,BC BD 为折痕,则CBD ∠的度数为( )A .60︒B .75︒C .90︒D .95︒8.(0分)[ID :10144]如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b .若8ab =,大正方形的面积为25,则小正方形的边长为( )A .9B .6C .4D .39.(0分)[ID :10141]12751348)的结果是( ) A .6B .3C .3D .1210.(0分)[ID :10138]小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s (千米)与所用时间t (分)之间的关系( )A.B.C.D.11.(0分)[ID:10192]如图2,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是()A.BA=BC B.AC、BD互相平分C.AC=BD D.AB∥CD12.(0分)[ID:10166]如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是()A.6B.12C.24D.不能确定13.(0分)[ID:10161]如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为()A.10m B.15m C.18m D.20m14.(0分)[ID:10159]将根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,设筷子露在杯子外面的长度hcm,则h的取值范围是( )A .h 17cm ≤B .h 8cm ≥C .7cm h 16cm ≤≤D .15cm h 16cm ≤≤15.(0分)[ID :10150]如图,已知点E 在正方形ABCD 内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )A .48B .60C .76D .80二、填空题16.(0分)[ID :10332]如图,BD 是△ABC 的角平分线,DE∥BC,交AB 于点E ,DF∥AB,交BC 于点F ,当△ABC 满足_________条件 时,四边形BEDF 是正方形.17.(0分)[ID :10331]如图,在ABC 中,AC BC =,点D E ,分别是边AB AC ,的中点,延长DE 到点F ,使DE EF =,得四边形ADCF .若使四边形ADCF 是正方形,则应在ABC 中再添加一个条件为__________.18.(0分)[ID :10320]如图所示,BE AC ⊥于点D ,且AB BC =,BD ED =,若54ABC ∠=,则E ∠=___.19.(0分)[ID :10300]如图,在平面直角坐标系xOy 中,点(0,6)C ,射线//x CE 轴,直线y x b =-+交线段OC 于点B ,交x 轴于点A ,D 是射线CE 上一点.若存在点D ,使得ABD △恰为等腰直角三角形,则b 的值为_______.20.(0分)[ID :10294]如图,矩形ABCD 的对角线AC 、BD 相交于点O ,∠AOB=120°,CE//BD ,DE//AC ,若AD=5,则四边形CODE 的周长______.21.(0分)[ID :10290]一个三角形的三边长分别为15cm 、20cm 、25cm ,则这个三角形最长边上的高是_____ cm .22.(0分)[ID :10284]如图,将周长为8的△ABC 沿BC 方向向右平移1个单位得到△DEF ,则四边形ABFD 的周长为 .23.(0分)[ID :10274]如果一组数据1,3,5,a ,8的方差是0.7,则另一组数据11,13,15,10a +,18的方差是________.24.(0分)[ID :10252]有一组数据如下:2,3,a ,5,6,它们的平均数是4,则这组数据的方差是 .25.(0分)[ID :10240]已知一组数据1,2,3,4,5的方差为2,则另一组数据11,12,13,14,15的方差为___.三、解答题26.(0分)[ID :10380]如图,在平面直角坐标系xOy 中,一次函数y 1=−23x+2与x 轴、y轴分别相交于点A 和点B ,直线y 2=kx+b(k≠0)经过点C(1,0)且与线段AB 交于点P ,并把△ABO 分成两部分. (1)求A 、 B 的坐标; (2)求△ABO 的面积;(3)若△ABO 被直线CP 分成的两部分的面积相等,求点P 的坐标及直线CP 的函数表达式.27.(0分)[ID :10379]如图①,在正方形ABCD 中,P 是对角线AC 上的一点,点E 在BC 的延长线上,且PE=PB(1)求证:△BCP ≌△DCP ; (2)求证:∠DPE=∠ABC ;(3)把正方形ABCD 改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.28.(0分)[ID :10347]先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,形如2a b ±,如果你能找到两个数m 、n ,使22m n a +=,且mn b =,则2a b ±可变形为2222()m n mn m n m n +±=±=±,从而达到化去一层根号的目的.例如:22232212221(2)212(12)-=+-=+-⨯⨯=-1221=-=-仿照上例完成下面各题: 填上适当的数:29.(0分)[ID :10346]011)1235-+⨯--.30.(0分)[ID :10340]设a =b =c =.(1)当x 取什么实数时,a ,b ,c 都有意义;(2)若Rt △ABC 三条边的长分别为a ,b ,c ,求x 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.C 2.A 3.A 4.B 5.B 6.A 7.C 8.D 9.D 10.D 11.B 12.B 13.C 14.C 15.C二、填空题16.∠ABC=90°【解析】分析:由题意知四边形DEBF是平行四边形再通过证明一组邻边相等可知四边形DEBF是菱形进而得出∠ABC=90°时四边形BEDF是正方形详解:当△ABC满足条件∠ABC=90°17.答案不唯一如∠ACB=90°或∠BAC=45°或∠B=45°【解析】【分析】先证明四边形ADCF 是平行四边形再证明AC=DF即可再利用∠ACB=90°得出答案即可【详解】∠ACB=90°时四边形AD18.27°【解析】【分析】连接AE先证Rt△ABD≌Rt△CBD得出四边形ABCE是菱形根据菱形的性质可推导得到∠E的大小【详解】如下图连接AE∵BE⊥AC∴∠ADB=∠BDC=90°∴△ABD 和△CB19.3或6【解析】【分析】先表示出AB坐标分①当∠ABD=90°时②当∠ADB=90°时③当∠DAB=90°时建立等式解出b即可【详解】解:①当∠ABD=90°时如图1则∠DBC+∠ABO=90°∴∠D20.20【解析】【分析】通过矩形的性质可得再根据∠AOB=120°可证△AOD是等边三角形即可求出OD的长度再通过证明四边形CODE是菱形即可求解四边形CODE的周长【详解】∵四边形ABCD是矩形∴∵∠21.【解析】【分析】过C作CD⊥AB于D根据勾股定理的逆定理可得该三角形为直角三角形然后再利用三角形的面积公式即可求解【详解】如图设AB=25是最长边AC=15BC=20过C作CD ⊥AB于D∵AC2+B22.【解析】试题解析:根据题意将周长为8的△ABC沿边BC向右平移1个单位得到△DEF则AD=1BF=BC+CF=BC+1DF=AC又∵AB+BC+AC=10∴四边形ABFD的周长=AD+AB+BF+D23.7【解析】【分析】根据题目中的数据和方差的定义可以求得所求数据的方差【详解】设一组数据135a8的平均数是另一组数据111315+1018的平均数是+10∵=07∴==07故答案为07【点睛】本题考24.2【解析】试题分析:先由平均数计算出a=4×5-2-3-5-6=4再计算方差(一般地设n个数据x1x2…xn的平均数为=()则方差=)==2考点:平均数方差25.2【解析】试题分析:根据方差的性质当一组数据同时加减一个数时方差不变进而得出答案∵一组数据12345的方差为2∴则另一组数据1112131415的方差为2故答案为2考点:方差三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.C解析:C【解析】分析:商场经理要了解哪些型号最畅销,所关心的即为众数.详解:根据题意知:对商场经理来说,最有意义的是各种型号的衬衫的销售数量,即众数.故选C.点睛:此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.2.A解析:A【解析】试题分析:作辅助线构造出全等三角形是解题的关键,也是本题的难点.如图:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD和△OCE全等,根据全等三角形对应边相等可得OE=AD,CE=OD,然后根据点C在第二象限写出坐标即可.∴点C的坐标为(-,1)故选A.考点:1、全等三角形的判定和性质;2、坐标和图形性质;3、正方形的性质.3.A解析:A【解析】 【分析】观察函数图象结合点P 的坐标,即可得出不等式的解集. 【详解】解:观察函数图象,可知:当3x ≤时,4kx b +≤. 故选:A . 【点睛】考查了一次函数与一元一次不等式以及一次函数的图象,观察函数图象,找出不等式4kx b +≤的解集是解题的关键. 4.B解析:B 【解析】 【分析】依据作图即可得到AC =AN =4,BC =BM =3,AB =2+2+1=5,进而得到AC 2+BC 2=AB 2,即可得出△ABC 是直角三角形. 【详解】如图所示,AC =AN =4,BC =BM =3,AB =2+2+1=5, ∴AC 2+BC 2=AB 2,∴△ABC 是直角三角形,且∠ACB =90°, 故选B .【点睛】本题主要考查了勾股定理的逆定理,如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2,那么这个三角形就是直角三角形.5.B解析:B 【解析】 【分析】根据两函数图象平行k 相同,以及平移规律“左加右减,上加下减”即可判断 【详解】∵将直线1l 向下平移若干个单位后得直线2l , ∴直线1l ∥直线2l ,∴12k k =,∵直线1l 向下平移若干个单位后得直线2l ,∴12b b >,∴当x 5=时,12y y >故选B .【点睛】本题考查图形的平移变换和函数解析式之间的关系,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标左移加,右移减;纵坐标上移加,下移减.平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.6.A解析:A【解析】【分析】利用正方形的判定方法分别判断后即可确定正确的选项.【详解】A 、对角线相等的菱形是正方形,正确,是真命题;B 、对角线相等的平行四边形是矩形,故错误,是假命题;C 、对角线互相垂直的平行四边形是菱形,故错误,是假命题;D 、对角线互相垂直平分的四边形是菱形,故错误,是假命题,故选:A .【点睛】考查了命题与定理的知识,解题的关键是了解正方形的判定方法.7.C解析:C【解析】【分析】根据图形,利用折叠的性质,折叠前后形成的图形全等,对应角相等,利用平角定义ABC ∠+A BC '∠+E BD '∠+EBD ∠=180°,再通过等量代换可以求出CBD ∠. 【详解】解:∵长方形纸片按如图所示的方式折叠,,BC BD 为折痕∴A BC ABC '∠=∠,E BD EBD '∠=∠∵ABC ∠+A BC '∠+E BD '∠+EBD ∠=180°(平角定义)∴A BC '∠+A BC '∠+E BD '∠+E BD '∠=180°(等量代换)A BC '∠+E BD '∠=90°即CBD ∠=90°故选:C .【点睛】本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.8.D解析:D【解析】【分析】由题意可知:中间小正方形的边长为:-a b ,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.【详解】解:由题意可知:中间小正方形的边长为:-a b每一个直角三角形的面积为:118422ab =⨯= 214()252ab a b ∴⨯+-= 2()25169a b ∴-=-=3a b ∴-=故选:D【点睛】本题考查勾股定理的运用,稍有难度;利用大正方形与小正方形、直角三角形面积之间的等量关系是解答本题的关键.9.D解析:D【解析】【分析】【详解】12===. 故选:D. 10.D解析:D【解析】【分析】根据描述,图像应分为三段,学校离家最远,故初始时刻s最大,到家,s为0,据此可判断.【详解】因为小明家所在学校离家距离为2千米,某天他放学后骑自行车回家,行使了5分钟后,因故停留10分钟,继续骑了5分钟到家,所以图象应分为三段,根据最后离家的距离为0,由此可得只有选项DF符合要求.故选D.【点睛】本题要求正确理解函数图象与实际问题的关系,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.11.B解析:B【解析】【分析】【详解】解:对角线互相垂直平分的四边形为菱形.已知对角线AC、BD互相垂直,则需添加条件:AC、BD互相平分故选:B12.B解析:B【解析】【分析】由矩形ABCD可得:S△AOD=14S矩形ABCD,又由AB=15,BC=20,可求得AC的长,则可求得OA与OD的长,又由S△AOD=S△APO+S△DPO=12OA•PE+12OD•PF,代入数值即可求得结果.【详解】连接OP,如图所示:∵四边形ABCD是矩形,∴AC=BD,OA=OC=12AC,OB=OD=12BD,∠ABC=90°,S△AOD=14S矩形ABCD,∴OA =OD =12AC , ∵AB =15,BC =20, ∴AC =22AB BC +=221520+=25,S △AOD =14S 矩形ABCD =14×15×20=75, ∴OA =OD =252, ∴S △AOD =S △APO +S △DPO =12OA •PE +12OD •PF =12OA •(PE +PF )=12×252(PE +PF )=75,∴PE +PF =12. ∴点P 到矩形的两条对角线AC 和BD 的距离之和是12.故选B .【点睛】本题考查了矩形的性质、勾股定理、三角形面积.熟练掌握矩形的性质和勾股定理是解题的关键.13.C解析:C【解析】∵树的折断部分与未断部分、地面恰好构成直角三角形,且BC=5m ,AB=12m , ∴22AB BC +22125+=13m ,∴这棵树原来的高度=BC+AC=5+13=18m.故选C.14.C解析:C【解析】【分析】观察图形,找出图中的直角三角形,利用勾股定理解答即可.【详解】首先根据圆柱的高,知筷子在杯内的最小长度是8cm ,则在杯外的最大长度是24-8=16cm ;再根据勾股定理求得筷子在杯内的最大长度是(如图)2222158AB BC +=+,则在杯外的最小长度是24-17=7cm ,所以h 的取值范围是7cm ≤h ≤16cm ,故选C.【点睛】本题考查了勾股定理的应用,注意此题要求的是筷子露在杯外的取值范围.主要是根据勾股定理求出筷子在杯内的最大长度.15.C解析:C【解析】试题解析:∵∠AEB=90°,AE=6,BE=8,∴22226810AE BE+=+=∴S阴影部分=S正方形ABCD-S Rt△ABE=102-168 2⨯⨯=100-24=76.故选C.考点:勾股定理.二、填空题16.∠ABC=90°【解析】分析:由题意知四边形DEBF是平行四边形再通过证明一组邻边相等可知四边形DEBF是菱形进而得出∠ABC=90°时四边形BEDF是正方形详解:当△ABC满足条件∠ABC=90°解析:∠ABC=90°【解析】分析: 由题意知,四边形DEBF是平行四边形,再通过证明一组邻边相等,可知四边形DEBF是菱形, 进而得出∠ABC=90°时,四边形BEDF是正方形.详解: 当△ABC满足条件∠ABC=90°,四边形DEBF是正方形.理由:∵DE∥BC,DF∥AB,∴四边形DEBF是平行四边形∵BD是∠ABC的平分线,∴∠EBD=∠FBD,又∵DE∥BC,∴∠FBD=∠EDB,则∠EBD=∠EDB,∴BE=DE.故平行四边形DEBF是菱形,当∠ABC=90°时,菱形DEBF是正方形.故答案为:∠ABC=90°.点睛: 本题主要考查了菱形、正方形的判定,正确掌握菱形以及正方形的判定方法是解题关键.17.答案不唯一如∠ACB=90°或∠BAC=45°或∠B=45°【解析】【分析】先证明四边形ADCF是平行四边形再证明AC=DF即可再利用∠ACB=90°得出答案即可【详解】∠ACB=90°时四边形AD解析:答案不唯一,如∠ACB=90°或∠BAC=45°或∠B=45°【解析】【分析】先证明四边形ADCF是平行四边形,再证明AC=DF即可,再利用∠ACB=90°得出答案即可.【详解】∠ACB=90°时,四边形ADCF是正方形,理由:∵E是AC中点,∴AE=EC,∵DE=EF,∴四边形ADCF是平行四边形,∵AD=DB,AE=EC,∴DE=12 BC,∴DF=BC,∵CA=CB,∴AC=DF,∴四边形ADCF是矩形,点D. E分别是边AB、AC的中点,∴DE//BC,∵∠ACB=90°,∴∠AED=90°,∴矩形ADCF是正方形.故答案为∠ACB=90°.【点睛】此题考查正方形的判定,解题关键在于掌握判定法则18.27°【解析】【分析】连接AE先证Rt△ABD≌Rt△CBD得出四边形ABCE是菱形根据菱形的性质可推导得到∠E的大小【详解】如下图连接AE∵BE⊥AC∴∠ADB=∠BDC=90°∴△ABD和△CB解析:27°【解析】【分析】连接AE,先证Rt△ABD≌Rt△CBD,得出四边形ABCE是菱形,根据菱形的性质可推导得到∠E 的大小.【详解】如下图,连接AE∵BE ⊥AC ,∴∠ADB=∠BDC=90°∴△ABD 和△CBD 是直角三角形在Rt △ABD 和Rt △CBD 中AB BC BD BD=⎧⎨=⎩ ∴Rt △ABD ≌Rt △CBD∴AD=DC∵BD=DE∴在四边形ABCE 中,对角线垂直且平分∴四边形ABCE 是菱形∵∠ABC=54°∴∠ABD=∠CED=27°故答案为:27°【点睛】本题考查菱形的证明和性质的运用,解题关键是先连接AE ,然后利用证Rt △ABD ≌Rt △CBD 推导菱形.19.3或6【解析】【分析】先表示出AB 坐标分①当∠ABD=90°时②当∠ADB=90°时③当∠DAB=90°时建立等式解出b 即可【详解】解:①当∠ABD=90°时如图1则∠DBC+∠ABO=90°∴∠D解析:3或6【解析】【分析】先表示出A 、B 坐标,分①当∠ABD=90°时,②当∠ADB=90°时,③当∠DAB=90°时,建立等式解出b 即可.【详解】解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,,∴∠DBC=∠BAO ,由直线y x b =-+交线段OC 于点B ,交x 轴于点A 可知OB=b ,OA=b ,∵点C (0,6),∴OC=6,∴BC=6-b ,在△DBC 和△BAO 中,DBC BAO DCB AOB BD AB ∠∠⎧⎪∠∠⎨⎪⎩=== ∴△DBC ≌△BAO (AAS ),∴BC=OA ,即6-b=b ,∴b=3;②当∠ADB=90°时,如图2,作AF ⊥CE 于F ,同理证得△BDC ≌△DAF ,∴CD=AF=6,BC=DF ,∵OB=b ,OA=b ,∴BC=DF=b-6,∵BC=6-b ,∴6-b=b-6,∴b=6;③当∠DAB=90°时,如图3,作DF ⊥OA 于F ,同理证得△AOB ≌△DFA ,∴OA=DF ,∴b=6;综上,b 的值为3或6,故答案为3或6.【点睛】本题考查了一次函数图像上点的坐标特征,等腰直角三角形的性质,三角形全等的判定和性质,作辅助线构建求得三角形上解题的关键.20.20【解析】【分析】通过矩形的性质可得再根据∠AOB=120°可证△AOD 是等边三角形即可求出OD 的长度再通过证明四边形CODE 是菱形即可求解四边形CODE 的周长【详解】∵四边形ABCD 是矩形∴∵∠解析:20【解析】【分析】通过矩形的性质可得OD OA OB OC ===,再根据∠AOB=120°,可证△AOD 是等边三角形,即可求出OD 的长度,再通过证明四边形CODE 是菱形,即可求解四边形CODE 的周长.【详解】∵四边形ABCD 是矩形∴OD OA OB OC ===∵∠AOB=120°∴18060AOD AOB =︒-=︒∠∠∴△AOD 是等边三角形∵5AD =∴5OD OA ==∴5OD OC ==∵CE//BD ,DE//AC∴四边形CODE 是平行四边形∵5OD OC ==∴四边形CODE 是菱形∴5OD OC DE CE ====∴四边形CODE 的周长20OD OC DE CE =+++=故答案为:20.【点睛】本题考查了四边形的周长问题,掌握矩形的性质、等边三角形的性质、菱形的性质以及判定定理是解题的关键.21.【解析】【分析】过C作CD⊥AB于D根据勾股定理的逆定理可得该三角形为直角三角形然后再利用三角形的面积公式即可求解【详解】如图设AB=25是最长边AC=15BC=20过C作CD⊥AB于D∵AC2+B解析:【解析】【分析】过C作CD⊥AB于D,根据勾股定理的逆定理可得该三角形为直角三角形,然后再利用三角形的面积公式即可求解.【详解】如图,设AB=25是最长边,AC=15,BC=20,过C作CD⊥AB于D.∵AC2+BC2=152+202=625,AB2=252=625,∴AC2+BC2=AB2,∴∠C=90°.∵S△ACB=12AC×BC=12AB×CD,∴AC×BC=AB×CD,∴15×20=25CD,∴CD=12(cm).故答案为12.【点睛】本题考查了勾股定理的逆定理和三角形的面积公式的应用.根据勾股定理的逆定理判断三角形为直角三角形是解答此题的突破点.22.【解析】试题解析:根据题意将周长为8的△ABC沿边BC向右平移1个单位得到△DEF则AD=1BF=BC+CF=BC+1DF=AC又∵AB+BC+AC=10∴四边形ABFD的周长= AD+AB+BF+D解析:【解析】试题解析:根据题意,将周长为8的△ABC沿边BC向右平移1个单位得到△DEF,则AD=1,BF=BC+CF=BC+1,DF=AC,又∵AB+BC+AC=10,∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.考点:平移的性质.23.7【解析】【分析】根据题目中的数据和方差的定义可以求得所求数据的方差【详解】设一组数据135a8的平均数是另一组数据111315+1018的平均数是+10∵=07∴==07故答案为07【点睛】本题考解析:7【解析】【分析】根据题目中的数据和方差的定义,可以求得所求数据的方差.【详解】设一组数据1,3,5,a,8的平均数是x,另一组数据11,13,15,x+10,18的平均数是x+10,∵22222 (1)(3)(5)()(8)5x x x a x x-+-+-+-+-=0.7,∴222 (1110)(1310)(1810)5x x x--+--+⋯--=22222 (1)(3)(5)()(8)5x x x a x x -+-+-+-+-=0.7,故答案为0.7.【点睛】本题考查方差,解答本题的关键是明确题意,利用方差的知识解答.24.2【解析】试题分析:先由平均数计算出a=4×5-2-3-5-6=4再计算方差(一般地设n个数据x1x2…xn的平均数为=()则方差=)==2考点:平均数方差解析:2【解析】试题分析:先由平均数计算出a=4×5-2-3-5-6=4,再计算方差(一般地设n个数据,x1,x2,…x n的平均数为x,x=1n(12nx x x++⋯+),则方差2 S=1n[222 12nx xx x x x-+-+⋯+-()()()]),2 S=15[222222434445464-+-+-+-+-()()()()()]=2.考点:平均数,方差25.2【解析】试题分析:根据方差的性质当一组数据同时加减一个数时方差不变进而得出答案∵一组数据12345的方差为2∴则另一组数据1112131415的方差为2故答案为2考点:方差解析:2【解析】试题分析:根据方差的性质,当一组数据同时加减一个数时方差不变,进而得出答案.∵一组数据1,2,3,4,5的方差为2,∴则另一组数据11,12,13,14,15的方差为2.故答案为2考点:方差三、解答题26.(1)A(3,0),B(0,2);(2)3;(3)P (34,32),y=-6x+6 【解析】【分析】(1)已知直线y 1的解析式,分别令x=0和y=0即可求出A 和B 的坐标;(2)根据(1)中求出的A 和B 的坐标,可知OA 和OB 的长,利用三角形的面积公式即可求出S △ABO ;(3)由(2)中的S △ABO ,可推出S △APC 的面积,求出y p ,继而求出点P 的坐标,将点C 和点P 的坐标联立方程组求出k 和b 的值后即可求出函数解析式.【详解】解:(1)∵一次函数的解析式为y 1=-23x+2, 令x=0,得y 1=2,∴B(0,2),令y 1=0,得x=3,∴A(3,0);(2)由(1)知:OA=3,OB=2,∴S △ABO =12OA•OB=12×3×2=3; (3)∵12S △ABO =12×3=32,点P 在第一象限, ∴S △APC =12AC•y p =12×(3-1)×y p =32, 解得:y p =32, 又点P 在直线y 1上, ∴32=-23x+2, 解得:x=34, ∴P 点坐标为(34,32), 将点C(1,0)、P(34,32)代入y=kx+b 中,得 03324k b k b =+⎧⎪⎨=+⎪⎩,解得:66kb=-⎧⎨=⎩.故可得直线CP的函数表达式为y=-6x+6.【点睛】本题是一道一次函数综合题,考查了一次函数的性质、三角形的面积公式、待定系数法求解一次函数的解析式等知识点,解题关键是根据S△APC =12AC•y p求出点P的纵坐标,难度中等.27.(1)详见解析(2)详见解析(3)58【解析】【分析】(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCP=∠DCP,然后利用“边角边”证明即可.(2)根据全等三角形对应角相等可得∠CBP=∠CDP,根据等边对等角可得∠CBP=∠E,然后求出∠DPE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证.(3)根据(2)的结论解答:与(2)同理可得:∠DPE=∠ABC=58°.【详解】解:(1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,∵在△BCP和△DCP中,BC DCBCP DCPPC PC=⎧⎪∠=∠⎨⎪=⎩,∴△BCP≌△DCP(SAS).(2)证明:由(1)知,△BCP≌△DCP,∴∠CBP=∠CDP.∵PE=PB,∴∠CBP=∠E.∴∠CDP=∠E.∵∠1=∠2(对顶角相等),∴180°﹣∠1﹣∠CDP=180°﹣∠2﹣∠E,即∠DPE=∠DCE.∵AB ∥CD ,∴∠DCE=∠ABC .∴∠DPE=∠ABC .(3)解:在菱形ABCD 中,BC=DC ,∠BCP=∠DCP ,在△BCP 和△DCP 中,BC DC BCP DCP PC PC =⎧⎪∠=∠⎨⎪=⎩∴△BCP ≌△DCP (SAS ),∴∠CBP=∠CDP ,∵PE=PB ,∴∠CBP=∠E ,∴∠DPE=∠DCE ,∵AB ∥CD ,∴∠DCE=∠ABC ,∴∠DPE=∠ABC=58°,故答案为:58.28.-【解析】【分析】①直接利用完全平方公式将原式变形进而得出答案;②直接利用完全平方公式将原式变形进而得出答案.【详解】先阅读下列材料,再解决问题:①填上适当的数:====②解:原式==325=+=【点睛】本题主要考查了二次根式的性质与化简,正确应用完全平方公式时关键是记住公式形式,把握公式特征. 29.【解析】【分析】原式第一项利用平方根定义计算,第二项利用零指数幂法则计算,第三项利用负指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果.【详解】解:原式=8-1+4-5=6.【点睛】本题考查实数的运算;零指数幂;负整数指数幂.30.(1)483x-≤≤;(2)x=25或2.【解析】【分析】(1)根据二次根式的被开方数为非负数,列不等式组求解;(2)根据a、b、c分别作直角三角形的斜边,由勾股定理分别求解.【详解】解:(1)由二次根式的性质,得80 34020xxx-≥⎧⎪+≥⎨⎪+≥⎩,解得48 3x-≤≤;(2)当c为斜边时,由a2+b2=c2,即8-x+3x+4=x+2,解得x=-10,当b为斜边时,a2+c2=b2,即8-x+x+2=3x+4,解得x=2,当a为斜边时,b2+c2=a2,即3x+4+x+2=8-x,解得x=2 5∵48 3x-≤≤∴x=25或2.【点睛】本题考查二次根式的性质及勾股定理的运用.在没有指定直角三角形的斜边的情况下,注意分类讨论.。
八年级下册语文期末考试试题 2

期末考试试题(二)一、语文积累1.阅读下面文字,把文中拼音所表示的汉字依次写在文下横线上。
在生命的旅途中,能拥有来自四面八方的各种提醒,该是多么令人欢xīn 鼓舞啊。
那是一双双关切的眼睛在注视着我们的前行;那是一块块清xī的路标;指引我们前进的方向,那是迷茫中的一zhǎn 灯,那是陶醉时的一lǚ清风,那是求索中的一份勉励,那是落寞时的一语问询……2.下列加横线词语使用正确的一项是 ( )A.他的事迹如此感人,我们觉得应该大肆宣扬。
B.春天来了,天空中的鸟儿都销声匿迹了。
C.沙漠地区并不完全是不毛之地,其中也有一些草木葱茏的绿州。
D.举世闻名的恐怖头子近日被边防军击毙了。
3.下边是病句的一项()A.我们应该探骊得珠,进一步寻求余光中的《乡愁》大获成功的深层原因,这样不仅可以把此诗的解读引向深入,而且还可以引申出新诗艺术成败的规律性因素。
B.一部作品是否真实,不在于它“如实地”描写了事实或现象,而在于它通过生活现象的描写反映了生活的真实面貌。
C.在老师和同学们的帮助下,他的学习成绩有了很大进步。
D.只有坚持不懈的刻苦努力,才能取得优异的成绩。
4.口语交际:小明向外人介绍家人,下列哪一项称谓的使用是正确的()A.先父..目前任职私人企业,工作非常忙碌。
B.令堂..喜爱阅读,营造了家中浓郁的读书风气。
C.尊兄..擅长运动,尤其热衷篮球。
D.敝妹..活泼可爱,是全家人的开心果。
5.下面语句排序最恰当的是()①首先设法安慰自己,树立信心,镇定情绪,消除心理障碍。
②遇到无法下笔,思路阻塞,判断不清的难题时,不要着急。
③心里平静后再冷静思考就不怕难题了。
④这时候,你应该想:我难,别人也难,何必畏惧呢?A.②③④① B.①④②③ C.②①④③ D.①④③②二、知识积累及运用6.默写、理解识记①辛苦遭逢起一经,。
②,下者飘转沉塘坳。
③,愁云惨淡万里凝。
④,西出阳关无故人。
⑤《己亥杂诗》中,作者以落花为喻,表明心志的句子是:__________ ___,。
人教版语文八年级(下)期末质量测试卷2(附答案)

语文八年级(下)期末质量测试卷注意事项:1.答卷前,考生务必将自己的学校、班级、姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
非网阅学校的考生,请将相关信息填在答题卡密封线内。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.非选择题用0.5毫米黑色墨水签字笔将答案直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、积累与运用。
(26分,1—7题各3分,第8题5分。
)1.下列选项中,加点字注音完全正确的一项是()。
A.束缚.(fù)拾.级(shí)狩.猎(shǒu)风雪载.途(zài)B.颠簸(bō)瞭.望(liào)褶.皱(zhé)强.词夺理(qiǎn g)C.闭塞.(sè)脑畔.(pàn)拙.劣(zhuō)悄怆幽邃.(suì)D.斡.旋(wò)腈.纶(qín g)归省.(xĭn)怒不可遏.(è)2.下列选项中,词语书写完全正确的一项()。
A.狡辩震憾自圆其说周而覆始B.羁绊抉择戛然而止纷至沓来C.巉竣诬蔑相辅相承不修边幅D.绚丽维幕人情事故名副其实3.依次填入下面句中横线处的词语最恰当的一项是()。
周国平说,我不认为读书可以成为时尚,并且对一切成为时尚的读书持态度。
读书属于个人的精神生活,必定是非常个人化的。
可以成为时尚的不是读书,而是买书和谈书。
譬如说,在媒体的下,某一时期有某一本书特别畅销,谈论它显得很,插不上嘴便显得很。
A.怀疑指导前卫守旧B.疑惑干扰合群落伍C.疑惑熏陶现代保守D.怀疑影响时髦落后4.下列句子中加点的成语使用不正确的一项是()。
A.没有一个人的成功是容易的,每一个成功者的背后,总有一些鲜为人知....的心酸故事。
人教版八年级数学下册期末测试卷(二)(原卷+解析)

人教版八年级数学下册期末测试卷(二)一.选择题(共10小题,满分30分,每小题3分)1.(3分)已知|a|=5,=7,且|a+b|=a+b,则a﹣b的值为()A.2或12B.2或﹣12C.﹣2或12D.﹣2或﹣12 2.(3分)一组数据3、2、1、2的方差是()A.0.25B.0.5C.1D.23.(3分)已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD 是平行四边形的是()A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B 4.(3分)已知关于x的一次函数y=(k2+1)x﹣2图象经过点A(3,m)、B(﹣1,n),则m,n的大小关系为()A.m≥n B.m>n C.m≤n D.m<n5.(3分)一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为t,剩下的水量为s.下面能反映s与t之间的关系的大致图象是()A.B.C.D.6.(3分)函数y=+(x﹣5)﹣2中自变量x的取值范围是()A.x≥3且x≠5B.x>3且x≠5C.x<3且x≠5D.x≤3且x≠5 7.(3分)在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是()A.96分、98分B.97分、98分C.98分、96分D.97分、96分8.(3分)下列各组线段中,不能构成直角三角形的是()A.1、、B.、、C.2、、D.1、2、9.(3分)如图,在矩形ABCD中,点M从点B出发沿BC向点C运动,点E、F分别是AM、MC的中点,则EF的长随着M点的运动()A.不变B.变长C.变短D.先变短再变长10.(3分)如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB 上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是()A.1.2B.1.5C.2.4D.2.5二.填空题(共6小题,满分18分,每小题3分)11.(3分)计算(+2)2的结果等于.12.(3分)如图,把一张平行四边形纸片ABDC沿BC对折,使点D落在E处,BE与AC 相交于点O,若∠DBC=15°,则∠BOC=度.13.(3分)李刚师范大学毕业后参加了某市教育局组织的教师招聘考试,这次考试包括笔试、面试两项,其笔试、面试成绩按3:7的比例确定各人的最终成绩.考试结束后他笔试、面试的成绩分别为90分、96分,那么李刚参加这次招聘考试的最终成绩为分.14.(3分)已知直线y=kx+b在y轴上的截距为3,且经过点(1,4),那么这条直线的表达式为.15.(3分)如图,E,F,M分别是正方形ABCD三边的中点,CE与DF交于N,连接AM,AN,MN对于下列四个结论:①AM∥CE;②DF⊥CE;③AN=BC;④∠AND=∠CMN.其中正确的是.(填序号)16.(3分)如图,在边长为6的等边△ABC中,D为AC上一点,AD=2,P为BD上一点,连接CP,以CP为边,在PC的右侧作等边△CPQ,连接AQ交BD延长线于E,当△CPQ面积最小时,QE=.三.解答题(共8小题,满分72分)17.(8分)计算:(1)﹣﹣;(2)×÷;(3)(﹣3)÷2.18.(8分)元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.(1)求小黄出发0.5小时时,离家的距离;(2)求出AB段的图象的函数解析式;(3)小黄出发1.5小时时,离目的地还有多少千米?19.(8分)如图,一次函数y1=﹣x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数y2=﹣x图象交于点C(﹣2,n).(1)求m和n的值;(2)求△OAC的面积;(3)问:在y轴上,是否存在一点P,使得S△BCP=S△OAC?若存在,直接写出点P的坐标;若不存在,请说明理由.20.(10分)如图,在▱ABCD中,∠BAD,∠ADC的平分线AF,DE分别与线段BC交于点F,E,AF与DE交于点G.(1)求证:AF⊥DE,BF=CE.(2)若AD=10,AB=6,AF=8,求DE的长度.21.(8分)某工厂生产某种产品,3月份的产量为6000件,4月份的产量为9000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.(1)4月份随机抽取的若干件产品中位数在组;(2)4月份生产的该产品抽样检测的合格率是;(3)在3月份和4月份生产的产品中,估计哪个月的不合格件数多?为什么?22.(8分)如图,在△ABC中,AB=AC,∠ABC的角平分线交AC于点D,过点A作AE ∥BC交BD的延长线于点E.(1)若∠BAC=50°,求∠E的度数.(2)若F是DE上的一点,且AD=AF,求证:BF=DE.23.(10分)(1)观察猜想:如图1,在△ABC中,tan B=1,AB=AC=3,AD是∠BAC的平分线,以CD为一边作正方形CDEF,点E与点A重合,则=.(2)类比探究:在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE、CE、AF,(1)中的结论是否成立?请按图2加以证明.(3)问题解决:当正方形CDEF旋转到B、E、F三点共线时,请直接写出线段AF的长.24.(12分)如图,平面直角坐标系xOy中,直线y=﹣x+3交x轴于点A,交y轴于点B,点P是线段OA上一动点(不与点A重合),过点P作PC⊥AB于点C.(1)当点P是OA中点时,求△APC的面积;(2)连接BP,若BP平分∠ABO,求此时点P的坐标;(3)设点D是x轴上方的坐标平面内一点,若以点O,B,C,D为顶点的四边形是菱形,求点D的坐标及此时OP的长.2021年人教版八年级数学下册期末测试卷(二)参考答案与试题解析一.选择题(共10小题,满分30分,每小题3分)1.(3分)已知|a|=5,=7,且|a+b|=a+b,则a﹣b的值为()A.2或12B.2或﹣12C.﹣2或12D.﹣2或﹣12【分析】首先分别根据绝对值的和算术平方根的定义可求出a,b的值,然后把a,b的值代入|a+b|=a+b中,最终确定a,b的值,然后求解.【解答】解:∵|a|=5,∴a=±5,∵=7,∴b=±7,∵|a+b|=a+b,∴a+b>0,所以当a=5时,b=7时,a﹣b=5﹣7=﹣2,当a=﹣5时,b=7时,a﹣b=﹣5﹣7=﹣12,所以a﹣b的值为﹣2或﹣12.故选:D.【点评】此题主要考查了绝对值的意义:即正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值还是0.也利用了算术平方根的定义.2.(3分)一组数据3、2、1、2的方差是()A.0.25B.0.5C.1D.2【分析】先求出这组数据的平均数,然后代入方差公式求出即可.【解答】解:这组数据的平均数为:(3+2+1+2)÷4=2;则方差为:S2==,故选:B.【点评】此题主要考查了方差的有关知识,正确的求出平均数,并正确代入方差公式是解决问题的关键.3.(3分)已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD 是平行四边形的是()A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.【解答】解:如图所示:∵AB∥CD,∴∠B+∠C=180°,当∠A=∠C时,则∠A+∠B=180°,故AD∥BC,则四边形ABCD是平行四边形.故选:C.【点评】此题主要考查了平行线的判定与性质以及平行四边形的判定,得出AD∥BC是解题关键.4.(3分)已知关于x的一次函数y=(k2+1)x﹣2图象经过点A(3,m)、B(﹣1,n),则m,n的大小关系为()A.m≥n B.m>n C.m≤n D.m<n【分析】由偶次方非负可得出k2+1>0,利用一次函数的性质可得出y值随x值的增大而增大,再结合3>﹣1可得出m>n,此题得解.【解答】解:∵k2≥0,∴k2+1>0,∴y值随x值的增大而增大.又∵3>﹣1,∴m>n.故选:B.【点评】本题考查了一次函数的性质,牢记“k>0,y随x的增大而增大;k<0,y随x 的增大而减小”是解题的关键.5.(3分)一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为t,剩下的水量为s.下面能反映s与t之间的关系的大致图象是()A.B.C.D.【分析】根据抽水时间的增加,剩下的水量逐渐减少;停止时剩下的水量不变,两台抽水机同时工作抽水速度增大,剩下的水量迅速减少,可得答案.【解答】解:由题意,随着抽水时间的增加,剩下的水量逐渐减少;停止时剩下的水量不变,两台抽水机同时工作抽水速度增大,剩下的水量迅速减少,可得答案.故选:D.【点评】本题考查了函数图象,利用抽水时间确定剩下的水量是解题关键,注意两台抽水机同时工作的剩余水量迅速减少.6.(3分)函数y=+(x﹣5)﹣2中自变量x的取值范围是()A.x≥3且x≠5B.x>3且x≠5C.x<3且x≠5D.x≤3且x≠5【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.【解答】解:依题意有x﹣3>0且x﹣5≠0,解得:x>3且x≠5.故选:B.【点评】本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.7.(3分)在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是()A.96分、98分B.97分、98分C.98分、96分D.97分、96分【分析】利用众数和中位数的定义求解.【解答】解:98出现了9次,出现次数最多,所以数据的众数为98分;共有25个数,最中间的数为第13数,是96,所以数据的中位数为96分.故选:A.【点评】本题考查了众数:一组数据中出现次数最多的数据叫做众数.也考查了中位数.8.(3分)下列各组线段中,不能构成直角三角形的是()A.1、、B.、、C.2、、D.1、2、【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【解答】解:A、12+()2=()2,故能构成直角三角形;B、()2+()2=()2,故能构成直角三角形;C、22+()2≠()2,故不能构成直角三角形;D、12+()2=22,故能构成直角三角形.故选:C.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.9.(3分)如图,在矩形ABCD中,点M从点B出发沿BC向点C运动,点E、F分别是AM、MC的中点,则EF的长随着M点的运动()A.不变B.变长C.变短D.先变短再变长【分析】证明EF为三角形AMC的中位线,那么EF长恒等于定值AC的一半.【解答】解:连接AC,如图所示:∵E,F分别是AM,MC的中点,∴EF=AC,∵C是定点,∴AC是定长,∴无论M运动到哪个位置EF的长不变,故选:A.【点评】此题考查的是进行的性质、三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.10.(3分)如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB 上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是()A.1.2B.1.5C.2.4D.2.5【分析】先由勾股定理求出AB=5,再证四边形CEMF是矩形,得EF=CM,当CM⊥AB时,CM最短,此时EF也最小,则CP最小,然后由三角形面积求出CM=2.4,即可得出答案.【解答】解:连接CM,如图所示:∵∠ACB=90°,AC=3,BC=4,∴AB===5,∵ME⊥AC,MF⊥BC,∠ACB=90°,∴四边形CEMF是矩形,∴EF=CM,∵点P是EF的中点,∴CP=EF,当CM⊥AB时,CM最短,此时EF也最小,则CP最小,∵△ABC的面积=AB×CM=AC×BC,∴CM===2.4,∴CP=EF=CM=1.2,故选:A.【点评】本题考查了矩形的判定与性质、勾股定理、三角形面积以及最小值等知识;熟练掌握矩形的判定与性质是解题的关键.二.填空题(共6小题,满分18分,每小题3分)11.(3分)计算(+2)2的结果等于7+4.【分析】根据完全平方公式可以解答本题.【解答】解:(+2)2=3+4+4=7+4,故答案为:7+4.【点评】本题考查二次根式的混合运算,解答本题的关键是明确二次根式的混合运算的计算方法.12.(3分)如图,把一张平行四边形纸片ABDC沿BC对折,使点D落在E处,BE与AC 相交于点O,若∠DBC=15°,则∠BOC=150度.【分析】由折叠易得∠OCB=∠DBC=15°,由平行四边形对边平行易得∠ACB=∠DBC =15°,利用三角形内角和即可求得所求的角的度数.【解答】解:∵△BEC是△BDC翻折变换的三角形,∴△BEC≌△BDC,∠EBC=∠DBC=15°,∵AC∥BD,∴∠OCB=∠DBC=15°,∴∠BOC=180°﹣∠OCB﹣∠EBC=180°﹣15°﹣15°=150°.故答案为150.【点评】本题考查的是经过翻折变换后的图形与原图形全等的性质,及平行四边形的性质.13.(3分)李刚师范大学毕业后参加了某市教育局组织的教师招聘考试,这次考试包括笔试、面试两项,其笔试、面试成绩按3:7的比例确定各人的最终成绩.考试结束后他笔试、面试的成绩分别为90分、96分,那么李刚参加这次招聘考试的最终成绩为94.2分.【分析】根据笔试和面试所占的权重以及笔试成绩和面试成绩,列出算式,进行计算即可.【解答】解:李刚参加这次招聘考试的最终成绩为=94.2(分).故答案为:94.2.【点评】此题考查了加权平均数,关键是根据加权平均数的计算公式列出算式,用到的知识点是加权平均数.14.(3分)已知直线y=kx+b在y轴上的截距为3,且经过点(1,4),那么这条直线的表达式为y=x+3.【分析】根据“在y轴上的截距为3”计算求出b值,然后代入点(1,4)即可得解.【解答】解:∵直线y=kx+b在y轴上的截距为3,∴b=3,∴y=kx+3,∵经过点(1,4),∴4=k+3,∴k=1,∴这条直线的解析式是y=x+3.故答案是:y=x+3.【点评】本题考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.15.(3分)如图,E,F,M分别是正方形ABCD三边的中点,CE与DF交于N,连接AM,AN,MN对于下列四个结论:①AM∥CE;②DF⊥CE;③AN=BC;④∠AND=∠CMN.其中正确的是①②③.(填序号)【分析】①通过证明四边形AMCE是平行四边形,可得AM∥CE;②由“SAS”可证△DCF≌△CBE,可得∠BCE=∠CDF,由直角三角形的性质可求∠CND=90°;③由直角三角形的性质可得DM=MN,由等腰三角形的性质可得AM垂直平分DN,可得AN=AD=BC;④由等腰三角形的性质和余角的性质可得∠ADN=∠DCN=∠AND=∠CNM,即可求解.【解答】解:∵E,F,M分别是正方形ABCD三边的中点,∴AE=BE=BF=CF=DM=CM,CD∥AB,∴四边形AMCE是平行四边形,∴AM∥CE,故①正确;在△DCF和△CBE中,,∴△DCF≌△CBE(SAS),∴∠BCE=∠CDF,∵∠DCE+∠BCE=90°,∴∠CDF+∠DCN=90°,∴∠CND=90°,∴DF⊥CE,故②正确;∵DF⊥CE,DM=CM,∴DM=MN=CM,∵AM∥CE,∴AM⊥DN,∴AM垂直平分DN,∴AD=AN,∴AN=BC,故③正确;∵AN=BC,∴∠ADN=∠AND,∵DM=MN=CM,∴∠DNM=∠NDM,∠MCN=∠MNC,∵∠ADN+∠CDN=90°,∠CDN+∠DCN=90°,∴∠ADN=∠DCN=∠AND=∠CNM,故④错误,故答案为:①②③.【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质以及垂直平分线的性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.16.(3分)如图,在边长为6的等边△ABC中,D为AC上一点,AD=2,P为BD上一点,连接CP,以CP为边,在PC的右侧作等边△CPQ,连接AQ交BD延长线于E,当△CPQ面积最小时,QE=.【分析】如图,过点D作DF⊥BC于F,由“SAS”可证△ACQ≌△BCP,可得AQ=BP,∠CAQ=∠CBP,由直角三角形的性质和勾股定理可求BD的长,由锐角三角函数可求BP的长,由相似三角形的性质可求AE的长,即可求解.【解答】解:如图,过点D作DF⊥BC于F,∵△ABC,△PQC是等边三角形,∴BC=AC,PC=CQ,∠BCA=∠PCQ=60°,∴∠BCP=∠ACQ,且AC=BC,CQ=PC,∴△ACQ≌△BCP(SAS)∴AQ=BP,∠CAQ=∠CBP,∵AC=6,AD=2,∴CD=4,∵∠ACB=60°,DF⊥BC,∴∠CDF=30°,∴CF=CD=2,DF=CF=2,∴BF=4,∴BD===2,∵△CPQ是等边三角形,∴S△CPQ=CP2,∴当CP⊥BD时,△CPQ面积最小,∴cos∠CBD=,∴,∴BP=,∴AQ=BP=,∵∠CAQ=∠CBP,∠ADE=∠BDC,∴△ADE∽△BDC,∴,∴,∴AE=,∴QE=AQ﹣AE=.【点评】本题考查了全等三角形的判定和性质,等边三角形的性质,锐角三角函数,相似三角形的判定和性质,直角三角形的性质,勾股定理等知识,求出BP的长是本题的关键.三.解答题(共8小题,满分72分)17.(8分)计算:(1)﹣﹣;(2)×÷;(3)(﹣3)÷2.【分析】(1)先化简二次根式,再合并同类二次根式;(2)按二次根式的乘除法法则计算求值即可;(3)先算括号里面的,再除法运算.【解答】解:(1)原式=3﹣×3﹣2=﹣;(2)原式===;(3)原式=(4﹣9)÷2==﹣.【点评】本题考查了二次根式的混合运算,掌握二次根式的运算法则是解决本题的关键.18.(8分)元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.(1)求小黄出发0.5小时时,离家的距离;(2)求出AB段的图象的函数解析式;(3)小黄出发1.5小时时,离目的地还有多少千米?【分析】(1)先运用待定系数法求出OA的解析式,再将x=0.5代入,求出y的值即可;(2)设AB段图象的函数表达式为y=k′x+b,将A、B两点的坐标代入,运用待定系数法即可求解;(3)先将x=1.5代入AB段图象的函数表达式,求出对应的y值,再用156减去y即可求解.【解答】解:(1)设OA段图象的函数表达式为y=kx.∵当x=0.8时,y=48,∴0.8k=48,∴k=60.∴y=60x(0≤x≤0.8),∴当x=0.5时,y=60×0.5=30.故小黄出发0.5小时时,离家30千米;(2)设AB段图象的函数表达式为y=k′x+b.∵A(0.8,48),B(2,156)在AB上,,解得,∴y=90x﹣24(0.8≤x≤2);(3)∵当x=1.5时,y=90×1.5﹣24=111,∴156﹣111=45.故小黄出发1.5小时时,离目的地还有45千米.【点评】本题考查了一次函数的应用及一次函数解析式的确定,解题的关键是通过仔细观察图象,从中整理出解题时所需的相关信息,本题较简单.19.(8分)如图,一次函数y1=﹣x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数y2=﹣x图象交于点C(﹣2,n).(1)求m和n的值;(2)求△OAC的面积;(3)问:在y轴上,是否存在一点P,使得S△BCP=S△OAC?若存在,直接写出点P的坐标;若不存在,请说明理由.【分析】(1)直接利用待定系数法可先确定n的值,然后再把C的坐标代入一次函数y =﹣x+m可得m的值;(2)首先确定A点坐标,进而可得AO的长,再集合C点坐标可得△OAC的面积;(3)根据题意可得S△BCP=PB•|x C|=S△OAC=6,解出PB的值,进而可得P点的坐标.【解答】解:(1)∵点C(﹣2,n)在正比例函数y2=﹣x图象上,∴n=﹣×(﹣2)=3,∴点C的坐标为(﹣2,3).∵点C(﹣2,3)在一次函数y=﹣x+m的图象上,∴3=﹣(﹣2)+m,解得:m=2,∴一次函数解析式为y=﹣x+2.∴m的值为2,n的值为3.(2)当y=0时,0=﹣x+2,解得x=4,∴点a的坐标为(4,0),∴S△OAC=OA•y C=×4×3=6.(3)存在.当x=0时,y=﹣x+2=2,∴B(0,2),∵S△BCP=PB•|x C|=S△OAC=6,∴PB•2=6,∴PB=6,∴点P的坐标为(0,8)或(0,﹣4).【点评】此题主要考查了两直线相交问题,关键是掌握待定系数法求函数解析式,掌握凡是函数图象经过的点必能满足解析式.20.(10分)如图,在▱ABCD中,∠BAD,∠ADC的平分线AF,DE分别与线段BC交于点F,E,AF与DE交于点G.(1)求证:AF⊥DE,BF=CE.(2)若AD=10,AB=6,AF=8,求DE的长度.【分析】(1)根据平行四边形的性质和平行线的性质得到∠BAD+∠ADC=180°;然后根据角平分线的性质推知∠DAE+∠ADF=∠BAD+∠ADC=90°,即∠AGD=90°.证得∠BAF=∠AFB,由等腰三角形的判定可得出AB=BF,同理可得CD=CE,则可得出结论;(2)过点C作CK∥AF交AD于K,交DE于点I,证明四边形AFCK是平行四边形,∠AGD=∠KID=90°,得出AF=CK=8,由勾股定理求出DI,则可得出答案.【解答】(1)证明:在平行四边形ABCD中,AB∥DC,∴∠BAD+∠ADC=180°.∵AE,DF分别是∠BAD,∠ADC的平分线,∴∠DAE=∠BAE=∠BAD,∠ADF=∠CDF=∠ADC.∴∠DAE+∠ADF=∠BAD+∠ADC=90°.∴∠AGD=90°.∴AE⊥DF.∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,∴∠DAF=∠AFB,又∵∠DAF=∠BAF,∴∠BAF=∠AFB,∴AB=BF,同理可得CD=CE,∴BF=CE;(2)解:过点C作CK∥AF交AD于K,交DE于点I,∵AK∥FC,AF∥CK,∴四边形AFCK是平行四边形,∠AGD=∠KID=90°,∴AF=CK=8,∵∠KDI+∠DKI=90°,∠DIC+∠DCI=90°,∠IDK=∠IDC,∴∠DKI=∠DCI,∴DK=DC=6,∴KI=CI=4,∵AD∥BC,∴∠ADE=∠DEC=∠CDE,∴CE=CD,∵CI⊥DE,∴EI=DI,∵DI===2,∴DE=2DI=4.【点评】本题考查了平行四边形的判定与性质,平行线的性质,等腰三角形的判定与性质,勾股定理,熟练掌握平行四边形的判定与性质是解题的关键.21.(8分)某工厂生产某种产品,3月份的产量为6000件,4月份的产量为9000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.(1)4月份随机抽取的若干件产品中位数在80<x≤90组;(2)4月份生产的该产品抽样检测的合格率是98.4%;(3)在3月份和4月份生产的产品中,估计哪个月的不合格件数多?为什么?【分析】(1)根据频数分布直方图中的数据,可以得到4月份随机抽取的若干件产品中位数在哪一组;(2)根据频数分布直方图中的数据,可以得到4月份生产的该产品抽样检测的合格率;(3)根据统计图中的数据,可以分别计算出3月和4月不合格的件数,然后比较大小即可解答本题.【解答】解:(1)4月份随机抽取的产品数为:8+132+160+200=500,则4月份随机抽取的若干件产品中位数在80<x≤90这一组,故答案为:80<x≤90;(2)4月份生产的该产品抽样检测的合格率为:×100%=98.4%,故答案为:98.4%;(3)4月的不合格件数多,理由:由题意可得,3月的不合格件数为:6000×2%=120,4月的不合格件数为:9000×(1﹣98.4%)=144,∵144>120,∴4月的不合格件数多.【点评】本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.22.(8分)如图,在△ABC中,AB=AC,∠ABC的角平分线交AC于点D,过点A作AE ∥BC交BD的延长线于点E.(1)若∠BAC=50°,求∠E的度数.(2)若F是DE上的一点,且AD=AF,求证:BF=DE.【分析】(1)根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD的度数,最后根据两直线平行,内错角相等求出;(2)根据AAS先证明△ABD≌△AEF,根据全等三角形的对应边相等得出BD=EF,再根据等式的基本性质证出BF=DE.【解答】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵∠BAC=50°,∴∠ABC=(180°﹣∠BAC)=65°,∵BD平分∠ABC,∴∠CBD=∠ABC=32.5°,∵AE∥BC,∴∠E=∠CBD=32.5°.(2)∵BD平分∠ABC,∴∠ABD=∠CBD,∵AE∥BC,∴∠AEF=∠CBD,∴∠ABD=∠AEF,∵AD=AF,∴∠ADF=∠AFD,∵∠ADB=180°﹣∠ADF,∠AFE=180°﹣∠AFD,∴∠ADB=∠AFE,在△ABD与△AEF中,,∴△ABD≌△AEF(AAS),∴BD=EF,∴BD+DF=EF+DF,∴BF=DE.【点评】本题考查了等腰三角形的性质,平行线的性质,角平分线的定义,三角形全等,考核学生的推理能力,证明三角形全等是解题的关键.23.(10分)(1)观察猜想:如图1,在△ABC中,tan B=1,AB=AC=3,AD是∠BAC的平分线,以CD为一边作正方形CDEF,点E与点A重合,则=.(2)类比探究:在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE、CE、AF,(1)中的结论是否成立?请按图2加以证明.(3)问题解决:当正方形CDEF旋转到B、E、F三点共线时,请直接写出线段AF的长.【分析】(1)先判断出△ABD为等腰直角三角形,进而得出AB=AD,即可得出结论;(2)先利用三角函数得出,证明夹角相等即可得出△ACF∽△BCE,进而得出结论;(3)分两种情况计算,当点E在线段BF上时,如图3,先利用勾股定理求出EF=CF =CD=,BF=,即可得出BE的长,借助(2)得出的结论,当点E在线段BF的延长线上,同前一种情况一样即可得出结论.【解答】解:(1)=,理由是:在Rt△ABC中,AB=AC,根据勾股定理得,BC=AB,又∵点D为BC的中点,∴AD⊥BC,∴AB=AD,∵四边形CDEF是正方形,∴AF=EF=AD,∴AB=AF,即=,故答案为:;(2)(1)中的结论成立.证明:∵tan B=1,∴∠ABC=45°,∵AB=AC=3,∴∠ABC=∠ACB=45°,∴∠BAC=90°,∴sin45°=,∴,∵四边形CDEF是正方形,∴∠FEC=45°,∴sin45°==,∴,∵∠FCA=∠ECB,∴△ACF∽△BCE,∴;(3)或.如图2,当点E在线段BF上时,由(1)知CF=EF=CD=,∵在Rt△BCF中,CF=,CB=3,∴BF==,∴BE=BF﹣EF==.由(2)知,∴BE=AF,∴=AF,∴AF=,如图3,当点E在线段BF的延长线上时,同理可得BE=BF+EF=,∴,∴AF=,综上所述,当正方形CDEF旋转到B,E,F三点共线时,线段AF的长为或.【点评】此题是四边形综合题,主要考查了等腰直角三角形的性质,正方形的性质,旋转的性质,相似三角形的判定和性质,熟练掌握正方形的性质及相似三角形的性质是解题的关键.24.(12分)如图,平面直角坐标系xOy中,直线y=﹣x+3交x轴于点A,交y轴于点B,点P是线段OA上一动点(不与点A重合),过点P作PC⊥AB于点C.(1)当点P是OA中点时,求△APC的面积;(2)连接BP,若BP平分∠ABO,求此时点P的坐标;(3)设点D是x轴上方的坐标平面内一点,若以点O,B,C,D为顶点的四边形是菱形,求点D的坐标及此时OP的长.【分析】(1)连接BP,先求出点A(4,0),点B(0,3),可得AO=4,OB=3,由勾股定理可求AB的长,由面积法可求PC的长,由勾股定理可求AC的长,即可求解;(2)由“AAS”可证△BOP≌△BCP,可得BO=BC=3,OP=CP,由勾股定理可求OP 的值,即可求点P坐标;(3)分OB为边和OB为对角线两种情况讨论,利用菱形的性质两点距离公式先求出点C坐标,再求出CP解析式,即可求解.【解答】解:(1)如图,连接BP,∵直线y=﹣x+3交x轴于点A,交y轴于点B,∴点A(4,0),点B(0,3),∴AO=4,OB=3,∴AB===5,∵点P是OA中点,∴AP=OP=2,∵S△ABP=×AP×OB=×AB×CP,∴CP=,∴AC===,∴S△APC=×AC×PC=;(2)∵BP平分∠ABO,∴∠OBP=∠CBP,又∵BP=BP,∠BOP=∠BCP=90°,∴△BOP≌△BCP(AAS),∴BO=BC=3,OP=CP,∴AC=AB﹣BC=5﹣3=2,∵AP2=PC2+AC2,∴(4﹣OP)2=OP2+4,∴OP=,∴点P(,0);(3)若OB为边,如图2,设点C(a,﹣a+3),连接OD,∵四边形OCDB是菱形,∴OC=CD=BD=OB=3,BO∥CD,OD⊥BC,∴(a﹣0)2+(﹣a+3﹣0)2=9,∴a1=0(不合题意舍去),a2=,∴点C(,),∵BO∥CD,OB=CD=3,∴点D(,),∴直线OD解析式为:y=x,∵PC∥OD,∴设直线PC解析式为y=x+b,∴=×+b,∴b=﹣3,∴直线PC解析式为y=x﹣3,∴当y=0时,x=,∴点P(,0),∴OP=;若OB为对角线,如图3,设点C(a,﹣a+3),连接CD,∵四边形OCBD是菱形,∴OB与CD互相垂直平分,∴点C在OB的垂直平分线上,∴=﹣a+3,∴a=2,∴点C(2,),∵BO垂直CD,∴点D(﹣2,),设直线PC解析式为y=x+b,∴=×2+b,∴b=﹣,∴设直线PC解析式为y=x﹣,当y=0时,x=,∴点P(,0),∴OP=;综上所述:当OP=时,点D(﹣2,)或当OP=时,点D(,).【点评】本题是一次函数综合题,考查了待定系数法求解析式,全等三角形的判定和性质,勾股定理,菱形的性质等知识,利用分类讨论思想解决问题是本题的关键.。
【期末卷】四川成都市八年级英语下册期末质量检测卷(二)含答案与解析

四川成都市八年级下册期末质量检测卷(二)英语学校:___________姓名:___________班级:___________考号:___________注意事项:1. 本试卷共四部分,共七大题,满分120分,考试时间100分钟。
2. 请务必在答题卡上答题,在试卷上答题无效。
3. 考试结束后,请将试卷和答题卡一并交回。
一、单选题1.—Alex, don't make a noise. Your brother________ English in the room at the moment.— Sorry, mum. I didn't know that.A.practiced B.practices C.is practicing2.Our teacher kept _______ us that the future would be great for the well-educated. A.asking B.to teach C.telling3.—I wonder in the past.—He was very quiet.A.what was he like B.what he was like C.what does he look like 4.Jenny can play ________ guitar, but she hasn't got ________ guitar at home.A.the, an B.the, a C.a, the5.As a student, we________ be hard-working enough to get good grades in all the subjects. A.can B.should C.may6._________ the player tried his best,he lost the game at last.A.Also B.But C.Although7.—Could you please tell me __________?—Yes. There is one on Center Street.A.where can I buy some stampsB.when you will take your vacationC.if there are any good restaurants here8.Kung Fu League seems much________than Hichki, because few people went to the cinema to watch it.A.less interesting B.interesting C.more interesting9.The beautiful park is situated in Qingcheng mountain and it’s fr ee to everyone.A.is set up B.set in C.is located10.You’d better eat hamburgers, French fries and chocolate less. of them are good for your health.A.None B.All C.Each二、补全对话(五选五)A: Hello, Kevin. You didn't come to my birthday party yesterday. Why?B: 11.A: Your cousin Edison? Do you look alike?B: 12.But Edison is a little taller and stronger than me. He always beats me in basketball.A: 13.B: Yes, we both like reading books and playing computer games.A: That sounds great. 14.Is he outgoing?B: Yes, he's more outgoing than me. He likes making friends.A: Can you introduce him to me?B: Sure. 15.三、完形填空AIt's necessary for young people to improve your sense of direction(方向感). Here 16 the ways to help you.If you are using a map, turn it so it tells the way you are facing.If you leave your bike in a strange place, put it 17 something like a big stone or a tree.Note landmarks (地标)on the way as you go away from your bike. When you return, go back along the 18 road.Count your steps so that you know how 19 you have gone and remember some landmarks 20 buildings or stores. It can help to find out where you are.Now, it's not easy for you to get lost again.16.A.be B.is C.are17.A.beside B.with C.on18.A.wide B.same C.beautiful19.A.fast B.far C.long20.A.at least B.more than C.such asBMy name is Toby. I'm an old man, eighty-three this spring. My house is right in the middle of Stratford-upon-Avon, and I can watch the street market from my window. But I live a very 21 life now. I'm just a man, sitting in a chair.I once knew the 22 man in England. For thirty years I was his friend. I worked with him in the theatre, through 23 the good times and the bad times. He was a good friend to me. He was also the best рlaywright (剧作家) , the best poet, that ever lіved іn Еngland. Willian Ѕhakespeare was his name.I saw all his 24 in the theatre. People loved them. They shouted, laughed and cried, ate oranges, and called for more. 25 kinds of people, kings, queens, princes, great lords and ladies, poor people, the boys who held the horses...everyone came to the theatre. William Shakespeare could please them all.He put me in a play. Well, he 26 my name-Toby. Twelfth Night was 27 play,I remember Sir Toby Belch. He was a big fat man, who 28 drinking too much, staying ina bar and having a good time. Queen Elizabeth the First watched that play-on Twelfth Night, the 6th of January, 1601. She liked it, too.Will's dead now, of course. He's been dead for more than thirty years, and 29 sees his plays now. The Puritans(清教徒) 30 all the theatres. There's no singing, no dancing, no plays. It wasn't like that in my you ng days. We had a good time in London, Will and I…21.A.happy B.quiet C.busy22.A.most different B.healthiest C.greatest23.A.either B.both C.only24.A.diaries B.letters C.plays25.A.All B.Some C.Few26.A.reached B.organized C.used27.A.the B.my C.her28.A.hated B.liked C.started29.A.everyone B.anyone C.no one30.A.closed B.made C.opened四、阅读判断阅读下面短文, 根据短文内容判断句子正误。
2021_2022学年度八年级上学期期末检测卷(二)道德与法治试卷

2021~2022学年度八年级上学期期末检测卷(二)道德与法治试卷(考试范围:上册全部)注意事项:总分70分,考试时间60分钟。
一、单项选择(每小题只有一个最符合题意的选项。
每小题2分,共34分)1.中学生小鄱在2020年国庆期间观看了电影《我和我的家乡》后心潮澎湃,为祖国各地城乡发生的翻天覆地的变化与全面建成小康社会而感到自豪和骄傲。
这体现了亲社会行为中的()A.谦让B.关心社会发展C.分享D.帮助他人2.从不同的角度,根据不同的标准,我们可将社会关系分为不同的类型。
下列体现了业缘关系的是()A.小鄱和小明是邻居B.小梅和小兰是老乡C.小敏和小明是同事D.小军和小红是兄妹3.直播卖酒水单场成交1080万元,这是主播吴一在2020年8月26日的快手百亿补贴专场交出的成绩单。
这体现了()A.网络促进民主政治的进步B.网络为文化传播搭建新平台C.网络为科技创新搭建新平台D.网络为经济发展注入新的活力4.阅读下边漫画,你能从中获得的感悟有()①散布网络谣言是刑事违法行为②增强自我保护意识,自觉远离网络③学会辨析网络信息,让谣言止于智者④自觉遵守道德与法律,做负责任的网民A.①②B.③④C.②④D.①③5.疫情期间,人们进出火车站、高铁站等都要配合进行安全检查、测量体温、佩戴口罩、扫健康码等,体现了人们遵守()A.社会管理秩序B.生产秩序C.交通秩序D.课堂教学秩序6.2020年9月7日,陕西有一家“网红”书店(西安方所创联中心)因为拒绝农民工进店,在网上引发了热议。
当事人李先生说:“保安问我是不是旁边工地上的农民工,我说不是,而且他问了我两遍……”最终,李先生被放行,进入了书店。
这件事让李先生的心里五味杂陈。
这件事警示我们要()①关心他人,物质上帮助他人②平等待人,尊重他人的人格③尊重他人,体会他人的感受④欣赏他人,赞美他人的优点A.①③B.②④C.②③D.①④7.有网友曝光了一组视频,一名网红在高铁上拍视频,不仅外放声音,而且脱了鞋用脚蹬着座椅,做各种夸张的动作和表情,丝毫不顾及他人的感受。
最新八年级英语下学期期末考试卷 (2)

英语试卷卷Ⅰ一、单项选择(15分)1.youto the aquarium last Monday?A.Were,go B.Do,went C.Did,went D.Did,go2.Don't watch TV.It's too late.Pleaseand go to bed right away.A.turn down it B.turn off itC.turn it off D.turn it down3.There is something wrong with my ears.I can't hear.A.clear enough B.clearly enoughC.enough clear D.enough clearly4.Look out!The traffic is moving fast.It's dangerous cross thestreet.A.very;to B.so;that C.enough;to D.too;to5.This is a big class,and of the students are girls.A.two third B.second three C.two thirds D.twothree6.My aunt has two children.But of them lives with her.A.each B.neither C.either D.both7.--I can not see Tom recently.--Oh,heto Canada with his parents.A.went B.has been C.has gone D.have been gone8.Alice has to go to work now,?A.has she B.hasn't she C.doesn't she D.does she9.--Excuse me,can I the book from you?---Sure But you canit for only one week.A.keep,keep B borrow,keep C.borrow,borrowD.keep,borrow10.Whatyouat eight yesterday evening?A.have,done B.did,do C.were,doing D.will,do11.I'm sorry,but Imy homework at home.A.1eft B.forgot C.remembered D.lost12.I saw the teacher come ina few books under his arm.A.to B.for C.behind D.with13.--Do you think theremany people in the theatre?--Yes,there will.A.will be B.will have C.are D.have 14.Remember,boys and girls.you work,you will get.A.The better;the harder B.The harder;the better C.The hard;the better D.The hard;the good 15.I don't like this pair of shoes.Please show me another.A.one B.shoes C.pair D.it二、完形填空(10分)Young people are often unhappy when they are with their parents.They say that theirparents don't 1 them.They often think their parents are too strict with them,and they are never given a 2 hand.Parents often find 3 difficult to win their children's trust (信任)and they seem toforget how they themselves 4 when they were young.For example,young people like todo things without much thinking.It is one of their ways to 5 that theygrow up and theycan do with any difficult things.Older people worry more easily.Most of them plan thingsahead and don't like their plans to be changed.When you want your parents to let you dosomething,you will have better success 6 you ask before you really start doing it.Young people often make their parents angry by clothes they want,the music they enjoyand something else.But they don't 7 to cause any trouble(惹麻烦).They just feel thatin this way they can be cut off(切断)from the old people,s world and they want to make anew culture(文化)of their own.And if their parents don,t like their music or their clothesor their manner of speech,the young people feel very 8 .Sometimes you even don't wantyour parents to say“9 ”to what you do.You want to stay at home alone and do whatyou like.If you plan to control(控制)your 10,you'd better win your parentsover and try toget them to understand you.If your parents see that you have high sense of responsibility(高度责任感),they will certainly give you the right(权利)to do what you want to do.1.A.remember B.help C.understand D.like 2.A.helpful B.useful C.free D.strong 3.A.that B.them C.one D.it 4.A.thought B.wanted C.needed D.felt 5.A.learn B.see C.find D.show 6.A.since B.if C.because D.though 7.A.mean B.care C.like D.decide 8.A.lonely B.happy C.worried D.strange 9.A.Yes B.No C.Sorry D.That's right 10.A.life B.work C.study D.health三、阅读理解(15分)AI can still remember my first day at school.I was only 6 years old at that time.It was avery big room.I sat at the desk near the window,but I couldn't see anything because thewindow was too high.There was a big map of world on the wall and an old blackboard.Idon't think I was worried or afraid at that time.There was another little boy next to me.Hesat there and kept silent at first.Then he began to cry,because hedidn't want to stay there.More and more students came in,but the boy didn't stop crying.“Mom,I want to gohome.”He cried again and again.Later,the teacher came in.She went to the little boy,andsaid something to him.I couldn't hear what she said.Soon the boy stopped crying and beganto smile.To this day,I still don't know what the teacher said to the little boy.判断下列句子的正(T)误(F):1.The writer went to school when he was 6 years old.2.She sat near the window,so she could look outside.3.She was not worried.She was afraid.4.When the teacher came in,the little boy stopped crying.5.The writer knew what the teacher said to the little boy.BThere are many kinds of cars in this world.My grandfather thinks this is because carsare like their drivers.He says,“Rich people have expensive cars,big people have large cars,and old people drive old cars.”But I don't agree with him.My neighbor,Mrs. Hill,is 82 years old.She drives only onTuesday,and then shedrives only to the bank.She never drives more than 30 kilometers an hour.Do you thinkMrs. Hill has a very old and small car?No!Her car is new.It's very large,and it can go 200kilometers an hour!My friend Mike is an artist.He paints beautiful pictures with lots of colors.But his caris black.Mrs.Bates has a very,very old car.It often has some trouble.Does she drive thatkind of car because she is poor?No,she has four restaurants and two million dollars in thebank.My uncle Joe has a very small car.Every Sunday,he drives to the country with hiswife,his three children,his mother and his dog.Now,you have read about my friends and their cars.Do you agree with my grandfather?Maybe you have a car.Does it say something about you?6.The writer's grandfather thinks.A.a person has the same kind of car as himself(herself)B.different people have cars of the same kindC.poor people have large carsD.artists have black cars7.Mrs.Bates has an old car.A.because she is poor B.because she is richC.because she likes old cars D.the passage doesn't tell us why8.Though Uncle Joe has a very small car,.A.he has a dog B.he has a large familyC.he has no children D.he has few members in his family9.The writer's friend Mike paints .A.pictures in black.B.colorful picturesC.colorless pictures D.pictures with only a few colors 10.The writer thinks.A.his grandfather's idea about cars is rightB.cars are often the same as their drivers in many ways C.artists shouldn't drive black carsD.a car doesn't say anything about its ownerCSally was a student.It was going to be her mother's birthday.She wanted to buy her apresent that would be niceand useful but not expensive.A week before her mother's birthday,she went shopping after a quick and simple lunch.When she had been looking for half an hour,she found a shop that was selling cheap umbrellas(伞),and decided to take a black one,since her mother had lost hers the month before.She thought,“You could carry that when you are wearing clothes of any color.”So she decided to buy a lovely black umbrella and took it back to school with her until her classes hadfinished.On her way back home in the train that evening,she felt hungry because she had such asmall lunch that she went along to the buffet car(餐车)for another sandwich and cup ofcoffee.She had left the black umbrella above her seat in the compartment(车厢),but whenshe got back,it had gone!When she had left the compartment,there had been no other passengers(乘客)in it,but now there were three.Sally began to cry when she saw that the umbrella was no longer there.The other passengers felt very sorry for her and asked what the matter was.She told them that theblackumbrella she had bought for her mother was gone,and that she had to get out at the nextstation.After the three other passengers heard it,they asked her for her mother's address so that they could sent the umbrella to her if someone had taken it by mistake and brought itback after Sally had got out of the train.The next week,Sally heard from her mother.It said,“Thank you very much for yourlovely presents,but why did you send me three black umbrellas?”11.Which is of the following is the best for the sentence “You could carry that when you are wearing clothes of anycolor?”A.You can carry it when you are wearing any clothes.B.Any color of your clothes will be all right.C.The umbrella will be OK for your clothes in any colors.D.You can take any clothes that you like to wear.12.What does the story infer(推断)?A.Her mother would write to her if she didn't receive the presents.B.The three umbrella were sent by the girl.C.Only four people had ever been to the compartment.D.Nobody brought the umbrella back.13.How many umbrellas did Sally's mother get at last?A.No.B.Only one.C.Three.D.Four.14.The best name of the story is.A.A Lucky Girl B.The Missing UmbrellaC.A Happy Mother D.Mothers Present15.What does the writer want to tell us?A.You should take care of your things when you are traveling.B.Show your love to others,and they will bring you love.C.Children should often come back to see their parents.D.It's no use crying when you are in trouble.四、情景反应(5分)A:Have you seen Jim these two days?B: 1 He's gone to Japan to see his grandfather.A:2B:Of course!He lived there before he came here.A:3B:Yes,I've just received a letter from himA:4B:He said he had a good time there and would stay for another month.Then he wasgoing to return toEngland.He also wanted me to give his best wishes toyou.A:Oh,well.5卷Ⅱ一、根据首字母填空(7分)1.Beijing is the c of China.2.How much does a bus ticket c?3.In fact,we should also take care not to cough or sneeze loudly in p.4.My English writing is good,but I need to imy listening skills.5.If you study hard,you will have a good cto go to college.6.Ten hundred is one t.7.I often get awhen someone cut in line.二、用动词的适当形式填空(8分)1.I'll go to the park if it(not rain)tomorrow.2.There(be)a football game in our school tomorrow.3.We(study)English for two years.4.My father came into the bedroom while I (dance).5.I think(do)something for someone is the best gift.6.Some students have been skating (raise)money for charity.7.The teacher——(take)away my mobile phone because I used it in class.8.Thank you for(help)me with my English.三、句型转换(10分)1.American fast food seems to be the most popular in theworld.(改为同义句)American fast food is the most popular in the world.2.You sister has never been to Guangzhou.(改为反意疑问句)You sister has never been to Guangzhou,?3.She has been swimming since 2004.(就划线部分提问)has she been swimming?4.He was so happy that he couldn't say a word when he was told the news.(改为简单句)He washappysay a word when he was told the news.5.She says:“I'm going to her house on Friday night.”(变为间接引语)She said going to her house on Friday night.6.I've been a flight attendant for two years.(同意句转换)I a flight attendant two years.7.I think there is going to be an English test next week.(改为否定句)I there going to be an English test next week.8.I have already had my lunch.(变为一般疑问句)youyour lunch?9.He's flying a kite happily.(改为感叹句)he is flying a kite!四、英汉互译(15分)1.你曾经去过游乐园吗?不,没去过。
最新八年级下学期期末数学考试试卷 (解析版) (2)

一、选择题1.下列标志既是轴对称图形又是中心对称图形的是()A.B.C.D.2.已知x>y,则下列不等式成立的是()A.2x<2y B.x﹣6<y﹣6 C.x+5>y+5 D.﹣3x>﹣3y 3.分式的值为0,则x的值为()A.0 B.1 C.﹣1 D.24.若正多边形的内角和是1080°,则该正多边形的一个外角为()A.45°B.60°C.72°D.90°5.下列等式中,从左到右的变形是因式分解的是()A.x(x+1)=x2+x B.x2+xy﹣3=x(x+y)﹣3C.x2+6x+4=(x+3)2﹣5 D.x2+2x+1=(x+1)2 6.关于x的不等式2x﹣a≤﹣1的解集如图所示,则a的取值是()A.﹣1 B.﹣2 C.﹣3 D.07.如图,在▱ABCD中,AB=4,BC=7,∠ABC的平分线交AD 于点E,则ED等于()A.2 B.3 C.4 D.58.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠DBC的度数是()A.36°B.45°C.54°D.72°9.点P到△ABC的三个顶点的距离相等,则点P是△ABC()的交点.A.三条高B.三条角平分线C.三边的垂直平分线D.三条中线10.已知关于x的分式方程=1的解是负数,则m的取值范围是()A.m≤3 B.m≤3且m≠2 C.m<3D.m<3且m≠2二、填空题(每小题4分,共16分)11.分解因式:4﹣m2=.12.如图,在△ABC中,D、E分别为AB、AC边的中点,若DE=2,则BC边的长为.13.如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为.14.如图,在矩形ABCD中,对角线AC与BD交于点O,过点A 作AE⊥BD于点E,已知∠EAD=3∠BAE,则∠EOA=°.三、解答题(本大题共6小题,共54分,答题应写出文字说明、证明过程或演算步骤)15.计算(1)分解因式:x2y﹣2xy2+y3;(2)解不等式组.16.化简:.17.△ABC在平面直角坐标系中的位置如图所示.(1)将△ABC向左平移4个单位长度后得到△A1B1C1,点A1、B1、C1分别是A、B、C的对应点,请画出△A1B1C1,并写出C1的坐标;(2)将△ABC绕点O顺时针旋转90°,得到△A2B2C2,点A2、B2、C2分别是A、B、C的对应点,请画出△A1B1C1,并写出C2的坐标.18.列方程解应用题今年1月下旬以来,新冠肺炎疫情在全国范围内迅速蔓延,而比疫情蔓延速度更快的是口罩恐慌.企业复工复产急需口罩,某大型国有企业向生产口罩的A、B两厂订购口罩,向A厂支付了1.32万元,向B厂支付了2.4万元,且在B厂订购的口罩数量是A厂的2倍,B厂的口罩每只比A厂低0.2元.求A、B两厂生产的口罩单价分别是多少元?19.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数y=k1x+b1和y=kx+b的图象,分别与x 轴交于点A、B,两直线交于点C.已知点A(﹣1,0),B(2,0),观察图象并回答下列问题:(1)关于x的方程k1x+b1=0的解是;关于x的不等式kx+b<0的解集是;(2)直接写出关于x的不等式组的解集;(3)若点C(1,3),求关于x的不等式k1x+b1>kx+b的解集和△ABC的面积.20.如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE,DF.(1)试判断四边形AEDF的形状,并证明你的结论;(2)若∠BAC=60°,AE=6,求四边形AEDF的面积;(3)△ABC满足什么条件时,四边形AEDF是正方形?请说明理由.四、填空题(每小题4分,共20分)21.232﹣1可以被10和20之间某两个整数整除,则这两个数是.22.两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP=cm.23.若关于x的分式方程+=﹣1无解,则常数n的值是.24.如图,Rt△OAB的两直角边OA、OB分别在x轴和y轴上,A (﹣2,0),B(0,4),将△OAB绕O点顺时针旋转90°得到△OCD,直线AC、BD交于点E.点M为直线BD上的动点,点N 为x轴上的点,若以A,C,M,N四点为顶点的四边形是平行四边形,则符合条件的点M的坐标为.25.如图,已知边长为6的菱形ABCD中,∠ABC=60°,点E,F 分别为AB,AD边上的动点,满足BE=AF,连接EF交AC于点G,CE、CF分别交BD于点M,N,给出下列结论:①△CEF是等边三角形;②∠DFC=∠EGC;③若BE=3,则BM=MN=DN;④EF2=BE2+DF2;⑤△ECF面积的最小值为.其中所有正确结论的序号是.五、解答题(本大题共3小题,共30分.其中26题8分,27题10分,28题12分)26.2020年初,“新型冠状病毒”肆虐全国,武汉“封城”.大疫无情人有情,四川在做好疫情防控的同时,向湖北特别是武汉人们伸出了援手,医疗队伍千里驰援、社会各界捐款捐物.某运输公司现有甲、乙两种货车,要将234吨生活物资从成都运往武汉,已知2辆甲车和3辆乙车可运送114吨物资;3辆甲车和2辆乙车可运送106吨物资.(1)求每辆甲车和每辆乙车一次分别能装运多少吨生活物资?(2)从成都到武汉,已知甲车每辆燃油费2000元,乙车每辆燃油费2600元.在不超载的情况下公司安排甲、乙两种车共10辆将所有生活物资运到武汉,问公司有几种派车方案?哪种方案所用的燃油费最少?最低燃油费是多少?27.先阅读下面的内容,再解决问题:问题:对于形如x2+2ax+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2ax﹣3a2,就不能直接运用公式了.此时,我们可以在二次三项式x2+2ax﹣3a2中先加上一项a2,使它与x2+2ax成为一个完全平方式,再减去a2,整个式子的值不变,于是有:x2+2ax﹣3a2=(x2+2ax+a2)﹣a2﹣3a2=(x+a)2﹣4a2=(x+a)2﹣(2a)2=(x+3a)(x﹣a)像这样,先添一适当项,使式中出现完全平方式,再减去这项,使整个式子的值不变的方法称为“配方法”.利用“配方法”,解决下列问题:(1)分解因式:a2﹣8a+15=;(2)若△ABC的三边长是a,b,c,且满足a2+b2﹣14a﹣8b+65=0,c边的长为奇数,求△ABC的周长的最小值;(3)当x为何值时,多项式﹣2x2﹣4x+3有最大值?并求出这个最大值.28.如图1,▱ABCD在平面直角坐标系xOy中,已知点A(﹣1,0)、B(0,4)、C(3,2),点G是对角线AC的中点,过点G 的直线分别与边AB、CD交于点E、F,点P是直线EF上的动点.(1)求点D的坐标和S四边形BEFC的值;(2)如图2,当直线EF交x轴于点H(5,0),且S△PAC=S四边形BEFC时,求点P的坐标;(3)如图3,当直线EF交x轴于点K(3,0)时,在坐标平面内是否存在一点Q,使得以P、A、Q、C为顶点的四边形是矩形?若存在,直接写出点P的坐标;若不存在,请说明理由.参考答案一、选择题(每小题3分,共30分.下列各小题给出的四个选项中,只有一个符合题目要求)1.下列标志既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形与轴对称图形的概念判断即可.解:A、既是轴对称图形,又是中心对称图形.故正确;B、是轴对称图形,不是中心对称图形.故错误;C、不是轴对称图形,是中心对称图形.故错误;D、不是轴对称图形,不是中心对称图形.故错误.故选:A.2.已知x>y,则下列不等式成立的是()A.2x<2y B.x﹣6<y﹣6 C.x+5>y+5 D.﹣3x>﹣3y 【分析】根据不等式的性质逐个判断即可.解:A、∵x>y,∴2x>2y,故本选项不符合题意;B、∵x>y,∴x﹣6>y﹣6,故本选项不符合题意;C、∵x>y,∴x+5>y+5,故本选项符合题意;D、∵x>y,∴﹣3x<﹣3y,故本选项不符合题意;故选:C.3.分式的值为0,则x的值为()A.0 B.1 C.﹣1 D.2【分析】直接利用分式的值为零,则分子为零,且分母不为零,进而得出答案.解:由题意,得x2﹣1=0且x﹣1≠0,解得x=﹣1,故选:C.4.若正多边形的内角和是1080°,则该正多边形的一个外角为()A.45°B.60°C.72°D.90°【分析】首先设这个正多边形的边数为n,根据多边形的内角和公式可得180(n﹣2)=1080,继而可求得答案.解:设这个正多边形的边数为n,∵一个正多边形的内角和为1080°,∴180(n﹣2)=1080,解得:n=8,∴这个正多边形的每一个外角是:360°÷8=45°.故选:A.5.下列等式中,从左到右的变形是因式分解的是()A.x(x+1)=x2+x B.x2+xy﹣3=x(x+y)﹣3C.x2+6x+4=(x+3)2﹣5 D.x2+2x+1=(x+1)2【分析】根据因式分解的定义逐个判断即可.解:A、不是因式分解,故本选项不符合题意;B、不是因式分解,故本选项不符合题意;C、不是因式分解,故本选项不符合题意;D、是因式分解,故本选项符合题意;故选:D.6.关于x的不等式2x﹣a≤﹣1的解集如图所示,则a的取值是()A.﹣1 B.﹣2 C.﹣3 D.0【分析】解关于x的不等式得出x≤,由数轴知不等式的解集即可得出关于a的方程,解之即可.解:移项,得:2x≤a﹣1,系数化为1,得:x≤,由数轴可知=﹣1,解得:a=﹣1,故选:A.7.如图,在▱ABCD中,AB=4,BC=7,∠ABC的平分线交AD 于点E,则ED等于()A.2 B.3 C.4 D.5【分析】由四边形ABCD为平行四边形,得到AD与BC平行,AD=BC,利用两直线平行得到一对内错角相等,由BE为角平分线得到一对角相等,等量代换得到∠ABE=∠AEB,利用等角对等边得到AB=AE=4,由AD﹣AE求出ED的长即可.解:∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC=7,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠AEB=∠ABE,∴AB=AE=4,∴ED=AD﹣AE=BC﹣AE=7﹣4=3.故选:B.8.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠DBC的度数是()A.36°B.45°C.54°D.72°【分析】由已知条件开始,通过线段相等,得到角相等,再由三角形内角和求出各个角的大小.解:设∠A=x°.∵BD=AD,∴∠A=∠ABD=x°,∠BDC=∠A+∠ABD=2x°,∵BD=BC,∴∠BDC=∠BCD=2x°,∵AB=AC,∴∠ABC=∠BCD=2x°,在△ABC中x+2x+2x=180,解得:x=36,∴∠C=∠BDC=72°,∴∠DBC=36°,故选:A.9.点P到△ABC的三个顶点的距离相等,则点P是△ABC()的交点.A.三条高B.三条角平分线C.三边的垂直平分线D.三条中线【分析】根据线段垂直平分线的判定定理解答.解:∵点P到A、B两点的距离相等,∴点P在线段AB的垂直平分线上,同理,点P在线段AC、BC的垂直平分线上,则点P是△ABC三边的垂直平分线的交点,故选:C.10.已知关于x的分式方程=1的解是负数,则m的取值范围是()A.m≤3 B.m≤3且m≠2 C.m<3D.m<3且m≠2【分析】直接解方程得出分式的分母为零,再利用x≠﹣1求出答案.解:=1解得:x=m﹣3,∵关于x的分式方程=1的解是负数,∴m﹣3<0,解得:m<3,当x=m﹣3=﹣1时,方程无解,则m≠2,故m的取值范围是:m<3且m≠2.故选:D.二、填空题(每小题4分,共16分)11.分解因式:4﹣m2=(2+m)(2﹣m).【分析】原式利用平方差公式分解即可.解:原式=(2+m)(2﹣m),故答案为:(2+m)(2﹣m).12.如图,在△ABC中,D、E分别为AB、AC边的中点,若DE=2,则BC边的长为 4 .【分析】根据三角形中位线定理解答即可.解:∵D、E分别为AB、AC边的中点,∴DE是△ABC的中位线,∴BC=2DE=4,故答案为:4.13.如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为144米2 .【分析】将道路分别向左、向上平移,得到草地为一个长方形,分别求出长方形的长和宽,再用长和宽相乘即可.解:将道路分别向左、向上平移,得到草地为一个长方形,长方形的长为20﹣2=18(米),宽为10﹣2=8(米),则草地面积为18×8=144米2.故答案为:144米2.14.如图,在矩形ABCD中,对角线AC与BD交于点O,过点A 作AE⊥BD于点E,已知∠EAD=3∠BAE,则∠EOA=45 °.【分析】根据矩形的性质得出∠BAD=90°,AC=BD,OA=OC,OB=OD,求出OA=OB,求出∠OAB=∠ABO,求出∠ABO即可.解:∵四边形ABCD是矩形,∴∠BAD=90°,∵∠EAD=3∠BAE,∴∠BAE=×90°=22.5°,∵AE⊥BD,∴∠AEB=90°,∴∠ABO=180°﹣∠AEB﹣∠BAE=180°﹣90°﹣22.5°=67.5°,∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OA=OB,∴∠OAB=∠ABO=67.5°,∴∠EOA=180°﹣67.5°﹣67.5°=45°,故答案为:45.三、解答题(本大题共6小题,共54分,答题应写出文字说明、证明过程或演算步骤)15.计算(1)分解因式:x2y﹣2xy2+y3;(2)解不等式组.【分析】(1)直接提取公因式y,再利用公式法分解因式得出答案;(2)分别解不等式进而得出不等式组的解集.解:(1)x2y﹣2xy2+y3=y(x2﹣2xy+y2)=y(x﹣y)2;(2),解①得:x<2,解②得:x≥﹣3,故不等式组的解集为:﹣3≤x<2.16.化简:.【分析】直接将括号里面通分运算,再将原式的分子与分母分解因式,进而化简得出答案.解:原式=•=•=.17.△ABC在平面直角坐标系中的位置如图所示.(1)将△ABC向左平移4个单位长度后得到△A1B1C1,点A1、B1、C1分别是A、B、C的对应点,请画出△A1B1C1,并写出C1的坐标;(2)将△ABC绕点O顺时针旋转90°,得到△A2B2C2,点A2、B2、C2分别是A、B、C的对应点,请画出△A1B1C1,并写出C2的坐标.【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.(2)分别作出A,B,C的对应点A2,B2,C2即可.解:(1)如图△A1B1C1即为所求.并写出C1的坐标(﹣1,4).(2)如图△A2B2C2,即为所求并写出C2的坐标(4,﹣3).18.列方程解应用题今年1月下旬以来,新冠肺炎疫情在全国范围内迅速蔓延,而比疫情蔓延速度更快的是口罩恐慌.企业复工复产急需口罩,某大型国有企业向生产口罩的A、B两厂订购口罩,向A厂支付了1.32万元,向B厂支付了2.4万元,且在B厂订购的口罩数量是A厂的2倍,B厂的口罩每只比A厂低0.2元.求A、B两厂生产的口罩单价分别是多少元?【分析】设B厂生产的口罩单价为x元,则A厂生产的口罩单价为(x+0.2)元,根据数量=总价÷单价结合在B厂订购的口罩数量是A厂的2倍,即可得出关于x的分式方程,解之经检验后即可得出结论.解:设B厂生产的口罩单价为x元,则A厂生产的口罩单价为(x+0.2)元,依题意,得:=2×,解得:x=2,经检验,x=2是原方程的解,且符合题意,∴x+0.2=2.2.答:A厂生产的口罩单价为2.2元,B厂生产的口罩单价为2元.19.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数y=k1x+b1和y=kx+b的图象,分别与x 轴交于点A、B,两直线交于点C.已知点A(﹣1,0),B(2,0),观察图象并回答下列问题:(1)关于x的方程k1x+b1=0的解是x=﹣1 ;关于x的不等式kx+b<0的解集是x>2 ;(2)直接写出关于x的不等式组的解集;(3)若点C(1,3),求关于x的不等式k1x+b1>kx+b的解集和△ABC的面积.【分析】(1)利用直线与x轴交点即为y=0时,对应x的值,进而得出答案;(2)利用两直线与x轴交点坐标,结合图象得出答案;(3)利用三角形面积公式求得即可.解:(1)∵一次函数y=k1x+b1和y=kx+b的图象,分别与x轴交于点A(﹣1,0)、B(2,0),∴关于x的方程k1x+b1=0的解是x=﹣1,关于x的不等式kx+b <0的解集,为x>2,故答案为x=﹣1,x>2;(2)根据图象可以得到关于x的不等式组的解集﹣1<x<2;(3)∵AB=3,∴S△ABC=•yC==.20.如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE,DF.(1)试判断四边形AEDF的形状,并证明你的结论;(2)若∠BAC=60°,AE=6,求四边形AEDF的面积;(3)△ABC满足什么条件时,四边形AEDF是正方形?请说明理由.【分析】(1)由∠BAD=∠CAD,AO=AO,∠AOE=∠AOF=90°证△AEO≌△AFO,推出EO=FO,得出平行四边形AEDF,根据EF ⊥AD得出菱形AEDF;(2)根据菱形的性质和菱形的面积公式即可得到结论;(3)根据有一个角是直角的菱形是正方形可得∠BAC=90°时,四边形AEDF是正方形.解:(1)四边形AEDF是菱形,∵AD平分∠BAC,∴∠1=∠2,又∵EF⊥AD,∴∠AOE=∠AOF=90°∵在△AEO和△AFO中∵,∴△AEO≌△AFO(ASA),∴EO=FO,∵EF垂直平分AD,∴EF、AD相互平分,∴四边形AEDF是平行四边形又EF⊥AD,∴平行四边形AEDF为菱形;(2)∵四边形AEDF为菱形,∴AE=AF,∵∠BAC=60°,∴△AEF是等边三角形,∠1=30°,∴AO=3,EF=AE=6,∴AD=6,∴四边形AEDF的面积=AD•EF=6×6=18;(3)在△ABC中,当∠BAC=90°时,四边形AEDF是正方形;∵∠BAC=90°,∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).四、填空题(每小题4分,共20分)21.232﹣1可以被10和20之间某两个整数整除,则这两个数是15和17 .【分析】先对原式进行因式分解,然后即可求出这两个整数.解:原式=(216+1)(216﹣1)=(216+1)(28+1)(24+1)(24﹣1)=(216+1)(28+1)×17×15.则这两个数是15和17.故答案是:15和17.22.两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP=4cm.【分析】由“HL”可证Rt△OMP≌Rt△ONP,可得∠MOP=∠NOP =30°,由直角三角形的性质可求解.解:在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,∴Rt△OMP≌Rt△ONP(HL),∴∠MOP=∠NOP,∵∠AOB=60°,∴∠MOP=∠NOP=30°,∵∠OMP=90°,∴OP=2MP,OM=MP=6cm,∴MP=2cm,∴OP=4cm,故答案为:4.23.若关于x的分式方程+=﹣1无解,则常数n的值是1或..【分析】分式方程去分母转化为整式方程,由分式方程无解得到x ﹣3=0,确定出x的值,代入整式方程计算即可求出n的值.解:两边都乘(x﹣3),得3﹣2x+nx﹣2=﹣x+3,解得x=,n=1时,整式方程无解,分式方程无解,∴当x=3时分母为0,方程无解,即,∴时方程无解.故答案为:1或.24.如图,Rt△OAB的两直角边OA、OB分别在x轴和y轴上,A (﹣2,0),B(0,4),将△OAB绕O点顺时针旋转90°得到△OCD,直线AC、BD交于点E.点M为直线BD上的动点,点N 为x轴上的点,若以A,C,M,N四点为顶点的四边形是平行四边形,则符合条件的点M的坐标为(2,2)或(6,﹣2).【分析】由A、B的坐标可求得AO和OB的长,由旋转的性质可求得OC、OD的长,从而可求得∠AEB=90°,再由勾股定理可求得CD和AB的长,可求得AB=CD,可证得△ABE≌△DCE,得到OD=OB,由B、D坐标可求得直线BD解析式,当M点在x轴上方时,则有CM∥AN,则可求得M点纵坐标,代入直线BD解析式可求得M点坐标,当M点在x轴下方时,同理可求得M点纵坐标,则可求得M点坐标.解:∵A(﹣2,0),B(0,4),∴OA=2,OB=4,∵将△OAB绕O点顺时针旋转90°得△OCD,∴OC=OA=2,OD=OB=4,AB=CD,∴∠ACO=∠ECB=∠CBE=45°,∴∠CEB=90°,∴∠AEB=∠CED,且CE=BE,在Rt△ABE和Rt△DCE中,∴Rt△ABE≌Rt△DCE(HL),∴OD=OB=4,∴D(4,0),且B(0,4),∴直线BD解析式为y=﹣x+4,当M点在x轴上方时,则有CM∥AN,即CM∥x轴,∴M点到x轴的距离等于C点到x轴的距离,∴M点的纵坐标为2,在y=﹣x+4中,令y=2可得x=2,∴M(2,2);当M点在x轴下方时,同理可得M点的纵坐标为﹣2,在y=﹣x+4中,令y=﹣2可求得x=6,∴M点的坐标为(6,﹣2);综上可知M点的坐标为(2,2)或(6,﹣2),故答案为:(2,2)或(6,﹣2).25.如图,已知边长为6的菱形ABCD中,∠ABC=60°,点E,F 分别为AB,AD边上的动点,满足BE=AF,连接EF交AC于点G,CE、CF分别交BD于点M,N,给出下列结论:①△CEF是等边三角形;②∠DFC=∠EGC;③若BE=3,则BM=MN=DN;④EF2=BE2+DF2;⑤△ECF面积的最小值为.其中所有正确结论的序号是①②③⑤.【分析】由“SAS”可证△BEC≌△AFC,可得CF=CE,∠BCE=∠ACF,可证△EFC是等边三角形,由三角形内角和定理可证∠DFC =∠EGC;由等边三角形的性质和菱形的性质可求MN=DN=BM =2;由勾股定理即可求解EF2=BE2+DF2不成立;由等边三角形的性质可得△ECF面积的EC2,则当EC⊥AB时,△ECF的最小值为.解:∵四边形ABCD是菱形,∴AB=BC=CD=AD=6,∵AC=BC,∴AB=BC=CD=AD=AC,∴△ABC,△ACD是等边三角形,∴∠ABC=∠BAC=∠ACB=∠DAC=60°,∵AC=BC,∠ABC=∠DAC,AF=BE,∴△BEC≌△AFC(SAS)∴CF=CE,∠BCE=∠ACF,∴∠ECF=∠BCA=60°,∴△EFC是等边三角形,故①正确;∵∠ECF=∠ACD=60°,∴∠ECG=∠FCD,∵∠FEC=∠ADC=60°,∴∠DFC=∠EGC,故②正确;若BE=3,菱形ABCD的边长为6,∴点E为AB中点,点F为AD中点,∵四边形ABCD是菱形,∴AC⊥BD,AO=CO,BO=DO,∠ABO=∠ABC=30°,∴AO=AB=3,BO=AO=3,∴BD=6,∵△ABC是等边三角形,BE=AE=3,∴CE⊥AB,且∠ABO=30°,∴BE=EM=3,BM=2EM,∴BM=2,同理可得DN=2,∴MN=BD﹣BM﹣DN=2,∴BM=MN=DN,故③正确;∵△BEC≌△AFC,∴AF=BE,同理△ACE≌△DCF,∴AE=DF,∵∠BAD≠90°,∴EF2=AE2+AF2不成立,∴EF2=BE2+DF2不成立,故④错误,∵△ECF是等边三角形,∴△ECF面积的EC2,∴当EC⊥AB时,△ECF面积有最小值,此时,EC=3,△ECF面积的最小值为,故⑤正确;故答案为:①②③⑤.五、解答题(本大题共3小题,共30分.其中26题8分,27题10分,28题12分)26.2020年初,“新型冠状病毒”肆虐全国,武汉“封城”.大疫无情人有情,四川在做好疫情防控的同时,向湖北特别是武汉人们伸出了援手,医疗队伍千里驰援、社会各界捐款捐物.某运输公司现有甲、乙两种货车,要将234吨生活物资从成都运往武汉,已知2辆甲车和3辆乙车可运送114吨物资;3辆甲车和2辆乙车可运送106吨物资.(1)求每辆甲车和每辆乙车一次分别能装运多少吨生活物资?(2)从成都到武汉,已知甲车每辆燃油费2000元,乙车每辆燃油费2600元.在不超载的情况下公司安排甲、乙两种车共10辆将所有生活物资运到武汉,问公司有几种派车方案?哪种方案所用的燃油费最少?最低燃油费是多少?【分析】(1)设每辆甲车一次能装运x吨生活物资,每辆乙车一次能装运y吨生活物资,根据“2辆甲车和3辆乙车可运送114吨物资;3辆甲车和2辆乙车可运送106吨物资”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设该公司安排m辆甲车,则安排(10﹣m)辆乙车,根据10辆车的总运载量不少于234吨,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,结合m为正整数即可得出各派车方案,设总燃油费为w元,根据总燃油费=每辆车的燃油费×派车辆数,即可得出w关于m的函数关系式,再利用一次函数的性质,即可解决最值问题.解:(1)设每辆甲车一次能装运x吨生活物资,每辆乙车一次能装运y吨生活物资,依题意,得:,解得:.答:每辆甲车一次能装运18吨生活物资,每辆乙车一次能装运26吨生活物资.(2)设该公司安排m辆甲车,则安排(10﹣m)辆乙车,依题意,得:18m+26(10﹣m)≥234,解得:m≤.又∵m为正整数,∴m可以为1,2,3,∴公司有3种派车方案,方案1:安排1辆甲车,9辆乙车;方案2:安排2辆甲车,8辆乙车;方案3:安排3辆甲车,7辆乙车.设总燃油费为w元,则w=2000m+2600(10﹣m)=﹣600m+26000,∵k=﹣600,∴w随m的增大而减小,∴当m=3时,w取得最小值,最小值=﹣600×3+26000=24200.答:公司有3种派车方案,安排3辆甲车,7辆乙车时,所用的燃油费最少,最低燃油费是24200.27.先阅读下面的内容,再解决问题:问题:对于形如x2+2ax+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2ax﹣3a2,就不能直接运用公式了.此时,我们可以在二次三项式x2+2ax﹣3a2中先加上一项a2,使它与x2+2ax成为一个完全平方式,再减去a2,整个式子的值不变,于是有:x2+2ax﹣3a2=(x2+2ax+a2)﹣a2﹣3a2=(x+a)2﹣4a2=(x+a)2﹣(2a)2=(x+3a)(x﹣a)像这样,先添一适当项,使式中出现完全平方式,再减去这项,使整个式子的值不变的方法称为“配方法”.利用“配方法”,解决下列问题:(1)分解因式:a2﹣8a+15=(a﹣3)(a﹣5);(2)若△ABC的三边长是a,b,c,且满足a2+b2﹣14a﹣8b+65=0,c边的长为奇数,求△ABC的周长的最小值;(3)当x为何值时,多项式﹣2x2﹣4x+3有最大值?并求出这个最大值.【分析】(1)根据题目中的例子,可以对题目中的式子配方后分解因式;(2)根据题目中的式子,利用配方法可以求得a、b的值,根据三角形三边关系确定c的值,由三角形周长可得结论;(3)根据配方法即可求出答案.解:(1)a2﹣8a+15=(a2﹣8a+16)﹣1=(a﹣4)2﹣12=(a ﹣3)(a﹣5);故答案为:(a﹣3)(a﹣5);(2)∵a2+b2﹣14a﹣8b+65=0,∴(a2﹣14a+49)+(b2﹣8b+16)=0,∴(a﹣7)2+(b﹣4)2=0,∴a﹣7=0,b﹣4=0,解得,a=7,b=4,∵△ABC的三边长是a,b,c,∴3<c<11,又∵c边的长为奇数,∴c=5,7,9,当a=7,b=4,c=5时,△ABC的周长最小,最小值是:7+4+5=16;(3)﹣2x2﹣4x+3,=﹣2(x2+2x+1﹣1)+3,=﹣2(x+1)2+5,∴当x=﹣1时,多项式﹣2x2﹣4x+3有最大值,最大值是5.28.如图1,▱ABCD在平面直角坐标系xOy中,已知点A(﹣1,0)、B(0,4)、C(3,2),点G是对角线AC的中点,过点G 的直线分别与边AB、CD交于点E、F,点P是直线EF上的动点.(1)求点D的坐标和S四边形BEFC的值;(2)如图2,当直线EF交x轴于点H(5,0),且S△PAC=S四边形BEFC时,求点P的坐标;(3)如图3,当直线EF交x轴于点K(3,0)时,在坐标平面内是否存在一点Q,使得以P、A、Q、C为顶点的四边形是矩形?若存在,直接写出点P的坐标;若不存在,请说明理由.【分析】(1)根据平行线的性质可求点D的坐标,根据重心的定义可得S四边形BEFC=S▱ABCD,从而求解;(2)分两种情况:①点P在AC左边,②点P在AC右边,进行讨论即可求解;(3)先作出图形,再根据矩形的性质即可求解.解:(1)∵▱ABCD在平面直角坐标系xOy中,点A(﹣1,0)、B(0,4)、C(3,2),∴点D的坐标为(2,﹣2),∴S▱ABCD=6×4﹣×1×4﹣×3×2﹣×1×4﹣×3×2=14,∵点G是对角线AC的中点,∴S四边形BEFC=S▱ABCD=7;(2)∵点G是对角线AC的中点,∴G(1,1),设直线GH的解析式为y=kx+b,则,解得,∴直线GH的解析式为y=﹣x+;①点P在AC右边,S△ACH=×6×2=6,∵S△PAC=S四边形BEFC,1+4×=,当x=时,y=﹣×+=﹣;∴P(,﹣);②点P在AC左边,由中点坐标公式可得P(﹣,).综上所述,点P的坐标为(,﹣)或(﹣,);(3)如图,设直线GK的解析式为y=kx+b,则,解得.则直线GK的解析式为y=﹣x+;CP⊥AP时,点P的坐标为(3,0)或(﹣1,2);CP⊥AC时,直线AC的解析式为y=x+直线CP的解析式为y=﹣2x+8故点P的坐标为(,﹣);AP⊥AC时,同理可得点P的坐标为(﹣,).综上所述,点P的坐标为(3,0)或(﹣1,2)或(,﹣)或(﹣,).。
2020年八年级下册生物期末考试卷2

2020年八年级生物期末考试卷一、选择题(本大题共25个小题,每小题2分,共50分。
每小题的四个选项中,只有一个最符合题目要求)1.生物圈中的生物都具有的共同特征是()A.能进行活动 B.能繁殖后代C.能进行反射 D.能呼吸并消耗氧气2.关于显微镜的结构和使用的叙述错误的是()A.观察材料应该薄而透明B.视野中光线较暗时,可以换用大光圈C.放大倍数越小,视野中细胞数目越少D.要使物像更清晰,应该调节细准焦螺旋3.关于细胞分裂和分化的叙述错误的是()A.细胞分裂是细胞核先一分为二,然后再进行遗传物质的复制B.经过细胞的分化,细胞形态、结构和功能都可能发生变化C.细胞分裂使细胞数目增多,细胞分化使生物体形成不同组织D.细胞的分裂和分化是生物体生长发育和繁殖的基础4.不是每一朵花都能结出果实,能结出果实的花一定()①长有雌蕊和雄蕊②长有雌蕊③经历了自花传粉④经历了传粉⑤经历了受精A.①④⑤ B.①③⑤ C.②③⑤ D.②④⑤5.下图是菜豆发育过程中的相关结构,以下叙述正确的是()A.菜豆种子的胚由甲图中的①②③组成B.乙图中的a是由甲图中的③发育成的C.乙图中的b是由甲图中的②发育成的D.由甲图发育到乙图时最先突破种皮的是①6.下图是花生果实的部分结构,据此可判断花生属于()A.苔藓植物B.蕨类植物C.裸子植物D.被子植物7.“藕断丝连”是常见的现象,这里的“丝”来自植物体的()A.保护组织B.营养组织C.分生组织 D.输导组织8.“沙漠植被之王”梭梭的种子,萌发所用时间是最短的,只需两三个小时。
对于沙漠植物来说,影响萌发的最重要的环境因素是( )A.温度 B.水分 C.空气 D.光照9.森林地区往往比沙漠地区降雨更多,从生物学角度分析,主要原因是()A.蒸腾作用使大气湿度增加 B.根系保持水土,蓄水过多C.呼吸作用旺盛,产生水分多 D.光合作用旺盛,释放水汽多10.制造“试管婴儿”和“克隆动物”所采用的生殖方式分别是( )A.都属于有性生殖 B.前者属于有性生殖,后者属于无性生殖C.都属于无性生殖 D.前者属于无性生殖,后者属于有性生殖11.某同学的妈妈因病手术,他为妈妈准备了以下食物,其中最有利于伤口愈合的是( )A.苹果、香蕉 B.牛奶、鸡蛋C.巧克力、橙汁 D.面包、饼干12.图为胸腔和肺的示意图,当肋间外肌和膈肌收缩时,图中三部位压力由小到大的顺序是()A.b<c<aB.a<b<cC.a<c<bD.c<a<b13.如图所示曲线表示人体血液中某些物质含量的变化情况,下列说法错误的是() A.若b为包绕在肺泡外的毛细血管,则c的名称是肺静脉,表示二氧化碳变化的是曲线②B.若b是组织处的毛细血管,表示氧气变化的是曲线②C.若b是小肠绒毛内的毛细血管,曲线①可表示营养物质的变化D.若b为肾小球处的毛细血管网,曲线②为蛋白质和血细胞14.如图为身高110厘米的广东男子与身高70厘米的“袖珍新娘”喜结连理的幸福画面。
安徽省2023年八年级下学期期末考试数学试卷 (2)

安徽省八年级下学期期末考试数学试卷一、精心选一选,慧眼识金(每小题3分,共30分)1.(3分)下列各式是最简二次根式的是()A.B.C.D.考点:最简二次根式.专题:常规题型.分析:先根据二次根式的性质化简,再根据最简二次根式的定义判断即可.解答:解:A、=3,故不是最简二次根式,故A选项错误;B、是最简二次根式,符合题意,故B选项正确;C、=2,故不是最简二次根式,故C选项错误;D、=,故不是最简二次根式,故D选项错误;故选:B.点评:本题考查了对最简二次根式的定义的理解,能理解最简二次根式的定义是解此题的关键.2.(3分)下列各组数中,能构成直角三角形的是()A.4,5,6 B.1,1,C.6,8,11 D.5,12,23考点:勾股定理的逆定理.专题:计算题.分析:根据勾股定理逆定理:a2+b2=c2,将各个选项逐一代数计算即可得出答案.解答:解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;B、∵12+12=,∴能构成直角三角形,故B正确;C、∵62+82≠112,∴不能构成直角三角形,故C错误;D、∵52+122≠232,∴不能构成直角三角形,故D错误.故选:B.点评:此题主要考查学生对勾股定理的逆定理的理解和掌握,要求学生熟练掌握这个逆定理.3.(3分)已知一次函数y=kx+b的图象如图所示,则k、b的符号是()A.k<0,b<0 B.k>0,b<0 C.k<0,b>0 D.k>0,b>0考点:一次函数图象与系数的关系.专题:数形结合.分析:由图可知,一次函数y=kx+b的图象经过二、三、四象限,根据一次函数图象在坐标平面内的位置与k、b的关系作答.解答:解:由一次函数y=kx+b的图象经过二、三、四象限,当k<0时,直线必经过二、四象限,故k<0,直线与y轴负半轴相交,故b<0.故选:A.点评:本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.4.(3分)(•潍坊)在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.方差C.平均数D.中位数考点:统计量的选择.分析:9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.解答:解:由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.故选:D.点评:此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.5.(3分)连接对角线互相垂直的四边形的四边中点,所构成的四边形一定是()A.矩形B.菱形C.正方形D.梯形考点:中点四边形.专题:探究型.分析:根据中位线的与对角线平行的性质,因此顺次连接四边中点可以得到一个相邻的边互相垂直的四边形,根据矩形的定义,邻边垂直的四边形为矩形.解答:已知:AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.求证:四边形EFGH是矩形.证明:∵E、F、G、H分别为各边的中点,∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,(三角形的中位线平行于第三边)∴四边形EFGH是平行四边形,(两组对边分别平行的四边形是平行四边形)∵AC⊥BD,EF∥AC,EH∥BD,∴∠EMO=∠ENO=90°,∴四边形EMON是矩形(有三个角是直角的四边形是矩形),∴∠MEN=90°,∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).故选:A.点评:本题考查的是矩形的判定方法,常用的方法有三种:①一个角是直角的平行四边形是矩形.②三个角是直角的四边形是矩形.③对角线相等的平行四边形是矩形.6.(3分)若的整数部分为x,小数部分为y,则的值是()A.B.C.1D.3考点:二次根式的加减法.专题:计算题.分析:因为的整数部分为1,小数部分为﹣1,所以x=1,y=﹣1,代入计算即可.解答:解:∵的整数部分为1,小数部分为﹣1,∴x=1,y=﹣1,∴=﹣(﹣1)=1.故选:C.点评:关键是会表示的整数部分和小数部分,再二次根式的加减运算,即将被开方数相同的二次根式进行合并.7.(3分)将直线y=﹣2x向右平移2个单位所得直线的解析式为()A.y=﹣2x+2 B.y=﹣2x﹣4 C.y=﹣2x﹣2 D.y=﹣2x+4考点:一次函数图象与几何变换.分析:根据“左加右减”的平移规律可由已知的解析式写出新的解析式.解答:解:将直线y=﹣2x向右平移2个单位所得直线的解析式为y=﹣2(x﹣2),即y=﹣2x+4.故选:D.点评:本题考查了一次函数图象与几何变换,掌握解析式“左加右减”的平移规律是解题的关键.8.(3分)某班50名学生身高测量结果如下表:身高 1.51 1.52 1.53 1.54 1.55 1.56 1.57 1.58 1.59 1.60 1.64人数 1 1 3 4 3 4 4 6 8 10 6该班学生身高的众数和中位数分别是()A.1.60,1.56 B.1.59,1.58 C.1.60,1.58 D.1.60,1.60考点:众数;中位数.专题:图表型.分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.解答:解:表图为从小到大排列,数据1.60出现了10次,出现最多,故1.60为众数;1.58和1.58处在第25、26位,其平均数1.58,故1.58为中位数.所以本题这组数据的中位数是1.58,众数是1.60.故选:C.点评:本题属于基础题,考查了确定一组数据的中位数和众数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.9.(3分)(•南昌)某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是()A.B.C.D.考点:函数的图象.专题:图表型.分析:根据某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间,休息时油量不再发生变化,再次出发油量继续减小,即可得出符合要求的图象.解答:解:某人驾车从A地上高速公路前往B地,油量在减小;中途在服务区休息了一段时间,休息时油量不发生变化;再次出发油量继续减小;到B地后发现油箱中还剩油4升;只有C符合要求.故选:C.点评:本题考查了利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.10.(3分)(1998•内江)能判定四边形是平行四边形的条件是()A.一组对边平行,另一组对边相等B.一组对边相等,一组邻角相等C.一组对边平行,一组邻角相等D.一组对边平行,一组对角相等考点:平行四边形的判定.专题:证明题.分析:平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.根据判定定理进行推导即可.解答:解:如图所示,若已知一组对边平行,一组对角相等,易推导出另一组对边也平行,两组对边分别平行的四边形是平行四边形.故根据平行四边形的判定,只有D符合条件.故选:D.点评:此题主要考查学生对平行四边形的判定的掌握情况.在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.二、耐心填一填,一锤定音(每小题3分,共21分)11.(3分)(•襄阳)使代数式有意义的x的取值范围是x≥且x≠3.考点:二次根式有意义的条件;分式有意义的条件.专题:计算题.分析:根据被开方数大于等于0,分母不等于0列式进行计算即可得解.解答:解:根据题意得,2x﹣1≥0且3﹣x≠0,解得x≥且x≠3.故答案为:x≥且x≠3.点评:本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.12.(3分)请你写出同时具备下列两个条件的一次函数的表达式(写出一个即可)y=﹣x ﹣6.(1)y随x的增大而减小;(2)图象经过点(2,﹣8)考点:一次函数的性质.专题:开放型.分析:由题可知,需求的一次函数只要满足k<0且经过点(2,﹣8)即可.解答:解:设函数关系式是y=kx+b(k≠0)由y随着x的增大而减小得k<0可设k=﹣1,将(2,﹣8)代入函数关系式,得b=﹣6因此一次函数表达式为y=﹣x﹣6.(此题答案不唯一)故答案为:y=﹣x﹣6.点评:本题考查了一次函数的性质.此类题要首先运用待定系数法确定k,b应满足的一个确定的关系式,再根据条件确定k的值,进一步确定b的值,即可写出函数关系式.13.(3分)已知,则x3y+xy3=10.考点:二次根式的化简求值.专题:计算题.分析:由已知得x+y=2,xy=1,把x3y+xy3分解因式再代入计算.解答:解:∵,∴x+y=2,xy=1,∴x3y+xy3=xy(x2+y2)=xy[(x+y)2﹣2xy]=(2)2﹣2=10.点评:解题时注意,灵活应用二次根式的乘除法法则,切忌把x、y直接代入求值.14.(3分)已知一组数据为:10;8,10,10,7,则这组数据的方差是 1.6.考点:方差.专题:计算题.分析:结合方差公式先求出这组数据的平均数,然后代入公式求出即可.解答:解:平均数为:(10+8+10+10+7)÷5=9,S2=[(10﹣9)2+(8﹣9)2+(10﹣9)2+(10﹣9)2+(7﹣9)2],=(1+1+1+1+4),=1.6,故答案为:1.6.点评:此题主要考查了方差的有关知识,正确的求出平均数,并正确代入方差公式是解决问题的关键.15.(3分)已知一次函数y=2x+1,则它的图象与坐标轴围成的三角形面积是.考点:一次函数图象上点的坐标特征.专题:数形结合.分析:求得函数与坐标轴的交点,然后根据三角形的面积公式即可求得三角形的面积.解答:解:一次函数的关系式是y=2x+1,当x=0时,y=1;当y=0时,x=﹣,它的图象与坐标轴围成的三角形面积是:×1×|﹣|=.故答案是:.点评:本题主要考查了一次函数图象上点的坐标特征.求线段的长的问题一般是转化为求点的坐标的问题解决.16.(3分)一个三角形的三边长分别为15cm、20cm、25cm,则这个三角形最长边上的高是12cm.考点:勾股定理的逆定理.专题:数形结合.分析:过C作CD⊥AB于D,根据勾股定理的逆定理可得该三角形为直角三角形,然后再利用三角形的面积公式即可求解.解答:解:如图:设AB=25是最长边,AC=15,BC=20,过C作CD⊥AB于D,∵AC2+BC2=152+202=625,AB2=252=625,∴AC2+BC2=AB2,∴∠C=90°,∵S△ACB=AC×BC=AB×CD,∴AC×BC=AB×CD15×20=25CD,∴CD=12(cm);故答案为:12.点评:本题考查勾股定理的逆定理和三角形的面积公式的应用.根据勾股定理的逆定理判断三角形为直角三角形是解答此题的突破点.17.(3分)如图,在直角坐标系中,正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…A n B n C n C n 的顶点A1、A2、A3、…、A n均在直线y=kx+b上,顶点C1、C2、C3、…、C n在x轴上,﹣1若点B1的坐标为(1,1),点B2的坐标为(3,2),那么点B4的坐标为(15,8).考点:一次函数图象上点的坐标特征;正方形的性质.专题:规律型.分析:首先利用待定系数法求得直线A1A2的解析式,然后分别求得B1,B2,B3…的坐标,可以得到规律:B n(2n﹣1,2n﹣1),据此即可求解.解答:解:∵B1的坐标为(1,1),点B2的坐标为(3,2),∴正方形A1B1C1O边长为1,正方形A2B2C2C1边长为2,∴A1的坐标是(0,1),A2的坐标是:(1,2),代入y=kx+b得:,解得:,则直线A1A2的解析式是:y=x+1.∵A1B1=1,点B2的坐标为(3,2),∴点A3的坐标为(3,4),∴A3C2=A3B3=B3C3=4,∴点B3的坐标为(7,4),∴B1的纵坐标是:1=20,B1的横坐标是:1=21﹣1,∴B2的纵坐标是:2=21,B2的横坐标是:3=22﹣1,∴B3的纵坐标是:4=22,B3的横坐标是:7=23﹣1,∴B n的纵坐标是:2n﹣1,横坐标是:2n﹣1,则B n(2n﹣1,2n﹣1).∴B4的坐标是:(24﹣1,24﹣1),即(15,8).故答案为:(15,8).点评:此题主要考查了待定系数法求函数解析式和坐标的变化规律.此题难度较大,注意正确得到点的坐标的规律是解题的关键.三、用心做一做,马到成功(本大题共49分)18.(15分)计算(1)(﹣4)﹣(3﹣2);(2)(﹣)2+2×3;(3)5•(﹣4)(a≥0,b≥0).考点:二次根式的混合运算.专题:计算题.分析:(1)先把各二次根式化为最简二次根式,然后去括号后合并即可;(2)先利用完全平方公式和二次根式的乘法法则运算,然后合并即可;(3)利用二次根式的乘法法则运算.解答:解:(1)原式=4﹣﹣+=3;(2)原式=2﹣2+3+×3=5﹣2+2=5;(3)原式=﹣20=﹣20a2b.点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.19.(8分)如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.考点:翻折变换(折叠问题);勾股定理.专题:几何图形问题.分析:根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到∴42+x2=(8﹣x)2,然后解方程即可.解答:解:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°,∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),∴AF=AD=10,DE=EF,在Rt△ABF中,AB=8,AF=10,∴BF==6,∴CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中,∵CF2+CE2=EF2,∴42+x2=(8﹣x)2,解得x=3,即EC的长为3cm.点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.20.已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交于BE的延长线于点F,且AF=DC,连接CF.(1)求证:D是BC的中点;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.考点:矩形的判定;全等三角形的判定与性质;等腰三角形的性质;平行四边形的性质.专题:证明题.分析:(1)可证△AFE≌△DBE,得出AF=BD,进而根据AF=DC,得出D是BC中点的结论;(证法2:可根据AF平行且相等于DC,得出四边形ADCF是平行四边形,从而证得DE是△BCF的中位线,由此得出D是BC中点)(2)若AB=AC,则△ABC是等腰三角形,根据等腰三角形三线合一的性质知AD⊥BC;而AF与DC平行且相等,故四边形ADCF是平行四边形,又AD⊥BC,则四边形ADCF是矩形.解答:(1)证明:∵E是AD的中点,∴AE=DE.∵AF∥BC,∴∠FAE=∠BDE,∠AFE=∠DBE.在△AFE和△DBE中,,∴△AFE≌△DBE(AAS).∴AF=BD.∵AF=DC,∴BD=DC.即:D是BC的中点.(2)解:四边形ADCF是矩形;证明:∵AF=DC,AF∥DC,∴四边形ADCF是平行四边形.∵AB=AC,BD=DC,∴AD⊥BC即∠ADC=90°.∴平行四边形ADCF是矩形.点评:此题主要考查了全等三角形的判定和性质,等腰三角形的性质,平行四边形、矩形的判定等知识综合运用.21.(9分)在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港.最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.(1)填空:A、C两港口间的距离为120km,a=4;(2)请分别求出y1、y2与x的函数关系式,并求出交点P的坐标;(3)若两船的距离不超过10km时能够相互望见,求甲、乙两船经过多长时间正好相距10千米?考点:一次函数的应用.专题:综合题;分类讨论.分析:(1)从图中可以看出A、B两港是30km,B、C两港是90km,A、C两港口间的距离为30+90=120km,根据路程÷时间求出甲的速度,进而求出a的值;(2)利用待定系数法求出y1=,y2=15x(0≤x≤6),解方程组,即可求出点P的坐标.(3)先根据一次函数的图象求出乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.解答:解:(1)从图中可以看出A、B两港是30km,B、C两港是90km,所以A、C两港口间的距离为30+90=120(km);甲的速度为:30÷1=30(km/h),a=120÷30=4.故答案为:120,4;(2)当0≤x≤1时,由点(0,30),(1,0)求得y1=﹣30x+30;当1<x≤4时,由点(1,0),(4,90)求得y1=30x﹣30;即y1与x的函数关系式为y1=;由点(6,90)求得,y2=15x(0≤x≤6),即y2与x的函数关系式为y2=15x(0≤x≤6);由图象可知,交点P的横坐标x>1,此时y1=y2,解方程组,得,所以点P的坐标为(2,30);(3)由函数图象可知,乙船的速度为:90÷6=15(km/m).①甲在乙后10km,设行驶时间为xh,则x<2.如果0≤x≤1,那么(﹣30x+30)+15x=10,解得x=,不合题意舍去;如果1≤x<2,那么15x﹣(30x﹣30)=10,解得x=,符合题意;②甲超过乙后,甲在乙前10km,设行驶时间为xh,则x>2.由题意,得30x﹣30﹣15x=10,解得x=,符合题意;③甲船已经到了而乙船正在行驶,则4≤x<6.由题意,得90﹣15x=10,解得x=,符合题意;即甲、乙两船经过小时或小时或小时,正好相距10千米.点评:本题考查的是一次函数的图象及一次函数的应用,解答此题时要注意运用分类讨论的思想,不要漏解.22.(9分)如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG 并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.(1)证明:四边形MPBG是平行四边形;(2)设BE=x,四边形MNBG的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;(3)如果按题设作出的四边形BGMP是菱形,求BE的长.考点:四边形综合题;平行线的判定.专题:几何综合题.分析:(1)分别证得DB∥ME和MN∥CB后利用两组对边分别相等的四边形是平行四边形即可证得结论;(2)根据正方形BEFG,从而可得CM=1﹣x,然后得y=(BG+MN)•BN即可.(3)由已知易得四边形BGMP是平行四边形,要使四边形BGMP是菱形则BG=MG,可得x=(1﹣x),解得x即可.解答:证明:(1)∵ABCD、BEFG是正方形∴∠CBA=∠FEB=90°,∠ABD=∠BEG=45°,∴DB∥ME(同位角相等,两直线平行).∵MN⊥AB,CB⊥AB,∴MN∥CB.∴四边形MPBG是平行四边形;(2)∵正方形BEFG,∴BG=BE=x.∵∠CMG=∠BEG=45°,∴CG=CM=BN=1﹣x.∴y=(GB+MN)•BN=(1+x)(1﹣x)=﹣x2(0<x<1);(3)∵四边形BGMP是菱形,∴BG=MG,∴x=(1﹣x),∴x=2﹣,∴BE=2﹣.点评:此题考查了四边形的综合知识,较复杂,但充分利用题目所给的条件,根据四边形性质列出方程即可解答.解答此题,不要局限于一种方法,可以多试几种方法,以提高解题的“含金量”.教师的职务是‘千教万教,教人求真’;学生的职务是‘千学万学,学做真人’。
湖南长沙明德集团2024届英语八年级第二学期期末考试试题含答案

湖南长沙明德集团2024届英语八年级第二学期期末考试试题满分120分,时间90分钟一、完形填空(10分)1、通读下面短文,掌握其大意,然后在每小题所给的四个选项中,选出一个最佳答案。
When I was 12 years old, my mother sent me to a Chinese school in California. I ____1____ spending my Saturdays in a three-hour Chinese class, because I thought it was difficult and boring.However, my mum thought that I should develop and improve my Chinese language skills. I seemed to know that it would bring me ____2____ good in the future, but at that time I was so busy finishing my homework at school. So I couldn’t realize the ____3____ of learning a second language.Many years later, I had a ____4____ to work in Asia. I chose to work in China mainly because I know a little about Chinese. After all, I learned Chinese when I was ____5____. I am also very confident that I can read street signs, buy food and talk to people there.Shortly after I arrived in China, my Chinese language ____6____ came back soon and improved very quickly. I can’t make so much progress without my mother’s ____7____. Thinking of the experience of learning Chinese and staying in China, I am always ____8____ for what she did to me. A long time ago, I wanted to ____9____ learning Chinese, but my mother encouraged me to learn Chinese. Because of learning Chinese, I made a lot of new friends. ____10____, I’m glad that it has helped me a lot in my work. My life is getting more and more colourful.1. A. hated B. advised C. enjoyed D. forgot2. A. something B. nothing C. anything D. everything3. A. mistakes B. places C. weather D. advantages4. A. habit B. chance C. skill D. suggestion5. A. busy B. young C. successful D. experienced6. A. tools B. skills C. points D. difficulties7. A. care B. plan C. idea D. help8. A. helpful B. careful C. thankful D. useful9. A. give out B. give up C. give in D. give away10. A. Finally B. However C. Besides D. Quickly二、短文填空(10分)2、根据短文内容,从短文后的选项中选出能填入小题横线上的最佳选项。
八年级下学期数学期末测试卷 试题试卷 含答案解析(2)

八年级下期数学期末测试一.选择题1.9的平方根为()A.3B.﹣3C.±3D.2.下列式子中,为最简二次根式的是()A.B.C.D.3.直线y=3x+1向下平移2个单位,所得直线的解析式是()A.y=3x+3B.y=3x﹣2C.y=3x+2D.y=3x﹣14.若式子在实数范围内有意义,则x的取值范围是()A.x≥1且x≠2B.x≤1C.x>1且x≠2D.x<15.某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是()A.1.95元B.2.15元C.2.25元D.2.75元6.下表是我市6个县(市)区今年某日最高气温(℃)的统计结果:地区孟州温县沁阳博爱武陟修武平均气温温度(℃)■302729283029则6个县(市)区该日最高气温(℃)的众数和中位数分别是()A.29,31B.30,29.5C.30,29D.30,37.如图,直线y=﹣x+b经过点(0,3),则关于x的不等式﹣x+b>0的解集是()A.x>2B.x<2C.x≥2D.x≤28.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB 的长度为()A.5B.6C.7D.259.如果△ABC的三个顶点A,B,C所对的边分别为a,b,c,那么下列条件中,不能判断△ABC是直角三角形的是()A.∠A=25°,∠B=65°B.∠A:∠B:∠C=2:3:5C.a:b:c=::D.a=6,b=10,c=1210.四边形ABCD的对角线AC与BD相交于点O,下列四组条件中,一定能判定四边形ABCD为平行四边形的是()A.AD∥BC B.OA=OC,OB=ODC.AD∥BC,AB=DC D.AC⊥BD11.如图,正方形ABCD的边长为2,动点P从点B出发,在正方形的边上沿B→C→D的方向运动到点D停止,设点P的运动路程为x,在下列图象中,能表示△P AD的面积y 关于x的函数关系的图象是()A.B.C.D.二.填空题12.甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.14,乙的方差是0.06,这5次短跑训练成绩较稳定的是.(填“甲”或“乙”)13.化简:=.14.如图,菱形ABCD的对角线AC、BD相交于点O,OE⊥AD,垂足为E,AC=8,BD=6,则OE的长为.15.如图,菱形ABCD的两条对角线AC、BD相交于点O,若AB=cm,BD=6cm,则菱形ABCD的面积是.16.若一组数据4,a,7,8,3的平均数是5,则这组数据的中位数是.17.一次函数y=kx﹣2的图象经过第一、三、四象限,且与两坐标轴围成的三角形的面积等于4,则k的值等于.18.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE =30°,DF=3,则AF的长为.19.如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC,若∠ADF=25°,则∠ECD=°.三.解答题20.计算:.21.计算:(﹣2)2+﹣÷.22.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.23.在平面直角坐标系xOy中,已知一次函数y=kx+4与y=﹣x+b的图象都经过A(﹣2,0),且分别与y轴交于点B和点C.(1)填空:k=,b=;(2)设点D在直线y=﹣x+b上,且在y轴右侧,当△ABD的面积为15时,求点D 的坐标.24.小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A、B两种水果进行销售,并分别以每箱35元与60元的价格售出,设购进A水果x箱,B水果y箱.(1)若小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A、B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?25.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)当∠BOD=°时,四边形BECD是菱形;(3)当∠A=50°,则当∠BOD=°时,四边形BECD是矩形.26.如图,正方形ABCD中,M为BC上的点,E是AD的延长线的点,且AE=AM,过E作EF⊥AM垂足为F,EF交DC于点N.(1)求证:AF=BM;(2)若AB=12,AF=5,求DE的长.27.某校七、八年级各有400名学生,为了了解疫情期间线上教学学生的学习情况,复学后,某校组织了一次数学测试,刘老师分别从七、八两个年级随机抽取各50名同学的成绩(百分制),并对数据(成绩)进行了整理、描述和分析,部分信息如下:a.七、八年级的频数分布直方图如下(数据分为5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):b.七年级学生成绩在80≤x<90的这一组是:808081818182828283858586868888899090c.七、八年级学生成绩的平均数、中位数如下:年级平均数中位数七年级80.3m八年级78.276根据以上信息,回答下列问题:(1)表中m的值为;(2)在这次测试中,八年级80分以上(含80分)有人;(3)小江说:“这次考试没考好,只得了79分,但年级排名仍属于前50%”,请判断小江所在年级,并说明理由;(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.28.如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE,连接BE.(1)发现问题如图①,若E是线段AC的中点,连接EF,其他条件不变,填空:线段BE与EF的数量关系是;(2)探究问题如图②,若E是线段AC上任意一点,连接EF,其他条件不变,猜想线段BE与EF的数量关系是什么?请证明你的猜想;(3)解决问题如图③,若E是线段AC延长线上任意一点,其他条件不变,且∠EBC=30°,AB=1,请直接写出AF的长度.参考答案一.选择题1.C.2.B.3.D.4.A.5.C.6.B.7.B.8.A.9.D.10.B.11.D.二.填空题12.乙.13..14..15.12cm2.16.4.17..18.3.19.57.5.三.解答题20.解:原式=﹣﹣2=4﹣﹣2=4﹣3.21.解:原式=3﹣4+2+2﹣3=7﹣5.22.解:(1)∵D、E分别为AB、AC的中点,∴DE∥BC,DE=BC,∵EF∥CD∴四边形DEFC是平行四边形,∴DE=CF.(2)∵四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.23.解:(1)将A(﹣2,0)代入y=kx+4得﹣2k+4=0,解得k=2,将A(﹣2,0)代入y=﹣x+b得1+b=0,解得b=﹣1;故答案为2,﹣1;(2)如图,过D作DE⊥BC于E,在y=2x+4中,令x=0,则y=4,∴B(0,4),在y=﹣x﹣1中,令x=0,则y=﹣1,∴C(0,﹣1),∴BC=5,+S△BCD=15,当△ABD的面积为15时,S△ABC即AO×BC+DE×BC=15,∴×2×5+×DE×5=15,∴DE=4,在y=﹣x﹣1中,令x=4,则y=﹣3,∴D(4,﹣3).24.解:(1)由题意可得,,解得,答:小王共购进A种水果25箱,B种水果9箱.(2)设利润为W元,W=(35﹣30)x+(60﹣50)y=5x+10×=﹣x+240.∵购进A水果的数量不得少于B水果的数量,∴x≥,解得:x≥15.∵﹣1<0,∴W随x的增大而减小,∴当x=15时,W取最大值,最大值为225,此时y=(1200﹣30×15)÷50=15.答:购进水果A、B的数量均为15箱并全部售出才能获得最大利润,此时最大利润为225元.25.(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC,AB=CD,∴∠OEB=∠ODC,又∵O为BC的中点,∴BO=CO,在△BOE和△COD中,,∴△BOE≌△COD(AAS);∴OE=OD,∴四边形BECD是平行四边形;(2)解:当∠BOD=90°时,四边形BECD是菱形;理由:∵四边形BECD是平行四边形,∴当∠BOD=90°时,四边形BECD是菱形;(3)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:∵四边形ABCD是平行四边形,∴∠BCD=∠A=50°,∵∠BOD=∠BCD+∠ODC,∴∠ODC=100°﹣50°=50°=∠BCD,∴OC=OD,∵BO=CO,OD=OE,∴DE=BC,∵四边形BECD是平行四边形,∴四边形BECD是矩形;故答案是:(2)90°;(3)100°.26.证明:(1)∵四边形ABCD是正方形∴∠ABC=90°,AD∥BC∴∠EAF=∠AMB,∵∠AFE=∠ABC=90°,AE=AM,∴△ABM≌△EF A(AAS)∴AF=BM(2)∵在Rt△ABM中,AB=12,AF=BM=5∴AM==13∵△ABM≌△EF A,∴AM=AE=13,∵四边形ABCD是正方形,∴AB=AD,∴DE=AE﹣AD=13﹣12=127.解:(1)由直方图中的数据可知,中位数是80≤x<90这一组第一个和第二个数的平均数,故m=(80+80)÷2=80,故答案为:80;(2)由频数分布直方图可得,在这次测试中,八年级80分以上(含80分)有400×=160(人),故答案为:160;(3)小江属于八年级,因为小江的成绩大于八年级成绩的中位数,而小于七年级成绩的中位数,故小江属于八年级;(4)400×=136(人),即七年级达到“优秀”的有136人.28.解:(1)猜想线段BE与EF的数量关系为:BE=EF;理由如下:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴∠BCA=60°,∵E是线段AC的中点,∴∠CBE=∠ABE=30°,AE=CE,∵CF=AE,∴CE=CF,∴∠F=∠CEF=∠BCA=30°,∴∠CBE=∠F=30°,∴BE=EF.故答案为BE=EF.(2)猜想线段BE与EF的数量关系为:BE=EF;理由如下:过点E作EG∥BC交AB于点G,如图②所示:∵四边形ABCD为菱形,∠ABC=60°,∴AB=BC,∠BCD=120°,AB∥CD,△ABC与△ACD都是等边三角形,∴∠ACD=60°,∠DCF=∠ABC=60°,AB=AC,∴∠ECF=120°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE,∴BG=CE,∠BGE=120°=∠ECF,又∵CF=AE,∴GE=CF,在△BGE和△CEF中,,∴△BGE≌△ECF(SAS),∴BE=EF.(3)连接EF,过点E作EG∥BC交AB延长线于点G,如图③所示:∵四边形ABCD为菱形,∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,∴∠ECF=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE,∴BG=CE,∠AGE=∠ECF,又∵CF=AE,∴GE=CF,在△BGE和△CEF中,,∴△BGE≌△ECF(SAS),∴BE=EF,∵∠ABC=60°,∠EBC=30°,∴∠ABE=∠ABC+∠EBC=60°+30°=90°,∵△ABC是等边三角形,∴∠BAC=60°,∴∠BEA=180°﹣∠ABE﹣∠BAC=180°﹣90°﹣60°=30°,在Rt△ABE中,∠BEA=30°,∴AE=2AB=2×1=2,BE=,∴EF=,∵BE=EF,∴∠EBC=∠EFB=30°,∴∠BEF=180°﹣30°﹣30°=120°,∴∠AEF=∠BEF﹣∠BEA=120°﹣30°=90°,由勾股定理得:AF===.。
2023八年级下学期期末考试语文试卷2

2023-2023八年级下学期期末考试语文试卷2023-2023八年级下学期期末考试语文试卷2023-2023八年级下学期期末考试语文试卷1 一、选择题〔题文〕以下词语中加点字的注音完全正确的一组是〔〕A、翘望〔qiáo〕嫉妒〔jí〕箴言〔zhēn〕拈轻怕重〔niān〕B、摒弃〔bìng〕遴选〔lián〕粗糙〔cāo〕锲而不舍〔qiè〕C、精华〔suí〕雕镂〔lòu〕吮吸〔shǔn〕鳞次栉比〔zhì〕D、抽噎〔yē〕踮脚〔diǎn〕叱咤〔chà〕半身不遂〔suí〕以下各句中,加点的成语使用不恰当的一项为哪一项〔〕A、这位教师教学有方,经常在课堂上故弄玄虚,以启发学生,收到了深化浅出的效果。
B、罕见雪灾袭向神州大地,一个个雪中送炭的场面立马再现。
C、就目前而言,南水北调工程正在如火如荼地进展,地方间跨流域调水也变得屡见不鲜。
D、这虽是几句无稽之谈,但他听后却很快乐,拼命地钻研《美国十大富豪传》,找发财致富的门径。
选择以下对课文描绘有错误的一项〔〕A.《白杨礼赞》,是现代作家茅盾的作品,文章以象征的手法,讴歌了中国____领导下的北方抗日军民以及中华民族的精神和意志。
B.《马说》、《陋室铭》,文体即题目所说的“说”“铭”,它们的作者分别是唐朝的韩愈、宋朝的刘禹锡。
C.《沙漠里的奇怪现象》是一篇科学小品文,文章由现象到本质,诠释了“魔鬼的海”和鸣沙原理;蒲松龄的《山市》那么着重表现了山市空虚缥缈、瞬息万变的特点。
D.《人的高贵在于灵魂》,作者周国平运用了比喻、引用等论证方法,说明了“人的高贵在于灵魂”的道理,提倡人们在生活中应该保持纯粹的精神追求。
以下句子顺序排列正确的一项为哪一项〔〕。
①有一些微生物发现,牛的胃是它们生长的乐园。
②于是,这些小家伙纷纷光临这里,居住下来。
③自然界存在着各种各样的微生物,它们总是各就各位,在适宜它们生长的地方安家落户。
人教版(Go for it)八年级下册期末试卷2

人教版(Go for it)八年级英语下册期末考试试卷(二)说明:本试卷分为听力和笔试两部分,满分120分,考试时间100分钟。
所有试题的答案都对应写在答题卡相应位置的横线上,不得答在试卷上。
一、听力部分(20分)第一节听音选图(每小题1分,共5分)听句子,选出你所听句子内容相符的图片,每小题读两遍。
1. A. B. C.2. A. B. C.3. A. B. C.4. A. B. C.5. A. B. C.第二节情景反应。
(每小题1分,共5分)根据你所听到的句子,选择正确的答语,每小题读两遍。
6. A. It‟s a pleasure. B. It‟s rainy. C. It‟s big.7. A. Three times a day. B. 2 pills at a time. C. for 4 hours.8. A. I‟m 14 years old. B. I like apples. C.I had a fight with my brother.9. A. Yes, I do. B. No, I can‟t. C. No, I won‟t.10. A. They‟re Jack‟s. B. They‟re beautiful. C. They‟re 40 yu an.第三节对话理解。
(每小题1分,共5分)根据所听对话内容,选择正确的答案,每小题读两遍。
听第一段对话,完成11-12小题。
11. What‟s Jenny going to do?A. She is going to the park.B. She is going to the movie.C. She is going to finish her homework.12. What will happen if Tom copies Jenny‟s homework?A. His mother will be mad at him.B. His mother won‟t ta ke him to the park.C. Hi s mother won‟t take him to the movie.听第二段对话,完成13—15 小题。
内蒙古自治区呼和浩特市四中学2024届英语八年级第二学期期末考试试题含答案

内蒙古自治区呼和浩特市四中学2024届英语八年级第二学期期末考试试题满分120分,时间90分钟一、单项选择(共10小题,满分10分)1、— What can you do for the charity?— We can ________ the leaflets to raise money for the people in need.A. put outB. hand outC. find outD. cut out2、—We have few vegetables for dinner. Will you go and buy ________ please?—OK, no problem.A. anyB. itC. someD. few3、—What’s the matter ________ your computer?—It doesn’t work.A. forB. toC. withD. about4、—Can you tell me ________?—No worry! I can make it myself.A. if you need help to complete the workB. when can you finish the workC. what you needed to complete the work5、Tom didn’t listen to the teacher carefully. ________, he failed the exam.A. In a wordB. In factC. As a result6、B【解析】【详解】句意:——汤姆当时在哪里?——他在网上和老师讨论一道数学题。
考查时态。
根据“ at that moment”可知此处用过去进行时,表“过去某个时间点发生的动作”。
故选B。
7、—Look at the cloud! It is in the shape of a rabbit.—Yes, and it seems to be eating a carrot.A. looks forB. looks upC. looks like8、Can you work out this math problem ________ (正确)?9、— What________ the number of the students in your school?—About two thousand. A number of them ________ from the country.A. is; areB. is; isC. are; isD. are; are10、Billy really ________ his father. They both have blonde hair and blue eyes.A. feels likeB. looks afterC. takes afterD. cares about二、补全对话(10分)11、根据下面的对话情景,在每个空白处填上一个适当的句子,使对话的意思连贯、完整。
北京市2023年八年级下学期期末考试数学试卷 (2)

北京市 八年级下学期期末考试数学试卷一、选择题(共24分,每小题3分)下列各题均有四个选项,其中只有一个是符合题意的.1.函数y =x 的取值范围是( )A .2x ≠B .2x ≤C .2x >D .2x ≥ 2.五边形的内角和为( )A .180°B .360°C .540°D .720°3.在平面直角坐标系中,点A (1,2)关于x 轴对称的点的坐标是( ) A .(1,2) B .(1,-2) C .(-1,2) D .(-1,-2) 4.下列图形中,既是中心对称图形又是轴对称图形的是( )A .等边三角形B .平行四边形C .等腰梯形D .矩形 5.已知2x =是一元二次方程2+80x mx -=的一个解,则m 的值是( )A .2B .2-C .4-D .2或4-6.某工厂由于管理水平提高,生产成本逐月下降. 原来每件产品的成本是1600元,两个月后,降至900元.如果产品成本的月平均降低率是x ,那么根据题意所列方程正确的是( )A .1600(1)900x -=B .900(1)1600x +=C .21600(1)900x -=D .2900(1)1600x += 7. 10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm )如下表所示:设两队队员身高的平均数依次为x 甲,x 乙,身高的方差依次为2S 甲,2S 乙,则下列关系中完全 正确的是( ) A .x x =甲乙,22S S >乙甲B .x x =甲乙,22S S<乙甲C .x x >甲乙,22S S>乙甲D .x x <甲乙,22S S<乙甲8.如图,菱形ABCD 中,AB =2,∠B =120°,点M 是AD 的中点,点P 由点A 出发,沿A →B →C →D 作匀速运动,到达点D 停止,则△APM 的面积y 与点P 经过的路程x 之间的函数关系的图象大致是( )二、填空题(共18分,每小题3分)9.如图,在△ABC 中,D ,E 分别是边AB ,AC 的中点,如果BC =8,那么DE = .11. 如图,在菱形ABCD 中,AC ,BD 是对角线,如果∠BAC =70°, 那么∠ADC 等于 .A BCD12. 如果把代数式x 2-2x+3化成2()x h k -+的形式,其中h ,k 为常数,那么h +k 的值是 . 13.如图,在梯形ABCD 中,AD ∥BC ,如果∠ABC =60º,BD 平分∠ABC ,且BD ⊥DC ,CD =4, 那么梯形ABCD的周长是 .14.如图,在平面直角坐标系中有一个边长为1的正方形OABC ,边OA ,OC 分别在x 轴、y 轴上,如果以对角线OB 为边作第二个正方形11OBB C ,再以对角线1OB 为边作第三个正方形122OB B C ,……,照此规律作下去,则点2B 的坐标为_________;点2014B 的坐标为_________.三、解答题(共20分,每小题5分)15.解方程:2450x x --=.16. 如图,将△ABC 置于平面直角坐标系中,点A (-1,3),B (3,1),C (3,3).(1)请作出△ABC 关于原点O 的中心对称图形△A ’B ’C ’;(点A 的对称点是点A ’, 点B 的对称点是点B ’, 点C 的对称点是点C ’)(2)判断以A ,B ’,A ’ ,B 为顶点的四边形的形状,并直接写出这个四边形的周长.17.已知一次函数112y x =+的图象与x 轴交于点A ,与y 轴交于点B . (1)求A ,B 两点的坐标;(2)过B 点作直线B P 与x 轴交于点P ,且使△A B P 的面积为2,求点P 的坐标. 18.【题设】已知:如图,点E ,F 是□ABCD 中AB ,DC 边上的点,且AE =CF ,联结DE ,BF .求证:DE =BF .ABCD EF四、解答题(共24分,每小题6分)19. 已知关于x 的一元二次方程04222=-++k x x 有两个不相等的实数根. (1)求k 的取值范围;(2)若k 为正整数,且该方程的根都是整数,求k 的值.20.为了解某校学生的身高情况,随机抽取该校若干名学生测量他们的身高,已知抽取的学生中,男生、女生的人数相同....,利用所得数据绘制如下统计图表: 身高分组表 女生身高频数分布表 男生身高频数分布直方图组别 身高/cmA 155x <B 155160x ≤<C 160165x ≤<D 165170x ≤<E170x ≥组别频数 频率A8 aB12 0.30 C100.25 Dc0.15 E40.10 合计b1.00身高/cm146102EDCB4812频数A请根据以上图表提供的信息,解答下列问题:(1)在女生身高频数分布表中:a = ,b = ,c = ; (2)补全男生身高频数分布直方图;(3)已知该校共有女生400人,男生380人,请估计身高在165≤x <170之间的学生约有多少人. 21.为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.(1)设每年用水量为x 立方米,按“阶梯水价”应缴水费y 元,请写出y (元)与x (立方米)之间的函数解析式;(2)明明家预计202X 年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元? 22.如图,矩形ABCD 的对角线AC ,BD 交于点O , DE ∥AC 交BA 的延长线于点E ,点F 在BC 上,BF =BO ,且AE =6,AD =8.(1)求BF 的长;(2)求四边形OFCD 的面积.五、解答题(共14分,每小题7分)23. 如图,在平面直角坐标系xOy 中,直线1l 与x 轴交于点A (3-,0),与y 轴交于点B ,且与直线2l :43y x =的交点为C (a ,4) . (1)求直线1l 的解析式;(2)如果以点O ,D ,B ,C 为顶点的四边形是平行四边 形,直接写出点D 的坐标;(3)将直线1l 沿y 轴向下平移3个单位长度得到直线3l ,点P (m ,n )为直线2l 上一动点,过点P 作x轴的垂线, 分别与直线1l ,3l 交于M ,N.当点P 在线段..MN 上时,请直接写出m 的取值范围.24.把一个含45°角的直角三角板BEF 和一个正方形ABCD 摆放在一起,使三角板的直角顶点和正方形的顶点B 重合,联结DF ,点M ,N 分别为DF ,EF 的中点,联结MA ,MN .(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接写出结论;(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.教师的职务是‘千教万教,教人求真’;学生的职务是‘千学万学,学做真人’。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
朝阳七中八年级(下)期末测试卷
时间 120 分钟 共24分) ) 满分 150 分 成绩 :_________________ 10.函数 y=
2x 1 x -1
的自变量 x 的取值范围是______________
8 3
一、选择(每小题3分
11.如图,直线 L1:y=x+b 与直线 L2:y=ax+
相交于点 P(1,2) ,则关于 x 的不等式 x+b>ax+
8 3
的解集
1.已知 a、b 是有理数,且 a<b,则下列式子不正确的是-------------------( A.a+3<b+3 B.a-3<b-3 C.3a<3b D.-3a<-3b
2.下列由左边到右边的变形是因式分解的是-------------------------------( A. (a+3) (a-3)= a -9 C.a - b +1=(a+b) (a-b)+1
2 2 2
)
为______________ 12.下列命题:①有一个锐角相等的两个直角三角形相似;②斜边和一直角边对应成比例的两个直角三角形 相似;③两个等边三角形一定相似;④任意两个矩形一定相似.其中真命题有__________(填序号) .
B.m -4=(m+2) (m-2) D.2π R+2π r+2=2π (R+r) )
2
3. 若 x:y:z=3:5:7,3x+2y-4z=9,则 x+y+z 的值为--------------------------( A.-3 B.-5 C.-7 D. -15
13.已知两个相似三角形的相似比为 2:3,面积之差为 25cm ,则较大三角形的面积为__________. 14.已知一组数据 1,2,3,5,x,它的平均数是 3,则这组数据的方差是___________.
2
4.如图,下列条件不能判定直线 L1∥L2 的是-----------------------------------------------( A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
)
15. 若不等式 x<a 只有 4 个正整数解,则 a 的取值范围是_____________ 16.用黑白两种正六边形地面瓷砖,按如图规律拼成若干图案,则第 n 个图案中有白色地面瓷砖 块。
5.已知 C 是线段 AB 的黄金分割点(AC>BC), 则 AC∶BC =------------------------( A .(
5
)
-1)∶2
B.(
5
+1)∶2
C.(3-
5
)∶2
D.(3+
5
)∶2 ) 三、 解答题 )
x 4 3 x 2 17. 分)解不等式组 1 2 x (8 1 x 3
6.如果关于 x 的不等式(a+1)x>a+1 的解集为 x<1,那么 a 的取值范围是---( A.a>0 B.a<0
0
第1个
第2个
第3个
C.a>-1
D.a<-1
7.如图,∠APD=90 ,AP=PB=BC=CD,则下列结论成立的是------------------( A. Δ PAB∽Δ PCA C. Δ ABC ∽ Δ DBA B. Δ PAB∽Δ PDA D. Δ ABC∽Δ DCA
并求其整数解。
8. 如图,在□ABCD 中,点 M 是 BC 的中点,且 S△BME=1,则□ABCD 的面积为---( A.12 B.13
A
)
C.14
D.15
P
B
C
D
二、填空题 (每题 3 分
共 24 分) .
9.分解因式:2x2-12x+18=
18. 分)先化简,再求值: (8
x -3 x -2
÷(
5 x -2
- 2 - x)
其中 x = 2 - 3
20. (10 分)如图,在△ABC 中,DE∥BC,且 S△ADE :S 四边形 BCED=1:2,BC=2 6 , 求 DE 的长。
A
D
E
B
C
19. 分)如图,在边长为 1 个单位长度的小正方形组成的网格中,按要求画出△A1B1C1 和△A2B2C2; (8 (1)将△ABC 向右平移 4 个单位,再向上平移 1 个单位,得到△A1B1C1; (2)以图中的 O 为位似中心,将△A1B1C1 作位似变换且放大到原来的两倍,得到△A2B2C2.
21.(10 分)某市为了治理城市污水,需要铺设一段全长为 300 米的污水排放管道,铺设 120 米后,为了尽 可能减少施工对城市交通所造成的影响, 后来实际每天的工作量比原计划增加 20%, 结果共用了 27 天完成了 这项任务,求后来实际每天铺设管道多少米?
C B A O
22. (10 分)如图,在梯形 ABCD 中,AD⊥BC,∠BAD=90°,对角线 BD⊥DC. (1) Δ ABD 与Δ DCB 相似吗?请说明理由. (2) 如果 AD=4,BC=9,求 BD 的长.
24. (12 分)如图:△ABC 是等边三角形,点 D,E 分别在 BC,AC 上,且 BD=CE,AD 与 BE 相交于点 P (1)求证:△ABD≌△BCE
(2)求证:△AEP∽△BEA
(3)求证: BD
2
=AD×DP
23. (10 分)为了了解全市今年 8 万名初中毕业生的体育升学考试成绩状况, (满分 30 分,得分均是整数) 从中随机抽取了部分学生的体育升学考试成绩制成下面频数直方图(尚不完整) ,已知第一小组的频率为 0.12,回答下列问题: (1) 在这个问题中, 总体是___________________________________________ , 样本的容量为________; (2)第四小组的频率为__________,请补全频数直方图; (3)被抽取的样本的中位数落在第_______小组内; (4)若成绩在 24 分以上的为“优秀” ,请估计今年全市初中毕业生的体育升学考试成绩为“优秀”的 人数.
25. (12 分)某运输公司用 10 辆相同的汽车将一批苹果运到外地,每辆汽车能装 8 吨甲种苹果,或 10 吨乙 种苹果,或 11 吨丙种苹果.公司规定每辆车只能装同一种苹果,而且必须满载.已知公司运送了甲、乙、 丙三种苹果共 100 吨,且每种苹果不少于一车. (1)设用 x 辆车装甲种苹果,y 辆车装乙种苹果,求 y 与 x 之间的函数关系式,并求出自变量 x 的取 值范围; (2)若运送三种苹果所获利润的情况如下表所示:设此次运输的利润为 W(万元) ,如何安排车辆分配 方案才能使运输利润 W 最大,并求出最大利润.
26. (14 分)等腰△ABC,AB=AC,∠BAC=120° ,P 为 BC 的中点,小慧拿着含 30° 角的透明三角板,使 30° 角的顶点落在点 P,三角板绕 P 点旋转. (1)如图 a,当三角板的两边分别交 AB、AC 于点 E、F 时.求证:△BPE∽△CFP; (2)操作:将三角板绕点 P 旋转到图 b 情形时,三角板的两边分别交 BA 的延长线、边 AC 于点 E、F. ①探究 1:△BPE 与△CFP 还相似吗?(只需写出结论) ②探究 2:连接 EF,△BPE 与△PFE 是否相似?请说明理由;
。
