2011年广东高考文科数学选择填空

合集下载

2011年高考数学(新课标)文科真题及答案

2011年高考数学（新课标）文科真题及答案参考答案一、选择题B C B D B AB DC CD A二、填空题1 -6三、解答题解：因为所以所以的通项公式为(18)解：因为，由余弦定理得从而BD2+AD2= AB2，故BD AD又PD 底面ABCD，可得BD PD所以BD 平面PAD. 故PA BD如图，作DE PB，垂足为E。

已知PD 底面ABCD，则PD BC。

由知BD AD，又BC//AD，所以BC BD。

故BC 平面PBD，BC DE。

则DE 平面PBC。

由题设知，PD=1，则BD= ，PB=2，根据BEPB=PDBD，得DE= ，即棱锥DPBC的高为解由试验结果知，用A配方生产的产品中优质的频率为，所以用A配方生产的产品的优质品率的估计值为0.3。

由试验结果知，用B配方生产的产品中优质品的频率为，所以用B 配方生产的产品的优质品率的估计值为0.42由条件知用B配方生产的一件产品的利润大于0当且仅当其质量指标值t94，由试验结果知，质量指标值t94的频率为0.96，所以用B 配方生产的一件产品的利润大于0的概率估计值为0.96.用B配方生产的产品平均一件的利润为(20）解：曲线与y轴的交点为，与x轴的交点为，则有解得t=1. 则圆C的半径为所以圆C的方程为设A，B，其坐标满足方程组：消去y，得到方程由已知可得，判别式因此，从而①由于OAOB，可得又所以②由①，②得，满足故解：由于直线的斜率为，且过点，故即解得，。

由知，所以考虑函数，则所以当时，故当时，当时，从而当解：连接DE，根据题意在△ADE和△ACB中，ADAB=mn=AEAC，即.又DAE=CAB，从而△ADE∽△ACB因此ADE=ACB所以C，B，D，E四点共圆。

m=4，n=6时，方程x2-14x+mn=0的两根为x1=2，x2=12.故AD=2，AB=12.取CE的中点G，DB的中点F，分别过G，F作AC，AB的垂线，两垂线相交于H点，连接DH.因为C，B，D，E四点共圆，所以C，B，D，E四点所在圆的圆心为H，半径为DH.由于A=900，故GH∥AB，HF∥AC. HF=AG=5，DF= (12-2)=5.故C，B，D，E四点所在圆的半径为5解：设P(x，y)，则由条件知M( ).由于M点在C1上，所以即从而的参数方程为曲线的极坐标方程为，曲线的极坐标方程为。

2011年高考文科数学(广东)考试答案

2011年普通高等学校招生全国统一考试（广东卷）数学（文科）答案本试卷共4页，21小题，满分150分．考试用时120分钟．一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、【解析】A.由题得,1i iz -==所以选A. 2、【解析】 C.方法一：由题得⎩⎨⎧==⎩⎨⎧==∴⎩⎨⎧=+=+10011122y x y x y x y x 或，)}1,0(),0,1(|),{(y x B A = ，所以选C.方法二：直接作出单位圆221x y +=和直线1=+y x ，观察得两曲线有两个交点，所以选C. 3、【解析】B.)2,1()0,()2,1(λλλ+=+=+b a ，()//a b c λ+210324)1(=∴=⨯-⨯+∴λλ 所以选B. 4、【解析】C.由题得），，（）函数的定义域为（且∞+∴≠->∴⎩⎨⎧>+≠-11,1-110101 x x x x 所以选C. 5、 6、OABC,||||cos 3||cos 3||z OM OA OM OA AOM OM AOM ON =⋅=⋅∠=∠=，所以就是求||ON 的最大值，||ON 表示方向上的投影，在OA OM 数形结合观察得当点M 在点B 的地方时，||ON 才最大。

222236124cos 23236AOM AOM +-∆+∴∠==2在中，OA=2+1=3,OB=2=6,AB=2-1=1,,所以423263max =∙∙=z ，所以选择B7、【解析】A.先从5个侧面中任意选一个侧面有15C 种选法，再从这个侧面的4个顶点中任意选一个顶点有14C 种选法，由于不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，所以除去这个侧面上、相邻侧面和同一底面上的共8个点，还剩下2个点，把这个点和剩下的两个点连线有12C 种方法，但是在这样处理的过程中刚好每一条对角线重复了一次，所以最后还要乘以,21所以这个正五棱柱对角线的条数共有2021121415=∙∙∙C C C ,所以选择A.8、【解析】A.设圆C 圆心C ),(y x ，半径为R,A(0,3),点C 到直线y=0的距离为|CB|，由题得1811)3(11||222+=∴+=-+∴+=+=x y y y x y R CA ,所以圆C 的圆心C 轨迹是抛物线，所以选A.9、【解析】C.由题得该几何体是如图所示的四棱锥P-ABCD ，，棱锥的高，3232322131331233231222=⨯⨯⨯⨯⨯=∴=-=-==∴=-=V PO h AO所以选择C.10、【解析】B.由()()())(x g f x g f = 得选择支B 左边=()()()))()((x h g f x h g f ∙=∙ 由()()())(x g x f x g f =∙得))(())(())()((x h g x h f x h g f =∙;由()()())(x g x f x g f =∙得选择支B 右边==∙))(()((x h g h f 。

2011年广东高考数学试题(文科)

初一语文模拟试卷（11.20）一、语言的积累与运用：（5分）1、给下面加点字注音，或根据拼音写汉字。

（2.5分）①骸．（）骨②潜．（）行③静谧．（）④篡．（）夺⑤一霎．（）时⑥xī（）sū（）作响⑦喧xiāo（）⑧shǒu（）猎⑨kù（）爱⑩dǎo（）告2、完词填空（2.5分）①海枯石（）②千（）百态③（）首挺立④更胜一（）⑤销声（）迹二、古诗文默写：（10分）3、海日生残夜，。

4、开轩面场圃，。

5、，听取蛙声一片。

6、《泊秦怀》一诗中哪两句渲染了一幅迷茫、冷落的水上夜景图，。

7、张若虚在《春江花月夜》一诗云：“此时相望不相闻，但愿月华流照君”。

《闻王昌龄左迁龙标遥有此寄》中亦有与此句意境相类似的诗句是：，。

8、崔颢《黄鹤楼》中有诗句“日暮乡关何处是，烟波江上使人愁”，马志远《天净沙秋思》中与此意境相似的名句是：，。

9、《论语十则》中鲜明的指导我们学习中要紧密的把学与思结合起来的句子是：，。

三、阅读。

（42分）（一）课内古文阅读。

（10分）《陈太丘与友期》陈太丘与友期行，期日中，过中不至，太丘舍去，去后乃至。

元方时年七岁，门外戏。

客问元方：“尊君在不？”答曰：“待君久不至，已去。

”友人便怒：“非人哉！与人期行，相委而去。

”元方曰：“君与家君期日中。

日中不至，则是无信；对子骂父，则是无礼。

”友人惭，下车引之，元方入门不顾。

10、解释下列加点字在文中的含义。

（2分）①期．日中（）②舍．去（）③相委．而去（）④友人惭．（）11、友人“下车引之”的原因是什么？（用文中的话回答）（2分）。

12、当自己的父亲遭到朋友的指责时，元方有理有据地对友人进行了批驳，从中可以看出元方是个什么样的孩子？（2分）13、友人来迟，却对子骂父，遭到了一个孩子的有力批驳。

看来有理真的未必在年高，那么面对这样的突发事件，你会怎么做呢？你从元方的做法中能得到什么启发呢？（4分）（二）课外古文阅读（6分）天地浑沌如鸡子盘古生其中万八千岁天地开辟阳清为天，阴浊为地。

高考文科数学试题及答案广东

6 号打篮
（二）选择题（ 14-15 题，考生只能从中选做一题）
14 ．（坐标系与参数方程选做题）已知两曲线参数方程分别为
5 cos
（0
y sin
< ）和
x 5t2
4 （ t R ），它们的交点坐标为
。
yt
15．（集合证明选讲选做题）如图 4，在梯形 ABCD中， AB∥ CD，AB=4，CD=2．E,F分别为 AD，BC 上点，且 EF=3， EF∥AB，则梯形 ABFE与梯形 EFCD的面积比为
18．（本小题满分 13 分）
图 5 所示的集合体是将高为 2，底面半径为 1 的直圆柱沿过轴的平面切开后，将其中一半沿
切面向右水平平移后得到的． A，A′，B，B′分别为 CD , C'D ' , DE , D 'E ' 的中点， O1, O1' ,O2, O2'
分别为 CD ,C ' D ', DE , D ' E ' 的中点．
2 13
5
）的值
17．（本小题满分 13 分）在某次测验中，有 6 位同学的平均成绩为成绩，且前 5 位同学的成绩如下：
75 分。用 xn 表示编号为 n（n=1,2, …,）6 的同学所得
编号 n
1
2
3
4
5
成绩 xn
70
76
72
70
72
（ 1）求第 6 位同学的成绩 x6，及这 6 位同学成绩的标准差 s; （ 2）从前 5 位同学中，随机地选 2 位同学，求恰有 1 位同学成绩在区间（ 68，75）中的概率。
D． (( f g) h)( x) (( f h) ( g h))( x)

2011年高考新课标卷文科数学试题(解析版)

2011年普通高等学校招生全国统一考试(新课标全国卷）文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题)两部分，其中第Ⅱ卷第22～24题为选考题，其他题为必考题第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{0,1,2,3,4}M =,{1,3,5}N =，P MN =,则P 的子集共有A ．2个B ．4个C ．6个D ．8个【答案】B 【解析】P M N =={1,3}，故P 的子集有224=个．2．复数5i12i=- A ．2i - B ．12i - C ．2i -+ D ．12i -+ 【答案】C 【解析】5i 5i(12i)2i 12i (12i)(12i)+==-+--+． 3．下列函数中,既是偶函数又在(0,)+∞单调递增的函数是A ．3y x = B ．||1y x =+ C ．21y x =-+ D ．||2x y -=【答案】B【解析】3y x =为奇函数，21y x =-+在(0,)+∞上为减函数,||2x y -=在(0,)+∞上为减函数，故选B ．4．椭圆221168x y +=的离心率为A ．13 B ．12C D ．2【答案】D【解析】由221168x y +=可知216a =，28b =，∴2228c a b =-=，∴22212c e a ==,∴22e =． 5．执行右面的程序框图，如果输入的N 是6,那么输出的p 是A ．120B ．720C ．1440D ．5040 【答案】B【解析】由程序框图可得，输出的123456720p =⨯⨯⨯⨯⨯=，选B6．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 A ．13 B ．12 C ．23 D ．34【答案】A【解析】记三个兴趣小组分别为1、2、3,甲参加1组记为“甲1”，则基本事件为“甲1，乙1；甲1,乙2;甲1，乙3；甲2，乙1；甲2，乙2;甲2，乙3；甲3，乙1；甲3，乙2;甲3,乙3”，共9个．记事件A 为“甲、乙两位同学参加同一个兴趣小组"，其中事件A 有“甲1，乙1;甲2，乙2；甲3，乙3”,共3个．因此31()93P A ==． 7．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=A ．45-B ．35-C ．35D ．45【答案】B【解析】由题知tan 2θ=，222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++,选B ．8．在一个几何体的三视图中,正视图与俯视图如右图所示，则相应的侧视图可以为俯视图正视图DCB A【答案】D【解析】通过正视图及俯视图可看出该几何体为半个圆锥和一个三棱锥组合在一起，故侧视图为D ．9．已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于,A B 两点,||AB =12，P 为C 的准线上一点，则ABP ∆的面积为_____．A ．18B ．24C ．36D ．48 【答案】C【解析】设抛物线方程为22y px =,则焦点坐标为(,0)2p ，将2px =代入22y px =可得22y p =，||AB =12，即2p =12，∴p =6．点P 在准线上，到AB 的距离为p =6，所以ABP ∆面积为1612362⨯⨯=． 10．在下列区间中，函数()43xf x e x =+-的零点所在的区间为_____． A ．1(,0)4- B ．1(0,)4 C ．11(,)42 D ．13(,)24【答案】C【解析】因为114411()432044f e e =+⨯-=-<,112211()431022f e e =+⨯-=->,所以()43x f x e x =+-的零点所在的区间为11(,)42．11．设函数()sin(2)cos(2)44f x x x ππ=+++，则 A ．()y f x =在(0,)2π单调递增,其图象关于直线4x π=对称 B ．()y f x =在(0,)2π单调递增，其图象关于直线2x π=对称 C ．()y f x =在(0,)2π单调递减，其图象关于直线4x π=对称 D ．()y f x =在(0,)2π单调递减，其图象关于直线2x π=对称【答案】D【解析】因为()sin(2)cos(2)44f x x x ππ=+++=2sin(2)2x π+=2cos 2x ，所以2cos 2y x =，在(0,)2π单调递减，对称轴为2x k π=，即2k x π=(k ∈Z ）．12．已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =，那么函数()y f x =的图象与函数|lg |y x =的图象的交点共有_____．A ．10个B ．9个C ．8个D ．1个【答案】A【解析】画出两个函数图象可看出交点有10个．第Ⅱ卷本卷包括必考题和选考题两部分．第13题—第21题为必考题,每个试题考生都必须做答．第22题—第24题为选考题,考生根据要求做答．二、填空题：本大题共4小题,每小题5分．13．已知a 与b 为两个不共线的单位向量,k 为实数,若向量+a b 与向量k -a b 垂直，则k = ．【答案】1【解析】∵+a b 与k -a b 垂直，∴(+a b )·(k -a b ) =0，化简得(1)(1)0k -⋅+=a b ,根据a 、b 向量不共线，且均为单位向量得10⋅+≠a b ，得10k -=，即1k =．14．若变量x ,y 满足约束条件32969x y x y ≤+≤⎧⎨≤-≤⎩，则2z x y =+的最小值是_________．【答案】－6【解析】画出区域图知，当直线2z x y =+过239x y x y +=⎧⎨-=⎩的交点(4，—5)时，min 6z =-．15．ABC ∆中，120,7,5B AC AB =︒==，则ABC ∆的面积为_________．153【解析】根据sin sin AB ACC B=得5353sin sin 7AB C B AC === 25311cos 1()1414C =-=，所以sin sin[()]sin cos sin cos A B C B C C B π=-+=+3111533321421414=⨯-⨯=．因此ABC S ∆=1133153sin 7522144AB AC A ⨯⨯⨯=⨯⨯⨯= 16．已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的316,则这两个圆锥中，体积较小者的高与体积较大者的高的比值为______________．【答案】13【解析】设球心为1O ,半径为1r ,圆锥底面圆圆心为2O ,半径为2r ，则有22123416r r ππ⨯=，即212r r =，所以1122r O O ==，设两个圆锥中，体积较小者的高与体积较大者的高分别为1h 、2h ，则1111211232r r h r h r -==+．三、解答题：解答应写文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知等比数列{}n a 中，113a =,公比13q =．（Ⅰ)n S 为{}n a 的前n 项和，证明：12nn a S -=；（Ⅱ)设31323log log log n n b a a a =+++，求数列{}n b 的通项公式．【解析】(Ⅰ）因为.31)31(311n n n a =⨯=- ,2311311)311(31nn n S -=--= 所以,21nn a S --(Ⅱ）n n a a a b 32313log log log +++=)21(n +++-=2)1(+-=n n 所以}{n b 的通项公式为.2)1(+-=n n b n18．（本小题满分12分）如图,四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB AD =,PD ⊥底面ABCD ．（Ⅰ)证明：PA BD ⊥;(Ⅱ)若1PD AD ==，求棱锥D PBC -的高．【解析】（Ⅰ)因为60,2DAB AB AD ∠=︒=，由余弦定理得3BD AD =从而222BD AD AB +=，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面P AD. 故 P A ⊥BD(Ⅱ）如图，作DE ⊥PB ，垂足为E ．已知PD ⊥底面ABCD ，则PD ⊥BC ．由（Ⅰ)知BD ⊥AD ，又BC //AD ，所以BC ⊥BD ．故BC ⊥平面PBD ，BC ⊥DE ．则DE ⊥平面PBC ．由题设知，PD =1，则BD =3，PB =2，根据BE ·PB =PD ·BD ，得DE =23，即棱锥D —PBC 的高为.2319．（本小题满分12分）某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好,且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A 配方和B 配方)做试验,各生产了100件这种产品，并测量了每件产品的质量指标值，得到时下面试验结果：A 配方的频数分布表B 配方的频数分布表(Ⅰ)分别估计用A 配方,B 配方生产的产品的优质品率;（Ⅱ）已知用B 配方生产的一种产品利润y (单位：元)与其质量指标值t 的关系式为2,942,941024,102t y t t -<⎧⎪=≤<⎨⎪≥⎩，估计用B 配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述100件产品平均一件的利润．【解析】（Ⅰ)由试验结果知,用A 配方生产的产品中优质品的频率为2280.3100+=，所以用A 配方生产的产品的优质品率的估计值为0.3．由试验结果知,用B 配方生产的产品中优质品的频率为32100.42100+=，所以用B 配方生产的产品的优质品率的估计值为0.42．(Ⅱ）由条件知，用B 配方生产的一件产品的利润大于0当且仅当其质量指标值94t ≥，由试验结果知，质量指标值94t ≥的频率为0．96．所以用B 配方生产的一件产品的利润大于0的概率估计值为0．96．用B 配方生产的产品平均一件的利润为1[4(2)542424] 2.68100⨯⨯-+⨯+⨯=（元）．20．(本小题满分12分）在平面直角坐标系xOy 中，曲线261y x x =-+与坐标轴的交点都在圆C 上． (Ⅰ)求圆C 的方程;（Ⅱ)若圆C 与直线0x y a -+=交于,A B 两点,且OA OB ⊥,求a 的值．【解析】（Ⅰ）曲线162+-=x x y 与y 轴的交点为（0,1)，与x 轴的交点为（).0,223(),0,223-+故可设C 的圆心为（3，t ）,则有,)22()1(32222t t +=-+解得t =1.则圆C 的半径为.3)1(322=-+t 所以圆C 的方程为.9)1()3(22=-+-y x（Ⅱ）设A (11,y x )，B (22,y x )，其坐标满足方程组：⎪⎩⎪⎨⎧=-+-=+-.9)1()3(,022y x a y x 消去y,得到方程.012)82(222=+-+-+a a x a x由已知可得，判别式.0416562>--=∆a a因此，,441656)28(22,1a a a x --±-=从而2120,422121+-=-=+a a x x a x x①由于OA ⊥OB ，可得,02121=+y y x x 又,,2211a x y a x y +=+=所以.0)(222121=+++a x x a x x②由①,②得1-=a ,满足,0>∆故.1-=a21．(本小题满分12分）已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=．（Ⅰ)求a ,b 的值；(Ⅱ）证明：当0x >,且1x ≠时，ln ()1xf x x >-．【解析】（Ⅰ）221(ln )'()(1)x x b x f x x x α+-=-+由于直线230x y +-=的斜率为12-，且过点(1,1)，故(1)1,1'(1),2f f =⎧⎪⎨=-⎪⎩即1,1,22b a b =⎧⎪⎨-=-⎪⎩解得1a =，1b =．(Ⅱ）由（Ⅰ）知ln 1f ()1x x x x=++，所以 )1ln 2(111ln )(22xx x x x x x f -+-=-=考虑函数()2ln h x x =+xx 12-(0)x >,则22222)1()1(22)(xx x x x x x h --=---=' 所以当1≠x 时，,0)1(,0)(=<'h x h 而故当)1,0(∈x 时，;0)(11,0)(2>->x h x x h 可得当),1(+∞∈x 时，;0)(11,0)(2>-<x h xx h 可得从而当.1ln )(,01ln )(,1,0->>--≠>x xx f x x x f x x 即且请考生在第（22）、（23）、（24）三题中任选一题做答,如果多做，则按所做的第一题记分．22．(本小题满分10分)选修4—1:几何证明选讲如图，D ，E 分别为ABC ∆的边AB ,AC 上的点,且不与ABC ∆的顶点重合．已知AE 的长为m ，AC 的长为n ,AD ,AB 的长是关于x 的方程2140x x mn -+=的两个根．EB(Ⅰ)证明：,,,C B D E 四点共圆；(Ⅱ）若90A ∠=︒，且4,6,m n ==求,,,C B D E 所在圆的半径．【解析】(Ⅰ)连结DE ，根据题意在ADE ∆和ACB ∆中，AD AB mn AE AC ⨯==⨯，即AD AEAC AB=．又DAE CAB ∠=∠,从而ADE ∆∽ACB ∆．因此ADE ACB ∠=∠．所以C ，B ，D ，E 四点共圆．(Ⅱ)4m =,6n =时，方程2140x x mn -+=的两根为12x =，212x =．故2AD =，12AB =．取CE 的中点G ,DB 的中点F ，分别过G ，F 作AC ，AB 的垂线，两垂线相交于H 点,连结DH ．因为C ，B ，D ，E 四点共圆，所以C ，B ，D ，E 四点所在圆的圆心为H ，半径为DH ．由于90A ∠=︒，故//GH AB ，//HF AC ，从而5HF AG ==，()112252DF =-=．故C ，B ,D ，E 四点所在圆的半径为23．(本小题满分10分）选修4—4:坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为2cos (22sin x y ααα=⎧⎨=+⎩为参数），M 为1C 上的动点,P 点满足2OP OM =，点P 的轨迹为曲线2C ．（Ⅰ）求2C 的方程；ADB C GEM（Ⅱ)在以O 为极点，x 轴的正半轴为极轴的极坐标系中,射线3πθ=与1C 的异于极点的交点为A ，与2C 的异于极点的交点为B ,求||AB .【解析】(Ⅰ)设(),P x y ,则由条件知,22x y M ⎛⎫⎪⎝⎭，由于M 点在1C 上，所以2cos 222sin 2xy αα⎧=⎪⎪⎨⎪=+⎪⎩,即4cos 44sin x y αα=⎧⎨=+⎩．从而2C 的参数方程为4cos 44sin x y αα=⎧⎨=+⎩(α为参数）．（Ⅱ)曲线1C 的极坐标方程为4sin ρθ=，曲线2C 的极坐标方程为8sin ρθ=．射线3πθ=与1C 的交点A 的极径为14sin 3πρ=，射线3πθ=与2C 的交点B 的极径为28sin3πρ=，所以12AB ρρ=-=24．（本小题满分10分）选修4-5：不等式选讲设函数()||3f x x a x =-+，其中0a >． (Ⅰ)当1a =时，求不等式()32f x x ≥+的解集．（Ⅱ)若不等式()0f x ≤的解集为｛x |1}x ≤-，求a 的值．【解析】（Ⅰ)当1a =时，()32f x x ≥+可化为12x -≥由此可得3x ≥或1x ≤-，故不等式()32f x x ≥+的解集为{3x x ≥或}1x ≤-． (Ⅱ）由()0f x ≤得30x a x -+≤，此不等式化为不等式组 30x a x a x ≥⎧⎨-+≤⎩或30x a a x x ≤⎧⎨-+≤⎩即4x a a x ≥⎧⎪⎨≤⎪⎩或2x aa x ≤⎧⎪⎨≤-⎪⎩．由于0a >，所以不等式组的解集为2a x x ⎧⎫≤-⎨⎬⎭⎩．由题设可得12a-=-,故2a =．。

2011年广东数学高考题(编辑版)

2011年广东文数高考题一、单选题（10×5=50分）：1、设i z=1，则复数z=（）：A 、—iB 、iC 、—1D 、12、若x 、y ∈R ，集A={（x ，y ）∣22x y +=1}，B={（x ，y ）∣x +y =1}，则A ∩B 的元素个数为（）：A 、4B 、3C 、2D 、13、若λ∈R ，向量a =（1，2），b =（1，0），c =（3，4）；（a +λb ）∥c，则λ=（）：A 、14 B 、12C 、1D 、2 4、()f x =11x -+()lg 1x +的定义域是（）：A 、（—∞，—1）B 、（1，+∞）C 、（—1，1）∪（1，+∞）D 、R5、不等式22x —x —1>0的解集是（）： A 、1(,1)2-B 、（1，+∞）C 、（—∞，1）∪（2，+∞）D 、（—∞，—12）∪（1，+∞） 6、若A ，动点M (),x y在平面区域02x y x ⎧≤≤⎪≤⎨⎪≤⎩则z=OA ·OM的最大值为（）： A 、3 B 、4 C 、D 、7、正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为其对角线，则一个正五棱柱对角线的条数是（）：A 、20B 、15C 、12D 、108、与圆2x +()23y -=1外切、且与直线y =0相切的动圆C 的圆心的轨迹为（）：A 、抛物线B 、双曲线C 、椭圆D 、圆9、正、侧、俯视图分别是正Δ、等腰Δ和菱形的几何体体积为（）： A 、B 、4C 、D 、210、设()f x 、()g x 、()h x 是R 上的任意实值函数，x ∀∈R ，定义()()f g x =[()]f g x ，()()f x x ∙=()()f x g x 。

则下列恒成立的是（）：A 、[（f g ）·h]（x ）=[（f·h ）（g·h ）]（x ）B 、[（f·g ） h]（x ）=[（f h ）·（g h ）]正视图俯视图（x ）C 、[（f g ） h]（x ）=[（f h ）（g h ）]（x ）D 、[（f·g ）·h]（x ）=[（f·h ）·（g·h ）]（x ）二、填空题（4×5=20分，其中第14∽15题二选一）： 11、若{}n a 是递增等比数列，2a =2，43a a -=4，则公比q =______ 12、设()f x =1+3cos x x ，若()f a =11，则()f a -=_______13、为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x （单位：小时）与当天投篮命中率y 之间的关系：小李这5天的平均投篮命中率为_________；用线性回归分析法，预测小李每月6号打篮球6小时的投篮命中率为________。

2011年广东省高考数学试卷(文科)答案与解析

2011年广东省高考数学试卷（文科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分）1．（5分）（2011•广东）设复数z满足iz=1，其中i为虚数单位，则z=（）A．﹣i B．i C．﹣1 D．1【考点】复数代数形式的乘除运算．【专题】数系的扩充和复数．【分析】我们可以利用待定系数法求出Z，我们设Z=x+yi，结合已知中iz=1，结合复数相等的充要条件，我们易构造出一个关于x，y的方程组，解方程组即可求出满足条件的复数Z的值．【解答】解：设Z=x+yi∵iz=1，∴i（x+yi）=﹣y+xi=1故x=0，y=﹣1∴Z=﹣i故选A【点评】本题考查的知识点是复数代数形式的乘除运算，其中利用复数相等的充要条件，构造出一个关于x，y的方程组，是解答本题的关键．2．（5分）（2011•广东）已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B=|（x，y）|x，y为实数，且x+y=1}，则A∩B的元素个数为（）A．4 B．3 C．2 D．1【考点】交集及其运算．【专题】集合．【分析】观察两集合发现，两集合表示两点集，要求两集合交集元素的个数即为求两函数图象交点的个数，所以联立两函数解析式，求出方程组的解，有几个解就有几个交点即为两集合交集的元素个数．【解答】解：联立两集合中的函数关系式得：，由②得：x=1﹣y，代入②得：y2﹣y=0即y（y﹣1）=0，解得y=0或y=1，把y=0代入②解得x=1，把y=1代入②解得x=0，所以方程组的解为或，有两解，则A∩B的元素个数为2个．故选C【点评】此题考查学生理解交集的运算，考查了求两函数交点的方法，是一道基础题．本题的关键是认识到两集合表示的是点坐标所构成的集合即点集．3．（5分）（2011•广东）已知向量=（1，2），=（1，0），=（3，4）．若λ为实数，（+λ）∥，则λ=（）A．B．C．1 D．2【考点】平面向量共线（平行）的坐标表示．【专题】平面向量及应用．【分析】根据所给的两个向量的坐标，写出要用的+λ向量的坐标，根据两个向量平行，写出两个向量平行的坐标表示形式，得到关于λ的方程，解方程即可．【解答】解：∵向量=（1，2），=（1，0），=（3，4）．∴=（1+λ，2）∵（+λ）∥，∴4（1+λ）﹣6=0，∴故选B．【点评】本题考查两个向量平行的坐标表示，考查两个向量坐标形式的加减数乘运算，考查方程思想的应用，是一个基础题．4．（5分）（2011•广东）函数f（x）=+lg（1+x）的定义域是（）A．（﹣∞，﹣1）B．（1，+∞）C．（﹣1，1）∪（1，+∞）D．（﹣∞，+∞）【考点】函数的定义域及其求法．【专题】函数的性质及应用．【分析】根据题意，结合分式与对数函数的定义域，可得，解可得答案．【解答】解：根据题意，使f（x）=+lg（1+x）有意义，应满足，解可得（﹣1，1）∪（1，+∞）；故选：C．【点评】本题考查函数的定义域，首先牢记常见的基本函数的定义域，如果涉及多个基本函数，取它们的交集即可．5．（5分）（2011•广东）不等式2x2﹣x﹣1＞0的解集是（）A．（﹣，1）B．（1，+∞）C．（﹣∞，1）∪（2，+∞）D．（﹣∞，﹣）∪（1，+∞）【考点】一元二次不等式的解法．【专题】不等式的解法及应用．【分析】将不等式的左边分解因式得到相应的方程的根；利用二次方程解集的形式写出解集．【解答】解：原不等式同解于（2x+1）（x﹣1）＞0∴x＞1或x＜故选：D【点评】本题考查二次不等式的解法：判断相应的方程是否有根；若有根求出两个根；据二次不等式解集的形式写出解集．6．（5分）（2011•广东）已知平面直角坐标系xOy上的区域D由不等式组给定．若M（x，y）为D上的动点，点A的坐标为，则z=•的最大值为（）A．3 B．4 C．3D．4【考点】二元一次不等式（组）与平面区域；数量积的坐标表达式．【专题】不等式的解法及应用．【分析】首先做出可行域，将z=•的坐标代入变为z=，即y=﹣x+z，此方程表示斜率是﹣的直线，当直线与可行域有公共点且在y轴上截距最大时，z有最大值．【解答】解：首先做出可行域，如图所示：z=•=，即y=﹣x+z做出l0：y=﹣x，将此直线平行移动，当直线y=﹣x+z经过点B时，直线在y轴上截距最大时，z有最大值．因为B（，2），所以z的最大值为4故选：B【点评】本题考查线性规划、向量的坐标表示，考查数形结合思想解题．7．（5分）（2011•广东）正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有（）A．20 B．15 C．12 D．10【考点】棱柱的结构特征．【专题】立体几何．【分析】抓住上底面的一个顶点，看从此顶点出发的对角线有多少条即可解决．【解答】解：由题意正五棱柱对角线一定为上底面的一个顶点和下底面的一个顶点的连线，因为不同在任何侧面内，故从一个顶点出发的对角线有2条．正五棱柱对角线的条数共有2×5=10条．故选D【点评】本题考查计数原理在立体几何中的应用，考查空间想象能力．8．（5分）（2011•广东）设圆C与圆x2+（y﹣3）2=1外切，与直线y=0相切，则C的圆心轨迹为（）A．抛物线B．双曲线C．椭圆 D．圆【考点】圆的切线方程；圆与圆的位置关系及其判定；抛物线的定义．【专题】直线与圆．【分析】由动圆与定圆相外切可得两圆圆心距与半径的关系，然后利用圆与直线相切可得圆心到直线的距离与半径的关系，借助等量关系可得动点满足的条件，即可的动点的轨迹．【解答】解：设C的坐标为（x，y），圆C的半径为r，圆x2+（y﹣3）2=1的圆心为A，∵圆C与圆x2+（y﹣3）2=1外切，与直线y=0相切∴|CA|=r+1，C到直线y=0的距离d=r ∴|CA|=d+1，即动点C定点A的距离等于到定直线y=﹣1的距离由抛物线的定义知：C的轨迹为抛物线．故选A【点评】本题考查了圆的切线，两圆的位置关系及抛物线的定义，动点的轨迹的求法，是个基础题．9．（5分）（2011•广东）如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为（）A．B．4 C． D．2【考点】由三视图求面积、体积．【专题】立体几何．【分析】根据已知中的三视图及相关视图边的长度，我们易判断出该几何体的形状及底面积和高的值，代入棱锥体积公式即可求出答案．【解答】解：由已知中该几何中的三视图中有两个三角形一个菱形可得这个几何体是一个四棱锥由图可知，底面两条对角线的长分别为2，2，底面边长为2故底面棱形的面积为=2侧棱为2，则棱锥的高h==3故V==2故选C【点评】本题考查的知识点是由三视图求面积、体积其中根据已知求出满足条件的几何体的形状及底面面积和棱锥的高是解答本题的关键．10．（5分）（2011•广东）设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（（f•g）（x）对任意x∈R，（f°g）（x）=f（g（x））；（f•g）（x）=f（x）g （x），则下列等式恒成立的是（）A．（（f°g）•h）（x）=（（f•h）°（g•h））（x）B．（（f•g）°h）（x）=（（f°h）•（g°h））（x）C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）D．（（f•g）•h）（x）=（（f•h）•（g•h））（x）【考点】抽象函数及其应用．【专题】函数的性质及应用．【分析】根据定义两个函数（f°g）（x）和（（f•g）（x）对任意x∈R，（f°g）（x）=f（g（x））；（f•g）（x）=f（x）g（x），然后逐个验证即可找到答案．【解答】解：A、∵（f°g）（x）=f（g（x）），（f•g）（x）=f（x）g（x），∴（（f°g）•h）（x）=（f°g）（x）h（x）=f（g（x））h（x）；而（（f•h）°（g•h））（x）=（f•h）（（g•h）（x））=f（g（x）h（x））h（g（x）h（x））；∴（（f°g）•h）（x）≠（（f•h）°（g•h））（x）B、∵（（f•g）°h）（x）=（f•g）（h（x））=f（h（x））g（h（x））（（f°h）•（g°h））（x）=（f°h）•（x）（g°h）（x）=f（h（x））g（h（x））∴（（f•g）°h）（x）=（（f°h）•（g°h））（x）C、（（f°g）°h）（x）=（（f°g）（h（x））=f（g（h（x））），（（f°h）°（g°h））（x）=f（h（g（h（x））））∴（（f°g）°h）（x）≠（（f°h）°（g°h））（x）；D、（（f•g）•h）（x）=f（x）g（x）h（x），（（f•h）•（g•h））（x）=f（x）h（x）g（x）h（x），∴（（f•g）•h）（x）≠（（f•h）•（g•h））（x）．故选B．【点评】此题是个基础题．考查学生分析解决问题的能力，和知识方法的迁移能力．二、填空题（共5小题，考生作答4小题每小题5分，满分20分）11．（5分）（2011•广东）已知{a n}是递增等比数列，a2=2，a4﹣a3=4，则此数列的公比q= 2．【考点】等比数列的通项公式．【专题】等差数列与等比数列．【分析】由已知{a n}是递增等比数列，a2=2，我们可以判断此数列的公比q＞1，又由a2=2，a4﹣a3=4，我们可以构造出一个关于公比q的方程，解方程即可求出公比q的值．【解答】解：∵{a n}是递增等比数列，且a2=2，则公比q＞1又∵a4﹣a3=a2（q2﹣q）=2（q2﹣q）=4即q2﹣q﹣2=0解得q=2，或q=﹣1（舍去）故此数列的公比q=2故答案为：2【点评】本题考查的知识点是等比数列的通项公式，其中利用等比数列的通项公式及a2=2，a4﹣a3=4，构造出一个关于公比q的方程，是解答本题的关键．12．（5分）（2011•广东）设函数f（x）=x3cosx+1，若f（a）=11，则f（﹣a）=﹣9．【考点】函数奇偶性的性质．【专题】函数的性质及应用．【分析】由于函数f（x）=x3cosx+1，是一个非奇非偶函数，故无法直接应用函数奇偶性的性质进行解答，故可构造函数g（x）=f（x）﹣1=x3cosx，然后利用g（x）为奇函数，进行解答．【解答】解：令g（x）=f（x）﹣1=x3cosx则g（x）为奇函数，又∵f（a）=11，∴g（a）=f（a）﹣1=11﹣1=10∴g（﹣a）=﹣10=f（﹣a）﹣1∴f（﹣a）=﹣9故答案为：﹣9【点评】本题考查的知识点是函数奇偶性的性质，其中构造出奇函数g（x）=f（x）﹣1=x3cosx，是解答本题的关键．13．（5分）（2011•广东）工人月工资y（元）与劳动生产率x（千元）变化的回归方程为=50+80x，下列判断正确的是②①劳动生产率为1千元时，工资为130元；②劳动生产率提高1千元，则工资提高80元；③劳动生产率提高1千元，则工资提高130元；④当月工资为210元时，劳动生产率为2千元．【考点】线性回归方程．【专题】概率与统计．【分析】回归方程═50+80x变量x增加一个单位时，变量产生相应变化，从而对选项一一进行分析得到结果．【解答】解：：∵对x的回归直线方程=50+80x，∴=（x+1）+50，∴﹣=80（x+1）+50﹣80x﹣50=80．所以劳动生产率提高1千元，则工资提高80元，②正确，③不正确．①④不满足回归方程的意义．故答案为：②．【点评】主要考查知识点：统计．本题主要考查线性回归方程的应用，考查线性回归方程自变量变化一个单位，对应的预报值是一个平均变化，这是容易出错的知识点．14．（5分）（2011•广东）已知两曲线参数方程分别为（0≤θ＜π）和（t∈R），它们的交点坐标为（1，）．【考点】参数方程化成普通方程；直线的参数方程；椭圆的参数方程．【专题】坐标系和参数方程．【分析】利用同角三角函数的基本关系及代入的方法，把参数方程化为普通方程，再利用消去参数t化曲线的参数方程为普通方程，最后解方程组求得两曲线的交点坐标即可．【解答】解：曲线参数方程（0≤θ＜π）的直角坐标方程为：；曲线（t∈R）的普通方程为：；解方程组：得：∴它们的交点坐标为（1，）．故答案为：（1，）．【点评】本题考查同角三角函数的基本关系，参把数方程化为普通方程的方法，以及求两曲线的交点坐标的方法，考查运算求解能力．属于基础题．15．（2011•广东）如图，在梯形ABCD中，AB∥CD，AB=4，CD=2．E，F分别为AD，BC上点，且EF=3，EF∥AB，则梯形ABFE与梯形EFCD的面积比为7：5．【考点】相似三角形的性质．【专题】解三角形．【分析】根据EF的长度和与上下底平行知是梯形的中位线，设出中位线分成的两个梯形的高，根据梯形的面积公式写出两个梯形的面积，都是用含有高的代数式来表示的，求比值得到结果．【解答】解：∵E，F分别为AD，BC上点，且EF=3，EF∥AB，∴EF是梯形的中位线，设两个梯形的高是h，∴梯形ABFE的面积是，梯形EFCD的面积∴梯形ABFE与梯形EFCD的面积比为=，故答案为：7：5【点评】本题考查梯形的中位线，考查梯形的面积公式是一个基础题，解题的时候容易出的一个错误是把两个梯形看成相似梯形，根据相似多边形的面积之比等于相似比的平方．三、解答题（共6小题，满分80分）16．（12分）（2011•广东）已知函数f（x）=2sin（x﹣），x∈R．（1）求f（0）的值；（2）设α，β∈，f（3）=，f（3β+）=．求sin（α+β）的值．【考点】两角和与差的正弦函数．【专题】三角函数的图像与性质．【分析】（1）把x=0代入函数解析式求解．（2）根据题意可分别求得sinα和sinβ的值，进而利用同角三角函数基本关系求得cosα和cosβ的值，最后利用正弦的两角和公式求得答案．【解答】解：（1）∵f（x）=2sin（x﹣），x∈R，∴f（0）=2sin（﹣）=﹣1（2）∵f（3）=2sinα=，f（3β+）=2sinβ=．∴sinα=，sinβ=∵α，β∈，∴cosα==，cosβ==∴sin（α+β）=sinαcosβ+cosαsinβ=【点评】本题主要考查了两角和与差的正弦函数．考查了对三角函数基础公式的熟练记忆．17．（13分）（2011•广东）在某次测验中，有6位同学的平均成绩为75分．用x n表示编号为n（n=1，2，…，6）的同学所得成绩，且前5位同学的成绩如下：编号n 1 2 3 4 5成绩x n70 76 72 70 72（1）求第6位同学的成绩x6，及这6位同学成绩的标准差s；（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．【考点】极差、方差与标准差；古典概型及其概率计算公式．【专题】概率与统计．【分析】（1）根据平均数公式写出这组数据的平均数表示式，在表示式中有一个未知量，根据解方程的思想得到结果，求出这组数据的方差，再进一步做出标准差．（2）本题是一个古典概型，试验发生包含的事件是从5位同学中选2个，共有C52种结果，满足条件的事件是恰有一位成绩在区间（68，75）中，共有C41种结果，根据概率公式得到结果．【解答】解：（1）根据平均数的个数可得75=，∴x6=90，这六位同学的方差是（25+1+9+25+9+225）=49，∴这六位同学的标准差是7（2）由题意知本题是一个古典概型，试验发生包含的事件是从5位同学中选2个，共有C52=10种结果，满足条件的事件是恰有一位成绩在区间（68，75）中，共有C41=4种结果，根据古典概型概率个数得到P==0.4．【点评】本题考查一组数据的平均数公式的应用，考查求一组数据的方差和标准差，考查古典概型的概率公式的应用，是一个综合题目．18．（13分）（2011•广东）如图所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，A，A′，B，B′分别为的中点，O1，O1′，O2，O2′分别为CD，C′D′，DE，D′E′的中点．（1）证明：O1′，A′，O2，B四点共面；（2）设G为A A′中点，延长A′O1′到H′，使得O1′H′=A′O1′．证明：BO2′⊥平面H′B′G．【考点】直线与平面垂直的判定；棱柱的结构特征；平面的基本性质及推论．【专题】空间位置关系与距离；立体几何．【分析】（1）要证O1′，A′，O2，B四点共面，即可证四边形BO2A′O1′为平面图形，根据A′O1′与B′O2′在未平移时属于同一条直径知道A′O1′∥B′O2′即BO2∥A′O1′再根据BO2=A′O1′=1即可得到四边形BO2A′O1′是平行四边形，则证．（2）建立空间直角坐标系，要证BO2′⊥平面H′B′G只需证，，根据坐标运算算出•，的值均为0即可【解答】证明：（1）∵B′，B分别是中点∴BO2∥B′O2′∵A′O1′与B′O2′在未平移时属于同一条直径∴A′O1′∥B′O2′∴BO2∥A′O1′∵BO2=A′O1′=1∴四边形BO2A′O1′是平行四边形即O1′，A′，O2，B四点共面（2）以D为原点，以向量DE所在的直线为X轴，以向量DD′所在的直线为Z轴，建立如图空间直角坐标系，则B（1，1，0），O2′（0，1，2），H′（1，﹣1，2），A（﹣1，﹣1，0），G（﹣1，﹣1，1），B′（1，1，2）则=（﹣1，0，2），=（﹣2，﹣2，﹣1），=（0，﹣2，0）∵•=0，=0∴BO2′⊥B′G，BO2′⊥B′H′即，∵B′H′∩B′G=B′，B′H′、B′G⊂面H′GB′∴BO2′⊥平面H′B′G【点评】本题考查了直线与平面垂直的判定，棱柱的结构特征，平面的基本性质及推论以及空间向量的基本知识，属于中档题．19．（14分）（2011•广东）设a＞0，讨论函数f（x）=lnx+a（1﹣a）x2﹣2（1﹣a）x的单调性．【考点】利用导数研究函数的单调性．【专题】导数的综合应用．【分析】求出函数的定义域，求出导函数，设g（x）=2a（1﹣a）x2﹣2（1﹣a）x+1，x∈（0，+∞），讨论a=1，a＞1与0＜a＜1三种情形，然后利用函数的单调性与导函数符号的关系求出单调性．【解答】解：定义域{x|x＞0}f′（x）==设g（x）=2a（1﹣a）x2﹣2（1﹣a）x+1，x∈（0，+∞）①若a=1，则g（x）=1＞0∴在（0，+∞）上有f'（x）＞0，即f（x）在（0，+∞）上是增函数．②若a＞1则2a（1﹣a）＜0，g（x）的图象开口向下，此时△=[﹣2（1﹣a）]2﹣4×2a（1﹣a）×1=4（1﹣a）（1﹣3a）＞0方程2a（1﹣a）x2﹣2（1﹣a）x+1=0有两个不等的实根不等的实根为x1=，x2=且x1＜0＜x2∴在（0，）上g（x）＞0，即f'（x）＞0，f（x）是增函数；在（，+∞）上g（x）＜0，即f'（x）＜0，f（x）是减函数；③若0＜a＜1则2a（1﹣a）＞0，g（x）的图象开口向上，此时△=[﹣2（1﹣a）]2﹣4×2a（1﹣a）×1=4（1﹣a）（1﹣3a）可知当≤a＜1时，△≤0，故在（0，+∞）上，g（x）≥0，即f'（x）≥0，f（x）是增函数；当0＜a＜时，△＞0，方程2a（1﹣a）x2﹣2（1﹣a）x+1=0有两个不等的实根不等的实根满足＞＞0故在（0，）和（，+∞）上g（x）＞0，即f'（x）＞0，f（x）是增函数；在（，）上g（x）＜0，即f'（x）＜0，f（x）是减函数．【点评】本题考查利用导函数讨论函数的单调性：导函数为正函数递增；导函数为负，函数递减，同时考查了分类讨论的数学思想方法，属于难题．20．（14分）（2011•广东）设b＞0，数列{a n}满足a1=b，a n=（n≥2）（1）求数列{a n}的通项公式；（2）证明：对于一切正整数n，2a n≤b n+1+1．【考点】数列递推式；数列与不等式的综合．【专题】等差数列与等比数列．【分析】（1）由题设形式可以看出，题设中给出了关于数列a n的面的一个方程，即一个递推关系，所以应该对此递推关系进行变形整理以发现其中所蕴含的规律，观察发现若对方程两边取倒数则可以得到一个类似等差数列的形式，对其中参数进行讨论，分类求其通项即可．（2）由于本题中条件较少，解题思路不宜用综合法直接分析出，故求解本题可以采取分析法的思路，由结论探究其成立的条件，再证明此条件成立，即可达到证明不等式的目的．【解答】解：（1）∵（n≥2），∴（n≥2），当b=1时，（n≥2），∴数列{}是以为首项，以1为公差的等差数列，∴=1+（n﹣1）×1=n，即a n=1，当b＞0，且b≠1时，（n≥2），即数列{}是以=为首项，公比为的等比数列，∴=×=，即a n=，∴数列{a n}的通项公式是（2）证明：当b=1时，不等式显然成立当b＞0，且b≠1时，a n=，要证对于一切正整数n，2a n≤b n+1+1，只需证2×≤b n+1+1，即证∵==（b n+1+1）×（b n﹣1+b n﹣2+…+b+1）=（b2n+b2n﹣1+…+b n+2+b n+1）+（b n﹣1+b n﹣2+…+b+1）=b n[（b n+b n﹣1+…+b2+b）+（++…+）]≥b n（2+2+…+2）=2nb n所以不等式成立，综上所述，对于一切正整数n，有2a n≤b n+1+1，【点评】本题考点是数列的递推式，考查根据数列的递推公式求数列的通项，研究数列的性质的能力，本题中递推关系的形式适合用取倒数法将所给的递推关系转化为有规律的形式，两边取倒数，条件许可的情况下，使用此技巧可以使得解题思路呈现出来．数列中有请多成熟的规律，做题时要注意积累这些小技巧，在合适的情况下利用相关的技巧，可以简化做题．在（2）的证明中，采取了分析法的来探究解题的思路，通过本题希望能进一步熟悉分析法证明问题的技巧．21．（14分）（2011•广东）在平面直角坐标系xOy中，直线l：x=﹣2交x轴于点A，设P 是l上一点，M是线段OP的垂直平分线上一点，且满足∠MPO=∠AOP．（1）当点P在l上运动时，求点M的轨迹E的方程；（2）已知T（1，﹣1），设H是E上动点，求|HO|+|HT|的最小值，并给出此时点H的坐标；（3）过点T（1，﹣1）且不平行与y轴的直线l1与轨迹E有且只有两个不同的交点，求直线l1的斜率k的取值范围．【考点】轨迹方程；直线与圆锥曲线的综合问题．【专题】综合题；压轴题；转化思想．【分析】（1）由于直线l：x=﹣2交x轴于点A，所以A（﹣2，0），由于P是l上一点，M 是线段OP的垂直平分线上一点，且满足∠MPO=∠AOP，可以设点P，由于满足∠MPO=∠AOP，所以分析出MN∥AO，利用相关点法可以求出动点M的轨迹方程；（2）由题意及点M的轨迹E的方程为y2=4（x+1），且已知T（1，﹣1），又H是E 上动点，点O及点T都为定点，利用图形即可求出；（3）由题意设出过定点的直线方程l1并与点M的轨迹E的方程联立，利用有两个交点等价与联立之后的一元二次方程的判别式大于0，即可得到所求．【解答】解：（1）如图所示，连接OM，则|PM|=|OM|，∵∠MPO=∠AOP，∴动点M满足MP⊥l或M在x的负半轴上，设M（x，y）①当MP⊥l时，|MP|=|x+2|，|om|=，|x+2|=，化简得y2=4x+4 （x≥﹣1）②当M在x的负半轴上时，y=0（x≤﹣1），综上所述，点M的轨迹E的方程为y2=4x+4（x≥﹣1）或y=0（x＜﹣1）．（2）由题意画出图形如下：∵由（1）知道动点M 的轨迹方程为：y2=4（x+1）．是以（﹣1，0）为顶点，以O（0，0）为焦点，以x=﹣2为准线的抛物线，由H引直线HB垂直准线x=﹣2与B点，则利用抛物线的定义可以得到：|HB|=|HO|，∴要求|HO|+|HT|的最小值等价于求折线|HB|+|HT|的最小值，由图可知当由点T直接向准线引垂线是与抛物线相交的H使得HB|+|HT|的最小值，故|HO|+|HT|的最小值时的H．（3）如图，设抛物线顶点A（﹣1，0），则直线AT的斜率，∵点T（1，﹣1）在抛物线内部，∴过点T且不平行于x，y轴的直线l1必与抛物线有两个交点，则直线l1与轨迹E的交点个数分以下四种情况讨论：①当K时，直线l1与轨迹E有且只有两个不同的交点，②当时，直线l1与轨迹E有且只有一个不同的交点，③当K=0时，直线l1与轨迹E有且只有一个交点，④当K＞0时，直线l1与轨迹E有且只有两个不同的交点．综上所述，直线l1的斜率K的取值范围是（﹣]∪（0，+∞）．【点评】此题重点考查了利用相关点法求动点的轨迹方程，还考查了利用抛物线的定义求出HO|+|HT|的最小值时等价转化的思想，还考查了直线与曲线有两个交点的等价转化思想．。

2011年高考广东卷文科数学答案和解析版

2011年高考广东卷文科数学解析版一、选择题 1．【命题意图】本题考查复数的运算，是容易题. 【解析】∵1iz =，∴z =1i=i -，故选A. 2．【命题意图】本题考查集合的运算、直线与圆的位置关系，是容易题. 【解析】集合A 表示由圆221x y +=上所有点组成的集合，集合B 表示直线1x y +=上所有点的集合，∵直线过园内点（12,12），∴直线与圆有两个交点，故选C . 3．【命题意图】本题考查向量平行的充要条件，是容易题. 【解析】∵(1,2),(1,0),(3,4)a b c ===，∴a b λ+ =（1λ+，2）， ∵()//a b c λ+， ∴32(1)40λ⨯-+⨯=，解得λ= 12，故选B 4 ．【命题意图】本题考查函数的定义域求法和不等式解法，是容易题.【解析】要使式子有意义，则1010x x -≠⎧⎨+>⎩，解得11x x >-≠且，故选C.5．【命题意图】本题考查一元二次不等式解法，是容易题.【解析】2210x x -->⇔(21)(1)0x x +->，解得112x x <->或，故选D. 6．【命题意图】本题考查数量积的坐标运算、简单线性规划，是容易题. 【解析】如图,区域D 为四边形OABC 及其内部区域,目标函数为z =(,)x y ⋅y +,z 即为y z =+在y 轴的截距，由图知，当直线y z =+过B 时，2max z 2=+=4，故选B.7．【命题意图】本题考查学生的空间想象能力，难度较大.【解析】下底面有5个点，每个下底面的点对应上底面的5个点中，符合条件的只有2个，故总共有10条，选D.8．【命题意图】本题考查直线与圆的位置关系、圆与圆的位置关系、轨迹问题，难度较大.【解析】设圆心C(,x y )，则圆C 的半径为y ， ∵设圆C 与圆错误！未找到引用源。

外切，∴1y =+，整理得28(1)x y =-，故选A. 9．【命题意图】本题考查简单几何体的三视图和体积计算，是中档题. 【解析】由三视图知，此几何体是底面边长为2，短对角线为2的菱形，顶点在底面上的射影为菱形的中心，一条侧棱长为，∴底面积为14⨯⨯==3，故133V =⨯=，故选C.10．【命题意图】本题是新定义型题，考查学生学习、理解新知识、运用新知识的能力，属难度.【解析】由题知()()x g f 表示两个函数复合，()()x g f ∙表示两个函数相乘，故对A ：左=()()()f g h x ∙=(())()f g x h x ，右=()()()()f h g h x ∙∙=(()())(()())f x h x g x h x =((()())(()()))f g x h x h g x h x ，显然不等，对B ：左=(())()f g h x ∙=(())(())f h x g h x ，右=(()())()f h g h x ∙=()()()()f h x g h x =(())(())f h x g h x ，显然正确，对C ：左=(())()f g h x =((()))f g h x ，右=(()())()f h g h x =(((())))f h g h x ，显然不等，对D ：左=(())()f g h x ∙∙=()()()f x g x h x ，右=(()())()f h g h x ∙∙∙=2()()()f x g x h x ，显然不等，故选B. 二、填空题（一）必做题（11～13题）11．【命题意图】本题考查等比数列的通项公式、数列的单调性，是容易题. 【解析】∵4,2342=-=a a a ,∴2224q q -=，解得q =2或－1（舍），故q =2. 【答案】2 12．【命题意图】本题考查函数的奇偶性和函数求值,是简单题. 【解析】∵3()cos 111f a a a =+=，=-)(a f 3()cos()1a a --+=3cos 1a a -+， ∴两式相加得()112f a -+=，∴=-)(a f －9. 【答案】－9 13．【命题意图】本题考查线性回归分析方法及运算求解能力，是中档题. 【解析】平均命中率为y =0.40.50.60.60.45++++=0.5，平均训练时间x =12345++++=3，∴ˆb=51521()()()iii i i x x y y x x ==---∑∑=0.110=0.01，ˆa=ˆy bx -=0.5—0.01×3=0.47，样本回归方程为ˆy=0.470.01x +，当x =6时，ˆy=0.47+0.01×6=0.53. 【答案】0.5 0.53 （二）选做题 14．【命题意图】本题考查参数方程与普通方程互化、求两曲线的交点及运算求解能力，是中档题.【解析】化为普通方程分别为221(0)5x y x +=>，245y x =，联立解得1x y =⎧⎪⎨=⎪⎩交点（1. 【答案】（1）15．【命题意图】本题考查合情推理，是容易题.【解析】∵AB ∥CD ，AB ＝4，CD ＝2, EF ＝3，EF ∥AB ，∴2EF=AB+CD ，∴EF 是梯形ABCD 的中位线，设梯形ABEF EFCD S S 梯形梯形=(4+3)2(32)2hh +=75.【答案】7516【命题意图】本题考查诱导公式、同角三角函数基本关系式、两角和的余弦公式等基本知识，考查运算能力，是容易题. 【解析】(1)1)6sin(2)0(-=-=πf(2) ∵10(3)2sin 213f παα+==，∴5sin 13α=，又∵[0,]2πα∈，∴12cos 13α=，∵6(32)2sin()2cos 25f πβπββ+=+==， ∴3cos 5β=，又∵[0,]2πβ∈，∴4sin 5β=，∴16cos()cos cos sin sin 65αβαβαβ+=-=.17【命题意图】本题考查样本的均值与方差，等可能事件的概率计算，是容易题. 【解析】(1)由题意得：75=90,6727072767066=+++++x x 得S=76)7590()7572()7570()7572()7576()7570(222222=-+-+-+-+-+-(2)设5位同学为：A, B,C, D, E 其中A70分，B76分，C72分，D70分，E72分基本事件：AB, AC,AD,AE, BC,BD,BE,CD,CE, DE ,共10种。

2011广东数学高考试题和答案

2011普通高等学校统一考试数学(广东卷)一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数z 满足(1＋i)z ＝2，其中i 为虚数单位，则z 等于( ) A ．1＋i B ．1－i C ．2＋2i D ．2－2i2．已知集合A ＝{(x ，y )|x ，y 为实数，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y 为实数，且y ＝x }，则A ∩B 的元素个数为( )A ．0B ．1C ．2D ．3 3．若向量a ，b ，c 满足a ∥b 且a ⊥c ，则c ·(a ＋2b )等于 ( ) A ．4 B ．3 C ．2 D ．04．设函数f (x )和g (x )分别是R 上的偶函数和奇函数，则下列结论恒成立的是( ) A ．f (x )＋|g (x )|是偶函数 B ．f (x )－|g (x )|是奇函数 C ．|f (x )|＋g (x )是偶函数 D ．|f (x )|－g (x )是奇函数5．已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧≤≤⎪≤⎨⎪≤⎩给定．若M (x ，y )为D 上的动点，点A 的坐标为(2，1)，则z OM OA =⋅的最大值为( )A ．42B ．32C ．4D ．36．甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军．若两队胜每局的概率相同，则甲队获得冠军的概率为( )A ．12B ．35C ．23D ．347．如图1～3，某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为… ()A ．63B ．93C ．123D ．1838．设S 是整数集Z 的非空子集，如果∀a ，b ∈S ，有ab ∈S ，则称S 关于数的乘法是封闭的．若T ，V 是Z 的两个不相交的非空子集，T ∪V ＝Z ，且∀a ，b ，c ∈T ，有abc ∈T ；∀x ，y ，z ∈V ，有xyz ∈V ，则下列结论恒成立的是( )A ．T ，V 中至少有一个关于乘法是封闭的B ．T ，V 中至多有一个关于乘法是封闭的C ．T ，V 中有且只有一个关于乘法是封闭的D ．T ，V 中每一个关于乘法都是封闭的二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． (一)必做题(9～13题)9．不等式|x ＋1|－|x －3|≥0的解集是____________．10．72()x x x-的展开式中，x 4的系数是________．(用数字作答)11．等差数列{a n }前9项的和等于前4项的和．若a 1＝1，a k ＋a 4＝0，则k ＝________. 12．函数f (x )＝x 3－3x 2＋1在x ＝________处取得极小值． 13．某数学老师身高176 cm ，他爷爷、父亲和儿子的身高分别是173 cm 、170 cm 和182 cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________ cm.(二)选做题(14～15题，考生只能从中选做一题)14．(坐标系与参数方程选做题)已知两曲线参数方程分别为5cos sin x y θθ⎧=⎪⎨=⎪⎩ (0≤θ＜π)和254x t y t⎧=⎪⎨⎪=⎩ (t ∈R )，它们的交点坐标为________． 15．(几何证明选讲选做题)如图，过圆O 外一点P 分别作圆的切线和割线交圆于A ，B ，且PB ＝7，C 是圆上一点使得BC ＝5，∠BAC ＝∠APB ，则AB ＝________.三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．已知函数1()2sin()36f x x π=-，x ∈R .(1)求5()4f π的值； (2)设α，β∈[0，2π]，10(3)213f a π+=，6(32)5f βπ+=，求cos(α＋β)的值．17．为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中微量元素x ，y 的含量(单位：毫克)．下表是乙厂的5件产品的测量数据：编号1 2 3 4 5 x 169 178 166 175 180 y 75 80 77 7081(1)已知甲厂生产的产品共有98件，求乙厂生产的产品数量；(2)当产品中的微量元素x ，y 满足x ≥175且y ≥75时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量；(3)从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数ξ的分布列及其均值(即数学期望)．18．如图，在锥体P －ABCD 中，ABCD 是边长为1的菱形，且∠DAB ＝60°，P A ＝PD ＝2，PB ＝2，E 、F 分别是BC 、PC 的中点．(1)证明：AD ⊥平面DEF ；(2)求二面角P －AD －B 的余弦值．19．设圆C 与两圆22(5)4x y ++=，22(5)4x y -+=中的一个内切，另一个外切．(1)求C 的圆心轨迹L 的方程；(2)已知点M (355，455)，F (5，0)，且P 为L 上动点．求||MP |－|FP ||的最大值及此时点P 的坐标．20．设b ＞0，数列{a n }满足a 1＝b ，1122n n n nba a a n --=+-(n ≥2)．(1)求数列{a n }的通项公式；(2)证明：对于一切正整数n ，1112n n n b a ++≤+.21．在平面直角坐标系xOy 上，给定抛物线L ：214y x =.实数p ，q 满足p 2－4q ≥0，x 1，x 2是方程x 2－px ＋q ＝0的两根，记φ(p ，q )＝ma x {|x 1|，|x 2|}．(1)过点A (p 0，2014p )(p 0≠0)作L 的切线交y 轴于点B ．证明：对线段AB 上的任一点Q (p ，q )，有0(,)2p p q ϕ=；(2)设M (a ，b )是定点，其中a ，b 满足a 2－4b ＞0，a ≠0.过M (a ，b )作L 的两条切线l 1，l 2，切点分别为E (p 1，2114p )，E ′(p 2，2214p )，l 1，l 2与y 轴分别交于F ，F ′.线段EF 上异于两端点的点集记为X .证明：M (a ，b )∈X ⇔|p 1|＞|p 2|⇔1(,)2p a b ϕ=；(3)设D ＝{(x ，y )|y ≤x －1，215(1)44y x ≥+-}．当点(p ，q )取遍D 时，求φ(p ，q )的最小值(记为φmin )和最大值(记为φma x )．参考答案1．B 2．C 3．D 4．A 5．C 6．D 7．B 8．A 9．答案：{x |x ≥1} 10．答案：84 11．答案：10 12．答案：2 13．答案：185 14．答案：(1，255) 15．答案：3516．解：(1)55()2sin()2sin 241264f ππππ=-==. (2)10(3)2sin 213f παα+==，∴5sin 13α=，又α∈[0，2π]，∴12cos 13α=，6(32)2sin()2cos 25f πβπββ+=+==，3cos 5β=，又β∈[0，2π]，∴4sin 5β=，16cos()cos cos sin sin 65αβαβαβ+=-=. 17．解：(1)乙厂生产的产品总数为5÷1498＝35. (2)样品中优等品的频率为25，乙厂生产的优等品的数量为35×25＝14. (3)ξ＝0，1，2，22325=i i i C C P C ξ-（）=(i ＝0，1，2)，ξ的分布列为ξ 012P310 35 110均值E (ξ)＝1×35＋2×110＝45. 18．解：(1)取AD 的中点G ，又P A ＝PD ，∴PG ⊥AD ，由题意知△ABC 是等边三角形，∴BG ⊥AD ．又PG ，BG 是平面PGB 的两条相交直线， ∴AD ⊥平面PGB ， ∴EF ∥PB ，DE ∥GB ， ∴平面DEF ∥平面PGB ， ∴AD ⊥平面DEF .(2)由(1)知∠PGB 为二面角P —AD —B 的平面角，在Rt △PGA 中，PG 2＝(2)2－(12)2＝74；在Rt △BGA 中，BG 2＝12－(12)2＝34；在△PGB 中，22221cos 27PG BG PB PGB PG BG +-∠==-⋅.19．解：(1)两圆的圆心分别为A (－5，0)，B (5，0)，半径为2，设圆C 的半径为r .由题意得|CA |＝r －2，|CB |＝r ＋2或|CA |＝r ＋2，|CB |＝r －2，两式相减得|CA |－|CB |＝－4或|CA |－|CB |＝4，即||CA |－|CB ||＝4.则C 的轨迹为双曲线，其中2a ＝4，c ＝5，b 2＝1∴圆C 的圆心轨迹L 的方程为2214x y -=. (2)由(1)知F 为双曲线L 的一个焦点，如图，连MF 并延长交双曲线于一点P ，此时|PM |－|PF |＝|MF |为||PM |－|FP ||的最大值．又2235455=255MF =-+（）（） MF 的方程为2(5)y x =--即252y x =-代入x 2－4y 2＝4并整理得215325840x x -+=，解得x ＝14515或x ＝18515＝655，显然x ＝655为点P 的横坐标，点P 的纵坐标为125252555p y =-=-. 即||MP |－|FP ||的最大值为2，此时点P 的坐标为(655，－255)．20．解：(1)法一：112(1)n n n a ba n a n --=+-，得1112(1)121n n n n a n n n a ba b b a ---+--==+⋅，设n n n b a =，则121n n b b b b-=⋅+(n ≥2)，设12()n n b b b λλ-+=⋅+，则122(1)n n b b b bλ-=⋅+-，当b ≠2时令21(1)b b λ-=，得12b λ=-，∴1121()22n n b b b b b -+=⋅+--(n ≥2)，知12n b b +-是等比数列，∴11112()()22n n b b b b b -+=+⋅--，又11b b =，∴12112()222n n n n n b b b b b b b -=⋅-=⋅---，∴(2)2n n n nnb b a b-=-. 当b ＝2时，2n n b =，a n ＝2，∴(2)(2)22(2)n n nnnb b a b b b ⎧-=≠⎪-⎨⎪=⎩. 法二：当b ＝2时，a n ＝2；当b ≠2时a 1＝b ，2222222(2)22b b b a b b -==+-，33323333(2)242b b b a b b b -==++-，猜想(2)(2)2n n n nnb b a b b-=≠-，下面用数学归纳法证明： ①当n ＝1时，猜想显然成立；②假设当n ＝k 时，(2)2k k k kkb b a b -=-，则1111(1)(1)(2)(1)(2)2(1)(2)2(2)2k k k k k k kk k k k b a k b kb b k b b a a n kb b k b b +++++⋅+⋅-+-===+--+⋅--，所以当n ＝k ＋1时，猜想成立．由①②知，∀n ∈N *，(2)2n n n nnb b a b -=-. (2)b 2n ＋22n ≥2222nn b⋅＝2n ＋1b n ，b 2n －1·2＋b ·22n －1≥2222nn b ⋅＝2n ＋1b n ，…b n ＋1·2n －1＋b n －1·2n ＋1≥2222nnb ⋅＝2n ＋1b n ，以上n 个式子相加得b 2n ＋b 2n －1·2＋…＋b n ＋1·2n －1＋b n －1·2n ＋1＋…＋b ·22n －1＋22n ≥n ·2n ＋1b n ，221212111(222)2(2)2(2)2(2)2(2)n n n n n n n n n n n n n n n b b b b b n b b a b b ----+⎡⎤+⋅++⋅+-⋅-⋅-⎣⎦=≤-- 2212121(222)(2)2(2)2(2)n n n n n n n n n b b b b b b b --+⎡⎤+⋅++⋅+--⋅-⎣⎦=- 2121111(2)222(2)n n n n n n n n n b b b b +++-+--⋅+⋅=-2111211(2)(22)2(2)n n n n n n n n n b b b b +++++-+⋅-=-1112n n b ++=+. 21．解：(1) 0001|()|2AB x p x p k y x p '＝＝＝＝＝，直线AB 的方程为200011()42y p p x p -=-，即2001124y p x p =-，∴2001124q p p p =-，方程x 2－px ＋q ＝0的判别式Δ＝p 2－4q ＝(p －p 0)2，两根001,222p p p p x ±-==或02pp -，∵p ·p 0≥0，∴0022p pp p -=-，又0≤|p |≤|p 0|，∴000222p p p p -≤-≤，得000222p p p p p -=-≤，∴φ(p ，q )＝02p.(2)由a 2－4b ＞0知点M (a ，b )在抛物线L 的下方．①当a ＞0，b ≥0时，作图可知，若M (a ，b )∈X ，则p 1＞p 2≥0，得|p 1|＞|p 2|；若|p 1|＞|p 2|，显然有点M (a ，b )∈X ；∴M (a ，b )∈X ⇔|p 1|＞|p 2|. ②当a ＞0，b ＜0时，点M (a ，b )在第二象限，作图可知，若M (a ，b )∈X ，则p 1＞0＞p 2，且|p 1|＞|p 2|；若|p 1|＞|p 2|，显然有点M (a ，b )∈X ； ∴M (a ，b )∈X ⇔|p 1|＞|p 2|.根据曲线的对称性可知，当a ＜0时，M (a ，b )∈X ⇔|p 1|＞|p 2|. 综上所述，M (a ，b )∈X ⇔|p 1|＞|p 2|(*)由(1)知点M 在直线EF 上，方程x 2－ax ＋b ＝0的两根x 1，2＝12p 或12p a -，同理点M 在直线E ′F ′上，方程x 2－ax ＋b ＝0的两根x 1，2＝22p 或22pa -，若φ(a ，b )＝12p ，则12p |不比12p a -、22p 、22pa -小，∴|p 1|＞|p 2|，又|p 1|＞|p 2|⇔M (a ，b )∈X ，∴φ(a ，b )＝12p ⇔M (a ，b )∈X ；又由(1)知，M (a ，b )∈X ⇔φ(a ，b )＝12p ； ∴φ(a ，b )＝12p⇔ M (a ，b )∈X ，综合(*)式，得证．(3)联立y ＝x －1，215(1)44y x =+-得交点(0，－1)，(2，1)，可知0≤p ≤2，过点(p ，q )作抛物线L 的切线，设切点为(x 0，2014x )，则20001142x qx x p -=-，得200240x px q -+=，解得204x p p q =+-，又215(1)44q p ≥+-，即p 2－4q ≤4－2p ， ∴042x p p ≤+-，设42p t -=，∴2201152(1)222x t t t ≤-++=--+， ∵0max max2x ϕ=，又052x ≤，∴max 54ϕ=； ∵q ≤p －1，∴204422x p p p p p ≥+-+=+-=，∴0min min12x ϕ==.。

2011年广东高考文科数学真题及答案

2011年广东高考文科数学真题及答案一、选择题（共10小题，每小题5分，满分50分）1．（5分）设复数z满足iz=1，其中i为虚数单位，则z=（）A．﹣i B．i C．﹣1 D．1【解答】解：设Z=x+yi∵iz=1，∴i（x+yi）=﹣y+xi=1故x=0，y=﹣1∴Z=﹣i故选A2．（5分）已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B=|（x，y）|x，y为实数，且x+y=1}，则A∩B的元素个数为（）A．4 B．3 C．2 D．1【解答】解：联立两集合中的函数关系式得：，由②得：x=1﹣y，代入②得：y2﹣y=0即y（y﹣1）=0，解得y=0或y=1，把y=0代入②解得x=1，把y=1代入②解得x=0，所以方程组的解为或，有两解，则A∩B的元素个数为2个．故选C3．（5分）已知向量=（1，2），=（1，0），=（3，4）．若λ为实数，（+λ）∥，则λ=（）A．B．C．1 D．2【解答】解：∵向量=（1，2），=（1，0），=（3，4）．∴=（1+λ，2）∵（+λ）∥，∴4（1+λ）﹣6=0，∴故选B．4．（5分）函数f（x）=+lg（1+x）的定义域是（）A．（﹣∞，﹣1） B．（1，+∞）C．（﹣1，1）∪（1，+∞）D．（﹣∞，+∞）【解答】解：根据题意，使f（x）=+lg（1+x）有意义，应满足，解可得（﹣1，1）∪（1，+∞）；故选：C．5．（5分）不等式2x2﹣x﹣1＞0的解集是（）A．（﹣，1）B．（1，+∞）C．（﹣∞，1）∪（2，+∞）D．（﹣∞，﹣）∪（1，+∞）【解答】解：原不等式同解于（2x+1）（x﹣1）＞0∴x＞1或x＜故选：D6．（5分）已知平面直角坐标系xOy上的区域D由不等式组给定．若M（x，y）为D上的动点，点A的坐标为，则z=•的最大值为（）A．3 B．4 C．3 D．4【解答】解：首先做出可行域，如图所示：z=•=，即y=﹣x+z做出l0：y=﹣x，将此直线平行移动，当直线y=﹣x+z经过点B时，直线在y轴上截距最大时，z有最大值．因为B（，2），所以z的最大值为4故选：B7．（5分）正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有（）A．20 B．15 C．12 D．10【解答】解：由题意正五棱柱对角线一定为上底面的一个顶点和下底面的一个顶点的连线，因为不同在任何侧面内，故从一个顶点出发的对角线有2条．正五棱柱对角线的条数共有2×5=10条．故选D8．（5分）设圆C与圆x2+（y﹣3）2=1外切，与直线y=0相切，则C的圆心轨迹为（）A．抛物线B．双曲线C．椭圆 D．圆【解答】解：设C的坐标为（x，y），圆C的半径为r，圆x2+（y﹣3）2=1的圆心为A，∵圆C与圆x2+（y﹣3）2=1外切，与直线y=0相切∴|CA|=r+1，C到直线y=0的距离d=r ∴|CA|=d+1，即动点C定点A的距离等于到定直线y=﹣1的距离由抛物线的定义知：C的轨迹为抛物线．故选A9．（5分）如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为（）A．B．4 C．D．2【解答】解：由已知中该几何中的三视图中有两个三角形一个菱形可得这个几何体是一个四棱锥由图可知，底面两条对角线的长分别为2，2，底面边长为2故底面棱形的面积为=2侧棱为2，则棱锥的高h==3故V==2故选C10．（5分）设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（（f•g）（x）对任意x∈R，（f°g）（x）=f（g（x））；（f•g）（x）=f（x）g（x），则下列等式恒成立的是（）A．（（f°g）•h）（x）=（（f•h）°（g•h））（x）B．（（f•g）°h）（x）=（（f°h）•（g°h））（x）C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）D．（（f•g）•h）（x）=（（f•h）•（g•h））（x）【解答】解：A、∵（f°g）（x）=f（g（x）），（f•g）（x）=f（x）g（x），∴（（f°g）•h）（x）=（f°g）（x）h（x）=f（g（x））h（x）；而（（f•h）°（g•h））（x）=（f•h）（（g•h）（x））=f（g（x）h（x））h（g（x）h（x））；∴（（f°g）•h）（x）≠（（f•h）°（g•h））（x）B、∵（（f•g）°h）（x）=（f•g）（h（x））=f（h（x））g（h（x））（（f°h）•（g°h））（x）=（f°h）•（x）（g°h）（x）=f（h（x））g（h（x））∴（（f•g）°h）（x）=（（f°h）•（g°h））（x）C、（（f°g）°h）（x）=（（f°g）（h（x））=f（g（h（x））），（（f°h）°（g°h））（x）=f（h（g（h（x））））∴（（f°g）°h）（x）≠（（f°h）°（g°h））（x）；D、（（f•g）•h）（x）=f（x）g（x）h（x），（（f•h）•（g•h））（x）=f（x）h（x）g（x）h（x），∴（（f•g）•h）（x）≠（（f•h）•（g•h））（x）．故选B．二、填空题（共5小题，考生作答4小题每小题5分，满分20分）11．（5分）已知{a n}是递增等比数列，a2=2，a4﹣a3=4，则此数列的公比q= 2 ．【考点】等比数列的通项公式．【专题】等差数列与等比数列．【分析】由已知{a n}是递增等比数列，a2=2，我们可以判断此数列的公比q＞1，又由a2=2，a4﹣a3=4，我们可以构造出一个关于公比q的方程，解方程即可求出公比q的值．【解答】解：∵{a n}是递增等比数列，且a2=2，则公比q＞1又∵a4﹣a3=a2（q2﹣q）=2（q2﹣q）=4即q2﹣q﹣2=0解得q=2，或q=﹣1（舍去）故此数列的公比q=2故答案为：2【点评】本题考查的知识点是等比数列的通项公式，其中利用等比数列的通项公式及a2=2，a4﹣a3=4，构造出一个关于公比q的方程，是解答本题的关键．12．（5分）设函数f（x）=x3cosx+1，若f（a）=11，则f（﹣a）= ﹣9 ．【考点】函数奇偶性的性质．【专题】函数的性质及应用．【分析】由于函数f（x）=x3cosx+1，是一个非奇非偶函数，故无法直接应用函数奇偶性的性质进行解答，故可构造函数g（x）=f（x）﹣1=x3cosx，然后利用g（x）为奇函数，进行解答．【解答】解：令g（x）=f（x）﹣1=x3cosx则g（x）为奇函数，又∵f（a）=11，∴g（a）=f（a）﹣1=11﹣1=10∴g（﹣a）=﹣10=f（﹣a）﹣1∴f（﹣a）=﹣9故答案为：﹣9【点评】本题考查的知识点是函数奇偶性的性质，其中构造出奇函数g（x）=f（x）﹣1=x3cosx，是解答本题的关键．13．（5分）工人月工资y（元）与劳动生产率x（千元）变化的回归方程为=50+80x，下列判断正确的是②①劳动生产率为1千元时，工资为130元；②劳动生产率提高1千元，则工资提高80元；③劳动生产率提高1千元，则工资提高130元；④当月工资为210元时，劳动生产率为2千元．【考点】线性回归方程．【专题】概率与统计．【分析】回归方程═50+80x变量x增加一个单位时，变量产生相应变化，从而对选项一一进行分析得到结果．【解答】解：：∵对x的回归直线方程=50+80x，∴=（x+1）+50，∴﹣=80（x+1）+50﹣80x﹣50=80．所以劳动生产率提高1千元，则工资提高80元，②正确，③不正确．①④不满足回归方程的意义．故答案为：②．【点评】主要考查知识点：统计．本题主要考查线性回归方程的应用，考查线性回归方程自变量变化一个单位，对应的预报值是一个平均变化，这是容易出错的知识点．14．（5分）已知两曲线参数方程分别为（0≤θ＜π）和（t∈R），它们的交点坐标为（1，）．【考点】参数方程化成普通方程；直线的参数方程；椭圆的参数方程．【专题】坐标系和参数方程．【分析】利用同角三角函数的基本关系及代入的方法，把参数方程化为普通方程，再利用消去参数t化曲线的参数方程为普通方程，最后解方程组求得两曲线的交点坐标即可．【解答】解：曲线参数方程（0≤θ＜π）的直角坐标方程为：；曲线（t∈R）的普通方程为：；解方程组：得：∴它们的交点坐标为（1，）．故答案为：（1，）．【点评】本题考查同角三角函数的基本关系，参把数方程化为普通方程的方法，以及求两曲线的交点坐标的方法，考查运算求解能力．属于基础题．15．如图，在梯形ABCD中，AB∥CD，AB=4，CD=2．E，F分别为AD，BC上点，且EF=3，EF∥AB，则梯形ABFE与梯形EFCD的面积比为7：5 ．【考点】相似三角形的性质．【专题】解三角形．【分析】根据EF的长度和与上下底平行知是梯形的中位线，设出中位线分成的两个梯形的高，根据梯形的面积公式写出两个梯形的面积，都是用含有高的代数式来表示的，求比值得到结果．【解答】解：∵E，F分别为AD，BC上点，且EF=3，EF∥AB，∴EF是梯形的中位线，设两个梯形的高是h，∴梯形ABFE的面积是，梯形EFCD的面积∴梯形ABFE与梯形EFCD的面积比为=，故答案为：7：5【点评】本题考查梯形的中位线，考查梯形的面积公式是一个基础题，解题的时候容易出的一个错误是把两个梯形看成相似梯形，根据相似多边形的面积之比等于相似比的平方．三、解答题（共6小题，满分80分）16．（12分）已知函数f（x）=2sin（x﹣），x∈R．（1）求f（0）的值；（2）设α，β∈，f（3）=，f（3β+）=．求sin（α+β）的值．【考点】两角和与差的正弦函数．【专题】三角函数的图像与性质．【分析】（1）把x=0代入函数解析式求解．（2）根据题意可分别求得sinα和sinβ的值，进而利用同角三角函数基本关系求得cosα和cosβ的值，最后利用正弦的两角和公式求得答案．【解答】解：（1）∵f（x）=2sin（x﹣），x∈R，∴f（0）=2sin（﹣）=﹣1（2）∵f（3）=2sinα=，f（3β+）=2sinβ=．∴sinα=，sinβ=∵α，β∈，∴cosα==，cosβ==∴sin（α+β）=sinαcosβ+cosαsinβ=【点评】本题主要考查了两角和与差的正弦函数．考查了对三角函数基础公式的熟练记忆．17．（13分）在某次测验中，有6位同学的平均成绩为75分．用x n表示编号为n（n=1，2，…，6）的同学所得成绩，且前5位同学的成绩如下：编号n 1 2 3 4 5成绩x n70 76 72 70 72（1）求第6位同学的成绩x6，及这6位同学成绩的标准差s；（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．【考点】极差、方差与标准差；古典概型及其概率计算公式．【专题】概率与统计．【分析】（1）根据平均数公式写出这组数据的平均数表示式，在表示式中有一个未知量，根据解方程的思想得到结果，求出这组数据的方差，再进一步做出标准差．（2）本题是一个古典概型，试验发生包含的事件是从5位同学中选2个，共有C52种结果，满足条件的事件是恰有一位成绩在区间（68，75）中，共有C41种结果，根据概率公式得到结果．【解答】解：（1）根据平均数的个数可得75=，∴x6=90，这六位同学的方差是（25+1+9+25+9+225）=49，∴这六位同学的标准差是7（2）由题意知本题是一个古典概型，试验发生包含的事件是从5位同学中选2个，共有C52=10种结果，满足条件的事件是恰有一位成绩在区间（68，75）中，共有C41=4种结果，根据古典概型概率个数得到P==0.4．【点评】本题考查一组数据的平均数公式的应用，考查求一组数据的方差和标准差，考查古典概型的概率公式的应用，是一个综合题目．18．（13分）如图所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，A，A′，B，B′分别为的中点，O1，O1′，O2，O2′分别为CD，C′D′，DE，D′E′的中点．（1）证明：O1′，A′，O2，B四点共面；（2）设G为A A′中点，延长A′O1′到H′，使得O1′H′=A′O1′．证明：BO2′⊥平面H′B′G．【考点】直线与平面垂直的判定；棱柱的结构特征；平面的基本性质及推论．【专题】空间位置关系与距离；立体几何．【分析】（1）要证O1′，A′，O2，B四点共面，即可证四边形BO2A′O1′为平面图形，根据A′O1′与B′O2′在未平移时属于同一条直径知道A′O1′∥B′O2′即BO2∥A′O1′再根据BO2=A′O1′=1即可得到四边形BO2A′O1′是平行四边形，则证．（2）建立空间直角坐标系，要证BO2′⊥平面H′B′G只需证，，根据坐标运算算出•，的值均为0即可【解答】证明：（1）∵B′，B分别是中点∴BO2∥B′O2′∵A′O1′与B′O2′在未平移时属于同一条直径∴A′O1′∥B′O2′∴BO2∥A′O1′∵BO2=A′O1′=1∴四边形BO2A′O1′是平行四边形即O1′，A′，O2，B四点共面（2）以D为原点，以向量DE所在的直线为X轴，以向量DD′所在的直线为Z轴，建立如图空间直角坐标系，则B（1，1，0），O2′（0，1，2），H′（1，﹣1，2），A（﹣1，﹣1，0），G（﹣1，﹣1，1），B′（1，1，2）则=（﹣1，0，2），=（﹣2，﹣2，﹣1），=（0，﹣2，0）∵•=0，=0∴BO2′⊥B′G，BO2′⊥B′H′即，∵B′H′∩B′G=B′，B′H′、B′G⊂面H′GB′∴BO2′⊥平面H′B′G【点评】本题考查了直线与平面垂直的判定，棱柱的结构特征，平面的基本性质及推论以及空间向量的基本知识，属于中档题．19．（14分）设a＞0，讨论函数f（x）=lnx+a（1﹣a）x2﹣2（1﹣a）x的单调性．【考点】利用导数研究函数的单调性．【专题】导数的综合应用．【分析】求出函数的定义域，求出导函数，设g（x）=2a（1﹣a）x2﹣2（1﹣a）x+1，x∈（0，+∞），讨论a=1，a＞1与0＜a＜1三种情形，然后利用函数的单调性与导函数符号的关系求出单调性．【解答】解：定义域{x|x＞0}f′（x）==设g（x）=2a（1﹣a）x2﹣2（1﹣a）x+1，x∈（0，+∞）①若a=1，则g（x）=1＞0∴在（0，+∞）上有f'（x）＞0，即f（x）在（0，+∞）上是增函数．②若a＞1则2a（1﹣a）＜0，g（x）的图象开口向下，此时△=[﹣2（1﹣a）]2﹣4×2a（1﹣a）×1=4（1﹣a）（1﹣3a）＞0方程2a（1﹣a）x2﹣2（1﹣a）x+1=0有两个不等的实根不等的实根为x1=，x2=且x1＜0＜x2∴在（0，）上g（x）＞0，即f'（x）＞0，f（x）是增函数；在（，+∞）上g（x）＜0，即f'（x）＜0，f（x）是减函数；③若0＜a＜1则2a（1﹣a）＞0，g（x）的图象开口向上，此时△=[﹣2（1﹣a）]2﹣4×2a（1﹣a）×1=4（1﹣a）（1﹣3a）可知当≤a＜1时，△≤0，故在（0，+∞）上，g（x）≥0，即f'（x）≥0，f（x）是增函数；当0＜a＜时，△＞0，方程2a（1﹣a）x2﹣2（1﹣a）x+1=0有两个不等的实根不等的实根满足＞＞0故在（0，）和（，+∞）上g（x）＞0，即f'（x）＞0，f（x）是增函数；在（，）上g（x）＜0，即f'（x）＜0，f（x）是减函数．【点评】本题考查利用导函数讨论函数的单调性：导函数为正函数递增；导函数为负，函数递减，同时考查了分类讨论的数学思想方法，属于难题．20．（14分）设b＞0，数列{a n}满足a1=b，a n=（n≥2）（1）求数列{a n}的通项公式；（2）证明：对于一切正整数n，2a n≤b n+1+1．【考点】数列递推式；数列与不等式的综合．【专题】等差数列与等比数列．【分析】（1）由题设形式可以看出，题设中给出了关于数列a n的面的一个方程，即一个递推关系，所以应该对此递推关系进行变形整理以发现其中所蕴含的规律，观察发现若对方程两边取倒数则可以得到一个类似等差数列的形式，对其中参数进行讨论，分类求其通项即可．（2）由于本题中条件较少，解题思路不宜用综合法直接分析出，故求解本题可以采取分析法的思路，由结论探究其成立的条件，再证明此条件成立，即可达到证明不等式的目的．【解答】解：（1）∵（n≥2），∴（n≥2），当b=1时，（n≥2），∴数列{}是以为首项，以1为公差的等差数列，∴=1+（n﹣1）×1=n，即a n=1，当b＞0，且b≠1时，（n≥2），即数列{}是以=为首项，公比为的等比数列，∴=×=，即a n=，∴数列{a n}的通项公式是（2）证明：当b=1时，不等式显然成立当b＞0，且b≠1时，a n=，要证对于一切正整数n，2a n≤b n+1+1，只需证2×≤b n+1+1，即证∵==（b n+1+1）×（b n﹣1+b n﹣2+…+b+1）=（b2n+b2n﹣1+…+b n+2+b n+1）+（b n﹣1+b n﹣2+…+b+1）=b n[（b n+b n﹣1+…+b2+b）+（++…+）]≥b n（2+2+…+2）=2nb n所以不等式成立，综上所述，对于一切正整数n，有2a n≤b n+1+1，【点评】本题考点是数列的递推式，考查根据数列的递推公式求数列的通项，研究数列的性质的能力，本题中递推关系的形式适合用取倒数法将所给的递推关系转化为有规律的形式，两边取倒数，条件许可的情况下，使用此技巧可以使得解题思路呈现出来．数列中有请多成熟的规律，做题时要注意积累这些小技巧，在合适的情况下利用相关的技巧，可以简化做题．在（2）的证明中，采取了分析法的来探究解题的思路，通过本题希望能进一步熟悉分析法证明问题的技巧．21．（14分）在平面直角坐标系xOy中，直线l：x=﹣2交x轴于点A，设P是l上一点，M 是线段OP的垂直平分线上一点，且满足∠MPO=∠AOP．（1）当点P在l上运动时，求点M的轨迹E的方程；（2）已知T（1，﹣1），设H是E上动点，求|HO|+|HT|的最小值，并给出此时点H的坐标；（3）过点T（1，﹣1）且不平行与y轴的直线l1与轨迹E有且只有两个不同的交点，求直线l1的斜率k的取值范围．【考点】轨迹方程；直线与圆锥曲线的综合问题．【专题】综合题；压轴题；转化思想．【分析】（1）由于直线l：x=﹣2交x轴于点A，所以A（﹣2，0），由于P是l上一点，M 是线段OP的垂直平分线上一点，且满足∠MPO=∠AO P，可以设点P，由于满足∠MPO=∠AOP，所以分析出MN∥AO，利用相关点法可以求出动点M的轨迹方程；（2）由题意及点M的轨迹E的方程为y2=4（x+1），且已知T（1，﹣1），又H是E 上动点，点O及点T都为定点，利用图形即可求出；（3）由题意设出过定点的直线方程l1并与点M的轨迹E的方程联立，利用有两个交点等价与联立之后的一元二次方程的判别式大于0，即可得到所求．【解答】解：（1）如图所示，连接OM，则|PM|=|OM|，∵∠MPO=∠AOP，∴动点M满足MP⊥l或M在x的负半轴上，设M（x，y）①当MP⊥l时，|MP|=|x+2|，|om|=，|x+2|=，化简得y2=4x+4 （x≥﹣1）②当M在x的负半轴上时，y=0（x≤﹣1），综上所述，点M的轨迹E的方程为y2=4x+4（x≥﹣1）或y=0（x＜﹣1）．（2）由题意画出图形如下：∵由（1）知道动点M 的轨迹方程为：y2=4（x+1）．是以（﹣1，0）为顶点，以O（0，0）为焦点，以x=﹣2为准线的抛物线，由H引直线HB垂直准线x=﹣2与B点，则利用抛物线的定义可以得到：|HB|=|HO|，∴要求|HO|+|HT|的最小值等价于求折线|HB|+|HT|的最小值，由图可知当由点T直接向准线引垂线是与抛物线相交的H使得HB|+|HT|的最小值，故|HO|+|HT|的最小值时的H．（3）如图，设抛物线顶点A（﹣1，0），则直线AT的斜率，∵点T（1，﹣1）在抛物线内部，∴过点T且不平行于x，y轴的直线l1必与抛物线有两个交点，则直线l1与轨迹E的交点个数分以下四种情况讨论：①当K时，直线l1与轨迹E有且只有两个不同的交点，②当时，直线l1与轨迹E有且只有一个不同的交点，③当K=0时，直线l1与轨迹E有且只有一个交点，④当K＞0时，直线l1与轨迹E有且只有两个不同的交点．综上所述，直线l1的斜率K的取值范围是（﹣]∪（0，+∞）．【点评】此题重点考查了利用相关点法求动点的轨迹方程，还考查了利用抛物线的定义求出HO|+|HT|的最小值时等价转化的思想，还考查了直线与曲线有两个交点的等价转化思想．21。

2011年普通高等学校招生全国统一考试(广东卷)数学试题 (文科)(解析版)

绝密★启用前试卷类型：B2011年普通高等学校招生全国统一考试（广东卷）数学（文）试题解析本试题共4页，21小题，满分150分，考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。

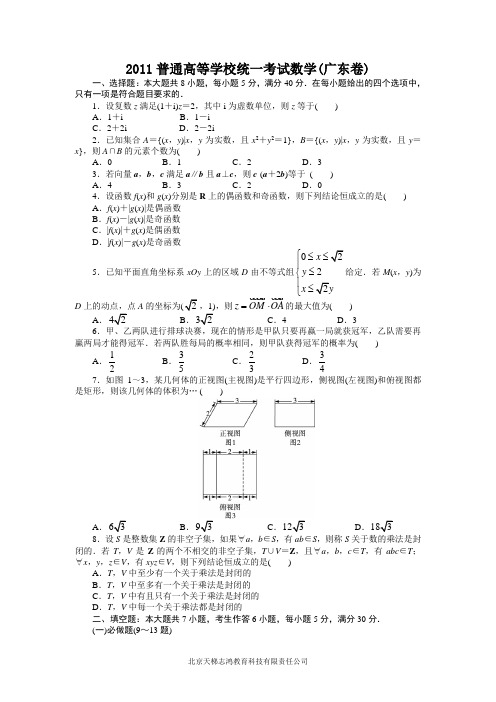
考试结束后，将试卷和答题卡一并交回。

参考公式：锥体体积公式13V Sh =，其中S 为锥体的底面积，h 为锥体的高．线性回归方程$$y bxa =+$中系数计算公式121()()()niii nii x x y y b x x ==--=-∑∑$，$ay bx =-$，样本数据12,,,n x x x L的标准差，s = 其中x ，y 表示样本均值．n 是正整数，则1221()()n n n n n n a b a b a a b ab b -----=-++++L ．一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数z 满足1iz =，其中i 为虚数单位，则z =（）A ．i -B ．iC ．1-D ．1解析：（A ）．1()iz i i i i -===-⨯-2．已知集合{(,)|,A x y x y =为实数，且221}x y +=，{(,)|,B x y x y =为实数，且1}x y +=，则A B ⋂的元素个数为（）A ．4B ．3C ．2D ．1解析：（C ）．A B ⋂的元素个数等价于圆221x y +=与直线1x y +=的交点个数，显然有2个交点3．已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+a b ∥c ，则λ=（）A ．14 B ．12C ．1D ．2解析：（B ）．(1,2)λλ+=+a b ，由()λ+a b ∥c ，得64(1)0λ-+=，解得λ=124．函数1()lg(1)1f x x x=++-的定义域是（） A ．(,1)-∞- B ．(1,)+∞ C ．(1,1)(1,)-⋃+∞ D ．(,)-∞+∞解析：（C ）．10110x x x -≠⎧⇒>-⎨+>⎩且1x ≠，则()f x 的定义域是(1,1)(1,)-⋃+∞5．不等式2210x x -->的解集是（）A ．1(,1)2-B ．(1,)+∞C ．(,1)(2,)-∞⋃+∞D ．1(,)(1,)2-∞-⋃+∞ 解析：（D ）．21210(1)(21)02x x x x x -->⇒-+>⇒<-或1x >，则不等式的解集为1(,)(1,)2-∞-⋃+∞6．已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧⎪⎨⎪⎩≤≤≤≤给定．若(,)M x y 为D 上的动点，点A 的坐标为(2,1)，则z OM OA u u u u r u u u r=⋅的最大值为（）A ．3B ．4C ．32D ．42解析：（B ）．2z x y =+，即2y x z =-+，画出不等式组表示的平面区域，易知当直线2y x z =-+经过点(2,2)时，z 取得最大值，max 2224z =⨯+=7．正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有（）A ．20B ．15C ．12D ．10 解析：（D ）．正五棱柱中，上底面中的每一个顶点均可与下底面中的两个顶点构成对角线，所以一个正五棱柱对角线的条数共有5210⨯=条8．设圆C 与圆22(3)1x y +-=外切，与直线0y =相切，则C 的圆心轨迹为（）A ．抛物线B ．双曲线C ．椭圆D ．圆解析：（A ）．依题意得，C 的圆心到点(0,3)的距离与它到直线1y =-的距离相等，则C 的圆心轨迹为抛物线9．如图1 ~ 3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为A ．43B ．4C ．23D ．2解析：（C ）．该几何体是一个底面为菱形的四棱锥，菱形的面积122S =⨯⨯=3，则该几何体的体积11333V Sh ==⨯=10．设(),(),()f x g x h x 是R 上的任意实值函数，如下定义两个函数()f g o ()x 和()f g g ()x ：对任意x ∈R ，()f g o ()x =(())f g x ；()f g g ()x =()()f x g x ，则下列等式恒成立的是A ．(()f g o g h )()x =(()f h g o ()g h g )()xB ．(()f g g o h )()x =(()f h o g ()g h o )()xC ．(()f g o o h )()x =(()f g o o()g h o )()x D ．(()f g g g h )()x =(()f g g g ()g h g )()x解析：（B ）．对A 选项 (()f g o g h )()x =()f g o ()()x h x (())()f g x h x = (()f h g o ()g h g )()x =()f h g (()()g h x g )=()f h g ((()()g x h x g ) (()())(()())f g x h x h g x h x =g g ，故排除A对B 选项 (()f g g o h )()x =()(())f g h x =g (())(())f h x g h x (()f h o g 　()g h o )()x =()()()()f h x g h x o o (())(())f h x g h x =，故选B 对C 选项 (()f g o o h )()x =()(())f g h x o ((()))f g h x =(()f g o o ()g h o )()x =()(()())()((()))f g g h x f g g h x =o o o (((())))f g g h x =，故排除C对D 选项 (()f g g g h )()x =()()()()()()f g x h x f x g x h x =g (()f g g g 　()g h g )()x =()()()()()()()()f g x g h x f x g x g x h x =g g ，故排除D二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（9 ~ 13题）11．已知{}n a 是递增的等比数列，若22a =，434a a -=，则此数列的公比q = ．解析：2．2243224422402(2)(1)0a a a q a q q q q q -=⇒-=⇒--=⇒-+=2q ⇒=或1q =-∵{}n a 是递增的等比数列，∴2q =12．设函数3()cos 1f x x x =+．若()11f a =，则()f a -= ．解析：9-3()cos 111f a a a =+=，即3()cos 10f a a a ==，则33()()cos()1cos 11019f a a a a a -=--+=-+=-+=-13．为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x （单位：小时）与当天投篮命中率y 之间的关系：天的平均投篮命中率为；用线性回归分析的方法，预测小李该月打6小时篮球的投篮命中率为．解析：0.5；0.53图4BAC DE F小李这5天的平均投篮命中率1(0.40.50.60.60.4)0.55y =++++= 3x =，1222221()()0.2000.1(0.2)0.01(2)(1)012()niii nii x x y y bx x ==--++++-===-+-+++-∑∑$，$0.47a y bx =-=$ ∴线性回归方程$0.010.47y x =+，则当6x =时，0.53y = ∴预测小李该月6号打6小时篮球的投篮命中率为0.53（二）选做题（14 ~ 15题，考生只能从中选做一题） 14．（坐标系与参数方程选做题）已知两曲线参数方程分别为5cos sin x y θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t⎧=⎪⎨⎪=⎩ (t ∈)R ，它们的交点坐标为___________．解析：25(1,)． 5cos sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(5501)x y -<≤≤≤且，254x t y t ⎧=⎪⎨⎪=⎩表示抛物线245y x = 22221(5501)5450145x y x y x x x y x ⎧+=-<≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩且或5x =-（舍去），又因为01y ≤≤，所以它们的交点坐标为25(1,)515．（几何证明选讲选做题）如图4，在梯形ABCD 中，AB ∥CD ， 4AB =，2CD =，,E F 分别为,AD BC 上的点，且3EF =，EF ∥AB ，则梯形ABFE 与梯形EFCD 的面积比为________．解析：75如图，延长,AD BC ，AD BC P =I∵23CD EF =，∴49PCD PEF S S ∆∆= ∵24CD AB =，∴416PCD PEF S S ∆∆=∴75ABEF EFCD S S =梯形梯形PBAC DE F三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）已知函数1()2sin()36f x x π=-，x ∈R ．（1）求(0)f 的值；（2）设,0,2παβ⎡⎤∈⎢⎥⎣⎦，10(3)213f πα+=，6(32)5f βπ+=，求sin()αβ+的值．16. 解：（1）(0)2sin()16f π=-=-（2）110(3)2sin[(3)]2sin 232613f πππααα+=+-==，即5sin 13α= 16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=，即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦，∴12cos 13α==，4sin 5β==∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=17．（本小题满分13分）在某次测验中，有6位同学的平均成绩为75分．用n x 表示编号为n (n 的同学所得成绩，且前5位同学的成绩如下：（1）求第6位同学的成绩6，及这6位同学成绩的标准差；（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．17．解：（1）61(7076727072)756x +++++=，解得690x =标准差7s === （2）前5位同学中随机选出的2位同学记为(,)a b ，,{1,2,3,4,5}a b ∈且a b ≠则基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)共10种这5位同学中，编号为1、3、4、5号的同学成绩在区间（68，75）中设A 表示随机事件“从前5位同学中随机选出2位同学，恰有1位同学成绩在区间（68，75）中” 则A 中的基本事件有(1,2)、(2,3)、(2,4)、(2,5)共4种，则42()105P A == 18．（本小题满分13分）图5所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的．,,,A A B B ''分别为»CD,¼C D '',»DE ,¼D E ''的中点，EE '图5C C E'1122,,,O O O O ''分别为CD ,C D '', DE ,D E ''的中点．（1）证明：12,,,O A O B ''四点共面；（2）设G 为AA '中点，延长1A O ''到H '，使得11O H A O ''''=．证明：2BO '⊥平面H B G ''．证明：（1）连接2,BO 22,O O '依题意得1122,,,O O O O ''是圆柱底面圆的圆心 ∴,,,CD C D DE D E ''''是圆柱底面圆的直径∵,,A B B ''分别为¼CD '',»DE ,¼D E ''的中点 ∴1290A O D B O D ''''''∠=∠=o∴1A O ''∥2BO '∵BB '//22O '，四边形22O O B B ''是平行四边形 ∴2BO ∥2BO ' ∴1A O ''∥2BO∴12,,,O A O B ''四点共面（2）延长1A O '到H ，使得11O H AO ''=，连接1,,HH HO HB ''∵11O H A O ''''=∴1O H ''2B ''，四边形12O O B H ''''是平行四边形 ∴12O O ''∥H B ''∵1222O O O O '''⊥，122O O B O ''''⊥，2222O O B O O ''''=I ∴12O O ''⊥面22O O B B ''∴H B ''⊥面22O O B B ''，2BO '⊂面22O O B B '' ∴2BO H B '''⊥易知四边形AA H H ''是正方形，且边长2AA '=∵11tan 2HH HO H O H '''∠==''，1tan 2A G A H G A H '''∠==''∴1tan tan 1HO H A H G ''''∠⋅∠= ∴190HO H A H G ''''∠+∠=o ∴1HO H G ''⊥易知12O O ''HB ，四边形12O O BH ''是平行四边形 ∴2BO '∥1HO '∴2BO H G ''⊥，H G H B H ''''=I∴2BO '⊥平面H B G ''．19．（本小题满分14分）设0a >，讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性．19. 解：函数()f x 的定义域为(0,)+∞212(1)2(1)1()2(1)2(1)a a x a x f x a a x a x x---+'=+---=令2()2(1)2(1)1g x a a x a x =---+224(1)8(1)121644(31)(1)a a a a a a a ∆=---=-+=--① 当103a <<时，0∆>，令()0f x '=，解得x =则当0x <<或x >()0f x '>x <<时，()0f x '<则()f x 在，)+∞上单调递增，在上单调递减② 当113a ≤≤时，0∆≤，()0f x '≥，则()f x 在(0,)+∞上单调递增③ 当1a >时，0∆>，令()0f x '=，解得x =∵0x >，∴x =则当0x <<时，()0f x '>当x >时，()0f x '<则()f x 在上单调递增，在)+∞上单调递减20．（本小题满分14分）设0b >，数列{}n a 满足1a b =，111n n n nba a a n --=+-(n ≥2)．（1）求数列{}n a 的通项公式；（2）证明：对于一切正整数n ，2n a ≤11n b ++．20. 解：（1）∵111n n n nba a a n --=+-∴111n n n a ba n a n --=+- ∴1111n n n n a b a b--=⋅+ ① 当1b =时，111n n n n a a ---=，则{}nn a 是以1为首项，1为公差的等差数列 ∴1(1)1nnn n a =+-⨯=，即1n a = ② 当0b >且1b ≠时，11111()11n n n n a b b a b--+=+-- 当1n =时，111(1)n n a b b b +=-- ∴1{}1n n a b +-是以1(1)b b -为首项，1b 为公比的等比数列∴111()11n n n a b b b+=⋅-- ∴111(1)1(1)n n nn n b a b b b b b-=-=--- ∴(1)1nn nn b b a b -=-综上所述(1),01111nn n n b b b b a b b ⎧->≠⎪=-⎨⎪=⎩　且，（2）证明：① 当1b =时，1212n n a b +=+=；② 当0b >且1b ≠时，211(1)(1)n n n b b b bb ---=-++++L要证121n n a b +≤+，只需证12(1)11n n nn b b b b+-≤+-，即证2(1)11n nn b b b b-≤+- 即证21211n n nn b b b b b --≤+++++L即证211()(1)2n n n b b b b n b--+++++≥L即证21121111()()2n nn n b b b b n b b b b--+++++++++≥L L∵21121111()(n n n n b b b b b b b b--+++++++++L L 21211111(((()n n n n b b b b --=++++++++L2n ≥+=L ，∴原不等式成立∴对于一切正整数n ，2n a ≤11n b ++．21．（本小题满分14分）在平面直角坐标系xOy 上，直线l ：2x =-交x 轴于点A ．设P 是l 上一点，M 是线段OP 的垂直平分线上一点，且满足MPO AOP ∠=∠．（1）当点P 在l 上运动时，求点M 的轨迹E 的方程；（2）已知(1,1)T -，设H 是E上动点，求HO HT +的最小值，并给出此时点H 的坐标；（3）过点(1,1)T -且不平行于y 轴的直线1l 与轨迹E 有且只有两个不同的交点，求直线1l 的斜率k 的取值范围． 21.解：（1）如图所示，连接OM ，则PM OM = ∵MPO AOP ∠=∠，∴动点M 满足MP l ⊥或M 在x 的负半轴上，设(,)M x y ① 当MP l ⊥时，2MP x =+，OM =2x +=，化简得244y x =+(1)x ≥- ② 当M 在x 的负半轴上时，0y =(1)x <-综上所述，点M 的轨迹E 的方程为244y x =+(1)x ≥-或0y =(1)x <-（2）由（1）知M 的轨迹是顶点为(1,0)-，焦点为原点的抛物线和x 的负半轴0y =(1)x <- ① 若H 是抛物线上的动点，过H 作HN l ⊥于N由于l 是抛物线的准线，根据抛物线的定义有HO HN =则HO HT HN HT +=+当,,N H T 三点共线时，HN HT +有最小值3TN =求得此时H 的坐标为3(,1)4-- ② 若H 是x 的负半轴0y =(1)x <-上的动点显然有3HO HT +>综上所述，HO HT +的最小值为3，此时点H 的坐标为3(,1)4-- （3）如图，设抛物线顶点(1,0)A -，则直线AT 的斜率12AT k =-∵点(1,1)T -在抛物线内部，∴过点T 且不平行于,x y 轴的直线1l 必与抛物线有两个交点则直线1l 与轨迹E 的交点个数分以下四种情况讨论： ① 当12k ≤-时，直线1l 与轨迹E 有且只有两个不同的交点② 当102k -<<时，直线1l 与轨迹E 有且只有三个不同的交点 ③ 当0k =时，直线1l 与轨迹E 有且只有一个交点④ 当0k >时，直线1l 与轨迹E 有且只有两个不同的交点综上所述，直线1l 的斜率k 的取值范围是1(,](0,)2-∞-+∞U。

《2011年高考真题解析版—文科数学(广东卷)解析版》

绝密★启用前试卷类型：B2011年普通高等学校招生全国统一考试（广东卷）数学（文科）本试题共4页，21小题，满分150分，考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式：锥体体积公式13V Sh =，其中S 为锥体的底面积，h 为锥体的高．线性回归方程y bx a =+中系数计算公式121()()()niii nii x x y y b x x ==--=-∑∑，a y bx =-，样本数据12,,,n x x x 的标准差，222121[()()()]n s x x x x x x n=-+-++-，其中x ，y 表示样本均值．n 是正整数，则1221()()n n n n n n a b a b a a b ab b -----=-++++．一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设复数z 满足1iz =，其中i 为虚数单位，则z =A ．i -B ．iC ．1-D ．1 1．（A ）．1()iz i ii i -===-⨯- 2．已知集合{(,)|,A x y x y =为实数，且221}x y +=，{(,)|,B x y x y =为实数，且1}x y +=，则A B ⋂的元素个数为A ．4B ．3C ．2D ．1 2．（C ）．A B ⋂的元素个数等价于圆221x y +=与直线1x y +=的交点个数，显然有2个交点3．已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+a b ∥c ，则λ= A ．14B ．12C ．1D ．2 3．（B ）．(1,2)λλ+=+a b ，由()λ+a b ∥c ，得64(1)0λ-+=，解得λ=124．函数1()lg(1)1f x x x=++-的定义域是 A ．(,1)-∞- B ．(1,)+∞ C ．(1,1)(1,)-⋃+∞ D ．(,)-∞+∞ 4．（C ）．10110x x x -≠⎧⇒>-⎨+>⎩且1x ≠，则()f x 的定义域是(1,1)(1,)-⋃+∞5．不等式2210x x -->的解集是A ．1(,1)2-B ．(1,)+∞C ．(,1)(2,)-∞⋃+∞D ．1(,)(1,)2-∞-⋃+∞5．（D ）．21210(1)(21)02x x x x x -->⇒-+>⇒<-或1x >，则不等式的解集为1(,)(1,)2-∞-⋃+∞6．已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧⎪⎨⎪⎩≤≤≤≤给定．若(,)M x y 为D 上的动点，点A 的坐标为(2,1)，则z OM OA =⋅的最大值为A ．3B ．4C ．32D ．42 6．（B ）．2z x y =+，即2y x z =-+，画出不等式组表示的平面区域，易知当直线2y x z =-+经过点(2,2)时，z 取得最大值，max 2224z =⨯+=7．正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有A ．20B ．15C ．12D ．107．（D ）．正五棱柱中，上底面中的每一个顶点均可与下底面中的两个顶点构成对角线，所以一个正五棱柱对角线的条数共有5210⨯=条8．设圆C 与圆22(3)1x y +-=外切，与直线0y =相切，则C 的圆心轨迹为 A ．抛物线 B ．双曲线 C ．椭圆 D ．圆 8．（A ）．依题意得，C 的圆心到点(0,3)的距离与它到直线1y =-的距离相等，则C23正视图图1侧视图图22 俯视图2图3 的圆心轨迹为抛物线9．如图1 ~ 3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为 A ．43 B ．4 C ．23 D ．29．（C ）．该几何体是一个底面为菱形的四棱锥，菱形的面积1223232S =⨯⨯=，四棱锥的高为3，则该几何体的体积112332333V Sh ==⨯⨯=10．设(),(),()f x g x h x 是R 上的任意实值函数，如下定义两个函数()f g ()x 和()f g ()x ：对任意x ∈R ，()f g ()x =(())f g x ；()f g ()x =()()f x g x ，则下列等式恒成立的是A ．(()f g h )()x =(()f h ()g h )()xB ．(()f g h )()x =(()f h ()g h )()xC ．(()f g h )()x =(()f g ()g h )()x D ．(()f g h )()x =(()f g 　()g h )()x 10．（B ）．对A 选项 (()f g h )()x =()f g ()()x h x (())()f g x h x =(()f h ()g h )()x =()f h (()()g h x )=()f h ((()()g x h x )(()())(()())f g x h x h g x h x =，故排除A对B 选项 (()f g h )()x =()(())f g h x =(())(())f h x g h x(()f h ()g h )()x =()()()()f h x g h x (())(())f h x g h x =，故选B对C 选项 (()f g h )()x =()(())f g h x ((()))f g h x =(()f g ()g h )()x =()(()())()((()))f g g h x f g g h x = (((())))f g g h x =，故排除C对D 选项 (()f g h )()x =()()()()()()f g x h x f x g x h x =(()f g ()g h )()x =()()()()()()()()f g x g h x f x g x g x h x =，故排除 D二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（9 ~ 13题）11．已知{}n a 是递增的等比数列，若22a =，434a a -=，则此数列的公比q = ．11．2．2243224422402(2)(1)0a a a q a q q q q q -=⇒-=⇒--=⇒-+=2q ⇒=或1q =-∵{}n a 是递增的等比数列，∴2q =12．设函数3()cos 1f x x x =+．若()11f a =，则()f a -= ． 12．9-3()cos 111f a a a =+=，即3()cos 10f a a a ==，则33()()cos()1cos 11019f a a a a a -=--+=-+=-+=-13．为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x （单位：小时）与当天投篮命中率y 之间的关系：时间x 1 2 3 4 5 命中率y0.40.50.60.60.4小李这5天的平均投篮命中率为；用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率为． 13．0.5；0.53小李这5天的平均投篮命中率1(0.40.50.60.60.4)0.55y =++++=3x =，1222221()()0.2000.1(0.2)0.01(2)(1)012()niii nii x x y y b x x ==--++++-===-+-+++-∑∑，0.47a y bx =-=∴线性回归方程0.010.47y x =+，则当6x =时，0.53y = ∴预测小李该月6号打6小时篮球的投篮命中率为0.53（二）选做题（14 ~ 15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）已知两曲线参数方程分别为图4BAC DEF 5cos sin x y θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t⎧=⎪⎨⎪=⎩ (t ∈)R ，它们的交点坐标为___________． 14．25(1,)5． 5cos sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(5501)x y -<≤≤≤且，254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =22221(5501)5450145x y x y x x x y x ⎧+=-<≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩且或5x =-（舍去），又因为01y ≤≤，所以它们的交点坐标为25(1,)515．（几何证明选讲选做题）如图4，在梯形ABCD 中，AB ∥CD ，4AB =，2CD =，,E F 分别为,AD BC 上的点，且3EF =，EF ∥AB ，则梯形ABFE 与梯形EFCD 的面积比为________． 15．75如图，延长,AD BC ，AD BC P = ∵23CD EF =，∴49PCD PEF S S ∆∆=∵24CD AB =，∴416PCD PEF S S ∆∆=∴75ABEF EFCDS S =梯形梯形 PBAC DE F三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）已知函数1()2sin()36f x x π=-，x ∈R ．（1）求(0)f 的值；（2）设,0,2παβ⎡⎤∈⎢⎥⎣⎦，10(3)213f πα+=，6(32)5f βπ+=，求sin()αβ+的值． 16．解：（1）(0)2sin()16f π=-=-（2）110(3)2sin[(3)]2sin 232613f πππααα+=+-==，即5sin 13α=16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=，即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦，∴212cos 1sin 13αα=-=，24sin 1cos 5ββ=-= ∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=17．（本小题满分13分）在某次测验中，有6位同学的平均成绩为75分．用n x 表示编号为n (1,2,,6)n =的同学所得成绩，且前5位同学的成绩如下：编号n 1 2 3 4 5 成绩n x7076727072（1）求第6位同学的成绩6x ，及这6位同学成绩的标准差s ；BAB 'A 'CC 'DD 'EE 'GH '1O2O1O '2O '图5（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．17．解：（1）61(7076727072)756x +++++=，解得690x =标准差22222222212611[()()()](5135315)766s x x x x x x =-+-++-=+++++= （2）前5位同学中随机选出的2位同学记为(,)a b ，,{1,2,3,4,5}a b ∈且a b ≠ 则基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)共10种这5位同学中，编号为1、3、4、5号的同学成绩在区间（68，75）中设A 表示随机事件“从前5位同学中随机选出2位同学，恰有1位同学成绩在区间（68，75）中”则A 中的基本事件有(1,2)、(2,3)、(2,4)、(2,5)共4种，则42()105P A == 18．（本小题满分13分）图5所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的．,,,A A B B ''分别为CD ,C D '',DE ,D E ''的中点，1122,,,O O O O ''分别为CD ,C D '',DE ,D E ''的中点．（1）证明：12,,,O A O B ''四点共面；（2）设G 为AA '中点，延长1A O ''到H '，使得11O H A O ''''=．证明：2BO '⊥平面H B G ''．BAB 'A 'CC 'DD 'EE 'GH '1O2O1O '2O 'H18．证明：（1）连接2,BO 22,O O '依题意得1122,,,O O O O ''是圆柱底面圆的圆心∴,,,CD C D DE D E ''''是圆柱底面圆的直径∵,,A B B ''分别为C D '',DE ,D E ''的中点∴1290A O D B O D ''''''∠=∠= ∴1A O ''∥2BO '∵BB '//22O O '，四边形22O O B B ''是平行四边形 ∴2BO ∥2BO '∴1A O ''∥2BO ∴12,,,O A O B ''四点共面（2）延长1A O '到H ，使得11O H AO ''=，连接1,,HH HO HB '' ∵11O H A O ''''=∴1O H ''//2O B ''，四边形12O O B H ''''是平行四边形 ∴12O O ''∥H B ''∵1222O O O O '''⊥，122O O B O ''''⊥，2222O O B O O ''''= ∴12O O ''⊥面22O O B B ''∴H B ''⊥面22O O B B ''，2BO '⊂面22O O B B '' ∴2BO H B '''⊥易知四边形AA H H ''是正方形，且边长2AA '= ∵11tan 2HH HO H O H '''∠==''，1tan 2A G A H G A H '''∠=='' ∴1tan tan 1HO H A H G ''''∠⋅∠= ∴190HO H A H G ''''∠+∠=∴1HO H G ''⊥易知12O O ''//HB ，四边形12O O BH ''是平行四边形 ∴2BO '∥1HO '∴2BO H G ''⊥，H G H B H ''''= ∴2BO '⊥平面H B G ''．19．（本小题满分14分）设0a >，讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性． 19．解：函数()f x 的定义域为(0,)+∞212(1)2(1)1()2(1)2(1)a a x a x f x a a x a x x---+'=+---=令2()2(1)2(1)1g x a a x a x =---+224(1)8(1)121644(31)(1)a a a a a a a ∆=---=-+=--① 当103a <<时，0∆>，令()0f x '=，解得1(31)(1)2(1)a a a x a a -±--=-则当1(31)(1)02(1)a a a x a a ----<<-或1(31)(1)2(1)a a a x a a -+-->-时，()0f x '>当1(31)(1)1(31)(1)2(1)2(1)a a a a a a x a a a a -----+--<<--时，()0f x '< 则()f x 在1(31)(1)(0,)2(1)a a a a a -----，1(31)(1)(,)2(1)a a a a a -+--+∞-上单调递增，在1(31)(1)1(31)(1)(,)2(1)2(1)a a a a a a a a a a -----+----上单调递减② 当113a ≤≤时，0∆≤，()0f x '≥，则()f x 在(0,)+∞上单调递增 ③ 当1a >时，0∆>，令()0f x '=，解得1(31)(1)2(1)a a a x a a -±--=-∵0x >，∴1(31)(1)2(1)a a a x a a ----=-则当1(31)(1)02(1)a a a x a a ----<<-时，()0f x '>当1(31)(1)2(1)a a a x a a ---->-时，()0f x '<则()f x 在1(31)(1)(0,)2(1)a a a a a -----上单调递增，在1(31)(1)(,)2(1)a a a a a ----+∞-上单调递减20．（本小题满分14分）设0b >，数列{}n a 满足1a b =，111n n n nba a a n --=+-(n ≥2)．（1）求数列{}n a 的通项公式；（2）证明：对于一切正整数n ，2n a ≤11n b ++． 20．（1）解：∵111n n n nba a a n --=+-∴111n n n a ba n a n --=+- ∴1111n n n n a b a b--=⋅+ ① 当1b =时，111n n n n a a ---=，则{}nn a 是以1为首项，1为公差的等差数列∴1(1)1nnn n a =+-⨯=，即1n a = ② 当0b >且1b ≠时，11111()11n n n n a b b a b--+=+-- 当1n =时，111(1)n n a b b b +=-- ∴1{}1n n a b +-是以1(1)b b -为首项，1b为公比的等比数列 ∴111()11n n n a b b b+=⋅-- ∴111(1)1(1)n n nn n b a b b b b b-=-=--- ∴(1)1nn nn b b a b -=-综上所述(1),01111nn n n b b b b a bb ⎧->≠⎪=-⎨⎪=⎩　且，（2）证明：① 当1b =时，1212n n a b +=+=；② 当0b >且1b ≠时，211(1)(1)n n n b b b b b ---=-++++要证121n n a b +≤+，只需证12(1)11n n nn b b b b+-≤+-，即证2(1)11n nn b b b b -≤+- 即证21211n n nn b b b b b--≤+++++ 即证211()(1)2n n n b b b b n b--+++++≥即证21121111()()2n n n n b b b b n b b b b --+++++++++≥∵21121111()()n n n n b b b b b b b b--+++++++++21211111()()()()n n n n b b b b b b b b--=++++++++xy O 2x =-APlMMxy O2x =-TNlHNH ∙H2121111122222n n n nb b b b n b bb b --≥⋅+⋅++⋅+⋅=，∴原不等式成立 ∴对于一切正整数n ，2n a ≤11n b ++．21．（本小题满分14分）在平面直角坐标系xOy 上，直线l ：2x =-交x 轴于点A ．设P 是l 上一点，M 是线段OP 的垂直平分线上一点，且满足MPO AOP ∠=∠．（1）当点P 在l 上运动时，求点M 的轨迹E 的方程；（2）已知(1,1)T -，设H 是E 上动点，求HO HT +的最小值，并给出此时点H的坐标；（3）过点(1,1)T -且不平行于y 轴的直线1l 与轨迹E 有且只有两个不同的交点，求直线1l 的斜率k 的取值范围．21．解：（1）如图所示，连接OM ，则PM OM =∵MPO AOP ∠=∠，∴动点M 满足MP l ⊥或M 在x 的负半轴上，设(,)M x y① 当MP l ⊥时，2MP x =+，22OM x y =+222x x y +=+，化简得244y x =+(1)x ≥-② 当M 在x 的负半轴上时，0y =(1)x <-综上所述，点M 的轨迹E 的方程为244y x =+(1)x ≥-或0y =(1)x <-（2）由（1）知M 的轨迹是顶点为(1,0)-，焦点为原点的抛物线和x 的负半轴0y =(1)x <-① 若H 是抛物线上的动点，过H 作HN l ⊥于N由于l 是抛物线的准线，根据抛物线的定义有HO HN =xy OTA 1l1l1l 则HO HT HN HT +=+当,,N H T 三点共线时，HN HT +有最小值3TN = 求得此时H 的坐标为3(,1)4--② 若H 是x 的负半轴0y =(1)x <-上的动点显然有3HO HT +>综上所述，HO HT +的最小值为3，此时点H 的坐标为3(,1)4-- （3）如图，设抛物线顶点(1,0)A -，则直线AT 的斜率12AT k =- ∵点(1,1)T -在抛物线内部，点∴过点T 且不平行于,x y 轴的直线1l 必与抛物线有两个交则直线1l 与轨迹E 的交点个数分以下四种情况讨论：① 当12k ≤-时，直线1l 与轨迹E 有且只有两个不同的交点 ② 当102k -<<时，直线1l 与轨迹E 有且只有三个不同的交点 ③ 当0k =时，直线1l 与轨迹E 有且只有一个交点 ④ 当0k >时，直线1l 与轨迹E 有且只有两个不同的交点综上所述，直线1l 的斜率k 的取值范围是1(,](0,)2-∞-+∞。

2011年高考真题详解——广东卷(文科数学)

2011年普通高等学校招生全国统一考试【广东卷】（文科数学）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至第2页，第Ⅱ卷第3页至第4页．全卷满分150分，考试时间120分钟．第Ⅰ卷（选择题共50分）一、选择题：（每小题5分，共50分）【2011⋅广东文，1】1．设复数z 满足1iz =，其中i 为虚数单位，则z = ( )． A ．i - B ．i C ．1 D ．1- 【答案】A ．【解析】 1()iz i i i i -===-⨯-．【2011⋅广东文，2】2．已知集合(){,|A x y x y =、为实数，且}221xy +=，(){,|B x y x y=、为实数，且}1x y +=，则A B 的元素个数为( )．A ．4B ．3C ．2D ．1 【答案】C ．【解析】A B 的元素个数等价于圆221x y +=与直线1x y +=的交点个数，显然有2个交点．【2011⋅广东文，3】3．已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+a b ∥c ，则λ= ( )． A ．14 B ．12C ．1D ．2 【答案】B ．【解析】 (1,2)λλ+=+a b ，由()λ+a b ∥c ，得64(1)0λ-+=，解得λ=12．【2011⋅广东文，4】4．函数1()lg(1)1f x x x=++-的定义域是( )． A ．(,1)-∞- B ．(1,)+∞ C ．(1,1)(1,)-+∞ D ．(,)-∞+∞ 【答案】C ．【解析】 10110x x x -≠⎧⇒>-⎨+>⎩且1x ≠，则()f x 的定义域是(1,1)(1,)-+∞ ．【2011⋅广东文，5】5．不等式2210x x -->的解集是( )． A ．1(,1)2-B ．(1,)+∞C ．(,1)(2,)-∞+∞D ．1(,)(1,)2-∞-+∞ 【答案】D ．【解析】21210(1)(21)02x x x x x -->⇒-+>⇒<-或1x >，则不等式的解集为1(,)(1,)2-∞-+∞ ．【2011⋅广东文，6】6．已知平面直角坐标系xOy 上的区域D由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩给定，若(),M x y 为D 上的动点，点A的坐标为)，则z OM OA =⋅的最大值为( )．A ．3B ．4 C． D．【答案】B ．【解析】z y =+，即y z =+，画出不等式组表示的平面区域，易知当直线y z =+经过点时，z取得最大值，max 24z =．【2011⋅广东文，7】7．正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有( )．A ．20B ．15C ．12D ．10 【答案】D ．【解析】正五棱柱中，上底面中的每一个顶点均可与下底面中的两个顶点构成对角线，所以一个正五棱柱对角线的条数共有5210⨯=条．【2011⋅广东文，8】8．设圆C 与圆22(3)1x y +-=外切，与直线0y =相切．则C 的圆心轨迹为( )．A ．抛物线B ．双曲线C ．椭圆D ．圆【答案】A ．【解析】依题意得，C 的圆心到点(0,3)的距离与它到直线1y =-的距离相等，则C 的圆心轨迹为抛物线．【2011⋅广东文，9】9．如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别为等边三角形、等腰三角形和菱形，则该几何体体积为( )．A ．B ．4C ．D ． 2【答案】C ．【解析】该几何体是一个底面为菱形的四棱锥，菱形的面积122S =⨯⨯=，四棱锥的高为3，则该几何体的体积11333V Sh ==⨯=．【2011⋅广东文，10】10．设||||HO HT +是R 上的任意实值函数．如下定义两个函数()()f g x 和()()f g x ；对任意x R ∈,()()()()f g x f g x = ；()()()()f g x f x g x = ．则下列等式恒成立的是( )． A ．()()()()()()()f g h x f h g h x = B ． ()()()()()()()f g h x f h g h x = C ． ()()()()()()()f g h x f h g h x =D ．()()()()()()()f g h x f h g h x =【答案】B ．【解析】对A 选项 (()f g h )()x =()f g ()()x h x (())()f g x h x =， (()f h ()g h )()x =()f h (()()g h x )=()f h ((()()g x h x ) (()())(()())f g x h x h g x h x = ，故排除A ；对B 选项 (()f g h )()x =()(())f g h x = (())(())f h x g h x ，(()f h ()g h )()x =()()()()f h x g h x (())(())f h x g h x =，故选B ；对C 选项 (()f g h )()x =()(())f g h x ((()))f g h x =，(()f g ()g h )()x =()(()())()((()))f g g h x f g g h x = ． (((())))f g g h x =，故排除C ；对D 选项 (()f g h )()x =()()()()()()f g x h x f x g x h x = ，(()f g ()g h )()x =()()()()()()()()f g x g h x f x g x g x h x = ，故排除D ．解析二：二、填空题：本大题共5小题．考生作答4小题．每小题5分，满分20分．（一）必做题（11～13题）第Ⅱ卷（非选择题共100分）二、填空题：（每小题5分，共20分）【2011⋅广东文，11】11．已知{}n a 是递增等比数列，2432,4a a a =-=，则此数列的公比=q ．【答案】 2．【解析】 2243224422402(2)(1)0a a a q a q q q q q -=⇒-=⇒--=⇒-+=2q ⇒=或1q =- ∵{}n a 是递增的等比数列，∴2q =．【2011⋅广东文，12】12．设函数3()cos 1.f x x x =+若()11f a =，则()f a -= ．【答案】 9-．【解析】3()cos 111f a a a =+=，即3()cos 10f a a a ==，则33()()cos()1cos 11019f a a a a a -=--+=-+=-+=-．【2011⋅广东文，13】13．为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打时间x （单位：小时）与当于投篮命中率y 之间的关系：小李这 5天的平均投篮命中率为，用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率为．【答案】 0.5；0.53．【解析】小李这5天的平均投篮命中率1(0.40.50.60.60.4)0.55y =++++= 3x =，1222221()()0.2000.1(0.2)0.01(2)(1)012()niii nii x x y y bx x ==--++++-===-+-+++-∑∑ ， 0.47a y bx =-= ∴线性回归方程 0.010.47y x =+，则当6x =时，0.53y = ∴预测小李该月6号打6小时篮球的投篮命中率为0.53．（二）选做题（14、15题，考生只能从中选做一题）【2011⋅广东文，14】14．（坐标系与参数方程选做题）已知两曲线参数方程分别为⎩⎨⎧==θθsin cos 5y x （0≤θ ＜π) 和254x ty t⎧=⎪⎨⎪=⎩（t ∈R ），它们的交点坐标为．【答案】 (1,)5．【解析】 sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(01)x y <≤≤≤，254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =，22221(01)5450145x y x y x x x y x ⎧+=≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩或5x =-（舍去），又因为01y ≤≤，所以它们的交点坐标为．【2011⋅广东文，15】15．（几何证明选讲选做题）如图4，在梯形ABCD 中，AB ∥CD ，AB ＝4，CD ＝2，E 、F 分别为AD 、BC 上点，且EF ＝3，EF ∥AB ，则梯形ABFE 与梯形EFCD 的面积比为．【答案】75．【解析】如图，延长,AD BC ，AD BC P = ，∵23CD EF =，∴49PCD PEF S S ∆∆= ∵24CD AB =，∴416PCD PEF S S ∆∆= ∴75ABEF EFCDS S =梯形梯形．三、解答题：（本大题共6小题，共80分）【2011⋅广东文，16】16．（本小题满分12分）已知函数()12sin()36f x x π=-，x R ∈．(Ⅰ) 求()0f 的值； (Ⅱ) 设10,0,,(3),2213f ππαβα⎡⎤∈+=⎢⎥⎣⎦6(3),25f πβ+=求()sin αβ+的值．【解析】． (Ⅰ) (0)2sin()16f π=-=-；(Ⅱ) 110(3)2sin[(3)]2sin 232613f πππααα+=+-==，即5sin 13α=16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=，即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦，∴12cos 13α==，4sin 5β== ∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=．【2011⋅广东文，17】17．（本小题满分13分）在某次测验中，有6位同学的平均成绩为75分．用n x 表示编号为()1,2,,6n n = 的同学所得成绩，且前5(Ⅰ) 求第6位同学成绩6，及这6位同学成绩的标准差；(Ⅱ) 从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间()68,75中的概率．【解析】．(Ⅰ) 611756n n x x ===∑5616675707672707290,n n x x x =∴=-=⨯-----=∑622222222111()(5135315)4966n n s x x ==-=+++++=∑，7.s ∴=(Ⅱ) 从5位同学中随机选取2位同学，共有如下10种不同的取法： {1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}，{3，4}，{3，5}，{4，5}，选出的2位同学中，恰有1位同学的成绩位于（68，75）的取法共有如下4种取法： {1，2}，{2，3}，{2，4}，{2，5}，故所求概率为25．解法二：（1）61(7076727072)756x +++++=，解得690x =，标准差7s =．（2）前5位同学中随机选出的2位同学记为(,)a b ，,{1,2,3,4,5}a b ∈且a b ≠，则基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)共10种，这5位同学中，编号为1、3、4、5号的同学成绩在区间（68，75）中设A 表示随机事件“从前5位同学中随机选出2位同学，恰有1位同学成绩在区间（68，75）中”，则A 中的基本事件有(1,2)、(2,3)、(2,4)、(2,5)共4种，则42()105P A ==．【2011⋅广东文，18】18．（本小题满分12分）如图所示，将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右平移到的,,,A A B B ''分别为,,,,CD C D DE D E ''''的中点，1122,,,O O O O ''分别为,,,CD C D DE D E ''''的中点． (Ⅰ) 证明：12,,,O A O B ''四点共面；(Ⅱ) 设G 为AA '中点，延长1A O ''到H ',使得11O H A O ''''=,证明：2BO H B G '''⊥面．【解析】．// (Ⅰ) ,,A A CDC D ''' 分别为中点， 11//O A O A ''∴连接BO 2直线BO 2是由直线AO 1平移得到12//AO BO ∴12//O A BO ''∴ 12,,,O A O B ''∴共面．(Ⅱ) 将AO 1延长至H 使得O 1H=O 1A ，连接1,,HO HB H H '' ∴由平移性质得12O O ''=HB21//BO HO ''∴11,,2A G H O H H A H O H H GA H π''''''''''==∠=∠=1GA H O H H ''''∴∆≅∆12H O H GH A π'''∴∠+=1O H H G ''∴⊥ 2BO H G ''∴⊥12212222222,,O O B O O O O O B O O O O '''''''''''⊥⊥⋂= 1222O O B BO O ''''∴⊥平面122O O BO '''∴⊥ 2BO H B '''∴⊥ H B H G H ''''⋂=2.BO H B G '''∴⊥平面解法二：证明：（1）连接2,BO 22,O O '依题意得1122,,,O O O O ''是圆柱底面圆的圆心 ∴,,,CD C D DE D E ''''是圆柱底面圆的直径∵,,A B B ''分别为 CD '', DE , D E ''的中点 ∴1290A O D B O D ''''''∠=∠=∴1A O ''∥2BO '∵BB '//22O '，四边形22O O B B ''是平行四边形 ∴2BO ∥2BO ' ∴1A O ''∥2BO∴12,,,O A O B ''四点共面（2）延长1A O '到H ，使得11O H AO ''=，连接1,,HH HO HB '' ∵11O H A O ''''=∴1O H ''2B ''，四边形12O O B H ''''是平行四边形 ∴12O O ''∥H B ''∵1222O O O O '''⊥，122O O B O ''''⊥，2222O O B O O ''''= ∴12O O ''⊥面22O O B B ''∴H B ''⊥面22O O B B ''，2BO '⊂面22O O B B '' ∴2BO H B '''⊥易知四边形AA H H ''是正方形，且边长2AA '=，∵11tan 2HH HO H O H'''∠==''，1tan 2A G A H G A H '''∠==''， ∴1tan tan 1HO H A H G ''''∠⋅∠=， ∴190HO H A H G ''''∠+∠= ， ∴1HO H G ''⊥易知12O O ''HB ，四边形12O O BH ''是平行四边形， ∴2BO '∥1HO '，∴2BO H G ''⊥，H G H B H ''''= ， ∴2BO '⊥平面H B G ''．【2011⋅广东文，19】19．（本小题满分14分）设0a >,讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性．【解析】．函数()f x 的定义域为(0,)+∞．22(1)2(1)1(),a a x a x f x x---+'=当212(1)2(1)1a a a x a x ≠---+时,方程的判别式112(1)()3a a ∆=--．①当10,0,()3a f x '<<∆>时有两个零点，12110,22x x a a =>= 且当12120,()0,()(0,)(,)x x x x f x f x x x '<<>>+∞或时在与内为增函数；当1212,()0,()(,)x x x f x f x x x '<<<时在内为减函数；②当11,0,()0,()(0,)3a f x f x '≤<∆≤≥+∞时所以在内为增函数；③当11,()0(0),()(0,)a f x x f x x'==>>+∞时在内为增函数；④当111,0,0,2a x a >∆>=>时210,()2x f x a '=+<所以在定义域内有唯一零点1x ，且当110,()0,()(0,)x x f x f x x '<<>时在内为增函数；当1x x >时，1()0,()(,)f x f x x '<+∞在内为减函数。

2011年普通高等学校招生全国统一考试文科数学(广东卷)

14. 已知两曲线参数方程分别为
（0≤θ＜π）和
（t∈R），它们的交点坐标为．
15. 如图，在梯形ABCD中，AB∥CD，AB=4，CD=2．E，F分别为AD，BC上点，且EF=3，EF∥AB，则梯形ABFE与梯形EFCD的面积比为．
三、解答题
16. f(x)=2sin（ x﹣ ），x∈R．
（1）求f（0）的值；
C．2
D．1
3. （5分）（2011•广东）已知向量 =（1，2）， =（1，0）， =（3，4）．若λ为实数，（ +λ ）∥ ，则λ=（）
A．
B．
C．1
D．2
4. 函数f(x)＝＋lg(1＋x)的定义域是（）
A．(－∞，－1)
B．(1，＋∞)
C．(－1，1)∪(1，＋∞)
D．(－∞，＋∞)
5. （5分）（2011•广东）不等式2x2﹣x﹣1＞0的解集是（） B．（1，+∞）
2011年普通高等学校招生全国统一考试文科数学（广东卷）
一、单选题
1. 设复数z满足iz=1，其中i为虚数单位，则z=（）
A．﹣i
B．i
C．﹣1
D．1
2. 已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B=|（x，y）|x，y为实数，且x+y=1}，则A∩B的元素个数为（）
A．4
B．3
二、填空题
11. 已知{an}是递增等比数列，a2=2，a4﹣a3=4，则此数列的公比q= ．
12. =x3cosx+1，若f（a）=11，则f（﹣a）= ．
13. 工人月工资y（元）与劳动生产率x（千元）变化的回归方程为 =50+80x，下列判断正确的是 ①劳动生产率为1千元时，工资为130元；②劳动生产率提高1千元，则工资提高80元；③劳动生产率提高1千元，则工资提高130元；④当月工资为210元时，劳动生产率为2千元．