角谷猜想的斐波那契数列现象

合集下载

斐波那契数列的6大结论

斐波那契数列的6大结论斐波那契数列，这个名字听起来就像是数学界的魔法。

没错，斐波那契数列的魅力就在于它看似简单，却藏着无尽的奥秘。

今天咱们就来聊聊这条神秘的数字之路，顺便带点幽默，轻松一下。

1. 斐波那契数列是什么？1.1 说白了，斐波那契数列就是这样一串数字：0、1、1、2、3、5、8、13、21，依此类推。

你可能会问，这数字有什么了不起的？其实，这串数字的产生规则非常简单：前两个数相加，得到下一个数。

就像做饭，先放盐再放胡椒，最后成了一道美味的菜。

1.2 你看，这数列不光是数学家们的心头好，艺术家、建筑师也爱得不得了。

比如，著名的“黄金比例”就跟它有千丝万缕的联系。

可以说，斐波那契数列就像是宇宙的乐谱，处处都能听到它的旋律。

2. 自然界的魅力2.1 斐波那契数列在自然界中无处不在，这可不是我随便说说。

你注意过向日葵的花瓣吗？它们的排列方式就遵循这个数列，真是神奇得让人赞叹不已。

就像大自然的设计师，精心安排了一切。

2.2 除了花瓣，松果、贝壳甚至是一些水果的种子分布也都跟斐波那契数列有关。

这让人不禁想，难道自然界也在暗自欣赏这串数字的美妙？就像人们欣赏一幅完美的画作，心里忍不住咯噔一下。

3. 斐波那契与生活3.1 在我们的日常生活中，斐波那契数列其实也无处不在。

比如说，咱们日常见到的许多设计和建筑，往往都运用了这个数列的美学原则。

你看看那些高楼大厦，有的外形简直就是一幅现代艺术画，背后其实都有数学的影子。

3.2 另外，许多经济学模型也利用了斐波那契数列来预测市场走势。

这就像在打麻将，灵活运用每一张牌，才能获得胜利。

数列的神秘力量在这里展露无遗，让人不禁感慨：数字背后藏着多少智慧呀！4. 学习与探索4.1 学习斐波那契数列，简直就像是一场冒险旅行。

起初可能有点不知所措，但随着深入，真的会发现不少惊喜。

就像走进一个藏满宝藏的洞穴，越走越想探索下去。

4.2 斐波那契数列的应用范围广泛，甚至可以帮助我们理解一些复杂的现象。

斐波那契数列结论

斐波那契数列结论1斐波那契数列：斐波那契数列（又译作费氏数列），又称黄金分割数列，是指满足以下公式的数列：F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2)，由此产生的递推数列。

它是在现代数学中非常引人关注的数列，历来被用于理解各种问题。

2斐波那契数列的历史：斐波那契数列是意大利数学家费马在公元1790年公布的，当时它用该数字列解决一个关于“早期出生者死后仍有死亡率升高”的统计问题。

费马在当时就发现了斐波那契数列的出现模式，并对它的运用和研究取得了重要的成果。

3斐波那契数列的性质：斐波那契数列是一个由递推公式确定的数列，它具有如下几个特性：（1）斐波那契数列以1,1开头，经过多次运算后，任一项与其前两项之和相同；（2）斐波那契数列具有前后对称的属性，也就是1,1，2,3,5,8,13,21,34，它的前半部分与后半部分对称；（3）斐波那契数列有许多和自身有关的数论定理，它的计算方法包含了数论的各种定理；（4）斐波那契数列有着很强的数学关联和规律性，它不仅能被用在数学上，而且根据其特性，可以在很多技术领域都取得一定成果。

4斐波那契数列的应用：斐波那契数列广泛应用于计算机和数学领域，是一种算法的基础。

它不仅被广泛应用于程序控制，多步判决等算法，而且仍在发展着新的应用，如生物学，多媒体等。

斐波那契数列同样是研究图论的重要素材，而在图的最短路径问题，网络流量分析，判断图的联通性，求解图的最大完全子图，检测图的完全性等问题上，都可以利用斐波那契数列的性质来获得解决方案。

在实际工程中，斐波那契数列也有着重要的应用，它可以用来产生比例等级及索引，如在影视制作中作为比例等级，在报纸版面排，布局设计、调剂，以及建筑等工程设计中都能利用它来调整，提高效率，更有利于减少错误。

此外，斐波那契数列也可以被用于统计分析，可以用来计算概率等数据，研究复杂性系统中的模式及规律，从而推测未来发展趋势。

斐波那契数列的趣味介绍

斐波那契数列的趣味介绍
斐波那契数列是许多数学家试图解答的自然现象。

它是以著名的数学家斐波那契在公元前一世纪所创造出来的。

斐波那契数列也被称为费布拉斯圆周率序列，它有着令人神往的特点，更是数学界的一大研究课题。

斐波那契数列以兔子繁殖为例而产生，假定有一对1岁的兔子，在每个月都会孕育一对小兔，假设不会有死亡的情况，那么经过第n个月后，一共就会有多少只兔子？
事实上，一共有1，1，2，3，5，8，13，21，34...这样的一系列数字，这就是著名的斐波那契数列。

可以发现，任意一个数字都等于其前两项之和，可以用如下伪码表示： f(1)=1, f(2)=1, f(n)=f(n-1)+f(n-2).
令人吃惊的是，在自然界中，看到许多生物的繁殖工作也属于斐波那契数列的范畴，比如几种物种的年龄结构、植物的芽孢分裂，甚至人口的统计、金融投资等也会隐隐具备斐波那契序列的特征。

斐波那契数列与不同领域有着紧密的关系，这其中蕴藏了很多有趣的现象，比如说，任何一个斐波那契数列的数字，都等于其前两项数字的总和，这其实就是有趣的金字塔方阵数学令人神奇的特征，再或者，斐波那契数字与黄金分割比，它是某个整数加1除以该整数的结果，正好是1.618的比率，可以发现前面的斐波那契数字与黄金分割比有着很密切的关系，这也就直观地体现了自然界蕴藏的美感和数学上封装的流畅。

斐波那契数列是数学界的一大课题，自然界中也蕴藏了不少它的痕迹。

它有着非常有趣的现象，涉及的领域也甚广，很多学者都在一直解答这一种现象，希望能够用唯一的数学理论拟合出它的惊人之处。

有趣的斐波那契数列例子

……
F(3)-r*F(2)=s*[F(2)-r*F(1)]。
联立以上n-2个式子，得：
F(n)-r*F(n-1)=[s^(n-2)]*[F(2)-r*F(1)]。
∵s=1-r，F(1)=F(2)=1。
上式可化简得：
F(n)=s^(n-1)+r*F(n-1)。
那么：
F(n)=s^(n-1)+r*F(n-1)。
157
…
F[1,3]n
1
3
4
7
11
18
29
47
76
123
…
F[1,4]n-F[1,3]n
0
1
1
2
3
5
8
13
21
34
…
F[1,4]n+F[1,3]n
2
7
9
16
25
41
66
107
173
280
…
②任何一个斐波那契—卢卡斯数列都可以由斐波那契数列的有限项之和获得，如
n
1
2
3
4
5
6
7
8
9
10
…
F[1,1](n)
1
1
2
3
5
8
13
21
34
55
…
F[1,1](n-1)
0
1
1
2
3
5
8
13
21
34
…
F[1,1](n-1)
0
1
1
2
3
5
8
13
21
34
…
F[1,3]n
1
3

斐波那契数列的十六个性质

斐波那契数列的十六个性质
斐波那契数列的十六个性质为：
性质一：模除周期性
数列的数模除某个数的结果会呈现一定周期性，因为数列中的某个数取决与前两个数，一旦有连着的两个数的模除结果分别等于第0第一项的模除结果，那麽代表着一个新的周期的的开始，如果模除n，则每个周期中的元素不会超过n×n。

性质二：黄金分割
随着i的增大Fi/Fi－1接近于0.618.
性质三：平方与前后项
从第二项开始，每个奇数项的平方都比前后两项之积多一，每个偶数项的平方比前后两项之积少一。

性质四：斐波那契数列的第n＋2项代表了集合{1，2，...n}中所有不包含相邻正整数的子集的个数。

性质五：求和。

斐波那契数列的特点：
斐波那契数具有很多有趣且令人惊讶的特性，在此我将举例说明和证明其中两个。

两种证明都将使用数学归纳法
1．数学归纳法
如果您不熟悉数学归纳法，请这样考虑。

想象一下，我拥有一套永无止境的多米诺骨牌，而我将把它们全都站起来，形成一串多米诺
骨牌，它们将永远相互撞倒。

为确保发生这种情况，我需要了解以下内容：
第一个多米诺骨牌被击倒了。

2．碰到任何多米诺骨牌都会导致下一个多米诺骨牌被碰倒。

以类似的方式，我们可以通过证明以下事实来证明对于所有数字n都是正确的：
1．n＝1时成立（称为归纳开始）
2．如果n＝k成立，那么n＝k＋1也成立。

（这被称为归纳步骤。

即证明如果所有n≤k都成立，那么n＝k＋1也成立。

）。

斐波那契递推公式推导证明

斐波那契递推公式推导证明斐波那契数列，这玩意儿可有意思啦！好多同学一开始接触可能会觉得有点头疼，但其实只要咱们耐心点儿，一步一步来，就能把它整明白。

咱先来说说啥是斐波那契数列。

它就是这么一串数：0、1、1、2、3、5、8、13、21、34、55、89、144…… 瞧见没，从第三个数开始，每个数都是前两个数相加得到的。

那咱们来推导证明一下斐波那契递推公式。

假设斐波那契数列的第n 个数用 F(n) 来表示。

当 n = 0 时，F(0) = 0；当 n = 1 时，F(1) = 1。

这俩是最开始给定的，是这个数列的基础。

接下来，对于n ≥ 2 的情况，F(n) = F(n - 1) + F(n - 2)。

这就是斐波那契数列的递推公式。

咱们来仔细瞅瞅这个公式是咋来的。

比如说，到了第 3 个数，按照前面的规律，是前两个数 1 和 1 相加，也就是 2。

用公式表示就是 F(3) = F(2) + F(1)，而 F(2)就是 1，F(1)也是 1，所以 F(3)就是 2，没问题吧？再往后，第 4 个数，是 2 和 1 相加得 3。

公式就是 F(4) = F(3) + F(2)，F(3)是 2，F(2)是 1，所以 F(4)就是 3。

就这么一直推下去，这个递推公式都能成立。

我记得有一次，我给学生们讲这个斐波那契数列。

有个小家伙特别较真儿，非得让我给他一遍又一遍地解释为啥会有这个递推公式。

我就耐心地陪着他，从最开始的数开始，一个一个地加给他看，直到他终于恍然大悟，那小眼神儿里透出来的兴奋劲儿，让我觉得当老师可真有成就感。

咱们再从数学的角度深入点儿说。

这个斐波那契数列在很多地方都有神奇的应用。

比如在自然界中，一些植物的花瓣数量、叶子的排列方式，都可能遵循着斐波那契数列的规律。

而且在计算机编程里，要实现斐波那契数列的计算，就得靠这个递推公式。

通过一个简单的循环，就能轻松算出数列中的每个数。

总之啊，斐波那契递推公式虽然看起来简单，但是背后的学问可大着呢！同学们只要认真琢磨，就能发现其中的乐趣和奥秘。

斐波那契数列

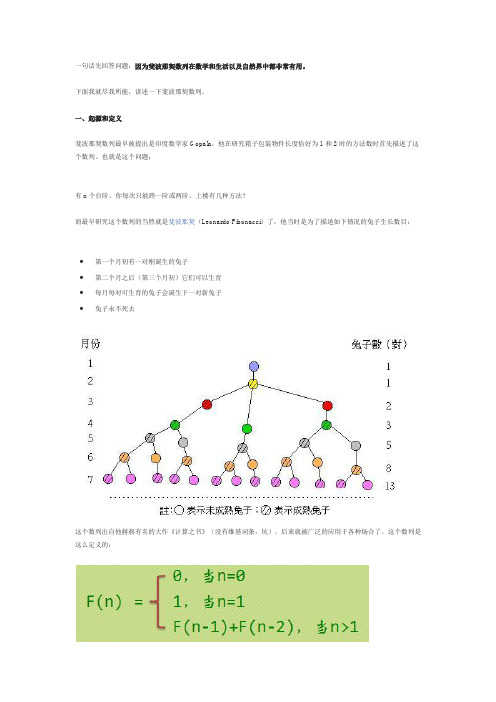
一句话先回答问题：因为斐波那契数列在数学和生活以及自然界中都非常有用。

下面我就尽我所能，讲述一下斐波那契数列。

一、起源和定义斐波那契数列最早被提出是印度数学家Gopala，他在研究箱子包装物件长度恰好为1和2时的方法数时首先描述了这个数列。

也就是这个问题：有n个台阶，你每次只能跨一阶或两阶，上楼有几种方法？而最早研究这个数列的当然就是斐波那契（Leonardo Fibonacci）了，他当时是为了描述如下情况的兔子生长数目：•第一个月初有一对刚诞生的兔子•第二个月之后（第三个月初）它们可以生育•每月每对可生育的兔子会诞生下一对新兔子•兔子永不死去这个数列出自他赫赫有名的大作《计算之书》（没有维基词条，坑），后来就被广泛的应用于各种场合了。

这个数列是这么定义的：The On-Line Encyclopedia of Integer Sequences® (OEIS®)序号为A000045 - OEIS（注意，并非满足第三条的都是斐波那契数列，卢卡斯数列（A000032 - OEIS）也满足这一特点，但初始项定义不同）二、求解方法讲完了定义，再来说一说如何求对应的项。

斐波那契数列是编程书中讲递归必提的，因为它是按照递归定义的。

所以我们就从递归开始讲起。

1.递归求解int Fib(int n){return n < 2 ? 1 : (Fib(n-1) + Fib(n-2));}这是编程最方便的解法，当然，也是效率最低的解法，原因是会出现大量的重复计算。

为了避免这种情况，可以采用递推的方式。

2.递推求解int Fib[1000];Fib[0] = 0;Fib[1] = 1;for(int i = 2;i < 1000;i++) Fib[i] = Fib[i-1] + Fib[i-2];递推的方法可以在O(n)的时间内求出Fib(n)的值。

但是这实际还是不够好，因为当n很大时这个算法还是无能为力的。

斐波那契数列常用结论

斐波那契数列常用结论
1斐波那契数列
斐波那契数列又称黄金分割数列，是指从0和1开始，之后的每一项都是前两项之和的自然数序列，即：F(0)=0，F(1)=1，F(n)=F(n-1)+F(n-2)（n>1，n∈N*），那么形成了如下数列：0，1，1，2，3，5，8，13，21，34，55，89，144，……
斐波那契数列可以用来表示各种有规律变化的现象，如天文学中行星轨道运行的规律、物理学中光衍射和电磁波传播的规律、生物学中由细胞分裂形成的规律等。

2常用结论
1.黄金比例
斐波那契数列中的两个相邻数的比值，比如5和8的比为8/5等于1.618，34和55的比为55/34也等于1.618。

这就是著名的黄金分割比例，也常被称为黄金比例，具有美观耐看性，在艺术、建筑中广泛应用。

2.斐波那契数列的通项公式
从斐波那契数列的定义可以发现，任何一项的斐波那契数都可以用前两项来计算出来，比如F(5)=F(4)+F(3)，那么我们可以用下面这个公式来表示斐波那契数列的每一项：F(n)=F(n-1)+F(n-2)，这就可以用来计算出任意的项的斐波那契数了。

3.斐波那契数列的正则表达式
斐波那契数列可以用下面的正则表达式完美地描述出来：
F(n)=2*F(n-1)+F(n-2)，用此正则表达式可以轻松实现斐波那契数列的自动构建。

4.完美数
斐波那契数列中的完美数是指那些满足F(n)=2^n-1的斐波那契数，即F(0)=0，F(1)=1，F(2)=3，F(3)=7，F(4)=15，F(5)=31，如果除了0和1外，它们都等于2的次方数减1，都称之为完美数。

从上面几条结论来看，斐波那契数列不仅应用于数学领域，在多个领域也有着广泛的应用，对于研究具有重要意义。

大自然的神奇数列—斐波那契数列详解

大自然的神奇数列—斐波那契数列详解斐波那契是专业交易者可以使用的最重要的工具之一。

本文将介绍：什么是斐波那契？斐波那契序列水平，斐波那契策略以及如何通过三种不同的方法正确使用斐波那契工具，这将提高你的交易策略的有效性。

列奥纳多·波纳契列奥纳多·波纳契又名斐波那契，大约1170年出生于比萨，是一位富商的儿子。

他是一位意大利数学家，被认为是中世纪最有才华的西方数学家。

他的书“ Liber Abaci”介绍了印度－阿拉伯数字系统。

什么是斐波那契？斐波那契数列是指一组数字，该数字以数字1或数字0开头，后接另一个数字1，然后该模式根据以下规则继续：数字（或斐波那契数字）将等于它们前面两个数字的总和（或之前两个数字的总和）。

如今，斐波那契水平被用于所有类型的交易中，包括股票，期货，商品，加密货币以及外汇交易。

斐波那契水平及其回撤和目标是整个技术分析领域中最好的工具之一。

其强大的支撑和阻力位是精确而明确的。

最重要的是，斐波那契提供非常明确和精确的出入点。

斐波那契水平是从斐波那契数列得出的。

斐波那契序列水平斐波那契数列如下：0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597等。

通过始终将最后两个数字加在一起来创建：•0 +1 = 1•1 +1 = 2•1 + 2 = 3•2 + 3 = 5•3 + 5 = 8等如果我们将其应用于更高的数字，我们将仍然具有相同的完美序列。

•89 + 144 = 233，•144 + 233 = 377，依此类推您可能想知道为什么这些斐波那契序列号如此重要。

原因有很多，包括：•交易图表上强烈尊重斐波那契数列，因为绝大多数交易者都在使用它们。

•斐波那契序列水平用于计算斐波那契回撤和斐波那契目标，这是市场上经常使用的水平。

•这些数字不仅用于交易市场，而且实际上可以在我们周围观察到：在晶体形式中，或通过演奏音乐进行演奏。

无处不在的斐波那契数列

无处不在的斐波那契数列斐波那契数列是一个非常美丽、和谐的数列，它的形状可以用排成螺旋状的一系列正方形来说明，起始的正方形的边长为1，在它左边的那个正方形的边长也是1，在这两个正方形的上方再放一个正方形，其边长为2，以后顺次加上边长为3、5、8、13、2l……等等的正方形。

这些数字每一个都等于前面两个数之和，它们正好构成了斐波那契数列。

1.斐波那契数列的提出斐波那契是意大利的数学家，他是一个商人的儿子，儿童时代跟随父亲到了阿尔及利亚，在那里学到了许多阿拉伯的算术和代数知识，从而对数学产生了浓厚的兴趣。

长大以后,因为商业贸易关系,他走遍了许多国家,到过埃及,叙利亚,希腊,西西里和法兰西.每到一处他都留心搜集数学知识。

回国后,他把搜集到的算术和代数材料,进行研究,整理,编写成一本书,取名为《算盘之书》,于1202年正式出版。

这本书是欧洲人从亚洲学来的算术和代数知识的整理和总结,它推动了欧洲数学的发展.其中有一道“兔子数目”的问题是这样的: 一个人到集市上买了一对小兔子,一个月后,这对小兔子长成一对大兔子.然后这对大兔子每过一个月就可以生一对小兔子,而每对小兔子也都是经过一个月可以长成大兔子,长成大兔后也是每经过一个月就可以生一对小兔子.那么,从此人在市场上买回那对小兔子算起,每个月后,他拥有多少对小兔子和多少对大兔子?这是一个有趣的问题.当你将小兔子和大兔子的对数算出以后,你将发现这是一个很有规律的数列,而且这个数列与一些自然现象有关.人们为了纪念这位兔子问题的创始人,就把这个数列称为"斐波那契数列".你能把兔子的对数计算出来吗?解:可以这么推算:第一个月后,小兔子刚长成大兔子,还不能生小兔子,所以只有一对大兔子。

第二个月后,大兔子生了一对小兔子,他有了一对小兔子和一对大兔子。

第三个月后,原先的大兔子又生了一对小兔子,上月出生的小兔子也长成了大兔子,他共有一对小兔子和两对大兔子。

第四个月后,两对大兔子各生一对小兔子,上月出生的小兔子又长成了大兔子,他共有两对小兔子和三对大兔子。

斐波那契数列知识总结

斐波那契数列是一系列数字，其中每个数字都是前两个数字的总和，通常以0 和1 开头。

它以意大利数学家比萨的莱昂纳多的名字命名，他也被称为斐波那契。

斐波那契数列出现在许多自然现象中，例如树的分枝和叶子在茎上的排列。

在数学术语中，斐波那契数列可以定义为递归关系，其中数列中的每个数都是前两个数的和，初始条件为F0 = 0 和F1 = 1。

数学上该数列定义为递归关系：
Fn = Fn-1 + Fn-2
其中n 是序列中的位置，F 是该位置的斐波那契数。

斐波那契数列有许多有趣的特性，包括：
•随着数字变大，连续斐波那契数的比率接近黄金比例（大约1.6180339887）
•斐波那契数与斐波那契螺旋有关，可以在许多自然物体的形状中找到它。

•斐波那契数列已被用于模拟人口增长和金融市场。

斐波那契数列还与斐波那契螺线有关，斐波那契螺线出现在许多自然现象中，例如贝壳、松果、菠萝的形状。

总的来说，斐波那契数列有很多实际应用，包括计算机科学、生物学和金融学。

有许多方法可以计算斐波那契数列，例如使用递归函数、封闭式公式或矩阵求幂。

计算斐波那契数列中大数的最有效方法是使用矩阵求幂，这需要O(log n) 时间。

总的来说，斐波那契数列是一个迷人而美丽的数学概念，出现在许多自然现象中。

它具有许多有趣的特性和广泛的实际应用。

斐波那契数列的

斐波那契数列的斐波那契数列是一个有趣而又复杂的数学问题，它可以用一组有规则的数字序列来描述，并且在各个领域都有广泛的应用。

斐波那契数列是从第三项开始的一个等比数列，每一项的值都是前两项的和。

由于它有很多有趣的性质，因此受到了众多学者的关注和研究，而且被广泛应用到工程、经济学、生物学等不同领域。

首先，让我们来看一下斐波那契数列的定义，它是由以下等式定义的：f(n)=f(n-1)+f(n-2)，其中n≥3，f(1)=f(0)=1。

从这里可以看出，斐波那契数列是一个等比数列，每一项的值都是前两项之和。

斐波那契数列也可以用图表来表示：1，1，2，3，5，8，13，21，34，55，89，144，233……斐波那契数列有很多有趣的性质，其中最常见的一个就是每个数字都是前面两个数字的和。

由此可以推出后面的数字，这样就可以生成一个无限的等比数列。

此外，斐波那契数列还有一种特殊的性质，就是其中每两个相邻的数字都是有一定比例关系的，这个比例称为黄金分割比，即前后两个数字的比值约为1.618，被称为黄金分割比。

此外，斐波那契数列还有一个很有趣的性质，就是它的前面的数字中，每次出现的数字都是它的因数，例如：144的因数有1，2，3，4，6，8，9，12，16，18，24，36，48，72，144，而斐波那契数列前面的几个数字正是这些因数，即1，1，2，3，5，8，13，21，34，55，89。

斐波那契数列不仅有着许多独特的性质，而且也因其强大的应用性而受到了学术界的广泛研究。

斐波那契数列在工程，经济，生物学等各个领域都有广泛的应用，比如在工程中，我们可以使用斐波那契数列来分析结构物的稳定性，在经济学中，它可以帮助我们了解货币市场的变化趋势，而在生物学领域，它可以帮助我们研究突变和定型等诸多问题。

总之，斐波那契数列是一个具有深远影响的数学问题，它的出现不仅创造了许多有趣的数学性质，而且还被广泛应用到了工程、经济学、生物学等多个领域，成为了研究突变和定型等各种问题的重要工具。

斐波那契数列的介绍

斐波那契数列的介绍
嘿，朋友们！今天咱来聊聊斐波那契数列。

你说这斐波那契数列啊，就像是一个神秘又有趣的小伙伴。

它是从兔子繁殖问题里蹦出来的呢！想象一下，兔子们一代代繁衍，那数量的变化可有意思啦。

一开始只有一对小兔子，过一个月它们长大啦，又过一个月它们就生了新的小兔子，就这样，兔子的数量按照一种特别的规律增长着，这就是斐波那契数列的来历。

这个数列呢，前两个数是 0 和 1，然后后面的每个数都是前两个数相加得到的。

听起来好像挺简单，但你仔细研究研究，就会发现它可神奇啦！比如说，你看大自然里的很多现象都和它有关系呢。

像那些花儿的花瓣数量呀，有的就是斐波那契数列里的数。

斐波那契数列还常常在艺术和设计里冒出来呢。

设计师们有时候就会根据它来设计一些好看的图案，让作品变得特别又吸引人。

而且啊，在一些音乐作品里居然也能找到它的影子，真是太奇妙啦！就好像这个数列偷偷藏在各种地方，等着我们去发现它。

它就像是一个宝藏，越挖越有意思。

有时候我都在想，这斐波那契数列是不是老天给我们的一个特别礼物呀，让我们在探索中找到乐趣和惊喜。

哎呀呀，说了这么多，总之呢，斐波那契数列就是这么一个特别的存在。

它不是那种高高在上、让人摸不着头脑的东西，而是贴近我们生活，能给我们带来乐趣和新奇的小伙伴。

希望大家也能像我一样，发现它的美妙之处，和它成为好朋友哟！好啦，今天关于斐波那契数列就先聊到这儿啦，下次再和你们分享更多好玩的事儿哦！。

斐波那契数列的现实存在的例子，你知道的有哪些？

斐波那契数列的现实存在的例子，你知道的有哪些？斐波那契数列是一种递归序列，序列中每一个数字都是通过将前两个数字相加而产生的。

0、1、1、2、3、5、8、13、21、34、55、89、144、233、377，610、987 ...黄金分割率和斐波那契数列的数学联系紧密。

斐波那契数列的发现斐波那契数列是由一位13世纪的意大利比萨的数学家列奥纳多·斐波那契发现的，他的功绩还包括在整个欧洲大部分地区推广了印度-阿拉伯数字系统。

斐波那契的书《Liber abaci》（1202年）还解决了许多有的数学问题。

这些问题之一就论及兔子的繁殖速度相关的问题：假设整个过程中没有兔子死亡，并且雌兔总是繁殖出一对仔兔且雌雄各一。

兔子可以在一个月大的时候繁殖，所以在第二个月月底，雌性仔兔可以生下另一对兔子。

每个月初兔子的总数遵循以下模式：1、1、2、3、5、8、13、21、34、55、89、144，依此类推。

每个数字都是前两个数字的和，数字很快变大，并且序列是无限的。

直到很久以后，法国数学家爱德华·卢卡斯（Edouard Lucas）在研究自己的相似数字序列并对斐波那契的描述进行更详细的研究之后，才明白了这些数字的意义，因此他给斐波那契数列定了名。

继卢卡斯的研究之后，在自然界中越来越多地观察到这些数字所描述的规律，从松果的螺旋片状结构、花椰菜上的小花到向日葵上的种子排列的方式。

实际上该序列描述的东西比兔子的繁殖模式复杂得多。

自然增长模式斐波那契数列似乎总是与自然界的增长规律有关。

这种规律适用于所有生物的生长，从单个植物细胞到蜜蜂的繁殖；大自然依靠简单的规律来构建极其复杂，而且通常很漂亮的构造，斐波那契数列正反映了这一点。

直到1993年，斐波那契数才被科学证明存在于自然界中。

黄金比例与斐波纳契数列密切相关的是黄金比例。

黄金比例似乎是人类潜意识进行审美过程中识别出的一种模式，这意味着人脑中对于黄金比例非常敏感，复合黄金比例的视觉模式可以激发人类的审美情绪（某种神经和谐状态）。

数学奇趣录探索数学中的奇特现象

数学奇趣录探索数学中的奇特现象【数学奇趣录：探索数学中的奇特现象】引言：数学作为一门古老而又精巧的学科，不仅仅是应用于日常生活中的计算工具，更是隐藏着种种奇特现象的探索领域。

在本文中，我们将一同探索一些数学中的奇趣现象，揭示其中的玄妙之处。

一、斐波那契数列：数学之美的黄金分割斐波那契数列，是一个从古希腊开始出现的数学数列，最为人熟知的特点是任意两个相邻的数之比，都接近于1.618，被称为黄金分割。

斐波那契数列在自然界中也大量出现，例如植物的枝干分支、线条的美感等都与这个比例密切相关。

斐波那契数列之所以如此神奇，是因为它从简单的规则中展现出了数学之美。

二、柯赫曲线：一线之旅的无限和谐柯赫曲线是一种分形几何图形，其由一小段线段构成，每次对线段进行分割，再在其上构建一个等边三角形，最终形成一个无限细分的曲线。

奇妙之处在于，无论曲线怎样细分下去，其总长度仍旧有限。

柯赫曲线表现出了无限和谐的美感，让人感叹数学的神秘力量。

三、时间旅行者：莱布尼茨的微积分微积分是数学中的一门重要分支，描述了变化的本质。

在微积分的框架下，我们可以进行时间的旅行，探索过去、现在和未来之间的关系。

莱布尼茨的微积分理论揭示了时间的流动实际上是由无数个瞬间组成的，每个瞬间都是一个瞬时的现在。

微积分为我们理解时间的连续性提供了一种数学模型。

四、图论的魅力：七桥问题的解答图论是研究图的性质及其应用的数学分支。

七桥问题是欧拉在18世纪提出的一个经典问题，通过建模和图论的方法，欧拉成功解答了这个看似无解的难题。

他证明了一个连通图可以通过一笔画过每条边仅一次的路径实现。

这个简单问题背后蕴含了图论的魅力，揭示了数学中的智慧和探索的激情。

五、悖论与佯谬：佩亚诺悖论的思辨之旅佩亚诺悖论是一类逻辑悖论的代表，它将我们引向了思考自指和自我参照的问题。

佩亚诺悖论中最著名且简明的表达是“这句话是假话”。

这个看似简单的陈述却带来了无穷的矛盾和困惑，挑战了我们对逻辑和真理的理解。

奥数解谜数列中的猜想与证明

奥数解谜数列中的猜想与证明在奥数解谜的世界里，数列一直是一种让人着迷的对象。

数列中隐藏着各种猜想和规律，通过推理和证明，数学爱好者们不断探索其中奥秘。

本文将围绕奥数解谜数列中的猜想与证明展开讨论，揭示其中的数学美妙。

一、斐波那契数列与黄金分割斐波那契数列是一种非常著名的数列，它的特点是每一项都是前两项的和。

其前几项为1、1、2、3、5、8、13……这个数列被广泛应用于自然科学、艺术等领域，因为它与黄金分割有着紧密的联系。

黄金分割是指一条线段，分为两部分，其中一部分与整体的比值等于另一部分与这部分的比值。

这个比值约为1.6180339887，常用希腊字母φ表示。

斐波那契数列中，相邻两项的比值趋近于黄金分割。

这个奇妙的现象引发了数学家们的兴趣，他们通过数学证明发现，斐波那契数列中的比值确实无限接近黄金分割。

二、四平方和猜想与拉格朗日定理四平方和猜想是另一个引人入胜的数列问题。

根据这个猜想，任何一个正整数都可以表示为不超过四个整数的平方之和。

比如，5可以表示为1²+2²，7可以表示为1²+2²+1²+1²。

为了解决四平方和问题，法国数学家拉格朗日提出了著名的拉格朗日定理。

这个定理表明，任何一个正整数N都可以表示为四个整数的平方和的充分必要条件是N不能写成4^a(8b+7)的形式，其中a和b为任意非负整数。

三、康托尔的连续分数猜想与二次逼近康托尔是20世纪初著名的德国数学家，他提出了连续分数猜想。

这个猜想指出，在实数域中，每一个不是有理数的数都可以用连续分数的形式表示。

连续分数是指一个实数可以通过无限嵌套的分数表示出来，每一步都是取整和取倒数。

比如，√2可以表示为1+1/(2+1/(2+1/(2+...)))的形式。

证明康托尔的连续分数猜想是一个复杂而有趣的数学问题。

数学家们通过迭代算法和二次逼近方法，成功地证明了连续分数猜想的正确性。

综上所述，奥数解谜数列中的猜想与证明是数学世界中的一道亮丽风景线。

数的猜想发现数的规律

数的猜想发现数的规律在数学中，数的猜想是一种寻找数字规律和模式的方法。

通过观察和思考一系列数字，人们常常可以发现奇妙而且有趣的规律。

这些规律不仅在自然界中有所体现，同时也存在于我们的日常生活中。

本文将介绍一些常见的数的猜想以及发现的数的规律。

1. 斐波那契数列斐波那契数列是一种经典的数的猜想。

它的规律是每个数字都是前两个数字之和。

例如，数列的前几个数字是0, 1, 1, 2, 3, 5, 8, 13, 21...。

通过观察其中的规律，我们可以发现一些有趣的事实，例如相邻的两个数字的比值趋近于黄金比例等。

2. 哥德巴赫猜想哥德巴赫猜想是一个关于素数的猜想。

素数是只能被1和自身整除的数，例如2, 3, 5, 7, 11等。

哥德巴赫猜想提出了一个大胆的观点，即任意一个大于2的偶数都可以表示为两个素数之和。

虽然这个猜想已经提出了几百年，但至今没有被证明或者推翻。

3. 九九乘法表九九乘法表是我们学习数学时最常接触到的一种数字规律。

它展示了从1到9的数字两两相乘的结果。

通过观察九九乘法表，我们可以发现很多有趣的规律。

例如，每一行的数字递增，每一列的数字也递增。

此外，乘积为偶数的组合总是出现在左下和右上两个对角线上。

4. 黑洞数黑洞数是一种具有迷人规律的数字。

它的定义是将任意一串数字重新排列，得到两个升序数字和一个降序数字，并用降序减去升序。

重复这个过程，最终将会得到一个黑洞数。

例如，以数字6174为例，将得到以下的计算过程：7641 - 1467 = 61747641 - 1467 = 6174通过观察这个过程，我们可以发现不同的初始数字最终都会收敛到6174这个黑洞数。

5. 莱布尼茨猜想莱布尼茨猜想是一个关于连续分数的数学猜想。

连续分数是一个形如a+1/(b+1/(c+1/d))的分数，其中a、b、c、d均为整数。

莱布尼茨猜想提出了一个大胆的观点，即任意一个有理数都可以由连续分数表示。

虽然这个猜想也已经存在了几百年，但至今也没有被证明或者推翻。

斐波那契数的规律

斐波那契数的规律嘿，朋友们！今天咱来聊聊那神奇的斐波那契数呀！这斐波那契数啊，就像是数学世界里的一串神秘密码。

你看啊，从 1，1 开始，后面的每个数都等于前两个数的和。

就好像是一级一级的台阶，让我们不断往上爬，去探索更奇妙的数学天地。

咱可以把斐波那契数想象成是生活中的一些有趣现象。

比如说，兔子的繁殖！一对小兔子长大以后，每个月能生出一对小兔子，那兔子的数量增长不就有点像斐波那契数的增长嘛！刚开始可能就那么一两只，慢慢地越来越多，越来越多。

再想想大自然中的那些美丽图案，有些花朵的花瓣数，不也常常和斐波那契数有关系嘛！这难道不是大自然在向我们展示斐波那契数的神奇魅力吗？这多有意思呀！斐波那契数还有一个特别神奇的地方，就是它在很多领域都有出现呢！不只是数学，在艺术、建筑等方面也都能看到它的影子。

就好像它是一把万能钥匙，能打开各种不同领域的大门。

而且哦，斐波那契数的规律有时候还能帮我们解决一些实际问题呢！比如说在设计一些图案或者排列东西的时候，按照斐波那契数的规律来，可能会让整个布局看起来更加和谐、美观。

你说这斐波那契数是不是很神奇？它就像是一个隐藏在数学世界里的宝藏，等着我们去不断挖掘、发现。

我们在生活中不也常常会遇到这样看似简单却蕴含着大道理的事情吗？就像斐波那契数，一开始可能觉得不就是几个数字嘛，但深入了解后才发现它的奥秘无穷无尽。

那我们是不是也应该像对待斐波那契数一样，对生活中的各种事物都保持着好奇心和探索精神呢？不要轻易地就忽略那些看似普通的东西，说不定它们背后都有着让人惊叹的一面呢！斐波那契数，真的是让我们感受到了数学的魅力和神奇。

它不仅仅是一些数字的组合，更是一种智慧的体现，一种对世界的独特解读。

所以啊，朋友们，可别小看了这斐波那契数哦！。

认识斐波那契数列：什么是斐波那契数列？有何特点？

斐波那契数列，又被称为黄金分割数列或兔子数列，是一种在数学上极为著名且有趣的数列。

它由意大利数学家莱昂纳多·斐波那契在《计算之书》（Liber Abaci）中首次提出。

斐波那契数列不仅是数学领域的研究对象，更在日常生活中、自然界以及科学研究中展现出其独特魅力和重要性。

下面，我们将深入探讨斐波那契数列的定义、特点、以及其广泛的应用。

一、斐波那契数列的定义斐波那契数列是这样一组数列：1，1，2，3，5，8，13，21，34，……，其中每一个数字都是前两个数字的和。

具体来说，斐波那契数列的定义如下：F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2)，其中n≥2二、斐波那契数列的特点1. 递推公式：斐波那契数列的每一项都是其前两项的和，这是其最显著的特点。

这一特点使得斐波那契数列可以通过递推的方式轻松地计算出来。

2. 黄金分割率：斐波那契数列与黄金分割率（φ = (√5 - 1) / 2 ≈ 0.618）有着密切的联系。

当斐波那契数列的项数趋于无穷大时，相邻两项的比值会趋近于黄金分割率。

这一性质使得斐波那契数列在美学、建筑、艺术等领域具有广泛的应用。

3. 对称性：斐波那契数列具有一种神奇的对称性。

具体来说，对于任意正整数n，都有F(n) = F(n-1) + F(n-2) = F(n+1) - F(n-1)。

这种对称性使得斐波那契数列在数学上具有独特的美感。

4. 递归性质：斐波那契数列是一种递归数列，这意味着每一项都可以通过递归的方式来表示。

例如，F(5) = F(4) + F(3) = (F(3) + F(2)) + F(3) = 2F(3) + F(2) = 2(F(2) + F(1)) + F(2) = 3F(2) + 2F(1) = 3×1 + 2×1 = 5。

这种递归性质使得斐波那契数列在计算上具有较大的灵活性。

三、斐波那契数列的应用斐波那契数列作为一种重要的数学概念，其在各个领域都有着广泛的应用。

斐波那契数列知识点

斐波那契数列知识点《聊聊斐波那契数列那些事儿》嘿，朋友们！今天咱来聊聊一个特别有意思的知识点——斐波那契数列。

这可真是个神奇的玩意儿！斐波那契数列，听着好像挺高大上的，但其实啊，就是一串数字排排队。

可别小看了这串数字，它们背后藏着好多奥秘和乐趣呢！你看啊，这斐波那契数列一开始是0 和1，然后后面每个数都等于前两个数相加。

就这么简单的规则，却能变出好多花样儿来。

想象一下，就像一个数字小精灵在那蹦跶，一会儿加这个，一会儿加那个，就变出了一长串的数字。

就感觉特别神奇，是不是？我第一次接触斐波那契数列的时候，心里那叫一个好奇啊。

就琢磨着，这玩意儿到底有啥用啊？后来发现，用处可多啦！比如说在自然界里，很多东西的生长都跟斐波那契数列有关系。

像某些花朵的花瓣数量、松果的螺旋形状，都能看到斐波那契数列的影子。

有时候我就想，这大自然是不是也在跟我们玩数字游戏啊！还有呢，在一些艺术和设计领域，斐波那契数列也特别吃香。

它能给作品带来一种特别的美感和韵律。

就好像是给作品注入了灵魂一样，让它们变得更加吸引人。

而且啊，斐波那契数列还能用来解决一些实际问题呢！比如说排列组合啥的。

是不是感觉很厉害？我觉得学习斐波那契数列就像是在探索一个神秘的宝藏。

每发现一个它的新特点或者新用途，就像找到了一颗闪闪发光的宝石。

学习斐波那契数列还让我明白了一个道理，那就是很多看似简单的东西，背后可能藏着巨大的价值。

所以啊，朋友们，别小看了这些知识点。

它们就像隐藏在知识海洋里的小惊喜，等着你去发现呢！总之呢，斐波那契数列知识点真是太有趣啦！既能让我们感受到数字的魅力，又能让我们惊叹于自然和艺术的奇妙。

大家以后要是碰到了，可得好好研究研究，说不定还会有更多意想不到的收获哦！。