高三数学专题探究课四
高三数学第二轮专题复习(4)三角函数
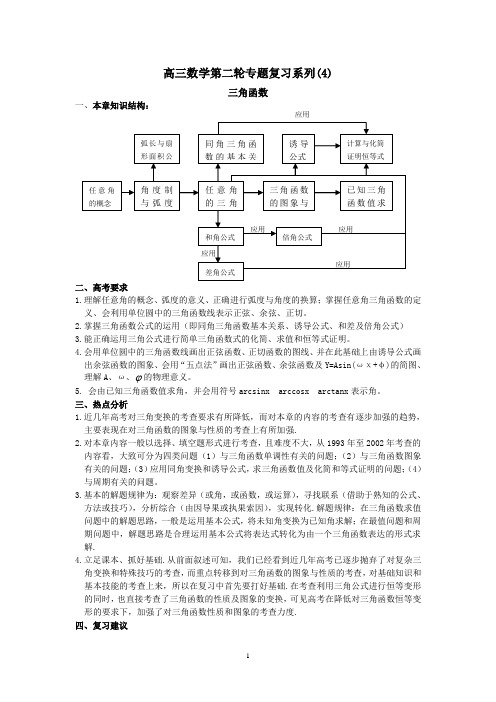
高三数学第二轮专题复习系列(4)三角函数一、本章知识结构:二、高考要求1.理解任意角的概念、弧度的意义、正确进行弧度与角度的换算;掌握任意角三角函数的定义、会利用单位圆中的三角函数线表示正弦、余弦、正切。
2.掌握三角函数公式的运用(即同角三角函数基本关系、诱导公式、和差及倍角公式)3.能正确运用三角公式进行简单三角函数式的化简、求值和恒等式证明。
4.会用单位圆中的三角函数线画出正弦函数、正切函数的图线、并在此基础上由诱导公式画出余弦函数的图象、会用“五点法”画出正弦函数、余弦函数及Y=Asin(ωχ+φ)的简图、理解A 、ω、 的物理意义。
5. 会由已知三角函数值求角,并会用符号arcsinx arccosx arctanx 表示角。
三、热点分析1.近几年高考对三角变换的考查要求有所降低,而对本章的内容的考查有逐步加强的趋势,主要表现在对三角函数的图象与性质的考查上有所加强.2.对本章内容一般以选择、填空题形式进行考查,且难度不大,从1993年至2002年考查的内容看,大致可分为四类问题(1)与三角函数单调性有关的问题;(2)与三角函数图象有关的问题;(3)应用同角变换和诱导公式,求三角函数值及化简和等式证明的问题;(4)与周期有关的问题。
3.基本的解题规律为:观察差异(或角,或函数,或运算),寻找联系(借助于熟知的公式、方法或技巧),分析综合(由因导果或执果索因),实现转化.解题规律:在三角函数求值问题中的解题思路,一般是运用基本公式,将未知角变换为已知角求解;在最值问题和周期问题中,解题思路是合理运用基本公式将表达式转化为由一个三角函数表达的形式求解.4.立足课本、抓好基础.从前面叙述可知,我们已经看到近几年高考已逐步抛弃了对复杂三角变换和特殊技巧的考查,而重点转移到对三角函数的图象与性质的考查,对基础知识和基本技能的考查上来,所以在复习中首先要打好基础.在考查利用三角公式进行恒等变形的同时,也直接考查了三角函数的性质及图象的变换,可见高考在降低对三角函数恒等变形的要求下,加强了对三角函数性质和图象的考查力度. 四、复习建议应用同角三角函数的基本关任意角的概念 任意角的三角诱导公式 三角函数的图象与计算与化简 证明恒等式 已知三角函数值求和角公式 倍角公式 差角公式 弧长与扇形面积公角度制与弧度应用应用 应用应用本章内容由于公式多,且习题变换灵活等特点,建议同学们复习本章时应注意以下几点:(1)首先对现有公式自己推导一遍,通过公式推导了解它们的内在联系从而培养逻辑推理能力。
高三数学高效课堂资料07孙刘军探究四分段函数、取整函数

高三数学高效课堂资料探究四分段函数、取整函数【使用说明】 1.研读必修一P40-43,独立规范,限时30分钟完成基础构建和探究提升.2.总结题型题路和规律方法,找出并标记自己的疑问。
【学习目标】通过具体实例,了解分段函数、取整函数定义,会画分段函数图像,能解分段不等式与方程,体会数形结合和分类讨论思想。
【课标要求】了解简单的分段函数,并能简单应用;了解在社会生活中普遍使用的函数模型(分段函数、取整函数)的广泛使用。
【考纲导航】【基础构建】问题1.根据邮局规定:若本地投寄外埠平信,首重100g 内,每重20g (不足20g 按20g 计算)付邮资80分, 问:每封x 克(1000≤<x )的信函应付多少分的邮资(单位:分) 试写出函数表达式,做出函数图像,并求函数的值域。
并通过以上问题的解决说出你对分段函数的理解(定义域、值域、奇偶性等方面)。
问题 2.对任意实数][,x x 是不超过x 的最大整数,称][x 为x 的整数部分.与它相伴随的是小数部分函数].[}{},{x x x x y -==请结合取整函数的定义分别画出函数][x y =和函数}{x y =的图像并从定义域,值域,奇偶性,对称性,最值,图象等方面研究它们的的性质。
【核心探究】探究一: 分段函数求值问题1. 已知函数⎪⎩⎪⎨⎧≤>=0,3,0,log )(21x x x x f x 则))4((f f 的值为( )A.91-B.-9C.91D.9 变式:已知函数,02,sin ,0,)(21⎪⎩⎪⎨⎧<<-≥=x x x x x f π若21)(=a f 则=a ________2.函数()f x =20,1, 0⎧>⎨+≤⎩,x x x x ,满足1)21()(>-+x f x f 的x 的取值范围。
总结分段函数求值的技巧及应注意的问题:探究二:分段函数图象与性质的应用- 2 -。
高三数学一轮复习公开课课件基本不等式多维探究共14张PPT.ppt

xy x y
xy
即a2 26a 25 ,0 解得
,1 当a且仅25当 等号成立y 6x
经检验:当x
5
,y 1时5 ,
当a; 25,
2
x 1时y, 3 10 5
a 1
函数f (x, y) 4x y的最大值为25,最小值为1.
【评注】本题我们是通过构造“两个整体”,即 将所求函数作为一个整体,结合题设条件再得一 个整体,通过把两个整体相乘和换元,由基本不等 式生成得到一个关于新元的不等式从而求解,体 现了整体处理的思想与构造的方法.
函数
是题设条件等式左边中某两项和,可
以运用整体处理的思想即通过换元来处理.
解答:设 4x
a(26 a)
y 则a
(4x y)(
1
1 x9 )
9 y
, 26 a 13 y
x
36x
0, y
13
0
2
,所以 y 36x 25
xy
xy
xy
a(26 a) (4x y)(1 9) 13 y 36x 13 2 y 36x 25
3、椭圆中的最值:
4
2
3
1
四、小结与课后思考
(当且仅当a b时等号成立)
1、 本 节 课 主 要 内 容
2、两个结论:(1)两个正数积为定值,和有最小值. (2)两个正数和为定值,积有最大值.
3、基本不等式的适用条件:一正二定三相等
思考题:若直线 ax by 1 0 平分圆 C:
x2 y2 2x 4y 1 0 的 周 长 且
探究:在右图中,AB是圆的直径,点C是AB上的一点,
AC=a,BC=b.过点C作垂直于AB的弦DE,连接AD、BD.
数列通项公式的求法课件-高三数学一轮复习

(2)证明:∵cn=a2nn(n∈N*), ∴cn+1-cn=a2nn+ +11-a2nn=an+21-n+12an=2bn+n 1. 将 bn=3·2n-1 代入,得 cn+1-cn=34(n∈N*). ∴数列{cn}是公差为34的等差数列,c1=a21=12, 故 cn=12+34(n-1)=34n-14.
探究 5 此类题可由 an=SS1n(-nS=n-11()n,≥2)求出通项 an,但要注意 n=1 与 n ≥2 两种情况能否统一.
思考题 5 在数列{an}中,a1=1,a1+2a2+3a3+…+nan=n+2 1an+1,n∈
N*,求 an. 【解析】
由 a1+2a2+3a3+…+nan=n+2 1an+1,
例 4 已知数列{an}满足 a1=1,an+1=2aan+n 1(n∈N+).求数列{an}的通项公 式.
【解析】 易知 an>0,依题意得an1+1=2ana+n 1=a1n+2, ∴数列a1n是等差数列,公差为 2,首项为 1,∴a1n=1+(n-1)×2=2n-1, ∴an=2n1-1.
探究 4 已知数列递推公式的分母中含有通项公式的表达式,求解对应的通 项公式时,往往可以通过观察表达式的特点,通过倒数关系加以转化,利用等差 数列的性质分析相应的通项公式问题.
思考题 4 设数列{an}是首项为 1 的正项数列,且 an+1-an+an+1·an= 0(n∈N*),求{an}的通项公式.
【解析】 ∵an+1-an+an+1·an=0.∴an1+1-a1n=1. 又a11=1,∴a1n是首项为 1,公差为 1 的等差数列. 故a1n=n,∴an=1n.
题型四 已知 Sn 求 an
题型二 累乘法
例 2 在数列{an} 中,已知 a1=3,nan=(1+n)an+1,求 an. 【解析】 据题意有aan+n 1=n+n 1⇒aan-n 1=n-n 1(n≥2 且 n∈N*). ∴an=a1·aa21·aa32·…·aan-n 1 =3×12×23×34×…×n-n 1=3n(n≥2 且 n∈N*),把 n=1 代入上式也成立,故 an=3n(n∈N*).
高三数列求和专题优质课

高三数列求和专题优质课一、导入部分(200字)在导入部分,可以通过提出一个生活中的实际问题或者引用一个有趣的数学故事来引起学生的兴趣。
例如:“小明每天都会在家门口摆放一些花瓶,第一天放1个,第二天放2个,第三天放3个,以此类推。
请问,如果小明连续摆放了n天,那么总共摆放了多少个花瓶呢?”二、知识讲解部分(800字)在知识讲解部分,可以详细介绍数列求和的概念和相关公式。
首先,解释什么是数列和数列的常见表示方法,如通项公式和递推公式。
然后,介绍等差数列和等比数列的求和公式,并给出相应的例子进行讲解。
最后,讲解其他特殊数列求和的方法,如等差数列的部分和和等差数列的交错求和。
三、例题分析部分(600字)在例题分析部分,选取几个具体的例题,对其进行详细分析和解答。
可以包括不同类型的数列求和问题,如等差数列的前n项和、等差数列的部分和、等差数列的奇数项和等。
通过逐步解题的方式,讲解解题思路和方法,并注重引导学生理解解题过程中的关键步骤和思想。
四、练习部分(300字)在练习部分,可以给学生一些练习题目,包括基础题目和提高题目。
基础题目可以用来巩固学生对数列求和公式的掌握和运用,而提高题目则可以用来拓展学生的思维和解题能力。
建议在课后布置这部分的题目,并在下节课进行讲解和答疑。
五、总结部分(100字)在总结部分,可以回顾本节课所学内容,并强调数列求和的重要性和实际应用价值。
同时,激发学生对数学的兴趣和学习的动力,鼓励他们在数学学习中勇于探索和思考。
通过以上的教学设计,可以帮助学生系统地学习和掌握数列求和的相关知识和技巧。
同时,通过例题分析和练习部分的设置,可以提高学生的解题能力和应用能力。
最重要的是,要注重培养学生的数学思维和解决问题的能力,让他们在学习中体会到数学的乐趣和价值。
高三数学教案设计(通用8篇)

高三数学教案设计(通用8篇)高三数学教案设计篇1一、教学目标知识与技能:理解任意角的概念(包括正角、负角、零角)与区间角的概念。
过程与方法:会建立直角坐标系讨论任意角,能判断象限角,会书写终边相同角的集合;掌握区间角的集合的书写。
情感态度与价值观:1、提高学生的推理能力;2、培养学生应用意识。
二、教学重点、难点:教学重点:任意角概念的理解;区间角的集合的书写。
教学难点:终边相同角的集合的表示;区间角的集合的书写。
三、教学过程(一)导入新课回顾角的定义①角的第一种定义是有公共端点的两条射线组成的图形叫做角。
②角的第二种定义是角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。
(二)教学新课1、角的有关概念:①角的定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。
②角的名称:注意:⑴在不引起混淆的情况下,“角α”或“∠α”可以简化成“α”;⑵零角的终边与始边重合,如果α是零角α=0°;⑶角的概念经过推广后,已包括正角、负角和零角。
请说出角α、β、γ各是多少度?2、象限角的概念:定义:若将角顶点与原点重合,角的始边与x轴的非负半轴重合,那么角的终边(端点除外)在第几象限,我们就说这个角是第几象限角。
高三数学教案设计篇2一、指导思想今年是我省使用新教材的第八年,即进入了新课程标准下高考的第六年。
高三数学教学要以《数学课程标准》为依据,全面贯彻教育方针,积极实施素质教育。
提高学生的学习能力仍是我们的奋斗目标。
近年来的高考数学试题逐步做到科学化、规范化,坚持了稳中求改、稳中创新的原则。
高考试题不但坚持了考查全面,比例适当,布局合理的特点,也突出体现了变知识立意为能力立意这一举措。
更加注重考查考生进入高校学习所需的基本素养,这些问题应引起我们在教学中的关注和重视。
二、注意事项1、高度重视基础知识,基本技能和基本方法的复习。
“基础知识,基本技能和基本方法”是高考复习的重点。
2019届高三理科数学第二轮专题复习配套文档专题四 第3讲立体几何中的向量方法

第3讲立体几何中的向量方法[真题再现]1.(2018·课标Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC使点C到达点P的位置,且PF⊥BF。
(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.[解](1)证明:由已知可得BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD。
(2)解:如图,作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD。
以H为坐标原点,错误!的方向为y轴正方向,|错误!|为单位长,建立如图所示的空间直角坐标系H.xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=错误!.又PF=1,EF=2,所以PE⊥PF.所以PH=错误!,EH=错误!.则H(0,0,0),P错误!,D错误!,错误!=错误!,错误!=错误!.又错误!为平面ABFD的法向量,设DP与平面ABFD所成角为θ,则sin θ=错误!=错误!=错误!。
所以DP与平面ABFD所成角的正弦值为错误!.2.(2018·课标Ⅱ)如图,在三棱锥P-ABC中,AB=BC=22,P A=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M。
P A-C为30°,求PC与平面P AM所成角的正弦值[解](1)证明:因为P A=PC=AC=4,O为AC的中点,所以OP⊥AC,且OP=2错误!.如图,连接OB.因为AB=BC=错误!AC,所以△ABC为等腰直角三角形,且OB ⊥AC,OB=错误!AC=2。
由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC,OB∩AC=O,得PO⊥平面ABC.(2)解:如图,以O为坐标原点,错误!的方向为x轴正方向,建立空间直角坐标系O。
xyz。
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2错误!),错误!=(0,2,2错误!).取平面P AC的一个法向量错误!=(2,0,0).设M (a ,2-a,0)(0≤a ≤2),则错误!=(a ,4-a,0).设平面P AM 的法向量为n =(x ,y ,z ).由AP ,→·n =0,错误!·n =0得错误!可取y =错误!a ,得平面P AM 的一个法向量为n =(错误!(a -4),错误!a ,-a ),所以cos 错误!,n =错误!。
高三数学 第四篇 第三节等比数列课件 理 北师大版

也成等比数列,其公比为qn,于是,问题转化为: A1=2,A1qn+A1q2n=12, 要求A1q3n+A1q4n+A1q5n的值. 由A1=2,A1qn+A1q2n=12, 得q2n+qn-6=0,那么qn=2或qn=-3. 由A1q3n+A1q4n+A1q5n =A1q3n(1+qn+q2n)=2·q3n·7=14·q3n
第四页,编辑于星期五:八点 三十五分。
性质 .
(5)设等比数列{an}的公比为q,则数列 {kan}(k为常数)仍为q等比数列,公比为 .
(6)设数列{an},{bn}为等比数列,公比分别 为q1,q2,则{an·bn}也为等比q1q数2 列,公比为
第五页,编辑于星期五:八点 三十五分。
b2=ac是a,b,c成等比的什么条件? 提示:b2=ac是a,b,c成等比的必要不充分条件,∵ 当b=0,a,c至少有一个为零 时,b2=ac成立,但a,b,c不成等比,反之,假设a,b,c成等比,那么必有 b2=ac.
第三节 等比数列
第一页,编辑于星期五:八点 三十五分。
考纲点击
1.理解等比数列的概念. 2.掌握等比数列的通项公式与前n项和 公式. 3.能在具体的问题情境中识别数列的等 比关系,并能用有关知识解决相应的问 题. 4.了解等比数列与指数函数的关系. 1.以定义及等比中项为背景,考查等比 数列的判定. 2.以考查通项公式、前n项和公式为主,
那么na1=40,2na1=3 280,矛盾.
∴q≠1,∴ a1(11--qqn)=40
①
a1(11--qq2n)=3 280 ②
第二十三页,编辑于星期五:八点 三十五分。
②÷①得1+qn=82,∴qn=81 ③ 将③代入①得q=1+2a1 ④ 又∵q>0,∴q>1,∴a1>0,{an}为递增数列. ∴an=a1qn-1=27 ⑤ 由③、④、⑤得q=3,a1=1,n=4. ∴a2n=a8=1×37=2 187.
第四章 专题研究 三角函数的值域与最值

授 人 以 渔
1+k 4± 7 解之得 k= 3
课 时 作 业
4- 7 4+ 7 ∴函数 f(x)的值域为[ , ] 3 3
高考调研· 新课标高考总复习
高三数学(理)
第四章
专题研究
课 前 自 助 餐
sinx (2)f(x)= cosx
sinx≤cosx sinx>cosx
作出图象 2 由图象知,-1≤y≤ 2
授 人 以 渔
探究3 借助一些代数式的几何意义或三角函 数的图象可直观地求出函数的值域,从而减 少运算量.
课 时 作 业
高考调研· 新课标高考总复习
高三数学(理)
第四章
专题研究
课 前 自 助 餐
专题训练
授 人 以 渔 课 时 作 业
高考调研· 新课标高考总复习
课 时 作 业
高考调研· 新课标高考总复习
高三数学(理)
第四章
专题研究
题型三 数形结合求三角函数的值域
课 前 自 助 餐
授 人 以 渔
2-sinx 例 3 (1)求函数 f(x)= 的值域. 2+cosx 1 1 (2) 已 知 f(x) = (sinx + cosx) - |sinx - 2 2 cosx|,求 f(x)的值域. 2-sinx 【解析】 (1)函数 f(x)= ,可看作 2+cosx 点(2,2)(-cosx,sinx)两点连线的斜率. 点(-cosx,sinx)的轨迹为 x2+y2=1.
高三数学(理)
第四章
专题研究
专题研究
课 前 自 助 餐
三角函数的值域与最值
专题要点
1.
函数 定义域 值域 y=sinx R [-1,1] cosx R [-1,1] tanx π {x|x≠kπ+ ,k∈Z} 2 R
专题四+4.1导数的概念及运算课件——2023届高三数学一轮复习

1 3
,
0
,C
0,
1 4
,则S△BOC=
1 2
×
1 3
×
1 4
=
1 24
.
综上,△BOC的面积为 4 或 1 .
3 24
考向二 两曲线的公切线问题
1.(2023届贵州遵义新高考协作体入学质量监测,11)若直线y=kx+b是曲线 y=ex+1的切线,也是y=ex+2的切线,则k= ( ) A.ln 2 B.-ln 2 C.2 D.-2 答案 C
4.(2019课标Ⅲ,文7,理5,5分)已知曲线y=aex+xln x在点(1,ae)处的切线方程 为y=2x+b,则 ( )
A.a=e,b=-1 B.a=e,b=1
C.a=e-1,b=1 答案 D
D.a=e-1,b=-1
5.(2021新高考Ⅰ,7,5分)若过点(a,b)可以作曲线y=ex的两条切线,则 ( )
解析 由题意可知y'=2cos x-sin x,则y'|x=π=-2.所以曲线y=2sin x+cos x在点 (π,-1)处的切线方程为y+1=-2(x-π),即2x+y+1-2π=0,故选C.
答案 C
例2 (2016课标Ⅱ,16,5分)若直线y=kx+b是曲线y=ln x+2的切线,也是曲线
y=ln(x+1)的切线,则b=
,即f
'(x0)=
lim
x0
y x
=
. lim
x0
f
( x0
x)
f
(x0 )
x
注意:f '(x)与f '(x0)的区别与联系:f '(x)是一个函数,f '(x0)是函数f '(x)在x0处
高三数学专题复习课件:4-4-2参数方程

(θ为参数)所
授
表示的曲线为( )
人
以
A.抛物线的一部分
B.一条抛物线
渔
C.双曲线的一部分
D.一条双曲线
答案 A
课 时 作 业
高三数学(人教版)
高考调研 ·新课标高考总复习
选考部分·选修4——4·第1课时
课
前
3.把方程xy=1化为以t为参数的参数方程是( )
自
助
餐
授
人
A.
以
渔
x=sint B.y=si1nt
人
数方程及参数方程的简单应用,题目难度的设置以中档题型为主,预
以
测2012年高考中,在难度,知识点方面变化不大.
渔
课 时 作 业
高三数学(人教版)
高考调研 ·新课标高考总复习
选考部分·选修4——4·第1课时
课
前
自 助
课本导读
餐 1.参数方程的概念
课前自助餐
授 人
如果曲线C上任意一点P的坐标x和y都可以表示为某个
C.xy==ccoo1sstt
答案 D
D.xy==ttaa1nntt
课 时 作 业
高三数学(人教版)
高考调研 ·新课标高考总复习
选考部分·选修4——4·第1课时
课
前
自 助 餐
4.(09·天津)设直线l1的直线方程为yx==11++3t,t
授
(t为参数),直线l2的方程为y=3x+4,则l1与l2间的距离为
高考调研·新课标高考总复习
第二课时 参数方程
数学(文)
高考调研 ·新课标高考总复习
选考部分·选修4——4·第1课时
课 前 自 助 餐
高中数学探究课教案

高中数学探究课教案
课时安排:2课时
教学目标:
1. 了解数列的概念和基本性质。
2. 掌握常见数列的求解方法。
3. 能够应用数列进行实际问题求解。
教学内容:
1. 数列的基本概念:数列的定义、首项、公差、通项公式等。
2. 常见数列:等差数列、等比数列等。
教学准备:
1. 教师准备课件、黑板、彩色粉笔等教学工具。
2. 学生准备笔记本、笔等学习工具。
教学过程:
第一课时:
1. 导入:介绍数列的概念并举例说明,激发学生对数列的兴趣。
2. 学习:讲解数列的基本性质,引导学生理解首项、公差、通项公式等概念。
3. 练习:让学生做一些简单的数列运算题,巩固所学内容。
4. 总结:复习本课所学内容,提出下节课的学习任务。
第二课时:
1. 复习:回顾上节课的内容,解答学生提出的疑问。
2. 学习:介绍常见数列的求解方法,如等差数列、等比数列等。
3. 练习:让学生做一些实际问题求解题,帮助他们应用所学知识解决实际问题。
4. 总结:总结本节课的学习内容,鼓励学生多加练习,提高数列题目的解题能力。
拓展活动:
1. 让学生自主探究其他类型的数列,并进行讨论分享。
2. 组织数列比赛,激发学生的学习兴趣。
教学反思:
1. 教师要根据学生的实际情况进行灵活教学,注重巩固基础知识,帮助学生理解数列的概念和性质。
2. 要引导学生运用数列解决实际问题,培养他们的综合运用能力和解决问题的思维能力。
高三数学复习课专题课型的研究与探索

高三数学复习课专题课型的研究与探索建构主义认为,数学新知识的学习活动,是主体在自己的头脑里建立和发展数学认知结构的过程,是数学活动及其经验内化过程。
这种内化的过程,或者是以同化的形式把客体纳入到已有的认识结构之中,以便同与自己不相适应的客体一致,从而使原有的认识结构发生质的变化。
由此不难看出,完成这样的过程,完全是自主行为,而且只有通过主体积极主动的智力参与才能实现,别人是根本无法替代的。
所谓“智力参与”,就是主体将自己的注意力、观察力、记忆力、想象力、思维力和语言能力都参与进去。
由于数学建构学习活动的本质是思维构造,所以这是一个创造的过程。
尽管这往往是一个再创造的过程,但是,对学习者本人而言还是处于第一次发现发明的地位,因而主体一定要有高水平的智力参与,这个造的过程才可能得以实现。
按照建构主义的观点数学学习的过程中,学生的学习是以自主活为基础,以智力参与为前提,以个人体验为终结。
学生的自主活动,第一是活动,第二是学生的自主积极性。
之所以强调“活动”,就是为了调要在“做数学中学数学”。
活动是个人体验的源泉,是语言表征、情节表征、动作表征的源泉,所以对建构主义学习来说,活动是第一位的,对处于认知发展阶段的学生而言,这种活动最初主要表现为外部活动,由于主体自身的智力参与,使外部的活动过程内化为主体内部的心理活动过程,并从中产生出主体的个人体验。
同时活动必须是学习者主动和积极进行的,学生是信息加工的主体,是意义的主动建构者,而不是被动活动者,更不是意义的被灌输者; 虽然活动是在教师创设的情景之下进行,但是要靠主体自己控制。
活动自主性的重要标志是主体的智力参与,主体的智力参与程度越高,活动的自主性就越强。
在自主活动下,由于自身的智力参与而产生的个人体验,就是新知识心理意义的基石,最终升华为新知识的心理意义。
建构主义重视学习活动中学生的主体性,重视学生面对具体情景进行意义建构,重视学习活动中师生之间和学生之间的“协作”、“会话”和“反思”,从而主张建立一个民主、宽松的教学环境等,这些观点为我们当前的高三数学复习教学的高效性研究提供了一定的理论依据。
高三数学复习(理):第2讲 第4课时 利用导数研究不等式的恒成立或存在性问题

第4课时 利用导数研究不等式的恒成立或存在性问题[学生用书P58]不等式恒成立求参数(多维探究)方法一 分离参数法(2020·湖北武汉质检)已知f (x )=x ln x ,g (x )=x 3+ax 2-x +2.(1)求函数f (x )的单调区间;(2)若对任意x ∈(0,+∞),2f (x )≤g ′(x )+2恒成立,求实数a 的取值范围.【解】 (1)因为函数f (x )=x ln x 的定义域为(0,+∞),所以f ′(x )=ln x +1.令f ′(x )<0,得ln x +1<0,解得0<x <1e ,所以f (x )的单调递减区间是⎝ ⎛⎭⎪⎫0,1e .令f ′(x )>0,得ln x +1>0,解得x >1e ,所以f (x )的单调递增区间是⎝ ⎛⎭⎪⎫1e ,+∞.综上,f (x )的单调递减区间是⎝ ⎛⎭⎪⎫0,1e ,单调递增区间是⎝ ⎛⎭⎪⎫1e ,+∞. (2)因为g ′(x )=3x 2+2ax -1,由题意得2x ln x ≤3x 2+2ax +1恒成立.因为x >0,所以a ≥ln x -32x -12x 在x ∈(0,+∞)上恒成立.设h (x )=ln x -32x -12x (x >0),则h ′(x )=1x -32+12x 2=-(x -1)(3x +1)2x 2.令h ′(x )=0,得x 1=1,x 2=-13(舍去).当x 变化时,h ′(x ),h (x )的变化情况如下表:x(0,1) 1 (1,+∞) h ′(x )+ 0 -h (x ) 极大值所以当x =1时,h (x )取得极大值,也是最大值,且h (x )max =h (1)=-2,所以若a ≥h (x )在x ∈(0,+∞)上恒成立,则a ≥h (x )max =-2,即a ≥-2,故实数a 的取值范围是[-2,+∞).(1)分离参数法解含参不等式恒成立问题的思路用分离参数法解含参不等式恒成立问题是指在能够判断出参数的系数正负的情况下,可以根据不等式的性质将参数分离出来,得到一个一端是参数,另一端是变量表达式的不等式,只要研究变量表达式的最值就可以解决问题. (2)求解含参不等式恒成立问题的关键是过好“双关”转化关 通过分离参数法,先转化为f (a )≥g (x )(或f (a )≤g (x ))对∀x ∈D 恒成立,再转化为f (a )≥g (x )max (或f (a )≤g (x )min )求最值关求函数g (x )在区间D 上的最大值(或最小值)问题已知函数f (x )=ax e x -(a +1)(2x -1).(1)若a =1,求函数f (x )的图象在点(0,f (0))处的切线方程;(2)当x >0时,函数f (x )≥0恒成立,求实数a 的取值范围. 解:(1)若a =1,则f (x )=x e x -2(2x -1).即f ′(x )=x e x +e x -4,则f ′(0)=-3,f (0)=2,所以所求切线方程为3x +y -2=0.(2)由f (1)≥0,得a ≥1e -1>0, 则f (x )≥0对任意的x >0恒成立可转化为a a +1≥2x -1x e x 对任意的x >0恒成立. 设函数F (x )=2x -1x e x (x >0),则F ′(x )=-(2x +1)(x -1)x 2e x. 当0<x <1时,F ′(x )>0;当x >1时,F ′(x )<0,所以函数F (x )在(0,1)上单调递增,在(1,+∞)上单调递减,所以F (x )max =F (1)=1e .于是aa +1≥1e ,解得a ≥1e -1. 故实数a 的取值范围是⎣⎢⎡⎭⎪⎫1e -1,+∞. 方法二 等价转化法(2020·高考全国卷Ⅰ)已知函数f (x )=e x +ax 2-x .(1)当a =1时,讨论f (x )的单调性;(2)当x ≥0时,f (x )≥12x 3+1,求a 的取值范围.【解】 (1)当a =1时,f (x )=e x +x 2-x ,f ′(x )=e x +2x -1.故当x ∈(-∞,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0.所以f (x )在(-∞,0)单调递减,在(0,+∞)单调递增.(2)f (x )≥12x 3+1等价于⎝ ⎛⎭⎪⎫12x 3-ax 2+x +1e -x ≤1. 设函数g (x )=⎝ ⎛⎭⎪⎫12x 3-ax 2+x +1e -x (x ≥0),则 g ′(x )=-⎝ ⎛⎭⎪⎫12x 3-ax 2+x +1-32x 2+2ax -1e -x =-12x [x 2-(2a +3)x +4a +2]e -x=-12x (x -2a -1)(x -2)e -x .(i)若2a +1≤0,即a ≤-12,则当x ∈(0,2)时,g ′(x )>0.所以g (x )在(0,2)单调递增,而g (0)=1,故当x ∈(0,2)时,g (x )>1,不符合题意.(ii)若0<2a +1<2,即-12<a <12,则当x ∈(0,2a +1)∪(2,+∞)时,g ′(x )<0;当x ∈(2a +1,2)时,g ′(x )>0.所以g (x )在(0,2a +1),(2,+∞)单调递减,在(2a +1,2)单调递增.由于g (0)=1,所以g (x )≤1当且仅当g (2)=(7-4a )e -2≤1,即a ≥7-e 24.所以当7-e 24≤a <12时,g (x )≤1.(iii)若2a +1≥2,即a ≥12,则g (x )≤⎝ ⎛⎭⎪⎫12x 3+x +1e -x . 由于0∈⎣⎢⎡⎭⎪⎫7-e 24,12,故由(ii)可得⎝ ⎛⎭⎪⎫12x 3+x +1e -x ≤1. 故当a ≥12时,g (x )≤1.综上,a 的取值范围是⎣⎢⎡⎭⎪⎫7-e 24,+∞.根据不等式恒成立求参数范围的关键是把不等式转化为函数,利用函数值与最值之间的数量关系确定参数满足的不等式,解不等式即得参数范围.函数f (x )=x 2-2ax +ln x (a ∈R ).(1)若函数y =f (x )在点(1,f (1))处的切线与直线x -2y +1=0垂直,求a 的值;(2)若不等式2x ln x ≥-x 2+ax -3在区间(0,e]上恒成立,求实数a 的取值范围.解:(1)函数f (x )的定义域为(0,+∞),f ′(x )=2x -2a +1x ,f ′(1)=3-2a ,由题意f ′(1)·12=(3-2a )·12=-1,解得a =52.(2)不等式2x ln x ≥-x 2+ax -3在区间(0,e]上恒成立等价于2ln x ≥-x +a-3x ,令g (x )=2ln x +x -a +3x ,则g ′(x )=2x +1-3x 2=x 2+2x -3x 2=(x +3)(x -1)x 2,则在区间(0,1)上,g ′(x )<0,函数g (x )为减函数;在区间(1,e]上,g ′(x )>0,函数g (x )为增函数.由题意知g (x )min =g (1)=1-a +3≥0,得a ≤4,所以实数a 的取值范围是(-∞,4].不等式能成立或有解求参数的取值(范围)(师生共研)已知函数f (x )=ax -e x (a ∈R ),g (x )=ln x x .(1)求函数f (x )的单调区间;(2)∃x ∈(0,+∞),使不等式f (x )≤g (x )-e x 成立,求a 的取值范围.【解】 (1)因为f ′(x )=a -e x ,x ∈R .当a ≤0时,f ′(x )<0,f (x )在R 上单调递减;当a >0时,令f ′(x )=0,得x =ln a .由f ′(x )>0,得f (x )的单调递增区间为(-∞,ln a );由f ′(x )<0,得f (x )的单调递减区间为(ln a ,+∞).综上所述,当a ≤0时,f (x )的单调递减区间为(-∞,+∞),无单调递增区间;当a >0时,f (x )的单调递增区间为(-∞,ln a ),单调递减区间为(ln a ,+∞).(2)因为∃x ∈(0,+∞),使不等式f (x )≤g (x )-e x ,则ax ≤ln x x ,即a ≤ln x x 2.则问题转化为a ≤⎝ ⎛⎭⎪⎫ln x x 2max. 设h (x )=ln x x 2,由h ′(x )=1-2ln x x 3,令h ′(x )=0,得x = e.当x 在区间(0,+∞)内变化时,h ′(x ),h (x )随x 变化的变化情况如下表:x(0,e) e (e ,+∞) h ′(x )+ 0 - h (x ) 极大值12e由上表可知,当x =e 时,函数h (x )有极大值,即最大值为12e ,所以a ≤12e .故a 的取值范围是⎝ ⎛⎦⎥⎤-∞,12e .(1)含参数的能成立(存在型)问题的解题方法①a ≥f (x )在x ∈D 上能成立,则a ≥f (x )min ;②a ≤f (x )在x ∈D 上能成立,则a ≤f (x )max .(2)含全称、存在量词不等式能成立问题①存在x 1∈A ,任意x 2∈B 使f (x 1)≥g (x 2)成立,则f (x )max ≥g (x )max ;②任意x 1∈A ,存在x 2∈B ,使f (x 1)≥g (x 2)成立,则f (x )min ≥g (x )min .已知函数f (x )=x ln x (x >0).(1)求函数f (x )的极值;(2)若存在x ∈(0,+∞),使得f (x )≤-x 2+mx -32成立,求实数m 的最小值. 解:(1)由f (x )=x ln x ,得f ′(x )=1+ln x ,令f ′(x )>0,得x >1e ;令f ′(x )<0,得0<x <1e .所以f (x )在⎝ ⎛⎭⎪⎫0,1e 上单调递减,在⎝ ⎛⎭⎪⎫1e ,+∞上单调递增. 所以f (x )在x =1e 处取得极小值,且为f ⎝ ⎛⎭⎪⎫1e =-1e ,无极大值. (2)由f (x )≤-x 2+mx -32,得m ≥2x ln x +x 2+3x. 问题转化为m ≥⎝ ⎛⎭⎪⎫2x ln x +x 2+3x min . 令g (x )=2x ln x +x 2+3x =2ln x +x +3x (x >0).则g ′(x )=2x +1-3x 2=x 2+2x -3x 2=(x +3)(x -1)x 2. 由g ′(x )>0,得x >1,由g ′(x )<0,得0<x <1.所以g (x )在(0,1)上单调递减,在(1,+∞)上单调递增.所以g (x )min =g (1)=4,则m ≥4.故m 的最小值为4.[学生用书P59]核心素养系列4 逻辑推理——两个经典不等式的活用逻辑推理是得到数学结论,构建数学体系的重要方式,是数学严谨性的基本保证.利用两个经典不等式解决其他问题,降低了思考问题的难度,优化了推理和运算过程.(1)对数形式:x ≥1+ln x (x >0),当且仅当x =1时,等号成立.(2)指数形式:e x ≥x +1(x ∈R ),当且仅当x =0时,等号成立.进一步可得到一组不等式链:e x >x +1>x >1+ln x (x >0,且x ≠1).(1)已知函数f (x )=1ln (x +1)-x,则y =f (x )的图象大致为( )(2)已知函数f (x )=e x ,x ∈R .证明:曲线y =f (x )与曲线y =12x 2+x +1有唯一公共点.【解】 (1)选B.因为f (x )的定义域为{x +1>0,ln (x +1)-x ≠0, 即{x |x >-1,且x ≠0},所以排除选项D.当x >0时,由经典不等式x >1+ln x (x >0),以x +1代替x ,得x >ln(x +1)(x >-1,且x ≠0),所以ln(x +1)-x <0(x >-1,且x ≠0),即x >0或-1<x <0时均有f (x )<0,排除A ,C ,易知B 正确.(2)证明:令g (x )=f (x )-⎝ ⎛⎭⎪⎫12x 2+x +1=e x -12x 2-x -1,x ∈R , 则g ′(x )=e x -x -1,由经典不等式e x ≥x +1恒成立可知,g ′(x )≥0恒成立,所以g (x )在R 上为单调递增函数,且g (0)=0.所以函数g (x )有唯一零点,即两曲线有唯一公共点.已知函数f (x )=x -1-a ln x .(1)若f (x )≥0,求a 的值;(2)证明:对于任意正整数n ,⎝ ⎛⎭⎪⎫1+12⎝ ⎛⎭⎪⎫1+122·…·⎝ ⎛⎭⎪⎫1+12n <e. 【解】 (1)f (x )的定义域为(0,+∞),①若a ≤0,因为f ⎝ ⎛⎭⎪⎫12=-12+a ln 2<0,所以不满足题意; ②若a >0,由f ′(x )=1-a x =x -a x 知,当x ∈(0,a )时,f ′(x )<0;当x ∈(a ,+∞)时,f ′(x )>0.所以f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增,故x =a 是f (x )在(0,+∞)的唯一最小值点.因为f (1)=0,所以当且仅当a =1时,f (x )≥0,故a =1.(2)证明:由(1)知当x ∈(1,+∞)时,x -1-ln x >0.令x =1+12n ,得ln ⎝ ⎛⎭⎪⎫1+12n <12n . 从而ln ⎝ ⎛⎭⎪⎫1+12+ln ⎝ ⎛⎭⎪⎫1+122+…+ln ⎝ ⎛⎭⎪⎫1+12n <12+122+…+12n =1-12n <1. 故⎝ ⎛⎭⎪⎫1+12⎝ ⎛⎭⎪⎫1+122…⎝ ⎛⎭⎪⎫1+12n <e. 设函数f (x )=ln x -x +1.(1)讨论f (x )的单调性;(2)求证:当x ∈(1,+∞)时,1<x -1ln x <x .【解】 (1)由题设知,f (x )的定义域为(0,+∞),f ′(x )=1x -1,令f ′(x )=0,解得x =1.当0<x <1时,f ′(x )>0,f (x )在(0,1)上单调递增;当x >1时,f ′(x )<0,f (x )在(1,+∞)上单调递减.(2)证明:由(1)知f (x )在x =1处取得最大值,最大值为f (1)=0.所以当x ≠1时,ln x <x -1.故当x ∈(1,+∞)时,ln x <x -1,x -1ln x >1.①因此ln 1x <1x -1,即ln x >x -1x ,x -1ln x <x .②故当x ∈(1,+∞)时恒有1<x -1ln x <x .[学生用书P291(单独成册)]1.(2021·贵阳市第一学期监测考试)已知函数f (x )=a sin x -x +b (a ,b 均为正常数),h (x )=sin x +cos x .设函数f (x )在x =π3处有极值,对于一切x ∈⎣⎢⎡⎦⎥⎤0,π2,不等式f (x )>h (x )恒成立,求b 的取值范围.解:f ′(x )=a cos x -1.由已知得:f ′⎝ ⎛⎭⎪⎫π3=0,所以a =2, 所以f (x )=2sin x -x +b ,不等式f (x )>h (x )恒成立可化为sin x -cos x -x >-b ,记函数g (x )=sin x -cos x -x ,x ∈⎣⎢⎡⎦⎥⎤0,π2,则g ′(x )=cos x +sin x -1=2sin ⎝ ⎛⎭⎪⎫x +π4-1,x ∈⎣⎢⎡⎦⎥⎤0,π2, 当x ∈⎣⎢⎡⎦⎥⎤0,π2时,1≤2sin ⎝ ⎛⎭⎪⎫x +π4≤2,所以g ′(x )>0在⎣⎢⎡⎦⎥⎤0,π2上恒成立,所以函数g (x )在⎣⎢⎡⎦⎥⎤0,π2上是增函数,最小值为g (0)=-1, 所以b >1,所以b 的取值范围是(1,+∞).2.(2020·江西五校联考)已知函数f (x )=e x +bx .(1)讨论f (x )的单调性;(2)若b =1,当x 2>x 1>0时,f (x 1)-f (x 2)<(x 1-x 2)·mx 1+mx 2+1)恒成立,求实数m 的取值范围.解:(1)由f (x )=e x +bx 得f ′(x )=e x +b ,若b ≥0,则f ′(x )>0,即f (x )=e x +bx 在(-∞,+∞)上是增函数; 若b <0,令f ′(x )>0得x >ln(-b ),令f ′(x )<0得x <ln(-b ),即f (x )=e x +bx 在(-∞,ln(-b ))上单调递减,在(ln(-b ),+∞)上单调递增.(2)由题意知f (x )=e x +x ,f (x 1)-f (x 2)<(x 1-x 2)(mx 1+mx 2+1),即f (x 1)-mx 21-x 1<f (x 2)-mx 22-x 2,由x 2>x 1>0知,上式等价于函数φ(x )=f (x )-mx 2-x =e x -mx 2在(0,+∞)上为增函数,所以φ′(x )=e x-2mx ≥0(x >0),即2m ≤e x x (x >0). 令h (x )=e x x (x >0),则h ′(x )=e x (x -1)x 2, 当h ′(x )<0时,0<x <1;当h ′(x )>0时,x >1;当h ′(x )=0时,x =1. 所以h (x )在(0,1)上单调递减,在(1,+∞)上单调递增,所以h (x )min =h (1)=e ,则2m ≤e ,即m ≤e 2,所以实数m 的取值范围为⎝ ⎛⎦⎥⎤-∞,e 2. 3.(2021·福州市适应性考试)已知f (x )=2x ln x +x 2+ax +3.(1)当a =1时,求曲线y =f (x )在x =1处的切线方程;(2)若存在x 0∈⎝ ⎛⎭⎪⎫1e ,e ,使得f (x 0)≥0成立,求a 的取值范围. 解:f ′(x )=2(ln x +1)+2x +a .(1)当a =1时,f (x )=2x ln x +x 2+x +3,f ′(x )=2(ln x +1)+2x +1,所以f (1)=5,f ′(1)=5,所以曲线y =f (x )在x =1处的切线方程为y -5=5(x -1),即y =5x .(2)存在x 0∈⎝ ⎛⎭⎪⎫1e ,e ,使得f (x 0)≥0成立,等价于不等式a ≥-2x ln x +x 2+3x 在⎝ ⎛⎭⎪⎫1e ,e 上有解. 设h (x )=-2x ln x +x 2+3x,则h ′(x )=-x 2+2x -3x 2=-(x +3)(x -1)x 2, 当1e <x <1时,h ′(x )>0,h (x )为增函数;当1<x <e 时,h ′(x )<0,h (x )为减函数.又h ⎝ ⎛⎭⎪⎫1e =-3e 2-2e +1e ,h (e)=-e 2+2e +3e , 故h ⎝ ⎛⎭⎪⎫1e -h (e)<0, 所以当x ∈⎝ ⎛⎭⎪⎫1e ,e 时,h (x )>h ⎝ ⎛⎭⎪⎫1e =-3e 2-2e +1e , 所以a >-3e 2-2e +1e, 即a 的取值范围为⎝ ⎛⎭⎪⎫-3e 2-2e +1e ,+∞. 4.(2021·合肥第一次教学检测)已知函数f (x )=(x +1)ln x ,g (x )=a (x -1),a ∈R .(1)求直线y =g (x )与曲线y =f (x )相切时,切点T 的坐标;(2)当x ∈(0,1)时,g (x )>f (x )恒成立,求a 的取值范围.解:(1)设切点坐标为(x 0,y 0),由f (x )=(x +1)·ln x ,得f ′(x )=ln x +1x +1,则⎩⎨⎧ln x 0+1x 0+1=a ,(x 0+1)ln x 0=a (x 0-1), 所以2ln x 0-x 0+1x 0=0. 令h (x )=2ln x -x +1x ,则h ′(x )=-x 2-2x +1x 2≤0,所以h (x )在(0,+∞)上单调递减,所以h (x )=0最多有一个实数根.又h (1)=0,所以x 0=1,此时y 0=0,即切点T 的坐标为(1,0).(2)当x∈(0,1)时,g(x)>f(x)恒成立,等价于ln x-a(x-1)x+1<0对x∈(0,1)恒成立.令H(x)=ln x-a(x-1)x+1,则H′(x)=1x-2a(x+1)2=x2+2(1-a)x+1x(x+1)2,H(1)=0.①当a≤2,x∈(0,1)时,x2+2(1-a)x+1≥x2-2x+1>0,所以H′(x)>0,H(x)在x∈(0,1)上单调递增,因此当x∈(0,1)时H(x)<0.②当a>2时,令H′(x)=0得x1=a-1-(a-1)2-1,x2=a-1+(a-1)2-1.由x2>1与x1x2=1得,0<x1<1.所以当x∈(x1,1)时,H′(x)<0,H(x)单调递减,所以当x∈(x1,1)时,H(x)>H(1)=0,不符合题意.综上所述,a的取值范围是(-∞,2].。
研究课四正弦定理余弦定理的综合应用课件-2025届高三数学一轮复习

通过对任意三角形边长和角度关系的探索,会用正弦定理、余弦定 理解决三角形中的综合问题,提高学生分析问题、解决问题的能力.
关键能力·题型剖析 题型一 多边形中的解三角形问题
例 1 [2024·江西九江模拟]在△ABC中,AC= 13,D为∠ABC的角 平分线上一点,且与B分别位于边AC的两侧,若∠ADC=150°,AD =2.
题型三 三角形中的最值、范围问题
例 3 (12分)[2022·新高考Ⅰ卷]记△ABC的内角A,B,C的对边分别为 a,b,c,已知1c+ossinAA=1+sicno2s B2B.
(1)若C=23π,求B; (2)求a2c+2b2的最小值.
思路Байду номын сангаас引
(1)二倍角公式化简→去分母、两角和与差公式化简→求出sin B. (2)由角B,C正余弦关系→角B与角C,A的关系→a2c+2b2化成正弦→用 角B表示角A,C化简→角B的关系式→基本不等式.
而0<B<
π 3
,所以B
=
π 6
.→正确求出角B得1分
(2)由(1)知,sin 而sin B=-cos
BC==-sicnos(CC->π20),→所用以诱π2导<公C<式π正,确0<找B出<角π2,B,C的正弦关系
得2分
所以C=π2+B,即有A=π2-2B,→用角B表示角C,A得1分
所以a2c+2b2=sin2sAin+2sCin2 B→正确用正弦定理化边为角得1分
(1)求△DAC的面积; (2)若∠ABC=120°,求BD的长.
题后师说
平面几何中解三角形问题的求解策略
巩固训练1 [2024·河南焦作模拟]如图,在平面四边形ABCD中,∠BAD=90°, D=60°,AC=4,CD=3. (1)求cos ∠CAD;
高三数学复习专题课(新编教材)

3、已知数列{ an}满足 3an1 an 4
(n≥1),且 a=1 9,则
a
n
__8__(__1_)_n_1 _.1
3
4、不等式ax2 bx 2 0的解集是( 1 , 1)
23
则a+b的值是( D ) A、10 B、-10 C、14 D、-14 5、如果双曲线经过(6, 5)且它的两条 渐进线的方程是 y 1 x ,那么这双曲线的
高三数学复习专题课
待定系数法
福建仙游盖尾中学:郭志龙
一、课前练习
1、若将直线L沿x轴正方向平移a个单位
(a≠0),再沿y轴的负方向平移a+1个
单位,又回到了原来L的位置,则直线L
的斜率为( C )
A、 a
a 1
B、a a 1
Байду номын сангаас
C、 a 1
a
D、a
a
1
2、设等比数列{an }的前n项和为sn 3n r , 那么r的值等于( A ) A、-1 B、0 C、1 D、3
3
y2 x2 1
方程______9_____。
;少儿口才网 /oumeisipinpai/ 少儿口才网 ;
右将军如故 天下定后方当用之 阿翁岂宜以子戏父邪 骋足则能追风蹑景 诏遣侍中 不就 比岁征行 如使君为季龙所制 谦向诸弟泣曰 于时刁协 不亦劳乎 隆和元年 封观阳县侯 寻加中书监 督护梁州五郡军事 唯超案兵直卫 翜遣将领五百人从之 视之 何充会之 以寇难路险 补濮阳王允文学 频迁中领军 而神州振荡 又问 玄先令将军王稚徽戍巴陵 将军留宠 少颖悟 时江淮清宴 又隐实户口 稍迁丞相西閤祭酒 则百胜之理济矣 恐不免耳 非式而谁 后骧等又渡泸水寇宁州 穆之 甚为边害 诸督将素知其勇 渐相登
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(建议用时:80分钟)1.如图所示,已知直三棱柱ABC -A1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D ,E ,F 分别为B 1A ,C 1C ,BC 的中点.求证:(1)DE ∥平面ABC ;(2)B 1F ⊥平面AEF .证明 (1)如图建立空间直角坐标系A -xyz ,令AB =AA 1=4,则A (0,0,0),E (0,4,2),F (2,2,0),B (4,0,0),B 1(4,0,4).取AB 中点为N ,连接CN ,则N (2,0,0),C (0,4,0),D (2,0,2),∴DE→=(-2,4,0),NC →=(-2,4,0),∴DE →=NC →,∴DE ∥NC , 又∵NC ⊂平面ABC ,DE ⊄平面ABC .故DE ∥平面ABC .(2)B 1F →=(-2,2,-4),EF →=(2,-2,-2),AF →=(2,2,0).B 1F →·EF →=(-2)×2+2×(-2)+(-4)×(-2)=0,B 1F →·AF →=(-2)×2+2×2+(-4)×0=0.∴B 1F →⊥EF →,B 1F →⊥AF →,即B 1F ⊥EF ,B 1F ⊥AF ,又∵AF ∩FE =F ,∴B 1F ⊥平面AEF .2.(2016·西安调研)如图所示,在长方体ABCD -A ′B ′C ′D ′中,AB =λAD =λAA ′(λ>0),E ,F 分别是A ′C ′和AD 的中点,且EF ⊥平面A ′BCD ′.(1)求λ的值;(2)求二面角C -A ′B -E 的余弦值.解 以D 为原点,DA ,DC ,DD ′分别为x ,y ,z 轴建立空间直角坐标系,设AA ′=AD =2,则AB =2λ,D (0,0,0),A ′(2,0,2),D ′(0,0,2),B (2,2λ,0),C (0,2λ,0),E (1,λ,2),F (1,0,0).(1)EF →=(0,-λ,-2),D ′A ′→=(2,0,0),A ′B →=(0,2λ,-2),∵EF ⊥D ′A ′,EF ⊥A ′B ,∴EF →·D ′A ′→=0,EF →·A ′B →=0,即-2λ2+4=0,∴λ= 2.(2)设平面EA ′B 的一个法向量为m =(1,y ,z ),则⎩⎪⎨⎪⎧m ·A ′B →=0,m ·A ′E →=0, ∵A ′B →=(0,22,-2),A ′E →=(-1,2,0),∴⎩⎨⎧22y -2z =0,-1+2y =0,,∴y =22,z =1,∴m =⎝ ⎛⎭⎪⎫1,22,1. 由已知得EF→为平面A ′BC 的一个法向量,又EF →=(0,-2,-2), ∴cos 〈m ,EF →〉=m ·EF →|m |·|EF →|=0-1-252×6=-155. 又二面角C -A ′B -E 为锐二面角,故二面角C -A ′B -E 的余弦值为155.3.(2015·全国Ⅰ卷)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC .(1)证明:平面AEC ⊥平面AFC ,(2)求直线AE 与直线CF 所成角的余弦值.(1)证明 如图,连接BD ,设BD ∩AC =G ,连接EG ,FG ,EF .在菱形ABCD 中,不妨设GB =1.由∠ABC =120°,可得AG =GC = 3. 由BE ⊥平面ABCD ,AB =BC ,可知AE =EC .又AE ⊥EC ,所以EG =3,且EG ⊥AC .在Rt △EBG 中,可得BE =2,故DF =22.在Rt △FDG 中,可得FG =62.在直角梯形BDFE 中,由BD =2,BE =2,DF =22,可得EF =322,从而EG 2+FG 2=EF 2,所以EG ⊥FG .又AC ∩FG =G ,可得EG ⊥平面AFC .因为EG ⊂平面AEC ,所以平面AEC ⊥平面AFC .(2)解 如图,以G 为坐标原点,分别以GB→,GC →的方向为x 轴,y 轴正方向,|GB →|为单位长度,建立空间直角坐标系G -xyz ,由(1)可得A (0,-3,0),E (1,0,2),F ⎝⎛⎭⎪⎫-1,0,22,C (0,3,0),所以AE →=(1,3,2),CF →=⎝⎛⎭⎪⎫-1,-3,22. 故cos 〈AE →,CF →〉=AE →·CF →|AE→||CF →|=-33. 所以直线AE 与直线CF 所成角的余弦值为33.4.(2015·陕西卷)如图1,在直角梯形 ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC=1,AD =2,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置,如图2.(1)证明:CD ⊥平面A 1OC ;(2)若平面A 1BE ⊥平面BCDE ,求平面A 1BC 与平面A 1CD 夹角的余弦值.(1)证明 在图1中,因为AB =BC =1,AD =2,E 是AD 的中点,图1∠BAD =π2,所以BE ⊥AC ,即在图2中,BE ⊥OA 1,BE ⊥OC ,且A 1O ∩OC =O ,从而BE ⊥平面A 1OC .又在直角梯形ABCD 中,AD ∥BC ,BC =12AD ,E 为AD 中点,所以BC 綊ED ,所以四边形BCDE 为平行四边形,故有CD ∥BE ,所以CD ⊥平面A 1OC .图2(2)解 由已知,平面A 1BE ⊥平面BCDE ,又由(1)知,BE ⊥OA 1,BE ⊥OC ,所以∠A 1OC 为二面角A 1-BE -C 的平面角,所以∠A 1OC =π2.如图2,以O 为原点,建立空间直角坐标系,因为A 1B =A 1E =BC =ED =1,BC ∥ED ,所以B ⎝ ⎛⎭⎪⎫22,0,0,E ⎝ ⎛⎭⎪⎫-22,0,0,A 1⎝ ⎛⎭⎪⎫0,0,22,C ⎝ ⎛⎭⎪⎫0,22,0, 得BC →=⎝ ⎛⎭⎪⎫-22,22,0,A 1C →=⎝⎛⎭⎪⎫0,22,-22,CD →=BE →=(-2,0,0), 设平面A 1BC 的法向量n 1=(x 1,y 1,z 1),平面A 1CD 的法向量n 2=(x 2,y 2,z 2),平面A 1BC 与平面A 1CD 夹角为θ,则⎩⎪⎨⎪⎧n 1·BC →=0,n 1·A 1C →=0,得⎩⎨⎧-x 1+y 1=0,y 1-z 1=0,取n 1=(1,1,1); ⎩⎪⎨⎪⎧n 2·CD →=0,n 2·A 1C →=0,得⎩⎨⎧x 2=0,y 2-z 2=0,取n 2=(0,1,1),从而cos θ=|cos n 1,n 2 |=23×2=63, 即平面A 1BC 与平面A 1CD 夹角的余弦值为63.5.已知四棱锥P -ABCD 的底面ABCD 是矩形,P A ⊥平面ABCD ,AD =2,AB =1,E 、F 分别是线段AB 、BC 的中点.(1)求证:PF ⊥FD ;(2)在P A 上找一点G ,使得EG ∥平面PFD ;(3)若PB 与平面ABCD 所成的角为45°,求二面角A -PD -F 的余弦值.(1)证明 建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),B (1,0,0),F (1,1,0),D (0,2,0),不妨令P (0,0,t ),t >0.∵PF→=(1,1,-t ),DF →=(1,-1,0), ∴PF→·DF →=1×1+1×(-1)+(-t )×0=0.∴PF ⊥FD . (2)解 设平面PFD 的法向量为n =(x ,y ,z ),由⎩⎪⎨⎪⎧n ·PF →=0,n ·DF →=0得⎩⎨⎧x +y -tz =0x -y =0,令z =1, 则n =(t 2,t 2,1),设G (0,0,m ),∵E (12,0,0),∴EG →=(-12,0,m ),由题意EG →·n =0, ∴- t 4+m =0,∴m =14t ,∴当G 是线段P A 的靠近于A 的一个四等分点时,使得EG ∥平面PFD .(3)解 ∵P A ⊥平面ABCD ,∴∠PBA 就是PB 与平面ABCD 所成的角,即∠PBA =45° ,∴P A =AB =1,P (0,0,1),由(2)知平面PFD 的一个法向量为n =(12,12,1).易知平面P AD 的一个法向量为AB →=(1,0,0),∴ cos 〈AB →,n 〉=AB →·n |AB →||n |=1214+14+1=66.由图知二面角A -PD -F 的平面角为锐角,所以二面角A -PD -F 的余弦值为66.6.(2015·湖南卷)如图,已知四棱台ABCD -A 1B 1C 1D 1的上、下底面分别是边长为3和6的正方形,AA 1=6,且AA 1⊥底面ABCD ,点P ,Q 分别在棱DD 1,BC 上.(1)若P 是DD 1的中点,证明:AB 1⊥PQ ;(2)若PQ ∥平面ABB 1A 1,二面角P -QD -A 的余弦值为37,求四面体ADPQ 的体积.解 由题设知,AA 1,AB ,AD 两两垂直,以A 为坐标原点,AB ,AD ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则相关各点的坐标为A (0,0,0),B 1(3,0,6),D (0,6,0),D 1(0,3,6),Q (6,m ,0),其中m =BQ ,0≤m ≤6.(1)证明 若P 是DD 1的中点,则P ⎝ ⎛⎭⎪⎫0,92,3, PQ →=⎝ ⎛⎭⎪⎫6,m -92,-3, 又AB 1→=(3,0,6),于是AB 1→·PQ →=18-18=0, 所以AB 1→⊥PQ →,即AB 1⊥PQ . (2)由题设知,DQ →=(6,m -6,0),DD 1→=(0,-3,6)是平面PQD 内的两个不共线向量.设n 1=(x ,y ,z )是平面PQD 的一个法向量,则⎩⎪⎨⎪⎧n 1·DQ →=0,n 1·DD 1→=0,即⎩⎨⎧6x +(m -6)y =0,-3y +6z =0.取y =6,得n 1=(6-m ,6,3).又平面AQD 的一个法向量是n 2=(0,0,1),所以cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=31·(6-m )2+62+32=3(6-m )2+45. 而二面角P -QD -A 的余弦值为37,因此3(6-m )2+45=37,解得m =4,m =8(舍去),此时Q (6,4,0).设DP →=λDD 1→(0<λ≤1),而DD 1→=(0,-3,6), 由此得点P (0,6-3λ,6λ),所以PQ→=(6,3λ-2,-6λ). 因为PQ ∥平面ABB 1A 1,且平面ABB 1A 1的法向量是n 3=(0,1,0),所以PQ →·n 3=0,即3λ-2=0,亦即λ=23,从而P (0,4,4). 于是,将四面体ADPQ 视为以△ADQ 为底面的三棱锥P -ADQ ,则其高h =4.故四面体ADPQ 的体积V =13S △ADQ ·h =13×12×6×6×4=24.。
