备战高考之文科数学空间点线面位置关系
2022年高考数学总复习:空间点、直线、平面之间的位置关系

第 1 页 共 16 页 2022年高考数学总复习:空间点、直线、平面之间的位置关系
1.四个公理
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
公理2:过不在一条直线上的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 公理
4:平行于同一条直线的两条直线互相平行.
2.直线与直线的位置关系
(1)位置关系的分类
⎩⎨⎧ 共面直线⎩⎪⎨⎪⎧ 平行直线相交直线异面直线:不同在任何一个平面内,没有公共点
(2)异面直线所成的角
①定义:设a ,b 是两条异面直线,经过空间任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).
②范围:⎝⎛⎦
⎤0,π2. 3.直线与平面的位置关系有直线在平面内、直线与平面相交、直线与平面平行三种情况.
4.平面与平面的位置关系有平行、相交两种情况.
5.等角定理
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
知识拓展
1.唯一性定理
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)过直线外一点有且只有一个平面与已知直线垂直.
(3)过平面外一点有且只有一个平面与已知平面平行.
(4)过平面外一点有且只有一条直线与已知平面垂直.
2.异面直线的判定定理
经过平面内一点的直线与平面内不经过该点的直线互为异面直线.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)。
高考冲刺 空间点线面的位置关系(提高)
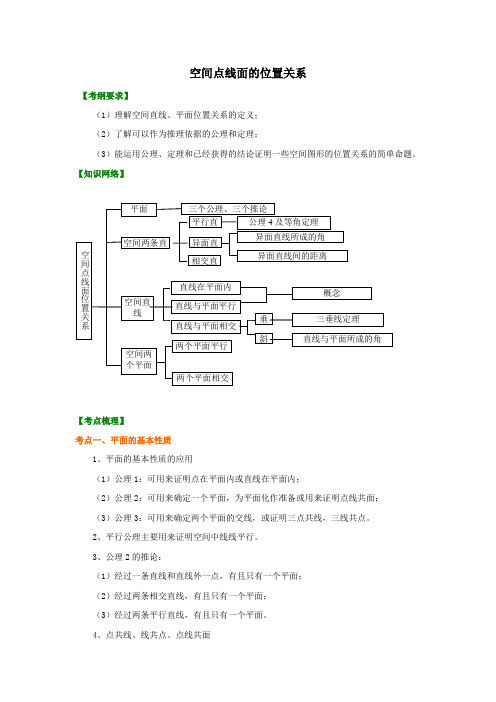
空间点线面的位置关系【考纲要求】(1)理解空间直线、平面位置关系的定义; (2)了解可以作为推理依据的公理和定理;(3)能运用公理、定理和已经获得的结论证明一些空间图形的位置关系的简单命题。
【知识网络】【考点梳理】考点一、平面的基本性质1、平面的基本性质的应用(1)公理1:可用来证明点在平面内或直线在平面内;(2)公理2:可用来确定一个平面,为平面化作准备或用来证明点线共面; (3)公理3:可用来确定两个平面的交线,或证明三点共线,三线共点。
2、平行公理主要用来证明空间中线线平行。
3、公理2的推论:(1)经过一条直线和直线外一点,有且只有一个平面; (2)经过两条相交直线,有且只有一个平面; (3)经过两条平行直线,有且只有一个平面。
4、点共线、线共点、点线共面空间点线面位置关系三个公理、三个推论 平面平行直异面直相交直公理4及等角定理 异面直线所成的角 异面直线间的距离直线在平面内直线与平面平行 直线与平面相交 空间两条直概念垂斜空间直线 与平面 空间两个平面两个平面平行两个平面相交三垂线定理 直线与平面所成的角(1)点共线问题证明空间点共线问题,一般转化为证明这些点是某两个平面的公共点,再根据公理3证明这些点都在这两个平面的交线上。
(2)线共点问题证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上。
要点诠释:证明点线共面的常用方法①纳入平面法:先确定一个平面,再证明有关点、线在此平面内;②辅助平面法:先证明有关的点、线确定平面α,再证明其余元素确定平面β,最后证明平面α、β重合。
考点二、直线与直线的位置关系(1)位置关系的分类⎧⎧⎪⎨⎨⎩⎪⎩相交直线共面直线平行直线异面直线:不同在任何一个平面内,没有公共点(2)异面直线所成的角①定义:设a,b 是两条异面直线,经过空间中任一点O 作直线a ’∥a,b ’∥b,把a ’与b ’所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角)②范围:02π⎛⎤ ⎥⎝⎦,要点诠释:证明两直线为异面直线的方法:1、定义法(不易操作)2、反证法:先假设两条直线不是异面直线,即两直线平行或相交,由假设的条件出发,经过严密的推理,导出矛盾,从而否定假设肯定两条直线异面。
高三-空间点线面位置关系.doc

辅导讲义学员编号: 年 级: 高三 课 时 数:3 学员姓名: 辅导科目: 数学 学科教师:授课类型 三角函数图像 三角函数图像平移 三角函数图像综合授课日期及时段教学内容空间点、直线、平面之间的位置关系基础梳理1.平面的基本性质(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. (2)公理2:经过不在同一条直线上的三点,有且只有一个平面.(3)公理3:如果两个平面(不重合的两个平面)有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.(4)公理4:平行于同一条直线的两条直线平行。
推论1:经过一条直线和这条直线外一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面. 2.直线与直线的位置关系 (1)位置关系的分类⎩⎨⎧共面直线⎩⎪⎨⎪⎧平行相交异面直线:不同在任何一个平面内(2)异面直线所成的角①定义:设a ,b 是两条异面直线,经过空间任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角或直角叫做异面直线a ,b 所成的角(或夹角). ②范围:]2,0(π.3.直线与平面的位置关系有平行、相交、在平面内三种情况.4.平面与平面的位置关系有平行、相交两种情况.5.等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.基础自测1.下列命题是真命题的是________①.空间中不同三点确定一个平面 ②.空间中两两相交的三条直线确定一个平面 ③.一条直线和一个点能确定一个平面 ④.梯形一定是平面图形 解析:空间中不共线的三点确定一个平面,①错;空间中两两相交不交于一点的三条直线确定一个平面,②错; 经过直线和直线外一点确定一个平面,③错 答案:④2.已知a ,b 是异面直线,直线c 平行于直线a ,那么下列c 与b 位置关系一定正确的是________ ①.一定是异面直线 ②.一定是相交直线 ③.不可能是平行直线 ④.不可能是相交直线解析:由已知直线c 与b 可能为异面直线也可能为相交直线,但不可能为平行直线,若b ∥c ,则a ∥b ,与已知a 、b 为异面直线相矛盾. 答案:③4.如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线解析:如图所示,与AB 异面的直线有B 1C 1;CC 1,A 1D 1,DD 1四条,因为各棱具有相同的位置且正方体共有12条棱,排除两棱的重复计算,共有异面直线12×42=24(对).答案:24对5.两个不重合的平面可以把空间分成________部分. 答案:3或46.在正方体1111ABCD A B C D 各个表面的12条对角线中,与1BD 垂直的有____ _ 条. 答案:6一、专题精讲考点一平面的基本性质例题1.正方体ABCDA1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点,那么,正方体的过P、Q、R的截面图形是什么图形。
点线面位置关系(知识点加典型例题)+大一高数知识点-重难点整理

点线面位置关系(知识点加典型例题)+大一高数知识点-重难点整理2.1空间中点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系 1、教学重点和难点重点:空间直线、平面的位置关系。
难点:三种语言(文字语言、图形语言、符号语言)的转换 2、三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号表示为A ∈LB ∈L => L α ,A ∈α ,B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
推论:① 一条直线和其外一点可确定一个平面②两条相交直线可确定一个平面 ③两条平行直线可确定一个平面(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈LLA ·α C ·B·A· α P· αLβ公理3作用:判定两个平面是否相交的依据 (4)公理 4:平行于同一条直线的两条直线平行等角定理:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.2、空间两条不重合的直线有三种位置关系:相交、平行、异面3、异面直线所成角θ的范围是 00<θ≤900 2.1.2 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点。
2 公理4:平行于同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线a ∥bc ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
高三数学 空间点线面之间的位置关系

课堂互动讲练
【名师点评】 题中是先说明D1、 E、F确定一平面,再说明B在所确定 的平面内,也可证明D1E∥BF,从而 说明四点共面.
课堂互动讲练
考点四 异面直线的判定
证明两直线为异面直线的方法: 1.定义法(不易操作). 2.反证法:先假设两条直线不 是异面直线,即两直线平行或相交, 由假设的条件出发,经过严密的推理, 导出矛盾,从而否定假设肯定两条直 线异面.此法在异面直线的判定中经 常用到.
A.A∈l,A∈α,B∈l, B∈α⇒l⊂α
B.A∈α,A∈β,B∈α, B∈β⇒a∩β=AB
C.l⊄α,A∈l⇒A∉α D.A∈α,A∈l,l⊄α⇒l∩α=A 答案:C
三基能力强化
4.如图所示,在正方体ABCD-
A1B1C1D1中,异面直线AC与B1C1
所成的角为
.
答案:45°
5.三条直线两两相交,可以确 定3进一步反映了平面的延展 性.其作用是:(1)判定两平面相交;(2) 作两平面相交的交线(当知道两个平面 的两个公共点时,这两点的连线就是交 线);(3)证明多点共线(如果几个点都是 某两个平面的公共点,则这几个点都在 这两个平面的交线上).
随堂即时巩固
点击进入
课时活页训练
PQ、CB的延长线交于M,RQ、DB的延
长线交于N,RP、DC的延长线交于K.求
证:M、N、K三点共线.
课堂互动讲练
【思路点拨】 要证明M、N、K 三点共线,由公理3可知,只要证明M、 N、K都在平面BCD与平面PQR的交 线上即可.
课堂互动讲练
【证明】
PQ∩CB=M
RQ∩DB=N⇒
RP∩DC=K
课堂互动讲练
解:选取平面BCF,该 平面有以下两个特点:①该 平面包含直线CF;②该平面 与DE相交于点E.在平面BCF 中,过点E作CF的平行线交 BF于点N,连结ND,可以看 出:EN与ED所成的角即为 异面直线FC与ED所成的角. 10分
2024年高考数学专题复习第19讲空间点、线、面之间的位置关系

置关系
利用某些特殊空间图形判断空间
点、直线、平面的位置关系
能说明直线与直线平行的基本事
实,能归纳出直线与平面、平面
判断或证明空 间中的平行关 系
与平面平行的判定定理;能从定 义出发归纳并证明直线与平面、 平面与平面平行的性质定理,能 利用直线与平面、平面与平面平
理解
行的判定定理和性质定理解决有 关问题
课标导引
知知识识聚聚焦焦
核心考点
(2)线面平行的性质定理 一条直线与一个平面平行,如果过该直线的
文字语言 平面与此平面交于一条直线,那么该直线与 交线平行
符号语言 a∥α,a⊂β,α∩β=b⇒a∥b
图形语言
-8-
第19讲 空间点、线、面之间的 位置关系
课标导引
知知识识聚聚焦焦
核心考点
5.平面与平面平行的判定与性质
点的公共直线
图形语言
符号语言 (数学语言) A,B,C三点不共 线⇒存在唯一的 平面α使得 A,B,C∈α
A∈l,B∈l,且 A∈α,B∈α⇒l⊂α
P∈α,P∈β⇒α∩ β=l,且P∈l
-3-
第19讲 空间点、线、面之间的 位置关系
课标导引
知知识识聚聚焦焦
核心考点
三个推论: 推论1:经过一条直线和这条直线外一点,有且只有一个平面(图1). 推论2:经过两条相交直线,有且只有一个平面(图2). 推论3:经过两条平行直线,有且只有一个平面(图3).
(1)面面平行的判定定理
文字语言
如果一个平面内的两条相交直线与另一个平面平行, 那么这两个平面平行
符号语言 a,b⊂α,a∩b=P,a∥β,b∥β⇒α∥β
图形语言
-9-
第19讲 空间点、线、面之间的 位置关系
2020年高考数学必刷题《34 空间点、线、面的位置关系》(解析版)

专题八 立体几何34 空间点、线、面的位置关系1.空间中可以确定一个平面的条件是 A .三个点 B .四个点 C .三角形D .四边形【答案】C【解析】在A 中,不共线的三个点能确定一个平面,共线的三个点不能确定一个平面,故A 错误; 在B 中,不共线的四个点最多能确定四个平面,故B 错误;在C 中,由于三角形的三个顶点不共线,因此三角形能确定一个平面,故C 正确; 在D 中,四边形有空间四边形和平面四边形,空间四边形不能确定一个平面,故D 错误. 2.已知异面直线,a b 分别在平面,αβ内,且c αβ=,那么直线c 一定A .与a b ,都相交B .只能与a b ,中的一条相交C .至少与a b ,中的一条相交D .与a b ,都平行【答案】C【解析】若 与 , 都不相交,则 与 , 都平行. 根据公理4,则 ,与 , 异面矛盾. 故直线c 一定至少与a b ,中的一条相交.3.已知 , 是异面直线,直线 平行于直线 ,那么 与 A .一定是异面直线 B .一定是相交直线 C .不可能...是相交直线 D .不可能...是平行直线 【答案】D【解析】∵直线a 与b 是异面直线,直线c ∥a ,∴直线b 和c 有可能在同一平面上,也有可能不在同一平面上, 如果b 和c 在同一平面上,二者的位置关系为相交; 如果b 和c 不在同一平面上,二者的位置关系为异面.如果b ∥c ,则a ∥b ,与已知a ,b 是异面直线矛盾,故答案为D. 4.已知直线 和平面 ,若 , ,则过点 且平行于 的直线 A .只有一条,不在平面 内 B .只有一条,且在平面 内 C .有无数条,一定在平面 内 D .有无数条,不一定在平面 内【答案】B【解析】假设过点P 且平行于l 的直线有两条m 与n ,则m ∥l 且n ∥l , 由平行公理得m ∥n ,这与两条直线m 与n 相交于点P 相矛盾, 故过点 且平行于 的直线只有一条,又因为点P 在平面内,所以过点P 且平行于l 的直线只有一条且在平面内. 故选B.5.如图,在正方体ABCD −A 1B 1C 1D 1中,E 、F 分别为BC 、BB 1的中点,则下列直线中与直线EF 相交的是A .直线AA 1B .直线A 1B 1C .直线A 1D 1 D .直线B 1C 1【答案】D【解析】只有11B C 与EF 在同一平面内,是相交的,其他A ,B ,C 选项中的直线与EF 都是异面直线,故选D .6.如图所示,平面 平面 , , , , ,则平面 和平面 的交线是A .直线B .直线C .直线D .直线ABC D E F A 1B 1C 1D 1【答案】D【解析】∵l α⊂, ,∴ , 又 ,∴CD α⊂.又 在平面 内,∴ 为平面 与平面 的交线.故选D. 7.设直线l 与平面α平行,直线m 在平面α上,那么 A .直线l 不平行于直线m B .直线l 与直线m 异面 C .直线l 与直线m 没有公共点 D .直线l 与直线m 不垂直【答案】C【解析】∵直线l 与平面α平行,∴由线面平行的定义可知:直线l 与平面α无公共点, 又直线m 在平面α上, ∴直线l 与直线m 没有公共点, 故选C .8.在空间四边形 的边 , , , 上分别取 , , , 四点,如果 , 交于一点 ,则 A . 一定在直线 上 B . 一定在直线 上C . 一定在直线 或 上D . 既不在直线 上,也不在直线 上 【答案】B【解析】由题意, , 相交于点 ,则点 ,且 , 又 平面 , 平面 ,则 平面 ,且 平面 , 则点 必在平面 与平面 的交线上,即点 一定在直线 上. 故选 .9.空间中A B C D E ,,,,五点不共面,已知A B C D ,,,在同一平面内,B C D E ,,,在同一平面内,那么B C D ,,三点 A .一定构成三角形 B .一定共线 C .不一定共线D .与AE ,共面 【答案】B【解析】设平面ABCD 为α,平面BCDE 为β,且A B C D E ,,,,不共面,则,BC CD αα⊂⊂,,BC CD ββ⊂⊂,则,αβ必相交于直线l ,且,,B l C l D l ∈∈∈,故B C D ,,三点一定共线且位于平面ABCD 与平面BCDE 的交线上. 故选B.10.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的余弦值为A .23-B .53 C .23D .255【答案】C【解析】如图,连结BE ,∵在正方体1111ABCD A B C D -中,E 为棱1CC 的中点, ∴CD AB ∥,∴BAE ∠是异面直线AE 与CD 所成的角(或所成角的补角), 设正方体1111ABCD A B C D -的棱长为2, 则2AB =,415BE =+=,AB BE ⊥,则22453AE AB BE =+=+=,∴异面直线AE 与CD 所成角的余弦值为2cos 3AB BAE AE ∠==. 故异面直线AE 与CD 所成角的余弦值为23. 故选C .11.平面 内有不共线的三点到平面 的距离相等且不为零,则 与 的位置关系为 _____ .【答案】平行或相交【解析】若三点分布于平面β的同侧,则α与β平行; 若三点分布于平面β的两侧,则α与β相交. 故 与 的位置关系为平行或相交.12.若直线 和平面 平行,且直线 ,则两直线 和 的位置关系为 _____ . 【答案】平行或异面【解析】由条件可知直线 和 没有公共点,故直线 和 的位置关系为平行或异面.13.若直线l 1与l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则下列命题正确的是A .l 与l 1,l 2都不相交B .l 与l 1,l 2都相交C .l 至多与l 1,l 2中的一条相交D .l 至少与l 1,l 2中的一条相交【答案】D【解析】可用反证法. 假设l 与1l ,2l 都不相交,因为l 与1l 都在平面 内,于是1l l ∥,同理2l l ∥,于是12l l ∥,与已知矛盾,故l 至少与1l ,2l 中的一条相交,故选D .14.已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是A .若 , ,则B .若 , ,则C .若 , ,则D .若 , ,则【答案】D【解析】对于A ,若 ,则m ,n 可能相交、平行、异面,A 错; 对于B ,若 ,则 、 可能相交、平行,B 错; 对于C ,若 ,则 、 可能相交、平行,C 错;对于D ,若 ,根据线面垂直的性质定理可得 ,D 正确. 故选D.15.设,a b 是异面直线,则以下四个命题:①存在分别经过直线,a b 的两个互相垂直的平面;②存在分别经过直线,a b 的两个平行平面;③经过直线a 有且只有一个平面垂直于直线b ;④经过直线a 有且只有一个平面平行于直线b ,其中正确的个数有 A .1 B .2 C .3 D .4【答案】C【解析】对于①,可以在两个互相垂直的平面中,分别画一条直线,当这两条直线异面时,可判断①正确;对于②,可在两个平行平面中,分别画一条直线,当这两条直线异面时,可判断②正确;对于③,当这两条直线不是异面垂直时,不存在这样的平面满足题意,可判断③错误;对于④,假设过直线a有两个平面α、β与直线b平行,则平面α、β相交于直线a,过直线b作一平面γ与平面α、β相交于两条直线m、n,则直线m、n相交于一点,且都与直线b平行,这与“过直线外一点有且只有一条直线与已知直线平行”矛盾,所以假设不成立,所以④正确.故选C.16.我国古代《九章算术》里,记载了一个例子:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”该问题中的羡除是如图所示的五面体,其三个侧面皆为等腰梯形,两个底面为直角三角形,其中尺,尺,尺,间的距离为尺,间的距离为尺,则异面直线与所成角的正弦值为A.9130130B.7130130C.97D.79【答案】B【解析】过点作,如图:根据题意知,所以是异面直线与所成的角,又因为 尺, 尺,且侧面为等腰梯形,则 尺, 间的距离为 尺,故 尺,由勾股定理得 尺, 所以77130sin 130130FDC ∠==. 故选B.17.在长方体1111ABCD A B C D -中,O 是DB 的中点,直线1A C 交平面1C BD 于点M ,则下列结论正确的是①1C 、M 、O 三点共线; ②1C 、M 、A 、C 四点共面; ③1C 、O 、1B 、B 四点共面;④1D 、D 、O 、M 四点共面.A .①②③B .①②③④C .①②D .③④【答案】C【解析】∵O AC ∈,AC ⊂平面11ACC A ,∴O ∈平面11ACC A , ∵O BD ∈,BD ⊂平面1C BD ,∴O ∈平面1C BD , ∴O 是平面11ACC A 和平面1C BD 的公共点;同理可得,点M 和1C 都是平面11ACC A 和平面1C BD 的公共点,根据公理3可得1C 、M ,O 在平面11ACC A 和平面1C BD 的交线上,因此①正确. ∵11AA BB ∥,11BB CC ∥,∴11AA CC ∥,1AA ,1CC 确定一个平面,又1M A C ∈,1AC ⊂平面11ACC A ,∴M ∈平面11ACC A ,故②正确. 根据异面直线的判定定理可得1BB 与1C O 为异面直线,故1C 、O 、1B 、B 四点不共面,故③不正确. 根据异面直线的判定定理可得1DD 与MO 为异面直线, 故1D 、D 、O 、M 四点不共面,故④不正确. 故选C .18.不在同一条直线上的三点A 、B 、C 到平面α的距离相等,且A ∉α,给出以下三个命题:①△ABC 中至少有一条边平行于α;②△ABC 中至多有两边平行于α;③△ABC 中只可能有一条边与α相交.其中真命题是_____________.(填序号) 【答案】①【解析】如图,三点A 、B 、C 可能在α的同侧,也可能在α两侧,其中真命题是①.19.如图所示,若,,,G H M N 分别是三棱柱的顶点或所在棱的中点,则表示直线,GH MN 是异面直线的图形有_____________.(填序号)【答案】②④【解析】①中,GH MN ∥,③中,连接GM ,则GM HN ∥且GM HN ≠,故GH ,MN 必相交,②④符合题意.20.如图,在四棱柱1111ABCD A B C D -中,侧面都是矩形,底面四边形ABCD 是菱形且23AB BC ==,120ABC ∠=︒,若异面直线1A B 和1AD 所成的角为90︒,则1AA 的长为_____________.【答案】6【解析】如图,连接1CD AC ,.由题意得四棱柱1111ABCD A B C D -中,11∥A D BC ,11A D BC =, ∴四边形11A BCD 是平行四边形,11A B CD ∴∥,1AD C ∴∠(或其补角)为1A B 和1AD 所成的角.∵异面直线1A B 和1AD 所成的角为90︒,190AD C ∴∠=︒.∵四棱柱1111ABCD A B C D -中,侧面都是矩形,底面四边形ABCD 是菱形,1△ACD ∴是等腰直角三角形,122AD AC ∴=.∵底面四边形ABCD 是菱形且23AB BC ==,120ABC ∠=︒,23sin 6026AC ∴=⨯︒⨯=,12322AD AC ==, ()()2222111132236AA AD A D ∴=-=-=.21.(2019年高考全国Ⅲ卷理数)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线 【答案】B【解析】如图所示,作EO CD ⊥于O ,连接ON ,BD ,易得直线BM ,EN 是三角形EBD 的中线,是相交直线.过M 作MF OD ⊥于F ,连接BF ,平面CDE ⊥平面ABCD ,,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴△与EON △均为直角三角形.设正方形边长为2,易知3,12EO ON EN ===,,35,,722MF BF BM ==∴=,BM EN ∴≠. 故选B .【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.22.(2018新课标全国Ⅱ理科)在长方体1111ABCD A B C D -中,1AB BC ==,13AA =,则异面直线1AD 与1DB 所成角的余弦值为A .15B .56C .55D .22【答案】C【解析】用一个与原长方体相同的长方体拼到原长方体的前面, 如图,则11B P AD ∥,连接DP ,易求得1=5DB DP =,12B P =,则1DB P ∠是异面直线1AD 与1DB 所成的角,由余弦定理可得222111115455cos 2545DB B P DP DB P DB PB +-+-∠===⋅. 故选C.23.(2017新课标全国Ⅱ理科)已知直三棱柱111ABC A B C -中,120ABC ∠=︒,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为A .32B .155 C .105D .33【答案】C【解析】如图所示,补成直四棱柱1111ABCD A B C D -, 则所求角为21111,2,21221cos603,5BC D BC BD C D AB ∠==+-⨯⨯⨯︒===,易得22211C D BD BC =+,因此111210cos 55BC BC D C D ∠===. 故选C .【名师点睛】平移法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角; ②认定:证明作出的角就是所求异面直线所成的角; ③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是(0,]2π,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.求异面直线所成的角要特别注意异面直线之间所成角的范围.24.(2015安徽理科)已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是A .若α,β垂直于同一平面,则α与β平行B .若m ,n 平行于同一平面,则m 与n 平行C .若α,β不平行,则在α内不存在与β平行的直线D .若m ,n 不平行,则m 与n 不可能垂直于同一平面 【答案】D【解析】由A ,若α,β垂直于同一平面,则α,β可以相交、平行,故A 不正确; 由B ,若m ,n 平行于同一平面,则m ,n 可以平行、重合、相交、异面,故B 不正确;由C ,若α,β不平行,但α平面内会存在平行于β的直线,如α平面中平行于α,β交线的直线,故C 不正确;由D ,其逆否命题为“若m 与n 垂直于同一平面,则m ,n 平行”是真命题,故D 项正确. 所以选D.25.(2016新课标全国Ⅰ理科)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α//平面CB 1D 1,αI 平面ABCD =m ,αI 平面ABB 1 A 1=n ,则m ,n 所成角的正弦值为A .32B .22C .33D .13【答案】A【解析】如图,设平面11CB D 平面ABCD ='m ,平面11CB D 平面11ABB A ='n ,因为α∥平面11CB D ,所以','m m n n ∥∥,则,m n 所成的角等于','m n 所成的角. 过1D 作11D E B C ∥,交AD 的延长线于点E ,连接CE ,则CE 为'm . 连接1A B ,过B 1作111B F A B ∥,交1AA 的延长线于点1F ,则11B F 为'n . 连接BD ,则111,BD CE B F A B ∥∥,则','m n 所成的角即为1,A B BD 所成的角,为60︒, 故,m n 所成角的正弦值为32, 选A.【名师点睛】求解本题的关键是作出异面直线所成的角,求异面直线所成角的步骤是:平移定角、连线成形、解形求角、得钝求补.26.(2017新课标全国Ⅲ理科) a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角; ②当直线AB 与a 成60°角时,AB 与b 成60°角; ③直线AB 与a 所成角的最小值为45°; ④直线AB 与a 所成角的最大值为60°.其中正确的是________.(填写所有正确结论的编号) 【答案】②③【解析】设1AC BC ==.由题意,AB 是以AC 为轴,BC 为底面半径的圆锥的母线,由,AC a AC b ⊥⊥,又AC ⊥圆锥底面,所以在底面内可以过点B ,作BD a ∥,交底面圆C 于点D ,如图所示,连接DE ,则DE ⊥BD ,DE b ∴∥,连接AD ,等腰ABD △中,2AB AD ==,当直线AB 与a 成60°角时,60ABD ∠=,故2BD =,又在Rt BDE △中,2,2BE DE =∴=,过点B 作BF ∥DE ,交圆C于点F ,连接AF ,由圆的对称性可知2BF DE ==,ABF ∴△为等边三角形,60ABF ∴∠=,即AB 与b 成60°角,②正确,①错误.由图可知③正确;很明显,可以满足平面ABC ⊥直线a ,则直线AB 与a 所成角的最大值为90°,④错误.故正确的是②③.【名师点睛】(1)平移直线法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角;②认定:证明作出的角就是所求异面直线所成的角;③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是π0,2⎛⎤⎥⎝⎦,可知当求出的角为钝角时,应取它的补角作为两条异面直线所成的角.(2)求异面直线所成的角要特别注意异面直线之间所成角的范围.。
文科数学学霸笔记29 空间点、直线、平面之间的位置关系

两条直线互相垂直.两条互相垂直的异面直线a,b,记作a⊥b.4.常用结论(1)唯一性定理①过直线外一点有且只有一条直线与已知直线平行.②过直线外一点有且只有一个平面与已知直线垂直.③过平面外一点有且只有一个平面与已知平面平行.④过平面外一点有且只有一条直线与已知平面垂直.(2)异面直线的判定方法经过平面内一点的直线与平面内不经过该点的直线互为异面直线.二、平面的基本性质及应用(1)证明点共线问题,就是证明三个或三个以上的点在同一条直线上,主要依据是公理 3.常用方法有:①首先找出两个平面,然后证明这些点都是这两个平面的公共点,根据公理3知这些点都在这两个平面的交线上;②选择其中两点确定一条直线,然后证明其他点也在这条直线上.(2)证明三线共点问题,一般先证明待证的三条直线中的两条相交于一点,再证明第三条直线也过该点.常结合公理3,证明该点在不重合的两个平面内,故该点在它们的交线(第三条直线)上,从而证明三线共点.(3)证明点或线共面问题,主要有两种方法:①首先由所给条件中的部分线(或点)确定一个平面,然后再证其余的线(或点)在这个平面内;②将所有条件分为两部分,然后分别确定平面,再证两平面重合.三、空间线面位置关系的判断1.异面直线的判定方法:(1)反证法:先假设两条直线不是异面直线,即两条直线平行或相交,由假设出发,经过严格的推理,导出矛盾,从而否定假设,肯定两条直线异面.(2)定理:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.2.点、线、面位置关系的判定,要注意几何模型的选取,常借助正方体为模型,以正方体为主线直观感知并认识空间点、线、面的位置关系.四、异面直线所成的角求异面直线所成的角的常见策略:(1)求异面直线所成的角常用平移法.平移法有三种类型,利用图中已有的平行线平移,利用特殊点(线段的端点或中点)作平行线平移,利用补形平移.(2)求异面直线所成角的步骤①一作:即根据定义作平行线,作出异面直线所成的角;②二证:即证明作出的角是异面直线所成的角;③三求:解三角形,求出作出的角.如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角.。
高考数学复习空间点、直线、平面之间的位置关系

第2讲 空间点、直线、平面之间的位置关系最新考纲考向预测借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系的定义,了解公理1~4及其相关定理.命题趋势主要考查与点、线、面位置关系有关的命题真假判断和求解异面直线所成的角,主要以选择题和填空题的形式出现,主要为中低档题.核心素养 直观想象、逻辑推理1.四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 公理2:过不在一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.公理4:平行于同一条直线的两条直线互相平行. 2.空间直线的位置关系 (1)位置关系的分类⎩⎨⎧共面直线⎩⎨⎧平行相交异面直线:不同在任何一个平面内 (2)异面直线所成的角①定义:设a ,b 是两条异面直线,经过空间中任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).②范围:⎝ ⎛⎥⎤0,π2.(3)等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. 3.空间中直线与平面、平面与平面的位置关系(1)空间中直线和平面的位置关系位置关系图形表示符号表示公共点直线a在平面α内a⊂α有无数个公共点直线在平面外直线a与平面α平行a∥α没有公共点直线a与平面α斜交a∩α=A有且只有一个公共点直线a与平面α垂直a⊥α(2)空间中两个平面的位置关系位置关系图形表示符号表示公共点两平面平行α∥β没有公共点两平面相交斜交α∩β=l有一条公共直线垂直α⊥β且α∩β=a常用结论1.公理2的三个推论推论1:经过一条直线和这条直线外一点有且只有一个平面;推论2:经过两条相交直线有且只有一个平面;推论3:经过两条平行直线有且只有一个平面.2.异面直线判定的一个定理过平面外一点和平面内一点的直线,与平面内不过该点的直线是异面直线.常见误区1.异面直线易误解为“分别在两个不同平面内的两条直线为异面直线”,实质上两异面直线不能确定任何一个平面,因此异面直线即不平行,也不相交.2.在判断直线与平面的位置关系时最易忽视“线在平面内”.1.判断正误(正确的打“√”,错误的打“×”)(1)若P∈α∩β且l是α,β的交线,则P∈l.()(2)三点A,B,C确定一个平面.()(3)若直线a∩b=A,则直线a与b能够确定一个平面.()(4)若A∈l,B∈l且A∈α,B∈α,则l⊂α.()(5)分别在两个平面内的两条直线是异面直线.()答案:(1)√(2)×(3)√(4)√(5)×2.(多选)α是一个平面,m,n是两条直线,A是一个点,若m⊄α,n⊂α,且A∈m,A∈α,则m,n的位置关系可能是()A.垂直B.相交C.异面D.平行解析:选ABC.依题意,m∩α=A,n⊂α,所以m与n可能异面、相交(垂直是相交的特例),一定不平行.3.若∠AOB=∠A1O1B1,且OA∥O1A1,OA与O1A1的方向相同,则下列结论中正确的是()A.OB∥O1B1且方向相同B.OB∥O1B1C.OB与O1B1不平行D.OB与O1B1不一定平行解析:选 D.两角相等,角的一边平行且方向相同,另一边不一定平行,故选D.4.(易错题)如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD 的中点,则异面直线B1C与EF所成角的大小为________.解析:连接B1D1,D1C,则B1D1∥EF,故∠D1B1C为所求角,又B1D1=B1C =D1C,所以∠D1B1C=60°.答案:60°5.如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA 的中点,则(1)当AC,BD满足条件________时,四边形EFGH为菱形;(2)当AC,BD满足条件________时,四边形EFGH为正方形.解析:(1)因为四边形EFGH为菱形,所以EF=EH,故AC=BD.(2)因为四边形EFGH为正方形,所以EF=EH且EF⊥EH,因为EF綊12AC,EH綊12BD,所以AC=BD且AC⊥BD.答案:(1)AC=BD(2)AC=BD且AC⊥BD平面的基本性质如图所示,在正方体ABCD-A1B1C1D中,E,F分别是AB和AA1的中点,求证:E,C,D1,F四点共面.【证明】如图所示,连接CD1,EF,A1B,因为E,F分别是AB和AA1的中点,所以EF∥A1B且EF=12A1B.又因为A1D1綊BC,所以四边形A1BCD1是平行四边形,所以A1B∥CD1,所以EF∥CD1,所以EF与CD1确定一个平面α,所以E,F,C,D1∈α,即E,C,D1,F四点共面.【引申探究】(变问法)若本例条件不变,如何证明“CE,D1F,DA交于一点”?证明:如图,由本例知EF∥CD1,且EF=12CD1,所以四边形CD1FE是梯形,所以CE与D1F必相交,设交点为P,则P∈CE且P∈D1F,又CE⊂平面ABCD,且D1F⊂平面A1ADD1,所以P∈平面ABCD,且P∈平面A1ADD1.又平面ABCD∩平面A1ADD1=AD,所以P∈AD,所以CE,D1F,DA三线交于一点.共面、共线、共点问题的证明方法(1)证明点或线共面:①首先由所给条件中的部分线(或点)确定一个平面,然后再证其余的线(或点)在这个平面内;②将所有条件分为两部分,然后分别确定平面,再证两平面重合.(2)证明点共线:①先由两点确定一条直线,再证其他各点都在这条直线上;②直接证明这些点都在同一条特定的直线上.(3)证明线共点:先证其中两条直线交于一点,再证其他直线经过该点. [提醒] 点共线、线共点等都是应用公理3,证明点为两平面的公共点,即证明点在交线上.1.(多选)如图,在长方体ABCD -A 1B 1C 1D 1中,O 是DB 的中点,直线A 1C 交平面C 1BD 于点M ,则下列结论正确的是( )A .C 1,M ,O 三点共线B .C 1,M ,O ,C 四点共面 C .C 1,O ,A 1,M 四点共面D .D 1,D ,O ,M 四点共面解析:选ABC.连接A 1C 1,AC ,则AC ∩BD =O ,又A 1C ∩平面C 1BD =M ,所以三点C 1,M ,O 在平面C 1BD 与平面ACC 1A 1的交线上,所以C 1,M ,O 三点共线,所以选项A ,B ,C 均正确,选项D 错误.2.如图,空间四边形ABCD 中,E ,F 分别是AB ,AD 的中点,G ,H 分别在BC ,CD 上,且BG ∶GC =DH ∶HC =1∶2.(1)求证:E ,F ,G ,H 四点共面;(2)设EG 与FH 交于点P ,求证:P ,A ,C 三点共线.证明:(1)因为E ,F 分别为AB ,AD 的中点,所以EF ∥BD .在△BCD 中,BG GC =DH HC =12,所以GH ∥BD ,所以EF ∥GH ,所以E ,F ,G ,H 四点共面.(2)因为EG ∩FH =P ,P ∈EG ,EG ⊂平面ABC ,所以P∈平面ABC.同理P∈平面ADC .所以P为平面ABC与平面ADC的公共点,又平面ABC∩平面ADC=AC,所以P∈AC,所以P,A,C三点共线.空间两直线的位置关系(2019·高考全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线【解析】如图,取CD的中点F,连接EF,EB,BD,FN,因为△CDE 是正三角形,所以EF⊥CD.设CD=2,则EF= 3.因为点N是正方形ABCD的中心,所以BD=22,NF=1,BC⊥CD.因为平面ECD⊥平面ABCD,所以EF⊥平面ABCD,BC⊥平面ECD,所以EF⊥NF,BC⊥EC,所以在Rt△EFN中,EN=2,在Rt△BCE中,EB=22,所以在等腰三角形BDE中,BM=7,所以BM≠EN.易知BM,EN是相交直线.故选B.【答案】 B1.已知a,b是异面直线,A,B是a上的两点,C,D是b上的两点,M,N分别是线段AC,BD的中点,则MN和a的位置关系是()A.异面B.平行C.相交D.以上均有可能解析:选A.若MN与AB平行或相交,则MN与AB共面,设该平面为α.因为C∈直线AM,D∈直线BN,所以C∈α,D∈α,所以b⊂α.又因为A∈α,B ∈α,所以a⊂α.这与a,b异面矛盾.故选A.2.(多选)如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C 的中点,下列说法正确的有()A.直线AM与CC1是相交直线B.直线AM与BN是平行直线C.直线BN与MB1是异面直线D.直线AM与DD1是异面直线解析:选CD.因为点A在平面CDD1C1外,点M在平面CDD1C1内,直线CC1在平面CDD1C1内,CC1不过点M,所以AM与CC1是异面直线,故A错;取DD1的中点E,连接AE(图略),则BN∥AE,但AE与AM相交,故B错;因为B1与BN都在平面BCC1B1内,M在平面BCC1B1外,BN不过点B1,所以BN 与MB1是异面直线,故C正确;同理D正确,故选CD.异面直线所成的角(1)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB 的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为________.(2)四面体ABCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=1,则EF的长为________.【解析】(1)取圆柱下底面弧AB的另一中点D,连接C1D,AD,因为C是圆柱下底面弧AB的中点,所以AD∥BC,所以直线AC1与AD所成的角即为异面直线AC1与BC所成的角,因为C1是圆柱上底面弧A1B1的中点,所以C1D垂直于圆柱下底面,所以C1D⊥AD.因为圆柱的轴截面ABB1A1是正方形,所以C1D=2AD,所以直线AC1与AD所成角的正切值为2,所以异面直线AC1与BC所成角的正切值为 2.(2)如图,取BC的中点O,连接OE,OF,因为OE∥AC,OF∥BD,所以OE与OF所成的锐角(或直角)即为AC与BD所成的角,而AC,BD所成角为60°,所以∠EOF =60°或∠EOF =120°.当∠EOF =60°时,EF =OE =OF =12.当∠EOF =120°时,取EF 的中点M ,则OM ⊥EF , EF =2EM =2×34=32. 【答案】 (1)2 (2)12或32平移法求异面直线所成角的步骤具体步骤如下:1.直三棱柱ABC -A 1B 1C 1中,若∠BAC =90°,AB =AC =AA 1,则异面直线BA 1与AC 1所成的角等于( )A .30°B .45°C .60°D .90°解析:选C.如图,可补成一个正方体,所以AC 1∥BD 1.所以BA 1与AC 1所成的角为∠A 1BD 1.又易知△A1BD1为正三角形.所以∠A1BD1=60°.即BA1与AC1所成的角为60°.2.(2021·济南市学习质量评估)如图,在正方形ABCD中,点E,F分别为BC,AD的中点,将四边形CDFE沿EF翻折,使得平面CDFE⊥平面ABEF,则异面直线BD与CF所成角的余弦值为________.解析:如图,连接DE交FC于点O,取BE的中点G,连接OG,CG,则OG∥BD且OG=12BD,所以∠COG为异面直线BD与CF所成的角或其补角.设正方形ABCD的边长为2,则CE=BE=1,CF=DE=CD2+CE2=5,所以CO=12CF=52.易得BE⊥平面CDFE,所以BE⊥DE,所以BD=DE2+BE2=6,所以OG=12BD=62.易知CE⊥平面ABEF,所以CE⊥BE,又GE=12BE=12,所以CG=CE2+GE2=52.在△COG中,由余弦定理得,cos∠COG=OC2+OG2-CG22OC·OG=⎝⎛⎭⎪⎫522+⎝⎛⎭⎪⎫622-⎝⎛⎭⎪⎫5222×52×62=3010,所以异面直线BD与CF所成角的余弦值为30 10.答案:3010[A级基础练]1.已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面解析:选D.依题意,直线b和c的位置关系可能是相交、平行或异面.故选D.2.(多选)下列命题正确的是()A.梯形一定是平面图形B.若两条直线和第三条直线所成的角相等,则这两条直线平行C.两两相交的三条直线最多可以确定三个平面D.若两个平面有三个公共点,则这两个平面重合解析:选AC.对于A,由于两条平行直线确定一个平面,所以梯形可以确定一个平面,故A正确;对于B,两条直线和第三条直线所成的角相等,则这两条直线平行或异面或相交,故B错误;对于C,两两相交的三条直线最多可以确定三个平面,故C正确;对于D,若两个平面有三个公共点,则这两个平面相交或重合,故D错误.3.(2021·安徽蚌埠第二中学期中)在四面体ABCD中,点E,F,G,H分别在直线AD,AB,CD,BC上,若直线EF和GH相交,则它们的交点一定() A.在直线DB上B.在直线AB上C.在直线CB上D.都不对解析:选A.直线EF和GH相交,设其交点为M.因为EF⊂平面ABD,HG ⊂平面CBD,所以M∈平面ABD且M∈平面CBD.因为平面ABD∩平面BCD=BD,所以M∈BD,所以EF与HG的交点在直线BD上.故选A.4.如图所示,平面α∩平面β=l,A∈α,B∈α,AB∩l=D,C∈β,C∉l,则平面ABC与平面β的交线是()A.直线AC B.直线ABC.直线CD D.直线BC解析:选C.由题意知,D∈l,l⊂β,所以D∈β,又因为D∈AB,所以D∈平面ABC,所以点D在平面ABC与平面β的交线上.又因为C∈平面ABC,C∈β,所以点C在平面β与平面ABC的交线上,所以平面ABC∩平面β=CD.5.如图,在三棱柱ABC-A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是()A.CC1与B1E是异面直线B.C1C与AE共面C.AE与B1C1是异面直线D.AE与B1C1所成的角为60°解析:选C.由于CC1与B1E都在平面C1B1BC内,故C1C与B1E是共面的,所以A错误;由于C1C在平面C1B1BC内,而AE与平面C1B1BC相交于E点,点E不在C1C上,故C1C与AE是异面直线,B错误;同理AE与B1C1是异面直线,C正确;而AE与B1C1所成的角就是AE与BC所成的角,E为BC中点,△ABC为正三角形,所以AE⊥BC,D错误.6.已知棱长为a的正方体ABCD-A′B′C′D′中,M,N分别为CD,AD的中点,则MN与A′C′的位置关系是________.解析:如图,由题意可知MN∥AC.又因为AC ∥A ′C ′,所以MN ∥A ′C ′.答案:平行7.(2020·高考全国卷Ⅰ)如图,在三棱锥P -ABC 的平面展开图中,AC =1,AB =AD =3,AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB =________.解析:依题意得,AE =AD =3,在△AEC 中,AC =1,∠CAE =30°,由余弦定理得EC 2=AE 2+AC 2-2AE ·AC cos ∠EAC =3+1-23cos 30°=1,所以EC =1,所以CF =EC =1.又BC =AC 2+AB 2=1+3=2,BF =BD =AD 2+AB 2=6,所以在△BCF 中,由余弦定理得cos ∠FCB =BC 2+CF 2-BF 22BC ×CF =22+12-(6)22×2×1=-14. 答案:-148.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,则异面直线AP 与BD 所成的角为________.解析:如图,将原图补成正方体ABCD -QGHP ,连接AG ,GP ,则GP ∥BD ,所以∠APG 为异面直线AP 与BD 所成的角,在△AGP 中,AG =GP =AP ,所以∠APG =π3.答案:π39.如图,在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N三点的平面与正方体的下底面相交于直线l.(1)画出l的位置;(2)设l∩A1B1=P,求PB1的长.解:(1)如图,延长DM与D1A1交于点O,连接NO,则直线NO即为直线l.(2)因为l∩A1B1=P,则易知直线NO与A1B1的交点即为P.所以A1M∥DD1,且M,N分别是AA1,D1C1的中点,所以A1也为D1O的中点.由图可知A1PD1N=OA1OD1=12,所以A1P=a4,从而可知PB1=3a4.10.如图所示,A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.(1)求证:直线EF与BD是异面直线;(2)若AC⊥BD,AC=BD,求EF与BD所成的角.解:(1)证明:假设EF与BD不是异面直线,则EF与BD共面,从而DF 与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内,这与A是△BCD 所在平面外的一点相矛盾.故直线EF与BD是异面直线.(2)取CD的中点G,连接EG,FG,则AC∥FG,EG∥BD,所以相交直线EF与EG所成的角,即为异面直线EF与BD所成的角.又因为AC⊥BD,则FG⊥EG.在Rt△EGF中,由EG=FG=12AC,求得∠FEG=45°,即异面直线EF与BD所成的角为45°.[B级综合练]11.已知直线l⊄平面α,直线m⊂平面α,给出下面四个结论:①若l与m 不垂直,则l与α一定不垂直;②若l与m所成的角为30°,则l与α所成的角也为30°;③l∥m是l∥α的必要不充分条件;④若l与α相交,则l与m一定是异面直线.其中正确结论的个数为()A.1B.2C.3D.4解析:选A.对于①,当l与m不垂直时,假设l⊥α,那么由l⊥α一定能得到l⊥m,这与已知条件矛盾,因此l与α一定不垂直,故①正确;对于②,易知l与m所成的角为30°时,l与α所成的角不一定为30°,故②不正确;对于③,l∥m可以推出l∥α,但是l∥α不能推出l∥m,因此l∥m是l∥α的充分不必要条件,故③不正确;对于④,若l与α相交,则l与m相交或异面,故④不正确.故正确结论的个数为1,选A.12.如图,在正方体ABCD-A′B′C′D′中,平面α垂直于对角线AC′,且平面α截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则()A.S为定值,l不为定值B.S不为定值,l为定值C.S与l均为定值D.S与l均不为定值解析:选B.设平面α截得正方体的六个表面得到截面六边形ω,ω与正方体的棱的交点分别为I,J,N,M,L,K(如图).将正方体切去两个正三棱锥AA′BD和C′B′CD′,得到一个几何体V,则V的上、下底面B′CD′与A′BD互相平行,每个侧面都是等腰直角三角形,截面六边形ω的每一条边分别与V的底面上的每一条边平行.设正方体的棱长为a ,A ′K A ′B ′=γ,则IK =γB ′D ′=2aγ,KL =(1-γ)A ′B =2a (1-γ),故IK +KL =2aγ+2a (1-γ)=2a .同理可证LM +MN =NJ +IJ =2a ,故六边形ω周长为32a ,即周长为定值.当I ,J ,N ,M ,L ,K 都在对应棱的中点时,ω是正六边形.其面积S =6×12×⎝ ⎛⎭⎪⎫22a 2×32=334a 2,△A ′BD 的面积为12×(2a )2×32=32a 2,当ω无限趋近于△A ′BD 时,ω的面积无限趋近于32a 2,故ω的面积一定会发生变化,不为定值.故选B.13.如图,四边形ABEF 和ABCD 都是直角梯形,∠BAD =∠F AB =90°,BC 綊12AD ,BE 綊12F A ,G ,H 分别为F A ,FD 的中点.(1)证明:四边形BCHG 是平行四边形;(2)C ,D ,F ,E 四点是否共面?为什么?解:(1)证明:由已知FG =GA ,FH =HD 可得GH 綊12AD .又BC 綊12AD ,所以GH 綊BC .所以四边形BCHG 为平行四边形.(2)C ,D ,F ,E 四点共面,理由如下:由BE 綊12AF ,G 为F A 的中点知,BE 綊FG ,所以四边形BEFG 为平行四边形,所以EF ∥BG .由(1)知BG ∥CH ,所以EF ∥CH ,所以EF 与CH 共面,又D ∈FH ,所以C ,D ,F ,E 四点共面.14.如图,E ,F ,G ,H 分别是空间四边形ABCD 各边上的点,且AE ∶EB =AH ∶HD =m ,CF ∶FB =CG ∶GD =n .(1)证明:E,F,G,H四点共面;(2)m,n满足什么条件时,四边形EFGH是平行四边形?(3)在(2)的条件下,若AC⊥BD,试证明:EG=FH.解:(1)证明:因为AE∶EB=AH∶HD,所以EH∥BD.又CF∶FB=CG∶GD,所以FG∥BD.所以EH∥FG.所以E,F,G,H四点共面.(2)当m=n时,四边形EFGH为平行四边形,理由如下:当EH∥FG,且EH=FG时,四边形EFGH为平行四边形.因为EHBD=AEAE+EB=mm+1,所以EH=mm+1BD.同理可得FG=nn+1BD,由EH=FG,得m=n.故当m=n时,四边形EFGH为平行四边形.(3)证明:当m=n时,AE∶EB=CF∶FB,所以EF∥AC,又EH∥BD,所以∠FEH是AC与BD所成的角(或其补角),因为AC⊥BD,所以∠FEH=90°,从而平行四边形EFGH为矩形,所以EG=FH.[C级创新练]15.平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为()A.32 B.22 C.33 D.13解析:选A.如图所示,设平面CB1D1∩平面ABCD=m1,因为α∥平面CB1D1,则m1∥m,又因为平面ABCD∥平面A1B1C1D1,平面CB1D1∩平面A1B1C1D1=B1D1,所以B 1D 1∥m 1,所以B 1D 1∥m ,同理可得CD 1∥n .故m ,n 所成角的大小与B 1D 1,CD 1所成角的大小相等,即∠CD 1B 1的大小. 又因为B 1C =B 1D 1=CD 1(均为面对角线),所以∠CD 1B 1=π3, 得sin ∠CD 1B 1=32,故选A.16.(2020·新高考卷Ⅰ)已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.解析:如图,连接B 1D 1,易知△B 1C 1D 1为正三角形,所以B 1D 1=C 1D 1=2.分别取B 1C 1,BB 1,CC 1的中点M ,G ,H ,连接D 1M ,D 1G ,D 1H ,则易得D 1G =D 1H =22+12=5,D 1M ⊥B 1C 1,且D 1M = 3.由题意知G ,H 分别是BB 1,CC 1与球面的交点.在侧面BCC 1B 1内任取一点P ,使MP =2,连接D 1P ,则D 1P = D 1M 2+MP 2=(3)2+(2)2=5,连接MG ,MH ,易得MG =MH =2,故可知以M 为圆心,2为半径的圆弧GH 为球面与侧面BCC 1B 1的交线.由∠B 1MG =∠C 1MH =45°知∠GMH =90°,所以GH ︵的长为14×2π×2=2π2.答案:2π2第2讲 空间点、直线、平面之间的位置关系 最新考纲考向预测 借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系的定义,了解公理1~4及其相关定理. 命题趋势 主要考查与点、线、面位置关系有关的命题真假判断和求解异面直线所成的角,主要以选择题和填空题的形式出现,主要为中低档题. 核心素养 直观想象、逻辑推理1.四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 公理2:过不在一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.公理4:平行于同一条直线的两条直线互相平行.2.空间直线的位置关系(1)位置关系的分类⎩⎨⎧共面直线⎩⎨⎧平行相交异面直线:不同在任何一个平面内(2)异面直线所成的角①定义:设a ,b 是两条异面直线,经过空间中任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).②范围:⎝⎛⎦⎥⎤0,π2. (3)等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.3.空间中直线与平面、平面与平面的位置关系(1)空间中直线和平面的位置关系位置关系图形表示符号表示公共点直线a在平面α内a⊂α有无数个公共点直线在平面外直线a与平面α平行a∥α没有公共点直线a与平面α斜交a∩α=A有且只有一个公共点直线a与平面α垂直a⊥α(2)空间中两个平面的位置关系位置关系图形表示符号表示公共点两平面平行α∥β没有公共点两平面相交斜交α∩β=l有一条公共直线垂直α⊥β且α∩β=a常用结论1.公理2的三个推论推论1:经过一条直线和这条直线外一点有且只有一个平面;推论2:经过两条相交直线有且只有一个平面;推论3:经过两条平行直线有且只有一个平面.2.异面直线判定的一个定理过平面外一点和平面内一点的直线,与平面内不过该点的直线是异面直线.常见误区1.异面直线易误解为“分别在两个不同平面内的两条直线为异面直线”,实质上两异面直线不能确定任何一个平面,因此异面直线即不平行,也不相交.2.在判断直线与平面的位置关系时最易忽视“线在平面内”.1.判断正误(正确的打“√”,错误的打“×”)(1)若P∈α∩β且l是α,β的交线,则P∈l.()(2)三点A,B,C确定一个平面.()(3)若直线a∩b=A,则直线a与b能够确定一个平面.()(4)若A∈l,B∈l且A∈α,B∈α,则l⊂α.()(5)分别在两个平面内的两条直线是异面直线.()答案:(1)√(2)×(3)√(4)√(5)×2.(多选)α是一个平面,m,n是两条直线,A是一个点,若m⊄α,n⊂α,且A∈m,A∈α,则m,n的位置关系可能是()A.垂直B.相交C.异面D.平行解析:选ABC.依题意,m∩α=A,n⊂α,所以m与n可能异面、相交(垂直是相交的特例),一定不平行.3.若∠AOB=∠A1O1B1,且OA∥O1A1,OA与O1A1的方向相同,则下列结论中正确的是()A.OB∥O1B1且方向相同B.OB∥O1B1C.OB与O1B1不平行D.OB与O1B1不一定平行解析:选 D.两角相等,角的一边平行且方向相同,另一边不一定平行,故选D.4.(易错题)如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD 的中点,则异面直线B1C与EF所成角的大小为________.解析:连接B1D1,D1C,则B1D1∥EF,故∠D1B1C为所求角,又B1D1=B1C =D1C,所以∠D1B1C=60°.答案:60°5.如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA 的中点,则(1)当AC,BD满足条件________时,四边形EFGH为菱形;(2)当AC,BD满足条件________时,四边形EFGH为正方形.解析:(1)因为四边形EFGH为菱形,所以EF=EH,故AC=BD.(2)因为四边形EFGH为正方形,所以EF=EH且EF⊥EH,因为EF綊12AC,EH綊12BD,所以AC=BD且AC⊥BD.答案:(1)AC=BD(2)AC=BD且AC⊥BD平面的基本性质如图所示,在正方体ABCD-A1B1C1D中,E,F分别是AB和AA1的中点,求证:E,C,D1,F四点共面.【证明】如图所示,连接CD1,EF,A1B,因为E,F分别是AB和AA1的中点,所以EF∥A1B且EF=12A1B.又因为A1D1綊BC,所以四边形A1BCD1是平行四边形,所以A1B∥CD1,所以EF∥CD1,所以EF与CD1确定一个平面α,所以E,F,C,D1∈α,即E,C,D1,F四点共面.【引申探究】(变问法)若本例条件不变,如何证明“CE,D1F,DA交于一点”?证明:如图,由本例知EF∥CD1,且EF=12CD1,所以四边形CD1FE是梯形,所以CE与D1F必相交,设交点为P,则P∈CE且P∈D1F,又CE⊂平面ABCD,且D1F⊂平面A1ADD1,所以P∈平面ABCD,且P∈平面A1ADD1.又平面ABCD∩平面A1ADD1=AD,所以P∈AD,所以CE,D1F,DA三线交于一点.共面、共线、共点问题的证明方法(1)证明点或线共面:①首先由所给条件中的部分线(或点)确定一个平面,然后再证其余的线(或点)在这个平面内;②将所有条件分为两部分,然后分别确定平面,再证两平面重合.(2)证明点共线:①先由两点确定一条直线,再证其他各点都在这条直线上;②直接证明这些点都在同一条特定的直线上.(3)证明线共点:先证其中两条直线交于一点,再证其他直线经过该点. [提醒] 点共线、线共点等都是应用公理3,证明点为两平面的公共点,即证明点在交线上.1.(多选)如图,在长方体ABCD -A 1B 1C 1D 1中,O 是DB 的中点,直线A 1C 交平面C 1BD 于点M ,则下列结论正确的是( )A .C 1,M ,O 三点共线B .C 1,M ,O ,C 四点共面 C .C 1,O ,A 1,M 四点共面D .D 1,D ,O ,M 四点共面解析:选ABC.连接A 1C 1,AC ,则AC ∩BD =O ,又A 1C ∩平面C 1BD =M ,所以三点C 1,M ,O 在平面C 1BD 与平面ACC 1A 1的交线上,所以C 1,M ,O 三点共线,所以选项A ,B ,C 均正确,选项D 错误.2.如图,空间四边形ABCD 中,E ,F 分别是AB ,AD 的中点,G ,H 分别在BC ,CD 上,且BG ∶GC =DH ∶HC =1∶2.(1)求证:E ,F ,G ,H 四点共面;(2)设EG 与FH 交于点P ,求证:P ,A ,C 三点共线.证明:(1)因为E ,F 分别为AB ,AD 的中点,所以EF ∥BD .在△BCD 中,BG GC =DH HC =12,所以GH ∥BD ,所以EF ∥GH ,所以E ,F ,G ,H 四点共面.(2)因为EG ∩FH =P ,P ∈EG ,EG ⊂平面ABC ,所以P∈平面ABC.同理P∈平面ADC .所以P为平面ABC与平面ADC的公共点,又平面ABC∩平面ADC=AC,所以P∈AC,所以P,A,C三点共线.空间两直线的位置关系(2019·高考全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线【解析】如图,取CD的中点F,连接EF,EB,BD,FN,因为△CDE 是正三角形,所以EF⊥CD.设CD=2,则EF= 3.因为点N是正方形ABCD的中心,所以BD=22,NF=1,BC⊥CD.因为平面ECD⊥平面ABCD,所以EF⊥平面ABCD,BC⊥平面ECD,所以EF⊥NF,BC⊥EC,所以在Rt△EFN中,EN=2,在Rt△BCE中,EB=22,所以在等腰三角形BDE中,BM=7,所以BM≠EN.易知BM,EN是相交直线.故选B.【答案】 B1.已知a,b是异面直线,A,B是a上的两点,C,D是b上的两点,M,N分别是线段AC,BD的中点,则MN和a的位置关系是()A.异面B.平行C.相交D.以上均有可能解析:选A.若MN与AB平行或相交,则MN与AB共面,设该平面为α.因为C∈直线AM,D∈直线BN,所以C∈α,D∈α,所以b⊂α.又因为A∈α,B ∈α,所以a⊂α.这与a,b异面矛盾.故选A.2.(多选)如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C 的中点,下列说法正确的有()A.直线AM与CC1是相交直线B.直线AM与BN是平行直线C.直线BN与MB1是异面直线D.直线AM与DD1是异面直线解析:选CD.因为点A在平面CDD1C1外,点M在平面CDD1C1内,直线CC1在平面CDD1C1内,CC1不过点M,所以AM与CC1是异面直线,故A错;取DD1的中点E,连接AE(图略),则BN∥AE,但AE与AM相交,故B错;因为B1与BN都在平面BCC1B1内,M在平面BCC1B1外,BN不过点B1,所以BN 与MB1是异面直线,故C正确;同理D正确,故选CD.异面直线所成的角(1)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB 的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为________.(2)四面体ABCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=1,则EF的长为________.【解析】(1)取圆柱下底面弧AB的另一中点D,连接C1D,AD,因为C是圆柱下底面弧AB的中点,所以AD∥BC,所以直线AC1与AD所成的角即为异面直线AC1与BC所成的角,因为C1是圆柱上底面弧A1B1的中点,所以C1D垂直于圆柱下底面,所以C1D⊥AD.因为圆柱的轴截面ABB1A1是正方形,所以C1D=2AD,所以直线AC1与AD所成角的正切值为2,所以异面直线AC1与BC所成角的正切值为 2.(2)如图,取BC的中点O,连接OE,OF,因为OE∥AC,OF∥BD,所以OE与OF所成的锐角(或直角)即为AC与BD所成的角,而AC,BD所成角为60°,所以∠EOF =60°或∠EOF =120°.当∠EOF =60°时,EF =OE =OF =12.当∠EOF =120°时,取EF 的中点M ,则OM ⊥EF , EF =2EM =2×34=32. 【答案】 (1)2 (2)12或32平移法求异面直线所成角的步骤具体步骤如下:1.直三棱柱ABC -A 1B 1C 1中,若∠BAC =90°,AB =AC =AA 1,则异面直线BA 1与AC 1所成的角等于( )A .30°B .45°C .60°D .90°解析:选C.如图,可补成一个正方体,所以AC 1∥BD 1.所以BA 1与AC 1所成的角为∠A 1BD 1.又易知△A1BD1为正三角形.所以∠A1BD1=60°.即BA1与AC1所成的角为60°.2.(2021·济南市学习质量评估)如图,在正方形ABCD中,点E,F分别为BC,AD的中点,将四边形CDFE沿EF翻折,使得平面CDFE⊥平面ABEF,则异面直线BD与CF所成角的余弦值为________.解析:如图,连接DE交FC于点O,取BE的中点G,连接OG,CG,则OG∥BD且OG=12BD,所以∠COG为异面直线BD与CF所成的角或其补角.设正方形ABCD的边长为2,则CE=BE=1,CF=DE=CD2+CE2=5,所以CO=12CF=52.易得BE⊥平面CDFE,所以BE⊥DE,所以BD=DE2+BE2=6,所以OG=12BD=62.易知CE⊥平面ABEF,所以CE⊥BE,又GE=12BE=12,所以CG=CE2+GE2=52.在△COG中,由余弦定理得,cos∠COG=OC2+OG2-CG22OC·OG=⎝⎛⎭⎪⎫522+⎝⎛⎭⎪⎫622-⎝⎛⎭⎪⎫5222×52×62=3010,。
§8.2 空间点、线、面的位置关系

§8.2 空间点、线、面的位置关系
考点 空间点、线、面的位置关系
一、空间点、线、面的位置关系 1.双基表
2.如图,直线AB、BC、CA两两相交,交点分别为A、B、C,判断这三条直线是否共面并说明 理由.回答是肯定的,这三条直线共面,理由如下:
∵直线AB和AC相交于点A, ∴直线AB和AC确定一个平面α(推论2). ∵ B∈直线AB,C∈直线AC, ∴B∈α,C∈α,∴ BC⊂α(公理1). 因此,直线AB、BC、CA都在平面α内,即它们共面.
3.空间两条直线的位置关系
位置关系 共面 直线
异面直线
相交直线 平行直线
公共点的个数 有且仅有一个公共点 没有公共点 不同在任何一个平面内,没有公共点
ቤተ መጻሕፍቲ ባይዱ
4.平行直线 平行于同一条直线的两条直线互相平行,这就是公理4.用符号表示如下:设a、b、c为三条不同 的直线,a∥b且b∥c,则a∥c. 5.等角定理 如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等. 6.注意四个公理及三个推论的文字语言、图形语言、符号语言的转换和交替使用. (1)公理1:A∈l,B∈l,A∈α,B∈α⇒l⊂α.运用公理1可证明直线是否在某一平面内. (2)公理2:A、B、C不共线⇒A、B、C确定α. 推论1:A∉l⇒A,l确定α. 推论2:a∩b=A⇒a,b确定α. 推论3:a∥b⇒a,b确定α. 公理2及其三个推论是四个等价命题,是确定平面的依据.确定一个平面,包括两层意思:一是存在 一个平面,二是只有一个平面. (3)公理3:A∈α,A∈β⇒α∩β=l且A∈l.这是确定两个平面相交于一条直线的依据,运用公理3可判
重视两个问题:一是画图与识图,即能正确运用实、虚线画出结构合理的直观示意图,能正确识 别点、线、面的位置关系;二是要重视改变视角的非常规位置的画法训练(如倒置或横、竖放 置等),借助图形思考,能正确判定空间图形位置、形状及存在的数量关系,寻找解题思路或途径.
高考数学复习考点知识与题型专题讲解48---空间点、直线、平面之间的位置关系

高考数学复习考点知识与题型专题讲解空间点、直线、平面之间的位置关系考试要求1.理解空间直线、平面位置关系的定义.2.了解可以作为推理依据的公理和定理.3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.知识梳理 1.四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 公理2:过不在一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 公理4:平行于同一条直线的两条直线互相平行. 2.空间中直线与直线的位置关系⎩⎪⎨⎪⎧共面直线⎩⎨⎧ 平行直线相交直线异面直线:不同在任何一个平面内,没有 公共点3.空间中直线与平面的位置关系直线与平面的位置关系有:直线在平面内、直线与平面相交、直线与平面平行三种情况.4.空间中平面与平面的位置关系平面与平面的位置关系有平行、相交两种情况.5.等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)两个平面α,β有一个公共点A,就说α,β相交于过A点的任意一条直线.(×)(2)两两相交的三条直线最多可以确定三个平面.(√)(3)如果两个平面有三个公共点,那么这两个平面重合.(×)(4)没有公共点的两条直线是异面直线.(×)教材改编题1.如图是一个正方体的展开图,如果将它还原为正方体,则下列说法不正确的是()A.AB与CD是异面直线B.GH与CD相交C.EF∥CDD.EF与AB异面答案D解析把展开图还原成正方体,如图所示.还原后点G与C重合,点B与F重合,由图可知ABC正确,EF与AB相交,故D错.2.如果直线a⊂平面α,直线b⊂平面β.且α∥β,则a与b()A.共面B.平行C.是异面直线D.可能平行,也可能是异面直线答案D解析α∥β,说明a与b无公共点,∴a与b可能平行也可能是异面直线.3.如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则(1)当AC,BD满足条件________时,四边形EFGH为菱形;(2)当AC,BD满足条件________时,四边形EFGH为正方形.答案(1)AC=BD(2)AC=BD且AC⊥BD解析(1)∵四边形EFGH为菱形,∴EF=EH,∵EF 綉12AC ,EH 綉12BD , ∴AC =BD .(2)∵四边形EFGH 为正方形, ∴EF =EH 且EF ⊥EH , ∵EF 綉12AC ,EH 綉12BD ,∴AC =BD 且AC ⊥BD .题型一 平面基本性质的应用例1如图所示,已知在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为D 1C 1,C 1B 1的中点,AC ∩BD =P ,A 1C 1∩EF =Q .求证:(1)D ,B ,F ,E 四点共面;(2)若A 1C 交平面DBFE 于R 点,则P ,Q ,R 三点共线. 证明(1)∵EF 是△D 1B 1C 1的中位线, ∴EF ∥B 1D 1.在正方体ABCD -A 1B 1C 1D 1中,B 1D 1∥BD , ∴EF ∥BD .∴EF,BD确定一个平面,即D,B,F,E四点共面.(2)在正方体ABCD-A1B1C1D1中,设平面A1ACC1为α,平面BDEF为β.∵Q∈A1C1,∴Q∈α.又Q∈EF,∴Q∈β,则Q是α与β的公共点,同理,P是α与β的公共点,∴α∩β=PQ.又A1C∩β=R,∴R∈A1C.∴R∈α,且R∈β,则R∈PQ,故P,Q,R三点共线.教师备选如图所示,在正方体ABCD-A1B1C1D1中,点E,F分别是AB,AA1的中点,连接D1F,CE.求证:(1)E,C,D1,F四点共面;(2)CE ,D 1F ,DA 三线共点.证明(1)如图所示,连接CD 1,EF ,A 1B , ∵E ,F 分别是AB ,AA 1的中点, ∴EF ∥A 1B ,且EF =12A 1B . 又∵A 1D 1∥BC ,A 1D 1=BC , ∴四边形A 1BCD 1是平行四边形, ∴A 1B ∥CD 1,∴EF ∥CD 1,∴EF 与CD 1能够确定一个平面ECD 1F , 即E ,C ,D 1,F 四点共面.(2)由(1)知EF ∥CD 1,且EF =12CD 1, ∴四边形CD 1FE 是梯形,∴CE 与D 1F 必相交,设交点为P , 则P ∈CE ,且P ∈D 1F ,∵CE ⊂平面ABCD ,D 1F ⊂平面A 1ADD 1, ∴P ∈平面ABCD ,且P ∈平面A 1ADD 1.又∵平面ABCD∩平面A1ADD1=AD,∴P∈AD,∴CE,D1F,DA三线共点.思维升华共面、共线、共点问题的证明(1)证明共面的方法:先确定一个平面,然后再证其余的线(或点)在这个平面内.(2)证明共线的方法:先由两点确定一条直线,再证其他各点都在这条直线上.(3)证明共点的方法:先证其中两条直线交于一点,再证其他直线经过该点.跟踪训练1(1)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的图是()答案D解析对于A,PS∥QR,故P,Q,R,S四点共面;同理,B,C图中四点也共面;D中四点不共面.(2)在三棱锥A-BCD的棱AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG =P,则点P()A.一定在直线BD上B.一定在直线AC上C.在直线AC或BD上D.不在直线AC上,也不在直线BD上答案B解析如图所示,因为EF⊂平面ABC,HG⊂平面ACD,EF∩HG=P,所以P∈平面ABC,P∈平面ACD.又因为平面ABC∩平面ACD=AC,所以P∈AC.题型二空间位置关系的判断例2(1)下列推断中,错误的是()A.若M∈α,M∈β,α∩β=l,则M∈lB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A,B,C∈α,A,B,C∈β,且A,B,C不共线⇒α,β重合答案C解析对于A,因为M∈α,M∈β,α∩β=l,由公理3可知M∈l,A对;对于B,A∈α,A∈β,B∈α,B∈β,故直线AB⊂α,AB⊂β,即α∩β=AB,B对;对于C,若l∩α=A,则有l⊄α,A∈l,但A∈α,C错;对于D,有三个不共线的点在平面α,β中,故α,β重合,D对.(2)已知在长方体ABCD-A1B1C1D1中,M,N分别是长方形A1B1C1D1与长方形BCC1B1的中心,则下列说法正确的是()A.直线MN与直线A1B是异面直线B.直线MN与直线DD1相交C.直线MN与直线AC1是异面直线D.直线MN与直线A1C平行答案C解析如图,因为M,N分别是长方形A1B1C1D1与长方形BCC1B1的中心,所以M,N分别是A1C1,BC1的中点,所以直线MN与直线A1B平行,所以A错误;因为直线MN经过平面BB1D1D内一点M,且点M不在直线DD1上,所以直线MN与直线DD1是异面直线,所以B错误;因为直线MN经过平面ABC1内一点N,且点N不在直线AC1上,所以直线MN与直线AC1是异面直线,所以C正确;因为直线MN经过平面A1CC1内一点M,且点M不在直线A1C上,所以直线MN与直线A1C是异面直线,所以D错误.教师备选1.设a,b,c是三条不同的直线,α,β是两个不同的平面,则下列结论正确的是() A.若a⊂α,b⊂β,则a与b是异面直线B.若a与b异面,b与c异面,则a与c异面C.若a,b不同在平面α内,则a与b异面D.若a,b不同在任何一个平面内,则a与b异面答案D2.如图所示,G,N,M,H分别是正三棱柱的顶点或所在棱的中点,则表示直线GH与MN是异面直线的图形有________.(填序号)答案②④思维升华(1)点、直线、平面位置关系的判定,注意构造几何体(长方体、正方体)模型来判断,常借助正方体为模型.(2)对异面直线的判定常用到以下结论:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.跟踪训练2(1)空间中有三条线段AB,BC,CD,且∠ABC=∠BCD,那么直线AB与CD 的位置关系是()A.平行B.异面C.相交或平行D.平行或异面或相交均有可能答案D解析根据条件作出示意图,容易得到以下三种情况均有可能,如图可知AB与CD有相交、平行、异面三种情况.(2)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列结论正确的是()A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交答案D解析如图1,l1与l2是异面直线,l1与l平行,l2与l相交,故A,B不正确;如图2,l1与l2是异面直线,l1,l2都与l相交,故C不正确.图1图2题型三空间几何体的切割(截面)问题例3(1)在正方体ABCD-A1B1C1D1中,M,N分别是棱DD1和BB1上的点,MD=13DD1,NB=13BB1,那么正方体中过M,N,C1的截面图形是()A.三角形B.四边形C.五边形D.六边形答案C解析先确定截面上的已知边与几何体上和其共面的边的交点,再确定截面与几何体的棱的交点.如图,设直线C1M,CD相交于点P,直线C1N,CB相交于点Q,连接PQ交直线AD于点E,交直线AB于点F,则五边形C1MEFN为所求截面图形.(2)已知正方体ABCD-A1B1C1D1的棱长为2.以D1为球心,5为半径的球面与侧面BCC1B1的交线长为______.答案π2解析以D1为球心,5为半径的球面与侧面BCC1B1的交线是以C1为圆心,1为半径的圆与正方形BCC1B1相交的一段弧(圆周的四分之一),其长度为14×2π×1=π2.延伸探究将本例(2)中正方体改为直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°.以D1为球心,5为半径的球面与侧面BCC1B1的交线长为________.答案2π2解析如图,设B1C1的中点为E,球面与棱BB1,CC1的交点分别为P,Q,连接DB,D1B1,D1P,D1E,EP,EQ,由∠BAD=60°,AB=AD,知△ABD为等边三角形,∴D1B1=DB=2,∴△D1B1C1为等边三角形,则D1E=3且D1E⊥平面BCC1B1,∴E为球面截侧面BCC1B1所得截面圆的圆心,设截面圆的半径为r,则r=R2球-D1E2=5-3= 2.又由题意可得EP=EQ=2,∴球面与侧面BCC1B1的交线为以E为圆心的圆弧PQ.又D1P=5,∴B1P=D1P2-D1B21=1,同理C1Q=1,∴P,Q分别为BB1,CC1的中点,∴∠PEQ=π2,知PQ︵的长为π2×2=2π2,即交线长为2π2.教师备选如图,在正方体ABCD-A1B1C1D1中,E是BC的中点,平面α经过直线BD且与直线C1E平行,若正方体的棱长为2,则平面α截正方体所得的多边形的面积为________.答案9 2解析如图,过点B作BM∥C1E交B1C1于点M,过点M作BD的平行线,交C1D1于点N,连接DN,则平面BDNM即为符合条件的平面α,由图可知M,N分别为B1C1,C1D1的中点,故BD=22,MN=2,且BM=DN=5,∴等腰梯形MNDB的高为h =(5)2-⎝ ⎛⎭⎪⎫222=322,∴梯形MNDB 的面积为 12×(2+22)×322=92.思维升华 (1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线. (2)作交线的方法有如下两种:①利用公理3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.跟踪训练3(1)如图,在正方体ABCD -A 1B 1C 1D 1中,E 为棱BB 1的中点,用过点A ,E ,C 1的平面截去该正方体的下半部分,则剩余几何体的正视图是()答案A解析在正方体ABCD -A 1B 1C 1D 1中,过点A,E,C1的平面截去该正方体的下半部分后,剩余部分的直观图如图.则该几何体的正视图为图中粗线部分,故选A.(2)(2022·兰州模拟)如图,正方体A1C的棱长为1,点M在棱A1D1上,A1M=2MD1,过M的平面α与平面A1BC1平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为________.答案3 2解析在平面A1D1DA中寻找与平面A1BC1平行的直线时,只需要ME∥BC1,如图所示,因为A1M=2MD1,故该截面与正方体的交点位于靠近D1,A,C的三等分点处,故可得截面为MIHGFE,设正方体的棱长为3a,则ME=22a,MI=2a,IH=22a,HG=2a,FG=22a,EF=2a,所以截面MIHGFE的周长为ME+EF+FG+GH+HI+IM=92a,又因为正方体A1C的棱长为1,即3a=1,故截面多边形的周长为3 2.课时精练1.给出以下四个命题:①依次首尾相接的四条线段必共面;②过不在同一条直线上的三点,有且只有一个平面;③空间中如果一个角的两边与另一个角的两边分别对应平行,那么这两个角必相等;④垂直于同一直线的两条直线必平行.其中正确命题的个数是()A.0B.1C.2D.3答案B解析①中,空间四边形的四条线段不共面,故①错误.②中,由公理2知道,过不在同一条直线上的三点,有且只有一个平面,故②正确.③中,由空间角的等角定理知,空间中如果一个角的两边与另一个角的两边分别对应平行,那么这两个角相等或互补,故③错误.④中,空间中,垂直于同一直线的两条直线可相交、可平行、可异面,故④错误.2.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列判断正确的是() A.若m⊥α,n⊥β,α⊥β,则直线m与n可能相交或异面B.若α⊥β,m⊂α,n⊂β,则直线m与n一定平行C.若m⊥α,n∥β,α⊥β,则直线m与n一定垂直D.若m∥α,n∥β,α∥β,则直线m与n一定平行答案A解析m,n是两条不同的直线,α,β是两个不同的平面,对于A,若m⊥α,n⊥β,α⊥β,则直线m与n相交垂直或异面垂直,故A正确;对于B,若α⊥β,m⊂α,n⊂β,则直线m与n相交、平行或异面,故B错误;对于C,若m⊥α,n∥β,α⊥β,则直线m与n相交、平行或异面,故C错误;对于D,若m∥α,n∥β,α∥β,则直线m与n平行或异面,故D错误.3.(2022·营口模拟)已知空间中不过同一点的三条直线a,b,l,则“a,b,l两两相交”是“a,b,l共面”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案A解析空间中不过同一点的三条直线a,b,l,若a,b,l在同一平面,则a,b,l相交或a ,b ,l 有两个平行,另一直线与之相交,或三条直线两两平行. 所以a ,b ,l 在同一平面,则a ,b ,l 两两相交不一定成立; 而若a ,b ,l 两两相交,则a ,b ,l 在同一平面成立.故“a ,b ,l 两两相交”是“a ,b ,l 共面”的充分不必要条件.4.如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 是平面ADD 1A 1的中心,M ,N ,F 分别是B 1C 1,CC 1,AB 的中点,则下列说法正确的是()A .MN =12EF ,且MN 与EF 平行 B .MN ≠12EF ,且MN 与EF 平行 C .MN =12EF ,且MN 与EF 异面 D .MN ≠12EF ,且MN 与EF 异面 答案D解析设正方体ABCD -A 1B 1C 1D 1的棱长为2a ,则MN =MC 21+C 1N 2=⎝ ⎛⎭⎪⎫2a 22+⎝ ⎛⎭⎪⎫2a 22=2a , 作点E 在平面ABCD 内的射影点G ,连接EG ,GF ,所以EF =EG 2+GF 2=⎝ ⎛⎭⎪⎫2a 22+(2a )2 =3a ,所以MN ≠12EF ,故选项A ,C 错误; 连接DE ,因为E 为平面ADD 1A 1的中心, 所以DE =12A 1D ,又因为M ,N 分别为B 1C 1,CC 1的中点, 所以MN ∥B 1C ,又因为B 1C ∥A 1D ,所以MN ∥ED , 且DE ∩EF =E ,所以MN 与EF 异面,故选项B 错误.5.如图所示,平面α∩平面β=l ,A ∈α,B ∈α,AB ∩l =D ,C ∈β,C ∉l ,则平面ABC 与平面β的交线是()A.直线AC B.直线ABC.直线CD D.直线BC答案C解析由题意知,D∈l,l⊂β,所以D∈β,又因为D∈AB,所以D∈平面ABC,所以点D在平面ABC与平面β的交线上.又因为C∈平面ABC,C∈β,所以点C在平面β与平面ABC的交线上,所以平面ABC∩平面β=CD.6.(2022·厦门模拟)下列说法正确的是()A.两组对边分别相等的四边形确定一个平面B.和同一条直线异面的两直线一定共面C.与两异面直线分别相交的两直线一定不平行D.一条直线和两平行线中的一条相交,也必定和另一条相交答案C解析两组对边分别相等的四边形可能是空间四边形,故A错误;如图1,直线DD1与B1C1都是直线AB的异面直线,同样DD1与B1C1也是异面直线,故B错误;如图2,设直线AB与CD是异面直线,则直线AC与BD一定不平行,否则若AC∥BD,有AC 与BD 确定一个平面α,则AC ⊂α,BD ⊂α,所以A ∈α,B ∈α,C ∈α,D ∈α,所以AB ⊂α,CD ⊂α,这与假设矛盾,故C 正确;如图1,AB ∥CD ,而直线AA 1与AB 相交,但与直线CD 不相交,故D 错误.图1图27.已知a ,b 是两条不同的直线,α,β是两个不同的平面,在下列命题①⎭⎬⎫a ∥αa ∥β⇒α∥β;②⎭⎬⎫a ⊥αa ⊥β⇒α∥β;③ ⎭⎬⎫a ∥αb ∥α⇒a ∥b ;④⎭⎬⎫a ⊥αb ⊥α⇒a ∥b 中,正确的命题是________(只填序号). 答案②④解析①与同一条直线平行的两个平面不一定平行,在本题的条件下,两平面可能相交,所以①是假命题;②根据直线与平面的位置关系,由a ⊥α,a ⊥β可得出α∥β,所以②是真命题; ③根据直线与平面的位置关系,可得a 与b 可以是平行或相交或异面,所以③是假命题; ④垂直于同一个平面的两条直线平行,所以④是真命题.8.(2022·渭南模拟)在空间中,给出下面四个命题,其中假命题为________.(填序号) ①过平面α外的两点,有且只有一个平面与平面α垂直;②若平面β内有不共线三点到平面α的距离都相等,则α∥β;③若直线l与平面α内的任意一条直线垂直,则l⊥α;④两条异面直线在同一平面内的射影一定是两条相交直线.答案①②④解析对于①,当平面α外两点的连线与平面α垂直时,此时过两点有无数个平面与平面α垂直,所以①不正确;对于②,若平面β内有不共线三点到平面α的距离都相等,平面α与β可能平行,也可能相交,所以②不正确;对于③,直线l与平面内的任意直线垂直时,得到l⊥α,所以③正确;对于④,两条异面直线在同一平面内的射影可能是两条相交直线或两条平行直线或直线和直线外的一点,所以④不正确.9.如图,平面ABEF⊥平面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠F AB=90°,BC∥AD且BC=12AD,BE∥AF且BE=12AF,G,H分别为F A,FD的中点.(1)证明:四边形BCHG是平行四边形;(2)C,D,F,E四点是否共面?为什么?(1)证明∵G,H分别是F A,FD的中点,∴GH綉12AD.又BC綉12AD,∴GH綉BC.∴四边形BCHG为平行四边形.(2)解∵BE綉12AF,G是F A的中点,∴BE綉FG,∴四边形BEFG为平行四边形,∴EF∥BG.由(1)知BG綉CH,∴EF∥CH,∴EF与CH共面.又D∈FH,∴C,D,F,E四点共面.10.如图,四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,四边形ABCD为菱形,E,F分别为AA1,CC1的中点,M为AB上一点.(1)若D1E与CM相交于点K,求证D1E,CM,DA三条直线相交于同一点;(2)若AB=2,AA1=4,∠BAD=π3,求点D1到平面FBD的距离.(1)证明∵D1E与CM相交于点K,∴K∈D1E,K∈CM,而D1E⊂平面ADD1A1,CM⊂平面ABCD,且平面ADD1A1∩平面ABCD=AD,∴K∈AD,∴D1E,CM,DA三条直线相交于同一点K.(2)解∵四边形ABCD为菱形,AB=2,∴BC=CD=2,而四棱柱的侧棱AA1⊥底面ABCD,∴CC1⊥底面ABCD,又∵F是CC1的中点,CC1=4,∴CF=2,∴BF=DF=22,又∵四边形ABCD 为菱形,∠BAD =π3, ∴BD =AB =2, ∴S △FBD =12×2×(22)2-1=7.设点D 1到平面FBD 的距离为h ,点B 到平面DD 1F 的距离为d , 则d =2sin π3=3, 又∵11D FBD B DD F V V --=,∴13×S △FBD ×h =13×1DD F S △×d , ∴13×7×h =13×12×4×2×3, 解得h =4217.即点D 1到平面FBD 的距离为4217.11.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则()A .BM =EN ,且直线BM ,EN 是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线答案B解析如图,取CD的中点O,连接ON,EO,因为△ECD为正三角形,所以EO⊥CD,又平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,所以EO⊥平面ABCD.设正方形ABCD的边长为2,则EO=3,ON=1,所以EN2=EO2+ON2=4,得EN=2.过M作CD的垂线,垂足为P,连接BP,则MP=32,CP=32,所以BM2=MP2+BP2=⎝⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322+22=7,得BM=7,所以BM≠EN.连接BD,BE,因为四边形ABCD为正方形,所以N为BD的中点,即EN,MB均在平面BDE内,所以直线BM,EN是相交直线.12.(2022·广州六校联考)如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,下列结论正确的是()A.AP与CM是异面直线B.AP,CM,DD1相交于一点C.MN∥BD1D.MC∥平面BB1D1D答案B解析如图,连接MP,AC,因为MP∥AC,MP≠AC,所以AP与CM是相交直线,又平面A1ADD1∩平面C1CDD1=DD1,所以AP,CM,DD1相交于一点,则A不正确,B正确;令AC∩BD=O,连接OD1,ON.因为M,N分别是C1D1,BC的中点,所以ON∥D1M∥CD,ON=D1M=12CD,则四边形MNOD1为平行四边形,所以MN∥OD1,因为MN⊄平面BB1D1D,OD1⊂平面BB1D1D,所以MN ∥平面BB 1D 1D ,C 不正确,D 不正确.13.棱长均为1m 的正三棱柱透明封闭容器盛有a m 3水,当侧面AA 1B 1B 水平放置时,液面高为h m(如图1);当转动容器至截面A 1BC 水平放置时,容器中的水恰好充满三棱锥A -A 1BC (如图2),则a =________,h =________.图1图2答案31232-22解析由题意得S △ABC =12×1×1×sin60° =12×1×1×32=34, AA 1=1.∴1A A BC V -=13S △ABC ·AA 1=13×34×1=312=a . 由1111ABED A B E D V -=1A A BC V -得S 四边形ABED ·AA 1 =13S △ABC ·AA 1, ∴S 四边形ABED =13S △ABC , ∴S △CDE =23S △ABC ,∴34DE2=23×34AB2,∴DEAB=23=63.∵DCAC=DEAB=63,∴DC=63,∴AD=1-63,在等边△ABC中,AB边上的高为32.∵h32=ADAC=1-631,∴h=32-22.14.(2022·盐城模拟)在棱长为4的正方体ABCD-A1B1C1D1中,P,Q分别为棱A1D1,CC1的中点,过P,Q,A作正方体的截面,则截面多边形的周长是________.答案25+95+2133解析如图所示,过Q作QM∥AP交BC于M,由A 1P =CQ =2,tan ∠AP A 1=2,则tan ∠CMQ =2,CM =CQ tan ∠CMQ=1, 延长MQ 交B 1C 1的延长线于E 点,连接PE ,交D 1C 1于N 点,则多边形AMQNP 即为截面,根据平行线性质有C 1E =CM =1,C 1N ND 1=C 1E PD 1=12,则C 1N =43,D 1N =83,因此NQ =22+⎝ ⎛⎭⎪⎫432=2133, NP =22+⎝ ⎛⎭⎪⎫832=103, 又AP =42+22=25,AM =42+32=5, MQ =12+22=5, 所以多边形AMQNP 的周长为AM +MQ +QN +NP +P A =5+5+2133+103+2 5=25+95+2133.15.(2022·山西康杰中学模拟)如图,直四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1=3,E,F分别是AB,BC的中点,过点D1,E,F的平面记为α,则下列说法中错误的是()A.点B到平面α的距离与点A1到平面α的距离之比为1∶2B.平面α截直四棱柱ABCD-A1B1C1D1所得截面的面积为73 2C.平面α将直四棱柱分割成的上、下两部分的体积之比为47∶25D.平面α截直四棱柱ABCD-A1B1C1D1所得截面的形状为四边形答案D解析对于A,因为平面α过线段AB的中点E,所以点A到平面α的距离与点B到平面α的距离相等.由平面α过A1A的三等分点M可知,点A1到平面α的距离是点A到平面α的距离的2倍,因此,点A1到平面α的距离是点B到平面α的距离的2倍.故选项A正确;延长DA ,DC 交直线EF 的延长线于点P ,Q ,连接D 1P ,D 1Q ,交棱A 1A ,C 1C 于点M ,N .连接ME ,NF ,可得五边形D 1MEFN ,故选项D 错误;由平行线分线段成比例可得AP =BF =1,故DP =DD 1=3,则△DD 1P 为等腰三角形.由相似三角形可知,AM =AP =1,A 1M =2,则D 1M =D 1N =22,ME =EF =FN = 2.连接MN ,则MN =22,因此五边形D 1MEFN 可分为等边三角形D 1MN 和等腰梯形MEFN .等腰梯形MEFN 的高h =(2)2-⎝ ⎛⎭⎪⎫22-222=62, 则等腰梯形MEFN 的面积为22+22×62=332.又1D MN S △=12×22×6=23,所以五边形D 1MEFN 的面积为332+23=732,故选项B 正确;记平面将直四棱柱分割成上、下两部分的体积分别为V 1,V 2,则V 2=1D DPQ M PAE N CFQ V V V ----- =13×12×3×3×3-13×12×1×1×1-13×12×1×1×1=256,所以V 1=1111ABCD A B C D V --V 2=12-256=476, V 1∶V 2=47∶25,故选项C 正确.16.如图1,在边长为4的正三角形ABC 中,D ,F 分别为AB ,AC 的中点,E 为AD 的中点.将△BCD 与△AEF 分别沿CD ,EF 同侧折起,使得二面角A -EF -D 与二面角B -CD -E 的大小都等于90°,得到如图2所示的多面体.图1图2(1)在多面体中,求证:A ,B ,D ,E 四点共面;(2)求多面体的体积.(1)证明因为二面角A -EF -D 的大小等于90°,所以平面AEF ⊥平面DEFC ,又AE ⊥EF ,AE ⊂平面AEF ,平面AEF ∩平面DEFC =EF ,所以AE ⊥平面DEFC , 同理,可得BD ⊥平面DEFC ,所以AE∥BD,故A,B,D,E四点共面.(2)解因为AE⊥平面DEFC,BD⊥平面DEFC,EF∥CD,AE∥BD,DE⊥CD,所以AE是四棱锥A-CDEF的高,点A到平面BCD的距离等于点E到平面BCD的距离,又AE=DE=1,CD=23,EF=3,BD=2,所以V=V A-CDEF+V A-BCD=13S梯形CDEF ·AE+13S△BCD·DE=736.。
苏教版(文科)高中数学高考总复习知识讲解_空间点线面的位置关系(基础)
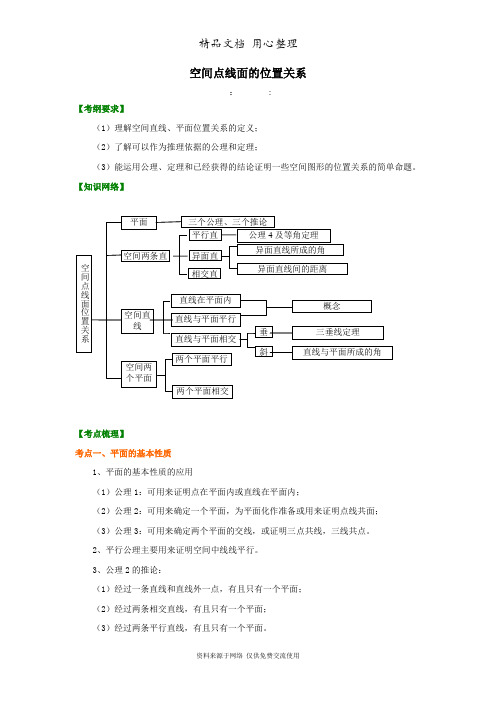
空间点线面的位置关系: :【考纲要求】(1)理解空间直线、平面位置关系的定义; (2)了解可以作为推理依据的公理和定理;(3)能运用公理、定理和已经获得的结论证明一些空间图形的位置关系的简单命题。
【知识网络】【考点梳理】考点一、平面的基本性质1、平面的基本性质的应用(1)公理1:可用来证明点在平面内或直线在平面内;(2)公理2:可用来确定一个平面,为平面化作准备或用来证明点线共面; (3)公理3:可用来确定两个平面的交线,或证明三点共线,三线共点。
2、平行公理主要用来证明空间中线线平行。
3、公理2的推论:(1)经过一条直线和直线外一点,有且只有一个平面; (2)经过两条相交直线,有且只有一个平面; (3)经过两条平行直线,有且只有一个平面。
空间点线面位置关系三个公理、三个推论平面平行直异面直相交直公理4及等角定理 异面直线所成的角 异面直线间的距离直线在平面内直线与平面平行 直线与平面相交 空间两条直概念垂斜空间直线 与平面 空间两个平面两个平面平行两个平面相交三垂线定理 直线与平面所成的角4、点共线、线共点、点线共面 (1)点共线问题证明空间点共线问题,一般转化为证明这些点是某两个平面的公共点,再根据公理3证明这些点都在这两个平面的交线上。
(2)线共点问题证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上。
要点诠释:证明点线共面的常用方法①纳入平面法:先确定一个平面,再证明有关点、线在此平面内;②辅助平面法:先证明有关的点、线确定平面α,再证明其余元素确定平面β,最后证明平面α、β重合。
考点二、直线与直线的位置关系(1)位置关系的分类⎧⎧⎪⎨⎨⎩⎪⎩相交直线共面直线平行直线异面直线:不同在任何一个平面内,没有公共点(2)异面直线所成的角①定义:设a,b 是两条异面直线,经过空间中任一点O 作直线a ’∥a,b ’∥b,把a ’与b ’所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).②范围:02π⎛⎤ ⎥⎝⎦,要点诠释:证明两直线为异面直线的方法:1、定义法(不易操作)2、反证法:先假设两条直线不是异面直线,即两直线平行或相交,由假设的条件出发,经过严密的推理,导出矛盾,从而否定假设肯定两条直线异面。
高考文科数学《空间点、线、面之间的位置关系》课件

B.OB∥O1B1 C.OB 与 O1B1 不平行 D.OB 与 O1B1 不一定平行
解:两角相等,角的一边平行且方向相同,另一边不一定平行,
如圆锥的母线与轴的夹角.故选 D.
(辽宁葫芦岛六中 2018 二检)下列四个命题: ①若两条不同的直线垂直于同一平面,则这两条直线平行; ②若一条直线与平面内的无数条直线垂直,则这条直线垂直于这 个平面; ③若一个平面内的三个不共线的点到另一个平面的距离都相等, 则这两个平面平行; ④若一条直线不垂直于平面,则这个平面内没有与这条直线垂直
即 B,D,O 三点共线.
点 拨: ①本题是一道经典的点共线问题,它体现了证明点共线的基本思路:首 先由其中的两个点 B 和 D 确定一条直线,然后证明点 O 也是直线 BD 上的点,
也就是证明点 O 是两个平面的交线上的点.在证明点 O 也是直线 BD 上的点 时,运用了公理 1 以及公理 3,这种方法是证明点共线的通用方法.②证明空
证明:在图 3 中,因为直线 EN∥BF,所以 B、N、E、F 四点共面,因此 EF 与 BN 相交,交点为 M.因为 M∈EF,且 M∈NB,而 EF⊂平面 AEF,NB⊂平面 ABCD, 所以 M 是平面 ABCD 与平面 AEF 的公共点.又因为点 A 是平面 AEF 和平面 ABCD 的 公共点,故 AM 为两平面的交线.
在图 4 中,C1M 在平面 DCC1D1 内,因此与 DC 的延长线相交,交点为 M,则点 M 为平面 A1C1B 与平面 ABCD 的公共点,又点 B 是这两个平面的公共点,因此直线 BM 是两平面的交线.
点 拨: 本题解题的关键在于构造平面,可考虑过一条直线及另一条直线上
的点作平面,进而找出两面相交的交线.
高考数学总复习第三节 空间点、线、面之间的位置关系

1.(2018·江西七校联考)已知直线a和平面α,β,α∩β=l,
a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线
b和c的位置关系是
()
A.相交或平行
B.相交或异面
C.平行或异面
D.相交、平行或异面
解析:依题意,直线b和c的位置关系可能是相交、 平行或异面.
答案:D
返回
2.(2019·杭州诊断)设l,m,n表示三条直线,α,β,γ表示
答案:③④
返回
必过易错关
返回
1.异面直线易误解为“分别在两个不同平面内的两条直线为 异面直线”,实质上两异面直线不能确定任何一个平面, 因此异面直线既不平行,也不相交.
2.直线与平面的位置关系在判断时最易忽视“线在面内”. 3.不共线的三点确定一个平面,一定不能丢掉“不共线”
条件.
返回
[小题纠偏]
返回
2.有关平移的3种技巧 求异面直线所成的角的方法为平移法,平移的方法一般 有3种类型: (1)利用图形中已有的平行线平移; (2)利用特殊点(线段的端点或中点)作平行线平移; (3)补形平移.计算异面直线所成的角通常放在三角形中 进行.
[即时应用]
返回
如图所示,在正方体ABCD-A1B1C1D1中, (1)求AC与A1D所成角的大小; (2)若E,F分别为AB,AD的中点,求A1C1 与EF所成角的大小.
2.证明多线共点问题的2个步骤 (1)先证其中两条直线交于一点;
(2)再证交点在第三条直线上.证交点在第三条直线上时,
第三条直线应为前两条直线所在平面的交线,可以利用公理3
证明.
[即时应用]
返回
如图,在四边形ABCD中,已知AB∥CD,
直线AB,BC,AD,DC分别与平面α相交于
高考文科数学空间点直线平面之间位置关系考点讲解

高考复习讲义 考点全通关 5
3.公理3
空间点、直线、平面之间的位置关系 考点一 平面的性质
(1)自然语言:如果两个不重合的平面有一个公共点,那么它们有且只有一 直线. (2)图形语言:如图所示. (3)符号语言:P∈α,且P∈β⇒α∩β=l,且P∈l. (4)作用:①判断两个平面相交的依据;②证明点共线的依据;③证明线共点
三点不一定能确定一个平面.当三点共线时,过这三点的平面有无数个,所 以必须是不在一条直线上的三点才能确定一个平面. 所有理想化模型均忽略对所研究问 题无影响的因素,是研究问题的一种 理想方法.在高中学习的理想模型还 有:点电荷、理想气体、弹簧振子、 点光源等.
高考复习讲义 考点全通关 4 2.公理2
考纲解读
命题规律
命题趋势
空间点、直线、平面之间的位置关系
考查内容
平面的性质
空间中直线间 的位置关系 直线与平面的
位置关系 两个平面的位
置关系
平ห้องสมุดไป่ตู้的性质
考查频次 3年2考 3年22考 3年2考 3年2考 3年2考
考查题型 选择题、填空题或解答
题的一小问 选择题、填空题或解答
题的一小问
选择题、填空题
选择题、填空题
所异有面理直想线化所模成型的均角忽的略范对围所是研(0究,90问°],所以垂直有两种情况——异面垂直 题 理和无 想相影 方交响 法垂.的直在因.高素中,是学习研的究理问想题模的型一还种 有:点电荷、理想气体、弹簧振子、 点光源等.
高考复习讲义 考点全通关 8 3.公理4
考点二 空间中直线间的位置关系
此异面直线既不平行,也不相交; 所 题(2有 无)不理 影能想 响把化 的异模 因面型素直,均是线忽研误略究解对问为所题分研的别究一在问种不同平面内的两条直线为异面直线. 理(3想)异方面法直.在线高不中具学有习传的递理性想,即模若型直还线a与b异面,b与c异面,则a与c不一定是 有 点异:光点面源电直等荷线.、. 理想气体、弹簧振子、
高考备考指南文科数学第8章第3讲空间点、线、面的位置关系

第八章第3讲[A级基础达标]1.l1,l2表示空间中的两条直线,若p:l1,l2是异面直线;q:l1,l2不相交,则() A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充要条件D.p既不是q的充分条件,也不是q的必要条件【答案】A【解析】直线l1,l2是异面直线,一定有l1与l2不相交,因此p是q的充分条件;若l1与l2不相交,那么l1与l2可能平行,也可能是异面直线,所以p不是q的必要条件.故选A.2.(2018年西安二模)下列命题正确的是()①三点确定一个平面;②两两相交且不共点的三条直线确定一个平面;③如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面;④如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面.A.①③B.①④C.②④D.②③【答案】C【解析】在①中,不共线的三点确定一个平面,故①错误;在②中,两两相交且不共点的三条直线确定一个平面,故②正确;在③中,如果两个平面垂直,那么其中一个平面内的直线与另一个平面相交、平行或在另一个平面内,故③错误;在④中,如果两个平面平行,那么由面面平行的性质得其中一个平面内的直线一定平行于另一个平面,故④正确.故选C.3.(2018年钦州三模)在正方体ABCD-A1B1C1D1中,下列几种说法正确的是() A.A1C1与B1C成60°角B.D1C1⊥ABC.AC1与DC成45°角D.A1C1⊥AD【答案】A【解析】如图,因为AC∥A1C1,所以∠ACB1即为A1C1与B1C所成的角,在正△AB1C中易得,∠ACB1=60°,故A正确;选项B,由正方体的性质易得D1C1∥AB,故错误;选项C,可得DC∥D1C1,∠AC1D1即为AC1与DC所成的角,在Rt△AC1D1中,∠C1D1A=90°,AD1≠D1C1,故AC1与DC不可能成45°角,故错误;选项D,易得∠D1A1C1为A1C1与AD所成的角,在等腰直角三角形D1A1C1中易得∠D1A1C1=45°,故A1C1与AD不可能垂直,故错误.故选A.4.(2017年济南模拟)a,b,c是两两不同的三条直线,下面四个命题中,真命题是() A.若直线a,b异面,b,c异面,则a,c异面B.若直线a,b相交,b,c相交,则a,c相交C.若a∥b,则a,b与c所成的角相等D.若a⊥b,b⊥c,则a∥c【答案】C【解析】若直线a,b异面,b,c异面,则a,c相交、平行或异面;若a,b相交,b,c相交,则a,c相交、平行或异面;若a⊥b,b⊥c,则a,c相交、平行或异面;由异面直线所成的角的定义知C正确.故选C.5.如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是()A.A,M,O三点共线B.A,M,O,A1不共面C.A,M,C,O不共面D.B,B1,O,M共面【答案】A【解析】连接A1C1,AC,则A1C1∥AC,所以A1,C1,C,A四点共面.所以A1C⊂平面ACC1A1.因为M∈A1C,所以M∈平面ACC1A1.又M∈平面AB1D1,所以M在平面ACC1A1与平面AB1D1的交线上.同理O在平面ACC1A1与平面AB1D1的交线上,所以A,M,O三点共线.故选A.6.已知正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为BB 1,CC 1的中点,那么异面直线AE 与D 1F 所成角的余弦值为( )A .45B .35C .23D .57【答案】B【解析】依题作出正方体ABCD -A 1B 1C 1D 1,如图,连接DF ,则AE ∥DF ,所以∠D 1FD 为异面直线AE 与D 1F 所成的角.设正方体棱长为a ,则D 1D =a ,DF =D 1F =52a ,所以cos ∠D 1FD =⎝⎛⎭⎫52a 2+⎝⎛⎭⎫52a 2-a 22·52a ·52a =35.故选B .7.如果两条直线a 和b 没有公共点,那么a 与b 的位置关系是________. 【答案】平行或异面【解析】空间中两条直线的位置关系有三种:相交,有且只有一个公共点;平行,没有公共点;异面,没有公共点.由此可知,如果两条直线a 和b 没有公共点,那么a 与b 的位置关系是平行或异面.8.(2018年渭南二模)已知m ,n 是空间两条不同直线,α,β是空间两个不同平面,下面有四个命题:①若m ∥α,n ∥β且α∥β,则m ∥n ; ②若m ⊥α,n ⊥β且α⊥β,则m ⊥n ; ③若m ⊥α,n ∥β且α∥β,则m ⊥n ; ④若m ∥α,n ⊥β且α⊥β,则m ∥n .其中真命题的编号是________.(写出所有真命题的编号) 【答案】②③【解析】在①中,若m ∥α,n ∥β且α∥β,则m 与n 相交、平行或异面,故①错误;在②中,若m ⊥α,n ⊥β且α⊥β,则由线面垂直的性质得m ⊥n ,故②正确;在③中,若m ⊥α,n ∥β且α∥β,则由线面垂直的性质得m ⊥n ,故③正确;在④中,若m ∥α,n ⊥β且α⊥β,则m 与n 相交、平行或异面,故④错误.故答案为②③.9.(2017年成都月考)如图所示,在三棱锥P -ABC 中,P A ⊥底面ABC ,D 是PC 的中点.已知∠BAC =π2,AB =2,AC =23,P A =2.求:(1)三棱锥P -ABC 的体积;(2)异面直线BC 与AD 所成角的余弦值. 【解析】(1)S △ABC =12×2×23=23,三棱锥P -ABC 的体积为 V =13S △ABC ·P A =13×23×2=433.(2)如图,取PB 的中点E ,连接DE ,AE ,则ED ∥BC ,所以∠ADE 是异面直线BC 与AD 所成的角(或其补角).在△ADE 中,DE =2,AE =2,AD =2, cos ∠ADE =22+22-22×2×2=34.故异面直线BC 与AD 所成角的余弦值为34.[B 级 能力提升]10.以下四个命题中,①不共面的四点中,其中任意三点不共线;②若点A ,B ,C ,D 共面,点A ,B ,C ,E 共面,则点A ,B ,C ,D ,E 共面; ③若直线a ,b 共面,直线a ,c 共面,则直线b ,c 共面; ④依次首尾相接的四条线段必共面. 正确命题的个数是( ) A .0 B .1 C .2D .3【答案】B【解析】①假设其中有三点共线,则该直线和直线外的另一点确定一个平面,这与四点不共面矛盾,故其中任意三点不共线,所以①正确;②从条件看出两平面有三个公共点A ,B ,C ,但是若A ,B ,C 共线,则结论不正确;③不正确;④因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形,④不正确.故选B .11.若空间中四条两两不同的直线l 1,l 2,l 3,l 4,满足l 1⊥l 2,l 2⊥l 3,l 3⊥l 4,则下列结论一定正确的是( )A .l 1⊥l 4B .l 1∥l 4C .l 1与l 4既不垂直也不平行D .l 1与l 4的位置关系不确定 【答案】D【解析】如图所示,在长方体ABCD -A 1B 1C 1D 1中,记l 1=DD 1,l 2=DC ,l 3=DA .若l 4=AA 1,满足l 1⊥l 2,l 2⊥l 3,l 3⊥l 4,此时l 1∥l 4,可以排除选项A 和C .若取C 1D 为l 4,则l 1与l 4相交;若取BA 为l 4,则l 1与l 4异面;取C 1D 1为l 4,则l 1与l 4相交且垂直.因此l 1与l 4的位置关系不能确定.故选D .12.(2018年永州三模)三棱锥A -BCD 的所有棱长都相等,M ,N 分别是棱AD ,BC 的中点,则异面直线BM 与AN 所成角的余弦值为( )A .13B .24C .33D .23【答案】D【解析】作图,取DN 中点O ,连接MO ,BO ,因为三棱锥A -BCD 的所有棱长都相等,M ,N 别是棱AD ,BC 的中点,所以MO ∥AN ,所以∠BMO 是异面直线BM 与AN 所成角(或其补角).设三棱锥A -BCD 的所有棱长为2,则AN =BM =DN =22-12=3,MO=12AN =32=NO =12DN ,BO =BN 2+NO 2=72,所以cos ∠BMO =BM 2+MO 2-BO 22×BM ×OM=3+34-742×3×32=23.所以异面直线BM 与AN 所成角的余弦值为23.故选D .13.已知正方体ABCD -A 1B 1C 1D 1的棱长为2,点P 是平面AA 1D 1D 的中心,点Q 是上底面A 1B 1C 1D 1上一点,且PQ ∥平面AA 1B 1B ,则线段PQ 的长的最小值为________.【答案】1【解析】作图,由PQ ∥平面AA 1B 1B 知Q 在过点P 且平行于平面AA 1B 1B 的平面上,易知点Q 在A 1D 1,B 1C 1中点的连线MN 上,故PQ 的最小值为PM =12AA 1=1.14.如图所示,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,F ,G 分别是线段AE ,BC 的中点,则AD 与GF 所成的角的余弦值为________.【答案】36【解析】如图,取DE 的中点H ,连接HF ,GH .由题设,HF 12AD .所以∠GFH 为异面直线AD 与GF 所成的角(或其补角).在△GHF 中,可求得HF =2,GF =GH =6,所以cos ∠HFG =2+6-62×2×6=36.15.如图所示,在三棱柱ABC -A 1B 1C 1中,底面是边长为2的正三角形,侧棱A 1A ⊥底面ABC ,点E ,F 分别是棱CC 1,BB 1上的点,点M 是线段AC 上的动点,EC =2FB =2.(1)当点M 在何位置时,BM ∥平面AEF?(2)若BM ∥平面AEF ,判断BM 与EF 的位置关系,说明理由;并求BM 与EF 所成的角的余弦值.【解析】(1)如图所示,取AE 的中点O ,连接OF ,过点O 作OM ⊥AC 于点M .因为侧棱A 1A ⊥底面ABC ,所以C 1C ⊥底面ABC ,所以C 1C ⊥AC . 又因为EC =2FB =2,所以OM ∥EC ∥FB 且OM =12EC =FB .所以四边形OMBF 为矩形,BM ∥OF . 因为OF ⊂平面AEF ,BM ⊄平面AEF , 故BM ∥平面AEF ,此时点M 为AC 的中点.(2)由(1)知,BM 与EF 异面,∠OFE 就是异面直线BM 与EF 所成的角或其补角. 易求得AF =EF =5,OF =3,EO =2,又O 为AE 的中点,所以OF ⊥AE . 所以cos ∠OFE =OF EF =35=155.所以BM 与EF 所成的角的余弦值为155.。
(高三文科)空间点、线、面之间的位置关系

【解答】(1) 因为 E,F 分别为 AB,AD 的中点,所以 EF∥BD.
(变式)
BG DH 1 在△BCD 中,GC=HC =2,
所以 GH∥BD,所以 EF∥GH, 所以 E,F,G,H 四点共面.
第24页
栏目导航
高考总复习 一轮复习导学案 ·数学文科
第八章
立体几何
(2) 因为 EG∩FH=P,P∈EG,EG⊂平面 ABC,所以 P∈平面 ABC.同理 P∈平 面 ADC.
高考总复习 一轮复习导学案 ·数学文科
第八章
立体几何
3. 如图, 在长方体 ABCDA1B1C1D1 中, O 是 B1D1 的中点, 直线 A1C 交平面 AB1D1 于点 M,则下列结论正确的是( A ) A. A,M,O 三点共线 B. A,M,O,A1 不共面 C. A,M,C,O 不共面 D. B,B1,O,M 共面
第八章
立体几何
因为 M,N 分别是 A1B1,B1C1 的中点,所以 MN∥A1C1. 又因为 A1A∥C1C,且 A1A=C1C, 所以四边形 A1ACC1 为平行四边形,
所以 A1C1∥AC,所以 MN∥AC,
所以 A,M,N,C 在同一平面内, 故 AM 和 CN 不是异面直线. (2) 是异面直线.理由如下: 因为 ABCDA1B1C1D1 是正方体,
第八章
立体几何
目标 1 平面的基本性质 已知在正方体 ABCDA1B1C1D1 中,E,F 分别为 D1C1,C1B1 的中点, AC∩BD=P,A1C1∩EF=Q. (1) 求证:D,B,F,E 四点共面; (2) 若 A1C 交平面 DBFE 于点 R,则 P,Q,R 三点共线; (3) 求证:直线 DE,BF,CC1 交于同一点 M.
考点25 空间点、线、面的位置关系-备战2021年新高考数学一轮复习考点一遍过

考点25空间点、线、面的位置关系【命题解读】空间点、直线、平面的位置关系是高考常考知识点之一,它的出题形式多样,在选择题或者填空或者解答都有可能涉及,这部分以简单和中档题为主,主要是考察空间想象力和空间思维能力。
【命题预测】预计2021年的高考对于空间点、线、面的位置关系出选择题的可能性比较大,对于异面直线所成的角解答题有可能涉及到,因此这部分要加强复习。
【复习建议】1.能直观认识空间点、线、面的位置关系,并能抽象出空间点、线、面的位置关系;2.掌握4个基本事实和1个定理。
考向一空间点、线、面的位置关系1.四个基本事实文字语言图形语言符号语言作用基本事实1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内A∈l,B∈l,A∈α,B∈α}⇒l⊂α可用来证明点、直线在平面内基本事实2 过不在一条直线上的三点,有且只有一个平面A,B,C三点不共线⇒有且只有一个平面α,使A∈α,B∈α,C∈α①可用来确定一个平面;②证明点、线共面基本事实3 如果两个不重合的平面有一个公共点,那么P∈α,且P∈β⇒α∩β=l,且P∈l①可用来确定两个平面的交线;②判断或证明多它们有且只有一条过该点的公共直线点共线;③判断或证明多线共点基本事实4平行于同一条直线的两条直线互相平行a ∥b ,b ∥c ⇒a ∥c证明空间中两条直线平行2.基本事实2的三个推论推论1:经过一条直线和这条直线外一点有且只有一个平面; 推论2:经过两条相交直线有且只有一个平面; 推论3:经过两条平行直线有且只有一个平面. 3.空间直线的位置关系 (1)位置关系的分类 空间直线{共面{平行直线相交直线异面——异面直线4.空间中直线与平面、平面与平面的位置关系图形语言符号语言 公共点 直线与平面相交a ∩α=A1个平行a ∥α0个在平面内a ⊂α无数个平面与平面 平行 α∥β 0个相交α∩β=l无数个1.【2020四川高三期中】 m ,n 是不同的直线,α,β是不重合的平面,下列说法正确的是( )A .若m ,n a ⊂,//m β,βn//,则//αβ;B .若//αβ,m a ⊂,n β⊂,则//m n ;C .若//αβ,//m α,则//m β;D .m ,n 是异面直线,若//m α,//m β,n ⊂α,βn//则//αβ. 【答案】D【解析】对于A ,若m ,n ⊂α,当//m n 时,可能有两个面相交.所以A 不正确 若//αβ,m α⊂,n β⊂,则//m n ,也可能m ,n 是异面直线,所以A 不正确; 对于B ,若//αβ,m α⊂,n β⊂,则//m n ,也可能m ,n 是异面直线,所以B 不正确;对于C ,若//αβ,//m α,则//m β,也可能m β⊂,所以C 不正确;对于D ,过A 作//a m ,//b n ,直线a ,b 是相交直线,确定平面γ,由题意可得,//γβ,//γα,//αβ∴,所以D 正确;故选:D .2. 【2020山西省古县第一中学高二期中】若直线a 与平面α不垂直,那么在平面α内与直线a 垂直的直线( ) A .只有一条B .无数条C .是平面α内的所有直线D .不存在【答案】B【解析】直线a 与平面α不垂直,一定存在b α⊂,使得a b ⊥成立,因此在平面α内,与b 平行的所有直线都与直线a 垂直,因此有无数条直线在平面α内与直线a 垂直. 故选:B考向二 异面直线所成的角1.异面直线所成的角①定义:设a ,b 是两条异面直线,经过空间中任一点O 作直线a'∥a ,b'∥b ,把a'与b'所成的锐角(或直角)叫作异面直线a 与b 所成的角(或夹角).②范围: (0,π2].2.等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.1.【2020北京四中高二期中】设a 、b 是异面直线,给出下列命题: ①经过直线a 有且仅有一个平面平行于直线b ; ②经过直线a 有且仅有一个平面垂直于直线b ; ③存在分别经过直线a 和直线b 的两个平行平面; ④存在分别经过直线a 和直线b 的两个互相垂直的平面. 其中错误的命题为( ) A .①与② B .②与③C .②与④D .仅②【答案】D【解析】对于①,选一条直线c 与b 平行,且c 与a 相交,则由公理2的推论可知,通过a 与c 有且仅有一个平面α,此时//b α,故①正确;对于②,若a 与b 不垂直,则直线b 不可能垂直于直线a 所在的平面,故②错; 对于③,取平面α与平面β,且使//αβ,若a α⊂,b β⊂,且a 与b 不平行,则,a b 异面,故③正确;对于④,若a 、b 异面,则存在一条直线c ,使得a c ⊥,b c ⊥,设由a 、c 所确定的平面为α,则一定可以过直线b 作一个平面β,使得αβ⊥,故④正确. 故选:D.2. 【2020河北高三期中】如图,在三棱锥D-ABC 中,AC BD ⊥,一平面截三棱锥D-ABC 所得截面为平行四边形EFGH .已知2EF =,5EH =,则异面直线EG 和AC所成角的正弦值是( )A .147B .77C .357D .27【答案】A【解析】EFGH 是平行四边形,所以//EH FG ,因为EH ⊄平面ACD ,FG ⊂平面ACD ,所以//EH 平面ACD ,又EH ⊂平面ABC ,平面ABC平面ACD AC =,所以//EH AC ,所以HEG ∠(或其补角)就是异面直线EG 和AC 所成的角,因为AC BD ⊥,所以90EHG ∠=, 因为2HG EF ==,5EH =,所以7EG =,故14sin 7HG HEG EG ∠==. 故选:A3. 【2020湖北高三月考】在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 分别为BC ,CC 1,BB 1的中点,则( )A .D 1D ⊥AFB .A 1G ∥平面AEFC .异面直线A 1G 与EF 10D .点G 到平面AEF 的距离是点C 到平面AEF 的距离的2倍 【答案】BCD【解析】A 选项,由11//DD CC ,即1CC 与AF 并不垂直,所以D 1D ⊥AF 错误. B 选项,如下图,延长FE 、GB 交于G’连接AG’、GF ,有GF//BE 又E ,F ,G 分别为BC ,CC 1,BB 1的中点,所以11GG BB AA '==,而1//AA GG ',即1//A G AG ';又因为面11ABB A 面AEF =AG ,且1AG ⊄面AEF ,1AG ⊂面11ABB A ,所以A 1G ∥平面AEF ,故正确.C 选项,取11B C 中点H ,连接GH ,由题意知GH 与EF 平行且相等,所以异面直线A 1G 与EF 所成角的平面角为1AGH ∠,若正方体棱长为2,则有112,5GH AG A H ===,即在1A GH 中有110cos 10AGH ∠=,故正确.D 选项,如下图若设G 到平面AEF 的距离、C 到平面AEF 的距离分别为1h 、2h ,则由11133A GEF GEF G AEF AEF V AB S V h S --=⋅⋅==⋅⋅且21133A CEFCEF C AEF AEF V AB S V h S --=⋅⋅==⋅⋅,知122GEF CEF S h h S ==,故正确.故选:BCD题组一(真题在线)1. 【2020年高考浙江】已知空间中不过同一点的三条直线l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件2. 【2020年高考全国Ⅱ卷理数】设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内. p 2:过空间中任意三点有且仅有一个平面. p 3:若空间两条直线不相交,则这两条直线平行. p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l . 则下述命题中所有真命题的序号是__________.①14p p ∧ ②12p p ∧ ③23p p ⌝∨ ④34p p ⌝∨⌝3. 【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面4. 【2019年高考全国Ⅲ卷理数】如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线5. 【2019年高考北京卷理数】已知l ,m 是平面α外的两条不同直线.给出下列三个论断: ①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.题组二1. 【2020全国高三(理)】在正方体1111ABCD A B C D -中,点E 是棱11B C 的中点,点F 是线段1CD 上的一个动点.有以下三个命题:①异面直线1AC 与1B F 所成的角是定值; ②三棱锥1B A EF -的体积是定值;③直线1A F 与平面11B CD 所成的角是定值. 其中真命题的个数是 A .3 B .2C .1D .02. 【2020福建师大附中高三期中】在正方体1111ABCD A B C D -中,记平面11CB D 为α,若α平面ABCD m =, α⋂平面11ABB A n =,则m ,n 所成角的余弦值为( )A .2B .2C .3D .123. 【2020吉林高二期中(理)】设m ,n 是两条不同的直线,α,β,γ是三个不同的平面,给出如下命题: ①若αβ⊥,m αβ=,n ⊂α,n m ⊥,则n β⊥;②若αγ⊥,βγ⊥,则//αβ;③若αβ⊥,m β⊥,m α⊄,则//m α; ④若αβ⊥,//m α,则m β⊥. 其中正确命题的个数为( ) A .1B .2C .3D .44. 【2020河南高三月考(理)】在长方形ABCD 中,AB =2AD ,过AD ,BC 分别作异于平面ABCD 的平面α,β,若l αβ=,则l 与BD 所成角的正切值是( )A .12B .1C .2D .45. 【2020东台创新高级中学高一月考】设m ,n 是两条不同的直线,α,β是两个不重合的平面,下列说法正确的是( ) A .若m n ⊥,n ⊂α,则m α⊥ B .若m α⊥,m β⊂,则αβ⊥ C .若m α⊥,n α⊥,则//m nD .若m α⊂,n β⊂,//αβ,则//m n6. 【2020山东济宁·高三其他模拟】如图,在四棱锥P ABCD -中,底面ABCD 为菱形,且60DAB ∠=,侧面PAD 为正三角形,且平面PAD ⊥平面ABCD ,则下列说法正确的是( )A .在棱AD 上存在点M ,使AD ⊥平面PMB B .异面直线AD 与PB 所成的角为90C .二面角P BC A --的大小为45D .BD ⊥平面PAC7. 【2020北京四中高二期中】正方形ABCD 与正方形ABEF 有公共边AB ,平面ABCD 与平面ABEF 所成角为60°,则异面直线AB 与FC 所成角大小等于______. 8. 【2020重庆南开中学高三期中(理)】正三棱柱111ABC A B C -中,2AB =,122AA =,D 为棱11A B 的中点,则异面直线AD 与1CB 成角的大小为_______.9. 【2020浙江温州高二期中】如图所示,在三棱锥D ABC -中,AD ⊥平面DBC ,120BDC ∠=,且1AD =,2DB DC ==,E 是DC 的中点.(1)求异面直线AE 与BD 所成角的余弦值; (2)求二面角A BE C --的正切值.题组一1.B【解析】依题意,,m n l 是空间不过同一点的三条直线,当,,m n l 在同一平面时,可能////m n l ,故不能得出,,m n l 两两相交.当,,m n l 两两相交时,设,,m n A m l B n l C ⋂=⋂=⋂=,根据公理2可知,m n 确定一个平面α,而,B m C n αα∈⊂∈⊂,根据公理1可知,直线BC 即l α⊂,所以,,m n l 在同一平面.综上所述,“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件.故选:B2. ①③④【解析】对于命题1p ,可设1l 与2l 相交,这两条直线确定的平面为α;若3l 与1l 相交,则交点A 在平面α内,同理,3l 与2l 的交点B 也在平面α内,所以,AB α⊂,即3l α⊂,命题1p 为真命题;对于命题2p ,若三点共线,则过这三个点的平面有无数个,命题2p 为假命题;对于命题3p ,空间中两条直线相交、平行或异面,命题3p 为假命题;对于命题4p ,若直线m ⊥平面α,则m 垂直于平面α内所有直线,直线l ⊂平面α,∴直线m ⊥直线l ,命题4p 为真命题. 综上可知,,为真命题,,为假命题,14p p ∧为真命题,12p p ∧为假命题,23p p ⌝∨为真命题,34p p ⌝∨⌝为真命题.故答案为:①③④.3. B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B .4. B【解析】如图所示,作EO CD ⊥于O ,连接ON ,BD ,易得直线BM ,EN 是三角形EBD 的中线,是相交直线.过M 作MF OD ⊥于F ,连接BF ,平面CDE ⊥平面ABCD ,,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴△与EON △均为直角三角形.设正方形边长为2,易知3,12EO ON EN ===,,35,,722MF BF BM ==∴=BM EN ∴≠,故选B .故选:B .5. 如果l ⊥α,m ∥α,则l ⊥m .【解析】将所给论断,分别作为条件、结论,得到如下三个命题:(1)如果l ⊥α,m ∥α,则l ⊥m ,正确;(2)如果l ⊥α,l ⊥m ,则m ∥α,不正确,有可能m 在平面α内;(3)如果l ⊥m ,m ∥α,则l ⊥α,不正确,有可能l 与α斜交、l ∥α.故答案为:如果l ⊥α,m ∥α,则l ⊥m.6. C【解析】由题可得i,i (1)i,z x y z x y =+-=+-22i (1)1,z x y -=+-=则22(1)1x y +-=.故选C .7. C【解析】由32i,z =-+得32i,z =--则32i z =--对应的点(-3,-2)位于第三象限.故选C .8. D 【解析】()(2i 2i 1i 1i 1i 1i 1i )()z -===+++-.故选D . 13【解析】5i (5i)(1i)|||||23i |131i (1i)(1i)---==-=++-.【解析】 由题可得1|||1i |2z ===+. 11. 2【解析】2(2i)(1i)i 2i 2i 2(2)i a a a a a ++=+++=-++,令20a -=,解得2a =.题组二1.B【解析】以A 点为坐标原点,AB,AD,1AA 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,设正方体棱长为1,可得B (1,0,0),C (1,1,O ),D (0,1,0),1A (0,0,1),1B (1,0,1),1C (1,1,1),1D (0,1,1),设F (t ,1,1-t ),(0≤t ≤1), 可得1AC =(1,1,1),1B F =(t -1,1,-t ),可得11AC B F =0,故异面直线1AC 与1B F 所的角是定值,故①正确;三棱锥1B A EF -的底面1A BE 面积为定值,且1CD ∥1BA ,点F 是线段1CD 上的一个动点,可得F 点到底面1A BE 的距离为定值,故三棱锥1B A EF -的体积是定值,故②正确;可得1A F =(t ,1,-t ),1B C =(0,1,-1),11B D =(-1,1,0),可得平面11B CD 的一个法向量为n =(1,1,1),可得1cos ,A F n 不为定值,故③错误;故选B .2.D 【解析】如图,连接11,,BD A B A D , 可得在正方体中,111B B CC DD ,即四边形11BB D D 是平行四边形,11//B D BD ∴,BD ⊂平面ABCD ,11B D ⊄平面ABCD ,∴11//B D 平面ABCD , 又α平面ABCD m =,11B D α⊂,11//B D m ∴,//BD m ∴,同理可得1//CD 平面11ABB A ,α⋂平面11ABB A n =,1CD α⊂, 1//CD n ∴,1//A B n ,1A BD ∴∠即为m ,n 所成角,1A BD 为等边三角形,160A BD ∴∠=,11cos 2A BD ∴∠=. 故选:D.3.B 【解析】对于①,由平面与平面垂直的性质知n β⊥,所以①正确;对于②中,α,β可能平行,也可能相交,所以②不正确;对于③中,αβ⊥,m β⊥,m α⊄时,只可能有//m α,所以③正确;对于④中,m 与β的位置关系可能是//m β或m β⊂或m 与β相交,所以④不正确; 综上,可知正确命题的个数为2.故选:B.4. C 【解析】由//AD BC 及线面平行的判定定理,得//AD β,再由线面平行的性质定理,得//AD l .所以l 与BD 所成角是ADB ∠,从而tan 2ADB ∠=.故选:C .5.BC【解析】若m n ⊥,n ⊂α,推不出m α⊥,故A 错误;若m α⊥,m β⊂,则αβ⊥,故B 正确若m α⊥,n α⊥,则//m n ,故C 正确若m α⊂,n β⊂,//αβ,则,m n 可以平行、相交、异面,故D 错误故选:BC6.ABC【解析】如图,取AD 的中点M ,连接,PM BM ,∵侧面PAD 为正三角形,PM AD ∴⊥,又底面ABCD 是菱形,60DAB ︒∠=,ABD ∴是等边三角形,AD BM ∴⊥,又PM BM M ⋂=,,PM BM ⊂平面PMB ,AD ∴⊥平面PMB ,AD PB ⊥,故A ,B 正确;对于C ,∵平面PBC 平面ABCD BC =,//BC AD ,BC ∴⊥平面PMB ,BC PB ∴⊥,BC BM ⊥,PBM ∴∠是二面角P BC A --的平面角,设1AB =,则3BM =,3PM =, 在Rt PBM △中,tan 1PM PBM BM∠==,即45PBM ︒∠=,故二面角P BC A --的大小为45︒,故C 正确;对于D ,假设BD ⊥平面PAC ,则BD PA ⊥,又依题意平面PAD ⊥平面ABCD ,AD BM ⊥,则BM ⊥平面PAD ,故BM PA ⊥,而BD ,BM 相交,且在平面ABCD 内,故PA ⊥平面ABCD ,与PM ⊥平面ABCD 矛盾,因此BD 与平面PAC 不垂直,故D 错误.故选:ABC.7. 45︒【解析】 面ABCD 面ABEF AB =,且,,BC AB BE AB BC BE B ⊥⊥⋂=,60CBE ∴∠=︒,AB ⊥面BCE连接CE ,如图所示,则BC BE CE EF ===,又//EF AB ,则EF ⊥面BCE ,CE ⊂面BCE ,EF CE ∴⊥即CEF △是等腰直角三角形,45CFE ∠=︒则异面直线AB 与FC 所成角大小等于45︒故答案为:45︒ 8. 6π 【解析】如图,1111111122AD AA A D AA A B AA AB =+=+=+,111CB CA AB BB AA AC AB =++=-+, 且12,22AB AC BC AA ==== ∴1111()2AD CB AA AB AA AC AB ⎛⎫⋅=+⋅-+ ⎪⎝⎭ 2211122AA AB AC AB =-⋅+ 11182249222=-⨯⨯⨯+⨯=, 1813,8423AD CB =+==+=∴13cos ,2323AD CB <>==⨯,且[]1,0,AD CB π<>∈, ∴1,6AD CB π<>=,∴异面直线AD 与1CB 成角的大小为6π. 故答案为:6π. 9. 见解析 【解析】(1)取线段BC 中点F ,连接EF 、AF 、DF ,则//EF BD ,且112EF BD ==,从而AEF ∠或其补角就是直线AE 与BD 所成的角.AD ⊥平面BCD ,CD ⊂平面BCD ,AD CD ∴⊥,同理可得AD DF ⊥, E 为CD 的中点,则112DE CD ==,222AE AD DE =+=, 2BD CD ==,F 为BC 的中点,则DF BC ⊥,120BDC ∠=,30CBD ∴∠=,sin301DF BD ∴==,则222AF AD DF =+=,由余弦定理可得2222cos 24AE EF AF AEF AE EF +-∠==⋅, 因此,异面直线AE 与BD 所成角的余弦值为24; (2)可知二面角A BE C --的平面角与二面角A BE D --的平面角互补. 在平面BCD 内作直线DG BE ⊥于G ,连接AG ,AD ⊥平面BCD ,BE ⊂平面BCD ,BE AD ∴⊥,同理可得AD DG ⊥, BE DG ⊥,AD DG D =,BE ∴⊥平面ADG ,AG ⊂平面ADG ,AG BE ∴⊥,所以,二面角A BE D --的平面角为AGD ∠,在DBE 中,由余弦定理得cos1207BE == 由等面积法可得11sin12022BDE S BD DE BE DG =⋅=⋅△,sin12021BD DE DG BE ⋅∴==,在Rt ADG 中,tan 3AD AGD DG ∠==,∴二面角A BE C --的正切值为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间线面关系
一、选择题:
1.在下列命题中,不是公理..
的是( ) A .平行于同一个平面的两个平面相互平行
B .过不在同一条直线上的三点,有且只有一个平面
C .如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内
D .如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线
2.设平面α与平面β相交于直线m ,直线a 在平面α内,直线b 在平面β内,且b m ⊥,则“αβ⊥”是“a b ⊥”的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .即不充分不必要条件
3.下列命题正确的是( )
A .若两条直线和同一个平面所成的角相等,则这两条直线平行
B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D .若两个平面都垂直于第三个平面,则这两个平面平行
4.已知矩形ABCD ,1AB =,BC ABD ∆沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中( )
A .存在某个位置,使得直线AC 与直线BD 垂直
B .存在某个位置,使得直线AB 与直线CD 垂直
C .存在某个位置,使得直线A
D 与直线BC 垂直
D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直
5.已知n m ,为异面直线,⊥m 平面α,⊥n 平面β,直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则( )
A .βα//,且α//l
B .βα⊥,且β⊥l
C .α与β相交,且交线垂直于l
D .α与β相交,且交线平行于l
6.已知正四棱柱1111ABCD A BC D -中 ,
2AB =,1CC =E 为1CC 的中点,则直线1AC 与平面BED 的距离为( )
A .2
B
C
D .1
7.设四面体的六条棱的长分别为1,1,1,1a 且长为a 则a 的取值范围是( )
A .
B .
C .
D .(1
8.如图,在正方体1111ABCD A BC D -中,
E 、
F 分别为BC 、1BB 的中点,则下列直线中与直线EF 相交的是( )
A .直线1AA
B .直线11A B
C .直线11A
D D .直线11B C
9.已知直三棱柱111ABC A B C -中,120ABC ∠=︒,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为( )
A B C D 10.若空间中n 个不同的点两两距离都相等,则正整数n 的取值( )
A .大于5
B .等于5
C .至多等于4
D .至多等于3
11.平面α过正方体1111ABCD A BC D -的顶点
A ,//α平面11C
B D ,α 平面ABCD m =,α 平面11ABB A n =,则m ,n 所成角的正弦值为( )
A B C D .13 12.已知正四棱锥S ABCD -所有棱长都为1,点E 是侧棱SC 上一动点,过点E 垂直于SC 的截面将正四棱锥分成上、下两部分,记SE x =(01x <<),截面下面部分的体积为()V x ,则函数()y V x =的图像大致为( )
二、填空题:
13.如图,在正方体1111ABCD A BC D -中,
M 、N 分别是CD 、1CC 的中点,则异面直线
1A M 与DN 所成的角的大小是____________
N
A 1
14.已知正方体1111ABCD A BC D -中,
E 、
F 分别为11BB CC 、的中点,那么异面直线AE 与1D F 所成角的余弦值为____________.
15.如图,已知平面四边形ABCD ,3AB BC ==,1CD =,AD =90ADC ∠=︒.
沿直线AC 将ACD ∆翻折成1ACD ∆,直线AC 与1BD 所成角的余弦的最大值是______.
16.若四面体ABCD 的三组对棱分别相等,即AB CD =,AC BD =,AD BC =,则______(写出所有正确结论编号).
①四面体ABCD 每组对棱相互垂直;
②四面体ABCD 每个面的面积相等;
③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90。
而小于180。
; ④连接四面体ABCD 每组对棱中点的线段互垂直平分;
⑤从四面体ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长.
答案:
AACB ;DDAD ;CCAA ;
2π;53②④⑤
强化练习
1.体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )
A .12π
B .
323π
C .8π
D .4π 2.已知空间三条直线l 、m 、n ,若l 与m 异面,且l 与n 异面,则( )
A .m 与n 异面
B .m 与n 相交
C .m 与n 平行
D .m 与n 异面、相交、平行均有可能 3.已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足//m α,n β⊥,则( )
A .//m l
B .//m n
C .n l ⊥
D .m n ⊥
4.已知直线a ,b 分别在两个不同的平面α,β内,则“直线a 和直线b 相交”是“平面α和平面β相交”的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
5.已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )
A .若α,β垂直于同一平面,则α与β平行
B .若m ,n 平行于同一平面,则m 与n 平行
C .若α,β不平行,则在α内不存在与β平行的直线
D .若m ,n 不平行,则m 与n 不可能垂直于同一平面
6.设α,β是两个不同的平面,m 是直线且m α⊂.“m β∥”是“αβ∥”的( )
A .充分而不必要条件
B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
7.若,l m 是两条不同的直线,m 垂直于平面α,则“l m ⊥”是“//l α”的 ( )
A .充分而不必要条件
B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
8.若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )
A .l 至少与1l ,2l 中的一条相交
B .l 与1l ,2l 都相交
C .l 至多与1l ,2l 中的一条相交
D .l 与1l ,2l 都不相交
9.如图,若Ω是长方体ABCD -A 1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体,其中E 为线段A 1B 1上异于B 1的点,F 为线段BB 1上异于B 1的点,且EH ∥A 1D 1,则
下列结论中不正确的是( )
A .EH ∥FG
B .四边形EFGH 是矩形
C .Ω是棱柱
D .四边形EFGH 可能为梯形
10.如图,四棱锥P ABCD -中,090ABC BAD ∠=∠=,2BC AD =,PAB ∆和PAD ∆都是等边三角形,则异面直线CD 和PB 所成角的大小为( )
A .090
B .075
C .060
D .045
11.三棱柱111ABC A B C -侧棱与底面垂直,体积为94,底面是正三角形,若P 是111A B C ∆中心,则PA 与平面ABC 所成的角大小是( ) A. 12π
B. 3π
C. 4π
D. 6π
12.在长方体1111ABCD A B C D -中,AB =,11BC AA ==,点P 为对角线1AC 上的动点,点Q 为底面ABCD 上的动点(点P ,Q 可以重合),则1B P PQ +的最小值为( )
A B C .
32
D .2 二、填空题:
13.一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为______________.
14.设甲,乙两个圆柱的底面面积分别为12,S S ,体积为12,V V ,若它们的侧面积相等且1294S S =,则12
V V 的值是 . 15.
已知边长为的菱形ABCD 中,60BAD ∠= ,沿对角线BD 折成二面角为120 的四面体,则四面体的外接球的表面积为________.
16.已知在直角梯形ABCD 中,222,,===⊥⊥CD AD AB AD CD AD AB ,将直角梯形ABCD 沿AC 折叠成三棱锥ABC D -,当三棱锥ABC D -的体积取最大值时,其外接球的体积为______.
答案:ADCA ;DBBA ;DABC ;21π;
32;π28;34π。
