曲面的第二基本形式与几何性质
大学微分几何的曲率与曲面积分计算

大学微分几何的曲率与曲面积分计算微分几何是数学中的一个分支,研究的是曲线、曲面等几何对象的性质及其与微积分的关系。
曲率和曲面积分是微分几何中的两个重要概念,在研究曲线和曲面特征时起到了关键作用。
一、曲线上的曲率计算曲线上的曲率是描述曲线弯曲程度的量度,可以通过计算曲线的曲率半径来确定。
假设有一个平面曲线C,其参数方程为r(t)=(x(t), y(t)),其中t是曲线上的参数。
我们可以通过以下步骤计算曲线C上的曲率:1. 计算曲线的切向量T(t)。
切向量是曲线在某一点的切线的方向向量,可以表示为:T(t) = (dx/dt, dy/dt) / √((dx/dt)^2 + (dy/dt)^2)2. 计算曲线的单位切向量T'(t)。
单位切向量是切向量的归一化,即除以其模,可以表示为:T'(t) = T(t) / ||T(t)||3. 计算曲线的曲率K(t)。
曲率是刻画切线转动速度的量度,可以表示为:K(t) = ||T'(t)|| / ||r'(t)||4. 计算曲线的曲率半径R(t)。
曲率半径是曲率的倒数,可以表示为:R(t) = 1 / K(t)二、曲面上的曲率计算与曲线不同,曲面上的曲率不再是一个标量,而是一个张量。
曲面的曲率在每个点上有两个主曲率和两个主曲率方向。
设有一个曲面S,其参数方程为r(u, v) = (x(u, v), y(u, v), z(u, v)),其中u和v是曲面上的参数。
我们可以通过以下步骤计算曲面S上的曲率:1. 计算曲面的法向量N(u, v)。
法向量是曲面在某一点的垂直于切平面的向量,可以表示为:N(u, v) = (rxu × rxv) / ||rxu × rxv||其中rxu和rxv分别表示对u和v求偏导数得到的向量,×表示向量的叉乘。
2. 计算曲面的第一基本形式E(u, v)、F(u, v)和G(u, v)。
曲面第一第二基本形式

曲面第一第二基本形式曲面的第一第二基本形式是曲面微分几何中的重要概念,用于描述曲面的局部性质。
曲面的第一基本形式是一个二次型,描述了曲面上的长度和角度的变化;而第二基本形式是一个线性映射,描述了曲面上的曲率信息。
对于一个曲面上的点,可以通过两个正交曲线来描述它的局部性质。
这两条曲线称为曲面上的曲线坐标线,在该点处与坐标轴相切。
通过这两条曲线,可以定义曲线的长度、角度和曲率等重要几何量。
曲面的第一基本形式是一个二次型,可以表示为:[ds^2 = E du^2 + 2F du dv + G dv^2]其中,(E)、(F) 和 (G) 是曲面上的度量系数。
它们描述了曲线坐标线上的长度和夹角变化。
具体而言,(E) 表示曲线坐标线在 (u) 方向上的长度的平方,(G) 表示曲线坐标线在 (v) 方向上的长度的平方,而 (F) 则表示曲线坐标线在 (u) 和 (v) 方向上的长度乘积。
曲面的第二基本形式是一个线性映射,可以表示为:[dN = L du^2 + 2M du dv + N dv^2]其中,(L)、(M) 和 (N) 是曲面上的切向量与法向量之间的内积。
它们描述了曲面上的曲率信息。
具体而言,(L) 表示曲面的法向量在 (u) 方向上的变化率,(N) 表示曲面的法向量在 (v) 方向上的变化率,而 (M) 则表示曲面的法向量在 (u) 和 (v) 方向上的变化率乘积。
通过第一第二基本形式,我们可以计算曲面上的各种几何量,如曲率、高斯曲率和平均曲率等。
这些几何量对于曲面的形状和性质具有重要的意义,并在计算机图形学、物理学和工程学等领域中得到广泛应用。
总之,曲面的第一第二基本形式是描述曲面局部性质的重要工具,它们提供了曲面上的长度、角度和曲率等几何信息。
通过研究这些信息,我们可以深入理解曲面的形状和性质,并应用于各种实际问题的解决中。
最新第四章曲面的第二基本形式与曲面上的曲率

第四章 曲面的第二基本形式与曲面上的曲率§5 曲面上的曲率概念利用上一节所作的准备,围绕曲面弯曲状况的刻画,本节将引入曲面上的基本的和重要的曲率概念,并简要讨论相关的几何体.一.主曲率定义1 曲面 S 上的点 P 处的法曲率关于切方向的两个最值,分别称为曲面 S 在点 P 处的主曲率;使得法曲率达到最值的两个切方向,分别称为曲面 S 在点 P 处的主方向.注记1 ① Weingarten 变换的特征值和特征方向,分别是曲面的主曲率和主方向.② 当两个主曲率 1(P ) 2(P ) 时,曲面在点 P 处有且仅有正交的两组主方向,每一组的单位化向量分别就是Weingarten 变换的单位正交特征向量.而当两个主曲率 1(P ) 2(P ) 时,曲面在点 P 处的任何非零切向都是主方向,Weingarten 矩阵 (P ) 1(P )I 2 ,即 (P )1(P )g (P ) .主曲率和主方向的计算,自然归结为Weingarten 变换的特征值和特征方向的计算,也就是Weingarten 矩阵的特征值和特征方向的计算.即:① 对于主曲率的算法,当易知Weingarten 矩阵 之时,方程为 (4.3) 式,或直接写为(5.1)I 2 0 ; 等价地,当易知系数矩阵 和 g 之时,其方程可变形为(5.2) g 0 . ② 对于主方向的算法,各种等价算式为a a i r i 0 为主方向,即非零切方向 a 1:a 2 为主方向, (a 1, a 2) (a 1, a 2) , (a 1, a 2) (0, 0), (a 1, a 2) (a 1, a 2)g , (a 1, a 2) (0, 0) det. ⎝⎛⎭⎫(a 1, a 2) (a 1, a 2)g 0(a2)2a1a2 (a1)2g11g12g22Ω11 12 220 .主方向所对应的微分方程通常写为(5.3)(d u2)2d u1d u2 (d u1)2g11g12g22Ω11 12 220 .定义2若曲面S在点P处的两个主曲率相等,则称点P为曲面S上的一个脐点.若曲面S处处为脐点,则称曲面S为全脐曲面.若脐点处的主曲率为零,则称之为平点;若脐点处的主曲率不为零,则称之为圆点.注记2全脐曲面S的法曲率只与点有关而不依赖于切向选取,故只有平面和球面两类;平面上各点为平点,球面上各点为圆点.全脐曲面主方向所对应的微分方程是蜕化的恒等式.二.Gauss曲率和平均曲率定义3对于正则曲面S,其在点P处的两个主曲率的乘积 ,称为其在点P处的Gauss曲率或总曲率;其在点P处的两个主曲率的算术平均值H,称为其在点P处的平均曲率.注记3①注意到(4.4)-(4.5) 式,Gauss曲率和平均曲率分别具有用Weingarten矩阵或两个基本形式系数的表达式,分别列为(5.4) |Ω||g|LN-M2EG-F2,(5.5) H tr.2LG- 2MF NE2(EG-F2).②主曲率方程 (4.3) 式现可改写为(5.6) 2 2H 0 ;其中H 2 ( 1 2)24≥0 .③Gauss曲率在容许参数变换下不变;平均曲率在保向参数变换下不变,在反向参数变换下变号.④当曲面三阶连续可微时,Gauss曲率和平均曲率分别是连续可微函数;此时,两个主曲率函数(5.7) i H H2 , i 1, 2处处连续,并且在非脐点处连续可微.⑤ 平均曲率等于法曲率按切方向的积分平均值(留作习题).⑥ 平均曲率不是等距不变量.反例如圆柱面和平面.例1 证明可展曲面的Gauss 曲率 0 .证明 对可展曲面 S 的直纹面参数化 r (u , v ) a (u )v l (u ) ,由可展定义得知 n v 0 ,故其第二基本形式系数满足M r u n v 0 , N r v n v 0 ,于是LN - M 2 EG - F 20 . □ 在上例中,若取准线使 a l 0 且 l 1 ,则可展曲面 S 的第一和第二基本形式系数矩阵同时对角化,Weingarten 矩阵则为特征值对角阵,而且(5.8) 1 L E, 2 0 . 三.Gauss 映射和第三基本形式Gauss 在考察曲面的弯曲程度刻画时,注意到曲面的单位法向在单位球面上的行为对于曲面弯曲状况的反映,并进一步明确了两者的依赖程度,进而在曲面论中做出了卓有成效的工作.观察熟知的一些曲面,比如平面、圆柱面、圆锥面、椭球面、双叶双曲面、双曲抛物面等等,可以直观感受到单位法向不同的行为和曲面不同的弯曲状况之间有着密切联系.定义4 对于 C 3 正则曲面 S : r (u 1, u 2) 及其单位法向量场 n (u 1, u 2) ,曲面 S 到以原点为心的单位球面 S 2(1) 上的映射(5.9) G : S S 2(1) r (u 1, u 2) G (r (u 1, u 2)) n (u 1, u 2)称为曲面 S 的Gauss 映射.二次微分形式图4-5(5.10) Ⅲ d n d n称为曲面S的第三基本形式.性质①n1 n2 r1 r2.② (P) limU收缩至P A(G(U))A(U),其中P U S , U为单连通区域,A(G(U)) 是G(U)⊂S2(1) 的面积,A(U) 是U S的面积.③Ⅲ 2HⅡ Ⅰ 0 .证明①由Weingarten公式得n1 n2 [( 11r1 12r2)] [( 21r1 22r2)]r1 r2 r1 r2.②A(U)r1(U)| r1 r2| d u1d u2 ,A(G(U))r1(U) | n1 n2| d u1d u2r1(U)|K|| r1 r2|d u1d u2.而由积分中值定理,P* U使r1(U) |K||r1 r2|d u1d u2 |K (P*)|r1(U)|r1 r2|d u1d u2.故而lim U收缩至P A(G(U))A(U)limP* P|K (P*)| |K (P)|.③结论用系数矩阵等价表示为( g1)g( g1)T 2H g 0g1 2H g 0g1 g1 2H g1 I2 0(tr. ) I2 0 .而最后的等式对于二阶方阵总成立(用特征值理论则知是显然的),用元素计算可直接验证为i k k j (tr. ) i j i ji1 1j i2 2j ( 11 22) i j ( 11 22 12 21) i j 0 .□习题⒈对于螺面r= (u cos v , u sin v , u v) ,试求:①主曲率 1和 2;②Gauss曲率和平均曲率.⒉试求球面的Gauss曲率和平均曲率与球面半径的关系.⒊试证:平均曲率等于法曲率按切方向的积分平均值,即 2 H(P) 2πκ(P, ) d .⒋试证:直纹面的Gauss曲率处处非正.⒌设正则曲面S: r(u1, u2) 当常数 足够小时 1 2 H 2 0 .按参数相同作对应曲面S*: r*(u1, u2) r(u1, u2) n(u1, u2) ,其中n为曲面S的单位法向量场.试证:①S和S* 在对应点具有相同的单位法向和法线;②S和S* 在对应点的Weingarten矩阵具有关系式 * (I2 )1;③S和S* 在对应点的Gauss曲率和平均曲率具有关系式*1 2 H 2,H*H1 2 H 2;④S的曲率线对应于S* 的曲率线.⒍已知曲面S在一点处沿着一组等分周角的m个切方向的法曲率分别为 n(1), …,n (m),m 2 .试证:S在该点的平均曲率Hn(1)… n(m)m.⒎试证:曲面S的第三基本形式恒为零的充要条件为S是平面.工作总结-财务处长个人工作总结[工作总结-财务处长个人工作总结]工作总结-财务处长个人工作总结(范文)工作总结-财务处长个人工作总结2009-07-06 11:52财务处长个人工作总结光阴似箭、岁月如梭,转眼之间一年过去了,新的一年已经开始,工作总结-财务处长个人工作总结。
微分几何科普(1)浅谈度规和曲率

微分几何科普(1):浅谈度规和曲率Shanqin(萍踪浪迹)前言:从现在开始,写一些大学理科生可以轻松看得懂的科普帖子,作出的牺牲就是让其他更高学历的人看起来很平庸.从现在开始,要把看起来要写比较长的文章分开写,不在一个帖子里搞连载。
这样主要是为了避免没有时间续写自己的主题而让自己的帖子变成TJ帖(啥叫TJ呢?就是和DJ有一定联系的……)。
正文:初步的微分几何,必须掌握基本的曲线论,必须适应以弧长为参数的方程.Frenet公式是曲线论基本公式, Frenet标架是活动标架在曲线时的特殊情形.两条曲率和挠率都一样的曲线可以通过刚体运动重合在一起,这是曲线论基本定理.曲线的内蕴曲率为零。
所以所有曲线都可以拉直而不改变其上任意两点间弧长.我们知道,曲面论中这一点通常不能成立,除非此曲面可以等距映射为平面,我们称这种可以和平面进行等距映射的曲面为平坦曲面,如柱面.因此,我们必须深入研究曲面的曲率问题,首先要熟悉曲线坐标,在切平面上讨论问题,这个是整个微分几何的基础.因为即使到高维情形,我们仍要讨论切空间及其上的Levi-Civita联络.在切平面上任意点引入切矢量基(du,dv),切向量在这个基下的分量则为r_u,r_v,定义切向量内积系数:E=< r_u. r_u>=g_11,F=< r_u. r_v>=< r_v. r_u>=g_12,G=< r_v. r_v>=g_22,这三个量就是极其重要的度量(度规)系数.曲面的第一基本形式于是可以写成:Ⅰ=<dr.dr>=Edudu+2Fdudv+Gdvdv=g_ijdu_idu_j最后一式我们将du,dv写成du_1,du_2,i,j取值为1,2,这里采用了Einstein求和约定:重复指标自动求和.这样的符号约定和求和约定可以让我们轻松将2维情形推广到n维流形的n维切空间,其上切向量内积系数(度量系数)就是g_ij(i,j=1,2,…,n),若n等于4,就是广义相对论中的度规张量情形.我们开始讨论曲面的第二基本形式.引入曲面上任意点的法向量n,定义两点间法向量的变化: dn=n_udu+n_vdv.其中n_u,n_v为dn在基(du,dv)下的展开系数.则我们可以定义内积:L=-< r_u. n_u>=h_11M=-< r_u. n_v>=< r_v. n_u>h_12N=-< r_v. n_v>=h_22L,M,N(h_11, h_12, h_22)称为第二形式基本量,于是第二基本形式可以写成:Ⅱ= -<dr.dn>= Ldudu+2Mdudv+Ndvdv= h_ijdu_idu_j.最后一个等式采用的符号和求和约定同上.第一基本形式决定了曲面的内蕴结构,以后我们会发现,联络系数(Christoffel符号)由度规张量和度规张量的一次导数决定,而曲面的Gauss曲率(广而言之,流形的Riemann截面曲率)由联络系数及其一阶导数决定.什么是Gauss曲率和Riemann截面曲率?我们可以从曲面的法曲率出发,定义主曲率.我们想象拿着一把刀,贴着曲面上某点(u,v)的法线往下切,在曲面上切出一条曲线,这条曲线的曲率就是曲面在该点(u,v)沿(du,dv)方向的法曲率.如果想象我们切一个椭球面,在同一点贴着法线,沿不同方向切下去,切出的所有曲线(称为法截线,相应的这一刀所在的平面称为法截面)的曲率不一定一样.我们把这些曲线的曲率进行比较,最大和最小的法曲率称为主曲率,记为k_1, k_2.这两个法曲率对应的法截线必定垂直.定义Gauss曲率为k_1, k_2的乘积:K= k_1.k_2. 若K=0,则曲面必然平坦.定义平均曲率为k_1, k_2的算术平均: H=( k_1+_2)/2.若H=0,则该曲面就是极小曲面.Gauss绝妙定理指出, Gauss曲率K在曲面的等距变换下保持不变.即曲面的内蕴性质由第一基本形式决定决定,与它在外围空间中的形状无关.而曲面的第二基本形式则决定了曲面在外围空间中的形状.这些结论可以可以推广到高维空间中的超曲面(维数比外围空间低一的曲面称为超曲面).1854年Riemann推广了Gauss的想法,将抽象曲面研究推广到高维抽象弯曲空间(流形)进行研究.在高维情形,我们将面对切空间.与前面类似,我们定义度规系数g_ij(i,j=1,2,…,n),此时我们可以让其他方向都退化,留下两个方向,用曲面论观点看问题.这样就可以将Gauss曲率搬到这里,由于方向很多,我们将面对不止一个的Gauss曲率,我们将这些曲率称为Riemann截面曲率.显然,当弯曲空间为2维曲面时, Riemann 截面曲率就是Gauss曲率.Riemann截面曲率为常数的空间称为常曲率空间,如果这个常曲率空间是单连通的,我们就称为“空间形式”,最重要的三种空间形式分别是正曲率的球空间,零曲率的欧空间,负曲率的双曲空间.Riemann在世时,并未将这个想法进行详细发展,后世的Christoffel进行了很大的扩充,这个曲率由Christoffel符号的导数和乘积表示, 所以Riemann截面曲率也称为Riemann-Christoffel曲率.将Riemann截面曲率缩并(取迹,即让R_ijkl中的两个字母相同而求和),就得到了Ricci曲率R_ij,将Ricci 曲率缩并,就得到标量曲率(数量曲率,纯量曲率)R.这些概念在后来Einstein创立的引力论(GR)之中都成为核心概念.GR确定了时空曲率和物质分布的关系.其基本方程就是Einstein方程:R_ij-1/2 R g_ij+Λg_ij=8πT_ij其中R_ij为时空的Ricci曲率,R为时空的标量曲率, g_ij为时空的度规张量. Λ为宇宙学常数, T_ij为物质的物质的能-动张量.我们可以记G_ij=R_ij-1/2 R g_ij, G_ij就是通常所说的Einstein张量.因此我们研究四维时空时,只要知道它的度规张量(第一基本形式系数),就可以直接以这个四维时空为研究对象,而不用考虑将这个时空嵌入更高维数的空间进行研究.所以不管是Minkowski空间,de Sitter空间还是反de Sitter空间,都是写成度规后进行研究.但是在很多时候,我们要研究时空中的超曲面. 即使是de Sitter空间和反de Sitter空间,我们也可以将它们分别嵌入五维欧氏空间R^5里面的双曲面.而在广义相对论中我们以Lorentz流形作为基本研究框架(尽管我们可以赋予时空其他形式的度规结构,但是我们最经常使用的还是Lorentz度规.)我们通常要研究Lorentz流形中的类空超曲面M^3,为了研究其上的内蕴特征和外在特征在时间演化下的变化,就必须引入初始数据集(M^3,g_ij, h_ij),此处g_ij, h_ij 分别为M^3上的度规张量和第二基本形式量. g_ij和h_ij必须满足的相容性条件是著名的Gauss-Codazzi方程.因为Gauss-Codazzi方程是(超)曲面存在的充分必要条件.因此可见看似初等的微分几何曲面论中的一些概念在广义相对论的现代研究中实际上是非常重要的.但是在很多时候,我们要研究时空中的超曲面. 即使是de Sitter空间和反de Sitter空间,我们也可以将它们分别嵌入五维欧氏空间R^5里面的双曲面.===================================================昌海兄,请将上面这一段替换成下面这一段,然后删除此回帖:但是在很多时候,我们要研究时空中的超曲面. 即使是de Sitter空间和反de Sitter空间,我们也可以将它们分别嵌入五维伪欧氏空间(pseudo-Euclidean spaces)R^5里面的双曲面。
《微分几何》教学大纲

《微分几何》课程教学大纲课程名称:《微分几何》课程编码:074112303适用专业及层次:数学与应用数学(本科)课程总学时:72学时课程总学分:4一、课程的性质、目的与任务等。
1、微分几何简介及性质微分几何是高等院校数学和数学教育各专业主要专业课程之一,是运用微积分的理论研究空间的几何性质的数学分支学科。
古典微分几何研究三维空间中的曲线和曲面,而现代微分几何开始研究更一般的空间--流--形。
微分几何与拓扑学等其他数学分支有紧密的联系,对物理学的发展也有重要影响,爱因斯坦的广义相对论就以微分几何中的黎曼几何作为其重要的数学基础。
本课程的前导课程为解析几何、高等代数、数学分析和常微分方程。
2、教学目的:通过本课程的教学,使学生掌握三维欧氏空间中的曲线和曲面的局部微分理论和方法,分析和解决初等微分几何问题,并为进一步学习微分几何的近代内容打下良好的基础。
3、教学内容与任务:本课程主要应用向量分析的方法,研究一般曲线和曲面的局部理论,同时还采用了张量的符号讨论曲面论的基本定理和曲面的内蕴几何内容,并且讨论了属于整体微分几何的高斯崩尼(B公式。
重点让学生把握理解本教材的前二章。
二、教学内容、讲授大纲与各章的基本要求第一章曲线论教学要点:本章主要研究内容为向量分析,曲线的切线,法平面,曲线的弧长参数表示,空间曲线的基本三棱形,曲率和挠率的概念和计算,曲线论的基本公式和基本定理,从而对空间曲线在一点邻近的形状进行研究,同时对特殊曲线特别是一般螺线和贝特朗曲线进行研究。
通过本章的教学,使学生理解和熟记有关概念,掌握理论体系和思想方法,能够证明和计算有关问题教学时数:22学时。
教学内容:第一节向量函数1.1向量函数的极限1.2向量函数的连续性1.3向量函数的微商向量函数的泰勒()公式1.5向量函数的积分第二节曲线的概念2.1曲线的概念2.2光滑曲线、曲线的正常点2.3曲线的切线和法面2.4曲线的弧长、自然参数第三节空间曲线3.1空间曲线的密切平面3.2空间曲线的基本三棱形空间曲线的曲率、挠率和伏雷内公式3.4空间曲线在一点邻近的结构3.5空间曲线论的基本定理3.一6般螺线考核要求:i理解向量函数的极限、连续性、微商、泰勒(L公式和积分等概念,能推导和熟记有关公式,并能使用它们熟练地进行运算。
微分几何陈维桓第四章讲稿

微分⼏何陈维桓第四章讲稿⽬录第四章曲⾯的第⼆基本形式 (50)§ 4.1 第⼆基本形式 (50)§ 4.2 法曲率 (52)§ 4.3 Weingarten映射和主曲率 (55)⼀、Gauss映射和W eingarten变换 (55)⼆、主曲率和主⽅向 (55)§ 4.4 主⽅向和主曲率的计算 (57)⼀、Gauss曲率和平均曲率 (57)⼆、Weingarten变换在⾃然基底下的矩阵 (59)三、第三基本形式 (61)§ 4.5 Dupin标形和曲⾯参数⽅程在⼀点的标准展开 (61)§ 4.6 某些特殊曲⾯ (64)⼀、Gauss曲率K为常数的旋转曲⾯ (65)⼆、旋转极⼩曲⾯ (66)第四章曲⾯的第⼆基本形式本章内容:第⼆基本形式,法曲率,Gauss 映射和Weingarten 变换,主⽅向与主曲率,Dupin 标形,某些特殊曲⾯计划学时:12学时,含习题课3学时. 难点:主⽅向与主曲率§ 4.1 第⼆基本形式设:(,)S r r u v = 为正则曲⾯,(,)n n u v = 是单位法向量. 向量函数(,)r u v的⼀阶微分为u v dr r du r dv =+,⼆阶微分为()222222u v u v uu uv vv d r d r du r dv r d u r d v r du r dudv r dv =+=++++ .由于0dr n ?= ,再微分⼀次,得2d r n dr dn ?=-? .定义⼆次微分式222II 2d r n dr dn Ldu Mdudv Ndv =?=-?=++ (1.6)称为曲⾯S 的第⼆基本形式(second fundamental form),其中uu u u L r n r n =?=-? ,uv u v v u M r n r n r n =?=-?=-?,vv v v N r n r n =?=-? (1.4-5) 称为曲⾯S 的第⼆类基本量.第⼆基本形式的⼏何意义:刻划了曲⾯偏离切平⾯的程度,也就是曲⾯的弯曲程度.由微分的形式不变性可知第⼆基本形式在保持定向的参数变换下是不变的,⽽在改变定向的参数变换下会相差⼀个符号. 但是,在参数变换下第⼆类基本量,,L M N ⼀般都会改变.第⼆基本形式与空间坐标系的选取⽆关. 对曲⾯:(,)S r r u v =作参数变换(,),(,)u u uv v v uv == (1.7) 在新的参数下,u u v u v r r r u u ??=+?? ,v u v u v r r r v v=+ .因此(,)(,)u v uv uv u vu v u v r r r r r r u v v u u v=-=. (1.10)当(,)0(,)u v uv ?>? 时,n n = ,从⽽ I I ,,I Id r d nd r d n =-=-=;当(,)0(,)u v uv ?n =- ,从⽽ II ,,II dr d n dr dn =-==- . 在保持定向的参数变换下,第⼆类基本量有和第⼀类基本量相同的变化规律. 事实上,记参数变换(1.7)的Jacobi 矩阵为u vu uu v vvJ =. 则()()(),,,u vu uu v vvdu dv dudv dudv J== ??. (1.14) 从⽽T II (,)(,)(,)II LM du L M dudu L M du dv du dv J J du dv MN dv M N dv dvMN ==== ?,即有T L M L M J J M N M N = ? ?. (1.13) 例求平⾯(,,0)r u v =和圆柱⾯()cos ,sin ,u u a ar a a v = 的第⼆基本形式. 解. (1) 对平⾯,(1,0,0)(0,1,0)dr du dv =+ ,20d r =,所以II 0=.(2) 对圆柱⾯,()sin ,cos ,0u uu a a r =- ,()0,0,1v r = ,()cos ,sin ,0u u u v a a n r r =?= . 因此 ()11sin ,cos ,0u u u a a a a dn du r du =-= , ()()211 II u v u a a dr dn r du r dv r du du =-?=-+?=- . □定理1.1 正则曲⾯S 是平⾯(或平⾯的⼀部分),当且仅当S 的第⼆基本形式II 0≡. 证明 “?”平⾯S 的单位法向量n是常向量,故II 0dr dn =-?=. “?” 由0u n n ?= ,0u u n r L ?=-= ,0u v n r M ?=-= 得0u n = . 同理有0v n =. 所以0n n =是常向量. 于是0()0dr n d r n ?=?=. 故0r n C ?=. □定理 1.2正则曲⾯S 是球⾯(或球⾯的⼀部分),当且仅当S 的第⼆基本形式是第⼀基本形式的⾮零倍数:II I λ≡,其中(,)u v λλ=是⾮零函数.证明 “?”不妨设球⼼为原点,半径为a . 则22r a = ,0r dr ?= ,1an r =. 从⽽211II I aadr dn dr =-?=-=-.“?”由条件,L E λ=,M F λ=,N G λ=(因为,du dv 是独⽴的变量). 所以()0u u u n r r L E λλ+?=-+= ,()0u u v n r r M F λλ+?=-+=.⼜()0u u n r n λ+?=. 故u u n r λ=-. (1) 同理有v v n r λ=-. (2)因为S 是三次以上连续可微的,uv vu n n =. 于是v u uv uv vu u v vu r r n n r r λλλλ--===--,即有v u u v r r λλ=. 由于,u v r r线性⽆关,0,0u v λλ==. 故λ是⾮零常数. 由(1)和(2)得()0u n r λ+= ,()0v n r λ+=.所以110()n r n r r λλλ+=+=是常向量. 从⽽S 上的点满⾜球⾯⽅程2210()r r λ-= . □课外作业:习题1(1,4,5),2(3),3,6§ 4.2 法曲率设:(),()C u u s v v s ==是曲⾯:(,)S r r u v =上过点p 的⼀条正则曲线,s 是C 的弧长参数,00(,)((0),(0))u v u v =为p 点的曲纹坐标. 则C 的单位切向量为du dvu v ds ds dr ds r r r α===+ . (2.3) 根据Frenet 公式,C 的曲率向量22222222()2()d r d u d vdu du dv dv u vuu uv vv ds ds ds ds dsds dsr r r r r κβα===++++ , (2.4) 其中κ是C 的曲率. 设n 为S 的单位法向量,(,)n θβ=∠,则cos n θβ=? .定义函数000000(,,,):(0)cos (0)(0)(,)(0)(,)n n u v du dv n u v r n u v κκκθκβ===?=?(2.6)22000000(,)()2(,)(,)()du du dvdv ds ds ds dsL u v M u v N u v =++ (2.5) 称为曲⾯S 在p 点沿着切⽅向(,)du dv (即d r)的法曲率(normal curvature).注曲⾯上所有在p 点相切的曲线在p 点有相同的法曲率,并且在p 点这些曲线的曲率中⼼位于垂直于切⽅向的平⾯(C 的法平⾯∏)内的⼀个直径为1/||n κ的圆周上:曲率中⼼为11((0),(0))(0)((0),(0))cos (0)(0)nc r u v r u v βθβκκ=+=+.沿着曲线C ,有dr rds= . 由于s 是弧长参数,因此在p 点成⽴ 22200000(,)2(,)(,)d s d r d r E u v d u F u v d u d v G u vd v=?=++.定义2.1 在曲⾯S 上对应于参数(,)u v 的点p 处,沿着切⽅向(,)du dv 的法曲率为22222II (,,,)2In n Ldu M dudv Ndv u v du dv Edu Fdudv G dvκκ++===++. (2.8)注法曲率除了与点p 有关,还与切⽅向即⽐值:du dv 有关. 但是与切向量d r的⼤⼩⽆关. 上⾯的定义不要求以d r为切向量的曲线C 以弧长s 为参数.定义曲⾯S 上过p 点的⼀个切⽅向(,)d u d v 与p 点的法线确定的平⾯π称为由切⽅向(,)du dv 确定的法截⾯. 法截⾯π与曲⾯S 的交线称为该点的⼀条法截线.定理2.1 曲⾯S 在(,)u v 点,沿切⽅向(,)du dv 的法曲率n κ等于该切⽅向确定的法截线C 在相应的有向法截⾯π(以d r n ?为平⾯π的定向)中的相对曲率,即有n r κκ=.证明设该点是000(,)r r u v =,沿切⽅向(,)du dv 的单位切向量为000(,)()|u v uv r du r dv α=+,在00(,)u v 点的单位法向量为000(,)n n u v =. 则法截⾯的定向是00n α?,从⽽法截线C 的弧长参数⽅程为000()()()r s r x s y s n α=++,其中(0)(0)0x y ==. 因为00(0)(0)(0)r x y n α=+ 是S 的切向量,0(0)(0)0y r n =?= . 从⽽(0)1x = . 因此0(0)r α= 是由(,)du dv 确定的切⽅向. 由定义,沿切⽅向(,)du dv 的法曲率 0000(0)[(0)(0)](0)n r n x y n n y κα=?=+?=.另⼀⽅⾯,法截线C 在该点的相对曲率(0)(0)(0)(0)(0)r x y x y y κ=-= . 所以有n r κκ=. □例 (1) 平⾯的法曲率.在平⾯S 上,II 0≡. 所以在任意点p S ∈,沿任意切⽅向(,)du dv ,都有法曲率0n κ=.(2) 圆柱⾯()cos ,sin ,u u a ar a a v =的法曲率. 对圆柱⾯,由上⼀节的例,22I du dv =+,21II adu =-,所以222()dun a du dv κ+=-.(3) 球⾯()2():cos cos ,cos sin ,sin S a r a u v a u v a u = 的法曲率.由定理1.2,1II I a =-. 所以1n aκ=-是⾮零常数. □定理2.2 在曲⾯S 上任意⼀点p 处,法曲率必定在两个彼此正交的切⽅向上分别取到最⼤值和最⼩值.证明在固定点p ,,,,,,E F G L M N 都是常数,法曲率n κ仅与⽐值:du dv 有关. 取p 点邻近的正交参数⽹. 则任意单位切向量p dr T S ∈,可以写成12cos sin u v dr r du r dv e e θθ=+=+,其中12,u v e e ==,1(,)dr e θ=∠即,du dv θθ==.沿着切⽅向:du dv 的法曲率22()cos sin sinn n L N E G κκθθθθθ==++ ()θ∈R是R 上的连续可微周期函数,必定在闭区间[0,2]π上取到最⼤值和最⼩值.如果n κ是常值函数,则n κ在任意两个彼此正交的切⽅向上分别取到最⼤值和最⼩值. 设()n κθ不是常值函数,则它的最⼤值和最⼩值不相等. 通过对曲⾯作参数变换00cos sin u uv θθ=- ,00sin cos v u v θθ=+ ,不妨设在0θ=处()n κθ取到最⼤值(0)/n L E κ=. 由于()sin 22nN L G E κθθθ??'=-+ ?,(0)0n κ'==,并且/(/2)(0)/n n N G L E κπκ=≤=,有222()cos sin cos n L N NL N N E GG E G G κθθθθ??=+=+-≥ ?. 所以()n κθ在/2θπ=±处取到最⼩值/N G . □定义2.2在曲⾯S 上⼀个固定点p 处,法曲率取最⼤值和最⼩值的切⽅向称为曲⾯S 在该点的主⽅向(principal direction),相应的法曲率称为S 在该点的主曲率(principal curvature).注由上⾯的推导过程可知,如果在p 点n κ不是常值函数,()()sin 2NL nGEκθθ'=-在闭区间[0,2]π上只有4个零点,所以在p 点n κ只有两个主曲率1/L E κ=,2/N G κ=. 于是有下⾯的Euler 公式:2212()cos sin n κθκθκθ=+,其中(,)u dr r θ=∠,12κκ>,并且12()n κκθκ≥≥.定义 2.3 (1) 在曲⾯S 上⼀点,使法曲率为零的切⽅向(,)du dv 称为该点的⼀个渐近⽅向(asymptotic direction).(2) 设C 是曲⾯S 上的⼀条曲线. 若C 上每⼀点的切向量都是曲⾯在该点的渐近⽅向,则称C 是曲⾯S 上的⼀条渐近曲线(asymptotic curve).在⼀点(,)u v 处,渐近⽅向(,)du dv 是⼆次⽅程 2220Ldu Mdudv Ndv ++= (2.5) 的解. 当20LN M-<时,有两个实渐近⽅向::du dv M L N M =-±=-当20LN M -=时,只有⼀个实渐近⽅向:::du dv M L N M =-=-;当20LN M ->时,没有实渐近⽅向.让(,)u v 变动,则(2.5)就是渐近曲线的微分⽅程. 如果在曲⾯上每⼀点,20LN M -<,则曲⾯上存在两个处处线性⽆关的渐近⽅向向量场. 根据第三章定理4.1,在曲⾯上有由渐近曲线构成的参数曲线⽹,称为渐近线⽹.定理2.3 参数曲线⽹是渐近线⽹的充分必要条件是:0L N ==.证明 “?” 在u -曲线上0,0dv du =≠. 由(2.5)得0L =. 同理可得0N =. “?” (2.5)现在成为0M dudv =. 因此u -曲线和v -曲线都是渐近曲线. □定理 2.4 设C 是曲⾯S 上的⼀条曲线. 则C 是渐近线,当且仅当C 是直线,或C 的密切平⾯与曲⾯的切平⾯重合.证明由公式cos (,)n n κκβ=∠可得. □课外作业:习题1,4,7.§ 4.3 Weingarten 映射和主曲率⼀、Gauss 映射和W eingarten 变换设:(,)S r r u v = (2(,)u v ∈Ω? )是⼀个正则曲⾯,(,)n n u v =是它的单位法向量. 向量函数(,)n u v 定义了⼀个映射2::(,)(,)n S u v n u v Ω→,其中2S 是3E 中的单位球⾯. 因为空间3E 中的点与它的位置向量是⼀⼀对应的,映射n诱导了映射12::(,)((,))(,)g n r S S r u v g r u v n u v -=→= . (3.1)这个映射2:g S S →称为Gauss 映射. 注意Gauss 映射的象不⼀定是2S 的⼀个区域.Gauss 映射g 的切映射2():p g p g T S T S *→是⼀个线性映射,满⾜()g dr dn *=,即 ()u v u v g r du r du n du n dv *+=+,p dr T S ?∈,p S ?∈. (3.2)特别有()u u g r n *= ,()v v g r n *=. (3.4)因为(,)n u v同时也是2()g p T S 的法向量,S 在(,)p u v 点的切平⾯与2S 在()g p 点的切平⾯是平⾏的,从⽽在⾃由向量的意义下可将2()g p T S 与p T S 等同.定义线性映射2():p p g p W g T S T S T S *=-→≡称为曲⾯S 在p 点的Weingarten 变换(Weingarten transformation).事实上,因为0u v n n n n ?=?= ,所以,u u p n n T S ∈. 由定义可知, ()()()u v uv p W d r W r d u r d v d n n d un d v T S =+=-=-+∈,p dr T S ?∈. (3.5)⼆、主曲率和主⽅向定理3.1 II ()W dr dr =?. □定理3.2 相对于切空间的内积,Weingarten 变换:p p W T S T S →是⾃共轭(对称)的,即()()W dr r dr W r δδ?=?,,p dr r T S δ?∈ .证明 ()()()u v u v W dr r dn r n du n dv r u r v δδδδ?=-?=-+?+L d u u M d u v M d v u N dδδδδ=+++ ()()()(u v uvr d u r d v n u n v d r n d r W r δδδδ=-+?+=?-=?. □根据线性变换理论,Weingarten 变换W 的2个特征值12,λλ都是实的(这2个特征值可能相等). 设12,p X X T S ∈分别是从属于它们的特征向量,即111()W X X λ= ,222()W X X λ= . 当12λλ≠时,12,X X所确定的切⽅向:du dv 和:u v δδ是唯⼀的,且相互正交. 当12λλ=时,p T S 中的任何⾮零向量都是特征向量. 因此仍然有两个相互正交的特征⽅向.定理3.3在曲⾯S 上任意⼀点p 处,W 的2个特征值12,λλ正好是曲⾯S 在p 点的主曲率,对应的特征⽅向是曲⾯S 在p 点的主⽅向.证明取p T S 的由W 的特征向量构成的单位正交基{}12,e e,使得111()W e e λ= ,222()W e e λ=, (3.12)并设12λλ≥.对任意⼀个单位切向量p e T S ∈,可设 12cos sin e e e θθ=+. (3.13)则有121122()cos ()sin ()cos sin W e W e W e e e θθλθλθ=+=+. (3.14)于是沿切⽅向e的法曲率为2211221212II ()()I (cos sin )(cos sin )cos sin .n n W e ee ee e e e κκθλθλθθθλθλθ?===?=+?+=+由12λλ≥可知2222121121()cos ()()sin n λλλλθκθλλλθλ≤+-==--≤,并且()n κθ在0θ=时取最⼤值1λ,在/2θπ=时取最⼩值2λ. 所以12,λλ就是曲⾯S 在p 点的主曲率12,κκ,相应的切⽅向12,e e就是主⽅向. □注1 由定理可知沿特征⽅向:du dv 的法曲率n κ就是对应于特征向量d r的特征值:II()()I nW dr dr dr drdr dr dr dr λκλ??====?? . 注2 曲⾯S 在每⼀点p 有2个主曲率12,κκ. 当12κκ≠时,只有2个主⽅向,它们相互正交. 此时可取2个单位特征向量12,e e. 当12κκ=时,任何⽅向都是主⽅向. 此时可任取2个正交的单位特征向量12,e e.定理3.4(Euler 公式) 设{}12,e e是p 点的2个正交的单位特征向量,对应的主曲率为12,κκ.则对任意单位切向量12cos sin p X e e T S θθ=+∈,沿着X ⽅向的法曲率为2212()cos sin n κθκθκθ=+. (3.15)在曲⾯S 上⼀点p 处,如果12κκλ==,则由Euler 公式可知沿任何切⽅向:du dv ,都有II In κλ==, (3.16)即II I λ=. 这样的点称为脐点(umbilical point). 此时在该点有:::L E M F N G λ===. (3.17)当0λ=时,该点称为平点(planar point);当0λ≠时,该点称为圆点(circle point).定理1.1和定理1.2的推论曲⾯S 是平⾯(或其⼀部分),当且仅当S 上的点都是平点;曲⾯S 是球⾯(或其⼀部分),当且仅当S 上的点都是圆点.定义3.1 设C 是曲⾯S 上的⼀条曲线. 若C 上每⼀点的切向量都是曲⾯在该点的主⽅向,则称C 是曲⾯S 上的⼀条曲率线(curvature line).定理 3.5(Rodriques 定理) 曲⾯:(,)S r r u v =上⼀条正则曲线:(),()C u u t v v t ==是曲率线的充分必要条件是:沿着曲线C ,()//()dn t dr t ,即((),())//((),())dn u t v t dr u t v t. 证明. 由定义,C 是曲率线,当且仅当对所有的t ,()dr t是Weingarten 变换的特征向量,即()()()()W dr t t dr t λ= ,也就是()()()()()dn t W dr t t dr t λ=-=-. □定理3.6 曲⾯S 上⼀条曲线C 是曲率线的充分必要条件是:曲⾯S 的沿着曲线C 的法线构成可展曲⾯.证明. 对曲⾯S 上任意⼀条曲线C ,曲⾯S 的沿着曲线C 的法线构成直纹⾯1:(,)((),())((),())S X X s t r u s v s t n u s v s ==+,其中s 是C 的弧长参数. 由于()()r s s α= 和()n s 是相互正交的单位向量,从⽽是线性⽆关的.1S 是可展曲⾯?()(),(),()0s n s n s α'≡()()()()(n s s s s n s λαµ'=+. 上式两边与()n t作内积可得()0s µ=,从⽽上式等价于 ()()()n s s s λα'=,这正好是曲线C 是曲率线的充分必要条件. □例3.1 求旋转⾯上的曲率线.解设旋转⾯的⽅程为()(,)()cos ,()sin ,()r u v f v u f v u g v =. 其中()0f v >,并且v 是经线的弧长参数,221f g ''+=. 则()sin ,cos ,0u r f u u =- ,()cos ,sin ,v r f u f u g '''=, ()cos ,sin ,u v r r f g u g u f '''?=- ,()cos ,sin ,n g u g u f '''=-. 由于()sin ,cos ,0u n g u u '=- ,()cos ,sin ,v n g u g u f ''''''=-,并且0f fg g ''''''+=,有0v v n r ?= ,0v v n r ?=. 所以u -曲线(纬线圆)和v -曲线(经线)都是曲率线. 当0g '=时,这个旋转⾯是平⾯,任何曲线都是曲率线. 当0g '≠时,1 g g f f -''''''=-. 如果f g f g a ''''''-=是常数,即经线是圆弧,则旋转⾯是球⾯.此时任何曲线都是曲率线. □例3.2 求可展曲⾯上的曲率线.解设可展曲⾯⽅程为(,)()()r u v a u vl u =+ . 已经知道它的单位法向量()n n u =与v ⽆关,沿着v -曲线(直母线)有0//v v n r =. 所以v -曲线是它的⼀族曲率线. 于是v -曲线的正交轨线是它的另⼀族曲率线. 如果可展曲⾯是平⾯,任何曲线都是曲率线. □课外作业:习题1,4,5§ 4.4 主⽅向和主曲率的计算⼀、Gauss 曲率和平均曲率设曲⾯S 的参数⽅程为(,)r r u v =,,,E F G 和,,L M N 分别是S 的第⼀、第⼆类基本量. 引理设λ是(,)p u v 点的主曲率,则λ满⾜0L E M F M FN Gλλλλ--=--, (4.4)即λ是⼆次⽅程222()(2)()0EG F LG M F NE LN M λλ---++-=的根,也就是⽅程220H K λλ-+= (4.8)的根,其中222()LG M F NEH EG F -+=-,22LN MK EG F -=-,分别称为曲⾯S 的平均曲率(或中曲率)(mean curvature)和Gauss 曲率(或总曲率)(Gaussian curvature). 换句话说,H λ= (4.9)证明. 设:du dv 是对应的主⽅向. 则有()W dr dr λ=,即()()u v u u n du n dv r du r dv λ-+=+.分别⽤,u v r r与上式两边作内积,得()Ldu M dv Edu Fdv λ+=+,()M du Ndv Fdu Gdv λ+=+.所以主⽅向:du dv 满⾜ ()()0,()()0.L E d u M F d v M F d uN G d v λλλλ-+-=??-+-=? (4.3)由于,du dv 不全为零,可得(4.4)式. □设12,κκ是(,)p u v 点的两个主曲率. 由根与系数的关系可得12222L G M F N EH E G Fκκ-++==-,2122LN M K EG Fκκ-==-. (4.6-7)因此1H κ=+,2H κ=-(4.9)p 点是脐点的充分必要条件是在p 点成⽴20H K ==.注⽅程(4.4)即(4.8)是Weingarten 变换的特征⽅程,在保持定向的参数变换下保持不变. 事实上,主曲率在保持定向的参数变换下不变,在反转定向的参数变换下相差⼀个符号. 因此平均曲率12()/2H κκ=+在保持定向的参数变换下不变,在反转定向的参数变换下相差⼀个符号. ⽽Gauss 曲率12K κκ=在参数变换下保持不变.定理4.1 假定曲⾯S 是3r ≥次连续可微的. 则主曲率函数12,κκ是连续的,且在⾮脐点邻近是2r -次连续可微的. □在脐点,20K H=≥,12H κκ==. 从⽽由II I H =可知L H E =,M HF =,N H G =,(4.3)中的两个⽅程成为恒等式. 此时,任何⽅向都是主⽅向.在⾮脐点,分别⽤1λκ=和2λκ=代⼊(4.3),得到相应的主⽅向1111:():()():()d u d vM F L E N G M F κκκκ=---=--- (4.10) 和2222:():()():()u v M F L E N G M F δδκκκκ=---=---. (4.11)将(4.3)改写成()()0,()()0.L d u M d v E d u F d v M d u N d v F d uG d v λλ+-+=??+-+=? (4.12)由于1,λ-不全为零,有 0Ldu M dv E du F dv M du N dv F du G dv++=++, (4.14)即22()()()0FL EM du G L EN dudv G M FN dv -+-+-=. (4.15) 上式可写成220dv dudv du E F G LMN-=. (4.16)(4.14)或(4.15)或(4.16)就是曲⾯上曲率线的微分⽅程.定理4.2 设p 是曲⾯:(,)S r r u v =上⼀个固定点,它的曲纹坐标为00(,)u v . 则在该点参数曲线的切⽅向是相互正交的主⽅向,当且仅当在该点有00(,)0F u v =,00(,)0M u v =. 此时,曲⾯S 在该点的两个主曲率分别为00100(,)(,)L u v E u v κ=,00200(,)(,)N u v G u v κ=.证明必要性. 在00(,)p u v 点,u -曲线和v -曲线相互正交,故000000(,)(,)(,)0u v F u vr u v r u v =?=. (1) ⼜00(,)u r u v ,00(,)v r u v是W 的特征向量,故()0000100(,)(,)(,)u u un u v W r u v r u v κ-==, ()0000200(,)(,)(,)v v vn u v W r u v r u v κ-==. 分别⽤,u v r r与上⾯两式作内积得00(,)0M u v =,并且00100(,)(,)L u v E u v κ=,00200(,)(,)N u v G u v κ=. (4.17)充分性. 由条件,0000(,)(,)0u v r u v r u v ?= ,即00(,)u r u v ,00(,)v r u v相互正交. ⼜00000000(,)(,)(,)(,)0u v v u n u v r u v n u v r u v ?=?=.因此()000000(,)(,)//(,)u u u n u v W r u v r u v -= ,()000000(,)(,)//(,)v v vn u v W r u v r u v -=,即00(,)u r u v ,00(,)v r u v是W 的特征向量. □下⾯的两个定理是定理4.2的直接推论.定理4.3 参数曲线⽹是正交的曲率线⽹的充分必要条件是0F M ==,此时222212I ,II Edu G dv Edu G dv κκ=+=+. (4.18) 定理4.4 在⾮脐点,定理4.3中的参数曲线⽹局部总是存在的. □注若曲⾯S 上没有脐点,则可取正交的曲率线⽹作为参数曲线⽹. 事实上,此时由(4.10)和(4.11)可确定两个相互正交的主⽅向:du dv 和:u v δδ. 从⽽有两个相互正交的⾮零向量场u v dr r du r dv =+ 和u v r r u r v δδδ=+,它们是连续可微的. 根据第三章定理4.1,这样的参数曲线⽹是存在的.若曲⾯S 上的点都是脐点,则曲⾯上任意曲线都是曲率线,此时任何正交参数曲线⽹都是曲率线⽹. 但是在孤⽴脐点邻近,未必有正交的曲率线⽹作为参数曲线⽹.⼆、W eingarten 变换在⾃然基底下的矩阵我们知道{},u v r r是切空间p T S 的基,称为p T S 的⾃然基. 在这组基下,设Weingarten 变换的矩阵为11211222a a A a a ??=,即()()()11211222,(),(),u v u v u v a a n n W r W r r r a a ??--==, (4.19) 也就是11122122(),().u u u v v v u v n W r a r a r n W r a r a r -==+??-==+? 分别⽤,u v r r与上⾯⼆式作内积得11211222a a L M E F a a MN FG ??= ? ? ???. 因此11121212221a aE F LM G F LM A a a F G MN FE MN EG F --===--21G L F M G M F NE MF L E NF ME GF --??=---. (4.21) 代⼊(4.19)得()()1,,u v u v E F L M W r r r r F G MN -=()21,u v G L FM G M FN r r EM FL EN FM EG F --?=---. (4.22)我们知道Weingarten 变换W 的特征多项式 ()10()d e t 0EF L M f I A FG M N λλλλ-=-=- ?121E F E L F M E L F MF GF MG NF MG NEG F λλλλλλλλ-----==-----.其中I 是单位矩阵. W 的特征值12,κκ是特征多项式()f λ的根,与基的取法⽆关,从⽽Gauss 曲率2122det LN M K A EG Fκκ-===-和平均曲率12212trace 222()LG M F NE H A EG F κκ+-+===-与参数取法⽆关,是曲⾯的⼏何不变量.Gauss 曲率K 的⼏何意义:从(4.19)可得1112212211221221()()()u v u v u v u v u v n n a r a r a r a r a a a a r r K r r ?=+?+=-?=? .因此曲⾯S 上⼀个区域D 在Gauss 映射g 下的像()g D 的⾯积元素 0||||||||u v u v d n n dudv K r r dudv K d σσ=?=?= . (4.23)所以()g D 的⾯积()0()||()g D DA d K d g D σσ==.根据积分中值定理,存在pD ∈使得 ()|()|||()()()DA K pd K p A D g D σ==? .让区域D 收缩到⼀点p D ∈,取极限得到(())|()|lim()D pA g D K p A D →=. (4.25)这个公式是曲线论中||()limlim||s s s s sθθκ?→?→??==??的⼀个推⼴,其中θ?是曲线上⼀段由s 到s ?的弧在切线像α下的弧长.三、第三基本形式定义设(,)n u v 是曲⾯:(,)S r r u v =的单位法向量. ⼆次微分式22III 2dn dn e du f dudv g dv =?=++ (4.27)称为曲⾯S 的第三基本形式,其中()()22,,u u v v e n f n n g n ==?= . (4.28)注利⽤Gauss 映射,第三基本形式0III I g *=,其中0I 是单位球⾯2S 的第⼀基本形式. 定理4.5 曲⾯:(,)S r r u v =上的三个基本形式满⾜III 2II I 0H K -+=. 证明因为Weingarten 变换W 的特征多项式为2()2f H K λλλ=-+,所以 220W H W K I -+=.其中::p pI T S T S X X →是单位变换. 于是有 ()()()()()2()()()(2)()22.u u u u u u u uu u u e n n W r W r W r r H W K I r r H n K r r H L K E =?=?=?=-?=--?=-同理可得2u v f n n HM KF =?=- ,2u v g n n HN KG =?=-课外作业:习题2,4,6§ 4.5 Dupin 标形和曲⾯参数⽅程在⼀点的标准展开设(,)p u v 是曲⾯:(,)S r r u v = 上⼀个固定点,12,e e是p 点的两个相互正交的单位主向量 (即Weingarten 变换的特征向量),对应的主曲率为12,κκ. 对单位切向量12cos sin e e e θθ=+([0,2]θπ∈),沿该⽅向的法曲率为2212()cos sin n κθκθκθ=+. 当()0n κθ≠时,在p 点的切平⾯π中取⼀点q 使得)1211cos sin pq e e θθ==+. (5.3)p 点切平⾯π中这样的点q 的轨迹称为曲⾯S 在p 点的Dupin 标形(或标线indicatrix ).在平⾯π中取直⾓标架{}12;,p e e, 现在来导出Dupin 标线的⽅程.设轨迹上的点q 在此坐标系中的坐标为(,)x y . 则)1212cos sin xe ye pq e e θθ+==+.因此1x θ=,1y θ=. (5.4)由Euler 公式得到2212sgn(())n x y κκκθ+=. (5.5)这就是Dupin 标线的直⾓坐标⽅程,它是平⾯π中的⼆次曲线. 如果在平⾯π中取极坐标系,那么Dupin 标线的极坐标⽅程可由(5.3)⽴即得到:()ρρθ==当p 点的Gauss 曲率120K κκ=>时,()n κθ,1κ,2κ同号,Dupin 标线(5.5)是⼀个椭圆2212||||1x y κκ+=. (5.6) 当120K κκ=<时,1κ,2κ异号,Dupin 标线(5.5)是两对共轭双曲线2212||||1x y κκ-=±. (5.7)它们的公共渐近线的⽅向正是曲⾯S 在p 点的渐近⽅向00:cos :sin du dv θθ=.当120K κκ==时,若1κ,2κ不全为零,Dupin 标线(5.5)是两条平⾏直线x =±(20κ=) 或y =±(10κ=). (5.8)当p 点为平点,即120κκ==时,Dupin 标线不存在.定义. 设p S ∈,若()0K p >,则称p 点为曲⾯S 上的椭圆点;若()0K p <,则称p 点为曲⾯S 上的双曲点;若()0K p =,则称p 点为曲⾯S 上的抛物点.下⾯考察曲⾯S 在⼀点p 邻近的形状. 在p 点邻近取正交参数曲线⽹(,)u v ,使得p 点对应的参数为(0,0),且(0,0)u r,(0,0)v r是p 点的两个单位主向量. 则(0,0)(0,0)(0,0)u v n r r =?,且在p 点有(0,0)(0,0)E G ==,(0,0)(0,0)0F M ==,1(0,0)L κ=,2(0,0)N κ=. (5.9)以标架{}123;(0,0),(0,0),(0,0)u v p e r e r e n === 建⽴3E 的坐标系. 根据Taylor 公式,(,)(0,0)(0,0)(0uvr u v r r u r v =++22212(0,0)2(0,0)(0,0)()u u u v v v r u r u v r v o ρ??+ +++?, (5.10)其中ρ=. 由于(0,0)0r p p == ,31(0,0)(0,0)uu r e L κ?==, 3(0,0)(0,0)0uv r e M ?==,32(0,0)(0,0)vv r e N κ?==, (5.11)(5.10)可化为()()()2221121232(,)()()()r u v u o e v o e u v oe ρρκκρ=++++++. (5.12)(5.12)称为曲⾯S 在p 点的标准展开.当ρ=我们得到S 的近似曲⾯S *,在标架{}123;,,p e e e 下,S *的参数⽅程为()221122(,),,()r u v u v u v κκ*=+ ,显式⽅程为 221122()z x y κκ=+. (5.14)直接计算可知近似曲⾯S *与原曲⾯S 在p 点相切(即它们的切平⾯相同). 并且沿着p 点切空间的任何相同的切⽅向,两者有相同的法曲率,即在p 点具有公共切⽅向的法截线有相同的曲率和相同的弯曲⽅向.在椭圆点p ,近似曲⾯S *是椭圆抛物⾯. S *在p 点是凸的.在双曲点p ,S *是双曲抛物⾯. S *在p 点不是凸的,且p 点的切平⾯与S *相交成两条直线,它们是S *上过p 点的两条渐近曲线.在⾮平点的抛物点p ,S *是抛物柱⾯,p 点的切平⾯与S *相交成⼀条直线,是S *上过p 点的渐近曲线.在平点p ,S *是平⾯. 此时,要考察曲⾯S 的近似形状,需要将Taylor 展式(5.10)展开到更⾼阶的项. 见例5.2.⽤平⾯12z =±去截近似曲⾯S *,再投影到p 点的切平⾯上,就得到p 点的Dupin 标线.例5.1 考察圆环⾯()(cos )cos ,(cos )sin ,sin r a r u v a r u v r u =++,2(,)u v ∈R上各种类型点的分布,其中常数,a r 满⾜0a r >>.解 ()sin cos ,sin sin ,cos u r r u v u v u =-- ,()(cos )sin ,cos ,0v r a r u v v =+-, ()(cos )cos cos ,cos sin ,sin u v r r r a r u u v u v u ?=-+ ,()cos cos ,cos sin ,sin n u v u v u =-.()1sin cos ,sin sin ,cos u u n u v u v u r r =-=- ,()cos cos sin ,cos ,0cos v v u n u v v r a r u=-=-+.所以两个主曲率为121cos ,cos u r a r uκκ=-=-+.Gauss 曲率和平均曲率分别为其中0a ≥. 它的母线是xO z 平⾯上的曲线:()z f x =. 则由()cos ,sin ,()u r v v f u '= ,()sin ,cos ,0v r u v u v =-.)()cos ,()sin ,1n f u v f u v ''=-- ,()0,0,()uu r f u ''= ,()sin ,cos ,0uv r v v =-,()cos ,sin ,0vv r u v u v =--.可得()21E f '=+,0F =,2G u =, (6.2)L ''=,0M =,N '=. (6.3)因此参数曲线⽹是正交的曲率线⽹. 由定理4.2,主曲率为()13/221L f E f κ''=='+, ()21/221N f Gu f κ'=='+.于是Gauss 曲率和平均曲率分别为 ()221f f K u f '''='+, ()23/22(1)21f f uf H u f ''''++='+. (6.4)⼀、Gauss 曲率K 为常数的旋转曲⾯如果K 是常数,则函数()f u 应满⾜()2211K u f ''=-??'+??. (6.5) 积分得到2211C K u f =-'+, (6.6)其中C 为积分常数. 即有2221C Ku f C Ku-+'=-.于是()f u =±?. (6.7)1.若0K =,则()f u Au B =+,其中A =,B 为积分常数. 当0A =时,S 是平⾯;当0A ≠时,S 是圆锥⾯. 另⼀个0K =的旋转曲⾯是圆柱⾯()cos ,sin ,r a v a v u =,它不能写成(6.1)的形式.2.若0K >,令21a K =(0a >). 则由(6.6)可知0C >. 设2C b =(0b >). (6.7)化为()f u =±?. (6.9)若21b =,则()f u c =±=+?. (6.10)于是S 是由xO z 平⾯上的半圆弧222()x z c a +-=(0x u =>)绕z 轴旋转⽽成的球⾯.当21b >或201b <<时,由(6.9)定义的函数()f u 仍然存在,但旋转曲⾯S 不是球⾯,虽然S 的Gauss 曲率也是常数21a K =.3.若0K <,令21aK =-(0a >).则由(6.6)可知1C <.设21C b =-(0b >). (6.7)可化为()f u =±?. (6.11)若21b =,则[]()ln(sec tan )sin f u a c u=±=±+-+?,其中arccosu a=. 不妨设积分常数0c =. 则旋转曲⾯S 的母线是xO z 平⾯上的两条曳物线[]c o s ,l n (s ec t a n )s i n .x u az a ==??=±+-? (6.13)其中0z >的⼀⽀绕z 轴旋转⽽得的旋转曲⾯S 称为伪球⾯,它的参数⽅程为[]()c o s c o s ,c o s s i n ,l n (s e c t a n )s i n r a a a ?θ?θ=+-, (,)(0,/2)(0,?θππ∈?. (6.14)当21b >或201b <<时,由(6.11)定义的函数()f u 给出Gauss 曲率为负常数的旋转曲⾯的其他例⼦.⼆、旋转极⼩曲⾯平均曲率0H ≡的曲⾯称为极⼩曲⾯. 现在我们来研究有哪些旋转极⼩曲⾯. 由(6.4)可知函数()f u 应满⾜2(1)0f f uf ''''++=. (6.16)也就是()211f uf f ''=-''+.则()()222222ln()ln(1)2ln 1f f f f u uf f '''''''??-+==-=-??'+.积分得2221f Cf u'='+, (6.17)其中积分常数0C ≥.如果0C =,则()f u A =是常数,从⽽S 是平⾯z A =.如果2C a =,0a >. 则22211u C f u-='+,即f '=±故(()ln f u a u c ??=±=±++. (6.19)不妨设积分常数ln c a =-. 令(ln ua. 则cosh u a t =,S 的参数⽅程可改写为()cosh cos ,cosh sin ,r a t v a t v at =,(,)(0,2)t v π∈? .这个旋转极⼩曲⾯S 称为悬链⾯.⽤变分法可以证明,如果在所有以给定曲线C 为边界的曲⾯中,S 的⾯积达到最⼩值,则S ⼀定是极⼩曲⾯.极⼩曲⾯是微分⼏何研究的重要课题之⼀. ⼀百多年来,数学家们在关于以已知曲线为边界的极⼩曲⾯的存在性的Plateau 问题,⼤范围极⼩曲⾯的性质,极⼩曲⾯在⾼维的推⼴⽅⾯作了⼤量的⼯作,取得了丰富的成果.在极⼩曲⾯上,Gauss 曲率21210K κκκ==-≤,只有平点或双曲点. 在双曲点,2个渐进⽅向是正交的. 事实上,根据Euler 公式,渐近⽅向与主⽅向的夹⾓θ满⾜cos 20θ=.著名的Bernstein 定理是说:极⼩图只能是平⾯,即习题6中的⼆阶偏微分⽅程22(1)2(1)0y xx x y xy x yy f f f f f f f +-++=的定义在全平⾯上的解只能是线性函数.平均曲率H 为⾮零常数的曲⾯,即常平均曲率曲⾯,也是微分⼏何研究的⼀个重要课题. 课外作业:习题2,4,6。
空间曲面与曲面积分

空间曲面与曲面积分在数学中,曲面是一种在三维空间中展开的二维对象。
曲面可以通过参数方程或隐函数方程来描述。
与平面不同,曲面具有曲率和形状的变化。
空间曲面的研究是数学分析和几何学的重要领域之一。
1. 曲面的定义与性质曲面可以通过参数方程来定义,常见的参数方程有笛卡尔坐标系参数方程、球坐标系参数方程和柱坐标系参数方程等。
曲面的性质包括曲面的方向、切平面、法线和曲率等。
2. 曲面积分的概念曲面积分是将函数沿着曲面进行积分的一种方法。
常见的曲面积分有第一类曲面积分和第二类曲面积分。
第一类曲面积分是将函数在曲面上的数值进行积分,而第二类曲面积分则是将函数乘以曲面的微元进行积分。
3. 第一类曲面积分第一类曲面积分的计算涉及到曲面的面积元素和函数的数值。
具体而言,可以通过将曲面分割成小区域,计算每个小区域的贡献,然后将贡献进行累加来得到曲面积分的结果。
常见的例子包括曲面面积的计算和质量分布的求解。
4. 第二类曲面积分第二类曲面积分的计算需要考虑曲面的方向和曲面的法向量。
根据曲面的方向和法向量的关系,第二类曲面积分可以分为曲面的左侧区域和右侧区域两种情况。
具体而言,可以通过将曲面分割成小区域,计算每个小区域的贡献,然后将贡献进行累加来得到曲面积分的结果。
常见的例子包括曲面的通量计算和曲面的旋度计算等。
5. 曲面积分的应用曲面积分在物理学和工程学等领域有广泛的应用。
例如,在电动力学中,曲面积分可以用来计算电场通过曲面的总通量。
在流体力学中,曲面积分可以用来计算流体通过曲面的总流量。
在声学中,曲面积分可以用来计算声波通过曲面的总能量等。
总结起来,空间曲面与曲面积分是数学分析和几何学的重要研究内容。
通过曲面的定义与性质的理解,我们可以深入探讨曲面积分的概念和计算方法。
曲面积分在物理学和工程学等应用中起着至关重要的作用。
数学与应用数学专业(本科)课程说明1.国家开放大学学习指南本课程1

数学与应用数学专业(本科)课程说明1.国家开放大学学习指南本课程1学分,18学时,开设一学期。
本课程是国家开放大学(中央广播电视大学)在本科、专科、“一村一名大学生计划”的所有专业中开设的一门统设必修课。
本课程的教学目的是使接受国家开放大学远程教育的学生在进入专业(课程)学习之前,了解和熟悉远程教育新的学习环境,建立与远程教育模式相适应的新学习理念,了解并尽快适应远程教育教与学的方式,掌握基本的学习技能,逐步培养自主学习的习惯和能力。
本课程的主要内容:以完成学习任务的过程为导向,从学习者如何完成国家开放大学规定的专业学习任务的角度,让学习者学会如何完成一门课程的学习、一个专业的学习,同时描述国家开放大学的基本学习方式,说明国家开发大学的学习环境,解释国家开发大学学习平台上基本术语的含义,使学生能使用学习平台的基本工具辅助完成学习活动,并且了解国家开放大学学生相关事务与管理规定,使学生初具备利用现代远程技术在国家开放大学进行学习的能力。
2.数学分析专题研究本课程4学分,72学时,开设一学期。
本课程分为六个部分。
第一部分是集合与映射,包括集合及其运算,关系与映射,等价关系,序关系,基数;第二部分介绍数集,包括整数理论和实数理论等;第三部分介绍函数及其性质,特别是初等函数与超越函数;第四部分介绍指数函数与对数函数,以及深入地分析其性质;第五部分专题研究三角函数,及其公理化体系;第六部分专题研究极值问题,包括凸函数与极值,泛函数值与欧拉方程以及等周问题。
通过本课程的学习,使学员对实数理论,初等函数有一个系统的认识,能居高临下地看待中学数学中的教学内容,并指导中学数学教学。
3.英语II(1)(2)本课程6学分,108学时,开设一学年。
该课程为广播电视大学公共英语课。
通过语音、语法、词汇等知识的学习和读、听、说、写基本技能训练,培养学生运用英语的能力,侧重培养学生的阅读能力,为学生进一步学习和运用英语打好基础。
《微分几何》教学大纲09
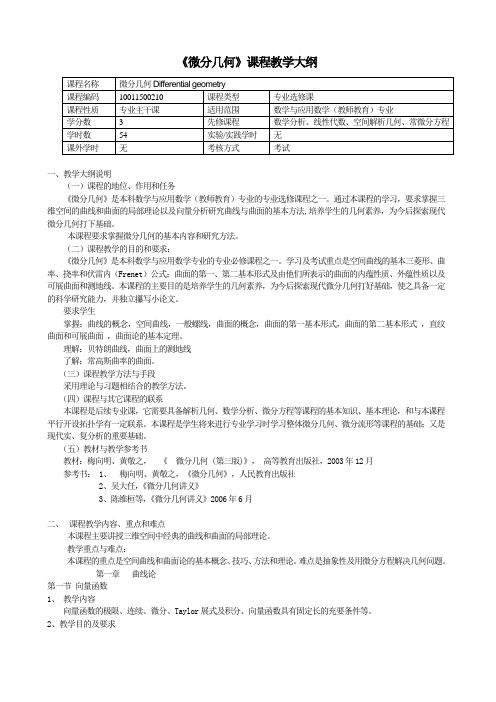
《微分几何》课程教学大纲一、教学大纲说明(一)课程的地位、作用和任务《微分几何》是本科数学与应用数学(教师教育)专业的专业选修课程之一。
通过本课程的学习,要求掌握三维空间的曲线和曲面的局部理论以及向量分析研究曲线与曲面的基本方法,培养学生的几何素养,为今后探索现代微分几何打下基础。
本课程要求掌握微分几何的基本内容和研究方法。
(二)课程教学的目的和要求:《微分几何》是本科数学与应用数学专业的专业必修课程之一。
学习及考试重点是空间曲线的基本三菱形、曲率、挠率和伏雷内(Frenet)公式;曲面的第一、第二基本形式及由他们所表示的曲面的内蕴性质、外蕴性质以及可展曲面和测地线。
本课程的主要目的是培养学生的几何素养,为今后探索现代微分几何打好基础,使之具备一定的科学研究能力,并独立攥写小论文。
要求学生掌握:曲线的概念,空间曲线,一般螺线,曲面的概念,曲面的第一基本形式,曲面的第二基本形式,直纹曲面和可展曲面,曲面论的基本定理。
理解:贝特朗曲线,曲面上的测地线了解:常高斯曲率的曲面。
(三)课程教学方法与手段采用理论与习题相结合的教学方法。
(四)课程与其它课程的联系本课程是后续专业课,它需要具备解析几何、数学分析、微分方程等课程的基本知识、基本理论,和与本课程平行开设拓扑学有一定联系。
本课程是学生将来进行专业学习时学习整体微分几何、微分流形等课程的基础;又是现代实、复分析的重要基础。
(五)教材与教学参考书教材:梅向明、黄敬之,《微分几何 (第三版)》,高等教育出版社,2003年12月参考书: 1、梅向明、黄敬之,《微分几何》,人民教育出版社2、吴大任,《微分几何讲义》3、陈维桓等,《微分几何讲义》2006年6月二、课程教学内容、重点和难点本课程主要讲授三维空间中经典的曲线和曲面的局部理论。
教学重点与难点:本课程的重点是空间曲线和曲面论的基本概念、技巧、方法和理论。
难点是抽象性及用微分方程解决几何问题。
第一章曲线论第一节向量函数1、教学内容向量函数的极限、连续、微分、Taylor展式及积分、向量函数具有固定长的充要条件等。
微分几何曲面局部理论

那么对于 P 点附近的任意一个正则参数表示 x (u , v )
有
nu nv 0.
由连通性可以得出 n 是常向量,即曲面是平面。
■
第二章 曲面:局部理论
例1 M是半径为 ,a 中心在原点的的球面,则
在局部参数表示下Gauss映射为
n 1 x(u, v). a
它的形状算子满足
S P (x u ) n u 1 a x u, S P (x v ) n v 1 a x v .
也都是渐近线。
第二章 曲面:局部理论
事实上,如右图所示,在点 P
处的沿圆柱螺线单位切向量的
法截线在点 P 为拐点。因此,
圆柱螺线是圆柱螺面上的渐近 线。
具体计算为作业。
第二章 曲面:局部理论
假设 ( s为) 曲面 上M 一条弧长参数曲线,满足
(0)P , (0)V.
那么由之前的计算得到 P(V,V)Nn.
第二章 曲面:局部理论
定义 曲面 M在点 处P 的主曲率满足 则称为点 P 为曲面 的M 脐点。 特别的,k1 k2 称 0为平P 点。
k1 k2
如果 K ,0 且 不P是平点,则称 为抛P 物点; 如果 K ,0 则称 为P椭圆点; 如果 K ,0 则称 为P双曲点。
第二章 曲面:局部理论
曲面在任意点 P 的两个主方向是正交的,于是
我们可以选择了切平面 T p M的一个正交基底恰
好由主方向向量构成。
第二章 曲面:局部理论
定理(Euler公式)令 e 1 , e为2 曲面 在M 点 的单P 位
主方向,分别对应主曲率 和 k 。1 假设k 2 切向
量
Vco,s其e1中sine2。 [0,2)
微分几何第二章曲面论曲面的概念

VS
高斯曲率
设曲面$S$在点$P$处的两个主曲率分别为 $k_1, k_2$,则称$K = k_1k_2$为曲面在 点$P$处的高斯曲率。高斯曲率是曲面内蕴 几何量的重要代表,反映了曲面在一点处 的弯曲程度。
法截线和法截线族
法截线
设曲面$S$在点$P$处的法向量为 $mathbf{n}$,过点$P$且与法向量 $mathbf{n}$垂直的平面称为法截面。 法截面与曲面交于一条曲线,该曲线 称为法截线。
曲面性质
曲面具有连续性、光滑性、可定向性等性质。其中连续性指 曲面上任意两点都可以用一条连续曲线连接;光滑性指曲面 上任意一点都存在切线平面;可定向性指曲面存在连续的单 位法向量场。
曲面分类与举例
曲面分类
根据曲面的形状和性质,可以将曲面分为闭曲面、开曲面、紧致曲面、非紧致曲面等类 型。
举例
球面、环面、柱面、锥面等都是常见的曲面类型。例如,球面可以表示为 $mathbf{r}(theta, varphi) = (Rcosthetasinvarphi, Rsinthetasinvarphi,
法截线族
过曲面上一点的所有法截线构成的集 合称为该点的法截线族。法截线族在 微分几何中具有重要的研究价值,与 曲面的形状和性质密切相关。
04
曲面局部理论:可 展曲面与极小曲面
可展曲面定义及性质
定义
可展曲面是一类特殊的曲面,它可以在不改 变距离的情况下完全展开到一个平面上。也 就是说,它的高斯曲率为零。
02
第一基本形式与度 量性质
第一基本形式定义及性质
第一基本形式定义
第一基本形式是微分几何中曲面论的基本概念,用于描述曲面上的度量性质。它是一个二次微分形式,记作$I = Edu^2 + 2Fdudv + Gdv^2$,其中$E, F, G$是曲面上的系数函数。
§2 法曲率

第四章 曲面的第二基本形式与曲面上的曲率§2 法曲率曲面上的曲线的行为,必然受到曲面几何性质的制约,而反过来又可以表现出曲面的某些几何性质.在Euler 时代,曲面通常理解为由曲线构成,曲面的截线往往成为关注的对象;同时,截线法自然成为揭示曲面几何性质的重要方法——至今仍然是最具直观的基本方法之一.一.曲面上曲线的曲率考虑曲面 S : r = r (u , v ) 上的弧长 s 参数化曲线 C : {u = u (s )v = v (s )的曲率向量的行为.C 的单位切向为T (s ) = r u (u (s ), v (s )) d u d s + r v (u (s ), v (s )) d v d s ,沿曲线 C 满足d s 2 = (E d u 2 + 2F d u d v + G d v 2)|u = u (s ), v = v (s ) .沿曲线 C 的单位正交右手标架场{r (u (s ), v (s )); n (u (s ), v (s )), T (s ), n (u (s ), v (s ))×T (s )}n ×T 及其运动公式,将曲线和曲面的弯曲程度紧紧联系在一起;其中曲线的曲率向量T ′(s ) 在此标架下的分量,可预期成为重要的几何量.事实上,利用曲面的两个基本形式,曲率向量的上图4-3述分量有下列沿曲线 C 的计算:T ′(s )•n (u (s ), v (s ))= d d s ⎝⎛⎠⎞r u (u (s ), v (s )) d u d s + r v (u (s ), v (s )) d v d s • n (u (s ), v (s )) = ⎝⎛⎠⎞r uu •n ⎝⎛d u d s 2 + 2r uv •n d u d s d v d s + r vv •n ⎝⎛⎠⎞d v d s 2 |u = u (s ), v = v (s ) = ⎝⎛⎠⎞L ⎝⎛⎠⎞d u d s 2 + 2M d u d s d v d s + N ⎝⎛⎠⎞d v d s 2 |u = u (s ), v = v (s ) = Ⅱ d s 2 |u = u (s ), v = v (s ) = Ⅱ Ⅰ|u = u (s ), v = v (s ) ; T ′(s )•[n (u (s ), v (s ))×T (s )] = (T ′(s ), n (u (s ), v (s )), T (s )) .定义1 曲面 S : r = r (u , v ) 上的曲线 C 在点 r (u , v ) 处的曲率向量分解为(2.1) d T d s = κn n + κg n ×T ,则称 κn n 为曲线 C 在曲面 S 上的法曲率向量(场),称 κn 为曲线 C 在曲面 S 上的法曲率(函数);称 κg n ×T 为曲线 C 在曲面 S 上的测地曲率向量(场),称 κg 为曲线 C 在曲面 S 上的测地曲率(函数).例1 以下各条事实具有明显的几何直观,通过简单运算也可验证. ① 曲面 S 上若有直线 C ,则 C 在曲面 S 上的法曲率和测地曲率恒为零;反之亦然.② 对于圆柱面 S 上的纬圆 C ,C 的曲率向量是 S 的内法向,C 的测地曲率恒为零,法曲率为非零常数.③ 对于平面 S 上的曲线 C ,C 在 S 上的法曲率恒为零,测地曲率即为相对曲率.④ 曲面 S 上曲线的法曲率不是曲面的等距不变量.⑤ 球面上的圆周的法曲率和测地曲率都是常数. □本节着重讨论法曲率的概念,而测地曲率将留待下一节以及第六章中进行详细讨论.根据前面的计算结果,法曲率(2.2) κn = T ′(s )•n (u (s ), v (s )) = Ⅱ Ⅰ |u = u (s ), v = v (s )只依赖于点 r (u (s ), v (s )) 以及曲线 C 的切向 (d u , d v )|u = u (s ), v = v (s ) .因此,法曲率可以改写为点 P : r (u (s ), v (s )) 和切向微元 d r |u = u (s ), v = v (s ) 的函数κn = κn (P ; d u (s ):d v (s )) ,并导致下述结果.定理1(Meusnier) 若曲面上的两条曲线在点 P 相切,则它们在点 P 处具有相同的法曲率.定义2 过曲面 S 上点 P 处法线的平面称为曲面 S 的法截面;法截面与曲面 S 的交线称为曲面 S 的法截线.注记1 给定曲面 S 上点 P 处的切向微元 d r ,存在曲面 S 的唯一一条法截线以 d r 为切向.n (P )=N(P ) ) 图4-4推论 曲面 S 上的曲线 C 在点 P 处的法曲率,等于曲面 S 上的与曲线 C 在点P 处具有相同切向的法截线 C * 在点 P 处的法曲率,等于 C * 在法截面标以正向(T ×n )|P 时的相对曲率. 二.曲面的法曲率由于法曲率只依赖于曲面的点和切向,可以脱离曲线而存在,故可用以定义曲面上的相应概念.定义3 给定曲面 S 上在点 P 处的任一切向 d r ∈T P −{0} , S 上过点 P 且以 d r 为切向的曲线在点 P 处的法曲率,称为曲面 S 在点 P 处沿切向 d r 的法曲率.注记2 给定曲面 S 上点 P 处的切向微元 d r ,法曲率可以改写为点 P : r (u , v ) 和切向微元 d r 的函数(2.3) κn = κn (P ; d r ) = κn (P ; d u :d v ) = ⅡⅠ|P , d u :d v . 例2 ① 平面的法曲率恒为零.② 球面的法曲率恒为常数,其绝对值是球面的半径的倒数.③ 对于 a , b = const. , 0 < a < b ,圆环面r (θ, ϕ) = ((b + a cos ϕ ) cos θ , (b + a cos ϕ ) sin θ , a sin ϕ)具有第一基本形式Ⅰ = (b + a cos ϕ )2 d θ 2 + a 2 d ϕ2和第二基本形式Ⅱ=−(b+a cosϕ ) cosϕ dθ 2−a dϕ2.此圆环面的法曲率κn=κn(P; dθ:dϕ)=ⅡⅠ=−(b+a cosϕ ) cosϕ dθ 2−a dϕ2(b+a cosϕ )2 dθ 2+a2 dϕ2;沿着其经线圆周ϕ线切向的法曲率为κn(P; 0:1) =−(b+a cosϕ ) cosϕ dθ 2−a dϕ2(b+a cosϕ )2 dθ 2+a2 dϕ2|dθ:dϕ= 0:1=−1a;沿着其纬线圆周θ线切向的法曲率为κn(P; 1:0) =−(b+a cosϕ ) cosϕ dθ 2−a dϕ2(b+a cosϕ )2 dθ 2+a2 dϕ2|dθ:dϕ= 1:0=−cosϕb+a cosϕ .例3已知曲面S: r=r(u, v) 的两个基本形式的全部系数,则在点P0: r(u0, v0) 处沿切向r u的法曲率为κn(P0; r u(u0, v0))=L(u0, v0)E(u0, v0) ;在点P0处沿切向r v的法曲率为κn(P0; r v(u0, v0))=N(u0, v0)G(u0, v0) . □习 题⒈ 求下列正则曲面的法曲率:①r= (cos v , sin v , u+v) ;② r= (u cos v , u sin v , v) ;③ r= (u , v , f(u, v)) ;④ r= (f(u) cos v , f(u) sin v , g(u)) .⒉对于例2中的圆环面,讨论其法曲率在何处、沿何切向取到最大值或最小值.⒊ 取定正则曲面S: r(u, v) 上过点P0: r(u0, v0) 的正则曲线C;S的过点P0与C相切于点P0的法截面记为Π0;C向Π0的垂直投影曲线记为C* .试证:C在点P0关于S 的法曲率,等于C* 在点P0关于适当定向后的Π0的相对曲率.⒋对正则曲面S: r(u1, u2) 上的正则曲线C,沿C取S的切平面构成单参数平面族;已知该族平面具有包络面S* .试证:C关于S的测地曲率,等于C关于S* 的测地曲率.⒌已知正则曲面S的法曲率只与点有关而不依赖于切向选取.试证:S或是平面片,或是球面片.⒍设两张正则曲面S和S* 的交线C具有曲率κ,并且C关于S的法曲率为κn,C关于S* 的法曲率为κn* .记曲面S和S* 沿交线C各点有交角θ.试证:κ2 sin2θ= (κn)2+ (κn*)2− 2κnκn* cosθ.⒎ 当曲面的第二基本形式是自变量微分的正定的二次型时,曲面的局部形状大致如何?对于二次型的其他情形,相应进行讨论.。
第三章曲面的第二基本形式

v = v( s) 是 S 上过 P 点,且在 P 点以 du : dv 为切方向的一条曲线,仍记曲面在 P 点的单位
法 向 量 为 n , α 、 β 分 别 表 示 曲 线 在 P 点 处 的 单 位 切 向 量 和 单 位 主 法 向 量, 且 记
θ = ∠( β , n) 。我们考察 C 的曲率向量 kβ 在 n 上的投影
n = ( 0,0,1)
所以
? = dr ⋅ dr = du 2 + dv 2 , ? = −dr ⋅ dn = 0
设圆柱面 S2 的方程是
(15)
u u r = (a cos , a sin , v) a a
故
u u ru = − sin , cos , 0 a a rv = (0,0,1) u u ru × rv = cos , sin , 0 = n a a u 1 u 1 ruu = − cos , − sin ,0 a a a a ruv = rvv = 0
一方面,
kβ ⋅ n = k cosθ
另一方面
kβ ⋅ n = n ⋅
结合两方面,我们看到
d 2r ? = , ds 2 ?
(1)
k cosθ = ? /?
[注 1]( 1)式右端只是点和方向的函数,给定点处,其值仅由方向 du : dv 决定,因此, 对于过点 P 且具有相同切线的诸多曲线而言, 尽管它们在 P 点的曲率 k 不同; 对应的 θ 也不 相同,但乘积 k cosθ 却是个固定值。 [注 2] ( 1 )式左端含有反映曲线弯曲程序的曲率项,而右端有反映曲面弯曲程度的第 二基本型,因此, ( 1)式把曲线与曲面的弯曲性联系起来,为我们利用曲线来研究曲面的弯 曲程序提供了方便 定义 1 称 k cosθ 为曲线 C 在 P 点处的法曲率,记为
球面的第一第二基本形式

球面的第一第二基本形式球面是一种特殊的曲面,经常被用来描述三维空间中的形状和物体。
对于每个点P,我们可以将球面视为由该点为中心,半径为R的球体的表面。
球面有两个重要的度量表示方法:第一基本形式和第二基本形式。
第一基本形式:球面的第一基本形式是一个张量,它用于描述Tangential to the surface of a sphere(曲面的切向)在点P处的内部几何信息。
它由曲面上两个切向(u和v,或者其他任意的切向向量)的内积构成,如下所示:g_1 = E du^2 + 2F du dv + G dv^2其中,E、F和G是函数,也就是曲面的基本形式系数。
- E和G表示切向量距离中心点P的距离的平方。
- F表示切向量之间夹角的余弦值。
第一基本形式允许我们计算沿曲面走过的距离和夹角。
例如,曲面的弧长可以通过积分式计算:L = ∫a^b√(E(du/dt)^2+2F(du/dt)(dv/dt)+G(dv/dt)^2) dt 这里du/dt和dv/dt是曲面上从点a到点b的切向量u和v的导数,t是曲线上的参数(例如弧长)。
第二基本形式:球面的第二基本形式描述了曲面在 P点的法向量方向上的几何信息。
它是一个2 x 2张量,在 P点的曲面切向量域和法向量域上定义。
它的定义与高斯曲率和平均曲率以及曲面上任意法向量方向的方向导数(曲线的曲率)有关。
第二基本形式的计算公式为:h_ij = -n · ∂^2X/∂u^i∂u^j其中,∂^2X/∂u^i∂u^j 是曲面上的二阶偏导数,n是曲面上某一点的单位法向量。
第二基本形式的主要应用之一是计算曲面上的最小曲率半径(或曲率半径的倒数k),或者曲面上任意方向的方向导数(平均曲率H)。
在球面上,由于曲率是固定的,第二基本形式有一个很特殊的形式:h_ij = -R^2 δ_ij其中, R 是球面半径,δ_ij 是克罗内克δ 称为Kronecker Delta。
第三节+++++曲面的第二

二 .曲面的第二基本形式
2 Ⅱ= n r ds 2 2 n ruu du 2 n ruv dudv n rvv dv Ldu 2 Mdudv Ndv
2 2
第二类基本量 : L n ruu , M n ruv , N n rvv
三.曲面的法曲率 1.曲面上曲线的曲率 在引入曲面的第二基本形式时, 我们已经 了解到曲面在已知点邻近的弯曲性可以 由曲面离开它的切平面的快慢程度来决 定. 但是在给定点处, 曲面沿不同方向的 弯曲程度不同,也就是说沿不同方向曲 面以不同的速度离开切平面. 因此当我 们想刻画曲面在已知点邻近的弯曲性时, 就需要用曲面上过该点的不同的曲线的 曲率来进行研究, 并由此引进法曲率的 概念, 以起到承上启下的作用.
( EN GL ) 4 ( EM FL )( FN GM )
2
[( EN GL ) 4 ( EG F )
2
2F E
( EM FL )]
2
2
E
2
( EM FL ) 0
当且仅当
EN-GL=EM-FL=0------(2.36) 或 E:F:G=L:M:N时,Δ=0. 除此外, Δ>0,曲面有且只有两个(实)主方向; 而当E:F:G=L:M:N时,(2.35)’’是恒等式,这时 每一方向都是主方向. 3.脐点,平点,圆点. 曲面上满足E:F:G=L:M:N的点称为曲面的 脐点. L=M=N=0的脐点称为平点. L,M,N,不全为零的脐点称为圆点. [脐点处每一方向都是主方向]
六.曲面的渐近方向,渐近曲线,渐近网 1.满足方程
的方向du:dv叫做曲面(在点P)处的渐近方 向. 例.求球面在点(450,450)处的渐近方向.
曲面论的概念

曲面论的概念曲面论是微分几何学的一个分支,研究的对象是曲面及其在空间中的性质和变化。
曲面是三维空间中的一个二维物体,可以用参数方程或隐函数方程来描述。
曲面论的核心思想是通过微分几何工具来研究曲面的几何性质和变化规律。
首先,我们来看曲面的定义。
对于一个三维空间中的点P,如果存在一个邻域使得这个邻域内的点可以由两个独立的参数u和v来唯一确定,则这个邻域就构成了一个曲面。
曲面可以用参数方程表示为:\[\begin{cases}x = x(u,v) \\y = y(u,v) \\z = z(u,v)\end{cases}\]或者用隐函数方程表示为F(x,y,z)=0。
曲面论主要研究的内容可以分为以下几个方面:1. 曲面的基本性质:曲面论研究曲面的局部性质,例如曲面上的切向量、法向量、曲率等。
曲面上每一点都有一个与之相切的平面,称为切平面。
曲面的法向量是垂直于切平面的向量,它可以用曲面的参数方程来表示。
2. 第一基本形式:第一基本形式是曲面的内禀度量,描述了曲面上切向量的内积。
它反映了曲面的长度、角度、曲线弯曲等性质。
第一基本形式可以通过曲面的参数方程来计算。
3. 第二基本形式:第二基本形式是曲面对于切平面的曲率性质。
它与曲面的法向量和曲面的法向量的导数相关。
第二基本形式可以用曲面的方程来计算。
4. 高斯曲率和平均曲率:高斯曲率和平均曲率是曲面论中的重要概念。
高斯曲率是曲面上局部形状的量度,描述了曲面的弯曲程度。
平均曲率反映了曲面在某一点的整体弯曲情况。
5. 曲面的变化:曲面论还研究了曲面的变化规律,包括曲面的平移、旋转、放缩等。
这些变化可以通过微分几何的方法来描述和研究。
应用方面,曲面论在计算机图形学、计算机辅助设计、物理学、生物学等领域都有广泛的应用。
在计算机图形学中,曲面论可以用来构造和渲染三维模型。
在计算机辅助设计中,曲面论可以用来建立和分析复杂曲面形状。
在物理学中,曲面论可以用来描述空间中的电磁场、引力场等。
微分几何背景下 Dini曲面的几何性质研究

微分几何背景下 Dini曲面的几何性质研究朱红桃;梁馨月;梁林【摘要】曲面是经典微分几何研究的主要对象,它的性质很丰富。
本文以Dini曲面为背景,以微分几何为工具,讨论了三维欧氏空间中Dini曲面的有关几何性质,给出了Dini曲面的主曲率、高斯曲率、平均曲率等几何性质;再由高斯曲率、平均曲率,得到Dini曲面的极小轨迹。
%Surface is main object of the classic differential geometry,which has a lot of differential ge-ometry,Based onthe Dini surface as the background,Dini in three dimensional Euclidean space were dis-cussed about the geometric properties of the surface. Gives the Dini surface asymptote,main curvature , gaussian curvature and mean curvature geometry properties;Again by gaussian curvature and mean curva-ture,obtained the Dini tiny trajectory of the surface.【期刊名称】《楚雄师范学院学报》【年(卷),期】2016(031)009【总页数】6页(P1-6)【关键词】Dini曲面;主曲率;高斯曲率;极小轨迹【作者】朱红桃;梁馨月;梁林【作者单位】云南师范大学,云南昆明 650500;云南师范大学,云南昆明 650500;楚雄师范学院科技处,云南楚雄 675000【正文语种】中文【中图分类】O186.16微分几何是以数学分析的方法为基础,应用微积分的理论对空间几何性质进行研究的学科,而曲面是微分几何研究的主要对象,它有许多丰富的性质。
