理工概率08-10
高考数学中的概率题如何解答

我们通过一个具体的例子来看看。
题目:在一次抽奖活动中,盒子里有10张奖券,其(1)甲抽到一等奖的概率;
(2)在甲抽到一等奖的情况下,乙抽到一等奖的概率。
对于第一问,甲从10张奖券中抽一张,抽到一等奖的概率就是3/10。
对于第二问,在甲抽到一等奖后,剩下9张奖券,其中2张是一等奖,所以乙抽到一等奖的概率就是2/9。
高考数学中的概率题如何解答
在高考数学中,概率题是一个重要的考点,也是不少同学感到头疼的部分。但其实,只要掌握了正确的方法和思路,概率题并没有想象中那么难。接下来,咱们就一起探讨一下高考数学中概率题的解答方法。
首先,我们要清楚概率的基本概念。概率,简单来说,就是某一事件发生的可能性大小。比如抛一枚硬币,正面朝上的概率就是05。在概率的计算中,我们常常会用到排列组合的知识。所以,熟练掌握排列组合的公式和计算方法是解答概率题的基础。
那么,在面对具体的概率题时,我们该怎么做呢?第一步,一定要认真读题,弄清楚题目所描述的事件和条件。很多同学在这一步就出错,没有理解题目意思就盲目做题,结果可想而知。比如,题目说从5个不同颜色的球中取出2个,这是组合问题;如果说取出2个球依次取出,这就是排列问题。
第二步,选择合适的计算方法。如果是等可能事件的概率,我们通常用事件包含的基本事件数除以总的基本事件数。举个例子,一个袋子里有3个红球和2个白球,从中随机取出一个球是红球的概率,这里总的基本事件数是5,红球的基本事件数是3,所以概率就是3/5。
如果涉及到相互独立事件同时发生的概率,就用乘法原理。比如,甲投篮命中的概率是08,乙投篮命中的概率是07,两人投篮相互独立,那么两人都命中的概率就是08×07=056。
秘籍08统计与概率(原卷版)

秘籍08 统计与概率统计与概率是全国中考的必考内容!但总有一部分学生,因为粗心,因为混淆概念等的小错误就丢了分数。
1.从考点频率看,统计与概率是高频考点,通常考查条形统计图、扇形统计图和树状图。
2.从题型角度看,选择题、填空题较多,同时考查多个考点的综合性题目以解答题为主,分值9分左右!中考数学关于统计与概率的知识点考察分析1.平均数2.中位数:几个数据按从小到大的顺序排列时,处于最中间的一个数据(或是中间两个数据的平均数)是这组数据的中位数.3.众数:一组数据中出现次数最多的那个数据.4.方差典例1.家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康,某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭进行一次简单随机抽样调查.(1)下列选取样本的方法最合理的一种是.(只需填上正确答案的序号)①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.(2)本次抽样调查发现,接受调查的家庭都有过期药品.现将有关数据呈现如图:①m=,n=;②补全条形统计图;③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期参加四个社团活动人数扇形统计图请根据以上信息,回答下列问题:(1)抽取的学生共有人,其中参加围棋社的有人;(2)若该校有3200人,估计全校参加篮球社的学生有多少人?(3)某班有3男2女共5名学生参加足球社,现从中随机抽取2名学生参加学校足球队,请用树状图或列表法说明恰好抽到一男一女的概率.中考统计与概率是基础题。
条形统计图和扇形统计图的结合经常考查求总量、画条形统计图、求扇形度数和估计等。
数据整理和分析常考的知识点有众数、中位数、平均数和方差。
有时也会考查频率和频数。
典例4.教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并请根据所给信息解答下列问题:a____________,②b=____________,③θ=____________度;(1)填空:①=(2)若把统计表每组中各个成绩用这组数据的中间值代替(例如:A组数据中间值为55分),请估计被选取的200名学生成绩的平均数;(3)规定海选成绩不低于90分记为“优秀”,请估计该校参加这次海选比赛的2000名学生中成绩“优秀”的有多少人?1.(2023·甘肃张掖·校联考一模)中国古典长篇小说四大名著是指《水浒传》、《三国演义》、《西游记》、《红楼梦》这四部巨著,它们承载着无数文化精华,代表了中国古典小说的巅峰,是悠悠中国文学史上灿烂辉煌的一笔.甲、乙两人从四大名著中随机选择一本进行研读,假设选择时不受四本名著封面厚度等影响,且每一本被选到的可能性相同.(1)求甲选择研读《三国演义》的概率;(2)若甲先从四本名著中随机选择一本(不放回),乙从剩余三本中随机选择一本,求甲、乙两人选到的是《三国演义》和《红楼梦》的概率. 2.(2023·广东广州·统考一模)为锻炼学生的社会实践能力,某校开展五项社会实践活动,要求每名学生在规定时间内必须且只能参加其中一项活动,该校从全体学生中调查他们参加活动的意向,将收集的数据整理后,绘制成如下两幅不完整的统计图(五个综合实践活动分别用A B C D E ,,,,表示):(1)扇形统计图中的%n =________%,B 项活动所在扇形的圆心角的大小是________︒.(2)甲同学想参加A 、B 、C 三个活动中的一个,乙同学想参加B 、C 、E 这三个活动中的一个,若他们随机抽选其中一个活动的概率相同,请用列表法或画树状图法,求他们同时选中同一个活动的概率. 3.(2023·安徽宿州·统考二模)自2023年3月1日起,《安徽省电动自行车管理条例》正式实施.某校为了解本校学生对该条例的知晓情况,对本校所有的学生进行了知识测试,并随机抽取了m 名学生的成绩,将测试成绩进行整理,分成以下六组(得分用x 表示):A .7075x ≤<,B .7580x ≤<,C .8085x ≤<,D .8590x ≤<,E .9095x ≤<;F .95100x ≤<. 根据统计的结果将成绩制成如下统计图,部分信息如图:已知测试成绩F 组的全部数据为96,95,97,96,99,98.请根据图表中的信息,解答下列问题:(1)填空:b = ,抽取的学生竞赛成绩的中位数落在 组;(2)补全频数分布直方图,并求此次抽取的学生竞赛成绩的平均数;(3)若学校规定此次竞赛成绩在90分(含90分)以上为“优秀”,请你估计全校1800名学生中,此次竞赛成绩为“优秀”的学生人数.5.(2023·江苏徐州·统考一模)校园安全问题受到全社会的广泛关注,教育局要求各学校加强对学生的安全教育,某中学为了了解学生对校园安全知识的了解程度(程度分为:A.十分熟悉、B.了解较多、C.了解较少、D.不了解),随机抽取了该校部分学生进行调查,统计整理并绘制成如下两幅不完整的统计图.根据以上信息解答下列问题:(1)本次接受调查的学生共有人,扇形统计图中A部分所对应的扇形圆心角是;(2)请补全条形统计图;(3)若该中学共有学生1800人,估计该校学生中对校园安全知识的了解程度达到A和B的总人数.6.(2023·江苏苏州·统考二模)2023年春节假期,苏州文旅全面复苏,接待人次、旅游收入双创新高:重点景区人气爆棚,持续高位运行.据统计,2023年1月21日到1月27日期间,苏州共接待游客约221万人次.其中著名打卡景区有,A:穹窿山景区,B:虎丘景区,C:灵岩山景区,D:西山景区,E:东山景区,F:其他.小志为了解哪个景区最受欢迎,随机调查了自己学校的部分同学,并根据调查结果绘制了两幅不完整的统计图.请你根据统计图中的信息,解决下列问题:(1)这次调查一共抽取了___名同学:扇形统计图中,旅游地点D所对应的扇形圆心角的度数____,并补全条形统计图.(2)若小志所在学校共有3000名学生,请你根据调查结果估计该校最喜爱“穹窿山景区”与“灵岩山景区”的学根据以上信息,回答下列问题:(1)表中m=______,n=______;(2)下列推断合理的是______;①样本中两个年级数据的平均数相同,八年级数据的方差较小,由此可以推断该校八年级学生成绩的波动程度较小;②若八年级小明同学的成绩是84分,可以推断他的成绩超过了该校八年级一半以上学生的成绩.(3)竞赛成绩80分及以上记为优秀,该校七年级有600名学生,估计七年级成绩优秀的学生人数.13.(2023·四川成都·统考二模)2019年11月,联合国教科文组织将每年的3月14日定为“国际数学日”,也被许多人称为“π节”.我区某校在今年的“数学π节”活动中开展了如下四项活动:A.趣味魔方;B.折纸活动;C.数独比赛;D.唱响数学.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:(1)这次被调查的学生共有_______人;(2)请补全条形统计图;(3)在数独比赛项目中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中随机选取两名参加数独决赛,请利用画树状图或列表的方法,求恰好选中甲、乙两位同学的概率.14.(2023·四川成都·统考一模)某学校在推进新课改的过程中,开设的体育社团活动课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了如图所示的两幅不完整的统计图.(1)则该班的总人数为______人,其中学生选D“羽毛球”所在扇形的圆心角的度数是______度;(2)补全条形统计图;(3)该班班委4人中,2人选修篮球,1人选修足球,1人选修排球,李老师要从这4人中选2人了解他们对体育社团活动课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.15.(2023·浙江金华·统考一模)某校为提高九年级学生的体育成绩,针对跳绳项目进行了专门训练.为了解训练效果,在训练前后各组织了一次测试,并从中抽取了50名学生的数据制成了如下条形统计图,请回答下列问题:某校九年级50名学生训练前后跳绳成绩条形统计图(1)训练前成绩的中位数是分,训练后成绩的众数是分.(2)训练后比训练前平均分增加了多少分?(3)如果该校九年级有400名学生,那么估计训练后成绩为满分的人数有多少人?。
08-09概率论期末考试试卷A (1)

《概率论与数理统计》期末考试试卷(A1)2、下列叙述中正确的是( A ). (A) ()1X EX D DX -= (B) ~(0,1)X EXN DX- (C) 22)(EX EX = (D) 22()EX DX EX =-3、设θ是总体X 中的参数,称),(θθ为θ的置信度a -1的置信区间,下面说话正确的是( D ).(A) 以),(θθ估计θ的范围,不正确的概率是a -1 (B) θ 以概率a -1落入),(θθ (C) θ以概率a 落在),(θθ之外 (D) ),(θθ以概率a -1包含θ4、设(,)0,(,)(,)~(,)0,g x y x y GX Y f x y ≠∈⎧=⎨⎩其它,D 为一平面区域,记G,D 的面积分别为,G D S S ,则{(,)}(B )P x y D ∈=.(A)GD S S (B) ⎰⎰Ddxdy y x f ),( (C) (,)G g x y dxdy ⎰⎰ (D) G G D S S5、设总体分布为),(2σμN ,若μ未知,则要检验20:100H σ≥,应采用统计量( B ).(A)nS X /μ- (B)100)(21∑=-ni iX X(C)100)(21∑=-ni iXμ (D)22)1(σS n -6、有三类箱子,箱中装有黑、白两种颜色的小球,各类箱子中黑球、白球数目之比为,2:3,2:1,1:4已知这三类箱子数目之比为1:3:2,现随机取一个箱子,再从中随机取出一个球,则取到白球的概率为( A ).(A)157 (B)4519 (C)135(D)3019 7、设随机变量X 的概率密度函数为(),()(),()f x f x f x F x =-是X 的分布函数,则对任意实数a 有( B ). (A) ⎰-=-adx x f a F 0)(1)((B) ∑⎰-=-adx x f a F 0)(21)((C) )()(a F a F =- (D) 1)(2)(-=-a F a F题目 一 二 三 四 五 六 七 八 九 十 总分 得分一.填空题:(本大题共7小题,每小题3分,共21分)1. 已知样本1621,,,X X X 取自正态分布总体(3,1)N ,X 为样本均值,已知{}0.5P X λ<=,则=λ 3 。
《概率论与数理统计》考试试卷

填空题(每空2分, 2×12=24分)1、 设 A.B.C 为三事件, 事件 A.B.C 恰好有两个事件发生可表示为__________________。
2、 已知 =0.5, =0.3, =0.6, 则 =__________________。
3、 设 , 则 的密度函数为____________________。
4、 设 服从区间 上的均匀分布, 则 ______________, _______________。
5、 设 是X 的一个随机样本, 则样本均值 _______________, 且 服从的分布为_____________________。
6、 若二维连续型随机变量密度函数为 , 则 。
7、 总体 且 已知, 用样本检验假设 时, 采用统计量_________________________。
8、 评选估计量的标准有_______________、_____________和一致性。
9、 切贝雪夫不等式应叙述为_______________判断题(每小题2分, 2×8=16分)1、 互不相容的随机事件一定相互独立。
( )2、 若连续型随机变量 的概率密度为 , 则 。
( )3、 二维随机变量的边缘分布可以确定联合分布。
( )4、 对于任意随机变量 , 有 。
( )5、 不相关的两个随机变量一定是相互独立的。
( )6、 对任意随机变量 , 若 存在, 则 。
( )7、 若 , 则 。
( )若 , , 密度函数分别为 及 , 则 。
( )概率计算题(每题10分, 4×10=40分)在1-2000的整数中随机地取一个数, 问取到的整数即不能被4整除又不能被6整除的概率是多少? (10分)设两台车床加工同样的零件, 第一台车床的优质品率为0.6, 第二台车床的优质品率为0.9, 现把加工的零件放在一起, 且已知第一台加工的零件比第二台加工的零件多一倍, 求: (1)从产品中任取一件是优质品的概率。
《概率初步——利用频率估计概率》数学教学PPT课件(3篇)

你能估计图钉尖朝上的 概率吗?
5、(1) 计算并完成表格:
转动转盘的次数n 100 150 200 500 800 1 000 落在“铅笔”的次数m 68 111 136 345 546 701
m
落在“铅笔”的频率n 0.68 0.74 0.68 0.69 0.6825 0.701
235
0.870
400
369
0.923
750
662
0.883
1500
1335
0.890
3500 7000 9000
3203 6335 8073
0.915 0.905 0.897
14000
12628
0.902
估计移植成活率
由下表可以发现,幼树移植成活的频率在_0_.9__左右 摆动,并且随着移植棵数越来越大,这种规律愈加明显.
500 51.54 0.103
共同练习
完成下表, 利用你得到的结论解答下列问题:
柑橘损坏的频率(
m n
)
50
5.50
0.110
100
10.5
0.105
150
15.15
0.101
2为00简单起见,我们能19.否42 直接把表中的 0.097
502050千克柑橘对应的柑24.橘25 损坏的频率看作0.097
的成本进了10000千克柑橘, 300
则这批柑橘中完好柑橘的质 量是_9_0_0_0__,若公司希望这
350
些柑橘能够
400
15.15 19.42 24.35 30.32 35.32 39.24
0.101 0.097 0.097 0.101 0.101 0.098
概率论与数理统计模拟试题及答案

概率论与数理统计试题 考试时间:120分钟 试卷总分100分 题号 一 二 三 四 五 六 七 八 九 十 总分 得分 评卷教师一、填空题(满分15分)1.已知3.0)(=B P ,7.0)(=⋃B A P ,且A 与B 相互独立,则=)(A P 。
2.设随机变量X 服从参数为二项分布,且21}0{==X P ,则=p 。
3.设),3(~2σN X ,且1.0}0{=<X P ,则=<<}63{X P4.已知DX=1,DY=2,且X 和Y 相互独立,则D(2X-Y)=5.已知随机变量X 服从自由度为n 的t 分布,则随机变量2X 服从的分布是 。
二、选择题(满分15分)1.抛掷3枚均匀对称的硬币,恰好有两枚正面向上的概率是 。
装订线(A )0.125, (B )0.25, (C )0.375, (D )0.5 2.有γ个球,随机地放在n 个盒子中(γ≤n),则某指定的γ个盒子中各有一球的概率为 。
(A )γγn ! (B )γγn C r n ! (C )nn γ! (D) n n n C γγ! 3.设随机变量X 的概率密度为||)(x ce x f -=,则c = 。
(A )-21(B )0 (C )21 (D )14.掷一颗骰子600次,求“一点” 出现次数的均值为 。
(A )50 (B )100 (C )120 (D )1505.设总体X 在),(ρμρμ+-上服从均匀分布,则参数μ的矩估计量为 。
(A )x 1 (B )∑=-n i i X n 111 (C )∑=-n i i X n 1211 (D )x 三、计算题(满分60分)1.某商店拥有某产品共计12件,其中4件次品,已经售出2件,现从剩下的10件产品中任取一件,求这件是正品的概率。
2.设某种电子元件的寿命服从正态分布N (40,100),随机地取5个元件,求恰有两个元件寿命小于50的概率。
(8413.0)1(=Φ,9772.0)2(=Φ)3.在区间(0,1)中随机地取两个数,求事件“两数之和小于56”的概率。
概率论与数理统计答案 第三章习题

解
f
X
(
x)
fY
(
y)
2x(1
0,
|
y |),0
x 1,| y|1 其它
f (x, y)
故X和Y不相互独立.
14.设X和Y是相互独立的随机变量,X在(0,1)上服从均匀分布,
Y的概率密度为
fY
(
y)
1 2
e
y
2
,
y
0
(1)求X和Y的联合概率密度;
0, y 0
(2)设含有a的二次方程为a2+2Xa+Y=0,试求a有实根的概率.
(X,Y)关于Y的边缘分布律可用Y= j时 X取所有可能取的值的概率相加而得. 也可以单独列表如下:
X0 1 2
pk 1 2 1
4 44
Y0 1 2 3
pk 1 3 3 1
8 88 8
X Y0123
012
1 10 0 88
0 220
88
00 11
88
1 P{Y=j} 8
3 8
3 8
1 8
P{X=i}
0 25/36 5/36 5/6
0 45/66 10/66 5/6
1 5/36 1/36 1/6
1 10/66 1/66 1/6
P{X=i} 5/6 1/6 1
P{X=i} 5/6 1/6 1
13(1)问第1题中的随机变量X和Y是否相互独立?(需说明理由) 解 (1)P{X=i,Y=j}=P{X=i}P{Y=j}对(X,Y)所有可能取值 (i,j)( i ,j =0,1)都成立,故放回抽样X和Y相互独立.
y)dy y (4)
4
(2)
2
08-09I概率论与数理统计试卷(A)参考答案

| | | | | | | |装| | | | |订| | | | | |线| | | | | | | | ||防灾科技学院2008~2009学年 第一学期期末考试概率论与数理统计试卷(A )使用班级07601/ 07602/07103 答题时间120分钟一填空题(每题2分,共20分)1、已知事件A ,B 有概率4.0)(=A P ,条件概率3.0)|(=A B P ,则=⋂)(B A P 0.28 ;2、设),(~1p n b X ,),(~2p n b Y 则~Y X +),(21p n n b +;3、若)2(~πX ,则=)(2X E 6 ;4、随机变量X 的分布函数是⎪⎪⎩⎪⎪⎨⎧≤<≤<≤--<=x x x x x F 3,131,8.011,6.01,0)(,则=≤<-)31(X P0.4 ;5、连续型随机变量的概率密度函数为)0(0,)(>⎩⎨⎧≤>=-λλλx x ex f x,则分布函数为⎩⎨⎧≤>-=-000,1)(x x e x F x λ;6、若)1,0(~),1,0(~N Y N X 且X 与Y 相互独立,则~2/)(22Y X X +)2(t ;7、若随机变量X ,1)(,2)(==X D X E ,则利用切比雪夫不等式估计概率()≥<-32X P 98;8、若总体),(~2σμN X ,则样本方差的期望=)(2S E 2σ;9、设随机变量)2,1(~-U X ,令⎩⎨⎧<≥=.0,0,0,1X X Y ,则Y10、已知灯泡寿命)100,(~2μN X ,今抽取25只灯泡进行寿命测试,得样本1200=x 小时,则μ的置信度为95%的置信区间是 (1160.8,1239.2) (96.1025.0=z )。
二、单项选择题(本大题共5小题,每题2分,共10分)1、若6.0)(,4.0)(,5.0)(===B A P B P A P ,则=)(A B P ( C )(A) 0.2 ; (B) 0.45; (C) 0.6; (D) 0.75;2、设离散型随机变量X 的分布律为k k X P αβ==}{, ,2,1=k 且0>α,则参数=β( C )(A )11-=αβ ;(B )1+=αβ;(C )11+=αβ;(D )不能确定; 3、设随机变量X 和Y 不相关,则下列结论中正确的是( B )(A )X 与Y 独立; (B ))(4)()2(Y D X D Y X D +=-;(C ))(2)()2(Y D X D Y X D +=-; (D ))(4)()2(X D Y D Y X D -=-;4、若)1,0(~N X ,则)2|(|>X P =( A )(A ))]2(1[2Φ-;(B )1)2(2-Φ;(C ))2(2Φ-;(D ))2(21Φ-; 5、下列不是评价估计量三个常用标准的是( D ))(A 无偏性; )(B 有效性; )(C 相合性; )(D 正态性。
概率-抽样(简单随机、系统、分层)

简单随机抽样教学目标:1、知识与技能:(1)正确理解随机抽样的概念,掌握抽签法、随机数表法的一般步骤;2、过程与方法:(1)能够从现实生活或其他学科中提出具有一定价值的统计问题;(2)在解决统计问题的过程中,学会用简单随机抽样的方法从总体中抽取样本。
3、情感态度与价值观:通过对现实生活和其他学科中统计问题的提出,体会数学知识与现实世界及各学科知识之间的联系,认识数学的重要性。
4、重点与难点:正确理解简单随机抽样的概念,掌握抽签法及随机数法的步骤,并能灵活应用相关知识从总体中抽取样本。
教学设想:假设你作为一名食品卫生工作人员,要对某食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?显然,你只能从中抽取一定数量的饼干作为检验的样本。
(为什么?)那么,应当怎样获取样本呢?【探究新知】一、简单随机抽样的概念一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就把这种抽样方法叫做简单随机抽样,这样抽取的样本,叫做简单随机样本。
【说明】简单随机抽样必须具备下列特点:(1)简单随机抽样要求被抽取的样本的总体个数N是有限的。
(2)简单随机样本数n小于等于样本总体的个数N。
(3)简单随机样本是从总体中逐个抽取的。
(4)简单随机抽样是一种不放回的抽样。
(5)简单随机抽样的每个个体入样的可能性均为n/N。
思考?下列抽样的方式是否属于简单随机抽样?为什么?(1)从无限多个个体中抽取50个个体作为样本。
(2)箱子里共有100个零件,从中选出10个零件进行质量检验,在抽样操作中,从中任意取出一个零件进行质量检验后,再把它放回箱子。
二、抽签法和随机数法1、抽签法的定义。
一般地,抽签法就是把总体中的N个个体编号,把号码写在号签上,将号签放在一个容器中,搅拌均匀后,每次从中抽取一个号签,连续抽取n次,就得到一个容量为n的样本。
【说明】抽签法的一般步骤:(1)将总体的个体编号。
复合Poisson-Geometric过程风险模型的破产概率满足的Pollazek-Khinchin公式

1 一 P
其 中:
():∑ ( 一 ) x() 1 pp ‘ , F
() =∑ ( 一 ) () 1p 一
() 与 ( ) 分别表示 () 与^( ) 的 k重卷积 .
定义 2 令
一 —
定义 ( , )=E ( ( ) , “W [ U T ) T<∞ I ( ) o v =n 为破产发生 时的盈余惩罚期望. ] 由文献[ ] 2
我们 有模 型满 足 的更 新方 程 :
(加= z)) 一 ( yd “) I , ( ) ; ‘ ; 1 一) y
+ ( y( 一 ( 一 ) 1 “+y )y ) d 当 “:0时, 模型( ) 1 满足的更新方程变为:
—
4 8 2.
苎 ( !
“ ( )=
一 (. 然 显 当p= 时 ) o ,
( , ) 此时上述公式就是经典风险模
[ ] 廖 基定 , 1 3 龚 3 朝等. 复合 Pi o —G o ei 风险模型 G r r o sn em tc s r ee b
—
Si 折现惩罚 函数[ ] 应用数学 学报 , 0 ,0 6 ;06 h u J. 2 7 3 ( ) 17 0
关键 词 : 破 产概 率 ; 险模 型 ; 风 复合 Pio o sn—G o tc过程 ;oae s emei r P lzk—K ici 式 l hnhn公
中图分类号 : 0 1 . 2 16 文 献标识码 : A
1 模 型建 立
近年来 , 越来越多的人对经典风险模型进行了 研究 , 得 到许 多 有 用 的结 论 , 主要 考 虑 的都 是 并 但 赔付服从 Pio os s n过程的风险模型…. Pio 过 而 os sn 程的期望和方差是相等的, 但是在实际情况中方差 往往又是大于期望 , 基于这一点 , 文献 [ ] 出了 2提 种复合 Pio —G o e i o sn em t s r c过程 , 该过程 的方差 大于 等 于期 望 . 因此 我 们 考 虑 赔 付 为 复 合 Pio os n s G o e i过程 的风险模型便更具有现实意义. e tc mr 基 于上述 原 因 , 文 考虑 如下 风险模 型 : 本
10概率学案

概率小结与复习一、知识梳理1. 概率:随机事件A 的概率是频率的稳定值,反之,频率是概率的近似值.2. 等可能性事件的概率:如果一次试验中可能出现的结果有n 个,且所有结果出现的可能性都相等,那么,每一个基本事件的概率都是n 1,如果某个事件A 包含的结果有m 个,那么事件A 的概率nm P(A)=. 3. ①互斥事件:不可能同时发生的两个事件叫互斥事件. 如果事件A 、B 互斥,那么事件A+B 发生(即A 、B 中有一个发生)的概率,等于事件A 、B 分别发生的概率和,即P(A+B)=P(A)+P(B),推广:)P(A )P(A )P(A )A A P(A n 21n 21+++=+++ .②对立事件:两个事件必.....有一个发生的互斥事件..........叫对立事件. 例如:从1~52张扑克牌中任取一张抽到“红桃”与抽到“黑桃”互为互斥事件,因为其中一个不可能同时发生,但又不能保证其中一个必然发生,故不是对立事件.而抽到“红色牌”与抽到黑色牌“互为对立事件,因为其中一个必发生. 注意:i.对立事件的概率和等于1:1)A P(A )A P(P(A)=+=+. ii.互为对立的两个事件一定互斥,但互斥不一定是对立事件.③相互独立事件:事件A(或B)是否发生对事件B(或A)发生的概率没有影响.这样的两个事件叫做相互独立事件. 如果两个相互独立事件同时发生的概率,等于每个事件发生的概率的积,即P(A·B)=P(A)·P(B). 由此,当两个事件同时发生的概率P (AB )等于这两个事件发生概率之和,这时我们也可称这两个事件为独立事件.例如:从一副扑克牌(52张)中任抽一张设A :“抽到老K”;B :“抽到红牌”则 A 应与B 互为独立事件[看上去A 与B 有关系很有可能不是独立事件,但261P(B)P(A),215226P(B),131524P(A)=⋅====.又事件AB 表示“既抽到老K 对抽到红牌”即“抽到红桃老K 或方块老K”有261522B)P(A ==⋅,因此有)B P(A P(B)P(A)⋅=⋅.推广:若事件n 21,A ,,A A 相互独立,则)P(A )P(A )P(A )A A P(A n 21n 21 ⋅=⋅.注意:i. 一般地,如果事件A 与B 相互独立,那么A 与A B ,与B ,A 与B 也都相互独立. ii. 必然事件与任何事件都是相互独立的.iii. 独立事件是对任意多个事件来讲,而互斥事件是对同一实验来讲的多个事件,且这多个事件不能同时发生,故这些事件相互之间必然影响,因此互斥事件一定不是独立事件.④独立重复试验:若n 次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n 次试验是独立的. 如果在一次试验中某事件发生的概率为P ,那么在n 次独立重复试验中这个事件恰好发生k 次的概率:kn k k n n P)(1P C (k)P --=. 4. 对任何两个事件都有)()()()(B A P B P A P B A P ⋅-+=+5.解决概率问题的步骤:第一步,确定事件性质(等可能事件、互斥事件、独立事件、n 次独立重复试验))即所给的问题归结为四类事件中的某一种.第二步,判断事件的运算(和事件、积事件)即是至少有一个发生,还是同时发生,分别运用相加或相乘事件.第三步,运用公式()()()()()()()()(1)k k n k n n m P A nP A B P A P B P A B P A P B P k C p p -⎧=⎪⎪⎪+=+⎨⎪⋅=⋅⎪=-⎪⎩等可能事件: 互斥事件: 独立事件: n 次独立重复试验:求解第四步,答,即给提出的问题有一个明确的答复. 题型一 频率与概率例1.某企业生产的乒乓球被08年北京奥委会指定为乒乓球比赛专用球.日前有关部门对某批产品进行了抽样检测,检查结果如下表所示.互斥对立(1)计算表中乒乓球优等品的频率;(2)从这批乒乓球产品中任取一个,质量检查为优等品的概率是多少?(结果保留到小数点后三位)(1)计算表中进球的频率;(2)这位运动员投篮一次,进球的概率是多少?题型二随机事件间的关系例2.从一副桥牌(52张)中任取1张.判断下列每对事件是否为互斥事件,是否为对立事件.(1)“抽出红桃”与“抽出黑桃”;(2)“抽出红色牌”与“抽出黑色牌”;(3)“抽出的牌点数为3的倍数”与“抽出的牌点数大于10”.【变式训练】抽查10件产品,设事件A:至少有两件次品,则A的对立事件为()A.至多两件次品B.至多一件次品C.至多两件正品D.至少两件正品题型三概率概念的应用例3... (1)请完成上面列联表;已知从全部105人中随机抽取1人为优秀的概率为7(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”(参考数据P(K2>6.635)=0.05);(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10人按2到11进行编号,然后两次掷一枚均匀的骰子,出现的点数之和为被抽取人的编号.试求抽到6号或10号的概率.【变式训练】袋内有35个球,每个球上都记有从1~35中的一个号码,设号码为n 的球的重量为32n -5n +20克,这些球以等可能性从袋里取出(不受重量、号码的影响).(1)如果取出1球,试求其重量比号码数大5的概率;(2)如果任意取出2球,试求它们重量相等的概率.题型四 古典概率模型的计算问题例4.),现按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A 类10辆.(1)求z 的值;(2)用分层抽样的方法在C 类轿车中抽取一个容量为5的样本,将该样本视为一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;(3)用随机抽样方法从B 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2把这8辆车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.【变式训练】已知△ABC 的三边是10以内(不包含10)的三个连续的正整数,求任取一个△ABC 是锐角三角形的概率.题型五 有放回抽样与不放回抽样例5.现有一批产品共有10件,其中8件为正品,2件为次品.(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率; (2)如果从中一次取3件,求3件都是正品的概率.【点拨】关于不放回抽样,计算基本事件个数时,既可以看作是有顺序的,也可以看作是无顺序的,其结果是一样【变式训练】有5张卡片,上面分别写有0,1,2,3,4中的1个数.求:(1)从中任取两张卡片,两张卡片上的数字之和等于4的概率;(2)从中任取两次卡片,每次取一张,第一次取出卡片,记下数字后放回,再取第二次,两次取出的卡片上的数字之和恰好等于4的概率.题型六 古典概型问题的综合应用例6.甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n 个白球.从甲、乙两袋中各任取2个球.(1)若n =3,求取到的4个球全是红球的概率;(2)若取到的4个球中至少有2个红球的概率为34,求n .例7.某单位组织4个部门的职工旅游,规定每个部门只能在峨眉山、泰山、华山3个景区中任选一个,假设各部门选择每个景区是等可能的.(Ⅰ)求3个景区都有部门选择的概率;(Ⅱ)求恰有2个景区有部门选择的概率.例8.一个盒子装有六张卡片,上面分别写着如下六个定义域为R 的函数:f 1(x )=x ,f 2(x )=x 2,f 3(x )=x 3,f 4(x )=sin x ,f 5(x )=cos x ,f 6(x )=2.(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取3次的概率.例9.一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.(1)求这箱产品被用户接收的概率;(2)抽检的产品数为ξ,求ξ分别为1、2、3的概率【变式训练】甲、乙二人参加普法知识竞赛,共有10道不同的题目,其中选择题6道,判断题4道,甲、乙二人一次各抽取一题.(1)甲抽到选择题,乙抽到判断题的概率是多少?(2)甲、乙二人至少有一个抽到选择题的概率是多少?总结提高1.对古典概型首先必须使学生明确判断两点:①对于每个随机试验来说,所有可能出现的试验结果数n 必须是有限个;②出现的各个不同的试验结果数m 其可能性大小必须是相同的.只有在同时满足①、②的条件下,运用的古典概型计算公式P (A )=m n 得出的结果才是正确的.使用公式P (A )=mn 计算时,确定m 、n 的数值是关键所在.2.对于n 个互斥事件A 1,A 2,…,A n ,其加法公式为P (A 1+A 2+…+A n )=P (A 1)+P (A 2)+…+P (A n ).3.分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想.4.在应用题背景条件下,能否把一个复杂事件分解为若干个互相排斥或相互独立、既不重复又不遗漏的简单事件是解答这类应用题的关键,也是考查学生分析问题、解决问题的能力的重要环节. 题型七 几何概型长度问题例10.如图,∠AOB =60°,OA =2,OB =5,在线段OB 上任取一点C ,试求:(1)△AOC 为钝角三角形的概率; (2)△AOC 为锐角三角形的概率.【点拨】我们把每一个事件理解为从某个特定的区域内随机地取一点,该区域中每一点被取到的机会都一样,而一个事件发生则理解为恰好在上述区域内的某个指定的区域内的点,这样的概率模型就可以用几何概型求解. 【变式训练】点A 为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B ,则劣弧AB 的长度小于1的概率为 .题型八 几何概型面积问题例11. 两个CB 对讲机(CB 即CitizenBand 民用波段的英文缩写)持有者,莉莉和霍伊都为卡尔货运公司工作,他们的对讲机的接收范围为25公里,在下午3:00时莉莉正在基地正东距基地30公里以内的某处向基地行驶,而霍伊在下午3:00时正在基地正北距基地40公里以内的某地向基地行驶,试问在下午3:00时他们能够通过对讲机交谈的概率有多大?【变式训练】如图,以正方形ABCD 的边长为直径作半圆,重叠部分为花瓣.现在向该正方形区域内随机地投掷一飞镖,求飞镖落在花瓣内的概率.题型九 体积问题例12. 在线段[0,1]上任意投三个点,设O 至三点的三线段长为x 、y 、z ,研究方法表明:x ,y ,z 能构成三角形只要点(x ,y ,z )落在棱长为1的正方体T 的内部由△ADC ,△ADB ,△BDC ,△AOC ,△AOB ,△BOC 所围成的区域G 中(如图),则x ,y ,z 能构成三角形与不能构成三角形这两个事件中哪一个事件的概率大?【变式训练3】已知正方体ABCD —A 1B 1C 1D 1内有一个内切球O ,则在正方体ABCD —A 1B 1C 1D 1内任取点M ,点M 在球O 内的概率是( )A.π4B.π8C.π6D.π12总结提高1.几何概型是一种概率模型,它与古典概型的区别是试验的可能结果不是有限个.其特点是在一个区域内均匀分布,概率大小与随机事件所在区域的形状和位置无关,只与该区域的大小有关.如果随机事件所在区域是一个单点,其测度为0,则它出现的概率为0,但它不是不可能事件. 如果随机事件所在区域是全部区域扣除一个单点, 其测度为1,则它出现的概率为1,但它不是必然事件.2.若试验的全部结果是一个包含无限个点的区域(长度,面积,体积),一个基本事件是区域中的一个点.此时用点数度量事件A 包含的基本事件的多少就毫无意义.“等可能性”可以理解成“对任意两个区域,当它们的测度(长度,面积,体积,…)相等时,事件A 对应点落在这两区域上的概率相等,而与形状和位置都无关”.3.几何概型并不限于向平面(或直线、空间)投点的试验,如果一个随机试验有无限多个等可能的基本结果,每个基本结果可以用平面(或直线、空间)中的一点来表示,而所有基本结果对应于一个区域Ω,这时,与试验有关的问题即可题型十 条件概率的求法例13.一张储蓄卡的密码共6位数字,每位数字都可从0~9中任选一个.某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求:(1)任意按最后一位数字,不超过2次就按对的概率;(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率.【变式训练】设某种动物从出生算起活到20岁以上的概率为0.8,活到25岁以上的概率为0.4.现有一只20岁的这种动物,问它能活到25岁以上的概率是 .题型十一 相互独立事件的概率例14.三人独立破译同一份密码,已知三人各自破译出密码的概率分别为15,14,13,且他们是否破译出密码互不影响.(1)求恰有二人破译出密码的概率;(2)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.【变式训练】甲、乙、丙三个口袋内都分别装有6个只有颜色不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球,求恰好摸出红球、黑球和无色球各1个的概率.题型十二 综合问题例15.某公司招聘员工,指定三门考试课程,有两种考试方案.方案一:三门课程中至少有两门及格为考试通过;方案二:在三门课程中随机选取两门,这两门都及格为考试通过.假设某应聘者对三门指定课程考试及格的概率分别是a ,b ,c ,且三门课程考试是否及格相互之间没有影响. (1)分别求该应聘者在方案一和方案二下考试通过的概率;(2)试比较该应聘者在上述两种方案下考试通过的概率的大小,并说明理由.【变式训练】甲,乙,丙三人分别独立地进行某项体能测试,已知甲能通过测试的概率是25,甲,乙,丙三人都能通过测试的概率是320,甲,乙,丙三人都不能通过测试的概率是340,且乙通过的概率比丙大.(1)求乙,丙两人各自通过测试的概率分别是多少?(2)测试结束后,最容易出现几人通过的情况?总结提高1.互斥事件、对立事件、相互独立事件的区别:对于事件A 、B ,在一次试验中,A 、B 如果不能同时发生,则称A 、B 互斥.一次试验中,如果A 、B 互斥且A 、B 中必有一个发生,则称A 、B 对立.显然,A +A 为必然事件,A 、B 互斥则不能同时发生,但可能同时不发生.两事件相互独立是指一个事件的发生与否对另一事件的发生的概率没有影响.事实上:A 、B 互斥,则P (AB )=0; A 、B 对立,则P (AB )=0且P (A )+P (B )=1; A 、B 相互独立,则P (AB )=P (A )P (B ). 它们是不相同的.2.由于当事件A 、B 相互独立时,P (AB )=P (A )P (B ),因此式子1-P (A )P (B )表示相互独立事件A 、B 中至少有一个不发生的概率.对于n 个随机事件A 1,A 2,…,A n ,有P (A 1+A 2+…+A n )=1-P (1A ∩2A ∩…∩n A ),此称为概率的和与积的互补公式.例16.从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A :“取出的2件产品中至多有1件是二等品”的概率()0.96P A .(1)求从该批产品中任取1件是二等品的概率p ;(2)若该批产品共100件,从中任意抽取2件,求事件B :“取出的2件产品中至少有一件二等品”的概率()P B .例17.甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n 个白球.由甲,乙两袋中各任取2个球.(Ⅰ)若n=3,求取到的4个球全是红球的概率;(Ⅱ)若取到的4个球中至少有2个红球的概率为43,求n.例18.某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率.例19.盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率: (1)2只都是次品;(2)2只中正品、次品各一只;(3)2只中至少有一只正品。
大连理工大学概率上机作业

大连理工大学概率上机作业————————————————————————————————作者: ————————————————————————————————日期:ﻩ第一次上机作业1.利用Matlab自带命令产生1000个均匀随机变量服从U(0,1)。
>>unifrnd(0,1,20,50)ans=Columns 1 through 100.81470.65570.4387 0.75130.3517 0.16220.10670.85300.78030.54700.9058 0.03570.3816 0.25510.8308 0.7943 0.9619 0.6221 0.3897 0.29630.1270 0.84910.7655 0.50600.58530.3112 0.0046 0.35100.24170.74470.9134 0.93400.79520.6991 0.5497 0.5285 0.7749 0.5132 0.4039 0.18900.6324 0.6787 0.1869 0.8909 0.9172 0.1656 0.8173 0.40180.0965 0.68680.09750.75770.48980.9593 0.28580.6020 0.86870.07600.1320 0.18350.2785 0.74310.44560.5472 0.75720.26300.08440.23990.94210.36850.5469 0.39220.64630.13860.75370.6541 0.3998 0.1233 0.9561 0.62560.9575 0.6555 0.7094 0.1493 0.3804 0.6892 0.25990.18390.5752 0.78020.9649 0.1712 0.75470.25750.56780.7482 0.80010.24000.05980.08110.15760.7060 0.2760 0.8407 0.0759 0.4505 0.4314 0.41730.2348 0.92940.97060.03180.67970.2543 0.05400.08380.9106 0.0497 0.35320.77570.9572 0.2769 0.65510.8143 0.5308 0.22900.18180.9027 0.8212 0.48680.4854 0.0462 0.1626 0.2435 0.7792 0.9133 0.2638 0.94480.01540.43590.8003 0.0971 0.11900.92930.9340 0.1524 0.1455 0.4909 0.0430 0.44680.1419 0.82350.4984 0.3500 0.12990.82580.13610.4893 0.1690 0.30630.4218 0.69480.9597 0.19660.56880.5383 0.8693 0.3377 0.6491 0.50850.9157 0.31710.3404 0.2511 0.4694 0.99610.57970.90010.7317 0.51080.7922 0.95020.5853 0.61600.01190.07820.54990.3692 0.6477 0.81760.95950.0344 0.2238 0.4733 0.3371 0.44270.1450 0.11120.4509 0.7948Columns 11 through 200.6443 0.31110.0855 0.0377 0.03050.0596 0.17340.95160.0326 0.25180.3786 0.92340.26250.8852 0.74410.68200.3909 0.92030.56120.29040.8116 0.4302 0.8010 0.91330.50000.0424 0.83140.05270.8819 0.61710.5328 0.18480.0292 0.79620.47990.07140.8034 0.7379 0.66920.26530.3507 0.9049 0.9289 0.0987 0.90470.52160.06050.26910.19040.82440.9390 0.9797 0.7303 0.26190.60990.09670.39930.42280.3689 0.98270.8759 0.4389 0.4886 0.3354 0.6177 0.81810.5269 0.54790.4607 0.73020.55020.1111 0.5785 0.6797 0.8594 0.81750.41680.94270.9816 0.34390.62250.2581 0.23730.1366 0.8055 0.7224 0.65690.4177 0.15640.58410.5870 0.4087 0.45880.7212 0.57670.14990.6280 0.98310.8555 0.10780.20770.5949 0.96310.10680.18290.6596 0.2920 0.3015 0.6448 0.90630.3012 0.2622 0.54680.6538 0.23990.5186 0.43170.7011 0.3763 0.87970.4709 0.60280.52110.49420.8865 0.97300.0155 0.6663 0.19090.81780.23050.7112 0.23160.77910.02870.6490 0.9841 0.5391 0.4283 0.26070.84430.2217 0.48890.7150 0.4899 0.8003 0.1672 0.69810.4820 0.59440.1948 0.1174 0.6241 0.90370.16790.4538 0.10620.66650.1206 0.02250.22590.2967 0.6791 0.8909 0.9787 0.43240.3724 0.1781 0.58950.42530.1707 0.3188 0.3955 0.3342 0.7127 0.8253 0.1981 0.1280 0.2262 0.31270.2277 0.4242 0.3674 0.6987 0.5005 0.0835 0.48970.9991 0.3846 0.16150.4357 0.5079 0.98800.19780.47110.1332 0.33950.17110.5830 0.1788Columns21through 300.42290.7788 0.25480.1759 0.6476 0.5822 0.4046 0.3477 0.82170.51440.0942 0.42350.2240 0.7218 0.67900.54070.4484 0.1500 0.42990.88430.59850.09080.66780.47350.6358 0.86990.3658 0.5861 0.88780.58800.47090.2665 0.8444 0.1527 0.94520.26480.76350.2621 0.3912 0.15480.6959 0.15370.34450.34110.2089 0.3181 0.62790.04450.7691 0.19990.69990.2810 0.78050.60740.70930.11920.7720 0.7549 0.3968 0.40700.63850.44010.6753 0.19170.23620.9398 0.93290.2428 0.8085 0.74870.03360.52710.0067 0.73840.11940.64560.9727 0.44240.7551 0.82560.0688 0.45740.6022 0.24280.6073 0.4795 0.19200.68780.37740.79000.3196 0.87540.38680.9174 0.4501 0.63930.13890.35920.2160 0.31850.53090.5181 0.91600.2691 0.45870.5447 0.69630.7363 0.7904 0.53410.6544 0.9436 0.0012 0.7655 0.6619 0.64730.0938 0.3947 0.94930.09000.4076 0.6377 0.4624 0.1887 0.77030.5439 0.5254 0.6834 0.32760.11170.8200 0.95770.42430.28750.3502 0.7210 0.53030.7040 0.6713 0.13630.71840.24070.46090.0911 0.6620 0.5225 0.8611 0.4423 0.43860.67870.96860.6761 0.77020.5762 0.41620.9937 0.4849 0.0196 0.8335 0.49520.5313 0.28910.3225 0.68340.84190.21870.39350.3309 0.7689 0.18970.3251 0.67180.7847 0.5466 0.83290.1058 0.67140.4243 0.16730.49500.10560.69510.4714 0.4257 0.25640.10970.7413 0.2703 0.8620 0.14760.6110 0.06800.03580.6444 0.61350.06360.52010.1971 0.9899 0.0550Columns 31 through 400.85070.73860.55230.12390.73780.5590 0.1781 0.89490.6311 0.69250.56060.58600.62990.4904 0.06340.8541 0.3596 0.07150.08990.55670.9296 0.24670.03200.8530 0.86040.3479 0.0567 0.2425 0.08090.39650.69670.6664 0.61470.87390.93440.4460 0.5219 0.0538 0.77720.06160.58280.08350.3624 0.2703 0.9844 0.0542 0.3358 0.44170.9051 0.78020.8154 0.62600.04950.2085 0.8589 0.17710.17570.01330.53380.33760.8790 0.6609 0.4896 0.5650 0.7856 0.6628 0.20890.89720.10920.60790.98890.7298 0.19250.6403 0.51340.33080.90520.1967 0.82580.74130.00050.89080.12310.41700.17760.8985 0.6754 0.09340.3381 0.10480.86540.98230.20550.2060 0.39860.1182 0.4685 0.3074 0.2940 0.12790.6126 0.76900.14650.94790.13390.9884 0.91210.4561 0.7463 0.54950.99000.58140.1891 0.0821 0.03090.54000.10400.1017 0.0103 0.48520.5277 0.9283 0.0427 0.10570.9391 0.7069 0.74550.9954 0.0484 0.89050.4795 0.5801 0.6352 0.14200.30130.9995 0.7363 0.3321 0.66790.79900.8013 0.0170 0.2819 0.1665 0.29550.28780.5619 0.2973 0.6035 0.73430.2278 0.1209 0.5386 0.62100.3329 0.4145 0.18420.06200.52610.05130.4981 0.8627 0.6952 0.57370.4671 0.4648 0.5972 0.2982 0.72970.07290.90090.4843 0.4991 0.0521 0.64820.7640 0.2999 0.0464 0.70730.08850.57470.84490.53580.9312 0.0252 0.81820.13410.50540.7814 0.79840.8452 0.20940.4452 0.7287 0.8422 0.10020.21260.76140.28800.9430Columns 41 through 500.6837 0.78940.1123 0.6733 0.09860.9879 0.5975 0.75930.80920.75190.1321 0.36770.78440.42960.14200.1704 0.3353 0.7406 0.7486 0.22870.7227 0.2060 0.2916 0.4517 0.1683 0.2578 0.2992 0.74370.12020.06420.11040.0867 0.60350.6099 0.19620.3968 0.4526 0.10590.5250 0.76730.11750.77190.9644 0.0594 0.31750.0740 0.4226 0.68160.3258 0.67120.6407 0.2057 0.43250.3158 0.31640.6841 0.35960.46330.5464 0.71520.3288 0.38830.6948 0.7727 0.2176 0.4024 0.5583 0.21220.3989 0.64210.65380.5518 0.75810.6964 0.25100.9828 0.74250.09850.4151 0.41900.7491 0.2290 0.4326 0.12530.8929 0.4022 0.4243 0.82360.1807 0.39080.58320.6419 0.65550.1302 0.70320.6207 0.4294 0.1750 0.2554 0.81610.74000.48450.10980.0924 0.5557 0.1544 0.1249 0.1636 0.0205 0.31740.2348 0.15180.93380.00780.1844 0.3813 0.0244 0.66600.9237 0.81450.7350 0.78190.1875 0.42310.21200.1611 0.2902 0.8944 0.65370.78910.97060.10060.2662 0.65560.07730.75810.3175 0.5166 0.93260.85230.8669 0.29410.7978 0.7229 0.91380.8711 0.65370.70270.1635 0.50560.08620.23740.48760.53120.70670.35080.9569 0.1536 0.9211 0.63570.3664 0.5309 0.76900.10880.5578 0.68550.9357 0.95350.79470.95090.3692 0.0915 0.3960 0.63180.31340.2941 0.4579 0.54090.57740.44400.6850 0.40530.27290.12650.1662 0.53060.24050.67970.4400 0.06000.5979 0.10480.0372 0.1343 0.6225 0.83240.76390.03660.25760.86672.参考课本综合例题2.5.4和2.5.5中的方法,模拟产生1000个随机变量,使其服从参数为2的指数分布,进而计算这1000个随机数的均值和方差。
哈尔滨工程大学概率论历年考题综合

Ch1摸球问题、几何概型1. 袋中有5个白球和3个黑球,从中任取2个球,则取得的两球恰有一黑球的概率为 。
(07’)1、10把钥匙中有3把能打开门锁,今任取两把钥匙,则打不开门锁的概率为 。
(08’)3. 在区间)1,0(中随机的取两个数,则这两个数之差的绝对值小于21的概率为 。
(07’)2、在区间()1,0之间随机地取两个数,则事件{两数的最大值大于23}发生的概率 为 。
(08’)1、某人忘记了电话号码的最后一个数字,因而随意拨号,则拨号不超过三次而接通电话的概率为 。
(09’)(A ) 101 (B ) 103 (C ) 109 (D ) 811、在区间[0,]L 之间随机地投两点,则两点间距离小于2L的概率为 。
(09’)1、设两事件A ,B 满足条件)()(B A P AB P =,且)10()(<<=p p A P ,则)(B P = 。
(06’)1. 10件产品中有8件正品,2件次品,任选两件产品,则恰有一件为次品的概率为 .(10’)2. 在区间()1,0中随机地取两个数,则事件{两数之和大于54}的概率为(10’).1. 设,A B 为随机事件,且()0,(|)1P B P A B >=,则必有 。
(07’) (A )()()P A B P A ⋃> (B )()()P A B P B ⋃>(C )()()P A B P A ⋃=(D )()()P A B P B ⋃=1. 设,A B 为两个随机事件,若事件,A B 的概率满足0()1,0()1P A P B ,且有等式()()P A B P A B 成立,则事件B A ,_______.(10’)(A ) 互斥 (B ) 对立 (C ) 相互独立 (D ) 不独立三、计算题1、设B A ,为两事件,4.0)(,6.0)(,7.0)(===A B P B P A P ,求)(B A P ⋃。
(06’) (05’)已知随机事件A 的概率5.0)(=A P ,随机事件B 的概率6.0)(=B P ,条件概率8.0)(=A B P ,求)(B A P 。
概率与统计试题08-09(2)A-B

试卷 (A 卷)一﹑单项选择题1.设事件B A ,,满足A B ⊂,则下列式子正确的是(A ))()(A P B A P = (B ) )()(A P AB P =(C ) )()(B P A B P = (D ) )()()(A P B P A B P -=-2.某学生做电路实验,成功的概率是10(<<p p ),则在3次重复实验中至少失败1次的概率是(A )3p (B )3)1(p -(C )31p - (D )3)1(p -)1()1(22p p p p -+-+ 3.设Y X ,是任意随机变量,C 为常数,则下列各式中正确的是(A ))()()(Y D X D Y X D +=+ (B )C X D C X D +=+)()( (C ))()()(Y D X D Y X D -=+(D ))()(X D C X D =-4.已知1)(-=X E ,3)(=X D ,则=-)]2(3[2X E (A ) 9 (B ) 6 (C )30 (D )36 5.设随机变量)2(~2χX ,)3(~2χY ,且Y X ,相互独立,则YX 23服从的分布为(A )F (2,2) (B )F (3,2) (C )F (2,3)(D )F (3,3)二﹑填空题1、已知()0.5,()0.8P A P B ==且(|)0.8 P B A =,则=)(B A P .2、设随机变量X 服从),2(2σN 分布,且{}3.042=<<X P ,则{}0<X P = .3、1621,,,X X X 是来自总体),2(~2σN X 的一个样本,∑==161161i iX X ,则~84σ-X .三、计算题已知一批产品90%是合格品,其余是次品。
检查产品时,一个合格品被误认为是次品的概率为03.0,而一个次品被误认为是合格品的概率为06.0,求在检查中一个产品被认为是合格品的概率? 四、计算题某工厂生产的电子管的寿命为X (小时),其概率密度函数为⎪⎩⎪⎨⎧≤>=120,0120,120)(2x x x x f ,假定电子管的寿命不到150小时就不合格,现任取3只电子管,求其中恰好有1只不合格的概率? 五、计算题设随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧≤≤≥=-其他,0510,0,25),(5y x e y x f x ,(1)求边缘概率密度函数)(),(y f x f Y X . (2)判别Y X ,是否相互独立. 六﹑计算题设10021,,,X X X 相互独立同分布,且100)(=i X E ,100)(=i X D ()100,,2,1 =i ,试用中心极限定理近似计算∑=>1001}10200{i i X P .七、计算题设总体X 的概率密度函数为⎪⎩⎪⎨⎧<<-=其他,01,)1(2)(322θθθx x x f ,其中θ是未知参数.n X X X ,,,21 是取自总体X 的一个容量为n 的简单随机样本,用矩估计法求θ的估计量. 八、计算题随机从一批灯泡中抽查16个灯泡,测得其使用时数的平均值为x =1500(小时), 样本方差2220=s (小时2), 设灯泡使用时数服从正态分布。
大学理工科专业目录新旧对照表
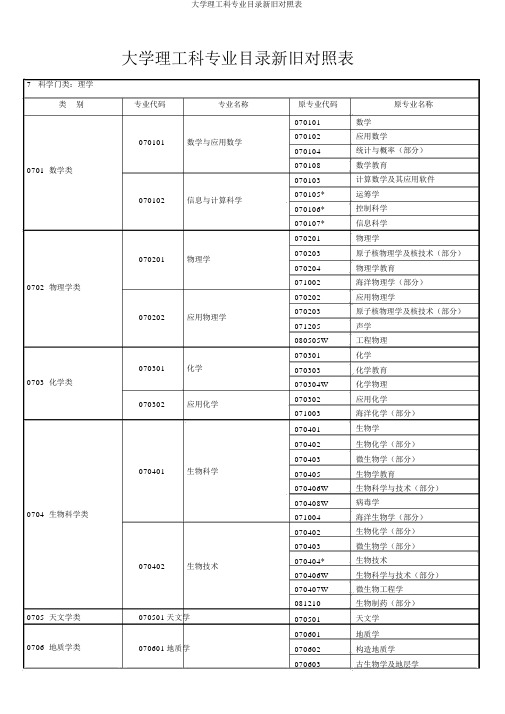
大学理工科专业目录新旧对照表7科学门类:理学类别专业代码专业名称070101数学与应用数学0701 数学类070102信息与计算科学070201物理学0702 物理学类070202应用物理学070301化学0703 化学类070302应用化学070401生物科学0704 生物科学类070402生物技术0705 天文学类070501天文学0706 地质学类070601地质学原专业代码原专业名称070101 数学070102 应用数学070104 统计与概率(部分)070108 数学教育070103 计算数学及其应用软件070105* 运筹学070106* 控制科学070107* 信息科学070201 物理学070203 原子核物理学及核技术(部分)070204 物理学教育071002 海洋物理学(部分)070202 应用物理学070203 原子核物理学及核技术(部分)071205 声学080505W 工程物理070301 化学070303 化学教育070304W 化学物理070302 应用化学071003 海洋化学(部分)070401 生物学070402 生物化学(部分)070403 微生物学(部分)070405 生物学教育070406W 生物科学与技术(部分)070408W 病毒学071004 海洋生物学(部分)070402 生物化学(部分)070403 微生物学(部分)070404* 生物技术070406W 生物科学与技术(部分)070407W 微生物工程学081210 生物制药(部分)070501 天文学070601 地质学070602 构造地质学070603 古生物学及地层学070602070701 0707 地理科学类070702070703 0708 地球物理学类070801071001 0709 大气科学类070902071001 0710 海洋科学类071002 0711 力学类071101071201 0712 电子信息科学类071202071203071301 0713 材料科学类071302071401 0714 环境科学类071402071501 0715 心理学类071502 0716 统计学类071601 8学科门类:工学类别专业代码地球化学地理科学资源环境与城乡规划管理地理信息系统地球物理学大气科学应用气象学海洋科学海洋技术理论与应用力学电子信息科学与技术微电子学光信息科学与技术材料物理材料化学环境科学生态学心理学应用心理学统计学专业名称070605W 地震地质学070604 地球化学070701 地理学070702* 地貌学与第四纪地质学070706 地理学教育070703 资源环境区划与管理070704 经济地理学与城乡区域规划070705 地理信息系统与地图学070801 地球物理学070802 空间物理学070901 气象学(部分)070902 气候学070903 大气物理学与大气环境070905W 大气科学070901 气象学(部分)070904 农业气象(部分)071001 海洋学071002 海洋物理学(部分)071003 海洋化学(部分)071004 海洋生物学(部分)071002 海洋物理学(部分)071003 海洋化学(部分)071004 海洋生物学(部分)071101 理论与应用力学071201 无线电物理学071202 电子学与信息系统071206W 信息与电子科学071203 微电子学071204 应用光学071301 材料物理071303W 矿物岩石材料071302 材料化学071401 环境学081103 环境规划与管理(部分)071402 生态学071501 心理学071502 应用心理学020103 统计学070104 统计与概率(部分)原专业代码原专业名称080101采矿工程080102石油工程080103矿物加工工程0801 地矿类080104勘查技术与工程080105资源勘查工程080201冶金工程080202金属材料工程0802 材料类080203无机非金属材料工程080204高分子材料与工程0803 机械类080301机械设计制造及其自动化080106080110080111080113W080103080104080105080108080101080102080104080201080202080203080213W080204080205080209080210080211080303080304080305080206080207080210080208080210080215W080301080306080309080310080312080314080315080317081502采矿工程石油工程选矿工程矿物加工工程水文地质与工程地质(部分)应用地球化学(部分)应用地球物理勘察工程地质矿产勘查石油与天然气地质勘查应用地球化学(部分)钢铁冶金有色金属冶金冶金物理化学冶金金属材料与热处理(部分)金属压力加工粉末冶金复合材料(部分)腐蚀与防护铸造(部分)塑性成形工艺及设备(部分)焊接工艺及设备(部分)无机非金属材料硅酸盐工程复合材料(部分)高分子材料与工程复合材料(部分)高分子材料及化工(部分)机械制造工艺与设备机械设计及制造(部分)汽车与拖拉机机车车辆工程流体传动及控制(部分)真空技术及设备机械电子工程设备工程与管理林业与木工机械080302080303080304 0804 仪器仪表类080401080501 0805 能源动力类080502080601 0806 电气信息类080602 材料成型及控制工程工业设计过程装备与控制工程测控技术与仪器热能与动力工程核工程与核技术电气工程及其自动化自动化080204 金属材料与热处理(部分)080302 热加工工艺及设备080303 铸造(部分)080304 塑性成形工艺及设备080305 焊接工艺及设备(部分)080316 工业设计080307 化工设备与机械080401 精密仪器080402 光学技术与光电仪器080403 检测技术及仪器仪表080404 电子仪器及测量技术080405* 几何量计量测试080406* 热工计量测试080407* 力学计量测试080408* 光学计量测试080409* 无线电计量测试080410W 检测技术与精密仪器080411W 测控技术与仪器080311 热力发动机080313 流体机械及流体工程080319W 热能工程与动力机械080501 热能工程080502 制冷与低温技术080506W 能源工程080507W 工程热物理080903 水利水电动力工程081409 冷冻冷藏工程(部分)080503 核技术080504 核工程080602 电力系统及其自动化080603 高电压与绝缘技术080605 电气技术(部分)080601 电机电器及其控制080718W 光源与照明080606W 电气工程及其自动化080312 流体传动及控制(部分)080605 电气技术(部分)080604 工业自动化080603电子信息工程080604通信工程080605计算机科学与技术080607生物医学工程080607生物医学工程080701建筑学080702城市规划0807 土建类080703土木工程080607W 自动化080711 自动控制081806 飞行器制导与控制(部分)080703 电子工程080704 应用电子技术080705 信息工程080706 电磁场与微波技术080715W 广播电视工程080716W 电子信息工程080720W 无线电技术与信息系统080723W 电子与信息技术081003 摄影测量与遥感(部分)082009 公共安全图像技术080712 通信工程080724W 计算机通信080709 计算机及应用080710 计算机软件080714 计算机科学教育080717W 软件工程080719W 计算机器件及设备080722W 计算机科学与技术080701 电子材料与元器件080702 微电子技术080707 物理电子技术080708 光电子技术080721W 物理电子和光电子技术080713 生物医学工程080801 建筑学080802 城市规划080804 城镇建设(部分)081708总图设计与运输工程(部分)090302 风景园林(部分)080109 矿井建设080803 建筑工程080804 城镇建设(部分)080805 交通土建工程080809* 工业设备安装工程080810W 饭店工程0808 水利类0809 测绘类0810 环境与安全类0811 化工与制药类0812 交通运输类080811W 涉外建筑工程080812W 土木工程080806 供热通风与空调工程080704 建筑环境与设备工程080807 城市燃气工程080813W 供热空调与燃气工程080705 给水排水工程080808 给水排水工程080801 水利水电工程080902 水利水电建筑工程080906W 水利水电工程080802 水文与水资源工程080901 水文与水资源利用080803 港口航道与海岸工程080904 港口航道及治河工程080905 海岸与海洋工程(部分)081001 大地测量081002 测量工程080901 测绘工程081003 摄影测量与遥感(部分)081004 地图学081005W 地理信息系统与地图081101 环境工程081102 环境监测081001 环境工程080103水文地质与工程地质(部分)090305 农业环境保护(部分)081002 安全工程080107 矿山通风与安全082206* 安全工程081201 化学工程081202 化工工艺081203 高分子化工081204 精细化工081205 生物化工(部分)081101 化学工程与工艺081206 工业分析081207 电化学工程081208 工业催化081214W 化学工程与工艺081215W 高分子材料及化工(部分)081216W 生物化学工程(部分)081209 化学制药081102 制药工程081210 生物制药(部分)081213 中药制药(部分)081217W 制药工程081201 交通运输081701 交通运输081202081203081204081205081206 0812 海洋工程类0813010814010814 轻工纺织食品类081402081403081404081405081406 0815 航空航天类081501081702 载运工具运用工程082004 道路交通管理工程081703 交通工程交通工程081708总图设计与运输工程(部分)082005 道路交通事故防治工程油气储运工程081707 石油天然气储运工程飞行技术081706 飞机驾驶航海技术081704 海洋船舶驾驶轮机工程081705 轮机管理船舶与海洋工程080308 船舶工程080905 海岸与海洋工程(部分)081301 制糖工程081305 粮食工程081306 油脂工程081307 食品科学与工程081310 烟草工程食品科学与工程081311W 食品科学与工程081313W 粮油储藏081407 农产品贮运与加工081408 水产品贮藏与加工081409 冷冻冷藏工程(部分)090405 蜂学(部分)081302 皮革工程轻化工程081303 制浆造纸工程(部分)081604 染整工程包装工程081309 包装工程印刷工程081304 印刷技术081601 纺织工程081602 丝绸工程纺织工程081603 针织工程081605 纺织材料及纺织品设计081312W 棉花加工与检验服装设计与工程081606 服装050419 服装艺术设计(部分)081801 航空飞行器设计飞行器设计与工程081802 空间飞行器设计081803 飞行器强度与实验技术081802 空气动力学与飞行力学0816 武器类0817 工程力学类0818 生物工程类0819 农业工程类0820 林业工程类0821 公安技术类081502 飞行器动力工程081804 飞行器动力工程081503 飞行器制造工程081805* 飞行器制造工程081504飞行器环境与生命保障工程081808飞行器环境控制与安全救生081807 火箭导弹发射技术与设备081901 火炮与自动武器(部分)081601 武器系统与发射工程081902 火箭武器081904 弹道工程081905 鱼雷水雷工程(部分)082205 系统工程(部分)081806 飞行器制导与控制(部分)081602 探测制导与控制技术081905 鱼雷水雷工程(部分)081906 火控与指挥系统工程081908 引信技术081603 弹药工程与爆炸技术081903 弹药工程081909 爆炸技术及应用081604 特种能源工程与烟火技术081907 火炸药081910 火工与烟火技术081605 地面武器机动工程081901 火炮与自动武器(部分)081911 军用车辆工程081606 信息对抗技术[新增 ]081701 工程力学081701 工程力学081205 生物化工(部分)081801 生物工程051211 微生物制药081216W 生物化学工程(部分)081308 发酵工程081901 农业机械化及其自动化080306 机械设计及制造(部分)081401 农业机械化081902 农业电气化与自动化081403 农业电气化自动化081903 农业建筑环境与能源工程081402 农业建筑与环境工程081406 农村能源开发与利用081904 农业水利工程081404 农田水利工程082001 森林工程081501 森林工程081503 木材加工082002 木材科学与工程081505 室内与家具设计(部分)081303 制浆造纸工程(部分)082003林产化工081504 林产化工082101 刑事科学技术082006 痕迹检验082102消防工程9学科门类:农学类别专业代码专业名称090101农学0901 植物生产类090102园艺090103 植物保护090104 茶学0902 草业科学类090201 草业科学090301林学0903 森林资源类090302森林资源保护与游憩090303野生动物与自然保护区管理090401园林090402水土保持与荒漠化防治0904 环境生态类090403农业资源与环境082007文件鉴定082008法化学082001防火工程082002灭火技术082003火灾原因技术鉴定原专业代码原专业名称090101 农业090102 热带作物090109 药用植物(部分)090108 土壤与农业化学(部分)090112W 烟草090103 园艺090104 果树090105 蔬菜090106 观赏园艺(部分)060107 植物保护090110 茶学090111 草学090201 林学090202 森林保护090203 经济林090204野生植物资源开发与利用(部分)090204野生植物资源开发与利用(部分)090206W 森林旅游090205 野生动物保护与利用090605 自然保护区资源管理090106 观赏园艺(部分)090301 园林090302 风景园林(部分)090303 水土保持090304 沙漠治理090108 土壤与农业化学(部分)090305 农业环境保护(部分)090604渔业资源与渔政管理(部分)070904 农业气象(部分)0905 动物生产类0906 动物医学类0907 水产类10学科门类:医学类别1001 基础医学类1002 预防医学类1003 临床医学与医学技术类1004 口腔医学类1005 中医学类090401 畜牧兽医(部分)090501 动物科学090402 畜牧090405 蜂学(部分)090406 动物营养与饲料加工090502 蚕学090404 蚕学090401 畜牧兽医(部分)090103 实验动物090601 动物医学090407 兽医090408 中兽医090409 动物药学090701 水产养殖学090501 淡水渔业090502 海水养殖090503 海洋渔业090702 海洋渔业科学与技术090604渔业资源与渔政管理(部分)专业代码专业名称原专业代码原专业名称100101 基础医学100101 基础医学100201 预防医学100202 环境医学100201 预防医学100203 卫生检验100204 营养与食品卫生100205* 妇幼卫生100301 临床医学100302 儿科医学100301 临床医学100303 精神病学与精神卫生100304 放射医学100307 医学营养学100302 麻醉学100308* 麻醉学100303 医学影像学100305* 医学影像学100304 医学检验100306* 医学检验100401 口腔医学100401 口腔医学100501 中医学100502 中医五官科学100501 中医学100503 中医骨伤科学100504* 中医外科学100505* 中医养生康复学100508* 中医文献学大学理工科专业目录新旧对照表1006 法医学类1007 护理学类1008 药学类100502 针灸推拿学100506 针灸学100507 推拿学100503 蒙医学100509 蒙医学100504 藏医学100510 藏医学100601 法医学100601 法医学100701 护理学100701 护理学100801 药学100803 药物分析100801 药学100804 药理学100805* 临床药学100802 药物化学100806 中药学100807 中药检定100802 中药学100808 中药药理学100809 中药资源081213 中药制药(部分)090109 药用植物(部分)100803 药物制剂081212 药物制剂。
陈希孺概率论答案

陈希孺概率论答案【篇一:概率统计参考书推荐】>概率论、数理统计、随机过程、随机分析等“随机数学”,近来在经济管理及金融领域应用火爆,有志在这些领域深造的同学,必须要把这随机数学学得炉火纯青。
以下书籍难度基本由低至高。
各类别中列举数种,也不必全看,重点阅读一两本即可。
关键是要有毅力,随便一本书,坚持读到底,做完上边的全部习题,功夫即可小成。
最忌讳贪多求新,得陇望蜀,一本没完,另开一本,读书变成了赏书,结果一本都不可得。
记住:一本书读三遍,胜过三本书读一遍。
各书均可在卓越、当当等处购买,凡市面上难见者,以图书馆藏书为限。
大致印象:国人编书,篇幅短小重点突出,但过于中规中矩,缺乏自由发挥,好在价格便宜。
老外作书,篇幅浩瀚,无拘无束自由挥洒,表面上絮絮叨叨,可是思想火花恰在此絮叨中显现,价格一般偏贵。
一般认为,国人教材适合入门,老外教材适合巩固和进阶之用。
(一)概率论:1。
陈希孺《概率论与数理统计》,中国科技大学出版社作者为院士。
这本是适合工科学生的初级教程。
优点在于基本概念基本思想交代得细致平淡自然,不搞那些故弄玄虚的花架子。
习题稍难,后附简答。
2。
李贤平《概率论基础》配套辅导概率论基础学习指导书(第三版)高等教育出版社2010-4经典教材,数学专业初学适用。
只涉及概率论,不讲数理统计。
叙述清晰,深度适当,例题丰富多彩。
极限定理一章比较难,需要有高度的毅力和决心。
课后题极多,书后只给计算题的结果。
3。
王梓坤《概率论基础及其应用》(第三版)北京师范大学出版社2007-3 作者是资深院士,曾留学苏联,北师大原校长。
此书绝版多年,终于再版。
只涉及概率论,书较厚,观点比较高。
课后答案极其详细,适合自学。
著名的入门教程,作者是应用概率论的专家。
其书内容结构要比本土教程扩展很多,例题、习题极富新意。
5。
[美]a.帕普里斯等《概率、随机变量与随机过程》第四版,保铮等译。
西安交通大学出版社,2004年。
经典名著。
全概率公式与贝叶斯公式

比如原来认为作案可能性较小的某丙,现在变成了重
点嫌疑犯.
最
大
15
在医疗诊断中,为了诊断病人到底患了毛病
A1 , A2 ,, An 中 的 哪 一 种 ,对 病 人 进 行 检 查 ,确 定 了
某个指标 B(比如体温 ).
根 据 以 往 资 料 可 知 P( A1 ), P( A2 ),, P( An ) ,
13
解 释 :事 件 A1 , A2 ,, An 看 作 是 导 致 事 件 B 发 生 的“ 原
因 ”,在 不 知 事 件 B 是 否 发 生 的 情 况 下 ,它 们 的 概 率 为 P( A1), P( A2 ),, P( An ) , 通 常 称 为 先 验 概 率 .
现 在 有 了 新 的 信 息 已 知 ( B 发 生 ),我 们 对 A1 , A2 ,, An
4
全概率公式
n
P(B) P( Ai ) P(B | Ai ) i 1
利用全概率公式,可以把较复杂事件概率的 计算问题,化为若干互不相容的较简单情形,分 别求概率然后求和.
5
例1库房内有三家工厂生产的同类产品,其中第一、二、 三家工厂的产品各占库房总量的50%、30%、 20%,且 三家工厂的次品率分别为 0.01、0.02、0.04,现从库房 中任取一件产品,问取出的是次品的概率有多大.
a(a 1)
ab
a,
(a b)(a b 1) (a b)(a b 1) a b
由于 P(B | A) P(B) , 所以A,B不相互独立.
9
在上面例1中,如买到一件次品,问它是甲厂生产 的概率为多大?这就要用到贝叶斯公式.
定理(贝叶斯公式) 设 A1, A2 ,, An 为 一 个 完 备 事 件 组 , P( Ai ) 0 , i 1,, n , 对 任 一 事 件 B,若 P(B) 0 ,有
08-11年中考及模拟概率大题答案
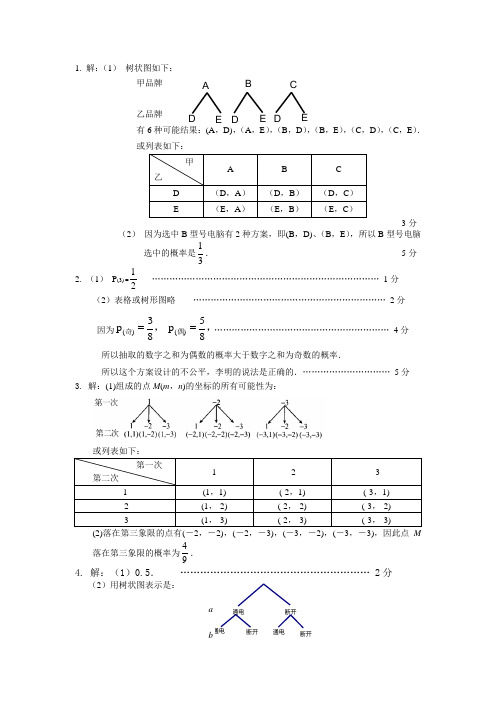
1. 解:(1) 树状图如下: 甲品牌乙品牌有6种可能结果:(A ,D),(A ,E ),(B ,D ),(B ,E ),(C ,D ),(C ,E ). 或列表如下:·························· 3分(2) 因为选中B 型号电脑有2种方案,即(B ,D)、(B ,E ),所以B 型号电脑选中的概率是31. ················································································ 5分 2. (1) P (3) =21…………………………………………………………………… 1分 (2)表格或树形图略 ………………………………………………………… 2分 因为 )(83p ,奇= )(85p ,偶=…………………………………………………… 4分 所以抽取的数字之和为偶数的概率大于数字之和为奇数的概率.所以这个方案设计的不公平,李明的说法是正确的.………………………… 5分 3. 解:(1)组成的点M (m ,n )的坐标的所有可能性为:或列表如下:(2)落在第三象限的点有(-2,-2),(-2,-3),(-3,-2),(-3,-3),因此点M落在第三象限的概率为94. 4. 解:(1)0.5. ………………………………………………… 2分(2)用树状图表示是:DDE E DC B A 断开通电断开断开通电或用列表法表示是:P 、Q 之间电流通过的概率是4. …………………………………………… 4分 (3)87. ……………………………………………………………………6分 5. 解:A B C D B C D C A B D B ABACADBABCBDCACBCDDADBDC………………………3分∴P (得到奖励)31124==.………………………5分(说明:列表法同理给分) 6. 解:(1)树状图如图①:①∴P (吃到两只粽子都是什锦馅)61122==. (2)模拟试验的树状图如图②:∴P (吃到两只粽子都是什锦馅)41164==6141=/, ∴这样模拟不正确. 7. (1)树状图如图:第19题答图所有可能的结果有(白,白)、(白,红)、(白,黑)、(红,白)、(红,红)、(红,黑)、(黑,白)、(黑,红)、(黑,黑). (2)P (甲、乙颜色相同)3193==. 8. 解:列表如下:正好是她喜欢搭配的颜色的概率是9. (也可用树形图法解)9. 解:用画树状图的方法,列出两次抽得的卡片上所标数字的所有可能结果如下.第21题答图∵所有可能的结果有12个,它们出现的可能性相等,所有的结果中,满足抽得的两张卡片上的数字按题目要求组成的两位数大于22的结果有7个,∴P (两位数大于22)=127. 10. 解:(1)P (抽到牌面数字4)=31(2)游戏规则对双方不公平. 理由如下:或第19题答图由上述表格或树状图知:所有可能出现的结果共有9种.P (抽到牌面数字相同)3193==, P (抽到牌面数字不相同)3296==.3231< ,此游戏规则不公平,小李赢的可能性大. 11. 解:(1)由于关于x 的一元二次方程x 2+2ax +b 2=0有实数根,所以(2a )2-4b 2≥0,有a 2≥b 2. 由于a ≥0,b ≥0,所以a ≥b .共有12种情况,其中a ≥b 的有9种,则上述方程有实数根的概率是4. 12. 解法一:一次游戏,甲、乙两人随机出手势的所有可能的结果如图所示:第20题答图所有可能出现的结果为(S ,S)、(S ,J)、(S ,B)、(J ,S)、(J ,J)、(J ,B)、(B ,S)、(B ,J)、(B ,B).从上面树状图可以看出,一次游戏可能出现的结果共有9种,而且每种结果出现的可能性相同.所以,P (出同种手势)=3193=;P (甲获胜)=3193=. 解法二:一次游戏,甲、乙两人随机出手势的所有可能的结果如下表所示:以下同解法一.。
概率统计

1.列举是处理古典概型的基本方法. 2.列举时,要注意分清“有序”还是 “无序”,按一定次序进行列举,防止重复和 遗漏.采用列表、“树图”等直观手段是防止 重复与遗漏的有效方法. 3.具体事件的给出常常和其他数学知识 相联系,要注意联系相关知识找到相应事件的 基本事件数.
8
题型三:几何概型
例 3、在区间 使得函数 [ , ]内随机取两个数分别记
知识树
系统抽 样 简单随 机抽样
分层抽 样
用样本 的频率 分布估 计总体 分布
随机抽 样
相关性检验
用样本 估计总 体
用样本 的数字 特征估 计总体 的数字 特征 回归直线方 程
变量间的 相关关系
统计
随机事 件的概 率
古典概型
频率和概 率的联系 区别
独立性检 验
概率
古典概型 方法步骤
几何概型
几何概型方 法步骤
[答案] 6 000
频率分布直方图和程序框图是高考考查的一个 热点,弄清二者的结合点是处理好互斥事件等概率模 型的计算方法与步骤 2.掌握三种抽样方法、会识别统计图表、会计算 各种样本数字特征 3.掌握回归直线方程和独立性检验的意义
从表中看,每年至少一个小题和一个大题, 总分值为17~21分,题型稳定,分值固定,大题 08、10、11三年为18题,09、12两年为19题,位 置相对固定,难度为中档题,且都是应用题,材 料背景基本相同,除独立性检验、茎叶图、随机 模拟外,其余知识点都考过. 小题主要考查统计的有关知识(如抽样方法、 统计图表、样本数学特征、线性回归分析等)和几 何概型,几何概型往往与其它章节的知识进行综 合考查,一般属于中档题。解答题的命题重点是 古典概型、互斥事件的概率,有时与统计的有关 知识综合进行考查。加大了统计知识、方法的考 查,08~10年分值为4~5分, 11~12年分值为9 分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福州大学《概率论与数理统计》期末考试试卷(200806理)专业 班 姓名 学号一.单项选择(每小题2分,共20分)1.袋中有8只红球,2只白球,从中任取2只,颜色不同的概率为( ) (A)101 (B)4516 (C)102 (D)4529 2.设A B ⊂且相互独立,则( )(A )()0P A = (B )()1P A =(C )()0()1P A P B ==或 (D )上述都不对3.每次试验成功概率为(01)p p <<,则在3次重复试验中至少成功1次的概率为( ) (A) 31(1)p -- (B) 31p - (C) 3(1)p - (D) 322(1)(1)(1)p p p p p -+-+-4.设随机变量X 的分布列为 X 0 1 2 ,分布函数()F x ,则(1.5)F =( )P 0.3 0.5 0.2(A) 0 (B)0.3 (C)0.8 (D)1 5.随机变量()2~(2,),00.35X N P X σ<=,则()04P X <<=( )(A )0.5 (B )0.7 (C )0.35 (D )0.36.设随机变量X 服从二项分布)2.0,10(B ,Y 服从参数为2的泊松分布,且X ,Y 相互独立,则(231)D X Y -+=( )(A) 9.2 (B)-10.6 (C)24.4 (D) 25.4 7.设,X Y 为任意两个随机变量,则下列等式一定成立有( ) (A))()()(Y E X E XY E = (B)()()()E X Y E X E Y -=- (C))()()(Y D X D XY D = (D)()()()D X Y D X D Y -=+8.设~(1,4)X N ,2~(1)Y n χ-,X 与Y)(A) 自由度为1-n 的t 分布 (B) 自由度为n 的2χ分布 (C) 自由度为n 的t 分布 (D) 自由度为1-n 的2χ分布9.设n 个随机变量12,,n X X X 独立同分布,且()1D X =2σ,,11i ni X n X ∑==,)(11212X X n S i ni --=∑=则( ) (A) S 与X 相互独立 (B) S 是σ的极大似然估计量 (C) S 是σ的无偏估计量 (D) 2S 是2σ的无偏估计量10.总体平均值μ的置信度为α-1的置信区间是),(21μμ,这意味着( )(A) 区间),(21μμ包含总体平均值μ真值的概率为α-1; (B) 有100(α-1)%的样本平均值将落在),(21μμ; (C) 总体平均值μ位于),(21μμ的概率为α-1; (D) 区间),(21μμ包含样本平均值的概率为α-1.二.填空题(每小题2分,共20分)1.两封信随机地投入4个邮筒,则前两个邮筒各有一封信的概率为___________. 2.若1()4P A =,31)(=B P 且B A ⊃,则)(B A P ⋃= __________. 3.设随机变量X 的分布函数为()5(0)xF x A e x -=+≤<∞,则A =______________. 4.已知随机变量X 只能取-1,0,1,2,3五个数值,其相应的概率依次为cc c c c 161,161,81,41,21,则=c ___________.5.设随机变量X 的概率密度为⎪⎩⎪⎨⎧<≤-<≤=其他,,0,21,2,10,)(x x x x x f 则()1/43/2P X <<= .6.已知~()X E λ,且1()3E X =,则λ=__________. 7.设X ,Y 为两个相互独立的随机变量,且1)(=X E ,2)(=Y E ,3)(2=X E ,5)(2=Y E ,则(2)D X Y +=____ .8.已知~(2,9)X N ,~(1,16)Y N ,相关系数0.15XY ρ=,则ov(,)C X Y =________.9.当2σ已知时,正态总体均值μ的90%的置信区间的长度为___________.10.设总体X 服从正态分布),(2σμN ,其中2σ未知,n X X X ,,,21 为其的样本,则对假 设0:μμ=H 进行检验时,采用的检验统计量为 .三.计算题(每小题9分,共18分)1.甲,乙两人各射一次靶,他们各自中靶与否相互独立,且已知他们各自中靶的概率分别为0.6,0.8,求下列事件的概率.(1)两人中靶的事件(2)至少有一人中靶(3)恰有一人中靶. 2.设随机变量X 在[2,5]上服从均匀分布,现在对X 进行三次独立观测,试求至少有两次观测 值大于3的概率.四.计算题(每小题8分,共16分)1.设某厂产品的合格率为0.96,现采用新方法测试,一件合格产品经检查而获准出厂的概率 为0.95,而一件废品经检查而获准出厂的概率为0.05,试求使用这种方法后,获得出厂许可的 产品是合格品的概率及未获得出厂许可的产品是废品的概率.2.随机变量X的概率密度为|1,()0,x f x <=⎩其它求:(1)常数C ;(2)X 的分布函数.五.计算题(第一小题10分,第二小题8分,共18分) 1.设二维随机变量),(Y X 在矩形域d y c b x a ≤≤≤≤,内服从均匀分布,求(1)求联合概率密度函数;(2)求Y X ,的边缘概率密度;(3)判断随机变量Y X ,是否独立.2.设总体X 的概率密度为1,01,()0,xe xf x θθ-⎧<<⎪=⎨⎪⎩其他且0θ>,12,,n X X X …,为X 的样本,求θ的极大似然估计量. 六.计算题(8分)早稻收割根据长势估计平均亩产为310kg ,收割时,随机抽取了10块,测出每块的实际亩产量为1021,,,X X X ,计算得∑===101320101i i X X ,如果已知早稻亩产量X服从正态分布(),144N μ,试问所估产量是否正确?(05.0=α)(0.0251.96u =,0.05 1.64u =)福州大学《概率论与数理统计》期末考试试卷(200905理)专业 班 姓名 学号一.单项选择(每小题2分,共20分)1.从一大批产品中任抽5件产品,事件A 表示:“这5件中至多有1件废品”, 事件B 表示“这5件产品都是合格品”,则AB 表示( )(A )所抽5件均为合格品 (B )所抽5件均为废品 (C )不可能事件 (D )必然事件 2.设A ,B 均为非零概率事件,且A B ⊃,则成立( )(A ))()()(B P A P B A P +=⋃ (B ))()()(B P A P AB P ⋅= (C ))()()|(B P A P B A P =(D ))()()(B P A P B A P -=- 3.设随机变量X 的分布列为 X 0 1 2 ,分布函数()F x ,则(0.8)F =( )p 0.3 0.5 0.2(A )0 (B )0.3 (C )0.8 (D )1 4.设随机变量X 的概率密度为()X f x ,则13+=X Y 的概率密度为( ) (A )11()33X f y - (B )(31)X f y + (C )111()333X f y - (D )11()33X f y - 5.若离散型二维随机变量(,)X Y 的联合分布律为(,1,2,)ij p i j = ,则二维随机变量(,)X Y 关于Y 的边缘分布律为( ) (A ),1,2,iji p j =∑ (B ),1,2,ijj p i =∑ (C ),1,2,ij i p i =∑ (D ),1,2,ijjp j =∑6.设二维随机变量(,)X Y 服从G 上的均匀分布,G 的区域由直线x y =,x 轴及2x =所围,则(,)X Y 的联合概率密度函数为( )(A )⎩⎨⎧∈=他其,0),(,6),(G y x y x f ; (B )⎩⎨⎧∈=他其,0),(,6/1),(Gy x y x f(C )⎩⎨⎧∈=他其,0),(,2),(G y x y x f ; (D )⎩⎨⎧∈=他其,0),(,2/1),(Gy x y x f7.设随机变量X 服从指数分布(12)E ,Y 服从正态分布2(5,2)N ,且,X Y 相互独立,则(22)D X Y -+=( ) (A )12 (B )20 (C )22 (D )68.设)2,0(~N X ,2~(4)Y χ,且X 与Y服从( ) (A )自由度为2的t 分布 (B )自由度为2的2χ分布 (C )自由度为4的t 分布 (D )自由度为4的2χ分布9.设1ˆθ,2ˆθ是θ的两个估计量,当( )时,称1ˆθ比2ˆθ有效 (A )1ˆ()D θ<)ˆ(2θD (B ) 1ˆ()D θ>)ˆ(2θD (C )1ˆθ无偏且)ˆ(1θD ≤)ˆ(2θD (D )1ˆθ,2ˆθ均无偏且1ˆ()D θ<)ˆ(2θD10.点估计量是( )(A )总体的函数 (B )无偏估计 (C )样本的函数 (D )有偏估计 二.填空题(每小题2分,共20分)1. 掷两颗骰子,它们出现的点数之和等于8的概率是__________.2.设,A B 两事件相互独立,11(),()32P A P B ==,则,A B 中恰有一个发生的概率是________. 3.设随机变量X 的分布列为6sin )(πk A k X P ==,1,3,5,13,15,17k =,则A =__________.4.设X ~)2,7(2N ,()x Φ为标准正态函数且{3}()P X a >=Φ,则a = .5.设(,)X Y 的联合概率密度为(2)20,0(,)0x y e x y f x y -+⎧>>=⎨⎩其它,则(,)X Y 关于Y 的边缘概率密度为_________________.6.设随机变量X 的分布列为10120.20.30.20.3X -⎛⎫ ⎪⎝⎭,22X Y =,则()E Y =___________. 7.~(3,9)X N ,~(2,16)Y N ,相关系数0.25XY ρ=,则ov(,)C X Y =__________. 8.设总体()X t n ,则2X ____________. 9.设有来自正态总体209XN μ~.(,)容量为9的简单随机样本,得样本均值5X =,则未知参数μ的置信度为0.95的置信区间是___________.(1.96)0.975,(1.64)0.95Φ=Φ= 10.设总体X 服从二项分布(,)B n p ,其中p 未知,12,,,n X X X 是总体的一个样本,则未知参数p 的矩估计量________________.三.计算题(每小题7分,共14分)1.对以往数据分析的结果表明,当机器调整为良好时,产品的合格率为90%,而当机器发生故障时,其合格率为30%.每天早上机器启动时,机器调整为良好的概率为75%,试求已知某日早上第一件产品是合格品时,机器发生故障的概率. 2.某元件寿命X 服从为λ)1000(1小时=-λ的指数分布.3个这样的元件使用1000小时后,恰有一个损坏的概率是多少?四.计算题(每小题8分,共16分) 1.设随机变量X 的概率密度为||()(),x f x Cex -=-∞<<+∞求:(1)常数C ; (2)(11)P X -≤≤;(3)X 的分布函数.2.设袋中装有4个球,分别标有数字1,2,2,3,从袋中任取一球(其上数字记为X )之后不再放回,再从袋中任取一球(其上数字记为Y ),求: (1)),(Y X 的联合分布律;(2)关于,X Y 的边缘分布律;(3)判别,X Y 是否独立. 五.计算题(每小题7分,共14分)1.随机变量X 的分布函数为0111()arcsin 11211x F x x x x π<-⎧⎪⎪=+-≤<⎨⎪≥⎪⎩求:)(X E 及)(X D2.某互联网站有10000个相互独立的用户,已知每个用户在平时任一时刻访问网站的概率为0.2,试用中心极限定理计算在任一时刻有19002100 用户访问该网站的概率.)9938.0)5.2(,9893.0)3.2(,9772.0)0.2((=Φ=Φ=Φ六.计算题(每小题8分,共16分)1.设总体X 服从参数为λ(0,)λ>未知的泊松分布,求未知参数λ的极大似然估计.(提示:(;),0,1,2,!xp x ex x λλλ-== )2. 某种型号的电池,其寿命(以小时计)长期以来服从方差26000σ=的正态分布,现随机取17只电池,测出其寿命的样本标准差为90s =.问根据这一数据能否推断这批电池的寿命的波动性较以往的有显著的变化?(取0.05α=)220.9750.025((16) 6.908,(16)28.25,χχ==220.950.05(16)7.962,(16)26.3)χχ==福州大学《概率论与数理统计》期末考试试卷(201006理)专业 班 姓名 学号一、单项选择题(每小题3分,共24分)1、已知()P A a =, ()P B b =, ()P AB c =,则()P A B =( ) (A )()()11a b -- (B) 1c - (C) 1a b c --+ (D) a b c +-2、每次试验成功概率为(01)p p <<,则在3次重复试验中至少失败1次的概率为( )(A) ()31p - (B) 313p - (C) 3(1)p - (D) 322(1)3(1)3(1)p p p p p -+-+-3、设随机变量~()X P λ,且(0)(1)P X P X ===,则(2)P X ==( )(A )112e - (B )223e - (C )12e - (D )123e - 4、设随机变量X ~23[0,]()0x x A f x ⎧∈=⎨⎩其它,则常数A =( )(A)41 (B) 21(C) 2 (D) 1 5、随机变量X 和Y 相互独立,都服从于01-分布:2(0)(0)3P X P Y ====, 则()P X Y ==( )(A )0 (B )59 (C )79(D )1 6、设随机变量X 服从指数分布(1E ,Y 服从正态分布2(2,3)N ,且,X Y 相互独立,则(21)D X Y -+=( ) (A )45(B )46 (C )10(D )267、设2~(1,2)X N ,2~(12)Y χ,且X 与Y服从( ) (A )自由度为3的t 分布 (B )自由度为12的2χ分布 (C )自由度为12的t 分布 (D )自由度为3的2χ分布 8、在假设检验中,记0H 为原假设,第一类错误为( )(A)0H 为真,接受0H (B) 0H 不真,拒绝0H (C)0H 为真,拒绝0H (D )0H 不真,接受0H二、填空题(每小题2分,共16分)1、袋中有8只红球,2只白球,从中任取2只,颜色相同的概率为_________2、设随机事件A 与B 相互独立,A 发生B 不发生的概率与B 发生A 不发生的概率相等,且1(),()3P A P B ==则 3、随机变量X 服从()0,1上的均匀分布,则随机变量函数X Y ln 2-=的概率密度为()________Y f y =4、设随机变量X 的密度函数为0()0x e x f x x -⎧>⎪=⎨≤⎪⎩,2x Y e -=,则()________E Y =5、已知~(2,9)X N ,~(1/4)Y E ,相关系数0.25XY ρ=,则ov(,)C X Y =________6、设随机变量~(,)X F m n ,则1~X____________ 7、设有来自正态总体()2~,X N μσ容量为9的简单随机样本,得样本均值5,1X S ==,则未知参数μ的置信度为0.95的置信区间是________________.()0.0250.0250.05(8) 2.31,(9) 2.26,(8) 1.86t t t === 8、设总体X 以概率1θ取值1,2,...,θ,则未知数θ的矩估计量为_______________三、计算题(每小题7分,共14分)1、若发报机分别以0.7与0.3的概率发出信号“0”与“1”,由于随机干扰,当发出信号“0”时,接收机收到的信号“0”与“1”的概率分别是0.8与0.2;当发出信号“1”时,接收机收到的信号“1”与“0”的概率分别是0.9与0.1.试问:假定已收到信号“0”,发报机恰好发出信号“0”的概率是多少?2、某厂生产的电子管寿命X (单位:h )服从2(1600,)N σ,若电子管寿命在1200小时以上的概率不小于0.96,求σ的值. ()()1.760.96Φ=四、计算题(每小题8分,共16分) 1、设随机变量X 的分布函数为()1xAF x e-=+求(1)常数A ;(2)X 的概率密度;(3)()0P X ≤2、设(),X Y 在区域G 上服从均匀分布,G 由直线12xy +=及x 轴y 轴围成,求: (1)(),X Y 的联合概率密度;(2)(),X Y 的边缘概率密度;(3)判别,X Y 是否独立五、计算题(每小题7分,共14分) 1、设随机变量X 的概率密度为()()2xef x x -=-∞<<+∞,求()(),E X D X2、某种电器元件的寿命服从均值为100小时的指数分布.现随机地取25只,设它们的寿命是相互独立的.求这25只元件寿命的总和大于2750小时的概率.()()0.50.6915Φ=六、计算题(每小题8分,共16分)1、设总体X 的概率密度为()()1,01;0;0,x f x θθ≤≤=>⎪⎩,其它12,,...,n X X X 是总体X 的一个样本,求总体X 的参数θ的极大似然估计.2、某厂生产乐器用合金弦线,其抗拉强度服从均值为10560(公斤/厘米2)的正态分布,现从一批产品中抽取10根,测得其抗拉强度(单位:公斤/厘米2)如下:10512,10623,10668,10554,10776, 10707,10557,10581,10666,10670 问这批产品的抗拉强度有无显著变化?(0.01α=)()0.010.0050.005(9) 2.82,(9) 3.25,(10) 3.17t t t ===。
