印七全年级复习卷
七年级数学总复习试卷与答案

七年级数学(满分:150分 时间:120分钟)一、选择题(本大题共8小题,每小题3分,共24分,每小题仅有一个答案正确,请把你认为正确的答案前的字母填入答题纸中表格相应的空格内 ) 1.把方程20.3120.30.7x x +--=的分母化为整数,结果应为( ▲ ) A. 231237x x +--= B. 10203102037x x +--=C. 1020310237x x +--=D. 2312037x x +--=2.下列说法中:①棱柱的上、下底面的形状相同;②若AB =BC ,则点B 为线段AC 的中点;③相等的两个角一定是对顶角;④不相交的两条直线叫做平行线;⑤直线外一点与直线 上各点连接的所有线段中,垂线段最短。
正确的有( ▲ ) 3.下列运算中,正确的是( ▲ )A .b a b a b a 2222=+- B .22=-a a C .422523a a a =+ D .ab b a 22=+4.如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四 位同学补画,其中正确的是 ( ▲ )A.B.C.D.5.下列各数是无理数的是( ▲ ) A .-2 B .227C .0.010010001D . π6.如图,AD ⊥BC ,ED ⊥AB ,表示点D 到直线AB 距离的是( ▲ )A .线段AD 的长度B .线段AE 的长度C .线段BE 的长度D .线段DE 的长度7.如图是我市十二月份某一天的天气预报,该天最高气温比最低气温高( ▲ ) A.-3℃A BE D CB. 7℃C. 3℃D.-7℃A .1个B .2个C .3个D .4个8.如图,由白色小正方形和黑色小正方形组成的图形.则第6个图形中白色小正方形和黑 色小正方形的个数总和等于( ▲ ) A.60 B.58 C.45 D.40二、填空题(每题3分,计30分,请把你的正确答案填入答题纸中相应的横线上)9.据统计,全球每分钟约有8500000吨污水排入江河湖海,则每分钟的排污量用科学记数 法表示应是 吨. 10.单项式34a b π-的次数是 次.11.如果A 2618'∠=︒,那么A ∠的余角为 °(结果化成度).12.已知3x y -=,则()()12+-+-x y y x 的值为___________ .13.用边长为1的正方形,做了一套七巧板,拼成如图(1)所示的图形,则图②中阴影部 分的面积为 .14.得到折痕EF ,如果∠DFE =36°, 则∠DF A = °.15.甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%; 乙超市连续两次降价15%;丙超市一次降价30%。
七年级数学系列复习试卷7(共8份-含答案)

数学系列学习7本试卷共有30题,满分100分,考试时间90分钟题号 一二三四五六七总分得分 评卷人一、填空(每空1分,共17分)1.在下列图案中可以用平移得到的是___________(填代号).2.有一种原子的直径约为0.00000053米, 用科学记数法表示为. 3.()22--=___ __;23x x -⋅=_;23(-3y )=__ ___;4()()xy xy ÷=.4.73x x =⋅; 2+1n a÷=3a .5.比较大小:4273816.如图,直线l 1∥l 2,AB ⊥l 1,垂足为O ,BC 与l 2相交于点E ,若∠1=43°,则∠2=__°.7.如图,将一张长方形纸片沿EF 折叠后,点D 、C 分别落在D′、C′的位置,ED ′的延长线与BC 交于点G .若∠EFG=55°,则∠1=_______°.8.已知△ABC 的三个内角分别是∠A 、∠B 、∠C ,若∠A=30°,∠C=2∠B ,则∠B=°.9. 一个多边形的每一个外角都是60°,则这个多边形是__ _边形,它的内角和是____°.10.一个三角形的两边长分别是2和7,另一边长a 为偶数,且28a <<,则这个三角形的周长为____________.11.用等腰直角三角板画45AOB =∠,并将三角板沿OB 方向平移到如图所示的虚线处后绕点M 逆时针方向旋转22,则三角板的斜边与射线OA 的夹角α为______. 12.如果等式()2x21x -=,则x=.第6题 第7题 第11题 二、选择题(每题2分,共20分)13.(-3a 3)2的计算结果是( )A .-9a 5 B. 6a 6 C. 9a 6 D. 6a 514.下列各式(1)55b b ⋅52b = (2) (-2a 2)2=4-4a (3) (1-n a )3=13-n a(4) 333)(y x y x -=-其中计算错误的有 ( )A.1个B.2个C.3个D.4个OA22α15.如果(),990-=a ()11.0--=b ,235-⎪⎭⎫⎝⎛-=c ,那么c b a ,,三数的大小为( )A.c b a >>B.b a c >>C.b c a >>D.a b c >> 16.下列说法正确的是( )A .同位角相等 B.同角的补角相等C.两直线平行,同旁内角相等D.相等的角是对顶角17.小明同学在计算某n 边形的内角和时,不小心少输入一个内角,得到和为2005°,则n 等于 ( )A .11B .12C .13D .1418.现有3cm 、4cm 、7cm 、9cm 长的四根木棒,任选其中三根组成一个三角形,那么可以组成的三角形的个数是( )A .1B .2C .3D .4 19.如图,下列判断正确的是 ( ) A .若∠1=∠2,则AD ∥BC B .若∠1=∠2.则AB ∥CD C .若∠A=∠3,则 AD ∥BC D .若∠A+∠ADC=180°,则AD ∥BC20.如图,在△ABC 中,已知点D 、E 分别为边BC 、AD 、上的中点,且S △ABC =4cm 2,则S △BEC 的值为( )A.2cm 2B.1cm 22 D.0.25cm 221.如图,AB ∥CD ∥EF ,BC ∥AD ,AC 平分∠BAD 且与EF 交于点O ,那么与∠AOE 相等的角有( )A.5个B.4 个C.3个D.2个22.大于1的正整数m 的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m 3分裂后,其中有一个奇数是2013,则m 的值是 ( )A .43B .44C .45D .4第19题 第20题 第21题 三、计算(每题4分,共24分) 23. ()()-1201-1+-2+7--3π⎛⎫⎪⎝⎭24.3223)()(a a -⋅-25.23324()2x x x x x x -⋅+⋅-⋅ 26.(b 2n )3 (b 3)4n ÷(b 5)nAB DCO FE27. 234)()()(q p p q q p -⋅-÷- 28. ()2006200721-0.63⎛⎫⨯ ⎪⎝⎭四、解答题(29题11分,30题6分,31题8分,32题14分,共39分)29.(1)已知m2,3na a ==,求①m n a +的值;②3m-2na 的值(2)已知2328162x⨯⨯=,求x 的值.30.如图,在四边形ABCD 中,∠B =∠D =90°,E 是BC 边上的一点,且∠AEC =∠BAD.试说明:AE ∥DC.31.如图,在△ABC 中,∠B=24°,∠ACB=104°,AD ⊥BC 于D ,AE 平分∠BAC ,求∠DAE 的度数.32.(1)如图(1),在△ABC 中,∠A=62°,∠ABD=20°,∠ACD=35°,求∠BDC的度数.A B C E DD C B AE DC B A Z YX C BA (2)图(1)所示的图形中,有像我们常见的学习用品——圆规。
2023年人教版七年级下册期末复习检测卷(四)(考试版A4)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!2023年人教版七年级下册复习检测卷(四)英语(时间:120分钟满分:120分)注意事项:1.本试卷共四部分,十大题,满分120 分。
考试时间为120分钟。
2全卷包括“试题卷”和“答题卡”两部分。
3.请务必在“答题卡”上答题,在“试题卷”上答题无效。
4考试结束后,请将“试题卷”和“答题卡”一并交回。
第一部分听力(共四大题,满分20分)Ⅰ.短对话理解(共5小题;每小题1分,满分5分)你将听到五段对话,每段对话后有一个小题。
请在每小题所给的A、B、C三个选项中选出一个最佳选项。
每段对话读两遍。
1. What animals does Mike's friend like?A. B. C.2. Where does the woman want to go?A. B. C.3. What did Sam do last Sunday?A. He drove to the town.B. He visited his dad.C. He cleaned the yard.4. What are the two speakers talking about?A. The weather.B. The radio.C. The time.5. What does the man usually do on Sunday afternoon?A. He goes to the park.B. He works in the garden.C. He reads newspapers.Ⅱ.长对话理解(共5小题;每小题1分,满分5分)你将听到两段对话,每段对话后几个小题。
人教版七年级上册数学全册单元试卷复习练习(Word版 含答案)
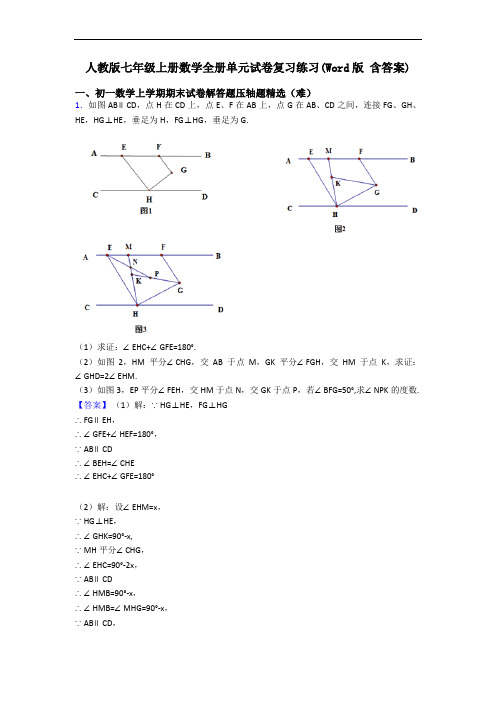
人教版七年级上册数学全册单元试卷复习练习(Word版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.(1)求证:∠EHC+∠GFE=180°.(2)如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.(3)如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数. 【答案】(1)解:∵HG⊥HE,FG⊥HG∴FG∥EH,∴∠GFE+∠HEF=180°,∵AB∥CD∴∠BEH=∠CHE∴∠EHC+∠GFE=180°(2)解:设∠EHM=x,∵HG⊥HE,∴∠GHK=90°-x,∵MH平分∠CHG,∴∠EHC=90°-2x,∵AB∥CD∴∠HMB=90°-x,∴∠HMB=∠MHG=90°-x,∵AB∥CD,∴∠BMH+∠DHM=180°,即∠BMH+∠GHM+∠GHD =180°,∴90°-x+90°-x+∠GHD =180°,解得,∠GHD =2x,∴∠GHD=2∠EHM;(3)解:延长FG,GK,交CD于R,交HE于S,如图,∵AB∥CD,∠BFG=50°∴∠HRG=50°∵FG⊥HG,∴∠GHR=40°,∵HG⊥HE,∴∠EHG=90°,∴∠CHE=180°-90°-40°=50°,∵AB∥CD,∴∠FEH=∠CHE=50°,∵EP是∠HEF的平分线,∴∠SEP= ∠FEH=25°,∵GH平分∠HGF,∴∠HGS= ∠HGF=45°,∴∠HSG=45°,∵∠SEP+∠SPE=∠HSP=45°,∴∠EPS=20°,即∠NPK=20°.【解析】【分析】(1)根据HG⊥HE,FG⊥HG可证明FG∥EH,从而得∠GFE+∠HEF=180°,再根据AB∥CD可得∠BEH=∠CHE,进而可得结论;(2)设∠EHM=x,根据MH是∠CHG的平分线可得∠MHG=90°-x,∠EHC=90°-2x,根据平行线的性质得∠HMB=90°-x,从而得∠HMB=∠MHG,再由平行线的性质得∠BMH+∠DHM=180°,从而可得结论;(3)分别延长FG,GK,交CD于R,交HE于S,由AB∥CD得∠HRG=50°,由FG⊥HG得∠GHR=40°,由MH平分∠CHG得∠CHE=50°,由AB∥CD得∠MEH=∠CHE=50°,可得∠SEP=25°,最后由三角形的外角可得结论.2.如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.(1)若BC=15,求a、b的值;(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.①用含t代数式表示PQ、 MN;②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.【答案】(1)∵BC=15,点C对应的数是10,∴c-b=15,∴b=-5,∵c-b=b-a=15,∴a=-20;(2)①∵OQ=10+t,OP=20+2t,∴PQ=(10+t)+( 20+2t)=30+3t;∵OB=5, OQ=10+t,∴BQ=15+t,∵M为BQ的中点,∴BM=7.5+0.5t,∴OM=7.5+0.5t-5=2.5+0.5t.∵OP=20+2t, N为OP的中点,∴ON=10+t,∴MN=OM+ON=12.5+1.5t;②PQ-2MN=5.∵PQ=30+3t,MN= 12.5+1.5t,∴PQ-2MN=(30+3t)-2(12.5+1.5t)=5.【解析】【分析】(1)利用数轴上所表示的数,右边的总比左边的大及数轴上任意两点间的距离等于这两点所表示数的差的绝对值,由BC=15,点C对应的数是10,即可算出点B 所表示的数,即b的值,进而根据 c-b=b-a 即可算出点A所表示的数a的值;(2)① 根据路程等于速度乘以时间,得出PA=2t,CQ=t,所以OQ=OC+CQ=10+t,OP==OA+PA=20+2t, 进而根据PQ=OQ+OP,根据整式加减法法则算出PQ的长;根据BQ=OB+OQ得出 BQ=15+t, genuine线段中点的定义得出 BM=7.5+0.5t, ON=10+t, 根据MN=OM+ON ,由整式加减法法则即可算出答案;②PQ-2MN=5,理由如下:由PQ=30+3t,MN= 12.5+1.5t,故利用整式家家爱你法法则即可算出PQ-2MN=5。
初一语文复习试卷及详细答案

初一语文复习试卷及详细答案初一语文复习试卷及详细答案初一的学生平时应该多做一些复习试卷,这样可以对自己的掌握对知识点进行的检测、反馈、巩固和提高。
店铺为大家力荐了初一语文复习试卷以及参考答案,给大家作为参考,欢迎阅读!初一语文复习试卷一、积累及运用(25分)(1—8题,每题2分;第9题每空1分)1.加点字注音完全正确的一项是( )A. 嫉妒(jí) 魁梧(wǔ) 模样(mú) 鲜为人知(xiǎn)B. 脑髓(suí) 归省(xǐng)哺育(bǔ) 呕心沥血(ǒu)C. 发酵(jiào) 重荷(hè) 沮丧(jǔ) 戛然而止(jiá)D. 纤维(qiān) 潜水(qián) 狭隘(ài) 一蹴而就(cù)2.下列词语中没有错别字的一项是 ( )A. 懊悔鉴赏锲而不舍小心冀冀B. 怪涎蓦然来势汹汹肆无忌惮C. 震撼嗔视兴高采烈语无伦次D. 抵御余暇姗姗来迟不可思意3.下面句子中加点词语使用正确的一项是( )A、一阵轻风拂过,枝头的果子津津有味,令人垂涎。
B、深海和远洋中还有许许多多尚未被我们充分开发利用的海洋生物,其巨大潜力是不言而喻的。
C、柜台里的点心有二十几种,真是不计其数。
D、全校同学聚精会神,目不暇接地聆听着科学家精彩的学术报告。
4.下面语段横线处应填入的恰当句子是( )第一次真好,第一次的感觉真奇妙。
细细回想:在你的生命中,有多少“第一次”值得你留恋回味?A、有多少“第一次”把不可磨灭的印象给你留下啊!B、有多少“第一次”给你留下不可磨灭的印象?C、有无数个“第一次”给你留下不可磨灭的印象。
D、难道没有无数个“第一次”给你留下不可磨灭的印象吗?5.对诗歌《木兰诗》分析错误的一项是( )A. 《木兰诗》写的是一位女子代父从军的故事,充满传奇色彩。
B. “旦辞爷娘去,暮至黄河边,不闻爷娘唤女声,但闻黄河流水鸣溅溅。
印刷七年级模拟一1

2011-2012学年度下学期期末质量检测七年级语文试卷第一卷:选择题(50分)1、下列词语中加点的字读音没有错误的一项是( )A 、窥伺(ku ī) 彪悍(h àn ) 阔绰(chu î) 庇荫(b ì)B 、恍惚(hu ǎng ) 羁绊(j ī) 畸形(q ī) 告罄(q ìng)C 、阴霾(l í) 踌躇(ch ïu ) 菜畦(q í) 骊歌(l í)D 、嫉妒(j ì) 沟壑 (hu î) 缀行(chu î) 亢奋(k àng ) 2、下列词语书写有错别字的一项是( )A 、妇孺皆知 锲而不舍 浑身解数 人声鼎沸B 、迫不及待 语无轮次 养精蓄锐 耀武扬威C 、郑重其事 精打细算 漠不关心 姗姗来迟D 、毛骨悚然 孜孜不倦 梦寐以求 眼花缭乱 3、下列成语使用有误的一项是( )A 、闻一多先生在群众大会上,大骂特务,慷慨淋漓。
B 、她使出浑身解数,用她灵活的四肢五官,来讲说印度古代的优美故事。
C 、他们怏怏不乐地在阿蒙森的胜利旗帜旁边插上英国国旗。
D 、现代科学技术的发展日新月异,让人目膯口呆。
4、选出和“树林一直在唱着那首愉快的歌”修辞方法相同的一项是( ) A.这里的人们非常好客,火一般热情。
B.一路上,稻田绿、菜花黄、江水银,绘成了一幅幅田园巨画。
C.生命是一条河流,有奔腾也有平缓。
D.天气炎热,那张乒乓球桌子也在睡觉。
5、填入下面横线处,最恰当的一项是( )全村的干部群众,都捐出了棉被、蚊帐、衣服等生活用品支援灾区。
虽然少了些,虽然旧些破些,便是。
A 、多一声响多一个铃铛,多一支蜡烛多一分光B 、多一个铃铛多一声响,多一支蜡烛多一分光C 、多一声响多一个铃铛,多一分光多一支蜡烛D 、多一个铃铛多一声响,多一分光多一支蜡烛 6、下列说法不得体的一项( )A 、当同学向你请教问题时,你说:“有什么问题,请说吧,我们一起来讨论。
2019年人教版最全七年级下册全册同步练习及单元测验卷及答案-精品
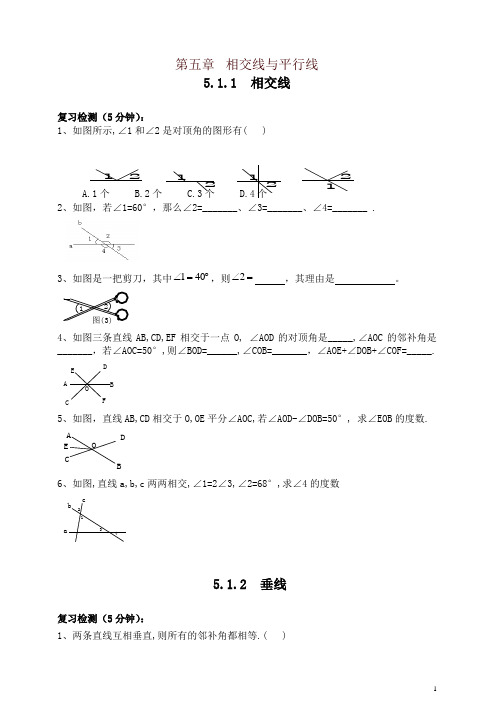
第五章 相交线与平行线5.1.1 相交线复习检测(5分钟):1、如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个2、如图,若∠1=60°,那么∠2=_______、∠3=_______、∠4=_______ .3、如图是一把剪刀,其中︒=∠401,则=∠2 ,其理由是 。
图(3)214、如图三条直线AB,CD,EF 相交于一点O, ∠AOD 的对顶角是_____,∠AOC 的邻补角是_______,若∠AOC=50°,则∠BOD=______,∠COB=_______,∠AOE+∠DOB+∠COF=_____.OF E D CBA5、如图,直线AB,CD 相交于O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•求∠EOB 的度数.OE D CBA6、如图,直线a,b,c 两两相交,∠1=2∠3,∠2=68°,求∠4的度数cba34125.1.2 垂线复习检测(5分钟):1、两条直线互相垂直,则所有的邻补角都相等.( )12121221E(3)O D CBA (2)O D CBA (1)ODC BA2、一条直线不可能与两条相交直线都垂直.( )3、两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( )4、两条直线相交有一组对顶角互补,那么这两条直线互相垂直.( ).5、如图1,OA ⊥OB,OD ⊥OC,O 为垂足,若∠AOC=35°,则∠BOD=________.6、如图2,AO ⊥BO,O 为垂足,直线CD 过点O,且∠BOD=2∠AOC,则∠BOD=________.7、如图3,直线AB 、CD 相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB 的位置关系是_________.8、已知:如图,直线AB,射线OC 交于点O,OD 平分∠BOC,OE 平分∠AOC.试判断OD 与OE 的位置关系.9、如图,AC ⊥BC,C 为垂足,CD ⊥AB,D 为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C 到AB 的距离是_______,点A 到BC 的距离是________,点B 到CD 的距离是_____,A 、B 两点间的距离是_________.10、如图,在线段AB 、AC 、AD 、AE 、AF 中AD 最短.小明说垂线段最短, 因此线段AD 的长是点A 到BF 的距离,对小明的说法,你认为对吗?11、用三角尺画一个是30°的∠AOB,在边OA 上任取一点P,过P 作PQ ⊥OB, 垂足为Q,量一量OP 的长,你发现点P 到OB 的距离与OP 长的关系吗?5.1.3同位角、内错角、同旁内角E ODC BAFE D C B AD CB A复习检测(5分钟):1、如图(4),下列说法不正确的是()A.∠1与∠2是同位角B.∠2与∠3是同位角C.∠1与∠3是同位角D.∠1与∠4不是同位角2、如图(5),直线AB、CD被直线EF所截,∠A和是同位角,∠A和是内错角,∠A和是同旁内角.3、如图(6), 直线DE截AB, AC, 构成八个角:①、指出图中所有的同位角、内错角、同旁内角.②、∠A与∠5, ∠A与∠6, ∠A与∠8, 分别是哪一条直线截哪两条直线而成的什么角?4、如图(7),在直角 ABC中,∠C=90°,DE⊥AC于E,交AB于D .①、指出当BC、DE被AB所截时,∠3的同位角、内错角和同旁内角.②、若∠3+∠4=180°试说明∠1=∠2=∠3的理由.5.2.1平行线复习检测(5分钟):1、在同一平面内,两条直线的位置关系有_________2、两条直线L1与L2相交点A,如果L1//L,那么L2与L()3、在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必__________.8765c b a 34124、两条直线相交,交点的个数是________,两条直线平行,交点的个数是_____个. 判断题5、6、7、85、不相交的两条直线叫做平行线.( )6、如果一条直线与两条平行线中的一条直线平行, 那么它与另一条直线也互相平行.( )7、过一点有且只有一条直线平行于已知直线.( )8、读下列语句,并画出图形后判断.(1)直线a 、b 互相垂直,点P 是直线a 、b 外一点,过P 点的直线c 垂直于直线b. (2)判断直线a 、c 的位置关系,并借助于三角尺、直尺验证.9、试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况.5.2.2平行线的判定复习检测(10分钟):1、如图1所示,下列条件中,能判断AB ∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD(1) (2) (3) (4)2、如图2所示,如果∠D=∠EFC,那么( )A.AD ∥BCB.EF ∥BCC.AB ∥DCD.AD ∥EF3、下列说法错误的是( ) A.同位角不一定相等 B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行 4、如图5,直线a,b 被直线c 所截,现给出下列四个条件: •①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a ∥b 的条件序号为( ) (5) A.①② B.①③ C.①④ D.③④5、如图5,如果∠3=∠7,那么______ ,理由是 ;如果∠5=∠3,那么________, 理由是______________;34D C B A 21F E D C B A 876543219654321D C B A D CBA 21如果∠2+ ∠5= ______ 那么a ∥b,理由是________ .6、如图4,若∠2=∠6,则______∥______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______,如果∠9=_____,那么AD ∥BC;如果∠9=_____,那么AB ∥CD.7、在同一平面内,若直线a,b,c 满足a ⊥b,a ⊥c,则b 与c 的位置关系是______.8、如图所示,BE 是AB 的延长线,量得∠CBE=∠A=∠C.(1)由∠CBE=∠A 可以判断______∥______,根据是_________.(2)由∠CBE=∠C 可以判断______∥______,根据是_________.9、已知直线a 、b 被直线c 所截,且∠1+∠2=180°,试判断直线a 、b 的位置关系,并说明理由.10、如图,已知DG AEM ∠=∠,21∠=∠,试问EF 是否平行GH ,并说明理由.11、如图所示,已知∠1=∠2,AC 平分∠DAB,试说明DC ∥AB.12、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=30°,试说明AB ∥CD.E DC B A c ba321D C B A OF E DC B AD C B A 187654321DC B A 56 北乙甲北G F E DC B A 12GHKFEDC B A13、提高训练:如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?•为什么?d ecb a 34125.3.1平行线的性质复习检测(10分钟):1、如图1所示,AB ∥CD,则与∠1相等的角(∠1除外)共有( )A.5个B.4个C.3个D.2个(1) (2) (3)2、如图2所示,CD ∥AB,OE 平分∠AOD,OF ⊥OE,∠D=50°,则∠BOF 为( ) A.35° B.30° C.25° D.20°3、如图3所示,AB ∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______, ∠ACD=•_______.4、如图4,若AD ∥BC,则∠______=∠_______,∠_______=∠_______, ∠ABC+∠_______=180°; 若DC ∥AB,则∠______=∠_______,∠________=∠__________,∠ABC+∠_________=180°.(4) (5) (6)E 21D C B N MGF E D C BA5、如图5,在甲、乙两地之间要修一条笔直的公路, 从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通, 则乙地所修公路的走向是_________,因为____________.6、河南)如图6所示,已知AB ∥CD,直线EF 分别交AB,CD 于E,F,EG•平分∠B-EF,若∠1=72°,则∠2=_______.7、如图,AB ∥CD ,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据?8、如图,EF 过△ABC 的一个顶点A ,且EF ∥BC ,如果∠B =40°,∠2=75°,那么∠1、∠3、∠C 、∠BAC +∠B +∠C 各是多少度,并说明依据?9、如图,已知:DE ∥CB,∠1=∠2,求证:CD 平分∠ECB.10、如图所示,把一张长方形纸片ABCD 沿EF 折叠,若∠EFG=50°,求∠DEG 的度数.11、如图所示,已知:AE 平分∠BAC ,CE 平分∠ACD ,且AB ∥CD .求证:∠1+∠2=90°. 证明:∵ AB ∥CD ,(已知)∴∠BAC +∠ACD =180°,( ) 又∵ AE 平分∠BAC ,CE 平分∠ACD ,( )∴112B AC ∠=∠,122A C D ∠=∠,( )∴001112()1809022B AC A CD ∠+∠=∠+∠=⨯=. 即 ∠1+∠2=90°.结论:若两条平行线被第三条直线所截,则一组同旁内角的平分线互相 . 推广:若两条平行线被第三条直线所截,则一组同位角的平分线互相 .5.3.2命题、定理、证明复习检测(5分钟):1、判断下列语句是不是命题(1)延长线段AB ( ) (2)两条直线相交,只有一交点( ) (3)画线段AB 的中点( ) (4)若|x|=2,则x=2( ) (5)角平分线是一条射线( ) 2、下列语句不是命题的是( )A.两点之间,线段最短B.不平行的两条直线有一个交点C.x 与y 的和等于0吗?D.对顶角不相等. 3、下列命题中真命题是( )A.两个锐角之和为钝角B.两个锐角之和为锐角C.钝角大于它的补角D.锐角小于它的余角4、命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )A.1个B.2个C.3个D.4个 5、分别指出下列各命题的题设和结论(1)如果a ∥b ,b ∥c ,那么a ∥c (2)同旁内角互补,两直线平行 6、分别把下列命题写成“如果……,那么……”的形式(1)两点确定一条直线; (2)等角的补角相等; (3)内错角相等.7、如图,已知直线a 、b 被直线c 所截,在括号内为下面各小题的推理填上适当的根据:(1)∵a ∥b,∴∠1=∠3( ); (2)∵∠1=∠3,∴a ∥b( ); (3)∵a ∥b,∴∠1=∠2( ); (4) ∵a ∥b,∴∠1+∠4=180º ( ) (5)∵∠1=∠2,∴a ∥b( ); (6)∵∠1+∠4=180º,∴a ∥b( ). 8、已知:如图AB ⊥BC ,BC ⊥CD 且∠1=∠2,求证:BE ∥CF证明:∵AB ⊥BC ,BC ⊥CD (已知)∴ = =90°( ) ∵∠1=∠2(已知)∴ = (等式性质)ab 1 23c4C A BDEF1 2∴BE ∥CF ( )9、已知:如图,AC ⊥BC ,垂足为C ,∠BCD 是∠B 的余角.求证:∠ACD=∠B证明:∵AC ⊥BC (已知)∴∠ACB=90°( ) ∴∠BCD 是∠ACD 的余角∵∠BCD 是∠B 的余角(已知)∴∠ACD=∠B ( )5.4 平移复习检测(5分钟):1、下列哪个图形是由左图平移得到的( )A BCD2、如图所示,△FDE 经过怎样的平移可得到△ABC.( ) A.沿射线EC 的方向移动DB 长; B.沿射线EC 的方向移动CD 长C.沿射线BD 的方向移动BD 长;D.沿射线BD 的方向移动DC 长3、下列四组图形中,•有一组中的两个图形经过平移其中一个能得到-另一个,这组图形是( )4、如图所示,△DEF 经过平移可以得到△ABC,那么∠C的对应角和ED 的对应边分-别是( )A.∠F,ACB.∠BOD,BA;C.∠F,BAD.∠BOD,AC5、在平移过程中,对应线段( ) A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等6、在平移过程中,平移后的图形与原来的图形________和_________都相同,•因-此对应线段和对应角都________.7、如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=•____-度,∠EDF=_______度, ∠F=______度,∠DOB=_______度.8、将正方形ABCD 沿对角线AC 方向平移,且平移后的图形的一个顶点恰好在AC 的中点O 处,则移动前后两个图形的重叠部分的面积是原正方形面积的_______BD ACFE D C B A O FE C B ADABC D OF E C B AD9、直角△ABC 中,AC =3cm ,BC =4cm ,AB =5cm ,将△ABC 沿CB 方向平移3cm ,则边AB 所经过的平面面积为____cm 2。
人教版七年级上册数学全册单元试卷复习练习(Word版 含答案)

人教版七年级上册数学全册单元试卷复习练习(Word版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.已知长方形纸片ABCD,点E,F,G分别在边AB,DA,BC上,将三角形AEF沿EF翻折,点A落在点处,将三角形EBG沿EG翻折,点B落在点处.(1)点E,,共线时,如图,求的度数;(2)点E,,不共线时,如图,设,,请分别写出、满足的数量关系式,并说明理由.【答案】(1)解:如图中,由翻折得: ,(2)解:如图,结论: .理由:如图中,由翻折得:,如图,结论:,理由: ,,.【解析】【分析】(1)根据翻折不变性得:,由此即可解决问题.(2)根据翻折不变性得到:,根据分别列等式可得图和的结论即可.2.点在线段上, .(1)如图1,,两点同时从,出发,分别以,的速度沿直线向左运动;①在还未到达点时,求的值;②当在右侧时(点与不重合),取中点,的中点是,求的值;(2)若是直线上一点,且 .求的值.【答案】(1)解:①AP=AC-PC,CQ=CB-QB,∵BC=2AC,P、Q速度分别为1cm/s、2cm/s,∴QB=2PC,∴CQ=2AC-2PC=2AP,∴②设运动秒,分两种情况A: 在右侧,,分别是,的中点,,∴B: 在左侧,,分别是,的中点,,∴(2)解:∵BC=2AC.设AC=x,则BC=2x,∴AB=3x,①当D在A点左侧时,|AD-BD|=BD-AD=AB= CD,∴CD=6x,∴;②当D在AC之间时,|AD-BD|=BD-AD= CD,∴2x+CD-x+CD= CD,x=- CD(不成立),③当D在BC之间时,|AD-BD|=AD-BD= CD,∴x+CD-2x+CD= CD,CD= x,∴;|AD-BD|=BD-AD= CD,∴2x-CD-x-CD= CD,∴CD=;④当D在B的右侧时,|AD-BD|=BD-AD= CD,∴2x-CD-x-CD= CD,CD=6x,∴ .综上所述,的值为或或或【解析】【分析】(1)由线段的和差关系,以及QB=2PC,BC=2AC,即可求解;(2)设AC=x,则BC=2x,∴AB=3x,D点分四种位置进行讨论,①当D在A点左侧时,②当D在AC之间时,③当D在BC之间时,④当D在B的右侧时求解即可.3.如图(1)观察思考如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;(2)模型构建如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;(3)拓展应用8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.【答案】(1)解:∵以点A为左端点向右的线段有:线段AB、AC、AD,以点C为左端点向右的线段有线段CD、CB,以点D为左端点的线段有线段DB,∴共有3+2+1=6条线段(2)解:,理由:设线段上有m个点,该线段上共有线段x条,则x=(m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x=1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= =m(m-1),∴x=(3)解:把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作为一条线段,直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行场比赛【解析】【分析】(1)线段AB上共有4个点A、B、C、D,得到线段共有4×(4-1)÷2条;(2)根据规律得到该线段上共有m(m-1)÷2条线段;(3)由每两位同学之间进行一场比赛,得到要进行8×(8-1)÷2场比赛.4.如图(1),将两块直角三角板的直角顶点C叠放在一起.(1)试判断∠ACE与∠BCD的大小关系,并说明理由;(2)若∠DCE=30°,求∠ACB的度数;(3)猜想∠ACB与∠DCE的数量关系,并说明理由;(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)【答案】(1)解:∠ACE=∠BCD,理由如下:∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,∴∠ACE=∠BCD;(2)解:若∠DCE=30°,∠ACD=90°,∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,∵∠BCE=90°且∠ACB=∠ACE+∠BCE,∠ACB=90°+60°=150°(3)解:猜想∠ACB+∠DCE=180°.理由如下:∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°(4)解:成立.【解析】【分析】(1)根据余角的性质,可得答案;(2)根据余角的定义,可得∠ACE,根据角的和差,可得答案;(3)根据角的和差,可得答案;(4)根据角的和差,可得答案.5.如图,直线AB、CD相交于点O,已知,OE把分成两个角,且::3(1)求的度数;(2)过点O作射线,求的度数.【答案】(1)解:,,::3,;(2)解:,,,OF在的内部时,,,,OF在的内部时,,,,综上所述或【解析】【分析】(1)根据对顶角相等得出,然后根据::3 即可算出∠BOE的度数;(2)根据角的和差,由算出∠DOE的度数,根据垂直的定义得出∠EOF=90°;当OF在的内部时,根据,算出答案;OF在的内部时,根据,算出但,综上所述即可得出答案。
七年级数学下学期期末复习卷试题

智才艺州攀枝花市创界学校射阳县特庸初级七年级数学下学期期末复习卷本套试卷由选择题、填空题和解答题三大题组成,一共28题,总分值是130分.考试用时120分钟.本卷须知:2.考生答题必须在答题卷上,答在试卷和草稿纸上一律无效,一、选择题:〔本大题一一共有10小题,每一小题3分,一共30分,以下各题都有四个选项,其中只有一个是正确的,选出正确答案,并填写上在答题卷上相应的表格内.〕1.在以下四个汽车标志图案中,能用平移变换来分析其形成过程的图案是2.以下计算正确的选项是A.a+2a2=3a2B.a8÷a2=a4 C.a3·a2=a6D.(a3)2=a63.把一个不等式组的解集表示在数轴上,如下列图,那么该不等式组的解集为A.0<x≤1 B.x≤1C.0≤x<1 D.x>04.等腰三角形的两条边长分别为2和3,那么它的周长为A.7 B.8 C.5 D.7或者85.以下等式由左边到右边的变形中,属于因式分解的是A.x2+5x-1=x(x+5)-1 B.x2-4+3x=(x+2)(x-2)+3xC.x2-9=(x+3)(x-3) D.(x+2)(x-2)=x2-46.如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中能断定AB∥CD的条件的个数有A.1 B.2 C.3 D.47.甲和乙两人玩“打弹珠〞游戏,甲对乙说:“把你珠子的一半给我,我就有10颗珠子〞,乙却说:“只要把你的善给我,我就有10颗〞,假设设乙的弹珠数为x颗,甲的弹珠数为y颗,那么列出方程组正确的选项是A.210330x yx y+=⎧⎨+=⎩B.210310x yx y+=⎧⎨+=⎩C.220310x yx y+=⎧⎨+=⎩D.220330x yx y+=⎧⎨+=⎩①同旁内角互补,两直线平行;②假设a=b,那么a=b;③直角都相等;④相等的角是对项角.A.4个B.3个C.2个D.1个9.假设M=〔x-3〕〔x-5〕,N=(x-2)(x-6〕,那么M与N的关系为A.M=NB.M>NC.M<ND.M与N的大小由x的取值而定10.方程5x+3y=54一共有▲组正整数解.A.2 B.3 C.4 D.5二、填空题:〔本大题一一共8小题,每一小题3分,一共24分,把答案直接填在答题卷相对应的位置上.〕11.5-2表示成分数是▲.12.我们知道冥王星离太阳平均间隔约为5,910,000,000千米,用科学记数法,可以把5,910,000,000千米写成▲千米.13.一个n边形的内角和是1260°,那么n=▲.14.假设(x+k)(x-4〕的展开式中不含有x的一次项,那么k的值是▲.15.如图,装修工人向墙上钉木条.假设∠2=100°,要使木条b与a平行,那么∠1的度数等于▲.16.m x=8,m y=4,那么m x+2y=▲.17.假设关于x的不等式组2xx m>⎧⎨>⎩的解集是x>2,那么m的取值范围是▲.18.如图a是长方形纸带,∠DEF=19°,将纸带沿EF折叠成图b,再沿BF折叠成图c,那么图c中的∠DHF的度数是▲.三、解答题:〔本大题一一共10小题,一共76分.把解答过程写在答题卷相应的位置上,解答时应写出必要的计算过程、推演步骤或者文字说明.〕19.〔此题总分值是12分,每一小题4分〕计算:(1)(x +2)(4x -2〕;(2)()()2223a a a -•÷; (3)()10001011320133⎛⎫-⨯-- ⎪⎝⎭.20.〔此题总分值是5分〕先化简,再求值:2b 2+(a +b)(a -b)-(a -b)2,其中a =-3,b =12. 21.〔此题总分值是8分,每一小题4分〕解方程组: (1)()15551x y x y -=+⎧⎪⎨+=-⎪⎩ (2)542311316x y z x y z x y z --=⎧⎪+-=⎨⎪++=⎩22.〔此题总分值是8分,每一小题4分〕因式分解:(1)2x 2-8xy +8y 2; (2)4x 3-4x 2y -(x -y). 23.〔此题总分值是6分〕解不等式组()5931311122x x x x ⎧-<-⎪⎨-≤-⎪⎩并写出它的整数解. 24.〔此题总分值是7分〕如图,∠ABC 的平分线BD 交于AC 于点D ,DE//CB ,交AB 于点E ,∠A =45°,∠BDC =60°,求△BDE 各内角的度数.25.〔此题总分值是7分〕,关于x ,y 的方程组325x y a x y a-=+⎧⎨+=⎩解满足x>y>0.(1)求a 的取值范围;(2)化简2a a --.26.〔此题总分值是7分〕如下几个图形是五角星和它的变形.(1)图甲是一个五角星ABCDE ,那么∠A +∠B +∠C +∠D +∠E 的度数为▲;〔不必写过程〕(2)如图乙,假设点B 向右挪动到AC 上时,那么∠A +∠EBD +∠C +∠D +∠E 度数为▲;〔不必写过程〕(3)如图丙,点B 向右挪动到AC 的另一侧时,(1)的结论成立吗?为什么?(4)如图丁,点B ,E 挪动到∠CAD 的内部时,结论又如何?〔不必写过程〕27.〔此题总分值是8分〕一天,小明在玩纸片拼图游戏时,发现利用图①中的三种材料各假设干,可以拼出一些长方形来解释某些等式,比方图②可以解释为等式:(a +2b)(a +b)=a 2+3ab +2b 2. (1)那么图③可以解释为等式:▲. (2)在虚线框中用图①中的根本图形假设干块〔每种至少用 一次〕拼成一个长方形,使拼出的长方形面积为2a 2+7ab +3b 2,并请在图中标出这个长方形的长 和宽.(3)如图④,大正方形的边长为m ,小正方形的边长为n ,假设用x ,y 表示四个长方形的两边长(x>y 〕,观察图案,指出以下关系式:(a)x y n -=; (b)224m n xy -=; (c)22x y mn -=; (d)22222m n x y ++=. 其中正确的关系式的个数有▲个.28.〔此题总分值是8分〕李大爷一年前买入了A 、B 两种兔子一共46只,目前,他所养的这两种兔子数量一样,且A 种兔子的数量比买入时减少了3只,B 种兔子的数量比买入时减少a 只.(1)那么一年前李大爷买入A 种兔子▲只,目前A 、B 两种兔子一共▲只;〔用含a 的代数式表示〕(2)假设一年前买入的A 种兔子数量多于B 种兔子数量,那么目前A 、B 两种兔子一共有多少只?(3)李大爷目前准备卖出30只兔子,卖A 种兔子可获利15元/只,卖B 种兔子可获利6元/只,假设卖出的A 种兔子少于15只,且总一共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?恳求出最大获利.。
人教版最全七年级下册全册同步练习及单元测验卷及答案

第五章相交线与平行线相交线复习检测(5分钟):1、如图所示,∠1和∠2是对顶角的图形有( )~个 个 个 个2、如图,若∠1=60°,那么∠2=_______、∠3=_______、∠4=_______ .3、如图是一把剪刀,其中︒=∠401,则=∠2 ,其理由是 。
图(3)21~4、如图三条直线AB,CD,EF 相交于一点O, ∠AOD 的对顶角是_____,∠AOC 的邻补角是_______,若∠AOC=50°,则∠BOD=______,∠COB=_______,∠AOE+∠DOB+∠COF=_____.OF E D CBA5、如图,直线AB,CD 相交于O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•求∠EOB 的度数.OE D CBA6、如图,直线a,b,c 两两相交,∠1=2∠3,∠2=68°,求∠4的度数12121221E(3)O D CBA (2)O D CBA (1)ODC Bcba3412$垂线复习检测(5分钟):1、两条直线互相垂直,则所有的邻补角都相等.( )2、一条直线不可能与两条相交直线都垂直.( )3、两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( )4、两条直线相交有一组对顶角互补,那么这两条直线互相垂直.( ).5、如图1,OA ⊥OB,OD ⊥OC,O 为垂足,若∠AOC=35°,则∠BOD=________.。
6、如图2,AO ⊥BO,O 为垂足,直线CD 过点O,且∠BOD=2∠AOC,则∠BOD=________.7、如图3,直线AB 、CD 相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB 的位置关系是_________.8、已知:如图,直线AB,射线OC 交于点O,OD 平分∠BOC,OE 平分∠AOC.试判断OD与OE 的位置关系.(9、如图,AC ⊥BC,C 为垂足,CD ⊥AB,D 为垂足,BC=8,CD=,BD=,AD=,AC= 6,那么点C 到AB 的距离是_______,点A 到BC 的距离是________,点B 到CD 的距离是EODC BACB A_____,A、B两点间的距离是_________.!10、如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为对吗11、用三角尺画一个是30°的∠AOB,在边OA上任取一点P,过P作PQ⊥OB, 垂足为Q,量一量OP的长,你发现点P到OB的距离与OP长的关系吗同位角、内错角、同旁内角.复习检测(5分钟):1、如图(4),下列说法不正确的是()A.∠1与∠2是同位角B.∠2与∠3是同位角C.∠1与∠3是同位角D.∠1与∠4不是同位角2、如图(5),直线AB、CD被直线EF所截,∠A和是同位角,∠A和是内错角,∠A和是同旁内角.,3、如图(6), 直线DE截AB, AC, 构成八个角:①、指出图中所有的同位角、内错角、同旁内角.②、∠A与∠5, ∠A与∠6, ∠A与∠8, 分别是哪一条直线截哪两条直线而成的什么角-A4、如图(7),在直角 ABC中,∠C=90°,DE⊥AC于E,交AB于D .①、指出当BC、DE被AB所截时,∠3的同位角、内错角和同旁内角.②、若∠3+∠4=180°试说明∠1=∠2=∠3的理由.、平行线、复习检测(5分钟):1、在同一平面内,两条直线的位置关系有_________2、两条直线L1与L2相交点A,如果L14、两条直线相交,交点的个数是________,两条直线平行,交点的个数是_____个.判断题5、6、7、85、不相交的两条直线叫做平行线.( )6、如果一条直线与两条平行线中的一条直线平行, 那么它与另一条直线也互相平行.( )7、过一点有且只有一条直线平行于已知直线.( );8、读下列语句,并画出图形后判断.(1)直线a、b互相垂直,点P是直线a、b外一点,过P点的直线c垂直于直线b.(2)判断直线a、c的位置关系,并借助于三角尺、直尺验证.9、试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况.)8765cba3412平行线的判定复习检测(10分钟):1、如图1所示,下列条件中,能判断AB ∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD%(1) (2) (3) (4)2、如图2所示,如果∠D=∠EFC,那么( ) ;∥BC ∥BC ∥DC ∥EF 3、下列说法错误的是( )A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行 4、如图5,直线a,b 被直线c 所截,现给出下列四个条件:•①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明 a ∥b 的条件序号为( )(5)A.①②B.①③C.①④D.③④ 》5、如图5,如果∠3=∠7,那么______ ,理由是 ;如果∠5=∠3,那么________, 理由是______________; 如果∠2+ ∠5= ______ 那么a ∥b,理由是________ .6、如图4,若∠2=∠6,则______∥______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______,如果∠9=_____,那么AD ∥BC;如果∠9=_____,那么AB ∥CD.7、在同一平面内,若直线a,b,c 满足a ⊥b,a ⊥c,则b 与c 的位置关系是______.8、如图所示,BE 是AB 的延长线,量得∠CBE=∠A=∠C.(1)由∠CBE=∠A 可以判断______∥______,根据是_________.; (2)由∠CBE=∠C 可以判断______∥______,根据是_________.9、已知直线a 、b 被直线c 所截,且∠1+∠2=180°, 试判断直线a 、b 的位置关系,并说明理由.34DC B A21F E DC B A 876543219654321DC B AEDCBADCBA21%10、如图,已知DG AEM ∠=∠,21∠=∠,试问EF 是否平行GH ,并说明理由.'11、如图所示,已知∠1=∠2,AC 平分∠DAB,试说明DC ∥AB.,12、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=30°,试说明AB ∥CD.GHKFEDC B A…13、提高训练:如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗•为什么DCBAOFEDC BAD CB A187654321DCBACA d ecb a 3412平行线的性质复习检测(10分钟):1、如图1所示,AB ∥CD,则与∠1相等的角(∠1除外)共有( )%个 个 个 个(1) (2) (3)2、如图2所示,CD ∥AB,OE 平分∠AOD,OF ⊥OE,∠D=50°,则∠BOF 为( ) ^° ° ° °3、如图3所示,AB ∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______, ∠ACD=•_______.4、如图4,若AD ∥BC,则∠______=∠_______,∠_______=∠ABC+∠_______=180°; 若DC ∥AB,则∠______=∠∠________=∠__________,∠ABC+∠_________=180°.【(4) (5) (6) 5、如图5,在甲、乙两地之间要修一条笔直的公路, 从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通, 则乙地所修公路的走向是_________,因为____________.6、河南)如图6所示,已知AB ∥CD,直线EF 分别交AB,CD 于E,F,EG•平分∠B-EF,若∠1=72°,则∠2=_______.7、如图,AB ∥CD ,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据E21DCBNM G F E D CB A》8、如图,EF 过△ABC 的一个顶点A ,且EF ∥BC ,如果∠B =40°,∠2=75°,那么∠1、∠3、∠C 、∠BAC +∠B +∠C 各是多少度,并说明依据 )9、如图,已知:DE ∥CB,∠1=∠2,求证:CD 平分∠ECB.:10、如图所示,把一张长方形纸片ABCD 沿EF 折叠,若∠EFG=50°,求∠DEG 的度数.¥11、如图所示,已知:AE 平分∠BAC ,CE 平分∠ACD ,且AB ∥CD .求证:∠1+∠2=90°.证明:∵ AB ∥CD ,(已知)∴∠BAC +∠ACD =180°,( ) 又∵ AE 平分∠BAC ,CE 平分∠ACD ,( )∴112B AC ∠=∠,122A C D ∠=∠,( ))∴001112()1809022B AC A CD ∠+∠=∠+∠=⨯=. 即 ∠1+∠2=90°.结论:若两条平行线被第三条直线所截,则一组同旁内角的平分线互相 .推广:若两条平行线被第三条直线所截,则一组同位角的平分线互相 .命题、定理、证明)复习检测(5分钟):1、判断下列语句是不是命题(1)延长线段AB ( ) (2)两条直线相交,只有一交点( ) (3)画线段AB 的中点( ) (4)若|x|=2,则x=2( ) (5)角平分线是一条射线( ) 2、下列语句不是命题的是( ) A.两点之间,线段最短 B.不平行的两条直线有一个交点 与y 的和等于0吗 D.对顶角不相等. `3、下列命题中真命题是( ) A.两个锐角之和为钝角 B.两个锐角之和为锐角 C.钝角大于它的补角 D.锐角小于它的余角4、命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )个 个 个 个 5、分别指出下列各命题的题设和结论(1)如果a ∥b ,b ∥c ,那么a ∥c (2)同旁内角互补,两直线平行 6、分别把下列命题写成“如果……,那么……”的形式 、(1)两点确定一条直线; (2)等角的补角相等; (3)内错角相等.7、如图,已知直线a 、b 被直线c 所截,在括号内为下面各小题的推理填上适当的根据:(1)∵a ∥b,∴∠1=∠3( ); (2)∵∠1=∠3,∴a ∥b( ); (3)∵a ∥b,∴∠1=∠2( ); (4) ∵a ∥b,∴∠1+∠4=180º ( ) (5)∵∠1=∠2,∴a ∥b( );ab 1 23c4(6)∵∠1+∠4=180º,∴a ∥b( ).|8、已知:如图AB ⊥BC ,BC ⊥CD 且∠1=∠2,求证:BE ∥CF证明:∵AB ⊥BC ,BC ⊥CD (已知)∴ = =90°( ) ∵∠1=∠2(已知)∴ = (等式性质)∴BE ∥CF ( )9、已知:如图,AC ⊥BC ,垂足为C ,∠BCD 是∠B 的余角.求证:∠ACD=∠B证明:∵AC ⊥BC (已知)∴∠ACB=90°( ) ∴∠BCD 是∠ACD 的余角∵∠BCD 是∠B 的余角(已知) {∴∠ACD=∠B ( )平移复习检测(5分钟):1、下列哪个图形是由左图平移得到的( )2、如图所示,△FDE 经过怎样的平移可得到△ABC.( ) 、A.沿射线EC 的方向移动DB 长;B.沿射线EC 的方向移动CD 长C.沿射线BD 的方向移动BD 长;D.沿射线BD 的方向移动DC 长 3、下列四组图形中,•有一组中的两个图形经过平移其中一个能得到-另一个,这组图形是( )^4、如图所示,△DEF 经过平移可以得到△ABC,那么∠C 的对应角和ED 的对应边分-别是( )A.∠F,ACB.∠BOD,BA;C.∠F,BAD.∠BOD,ACB|ACFB A OCB ADABCD5、在平移过程中,对应线段( )A.互相平行且相等;B.互相垂直且相等C.互相平行(或在同一条直线上)且相等6、在平移过程中,平移后的图形与原来的图形________和_________都相同,•因-此对应线段和对应角都________.¥7、如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=•____-度,∠EDF=_______度, ∠F=______度,∠DOB=_______度.8、将正方形ABCD 沿对角线AC 方向平移,且平移后的图形的一个顶点恰好在AC 的中点O 处,则移动前后两个图形的重叠部分的面积是原正方形面积的_______9、直角△ABC 中,AC =3cm ,BC =4cm ,AB =5cm ,将△ABC 沿CB 方向平移3cm ,则边AB 所经过的平面面积为____cm 2。
七年级语文下学期复习检测卷(初中一年级语文)

七年级语文下学期复习检测卷(初中一年级语文)七年级语文下学期复习检测卷一、语言积累与运用(20分)1、根据拼音写汉字。
(4分)是那不定的风把那无人采撷的种子撒落到海角天yá()。
当它们不能再找到泥土,它们便把最后一线生的希望寄托在这一线石缝里。
尽管它们也能从阳光中分享到温暖,从雨水里得到湿rùn(),而唯有那一切生命lài()以生存的土壤却要自己去寻找。
它们面对着的现实该是多么严jùn()。
2、填入文中的横线上最恰当的一组词语是()(3分)⑴巴勒斯坦人民________________ 和平的愿望何时才能变为现实?⑵我们要努力学习谋篇布局的________________ ,以加强作品的表现力。
⑶________________ 真诚有助于我们创造金色的人生。
A、乞求技巧严守B、祈求技巧恪守C、乞求技能恪守D、祈求技能严守3、古诗文填空(①——④题必做,⑤⑥两题任选一题。
(6分)①,思而不学则殆。
②几处早莺争暖树,。
③商女不知亡国恨,。
④何当共剪西窗烛,。
⑤《题破山寺后禅院》中以声衬静,可以与“蝉噪林逾静,鸟鸣山更幽”相媲美的诗句是:,。
⑥请写出古诗文中描写雪景的诗句:,。
4、仿写句子。
(2分)例句:如果我是春雨,我将滋润万物。
仿写:,。
5、名著知识(2分)在(作品)中有一位英雄,他曾温酒斩华雄、千里走单骑、刮骨疗毒,被后人敬仰并尊为中国的“武圣”,这位英雄是。
6、综合性学习(3分)小刚要参加全区朗诵比赛,每天晚上都练习得很晚。
一天,邻居张伯伯对他说:“小刚,你学习真刻苦,每天我们都睡了,你还在大声念书。
”小刚说:“伯伯过奖了,我还差得很远,还需要继续努力!”①张伯伯的话言外之意是。
②小刚对张伯伯话的意思理解是。
③如果你是小刚,应怎样回答。
二、现代文阅读(23分)(一)(10分)后来发生了分歧:母亲要走大路,大路平顺;我的儿子要走小路,小路有意思。
不过,一切都取决于我。
七年级下学期数学全册单元期末试卷及答案-百度文库doc

七年级下学期数学全册单元期末试卷及答案-百度文库doc一、选择题1.用白铁皮做罐头盒,每张铁皮可制盒身10个或制盒底16个,一个盒身与两个盒底配成一套罐头盒,现有18张白铁皮,设用x 张制作盒身,y 张制作盒底,可以使盒身和盒底正好配套,则所列方程组正确的是( )A .181016x y x y +=⎧⎨=⎩B .1821016x y x y +=⎧⎨⨯=⎩C .1810216x y x y +=⎧⎨=⨯⎩D .181610x y x y +=⎧⎨=⎩2.下列运算正确的是 ()A .()23524a a -=B .()222a b a b -=- C .61213a a +=+ D .325236a a a ⋅=3.以下列各组线段为边,能组成三角形的是( ) A .2cm 、2cm 、4cm B .2cm 、6cm 、3cm C .8cm 、6cm 、3cmD .11cm 、4cm 、6cm4.新冠病毒(2019﹣nCoV )是一种新的Sarbecovirus 亚属的β冠状病毒,它是一类具有囊膜的正链单股RNA 病毒,其遗传物质是所有RNA 病毒中最大的,也是自然界广泛存在的一大类病毒.其粒子形状并不规则,直径约60﹣220nm ,平均直径为100nm (纳米).1米=109纳米,100nm 可以表示为( )米. A .0.1×10﹣6 B .10×10﹣8 C .1×10﹣7 D .1×1011 5.等腰三角形的两边长分别为3和6,那么该三角形的周长为( )A .12B .15C .10D .12或156.科学家发现2019﹣nCoV 冠状肺炎病毒颗粒的平均直径约为0.00000012m .数据0.00000012用科学记数法表示为( ) A .1.2×107 B .0.12×10﹣6 C .1.2×10﹣7 D .1.2×10﹣8 7.若(2x+3y)(mx-ny)=9y 2-4x 2,则m 、n 的值为 ( )A .m=2,n=3B .m=-2,n=-3C .m=2,n=-3D .m=-2,n=38.若25a =,23b =,则232a b -等于( )A .2725B .109C .35D .25279.下列不等式:ac bc >;ma mb -<-;22ac bc >;22ac bc ->-,其中能推出a b >的是( ) A .ac bc > B .ma mb -<- C .22ac bc > D .22ac bc ->- 10.比较255、344、433的大小( )A .255<344<433B .433<344<255C .255<433<344D .344<433<255二、填空题11.计算:20202019120192019⎛⎫⨯- ⎪⎝⎭=________.12.若(3x+2y )2=(3x ﹣2y )2+A ,则代数式A 为______.13.如果()()2x 1x 4ax a +-+的乘积中不含2x 项,则a 为______ .14.已知12x y =⎧⎨=⎩是关于x 、y 的二元一次方程mx ﹣y =7的一个解,则m =_____. 15.已知一个多边形的每个外角都是24°,此多边形是_________边形. 16.已知2x =3,2y =5,则22x+y-1=_____.17.如图,ABC 三边的中线AD 、BE 、CF 的公共点为G ,18ABCS =,则图中阴影部分的面积是 ________.18.若等式0(2)1x -=成立,则x 的取值范围是_________.19.已知关于x 的不等式3()50a b x a b -+->的解集是1x <,则关于x 的不等式4ax b >的解集为_______.20.某校七年级社会实践小组去商场调查商品的销售情况,了解到该商场以每件80元的价格购进某品牌衬衫500件,并以每件120元的价格销售400件.该商场准备采取促销措施,将剩下的衬衫降价销售,每件衬衫至多降价______元,销售完这批衬衫才能达到盈利45%的预期目标. 三、解答题21.计算:(1)2x 3y •(﹣2xy )+(﹣2x 2y )2; (2)(2a +b )(b ﹣2a )﹣(a ﹣3b )2.22.如图1是一个长为 4a ,宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).(1)图2中的阴影部分的面积为 ;(2)观察图2请你写出 ()2a b +,()2a b -,ab 之间的等量关系是 ; (3)根据(2)中的结论,若 6x y +=,114x y ⋅=,则 x y -= ; (4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式()()2222252a b a b a ab b ++=++.在图形上把每一部分的面积标写清楚.23.如图1,在ABC 中,BD 平分ABC ∠,CD 平分ACB ∠. (1)若80A ∠=︒,则BDC ∠的度数为______; (2)若A α∠=,直线MN 经过点D .①如图2,若//MN AB ,求NDC MDB ∠-∠的度数(用含α的代数式表示); ②如图3,若MN 绕点D 旋转,分别交线段,BC AC 于点,M N ,试问在旋转过程中NDC MDB ∠-∠的度数是否会发生改变?若不变,求出NDC MDB ∠-∠的度数(用含α的代数式表示),若改变,请说明理由:③如图4,继续旋转直线MN ,与线段AC 交于点N ,与CB 的延长线交于点M ,请直接写出NDC ∠与MDB ∠的关系(用含α的代数式表示).24.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.(探究1):如图1,在ΔABC 中,O 是∠ABC 与∠ACB 的平分线BO 和CO 的交点,通过分析发现∠BOC=90º+12∠A ,(请补齐空白处......) 理由如下:∵BO 和CO 分别是∠ABC 和∠ACB 的角平分线,∴∠1=12∠ABC ,_________________, 在ΔABC 中,∠A+∠ABC+∠ACB=180º. ∴∠1+∠2=12(∠ABC+∠ACB )=12(180º-∠A )=90º-12∠A , ∴∠BOC=180º-(∠1+∠2)=180º-(________)=90º+12∠A . (探究2):如图2,已知O 是外角∠DBC 与外角∠ECB 的平分线BO 和CO 的交点,则∠BOC 与∠A 有怎样的关系?请说明理由.(应用):如图3,在RtΔAOB 中,∠AOB=90º,已知AB 不平行与CD ,AC 、BD 分别是∠BAO 和∠ABO 的角平分线,又CE 、DE 分别是∠ACD 和∠BDC 的角平分线,则∠E=_______;(拓展):如图4,直线MN 与直线PQ 相交于O ,∠MOQ=60º,点A 在射线OP 上运动,点B 在射线OM 上运动,延长BA 至G ,已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线及其延长线交于E 、F ,在ΔAEF 中,如果有一个角是另一个角的4倍,则∠ABO=______.25.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是 .(请选择正确的选项) A .a 2﹣b 2=(a +b )(a ﹣b ) B .a 2﹣2ab +b 2=(a ﹣b )2 C .a 2+ab =a (a +b )(2)若x 2﹣y 2=16,x +y =8,求x ﹣y 的值; (3)计算:(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020).26.好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在ABC ∆中,点I 是ABC ∠、ACB ∠的平分线的交点,点D 是MBC ∠、NCB ∠平分线的交点,,BI DC 的延长线交于点E .(1)若50BAC ∠=︒,则BIC ∠= °;(2)若BAC x ∠=︒ (090x <<),则当ACB ∠等于多少度(用含x 的代数式表示)时,//CE AB ,并说明理由; (3)若3D E ∠=∠,求BAC ∠的度数. 27.阅读材料:求1+2+22+23+24+…+22020的值.解:设S =1+2+22+23+24+...+22020,将等式两边同时乘以2得, 2S =2+22+23+24+25+ (22021)将下式减去上式,得2S ﹣S =22021﹣1,即S =22021﹣1. 即1+2+22+23+24+…+22020=22021﹣1 仿照此法计算: (1)1+3+32+33+…+320; (2)2310011111 (2222)+++++. 28.定义:若实数x ,y 满足22x y t =+,22y x t =+,且x ≠y ,则称点M (x ,y )为“好点”.例如,点(0,-2)和 (-2,0)是“好点”.已知:在直角坐标系xOy 中,点P (m ,n ).(1)P 1(3,1)和P 2(-3,1)两点中,点________________是“好点”. (2)若点P (m ,n )是“好点”,求m +n 的值.(3)若点P 是“好点”,用含t 的代数式表示mn ,并求t 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据题意可知,本题中的相等关系是:(1)盒身的个数2⨯=盒底的个数;(2)制作盒身的白铁皮张数+制作盒底的白铁皮张数18=,再列出方程组即可.【详解】解:设用x张制作盒身,y张制作盒底,根据题意得:18 21016x yx y+=⎧⎨⨯=⎩.故选:B.【点睛】此题考查从实际问题中抽出二元一次方程组,根据题目给出的条件,找出合适的等量关系注意运用本题中隐含的一个相等关系:“一个盒身与两个盒底配成一套盒”.2.D解析:D【解析】A选项:(﹣2a3)2=4a6,故是错误的;B选项:(a﹣b)2=a2-2ab+b2,故是错误的;C选项:6123aa+=+13,故是错误的;故选D.3.C解析:C【分析】根据三角形三条边的关系计算即可,三角形任意两边之和大于第三边,任意两边之差小于第三边.【详解】A. ∵2+2=4,∴ 2cm、2cm、4cm不能组成三角形,故不符合题意;B. ∵2+3<6,∴2cm、6cm、3cm不能组成三角形,故不符合题意;C. ∵3+6>8,∴8cm、6cm、3cm能组成三角形,故符合题意;D. ∵4+6<11,∴11cm、4cm、6cm不能组成三角形,故不符合题意;故选C.【点睛】本题考查了三角形三条边的关系,熟练掌握三角形三条边的关系是解答本题的关键. 4.C解析:C【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:100nm=100×10﹣9m=1×10﹣7m,故选:C.【点睛】本题是对科学记数法知识的考查,熟练掌握负指数幂知识是解决本题的关键.5.B解析:B【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为3和6,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】由题意,分以下两种情况:(1)当等腰三角形的腰为3时,三边为3,3,6+=,不满足三角形的三边关系定理此时336(2)当等腰三角形的腰为6时,三边为3,6,6+>,满足三角形的三边关系定理此时366++=则其周长为36615综上,该三角形的周长为15故选:B.【点睛】本题考查了等腰三角形的定义、三角形的三边关系定理,依据题意,正确分两种情况讨论是解题关键.6.C解析:C【分析】用科学计数法将0.00000012表示为a×10-n即可.【详解】解:0.00000012=1.2×10﹣7,故选:C.【点睛】本题考查用科学计数法表示较小的数,绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.7.B解析:B【解析】【分析】先把等式左边利用多项式乘多项式的法则展开并整理,根据对应项系数相等列出等式,求解即可.【详解】解:将(2x+3y)(mx-ny)展开,得2mx2-2nxy+3mxy-3ny2,根据题意可得2mx 2-2nxy+3mxy-3ny 2=9y 2-4x 2,根据多项式相等,则对应项及其系数相等,可得2m=-4,-3n=9, 解得m=-2,n=-3 故选B . 【点睛】本题是一道有关多项式乘法的题目,明确多项式的乘法法则是解题的关键.8.D解析:D 【分析】根据同底数幂的除法的逆运算法则及幂的乘方运算法则,进行代数式的运算即可求解. 【详解】222233332(2)5252=2(2)327a a a bb b -=== 故选:D 【点睛】本题考查了同底数幂的除法的逆运算法,一般地,(0mm nn a a a a-=≠,m ,n 都是正整数,并且m >n),还考查了幂的乘方运算法则,(a m )n =a mn (m ,n 都是正整数). 9.C解析:C 【分析】根据不等式的性质逐项判断即可. 【详解】解:A. ac bc >,由于不知道c 的符号,故无法得到a b >,故该选项不合题意; B. ma mb -<-,由于不知道-m 的符号,故无法得到a b >,故该选项不合题意; C. 22ac bc >,∵20c ≠,∴2c >0,∴a b >,故该选项符合题意; D. 22ac bc ->-,∵20c ≠,∴20c -<,∴a b <,故该选项不合题意. 故选:C 【点睛】本题考查了不等式的性质,熟知不等式的性质是解题关键.10.C解析:C 【分析】根据幂的乘方的知识,可得255=(25)11=3211,344=(34)11=8111,433=(43)11=6411,再比较底数的大小,即可得结论. 【详解】解:∵255=(25)11=3211,344=(34)11=8111,433=(43)11=6411,又∵32<64<81, ∴255<433<344. 故选C . 【点睛】本题考查了幂的乘方,解题的关键是根据幂的乘方的公式,转化为底数相同的幂.二、填空题11.【分析】先利用幂的乘方进行分解,再根据同底数幂相乘,进行计算即可. 【详解】 = 故答案为. 【点睛】此题考查幂的乘方,同底数幂相乘,解题关键在于掌握运算法则. 解析:12019【分析】先利用幂的乘方进行分解,再根据同底数幂相乘,进行计算即可. 【详解】20202019201920191112019=2019201920192019⎛⎫⨯-⨯⨯⎪⎝⎭=12019故答案为12019. 【点睛】此题考查幂的乘方,同底数幂相乘,解题关键在于掌握运算法则.12.24xy 【解析】∵(3x+2y )2=(3x ﹣2y )2+A ,∴(3x )2+2×3x×2y+(2y)2=(3x )2-2×3x×2y+(2y)2+A, 即9x2+12xy+4y2=9x2-12xy+解析:24xy 【解析】∵(3x+2y )2=(3x ﹣2y )2+A ,∴(3x )2+2×3x×2y+(2y)2=(3x )2-2×3x×2y+(2y)2+A, 即9x 2+12xy+4y 2=9x 2-12xy+4y 2+A ∴A=24xy, 故答案为24xy.【点睛】本题考查了完全平方公式,熟记完全平方公式是解题的关键. 完全平方公式:(a±b)2=a 2±2ab+b 2.13.【分析】先根据多项式乘以多项式法则展开,合并同类项,根据已知得出,求出即可; 【详解】 解: ,的乘积中不含项, , 解得:. 故答案为:. 【点睛】本题考查了多项式乘以多项式法则和解一元解析:14【分析】先根据多项式乘以多项式法则展开,合并同类项,根据已知得出4a 10-+=,求出即可; 【详解】解:()()2x 1x 4ax a +-+322x 4ax ax x 4ax a =-++-+()32x 4a 1x 3ax a =+-+-+,()()2x 1x 4ax a +-+的乘积中不含2x 项,4a 10∴-+=,解得:1a 4=.故答案为:14.【点睛】本题考查了多项式乘以多项式法则和解一元一次方程,掌握多项式乘以多项式法则是解此题的关键.14.9 【分析】根据题意直接将 代入方程mx ﹣y =7得到关于m 的方程,解之可得答案. 【详解】解:将代入方程mx﹣y=7,得:m﹣2=7,解得m=9,故答案为:9.【点睛】本题主要考查二元解析:9【分析】根据题意直接将12xy=⎧⎨=⎩代入方程mx﹣y=7得到关于m的方程,解之可得答案.【详解】解:将12xy=⎧⎨=⎩代入方程mx﹣y=7,得:m﹣2=7,解得m=9,故答案为:9.【点睛】本题主要考查二元一次方程的解,解题的关键是掌握使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.15.十五【分析】任何多边形的外角和是360°,用外角和除以每个外角的度数即可得到边数.【详解】多边形的外角和是360°,每个外角的度数是24°360°24=15故答案:十五【点睛】此题主解析:十五【分析】任何多边形的外角和是360°,用外角和除以每个外角的度数即可得到边数.【详解】多边形的外角和是360°,每个外角的度数是24°360°÷24=15故答案:十五【点睛】此题主要考查了多边形的外角和,关键是掌握任何多边形的外角和都是360°,已知每个外角度数就可以求出多边形边数.16.【分析】根据同底数幂的乘法,底数不变,指数相加;同底数幂的除法,底数不变,指数相减,可得答案.【详解】解:22x+y-1=22x×2y÷2=(2x)2×2y÷2=9×5÷2=故答案为解析:45 2【分析】根据同底数幂的乘法,底数不变,指数相加;同底数幂的除法,底数不变,指数相减,可得答案.【详解】解:22x+y-1=22x×2y÷2=(2x)2×2y÷2=9×5÷2=45 2故答案为:452.【点睛】本题考查了同底数幂的乘法与除法的逆用,熟记法则并根据法则计算是解题关键.17.【分析】利用三角形重心的性质证明图中个小三角形的面积相等即可得到答案.【详解】解:三边的中线AD、BE、CF的公共点为G,图中阴影部分的面积是故答案为:6.【点睛】解析:6.【分析】利用三角形重心的性质证明图中6个小三角形的面积相等即可得到答案.【详解】 解: ABC 三边的中线AD 、BE 、CF 的公共点为G ,,,,GBDGCD GCE AGE AGF BGF S S S S S S ∴=== 2,BG GE = 2,BGCGEC S S ∴= ,DGC CGE S S ∴=GBD GCD GCE AGE AGF BGF S S S S S S ∴=====∴ 图中阴影部分的面积是182 6.6⨯= 故答案为:6.【点睛】 本题考查的是三角形中线的性质,三角形重心的性质,掌握以上知识解决三角形的面积问题是解题的关键.18.【分析】根据非0数的0次幂等于1列出关于的不等式,求出的取值范围即可.【详解】解:成立,,解得.故答案为:.【点睛】本题考查了0指数幂的意义,即非0数的0次幂等于1,0的0次幂无意义 解析:2x ≠【分析】根据非0数的0次幂等于1列出关于x 的不等式,求出x 的取值范围即可.【详解】解:0(2)1x -=成立,20x ∴-≠,解得2x ≠.故答案为:2x ≠.【点睛】本题考查了0指数幂的意义,即非0数的0次幂等于1,0的0次幂无意义.19.【分析】根据已知不等式的解集,即可确定a,b 之间得关系以及b 的符号,从而解不等式.【详解】解:∵的解集是,∴=1,a -b<0,∴a=2b,b<0.则不等式可以化为2bx>4b.∵b<解析:2x <【分析】根据已知不等式的解集,即可确定a,b 之间得关系以及b 的符号,从而解不等式.【详解】解:∵3()50a b x a b -+->的解集是1x <,∴()53a b a b --=1,a-b<0, ∴a=2b,b<0.则不等式4ax b >可以化为2bx>4b.∵b<0.∴x<2.即关于x 的不等式4ax b >的解集为x<2.【点睛】本题考查了不等式的解法,正确确定b 的符号是关键.20.【分析】设每件衬衫降价x 元,正好达到预期目标,根据销售收入-成本=利润,即可得出关于x 的一元一次方程,解之即可得出结论.【详解】解:设每件衬衫降价x 元,正好达到预期目标,根据题意得:120解析:20【分析】设每件衬衫降价x 元,正好达到预期目标,根据销售收入-成本=利润,即可得出关于x 的一元一次方程,解之即可得出结论.【详解】解:设每件衬衫降价x 元,正好达到预期目标,根据题意得:120×400+(120-x )×(500-400)-80×500=80×500×45%,解得:x=20.答:每件衬衫降价10元,正好达到预期目标.【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.三、解答题21.(1)0;(2)﹣5a 2+6ab ﹣8b 2.【分析】(1)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;(2)原式利用平方出根是,以及完全平方公式化简,去括号合并即可得到结果.【详解】解:(1)原式=﹣4x 4y 2+4x 4y 2=0;(2)原式=﹣4a 2+b 2﹣(a 2﹣6ab +9b 2)=﹣4a 2+b 2﹣a 2+6ab ﹣9b 2=﹣5a 2+6ab ﹣8b 2.【点睛】此题考查了整式的混合运算,熟练掌握运算法则及公式是解本题的关键.22.(1)2()b a -;(2)22()()4a b a b ab +=-+;(3)±5;(4)详见解析 【分析】(1)表示出阴影部分正方形的边长,然后根据正方形的面积公式列式即可;(2)根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可; (3)将(x -y )2变形为(x +y )2—4xy ,再代入求值即可;(4)由已知的恒等式,画出相应的图形,如图所示.【详解】解:(1)阴影部分为一个正方形,其边长为b -a ,∴其面积为:2()b a -,故答案为:2()b a -;(2)大正方形面积为:()2a b +小正方形面积为:2()b a -=2()a b -, 四周四个长方形的面积为:4ab ,∴22()()4a b a b ab +=-+,故答案为:22()()4a b a b ab +=-+;(3)由(2)知,22()()4x y x y xy +=-+, ∴22()()4x y x y xy -=+-,∴x y -=5=±, 故答案为:±5;(4)符合等式()()2222252a b a b a ab b ++=++的图形如图所示,【点睛】本题考查了完全平方公式的几何背景,此类题目关键在于同一个图形的面积用两种不同的方法表示.23.(1)130°;(2)①90︒-α;②不变,90︒-α;③∠NDC+∠MDB=90︒-1α2.【分析】(1)根据已知,以及三角形内角和等于180︒,即可求解;(2)①根据平行线的性质可以证得∠ABD=∠BDM=∠MBD,∠CND=∠A=α,再利用含有α的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;②延长BD交AC于点E,则∠NDE=∠MDB,因此∠NDC-∠MDB=∠NDC-∠NDE=∠EDC,再利用三角形内角和为180︒,即可求解;③如图可知,∠NDC+∠MDB=180︒-∠BDC,利用平角的定义,即可求解代数式.【详解】解:(1)∵∠A=80︒∴∠ABC+∠ACB=180︒-80︒=100︒又∵ BD平分∠ABC,CD平分∠ACB,∴∠DBC+∠DCB=12⨯100︒=50︒.∴∠BDC=180︒-50︒=130︒.(2)①∵MN//AB,BD平分∠ABC,CD平分∠ACB,∴∠ABD=∠BDM=∠MBD,∠CND=∠A=α,∴∠NDC=180︒-α-12∠ACB,∠MDB=12∠ABC,∴∠NDC-∠MDB=180︒-α-12∠ACB-12∠ABC=180︒-α-12(∠ACB+∠ABC)=180︒-α-12(180︒-α)=90︒-α.②不变;延长BD交AC于点E,如图:∴∠NDE=∠MDB,∵∠BDC=180︒-12(∠ACB+∠ABC)=180︒-12(180︒-α)=90︒+1α2,∴∠NDC-∠MDB=∠NDC-∠NDE=∠EDC=180︒-∠BDC=180︒-(90︒+1α2)=90︒-α,同①,说明MN在旋转过程中∠NDC-∠MDB的度数只与∠A有关系,而∠A始终不变,故:MN在旋转过程中∠NDC-∠MDB的度数不会发生改变.③如图可知,∠NDC+∠MDB=180︒-∠BDC,由②知∠BDC=90︒+1α2,∴∠NDC+∠MDB=180︒-(90︒+1α2)=90︒-1α2.故∠NDC与∠MDB的关系是∠NDC+∠MDB=90︒-1α2.【点睛】本题目考查平行线与三角形的综合,涉及知识点有平行线的性质,三角形内角和等于180°等,是中考的常考知识点,难度一般,熟练掌握以上知识点的综合运用是顺利解题的关键.24.【探究1】∠2=12∠ACB,90º-12∠A;【探究2】∠BOC=90°﹣12∠A,理由见解析;【应用】22.5°;【拓展】45°或36°.【分析】【探究1】根据角平分线的定义可得∠1=12∠ABC,∠2=12∠ACB,根据三角形的内角和定理可得∠1+∠2=90º-12∠A,再根据三角形的内角和定理即可得出结论;【探究2】如图2,由三角形的外角性质和角平分线的定义可得∠OBC=1 2(∠A+∠ACB),∠OCB=12(∠A+∠ABC),然后再根据三角形的内角和定理即可得出结论;【应用】延长AC与BD,设交点为G,如图5,由【探究1】的结论可得∠G的度数,于是可得∠GCD+∠GDC的度数,然后根据角平分线的定义和角的和差可得∠1+∠2的度数,再根据三角形的内角和定理即可求出结果;【拓展】根据角平分线的定义和平角的定义可得∠EAF=90°,然后分三种情况讨论:若∠EAF=4∠E,则∠E=22.5°,根据角平分线的定义和三角形的外角性质可得∠ABO=2∠E,于是可得结果;若∠EAF=4∠F,则∠F=22.5°,由【探究2】的结论可求出∠ABO=135°,然后由三角形的外角性质即可判断此种情况不存在;若∠F=4∠E,则∠E=18°,然后再由第一种情况的结论∠ABO=2∠E即可求出结果,进而可得答案.【详解】解:【探究1】理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=12∠ABC,∠2=12∠ACB,在ΔABC中,∠A+∠ABC+∠ACB=180º.∴∠1+∠2=12(∠ABC+∠ACB)=12(180º-∠A)=90º-12∠A,∴∠BOC=180º-(∠1+∠2)=180º-(90º-12∠A)=90º+12∠A;故答案为:∠2=12∠ACB,90º-12∠A;【探究2】∠BOC=90°﹣12∠A;理由如下:如图2,由三角形的外角性质和角平分线的定义,∠OBC=12(∠A+∠ACB),∠OCB=12(∠A+∠ABC),在△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣12(∠A+∠ACB)﹣12(∠A+∠ABC),=180°﹣12(∠A+∠ACB+∠A+∠ABC),=180°﹣12(180°+∠A),=90°﹣12∠A;【应用】延长AC与BD,设交点为G,如图5,由【探究1】的结论可得:∠G=1901352O︒+∠=︒,∴∠GCD+∠GDC=45°,∵CE 、DE 分别是∠ACD 和∠BDC 的角平分线,∴∠1=12∠ACD=()11802GCD ︒-∠,∠2=12∠BDC=()11802GDC ︒-∠, ∴∠1+∠2=()11802GCD ︒-∠+()11802GDC ︒-∠=()136045157.52︒-︒=︒, ∴()1801222.5E ∠=︒-∠+∠=︒;故答案为:22.5°;【拓展】如图4,∵AE 、AF 是∠BAO 和∠OAG 的角平分线,∴∠EAQ+∠FAQ=()111809022BAO GAO ∠+∠=⨯︒=︒, 即∠EAF=90°,在Rt △AEF 中,若∠EAF=4∠E ,则∠E=22.5°,∵∠EOQ=∠E+∠EAQ ,∠BOQ=2∠EOQ ,∠BAO=2∠EAQ ,∴∠BOQ=2∠E+∠BAO ,又∠BOQ=∠BAO+∠ABO ,∴∠ABO=2∠E=45°;若∠EAF=4∠F ,则∠F=22.5°,则由【探究2】知:19022.52F ABO ∠=︒-∠=︒,∴ ∠ABO=135°, ∵∠ABO <∠BOQ=60°,∴此种情况不存在;若∠F=4∠E ,则∠E=18°,由第一种情况可知:∠ABO=2∠E ,∴∠ABO=36°;综上,∠ABO=45°或36°;故答案为:45°或36°.【点睛】本题主要考查了角平分线的定义、三角形的内角和定理、平角的定义和三角形的外角性质等知识,具有一定的综合性,熟练掌握上述知识、灵活应用整体思想是解题的关键.25.(1)A ;(2)2;(3)20214040 【分析】(1)由题意直接根据拼接前后的面积相等进行分析计算即可得出答案;(2)根据题意可知x 2﹣y 2=16,即(x +y )(x ﹣y )=16,又x +y =8,可求出x ﹣y 的值;(3)根据题意利用平方差公式将算式转化为分数的乘积的形式,根据数据规律得出答案.【详解】解:(1)图1的剩余面积为a 2﹣b 2,图2拼接得到的图形面积为(a +b )(a ﹣b ) 因此有,a 2﹣b 2=(a +b )(a ﹣b ),故答案为:A.(2)∵x 2﹣y 2=(x +y )(x ﹣y )=16,又∵x +y =8,∴x ﹣y =16÷8=2;(3)(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020) =(1﹣12)(1+12)(1﹣13)(1+13)(1﹣14)(1+14)……(1﹣12019)(1+12019)(1﹣12020)(1+12020) =12×32×23×43×34×54×……×20182019×20202019×20192020×20212020 =12×20212020 =20214040. 【点睛】本题考查平方差公式的几何意义及应用,掌握公式的结构特征是正确应用的前提,利用公式进行适当的变形是解题的关键.26.(1)115;(2)180-2x ,理由见解析;(3)45°.【分析】(1)已知点I 是两角∠ABC 、∠ACB 平分线的交点,故()()()11118018018018090222BIC IBC ICB ABC ACB A BAC ∠=︒-∠+∠=︒-∠+∠=︒-︒-∠=+∠ ,由此可求∠BIC ;(2)当CE ∥AB 时, ∠ACE=∠A=x °,根据∠ACE=∠A=x °,根据CE 是∠ACG 的角平分线,推出∠ACG=2x °,∠ABC=∠BAC=x °,即可求出ACB ∠的度数.(3)由题意知:△BDE 是直角三角形∠D+∠E=90°,可求出若∠D=3∠E 时,∠BEC=22.5°,再推理出12BEC BAC ∠=∠,即可求出BAC ∠的度数. 【详解】(1)∵点I 是两角∠ABC 、∠ACB 平分线的交点,∴()180BIC IBC ICB ∠=︒-∠+∠ ()11802ABC ACB =-∠+∠︒ ()11801802A =-︒︒-∠ 1901152BAC =+∠=︒; 故答案为:115.(2)当∠ACB 等于(180-2x )°时,CE ∥AB .理由如下:∵CE ∥AB ,∴∠ACE=∠A=x °,∵∠ACE=∠A=x °,CE 是∠ACG 的角平分线,∴∠ACG=2∠ACE=2x °,∴∠ABC=∠ACG-∠BAC=2x °-x °=x °,∴∠ACB=180°-∠BAC-∠ABC=(180-2x )°;(3)由题意知:△BDE 是直角三角形∠D+∠E=90°若∠D=3∠E 时∠BEC=22.5°,∵90BEC BDC ∠=︒-∠190902BAC ⎛⎫=︒-︒-∠ ⎪⎝⎭ 12BAC =∠, ∴45BAC ∠=︒.【点睛】本题考查了三角形的内角、外角平分线的夹角大小与原三角形内角的关系,要充分运用三角形内角和定理,角平分线性质转换.27.(1)21312-;(2)101100212-. 【分析】(1)仿照阅读材料中的方法求出所求即可;(2)仿照阅读材料中的方法求出所求即可.【详解】解:(1)设S =1+3+32+33+ (320)则3S =3+32+33+ (321)∴3S ﹣S =321﹣1,即S =21312-, 则1+3+32+33+…+320=21312-; (2)设S =1+2310011112222+++⋯+, 则12S =231001011111122222+++⋯++, ∴S ﹣12S =1﹣10112=101101212-,即S =101100212-, 则S =1+2310011112222+++⋯+=101100212-. 【点睛】此题考查的是探索运算规律题,根据已知材料中的方法,探索出运算规律是解决此题的关键.28.(1)2P ;(2)2-;(3)3t >【分析】(1)将P 1(3,1)和P 2(-3,1)分别代入等式即可得出结果;(2)将点P (m ,n )代入等式即可得出m+n 的值;(3)根据“好点”的定义,将P 点代入即可得到关于m 和n 的等式,将两个等式结合即可得出结果.【详解】解:(1)对于1(3,1)P ,2321,7t t =⨯+=,2123,5t t =⨯+=-对于2(3,1)P -,2(3)21,7t t -=⨯+=,212(3),7t t =⨯-+=,所以2P 是“好点” (2)∵点(,)P m n 是好点,∴222,2m n t n m t =+=+, 222()m n n m -=-,∴2m n +=-(3)∵222,2m n t n m t =+=+,2222m n n t m t -=+--①,2222m n m t n t +=+++②,得()()2()0m n m n m n -++-=,即()(2)0m n m n -++=,由题知,,2m n m n ≠∴+=-,由②得2()22()2m n mn m n t +-=++,∴4242,4mn t mn t -=-+=-, ∵m n ≠,∴2()0m n ->, ∴2()40m n mn +->, ∴44(4)0t -->,所以3t >,【点睛】本题主要考查的是新定义“好点”,正确的掌握整式的乘法解题的关键.。
数学七年级下册数学全册单元期末试卷及答案-百度文库

数学七年级下册数学全册单元期末试卷及答案-百度文库一、选择题1.下列计算正确的是( ) A .a 3.a 2=a 6B .a 2+a 4=2a 2C .(a 3)2=a 6D .224(3)6a a =2.在如图所示的四个汽车标识图案中,能用平移变换来分析其形成过程的是( )A .B .C .D .3.如图,P 1是一块半径为1的半圆形纸板,在P 1的右上端剪去一个直径为1的半圆后得到图形P 2,然后依次剪去一个更小的半圆(其直径为前一个被剪去的半圆的半径)得到图形P 3、P 4…P n …,记纸板P n 的面积为S n ,则S n -S n +1的值为( )A .12nπ⎛⎫ ⎪⎝⎭B .14nπ⎛⎫ ⎪⎝⎭C .2112n π+⎛⎫ ⎪⎝⎭D .2112n π-⎛⎫ ⎪⎝⎭4.把多项式228x -分解因式,结果正确的是( )A .22(8)x -B .22(2)x -C .D .42()x x x-5.新冠病毒(2019﹣nCoV )是一种新的Sarbecovirus 亚属的β冠状病毒,它是一类具有囊膜的正链单股RNA 病毒,其遗传物质是所有RNA 病毒中最大的,也是自然界广泛存在的一大类病毒.其粒子形状并不规则,直径约60﹣220nm ,平均直径为100nm (纳米).1米=109纳米,100nm 可以表示为( )米. A .0.1×10﹣6B .10×10﹣8C .1×10﹣7D .1×10116.如图所示的四个图形中,∠1和∠2不是同位角的是( ) A .B .C .D .7.将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )A .90°B .120°C .135°D .150°8.下列四个等式从左到右的变形是因式分解的是 ( ) A .22()()a b a b a b +-=-B .2()ab a a b a -=-C .25(1)5x x x x +-=+-D .21()x x x x x+=+9.如果多项式x 2+2x+k 是完全平方式,则常数k 的值为( ) A .1B .-1C .4D .-410.如图,在△ABC 中,BC =6,∠A =90°,∠B =70°.把△ABC 沿BC 方向平移到△DEF 的位置,若CF =2,则下列结论中错误的是( )A .BE =2B .∠F =20°C .AB ∥DED .DF =6二、填空题11.计算:2202120192020⨯-=__________12.若(3x+2y )2=(3x ﹣2y )2+A ,则代数式A 为______.13.计算:312-⎛⎫ ⎪⎝⎭= . 14.已知:实数m,n 满足:m+n=3,mn=2.则(1+m)(1+n)的值等于____________. 15.如图,一个宽度相等的纸条按如图所示方法折叠一下,则1∠=________度.16.已知关于x ,y 的方程22146m n m n xy --+++=是二元一次方程,那么点(),M m n 位于平面直角坐标系中的第______象限.17.已知21x y =⎧⎨=⎩是方程2x ﹣y +k =0的解,则k 的值是_____.18.如图,已知AE 是△ABC 的边BC 上的中线,若AB=8cm,△ACE 的周长比△AEB 的周长多2cm,则AC=_____.19.对有理数x ,y 定义运算:x*y=ax+by ,其中a ,b 是常数.例如:3*4=3a+4b ,如果2*(﹣1)=﹣4,3*2>1,则a 的取值范围是_______.20.已知满足不等式()()325416x x -+<-+的最小整数解是方程23x ax -=的解,则a 的值为________.三、解答题21.(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b )2=a 2+2ab+b 2,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式: .(2)利用(1)中得到的结论,解决下面的问题:若a+b+c =10,ab+ac+bc =35,则a 2+b 2+c 2= .(3)小明同学用图3中x 张边长为a 的正方形,y 张边长为b 的正方形,z 张宽、长分别为a 、b 的长方形纸片拼出一个面积为(2a+b )(a+2b )长方形,则x+y+z = . (知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .22.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x 、y 的等式表示) ;(2)若2(32)5x y -=,2(32)9x y +=,求xy 的值; (3)若25,2x y xy +==,求2x y -的值. 23.阅读理解并解答:为了求1+2+22+23+24+…+22009的值. 可令S =1+2+22+23+24+…+22009 则2S =2+22+23+24+…+22009+22010因此2S ﹣S =(2+22+23+24+…+22009+22010)﹣(1+22+23+24+…+22009)=22010﹣1所以S =22010﹣1即1+2+22+23+24+…+22009=22010﹣1 请依照此法,求:1+5+52+53+54+…+52020的值. 24.因式分解:(1)3()6()x a b y b a ---(2)222(1)6(1)9y y ---+25.同一平面内的两条直线有相交和平行两种位置关系.(1)如图a ,若//AB CD ,点P 在AB 、CD 外部,我们过点P 作AB 、CD 的平行线PE ,则有////AB CD PE ,则BPD ∠,B ,D ∠之间的数量关系为_________.将点P 移到AB 、CD 内部,如图b ,以上结论是否成立?若成立,说明理由;若不成立,则BPD ∠、B 、D ∠之间有何数量关系?请证明你的结论.(2)迎“20G ”科技节上,小兰制作了一个“飞旋镖”,在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图c ,他很想知道BPD ∠、ABP ∠、D ∠、BQD ∠之间的数量关系,请你直接写出它们之间的数量关系:__________.(3)设BF 交AC 于点P ,AE 交DF 于点Q ,已知126APB ∠=︒,100AQF ∠=︒,直接写出B E F ∠+∠+∠的度数为_______度,A ∠比F ∠大______度.26.当,m n 都是实数,且满足28m n =+,就称点21,2n P m +⎛⎫- ⎪⎝⎭为“爱心点”. (1)判断点()5,3A 、()4,8B 哪个点为“爱心点”,并说明理由;(2)若点(),4A a -、()4,B b 是“爱心点”,请判断A 、B 两点的中点C 在第几象限?并说明理由;(3)已知P 、Q 为有理数,且关于x 、y 的方程组333x y q x y q⎧+=+⎪⎨-=-⎪⎩解为坐标的点(),B x y 是“爱心点”,求p 、q 的值.27.已知:方程组2325x y ax y +=-⎧⎨+=⎩,是关于x 、y 的二元一次方程组.(1)求该方程组的解(用含a 的代数式表示);(2)若方程组的解满足0x <,0y >,求a 的取值范围. 28.阅读材料:求1+2+22+23+24+…+22020的值.解:设S =1+2+22+23+24+...+22020,将等式两边同时乘以2得, 2S =2+22+23+24+25+ (22021)将下式减去上式,得2S ﹣S =22021﹣1,即S =22021﹣1. 即1+2+22+23+24+…+22020=22021﹣1 仿照此法计算: (1)1+3+32+33+…+320; (2)2310011111 (2222)+++++.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据同底幂的运算法则依次判断各选项. 【详解】A 中,a 3.a 2=a 5,错误;B 中,不是同类项,不能合并,错误;C 中,(a 3)2=a 6,正确;D 中,224(3)9a a =,错误 故选:C . 【点睛】本题考查同底幂的运算,注意在加减运算中,不是同类项是不能合并的.2.D解析:D 【分析】根据平移作图是一个基本图案按照一定的方向平移一定的距离,连续作图设计出的图案进行分析即可. 【详解】解:A、不能用平移变换来分析其形成过程,故此选项错误;B、不能用平移变换来分析其形成过程,故此选项错误;C、不能用平移变换来分析其形成过程,故此选项正确;D、能用平移变换来分析其形成过程,故此选项错误;故选:D.【点睛】本题考查利用平移设计图案,解题关键是掌握图形的平移只改变图形的位置,而不改变图形的形状、大小和方向.3.C解析:C【分析】首先分析题意,找到规律,并进行推导得出答案.【详解】根据题意得,n≥2,S1=12π×12=12π,S2=12π﹣12π×(12)2,…S n=12π﹣12π×(12)2﹣12π×[(12)2]2﹣…﹣12π×[(12)n﹣1]2,S n+1=12π﹣12π×(12)2﹣12π×[(12)2]2﹣…﹣12π×[(12)n﹣1]2﹣12π×[(12)n]2,∴S n﹣S n+1=12π×(12)2n=(12)2n+1π.故选C.【点睛】考查学生通过观察、归纳、抽象出数列的规律的能力.4.C解析:C【解析】试题分析:首先进行提取公因式,然后利用平方差公式进行因式分解.原式=2(2x-4)=2(x+2)(x-2).考点:因式分解.5.C解析:C【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:100nm=100×10﹣9m=1×10﹣7m,故选:C.【点睛】本题是对科学记数法知识的考查,熟练掌握负指数幂知识是解决本题的关键.6.C解析:C【分析】根据同位角的定义,逐一判断选项,即可得到答案.【详解】A. ∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角,不符合题意;B. ∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角,不符合题意;C. ∠1与∠2分别是四条直线中的两对直线的夹角,不符合同位角的定义,故它们不是同位角,符合题意;D. ∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角,不符合题意.故选C.【点睛】本题主要考查同位角的定义,掌握同位角的定义:“两条直线被第三条直线所截,在两条直线的同侧,在第三条直线的同旁的两个角,叫做同位角”,是解题的关键.7.B解析:B【详解】解:根据题意得:∠1=180°-60°=120°.故选:B【点睛】本题考查直角三角板中的角度的计算,难度不大.8.B解析:B【分析】根据因式分解的概念:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,即可求解.【详解】解:根据因式分解的概念,A选项属于整式的乘法,错误;B 选项符合因式分解的概念,正确;C 选项不符合因式分解的概念,错误;D 选项因式分解错误,应为2(1)x x x x +=+,错误. 故选B . 【点睛】本题目考查因式分解的概念,难度不大,熟练区分因式分解与整数乘法的关系是解题的关键.9.A解析:A 【分析】根据完全平方公式的乘积二倍项和已知平方项先确定出另一个数是1,平方即可. 【详解】解:∵2x=2×1•x , ∴k=12=1, 故选A . 【点睛】本题考查了对完全平方公式的应用,由乘积二倍项确定做完全平方运算的两个数是解题的关键.10.D解析:D 【分析】根据平移的性质可得BC=EF ,然后求出BE=CF . 【详解】∵△ABC 沿BC 方向平移得到△DEF , ∴BC=EF , ∴BC-EC=EF-EC , 即BE=CF , ∵CF=2cm , ∴BE=2cm .∵BC=6,∠A=90°,∠B=70°, ∴∠ACB=20°,根据平移的性质可得AB ∥DE , ∴∠F=20°; 故选:D . 【点睛】本题考查了平移的性质,主要利用了平移对应点所连的线段平行且相等.二、填空题11.-1 【分析】根据平方差公式即可求解. 【详解】 =-1故答案为:-1. 【点睛】此题主要考查整式乘法公式的应用,解题的关键是熟知其运算法则.解析:-1 【分析】根据平方差公式即可求解. 【详解】2202120192020⨯-=()()22220201202012020202012020+⨯--=--=-1故答案为:-1. 【点睛】此题主要考查整式乘法公式的应用,解题的关键是熟知其运算法则.12.24xy 【解析】∵(3x+2y )2=(3x ﹣2y )2+A ,∴(3x )2+2×3x×2y+(2y)2=(3x )2-2×3x×2y+(2y)2+A, 即9x2+12xy+4y2=9x2-12xy+解析:24xy 【解析】∵(3x+2y )2=(3x ﹣2y )2+A ,∴(3x )2+2×3x×2y+(2y)2=(3x )2-2×3x×2y+(2y)2+A, 即9x 2+12xy+4y 2=9x 2-12xy+4y 2+A ∴A=24xy, 故答案为24xy.【点睛】本题考查了完全平方公式,熟记完全平方公式是解题的关键. 完全平方公式:(a±b)2=a 2±2ab+b 2.13.8 【解析】分析:根据幂的负整数指数运算法则进行计算即可. 解:原式==8. 故答案为8.点评:负整数指数幂的运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.解析:8 【解析】分析:根据幂的负整数指数运算法则进行计算即可.解:原式=3112⎛⎫ ⎪⎝⎭=8.故答案为8.点评:负整数指数幂的运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.14.6 【分析】根据多项式乘以多项式的法则展开,再代入计算即可. 【详解】∵m+n=3,mn=2,∴(1+m)(1+n)=1+n+m+mn=1+3+2=6. 故答案为:6. 【点睛】 本题考查了多解析:6 【分析】根据多项式乘以多项式的法则展开,再代入计算即可. 【详解】 ∵m +n =3,mn =2,∴(1+m )(1+n )=1+n +m +mn =1+3+2=6. 故答案为:6. 【点睛】本题考查了多项式乘以多项式,掌握多项式乘以多项式的法则是解答本题的关键.注意不要漏项,漏字母,有同类项的合并同类项.15.65 【分析】根据两直线平行内错角相等,以及折叠关系列出方程求解则可. 【详解】解:如图,由题意可知, AB∥CD,∴∠1+∠2=130°, 由折叠可知,∠1=∠2,∴2∠1=130°,解解析:65【分析】根据两直线平行内错角相等,以及折叠关系列出方程求解则可.【详解】解:如图,由题意可知,AB∥CD,∴∠1+∠2=130°,由折叠可知,∠1=∠2,∴2∠1=130°,解得∠1=65°.故答案为:65.【点睛】本题考查了平行线的性质和折叠的知识,题目比较灵活,难度一般.16.四【分析】根据题意得到关于m、n的二元一次方程组,确定点M坐标,判断M所在象限即可.【详解】解:由题意得,解得,∴点M坐标为,∴点M在第四象限.故答案为:四【点睛】本题考查了二元解析:四【分析】根据题意得到关于m、n的二元一次方程组,确定点M坐标,判断M所在象限即可.【详解】解:由题意得22111m n m n --=⎧⎨++=⎩, 解得11m n =⎧⎨=-⎩, ∴点M 坐标为()1,1-,∴点M 在第四象限.故答案为:四【点睛】本题考查了二元一次方程定义,二元一次方程组解法,点的坐标等知识,综合性较强,根据题意列出方程组是解题关键.17.-3【分析】把x 与y 的值代入方程计算即可求出k 的值.【详解】解:把代入方程得:4﹣1+k =0,解得:k =﹣3,则k 的值是﹣3.故答案为:﹣3.【点睛】此题考查的是根据二元一次方程的解析:-3【分析】把x 与y 的值代入方程计算即可求出k 的值.【详解】解:把21x y =⎧⎨=⎩代入方程得:4﹣1+k =0, 解得:k =﹣3,则k 的值是﹣3.故答案为:﹣3.【点睛】此题考查的是根据二元一次方程的解,求方程中的参数,掌握二元一次方程解的定义是解决此题的关键.18.10cm【分析】依据AE 是△ABC 的边BC 上的中线,可得CE =BE ,再根据AE =AE ,△ACE 的周长比△AEB 的周长多2cm ,即可得到AC 的长.【详解】解:∵AE是△ABC的边BC上的中线,解析:10cm【分析】依据AE是△ABC的边BC上的中线,可得CE=BE,再根据AE=AE,△ACE的周长比△AEB 的周长多2cm,即可得到AC的长.【详解】解:∵AE是△ABC的边BC上的中线,∴CE=BE,又∵AE=AE,△ACE的周长比△AEB的周长多2cm,∴AC−AB=2cm,即AC−8cm=2cm,∴AC=10cm,故答案为10cm.【点睛】本题考查了三角形中线的有关计算,分析得到两个三角形的周长的差等于两边的差是解题的关键.19.a>﹣1【分析】根据新运算法则可得关于a、b的方程与不等式:2a﹣b=﹣4①,3a+2b>1②,于是由①可用含a的代数式表示出b,所得的式子代入②即得关于a的不等式,解不等式即得答案.【详解】解析:a>﹣1【分析】根据新运算法则可得关于a、b的方程与不等式:2a﹣b=﹣4①,3a+2b>1②,于是由①可用含a的代数式表示出b,所得的式子代入②即得关于a的不等式,解不等式即得答案.【详解】解:∵2*(﹣1)=﹣4,3*2>1,∴2a﹣b=﹣4①,3a+2b>1②,由①得,b=2a+4③,把③代入②,得3a+2(2a+4)>1,解得:a>﹣1.故答案为:a>﹣1.【点睛】本题是新运算题型,主要考查了一元一次不等式的解法,正确理解运算法则、熟练掌握一元一次不等式的解法是关键.20.【分析】首先解不等式求的不等式的解集,然后确定解集中的最小整数值,代入方程求得a 的值即可;【详解】解不等式,去括号,得,移项,得,合并同类项,得,系数化为1,得,则最小的整数解为- 解析:72【分析】首先解不等式求的不等式的解集,然后确定解集中的最小整数值,代入方程求得a 的值即可;【详解】解不等式()()325416x x -+<-+,去括号,得365446-+<-+x x ,移项,得344665-<-++-x x ,合并同类项,得3x -<,系数化为1,得3x >-,则最小的整数解为-2.把2x =-代入23x ax -=中,得423a -+=, 解得:72a =. 故答案为72. 【点睛】本题主要考查了一元一次方程的解与一元一次不等式的整数解,准确计算是解题的关键.三、解答题21.(1)(a+b+c )2=a 2+b 2+c 2+2ab+2ac+2bc ;(2)30;(3)9;(4)x 3﹣x =(x+1)(x ﹣1)x【分析】(1)依据正方形的面积=(a+b+c )2;正方形的面积=a 2+b 2+c 2+2ab+2ac+2bc ,可得等式;(2)依据a 2+b 2+c 2=(a+b+c )2﹣2ab ﹣2ac ﹣2bc ,进行计算即可;(3)依据所拼图形的面积为:xa 2+yb 2+zab ,而(2a+b )(a+2b )=2a 2+4ab+ab+2b 2=2a 2+5b 2+2ab ,即可得到x ,y ,z 的值.(4)根据原几何体的体积=新几何体的体积,列式可得结论.【详解】(1)由图2得:正方形的面积=(a+b+c )2;正方形的面积=a 2+b 2+c 2+2ab+2ac+2bc , ∴(a+b+c )2=a 2+b 2+c 2+2ab+2ac+2bc ,故答案为:(a+b+c )2=a 2+b 2+c 2+2ab+2ac+2bc ;(2)∵(a+b+c )2=a 2+b 2+c 2+2ab+2ac+2bc ,∵a+b+c =10,ab+ac+bc =35,∴102=a 2+b 2+c 2+2×35,∴a 2+b 2+c 2=100﹣70=30,故答案为:30;(3)由题意得:(2a+b )(a+2b )=xa 2+yb 2+zab ,∴2a 2+5ab+2b 2=xa 2+yb 2+zab ,∴225x y z =⎧⎪=⎨⎪=⎩,∴x+y+z =9,故答案为:9;(4)∵原几何体的体积=x 3﹣1×1•x =x 3﹣x ,新几何体的体积=(x+1)(x ﹣1)x ,∴x 3﹣x =(x+1)(x ﹣1)x .故答案为:x 3﹣x =(x+1)(x ﹣1)x .【点睛】本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.22.(1)224()()xy x y x y =+--;(2)16xy =;(3)23x y -=±. 【分析】(1)阴影部分的面积可以由边长为x+y 的大正方形的面积减去边长为x-y 的小正方形面积求出,也可以由4个长为x ,宽为y 的矩形面积之和求出,表示出即可;(2)先利用完全平方公式展开,然后两个式子相减,即可求出答案;(3)利用完全平方变形求值,即可得到答案.【详解】解:(1)图中阴影部分的面积为: 224()()xy x y x y =+--;故答案为:224()()xy x y x y =+--;(2)∵2(32)5x y -=, ∴2291245x xy y -+=①,∵2(32)9x y +=,∴2291249x xy y ++=②,∴由②-①,得 24954xy =-=, ∴16xy =; (3)∵25,2x y xy +==, ∴222(2)4425x y x xy y +=++=,∴224254217x y +=-⨯=,∴222(2)4417429x y x y xy -=+-=-⨯=;∴23x y -=±;【点睛】本题考查了完全平方公式的几何背景,准确识图,以及完全平方公式变形求值,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键. 23.2021514- 【分析】根据题目信息,设S =1+5+52+53+…+52020,求出5S ,然后相减计算即可得解.【详解】解:设S =1+5+52+53+ (52020)则5S =5+52+53+54 (52021)两式相减得:5S ﹣S =4S =52021﹣1, 则202151.4S -= ∴1+5+52+53+54+…+52020的值为2021514-. 【点睛】本题考查了有理数的乘方,读懂题目信息,理解求和的运算方法是解题的关键.24.(1)3()(2)a b x y -+;(2)22(2)(2)y y +-【分析】(1)提取公因式3(a-b),即可求解.(2)将(y 2-1)看成一项,根据完全平方公式进行因式分解,之后再利用平方差公式即可求解.【详解】(1)原式=3()6()x a b y b a ---=3()(2)a b x y -+故答案为:3()(2)a b x y -+(2)原式=222(1)6(1)9y y ---+=22(y 13)--=22(4)y -=22(2)(2)y y +-故答案为:22(2)(2)y y +-【点睛】本题考查了因式分解的方法,本题分别采用了提取公因式法和公式法进行因式分解,一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法.运用公式法因式分解,一般有平方差公式,完全平方公式,立方和公式,完全立方公式.25.(1)∠BPD=∠B-∠D ;将点P 移到AB 、CD 内部,∠BPD=∠B-∠D 不成立,∠BPD=∠B+∠D ,证明见解析;(2)∠BPD=∠ABP+∠D+∠BQD ;(3)80,46.【分析】(1)由平行线的性质得出∠B=∠BPE ,∠D=∠DPE ,即可得出∠BPD=∠B-∠D ;将点P 移到AB 、CD 内部,延长BP 交DC 于M ,由平行线的性质得出∠B=∠BMD ,即可得出∠BPD=∠B+∠D ;(2)由平行线的性质得出∠A ′BQ=∠BQD ,同(1)得:∠BPD=∠A ′BP+∠D ,即可得出结论;(3)过点E 作EN ∥BF ,则∠B=∠BEN ,同(1)得:∠FQE=∠F+∠QEN ,得出∠EQF=∠B+∠E+∠F ,求出∠EQF=180°-100°=80°,即∠B+∠E+∠F=80°,由∠AMP=∠APB-∠A=126°-∠A ,∠FMQ=180°-∠AQF-∠F=180°-100°-∠F=80°-∠F ,∠AMP=∠FMQ ,得出126°-∠A=80°-∠F ,即可得出结论.【详解】解(1)∵AB ∥CD ∥PE ,∴∠B=∠BPE ,∠D=∠DPE ,∵∠BPE=∠BPD+∠DPE ,∴∠BPD=∠B-∠D ,故答案为:∠BPD=∠B-∠D ;将点P 移到AB 、CD 内部,∠BPD=∠B-∠D 不成立,∠BPD=∠B+∠D ,理由如下:延长BP 交DC 于M ,如图b 所示:∵AB ∥CD ,∴∠B=∠BMD ,∵∠BPD=∠BMD+∠D ,∴∠BPD=∠B+∠D ;(2)∵A ′B ∥CD ,∴∠A ′BQ=∠BQD ,同(1)得:∠BPD=∠A ′BP+∠D ,∴∠BPD=∠ABP+∠D+∠BQD ,故答案为:∠BPD=∠ABP+∠D+∠BQD ;(3)过点E 作EN ∥BF ,如图d 所示:则∠B=∠BEN ,同(1)得:∠FQE=∠F+∠QEN ,∴∠EQF=∠B+∠E+∠F ,∵∠AQF=100°,∴∠EQF=180°-100°=80°,即∠B+∠E+∠F=80°,∵∠AMP=∠APB-∠A=126°-∠A ,∠FMQ=180°-∠AQF-∠F=180°-100°-∠F=80°-∠F ; ∵∠AMP=∠FMQ ,∴126°-∠A=80°-∠F ,∴∠A-∠F=46°,故答案为:80,46.【点睛】本题考查了平行线性质,三角形外角性质、三角形内角和定理等知识,熟练掌握平行线的性质是解题的关键.26.(1)()5,3A 为爱心点,理由见解析;(2)第四象限,理由见解析;(3)0p =,q =23- 【分析】(1)分别把A 、B 点坐标,代入(m ﹣1,22n +)中,求出m 和n 的值,然后代入2m =8+n 检验等号是否成立即可;(2)把点A(a,﹣4)、B(4,b)各自代入(m﹣1,22n+)中,分别用a、b表示出m、n,再代入2m=8+n中可求出a、b的值,则可得A和B点的坐标,再根据中点坐标公式即可求出C点坐标,然后即可判断点C所在象限;(3)解方程组,用q和p表示x和y,然后代入2m=8+n可得关于p和q的等式,再根据p,q为有理数,即可求出p、q的值.【详解】解:(1)A点为“爱心点”,理由如下:当A(5,3)时,m﹣1=5,22n+=3,解得:m=6,n=4,则2m=12,8+n=12,所以2m=8+n,所以A(5,3)是“爱心点”;当B(4,8)时,m﹣1=4,22n+=8,解得:m=5,n=14,显然2m≠8+n,所以B点不是“爱心点”;(2)A、B两点的中点C在第四象限,理由如下:∵点A(a,﹣4)是“爱心点”,∴m﹣1=a,22n+=﹣4,解得:m=a+1,n=﹣10.代入2m=8+n,得2(a+1)=8﹣10,解得:a=﹣2,所以A点坐标为(﹣2,﹣4);∵点B(4,b)是“爱心点”,同理可得m=5,n=2b﹣2,代入2m=8+n,得:10=8+2b﹣2,解得:b=2.所以点B坐标为(4,2).∴A、B两点的中点C坐标为(2442,22-+-+),即(1,﹣1),在第四象限.(3)解关于x,y的方程组3x y qx y q⎧+=+⎪⎨-=-⎪⎩,得:2x qy q⎧=-⎪⎨=⎪⎩.∵点B(x,y)是“爱心点”,∴m﹣1﹣q,22n+=2q,解得:m﹣q+1,n=4q﹣2.代入2m=8+n,得:﹣2q+2=8+4q﹣2,整理得﹣6q=4.∵p ,q 为有理数,若使p ﹣6q 结果为有理数4,则P =0,所以﹣6q =4,解得:q =﹣23. 所以P =0,q =﹣23. 【点睛】本题是新定义题型,以“爱心点”为载体,主要考查了解二元一次方程组、中点坐标公式等知识以及阅读理解能力和迁移运用能力,正确理解题意、熟练掌握二元一次方程组的解法是关键. 27.(1)1213x a y a=+⎧⎨=-⎩;(2)12a <- 【分析】(1)利用加减消元法求解可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】(1)①2⨯,得2242x y a +=-.③②-③,得12x a =+把12x a =+代入①,得13y a =-所以原方程组的解是1213x a y a=+⎧⎨=-⎩ (2)根据题意,得 120130a a +<⎧⎨->⎩解不等式组,得,12a <- 所以a 的取值范围是:12a <-. 【点睛】 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.28.(1)21312-;(2)101100212-. 【分析】(1)仿照阅读材料中的方法求出所求即可;(2)仿照阅读材料中的方法求出所求即可.【详解】解:(1)设S =1+3+32+33+ (320)则3S =3+32+33+ (321)∴3S ﹣S =321﹣1,即S =21312-, 则1+3+32+33+…+320=21312-; (2)设S =1+2310011112222+++⋯+, 则12S =231001011111122222+++⋯++, ∴S ﹣12S =1﹣10112=101101212-,即S =101100212-, 则S =1+2310011112222+++⋯+=101100212-. 【点睛】此题考查的是探索运算规律题,根据已知材料中的方法,探索出运算规律是解决此题的关键.。
七年级下学期数学全册单元期末试卷及答案-百度文库

七年级下学期数学全册单元期末试卷及答案-百度文库一、选择题1.如图1的8张长为a ,宽为b (a <b )的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD 内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S ,当BC 的长度变化时,按照同样的放置方式,S 始终保持不变,则a ,b 满足( )A .b =5aB .b =4aC .b =3aD .b =a2.下列各式从左到右的变形中,是因式分解的是( )A .2(3)(3)9a a a +-=-B .2323(2)a a a a a--=-- C .245(4)5a a a a --=-- D .22()()a b a b a b -=+- 3.冠状病毒是引起病毒性肺炎的病原体的一种,可以在人群中扩散传播,某冠状病毒的直径大约是0.000000081米,用科学计数法可表示为( )A .-98.110⨯B .-88.110⨯C .-98110⨯D .-78.110⨯ 4.若(x-2y)2 =(x+2y)2+M,则M= ( ) A .4xyB .- 4xyC .8xyD .-8xy 5.下列各式中,计算结果为x 2﹣1的是( )A .()21x -B .()(1)1x x -+-C .()(1)1x x +-D .()()12x x -+ 6.下列图形中,不能通过其中一个四边形平移得到的是( )A .B .C .D .7.将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )A .22()()a b a b a b +-=-B .222()a b a b -=-C .2()b a b ab b -=-D .2()ab b b a b -=-8.不等式3+2x>x+1的解集在数轴上表示正确的是( )A .B .C .D .9.能把一个三角形的面积分成相等的两部分的线是这个三角形的( ) A .一条高 B .一条中线 C .一条角平分线D .一边上的中垂线 10.七边形的内角和是( )A .360°B .540°C .720°D .900° 二、填空题11.分解因式:29a -=__________.12.已知一个多边形的内角和与外角和的差是1260°,则这个多边形边数是 .13.三角形的周长为10cm ,其中有两边的长相等且长为整数,则第三边长为______cm .14.一个等腰三角形的两边长分别为4cm 和9cm ,则它的周长为__cm .15.阅读材料:①1的任何次幂都等于1;②﹣1的奇数次幂都等于﹣1;③﹣1的偶数次幂都等于1;④任何不等于零的数的零次幂都等于1,试根据以上材料探索使等式(2x+3)x+2016=1成立的x 的值为_____.16.计算:x (x ﹣2)=_____17.如图,若AB ∥CD ,∠C=60°,则∠A+∠E=_____度.18.如图,一个宽度相等的纸条按如图所示方法折叠一下,则1∠=________度.19.已知(a +b )2=7,a 2+b 2=5,则ab 的值为_____.20.有两个正方形,A B ,现将B 放在A 的内部得图甲,将,A B 并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形,A B 的边长之和为________.三、解答题21.如图,在△ABC 中,∠ABC =56º,∠ACB =44º,AD 是BC 边上的高,AE 是△ABC 的角平分线,求出∠DAE 的度数.22.先化简,再求值:(3x +2)(3x -2)-5x (x +1)-(x -1)2,其中x 2-x -10=0.23.先化简,再求值:(2a ﹣b )2﹣(a +1﹣b )(a +1+b )+(a +1)2,其中a =12,b =﹣2. 24.如图 1,直线GH 分别交,AB CD 于点 ,E F (点F 在点E 的右侧),若12180︒∠+∠= (1)求证://AB CD ;(2)如图2所示,点M N 、在,AB CD 之间,且位于,E F 的异侧,连MN , 若23M N ∠=∠,则,,AEM NFD N ∠∠∠三个角之间存在何种数量关系,并说明理由.(3)如图 3 所示,点M 在线段EF 上,点N 在直线CD 的下方,点P 是直线AB 上一点(在E 的左侧),连接,,MP PN NF ,若2,2MPN MPB NFH HFD ∠=∠∠=∠,则请直接写出PMH ∠与N ∠之间的数量25.计算 (1)1012(2)3π-⎛⎫---+- ⎪⎝⎭; (2)52482(2)()()x x x x +-÷-.26.如图所示,点B ,E 分别在AC ,DF 上,BD ,CE 均与AF 相交,∠1=∠2,∠C =∠D ,求证:∠A =∠F .27.已知有理数,x y 满足:1x y -=,且221x y ,求22x xy y ++的值.28.如图,一个三角形的纸片ABC ,其中∠A=∠C ,(1)把△ABC 纸片按 (如图1) 所示折叠,使点A 落在BC 边上的点F 处,DE 是折痕.说明 BC ∥DF ;(2)把△ABC 纸片沿DE 折叠,当点A 落在四边形BCED 内时 (如图2),探索∠C 与∠1+∠2之间的大小关系,并说明理由;(3)当点A 落在四边形BCED 外时 (如图3),探索∠C 与∠1、∠2之间的大小关系.(直接写出结论)【参考答案】***试卷处理标记,请不要删除一、选择题1.A【分析】分别表示出左上角阴影部分的面积S 1和右下角的阴影部分的面积S 2,两者求差,根据当BC 的长度变化时,按照同样的放置方式,S 始终保持不变,即可求得a 与b 的数量关系.【详解】解:设左上角阴影部分的面积为1S ,右下角的阴影部分的面积为2S ,12S S S =-225315[()]AD AB a AD a AB a BC AB b BC AB b 225315()BC AB a BCa AB a BC ABb BC AB b 22(5)(3)15a b BC b a AB a b . AB 为定值,当BC 的长度变化时,按照同样的放置方式,S 始终保持不变,50a b, 5b a .故选:A .【点睛】本题考查了整式的混合运算在几何图形问题中的应用,数形结合并根据题意正确表示出两部分阴影的面积之差是解题的关键.2.D解析:D【分析】根据因式分解的定义,需要将式子变形为几个整式相乘的形式,据此可判断.【详解】A 、C 不是几个式子相乘的形式,错误;B 中,32a a--不是整式,错误; D 是正确的故选:D .【点睛】本题考查因式分解的定义,注意一定要化成多个整式相乘的形式才叫因式分解. 3.B解析:B【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.000000081=-88.110⨯;故选B .本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.4.D解析:D【分析】根据完全平方公式的运算法则即可求解.【详解】∵(x-2y)2 =(x+2y)2+M∴M=(x-2y)2 -(x+2y)2=x2-4xy+4y2-x2-4xy-4y2=-8xy故选D.【点睛】此题主要考查完全平方公式的运算,解题的关键是熟知完全平方公式的运算法则.5.C解析:C【分析】运用多项式乘法法则对各个算式进行计算,再确定答案.【详解】解:A.原式=x2﹣2x+1,B.原式=﹣(x﹣1)2=﹣x2+2x﹣1;C.(x+1)(x﹣1)=x2﹣1;D.原式=x2+2x﹣x﹣2=x2+x﹣2;∴计算结果为x2﹣1的是C.故选:C.【点睛】此题考查了平方差公式,多项式乘多项式,以及完全平方公式,熟练掌握公式及法则是解本题的关键.6.D解析:D【详解】解:A、能通过其中一个四边形平移得到,不符合题意;B、能通过其中一个四边形平移得到,不符合题意;C、能通过其中一个四边形平移得到,不符合题意;D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意.故选D.7.A解析:A【分析】根据长方形的面积=长 宽,分别表示出甲乙两个图形的面积,即可得到答案.解:()()=S a b a b +-甲,()()2222==S a a b b a b a ab ab b a b -+-=-+--乙. 所以()()a b a b +-22=a b -故选A .【点睛】本题考查平方差公式,难度不大,通过计算两个图形的面积即可顺利解题.8.A解析:A【分析】先解不等式求出不等式的解集,然后根据不等式的解集在数轴上的表示方法判断即可.【详解】解:移项,得2x -x >1-3,合并同类项,得x >﹣2,不等式的解集在数轴上表示为:.故选:A .【点睛】本题考查了一元一次不等式的解法和不等式的解集在数轴上的表示,属于基础题型,熟练掌握一元一次不等式的解法是关键.9.B解析:B【分析】根据三角形中线的性质作答即可.【详解】解:能把一个三角形的面积分成相等的两部分的线是这个三角形的一条中线. 故选:B .【点睛】本题考查了三角形中线的性质,属于应知应会题型,熟知三角形的一条中线将三角形分成面积相等的两部分是解题的关键.10.D解析:D【分析】n 边形的内角和是(n ﹣2)•180°,把多边形的边数代入公式,就得到多边形的内角和.【详解】(7﹣2)×180°=900°.故选D .【点睛】本题考查了多边形的内角和与外角和定理,解决本题的关键是正确运用多边形的内角和公式,是需要熟记的内容.二、填空题11.【解析】试题分析:本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式.在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止.先把式子写成a2-32,符合平方差公式的特点解析:()()33a a +-【解析】试题分析:本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式.在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止.先把式子写成a 2-32,符合平方差公式的特点,再利用平方差公式分解因式.a 2-9=a 2-32=(a+3)(a-3).故答案为(a+3)(a-3).考点:因式分解-运用公式法.12.12【解析】试题解析:根据题意,得(n-2)•180-360=1260,解得:n=11.那么这个多边形是十一边形.考点:多边形内角与外角.解析:12【解析】试题解析:根据题意,得(n-2)•180-360=1260,解得:n=11.那么这个多边形是十一边形.考点:多边形内角与外角.13.或 2【分析】可分相等的两边的长为1cm ,2cm ,3cm ,4cm ,依此讨论,根据三角形三边关系(三角形两边之和大于第三边,两边只差小于第三边)即可求解.【详解】解:相等的两边的长为1cm ,则解析:或 2【分析】可分相等的两边的长为1cm,2cm,3cm,4cm,依此讨论,根据三角形三边关系(三角形两边之和大于第三边,两边只差小于第三边)即可求解.【详解】解:相等的两边的长为1cm,则第三边为:10-1×2=8(cm),1+1<8,不符合题意;相等的两边的长为2cm,则第三边为:10-2×2=6(cm),2+2<6,不符合题意;相等的两边的长为3cm,则第三边为:10-3×2=4(cm),3+3>4,符合题意;相等的两边的长为4cm,则第三边为:10-4×2=2(cm),2+4>4,符合题意.故第三边长为4或2cm.故答案为:4或2.【点睛】此题考查了三角形三边关系(三角形两边之和大于第三边,两边只差小于第三边),等腰三角形的性质和周长计算,分类思想的运用是解题的关键.14.22【解析】【分析】底边可能是4,也可能是9,分类讨论,去掉不合条件的,然后可求周长. 【详解】试题解析:①当腰是4cm,底边是9cm时:不满足三角形的三边关系,因此舍去.②当底边是4cm解析:22【解析】【分析】底边可能是4,也可能是9,分类讨论,去掉不合条件的,然后可求周长.【详解】试题解析:①当腰是4cm,底边是9cm时:不满足三角形的三边关系,因此舍去.②当底边是4cm,腰长是9cm时,能构成三角形,则其周长=4+9+9=22cm.故填22.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答.15.﹣1或﹣2或﹣2016【分析】根据1的乘方,﹣1的乘方,非零的零次幂,可得答案.【详解】解:①当2x+3=1时,解得:x=﹣1,此时x+2016=2015,则(2x+3)x+2016=12解析:﹣1或﹣2或﹣2016【分析】根据1的乘方,﹣1的乘方,非零的零次幂,可得答案.【详解】解:①当2x+3=1时,解得:x=﹣1,此时x+2016=2015,则(2x+3)x+2016=12015=1,所以x=﹣1.②当2x+3=﹣1时,解得:x=﹣2,此时x+2016=2014,则(2x+3)x+2016=(﹣1)2014=1,所以x=﹣2.③当x+2016=0时,x=﹣2016,此时2x+3=﹣4029,则(2x+3)x+2016=(﹣4029)0=1,所以x=﹣2016.综上所述,当x=﹣1,或x=﹣2,或x=﹣2016时,代数式(2x+3)x+2016的值为1.故答案为:﹣1或﹣2或﹣2016.【点睛】本题考查的是乘方运算,特别是乘方的结果为1的情况,分类讨论的思想是解题的关键.16.x2﹣2x【分析】根据单项式乘多项式法则即可求出答案.【详解】解:原式=x2﹣2x故答案为:x2﹣2x.【点睛】此题考查的是整式的运算,掌握单项式乘多项式法则是解决此题的关键.解析:x2﹣2x【分析】根据单项式乘多项式法则即可求出答案.【详解】解:原式=x2﹣2x故答案为:x2﹣2x.【点睛】此题考查的是整式的运算,掌握单项式乘多项式法则是解决此题的关键.17.60【解析】先由AB∥CD,求得∠C的度数,再根据三角形的外角等于与它不相邻的两内角之和可求∠A+∠E的度数.【详解】∵AB∥CD,∴∠C与它的同位角相等,根据三角形的外角等于解析:60【解析】【分析】先由AB∥CD,求得∠C的度数,再根据三角形的外角等于与它不相邻的两内角之和可求∠A+∠E的度数.【详解】∵AB∥CD,∴∠C与它的同位角相等,根据三角形的外角等于与它不相邻的两内角之和,所以∠A+∠E=∠C=60度.故答案为60.【点睛】本题考查了平行线的性质,三角形的外角等于和它不相邻的两个内角的和. ①两直线平行同位角相等;②两直线平行内错角相等;③两直线平行同旁内角互补;④夹在两平行线间的平行线段相等.在运用平行线的性质定理时,一定要找准同位角,内错角和同旁内角.18.65【分析】根据两直线平行内错角相等,以及折叠关系列出方程求解则可.【详解】解:如图,由题意可知,AB∥CD,∴∠1+∠2=130°,由折叠可知,∠1=∠2,∴2∠1=130°,解解析:65【分析】根据两直线平行内错角相等,以及折叠关系列出方程求解则可.【详解】解:如图,由题意可知,∴∠1+∠2=130°,由折叠可知,∠1=∠2,∴2∠1=130°,解得∠1=65°.故答案为:65.【点睛】本题考查了平行线的性质和折叠的知识,题目比较灵活,难度一般.19.1【分析】利用完全平方公式得到a2+2ab+b2=7,然后把a2+b2=5代入可计算出ab的值.【详解】解:∵(a+b)2=7,∴a2+2ab+b2=7,∵a2+b2=5,∴5+2ab解析:1【分析】利用完全平方公式得到a2+2ab+b2=7,然后把a2+b2=5代入可计算出ab的值.【详解】解:∵(a+b)2=7,∴a2+2ab+b2=7,∵a2+b2=5,∴5+2ab=7,∴ab=1.故答案为1.【点睛】本题主要考查了完全平方差公式的运用,掌握完全平方差公式是解题的关键.20.5【分析】设正方形A,B的边长分别为a,b,根据图形构建方程组即可解决问题.解:设正方形A ,B 的边长分别为a ,b .由图甲得:,由图乙得:,化简得,∴,∵a+b>0,∴a+b解析:5【分析】设正方形A ,B 的边长分别为a ,b ,根据图形构建方程组即可解决问题.【详解】解:设正方形A ,B 的边长分别为a ,b .由图甲得:2()1a b -=,由图乙得:22()()12+--=a b a b ,化简得6ab =,∴22()()412425+=-+=+=a b a b ab ,∵a +b >0,∴a +b =5,故答案为:5.【点睛】本题考查完全平方公式,正方形的面积等知识,解题的关键是学会利用参数,构建方程组解决问题,属于中考常考题型. 三、解答题21.6°【解析】试题分析:先根据三角形内角和求出∠BAC 的度数,由AE 是△ABC 的角平分线,求出∠DAC 的度数,由AD 是BC 边上的高,求出∠EAC 的度数,再利用角的和差求出∠DAE 的度数.解:∵在△ABC 中,∠ABC =56°,∠ACB =44°∴∠BA C =180°-∠ABC-∠ACB =80°∵AE 是△ABC 的角平分线∴∠EAC=12∠BA C =40° ∵AD 是BC 边上的高,∠ACB =44°∴∠DAC=90°-∠ACB =46°∴∠DAE=∠DAC-∠EAC=6°22.3x 2-3x -5,25原式第一项利用平方差公式化简,第二项利用单项式乘以多项式法则计算,最后一项利用完全平方公式展开,去括号合并得到最简结果,将已知的方程变形后代入即可求值.【详解】原式=()222945521x x x x x -----+=222945521x x x x x ----+-=2335x x --,当2100x x =--,即210x x =-时,原式=()235310525x x -=⨯-=-【点睛】本题考查整式的混合运算-化简求值,涉及的知识点有:完全平方公式、平方差公式、去括号法则及合并同类项法则,熟练掌握以上公式及法则是解题的关键.23.22442a ab b -+;13【分析】原式利用平方差公式及完全平方公式展开,去括号合并得到最简结果,把a 与b 的值代入计算即可求出值.【详解】解:原式=4a 2﹣4ab+b 2﹣(a 2+2a+1﹣b 2)+a 2+2a+1=4a 2﹣4ab+b 2﹣a 2﹣2a ﹣1+b 2+a 2+2a+1=4a 2﹣4ab+2b 2, 当a =12,b =﹣2时,原式=1+4+8=13. 【点睛】 此题考查了整式的混合运算−化简求值,熟练掌握运算法则是解本题的关键.24.(1)证明过程见解析;(2)12N AEM NFD ∠=∠-∠,理由见解析;(3)13∠N+∠PMH=180°. 【分析】(1)根据同旁内角互补,两直线平行即可判定AB ∥CD ;(2)设∠N=2α,∠M=3α,∠AEM=x ,∠NFD=y ,过M 作MP ∥AB ,过N 作NQ ∥AB 可得∠PMN=3α-x ,∠QNM=2α-y ,根据平行线性质得到3α-x =2α-y ,化简即可得到12N AEM NFD ∠=∠-∠; (3)过点M 作MI ∥AB 交PN 于O ,过点N 作NQ ∥CD 交PN 于R ,根据平行线的性质可得∠BPM=∠PMI ,由已知得到∠MON=∠MPN+∠PMI=3∠PMI 及∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD ,根据对顶角相等得到∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM ,化简得到∠FNP+2∠PMI-2∠RFM=180°-∠PMH ,根据平行线的性质得到3∠PMI+∠FNP+∠FNH=180°及3∠RFM+∠FNH=180°,两个等式相减即可得到∠RFM-∠PMI=13∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到1 3∠FNP=180°-∠PMH,即13∠N+∠PMH=180°.【详解】(1)证明:∵∠1=∠BEF,12180︒∠+∠=∴∠BEF+∠2=180°∴AB∥CD.(2)解:12N AEM NFD ∠=∠-∠设∠N=2α,∠M=3α,∠AEM=x,∠NFD=y 过M作MP∥AB,过N作NQ∥AB∵//AB CD,MP∥AB,NQ∥AB∴MP∥NQ∥AB∥CD∴∠EMP=x,∠FNQ=y∴∠PMN=3α-x,∠QNM=2α-y∴3α-x=2α-y即α=x-y∴12N AEM NFD ∠=∠-∠故答案为12N AEM NFD ∠=∠-∠(3)解:13∠N+∠PMH=180°过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R.∵//AB CD,MI∥AB,NQ∥CD∴AB∥MI∥NQ∥CD∴∠BPM=∠PMI∵∠MPN=2∠MPB∴∠MPN=2∠PMI∴∠MON=∠MPN+∠PMI=3∠PMI∵∠NFH=2∠HFD∴∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD∵∠RFN=∠HFD∴∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM∴∠MON+∠PRF+∠RFM=360°-∠OMF即3∠PMI+∠FNP+180°-3∠RFM+∠RFM=360°-∠OMF ∴∠FNP+2∠PMI-2∠RFM=180°-∠PMH∵3∠PMI+∠PNH=180°∴3∠PMI+∠FNP+∠FNH=180°∵3∠RFM+∠FNH=180°∴3∠PMI-3∠RFM+∠FNP=0°即∠RFM-∠PMI=13∠FNP∴∠FNP+2∠PMI-2∠RFM=∠FNP-2(∠RFM-∠PMI)=180°-∠PMH∠FNP-2×13∠FNP=180°-∠PMH13∠FNP=180°-∠PMH即13∠N+∠PMH=180°故答案为13∠N+∠PMH=180°【点睛】本题主要考查了平行线的判定与性质.解题的关键是正确作出辅助线,通过运用平行线性质得到角之间的关系.25.(1)2- ;(2)103x【分析】(1)根据负整数指数幂以及零指数幂运算即可求解;(2)根据同底数幂相乘(除),底数不变,指数相加(减),即可求解.【详解】解:(1)原式=213=2---;(2)原式12252481010122101010221=24443x xx x x x x x x x x ⨯+-⎛⎫⋅+⋅-=-=-=-= ⎪⎝⎭. 【点睛】本题目考查整数指数幂,涉及知识点有正整数指数幂、零指数幂、负整数指数幂等,难度一般,熟练掌握整数指数幂的运算法则是顺利解题的关键.26.证明见解析.【分析】根据对顶角的性质得到BD ∥CE 的条件,然后根据平行线的性质得到∠B=∠C ,已知∠C=∠D ,则得到满足AB ∥EF 的条件,再根据两直线平行,内错角相等得到∠A=∠F .【详解】证明:∵∠2=∠3,∠1=∠2,∴∠1=∠3,∴BD ∥CE ,∴∠C=∠ABD ;又∵∠C=∠D ,∴∠D=∠ABD ,∴AB ∥EF ,∴∠A=∠F .考点:平行线的判定与性质;对顶角、邻补角.27.【分析】利用1x y -=将221x y 整理求出xy 的值,然后将22x xy y ++利用完全平方公式变形,将各自的值代入计算即可求出值. 【详解】∵221x y ,∴化简得:241xy x y , ∵1x y -=,∴241xy x y 可化为:241xy ,即有:5xy =,∴2222313516x xy y x y xy .【点睛】此题考查了整式的混合运算 化简求值,熟练掌握运算法则是解本题的关键.28.(1)见解析;(2)∠1+∠2=2∠C;(3)∠1-∠2=2∠C.【分析】(1)根据折叠的性质得∠DFE=∠A,由已知得∠A=∠C,于是得到∠DFE=∠C,即可得到结论;(2)先根据四边形的内角和等于360°得出∠A+∠A′=∠1+∠2,再由图形翻折变换的性质即可得出结论;(3)∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β),于是得到∠2+2α=180°,∠1=β-∠BDE=β-(∠A+α),推出∠2-∠1=180°-(α+β)+∠A,根据三角形的内角和得到∠A=180°-(α+β),证得∠2-∠1=2∠A,于是得到结论.【详解】解:(1) 由折叠知∠A=∠DFE,∵∠A=∠C,∴∠DFE=∠C,∴BC∥DF;(2)∠1+∠2=2∠A.理由如下:∵∠1+2∠AED=180°,∠2+2∠ADE=180°,∴∠1+∠2+2(∠ADE+∠AED)=360°.∵∠A+∠ADE+∠AED=180°,∴∠ADE+∠AED=180°-∠A,∴∠1+∠2+2(180°-A)=360°,即∠1+∠2=2∠C.(3)∠1-∠2=2∠A.∵2∠AED+∠1=180°,2∠ADE-∠2=180°,∴2(∠ADE+∠AED)+∠1-∠2=360°.∵∠A+∠ADE+∠AED=180°,∴∠ADE+∠AED=180°-∠A,∴∠1-∠2+2(180°-∠A)=360°,即∠1-∠2=2∠C.【点睛】考查了翻折变换的性质,三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和等于180°,综合题,但难度不大,熟记性质准确识图是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七下期中考前语文练习题(一)1.下列词语中加点的字注意完全正确的一项是()A 讪.笑(shàn)叮嘱.(zhǔ)冰雹.(pào) 澎湃.(pài)B 秕.谷(bǐ)炽.痛(chì)宿儒.(rú) 惬.意(qiâ)C 亘.古(gâng)蝉蜕.(duì)迸.出(bâng)归省.(shěng)D 确凿.(záo)畸.形(qí)滞.留(zhì)参差.(cī)2.下列句子中,没有错别字的一项是()A .来势凶凶锲而不舍荒草萋萋家喻户晓B. 九曲连环心会神疑锋芒必露亦复如是C .历尽心血人声鼎沸炯炯有神秩序井然D .当之无愧杂乱无章惹人注目慷慨淋漓3.下列句子加点词语运用正确的一项是()A.2009年7月5日乌鲁木齐发生严重的打砸抢烧暴力事件,真是骇人听闻....。
B.云台山神奇秀美,真是巧夺天工....,令人赞叹不已。
C.通过模拟考试,他发现了学习语文的蛛丝马迹....。
D.建筑工地上机器轰鸣,人声鼎沸,好一派热闹的场面。
4.下列作品、作家和朝代(国籍)搭配有误一的项是()。
A.《春夜洛城闻笛》——唐——李白 B.《音乐巨人贝多芬》——当代——何为。
C.《山中杂诗》——唐——王维 D.《逢入京使》——唐——岑参5.下列句子的顺序已打乱,如将其还原,则顺序正确的一项是:()①可是,这个因素常常不是每个人都会注意到的。
②这种情况就比食物本身的不清洁,更容易被人所忽略。
③不洁的饮食,或者说,微生物的感染,是引起急性胃肠病的最多见的因素。
④特别是有的时候,食物本身本来很清洁,可是由于手的不清洁,或者菜刀、案板、抹布的不清洁,而致使人受到感染。
A.①②③④ B. ②①④③ C. ③①④② D. ④②③①语文练习(二)1.加点字注音有误的一项是( )A.蝉蜕(tuì)尴尬(ɡān ɡà)木屐(jī)玉簪花( zān )B.系上(jì)斑蝥(máo)缠络(luî)攒成(zǎn )C.桑葚(shân)臃肿( yōng )花圃(pǔ)掸子( dǎn )D. 菜畦(qí) 倜傥(tìtǎnɡ)拗过去(ǎo)弥漫(mí)2.下列词语字形有误的一项是()A.相宜丑陋瞬息人迹罕至 B.确凿讪笑肿胀荒草萋萋C.书塾幽寂搏学来势凶凶 D.瞬息嫉妒叮嘱骇人听闻3.下列句子中成语使用有误的一项是()A.B.C.奥本海默是一个拔尖的人物,锋芒毕露。
D.风小心翼翼的吹过来,唯恐弄乱了他的头发。
4.没有运用比喻的—句是( )A.村落啦,树林子啦,坑洼啦,沟渠啦,好像一下子全都掉进了神秘的沉寂里。
B.那些树仍旧浑然不觉地,在飘送那些小型的云朵,倒好像是一座无限的云库似的。
C.他把自己吹得像一条鼓满了风的风帆。
D.天上的云有的像羽毛,轻轻飘在空中;有的像羊群,来来去去。
5.下列说法不正确的一项是( )A.《假如生活欺骗了你》选自戈宝权译的《普希金诗集》,作者普希金是俄国著名诗人。
B.《爸爸的花儿落了》“爸爸的花儿落了”这个题目语带双关,含义丰富,既指指夹竹桃花的败落,又暗示天性爱花的爸爸离开人世。
C.《伤仲永》选自《临川先生文集》,作者王安石是唐朝的政治家、文学家、思想家。
他还是“唐宋八大家”之一。
D. 《艰难的国运与雄健的国民》作者是李大钊,这是一篇用杂文(散文)形式写的民族精神颂。
语文练习(三)1.选择注音不正确的一组 ( )A、确凿(záo) 骊歌(lí)花圃(pǔ) 菜畦(qí)人迹罕至(hǎn)B、嫉妒(jí)嗥鸣(háo)炽痛(chì)模样(mú)鲜为人知(xiǎn)C、踱步(duï)深邃(suì) 喧嚣(xiāo) 收敛(liǎn)鞠躬尽瘁(jū)D、讪笑(shàn)伫立(zhù)重荷(hâ)殷红(yīn)锲而不舍(qiâ)2.选择字形完全正确的一组 ( )A.仁慈人迹罕致似曾相识 B.迷惑绅士风度茫然若失C.和蔼白驹过隙摹然回首 D.琢磨清翠笑声蓝色绒衣3.下列词语解释不正确的一项是(A.B. 今年2此前赛事成绩平平、鲜为人知....的他成为全球关注的焦点。
C.“鞠躬尽瘁,死而后已”这几个字是对孔繁森一生最好的评价。
D.几年没见,调皮的小军变成了一个品学兼优的小伙子,再也不是当年的吴下阿蒙了。
4.下面对课文内容分析有误的一项是()A. 《童年》是德国作家高尔基创作的自传体小说三部曲中的第一部。
B. 《爸爸的花儿落了》节选自《城南旧事》,作者是台湾作家林海音,主要记叙了“我”的成长体验,同时也给我们塑造了一位可亲可敬的父亲形象。
C.《无选择的路》选自《中外哲理诗精选》,美国诗人弗罗斯特。
D. 《丑小鸭》是一则童话,作者是丹麦的安徒生。
5.选择修辞判断正确的一项填入括号内 ( )(1) 我常想,北大就是一条生命饱满的河流。
(2) 他们部队自己会配制农药,会往山上撒化肥,会开拖拉机,会做小生意。
(3) 手掌大的地方怎么能做游戏?(4) 柳树病了,枝条儿全都垂下来。
A.比喻排比夸张拟人 B.夸张排比比喻拟人C.拟人夸张比喻排比 D.比喻排比拟人夸张语文练习(四)1、下列加点字注音完全正确的一项是()。
A.救济.(jì))嫉.(jí)妒环谒.(yâ)憎.(zēng)恶B.炽.(chì)痛默契.(qì)祈.(qĭ)祷脑髓.(suǐ)C.哽咽.(yâ) 蝉蜕.(tuì) 可汗.(hán) 九曲.(qŭ)连环D.确凿.(záo)气氛.(fân)泥泞.(nìng)讪.笑(shàn)2 下列没有错别字的一项是()A.菜畦狂斓臃肿人迹罕至 B.叮嘱逼狹丑陋来势汹汹C.阻仰崎岖屏嶂荒草萋萋 D.澎湃怪诞谰语一泄万里3. 下面句子中加点的词语解释不正确...的一项是( )A.他处处挨啄,被排挤,被讪笑..,不仅在鸭群中是如此,连在鸡群中也是这样。
(讥笑,即讥讽和嘲笑)B.愿为市鞍马,从此替爷.征。
(爷:父亲。
)C.于是大家放开喉咙读一阵书,真是人声鼎沸....。
(人声鼎沸:形容人声喧闹。
鼎,古代的一种铜鋳的锅,一般是三足两耳。
沸,水开。
鼎沸,本意是锅里的水烧开了,发出响声。
)D.我对他很恭敬,因为我听说,他是本城中极方正..,质朴,博学的人。
(方正:做事情呆板,不知变通。
)4.对下面的句子所使用的修辞方法,判断正确的一项是()①将军百战死,壮士十年归。
②军书十二卷,卷卷有爷名。
③油蛉在这里低唱,蟋蟀们在这里弹琴。
④问女何所思,问女何所欲。
A .①拟人②比喻③夸张④复沓 B.①互文、排比②对偶③比喻④对偶C .①比喻②对偶③夸张④对偶 D.①互文、对偶②顶真③拟人④复沓5. 请选出下列说法错误的一项()A.《从百草园到三味书屋》选自鲁迅的《朝花夕拾》,文章通过对百草园和三味书屋的回忆,表现作者儿童时代对自然的热爱,对知识的追求,以及天真、幼稚、欢乐的心理。
B.《最后一课》是德国作家都德创作的短篇小说,韩麦尔先生是一位恪尽职守、道德高尚的教师形象和感人至深的爱国志士形象。
C.《木兰诗》选自宋朝郭茂倩编辑的《乐府诗集》,是南北朝时北方的一首乐府民歌。
D.《闻一多先生的说和做》作者是现代著名诗人臧克家。
闻一多,诗人、学者、民主战士,著作收在《闻一多全集》语文练习(五)1、加点字注音有误的一项是()A.狂澜.lán 督学dū炽痛chì回环曲.折qūB.嗥呜áo 哽咽 gěng 哺育 pǔ亦.复如是yìC.默契.qì崎岖 qí祈.祷 qí高山之巅.diānD.郝叟. sǒu 田垄. lǒng 镐头gǎo 惊涛澎湃.pài2、没有错别字的一组是()A. 紫滕亘古斑斓妇儒皆知B. 丰饶土壤鞠躬尽碎C. 默契屏障污秽疲惫不堪D.耻辱懊诲蚱蜢畏宿不前3.对词语解释的错误的一项是〔〕A骊歌:告别的歌。
迥乎不同:很不一样B弥高:更高踌躇: 犹豫不决地走来走去。
C叹为观止:赞美看到的事物好到了极点。
亢奋:极度兴奋。
D谰语:梦话污秽:肮脏的东西。
4.写出下列诗句没有用到修辞手法的是()A.朔气传金柝,寒光照铁衣。
B.我们民族的伟大精神,将要在你的哺育下/发扬滋长!C.东市买骏马,西市买鞍鞯,南市买辔头,北市买长鞭。
D.可汗问所欲,木兰不用尚书郎。
5.下列说法不正确的是()A. 阿廖莎是高尔基的乳名,也是《童年》中的主人公。
小说生动的再现了19世纪七八十年代俄罗斯下层人民的悲惨的生活状况B.贝多芬是德国作曲家,他的代表作有《田园交响曲》、《命运交响曲》。
C.《福楼拜的星期天》的作者是莫泊桑,他是法国作家,被称为短篇小说巨匠,代表作有《项链》、《羊脂球》等。
D.《孙权劝学》节选自南宋政治家、史学家司马光编的《资治通鉴》。
语文练习(六)1、下列加点词注音完全正确的一项是()A、确凿.(zuî)哽.咽(gěng)倜.傥.(tì dǎng) 迥(jiōng)乎不同B、执拗.(ǎo) 骊.歌(lí) 骇.人(gāi) 锲(qí)而不舍C、盔.甲(kuí) 花圃.(pǔ) 迸.溅(bâng) 兀兀(wù)穷年D、系.绳(jì) 伫.立(zhù) 沮.丧(jǔ) 兽铤(tǐng)亡群2..下列各组词语书写准确无误的一项是()A.马革果尸妇儒皆知心会神凝彷徨 B.博学多识燕然勒功忘乎所已迭起C.一拍即合当之无愧惹人注目磐石 D.和爱可亲死而后己一反既往滑稽3.下面词语运用恰当的一项是 ( )A.小宁在语文课上答错了一个题目,弄得面红耳赤,声名狼藉。
B.我们的班长德高望重,这次被评为全市优秀共青团员。
C. 奥运“样云”火炬所经之处,“中国加油、四川加油”的口号络绎不绝。
D. 做学问是一项艰辛的劳动,应踏踏实实,不能好高骛远。
4.请选出下列句子排序正确..的一项()①日子久了,他闭上眼睛,竹子的各种形象就像电影画面一样,一幕一幕地浮现在他的脑子里,画起竹来自然就容易了。
②据说,古代有个画家,善于画竹子。
③原来他在院子里种了许多竹子,经常观察竹子的形态。
④因此人们夸他胸有成竹。
⑤他随手挥几笔,就能画出一枝形态逼真、栩栩如生的竹子来。
A.①③②⑤④B. ②⑤④③①C. ②④⑤③①D. ③①④②⑤5.下列说法不正确的是()。
A.《黄河大合唱》选自《黄河大合唱》的第二部《黄河颂》,是一部大型合唱音乐作品,词作者是光未然,曲作者是冼星海。
