第四章习题点评修改(化原) [兼容模式]

合集下载

高等数学第四章不定积分课后习题详解.doc

第4章不定积分内容概要课后习题全解习题4-11.求下列不定积分：知识点：直接积分法的练习——求不定积分的基本方法。

思路分析：利用不定积分的运算性质和基本积分公式，直接求出不定积分！★(1)思路: 被积函数52x -=，由积分表中的公式（2）可解。

解：532223x dx x C --==-+⎰★(2)dx-⎰ 思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：1141113332223()24dx x x dx x dx x dx x x C --=-=-=-+⎰⎰⎰⎰ ★(3)22x x dx +⎰（）思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：2232122ln 23x x x x dx dx x dx x C +=+=++⎰⎰⎰（）★(4)3)x dx -思路:根据不定积分的线性性质，将被积函数分为两项，分别积分。

解：3153222223)325x dx x dx x dx x x C -=-=-+⎰⎰⎰ ★★(5)4223311x x dx x +++⎰思路:观察到422223311311x x x x x ++=+++后，根据不定积分的线性性质，将被积函数分项，分别积分。

解：42232233113arctan 11x x dx x dx dx x x C x x ++=+=++++⎰⎰⎰ ★★(6)221x dx x +⎰思路:注意到222221111111x x x x x +-==-+++，根据不定积分的线性性质，将被积函数分项，分别积分。

解：2221arctan .11x dx dx dx x x C x x =-=-+++⎰⎰⎰ 注：容易看出(5)(6)两题的解题思路是一致的。

一般地，如果被积函数为一个有理的假分式，通常先将其分解为一个整式加上或减去一个真分式的形式，再分项积分。

★(7)x dx x x x⎰34134（-+-）2 思路:分项积分。

线性代数课后习题详解第四章

第四章矩阵的初等变换与线性方程组1．把下列矩阵化为行最简形矩阵：(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320;(3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--3403130212011312)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020********* )2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320 1312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫⎝⎛---310031001320 21233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫ ⎝⎛000031005010(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311 141312323~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311 )5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----221002210022100343112423213~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛-----1187701298804202111110 141312782~r r r r r r --+⎪⎪⎪⎪⎪⎭⎫⎝⎛--4100041000202011111034221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102021 32~r r +⎪⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012．在秩是r 的矩阵中,有没有等于0的1-r 阶子式?有没有等于0的r 阶子式?解在秩是r 的矩阵中,可能存在等于0的1-r 阶子式,也可能存在等于0的r 阶子式.例如，⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000000010000100001α3)(=αR 同时存在等于0的3阶子式和2阶子式.3．从矩阵A 中划去一行得到矩阵B ,问B A ,的秩的关系怎样? 解 )(A R ≥)(B R设r B R =)(，且B 的某个r 阶子式0≠D r .矩阵B 是由矩阵A 划去一行得到的，所以在A 中能找到与D r 相同的r 阶子式D r ，由于0≠=D D r r ，故而)()(B R A R ≥.4．求作一个秩是4的方阵,它的两个行向量是)0,0,1,0,1(,)0,0,0,1,1(- 解设54321,,,,ααααα为五维向量,且)0,0,1,0,1(1=α,)0,0,0,1,1(2-=α,则所求方阵可为,54321⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=αααααA 秩为4,不妨设⎪⎩⎪⎨⎧===)0,0,0,0,0(),0,0,0,0()0,,0,0,0(55443αααx x 取154==x x 故满足条件的一个方阵为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-00000100000100000011001015．求下列矩阵的秩,并求一个最高阶非零子式：(1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013; (2) ⎪⎪⎪⎭⎫⎝⎛-------815073131213123； (3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013r r 21~↔⎪⎪⎪⎭⎫ ⎝⎛---443120131211 ⎪⎪⎪⎭⎫⎝⎛------564056401211~12133r r r r 2000056401211~23秩为⎪⎪⎪⎭⎫ ⎝⎛----r r 二阶子式41113-=-．(2) ⎪⎪⎪⎭⎫⎝⎛-------815073131223123⎪⎪⎪⎭⎫ ⎝⎛---------152********117014431~27122113r r r r r r 200000591170144313~23秩为⎪⎪⎪⎭⎫ ⎝⎛-----r r .二阶子式71223-=-．(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---02301085235703273812434241322~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------023010********071210 131223~r r r r ++⎪⎪⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210344314211614~r r r r r r r r -÷÷↔↔⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000010*******002301秩为3 三阶子式07023855023085570≠=-=-．6．求解下列齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+++=-++=-++;0222,02,02432143214321x x x x x x x x x x x x (2)⎪⎩⎪⎨⎧=-++=--+=-++;05105,0363,02432143214321x x x x x x x x x x x x (3) ⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+;0742,0634,0723,05324321432143214321x x x x x x x x x x x x x x x x (4)⎪⎪⎩⎪⎪⎨⎧=++-=+-+=-+-=+-+.0327,01613114,02332,075434321432143214321x x x x x x x x x x x x x x x x解 (1) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛--212211121211⎪⎪⎪⎪⎭⎫⎝⎛---3410013100101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-==4443424134334x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x(2) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛----5110531631121⎪⎪⎪⎭⎫ ⎝⎛-000001001021~ 即得⎪⎪⎩⎪⎪⎨⎧===+-=4432242102x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10010*********k k x x x x(3) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132⎪⎪⎪⎪⎪⎭⎫⎝⎛1000010000100001~即得⎪⎪⎩⎪⎪⎨⎧====00004321x xx x故方程组的解为⎪⎪⎩⎪⎪⎨⎧====00004321x x x x(4) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--000000001720171910171317301~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x x x x故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛1017201713011719173214321k k x x x x7．求解下列非齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+=+-=-+;8311,10213,22421321321x x x x x x x x (2) ⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++;694,13283,542,432z y x z y x z y x z y x(3) ⎪⎩⎪⎨⎧=--+=+-+=+-+;12,2224,12w z y x w z y x w z y x (4) ⎪⎩⎪⎨⎧-=+-+=-+-=+-+;2534,4323,12w z y x w z y x w z y x解 (1) 对系数的增广矩阵施行行变换,有⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--60003411100833180311102132124~2)(=A R 而3)(=B R ,故方程组无解．(2) 对系数的增广矩阵施行行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201~ 即得⎪⎩⎪⎨⎧=+=--=zz z y z x 212亦即⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛021112k z y x(3) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫ ⎝⎛----111122122411112⎪⎪⎪⎭⎫ ⎝⎛-000000100011112~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧===++-=0212121w z z y y z y x 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00021010210012121k k w z y x(4) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛-----000007579751025341253414312311112~⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----000007579751076717101~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=++=w w z z w z y w z x 757975767171 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00757610797101757121k k w z y x8．λ取何值时,非齐次线性方程组 ⎪⎩⎪⎨⎧=++=++=++2321321321,,1λλλλλx x x x x x x x x (1)有唯一解；(2)无解；(3)有无穷多个解?解 (1) 0111111≠λλλ,即2,1-≠λ时方程组有唯一解.(2) )()(B R A R < ⎪⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011~λλλλλλλλλλ由0)1)(1(,0)2)(1(2≠+-=+-λλλλ 得2-=λ时,方程组无解.(3) 3)()(<=B R A R ,由0)1)(1()2)(1(2=+-=+-λλλλ, 得1=λ时,方程组有无穷多个解.9．非齐次线性方程组⎪⎩⎪⎨⎧=-+=+--=++-23213213212,2,22λλx x x x x x x x x 当λ取何值时有解？并求出它的解．解 ⎪⎪⎪⎪⎭⎫ ⎝⎛+-----⎪⎪⎪⎭⎫ ⎝⎛----=)2)(1(000)1(321101212111212112~2λλλλλλB方程组有解，须0)2)(1(=+-λλ得2,1-==λλ当1=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛001111321k x x x当2-=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛022111321k x x x10．设⎪⎩⎪⎨⎧--=-+--=--+=-+-,1)5(42,24)5(2,122)2(321321321λλλλx x x x x x x x x问λ为何值时,此方程组有唯一解、无解或有无穷多解？并在有无穷多解时求解．解 ⎪⎪⎪⎭⎫ ⎝⎛---------154224521222λλλλ初等行变换~⎪⎪⎪⎪⎪⎭⎫⎝⎛---------2)4)(1(2)10)(1(00111012251λλλλλλλλ 当0≠A ,即02)10()1(2≠--λλ 1≠∴λ且10≠λ时，有唯一解.当02)10)(1(=--λλ且02)4)(1(≠--λλ，即10=λ时，无解.当02)10)(1(=--λλ且02)4)(1(=--λλ，即1=λ时，有无穷多解.此时，增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛-000000001221原方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛00110201221321k k x x x (R k k ∈21,)11．试利用矩阵的初等变换，求下列方阵的逆矩阵：(1) ⎪⎪⎪⎭⎫⎝⎛323513123; (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023. 解（1）⎪⎪⎪⎭⎫ ⎝⎛100010001323513123⎪⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----10121121023200010023~⎪⎪⎪⎪⎪⎭⎫⎝⎛----2102121129227100010003~⎪⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267100010001~故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267(2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001~ 故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------1061263111010421112．(1) 设⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=132231,113122214B A ,求X 使B AX =;(2) 设⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛---=132321,433312120B A ,求X 使B XA =. 解 (1) ()⎪⎪⎪⎭⎫ ⎝⎛----=132231113122214B A 初等行变换~⎪⎪⎪⎭⎫ ⎝⎛--412315210100010001 ⎪⎪⎪⎭⎫ ⎝⎛--==∴-4123152101B A X (2) ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛132321433312120B A 初等列变换~⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---474112100010001 ⎪⎪⎭⎫ ⎝⎛---==∴-4741121BA X ．。

【新版】组合数学第四章习题解答范文

GG'{g(,g')gG,g'G'}, (g1,g1')(g2,g2')(g1g2,g1'g2'),
G×G’的单位元素是(e,e’),试证G×G’是群
(1)封闭性显然 (2)结合律显然
(3)逆元素显然 (4)单位元显然
优选
27
4.27 一个项链由7颗珠子装饰成的，其中两颗珠
子是红的，3颗是蓝的，其余两颗是绿的，问有多少
显然
优选
10
4.11 有一个3×3的正方形棋盘，若用红蓝色对这9 个格进行染色，要求两个格着红色，其余染蓝色，问有多少种着色方案。
P(x)1[1(x)94(1x)3(1x2)3 8
2(1x)1(x4)2(1x)1(x2)4]
(1+x)9中x2项的系数是c(9,2)=36
4(1+x)3(1+x2)3中x2项的系数是 4[c(3,2)c(3,0)+c(3,0)c(3,1)]=24
优选
4
证明：如果ak的阶为n, 则k与n互素，
证明：akn=e,且不存在m<n,使akm=e,则k与n互素, 设k与n不互素，存在h>1,k=hb,n=hc, kn=(hb)(hc),则(hb)c=kc=bn 因此akc=abn=e,c<n矛盾
优选
5
4.5 试证循环群的子群也是循环群。显然。
(1)不换色不动：p1=(1)(2)(3)(4)(5)(6)(7)(8)(9)…(13)(14)(15)(16) 逆时针转90 :p2=(1)(2)(3456)(789 10)(11 12)(13 14 15 16) 顺时针转90 :p3=(1)(2)(6543)(10 987)(11 12)(16 15 14 13) 转180 :p4=(1)(2)(35)(46)(79)(8 10)(11 12)(13 15)(14 16) (2)换色不动：p5=(12)(37)(48)(59)(6 10)(11 12)(13 14)(15 16) 逆时针转90 :p6=(12)(385 10)(6749)(11)(12)(16 15 14 13) 顺时针转90 :p7=(12)(10 583)(9476)(11)(12)(13 14 15 16) 转180 :p8=(12)(39)(4 10)(57)(68)(11 12)(13)(14)(15)(16) (16+2+2+4+0+2+2+4)/8=4(种方案)

有机化学第四章习题答案

p941.解释下列名词。

共轭效应互变异构1,4-加成亲核加成乙烯基化反应氢化热离域能(共轭能)超共轭效应双烯合成亲双烯体红外活性键的伸缩振动键的弯曲振动解：共轭效应：由于结构的原因，双键π电子云不再只定域在双键上，也有部分离域到分子的其它部分，即发生了键的离域。

这种离域效应叫共轭效应。

互变异构：在一般条件下，两个构造异构体可以迅速地相互转变的异构现象。

1,4-加成：一分子试剂加在共轭双键两端的加成反应。

亲核加成：由亲核试剂进攻而引起的加成反应。

乙烯基化反应：反应物分子中的氢原子被乙烯基取代的反应。

氢化热：每一摩尔烯烃催化加氢时放出的能量叫氢化热。

离域能(共轭能)：共轭分子中由于键的离域而导致分子的额外的稳定能，称为离域能。

超共轭效应：σ轨道与π轨道相互作用而引起的离域效应。

双烯合成：共轭二烯和某些具有碳碳双键的化合物发生1,4-加成，生成环状化合物的反应。

亲双烯体：在双烯合成中能和共轭二烯反应的重键化合物叫做亲双烯体。

红外活性：能吸收红外辐射的性质。

键的伸缩振动：只改变键长，而不改变键角的振动。

键的弯曲振动：只改变键角，而不改变键长的振动。

2．用系统命名法命名下列化合物：(1) (CH3)3CC≡CCH2CH3(2) HC≡CCH2Br (3) CH2=CHC≡CH (4)CH2=CHCH2CH2C≡CH (5) CH3CHClC≡CCH2CH3(6) CH3C≡CC(CH=CH2)=CHCH2CH3(7)解：(1) 2,2-二甲基-3-己炔(2) 3-溴丙炔(3) 1-丁烯-3-炔(4) 1-己烯-5-炔(5) 2-氯-3-己炔(6) 4 –乙烯基-4 –庚烯-2-炔(7) 1,3,5-己三烯3．写出下列化合物的构造式。

(1) 4 –甲基-1-戊炔(2) 3 –甲基-3-戊烯-1-炔(3) 二异丙基乙炔(4) 1,5 –己二炔(5) 异戊二烯(6) 丁苯橡胶(7) 乙基叔丁基乙炔解：(1) CH≡CCH2CH(CH3)CH3(2) CH≡CC(CH3)=CHCH3(3) (CH3)2CHC≡CCH(CH3)2(4) CH≡CCH2CH2C≡CH (5) CH2=C(CH3)CH=CH2(6) -[-CH2CH=CHCH2CH(C6H5)CH2-〕n- （7）CH3CH2C≡CC(CH3)34．写出1-丁炔与下列试剂作用的反应式。

程稼夫电磁学第二版第四章习题解析

前言：特别感谢质心教育的题库与解析，以及“程稼夫力学、电磁学习题答案详解”的作者前辈和血色の寂宁前辈的资料.4-1动生电动势，电路中的电流要使功率最大，应取最小值1，即.4-2原题图片和答案结果不符，现分两种情况：（1）按答案来：整体绕过o点且于磁感应强度平行的轴转动将运动分解为绕c的平动和转动，转动对电势差无贡献4-3（1）OP电势相等时，OP速度沿磁场方向，显然当OP位于YOZ平面时，OP电势相等（2）当OP在YOZ平面右侧即X＞0时，电势差（3）当OP在XOZ平面第一象限时，电势差最大4-4在任意时刻t，线圈中的电流为，则由电磁感应定律和欧姆定律得，该式也可以由能量得到4-5其中后一项式中与直杆平行，当与直杆方向垂直时，电动势绝对值最大故有.4-6对于回路有，故有力矩平衡故有.4-7（1）当转轮在磁场中旋转时，每一根轮辐上的感应电动势为四根辐条作为电源是并联的，轮子产生的感应电动势不变（2）根据戴维宁定理，将轮子作为电源，此时将外电路断路计算等效电动势. 4-8式中当转轮1和转轮2分别以ω1和ω2旋转并达到稳定时，闭合回路中感应电流为注意，因转轮1的四根轮辐并联，总电阻为；转轮2类似，其余连接导线、电刷、轮边缘的电阻均忽略不计.又，因转轮1和转轮2同方向旋转，ε1和ε2同方向，但在电路中的作用是彼此减弱的稳定转动时，转轮2所受磁力矩应与阻力矩抵消.磁力矩是四轮辐所受安培力产生的力矩，为式中是转轮2每根轮辐中的电流.阻力矩是阻力闸提供的力矩，因阻力恒为F，故有稳定将要向下滑动时安培力加滑动摩擦力等于重力分力解得可变电阻最大值匀速向上滑动时，电路中同时杆受力平衡，有联立解得.4-11注意题文描述中磁场竖直向上而所给图垂直于轨道平面，此处以文字为正.（1）下滑时，动生电动势与电源同向，故当加速下滑时，电流增大，V2读数增大，V1减小.（2）由牛顿第二定律及欧姆定律得：4-4-4-内电阻阻值负载电阻与内阻相等时，负载上功率最大.4-15平板的宽度d切割磁感线产生感应电动势，积累电荷产生电场，使自由电荷磁场力和4-16由受力平衡，；由力矩平衡，解得.4-17由于圆盘有厚度D，故当圆盘在磁场区域内竖直下落的速度为v时，在圆盘的厚度方向分离变量：两边积分：又初态，代入得：最大焦耳热：4-23（1）如图所示，当小球在管中任意位置x时，设该处的涡旋电场为E，则故式中r是小球在x位置时与O′的距离，式中的负号表示E的方向如图所示，即E与B的变化构成左手螺旋.因此，E的x分量为其中用到几何关系表示沿y轴正方向.小球所受洛仑兹力沿y方向，无x分量，为可见，即洛仑兹力沿y轴负方向小球在y方向还受管的支持力，因三力平衡，故管对小球的支持力为，于是，小球对管的作用力为.4-24法一：cd法二：记圆心为O，连接，.封闭回路中，与段无感生电动势，则.4-25由图中磁场方向及均匀减小，可知圆周上感应电动势方向为顺时针，大小为已知，联立解出故A、B两点电势差.4-26磁场变化产生感应电动势（负号代表逆时针方向）圆环电阻阻值，感应电流电功率.4-27回路以逆时针指向纸外为正，则磁通ab上解得做功.4-29K反向时，励磁电流反向，磁场反向，磁通量变化量大小为原来的两倍，方向相反.4-32根据自感定义，单匝线圈磁通为.4-36设原线圈电路电流为，副线圈电路电流为，由理想变压器性质由题整理得要求灯正常发光，所以算出额定电流，然后能得到每个回路上的电流.4-38（1）如图，由输入等效电路原理（2）原线圈上的电压；副线圈上的电压（3）变压比为.4-39（1）由题，安培力等于阻力（2）代入，（3）单位时间克服阻力做功单位时间电路中消耗代入得（2）当C2断路时，没有感应电流，C1中无互感电动势此时C2中只有互感电动势，a′、b′两端的电压为.。

编译原理(第三版)第4章课后练习及参考答案中石大版第4章课后练习及参考答案

第4章练习P72作业布置：P723，7，9，11提示1：判断两个正规式是否相等，应判断两个正规式所产生的正规集是否一样。

完成此项任务需要经过四个阶段：第一，画出正规式的NFA；第二，由NFA变换到DFA；第三，将DFA最小化；第四，画出最小化DFA的有限自动机。

如果要判断的正规式的最小化DFA的有限自动机是一样的，则正规式等价；反之，则不等价。

提示2：构造正规表达式的最小化的DFA方法是：首先，按规则将正规表达式用NFA表示；其次，使用ε-closure(Move())将NFA转变为DFA；最后使用子集法将DFA最小化。

对于这类题目要多做练习，熟能生巧。

解：由于从S 出发任何输入串都不能到达状态E 和F ，所以，状态E ，F 为多余的状态，不予考虑。

这样，可以写出文法G[S]对应的NFA M ：NFA M={k, Σ, f, S, Z}K={S, A, B, Q, D, Z} S={S} Z={Z} F(S, a)=A f(S, b)=Q F(A, a)=A f(A, b)=B f(A,b)=ZF(B, b)=D f(B, a)=QF(Q, a)=Q f(Q, b)=D f(Q,b)=Z F(D, b)=B f(D, a)=A NFA M 的状态转换图为：下表由子集法将NFA 转换为DFA ：a由上表可知：(1)因为C、D是DFA的终态，其他是非终态，可将状态集分成两个子集：P1={S, A, B, E, F}，P2={C, D}。

(2)因为{A, B}b={C, D}为终态，{S, E, F}b={B, E, F}为非终态，所以P1可划分为：P11={S, E, F}，P12={A, B}。

【免费下载】第四章课后习题解答

4.2.2 本题图表示测定运动体能的装置。

绳拴在腰间沿水平展开跨过理想滑轮，下悬重物50kg ，人用力向后蹬传送带而人的质心相对于地面不动，设传送带上侧以2m/s 的速率向后运动，问运动员对传送带做功否？功率如何？解：人作用在传送带上的力有向下的压力和水平向后的静摩擦力，压力方向与传送带位移方向垂直，所以压力不做功，但静摩擦力方向与传送带位移方向相同，所以静摩擦力对传送带做正功。

分析人受力情况，由质心定理可知，人与传送带之间的静摩擦力的大小f=mg ，所以，人对传送带做功的功率为：N = fv = mgv = 50×9.8×2 = 9.8×102（瓦）4.2.4一细线系一小球，小球在光滑水平桌面上沿螺旋线运动，线穿过桌中心光滑圆孔，用力F 向下拉绳，证明力F 对线做的功等与线作用于小球的拉力所做的功，线不可伸长。

证明：以圆孔为顶点建立极坐标，设小球的位置由r 1,θ1变为r 2,θ2，由于忽略绳的质量、伸长，不计摩擦，所以绳对球的拉力T=FFT F r r r r r r r T A A r r T r r F A r r T dr T Tdr dr F A =∴-=-=-==-==⎰⎰⎰),()()(2121211221214.3.1质量为m=0.5kg 的木块可在水平光滑直杆上滑动，木块与一不可伸长的轻绳相连，绳跨过一固定的光滑小环，绳端作用着大小不变的力T=50N ，木块在A 点时具有向右的速率v 0=6m/s ，求力T 将木块从A 拉至B 点时的速度。

解：以A 为原点建立图示坐标o-x ，木块由A 到B ，只有拉力T 做功：⎰⎰⎰+--===403)4()4(404022cos x dxx x T dx T dx F A θJx x x d x T 100)35(50|9)4(50|]9)4[(2]9)4[(]9)4[(402402/122504022/122=-⨯=+-=+-⨯-=+-+--=⎰-设木块到达B 时的速度为v ，由动能定理：221221mv mv A -=，方向向右s m v m A v /88.2065.0/1002/2220≈+⨯=+=ABx4.3.3 质量为m 的物体与轻弹簧相连，最初m 处于使弹簧既未压缩也未伸长的位置，并以速度v 0μ求证物体能达到的最远距离l 为=kmgl μ证明：质点m 由弹簧原长位置运动到最远位置l ，弹力F 和滑动摩擦力f 对质点做负功，导致质点动能由mv 02/2变为0。

并行程序设计导论第四章课后题答案-2024鲜版

2024/3/28
分布性
数据分布在多个处理单元中。
8
常见并行计算模型介绍
共享内存模型
所有处理器共享同一物理内存，通过读写共享内存实现处理器间的通信和同步。
消息传递模型
处理器拥有自己独立的内存空间，通过发送和接收消息实现处理器间的通信和同步。
数据并行模型
数据被划分为多个子集，每个子集分配给一个处理器进行处理，处理器之间无需通信和同步。
02
2024/3/28
03
任务同步
在并行执行任务过程中，需要确保任务之间的同步和协调，以避免任务之间的干扰和错误。
13
混合并行编程策略探讨
2024/3/28
混合并行模式
结合数据并行和任务并行的优点，将数据划分和任务划分相结合，实现更高效的并行处理。
并行算法设计
针对具体问题和应用场景，设计合适的并行算法，以充分利用混合并行的优势。
并行性能优化
通过分析并行程序的性能瓶颈，采用合适的优化策略，如减少通信开销、提高缓存利用率等，提高并行程序的执行效率。
14
04 同步与通信机制在并行程序中的应用
2024/3/28
15
同步机制原理及作用
2024/3/28
同步机制原理
通过设定同步点或同步操作，确保并行程序中的各个进程或线程在关键点上达到一致状态，避免数据竞争和结果不确定性。
重点复习并行程序设计的基本概念、原理和方法，理解并掌握相关术语和定义。通过对比和分析选项，找出正确答案。
简答题
在理解基本概念的基础上，结合实际应用场景和问题背景，进行深入分析和思考。注意答案的条理性和逻辑性，尽量用简洁明了的语言进行表述。
编程题

流体力学实验_第四章流速与流量测量 [兼容模式]

流体粘性的影响：需满足Re>200，在小雷诺数时，毕托管的标定系数将随雷诺数的变化而变化
管柄堵塞的影响：毕托管管柄堵塞使流体过流面积减小，流速增加，静压减小，总压不变。毕托管管柄直径≤1/50管道直径且插入深度≤管道半径时可忽略
横向流速梯度的影响：毕托管头部与流体之间的相互作用引起邻近流线的微小位移，使较高流速区的流线移至总压孔处，总压增大。通过测压位置修正。
考虑温度效应，可采用
E 2 (Tw Te )( A BU n )
n
分段拟合多项式，即 E 2 ( Ai BiU CiU 2 DiU 3 ) 1 40
将热线风速仪的输出电压E和已知流动速度U直接联系在一起，对每一个流速U，对应一个电压E值做出E-U曲线，也
就是校准曲线。
(1) 校准的原因
热线热膜探针的性能是随制造工艺、探针尺寸和金属丝、膜的材料而异的，即使是相同的材料、制造工艺、尺寸，其性能也不可能完全一样；
探针的性能和流体的温度、密度以及测量时的气压有关；探针的性能也和实验室环境条件、污染情况有关；探针使用后会发生老化；探针的性能和流速范围有关；探针在测量中是和仪器结合在一起使用的，真正的相应
对于给定的热线，e , R0 , A, B都为常数，因此 Iw, Rw,U 之间
存在确定的函数关系。
恒流静态方程
当工作电流 Iw＝常数时，Rw和U之间具有如下关系：
Rw

R0 ( A B Iw2e R0 ( A
U B
) U
)
恒流式热线风速仪
27
恒温静态方程
当工作电阻 Rw ＝常数时，Iw 和U之间具有如下关系：
Rw

第四章习题答案

复习题答案4.1 说明数据库开发的三个阶段以及各个阶段的主要任务？.•需求: 设计者和用户交流，获取抽样表单、报表、查询以及有关数据更新活动的说明。

这些需求将用于创建数据模型.•设计: 数据模型被转换成特定的数据库设计，包括数据库中各种表的设计、关联和约束设计等。

.•实现: 构建数据库，并向其中填充数据；同时建立各种查询、表单和报表。

4.2 什么是数据模型, 它的作用是什么?数据模型（Data Model）是数据特征的抽象，是数据库管理的教学形式框架。

数据库系统中用以提供信息表示和操作手段的形式构架。

数据模型包括数据库数据的结构部分、数据库数据的操作部分和数据库数据的约束条件。

4.3 什么是原型,它的作用是什么?A prototype is a working demonstration of selected portions of a future system. Aprototype is an easy way to show elements of the database model design to users and to get their feedback.原型是对将要开发的系统某些部分的模拟展示。

原型提供了一种简便的方法，使得我们可以更早向客户展示我们的数据库内部的元素并得到他们的反馈。

4.4 什么是用例,它的作用是什么?用例描述用户将如何使用新信息系统的各个特性和功能。

用例提供了需求的来源，并且可以用于验证数据模型、设计和实现方案。

4.5 举一个数据约束的示例工作时间必须大于0小时，小于65小时.4.6 举一个在数据库开发项目中需要记录业务规则的示例t.学生必须选择一个专业方向，但可以选择任何一个班级.4.7 什么是实体，请举例说明。

.实体是用户希望跟踪的对象. 例如对于Pacific Northwest Real Estate Agency(PNREA). 实体实例包括AGENT John Smith, PROPERTY 568 12th Street, andCASH_RECEIPT CR2004001.4.8 说明实体集和实体实例的区别.给定类型的实体被分为实体集。

离散数学_第_4_章习题解答讲解

第四章归结法原理习题与解答1. 用归结法证明：(1)(2)(3)(4)(5)(6)解(1) 首先将p→q,p→r，¬(p→q∧r)化为合取范式。

p→q⇔¬p∨qp→r⇔¬p∨r¬(p→q∧r)⇔¬(¬p∨(q∧r))⇔p∧(¬q∨¬r) 给出子句集{¬p∨q,¬p∨r,p,¬q∨¬r}的反驳如下。

⑴ ¬p∨q⑵ ¬p∨r⑶ p⑷ ¬q∨¬r⑸ q 由⑴和⑶由⑵和⑶⑹ r⑺ ¬r 由⑷和⑸⑻ □ 由⑹和⑺因此，p→q,p→r|=p→q∧r(2) 首先将p→r，q→r，¬(p∨q→r)化为合取范式。

p→r⇔¬p∨rq→r⇔¬q∨r¬(p∨q→r)⇔(p∨q)∧¬r给出子句集{¬p∨r,¬q∨r,p∨q,¬r}的反驳如下。

p→q∨r⇔¬p∨q∨r¬((p→q)∨(p→r))⇔¬((¬p∨q)∨(¬p∨r))⇔p∧¬q∧¬r 给出子句集{¬p∨q∨r,p,¬q,¬r}的反驳如下。

⑴ ¬p∨q∨r⑵ p⑶ ¬q⑷ ¬r⑸ q∨r 由⑴和⑵⑹ r 由⑶和⑸⑺ □ 由⑷和⑹因此，p→q∨r|=(p→q)∨(p→r)(4) 首先将p∧q→r,¬((p→r)∨(q→r))化为合取范式。

离散数学-第四章一阶逻辑的基本概念课后练习习题及答案

离散数学-第四章⼀阶逻辑的基本概念课后练习习题及答案第四章作业评分要求：1. 合计36分2. 给出每⼩题得分(注意: 写出扣分理由).3. 总得分在采分点1处正确设置.(解答时的具体格式参照教材及幻灯⽚)⼀在⼀阶逻辑中将下列命题符号化1 ⽕车都⽐轮船快.2 有的⽕车⽐有的汽车快.3 不存在⽐所有⽕车都快的汽车.4 说凡是汽车就⽐⽕车慢是不对的.(4⼩题，每题3分，总计12分。

每⼀⼩题正确设定谓词得1分，正确符号化得2分。

)1 设是⽕车, 是轮船, ⽐快x ( F(x) → (⽕车x⽐所有的轮船快) )x ( F(x) → (?y(G(y)→ H(x,y)) ) )xy(F(x)∧G(y)→H(x,y))2设是⽕车, 是汽车, ⽐快x ( F(x) ∧ (⽕车x⽐有的汽车快) )x ( F(x) ∧ (?y(G(y)∧H(x,y)) ))xy ( F(x)∧G(y)∧H(x,y) )3设是汽车, 是⽕车, ⽐快x ( F(x) ∧ (汽车x⽐所有⽕车都快) )x ( F(x) ∧ ( ?y(G(y)→H(x,y)) ))x ( F(x) ∧ ( ?y(G(y)→H(x,y)) ))xy ( F(x) ∧ ( G(y)→ H(x,y) ) )x?y ( F(x) ∧ ( G(y)→ H(x,y) ) )4 设是汽车, 是⽕车, ⽐慢x ( F(x) → (汽车x⽐所有⽕车慢) )x ( F(x) → ( ?y(G(y)→ H(x,y)) ))x ( F(x) → ( ?y(G(y)→ H(x,y)) ))x?y ( F(x)∧G(y)→ H(x,y) )⼆给定解释I如下.a) 个体域.b) 特定元素.c) 上的函数.d) 上的谓词.给出下列各式在I下的解释, 并讨论它们的真值. 1234(4⼩题，每题3分，总计12分。

每⼀⼩题正确写出解释下的公式得2分，正确给出真值得1分。

)1 “对任意⾃然数, ”假2 “对任意⾃然数, 如果, 则.”假3 “对任意⾃然数, 存在⾃然数, 使得.”真4 “存在⾃然数, 使得.”真三判断下列各式的类型1234(4⼩题，每题3分，总计12分。

物理学简明教程第四章课后习题答案高等教出版社

物理学简明教程第四章课后习题答案高等教出版社第四章机械振动与机械波4-1 一个质点作简谐运动，振幅为A ，在起始时刻质点的位移为2A -，且向x 轴正方向运动，代表此简谐运动的旋转矢量为（）题4-１图分析与解（B ）图中旋转矢量的矢端在x 轴上投影点的位移为－A /2，且投影点的运动方向指向Ox 轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为（B ）．4-2 一简谐运动曲线如图（a ）所示，则运动周期是（）(A) 2.62 s (B) 2.40 s (C) 2.20 s （D ）2.00 s题4-２图分析与解由振动曲线可知，初始时刻质点的位移为A /2，且向x 轴正方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为-．振动曲线上给出质点从A /2 处运动到x =0处所需时间为1 s ，由对应旋转矢量图可知相应的相位差65232πππϕ=+=∆，则角频率1s rad 65Δ/Δ-⋅==πϕωt ，周期s 40.22==ωπT .故选（B ）．4-3 两个同周期简谐运动曲线如图（a ）所示， x 1的相位比x 2的相位（）3/π2（A ）落后2π（B ）超前2π（C ）落后π（D ）超前π 分析与解由振动曲线图作出相应的旋转矢量图（b ）即可得到答案为（B ）．题4 -３图4-4 两个同振动方向、同频率、振幅均为A 的简谐运动合成后，振幅仍为A ，则这两个简谐运动的相位差为（）（A ）60 （B ）90 （C ）120 （D ）180分析与解由旋转矢量图可知两个简谐运动1和2的相位差为120 时，合成后的简谐运动3的振幅仍为A .正确答案为（C ）．题4-4图4-5 若简谐运动方程为⎪⎭⎫ ⎝⎛+=4ππ20cos 10.0t x ，式中x 的单位为m ，t 的单位为s.求：（1）振幅、频率、角频率、周期和初相；（2）s 2=t 时的位移、速度和加速度．分析可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果．解（1）将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得：振幅A ＝0.10m ，角频率1s rad π20-⋅=ω，初相ϕ＝0.25π，则周期s 1.0/π2==ωT ，频率Hz /1T =v ．（２）s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a4-6 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T ＝0.50ｓ．当t ＝0 时，（1）物体在正方向端点；（2）物体在平衡位置、向负方向运动；（3）物体在x ＝-1.0×10-2m 处，向负方向运动；（4）物体在x ＝-1.0×10-2 m 处，向正方向运动．求以上各种情况的运动方程．分析在振幅A 和周期T 已知的条件下，确定初相φ是求解简谐运动方程的关键．初相的确定通常有两种方法．（1）解析法：由振动方程出发，根据初始条件，即t ＝0 时，x ＝x 0和v ＝v 0来确定φ值．（2）旋转矢量法：如图（a ）所示，将质点P 在Ox 轴上振动的初始位置x 0和速度v 0的方向与旋转矢量图相对应来确定φ．旋转矢量法比较直观、方便，在分析中常采用．题4-6图解由题给条件知A ＝2.0 ×10-2 m ，1s π4/2-==T ω，而初相φ可采用分析中的两种不同方法来求．解析法：根据简谐运动方程()ϕω+=t A x cos ，当0t =时有()ϕω+=t A x cos 0，sin 0ϕωA -=v ．当（1）A x =0时，1cos 1=ϕ，则01=ϕ；（2）00=x 时，0cos 2=ϕ，2π2±=ϕ，因00<v ，取2π2=ϕ；（3）m 100120-⨯=.x 时，50cos 3.=ϕ，3π3±=ϕ，由00<v ，取3π3=ϕ；（4）m 100120-⨯-=.x 时，50cos 4.-=ϕ，3ππ4±=ϕ，由00>v ，取3π44=ϕ．旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b ）所示，它们所对应的初相分别为01=ϕ，2π2=ϕ，3π3=ϕ，3π44=ϕ．振幅A 、角频率ω、初相φ均确定后，则各相应状态下的运动方程为（1）()m t πcos4100.22-⨯=x（2）()()m /2πt π4cos 100.22+⨯=-x（3）()()m /3πt π4cos 100.22+⨯=-x（4）()()m /3π4t π4cos 100.22+⨯=-x 4-7 有一弹簧，当其下端挂一质量为m 的物体时，伸长量为9.8 ×10-2 m ．若使物体上、下振动，且规定向下为正方向．（1）当t ＝0 时，物体在平衡位置上方8.0 ×10-2ｍ处，由静止开始向下运动，求运动方程．（2）当t ＝０时，物体在平衡位置并以0.6ｍ·s -1的速度向上运动，求运动方程．分析求运动方程，也就是要确定振动的三个特征物理量A 、ω和φ．其中振动的角频率是由弹簧振子系统的固有性质（振子质量m 及弹簧劲度系数k ）决定的，即ω=k 可根据物体受力平衡时弹簧的伸长来计算；振幅A 和初相φ需要根据初始条件确定．题4-7图解物体受力平衡时，弹性力F 与重力P 的大小相等，即F ＝mg ．而此时弹簧的伸长量Δl ＝9.8 ×10-2m ．则弹簧的劲度系数k ＝F ／Δl ＝mg ／Δl ．系统作简谐运动的角频率为1s 10-=∆==l g m k //ω（1）设系统平衡时，物体所在处为坐标原点，向下为x 轴正向．由初始条件t ＝0 时，x 10＝8.0 ×10-2 m 、v 10＝0 可得振幅()m 10082210210-⨯=+=./ωv x A ；应用旋转矢量法可确定初相π1=ϕ［图（a ）］．则运动方程为()()m π10t cos 100.821+⨯=-x（2）t ＝０时，x 20＝0、v 20＝0.6 ｍ·s -1，同理可得()m 100622202202-⨯=+=./ωv x A ；2/π2=ϕ［图（b ）］．则运动方程为 ()()m π5.010t cos 100.622+⨯=-x4-8 某振动质点的x -t 曲线如图（a ）所示，试求：（1）运动方程；（2）点P 对应的相位；（3）到达点P 相应位置所需的时间．分析由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题．本题就是要通过x －t 图线确定振动的三个特征量A 、ω和0ϕ，从而写出运动方程．曲线最大幅值即为振幅A ；而ω、0ϕ通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比较方便．解（1）质点振动振幅A ＝0.10 ｍ．而由振动曲线可画出t 0＝0 和t 1＝4 ｓ时旋转矢量，如图（b ）所示．由图可见初相3/π0-=ϕ（或3/π50=ϕ），而由()3201//ππω+=-t t 得1s 24/π5-=ω，则运动方程为()m 3/π24π5cos 10.0⎪⎭⎫ ⎝⎛-=t x题4-8图（2）图（a ）中点P 的位置是质点从A ／2 处运动到正向的端点处．对应的旋转矢量图如图（c ）所示．当初相取3/π0-=ϕ时，点P 的相位为()000=-+=p p t ωϕϕ（如果初相取成3/π50=ϕ，则点P 相应的相位应表示为()π200=-+=p p t ωϕϕ．（3）由旋转矢量图可得()3/π0=-p t ω，则s 61.=p t ．4-9 质量为10 g 的物体沿x 的轴作简谐运动，振幅A =10 cm ，周期T =4.0 s ，t =0 时物体的位移为，cm 0.50-=x 且物体朝x 轴负方向运动，求（1）t =1.0 s时物体的位移；（2）t =1.0 s 时物体受的力；（3）t =0之后何时物体第一次到达x =5.0 cm 处；（4）第二次和第一次经过x =5.0 cm 处的时间间隔.分析：根据题给条件可以先写出物体简谐运动方程)cos(ϕω+=t A x .其中振幅A ，角频率Tπ2=ω均已知，而初相ϕ可由题给初始条件利用旋转矢量法方便求出. 有了运动方程，t 时刻位移x 和t 时刻物体受力x m ma F 2ω-==也就可以求出. 对于（3）、（4）两问均可通过作旋转矢量图并根据公式t ∆=∆ωϕ很方便求解.解由题给条件画出t =0时该简谐运动的旋转矢量图如图（a ）所示，可知初相3π2=ϕ.而A =0.10 m ，1s 2ππ2-==T ω.则简谐运动方程为 m )3π22πcos(10.0+=t x (1)t =1.0 s 时物体的位移m 1066.8m )3π22π0.1cos(10.02-⨯-=+⨯=x（2）t =1.0 s 时物体受力N1014.2N )1066.8()2π(101032232---⨯=⨯-⨯⨯⨯-=-=x m F ω （3）设t =0时刻后，物体第一次到达x =5.0 cm 处的时刻为t 1，画出t =0和t =t 1时刻的旋转矢量图，如图（b ）所示，由图可知，A 1与A 的相位差为π，由t ∆=∆ωϕ得s 2s 2/ππ1==∆=ωϕt （4）设t =0时刻后，物体第二次到达x =5.0 cm 处的时刻为t 2,画出t =t 1和t = t 2时刻的旋转矢量图，如图（c ）所示，由图可知，A 2与A 1的相位差为3π2，故有 s 34s 2/π3/π212==∆=-=∆ωϕt t t题 4-9 图4-10 图（a ）为一简谐运动质点的速度与时间的关系曲线，且振幅为2cm ，求（1）振动周期；（2）加速度的最大值；（3）运动方程．分析根据v -t 图可知速度的最大值v max ，由v max ＝A ω可求出角频率ω，进而可求出周期T 和加速度的最大值a max ＝A ω2．在要求的简谐运动方程x ＝A cos（ωt ＋φ）中，因为A 和ω已得出，故只要求初相位φ即可．由v －t 曲线图可以知道，当t ＝0 时，质点运动速度v 0＝v max /2 ＝A ω/2，之后速度越来越大，因此可以判断出质点沿x 轴正向向着平衡点运动．利用v 0＝－A ωsin φ就可求出φ．解（1）由ωA v =max 得1s 51-=.ω，则s 2.4/π2==ωT（2）222max s m 1054--⋅⨯==.ωA a（3）从分析中已知2/sin 0ωA ωA =-=v ，即21sin /-=ϕ6/π5,6/π--=ϕ因为质点沿x 轴正向向平衡位置运动，则取6/π5-=，其旋转矢量图如图（b ）所示．则运动方程为()cm 6π55.1cos 2⎪⎭⎫ ⎝⎛-=t x题4-10图4-11 有一单摆，长为1.0m ，最大摆角为5°，如图所示．（1）求摆的角频率和周期；（2）设开始时摆角最大，试写出此单摆的运动方程；（3）摆角为3°时的角速度和摆球的线速度各为多少？题4-11图分析单摆在摆角较小时（θ＜5°）的摆动，其角量θ与时间的关系可表示为简谐运动方程()ϕωθθ+=t cos max ，其中角频率ω仍由该系统的性质（重力加速度g 和绳长l ）决定，即l g /=ω．初相φ与摆角θ，质点的角速度与旋转矢量的角速度（角频率）均是不同的物理概念，必须注意区分．解（1）单摆角频率及周期分别为s 01.2/π2;s 13.3/1====-ωT l g ω（2）由0=t 时o max 5==θθ可得振动初相0=ϕ，则以角量表示的简谐运动方程为t θ13.3cos 36π= （３）摆角为3°时，有()60cos max ./==+θθϕωt ，则这时质点的角速度为()()1max 2max max s 2180800cos 1sin /d d --=-=+--=+-=..ωθϕωωθϕωωθθt t t线速度的大小为1s m 218.0/d d -⋅-==t l v θ讨论质点的线速度和角速度也可通过机械能守恒定律求解，但结果会有极微小的差别．这是因为在导出简谐运动方程时曾取θθ≈sin ，所以，单摆的简谐运动方程仅在θ较小时成立．4-12 如图（a ）所示，质量为1.0 ×10-2kg 的子弹，以500m ·s -1的速度射入木块，并嵌在木块中，同时使弹簧压缩从而作简谐运动，设木块的质量为4.99 kg ，弹簧的劲度系数为8.0 ×103 N ·m -1，若以弹簧原长时物体所在处为坐标原点，向左为x 轴正向，求简谐运动方程．题4-12图分析可分为两个过程讨论．首先是子弹射入木块的过程，在此过程中，子弹和木块组成的系统满足动量守恒，因而可以确定它们共同运动的初速度v 0，即振动的初速度．随后的过程是以子弹和木块为弹簧振子作简谐运动．它的角频率由振子质量m 1＋m 2和弹簧的劲度系数k 确定，振幅和初相可根据初始条件（初速度v 0和初位移x 0）求得．初相位仍可用旋转矢量法求．解振动系统的角频率为 ()121s 40-=+=m m k /ω 由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v 0为12110s m 0.1-⋅=+=m m v m v 又因初始位移x 0＝0，则振动系统的振幅为 ()m 105.2//202020-⨯==+=ωωx A v v 图（b ）给出了弹簧振子的旋转矢量图，从图中可知初相位2/π0=ϕ，则简谐运动方程为()()m π0.540cos 105.22+⨯=-t x4-13 如图（a ）所示，一劲度系数为k 的轻弹簧，其下挂有一质量为m 1的空盘．现有一质量为m 2的物体从盘上方高为h 处自由落入盘中，并和盘粘在一起振动．问：（1）此时的振动周期与空盘作振动的周期有何不同？（2）此时的振幅为多大？题4-13图分析原有空盘振动系统由于下落物体的加入，振子质量由m 1变为m 1 + m 2，因此新系统的角频率（或周期）要改变．由于()2020/ωx A v +=，因此，确定初始速度v 0和初始位移x 0是求解振幅A 的关键．物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度v 0，这也是该振动系统的初始速度．在确定初始时刻的位移x 0时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置．因此，本题中初始位移x 0，也就是空盘时的平衡位置相对新系统的平衡位置的位移．解（1）空盘时和物体落入盘中后的振动周期分别为k m ωT /π2/π21== ()k m m ωT /π2/π221+='='可见T ′＞T ，即振动周期变大了．（2）如图（b ）所示，取新系统的平衡位置为坐标原点O ．则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即g km g k m m k g m l l x 2211210-=+-=-= 式中k g m l 11=为空盘静止时弹簧的伸长量，l 2＝g km m 21+为物体粘在盘上后，静止时弹簧的伸长量．由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度gh m m m m m m 22122120+=+=v v 式中gh 2=v 是物体由h 高下落至盘时的速度．故系统振动的振幅为 ()gm m kh k g m x A )(21/2122020++='+=ωv 本题也可用机械能守恒定律求振幅A ．4-14 质量为0.10kg 的物体，以振幅1.0×10-2 m 作简谐运动，其最大加速度为4.0 ｍ·s -1求：（1）振动的周期；（2）物体通过平衡位置时的总能量与动能；（3）物体在何处其动能和势能相等？（4）当物体的位移大小为振幅的一半时，动能、势能各占总能量的多少？分析在简谐运动过程中，物体的最大加速度2max ωA a =，由此可确定振动的周期T ．另外，在简谐运动过程中机械能是守恒的，其中动能和势能互相交替转化，其总能量E ＝kA 2/2．当动能与势能相等时，E k ＝E P ＝kA 2/4．因而可求解本题．解（1）由分析可得振动周期s 314.0/π2/π2max ===a A ωT（2）当物体处于平衡位置时，系统的势能为零，由机械能守恒可得系统的动能等于总能量，即J 100221213max 22k -⨯====.m Aa m A E E ω （3）设振子在位移x 0处动能与势能相等，则有42220//kA kx = 得m 100772230-⨯±=±=./A x（４）物体位移的大小为振幅的一半（即2x A =/）时的势能为4221212P /E A k kx E =⎪⎭⎫ ⎝⎛== 则动能为43P K /E E E E =-=4-15 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ；()()m π25.010cos 06.02+=t x ．求：（1）合振动的振幅及初相；（2）若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .，则3ϕ为多少时，x 1＋x 3的振幅最大？又3ϕ为多少时，x 2＋x 3的振幅最小？题4-15图分析可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动的合成仍为一简谐运动，其角频率不变；合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ，其大小与两个分振动的初相差12ϕϕ-相关．而合振动的初相位()()[]22112211cos cos sin sin arctanϕϕϕϕϕA A A A ++=/ 解（1）作两个简谐运动合成的旋转矢量图（如图）．因为2/πΔ12-=-=ϕϕϕ，故合振动振幅为 ()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A合振动初相位()()[]rad 1.48arctan11cos cos sin sin arctan22112211==++=ϕϕϕϕϕA A A A /（2）要使x 1＋x 3振幅最大，即两振动同相，则由π2Δk =ϕ得,...2,1,0,π75.0π2π213±±=+=+=k k k ϕϕ要使x 1＋x 3的振幅最小，即两振动反相，则由()π12Δ+=k ϕ得(),...2,1,0,π25.1π2π1223±±=+=++=k k k ϕϕ4-16 两个同频率的简谐运动1 和2 的振动曲线如图（a ）所示，求（1）两简谐运动的运动方程x 1和x 2；（2）在同一图中画出两简谐运动的旋转矢量，并比较两振动的相位关系；（3）若两简谐运动叠加，求合振动的运动方程．分析振动图已给出了两个简谐运动的振幅和周期，因此只要利用图中所给初始条件，由旋转矢量法或解析法求出初相位，便可得两个简谐运动的方程．解（1）由振动曲线可知，A ＝0.1 ｍ，T ＝2ｓ，则ω＝2π／T ＝πｓ-1．曲线1表示质点初始时刻在x ＝0 处且向x 轴正向运动，因此φ1＝－π／2；曲线2 表示质点初始时刻在x ＝A /2 处且向x 轴负向运动，因此φ2＝π／3．它们的旋转矢量图如图（b ）所示．则两振动的运动方程分别为()()m 2/ππcos 1.01-=t x 和（2）由图（b ）可知振动2超前振动1 的相位为5π／6．（3）()ϕω+'=+=t A x x x cos 21其中()m 0520cos 212212221.=-++='ϕϕA A A A A ()12π0.268arctan cos cos sin sin arctan 22112211-=-=++=ϕϕϕϕϕA A A A 则合振动的运动方程为 ()()m π/12πc o s 052.0-=t x题4-16 图4-17 图（a ）表示t ＝0 时的简谐波的波形图，波沿x 轴正方向传播，图（b ）为一质点的振动曲线．则图（a ）中所表示的x ＝0 处振动的初相位与图（b ）所表示的振动的初相位分别为（）()()m 3/ππcos 1.02+=t x题4-17 图（Ａ）均为零（Ｂ）均为2π （Ｃ）均为2π- （Ｄ）2π与2π-（Ｅ）2π-与2π 分析与解本题给了两个很相似的曲线图，但本质却完全不同．求解本题要弄清振动图和波形图不同的物理意义．图（a ）描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态．其中原点处质点位移为零，其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向，利用旋转矢量法可以方便的求出该质点振动的初相位为π/2．而图（b ）是一个质点的振动曲线图，该质点在t ＝0 时位移为0，t ＞0 时，由曲线形状可知，质点向y 轴正向运动，故由旋转矢量法可判知初相位为－π/2，答案为（D ）．4-18一横波以速度u 沿x 轴负方向传播，t 时刻波形曲线如图（a ）所示，则该时刻（）（A ）A 点相位为π（B ）B 点静止不动（C ）C 点相位为2π3（D ）D 点向上运动分析与解由波形曲线可知，波沿x 轴负向传播，B 、D 处质点均向y 轴负方向运动，且B 处质点在运动速度最快的位置. 因此答案（B ）和（D ）不对. A 处质点位于正最大位移处，C 处质点位于平衡位置且向y 轴正方向运动，它们的旋转矢量图如图（b ）所示.A 、C 点的相位分别为0和2π3.故答案为（C ）题 4-18 图4-19 如图所示，两列波长为λ的相干波在点P 相遇．波在点S 1振动的初相是φ1，点S 1到点P 的距离是r 1．波在点S 2的初相是φ2，点S 2到点P 的距离是r 2，以k 代表零或正、负整数，则点P 是干涉极大的条件为（）()()()()()()π2/π2A π2/π2A π2A πA 211212121212k r r k r r k k r r =-+-=-+-=-=-λϕϕλϕϕϕϕ 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =，而两列波传到P 点时的两分振动相位差为()λϕϕϕ/π2Δ1212r r ---=，故选项（D ）正确．题4-19图4-20 一横波在沿绳子传播时的波动方程为()x y ππ5.2cos 20.0-=，式中y 的单位为m ，t 的单位为s ．（1）求波的振幅、波速、频率及波长；（2）求绳上质点振动时的最大速度；（3）分别画出t ＝1s 和t ＝2 s 时的波形，并指出波峰和波谷．画出x ＝1.0 ｍ处质点的振动曲线并讨论其与波形图的不同．分析（1）已知波动方程（又称波函数）求波动的特征量（波速u 、频率υ、振幅A 及波长λ等），通常采用比较法．将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写，然后通过比较确定各特征量（式中u x 前“-”、“+”的选取分别对应波沿x 轴正向和负向传播）．比较法思路清晰、求解简便，是一种常用的解题方法．（2）讨论波动问题，要理解振动物理量与波动物理量之间的内在联系与区别．例如区分质点的振动速度与波速的不同，振动速度是质点的运动速度，即v ＝d y /d t ；而波速是波线上质点运动状态的传播速度（也称相位的传播速度、波形的传播速度或能量的传播速度），其大小由介质的性质决定．介质不变，波速保持恒定．（3）将不同时刻的t 值代入已知波动方程，便可以得到不同时刻的波形方程y ＝y （x ），从而作出波形图．而将确定的x 值代入波动方程，便可以得到该位置处质点的运动方程y ＝y （t ），从而作出振动图．解（1）将已知波动方程表示为()[]()m 5.2/π5.2cos 20.0x t y -=与一般表达式()[]0cos ϕω+-=u x t A y /比较，可得0s m 52m 20001=⋅==-ϕ,.,.u A则m 0.2/,Hz 25.1π2/====v u λωv（2）绳上质点的振动速度()[]()1s m 5.2/π5.2sin π5.0d /d -⋅--==x t t y v则1max s m 57.1-⋅=v（3）t ＝1ｓ和t ＝2ｓ时的波形方程分别为 ()()()()m ππ5cos 20.0m ππ5.2cos 20.021x y x y -=-=波形图如图（a ）所示． x ＝1.0m 处质点的运动方程为()()m π5.2cos 20.0t y -=振动图线如图（b ）所示．波形图与振动图虽在图形上相似，但却有着本质的区别．前者表示某确定时刻波线上所有质点的位移情况，而后者则表示某确定位置的一个质点，其位移随时间变化的情况．题4-20图4-21 波源作简谐运动，其运动方程为()m t πcos240100.43-⨯=y ，它所形成的波形以30ｍ·ｓ-1的速度沿一直线传播．（1）求波的周期及波长；（2）写出波动方程．分析已知波源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式进行比较，求出振幅A 、角频率ω及初相φ0，而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的．再利用题中已知的波速u 及公式ω＝2πν＝2π／T 和λ＝uT 即可求解．解（1）由已知的运动方程可知，质点振动的角频率1s π240-=ω．根据分析中所述，波的周期就是振动的周期，故有s 1033.8/π23-⨯==ωT波长为λ＝uT ＝0.25 ｍ（２）将已知的波源运动方程与简谐运动方程的一般形式比较后可得A ＝4.0 ×10-3m ，1s π240-=ω，φ0＝0故以波源为原点，沿x 轴正向传播的波的波动方程为()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=-4-22 图示为平面简谐波在t ＝0 时的波形图，设此简谐波的频率为250Hz ，且此时图中质点P 的运动方向向上．求：（1）该波的波动方程；（2）在距原点O 为7.5 m 处质点的运动方程与t ＝0 时该点的振动速度．分析（1）从波形曲线图获取波的特征量，从而写出波动方程是建立波动方程的又一途径．具体步骤为：1. 从波形图得出波长λ、振幅A 和波速u ＝λυ；2. 根据点P 的运动趋势来判断波的传播方向，从而可确定原点处质点的运动趋向，并利用旋转矢量法确定其初相φ0．（2）在波动方程确定后，即可得到波线上距原点O 为x 处的运动方程y ＝y （t ），及该质点的振动速度υ＝d y /d t ．解（1）从图中得知，波的振幅A ＝0.10 m ，波长λ＝20.0m ，则波速u ＝λυ＝5.0 ×103ｍ·ｓ-1．根据t ＝0 时点P 向上运动，可知波沿Ox 轴负向传播，并判定此时位于原点处的质点将沿Oy 轴负方向运动．利用旋转矢量法可得其初相φ0＝π/3．故波动方程为()[]()[]()m 3/π5000/π500cos 10.0/cos 0++=++=x t u x t A y ϕω()ϕω+=t cos A y（2）距原点O 为x ＝7.5ｍ处质点的运动方程为()()m 12π13π5000.10cosy /t +=t ＝0 时该点的振动速度为 ()-10s m 40.6/12π13sin π50/d d ⋅=-===t t y v题4-22图4-23 平面简谐波的波动方程为()x t y π2π4cos 08.0-=,式中y 和x 的单位为m ，t 的单位为s,求：（1） t ＝2.1 s 时波源及距波源0.10m 两处的相位；（2）离波源0.80 m 及0.30 m 两处的相位差．解（1）将t ＝2.1 s 和x ＝0 代入题给波动方程，可得波源处的相位π4.81=ϕ将t ＝2.1 s 和x ′＝0.10 m 代入题给波动方程，得0.10 m 处的相位为π2.82=ϕ（2）从波动方程可知波长λ＝1.0 m ．这样，x 1＝0.80 m 与x 2＝0.30 m 两点间的相位差πΔπ2Δ=⋅=λϕx4-24 两相干波波源位于同一介质中的A 、B 两点，如图（a ）所示．其振幅相等、频率皆为100 Hz ，B 比A 的相位超前π．若A 、B 相距30.0m ，波速为u ＝400 m ·s -1，试求AB 连线上因干涉而静止的各点的位置．题4-24图分析两列相干波相遇时的相位差λϕϕϕr Δπ2Δ12--=．因此，两列振幅相同的相干波因干涉而静止的点的位置，可根据相消条件()π12Δ+=k ϕ获得．解以A 、B 两点的中点O 为原点，取坐标如图（b ）所示．两波的波长均为λ＝u /υ＝4.0 m ．在A 、B 连线上可分三个部分进行讨论．1. 位于点A 左侧部分()π14π2ΔA B A B -=---=r r ϕϕϕ因该范围内两列波相位差恒为2π的整数倍，故干涉后质点振动处处加强，没有静止的点．2. 位于点B 右侧部分()π16π2ΔA B A B =---=r r ϕϕϕ显然该范围内质点振动也都是加强，无干涉静止的点．3. 在A 、B 两点的连线间，设任意一点P 距原点为x ．因x r -=15B ，x r +=15A ，则两列波在点P 的相位差为()()π1/π2ΔA B A B +=---=x r r λϕϕϕ根据分析中所述，干涉静止的点应满足方程()()π152π1+=+k x x得()2,...1,0,k m 2±±==k x因x ≤15 m ，故k ≤7．即在A 、B 之间的连线上共有15 个静止点．4-25图（a ）是干涉型消声器结构的原理图，利用这一结构可以消除噪声．当发动机排气噪声声波经管道到达点A 时，分成两路而在点B 相遇，声波因干涉而相消．如果要消除频率为300 Hz 的发动机排气噪声，则图中弯管与直管的长度差Δr ＝r 2－r 1至少应为多少？（设声波速度为340 m ·s -1）题4-25图分析一列声波被分成两束后再相遇，将形成波的干涉现象．由干涉相消条件，可确定所需的波程差，即两管的长度差Δr ．解由分析可知，声波从点A 分开到点B 相遇，两列波的波程差Δr ＝r 2 - r 1，故它们的相位差为()λλϕ/Δπ2/π2Δ12r r r =-=由相消静止条件Δφ＝（2k ＋1）π，（k ＝0，±1，±2，…）得 Δr ＝（2k ＋1）λ／2根据题中要求令k ＝0 得Δr 至少应为m 57022.//===∆v u r λ讨论在实际应用中，由于噪声是由多种频率的声波混合而成，因而常将具有不同Δr 的消声单元串接起来以增加消除噪声的能力．图（b ）为安装在摩托车排气系统中的干涉消声器的结构原理图．4-26 一警车以25 m ·s -1的速度在静止的空气中行驶，假设车上警笛的频率为v =800 Hz ．求：（1）静止站在路边的人听到警车驶近和离去时的警笛声波频率；（2）如果警车追赶一辆速度为15m ·s -1的客车，则客车上人听到的警笛声波的频率是多少？（设空气中的声速u ＝330m ·s -1）分析由于声源与观察者之间的相对运动而产生声多普勒效应，由多普勒频率公式可解得结果．在处理这类问题时，不仅要分清观察者相对介质（空气）是静止还是运动，同时也要分清声源的运动状态．解（1）根据多普勒频率公式，当声源（警车）以速度υs ＝25 m ·s -1运动时，静止于路边的观察者所接收到的频率为su u v v υ =' 警车驶近观察者时，式中υs 前取“－”号，故有Hz 6.8651=-='su u v v υ 警车驶离观察者时，式中υs 前取“＋”号，故有Hz 7.7432=+='su u v v υ （2）客车的速度为0υ=15m ·s -1,声源（警车）与客车上的观察者作同向运动时，观察者收到的频率为Hz 2.82603=--='su u v v υυ 4-27 蝙蝠在洞穴中飞来飞去，能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39 kHz ，当它以声速的401的速度朝着表面平直的岩壁飞去时，试求它听到的从岩壁反射回来的超声波频率为多少？分析：由题意可知，蝙蝠既是波的发出者，又是波的接收者.设超声波的传播速度为u .首先，蝙蝠是声源，发出信号频率为v ，运动速度为40s u =υ，岩壁是接收者，利用多普勒频率公式，即可求得岩壁接收到的信号频率v '.经岩壁反射后频率不变，即岩壁发射信号频率为v '，这时蝙蝠是波的接收者，其运动速度为400u =υ，再次利用多普勒频率公式，可求得蝙蝠接收到的信号频率v ''. 解：将蝙蝠看成波源，则由分析可知，岩壁接收到的信号频率为sυ-='u uv v ，在蝙蝠接收岩壁反射信号时，又将它看成接收者.则蝙蝠接收到的信号频率为 kHz 41kHz 3940/1140/11/1/1s 0s 00=⨯-+=-+=-+='+=''v u u v u u v u u v υυυυυ。

无机化学第四章课后习题参考答案

第四章氧化和还原1、在下列两种物质中，分别按Mn,N元素的氧化值由低到高的顺序将各物质进行排列：（1）MnO, MnSO4, KMnO4, MnO(OH), K2MnO4, Mn(2) N2, NO2, N2O5, N2O, NH3, N2H42、指出下列反应中的氧化剂，还原剂以及它们相应的还原，氧化产物。

（1）SO2+ I2 + 2H2O →H2SO4 + 2HI（2）SnCl2 + 2HgCl2→SnCl4 + Hg2Cl2(3) 3I2 + 6NaOH →5NaI + NaIO3 + 3H2O3、用氧化值法配平下列氧化还原反应方程式：（1）Cu + H2SO4 (浓)→CuSO4 + SO2 + H2O（2）KMnO4 + S →MnO2 + K2SO4(3) As2S3+ HNO3 + H2O →H3AsO4 + H2SO4 + NO(4) (NH4)2Cr2O7→N2 + Cr2O3 + H2O(5) P4 + NaOH →PH3+ NaH2PO24、用离子-电子法配平下列氧化还原反应方程式：（1）Cr2O72-+ SO32+ + H+→Cr3+ + SO42-(2) PbO2(s) + Cl- + H+→Pb2+ (实际是PbCl42-) + Cl2(3) H2S + I2→I- + S(4) CrO2- + H2O2 + OH-→CrO42-(5) ClO3- + S2-→Cl- + S + OH-(6) KMnO4 + FeSO4 + H2SO4→MnSO4 + Fe2(SO4)3 + K2SO4 + H2O(7) KI + KIO3 + H2SO4→I2+ K2SO4(8) Ca(OH)2 + Cl2→Ca(ClO) 2 + CaCl2(9) Fe(OH)2 + H2O2→Fe(OH)3(10) Al + NO3-→[Al(OH) 4] - + NH3(11) ClO- + Fe(OH)3→Cl- + FeO42-(12) P + CuSO4→Cu3P + H3PO4 + H2SO45、把镁片和铁片分别放入浓度均为1 mol .L-1的镁盐和亚铁盐的溶液中，并组成一个原电池。

高等数学第4章课后习题答案(科学出版社)

第四章习题解答习题 4-11.求下列不定积分：(1)；(2) 2(23)d x x x +⎰；(3)⎰+)1(d 22x x x；(4) 2cot d x x ⎛⎫+⎪⎭⎰；(6) 21(1)x x -⎰； (7)1d 1cos 2xx +⎰；(9)221d sin cos x x x ⎰；(10){}max ||,1d x x ⎰.2.设某曲线上任意点处的切线的斜率等于该点横坐标的立方，又知该曲线通过原点，求此曲线方程.3.验证函数21sin 2x ，21cos 2x -，1cos 24x -是某同一函数的原函数.解答：1.求下列不定积分：（1）解53225125212d 1()3x x x C x C --+-==+=-++-⎰．（2）解：⎰+x x xd )32(2C xx x +3ln 29+6ln 62+2ln 24=（3）=+-=+⎰⎰⎰22221d d )1(d x x x x x x x C x x+--arctan 1(4) 解：⎰⎰⎰-+-=+-x x x x x x x d )1(csc d 11d )cot 11(2222=C x xx +cot arcsin（5）1131352222222242(2)d 235x x x x x x x x x C -==-+=-++⎰⎰(6) 33571244444214(1)(1)d ()d 47x x x x x x x x x C x ----=-⋅=-=++⎰⎰⎰(7) 解2111d d tan 1cos 22cos 2x x x C x x ==++⎰⎰ (8) 解：⎰x x x x d sin cos 2cos 22⎰⎰-=-=x xx x x x x x d )cos 1sin 1(d sin cos sin cos 222222 C x x +--=tan cot(9) 解：222222221sin cos 11d d d d sin cos sin cos cos sin x x x x x x x x x x x x +==+⎰⎰⎰⎰ 22sec d csc d tan cot x x x x x x C =+=-+⎰⎰(10) 解：},,1max{)(x x f =设⎪⎩⎪⎨⎧>≤≤--<-=1,11,11,)(x x x x x x f 则.上连续在),()(+∞-∞x f ，)(x F 则必存在原函数，1>,+211≤≤1,+1<,+21=)(32212x C x x C x x C x x F 须处处连续，有又)(x F)+21(lim =)+(lim 121→21→+C x C x x x ，,21112C C +-=+-即 )(lim )21(lim 21321C x C x x x +=+-+→→ ，,12123C C +=+即 ,1C C =联立并令.1,2132C C C C +==＋可得.1,12111,211,21},1max{22⎪⎪⎪⎩⎪⎪⎪⎨⎧>++≤≤-++-<+-=⎰x C x x C x x C x dx x 故2. 解：设所求曲线方程为)(x f y =，其上任一点),(y x 处切线的斜率为3d d x xy=，从而 ⎰+==C x x x y 4341d .由0)0(=y ，得0=C ，因此所求曲线方程为441x y =. 3.解：x 2sin 21x x cos sin =， x x x sin cos cos 212='⎪⎭⎫ ⎝⎛- x x x x cos sin 2sin 212cos 41=='⎪⎭⎫⎝⎛-所以x 2sin 21、 x 2cos 21-、 x 2cos 41-都是x x cos sin 的原函数.习题 4-2 1.求下列不定积分： (1) 1d 12x x -⎰; (2) 100(23)d x x -⎰;(3) 12ed xx x ⎰; (4)211sin()d x x x ⎰;(5) ⎰-294d x x;(7) 1d ln lnln x x x x⎰;(8)x e x d 11⎰+;(9)⎰+3xx dx ; (10)x x x x x d )cos 2(sin sin 2cos 2⎰+-; (11)3cos d x x ⎰; (12)⎰+x x d 412;(14)2sin d cos 6cos 12x xx x -+⎰;(15)x ; (16) dx x ⎰5cos(17) ⎰x x x d cos sin 52(18)cos5sin 4d x x x ⎰;(19)⎰+x xx d sin 1sin ; (20)x exd 112⎰+(21) xx ⎰;(22)x x⎰. 2. 求下列积分：（1） sin 2d x x x ⎰；（2）⎰-x e x xd 2；（3）()⎰-x x x d 1ln ；（4）(31)sin 3d x x x +⎰；（5）x x d sin3⎰；（6） e sin 2d x x x -⎰；（7） 2arctan d x x x ⎰；（8） 2cos d x x x ⎰；（9）x ；（10）⎰x x e xd sin ；（11）3csc d x x ⎰；（12）()d xf x x ''⎰.3.已知x x f 22tan )(sin ='，求函数)(x f .4. 已知xe xf -=)(，求不定积分⎰'x xx f d )(ln . 5. 求e d n xn I x x =⎰的递推公式，其中n 为自然数，并计算2I 的值．6. 已知)(u f 有二阶连续的导数，求∫d )e (′′e2x f x x；解答：1.求下列不定积分：(1) 解：令2u x =，有2sin 2d sin 2(2)d sin d cos x x x x x u u u C '===-+⎰⎰⎰，将2u x =回代，得2sin 2d x x ⎰cos 2x C =-+. (2) 解 10010010111(23)d (23)d(23)(23)3303x x x x x C -=---=--+⎰⎰ (3) 解：⎰x xexd 21C e x e x x +=)1-d( =11∫(4) 解：211111sin()d sin d()cos x C x x x x x=-=+⎰⎰ (5) 解：=-⎰294d x xc xx x x x +|323+2|ln 121=d 321+3+2141∫ (6) 解：x x x x d )ln (ln 12⎰+C xx x x x x +-==⎰ln 1)ln d()ln (12(7) 解：x x x x d ln ln ln 1⎰C x x x x x x +===⎰⎰ln ln ln )ln d(ln ln ln 1)d(ln ln ln ln 1(8) 解：x ee x e e e x e xxx x x x d )11(d 11d 11⎰⎰⎰+-=+-+=+=C e x x ++-)1ln( (9) 解令)0( 6>=t t x ，则⎰⎰+=+23536t t dtt x x dxdt tt t )111(62⎰+-+-=C t t t t ++-+-=))1ln(23(623C x x x x ++-+-=)1ln(6 6 32663(10) 解：)cos 2+(sin d )cos 2+(sin 1 =d )cos 2+(sin sin 2cos∫∫22x x x x x x x x x =C xx ++-cos 2sin 1(11) 解：⎰x x d cos 3⎰=x x x d cos cos 2)d(sin sin 12⎰-=x x C xx +-=3sin sin 3 (12) 解：∫∫2d 2+1121=d +4122x xx x =C x +2arctan 21. (13)解：2x 231arcsin d(arcsin )(arcsin )3x x x C ==+⎰．(14)解：22sin d d(cos 3)cos 6cos 12(cos 3)3x x x C x x x -=-=-+-+⎰⎰ (15) 解：x x x xd )1(arctan ⎰+)d()(1arctan 2d 1arctan 22x x xx x x ⎰⎰+=+=C x x x +==⎰2)(arctan)d(arctan arctan2(16) x x x x x x sin d )sin -1( =sin d cos =d cos ∫∫∫2245=C x x x ++-52sin 51sin 32sin .(17) ⎰⎰⎰+-=-=x x x x x x x x x x sin d )sin sin 2(sin sin d )sin 1(sin d cos sin 64222252c x x x ++-=753sin 71sin 52sin 31 (18) 解：C x x x x x x x x ++-=-=⎰⎰cos 219cos 181d 2sin 9sin d 4sin 5cos (19) 解：∫∫∫d )tan +sec (tan =d sin -1)sin +1(sin =d sin +1sin 22x x x x x xx x x x x ⎰-+=x x x x d )1sec sec (tan 2=C x x x +-+tan sec .(20) 解：令)1ln(212-=t x ，则t t t x d 1d 2-=，于是C t t t t t t t t x ex ++-=-=-⋅=+⎰⎰⎰11ln 21d 11d 11d 11222 =C x e e x x +-++-)212ln(2122(21) 解：设sin (0)2x a t t π=<<，d cos d x a t t =，则22421sin cos cos d sin 2d 4x x a t a t a t t a t t =⋅⋅=⋅⎰⎰⎰ 444111(1cos 4)d sin 48832a t t a t a t C =-=-+⎰ 44211sin cos (12sin )88a t a t t t C =--+42211arcsin 2)88x a a x C a =--+． (22) 解：令sec x a t =，d sec tan d x a t t t =⋅，则22tan sec tan d tan d (sec 1)d sec a t a t t t a t t a t t a t =⋅⋅==-⎰⎰⎰ (tan )a t t C =-+arccos )a a C x=-+．2.求下列不定积分（1）解：⎰x x x d 2sin )2cos d(21⎰-=x x ⎰+-=x x x x d 2cos 212cos 2 C x x x ++-=2sin 412cos 2（2）解：⎰-x e x x d 2⎰⎰---+-=-=x xe e x e x xx x d 2d 22⎰⎰-----+--=--=x e xe e x e x e x xx x x x d 22d 222C e xe ex x x x+---=---222（3）解：()⎰-x x x d 1ln ()⎰⎪⎪⎭⎫⎝⎛-=2d 1ln 2x x()⎰---=x x x x x d 11211ln 222 ()⎰⎪⎭⎫⎝⎛-++--=x x x x x d 111211ln 22()()C x x x x x +-----=1ln 2121411ln 222（4）(31)sin 3d x x x +⎰1(31)d(cos3)3x x =+-⎰ 1(31)cos3cos3d 3x x x x =-++⎰11(31)cos3sin 333x x x C =-+++.（5）解：令t x =3，则3t x =，t t dx d 32=原式⎰⎰-=⋅=t t t t t cos d 3d 3sin 22∫∫sin d 6+cos 3=d 2cos 3+cos 3=22t t t t t t tt t⎰-+-=t t t t t t d sin 6sin 6cos 32C t t t t t +++-=cos 6sin 6cos 32C x x x x x +++-=333332cos 6sin 6cos 3（6）解：因为⎰-x x e x d 2sin ⎰--=x e x d 2sin )2d(sin 2sin ⎰--+-=x e x e xx)d(2cos 22sin ⎰----=x x e x x e )2d(cos 22cos 22sin ⎰---+--=x e x e x e x x x⎰------=x x e x e x e x x x d 2sin 42cos 22sin于是⎰-x x exd 2sin C xe x e x x +--=--52cos 22sin（7）解：⎰x x x d arctan 2⎰⎰-==x x x x x x arctan d 3arctan 33d arctan 333∫d +131arctan 3=233x x x x x ⎰+-+-=x x xx x x x d 131arctan 3233 C x x x x +++-=)1ln(31arctan 3223 （8）解：⎰x x x d cos 2⎰⎰+=+=x x x x x x xd )2cos (21d 22cos 1⎰+=x x x x d 2cos 2142 ⎰+=x x x 2sin d 4142⎰-+=x x x x x d 2sin 412sin 4142 C x x x x +-+=2cos 812sin 4142 （9）解：⎰x x xd arcsin 1⎰⎰-==x x x x x x arcsind 2arcsin2d arcsin2∫d 11arcsin 2=x xxx C x x x +-+=12arcsin 2 （10）解：e sin d sin d e x xx x x =⎰⎰e sin e d sin x x x x =-⎰e sin e cos d x x x x x =-⎰e sin cos d e x x x x =-⎰e sin (e cos e d cos )x x x x x x =--⎰ e sin e cos e sin d x x x x x x x =--⎰.因此得2e sin d e (sin cos )x xx x x x =-⎰.即1e sin d e (sin cos )2xxx x x x C =-+⎰.（11）解：32csc d csc (csc )d csc d(cot )x x x x x x x ==-⎰⎰⎰2csc cot cot csc d x x x x x =--⋅⎰3csc cot csc d csc d x x x x x x =--+⎰⎰ 3csc cot csc d ln csc cot x x x x x x =--+-⎰，从而 31csc d (csc cot ln csc cot )2x x x x x x C =---+⎰（12）解 ⎰''x x f x d )(C x f x f x x x f x f x x f x +-'='-'='=⎰⎰)()(d )()()(d3.已知x x f 22tan )(sin ='，求函数)(x f .解依题求得xx x f -='1)(，因此 C x x x x xx x x x f +---=--=-=⎰⎰⎰|1|ln d d 11d 1)(. 4. 已知xe xf -=)(，求不定积分⎰'x xx f d )(ln . 解=+='='⎰⎰C x f x x f x xx f )(ln ln d )(ln d )(ln C x +1.5. 解 11e d de e e d e n x n x n x n x n xn n I x x x x n x x x nI --===-=-⎰⎰⎰，即1e n x n n I x nI -=-为所求递推公式．而221e 2x I x I =-，11e d de e e d e e x x x x x xI x x x x x x C ===-=-+⎰⎰⎰，故22(22)e x I x x C =-++．(12C C =-)6. 解⎰''x f x xd )e (e2()⎰''=x x x f e d )e (e []⎰'=)e (d e x x f⎰'-'=)e (d )e ()e (e x x xx f f C f f x x x +-'=)e ()e (e习题 4-31. 求下列积分：（1） sin 2d x x x ⎰；（2）⎰-x e x xd 2；（3）()⎰-x x x d 1ln ；（4）(31)sin 3d x x x +⎰；（5）x x d sin3⎰；（6） e sin 2d x x x -⎰；（7） 2arctan d x x x ⎰；（8） 2cos d x x x ⎰；（9）x ；（10）⎰x x e xd sin ；（11）3csc d x x ⎰；（12）()d xf x x ''⎰.2. 求e d n xn I x x =⎰的递推公式，其中n 为自然数，并计算2I 的值．3. 已知)(u f 有二阶连续的导数，求⎰''x f x xd )e (e2；解答1.求下列不定积分（1）解：⎰x x x d 2sin )2cos d(21⎰-=x x ⎰+-=x x x x d 2cos 212cos 2 C x x x ++-=2sin 412cos 2（2）解：⎰-x e x x d 2⎰⎰---+-=-=x xe e x e x xx x d 2d 22⎰⎰-----+--=--=x e xe e x e x e x xx x x x d 22d 222C e xe ex x x x+---=---222（3）解：()⎰-x x x d 1ln ()⎰⎪⎪⎭⎫⎝⎛-=2d 1ln 2x x()⎰---=x x x x x d 11211ln 222()⎰⎪⎭⎫⎝⎛-++--=x x x x x d 111211ln 22()()C x x x x x +-----=1ln 2121411ln 222（4）(31)sin 3d x x x +⎰1(31)d(cos3)3x x =+-⎰ 1(31)cos3cos3d 3x x x x =-++⎰11(31)cos3sin 333x x x C =-+++.（5）解：令t x =3，则3t x =，t t dx d 32=原式⎰⎰-=⋅=t t t t t cos d 3d 3sin 22∫∫sin d 6+cos 3=d 2cos 3+cos 3=22t t t t t t tt t⎰-+-=t t t t t t d sin 6sin 6cos 32C t t t t t +++-=cos 6sin 6cos 32C x x x x x +++-=333332cos 6sin 6cos 3（6）解：因为⎰-x x e x d 2sin ⎰--=x e x d 2sin )2d(sin 2sin ⎰--+-=x e x e xx)d(2cos 22sin ⎰----=x x e x x e )2d(cos 22cos 22sin ⎰---+--=x e x e x e x x x ⎰------=x x e x e x e x x x d 2sin 42cos 22sin于是⎰-x x exd 2sin C xe x e x x +--=--52cos 22sin（7）解：⎰x x x d arctan 2⎰⎰-==x x x x x x arctan d 3arctan 33d arctan 333∫d +131arctan 3=233x x x x x ⎰+-+-=x x xx x x x d 131arctan 3233 C x x x x +++-=)1ln(31arctan 3223 （8）解：⎰x x x d cos 2⎰⎰+=+=x x x x x x xd )2cos (21d 22cos 1⎰+=x x x x d 2cos 2142⎰+=x x x 2sin d 4142⎰-+=x x x x x d 2sin 412sin 4142 C x x x x +-+=2cos 812sin 4142 （9）解：⎰x x xd arcsin 1⎰⎰-==x x x x x x arcsind 2arcsin2d arcsin2∫d 11arcsin 2=x xxx C x x x +-+=12arcsin 2 （10）解：e sin d sin d e x xx x x =⎰⎰e sin e d sin x x x x =-⎰e sin e cos d x x x x x =-⎰e sin cos d e x x x x =-⎰e sin (e cos e d cos )x x x x x x =--⎰ e sin e cos e sin d x x x x x x x =--⎰.因此得2e sin d e (sin cos )x xx x x x =-⎰.即1e sin d e (sin cos )2xxx x x x C =-+⎰. （11）解：32csc d csc (csc )d csc d(cot )x x x x x x x ==-⎰⎰⎰2csc cot cot csc d x x x x x =--⋅⎰3csc cot csc d csc d x x x x x x =--+⎰⎰ 3csc cot csc d ln csc cot x x x x x x =--+-⎰，从而 31csc d (csc cot ln csc cot )2x x x x x x C =---+⎰（12）解 ⎰''x x f x d )(C x f x f x x x f x f x x f x +-'='-'='=⎰⎰)()(d )()()(d2. 解 11e d de e e d e n x n x n x n x n xn n I x x x x n x x x nI --===-=-⎰⎰⎰，即1e n x n n I x nI -=-为所求递推公式．而221e 2x I x I =-，11e d de e e d e e x x x x x xI x x x x x x C ===-=-+⎰⎰⎰，故22(22)e x I x x C =-++．(12C C =-)3. 解⎰''x f x x d )e (e 2()⎰''=x x x f e d )e (e []⎰'=)e (d e x x f⎰'-'=)e (d )e ()e (e x x xx f f C f f x x x +-'=)e ()e (e ．习题4-4求下列不定积分：(1)23d 56x x x x +-+⎰； (2)21d (1)x x x -⎰；(3)22d (1)(1)xx x x +++⎰； (4)3224d 56x x x x x +++⎰．x x x d )+1(1 5∫28）（；（6）2d 3sin xx+⎰；（7）⎰++311d xx(8)sin d 1cos x xx x ++⎰.解答 (1) 解233(3)(2)56(2)(3)23(2)(3)x x A B A x B x x x x x x x x x ++-+-==+=-+------，即3(3)(2)x A x B x +=-+-，比较系数知1323A B A B +=⎧⎨--=⎩(或者用赋值法：分别在3(3)(2)x A x B x +=-+-中令3x =与2x =，也可解出A 与B )，解之得56A B =-⎧⎨=⎩，于是62356d ()d ln(3)5ln 25623x x x x x C x x x x +-=+=---+-+--⎰⎰65(3)ln 2x C x -=+-．(2) 解令221(1)1(1)A B Cx x x x x =++---，用待定系数法或者用赋值法可求出1A =，1B =-，1C =，故221111d []d (1)1(1)x x x x x x x =-+---⎰⎰2111d d d 1(1)x x x x x x =-+--⎰⎰⎰1ln ln 11x x C x =---+-． (3) 解因为222211(1)(1)11x x x x x x x x -+=+++++++，所以 2222d 1()d (1)(1)11x x x x x x x x x x -+=+++++++⎰⎰222221d(1)1d(1)1d 212121x x x x x x x x x +++=-+++++++⎰⎰⎰2221d()1112ln(1)ln(1)13222()24x x x x x +=-+++++++⎰2211ln 21x C x x +=-++++．(4) 解由于32224615656x x x x x x x x +-=--++++ 98132x x x =--+++，则 322498d (1)d 5632x x x x x x x x x +=--+++++⎰⎰219ln 38ln 22x x x x C =--++++．（5）解 ⎰⎰⎰+=+=+2888288728)1()1()1(1x x dx dx x x x dx x x =C xx +)1+1ln(+118188（6）解⎰+x x 2sin 3d ⎰-=x x 2cos 7d 2x u tan =⎰+243d u u ⎰+=2)32(1d 31u uC x +=3tan 2arctan 321（7）解 ⎰++311d xx31x t +=⎰+t t t 1d 32t t t d )111(3⎰++-=C t t t +++-=1ln 232 (8)解注意到sin d d(1cos )x x x =-+及211d d d(tan )1cos 22cos2xx x x x ==+，可将原来的积分拆为两项，然后积分，即sin sin d d d 1cos 1cos 1cos x x x x x x x x x x +=++++⎰⎰⎰1d(tan )d(1cos )21cos x x x x=-++⎰⎰tantan d ln(1cos )22x xx x x =--+⎰1tan 2ln cos ln(1cos )22x xx x C =+-++21tan 2ln cos ln(2cos )222x x xx C =+-+1tan (ln 2)2x x CC C =+=-．习题4-5利用积分表计算下列不定积分：（1）；（2）3ln d x x ⎰；（3）221d (1)x x +⎰；（4）；（5）x x ⎰；（6）（7） 6cos d x x ⎰；（8）2e sin3d x x x -⎰.解答（1）解：因为⎰+-245d xx x ⎰-+-=2)2(1)2d(x x在积分表中查得公式（73）C a x x a x x +++=+⎰)ln(d 2222现在1=a ，2-=x x ，于是⎰+-245d x x xC x x x +-+-+=)245ln(2（2）⎰x x d ln 3解：在积分表中查得公式（135）⎰⎰--=x x n x x x x n n n d ln )(ln d ln 1 现在3=n ，重复利用此公式三次，得⎰x x d ln3C x x x x x x x +-+-=6ln 6ln 3ln 23.（3）=+⎰x x d )1(122解：在积分表中查得公式（28）⎰⎰+++=+bax xb b ax b x x ax b 2222d 21)(2d )(1 于是现在1=a ，1=b ，于是=+⎰x x d )1(122 C x x xx x x x +++=+++⎰arctan )1(21d 21)1(2222 （4）⎰-1d 2x xx解：在积分表中查得公式（51）C xaa x ax x+=-⎰arccos 1d 12 于是现在1=a ，于是⎰-1d 2x xx C x+=1arccos（5）x x x xd 222-⎰解：令1-=x t ，因为x x x xd 222-⎰x x x d 1)1(22--=⎰t t t t d 1)12(22-++=⎰由积分表中公式（56）、（55）、（54）C a x x a a x a x x x a x x+-+---=-⎰2222222222ln 8)2(8dC a x x a x x +-=-⎰32222)(31dC a x x a a x x x a x +-+--=-⎰2222222ln 22d于是x x x x d 222-⎰2222)1())1(2[81a x a x x -----= C a x a x x a +--+--+--322222])1[(31)1(1ln 85. （6）⎰-12d 2x xx解：在积分表中查得公式（16）、（15）⎰⎰+-+-=+b ax x xb a bx b ax b ax xxd 2d 2C bbax b bax xx +-+-=+⎰arctan2d 于是现在2=a ，1-=b ，于是=-⎰12d 2x x x⎰-+-12d 12x x xx x C x x x +-+-=12arctan 212 （7） ⎰x x d cos 6解：在积分表中查得公式（135）⎰⎰----=x x nn x x n x x n n n d cos 1sin cos 1d cos 21 现在6=n ，重复利用此公式三次，得⎰x x d cos 6C x x x x •x x ++++=)22sin 41(2415sin cos 245sin cos 6135. （8）x x e xd 3sin 2⎰-解：在积分表中查得公式（128）C bx b bx a e ba x bx e axax +-+=⎰)cos sin (1d sin 22 现在2-=a ，3=b ，于是C x x e x x e axx+--=⎰-)3cos 33sin 2(131d 3sin 2 C x x e ax++-=)3cos 33sin 2(131复习题A一、选择题1. 设)(x F 是)(x f 的一个原函数，则等式（）成立。

编译原理教程课后习题答案——第四章

第四章语义分析和中间代码生成4.1 完成下列选择题：(1) 四元式之间的联系是通过实现的。

a. 指示器b. 临时变量c. 符号表d. 程序变量(2) 间接三元式表示法的优点为。

a. 采用间接码表，便于优化处理b. 节省存储空间，不便于表的修改c. 便于优化处理，节省存储空间d. 节省存储空间，不便于优化处理(3) 表达式(┐A∨B)∧(C∨D)的逆波兰表示为。

a. ┐AB∨∧CD∨b. A┐B∨CD∨∧c. AB∨┐CD∨∧d. A┐B∨∧CD∨(4) 有一语法制导翻译如下所示：S→bAb {print″1″}A→(B {print″2″}A→a {print″3″}B→Aa) {print″4″}若输入序列为b(((aa)a)a)b，且采用自下而上的分析方法，则输出序列为。

a. 32224441 b. 34242421c. 12424243d. 34442212【解答】(1) b (2) a (3) b (4) b4.2 何谓“语法制导翻译”？试给出用语法制导翻译生成中间代码的要点，并用一简例予以说明。

【解答】语法制导翻译(SDTS)直观上说就是为每个产生式配上一个翻译子程序(称语义动作或语义子程序)，并且在语法分析的同时执行这些子程序。

也即在语法分析过程中，当一个产生式获得匹配(对于自上而下分析)或用于归约(对于自下而上分析)时，此产生式相应的语义子程序进入工作，完成既定的翻译任务。

用语法制导翻译(SDTS)生成中间代码的要点如下：(1) 按语法成分的实际处理顺序生成，即按语义要求生成中间代码。

(2) 注意地址返填问题。

(3) 不要遗漏必要的处理，如无条件跳转等。

例如下面的程序段：if (i>0) a=i+e-b*d; else a=0;在生成中间代码时，条件“i>0”为假的转移地址无法确定，而要等到处理“else”时方可确定，这时就存在一个地址返填问题。

此外，按语义要求，当处理完(i>0)后的语句(即“i>0”为真时执行的语句)时，则应转出当前的if语句，也即此时应加入一条无条件跳转指令，并且这个转移地址也需要待处理完else之后的语句后方可获得，就是说同样存在着地址返填问题。

管理运筹学(第四版)第四章习题答案

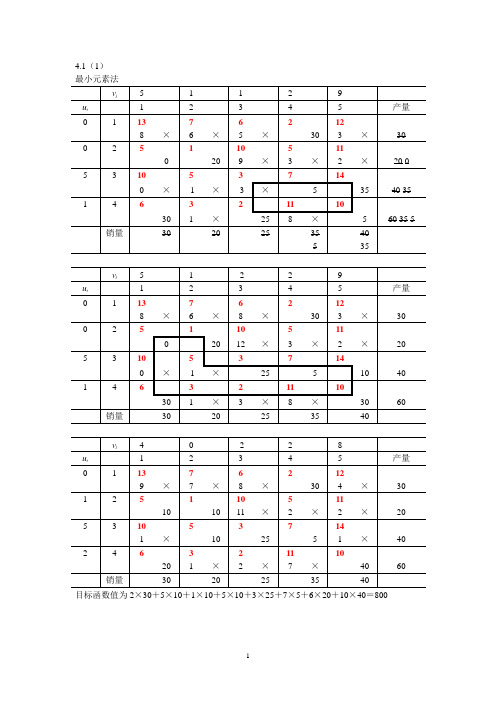
目标函数值为2×30＋5×10＋1×10＋5×10＋3×25＋7×5＋6×20＋10×40＝800目标函数值为2×30＋5×10＋1×10＋5×10＋3×25＋7×5＋6×20＋10×40＝800（2）最小元素法：先从311=c 开始分配先从325=c 开始分配，需迭代4次，具体见QM 的迭代逼近法（结果同最小元素法——先从313=c 开始分配）v j 2 2 0 u i 1 2 3 产量 0 1 2 10 7 2 8 × 7 × 2 1 2 3 2 1 0 × 2 2 4 1 3 11 3 8 8 × 3 7 × 3 2 4 4 9 2 1 5 × 5 6 -2 5 0 0 0 4 0 × 2 × 4销量757目标函数值为33。

A B C 产量甲 18 16 21 180 乙 16 18 22 250 丙 19 14 19 320 销量 250300200用QM 解得玩具利润工人A B C 产量甲52 64 49 180乙54 62 48 250丙51 66 51 320销量250 300 200用QM解得即甲工人做C玩具180个，乙工人做B玩具250个，丙工人做A玩具250个，做B玩具50个，做C玩具20个。

最大利润为：70×250＋80×300＋70×200－41390＝14110元甲乙丙产量A 15 18 22 400B 21 25 16 450最低需求290 250 270最高需求320 250 350甲1 甲2 乙丙1 丙2 产量A 15 15 18 22 22 400B 21 21 25 16 16 450C M 0 M M 0 70需求290 30 250 270 80用QM解得玩具费用工人地区运费厂家地区运费厂家即A厂供给甲地区化肥150万吨，供给乙地区化肥250万吨；B厂供给甲地区化肥140万吨，供给丙地区化肥310万吨，总运费为14650万元。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解 : t = (20 + 60） / 2 = 400 C查水的物性数据得： ρ = 992.2Kg / m 3 , C P = 4.174kJ / kg ⋅0 C, λ = 0.6338W / m ⋅0 C µ = 0.6560 × 10−3 Pa ⋅ s, Pr = 4.32 Re = d i uρ / µ = 0.053× 1.8 × 992.2 /(0.650 × 10−3 ) = 144292.5 α i = 0.023λRe Pr
t0 t1 t2 t3
180℃ 35℃
r0 r1 r2 r3 Q
δ1 δ2 50 10
2 × 3.14 × (180 − 35) = 1 19 1 69 1 79 ln + ln + ln 45 16.5 0.07 19 0.15 69
= 47.1 W/m ② Q = 2π L(t2 − t3 ) 1 r3 ln λ2 r2
●
A=1.89m2
A=2.89m2
55℃
20℃ 95℃
50℃
△t1=35℃
△t2=45℃
Q=KA△tm= Qh=Wh Cph(T1-T2)
●
∆ t 2 − ∆ t1 ∆ tm = ∆ t2 ln ∆ t1 45 − 35 = = 39.8 45 ln 35 Q=KA△tm= Qh=Wh Cph(T1-T2)
do bd o 1 1 = + Ri + + Ro + K o α i di λ dm α0
热阻分配：管内： o
d α i di 25 (100 × 20) = = 81.06% 1 Ko 0.01542
Ri + Ro 0.00118 + 0.00118 污垢： = = 15.30% 1 Ko 0.01542 bd o λ d m (0.0025 × 25) /(45 × 22.5) = = 0.40% 管壁： 1 Ko 0.01542
●
2.8 × 103 × A × 39.8 = (4.5 ×103 ) × 4.181× 103 × (95 − 55) 3600
A = 1.89m
2
A=1.89m2
95℃
20℃ 55℃
50℃
△t2=75℃
△t1=5℃
∆ t 2 − ∆ t1 ∆ tm = ∆ t2 ln ∆ t1 75 − 5 = = 25.85 ℃ 75 ln 5 Q=KA△tm= Qh=Wh Cph(T1-T2)
水蒸气
di 1 1 bdi = + + Ki α i λ d m α o do 1 0.002 × 31 31 = + + 4 420 45 × 33 10 × 35
do bd o 1 1 = + + K o α i di λ d m α 0 35 0.002 × 35 1 = + + 4 420 × 31 45 × 33 10
Cph=4.181 kJ/kg·℃ 解： ①Qh=Qc
Cpc=4.174 kJ/kg·℃
WhCph(T1-T2)= WcCpc(t2-t1) (4.5×103)×4.181×(95 (95-55)= Wc×4.174×(50 (50-20) Wc=6010 kg/h
55℃
20℃ 95℃
50℃
55℃
= 247.81 W/m2
【4-5】Φ38×2.5mm的钢管用作蒸汽管。为了减少热损失，在管外保温。第1层是50 mm厚的氧化锌粉，其平均热导率(导热系数)为0.07 W/(m·℃)；第2层是10mm厚的石棉层，其平均热导率(导热系数)为0.15 W/(m·℃)。若管内壁温度为180℃，石棉层外表面温度为35℃，试求每米管长的热损失及两保温层 t0 t1 t2 t3 界面处的温度？ 180℃ 35℃ 解： ①r0=16.5mm, r1=16.5+2.5=19mm r2=r1+ δ1 =19+50=69mm r0 r3=r2+ δ2 =69+10=79mm λ0=45 W/(m·℃) 2π L(t0 − t3 ) Q= 1 r1 1 r2 1 r2 ln + ln + ln λ0 r0 λ1 r1 λ2 r1
解： Q
t1 − t4 = b3 b1 b2 + + λ1 A λ2 A λ3 A
1000℃
55℃
Q
Q t1 − t4 1000 − 55 = = A b1 + b2 + b3 0.5 + 0.5 + 0.25 λ1 λ2 λ3 1.2 0.16 0.92
b λ
0.5 0.5 0.25 1.2 0.16 0.92
do bd o 1 1 = + Ri + + Ro + K o α i di λ dm α0
25 0.0025 × 25 1 = + 0.00118 + + 0.00118 + 100 × 20 45 × 22.5 2000
= 0.01542 1/[W/(m2·℃)]
K o = 64.84 W/(m2·℃)
= 0.0025111/[W/(m2·℃)]
Ki = 398.3 W/(m2·℃)
= 0.002835 1/[W/(m2·℃)]
K o = 352.7 W/(m2·℃)
水蒸气原油
d 1 1 bd = + i + i Ki α i λ d m α o do
1 αi 1 420 管内： = = 94.83% 1 K i 1 398.3
95℃
20℃ 95℃
50℃
20℃ 55℃
50℃
△t1=35℃
△t2=45℃
△t2=75℃
△t1=5℃
∆ t 2 − ∆ t1 ∆ tm = ∆ t2 ln ∆ t1 45 − 35 = = 39.8 ℃ 45 ln 35 Q=KA△tm= Qh=Wh Cph(T1-T2)
●
∆ t 2 − ∆ t1 ∆ tm = ∆ t2 ln ∆ t1 75 − 5 = = 25.85 ℃ 75 ln 5 Q=KA△tm= Qh=Wh Cph(T1-T2)
习题点评
第四章
【4-3】某燃烧炉的平壁由耐火砖、绝热砖和普通砖三种砖砌成，它们的热导率(导热系数)分别为1.2W/(m·℃)，0.16 W/(m·℃)和 0.92 W/(m·℃)，耐火砖和绝热砖厚度都是0.5m，普通砖厚度为 0.25m。已知炉内壁温为1000℃，外壁温度为55℃，设各层砖间接触良好，求每平方米炉壁散热速率。 t1 t2 t3 t4
d bd 1 1 = o + o + K o α i di λ d m α 0
d o α i d i 35 (420 × 31) 管内： 1 K = 1 352.7 = 94.81% o
bd o λ d m (0.002 × 35) /(45 × 33) bd λ d (0.002 × 31) /(45 × 33) i m = 管壁：管壁： = 1 Ko 1 352.7 1 Ki 1 398.3
0.8 0.4
/ di
= 0.023× 0.6338× 144292.50.8 × 4.320.4/0.053 = 6622w /(m 2 ⋅0 C )
【4-23】为保证原油管道的输送，在管外设置蒸汽夹套。对一段管路来说，设原油的给热系数为420 W/(m2·℃)，水蒸气冷凝给热系数为104 W/(m2·℃)。管子规格为φ35×2mm钢管。试分别计算Ki和K0，并计算各项热阻占总热阻的分率。解： α原油= αi =420 原油 α水蒸气= αo =104 W/(m2·℃) di=31mm do=35mm b=2mm λ=45 W/(m·℃) dm=(di+do)/2=(31+35)/2=33mm W/(m2·℃)
●
甲苯 80℃
d bd 1 1 = o + o + K o α i di λ d m α 0 ∆t2 − ∆t1 ∆tm = ∆t ln 2 ∆t1
30℃
KoAo △tm= Qh=Wh Cph(T1-T2)
●
水
15℃ 45℃ ∆ t 2 − ∆ t1 35 − 15 ∆ tm = = = 23.6℃ ∆ t2 35 甲苯 80℃ ln ln 15 ∆ t1 △t1=15℃ △t2=35℃ do bd o 1 1 di + d o 32 + 38 = + + dm = = = 35mm K o α i di λ d m α 0 2 2 38 0.003 × 38 1 = + + 2500 × 32 45 × 35 900 = 0.00165851/[W/(m2·℃)] Ko=603 W/(m2·℃)
= 1.66%
= 1.66%
1 α0 1 104 di α o d o 31/(104 × 35) = = 3.53% = = 3.51% 管外：管外： 1 K o 1 352.7 1 Ki 1/ 398.3
【4-25】一列管换热器，管子规格为φ25×2.5mm，管内流体的对流给热系数为100 W/(m2·℃)，管外流体的对流给热系数为2000 W/(m2·℃)，已知两流体均为湍流流动，管内外两侧污垢热阻均为0.00118 m2·℃/W。试求：①传热系数Ko及各部分热阻的分配；②若管内流体流量提高一倍，传热系数有何变化？解： ①Ri=Ro=0.00118 (m2·℃)/ W λ=45 W/(m·℃) dm=(di+do)/2=(20+25)/2=22.5mm αi =100 W/(m2·℃) αo =2000W/(m2·℃)
●
Q=KA△tm= Qh=Wh Cph(T1-T2)