标准正态分布函数的拟合方法
第7章分布拟合
第7章分布拟合统计学的任务之一是由样本(Sample)推断总体(Population),因而,样本资料的总体分布(Distribution)是人们十分关注的问题。
实际工作中,人们也是根据资料的分布形态选择适当的统计指标的。
SAS/Win(v8)系统提供了多种分布拟合(Distribution Fit),包括正态分布(Normal)拟合,对数正态分布(Lognormal)拟合,指数分布(E3cPonential)拟合和威布尔分布(Weibull)拟合等。
7.1 正态分布拟合正态分布或近似正态分布是一种最常见的分布,也是一种最重要的连续型分布。
正态分布又称高斯分布(Gaussian Distribution),它以均数为对称轴呈对称的钟形分布。
同时有些资料在一定条件下,也可以用正态分布或近似正态分布分析。
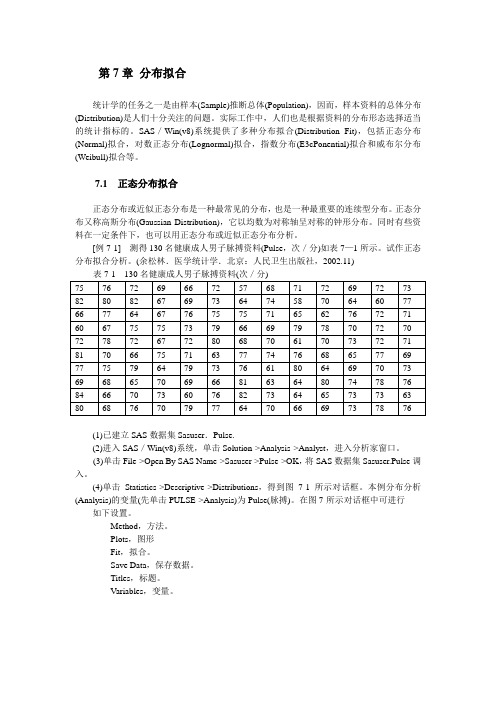
[例7-1] 测得130名健康成人男子脉搏资料(Pulse,次/分)如表7—1所示。
试作正态分布拟合分析。
(余松林.医学统计学.北京:人民卫生出版社,2002.11)(1)已建立SAS数据集Sasuser.Pulse.(2)进入SAS/Win(v8)系统,单击Solution->Analysis->Analyst,进入分析家窗口。
(3)单击File->Open By SAS Name->Sasuser->Pulse->OK,将SAS数据集Sasuser.Pulse调入。
(4)单击Statistics->Descriptive->Distributions,得到图7-1所示对话框。
本例分布分析(Analysis)的变量(先单击PULSE->Analysis)为Pulse(脉搏)。
在图7-所示对话框中可进行如下设置。
Method,方法。
Plots,图形Fit,拟合。
Save Data,保存数据。
Titles,标题。
Variables,变量。
图7-1 Distributions:Pulse(分布)对话框(5)在图7-1所示对话框中,单击Method按钮,得到图7-2所示对话框。
matlab拟合方法

matlab拟合方法Matlab拟合方法摘要:拟合是一种常见的数据分析方法,用于通过数学模型来描述和预测数据的趋势。
Matlab是一种功能强大的数学软件,提供了多种拟合方法来处理不同类型的数据。
本文将介绍几种常用的Matlab 拟合方法,并给出实际案例来说明其应用。
1. 多项式拟合多项式拟合是一种基于多项式函数的拟合方法,通过拟合数据点来获得一个多项式函数,从而近似描述数据的趋势。
Matlab中的polyfit函数可以实现多项式拟合,用户可以指定多项式的阶数,从而控制拟合的复杂程度。
通过最小二乘法,polyfit函数可以找到最佳拟合曲线。
2. 曲线拟合除了多项式拟合,Matlab还提供了其他的曲线拟合方法,包括指数、对数、幂函数等。
这些方法可以根据数据的特点选择适当的曲线形式来进行拟合。
例如,使用fittype函数可以指定拟合的曲线类型,然后使用fit函数进行拟合。
用户还可以根据拟合结果进行参数估计和预测。
3. 非线性拟合当数据无法用简单的线性模型拟合时,可以使用非线性拟合方法。
Matlab提供了lsqcurvefit函数来实现非线性拟合,用户需要提供一个自定义的非线性函数,并指定初始参数值。
lsqcurvefit函数会通过最小二乘法来求解最佳参数值,从而得到最佳拟合曲线。
4. 插值插值是一种通过已知数据点来估计未知点的方法。
Matlab中的interp1函数可以实现插值拟合,用户需要提供已知数据点的坐标和对应的函数值,然后可以使用interp1函数来估计未知点的函数值。
interp1函数支持不同的插值方法,包括线性插值、样条插值等。
5. 统计拟合除了数学模型拟合,Matlab还提供了统计拟合方法,用于分析数据的概率分布。
Matlab中的normfit函数可以根据数据点的均值和标准差来拟合正态分布曲线。
用户还可以使用histfit函数来绘制数据的直方图和拟合曲线,从而比较数据的分布和理论模型的拟合程度。
python 正态分布拟合优度检验

主题:Python 正态分布拟合优度检验引言在统计学中,正态分布是一种重要的概率分布,在许多领域都有广泛应用。
Python作为一种强大的编程语言,提供了许多用于概率分布拟合和优度检验的函数和库。
本文将探讨Python中如何使用正态分布拟合优度检验方法,并提供个人观点和理解。
正态分布简介正态分布是一种连续的对称概率分布,常用来描述自然界和社会现象中的许多随机变量。
正态分布的概率密度函数可表示为:f(x) = (1 / (σsqrt(2π))) * e^(-(x-μ)² / (2σ²))其中,μ是均值,σ是标准差。
正态分布的特点是呈钟形曲线,均值处为对称轴。
正态分布的拟合优度检验拟合优度检验可以判断数据是否服从正态分布。
在Python中,可以使用scipy库的stats模块来进行正态分布的拟合优度检验。
下面将介绍一种常用的方法——卡方检验。
卡方检验的原理是通过比较观测值与期望值之间的差异来判断数据的拟合优度。
步骤如下:1.准备一组数据,假设为样本数据。
2.计算样本数据的均值和标准差,作为正态分布的参数。
3.利用正态分布的参数生成一组期望值,与样本数据的长度相同。
4.利用scipy库的stats模块中的chisquare函数进行卡方检验。
5.根据卡方统计量和自由度,得出拟合优度检验的结果。
在Python中,拟合优度检验代码示例如下:import numpy as npfrom scipy import stats# 样本数据data = np.array([1, 2, 3, 4, 5])# 计算均值和标准差mean = np.mean(data)std = np.std(data)# 生成期望值expected = stats.norm(mean, std).pdf(data)# 进行卡方检验chi2, p = stats.chisquare(data, expected)# 输出拟合优度检验结果if p < 0.05:print("样本数据不服从正态分布")else:print("样本数据服从正态分布")个人观点和理解正态分布是统计学中非常重要的一种概率分布,对于理解和分析数据具有重要意义。
正态分布拟合优度检验

正态分布拟合优度检验正态分布是概率论中非常重要的一种概率分布,也被称为高斯分布。
它在自然界和社会科学中的许多现象中都有广泛的应用。
正态分布的特点是对称、钟形曲线,均值和标准差分别决定了曲线的中心位置和形态。
在实际应用中,我们经常需要通过样本数据来推断总体数据是否服从正态分布,这就需要用到正态分布的拟合优度检验。
拟合优度检验是一种用来判断一组观测数据是否符合某种理论分布的统计方法。
在正态分布的拟合优度检验中,我们假设总体数据服从正态分布,然后利用样本数据来验证这一假设的合理性。
具体的步骤是先计算样本数据的均值和标准差,然后利用这些统计量来构造正态分布的理论曲线。
最后,我们使用某种统计量来衡量观测数据与理论曲线的拟合程度,从而判断总体数据是否服从正态分布。
常用的拟合优度检验统计量有卡方统计量。
卡方统计量是一种衡量观测数据与理论分布之间差异的统计量,它的计算方法是将观测频数与理论频数之间的差异进行平方后除以理论频数再求和。
卡方统计量越小,表示观测数据与理论分布的拟合程度越好。
在进行正态分布的拟合优度检验时,我们首先需要确定显著性水平。
显著性水平是指在进行假设检验时,所能容忍的拒绝原假设的错误概率。
常用的显著性水平有0.05和0.01两种。
然后,我们需要根据样本数据计算出卡方统计量。
计算卡方统计量时,需要根据样本数据的频数和理论频数来计算每个类别的差异平方和。
最后,我们需要根据卡方统计量和自由度来确定拟合优度检验的结果。
自由度是指在进行假设检验时可以自由变动的数据个数。
拟合优度检验的结果可以有三种情况。
一种情况是拟合优度检验的P值大于显著性水平,这时我们不能拒绝原假设,即认为总体数据符合正态分布。
另一种情况是拟合优度检验的P值小于显著性水平,这时我们可以拒绝原假设,即认为总体数据不符合正态分布。
还有一种情况是拟合优度检验的P值非常接近显著性水平,这时我们需要进一步进行判断,可以考虑增加样本容量或者使用其他的拟合优度检验方法来进行验证。
matlab正态分布拟合曲线

matlab正态分布拟合曲线Matlab正态分布拟合曲线正态分布是一种常见的概率分布,通常也被称为高斯分布或正态曲线。
正态分布曲线是一个钟形曲线,以均值μ为对称轴,在3σ处有极值点。
Matlab是一个强大的数学软件,可以很方便地用来进行正态分布拟合曲线的绘制和分析。
下面是在Matlab上进行正态分布拟合曲线的步骤:1.准备数据首先,需要准备一组数据来拟合正态分布曲线。
可以使用Matlab 中的randn函数生成一个随机的样本数据,例如生成一个1000个元素的随机向量:x = randn(1000,1);2.计算均值和标准差接下来,需要计算数据的均值和标准差,这是计算正态分布曲线的必要参数。
可以使用Matlab中的mean和std函数进行计算:mu = mean(x);sigma = std(x);3.绘制直方图可以使用Matlab中的hist函数绘制数据的直方图,以便更好地了解数据的分布情况。
可以选择适当的bin值和归一化参数,以获得更好的分布情况:[n,edges] = histcounts(x,'Normalization','pdf'); binwidth = edges(2)-edges(1);bins = edges(1:end-1)+binwidth/2;bar(bins,n,1);4.绘制正态分布曲线使用Matlab的normpdf函数绘制正态分布曲线,传递计算出的参数mu和sigma以及样本数据的范围:range = min(x):0.01:max(x);y = normpdf(range,mu,sigma);hold on;plot(range,y,'r-');hold off;5.进行适当调整最后,可以对绘制的直方图和正态分布曲线进行调整,以便更好地呈现数据分布情况。
可以添加适当的标签,标题和注释等,以便更好地呈现分析结果。
总结:通过Matlab进行正态分布拟合曲线的绘制和分析,可以方便地了解数据的分布情况,并对数据进行更深入的分析。
标准正态分布函数公式

标准正态分布函数公式标准正态分布函数是统计学中一个重要的概率密度函数,它在实际应用中有着广泛的用途。
标准正态分布函数的概念和公式是统计学习和应用的基础,下面将对标准正态分布函数的概念、性质和公式进行详细介绍。
标准正态分布函数又称为正态分布曲线,是一种钟形曲线,其形状由均值和标准差决定。
标准正态分布函数的均值为0,标准差为1,其概率密度函数可以用数学公式来表示:f(x) = (1/√(2π)) e^(-x^2/2)。
其中,f(x)表示随机变量X落在x附近的概率密度,e为自然对数的底,π为圆周率。
这个公式描述了标准正态分布函数曲线的形状和特点。
标准正态分布函数的曲线呈现出对称的特点,以均值为中心向两侧逐渐减小,呈现出类似钟形的分布。
在均值处取得最大值,随着离均值越远,概率密度逐渐减小。
这种对称性和集中性使得标准正态分布函数在实际应用中有着重要的作用。
标准正态分布函数的性质还包括了68-95-99.7法则,即在标准正态分布曲线上,约有68%的数据落在均值附近的一个标准差范围内,约有95%的数据落在两个标准差范围内,约有99.7%的数据落在三个标准差范围内。
这一法则在统计学中有着重要的应用,可以帮助分析数据的分布情况。
标准正态分布函数的公式中包含了自然对数和圆周率等数学常数,这些常数的存在使得标准正态分布函数具有一定的特殊性。
它的概率密度函数在数学上具有较高的复杂性,但在实际应用中,可以通过数值计算或统计软件进行快速计算和分析。
总之,标准正态分布函数是统计学中一个重要的概率密度函数,它的概念、性质和公式对于理解统计学知识和进行实际应用有着重要的意义。
通过对标准正态分布函数的深入了解,可以更好地理解和分析各种随机变量的分布规律,为数据分析和统计推断提供重要的理论基础。
正态分布拟合matlab

正态分布拟合matlab摘要:I.引言- 介绍正态分布拟合的概念- 说明matlab 在正态分布拟合中的作用II.matlab 正态分布拟合的原理- 讲解正态分布的数学模型- 阐述matlab 如何通过数学模型生成正态分布随机数III.matlab 正态分布拟合的步骤- 详述使用matlab 进行正态分布拟合的步骤- 说明每一步骤的目的和意义IV.matlab 正态分布拟合的实例- 提供一个使用matlab 进行正态分布拟合的实例- 分析实例的结果,说明其含义和应用V.总结- 总结正态分布拟合在matlab 中的重要性- 提出进一步研究的建议正文:I.引言正态分布,也被称为高斯分布,是一种常见的数学分布。
在自然界和社会科学中,许多现象都遵循正态分布。
因此,对于正态分布的研究和应用具有重要的意义。
matlab 是一种强大的数学软件,可以用于进行各种数学计算和模拟。
在正态分布的拟合中,matlab 也发挥着重要的作用。
II.matlab 正态分布拟合的原理正态分布是一种连续型概率分布,其概率密度函数为:f(x) = (1 / (√(2π)σ)) * exp(-(x-μ) / 2σ)其中,μ为均值,σ为标准差。
正态分布的形状取决于均值和标准差的大小。
当均值μ=0,标准差σ=1 时,正态分布就是标准正态分布,其概率密度函数为:f(x) = (1 / √(2π)) * exp(-x / 2)matlab 可以使用上述概率密度函数生成正态分布的随机数。
此外,matlab 还可以通过参数估计方法,根据给定的数据集,估计正态分布的均值和标准差,从而拟合正态分布。
III.matlab 正态分布拟合的步骤使用matlab 进行正态分布拟合的步骤如下:1.导入数据:首先,需要将需要拟合的数据导入matlab。
可以使用matlab 的`readtable`或`readmatrix`函数读取数据文件。
2.计算均值和标准差:使用matlab 的`mean`和`std`函数计算数据的均值和标准差。
标准正态分布特征函数

标准正态分布特征函数标准正态分布,又称标准正态积分或高斯分布,是一种连续概率分布,用来对未知的随机变量的取值进行建模。
它是普遍存在的,可以用来统计测量各种规模的事件中出现的概率情况。
标准正态分布由其函数描述: $$f(x)=\frac{1}{{\sqrt {2\pi \sigma^2 }}}\mathrme^{ \frac{-(x-\mu )^2}{2\sigma^2} }$$其中,$\mu$ 为随机变量的期望,$\sigma^2$为随机变量的方差。
从函数形式上可以看出,标准正态分布出现了一种抛物线形状,当取值越接近$\mu$时,随机变量出现的概率也会越大,而当取值越偏离$\mu$时,就越小。
标准正态分布的方差衡量的是随机变量的概率集中程度,也就是变量出现在$\mu$附近的概率有多大。
当$\sigma^2$越小,就表示概率集中程度越高,变量出现在期望$\mu$附近的概率也越高;而$\sigma^2$越大,概率集中程度相对就越低,变量出现在期望附近的概率就会变小。
标准正态分布的偏度和峰度分别可以用偏斜系数来衡量,偏斜系数恒定等于零,表示经验历史资料的非对称强度,也表明随机变量的分布具有正态性。
峰度系数也恒定等于三,表示随机变量的波动性要比正态分布偏度低。
标准正态分布有着多种应用。
首先,它可以用来度量特定事件出现概率。
比如在机器学习中,用来使用正态分布可以广泛用来定义各种机会,根据其概率密度函数来计算特定输入下模型输出的概率有多大。
标准正态分布还可以用来拟合众多实际问题,比如人体身高体重分布等。
把实际测量的数据和标准正态分布的模型进行拟合,也就可以得出模型的期望、方差等等参数,进而决定实验测量的概率分布。
标准正态分布对统计分析也有重要的意义。
比如,在进行t检验的时候,就用到了它的假设,即总体均值服从标准正态分布。
这样就可以拿到一个t检验解,来判断实验观测结果是否和总体一致。
标准正态分布也可以用来进行贝叶斯定理中的概率更新,有助于估计未知参数。
如何化标准正态分布

如何化标准正态分布标准正态分布是统计学中非常重要的概念,它在各个领域都有着广泛的应用。
在实际应用中,我们经常需要将非正态分布的数据转化为标准正态分布,以便进行统计分析和推断。
本文将介绍如何将非标准正态分布转化为标准正态分布的方法和步骤。
首先,我们需要了解标准正态分布的概念。
标准正态分布是一种均值为0,标准差为1的正态分布。
其概率密度函数可以用数学公式表示为:\[ f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \]其中,\( \pi \) 是圆周率,\( e \) 是自然对数的底数。
标准正态分布的特点是钟型曲线,且均值为0,标准差为1。
接下来,我们将介绍如何将非标准正态分布转化为标准正态分布。
假设我们有一个非正态分布的随机变量X,其均值为\( \mu \),标准差为\( \sigma \)。
我们可以使用以下公式将X转化为标准正态分布的随机变量Z:\[ Z = \frac{X \mu}{\sigma} \]通过这个公式,我们可以将X转化为标准正态分布的随机变量Z。
这样做的好处是,我们可以利用标准正态分布的性质进行统计分析,而不需要考虑原始数据的分布情况。
在实际操作中,我们可以按照以下步骤将非标准正态分布转化为标准正态分布:1. 计算原始数据的均值\( \mu \)和标准差\( \sigma \);2. 使用上述公式,将原始数据转化为标准正态分布的数据;3. 对转化后的数据进行统计分析和推断。
需要注意的是,在转化数据时,我们要确保原始数据的分布是近似正态分布的。
否则,转化后得到的标准正态分布数据可能无法准确反映原始数据的特征。
除了上述方法外,我们还可以使用统计软件进行标准正态分布的转化。
常见的统计软件如SPSS、R、Python等都提供了相关的函数和工具,可以方便地进行数据转化和分析。
总之,标准正态分布在统计学中具有重要的意义,我们可以通过一定的方法将非标准正态分布的数据转化为标准正态分布,以便进行统计分析和推断。
正态分布如何标准化

正态分布如何标准化首先,我们需要了解正态分布的特点。
正态分布的均值为μ,标准差为σ,其概率密度函数为:f(x) = (1/(σ√(2π))) exp(-((x-μ)²/(2σ²)))。
其中,exp表示自然对数的底e的幂次方。
在正态分布中,约68%的数据落在均值±1个标准差的范围内,约95%的数据落在均值±2个标准差的范围内,约99.7%的数据落在均值±3个标准差的范围内。
这些特点对于我们理解正态分布的形状和分布规律非常重要。
接下来,我们来介绍正态分布的标准化方法。
标准化的目的是将原始数据转化为均值为0,标准差为1的标准正态分布。
标准化的公式为:Z = (X-μ)/σ。
其中,Z为标准化后的数值,X为原始数据,μ为原始数据的均值,σ为原始数据的标准差。
通过这个公式,我们可以将原始数据转化为标准正态分布,方便进行统计分析和比较。
在实际应用中,标准化的方法非常常见。
例如,在进行数据挖掘和机器学习时,我们通常会对数据进行标准化处理,以便更好地进行模型训练和预测。
另外,在统计学中,标准化也是非常重要的一步,能够帮助我们更好地理解数据的分布规律和特征。
需要注意的是,标准化只是一种数据处理的方法,它并不改变数据的分布形态和特征。
因此,在进行标准化处理后,我们仍然可以通过均值和标准差来判断数据的分布情况,只是数据的数值发生了变化而已。
总之,正态分布的标准化方法是统计学中非常重要的一步,它能够帮助我们更好地理解和分析数据。
通过标准化,我们可以将原始数据转化为标准正态分布,方便进行统计分析和比较。
希望本文能够帮助您更好地理解正态分布的标准化方法,为实际应用提供一定的参考价值。
hist 拟合曲线

hist 拟合曲线
拟合直方图(hist)的曲线通常使用概率密度函数(Probability Density Function, PDF)来描述数据的分布情况。
常见的拟合方法包括使用正态分布函数、指数分布函数、均匀分布函数等等。
具体的拟合步骤如下:
1. 统计直方图的数据:首先,根据数据集统计直方图的频率分布。
将数据按照一定的区间范围划分为多个区间(bin),并统计每个区间内数据的数量。
2. 选择拟合函数:根据数据的特点和拟合目的,选择合适的拟合函数。
常用的拟合函数包括正态分布函数、指数分布函数、均匀分布函数等。
对于正态分布,拟合函数为:
`f(x) = A * exp(-((x - μ)^2) / (2 * σ^2))`
其中 A 为幅度(高度),μ 为均值,σ 为标准差。
3. 参数估计:根据选择的拟合函数,需要估计拟合函数的参数值。
一般采用最小二乘法或最大似然估计来估计参数值。
4. 拟合曲线绘制:利用估计得到的参数,将拟合函数绘制在直方图上,形成拟合曲线。
需要注意的是,直方图的拟合曲线只是对实际数据的一个近似
描述,并不能完全准确地描述数据的分布情况。
拟合曲线的好坏也需要根据实际数据的分布情况和拟合效果来进行评估。
拟合曲线高斯法

拟合曲线高斯法拟合曲线是一种常见的数据分析技术,它用于通过数学模型来描述和预测数据变化的模式。
高斯法(Gaussian fitting)是其中一种常用的拟合方法,它基于高斯函数(正态分布)进行拟合,适用于许多实际问题和科学研究领域。
在探讨拟合曲线高斯法时,首先我们需要了解高斯函数以及它的数学表达式。
高斯函数又被称为正态分布函数,它的形式类似于一个钟形曲线。
数学表达式如下:\(f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)其中,\(x\) 是自变量,\(f(x)\) 是函数在某一点 \(x\) 处的取值。
参数\(\mu\) 是均值(代表着钟形曲线的中心位置),\(\sigma\) 是标准差(决定了曲线的宽度)。
接下来,我们可以利用高斯函数进行数据拟合。
拟合过程基于最小二乘法,即通过调整高斯函数的参数,使得函数曲线与实际数据的残差最小化。
这样就可以得到最佳拟合曲线,用来描述数据的整体趋势。
在实际应用中,拟合曲线高斯法常用于解决以下几类问题:1. 数据分布的分析与模式挖掘:通过拟合曲线可以更好地了解数据分布的特征,例如中心位置、峰值、宽度等。
这对于统计分析、数据挖掘以及自然科学研究中的模式识别非常有用。
2. 信号处理与滤波:高斯函数在信号处理领域有着广泛应用。
通过对信号进行高斯拟合,可以滤除噪声并提取出信号的主要成分。
这在通信工程、图像处理以及生物医学信号处理等领域具有重要意义。
3. 实验数据分析与参数估计:在实验研究中,拟合曲线高斯法可以用来分析实测数据,并估计出需要的参数值。
在物理学的研究中,科学家经常使用高斯拟合来确定粒子的质量以及其他物理量。
需要注意的是,拟合曲线高斯法也存在一些限制和注意事项。
在应用高斯拟合时,数据必须满足一定的前提条件,例如数据在一定程度上服从正态分布,并且不受过多的异常值干扰。
在参数估计过程中,需要注意拟合结果的可靠性和统计意义,以及合适的模型选择。
matlab正态分布拟合曲线

matlab正态分布拟合曲线
本篇文章将介绍如何使用MATLAB对一组数据进行正态分布拟合,并绘制出拟合曲线。
正态分布是一种常见的概率分布,它在统计学中有着广泛的应用。
我们将通过以下步骤来实现正态分布拟合曲线:
1. 导入数据:我们首先需要将数据导入到 MATLAB 中。
可以使
用 MATLAB 中的“readtable”函数来读取数据文件,并将数据存储
到表格中。
2. 统计数据:在拟合曲线前,我们需要对数据进行一些统计分析。
可以使用 MATLAB 中的“mean”和“std”函数来计算样本均值
和样本标准差。
3. 计算概率密度函数:根据正态分布的定义,我们可以使用计
算公式计算概率密度函数。
可以使用 MATLAB 中的“normpdf”函数
来计算。
4. 拟合曲线:使用 MATLAB 中的“fit”函数可以对数据进行正态分布拟合。
该函数将返回一个包含拟合参数的结构体。
5. 绘制拟合曲线:使用 MATLAB 中的“plot”函数将拟合曲线
绘制出来。
通过以上步骤,我们可以很容易地在 MATLAB 中实现正态分布拟合曲线。
这对于进行统计分析和数据可视化是非常有帮助的。
- 1 -。
函数拟合 分布拟合

函数拟合分布拟合
函数拟合和分布拟合是数据分析中常用的方法。
函数拟合是通过选择一个合适的函数模型,拟合数据并得到函数参数的过程。
分布拟合则是通过选择一个合适的分布模型,拟合数据并得到分布参数的过程。
函数拟合可以用来对数据进行预测和推断,例如可以利用线性回归模型拟合数据并预测新数据的结果。
而分布拟合可以用来研究数据的概率分布特征,例如可以利用正态分布拟合数据并得到均值和标准差等参数。
在进行函数拟合和分布拟合时,需要考虑选择合适的模型和参数估计方法。
常用的函数模型包括线性函数、多项式函数、指数函数等;常用的分布模型包括正态分布、伽马分布、泊松分布等。
参数估计方法包括最小二乘法、极大似然估计等。
在选择模型和参数估计方法时,需要考虑数据的特征和需求。
例如,如果数据具有线性关系,则可以选择线性函数模型并使用最小二乘法进行参数估计;如果数据具有时间序列特征,则可以选择ARIMA 模型并使用极大似然估计方法。
总之,函数拟合和分布拟合是数据分析中常用的方法,可以帮助我们研究数据的特征和预测未来趋势。
在进行拟合时,需要选择合适的模型和参数估计方法,并注意数据的特征和需求。
- 1 -。
gaussamp拟合方程

gaussamp拟合方程高斯函数是一种常见的数学函数形式,它在统计学、物理学、工程学等领域中被广泛应用。
而高斯拟合则是一种利用高斯函数来拟合实际数据的方法。
在本文中,我们将介绍高斯拟合的原理和应用,并通过一个案例来说明其具体的实施过程。
高斯函数,也称为正态分布函数,是一个关于自变量x的连续函数。
其数学形式可以用以下公式表示:\[ f(x) = A \cdot e^{-\frac{(x - \mu)^2}{2\sigma^2}} \]其中,A代表高斯函数的幅度,即函数在峰值处的取值;μ代表高斯函数的均值,即函数的中心位置;σ代表高斯函数的标准差,即函数的宽度。
高斯拟合是指利用高斯函数来拟合实际观测数据,从而找到最佳的参数估计。
在实际应用中,我们往往有一组离散的数据点,我们的目标是找到一个高斯函数,使其能够最好地拟合这些数据点。
具体而言,我们需要通过最小化拟合误差的方法,来确定高斯函数的参数A、μ和σ。
在实际操作中,我们可以使用最小二乘法来进行高斯拟合。
最小二乘法是一种常见的参数估计方法,它的基本思想是通过最小化观测值与模型预测值之间的误差平方和,来确定模型的参数。
对于高斯拟合来说,我们可以将观测值与高斯函数的预测值之间的差值作为误差,然后通过最小二乘法来求解最佳参数估计。
接下来,我们通过一个具体的案例来说明高斯拟合的实施过程。
假设我们有一组实际观测数据,表示某个物理量在不同位置上的取值。
我们的目标是找到一个高斯函数,使其能够最好地拟合这些观测数据。
我们需要在计算机上编写一个高斯拟合的程序。
然后,我们将观测数据输入程序,并设定初始参数值。
接下来,程序将通过最小二乘法来不断调整参数,直到找到最佳的拟合结果。
在实际操作中,我们可以使用一些数值计算软件或编程语言来实现高斯拟合。
例如,MATLAB、Python中的SciPy库、R语言等都提供了相应的函数或包来进行高斯拟合。
完成高斯拟合后,我们可以得到最佳的参数估计,即高斯函数的幅度A、均值μ和标准差σ。
标准正态函数

标准正态函数标准正态函数(Standard Normal Distribution)是统计学中常用的一种概率分布函数,也称为正态分布函数(Normal Distribution)。
它是数学家高斯(Gauss)在自然科学和社会科学中的研究中首次提出的。
标准正态函数在各个领域都有着广泛的应用,特别是在自然科学、社会科学和工程技术领域中,被广泛地应用于数据分析、模型拟合、风险评估等方面。
标准正态函数的概率密度函数(Probability Density Function,简称PDF)是一个关于随机变量的函数,用来描述随机变量落在某个区间内的概率。
它的数学表达式为:\[f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}\]其中,\(x\) 是随机变量,\(\pi\) 是圆周率,\(e\) 是自然对数的底。
标准正态函数的特点之一是其均值为0,标准差为1。
这意味着标准正态函数的曲线关于均值对称,且其形状由标准差决定。
当标准差较小时,曲线较为陡峭;当标准差较大时,曲线较为平缓。
在实际应用中,我们经常需要计算标准正态函数在某个区间内的概率值。
这时,我们可以利用标准正态分布表来进行计算。
标准正态分布表是一个预先计算好的表格,其中包含了标准正态函数在不同区间内的概率值。
通过查表,我们可以方便地获取所需的概率值,从而进行相应的数据分析和决策。
除了概率密度函数和概率分布表之外,标准正态函数还有一些重要的性质和应用。
例如,标准正态函数与正态分布函数之间存在着一定的数学关系,通过线性变换,我们可以将任意正态分布转化为标准正态分布,从而简化问题的求解过程。
此外,标准正态函数还与中心极限定理密切相关,中心极限定理指出,大量独立同分布的随机变量的均值近似服从正态分布,而标准正态函数则是中心极限定理的一个重要特例。
在实际应用中,我们经常需要利用标准正态函数进行数据分析和模型拟合。
例如,在金融领域中,我们可以利用标准正态函数来对股票价格的波动进行建模,从而进行风险评估和投资决策。
正态分布怎么标准化

正态分布怎么标准化首先,我们需要了解正态分布的特点。
正态分布的概率密度函数呈钟形曲线,均值μ决定了曲线的中心位置,标准差σ决定了曲线的宽窄程度。
正态分布的曲线在均值μ处达到最高点,然后向两侧逐渐下降,呈对称分布。
在标准正态分布中,均值μ为0,标准差σ为1。
接下来,我们来看如何对正态分布进行标准化。
标准化的目的是将原始的正态分布转化为标准正态分布,以便进行统计推断和比较。
标准化的过程是将原始数值减去均值,然后除以标准差。
具体步骤如下:1. 计算原始数据的均值μ和标准差σ。
2. 对原始数据进行标准化处理,使用以下公式:Z = (X μ) / σ。
其中,Z为标准化后的数值,X为原始数据,μ为均值,σ为标准差。
3. 标准化后的数据Z符合标准正态分布,其均值为0,标准差为1。
通过标准化,我们可以将不同均值和标准差的正态分布转化为具有相同均值和标准差的标准正态分布,从而方便进行比较和分析。
标准化后的数据可以直接利用标准正态分布表进行概率计算,也可以进行统计推断和假设检验。
需要注意的是,标准化并不改变原始数据的分布形态,只是改变了数值的尺度。
因此,在进行标准化时,我们需要保留原始数据的分布特点和含义,以便正确解释和应用标准化后的结果。
总之,正态分布的标准化是统计学中常见的数据处理方法,通过将原始数据转化为标准正态分布,方便进行统计分析和推断。
标准化的过程简单直观,但在实际应用中需要注意保留原始数据的含义和特点。
希望本文能够帮助您更好地理解正态分布的标准化方法,提高数据分析和统计推断的准确性和可靠性。
高斯拟合的原理和应用

高斯拟合的原理和应用1. 什么是高斯拟合?高斯拟合,也称为高斯曲线拟合,是一种常用的数据拟合方法。
它基于高斯函数,通过调整函数参数来最优化拟合数据。
高斯函数又称为正态分布函数,具有钟形曲线的特征。
2. 高斯函数的数学表达式高斯函数的数学表达式为:f(x) = a * exp(-((x-b)/c)^2/2)其中,a代表曲线的幅度,b代表曲线的中心位置,c代表曲线的宽度。
3. 高斯拟合的原理高斯拟合的原理基于最小二乘法,即通过调整曲线的参数,使拟合曲线与实际数据的残差平方和最小。
具体步骤如下:1.初始化曲线参数a、b、c的初值。
2.根据当前曲线参数计算拟合曲线的值。
3.计算拟合曲线与实际数据的残差平方和。
4.通过优化算法(如梯度下降法、Levenberg-Marquardt算法等)调整参数,使残差平方和最小化。
5.迭代步骤2-4,直到达到收敛条件(如残差平方和小于某个阈值)。
4. 高斯拟合的应用高斯拟合在各个领域都有广泛的应用。
以下是一些常见的应用场景:4.1 数据分析与建模高斯拟合可以用于对实际数据进行分析与建模。
通过拟合实际数据,可以找到合适的高斯函数参数,从而对数据进行描述和预测。
4.2 信号处理在信号处理中,高斯拟合可以用于滤波、信号噪声去除等方面。
通过拟合信号数据,可以获取信号的特征参数,进而进行信号处理操作。
4.3 图像处理图像处理中常常需要对图像的亮度分布进行建模或调整。
高斯拟合可以用于对图像亮度分布进行建模,并通过调整参数实现图像的增强、平滑等效果。
4.4 计量学在计量学中,高斯拟合常常用于对实验数据进行分析。
通过拟合实验数据,可以估计实验结果的精确性和可靠性。
4.5 金融学高斯拟合在金融学中有重要应用。
通过对金融数据进行高斯拟合,可以得到风险价值、收益率分布等重要参数,为投资决策提供依据。
4.6 医学影像处理在医学影像处理中,高斯拟合可以用于对图像中的病变或结构进行分析与描述。
通过拟合图像数据,可以提取重要的特征参数,用于医学诊断与研究。
正态分布拟合matlab

正态分布拟合matlab
在MATLAB中,可以使用normfit函数对数据进行正态分布拟合。
该函数返回给定数据的正态分布拟合参数,包括均值、标准差和拟合优度。
以下是一个简单的示例:
matlab% 生成一些随机数据data = randn(1000,1);% 进行正态分布拟合params = normfit(data);% 输出拟合参数mean =
params(1);stddev = params(2);gof = params(3);disp(['均值:', num2str(mean)]);disp(['标准差:', num2str(stddev)]);disp(['拟合优度:', num2str(gof)]);
在上面的示例中,randn函数用于生成1000个标准正态分布的随机数。
然后,使用normfit函数对这些数据进行正态分布拟合,并将返回的拟合参数存储在params变量中。
最后,通过索引将拟合参数的均值、标准差和拟合优度提取出来,并使用disp函数将其输出到命令窗口。
除了normfit函数,还有其他一些函数可以用于正态分布拟合,例如fitdist和pdfndist。
这些函数的使用方法可能会有所不同,但它们的基本原理都是通过对数据进行最小二乘拟合来计算正态分
布的参数。
需要注意的是,正态分布拟合并不一定能够完全拟合数据,因为数据通常不是完全符合正态分布的。
因此,在进行正态分布拟合时,
需要谨慎评估数据的拟合程度,并使用适当的的方法对数据进行处理和分析。
