八年级上册期末试卷(A.B卷)及答案
八年级(上)期末数学试卷(含答案)

八年级(上)期末数学试卷(含答案)一、选择题1.低碳环保理念深入人心,共享单车已经成为出行新方式下列共享单车图标中,是轴对称图形的是( )A .B .C .D .2.已知实数,a b 满足2|2|(4)0a b -+-=,则以,a b 的值为两边的等腰三角形的周长是( ) A .10 B .8或10 C .8 D .以上都不对3.若分式15x -在实数范围内有意义,则实数x 的取值范围是( ) A .5x ≠ B .5x = C .5x > D .5x < 4.下列各点中在第四象限的是( )A .()2,3--B .()2,3-C .()3,2-D .()3,25.若2149x kx ++是完全平方式,则实数k 的值为( ) A .43B .13C .43±D .13±6.某种产品的原料提价,因而厂家决定对产品提价,现有三种方案: 方案(一):第一次提价%p ,第二次提价%q ; 方案(二):第一次提价%q ,第二次提价%p ; 方案(三):第一、二次提价均为2%p q+; 其中p ,q 是不相等的正数. 有以下说法:①方案(一)、方案(二)提价一样;②方案(一)的提价也有可能高于方案(二)的提价; ③三种方案中,以方案(三)的提价最多;④方案(三)的提价也有可能会低于方案(一)或方案(二)的提价. 其中正确的有( ) A .②③B .①③C .①④D .②④7.正比例函数y kx =的图象经过第一、三象限,则一次函数y x k =+的图象大致是()A .B .C .D .8.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()1,1,第2次接着运动到点()2,0,第3次接着运动到点()3,2,···,按这样的运动规律,经过第2020次运动后,动点P 的坐标是( )A .()2020,1B .()2020,0C .()2020,2D .()2019,09.一辆货车从甲地匀速驶往乙地用了2.7h ,到达后用了0.5h 卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的1.5倍,货车离甲地的距离y (km )关于时间x (h )的函数图象如图所示,则a 等于( )A .4.7B .5.0C .5.4D .5.8 10.在下列黑体大写英文字母中,不是轴对称图形的是( )A .B .C .D .二、填空题11.圆周率π=3.1415926…精确到千分位的近似数是_____. 12.比较大小:10_____3.(填“>”、“=”或“<”)13.如图,在平面直角坐标系中,点P 的坐标为(0,4),直线y =34x -3与x 轴、y 轴分别交于点A 、B ,点M 是直线AB 上的一个动点,则PM 的最小值为________.14.如图,在ABC ∆和EDB ∆中,90C EBD ∠=∠=︒,点E 在AB 上.若ABC EDB ∆∆≌,4AC =,3BC =,则DE =______.15.如图,直线l 上有三个正方形,,a b c ,若,a c 的面积分别为5和11,则b 的面积为__________.16.如图,在长方形ABCD 中,5,6AB BC ==,将长方形ABCD 沿BE 折叠,点A 落在'A 处,若'EA 的延长线恰好过点C ,则AE 的长为__________.17.已知点M (1,a )和点N (2,b )是一次函数y =-2x +1图象上的两点,则a 与b 的大小关系是_________.18.将一次函数y =2x +2的图象向下平移2个单位长度,得到相应的函数表达式为____. 19.将矩形纸片ABCD 按如图所示的方式折叠,恰好得到菱形AECF .若AB=6,则菱形AECF 的面积为__________.20.若代数式321xx -+有意义,则x 的取值范围是______________. 三、解答题21.如图,已知函数12y x =+的图像与y 轴交于点A ,一次函数2y kx b =+的图像经过点(0,4)B ,与x 轴交于点C ,与12y x =+的图像交于点D ,且点D 的坐标为2,3n ⎛⎫ ⎪⎝⎭.(1)求k 和b 的值;(2)若12y y >,则x 的取值范围是__________. (3)求四边形AOCD 的面积.22.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x 小时,两车之间的距离为y 千米,图中折线表示y 与x 之间的函数图象,请根据图象解决下列问题:(1)甲乙两地之间的距离为 千米; (2)求快车和慢车的速度;(3)求线段DE 所表示的y 与x 之间的函数关系式,并写出自变量x 的取值范围.23.(模型建立)如图1,等腰直角三角形ABC 中,90ACB ∠=︒,CB CA =,直线ED 经过点C ,过A 作AD ED ⊥于点D ,过B 作BE ED ⊥于点E .求证:BEC CDA ∆∆≌; (模型应用) ①已知直线1l :443y x =+与x 轴交于点A ,与y 轴交于点B ,将直线1l 绕着点A 逆时针旋转45︒至直线2l ,如图2,求直线2l 的函数表达式;②如图3,在平面直角坐标系中,点()8,6B,作BA y ⊥轴于点A ,作BC x ⊥轴于点C ,P 是线段BC 上的一个动点,点Q 是直线26y x =-上的动点且在第一象限内.问点A 、P 、Q 能否构成以点Q 为直角顶点的等腰直角三角形,若能,请直接写出此时点Q的坐标,若不能,请说明理由.24.(131232)36+(2)因式分解:3312x x - (3)计算:2(1)(2)(3)x x x x -+-+(4)计算:2(21)2(1)(1)x x x +-+-25.如图,平面直角坐标系中,直线AB :y =kx +3(k ≠0)交x 轴于点A (4,0),交y 轴正半轴于点B ,过点C (0,2)作y 轴的垂线CD 交AB 于点E ,点P 从E 出发,沿着射线ED向右运动,设PE=n.(1)求直线AB的表达式;(2)当△ABP为等腰三角形时,求n的值;(3)若以点P为直角顶点,PB为直角边在直线CD的上方作等腰Rt△BPM,试问随着点P 的运动,点M是否也在直线上运动?如果在直线上运动,求出该直线的解析式;如果不在直线上运动,请说明理由.四、压轴题26.直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.27.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.28.观察下列两个等式:5532321,44133+=⨯-+=⨯-,给出定义如下:我们称使等式1a b ab +=-成立的一对有理数,a b 为“白马有理数对”,记为(,)a b ,如:数对5(3,2),4,3⎛⎫⎪⎝⎭都是“白马有理数对”.(1)数对3(2,1),5,2⎛⎫- ⎪⎝⎭中是“白马有理数对”的是_________; (2)若(,3)a 是“白马有理数对”,求a 的值;(3)若(,)m n 是“白马有理数对”,则(,)n m --是“白马有理数对”吗?请说明理由. (4)请再写出一对符合条件的“白马有理数对”_________(注意:不能与题目中已有的“白马有理数对”重复)29.在ABC 中,AB AC =,D 是直线AB 上一点,E 在直线BC 上,且DE DC =. (1)如图1,当D 在AB 上,E 在CB 延长线上时,求证:EDB ACD ∠=∠; (2)如图2,当ABC 为等边三角形时,D 是BA 的延长线上一点,E 在BC 上时,作//EF AC ,求证:BE AD =;(3)在(2)的条件下,ABC ∠的平分线BF 交CD 于点F ,连AF ,过A 点作AH CD ⊥于点H ,当30EDC ∠=︒,6CF =时,求DH 的长度.30.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线1l ,2l ,3l 上,90BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B 、C 向1l 作垂线,就能利用全等三角形的知识求出AB 的长. (2)小林说:“我们可以改变ABC 的形状.如图2,AB AC =,120BAC ∠=︒,且每两条平行线之间的距离为1,求AB的长.”(3)小谢说:“我们除了改变ABC的形状,还能改变平行线之间的距离.如图3,等边三角形ABC三个顶点分别落在三条平行线1l,2l,3l上,且1l与2l之间的距离为1,2l与3l 之间的距离为2,求AB的长、”请你根据3位同学的提示,分别求出三种情况下AB的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】【分析】根据轴对称图形的概念求解.【详解】A、是轴对称图形.故选项正确;B、不是轴对称图形.故选项错误;C、不是轴对称图形.故选项错误;D、不是轴对称图形.故选项错误.故选:A.【点睛】此题主要考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,两边图象折叠后可重合.2.A解析:A 【解析】 【分析】先根据非负数的性质求出a 和b 的值,然后分两种情况求解即可. 【详解】∵2|2|(4)0a b -+-=, ∴a-2=0,b-4=0, ∴a=2,b=4,当a 为腰时,2+2=4,不合题意,舍去; 当b 为腰时,2+4>4,符合题意, ∴周长=4+4+2=10. 故选A. 【点睛】此题主要考查了等腰三角形的性质及三角形三边关系的运用;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.3.A解析:A 【解析】 【分析】根据分式的定义即可求解. 【详解】依题意得50x -≠,解得5x ≠, 故选A. 【点睛】此题主要考查分式的性质,解题的关键是熟知分式的性质.4.C解析:C 【解析】 【分析】根据第四象限点的坐标特点,在选项中找到横坐标为正,纵坐标为负的点即可. 【详解】解:A .(-2,-3)在第三象限; B .(-2,3)在第二象限; C .(3,-2)在第四象限; D .(3,2)在第一象限; 故选:C . 【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,用到的知识点为:点在第四象限内,那么横坐标大于0,纵坐标小于0.5.C解析:C 【解析】 【分析】本题是已知平方项求乘积项,根据完全平方式的形式可得出k 的值. 【详解】由完全平方式的形式(a±b )2=a 2±2ab+b 2可得: kx=±2•2x•13, 解得k=±43. 故选:C 【点睛】本题关键是有平方项求乘积项,掌握完全平方式的形式(a±b )2=a 2±2ab+b 2是关键.6.B解析:B 【解析】 【分析】根据提价方案求出提价后三种方案的价格,得到方案(一)、方案(二)、方案(三)提价情况,进行对比即可得解. 【详解】∵方案(一):(1%)(1%)1%%%%p q p q p q ++=+++ 方案(二):(1%)(1%)1%%%%q p q p q p ++=+++ ∴方案(一)、方案(二)提价一样 ∴①对,②错; ∵方案(三):2(1%)(1%)1%%(%)222p q p q p q p q +++++=+++ ∴可知:21%%(%)(1%%%%)2p q p q p q p q ++++-+++2(%)%%2p q p q +=-2(%)2p q -= ∵p ,q 是不相等的正数 ∴2(%)02p q -> ∴方案(三)提价最多 ∴③对,④错 ∴①③对故选:B.【点睛】本题主要考查了销售问题中的增长率问题,熟练掌握增长率的相关知识及整式的乘法化简是解决本题的关键.7.A解析:A【解析】【分析】根据正比例函数的图象及性质即可求出k 的取值范围,然后根据一次函数的图象及性质即可判断.【详解】解:∵正比例函数y kx =的图象经过第一、三象限,∴0k >∵一次函数y x k =+中,1>0, 0k >∴一次函数y x k =+经过一、二、三象限故选A .【点睛】此题考查的是正比例函数的图象及性质和一次函数的图象及性质,掌握一次函数的图象及性质与各项系数的关系是解决此题的关键.8.B解析:B【解析】【分析】观察可得点P 的变化规律,“()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++,,, (n 为自然数)”,由此即可得出结论.【详解】观察, ()()()()()()0123450,01,12,0,3,2,4,0,5,1....P P P P P P ,,,, 发现规律:()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++,,, (n 为自然数) .∵20204505=⨯∴2020P 点的坐标为()2020,0.故选: B.【点睛】本题考查了规律型中的点的坐标,解题的关键是找出规律“()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++,,, (n 为自然数)”,本题属于中档题,难度不大,解决该题型题目时,根据点P 的变化罗列出部分点的坐标,再根据坐标的变化找出规律是关键.9.B解析:B【解析】【分析】先根据路程、速度和时间的关系题意可得甲地到乙地的速度和从乙地到甲地的时间,再由货车返回的速度是它从甲地驶往乙地的速度的1.5倍,列出方程组求得从乙地到甲地的时间t,进而求得a的值.【详解】解:设甲乙两地的路程为s,从甲地到乙地的速度为v,从乙地到甲地的时间为t,则2.71.5v svt s=⎧⎨=⎩解得,t=1.8∴a=3.2+1.8=5(小时),故选B.【点睛】本题考查了一次函数的图像的应用、方程组的应用,根据一次函数图像以及路程、速度和时间的关系列出方程组是解答本题的关键.10.C解析:C【解析】【分析】根据轴对称图形的概念对各个大写字母判断即可得解.【详解】A.“E”是轴对称图形,故本选项不合题意;B.“M”是轴对称图形,故本选项不合题意;C.“N”不是轴对称图形,故本选项符合题意;D.“H”是轴对称图形,故本选项不合题意.故选:C.【点睛】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.二、填空题11.142【解析】【分析】近似数π=3.1415926…精确到千分位,即是保留到千分位,由于千分位1后面的5大于4,故进1,得3.142.【详解】解:圆周率π=3.1415926…精确到千分解析:142【解析】【分析】近似数π=3.1415926…精确到千分位,即是保留到千分位,由于千分位1后面的5大于4,故进1,得3.142.【详解】解:圆周率π=3.1415926…精确到千分位的近似数是3.142.故答案为3.142.【点睛】本题考查了近似数和精确度,精确到哪一位,就是对它后边的一位进行四舍五入.12.>.【解析】【分析】先求出3=,再比较即可.【详解】∵32=9<10,∴>3,故答案为:>.【点睛】本题考查了实数的大小比较和算术平方根的应用,用了把根号外的因式移入根号内的方法.解析:>.【解析】【分析】先求出【详解】∵32=9<10,3,故答案为:>.【点睛】本题考查了实数的大小比较和算术平方根的应用,用了把根号外的因式移入根号内的方法.13.【解析】【分析】认真审题,根据垂线段最短得出PM⊥AB时线段PM最短,分别求出PB、OB、OA、AB的长度,利用△PBM∽△ABO,即可求出本题的答案【详解】解:如图,过点P作PM⊥AB,解析:28 5【解析】【分析】认真审题,根据垂线段最短得出PM⊥AB时线段PM最短,分别求出PB、OB、OA、AB的长度,利用△PBM∽△ABO,即可求出本题的答案【详解】解:如图,过点P作PM⊥AB,则:∠PMB=90°,当PM⊥AB时,PM最短,因为直线y=34x﹣3与x轴、y轴分别交于点A,B,可得点A的坐标为(4,0),点B的坐标为(0,﹣3),在Rt△AOB中,AO=4,BO=3,22345+=,∵∠BMP=∠AOB=90°,∠B=∠B,PB=OP+OB=7,∴△PBM∽△ABO,∴PB PMAB AO=,即:754PM =,所以可得:PM=285.14.5【解析】【分析】先根据勾股定理求得AB的长度,再由全等三角形的性质可得DE的长度. 【详解】解:在Rt△ACB中,∠C=90°,AC=4,BC=3,由勾股定理得:AB=5,∵△ABC≌解析:5【解析】【分析】先根据勾股定理求得AB的长度,再由全等三角形的性质可得DE的长度.【详解】解:在Rt△ACB中,∠C=90°,AC=4,BC=3,由勾股定理得:AB=5,∵△ABC≌△EDB,∴DE=AB=5.【点睛】本题考查勾股定理,全等三角形的性质.熟记全等三角形对应边相等是解决此题的关键. 15.16【解析】【分析】运用正方形边长相等,再根据同角的余角相等可得∠ABC=∠DAE,然后证明△ΔBCA≌ΔAED,结合全等三角形的性质和勾股定理来求解即可.【详解】解:∵AB=AD,∠BC解析:16【解析】【分析】运用正方形边长相等,再根据同角的余角相等可得∠ABC=∠DAE,然后证明△ΔBCA≌ΔAED,结合全等三角形的性质和勾股定理来求解即可.【详解】解:∵AB=AD,∠BCA=∠AED=90°,∴∠ABC=∠DAE,∴ΔBCA≌ΔAED(ASA),∴BC=AE,AC=ED,故AB²=AC²+BC²=ED²+BC²=11+5=16,即正方形b的面积为16.点睛:此题主要考查对全等三角形和勾股定理的综合运用,解题的重点在于证明ΔBCA≌ΔAED,而利用全等三角形的性质和勾股定理得到b=a+c则是解题的关键. 16.【解析】【分析】结合长方形与折叠的性质在在中根据勾股定理可得的长,设设,可知,中,由勾股定理得方程,求出x 值即可.【详解】解:四边形ABCD 是长方形由折叠的性质可得在中,根据勾股解析:6【解析】【分析】结合长方形与折叠的性质在在'Rt BAC 中根据勾股定理可得'AC 的长,设设AE x =,可知',6,A E x DE x CE x ==-=+Rt CDE △中,由勾股定理得方程222(6)5(x x -+=+,求出x 值即可.【详解】 解:四边形ABCD 是长方形90,5,6A D AB CD AD BC ︒∴∠=∠=====由折叠的性质可得''',5,90A E AE A B AB EA B A ︒===∠=∠=在'Rt BAC 中,根据勾股定理得'AC ==设AE x =,则',6,A E x DE x CE x ==-=+在Rt CDE △中,根据勾股定理得222DE CD CE +=即222(6)5(x x -+=+可得2236122511x x x -++=++12)50x ∴=6)6x ∴====-=故答案为:6【点睛】本题考查了勾股定理,灵活利用折叠三角形的性质结合勾股定理求线段长是解题的关键. 17.a>b【解析】【分析】【详解】解:∵一次函数y=﹣2x+1中k=﹣2,∴该函数中y 随着x 的增大而减小,∵1<2,∴a >b .故答案为a>b.【点睛】本题考查一次函数图象上点的坐标特征解析:a>b【解析】【分析】【详解】解:∵一次函数y=﹣2x+1中k=﹣2,∴该函数中y随着x的增大而减小,∵1<2,∴a>b.故答案为a>b.【点睛】本题考查一次函数图象上点的坐标特征.18.y=2x【解析】【分析】直接利用一次函数平移规律:左右平移,x左加右减;上下平移,b上加下减,得出答案.【详解】解:将函数y=2x+2的图象向下平移2个单位长度后,所得图象的函数关系式为y解析:y=2x【解析】【分析】直接利用一次函数平移规律:左右平移,x左加右减;上下平移,b上加下减,得出答案.【详解】解:将函数y=2x+2的图象向下平移2个单位长度后,所得图象的函数关系式为y=2x+2﹣2=2x.故答案为:y=2x.【点睛】本题考查的知识点是一次函数图象与几何变换,掌握一次函数图象平移的规律“左右平移,x左加右减;上下平移,b上加下减”是解此题的关键.19.8【解析】【分析】根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求得BC的长,则利用菱形的面积公式即可求解.【详解】解:∵四边形解析:【解析】【分析】根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求得BC的长,则利用菱形的面积公式即可求解.【详解】解:∵四边形AECF是菱形,AB=6,∴设BE=x,则AE=6-x,CE=6-x,∵四边形AECF是菱形,∴∠FCO=∠ECO,∵∠ECO=∠ECB,∴∠ECO=∠ECB=∠FCO=30°,2BE=CE,∴CE=2x,∴2x=6-x,解得:x=2,∴CE=AE=4.利用勾股定理得出:∴菱形的面积=AE•故答案为:【点睛】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.20.【解析】【分析】代数式有意义,则它的分母2x+1≠0,由此求得x的取值范围.【详解】∵代数式有意义,∴2x+1≠0,解得x≠.故答案为:x≠.【点睛】本题考查了分式有意义的条件.解析:12 x≠-【解析】【分析】代数式321x x -+有意义,则它的分母2x+1≠0,由此求得x 的取值范围. 【详解】 ∵代数式321x x -+有意义, ∴2x+1≠0, 解得x≠12-. 故答案为:x≠12-. 【点睛】本题考查了分式有意义的条件.分式有意义的条件是分母不等于零.三、解答题21.(1)k 和b 的值分别为2-和4;(2)23x >;(3)103. 【解析】【分析】(1)根据点D 在函数y =x +2的图象上,即可求出n 的值;再利用待定系数法求出k ,b 的值;(2)根据图象,直接判断即可;(3)用三角形OBC 的面积减去三角形ABD 的面积即可.【详解】(1)函数12y x =+的图像过点D ,且点D 的坐标为2(,)3n ,则有28233n =+=. 所以点D 的坐标为28(,)33. 所以有4,28.33b k b =⎧⎪⎨+=⎪⎩ 解得2,4.k b =-⎧⎨=⎩所以k 和b 的值分别为2-和4. (2)由图象可知,函数y =kx +b 大于函数y =x +2时,图象在直线x =23的左侧, ∴x <23, 故答案为:x <23. (3)已知函数12y x =+的图像与y 轴交于点A ,则点A 坐标为(0,2).所以422AB OB OA =-=-=.函数2y kx b =+的图像与x 轴交于点C ,令20y =,则240x -+=.2x =.所以点C 坐标为(2,0).∴2OC =.则四边形AOCD 的面积等于112104222233BOC BAD S S ∆∆-=⨯⨯-=⨯⨯. 【点睛】本题主要考查一次函数的交点,解决此题时,明确二元一次方程组与一次函数的关系是解决此类问题的关键.第(3)小题中,求不规则图形的面积时,可以利用整体减去部分的方法进行计算.22.(1)560;(2)快车的速度是80km/h ,慢车的速度是60km/h .(3)y=-60x+540(8≤x≤9).【解析】【分析】(1)根据函数图象直接得出甲乙两地之间的距离;(2)根据题意得出慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;(3)利用(2)所求得出D ,E 点坐标,进而得出函数解析式.【详解】(1)由题意可得出:甲乙两地之间的距离为560千米;故答案为:560;(2)由题意可得出:慢车和快车经过4个小时后相遇,相遇后停留了1个小时,出发后两车之间的距离开始增大,快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,∴设慢车速度为3xkm/h ,快车速度为4xkm/h ,∴(3x+4x )×4=560,x=20,∴快车的速度是80km/h ,慢车的速度是60km/h .(3)由题意可得出:快车和慢车相遇地离甲地的距离为4×60=240km ,当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240-3×60=60km , ∴D (8,60),∵慢车往返各需4小时,∴E (9,0),设DE 的解析式为:y=kx+b , ∴90860k b k b +⎧⎨+⎩==, 解得:60540k b -⎧⎨⎩==.∴线段DE 所表示的y 与x 之间的函数关系式为:y=-60x+540(8≤x≤9).【点睛】此题主要考查了待定系数法求一次函数解析式以及一次函数的应用,根据题意得出D ,E 点坐标是解题关键.23.【模型建立】详见解析;【模型应用】①721y x =--;②Q 点坐标为(4,2)或(203,223). .【解析】【分析】模型建立:根据△ABC 为等腰直角三角形,AD ⊥ED ,BE ⊥ED ,可判定△ACD ≌△CBE ;模型应用:①过点B 作BC ⊥AB ,交l 2于C ,过C 作CD ⊥y 轴于D ,根据△CBD ≌△BAO ,得出BD=AO=2,CD=OB=3,求得C (-3,5),最后运用待定系数法求直线l 2的函数表达式;②分两种情况考虑:如图3,∠AQP=90°,AQ=PQ ,设Q 点坐标为(a ,2a-6),利用三角形全等得到a+6-(2a-6)=8,得a=4,易得Q 点坐标;如图4,同理求出Q 的坐标.【详解】模型建立:证明:∵AD CD ⊥,BE EC ⊥∴90D E ∠=∠=︒.∵CB CA =,∠ACB=90°.∴1809090ACD BCE ︒︒∠+∠=-=︒.又∵90EBC BCE ∠+∠=︒,∴ACD EBC ∠=∠.在ACD ∆与CBE ∆中, D E ACD EBC CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BEC CDA ∆∆≌.模型应用:如图2,过点B 作BC AB ⊥交2l 于C ,过C 作CD y ⊥轴于D ,∵45BAC ∠=︒,∴ABC ∆为等腰直角三角形.由(1)可知:CBD BAO ∆∆≌,∴BD AO =,CD OB =.∵144,3:l y x =+ ∴令0y =,得3x =-,∴()30A -,, 令0x =,得4y =,∴()0,4B .∴3BD AO ==,4CD OB ==,∴437OD =+=.∴()4,7C -.设2l 的解析式为y kx b =+∴7403k b k b =-+⎧⎨=-+⎩∴721k b =-⎧⎨=-⎩ 2l 的解析式:721y x =--.分以下两种情况:如图3,当∠AQP=90°时,AQ=PQ ,过点Q 作EF ⊥y 轴,分别交y 轴和直线BC 于点E 、F .在△AQE 和△QPF 中,由(1)可得,△AQE ≌△QPF (AAS ),AE=QF ,设点Q 的坐标为(a,2a-6),即6-(2a-6)=8-a ,解得a=4.此时点Q 的坐标为(4,2).如图4:当∠AQP=90°时,AQ=PQ 时,过点Q 作EF ⊥y 轴,分别交y 轴和直线BC 于点E 、F ,设点Q 的坐标为(a,2a-6),则AE=2a-12,FQ=8-a .,在△AQE 和△QPF 中,同理可得△AQE ≌△QPF (AAS ),AE=QF ,即2a-12=8-a ,解得a=203. 此时点Q 的坐标为(203,223). 综上所述:A 、P 、Q 可以构成以点Q 为直角顶点的等腰直角三角形,点Q 的坐标为 (4,2)或(203,223). 【点睛】 本题考查一次函数综合题,主要考查了点的坐标、矩形的性质、待定系数法、等腰直角三角形的性质以及全等三角形等相关知识的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的性质进行计算,需要考虑的多种情况,解题时注意分类思想的运用.24.(1)6;(2)()()322x x x +-;(3)236x x --;(4)2243x x ++【解析】【分析】(1)根据二次根式乘法法则运算;(2)先提公因式,再套用公式;(3)根据整式乘法法则运算;(4)运用乘法公式运算.【详解】解:(13(1232)36+=3(2332)36+ =63636-=6(2)()()()3231234322x x x x x x x -=-=+- (3)2(1)(2)(3)x x x x -+-+=22226x x x x -++-=236x x --(4)2(21)2(1)(1)x x x +-+-=224412(1)x x x ++--=2244122x x x ++-+ =2243x x ++ 【点睛】考核知识点:因式分解,整式乘法.掌握相应法则是关键.25.(1)y =﹣34x +3;(2)n =56或83+21或﹣43+26;(3)在直线上,理由见解析 【解析】【分析】 (1)将点A 的坐标代入直线AB :y =kx +3并解得:k =﹣34,即可求解; (2)分AP =BP 、AP =AB 、AB =BP 三种情况,分别求解即可;(3)证明△MHP ≌△PCB (AAS ),求出点M (n +73,n +103),即可求解. 【详解】 (1)将点A 的坐标代入直线AB :y =kx +3并解得:k =﹣34, 故AB 的表达式为:y =﹣34x +3; (2)当y =2时,x =43,故点E (43,2),则点P (n +43,2), 而点A 、B 坐标分别为:(4,0)、(0,3),则AP 2=(43+n ﹣4)2+4;BP 2=(n +43)2+1,AB 2=25, 当AP =BP 时,(43+n ﹣4)2+4=(n +43)2+1,解得:n =56; 当AP =AB 时,同理可得:n =8213+(不合题意值已舍去); 当AB =BP 时,同理可得:n =﹣43+26; 故n =56或83+21或﹣43+26; (3)在直线上,理由:如图,过点M 作MD ⊥CD 于点H ,∵∠BPC +∠PBC =90°,∠BPC +∠MPH =90°,∴∠CPB =∠MPH ,BP =PM ,∠MHP =∠PCB =90°∴△MHP ≌△PCB (AAS ),则CP =MH =n +43,BC =1=PH , 故点M (n +73,n +103), n +73+1= n +103, 故点M 在直线y =x +1上.【点睛】此题主要考查了平面直角坐标系中一次函数与全等三角形、等腰三角形的综合应用,熟练掌握,即可解题.四、压轴题26.(1)证明见解析;(2)①CM =8t -,CN =63t -;②t =3.5或5或6.5.【解析】【分析】(1)根据垂直的定义得到∠DAC=∠ECB ,利用AAS 定理证明△ACD ≌△CBE ;(2)①由折叠的性质可得出答案;②动点N 沿F→C 路径运动,点N 沿C→B 路径运动,点N 沿B→C 路径运动,点N 沿C→F 路径运动四种情况,根据全等三角形的判定定理列式计算.【详解】(1)∵AD ⊥直线l ,BE ⊥直线l ,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB ,在△ACD 和△CBE 中,ADC CEB DAC ECB CA CB ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△CBE (AAS );(2)①由题意得,AM=t ,FN=3t ,则CM=8-t ,由折叠的性质可知,CF=CB=6,∴CN=6-3t ;故答案为:8-t ;6-3t ;②由折叠的性质可知,∠BCE=∠FCE ,∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,∴∠NCE=∠CMD ,∴当CM=CN 时,△MDC 与△CEN 全等,当点N 沿F→C 路径运动时,8-t=6-3t ,解得,t=-1(不合题意),当点N 沿C→B 路径运动时,CN=3t-6,则8-t=3t-6,解得,t=3.5,当点N 沿B→C 路径运动时,由题意得,8-t=18-3t ,解得,t=5,当点N 沿C→F 路径运动时,由题意得,8-t=3t-18,解得,t=6.5,综上所述,当t=3.5秒或5秒或6.5秒时,△MDC 与△CEN 全等.【点睛】本题考查了折叠的性质,全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用分情况讨论思想是解题的关键.27.(1)AB ∥CD ,理由见解析;(2)证明见解析;(3)45°.【解析】【分析】(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF 、∠CFE 互补,所以易证AB ∥CD ;(2)利用(1)中平行线的性质推知∠BEF+∠EFD=180°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG ⊥PF ,故结合已知条件GH ⊥EG ,易证PF ∥GH ; (3)利用三角形外角定理、三角形内角和定理求得90902KPG PKG HPK ︒︒∠=-∠=-∠;然后由邻补角的定义、角平分线的定义推知1452QPK EPK HPK ︒∠=∠=+∠;最后根据图形中的角与角间的和差关系求得∠HPQ =45°.【详解】(1)AB ∥CD ,理由如下:∵∠1与∠2互补,∴∠1+∠2=180°,又∵∠1=∠AEF ,∠2=∠CFE ,∴∠AEF +∠CFE =180°,∴AB ∥CD ;(2)由(1)知,AB ∥CD ,∴∠BEF +∠EFD =180°.又∵∠BEF 与∠EFD 的角平分线交于点P , ∴1()902FEP EFP BEF EFD ︒∠+∠=∠+∠=∴∠EPF=90°,即EG⊥PF.∵GH⊥EG,∴PF∥GH;(3)∵∠PHK=∠HPK,∴∠PKG=2∠HPK.又∵GH⊥EG,∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK,∴∠EPK=180°﹣∠KPG=90°+2∠HPK.∵PQ平分∠EPK,∴1452QPK EPK HPK︒∠=∠=+∠,∴∠HPQ=∠QPK﹣∠HPK=45°.答:∠HPQ的度数为45°.【点睛】本题考查了平行线的判定与性质.解题过程中,注意“数形结合”数学思想的运用.28.(1)35,2⎛⎫⎪⎝⎭;(2)2;(3)不是;(4)(6,75)【解析】【分析】(1)根据“白马有理数对”的定义,把数对3(2,1),5,2⎛⎫- ⎪⎝⎭分别代入1a b ab+=-计算即可判断;(2)根据“白马有理数对”的定义,构建方程即可解决问题;(3)根据“白马有理数对”的定义即可判断;(4)根据“白马有理数对”的定义即可解决问题.【详解】(1)∵-2+1=-1,而-2×1-1=-3,∴-2+1≠-3,∴(-2,1)不是“白马有理数对”,∵5+32=132,5×32-1=132,∴5+32=5×32-1,∴35,2⎛⎫⎪⎝⎭是“白马有理数对”,故答案为:3 5,2⎛⎫ ⎪⎝⎭;(2)若(,3)a是“白马有理数对”,则a+3=3a-1,解得:a=2,故答案为:2;(3)若(,)m n是“白马有理数对”,则m+n=mn-1,那么-n+(-m)=-(m+n)=-(mn-1)=-mn+1,∵-mn+1 mn-1∴(-n,-m)不是“白马有理数对”,故答案为:不是;(4)取m=6,则6+x=6x-1,∴x=75,∴(6,75)是“白马有理数对”,故答案为:(6,75).【点睛】本题考查了“白马有理数对”的定义,有理数的加减运算,一次方程的列式求解,理解“白马有理数对”的定义是解题的关键.29.(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E作EF∥AC交AB于F,根据已知条件得到△ABC是等边三角形,推出△BEF是等边三角形,得到BE=EF,∠BFE=60°,根据全等三角形的性质即可得到结论;(3)连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=12CF=3.【详解】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵DE=DC,∴∠E=∠DCE,∴∠ABC-∠E=∠ACB-∠DCB,即∠EDB=∠ACD;(2)∵△ABC是等边三角形,∴∠B=60°,∴△BEF是等边三角形,∴BE=EF,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD,在△DEF与△CAD中,。
人教版八年级上册数学期末考试试题带答案

人教版八年级上册数学期末考试试卷一、选择题。
(每小题只有一个正确答案)1.下列四个图案中,是轴对称图形的是()A .B .C .D .2.如果线段a ,b ,c 能组成三角形,那么它们的长度比可能是()A .1∶2∶4B .2∶3∶4C .3∶4∶7D .1∶3∶43.石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是0.00000000034m ,这个数用科学记数法表示正确的是()A .3.4×10-9m B .0.34×10-9mC .3.4×10-10mD .3.4×10-11m 4.下列运算中,正确的是()A .22a a a ⋅=B .224()a a =C .236a a a ⋅=D .2323()a b a b =⋅5.如图,点P 是∠AOB 的平分线OC 上一点,PD ⊥OA ,垂足为D ,若PD =2,则点P 到边OB 的距离是()A .4B C .2D .16.若分式13x +有意义,则x 的取值范围是()A .x >3B .x <3C .x ≠-3D .x =37.如图,在△ABC 中,∠A =80°,∠C =60°,则外角∠ABD 的度数是()A .100°B .120°C .140°D .160°8.下列各式是完全平方式的是()A .214x x -+B .21x +C .22x xy y -+D .221a a +-9.已知一个多边形的内角和是1080°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形10.如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.其中正确的是()A.①②③④B.②③④C.①③④D.①②③二、填空题11.点()2,1M-关于y轴的对称点的坐标为______.12.如果多边形的每个内角都等于150︒,则它的边数为______.13.如图,△ABC≌△DCB,A、B的对应顶点分别为点D、C,如果AB=6cm,BC=12cm,AC=10cm,DO=3cm,那么OC的长是_____cm.14.在△ABC中,AB=AC,AB的垂直平分线交AC于D,交AB于E,连接BD,若∠ADE =40°,则∠DBC=_____.15.已知13aa+=,则221+=aa_____________________;16.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β=_____.三、解答题17.解方程:21133xx x-=---.18.先化简,再求值:(3x+2)(3x﹣2)﹣10x(x﹣1)+(x﹣1)2,其中x=﹣1.19.如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.20.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.21.甲、乙两工程队共同完成一项工程,乙队先单独做1天后,再由甲、乙两队合作2天就完成了全部工程,已知甲队单独完成这项工程所需的天数是乙队单独完成工程所需天数的2倍,则甲、乙两工程队单独完成工程各需多少天?22.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.23.如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.求证:(1)AE=CD.(2)若AC=12cm,求BD的长.24.某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?25.如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.(1)若点Q与点P的运动速度相等,经过3秒后,△BPD与△CQP是否全等?请说明理由;(2)若点Q与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?参考答案1.C【解析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,对各项进行判断找出不是轴对称图形即可.【详解】A.不是轴对称图形;B.不是轴对称图形;C.是轴对称图形;D.不是轴对称图形;故选:C .【点睛】考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.B【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析求解.【详解】A 、1+2<4,不能组成三角形;B 、2+3>4,能组成三角形;C 、3+4=7,不能够组成三角形;D 、1+3=4,不能组成三角形.故选B .【点睛】考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.3.C【详解】试题分析:根据科学记数法的概念可知:用科学记数法可将一个数表示10n a ⨯的形式,所以将0.00000000034用科学记数法表示103.410-⨯,故选C .考点:科学记数法4.B【解析】【分析】根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘,对各选项分析判断后利用排除法求解.【详解】A 选项:23a a a ⋅=,故是错误的;B选项:()224a a=,故是正确的;C选项:235a a a⋅=,故是错误的;D选项:()3243=⋅,故是错误的;a b a b故选:B.【点睛】考查了同底数幂乘法和幂的乘方,解题关键是运用了同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘.5.C【分析】根据角平分线的性质解答.【详解】解:如图,作PE⊥OB于E,∵点P是∠AOB的角平分线OC上一点,PD⊥OA,PE⊥OB,∴PE=PD=2,故选C.【点睛】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.6.C【解析】【分析】考查分式有意义的条件:分母≠0,即x+3≠0,解得x的取值范围.【详解】∵x+3≠0,∴x≠-3.故选:C.考查的是分式有意义的条件:当分母不为0时,分式有意义.7.C【解析】【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】由三角形的外角性质得,∠ABD=∠A+∠C=80°+60°=140°.故选C.【点睛】考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.8.A【解析】【分析】根据完全平方式(a2+2ab+b2和a2-2ab+b2)进行判断.【详解】A、是完全平方式,故本选项正确;B、不是完全平方式,故本选项错误;C、不是完全平方式,故本选项错误;D、不是完全平方式,故本选项错误;故选:A.【点睛】考查了对完全平方式的应用,主要考查学生的判断能力.9.D【分析】根据多边形的内角和=(n﹣2)•180°,列方程可求解.【详解】设所求多边形边数为n,∴(n﹣2)•180°=1080°,解得n=8.【点睛】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.10.A【分析】由已知条件运用等边三角形的性质得到三角形全等,进而得到更多结论,然后运用排除法,对各个结论进行验证从而确定最后的答案.【详解】∵△ABC和△CDE是正三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ADC≌△BEC(SAS),故①正确,∴AD=BE,故②正确;∵△ADC≌△BEC,∴∠ADC=∠BEC,∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,故③正确;∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,∴△CPQ是等边三角形,故④正确;故选A.【点睛】考查等边三角形的性质及全等三角形的判定等知识点;得到三角形全等是正确解答本题的关键.11.()2,1【分析】关于y 轴对称的点,纵坐标相同,横坐标互为相反数.【详解】∵关于y 轴对称的点,纵坐标相同,横坐标互为相反数∴点()2,1M -关于y 轴的对称点的坐标为()2,1.故答案为:()2,1【点睛】考核知识点:轴对称与点的坐标.理解轴对称和点的坐标关系是关键.12.12【分析】先求出这个多边形的每一个外角的度数,再用360°除以外角的度数即可得到边数.【详解】∵多边形的每一个内角都等于150°,∴多边形的每一个外角都等于180°﹣150°=30°,∴边数n =360°÷30°=12.故答案为12.【点睛】本题考查了多边形的内角与外角的关系,求出每一个外角的度数是解答本题的关键.13.7【解析】【分析】根据△ABC ≌△DCB 可证明△AOB ≌△DOC ,从而根据已知线段即可求出OC 的长.【详解】∵△ABC ≌△DCB ,∴AB=DC ,∠A=∠D ,又∵∠AOB=∠DOC (对顶角相等),∴△AOB ≌△DOC ,∴OC=BO=BD-DO=AC-DO=7.故答案是:7.【点睛】考查了全等三角形的性质解题的关键是注意掌握全等三角形的对应边相等,注意对应关系.14.15°.【分析】先根据线段垂直平分线的性质得出DA=DB ,∠AED=∠BED=90︒,即可得出∠A=∠ABD ,∠BDE =∠ADE ,然后根据直角三角形的两锐角互余和等腰三角形的性质分别求出∠ABD ,∠ABC 的度数,即可求出∠DBC 的度数.【详解】∵AB 的垂直平分线交AC 于D ,交AB 于E ,∴DA=DB ,∠AED=∠BED=90︒,∴∠A=∠ABD ,∠BDE =∠ADE ,∵∠ADE =40︒,∴∠A=∠ABD=9040︒-︒=50︒,∵AB =AC ,∴∠ABC=150652︒-︒=︒,∴∠DBC =∠ABC-∠ABD=15︒.故答案为15︒.【点睛】本题考查线段垂直平分线的性质,等腰三角形的性质.15.7【分析】把已知条件平方,然后求出所要求式子的值.【详解】∵13a a +=,∴219a a ⎛⎫+= ⎪⎝⎭,∴2212+a a +=9,∴221+=a a =7.故答案为7.【点睛】此题考查分式的加减法,解题关键在于先平方.16.240°【详解】已知等边三角形的顶角为60°,根据三角形的内角和定理可得两底角和=180°-60°=120°;再由四边形的内角和为360°可得∠α+∠β=360°-120°=240°.故答案是:240°.17.无解【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】21133x x x -=---2-x=x-3-1-2x=-3-1-2x=3当x=3时,x-3=0,所以原分式方程无解.【点睛】考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.18.8x -3,-11【解析】【分析】原式利用平方差公式,完全平方公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果.【详解】原式=9x 2-4-10x 2+10x+x 2+1-2x=8x-3当x=-1时,原式=-8-3=-11.【点睛】考查了整式的混合运算,平方差公式,以及完全平方公式,熟练掌握运算法则是解本题的关键.19.见解析【分析】先作CD的垂直平分线和∠AOB的平分线,它们的交点为P点,则根据线段垂直平分线的性质和角平分线的性质得到PC=PD,且P到∠AOB两边的距离相等.【详解】解:如图,点P为所作.【点睛】本复考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.20.50°【分析】先利用平行线求出∠CBG,再用邻补角的定义求出∠CBD,最后用三角形的内角和定理即可得出结论.【详解】解:∵EF∥GH,∴∠CBG=∠EAB,∵∠EAB=110°,∴∠CBG=110°,∴∠CBD=180°﹣∠CBG=70°,在△BCD中,∵∠C=60°,∴∠BDC=180°﹣∠C﹣∠CBD=180°﹣60°﹣70°=50°,即:∠BDC的度数为50°.【点睛】此题主要考查了平行线的性质,邻补角的定义,三角形内角和定理,求出∠CBD=70°是解本题的关键.21.甲需8天,乙需4天【解析】【分析】根据乙队先单独做1天后,再由两队合作2天就完成了全部工程则等量关系为:乙一天的工作量+甲乙合作2天的工作量=1,再设未知数列方程,解方程即可.【详解】设乙队单独完成所需天数x天,则甲队单独完成需2x天,1112(1++=2x x x解得:x=4,当x=4时,分式方程有意义,所以x=4是分式方程的解,所以甲、乙两队单独完成工程各需8天和4天.答:甲、乙两队单独完成工程各需8天和4天.【点睛】考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.22.证明见解析【详解】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.试题解析:∵AB=AC=AD,∴∠C=∠ABC,∠D=∠ABD.∴∠ABC=∠CBD+∠D.∵AD∥BC,∴∠CBD=∠D.∴∠ABC=2∠D.又∵∠C=∠ABC,∴∠C=2∠D.23.(1)见解析;(2)6【分析】(1)根据DB ⊥BC ,CF ⊥AE ,得出∠D =∠AEC ,再结合∠DBC =∠ECA =90°,且BC =CA ,证明△DBC ≌△ECA ,即可得证;(2)由(1)可得△DBC ≌△ECA ,可得CE=BD ,根据BC=AC=12cm AE 是BC 的中线,即可得出12CE BC =,即可得出答案.【详解】证明:(1)证明:∵DB ⊥BC ,CF ⊥AE ,∴∠DCB +∠D =∠DCB +∠AEC =90°.∴∠D =∠AEC .又∵∠DBC =∠ECA =90°,且BC =CA ,在△DBC 和△ECA 中90D AEC DBC ECA BC AC ∠∠∠∠⎪⎩︒⎧⎪⎨====,∴△DBC ≌△ECA (AAS ).∴AE =CD ;(2)由(1)可得△DBC ≌△ECA∴CE=BD ,∵BC=AC=12cm AE 是BC 的中线,∴162CE BC cm ==,∴BD=6cm .【点睛】本题考查了全等三角形的判定和性质,直角三角形斜边上的中线,证明△DBC ≌△ECA 解题关键.24.(1)商场两次共购进这种运动服600套;(2)每套运动服的售价至少是200元【分析】(1)设该商场第一次购进这种运动服x 套,第二次购进2x 套,然后根据题意列分式解答即可;(2)设每套售价是y 元,然后根据“售价-两次总进价≥成本×利润率”列不等式并求解即可.【详解】解:(1)设商场第一次购进x 套运动服,由题意得6800032000102x x-=解这个方程,得200x =经检验,200x =是所列方程的根22200200600x x +=⨯+=;答:商场两次共购进这种运动服600套;(2)设每套运动服的售价为y 元,由题意得600320006800020%3200068000y --+ ,解这个不等式,得200y ≥.答:每套运动服的售价至少是200元.【点睛】本题主要考查了分式方程和一元一次不等式的应用,弄清题意、确定量之间的关系、列出分式方程和不等式是解答本题的关键.25.(1)全等;(2)当点Q 的运动速度为54厘米/秒时,能够使△BPD 与△CQP 全等.【分析】(1)根据时间和速度分别求得两个三角形中的边的长,根据SAS 判定两个三角形全等;(2)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P 运动的时间,再求得点Q 的运动速度.【详解】(1)因为t =3秒,所以BP =CQ =1×3=3(厘米),因为AB =10厘米,点D 为AB 的中点,所以BD =5厘米.又因为PC =BC BP -,BC =8厘米,所以PC =835-=(厘米),所以PC =BD .因为AB =AC ,所以∠B=∠C,所以△BPD≌△CQP(SAS).(2)因为P v≠Q v,所以BP≠CQ,当△BPD≌△CPQ时,因为∠B=∠C,AB=10厘米,BC=8厘米,所以BP=PC=4厘米,CQ=BD=5厘米,所以点P,点Q运动的时间为4秒,所以54Qv 厘米/秒,即当点Q的运动速度为54厘米/秒时,能够使△BPD与△CQP全等.【点睛】考查了全等三角形的判定,等腰三角形的性质.解题时,主要是运用了路程=速度×时间的公式.熟练运用全等三角形的判定和性质,能够分析出追及相遇的问题中的路程关系.。
八年级上册期末试卷(AB卷)及答案.docx

八年级上册期末试卷(A卷)(满分120分时间100分钟)一. 选择题:(30分)1.做完“装满水的杯子里还能放多少回形针”的实验,强强对实验的结果感到非常吃惊,同时对决定放入回形针多少的因素进行了猜想。
指出列出的猜想中,肯定不合理的是:()A.杯子的组成材料;B.杯口的大小;C.杯里所盛的液体;2.将正在发声的手机.电铃或接通电源的音乐芯片悬挂在广口瓶内,再把瓶内的空气抽出如图所示,声音逐渐变小,但始终能听到声音。
原因是:()A.瓶内已被抽成真空,真空亦能传声;B.声源发声太强,换用发声较弱的声源;C.离实验瓶远一点,就可以听不到声音;D.瓶内仍有少量空气,悬挂声源的固体亦能传声3.“影”是我们日常生活中常见的光现象,如做光学游戏形成的“手影”,剧院放映的电影; 湖岸景色在水中形成的倒影,春游时留下美好记忆的照片一摄影等,以下列出的“影”与物理知识对应()关系不牙硕的是\ )A.手影一光的直线传播;B.倒影一平面镜成像;C.电影一凸透镜成像;D.摄影一光的反射4.在班级进行的物理知识抢答比赛中,坐在前排座位的同学,不用回头,根据说话的声音就能判断出是谁在抢答,这是因为不同人的声音具有不同的()A.振幅B.频率C.响度D.音色5.小明学过平面镜成像知识后,概括了几个特点,其中镜谡的是()A.物体在平面镜里成的像与物体的大小相等B.平面镜里物体成的像可以用白纸做的屏幕接收到C.像与物到镜面的距离相等D.像与物对应的连线与镜面垂直6.下列说法中,能证实红外线存在的是()A.红外线显红色B.在红光的内侧能观察到C.温度高的物体有红外线D.红外线使物体发热7.战斗机在空中加油时,已知加油机的速度是8000km/h,则在加油过程中,战斗机飞行的路程与加油机飞行的路程之比是A.等于1: 1B.大于1: 1D.杯子的价格C.小于1: 1D.无法判断8.目前有些饭店安装了热风干手器,打开它就有热风吹到手上,使手上的水很快蒸发掉,使水快速蒸发的原因是( )A.加快了水面附近空气的流动并提高了水的温度B.提高了水的温度并增大了水的表面积C.加快了水面附近空气的流动并增大了水的表面积D.加快了水面附近空气的流动,提高了水的温度并增大了水的表面积9.下列说法中正确的是( )A.恰当的放大镜可使5°的角度放大成8°或10°B.人离平面镜越远,平面镜中的像越小C.实像可以用光屏承接,虚像不可以用光屏承接D.不论什么光,通过凸透镜后总可以会聚到一点10.下列关于光现象的说法中,正确的是( )A.我国古代使用的铜镜能成正立放大的实像B.老花镜是利用凹透镜对光线的会聚作用C.不能用望远镜直接观察太阳或其他强光源D.清晨,地平线下的太阳我们也能看到,这是由于光的反射形成的二. 填空题(28分)1.为测量书本中一张纸的大致厚度,有位同学这样做:先测整个课本的厚度,结果为0. 72cm, 然后他翻到课本最后一页,看到页码为17&于是,他计算得到的厚度为:唏21=0. 004cm;(1)他计算中存在的错误是:_______________________________ ;(2)正确的计算应当是:_______________________________ o2.亚洲最大沉管隧道一上海外环隧道于2003年6月21日通车,隧道的江中管段长736m。
人教版八年级上学期英语《期末测试卷》附答案

A. To give students more knowledge about safety and make sure their lives safe.
The young man swallowed(吞咽)and said nothing. He lifted the kid's brother back into the wheelchair. Then the little boy pushed his brother towards their home.
He didn't hesitate(犹豫). "I'm John Blanchard and you must be Miss Maynell. I am so glad you could meet me. May I take you to dinner?" he asked.
The woman had a kind smile on her face. "I don't know,what this is about,dear," she answered,"But the young lady in the green coat just asked me to wear this rose on my coat. She said if you asked me out to dinner,I should tell you that she is waiting for you in the big restaurant across the street. She said it was a kind of test! "
八年级(上)期末数学试卷(含答案)

八年级(上)期末数学试卷(含答案) 一、选择题1.摩托车开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油量y (升)与它工作时间t (时)之间函数关系的图象是( )A .B .C .D .2.如图,已知ABC DCB ∠=∠,添加以下条件,不能判定ABC DCB ∆≅∆的是( )A .AB DC = B .BE CE = C .AC DB =D .A D ∠=∠3.如图,在ABC ∆中,31C ∠=︒,ABC ∠的平分线BD 交AC 于点D ,如果DE 垂直平分BC ,那么A ∠的度数为( )A .31︒B .62︒C .87︒D .93︒ 4.下列无理数中,在﹣1与2之间的是( )A .﹣3B .﹣2C .2D .5 5.若b >0,则一次函数y =﹣x +b 的图象大致是( )A .B .C .D .6.下列四组线段a 、b 、c ,能组成直角三角形的是( )A .4a =,5b =,6c =B .3a =,4b =,5c =C .2a =,3b =,4c =D .1a =,2b =3c =7.人的眼睛可以看见的红光的波长约为5810cm -⨯,近似数5810-⨯精确到( ) A .0.001cm B .0.0001cm C .0.00001cm D .0.000001cm8.在平面直角坐标系中,把直线34y x =-+沿x 轴向左平移2个单位长度后,得到的直线函数表达式为( )A .31y x =-+B .32y x =-+C .31y x =--D .32y x =--9.下列关于10的说法中,错误的是( )A .10是无理数B .3104<<C .10的平方根是10D .10是10的算术平方根10.工人师傅常用角尺平分一个任意角做法如下:如图所示,在∠AOB 的两边OA ,OB 上分别取OM =ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合,过角尺顶点C 的射线OC 即是∠AOB 的平分线画法中用到三角形全等的判定方法是( )A .SSSB .SASC .ASAD .HL二、填空题11.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了__________步路(假设2步为1米),却踩伤了花草.12.计算:32()x y -=__________.13.在平面直角坐标系中,(2,3)A -、(4,4)B ,点P 是x 轴上一点,且PA PB =,则点P 的坐标是__________.14.如图,已知直线3y x b =+与2y ax =-的交点的横坐标为-2,则关于x 的不等式32x b ax +>-的解集为______.15.如图①,四边形ABCD 中,//,90BC AD A ∠=︒,点P 从A 点出发,沿折线AB BC CD →→运动,到点D 时停止,已知PAD △的面积s 与点P 运动的路程x 的函数图象如图②所示,则点P 从开始到停止运动的总路程为________.16.如图,在平面直角坐标系xOy 中,点A 的坐标为(1,3),点B 的坐标为(2,-1),点C 在同一坐标平面中,且△ABC 是以AB 为底的等腰三角形,若点C 的坐标是(x ,y ),则x 、y 之间的关系为y =______(用含有x 的代数式表示).17.如图,已知直线l 1:y=kx+4交x 轴、y 轴分别于点A (4,0)、点B (0,4),点C 为x 轴负半轴上一点,过点C 的直线l 2:12y x n =+经过AB 的中点P ,点Q (t ,0)是x 轴上一动点,过点Q 作QM ⊥x 轴,分别交l 1、l 2于点M 、N ,当MN=2MQ 时,t 的值为_____.18.小明体重约为62.36千克,如果精确到0.1千克,其结果为____千克.19.如图,在ABC ∆中,AC AD BD ==,28B ∠=,则CAD ∠的度数为__________.20.若等腰三角形的顶角为30°,那么这个等腰三角形的底角为_____°三、解答题21.如图所示,在ABC ∆中,BAC ∠的平分线AD 交BC 于点D ,DE 垂直平分AC ,垂足为点E .求证:BAD C ∠=∠.22.小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:?1322x x+=--. (1)她把这个数“?”猜成5,请你帮小华解这个分式方程; (2)小华的妈妈说:“我看到标准答案是:方程的增根是2x =,原分式方程无解”,请你求出原分式方程中“?”代表的数是多少?23.如图,直角坐标系xOy 中,一次函数y=﹣12x+5的图象l 1分别与x ,y 轴交于A ,B 两点,正比例函数的图象l 2与l 1交于点C (m ,4). (1)求m 的值及l 2的解析式;(2)求S △AOC ﹣S △BOC 的值;(3)一次函数y=kx+1的图象为l 3,且11,l 2,l 3不能围成三角形,直接写出k 的值.24.定义:到一个三角形三个顶点的距离相等的点叫做该三角形的外心.(1)如图①,小海同学在作△ABC 的外心时,只作出两边BC ,AC 的垂直平分线得到交点O ,就认定点O 是△ABC 的外心,你觉得有道理吗?为什么?(2)如图②,在等边三角形ABC 的三边上,分别取点D ,E ,F ,使AD =BE =CF ,连接DE ,EF ,DF ,得到△DEF .若点O 为△ABC 的外心,求证:点O 也是△DEF 的外心.25.如图,已知直线y=kx+6经过点A(4,2),直线与x轴,y轴分别交于B、C两点.(1)求点B的坐标;(2)求△OAC的面积.四、压轴题26.如图,直线11 2y x b=-+分别与x轴、y轴交于A,B两点,与直线26y kx=-交于点()C4,2.(1)b= ;k= ;点B坐标为;(2)在线段AB上有一动点E,过点E作y轴的平行线交直线y2于点F,设点E的横坐标为m,当m为何值时,以O、B、E、F为顶点的四边形是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得P,Q,A,B四个点能构成一个菱形.若存在,直接写出所有符合条件的Q点坐标;若不存在,请说明理由.27.在平面直角坐标系中点A(m−3,3m+3),点 B(m,m+4)和 D(0,−5),且点 B 在第二象限.(1)点B 向平移单位,再向下平移(用含m 的式子表达)单位可以与点A 重合;(2)若点B 向下移动 3 个单位,则移动后的点B 和点A 的纵坐标相等,且有点 C(m−2,0).①则此时点A、B、C 坐标分别为、、.②将线段AB 沿y 轴负方向平移n 个单位,若平移后的线段AB 与线段CD 有公共点,求n 的取值范围.③当m<−1 式,连接AD,若线段AD 沿直线AB 方向平移得到线段BE,连接DE 与直线y=−2 交于点F,则点F 坐标为.(用含m 的式子表达)28.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.29.阅读下面材料,完成(1)-(3)题.数学课上,老师出示了这样一道题:如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.同学们经过思考后,交流了自已的想法:小明:“通过观察和度量,发现∠DFC的度数可以求出来.”小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”......老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”(1)求∠DFC的度数;(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.30.如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两直线的交点为P点.(1)求P点的坐标;(2)求△APB的面积;(3)x轴上存在点T,使得S△ATP=S△APB,求出此时点T的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】由题意根据剩余油量等于油箱中的原有的油量减去用去的油量,列出y、x的关系式,然后根据一次函数的图象选择答案即可.【详解】解:∵油箱中有油4升,每小时耗油0.5升,∴y=4-0.5x,∵4-0.5x≥0,∴x≤8,∴x的取值范围是0≤x≤8,所以,函数图象为:故选:D.【点睛】本题考查一次函数的应用,一次函数的图象,比较简单,难点在于根据实际意义求出自变量x的取值范围.2.C解析:C【解析】【分析】全等三角形的判定方法有SAS,ASA,AAS,SSS,根据定理逐个判断即可.【详解】A.AB=DC,∠ABC=∠DCB,BC=BC,符合SAS,即能推出△ABC≌△DCB,故本选项错误;B.∵BE=CE,∴∠DBC=∠ACB.∵∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合ASA,即能推出△ABC≌△DCB,故本选项错误;C.∠ABC=∠DCB,AC=BD,BC=BC,不符合全等三角形的判定定理,即不能推出△ABC≌△DCB,故本选项正确;D.∠A=∠D,∠ABC=∠DCB,BC=BC,符合AAS,即能推出△ABC≌△DCB,故本选项错误.故选:C.【点睛】本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,能正确根据全等三角形的判定定理进行推理是解答此题的关键,注意:全等三角形的判定方法有SAS,ASA,AAS,SSS.3.C解析:C【分析】根据垂直平分线的性质,可以得到∠C=∠ABC ,再根据角平分线的性质,得到∠ABC 的度数,最后利用三角形内角和即可解决.【详解】∵DE 垂直平分BC ,DB DC ∴=,31C DBC ︒∴∠=∠=,∵BD 平分ABC ∠,262ABC DBC ︒∴∠=∠=,180A ABC C ︒∴∠+∠+∠=,180180623187A ABC C ︒︒︒︒︒∴∠=-∠-∠=--=故选C【点睛】本题考查了垂直平分线的性质,角平分线的性质和三角形内角和,解决本题的关键是熟练掌握三者性质,正确理清各角之间的关系.4.C解析:C【解析】试题分析:A 1,故错误;B <﹣1,故错误;C .﹣1<2,故正确;2,故错误;故选C .【考点】估算无理数的大小.5.C解析:C【解析】分析:根据一次函数的k 、b 的符号确定其经过的象限即可确定答案.详解:∵一次函数y x b =+中100k b =-,,∴一次函数的图象经过一、二、四象限,故选C .点睛:主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y kx b =+的图象有四种情况:①当k >0,b >0,函数y =kx +b 的图象经过第一、二、三象限;②当k >0,b <0,函数y =kx +b 的图象经过第一、三、四象限;③当k <0,b >0时,函数y =kx +b 的图象经过第一、二、四象限;④当k <0,b <0时,函数y =kx +b 的图象经过第二、三、四象限.6.B【解析】【分析】根据勾股定理的逆定理,依次对各选项进行分析即可得答案.【详解】解:A.因为42+52≠62,所以不能围成直角三角形,此选项错误;B.因为32+42=52,所以能围成直角三角形,此选项正确;C. 因为22+32≠42,所以不能围成直角三角形,此选项错误;D. 因为12+2≠32,所以不能围成直角三角形,此选项错误;故选:B.【点睛】本题考查了勾股定理的逆定理. 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.能依据这一定理判断三角形是否为直角三角形是解决此题的关键.7.C解析:C【解析】【分析】把数还原后,再看首数8的最后一位数字8所在的位数是十万分位,即精确到十万分位.【详解】∵5⨯=0.00008,810-∴近似数5⨯是精确到十万分位,即0.00001.810-故选:C.【点睛】此题主要考查了科学记数法与有效数字,正确还原数据是解题关键.8.D解析:D【解析】【分析】求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.上下平移时只需让b的值加减即可.【详解】y=-3x+4的k=-3,b=4,沿x轴向左平移2个单位后,新直线解析式为:y=-3(x+2)+4=-3x-2.故选:D.【点睛】本题考查了一次函数的平移变换,属于基础题,关键掌握将直线上下平移时k的值不变,只有b发生变化.9.C解析:C【解析】试题解析:A是无理数,说法正确;B、3<4,说法正确;C、10,故原题说法错误;D是10的算术平方根,说法正确;故选C.10.A解析:A【解析】【分析】根据全等三角形的判定方法即可解决问题.【详解】由题意:OM=ON,CM=CN,OC=OC,∴△COM≌△CON(SSS),∴∠COM=∠CON,故选:A.【点睛】此题主要考查三角形全等判定的应用,熟练掌握,即可解题.二、填空题11.8【解析】【分析】先根据勾股定理求出斜边的长,与直角边进行比较即可求得结果.【详解】解:由题意得,斜边长AB===10米,则少走(6+8-10)×2=8步路,故答案为8.【点睛】本解析:8【解析】【分析】先根据勾股定理求出斜边的长,与直角边进行比较即可求得结果.【详解】解:由题意得,斜边长米,则少走(6+8-10)×2=8步路,故答案为8.【点睛】本题考查的是勾股定理的应用,属于基础应用题,只需学生熟练掌握勾股定理,即可完成.12.【解析】【分析】根据积的乘方法则进行计算.【详解】故答案为:【点睛】考核知识点:积的乘方.理解积的乘方法则是关键.解析:62x y【解析】【分析】根据积的乘方法则进行计算.【详解】()2323262()x y x y x y-=-=故答案为:62x y【点睛】考核知识点:积的乘方.理解积的乘方法则是关键.13.(,0)【解析】【分析】画图,设点的坐标是(x,0),因为PA=OB,根据勾股定理可得:AC2+PC2=BD2+ PD2.【详解】已知如图所示;设点的坐标是(x,0),因为PA=OB根据勾解析:(1912,0)【解析】【分析】画图,设点P的坐标是(x,0),因为PA=OB,根据勾股定理可得:AC2+PC2=BD2+PD2.【详解】已知如图所示;设点P的坐标是(x,0),因为PA=OB 根据勾股定理可得:AC2+PC2=BD2+PD2所以32+(x+2)2=42+(4-x)2解得1912 x所以点P的坐标是(1912,0)故答案为:(1912,0)【点睛】考核知识点:勾股定理.数形结合,根据勾股定理建立方程是关键.14.x>−2【解析】【分析】直线y=3x+b与y=ax−2的交点的横坐标为−2,求不等式3x+b>ax−2的解集,就是看函数在什么范围内y=3x+b的图象在函数y=ax−2的图象上方.【详解】解析:x>−2【解析】【分析】直线y=3x+b与y=ax−2的交点的横坐标为−2,求不等式3x+b>ax−2的解集,就是看函数在什么范围内y=3x+b的图象在函数y=ax−2的图象上方.【详解】解:从图象得到,当x>−2时,y=3x+b的图象在y=ax−2的图象上方,∴不等式3x+b>ax−2的解集为:x>−2.故答案为x>−2.【点睛】本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.【解析】【分析】根据函数图象可以直接得到AB、BC和三角形ADB的面积,从而可以求得AD的长,作辅助线CE⊥AD,从而可得CD的长,进而求得点P从开始到停止运动的总路程,本题得以解决.【解析:11【解析】【分析】根据函数图象可以直接得到AB、BC和三角形ADB的面积,从而可以求得AD的长,作辅助线CE⊥AD,从而可得CD的长,进而求得点P从开始到停止运动的总路程,本题得以解决.【详解】解:作CE⊥AD于点E,如下图所示,由图象可知,点P从A到B运动的路程是3,当点P与点B重合时,△PAD的面积是212,由B到C运动的路程为3,∴321 222 AD AB AD⨯⨯==解得,AD=7,又∵BC//AD,∠A=90°,CE⊥AD,∴∠B=90°,∠CEA=90°,∴四边形ABCE是矩形,∴AE=BC=3,∴DE=AD-AE=7-3=4,∴2222345,CD CE DE=+=+=∴点P从开始到停止运动的总路程为: AB+BC+CD=3+3+5=11.故答案为:11【点睛】本题考查了根据函数图象获取信息,解题的关键是明确题意,能从函数图象中找到准确的信息,利用数形结合的思想解答问题.16.【解析】设的中点为,过作的垂直平分线,通过待定系数法求出直线的函数表达式,根据可以得到直线的值,再求出中点坐标,用待定系数法求出直线的函数表达式即可.【详解】解:设的中点为,过作的解析:1548x+【解析】【分析】设AB的中点为D,过D作AB的垂直平分线EF,通过待定系数法求出直线AB的函数表达式,根据EF AB⊥可以得到直线EF的k值,再求出AB中点坐标,用待定系数法求出直线EF的函数表达式即可.【详解】解:设AB的中点为D,过D作AB的垂直平分线EF∵A(1,3),B(2,-1)设直线AB的解析式为11y k x b=+,把点A和B代入得:321k bk b+=⎧⎨+=-⎩解得:1147kb=-⎧⎨=⎩∴47y x=-+∵D为AB中点,即D(122+,312-)∴D(32,1)设直线EF的解析式为22y k x b=+∵EF AB⊥∴121k k=-∴214k=∴把点D 和2k 代入22y k x b =+可得:213142b =⨯+ ∴258b =∴1548y x =+ ∴点C(x ,y )在直线1548y x =+上 故答案为1548x + 【点睛】 本题主要考查了等腰三角形的性质,中垂线的性质,待定系数法求一次函数的表达式,根据题意作出中垂线,再用待定系数法求出一次函数的解析式是解题的关键.17.10或【解析】【分析】先求出的值,确定的关系式,然后根据一次函数图象上点的坐标特征求得点M 、N 的坐标,由两点间的距离公式求得MN ,MQ 的代数式,由已知条件,列出方程,借助于方程求得t 的值即可;解析:10或227 【解析】【分析】先求出k n ,的值,确定12l l ,的关系式,然后根据一次函数图象上点的坐标特征求得点M 、N 的坐标,由两点间的距离公式求得MN ,MQ 的代数式,由已知条件,列出方程,借助于方程求得t 的值即可;【详解】解:把()40A ,代入到4y kx =+中得:440k +=,解得:1k =-, ∴1l 的关系式为:4y x =-+,∵P 为AB 的中点,()40A ,,()0,4B ∴由中点坐标公式得:()2,2P ,把()2,2P 代入到12y x n =+中得:1222n ⨯+=,解得:1n =, ∴2l 的关系式为:112y x =+,∵QM x ⊥轴,分别交直线1l ,2l 于点M N 、,()0Q t ,, ∴(),4M t t -+,1,12N t t ⎛⎫+ ⎪⎝⎭,∴()1341322MN t t t ⎛⎫=-+-+=- ⎪⎝⎭,44MQ t t =-+=-, ∵2MN MQ =, ∴33242t t -=-, 分情况讨论得:①当4t ≥时,去绝对值得:()33=242t t --, 解得:10t =;②当24t ≤<时,去绝对值得:()33=242t t --, 解得:227t =; ③当2t <时,去绝对值得:()33=242t t --, 解得:102t =>,故舍去;综上所述:10t =或227t =; 故答案为:10或227. 【点睛】本题属于一次函数综合题,需要熟练掌握待定系数法确定函数关系式,一次函数图象上点的坐标特征,两点间的距离公式等知识点,能够表示出线段的长度表达式,合理的使用分类讨论思想是解决本题的关键,有一定的难度.18.4.【解析】【分析】把百分位上的数字6进行四舍五入即可.【详解】62.36千克精确到0.1千克为62.4千克.故答案为:62.4.本题考查了近似数和有效数字:近似数与精确数的解析:4.【解析】【分析】把百分位上的数字6进行四舍五入即可.【详解】62.36千克精确到0.1千克为62.4千克.故答案为:62.4.【点睛】本题考查了近似数和有效数字:近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.19.68°【解析】【分析】由在△ABC中,AC=AD=BD,∠B=28°,根据等腰三角形的性质,即可求得∠ADC 的度数,接着求得∠C的度数,可得结论.【详解】解:∵AD=BD,∴∠BAD=∠解析:68°【解析】【分析】由在△ABC中,AC=AD=BD,∠B=28°,根据等腰三角形的性质,即可求得∠ADC的度数,接着求得∠C的度数,可得结论.【详解】解:∵AD=BD,∴∠BAD=∠B=28°,∴∠ADC=∠B+∠BAD=28°+28°=56°,∵AD=AC,∴∠C=∠ADC=56°,∴∠CAD=180°-∠ADC-∠C=180°-56°-56°=68°,故答案为:68°.【点睛】此题考查了等腰三角形的性质与三角形外角的性质.此题难度不大,注意掌握数形结合思想的应用.20.75【解析】根据等腰三角形两个底角相等可得解.【详解】依题意知,等腰三角形两个底角相等.当顶角=30°时,两底角的和=180°-30°=150°.所以每个底角=75°.故答案解析:75【解析】【分析】根据等腰三角形两个底角相等可得解.【详解】依题意知,等腰三角形两个底角相等.当顶角=30°时,两底角的和=180°-30°=150°.所以每个底角=75°.故答案为75.考点:三角形内角和与等腰三角形性质.点评:本题难度较低.已知角为顶角,根据等腰三角形性质与三角形内角和性质计算即可.三、解答题21.见解析【解析】【分析】利用角平分线的定义得到BAD DAE ∠=∠,然后利用垂直平分线的性质得到DA DC =,则DAE C ∠=∠,从而使问题得解.【详解】解:∵AD 平分BAC ∠∴BAD DAE ∠=∠,∵DE 垂直平分AC ,∴DA DC =,∴DAE C ∠=∠,∴BAD C ∠=∠【点睛】本题考查角平分线的定义和垂直平分线的性质,掌握相关性质正确推理论证是本题的解题关键.22.(1)0x =;(2)原分式方程中“?”代表的数是-1.【解析】(1)“?”当成5,解分式方程即可,(2)方程有增根是去分母时产生的,故先去分母,再将x=2代入即可解答.【详解】(1)方程两边同时乘以()2x -得()5321x +-=-解得 0x =经检验,0x =是原分式方程的解.(2)设?为m ,方程两边同时乘以()2x -得()321m x +-=-由于2x =是原分式方程的增根,所以把2x =代入上面的等式得()3221m +-=-1m =-所以,原分式方程中“?”代表的数是-1.【点睛】本题考查了分式方程解法和增根的定义及应用.增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.增根确定后可按如下步骤进行: ①化分式方程为整式方程; ②把增根代入整式方程即可求得相关字母的值.23.(1)m=2,l 2的解析式为y=2x ;(2)S △AOC ﹣S △BOC =15;(3)k 的值为32或2或﹣12. 【解析】【分析】(1)先求得点C 的坐标,再运用待定系数法即可得到l 2的解析式;(2)过C 作CD ⊥AO 于D ,CE ⊥BO 于E ,则CD=4,CE=2,再根据A (10,0),B (0,5),可得AO=10,BO=5,进而得出S △AOC ﹣S △BOC 的值;(3)分三种情况:当l 3经过点C (2,4)时,k=32;当l 2,l 3平行时,k=2;当11,l 3平行时,k=﹣12;故k 的值为32或2或﹣12. 【详解】(1)把C (m ,4)代入一次函数y=﹣12x+5,可得 4=﹣12m+5, 解得m=2,∴C (2,4),设l 2的解析式为y=ax ,则4=2a ,解得a=2,∴l 2的解析式为y=2x ;(2)如图,过C 作CD ⊥AO 于D ,CE ⊥BO 于E ,则CD=4,CE=2,y=﹣12x+5,令x=0,则y=5;令y=0,则x=10, ∴A (10,0),B (0,5),∴AO=10,BO=5, ∴S △AOC ﹣S △BOC =12×10×4﹣12×5×2=20﹣5=15;(3)一次函数y=kx+1的图象为l 3,且11,l 2,l 3不能围成三角形,∴当l 3经过点C (2,4)时,k=32; 当l 2,l 3平行时,k=2;当11,l 3平行时,k=﹣12; 故k 的值为32或2或﹣12. 【点睛】本题主要考查一次函数的综合应用,解决问题的关键是掌握待定系数法求函数解析式、等腰直角三形的性质、全等三角形的判定和性质、勾股定理及分类讨论思想等.24.(1)定点O 是△ABC 的外心有道理,理由见解析;(2)见解析【解析】【分析】(1)连接OA 、OB 、OC ,如图①,根据线段垂直平分线的性质得到OB OC =,OC OA =,则OA OB OC ==,从而根据三角形的外心的定义判断点O 是ABC ∆的外心;(2)连接OA 、OD 、OC 、OF ,如图②,利用等边三角形的性质得到OA OC =,2120AOC B ∠=∠=︒,再计算出30OAD OCF OAD ∠=∠=∠=︒,接着证明AOD COF ∆≅∆得到OD OC =,同理可得OD OE =,所以OD OE OF ==,然后根据三角形外心的定义得到点O 是DEF ∆的外心.【详解】(1)解:定点O是ABC∆的外心有道理.理由如下:连接OA、OB、OC,如图①,BC,AC的垂直平分线得到交点O,OB OC∴=,OC OA=,OA OB OC∴==,∴点O是ABC∆的外心;(2)证明:连接OA、OD、OC、OF,如图②,点O为等边ABC∆的外心,OA OC∴=,2120AOC B∠=∠=︒,30OAD OCF∴∠=∠=︒,30OAD∴∠=︒,在AOD∆和COF∆中OA OCOAD OCFAD CF=⎧⎪∠=∠⎨⎪=⎩,()AOD COF SAS∴∆≅∆,OD OC∴=,同理可得OD OE=,OD OE OF∴==,∴点O是DEF∆的外心.【点睛】本题考查了线段垂直平分线性质和全等三角形的判定、等边三角形的性质.掌握线段垂直平分线性质和构造三角形全等是解题关键.25.(1)B(6,0);(2)12【解析】【分析】(1)根据待定系数法求得直线解析式,然后根据图象上点的坐标特征即可求得B的坐标;(2)令x=0,求得C的坐标,然后根据三角形面积公式即可求得.【详解】解:(1)∵直线y=kx+6经过点A(4,2),∴2=4k+6,解得k=﹣1∴直线为y=﹣x+6令y=0,则﹣x+6=0,解得x=6,∴B(6,0);(2)令x=0,则y=6,∴C(0,6),∴CO=6,∴△OAC的面积=162⨯×4=12.【点睛】本题考查的知识点是一次函数的图象上点的坐标特征,属于基础题目,易于掌握.四、压轴题26.(1)4;2;(0,4);(2)125m=或285m=;(3)存在.Q点坐标为()-,()4,()0,4-或()5,4.【解析】【分析】(1)根据待定系数法,将点C(4,2)代入解析式可求解;(2)设点E(m,142m+),F(m,2m-6),得()154261022EF m m m=-+--=-,由平行四边形的性质可得BO=EF=4,列出方程即可求解;(3)分两种情况讨论,由菱形的性质按照点平移的坐标规律,先确定P点坐标,再确定O 点坐标即可求解.【详解】解:(1)(1)∵直线y2=kx-6交于点C(4,2),∴2=4k-6,∴k=2,∵直线212y x b =-+过点C (4,2), ∴2=-2+b ,∴b =4, ∴直线解析式为:212y x b =-+,直线解析式为y 2=2x -6, ∵直线212y x b =-+分别与x 轴、y 轴交于A ,B 两点, ∴当x =0时,y =4,当y =0时,x =8,∴点B (0,4),点A (8,0),故答案为:4;2;(0,4)(2)∵点E 在线段AB 上,点E 的横坐标为m ,∴1,42E m m ⎛⎫-+ ⎪⎝⎭,(),26F m m -, ∴()154261022EF m m m =-+--=-. ∵四边形OBEF 是平行四边形,∴EF BO =,∴51042m -=, 解得:125m =或285m =时, ∴当125m =或285m =时,四边形OBEF 是平行四边形. (3)存在.此时Q 点坐标为()45,4-,()45,4,()0,4-或()5,4.理由如下:假设存在.以P ,Q ,A ,B 为顶点的菱形分两种情况:①以AB 为边,如图1所示.因为点()8,0A ,()0,4B ,所以45AB =.因为以P ,Q ,A ,B 为顶点的四边形为菱形,所以AP AB =或BP BA =.当AP AB =时,点()845,0P -或()845,0+;当BP BA =时,点()8,0P -. 当()845,0P -时,()8458,04Q --+,即()45,4-; 当()845,0P +时,()8458,04Q +-+,即()45,4; 当()8,0P -时,()880,004Q -+-+-,即()0,4-.②以AB 为对角线,对角线的交点为M ,如图2所示.可得5AP =,点P 坐标为()3,0.因为以P ,Q ,A ,B 为顶点的四边形为菱形,所以点Q 坐标为()5,4.综上可知:若点P 为x 轴上一点,则在平面直角坐标系中存在一点Q ,使得P ,Q ,A ,B 四个点能构成一个菱形,此时Q 点坐标为()45,4-,()45,4,()0,4-或()5,4.【点睛】本题是一次函数综合题,利用待定系数法求解析式,平行四边形的性质,菱形的性质,利用分类讨论思想解决问题是本题的关键.27.(1)左;3;(1-2m );(2)①(-4,0);(-1,0)(-3,0); ②当平移后的线段 AB 与线段 CD 有公共点时,1913n ≤≤;③ F 9(,2)12m--. 【解析】【分析】(1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B 点向下平移后,点B 和点A 的纵坐标相等得到等量关系,可求出m 的值,从而求出A 、B 、C 三点坐标;②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点,设出K 点坐标,作 KH ⊥BM 与 H 点,表示出H 点坐标,然后利用面积关系ABM AKM BKM S S S ∆∆∆=+求出距离;当 B '在线段 CD 上时,BB '交 x 轴于 M 点,过 B '做B 'E ⊥OD ,利用S △COD = S △OB'C + S △OB'D ,求出n 的值,从而求出n 的取值范围;③通过坐标平移法用m 表示出E 点的坐标,利用D 、E 两点坐标表示出直线DE 的函数关系式,令y=﹣2,求出x 的值即可求出F 点坐标.【详解】解:(1)根据平移规律可得:B 向左平移;m -(m -1)=3,所以平移3个单位;m+4-(3m+3)=1-2m ,所以再向下平移(1-2m )个单位;故答案为:左;3;(1-2m )(2)①点 B 向下移动 3 个单位得:B (m ,m+1)∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A (-4,0);B (-1,0);C (-3,0);②如图 1,过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点,设 K 点坐标为(-3,a )M 点坐标为(-1,0)作 KH ⊥BM 与 H 点,H 点坐标为(-1,a )AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+ ∴222AM BM KC AM KH BM ⨯⨯⨯=+ ∴33323222a ⨯⨯⨯=+ 解得:1a =,∴当线段 AB 向下平移 1 个单位时,线段 AB 和 CD 开始有交点,∴ n ≥ 1,当 B'在线段 CD 上时,如图 2BB'交 x 轴于 M 点,过 B'做 B'E⊥OD,B'M=n-3,B'E=1,OD=5,OC=3∵ S△COD = S△OB'C + S△OB'D∴'' 222 CO OD CO B M OD B E ⨯⨯⨯=+∴353(3)51 222n⨯⨯-⨯=+解得:193n=,综上所述,当平移后的线段 AB 与线段 CD 有公共点时,1913n≤≤.③∵A(m−3,3m+3), B(m,m+4) D(0,−5)且AD 沿直线 AB 方向平移得到线段BE,∴E点横坐标为:3E点纵坐标为:﹣5+m+4-(3m+3)=﹣4-2m∴E(3,﹣4-2m),设DE:y=kx+b,把D(0,﹣5),E(3,﹣4-2m)代入y=kx+b∴3k+b=42mb=5⎧⎨⎩﹣-﹣∴1-2mk=3b=-5⎧⎪⎨⎪⎩,∴y=12mx53--,把y=﹣2代入解析式得:﹣2=12mx53--,x=912m-,∴F9(,2) 12m--.【点睛】本题考查平面直角坐标系中点的平移计算及一次函数解析式求法,解题关键在于理解掌握平面直角坐标系中点平移计算方法以及用待定系数法求函数解析式方法的应用.28.(1)AB ∥CD ,理由见解析;(2)证明见解析;(3)45°.【解析】【分析】(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF 、∠CFE 互补,所以易证AB ∥CD ;(2)利用(1)中平行线的性质推知∠BEF+∠EFD=180°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG ⊥PF ,故结合已知条件GH ⊥EG ,易证PF ∥GH ; (3)利用三角形外角定理、三角形内角和定理求得90902KPG PKG HPK ︒︒∠=-∠=-∠;然后由邻补角的定义、角平分线的定义推知1452QPK EPK HPK ︒∠=∠=+∠;最后根据图形中的角与角间的和差关系求得∠HPQ =45°.【详解】(1)AB ∥CD ,理由如下:∵∠1与∠2互补,∴∠1+∠2=180°,又∵∠1=∠AEF ,∠2=∠CFE ,∴∠AEF +∠CFE =180°,∴AB ∥CD ;(2)由(1)知,AB ∥CD ,∴∠BEF +∠EFD =180°.又∵∠BEF与∠EFD的角平分线交于点P,∴1()902FEP EFP BEF EFD︒∠+∠=∠+∠=∴∠EPF=90°,即EG⊥PF.∵GH⊥EG,∴PF∥GH;(3)∵∠PHK=∠HPK,∴∠PKG=2∠HPK.又∵GH⊥EG,∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK,∴∠EPK=180°﹣∠KPG=90°+2∠HPK.∵PQ平分∠EPK,∴1452QPK EPK HPK︒∠=∠=+∠,∴∠HPQ=∠QPK﹣∠HPK=45°.答:∠HPQ的度数为45°.【点睛】本题考查了平行线的判定与性质.解题过程中,注意“数形结合”数学思想的运用.29.(1)60°;(2)EF=AF+FC,证明见解析;(3)AF=EF+2DF,证明见解析.【解析】【分析】(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.【详解】解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,又△ABE为等边三角形,∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,在△ACE中,2α+60°+2β=180°,∴α+β=60°,∴∠DFC=α+β=60°;(2)EF=AF+FC,证明如下:∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,∵∠CFD=60°,则∠DCF=30°,∴CF=2DF,在EC上截取EG=CF,连接AG,。
最新人教版八年级数学上册第一学期期末考试试卷及答案(AB卷)
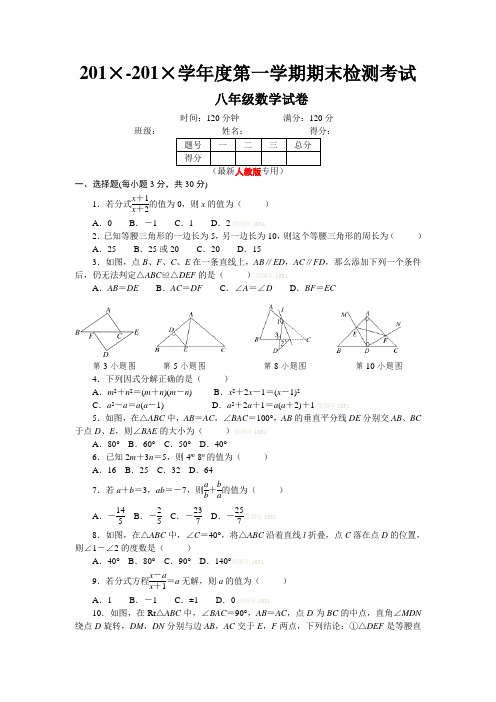
201×-201×学年度第一学期期末检测考试八年级数学试卷时间:120分钟 满分:120分班级:__________ 姓名:__________ 得分:__________(最新人教版专用)一、选择题(每小题3分,共30分)1.若分式x +1x +2的值为0,则x 的值为( )A .0B .-1C .1D .2周国年1031 2.已知等腰三角形的一边长为5,另一边长为10,则这个等腰三角形的周长为( ) A .25 B .25或20 C .20 D .153.如图,点B 、F 、C 、E 在一条直线上,AB ∥ED ,AC ∥FD ,那么添加下列一个条件后,仍无法判定△ABC ≌△DEF 的是( )周国年1031A .AB =DE B .AC =DF C .∠A =∠D D .BF =EC第3小题图 第5小题图 第8小题图 第10小题图 4.下列因式分解正确的是( )A .m 2+n 2=(m +n )(m -n )B .x 2+2x -1=(x -1)2C .a 2-a =a (a -1)D .a 2+2a +1=a (a +2)+1周国年1031 5.如图,在△ABC 中,AB =AC ,∠BAC =100°,AB 的垂直平分线DE 分别交AB 、BC 于点D 、E ,则∠BAE 的大小为( )周国年1031A .80°B .60°C .50°D .40° 6.已知2m +3n =5,则4m ·8n 的值为( ) A .16 B .25 C .32 D .647.若a +b =3,ab =-7,则a b +ba 的值为( )A .-145B .-25C .-237D .-257周国年10318.如图,在△ABC 中,∠C =40°,将△ABC 沿着直线l 折叠,点C 落在点D 的位置,则∠1-∠2的度数是( )A .40°B .80°C .90°D .140°周国年10319.若分式方程x -a x +1=a 无解,则a 的值为( )A .1B .-1C .±1D .0周国年1031 10.如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D 为BC 的中点,直角∠MDN 绕点D 旋转,DM ,DN 分别与边AB ,AC 交于E ,F 两点,下列结论:①△DEF 是等腰直角三角形;②AE =CF ;③△BDE ≌△ADF ;④BE +CF =EF ,其中正确结论是( )A .①②④B .②③④C .①②③D .①②③④周国年1031二、填空题(每小题3分,共24分)11.如图,∠ACD 是△ABC 的外角,若∠ACD =125°,∠A =75°,则∠B =__________. 12.计算:(-8)2016×0.1252015=__________.13.计算:x x +3-69-x 2÷2x -3=__________. 14.如图所示,AB =AC ,AD =AE ,∠BAC =∠DAE ,点D 在线段BE 上.若∠1=25°,∠2=30°,则∠3=__________.周国年103115.如图,AC 是正五边形ABCDE 的一条对角线,则∠ACB =36°.周国年1031第11小题图周国年1031 第14小题图 周国年1031 第15小题图周国年1031 第18小题图 16.若x 2+bx +c =(x +5)(x -3),则点P (b ,c )关于y 轴对称点的坐标是________. 17.已知甲、乙两地间的铁路长1480千米,列车大提速后,平均速度增加了70千米/时,列车的单程运行时间缩短了3小时,设原来的平均速度为x 千米/时,根据题意,可列方程为________.18.如图,△ABC 是等边三角形,AE =CD ,AD 、BE 相交于点P ,BQ ⊥DA 于Q ,PQ =3,EP =1,则DA 的长是________.周国年1031三、解答题(共66分)19.(8分)计算或因式分解:(1)计算:(a 2-4)÷a +2a ; (2)因式分解:a (n -1)2-2a (n -1)+a .20.(8分)现要在三角地ABC 内建一中心医院,使医院到A 、B 两个居民小区的距离相等,并且到公路AB 和AC 的距离也相等,请确定这个中心医院的位置.周国年103121.(10分)(1)解方程:1x -3-2=3x 3-x;周国年1031(2)设y =kx ,且k ≠0,若代数式(x -3y )(2x +y )+y (x +5y )化简的结果为2x 2,求k 的值.22.(10分)(1)已知a +b =7,ab =10,求a 2+b 2,(a -b )2的值;周国年1031(2)先化简⎝ ⎛⎭⎪⎫2a 2+2a a 2-1-a 2-a a 2-2a +1÷a a +1,并回答:原代数式的值可以等于-1吗?为什么?周国年103123.(8分)某校学生利用双休时间去距离学校10km 的炎帝故里参观.一部分学生骑自行车先走,过了20min 后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.周国年103124.(10分)如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于F ,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连接EG,EF.(1)求证:BG=CF;周国年1031(2)请你判断BE+CF与EF的大小关系,并说明理由.周国年103125.(12分)如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.(1)求证:BE=AD;(2)用含α的式子表示∠AMB的度数;(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.周国年1031期末参考答案与解析1.B 2.A 3.C 4.C 5.D 6.C 7.C 8.B9.C 解析:在方程两边乘(x +1),得x -a =a (x +1),整理得x (1-a )=2a .当1-a =0时,即a =1,整式方程无解;当x +1=0,即x =-1时,分式方程无解,把x =-1代入x (1-a )=2a ,得-(1-a )=2a ,解得a =-1.故选C.10.C 解析:∵在Rt △ABC 中,∠BAC =90°,AB =AC ,点D 为BC 的中点,∴AD ⊥BC ,∠B =∠C =∠BAD =∠CAD =45°,∴∠ADB =∠ADC =90°,AD =CD =BD .∵∠MDN 是直角,∴∠ADF +∠ADE =90°.∵∠BDE +∠ADE =∠ADB =90°,∴∠ADF =∠BDE .在△BDE 和△ADF 中,⎩⎪⎨⎪⎧∠B =∠CAD ,BD =AD ,∠BDE =∠ADF ,∴△BDE ≌△ADF (ASA),∴DE =DF ,BE =AF ,∴△DEF是等腰直角三角形,故①③正确;∵AE =AB -BE ,CF =AC -AF ,AB =AC ,BE =AF ,∴AE=CF ,故②正确;∵BE +CF =AF +AE ,AF +AE >EF ,∴BE +CF >EF ,故④错误;综上所述,正确的结论有①②③.故选C.11.50 12.8 13.1 14.55° 15.36°16.(-2,-15) 17.1480x =1480x +70+318.7 解析:∵△ABC 为等边三角形,∴AB =CA ,∠BAE =∠C =60°.在△AEB 和△CDA中,AB =CA ,∠BAE =∠C ,AE =CD ,∴△AEB ≌△CDA (SAS),∴∠ABE =∠CAD ,AD =BE ,∴∠BPQ =∠BAD +∠ABE =∠BAD +∠CAD =∠BAC =60°.∵BQ ⊥AD ,∴∠BQP =90°,∴∠PBQ =30°,∴BP =2PQ =6.∵EP =1,∴BE =BP +PE =7,∴DA =BE =7.19.解:(1)原式=(a +2)(a -2)·aa +2=a (a -2)=a 2-2a ;(4分)(2)原式=a [(n -1)2-2(n -1)+1]=a (n -1-1)2=a (n -2)2.(8分)20.解:如图,作AB 的垂直平分线EF ,(3分)作∠BAC 的平分线AM ,两线交于P ,(7分)则P 为这个中心医院的位置.(8分)21.解:(1)方程两边乘(x -3),得1-2(x -3)=-3x ,解得x =-7.(4分)检验:当x =-7时,x -3≠0,∴原分式方程的解为x =-7.(5分)(2)∵(x -3y )(2x +y )+y (x +5y )=2x 2+xy -6xy -3y 2+xy +5y 2=2x 2-4xy +2y 2=2(x -y )2=2(x -kx )2=2x 2(1-k )2=2x 2,(8分)∴(1-k )2=1,则1-k =±1,解得k =0(不合题意,舍去)或k =2.∴k 的值为2.(10分)22.解:(1)a 2+b 2=(a +b )2-2ab =72-2×10=49-20=29,(2分)(a -b )2=(a +b )2-4ab =72-4×10=49-40=9.(5分)(2)原式=⎣⎢⎡⎦⎥⎤2a (a +1)(a +1)(a -1)-a (a -1)(a -1)2·a +1a =⎝⎛⎭⎫2a a -1-a a -1·a +1a =a a -1·a +1a =a +1a -1.(8分)当a +1a -1=-1时,解得a =0,这时除式aa +1=0,没有意义,∴原代数式的值不能等于-1.(10分)23.解:设骑车学生的速度为x km/h ,则汽车的速度为2x km/h ,由题意得10x =102x +错误!,解得x =15.(6分)经检验,x =15是原方程的解,2x =2×15=30.(7分)答:骑车学生的速度和汽车的速度分别是15km/h ,30km/h.(8分) 24.(1)证明:∵BG ∥AC ,∴∠DBG =∠DCF .∵D 为BC 的中点,∴BD =CD .(2分)在△BGD 与△CFD 中,⎩⎪⎨⎪⎧∠DBG =∠DCF ,BD =CD ,∠BDG =∠CDF ,∴△BGD ≌△CFD (ASA),∴BG =CF .(5分)(2)解:BE +CF >EF .(6分)理由如下:∵△BGD ≌△CFD ,∴GD =FD ,BG =CF .又∵DE ⊥FG ,∴EG =EF (垂直平分线上的点到线段端点的距离相等).(8分)∵在△EBG 中,BE +BG >EG ,∴BE +CF >EF .(10分)25.(1)证明:如图①,∵∠ACB =∠DCE =α,∴∠ACD =∠BCE .(1分)在△ACD 和△BCE 中,⎩⎪⎨⎪⎧CA =CB ,∠ACD =∠BCE ,CD =CE ,∴△ACD ≌△BCE (SAS),∴BE =AD .(3分)(2)解:如图①,∵△ACD ≌△BCE ,∴∠CAD =∠CBE .∵∠BAC +∠ABC =180°-α,∴∠BAM +∠ABM =180°-α,∴∠AMB =180°-(180°-α)=α.(6分)(3)解:△CPQ 为等腰直角三角形.(7分)证明:如图②,由(1)可得,BE =AD .∵AD ,BE 的中点分别为点P ,Q ,∴AP =BQ .∵△ACD ≌△BCE ,∴∠CAP =∠CBQ .在△ACP 和△BCQ 中,⎩⎪⎨⎪⎧CA =CB ,∠CAP =∠CBQ ,AP =BQ ,∴△ACP ≌△BCQ (SAS),∴CP =CQ 且∠ACP =∠BCQ .(10分)又∵∠ACP +∠PCB =90°,∴∠BCQ +∠PCB =90°,∴∠PCQ =90°,∴△CPQ 为等腰直角三角形.(12分)201×-201×学年度第一学期期中检测考试八年级数学试卷时间:120分钟满分:120分班级:__________姓名:__________得分:__________(最新人教版专用)一、选择题(每小题3分,共30分)1.等腰三角形的两边长分别为4cm和8cm,则它的周长为()A.16cm B.17cm C.20cm D.16cm或20cm2.下列图形中不是轴对称图形的是()3.如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有()A.2对B.3对C.4对D.5对第3题图第6题图第7题图4.正n边形每个内角的大小都为108°,则n的值为()A.5 B.6 C.7 D.85.在△ABC中,∠ABC与∠ACB的平分线相交于I,且∠BIC=130°,则∠A的度数是()A.40°B.50°C.65°D.80°6.如图,AD是△ABC的角平分线,且AB∶AC=3∶2,则△ABD与△ACD的面积之比为()A.3∶2 B.9∶4 C.2∶3 D.4∶97.如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为()A.1 B.2 C.3 D.48.如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为()A.4cm B.3cm C.2cm D.1cm9.如图是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于()A.90°B.120°C.150°D.180°10.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A.4个B.3个C.2个D.1个二、填空题(每小题3分,共24分)11.点A(3,-2)关于x轴对称的点的坐标是________.12.已知三角形两边长分别是3cm,5cm,设第三边的长为x cm,则x的取值范围是________.13.如图所示是某零件的平面图,其中∠B=∠C=30°,∠A=40°,则∠ADC的度数为________.第13题图第14题图第15题图14.如图,△ABC≌△DFE,CE=6,FC=2,则BC=________.15.如图是一枚“八一”建军节纪念章,其外轮廓是一个正五边形,则图中∠1的大小为________.16.如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=________.17.如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕点M转动△ABC,使其直角顶点C 恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是________.18.如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=________.三、解答题(共66分)19.(8分)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.20.(8分)解答下面2个小题:(1)已知等腰三角形的底角是顶角的2倍,求这个三角形各个内角的度数;(2)已知等腰三角形的周长是12,一边长为5,求它的另外两边长.21.(8分)图①、图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,A、B、C三点均在小正方形的顶点上.(1)在图①中画出凸四边形ABCD,点D在小正方形的顶点上,且使四边形ABCD是只有一条对称轴的轴对称图形;(2)在图②中画出凸四边形ABCE,点E在小正方形的顶点上,且使四边形ABCE是有四条对称轴的轴对称图形.22.(10分)如图,在△ABC中,∠A=40°,∠B=72°,CD是AB边上的高,CE是∠ACB 的平分线,DF⊥CE于F,求∠CDF的度数.23.(10分)已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分,求这个等腰三角形的底边长和腰长.24.(10分)如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F 作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.(1)求证:△ABC是等腰三角形;(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.25.(12分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.(1)若AC=10,求四边形ABCD的面积;(2)求证:CE=2AF.期中参考答案与解析1.C 2.C 3.C 4.A 5.D 6.A 7.A 8.C9.D 解析:∵图中是三个等边三角形,∴∠1=180°-60°-∠ABC =120°-∠ABC ,∠2=180°-60°-∠ACB =120°-∠ACB ,∠3=180°-60°-∠BAC =120°-∠BAC .∵∠ABC +∠ACB +∠BAC =180°,∴∠1+∠2+∠3=360°-180°=180°.故选D.10.A 解析:∵BF ∥AC ,∴∠C =∠CBF .∵BC 平分∠ABF ,∴∠ABC =∠CBF ,∴∠C =∠ABC ,∴AB =AC .∵AD 是△ABC 的角平分线,∴BD =CD ,AD ⊥BC ,故②③正确;在△CDE 与△BDF 中,⎩⎪⎨⎪⎧∠C =∠CBF ,CD =BD ,∠EDC =∠FDB ,∴△CDE ≌△BDF (ASA),∴DE =DF ,CE =BF ,故①正确;∵AE =2BF ,∴AC =3BF ,故④正确.故选A.11.(3,2) 12.2<x <8 13.100°14.8 15.108° 16.67.5°17.5 解析:如图,连接CC 1.∵两块三角板重叠在一起,较长直角边的中点为M ,∴M是AC 、A 1C 1的中点,AC =A 1C 1,∴CM =A 1M =C 1M =12AC =5,∴∠A 1CM =∠A 1=30°,∴∠CMC 1=60°,∴△CMC 1为等边三角形,∴CC 1=CM =5.18.1.5 解析:如图,连接CD ,BD ,∵AD 是∠BAC 的平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE ,∠F =∠DEA =∠DEB =90°.又∵AD =AD ,∴Rt △ADF ≌Rt △ADE (HL),∴AE=AF .∵DG 是BC 的垂直平分线,∴CD =BD .在Rt △CDF 和Rt △BDE 中,⎩⎪⎨⎪⎧CD =BD ,DF =DE ,∴Rt △CDF ≌Rt △BDE (HL),∴BE =CF ,∴AB =AE +BE =AF +BE =AC +CF +BE =AC +2BE .∵AB =6,AC =3,∴BE =1.5.19.证明:∵AB ∥CD ,∴∠B =∠C .(2分)在△ABE 和△DCF 中,⎩⎪⎨⎪⎧∠A =∠D ,∠B =∠C ,AE =DF ,∴△ABE ≌△DCF (AAS),(6分)∴AB =CD .(8分)20.解:(1)设等腰三角形的顶角为x °,则底角为2x °,由题意得x +2x +2x =180,解得x =36,∴这个三角形三个内角的度数分别为36°、72°、72°.(4分)(2)∵等腰三角形的一边长为5,周长为12,∴当5为底边长时,其他两边长都为3.5,5、3.5、3.5可以构成三角形;(6分)当5为腰长时,其他两边长为5和2,5、5、2可以构成三角形.(7分)∴另外两边长是3.5、3.5或5、2.(8分)21.解:(1)图①中两个图形画出一个即可.(4分)(2)如图②所示.(8分)22.解:∵∠A =40°,∠B =72°,∴∠ACB =180°-40°-72°=68°.(2分)∵CE 是∠ACB的平分线,∴∠BCE =12∠ACB =12×68°=34°.(4分)∵CD ⊥AB ,∴∠CDB =90°,∴∠BCD =180°-90°-72°=18°,∴∠DCE =∠BCE -∠BCD =34°-18°=16°.(8分)∵DF ⊥CE ,∴∠DFC =90°,∴∠CDF =180°-90°-16°=74°.(10分)23.解:如图,△ABC 是等腰三角形,AB =AC ,BD 是AC 边上的中线,则有AB +AD=9cm 或AB +AD =15cm.(2分)设△ABC 的腰长为x cm ,分下面两种情况:(1)x +12x =9,∴x =6.∵三角形的周长为9+15=24(cm),∴三边长分别为6cm ,6cm ,12cm.6+6=12,不符合三角形的三边关系,舍去;(6分)(2)x +12x =15,∴x =10.∵三角形的周长为24cm ,∴三边长分别为10cm ,10cm ,4cm ,符合三边关系.(9分)综上所述,这个等腰三角形的底边长为4cm ,腰长为10cm.(10分)24.(1)证明:∵AE ∥BC ,∴∠B =∠DAE ,∠C =∠CAE .(2分)∵AE 平分∠DAC ,∴∠DAE =∠CAE .(3分)∴∠B =∠C .∴△ABC 是等腰三角形.(4分)(2)解:∵点F 是AC 的中点,∴AF =CF .(5分)在△AEF 和△CGF 中,⎩⎪⎨⎪⎧∠F AE =∠C ,AF =FC ,∠AFE =∠CFG ,∴△AEF ≌△CGF (ASA).∴AE =GC =8.∵GC =2BG ,∴BG =4,∴BC =12.(9分)∴△ABC 的周长为AB +AC +BC =10+10+12=32.(10分)25.(1)解:∵∠BAD =∠CAE =90°,∴∠BAC +∠CAD =∠EAD +∠CAD ,∴∠BAC=∠EAD .(2分)在△ABC 和△ADE 中,⎩⎪⎨⎪⎧AB =AD ,∠BAC =∠DAE ,AC =AE ,∴△ABC ≌△ADE (SAS).∴S △ABC=S △ADE ,∴S 四边形ABCD =S △ABC +S △ACD =S △ADE +S △ACD =S △ACE =12×102=50.(6分) (2)证明:∵△ACE 是等腰直角三角形,∴∠ACE =∠AEC =45°.由△ABC ≌△ADE 得∠ACB =∠AEC =45°,∴∠ACB =∠ACE ,∴AC 平分∠ECF .(8分)过点A 作AG ⊥CG ,垂足为点G ,∵AC 平分∠ECF ,AF ⊥CB ,∴AF =AG .又∵AC =AE ,∴∠CAG =∠EAG =45°,∴∠CAG =∠EAG =∠ACE =∠AEC ,∴CG =AG =GE ,(11分)∴CE =2AG =2AF .(12分)。
2023-2024学年全国初中八年级上数学人教版期末考卷(含答案解析)

20232024学年全国初中八年级上数学人教版期末考卷一、选择题(每题2分,共20分)1. 下列各数中,是整数的是()A. 0.5B. 2C. 3.14D. 5/32. 若a、b是实数,且a+b=0,则下列选项中正确的是()A. a和b互为相反数B. a和b互为倒数C. a和b互为平方根D. a和b互为对数3. 已知a、b是实数,且a²=b²,则下列选项中正确的是()A. a=bB. a=bC. a+b=0D. a²+b²=04. 下列各数中,是无理数的是()A. 2B. 3.14C. √9D. √55. 已知a、b是实数,且a²+b²=0,则下列选项中正确的是()A. a=0,b≠0B. a≠0,b=0C. a=0,b=0D. a≠0,b≠06. 若a、b是实数,且a²+b²=1,则下列选项中正确的是()A. a=1,b=0B. a=0,b=1C. a²+b²=0D. a²+b²=27. 已知a、b是实数,且a²+b²=0,则下列选项中正确的是()A. a=0,b≠0B. a≠0,b=0C. a=0,b=0D. a≠0,b≠08. 若a、b是实数,且a²+b²=1,则下列选项中正确的是()A. a=1,b=0B. a=0,b=1C. a²+b²=0D. a²+b²=29. 已知a、b是实数,且a²+b²=0,则下列选项中正确的是()A. a=0,b≠0B. a≠0,b=0C. a=0,b=0D. a≠0,b≠010. 若a、b是实数,且a²+b²=1,则下列选项中正确的是()A. a=1,b=0B. a=0,b=1C. a²+b²=0D. a²+b²=2二、填空题(每题2分,共20分)1. 若a、b是实数,且a²+b²=0,则a=______,b=______。
人教版八年级上学期期末考试数学试卷(附带答案)精选全文

精选全文完整版(可编辑修改)人教版八年级上学期期末考试数学试卷(附带答案)学校:___________班级:___________姓名:___________考号:___________一.选择题(共10小题,满分40分,每小题4分)1.(4分)下列图形中,是轴对称图形的是()A.B.C.D.2.(4分)下列式子中是分式的是()A.B.C.D.3.(4分)下列各式中,由左向右的变形是分解因式的是()A.x2﹣2x+1=x(x﹣2)+1B.x2y﹣xy2=xy(x﹣y)C.﹣x2+(﹣2)2=(x﹣2)(x+2)D.(x+y)2=x2+2xy+y24.(4分)(mx+8)(2﹣3x)展开后不含x的一次项,则m为()A.3 B.0 C.12 D.245.(4分)下列选项中,能使分式值为0的x的值是()A.1 B.0 C.1或﹣1 D.﹣16.(4分)如图,在Rt△ACB中,∠ACB=90°,∠A=35°,点D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上B′处,则∠ADB′的度数为()A.25°B.30°C.35°D.20°7.(4分)若多项式4x2﹣(k﹣1)x+9是一个完全平方式,则k的值是()A.13 B.13或﹣11 C.﹣11 D.±118.(4分)若关于x的分式方程有增根,则m的值是()A.0 B.1 C.2 D.﹣19.(4分)如图,在△ABC中,AB=AC、BC=6,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,连接DE、EF、DF,△DEF的周长是11,则AB的长度为()A.5 B.6 C.7 D.810.(4分)已知两个分式:将这两个分式进行如下操作:第一次操作:将这两个分式作和,结果记为f1;作差,结果记为g1;(即,)第二次操作:将f1,g1作和,结果记为f2;作差,结果记为g2;(即f2=f1+g1,g2=f1﹣g1)第三次操作;将f2,g2作和,结果记为f3;作差,结果记为g3;(即f3=f2+g2,g3=f2﹣g2)…(依此类推)将每一次操作的结果再作和,作差,继续依次操作下去,通过实际操作,有以下结论:①g7=8g1;②当x=2时;③若f8=g4,则x=2;④在第2n(n为正整数)次操作的结果中:.以上结论正确的个数有()个.A.4 B.3 C.2 D.1二.填空题(共8小题,满分32分,每小题4分)11.(4分)计算:+(﹣2013)0+()﹣2+|2﹣|+(﹣2)2×(﹣3)=.12.(4分)若一个正多边形的一个内角与它相邻的一个外角的差是100°,则这个多边形的边数是.13.(4分)若5x﹣3y﹣2=0,则25x÷23y﹣1=.14.(4分)已知x2+y2=8,x﹣y=3,则xy的值为.15.(4分)已知,则代数式的值为.16.(4分)若关于x的不等式组有4个整数解,且关于y的分式方程=1的解为正数,则满足条件所有整数a的值之和为17.(4分)如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD于点E,过点B作CD 平行线,交AE的延长线于点F,在延长线上截得FG=CD,连接CG、DF.若BG=11,AF=8,则四边形CGFD的面积等于.18.(4分)对于一个各位数字都不为零的四位正整数N,若千位数字比十位数字大3,百位数字是个位数字的3倍,那么称这个数N为“三生有幸数”,例如:N=5321,∵5=2+3,3=1×3,∴5321是个“三生有幸数”;又如N=8642,∵8≠4+3,∴8642不是一个“三生有幸数”.则最小的“三生有幸数”是.若将N 的千位数字与个位数字互换,百位数字与十位数字互换,得到一个新的四位数,那么称这个新的数为数N的“反序数”,记作N',例如:N=5321,其“反序数”N′=1235.若一个“三生有幸数”N的十位数字为x,个位数字为y,设P(N)=,若P(N)除以6余数是1,则所有满足题意的四位正整数N的最大值与最小值的差是.三.解答题(共9小题,满分78分)19.(8分)计算:(1)(﹣3x+2)(﹣3x﹣2)﹣5x(1﹣x)+(2x+1)(x﹣5)(2).20.(8分)解方程:(1);(2).21.(8分)将下列各式因式分解(1)x2(m﹣2)+y2(2﹣m)(2)x2+2x﹣1522.(8分)先化简,再求值:(﹣)÷.其中a是x2﹣2x=0的根.23.(8分)重庆市2023年体育中考已经结束,现从某校初三年级随机抽取部分学生的成绩进行统计分析(成绩得分用x表示,共分成4个等级,A:30≤x<35,B:35≤x<40,C:40≤x<45,D:45≤x≤50),绘制了如下的统计图,请根据统计图信息解答下列问题:(1)本次共调查了名学生;(2)请补全条形统计图;(3)在扇形统计图中,m的值是;B对应的扇形圆心角的度数是;(4)若该校初三年级共有2000名学生,估计此次测试成绩优秀(45≤x≤50)的学生共有多少人?24.(8分)在学习了角平分线的性质后,小明想要去探究直角梯形的两底边与两非直角顶点所连腰的数量关系,于是他对其中一种特殊情况进行了探究:在直角梯形ABCD中,∠B=∠C=90°,AE平分∠BAD交BC于点E,连接DE,当DE平分∠ADC时,探究AB、CD与AD之间的数量关系.他的思路是:首先过点E作AD的垂线,将其转化为证明三角形全等,然后根据全等三角形的对应边相等使问题得到解决.请根据小明的思路完成下面的作图与填空:证明:用直尺和圆规,过点E作AD的垂线,垂足为点F.(只保留作图痕迹)∵∠B=90°∴EB⊥AB∵AE平分∠BAD,EF⊥AD∴(角平分线的性质)在Rt△ABE和Rt△AFE中∵∴Rt△ABE≌Rt△AFE(HL).∴同理可得:DC=DF∴AB+CD=即AB+CD=AD.25.(10分)为落实“双减政策”,某校购进“红色教育”和“传统文化”两种经典读本,花费分别是14000元和7000元,已知“红色教育”经典读本的订购单价是“传统文化”经典读本的订购单价的 1.4倍,并且订购的“红色教育”经典读本的数量比“传统文化”经典读本的数量多300本.(1)求该学校订购的两种经典读本的单价分别是多少元;(2)该学校拟计划再订购这两种经典读本共1000本,其中“传统文化”经典读本订购数量不超过400本且总费用不超过12880元,求该学校订购这两种读本的最低总费用.26.(10分)如图1,点A(0,a),B(b,0),且a,b满足|a﹣4|+=0.(1)求A,B两点的坐标.(2)如图2,点C(﹣3,n)在线段AB上,点D在y轴负半轴上,连接CD交x轴负半轴于点M,且S△MBC =S△MOD,求点D的坐标.(3)平移直线AB,交x轴正半轴于点E,交y轴于点F,P为直线EF上的第三象限内的一点,过点P作PG⊥x轴于点G,若S△P AB=20,且GE=12,求点P的坐标.27.(10分)△ABC中,点D为AC边上一点,连接BD,在线段BD上取一点E,连接EC.(1)如图1,若∠BAC=90°,BC=AB,tan∠ABC=2,点D,E分别为AC,BD中点,BC=a,求△CDE的面积(结果用含a的代数式表示);(2)如图2,若EB=EC,过点E作EF⊥AC于点F,F在线段AD上(F与A,D不重合),过点E作EG∥AC交BC于点G,∠ABD=30°,AF=CF,求证:2CG+EG=BC;(3)如图3,若△ABC是等边三角形,且AE⊥BD,∠DEC=60°,AB=2,直接写出线段DE的长.参考答案一.选择题(共10小题,满分40分,每小题4分)1.(4分)下列图形中,是轴对称图形的是()A.B.C.D.【答案】C2.(4分)下列式子中是分式的是()A.B.C.D.【答案】B3.(4分)下列各式中,由左向右的变形是分解因式的是()A.x2﹣2x+1=x(x﹣2)+1B.x2y﹣xy2=xy(x﹣y)C.﹣x2+(﹣2)2=(x﹣2)(x+2)D.(x+y)2=x2+2xy+y2【答案】B4.(4分)(mx+8)(2﹣3x)展开后不含x的一次项,则m为()A.3 B.0 C.12 D.24【答案】C5.(4分)下列选项中,能使分式值为0的x的值是()A.1 B.0 C.1或﹣1 D.﹣1【答案】D6.(4分)如图,在Rt△ACB中,∠ACB=90°,∠A=35°,点D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上B′处,则∠ADB′的度数为()A.25°B.30°C.35°D.20°【答案】D7.(4分)若多项式4x2﹣(k﹣1)x+9是一个完全平方式,则k的值是()A.13 B.13或﹣11 C.﹣11 D.±11【答案】B8.(4分)若关于x的分式方程有增根,则m的值是()A.0 B.1 C.2 D.﹣1【答案】D9.(4分)如图,在△ABC中,AB=AC、BC=6,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,连接DE、EF、DF,△DEF的周长是11,则AB的长度为()A.5 B.6 C.7 D.8【答案】D10.(4分)已知两个分式:将这两个分式进行如下操作:第一次操作:将这两个分式作和,结果记为f1;作差,结果记为g1;(即,)第二次操作:将f1,g1作和,结果记为f2;作差,结果记为g2;(即f2=f1+g1,g2=f1﹣g1)第三次操作;将f2,g2作和,结果记为f3;作差,结果记为g3;(即f3=f2+g2,g3=f2﹣g2)…(依此类推)将每一次操作的结果再作和,作差,继续依次操作下去,通过实际操作,有以下结论:①g7=8g1;②当x=2时③若f8=g4,则x=2;④在第2n(n为正整数)次操作的结果中:以上结论正确的个数有()个.A.4 B.3 C.2 D.1【答案】B二.填空题(共8小题,满分32分,每小题4分)11.(4分)计算:+(﹣2013)0+()﹣2+|2﹣|+(﹣2)2×(﹣3)=.【答案】见试题解答内容12.(4分)若一个正多边形的一个内角与它相邻的一个外角的差是100°,则这个多边形的边数是9.【答案】见试题解答内容13.(4分)若5x﹣3y﹣2=0,则25x÷23y﹣1=8.【答案】见试题解答内容14.(4分)已知x2+y2=8,x﹣y=3,则xy的值为﹣.【答案】见试题解答内容15.(4分)已知,则代数式的值为﹣2.【答案】﹣2.16.(4分)若关于x的不等式组有4个整数解,且关于y的分式方程=1的解为正数,则满足条件所有整数a的值之和为2【答案】见试题解答内容17.(4分)如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD于点E,过点B作CD 平行线,交AE的延长线于点F,在延长线上截得FG=CD,连接CG、DF.若BG=11,AF=8,则四边形CGFD的面积等于20.【答案】见试题解答内容18.(4分)对于一个各位数字都不为零的四位正整数N,若千位数字比十位数字大3,百位数字是个位数字的3倍,那么称这个数N为“三生有幸数”,例如:N=5321,∵5=2+3,3=1×3,∴5321是个“三生有幸数”;又如N=8642,∵8≠4+3,∴8642不是一个“三生有幸数”.则最小的“三生有幸数”是4311.若将N的千位数字与个位数字互换,百位数字与十位数字互换,得到一个新的四位数,那么称这个新的数为数N的“反序数”,记作N',例如:N=5321,其“反序数”N′=1235.若一个“三生有幸数”N的十位数字为x,个位数字为y,设P(N)=,若P(N)除以6余数是1,则所有满足题意的四位正整数N的最大值与最小值的差是2729.【答案】4311;3331.三.解答题(共9小题,满分78分)19.(8分)计算:(1)(﹣3x+2)(﹣3x﹣2)﹣5x(1﹣x)+(2x+1)(x﹣5)(2).【答案】16x2-14x-9;20.(8分)解方程:(1);(2).【答案】(1)x=4;(2)无解.21.(8分)将下列各式因式分解(1)x2(m﹣2)+y2(2﹣m)(2)x2+2x﹣15【答案】(m-2)(x+y)(x-y);(x+5)(x-3).22.(8分)先化简,再求值:(﹣)÷.其中a是x2﹣2x=0的根.【答案】见试题解答内容23.(8分)重庆市2023年体育中考已经结束,现从某校初三年级随机抽取部分学生的成绩进行统计分析(成绩得分用x表示,共分成4个等级,A:30≤x<35,B:35≤x<40,C:40≤x<45,D:45≤x≤50),绘制了如下的统计图,请根据统计图信息解答下列问题:(1)本次共调查了50名学生;(2)请补全条形统计图;(3)在扇形统计图中,m的值是10;B对应的扇形圆心角的度数是108°;(4)若该校初三年级共有2000名学生,估计此次测试成绩优秀(45≤x≤50)的学生共有多少人?【答案】(1)50;(3)10,108°;(4)估计此次测试成绩优秀(45≤x≤50)的学生共有800人.24.(8分)在学习了角平分线的性质后,小明想要去探究直角梯形的两底边与两非直角顶点所连腰的数量关系,于是他对其中一种特殊情况进行了探究:在直角梯形ABCD中,∠B=∠C=90°,AE平分∠BAD交BC于点E,连接DE,当DE平分∠ADC时,探究AB、CD与AD之间的数量关系.他的思路是:首先过点E作AD的垂线,将其转化为证明三角形全等,然后根据全等三角形的对应边相等使问题得到解决.请根据小明的思路完成下面的作图与填空:证明:用直尺和圆规,过点E作AD的垂线,垂足为点F.(只保留作图痕迹)∵∠B=90°∴EB⊥AB∵AE平分∠BAD,EF⊥AD∴①(角平分线的性质)在Rt△ABE和Rt△AFE中∵∴Rt△ABE≌Rt△AFE(HL).∴③同理可得:DC=DF∴AB+CD=④即AB+CD=AD.【答案】①EB=EF,②AE=AE③.AB=AF,④AF+FD.25.(10分)为落实“双减政策”,某校购进“红色教育”和“传统文化”两种经典读本,花费分别是14000元和7000元,已知“红色教育”经典读本的订购单价是“传统文化”经典读本的订购单价的 1.4倍,并且订购的“红色教育”经典读本的数量比“传统文化”经典读本的数量多300本.(1)求该学校订购的两种经典读本的单价分别是多少元;(2)该学校拟计划再订购这两种经典读本共1000本,其中“传统文化”经典读本订购数量不超过400本且总费用不超过12880元,求该学校订购这两种读本的最低总费用.【答案】(1)“红色教育”的订购单价是14元,“传统文化”经典读本的单价是10元;(2)12400元26.(10分)如图1,点A(0,a),B(b,0),且a,b满足|a﹣4|+=0.(1)求A,B两点的坐标.(2)如图2,点C(﹣3,n)在线段AB上,点D在y轴负半轴上,连接CD交x轴负半轴于点M,且S△MBC =S△MOD,求点D的坐标.(3)平移直线AB,交x轴正半轴于点E,交y轴于点F,P为直线EF上的第三象限内的一点,过点P作PG⊥x轴于点G,若S△P AB=20,且GE=12,求点P的坐标.【答案】(1)A(0,4),B(﹣6,0);(2)D(0,﹣4);(3)(﹣8,﹣8).27.(10分)△ABC中,点D为AC边上一点,连接BD,在线段BD上取一点E,连接EC.(1)如图1,若∠BAC=90°,BC=AB,tan∠ABC=2,点D,E分别为AC,BD中点,BC=a,求△CDE的面积(结果用含a的代数式表示);(2)如图2,若EB=EC,过点E作EF⊥AC于点F,F在线段AD上(F与A,D不重合),过点E作EG∥AC交BC于点G,∠ABD=30°,AF=CF,求证:2CG+EG=BC;(3)如图3,若△ABC是等边三角形,且AE⊥BD,∠DEC=60°,AB=2,直接写出线段DE的长.【答案】(1)a2;(3).。
八年级(上)期末数学试卷(附答案解析)

八年级(上)期末数学试卷一、选择题(每小题3分,共30分)1.下面四个交通标志图中为轴对称图形的是()A.B.C.D.2.使分式有意义的x的取值范围为()A.x>0 B.x≠﹣1 C.x≠1 D.任意实数3.下列计算正确的是()A.3a×2b=5ab B.﹣a2×a=﹣a2C.(﹣x)9÷(﹣x)3=x3D.(﹣2a3)2=4a6 4.已知△ABC中,AB=7,BC=4,那么边长AC的长不可能是()A.11 B.9 C.7 D.45.若等腰三角形的顶角为40°,则它的底角度数为()A.40°B.50°C.60°D.70°6.下列多边形中,内角和是外角和的两倍的是()A.四边形B.五边形C.六边形D.八边形7.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为()A.2 B.3 C.4 D.58.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC 的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°9.如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是()A.5 B.6 C.7 D.810.A、B两地相距80km,已知乙的速度是甲的1.5倍,甲先由A去B,1小时后,乙再从A地出发去追甲,追到B地时,甲已早到20分钟,则甲的速度为()A.40km/h B.45km/h C.50km/h D.60km/h二、填空题(每小题3分,共24分)11.计算:(π﹣2)0=.12.多项式3x2﹣6x的公因式为.13.若a2﹣b2=,a﹣b=,则a+b的值为.14.如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD 周长为19cm,AB=.15.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后来客户要求提前5天交货,为保证按时完成任务,则每天应多做件.16.已知关于x的分式方程的解是非负数,则m的取值范围是.17.若m为正实数,且m2﹣m﹣1=0,则m2+=.18.如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,且△A′B′C≌△ABC,则∠BCA′:∠BCB′=.三、解答题(共66分)19.分解因式:(1)4a2﹣36(2)(x﹣2y)2+8xy.20.先化简,再求值:÷(x+1+),其中x=2018.21.解方程:(1)﹣=1(2)=﹣1.22.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AB=DE.23.如图,已知△ABC的三个顶点的坐标为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2).(1)请在图中作出△ABC关于y轴对称的△A′B′C′;(2)分别写出点A′、B′、C′的坐标.24.2015年5月,某县突降暴雨,造成山林滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区,现有甲、乙两种货车,乙知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1000件帐篷所用的车辆与乙车货车装运800件帐篷所用车辆相等.(1)求甲、乙两种货车每辆车可装多少件帐篷?(2)如果这批帐篷有1490件,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其它装满,求甲、乙两辆汽车各有多少辆?25.如图,△ABC是等边三角形,D是三角形外一动点,满足∠ADB=60°,(1)当D点在AC的垂直平分线上时,求证:DA+DC=DB;(2)当D点不在AC的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由;(3)当D点在如图的位置时,直接写出DA,DC,DB的数量关系,不必证明.26.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣8a﹣4b+20=0.①求a、b的值;②如图1,在①的条件下,第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;(2)如图2,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.参考答案与试题解析一、选择题(每小题3分,共30分)1.下面四个交通标志图中为轴对称图形的是()A.B.C.D.【考点】P3:轴对称图形.【分析】根据轴对称图形的概念对各选项分析判断即可得解.【解答】解:A、不是轴对称图形,故本选项不符合题意;B、是轴对称图形,故本选项符合题意;C、不是轴对称图形,故本选项不符合题意;D、不是轴对称图形,故本选项不符合题意.故选B.2.使分式有意义的x的取值范围为()A.x>0 B.x≠﹣1 C.x≠1 D.任意实数【考点】62:分式有意义的条件.【分析】直接利用分式有意义则分母不为零,进而得出答案.【解答】解:要使分式有意义,则x﹣1≠0,解得:x≠1.故选:C.3.下列计算正确的是()A.3a×2b=5ab B.﹣a2×a=﹣a2C.(﹣x)9÷(﹣x)3=x3D.(﹣2a3)2=4a6【考点】49:单项式乘单项式;46:同底数幂的乘法;47:幂的乘方与积的乘方;48:同底数幂的除法.【分析】根据单项式的乘法,同底数幂的除法,积的乘方,可得答案.【解答】解:A、3a×2b=6ab,故A不符合题意;B、﹣a2×a=﹣a3,故B不符合题意;C、(﹣x)9÷(﹣x)3=(﹣x)3,故C不符合题意;D、积的乘方等于乘方的积,故D符合题意;故选:D.4.已知△ABC中,AB=7,BC=4,那么边长AC的长不可能是()A.11 B.9 C.7 D.4【考点】K6:三角形三边关系.【分析】根据三角形的三边关系定理:三角形两边之和大于第三边.三角形的两边差小于第三边可得AC的取值范围,即可求解.【解答】解:根据三角形的三边关系定理可得:7﹣4<AC<7+4,即3<AC<11,故选:A.5.若等腰三角形的顶角为40°,则它的底角度数为()A.40°B.50°C.60°D.70°【考点】KH:等腰三角形的性质.【分析】根据等腰三角形的性质和三角形内角和定理可直接求出其底角的度数.【解答】解:因为等腰三角形的两个底角相等,又因为顶角是40°,所以其底角为=70°.故选:D.6.下列多边形中,内角和是外角和的两倍的是()A.四边形B.五边形C.六边形D.八边形【考点】L3:多边形内角与外角.【分析】根据多边形的内角和公式(n﹣2)•180°以及多边形的外角和等于360°列方程求出边数,从而得解.【解答】解:设多边形边数为n,由题意得,(n﹣2)•180°=2×360°,解得n=6,所以,这个多边形是六边形.故选C.7.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为()A.2 B.3 C.4 D.5【考点】KA:全等三角形的性质.【分析】根据全等三角形的对应边相等解答即可.【解答】解:∵△ABE≌△ACF,∴AC=AB=5,∴EC=AC﹣AE=3,故选:B.8.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC 的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°【考点】KB:全等三角形的判定.【分析】本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;故选:C.9.如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是()A.5 B.6 C.7 D.8【考点】PA:轴对称﹣最短路线问题;KK:等边三角形的性质.【分析】先连接CF,再根据EB=EC,将FE+EB转化为FE+CE,最后根据两点之间线段最短,求得CF的长,即为FE+EB的最小值.【解答】解:连接CF,∵等边△ABC中,AD是BC边上的中线∴AD是BC边上的高线,即AD垂直平分BC∴EB=EC,当B、F、E三点共线时,EF+EC=EF+BE=CF,∵等边△ABC中,F是AB边的中点,∴AD=CF=6,∴EF+BE的最小值为6,故选B10.A、B两地相距80km,已知乙的速度是甲的1.5倍,甲先由A去B,1小时后,乙再从A地出发去追甲,追到B地时,甲已早到20分钟,则甲的速度为()A.40km/h B.45km/h C.50km/h D.60km/h【考点】B7:分式方程的应用.【分析】设甲的速度是x千米/小时,B的速度是1.5x千米/小时,根据甲、乙行使相等距离而时间不同可列分式方程求解.【解答】解:设甲的速度是x千米/小时,B的速度是1.5x千米/小时,﹣1+=,x=40,经检验x=40是分式方程的解.答:甲的速度40千米/小时.二、填空题(每小题3分,共24分)11.计算:(π﹣2)0=1.【考点】6E:零指数幂.【分析】根据非零的零次幂等于,可得答案.【解答】解:(π﹣2)0=1,故答案为:1.12.多项式3x2﹣6x的公因式为3x.【考点】52:公因式.【分析】根据因式分解,可得答案.【解答】解:3x2﹣6x=3x(x﹣2),公因式是3x,故答案为:3x.13.若a2﹣b2=,a﹣b=,则a+b的值为.【考点】4F:平方差公式.【分析】已知第一个等式左边利用平方差公式化简,将a﹣b的值代入即可求出a+b的值.【解答】解:∵a2﹣b2=(a+b)(a﹣b)=,a﹣b=,∴a+b=.故答案为:.14.如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD 周长为19cm,AB=8cm.【考点】K2:三角形的角平分线、中线和高.【分析】设AB=xcm,BD=ycm,由三角形中线的定义得到BC=2BD=2ycm,再根据△ABC的周长为27cm,△ABD周长为19cm列出关于x、y方程组,解方程组即可.【解答】解:设AB=xcm,BD=ycm,∵AD是BC边的中线,∴BC=2BD=2ycm.由题意得,解得,所以AB=8cm.故答案为8cm.15.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后来客户要求提前5天交货,为保证按时完成任务,则每天应多做24件.【考点】B7:分式方程的应用.【分析】设每天应多做x件.根据实际所用的时间比原计划所用的时间提前5天列方程求解.【解答】解:设每天应多做x件,则依题意得:﹣=5,解得:x=24.经检验x=24是方程的根,答:每天应多做24件,故答案为24.16.已知关于x的分式方程的解是非负数,则m的取值范围是m ≥2且m≠3.【考点】B2:分式方程的解;C6:解一元一次不等式.【分析】解出分式方程,根据解是非负数求出m的取值范围,再根据x=1是分式方程的增根,求出此时m的值,得到答案.【解答】解:去分母得,m﹣3=x﹣1,解得x=m﹣2,由题意得,m﹣2≥0,解得,m≥2,x=1是分式方程的增根,所有当x=1时,方程无解,即m≠3,所以m的取值范围是m≥2且m≠3.故答案为:m≥2且m≠3.17.若m为正实数,且m2﹣m﹣1=0,则m2+=3.【考点】4C:完全平方公式.【分析】在m2﹣m﹣1=0同时除以m,得到,然后利用完全平方公式展开整理即可得解.【解答】解:在m2﹣m﹣1=0同时除以m,得:m﹣1﹣=0∴,=3,故答案为:3.18.如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,且△A′B′C≌△ABC,则∠BCA′:∠BCB′=1:4.【考点】KA:全等三角形的性质.【分析】根据三角形的内角和定理分别求出,∠A、∠ABC、∠ACB,再根据全等三角形对应角相等求出∠B′,∠A′CB′,全等三角形对应边相等可得BC=B′C,再求出∠BC A′,∠BC B′,然后相比即可.【解答】解:∵∠A:∠ABC:∠ACB=3:5:10,∴∠A=30°,∠ABC=50°,∠ACB=100°,∵△A′B′C≌△ABC,∴∠B′=∠B=50°,∠A′CB′=∠C=100°,BC=B′C,∴∠BC B′=180°﹣2×50°=80°,∠BC A′=100°﹣80°=20°,∴∠BC A′:∠BC B′=1:4.故答案为:1:4三、解答题(共66分)19.分解因式:(1)4a2﹣36(2)(x﹣2y)2+8xy.【考点】55:提公因式法与公式法的综合运用.【分析】(1)原式提取4,再利用平方差公式分解即可;(2)原式整理后,利用完全平方公式分解即可.【解答】解:(1)原式=4(a2﹣9)=4(a+3)(a﹣3);(2)原式=x2﹣4xy+4y2+8xy=x2+4xy+4y2=(x+2y)2.20.先化简,再求值:÷(x+1+),其中x=2018.【考点】6D:分式的化简求值.【分析】根据分式的混合运算顺序和法则化简原式,再将x的值代入即可得.【解答】解:原式=÷(+)=•=,当x=2018时,原式=.21.解方程:(1)﹣=1(2)=﹣1.【考点】B3:解分式方程.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:x2﹣2x+2=x2﹣x,移项合并得:﹣x=﹣2,解得:x=2,经检验x=2是分式方程的解;(2)去分母得:15x﹣12=4x+10﹣3x+6,移项合并得:14x=28,解得:x=2,经检验x=2是增根,分式方程无解.22.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AB=DE.【考点】KD:全等三角形的判定与性质.【分析】先证明BC=EF,然后依据AAS证明△ABC≌△DEF,最后依据全等三角形的性质进行证明即可.【解答】证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,∴△ABC≌△DEF.∴AB=DE.23.如图,已知△ABC的三个顶点的坐标为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2).(1)请在图中作出△ABC关于y轴对称的△A′B′C′;(2)分别写出点A′、B′、C′的坐标.【考点】P7:作图﹣轴对称变换.【分析】(1)直接利用关于y轴对称点的性质得出答案;(2)利用(1)中图形得出各点坐标.【解答】解:(1)如图所示:△A′B′C′即为所求;(2)A′(1,2)、B′(4,1)、C′(2,﹣2).24.2015年5月,某县突降暴雨,造成山林滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区,现有甲、乙两种货车,乙知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1000件帐篷所用的车辆与乙车货车装运800件帐篷所用车辆相等.(1)求甲、乙两种货车每辆车可装多少件帐篷?(2)如果这批帐篷有1490件,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其它装满,求甲、乙两辆汽车各有多少辆?【考点】B7:分式方程的应用;9A:二元一次方程组的应用.【分析】(1)可设甲种货车每辆车可装x件帐蓬,乙种货车每辆车可装y件帐蓬,根据等量关系:①甲种货车比乙种货车每辆车多装20件帐篷;②甲种货车装运1000件帐篷所用车辆与乙种货车装运800件帐蓬所用车辆相等;列出方程组求解即可;(2)可设甲种汽车有z辆,乙种汽车有(16﹣z)辆,根据等量关系:这批帐篷有1490件,列出方程求解即可.【解答】解:(1)设甲种货车每辆车可装x件帐蓬,乙种货车每辆车可装y件帐蓬,依题意有,解得,经检验,是原方程组的解.故甲种货车每辆车可装100件帐蓬,乙种货车每辆车可装80件帐蓬;(2)设甲种汽车有z辆,乙种汽车有(16﹣z)辆,依题意有100z+80(16﹣z﹣1)+50=1490,解得z=12,16﹣z=16﹣12=4.故甲种汽车有12辆,乙种汽车有4辆.25.如图,△ABC是等边三角形,D是三角形外一动点,满足∠ADB=60°,(1)当D点在AC的垂直平分线上时,求证:DA+DC=DB;(2)当D点不在AC的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由;(3)当D点在如图的位置时,直接写出DA,DC,DB的数量关系,不必证明.【考点】KD:全等三角形的判定与性质;KG:线段垂直平分线的性质.【分析】(1)根据线段垂直平分线和等边三角形的性质可得AD=DC,∠ABD=30°,再由正弦定理可以证明DA+DC=DB;(2)延长DA到E,使得∠EBD=60,由已知可知△EBD是一个等边三角形,再证明△EBD≌△CBD,得出EA=DC,从而证明BD=ED=EA+AD=DC+AD;(3)可直接得DA,DC,DB的数量关系.【解答】证明:(1)点D只能在AC的下边,容易得到BD是AC的中垂线,因此AD=DC,∠ABD=30°,在三角形内由正弦定理可以得到=,可以很快得到BD=2AD=AD+AC;(2)延长DA到E,使得ED=BD,又因为∠ADB=60°因此△EBD是一个等边三角形,所以BE=ED=BD,∠EBD=60°,又因为△ABC是等边三角形,所以AB=BC,∠ABC=60°,所以∠EBA=∠DBC,在△EBA与△DBC中,因为,所以△ABE≌△CBD(SAS),因此EA=DC,所以BD=ED=EA+AD=DC+AD;(3)DC<DA+DB.26.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣8a﹣4b+20=0.①求a、b的值;②如图1,在①的条件下,第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;(2)如图2,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.【考点】KY:三角形综合题.【分析】(1)①根据非负数的性质列出算式,求出a、b的值;②根据等腰直角三角形的性质求出AC、BC,根据三角形的面积公式计算即可;(2)作FG⊥y轴,FH⊥x轴垂足分别为G、H,证明四边形FHOG是正方形,得到OG=FH,∠GFH=90°,证明△AFG≌△BFH,根据全等三角形的性质计算即可.【解答】解:(1)①∵a2+b2﹣8a﹣4b+20=0,∴(a﹣4)2+(b﹣2)2=0,∴a=4,b=2;②∵A(0,4),B(2,0),∴AB==2,∵△ABC是等腰直角三角形,∴AC=BC=,∴四边形AOBC的面积S=×OA×OB+×AC×BC=4+5=9;(2)结论:FA=FB,FA⊥FB,理由如下:如图2,作FG⊥y轴,FH⊥x轴垂足分别为G、H,∵A(0,a)向右平移a个单位到D,∴点D坐标为(a,a),点E坐标为(a+b,0),∴∠DOE=45°,∵EF⊥OD,∴∠OFE=90°,∠FOE=∠FEO=45°,∴FO=EF,∴FH=OH=HE=(a+b),∴点F坐标为(,),∴FG=FH,四边形FHOG是正方形,∴OG=FH=,∠GFH=90°,∴AG=AO﹣OG=a﹣=,BH=OH﹣OB=﹣b=,∴AG=BH,在△AFG和△BFH中,,∴△AFG≌△BFH,∴FA=FB,∠AFG=∠BFH,∴∠AFB=∠AFG+∠BFG=∠BFH+∠BFG=90°,∴FA=FB,FA⊥FB.第21页(共21页)。
八年级上册期末复习测试题(AB卷,含答案)1

杨河中学第二次月考试卷姓名 班级 学号A 卷(共100分)一、选择题:(每小题3分,共30分)1. 1.下列函数(1)y =πx ;(2)y =2x -1;(3)y =1x;(4)y =x 2-1中,是一次函数的有( )A .4个B .3个C .2个D .1个2.一次函数y =—2x +3的图象与两坐标轴的交点是( )A .(3,1)(1,23);B .(1,3)(23,1);C .(3,0)(0,23) ;D .(0,3)(23,0)3.一次函数y=2x-3的图象不经过的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 4.函数2y x =+中,自变量x 的取值范围是( )A .2x >-B .2x -≥C .2x ≠-D .2x -≤ 5.若正比例函数的图像经过点(-1,2),则这个图像必经过点( ) A .(1,2) B .(-1,-2) C .(2,-1) D .(1,-2)6. 若把直线y=2x -3向上平移3个单位长度,得到直线( ) A .y=2x B.y=2x -6 C. y=5x -3 D.y=-x -37. 已知一次函数y =(m +2)x +(1-m ),若y 随x 的增大而减小,且此函数图象与y 轴的交点在x 轴的上方,则m 的取值范围是( )A. m >-2B. m <1C. m <-2D. m <1且m ≠-28.已知等腰三角形的周长为20cm ,将底边长y (cm )表示成腰长x (cm )•的函数关系式是y=20-2x ,则其自变量x 的取值范围是( ).A .0<x<10B .5<x<10C .一切实数D .x>09.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,•弹簧的长度为( ).A .7cmB .8cmC .9cmD .10cm10.下列计算中正确的是 ( )A .5322a b a =+B .-332 =96b ay/cm12.520C .842a a a =⋅D .()632a a -=-二、填空题:(每小题3分,共30分)11.若9m m 21684=⋅⋅,则=m ________.12. 若1b -=,则=⋅-⋅-53223b )b (]b )2[(___________.13.若单项式22m x y 与313n x y -是同类项,则m n +的值是 .14.某一次函数的图象经过点(1-,3),且函数y 随x 的增大而减小,请你写出一个符合条件的函数解析式______________________.15.一次函数y=-x+a 与一次函数y=x+b 的图像的交点坐标为(m ,8),则a+b=___16. 函数25+-=x y 与两坐标轴围成的三角形面积是 。
初中八年级数学上册期末考试卷及答案【完美版】

初中八年级数学上册期末考试卷及答案【完美版】班级: 姓名:一、选择题(本大题共10小题, 每题3分, 共30分)1. -5的相反数是()A. B. C. 5 D. -52. 计算: (a-b)(a+b)(a2+b2)(a4-b4)的结果是( )A. a8+2a4b4+b8B. a8-2a4b4+b8C. a8+b8D. a8-b83.解分式方程时, 去分母变形正确的是()A. B.C. D.4.《孙子算经》中有一道题, 原文是: “今有木, 不知长短.引绳度之, 余绳四足五寸;屈绳量之, 不足一尺.木长几何?”意思是: 用一根绳子去量一根长木, 绳子还剩余尺.将绳子对折再量长木, 长木还剩余尺, 问木长多少尺, 现设绳长尺, 木长尺, 则可列二元一次方程组为()A. B. C. D.5.“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务, 为了迎接雨季的到来, 实际工作时每天的工作效率比原计划提高了25%, 结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米, 则下面所列方程中正确的是()A. B.C. D.6.欧几里得的《原本》记载, 形如的方程的图解法是: 画, 使, , , 再在斜边上截取.则该方程的一个正根是()A. 的长B. 的长C. 的长D. 的长7.如图, 某小区计划在一块长为32m, 宽为20m的矩形空地上修建三条同样宽的道路, 剩余的空地上种植草坪, 使草坪的面积为570m2.若设道路的宽为xm, 则下面所列方程正确的是()A. (32﹣2x)(20﹣x)=570B. 32x+2×20x=32×20﹣570C. (32﹣x)(20﹣x)=32×20﹣570D. 32x+2×20x﹣2x2=5708.如图, △ABC中, AB⊥BC, BE⊥AC, ∠1=∠2, AD=AB, 则下列结论不正确的是()A. BF=DFB. ∠1=∠EFDC. BF>EFD. FD∥BC9.如图, 在△ABC和△DEF中, ∠B=∠DEF, AB=DE, 若添加下列一个条件后, 仍然不能证明△ABC≌△DEF, 则这个条件是()A. ∠A=∠DB. BC=EFC. ∠ACB=∠FD. AC=DF10.如图, 点P是边长为1的菱形ABCD对角线AC上的一个动点, 点M, N分别是AB, BC边上的中点, 则MP+PN的最小值是()A. B. 1 C. D. 2二、填空题(本大题共6小题, 每小题3分, 共18分)1. 若, 则二次根式化简的结果为________.2. 将命题“同角的余角相等”, 改写成“如果…, 那么…”的形式_____.3. 若一个正数的两个平方根分别是a+3和2﹣2a, 则这个正数的立方根是________.4. 如图, 在△ABC中, AD⊥BC于D, BE⊥AC于E, AD与BE相交于点F, 若BF =AC, 则∠ABC=________度.5. 如图, 菱形ABCD中, ∠B=60°, AB=3, 四边形ACEF是正方形, 则EF的长为__________.6.如图, 已知正方形ABCD的边长为5, 点E、F分别在AD、DC上, AE=DF=2, BE与AF相交于点G, 点H为BF的中点, 连接GH, 则GH的长为_______.三、解答题(本大题共6小题, 共72分)1. 解不等式(1)7252x x-+≥(2)111 32x x-+-<2. (1)已知x=, y=, 试求代数式2x2-5xy+2y2的值.(2)先化简, 再求值:, 其中x=, y=.3. 已知关于x的方程x2 -(m+1)x+2(m-1)=0,(1)求证: 无论m取何值时, 方程总有实数根;(2)若等腰三角形腰长为4, 另两边恰好是此方程的根, 求此三角形的另外两条边长.4. 如图, 在四边形中, , , 对角线, 交于点, 平分, 过点作交的延长线于点, 连接.(1)求证: 四边形是菱形;(2)若, , 求的长.5. 已知和位置如图所示, , , .(1)试说明: ;(2)试说明:.6. 某学校为改善办学条件, 计划采购A.B两种型号的空调, 已知采购3台A型空调和2台B型空调, 需费用39000元;4台A型空调比5台B型空调的费用多6000元.(1)求A型空调和B型空调每台各需多少元;(2)若学校计划采购A.B两种型号空调共30台, 且A型空调的台数不少于B 型空调的一半, 两种型号空调的采购总费用不超过217000元, 该校共有哪几种采购方案?(3)在(2)的条件下, 采用哪一种采购方案可使总费用最低, 最低费用是多少元?参考答案一、选择题(本大题共10小题, 每题3分, 共30分)1.C2.B3.D4.B5.C6.B7、A8、B9、D10、B二、填空题(本大题共6小题, 每小题3分, 共18分)1.-2、如果两个角是同一个角的余角, 那么这两个角相等3.44.455.36.三、解答题(本大题共6小题, 共72分)1.(1);(2)2、(1)42, (2)3. 略 4和24.(1)略;(2)2.5、(1)略;(2)略.6、(1)A型空调和B型空调每台各需9000元、6000元;(2)共有三种采购方案, 方案一:采购A型空调10台, B型空调20台, 方案二:采购A型空调11台, B型空调19台, 案三:采购A型空调12台, B型空调18台;(3)采购A型空调10台, B型空调20台可使总费用最低, 最低费用是210000元.。
八年级数学(上)期末测试试卷含答案解析

八年级数学(上)期末测试试卷一、选择题(共10小题,每小题2分,满分20分)1.(2分)下列各实数是无理数的是()A.B.C.3. D.﹣π2.(2分)二元一次方程2y﹣x=1有无数多个解,下列四组值中是该方程的解的是()A.B.C.D.3.(2分)满足下列条件的三角形中,不是直角三角形的是()A.三个内角之比为1:1:2 B.三条边之比为1:2:C.三条边之比为5:12:13 D.三个内角之比为3:4:54.(2分)下列命题错误的是()A.所有实数都可以用数轴上的点表示B.同位角相等,两直线平行C.无理数包括正无理数、负无理数和0D.等角的补角相等5.(2分)请估计的值在()A.1与2之间B.2与3之间C.3与4之间D.4与5之间6.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=()度.A.70 B.65 C.60 D.557.(2分)现在父亲的年龄是儿子年龄的3倍,七年前父亲的年龄是儿子年龄的5倍,则父亲和儿子现在的年龄分别是()A.42岁,14岁B.48岁,16岁C.36岁,12岁D.39岁,13岁8.(2分)如果m是任意实数,那么点M(m﹣5,m+2)一定不在()A.第一象限 B.第二象限 C.第三象限 D.第四象限9.(2分)如图,已知△ABC是等腰直角三角形,∠ACB=90°,P为斜边AB上一点,PF⊥BC于点F,PE⊥AC于点E.若S△APE=7,S△PBF=2,则PC的长为()A.5 B.3C. D.310.(2分)在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是()A.B.C.D.二、填空题(共8小题,每小题2分,满分16分)11.函数中,自变量x的取值范围是.12.(2分)一组数据﹣1,0,2,4,x的极差为7,则x=.13.(﹣2)2的平方根是.14.直线y=2x+1与y=﹣x+4的交点是(1,3),则方程组的解是.15.(2分)一个两位数,个位数字比十位数字大4,个位数字与十位数字的和为8,则这个两位数是.16.(2分)如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是.17.(2分)若直线y=k x+b平行于直线y=﹣2x+3,且过点(5,9),则其解析式为.18.(2分)如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x 轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0).则依图中所示规律,A2016的坐标是.三、解答题(共7小题,满分64分)19.计算:(﹣2)×﹣6(2)解方程组:.20.(8分)在平面直角坐标系中,△ABC的顶点坐标是A(﹣4,1),B(﹣2,1),C(﹣2,3).(1)作△ABC关于y轴对称的图形△A1B1C1;(2)作△ABC向下平移4个单位长度的图形△A2B2C2;(3)如果△ABC与△ABD全等,则请直接写出点D坐标.21.(8分)丽水发生特大泥石流灾害后,某校学生会在全校1900名学生发起了“心系丽水”若捐款活动,为了解捐款情况,学生会随机调查了部分学生捐款情况,并用调查排水数据绘制了如图统计图,根据相关信息解答系列问题:(1)本次接受随机抽样调查的学生人数为人,图①中的值是.(2)求本次调查获取的样本数据的众数和中位数;(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.22.(10分)某工厂工人的工作时间为每月25天,每天8小时,每名工人每月有基本工资400元.该厂生产A、B两种产品,工人每生产一件A种产品,可得到报酬0.75元;每生产一件B种产品,可得到报酬1.40元,如表记录了工人小王的工作情况:生产A种产品件数生产B种产品件数合计用工时间(分钟)1 1 353 2 85(1)求小王每生产一件A种产品和一件B种产品,分别需要多少时间?(2)求小王每月工资额范围.23.(8分)如图,A、B、C、D四点在同一条直线上,∠AGD=90°,且∠1=∠D,∠2=∠A.求证:FB∥EC.24.(10分)小明和小亮在9:00同时乘坐由甲地到乙地的客车,途经丙地时小亮下车,处理个人事情后乘公交返回甲地;小明乘客车到达乙地;30分钟后乘出租车也返回甲地,两人同时回到甲地,设两人之间的距离为y千米,所用时间为x分钟,图中折线表示y与x之间函数关系图象,根据题中所给信息,解答下列问题:(1)甲、乙两地相距千米,客车的速度是千米/时;(2)小亮在丙地停留分钟,公交车速度是千米/时;(3)求两人何时相距28千米?25.(12分)如图所示,AB∥CD,直线EF与AB相交于点E,与CD相交于点F,FH是∠EFD的角平分线,且与AB相交于点H,GF⊥FH交AB于点G(GF>HP).(1)如图①,求证:点E是GH的中点;(2)如图②,过点E作EP⊥AB交GF于点P,请判断GP2=PF2+HF2是否成立?并说明理由;(3)如图③,在(1)的条件下,过点E作EP⊥EF交GF于点P,请猜想线段GP、PF、HP有怎样的数量关系,请直接写出你猜想的结果.参考答案与试题解析一、选择题(共10小题,每小题2分,满分20分)1.(2分)下列各实数是无理数的是()A.B.C.3. D.﹣π【考点】无理数.【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【解答】解:A、=是有理数,故A错误;B、是有理数,故B错误;C、3.是有理数,故C错误;D、﹣π是无理数,故D正确;故选:D.【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.(2分)二元一次方程2y﹣x=1有无数多个解,下列四组值中是该方程的解的是()A.B.C.D.【考点】二元一次方程的解.【专题】计算题;一次方程(组)及应用.【分析】把各项中x与y的值代入方程检验即可.【解答】解:A、把x=0,y=﹣代入方程得:左边=﹣1,右边=1,不相等,不合题意;B、把x=1,y=1代入方程得:左边=2﹣1=1,右边=1,相等,符合题意;C、把x=1,y=0代入方程得:左边=﹣1,右边=1,不相等,不合题意;D、把x=﹣1,y=﹣1代入方程得:左边=﹣3,右边=1,不相等,不合题意,故选B.【点评】此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.3.(2分)满足下列条件的三角形中,不是直角三角形的是()A.三个内角之比为1:1:2 B.三条边之比为1:2:C.三条边之比为5:12:13 D.三个内角之比为3:4:5【考点】勾股定理的逆定理;三角形内角和定理.【分析】根据三角形的内角和定理得出A是直角三角形,D不是直角三角形,由勾股定理的逆定理得出B、C是直角三角形,从而得到答案.【解答】解:A、三个内角之比为1:1:2,因为根据三角形内角和定理可求出三个角分别为45°,45°,90°,所以是直角三角形,故正确;B、三条边之比为1:2:,因为12+22=()2,其符合勾股定理的逆定理,所以是直角三角形,故正确;C、三条边之比为5:12:13,因为52+122=132,其符合勾股定理的逆定理,所以是直角三角形,故正确;D、三个内角之比为3:4:5,因为根据三角形内角和公式得三个角中没有90°角,所以不是直角三角形,故不正确.故选:D.【点评】本题考查了勾股定理的逆定理、三角形内角和定理、直角三角形的判定;熟练掌握勾股定理的逆定理和三角形内角和定理是解决问题的关键.4.(2分)下列命题错误的是()A.所有实数都可以用数轴上的点表示B.同位角相等,两直线平行C.无理数包括正无理数、负无理数和0D.等角的补角相等【考点】命题与定理.【分析】利用数轴上的点与实数一一对应可对A进行判断;根据平行线的判定方法对B进行判断;根据无理数的定义对C进行判断;根据补角的定义对D进行判断.【解答】解:A、所有实数都可以用数轴上的点表示,所以A选项为真命题;B、同位角相等,两直线平行,所以B选项为真命题;C、无理数包括正无理数、负无理数,所以C选项为假命题;D、等角的补角相等,所以D选项为真命题.故选C.【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.5.(2分)请估计的值在()A.1与2之间B.2与3之间C.3与4之间D.4与5之间【考点】估算无理数的大小.【分析】根据被开方数越大算术平方根越大,可得3<<4,再根据不等式的性质1,可得答案.【解答】解:由被开方数越大算术平方根越大,得<<,即3<<4,都减1,得2<﹣1<3.故选:B.【点评】本题考查了估算无理数的大小,利用被开方数越大算术平方根越大得出3<<4是解题关键.6.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=()度.A.70 B.65 C.60 D.55【考点】平行线的性质.【分析】先由垂直的定义,求出∠PEF=90°,然后由∠BEP=50°,进而可求∠BEF=140°,然后根据两直线平行同旁内角互补,求出∠EFD的度数,然后根据角平分线的定义可求∠EFP的度数,然后根据三角形内角和定理即可求出∠EPF的度数.【解答】解:如图所示,∵EP⊥EF,∴∠PEF=90°,∵∠BEP=50°,∴∠BEF=∠BEP+∠PEF=140°,∵AB∥CD,∴∠BEF+∠EFD=180°,∴∠EFD=40°,∵FP平分∠EFD,∴=20°,∵∠PEF+∠EFP+∠EPF=180°,∴∠EPF=70°.故选:A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.7.(2分)现在父亲的年龄是儿子年龄的3倍,七年前父亲的年龄是儿子年龄的5倍,则父亲和儿子现在的年龄分别是()A.42岁,14岁B.48岁,16岁C.36岁,12岁D.39岁,13岁【考点】一元一次方程的应用.【分析】可设儿子现在的年龄是x岁,则父亲现在的年龄是3x岁,根据等量关系:7年前父亲的年龄=7年前儿子的年龄×5,依此列出方程求解即可.【解答】解:设儿子现在的年龄是x岁,依题意得:3x﹣7=5(x﹣7).解得x=14.则3x=42.即父亲和儿子现在的年龄分别是42岁,14岁.故选:A.【点评】考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,由年龄的倍数问题找出合适的等量关系列出方程,再求解.8.(2分)如果m是任意实数,那么点M(m﹣5,m+2)一定不在()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】点的坐标.【分析】根据第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣),可得答案.【解答】解:m>5时,m﹣5>0,m+2>0,点位于第一象限,故A不符合题意;m=5时点位于y轴;﹣2<m<5时,m﹣5<0,m+2>0,点位于第二象限,故B不符合题意;m=﹣2时,点位于x轴;m<﹣2时,m﹣5<0,m+2<0,点位于第三象限,故C不符合题意;M(m﹣5,m+2)一定不在第四象限,故D符合题意;故选:D.【点评】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).9.(2分)如图,已知△ABC是等腰直角三角形,∠ACB=90°,P为斜边AB上一点,PF⊥BC于点F,PE⊥AC于点E.若S△APE=7,S△PBF=2,则PC的长为()A.5 B.3C. D.3【考点】等腰直角三角形.【分析】由等腰直角三角形的性质得出∠A=∠B=45°,证出四边形PECF是矩形,得出PF=CE,证出△APE和△BPF是等腰直角三角形,得出AE=PE,BF=PF,再由三角形的面积得出PE2=14,CE2=PF2=4,由勾股定理求出PC的长即可.【解答】解:∵△ABC是等腰直角三角形,∠ACB=90°,∴∠A=∠B=45°,∵PF⊥BC于点F,PE⊥AC于点E,∴∠PFB=∠PEA=90°,四边形PECF是矩形,∴△APE和△BPF是等腰直角三角形,PF=CE,∠PEC=90°,∴AE=PE,BF=PF,∵S△APE=AE•PE=PE2=7,S△PBF=PF•BF=PF2=2,∴PE2=14,CE2=PF2=4,∴PC===3;故选:B.【点评】本题考查了等腰直角三角形的判定与性质、矩形的判定与性质、勾股定理;熟练掌握等腰直角三角形的判定与性质,运用勾股定理求出PC是解决问题的关键.10.(2分)在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是()A.B.C.D.【考点】一次函数的图象;正比例函数的图象.【分析】根据正比例函数与一次函数的图象性质作答.【解答】解:当k>2时,正比例函数y=kx图象经过1,3象限,一次函数y=(k﹣2)x+k的图象1,2,3象限;当0<k<2时,正比例函数y=kx图象经过1,3象限,一次函数y=(k﹣2)x+k的图象1,2,4象限;当k<0时,正比例函数y=kx图象经过2,4象限,一次函数y=(k﹣2)x+k的图象2,3,4象限;故选B.【点评】此题考查一次函数的图象问题,正比例函数的性质:正比例函数y=kx的图象是过原点的一条直线.当k>0时,直线经过第一、三象限;当k<0时,直线经过第二、四象限.二、填空题(共8小题,每小题2分,满分16分)11.函数中,自变量x的取值范围是x≤2.【考点】函数自变量的取值范围.【分析】根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.【解答】解:根据题意得:2﹣x≥0,解得:x≤2.故答案是:x≤2.【点评】函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.12.(2分)一组数据﹣1,0,2,4,x的极差为7,则x=6或﹣3.【考点】极差.【分析】分别当x为最大值和最小值时,根据极差的概念求解.【解答】解:当x为最大值时,x﹣(﹣1)=7,解得:x=6,当x为最小值时,4﹣x=7,解得:x=﹣3.故答案为:6或﹣3.【点评】本题考查了极差的知识,极差是指一组数据中最大数据与最小数据的差.13.(﹣2)2的平方根是±2.【考点】平方根.【专题】计算题.【分析】先求出(﹣2)2的值,然后开方运算即可得出答案.【解答】解:(﹣2)2=4,它的平方根为:±2.故答案为:±2.【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.14.直线y=2x+1与y=﹣x+4的交点是(1,3),则方程组的解是.【考点】一次函数与二元一次方程(组).【分析】利用函数图象交点坐标为两函数解析式组成的方程组的解易得答案.【解答】解:∵直线y=2x+1与y=﹣x+4的交点是(1,3),∴方程组的解为.故答案为.【点评】本题考查了一次函数与一元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.15.(2分)一个两位数,个位数字比十位数字大4,个位数字与十位数字的和为8,则这个两位数是26.【考点】二元一次方程组的应用.【专题】数字问题.【分析】设这个两位数个位数为x,十位数字为y,根据个位数字比十位数字大4,个位数字与十位数字的和为8,列方程组求解.【解答】解:设这个两位数个位数为x,十位数字为y,由题意得,,解得:,则这个两位数为26.故答案为:26.【点评】本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.16.(2分)如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是cm.【考点】平面展开-最短路径问题.【分析】将图形展开,可得到AD较短的展法两种,通过计算,得到较短的即可.【解答】解:(1)如图1,BD=BC=6cm,AB=5+10=15cm,在Rt△ADB中,AD==3cm;(2)如图2,AN=5cm,ND=5+6=11cm,Rt△ADN中,AD===cm.综上,动点P从A点出发,在长方体表面移动到D点的最短距离是cm.故答案为:cm.【点评】本题考查了平面展开﹣﹣最短路径问题,熟悉平面展开图是解题的关键.17.(2分)若直线y=kx+b平行于直线y=﹣2x+3,且过点(5,9),则其解析式为y=﹣2x+19.【考点】两条直线相交或平行问题.【专题】计算题.【分析】根据两直线平行的问题得到k=﹣2,然后把(5,9)代入y=﹣2x+b,求出b的值即可.【解答】解:根据题意得k=﹣2,把(5,9)代入y=﹣2x+b得﹣10+b=9,所以直线解析式为y=﹣2x+19.故答案为y=﹣2x+19.【点评】本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.18.(2分)如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x 轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).【考点】规律型:点的坐标.【分析】由于2016是4的整数倍数,故A1﹣﹣A4;A5﹣﹣﹣A8;…每4个为一组,可见,A2016在x轴上方,横坐标为2,再根据纵坐标变化找到规律即可解答即可.【解答】解:∵2016是4的整数倍数,∴A1﹣﹣A4;A5﹣﹣﹣A8;…每4个为一组,∵2016÷4=504…0,∴A2016在x轴上方,横坐标为2,∵A4、A8、A12的纵坐标分别为2,4,6,∴A2016的纵坐标为2016×=1008.故答案为:(2,1008).【点评】本题考查了等腰直角三角形、点的坐标,主要是根据坐标变化找到规律,再依据规律解答.三、解答题(共7小题,满分64分)19.计算:(﹣2)×﹣6(2)解方程组:.【考点】二次根式的混合运算;解二元一次方程组.【专题】计算题.【分析】(1)先进行二次根式的乘法运算,然后合并即可;(2)利用加减消元法解二元一次方程组.【解答】解:(1)原式=3﹣6﹣3(2),①+②×5得:13y=13,解得y=1,把y=1代入②中得2x﹣1=1,解得x=1,所以原方程组的解是.【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程组.20.(8分)在平面直角坐标系中,△ABC的顶点坐标是A(﹣4,1),B(﹣2,1),C(﹣2,3).(1)作△ABC关于y轴对称的图形△A1B1C1;(2)作△ABC向下平移4个单位长度的图形△A2B2C2;(3)如果△ABC与△ABD全等,则请直接写出点D坐标.【考点】作图-轴对称变换;全等三角形的性质;作图-平移变换.【分析】(1)首先确定A、B、C三点关于y轴对称的点的位置,再连接即可;(2)首先确定A、B、C三点向下平移4个单位长度的对应点的位置,再连接即可;(3)首先确定D点位置,然后再写出坐标即可.【解答】解:(1)(2)如图所示:;(3)(﹣4,﹣1);(﹣2,﹣1);(﹣4,3).【点评】此题主要考查了作图﹣﹣平移变换,以及关于坐标轴对称,全等三角形的判定,关键是正确确定对称点和对应点的位置.21.(8分)丽水发生特大泥石流灾害后,某校学生会在全校1900名学生发起了“心系丽水”若捐款活动,为了解捐款情况,学生会随机调查了部分学生捐款情况,并用调查排水数据绘制了如图统计图,根据相关信息解答系列问题:(1)本次接受随机抽样调查的学生人数为50人,图①中的值是12.(2)求本次调查获取的样本数据的众数和中位数;(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.【考点】条形统计图;用样本估计总体;扇形统计图;中位数;众数.【专题】计算题.【分析】(1)利用条形统计图得各组的频数,然后把它们相加即可得到抽样调查的学生的总数,再用16除以50即可得到m的值;(2)根据众数和中位数的定义求解;(3根据样本估计总体,用样本中捐款10元所占的百分比表示全校捐款10元的百分比,然后计算1900×32%即可.【解答】解:(1)本次接受随机抽样调查的学生人数为4+16+12+10+8=50(人),m%=×100%=32%;故答案为50;32;(2)本次调查获取的样本数据的众数是10元;中位数是15元;(3)1900×32%=608(人),答:估计该校捐款10元的学生人数有608人.【点评】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.从条形图可以很容易看出数据的大小,便于比较.也考查了用样本估计总体、中位数和众数.22.(10分)某工厂工人的工作时间为每月25天,每天8小时,每名工人每月有基本工资400元.该厂生产A、B两种产品,工人每生产一件A种产品,可得到报酬0.75元;每生产一件B种产品,可得到报酬1.40元,如表记录了工人小王的工作情况:生产A种产品件数生产B种产品件数合计用工时间(分钟)1 1 353 2 85(1)求小王每生产一件A种产品和一件B种产品,分别需要多少时间?(2)求小王每月工资额范围.【考点】一次函数的应用;二元一次方程组的应用.【分析】(1)设生产一件A种产品需要x分钟,生产一件B种产品需要y分钟,根据等量关系为“1件A,1件B用时35分钟”和“3件A,2件B用时85分钟”,根据这两个等量关系可列方程组,再进行求解即可.(2)求小王每月工资额的范围,需要求助于函数,由(1)知生产A、B的单个时间,又每月工作总时间一定为25×8×60,所以可列一个二元一次方程,又工资计算方法已知,则可利用一个未知量,去表示另一个未知量,得到函数,进行解答.【解答】解:(1)设生产一件A种产品需要x分钟,生产一件B种产品需要y分钟,依题意得:,解得:,答:生产一件A种产品需要15分钟,生产一件B种产品需要20分钟.(2)设小王每月生产A、B两种产品的件数分别为m、n,月工资额为w,根据题意得:,即,因为m,n为非负整数,所以0≤m≤800,故当m=0时,w有最大值为1240,当m=800时,w有最小值为1000,则小王每月工资额最少1000元,每月工资额最多1240元.【点评】此题考查了一次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系:“1件A,1件B用时35分钟”和“3件A,2件B用时85分钟”,列出方程组,再求解.23.(8分)如图,A、B、C、D四点在同一条直线上,∠AGD=90°,且∠1=∠D,∠2=∠A.求证:FB∥EC.【考点】平行线的判定.【专题】证明题.【分析】先由∠AGD=90°,根据三角形内角和定理得出∠A+∠D=90°,再由∠1=∠D,∠ABF=∠1+∠D,得出∠ABF=2∠D,同理得出∠DCE=2∠A,那么∠DCE+∠ABF=2(∠A+∠D)=180°,根据邻补角定义得出∠ABF+∠DBF=180°,由同角的补角相等得到∠DCE=∠DBF,根据同位角相等,两直线平行得出FB∥EC.【解答】证明:∵∠AGD=90°,∴∠A+∠D=90°,∵∠1=∠D,∠ABF=∠1+∠D,∴∠ABF=2∠D,同理:∠DCE=2∠A,∴∠DCE+∠ABF=2(∠A+∠D)=180°,又∵∠ABF+∠DBF=180°,∴∠DCE=∠DBF,∴FB∥EC.【点评】本题考查了平行线的判定,三角形内角和定理,三角形外角的性质,邻补角定义,补角的性质,根据条件得出∠DCE=∠DBF是解题的关键.24.(10分)小明和小亮在9:00同时乘坐由甲地到乙地的客车,途经丙地时小亮下车,处理个人事情后乘公交返回甲地;小明乘客车到达乙地;30分钟后乘出租车也返回甲地,两人同时回到甲地,设两人之间的距离为y千米,所用时间为x分钟,图中折线表示y与x之间函数关系图象,根据题中所给信息,解答下列问题:(1)甲、乙两地相距80千米,客车的速度是80千米/时;(2)小亮在丙地停留48分钟,公交车速度是40千米/时;(3)求两人何时相距28千米?【考点】一次函数的应用;一次函数的图象;待定系数法求一次函数解析式.【专题】数形结合;分类讨论;函数思想;待定系数法;一次函数及其应用.【分析】(1)结合图象知,小明乘客车从丙地到乙地用时30分钟,行驶40千米可得客车速度,小明从甲到乙行驶1小时,可得甲乙间距离;(2)小亮在x=30到达丙地,x=78离开丙地,可得停留时间,根据小亮从丙地返回到甲地用时可得公交车速度;(3)两人相距28千米,即y=28,求出AB、DE函数解析式,令y=28可求得.【解答】解:(1)根据题意可知,当x=30时小明、小亮同时到达丙地,小亮停留在丙地;当x=60时y=40,即小明到达乙地,此时两人间的距离为40千米,∴小明乘客车从丙地到乙地用时30分钟,行驶40千米,∴客车的速度为:40÷0.5=80(千米/小时),∵小明乘客车从甲地到乙地用时60分钟,速度为80千米/小时,∴甲、乙两地相距80千米.(2)当x=78时小亮从丙地出发返回甲地,当x=138时小亮乘公交车从丙地出发返回到甲地,∴小亮在丙地停留78﹣30=48(分钟),公交车的速度为:40÷1=40(千米/小时).(3)①设AB关系式为:y1=k1x+b1由图象可得A(30,0)、B(60,40),代入得:则,解得,所以AB关系式为:(30≤x≤60),令y1=28,有,∴x=51.②设DE关系式为:y2=k2x+b2,∵(千米),∴D(90,48),由图象可得E(138,0),所以,解得:,所以DE关系式为:y2=﹣x+138 (90≤x≤138),令y2=28,有﹣x+138=28,∴x=110.所以两人在9:51和10:50相距28千米.故答案为:(1)80,80;(2)48,40.【点评】本题主要考查一次函数图象及待定系数法求一次函数解析式的能力,读懂函数图象各分段实际意义是关键,属中档题.25.(12分)如图所示,AB∥CD,直线EF与AB相交于点E,与CD相交于点F,FH是∠EFD 的角平分线,且与AB相交于点H,GF⊥FH交AB于点G(GF>HP).(1)如图①,求证:点E是GH的中点;(2)如图②,过点E作EP⊥AB交GF于点P,请判断GP2=PF2+HF2是否成立?并说明理由;(3)如图③,在(1)的条件下,过点E作EP⊥EF交GF于点P,请猜想线段GP、PF、HP有怎样的数量关系,请直接写出你猜想的结果.【考点】全等三角形的判定与性质;勾股定理.【分析】(1)根据平行线的性质和角平分线的定义求得∠EHF=∠EFH,证得EF=EH,根据∠EFG+∠EFH=90°,∠EGF+∠EHF=90°,得出∠EFG=∠EGF,根据等角对等边求得EG=EF,即可证得EH=EG,即E为HG的中点;(2)连接PH,根据垂直平分线的性质得出PG=PH,在Rt△PFH中,根据勾股定理得:PH2=PF2+HF2,即可得到GP2=PF2+HF2;(3)延长PE,使PE=EM,连接MH,MF,易证得△GPE≌△HME,从而得出GP=MH,∠1=∠2,进而证得EF垂直平分PM,根据垂直平分线的性质得出PF=MF,在RT△MHF中,MF2=MH2+FH2,即可得到PF2=GP2+FH2.【解答】(1)证明:∵AB∥CD,∴∠EHF=∠HFD,∵FH平分∠EFD,∴∠EFH=∠HFD,∴∠EHF=∠EFH,∴EF=EH,∵∠GFH=90°,∴∠EFG+∠EFH=90°,∠EGF+∠EHF=90°,∴∠EFG=∠EGF,∴EG=EF,∴EH=EG,∴E为HG的中点;(2)连接PH,如图②:∵EP⊥AB,又∵E是GH中点,∴PE垂直平分GH,∴PG=PH,在Rt△PFH中,∠PFH=90°,由勾股定理得:PH2=PF2+HF2,∴GP2=PF2+HF2;(3)如图③,延长PE,使PE=EM,连接MH,MF,在△GPE和△HME中,,∴△GPE≌△HME(SAS),∴GP=MH,∠1=∠2,∵GF⊥FH,∴∠1+∠3=90°,∴∠2+∠3=90°,∵EF⊥PM,PE=EM,∴PF=MF,在RT△MHF中,MF2=MH2+FH2,∴PF2=GP2+FH2.【点评】本题考查了全等三角形的判定和性质,线段的垂直平分线的性质,等腰三角形的判定和性质,勾股定理的应用等,找出辅助线,构建等腰三角形是解题的关键.。
部编人教版八年级数学上册期末考试卷及答案【完整版】

部编人教版八年级数学上册期末考试卷及答案【完整版】 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.3-的倒数是( )A .3B .13C .13-D .3-2.若关于x 的方程3m(x +1)+5=m(3x -1)-5x 的解是负数,则m 的取值范围是( )A .m >-54B .m <-54C .m >54D .m <543.若α、β为方程2x 2-5x-1=0的两个实数根,则2235++ααββ的值为( )A .-13B .12C .14D .154.把函数y x =向上平移3个单位,下列在该平移后的直线上的点是( )A .()2,2B .()2,3C .()2,4D .(2,5) 5.代数式131x x -+-中x 的取值范围在数轴上表示为( ) A .B .C .D .6.下列运算正确的是( )A .224a a a +=B .3412a a a ⋅=C .3412()a a =D .22()ab ab =7.如图,将▱ABCD 沿对角线AC 折叠,使点B 落在B ′处,若∠1=∠2=44°,则∠B 为( )A .66°B .104°C .114°D .124°8.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是()A.B.C.D.9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P 3,P4四个点中找出符合条件的点P,则点P有()A.1个B.2个C.3个D.4个10.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是()A.x>﹣2 B.x>0 C.x>1 D.x<1 二、填空题(本大题共6小题,每小题3分,共18分)1.已知直角三角形的两边长分别为3、4.则第三边长为________.2x有意义,则x的取值范围为__________.328n n为________.4.通过计算几何图形的面积,可表示一些代数恒等式,如图所示,我们可以得到恒等式:2232a ab b ++=________.5.如图所示,把一张长方形纸片沿EF 折叠后,点D C ,分别落在点D C '',的位置.若65EFB ︒∠=,则AED '∠等于________.6.如图,四边形ABCD 中,∠A=90°,AB=33,AD=3,点M ,N 分别为线段BC ,AB 上的动点(含端点,但点M 不与点B 重合),点E ,F 分别为DM ,MN 的中点,则EF 长度的最大值为 .三、解答题(本大题共6小题,共72分)1.解分式方程:33122x x x-+=--2.先化简,再求值:()()22322323a a b ab a a b ---,其中a ,b 满足()2130a b a b +-+--=3.已知关于x 的一元二次方程22(21)10x m x m +++-=有两不相等的实数根. ①求m 的取值范围.②设x 1,x 2是方程的两根且221212170x x x x ++-=,求m 的值.4.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.5.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;(2)求恒温系统设定的恒定温度;(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?6.某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;(2)经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、C2、A3、B4、D5、A6、C7、C8、C9、C10、C二、填空题(本大题共6小题,每小题3分,共18分)1、52、0x ≥且1x ≠. 3、74、()()2a b a b ++.5、50°6、3三、解答题(本大题共6小题,共72分)1、x=1.2、483、①54m >-,②m 的值为53.4、(1)略;(2)四边形BECD 是菱形,理由略;(3)当∠A =45°时,四边形BECD 是正方形,理由略5、(1)y 关于x 的函数解析式为210(05)20(510)200(1024)x x y x x x ⎧⎪+≤<⎪=≤<⎨⎪⎪≤≤⎩;(2)恒温系统设定恒温为20°C ;(3)恒温系统最多关闭10小时,蔬菜才能避免受到伤害.6、(1)两次下降的百分率为10%;(2)要使每月销售这种商品的利润达到510元,且更有利于减少库存,则商品应降价2.5元.。
八年级上册期末复习测试题(AB卷_含答案).docx

八年级上册期末复习测试题A卷一、选择题:1.下列图案是我国几家银行的标志,其中是轴对称图形的有().A. 1个B. 2个C. 3个D. 4个2.将平面直角坐标系内的AABC的三个顶点坐标的横坐标乘以-1,纵坐标不变,则所得的三角形与原三角形().A.关于x轴对称B.关于y轴对称;C,关于原点对称 D.无任何对称关系3.已知点Pi (a-1, 5)和P2 (2, b-1)关于x轴对称,则(a+b)览质的值为().A. 0B. -1C. 1D. (-3)20054.AABC %等腰直角三角形,ZC=90° , D为BC上一点,且AD=2CD,则ZDAB=().A. 30°B. 45°C. 60°D. 15°5.已知一次函数y=mx+ | m+1 |的图像与y轴交于点(0,3),且y随x的增大而增大,则m的值为().A. 2B. -4C. -2 或-4D. 2 或-46.已知等腰三角形的周长为20cm,将底边长y (cm)表示成腰长x (cm)的函数关系式是y=20-2x,则其自变量x的取值范围是().A. 0<x<10B. 5<x<10C. 一切实数D. x>07.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为().A. 7cmB. 8cmC. 9cmD. 10cm8.在2XMNP中,Q为MN中点,且PQXMN,那么下列结论中不正确的是().A. AMPQ^ANPQ;B. MP=NP;C. ZMPQ=ZNPQD. MQ=NP9.如图所示,AABC为等边三角形,AQ=PQ, PR=PS, PR1AB于R, PS±AC于S,则四个结论正确的是().①点P在/A的平分线上;②AS=AR;③QP〃AR;④△BRPMZXQSP.A.全部正确;B.仅①和②正确;C.仅②③正确;D.仅①和③正确10.如图所示,在一个月的四个星期天中,某校环保小组共搜集废电池226节,每个星期天所搜集的电池数量如下表:星期天次序 1 2 3 4 搜集电池节数80635132下面四幅关于四个星期天搜集废电池节数的统计图中,正确的是().二、填空题:1. 一次函数y=-x+a 与一次函数y=x+b 的图像的交点坐标为(m, 8),则a+b=.2. 如图,ZA0P=ZB0P=15° , PC//OA, PQXOA,若 PC=4,则 PQ=.3. 为美化烟台,市政府下大力气实施城市改造,今春改造市区主要街道,街道两侧统一铺 设长为20cm,宽为10cm 的长方形水泥砖,若铺设总面积为10. 8万平方米,那么大约需 水泥砖 块(用科学计数法表示).4. 分解因式:a 2b-b 3=.5. 根据某市去年7月份中某21天的各天最高气温(笆)记录,制作了如图所示的统计图, 由图中信息可知,最高气温达到35°C (包括35°C)以上的天数有 天.6. 如果AABC 的边BC 的垂直平分线经过顶点A,与BC 相交于点D,旦AB= 2AD,则AABC 中,最大一个内角的度数为.7. 如图所示,ABDC 是将长方形纸牌ABCD 沿着BD 折叠得到的,图中(包括实线、虚线在内) 共有全等三角形 对.8. 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三 角形的底边长是.9. 如图所示,观察规律并填空:2S 44 88三、解答题: 1 .化简求值: (1)己知 |a+- |+ (b-3) 2=0,求代数式[(2a+b) 2+ (2a+b) (b-2a) -6b] 4-2b 的值. 2C'A 0/(2)已知 x+y=a, x2+y2=b,求 4x2y2.(3)计算:(2+1) (22+l) (23 4 5+l) - (2128+1) +1.2.如图所示,在△ ABC中,ZABC和/ACB的平分线交于点0,过。
八年级(上)期末数学试卷(含答案)

八年级(上)期末数学试卷(含答案)一、选择题1.下列条件中,不能判断△ABC 是直角三角形的是( )A .a :b :c =3:4:5B .∠A :∠B :∠C =3:4:5 C .∠A +∠B =∠CD .a :b :c =1:2:3 2.如图,已知O 为ABC ∆三边垂直平分线的交点,且50A ∠=︒,则BOC ∠的度数为( )A .80︒B .100︒C .105︒D .120︒3.如图,若一次函数y =﹣2x +b 的图象与两坐标轴分别交于A ,B 两点,点A 的坐标为(0,3),则不等式﹣2x +b >0的解集为( )A .x >32B .x <32C .x >3D .x <34.如果等腰三角形两边长是5cm 和2cm ,那么它的周长是( )A .7cmB .9cmC .9cm 或12cmD .12cm5.如图:若△ABE ≌△ACD ,且AB =6,AE =2,则EC 的长为( )A .2B .3C .4D .6 6.将直线y =12x ﹣1向右平移3个单位,所得直线是( ) A .y =12x +2 B .y =12x ﹣4 C .y =12x ﹣52 D .y =12x +127.2的算术平方根是()A .4B .±4C 2D .2±8.下列各数:4,﹣3.14,227,2π,3无理数有()A.1个B.2个C.3个D.4个9.在平面直角坐标系xOy中,线段AB的两个点坐标分别为A(﹣1,﹣1),B(1,2).平移线段AB,得到线段A′B′.已知点A′的坐标为(3,1),则点B′的坐标为()A.(4,4)B.(5,4)C.(6,4)D.(5,3)10.如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为P n,则P2020的坐标是()A.(5,3) B.(3,5) C.(0,2) D.(2,0)二、填空题11.点P(﹣5,12)到原点的距离是_____.12.如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=_____.13.若关于x的方程233x mx+=-的解不小于1,则m的取值范围是_______.14.如图,△ABC中,5BC=,AB边的垂直平分线分别交AB、BC于点D、E,AC边的垂直平分线分别交AC、BC于点F、G,则△AEG周长为____.15.如果点P在第二象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为______.16.如图是某足球队全年比赛情况统计图:根据图中信息,该队全年胜了_______场.17.3的平方根是_________.18.计算:16=_______.19.如图,在ABC ∆中,AC AD BD ==,28B ∠=,则CAD ∠的度数为__________.20.如图,在△ABC 中,AB = AC ,∠BAC = 120º,AD ⊥BC ,则∠BAD = _____°.三、解答题21.通过对下面数学模型的研究学习,解决下列问题:(模型呈现)(1)如图1,90BAD ∠=︒,AB AD =,过点B 作BC AC ⊥于点C ,过点D 作DE AC ⊥于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90ACB AED ∠=∠=︒,可以推理得到ABC DAE ∆∆≌.进而得到AC = ,BC = .我们把这个数学模型称为“K 字”模型或“一线三等角”模型;(模型应用)(2)①如图2,90BAD CAE ∠=∠=︒,AB AD =,AC AE =,连接BC ,DE ,且BC AF ⊥于点F ,DE 与直线AF 交于点G .求证:点G 是DE 的中点;②如图3,在平面直角坐标系xOy 中,点A 的坐标为()2,4,点B 为平面内任一点.若AOB ∆是以OA 为斜边的等腰直角三角形,请直接写出点B 的坐标.22.(1)计算:04(51)+-(2)解方程:23(1)120x --=23.已知一次函数y=2x+b.(1)它的图象与两坐标轴所围成的图形的面积等于4,求b 的值;(2)它的图象经过一次函数y=-2x+1、y=x+4图象的交点,求b 的值.24.在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在正方形网格的格点(网格线的交点)上.(1)请在如图所示的网格平面内作出平面直角坐标系,使点A 坐标为(1,3)点B 坐标为(2,1);(2)请作出△ABC 关于y 轴对称的△A 'B 'C ',并写出点C '的坐标;(3)判断△ABC 的形状.并说明理由.25.解方程:21133x xx x=+++.四、压轴题26.如图1.在△ABC中,∠ACB=90°,AC=BC=10,直线DE经过点C,过点A,B分别作AD⊥DE,BE⊥DE,垂足分别为点D和E,AD=8,BE=6.(1)①求证:△ADC≌△CEB;②求DE的长;(2)如图2,点M以3个单位长度/秒的速度从点C出发沿着边CA运动,到终点A,点N 以8个单位长度/秒的速度从点B出发沿着线BC—CA运动,到终点A.M,N两点同时出发,运动时间为t秒(t>0),当点N到达终点时,两点同时停止运动,过点M作PM⊥DE 于点P,过点N作QN⊥DE于点Q;①当点N在线段CA上时,用含有t的代数式表示线段CN的长度;②当t为何值时,点M与点N重合;③当△PCM与△QCN全等时,则t=.27.如图,A,B是直线y=x+4与坐标轴的交点,直线y=-2x+b过点B,与x轴交于点C.(1)求A,B,C三点的坐标;(2)点D是折线A—B—C上一动点.①当点D是AB的中点时,在x轴上找一点E,使ED+EB的和最小,用直尺和圆规画出点E 的位置(保留作图痕迹,不要求写作法和证明),并求E点的坐标.②是否存在点D,使△ACD为直角三角形,若存在,直接写出D点的坐标;若不存在,请说明理由28.定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x =3+a c ,y =3+b d ,那么称点T 是点A 和B 的融合点.例如:M (﹣1,8),N (4,﹣2),则点T (1,2)是点M 和N 的融合点.如图,已知点D (3,0),点E 是直线y =x +2上任意一点,点T (x ,y )是点D 和E 的融合点.(1)若点E 的纵坐标是6,则点T 的坐标为 ;(2)求点T (x ,y )的纵坐标y 与横坐标x 的函数关系式:(3)若直线ET 交x 轴于点H ,当△DTH 为直角三角形时,求点E 的坐标.29.如图已知ABC 中,,8B C AB AC ∠=∠==厘米,6BC =厘来,点D 为AB 的中点.如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动,设运动时间为t (秒).(1)用含t 的代数式表示线段PC 的长度;(2)若点,P Q 的运动速度相等,经过1秒后,BPD △与CQP 是否全等,请说明理由; (3)若点,P Q 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP 全等?(4)若点Q 以(3)中的运动速度从点C 出发,点v 以原来的运动速度从点B 同时出发,都顺时针沿三边运动,求经过多长时间,点P 与点Q 第一次在ABC 的哪条边上相遇?30.已知,在平面直角坐标系中,(42,0)A ,(0,42)B ,C 为AB 的中点,P 是线段AB 上一动点,D 是线段OA 上一点,且PO PD =,DE AB ⊥于E .(1)求OAB ∠的度数;(2)当点P 运动时,PE 的值是否变化?若变化,说明理由;若不变,请求PE 的值. (3)若45OPD ∠=︒,求点D 的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】A 、根据比值结合勾股定理的逆定理即可判断出三角形的形状;B 、根据角的比值求出各角的度数,便可判断出三角形的形状;C 、根据三角形的内角和为180度,即可计算出∠C 的值;D 、根据比值结合勾股定理的逆定理即可判断出三角形的形状.【详解】A 、因为a :b :c=3:4:5,所以设a=3x ,b=4x ,c=5x ,则(3x )2+(4x )2=(5x )2,故为直角三角形,故A 选项不符合题意;B 、因为∠A :∠B :∠C=3:4:5,所以设∠A=3x ,则∠B=4x ,∠C=5x ,故3x+4x+5x=180°,解得x=15°,3x=15×3=45°,4x=15×4=60°,5x=15×5=75°,故此三角形是锐角三角形,故B 选项符合题意;C 、因为∠A+∠B=∠C ,∠A+∠B+∠C=180°,则∠C=90°,故为直角三角形,故C 选项不符合题意;D 、因为a :b :c=1:23,所以设a=x ,b=2x ,3x ,则x 2+3x )2=(2x )2,故为直角三角形,故D 选项不符合题意,故选B.【点睛】本题考查了解直角三角形的相关知识,根据勾股定理的逆定理、三角形的内角和定理结合解方程是解题的关键.2.B解析:B【解析】【分析】延长AO交BC于D,根据垂直平分线的性质可得到AO=BO=CO,再根据等边对等角的性质得到∠OAB=∠OBA,∠OAC=∠OCA,再由三角形的外角性质可求得∠BOD=∠OAB+∠OBA,∠COD=∠OAC+∠OCA,从而不难求得∠BOC的度数.【详解】延长AO交BC于D.∵点O在AB的垂直平分线上.∴AO=BO.同理:AO=CO.∴∠OAB=∠OBA,∠OAC=∠OCA.∵∠BOD=∠OAB+∠OBA,∠COD=∠OAC+∠OCA.∴∠BOD=2∠OAB,∠COD=2∠OAC.∴∠BOC=∠BOD+∠COD=2∠OAB+2∠OAC=2(∠OAB+∠OAC)=2∠BAC.∵∠A=50°.∴∠BOC=100°.故选:B.【点睛】此题主要考查:(1)线段垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.(2)三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.3.B解析:B【解析】【分析】根据点A的坐标找出b值,令一次函数解析式中y=0求出x值,从而找出点B的坐标,观察函数图象,找出在x轴上方的函数图象,由此即可得出结论.【详解】解:∵一次函数y=﹣2x+b的图象交y轴于点A(0,3),∴b=3,令y=﹣2x+3中y=0,则﹣2x+3=0,解得:x=32,∴点B(32,0).观察函数图象,发现:当x<32时,一次函数图象在x轴上方,∴不等式﹣2x+b>0的解集为x<32.故选:B.【点睛】本题考查了一次函数与一元一次不等式,解题的关键是找出交点B的坐标.本题属于基础题,难度不大,解决该题型题目时,根据函数图象的上下位置关系解不等式是关键.4.D解析:D【解析】【分析】因为题中没有说明已知两边哪个是底,哪个是腰,所以要分情况进行讨论.【详解】解:当三边是2cm,2cm,5cm时,不符合三角形的三边关系;当三角形的三边是5cm,5cm,2cm时,符合三角形的三边关系,此时周长是5+5+2=12cm.故选:D.【点睛】考查了等腰三角形的性质,此类题注意分情况讨论,还要看是否符合三角形的三边关系.5.C解析:C【解析】【分析】根据全等三角形的对应边相等解答即可.【详解】解:∵△ABE≌△ACF,∴AC=AB=6,∴EC=AC﹣AE=6-2=4,故选:C.【点睛】本题考查的知识点是全等三角形的性质,熟记性质内容是解此题的关键.6.C解析:C【解析】【分析】直接根据“左加右减”的原则进行解答即可.【详解】由“左加右减”的原则可知,将直线y=12x﹣1向右平移3个单位,所得直线的表达式是y=12(x﹣3)﹣1,即y=12x﹣52.故选:C.【点睛】此题主要考查一次函数的平移,熟练掌握平移规律,即可解题.7.C解析:C【解析】【分析】根据算术平方根的定义求解即可.【详解】解:2故选C.【点睛】本题主要考查了算术平方根的定义,熟练掌握概念是解题的关键.8.B解析:B【解析】【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,找出无理数的个数.【详解】无理数有2π2个.故选:B.【点睛】本题考查的是无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.9.B解析:B【解析】由题意可得线段AB平移的方式,然后根据平移的性质解答即可.【详解】解:∵A(﹣1,﹣1)平移后得到点A′的坐标为(3,1),∴线段AB先向右平移4个单位,再向上平移2个单位,∴B(1,2)平移后的对应点B′的坐标为(1+4,2+2),即(5,4).故选:B.【点睛】本题考查了平移变换的性质,一般来说,坐标系中点的平移遵循:上加下减,左减右加的规律,熟练掌握求解的方法是解题关键.10.D解析:D【解析】【分析】根据轴对称的性质分别写出点P1的坐标为、点P2的坐标、点P3的坐标、点P4的坐标,从中找出规律,根据规律解答.【详解】解:由题意得,点P1的坐标为(5,3),点P2的坐标为(3,5),点P3的坐标为(0,2),点P4的坐标为(2,0),点P5的坐标为(5,3),2020÷4=505,∴P2020的坐标为(2,0),故选:D.【点睛】本题主要考查了点的坐标、坐标与图形变化−−对称,正确找出点的坐标的变化规律是解题的关键.二、填空题11.13【解析】【分析】直接根据勾股定理进行解答即可.【详解】∵点P(-5,12),∴点P到原点的距离==13.故答案为13.本题考查的是勾股定理,熟知在任何一个直角三角形中,解析:13【解析】【分析】直接根据勾股定理进行解答即可.【详解】∵点P(-5,12),∴点P到原点的距离=13.故答案为13.【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.12.3cm.【解析】【分析】利用勾股定理列式求出AB,根据翻折变换的性质可得BC′=BC,C′D=CD,然后求出AC′,设CD=x,表示出C′D、AD,然后利用勾股定理列方程求解即可.【详解】解析:3cm.【解析】【分析】利用勾股定理列式求出AB,根据翻折变换的性质可得BC′=BC,C′D=CD,然后求出AC′,设CD=x,表示出C′D、AD,然后利用勾股定理列方程求解即可.【详解】解:∵∠C=90°,BC=6cm,AC=8cm,∴AB10cm,由翻折变换的性质得,BC′=BC=6cm,C′D=CD,∴AC′=AB﹣BC′=10﹣6=4cm,设CD=x,则C′D=x,AD=8﹣x,在Rt△AC′D中,由勾股定理得,AC′2+C′D2=AD2,即42+x2=(8﹣x)2,解得x=3,即CD=3cm.故答案为:3cm.【点睛】本题考查了翻折变换的性质,勾股定理,此类题目熟记性质并利用勾股定理列出方程是解题的关键.13.m≥-8 且m≠-6【解析】【分析】首先求出关于x的方程的解,然后根据解不小于1列出不等式,即可求出. 【详解】解:解关于x的方程得x=m+9因为的方程的解不小于,且x≠3所以m+解析:m≥-8 且m≠-6【解析】【分析】首先求出关于x的方程233x mx+=-的解,然后根据解不小于1列出不等式,即可求出.【详解】解:解关于x的方程233x mx+=-得x=m+9因为x的方程233x mx+=-的解不小于1,且x≠3所以m+9≥1 且m+9≠3解得m≥-8 且m≠-6 .故答案为:m≥-8 且m≠-6【点睛】此题主要考查了分式方程的解,是一个方程与不等式的综合题目,重点注意分式方程存在的意义分母不为零.14.【解析】【分析】根据线段垂直平分线的性质可得AE=BE,AG=GC,据此计算即可.【详解】解:∵ED,GF分别是AB,AC的垂直平分线,∴AE=BE,AG=GC,∴△AEG的周长为AE解析:【解析】【分析】根据线段垂直平分线的性质可得AE=BE ,AG=GC ,据此计算即可.【详解】解:∵ED ,GF 分别是AB ,AC 的垂直平分线,∴AE=BE ,AG=GC ,∴△AEG 的周长为AE+AG+EG=BE+CG+EG=BC=5.故答案是:5.【点睛】此题主要考查线段的垂直平分线的性质,掌握性质是解题关键.线段的垂直平分线上的点到线段的两个端点的距离相等.15.【解析】试题分析:由点P 在第二象限内,可知横坐标为负,纵坐标为正,又因为点P 到x 轴的距离是4,到y 轴的距离是3,可知横坐标为-3,纵坐标为4,所以点P 的坐标为(-3,4).考点:象限内点的坐标解析:()3,4-【解析】试题分析:由点P 在第二象限内,可知横坐标为负,纵坐标为正,又因为点P 到x 轴的距离是4,到y 轴的距离是3,可知横坐标为-3,纵坐标为4,所以点P 的坐标为(-3,4). 考点:象限内点的坐标特征.16.22【解析】【分析】【详解】解:用平的场次除以所占的百分比求出全年比赛场次:10÷25%=40(场), ∴胜场:40×(1﹣20%﹣25%)=40×55%=22(场).故答案为:22.【解析:22【解析】【分析】【详解】解:用平的场次除以所占的百分比求出全年比赛场次:10÷25%=40(场),∴胜场:40×(1﹣20%﹣25%)=40×55%=22(场).故答案为:22.【点睛】本题考查1.条形统计图;2.扇形统计图;3.频数、频率和总量的关系.17.【解析】试题解析:∵()2=3,∴3的平方根是.故答案为.解析:【解析】试题解析:∵(2=3,∴3的平方根是故答案为18.4【解析】【分析】根据算术平方根的概念去解即可.算术平方根的定义:一个非负数的正的平方根,即为这个数的算术平方根,由此即可求出结果.【详解】解:原式==4.故答案为4.【点睛】此题主解析:4【解析】【分析】根据算术平方根的概念去解即可.算术平方根的定义:一个非负数的正的平方根,即为这个数的算术平方根,由此即可求出结果.【详解】解:原式.故答案为4.【点睛】此题主要考查了算术平方根的定义,算术平方根的概念易与平方根的概念混淆而导致错误.19.68°【解析】【分析】由在△ABC中,AC=AD=BD,∠B=28°,根据等腰三角形的性质,即可求得∠ADC 的度数,接着求得∠C的度数,可得结论.【详解】解:∵AD=BD,∴∠BAD=∠解析:68°【解析】【分析】由在△ABC中,AC=AD=BD,∠B=28°,根据等腰三角形的性质,即可求得∠ADC的度数,接着求得∠C的度数,可得结论.【详解】解:∵AD=BD,∴∠BAD=∠B=28°,∴∠ADC=∠B+∠BAD=28°+28°=56°,∵AD=AC,∴∠C=∠ADC=56°,∴∠CAD=180°-∠ADC-∠C=180°-56°-56°=68°,故答案为:68°.【点睛】此题考查了等腰三角形的性质与三角形外角的性质.此题难度不大,注意掌握数形结合思想的应用.20.60°【解析】【分析】根据等腰三角形三线合一的性质得:AD平分∠BAC,由此根据角平分线的定义得出结论.【详解】如图,∵AB=AC,AD⊥BC,∴AD平分∠BAC,∴∠BAD=∠BA解析:60°【解析】【分析】根据等腰三角形三线合一的性质得:AD平分∠BAC,由此根据角平分线的定义得出结论.【详解】如图,∵AB=AC,AD⊥BC,∴AD平分∠BAC,∴∠BAD=12∠BAC,∵∠BAC=120°,∴∠BAD=12×120°=60°, 故答案为:60°.【点睛】 本题考查的知识点是等腰三角形的性质,解题关键是熟记等腰三角形三线合一的性质.三、解答题21.(1)DE ,AE ;(2)①见解析;②()3,1,()1,3-【解析】【分析】(1)根据全等三角形的性质即可得到结论;(2)①作DM ⊥AH 于M ,EN ⊥AH 于N ,根据余角的性质得到∠B=∠1,根据全等三角形的性质得到AH=DM ,同理AH=EN ,求得EN=DM ,由全等三角形的性质得到DG=EG ,于是得到点G 是DE 的中点;②过A 作AM ⊥y 轴,过B 作BN ⊥x 轴于N ,AM 与BN 相交于M ,根据余角的性质得到∠OBN=∠BAM ,根据全等三角形的性质得到AM=BN ,ON=BM ,设AM=x ,则BN=AM=x ,从而得到结论.【详解】解:(1)AC=DE ,BC=AE ;故答案为:DE ,AE(2)①如图,作DM AF ⊥于M ,EN AF ⊥于N ,∵BC AF ⊥,∴90BFA AMD ∠=∠=︒,∵90BAD ∠=︒,∴12190B ∠+∠=∠+∠=︒,∴1B ∠=∠,在ABF ∆与DAM ∆中,BFA AMD ∠=∠,2B ∠=∠,AB DA =,∴ABF DAM ∆∆≌(AAS ),∴AF DM =,同理AF EN =,∴EN DM =,∵DM AF ⊥,EN AF ⊥,∴90GMD GNE ∠=∠=︒,在DMG ∆与ENG ∆中,DMG ENG ∠=∠,MGD NGE ∠=∠,DM EN =, ∴DMG ENG ∆=(AAS ),∴DG EG =,∴点G 是DE 的中点;②如图,过A作AM⊥y轴,过B作BN⊥x轴于N,AM与BN相交于M,∴∠M=90°,∵∠OBA=90°,∴∠ABM+∠OBN=90°,∵∠ABM+∠BAM=90°,∴∠OBN=∠BAM,在△OBN与△BAM中,M ONBOBN BAM OB AB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△OBN≌△BAM(AAS),∴AM=BN,ON=BM,设AM=x,则BN=AM=x,∴ON= x+2,∴MB+NB=x+x+2=MN=4,∴x=1,x+2=3,∴点B的坐标(3,1);如图同理可得,点B 的坐标(-1,3),综上所述,点B 的坐标为()3,1,()1,3-【点睛】本题考查了全等三角形的判定和性质,垂直的定义,余角的性质,正确的作出辅助线是解题的关键.22.(1)3;(2)3x =或1x =-.【解析】【分析】(1)根据实数的运算法则将每一项进行化简然后计算求解即可.(2)根据一元二次方程的解法步骤,将12移到等号右边,然后进行开平方运算求出方程的解即可.【详解】解:(1)0451)原式21=+3=(2)解方程:23(1)120x --=2(1)4x -=12x -=±3x =或1x =-【点睛】本题考查了实数的运算和一元二次方程的解法,解决本题的关键是熟练掌握实数的运算法则,掌握一元二次方程的解法步骤,在选择解法时要注意灵活选择合适的方法.23.(1)±4;(2)5【解析】【分析】(1)分别求出一次函数y=2x+b 与坐标轴的交点,然后根据它的图象与坐标轴所围成的图象的面积等于4列出方程即可求出b 的值;(2)由题意可知:三条直线交于一点,所以可先求出一次函数y=-2x+1与y=x+4的交点坐标,然后代入y=2x+b 求出b 的值.【详解】解:(1)令x=0代入y=2x+b ,∴y=b ,令y=0代入y=2x+b ,∴x=-2b , ∵y=2x+b 的图象与坐标轴所围成的图象的面积等于4,∴12×|b|×|-2b |=4, ∴b 2=16,∴b=±4;(2)联立214y x y x =-+⎧⎨=+⎩, 解得:13x y =-⎧⎨=⎩, 把(-1,3)代入y=2x+b ,∴3=-2+b ,∴b=5,【点睛】本题考查了一次函数与坐标轴的交点,图形与坐标的性质,待定系数求一次函数的解析式,解题的关键是根据条件求出b 的值,本题属于基础题型.24.(1)如图见解析;(2)如图见解析,C'的坐标为(﹣5,5);(3)△ABC 是直角三角形.【解析】试题分析:(1)根据A B 、两点的坐标建立平面直角坐标系即可;(2)作出各点关于y 轴的对称点,顺次连接即可;(3)根据勾股定理的逆定理判断出ABC 的形状即可.试题解析:(1)如图所示:(2)如图所示:'''A B C 即为所求:C '的坐标为()55-,;(3)2221454162091625AB AC BC =+==+==+=,,,∴222AB AC BC +=,∴ABC 是直角三角形.点睛:一个三角形两条边的平方和等于第三条边的平方,那么这个三角形是直角三角形. 25.32x =-【解析】【分析】分式方程两边同乘3(x+1),解出x 的解,再检验解是否满足.【详解】解:方程两边都乘()31x +,得:()3231x x x -=+, 解得:32x =-, 经检验32x =-是方程的解, ∴原方程的解为32x =-. 【点睛】本题考查的知识点是分式方程的求解,解题关键是解出的解要进行检验.四、压轴题26.(1)①证明见解析;②DE =14;(2)①8t -10;②t =2;③t =10,211【解析】【分析】(1)①先证明∠DAC =∠ECB ,由AAS 即可得出△ADC ≌△CEB ;②由全等三角形的性质得出AD =CE =8,CD =BE =6,即可得出DE =CD +CE =14; (2)①当点N 在线段CA 上时,根据CN =CN−BC 即可得出答案;②点M 与点N 重合时,CM =CN ,即3t =8t−10,解得t =2即可;③分两种情况:当点N 在线段BC 上时,△PCM ≌△QNC ,则CM =CN ,得3t =10−8t ,解得t =1011;当点N 在线段CA 上时,△PCM ≌△QCN ,则3t =8t−10,解得t =2;即可得出答案.【详解】(1)①证明:∵AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°,∵∠ACB =90°,∴∠DAC +∠DCA =∠DCA +∠BCE =90°,∴∠DAC =∠ECB ,在△ADC和△CEB中ADC CEBDAC ECBAC CB∠∠∠∠⎧⎪⎨⎪⎩===,∴△ADC≌△CEB(AAS);②由①得:△ADC≌△CEB,∴AD=CE=8,CD=BE=6,∴DE=CD+CE=6+8=14;(2)解:①当点N在线段CA上时,如图3所示:CN=CN−BC=8t−10;②点M与点N重合时,CM=CN,即3t=8t−10,解得:t=2,∴当t为2秒时,点M与点N重合;③分两种情况:当点N在线段BC上时,△PCM≌△QNC,∴CM=CN,∴3t=10−8t,解得:t=1011;当点N在线段CA上时,△PCM≌△QCN,点M与N重合,CM=CN,则3t=8t−10,解得:t=2;综上所述,当△PCM与△QCN全等时,则t等于1011s或2s,故答案为:1011s或2s.【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的性质、直角三角形的性质、分类讨论等知识;本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键.27.(1)A(-4,0) ;B(0,4);C(2,0);(2)①点E的位置见解析,E(43-,0);②D点的坐标为(-1,3)或(45,125) 【解析】【分析】 (1)先利用一次函数图象上点的坐标特点求得点A 、B 的坐标;然后把B 点坐标代入y=−2x +b 求出b 的值,确定此函数解析式,然后再求C 点坐标;(2)①根据轴对称—最短路径问题画出点E 的位置,由待定系数法确定直线DB 1的解析式为y=−3x−4,易得点E 的坐标;②分两种情况:当点D 在AB 上时,当点D 在BC 上时.当点D 在AB 上时,由等腰直角三角形的性质求得D 点的坐标为(−1,3);当点D 在BC 上时,设AD 交y 轴于点F ,证△AOF 与△BOC 全等,得OF=2,点F 的坐标为(0,2),求得直线AD 的解析式为122y x =+,与y=−2x +4组成方程组,求得交点D 的坐标为(45,125). 【详解】 (1)在y=x +4中,令x =0,得y=4,令y =0,得x=-4,∴A(-4,0) ,B(0,4)把B(0,4)代入y=-2x+b ,得b =4,∴直线BC 为:y=-2x+4在y=-2x +4中,令y =0,得x=2,∴C 点的坐标为(2,0);(2)①如图∵点D 是AB 的中点∴D (-2,2)点B 关于x 轴的对称点B 1的坐标为(0,-4),设直线DB 1的解析式为y kx b =+,把D (-2,2),B 1(0,-4)代入,得224k b b -+=⎧⎨=-⎩, 解得k=-3,b=-4,∴该直线为:y=-3x-4,令y=0,得x=43 -,∴E点的坐标为(43-,0).②存在,D点的坐标为(-1,3)或(45,125).当点D在AB上时,∵OA=OB=4,∴∠BAC=45°,∴△ACD是以∠ADC为直角的等腰直角三角形,∴点D的横坐标为421 2,当x=-1时,y=x+4=3,∴D点的坐标为(-1,3);当点D在BC上时,如图,设AD交y轴于点F.∵∠FAO+∠AFO=∠CBO+∠BFD,∠AFO=∠BFD,∴∠FAO=∠CBO,又∵AO=BO,∠AOF=∠BOC,∴△AOF≌△BOC(ASA)∴OF=OC=2,∴点F的坐标为(0,2),设直线AD的解析式为y mx n=+,将A(-4,0)与F(0,2)代入得402m nn-+=⎧⎨=⎩,解得1,22m n==,∴122y x=+,联立12224y xy x⎧=+⎪⎨⎪=-+⎩,解得:45125xy⎧=⎪⎪⎨⎪=⎪⎩,∴D 的坐标为(45,125). 综上所述:D 点的坐标为(-1,3)或(45,125) 【点睛】本题是一次函数的综合题,难度适中,考查了利用待定系数法求一次函数的解析式、轴对称的最短路径问题、直角三角形问题,第(2)②题采用了分类讨论的思想,与三角形全等结合,解题的关键是灵活运用一次函数的图象与性质以及全等的知识.28.(1)(73,2);(2)y =x ﹣13;(3)E 的坐标为(32,72)或(6,8) 【解析】【分析】(1)把点E 的纵坐标代入直线解析式,求出横坐标,得到点E 的坐标,根据融合点的定义求求解即可;(2)设点E 的坐标为(a ,a+2),根据融合点的定义用a 表示出x 、y ,整理得到答案;(3)分∠THD=90°、∠TDH=90°、∠DTH=90°三种情况,根据融合点的定义解答.【详解】解:(1)∵点E 是直线y =x +2上一点,点E 的纵坐标是6,∴x +2=6,解得,x =4,∴点E 的坐标是(4,6),∵点T (x ,y )是点D 和E 的融合点,∴x =343+=73,y =063+=2, ∴点T 的坐标为(73,2), 故答案为:(73,2); (2)设点E 的坐标为(a ,a +2),∵点T (x ,y )是点D 和E 的融合点,∴x =33a +,y =023a ++, 解得,a =3x ﹣3,a =3y ﹣2,∴3x ﹣3=3y ﹣2,整理得,y =x ﹣13; (3)设点E 的坐标为(a ,a +2), 则点T 的坐标为(33a +,23a +),当∠THD =90°时,点E 与点T 的横坐标相同, ∴33a +=a , 解得,a =32, 此时点E 的坐标为(32,72), 当∠TDH =90°时,点T 与点D 的横坐标相同, ∴33a +=3, 解得,a =6, 此时点E 的坐标为(6,8),当∠DTH =90°时,该情况不存在,综上所述,当△DTH 为直角三角形时,点E 的坐标为(32,72)或(6,8) 【点睛】本题考查了一次函数图象上点的坐标特征、融合点的定义,解题关键是灵活运用分情况讨论思想.29.(1)6-2t ;(2)全等,理由见解析;(3)83;(4)经过24s 后,点P 与点Q 第一次在ABC 的BC 边上相遇【解析】【分析】(1)根据题意求出BP ,由PC=BC-BP ,即可求得;(2)根据时间和速度的关系分别求出两个三角形中,点运动轨迹的边长,由∠B=∠C ,利用SAS 判定BPD △和CQP 全等即可;(3)根据全等三角形的判定条件探求边之间的关系,得出BP=PC ,再根据路程=速度×时间公式,求点P 的运动时间,然后求点Q 的运动速度即得;(4)求出点P 、Q 的路程,根据三角形ABC 的三边长度,即可得出答案.【详解】(1)由题意知,BP=2t ,则PC=BC-BP=6-2t ,故答案为:6-2t ;(2)全等,理由如下:∵p Q V V =,t=1,∴BP=2=CQ ,∵AB=8cm ,点D 为AB 的中点,∴BD=4(cm ),又∵PC=BC-BP=6-2=4(cm ),在BPD △和CQP 中BD PC B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴BPD △≌CQP (SAS )故答案为:全等.(3)∵p Q V V ≠,∴BP CQ ≠,又∵BPD △≌CPQ ,∠B=∠C ,∴BP=PC=3cm ,CQ=BD=4cm ,∴点,P Q 运动时间322BP t ==(s ), ∴48332Q CQ V t===(cm/s ), 故答案为:83;(4)设经过t 秒时,P 、Q 第一次相遇,∵2/p V cm s =,8/3Q V cm s =, ∴2t+8+8=83t , 解得:t=24此时点Q 走了824643⨯=(cm ),∵ABC 的周长为:8+8+6=22(cm ),∴6422220÷=,∴20-8-8=4(cm ),经过24s 后,点P 与点Q 第一次在ABC 的BC 边上相遇,故答案为:24s ,在 BC 边上相遇.【点睛】考查了全等三角形的判定和性质,路程,速度,时间的关系,全等三角形中的动点问题,动点的追及问题,熟记三角形性质和判定,熟练掌握全等的判定依据和动点的运动规律是解题的关键,注意动点中追及问题的方向.30.(1)45°;(2)PE 的值不变,PE=4,理由见详解;(3)D(8-,0).【解析】【分析】(1)根据A,(0,B ,得△AOB 为等腰直角三角形,根据等腰直角三角形的性质,即可求出∠OAB 的度数;(2)根据等腰直角三角形的性质得到∠AOC=∠BOC=45°,OC ⊥AB ,再证明△POC ≌△DPE ,根据全等三角形的性质得到OC=PE ,即可得到答案;(3)证明△POB ≌△DPA ,得到PA=OB=,DA=PB ,进而得OD 的值,即可求出点D 的坐标.【详解】(1)A,(0,B ,∴OA=OB=∵∠AOB=90°,∴△AOB 为等腰直角三角形,∴∠OAB=45°;(2)PE 的值不变,理由如下:∵△AOB 为等腰直角三角形,C 为AB 的中点,∴∠AOC=∠BOC=45°,OC ⊥AB ,∵PO=PD ,∴∠POD=∠PDO ,∵D 是线段OA 上一点,∴点P 在线段BC 上,∵∠POD=45°+∠POC ,∠PDO=45°+∠DPE ,∴∠POC=∠DPE ,在△POC 和△DPE 中,90POC DPE OCP PED PO PD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△POC ≅△DPE(AAS),∴OC=PE ,∵OC=12AB=12××=4, ∴PE=4;(3)∵OP=PD ,∴∠POD=∠PDO=(180°−45°)÷2=67.5°,∴∠APD=∠PDO−∠A=22.5°,∠BOP=90°−∠POD=22.5°,∴∠APD=∠BOP ,在△POB 和△DPA 中,OBP PAD BOP APD OP PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△POB ≌△DPA(AAS),∴PA=OB=DA=PB,∴DA=PB=-,∴OD=OA−DA=8-,∴点D的坐标为(8,0).【点睛】本题主要考查等腰直角三角形的性质,三角形全等的判定与性质定理,图形与坐标,掌握等腰直角三角形的性质,是解题的关键.。
人教版八年级语文上册期末考试卷(附答案)

人教版八年级语文上册期末考试卷(附答案)(考试时间:120分钟;试卷满分:150分)一.(16分)阅读下面的文段,完成1~3题。
打开课本,我们看到了英勇的人民解放军横渡长江,锐不可当.;目睹.了北宋汴京街上行人摩肩接( zhǒng )的繁华景象;体会到我国科研人员面对封锁(dān )精竭虑搞科研的不易;感受到朱德对慈爱且一生劳(lù)的母亲的殷殷情怀;结识汉文帝口中(kè)尽职守的"真将军"——周亚夫;欣赏苏州园林中的"隔而未隔,界而未界"的镂.空的花墙廊子,像一幅幅的完美图画……还瞻.仰了巍峨、雄伟、庄严的人民英雄纪念碑……可以说,优秀的作品,不仅是知识的结晶,更是人类情感与思想的结晶。
这些优秀作品,激励我们前进的动力。
1.文段中加点字的读音和拼音处应填写的汉字书写不正确的一项是( )(3分)A. dāng 踵B. dǔ弹C. lóu 禄D. zhān 恪2.填入文段中画横线处的成语,最恰当的一项是( )(3分)A.别具一格B.自出心裁C.一丝不苟D.惟妙惟肖3.文中画横线句有语病,请选出修改正确的一项( )(3分)A.这些出色作品,激励我们前进的动力。
B.这些优秀作品,激起我们前进。
C.这些优异作品,鼓励我们前进的动力。
D.这些优秀作品,激发我们前进的动力。
4.互联网时代,数字阅读已经成为一种常见的阅读方式。
在活动中,小鲁从网上搜集到一些关于数字阅读的资料,下面是关于2023年中国数字阅读各年龄段用户阅读时长和阅读频率的统计图。
请阅读统计图,写出你的探究结果。
(3分)5.学校开展"书房文化"活动,作为本次活动的学生志愿者,请你根据要求完成以下任务。
(4分)在读书人的心目中,书房是不可或缺的治学休闲之所,更是读书人放牧思想的田园。
我国文人有给自己的书房命名的雅好。
梁启超变法维新,面对国家的内忧外患,临危受命,遂将自己的书斋取名"饮冰室"。
最新部编版八年级数学上册期末测试卷及答案【完美版】

最新部编版八年级数学上册期末测试卷及答案【完美版】班级: 姓名:一、选择题(本大题共10小题, 每题3分, 共30分)1. 多项式与多项式的公因式是()A. B. C. D.2.已知, , 则代数式的值是()A. 24B. ±C.D.3.下列倡导节约的图案中, 是轴对称图形的是()A. B. C. D.4.下列结论中, 矩形具有而菱形不一定具有的性质是()A. 内角和为360°B. 对角线互相平分C. 对角线相等D. 对角线互相垂直5. 已知点P(a+5, a-1)在第四象限, 且到x轴的距离为2, 则点P的坐标为()A.(4, -2) B.(-4, 2) C.(-2, 4) D.(2, -4)6. 估计的值应在()A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间7.如图, 在△ABC 中, AB=3, AC=4, BC=5, P 为边 BC 上一动点, PE⊥AB 于E, PF⊥AC于 F, M 为 EF 中点, 则 AM 的最小值为()A. 1B. 1.3C. 1.2D. 1.58.如图, 每个小正方形的边长为1, A.B.C是小正方形的顶点, 则∠ABC的度数为()A. 90°B. 60°C. 45°D. 30°9.如图, 在同一直角坐标系中, 正比例函数, , , 的图象分别为,, , , 则下列关系中正确的是()A. B.C. D.10.如图, AD, CE分别是△ABC的中线和角平分线.若AB=AC, ∠CAD=20°, 则∠ACE的度数是()A. 20°B. 35°C. 40°D. 70°二、填空题(本大题共6小题, 每小题3分, 共18分)1. 因式分解: x3﹣4x=________.2. 分解因式: =__________.3. 计算的结果是________.4. 如图, 将绕直角顶点C顺时针旋转, 得到, 连接AD, 若, 则________.5. 正方形、、、…按如图所示的方式放置.点、、、…和点、、、…分别在直线和轴上, 则点的坐标是__________. (为正整数)6. 已知∠AOB=60°, OC是∠AOB的平分线, 点D为OC上一点, 过D作直线DE⊥OA, 垂足为点E, 且直线DE交OB于点F, 如图所示. 若DE=2, 则DF=________.三、解答题(本大题共6小题, 共72分)1. 解下列方程组:(1)257320x yx y-=⎧⎨-=⎩(2)134342x yx y⎧-=⎪⎨⎪-=⎩2. 先化简, 再求值:(1)(2+a)(2-a)+a(a-5b)+3a5b3÷(-a2b)2, 其中ab=-;(2)[(x+2y)(x-2y)-(x+4y)2]÷4y, 其中x=-5, y=2.3. 已知, 求代数式的值.4. 如图, A(4, 3)是反比例函数y= 在第一象限图象上一点, 连接OA, 过A 作AB∥x轴, 截取AB=OA(B在A右侧), 连接OB, 交反比例函数y= 的图象于点P.(1)求反比例函数y=kx的表达式;(2)求点B的坐标;(3)求△OAP的面积.5. 如图, 有一个直角三角形纸片, 两直角边cm, cm, 现将直角边沿直线AD折叠, 使它落在斜边AB上, 且与AE重合, 你能求出CD的长吗?6. 为了提高产品的附加值, 某公司计划将研发生产的1200件新产品进行精加工后再投放市场. 现有甲、乙两个工厂都具备加工能力, 公司派出相关人员分别到这两个工厂了解情况, 获得如下信息:信息一: 甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;信息二: 乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.根据以上信息, 求甲、乙两个工厂每天分别能加工多少件新产品.参考答案一、选择题(本大题共10小题, 每题3分, 共30分)1、A2、C3、C4、C5、A6、B7、C8、C9、B10、B二、填空题(本大题共6小题, 每小题3分, 共18分)1.x(x+2)(x﹣2)2、()() x x3x3+-3、11 m-4、705、1 (21,2) n n--6、4.三、解答题(本大题共6小题, 共72分)1.(1);(2).2.(1)4-2ab, 5;(2)-2x-5y, 0.3. , -24、(1)反比例函数解析式为y= ;(2)点B的坐标为(9, 3);(3)△OAP的面积=5.5.CD的长为3cm.6.甲、乙两个工厂每天分别能加工40件、60件新产品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
()
A.恰当的放大镜可使5°的角度放大成8°或10°
B.人离平面镜越远,平面镜中的像越小
C.实像可以用光屏承接,虚像不可以用光屏承接
D.不论什么光,通过凸透镜后总可以会聚到一点
10.下列关于光现象的说法中,正确的是
()
A.我国古代使用的铜镜能成正立放大的实像
B.老花镜是利用凹透镜对光线的会聚作用
C.不能用望远镜直接观察太阳或其他强光源
3.明明有一支次品温度计,玻璃管的内径和刻度都很均匀,标度(最 小标度1℃)却不准确。用此温度计测量冰水混合物,示数是5℃, 放在 一标准大气压的沸水中,温度示数是95℃。据此推算(1)此温度计的 实际分度值是多少?(2)测得的温度是32℃时,实际温度是多少?
4.电视台把无线电信号传送到高空中的通信卫星上,卫星再把信号传 到地面上的其它地区,这样就实现了卫星电视传播。在调试过程中,电 视台本身了也需要接收卫星传来的信号,并和演播室用电缆传来的信号 进行比较。这时发现,卫星传来的画面上,人物动作的变化总比电缆传 来的画面上相应的动作变化发生得晚一些。 (1)解释卫星上传来的画面上动作晚一些的原因。 (2)已知通信卫星的高度大约是36000千米,无线电信号传播的速度与 光速相同,估算画面延迟的时间。
2.(13分)某个同学在做凸透镜成像的实验时,先将凸透镜正对太阳
光,在透镜的另一侧移动光屏,在距透镜10㎝时,屏幕上出现一个最小
最亮的光斑,然后开始在光具座上做有关实验:
(1)为了研究凸透镜的成像规律,先将蜡烛、
和
依次放
到光具座上,然后调节它们的高度,使它们的中心与
的中心
大致在
,这是为了使像
;
(2)此实验中用的这个凸透镜的焦距是 ㎝;
D.杯子的价格
2.将正在发声的手机.电铃或接通电源的音乐芯片悬挂在广口瓶
内,再把瓶内的空气抽出如图所示,声音逐渐变小,但始终能听到声
音。原因是: ( )
A.瓶内已被抽成真空,真空亦能传声;
B.声源发声太强,换用发声较弱的声源;
C.离实验瓶远一点,就可以听不到声音;
D.瓶内仍有少量空气,悬挂声源的固体亦能传声
8.目前有些饭店安装了热风干手器,打开它就有热风吹到手上,使手
上的水很快蒸发掉,使水快速蒸发的原因是
()
A.加快了水面附近空气的流动并ቤተ መጻሕፍቲ ባይዱ高了水的温度
B.提高了水的温度并增大了水的表面积
C.加快了水面附近空气的流动并增大了水的表面积
D.加快了水面附近空气的流动,提高了水的温度并增大了水的表面
积
9.下列说法中正确的是
2.(4分)呈球面形状的反射镜叫球面镜,用外表面做反射面的球 面镜叫凸面镜,简称凸镜。我们知道,用平行光对着平面镜照射,反射 光线也是平行光,也就是说,平面镜对光线既不起会聚作用也不起发散 作用,那么凸镜对光线有什么作用呢?小华将好几只激光手电筒捆绑在 一起,形成相互平行的光线对凸镜照射,发现平行光线经凸镜反射后形 成如图所示的图像。请回答: (1)由此你可以得出什么结论?
6.下列说法中,能证实红外线存在的是
()
A.红外线显红色
B.在红光的内侧能观察到
C.温度高的物体有红外线 D.红外线使物体发热
7.战斗机在空中加油时,已知加油机的速度是8000km/h,则在加油过
程中,战斗机飞行的路程与加油机飞行的路程之比是
()
A.等于1:1
B.大于1:1
C.小于1:1
D.无法判断
像
和
人是不能听到;同样,光人所能看到的是可见光,
除此之外,像
和
是人不能看到的。
7.在28届雅典奥运会上,我国著名运动员刘翔在110米栏的比赛中以12
秒91的成绩获得冠军,并打破奥运会记录。请你计算一下,他的平均速
度是______m/s。
8.“湖静映彩霞”和“潭清疑水浅”分别叙述了两种物理现象,前一
句说的是光的__
(2)正确的计算应当是:_______________________________。
2.亚洲最大沉管隧道—上海外环隧道于2003年6月21日通车,隧道的江
中管段长736m。记者乘坐“帕萨特”轿车从浦西入口到浦东出口只需行
驶1min,则轿车在江中管段的行驶速度为________m/s.若以________为
度为________m。若在太空中测距,则应该用____________的反射现象
来进行。
5.常用的温度计是根据____________的性质制成的;在北方寒冷的冬
天,应该用酒精温度计测气温,是因为酒精的____________较低。
6.声和光是人类赖以生存必不可少的,而人类对它的依赖和应用却是
有限的;在自然界的各种声音中,人们能听到的是可听声,除此之外,
A P B
四.实验题:(21分) 1.下面是使用温度计来测量液体温度的实验步骤:A.选择适当的温度 计,观察其测量范围及其最小分度值;B.估计被测液体的温度;C.让
玻璃泡与被测液体充分接触;D.取出温度计;E.观察温度计的示数;
F.整理实验仪器;
请在横线上将这些步骤按正确的顺序排列起来:
。
(2分)
3.“影”是我们日常生活中常见的光现象,如做光学游戏形成的“手
影”,剧院放映的电影;湖岸景色在水中形成的倒影,春游时留下美好
记忆的照片—摄影等,以下列出的“影”与物理知识对应关系不正确的
是
(
)
A.手影—光的直线传播;
B.倒影—平面镜成像;
C.电影—凸透镜成像;
D.摄影—光的反射
4.在班级进行的物理知识抢答比赛中,坐在前排座位的同学,不用回
现象;后一句则说的是光的
现象。
9.放映电影.幻灯的银幕常用粗糙的白布做成,目的在于,一是利用
,使剧院中各处的观众均能看到画面;二是白布能反射
颜色的光,使观众能看到色彩正常的画面。
10.常用的体温表是一个三棱体,其横截面如右图所示,其正面是圆弧
形,这样就可以看清体温表内极细的水银柱,以便读数。这是因为圆弧
(3)当蜡烛距凸透镜15㎝时,光屏应在透镜另一侧距透镜
移动,在某一位置上光屏上会呈现一个清晰、
,
的
像;如果蜡烛在使用的过程中不断被消耗而缩短,则在光屏上的像将随
之向
移动;
(4)某个同学在水平方向上无论怎样移动光屏,光屏上始终不会出现
烛焰的像,请你分析,发生这一现象的原因可能是:
①
。
②
。
3.取一定量的松香,加热使其熔化。温度升到60℃时,每隔2分钟记录
一次松香的温度(如表一)。将表中的数据标在图7的温度计上,并用
平滑的线把各次的温度值连接起来。(2分)
表一:松香熔化温度记录
时间min 0 2 4 6 8 10 12 14 16
温度℃ 60 68 74 78 82 85 87 88 91
4.为了探究声音产生的条件,有人建议利用以下几个实验现象:(4 分) (1)从音乐卡片上剪下音乐芯片,并让其发声,然后放入封闭的容积 为100ml的注射器内,当用力向个拉活塞时,音乐声明显减小; (2)使正在发声的音叉接触水面时,水面溅起水花; (3)吹笛子时,手指按住不同的指孔,便会发出不同的声音; (4)在吊着的大钟上固定一枝细小的笔,把钟敲响后用纸帖着笔尖迅 速拖过,可以在纸上画出一条来回弯曲的细线。
玻璃的作用相当于
,使我们看到水银柱的
像。
11.上物理课复习时,老师写了一副热学对联,上联是“杯中冰水,水
结冰冰温未变”;下联是“盘内水冰,冰化水水温不升”,对联中包含
的物理变化分别是
和
__________,反映一个共性是
。
12.右边表格是2001年10月21日起实行的厦门站旅客列车时刻表上海开
往厦门的K175次列车,全程运行1740千米,由表可知K175次列车全程运
动的时间是_______,列车全程平均速度约_______________千米/时。
(保留一位小数)
13.将一个生鸡蛋放进盛有清水的杯中如图所示,逐渐向水里加入食
盐,慢慢搅拌使其溶解。能观察到的现象是:
_____
,根据现象提出的问题:____ ___ _____ 。
三.作图题:(6分) 1.作出如图所示中潜水侦察兵看到岸上目标A的像的大致位置. 2.如图PB为一挡板,已知两条由挡板后某发光点发出的光经过镜子发 射的反射光线,请在图中找出发光点的位置。 3.作出一束激光在三棱镜内和离开三棱镜后行进的路线
头,根据说话的声音就能判断出是谁在抢答,这是因为不同人的声音具
有不同的
()
A.振幅
B.频率
C.响度
D.音色
5.小明学过平面镜成像知识后,概括了几个特点,其中错误的是
()
A.物体在平面镜里成的像与物体的大小相等
B.平面镜里物体成的像可以用白纸做的屏幕接收到
C.像与物到镜面的距离相等
D.像与物对应的连线与镜面垂直
你认为,能说明声音产生的条件的实验现象是哪一个或哪几个? 其他现象虽然不能说明声音产生的条件,但能分别说明什么问题?
五.阅读探究: (7分) 1.(3分)汽车遇到红灯就要停下来;在修马路时,到了晚上修理
点都亮起红灯;还有电影院的安全门上、高塔上等也都用红灯作标 识……
为什么要点红灯呢?是不是因为红光鲜艳,非常好看呢? 我们知道,白光里面包含着红、橙、黄、绿、青、蓝、紫七种颜色 的光,不同颜色的光,波长也不一样。其中,红光的波长最长,它能穿 过雨点、尘埃、雾珠等细小的微粒;紫光波长最短,它的穿透本领也比 较小。当光照到细小的微粒上时,就要发生散射的现象,即偏离原来的 方向而分散开来。不同波长的光,散射情况也不相同。波长较短的光, 像紫光、蓝光等都很不容易被散射,能透过微粒的光线就多。 所以,在有迷雾的天气,看到的太阳是红彤彤的。隔着毛玻璃看灯 光,灯光也特别红。 正是因为红光不易被散射,具有很强的穿透本领,所以,红光被广 泛的用来表示危险的信号。就连自行车尾灯也是红色的,使后面的人容 易看见前方有车行驶,不致发生交通事故。 请你回答: ⑴判断:自行车的尾灯是红色的,是因为红光鲜艳,非常好看。( ) ⑵请你解释为什么常用红光来表示危险信号。
