基本算法语句练习题
基本算法练习题

基本算法练习题算法,作为计算机科学的重要组成部分,是解决问题的实用方法和步骤。
它是计算机能够自主运作的核心。
基本算法是算法学习的第一步,通过解决一系列的练习题,我们能够深入理解算法的原理和应用。
本文将介绍几个基本算法练习题,并给出相应的解答。
1. 排序算法排序是最基本的算法之一,它将一组元素按照特定规则进行排列。
常见的排序算法包括冒泡排序、插入排序、选择排序、快速排序等。
下面以冒泡排序为例:```pythondef bubble_sort(arr):n = len(arr)for i in range(n-1):for j in range(n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]return arr# 测试代码arr = [4, 2, 6, 8, 3, 1, 5, 7]print(bubble_sort(arr))```2. 查找算法查找算法是在给定的数据集合中寻找特定元素的算法。
常见的查找算法包括线性查找、二分查找、哈希查找等。
下面以二分查找为例:```pythondef binary_search(arr, target):left = 0right = len(arr)-1while left <= right:mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] < target:left = mid + 1else:right = mid - 1return -1# 测试代码arr = [1, 2, 3, 4, 5, 6, 7, 8]target = 6print(binary_search(arr, target))```3. 递归算法递归是一种重要的算法设计技巧,它通过调用自身来解决问题。
递归算法可以更简洁地解决一些复杂的问题。
(推荐)高一数学必修三第一单元知识点及练习题

高一数学必修三第一章算法初步1.1 算法与程序框图1.2 基本算法语句1.3 中国古代数学中的算法案例1.1.1算法的概念1、算法概念:在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.2. 算法的特点:(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.(3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题.(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.(5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.1.1.2程序框图1、程序框图基本概念:(一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下: 1、使用标准的图形符号。
2、框图一般按从上到下、从左到右的方向画。
3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。
判断框具有超过一个退出点的唯一符号。
4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。
5、在图形符号内描述的语言要非常简练清楚。
(三)、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
1、顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。
C语言初学者练习题目10条

C语言初学者练习题目10条1. 关于C语言初学者练习题目10条在学习编程语言的过程中,练习题目是一个重要的环节,可以帮助初学者巩固基本知识和提升解决问题的能力。
本文将介绍10个适合C语言初学者的练习题目,并分析每个题目的解题思路。
题目一:输出Hello, World!这是C语言中最基础的练习题目,通过编写一个简单的程序来输出"Hello, World!",帮助初学者熟悉C语言的基本语法和编译运行过程。
题目二:计算两个整数之和编写一个程序,接收用户输入的两个整数,并输出它们的和。
这个练习可以让初学者熟悉C语言的基本输入输出操作和基本的数学运算。
题目三:判断一个数是否为素数编写一个程序,接收用户输入的一个整数,并判断该数是否为素数。
这个练习可以让初学者熟悉使用循环和条件语句进行判断,并学习如何优化算法以提高判断效率。
题目四:计算数组元素的平均值编写一个程序,接收用户输入的一个整型数组,并计算出数组元素的平均值。
这个练习可以让初学者熟悉数组的基本使用和循环的结合运用。
题目五:查找数组中的最大值和最小值编写一个程序,接收用户输入的一个整型数组,并找出数组中的最大值和最小值。
这个练习可以让初学者学习如何定义和使用函数,并加深对数组的理解。
题目六:实现简单的字符串翻转编写一个程序,接收用户输入的一个字符串,并将其翻转输出。
这个练习可以让初学者学习如何处理字符串类型的数据,并锻炼对数组和循环的综合运用能力。
题目七:实现简单的冒泡排序编写一个程序,接收用户输入的一个整型数组,并使用冒泡排序算法对数组进行排序。
这个练习可以让初学者深入理解冒泡排序算法的原理,并学习如何进行数组的元素交换。
题目八:实现简单的查找算法编写一个程序,接收用户输入的一个整型数组和一个目标值,在数组中查找目标值并输出其下标。
这个练习可以让初学者学习不同查找算法的实现原理,并熟悉如何使用循环进行遍历操作。
题目九:实现简单的递归算法编写一个程序,使用递归算法计算斐波那契数列的第n项值,并将其输出。
高中数学 第二章 算法初步 3.2 循环语句练习(含解析)北师大版必修3-北师大版高中必修3数学试题

3.2 循环语句填一填1.For语句(1)格式For ________________ To ________循环体Next(2)适用X围For语句适用于________________的循环结构.2.Do Loop语句(1)格式(2)适用X围Do Loop语句适用于________________的循环结构.判一判1.循环语句与算法框图中的循环结构相对应.( )2.For语句与Do Loop语句都是循环语句.( )3.所有的循环结构框图都可以用For语句与Do Loop语句描述.( )4.For语句不能用来描述循环次数不确定的循环结构.( )5.Until语句中先进行条件判断,再执行循环体;While语句中先执行循环体,再进行条件判断.( )6.循环语句中一定有条件语句,条件语句中一定有循环语句.( )7.直到型循环语句和当型循环语句执行循环体的次数都可能是零.( )8想一想1.提示:循环语句中一定有条件语句,条件语句是循环语句的一部分,离开条件语句,循环语句无法循环,但条件语句可以脱离循环语句单独存在.可以不依赖循环语句独立地解决问题.2.直到型循环语句的设计策略是什么?提示:(1)直到型循环语句中先执行一次循环体,再判断条件是否满足,以决定继续循环还是退出循环.(2)在循环体内要有控制条件的改变,否则会陷入死循环.(3)控制循环次数的变量要综合考虑初始化时和Loop Until后两处,若初始值为1,则循环体中控制循环次数的变量要累加,若初始值为循环的次数,则循环体中控制循环次数的变量要递减.3.当型循环语句的设计策略是什么?提示:(1)当型循环也叫“前测试循环”,也就是先判断后执行.(2)While语句中的条件是指循环体的条件,满足此条件时执行循环体,不满足时,则执行循环结构后面的语句.4.用循环语句编写程序的注意事项有哪些?提示:(1)解决具体问题构造循环语句的算法时,要尽可能少地引入循环变量,否则较多的变量会使设计程序比较繁杂,并且较多的变量会使计算机占用大量的系统资源、导致系统缓慢.(2)While循环与Until循环一般可以相互转化.(3)恰当地设置判断条件,以控制循环的次数.思考感悟练一练1.下列关于WHILE语句的叙述中,不正确的是( )A.当给定的条件成立(真)时,反复执行循环体,直到条件不成立(假)时,才停止循环B.WHILE语句有时也称为“前测试型”循环C.WHILE语句结构也叫直到型循环D.任何一种需要重复处理的问题都可以用WHILE语句来实现2.下面的程序,执行完毕后a的值为( )A.99 B.100C.101 D.1023.在上面的程序中,输出的结果应为( )A.7 B.8C.3,4,5,6,7 D.4,5,6,7,84.下列程序的功能是( )S=0For i=1 To 5S=S+1/(2]Next 输出S .A .计算S =12×1+12×2+12×3+12×4+12×5 B .计算S =12×1+12×3+12×5C .计算S =12×5D .无法确定5.下列程序中循环语句的循环终止条件是( ) m =1 Dom =m +3Loop While m <10 输出m .A .m =10B .m <10C .m >10D .m ≥10知识点一 For 语句的应用1.下列语句运行的结果是( ) S =0For i =-1 To 11 S =i *i Next 输出S .A .-1B .11C .100D .1212.画出求1+12+13+…+11 000的值的算法框图,并用For 语句描述该算法.知识点二 Do Loop 语句的应用3.当x =2时,下面程序运行后输出的结果是( )A .3B .7C .15D .174.下面是求满足1+3+5+…+n >2 020的最小自然数n 的程序框图,试把它设计成程序.综合知识循环语句5.写出下列框图所对应的算法语句.6.画出计算12+32+52+…+9992的程序框图,并写出程序.基础达标1)①输入每个同学的数学成绩,求全班60名同学的平均分;②求从1开始的连续100个整数的和;③求函数f(x)=|x|的函数值;④输入100个数,从中找出最大的数.A.1个 B.2个C.3个 D.4个2.For语句中,循环变量的初始值为2 002,终值为2 016,循环变量的值每次增加1,则循环体执行的次数为( )A.12 B.13C.14 D.153.以下算法运行的结果为( )t=2For i=2 To 8 Step 2t=t*iNext输出t.A.96 B.192C.394 D.7684.下列程序中的For语句终止循环时,S等于( )S=0For M=1 To 13 Step 3S=S+MNext输出S.A.1 B.5C.10 D.355.若i的初始值为0,当执行完Do i=i+1 Loop While i≤10后i的值变为( ) A.9 B.10C.11 D.126.下面算法语句的功能是( )S=0For i=1 To 100S=S+iNext输出S.A.求1×2×3×…×100的值B.求1×3×5×…×99的值C.求1+2+3+…+100的值D.求1+3+5+…+99的值A.程序不同,结果不同B.程序不同,结果相同C.程序相同,结果不同 D.程序相同,结果相同8.执行下面的程序,输出结果为________.S=0i=1DoS =S +iLoop While i <5 输出S .9.给出下列For 语句: S =0For i =1 To 10 S =S +i Next循环变量是________,循环变量的初始值是________,循环变量的终值是________,循环体是________.10.如图,把求11×4+12×5+13×6+…+150×53的值的程序补充完整,则(1)________;(2)________.11.分别写出下列算法语句A 和B 运行的结果:A :________;B :________.A : s =0 i =1Do s =s +i i =i +1Loop While s <20输出i .B : s =0 i =1Do i =i +1 s =s +iLoop While s <20输出i .12.执行下面的算法语句,输出的结果是________. A =1 B =1 DoA =A +B B =A +BLoop While B <15 C =A +B 输出C .13.以下给出的是用循环语句编写的一个算法,写出该算法的功能,并画出相应的算法框图.I =1 Doa =I Mod 2If a =0 ThenEnd IfI=I+1Loop While I<=10014.给出某班50名学生的数学测试成绩,60分及60分以上的为及格,要求统计及格人数、及格人数的平均分、全班同学的平均分,画出框图,并用语句描述该算法.能力提升15.根据如图所示的算法框图写出相应的程序.16.用分期付款的方式购买价格为1 150元的冰箱,如果购买时先付150元,以后每月付50元,加上欠款的利息,若一个月后付第一个月的分期付款,月利率为1%,那么购买冰箱的钱全部付清后,实际共付出多少元?画出程序框图,写出程序.3.2 循环语句一测基础过关填一填1.(1)循环变量=初始值终值(2)预先知道循环次数2.(1)条件为真(2)预先不知道循环次数判一判1.√ 2.√ 3.× 4.√ 5.× 6.×7.×8.×练一练1.C 2.B 3.D 4.A 5.D二测考点落实1.解析:S=11×11=121.答案:D2.解析:算法框图为:用For语句描述算法为:S=0For i=1 To 1 000S=S+1/iNext输出S.3.解析:0×2+1=1,1×2+1=3,3×2+1=7,7×2+1=15,i=5>4,跳出循环,故输出s的值为15.答案:C4.解析:程序如下:5.解析:用算法语句描述为:S=1For i=3 To 99 Step 2S=S*iNext输出S.6.解析:由题意知各项指数相同,底数相差2,可以借助于循环语句设计算法.①程序框图:②程序为:三测学业达标1.解析:①②④中涉及数目较多,算法应设计为循环结构,故可用循环语句来描述;函数f(x)=|x|可看作是分段函数,而求分段函数的函数值应选用条件语句,故用不到循环语句.答案:C2.解析:一共循环了(2 016-2 002)+1=15次.答案:D3.解析:第一次循环t=2×2=4,第二次循环t=4×4=16,第三次循环t=16×6=96,第四次循环t=96×8=768.答案:D4.解析:S=1+4+7+10+13=35.答案:D5.解析:由Do Loop语句的形式和执行条件易得循环结束后,i=11.答案:C6.解析:由“S=S+i”可知该算法解决的是累加问题;由循环变量i的增量为1,从1到100可知,求的是1+2+3+…+100的值.答案:C7.解析:S甲=1+2+3+…+1 000,S乙=1 000+999+…+2+1,即甲、乙的程序不同,结果相同.答案:B8.解析:输出结果为S=2+3+4+5=14.答案:149.解析:循环变量是i,循环变量的初始值是1,循环变量的终值是10,循环体是S=S+i.答案:i 1 10 S=S+i10.答案:(1)S=S+1/i*(i+3) (2)i<=5011.解析:A:s=21,i=7时终止循环;B:i=6,s=20时终止循环.答案:7 612.解析:如果没有循环条件的限制,程序中的循环结构连同初始值,将依次给A,B 赋值为1、1,2、3,5、8,13、21,…,其中第1,3,5,…个数为A的值,第2,4,6,…个数为B的值;可见,当B=21时,循环结束,此时A=13,所以C=A+B=34.答案:3413.解析:该算法的功能是输出1至100的正整数中的所有偶数.算法框图如图所示.14.解析:框图如图:用语句描述为:M=0i=1S=0T=0Do输入x;If x>=60 ThenS=S+xM=M+1End IfT=T+xi=i+1Loop While i<=50P=S/MT=T/50输出M,P,T.15.解析:由算法框图可知,算法的功能是求12+32+52+…+9992的值.法一:用Do Loop语句描述如下:S=0i=1DoS=S+i2i=i+2Loop While i<=999输出S.法二:用For语句描述如下:S=0For i=1 To 999 Step 2S=S+i2Next输出S .16.解析:购买时付款150元,余款1 000元分20次付清,每次付款数组成一系列数. a 1=50+(1 150-150)×1%=60,a 2=50+(1 150-150-50)×1%=59.5,…,a n =50+[1 150-150-(n -1)×50]×1%=60-12(n -1)(n =1,2,…,20). 所以a 20=60-12×19=50.5. 总和S =150+60+59.5+…+50.5=1 255(元).程序框图如图.程序:a =150m =60S =0S =S +ai =1DoS =S +mm =m -0.5i =i +1Loop While i <=20输出S .。
算法初步知识点及习题

算法算法是高中数学课程中的新增内容,是中国数学课程内容的一个新特色.“算法”过程是指机械式地按照某种确定的步骤行事,通过一系列小的简单计算操作完成复杂计算的过程.算法的学习内容大致可分为三个步骤:用自然语言描述算法;精确刻画算法(程序框图);计算机实现执行算法(程序语言的描述过程).算法思想贯穿高中数学课程的相关部分.【知识要点】1.算法:算法可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列能够解决一类问题.现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤.2.程序框图程序框图:用一些通用的符号构成一张图来表示算法,这种图称为程序框图(程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形).用框图表示算法步骤的一些常用的图形符号:程序框名称功能终端框(起止框) 表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框) 赋值、计算判断框判断某一条件是否成立,成立时在出口处标明“是”,不成立时标明“否”↓→流程线(指向线) 指引流程图的方向连接点连接另一页或另一部分的框图程序框图的三种基本逻辑结构:顺序结构:描述的是最简单的算法结构,语句与语句之间、框与框之间按从上到下的顺序进行(如图9-1).图9-1条件分支结构:依据指定条件选择执行不同指令的控制结构(如图9-2).图9-2循环结构:根据指定条件决定是否重复执行一条或多条指令的控制结构(如图9-3).图9-33.几种基本算法语句任何一个程序设计语言中,都包含五种基本的算法语句,即输入语句、输出语句、赋值语句、条件语句、循环语句.输入语句和输出语句分别用来实现算法的输入信息、输出结果的功能;赋值语句是用来表明赋给某一个变量一个具体的确定值的语句;条件语句是处理条件分支逻辑结构的算法语句;循环语句是用来处理算法中的循环结构的语句.4.中国古代算法案例:更相减损之术、辗转相除法:求两个正数的最大公因数的方法.辗转相除法算法步骤:第一步:用两数中较大数除以较小数,求商和余数.第二步:用除数除以余数.第三步:重复第二步,直到余数为0.第四步,得出两数的最大公约数,即余数0之前的余数.更相减损术算法步骤:第一步:用较大数减去较小数,得到差.第二步:比较减数与差的大小,再用较大数减去较小数.第三步:重复第二步,直到差与减数相等为止.第四步:相等数即为最大公约数.割圆术:用正多边形的面积逐渐逼近圆面积的算法求圆周率π. 秦九韶算法:求一元多项式的值的一种方法,递推关系为),,2,1(10n k a x v v a v k n k kn=⎩⎨⎧+==-- 【复习要求】1.了解算法的含义,了解算法的思想.2.理解程序框图的三种基本逻辑结构:顺序结构、条件分支结构、循环结构.3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.【例题分析】例1 如图(图9-4)所示,将一系列指令用框图的形式表示,箭头指向下一步的操作.请按照框图回答问题:图9-4(1)这个框图表示了怎样的算法?(2)输出的数是多少?【分析】由框图中的文字及图形符号表示的操作内容可知:此算法是“求1到50的和”,由此可以算出输出的数.解:(1)此框图表示的算法为:求1+2+3+…+50的和;(2)易知所求和为1275.【评析】程序框图主要包括三部分:表示相应操作的框,带箭头的流程线和框外必要的说明.读框图时要从这三个方面研究,流程线反映了命令执行的先后顺序,主要看箭头方向,框及内外的文字说明表明了操作内容.常用这种方式考察对算法的理解和应用.例2 (1)如图9-5所示的是一个算法的程序框图,已知a1=3,输出的结果为7,则a2的值为______.图9-5(2)如图9-6所示的是某个函数求值的程序框图,则满足该程序的函数解析式为_____.图9-6(3)如图9-7所示的是求某个数列和的程序框图,此程序输出的结果为_____.图9-7【分析】这三个小题的重点在于读懂框图.(1)只含有顺序结构,(2)含有条件分支结构,表明函数的定义域为R ,当x <0时,遵从解析式f (x )=3x -1,否则(即当x ≥0时),遵从解析式f (x )=2-5x ;(3)中有两个循环变量S 、I ,S 是累加变量,I 是计数变量;另外还要判断I 的奇偶性,以此决定是加还是减.解:(1)112=a ;(2)⎩⎨⎧≥-<-=)0(52)0(13)(x x x x x f ;(3)S =12-22+32-42+…+992-1002=-5050.【评析】题(1),只含有顺序结构,所表示的算法比较简单,只需按照框图箭头方向依次读出即可.题(2)含有条件分支结构,这是一个与分段函数有关的算法,框图中含有判断框.读包含有判断框的框图时,要特别重视判断框内的条件和框外的文字说明,对应的下一步操作会依条件不同而改变.题(3)含有循环结构,当解决一些有规律的科学计算问题,尤其是累加和累乘时,往往可以利用循环结构来实现算法.循环结构有两种,读包含有循环结构的框图时,除关注判断框内外的说明外,一般要从开始依顺序做几次循环,观察变量的变化规律来帮助读懂算法的含义.例3 (1)已知平面上的一点P 0(x 0,y 0)和直线l :Ax +By +C =0,求点P 0到直线l 的距离d ,并画出程序框图.(2)用条件分支结构写“已知三个数a 、b 、c ,找出其中最大数”的算法及框图.(3)写出求n131211++++的和的算法,画出程序框图,并写出相应程序(选做). 【分析】正确分析“算理”,才能选择恰当的算法结构,有条理的表达算法.(1)在已知点到直线距离公式的前提下,适合用顺序结构表示;(2)涉及比大小,必须用到条件分支结构;(3)中分母有规律的递增,可以引入累加变量S 和计数变量i ,且S =S +1/i 是反复进行的,可以用循环结构表示.解:(1)算法及框图为:S1 输入x 0,y 0;A ,B ,C ; S2 计算m =A 2+B 2;S3 计算n =Ax 0+By 0+C ; S4 计算mn d ||=; S5 输出d ;(2)算法及框图为:S1 输入a ,b ,c ; S2 令x =a ;S3 若b >x ,则令x =b ;否则,执行S4;S4 若c >x ,则令x =c ;否则,执行S5; S5 输出x ;(3)算法及框图为:S1 输入i =1,S =0; S2 当i ≤n 时,,1iS S += i =i +1;否则执行S3; S3 输出S ;程序如下; S =0For i =1:1:n S =S +1/i i =i +1 endprint(%io (2),S )【评析】书写算法时,一步一步的程序化步骤,即“算则”固然重要,但这些步骤的依据,即“算理”有着更基本的作用,“算理,,是“算则”的基础,“算则”是“算理”的表现.这三道小题由于算理不同,所蕴含的算法结构也不同.通过实例,模仿、操作、探索,经历通过设计程序框图表达解决问题的过程,可以更好的理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句,体会和理解算法的含义,了解算法语言的基本构成.本例中涉及的“利用公式求点到直线的距离”、“实数排序求最值问题”、“求数列的和或积的问题”,还包括“二分法求函数零点”、“质数的判定”,“求π的近似值”等等,都是算法的典型案例,学习时要给予充分的重视.一般算法的表示方法并不唯一.不同的算法语言的书写形式是有差别的.本书所采用的是Scilab 语言,学习时要了解赋值语句、输入输出语句、if 语句、while 和for 语句的基本含义及表达方式,能够读懂语句表示的算法过程.例4 (1)用辗转相除法计算56和264的最大公约数时,需要做的除法次数是______. (2)用更相减损术求56和98的最大公约数时,操作如下:(98,56)(56,42)(42,14)(28,14)(14,14),由此可知两数的最大公约数为______.(3)用秦九韶算法求得多项式f (x )=x 6-2x 5+3x 3+4x 2-6x +5当x =2时函数值为______.解:(1)8216816240164015640564264+⨯=+⨯=+⨯=+⨯=所以最大公约数为8,需做的除法次数是4;(2)最大公约数为14; (3)33. 【评析】书上所涉及的古代基本算法案例包括:更相减损术与辗转相除法、秦九韶算法、割圆术.辗转相除法与更相减损术都是求最大公约数的方法,辗转相除法又叫欧几里得方法,计算上以除法为主,更相减损术以减法为主,计算次数上,前者相对较少,特别是两个整数相差较大时区别尤其明显;辗转相除法以余数为0结束,更相减损术则以减数与差相等结束.秦九韶算法的特点是把求n 次多项式的值转化为求n 个一次多项式的值,运算时只有加法和乘法,而且运算的次数比较少,求一个n 次多项式的值最多需要进行n 次加法、n 次乘法.割圆术是由中国古代数学家刘徽提出的,是当时计算圆周率比较先进的算法,“算理”明确,即用圆内接正多边形和外切正多边形逼近圆周率,重点是确定递推关系.例5 (09辽宁)某店一个月的收入和支出总共记录了N 个数据,其中收入记为正数,支出记为负数.该店用下边的程序框图计算月总收入S 和月净盈利V .那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A .A >0,V =S -TB .A <0,V =S -TC .A >0,V =S +TD .A <0,V =S +T【分析】本题要注意三点:a k 有正有负;S 为总收入,是所有正数的和;T 为总支出,是所有非正数的和.答案为C【评析】本题结合实际背景,强调算法的应用价值,是一种比较新的题型,应引起关注.练习9一、选择题1.任何一个算法都必须有的基本结构是( )A.顺序结构B.条件分支结构C.循环结构D.以上三个都要有2.下面给出对程序框图的几种说法:①任何一个程序框图都必须有起止框;②判断框有一个入口,有不止一个出口;③对于一个算法来说,判断框内的条件表达方式是唯一的;其中正确的有( )A.0个B.1个C.2个D.3个3.在算法的逻辑结构中,要求进行逻辑判断并根据结果进行不同处理的是哪种结构( ) A.顺序结构B.条件分支结构和循环结构C.顺序结构和条件分支结构D.顺序结构和循环结构4.算法:S1 输入n;S2 判断n是否是2;若n=2,则n满足条件,若n>2,则执行S3;S3 依次从2到n-1检验能否整除n,若都不能整除,则n满足条件;满足上述算法的n是( )A.奇数B.偶数C.质数D.合数二、填空题5.阅读下面两个程序框图,框图1输出的结果为______;框图2输出的结果为______.框图1 框图26.(08广东)阅读图9-8的程序框图,若输入m=4,n=6,则输出a=______,i=______.图9-8 图9-97.阅读图9-9的程序框图,若输入的n是100,则输出的变量S和T的值依次是______.8.“x=3*5”和“x=x+1”是某个程序中的先后相邻两个语句,下列说法中①“x=3*5”是将数值15赋给x,而不是普通运算“x=3*5=15”;②“x=3*5”可以写成“3*5=x”③语句“x=x+1”在执行时,“=”右边x为15,“=”左边x为16;正确的有______.三、解答题9.分别用辗转相除法和更相减损术求189和81的最大公约数.10.用循环语句书写求1+2+3+…+n>1000的最小自然数n的算法,画出程序框图,并写出相应的程序(选做).11.(09宁夏)为了测量两山顶MN间的距离,飞机沿水平方向在AB两点进行测量,MN在同一个铅垂平面内(如图).飞机能够测量的数据有俯角和AB间的距离,请你设计一个方案,包括:指出需要测量的数据(用字母表示,并在图中标出);用文字和公式写出计算MN间距离的步骤.专题九 算法参考答案练习9一、选择题1.A 2.C 3.B 4.C 二、填空题5.27,21 6.12,3 7.2550,2500 8.①③. 三、解答题9.解:辗转相除法:3278127281189 ⨯=⨯=,所以最大公约数为27.更相减损术:189-81=108,108-81=27,81-27=54,54-27=27, 所以最大公约数为27. 10.解:S1 输入S =0,i =1; S2 S =S +i ,i =i +1;S3 若S ≤1000,重复执行S2; 若 S >1000,输出i .S =0,i =1; While S ≤1000 S =S +i ; i =i +1; endprint (%io (2),i )11.解:如图(1)需要测量的数据有:A 点到M 、N 的俯角α1,β1;B 点到M 、N 的俯角α 2,β 2;A 、B 的距离d .11 / 11 (2)第一步:计算BM ,由正弦定理)sin(sin 211ααα+=d BM ; 第二步:计算BN ,由正弦定理)sin(sin 121βββ-=d BN ; 第三步:计算MN ,由余弦定理 )cos(22122αβ+++=⋅⋅BN BM BN BM MN .。
高中数学必修三课后习题答案

高中数学必修三课后习题答案第一章 算法初步 1.1算法与程序框图练习(P5) 1、算法步骤:第一步,给定一个正实数r .第二步,计算以r 为半径的圆的面积2S r π=.第三步,得到圆的面积S .2、算法步骤:第一步,给定一个大于1的正整数n .第二步,令1i =.第三步,用i 除n ,等到余数r .第四步,判断“0r =”是否成立. 若是,则i 是n 的因数;否则,i 不是n 的因数. 第五步,使i 的值增加1,仍用i 表示.第六步,判断“i n >”是否成立. 若是,则结束算法;否则,返回第三步.练习(P19)算法步骤:第一步,给定精确度d ,令1i =.的到小数点后第i 位的不足近似值,赋给a 的到小数点后第i 位的过剩近似值,赋给b . 第三步,计算55b am =-.第四步,若m d <,则得到5a;否则,将i 的值增加1,仍用i 表示.返回第二步. 第五步,输出5a.程序框图:习题1.1 A 组(P20)1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7 m 3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m 3的部分,每立方收费1.5元,并加收0.4元的城市污水处理费.设某户每月用水量为x m 3,应交纳水费y 元,那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值.算法步骤:第一步:输入用户每月用水量x .第二步:判断输入的x 是否不超过7. 若是,则计算 1.2y x =;若不是,则计算 1.9 4.9y x =-.第三步:输出用户应交纳的水费y .程序框图:2、算法步骤:第一步,令i =1,S=0.第二步:若i ≤100成立,则执行第三步;否则输出S. 第三步:计算S=S+i 2.第四步:i = i +1,返回第二步.程序框图:3、算法步骤:第一步,输入人数x ,设收取的卫生费为m 元.第二步:判断x 与3的大小. 若x >3,则费用为5(3) 1.2m x =+-⨯;若x ≤3,则费用为5m =.第三步:输出m .程序框图:B 组 1、算法步骤:第一步,输入111222,,,,,a b c a b c ..第二步:计算21121221b c b c x a b a b -=-.第三步:计算12211221a c a c y ab a b -=-.第四步:输出,x y .程序框图:INPUT “a ,b=”;a ,bsum=a+b diff=a -b pro=a*b quo=a/bPRINT sum ,diff ,pro ,quoEND2、算法步骤:第一步,令n =1第二步:输入一个成绩r ,判断r 与6.8的大小. 若r ≥6.8,则执行下一步;若r<6.8,则输出r ,并执行下一步.第三步:使n 的值增加1,仍用n 表示.第四步:判断n 与成绩个数9的大小. 若n ≤9,则返回第二步;若n >9,则结束算法.程序框图:说明:本题在循环结构的循环体中包含了一个条件结构.1.2基本算法语句 练习(P24) 1、程序:2、程序:3、程序:练习(P29) 1、程序:INPUT “a ,b ,c=”;a ,b ,cIF a+b>c AND a+c>b AND b+c>a THEN PRINT “Yes.” ELSEPRINT “No.” END IF INPUT “a ,b ,c=”;a ,b ,cp=(a+b+c)/2 s=SQR(p*(p -a) *(p -b) *(p -c)) PRINT “s=”;s END INPUT “F=”;F C=(F -32)*5/9 PRINT “C=”;C END4、程序: INPUT “a ,b ,c=”;a ,b ,csum=10.4*a+15.6*b+25.2*c PRINT “sum =”;sum END2、本程序的运行过程为:输入整数x . 若x 是满足9<x <100的两位整数,则先取出x 的十位,记作a ,再取出x 的个位,记作b ,把a ,b 调换位置,分别作两位数的个位数与十位数,然后输出新的两位数. 如输入25,则输出52. 34练习(P32) 1 2习题1.2 A 组(P33)1、1(0)0(0)1(0)x x y x x x -+<⎧⎪==⎨⎪+>⎩23、程序: 习题1.2 B 组(P33) 1、程序:23 41.3算法案例 练习(P45) 1、(1)45; (2)98; (3)24; (4)17. 2、2881.75.3、2200811111011000=() ,820083730=() 习题1.3 A 组(P48) 1、(1)57; (2)55. 2、21324.3、(1)104; (2)7212() (3)1278; (4)6315().4、习题1.3 B 组(P48)1、算法步骤:第一步,令45n =,1i =,0a =,0b =,0c =.第二步,输入()a i .第三步,判断是否0()60a i ≤<. 若是,则1a a =+,并执行第六步. 第四步,判断是否60()80a i ≤<. 若是,则1b b =+,并执行第六步. 第五步,判断是否80()100a i ≤≤. 若是,则1c c =+,并执行第六步. 第六步,1i i =+. 判断是否45i ≤. 若是,则返回第二步.2、如“出入相补”——计算面积的方法,“垛积术”——高阶等差数列的求和方法,等等. 第二章复习参考题A组(P50)1、(1)程序框图:程序:1、(2)程序框图:程序:2、见习题1.2 B组第1题解答.INPUT “x=”;x IF x<0 THENy=0ELSEIF x<1 THENy=1ELSEy=xEND IFEND IFPRINT “y=”;y ENDINPUT “x=”;x IF x<0 THENy=(x+2)^2 ELSEIF x=0 THENy=4ELSEy=(x-2)^2 END IFEND IFPRINT “y=”;y END34、程序框图:程序:INPUT “t=0”;t IF t<0 THEN PRINT “Please input again.”ELSE IF t>0 AND t<=180 THENy=0.2ELSEIF (t -180) MOD 60=0 THENy=0.2+0.1*(t-180)/60ELSEy=0.2+0.1*((t-180)\60+1)END IFEND IFPRINT “y=”;yEND IF END INPUT “n=”;n i=1 S=0WHILE i<=n S=S+1/i i=i+1 WENDPRINT “S=”;S END5、 (1)向下的运动共经过约199.805 m (2)第10次着地后反弹约0.098 m (3)全程共经过约299.609 m 第二章 复习参考题B 组(P35)1、 2、3、算法步骤:第一步,输入一个正整数x 和它的位数n . 第二步,判断n 是不是偶数,如果n 是偶数,令2n m =;如果n 是奇数,令12n m -=. 第三步,令1i =i=100 sum=0 k=1 WHILE k<=10 sum=sum+i i=i /2 k=k+1 WEND PRINT “(1)”;sum PRINT “(2)”;i PRINT “(3)”;2*sum -100 ENDINPUT “n=”;n IF n MOD 7=0 THEN PRINT “Sunday ” END IF IF n MOD 7=1 THEN PRINT “Monday ” END IF IF n MOD 7=2 THEN PRINT “Tuesday ” END IF IF n MOD 7=3 THEN PRINT “Wednesday ” END IF IF n MOD 7=4 THEN PRINT “Thursday ” END IF IF n MOD 7=5 THEN PRINT “Friday ” END IF IF n MOD 7=6 THEN PRINT “Saturday ” END IF END第四步,判断x 的第i 位与第(1)n i +-位上的数字是否相等. 若是,则使i 的值增加1,仍用i 表示;否则,x 不是回文数,结束算法.第五步,判断“i m >”是否成立. 若是,则n 是回文数,结束算法;否则,返回第四步.第二章 统计 2.1随机抽样 练习(P57)1、.况之间有误差. 如抽取的部分个体不能很好地代表总体,那么我们分析出的结果就会有偏差. 2、(1)抽签法:对高一年级全体学生450人进行编号,将学生的名字和对应的编号分别写在卡片上,并把450张卡片放入一个容器中,搅拌均匀后,每次不放回地从中抽取一张卡片,连续抽取50次,就得到参加这项活动的50名学生的编号. (2)随机数表法:第一步,先将450名学生编号,可以编为000,001, (449)第二步,在随机数表中任选一个数. 例如选出第7行第5列的数1(为了便于说明,下面摘取了附表的第6~10行).16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28第三步,从选定的数1开始向右读,得到一个三位数175,由于175<450,说明号码175在总体内,将它取出;继续向右读,得到331,由于331<450,说明号码331在总体内,将它取出;继续向右读,得到572,由于572>450,将它去掉. 按照这种方法继续向右读,依次下去,直到样本的50个号码全部取出,这样我们就得到了参加这项活动的50名学生. 3、用抽签法抽取样本的例子:为检查某班同学的学习情况,可用抽签法取出容量为5的样本. 用随机数表法抽取样本的例子:部分学生的心理调查等.抽签法能够保证总体中任何个体都以相同的机会被选到样本之中,因此保证了样本的代表性.4、与抽签法相比,随机数表法抽取样本的主要优点是节省人力、物力、财力和时间,缺点是所产生的样本不是真正的简单样本. 练习(P59)1、系统抽样的优点是:(1)简便易行;(2)当对总体结构有一定了解时,充分利用已有信息对总体中的个体进行排队后再抽样,可提高抽样调查;(3)当总体中的个体存在一种自然编号(如生产线上产品的质量控制)时,便于施行系统抽样法.系统抽样的缺点是:在不了解样本总体的情况下,所抽出的样本可能有一定的偏差. 2、(1)对这118名教师进行编号;(2)计算间隔1187.37516k==,由于k不是一个整数,我们从总体中随机剔除6个样本,再来进行系统抽样. 例如我们随机剔除了3,46,59,57,112,93这6名教师,然后再对剩余的112位教师进行编号,计算间隔7k=;(3)在1~7之间随机选取一个数字,例如选5,将5加上间隔7得到第2个个体编号12,再加7得到第3个个体编号19,依次进行下去,直到获取整个样本.3、由于身份证(18位)的倒数第二位表示性别,后三位是632的观众全部都是男性,所以这样获得的调查结果不能代表女性观众的意见,因此缺乏代表性.练习(P62)1、略2、这种说法有道理,因为一个好的抽样方法应该能够保证随着样本容量的增加,抽样调查结果会接近于普查的结果. 因此只要根据误差的要求取相应容量的样本进行调查,就可以节省人力、物力和财力.3、可以用分层抽样的方法进行抽样. 将麦田按照气候、土质、田间管理水平的不同而分成不同的层,然后按照各层麦田的面积比例及样本容量确定各层抽取的面积,再在各层中抽取个体(这里的个体是单位面积的一块地).习题2.1 A组(P63)1、产生随机样本的困难:(1)很难确定总体中所有个体的数目,例如调查对象是生产线上生产的产品.(2)成本高,要产生真正的简单随机样本,需要利用类似于抽签法中的抽签试验来产生非负整值随机数.(3)耗时多,产生非负整数值随机数和从总体中挑选出随机数所对的个体都需要时间.2、调查的总体是所有可能看电视的人群.学生A的设计方案考虑的人数是:上网而且登录某网址的人群,那些不能上网的人群,或者不登录某网址的人群就被排除在外了. 因此A方案抽取的样本的代表性差.学生B的设计方案考虑的人群是小区内的居民,有一定的片面性. 因此B方案抽取的样本的代表性差.学生C的设计方案考虑的人群是那些有电话的人群,也有一定的片面性. 因此C方案抽取的样本的代表性.所以,这三种调查方案都有一定的片面性,不能得到比较准确的收视率.3、(1)因为各个年级学习任务和学生年龄等因素的不同,影响各年级学生对学生活动的看法,所以按年级分层进行抽样调查,可以得到更有代表性的样本.(2)在抽样的过程中可能遇到的问题如敏感性问题:有些学生担心提出意见对自己不利;又如不响应问题:由于种种原因,有些学生不能发表意见;等等.(3)前面列举的两个问题都可能导致样本的统计推断结果的误差.(4)为解决敏感性问题,可以采用阅读与思考栏目“如何得到敏感性问题的诚实反应”中的方法设计调查问卷;为解决不响应问题,可以事先向全体学生宣传调查的意义,并安排专人负责发放和催收调查问卷,最大程度地回收有效调查问卷.4、将每一天看作一个个体,则总体由365天组成. 假设要抽取50个样本,将一年中的各天按先后次序编号为0~364天用简单随机抽样设计方案:制作365个号签,依次标上0~364. 将号签放到容器内充分搅拌均匀,从容器中任意不放回取出50个号签. 以签上的号码所对应的那些天构成样本,检测样本中所有个体的空气质量.用系统抽样设计抽样方案:先通过简单随机抽样方法从365天中随机抽出15天,再把剩下的350天重新按先后次序编号为0~349. 制作7个分别标有0~7的号签,放在容器中充分搅拌均匀. 从容器中任意取出一个号签,设取出的号签的编号为a,则编号为7(050)a k k +≤<所对应的那些天构成样本,检测样本中所有个体的空气质量.显然,系统抽样方案抽出的样本中个体在一年中排列的次序更规律,因此更好实施,更受方案的实施者欢迎.5、田径队运动员的总人数是564298+=(人),要得到28人的样本,占总体的比例为27.于是,应该在男运动员中随机抽取256167⨯=(人),在女运动员中随机抽取281612-=(人).这样我们就可以得到一个容量为28的样本.6、以10为分段间隔,首先在1~10的编号中,随机地选取一个编号,如6,那么这个获奖者奖品的编号是:6,16,26,36,46.7、说明:可以按年级分层抽样的方法设计方案. 习题2.1 B 组(P64)1、说明:可以按年级分层抽样的方法设计方案,调查问卷由学生所关心的问题组成. 例如:(1)你最喜欢哪一门课程? (2)你每月的零花钱平均是多少? (3)你最喜欢看《新闻联播》吗? (4)你每天早上几点起床? (5)你每天晚上几点睡觉?要根据统计的结果和具体的情况解释结论,主要从引起结论的可能原因及结论本身含义来解释.2、说明:这是一个开放性的题目,没有一个标准的答案. 2.2用样本估计总体 练习(P71) 1、说明:由于样本的极差为364.41362.51 1.90-=,取组距为0.19,将样本分为10组. 可以按照书上的方法制作频率分布表、频率分布直观图和频率折线图. 2、说明:此题目属于应用题,没有标准的答案.3、茎叶图为:由该图可以看出30名工人的日加工零件个数稳定在120件左右. 练习(P74)这里应该采用平均数来表示每一个国家项目的平均金额,因为它能反应所有项目的信息. 但平均数会受到极端数据2000万元的影响,所以大多数项目投资金额都和平均数相差比较大.练习(P79)1、甲乙两种水稻6年平均产量的平均数都是900,但甲的标准差约等于23.8,乙的标准差约等于41.6,所以甲的产量比较稳定.2、(1)平均重量496.86x ≈,标准差 6.55s ≈.(2)重量位于(,)x s x s -+之间有14袋白糖,所占的百分比约为66.67%.3、(1)略. (2)平均分19.25x ≈,中位数为15.2,标准差12.50s ≈.这些数据表明这些国家男性患该病的平均死亡率约为19.25,有一半国家的死亡率不超过15.2,15.2x >说明存在大的异常数据,值得关注. 这些异常数据使标准差增大. 习题2.2 A 组(P81) 1、(1)茎叶图为:(2)汞含量分布偏向于大于1.00 ppm 的方向,即多数鱼的汞含量分布在大于1.00 ppm 的区域. (3)不一定. 因为我们不知道各批鱼的汞含量分布是否都和这批鱼相同. 即使各批鱼的汞含量分布相同,上面的数据只能为这个分布作出估计,不能保证平均汞含量大于1.00 ppm. (4)样本平均数 1.08x ≈,样本标准差0.45s ≈.(5)有28条鱼的汞含量在平均数与2倍标准差的和(差)的范围内.2比较短,所以在这批棉花中混进了一些次品.3、说明:应该查阅一下这所大学的其他招生信息,例如平均数信息、最低录取分数线信息等. 尽管该校友的分数位于中位数之下,而中位数本身并不能提供更多录取分数分布的信息.在已知最低录取分数线的情况下,很容易做出判断;在已知平均数小于中位数很多,则说明最低录取分数线较低,可以推荐该校友报考这所大学,否则还要获取其他的信息(如标准差的信息)来做出判断. 4、说明:(1)对,从平均数的角度考虑; (2)对,从标准差的角度考虑;(3)对,从标准差的角度考虑; (4)对,从平均数和标准差的角度考虑; 5、(1)不能. 因为平均收入和最高收入相差太多,说明高收入的职工只占极少数. 现在已知知道至少有一个人的收入为50100x =万元,那么其他员工的收入之和为4913.55010075ii x==⨯-=∑(万元)每人平均只有1.53. 如果再有几个收入特别高者,那么初进公司的员工的收入将会很低. (2)不能,要看中位数是多少.(3)能,可以确定有75%的员工工资在1万元以上,其中25%的员工工资在3万元以上.(4)收入的中位数大约是2万. 因为有年收入100万这个极端值的影响,使得年平均收入比中位数高许多.6、甲机床的平均数=1.5x 甲,标准差=1.2845s 甲;乙机床的平均数 1.2z y =,标准差0.8718z s =. 比较发现乙机床的平均数小而且标准差也比较小,说明乙机床生产出的次品比甲机床少,而且更为稳定,所以乙机床的性能较好. 7、(1)总体平均数为199.75,总体标准差为95.26. (2)可以使用抓阄法进行抽样. 样本平均数和标准差的计算结果和抽取到的样本有关. (3) (4)略 习题2.2 B 组(P82)1、(1)由于测试1T 的标准差小,所以测试1T 结果更稳定,所以该测试做得更好一些. (2)由于2T 测出的值偏高,有利于增强队员的信心,所以应该选择测试2T .2、说明:此题需要在本节开始的时候就布置,先让学生分头收集数据,汇总所收集的数据才能完成题目.2.3变量间的相关关系 练习(P85)1、从已经掌握的知识来看,吸烟会损害身体的健康. 但除了吸烟之外,还有许多其他的随机因素影响身体健康,人体健康是很多因素共同作用的结果. 我们可以找到长寿的吸烟者,也更容易发现由于吸烟而引发的患病者,所以吸烟不一定引起健康问题. 但吸烟引起健康问题的可能性大,因此“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法是不对的.2、从现在我们掌握的知识来看,没有发现根据说明“天鹅能够带来孩子”,完全可能存在既能吸引天鹅和又使婴儿出生率高的第3个因素(例如独特的环境因素),即天鹅与婴儿出生率之间没有直接的关系,因此“天鹅能够带来孩子”的结论不可靠.而要证实此结论是否可靠,可以通过试验来进行. 相同的环境下将居民随机地分为两组,一组居民和天鹅一起生活(比如家中都饲养天鹅),而另一组居民的附近不让天鹅活动,对比两组居民的出生率是否相同. 练习(P92)1、当0x =时,147.767y =,这个值与实际卖出的热饮杯数150不符,原因是:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差;即使截距和斜率的估计没有误差,也不可能百分之百地保证对应于x ,预报值y 能够等于实际值y . 事实上:y bx a e =++. (这里e 是随机变量,是引起预报值y 与真实值(1)散点图如下: y 之间的误差的原因之一,其大小取决于e 的方差.)2、数据的散点图为:从这个散点图中可以看出,鸟的种类数与海拔高度应该为正相关(事实上相关系数为0.793). 但是从散点图的分布特点来看,它们之间的线性相关性不强. 习题2.3 A 组(P94)1、教师的水平与学生的学习成绩呈正相关关系. 又如,“水涨船高”“登高望远”等.2、(3)基本成正相关关系,即食品所含热量越高,口味越好.(4)因为当回归直线上方的食品与下方的食品所含热量相同时,其口味更好. 3、(1)散点图如下:(2)回归方程为:0.66954.933y x =+.(2)回归直线如下图所示:(3)加工零件的个数与所花费的时间呈正线性相关关系. 4、(1)散点图为:(2)回归方程为:0.546876.425y x =+.(3)由回归方程知,城镇居民的消费水平和工资收入之间呈正线性相关关系,即工资收入水平越高,城镇居民的消费水平越高. 习题2.3 B 组(P95) 1、(1)散点图如下:(2)回归方程为: 1.44715.843y x =-.(3)如果这座城市居民的年收入达到40亿元,估计这种商品的销售额为42.037y ≈(万元). 2、说明:本题是一个讨论题,按照教科书中的方法逐步展开即可.第二章 复习参考题A 组(P100)1、A .2、(1)该组的数据个数,该组的频数除以全体数据总数; (2)nmN. 3、(1)这个结果只能说明A 城市中光顾这家服务连锁店的人比其他人较少倾向于选择咖啡色,因为光顾连锁店的人使一种方便样本,不能代表A 城市其他人群的想法. (2)这两种调查的差异是由样本的代表性所引起的. 因为A 城市的调查结果来自于该市光顾这家服装连锁店的人群,这个样本不能很好地代表全国民众的观点.4、说明:这是一个敏感性问题,可以模仿阅读与思考栏目“如何得到敏感性问题的诚实反应”来设计提问方法.5、表略. 可以估计出句子中所含单词的分布,以及与该分布有关的数字特征,如平均数、标准差等.6、(1)可以用样本标准差来度量每一组成员的相似性,样本标准差越小,相似程度越高. (2)A 组的样本标准差为 3.730A S ≈,B 组的样本标准差为11.789B S ≈. 由于专业裁判给分更符合专业规则,相似程度应该高,因此A 组更像是由专业人士组成的.7、(1)中位数为182.5,平均数为217.1875.(2)这两种数字特征不同的主要原因是,430比其他的数据大得多,应该查找430是否由某种错误而产生的. 如果这个大数据的采集正确,用平均数更合适,因为它利用了所有数据的信息;如果这个大数据的采集不正确,用中位数更合适,因为它不受极端值的影响,稳定性好. 8、(1)略.(2)系数0.42是回归直线的斜率,意味着:对于农村考生,每年的入学率平均增长0.42%.(3)城市的大学入学率年增长最快. 说明:(4)可以模仿(1)(2)(3)的方法分析数据.第二章 复习参考题B 组(P101)1、频率分布如下表:从表中看出当把指标定为17.46千元 时,月65%的推销员 经过努力才能完成销 售指标.2、(1)数据的散点图如下:(2)用y 表示身高,x 表示年龄,则数据的回归方程为 6.31771.984y x =+. (3)在该例中,斜率6.317表示孩子在一年中增加的高度.(4)每年身高的增长数略. 3~16岁的身高年均增长约为6.323 cm. (5)斜率与每年平均增长的身高之间之间近似相等.第三章 概率3.1随机事件的概率 练习(P113) 1、(1)试验可能出现的结果有3个,两个均为正面、一个正面一个反面、两个均为反面. (2)通过与其他同学的结果汇总,可以发现出现一个正面一个反面的次数最多,大约在50次左右,两个均为正面的次数和两个均为反面的次数在25次左右. 由此可以估计出现一个正面一个反面的概率为0.50,出现两个均为正面的概率和两个均为反面的概率均为0.25. 2、略 3、(1)例如:北京四月飞雪;某人花两元钱买福利彩票,中了特等奖;同时抛10枚硬币,10枚都正面朝上.(2)例如:在王府井大街问路时,碰到会说中文的人;去烤鸭店吃饭的顾客点烤鸭;在1~1000的自然数任选一个数,选到的数大于1. 练习(P118)1、说明:例如,计算机键盘上各键盘的安排,公交线路及其各站点的安排,抽奖活动中各奖项的安排等,其中都用到了概率. 学生可能举出各种各样的例子,关键是引导他们正确分析例子中蕴涵的概率思想.2、通过掷硬币或抽签的方法,决定谁先发球,这两种方法都是公平的. 而猜拳的方法不太公平,因为出拳有时间差,个人反应也不一样.3、这种说法是错误的. 因为掷骰子一次得到2是一个随机事件,在一次试验中它可能发生也可能不发生. 掷6次骰子就是做6次试验,每次试验的结果都是随机的,可能出现2也可能不出现2,所以6次试验中有可能一次2都不出现,也可能出现1次,2次,…,6次. 练习(P121)1、0.72、0.6153、0.44、D5、B 习题3.1 A 组(P123) 1、D . 2、(1)0; (2)0.2; (3)1.3、(1)430.067645≈; (2)900.140645≈; (3)7010.891645-≈.4、略5、0.136、说明:本题是想通过试验的方法,得到这种摸球游戏对先摸者和后摸者是公平的结论. 最好把全班同学的结果汇总,根据两个事件出现的频率比较近,猜测在第一种情况下摸到红球的概率为110,在第二种下也为110. 第4次摸到红球的频率与第1次摸到红球的频率应该相差不远,因为不论哪种情况,第4次和第1次摸到红球的概率都是1 10.习题3.1 B组(P124)1、D.2、略. 说明:本题是为了学生根据实际数据作出一些推断. 一般我们假定每个人的生日在12个月中哪一个月是等可能的,这个假定是否成立,引导学生通过收集的数据作出初步的推断.3.2古典概率练习(P130)1、110. 2、17. 3、16.练习(P133)1、38,38.2、(1)113;(2)1213;(3)14;(4)313;(5)0;(6)213;(7)12;(8)1.说明:模拟的方法有两种.(1)把1~52个自然数分别与每张牌对应,再用计算机做模拟试验.(2)让计算机分两次产生两个随机数,第一次产生1~4的随机数,代表4个花色;第二次产生1~13的随机数,代表牌号.3、(1)不可能事件,概率为0;(2)随机事件,概率为49;(3)必然事件,概率为1;(4)让计算机产生1~9的随机数,1~4代表白球,5~9代表黑球.4、(1)16;(2)略;(3)应该相差不大,但会有差异. 存在差异的主要原因是随机事件在每次试验中是否发生是随机的,但在200次试验中,该事件发生的次数又是有规律的,所以一般情况下所得的频率与概率相差不大.习题3.2 A组(P133)1、游戏1:取红球与取白球的概率都为12,因此规则是公平的.游戏2:取两球同色的概率为13,异色的概率为23,因此规则是不公平的.游戏3:取两球同色的概率为12,异色的概率为12,因此规则是公平的.2、第一位可以是1~9这9个数字中的一个,第二位可以是0~9这10个数字中的一个,所以(1)190;(2)18919090-=;(3)9919010-=3、(1)0.52;(2)0.18.4、(1)12;(2)16;(3)56;(4)16.5、(1)25;(2)825.6、(1)920;(2)920;(3)12.习题3.2 B组(P134)1、(1)13;(2)14.2、(1)35;(2)310;(3)910.说明:(3)先计算该事件的对立事件发生的概率会比较简单.3、具体步骤如下:①建立概率模型. 首先要模拟每个人的出生月份,可用1,2,…,11,12表示月份,用产生取整数值的随机数的办法,随机产生1~12之间的随机数. 由于模拟的对象是一个有10个人的集体,故把连续产生的10个随机数作为一组模拟结果,可模拟产生100组这样的结果.②进行模拟试验. 可用计算器或计算机进行模拟试验.如使用Excel软件,可参看教科书125页的步骤,下图是模拟的结果:其中,A,B,C,D,E,F,G,H,I,J的每一行表示对一个10人集体的模拟结果. 这样的试验一共做了100次,所以共有100行,表示随机抽取了100个集体.③统计试验的结果. K,L,M,N列表示统计结果. 例如,第一行前十列中至少有两个数相同,表示这个集体中至少有两个人的生日在同一月. 本题的难点是统计每一行前十列中至少有两个数相同的个数. 由于需要判断的条件态度,所以用K,L,M三列分三次完成统计.其中K列的公式为“=IF(OR(A1=B1,A1=C1,A1=D1,A1=E1,A1=F1,A1=G1,A1=H1,A1=I1,A1=J1,B1=C1,B1=D1,B1=E1,B1=F1,B1=G1,B1=H1,B1=I1,B1=J1,C1=D1,C1=E1,C1=F1,C1=G1,C1=H1,C1=I1,C1=J1,D1=E1,D1=F1,D1=G1,D1=H1,D1=I1,D1=J1),1,0)”,L列的公式为“=IF(OR(E1=F1,E1=G1,E1=H1,E1=I1,E1=J1,F1=G1,F1=H1,F1=I1,F1=J1,G1=H1,G1=I1,G1=J1,H1=I1,H1=J1,I1=J1),1,0)”,M列的公式为“=IF(OR(K1=1,L1=1),1,0)”,M列的值为1表示该行所代表的10人集体中至少有两个人的生日在同一个月. N1表示100个10人集体中至少有两个人的生日在同一个月的个数,其公式为“=SUM(M$1:M$100)”. N1除以100所得的结果0.98,就是用模拟方法计算10人集体中至少有两个人的生日在同一个月的概率的估计值. 可以看出,这个估计值很接近1.3.3几何概率。
高一数学 基本算法语句-赋值、输入、输出语句

高一数学 基本算法语句-赋值、输入、输出语句教学目标(1)正确理解赋值语句、输入语句、输出语句的结构;(2)让学生充分地感知、体验应用计算机解决数学问题的方法;(3)通过实例,使学生理解3种基本的算法语句(输入语句、输出语句和赋值语句)的表示方法、结构和用法,能用这三种基本的算法语句表示算法,进一步体会算法的基本思想. 教学重点正确理解输入语句、输出语句、赋值语句的作用.教学难点准确写出输入语句、输出语句、赋值语句.教学过程一、问题情境1.问题1:已知我班某学生上学期期末考试语文、数学和英语学科成绩分别为80、100、89,试设计适当的算法求出这名学生三科的平均分.二、学生活动1.学生讨论,教师引导学生写出算法并画出流程图.2.怎样将以上算法转换成计算机能理解的语言呢? 下面我们将通过伪代码学习基本的算法语句. 三、建构数学1.伪代码:伪代码是介于自然语言和计算机语言之间的文字和符号,是表达算法的简单而实用的好方法.为了今后能学好计算机语言,我们在伪代码中将使用一种计算机语言“BASIC 语言”的关键词.2.赋值语句:赋值语句是将表达式所代表的值赋给变量的语句.例如:“x y ←”表示将y 的值赋给x ,其中x 是一个变量,y 是一个与x 同类型的变量或表达式.说明:①赋值语句中的赋值号“←”的左右两边不能对换,它将赋值号右边的表达式的值赋给赋值号左边的变量;②赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个数据、常量或表达式; ③对于一个变量可以多次赋值.算法: S1 a ←80 S2 b ←100 S3 c ←89 S4 A ←(a+b+c)/3 S5 输出A流程图:例1.写出求23x =时多项式3273511x x x +-+的值的算法.算法1 322373511x p x x ←←+-+算法2 23((73)5)11x p x x x ←←+-+ 说明:①以上两种算法,算法1要做6次乘法,算法2只要做3次乘法,由此可见,算法的好坏会影响运算速度; ②算法2称为“秦九韶算法”,其算法特点是:通过一次式的反复计算,逐步得出高次多项式的值;对于一个n 次多项式,只要做n 次乘法和n 次加法.附:秦九韶(1202—1261年),字道古,普州安岳(今四川安岳)人.他是我国古代最有成就的数学家之一.著有数学名著《数书九章》(又名数学九章》).该书共十八卷,分为大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易等九大类,每类用九个例题全书共八十一题)来阐明各种算法.这部中世纪的数学杰作,许多方面都有创造,而书中最突出的成就是“大衍求一术”和高次方程的数值解法“正负开方术”,是具有世界意义的成就.3.输入、输出语句:输入、输出语句分别用“Input ”(或者“Read ”)和“Print ”来描述数据的输入和输出.(1)输入语句与赋值语句的区别在于:赋值语句可以将一个代数表达式的值赋于一个变量,而输入语句由于要求输入的值只能是具体的常数,不能是函数、变量或表达式,因此输入语句只能将读入的具体数据赋给变量.(2)输出语句的主要作用是:①输出常量、变量的值和系统信息;②输出数值计算的结果. 例如:可以将问题1中的算法改进为求任意三门功课的平均值的算法.流程图:说明:输入语句“Read a ,b ”表示输入的数据依次送给a ,b ;“Print A ”表示输出运算结果A . 四、数学运用1.例题:例2.“鸡兔同笼”是我国隋朝时期的数学著作《孙子算经》中的一个有趣而具有深远影响的题目:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?” 伪代码: Read a ,b ,c A ←(a+b+c)/3 Print A请你先列出解决这个问题的方程组,并设计一个解二元一次方程组的通用算法,并画出流程图,写出伪代码.解:设有x 只鸡,y 只兔子,则352494x y x y +=⎧⎨+=⎩.设二元一次方程组为1111221222,(0),a x b y c a b a b a x b y c +=⎧-≠⎨+=⎩用消元法解得2112122112211221b c b c x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩, 因此,只要输入相应的未知数的系数和常数项,就能计算出方程组的解,即可输出,x y 的值.2.练习:课本第17页 练习1题.五、回顾小结:1.赋值语句、输入语句、输出语句的结构和作用.六、课外作业:课本第17页 练习2、3题;课本第24页习题1.2 第1题.补充:1.将五进制数化为十进制数的方法是“按权展开”,如将(5)1403化为十进制数为321015450535228⨯+⨯+⨯+⨯=.试用输入输出语句、赋值语句表示将五进制数(5)abcd 化为十进制数的算法.2.请用伪代码编写程序,实现三个变量1,2,3A B C ===的值按顺序互换,即A B C A →→→之间的交换.。
noi练习题

NOI练习题一、基础算法1.1 递归算法1. 请编写一个C++函数,实现求斐波那契数列的第n项。
2. 编写一个C++函数,实现计算阶乘n!。
1.2 循环算法3. 编写一个C++程序,实现输出1到100之间所有偶数。
4. 编写一个C++程序,计算1到100之间所有奇数的和。
1.3 排序算法5. 编写一个C++程序,使用冒泡排序算法对数组进行从小到大排序。
6. 编写一个C++程序,使用快速排序算法对数组进行从小到大排序。
二、数据结构2.1 线性表7. 编写一个C++程序,实现单链表的创建、插入、删除和查找操作。
8. 编写一个C++程序,实现顺序表的创建、插入、删除和查找操作。
2.2 栈和队列9. 编写一个C++程序,实现栈的基本操作:入栈、出栈、查看栈顶元素。
10. 编写一个C++程序,实现队列的基本操作:入队、出队、查看队首元素。
2.3 树和图11. 编写一个C++程序,实现二叉树的创建、遍历(前序、中序、后序)。
12. 编写一个C++程序,实现图的邻接矩阵表示和邻接表表示。
三、数学问题3.1 素数问题13. 编写一个C++程序,判断一个整数是否为素数。
14. 编写一个C++程序,输出1到100之间的所有素数。
3.2 最大公约数和最小公倍数15. 编写一个C++程序,计算两个整数的最大公约数。
16. 编写一个C++程序,计算两个整数的最小公倍数。
四、搜索算法4.1 暴力搜索17. 编写一个C++程序,实现全排列算法。
18. 编写一个C++程序,实现组合算法。
4.2 深度优先搜索19. 编写一个C++程序,使用深度优先搜索解决迷宫问题。
20. 编写一个C++程序,使用深度优先搜索求解N皇后问题。
五、动态规划5.1 斐波那契数列21. 编写一个C++程序,使用动态规划求解斐波那契数列的第n项。
5.2 最长公共子序列22. 编写一个C++程序,使用动态规划求解两个字符串的最长公共子序列。
5.3 最小路径和23. 编写一个C++程序,使用动态规划求解二维数组中的最小路径和。
排序的练习题

排序的练习题排序是一种常见的问题解决方法,在计算机科学和算法设计中起着重要的作用。
本文将介绍一些常见的排序算法,并提供一些练习题,以便读者巩固对排序算法的理解和应用。
一、冒泡排序冒泡排序是一种简单但效率较低的排序算法。
它的基本思想是,通过反复交换相邻的两个元素,将较大的元素逐渐"浮"到数组的末端。
练习题1:请使用冒泡排序算法将以下一组数字按照从小到大的顺序进行排序:9, 5, 3, 7, 2练习题2:请分析冒泡排序算法的时间复杂度,并给出你的理解。
二、选择排序选择排序是一种简单且较高效的排序算法。
它的基本思想是,每次从待排序的数组中选择最小的元素,放置到已排序的数组的末尾,直到所有元素都排列完毕。
练习题3:请使用选择排序算法将以下一组数字按照从小到大的顺序进行排序:6, 1, 8, 4, 9练习题4:请分析选择排序算法的时间复杂度,并给出你的理解。
三、插入排序插入排序是一种简单且高效的排序算法。
它的基本思想是,将待排序的元素逐个插入到已排序的数组中的适当位置。
练习题5:请使用插入排序算法将以下一组数字按照从小到大的顺序进行排序:3, 7, 2, 9, 1练习题6:请分析插入排序算法的时间复杂度,并给出你的理解。
四、快速排序快速排序是一种高效的排序算法,被广泛应用于实际开发中。
它的基本思想是,通过一趟排序将待排序的数组分割成独立的两部分,其中一部分的所有元素都比另一部分的所有元素小,然后对这两部分分别进行排序。
练习题7:请使用快速排序算法将以下一组数字按照从小到大的顺序进行排序:5, 1, 9, 3, 7练习题8:请分析快速排序算法的时间复杂度,并给出你的理解。
五、归并排序归并排序是一种稳定且高效的排序算法。
它的基本思想是,将待排序的数组递归地分解成多个子数组,对每个子数组进行排序,然后再将排好序的子数组合并成一个有序的数组。
练习题9:请使用归并排序算法将以下一组数字按照从小到大的顺序进行排序:4, 2, 8, 6, 5练习题10:请分析归并排序算法的时间复杂度,并给出你的理解。
c编程练习题

c编程练习题C语言是一种广泛使用的计算机编程语言,以其高效性和灵活性而闻名。
为了帮助学习者更好地掌握C语言,以下是一些C编程练习题,它们覆盖了基础到中级的知识点。
# 基础练习题1. 数据类型转换编写一个程序,输入一个整数和一个浮点数,然后输出它们转换为字符型后的ASCII值。
2. 算术运算编写一个程序,接受两个整数作为输入,并计算它们的和、差、积、商以及余数。
3. 条件语句编写一个程序,根据用户输入的成绩(0-100),输出相应的等级(A-F)。
4. 循环结构使用for循环打印从1到100的所有整数,并找出3和5的公倍数。
5. 数组操作编写一个程序,接受用户输入的5个整数,存储到数组中,并找出最大值和最小值。
# 中级练习题1. 字符串处理编写一个程序,接受用户输入的字符串,然后反转该字符串并输出。
2. 函数定义与调用定义一个函数,计算两个数的最大公约数,并在主函数中调用它。
3. 指针应用编写一个程序,使用指针交换两个变量的值,并输出交换后的结果。
4. 结构体使用定义一个结构体来存储学生的信息(如学号、姓名、成绩),然后编写一个程序来输入和输出这些信息。
5. 文件操作编写一个程序,能够读取一个文本文件中的内容,并计算其中单词的数量。
# 进阶练习题1. 递归函数编写一个递归函数来计算阶乘,并在主函数中调用它。
2. 动态内存分配使用malloc或calloc动态分配内存,并编写一个程序来复制一个数组的内容到另一个数组。
3. 链表操作实现一个简单的链表,并提供插入、删除和遍历链表的函数。
4. 排序算法实现冒泡排序、选择排序或插入排序算法,并编写一个程序来对用户输入的一系列数字进行排序。
5. 二叉树遍历定义一个二叉树的结构,并实现前序、中序和后序遍历。
# 实践项目1. 简单计算器实现一个基本的计算器,能够进行加、减、乘、除等基本运算。
2. 图书管理系统设计一个简单的图书管理系统,能够添加、删除、查找和列出图书。
必修3第一章《算法初步》训练题(含答案)

必修③第一章《算法初步》练习题一、选择题:1.下面对算法描述正确的一项是:( )A .算法只能用自然语言来描述B .算法只能用图形方式来表示C .同一问题可以有不同的算法D .同一问题的算法不同,结果必然不同 2. 算法的三种基本结构是 ( )A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构 3.用二分法求方程022=-x 的近似根的算法中要用哪种算法结构( ) A .顺序结构 B .条件结构 C .循环结构 D .以上都用 4.对赋值语句的描述正确的是 ( )①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A .①②③ B .①② C .②③④ D .①②④5. 将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( ) A. B. C. D.6、下列程序语句不正确...的是( ) A 、INPUT “MATH=”;a+b+c B 、PRINT “MATH=”;a+b+c C 、c b a += D 、1a =c b - 7.下列给变量赋值的语句正确的是( )A. 5=aB.a +2=aC. a =b =4D. a =2*a8. 给出以下四个问题,①输入一个数x ,输出它的相反数.②求面积为6的正方形的周长.③求三个数a,b,c 中的最大数. ④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值.其中不需要用条件语句来描述其算法的有 ( )A. 1个B. 2个C. 3个D. 4个 9.给出以下四个问题: ①解不等式32-x a>23-x a(0>a 且1≠a ) .②求边长为6的正三角形的面积.③求函数21,0()43,0x x f x x x -≥⎧=⎨+<⎩的函数值 ④若集合}1,1{-=A ,}1|{==mx x B ,且A B A =⋃,求m 的值。
比修3 算法语句 练习题

必修3第一章 算法初步1.2 基本算法语句题卷设计:绵阳市开元中学 王小凤老师 学生姓名1.已知变量a ,b 已被赋值,要交换a ,b 的值,采用的算法是( ) A .a b =,b a =B .a c =,b a =,c b =C .a c =,b a =,c a =D .c a =,a b =,b c =2.当1a =,3b =时,执行完如下的一段程序后x 的值是( )IF a b < THENx a b =+ELSEx a b =-END IFA .1B .3C .4D .-23.当2x =时,下面的程序运行结果是( )A .3B .7C .15D .174.下面程序运行后,输出的值是( )A .42B .43C .44D .455. 下面程序运行的结果是( )i =1S =0WHILE i<=100 S =S +ii =i +1WEND PRINT S ENDA .5 050B .5 049C .3D .26.阅读下面的程序,当分别输入2x =,1x =,0x =时,输出的y 值分别为________、________、________.INPUT “x =”;x IF x>1 THEN y =1/(x -1)ELSEIF x =1 THEN y =x^2ELSEy =x^2+1/(x -1) END IF END IF PRINT y END7.下列程序运行的结果是____________.x =100i =1DOx =x +10PRINT i ,x i =i +1LOOP UNTIL x>=200ENDi =1s =0WHILE i<=4s =s*x +1i =i +1WEND PRINT s END i =0DO i =i +1LOOP UNTIL i*i>=2 000 i =i -1PRINT i END8.利用计算机计算:s=11×2+12×3+13×4+…+199×100,某同学编写的程序语句中,①处应填_______________.9.为了在运行下面的程序之后得到y=25,键盘输入的x应该是________.INPUT xIF x<0THENy=(x+1)*(x+1)ELSEy=(x-1)*(x-1)END IFPRINT yEND10.有一列数:1,1,2,3,5,8,13,21,…,这列数有下面的特点:前两个数都是1,从第三个数开始,每个数都是前两个数的和,这样的一列数一般称为斐波那契数.图中程序所描述的算法功能是输出前10个斐波那契数.则这个算法中的横线处应填__________.(备选题)现欲求1+13+15+…+12n-1的和(其中n的值由键盘输入),已给出了其程序框图,请将其补充完整并设计出程序(用算法语句编写).。
【整合&免费】高中人教版数学 Ⅰ 课本练习必修1 2 3 4 5 答案

4、程序:
INPUT “Please input a year:;y ” b=y MOD 4 c=y MOD 100 d=y MOD 400 IF b=0 AND c<>0 THEN PRINT “Leap year.” ELSE IF d=0 THEN PRINT “Leap year.” ELSE PRINT “Not leap year.” END IF END IF END
2
第三步,得到圆的面积 S . 2、算法步骤:第一步,给定一个大于 1 的正整数 n . 第二步,令 i 1 . 第三步,用 i 除 n ,等到余数 r . 第四步,判断“ r 0 ”是否成立. 若是,则 i 是 n 的因数;否则, i 不是 n 的因数. 第五步,使 i 的值增加 1,仍用 i 表示. 第六步,判断“ i n ”是否成立. 若是,则结束算法;否则,返回第三 步. 练习(P19)
-
7 左
整合
第一章 算法初步 1.1 算法与程序框图 练习(P5) 1、算法步骤:第一步,给定一个正实数 r . 第二步,计算以 r 为半径的圆的面积 S r .
INPUT “a,b,c=” ;a,b,c p=(a+b+c)/2 s=SQR(p*(p-a) *(p-b) *(p-c)) PRINT “s=” ;s END
程序: 4、
INPUT “a,b,c=” ;a,b,c sum=10.4*a+15.6*b+25.2*c PRINT “sum =” ;sum END
高三理科党整合, 仅供高三复习全部书参考,以及高一二订正,不建议直接抄袭。 只要努力 一切来得及 在高考吧 里 零基础 学生 逆袭高考 仅一年时间 考上一本 重点 的例子不少。 课本 是一切知识的基础, 万变不离其宗! 望广大学子加油 考上自己理想的大学!
高考数学 15.2 基本算法语句与算法案例

15、算法初步15.2 基本算法语句与算法案例【知识网络】1.理解用伪代码表示的几种基本算法语句:赋值语句、输入语句、输出语句、条件语句、循环语句。
2.能用自然语言、流程图和伪代码表述算法,会用“While循环”和“For循环”语句或GoTo语句实施循环(注意:优先使用While和For语句,尽量少用GoTo语句)。
【典型例题】[例1](1)下列问题所描述出来的算法,其中不包含条件语句的为()A.读入三个表示三条边长的数,计算三角形的面积B.给出两点的坐标,计算直线的斜率C.给出一个数x,计算它的常用对数的值D.给出三棱锥的底面积与高,求其体积(2)设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线①上不能填入下面的那一个数?答:()A.13B.13.5C.14D.14.5(3)若mod(m,3)=1,则m的取值不可以是()A.2005 B.2006 C.2008 D.2020(4)下面的表述:①6←p;②t←3×5+2;③b+3←5;④p←((3x+2)-4)x+3;⑤a←a3;⑥x,y,z←5;⑦ab←3;⑧x ←y+2+x .其中正确表述的赋值语句有 . (注:要求把正确的表述全填上)(5)下面程序的运行结果为4[例2] 某百货公司为了促销,采用打折的优惠办法:每位顾客一次购物①在100元以上者(含100元,下同),按九五折优惠; ②在200元以上者,按九折优惠; ③在300元以上者,按八五折优惠; ④在500元以上者,按八折优惠. 试写出算法、画出流程图、伪代码,以求优惠价.[例3] 定义运算“!”为:n!=1×2×3×…×n ,其中n 为正整数,并且读作“n 的阶乘”,例如,5!=1×2×3×4×5=120,10!=9!×10= 3628800. 计算2007!写出算法分析与伪代码,并画出流程图。
java方法的调用练习题

java方法的调用练习题Java是一种面向对象的编程语言,它在软件开发领域具有广泛的应用。
作为一名Java程序员,我们经常需要编写和调用各种方法来实现不同的功能。
这些练习题将帮助我们提升对Java方法调用的理解和熟练程度。
1. 阶乘计算编写一个方法,用于计算给定数值的阶乘。
阶乘的定义是n! = n * (n-1) * (n-2) * ... * 1。
例如,5的阶乘为5! = 5 * 4 * 3 * 2 * 1 = 120。
在方法中使用循环结构来实现阶乘的计算,并返回结果。
2. 字符串反转编写一个方法,用于将给定字符串进行反转,并返回反转后的字符串。
例如,给定字符串"Hello",反转后的字符串为"olleH"。
在方法中使用循环结构来实现字符串的反转,并返回结果。
3. 最大公约数计算编写一个方法,用于计算两个给定数值的最大公约数。
最大公约数是能够同时整除两个数的最大正整数。
在方法中使用循环结构和条件语句来实现最大公约数的计算,并返回结果。
4. 数组排序编写一个方法,用于对给定数组进行排序。
排序可以使用冒泡排序、选择排序或其他常用的排序算法。
在方法中使用循环结构和条件语句来实现数组的排序,并返回排序后的数组。
5. 链表操作链表是一种常见的数据结构,它由节点构成,每个节点包含数据和指向下一个节点的引用。
编写一个方法,用于在链表中插入新节点、删除指定节点或查询指定节点。
在方法中使用循环和条件语句来实现链表的操作,并返回操作后的链表。
这些练习题涵盖了常见的Java方法调用场景,同时也提供了不同的算法和数据结构应用。
通过解决这些练习题,我们可以加深对Java方法调用的理解和熟练程度,并提升我们的编程能力。
除了掌握基本的方法调用技巧,我们还应该注重代码的可读性和可维护性。
在编写方法时,我们可以使用有意义的命名、注释和适当的缩进来提高代码的可读性。
同时,我们还可以将大问题拆解为多个小问题,并编写独立的方法来解决每个小问题,以提高代码的可维护性。
高中信息技术《基本算法》练习题(附答案解析)

高中信息技术《基本算法》练习题(附答案解析)学校:___________姓名:___________班级:________________ 一、选择题1.下列VB表达式的值等于2016的是()A.2016 Mod 2 ^ 20B.Len(“2015”) + 1C.Str(2008) +“8”D.Mid(“20160501”,1,4)2.下列与数学表达式对应的python表达式,正确的是()。
A.( - b + math. sqrt (b * b – 4 * a * c)) /a * aB.- b + math. sqrt (b * b – 4 * a * c) /2*aC.( -b + math. sqrt (b * 2 – 4 * a * c)) /(2 * a)D.( -b + math. sqrt ( b * b – 4 * a * c)) / (2 * a)3.某查找算法的VB 程序如下:Private Sub Commandl_Click()Dim a(1 To 9) As Integer, key As Integer, i As Integer,j As IntegerDim mid 1 As Integer,mid 2 As Integera(1)=4:a(2)=22:a(3)=27:a(4)=32:a(5)=35:a(6)=44:a(7)=56:a(8)=59:a(9)=78key=Val(Textl.Text)i=1:j=9flag=FalseDo While i<=j And Not flagmidl=i+(j-i)\3mid 2=j-(j-i)\3If key=a(midl) Thenflag=TrueElseIf key<a(midl) Thenj=midl-lElseIf key=a(mid 2) Thenflag=TrueElseIf key>a(mid2) Theni=mid2+1Elsei=mid1+1j=mid2-1End IfLoopIf flag Then Labell.Caption=″查找成功!″Else Labell.Caption=″查找失败!″End Sub该程序段执行时,在文本框Text1中输入36,单击命令按钮Command1,程序运行结束后,i和j的值为()A.4,5 B.6,5 C.5,6 D.6,44.有如下Python程序段:import randomd=[0]*6i=0while i<=5:d[i]=random.randint(1,10)if d[i]%2==i%2:continuei=i+1print(d)该程序执行后,下列输出的结果不正确...的是()A.[5, 8, 9, 8, 9, 2] B.[8, 1, 8, 7, 2, 5]C.[9, 6, 7, 2, 9, 4] D.[3, 8, 7, 6, 5, 4]5.有如下程序段:n=int(input())s=0while n!=0:x=n%10s=x+sn=n//10若运行程序后输入“20220308”,s的结果为()A.17 B.22238 C.2022 D.96.某DataFrame对象score包含“准考证号”“学校名称”“姓名”“总分”“排名”等数据列,下列语句中,可以以学校为单位,输出各校学生“总分”平均值的是()A.print(score.groupby(“学校名称”,as_index=False).mean( ))B.print(score.groupby(“总分”,as_index=False).mean( ))C.print(score.groupby(“学校名称”,as_index=False).排名.mean( ))D.print(score.sort_index(“学校名称”,as_index=False).describe( ))7.下列Python赋值语句中,无法正确运行的是()A.a=b=c=5 B.a, b=c C.a+=b D.b=-c8.下列关于算法的描述正确的是()A.算法只能用流程图描述B.算法只能有一个输入C.一个算法的执行步骤可以是无限的D.一个算法至少要有一个输出9.【加试题】对分查找的VB程序段如下:key=78i=1j=8k=1Do While i<=jm= fix((i+j)/2)if d(m)=key ThenLabel1.Caption=kExit doEnd ifIf d(m)<key Theni=m+1elsej=m-1End Ifk=k+1Loop数组元素a(1)到a(8)的值依次为“22,34,41,53,66,71,78,91”。
算法初步练习题(附详细答案解析)
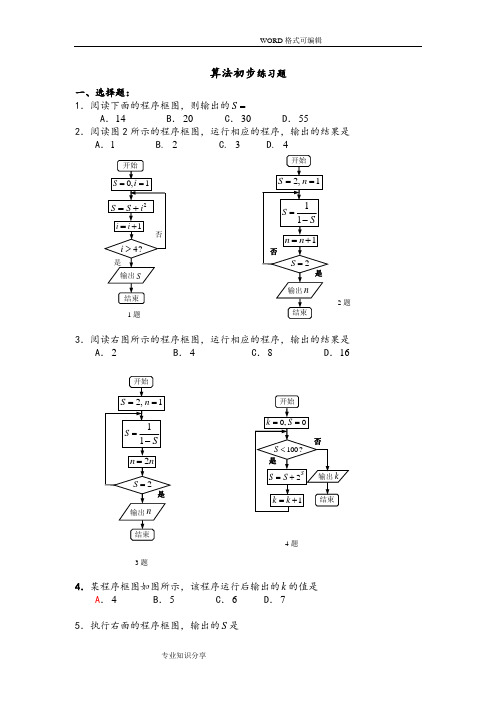
算法初步练习题一、选择题:1.阅读下面的程序框图,则输出的S =A .14B .20C .30D .552.阅读图2所示的程序框图,运行相应的程序,输出的结果是A .1 B. 2 C. 3 D. 43.阅读右图所示的程序框图,运行相应的程序,输出的结果是A .2B .4C .8D .164.某程序框图如图所示,该程序运行后输出的k 的值是A .4B .5C .6D .75.执行右面的程序框图,输出的S 是3题 2题1题4题A .378-B .378C .418-D .4186.如图的程序框图表示的算法的功能是A .计算小于100的奇数的连乘积B .计算从1开始的连续奇数的连乘积C .从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数D .计算100531≥⨯⋅⋅⋅⨯⨯⨯n 时的最小的n 值.7.右图是把二进制数)2(11111化为十进制数的一个程序框图,判断框内应填入的 条件是 A .4i > B .4i ≤ C .5i > D .5i ≤8.某程序框图如图所示,则该程序运行后输出的B 等于 A .15 B .29 C .31 D .635题6题9.如果执行右边的程序框图,输入2,0.5x h =-=,那么输出的各个数的和等于 A .3 B .3.5 C .4 D .4.510.某店一个月的收入和支出总共记录了N 个数据1a ,2,,N a a ⋅⋅⋅,其中 收入记为 正数,支出记为负数。
该店用右边的程序框图计算月总收入S 和月 净盈利V ,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中 的A .0,A V S T >=-B .0,A V S T <=-C .0,A V S T >=+D .0,A V S T <=+ 11. 如图1所示,是关于闰年的流程,则 以下年份是闰年的为A .1996年B .1998年C .2010年D .2100年12. 某流程如右上图所示,现输入如下四个函数,则可以输出的函数是11题A .2)(x x f =B .xx f 1)(=C .62ln )(-+=x x x fD .x x f sin )(=二、填空题:13.程序框图(即算法流程图)如图所示,其输出结果是_______. 14.执行右边的程序框图,输出的T = .14题12题13题15.下面的程序框图表示的算法的结果是 1616.阅读右上面的流程图,若输入6,1a b ==,则输出的结果是 217右面的程序框图,如果输入三个实数a ,b ,c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的 ①c x > ②x c > ③C .c b > ④b c >15题三、解答题:18.已知数列{a n }的各项均为正数,观察程序框图,若10,5==k k 时,分别有2110115==S S 和 (1)试求数列{a n }的通项; (2)令m a n b b b b n +++=...,221求的值.参考答案1.C .【解读与点评】当1=i 时, S =1;当i =2时, S =5;循环下去,当i =3时, S =14; 当i =4时,S =30;本试题考查了程序框图的运用.2.D 【解读与点评】本题考查是算法的重新框图与算法的语句识别.易错点是 不懂得运行顺序.当1,2n S ==代入程序中运行第一次是1S =-,然后赋值此时2n =;返回运 行第二次可得111(1)2S ==--,然后赋值3n =; 再返回运行第三次可得12112S ==-,然后赋值4n =,判断可知此时2S =,故输出4n =.故选D .3.C 【解读与点评】本题考查是算法的重新框图与算法的语句识别.考查学生 运算求解能力.本题的易错点是要注意是先赋值再输出.当1,2n S ==代入程序中运行第一次是1S =-,然后赋值此时2n =;返回运 行第二次可得111(1)2S ==--,然后赋值4n =; 再返回运行第三次可得12112S ==-,然后赋值8n =,判断可知此时2S =,故输出8n =.4.A .【解读与点评】对于0,1,k s ==1k ∴=.对于1,3,2k s k ==∴=,则2,38,3k s k ==+∴=,后面是113,382,4k s k ==++∴=,不符合条件时输出 的4k =.此题是新课程新增内容,考查了程序语言的概念和基本的应用,通 过对程序语言的考查,充分体现了数学程序语言中循环语言的关键. 9.B .【解读与点评】循环9次,对应输出值如下表。
codeforces 训练题单

codeforces 训练题单Codeforces是一个非常受欢迎的在线编程竞赛平台,每天都会举办一系列挑战性的算法竞赛。
Codeforces为程序员提供了一个学习和提高自己算法能力的好地方。
在这篇文章中,我将介绍一些适合初学者和进阶者的Codeforces训练题单。
对于初学者来说,从简单的问题开始是很重要的。
Codeforces为新手提供了大量的简单题目,它们有助于理解基本的算法和数据结构。
以下是一些适合初学者的Codeforces题目:1. Way Too Long Words:这个问题要求你将给定的单词进行简化。
它可以帮助你熟悉字符串操作和条件语句。
2. Next Round:这个问题要求你计算在一个竞赛中每个参赛选手的排名。
这个问题需要你使用数组和循环操作。
3. Beautiful Matrix:这个问题要求你通过交换相邻的元素,将一个矩阵变成一个特殊的形式。
这个问题可以帮助你理解二维数组的操作。
当你感觉对简单题目已经掌握了一些基本的算法和数据结构后,你可以尝试解决一些中等难度的问题。
以下是一些适合进阶者的Codeforces题目:1. Two Arrays:这个问题要求你找到两个数组中的相同元素。
这个问题需要你使用集合和哈希表。
2. Binary Strings:这个问题要求你计算给定字符串中0和1的最小数量,以使得字符串满足一些特定的条件。
这个问题需要你使用动态规划来解决。
3. Three Friends:这个问题要求你计算三个朋友之间的最小距离和最大距离。
这个问题需要你使用数学计算和条件语句。
除了解决问题以外,Codeforces还提供了一些很有趣的算法练习和竞赛。
你可以尝试参加Timus、AtCoder和HackerRank等竞赛,并与其他程序员交流和切磋。
要成为一名优秀的程序员,除了刷题,还需要不断地学习和提高自己的算法和编程技能。
你可以参考一些经典的算法教材,如《算法导论》和《编程珠玑》。
简单算法练习题

简单算法练习题算法是计算机科学中的基础概念,也是编程的核心内容之一。
通过解决一系列算法练习题,学习者可以锻炼逻辑思维、分析和解决问题的能力。
本文将介绍一些简单的算法练习题,帮助读者巩固基本算法知识。
1. 最大公约数计算题目描述:给定两个正整数,计算它们的最大公约数。
输入:两个正整数a和b(1 ≤ a, b ≤ 10^9)输出:输出a和b的最大公约数解题思路:最大公约数可以使用欧几里得算法(欧几里得定理)进行计算。
欧几里得算法的基本原理是:两个整数的最大公约数等于其中较小的数和两数的差的最大公约数。
算法实现如下:```pythondef gcd(a, b):if a < b:a, b = b, awhile b != 0:a, b = b, a % breturn a# 测试a = int(input("请输入第一个正整数:"))b = int(input("请输入第二个正整数:"))result = gcd(a, b)print("最大公约数为:", result)```2. 素数判断题目描述:给定一个正整数,判断它是否为素数。
输入:一个正整数n(1 ≤ n ≤ 10^6)输出:如果n是素数,则输出"Yes",否则输出"No"。
解题思路:素数是只能被1和自身整除的正整数。
判断一个数是否为素数,可以用试除法。
从2开始,依次判断2到n-1之间的整数是否能够整除n,若存在能整除n的数,则n不是素数,否则n是素数。
算法实现如下:```pythondef is_prime(n):if n < 2:return Falsefor i in range(2, int(n ** 0.5) + 1):if n % i == 0:return Falsereturn True# 测试n = int(input("请输入一个正整数:"))if is_prime(n):print("Yes")else:print("No")```3. 斐波那契数列题目描述:输出斐波那契数列的前n项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分层பைடு நூலகம்练
1、下面程序运行结束后M的值为:( )
程序:M←1
M←M+2
M←M+3
A.1 B. 3 C.5 D.6
2、下列程序段运行后,M的值为
a←5
b←10
m←a
if b>m then m←b
A.5 B.10 C.5和10 D.以上都不是
3、下列程序段运行后,变量a,b的值为
a←3
b←4
8、 某班有50名学生,现将某科的成绩分为3个等级:不低于80分为A,低于60分为C,其余为B,试用条件语句表示输出每个学生相应的成绩等级的算法。
本节学习疑点:
学生质疑
教师答复
习题5.3.1答案
1、D
2、B
3、B
4、a=-5,b=6,c=6
5、
6、a←1
b←-3
c←-4
△←b2-4ac
If △<0 Then
if a<b then
t←a
a←b
b←t
end if
A.3,4 B.4,3 C.3,3 D.4,4
4、 下列算法中,最后输出的a,b,c各是多少?
5、下列流程图表示的数学解析式是什么?
6、用算法语句给出用公式法求方程 的两个根的算法。
7、输入3个数a,b,c,如果这3个数能作为一个三角形的三边长,则输出 ,否则提示重新输入,试用算法语句表示上述过程。
Read n,a
If a Then
Print n,A
Else If a≥60 Then
Print n,B
Else
Print n,C
End If
I←I+1
End While
Print 原方程无实根
Else If △=0 Then
Print 原方程有等根x=-b/2a
Else
x1←
x2←
Print 原方程有两个不相等的实根
End If
7、Read a,b,c
If a+b>c且b+c>a且a+c>b Then
P
Else
Read a,b,c
End If
8、I←1
While I≤50
