初中数学几何题(超难)及答案分析-七年级几何题超难
初中数学几何题(超难)及答案分析

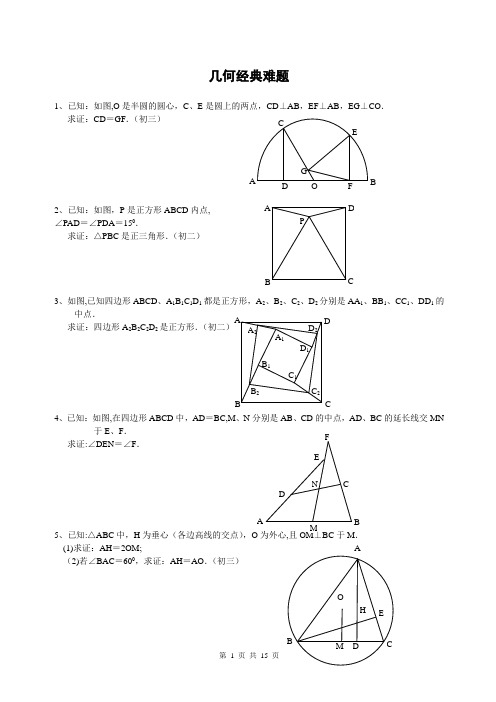
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
初中数学几何题(超难)及答案分析-七年级几何题超难

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .C D17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.CCD20、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.解答1.如下图做GH⊥AB,连接EO。
(完整版)初中数学几何题(超难)及答案分析

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
初中数学几何题超难与答案解析分析

几何经典难题1、:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .〔初三〕2、:如图,P 是正方形ABCD 点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.〔初二〕3、如图,四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.〔初二〕4、:如图,在四边形ABCD 中,AD =BC ,M 、N分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、:△ABC 中,H 为垂心〔各边高线的交点〕,O 〔1〕求证:AH =2OM ; 〔2〕假设∠BAC =600,求证:AH =AO .〔初三〕A P C D BA FGCE B O D D 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .〔初三〕7、如果上题把直线MN 由圆外平移至圆,那么由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 、Q . 求证:AP =AQ .〔初三 〕8、如图,分别以△ABC 的AC 和BC 为一边,在△,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .N求证:CE =CF .〔初二〕10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .〔初二〕12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .〔初三〕13、:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC =5. E EP求:∠APB 的度数.〔初二〕14、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .〔初二〕15、设ABCD 为圆接凸四边形,求证:AB ·CD +16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:≤L <2. 18、:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.C D19、P为正方形ABCD的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.20、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.解答1.如以下图做GH⊥AB,连接EO。
(完整版)初一几何难题_练习题(含答案)

1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
例1. 已知:如图1求证:DE = 分析:由∆ABC 连结CD ,易得CD = 证明:连结CDAC BC A BACB AD DBCD BD AD DCB B A AE CF A DCB AD CD=∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,∴≅∴=∆∆ADE CDFDE DF说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中线或高是常用的辅助线。
显然,在等腰直角三角形中,更应该连结CD ,因为CD 既是斜边上的中线,又是底边上的中线。
本题亦可延长ED 到G ,使DG =DE ,连结BG ,证∆EFG 是等腰直角三角形。
有兴趣的同学不妨一试。
例2. 已知:如图2所示,AB =CD ,AD =BC ,AE =CF 。
求证:∠E =∠FAB CD BC AD AC CA ABC CDA SSS B D AB CD AE CFBE DF===∴≅∴∠=∠==∴=,,,∆∆()在∆BCE 和∆DAF 中,BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意:(1)制造的全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到的两个全等三角形。
2、证明直线平行或垂直在两条直线的位置关系中,平行与垂直是两种特殊的位置。
证两直线平行,可用同位角、内错角或同旁内角的关系来证,也可通过边对应成比例、三角形中位线定理证明。
证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。
初中数学几何题(超难)及答案分析

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
初一几何难题练习题集(含答案解析)

1.证明线段相等或角相等两条线段或两个角相等就是平面几何证明中最基本也就是最重要得一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用得方法就是利用全等三角形得性质,其它如线段中垂线得性质、角平分线得性质、等腰三角形得判定与性质等也经常用到。
例1. 已知:如图1求证:DE =DF分析:由∆ABC 连结CD,易得CD = 证明:连结CDAC BC A BACB AD DBCD BD AD DCB B A AE CF A DCB AD CD=∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,∴≅∴=∆∆ADE CDFDE DF说明:在直角三角形中,作斜边上得中线就是常用得辅助线;在等腰三角形中,作顶角得平分线或底边上得中线或高就是常用得辅助线。
显然,在等腰直角三角形中,更应该连结CD,因为CD 既就是斜边上得中线,又就是底边上得中线。
本题亦可延长ED 到G,使DG =DE,连结BG,证∆EFG 就是等腰直角三角形。
有兴趣得同学不妨一试。
例2. 已知:如图2所示,AB =CD,AD =BC,AE =CF 。
求证:∠E =∠FAB CD BC AD AC CA ABC CDA SSS B DAB CD AE CF BE DF===∴≅∴∠=∠==∴=,,,∆∆()在∆BCE 与∆DAF 中,BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意: (1)制造得全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到得两个全等三角形。
2.证明直线平行或垂直在两条直线得位置关系中,平行与垂直就是两种特殊得位置。
证两直线平行,可用同位角、内错角或同旁内角得关系来证,也可通过边对应成比例、三角形中位线定理证明。
证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。
初中数学几何题(超难)及答案分析

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点, ∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)AP C DBAF GCE BODD 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP CB PA DCB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH⊥AB,连接EO。
初中数学几何题(超难)及答案分析

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD=∠PDA=150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)A P CDB4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.5、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC 于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初三)6、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初三)7、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初三)8、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)9、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)10、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)11、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)12、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)13、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)14、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)15、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)16、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)17、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L <2.18、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.19、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.20、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.解答1.如下图做GH⊥AB,连接EO。
初中数学几何题(超难)及答案分析
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点),(1)求证:AH =2OM; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A,自AEB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC上的任一点求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1。
初中数学几何题(超难)和答案分析

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .C D17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.CCD20、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.解答1.如下图做GH⊥AB,连接EO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、已知:如图,O 是半圆的圆心, 求证:CD= GF .(初三)2、已知:如图,P 是正方形 ABCD 内点, ∠ PAD =∠ PDA = 15°.求证:△ PBC 是正三角形.(初二)4、已知:如图,在四边形 ABCD 中,AD = BC , M 、N 分别是 AB 、CD 的中点,AD 、BCMN 于 E 、F . 求证:∠ DEN = ∠ F .5、已知:△ ABC 中,H 为垂心(各边高线的交点)(1) 求证:AH = 2OM ;(2) 若∠ BAC = 60°,求证:AH = AO .(初三)几何经典难题HE3、如图,已知四边形 ABCD 、A I B I C I D I 都是正方形,A 2、B 2、C ?、D ?分别是AA 1>BB 1、 CC 1∖ DD I的中点.求证:四边形 A 2B 2C 2D 2是正方形.的延长线交BC(初二),O 为外心,且OM 丄BC 于M .6、设MN 是圆O 外一直线,过 O 作OA 丄MN 于A ,自A 引圆的两条直线,交圆于 B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初三)7、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过 MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .8如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.(初二)求证:AP = AQ .(初三 )GN9、如图,四边形 ABCD 为正方形, 求证:CE = CF .(初二)11、设P 是正方形 ABCD 一边BC 上的任求证:PA = PF .(初二)12、如图,PC 切圆O 于C , AC 为圆的直径,证:AB = DC , BC = AD .(初三)求证: AE = AF .(初二)An10、如图,四边形 ABCD 为正方形, AF 与直线PO 相交于B 、D .求DE //AC ,DE //ACEPEF 为圆的割线,AE、13、已知:△ ABC 是正三角形,P 是三角形内一点, 求:∠APB 的度数.(初二)15、设ABCD 为圆内接凸四边形,求证: AB ∙ CD + AD ∙ BC = AC ∙ BD .(初三)16、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:∠ DPA =∠ DPC .(初二)14、设P 是平行四边形 ABCD 内部的一点,且∠ 求证:∠ PAB = ∠ PCB .(初二) PBA = ∠PDA .17、设P 是边长为1的正△ ABC 内任一点, L = PA + PB + PC ,求证:'≤ L V 2.18、已知:P是边长为1的正方形ABCD内的一点,求PA + PB + PC的最小值.19、P为正方形ABCD内的一点,并且PA = a, PB= 2a, PC = 3a,求正方形的边长.AD20、如图,△ ABC 中,∠ ABC =∠ ACB = 80°,=20°,求∠ BED的度数.D、E 分别是AB、AC 上的点,∠ DCA = 300,∠ EBA解答1•如下图做GH丄AB,连接E0。
由于GoFE四点共圆,所以∠ GFH =∠ OEG,2.如下图做厶DGC使与△ ADP全等,可得△ PDG为等边△,从而可得△ DGC ◎△ APD ◎△ CGP,得出PC=AD=DC,和∠ DCG= ∠ PCG = 15°所以∠ DCP=30°,从而得出△ PBC 是正三角形3.如下图连接BG和AB分别找其中点F,E.连接C2F与AE并延长相交于Q点, 连接EB并延长交QQ于H点,连接FB并延长交AQ于G点,由AE=壬AB i=壬BC= FB2 , EB=舟AB= ⅛ BC=F G ,又∠ GFQ+ ∠ Q=90°和∠ GE B⅛+∠ Q=90°,所以∠ GE B⅛=∠ GFQ 又∠ B⅛FC⅛= ∠ A⅛EB⅛ ,可得△ B⅛FC⅛BA A2EB2 ,所以A⅛B2=B⅛C2 ,又∠ GFQ+ ∠ HB2F=90°和∠ GFQ= ∠ EB2A2 ,从而可得∠ A2B2 C2=9O O ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形。
B C4.如下图连接AC并取其中点Q连接QN ffi QM所以可得∠ QMF= ∠ F, ∠ QNM= ∠ DEN和∠ QMN= ∠ QNM ,从而得出∠ DEN =∠ F。
5. (1)延长AD到F 连BF,做OQ AF,又∠ F= ∠ ACB= ∠ BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM ⑵连接OB OC既得∠ BOC=1200,从而可得∠ BOM=60 0,所以可得0B=20M=AH=A0,得证。
6. 证明:作E点关于GA的对称点F,连FQ、FA , FC, V OA 丄MN , EF 丄OA ,则有∠ FAP= ∠ EAQ , ∠ EAP= ∠ FAQ ,FA=EA , V∠ PAF= ∠ AFE= ∠ AEF=180- ∠FCD , V∠ PAF=180- ∠ FAQ , ∙∙∙∠ FCD= ∠FAQ , ∙∙∙ FCAQ四点共圆,∠ AFQ= ∠ ACQ= ∠ BED , 在厶EPA和厶FQA中∠ PEA= ∠ QFAAF=AE•••△ EPAFQA ,∠ PAE= ∠ QAF∙∙∙ AP=AQ .7. 作OFLCD OGLBE ,连接OP , OA , OF , AF , OG , AG , OQO 丄十AD AC CD 2FD FD 由于= = = =AB AE BE 2BG BG由此可得厶ADF ◎△ ABG ,从而可得∠ AFC= / AGE。
又因为PFQA与QGQA四点共圆,可得∠ AFC= / AQP和∠ AGE= / AQQ , / AQP= / AQQ ,从而可得AP=AQ。
由厶 EGA ◎△ AIC ,可得 EG=AlAB 29•顺时针旋转△ ADE ,到△ ABG ,连接CG 由于 ∠ ABG= ∠ ADE=90 °+45°=135°从而可得B , G , D 在一条直线上,可得△ AGB 也厶CGB 。
推出AE=AG=AC=GC ,可得△ AGC 为等边三角形。
∠ AGB=30 0,既得∠ EAC=30 0,从而可得∠ A EC=75 °。
从而可得PQ= AI + BI2从而得证。
EO由厶 BFH ◎△CBl可得FH=BI 。
又∠ EFC= ∠ DFA=450+3O0=750∙可证:CE=CF 。
10.连接BD乍CH⊥ DE ,可得四边形CGDH是正方形。
由AC=CE=2GC=2CH ,可得∠ CEH=30 0,所以∠ CAE= ∠ CEA= ∠ AED=15 0,又∠ FAE=900+450+150=1500,从而可知道∠ F=150,从而得出AE=AF。
D11.作FGL CD FE ⊥BE ,可以得出GFEC 为正方形。
令AB=Y ,BP=X ,CE=Z ,可得 PC=Y-X 。
tan ∠ BAP=tan ∠ EPF=—= ,可得 Y Y- X + Z即 Z(Y-X)=X(Y-X),既得 X=Z ,得出△ ABP 也厶 PEF , 得到PA = PF ,得证。
YZ=XY-X 2+XZ ,12. 证明:作CQ丄PD于Q,连接EO,EQ , EC , OF , QF , CF, 所以PC2=PQ?Po (射影定理),2又PC =PE?PF,所以EFOQ四点共圆,∠ EQF= ∠ EOF=2 ∠ BAD ,又∠ PQE= ∠ OFE= ∠ OEF= ∠ OQF ,而CQ丄PD ,所以∠ EQC= ∠ FQC ,因为∠ AEC= ∠ PQC=90 ,故B、E、C、Q四点共圆,所以∠ EBC=∠ EQC= 1/2∠ EQF=1/2 ∠ EOF= ∠ BAD ,∙∙∙ CB // AD ,所以BO=DO ,即四边形ABCD是平行四边形,∙∙∙ AB=DC , BC=AD .13. 顺时针旋转△ ABP 60°,连接PQ ,则△ PBQ是正三角形。
可得△ PQC是直角三角形。
所以∠ APB=150°。
14. 作过P点平行于AD的直线,并选一点E,使AE// DC BE // PC.可以得出/ ABP= / ADP= / AEP ,可得:AEBP共圆(一边所对两角相等)。
可得∠ BAP= / BEP= / BCP ,得证。
B C15.在 BD 取一点 E ,使 ∠ BCE= ∠ ACD ,既得△ BEC s ∖ ADC ,可得:又∠ ACB= ∠ DCE ,可得△ ABC s ∖ DEC ,既得 B E C17. ( 1)顺时针旋转△ BPC 60° ,可得△ PBE 为等边三角形。
既得PA+PB+PC=AP++PE+EF 要使最小只要 AP ,PE ,EF 在一条直线上,即如下图:可得最小BE _ ADBC = AC即 AD ?BC=BE ?AC, AB AC DEDC ,即 AB ?CD=DE ?AC ,由① + ②可得:AB?CD+AD ?BC=AC(BE+DE)= AC ∙ BD 16.过 D 作 AQL AE ,AEPQ AELPQ= , 2 2 可得DQ=DG ,可得∠由 AE=FC 。
,得证。
DPA =∠ DPC (角平分线逆定理)。
(2)过P点作BC的平行线交AB,AC与点D, F O由于∠ APD> ∠ ATP= ∠ ADP ,推出AD>AP ①又BP+DP>BP ②和PF+FOPC ③又DF=AF ④由①②③④可得:最大L< 2 ;18.顺时针旋转△ BPC 60°,可得△ PBE为等边三角形。
既得PA+PB+PC=AP+PE+EF要使最小只要AP , PE, EF在一条直线上, 即如下图:可得最小PA+PB+PC=AF o既得AF=I1+(^+1)2 =)2+ √3= j4+;^3(3+1)2由(1和(2)既得: ≤ L V 2.6+ 2219.顺时针旋转△ ABP 90°,可得如下图:既得正方形边长(2+7 )2+(;2)2L a = 5+2、「2U aO,可得∠ AFE=800 , 既得:∠ DFG=40°又BD=BC=BG 既得∠ BGD=80° ,既得∠ DGF=4O ° 推得:DF=DG ,得到:△ DFEDGE , 从而推得:∠ FED= ∠ BED=30° 。
