2007陕西中考预测试卷(二)
2007年中考模拟试卷(3份)[下学期]-2
![2007年中考模拟试卷(3份)[下学期]-2](https://img.taocdn.com/s3/m/d263e366336c1eb91a375d31.png)
2007年初中毕业生学业考试科学模拟试卷考生须知:1.本试卷分试题卷和答题卷两部分。
满分为200分,考试时间为120分钟。
2.答题前,必须在答题卷的密封区内填写校名、班级、姓名。
3.所有答案都必须写在答题卷标定的位置上,务必注意试题序号和答题序号相对应。
4.本卷可能用到的相对原子质量:H:1 C:12 O:16 Cl:35.5 Na:23 Ca:40 温馨提示:耐心点,再耐心点,耐心审题哦,赏你自己一个“金苹果”。
卷一一、选择题(每小题4分,共80分,每小题只有一个选项符合题意)1.有人说,森林象地球的头发,可能此说比较形象,但从功能上来说,森林更象是地球的 A.“肺” B.“肠” C.“肝” D.“脑”2.一项全国性的调查显示,很多学生是在晚上10时或11时之后才睡觉。
专家认为学生入睡最佳时间是在晚上9时到10时之间,并睡足9小时左右,这个习惯有利于学生的生长发...育.,这是因为人体在晚上能旺盛地分泌 A.生长激素 B.胰岛素 C.雄性激素 D.雌性激素 3.2005年11月13日,中石油吉林石化公司双苯厂发生爆炸事故,超过100吨的苯等有毒化学物质流入松花江。
为了过滤饮用水,人们使用了大量活性炭,活性炭的化学式是A.S B.CO 2 C.CO D.C4.高速磁悬浮列车是一种新型的轨道交通工具,它主要依靠电磁力使车体浮离轨道,具有“地面飞行器”的美誉,磁悬浮列车能悬起来的原因是A.异名磁极相排斥 B.同名磁极相排斥 C.S极与北极相排斥 D.N极和南极相排斥 5.下列实验中,哪一个实验可以更好地证明土壤中含有能燃烧的有机物A B C D 6.下列反射中,属于先天性行为的是A.谈虎色变 B.遇火缩手 C.望梅止渴 D.杯弓蛇影7.人体每个细胞内有二十三对染色体,右图模式化地展示 了其中的一个染色体。
下列有关叙述中,正确的是A.A是DNA B.A是脱氧核糖核酸C.B是染色体D.B是DNA8.下列词语中,一定包含有化学变化的是A.成云致雨 B.香气扑鼻 C.糯米酿酒 D.一刀两第9题图断9.以下能源中,属于可再生能源的是A.风能B.石油C.煤D.天然气10.煤燃烧产生的二氧化硫是大气污染物,而且二氧化硫还可以通过如下二个反应形成酸雨,从而污染水和土壤:SO2 + H2O= H2SO3 , 2H2SO3 +O2= 2H2SO4。
2007年陕西省初中毕业生学业考试

2007年陕西省初中毕业生学业考试数学模拟试卷(十七)(本卷共三个大题,考试时间:120分钟;全卷满分120分)6个小题,每题3分,满分18分)1、-31=2、函数y=2-x 的自变量取值范围是3、观察下列各式:212212+=⨯, 323323+=⨯, 434434+=⨯, 545545+=⨯…想一想,什么样的两数之积等于这两数之和?设n 表示正整数,用关于n 的等式表示这个规律为 4、如果反比例函数y=xk的图象经过点P (-3,1)那么k= 5、如果一个角的补角是1200,那么这个角的余角是6、如图:AB ∥CD ,直线EF 分别交AB 、CD 于E ∠1=720,则∠2= A B 二、选择题:(本大题共8个小题,每小题4分,满分32分)7、下列计算正确的是( ) A 、(-4x 2)(2x 2+3x -1)=-8x 4-12x 2-4x B 、(x+y )(x 2+y 2)=x 3+y 3 C 、(-4a -1)(4a -1)=1-16a 2 D 、(x -2y )2=x 2-2xy+4y 2 8、把x 2-1+2xy+y 2的分解因式的结果是( )A 、(x+1)(x -1)+y(2x+y)B 、(x+y+1)(x -y -1)C 、(x -y+1)(x -y -1)D 、(x+y+1)(x+y -1) 9、已知关于x 的方程x 2-2x+k=0有实数根,则k 的取值范围是( ) A 、k <1 B 、k ≤1 C 、k ≤-1 D 、k ≥110、某电视台举办的通俗歌曲比赛上,六位评委给1号选手的评分如下:90 96 91 96 95 94这组数据的众数和中位数分别是( )A 、94.5,95B 、95,95C 、96,94.5D 、2,9611、面积为2的△ABC ,一边长为x,这边上的高为y,则y 与x 的变化规律用图像表示大致是( )12、有如下结论(1)有两边及一角对应相等的两个三角形全等;(2)菱形既是轴对称图形又是中心对称图形;(3)对角线相等的四边形是矩形;(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧;(5)两圆的公切线最多有4条,其中正确结论的个数为( ) A 、1个B 、2个C 、3个D 、4个13、已知:如图梯形ABCD 中,AD ∥BC ,AB=DC,,AC 与BD 相交于点O ,那么图中全等三角形共有( )对。
2007年陕西初中毕业生学业考试

2007年陕西省初中毕业生学业考试数学模拟试卷(六)班级: 姓名: 座号: 评分:一、 选择题(每小题2分,共20分) 1、︱-32︱的值是( )A 、-3B 、3C 、9D 、-9 2、下列二次根式是最简二次根式的是( ) A 、21B 、8C 、7D 、以上都不是 3、下列计算中,正确的是( ) A 、X 3+X 3=X6B 、a 6÷a 2=a 3C 、3a+5b=8abD 、(—ab)3=-a 3b 34、1mm 为十亿分之一米,而个体中红细胞的直径约为0.0000077m ,那么人体中红细胞直径的纳米数用科学记数法表示为( )A 、7.7×103mm B 、7.7×102mm C 、7.7×104mm D 、以上都不对 5、如图2,天平右盘中的每个砝码的质量为10g ,则物体M 的质量m(g)的取值范围,在数轴上可表示为( )6、如图3,将∠BAC 沿DE 向∠BAC 内折叠,使AD 与A ’D 重合,A ’E 与AE 重合,若∠A =300,则∠1+∠2=( ) A 、500B 、60C 、450D 、以上都不对7、某校九(3)班的全体同学喜欢的球类运动用图4所示的统计图来表示,下面说法正确的是( )A 、从图中可以直接看出喜欢各种球类的具体人数;B 、从图中可以直接看出全班的总人数;C 、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况;D 、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系。
8、下列各式中,能表示y 是x 的函数关系式是( )A 、y=x x -+-12B 、y=x3C 、y=x x21- D 、y=x ±9、如图5,PA 为⊙O 的切线,A 为切点,PO 交⊙O 于点B ,PA =8,OA =6,则tan ∠APO 的值为( )A 、43 B 、53 C 、54 D 、34 10、在同一直角坐标系中,函数y=kx+k ,与y=xk-(k 0≠)的图像大致为( )二、 填空题(每小题2分,共20分)11、(-3)2-(л-3.14)0= 。
2007年数学陕西中考预测试卷13--16

2007年数学中考预测试卷(十三)一、选择题:(每题只有一个正确答案,请将正确答案的字母代号填入答题框内相应题号的下面,不填、填错或填写的答案不只一个都得0分,每题3分,本题满分30分) 1、 下列各组数中,相等的是( )A 、()31-和1 B 、()112--和 C 、()11---和 D 、()112--和2、对有理数230800精确到万位,用科学计数法表示为( )A 、23B 、2.3×105C 、2.31×105D 、2.30×1053、若方程()0422=+--m x m x 的两个实根互为相反数,则m 的值是( )A .0B .2C .-2D .-2或2 4、如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D '、C '的位置,若65EFB ∠=︒,则AED '∠等于( )A 、50︒B 、55︒C 、60︒D 、65︒5、两圆的半径分别为3cm 和4cm ,且两圆的圆心距为7cm ,则这两圆的公切线条数共有( )A 、1条B 、2条C 、3条D 、4条6、已知两个相似三角形的对应中线比为1:3,较大的三角形的周长为18cm ,则较小的三角形的周长为( )A 、6cmB 、2cmC 、9cmD 、63cm 7、在直角坐标系中,函数y= -3x 与y=x 2-1的图象大致是( )A B C D8、为了美化城市,建设中的某休闲广场准备用边长相同的正三角形与正方形两种地转镶嵌地面,在每一个顶点的周围,正三角形、正方形地转的个数分别是( )A 、3,2B 、2,3C 、4,1D 、2、29、在一个V 字形支架上摆放了两种口径不同的试管,如图,是它的轴截面,已知⊙O 1的半径是1,⊙O 2的半径是3,则图中阴影部分的面积是( ) A 、π438- B 、π61134- C 、π234- D 、π31138-10、抛物线c bx ax y ++=2的图象大致如图所示,有下列说法:①000<<>c ,b ,a ;②函数图象可以通过抛物线2ax y =向下平移,再向左平移得到;③直线y =ax +b 必过第一、EBC 'FCD65︒D 'A5题图二、三象限;④直线c ax y +=与此抛物线有两个交点,其中正确的有( )个 A 、1 B 、2 C 、3 D 、4二、填空题:(直接将答案填写在横线上,每题3分,共24分) 11、分解因式:xy y x 2422++-=_________________________. 12、函数312-++=x x y 的自变量x 的取值范围是___________________. 13、请你写出两个图象与x 轴没有公共点的函数解析式(不同类型)___________________. 14、圆锥的母线长为8cm ,底面半径为2cm ,则圆锥的表面积为____________________。
2007年陕西省初中毕业生学业考试

2007年陕西省初中毕业生学业考试数学模拟试卷(十七)(本卷共三个大题,考试时间:120分钟;全卷满分120分)6个小题,每题3分,满分18分)1、-31=2、函数y=2-x 的自变量取值范围是3、观察下列各式:212212+=⨯, 323323+=⨯, 434434+=⨯, 545545+=⨯…想一想,什么样的两数之积等于这两数之和?设n 表示正整数,用关于n 的等式表示这个规律为 4、如果反比例函数y=xk的图象经过点P (-3,1)那么k= 5、如果一个角的补角是1200,那么这个角的余角是6、如图:AB ∥CD ,直线EF 分别交AB 、CD 于E ∠1=720,则∠2= A B 二、选择题:(本大题共8个小题,每小题4分,满分32分)7、下列计算正确的是( ) A 、(-4x 2)(2x 2+3x -1)=-8x 4-12x 2-4x B 、(x+y )(x 2+y 2)=x 3+y 3 C 、(-4a -1)(4a -1)=1-16a 2 D 、(x -2y )2=x 2-2xy+4y 2 8、把x 2-1+2xy+y 2的分解因式的结果是( )A 、(x+1)(x -1)+y(2x+y)B 、(x+y+1)(x -y -1)C 、(x -y+1)(x -y -1)D 、(x+y+1)(x+y -1) 9、已知关于x 的方程x 2-2x+k=0有实数根,则k 的取值范围是( ) A 、k <1 B 、k ≤1 C 、k ≤-1 D 、k ≥110、某电视台举办的通俗歌曲比赛上,六位评委给1号选手的评分如下:90 96 91 96 95 94这组数据的众数和中位数分别是( )A 、94.5,95B 、95,95C 、96,94.5D 、2,9611、面积为2的△ABC ,一边长为x,这边上的高为y,则y 与x 的变化规律用图像表示大致是( )yyyy12、有如下结论(1)有两边及一角对应相等的两个三角形全等;(2)菱形既是轴对称图形又是中心对称图形;(3)对角线相等的四边形是矩形;(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧;(5)两圆的公切线最多有4条,其中正确结论的个数为( )A 、1个B 、2个C 、3个D 、4个13、已知:如图梯形ABCD 中,AD ∥BC ,AB=DC,,AC 与BD 相交于点O ,那么图中全等三角形共有( )对。
2007年中考第二次模拟考试

2007年中考第二次模拟考试理科综合试题B 卷Ⅰ一、选择题21.前几天大兴安岭又发生火灾,灭火飞机满载着灭火剂飞临火场上空,投下灭火剂后,灭火飞机仍以原来的高度和速度匀速飞行,则与投下灭火剂之前相比,飞机的A .动能增加,机械能不变B .动能减少,机械能减少C .动能不变,机械能不变D .动能不变,机械能增加22.演奏同一乐曲时,人能分辨出二胡和钢琴发出的声音,主要是因为它们的A 、响度不同B 、音调不同C 、音色不同D 、节奏不同23.室内温度为20℃,此时用浸有少量酒精的棉花裹在温度计的玻璃泡上,随着酒精的迅速蒸发,下图中哪幅图正确反映了温度计读数随时间的变化24.磁场是一种看不见的特殊物质,我们可以通过磁场对小磁针作用的效果来认识它.这是科学研究的一种常用方法.下列研究实例中不是采用这种研究方法的是A .比较温度的高低,我们可以通过液体受热后体积的变化来认识它B .学习电压,我们可以通过对比水压来认识它C .了解电磁铁磁性的强弱,我们可以通过观察它吸引大头针的多少来认识D .电路是否有电流,我们可以通过观察电路中电流表的指针是否偏转来认识25.如图所示,在探究并联电路中的电流关系时,小明同学用电流表测出A 、B 、C 三处的电流分别为I A =0.4A 、I B =0.2A 、I C =0.2A ,在表格中记录数据后,下一步应该做的是 A .整理器材,结束实验 B .分析数据,得出结论C .换用不同规格的小灯泡,再测出几组电流值D .换用电流表的另一量程,再测出一组电流值26.如图是用来研究凸透镜成像规律的实验装置示意图(屏未画出),当蜡烛和透镜放在图示位置时,通过移动光屏,可以在光屏上得到与物体等大的像。
若透镜位置不变,将蜡烛移到刻度为30cm 处,则A .移动光屏,可以在屏上得到倒立放大的像B .移动光屏,可以在屏上得到倒立缩小的像C .移动光屏,可以在屏上得到正立放大的像D .不论光屏移到什么位置,都不能在屏上得到清晰的像27.知识价值的体现之一是它可以让我们避免许多可以避免的事故。
2007陕西中考题以及答案【各科】

2007陕西中考题以及答案【各科】2007年陕西省中考历史试题第Ⅰ卷(非选择题共16分)13.我国历史上派遣张骞出使西域的是A.秦始皇 B.汉武帝 C.北魏孝文帝 D.唐太宗14.它的作者是贾思勰,它是我国现存的第一部完整的农学著作,在世界农学史上具有重要地位。
它是A.《齐民要术》 B.《水经注》 C.《本草纲目》 D.《天工开物》15.19世纪60~90年代,洋务派以“自强”求富”为口号,开展了洋务运动。
这场运动A.使民主共和观念深人人心B.客观上促进了中国资本主义的产生和发展C.推翻了清朝统治D.使中国富强起来16.抗击外来侵略、捍卫国家 ... 和民族尊严,是中华民族的优良传统。
下列图片所示历史事件,能够体现这一优良传统的是A.武昌起义士兵占领楚望 ... 械库 B.南昌起义C.中国守军在卢沟桥抗击日军 D.人民 ... 占领南京“总统府”17.某校九年级(2)班的同学以“中国共产党历次重要会议”为主题开展探究活动。
他们搜集到这样一则资料:这次会议作出了实行改革开放的战略决策,是我党历史上具有深远意义的伟大转折。
该会议是A.中国共产党第一次全国代表大会 B.遵义会议C.中国共产党第七次全国代表大会 D.中国共产党十一届三中全会18.学完中国现代史后,小华同学得出这样的认识:新中国成立以来,我国的国际地位不断提高。
下列叙述能够体现这一认识的有①在万隆会议上,周恩来总理提出“求同存异”的方针,促进了会议取得圆满成功②1971年,我国恢复在联合国的合法席位③我国在解决国际事务中发挥的作用越来越大④随着我国经济的发展,人民生活开始进入小康水平A.①②③ B.①②④ C.①③④ D.②③④19.某校准备举办“第一次工业革命成果图片展”,下列成果可供选用的有①电子计算机②珍妮机③汽车④“旅行者号”机车A.①② B.①③ C.③④ D.②④20.下列对世界经济全球化的有关叙述,正确的是A.主要表现为世界各国的经济联系日趋密切B.对发展中国家来说,有百利而无一害C.使各国经济互相排斥,孤立发展D.使人类不再面临战争的威胁第Ⅱ卷(非选择题共24分)本卷共7题,计60分。
2007年数学陕西中考预测试卷1--4
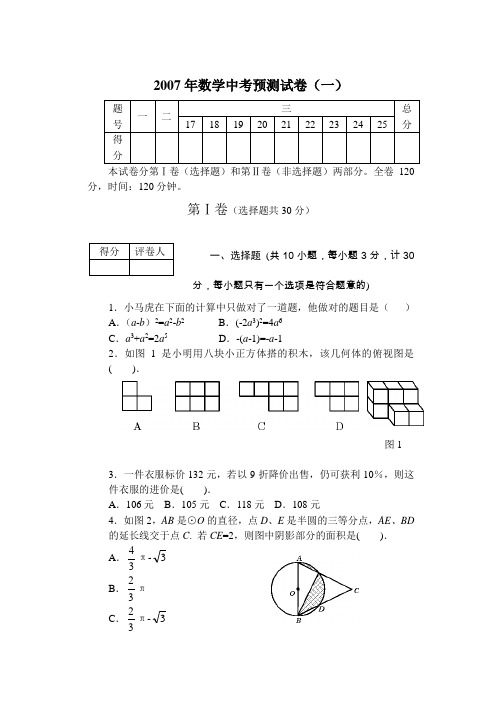
2007年数学中考预测试卷(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷120分,时间:120分钟。
第Ⅰ卷(选择题共30分)一、选择题(共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的)1.小马虎在下面的计算中只做对了一道题,他做对的题目是( ) A .(a -b )2=a 2-b 2 B .(-2a 3)2=4a 6 C .a 3+a 2=2a 5 D .-(a -1)=-a -12.如图1是小明用八块小正方体搭的积木,该几何体的俯视图是 ( ).图13.一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是( ).A .106元B .105元C .118元D .108元4.如图2,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE 、BD 的延长线交于点C . 若CE =2,则图中阴影部分的面积是( ).A .34π-3B .32πC .32π-3D .31π 5.小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽.如图3,圆锥帽底半径为9 cm ,母线长为36 cm ,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为( )A .648π cm 2B .432π cm 2C .324π cm 2D .216π cm 2 图36.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图4),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为( )A .8,8B .8,9C .9,9D .9,8 图4 7.已知矩形的面积为10,则它的长y 与宽x 之间的关系用图象大致可表示为( )A B C D 8.已知二次函数y =ax 2+bx +c 的图象如图5所示,则在“①a <0,②b >0,③c <0,④b 2-4ac >0”中正确的判断是( )A .①②③④B .④C .①②③D .①④ 9.将矩形ABCD 沿AE 折叠,得到如图6所示的图形,已知∠CED =60°,则∠AED 的大小是( )A .60°B .50°C .75°D.55° 10.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则!98!100的值为( ) A .4950 B .99!C .9 900D .2!第Ⅱ卷(非选择题共90分)二、填空题(共6小题,每小题3分,计18分)11.某公司成立3年以来,积极向国家上缴利税,由第一年的200万元增长到800万元,则平均每年增长的百分数是12.不等式3+2x ≤-1的解集是 .13.小芳画一个有两边长分别为5 cm 和6 cm 的等腰三角形,则这个等腰三角形的周长是 . 14.如图6,在边长为a 的正方形中剪去一个边长为b 的小正方形(a >b ),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式 .15.点M 既在一次函数y =-x -2的图象上,又在反比例函数y =-x3(x >0)的图象上,则M 点的坐标是 .16.下图是一组数据的折线统计图,这组数据的极差是 ,平均数是 .三、解答题(共9小题,计72分,解答应写出解题过程)17.(5分)解方程:1+x x +1=xx 22+. 18.(6分)(1)如图7,在方格纸中如何通过平移或旋转置这两种变换,由图形A 得到图形B ,再由图形B 得到图形C ?(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度)(2)如图7,如果点P 、P 3的坐标分别为(0,0)、(2,1),写出点P 2的坐标.(3)图8是某设计师设计图案的一部分,请你运用旋转变换的方法,在方格纸中将图形绕点O 顺时针依次旋转90°、180°、270°,依次画出旋转后所得到的图形,你会得到一个美丽的图案,但涂阴影时不要涂错了位置,否则不会出现理想的效果,你来试一试吧!注:方格纸中的小正方形的边长为1个单位长度.19.(7分)以下是小明本月的流水账:午餐:80元 零食和点心:30元 车费:60元 书籍:35元 水果:10元 文具:5元 看电影:5元 足球:20元 请对小明本月的支出进行分类,再设计一个统计图或统计表来反映他这个月的分类支出情况.从中你获得了哪些信息?20.(8分)某校需要添置某种教学仪器,有两种方案:方案1:到商家购买,每件需要8元;方案2:学校自己制作,每件4元,另外需要制作工具的租用费120元.设需要仪器x件,方案1与方案2的费用分别为y1,y2(元).(1)分别写出y1,y2的函数表达式.(2)当购置仪器多少件时,两种方案的费用相同?(3)需要仪器50件,采用哪种方案便宜?请说明理由.21.(8分)如图,在四边形ABCD中,对角线AC、BD相交于点O,已知∠ADC=∠BCD,AD=BC,求证:BO=CO.22.(8分)有一个抛两枚硬币的游戏,规则是:若出现两个正面,则甲赢;若出现一正一反,则乙赢;若出现两个反面,则甲、乙都不赢.(1)这个游戏是否公平?请说明理由;(2)如果你认为个游戏不公平,那么请你改变游戏规则,设计一个公平的游戏;如果你认为这个游戏公平,那么请你改变游戏规则,设计一个不公平的游戏.23.(本题满分8分)如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于点C,AE⊥CE且交⊙O于点D.求证:(1)DC=BC;(2)BC2=AB·DE.24.(本题满分10分)某自行车厂今年生产销售一种新型自行车,现向你提供以下有关的信息:(1)该厂去年已备有这种自行车车轮10 000只,车轮车间今年平均每月可生产车轮1 500只,每辆自行车需装配2只车轮;(2)该厂装配车间(自行车最后一道工序的生产车间)每月至少可装配这种自行车1 000辆,但不超过1 200辆;(3)该厂已收到各地客户今年订购这种自行车14 500 辆的订货单;(4)这种自行车出厂销售单价为500元/辆.设该厂今年这种自行车的销售金额为a万元.请你根据上述信息,判断a的取值范围是多少?25.(本题满分12分)正方形ABCD的边长为4,P是BC上一动点,QP⊥AP交DC于Q,设PB=x,△ADQ的面积为y.(1)求y与x之间的函数关系式,并写出自变量x的取值范围.(2)(1)中函数若是一次函数,求出直线与两坐标轴围成的三角形面积,若是二次函数,请利用配方法求出抛物线的对称轴和顶点坐标.(3)画出这个函数的图象.(4)点P 是否存在这样的位置,使△APB 的面积是△ADQ 的面积的32,若存在,求出BP 的长,若不存在,说明理由.2007中考数学预测试卷(二)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷120分,时间:120分钟第Ⅰ卷(选择题共30分)一、选择题 (共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的)1.冬季的一天室内温度是8℃,室外温度是-2℃,则室内外温度的差是( )A .4℃B .6℃C .10℃D .16℃2.如图1是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )A .4B .5 C.6 D .73.化简21y xy -+22y x yx -+的结果是( )A .)(1y x y - B .)(1y x y y -+ C.)(1y x y y -- D .)(1y x y +4.如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a 克,再称得剩余电线的质量为b 克,那么原来这卷电线的总长度是( )A .ab 1+米 B .⎪⎭⎫ ⎝⎛+1a b 米C .⎪⎭⎫⎝⎛++1a b a D .⎪⎭⎫⎝⎛+1b a 米5.如图2,⊙O 是△ABC 的外接圆,连接OA 、OC ,⊙O 的半径R =2,sin B =43,则弦AC 的长为( ) A .3B .7 C .23 D .436.小颖的家与学校的距离为s 0千米,她从家到学校先以匀速v 1跑步前进,后以匀速v 2(v 2<v 1)走完余下的路程,共用了t 0小时,下列能大致表示小颖离家的距离y (千米)与离家时间t (小时)之间关系的图象是( )A BCD7.如图3农村常搭建横截面为半圆形的全封闭塑料薄膜蔬菜大棚.如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( ).A .64π m 2B .72π m 2C .78π m 2D .80π m 28.已知抛物线y =2x 2-4x -1,下列说法中正确的是( ) A .当x =1时,函数取得最小值y =3 B .当x =-1时,函数取得最小值y =3C .当x =1时,函数取得最小值y =-3D .当x =-1时,函数取得最小值y =-39.为了美化校园,同学们要在一块正方形空地上种上草,他们设计了图4所示的图案,其中阴影部分为绿化面积,哪个图案的绿化面积与其他图案的绿化面积不相等( ).10.如图5,在□ABCD 中,EF//AB ,GH//AD ,EF 与GH 交于点O ,则该图中的平行四边形的个数共有( ).A .7B .8C .9D .11第Ⅱ卷(非选择题 共90分)二、填空题 (共6小题,每小题3分,计18分)11.如果关于x 的不等式(a -1)x <a +5和2x <4的解集相同,则a 的值为 .125(填“>”、“=”、“<”).13.杏花村现有手机188部,比2004年底的3倍还多17部,则该村2004年底有手机 部.14.若矩形的面积为6,则矩形的长y 关于宽x (x >0)的函数关系式为 .15.小明的身高是1.7 m,他的影长是2 m ,同一时刻学校旗杆的影长是10 m ,则旗杆的高是 m.16.如图,正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上一动点,则DN +MN 的最小值为 .三、解答题(共9小题,计72分,解答应写出过程)17.(5分)用换元法解分式方程:22222=-+-x xx x18.(本题满分6分)如图,作△ABC 的中线AD ,并将△ADC 绕点D 旋转180°,那么点C 与点B 重合,点A 转到A ′点,不难发现AC =A ′B ,AD =A ′D ,BD =DC ,如果知道AB =4 cm ,AC =3 cm,你能求出中线AD 的范围吗?19.(8分)甲乙两人掷一对骰子,若甲掷出的点数之和为6,则加一分,否则不得分;乙掷出的点数之和为7,则加一分,否则不得分;甲、乙各掷骰子10次,得分高者胜.(1)请用列表法求出甲获胜的概率;(2)这个游戏公平吗?若公平,说明理由;如果不公平,请你修改规则,使之公平.20.(8分)等腰梯形ABCD中,AD//BC,∠DBC=45°,翻折梯形ABCD,使点B 重合于点D,折痕分别交边AB、BC于点F、E.若AD=2,BC=8.求(1)BE的长;(2)∠CDE的正切值.21.(8分)如图1-6-16,l1、l2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(小时)的函数图象,假设两种灯的使用寿命都是2 000小时,照明效果一样.(1)根据图象分别求出l1、l2的函数关系式;(2)当照明时间为多少时,两种灯的费用相等?(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).22.(9分)某研究性学习小组,为了了解本校初一学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分钟),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:(1)这个研究性学习小组所抽取样本容量是多少?(2)在被调查的学生中,一天做家庭作业所用的大致时间超过.120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几?(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?23.(9分)已知某山区的平均气温与该山区的海拔高度的关系见下表:(1)若海拔高度用x(米)表示,平均气温用y(℃)表示,试写出y与x之间的函数关系式;(2)若某种植物适宜生长在18℃~20℃(包括18℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?24.(10分)已知:如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,在射线P A上截取PD=PC,连接CD,并延长交⊙O于点E.(1)求证:∠ABE=∠BCE;(2)当点P在AB的延长线上运动时,判断sin∠BCE的值是否随点P 位置的变化而变化,提出你的猜想并加以证明.25.(9分)在△CDE 中,∠C =90°,CD ,CE 的长分别为m ,n ,且DE ·cos D =cot E.(1)求证m 2=n ;(2)若m =2,抛物线y =a (x —m )2+n 与直线y =3x +4交于A (x 1,y 1)和B (x 2,y 2)两点,且△AOB 的面积为6(O 为坐标原点),求a 的值;(3)若是k 2=2mn,c +l-b =0,抛物线y =k (x 2+bx +c )与x 轴只有一个交点在原点的右侧,试判断抛物线与y 轴的交点在y 轴的正半轴还是负半轴,并证明你的结论.2007年中考数学预测试卷(三)本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共20分)注意事项:1.答卷I 前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回. 2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效. 一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.绝对值为4的实数是A .±4B . 4C .-4D . 22.下图是由一些相同的小正方体构成的几何体的三视图.这些相同的小正方体的个数是A .4个B .5个C .6个D .7个3.把不等式组110x x +⎧⎨-≤⎩>0 ,的解集表示在数轴上,正确的是A B C D 4.化简32()()x x --,结果正确的是A .6x -B .6x C .5x D .5x - 5.小明设计了一个关于实数运算的程序:输出的数比该数的平方小1,小刚按此程序输入A .10B .11C .12D .13 6.如图1,把一个正方形纸片三次对折后沿虚线剪下,打开铺平后,得到的图形是沿虚线剪开上折右折右下方折图1主视图 左视图 俯视图-1 -17.甲(#),乙(●),丙(■)表示的是三种不 同的物体,现用天平称了两次,如图2所示,那 么这三种物体按质量从大到小的顺序应是 A . 甲 乙 丙 B .乙 甲 丙C . 甲 丙 乙D .丙 乙 甲8.图3所示的两个圆盘中,指针落在每 一个数字所在的扇形区域上的机会是相 等的,那么两个指针同时落在偶数所在 的扇形区域上的概率是A .525 B .625 C .1025 D .19259.⊙O 1与⊙O 2的半径分别为2和5,当O 1O 2=3.5时,两圆的位置关系是A . 外切B .相交C . 内切D . 内含 10.若弹簧的总长度y (cm )是所挂重物x (千克)的一次函数, 图象如图4所示,由图可知,不挂重物时,弹簧的长度是 A .10cm B .9cm C .8. 5m D .7cmC A DB 图2图卷II (非选择题,共100分)注意事项:1.答卷II 前,将密封线左侧的项目填写清楚.2.答卷II 时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共5个小题;每小题3分,共15分.把答案写在题中横线上)11.分解因式2221x xy y -+-=.12.函数y =x 的取值范围是 . 13.如图5是用4个全等的等腰梯形镶嵌成的图形,则这个图形中等腰梯形上下两底边的比是 .14.用换元法解分式方程22301x x x x -++=-时,若设1xy x =-,则由原方程化成的关于y 的整式方程为 .15.如图6,一牧童在A 处牧马,牧童家在B 处,A ,B 处距河岸的距离AC ,BD 分别为500m 和700m ,且CD =500m ,天黑前牧童从A 处将马赶到河边去饮水后再回家,那么牧童最少要走 m .三、解答题(本大题共10个小题;共85分)图516.(本小题满分7分)已知:a=2,求(1+11a)·(a2-1)值.17.(本小题满分7分)如图7,小丽在观察某建筑物AB.(1)请你根据小亮在阳光下的投影,画出建筑物AB在阳光下的投影.(2)已知小丽的身高为1.65m,在同一时刻测得小丽和建筑物AB的投影长分别为1.2m和8m,求建筑物AB的高.试试基本功解答应写出文字说明、证明过程或演算步骤.请你一定要注意噢!图718.(本小题满分7分)观察右表中数字的排列规律,回答下面的问题①表中第1行第5列的数字是;②表中第5行第4列的数字是;③请用关于n的代数式表示表中第3列第n行的数为;④数字2006的位置是第行,第列.19.(本小题满分8分)个商场本周内总的获利情况;(2)在图8所示的网格图内画出两个商场每天归纳与猜想表中有规律!判断与决策星期日获利的折线图;(甲商场用虚线,乙商场用 实线)(3)根据折线图请你预测下周一哪个商场的获利会多一些?并简单说出你的理由.20.(本小题满分8分)某少儿活动中心在“六·一”活动中,举行了一次转盘摇奖活动.如图9是一个可以自由转动的转盘,当转动停止时,指针落在哪一个 区域就可以获得相应的奖品(落在分界线上时重新摇奖).下表是活动 进行中统计的有关数据. (1)计算并完成表格:(2)当转动转盘的次数n 很大时,概率将会接近多少? 图象与信息期一期二期三期四期五期六期日日期/天 图8图921.(本小题满分8分)某市自来水公司为鼓励居民节约用水,采取每月 用水量分段收费的办法,每户居民应交水费y (元) 与用水量x (吨)之间的函数关系如图10所示.(1)分别求出当0≤x ≤15和x ≥15时,y 与x 的函数关系式;(2)若一用户在某月的用水量为21吨,则应交水费多少元?22.(本小题满分8分)如图11—1,在△ABC 中,∠C=90°,AC =4,BC =3,四边形DEFG为△ABC 的内接正方形,若设正方形的边长为x ,容易算出x 的长为6037. 探究与计算:(1)如图11—2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC ,则正方形的边长为 ; (2)如图11—3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC ,则正方形的边长为 .猜想与证明:如图11—4,若三角形内有并排的n 个全等的正方形,它们组成的矩形内接于△ABC ,请你猜想正方形的边长是多少?并对你的猜想进行证明.操作与探究图11—1AD图11—2CDE23.(本小题满分8分)阅读理解:如图12—1中的△ABC 是直角三角形,∠C =90º.现将△ABC 补成矩形,使△ABC 的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合条件的矩形可以画出两个,如图12—2所示.解决问题:(1)设图12—2中的矩形ACBD 和矩形AEFB 的面积分别为S 1和S 2,则S 1 S 2(填“>”,“=”或“< ”;(2)如图12—3中的△ABC 是锐角三角形,且三边满足BC >AC >AB ,按短文中的要求把它补成矩形,那么 符合要求的矩形可以画出 个,并在图12—3中 把符合要求的矩形画出来. 猜想证明:实验与推理 BEB图12—1 ABC图12—3(1)在图12—3中所画出的矩形中,它们的面积之间具有怎样的关系?并说明你的理由;(2)猜想图12—3中所画的矩形的周长之间的大小关系.某商店经营一批进价为2综合与应用元的小商品,在市场营销的过程中发现:如果该商品按最低价3元销售,日销售量为18件,如果单价每提高1元,日销售量就减少2件.设销售单价为x(元),日销售量为y(件).(1)写出日销售量y(件)与销售单价x(元)之间的函数关系式;(2)设日销售的毛利润(毛利润=销售总额-总进价)为P(元),写出毛利润P(元)与销售单价x(元)之间的函数关系式;(3)在图13所示的坐标系中画出P关于x的函数图象的草图,并标出顶点的坐标;(4)观察图象,说出当销售单价为多少时,日销售的毛利润最高?是多少?25.(本小题满分12分)有一根直尺的短边长2cm ,长边长10cm ,还有一块锐角为45°的直角三角形纸板,其中直角三角形纸板的斜边长为12cm .按图14—1的方式将直尺的短边DE 放置在与直角三角形纸板的斜边AB 上,且点D 与点A 重合.若直尺沿射线AB 方向平行移动,如图14—2,设平移的长度为x (cm ),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S cm 2).(1)当x =0时,S =_____________;当x = 10时,S =______________; (2)当0<x ≤4时,如图14—2,求S 与x 的函数关系式; (3)当6<x <10时,求S 与x 的函数关系式;(4)请你作出推测:当x为何值时,阴影部分的面积最大?并写出最大值.(说明:问题(4)是额外加分题,加分幅度为1~4分)2007年中考数学预测试卷(三)参考答案及评分标准图14—1(D)A备选图一BA BC备选图二一、选择题(每小题2分,共20分)二、填空题(每小题3分,共15分)11.(1)(1)x y x y -+--; 12.x ≥2; 13.1∶2; 14.2320y y ++=; 15.1300.三、解答题(本大题共10个小题,共80分) 16.解:原式=1-a a(a +1)(a -1)=a (a +1)=a 2+a . ……………………………(4分)当a =2时,原式=a2+a =22+2=6.………………………………………………(7分) 17.解:(1)如图1;………………………………………………………………………(3分)(2)如图1,∵DE ,AF 都垂直于地面,且光线DF ∥AC ,∴Rt △DEF ∽Rt △ABC . ∴DE EFAB BC=.∴.28AB =. ∴AB =11(m ).即建筑物AB 的高为11m . ………(7分)18.答:①9;②112;③152n -⨯(n ≥1的整数);④2,502. ………………………(7分)19.解:(1)x 甲=1(2.5 2.4 2.83 3.2 3.5 3.6)37⨯++++++=(万元);x乙=1(1.9 2.3 2.7 2.634 4.5)37⨯++++++=(万元); ……………………(2分)图1 F E甲、乙两商场本周获利都是21万元; ……………………………………(4分)(2)甲、乙两商场本周每天获利的折线图如图2所示:…………………………………(6分)(3)从折线图上看到:乙商场后两天的销售情况都好于甲商场,所以,下周一乙商场获利会多一些. ………………………………………………………(8分)20.解:(1)填写下表:……………………………………………………………………(6分)(2)当转动转盘的次数n 很大时,概率将会接近0.70.………………………(8分)21.解:(1)由图象可知:当0≤x ≤15时,y 是x 的正比例函数,设y =kx .∵点A (15,27)在函数y =kx 的图象上,∴27=15k .∴k =95. ∴当≤x≤15时,95y x =.………………………………………………(2分)当x ≥15时,y 是x 的一次函数,设y =kx +b . ∵点A (15,27),B (20,39.5)在函数y =kx +b 的图象上,∴2715,39.520.k b k b =+⎧⎨=+⎩解得 2.5,10.5.k b =⎧⎨=-⎩期一期二期三期四期五期六期日日期(天)图2∴当x ≥15时,2.y x =-. …………………………………………(5分)(2)若一用户在某月的用水量为21吨,即x =21>15.将x =21代入 2.510.5y x =-得y =42(元).∴该用户在某月的用水21吨,应交水费42元.…………………………(8分) 22.解:(1)6049; …………………………………………………………………………(2分)(2)6061. …………………………………………………………………………(4分)若三角形内有并排的n 个全等的正方形,它们组成的矩形内接于△ABC ,正方形的边长是602512n +.………………………………………………………(6分)证明如下:如图3,过点C 作CN ⊥AB ,垂足为N ,交GF 于点M .设小正方形的边长为x . ∵四边形GDEF 为矩形,∴GF ∥AB .CM ⊥GF .容易算出125CD =. ∴CM GF CN AB =.即1251255xnx -=.∴x =602512n +. 即小正方形的边长是602512n+. …………………………………………(8分)23.解决问题:(1)=;………………………………………………………………………………图3DE N(2分)(2)3,…………………………………………(3分) 符合要求的矩形如图4所示.……………(4分)猜想证明: (1)图4中画出的矩形BCED 、矩形ABEG 和矩形AHIC 的面积相等. 理由:这三个矩形的面积都等于△ABC 面积的2倍. …………………………………………………(6分)(2)以AB 为边的矩形的周长最短,以BC 为边的矩形的周长最长.……………………………(8分)24.解:(1)182(y =-3分)(2)(2)(P x =-即22P x =-+(3)图象如图5所示;………………(9分) (4)观察图象可知,当销售单价为7元时,日销售的毛利润最高,是50元.(12分)25.解:(1)2,2;…………………………………………………………………………(4分)(2)2211(2)2222S x x x =+-=+,即图5A BC 图4D EFG H I22S x =+; …………………………(8分)(3)2211(12)(10)22222S x x x=---=-,即22S x =-; ………………(12分)(4)当x =5时,面积最大.……………………………………………………(加2分) 最大面积为11. …………………………………2007年中考数学预测试卷(四)本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共20分)注意事项:1.答卷I 前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回. 2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.计算2(3) ,结果正确的是A .-9B . 9C .-6D . 62.图1是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是3.一个盒子中装有标号为1,2,3,4的四张卡片,采用有放回的方式取出两张卡片,下列事件中,是必然事件的是A .和为奇数B .和为偶数C .和大于5D .和不超过8 4.如图2,数轴上点A ,B ,C ,D 表示的数中, 表示互为相反数的两个点是 A .点A 和点C B .点B 和点C C .点A 和点D D .点B 和点D 5.“神舟”五号载人飞船,绕地球飞行了14圈,共飞行约590200km ,用科学记数法表示590200,结果正确的是A .5.902×104B .5.902×105C .5.902×106D .0.5902×1066.如图3,在宽为20m ,长为30m 的矩形地面上修建两条 同样宽的道路,余下部分作为耕地.根据图中数据,耕地 的面积应为A .600m 2B .551m 2C .550 m 2D .500m 2图1A B C D图2 DA C 图37.如图4,两个正方体形状的积木摆成如图所示的塔形平放 于桌面上,上面正方体下底的四个顶点恰好是下面相邻正 方体的上底各边的中点,并且下面正方体的棱长为1,则能 够看到部分的面积为A .8B .172C .182D .78.方程(3)3x x x +=+的解是A .1x =B .10x =,23x =-C .11x =,23x =D .11x =,23x =-9.如图5,⊙O 的半径OA =6,以点A 为圆心,OA 为半径的弧交 ⊙O 于B ,C 两点,则BC 等于A. B. C. D.10.甲、乙两同学从A 地出发,骑自行车在同一条路上行驶到B 地,他们离出发地的距离s (千米)和行驶时间t (小时)之间的函数关系的图象如图6所示,根据图中提供的信息,有下列说法: (1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发了0.5小时;(4)相遇后,甲的速度小于乙的速度; (5)甲、乙两人同时到达目的地. 其中,符合图象描述的说法有A .2个B .3个C .4个D .5个t (小时) 图6图4图5卷II (非选择题,共100分)注意事项:1.答卷II 前,将密封线左侧的项目填写清楚.2.答卷II 时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共5个小题;每小题3分,共15分.把答案写在题中横线上)114的相反数是.12.如图7,有两棵树,一棵高10m ,另一棵高4m ,两树相距 8m .一只小鸟从一棵树的树尖飞到另一棵树的树尖,那么这只小鸟至少要飞行 m .13.某商店购进一批运动服,每件的售价为120元时,可获利20%,那么这批运动服的进价为是 .14.如图8,△ABC 是等腰直角三角形,BC 是斜边,点P 是 △ABC 内一定点,延长BP 至P /,将△ABP 绕点A 旋转后, 与△ACP /重合,如果AP =2,那么PP /= .15.图9是小明用火柴搭的1条、2条、3条“金鱼”……, 则搭n 条“金鱼”需要火柴 根.图`7 图81条2条3条图9……三、解答题(本大题共10个小题;共85分)16.(本小题满分7分)已知:13x=,求22()111x x xx x x-÷---的值.17.(本小题满分7分)(1)一木杆按如图10—1所示的方式直立在地面上,请在图中画出它在阳光下的影子(用线段CD表示);(2)图10—1是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点P表示);并在图中画出人在此光源下的影子(用线段EF表示).试试基本功解答应写出文字说明、证明过程或演算步骤.请你一定要注意噢!木杆图10—1 图10—218.(本小题满分7分)观察下面的图形(大正方形的边长为1)和相应的等式,探究其中的规律:①11122=-,②221111222+=-,③233111112222++=-,④234411111122222+++=-,(1)在下面的空格上写出第五个等式,与之对应的图示;(2)猜想并写出与第n个图形相对应的等式.19.(本小题满分8分)某电视台的娱乐节目有这样的翻奖游戏,正面为数字,背面写有祝福语或奖金数,如下面的表格.游戏的规则是:参加游戏的人可随意翻动一个数字牌,看背面对应的内容,就可以知道是得奖还是得到祝福语.归纳与猜想表中有规律!判断与决策……(1)写出“翻到奖金1000元”的概率; (2)写出“翻到奖金”的概率; (3)写出“翻不到奖金”的概率.20.(本小题满分8分)某学校为选派一名学生参加全市劳动技能竞赛,准备从A ,B 两位同学中选定一名.A ,B 两位同学在学校实习基地进行现场加工直径为20mm 的零件的测试,他俩各加工的10个零件的相关数据如图11和下面的表格所示(单位:mm ).根据测试得到的有关数据,请解答下面的问题: (1)考虑平均数与完全符合要求的零件的个数,你认为 的成绩好些; (2)计算出2B S 的大小,考虑平均数与方差,你认为的成绩好些;(3)根据折线图的走势,你认为派谁去参赛较合适?说明你的理由.B(件数) 图11 A。
陕西省2007年初中毕业学业考试(答案)

陕西省2007年初中毕业学业考试数学答案及评分参考第I 卷(选择题 共30分)一、选择题(共10小题,每小题3分,计30分) 题号 1 2 3 4 5 6 7 8 9 10 A 卷答案 A C D D C C B A B C B 卷答案CCABDBAACB第错误!未找到引用源。
卷(非选择题 共90分)二、填空题(共6小题,每小题3分,共18分) 11.33x y - 12.B 13.115°(填115不扣分) 14.(1)0.433(2)90.6 15.21 16.21 17.解:当A B =时,23111x x x =+--.311(1)(1)x x x x =+-+-. ···························································································· 1分 方程两边同时乘以(1)(1)x x +-,得(1)3(1)(1)x x x x +=++-. ························································································ 2分 2231x x x +=+-.2x =. ························································································································ 3分检验:当2x =时,(1)(1)30x x +-=≠.2x =∴是分式方程的根.···························································································· 4分 因此,当2x =时,A B =. ························································································ 5分18.解:(1)画图正确得4分.(2)最长线段的长是65个单位. ············································································· 6分 (第18题答案图)D ABCA 'B 'C 'D 'O19.(1)证明:90ACB ∠= ,C D C 是AB 边上的中线,C D A D D B ∴==. ···································································································· 1分30B ∠=,60A ∴∠=. ·············································································································· 2分 A C D ∴△是等边三角形. ···························································································· 3分C E 是斜边AB 上的高,AE ED ∴=. ·············································································································· 4分 (2)解:由(1)得2A C C D A D E D ===,又2A C =,21C D ED ∴==,. ··································································································· 5分 2213CE ∴=-=. ······························································································· 6分 C D E ∴△的周长21333C D ED C E =++=++=+. ·········································· 7分20.解:(1)这组数据的平均数:2932343382482553910++⨯+⨯+⨯+=;··········· 3分这组数据的中位数:3438362+=;············································································· 4分这组数据的众数是:34.····························································································· 5分 (2)这个目标可以定为每月39万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最大,可以认为,月销售额定为每月39万元是一个较高目标. ············ 8分 (说明:如果把中位数、众数作为月销售额目标,可以给1分,把其它数据作为月销售额目标不给分). 21.解:(1)证明:45AB D C D A AB B ⊥∠=∵∥,,°, 135C D A D E ∠=⊥∴°,. ························································································ 1分 又D E D A =∵,45E ∠=∴°. ············································································································· 2分 180C E ∠+∠=∴°. ·································································································· 3分 A E B C ∴∥. ············································································································· 4分(2)解:A E B C C E A B ∵∥,∥,∴四边形A B C E 是平行四边形. ·················································································· 5分3C E A B ==∴.2D A D E C E C D ==-=∴. ····················································································· 6分326ABCES C E AD ==⨯=∴·. ················································································ 7分22.解:(1)设y 与x 的函数关系式为y kx b =+, ····················································· 1分由题意,得2100180028002300k b k b +=⎧⎨+=⎩,, ··················································································· 3分解之,得57300k b ⎧=⎪⎨⎪=⎩,.······································································································· 5分 y ∴与x 的函数关系式为53007y x =+. ···································································· 6分 (2)当5600x =时,5560030043007y =⨯+=元. ················································ 7分 ∴王老师旅游这条线路的价格是4300元. ··································································· 8分 23.(1)证明:A C ∵是O 的切线,AB 是O 直径,A B A C ⊥∴.则1290∠+∠=°. ······································································································ 1分 又O C AD ⊥∵,190C ∠+∠=∴°. ····································································································· 2分2C ∠=∠∴. ············································································································· 3分而2BED ∠=∠,BED C ∠=∠∴. ······································································································· 4分(2)解:连接BD . A B ∵是O 直径,90A D B ∠=∴°.22221086BD AB AD =-=-=∴.…………5分O AC BD A ∴△∽△. ……………………………6分 ::O A BD AC D A =∴.即5:6:8A C =.……………………………………7分203A C =∴. ………………………………………8分24.解:(1)过点C 作C E O D ⊥于点E ,则四边形O B C E 为矩形. 8C E O B ==∴,1O E B C ==. 22221086DE CD CE=-=-=∴.7O D D E O E =+=∴.C D ∴,两点的坐标分别为(81)(07)C D ,,,.…………4分(2)P C P D ⊥∵, 1290∠+∠=∴°. 又1390∠+∠=°,23∠=∠∴.R t R t PO D C BP ∴△∽△.::P O C B O D B P =∴.即:17:(8)PO PO =-.2870PO PO -+=∴. 1P O =∴,或7P O =.CAOBED(第23题答案图)1 2DCBPOy x(第24题答案图)1 2E3∴点P 的坐标为(10),,或(70),. ··············································································· 6分 ①当点P 的坐标为(10),时,设经过D P C ,,三点的抛物线表达式为2y ax bx c =++, 则706481c a b c a b c =⎧⎪++=⎨⎪++=⎩,,.∴2528221287a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,,.∴所求抛物线的表达式为:22522172828y x x =-+. ···················································· 9分 ②当点P 为(70),时,设经过D P C ,,三点的抛物线表达式为2y ax bx c =++, 则749706481c a b c a b c =⎧⎪++=⎨⎪++=⎩,,.∴141147a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,,.∴所求抛物线的表达式为:2111744y x x =-+.························································10分(说明:求出一条抛物线表达式给3分,求出两条抛物线表达式给4分)25.解:(1)答案不唯一,如图①、②(只要满足题意,画对一个图形给2分,画对两个给3分)····································································································································· 3分 (2)过点A B ,分别作C D 的垂线,垂足分别为M N ,.11sin 22A C D S C D A M C D A E α==△∵···,AABBCCDOO(第25题答案图①) (第25题答案图②)11sin 22B C D S C D B N C D B E α==△···. ······································································ 5分 AC D BC D AC BD S S S =+△△四边形∴11sin sin 22C D A E C D B E αα=+····1()sin 2C D A E B E α=+·· 1sin 2C D A B α=··21sin 2m α=. ······································ 7分 (3)存在.分两种情况说明如下: ············································································· 8分 ①当AB 与C D 相交时, 由(2)及2AB CD R ==知21sin sin 2A CB D S ABCD R αα==四边形··. ···················· 9分②当AB 与C D 不相交时,如图④. 2AB CD R ==∵,O C O D O A O B R ====,90A O B C O D ∠=∠=∴°,而R t R t AO B O C D AO D BO C ABC D S S S S S =+++△△△△四边形2A O DB OC R S S =++△△.……………………………………10分延长B O 交O 于点E ,连接E C ,则132390∠+∠=∠+∠=°.12∠=∠∴.AO D C O E ∴△≌△.AO D O C E S S =△△∴.AOD BOC OCE BOC BCE S S S S S +=+=△△△△△∴.过点C 作C H B E ⊥,垂足为H , 则12B C E S B E C H R C H ==△··.∴当C H R =时,B C E S △取最大值2R . ······································································ 11分综合①、②可知,当1290∠=∠=°,即四边形A B C D 是边长为2R 的正方形时, 2222ABCD S R R R =+=四边形为最大值. ·······································································12分A CBD OMEN α(第25题答案图③)(第25题答案图④)132OBCE HAD。
2007年初中毕业暨升学考试模拟测试二

2007年初中毕业暨升学考试模拟测试㈡数 学 试 题注意事项:⒈本卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间为120分钟;⒉第Ⅰ卷的答案须填在第Ⅱ卷卷首“第Ⅰ卷答题卡”中,填在其它地方无效..; ⒊可以使用规定的计算器.第 Ⅰ 卷 ( 36分 )一、选择题(本大题共12题,每题3分,共36分.每题的四个选项中,只有一个选项是符合要求的,请将正确选项的代号字母填入第Ⅱ卷的选择题答题卡中,写在本试卷上无效) ⒈ 下列计算正确的是 A .a+2a 2=3a 2B .a 3-a 2=aC .(a 3)2=a 9D .a 3÷a 4=a -1(a ≠0)⒉ 当x =-2时,代数式122-+-x x 的值等于 A .9B .1C .-9D .-1⒊ 如果反比例函数xky =的图象经过点(-2,-1)和(4,b ),那么b 的值为 A .21 B .-21C .2D .-2⒋ 现有边长相等的正三角形、正方形、正六边形、正八边形形状的地砖,如果选择其中的两种铺满平整的地面,那么选择的两种地砖形状不能是下面的 A .正三角形和正方形 B .正三角形和正六边形 C .正方形和正六边形D .正方形和正八边形⒌ 不等式组⎪⎩⎪⎨⎧-≤--.,>x x x 28432的最小整数解是 A .-1B .0C .1D .4⒍ 如果圆锥的侧面积为20πcm 2,它的母线长为5cm ,那么此圆锥的底面半径的长等于 A .2cmB .22cmC .4cmD .8cm⒎如果a 为自然数,那么“a 2>2×a ”这一事件是 A .必然事情 B .随机事情C .不可能事情D .发生的可能性为0.5⒏ 把抛物线c bx x y ++=2向左平移2个单位,再向上平移3个单位,得到抛物线122+-=x x y ,则A .b=2,c=-2B .b=-6,c=6C .b=-8,c=14D .b=-8,c=18⒐ 三角形在正方形网格纸中的位置如图所示,则sinα的值是 A .43B .34C .53D .54 ⒑ 数据-2003,-2004,-2005,-2006,-2007的标准差为 A .-2B .2C .-2D .2⒒ 在如图的网格纸中,每个方格的边长均为1,互相垂直的直线的交点(如A 、B 、C 、D )叫做格点.则图中到AB 和CD 所在直线的距离相等的格点的个数为 A .2B .3C .4D .5 ⒓ 有人要上楼,此人每步能向上走1阶或2阶,如果楼梯有6阶,他不同的走法共有 A .12种 B .13种 C .14种 D .以上都不对ABCDα第9题图第11题图2007年初中毕业暨升学考试模拟测试㈡数 学 试 题第Ⅰ卷选择题答题卡第 Ⅱ 卷 ( 114分 )二、填空题(本大题共6题,每题4分,共24分.请把答案直接填在题中的横线上)⒔ 铁道部第六次全国铁路大提速于本月18日正式施行,其中时速250公里线路延展里程多达846公里,列车在此路段的运行时间压缩了24%,那么此次提速前列车在此路段运行的平均速度为________________公里/时.⒕ 两个同心圆的面积分别为8cm 2,18cm 2,则圆环的宽度(两半径之差)为________cm . ⒖ 如图,小正方形边长为1,则△ABC 中 AC 边上的高等于_____________.⒗ 袋子中原有10个除颜色外都相同的球,其中3白7红,现向其中放入______________,可使从袋子中任意摸出2个球,这两个球都是白球的概率为335. ⒘ 如图,点P 是边长为1的菱形ABCD 的对角线AC 上一个动点,点M 、N 分别是AB 、BC 边上的中点,MP+NP 的最小值是_______.⒙ cot22.5°的函数值等于_______________.(结果不取近似值,可含根号)第14题图B N MP DCAABC第15题图第17题图8题,共90分.解答应写出文字说明、证明过程或演算步骤)19.(本题满分8分)计算:1-.21122aaaaa+-÷-20.(本题满分10分)为美化环境,某小区有一块面积为40m2的等腰三角形草地,测得其一边长为10m,现要给这块三角形草地围上防护栅栏,则防护栅栏的长度至少为多少m?(不要求取近似值)21.(本题满分10分)如图,在△ABC中,∠ACB是直角,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.⑴设∠ABC=m°(0<m<90),试用m的代数式表示∠AFE的度数;⑵请你给△ABC再添加一个条件,使FE与FD的长度相等,并予以证明;⑶在⑵中,你认为“∠ACB是直角”的条件是否可以略去?直接判断,不必说明理由.22.(本题满分12分)现有一根长度为37cm 的铁丝.⑴从中截取长度分别为xcm ,xcm ,(x+1)cm 的3根铁丝,求x 的取值范围; ⑵你能在这根铁丝上截取4根长度都为整数的铁丝,使这4根铁丝中任意3根都不能构成一个三角形吗? (允许有剩余)若能,请写出你的一种截法.⑶如果要在这根铁丝上截取若干根长度都为整数的铁丝,使这些铁丝中任意3根都不能构成一个三角形(允许有剩余),那么你至多能截取多少根?请写出你的一种截法.23.(本题满分12分)有一块直角三角形铁皮,两条直角边长分别为30cm 和40cm ,现需在其内部裁出一块面积尽量大的矩形铁皮ABCD ,在分割时,小明和小亮的意见出现了分歧.⑴小明想利用图①的分割方法,设矩形铁皮的一边AB=xcm . ①AD 边的长度如何表示?②当x 取何值时,矩形铁皮的面积最大?最大值是多少?⑵小亮建议利用图②的分割方法,他认为能裁出面积更大的矩形铁皮,你认为他的想法能否实现?为什么?图① 图②24.(本题满分12分)北京奥组委将分三个阶段向境内公众销售门票.2007年4月至9月为第一阶段,其核心销售政策是“公开认购、抽签确认”.4月15日至6月30日为申购期, 公众可以通过登录北京奥运会官方票务网站或提交纸质订单预订门票. 7至8月票务系统将对全部有效门票预订单进行统计并对申购数量大于售票数量的场次采用电脑抽签系统进行门票分配,在抽签系统中特别设计了一个程序,假设某人订购某档的门票没有被抽中,计算机系统会自动把他的订单降至下一个价格档再次参与抽签,直至最低档.开幕式门票分为A、B、C、D、E五个档次,票价分别为人民币5000元、3000元、1500元、800元和200元.已知境内可售开幕式门票有A档2000张、B档4000张、C档8000张、D档10000张、E档16000张.假设所有境内可售开幕式门票均由100个门票代售网点代售.某网点第一周内开幕式门票的销售情况如图.⑴第一周售出的门票票价的众数和中位数各是多少元?由此能反映什么问题?⑵假设每周所有网点售票情况大致相同.张老师申购了1张A 档门票,试问张老师是否需通过电脑抽签才能分配到A 档门票?若需要,他分配到A 档门票的概率大约是多少?(精确到1%)⑶在⑵的假设下,王老师打算下周申购1张B 档门票,他分配到B 档门票的可能性有多大?⑷你认为⑵、⑶的估计是否合理?为什么?档(元) 数量(张)第一周开幕式门票销售情况统计图24 6 8 1012 5000 (数据来源:/) 3000 1500 800 20025.(本题满分12分)在Rt △ABC 和Rt △A ′B ′C ′中,∠ACB=∠A ′C ′B ′=90°. ⑴如图1,分割线CD 将Rt △ABC 分割成两个三角形△ADC 和△BDC ,且满足∠BCD=∠B ′.试在Rt △A ′B ′C ′的内部也作一条类似的分割线,使这条分割线把Rt △A ′B ′C ′分得的两个三角形分别与△ADC 和△BDC 相似,并说明你画法的正确性(作图工具不限,下同);⑵请在图2中画出与图1中不同的两条分割线,使得Rt △ABC 被分得的两个三角形与Rt △A ′B ′C ′被分得的两个三角形分别相似(直接画出分割线,写出相似三角形,不必说明理由);⑶如图3,已知任意△ABC 和△A ′B ′C ′,试分别在△ABC 和△A ′B ′C ′中画1条或两条分割线,使得△ABC 被分得的若干个三角形分别与△A ′B ′C ′被分得的若干个三角形相似(直接画出分割线,相等的角分别在图中用∠1、∠1′,∠2、∠2′,∠3、∠3′,……对应地标明,并写出所有相似三角形,不必说明理由).⑷由上面的操作,你得到什么一般性的经验?A B C C ′A ′B ′ 图1 AB C C ′A ′B ′ 图2A B C B ′C ′ A ′ 图3如图①,在矩形ABCD中,AB=10cm,BC=8cm.点P从点A出发,沿A→B→C→D 路线向点D运动,到达点D后停止;点Q从点D出发,沿D→C→B→A路线向点A运动,到达点A后停止.若点P、Q同时出发,点P的速度为1cm/s,点Q的速度为2cm/s,as时点P、Q同时改变速度,点P的速度变为bcm/s,点Q的速度变为dcm/s.图②、图③分别是点P、Q出发xs后△APD的面积S1(cm2)、△AQD的面积S2(cm2)与x(s)的关系图象.⑴仔细观察图象,求a、b、c、d的值;⑵当x为何值时,点P、Q相遇?⑶如果点P、Q分别为半径都是1cm的⊙P、⊙Q的圆心,那么在运动过程中,当x为何值时,⊙P和⊙Q相切?请说明理由.(图④仅供参考)④。
2007年第二次中考模拟考试

2007年第二次中考模拟考试数学试卷命题人:吉安县文山学校王辉明(说明:本卷共有六个大题,25个小题,全卷满分120分,考试时间120分钟.)一、填空题(本大题共10小题,每小题3分,共30分)1.计算:(—2)×(—3)=_________________。
2.如图,在△ABC中,D是AC延长线上一点,∠A=______度。
3.化简:2 —12=_______________。
4.图中是国光超市学生计算器的价格标签,请你横线上填出它的原价。
5.在压力不变的情况下,某物体当它的受力面积S为0.1m2时,所受的压强P为1000pa,则P与S的函数关系式为_________________。
6.抛物线y=x2—4的顶点坐标为________________。
7.已知(m—3)2=3—m,试写一个符合等式中m的值_________。
8.如图,圆与数轴相切于点A(A与坐标原点O重合),B、C为圆上的点,∠ACB=60°,若圆沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则数轴上与点B重合的点对应的实数是___________。
9.已知如图,A、B两点在面积为1个平方单位的小正三角形组成的虚线网格的格点上,请在格点上确定一点C,连结AB、AC、BC,使△ABC的面积为2个平方单位。
10.根据指令[s,α](s≥0, 0°≤α<360°)机器人在平面上能完成如下动作:先在原地逆时针旋转角度α,再朝其面对的方向沿直线行走距离s。
现机器人站在o点,不停地给机器人下相同的指令[10,60°],则机器人第一次回到o点时一共走的路程是_______________。
二、选择题(本大题共有6小题,每题3分,共18分)11. 下列运算正确的是()A.x2·x3 = x6 B. (-x2)3 = x6 C. x2+x3=x5 D. 6x5÷2x = 3x12.如图,在平面直角坐标系中,AB=2,AC=3,则A点坐标为(A.(—2,3) B.(2,—3) C.(—3,2) D.(3,—2)13.下图形是轴对称图形的是( )A B C D14. 已知如图,AB、MN为⊙O的直径,AB⊥MN,弦CD⊥AB于E,OE=EB,下列等式不成立...的是()A.CE=ED B.CB=BD C.MC=CB D.MC=ND15. 如图是一张简易活动餐桌,现测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌腿的张角∠COD的大小应为 ( )A.100°; B.120°; C.135°; D.150°.16.很早以前人们就对沿直线前进的马车车轮上的点的轨迹产生了浓厚的研究兴趣,有人认为这个轨迹是一段段周而复始的圆弧,也有人认为这个轨迹是一段段的抛物线。
2007年陕西中考模拟试题(二)

2007年陕西中考模拟试题(二)一、单项选择(每小题2分,共16分)1、小明同学在活动课上说出的下列观点,其中属于墨家思想的是A.仁者爱人,为政以德B.兼爱,非攻C.知己知彼,百战不殆D.顺其自然,无为而治2、“舟师识地理,夜则观星,昼则观日,阴晦则观指南针。
”我国制成指南针是什么时候?A.战国B.唐朝C.北宋D.南宋3、第二次鸦片战争中“既是帮凶,又单独作案”的是哪个帝国主义国家?A.英国B..法国C.俄国D.美国4、“大将筹边尚未还,湖湘子弟满天山。
新栽杨柳三千里,引得春风度玉关。
”你知道这首诗是在歌颂谁收复新疆的业绩吗?A.张之洞B.左宗棠C.曾国藩D.李鸿章5、社会主义制度在我国基本建立起来,我国开始进入社会主义初级阶段的标志是A.中华人民国和国的成立B.《中华人民共和国宪法》的制定C.十一届三中全会的召开D.三大改造的完成6、下列史实与华盛顿有关的是A.攻占巴士底狱B.建立君主立宪制C.签署《人权宣言》D.组建大陆军7、德国伟大音乐家贝多芬也是一位资产阶级革命运动的热情歌颂者,他“为纪念一个伟大的人物而作”的代表作品是A.《英雄交响曲》B.《命运交响曲》C.《合唱交响曲》D.《月光奏鸣曲》8、小刚同学在复习中通过抓住关键词了解和掌握历史知识。
他总结了“二战、第二战场”这两个关键词,你能判断他是在总结哪场战役吗?A、诺曼底登陆战B、斯大林格勒战役C、攻克柏林战役D、中途岛海战二、材料解析题(第9题8分,第10题8分,共16分)。
9、(8分)下边是15——16世纪世界上两次著名航海活动的示意图。
读图,结合所学知识回答问题:(1)图1、图2的航海活动的名称分别是什么?这两次航海活动的开始时间大约相差了多少年?(3分)图一(2)两次航海活动的主要目有何不同?(2分)图二(3)请你简要叙述图一中航海活动的意义。
(3分)10、(8分)看图,阅读材料,回答问题:材料一:“胶州亡矣,山东亡矣,国将不国矣!”——1919年5月2日,北京《晨报》发表《外交警报敬告国人》一书材料二“中国的土地可以被征服而不可以断送!中国的人民可以杀戮而不可以低头!”请回答:(1)上述材料描述的是哪一次运动?(1分)材料一反映出这场运动的导火线是什么?(1分)(2)图片中我们可以看到走在运动最前列的是什么人?(1分)材料二是他们散发的传单内容之一,你知道他们当时还有哪些其他的口号、标语或传单内容吗?举出最能反映这次运动性质的一条口号。
2007年中考模拟试题 2人教2007年中考模拟试题 2人教

2006年中考模拟试题(2)一、听力测试(一)听句子,选择与所听句子一致的画面。
每个句子听一遍。
1. A B C D2.A B C D3. A B C D4. A B C D(二)听问句,选出恰当的答语。
每个句子听一遍。
5. A. Yes, I am. B. Yes, you are. C. No, he isn’t.6. A. Yes, I can. B. No, I can’t. C. No, I don’t.7. A. For a week. B. In a week. C. Once a week.8. A. Two years ago. B. For two years. C. At once.9. A. Are you sure you have lost it?B. I’ve returned it to t he library.C. You must return it to the library on time.10. A. It’s very kind of you.B. Help yourself to some more, please.C. Oh, I’m afraid not.(三)听对话选择正确答案,每组对话读两遍。
11. How often does the boy write to his foreign friends?A.Once a year.B. Twice a year.C. Once a month.12. When can the boy come to see his teacher?A.Tuesday.B. Thursday.C. Sunday.13. What will the man probably do?A.Call again.B. Go back home.C. Cone to Sara’s house.14. How did the girl go to school yesterday?A.On foot.B. By bike.C. By bus.15. What will the woman do?A.She’ll call Sue.B. She’ll ring off.C. She’ll write down what the man says.16. What kind of books does the woman like reading?A.History books.B. Science books.C. Language books.17. Which house does the man like better?A.The old one.B. The new one.C. Neither.(四)对话理解:听第一段对话,回答第18—21小题。
2007最新模拟中考试题二及答案

12第4题图2007年中考模拟试题(二)这是一套综合性比较强、内容丰富多彩、技能性高、知识面比较广的具有现实性的新华师版的试题。
值得大家借鉴。
(时间120分钟,满分120分)山东省聊城东昌府区郑家中学 庞纪武 邮编:252035“没有比人更高的山,没有比脚更长的路”.亲爱的同学们,准备好了吗?请相信自己,沉着应答,你一定能愉快地完成这次测试之旅,祝你成功!一选择题(每小题3分,共30分,下列各题只有一个正确选项) 1 .下图是由10 把相同的折扇组成的“蝶恋花”(图 l )和梅花图案(图 2 )(图中的折扇无重叠), 则梅花图案中的五角星的五个锐角均为A . 36ºB . 42ºC . 45ºD . 48º第1题2.若反比例函数xky =的图象经过点)2,1(-,则这个函数的图象一定经过 A.)1,2(- B. )2,21(- C. )1,2(-- D.)2,21(3.若2123x x x -+-的值为零,则x 的值是( )A. 1±B. 1C. 1-D. 不存在4. 如图,将一等边三角形剪去一个角后,∠1+∠2等于( )A.1200B.2400C.3000D.36005. 下列图形中,不能..用同一种作平面镶嵌的是( ) A.正三角形 B. 正方形 C.正五边形 D.正六边形6.气象台预报“本市明天降水概率是80 %”.对此信息,下列说法正确的是(A)本市明天将有80%的地区降水 (B)本市明天将有80%的时间降水(C)明天肯定下雨 (D)明天降水的可能性比较大 7小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所 示.若返回时上坡、下坡的速度仍保持不变,那么小明从学 校骑车回家用的时间是( A ) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟8.据“保护长江万里行”考察队统计,仅2003年长江流域废水排放量已达163.9亿吨!治长江污染真是刻不容缓了!请将这个数据用四舍五入法,使其保留两个有效数字,再用科学记数法表示出来是( )(A) 31.610⨯亿吨 (B) 21.610⨯亿吨 (C) 31.710⨯亿吨 (D)21.710⨯ 亿吨9.如图是二次函数y 1=ax 2+bx +c 和一次函数y 2=mx +n 的图象,观察图象写出y 2≥y 1时,x 的取值范围( )A .x ≥0B .0≤x ≤1C .-2≤x ≤1D .x ≤10.2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a ,较短直角边为b ,则a 3+b 4的值为( ) A .35 B .43 C .89 D .97 二填空题(每小题3分,共30分)11.如图,三角形纸片ABC 中,∠A =65°,∠B =75°,将纸片的一角折叠,使点C 落在△ABC 内,若∠1=20°,则∠2的度数为______.12.为了估计湖里有多少条鱼,先从湖里捕捞100条鱼都做上标记,然后放回湖中去,经过一段时间,待有标记的鱼完全混合于鱼群后,第二次再捕捞100条鱼,发现其中10条有标记,那么你估计湖里大约有鱼_________条.13.诗云:“远望巍巍塔七层,灯光点点倍加增,共灯三百(第10题) (第11题)A BCDE FMC'D'B'八十七,试问尖头几盏灯?” 请回答: 。
【陕西中考数学试题及答案】2007

1二 00七年陕西省初中毕业学业考试数学试卷第Ⅰ卷(选择题共 30分一、选择题(共 10小题,每小题 3分,计 30分.每小题只有一个选项是符合题意的1. 2-的相反数为( A . 2B . 2-C .12D . 12-2.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是(3.不等式组 2030x x +>⎧⎨-⎩,≥ 的解集是(A . 23x -≤ ≤ B . 2x<-,或3x ≥ C . 23x -<< D . 23x -<≤该天这 11个市、区最高气温的平均数和众数分别是(A . 2121℃,℃ B . 2021℃, ℃ C . 2122℃, ℃ D . 2022℃, ℃ 5.中国人民银行宣布,从 2007年6月 5日起,上调人民币存款利率,一年定期存款利率上调到 3.06%.某人于 2007年 6月 5日存入定期为 1年的人民币 5000元(到期后银行将扣除 20%的利息锐.设到期后银行应向储户支付现金 x 元,则所列方程正确的是( A . 500050003.06%x -=⨯B . 500020%5000(13.06%x +⨯=⨯+C . 50003.06%20%5000(13.06%x +⨯⨯=⨯+D . 50003.06%20%50003.06%x +⨯⨯=⨯ 6.如图,圆与圆之间不同的位置关系有( A . 2种 B . 3种 C . 4种 D . 5种7.如图,一次函数图象经过点 A ,且与正比例函数 y x =-的A .B .D .(第 2题图(第 6题图(第 7题图2图象交于点 B ,则该一次函数的表达式为( A . 2y x =-+ B . 2y x =+C . 2y x =-D . 2y x =--8.抛物线 247y x x =--的顶点坐标是( A . (211 -,B . (27 -,C . (211,D . (23 -,9.如图,在矩形 ABCD 中, E 为 CD 的中点,连接 AE 并延长交 BC 的延长线于点F ,则图中全等的直角三角形共有(A . 3对B . 4对C . 5对D . 6对10.如图,在等边 ABC △中, 9AC =,点 O 在 AC 上, 且 3AO =,点 P 是 AB 上一动点,连结 OP ,将线段 OP 绕点 O 逆时针旋转 60得到线段 OD .要使点 D 恰好落在BC 上,则 AP 的长是(A . 4B . 5C . 6D . 8第Ⅱ卷(非选择题共 90分二、填空题(共 6小题,每小题 3分,计 18分 11.计算:221(3 3x y xy ⎛⎫-=⎪⎝⎭. 12.在 ABC △的三个顶点 (23 (45 (32 A B C ----,, , , , 中,可能在反比例函数 (0 ky k x=>的图象上的点是 .13.如图, 50ABC AD ∠=, 垂直平分线段 BC 于点 D ABC ∠, 的平分线 BE 交 AD 于点 E ,连结 EC ,则AEC ∠的度数是 .14.选作题 ... (要求在(1、(2中任选一题作答 (1用计算器计算:3sin38≈(结果保留三个有效数字.(2小明在楼顶点 A 处测得对面大楼楼顶点 C 处的FC(第 9题图PB(第 10题图D(第 13题图3仰角为 52 ,楼底点 D 处的俯角为 13.若两座楼 AB 与CD 相距 60米,则楼 CD 的高度约为(结果保留三个有效数字.(sin130.2250cos130.9744tan130.2309sin520.7880cos520.6157≈≈≈≈≈, , , , tan 521.2799≈15.小说《达芬奇密码》中的一个故事里出现了一串神密排列的数,将这串令人费解的数按从小到大的顺序排列为:112358, , , , , , … ,则这列数的第 8个数是 . 16.如图,要使输出值 y 大于 100,则输入的最小正整数是 .三、解答题(共 9小题,计 72分.解答应写出过程 17.(本题满分 5分设 23111x A B x x ==+--, ,当 x 为何值时, A 与 B 的值相等? 18.(本题满分 6分如图,横、纵相邻格点间的距离均为 1个单位.(1在格点中画出图形 ABCD 先向右平移 6个单位,再向上平移 2个单位后的图形; (2请写出平移前后两图形应对点之间的距离.19如图,在梯形 ABCD 中, 45AB DC DA AB B ∠=∥ , ⊥ , ,延长 CD 到点 E ,使 DE DA =,连接 AE .(1求证:AE BC ∥ ;(2若 31AB CD ==, ,求四边形 ABCE 的面积. 20.(本题满分 8分(第 18题图(第 16题图A(第 19题图4根据表格中的信息解答下列问题:(1求 2006年外省区市在陕投资总额; (2补全图①中的条形统计图;(3 2006年,外省区投资中有 81亿元用于西安高新技术产业开发区, 54亿元用于西安经济技术开发区,剩余资金用于我省其它地区. 请在图②中画出外省区市在我省投资金额使用情况的扇形统计图 (扇形统计图中的圆心角精确到 1,百分比精确到 1%.21.(本题满分 8分为了迎接暑期旅游,某旅行社推出了一种价格优惠方案:从现在开始,各条旅游线路的价格每人 y (元是原来价格每人 x (元的一次函数.现知道其中两条旅游线路原来旅游价格分别为每人 2100元和 2800元,而现在旅游的价格分别为每人 1800元和 2300元.(1求 y 与 x 的函数关系式(不要求写出 x 的取值范围; (2王老师想参加该旅行社原价格为 5600元的一条线路的暑期旅游,请帮王老师算出这条线路的价格. 22.(本题满分 8分在下列直角坐标系中, (1请写出在 ABCD 内 . (不包括边界横、纵坐标均为整数的点,且和为零的点的坐标; (2在 ABCD 内 . (不包括边界任取一个横、纵坐标均为整数的点,求该点的横、纵坐标之和为零的概率.23.(本题满分 8分如图, AB 是半圆 O 的直径,过点 O 作弦 AD 的垂线交切线 AC 于点 C OC , 与半圆 O 交于点 E ,连结 BE DE , . (1求证:BED C ∠=∠;(2若 58OA AD ==, ,求 AC 的长.(第 22题图 C AO B(第 23题图图①图②2006年外省区市在陕投资金额使用情况统计图 (第 20题图东建京江它2006年外省区市在陕投资金额统计图524.(本题满分 10分如图,在直角梯形 OBCD 中, 8110OB BC CD ===, , .(1求 C D , 两点的坐标; (2若线段 OB上存在点 P ,使 PDPC ⊥ ,求过 D P, , 三点的抛物线的表达式.25.(本题满分 12分如图, O 的半径均为 R . (1请在图①中画出弦 AB CD , ,使图①为轴对称图形而不是 ..中心对称图形;请在图②中画出弦 AB CD , , 使图②仍为中心对称图形;(2 如图③, 在 O 中, (02 AB CD m m R ==<<, 且 AB 与 CD 交于点 E , 夹角为锐角α. 求四边形 ACBD 面积(用含m α, 的式子表示;(3 若线段 AB CD , 是 O 的两条弦, 且 AB CD ==, 你认为在以点 A B C D , , , 为顶点的四边形中, 是否存在面积最大的四边形?请利用图④说明理由.陕西省基础教育课程改革实验区2007年初中毕业学业考试数学答案及评分标准一、选择题1. A2. B3. D4. A5. C6. C7. B8. A9. B 10. C 二、填空题11. 33x y - 12. B 13. 115°(填 115不扣分(第 24题图(第 25题图① (第 25题图②(第 25题图③ (第 25题图④14.(1 0.433 (2 90.615. 21 16. 21三、解答题17.解:当 A B =时, 23111x x x =+--.311(1(1 xx x x =+-+-. ···································································································· 1分方程两边同时乘以 (1(1 x x +-,得(1 3(1(1 x x x x +=++-. ······························································································· 2分2231x x x +=+-.2x=. ·································································································································· 3分检验:当 2x =时, (1(1 30x x +-=≠.2x =∴是分式方程的根. (4)分因此,当 2x =时, A B=. ································································································ 5分18.解:(1画图正确得 4分.(2个单位. ············································································································ 6分19.解:(1证明:45AB DC DA AB B ⊥∠=∵∥ , , °,135C DA DE ∠=⊥∴°, . ································································································ 1分又 DE DA =∵ ,45E ∠=∴°. ······················································································································ 2分 180C E ∠+∠=∴°. ·········································································································· 3分 AE BC ∴∥ . ······················································································································ 4分(2解:AE BC CE AB ∵∥ , ∥ ,∴四边形 ABCE 是平行四边形. ························································································· 5分 3CE AB ==∴ .2DA DE CE CD ==-=∴ . ···························································································· 6分326ABCE S CE AD ==⨯=∴ ·. ······················································································· 7分 (第 18题答案图20.解:(1 2006年外省区市在陕投资总额为:124676647119423++++=(亿元. ········································································· 2分(2如图①所示. ················································································································ 5分 2006年外省区市在陕投资金额计图 2006年外省区市在陕投资金额使用情况统计图(3如图②所示. ················································································································ 8分21.解:(1设 y 与 x 的函数关系式为 y kx b=+, ························································ 1分由题意,得 2100180028002300k b k b +=⎧⎨+=⎩,, ·························································································· 3分解之,得 57300k b ⎧=⎪⎨⎪=⎩, .··············································································································· 5分y ∴与 x 的函数关系式为 53007y x =+. ·········································································· 6分(2当 5600x =时, 5560030043007y =⨯+=元. ····················································· 7分∴王老师旅游这条线路的价格是 4300元. ········································································· 8分22.解:(1 (11 (00 (11 --, ,,, , . ···················································································· 3分(2 ∵在 ABCD 内横、纵坐标均为整数的点有 15个,其中横、纵坐标和为零的点有 3个, ··················································································· 6分 31155P==∴ . ···················································································································· 8分23.解:(1证明:AC ∵是 O 的切线, AB 是 O 直径,AB AC ⊥∴ .则1290∠+∠=°. ··············································································································· 1分又 OC AD ⊥∵ ,190C ∠+∠=∴°. ············································································································· 2分 2C∠=∠∴ . ······················································································································· 3分而 2BED ∠=∠,BED C∠=∠∴ . ················································································································ 4分(2解:连接 BD . (第 20题答案图① (第 20题答案图②东建京江它省区市13% 西安高新技术 19% CAB ∵是 O 直径,90ADB ∠=∴ °.6BD ===∴ . ·········································································· 5分OAC BDA ∴△∽△ . ········································································································ 6分 ::OA BD AC DA =∴ .即 5:6:8AC=. ·················································································································· 7分 203AC=∴ . ······················································································································· 8分24.解:(1过点 C 作 CE OD ⊥于点 E ,则四边形 OBCE 为矩形.8CE OB ==∴ , 1OE BC ==.6DE ===∴ . 7OD DE OE =+=∴ .C D ∴ , 两点的坐标分别为 (81(07 CD , , , . ··································································· 4分(2 PC PD ⊥∵ ,1290∠+∠=∴ °.又 1390∠+∠=°,23∠=∠∴ .Rt Rt POD CBP ∴△∽△ . ::PO CB OD BP =∴ .即 :17:(8 PO PO =-.2870PO PO -+=∴ .1PO =∴ ,或 7PO =.∴点 P 的坐标为 (10 , ,或(70 , . ······················································································ 6分①当点 P 的坐标为 (10 , 时,设经过 D P C , , 三点的抛物线表达式为 2y ax bx c =++,(第 24题答案图则 706481c a b c a b c =⎧⎪++=⎨⎪++=⎩, , . ∴ 2528221287a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,,.∴所求抛物线的表达式为:22522172828y x x =-+. ························································· 9分②当点 P 为 (70 , 时,设经过 D P C , , 三点的抛物线表达式为 2y ax bx c =++,则 749706481c a b c a b c =⎧⎪++=⎨⎪++=⎩, , . ∴ 141147a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,, .∴所求抛物线的表达式为:2111744y x x =-+. ···························································· 10分(说明:求出一条抛物线表达式给 3分,求出两条抛物线表达式给 4分25.解:(1答案不唯一,如图①、②(只要满足题意,画对一个图形给 2分,画对两个给 3分················································································································································ 3分(2过点 A B , 分别作 CD 的垂线,垂足分别为 M N , .11sin 22ACD S CD AM CD AE α==△∵ ···,11sin 22BCD S CD BN CD BEα==△ ···. ············································································ 5分 ACD BCD ACBD S S S =+△△四边形∴11sin sin 22CD AE CD BE αα=+····1( sin 2CD AE BE α=+··(第 25题答案图① (第 25题答案图②。
陕西省2007年初中毕业学业考试课改实验区模拟英语试卷

绝密★启用前某某省2007年初中毕业学业考试课改实验区模拟试题英语命题人:某某高新第二学校阮华婷本试卷分第Ⅰ卷和第Ⅱ卷两大部分。
第Ⅰ卷1-5页,第Ⅱ卷6-8页。
全卷满分120分,考试时间120分。
第Ⅰ卷(选择题共70分)听力部分Ⅰ. 听句子,选答题(共5小题,计5分)本题共有5个小题,每个小题你将听到一句话,读两遍,请从所给的三个选项中选出一个最恰当的答语。
( )1. A. Florida.B. I don’t like it.C. Summer.( )2.A. She is. B. Mine . C. It’s him.( )3.A. A policeman. B. A customer . C. A worker.( )4.A. She did her homework.B. She asked her teacher.C. She was listening to music.( )5.A. It is in the cinema. B. It doesn’t matter. C. It is boring.Ⅱ.听对话,选答案(共10小题,计10分)本题共有10个小题,每个小题有一段对话和一个问题,读两遍,请根据每段对话的内容和后面的问题,从所给的三个选项中选出最恰当的一项。
( )6. A. It is across from the library.B. It is between the library and the drug store.C. It is on Main Street.( )7. A. Yes. B. No. C. I don’t know.( )8. A. He played on the playground.B. He copied other’s homework.C. He ate in class.( )9. A. He used to be tall.B. He used to be shy.C.He used to be outgoing.( )10. A. She will listen to soft music before big exams.B. She will fail the exam.C. She will sleep.( )11. A. Every week. B. Every month. C. Every day.( )12. A. By memorizing the words and reading aloud.B. By making flash cards.C. By memorizing the grammar.( )13. A. People will learn at school.B. People will learn on puters.C. People will not learn.( )14. A. For 3 years. B. For 3,000 days. C. For 30 months.( )15. A. Clean the bedroom. B. Do her homework. C. Wash her clothes.Ⅲ.听短文,选答案(共5小题,计10分)本题你将听到一篇短文,读两遍,请从每个小题的三个选项中,选出能回答所提问题或完成所给句子的正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007陕西中考预测试卷(二)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷120分,时间:120分钟第Ⅰ卷(选择题共30分)一、选择题 (共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1.冬季的一天室内温度是8℃,室外温度是-2℃,则室内外温度的差是( ) A .4℃ B .6℃ C .10℃ D .16℃2.如图1是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )A .4B .5C .6D .73.化简21y xy -+22yx yx -+的结果是( ) A .)(1y x y -B .)(1y x y y -+C .)(1y x y y --D .)(1y x y +4.如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a 克,再称得剩余电线的质量为b 克,那么原来这卷电线的总长度是( )A .ab 1+米 B .⎪⎭⎫⎝⎛+1a b 米 C .⎪⎭⎫⎝⎛++1a b a 米D .⎪⎭⎫⎝⎛+1b a 米 5.如图2,⊙O 是△ABC 的外接圆,连接OA 、OC ,⊙O 的半径R =2,sin B =43,则弦AC 的长为( ) A .3B .7C .23 D .43 6.小颖的家与学校的距离为s 0千米,她从家到学校先以匀速v 1跑步前进,后以匀速v 2(v 2<v 1)走完余下的路程,共用了t 0小时,下列能大致表示小颖离家的距离y (千米)与离家时间t (小时)之间关系的图象是( )A B C D7.如图3农村常搭建横截面为半圆形的全封闭塑料薄膜蔬菜大棚.如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( ).A .64π m 2B .72π m 2C .78π m 2D .80π m 28.已知抛物线y =2x 2-4x -1,下列说法中正确的是( ) A .当x =1时,函数取得最小值y =3 B .当x =-1时,函数取得最小值y =3 C .当x =1时,函数取得最小值y =-3 D .当x =-1时,函数取得最小值y =-39.为了美化校园,同学们要在一块正方形空地上种上草,他们设计了图4所示的图案,其中阴影部分为绿化面积,哪个图案的绿化面积与其他图案的绿化面积不相等( ).10.如图5,在□ABCD 中,EF//AB ,GH//AD ,EF 与GH 交于点O ,则该图中的平行四边形的个数共有( ).A .7B .8C .9D .11第Ⅱ卷(非选择题 共90分)二、填空题 (共6小题,每小题3分,计18分)11.如果关于x 的不等式(a -1)x <a +5和2x <4的解集相同,则a 的值为. 125(填“>”、“=”、“<”). 13.杏花村现有手机188部,比2004年底的3倍还多17部,则该村2004年底有手机 部.14.若矩形的面积为6,则矩形的长y 关于宽x (x >0)的函数关系式为 .15.小明的身高是1.7 m,他的影长是2 m ,同一时刻学校旗杆的影长是10 m ,则旗杆的高是 m. 16.如图,正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上一动点,则DN +MN 的最小值为 .三、解答题(共9小题,计72分,解答应写出过程) 17.(5分)用换元法解分式方程: 22222=-+-x xx x18.(本题满分6分) 如图,作△ABC 的中线AD ,并将△ADC 绕点D 旋转180°,那么点C 与点B 重合,点A 转到A ′点,不难发现AC =A ′B ,AD =A ′D ,BD =DC ,如果知道AB =4 cm ,AC =3 cm,你能求出中线AD 的范围吗?19.(8分)甲乙两人掷一对骰子,若甲掷出的点数之和为6,则加一分,否则不得分;乙掷出的点数之和为7,则加一分,否则不得分;甲、乙各掷骰子10次,得分高者胜.(1)请用列表法求出甲获胜的概率;(2)这个游戏公平吗?若公平,说明理由;如果不公平,请你修改规则,使之公平.20.(8分)等腰梯形ABCD中,AD//BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E.若AD=2,BC=8.求(1)BE的长;(2)∠CDE的正切值.21.(8分)如图1-6-16,l1、l2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(小时)的函数图象,假设两种灯的使用寿命都是2 000小时,照明效果一样.(1)根据图象分别求出l1、l2的函数关系式;(2)当照明时间为多少时,两种灯的费用相等?(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).22.(9分)某研究性学习小组,为了了解本校初一学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分钟),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:(1)这个研究性学习小组所抽取样本容量是多少?(2)在被调查的学生中,一天做家庭作业所用的大致时间超过.120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几?(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?(2)若某种植物适宜生长在18℃~20℃(包括18℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?24.(10分)已知:如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,在射线P A上截取PD=PC,连接CD,并延长交⊙O于点E.(1)求证:∠ABE =∠BCE ;(2)当点P 在AB 的延长线上运动时,判断sin ∠BCE 的值是否随点P 位置的变化而变化,提出你的猜想并加以证明.25.(9分)在△CDE 中,∠C =90°,CD ,CE 的长分别为m ,n ,且DE ·cos D =cot E. (1)求证m 2=n ;(2)若m =2,抛物线y =a (x —m )2+n 与直线y =3x +4交于A (x 1,y 1)和B (x 2,y 2)两点,且△AOB 的面积为6(O 为坐标原点),求a 的值;(3)若是k 2=2mn,c +l-b =0,抛物线y =k (x 2+bx +c )与x 轴只有一个交点在原点的右侧,试判断抛物线与y 轴的交点在y 轴的正半轴还是负半轴,并证明你的结论.2007年陕西省中考数学预测试卷参考答案(二)一、选择题1.C 2.B 3.B 4.B 5.A 6.C 7.A 8.C 9.A 10.C 二、填空题11.解:由2x <4得x <2,∵(a -1)x <a +5与2x <4的解集相同∴⎪⎩⎪⎨⎧=-+-21501a aa ∴a =712.“<”;13.57. 14.9=x6; 15.8.5;16.10三、解答题17.解:设y x x =-22,则原方程可化为y +y1=2,即y 2-2y +1=0.解得y =1,则122=-x x .即x 2-x -2=0.解得x 1=2,x 2=-1.经检验原方程的解为x 1=2,x 2=-1.点评:本题考查用换元法解方程.18.解:由AC =A ′B ,AD =A ′D ,BD =DC ,可知△ADC ≌△A ′DB ,∴A ′B =AC=3 cm.在△ABA ′中,AB-A ′B <AA ′<AB +A ′B ,∴1<AA ′<7,则21<AD <27. 即中线AD 的长在21至27之间. 19.解:(1)每次游戏时,所有可能出现的结果如下:共36种结果,每种结果出现的可能性相同.①两骰子上点数和为6的结果有5种:(1,5)、(2,4)、(3,3)、(4,2)、(5,1),因此甲每次得分概率为365. ②两骰子上点数和为7的结果有6种:(1,6)、(2,5)、(3,4)、(4,3)、(5,2)、(6,1),因此乙每次得分概率为366=61. ∴366>365,且两人都掷10次,∴乙获胜概率大. (2)这个游戏不公平,因为两人获胜的概率不同,可将规则改为无论谁,只要投出的两骰子点数和为 6(或7)得1分,每人各投10次,得分多者获胜.20.解:(1)由题意得△BFE ≌△DFE ,∴DE =BE ,∵在△BDE 中,DE=BE ,∠DBE =45°∴∠BDE =∠DBE =45°,∴∠DEB =90°,即DE ⊥BC .∵在等腰梯形ABCD 中,AD =2,BC =8,易得CE =21(BC -AD )=3,∴BE =5. (2)由(1)得DE =BE =5.在△DEC 中,∠DEC =90°,DE =5,EC =3, ∴tan ∠CDE =ED EC =53. 21.解:(1)令l 1的方程为y =k 1x +b 1,l 2的方程为y =k 2x +b 2.对l 1上两点(0,2)和500,17)代入方程中⎩⎨⎧+==111500·172b k b ⇒⎩⎨⎧==203.011b k 由l 2上两点(0,20)和(500,26)代入方程l 2中⎩⎨⎧+==222500·2620b k b ⇒⎩⎨⎧==20012.022b k ∴l 1和l 2的方程分别为y =0.03x +2和y =0.012x +20 (2)⎩⎨⎧+=+=20012.0203.0x y x y ⇒⎩⎨⎧==321000y x即照明时间1000小时,两种灯费用相等. (3)2000小时的节能灯. 500小时的白炽灯. 22.解:(1)(3+4+6+8+9)=30∴这个研究性学习小组抽取样本容量为30. (2)(9+8+4)÷30=70%∴一天做作业超过120分钟人数占70% (3)中位数为8. 23.解:(1)经观察发现y 与x 满足的一次函数关系,设y =kx +b . 将x =0,y=22,及x =100,y =21.5分别代入y =kx +b ,得⎩⎨⎧+=+⨯=.1005.21,022b k b k 解得⎪⎩⎪⎨⎧-==.2001,22k b∴y =-2001x +22. (2)由题意得18≤y ≤20,即18≤-2001x +22≤20, ∴-4≤-2001x ≤-2, 即400≤x ≤800.故该植物适宜种植在海拔为400米至800米的山区. 24.证明:(1)∵PD=PC , ∴∠PDC =∠PCD .∵PC 切⊙O 于点C ,∴∠PCD =∠E .∵∠ABE =∠PDC -∠E ,∠BCE =∠PCD -∠PCB ,∴∠ABE =∠BCE . (2)猜想:sin ∠BCE 的值不随点P 位置的变化而变化. 证明:如图,连接AE .∵∠ABE =∠BCE ,∠BCE =∠A , ∴∠ABE =∠A .∵AB 是⊙O 的直径,∴∠AEB =90°. ∴∠BCE =∠A =45°. ∴sin ∠BCE =sin45°=22. ∴sin ∠BCE 的值不随点P 位置的变化而变化.第24题图点评:本题第(2)问的基本思路是:猜想sin ∠BCE 的值不变←∠BCE 不变←∠ABE 不变←证明∠ABE =45°,是考查圆的有关性质的一道探索性试题.25.(1)由DE ·cos D =cot E ,有DE ·.CDCEDE CD = ∴CD 2=CE ,∴m 2=n .(2)解⎩⎨⎧+=+-=434)2(2x y x a y ,得ax 2-(4a +3)x +4a =0∴x 1+x 2=aa 34+,x 1x 2=4. ∴|x 1-x 2|=212214)(x x x x -+=22292416)34(a a a a +=-+=||924a a + ∴|AB |=||90240a +.又直线y =3x +4与y 轴交于M (0,4),与x 轴交于N ⎪⎭⎫⎝⎛-0,34.设OH =h 垂直于MN ,则h =104 ∵.||3924,6104||9024021a a a a =+∴=∙+∙1∴a=3或a=.3。
