有限元考试精彩试题及问题详解——第一组
有限单元法考试题及答案

有限单元法考试题及答案一、选择题1. 有限元法是一种用于求解偏微分方程的数值方法,其基本思想是将连续域离散化成有限个互不重叠的子域。
这种说法正确吗?A. 正确B. 错误答案:A2. 在有限元法中,单元的选取通常遵循以下哪个原则?A. 单元越小越好B. 单元越大越好C. 单元大小应根据问题的具体需求来确定D. 单元大小固定不变答案:C3. 有限元分析中,边界条件的处理方式不包括以下哪一项?A. 强制边界条件B. 自然边界条件C. 忽略边界条件D. 周期性边界条件答案:C4. 在有限元法中,下列哪个不是常用的单元类型?A. 三角形单元B. 四边形单元C. 六面体单元D. 圆形单元答案:D5. 有限元法中,形函数的作用是什么?A. 描述单元的几何形状B. 描述单元的物理属性C. 用于构建单元的局部刚度矩阵D. 用于描述单元内部的位移场答案:D二、简答题1. 简述有限元法的基本步骤。
答案:有限元法的基本步骤包括:定义问题域和边界条件,划分网格,选择单元类型,定义形函数,组装全局刚度矩阵,施加边界条件,求解线性方程组,提取结果。
2. 有限元法中,局部刚度矩阵是如何构建的?答案:局部刚度矩阵是通过单元的形函数和材料属性来构建的。
首先,根据单元的形函数和材料属性,计算单元的应变和应力。
然后,利用应变和应力,通过积分得到单元的局部刚度矩阵。
三、计算题1. 给定一个简单的一维弹性杆问题,其长度为L,两端固定,中间受力P。
请使用有限元法求解该杆的位移和应力分布。
答案:首先,将杆划分为若干个单元,每个单元的长度为Δx。
然后,为每个单元定义形函数,通常是线性形函数。
接着,根据形函数和材料属性(如杨氏模量E),构建每个单元的局部刚度矩阵。
将所有单元的局部刚度矩阵组装成全局刚度矩阵。
由于杆两端固定,边界条件为位移为零。
最后,将力P施加到中间节点,求解全局刚度矩阵对应的线性方程组,得到节点位移。
应力可以通过位移和形函数计算得到。
西工大-有限元精彩试题
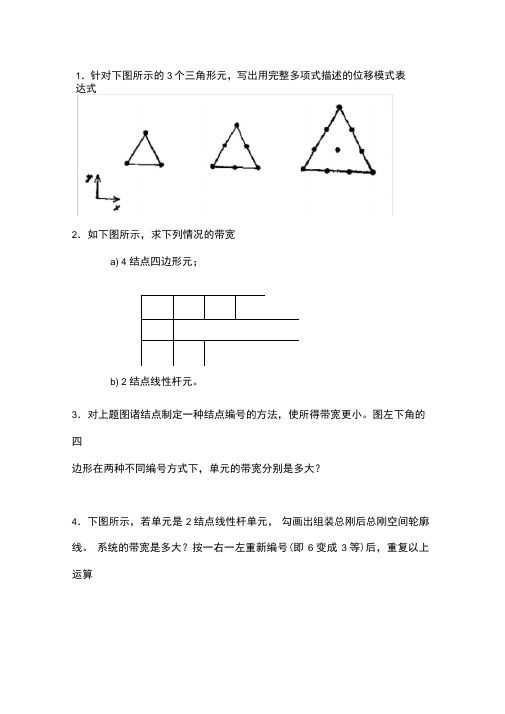
1.针对下图所示的3 个三角形元,写出用完整多项式描述的位移模式表达式2.如下图所示,求下列情况的带宽a) 4 结点四边形元;b) 2 结点线性杆元。
3.对上题图诸结点制定一种结点编号的方法,使所得带宽更小。
图左下角的四边形在两种不同编号方式下,单元的带宽分别是多大?4.下图所示,若单元是2 结点线性杆单元,勾画出组装总刚后总刚空间轮廓线。
系统的带宽是多大?按一右一左重新编号(即6 变成3 等)后,重复以上运算5.设杆件 1 -2 受轴向力作用,截面积为 A ,长度为L,弹性模量为E,试写出杆端力F1,F2 与杆端位移u1, u2 之间的关系式,并求出杆件的单元刚度矩阵[k](e)6.设阶梯形杆件由两个等截面杆件○1与○2所组成,试写出三个结点1 、2、3 的结点轴向力F1,F2,F3与结点轴向位移u1,u2, u3之间的整体刚度矩阵[K]。
7.在上题的阶梯形杆件中,设结点3 为固定端,结点1 作用轴向载荷F1=P ,求各结点的轴向位移和各杆的轴力。
8.下图所示为平面桁架中的任一单元,x, y 为局部坐标系,x,y 为总体坐标系,x轴与x 轴的夹角为。
1) 求在局部坐标系中的单元刚度矩阵[k](e)2) 求单元的坐标转换矩阵[T] ;3) 求在总体坐标系中的单元刚度矩阵[k](e)9.如图所示一个直角三角形桁架,已知E 3 107N /cm2,两个直角边长度l 100cm,各杆截面面积 A 10cm2,求整体刚度矩阵[K]。
10 .设上题中的桁架的支承情况和载荷情况如下图所示,按有限元素法求出各结点的位移与各杆的力。
11 .进行结点编号时,如果把所有固定端处的结点编在最后,那么在引入边界条件时是否会更简便些?12 .针对下图所示的 3 结点三角形单元,同一网格的两种不同的编号方式,单元的带宽分别是多大?13 .下图所示一个矩形单元,边长分别为2a 与2b ,坐标原点取在单元中心位移模式取为u 1 2 x 3 y 4xyv 5 6x 7 y 8xy 导出部任一点位移u,v 与四个角点位移之间的关系式。
有限元考试精彩试题及问题详解——第一组

有限元考试试题及答案一、简答题(5道,共计25分)。
1.有限单元位移法求解弹性力学问题的基本步骤有哪些?(5分)答:(1)选择适当的单元类型将弹性体离散化;(2)建立单元体的位移插值函数;(3)推导单元刚度矩阵;(4)将单元刚度矩阵组装成整体刚度矩阵;(5)代入边界条件和求解。
2. 在划分网格数相同的情况下,为什么八节点四边形等参数单元精度大于四边形矩形单元?(5分)答:在对于曲线边界的边界单元,其边界为曲边,八节点四边形等参数单元边上三个节点所确定的抛物线来代替原来的曲线,显然拟合效果比四边形矩形单元的直边好。
3.轴对称单元与平面单元有哪些区别?(5分)答:轴对称单元是三角形或四边形截面的空间的环形单元,平面单元是三角形或四边形平面单元;轴对称单元内任意一点有四个应变分量,平面单元内任意一点非零独立应变分量有三个。
4.有限元空间问题有哪些特征?(5分)答:(1)单元为块体形状。
常用单元:四面体单元、长方体单元、直边六面体单元、曲边六面体单元、轴对称单元。
(2)结点位移3个分量。
(3)基本方程比平面问题多。
3个平衡方程,6个几何方程,6个物理方程。
5.简述四节点四边形等参数单元的平面问题分析过程。
(5)分)答:(1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;(2)通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4)用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。
二、论述题(3道,共计30分)。
1. 简述四节点四边形等参数单元的平面问题分析过程。
(10分)答:(1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;(2) 通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变 分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4)用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。
(完整版)有限元考试试题及答案

e an dAl l t h i ng si nt he i rb ei n ga re go o2. 如图2所示,有一正方形薄板,沿对角承受压力作用,厚度t=1m ,载荷F=20KN/m ,设泊松比µ=0,材料的弹性模量为E ,试求它的应力分布。
(15分)图23. 图示结点三角形单元的124边作用有均布侧压力q ,单元厚度为t ,求单元的等效结点荷载。
图3图1一、简答题1. 答:1)合理安排单元网格的疏密分布2)为突出重要部位的单元二次划分3)划分单元的个数4)单元形状的合理性5)不同材料界面处及荷载突变点、支承点的单元划分6)曲线边界的处理,应尽可能减小几何误差7)充分利用结构及载荷的对称性,以减少计算量2. 答:形函数应满足的三个条件:a.必须能反映单元的刚体位移,就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。
b.能反映单元的常量应变,所谓常量应变,就是与坐标位置无关,单元内所有点都具有相同的应变。
当单元尺寸取小时,则单元中各点的应变趋于相等,也就是单元的形变趋于均匀,因而常量应变就成为应变的主要部分。
c.尽可能反映位移连续性;尽可能反映单元之间位移的连续性,即相邻单元位移协调。
3. 答:含义:所谓的等参数单元,就是在确定单元形状的插值函数和确定单元位移场的插值函数中采用了完全相同的形函数。
意义:构造出一些曲边地高精度单元,以便在给定地精度下,用数目较少地单元,解决工程实际地具体问题。
4. 答:有限单元法是基于变分原理的里兹(Ritz)法的另一种形式,从而使里兹法分析的所有理论基础都适用子有限单元法,确认了有限单元法是处理连续介质问题的一种普遍方法.利用变分原理建立有限元方程和经典里兹法的主要区别是有限单元法假设的近似函数不是在全求解域而是在单元上规定的,面且事先不要求满足任何边界条件,因此它可以用来处理很复杂的连续介质问题。
有nl⎥⎦⎤⎢⎣⎡5.0025.025.011212---==E k k ⎥⎦⎤⎢⎣⎡5.0025.0011313-==E k k ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡5.125.025.05.125.0005.05.00025.075.025.025.075.032222212222E E E E k k k k +=++=⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---5.025.025.0125.025.005.025.0025.05.032312323E E E k k k =+=⎥⎦⎤⎢⎣⎡---5.0025.025.022424E k k ==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡025.025.00025.0000025.0032522525E E E k k k =+=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡5.125.025.05.15.00025.075.025.025.075.025.0005.043333313333E E E E k k k k =++=⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---125.025.05.05.0025.025.05.025.0025.043533535E E E k k k =+=⎥⎦⎤⎢⎣⎡0025.0043636E k k ==⎥⎦⎤⎢⎣⎡75.025.025.075.024444E k k ==⎥⎦⎤⎢⎣⎡---25.0025.05.024545E k k == ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡5.125.025.05.175.025.025.075.05.00025.025.0005.045535525555E E E E k k k k =++=⎥⎦⎤⎢⎣⎡---25.0025.05.045656E k k ==⎥⎦⎤⎢⎣⎡25.0005.046666E k k ==把上面计算出的,…,对号入座放到总刚矩阵中去,于是得到11k 66k []K的具体表达式。
有限元期末考试题及答案

有限元期末考试题及答案一、选择题1. 有限元方法是一种数值分析方法,主要用于求解什么类型的数学问题?A. 线性代数方程B. 微分方程C. 积分方程D. 代数方程答案:B2. 在有限元分析中,单元的划分是基于什么原则?A. 单元数量B. 单元形状C. 问题域的几何特性D. 计算资源答案:C3. 下列哪项不是有限元分析中常用的单元类型?A. 三角形单元B. 四边形单元C. 六面体单元D. 圆形单元答案:D二、填空题4. 有限元方法中,______是指将连续的物理域离散成有限数量的小区域,这些小区域称为单元。
答案:离散化5. 在进行有限元分析时,通常需要定义材料属性,包括______、密度和弹性模量等。
答案:泊松比三、简答题6. 简述有限元方法的基本步骤。
答案:有限元方法的基本步骤包括:定义问题域、离散化问题域、选择单元类型、定义材料属性、构建全局刚度矩阵、施加边界条件、求解线性代数方程、提取结果。
7. 解释什么是有限元分析中的收敛性,并说明影响收敛性的因素。
答案:收敛性是指随着单元数量的增加,有限元分析结果逐渐接近真实解的性质。
影响收敛性的因素包括单元的类型、形状、大小以及网格的布局等。
四、计算题8. 假设有一个长度为2米的杆,两端固定,中间施加了一个向下的力F=1000N。
如果杆的材料是钢,其弹性模量E=210 GPa,泊松比ν=0.3,请计算杆的弯曲位移。
答案:首先,根据Euler-Bernoulli梁理论,可以写出弯曲位移的方程为:\[ w(x) = \frac{F}{384EI} L^3 \]其中,\( w(x) \) 是位移,\( F \) 是施加的力,\( L \) 是杆的长度,\( E \) 是弹性模量,\( I \) 是截面惯性矩。
对于一个矩形截面,\( I \) 可以表示为:\[ I = \frac{bh^3}{12} \]假设杆的截面宽度为b,高度为h,代入上述公式,可以计算出位移。
有限元试卷和答案

a
图1
1、解: 设图 1 所示的各点坐标为 点 1( a, 0) ,点 2(a,a) ,点 3(0,0) 于是,可得单元的面积为 (1) 形函数矩阵 N 为
1 (0 + ax − ay ) a2 1 N1 = 2 (0 + 0gx + ay ) a 1 N1 = 2 (a 2 − ax + 0gy ) a N1 =
判断正误 (×)1. 节点的位置依赖于形态,而并不依赖于载荷的位置 (√)2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元 (×)3. 不能把梁单元、壳单元和实体单元混合在一起作成模型 (√)4. 四边形的平面单元尽可能作成接近正方形形状的单元 (×)5. 平面应变单元也好,平面应力单元也好,如果以单位厚来作模型化 处理的话会得到一样的答案 (×)6. 用有限元法不可以对运动的物体的结构进行静力分析 (√)7. 一般应力变化大的地方单元尺寸要划的小才好 (×)8. 所谓全约束只要将位移自由度约束住,而不必约束转动自由度 (×)9. 线性应力分析也可以得到极大的变形 (√)10. 同一载荷作用下的结构,所给材料的弹性模量越大则变形值越小 (1)用加权余量法求解微分方程,其权函数 V 和场函数 u 的选择没有任何限 制。 ( × ) (2)四结点四边形等参单元的位移插值函数是坐标 x、y 的一次函数。 (√ ) (3)在三角形单元中,其面积坐标的值与三结点三角形单元的结点形函数值 相等。 续。 (√ ) (× ) (× ) (6)等参单元中 Jacobi 行列式的值不能等于零。 (√) (7)在位移型有限元中,单元交界面上的应力是严格满足平衡条件的。 (× ) (4)二维弹性力学问题的有限元法求解,其收敛准则要求试探位移函数 C1 连 (5)有限元位移法求得的应力结果通常比应变结果精度低。
有限元试题及答案[1]
![有限元试题及答案[1]](https://img.taocdn.com/s3/m/124aad996bec0975f465e211.png)
一、如图所示的1D 杆结构,试用取微单元体的方法建立起全部基本方程和边界条件,并求出它的所有解答。
注意它的弹性模量为E 、横截面积A解:如图1.1所示的1D 杆结构,其基本变量为 位移 x u 应变 x ε 应力 x σ取微单元体Adx ,其应力状态如图1.2,由泰勒展开式知()⋅⋅⋅⋅⋅+∂∂+⋅∂∂+=+22221dx x dx x dx x x x x σσσσ略去2阶以上的商阶微量知()dx xdx x xx ⋅∂∂+=+σσσ 由力的平衡知0=∑i x :0=-⎪⎭⎫ ⎝⎛∂∂+A A dx x x x x σσσ即力的平衡方程为:⋅⋅⋅⋅=0dxd xσ① 位移由图1.3知(泰勒展开,略去商阶微量)()dx xu u dx x u xx ⋅∂∂+=+ dxu dxdxdx u dx x uu ABABB A xx x x x ∂=-+-∂∂+=-=∴)(''ε应变 即几何方程为:⋅⋅⋅⋅=dxdu xx ε② 根据虎克定律知⋅⋅⋅⋅⋅⋅⋅=⋅=dxdu E E xx x εσ③ 由①、②、③知该1D 杆的基本方程为⎪⎪⎪⎩⎪⎪⎪⎨⎧====dx du E E dx du dx d x x xx xxεσεσ0 在节点1时位移:00==x x u 在节点2时应力:APlx x==σ即其边界条件为00==x x u on u SAPlx x==σ on P S 由①式知⋅⋅⋅⋅⋅=0c x σ ④ ④代入③解得:dxdu Ec x=0 ⋅⋅⋅⋅⋅⋅⋅+=10c x Ec u x ⑤ 0c 、1c 为待定系数结合边界条件知⎪⎪⎩⎪⎪⎨⎧==+A P c c x Ec 010解知得APc =0,01=c ∴⎪⎪⎪⎩⎪⎪⎪⎨⎧==⋅==EA P E x EA P u A P x xx x σεσ二、设平面问题中的应力问题y a x a a x 321++=σy a x a a y 654++=σ y a x a a xy 987++=τ其中i a (1、2、………9)为常数,令所有体积力为零,对下面特殊情况说明平衡是否满足?为什么?或者i a 之间有什么关系才满足平衡。
有限元例题及答案

例 8-1:E ,A ,L ,s σ 杆I 弹塑性; 杆II 弹性。
求s AF σ3=下2点位移。
解:(1)理论解在荷载s A F σ3=作用下,杆I 屈服而有内力(拉力)S A N σ=1,杆II 内力(压力)为s II A N σ2=,中点2位移δ取决于杆II 的变形,即*===∆=δσσδ22)2(EL AE L A l S S II式中E Ls σδ=*(屈服位移)(2)直接迭代法杆I 和杆II 的刚度分别为⎩⎨⎧=**≤〉)()(δδδδδσL EAAI S k L EA k II =①迭I 迭代步迭代从*=δδ0开始,这时有L EAk k K II I 20=+=*-====δσσδ5.15.123101EL L EA A F K S S②第2迭代步杆I 进入塑性,有L EA A k s I 67.01==δσ杆Ⅱ完全弹性,刚度不变。
因此,总刚为L EAk k K II I 67.11=+=*-====δσσδ8.18.167.13112E L LEA A F k S s 整个迭代过程见表8-1。
表8-1 直接迭代法各次迭代结果(3)切线刚度法杆Ⅰ和杆Ⅱ的切线刚度分别为⎩⎨⎧=**≤〉)()(0δδδδLEAI k L EA k II =①第1迭代步初始状态时,00=δ,杆Ⅰ,Ⅱ中应力、应变均匀为零。
总刚为:L EAk k K T TI T 21=+=由F K T -=δψ,得S A σψ30-=由n Tn n K ψδ1--=∆得,*=--=∆δσδ5.1)3(10S A L由式n n n δδδ∆+=+1得,s δδ5.11=杆中应力:S SI σσσσ5.111-==杆中内力:S SI A N A N σσ5.111-==②第2迭代步由于杆I 已进入塑性,杆Ⅱ仍处弹性,总刚:L EAk k K TIITI T =+=2由F K T -=δψ,得S S S A A A σσσψ5.035.21-=-=由n Tn n K ψδ1--=∆得,*=--=∆δσδ5.0)5.0(11S A LEA由式n n n δδδ∆+=+1得,*=∆+=σδδδ0.2112杆中应力:S II SI A N A N σσ0.222-==检验F K T -=δψ,有030.32=-=S S A A σσψ迭代平衡。
有限元考试复习题

第1章 杆件结构1.1 单元刚度如何叠加成结构的整体刚度矩阵?为什么这样叠加?如何从刚度矩阵的物理意义去理解此叠加关系?叠加成的整体刚度矩阵又有什么特点?答:(1)首先对杆件结构进行自然离散,并对其进行节点编号和单元编号,然后通过坐标转换公式将局部坐标系下的单元刚度矩阵转换为整体坐标系下的单元刚度矩阵。
将所得的单元刚度矩阵按节点编号进行组装,即可形成整体刚度。
(2)这样的叠加方法条理清晰,便于电脑程序编程,分块进行,效率较高,且尤其适用于大量杆件结构体系,将所有的计算程序化后,大大节省了时间,并且精度较高。
(3)刚度矩阵的物理意义是表示结构或构件单元在单位位移或变形下所能承受的力的大小。
通过单元刚度矩阵建立单元节点力与节点位移之间的关系,通过整体刚度矩阵建立所受外荷载与整体位移之间的关系。
通过单元刚度矩阵叠加构建整体刚度矩阵,则建立起了结构整体外荷载与整体位移之间的方程,进而通过求得的整体位移进一步求出单元之间的节点位移,并最终求得各单元之间的节点力。
(4)特点:1)对称性。
由于杆单元的单刚是对称矩阵,则由它们集成的总刚也具有对称性。
2)奇异性。
即无论是单刚还是总刚都是奇异的,它们不存在逆阵。
3)存在相当数量的零元素。
由于杆系结构的特点,一个节点可能只连接少数几个单元,因此可能与周围邻近的几个节点之间存在非零的元素。
1.2 如图所示的圆杆,由两个不同截面的杆件(1)与(2)组成,在节点1,2,3上作用有轴向节点载荷1Q 、2Q 、3Q 而平衡。
试写出3个轴向载荷与节点的轴向位移1u 、2u 、3u 之间的矩阵关系。
解:杆件1的单元刚度矩阵为:[]1111111EA k l -⎡⎤=⎢⎥-⎣⎦;杆件2的单元刚度矩阵为:[]2221111EA k l -⎡⎤=⎢⎥-⎣⎦; 结构的整体刚度矩阵为:1111111112112211222122111211222221222222EA EA l l k k EA EA EA EA K k k k k l l l l k k EA EA l l ⎡⎤-⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥=+=-+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦而又12l l L ==,所以11112222A A E K A A A A L A A -⎡⎤⎢⎥=-+-⎢⎥⎢⎥-⎣⎦令节点位移向量为{}123,,Tu u u δ=,节点力为{}123,,TF Q Q Q =,从而可得3个轴向载荷与节点的轴向位移其关系为11112112223223Q A A u E Q A A A A u L Q A A u -⎧⎫⎡⎤⎧⎫⎪⎪⎪⎪⎢⎥=-+-⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥-⎩⎭⎣⎦⎩⎭1.3 如图所示为三角桁架,已知25/101.2mm N E ⨯=,两直边的长度m l 1=,各杆的截面积21000mm A =,求此结构的整体刚度矩阵[]K ,若节点的编号改变后,问[]K 的有无变化?解:杆件的单元刚度矩阵为:[]1111ii iEA k l -⎡⎤'=⎢⎥-⎣⎦,从而可得各个单元在局部坐标系下的单元刚度矩阵为:[]11111EA k l -⎡⎤'=⎢⎥-⎣⎦;[]21111EA k l -⎡⎤'=⎢⎥-⎣⎦;[]31111k -⎡⎤'=⎢⎥-⎣⎦平面杆单元坐标转置矩阵:cos sin cos sin T αααα⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,而又00012390045ααα===-、和,从而各个单元的坐标转置矩阵分别为:10101T ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦;21010T ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦;3222T ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎢-⎢⎣⎦根据上面给出的坐标转置矩阵,可得各个单元在整体坐标系下的单元刚度矩阵为[][]1111000000101101000101001100010000010101T EA EA k T k T l l ⎡⎤⎡⎤⎢⎥⎢⎥--⎡⎤⎡⎤'⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦[][]2222101010001110000000011100101010000000T EA EA k T k T l l -⎡⎤⎡⎤⎢⎥⎢⎥-⎡⎤⎡⎤'⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦[][]3333101111101111001111011100111111011111T k T k T --⎡⎤⎡⎤⎢⎥⎢⎥-----⎡⎤⎡⎤'⎥⎢⎥===⎢⎥⎢⎥⎥⎢⎥----⎣⎦⎣⎦⎥⎢⎥---⎣⎦⎣⎦令节点位移向量为{}112233,,,,,Tu v u v u v δ=,节点力为{}112233,,,,,Tx y x y x y F q q q q q q =,按照整体刚度矩阵的拼装原则,可得[]1010000100011010000011 EAKl-⎡⎤⎢⎥-⎢⎥⎢⎥-+⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦若节点的编号改变后,[]K会发生变化,但是并不影响最终的计算结果。
有限元试题和答案

一。
简答题:1.轴对称体上作用正对称形式的载荷时,沿坐标,,r z θ的三个分量(,,)r P r z θ,z (,,)P r z θ和(,,)P r z θθ有何特点?(P85)(,,)r P r z θ和z (,,)P r z θ是偶函数,傅里叶级数展开式中不含sin k θ,(,,)P r z θθ是奇函数,傅里叶级数展开式中不含cos k θ。
2.某单元的节点上,既有位移自由度又有转动自由度,试述此单元的协调性要求?(P27) 在交界面上满足变形协调条件,变形后既不分裂,也不重叠,从而保证了整个结构的位移连续。
3.用泛函变分求解弹性力学的场问题时,为什么只需要考虑几何边界条件?(P179) 泛函求极值与求满足位移及力边界条件的平衡方程的解是完全等价的。
利用变分求解只需要满足位移边界条件,而力边界条件是在求解泛函的极值中自动满足的。
4.写出用位移梯度表示的格林应变张量和阿尔曼西应变张量,并证明他们的参考变形?(P201)格林应变张量1=+2j i k k ij j i i j u u u u E x x x x ∂∂∂∂∂∂∂∂(+) 阿尔曼西应变张量1=+2j i k k ij j i i ju u u u e x x x x ∂∂∂∂∂∂∂∂(-) 5.写出接触问题中的运动学条件和动力学条件?(P225)运动学条件:满足不可贯穿条件,对于两个接触物体,可表示为0ABV V ⋂=动力学条件:要求连个物体接触面的合力为零0ABq q += 二、三角形单元的位移为:012012(cos 1)(sin )(sin )(cos 1)u u x x v v x x θθθθ=+-+-=++-式中0u 和0v 分别为1x 和2x 方向的刚体位移,θ为逆时针绕原点的刚体转角。
计算单元的柯西应变和格林应变。
证明此位移为刚体运动。
(P201) 解:柯西应变:11=cos 1u x εθ∂=-∂,22=cos 1v x εθ∂=-∂,12212=+sin sin 0u v x x εθθ∂∂=-+=∂∂ 格林应变:1111111111=+(cos 1cos 1(cos 1)(cos 1)sin sin )022u u u u v v E x x x x x x θθθθθθ∂∂∂∂∂∂+-+-+--+=∂∂∂∂∂∂(+)=122121121211==+(sin sin (cos 1)(sin )sin (cos 1))022u v u u v v E E x x x x x x θθθθθθ∂∂∂∂∂∂+-++--+-=∂∂∂∂∂∂(+)=2222222211=+(cos 1cos 1(cos 1)(cos 1)sin sin )022v v u u v v E x x x x x x θθθθθθ∂∂∂∂∂∂+-+-+--+=∂∂∂∂∂∂(+)=三 周向有集中载荷作用的悬臂梁,弯曲刚度为EI ,(1)建立梁的总势能表达式,(2)假定瑞利-里茨能为2323w C x C x =+,计算梁的挠度表达式。
有限元分析与应用详细例题

试题1:图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;2)分别采用不同数量的三节点常应变单元计算;3)当选常应变三角单元时,分别采用不同划分方案计算。
一.问题描述及数学建模无限长的刚性地基上的三角形大坝受齐顶的水压作用可看作一个平面问题,简化为平面三角形受力问题,把无限长的地基看着平面三角形的底边受固定支座约束的作用,受力面的受力简化为受均布载荷的作用。
二.建模及计算过程1. 分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算下面简述三节点常应变单元有限元建模过程(其他类型的建模过程类似):进入ANSYS【开始】→【程序】→ANSYS →ANSYS Product Launcher →change the working directory →Job Name: shiti1→Run设置计算类型ANSYS Main Menu: Preferences →select Structural → OK选择单元类型单元是三节点常应变单元,可以用4节点退化表示。
ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete →Add →select Solid Quad 4 node 42 →OK (back to Element Types window)→Options… →select K3: Plane Strain →OK→Close (the Element Type window)定义材料参数材料为钢,可查找钢的参数并在有限元中定义,其中弹性模量E=210Gpa,泊松比v=。
ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear→Elastic→Isotropic→input EX:, PRXY:→ OK生成几何模型生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS→依次输入四个点的坐标:input:1(0,0),2(3,0),3(6,0),4(3,5),5(0,10),6(0,5)→OK生成坝体截面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS →依次连接1,2,6;2,3,4;2,4,6;4,5,6这三个特征点→OK网格划分ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) Global: Set →input NDIV: 1→OK →(back to the mesh tool window)Mesh: Areas, Shape: Tri, Free →Mesh →Pick All (in Picking Menu) → Close( the Mesh Tool window)模型施加约束分别给下底边和竖直的纵边施加x和y方向的约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→ On lines→选择底边→OK→select:ALL DOF → OK给斜边施加x方向的分布载荷ANSYS 命令菜单栏: Parameters→Functions →Define/Edit→1) 在下方的下拉列表框内选择x ,作为设置的变量;2) 在Result窗口中出现{X},写入所施加的载荷函数:1000*{X};3) File>Save(文件扩展名:func) →返回:Parameters→Functions →Read from file:将需要的.func文件打开,任给一个参数名,它表示随之将施加的载荷→OK →ANSYS Main Menu: Solution →Define Loads →Apply→Structural →Pressure →On Lines →拾取斜边;OK →在下拉列表框中,选择:Existing table (来自用户定义的变量)→OK →选择需要的载荷参数名→OK分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →OK结果显示确定当前数据为最后时间步的数据ANSYS Main Menu: General Postproc →Read Result→Last Set查看在外力作用下的变形ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape→select Def + Undeformed→OK查看节点位移分布情况Contour Plot→Nodal Solu…→select: DOF solution→Displacement vctor sum→Def + Undeformed→OK查看节点应力分布情况Contour Plot→Nodal Solu…→select: Stress→XY shear stress→ Def + Undeformed→OK退出系统ANSYS Utility Menu: File→ Exi t…→ Save Everything→OK 三.结果分析三节点常应变单元(6个节点,4个单元)几何模型图变形图,节点位移图,节点应力图,节点应变图六节点常应变单元(6个节点,4个单元)几何模型图变形图,节点位移图,节点应力图,节点应变图分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算结果比较单元划分方案变形大小应力大小应变大小值的比较分析三节点三角形单元DMX:SMX:DMX:SMN:2778SMX:8749DMX:SMN:SMX:1.最大变形值小;2.最大应力值小;3.最大应变值小。
有限元概念题解答

有限元概念题解答有限元复习第一章平面问题单元分析1.什么是平面应力问题?什么是平面应变问题?答:平面应力问题是指薄板受平行于板面且沿厚度均布载荷作用,只有xy面上三个应力分量σx,σy,τxy 非零。
平面应变问题是指长柱体受平行于横截面且沿长度均布载荷作用,只有xy面上三个应变分量εx,εy,γxy非零。
2.单元剖分时应注意哪些问题?答:规模适当、单元形状尽量接近正多边形、不同材料部分划分在不同单元、不同厚度或不同截面划分在不同单元、集中力作用点及分布载荷密度变化处设置节点、应力集中区域单元划分密度要大、疏密过渡要平缓、希望了解某处位移此处设置节点、边界点设置节点。
3.什么是位移模式?位移模式应满足哪些条件?答:位移模式是在单元范围内的位移函数,是坐标的函数。
位移模式通常应满足a)反映刚体位移;b)反映常变形;c)单元边界上位移连续,三个条件。
4.什么是节点力?什么是节点载荷?答:节点力是单元给节点的力或节点给单元的力,等于单元的弹性力;节点载荷是外界作用在弹性体节点上的力。
5.什么是单元分析?说说单元分析的大致过程。
答:单元分析就是寻求单元节点力与节点位移之间的关系。
单元分析的大致过程:设定位移模式即用节点位移表达单元内任意一点位移、建立应变与位移之间的几何方程、建立应力与应变之间的物理关系、由虚功原理建立节点力与单元内任意一点应力之间的平衡关系,从而得到单元刚度方程。
6.单元刚度矩阵有哪些特点?说说它们的物理意义。
答:单元刚度矩阵具有对称性、奇异性,可按节点分块。
对称性反映了功的互等关系,奇异性说明单元在无约束情况下可以发生刚体位移,由于每个节点具有相同的自由度,因此单元刚度矩阵可按节点分成若干相似的子块。
第二章平面问题整体分析1.如何引入约束条件?答:引入约束条件:a)对角元改1法,将刚度矩阵中有位移约束的自由度对应的行和列对角元改为1,其它元素改为0,载荷向量中对应元素置为已知位移值,其它载荷元素减去已知位移值与该行对应列刚度系数之积。
有限元题库讲解

有限元考试复习1. 平面应力/平面应变问题;空间问题/轴对称问题;杆梁问题;线性与非线性问题平面应力问题(1) 均匀薄板(2)载荷平行于板面且沿厚度方向均匀分布在六个应力分量中,只需要研究剩下的平行于XOY 平面的三个应力分量,即x y xy yx σσττ=、、(000z zx xz zy yz σττττ=====,,)。
一般0z σ=,z ε并不一定等于零,但可由x σ及y σ求得,在分析问题时不必考虑。
于是只需要考虑x y xy εεγ、、三个应变分量即可。
平面应变问题(1) 纵向很长,且横截面沿纵向不变。
(2)载荷平行于横截面且沿纵向均匀分布z yz zx εγγ===只剩下三个应变分量x y xy εεγ、、。
也只需要考虑x y xy σστ、、三个应力分量即可轴对称问题物体的几何形状、约束情况及所受外力都对称于空间的某一根轴 轴对称单元的特点(与平面三角形单元的区别):轴对称单元为圆环体,单元与单元间为节圆相连接;节点力与节点载荷是施加于节圆上的均布力;单元边界是一回转面;应变不是常量。
在轴对称问题中,周向应变分量θε是与r 有关。
板壳问题一个方向的尺寸比另外两个方向尺寸小很多,且能承受弯矩的结构称为板壳结构,并把平分板壳结构上下表面的面称为中面。
如果中面是平面或平面组成的折平面,则称为平板;反之,中面为曲面的称为壳。
杆梁问题杆梁结构是指长度远大于其横断面尺寸的构件组成的系统。
在结构力学中常将承受轴力或扭矩的杆件称为杆,而将承受横向力和弯矩的杆件称为梁。
线性问题/非线性问题线性问题:基于小变形假设,应力与应变方程、应力与位移关系方程、平衡方程都是线性的。
非线性问题:材料非线性(非线性弹性、非线性弹塑性),几何非线性(大变形大应变如金属橡胶,小应变大位移如薄壁结构)2.不同类型单元的节点自由度的理解:单元类型节点数节点自由度杆单元 2 1梁单元 2 3平面单元 3 2平面四边形 4 2轴对称问题 3 2板壳单元 4 3四面体单元 4 33.有限元法的基本思想与有限元分析的基本步骤(5步)有限元法的基本思想:离散、分片插值;其中离散的思想吸收了差分法的启示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元考试试题及答案一、简答题(5道,共计25分)。
1.有限单元位移法求解弹性力学问题的基本步骤有哪些?(5分)答:(1)选择适当的单元类型将弹性体离散化;(2)建立单元体的位移插值函数;(3)推导单元刚度矩阵;(4)将单元刚度矩阵组装成整体刚度矩阵;(5)代入边界条件和求解。
2. 在划分网格数相同的情况下,为什么八节点四边形等参数单元精度大于四边形矩形单元?(5分)答:在对于曲线边界的边界单元,其边界为曲边,八节点四边形等参数单元边上三个节点所确定的抛物线来代替原来的曲线,显然拟合效果比四边形矩形单元的直边好。
3.轴对称单元与平面单元有哪些区别?(5分)答:轴对称单元是三角形或四边形截面的空间的环形单元,平面单元是三角形或四边形平面单元;轴对称单元任意一点有四个应变分量,平面单元任意一点非零独立应变分量有三个。
4.有限元空间问题有哪些特征?(5分)答:(1)单元为块体形状。
常用单元:四面体单元、长方体单元、直边六面体单元、曲边六面体单元、轴对称单元。
(2)结点位移3个分量。
(3)基本方程比平面问题多。
3个平衡方程,6个几何方程,6个物理方程。
5.简述四节点四边形等参数单元的平面问题分析过程。
(5)分)答:(1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;(2)通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4)用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。
二、论述题(3道,共计30分)。
1. 简述四节点四边形等参数单元的平面问题分析过程。
(10分)答:(1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;(2)通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4)用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。
2.轴对称问题的简单三角形单元是否是常应力,常应变?为什么?(10分)答:不是常应力和常应变。
因为应变与位移分量的关系式为:⎭⎬⎫⎩⎨⎧⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=w u010rr u r u }{rz z r r z z r r w z u z w γεεεεθ,这里除含有微分算符外,还包含了r 的倒数项1/r ,则即使位移模式为线性的,但由于该项的存在,使得应变与坐标有关,即不会是常应变。
应力应变的物理关系为{}[]{}εσD = ,由于应变不是常应变,则所求得的应力也不会是常应力。
3.在薄板弯曲理论中做了哪些假设?薄板单元和厚板单元的基本假设有什么不同?(10分)答:四种假设: 1)变形前的中面法线在变形后仍为弹性曲面的法线。
2)变形前后板的厚度不变。
3)板变形时,中面无伸缩。
4)板各水平层间互不挤压。
不同点:薄板单元假设横向纤维无挤压,板的中面法线变形后仍保持为直线,该直线垂直于变形后的中面,但是厚板单元的假设考虑横向变形的影响,板的中面法线变形后仍 基本保持为直线,但该直线不再垂直于变形后的中面,法线绕坐标轴的转角不再是挠度的导数,而是独立的变量。
三、计算题(3道,共计45分)。
1.如图所示等腰直角三角形单元,其厚度为t ,弹性模量为E ,泊松比0ν=;单元的边长及结点编号见图中所示。
求(1) 形函数矩阵N (2) 应变矩阵B 和应力矩阵S(3) 单元刚度矩阵e K (12分)解:设图1所示的各点坐标为点1(a ,0),点2(a ,a ),点3(0,0)于是,可得单元的面积为 12A =2a ,及(1) 形函数矩阵N 为12122121(0a a )a1(00a )a 1(a a 0)a N x y N x y N x y =+-=++=-+ ;[][]123123 N N N ==N I I I N N N (2) 应变矩阵B 和应力矩阵S 分别为12a 010-a a -a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B ,220010a a a 0⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B ,32-a 0100a 0-a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B ; []123=B B B B12a 00-a a 11-a a 22E ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦S ,22000a a 1a 02E ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦S ,32-a 000a 10-a 2E ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦S ;[][]123123 ==S D B B B S S S(3) 单元刚度矩阵e K111213T 2122233132333110211312011110014020200200020111001e Et tA ---⎡⎤⎢⎥---⎢⎥⎡⎤--⎢⎥⎢⎥===⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥--⎣⎦K K K K B DB K K K K K K2.如图所示的四结点矩形单元,求出节点3的位移。
设厚度t =1m ,μ=0,E为常量。
(13分)注:对于四节点矩形单元有:()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+-=++=-+=--=ηξηξηξηξ1141114111411141.14321N N N N →)4,3,2,1()1)(1(41=++=i N i i i ηηξξ()[][][][]eT Aek k k k k k k k k k k k k k k k y x t B D B k ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎰⎰44434241343332312423222114131211d d .2,[][][][][][][]()()()()())4,3,2,1,( 3111311a 212123111311218d d d d 21111=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-===⎰⎰⎰⎰--j i b a b b a a b Et B D B abt y x t B D B k j i j i j i j i j i j i j i j i j i j i j i j i jTijTAiijηηξξμξξηηηξμξμηηξμξμηξξηημηηξξμηξ解:对于四节点矩形单元有:()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+-=++=-+=--=ηξηξηξηξ11411141114111414321N N N N →)4,3,2,1()1)(1(41=++=i N i i i ηηξξ[][][][]eT Aek k k k k k k k k k k k k k k k y x t B D B k ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎰⎰44434241343332312423222114131211d d , [][][][][][][]()()()()())4,3,2,1,( 3111311a 212123111311218d d d d 21111=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-+-+⎪⎭⎫⎝⎛+-+⎪⎭⎫ ⎝⎛+-===⎰⎰⎰⎰--j i b a b b a a b Et B D B abt y x t B D B k j i j i j i j i j i j i j i j i j i j i j i j i jTijTAiijηηξξμξξηηηξμξμηηξμξμηξξηημηηξξμηξ[]{}{}e e e R k =δ,代入边界条件μ1=ν1=μ2=ν2=μ4=ν4=0,将对应的行和列划掉没剩下的方程为:[]⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧P P k --νμ3333, 又)4,3,2,1()1)(1(41=++=i N i i i ηηξξ,且1133==ηξ,,a=1,b=1所以[]411483113112113113112833⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⨯=E E k 所以[]⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧P P k --νμ3333→⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡P P E --νμ4114833 解得⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧1158-νμ33E P 3.有一如图3(a)所示的剪力墙,墙顶作用竖向荷载P 。
将该剪力墙划分为两个三结点三角形常应力单元,单元和结点编号如图3(b)所示,并将荷载P 分成两个P/2作用在3、4结点。
已知单元厚度为t ,弹性模量为E ,泊松比μ=1/3。
求结点3和结点4的位移,以及单元①的应变和应力。
(20分)解:建立直角坐标系(注Y 轴向下为正),单元①i,j,m 对应的节点编号为3,1,4,单元②对应的节点编号为2,4,1。
对于单元①:i(0,0),j(0,4),m(2,0) bi=yi-ym=4;bj=ym-yi=0;bm=yi-yj=-4 ci=xm-xj=2;cj=xi-xm=-2;cm=xj-xi=0 三角形面积A=1/2*2*4=4几何矩阵[B]=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----40000204024202000481弹性矩阵[D]=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--2100010112μμμμE单元刚度矩阵∆=t B D B k T ]][[][][1=314)1(8001684)1(4)1(8)1(40816048)1(2)1(4)1(2)23(4)1(4)9(2)1(162⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------------+--μμμμμμμμμμμμμμEt132)1(8001684)1(4)1(8)1(40816048)1(2)1(4)1(2)23(4)1(4)9(2][][12⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------------+-==μμμμμμμμμμμμμk k然后合成总刚[K]。
整体节点力矢量为]0202[}{2211P PF F F F F yx y x =节点位移矢量为[]44330000}{v u v u d =}]{[}{d K F =,采用缩减矩阵法划去位移为零的行与列,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--------02/02/)23(4)1(4)1(88)9(2)1(416)23(40)9(2)1(1644332P P v u v u Et μμμμμμμμμ 解得[]T Et P v u v u 88.199.850.142.84433-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡单元①的应变{}[]T EtPd B 56.047.0285.0}]{[11-==ε 单元①的应力{}[]T tPd B D 84.068.158.0}]{][[11-==σ。
