实验三链表及其多项式相加(答案)(DOC)

合集下载

多项式链表加法

多项式链表加法要实现多项式链表的加法，我们可以按照指数的从小到大的顺序对两个多项式链表进行遍历，逐项相加生成新的链表。

具体步骤如下：1. 定义一个多项式链表的节点类，节点类中包含一个系数和指数作为节点的数据成员，并定义一个指向下一个节点的指针。

```pythonclass Node:def __init__(self, coefficient, exponent):self.coefficient = coefficientself.exponent = exponentself.next = None```2. 定义一个多项式链表类，类中包含一个头节点作为链表的起始位置，并定义相应的方法。

```pythonclass PolynomialLinkedList:def __init__(self):self.head = Node(0, 0) # 头节点的指数和系数均为0```3. 定义一个方法来插入节点到多项式链表中。

```pythondef insert(self, coefficient, exponent):new_node = Node(coefficient, exponent)current = self.headwhile current.next and current.next.exponent > exponent:current = current.nextif current.next and current.next.exponent == exponent:current.next.coefficient += coefficientelse:new_node.next = current.nextcurrent.next = new_node```4. 定义一个方法来将多项式链表进行加法运算，并返回一个新的多项式链表。

```pythondef add(self, other):result = PolynomialLinkedList()current1 = self.head.nextcurrent2 = other.head.nextwhile current1 and current2:if current1.exponent > current2.exponent:result.insert(current1.coefficient, current1.exponent)current1 = current1.nextelif current1.exponent < current2.exponent:result.insert(current2.coefficient, current2.exponent)current2 = current2.nextelse:result.insert(current1.coefficient + current2.coefficient, current1.exponent)current1 = current1.nextcurrent2 = current2.nextwhile current1:result.insert(current1.coefficient, current1.exponent) current1 = current1.nextwhile current2:result.insert(current2.coefficient, current2.exponent) current2 = current2.nextreturn result```以下是一个完整的示例代码：```pythonclass Node:def __init__(self, coefficient, exponent):self.coefficient = coefficientself.exponent = exponentself.next = Noneclass PolynomialLinkedList:def __init__(self):self.head = Node(0, 0)def insert(self, coefficient, exponent):new_node = Node(coefficient, exponent)current = self.headwhile current.next and current.next.exponent > exponent: current = current.nextif current.next and current.next.exponent == exponent: current.next.coefficient += coefficientelse:new_node.next = current.nextcurrent.next = new_nodedef add(self, other):result = PolynomialLinkedList()current1 = self.head.nextcurrent2 = other.head.nextwhile current1 and current2:if current1.exponent > current2.exponent:result.insert(current1.coefficient, current1.exponent)current1 = current1.nextelif current1.exponent < current2.exponent:result.insert(current2.coefficient, current2.exponent)current2 = current2.nextelse:result.insert(current1.coefficient + current2.coefficient, current1.exponent)current1 = current1.nextcurrent2 = current2.nextwhile current1:result.insert(current1.coefficient, current1.exponent)current1 = current1.nextwhile current2:result.insert(current2.coefficient, current2.exponent)current2 = current2.nextreturn result```通过以上的代码，我们就可以进行多项式链表的加法运算了。

实验三链表及其多项式相加 - 副本

实验三、链表及其多项式相加一、实验目的1.了解线性表的链式存储结构，熟练掌握链表。

2.了解作为链表的多项式存贮方式。

3.熟悉掌握多项式加法的算法。

二、实验原理顺序存储的线性表有一些弱点，其一，插入与删除元素需要大量移动元素；其二，预先分配存储空间时必须按最大的空间来分配。

其三，表长难以扩充。

所以，必须引入链式存储结构。

链式存储结构的特点是用一组任意的存储单元存储线性链表的数据元素，与顺序表的区别在于链式存储的存储单元可以是连续的，也可以是不连续的。

为了实现这种结构，链表采取由两部分信息组成数据元素a i的存储映像，称为结点。

结点包括两个域，其中存储数据信息的域称为数据域，存储直接后继信息的称为指针域。

指针域中存储的信息叫做指针或链。

这样，n个结点链接成一个链表，即为线性表（a1,a2,a3,···,a n）。

1.符号多项式的操作，已经成为表处理的典型用例，在数学上，一个一元多项式pn(x)可以按升幂写成：pn(x)=p0+p1·x+p2·（x的2次幂）+···+p n·（x的n次幂）。

它由n+1个系数唯一确定。

因此，在计算机里，它可用一个线性表P来表示：P=(p0,p1,p2,···,p n), 显然，此种表示仅适于顺序存储结构，在通常的应用中，多项式的次数变化很高且很大，将造成内存的很大浪费。

2.实现单链表就地逆置。

三、实验要求1．参照书上的原理说明分析程序，深入理解链表的物理存储模式和逻辑模式。

2．看懂书上算法，参考实验程序编出程序上机调试。

3．参考书上的程序，编写建立链表存储多项式，并实现两多项式相加。

四、代码实现：1.# include<stdio.h># include<stdlib.h>typedef struct Polynode{int coef;int exp;Polynode *next;}Polynode,* Polylist;Polylist polycreate(){Polynode * head,*rear,*s;int c,e;head=(Polynode *)malloc(sizeof(Polynode)); rear=head;scanf("%d,%d",&c,&e);while(c!=0){s=(Polynode *)malloc(sizeof(Polynode));s->coef=c;s->exp=e;rear->next=s;rear=s;scanf("%d,%d",&c,&e);}rear->next=NULL;return (head);}void polyadd(Polylist polya,Polylist polyb) {Polynode *p,*q,*tail,*temp;int sum;p=polya->next;q=polyb->next;tail=polya;while(p!=NULL && q!=NULL){if (p->exp<q->exp){tail->next=p;tail=p;p=p->next;}else if (p->exp==q->exp){sum=p->coef+q->coef;if (sum!=0){p->coef=sum;tail->next=p;tail=p;p=p->next;temp=q;q=q->next;free(temp);}else{temp=p;p=p->next;free(temp);temp=q;q=q->next;free(temp);}}else{tail->next=q;tail=q;q=q->next;}}if(p==NULL)tail->next=p;elsetail->next=q;}void main(){Polynode *p;printf("请输入第一个多项式,次数从低到高:\n"); Polylist A=polycreate();printf("\n多项式创建完成!\n");printf("\n请输入第二个多项式,次数从低到高:\n"); Polylist B=polycreate();printf("\n多项式创建完成!\n\n");polyadd(A,B);p=A->next;while(p!=NULL){printf("[%d %d] ",p->coef,p->exp);p=p->next;}printf("\n\n");}2.# include<stdio.h># include<stdlib.h>typedef struct Node{char data;struct Node * next;}Node,* Linklist;void Initlist(Linklist *L){*L=(Linklist)malloc(sizeof(Node));(*L)->next=NULL;}void CreateFromHead(Linklist L){Node *s;char c;int flag=1;while(flag){c=getchar();if (c!='$'){s=(Node *)malloc(sizeof(Node));s->data=c;s->next=L->next;L->next=s;}else flag=0;}}void Reverselist(Linklist L){Linklist p,q;p=L->next;L->next=NULL;while(p!=NULL){q=p->next;p->next=L->next;L->next=p;p=q;}}void main (){Linklist p;Linklist L;Initlist(&L);printf("Please input datas:\n");CreateFromHead(L);p=L;while (p->next!=NULL){p=p->next;printf("%c ",p->data);}Reverselist(L);printf("\n\n");}五：结果验证：1.2。

链表线性结构(多项式的加减乘除)

哈尔滨工业大学计算机科学与技术学院实验报告课程名称：数据结构与算法课程类型：必修实验项目：线性结构及其应用实验题目：多项式的加减乘除和特定值带入实验日期：2017/11/5班级：1603001学号：**********姓名：***一、实验目的设计线性表的链式存储结构，并实现一元多项式的代数运算。

二、实验要求及实验环境（1）实验要求：以链表存储一元多项式，在此基础上完成对多项式的代数操作。

1.能够输入多项式（可以按各项的任意输入顺序，建立按指数降幂排列的多项式）和输出多项式（按指数降幂排列）,以文件形式输入和输出，并显示。

2.能够计算多项式在某一点 x=x0 的值，其中 x0 是一个浮点型常量，返回结果为浮点数。

3.能够给出计算两个多项式加法、减法、乘法和除法运算的结果多项式，除法运算的结果包括商多项式和余数多项式。

4.要求尽量减少乘法和除法运算中间结果的空间占用和结点频繁的分配与回收操作。

（提示：利用循环链表结构和可用空间表的思想，把循环链表表示的多项式返还给可用空间表，从而解决上述问题）。

（2）实验环境：windows下的CB;三、设计思想（本程序中的用到的所有数据类型的定义，主程序的流程图及各程序模块之间的调用关系）1．逻辑设计:struct polynode{int coef;int exp;struct polynode * link;};//建立链表typedef struct polynode poly;poly* Attch(int c,int e,poly *d);//多项式插入poly *newPoly();//新链表poly *padd(poly *p1,poly *p2);//多项式加法poly *pmul(poly *p1,poly *p2);//乘法poly *inputPoly();//输入多项式poly *psub(poly *p1,poly *p2);//减poly *pdiv(poly *p1,poly *p2);//除poly *inputPoly1();double caculate(double x,poly *p);//计算多项式void sortPoly(poly *p);//多项式排序void outputPoly(poly*p);//输出多项式void delPoly(poly*p);//清空多项式2．物理设计：四、测试结果五、经验体会与不足不能连续输入多个多项式函数设计不够简洁算法过于直接简单加注释后修改代码方便六、附录：源代码（带注释）#include <stdio.h>#include <stdlib.h>struct polynode{int coef;int exp;struct polynode * link;};//建立新链表typedef struct polynode poly;poly* Attch(int c,int e,poly *d);//插入链表poly *newPoly();//建立新链表poly *padd(poly *p1,poly *p2);//加法poly *pmul(poly *p1,poly *p2);//乘法poly *inputPoly();//输入多项式poly *psub(poly *p1,poly *p2);//减法poly *pdiv(poly *p1,poly *p2);//除法poly *inputPoly1();//输入double caculate(double x,poly *p);//计算void sortPoly(poly *p);//排序void outputPoly(poly*p);//输出多项式void delPoly(poly*p);//除法void Insert(poly *p,poly *h){if(p->coef==0)free(p);else{poly *q1,*q2;q1=h;q2=h->link;while(q2&&p->exp<q2->exp){q1=q2;q2=q2->link;}/*判断两个指数是否相等*/if(q2&&p->exp==q2->exp){q2->coef+=p->coef;free(p);if(!q2->coef){q1->link=q2->link;free(q2);}}/*相等就加系数*/else{p->link=q2;q1->link=p;}}/*不等就插在后面*/}int main(){poly *p1,*p2,*padd1,*psub1,*pmul1; p1=newPoly();printf("第一个多项式\n");p1->link=inputPoly();outputPoly(p1);p2=newPoly();printf("第二个多项式\n");p2->link=inputPoly1();outputPoly(p2);padd1=newPoly();pmul1=newPoly();psub1=newPoly();padd1->link=padd(p1,p2);printf("padd\n");outputPoly(padd1);psub1->link=psub(p1,p2);printf("psub\n");outputPoly(psub1);pmul1->link=pmul(p1,p2);printf("pmul\n");outputPoly(pmul1);printf("输入x的值！");int x;scanf("%d",&x);x=caculate(x,p1);printf("%d\n",x);pdiv(p1,p2);return 0;}poly *newPoly(){poly *x;x=(poly*)malloc(sizeof(poly)); x->link=NULL;x->coef=0;x->exp=0;return x;}poly* Attch(int c,int e,poly *d) {poly *x;x=newPoly();x->coef=c;x->exp=e;d->link=x;return x;}poly *padd(poly *p1,poly *p2){poly *a, *b,*c,*d,*p;c=newPoly();d=c;p=c;a=p1->link;b=p2->link;while(a!=NULL&&b!=NULL){if(a->exp>b->exp)//如果a的系数大于b把a先输入 {c=Attch(a->coef,a->exp,c);a=a->link;}else if(a->exp<b->exp)//小于相反{c=Attch(b->coef,b->exp,c);b=b->link;}else//相等{c=Attch(b->coef+a->coef,a->exp,c);a=a->link;b=b->link;}}/*a b比较完成开始遍历剩下的未插入的*/while(a!=NULL){c=Attch(a->coef,a->exp,c);a=a->link;}while(b!=NULL){c=Attch(b->coef,b->exp,c);b=b->link;}c->link=NULL;d=d->link;p->link=NULL;delPoly(p);return d;}poly *psub(poly*p1,poly*p2)//加和减思路相同，b的系数得输入相反值{poly *a, *b,*c,*d,*p;c=newPoly();d=c;p=c;a=p1->link;b=p2->link;while(a!=NULL&&b!=NULL){if(a->exp>b->exp){c=Attch(a->coef,a->exp,c);a=a->link;}else if(a->exp<b->exp){c=Attch(b->coef*(-1),b->exp,c);b=b->link;}else{if((a->coef-b->coef)>0){c=Attch(a->coef-b->coef,a->exp,c); a=a->link;b=b->link;}else{a=a->link;b=b->link;}}}while(a!=NULL){c=Attch(a->coef,a->exp,c);a=a->link;}while(b!=NULL){c=Attch(b->coef*(-1),b->exp,c);b=b->link;}c->link=NULL;d=d->link;p->link=NULL;delPoly(p);return d;}/*乘法，先用第一个链表的第一个数据乘以第二个链表里的所有值，储存在新的链表中，之后遍历一中所有的值，最后把这些多项式加在一起。

《数据结构》实验3链表

二、源代码以及输入数据输出结果为：
三、源代码以及实验结果为
四、源代码以及实验结果为
五、源代码以及实验结果为
六、源代码以及实验结果为
七、附加题以及实验体会：
{
NODE *s; /*定义指向结点类型的指针*/
s=(NODE *)malloc(sizeof(NODE));
/*生成新结点*/
3
4
5
return 1;
}
/*删除P所指向的结点的后继结点*/
void DelLinkList(NODE *p)
{ NODE *q;
if(p->next!=0)
{ q=p->next; /* q指向p的后继结点*/
ch=getchar();
while(ch!='$')
{ p=(NODE *)malloc(sizeof(NODE));
p->data=ch;
1
2
ch=getchar();
}
return (head);
}
/*在链表的P指定结点之后插入值为x的结点*/
int InsLinkList(NODE *p, char x)
四、设有两个单链表A、B，其中元素递增有序，编写算法将A、B归并成一个按元素值递减（允许有相同值）有序的链表C，要求用A、B中的原结点形成，不能重新申请结点。
五、已知单链表表示的线性表中含有两类的数据元素（字母字符，数字字符）。试设计算法，按结点的值将单链表拆分成两个循环链表，分别只含有数字或字母。要求：利用原表中的结点空间作为这两个表的结点空间，头结点可另开辟空间。
附加题：如果换成循环单链表该如何实现？
即题目变成：已知单循环链表表示的线性表中含有两类的数据元素（字母字符，数字字符）。试设计算法，按结点的值将单链表拆分成两个循环链表，分别只含有数字或字母。

数据结构多项式相加实验报告doc

数据结构多项式相加实验报告篇一：数据结构实验多项式加法数据结构实验报告实验名称：多项式加减法学号：1XX10419姓名：林强实验日期：XX.5.05一、实验目的通过实现多项式的加减法，对链表有更深入的了解二、实验具体内容1、实验题目1：（1）题目设计一个一元稀疏多项式简单的加减法计算器实现要求：一元稀疏多项式简单计算器的基本功能是：（1）输入并建立多项式：A(x)?7?3x?9x8?5x17；B(x)?8x?22x7?9x8（2）输出多项式（3）多项式A和B相加，建立多项式C＝A＋B，并输出相加的结果多项式C（4）选作：多项式A和B相减，建立多项式C＝A－B，并输出相加的结果多项式D（2）分析1：本程序的任务是实现两个多项式的加法其中多项式的系数为浮点型，指数为整数，输出的结果也为系数和指数。

（1）输入的形式和输入值的范围：输入多项式的系数a和未知数X的指数b，当a和b都为零时，输入结束。

输入值的范围：a为实数，b为整数。

（2）输出形式：输出多项式的系数和多项式未知数X 的指数即(a,b)形式。

（3）程序所能达到的功能，实现两个多项式的加法，并输出最后的结果2：整个程序运行期间实行动态创建节点，一边输入数据，一边创建节点当将全部数据输入到单链表中后再调用多项式加法这个函数，并一边实现多项式的相加，一边释放节点，有效防止了在程序反复运行过程中可能出现系统空间不够分配的现象（3）实验代码typedef int Status;#define OVERFLOW -1#define null 0typedef struct Lnode{float coef; //存储项系数int expn;//存储项指数struct Lnode *next;}Lnode,*LinkList;typedef LinkList polynomial;Status InitList_L(LinkList &L) {//初始化头节点L=(LinkList)malloc(sizeof(Lnode));if(!L)return(-1);L->next=null;return 1;}void AddPolyn(polynomial pa, polynomial pb){ //实现两个多项式相加的算法float x;polynomial qa;polynomial qb;polynomial s;polynomial u;qa=pa->next; qb=pb->next; s=pa;while(qa&&qb){if(qa->expnexpn){s=qa;qa=qa->next;}else if(qa->expn==qb->expn){x=qa->coef+qb->coef;if(x!=0){qa->coef=x;s=qa;qa=qa->next;u=qb;qb=qb->next;free(u);}else{s->next=qa->next;free(qa);qa=s->next;u=qb;qb=qb->next;free(u);}}else if(qa->expn>qb->expn){ u=qb->next;s->next=qb;s=qb;qb->next=qa;qb=u;}}if(qb)qa->next=qb;free(pb);}void main(){float a;int b;polynomial L1;polynomial L2; LinkList q;LinkList p;LinkList m;LinkList n;InitList_L(L1);q=L1;InitList_L(L2);p=L2;cout 请输入数据：" for(;;){ cin>>a;cin>>b;if(a==0&&b==0) break;m=new Lnode;m->coef=a;m->expn=b;q->next=m;q=m;q->next=null;}//循环输入第一个多项式的系数与指数for(;;){cin>>a;cin>>b;if(a==0&&b==0)break;n=new Lnode;n->coef=a;n->expn=b;p->next=n;p=n;p->next=null;}//循环输入第二个多项式的系数与指数AddPolyn(L1,L2);//调用多项式相加的算法while((L1->next)!=null){coutnext->coefnext->expn L1=L1->next;}//输出计算结果}三、实验小结通过编写多项加法这个程序，我将自己所学到的创建链表，初始化链表和多项式加法算法都应用了一次，这使我们不仅仅只是理论化的学习书本上的知识，而是将学习到的理论知识应用到实际的操作中来增强我们的实际操作能力，这使我增加了实际操作经验，也使我通过实际操作来认识到自己在程序编写上的不足从而增强了我的实际编写程序的能力。

用链表实现多项式及其操作

通信韩若冰222010315220106实验项目：线性表及其应用实验内容：用单链表存储多项式；实现多项式的输出显示、相加、相乘、求导、求值运算。

算法设计与程序实现：由于存储多项式需要存储系数和指数，且其指数变化范围可能很大如果用顺序表就会浪费很大的空间，用单链表存取指针域，和数据域（系数和指数）就会节省很大空间。

要想实现多项式的显示，相加，相乘，求导，求值运算，首先得创建函数以实现上述功能，然后再在主函数中调用上述函数以得到运行结果。

算法描述：（实验内容的核心算法）创建链表：首先创建空表，然后将每个结点用尾插法依次插入。

每一项多项式的组成部分（系数和指数）输出程序：此程序需要遍历整个链表，通过判断p->next的系数的正负来确定输出“+”还是“-”很容易出现错误。

多项式相加：这个程序需要按照幂的排列顺序依次遍历寻找一个多项式与另一个多项式指数相同的，将其系数相加比较简单。

该程序写成升幂比较，其中可能出现如A多项式的前几项都比B中的指数小，那么以一个pre为头结点的链表先将其穿起来，找到相等的进行运算再串起来，最后可能会有链表剩余的指数更大的项不能和另一个相加再将剩余的串起来。

（第一项要先串起来，因为第一项之前没有多项式不用判断+ —号）多项式相乘：此程序需要循环语句，即将一个多项式的每一项分别和另一个多项式相乘，依次调用多项式相加的程序叠加起来。

多项式求导：需要依次将多项式的每一项的系数和指数相乘，指数减1，形成一个链表多项式求值：需要有x的幂次的表示，C语言不能识别“^”，所以需要用一个循环实现x^exp相乘的结果，容易出错核心程序：运行结果：实验总结：本次试验做了很长时间，也出现了很多错误。

总起来说有以下几种错误：1.输入错误：中英文状态下输入错误，其中还有运行时在中文状态下输入数据回车后就不能输了，应在英文状态下输入data , data↙2.多项式表示需要判断下一个多项式系数是正还是负然后分别写+, —（fabs），但是第一项必须先输出,因为第一项不需要写+ —号3.多项式相加，要注意写的程序是怎么比较的，升幂的话则p->exp < q->exp 则把p结点指数小的先穿起来。

链表两个多项式相加与相乘的解释

链表两个多项式相加与相乘的解释链表是一种数据结构，其中每个元素（称为节点）包含数据部分和一个指向下一个元素的指针。

在链表中表示多项式，每个节点包含一个系数和一个指示下一个节点在链表中的位置的指针。

多项式的每一项都存储在链表中。

对于两个多项式的相加和相乘，我们可以使用链表来表示这些操作。

1. 多项式相加：假设我们有两个多项式 P(x) 和 Q(x)，它们可以表示为链表：```cssP(x) = a_nx^n + a_n-1x^(n-1) + ... + a_1x + a_0Q(x) = b_mx^m + b_m-1x^(m-1) + ... + b_1x + b_0```多项式 P(x) 和 Q(x) 的相加可以通过简单的对应项相加来完成。

即对于每个i，我们找到 P(x) 的第 i 项和 Q(x) 的第 i 项，然后将它们相加并将结果存储在一个新的链表中。

注意，这可能会导致新的链表中的节点数少于原始链表中的节点数，因为如果某个指数在两个原始链表中都不存在，那么它就不会出现在结果链表中。

2. 多项式相乘：多项式相乘稍微复杂一些。

假设我们有两个多项式 P(x) 和 Q(x)，它们的链表表示如下：```cssP(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0Q(x) = b_mx^m + b_{m-1}x^{m-1} + ... + b_1x + b_0```P(x) 和 Q(x) 的相乘可以通过创建一个新的链表来完成，该链表包含所有可能的对应项乘积。

具体来说，结果链表的每个节点包含一个系数，该系数是原始链表中两个节点的系数的乘积。

对于每个 i 和 j（i 从 0 到 n，j 从 0 到m），我们将 P(x) 的第 i 项与 Q(x) 的第 j 项相乘并将结果添加到结果链表中。

注意，这可能会导致结果链表中的节点数多于原始链表中的节点数，因为每个节点可能与其它的多个节点相乘。

链式存储结构实现多项求和实验报告

链式存储结构实现多项求和实验报告课题设计目的：了解数据结构与算法的设计方法，独立分析和设计一元多项式加减的程序编码，通过程序编写掌握软件开发过程的问题分析、系统设计、程序编码、测试等基本方法和技能，提高综合运用所学的理论知识和方法独立分析和解决问题的能力，通过这次实践将实际问题中所涉及的对象在计算机中表示出来并对它们进行处理，掌握线性表的链式存储如何实现一元多项式的加减。

课题设计意义：通过完成此次课题，可以了解各种数据结构内在的逻辑关系，讨论它在计算机中的存储表示，以及在其上进行各种运算时的算法实现，并对算法的效率和优化进行简单的分析和讨论，不仅加强了学生对于线性表链式存储的理解，也提高了学生的思维能力，促进学生的综合应用能力和专业素质的提高。

数据结构实验-多项式的相加减

集美大学数据结构课程实验报告课程名称：数据结构班级：网络0911实验成绩：指导教师：姓名：实验项目名称：多项式的相加减学号上机实践日期：实验项目编号：组号：上机实践时间：学时一、目的(本次实验所涉及并要求掌握的知识点)学习和掌握如何运用链表来实现一元稀疏多项式的相加减。

多项式的输入和输出的应注意的要点，规定输出的多项式的顺序。

二、实验内容与设计思想(设计思路、主要数据结构、主要代码结构、)实验内容：一元稀疏多项式的相加减设计思路：建立数据结构存放常数和系数以及指向下一个节点的指数，用链表存放各个节点，通过对常数和系数的的运算，实现多项式的相加减主要数据结构：结构体，链表主要代码结构：struct Polyn;void addPolyn(Polyn * a,Polyn * b,int add);void display( );void tip()’Polyn * CreatPolyn(int m);三、实验使用环境(本次实验所使用的平台和相关软件)Dev-C++、windows XP四、实验步骤和调试过程(实验步骤、测试数据设计、测试结果分析)需说明出，加入必要的截图说明。

#include<iostream>#include<vector>using namespace std;struct Polyn{float coef;int expn;Polyn *next;};//构建结构体vector <Polyn *> ve;void addPolyn(Polyn * a,Polyn * b,int add);void display(Polyn *n);//打印void tip();//屏幕显示Polyn * CreatPolyn(int m); //建立多项式int main(){tip();system("pause");}void tip(){Polyn *first, *second,*s;int m;for( int i=1;i;){cout<<" 多项式运算.\n";cout<<"======================="<<"\n"; cout<<" 1------ 构造多项式.\n";cout<<" 2------ 多项式相加.\n";cout<<" 3------ 多项式相减.\n";cout<<" 0------ 结束.\n";cout<<"======================="<<"\n"; cout<<" 请输入您的选择.\n";cin>>i;switch(i){case 1:cout<<"请输入多项式的项数.\n";cin>>m;s=CreatPolyn(m);display(s);ve.push_back(s);break;case 2:first=ve.back();ve.pop_back();second=ve.back();addPolyn(first,second,0);break;case 3:first=ve.back();ve.pop_back();second=ve.back();addPolyn( first,second,1);break;case 0:cout<<" 再见"<<"\n";break;};}}Polyn* CreatPolyn(int m){Polyn* px=new Polyn[m];cout<<" 输入系数.\n";for(int i=0;i<m;i++)cin>>px[i].coef;cout<<"输入与系数相对应的指数.\n";for(int i=0;i<m;i++){cin>>px[i].expn;if(i!=m-1)px[i].next=&px[i+1];elsepx[i].next=NULL;}return px;}void display(Polyn *n){int q=0;Polyn * r;r=n;for(;r;r=r->next){if(r->coef)q++;if(r==n){if(r->coef!=0)cout<<r->coef<<"X"<<"^"<<r->expn;}else{if( r->coef>0)cout<<"+"<<r->coef<<"X"<<"^"<<r->expn;if(r->coef<0)cout<<r->coef<<"X"<<"^"<<r->expn;}}cout<<"\n";if(q==0)cout<<"0"<<"\n";}void addPolyn(Polyn * a,Polyn * b,int add)//两个多项式的加减{float c;int a1=1,b1=1,s,e;Polyn *ha,*hb,*p,*r;ha=a;hb=b;p=ha;r=hb;for(int i=0;ha[i].next;++i)a1++;for(int i=0;hb[i].next;++i)b1++;ha[a1-1].next=hb;for(int j=0;j<b1;j++){for(int i=0;i<a1;i++){if(a[i].expn-b[j].expn==0){if(add)ha[i].coef=ha[i].coef-hb[j].coef;elseha[i].coef=ha[i].coef+hb[j].coef;if(hb!=&hb[j])hb[j-1].next=hb[j].next;else{hb=hb[j].next;ha[a1-1].next=hb;}i=a1;}}}for(;p;p=p->next){for( Polyn * t=p->next;t;t=t->next)if( p->expn>t->expn){e=p->expn;p->expn=t->expn;t->expn=e;c=p->coef;p->coef=t->coef;t->coef=c;}}display(ha);}五、实验小结(实验中遇到的问题及解决过程、实验体会和收获)至少两点1.刚开始实现多项式的相加减运算时，申请一个新的空间来存放结果，结果指针乱了，后来改成了现在的程序。

(完整word版)链表线性结构(多项式的加减乘除)

二、实验要求及实验环境（1）实验要求：以链表存储一元多项式，在此基础上完成对多项式的代数操作。

1.能够输入多项式（可以按各项的任意输入顺序，建立按指数降幂排列的多项式）和输出多项式（按指数降幂排列）,以文件形式输入和输出，并显示。

2.能够计算多项式在某一点 x=x0 的值，其中 x0 是一个浮点型常量，返回结果为浮点数。

3.能够给出计算两个多项式加法、减法、乘法和除法运算的结果多项式，除法运算的结果包括商多项式和余数多项式。

4.要求尽量减少乘法和除法运算中间结果的空间占用和结点频繁的分配与回收操作。

（提示：利用循环链表结构和可用空间表的思想，把循环链表表示的多项式返还给可用空间表，从而解决上述问题）。

链表实现多项式的加和乘

if (lnode_tmp->exp!=0)
printf("x");
if (lnode_tmp->exp!=1 && lnode_tmp->exp!=0)
printf("^%d",lnode_tmp->exp);
if(lnode_tmp->next->coef>0)
printf("+");
}
else
scanf("%d",&l2_length) ;
CreatPolyn(l2,l2_length);
//创建相加链表的头节点，把链表l1，l2加入l_plus
Linklist l_plus=Create_lnode();
AddPolyn(l_plus,l1);
AddPolyn(l_plus,l2);
//创建相乘链表的头节点，l1，l2相乘生成链表l_mul
void MulPolyn(Linklist l_mul,Linklist l1,Linklist l2)
{
Linklist tmp_p = Create_lnode();
Linklist tmp_q = Create_lnode();
int zhishu,xishu;
tmp_p=l1->next;
InsertLnode(l_mul,p);
tmp_q = tmp_q->next;
}
tmp_p = tmp_p->next;
}
}
//PrintPolyn:打印链表l
Status PrintPolyn(Linklist l)
{

数据结构多项式相加实验报告

试验一多项式相加一. 实验内容：多项式相加二.实验目的和要求：利用双向链表实现通讯录的建立、删除、检索和列表，并可保存至文件，可重新装入。

用链式存储结构实现一元多项式的相加运算。

三．算法思想描述:1. 以单链表为存储结构插入多项式: 多项式输入：多项式按幂从高到低，以“系数，幂”的格式输入，并以“0，0”结束。

printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);while(i!=0){q=(pnode)malloc(sizeof(struct node));q->coef=i;q->exp=j;p->link=q;p=q;printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);}p->link=NULL;2. 多项式相加单链表合并:由两个多项式对应的单链表头节点开始，依次扫描各节点。

(1)若两表的节点均非空：比较二者的幂，按幂大者先入表。

如果幂相等，则系数相加再入表。

具体由以下代码实现：while(p!=NULL && q!=NULL){if(p->exp==q->exp){x=p->coef+q->coef;if(x!=0){s=(pnode)malloc(sizeof(struct node));s->coef=x;s->exp=p->exp;r->link=s;r=s;}p=p->link;q=q->link;}else if(p->exp<q->exp){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}else{s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}(2). 若有一链表已空，则将非空链表插入新表：while(p!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}while(q!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}3. 输出合并后的链表:while(head->link!=NULL){head=head->link;printf(" %d*x^%d",head->coef,head->exp);}4. 主函数调用，完成多项式相加。

多项式相加(含运行结果截图)

while (r){
printf("指数：%d系数：%f\n",r->expn,r->coef);
r=r->next;
}
}
main()
{
void creatpolyn(struct linklist *p,int n); //输入n项的系数，建立一个链表
struct linklist * addpolyn(struct linklist*p,struct linklist*q); //两个多项式相加,返回结果指针
la->coef=s; //此项不为0需要修改la中当前节点的系数值
la=la->next;
p=p->next;
lb=lb->next;
q=q->next;
}
else {
p->next=la->next;
r=la;
la=la->next;
free(r);
lb=lb->next;
q=q->next;
}
scanf("%d",&n);
creatpolyn(p,n);
printf("请输入第二个多项式的项数:\n");
scanf("%d",&n);
creatpolyn(q,n);
r=addpolyn(p,q);
print(r);
}
四．算法分析
多项式由系数和指数组成，建立两个链表分别存储系数和指数。为了方便实验过程，实验在输入的时候按照指数的由低到高输入，避免了排序。在相加过程中，将两个链表从头到尾进行比较，直到比到一个链表没有元素为止，将其中指数相同的系数进行加减运算。最后打印出多项式。

数据结构实验,用链表实现多项式加减乘

#include<stdio.h>#include<malloc.h>#include<stdlib.h>#include<math.h>#define ERROR 0#define POLY sizeof(Polynomial)typedef struct Polynomial /*用单链表存储多项式的结点结构*/{int coef; /*多项式的系数*/int exp; /*指数*/struct Polynomial *next;/*next是struct Polynomial类型中的一个成员，它又指向struct Polynomial类型的数据，以此建立链表*/}Polynomial;Polynomial * CreatPolyn(void)/*指针函数，返回指针类型；用尾插法建立一元多项式的链表的函数*/{Polynomial *head,*tail,*s;int c,e;head=(Polynomial *)malloc(POLY);/*建立多项式的头结点，为头结点分配存储空间*/if(!head)exit(ERROR);tail=head;/*tail指针始终动态指向链表的当前表尾，以便于做尾插入，其初值指向头结点*/ printf("系数:");scanf("%d",&c); /*输入系数*/printf("指数: ");scanf("%d",&e); /*输入指数*/if(c==0){printf("请重新输入");return NULL;}else{while(c!=0) /*输入系数为0时，表示多项式的输入结束*/{s=(Polynomial *) malloc(POLY); /*申请新结点*/s->coef=c; /*申请新结点后赋值*/s->exp=e; /*申请新结点后赋值*/tail->next=s; /*做尾插，插入新结点*/tail=s; /*tail始终指向单链表的表尾*/printf("系数:");scanf("%d",&c);printf("指数: ");scanf("%d",&e);}tail->next=NULL; /*将表的最后一个结点的next置NULL，以示表结束*/ return(head);}}void DestroyPolyn(Polynomial *p)//删除多项式{Polynomial *q;while(p->next!=NULL){q=p->next;free(p);p=q;}}int PolyLength(Polynomial *p){Polynomial *q;int i=0;q=p;while(q->next!=NULL){q=q->next;i++;}return(i);}void Order(Polynomial *p)/*多项式的升幂排序*/{Polynomial *q;int a,b,i=0;q=p;while(q->next!=NULL){if(q->exp>q->next->exp){a=q->coef;b=q->exp;q->coef=q->next->coef;q->exp=q->next->exp;q->next->coef=a;q->next->exp=b;}q=q->next;i++;}}void PaiXu(Polynomial *p)//重复调用升幂排序函数{int j;for(j=1;j<PolyLength(p);j++)Order(p);}void AddPolyn(Polynomial *polya, Polynomial *polyb)/*两个一元多项式相加，将和多项式存放在多项式polya中，并将多项式ployb删除*/ {Polynomial *p,*q,*he,*temp;int sum;p=polya->next;/*令p指向polya多项式链表中的第一个结点*/q=polyb->next;/*令q指向polyb多项式链表中的第一个结点*/he=polya; /*令he指向和多项式polya*/while(p!=NULL&&q!=NULL)/*当两个多项式均未扫描结束时，执行以下操作*/{if(p->exp<q->exp)/*若p指向的多项式指数小于q指的指数*/{he->next=p; /*将p结点加入到和多项式中*/he=he->next;p=p->next; /*将p指针后移一位*/}else if(p->exp==q->exp)/*若指数相等，则相应的系数相加*/{sum=p->coef+q->coef;if(sum!=0) /*系数和不为零，执行下列操作*/{p->coef=sum;he->next=p;he=he->next;p=p->next;temp=q->next;free(q);//q=q->next;q=temp; /*释放原q节点*/}else /*系数和为零，则删除结点p与q，并将指针指向下一个结点*/{temp=p->next;free(p);p=temp;temp=q->next;free(q);q=temp;}}else /*若p指数大于q指数*/{he->next=q; /*p结点不动，将q结点加入到和多项式中*/he=he->next;q=q->next;}}if(p!=NULL)/*多项式A中还有剩余，则将剩余的结点加入到和多项式中*/he->next=p;else /*否则将B的结点加入到和多项式中*/he->next=q;}void PrintPolyn(Polynomial *p) /*输出函数，打印出一元多项式*/{p=p->next;if(p->exp>0)printf("A(x)= %d*x^%d",p->coef,p->exp);else if(p->exp<0)printf("A(x)= %d*x^(%d)",p->coef,p->exp);elseprintf("A(x)= %d",p->coef);while(p->next!=NULL){p=p->next;if(p->coef>0){if(p->exp>0)printf(" + %d*x^%d",p->coef,p->exp);else if(p->exp<0)printf(" + %d*x^(%d)",p->coef,p->exp);elseprintf(" + %d",p->coef);}else{if(p->exp>0)printf(" %d*x^%d",p->coef,p->exp);else if(p->exp<0)printf(" %d*x^(%d)",p->coef,p->exp);elseprintf(" %d",p->coef);}}}void main() /*主函数*/{Polynomial *polya,*polyb;int i;printf(" !!两个多项式的相加!!");//printf("若输入的单项式为0，则表明多项式创建完毕\n");begin: printf("\n\t\t** ** ** ** ** ** * *** *** **");printf("\n\t\t* 1、输入第一个多项式 *");printf("\n\t\t* 2、输入第二个多项式 *");printf("\n\t\t* 3、输出两个多项式的和 *");printf("\n\t\t* 4、退出 *");printf("\n\t\t** ** ** ** ** ** * *** *** **");printf("\n请选择：");scanf("%d",&i);switch(i){case 1:printf("\n请输入多项式中的每一个单项式的系数和指数\n");printf(" 若输入的单项式为0，则表明多项式创建完毕:\n\n");polya=CreatPolyn(); /*调用函数，创建多项式*/if(polya==NULL)goto begin;else{PaiXu(polya);printf("输入的多项式:\n");PrintPolyn(polya);goto begin;}case 2:printf("\n请输入多项式中的每一个单项式的系数和指数:\n"); polyb=CreatPolyn(); /*同理，创建B*/if(polyb==NULL)goto begin;else{PaiXu(polyb);printf("输入的多项式:\n");PrintPolyn(polyb);goto begin;}case 3:printf("\n两个多项式的和为:\n");AddPolyn(polya,polyb); /*调用一元多项式相加函数*/PrintPolyn(polya);DestroyPolyn(polya);goto begin;case 4:printf("08计（3）谢世伟 080201031025\n");break;}}#include <cstdlib>#include <iostream>using namespace std;struct xiang{float xs,zs,x; //分别表示系数、指数、以及Xxiang *next;};class duoxiangshi{private:xiang *first,*p;public:duoxiangshi();~duoxiangshi();void add(float xs,float zs); //n代表多项式的项数个数xiang * operator+(const duoxiangshi & b); //重载多项式的相加xiang * operator-(const duoxiangshi & b);void print(xiang *athead); //输出多项式相加结果void printself(); //看一下};duoxiangshi::duoxiangshi(){first=new xiang;first->next=NULL;p=first;}duoxiangshi::~duoxiangshi(){while(p=first){first=first->next;delete p;}}void duoxiangshi::add(float xs,float zs) //增加多项式的项数，在插入的同时给它由指数的大小进行排序{xiang *q=new xiang;xiang *tmp; //临时指针。

多项式的链表表示及运算实验报告

多项式的链表表示及运算实验报告
一、实验目的
本次实验旨在了解多项式的链表表示及运算，学习应用链表实现多项式的加减乘除运算。

二、实验原理
多项式是数学中一种常见的运算方式，它由若干个单项式（即常数、未知数以及未知数不同次幂的积）求和组成。

多项式通常可以用数组或链表来表示。

本实验采用链表表示多项式。

链表表示多项式可以用一个链表来存储多项式中的每一项，链表节点存储着每一项的系数和指数。

链表的头节点指向第一项。

在链表表示多项式时，我们可以定义一个结构体来表示节点，包含两个成员变量：系数和指数。

当我们对多项式进行加减乘除运算时，首先需要将多项式转换成链表形式，然后按照运算规则进行运算，最后将运算结果转换为多项式形式。

三、实验步骤
1、定义多项式节点结构体，包含系数和指数两个成员变量；
2、编写函数从命令行读取用户输入的多项式，按照指数降序的方式将多项式转换成链表形式；
3、编写函数完成多项式相加、相减、相乘、相除等运算，每种运算均需要将两个多项式转换成链表形式后进行；
4、编写函数将链表形式的多项式转换成多项式字符串；
5、在主函数中调用上述函数，进行多项式的读取、运算、转换并输出结果。

四、实验总结
本次实验学习了多项式的链表表示及运算，掌握了链表的基本操作，了解了多项式的四则运算的实现。

在实验中，我们成功地用链表实现了多项式的加减乘除运算，实现了从命令行读取多项式，并将其转换为链表，最后将链表转换为多项式字符串输出。

通过本次实验，我更加深刻地理解了链表及其应用，学会了运用链表实现算法，提高了编码能力。

实验三.链表及其多项式相加(答案)

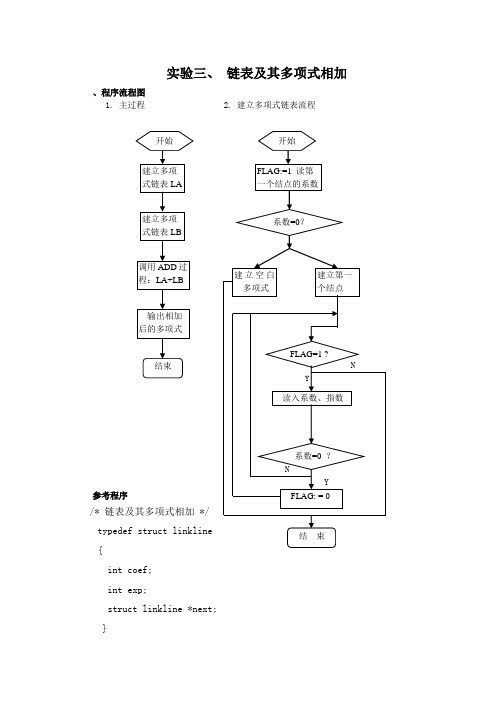
实验三、链表及其多项式相加、程序流程图1. 主过程2. 建立多项式链表流程参考程序/* 链表及其多项式相加 */typedef struct linkline{int coef;int exp;struct linkline *next;}line;line *creat(){ /*建立多项式列表*/int n;line *head;line *p1,*p2;n=0;printf("(输入的数必须是整数，指数须从小到大依次输入,系数为零表示多项式结束)\n");p1=p2=(line *)malloc(sizeof(line)); /*开辟一个新单元*/scanf("%d%d",&p1->coef,&p1->exp); /*录入多项式*/if (p1->coef==0) head=0;else{while(p1->coef!=0){ n++;if (n==1) head=p1;else p2->next=p1;p2=p1;p1=(line *)malloc(sizeof(line));scanf("%d%d",&p1->coef,&p1->exp);}p2->next=0;}return(head);}/* 以下是输出多项式的函数 */void print(line *p){line *p0;p0=p;printf(" ");if(p0!=0)do{printf("%dx的%d次幂",p0->coef,p0->exp);p0=p0->next;if(p0!=0) printf("+");}while(p0!=0);else printf(" 空多项式!!");printf("\n");}int compare(int m,int n) /*比较两个整数的大小的函数*/ {int j;if (m<n) j=-1;if (m==n) j=0;if (m>n) j=1;return(j);}void freeNode(line *w1) /* 释放一个表中的所有结点 */ {line *w2;w2=w1->next;while(w1){ free(w1);w1=w2;w2=w2->next; }}line *AddLine(line *ha,line *hb) /*两个非空多项式相加*/{line *la,*lb,*lc;int a,b,sum;lc=ha;la=ha;lb=hb;if ((ha==0)&&(hb!=0)) return(hb);while ((la!=0)&&(lb!=0)){ a=la->exp; b=lb->exp;switch( compare(a,b) ) /*比较当前结点指数的大小 */{ case -1:{ ha=la; /*只修改la的指针*/la=la->next;break;}case 0:{ sum=la->coef+lb->coef;if(sum!=0){ /* 将其不为零的系数和保存 */la->coef=sum;ha=la; la=la->next;} /* end if*/else{ /* 分别删除系数和为零的对应的两个结点 */if (lc==la) {lc=lc->next;ha=lc;la=ha;} /* 刚开始时特殊处理头结点 */else{ha->next=la->next;la=ha->next;}} /*end else*/hb=lb;lb=lb->next;break;}case 1:{ /* 将指数小的项插入到la的前部 */ hb=lb->next;if(ha==la) {lc=lb;lb->next=ha;la=la->next; } else{ha->next=lb;lb->next=la;ha=la;la=la->next;}lb=hb->next;break;}} /*end swtich*/} /*end while*/if (lb!=0) ha->next=lb;return(lc);} /*end AddLine *//*************以下为主程序**************/main(){line *la,*lb,*lc;printf("请输入多项式La: ");la=creat();printf("请输入多项式Lb: ");lb=creat();printf("多项式La:\n");print(la);printf("多项式Lb:\n");print(lb);printf("多项式La与Lb的和是: \n");lc=AddLine(la,lb);print(lc);freeNode(lb);}一、实验目的：1．了解栈存储结构的特点；2．掌握栈存储结构的应用。

（链表实现）写出两个一元多项式相加的算法

（链表实现）写出两个⼀元多项式相加的算法int c, e;head=new node; //⽣成头结点head->next=NULL;cout<<"请分别输⼊新的⼀项的系数、指数(以输⼊9999作为结束):"<<endl;cin>>c>>e;while(c!=9999 && e!=9999) //输⼊并检测结束{s=new node; //⽣成新结点s->co = c; //装⼊数据s->exp = e;p=head;while(p->next!=NULL){p=p->next;}p->next = s; //插到最后⼀个结点后s->next = NULL;cout<<"请分别输⼊新的⼀项的系数、指数(以输⼊9999作为结束):"<<endl;cin>>c>>e;}return head;}void Display(node * head){if(head==NULL){cout<<"多项式不存在！"<<endl;return ;}node* p;p=head->next;while(p!=NULL){if(p->co>0)cout<<p->co<<"x^"<<p->exp;elsecout<<"("<<p->co<<")"<<"x^"<<p->exp;if(p->next!=NULL)cout<<"+";p=p->next;}cout<<endl<<endl;}node* Add(node * A, node * B){node * C=new node;C->next=NULL;node * p1=A->next;node * p2=B->next;node * p3;node * rearC=C;while(p1!=NULL && p2!=NULL){。

数据结构-链表实现多项式求和

数据结构-链表实现多项式求和浙江⼤学数据结构课程第⼆讲练习：使⽤链表实现多项式求和与乘积，只写了求和，乘积暂时没写。

#include <iostream>#include <stdio.h>using namespace std;//Polynomial是typedef为PolyNode *类型声明的别名typedef struct PolyNode *Polynomial;struct PolyNode{int coef;int expon;Polynomial link;};void Attach(int c, int e, Polynomial *pRear) /* *pRear是指向指针的指针，这⾥是为了按值传递从⽽改变Rear的值 */{Polynomial P;P = (Polynomial)malloc(sizeof(struct PolyNode)); /*创建新节点，⽤于存储当前多项式*/P->link = NULL; /*因为插⼊每次的节点都是链表尾，所以要使其指针指向NULL*/P->coef = c; /*为新节点赋值*/P->expon = e;(*pRear)->link = P;*pRear = P; /*----------------改变Rear指向当前链表结尾-----------------*/}Polynomial ReadPoly(){Polynomial P,t;Polynomial Rear; /*当前结果表达式尾项指针*/int c, e, N;scanf("%d", &N); /*读⼊多项式总共有⼏项*/P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL; /*采⽤申请空节点作为链表头*/Rear = P; /*将当前节点的指针赋予Rear*/if (N < 1) /*检查数据是否输⼊正确*/cout << "input is error" << endl;while (N--) {scanf("%d %d", &c, &e); /*读⼊多项式的系数和指数*/Attach(c, e, &Rear); /*将当前项插⼊多项式*/}t = P; P = P->link; free(t); /*释放⼀开始申请的空节点*//*.................*/return P;}Polynomial Add(Polynomial P1, Polynomial P2){Polynomial t1, t2, P;Polynomial Rear;t1 = P1; t2 = P2; /*P1和P2指向表头，不能改变它的值，否则找不到链表*/P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL; /*采⽤申请空节点作为链表头*/Rear = P;while (t1&&t2) {if (t1->expon == t2->expon) {if ((t1->coef + t2->coef) != 0){Attach(t1->coef + t2->coef, t1->expon, &Rear);t1 = t1->link;t2 = t2->link;}else {t1 = t1->link;t2 = t2->link;}}else if (t1->expon > t2->expon) {Attach(t1->coef, t1->expon, &Rear);t1 = t1->link;}else {Attach(t2->coef, t2->expon, &Rear);t2 = t2->link;}}while (t1) {Attach(t1->coef, t1->expon, &Rear);t1 = t1->link;}while (t2){Attach(t2->coef, t2->expon, &Rear);t2 = t2->link;}Polynomial t;t = P; P = P->link; free(t);return P;}void PrintPoly(Polynomial P){int flag = 0;if (!P) { printf("0 0\n"); return; }while (P){if (!flag)flag = 1;elseprintf("");printf("%d %d", P->coef, P->expon);P = P->link;}printf("\n");}int main(){Polynomial P1, P2, P;P1 = ReadPoly();P2 = ReadPoly();P = Add(P1, P2);//Polynomial t; /*释放表头（为啥表头的空节点会没有释放）*///t = P; P = P->link; free(t);PrintPoly(P);printf("%d %d", P->coef, P->expon);return0;}总结：1.表头的指针不能动，否则会找不到链表的⼊⼝2.申请空节点作为表头时，插⼊数据后要把该节点的内存释放（free）3.使⽤malloc申请内存百度百科：申请⼀块连续的指定⼤⼩的内存块区域以void*类型返回分配的内存区域地址，当⽆法知道内存具体位置的时候，想要绑定真正的内存空间，就需要⽤到动态的分配内存⽤法举例：P = (Polynomial)malloc(sizeof(struct PolyNode)); //Polynomial是struct PolyNode*的typeof别名，P就是这块节点在内存⾥的存储位置4.关于链表的指针域，存放的是指针，该指针⼀般指向链表下⼀个节点的存储位置 P1 = (Polynomial)malloc(sizeof(struct PolyNode)); ⽐如P是当前节点，申请了P1节点后，令P->link = P1，即实现了为链表插⼊新节点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

int coef; int exp;struct lin kli ne实验三、链表及其多项式相加建立多项式链表流程2.{、程序流程图 1.主过程*n ext;{int n;line *head; line *p1,*p2; n=0;printf("( 输入的数必须是整数，指数须从小到大依次输入 , 系数为零表示多项式结束 )\n");p1=p2=(line *)malloc(sizeof(line)); /* scanf("%d%d",&p1->coef,&p1->exp); /* if (p1->coef==0) head=0; elsewhile(p1->coef!=0) { n++;if (n==1) head=p1; else p2->next=p1; p2=p1;p1=(line *)malloc(sizeof(line)); scanf("%d%d",&p1->coef,&p1->exp);p2->next=0;return(head);/* 以下是输出多项式的函数 */ void print(line *p)line ; line *creat()/*建立多项式列表 */开辟一个新单元 */录入多项式 */line*p0;p0=p;printf(" "); if(p0!=0)doprintf("%d x 的％(次幕",p 0->coef, pO->ex p);p0=p0->next;if(p0!=0) printf("+");while(p0!=0);else printf(" 空多项式!!");printf("\n ");int compare(int m,int n) /*比较两个整数的大小的函数*/intj;if (m<n) j=-1;if (m==n)j=0;if (m>n)j=1;return(j );void freeNode(line *w1) /*释放一个表中的所有结点*/line*w2;w2=w1->next; while(w1) { free(w1);w1=w2;w2=w2->next; } line *AddLine(line *ha,line *hb) /* line *la,*lb,*lc; int a,b,sum; lc=ha; la=ha; lb=hb;if ((ha==0)&&(hb!=0)) return(hb); while ((la!=0)&&(lb!=0)) { a=la->exp; b=lb->exp;switch( compare(a,b) ) /*比较当前结点指数的大小 */{ case -1:la=la->next; break;case 0:{ sum=la->coef+lb->coef; if(sum!=0)la->coef=sum; ha=la; la=la->next; } /* end if*/ elseif (lc==la) {lc=lc->next;ha=lc;la=ha;}理头结点 */两个非空多项式相加 */{ ha=la;/*只修改 la 的指针 *//*将其不为零的系数和保存 */{ /*分别删除系数和为零的对应的两个结点 *//* 刚开始时特殊处else{ha->next=la->next;la=ha->next;} /*end else*/hb=lb;lb=lb->next;break;case 1:/* 将指数小的项插入到la 的前部*/ hb=lb->next;if(ha==la) {lc=lb;lb->next=ha;la=la->next; }elseha->next=lb;lb->next=la;ha=la;la=la->next;lb=hb->next;break;} /*end swtich*/} /*end while*/if (lb!=0) ha->next=lb;return(lc);} /*end AddLine *//************* 以下为主程序**************/mai n()line*la,*lb,*lc;printf （" 请输入多项式La:"）; la=creat();printf （" 请输入多项式Lb:"）; lb=creat(); printf ("多项式 La:\n"); prin t(la); printf ("多项式 Lb:\n"); prin t(lb); printf (" 多项式 La 与Lb 的和是：\n"）; lc=AddL in e(la,lb); prin t(lc);freeNode(lb);} 一、实验目的： 1•了解栈存储结构的特点； 2.掌握栈存储结构的应用。

二、实验原理：栈是限制在表的一端进行插入和删除的线性表。

允许插入、删除的这一端称为栈顶，另一个固定端称为栈底。

由于栈的“先进先出” 结构来进行求解。

数制转换问题：将十进制数N 转换为r r=8为例转换方法如下：特点，在很多实际问题中都利用栈做一个辅助的数据进制的数，其转换方法利用辗转相除法: N=3456 N 3467 433 54 6N / 8433 546所以：(3456)10 = (整除)3 1 6 6 (6600) 8（求余）4我们看到所转换的8进制数按底位到高位的顺序产生的，而通常的输出是从高位到低位的，恰好与计算过程相反，因此转换过程中每得到一位8进制数则进栈保存，转换完毕后依次出栈则正好是转换结果。

算法思想如下：当N>0时重复1, 21.若N 工0,则将N %r 压入栈s 中，执行2;若N=0,将栈s 的内容依次出栈，算法结束。

2 .用N / r 代替N实验要求参照书上的原理说明分析程序，深入理解栈的物理存储模式和逻辑模式。

实验原理：一种"先进先出"(FIFO---First In First Out)的数据结构：即插入在队尾一端进行，而删除在队头进行。

键盘缓冲区问题：设计算法实现模拟键盘缓冲区问题。

假设有两个进程同时存在于一个应用程序之中，第1. 2. 看懂书上程序，编出程序上机调试。

参考代码：算法如下：typ edef int datat ype;void conv ersi on (i nt Nr){ SeqStack s; 义一个顺序栈*/ datet ype x; In it_SeqStack(&s); #define L 1 ,int r) vo id conv ersi on (i nt N{ int s[L],top int x; top while ( N ) { Push_SeqStack( &s , N %r );余数入栈*/N=N / r; 除数继续*/} } while ( Emp ty_SeqStack(& s )){ Pop_SeqStack (&s , &x );N=N / r; /*wh /*-1; /*{ s[++to p]=N%r; lile (top!=-1) x=s[to p-/*printf ( “％d ” x ); printf(,int初始化商作为被%d,x);}} 算法(a)算法(b)实验五、队列的应用一个进程连续在屏幕上显示字符“ X ” ,第二个进程不断检查键盘上是否有输入，若有则读入用户键入的字符，将其保存到键盘缓冲区之中。

程序约定当用户键入一个逗号“， ”，则表示第一进程结束，系统开始显示那些在键盘缓冲区中的字符；接着继续执行第一个进程，即，在屏幕上显示字符“ X ”；当用户输入“；”的时候，刚结束整个程序。

算法提示：为了充分利用缓冲区的空间往往将缓冲区设计成循环队列的结构，并为循环队列结构的缓冲区设置一个队首指针和一个队尾指针。

每输入法一个字符到缓冲区中，就将尾指针后移，链入缓冲区的循环队列之中；每输出一个字符号，就将队头指针前移，将它从缓冲队列中删除。

参考代码：/* 键盘缓冲区问题 */ #define MAXSIZE 20 #define TRUE 1 #define FALSE 0 #include "stdio.h" #include "conio.h" #include "dos.h"typedef structelemtype elem[MAXSIZE]; int front, rear; }queuetype;int enque(queuetype *s, elemtype x) if (( s->rear+1)%MAXSIZE==s->front )return (FALSE); elses->rear=(s->rear+1) % MAXSIZE;s->elem[s->rear]=x; return(true);typedef charelemtype;/* 数据入队列 *//* 队列已满 */return(NULL);s->front=(s->front+1)%MAXSIZE; return(s->elem[s->front]);main()char ch1,ch2; queuetype *p; int t,f;p=(queuetype *)malloc(sizeof(queuetype)); p->front=0; p->rear=0;if ( f== FALSE )elemtype delqueue (queuetype *s ) /*数据出队列 */ if (s-front==s->rear) /*队列为空 */ else /*队列非空 */ while(1)/* 开始交替执行 */while(1) /*第一个进程的执行 */ if(kbhit()) /*检测是否有键盘输入 */ ch1=bdos(7,0,0); /*中断调用 , 键入字符存入 ch1*/ f=enqueue( p, ch1 );/*字符入循环队列 */printf(" The queue is already full !\n");break;if ( ch1==';' || ch1==',' )/* 继续执行 */ /* 先置空 ch1*/实验目的：1、了解稀疏矩阵的三元组存储形式。