微观经济第五章作业(附答案)知识讲解
微观经济学高鸿业版第五章课后习题答案

第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+15OMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1 Q 2长期边际成本曲线与短期成本曲线A4已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MIN AVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时(1) 固定成本值:500 (2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A L A LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L (Q )+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC =100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q 2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC 函数、SAC 函数和AVC 函数。
微观经济学参考答案 第五章参考答案

[参考答案]一、判断题1.T2.F3.T4.T5.T6.T7.F8.F9.F 10. T二、填空题1.2000元2.20600元,33400元3.水平的4.边际成本5.递增6.等幅增加,保持不变7.过剩8.规模收益递增 9.大 10.等成本曲线三、选择题1.A2.D3.A4.D5.A6.B7.D8.A9.A 10.A四、名词解释1.机会成本:机会成本是指生产某种产品耗费的资源所能生产的其他产品的最高价值。
它是对资源配置的一种度量。
资源配置的效率高,则生产的机会成本就低。
2.隐性成本:隐性成本是指未通过市场购买,不进入会计成本计算的成本。
例如,企业所有者自身的工资、自有资金的利息。
3.显形成本:是厂商在生产过程中为生产而购买生产要素实际发生的费用。
如给工人支付的工资,购买原材料支付的资金。
4.生产成本:是厂商或企业在生产商品过程中所使用的生产要素的价格,也叫生产费用,包括显形成本和隐性成本。
5.短期成本:是指在生产者来不及调整某些生产要素数量的情况下,生产一定的产出数量所花费的成本。
短期成本包括固定成本和可变成本。
6.长期成本:是指生产者在可以调整所有生产要素数量的情况下,进行生产所花费的成本。
长期成本只包括可变成本。
它是短期成本中从长期角度看有最低值的那些成本所组成,长期总成本曲线、平均成本曲线分别是短期总成本曲线、平均成本曲线的包络线。
7.收益:是指厂商出售商品的收入,即商品的买价所得。
收益可分为三种:总收益、平均收益、边际收益。
8.经济利润:是指企业出售产品所得总收益与总成本之间的差额,而计入总成本的,除折旧费和其他一切实际支出的正常费用外,还包括正常利润,所以,经济利润实际上是超“正常利润”。
而会计利润所计入总成本的不包括正常利润,因此,即使经济利润为零,仍可能有会计利润存在。
9.成本函数:厂商生产一定量的产出与成本之间的对应关系,其形式为C =ƒ(Q )。
成本函数的大小主要取决于以下三个方面。
经济学原理 谭春枝微观第五章课后练习答案

微观第五章课后练习答案一、名词解释1. 边际生产力(MP)指在其他条件不变的情况下,每增加一个单位生产要素的投入所增加的产量。
边际生产力存在递减规律,即当某一个要素投入量不断增加,而其他要素不变,可变要素的边际产量在一个时期内可以增加或保持不变,但最终还是会递减。
2. 引致需求: 生产要素需求受到该产品和服务的供求状况影响,所以对生产要素的需求也称为引致需求。
3. 边际产品收益:产品边际收益是指在其他条件不变的情况下,每增加一个单位的实物产量所带来的收益增加值。
4. 洛仑兹曲线:(要求画图说明,详见图5-10)洛伦兹曲线是一条反映了社会个人收入或财产分布平等程度的曲线。
如图5-10所示,横轴OX表示人口百分比,纵轴OZ表示国民收入百分比,对角线OY为收入分配绝对平均曲线,曲线OBA代表实际的收入分配曲线,即洛仑兹曲线。
OHY离开对角线OY越远表示社会分配越不平均,越近则越平均。
5. 基尼系数:(要求画图说明,详见图5-10)基尼系数是利用洛仑兹曲线得到的衡量社会收入分配平等程度的一个指标。
如图5-10所示,A为洛仑兹曲线与对角线OY之间的面积,即阴影部分的面积,B为洛仑兹曲线与折线OXY之间的面积,而基尼系数G为:G=A/(A+B)(0≤G≤1)基尼系数的经济含义是:在全部居民收入中,用于进行不平均分配的那部分收入占总收入的百分比。
基尼系数最大为“1”,最小等于“0”。
前者表示居民之间的收入分配绝对不平均,即100%的收入被一个单位的人全部占有了;而后者则表示居民之间的收入分配绝对平均,即人与人之间收入完全平等,没有任何差异。
但这两种情况只是在理论上的绝对化形式,在实际生活中一般不会出现。
因此,基尼系数的实际数值只能介于0~1之间。
二、简答题1.完全竞争厂商在要素市场的生产原则。
一般来说,当厂商每增加一个单位的要素所增加的收益(MRP)与每增加一单位要素的购买所增加的成本(MFC)相等时,厂商得到最大的收益,生产要素的供求达到均衡。
微观经济学第五章答案

第五章1.下面表是一张关于短期生产函数)LQf,(K 的产量表:(1)在表1中填空(2)根据(1),在一张坐标图上作出TP L曲线,在另一张坐标图上作出AP L曲线和MP L曲线.(3)根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4)根据表2,在一张坐标图上作出TVC曲线,在另一张坐标图上作出AVC曲线和MC曲线.(5)根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.NO.1解答:(1)短期生产的产量表(表1)(3)短期生产的成本表(表2)(5)边际产量和边际成本的关系,边际MC 和边际产量MPL两者的变动方向是相反的。
总产量和总成本之间也存在着对应关系:当总产量TPL下凸时,总成本TC曲线和总可变成本TVC是下凹的;当总产量曲线存在一个拐点时,总成本TC曲线和总可变成本TVC 也各存在一个拐点。
平均可变成本和平均产量两者的变动方向相反。
MC曲线和AVC曲线的交点与MPL曲线和APL曲线的交点是对应的。
2.下图是一张某厂商的LAC曲线和LMC曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC曲线和SMC曲线.NO.2解答:在产量Q1和Q2上,代表最优生产规模的SAC曲线和SMC曲线是SAC1和SAC2以及SMC1和SMC2. SAC1和SAC2分别相切于LAC的A和B SMC1和SMC2则分别相交于LMC的A1和B1.3. 假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66:(1) 指出该短期成本函数中的可变成本部分和不变成本部分;(2) 写出下列相应的函数:TVC(Q) AC(Q)AVC(Q) AFC(Q)和MC(Q). NO.3解答:(1) 可变成本部分: Q 3-5Q 2+15Q 不可变成本部分:66(2)TVC(Q)= Q 3-5Q 2+15QOMCQLMCSMC 1SAC 1SAC 2SMC 2LACA 1B 1Q 1Q 2长期边际成本曲线与短期成本曲线AAC(Q)=Q 2-5Q+15+66/QAVC(Q)= Q 2-5Q+15 AFC(Q)=66/QMC(Q)= 3Q 2-10Q+154. 已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.NO.4解答:TVC(Q)=0.04 Q 3-0.8Q 2+10QAVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MINAVC5. 假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数.NO.5解答:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M当时,TC=1000 M =500(1) 固定成本值:500(2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100QAC(Q)= Q 2-15Q+100+500/QAVC(Q)= Q 2-15Q+1006.NO.6解答:11600)11200()22800(228002001120010002.01102=+-+=∆∴+=+=+=+=++==+⎰C C Q CC TVC Q C C TVC Q C Q Q MCdQ C TVC 时,时,7. 某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. NO.7解答:2122212min Q Q Q Q c -+=..t s 4021=+Q Q 构造拉格朗日函数:F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40) 令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F使成本最小的产量组合为Q 1=15,Q 2=258. 已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.NO.8解答:)2(111)1(4,164/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L Q MP L A A Q MP L A Q K L A L A L A =====∂∂∂∂==∂∂==∂∂===----所以所以因为 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16= Q 2/16+ Q 2/16+32= Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/49. 已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求:(1) 劳动的投入函数L=L(Q).(2) 总成本函数,平均成本函数和边际成本函数.(3) 当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? NO.9解答:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10.MP L =1/6L -2/3K 2/3MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L(Q)+r·50 =5·2Q+500 =10Q +500SAC= 10+500/QSMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L1/3K2/3,有Q=25.又π=TR-STC=100Q-10Q-500=1750所以,利润最大化时的产量Q=25,利润π=175010.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC函数、SAC函数和AVC函数。
微观经济学高鸿业版第五章课后习题答案
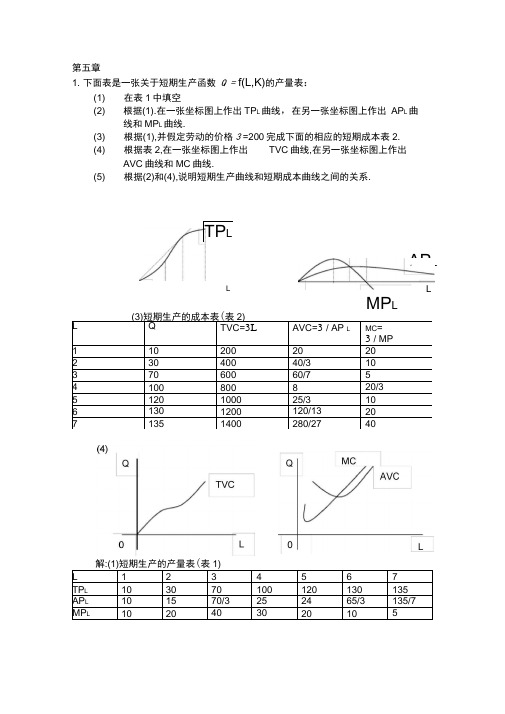
第五章1. 下面表是一张关于短期生产函数 Q = f(L,K)的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出 AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格3 =200完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出 TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.解:(1)短期生产的产量表(表1) L 1 2 3 45 6 7 TP L 10 30 70 100 120 130 135 AP L 10 15 70/3 25 24 65/3 135/7 MP L 10 2040 3020 105TP LAP LMP LL Q TVC=3L AVC=3 / AP L MC =3 / MP1 10 200 20 202 30 400 40/3 10 3 70 600 60/7 54 100 800 8 20/35 120 1000 25/3 106 130 1200 120/13 20 71351400280/2740LL(3)短期生产的成本表(表2)(5)边际产量和边际成本的关系,边际MC和边际产量MP L两者的变动方向是相反的•总产量和总成本之间也存在着对应系:当总产量TP L下凸时,总成本TC曲线和总可变成本TVC是下凹的;当总产量曲线存在一个拐点时,总成本TC曲线和总可变成本TVC也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的•MC曲线和AVC曲线的交点与MP L曲线和AP L曲线的交点是对应的•2. 下图是一张某厂商的LAC曲线和LMC曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC曲线和SMC曲线.解:在产量Q1和Q2上代表最优生产规模的SAC曲线和SMC曲线是SAC i 和SAC2以及SMC i和SMC2. SAC i和SAC?分别相切于LAC的A和B SMC i和SMC2则分别相交于LMC的A i和B i.SM LMCSAG SMC i SAC2Q2长期边际成本曲线与短期成本曲线3. 假定某企业的短期成本函数是TC(Q)=Q3-5Q2+i5Q+66:(i) 指出该短期成本函数中的可变成本部分和不变成本部分;⑵写出下列相应的函数:TVC(Q) AC(Q) AVC(Q) AFC(Q)和MC(Q).解⑴可变成本部分:Q3-5Q2+i5Q不可变成本部分:663 2(2) TVC(Q)= Q3-5Q2+i5QAC(Q)=Q2-5Q+i5+66/QAVC(Q)= Q2-5Q+i5AFC(Q)=66/QMC(Q)= 3Q2-i0Q+i53 24已知某企业的短期总成本函数是STC(Q)=0.04 Q -0.8Q +10Q+5,求最小的平均可变成本值.解:TVC(Q)=0.04 Q3-0.8Q2+10Q2AVC(Q)= 0.04Q2-0.8Q+10令AVC =0.08Q -0.8 =0得Q=10又因为AVC =0.08 0所以当Q=10 时,AVC MIN =65. 假定某厂商的边际成本函数MC=3Q 2-30Q+100且生产10单位产量时的总成本为1000.求:(1)固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数.2解:MC= 3Q -30Q+1003 2所以TC(Q)=Q -15Q +100Q+M当Q=10 时,TC=1000 =500(1) 固定成本值:500(2) TC(Q)=Q3-15Q2+100Q+500TVC(Q)= Q3-15Q2+100QAC(Q)= Q2-15Q+100+500/QAVC(Q)= Q2-15Q+1006. 某公司用两个工厂生产一种产品,其总成本函数为C=2Q12+Q22-Q1Q2,其中Q1表示第一个工厂生产的产量,Q2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合.解:构造F(Q)=2Q12+Q22-Q1Q2+ 入(G+ Q2-40):F4Q1 - Q21=0Q0^15令 --- =2Q2 -Qr + & = 0<Q2 = 25:Q2—-Q1 Q2 _40 =0C A H使成本最小的产量组合为Q1=15,Q2=257已知生产函数Q=A1/4L1/4K1/2;各要素价格分别为P A=1,P L=1.P K=2;假定厂商处于短期生产,且k二16 .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.解:因为 K =16,所以 Q =4A 1/4L 1/4(1)由(1)⑵可知L=A=Q 2/16又 TC(Q)=P A &A(Q)+P L &L(Q)+P K &16=Q 2/16+ Q 2/16+32 =Q 2/8+322AC(Q)=Q/8+32/Q TVC(Q)= Q /8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为 500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少 ? 解:(1)当 K=50 时,P K K=P K 50=500,所以P K =10.1 . .2/3 2/3L K MP L _ 6 MP K 2 L^K 」/36整理得K/L=1/1,即K=L.将其代入 Q=0.5L 1/3K 2/3,可得:L(Q)=2Q (2) STC=D ・ L(Q ) +r 50=5 2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3) 由(1)可知,K=L,且已知 K=50,所以.有 L=50•代入 Q=0.5L 1/3K 2/3,有 Q=25. 又 n =TRSTC=100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润n =1750MP L=:Q = A 1/4L ;/4;L:QMP A -:A A J /4L1/4_ P A MP L :QA 1/4L :/4_ P LQ " 3/4, 1/ 4MP AA _ L ;A.:L41所以L =A(2)MP L =1/6L MP K =2/6L -2/3K 1/3K2/3-1/3P LP K _109•假定某厂商短期生产的边际成本函数为 SMC(Q)=3Q 2-8Q+100,且已知当产量 Q=10时的总成本STC=2400,求相应的STC 函数、SAC 函数和AVC 函数。
微观经济学原理课后习题及答案-第五章-成本
当 时, ,带入生产函数
得, ,所以,
(3)生产函数 ,可得: ,
生产要素的最优组合
又因为 ,带入长期生产的扩展线方程得,
带入生产函数得:
(4) 是固定比例生产函数,厂商按照 的固定投入比例进行生产,且厂商的生产均衡点在直线 上,即长期生产的扩展线为 ,
,所以, ,
8.已知某企业的生产函数为 ,劳动的价格 ,资本的价格 。求:
(2) 平均成本函数为:AC= =Q2-10Q +17+ 平均可变成本函数为: AVC= =Q2-10Q+17 平均不变成本函数为:AFC= = ,边际成本函数为:MC(Q)=TC′(Q)=TVC′(Q)=3Q2-20Q+17
3.短期平均成本SAC曲线与长期平均成本LAC曲线都呈现出U形特征。请问:导致它们呈现这一特征的原因相同吗?为什么?
(1)该生产函数的平均产量为极大值时的L使用量。
(2)该生产函数的平均可变成本为极小值时的总产量。
解答: (1)该生产函数的平均产量函数AP(L)= =-0.1L2+2L+20
令AP' (L)= -0.2L+2=0,即L=10时, 平均产量为极大值.
(2)由于平均可变成本与平均产量呈对偶关系, 平均产量为极大值时, 生产函数的平均可变成本为极小值。即L=10时生产函数的平均可变成本为极小值。所以:
5-8长期半均成本曲线的移动
12.请比较消费者选择理论中的无差异曲线分析法与生产技术和成本理论中的等产量曲线分析法。
(5)一般来说,平均量与边际量之间的关系是:只要边际量大于平均量,则平均量上升;只要边际量小于平均量,则平均量下降;当边际量等于平均量时,则平均量达到最值点(即最大值或最小值点)。由此出发,可以根据MC曲线的U形特征来推导和解释AC曲线和AVC曲线。MC交AVC,AC的最低点。AC曲线与MC曲线一定相交于AC曲线的最低点C,在C点之前,MC<AC,则AC曲线是下降的;在C点之后,MC>AC,则AC曲线是上升的。类似地,AVC曲线与MC曲线相交于AVC曲线的最低点B。在B点之前,MC<AVC,则AVC曲线是下降的;在B点之后,MC>AVC,则AVC曲线是上升的。
微观经济学高鸿业版第五章课后习题答案

第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空(2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2.(4)根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.解:(1)短期生产的产量表(表1)(3)短期生产的成本表(表2)(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q) AC(Q) (3) AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/QOMCQLMCSMC 1SAC 1SAC 2SMC 2LACA 1B 1Q 1Q 2长期边际成本曲线与短期成本曲线AMC(Q)= 3Q 2-10Q+154已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV得Q=10又因为008.0>=''C AV所以当Q=10时,6=MINAVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000. 求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时(1) 固定成本值:500 (2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A L A LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10.MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L(Q )+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC =100Q-10Q-500 =1750所以利润最大化时的产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q 2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC 函数、SAC 函数和AVC 函数。
微观经济第五章作业(附答案)

1、已知某厂商的短期生产函数为32921L L L Q -+=。
(1)写出劳动的平均产量L AP 函数和边际产量L MP 函数;(2)分别计算总产量、平均产量和边际产量的最大值;(3)证明当平均产量达到极大时,劳动的平均产量和边际产量相等。
解:(1) 根据32921L L L TP L -+=可得:2921L L L TP AP L L -+== 231821L L dQdTP MP L L -+==(2)边际产量为零时,总产量最大即 0318212=-+L L解得 7=L (1-=L 不合题意)代入24592132=-+=L L L TP L同样,对于平均产量函数2921L L AP L -+=L AP dLd L 29-= 令 0=L AP dLd 即 029=-L 得 5.4=L(5.4=L 也可用L L MP AP =,即 2231821921L L L L -+=-+求得)又因为 02<-=⎪⎭⎫ ⎝⎛L AP dL d dL d 所以5.4=L 为平均产量达到极大时厂商雇用的劳动。
代入 2921L L AP L -+= 得平均产量AP L 的最大值为41.25 。
同样,对于231821L L MP L -+= L MP dLd L 618-= 令 0=L MP dLd 即 0618=-L 得 3=L又因为 06<-=⎪⎭⎫ ⎝⎛L MP dL d dL d 所以3=L 为边际产量达到极大时厂商雇用的劳动。
将3=L 代入231821L L MP L -+=得到边际产量MP L 的最大值为48。
(3)证明:从(2)中可知:当5.4=L 时劳动的平均产量达到极大值为41.25而当5.4=L 时,劳动的边际产量25.41318212=-+=L L MP L所以当平均产量达到极大时,劳动的平均产量和边际产量相等。
2、已知某企业的单一可变投入(X )与产出(Q )的关系如下:Q=1000X+10002X -23X ,当X 分别为200、300、400单位时,其边际产量和平均产量各为多少?它们分别属于哪一个生产阶段?该函数的三个生产阶段分界点的产出量分别为多少?解:TP=1000X+10002X -23X MP=1000+2000X-62X AP=1000+1000X-22X X=200 MP=161000 AP= 121000X=300 MP=61000 AP= 121000X=400 MP= -159000 AP= 81000MP= AP, X=250MP=0,1000+2000X-62X =0,610060001000+=X =334 第一阶段和第二阶段的分界点是X =250 ,第二阶段和第三阶段的分界点是334因此,X=200处于第一阶段,X=300处于第二阶段;X=400处于第三阶段。
微观经济学作业(5-7章)

第一部分习题第五章成本理论一、名词解释1.机会成本;2.显性成本;3.隐性成本;4.经济利润;5.正常利润;6.边际成本;7.短期总成本;8.长期总成本;9.规模经济; 10.规模不经济; 11.范围经济; 12.学习效应。
二、简答题1.为何短期平均成本曲线的最低点一定在平均可变成本曲线最低点的右边?2.为什么在SAC最小时,SAC=SMC?3.短期平均成本曲线和长期平均成本曲线都呈U形,请解释它们形成U形的原因有何不同?三、论述题1. 简述影响长期平均成本变动的因素。
2.(1)假定某行业中所有企业的成本函数都是C=Q+100,而且产品的市场需求量为1000,这时在一个占有40%市场份额的企业与一个占有20%市场份额的企业之间,哪一个企业在成本上占有优势?为什么?(2)从长期角度看,企业规模是否处于规模不经济?为什么?(3)有人认为该行业中企业产量水平越高,企业的利润也越高,这种想法正确吗?3. 为什么长期总成本在每一产量水平上都小于等于短期总成本?四、计算题1.已知某企业的短期总成本函数STC(Q)=5Q3-4Q2+3Q+50。
试求:(1)其中的可变成本和不变成本;(2)SAC(Q)、AFC(Q)、SMC(Q)的函数形式。
2.已知SMC=9Q 2+4Q+5,TFC=1000。
分别求STC、SAC、TVC和AVC的函数形式。
3.企业生产某产品的总固定成本为1000,平均总成本为50,平均可变成本是10,求企业现在的产量。
4.某厂商的短期生产函数为Q=-0.1L3+6L2+12L,其中单位劳动工资为2,试求平均可变成本最小时的产量是多少?5.设某企业的生产函数为Q=min(8L,4K),且P L=2,P K=3,试求当K=10时的STC、SAC分别为多少?第六章完全竞争市场一、名词解释1. 完全竞争市场;2. 总收益;3. 平均收益;4. 边际收益;5. 收支相抵点;6. 停止营业点;7. 成本递增行业; 8. 成本递减行业; 9. 成本不变行业;10. 生产者剩余。
微观经济学第五章 习题答案

网友可以在线阅读和下载这些文档让每个人平等地提升自我 By :麦群超2021年春季地理物理化学复习题 练习试卷 测试题\o(K,\s\up6(-)))的产量表: 表5—L 1 2 3 4 5 6 7 TP L 10 30 70 100 120 130 135 AP L MP L (2)根据(1),在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线。
(提示:为了便于作图与比较,TP L 曲线图的纵坐标的刻度单位大于AP L 曲线图和MP L 曲线图。
) (3)根据(1),并假定劳动的价格w =200,完成下面相应的短期成本表,即表5—2(即教材第147页的表5—3)。
L Q TVC =w·L A VC =\f(w AP L ) MC =\f(w MP L ) 1 10 2 30 3 70 4 100 5 120 6 130 7 135 线和MC 曲线。
(提示:为了便于作图与比较,TVC 曲线图的纵坐标的单位刻度大于A VC 曲线图和MC 曲线图。
) (5)根据(2)、(4),说明短期生产曲线和短期成本曲线之间的关系。
解答:(1)经填空完成的短期生产的产量表如表5—3所示: L 1 2 3 4 5 6 7 TP L 10 30 70 100 120 130 135 AP L 10 15 \f(70 3) 25 24 \f(65 3) eq \f(135 7) MP L 10 20 40 30 20 10 5 L L L 所示。
图5—1(3)令劳动的价格w=200,与(1)中的短期生产的产量表相对应的短期生产的成本表如表5—4所示:网友可以在线阅读和下载这些文档让每个人平等2021年春季地理物理化学教案等集合 1 10 200 20 20 2 30 400 \f(40 3) 10 3 70 600 \f(60 7) 5 4 100 800 8 \f(20 3) 5 120 1 000 \f(25 3) 10 6 130 1 200 \f(120 13) 20 7 135 1 400 \f(280 27) 40 (4)根据(3)中的短期生产成本表所绘制的TVC 曲线、A VC 曲线和MC 曲线如图5—2所示: 图5—2(5)公式A VC =eq \f(w,AP L )和MC =eq \f(w,MP L )已经清楚表明:在w 给定的条件下,A VC 值和AP L 值成相反方向的变化,MC 值和MP L 值也成相反方向的变化。
微观第五章习题及答案3上课讲义

一、名词解释机会成本沉没成本显性成本隐性成本成本函数短期总固定成本短期总可变成本短期边际成本长期总成本长期平均成本长期边际成本二、选择题1、经济学中短期与长期划分取决于(D )A.时间长短B.可否调整产量C.可否调整产品价格D.可否调整生产规模2、经济学中,生产的机会成本等于()A、显性成本+隐性成本B、显性成本+社会成本C、会计成本+隐性成本D、社会成本+隐性成本3、以下关于正常利润的说法不正确的是()A、正常利润是厂商对自己所提供的企业家才能所支付的报酬B、正常利润是隐性成本的一个组成部分C、正常利润是显性成本的一个组成部分D、经济利润中不包括正常利润4、下列说法哪个是正确的(A )A.如果连续的增加某种商品的产量,它的机会成本将递增B.短期平均成本呈现为“U”型,是由于机会成本递增C.经济分析中厂商的生产成本与机会成本这两个词是同义词D.如果一个人选择了上学而不是工作,那他的机会成本等于学习期间的学费5、短期可变成本曲线随着产量的增加而()A、不断上升B、不断下降C、先上升再下降D、先下降再上升6、当边际成本达到最低点时()A、平均成本曲线呈现递减状态B、平均可变成本曲线呈现递增状态C、平均产量曲线达到最大值D、总产量曲线达到最大值7、当边际成本曲线上升时,其对应的平均可变成本曲线一定是()A、上升B、下降C、既不上升,也不下降D、既可能上升,也可能下降8、短期内边际产量最高点对应于()A、边际成本最低点B、平均成本最低点C、平均可变成本最低点D、平均产量最高点9、长期边际成本曲线呈现U型形状的原因是()A、边际效用递减规律B 、边际收益递减规律C 、生产由规模经济向规模不经济变动D 、生产的一般规律10、从长期成本和短期成本曲线的关系来看,在对应LTC 与STC 切点处有( A ) A .LTC=STC 且LAC=SAC,LMC=SMC B .LTC=STC 但LAC<SAC,LMC<SMC C .LTC=STC 但LAC>SAC,LMC>SMC D .LTC=STC 且LAC=SAC 但LMC ≠SMC11、以下关于边际成本曲线、总成本曲线和可变成本曲线的说法正确的是( ) A 、当边际成本曲线下降时,总成本曲线以越来越慢的速度下降 B 、当边际成本曲线下降时,可变成本曲线以越来越快的速度下降 C 、当边际成本曲线上升时,总成本曲线以越来越快的速度上升 D 、当边际成本曲线上升时,可变成本曲线以越来越慢的速度上升12、若某个产量的长期平均成本等于短期平均成本,但高于长期边际成本,则( ) A 、规模报酬处于递减阶段 B 、长期平均成本正在下降 C 、短期平均成本最小D 、短期平均成本等于长期边际成本三、判断题1、由于固定成本不随产出的变化而变化,因而平均固定成本也不变化。
微观第五章习题和答案

第五章市场结构分析一、选择题完全竞争1.完全竞争的市场是指()A.市场参与者的购销量只占整个市场交易是量的极小一部分。
B.市场参与者只能接受价格,而不能影响价格C.交易的商品是同质的D.以上全对2.下列行业中哪一个最接近于完全竞争模式()A.飞机B.卷烟C.大米D.汽车3.在完全竞争的条件下,如果某行业中的厂商的商品价格等于平均成本,那么( )。
A.新的厂商要进入这个行业B.原有厂商要退出这个行业C.既没有厂商进入也没有厂商退出这个行业D.既有厂商进入也有厂商退出该行业4.在任何市场中,厂商的平均收益曲线可以由( )。
A.他的产品的供给曲线表示B.他的产品需求曲线表示C.行业的产品供给曲线表示D.行业的产品需求曲线表示5.假定在某一产量水平上,某厂商的平均成本达到了最小值,这意味着( )。
A.边际成本等于平均成本B.厂商获得了最大利润C.厂商获得了最小利润D.厂商的超额利润为零6.在完全竞争市场上,厂商短期均衡条件是( )。
A.P=ARB.P=MRC.P=MCD.P=AC7.在最好或最优短期产出水平情况下,厂商将( )。
A.取得最大利润B.使总损失最小C.使总损失最小,或使总盈利最大D.使单位产品中所获利润最大8.厂商在停止营业点( )。
A.P=AVCB.TR=TVCC.企业总损失等于TFCD.以上都对9.在一般情况下,厂商得到的价格若低于以下哪种成本将停止营业( )。
A.平均成本B.平均可变成本C.边际成本D.平均固定成本10.若在最优产出水平P 超过AVC,但小于AC时,则企业是在( )。
A.获取利润B.蒙受损失,但在短期内继续生产C.蒙受损失,应立即停产D.盈亏相等11.在完全竞争的条件下,如果厂商把产量调整到平均成本曲线最低点所对应的水平( )。
A.他将取得最大利润B.他没能获得最大利润C.他是否获得最大利润仍无法确定D.他一定亏损12.在完全竞争市场上,已知某厂商的产量是500单位,总收益是500元,总成本是800元,总不变成本是200元,边际成本是1元,按照利润最大化原则,他应该( )。
微观经济学第五章答案

第5 章需求和消费者行为二、问答题1.解释效用的含义。
总效用和边际效用之间有何差异?解释边际效用递减规律,并给出一个数字例子。
答:(1)效用的含义:参见本章概念题第1 题。
(2)边际效用与总效用之间的差异略。
(3)边际效用递减规律的内容:参见本章概念题第3 题。
根据基数效用论,边际效用递减规律成立的原因主要有两方面:一是由于随着相同消费品的连续增加,从人的生理和心理的角度讲,从每一单位消费品中所感受到的满足程度和对重复刺激的反应程度是递减的;二是由于在一种商品具有几种用途时,消费者总是将第一单位的消费品用在最重要的用途上,第二单位的消费品用在次重要的用途上,这样,消费品的边际效用便随着消费品的用途重要性的递减而递减。
假定消费者消费了三份食品,它们给消费者带来的效用分别为5、4、3,那么总效用就是第一、第二、第三份食品分别带给他的效用的总和12(=5+4+3);而边际效用则指消费的最后一份食品,也就是第三份食品带来的效用3。
当消费者开始连续消费食品时,第一份食品带给它的效用是很大的。
以后,随着它对食品数量的消费增加,虽然总效用是不断增加的,但每一份食品给他带来的效用增量(即边际效用)却是递减的。
当他完全吃饱时,总效用达到最大值,而边际效用则将为零。
这时如果他还继续吃,边际效用降为负值,总效用开始下降。
2.每周,汤姆·吴都以每个2 美元的价格购买两个汉堡包,以每瓶0.50 美元的价格购买8 瓶可口可乐,以每份1 美元的价格购买8 份比萨饼。
但是,在价格为每个1.50 美元时,他不购买任何热狗。
对于这4 种物品的每一种,你能算出汤姆的边际效用吗?答:根据等边际法则,以下等式成立:MU = MU = MU = MU2 0.5 1.5因此,只要已知每一美元货币收入的边际效用,就可以逐个算出汤姆对这四种物品的边际效用。
3.下列物品中哪一对可以划分为互补品、替代品和独立品:牛肉、番茄酱、羊肉、香烟、口香糖、猪肉、收音机、电视机、空中旅行、乘公共汽车旅行、出租车和平装书。
微观经济学高鸿业版第五章课后习题答案

第五章1.下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空(2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4)根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.解:(1)短期生产的产量表(表1)(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15QOMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1 Q 2长期边际成本曲线与短期成本曲线AAC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+154已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV得Q=10又因为008.0>=''C AV所以当Q=10时,6=MIN AVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时(1) 固定成本值:500 (2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A LA LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP 整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L(Q )+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L1/3K2/3, 有Q=25.又π=TR-STC=100Q-10Q-500=1750所以利润最大化时的产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC函数、SAC函数和AVC函数。
微观经济第五章课后习题分析解析

当AVC达到最小时,有:
dAVC 0.08Q 0.8 0 dQ
解得:Q=10
又由于 d 2 AVC 0.08 0 dQ 所以当Q=10时,AVC达到最小值。 将Q=10时代入平均可变成本函数
AVC 0.04Q2 0.8Q 10
解得
AVCmin 6
5、假定某厂商的边际成本函数为 MC 3Q2 30Q 100
TVC(Q)、AC(Q)、AVC(Q)、AFC(Q)和MC(Q)。
(1)可变成本部分:Q 5Q 15Q
3 2
不变成本部分:66
( 2)
TVC Q Q3 5Q2 15Q
TC Q 66 2 AC Q Q 5Q 15 Q Q
TVC Q AVC Q Q2 5Q 15 Q
(3)根据(1),并假定劳动价格w=200,完成下面 的相应的短期成本表,即表5-3。 表5-3 短期生产的成本表 L 1 2 3 4 Q 10 30 70 100 TVC=w.L
w w AVC MC MP AP L L
5
6 7
120
130 135
(4)根据表5-3,在一张坐标图上作出TVC曲线,在另 一张坐标图上作出AVC曲线和MC曲线。 (5)根据(2)和(4),说明短期生产曲线和短期成 本曲线之间的关系。
TVC AVC Q 2 15Q 100 Q
6、假定生产某产品的边际成本函数为 MC 110 0.04Q
求:当产量从100增加到200时总成本的变化量。
对MC积分可得TC,有:
TC 110 0.04Q dQ 110Q 0.02Q 常数
TFC 66 AFC Q Q Q
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同样 , 对于 MPL 21 18L 3L2
d MPL 18 6L
dL
仅供学习与交流,如有侵权请联系网站删除 谢谢 2
精品资料
令 d MPL 0 dL
即 18 6L 0 得 L 3
dd 又因为 dL dL MPL
60
所以 L 3为边际产量达到极大时厂商雇用的劳动。 将 L 3 代入 MPL 21 18L 3L2
精品资料
( 1)当产量 Q=36时, L 与 K 的值分别是多少? ( 2)如果生产要素的价格分别为 PL 2, PK 5, 则生产 480 单位产量时的最小成 本为多少? 答案:( 1)由 Q=2L= 3K=36,得 L=18;K=12
(2)Q =2L=3K=480,得 PLL+PKK=1280
( 1)当成本 C=3000时,企业实现最大产量时的 L、K和Q的均衡值。
( 2)当产量 Q=800时,企业实现最小成本时的 L、 K和C的均衡值。
21
1
1
解: Q=L 3 K 3 MPL = 2 K 3 L 3
3
2
2
MPK = 1 L 3 K 3
3
MPL / MPK =2K/L = 2 ,K/L=1 K=L
可解得, K
Q2 200
25,L=Q2/50 。
仅供学习与交流,如有侵权请联系网站删除 谢谢 4
精品资料
代入成本函数 TC=100L+400K,得, TC=4Q2+10000,此即为成本函数。
( 2) Q=20时,代入最佳资本规模 K
Q2 200
25 得, K=27 ,
从而 L=8。
3
2
5、已知某企业的短期成本函数为: STC=0.8Q -16 Q +100Q+50,求最小的平均
得到边际产量 MPL的最大值为 48。
( 3)证明:从( 2)中可知:
当 L 4.5 时劳动的平均产量达到极大值为 41.25 而当 L 4.5 时,劳动的边际产量 MPL 21 18L 3L2 41.25 所以当平均产量达到极大时,劳动的平均产量和边际产量相等。
2、已知某企业的单一可变投入( X)与产出( Q)的关系如下: Q=1000X+1000X 2 -2 X 3 ,当 X 分别为 200、300、400 单位时,其边际产量和平
令
d APL 0
dL
d APL 9 2L
dL
即 9 2L 0 得 L 4.5
( L 4.5 也可用 APL MPL ,即 21 9L L2 21 18L 3L2 求得 )
又因为
d dL
d dL
APL
20
所以 L 4.5 为平均产量达到极大时厂商雇用的劳动。
代入 APL 21 9L L2 得平均产量 APL 的最大值为 41.25 。
解:由 MC=3Q2+5Q+80得: TC= Q 3 +2.5 Q 2 +80Q+F 将 Q=3,TC=292代入,得 F=2.5
3
2
TC =Q +2.5 Q +80Q+2.5
AC=
Q 2 +2.5Q+80+2.5
Q
8、已知生产函数为 Q min 2L,3K 。求:
仅供学习与交流,如有侵权请联系网站删除 谢谢 5
3、已知某厂商的需求函数为: Q=6750-50P,总成本函数为: TC=12000+0.025Q2 。求: ( 1)利润最大化时的产量和价格。 ( 2)最大利润是多少? 解:( 1)已知 Q=6750-50P,P=135-(1/50 )Q
TR=PQ= [135- ( 1/50 ) Q]Q=135Q(- 1/50 ) Q 2 MR=135- ( 1/25 )Q
微观经济第五章作业 ( 附答案)
精品资料
1、已知某厂商的短期生产函数为 Q 21L 9L2 L3 。 (1)写出劳动的平均产量 APL 函数和边际产量 MPL 函数; ( 2)分别计算总产量、平均产量和边际产量的最大值; ( 3)证明当平均产量达到极大时,劳动的平均产量和边际产量相等。
解:( 1) 根据 TPL
MP= AP, X=250
MP=0,1000+2000X-6X24
6
第一阶段和第二阶段的分界点是 X =250 ,第二阶段和第三阶段的分界点是 334
仅供学习与交流,如有侵权请联系网站删除 谢谢 3
精品资料
因此, X=200处于第一阶段, X=300处于第二阶段; X=400处于第三阶段。
可变成本值。
解:由 STC 0.8Q 3 16Q 2 100Q 50
得 AVC 0.8Q 2 16Q 100
MC 2.4Q 2 32Q 100
平均成本最小时: AVC=MC
解得 Q=10 AVC MIN=20
21
6、已知某企业的生产函数为 Q=L3 K 3 ,劳动的价格ω =2,资本的价格γ=1。求:
( 1) C=2L+K=3000 将 K=L代入, K=L=1000,Q =1000
21
( 2) Q=L3 K 3 =800 将 K=L代入, K=L=800 C= 2L+K=2400
7、假设某产品的边际成本函数为 MC=32Q+5Q+80 当生产 3 单位产品时,总成本
为 292。试求总成本函数 . 平均成本函数和可变成本函数。
2
21L 9L
3
L
可得 : APL TPL 21 9L L2 L
MP L
dTPL dQ
21 18L 3L2
(2)边际产量为零时 , 总产量最大 即 21 18L 3L2 0
解得 L 7 ( L 1不合题意 )
代入 TPL 21L 9L2 L3 245
同样 , 对于平均产量函数 APL 21 9L L2
求:( 1)成本函数;( 2)Q=20时的最佳资本规模。
解:( 1)由要素最优组合公式:
,有 MPL=
dQ/dL=1/4.10L -3/4(K-25) 1/4 , MPK= dQ/dK=1/4.10L 1/4 (K-25) -3/4 。得 L= 4( K-
25),代回 Q=10L1/4 (K-25) 1/4
仅供学习与交流,如有侵权请联系网站删除 谢谢 6
均产量各为多少?它们分别属于哪一个生产阶段?该函数的三个生产阶段分界
点的产出量分别为多少?
解: TP=1000X+1000X2 -2 X 3 MP=1000+2000X-6 X 2 AP=1000+1000X-2 X 2
X=200 MP=161000 AP= 121000 X=300 MP=61000 AP= 121000 X=400 MP= -159000 AP= 81000
总成本函数为: TC=12000+0.025Q 2 ,MC = 0.05Q 令 MR=M,C即 135- (1/25 )Q= 0.05Q 解得: Q=1500, P=135-(1/50 )×1500=105 (2)π=TR-TC=[135Q-( 1/50 ) Q 2 ]-[12000+0.025 Q 2 ]=157500-68250=89250 4、某企业以劳动 L 和资本 K 的投入来生产产品 Q,生产函数为: Q=10L 1/4 (K-25) 1/4 (K ≥ 25) 其中 PL=100 P K=400。
