北京市昌平区2011-2012学年度第二学期高三年级第二次统一练习理(昌平二模理)-含答案
2024年北京市昌平区高三下学期高考二模物理试卷含答案
昌平区2024年高三年级第二次统一练习物理试卷2024.5本试卷共8页,共100分.考试时长90分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将答题卡交回.第一部分选择题(共42分)本部分共14小题,每小题3分,共42分.在每小题给出的四个选项中,只有一个选项是符合题意的,全部选对得3分,选错或不答的得0分.1.下列说法正确的是().A.水凝结成冰后,水分子的热运动停止B.一定质量的气体被压缩后,内能一定增加C.给自行车胎打气,越打越费力是因为分子间存在斥力D.显微镜下观察到悬浮在水中的花粉颗粒的无规则运动是布朗运动2.将两支铅笔并排放在一起,通过中间狭缝看与其平行的日光灯,观察到彩色条纹的现象属于光的().A.偏振现象B.衍射现象C.干涉现象D.全反射现象3由静止释放并开始计时,木筷就在水中上下振动,在一段时间内木筷在竖直方向可近似看做简谐运动.若取竖直向上为正方向,图中描述木筷振动的图像正确的是().A.B.C.D.4.如图所示,一交变电流通过理想变压器变压后对用电器供电,用电器铭牌上标有“220V,880W”字样,该用电器正常工作,输电线电阻忽略不计.已知交变电流的电压随时间变化关系为()=,下列说法正确的是().u tVA.原、副线圈的匝数比为1:5B.原线圈的输入功率为880WC.原线圈中电流的有效值为20A D.副线圈输出交流电的频率为100Hz5.如图为氢原子的能级示意图.若使处于基态的氢原子被激发后,可辐射能量为2.55eV的光,则激发氢原子的光子能量可能为().A.12.75eV B.12.09eV C.10.20eV D.2.55eV6.研究表明,2000年来地球自转周期累计慢了2个多小时.假设这种趋势持续下去,地球其他条件不变,未来人类发射的地球同步卫星与现在相比().A.距地面的高度变小B.向心加速度变大C.线速度变小D.角速度变大9.如图所示是一种电容式键盘,键盘上每个键子下面都连有一块小金属片,与该金属片隔有一定空气间隙的是另一块固定的小金属片,这样两块金属片就组成一个小电容器.该电容器的电容可用公式SCdε=计算,其中ε为一常量,S表示金属片的正对面积,d表示两金属片间的距离.连接电源,按下某个键时,与之相连的电子线路就给出与该键相关的信号,此时该电容器的().A.电容不变B.极板所带的电荷量变大C.极板间的电压变小D.极板间的场强不变8.如图所示,两个质量均为m的小木块A、B(可视为质点)放在水平圆盘上,A、B到转轴OO'的距离分别为l、2l.小木块与圆盘之间的动摩擦因数均为μ,可以认为小木块最大静摩擦力等于滑动摩擦力.若圆盘从静止开始绕轴转动,并缓慢地加速,用ω表示圆盘转动的角速度,用g表示重力加速度的大小,下列说法正确的是().A .圆盘对A 的作用力大小大于A 对圆盘的作用力大小B .当ω=A 所受摩擦力的大小为mg μC .A 、B 所受摩擦力的大小始终相等D .B 一定比A 先开始滑动9.在做“用油膜法估测油酸分子的大小”实验时,每1000mL 油酸酒精溶液中有纯油酸2mL ,用量筒测得1mL 上述溶液为100滴.在浅盘里盛上水,将爽身粉均匀地撒在水面上.把1滴上述溶液滴入浅盘里,等油膜形状稳定后,把带有坐标方格的玻璃板放在浅盘上,并描画出油膜的轮廓,油膜所占正方形方格数为75个,每个方格边长为2cm .下列说法正确的是().A .1滴油酸酒精溶液中含有的纯油酸的体积约为113210m -⨯B .油酸分子的直径约为96.710m-⨯C .若所撒爽身粉过厚,会导致估测出的分子直径偏小D .若描画油膜轮廓时油酸未完全散开,会导致估测出的分子直径偏小10.如图所示,水平放置的两平行金属板间存在着相互垂直的匀强电场和匀强磁场.一带电粒子(重力不计)从M 点沿水平方向射入到两板之间,恰好沿直线从N 点射出.电场强度为E ,磁感应强度为B .下列说法正确的是().A .粒子一定带正电B .粒子射入的速度大小Bv E=C .若只改变粒子射入速度的大小,其运动轨迹为曲线D .若粒子从N 点沿水平方向射入,其运动轨迹为直线11.某种力做功只与物体的起始和终点位置有关,而与物体运动所经过的具体路径无关,物理学中把这种E来表示.如力称为保守力.保守力做功所改变的是与系统的相对位置有关的能量,这种能量称为势能,用p图为某物体的势能随位置变化的曲线,该物体().A.在势能为0的位置时,受到的保守力也一定为零B.在1x位置时,受到保守力的方向沿x轴的负方向C.从1x位置运动到2x位置的过程中保守力做正功D.在1x位置受到保守力的大小小于在2x位置受到保守力的大小12.如图所示,在水平向右且场强大小为E的匀强电场中,两个半径相同、质量均为m的小球A、B静止q q>,B不带电,A、B之间的放置在光滑的水平面上,且A、B所在直线与电场线平行.A带电量为()0t=时刻开始,A在电场力的作用下开始沿直线运动,并与B发生弹性碰撞.碰撞过程中A、距离为L.0B之间没有电量转移,仅碰撞时才考虑A、B之间的相互作用.下列说法正确的是().An+次碰撞的时间间隔为2B.两球第n次碰撞到发生第1CD.两球连续两次碰撞的时间间隔均为13.将某物体沿与水平方向成一定角度斜向上抛出,经过一段时间,物体落回与抛出点事高处.在忽略空气阻力情况下,其运动轨迹如图中虚线所示,在考虑空气阻刀情况下,其运动轨迹如图中实线所示.在考虑空气阻力的情况下,().A .上升的时间一定小于下降的时间B .在最高点时的加速度等于重力加速度C .落回抛出点时的动能等于抛出时的动能D .上升阶段损失的机械能等于下降阶段损失的机械能14.如图为用于电真空器件的一种磁聚焦装置示意图.螺线管内存在磁感应强度为B 、方向平行于管轴的匀强磁场.电子枪可以射出速度大小均为v ,方向不同的电子,且电子速度v 与磁场方向的夹角非常小.电子电荷量为e 、质量为m .电子间的相互作用和电子的重力不计.这些电子通过磁场汇聚在荧光屏上P 点.下列说法错误..的是().A .电子在磁场中运动的时间可能为2πmeBB .荧光屏到电子入射点的距离可能为2πmveB C .若将电子入射速度变为12v ,这些电子一定能汇聚在P 点D .若将电子入射速度变为2v ,这些电子一定能汇聚在P 点第二部分非选择题(共58分)本部分共6小题,共58分.15.(8分)甲、乙两同学分别用不同的方案做“验证动量守恒定律”实验.(1)甲同学用如图所示的装置研究小球在斜槽末端碰撞时动量是否守恒.O 点是小球抛出点在地面上的垂直投影,实验时先让质量为1m 的入射小球多次从斜槽上位置S 由静止释放,通过白纸和复写纸找到其平均落地点的位置P ,测出平抛射程OP (称为第一次操作).然后,把半径相同质量为2m 的被碰小球静置于斜槽末端,仍将入射小球从斜槽上位置S 由静止释放,与被碰小球发生正碰,并多次重复该操作,两小球平均落地点位置分别为M 、N ,测出OM 、ON (称为第二次操作).在实验误差允许范围内,若满足关系式112m OP m OM m ON =+,则可以认为两球碰撞前后的动量守恒.①下列关于本实验条件的叙述,正确的是__________.(选填选项前的字母)A .同一组实验中,入射小球必须从同一位置由静止释放B .入射小球的质量必须大于被碰小球的质量C .斜槽倾斜部分必须光滑D .斜槽末端必须水平②若第二次操作时,入射小球从斜槽上静止释放的位置低于S ,其他操作都正确的情况下,实验结果为1m OP __________12m OM m ON +(选填“>”“<”或“=”).(2)乙同学用如图所示实验装置进行实验,两个带有等宽遮光条的滑块A 、B 间放置轻质弹簧,挤压两个滑块使弹簧压缩,并用一根细线将两个滑块固定,将其置于气垫导轨上.接通充气开关,烧断细线,A 、B 由静止向相反方向运动.利用光电计时器可记录下两遮光条通过光电门C 、D 的时间分别为1t 、2t .A 、B 的质量分别为1m 、2m .①在实验操作正确的前提下,若满足__________与__________近似相等(用所测物理量的字母表示),则可以认为两滑块被弹簧弹开前后动量守恒.②本实验__________(选填“需要”或者“不需要”)调节气垫导轨水平,判断气垫导轨水平的依据是__________.16.(10分)某同学分别用图甲和乙的电路测量同一节干电池的电动势和内阻.(1)利用图甲实验电路测电池的电动势E 和内阻r ,所测量的实际是下图中虚线框所示“等效电源”的电动势E '和内阻r '.若电流表内阻用A R 表示,用E 、r 和A R 表示E '=__________;r '=__________.(2)根据实验记录的数据得到如图所示的两条直线,图中直线Ⅰ对应电路是题图__________(选填“甲”或“乙”).(3)选择误差较小的实验电路,根据(2)图中对应的数据,该电池的电动势E =__________V (结果保留3位有效数字),内阻r =__________Ω(结果保留2位有效数字).17.(9分)质量为1kg 的物体在水平拉力的作用下,由静止开始在水平地面上沿x 轴运动,出发位置为0x =.拉力做的功W 与物体坐标x 的关系如图所示.物体与水平地面间的动摩擦因数为0.4,重力加速度大小取210m s .求:(1)物体在1m x =位置时,拉力的大小F ;(2)物体在1m x =位置时,拉力的功率P ;(3)物体从0x =运动到4m x =过程中,速度的最大值m v .18.(9分)如图所示,一单摆的摆长为l ,摆球质量为m ,固定在悬点O .将摆球向右拉至N 点,由静止释放,摆球将在竖直面内来回摆动,其中P 点为摆动过程中的最低位置.摆球运动到N 点时,摆线与竖直方向的夹角为θ(约为5︒),θ很小时可近似认为sin θθ≈、 PNPN ≈.重力加速度为g ,空气阻力不计.(1)请证明摆球的运动为简谐运动.(2)如图甲所示,若在O 点正下方34l 的O '处放置一细铁钉,当摆球摆至P 点时,摆线会受到铁钉的阻挡,继续在竖直面内摆动.a .求摆球摆动一个周期的时间T ;b .摆球向右运动到P 点时,开始计时,设摆球相对于P 点的水平位移为x ,且向右为正方向.在图乙中定性画出摆球在开始一个周期内的x t -关系图线.19.(10分)磁悬浮列车是一种高速运载的交通工具,它利用磁力使列车在轨道上悬浮起来从而减少阻力,同时利用磁场与固定在列车下方的金属线圈相互作用,使列车获得牵引力.如图为某种磁悬浮列车驱动原理的示意图.水平面上有两根平行直轨道,轨道间有垂直于轨道平面、方向相反的两种匀强磁场,两种磁场沿轨道方向的宽度均为L ,且相间排列.车厢下方固定着N 匝边长为L 的闭合正方形金属线圈abcd ,车厢与线圈绝缘.当所有磁场同时沿轨道方向运动时,线圈会带动车厢沿轨道运动.已知:轨道宽度为L ,两种磁场的磁感应强度大小均为B ,车厢运动中受到的阻力恒为f ,车厢及线圈的总质量为m ,线圈的总电阻为R .(1)若所有磁场同时沿轨道方向以速度v 做匀速运动,求:a .线圈中感应电流的最大值m I ;b .车厢速度的最大值m v .(2)若所有磁场同时沿轨道方向由静止做加速度为a 的匀加速运动,当磁场运动时间为t 时,车厢正在沿轨道做匀加速运动,求此时车厢的速度大小v 车.20.(12分)对同一个物理问题,常常可以从宏观与微观两个不同角度研究,从而更加深刻地理解其物理本质.如图所示,在竖直向下磁感应强度为B 的匀强磁场中,光滑U 型金属导轨abcd 固定放置在绝缘水平面内,导轨间距为L ,电阻不计.长度为L 的导体棒MN 与平行导轨垂直,且始终与导轨接触良好.导体棒MN 在水平向右拉力的作用下,以速度v 做匀速运动,运动过程中导体棒未滑出导轨.(1)利用法拉第电磁感应定律,推导导体棒MN 产生的感应电动势E BLv =;(2)利用电动势的定义W E q =非,推导导体棒MN 产生的感应电动势E BLv =;(3)利用拉力对导体棒MN 所做的功等于电路获得的电能,推导导体棒MN 产生的感应电动势E BLv =;(4)若bc 端断开,依然保持导体棒MN 以速度v 做匀速运动,利用导体棒MN 中的自由电子的受力情况,推导导体棒MIN 产生的感应电动势E BLv =.。
2012年昌平二模拟考试之化学篇含答案可编辑

北京昌平区2011—2012学年第二学期初三年级第二次统一练习化学试卷2012.6可能用到的相对原子质量H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 Si 28 Cl 35.5 Cu 64 Zn 65一、选择题(每小题只有1个选项符合题意。
共25个小题,每小题1分,共25分。
)1.下列家庭小实验中,主要发生物理变化的是A.生成炭黑B.用洗涤剂洗餐具C.鸡蛋壳放入食醋中D.牛奶制酸奶2.空气成分中,体积分数约占21%的是A.氧气B.氮气C.氢气D.二氧化碳3.决定元素种类的是A.中子数B.质子数C.核外电子数D.最外层电子数4.下列物质在氧气中燃烧,产生大量白烟的是A.木炭B.铁丝C.酒精D.红磷5.下列物质中,属于纯净物的是A.矿泉水B.苏打水C.白醋D.蒸馏水6.下列金属中,活动性最强的是A.镁B.铜C.锌D.铝7.将下列物质放入水中,能形成溶液的是A.大米B.面粉C.蔗糖D.胡椒粉8.水蒸发变成水蒸汽,这说明A.分子的间隔变大B.分子可再分C.分子质量变大D.分子体积变大9.下列各组气体中,均属于空气污染物的是A.CH4、CO2、H2B.CO2、HCl、N2C.SO2、CO、NO2D.HCl、N2、O210.下列数据是相应物质的近似pH,其中一定呈碱性的是(6.5~7.5) (4.0~4.4)(2.0~3.0) (9.5~10.5) A .饮用水 B .番茄汁C .柠檬汁D .液体肥皂11.下列操作中,与水净化无关..的是 A .过滤 B .电解 C .吸附 D .蒸馏 12.下列物质的化学式中,书写正确的是A .氧化镁MgO 2B .氯化铁FeCl 2C .氮气N 2D .火碱 Na 2CO 3 13.森林失火时,灭火队员通常要砍伐一些树木,开辟“防火隔离带”,其主要目的是A .隔离空气B .隔离可燃物C .降低可燃物温度D .开辟运输水的道路 14.喝牛奶可以补钙,这里的“钙”指的是A .分子B .原子C .元素D .单质15.下列实验操作中,正确的是A .滴加液体B .稀释浓硫酸C .移走蒸发皿D .检验装置的气密性16.能与无色硝酸银溶液反应,使溶液变为蓝色的金属是A .铝B .铁C .铜D .银17.薄荷香型牙膏中抗牙腐蚀药物的化学式为Na 2FPO 3,已知F 为-1价,则P 的化合价为A .+3B .+4C .+5D .+618.右图所示装置可用于测定空气中氧气的含量,实验前在集气瓶内加入少量水,并做上记号。
昌平区高三年级第二次统一练习

昌平区年高三年级第二次统一练习理科综合能力测试 物理试卷 ..一束单色光从真空斜射向某种介质的表面,如图所示。
下列说法中正确的是.介质的折射率等于2 .介质的折射率等于.介质的折射率等于22.增大入射角,可能发生全反射现象.钍核(23490Th )具有放射性,它能放出一个新的粒子而变为镤核(23491Pa ),同时伴随有γ射线产生,其方程为x Pa Th 2349123490+→。
则粒子为.质子 .中子 .α粒子 .β粒子.堵住打气筒的出气口,缓慢向下压活塞使气体体积减小,你会感到越来越费力。
设此过程中气体的温度保持不变。
对这一现象的解释正确的是.气体的密度增大,使得在相同时间内撞击活塞的气体分子数目增多 .气体分子间没有可压缩的间隙 .气体分子的平均动能增大.气体分子间相互作用力表现为斥力 .行星在太阳的引力作用下绕太阳公转,若把地球和水星绕太阳的运动轨迹都近似看作圆。
已知地球绕太阳公转的半径大于水星绕太阳公转的半径,则下列判断正确的是 .地球的线速度大于水星的线速度 .地球的角速度大于水星的角速度 .地球的公转周期大于水星的公转周期 .地球的向心加速度大于水星的向心加速度.一列简谐横波沿轴传播,图(甲)是时刻的波形图,图(乙)是处质点的振动图像,下列说法正确的是.该波的波长为.该波的周期为 .该波向轴负方向传播 .该波的波速为.如图所示,固定的竖直光滑长杆上套有质量为的小圆环,圆环与水平状态的轻质弹簧一端连接。
弹簧的另一端固定在墙上,并且处于原长状态。
现让圆环由静止开始下滑,已知弹簧原长为,圆环下滑到最低点时弹簧的长度为(未超过弹性限度),从圆环开始运动至第一次运动到最低点的过程中 .弹簧对圆环的冲量方向始终向上,圆环的动量先增大后减小.弹簧对圆环的拉力始终做负功,圆环的动能一直减小 .圆环下滑到最低点时,所受合力为零 .弹簧弹性势能变化了3mgL(乙)(甲)图介质真空 °°图图.著名物理学家费曼曾设计过这样一个实验:一块水平放置的绝缘体圆盘可绕过其中心的竖直轴自由转动,在圆盘的中部有一个线圈,圆盘的边缘固定着一圈带负电的金属小球,如图所示。
2012昌平高三(二模)数学(理)

昌平区2011-2012学年度第二学期高三年级第二次统一练习数学试卷(理科)2012. 4第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集U = R ,集合}{042≤-=x x |x A ,}2{<=x |x B ,则B A = A. {0≥x |x } B. {20<≤x |x } C. {42≤<x |x } D. {40≤≤x |x } 2. 在复平面内,与复数i+11对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限3. “1=a ” 是“002=-=+y a x y x 和直线直线垂直”的A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件4. 已知直线l :为参数)t t y t x (1⎩⎨⎧+==,圆C :2cos ρθ=,则圆心C 到直线l 的距离是 A. 2 B.3 C.2 D. 15.已知空间几何体的三视图如图所示,则该几何体的各侧面 图形中,是直角三角形的有 A. 0个 B. 1个C. 2个D. 3 个6. 某电视台曾在某时间段连续播放5个不同的商业广告,现在要在该时间段新增播一个商业广告与两个不同的公益宣传广告,且要求两个公益宣传广告既不能连续播放也不能在首尾播放,则在不改变原有5个不同的商业广告的相对播放顺序的前提下,不同的播放顺序共有 A. 60种 B. 120种 C. 144种 D. 300种 7.如图,在棱长为a 的正方体1111D C B A ABCD -中,P 为11D A 的中点,Q 为11B A 上 任意一点,F E 、为CD 上任意两点,且EF 的长为定值,则下面的四个值中不为定值的是 A. 点P 到平面QEF 的距离B. 直线PQ 与平面PEF 所成的角C. 三棱锥QEF P -的体积D.二面角Q EF P --的大小C 1A 1C主视图 左视图8. 设等差数列{}n a 的前n 项和为n S ,已知()37712012(1)1a a -+-=,()32006200612012(1)1a a -+-=-,则下列结论正确的是A .20122012S =,20127a a <B .20122012S =,20127a a >C .20122012S =-,20127a a <D .20122012S =-,20127a a >第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.在∆ABC 中,4,2,2π===A b a 那么角C =_________.10.已知双曲线的方程为1422=-y x ,则其渐近线的 方程为____________,若抛物线px y 22=的焦点与 双曲线的右焦点重合,则_______p =.11. 如图给出了一个程序框图,其作用是输入x 的值, 输出相应的y 值,若要使输入的x 值与输出的y 值相等, 则这样的x 值有 ___________个.12. 如图,AB 是⊙O 的直径,CD 切⊙O 于点D ,CA 切⊙O 于点A ,CD 交AB 的延长线于点E .若3AC =,2ED =,则BE =_____;AO =_____.13. 若变量 x , y 满足约束条件⎪⎩⎪⎨⎧≤-≥≤400x y y x 表示平面区域M ,则当-42≤≤a 时,动直线a y x =+所经过的平面区域M 的面积为____________. 14. 若对于定义在R 上的函数f (x ) ,其图象是连续不断的,且存在常数λ(∈λR )使得 f (x +λ) +λf (x ) = 0对任意实数x 都成立,则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论:①f (x ) =0 是常数函数中唯一个“λ—伴随函数”;②f (x ) = x 不是“λ—伴随函数”;③f (x ) = x 2是一个“λ—伴随函数”; ④“21—伴随函数”至少有一个零点. 其中不正..确.的序号是________________(填上所有不.正确..的结论序号).三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-. (Ⅰ)当b a ⊥时,求θ的值; (Ⅱ)求||b a +的取值范围.16.(本小题满分13分)某游乐场将要举行狙击移动靶比赛. 比赛规则是:每位选手可以选择在A 区射击3 次或选择在B 区射击2次,在A 区每射中一次得3分,射不中得0分; 在B 区每射中一次得2分,射不中得0分. 已知参赛选手甲在A 区和B 区每次射中移动靶的概率分别是41和)10(<<p p .(Ⅰ) 若选手甲在A 区射击,求选手甲至少得3分的概率; (Ⅱ) 我们把在A 、B 两区射击得分的数学期望高者作为选择射击区的标准,如果选手甲最终选择了在B 区射击,求p 的取值范围.17.(本小题满分14分)在正四棱柱1111ABCD A BC D -中, 122AA AB ==,E 为AD 中点,F 为1CC 中点.(Ⅰ)求证:1AD D F ⊥; (Ⅱ)求证://CE 平面1AD F ;(Ⅲ) 求平面1AD F 与底面ABCD 所成二面角的余弦值.18.(本小题满分13分) 已知函数∈+--=a x a xax x f ,ln )1()(R . (Ⅰ)当1>a 时,求)(x f 的单调区间;(Ⅱ)若)(x f 在]1[e ,上的最小值为2-,求a 的值. 19.(本小题满分14分)如图,已知椭圆M :)0(12222>>=+b a b y a x ,离心率36=e ,椭圆与x 正半轴交于点A ,直线l 过椭圆中心O ,且与椭圆交于B 、C 两点,B (1,1).(Ⅰ) 求椭圆M 的方程;(Ⅱ)如果椭圆上有两点Q P 、,使PBQ ∠的角平分线垂直于AO ,问是否存在实数)0(≠λλ使得AC PQ λ=成立?20. (本小题满分13分)实数列 3210a ,a ,a ,a ,由下述等式定义123,0,1,2,3,.n n n a a n +=-=(Ⅰ)若0a 为常数,求123,,a a a 的值; (Ⅱ)求依赖于0a 和n 的n a 表达式;(Ⅲ)求0a 的值,使得对任何正整数n 总有1n n a a +>成立.昌平区2011-2012学年度第二学期高三年级第二次统一练习数学( 理科)试卷2012.4 参考答案一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.)9.127π 10. x y 21±= , 52 11. 3 12. 1 , 2313. 7 14. ① ③三、解答题(本大题共6小题,共80分) 15.(本小题满分13分)解:(Ⅰ) a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分 得3tan =θ 又∵22π≤θ≤π-……… 4分 即:θ=3π………6分 (Ⅱ)||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ ……… 11分 21)3s i n (1≤π-≤-∴θ 4)3s i n (42≤π--≤-∴θ∴33≤+≤||b a ……… 13分16.(本小题满分13分)解:(Ⅰ)设“选手甲在A 区射击得0分”为事件M ,“选手甲在A 区射击至少得3分”为事件N ,则事件M 与事件N 为对立事件, 6427)411(41)(3003=-⋅⋅=)(C M P ………2分 6437642711=-=-=)M (P )N (P ………4分(Ⅱ) 设选手甲在A 区射击的得分为ξ,则ξ的可能取值为0,3,6,9.6427)41-(10)(3===ξP ;6427)411(41C 3)(213=-⋅⋅==ξP ; 649)411()41(6)(223=-==ξC P ; 641)41(9)(3===ξP所以ξ的分布列为49641964966427364270=⨯+⨯+⨯+⨯=ξ∴E 设选手甲在B 区射击的得分为η,则η的可能取值为0,2,4.2)-(10)(p P ==η;)1(2)1(C 2)(12p p p p P -=-⋅⋅==η;24)(p P ==η所以η的分布列为p p )p (p )p (E 441221022=⋅+-⋅+-⨯=η∴根据题意, 有 ξηE E > ∴1169494<<∴>p ,p ……… 13分 17.(本小题满分14分)(Ⅰ)证明:在正四棱柱1111ABCD A BC D -中四边形ABCD 是正方形, AD CD ∴⊥1DD ABCD AD ABCD ⊥⊂ 平面,平面1AD DD ∴⊥ 1DD CD D = 11AD CDD C ∴⊥平面111D F CDDC ⊂ 平面 1A D D F∴⊥ ……… 4分 (Ⅱ)证明:在正四棱柱1111ABCD A BC D -中,连结1A D ,交1AD 于点M ,连结,ME MF . M ∴为1AD 中点.E 为AD 中点,F 为1CC 中点. 111//2ME DD ME DD ∴=且……… 6分 又1121DD CF DD //CF =且 ∴四边形CEMF 是平行四边形. MF //CE ∴ ……… 8分CE ⊄ 平面1AD F ,MF ⊂平面1AD F .//CE ∴平面1AD F .………9分(Ⅲ)解:以D 为坐标原点,分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系如图. 则1(0,0,0),(1,0,0),(1,1,0),(0,1,0),(0,0,2),(0,1,1)D A B C D F……… 10分∴平面ABCD 的法向量为1(0,0,2)DD =………11分设平面1AD F 的法向量为(,,)x y z =n .1(1,1,1),(1,0,2)AF AD =-=-,分则有10,0.AF AD ⎧⋅=⎪⎨⋅=⎪⎩n n 所以 0,20.x y z x z -++=⎧⎨-+=⎩ 取1z =,得(2,1,1)=n .111cos ,6DD DD DD ⋅〈〉==n n n . ………13分 平面F AD 1与平面所成二面角为锐角.所以平面1AD F 与底面ABCD 所成二面角的余弦值为618.(本小题满分13分)解:(Ⅰ)f (x )的定义域为{x |0>x }……………1分.2222))(1()1(11)(x a x x x x a a x x a x a x f --=+-+=+-+='…………3分1>a 令0)(>'x f ,即a x x x a x x ><>--或得1,0))(1(2,∴)(x f 的增区间为(0,1),),(+∞a ……………4分 令0)(<'x f ,即a x xa x x <<<--1,0))(1(2得, ∴)(x f 的减区间为),1(a ……………5分 (Ⅱ)①当1≤a 时, 0)(≥'x f 在]1[e ,上恒成立, ∴)(x f 在]1[e ,恒为增函数. … 6分21)1()]([min -=-==∴a f x f ,得.(3舍去)=a ……… 7分②当e a <<1 时,令0)(='x f ,得1或a x =. 当a x <<1时,0)(<'x f ∴)(x f 在),1(a 上为减函数; 当e x a <<时,0)(>'x f ∴)(x f 在),(e a 上为增函数;2)ln()1(1)()]([min -=+--==∴a a a a f x f ,得(舍)……… 10分③当e a >时,0)(≤'x f 在],1[e 上恒成立,此时)(x f 在],1[e 恒为减函数.2)1()()]([min -=+--==∴a eae ef x f ,得 .e a = ………12分 综上可知 .e a = ……… 13分 19.(本小题满分14分)解:(Ⅰ)由题意可知2)(136abe -==,得 223b a = ……… 2分 )11(,B 点 在椭圆上11122=+ba 解得:34422==b ,a ……… 4分 故椭圆M 的方程为:143422=+y x ……… 4分 (Ⅱ)由于PBQ ∠的平分线垂直于OA 即垂直于x 轴,故直线PB 的斜率存在设为k ,则QB 斜率为 - k ,因此PB 、QB 的直线方程分别为y = k (x -1)+1, y = -k (x -1) +1 ……… 6分由⎪⎩⎪⎨⎧=++-=14341)1(22y x x k y 得01631631222=--+--+k k x )k (k x )k (①由0>∆ ,得31-≠k ……… 8分 点B 在椭圆上,x =1是方程①的一个根,设),(),,(Q Q p p y x Q y x P13163122+--=⋅∴k k k x P 即1316322+--=∴k k k x P ,同理1316322+-+=k k k x Q ………10分 ∴=PQk 311312213)13(22)(222=+--+-⋅=--+=--k k k k k k x x k x x k x x y y Q P Q P Q P Q P)1,1(),0,2(--C A 31=∴AC k 即:AC PQ k k =∴向量//,则总存在实数λ使λ=成立. ………13分20.(本小题满分13分)解:(Ⅰ)0131a a -=,0291a a +-=,03277a a -= ……… 2分(Ⅱ)由123,nn n a a +=-得1112(3)(3)(3)n n n n n n a a +++-=--- ……… 3分 令(3)n n n a b =-,所以112(3)nn n n b b ++-=-所以121321()()()n n n b b b b b b b b -=+-+-++-23112342222(3)(3)(3)(3)n nb -=+++++---- 2111222()[()()()]3333n b -=+--+-++-1122()(1())133()31()3n b ----=+--- 1122(1()),153n b -=+-- ……… 6分所以1122(1())(3)3153n n n a a -=+---- ……… 7分 所以1112(3)[(3)32]15n n n n a a --=⋅-+-+⋅ 1102(13)(3)[(3)32]15n n n a --=--+-+⋅101[2(1)3](1)35n n n n n a -=+-⋅+-⋅⋅ ……… 8分 (Ⅲ)1111101[2(1)3](1)35n n n n n n n a a a +++++-=+-⋅+-⋅⋅101[2(1)3](1)35n n n n n a --+-⋅--⋅⋅ 0112(1)43()55n n n a =⋅+-⋅⋅- 所以101121()()(1)4()3535n nn n n a a a +-=+-⋅⋅- ……… 10分如果0105a ->,利用n 无限增大时,2()3n的值接近于零,对于非常大的奇数n ,有10n n a a +-<;如果0105a -<,对于非常大的偶数n ,10n n a a +-<,不满足题目要求.当015a =时,112,5n n n a a +-=⋅于是对于任何正整数n ,1n n a a +>,因此015a =即为所求. ……… 13分。
昌平二模试题及答案

昌平区2011-2012学年第二学期初三第二次统一练习语文试卷一、选择。
下面各题均有四个选项,其中只有一个..符合题意,选出答案后在答题卡上用2B铅笔把对应题目的选项字母涂黑涂满。
(共12分,每小题2分)1.下列词语中加点字的读音完全正确的一项是A.屏蔽.(bì)呜咽. (yàn) 游弋.(yì)功亏一篑.(kuì)B.迂.腐(yū)贮.藏(chǔ)星宿.(xiù)力挽狂澜.(lán)C.剔.透(tì)狭隘.(ài)涉.猎 (shè) 言简意赅. (ɡāi)D.嘹.亮 (liáo) 缅.怀(miǎn)颈.椎 (jǐng ) 断壁残垣. (yuán )2.下列句子中加点词语使用有误的一项是A.他把中国20世纪文论的演进,放到本世纪世界文化和文论发展的大背景上进行纵横观察、比较、反思、高屋建瓴....,发人深思。
B.最后一年,道路依然不平坦,甚至充满荆棘,但是我们应该记住这样一条古训:行百里者半九十.......。
不可有任何松懈、麻痹和动摇。
C.发展生产力是当前首当其冲....的大事,是一切工作的重中之重。
D.教师要用发展的眼光全面公正地评价每一个学生,切不可一叶障目不见泰山........,这也是构建和谐师生关系的重要途径之一。
3.对下列病句修改正确的一项是A.通过《校车安全管理条例》的执行,可以解决我国学生上下学安全隐患问题。
修改:删去“问题”。
B.扩大内需的方法是我国经济长期平稳较快发展的根本立足点。
修改:删去“的方法”。
C.2012年,中国乒乓球男队以3比0横扫东道主德国队,连续六次夺得世界乒乓球团体锦标赛决赛。
修改:将“夺得”改为“创造”。
D.教育部能否公开选拔直属高校校长,是贯彻落实教育规划纲要、深化直属高校干部选拔任用制度改革的重要决策。
修改:在“是”字后面加上“能”。
4.下列句子的标点符号使用正确的一项是A.“在考场上千万别慌”,老师再三对我们说:“做题前一定要看清题目要求,答题要完整。
北京市昌平区高考二模文综地理试题成版
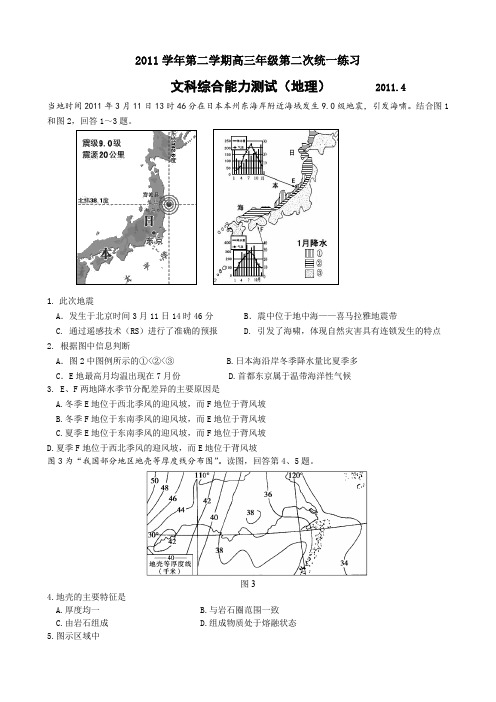
2011学年第二学期高三年级第二次统一练习文科综合能力测试(地理) 2011.41.此次地震A.发生于北京时间3月11日14时46分 B.震中位于地中海——喜马拉雅地震带C. 通过遥感技术(RS)进行了准确的预报D. 引发了海啸,体现自然灾害具有连锁发生的特点2. 根据图中信息判断A.图2中图例所示的①<②<③ B.日本海沿岸冬季降水量比夏季多C.E地最高月均温出现在7月份 D.首都东京属于温带海洋性气候3. E、F两地降水季节分配差异的主要原因是A.冬季E地位于西北季风的迎风坡,而F地位于背风坡B.冬季F地位于东南季风的迎风坡,而E地位于背风坡C.夏季E地位于东南季风的迎风坡,而F地位于背风坡D.夏季F地位于西北季风的迎风坡,而E地位于背风坡图3为“我国部分地区地壳等厚度线分布图”。
读图,回答第4、5题。
图34.地壳的主要特征是A.厚度均一B.与岩石圈范围一致C.由岩石组成D.组成物质处于熔融状态5.图示区域中A. 地壳越厚的地方地势就越高B. 44千米等厚度线为南北走向C. 地壳厚度大致由西向东递增D. 单位距离的地壳厚度差西部大于东部图4为“世界某区域示意图”,图中右侧分别表示甲河流R地河谷剖面示意图和P湖不同季节的蓄水面积分布图。
读图,回答第6、7题。
图46.图示区域A.Q湖位于外流区 B.沿岸海域有暖流经过C.R地河流东岸以侵蚀作用为主 D.P湖底的坡度南部大于北部7.乙河流域A.只参与陆地内循环 B.P湖最小湖面a出现于一月C.典型植被为亚热带常绿阔叶林 D.部分河段有结冰期和凌汛现象发生根据联合国标准,如果某地区65岁以上的人口达7%,则可视为进入老龄化社会。
图5为“1964~2000年中国各年龄段人口占总人口比重变化图”。
读图5,回答第8、9题。
图58.1964~2000年我国人口增长状况是A.人口的出生率迅速升高B.0~14岁年龄段人口比重持续增加C.15~64岁年龄段人口增长速度最快D.65岁及以上年龄段人口增长速度最快9.进入2000年,我国面对的主要人口问题是A.已进入老龄化社会,但就业压力仍较大B.人口老龄化日趋严重,劳动力严重短缺C.人口出现负增长,人口数量日趋减少D.人口自然增长率偏高,每年新增人口多图6为某企业以循环经济的新观念建立的循环经济产业链示意图。
昌平区2011-2012学年度第二学期高三年级第二次统一练习

昌平区2011-2012学年度第二学期高三年级第二次统一练习数 学 试 卷(文科) 2012. 4考生注意事项:1.本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,考试时间 120分钟.2.答题前,考生务必将学校、 班级、姓名、考试编号填写清楚.答题卡上第一部分(选择题)必须用2B 铅笔作答,第二部分(非选择题)必须用黑色字迹的签字笔作答,作图时必须使用2B 铅笔.3.修改时,选择题用塑料橡皮擦干净,不得使用涂改液.请保持卡面整洁,不要折叠、折皱、破损.不得在答题卡上作任何标记.4.请按照题号顺序在各题目的答题区域内作答,未在对应的答题区域作答或超出答题区域的作答均不得分.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 若集合}{0>=x |x A ,}4|{2<=x x B,则=B AA.{02<<-x |x } B . {20<<x |x } C. {22<<-x |x } D. {2->x |x }2. “1>x ” 是“0lg >x 垂直”的A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件3.下列函数在其定义域内既是奇函数又是增函数的是 A . lg y x = B .tan y x =C .3xy = D .13y x =4. 已知空间几何体的三视图如图所示,则该几何体的体积是 A.34 B. 38C. 4D. 8左视图5. 已知函数()()sin (0,0,)2f x A x A πωϕωϕ=+>><的部分图象如图所示,则ϕ=A. 4π- B.6πC.3π D.125π6. 爬山是一种简单有趣的野外运动,有益于身心健康,但要注意安全,准备好必需物品,控制好速度.现有甲、乙两人相约爬山,若甲上山的速度为1v ,下山的速度为2v (21v v ≠),乙上下山的速度都是221v v +(甲、乙两人中途不停歇),则甲、乙两人上下山所用的时间21,t t 的关系为A .21t t > B. 21t t < C. 21t t = D. 不能确定7. 四面体的四个面的面积分别为1S 、2S 、3S 、4S ,记其中最大的面积为S ,则SSi i341∑=的取值范围是A. ]231(, B. ]231[, C . (3432,] D. [3432,]8.设等差数列{}n a 的前n 项和为n S ,已知()37712012(1)1a a -+-=,()32006200612012(1)1a a -+-=-,有下列结论:①20122012S =-;②20122012S =;③20127a a >;④20127a a <.其中正确的结论序号是 A .①② B .①③ C .②③ D .②④第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9. i - (1-2 i ) =___________.10. 若向量b a ,满足32=⋅=b a a ,||, >=<b a,cos 43,则 |b | = ___________.11. 已知双曲线的方程为1422=-yx,则其渐近线的方程为___________,若抛物线px y 22=的焦点与双曲线的右焦点重合,则_______p =.12. 如图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值,若要使输入的x 值和输出的y 值相等,则这样的x 值有___________个.13.若变量 x , y 满足约束条件⎪⎩⎪⎨⎧≤-≥≤400x y y x 表示平面区域M ,则平面区域M 的面积是________;当 —42≤≤a 时,动直线a y x =+所经过的平面区域M 的面积为_____________.14. 若对于定义在R 上的函数f (x ) ,其图象是连续不断的,且存在常数λ(∈λR )使得 f (x +λ) +λf (x ) = 0对任意实数x 都成立,则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论:①f (x ) =0 是常数函数中唯一个“λ—伴随函数”;② f (x ) = x 2是一个“λ—伴随函数”;③ “21—伴随函数”至少有一个零点. 其中不正确...的序号是________________(填上所有不.正确..的结论序号).三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.) 15.(本小题满分13分)已知向量 (cos ,sin )θθ=a,(=b ,22π≤θ≤π-.(Ⅰ)当b a ⊥时,求θ的值; (Ⅱ)求b a ⋅的取值范围.某日用品按行业质量标准分成五个等级,等级系数X 依次为1,2,3,4,5.现从一批日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下表所示: (Ⅰ)若所抽取的20件日用品中,等级系数为2的恰有4件,求a,b,c 的值;(Ⅱ)在(Ⅰ)的条件下,从等级为4的2件日用品和等级为5的3件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.17.(本小题满分13分)在正四棱柱1111ABC D A B C D -中,E 为A D 中点,F 为11B C 中点.(Ⅰ)求证:1//A F 平面1EC C ;(Ⅱ)在C D 上是否存在一点G ,使B G ⊥平面1EC C ?若存在,请确定点G 的位置,并证明你的结论;若不存在,请说明理由.18.(本小题满分14分)已知函数2()4ln 6f x x ax x b =+-+(a ,b 为常数),且2x =为()f x 的一个极值点.(Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的单调区间;(Ⅲ) 若函数()y f x =有3个不同的零点,求实数b 的取值范围.F E D 1C 1B 1A 1DCBA已知椭圆C :22221(0)x y a b ab+=>>,过点B (0,1),离心率为3.(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(0,2)P 的直线l 与椭圆交于M ,N 两个不同的点,且使12PM PN= 成立?若存在,求出直线l 的方程;若不存在,请说明理由.20. (本小题满分13分)设数列}{n a 的首项211-=a ,前n 项和为n S ,且对任意*,N m n ∈都有)53()53(--=m m n n S S mn ,数列}{n a 中的部分项∈k a kb }({N *)成等比数列,且.4,221==b b(Ⅰ) 求数列}与{n n b a }{与的通项公式; (Ⅱ)令11)(+=n b n f ,并用x 代替n 得函数)(x f ,设)(x f 的定义域为R ,记))((...)2()1()0(*N n nn f nf n f f c n ∈++++=,求∑=+ni i i c c 111.昌平区2011-2012学年度第二学期高三年级第二次统一练习数学(文科)试卷参考答案及评分标准 2012.4一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.) 9. -2-i 10. 2 11. x y 21±= , 5212. 3 13.8 , 7 14. ①② 注:11,13题第一空2分.三、解答题(本大题共6小题,共80分)15.(本小题满分13分)解:(Ⅰ)b a ⋅0sin cos 3=+-=θθ ……… 2分 得3tan =θ 22π≤θ≤π-即:θ=3π ………6分(Ⅱ)由=⋅b a )sin(θθ32sin cos 3π-θ=+-……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ ……… 10分21)3s i n (1≤π-≤-∴θ 1)3s i n (22≤π-≤-∴θ……… 12分12≤⋅≤-∴b a ……… 13分16.(本小题满分13分)解:(Ⅰ)由频率分布表得115010450=++++...b a 即30.b a =+………2分 因为抽取20件日用品中,等级系数为2的恰有4件,所以20204.b ==解得10.a = , 21020=⨯=.c ………5分 从而10350.c b .a =--=所以22010===c ,.b ,.a ………6分 (Ⅱ) 从日用品21x ,x ,321y ,y ,y 中任取两件,所有可能的结果为}},{},{},{},{},{},{},{},{},{21323121322212312111x ,x {y ,y y y y y y ,x y ,x y ,x y ,x y ,x y ,x ,,………9分设事件A 表示“从日用品21x ,x ,321y ,y ,y 中任取两件,其等级系数相等”,则A 包含的基本事件}{},{},{},{22312121y ,y y ,y y ,y x ,x 共4个,基本事件总数为10, ……… 11分 故所求的概率 40104.)A (P ==……… 13分17.(本小题满分13分)(Ⅰ)证明:在正四棱柱1111ABC D A B C D -中,取B C 中点M ,连结,.AM FM11//B F BM B F BM ∴=且.∴四边形1B FM B 是平行四边形. 11//FM B B FM B B ∴=且.………2分11//FM A A FM A A = 且,∴四边形1AA FM 是平行四边形. 1//FA AM ∴. E 为A D 中点,//AE M C AE M C ∴=且.∴四边形A M C E 是平行四边形. ………4分 //C E A M ∴.1//C E A F ∴.11ECC F A 平面⊄ ,1EC EC C ⊂平面,11//A F EC C ∴平面. ……… 6分(Ⅱ) 证明:在C D 上存在一点G ,使B G ⊥平面1EC C取C D 中点G ,连结B G ………7分 在正方形A B C D 中, ,,,D E G C C D BC AD C BC D ==∠=∠C D E B C G ∴∆≅∆. E C D G B C ∴∠=∠. ………9分 90C G B G B C ∠+∠=︒ . 90C G B D C E ∴∠+∠=︒.GMF ED 1C 1B 1A 1DCBAB G EC ∴⊥. ………11分ABCD CC 平面⊥1 ,ABCD BG 平面⊂ 1C C BG ∴⊥,1EC C C C = .B G ∴⊥平面1EC C .故在CD 上存在中点G ,使得B G ⊥平面1EC C . ………13分18.(本小题满分14分)解: (Ⅰ) 函数f (x )的定义域为(0,+∞)……1分 ∵ f ′ (x ) =624-+ax x……2分∴06422=-+='a )(f ,则a = 1.………4分(Ⅱ)由(Ⅰ) 知b x x x x f +-+=6ln 4)(2∴ f ′ (x ) =xx x xx x x x)1)(2(24626242--=+-=-+ ………6分由f ′ (x ) > 0可得x >2或x <1,由f ′ (x ) < 0可得1< x <2. ∴ 函数f ( x ) 的单调递增区间为 (0 ,1) 和 (2,+ ∞ ),单调递减区间为 (1 , 2 ). ………9分(Ⅲ) 由(Ⅱ)可知函数f (x )在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.且当x =1或x =2时,f ′ (x ) = 0. ………10分 ∴ f (x ) 的极大值为 5611ln 4)1(-=+-+=b b f ………11分 f (x )的极小值为b b f +-=+-+=82ln 41242ln 4)2( ……12分由题意可知⎩⎨⎧<+-=>-=082ln 4)2(05)1(b f b f则 2ln 485-<<b ………14分19.(本小题满分14分) 解:(Ⅰ)由题意可知1=b ,32211)(122=-=-=aab ac 解得92=a故椭圆M 的方程为1922=+y x………4分(Ⅱ) 12PM PN =点M 为PN 的中点,设)()(2211y ,x N ,y ,x M 则 122x x = ① ……5分(1)当直线的斜率k 不存在时,P(0,2)),10()10(-,N ,,M ,易知不符合条件,此时直线方程不存在. ………7分 (2)当直线的斜率存在时,设直线的方程为2+=kx y由⎪⎩⎪⎨⎧=++=19222y x kx y ,消去y 得 027361922=+++kx x )k (得072)19(4)36(22>⋅+⋅-=∆k k 解得312>k (*) ……9分1936221+-=+k k x x ② ,1927221+=k x x ③由① ②③可得消去21x ,x ,可得532=k,故515±=k ……13分综上可知:存在这样直线l 的方程为: 2515+±=x y ………14分20.(本小题满分13分) 解:(Ⅰ) 由,2111-==a S 代入已知得1)53()53(1⨯--=n n S S n即n n S n 45432-=于是有⎪⎪⎩⎪⎪⎨⎧≥-=-=⎩⎨⎧≥-==-)2(,223)1(,21)2(,)1(,11n n n n S S n S a n n n 又2123211-⨯=-=a =1S所以数列}{n a 的通项公式为 223-=n a n …….3分由4,142==a a 知,数列}{kb a 是首项为1,公比为4的等比数列,14-=n b k a而kb a 为等差数列}{n a 中的第k b 项,是等比数列}{kb a 中的第k 项,所以有22341-=-k k b 即 34)4(321+=-n n b …….5分(Ⅱ)解由已知)241(23)(+=xx f ,则43])24(24241[23]241241[23)1()(1=+++=+++=-+-x xxxxx f x f…….8分),()1(...)2()1()1()0(nnf n n f n f n f n f f c n +-+++++=∴①),0(...)2()1()(f nn f n n f n n f c n ++-+-+=②①+②得 43)1(2+=n c n 即)1(83+=n c n …….10分 =+++=+=+∑13212111 (111)n n ni i ic c c c c c cc (18932964)211141313121+=⨯+-++-+-n n n n…….13分【 以上答案仅供参考,若有其它解法,请酌情给分】。
北京昌平区2011年高三年级第二学期统一练习(二)(数学理)

昌平区2010-2011学年第二学期高三年级第二次统一练习数学(理科)试卷 2011.4考生注意事项:1、本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,考试时间 120分钟。
2、答题前,考生务必将学校、姓名、考试编号填写清楚。
答题卡上第一部分(选择题)必须用2B 铅笔作答,第二部分(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔。
3、修改时,选择题用塑料橡皮擦干净,不得使用涂改液。
请保持卡面整洁,不要折叠、折皱、破损。
不得在答题卡上作任何标记。
4、请按照题号顺序在各题目的答题区域内作答,未在对应的答题区域作答或超出答题区域的作答均不得分。
第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)1.已知集合}0)4)(2(|{},3|{<--=≥=x x x B x x A ,则A B =A .}2|{<x xB .}43|{<≤x xC .}43|{≤≤x xD .}4|{>x x2.设向量)1,1(-=x a ,)3,1(+=x b ,则”“2=x 是b a //“”的A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分也不必要条件 3. 已知221)21(,2==b a ,运算原理如右图所示,则输出的值为A.241+ B.24+ C. 24 D. 424.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是A .πcm 3B .34πcm 3 C .35πcm 3 D .2π cm 35.根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100mL (不含80)之间,属于酒后驾车;血液酒精浓度在80mg/100mL (含80)以 上时,属醉酒驾车。
2012昌平高三(二模)数学(文)

昌平区2011-2012学年度第二学期高三年级第二次统一练习数 学 试 卷文科2012. 4第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 若集合}{0>=x |x A ,}4|{2<=x x B,则=B AA.{02<<-x |x }B. {20<<x |x }C. {22<<-x |x }D. {2->x |x }2. “1>x ” 是“0lg >x 垂直”的A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件 3.下列函数在其定义域内既是奇函数又是增函数的是A . lg y x =B .tan y x =C .3xy = D .13y x = 4. 已知空间几何体的三视图如图所示,则该几何体的体积是 A.34 B.38C. 4D. 85. 已知函数()()sin (0,0,)2f x A x A πωϕωϕ=+>><的部分图象如图所示,则ϕ=A. 4π- B.6πC.3π D.125π6. 爬山是一种简单有趣的野外运动,有益于身心健康,但要注意安全,准备好必需物品,控制好速度.现有甲、乙两人相约爬山,若甲上山的速度为1v ,下山的速度为2v (21v v ≠),乙上下山的速度都是221v v +(甲、乙两人中途不停歇),则甲、乙两人上下山所用的时间21,t t 的关系为A .21t t > B. 21t t < C. 21t t = D. 不能确定7. 四面体的四个面的面积分别为1S 、2S 、3S 、4S ,记其中最大的面积为S ,则SSi i341∑=的取值范围是A. ]231(, B. ]231[, C. (3432,] D. [3432,] 8.设等差数列{}n a 的前n 项和为n S ,已知()37712012(1)1a a -+-=,()32006200612012(1)1a a -+-=-,有下列结论:①20122012S =-;②20122012S =;③20127a a >;④20127a a <.其中正确的结论序号是 A .①② B .①③ C .②③ D .②④左视图第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9. i - (1-2 i ) =___________.10. 若向量b a ,满足32=⋅=b a a ,||, >=<b a,cos 43,则 |b | = ___________.11. 已知双曲线的方程为1422=-yx,则其渐近线的方程为若抛物线px y 22=的焦点与双曲线的右焦点重合,则p = . 12. 如图给出了一个程序框图,其作用是输入x 的值,输出 相应的y 值,若要使输入的x 值和输出的y 值相等,则这样 的x 值有___________个.13.若变量 x , y 满足约束条件⎪⎩⎪⎨⎧≤-≥≤400x y y x 表示平面区域M ,则平面区域M 的面积是________;当 —42≤≤a 时,动直线a y x =+所经过 的平面区域M 的面积为_____________.14. 若对于定义在R 上的函数f (x ) ,其图象是连续不断的,且存在常数λ(∈λR )使得f (x +λ) +λf (x ) = 0对任意实数x 都成立,则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论:①f (x ) =0 是常数函数中唯一个“λ—伴随函数”;② f (x ) = x 2是一个“λ—伴随函数”;③ “21—伴随函数”至少有一个零点. 其中不正确...的序号是________________(填上所有不.正确..的结论序号). 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)15.(本小题满分13分) 已知向量 (cos ,sin )θθ=a ,(=b ,22π≤θ≤π-.(Ⅰ)当b a ⊥时,求θ的值; (Ⅱ)求b a ⋅的取值范围.16.(本小题满分13分)某日用品按行业质量标准分成五个等级,等级系数X 依次为1,2,3,4,5.现从一批日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下表所示:(Ⅰ)若所抽取的20件日用品中,等级系数为2的恰有4件,求a,b,c 的值; (Ⅱ)在(Ⅰ)的条件下,从等级为4的2件日用品和等级为5的3件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.17.(本小题满分13分)在正四棱柱1111ABC D A B C D -中,E 为A D 中点, F 为11B C 中点. (Ⅰ)求证:1//A F 平面1EC C ;(Ⅱ)在C D 上是否存在一点G ,使B G ⊥平面1EC C ?若存在,请确定 点G 的位置,并证明你的结论;若不存在,请说明理由.18.(本小题满分14分)已知函数2()4ln 6f x x ax x b =+-+(a ,b 为常数), 且2x =为()f x 的一个极值点. (Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的单调区间;(Ⅲ) 若函数()y f x =有3个不同的零点,求实数b 的取值范围. 19.(本小题满分14分)已知椭圆C :22221(0)x y a b ab+=>>,过点B (0,1),离心率为3.(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(0,2)P 的直线l 与椭圆交于M ,N 两个不同的点,且使12PM PN = 成立?若存在,求出直线l 的方程;若不存在,请说明理由.20. (本小题满分13分)设数列}{n a 的首项211-=a ,前n 项和为n S ,且对任意*,N m n ∈都有)53()53(--=m m n n S S mn ,数列}{n a 中的部分项∈k a kb }({N *)成等比数列,且.4,221==b b(Ⅰ) 求数列}与{n n b a }{与的通项公式; (Ⅱ)令11)(+=n b n f ,并用x 代替n 得函数)(x f ,设)(x f 的定义域为R ,记))((...)2()1()0(*N n nn f nf n f f c n ∈++++=,求∑=+ni i i c c 111.F E D 1C 1B 1A 1DCBA昌平区2011-2012学年度第二学期高三年级第二次统一练习数学(文科)试卷2012.4 参考答案一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.) 9. -2-i 10. 2 11. x y 21±= , 5212. 3 13.8 , 7 14. ①② 注:11,13题第一空2分.三、解答题(本大题共6小题,共80分)15.解:(Ⅰ)b a ⋅0sin cos 3=+-=θθ 得3tan =θ 22π≤θ≤π-即:θ=3π(Ⅱ)由=⋅b a )sin(θθ32sin cos 3π-θ=+-22π≤≤π-θ 6365π≤π-≤π-∴θ 21)3sin(1≤π-≤-∴θ 1)3sin(22≤π-≤-∴θ 12≤⋅≤-∴b a16.(本小题满分13分)解:(Ⅰ)由频率分布表得115010450=++++...b a 即30.b a =+………2分 因为抽取20件日用品中,等级系数为2的恰有4件,所以20204.b ==解得10.a = , 21020=⨯=.c ………5分从而10350.c b .a =--=所以22010===c ,.b ,.a ………6分(Ⅱ) 从日用品21x ,x ,321y ,y ,y 中任取两件,所有可能的结果为}},{},{},{},{},{},{},{},{},{21323121322212312111x ,x {y ,y y y y y y ,x y ,x y ,x y ,x y ,x y ,x ,,………9分设事件A 表示“从日用品21x ,x ,321y ,y ,y 中任取两件,其等级系数相等”,则A 包含的基本事件}{},{},{},{22312121y ,y y ,y y ,y x ,x 共4个,基本事件总数为10, ……… 11分故所求的概率 40104.)A (P ==……… 13分17.(本小题满分13分)(Ⅰ)证明:在正四棱柱1111ABC D A B C D -中,取B C 中点M ,连结,.AM FM11//B F BM B F BM ∴=且.∴四边形1B FM B 是平行四边形.11//FM B B FM B B ∴=且.………2分 11//FM A A FM A A = 且,∴四边形1AA FM 是平行四边形. 1//FA AM ∴. E 为A D 中点,//AE M C AE M C ∴=且.∴四边形A M C E 是平行四边形. ………4分 //C E A M ∴.1//C E A F ∴.11ECC F A 平面⊄ ,1EC EC C ⊂平面,11//A F EC C ∴平面. ……… 6分(Ⅱ) 证明:在C D 上存在一点G ,使B G ⊥平面1EC C ,取C D 中点G ,连结B G ………7分 在正方形A B C D 中, ,,,D E G C C D BC AD C BC D ==∠=∠C D E B C G ∴∆≅∆. E C D G B C ∴∠=∠. ………9分90C G B G B C ∠+∠=︒ . 90C G B D C E ∴∠+∠=︒.B G E C ∴⊥. ………11分ABCD CC 平面⊥1 ,ABCD BG 平面⊂ 1C C BG ∴⊥,1EC C C C = . B G ∴⊥平面1EC C . 故在CD 上存在中点G ,使得B G ⊥平面1EC C . ………13分18.(本小题满分14分)解: (Ⅰ) 函数f (x )的定义域为(0,+∞)……1分∵ f ′ (x ) =624-+ax x……2分∴06422=-+='a )(f ,则a = 1.………4分(Ⅱ)由(Ⅰ) 知b x x x x f +-+=6ln 4)(2∴ f ′ (x ) =xx x xx x x x)1)(2(24626242--=+-=-+ ………6分由f ′ (x ) > 0可得x >2或x <1,由f ′ (x ) < 0可得1< x <2. ∴ 函数f ( x ) 的单调递增区间为 (0 ,1) 和 (2,+ ∞ ),单调递减区间为 (1 , 2 ). ………9分(Ⅲ) 由(Ⅱ)可知函数f (x )在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.且当x =1或x =2时,f ′ (x ) = 0. ………10分 ∴ f (x ) 的极大值为 5611ln 4)1(-=+-+=b b f ………11分 f (x )的极小值为b b f +-=+-+=82ln 41242ln 4)2( ……12分GMF E D 1C 1B 1A 1DCBA由题意可知⎩⎨⎧<+-=>-=082ln 4)2(05)1(b f b f 则 2ln 485-<<b ………14分19.(本小题满分14分) 解:(Ⅰ)由题意可知1=b ,32211)(122=-=-=aab ac 解得92=a故椭圆M 的方程为1922=+y x………4分(Ⅱ) 12PM PN =点M 为PN 的中点,设)()(2211y ,x N ,y ,x M 则 122x x = ① ……5分(1)当直线的斜率k 不存在时,P(0,2)),10()10(-,N ,,M ,易知不符合条件,此时直线方程不存在. ………7分 (2)当直线的斜率存在时,设直线的方程为2+=kx y由⎪⎩⎪⎨⎧=++=19222y x kx y ,消去y 得 027361922=+++kx x )k (得072)19(4)36(22>⋅+⋅-=∆k k 解得312>k (*) ……9分1936221+-=+k k x x ② ,1927221+=k x x ③由① ②③可得消去21x ,x ,可得532=k,故515±=k ……13分综上可知:存在这样直线l 的方程为: 2515+±=x y ………14分20.(本小题满分13分) 解:(Ⅰ) 由,2111-==a S 代入已知得1)53()53(1⨯--=n n S S n即n n S n 45432-=于是有⎪⎪⎩⎪⎪⎨⎧≥-=-=⎩⎨⎧≥-==-)2(,223)1(,21)2(,)1(,11n n n n S S n S a n n n 又2123211-⨯=-=a =1S ,所以数列}{n a 的通项公式为 223-=n a n …….3分由4,142==a a 知,数列}{kb a 是首项为1,公比为4的等比数列,14-=n b k a而kb a 为等差数列}{n a 中的第k b 项,是等比数列}{kb a 中的第k 项,所以有22341-=-k k b 即 34)4(321+=-n n b …….5分(Ⅱ)解由已知)241(23)(+=xx f ,则13113143()(1)[][]242422422(42)4xxxxxf x f x -+-=+=+=++++…….8分),()1(...)2()1()1()0(n nf n n f n f n f n f f c n +-+++++=∴①),0(...)2()1()(f nn f n n f n n f c n ++-+-+=②①+②得 43)1(2+=n c n 即)1(83+=n c n …….10分 =+++=+=+∑13212111 (111)n n ni i ic c c c c c cc (18932964)211141313121+=⨯+-++-+-n n n n…….13分。
2012年北京市昌平区高三年级第二次综合练习

昌平区2011-2012学年第二学期高三年级第二次统一练习英语试卷2012.4第一节单项填空(共15小题;每小题1分,共15分)从每题所给的A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. That ___ Seventh International Strawberry Festival was held in Changping is______great success.A. the ; aB. the ; theC. a; 不填D. a; a22.In the last few months, many practice exams _____ to sharpen the students’examination skills.A. were holdingB. were being heldC. have heldD. have been held23. It worried her a bit ____ her hair was turning grey.A. whenB. thatC. whichD. what24.________ the Internet is of great help, I don’t think it’s a good idea to spend too much time on it.A. WhileB. AsC. BecauseD. If25. — Which of those electronic dictionaries do you like most?— ____. They are all expensive and of little use.A. NoneB. BothC. NeitherD. All26. Some college students think V alentine’s Day is an opportunity _____ some pocketmoney by selling flowers.A. earnB. to earnC. earning D to have earned27. How beautiful your dress is! Could you please tell me ______you bought it? A.what B.which C.who D.where28. Betty went to the shopping mall alone. If she had invited me then, I _____with her.A. would goB. wentC. would have goneD. had gone29. The plane had already been away for quite some time when we ____ at the airport.A. have arrivedB. arrivedC. had arrivedD. arrive30. ---Where will you start your work after graduation?---Mmm, it’s not been decided yet. I ______ continue my study for a higher degree.A.needB. mustC. mightD. would31.---Did you watch the movie Mei Lanfang in the National Grand` Theater last night? ---I had planned to, but it _______ hard all the time.A. is rainingB. had rainedC. has rainedD. was raining32. Tom arranged to spend his winter vacation in Hawaii with his parents ______ hewould stay for a week.A. whoB. whereC. whichD. what33.______ a better position at IBM, he became more and more confident of his ability.A. To offerB. Having offeredC. OfferedD. Offering34. Only if you eat the correct foods _____ be able to keep fit and stay healthy.A. you willB. you doC. will youD. do you35. Can you take the path ______ to the deep forest?A.leading B.leads C.to be led D.led第二节完形填空(共20小题;每小题1.5分,共30分)阅读下面短文,掌握其大意,从每题所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
北京昌平区2012年高三二模理综试题及答案
北京2012年昌平区高考二模试题学校班级__________姓名__________成绩注意事项:1.本试卷配有答题卡,请同学们将题答在答题卡上,填写在试题卷上的无效。
2.本试卷满分共300分,考试时间150分钟。
3.试卷答题时可能用到的相对原子质量:H—1,C—12,O—16,N—14,Na—23,,Cl—35.5,Ca—40第I卷(选择题,共126分)一、选择题:(本题包括13小题,每小题6分。
每小题只有一个选项符合题意)1.在人体的内环境中,可以发生的生理过程是A.血浆蛋白和血红蛋白的合成B.丙酮酸氧化分解,产生二氧化碳和水C.神经递质从突触前膜扩散到突触后膜D.食物中的淀粉经消化,最终形成葡萄糖2.下图表示光合作用与呼吸作用过程中物质变化的关系,下列说法不正确...的是A.1、3和4过程产生的[H]都能与氧结合产生水B.各种生物体(病毒除外)都能进行的过程是3C.能提供给绿色植物各种生命活动所需能量最多的过程是5D.2过程需多种酶参与,且需ATP供能3.下图表示人体和人体细胞内某些信息传递机制的模式图,图示中箭头表示信息传递方向。
下列有关的叙述中,正确的是A.如果该图表示一个完整的反射弧,则a 表示感受器,b 表示神经中枢,c表示效应器,且其中的信息以局部电流的形式由a 传到cB.如果该图中a 为下丘脑,b 为垂体,c 为甲状腺,则c 分泌的激素过多对于a 分泌d , b 分泌e 均具有抑制作用C.如果该图表示细胞中的遗传信息的表达过程,则d 过程只发生在细胞核中D.如果a 表示抗原,b 表示吞噬细胞和T 细胞,c 为B 细胞,则该过程表示体液免疫的反应阶段4.下面有关生物实验的叙述中,有几项说法是错误的①西瓜汁中含有丰富的葡萄糖和果糖,是还原糖的鉴定实验的理想材料②用显微镜观察根尖细胞有丝分裂时,看到的分生区细胞在右下方,为使观察目标移至视野中央,应该将装片向右下方移动③在层析法分离叶绿体中色素的结果中,蓝绿色色带最宽,表明叶绿素a 的含量最多④DNA 的粗提取实验中,向鸡血细胞溶液中加蒸馏水的目的是为了降低NaCI 溶液浓度至0 . 1 4mol/L ,此时DNA 溶解度最小,以便析出DNA⑤在探究温度对酶活性影响的实验中,用到了相互对照原则A.四项B.三项C.两项D.一项5.有关通过发酵工程生产谷氨酸的叙述中不正确的是A.发酵时所采用的培养基为液体培养基B.往往采用连续培养法来提高产量C.发酵时,要不断通入无菌空气,否则会生成乳酸或琥珀酸D.扩大培养、接种和生产谷氨酸时所用的培养基,其C:N=4:16.下列有关叙述中正确的是A.胶体产生丁达尔效应是由胶粒的大小决定的B.同一主族元素的氢化物,相对分子质量越大,它的沸点一定越高C.分子晶体溶于水时,一定不破坏共价键D.具有相同质子数和电子数的粒子中,可能是一种原子和一种离子7.一定条件下,充分燃烧一定量的丁烷放出热量161.9 KJ,经测定完全吸收生成的二氧化碳需消耗5mol/L的KOH溶液100mL,恰好生成正盐。
北京市昌平区月高三第二次统一练习数学理试题含答案

昌平区 20XX 年高三年级第二次统一练习数学试卷(理科)(满分150分,考试时间 120分钟)2016.5考生须知:1. 本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
2. 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写。
3.答题卡上第I 卷(选择题)必须用2B 铅笔作答,第II 卷(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔。
请按照题号顺序在各题目的答题区内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
4. 修改时,选择题部分用塑料橡皮擦涂干净,不得使用涂改液。
保持答题卡整洁,不要折叠、折皱、破损。
不得在答题卡上做任何标记。
5. 考试结束后,考生务必将答题卡交监考老师收回,试卷自己妥善保存。
第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.) (1)复数i 1i=- A .1i 22+ B . 1i 22-+ C .1i 22-- D .1i 22-(2) 已知双曲线22:1C mx ny -=的一个焦点为(5,0)F -,实轴长为6,则双曲线C 的渐近线方程为A .43y x =± B. 34y x =± C. 53y x =± D. 35y x =±(3) 若,x y 满足2,10,20,x x y x y ≤⎧⎪-+≥⎨⎪+-≥⎩则2z x y =-的最小值为A .4 B. 1 C. 0 D. 12-(4)设,αβ是两个不同的平面,b 是直线且.b β⊂“b α⊥”是“αβ⊥”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件E DCB AO(5)如图,过点A 和圆心O 的直线交O 于,B C 两点(AB AC <),AD 与O 切于点D ,DE AC ⊥于.E 35,AD =3AB =,则BE 的长度为A. 1B. 2C. 2D. 5(6)执行如图所示的程序框图, 如果输出的S 值为3,则判断框 内应填入的判断条件为A. 2i <B. 3i < C .4i < D .5i <(7)已知函数f (x ) 是定义在[3,0)(0,3]-上的奇函数, 当(0,3]x ∈时,f (x ) 的图象如图所示,那么满足不等式()21x f x ≥-的x 的取值范围是A.[3,2][2,3]--B. [3,2](0,1]-- C. [2,0)[1,3]- D. [1,0)(0,1]-否是 0,1S i ==1i i =+开始2i S S =+2log (2)S S =+ 输出S结束俯视图侧(左)视图111正(主)视图11DCBAe 2e 1BAO(8)将一圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O ,并且12,.OA e OB e ==uu r u r uu u r u r若将点O 到正八角星16个顶点的向量,都写成为12,,R e e λμλμ+∈u r u r的形式,则λμ+的最大值为A .2 B. 2 C. 12+ D. 22第Ⅱ卷(非选择题 共110分) 二、填空题(本大题共6小题,每小题5分,共30分)(9)已知n S 是等比数列}{n a (n *∈N )的前n 项和,若314S =,公比 2q =,则数列}{n a 的通项公式n a = .(10)在极坐标系中,O 为极点,点A 为直线:sin cos 2l ρθρθ=+上一点,则||OA 的最小值为________.(11) 如图,点D 是ABC ∆的边BC 上一点,7,2,1,45.AB AD BD ACB ︒===∠=那么 ADB ∠=___________;AC =____________.(12) 某三棱锥的三视图如图所示,则该三棱 锥中最长棱的棱长为_________.(13)20XX 年3月12日,第四届北京农业嘉年华在昌平拉开帷幕.活动设置了“三馆两园一带一谷”七大板块.“三馆”即精品农业馆、创意农业馆、智慧农业馆;“两园”即主题狂欢乐园、农事体验乐园;“一带”即草莓休闲体验带;“一谷”即延寿生态观光谷.某校学生准备去参观,由于时间有限,他们准备选择其中的“一馆一园一带一谷”进行参观,那么他们参观的不同路线最多有______种. (用数字作答)(14)已知数列{}n a 中,1(01),a a a =<≤*11,1,().3,(1),2n n n n n a a a n a a +->⎧⎪=∈⎨-+≤⎪⎩N ①若31,6a =则a =_________;②记12...,n n S a a a =+++则2016S =____________.三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.) (15)(本小题满分13分)已知函数()sin()(0,0,||)2f x A x A ωϕωϕπ=+>><的部分图象如图所示. (Ⅰ)写出函数()f x 的解析式及0x 的值; (Ⅱ)求函数()f x 在区间ππ[, ]44-上的最大值与最小值.(16)(本小题满分13分)为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试. 现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:(I ) 比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小;(只需要写出结论) (II ) 如果将数学基础采用A 、B 、C 等级制,各等级对应的测试成绩标准如下表:(满分100分,所有学生成绩均在60分以上)甲校 乙校5 1 9 1 1 24 3 3 8 4 77 4 3 2 7 7 88 6 5 7 8C 1B 1A 1FEDCBA测试成绩 [85,100][70,85)(60,70)基础等级ABC假设每个新生的测试成绩互相独立.根据所给数据,以事件发生的频率作为相应事件发生的概率.从甲、乙两校新生中各随机抽取一名新生,求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.(17)(本小题满分14分)如图,三棱柱111ABC A B C -中,BC 垂直 于正方形11A ACC 所在平面,2,1AC BC ==,D 为AC 中点,E 为线段1BC 上的一点(端点除外),平面1AB E 与BD 交于点F .(I )若E 不是1BC 的中点,求证:1//AB EF ;(II )若E 是1BC 的中点,求AE 与平面D BC 1所成角的正弦值; (III )在线段1BC 上是否存在点E ,使得1,A E CE ⊥若存在,求出1BEEC 的值,若不存在,请说明理由.(18)(本小题满分13分)已知函数()e axf x =,2()(,,)g x x bx c a b c =-++∈R ,且曲线()y f x =与曲线()y g x =在它们的交点(0,)c 处具有公共切线. 设()()()=-h x f x g x . (I )求c 的值,及,a b 的关系式; (II )求函数()h x 的单调区间;(III )设0a ≥,若对于任意12,[0,1]x x ∈,都有12()()e 1h x h x -≤-,求a 的取值范围.(19)(本小题满分13分)已知椭圆M :()222210x y a b a b+=>>的焦距为2,点()0,3D 在椭圆M 上,过原点O 作直线交椭圆M 于A 、B 两点,且点A 不是椭圆M 的顶点,过点A 作x 轴的垂线,垂足为H ,点C 是线段AH 的中点,直线BC 交椭圆M 于点P ,连接AP .(Ⅰ)求椭圆M 的方程及离心率; (Ⅱ)求证:AB AP ⊥.(20)(本小题满分14分)定义{}123maxn x ,x ,x ,,x 表示123n x ,x ,x ,,x 中的最大值.已知数列1000=n a n ,2000=n b m ,1500=n c p,其中200++=n m p ,=m kn , ,,,∈n m p k *N .记{}max n n n n d a ,b ,c =.(I )求{}maxn n a ,b ;(II )当2=k 时,求n d 的最小值; (III )∀∈k *N ,求n d 的最小值.昌平区 20XX 年高三年级第二次统一练习数学试卷参考答案及评分标准 (理科) 2016.5一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.) 题号 1 2 3 4 5 6 7 8 答案BADACBBC二、填空题(本大题共6小题,每小题5分,共30分)(9)*2(N )n n ∈ (10)2 (11) 120︒;6 (12)5 (13)144 (14)1;15123三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)(15)(本小题满分13分) 解:(I )023()2sin(2),.324f x x x ππ=+=…………………7分z yxC 1B 1A 1F EDC BAG(II )由ππππ5π[,],2[, ]44366x x ∈-+∈-, ……………………9分 当π236x π+=-时,即4x π=-,min ()()1;4f x f π=-=-当232x ππ+=时,即12x π=,max ()() 2.12f x f π== ……………………13分(16)(本小题满分13分)解: (I )两校新生的数学测试样本成绩的平均值相同;甲校新生的数学测试样本成绩的方差小于乙校新生的数学测试样本成绩的方差. ……………………6分(II )设事件D =“从甲、乙两校新生中各随机抽取一名新生,甲校新生的数学基础等级高于乙校新生的数学基础等级”.设事件1E =“从甲校新生中随机抽取一名新生,其数学基础等级为A ”,11(),5P E = 设事件2E =“从甲校新生中随机抽取一名新生,其数学基础等级为B ”,27(),10P E =设事件1F =“从乙校新生中随机抽取一名新生,其数学基础等级为B ”,13(),10P F =设事件2F =“从乙校新生中随机抽取一名新生,其数学基础等级为C ”,23(),10P F =根据题意,111222,D E F E F E F =⋃⋃所以111222111222()()()()()()()()()()P D P E F P E F P E F P E P F P E P F P E P F =++=++131373335105101010100=⨯+⨯+⨯=. 因此,从甲、乙两校新生中各随机抽取一名新生,甲校新生的数学基础等级高于乙校新生的数学基础等级的概率为33.100……………………13分(17)(本小题满分14分)(I )证明:连接C B 1,交1BC 于点G ,连接GD . 在三棱柱111C B A ABC -中, G 为1B C 中点, 且D 为AC 中点, 所以1//GD AB . 因为1GD BC D ⊂平面, DBC AB 11平面⊄所以11//AB BC D 平面. ………………2分由已知,平面1AB E 与BD 交于点F , 所以1F AB ∈平面,E 从而1EF AB EF ⊂平面, 又1EF BC D ⊂平面, 所以11BC DAB EF EF =平面平面,所以1//AB EF . ……………………4分(II) 建立空间直角坐标系 11C ACB -如图所示.11(2,2,0),(2,0,0),(0,2,0),(0,0,0),1(0,2,1),(0,0,1),(0,1,),(1,2,0).2A A C CB B E D 1 111(2,1,),(0,2,1),(1,2,0)2AE C B C D =--==.设平面1BC D 的法向量为(,,)n x y z =由110,0,n C B n C D ==得20,20.y z x y +=⎧⎨+=⎩,令1,y =,得(2,1,2)n =--. ……………………6分421cos ,.63||||AE n AE n AE n <>== ……………………8分所以,AE 与平面1BC D 所成角的正弦值为42163. ……………………9分 (III) 在线段1BC 上存在点E ,使得1,A E CE ⊥且114BE EC =.理由如下: 假设在线段1BC 上存在点E ,使得1,A E C E ⊥设11(0,,)E y z ,1(0)BEEC λλ=>.则1BE EC λ=⋅,1111(0,2,1)(0,,)y z y z λ--=--.112,11,1y z λλ⎧=⎪⎪+⎨⎪=⎪+⎩ 21(0,,)11E λλ++. ………………11分 121(2,,)11A E λλ=-++,21(0,,)11CE λλλ-=++. 22410(1)(1)λλλ-+=++, 解得: 14λ=. ………………13分 所以,在线段1BC 上存在点E ,使得1,A E CE ⊥且114BE EC =.………………14分 (18)(本小题满分13分)解:(I )因为函数()e axf x =,2()=-++g x x bx c ,所以函数'()e ax f x a =,'()2=-+g x x b .又因为曲线()y f x =与曲线()y g x =在它们的交点(0,)c 处具有公共切线,所以(0)(0),'(0)'(0)=⎧⎨=⎩f g f g ,即1,.c a b =⎧⎨=⎩ ………………4分(II )由已知,2()()()e 1axh x f x g x x ax =-=+--. 所以'()e 2axh x a x a =+-.设()'()e 2axF x h x a x a ==+-,所以2'()e 2axF x a =+,∀∈a R ,'()0>F x ,所以'()h x 在(,)-∞+∞上为单调递增函数. ……………6分由(I )得,'(0)'(0),f g =所以'(0)'(0)'(0)0h f g =-=,即0是'()h x 的零点. 所以,函数()h x 的导函数'()h x 有且只有一个零点0.…………………………7分所以'()h x 及()h x 符号变化如下,x(,0)-∞0 (0,)+∞'()h x - 0+ ()h x ↘ 极小值 ↗所以函数()h x 的单调递减区间为(,0)-∞,单调递增区间为(0,)+∞.……………9分(III )由(II )知当[0,1]x ∈ 时,()h x 是增函数. 对于任意12,[0,1]x x ∈,都有12()()e 1h x h x -≤-等价于max min ()()(1)(0)e e 1a h x h x h h a -=-=-≤-,等价于当0a ≥时,()e (e 1)0aG a a =---≤,因为'()e 10aG a =-≥,所以()G a 在[0,)+∞上是增函数,又(1)0G =,所以[0,1]a ∈. ……………13分(19)(本小题满分13分)解:(I )由题意知1,c =3b =,则2224a b c =+=,所以椭圆M 的方程为22143x y +=,椭圆M 的离心率为12. ……………5分(II )设0011(,),(,)A x y P x y ,则0000(,),(,).2y B x y C x -- 由点,A P 在椭圆上,所以2200143x y +=① 2211143x y += ②点A 不是椭圆M 的顶点,②-①得 2210221034y y x x -=-- . 法一:又01001000332,,24PB BCy y y yk k x x x x +===+且点,,B C P 三点共线, 所以10010034y y y x x x +=+, 即 0100104().3()y y y x x x +=+所以,22010101010220101010104()4()43()1,3()3()34AB PAy y y y y y y y y k k x x x x x x x x x -+--====⨯-=--+-- 即 AB AP ⊥. ……………13分法二:由已知AB 与AP 的斜率都存在,2210101022101010PA PB y y y y y y k k x x x x x x -+-==-+-221022103()344x x x x --==-- 又03,4PB BC y k k x ==得00,PA x k y =-则0000()1AB PA y x k k x y -==-, 即 AB AP ⊥. ……………13分(20)(本小题满分14分)解:(I )由题意,{}10002000max max n n a ,b ,n kn ⎧⎫=⎨⎬⎩⎭, 因为1000200010002--=(k )n kn kn, 所以,当1=k 时,10002000<n kn,则{}2000max n n n a ,b b n ==, 当2=k 时,10002000=n kn,则{}1000max n n n a ,b a n ==, 当3≥k 时,10002000>n kn,则{}1000max n n n a ,b a n ==. ……………4分 (II )当2=k 时,{}{}10001500max max max 2003n n n n n n d a ,b ,c a ,c ,n n ⎧⎫===⎨⎬-⎩⎭, 因为数列{}n a 为单调递减数列,数列{}n c 为单调递增数列, 所以当100015002003=-n n时,n d 取得最小值,此时4009=n . 又因为40044459<<, 而{}44444444250max 11d a ,c a ===,454530013d c ==,有4445<d d . 所以n d 的最小值为25011. ……………8分 (III )由(II)可知,当2=k 时,n d 的最小值为25011. 当1=k 时,{}{}2000750max max max 100n n n n n n d a ,b ,c b ,c ,n n ⎧⎫===⎨⎬-⎩⎭. 因为数列{}n b 为单调递减数列,数列{}n c 为单调递增数列, 所以当2000750100=-n n时,n d 取得最小值,此时80011=n . 又因为800727311<<, 而72722509==d b ,73732509==d c . 此时n d 的最小值为2502502509911,>. ⑵当3≥k 时,15001500375200(1)200450≥=-+--k n n n,>n n a b ,所以{}{}1000375max max max 50n n n n n n d a ,b ,c a ,c ,n n ⎧⎫==≥⎨⎬-⎩⎭. 设1000375max 50n h ,n n ⎧⎫=⎨⎬-⎩⎭, 因为数列{}n a 为单调递减数列,数列375{}50-n为单调递增数列, 所以当100037550=-n n 时,n h 取得最小值,此时40011=n . 又因为400363711<<, 而36362509h a ==,3737525037513913h ,=<.此时n d 的最小值为2502502509911,>.综上,n d 的最小值为4425011=d . ……………14分。
2011年北京市昌平区高三物理二模考试(含答案)

19.等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中 a 点沿直线移到 b + 点,再从 b 点沿直线移到 c 点.则 A.从 a 点到 b 点,电势逐渐增大 •c a B.从 a 点到 b 点,检验电荷受电场力先增大后减小 •b • C.从 a 点到 c 点,检验电荷所受电场力的方向始终不变 D.从 a 点到 c 点,检验电荷的电势能先不变后增大 - 20.如图所示,匀强磁场的方向垂直于光滑的金属导轨平面向里,极板间距为 d 的平行板电容器与总阻值 为 2R0 的滑动变阻器通过平行导轨连接, 电阻为 R0 的导体棒 MN 可在外力的作用下沿导轨从左向右做 匀速直线运动。当滑动变阻器的滑动触头位于 a、b 的中间位置、导体棒 MN 的速度为 v0 时,位于电 容器中 P 点的带电油滴恰好处于静止状态. 若不计摩擦 M 和平行导轨及导线的电阻,重力加速度为 g,则下列判 × × × × 断正确的是 上 a· v 0 A.油滴带正电荷 × × R0 × × 2R0 •P d B.若将上极板竖直向上移动距离 d,油滴将向上加速 下 b · × × × × 运动,加速度 a = g/2 C.若将导体棒的速度变为 2v0,油滴将向上加速运动, N 加速度 a = 2g D. 若保持导体棒的速度为 v0 不变, 而将滑动触头置于 a 位置, 同时将电容器上极板向上移动距离 d/3, 油滴仍将静止 21. (18 分) ⑴ ①在做“用单摆测定重力加速度”的实验中,以下做法正确的有______。 A.选用约 1m 长、不易形变的细线充当摆线 B.质量相同,体积不同的摆球,应选用体积较大的 C.单摆偏离平衡位置的角度不能过大,应控制在 5°以内 D.当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆的振动周期 ②某同学通过游标卡尺测定某小球的直径, 测量的结果如图所示, 则该小球的直径为________mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
昌平区2011-2012学年度第二学期高三年级第二次统一练习数 学 试 卷(理科) 2012. 4考生注意事项:1.本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,考试时间 120分钟.2.答题前,考生务必将学校、班级、姓名、考试编号填写清楚.答题卡上第一部分(选择题)必须用2B 铅笔作答,第二部分(非选择题)必须用黑色字迹的签字笔作答,作图时必须使用2B 铅笔.3.修改时,选择题用塑料橡皮擦干净,不得使用涂改液.请保持卡面整洁,不要折叠、折皱、破损.不得在答题卡上作任何标记.4.请按照题号顺序在各题目的答题区域内作答,未在对应的答题区域作答或超出答题区域的作答均不得分.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集U = R ,集合}{42≤-=x x |x A ,}2{<=x |x B ,则B A =A. {0≥x |x } B . {20<≤x |x } C. {42≤<x |x } D. {40≤≤x |x } 2. 在复平面内,与复数i+11对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限3. “1=a ” 是“002=-=+y a x y x 和直线直线垂直”的A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件4. 已知直线l :为参数)t t y tx (1⎩⎨⎧+==,圆C :2cos ρθ=,则圆心C 到直线l 的距离是 A. 2 B.3 C.2 D. 15.已知空间几何体的三视图如图所示,则该几何体的各侧面图形中,是直角三角形的有 A. 0个 B. 1个C. 2个D. 3 个左视图6. 某电视台曾在某时间段连续播放5个不同的商业广告,现在要在该时间段新增播一个商业广告与两个不同的公益宣传广告,且要求两个公益宣传广告既不能连续播放也不能在首尾播放,则在不改变原有5个不同的商业广告的相对播放顺序的前提下,不同的播放顺序共有 A. 60种 B. 120种 C. 144种 D. 300种7.如图,在棱长为a 的正方体1111D C B A ABCD -中,P 为11D A 的中点,Q 为11B A 上 任意一点,F E 、为CD 上任意两点,且EF 的长为定值,则下面的四个值中不为定值的是 A. 点P 到平面QEF 的距离B . 直线PQ 与平面PEF 所成的角 C. 三棱锥QEF P -的体积 D.二面角Q EF P --的大小8. 设等差数列{}n a 的前n 项和为n S ,已知()37712012(1)1a a -+-=,()32006200612012(1)1a a -+-=-,则下列结论正确的是A .20122012S =,20127a a <B .20122012S =,20127a a >C .20122012S =-,20127a a <D .20122012S =-,20127a a >第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.在∆ABC 中,4,2,2π===A b a 那么角C =_________.10.已知双曲线的方程为1422=-y x ,则其渐近线的方程为____________,若抛物线px y 22=的焦点与双曲线的右焦点重合,则_______p =.C 1A 1C11. 如图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值,若要使输入的x 值与输出的y 值相等,则这样的x 值有 ___________个.12. 如图,AB 是⊙O 的直径,CD 切⊙O 于点D ,CA 切⊙O 于点A ,CD 交AB 的延长线于点E .若3AC =,2ED =,则BE =________;AO =________.13. 若变量 x , y 满足约束条件⎪⎩⎪⎨⎧≤-≥≤400x y y x 表示平面区域M ,则当-42≤≤a 时,动直线a y x =+所经过的平面区域M 的面积为_____________.14. 若对于定义在R 上的函数f (x ) ,其图象是连续不断的,且存在常数λ(∈λR )使得 f (x +λ) +λf (x ) = 0对任意实数x 都成立,则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论:①f (x ) =0 是常数函数中唯一个“λ—伴随函数”;②f (x ) = x 不是“λ—伴随函数”;③f (x ) = x 2是一个“λ—伴随函数”; ④“21—伴随函数”至少有一个零点. 其中不正确...的序号是________________(填上所有不.正确..的结论序号).三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-. (Ⅰ)当b a ⊥时,求θ的值; (Ⅱ)求||b a +的取值范围.EA某游乐场将要举行狙击移动靶比赛. 比赛规则是:每位选手可以选择在A 区射击3 次或选择在B 区射击2次,在A 区每射中一次得3分,射不中得0分; 在B 区每射中一次得2分,射不中得0分. 已知参赛选手甲在A 区和B 区每次射中移动靶的概率分别是41和)10(<<p p .(Ⅰ) 若选手甲在A 区射击,求选手甲至少得3分的概率;(Ⅱ) 我们把在A 、B 两区射击得分的数学期望高者作为选择射击区的标准,如果选手甲最终选择了在B 区射击,求p 的取值范围.17.(本小题满分14分)在正四棱柱1111ABCD A B C D -中, 122AA AB ==,E 为AD 中点,F 为1CC 中点.(Ⅰ)求证:1AD D F ⊥; (Ⅱ)求证://CE 平面1AD F ;(Ⅲ) 求平面1AD F 与底面ABCD 所成二面角的余弦值.18.(本小题满分13分) 已知函数∈+--=a x a xax x f ,ln )1()(R . (Ⅰ)当1>a 时,求)(x f 的单调区间;(Ⅱ)若)(x f 在]1[e ,上的最小值为2-,求a 的值.如图,已知椭圆M :)0(12222>>=+b a by a x ,离心率36=e ,椭圆与x 正半轴交于点A ,直线l 过椭圆中心O ,且与椭圆交于B 、C 两点,B (1,1).(Ⅰ) 求椭圆M 的方程;(Ⅱ)如果椭圆上有两点Q P 、,使PBQ ∠的角平分线垂直于AO ,问是否存在实数)0(≠λλ使得AC PQ λ=成立?20. (本小题满分13分)实数列 3210a ,a ,a ,a ,由下述等式定义123,0,1,2,3,.n n n a a n +=-=(Ⅰ)若0a 为常数,求123,,a a a 的值; (Ⅱ)求依赖于0a 和n 的n a 表达式;(Ⅲ)求0a 的值,使得对任何正整数n 总有1n n a a +>成立.昌平区2011-2012学年度第二学期高三年级第二次统一练习数学( 理科)试卷参考答案及评分标准 2012.4一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.)9.127π 10. x y 21±= , 52 11. 3 12. 1 , 2313. 714. ① ③ 注:10,12题第一空2分三、解答题(本大题共6小题,共80分) 15.(本小题满分13分) 解:(Ⅰ) a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分得3tan =θ 又∵22π≤θ≤π-……… 4分 即:θ=3π………6分 (Ⅱ)||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ ……… 11分 21)3s i n (1≤π-≤-∴θ 4)3sin(42≤π--≤-∴θ∴33≤+≤||b a ……… 13分16.(本小题满分13分)解:(Ⅰ)设“选手甲在A 区射击得0分”为事件M ,“选手甲在A 区射击至少得3分”为事件N ,则事件M 与事件N 为对立事件, 6427)411(41)(3003=-⋅⋅=)(C M P ………2分6437642711=-=-=)M (P )N (P ………4分 (Ⅱ) 设选手甲在A 区射击的得分为ξ,则ξ的可能取值为0,3,6,9.6427)41-(10)(3===ξP ;6427)411(41C 3)(213=-⋅⋅==ξP ; 649)411()41(6)(223=-==ξC P ; 641)41(9)(3===ξP 所以ξ的分布列为49641964966427364270=⨯+⨯+⨯+⨯=ξ∴E 设选手甲在B 区射击的得分为η,则η的可能取值为0,2,4.2)-(10)(p P ==η;)1(2)1(C 2)(12p p p p P -=-⋅⋅==η;24)(p P ==η所以η的分布列为p p )p (p )p (E 441221022=⋅+-⋅+-⨯=η∴根据题意, 有 ξηE E > ∴1169494<<∴>p ,p ……… 13分 17.(本小题满分14分)(Ⅰ)证明:在正四棱柱1111ABCD A B C D -中四边形ABCD 是正方形, AD CD ∴⊥1DD ABCD AD ABCD ⊥⊂平面,平面1AD DD ∴⊥ 1DD CD D = 11AD CDD C ∴⊥平面111D F CDD C ⊂平面 1A D D F∴⊥ ……… 4分 (Ⅱ)证明:在正四棱柱1111ABCD A B C D -中,连结1A D ,交1AD 于点M ,连结,ME MF .M ∴为1AD 中点.E 为AD 中点,F 为1CC 中点. 111//2ME DD ME DD ∴=且……… 6分 又1121DD CF DD //CF =且 ∴四边形CEMF 是平行四边形. MF //CE ∴ ……… 8分CE ⊄平面1AD F ,MF ⊂平面1AD F .//CE ∴平面1AD F . ………9分(Ⅲ)解:以D 为坐标原点,分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系如图. 则1(0,0,0),(1,0,0),(1,1,0),(0,1,0),(0,0,2),(0,1,1)D A B C D F……… 10分∴平面ABCD 的法向量为1(0,0,2)DD =………11分设平面1AD F 的法向量为(,,)x y z =n .1(1,1,1),(1,0,2)AF AD =-=-,分则有10,0.AF AD ⎧⋅=⎪⎨⋅=⎪⎩n n所以 0,20.x y z x z -++=⎧⎨-+=⎩取1z =,得(2,1,1)=n .1116cos ,DD DD DD ⋅〈〉==n n n . ………13分平面F AD 1与平面所成二面角为锐角.所以平面1AD F 与底面ABCD ……… 14分 18.(本小题满分13分)解:(Ⅰ)f (x )的定义域为{x |0>x }……………1分.2222))(1()1(11)(xa x x x x a a x x a x a x f --=+-+=+-+='…………3分 1>a 令0)(>'x f ,即a x x x a x x ><>--或得1,0))(1(2,∴)(x f 的增区间为(0,1),),(+∞a ……………4分 令0)(<'x f ,即a x xa x x <<<--1,0))(1(2得, ∴)(x f 的减区间为),1(a ………………5分(Ⅱ)①当1≤a 时, 0)(≥'x f 在]1[e ,上恒成立,∴)(x f 在]1[e ,恒为增函数. ……… 6分21)1()]([min -=-==∴a f x f ,得.(3舍去)=a ……… 7分②当e a <<1 时,令0)(='x f ,得1或a x =. 当a x <<1时,0)(<'x f ∴)(x f 在),1(a 上为减函数; 当e x a <<时,0)(>'x f ∴)(x f 在),(e a 上为增函数;2)ln()1(1)()]([min -=+--==∴a a a a f x f ,得(舍)……… 10分③当e a >时,0)(≤'x f 在],1[e 上恒成立,此时)(x f 在],1[e 恒为减函数.2)1()()]([min -=+--==∴a eae ef x f ,得 .e a = ………12分 综上可知 .e a = ……… 13分19.(本小题满分14分) 解:(Ⅰ)由题意可知2)(136abe -==,得 223b a = ……… 2分 )11(,B 点 在椭圆上11122=+ba 解得:34422==b ,a ……… 4分 故椭圆M 的方程为:143422=+y x ……… 4分 (Ⅱ)由于PBQ ∠的平分线垂直于OA 即垂直于x 轴,故直线PB 的斜率存在设为k ,则QB 斜率为 - k ,因此PB 、QB 的直线方程分别为y = k (x -1)+1, y = -k (x -1) +1 ……… 6分由⎪⎩⎪⎨⎧=++-=14341)1(22y x x k y 得01631631222=--+--+k k x )k (k x )k (①由0>∆ ,得31-≠k ……… 8分 点B 在椭圆上,x =1是方程①的一个根,设),(),,(Q Q p p y x Q y x P13163122+--=⋅∴k k k x P 即1316322+--=∴k k k x P ,同理1316322+-+=k k k x Q ………10分∴=PQk 311312213)13(22)(222=+--+-⋅=--+=--k k k k k k x x k x x k x x y y Q P Q P Q P Q P)1,1(),0,2(--C A 31=∴AC k 即:AC PQ k k =∴向量//,则总存在实数λ使λ=成立. ………13分20.(本小题满分13分)解:(Ⅰ)0131a a -=,0291a a +-=,03277a a -= ……… 2分(Ⅱ)由123,nn n a a +=-得1112(3)(3)(3)nn n n n n a a +++-=--- ……… 3分 令(3)n n na b =-,所以112(3)nn n n b b ++-=-所以121321()()()n n n b b b b b b b b -=+-+-++-23112342222(3)(3)(3)(3)n nb -=+++++---- 2111222()[()()()]3333n b -=+--+-++-1122()(1())133()231()3n b ----=+--- 1122(1()),153n b -=+-- ……… 6分所以1122(1())(3)3153n n n a a -=+---- ……… 7分 所以1112(3)[(3)32]15n n n n a a --=⋅-+-+⋅ 1102(13)(3)[(3)32]15n n n a --=--+-+⋅101[2(1)3](1)35n n n n n a -=+-⋅+-⋅⋅ ……… 8分(Ⅲ)1111101[2(1)3](1)35n n n n n n n a a a +++++-=+-⋅+-⋅⋅101[2(1)3](1)35n n n n n a --+-⋅--⋅⋅ 0112(1)43()55n n n a =⋅+-⋅⋅- 所以101121()()(1)4()3535n n n n n a a a +-=+-⋅⋅- ……… 10分 如果0105a ->,利用n 无限增大时,2()3n 的值接近于零,对于非常大的奇数n ,有10n n a a +-<;如果0105a -<,对于非常大的偶数n ,10n n a a +-<,不满足题目要求.当015a =时,112,5n n n a a +-=⋅于是对于任何正整数n ,1n n a a +>,因此015a =即为所求. ……… 13分【 以上答案仅供参考,若有其它解法,请酌情给分】。
