小波降噪及其在MATLAB中的仿真与比较
基于小波包的图像降噪及Matlab实现

第2 7卷增 - 7 1 J
、0 .7 S o ,1 u ol 2
辽宁工程技术大学学报 ( 自然科学版 )
J un l f io izT c nc l iest Nau a ce c o r a a nn e h ia v ri oL Un y( tr l in e) S
BI NG Y a y a Ⅵ W e b 2 u n u n, n o
( olg f o t sL a nn e h i l ie s y F xn1 3 0 , ia C l e mai , io ig c nc v ri , u i 2 0 0Chn ) e o Ge c T a Un t
2 0 年 5月 08
Ma 2 8 v 00
文章编号:lo-5; o8 0 8 6( o ) o 2 增刊 I02 — 一 43 2 0
基于小波包 的图像 降噪及 Ma a t b实现 l
邴媛媛 ,武文 波
( 宁工 程技术 大学 测 绘科学 与地理 科 学学院 ,辽 宁 阜新 130) 辽 200
r c n t c e ma e c n b b a n d b sn n e s v ltp c e o l c e c e t a d c mp e t h e o sr t d i g a e o t ie y u i g i v r e wa e e a k tf ra l o f i n s n o a d wi t e u i r h meh d o e al h e h l e o i g Tl x e me tlr s l r v a y u i g t i me o 。 o sn ma e t o f h l t r s o d d n sn . l e p r t e i na e u t p o e t t sn s s h b h t d n ii g i g s h c n b e u e fe t ey a d i g e i a eb t r r s r e . a er d c d e c i l n v a m e d t l c nb t e e v d a s e ep Ke r s wa ee a k t t r s o d i g e o sn y wo d : v lt c e ; h e h l ; ma ed n iig p
小波图像去噪及matlab分析
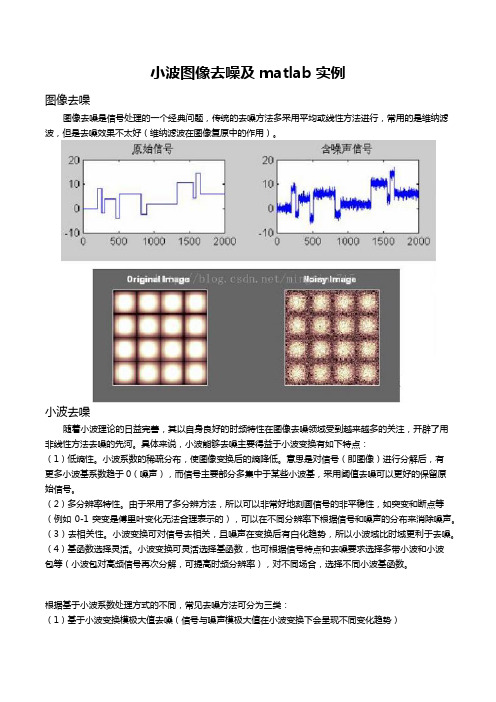
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题,传统的去噪方法多采用平均或线性方法进行,常用的是维纳滤波,但是去噪效果不太好(维纳滤波在图像复原中的作用)。
小波去噪随着小波理论的日益完善,其以自身良好的时频特性在图像去噪领域受到越来越多的关注,开辟了用非线性方法去噪的先河。
具体来说,小波能够去噪主要得益于小波变换有如下特点:(1)低熵性。
小波系数的稀疏分布,使图像变换后的熵降低。
意思是对信号(即图像)进行分解后,有更多小波基系数趋于0(噪声),而信号主要部分多集中于某些小波基,采用阈值去噪可以更好的保留原始信号。
(2)多分辨率特性。
由于采用了多分辨方法,所以可以非常好地刻画信号的非平稳性,如突变和断点等(例如0-1突变是傅里叶变化无法合理表示的),可以在不同分辨率下根据信号和噪声的分布来消除噪声。
(3)去相关性。
小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噪。
(4)基函数选择灵活。
小波变换可灵活选择基函数,也可根据信号特点和去噪要求选择多带小波和小波包等(小波包对高频信号再次分解,可提高时频分辨率),对不同场合,选择不同小波基函数。
根据基于小波系数处理方式的不同,常见去噪方法可分为三类:(1)基于小波变换模极大值去噪(信号与噪声模极大值在小波变换下会呈现不同变化趋势)(2)基于相邻尺度小波系数相关性去噪(噪声在小波变换的各尺度间无明显相关性,信号则相反)(3)基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法,应用广泛,因此重点介绍。
阈值函数选择阈值处理函数分为软阈值和硬阈值,设w是小波系数的大小,wλ是施加阈值后小波系数大小,λ为阈值。
(1)硬阈值当小波系数的绝对值小于给定阈值时,令其为0,而大于阈值时,保持其不变,即:(2)软阈值当小波系数的绝对值小于给定阈值时,令其为0,大于阈值时,令其都减去阈值,即:如下图,分别是原始信号,硬阈值处理结果,软阈值处理结果。
小波变换图像去噪方法MATLAB实现

小波变换图像去噪方法MATLAB实现本文的主要工作是:(1)对各种传统的图像去噪方法用MATLAB实现,并进行对比,总结各种方法的优缺点。
(2)阐述小波变换的发展历程、思想、概念和基于小波变换图像去噪的基本方法。
(3)研究小波分解层数、小波基的选择对图像去噪结果的影响。
(4)用MATLAB编程实现基于小波变换的图像去噪,并计算处理后图像的SNR和MSE。
关键词:图像去噪;小波变换;小波基;分解层数小波阈值去噪的原理从数学角度看小波去噪问题的实质是寻找最佳映射,即寻找从实际信号空间到小波函数空间的最佳映射,从而将原始信号和噪声信号分开,得到原始信号的最佳恢复。
从信号学的角来看,小波去噪实质是一个信号滤波问题,它可以看成是特征提取和低通滤波功能的综合,它既具有传统低通滤波器的功能,还能在去噪后保留信号的特征,其等效框图如下所示:图 3.2 小波去噪等效框小波阈值去噪的步骤如下:(1)根据信号特点和消噪要求选择合适的基小波和分解层数,对含有的噪声信号f(k)作小波变换,得到一组小波系数w j,k 。
图像经过采样后得到一系列的矩阵,然后将图像转换到小波域,此时的图像可以分为一个低通分量LL 和三个高通分量(HL ,LH ,HH),三个高通分量中一个为高通分量部分,剩下两个为次高频部分。
分解过程如下所示:图3.3 图像分解过程f(t)为一维信号,对其进行N 点采样后的离散信号为f(n),N 取0,1,2,...,N-1 ,其小波变换为: Wf (j,k )=2−j 2∑f (n )φ(2−j N−1n=0n −k) (11)其中Wf(j,k)为小波系数,简记为w j,k 。
小波系数可以分为两类:第一类 小波系数仅仅由噪声经过小波变换得到的;第二类 小波系数由信号经过小波变换的来,其中包含有噪声变换的结果。
(2)对w j,k进行阈值处理后得到估计的小波系数ŵj,k,使得‖ŵj,k−u j,k‖尽可能的小。
小波去噪理论及MATLAB实现研究

小波去噪理论及MATLAB实现研究作者:李平李卫国王志国来源:《现代商贸工业》2008年第09期摘要:阐述了小波变换去除信号噪声的基本原理和方法,研究利用小波变换技术对信号噪声进行抑制和去除非平稳信号的噪声。
然后利用MATLAB软件编制程序实现了基于小波变换的正弦信号的去噪仿真分析,仿真结果表明小波变换去除噪声具有很强的实用性。
关键词:小波变换;多分辨率分析;小波去噪;中图分类号:O4文献标识码:A文章编号:1672-3198(2008)09-0399-1 引言利用振动信号或状态量对设备进行诊断是设备故障诊断中最有效、最常用的方法,过去常用传统的基于快速傅里叶变换(FFT)的频谱分析方法进行振动信号处理,但是傅里叶分析存在着严重的不足,它只适于分析时不变系统的平稳信号,而不适于分析非平稳信号,且傅里叶变换对在检测信号中包含的趋势、突变事件的开始和结束等特征分析时也显得无能为力。
出于对非平稳信号和突变信号的分析的迫切要求,法国地球物理学家Morlet于1984年提出了一种新的线性时频分析方法——小波分析理论,为机械故障诊断中的非平稳信号分析,弱信号提取,信号滤波等提供了一条有效的途径。
本文我们利用小波分析所具有的时频局部化特性选择合适的小波函数,建立小波去噪模型,并结合当前在信号处理和分析领域应用广泛的MATLAB 7软件,通过计算机进行仿真,完成了小波去噪的MATLAB实现。
2 小波变换理论小波变换(Wavelet Transform)的基本思想和传统的傅里叶变换是一致的,它也是用一族函数来表示信号或函数,这一族函数称之为小波函数系,但是小波函数系与其它两种方法所用的简谐函数系不同,它是由一基本小波函数平移和伸缩构成的。
它是一种窗口面积恒定,窗口形状可变(时域窗口和频域窗口均可变)的时-频局域化分析方法。
2.1 连续小波变换理论设函数Ψ(t)为一平方可积函数,即Ψ(t)∈L2(R),其傅里叶变换Ψ(ω)满足允许条件:则称Ψ(t)为一个基小波(或小波母函数),我们称上式为小波函数的容许条件。
小波去噪及其在MATLAB中的实现

每次分解都能有效的去除一部分噪声。
其 中 为原始信号 , n分解步数 , /为小波基 函数 。该 函 ut f' 数分解 可得 C和 L两个 向量 , 其组成如图 2 :
c向量
三5 ()
() 5
() 5
L )
摘要 : 实际采样信号不可避免 的会 受到噪声的干扰 , 因此特征提取是故障诊断 中的一个重要环节。小波是一种信号的时间一频 率分
析方法 , 在去除噪声方面有着显著的效果 。文章对此在 MA L B环境 下做 了 TA 详尽 的仿真研 究, 有效的去除 了信号中的噪声 。
关键词 : 征提取 ; 波变换; 特 小 去噪 ; TL B MA A
E u p n Ma u a t n e h oo y No1 , 0 8 q i me t n f cr gT c n l g . 1 2 0 i
小波去噪及其在 MA L B中的实现 TA
吕 营, 朱成 实 , 李铁 军
( 沈阳化工学 院 机械工程学院 , 辽宁 沈 阳 104 ) 12 1
以有效 去除信号 中的噪声 。
其 中 d为含有 噪声 的信 号 为无噪 声的信号 , i 为独立
同分布 的高斯 白噪声 NO1, (, s为噪声水平 , ) Ⅳ为信号的长度 。 为 了从含 噪信 号中得 到 目标信号 ,可 以利用信号和噪声 在小波变换下的不 同特性对小波分解 的系数进行处理 ,达到
1 小 波变换
信 号和噪声分离 的 目的【 1 】 实际工程应用 中, 。在 有用 的信号通 常表现为低 频信 号或是一些相对平稳 的信号 ,而噪声信号则 通 常表现为高频信号 , 以可以先对含噪信号进行小波分解 , 所
以三层分解为例 , 如图 1 所示 :
基于小波变换的信号降噪研究及其MATLAB仿真(附源码)

5 总结
小波变换对平稳信号的去噪声,要比传统的滤波去噪声得到的效果好.用小波变换 进行信号降噪处理, 既降低了噪声同时又提高了信噪比,这说明小波降噪方法是切实 可行的方案, 但是由于小波函数很多,采用不同的小波进行分解, 得到的结果可能相 差很大, 而变换前并不能预知哪一种小波降噪效果更好,需反复试验比较才能得到良 好的效果,这也是小波变换的困难之处之一。另外信号降噪过程中阀值的选取是十分重 要的。本文利用两个小波( sym8 ,db 10 )以及将信号中的信噪分离开来,更加直观可 行,通过分别进行信号降噪处理对所得结果与原始信号进行比较可以得出 Sym8 小波以 及默认阈值处理后的重构信号与原始信号最为接近,与分离的结果相同。 小波分析是一种信号的视频分析方法,它具有多分辨率分析的特点 ,很适合探测正 常信号中夹带的瞬态反常现象并展示其成分,有效区分信号中的突变部分和噪声。通过 MATLAB 编制程序进行给定信号的噪声抑制和非平稳信号的噪声消除实验表明:基于小波 分析的消噪方法是一种提取有用信号、 展示噪声和突变信号的优越方法 ,具有广阔的实 用价值。在这个越来月信息化的社会中,基于小波分析的应用前景必将越来越广泛。
图1
图2
图3 图 1-1 为原始信号图形,1-2 为叠加随机噪声后的图形,而 1-3 和 1-4 为利用 db10 和 sym8 小波默认阈值降噪后的信号图形。从图 1-3 和 1-4 可以看出利用 db10 和 sym8 小波降噪后的信号基本上恢复了原始信号,去噪效果明显。但是滤波后的信号与原始信 号也有不同, 从图中可以很直观地看到采用阈值消噪后信号特征值较少无法准确还原原 始信号 这是由于为降噪过程中所用的分析小波和细节系数的阈值不恰当所致,如需要 更好的恢复信号,还可以采用其它种类小波对其进行分析,通过选取不同的阈值,分析 结果,得到一个合适的阈值。 从图 2 和图 3 中看出, 在经过用 db10 对信号进行 5 层分解, 然后分别对分解的第 5 层到第 1 层的低频系数和高频系数进行重构。 可以得出其主要基波函数和高频噪声函数 的图形,其中小分波分解的细节信号是有白噪声分解得到的,而正弦信号可以在图 2 中 的近似信号 a5 得到。因为在这一层的影响已经可以忽略了,所以获得的信号就是初始 信号的波形,从而把淹没在噪声中的有用信号有效地分离出来。
小波去噪方法分析与Matlab仿真

由小波变换是一种信号的时频分析,它具有多分辨率的特 点,可以方便地从混有强噪声பைடு நூலகம்信号中提取原始信号,被誉为分 析信号的显微镜。运用小波分析进行信号噪声去除是小波分析的 一个非常重要的应用之一。本文介绍小波消噪的基本原理及其几 种小波去噪方法,并利用 Matlab 软件在计算机上实现了几种方 法下信号的噪声消除,从混有噪声的实际信号中提取了原始信 号,具有非常实用的意义。对处理后的结果进行分析和比较。 1 小波消噪的基本原理
的平稳的高斯白噪声,其小波系数的平均功率与尺度成反比。并 且它的离散细节信号的幅值随着小波变换级数的增长而不断减 少。对于所有的尺度,白噪声小波变换的离散细节信号系数的反 差随着尺度的增加会有规律地减少。又因为小波变换是线性变 换,所以降质信号的小波系数是信号的小波系数和噪声的小波 系数的和;降质信号的离散逼近部分和离散细节部分分别是信 号变换后的离散逼近部分和离散细节部分与噪声变换后的离散 逼近部分和离散细节部分的和。因此在消噪过程中,利用信号与 白噪声在小波变换后,它们各自的小波系数的性质不同,可以消 除或减弱噪声。小波分析运用在信号去噪处理,主要表现在以下 方面:是针对信号经小波变换后在不同分辨率下呈现不同规律, 在不同分辨率下设定不同阈值门限,调整小波系数,达到去除噪 声的目的。
利用小波分解与重构去噪的步骤: 1)首先对含噪声信号 f(x)进行小波分解,得到小波变换之 后的逼近部分 c j,k 和细节部分 d j,k; 2)然后取出第 j 层的细节部分 d j,k,根据选定的阈值 δj,用下 列的公式进行处理
#d jk 当 d jk >δj
d jk = 0 当 d jk ≤δj 3)最后利用逼近部分 c j,k 和细节部分 d j,k 利用重构算法进 行重构,得到滤波后的信号。 2.2 小波变换阈值去噪 由于小波变换的小波基都是紧支集,因此小波变换具有一 种“集中”的能力,可以使信号的能量在小波变换域集中于少数 系数上,那么相对来说,对这些系数的取值必然大于在小波系数 域内能量分散于大量小波系数的噪声的小波系数值,这个意味 着对小波系数进行阀值处理可以在小波变换域中去除低于固定 幅度的噪声。小波阀值去噪方法可以分为硬阀值法和软阀值法 两种。 其中硬阀值的处理步骤如下: 1)先把信号做小波变换,得到小波系数; 2)计算出阀值,把小波系数的绝对值与阀值进行比较,小于 或等于阀值的点设为零,大于阀值的点保持不变;
小波变换降噪技术及其在Matlab中的实现

·54·文章编号:1006-1576(2006)02-0054-02小波变换降噪技术及其在Matlab 中的实现赵海英,纪超辉(海军潜艇学院 研究生队,山东 青岛 266071)摘要:小波降噪含模极大值、尺度空间滤波、域值滤波三种方法。
域值滤波法只对低频部分进一步分解,不考虑高频部分,因而用小波函数进行处理。
域值滤波方法的处理过程为:对信号进行小波分解;小波分解高频系数的域值量化;信号重组。
对潜艇获得的测量方位信号仿真结果分析表明,该方法可行。
关键词:小波变换;降噪;Matlab中图分类号:TP312 文献标识码:BNoise Reduction Technology Based on Wavelet Transform and Realization in MatlabZHAO Hai-ying, JI Chao-hui(Brigade of Graduate, Submarine Academy of PLA Navy, Qingdao 266071, China)Abstract: Modular maximum, scale space filtering and domain value filtering are three methods of wavelet noise reduction. Domain value filtering method only decompounded the low frequency, without considering the high frequency, so it can be disposed through wavelet function. The disposing process of domain value filtering method as follows: the wavelet decomposition of signals; the domain value quantification of high frequency coefficient in wavelet decomposition; recombination of signals. The simulation result of the submarine measure orientation proves that this method is reliable.Keywords: Wavelet transform; Noise reduction; Matlab1 引言傅里叶变换是降噪处理手段,对处理非平稳信号和暂态信号,傅里叶变换会忽略暂态信息。
小波阈值图像去噪算法及MATLAB仿真实验

小波阈值图像去噪算法及MATLAB仿真实验作者:刘钰马艳丽刘艳霞来源:《数字技术与应用》2010年第06期摘要:本文研究了小波阈值图像的去噪方法,并与其它图像去噪方法进行了比较。
对lena图像进行MATLAB仿真实验,得到了主观效果图和客观效果的PSNR。
研究发现,小波阈值图像去噪无论主观效果还是客观效果都优于其他图像去噪方法。
关键词:小波阈值去噪Wavelet Thresholding Algorithm of Image Denoising and MATLAB Simulation Experiments Liu Yu11,2Ma Yanli11Liu Yanxia11(1. College of Information Science and Project ,Hebei North University,Zhangjiakou075000;2. College of Electron Information Project,Tianjin University,Tianjin300072)Abstract:In this paper,research on wavelet thresholding algorithm of image denoising and compare with orther algorithms of image denoising.Then Lena on MATLAB simulation experiment images, receive the image of subjective effect and the PSNR of objective effect. Research found that waveletthresholding for image denoising effect regardless of the subjective or objective effect are superior to other algorithms of image denoising.Key words:wavelet;threshold;denoising1 引言近年来,小波图像去噪方法已成为去噪的一个重要分支和主要研究方向,具有“数字显微镜”之称的小波变换在时频域具有多分辨率的特性,可同时进行时频域的局部分析和灵活地对信号局部奇异特征进行提取以及时变滤波[1]。
改进的小波阈值去噪方法及其在MATLAB中的仿真

中图分类号: N 1.2 文献标识码: T 917 A
D I O 编码 :0 3 6 /.s .0 6—1 5 .0 0 0 .2 1 .9 9 ji n 10 s 3 5 2 1 .2 1 1
I pr v d W a e e m oe v l tThr s l n ii g M e ho nd e ho d De o sn t da I s S m u a i n Usng M ATLAB t i l to i
尖峰 、 断点 等 , 以便 于特征 提取 和保 护 ;
3 去相 关性 。 因为 小 波变 换 可 以对 信号 进 行 ) 去相关 , 噪 声 在 变 换 后 有 白化 趋 势 , 以 在 小 波 且 所
域 比在 时域更 利 于去 噪 ;
区分信号 中 的突变 部 分 和 噪声 , 从而 实 现 对 信号 的 降 噪 。小 波去 噪就 是 利用 具 体 问 题 的先 验 知 识 , 根
改进 的小 波 阈值 去 噪方法 及其 在 MA L B 中的仿 真 TA
11 2
文章编号 :0 615 (0 0 0 -1 1 4 10 —35 2 1 ) 2 2 - 0 0
改 进 的 小 波 阈值 去 噪 方 法 及 其 在 MA L B 中 的 仿 真 T A
李树 钰
( 西安 石 油大 学 机械 工程 学 院 , 西安
L h y IS u— u
( c ol f e h i a E gneig X ’ hyuU i r t, i n 7 0 6 C ia S ho o c na l n ier , i nS i nv sy X ’ 0 5, hn ) M c n a o ei a 1
Absr c t a t: I h sp p r e e a v ltd n ii g meh d r o a e nd a lz d.On t e e n t i a e ,s v r lwa e e e osn t o s a e c mp r d a nay e h s b s s,a n w h e h l u c in i o sr c e ae e t r s o d f n to sc n tu td.Th mp o e n ft r s od s l ci g i d e i r v me to h e h l ee tn sma e.S mu a i l— to x e i n f sg a e o sn s c ri d u sng MATL in e p rme to i n l d n iig i a re o t u i AB ot r T e a v na e o mp o e s fwae. h d a tg fi rv d wa e e e osn t o s d mo tae v ltd n ii g meh d i e nsr t d,a d betrd n ii g efc s g i e n te e osn fe ti a n d. Ke wor y ds: v b a in n wa e; wa ee ta so m ; t r s od e osn i r t a d o v v l t r n fr h e h l d n ii g; sg a t n ie in l o os
基于小波变换的信号降噪研究及matlab仿真程序

基于⼩波变换的信号降噪研究及matlab仿真程序基于⼩波变换的信号降噪研究及matlab 仿真程序 2 ⼩波分析基本理论设Ψ(t)∈L 2( R) ( L 2( R) 表⽰平⽅可积的实数空间,即能量有限的信号空间) ,其傅⽴叶变换为Ψ(t)。
当Ψ(t)满⾜条件[4,7]:2()R t dw w C ψψ=<∞? (1)时,我们称Ψ(t)为⼀个基本⼩波或母⼩波,将母⼩波函数Ψ(t)经伸缩和平移后,就可以得到⼀个⼩波序列:,()()a b t b t aψ-= ,,0a b R a ∈≠ (2)其中a 为伸缩因⼦,b 为平移因⼦。
对于任意的函数f(t)∈L 2( R)的连续⼩波变换为:,(,),()()f a b R t b W a b f f t dt aψψ-=<>=(3)其逆变换为: 211()(,)()f R R t b f t W a b dadb C a aψψ+-=?? (4)⼩波变换的时频窗是可以由伸缩因⼦a 和平移因⼦b 来调节的,平移因⼦b,可以改变窗⼝在相平⾯时间轴上的位置,⽽伸缩因⼦b 的⼤⼩不仅能影响窗⼝在频率轴上的位置,还能改变窗⼝的形状。
⼩波变换对不同的频率在时域上的取样步长是可调节的,在低频时,⼩波变换的时间分辨率较低,频率分辨率较⾼:在⾼频时,⼩波变换的时间分辨率较⾼,⽽频率分辨率较低。
使⽤⼩波变换处理信号时,⾸先选取适当的⼩波函数对信号进⾏分解,其次对分解出的参数进⾏阈值处理,选取合适的阈值进⾏分析,最后利⽤处理后的参数进⾏逆⼩波变换,对信号进⾏重构。
3 ⼩波降噪的原理和⽅法3.1 ⼩波降噪原理从信号学的⾓度看 ,⼩波去噪是⼀个信号滤波的问题。
尽管在很⼤程度上⼩波去噪可以看成是低通滤波 ,但由于在去噪后 ,还能成功地保留信号特征 ,所以在这⼀点上⼜优于传统的低通滤波器。
由此可见 ,⼩波去噪实际上是特征提取和低通滤波的综合 ,其流程框图如图所⽰[6]:⼩波分析的重要应⽤之⼀就是⽤于信号消噪 ,⼀个含噪的⼀维信号模型可表⽰为如下形式:(k)()()S f k e k ε=+* k=0.1…….n-1其中 ,f( k)为有⽤信号,s(k)为含噪声信号,e(k)为噪声,ε为噪声系数的标准偏差。
小波阈值图像降噪及MATLAB仿真

小波阈值图像降噪及MATLAB仿真图像信号在生成和传输过程中常常因受到各种噪声的干扰和影响而使图像降质,这对后续图像的处理(如分割、压缩和图像理解等)将产生不利影响。
为了抑制噪声,改善图像质量,便于更高层次的处理,必须对图像进行降噪预处理。
小波降噪的方法有多种,如利用小波分解与重构的方法滤波降噪、利用小波变换模极大值的方法去噪、利用信号小波变换后空域相关性进行信噪分离、非线性小波阈值方法去噪、平移不变量小波降噪法,以及多小波降噪等等。
归结起来主要有三类:模极大值检测法、阈值降噪法和屏蔽(相关)降噪法。
其中最常用的就是阈值法去噪,其基本思想就是利用图像小波分解后,各个子带图像的不同特性选取不同的阈值,从而达到较好的降噪目的。
而且,小波变换本身是一种线形变换,因而对于类似于高斯噪声的效果较好。
线性运算往往还会造成边缘模糊,小波分析技术正因其独特的时频局部化特性在图像信号和噪声信号的区分以及有效去除噪声并保留有用信息等方面较之传统的降噪具有明显的优势,且在降噪的同时实现了图像一定程度的压缩和边缘特征的提取。
所以小波降噪具有无可比拟的优越性。
小波降噪主要优点有:低熵性,小波系数的稀疏分布,使得图象变换后的熵降低;多分辨率,由于采用了多分辨率的方法,所以可以非常好地刻画信号的非平稳特征,如边缘、尖峰、断点等;去相关性,因为小波变换可以对信号进行去相关,且噪声在变换后有白化趋势,所以小波频域比时域更利于降噪;选基灵活性,由于小波变换可以灵活选择变换基,从而对不同应用场合、不同的研究对象,可以选用不同的小波函数,以获得最佳的效果。
一、阈值去噪法简述1992年,斯坦福大学的Donoho D L和Johnstone教授提出一种具有良好的统计优化特性的降噪方法,称作“Wavelet Shrinkage”(即阈值收缩法)。
该方法的主要思想是:基于图像和噪声在经小波变换后具有不同的统计特性:图像本身的能量对应着幅值较大的小波系数,主要集中在高频(LL);噪声能量则对应着幅值较小的小波系数,并分散在小波变换后的所有系数中。
小波阈值去噪及MATLAB仿真_毕业论文

⼩波阈值去噪及MATLAB仿真_毕业论⽂哈尔滨⼯业⼤学华德应⽤技术学院毕业设计(论⽂)毕业论⽂⼩波阈值去噪及MATLAB仿真摘要⼩波分析理论是⼀种新兴的信号处理理论,它在时间上和频率上都有很好的局部性,这使得⼩波分析⾮常适合于时—频分析,借助时—频局部分析特性,⼩波分析理论已经成为信号去噪中的⼀种重要的⼯具。
利⽤⼩波⽅法去噪,是⼩波分析应⽤于实际的重要⽅⾯。
⼩波去噪的关键是如何选择阈值和如何利⽤阈值来处理⼩波系数,通过对⼩波阈值化去噪的原理介绍,运⽤MATLAB 中的⼩波⼯具箱,对⼀个含噪信号进⾏阈值去噪,实例验证理论的实际效果,证实了理论的可靠性。
本⽂设计了⼏种⼩波去噪⽅法,其中的阈值去噪的⽅法是⼀种实现简单、效果较好的⼩波去噪⽅法。
关键词:⼩波变换;去噪;阈值-I-哈尔滨⼯业⼤学华德应⽤技术学院毕业设计(论⽂)AbstractWavelet analysis theory is a new theory of signal process and it has good localization in both frequency and time do-mains.It makes the wavelet analysis suitable for time-frequency analysis.Wavelet analysis has played a particularly impor-tant role in denoising,due to the fact that it has the property of time- frequency analysis. Using wavelet methods in de-noising, is an important aspect in the application of wavelet analysis. The key of wavelet de-noising is how to choose a threshold and how to use thresholds to deal with wavelet coefficients. It confirms the reliability of the theory through the wavelet threshold de-noising principle, the use of the wavelet toolbox in MATLAB, carrying on threshold de-noising for a signal with noise and actual results of the example confirmation theory.In this paper,the method of Wavelet Analysis is analyzed.and the method of threshold denoising is a good method of easy realization and effective to reduce the noise.Keywords:Wavelet analysis;denoising;threshold-II-哈尔滨⼯业⼤学华德应⽤技术学院毕业设计(论⽂)⽬录摘要........................................................................................................................... I Abstract ........................................................................................................................ I I第1章绪论 (1)1.1 研究背景和意义 (1)1.2 国内外研究历史和现状 (2)1.3 本⽂研究内容 (3)第2章⼩波变换的基本理论 (4)2.1 傅⽴叶变换 (5)2.2 加窗傅⽴叶变换 (5)2.3 ⼩波变换 (6)2.3.1 连续⼩波变换 (7)2.3.2 离散⼩波变换 (8)2.4 多分辨分析 (10)本章⼩结 (11)第3章经典噪声类型及去噪⽅法 (12)3.1 经典噪声类型 (12)3.2 常⽤滤波器 (15)3.2.1 线性滤波器 (15)3.2.2 均值滤波器 (15)3.2.3 顺序统计滤波器 (16)3.2.4 其他滤波器 (16)3.3 经典去噪⽅法 (16)-III-哈尔滨⼯业⼤学华德应⽤技术学院毕业设计(论⽂)3.4 Matlab⼯具 (18)3.4.1 Matlab 发展历程 (18)3.4.2 Matlab 简介 (18)本章⼩结 (19)第四章⼩波阈值去噪及MATLAB仿真 (19)4.1 ⼩波阈值去噪概述 (19)4.1.1 ⼩波阈值去噪⽅法 (20)4.1.2 图像质量评价标准 (21)4.2 基于MATLAB的⼩波去噪函数简介 (21)4.3⼩波去噪对⽐试验 (23)本章⼩结 (28)结论 (29)致谢 (29)附录1 译⽂ (31)附录2 英⽂参考资料 (32)-IV-哈尔滨⼯业⼤学华德应⽤技术学院毕业设计(论⽂)-V-第1章绪论1.1 研究背景和意义随着计算机技术的飞速发展,数字图像处理技术获得了飞速的发展。
小波去噪及其MATLAB中的函数

一、小波去噪中信号阈值的估算
信号去噪是信号处理领域的经典问题之一。 传统的去噪方法主要包括线性滤 波方法和非线性滤波方法,如中值滤波和 wiener 滤波等。传统去噪方法的不是 在于使信号变换后的熵增高、 无法刻画信号的非平稳特性并且无法得到信号的相 关性。为了克服上述缺点,人们开始使用小波变换解决信号去噪问题。 小波变换具有下列良好特性: (1) 低熵性:小波系数的稀疏分布,使信号变换后的熵降低; (2) 多分辨率特性:可以非常妤地刻画信号的非平稳特性,如边缘、尖峰、 断点等; (3) 去相关性:可取出信号的相关性,且噪声在小波变换后有白化趋势,所 以比时域更利于去噪; (4) 选基灵活性:由于小波变换可以灵活选择基函数,因此可根据信号特点 和去噪要求选择适合小波。 小波在信号去噪领域已得到越来越广泛的应用。 阈值去噪方法是一种实现简 单、效果较好的小波去噪方法。阈值去噪方法的思想就是对小波分解后的各层系 数中模大于和小于某阈值的系数分别处理, 然后对处理完的小波系数再进行反变 换,重构出经过去噪后的信号。下面从阈值函数和阈值估计两方面对阈值去噪方 法进行介绍。 1.阈值函数 常用的阈值函数主要是硬阈值函数和软阈值函数。 (1)硬阈值函数。表达式为 ( w) wI (| w | T ) ,如图 4.18 所示,其中横坐标 表示信号的原始小波系数,纵坐标表示阈值化后的小波系数。 (2)软阈值函数。 表达式为 ( w) ( w sgn( w)T ) I (| w | T ) , 如图 4.19 所示, 其中横坐标表示信号的原始小波系数,纵坐标表示阈值化后的小波系数。
2 2
/N。
/ N ,则
1 2 2 2 t (Y ) Y ER(t ) n E V , t (Y ) N N 1 2 2 E t (Y ) X X Y 2 t (Y ) X , X Y N 最后可得到风险函数的表达式: ET (t )
基于某MATLAB地小波变换地降噪原理及性能仿真

基于MATLAB的小波变换的降噪原理及性能仿真按小波变换的发展过程划分,大致可以划分三个阶段:第一阶段:孤立应用时间。
主要特征是一些特殊构造的小波在某些科学研究领域的特定问题上的应用。
这个时代最典型的代表工作是法国地球物理学家J.Morlet和A.Grossmann第一个把“小波”用于分析处理地质数据,引进了以他们的名字命名的时间—尺度小波,即Grossmann-Morlet小波。
这个时期的另一个代表性工作是1981年J.Stromberg对A.Haar在1910年所给出的Haar(哈尔)系标准正交小波基的改进。
同时,著名的计算机视觉专家D.Marr在他的“零交叉”理论中使用的可按“尺寸大小”变化的滤波算子,现在称为“墨西哥帽”的小波也是这个时期有名的工作之一,这部分工作和后来成为S.Mallat的正交小波构造理论支柱之“多尺度分析”或“多分辨分析”有密切联系。
这个时期一个有趣的现象是各个领域的专家、学者和工程师所从事的领域广泛分布于科学和技术研究的许多方面。
因此,这个现象从另一个侧面预示了小波分析理论研究和应用热潮的到来,说明了小波理论产生的历史必然性。
第二阶段:国家性研究热潮和统一构造时期。
真正的小波热潮开始与1986年,当时法国数学家Y.Meyer成功地构造出具有一定衰减性质的光滑函数,这个函数(算子)的二进尺度伸缩和二进整倍数平移产生的函数系构成著名的2-范数函数空间的标准正交基。
这项成果标志“小波分析”新时代的到来。
第三阶段:全面应用时期。
从1992年开始,小波分析方法进入全面应用阶段。
在前一阶段研究工作基础上,特别是数字信号和数字图像的Mallat分解和重构算法的确定,使小波分析的应用迅速波及科学研究和工程技术应用研究的几乎所有的领域。
编辑部是在美国的Texas A&M 大学的国际杂志《Applied and Computation Harmonic Analysis》从1993年创刊之日起就把小波分析的理论和应用研究作为其主要内容,编辑部的三位主编C.K.Chi、R.Coifman与I.Daubechies都在小波分析的研究和应用中有独到的贡献。
小波变换图像去噪MATLAB实现

基于小波图像去噪的MATLAB 实现一、 论文背景数字图像处理(Digital Image Processing ,DIP)是指用计算机辅助技术对图像信号进行处理的过程。
数字图像处理最早出现于 20世纪50年代,随着过去几十年来计算机、网络技术和通信的快速发展,为信号处理这个学科领域的发展奠定了基础,使得DIP 技术成为信息技术中最重要的学科分支之一。
在现实生活中,DIP 应用十分广泛,医疗、艺术、军事、航天等图像处理影响着人类生活和工作的各个方面。
然而,在图像的采集、获取、编码和传输的过程中,都存在不同程度被各种噪声所“污染”的现象。
如果图像被污染得比较严重,噪声会变成可见的颗粒形状,导致图像质量的严重下降。
根据研究表明,当一张图像信噪比(SNR)低于14.2dB 时,图像分割的误检率就高于0.5%,而参数估计的误差高于0.6%。
通过一些卓有成效的噪声处理技术后,尽可能地去除图像噪声,我们在从图像中获取信息时就更容易,有利于进一步的对图像进行如特征提取、信号检测和图像压缩等处理。
小波变换处理应用于图像去噪外,在其他图像处理领域都有着十分广泛的应用。
本论文以小波变换作为分析工具处理图像噪声,研究数字图像的滤波去噪问题,以提高图像质量。
二、 课题原理1.小波基本原理在数学上,小波定义为对给定函数局部化的新领域,小波可由一个定义在有限区域的函数()x ψ来构造,()x ψ称为母小波,(mother wavelet )或者叫做基本小波。
一组小波基函数,()}{,x b a ψ,可以通过缩放和平移基本小波 来生成:())(1,ab x a x b a -ψ=ψ (1) 其中,a 为进行缩放的缩放参数,反映特定基函数的宽度,b 为进行平移的平移参数,指定沿x 轴平移的位置。
当a=2j 和b=ia 的情况下,一维小波基函数序列定义为:()()1222,-ψ=ψ--x x j j j i (2) 其中,i 为平移参数,j 为缩放因子,函数f (x )以小波()x ψ为基的连续小波变换定义为函数f (x )和()x b a ,ψ的内积:()dx ab x a x f f x W b a b a )(1)(,,,-ψ=ψ=⎰+∞∞- (3) 与时域函数对应,在频域上则有: ())(,ωωa e a x j b a ψ=ψ- (4)可以看出,当|a|减小时,时域宽度减小,而频域宽度增大,而且()x b a ,ψ的窗口中心向|ω|增大方向移动。
小波去噪理论及MATLAB实现研究_李平

小波去噪理论及M AT L AB实现研究李平李卫国王志国(内蒙古工业大学机械学院,内蒙古呼和浩特010051)摘要:阐述了小波变换去除信号噪声的基本原理和方法,研究利用小波变换技术对信号噪声进行抑制和去除非平稳信号的噪声。
然后利用MATLAB软件编制程序实现了基于小波变换的正弦信号的去噪仿真分析,仿真结果表明小波变换去除噪声具有很强的实用性。
关键词:小波变换;多分辨率分析;小波去噪;MAT LAB中图分类号:O4文献标识码:A文章编号:1672-3198(2008)09-0399-021引言利用振动信号或状态量对设备进行诊断是设备故障诊断中最有效、最常用的方法,过去常用传统的基于快速傅里叶变换(FFT)的频谱分析方法进行振动信号处理,但是傅里叶分析存在着严重的不足,它只适于分析时不变系统的平稳信号,而不适于分析非平稳信号,且傅里叶变换对在检测信号中包含的趋势、突变事件的开始和结束等特征分析时也显得无能为力。
出于对非平稳信号和突变信号的分析的迫切要求,法国地球物理学家M orlet于1984年提出了一种新的线性时频分析方法)))小波分析理论,为机械故障诊断中的非平稳信号分析,弱信号提取,信号滤波等提供了一条有效的途径。
本文我们利用小波分析所具有的时频局部化特性选择合适的小波函数,建立小波去噪模型,并结合当前在信号处理和分析领域应用广泛的MAT LAB7软件,通过计算机进行仿真,完成了小波去噪的MAT LAB实现。
2小波变换理论小波变换(Wavelet T ransform)的基本思想和传统的傅里叶变换是一致的,它也是用一族函数来表示信号或函数,这一族函数称之为小波函数系,但是小波函数系与其它两种方法所用的简谐函数系不同,它是由一基本小波函数平移和伸缩构成的。
它是一种窗口面积恒定,窗口形状可变(时域窗口和频域窗口均可变)的时-频局域化分析方法。
2.1连续小波变换理论设函数7(t)为一平方可积函数,即7(t)I L2(R),其傅里叶变换7(X)满足允许条件:C7=Q]0|^7(w)|2w-1dw<]则称7(t)为一个基小波(或小波母函数),我们称上式为小波函数的容许条件。
小波变换降噪技术及其在Matlab中的实现

小波变换降噪技术及其在Matlab中的实现
赵海英;纪超辉
【期刊名称】《兵工自动化》
【年(卷),期】2006(25)2
【摘要】小波降噪含模极大值、尺度空间滤波、域值滤波三种方法.域值滤波法只对低频部分进一步分解,不考虑高频部分,因而用小波函数进行处理.域值滤波方法的处理过程为:对信号进行小波分解;小波分解高频系数的域值量化;信号重组.对潜艇获得的测量方位信号仿真结果分析表明,该方法可行.
【总页数】2页(P54-55)
【作者】赵海英;纪超辉
【作者单位】海军潜艇学院,研究生队,山东,青岛,266071;海军潜艇学院,研究生队,山东,青岛,266071
【正文语种】中文
【中图分类】TP312
【相关文献】
1.基于小波变换的图像融合及其MATLAB实现 [J], 柏春岚;刘豪
2.基于DFT、DCT和小波变换图像压缩与Matlab实现 [J], 张雅琪;才华
3.小波变换在信号降噪中的应用及MATLAB实现 [J], 朱来东;廉小亲;江远志
4.小波变换在遥感图像压缩中的应用及Matlab实现 [J], 易美华;朱自强;黄国祥;邹声杰
5.一种基于小波变换的数据位迭代纠错算法设计与Matlab实现 [J], 寇马可;钟升;唐磊
因版权原因,仅展示原文概要,查看原文内容请购买。
小波去噪及其在MATLAB中的实现

小波去噪及其在MATLAB中的实现
吕营;朱成实;李铁军
【期刊名称】《装备制造技术》
【年(卷),期】2008(000)011
【摘要】实际采样信号不可避免的会受到噪声的干扰.因此特征提取是故障诊断中的一个重要环节.小波是一种信号的时间一频率分析方法,在去除噪声方面有着显著的效果.文章对此在MATLAB环境下做了详尽的仿真研究,有效的去除了信号中的噪声.
【总页数】3页(P32-33,40)
【作者】吕营;朱成实;李铁军
【作者单位】沈阳化工学院机械工程学院,辽宁沈阳110142;沈阳化工学院机械工程学院,辽宁沈阳110142;沈阳化工学院机械工程学院,辽宁沈阳110142
【正文语种】中文
【中图分类】TN911.73
【相关文献】
1.传感器补偿系统中的小波去噪的应用及DSP的实现 [J], 裴峰;张志杰;王文廉;张雪峰
2.小波去噪及其在LabVIEW中的实现 [J], 郝张红;刘先勇;袁长迎
3.车辆声信号的小波去噪在TMS320F2812中的实现 [J], 胡美艳;杨卫;闫俊杰
4.Matlab在分子动力学中的应用——Matlab实现的波包含时演化 [J], 许继君;叶
叶;闵存高
5.小波去噪理论及MATLAB实现研究 [J], 李平;李卫国;王志国
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
w vl rso en in , r s tni a atm d l x m d—o ig n S F sa aysl te ae thehl d—o i t nl i — vr n, ou s et d s g a ao n i u mai e in dSN (pt l e c v mu ns a il e i
张 翠 芳
( 南京邮电大学通信 与信息工程学院 ,南京 200 ) 10 3
摘
要 :随着小 波理 论 的 日益 完善 ,小波 分 析在 信 号 降 噪领 域 已经得 到越 来越 广 泛 的应 用 。首
先讨论 了小波分析 的基 本特 点 ;其 次通过 理 论 分 析和 M T A A L B仿 真 实验 ,详 细讨 论 了四种 降噪
方 法 :闽值 降噪 法 、平 移 不变量 小 波 阈值 降噪 法、模 极 大值 降噪 法 、基 于各 尺度 下 小波 系数 相
关性 降噪 法。最后 ,对 这几种 算 法的降噪 效果进 行 了比较 。
关键词:小波分析;信号降噪;阈值 ;模极大值 ;M T A 仿真 A LB
S m u a i n a d c m p r s n o v lt d — o sn n M ATLAB i lt n o o a io f wa e e e n ii g i
收稿日期 :20 —0 0 7 6—1 3 基 金项 目:江苏省 自 然科学基金项 目 资助( K 06 5 ; B 202 )南京 邮电大 . 3 学项 目资助( "00 0 N/ 75 ) 2 作者简 介:张翠芳(94 ) 女 , 邮电大学通信与信 息工程学院 17 一 , 南京 讲 师, 要从 事 通 信 信 号处 理 等 方 面 的研 究 与 教 学 主
维普资讯
20 0 8年第3 期
中 图 分 类 号 :N 1 T91 文 献 标 识 码 : A 文章 编 号 : 0 1 9—25 {0 80 —0O —0 0 5220 )3 O4 2
小 波 降噪及 其在 M T A A L B中的仿 真 与 比较
adT l o mu i t n , aj g200 , n ) n e cm nc i s N ni 103 Oaa e ao n
Absr c :W a ee h oy h s b e d l s d i in l d . osn t i h oe ia o ltn s ta t v ltt e r a e n wiey u e n sg a e n ii g wih t t e r t l c mp ee es.At s c
d — osn r o ae e n ii g ae c mp r d. Ke r s: wa ee n lss i a e n iig; t rs o d;mo u u x mu ;MAT AB smu ain y wo d v lta ay i;sg ld — osn n h eh l d l sma i m L i lt o
噪 领域 已经得 到越 来越广 泛 的应用 。主要分 析 四种
征, 但重构信号不具有和原始信号一样的光滑性 。
2 平 移不变量小波阈值 降噪法
在信号急剧变化部分 , 运用 阈值法 降噪会产生 伪 吉布 斯 现象 。为 了 克 服 这 一 现 象 , 以采 用 “ 可 平 移——降噪——平均” 的思想 , 对原始信号进行 即: 定量 的循环平移 , 从而获得一个新的平移信号 ; 然
小 波变 换作 为一 种 新 的多 分 辨分 析 方 法 , 同 可 时进行 时域 和 频域 分 析 , 有 时— —频 局 部 化 和 多 具
阈值处理相对平滑, 但重构信号与原 始信号的逼近
程 度较 差 ; 阈值法 很 好 地保 留信号 边 缘 等局 部 特 硬
分辨特性。随着小波理论 的 日益完善 , 它在信号降
Z HANG ifn Cu —a g
(col f o S h o mmu ia o n fr t nE g e ̄ , a j g U i ri ot oC nc t n a d I o mai n mer i n o N ni nv s y o P s n e tf s
一
小波降噪方法, 并通过 M T A A L B仿真实 闯值 降噪 法
含噪信号经小波分解后 , 信号 的小波 系数 比较 大, 噪声的小波系数 比较小 。选择合适的阈值, 保留 信号的小波系数 , 而让大部分 噪声的小波 系数置为 零。具体步骤为: ①计算含噪信号 的正交小波变换 ; ②对分解得到的小波系数进行非线性 阈值处理 , 阈 值处理有软阈值和硬阈值两种方法 ; ③进行逆小波 变换 。 仿真过程为: 用极小极 大( imx) 采 Mn a 阈值 , i i 应
ni la o )b er aa s dMA L B s u tn i dt l i l ,t f c f em t si o eft t n yt o l i a T A i l i e i n l h eet o e o n s ir i h yn y sn m a o n a .F ay e f s t h h d
后对这个新信号作阈值降噪, 得到降噪后的新信号 ; 最后对 此信号 作相 反 的循 环 平移 , 而得 到 最终 的 从 降噪信 号 ; 变平移 量 , 改 采用 /次循 环平 移 , 7 , 并将 每 次平移 降 噪后 的结 果再进 行平均 。
仿真过程为: ①产生含噪信号 ( ha n 信 将 ev s e yi
i t h s n r u e a e r p r f s ,te te i it d c sw v ltpo e t S c n l ,h h s i u s s fu to s o in ld — o s g r h s o e y. e o dy te t e i d s s e o rmeh d fs a e n i n : s c g i
