最新人教版七年级数学下册试题 第七章 平面直角坐标系周周测2(7.1)
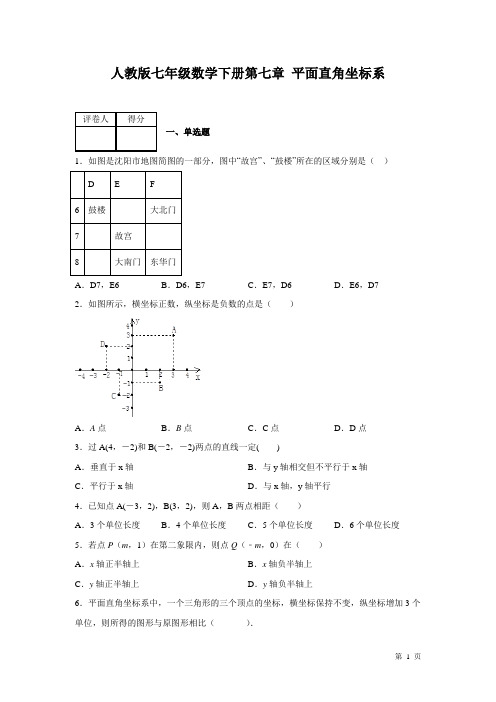
人教版七年下数学第七章平面直角坐标系测试题(最新整理)

考点1:点的坐标与象限的关系各个象限的点的坐标符号特征如下:(特别注意的是,坐标轴上的点不属于任何象限.)1、在平面直角坐标中,点M(-2,3)在()A.第一象限B.第二象限C.第三象限D.第四象限2、在平面直角坐标系中,点P(-2,-2x-1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3、若点P(a,b)在第四象限,则点M(b-a,a-b)在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4、点M(a,-a-1)不可能在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限5、如果b-a<0,且ab<0,那么点(a,b)在( )A.第一象限B.第二象限C.第三象限, D.第四象限.6、若点P(2,k-1)在第一象限,则k的取值范围是__________7、如果点A(x,y)在第三象限,则点B(-x,y-1)在考点2:点在坐标轴上的特点x轴上的点纵坐标为0, y轴上的点横坐标为0. 坐标原点(0,0)1、若点P(x ,y)的坐标满足xy=0,则点P在()A.原点上 B.x轴上 C.y轴上 D.坐标轴2、点P(m+3,m+1)在x轴上,则P点坐标为()A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)3、已知点P(m,2m-1)在y轴上,则P点的坐标是4、点P(a-1,a 2-9)在x轴负半轴上,则P点坐标是 _______考点3:点到直线的距离点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|,1、点M(-6,5)到x轴的距离是_____,到y轴的距离是______.2、已知点P(x,y)在第四象限,且│x│=3,│y│=5,则点P的坐标是()A.(-3,5) B.(5,-3) C.(3,-5) D.(-5,3)x y3、点P(x,y)位于x轴下方,y轴左侧,且=2 ,=4,点P的坐标是()A.(4,2) B.(-2,-4) C.(-4,-2) D.(2,4)4、若点P 到x 轴的距离为3,到y 轴的距离为5,则点P 的坐标是 ____ ____5、若点P 坐标为(2-a ,3a +6),且点P 到两坐标轴距离相等,则点P 的坐标是 _ _考点4:对称点的坐标关于x 轴对称: A (a ,b )关于x 轴对称的点的坐标为(a ,-b )。
人教版七年级数学下册第七章平面直角坐标系测试卷及参考答案

第七章《平面直角坐标系》检测题温馨提示:1.本卷共四道大题,满分100分;2.考试时量:90分钟。
一、选择题。
(每小题3分,共30分)1.在平面直角坐标系中有一个点A,过点A作x轴的垂线,垂足M在x轴上的坐标是7;过点A作y轴的垂线,垂足N在y轴上的坐标是5。
则点A的坐标是()A. (7,0)B. (0,5)C. (7,5)D. (5,7)2.在平面直角坐标系中有一个点B,点B到x轴、的y轴距离分别是6和3,则点B是()A. (6,3)B. (3,6)C. (6,3)或(-6,-3)D. (3,6)或(-3,-6)3.在平面直角坐标系中,点(x-2,2)在y轴上,则x的值为()A. 2B. -2C. 4D. -44.在平面直角坐标系中,点P(-2,12a)所在的象限是()A.第一象限B.第二象限C.第三象限D. 第四象限5.若点P(a,a-2)在第四象限,则a的取值范围是().A.-2<a<0 B.0<a<2 C.a>2 D.a<06.点P(m,1)在第二象限内,则点Q(-m,0)在()A.x轴正半轴上 B.x轴负半轴上C.y轴正半轴上 D.y轴负半轴上7.在平面直角坐标系中,将点A(-2,-3)向右平移3个单位长度得到点B,则点B的坐标是()A.(-5,-3)B.(-2,0)C.(1,-3)D. (1,-6)8.在平面直角坐标系中,将点A(4,-3)作三次平移。
第一次向左平移6个单位长度,得到点A1;第二次向上平移3个单位长度,得到点A2;第三次向右平移2个单位长度,得到点A3.则平移后的最后位置A3点在()A. 第一象限B. x轴的正半轴上C. y轴负半轴上D. 原点9.在矩形ABCD中,A,B,D三个顶点的坐标分别为(0,0),(5,0),(0,3),则C点的坐标是()A.(0,5) B. (5,0)C.(5,3) D.(3,0) 10.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为()A.(-4,0)B.(6,0)C.(-4,0)或(6,0)D.(0,12)或(0,-8)二、填空题。
新七年级下册数学第七章平面直角坐标系检测试卷(含答案)

人教版七年级下册第七课平面直角坐标系单元综合测试卷一.选择题(共10小题)1.在直角坐标系中,点A(-6,5)位于()A.第一象限B.第二象限C.第三象限D.第四象限2.如图,点A(-1,2),则点B的坐标为()A..(-2,2) B..(-2,-3) C..(-3,-2) D.(-2,-2)3.已知点A(-3,0),则A点在()A.x轴的正半轴上B.x轴的负半轴上C.y轴的正半轴上D.y轴的负半轴上4.在平面直角坐标系的第四象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是()A.(3,-4) B.(-4,3) C.(4,-3) D.(-3,4)5.在平面直角坐标系中,将点P(3,2)向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为()A.(1,0) B.(1,2) C.(5,4) D.(5,0)6.如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是()A.(1,0) B.(1,2) C.(2,1) D.(1,1)7.钓鱼岛历来就是中国不可分割的领土,中国对钓鱼岛及其附近海域拥有无可争辩的主权,能够准确表示钓鱼岛位置的是()A.北纬25°40′~26°B .东经123°~124°34′C .福建的正东方向D .东经123°~124°34′,北纬25°40′~26° 8.已知点M(a,1),N(3,1),且MN=2,则a 的值为( ) A .1B .5C .1或5D .不能确定9.如图所示是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),则黑棋②的坐标是( ) A .(0,-2)B .(1,-2)C .(2,-1)D .(1,2)10.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB 连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )A .(60,0)B .(72,0)C .⎝⎛⎭⎫67 15, 95D .⎝⎛⎭⎫79 15, 95二.填空题(共6小题)11.若4排3列用有序数对(4,3)表示,那么表示2排5列的有序数对为 . 12.在平面直角坐标系中,已知点A(2,3),点B 与点A 关于x 轴对称,则点B 坐标是 . 13.若点P(m+5,m-2)在x 轴上,则m= ;若点P(m+5,m-2)在y 轴上,则m= . 14.如图所示是轰炸机机群的一个飞行队形,如果其中两架轰炸机的平面坐标分别表示为A(-2,3)和B(2,1),那么轰炸机C 的平面坐标是 .15.将点P(x,4)向右平移3个单位得到点(5,4),则P点的坐标是.16.把自然数按如图的次序在直角坐标系中,每个点坐标就对应着一个自然数,例如点(0,0)对应的自然数是1,点(1,2)对应的自然数是14,那么点(1,4)对应的自然数是;点(n,n)对应的自然数是三.解答题(共6小题)17.在平面直角坐标系中,点A(2m-7,n-6)在第四象限,到x轴和y轴的距离分别为3,1,试求m+n的值.18.已知点P(2m+4,m-1),请分别根据下列条件,求出点P的坐标.(1)点P在x轴上;(2)点P的纵坐标比横坐标大3;(3)点P在过点A(2,-4)且与y轴平行的直线上.19.小王到公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示,可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),且一格表示一个单位长度.(1)在原图中建立直角坐标系,求出其它各景点的坐标;(2)在(1)的基础上,记原点为0,分别表示出线段AO和线段DO上任意一点的坐标.20.已知A(1,0)、B(4,1)、C(2,4),△ABC经过平移得到△A′B′C′,若A′的坐标为(-5,-2).(1)求B′、C′的坐标;(2)求△A′B′C′的面积.21.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为,B4的坐标为.(2)按以上规律将△OAB进行n次变换得到△OA n B n,则A n的坐标为,B n的坐标为;(3)△OA n B n的面积为.22.(1)在如图直角坐标系中,描出点(9,1)(11,6)(16,8)(11,10)(9,15)(7,10)(2,8)(7,6)(9,1),并将各点用线段顺次连接起来.(2)给图形起一个好听的名字,求所得图形的面积.(3)如果将原图形上各点的横坐标加2、纵坐标减5,猜一猜,图形会发生怎样的变化?(4)如果想让变化后的图形与原图形关于原点对称,原图形各点的坐标应该如何变化?答案:1-10 BDBCD DDCAA11. (2,5)12. (2,-3)13.-514. (-2,-1)15. (2,4)16.60 4n2-2n+117.解:∵点A(2m-7,n-6)在第四象限,到x轴和y轴的距离分别为3,1,∴2m-7=1,n-6=-3,解得m=4,n=3,所以,m+n=4+3=7.18.解:(1)∵点P(2m+4,m-1)在x轴上,∴m-1=0,解得m=1,∴2m+4=2×1+4=6,m-1=0,所以,点P的坐标为(6,0);(2)∵点P(2m+4,m-1)的纵坐标比横坐标大3,∴m-1-(2m+4)=3,解得m=-8,∴人教版七年级下册数学第七章平面直角坐标系达标检测卷一、选择题(每题3分,共30分)1.如果(7,3)表示电影票上“7排3号”,那么3排7号就表示为() A.(7,3) B.(3,7)C.(-7,-3) D.(-3,-7)2.在平面直角坐标系中,点(5,-2)所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限3.将三角形ABC的三个顶点的纵坐标都加上3,横坐标不变,表示将该三角形()A.沿x轴的正方向平移了3个单位长度B.沿x轴的负方向平移了3个单位长度C.沿y轴的正方向平移了3个单位长度D.沿y轴的负方向平移了3个单位长度4.如图,在平面直角坐标系中,三角形ABC的顶点都在方格纸的格点上,如果将三角形ABC先向右平移4个单位长度,再向下平移1个单位长度,得到三角形A1B1C1,那么点A的对应点A1的坐标为()A.(4,3) B.(2,4) C.(3,1) D.(2,5)(第4题)5.已知点P在x轴上,且点P到y轴的距离为1,则点P的坐标为() A.(0,1) B.(1,0)C.(0,1)或(0,-1) D.(1,0)或(-1,0)6.在下列各点中,与点A(-2,-4)的连线平行于y轴的是() A.(2,-4) B.(-2,4) C.(-4,2) D.(4,-2) 7.已知点A(-3,2m-4)在x轴上,点B(n+3,4)在y轴上,则m+n的值是() A.1 B.0 C.-1 D.78.如图,长方形ABCD的长为8,宽为4,分别以两组对边中点的连线为坐标轴建立平面直角坐标系,下列哪个点不在长方形上()A.(4,-2) B.(-2,4) C.(4,2) D.(0,-2) 9.已知点A(1,0),B(0,2),点P在x轴上,且三角形P AB的面积为5,则点P 的坐标是()A.(-4,0) B.(6,0)C.(-4,0)或(6,0) D.(0,12)或(0,-8)10.如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()(第8题) (第10题)A.2 B.3 C.4 D.5二、填空题(每题3分,共24分)11.点P(3,-4)到x轴的距离为________.12.若点P(a,b)在第四象限,则点Q(-a,-b)在第________象限.13.已知点M(x,y)与点N(-2,-3)关于x轴对称,则x+y=________.14.在平面直角坐标系中,点A(1,2a+3)在第一象限,且该点到x轴的距离与到y轴的距离相等,则a=________.15.已知A(a,-3),B(1,b),线段AB∥x轴,且AB=3.若a<1,则a+b=________.16.如图,点A,B的坐标分别为(1,2),(2,0),将三角形AOB沿x轴向右平移,得到三角形CDE,若DB=1,则点C的坐标为__________.(第16题)(第17题)(第18题)17.如图,在平面直角坐标系中,已知长方形ABCD的顶点坐标A(-1,-1),B(3,1.5),D(-2,0.5),则C点坐标为__________.18.如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.三、解答题(19,20,22题每题10分,21题8分,其余每题14分,共66分) 19.如图,已知单位长度为1的方格中有一个三角形ABC.(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标:B(____,____),B′(____,____).20.在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2).(1)线段AB,CD有什么关系?并说明理由.(2)顺次连接A,B,C,D四点组成的图形,你认为它像什么?21.张超设计的广告模板草图如图所示(单位:m),张超想通过电话征求李强的意见.假如你是张超,你如何把这个草图告诉李强呢?(提示:建立平面直角坐标系)22.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.23.如图,四边形ABCO在平面直角坐标系中,且A(1,2),B(5,4),C(6,0),O(0,0).(1)求四边形ABCO的面积;(2)将四边形ABCO四个顶点的横坐标都减去3,同时纵坐标都减去2,画出得到的四边形A′B′C′O′,你能从中得到什么结论?(3)直接写出四边形A′B′C′O′的面积.24.如图,正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD,B1D1都在x轴上,O,O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心),O为平面直角坐标系的原点.OD=3,O1D1=2.(1)如果O1在x轴上平移时,正方形A1B1C1D1也随之平移,其形状、大小没有改变,当中心O1在x轴上平移到两个正方形只有一个公共点时,求此时正方形A1B1C1D1各顶点的坐标;(2)如果O在x轴上平移时,正方形ABCD也随之平移,其形状、大小没有改变,当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时,求此时正方形ABCD各顶点的坐标.第7章达标测试卷参考答案一、1.B 2.D 3.C 4.D 5.D 6.B 7.C8B9.C10.B二、11.412.二13.114.-115.-516.(2,2)17.(2,3)18.(-505,505)点拨:由题图知,A4n的坐标为(-n,-n),A4n-1人教版七年级数学下册第七章平面直角坐标系培优巩固检测一.选择题(共10小题)1.平面直角坐标系内有一点P(-2019,-2019),则点P在()A.第一象限B.第二象限C.第三象限D.第四象限2.若点A(a,b)在第四象限,则点B(0,a)在()A.x轴的正平轴上B.x轴的负半轴上C.y轴的正半轴上D.y轴的负半轴上3.已知点P的坐标为(1,-2),则点P到x轴的距离是()A.1 B.2 C.-1 D.-24.如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是()A.(1,0) B.(1,2) C.(2,1) D.(1,1)5.已知点P位于第二象限,则点P的坐标可能是()A.(-3,0) B.(0,3) C.(-3,2) D.(-3,-3)6.在直角坐标系中,点M(-3,-4)先右移3个单位,再下移2个单位,则点M的坐标变为()A.(-6,-6) B.(0,-6) C.(0,-2,) D.(-6,-2)7.钓鱼岛历来就是中国不可分割的领土,中国对钓鱼岛及其附近海域拥有无可争辩的主权,能够准确表示钓鱼岛位置的是()A.北纬25°40′~26°B.东经123°~124°34′C.福建的正东方向D.东经123°~124°34′,北纬25°40′~26°8.如图,已知在△AOB中A(0,4),B(-2,0),点M从点(4,1)出发向左平移,当点M平移到AB 边上时,平移距离为()A.4.5 B.5 C.5.5 D.5.759.已知点M(a,1),N(3,1),且MN=2,则a的值为()A.1 B.5 C.1或5 D.不能确定10.在平面直角坐标系中,给出三点A,B,C,记其中任意两点的横坐标的差的最大值为a,任意两点的纵坐标差的最大值为h,定义“矩面积”S=ah,例如:给出A(1,2),B(-3,1),C(2,-2),则a=5,h=4,S=ah=20.若D(1,2),E(-2,1).F(0,t)三点的“矩面积”为18,则t=()A.-3或7 B.-4或6 C.-4或7 D.-3或6二.填空题(共6小题)11.若电影票上座位是“4排5号”记作(4,5),则(8,13)对应的座位是12.若P(a-2,a+1)在x轴上,则a的值是.13.若4排3列用有序数对(4,3)表示,那么表示2排5列的有序数对为.14.在平面直角坐标系中,将点A(-1,3)向左平移a个单位后,得到点A′(-3,3),则a的值是15.在平面直角坐标系中,点M在x轴的上方,y轴的左面,且点M到x轴的距离为4,到y轴的距离为7,则点M的坐标是.16.如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),…,根据这个规律,点P2019的坐标为三.解答题(共5小题)17.已知平面直角坐标系中有一点M(2m-3,m+1).(1)点M 到y 轴的距离为l 时,M 的坐标?(2)点N(5,-1)且MN ∥x 轴时,M 的坐标?18.六边形六个顶点的坐标为A(-4,0),B(-2,-2),C(1,-2),D(4,1),E(1,4),F(-2,4).(1)在所给坐标系中画出这个六边形;(2)写出各边具有的平行或垂直关系.(不说理由.)19.如图,三架飞机P 、Q 、R 保持编队飞行,30秒后飞机P 飞到1P 的位置,飞机Q 、R 飞到了新位置1Q 、1R .在直角坐标系中标出1Q 、1,R 并写出坐标.20.多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.知道马场的坐标为(-3,-3)、南门的坐标为(0,0),你能帮她建立平面直角坐标系并求出其他各景点的坐标?21.如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,写出B点的坐标;(2)在(1)的坐标系下将线段BA向右平移3个单位,再向上平移2个单位得线段CD,使得C点与点B对应,点D与点A对应.写出点C,D的坐标,并直接判断线段AB与CD之间关系?答案:1-5 CCBDC6-10 BDCCC11. 8排13号12. -113. (2,5)14.215. (-7,4)16. (505,505)17.解:(1)∵点M(2m-3,m+1),点M到y轴的距离为1,∴|2m-3|=1,解得m=1或m=2,当m=1时,点M的坐标为(-1,2),当m=2时,点M的坐标为(1,3);综上所述,点M的坐标为(-1,2)或(1,3);(2)∵点M(2m-3,m+1),点N(5,-1)且MN∥x轴,∴m+1=-1,解得m=-2,故点M的坐标为(-7,-1).18.解:(1)如图所示:(2)由图可得,AB∥DE,CD⊥DE,BC∥EF,CD⊥AB.19.解:由题意可知:P的坐标(-1,1),Q(-3,1),R(-1,-1)经过30秒后P1的坐标为(4,3),∴Q1的坐标(2,3),R1的坐标为(4,1)20.。
最新人教版七年级下册数学第七章平面直角坐标系测试卷及答案

人教版七年级数学下册第七章平面直角坐标系单元综合测试题及答案一、(本大题共10小题,每题3分,共30分. 在每题所给出的四个选项中,只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对!)1.根据下列表述,能确定位置的是()A.红星电影院2排B.北京市四环路C.北偏东30°D.东经118°,北纬40°2.点P(3,4)向上平移2个单位,向左平移3个单位,得到点P'的坐标是()A.(5,1)B.(5,7)C.(0,2)D.(0,6)3.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,若表示棋子“馬”和“車”的点的坐标分别为(3,2),(-3,0),则表示棋子“炮”的点的坐标为( )A.(1,2)B.(0,2)C.(2,1)D.(2,0)4.若点A(m,n)在第三象限,则点B(|m|,n)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限5.过点A(-3,2)和点B(-3,5)作直线则直线AB()A. 平行于Y轴B. 平行于X轴 C .与Y轴相交 D. 与y轴垂直6.在坐标系中,已知A(2,0),B(−3,−4),C(0,0),则△ABC的面积为()A.4B.6C.8D.37.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为().A.(-2,-5)B.(-2,5)C.(2,-5)D.(2,5)8.P点横坐标是-3,且到x轴的距离为5,则P点的坐标是()A.(5,-3)或(-5,-3)B.(-3,5)或(-3,-5)C.(-3,5)D.(-3,-5)9.在平面直角坐标系内,A、B、C三点的坐标分别是(0,0),(4,0),(3,2),以A、B、C三点为顶点画平面四边形,则第四个顶点不可能在()A.第一象限B.第二象限C.第三象限D.第四象限10.如图,已知三角形ABC在平面直角坐标系中的位置如图所示,将三角形ABC先向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是()A.(5,-2)B.(1,-2)C.(2,-1)D.(2,-2)二、细心填一填:(本大题共有8小题,每题3分,共24分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,积极思考,相信你一定会填对的!) 11.已知点A (0,1)、B (2,0)、C (0,0)、D (-1,0)、E (-3,0),则在轴上的点有 个。
人教版七年级下册数学第七章平面直角坐标系 综合测试试卷含答案

第7章平面直角坐标系测试题一.选择题(共8小题,满分40分)1.已知点M的坐标为(﹣2,1),则点M在直角坐标系中的位置位于()A.第一象限B.第二象限C.第三象限D.第四象限2.若点A(a+1,b﹣2)在第二象限,则点B(a,b+1)在()A.第一象限B.第二象限C.第三象限D.第四象限3.点P(3,﹣4)到x轴的距离是()A.3B.﹣4C.4D.54.已知点Q(a﹣1,a+2)在x轴上,那么Q点的坐标为()A.(﹣3,0)B.(3,0)C.(0,3)D.(0,﹣3)5.在平面直角坐标系内有一点A,若点A到x轴的距离为3,到y轴的距离为1.且点A在第二象限,则点A坐标为()A.(1,﹣3)B.(﹣1,3)C.(﹣3,1)D.(3,﹣1)6.已知点P的坐标为(2x,x+3),点M的坐标为(x﹣1,2x),PM平行于y轴,则P点的坐标()A.(﹣2,2)B.(6,6)C.(2,﹣2)D.(﹣6,﹣6)7.如图,象棋盘上,若“将”位于点(1,﹣1),“象”位于点(3,﹣1).则“炮”位于点()A.(﹣1,1)B.(﹣1,2)C.(﹣2,1)D.(﹣2,2)8.如图,在平面直角坐标系中,一动点从原点O出发,按“向上、向右、向下、向下、向右、向上…”的方向依次不断地移动,每次移动1个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(1,﹣1),…那么点A23的坐标是()A.(7,﹣1)B.(8,1)C.(7,1)D.(8,﹣1)二.填空题(共8小题,满分40分)9.已知点P(a,b),ab>0,a+b>0,则点P在第象限.10.如果点P(m+3,2m﹣4)在y轴上,那么m的值是.11.已知A点(﹣2a+6,a)在一三象限夹角平分线上,则a的值为.12.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是.13.在平面直角坐标系中,点A(m,﹣2),B(3,m﹣1),且直线AB∥x轴,则m的值是.14.如图,△OAB的顶点B的坐标是(5,0),把△OAB沿x轴向右平移得到△CDE,如果C点坐标是(3,0),那么OE的长为.15.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律经过第2021次运动后,动点P的坐标是.16.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的三.解答题(共4小题,满分40分)17.已知平面直角坐标系内的不同两点A(3,a﹣1),B(b+1,﹣2).(1)若点A在第一、三象限的角平分线上,求a的值;(2)若点B在第二、四象限的角平分线上,求b的值;(3)若直线AB平行于x轴,求a,b的值或取值范围;(4)若直线AB平行于y轴,且AB=5,求a,b的值.18.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣4,3),B(﹣2,4),C(﹣1,1),若把△ABC向右平移5个单位长度,再向下平移3个单位长度得到△A'B'C',点A,B,C的对应点分别为A',B',C'.(1)写出A',B',C'的坐标;(2)在图中画出平移后的△A'B'C';(3)求△A'B'C'的面积.19.△ABC与△A'B'C'在平面直角坐标系中的位置如图.20.如图,在平面直角坐标系中,点A(﹣3b,0)为x轴负半轴上一点,点B(0,4b)为y轴正半轴上一点,其中b满足方程:3(b+1)=6.(1)求点A、B的坐标;(2)点C为y轴负半轴上一点,且△ABC的面积为12,求点C的坐标;(3)在x轴上是否存在点P,使得△PBC的面积等于△ABC的面积的一半?若存在,求出相应的点P的坐标;若不存在,请说明理由.参考答案1.B.2.B.3.C.4.A.5.B.6.A.7.B.8.D.二.填空题(共8小题,满分40分)9.一.10.﹣3.11.:2.12.(1,8).13.﹣1.14.8.15.(2021,1).16.(﹣506,﹣506).三.解答题(共4小题,满分40分)17.解:(1)∵点A在第一、三象限的角平分线上,∴3=a﹣1,解得a=4;(2)∵点B在第二、四象限的角平分线上,∴b+1=2,解得b=1;(3)∵直线AB平行于x轴,∴a﹣1=﹣2,b+1≠3解得a=﹣1,b≠2;(4)∵直线AB平行于y轴,∴b+1=3,解得b=2,∵AB=5,∴a﹣1=3或a﹣1=﹣7,解得a=4或a=﹣6.18.解:(1)由平移可得,A'(1,0),B'(3,1),C'(4,﹣2).(2)平移后的△A'B'C'如图所示.,∴△A'B'C'的面积为3.5.19.解:(1)如图所示:A'(﹣3,1),B′(﹣2,﹣2),C′(﹣1,﹣1);故答案为:(﹣3,1),(﹣2,﹣2),(﹣1,﹣1);(2)△ABC先向左平移4个单位,再向下平移2个单位得到△A'B'C';故答案为:先向左平移4个单位,再向下平移2个单位;(3)若点P(a,b)是△ABC内部一点,则平移后△A'B'C'内的对应点P'的坐标为:(a ﹣4,b﹣2).故答案为:(a﹣4,b﹣2);(4)△ABC的面积为:S△ABC=6﹣×2×2﹣×1×3﹣×1×1=2.20.解:(1)解方程:3(b+1)=6,得:b=1,∴A(﹣3,0),B(0,4),(2)∵A(﹣3,0),∴OA=3,∵△ABC的面积为12,,∴BC=8,∵B(0,4),∴OB=4,∴OC=4,∴C(0,﹣4);(3)存在,∵△PBC的面积等于△ABC的面积的一半,C(0,﹣4),B(0,4),∴BC上的高OP为,∴点P的坐标(,0)或(﹣,0).。
人教版七年级下册数学试题第七章 平面直角坐标系周周测1(7.1-7.2)测试卷

第七章平面直角坐标系周周测1一选择题1.若P(-2,y)与Q(-2,-3)是不同的两点,且到x轴的距离相等,则y的值为()A.2B.3C.4D.52.若点P(a,b)在第四象限内,则a,b的取值范围是()A.a﹥0,b﹤0B.a﹥0,b>0C.a﹤0,b﹥0D.a﹤0,b﹤03.点P(m+3,m+1)在x轴上,则点P的坐标为()A.(2,0)B.(0,-2)C.(4,0)D.(0,-4)4.过点C(-1,-1)和点D(-1,5)作直线,则直线CD ()A.平行于y轴B.平行于x轴C.与y轴相交D.无法确定5.在平面直角坐标系中,点P(-2,5)在()A.第一象限B.第二象限C.第三象限D.第四象限6.若点A(2,m)在x轴上,则点B(m-1,m+1)在()A.第一象限B.第二象限C.第三象限D.第四象限二解答题7.已知点P(x,y)在第四象限,它到x轴的距离为2,到y轴的距离为3,求P点的坐标.8.若点P’(m,-1)与点P(2,n)在x轴两侧,且到x轴的距离相等,求m+n的值.9.(1)下图是某市旅游景点示意图,请建立适当的坐标系,写出各景点的坐标;(2)葛亮同学利用暑假参观了花峪村果树种植基地(如图).他从苹果园出发,沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(6,-3),(6,0),(6,4)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点,看看能得到什么图形?10.如图为某废墟示意图,由于雨水冲蚀,残缺不全,依稀可见钟楼坐标为A(5,-2),街口坐标为B(5,2),•资料记载阿明先生的祖居的坐标为(2,1),你能帮助阿明先生找到他家的老屋吗?第七章平面直角坐标系周周测1参考答案与解析一、选择题1.B2.A3.A4.A5.B6.B二、解答题7.解:∵点P(x,y)在第四象限,∴x>0,y<0.∵点P到x轴的距离为2,到y轴的距离为3,∴|y|=2,|x|=3,∴x=3,y=-2,则点P的坐标为(2,-3).8.解:∵点P’(m,-1)与点P(2,n)在x轴两侧,且到x轴的距离相等,∴m=2,n=1,则m+n=2+1=3.9.解:(1)答案不唯一.若以金斗山为原点建立平面直角坐标系,如图所示,则各景点的坐标分别为金斗山(0,0),市政府(0,-1),师兄墓(0,2),望驾山(4,4),汶河发源地(-2,5),青云山(3,-2),徂徕山(-6,-3),林放故居(-3,-5).(2)葛亮同学从苹果园出发,依次经过葡萄园,杏林,桃林,梅林,山楂林,枣林,梨园,最后回到苹果园,如图,连接他经过的地方得到了一个不规则多边形.10.解:阿明先生家的老屋位置如图所示.。
(完整)七年级数学下册第七章《平面直角坐标系》测试题

七年级数学下册第七章《平面直角坐标系》测试题(新人教版)班级姓名(时间 120 分满分 120 分)一、选择题:(每题 2.5 分,共 50 分)、若 a 5, b 4 ,且点 M ( a , b )在第二象限,则点 M 的坐标是()1A 、(5,4)B 、(- 5,4)C 、(- 5,- 4)D 、(5,- 4)2、过 A ( ,- )和 B (- ,- )两点的直线必定( )4 2 22A 、垂直于 x 轴B 、与 y 轴订交但不平于x 轴 C 、平行于 x 轴 D 、与 x 轴、 y 轴平行3、如右图所示的象棋盘上,若 帅位于点( 1,- 2)上,相位于点( 3,- 2)上,○ ○则炮○位于点()A 、(- 1,1)B 、(- 1, 2)C 、(- 2,1)D 、(- 2,2)炮帅 相4、一个长方形在平面直角坐标系中三个极点的坐标为(-图 31,- 1)、(- 1,2)、(3,- 1),则第四个极点的坐标为()A 、(2,2) B、( 3,2) C 、(3,3) D 、(2,3)5、若 x 轴上的点 P 到 y 轴的距离为 3,则点 P 的坐标为()A 、(3,0)B 、(3,0)或(– 3,0)C 、(0,3)D 、(0,3)或( 0,– 3)6、点 M (x ,y )知足 x=0那么点 M 的可能地点是()yA .x 轴上全部的点B .除掉原点后 x 轴上的点的全体C .y 轴上全部的点D .除掉原点后 y 轴上的点的全体7、假如两个点到 x 轴的距离相等,那么这两个点的坐标一定知足( )A 横坐标相等B 纵坐标相等C 横坐标的绝对值相等 D纵坐标的绝对值相等8、线段 CD 是由线段 AB 平移获得的 . 点 A (– 1,4)的对应点为 C ( 4, 7),则点 B (– 4 ,– 1 )的对应点 D 的坐标为( )A. (2,9)B. (5, 3)C. (1,2)D. (– 9 ,– 4 ) 9、已知三角形的三个极点坐标分别是(-1,4),(1,1),(- 4,- 1),现将这三个点先向右平移 2 个单位长度,再向上平移 3 个单位长度,则平移后三个极点的坐标是( )A 、(-2,2),(3,4),( 1,7)B 、(- 2,2),(4,3),(1,7)C 、(2,2),(3,4),(1,7) D、(2,- 2),(3,3),(1,7)10、在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形对比( )A 、向右平移了 3 个单位B 、向左平移了 3 个单位C 、向上平移了 3 个单位 D、向下平移了 3 个单位11、在平面直角坐标系中,点1,m 2 1 必定在()A .第一象限B .第二象限C .第三象限D .第四象限、若点 P m, n 在第二象限,则点 Q m, n 在( ) 12A .第一象限B .第二象限C .第三象限D .第四象限13、已知两圆的圆心都在 x 轴上, A 、B 为两圆的交点,若点 A 的坐标为 1, 1 ,则点 B 坐标为()A . 1,1B . 1,1C . 1,1D .没法求出14、已知点 A 2, 2 ,假如点 A 对于 x 轴的对称点是 B ,点 B 对于原点的对称点是 C ,那么 C点的坐标是()A . 2,2B .2,2C . 1,1D .2, 2、在平面直角坐标系中,以点 P 1,2 为圆心, 1 为半径的圆必与 x 轴有 个公共点15 ()A .0B .1C .2D .316、已知点 A 3a,2b 在 x 轴上方, y 轴的左边,则点 A 到 x 轴. y 轴的距离分别为()A . 3a, 2bB . 3a,2bC . 2b, 3aD . 2b,3a17、若点 P ( a , b )到 x 轴的距离是 2 ,到 y 轴的距离是 3 ,则这样的点 P 有 ()A.1个 B.2个 C.3个 D.4个18、点( x , x 1 )不行能在 ( )A .第一象限B .第二象限C .第三象限D .第四象限、假如点 P ( m , 3 )与点 P 1( 5 , n )对于 y 轴对称,则 m , n 的值分别为 ( )19A . m5,n3B . m 5, n 3C . m 5, n 3D . m 3, n 520、一艘轮船从港口 O 出发,以 15 海里 / 时的速度沿北偏东 60°的方向航行 4 小时后抵达 A 处,此时观察到其正西方向 50 海里处有一座小岛 B .若以港口 O 为坐标原点,正东方向为 x 轴的正方向,正北方向为y 轴的正方向, 1 海里为 1 个单位长度成立平面直角坐标系(如图),则小岛 B 所在地点的坐标是() AA . (30 3 50,30) B. (30,30 3 50)C . (30 3,30)D . (30,30 3)yAO x第 20题图二、填空题:(每空 2 分,共 54 分)1、按以下条件确立点 P ( x ,y )的地点:⑴ x =0, y <0,则点 P 在_____;⑵ xy =0, 则点 P 必定在____;⑶| x |+| y |=0,则点 P 在_____;⑷若 xy >0,则点 P在____.2、己知点 P (x ,y )位于第二象限,而且知足 y ≤x +4, x 、y 为整数,写出一个切合上述 条件的点 P 的坐标___。
最新人教版七年级数学下册第七章 平面直角坐标系 7.1.2 平面直角坐标系 基础训练题(含答案)

最新人教版七年级数学下册第七章平面直角坐标系基础训练题(含答案)7.1.2 平面直角坐标系1.下列说法错误的是()A.平面内两条互相垂直的数轴就构成了平面直角坐标系B.平面直角坐标系中两条坐标轴是相互垂直的C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限D.坐标轴上的点不属于任何象限2.在平面直角坐标系中,点(1,5)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3.如图,下列各点在阴影区域内的是()A.(3,2) B.(-3,2) C.(3,-2) D.(-3,-2)4.如图,点A(-2,1)到y轴的距离为()A.-2 B.1 C.2 D.55.点P在第三象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为()A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)6.已知点A(1,2),AC⊥x轴于C,则点C的坐标为()A.(2,0) B.(1,0) C.(0,2) D.(0,1)7.在平面直角坐标系中,点(0,-10)在()A.x轴的正半轴上B.x轴的负半轴上C.y轴的正半轴上D.y轴的负半轴上8.写出一个平面直角坐标系中第三象限内的点的坐标:_______________________.9.点P(4,-3)到x轴的距离是________个单位长度,到y轴的距离是________个单位长度.10.平面直角坐标系内有一点P(x,y),若点P在横轴上,则____________;若点P在纵轴上,则____________;若P为坐标原点,则____________。
11.写出图中A,B,C,D,E,F,O各点的坐标.12.在平面直角坐标系中,点P(2,x2)在()A.第一象限B.第四象限C.第一或者第四象限D.以上说法都不对13.如果点P(m+3,m+1)在直角坐标系的x轴上,那么P点坐标为()A.(0,2) B.(2,0) C.(4,0) D.(0,-4)14.已知坐标平面内点M(a,b)在第三象限,那么点N(b,-a)在()A.第一象限B.第二象限C.第三象限D.第四象限15.点P(a,b)满足ab>0,则点P在第____________象限;点P(a,b)满足ab<0,则点P在第____________象限;点P(a,b)满足ab=0,则点P在____________.16.已知点M到x轴的距离为3,到y轴的距离为4.(1)若M点位于第一象限,则其坐标为____________;(2)若M点位于x轴的上方,则其坐标为________________________;(3)若M点位于y轴的右侧,则其坐标为________________________.17.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是____________.18.请写出点A,B,C,D的坐标.并指出它们的横坐标和纵坐标.参考答案:1.A2.A3.A4.C5.B6.B7.D8.答案不唯一,如:(-3,-6)9.3 410.y=0 x=0 x=y=011.解:观察图,得A(2,3),B(3,2),C(-2,1),D(-1,-2),E(2.5,0),F(0,-2),O(0,0).12.D13.B14.B15.一、三二、四坐标轴上16.(4,3) (4,3)或(-4,3) (4,3)或(4,-3)17.(-3,5)18.解:A(3,2),横坐标是3,纵坐标是2;B(-3,4),横坐标是-3,纵坐标是4;C(-4,-3),横坐标是-4,纵坐标是-3;D(3,-3),横坐标是3,纵坐标是-3.。
人教版数学七年级下册 第七章《平面直角坐标系》全章测试题(含答案)

第七章《平面直角坐标系》检测卷题号一二三总分21 22 23 24 25 26 27 28分数一.选择题(共12小题)1、点M在ⅹ轴下方,y轴右侧,它到X轴、Y轴的距离分别为8和5,则点M的坐标为()A(8,5) B(5,-8) C(-5,8) D(-8,5)2、过点A(-3,2)和点B(-3,5)作直线则直线AB()A 平行于Y轴B 平行于X轴C 与Y轴相交D 与y轴垂直3、若点P(a,b)的坐标满足关系式ab>0,则点P在( )。
(A)第一象限(B)第三象限(C)第一、三象限(D)第二、四象限4、已知A(-4,2),B(1,2),则A,B两点的距离是()。
A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度5.小米同学乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(小圆半径是1km).若小艇C相对于游船的位置可表示为(270°,-1.5),则描述图中另外两个小艇A,B的位置,正确的是()A.小艇A(60°,3),小艇B(-30°,2)B.小艇A(60°,3),小艇B(60°,2)C.小艇A(60°,3),小艇B(150°,2)D.小艇A(60°,3),小艇B(-60°,2)6.在平面直角坐标系中,点(-1,2m+1)一定在( )A.第一象限B.第二象限C.第三象限D.第四象限7.已知坐标平面内,线段AB∥x轴,点A(﹣2,4),AB=1,则B点坐标为()A.(﹣1,4)B.(﹣3,4)C.(﹣1,4)或(﹣3,4)D.(﹣2,3)或(﹣2,5)8.已知过A(﹣1,a),B(2,﹣2)两点的直线平行于x轴,则a的值为()A.﹣1 B.1 C.2 D.﹣29.如图,下列说法正确的是()A.A与D的横坐标相同B.C与D的横坐标相同C.B与C的纵坐标相同D.B与D的纵坐标相同10.已知点A的坐标为(1,3),点B的坐标为(3,1),将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1),则点B的对应点的坐标为()A.(6,3)B.(0,3)C.(6,﹣1)D.(0,﹣1)11.将点(﹣3,2)先向右平移3个单位,再向下平移4个单位后与N点重合,则点N坐标为()A.(﹣3,﹣2)B.(0,﹣2)C.(0,2)D.(﹣6,﹣2)12.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2,再向正东方向走6m到达点A3,再向正南方向走8m到达点A4,再向正西方向走10m到达点A5,按如此规律走下去,当机器人走到点A9时,点A9在第()象限A.一B.二C.三D.四二.填空题(共4小题)13.如果将电影票上“8排5号”简记为(8,5),那么“11排10号”可表示为;(5,6)表示的含义是.14.边长为1的正方形网格在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为A(3,3),B(5,0),若A1的坐标为(﹣5,﹣3),则B1的坐标为.15.点M(3,4)与x轴的距离是个单位长度,与原点的距离是个单位长度.16.已知,点A(a﹣1,b+2),B(3,4),C(﹣1,﹣2)在同一个坐标平面内,且AB所在的直线平行于x轴,AC所在的直线平行于y轴,则a+b=.三.解答题(共4小题)17.在平面直角坐标系中,有点A(a+1,2),B(﹣a﹣5,2a+1).(1)若线段AB∥y轴,求点A、B的坐标;(2)当点B在第二、四象限的角平分线上时,求A点坐标.18.已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3),请回答如下问题:(1)在平面直角坐标系内描出点A、B、C;(2)在坐标系内存在点P,使以A、B、C、P四个点组成的四边形中,相对的两边互相平行且相等,则点P的坐标为.(直接写出答案)(3)平移线段BC,使得C点的对应点刚好与坐标原点重合,求出线段BC在平移的过程中扫过的面积.19.已知平面直角坐标系中有一点M(2m﹣3,m+1).(1)若点M到y轴的距离为2时,求点M的坐标;(2)点N(5,﹣1)且MN∥x轴时,求点M的坐标.20.对于实数a,b定义两种新运算“※”和“*”:a※b=a+kb,a*b=ka+b(其中k 为常数,且k≠0),若对于平面直角坐标系xOy中的点P(a,b),有点P′的坐标(a※b,a*b)与之对应,则称点P的“k衍生点”为点P′.例如:P(1,3)的“2衍生点”为P′(1+2×3,2×1+3),即P′(7,5).(1)点P(﹣1,5)的“3衍生点”的坐标为;(2)若点P的“5衍生点”P的坐标为(9,﹣3),求点P的坐标;(3)若点P的“k衍生点”为点P′,且直线PP′平行于y轴,线段PP′的长度为线段OP长度的3倍,求k的值.参考答案与试题解析一.选择题(共12小题)1.【解答】解:将点(2,3)向下平移1个单位长度,所得到的点的坐标是(2,2),故选:B.2.【解答】解:A、东经37°,北纬21°物体的位置明确,故本选项错误;B、电影院某放映厅7排3号物体的位置明确,故本选项错误;C、芝罘区南大街无法确定物体的具体位置,故本选项正确;D、烟台山灯塔北偏东60°方向,距离灯塔3千米物体的位置明确,故本选项错误;故选:C.3.【解答】解:如图所示:点C的坐标为(5,3),故选:D.4.【解答】解:∵A(﹣1,5)向右平移2个单位,向下平移1个单位得到A′(1,4),∴C(0,1)右平移2个单位,向下平移1个单位得到C′(2,0),故选:C.5.【解答】解:根据点A(m,n),且有mn≤0,所以m≥0,n≤0或m≤0,n≥0,所以点A一定不在第一象限,故选:A.6.【解答】解:在坐标系中,点(﹣3,2)先向右平移5个单位得(2,2),再把(2,2)向下平移3个单位后的坐标为(2,﹣1),则A点的坐标为(2,﹣1).故选:C.7.【解答】解:∵坐标平面内,线段AB∥x轴,∴点B与点A的纵坐标相等,∵点A(﹣2,4),AB=1,∴B点坐标为(﹣1,4)或(﹣3,4).故选:C.8.【解答】解:∵过A(﹣1,a),B(2,﹣2)两点的直线平行于x轴,∴a=﹣2,故选:D.9.【解答】解:根据题意,点Q的横坐标为:﹣2﹣3=﹣5;纵坐标为﹣3+2=﹣1;即点Q的坐标是(﹣5,﹣1).故选:C.10.【解答】解:∵A(1,3)的对应点的坐标为(﹣2,1),∴平移规律为横坐标减3,纵坐标减2,∴点B(3,1)的对应点的坐标为(0,﹣1).故选:D.11.【解答】解:如图,点A(﹣3,2)先向右平移3个单位得到B,再向下平移4个单位后与N点重合,观察图象可知N(0,﹣2),故选:B.12.【解答】解:由题可知,第一象限的规律为:3,7,11,15,19,23,27,…,3+4n;第二象限的规律为:2,6,10,14,18,22,26,…,2+4n;第三象限的规律为:1,5,9,13,17,21,25,…,1+4n;第四象限的规律为:4,8,12,16,20,24,…,4n;所以点A9符合第三象限的规律.故选:C.二.填空题(共4小题)13.【解答】解:∵8排5号简记为(8,5),∴11排10号表示为(11,10),(5,6)表示的含义是5排6号.故答案为:(11,10);5排6号.14.【解答】解:由点A到A1可知:各对应点之间的关系是横坐标加﹣8,纵坐标加﹣7,那点B到B1的移动规律也如此,则B1的横坐标为5+(﹣8)=﹣3;纵坐标为0+(﹣7)=﹣7;∴B1的坐标为(﹣3,﹣7).故答案为:(﹣3,﹣7).15.【解答】解:点M(3,4)与x轴的距离是4个单位长度,与原点的距离是5个单位长度,故答案为:4;516.【解答】解:由点A(a﹣1,b+2),B(3,4),C(﹣1,﹣2)在同一个坐标平面内,且AB所在的直线平行于x轴,AC所在的直线平行于y轴,可得:4=b+2,﹣1=a﹣1,解得:b=2,a=0,所以a+b=2,故答案为:2三.解答题(共4小题)17.【解答】解:(1)∵线段AB∥y轴,∴a+1=﹣a﹣5,解得:a=﹣3,∴点A(﹣2,2),B(﹣2,﹣5);(2)∵点B(﹣a﹣5,2a+1)在第二、四象限的角平分线上,∴(﹣a﹣5)+(2a+1)=0.解得a=4.∴点A的坐标为(5,2).18.【解答】解:(1)点A,B,C如图所示.(2)满足条件的点P的坐标为(8,3)或(﹣3,3)或(﹣1,﹣1).故答案为(8,3)或(﹣3,3)或(﹣1,﹣1).=2×(3×3﹣×1×3﹣×1×2(3)线段BC在平移的过程中扫过的面积=2S△OBC﹣×2×3)=7.19.【解答】解:(1)∵点M(2m﹣3,m+1),点M到y轴的距离为2,∴|2m﹣3|=2,解得m=2.5或m=0.5,当m=2.5时,点M的坐标为(2,3.5),当m=0.5时,点M的坐标为(﹣2,1.5);综上所述,点M的坐标为(2,3.5)或(﹣2,1.5);(2)∵点M(2m﹣3,m+1),点N(5,﹣1)且MN∥x轴,∴m+1=﹣1,解得m=﹣2,故点M的坐标为(﹣7,﹣1).20.【解答】解:(1)点P(﹣1,5)的“3衍生点”P′的坐标为(﹣1+3X5,﹣1X3+5),即(14,2),故答案为:(14,2);(2)设P(x,y)依题意,得方程组.解得.∴点P(﹣1,2);(3)设P(a,b),则P′的坐标为(a+kb,ka+b).∵PP′平行于y轴∴a=a+kb,即kb=0,又∵k≠0,∴b=0.∴点P的坐标为(a,0),点P'的坐标为(a,ka),∴线段PP′的长度为|ka|.∴线段OP的长为|a|.根据题意,有|PP′|=3|OP|,∴|ka|=3|a|.∴k=±3.。
新人教版七年级下册数学第七章平面直角坐标系检测试卷(含答案)(1)

人教七年级上册数学第7 章《平面直角坐标系》练习题 (A B 卷)人教版七年级数学下册第七章平面直角坐标系单元测试题班级姓名得分一、选择题( 4 分× 6=24 分)1.点 A (3,4 )所在象限为()A 、 第一象限B 、 第二象限C 、 第三象限D 、 第四象限2.点 B (3,0 )在()上A 、 在 x 轴的正半轴上B 、 在 x 轴的负半轴上C 、 在 y 轴的正半轴上D 、 在 y 轴的负半轴上3.点 C 在 x 轴上方, y 轴左边,距离x 轴 2 个单位长度,距离y 轴 3 个单位长度,则点C的坐标为()A 、( 2,3)B 、 (2, 3)C 、 (3,2) D 、(3, 2)4. 若点 P ( x,y )的坐标知足 xy =0,则点 P 的地点是()A 、 在 x 轴上B 、 在 y 轴上C 、 是坐标原点D 、在 x 轴上或在 y 轴上5.某同学的座位号为(2,4 ),那么该同学的所座地点是()A 、第 2排第 4列B 、第4 排第 2列C 、 第 2列第 4排D 、不好确立6.线段 AB 两头点坐标分别为 A ( 1,4 ), B ( 4,1 ),现将它向左平移 4 个单位长度,得 到线段 A 1B 1 ,则 A 1、 B 1 的坐标分别为()A 、A 1(5,0 ), B 1( 8, 3 )B 、 A 1( 3,7 ), B 1( 0,5)C 、 A 1( 5,4 ) B 1( -8, 1)D 、A 1( 3,4 )B 1( 0,1)二、填空题( 1 分× 50=50 分 )7.分别写出数轴上点的坐标:A E CB D -5 -4-3 -2 -10 12 345A ( )B ( )C ( )D ( )E ( )8.在数轴上分别画出坐标以下的点:A( 1) B(2) C (0.5) D( 0) E(2.5) F ( 6)-5-4-3 -2 -10123 4 59. 点 A(3, 4) 在第象限,点 B( 2, 3) 在第象限点 C( 3,4) 在第象限,点 D (2,3) 在第象限点 E( 2,0) 在第象限,点 F (0,3) 在第象限10.在平面直角坐标系上,原点O 的坐标是(), x 轴上的点的坐标的特色是 坐标为 0;y 轴上的点的坐标的特色是 坐标为 0。
最新人教版七年级下册数学第七章平面直角坐标系检测试卷及答案(2)

人教版七年级下册数学第七章平面直角坐标系达标检测卷一、选择题(每题3分,共30分)1.如果(7,3)表示电影票上“7排3号”,那么3排7号就表示为() A.(7,3) B.(3,7)C.(-7,-3) D.(-3,-7)2.在平面直角坐标系中,点(5,-2)所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限3.将三角形ABC的三个顶点的纵坐标都加上3,横坐标不变,表示将该三角形()A.沿x轴的正方向平移了3个单位长度B.沿x轴的负方向平移了3个单位长度C.沿y轴的正方向平移了3个单位长度D.沿y轴的负方向平移了3个单位长度4.如图,在平面直角坐标系中,三角形ABC的顶点都在方格纸的格点上,如果将三角形ABC先向右平移4个单位长度,再向下平移1个单位长度,得到三角形A1B1C1,那么点A的对应点A1的坐标为()A.(4,3) B.(2,4) C.(3,1) D.(2,5)(第4题)5.已知点P在x轴上,且点P到y轴的距离为1,则点P的坐标为() A.(0,1) B.(1,0)C.(0,1)或(0,-1) D.(1,0)或(-1,0)6.在下列各点中,与点A(-2,-4)的连线平行于y轴的是() A.(2,-4) B.(-2,4) C.(-4,2) D.(4,-2) 7.已知点A(-3,2m-4)在x轴上,点B(n+3,4)在y轴上,则m+n的值是() A.1 B.0 C.-1 D.78.如图,长方形ABCD的长为8,宽为4,分别以两组对边中点的连线为坐标轴建立平面直角坐标系,下列哪个点不在长方形上()A.(4,-2) B.(-2,4) C.(4,2) D.(0,-2) 9.已知点A(1,0),B(0,2),点P在x轴上,且三角形P AB的面积为5,则点P 的坐标是()A.(-4,0) B.(6,0)C.(-4,0)或(6,0) D.(0,12)或(0,-8)10.如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()(第8题) (第10题)A.2 B.3 C.4 D.5二、填空题(每题3分,共24分)11.点P(3,-4)到x轴的距离为________.12.若点P(a,b)在第四象限,则点Q(-a,-b)在第________象限.13.已知点M(x,y)与点N(-2,-3)关于x轴对称,则x+y=________.14.在平面直角坐标系中,点A(1,2a+3)在第一象限,且该点到x轴的距离与到y轴的距离相等,则a=________.15.已知A(a,-3),B(1,b),线段AB∥x轴,且AB=3.若a<1,则a+b=________.16.如图,点A,B的坐标分别为(1,2),(2,0),将三角形AOB沿x轴向右平移,得到三角形CDE,若DB=1,则点C的坐标为__________.(第16题)(第17题)(第18题)17.如图,在平面直角坐标系中,已知长方形ABCD的顶点坐标A(-1,-1),B(3,1.5),D(-2,0.5),则C点坐标为__________.18.如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.三、解答题(19,20,22题每题10分,21题8分,其余每题14分,共66分) 19.如图,已知单位长度为1的方格中有一个三角形ABC.(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标:B(____,____),B′(____,____).20.在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2).(1)线段AB,CD有什么关系?并说明理由.(2)顺次连接A,B,C,D四点组成的图形,你认为它像什么?21.张超设计的广告模板草图如图所示(单位:m),张超想通过电话征求李强的意见.假如你是张超,你如何把这个草图告诉李强呢?(提示:建立平面直角坐标系)22.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.23.如图,四边形ABCO在平面直角坐标系中,且A(1,2),B(5,4),C(6,0),O(0,0).(1)求四边形ABCO的面积;(2)将四边形ABCO四个顶点的横坐标都减去3,同时纵坐标都减去2,画出得到的四边形A′B′C′O′,你能从中得到什么结论?(3)直接写出四边形A′B′C′O′的面积.24.如图,正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD,B1D1都在x轴上,O,O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心),O为平面直角坐标系的原点.OD=3,O1D1=2.(1)如果O1在x轴上平移时,正方形A1B1C1D1也随之平移,其形状、大小没有改变,当中心O1在x轴上平移到两个正方形只有一个公共点时,求此时正方形A1B1C1D1各顶点的坐标;(2)如果O在x轴上平移时,正方形ABCD也随之平移,其形状、大小没有改变,当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时,求此时正方形ABCD各顶点的坐标.第7章达标测试卷参考答案一、1.B 2.D 3.C 4.D 5.D 6.B 7.C8B9.C10.B二、11.412.二13.114.-115.-516.(2,2)17.(2,3)18.(-505,505)点拨:由题图知,A4n的坐标为(-n,-n),A4n-1 人教版七年级下册数学第七章平面直角坐标系单元达标练习题一、选择题(每小题只有一个正确答案)1.如果7年2班记作,那么表示()A. 7年4班B. 4年7班C. 4年8班D. 8年4班2.在下列所给出的坐标中,在第二象限的是()A. (2,3)B. (2,-3)C. (-2,-3)D. (-2,3)3.在平面直角坐标系中,点M(-1,3),先向右平移2个单位,再向下平移4个单位,得到的点的坐标为()A. (-3,-1)B. (-3,7)C. (1,-1)D. (1,7)4.如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到CD,若点C的坐标为(6,3),则点D的坐标为()A. (2,6)B. (2,5)C. (6,2)D. (3,6)5.如图所示为某战役潜伏敌人防御工亭坐标地图的碎片,一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,4),由原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大概()A. A处B. B处C. C处D. D处6.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(﹣1,﹣1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,﹣1),则点B′的坐标为()A. (4,2)B. (5,2)C. (6,2)D. (5,3)7.观察下列数对:(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), (1,4), (2,3), (3,2), (4,1), (1,5), (2,4)...那么第32个数对是()A. (4,4)B. (4,5)C. (4,6)D. (5,4)8.若点P(x,y)的坐标满足xy=0(x≠y),则点P必在()A. 原点上B. x轴上C. y轴上D. x轴上或y轴上(除原点)9.若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是()A. (-4,3)B. (4,-3)C. (-3,4)D. (3,-4)10.P点横坐标是-3,且到x轴的距离为5,则P点的坐标是( )A. (-3,5)或(-3,-5)B. (5,-3)或(-5,-3)C. (-3,5)D. (-3,-5)11.若点P(a﹣2,a)在第二象限,则a的取值范围是()A. 0<a<2B. ﹣2<a<0C. a>2D. a<012.在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为()A. (1,2)B. (2,3)C. (3,2)D. (2,1)二、填空题13.点P(m−1,m+3)在平面直角坐标系的y轴上,则P点坐标为________.14.如果点P在第二象限内,点P到轴的距离是4,到轴的距离是3,那么点P的坐标为________.15.如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是,嘴唇C点的坐标为、,则此“QQ”笑脸右眼B的坐标________.16.如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2018的坐标为________.17.三角形ABC的三个顶点A(1,2),B(-1,-2),C(-2,3),将其平移到点A′(-1,-2)处,使A与A′重合,则B、C两点的坐标分别为________,________.18.如图,在直角坐标系中,右边的蝴蝶是由左边的蝴蝶飞过去以后得到的,左图案中左右翅尖的坐标分别是(-4,2)、(-`2,2),右图案中左翅尖的坐标是(3,4),则右图案中右翅尖的坐标是________.19.如下图,五间亭的位置是________,飞虹桥的位置是________,下棋亭的位置是________,碑亭的位置是________.20.如图所示,是象棋棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4,-1)上,则“炮”所在的点的坐标是________21.已知线段MN平行于x轴,且MN的长度为5,若M的坐标为(2,-2),那么点N的坐标是________;22.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点为整点,若整点P(,)在第四象限,则m的值为________;三、解答题23.如下图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?24.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?25.王林同学利用暑假参观了幸福村果树种植基地如图,他出发沿的路线进行了参观,请你按他参观的顺序写出他路上经过的地方,并用线段依次连接他经过的地点.26.如图,已知火车站的坐标为,文化宫的坐标为.(1)请你根据题目条件,画出平面直角坐标系;(2)写出体育场、市场、超市、医院的坐标.27.如图,这是某市部分简图,为了确定各建筑物的位置请完成以下步骤.(1)请你以火车站为原点建立平面直角坐标系;(2)写出市场的坐标是________;超市的坐标为________;(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.参考答案一、选择题D D C A B B B D C A A A二、填空题13. (0,4) 14.(﹣3,4)15. 16. (-505,-505)17.(-3,-6);(-4,-1)18. (5,4)19.(0,0);(-2,0);(-3,-1);(-2,-2)20.(-1,2)21.(7,-2)或(-3,-2)22.0三、解答题23.解:有6种走法分别为:①(2,4)→(3,4)→(4,4)→(4,3)→(4,2);②(2,4)→(3,4)→(3,3)→(4,3)→(4,2);③(2,4)→(3,4)→(3,3)→(3,2)→(4,2);④(2,4)→(2,3)→(3,3)→(4,3)→(4,2);⑤(2,4)→(2,3)→(3,3)→(3,2)→(4,2);⑥(2,4)→(2,3)→(2,2)→(3,2)→(4,2)24.解:如下图所示,可知小明与小刚相距3个格.25.解:由各点的坐标可知他路上经过的地方:葡萄园杏林桃林梅林山楂林枣林梨园苹果园.如图所示:26.(1)解:如图所示(2)解:体育场、市场、超市、医院.27.(1)解:如图所示:(2)(4,3);(2,﹣3)(3)解:如图所示:△A1B1C1的面积=3×6﹣×2×2﹣×4×3﹣×6×1=7.人教七年级上册数学第7章《平面直角坐标系》练习题(A B 卷)人教版七年级数学下册第七章平面直角坐标系单元测试题班级姓名得分一、选择题(4分×6=24分)1.点A (4,3-)所在象限为( )A 、 第一象限B 、 第二象限C 、 第三象限D 、 第四象限2.点B (0,3-)在()上A 、 在x 轴的正半轴上B 、 在x 轴的负半轴上C 、 在y 轴的正半轴上D 、 在y 轴的负半轴上3.点C 在x 轴上方,y 轴左侧,距离x 轴2个单位长度,距离y 轴3个单位长度,则点C 的坐标为()A 、(3,2)B 、 (3,2--)C 、 (2,3-)D 、(2,3-)4. 若点P (x,y )的坐标满足xy =0,则点P 的位置是()A 、 在x 轴上B 、 在y 轴上C 、 是坐标原点D 、在x 轴上或在y 轴上5.某同学的座位号为(4,2),那么该同学的所座位置是()A 、 第2排第4列B 、 第4排第2列C 、 第2列第4排D 、 不好确定6.线段AB 两端点坐标分别为A (4,1-),B (1,4-),现将它向左平移4个单位长度,得到线段A 1B 1,则A 1、B 1的坐标分别为()A 、 A 1(0,5-),B 1(3,8--) B 、 A 1(7,3), B 1(0,5)C 、 A 1(4,5-) B 1(-8,1)D 、 A 1(4,3) B 1(1,0)二、填空题( 1分×50=50分 )7.分别写出数轴上点的坐标:A ( )B ( )C ( )D ( )E ( )8.在数轴上分别画出坐标如下的点:)1(-A )2(B )5.0(C )0(D )5.2(E )6(-F9. 点)4,3(-A 在第 象限,点)3,2(--B 在第 象限点)4,3(-C 在第 象限,点)3,2(D 在第 象限点)0,2(-E 在第 象限,点)3,0(F 在第 象限10.在平面直角坐标系上,原点O 的坐标是( ),x 轴上的点的坐标的特点是 坐标为0;y 轴上的点的坐标的特点是 坐标为0。
人教版数学七年级下册 第七章《平面直角坐标系》全章测试题(含答案)

第七章平面直角坐标系检测卷一、选择题(每小题3分,共30分)1.在平面直角坐标系中,点(﹣8,2)所在的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限2.若x 轴上的点P 到y 轴的距离是3,则点P 的坐标为( ) A .(3,0) B .(3,0)或 (﹣3,0)C .(3,0)D .(0,3)或 (0,﹣3)3.若点P (m +3,m ﹣1)在x 轴上,则P 点的坐标为( ) A .(0,﹣4) B .(4,0)C .(0,4)D .(﹣4,0)4.在平面直角坐标系中,若点()2,3M -与点()2,N y -之间的距离是5,那么y 的值是( ) A .2-B .8C .2或8D .2-或85.点M 在第二象限,距离x 轴5个单位长度,距离y 轴3个单位长度,则M 点的坐标为( ) A .(5,﹣3)B .(﹣5,3)C .(3,﹣5)D .(﹣3,5)6.在平面直角坐标系中,线段CF 是由线段AB 平移得到的;点A (-1,4)的对应点为C (4,1);则点B (a ,b )的对应点F 的坐标为( )A .(a+3,b+5)B .(a+5,b+3)C .(a-5,b+3)D .(a+5,b-3) 7.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )A .(﹣3,3)B .(3,2)C .(1,3)D .(0,3)8.在平面直角坐标系xOy 中,线段AB 的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB 得到线段A’B’(点A 与A’对应),已知A’的坐标为(3,-1),则点B’的坐标为( ) A .(4,2)B .(5,2)C .(6,2)D .(5,3)9.将点A (-2,-3)向左平移3个单位长度得到点B ,则点B 的坐标是( ) A .(1,-3) B .(-2,0) C .(-5,-3) D .(-2,-6) 10.点()'2,1A -可以由点()2,1A -通过两次平移得到,正确的移法是( ) A .先向左平移4个单位长度,再向上平移2个单位长度 B .先向右平移4个单位长度,再向上平移2个单位长度 C .先向左平移4个单位长度,再向下平移2个单位长度 D .先向右平移4个单位长度,再向下平移2个单位长度二、填空题(每小题3分,共24分)11.已知点M(a+3,4-a)在y 轴上,则点M 的坐标为 .12.如图3,观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红方“马”走完“马3进4”后到达点B,则表示点B 位置的数对是 .图313.如图4,把笑脸放在平面直角坐标系中,已知眼睛A的坐标是(-2,3),嘴唇C 的坐标是(-1,1),则将此笑脸向右平移3个单位长度后,眼睛B的坐标是.图414.若点B的坐标为(2,1),AB∥y轴,且AB=4,则点A的坐标为.15.在平面直角坐标系中,正方形ABCD的顶点A,B,C的坐标分别为(-1,1),(-1,-1),(1,-1),则顶点D的坐标为________.16.在平面直角坐标系中,点A(1,2a+3)在第一象限,且到x轴的距离与到y轴的距离相等,则a=________.17.已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是________.18.如图,在平面直角坐标系中,点A1(1,2),A2(2,0),A3(3,-2),A4(4,0)……根据这个规律,探究可得点A2017的坐标是________.第14题图第18题图三、解答题(共66分)19.(7分)如图,已知单位长度为1的方格中有三角形ABC.(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.20.(7分)如图,长方形ABCD在坐标平面内,点A的坐标是A(2,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.(1)求B,C,D三点的坐标;(2)怎样平移,才能使A点与原点O重合?21.(8分)若点P(1-a,2a+7)到两坐标轴的距离相等,求6-5a的平方根.22.(10分)如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.(1)求这个四边形的面积;(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?23.(10分)如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A 与点D、点B与点E、点C与点F分别是对应点.观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说出三角形DEF 是由三角形ABC经过怎样的变换得到的;(2)若点Q(a+3,4-b)是点P(2a,2b-3)通过上述变换得到的,求a-b的值.24.(12分)已知A(0,1),B(2,0),C(4,3).(1)在坐标系中描出各点,画出三角形ABC;(2)求三角形ABC的面积;(3)设点P在坐标轴上,且三角形ABP与三角形ABC的面积相等,求点P的坐标.25.(12分)如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D路线运动到点D停止.若P,Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.(1)直接写出B,C,D三个点的坐标;(2)当P,Q两点出发112s时,试求三角形PQC的面积;(3)设两点运动的时间为t s,用含t的式子表示运动过程中三角形OPQ的面积S(单位:cm2).参考答案与解析1.B 2.B 3.B 4.D 5.D6.D 7.C 8.B 9.C10.D11. (0,7)12. (4,7)13. (3,3)14. (2,-3)或(2,5)15.(1,1) 16.-1 17.±418.(2017,2)19.解:(1)三角形A′B′C′如图所示.(3分)(2)建立的平面直角坐标系如图所示.(5分)点B的坐标为(1,2),点B′的坐标为(3,5).(7分)20.解:(1)∵A(2,1),AB=4,AD=2,∴BC到y轴的距离为4+2,(1分)CD到x轴的距离2+1=3,(2分)∴点B的坐标为(4+2,1),点C的坐标为(4+2,3),点D的坐标为(2,3).(5分)(2)由图可知,先向下平移1个单位长度,再向左平移2个单位长度(或先向左平移2个单位长度,再向下平移1个单位长度).(7分)21.解:由题意,得1-a=2a+7或1-a+2a+7=0,解得a=-2或-8,(4分)故6-5a=16或46,(6分)∴6-5a的平方根为±4或±46.(8分) 22.解:(1)过B作BF⊥x轴于F,过A作AG⊥x轴于G,如图所示.(2分)∴S四边形ABCO =S三角形BCF+S梯形ABFG+S三角形AGO=⎣⎢⎡⎦⎥⎤12×2×4+12×(4+6)×3+12×2×6×102=2500(平方米).(6分)(2)把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,即将这个四边形向右平移2个单位长度,(8分)故所得到的四边形的面积与原四边形的面积相等,为2500平方米.(10分)23.解:(1)A(2,4),D(-1,1),B(1,2),E(-2,-1),C(4,1),F(1,-2).(3分)三角形DEF是由三角形ABC先向左平移3个单位,再向下平移3个单位得到的(或先向下平移3个单位,再向左平移3个单位得到的).(5分)(2)由题意得2a-3=a+3,2b-3-3=4-b,(7分)解得a=6,b=103,(9分)∴a -b =83.(10分)24.解:(1)三角形ABC 如图所示.(3分)(2)如图,过点C 向x 轴、y 轴作垂线,垂足为D ,E .(4分)∴S长方形DOEC=3×4=12,S 三角形BCD =12×2×3=3,S 三角形ACE =12×2×4=4,S 三角形AOB =12×2×1=1.(6分)∴S三角形ABC=S 长方形DOEC -S 三角形ACE -S 三角形BCD -S 三角形AOB =12-4-3-1=4.(7分)(3)当点P 在x 轴上时,S 三角形ABP =12AO ·BP =4,即12×1×BP =4,解得BP =8.∵点B 的坐标为(2,0).∴点P 的坐标为(10,0)或(-6,0);(9分)当点P 在y 轴上时,S 三角形ABP =12BO ·AP =4,即12×2·AP =4,解得AP =4.∵点A 的坐标为(0,1),∴点P 的坐标为(0,5)或(0,-3).(11分)综上所述,点P 的坐标为(10,0)或(-6,0)或(0,5)或(0,-3).(12分)25.解:(1)B (4,5),C (4,2),D (8,2).(3分)(2)当t =112s 时,点P 运动的路程为112cm ,点Q 运动到点D 处停止,由已知条件可得BC =OA -DE =5-2=3(cm).∵AB +BC =7cm >112cm ,AB =4cm <112cm ,∴当t =112s 时,点P 运动到BC 上,且CP =AB +BC -112=4+3-112=32cm.∴S 三角形CPQ=12CP ·CD =12×32×4=3(cm 2).(6分) (3)①当0≤t <4时,点P 在AB 上,点Q 在OE 上,如图①所示,OA =5cm ,OQ =2t cm ,∴S 三角形OPQ =12OQ ·OA =12·2t ·5=5t (cm 2);(8分)②当4≤t ≤5时,点P 在BC 上,点Q 在ED 上,如图②所示,过P 作PM ∥x 轴交ED 延长线于M ,则OE =8cm ,EM =(9-t )cm ,PM =4cm ,EQ =(2t -8)cm ,MQ =(17-3t )cm ,∴S 三角形OPQ=S梯形OPME -S三角形PMQ -S三角形OEQ=12×(4+8)·(9-t )-12×4·(17-3t )-12×8·(2t -8)=(52-8t )(cm 2);(10分)③当5<t ≤7时,点P 在BC 上,点Q 停在D 点,如图③所示,过P 作PM ∥x 轴交ED 的延长线于M ,则MD =CP =(7-t )cm ,ME =(9-t )cm ,∴S三角形OPQ =S梯形OPME -S三角形PDM -S三角形DOE=12×(4+8)·(9-t )-12×4·(7-t )-12×8×2=(32-4t )(cm 2).综上所述,S =⎩⎨⎧5t (0≤t <4),52-8t (4≤t ≤5),32-4t (5<t ≤7).(12分)。
七年级数学下册《第七章 平面直角坐标系》单元测试卷-带答案(人教版)

七年级数学下册《第七章平面直角坐标系》单元测试卷-带答案(人教版)一、选择题(共8题)1.在平面直角坐标系中,点A(−2,−3)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.在平面直角坐标系中,在P(x−3,x+3)是x轴上一点,则点P的坐标是()A.(0,6)B.(0,−6)C.(−6,0)D.(6,0)3.在平面直角坐标系中,把点A(3,5)向下平移3个单位长度,再向左平移2个单位长度后,得对应点A1的坐标是()A.(1,2)B.(2,1)C.(−1,2)D.(−1,−2)4.已知点P(a,b)且ab=0,则点P在()A.x轴上B.y轴上C.坐标原点D.坐标轴上5.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(−2,2),黑棋(乙)的坐标为(−1,−2),则白棋(甲)的坐标是()A.(2,2)B.(0,1)C.(2,−1)D.(2,1)6.如图A,B的坐标为(1,0),(0,2)若将线段AB平移至A1B1,则a−b的值为()A.1B.−1C.0D.27.在直角坐标平面内,A是第二象限内的一点,如果它到x轴、y轴的距离分别是3和4,那么点A 的坐标是()A.(3,−4)B.(−3,4)C.(4,−3)D.(−4,3)8.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1,第2次移动到A2⋯第n 次移动到A n,则△OA3A2020的面积是()A.504.5m2B.505m2C.505.5m2D.1010m2二、填空题(共5题)9.点P(−3,2)到x轴的距离是.10.如果点P(a,2)在第二象限,那么点Q(−3,a−1)在第象限.11.坐标系中点M(a,a+1)在x轴上,则a=.12.如图,点A(1,0),B(2,0),C是y轴上一点,且三角形ABC的面积为1,则点C的坐标为13.在平面直角坐标系xOy中,对于点P(x,y),我们把点Pʹ(−y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4⋯⋯这样依次得到点A1,A2,A3⋯A n⋯.若点A1的坐标为(2,4),点A2021的坐标为.三、解答题(共6题)14.在平面直角坐标系中A,B,C三点的坐标分别为(−5,6),(−3,2),(0,5).(1) 在如图的坐标系中画出△ABC.(2) △ABC的面积为.(3) 将△ABC平移得到△AʹBʹCʹ,点A经过平移后的对应点为Aʹ(1,1),在坐标系内画出△AʹBʹCʹ,并写出点Bʹ,Cʹ的坐标.15.如图,在平面直角坐标系中,已知A(a,0),B(b,0)其中a,b满足∣a+2∣+(b−4)2=0.(1) 填空:a=,b=;(2) 如果在第三象限内有一点M(−3,m),请用含m的式子表示△ABM的面积;(3) 在(2)条件下,当m=−3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.16.已知点P(−3a−4,2+a),解答下列各题:(1) 若点P在x轴上,试求出点P的坐标;(2) 若Q(5,8),且PQ∥y轴,试求出点P的坐标.17.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均在格点上.点A的坐标为(2,3),点B的坐标为(3,0),点C的坐标为(0,2).(1) 以点C为旋转中心,将△ABC旋转180∘后得到△A1B1C,请画出△A1B1C.(2) 平移△ABC,使点A的对应点A2的坐标为(0,−1),请画出△A2B2C2.(3) 若将△A1B1C绕点P旋转可得到△A2B2C2,则点P的坐标为.18.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a,b,c满足关系式:∣a−2∣+(b−3)2+√c−4=0.(1) 求a,b,c的值.),请用含m的式子表示四边形ABOP的面积.(2) 如果在第二象限内有一点P(m,12(3) 在(2)的条件下,是否存在点P,使得四边形ABOP的面积不小于△ABC的面积的两倍?若存在,求出点P的坐标;若不存在,请说明理由.19.如图,点O为平面直角坐标系的原点,三角形ABC中∠BAC=90∘,AB=m顶点A,C的坐标分别为(1,0),(n,0)且∣m−3∣+(n−5)2=0.(1) 求三角形ABC的面积;(2) 动点P从点C出发沿射线CA方向以每秒1个单位长度的速度运动,设点P的运动时间为t秒,连接PB,请用含t的式子表示三角形ABP的面积;(3) 在(2)的条件下,当三角形ABP的面积为15时,直线BP与y轴相交于点D,求点D的坐标.2参考答案1. C2. C3. A4. D5. D6. C7. D8. B9. 210. 三11. −112. (0,2)或(0,−2)13. (2,4)14.(1) 略(2) 9(3) 略,点Bʹ(3,−3),Cʹ(6,0).15.(1) −2;4×6∣m∣=−3m.(2) S△ABM=12(3) P1(0,3),P2(0,−3).16.(1) ∵点P在x轴上∴2+a=0,∴a=−2∴−3a−4=2,∴P(2,0).(2) ∵Q(5,8),且PQ∥y轴∴−3a−4=5,a=−3∴2+a=−1∴P(5,−1).17.(1) 略(2) 略(3) (−1,0)18.(1) ∵∣a−2∣+(b−3)2+√c−4=0且∣a−2∣≥0,(b−3)2≥0,√c−4≥0∴∣a−2∣=0,(b−3)2=0,√c−4=0∴a=2,b=3,c=4.(2) 过P点作OA边上的高,设为ℎ由图可知:S ABOP=S△APO+S△ABO由(1)可得:A(0,2),B(3,0),C(3,4)∴OA=2,OB=3.又∵P点坐标(m,12)且P在第二象限∴m<0,ℎ=−m∴S ABOP=S△APO+S△ABO=12⋅OA⋅ℎ+12⋅OA⋅OB=12×2×(−m)+12×2×3=3−m,即四边形ABOP的面积为3−m.(3) P点是存在的.由(2)得:S ABOP=3−m过A点作BC边上的高,设为ℎ1∵BC=4,ℎ1=3∴S△ABC=12⋅BC⋅ℎ1=12×4×3=6.又∵S ABOP≥2S△ABC∴3−m≥2×6∴m≤−9此时P点坐标为(−9,12)即P点存在.19.(1) ∵∣m−3∣+(n−5)2=0.∴∣m−3∣=0,(n−5)2=0.∴m=3,n=5∴B(1,3)。
人教版七年级数学下册《第七章平面直角坐标系》测试卷-含有答案

人教版七年级数学下册《第七章平面直角坐标系》测试卷-含有答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.在平面直角坐标系中,点在()A.第一象限B.第二象限C.第三象限D.第四象限2.若点P(x, y)在第二象限,且,则x + y =()A.-1 B.1 C.5 D.-53.直角平坐标面内,如果点在第四象限,那么点所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限4.如图,是象棋盘的一部分,若“帅”位于点,“相”位于点上,则“炮”位于点()上.A.B.C.D.5.如图是天安门周围的景点分布示意图.在图中,分别以正东,正北方向为轴,轴的正方向建立平面直角坐标系.如果表示景山的点的坐标为,表示王府井的点的坐标为,则表示人民大会堂的点的坐标为()A.B.C.D.6.已知点与点在同一条平行于x轴的直线上,且N到y轴的距离等于4,则点N的坐标是()A.或B.或C.或D.或7.如图,已知A,B的坐标分别为和,将沿x轴正方向平移,使B平移到点E,得到,若,则点C的坐标为()A.B.C.D.8.四边形四个顶点的坐标分别为,和,琪琪把四边形平移后得到了四边形,并写出了它的四个顶点的坐标,和,琪琪所写四个顶点的坐标错误的是()A.B.C.D.二、填空题9.点(3,-3)在平面直角坐标系中第象限.10.剧院里5排2号可以用(5,2)表示,则(7,4)表示.11.点Q在第四象限内,并且到x轴的距离为4,到y轴的距离为3,则点Q的坐标为.12.课间操时,小明、小丽、小亮的位置如图所示,如果小明的位置用表示,小丽的位置用表示,那么小亮的位置可以表示成.13.在平面直角坐标系中,线段平行于轴,且 .若点的坐标为,点的坐标为,则.三、解答题14.已知点,根据下列条件,求出点的坐标.(1)点在轴上;(2)点的坐标为,直线轴.15.围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有4000多年的历史.如图是某围棋棋盘的一部分,若棋盘是由边长均为1的小正方形组成的,棋盘上两颗棋子的坐标分别为.(1)根据题意,画出相应的平面直角坐标系;(2)有一颗黑色棋子的坐标为,请标注出黑色棋子的位置.16.下图是利用平面直角坐标系画出的故宫博物院主要建筑分布图(图中的小方格均为边长为1的正方形),其中太和门的坐标为,九龙壁的坐标为.(1)在图中画出平面直角坐标系,并写出景仁宫的坐标;(2)如果养心殿的坐标是,在图中用点表示它的位置.17.如图,已知四边形ABCD(网格中每个小正方形的边长均为1).(1)写出点A,B,C,D的坐标;(2)求四边形ABCD的面积.18.在平面直角坐标系中,点的坐标为.(1)若点在过点且与轴平行的直线上时,求点的坐标;(2)将点向右平移个单位,再向上平移个单位后得到点,若点在第三象限,且点到轴的距离为,求点的坐标.参考答案:1.B2.B3.B4.D5.D6.D7.A8.D9.四10.7排4号11.12.13.5或-314.(1)解:∵点在x轴上∴a+4=0解得:a=−4∴=−2−1=−3则P(−3,0);(2)解:∵点Q的坐标为,直线轴∴=-5解得:a=-8∴a+4=-4则P(-5,-4).15.(1)正确画图(2)正确标注黑色棋子C的位置16.(1)解:平面直角坐标系如图,景仁宫的坐标为;(2)解:点的位置如图所示.17.(1)解:由图象可知A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2)(2)解:如图, S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF= ×1×3+×1×3+ ×2×4+3×3=16.18.(1)解:点在过点且与轴平行的直线上点的横坐标为解得点坐标为;(2)由题意知的坐标为在第三象限,且到轴的距离为点的横坐标为解得点的坐标为。
新人教版七年级下册数学第七章平面直角坐标系单元检测试题及答案

人教版七年级数学下册第7章平面直角坐标系能力提升卷一.选择题(共10小题)1.如图,小手盖住的点的坐标可能为()A.(5,2) B.(-7,9) C.(-6,-8) D.(7,-1)2.若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为()A.(5,1) B.(-1,1)C.(5,1)或(-1,1) D.(2,4)或(2,-2)3.若点A(a+1,b-2)在第二象限,则点B(1-b,-a)在()A.第一象限B.第二象限C.第三象限D.第四象限4.在平面直角坐标系中,点D(-5,4)到x轴的距离为()A.5 B.-5 C.4 D.-45.已知点A(2x-4,x+2)在坐标轴上,则x的值等于()A.2或-2 B.-2 C.2 D.非上述答案6.根据下列表述,能确定一个点位置的是()A.北偏东40°B.某地江滨路C.光明电影院6排D.东经116°,北纬42°7.如图是某动物园的平面示意图,若以大门为原点,向右的方向为x轴正方向,向上的方向为y轴正方向建立平面直角坐标系,则驼峰所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限8.若线段AB∥y轴,且AB=3,点A的坐标为(2,1),现将线段AB先向左平移1个单位,再向下平移两个单位,则平移后B点的坐标为()A.(1,2) B.(1,-4)C.(-1,-1)或(5,-1) D.(1,2)或(1,-4)9.课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成()A.(5,4) B.(4,5) C.(3,4) D.(4,3)10.已知点A(-1,2)和点B(3,m-1),如果直线AB∥x轴,那么m的值为()A.1 B.-4 C.-1 D.3二.填空题(共6小题)11.若P(a-2,a+1)在x轴上,则a的值是.12.在平面直角坐标系中,把点A(-10,1)向上平移4个单位,得到点A′,则点A′的坐标为.13.在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的3级关联点”为Q(3×1+4,1+3×4)即Q(7,13),若点B的“2级关联点”是B'(3,3),则点B的坐标为;已知点M(m-1,2m)的“-3级关联点”M′位于y轴上,则M′的坐标为.14.已知点A(m-1,-5)和点B(2,m+1),若直线AB∥x轴,则线段AB的长为.15.小刚家位于某住宅楼A座16层,记为:A16,按这种方法,小红家住B座10层,可记为.16.如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是.三.解答题(共7小题)17.如图,在平面直角坐标系中,三角形ABC的顶点A、B、C的坐标分别为(0,3)、(-2,1)、(-1,1),如果将三角形ABC先向右平移2个单位长度,再向下平移2个单位长度,会得到三角形A′B′C′,点A'、B′、C′分别为点A、B、C移动后的对应点.(1)请直接写出点A′、B'、C′的坐标;(2)请在图中画出三角形A′B′C′,并直接写出三角形A′B′C′的面积.18.已知平面直角坐标系中有一点M(m-1,2m+3)(1)当m为何值时,点M到x轴的距离为1?(2)当m为何值时,点M到y轴的距离为2?19.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.20.已知:点P(2m+4,m-1).试分别根据下列条件,求出P点的坐标.(1)点P在y轴上;(2)点P的纵坐标比横坐标大3;(3)点P在过A(2,-4)点且与x轴平行的直线上.21.阅读材料:象棋在中国有近三千年的历史,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.(1)若点A位于点(-4,4),点B位于点(3,1),则“帅”所在点的坐标为;"马”所在点的坐标为;"兵”所在点的坐标为.(2)若“马”的位置在点A,为了到达点B,请按“马”走的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.22.对有序数对(m,n)定义“f运算”:f(m,n)=11,,22m a n b⎛⎫+-⎪⎝⎭其中a、b为常数.f运算的结果也是一个有序数对,在此基础上,可对平面直角坐标系中的任意一点A(x,y)规定“F 变换”:点A(x,y)在F变换下的对应点即为坐标为f(x,y)的点A′.(1)当a=0,b=0时,f(-2,4)=;(2)若点P(4,-4)在F变换下的对应点是它本身,则a=,b=.答案:1-5 CCBCA6-10 DDDCD11.-112.(-10,5)13. (1,1)(0,-16)14.915. B1016. (-1,-1)17. 解:(1)根据题意知,点A′的坐标为(2,1)、B'的坐标为(0,-1)、C′的坐标为(1,-1);(2)如图所示,△A′B′C′即为所求,S△A′B′C′=1×1×2=1.218. 解:(1)∵|2m+3|=12m+3=1或2m+3=-1∴m=-1或m=-2;(2)∵|m-1|=2m-1=2或m-1=-2∴m=3或m=-1.19. 解:建立如图所示的平面直角坐标系:小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2).20. 解:(1)∵点P (2m+4,m-1),点P 在y 轴上, ∴2m+4=0, 解得:m=-2, 则m-1=-3, 故P (0,-3);21. 解:(1)由点A 位于点(-4,4人教七年级上册数学第7章《平面直角坐标系》练习题 (A B 卷)人教版七年级数学下册第七章平面直角坐标系 单元测试题班级 姓名 得分一、选择题(4分×6=24分) 1.点A (4,3-)所在象限为( )A 、 第一象限B 、 第二象限C 、 第三象限D 、 第四象限 2.点B (0,3-)在()上A 、 在x 轴的正半轴上B 、 在x 轴的负半轴上C 、 在y 轴的正半轴上D 、 在y 轴的负半轴上3.点C 在x 轴上方,y 轴左侧,距离x 轴2个单位长度,距离y 轴3个单位长度,则点C 的坐标为() A 、(3,2) B 、 (3,2--) C 、 (2,3-) D 、(2,3-) 4. 若点P (x,y )的坐标满足xy =0,则点P 的位置是()A 、 在x 轴上B 、 在y 轴上C 、 是坐标原点D 、在x 轴上或在y 轴上 5.某同学的座位号为(4,2),那么该同学的所座位置是()A 、 第2排第4列B 、 第4排第2列C 、 第2列第4排D 、 不好确定 6.线段AB 两端点坐标分别为A (4,1-),B (1,4-),现将它向左平移4个单位长度,得到线段A 1B 1,则A 1、B 1的坐标分别为()A 、 A 1(0,5-),B 1(3,8--) B 、 A 1(7,3), B 1(0,5)C 、 A 1(4,5-) B 1(-8,1)D 、 A 1(4,3) B 1(1,0) 二、填空题( 1分×50=50分 ) 7.分别写出数轴上点的坐标:A ( )B ( )C ( )D ( )E ( ) 8.在数轴上分别画出坐标如下的点:)1(-A )2(B )5.0(C )0(D )5.2(E )6(-F9. 点)4,3(-A 在第 象限,点)3,2(--B 在第 象限 点)4,3(-C 在第 象限,点)3,2(D 在第 象限 点)0,2(-E 在第 象限,点)3,0(F 在第 象限10.在平面直角坐标系上,原点O 的坐标是( ),x 轴上的点的坐标的特点 是 坐标为0;y 轴上的点的坐标的特点是 坐标为0。
人教版七年级下册数学第七章平面直角坐标系 测试题带答案
点睛:由于A,B两点的纵坐标相同,A,B两点的距离即为横坐标之差的绝对值;用较大的横坐标减去较小的横坐标即为所求.
5.A
【解析】
【分析】
先根据第二象限内点的坐标的特征得到m的范围,即可作出判断.
【详解】
∵点P(m,1)在第二象限
∴
∴
∴点Q(-m,o)在x轴正半轴上
故选A.
【点睛】
解题的关键是熟记平面直角坐标系内各个象限内的点的坐标的符号特征:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
12.(-3,2)
【解析】
【分析】
根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】
解:∵点P在第二象限,且到x轴的距离为2,到y轴的距离为3,
∴点P的横坐标是-3,纵坐标是2,
∴点P的坐标为(-3,2).
故答案为(-3,2).
解:电影票上的4排5号记作(4,5)则5排4号记作(5,4).
故答案为:(5,4).
【点睛】
此题主要考查了根据有序数对确定点的位置,解题的关键是理解题目的规定,知道有序数对与位置的对应关系.
10.三
【解析】
【分析】
根据所给点的横纵坐标的符号可得所在象限.
【详解】
解:∵所给点的横坐标是-3为负数,纵坐标是-1为负数,
故答案为:(-2,-3),(-1,3),(2,-2)
(2)以荷花池为原点,以水平向右为x轴的正方向,以竖直向上为y轴的正方向.用坐标表示下列景点的位置分别是:(1,6),(5,6).(答案不唯一).
故答案为:荷花池,(1,6),(5,6).(答案不唯一).
最新人教版七年级下册数学第七章平面直角坐标系测试题及答案(2)

人教版七年级数学下册第七章平面直角坐标系单元测试题人教版七年级数学下册第七章平面直角坐标系单元测试题一、选择题1.用 7 和 8 构成一个有序数对,能够写成 ( D )A.(7 ,8)B. (8,7)C.7,8 或 8,7D. (7 ,8) 或 (8 ,7)2.如图,一个方队正沿着箭头所指的方向行进, A 的地点为三列四行,表示为(3 ,4),那么C的地点是(D)A.(4 ,5)B. (5,4)C.(4 ,2)D.(4 ,3) 3.平面直角坐标系中,点(1 ,- 2) 在 ( D )A.第一象限B.第二象限C.第三象限D.第四象限4.如图是某游玩城的平面表示图,用(8 , 2) 表示进口处的地点,用(6 ,- 1) 表示球幕电影的地点,那么坐标原点表示的地点是( D )A.太空秋千B.梦幻艺馆C.海底世界D.激光战车5.在平面直角坐标系中,将点 P(3 ,- 2) 向下平移 4 个单位长度,获得点 P 的坐标为 ( B ) A.( -1,- 2)B. (3 ,- 6)C. (7 ,- 2)D. (3 ,- 2)6.点 N( - 1, 3) 能够看作由点 M(- 1,- 1)( A )A.向上平移 4 个单位长度所获得的B.向左平移 4 个单位长度所获得的C.向下平移 4 个单位长度所获得的D.向右平移 4 个单位长度所获得的8. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其次序为(1 , 0) , (2 ,0) , (2 ,1) ,(1 ,1) ,(1 ,2) ,(2 ,2) ,⋯,依据个律,第 2 018 个点的坐( C )A. (45 , 9)B. (45 , 11)C. (45 , 7)D. (46 , 0)9.王宁在班里的座位号(2 , 3) ,那么同学所坐的地点是( D )A.第 2排第 3列B.第 3排第 2列C.第 5排第 5列D.不好确立10.在平面直角坐系中,点(0 ,- 10) 在 ( D )A. x 的正半上B. x 的半上C. y 的正半上D. y 的半上二、填空11.如,在平面直角坐系中: A(1 ,1) ,B( - 1,1) ,C(- 1,- 2) ,D(1 ,- 2) ,把一条 2 018 个位度且没有性的 ( 的粗忽视不 ) 的一端固定在点 A ,并按A→B→C→D→A→⋯的律在四形ABCD的上,另一端所在地点的点的坐是(1,- 1).12.平面直角坐系内有一点P(x ,y) ,若点 P 在横上,y= 0;若点 P 在上,x =0;若点 P 坐原点,x= 0 且 y= 0.13.如是某学校的表示,若合楼在点(-2,-1),食堂在点(1,2),教课楼在点(-4,1) .14. 如,小在小明的北偏60°方向的500 m ,小明在小的南偏西60°方向的500 m . ( 用方向和距离描绘小明相于小的地点)15. 将点 A(1 ,1) 先向左平移 2 个位度,再向下平移 3 个位度获得点B,点 B 的坐是 ( -1,- 2) .16.如,点 P 在平面直角坐系中按中箭所示的方向运,第1次从原点运到点(1 ,1) ,第 2 次接着运到点(2 ,0) ,第 3 次接着运到点(3 ,2) ,⋯,按的运律,2 019次运后,点P 的坐(2__019 , 2) .三、解答17.五子珠棋和象棋、棋一,深受广大棋友的喜,其是:在15×15的正方形棋中,由黑方先行,流弈子,在任一方向上成五子者.如是两个五子棋好者甲和乙的弈 ( 甲黑子先行,乙白子后走 ) ,察棋思虑:若 A 点的地点作 (8 ,4) ,甲必在哪个地点上落子,才不会乙在短内?什么?解:甲必在 (1 ,7) 或 (5 ,3) 落子.因若甲不第一截断以上两之一,而乙在(1 ,7)或(5 , 3) 落子,不截断何,乙有一落子可成五子,乙必无疑.18.在以下图的平面直角坐标系中,描出以下各点,并将各点用线段挨次连结起来.(0,- 4) ,(3 ,- 5),(6 ,0) ,(0 ,- 1),( -6,0) ,( -3,- 5) ,(0 ,- 4).解:如图.19.如图, A(- 1, 0) ,C(1 , 4) ,点 B 在 x 轴上,且AB= 3.(1)求点 B的坐标;(2)求三角形 ABC的面积;(3) 在 y 轴上能否存在点P,使以 A, B, P 三点为极点的三角形的面积为10?若存在,请直接写出点P 的坐标;若不存在,请说明原因.解: (1) 当点 B 在点 A 的右侧时,点 B 的坐标为 (2 , 0) ;当点 B 在点 A 的左侧时,点 B 的坐标为 ( - 4, 0) .因此点 B 的坐标为 (2,0) 或( -4, 0) .1(2)三角形 ABC的面积为×3×4= 6. 2(3)设点 P到 x 轴的距离为 h,则1202×3h= 10,解得 h=3 .20①当点 P 在 y 轴正半轴时,点 P 的坐标为 (0, 3);②当点 P 在 y 轴负半轴时,点20P 的坐标为 (0 ,- ) .3综上所述,点 P 的坐标为 (0 ,20) 或(0 ,-20) .3 320.如图是某动物园平面表示图的一部分 ( 图中小正方形的边长代表 100 米 ) ,请问:(1) 在大门东南方向有哪些景点?(2) 从大门向东走 300 米,再向北走 200 米,抵达哪个景点?(3) 以大门为坐标原点,向东方向为x 轴正方向,向北方向为y 轴正方向成立平面直角坐标系,写出蛇山、水族馆及大象馆的坐标.解: (1) 猴山,大象馆.(2) 蛇山.(3)如图,蛇山的坐标为 (300,200),水族馆的坐标人教版七年级数学下册第七章平面直角坐标系培优测试一试卷一、单项选择题(共 10 题;共 30 分)1.在平面直角坐标系中, 将点 (-2,- 3)向上平移 3 个单位长度, 则平移后的点的坐标为 ( )A. (- 2, 0)B.-( 2, 1)C. (0,- 2)D. (1,- 1)2.点 P ( m+3, m+1)在直角坐标系的 x 轴上,则点 P 的坐标为()A. (2, 0)B. (0, -2)C. (4, 0)D. (0, -4)3.如图,在平面直角坐标系中, △ABC 位于第一象限,点 A 的坐标是( 4, 3),把 △ABC 向左平移 6 个单位长度,获得△A 1B 1 C 1 , 则点 B 1 的坐标是( )A. (﹣ 2, 3)B.(3,﹣ 1)C(.﹣ 3,1)D(.﹣ 5, 2)4.已知点 A 在x 轴上,且点 A 到y 轴的距离为4,则点 A 的坐标为()A. (4, 0)B. (0,4)C. (4, 0)或(- 4, 0)D. (0,4)或 (0,- 4)5.将点A(﹣ 1, 2)向右平移 4 个单位长度,再向下平移 3 个单位长度,则平移后点的坐标是()A. (3,1)B(.﹣ 3,﹣ 1)C(. 3,﹣ 1)D(.﹣ 3,1)6. 点A1(5,–7) 对于x 轴对称的点A2的坐标为().A.(– 5,–7)B.(– 7 ,– 5)C.(5, 7)D.(7,– 5)7.如图,在正方形ABCD 中, A,B,C三点的坐标分别是(﹣1,2)、(﹣1,0)、(﹣3,0),将正方形ABCD向右平移 3 个单位,则平移后点 D 的坐标是()A. (﹣ 6, 2)B(.0, 2)C(. 2, 0) D.( 2, 2)8.A( -3,4)和 B(4,-1)是平面直角坐标系中的两点,则由 A 点移到 B 点的路线可能是()A. 先向上平移 5 个单位长度,再向右平移7 个单位长度B. 先向上平移 5 个单位长度,再向左平移7 个单位长度C. 先向左平移7 个单位长度,再向上平移 5 个单位长度D. 先向右平移7 个单位长度,再向下平移 5 个单位长度9. a b(x y)我们商定“排数在前,列数在后”,若小张恰在小陈的正前面,则()A. a=xB. b=yC. a=yD. b=x10.如图是轰炸机机群的一个飞翔队形,假如最后两架轰炸机的平面坐标分别为A(﹣ 2,1)和 B(﹣ 2,﹣ 3),那么第一架轰炸机 C 的平面坐标是()A. (2,﹣ 1)B(.4,﹣ 2)C(. 4, 2)D(.2, 0)二、填空题(共 6 题;共 24分)11.线段 AB 两头点 A(-1, 2), B(4, 2),则线段 AB 上随意一点可表示为________.12.将点 P(x,4)向右平移 3 个单位获得点 (5, 4),则 P 点的坐标是 ________.13.点 A(1 - x, 5) 、 B(3 , y) 对于 y 轴对称,那么x+y =.14.在平面直角坐标系中,若点M( ﹣1,4)与点N(x, 4)之间的距离是5,则 x的值是________.15.如图是一个围棋棋盘(局部),把这个围棋棋盘搁置在一个平面直角坐标系中,白棋①的坐标是(- 2,- 1),白棋③的坐标是(- 1,- 3),则黑棋②的坐标是 ________.16.有一个英文单词的字母次序对应如图中的有序数对分别为(2,1),(2,2),(4,2),(5,1),请你把这个英文单词写出来(或许翻译成中文)为________。
最新人教版七年级下册数学第七章平面直角坐标系单元检测试题及答案

人教版七年级数学下册第七章平面直角坐标系期中复习检测试题 一、选择题(每题 3 分,共1. 在平面直角坐标系中,点30 分)P (-3 , 2)在(B )A .第一象限B .第二象限C .第三象限D .第四象限2. 经过两点 A ( 2, 3)、 B (﹣ 4, 3)作直线 AB ,则直线 AB ( B )A .经过原点B .平行于x 轴C .平行于y 轴 D .没法确立3.若y 轴上的点P 到 x 轴的距离为 3,则点 P 的坐标是( D )A.(3 , 0)B.(0, 3)C.(3, 0)或 (-3, 0)D.(0 , 3)或 (0, -3)4. 已知△ ABC 极点坐标分别是 A (0, 6), B (﹣ 3,﹣ 3), C ( 1, 0),将△ ABC 平移后顶 点 A 的对应点A 1 的坐标是(4, 10),则点 B 的对应点B 1 的坐标为(C )A .( 7, 1)B . B (1, 7)C .( 1, 1)D .( 2, 1)5.如图,在5×4 的方格纸中,每个小正方形边长为1,点 O ,A , B 在方格纸的交点(格点 )上,在第四象限内的格点上找点C ,使三角形ABC的面积为3,则这样的点C 共有 (B )A.2 个B.3 个C.4 个D.5 个6. 象棋在中国有三千多年的历史,因为器具简单,兴趣性强,成为流行极为宽泛的益智游戏.图 7-2- 1 是一局象棋残局,已知棋子“马”和“车”所在地点用坐标表示分别为(4 ,3) , ( - 2,1) ,则棋子“炮”所在地点用坐 标表示为(D )A .( -3,3)B . (3,2)C .(0 ,3)D .(1,3)7. 如图,线段 AB 经过平移获得线段 ′ ′,此中点 , B 的对应点分别为点′, ′,这A B A AB四个点都在网格的格点上.若线段 AB 上有一个点 P ( a , b ) ,则点 P 在线段 A ′ B ′上的对应点 P ′的坐标为 (A )A. ( a- 2,b+ 3) B. ( a- 2,b- 3) C. ( a+ 2,b+ 3) D. ( a+ 2,b- 3)8.将正整数按如所示的律摆列下去,如有序数(n, m)表示第n 排,从左到右第m 个数,如(4, 2)表示9,表示58 的有序数是(A)A.(11 , 3)9. 如,点的 (B.(3 , 11)A, B 的坐分A )C.(11 ,9)D.(9 , 11)(2 , 0) , (0 , 1) .若将段AB 平移至A1B1的地点,a+ bA.2 B.3 C.4 D.510.在平面直角坐系xOy中,于点,我把点叫做点陪伴点.已知点的陪伴点,点的陪伴点,点的陪伴点,⋯,挨次得到点,,,⋯,,⋯.若点的坐(2, 4),点的坐( D )A. (-3 , 3)B.(-2 , -2)C.(3 ,-1)二、填空(每空 3 分,共 18 分)D.(2 , 4)11.若点 P是第二象限内的点,且点 P 到 x 的距离是 4,到 y 的距离是 3,点 P 的坐是(3, 4)。
人教版七年级下册数学第七章平面直角坐标系--测试题有答案

人教版七年级数学下册第七章平面直角坐标系评卷人得分一、单选题1.若x轴上的点P到y轴的距离为3,则点P的坐标为()A.(3,0)B.(3,0)或(–3,0)C.(0,3)D.(0,3)或(0,–3)2.如图,将正整数按下图所示规律排列下去,若用有序数对(n,m)表示n排从左到右第m 个数.如(4,3)表示9,则(10,3)表示()A.46B.47C.48D.493.一个学生方队,B的位置是第8列第7行,记为(8,7),则学生A在第二列第三行的位置可以表示为()A.(2,1)B.(3,3)C.(2,3)D.(3,2)4.长方形OABC中,AB=3,BC=2,芳芳建立了如图所示的平面直角坐标系,则点B的坐标是()A.(3,2)B.(2,3)C.(-3,2)D.(-2,3)5.在直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P 的坐标为()A.(-3,-7)B.(-7,-3)C.(3,7)D.(7,3)6.下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是()A.图书馆B.教学楼C.实验楼D.食堂7.平面直角坐标系中,点(1,﹣2)在()A.第一象限B.第二象限C.第三象限D.第四象限8.如果用(2,3)表示电影院中的第2排3号位,那么(5,4)表示的意义是()A.4排5号B.5排4号C.4排或5排D.4号或5号评卷人得分二、填空题9.如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为________.10.点P(2,-3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是________.11.在平面直角坐标系中,已知点P在第二象限,距离x轴3个单位长度,距离y轴2个单位长度,则点P的坐标为________.12.线段AB的两个端点的坐标为A(m,2),B(3,5),将线段AB平移后得线段A′B′,其中A′(0,3),B′(6,n),则线段AB上的点C(-1,3)平移后的坐标是________.13.如果点P(a,b)在第三象限,则点Q(-a,-b)在第________象限.14.A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1,A1,B1的坐标分别为(﹣2,a),(b,5),则a+b的立方根是__.15.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是_____.16.若点P(m,n)在第三象限,则点Q(mn,m+n)在第________象限.评卷人得分三、解答题17.小强放学后,先向东走了300米,再向北走路200米,到书店A买了一本书,然后向西走了500米,再向南走了100米,到快餐店B买了零食,又向南走了400米,再向东走了800米,回到他家C,如图,以学校为原点建立坐标系,图中的每个单位长度表示100米.(1)请在图中的坐标系中标出A,B,C的位置,并写出A,B,C三点的坐标;(2)如果超市D的坐标为(-1,-3),邮局E的坐标为(4,2),请在图中标出超市和邮局的位置;(3)请求出小强家到超市的实际距离.18.已知三角形ABC的三个顶点坐标分别是A(-4,-1),B(-1,4),C(1,1),点A经过平移后对应点为A1(-2,1),将三角形ABC作同样的平移得到三角形A1B1C1,写出B1、C1两点的坐标.19.若点M(a-3,a+1)到x轴的距离是3,且它位于第三象限,求点M的坐标.20.多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?21.如果点P(m+3,m-2)在坐标轴上,求m的值和点P的坐标.参考答案1.B【解析】根据x轴上点的纵坐标为0,可得P点的纵坐标,根据点P到y轴的距离是点的横坐标的绝对值,可得答案.【详解】由x轴上的点P,得P点的纵坐标为0,由点P到y轴的距离为3,得P点的横坐标为3或-3,∴点P的坐标为(3,0)或(-3,0),故选B.【点睛】本题考查了点的坐标,利用y轴上点的横坐标为得出P点的横坐标是解题关键,注意点到x 轴的距离是点的纵坐标的绝对值.2.C【解析】【分析】根据排列规律解答.从图中可以发观,第n排的最后的数为:12n(n+1).【详解】从图中可以发观,第n排的最后的数为:12n(n+1)∵第9排最后的数为:12 9(9+1)=45,∴(10,3)表示第10排第3个数,则第10排第3个数为45+3=48.故选C.【点睛】本题考查了学生阅读理解及总结规律的能力,找到第n排的最后的数的表达式是解题的关键.3.C【解析】【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,据此即可解答.【详解】根据题干分析可得:B的位置是第8列第7行,记为(8,7),学生A在第二列第三行的位置可以表示为:(2,3).故选C.【点睛】本题考查了数对表示位置的方法,根据已知得出列与行的意义是解题的关键.4.C【解析】在长方形OABC中,∵AB=3,BC=2,BC⊥x轴于C,AB⊥y轴于A,∵点B在第二象限,∴B(-3,2),故选C.5.B【解析】【分析】根据点P所在象限先确定P点横纵坐标都是负数,根据P到x轴和y轴的距离确定点的坐标.【详解】∵点P(x,y)在第三象限,∴P点横纵坐标都是负数.∵P到x轴和y轴的距离分别为3、7,∴点P的坐标为(﹣7,﹣3).故选B.【点睛】本题考查了点的坐标,关键是掌握到x轴的距离=纵坐标的绝对值,到y轴的距离=横坐标的绝对值.6.A【解析】【分析】根据小明的坐标向右平移6个单位,再向上平移1个单位,可得原点,根据平面直角坐标系中点的坐标,可得答案.【详解】由小明的坐标向右平移6个单位,再向上平移1个单位,得:坐标(3,﹣2)在示意图中表示的是图书馆.故选A.【点睛】本题考查了坐标确定位置,利用小明的坐标平移得出原点的位置是解题的关键.7.D【解析】【分析】根据各象限内点的坐标特征解答即可.【详解】点(1,﹣2)在第四象限.故选D.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).8.B【解析】【分析】根据题意可以得到(5,4)表示的意义,本题得以解决.【详解】∵用(2,3)表示电影院中的第2排3号位,∴(5,4)表示电影院中的第5排4号位.故选B.【点睛】本题考查了坐标位置的确定,解题的关键是明确题目中坐标表示的意义.9.(6,120°)【解析】【分析】根据圆圈数表示横坐标,度数表示纵坐标,可得答案.【详解】目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).故答案为(6,120°).【点睛】本题考查了坐标确定位置,利用圆圈数表示横坐标,度数表示纵坐标是解题的关键.10.(-2,-2)【解析】解:点(2,﹣3),向左平移4个单位,横坐标:2﹣4=﹣2,向上平移1个单位,纵坐标:﹣3+1=﹣2,∴点P'(﹣2,﹣2).故答案为(﹣2,﹣2).11.(﹣2,3).【解析】【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.【详解】∵点P在第二象限,距离x轴3个单位长度,距离y轴2个单位长度,∴点P的横坐标为-2,纵坐标为3,∴点P的坐标为(-2,3).故答案是:(-2,3).【点睛】考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.12.(2,4)【解析】【分析】A的纵坐标由2变为3,说明新点的纵坐标应加1;B的横坐标由3变为6,说明新点的横坐标应加3,让点C的横纵坐标也做此变化即可.【详解】由题意可知:平移后点的横坐标为﹣1+(6﹣3)=2;纵坐标为3+(3﹣2)=4;∴线段AB上的点C(﹣1,3)平移后的坐标是(2,4).故答案为(2,4).【点睛】在平面直角坐标系中,图形的平移与图形上某点的平移相同,解决本题的关键是得到各点的平移规律.13.一【解析】【分析】根据第三象限点的横坐标是负数,纵坐标是负数判断出a、b的正负情况,载判断出点Q的横坐标与纵坐标的正负情况,然后解答即可.【详解】∵点P(a,b)在第三象限,∴a<0,b<0,∴-a>0,−b>0,∴点Q(-a,−b)在第一象限.故答案为一.【点睛】本题考查了象限及点的坐标的有关性质,解题的关键是熟练的掌握象限及点的坐标的有关性质.14.0【解析】∵A,B的坐标分别为(1,0),(0,2),将线段AB平移到A1B1后,A1,B1的坐标分别为(﹣2,a),(b,5),∴021052ba-=--⎧⎨-=-⎩,解得:33ab=⎧⎨=-⎩,∴a+b=3+(-3)=0,∴a+b的立方根是0.点睛:将一条线段平移后,线段上的每个点的横坐标与纵坐标的变化值是分别相等的. 15.(2,-1).【解析】试题分析:如图,根据A(-2,1)和B(-2,-3)确定平面直角坐标系,然后根据点C在坐标系中的位置确定点C的坐标为(2,-1).考点:根据点的坐标确定平面直角坐标系.16.四【解析】【分析】根据各象限内点的坐标特征解答即可.【详解】由题意,得:n<0,m<0,∴mn>0,m+n<0,点Q(mn,m+n)在第四象限.故答案为:四.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).17.(1)A(3,2),B(-2,1),C(6,-3)(2)见解析(3)700【解析】【分析】(1)利用小强所走路线可在坐标系中可标出A,B,C的位置,然后根据各象限点的坐标特征写出A,B,C三点的坐标;(2)利用D和E点坐标标出超市和邮局的位置;(3)求出CD的长即可得到小强家到超市的实际距离.【详解】(1)如图,A(3,2),B(﹣2,1),C(6,﹣3);(2)如图;(3)CD=700,所以小强家到超市的实际距离为700m.【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.18.B1(1,6),C1(3,3)【解析】【分析】根据点A(﹣4,﹣1)经平移后对应点为A1(﹣2,1),得出平移变换的规律即可得出B1、C1两点的坐标.【详解】∵点A(﹣4,﹣1)平移后点A1的坐标为(﹣2,1),∴平移规律为横坐标加2,纵坐标加2.∵B(﹣1,4),C(1,1),∴B1(1,6),C1(3,3).【点睛】本题考查了坐标与图形的变化,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.19.(-7,-3)【解析】【分析】根据到x轴的距离是3可得:|a+1|=3,再根据点M在第三象限可得a+1=﹣3,计算出a的值,再代入a﹣3可得点M的坐标.【详解】由题意知:|a+1|=3.∵点M位于第三象限,∴a+1=﹣3,∴a=﹣4.当a=﹣4时,a﹣3=﹣7,∴M的坐标为(﹣7,﹣3).【点睛】本题考查了点的坐标,关键是掌握到x轴的距离等于纵坐标的绝对值.20.A(0,4);B(﹣3,2);C(﹣2,﹣1);D(2,﹣2).【解析】试题分析:由牡丹园的坐标为(3,3),可以确定平面直角坐标系中原点的位置,以及坐标轴的位置,从而可以确定其它景点的坐标.解:由题意可知,本题是以点F为坐标原点(0,0),FA为y轴的正半轴,建立平面直角坐标系.则A、B、C、D的坐标分别为:A(0,4);B(﹣3,2);C(﹣2,﹣1);D(2,﹣2).【点评】本题考查了坐标确定位置.由已知条件正确确定坐标轴的位置是解决本题的关键.21.P(0,-5)或(5,0)【解析】【分析】根据坐标轴上的点坐标特征,分横坐标与纵坐标为零两种情况讨论求解.【详解】∵点P(m+3,m﹣2)在坐标轴上,∴m+3=0或m﹣2=0,∴m=﹣3或m=2,∴点P(0,﹣5)或(5,0).【点睛】本题考查了点的坐标,主要利用了坐标轴上的点坐标特征,注意要分情况讨论.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 平面直角坐标系周周测2
一 填空题
1.如图,如果点A 的位置为(3,2),那么点B 的位置为______ .点C 的位置为______ .
第1题图 第2题图
2.如图,从2街4巷到3街2巷,走最短的街、巷路线,共有 种走法.
3.如图,是象棋盘的一部分,若帥位于点(5
,1
)上,则炮所在点的坐标为 .
第3题图 第4题图
4.如图是一台雷达探测相关目标得到的结果,若记图中目标A 的位置为(1,90°),B 为(1,30°),C 为(2,240°),则目标D ,E 位置分别是 . 5.点A (2,7)到x 轴的距离为 ,到y 轴的距离为 ; 6.点P (a ,b )在第四象限内,则a ,b 的取值范围 .
7.点P (m 2-1, m +3)在直角坐标系的y 轴上,则点P 坐标为 . 8.已知AB ∥x 轴,A 点的坐标为(3,2),且AB=4,则B 点的坐标为 . 9.若点A 的坐标是(-3,5),则它到x 轴的距离是 ,到y 轴的距离是 . 10.点B在x 轴下方,y 轴右侧,距y 轴、x 轴分别是2、4个单位长度,点B 的坐标是 . 11.点P (a-1,a 2-9)在x 轴负半轴上,则P 点坐标是 .
12.如果点A (x ,y )在第三象限,则点B (-x ,y -1)在第 象限. 二 选择题
13.已知坐标平面内点M(a ,b)在第三象限,那么点N(b ,-a)在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限
14.已知点A (2,-3),线段AB 与坐标轴没有交点,则点B 的坐标可能是 ( ) A .(-1,-2) B .( 3,-2) C .(1,2) D .(-2,3) 15.已知点A (2,-3),线段AB 与坐标轴平行,则点B 的坐标可能是 ( ) A .(-1,-2) B .( 3,-2) C .(1,2) D .(-2,-3) 16.已知点P (x , |x|),则点P 一定( )
(街)
(巷)235411
4
53
2
A .在第一象限
B .在第一或第四象限
C .在x 轴上方
D .不在x 轴下方 17.点
E 与点
F 的纵坐标相同,横坐标不同,则直线EF 与y 轴的关系是( ) A .相交 B .垂直 C .平行 D .以上都不正确
18.在平面直角坐标系中,适合条件∣x ∣=6,∣x-y ∣=8的点p(x ,y)的个数是( ) A .2个 B .3个 C .4个 D .5个 19.已知点P (a ,b ),ab >0,a +b <0,则点P 在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限
20.在直角坐标系中有两个点C ,D ,且CD ⊥x 轴,那么C ,D 两点的横坐标( ) A.不相等 B.互为相反数 C.相等 D.相等或互为相反数 三 解答题
21.如图,在直角坐标系中,(15)A -,,(10)B -,,(43)C -,.
求三角形ABC 的面积.
22.建立适当的平面直角坐标系,表示边长为4的正方形各点的坐标.
23.画出以A(0,0) ,B(3,0) , C(5,4), D(2,4)为顶点的四边形ABCD ,并求其面积.
y
x
1
2
3
4
5
–1
1234–1
O
24.在平面直角坐标系中,点A(0,4),点B(0,-2),点C在x
轴上,如果三角形ABC的面积是9,求点C的坐标.
25.如图,写出三角形ABC各顶点的坐标并且求出三角形的面积.
y
x
1234
–1
–2
–3
–4
1
2
3
4
–1
–2
–3
O
第七章平面直角坐标系周周测2参考答案与解析
一、填空题
1.(2,5)(4,4)
2.3
3.(2,4)
4.(3,300°),(6,270°)
5.7 2
6.a>0,b<0
7.(0,4)或(0,2)
8.(-1,2)或(7,2)
9.5 3
10.(2,-4)11.(-4,0)12..四
二、选择题
13.B 14.B 15.D 16.D 17.B 18.C 19.C 20.C
三、解答题
21.解:由题意,三角形ABC的边AB=5,AB边上的高为3,则其面积为1
2
×5×3=
15
2
.
22.解:答案不唯一.若以点B为原点建立如图所示的平面直角坐标系,则A(0,4),B(0,0),C(4,0),D(4,4).
23.解:四边形ABCD如图所示,由题意可知,四边形ABCD为平行四边形,其面积为3×4=12.
24.解:如图,设点C的坐标为(x,0).
∵三角形ABC的面积为9,∴1
2
AC·OC=9,即
1
2
×6|x|=9,解得x=±3,∴点C的坐标为
(3,0)或(-3,0).
25.解:由图知,三角形ABC个顶点坐标分别为A(2,2),B(-2,-1),C(3,-2).三
角形ABC的面积为5×4-1
2
×3×4-
1
2
×1×5-
1
2
×1×4=9.5.。
