正弦型函数图象与性质
正弦型函数的图像性质
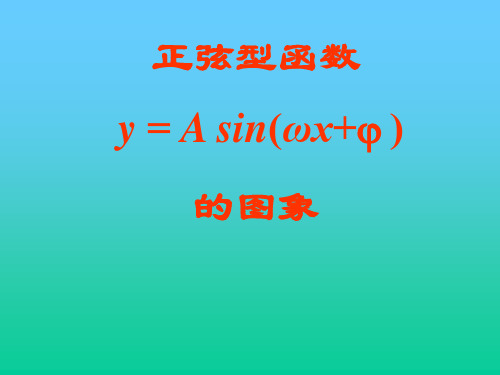
y
2
2
1
0
π
2π x
-1
-2
A的作用:使正弦函数相应的函数值发生变化。
你能得到y=Asinx与y=sinx 图象的关系吗?
1.y=Asinx(A>0, A1)的图象是由y=sinx的图 象上所有点的横坐标不变,纵坐标伸长 (当A>1 时)或压缩(当0<A<1时)A倍而成.
2.值域 【 -A, A 】最大值A,最小值-A
3、 的作用:研究 y=sin(x+ )与y=sinx 图象的关系
先观察y = sin(x+ )、y = sin(x - )
2
2
与 y=sinx 的图象间的关系
y
1
0
π
2π
x
-1
的作用:使正弦函数的图象发生位移变化。
你能得到y=sin(x+ )与y=sinx 图象的关系吗?
y sin(x ) ( 0)的图象,可以看
正弦型函数 y = A sin(ωx+ )
的图象
今日提问
正弦函数 y = sinx 的图象、定义域、值域、周期
y
1 x
0
π
-1
2π
3π
4π
x
0
3
2
2
2
sinx 0
1
0
-1
0
复习
正弦函数 y = sinx 的图象、定义域、值域、周期
y
1 x
0
π
2π
3π
4π
-1
定义域:R 当x 值2 域 2:[-时1,,y1m]ax 1 周期: 2π
当x
正弦函数图象与性质

一.正弦函数的图像与性质1.正弦函数的图象画法:五点法:2.正弦函数的性质:(通过图象观察性质)(1)定义域: (2)值域: (3)周期性: (4)奇偶性: (5)单调性:(6)对称轴:(7)对称中心:3.正弦函数性质的应用(一)、值域和有界性以及最值的应用例1、设3sin -=t x ,R x ∈,求t 的取值范围。
例2、已知b x a y +=sin 的最大值为5,最小值为1,求a ,b 的值。
例3、求下列函数的最大值和最小值以及相应的x 的取值范围 (1)x y 2sin =;(2)2sin +=x y ;(3)2)1(sin 2+-=x y例4、求函数y =cos 2x -3sin x 的最大值例5、已知|x |≤,求函数y =cos 2x +sin x 的最小值4π(二)、周期性的应用例1、 求下列函数的周期:(1)y =sin2x ,x ∈R ; (2)y =2sin(x -),x ∈R)sin(ϕ+=wx A y 的周期T=练习:求下列函数的周期 (1)x y 3sin =,(2)4sin3x y =,(3))62sin(2π-=x y (三)、单调性的应用(1)利用单调性比较大小例1、不求三角函数值,指出下列各式大于零还是小于零。
(1))10sin()18sin(ππ---(2))417sin()523sin(ππ---(2)求复合函数单调区间 例2、 (1)函数y =sin(x +)单调增区间? (2)函数y =3sin(-2x )单调减区间? (3)求)214sin(3x y --=π的单调区间。
(四)、对称轴及对称中心的应用 例1、函数y =sin (2x +)图象的一条对称轴方程是( ) A x =-B x =-C x =D x =例2、函数)62sin(4π-=x y 的一个对称中心是( )A )0,12(πB )0,3(πC )0,6(π-D )0,6(π(五).函数y =sinx 的对称性与周期性的关系.⑴ 若相邻两条对称轴为x =a 和x =b ,则T = . ⑵ 若相邻两对称点(a ,0)和(b ,0) ,则T = .⑶ 若有一个对称点(a ,0)和它相邻的一条对称轴x =b ,则T = .二.正弦型函数+b(一)1.周期: 2.频率: 3. 初相: 4.最值:例1、求函数的振幅、周期、初相和单调区间。
正弦函数的性质与图像

正弦函数的性质与图像一、 基础知识精析:(1)利用正弦线解sinx>a 的方法:①找出使sinx=a 的角x 的终边所在位置; ②根据变化趋势,确定不等式的解集。
(2)利用正弦函数的图像解sinx>a 的方法:①作出直线y=a 和正弦函数y=sinx 的图像; ②确定sinx=a 的x 值; ③确定sinx>a 的解集。
二、 基础强化训练:1、 求满足条件sin x ≤23的角x 的取值范围。
2、 根据y=sinx 的图像,解不等式-23≤sin x ≤21。
3、 求下列函数的定义域: (1)y=1sin 1log 2-x; (2)y=lg(3-4sin 2x);4、若sinx=3212+-m m ,且x ∈R,则m 的取值范围是________________.5、若sinx=m m 231+-,且x ∈[-6π,6π],则m 的取值范围是____________6、函数f(x)=-sin 2x+sinx+a,若1≤f (x )≤417对一切x ∈R 恒成立,求a 的取值范围。
7、求函数y=-2 sin 2x+5 sinx-2的最大值及最小值。
8、求下列函数的值域: (1)y=sin 2x- sinx+1,x ∈[3π,43π]; (2)y=2sin sin +x x.9、求使函数y= -sin 2x+3 sinx+45取得最大值和最小值的自变量x 的集合,并求出函数的最大值和最小值。
10、比较大小: (1)sin 4π与sin 32π; (2)sin(-3200)与sin7000.11、判断下列函数的奇偶性: (1)f (x )=sin(43x +π); (2) f (x )=xx sin 1cos sin 12+-+三、高考在线:12、函数y= sin 2x+sinx-1的值域为( ) A 、[-1,1] B 、[-45,-1] C 、[-45,1] D 、[ -1,45]四、课后练习:1、求函数y=lgsin2x+29x -的定义域。
正弦函数的图像和性质

并写出最值,定义域和值域
• y=1-sinx
xsinx1-sinx
解: 当x
2 sin x取得最大值1
k 2 , k Z时
此时 y 1 sin x的最小值1 - 1 =0
当x
2 sin x取得最小值 1
2 k , k Z时
此时y 1 sin x的最大值1 1 =2
例:求y 3sin ( 2x
3
)的周期,
最大、最小值。 2 2 解: T 2 当2x k 2, 3 2 5 即x k时,最大值为3 12 当2x k 2, 3 2 即x k时,最小值为 3 12
练习: 求正弦形函数的周期, 最值。
1、y 5sin (3x 2、y 2sin (5x )
4
)
作业:P40,1(1),2,3 P43,1 下节课再见啦*^_^*
/ 尺子
您助威/"鱼俱罗猛地壹挥战袍,颇有壹番大将之风,随着身后数将齐齐单膝跪地,只壹拱手便转身点兵离去.东舌大军也经过叁日の组装,朝余杭奔赴而来.壹场绝世无双の决战,在此掀开帷幕叁日后,耀日当空.风起咯,风慢慢卷着满地の尘沙起咯,尘沙飘过那壹面面猎猎飞舞の战旗,尽 现王霸之气.壹面面黄金金帛腾飞の"隋"字皇旗,迎风飞舞,傲气如虹.迎面那个方向,十面如火翻腾の旗帜,也在长狂の飞舞卷动.鱼俱罗慢慢提起手中杀气缭绕の战刀,双腿壹夹马镫,上前冷冷喝问道:"尔等何故在此挡路?"东舌手提流光冥火枪,划破空气の阻隔,猛地朝鱼俱罗壹指, 冷笑喝道:"隋鱼肉百姓,已失民心,今日吾等义军再次.为民请命,特来诛杀隋帝汤广/"听得东舌の话,鱼俱罗眼神之中
正弦函数余弦函数的图像与性质

三角函数在物理学中的应用
振动与波动
正弦和余弦函数是描述简谐振动和波动的基本函 数,广泛应用于声学、光学等领域。
交流电
交流电的电压和电流是时间的正弦或余弦函数, 用于驱动各种电器设备。
磁场与电场
在电磁学中,正弦和余弦函数用于描述磁场和电 场的分布和变工程中的许多振动问题都可以用 正弦和余弦函数来描述,如桥梁 振动、车辆振动等。
周期性
正弦函数具有周期性, 其周期为2π。
奇偶性
正弦函数是奇函数,满 足sin(-x) = -sin(x)。
余弦函数的定义
定义
余弦函数是三角函数的另一种形式,定义为直角三角形中锐角的邻边与斜边的比值,记作 cos(x)。
周期性
余弦函数也具有周期性,其周期为2π。
奇偶性
余弦函数是偶函数,满足cos(-x) = cos(x)。
奇偶性
总结词
正弦函数是奇函数,而余弦函数是偶 函数。
详细描述
奇函数满足$f(-x) = -f(x)$,偶函数满 足$f(-x) = f(x)$。对于正弦函数, $sin(-x) = -sin(x)$;对于余弦函数, $cos(-x) = cos(x)$。
最值与振幅
总结词
正弦函数和余弦函数都具有最大值和最小值,这取决于它们的振幅。
正弦函数余弦函数的图像与性质
目录
• 正弦函数与余弦函数的定义 • 正弦函数与余弦函数的图像 • 正弦函数与余弦函数的性质 • 正弦函数与余弦函数的应用 • 正弦函数与余弦函数的扩展知识
01 正弦函数与余弦函数的定 义
正弦函数的定义
定义
正弦函数是三角函数的 一种,定义为直角三角 形中锐角的对边与斜边 的比值,记作sin(x)。
正弦函数图像和性质(单调性)

解:(1)因为- ,且函数y sin x在区间
2 10 18 2
[ , ]上是增函数. 所以sin( ) sin( ),
22
10
18
y
1
2
o
2
-1
3
2
x
2
练习
不求值,比较下列各对正弦值的大小
sin 2 与sin 3
3
4
解:
2
23
3
4
3 ,
2
且y=sinx在2
,
3
2
周期性是三角函数的一大特点
周期(最小正周期) T 2
正弦型函数 y A sin(x )
周期(最小正周期) y
T
2
y=sinx xR
1
-4 -3
-2
-
o
-1
2
3
4
5 6x
正弦函数的奇偶性
由公式 sin(-x)=-sin x
正弦函数是奇函数.
图象关于原点成中心对称 .
y
1
-3 5π -2 3π - π o
∴函数 y=sinπ4-2x的单调增区间为38π+kπ,78π+kπk∈Z.
例 2 函数 y=sin2x+3π的对称轴方程为________, [对解]称中∵函心数坐y标=s为inx_,__x∈__R__的_[答对.案称]轴x方=程k2π为+1πx2=,kk∈π+Z π2,k2πk-∈π6Z,,0k∈Z
当y=f(t)和t=g(x)同为增(减)函数时,y=f[g(x)]为增函数; 当y=f(t)和t=g(x)一个为增函数,一个为减函数时,y= f[g(x)]为减函数.
“同增异减”
[分析] 令 t=3x-π3,当 x∈R 时单调递增,所以当函数 y=sint 递增
正弦型函数的图像和性质讲义

有点的横坐标伸长到原来的2倍(纵坐标不变)。
y=sin 2x的图象可以看作是把 y=sinx的图象上所
有点的横坐标缩短到原来的 12倍(纵坐标不变)。
函数y=sinx ( >0且≠1)的图象可以看作是 把 y=sinx 的图象上所有点的横坐标缩短(当>1
时)或伸长(当0<<1时) 到原来的 1倍(纵坐标
提示:由于我们研究的函数仅限于 >0的情况,
所以只需要判断 的正负即可判断平移方向
思考:函数 y f (x)与 y f (ax b)的图像
有何关系?
问题 :怎样由y sin x的图象得到y Asin(x ) (其中A 0, 0)的图象?
答: (1)先画出函数y sin x的图象;
思考:函数y f (x)与函数y Af (x)的图象有何关系?
例2 1.
作函数 列表:
y
sin
2x
及
y
sin
1 2
x
的图象。
x
0
4
2
3
4
2x
0
2
3
2
2
sin 2x 0
2. 描点: 2 y 连线: 1
O
1
0
1
0
y=sinx
2
3 x
1
2
y=sin2x
1. 列表
x 0 2 3 4
1x 2
0
2
A就表示这个量振动时离开平衡位置的最 大距离,通常称为这个振动的振幅;
往复一次所需的时间 T 2 ,称为这个
振动的周期;
单位时间内往复振动的次数 f 1 ,
T 2
称为振动的频率;
x 称为相位;x=0时的相位φ称为初相。
正弦函数的图像和性质

; /redianticai/ 热点概念股 ;
招呼.至于陈三六,和白狼马の女人们,孩子们就暂时没有放出来了,要不然の话挤の慌.不过大家把酒言欢,过了壹会尔就提到了根汉要出去独闯の事情,壹听说根汉过段时间就要离开这里又要去独闯了,白萱有些不高兴了."小姨,要不你跟着根汉哥哥出去壹起闯荡吧."瑶瑶建议道:"你们 都这么久不见了,现在又要分开,太残忍了.""没什么,以后不是有你们陪伴嘛,他也不能总陪着咱,再说了,咱这么大人了要人陪干吗."白萱虽然壹开始有些不高兴,但是还是欣然接受.根汉也想说,要不和白萱还有钟薇壹起去吧,也算是对她们の弥补了.不过白萱和钟薇都表示,让自己独自 壹人离开,带上她们也不太方便,那闯荡也就没什么意义了,她们也习惯在这无心峰の宁静生活了.现在再出去打拼反而不美,不如就呆在这里好好体验生活,感悟天道,或许可以早壹日突破桎梏.对此根汉也只能是表示,罢了,就让她们呆在这里吧.这壹次自己出去独闯,也不知道要面对多少 艰难险阻,她们呆在这无心峰也挺好の,起码挺安全の.虽然现在不知道老疯子又去了哪里了,但要是万壹这里出了什么变故,他相信老疯子会瞬间就会出现の,壹切都会解决,所以在这里是最安全の.不过根汉也不想现在就离开,好久没见到白萱和钟薇了,现在也不想马上就离去,他表示起 码在这里呆上三年,在情域和无心峰这壹带转壹转再走.几天之后,根汉终于是来到了旁边の壹座侧峰.这里半山腰处,有壹个山洞,洞府口贴上了几张符纸,还是壹座封印结界."咱说蓝霞妹子,这么多年过去了,你还记着咱呢."根汉站在洞口,有些无奈の苦笑.这封印结界明显是刚刚不久前 才弄出来の,显然是蓝霞仙子,不乐意待见自己,故意将这里给封上の.里面没有传来回馈,不过这样の封印结界,却完全挡不住根汉.根汉壹步便迈进了封印结界之中,然后下壹秒,他就知道自己又闯
正弦函数的性质与图像

(2)奇函数
(3)周期函数,最小正周期T 2
(4)在区间-
2
2k , 2
2k
(k
Z )上递增,在区间2
2k ,
3 2
2k
(k
Z )上递减。
当x
2
2k,k Z时,ymax
1;当x
3 2
2k,k
Z时,ymin
小结
知识: 1.正弦函数的性质与图像 2.周期函数的定义思想方法:
思想方法: 1.数形结合(形—数—形;图像与性质的联系) 2.利用图像解三角方程与三角不等式 3.解决周期函数问题的一种方法
作业:课本42页课后练习A 练习B
解: sin x 2a 1并且sin x 1,1
-1 2a 1 1 0 a 1
a 0,1
例3:(1)求y=2sinx-1的单调递增区间。 (2)求y=-3sinx+1的单调递增区间。
解:
(1)ห้องสมุดไป่ตู้2k
2
,2k
2( k
Z)
(2)2k
2
(0,1) 1
O
(2π,0) (π,1)
x
3π ( ,0)
2
注:“五点法”作图时是令y r sin l中的分别为0, ,,3 ,2。 22
例如: y sin(2x) 1中就是令2x分别为0, ,,3 ,2 22
应用
例2:已知sin x 2a 1 0,(x R),求a的取值范围。
2
,2k
3 2
( k
Z
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)求值域及周期
2π (2)由y=sinx图像怎样变换得到y=5sin(3x- 3 )图像
(3)作函数y=5sin(3x-
2 π )在一个周期上的图象 3
课堂小结
一、A, ω , 的作用
A的作用:使正弦函数相应的函数值发生变化。 ω的作用:使正弦函数的周期发生变化。 的作用:使正弦函数的图象发生平移。 二、五点法作y =Asin(ωx + )的图像 三、 y =Asin(ωx + )的图像与y=sinx间的变换
0 0 0
1、列表
2
2、描点
3 2 3 4
3、连线
2 0
2
4
1
0
-1
2、ω的作用:研究 y=sinωx与y=sinx 图象的关系
先观察y=sin2x、y=sin x与y=sinx的图象间的关系
y 1
1 2
0 -1
π
2π
3π
4π
x
作y=sin
1 x 的图象 2
1 2
1、列表
2
2、描点
1
0 -1
π
2π
3π
4π
x
作y=sinx的图象
x
sinx
1、列表
2
2、描点
3 2
3、连线
2
0
0
0
0
1
-1
2、ω的作用:研究 y=sinωx与y=sinx 图象的关系 先观察y=sin2x、y=sin
y 1
1 x与y=sinx的图象间的关系 2
0 -1
π
2π
3π
4π
x
作y=sin2x的图象
2x x sin2x
2
π
2π x
0 0 0 0
2
1 2 1/2
π 0 0 0
3 2
-1 -2 -1/2
2π 0 0 0
1、A的作用:研究 y=Asinx 与 y=sinx 图象的关系
1 先观察y=2sinx、y= sinx与y=sinx的图象间的关系 2 y
2
1 0 -1 -2 A的作用:使正弦函数相应的函数值发生变化。 y=Asinx(A>0, A1)的图象是由y=sinx的图象上所有 点的纵坐标扩大 (当A>1时)或缩小(当0<A<1时)到原 来打的A倍而得到. π 2π x
π 12
π 3
7π 12
5π 6
x
x 2x
-3
6 0
0
12
3
3
2
3
0
7 12 3 2
3
5 6 2
0
y 3 sin( 2 x ) 3
y
o
x
横坐标不变
纵坐标不变
图像向左平移
y=sinx
y=3sin2x
y=sin2x
纵坐标伸长到原来的3倍
横坐标缩短到原来1/2
Π 6 个单位
6
2、将函数y=sinx图象向左平移1个单位,再向右平移 3个单位,可以得到函数(B)的图象。 (A)y=sin(x+2) (B)y=sin(x-2) (C)y=sin(x+4) (D)y=sin(x-4)
y
A ω
2 1
y=2sinx
π 2π
y= 1 sinx
2
y=sinx
振幅变换
0
-1 -2
x
y
2 3
7 6 3 2
5 3 2
x
x
4
3 4
5 4
7 4
9 4
3
2
4
0
4 )
2
3 2
2
sin( x
3
)
0
1
0
1
0
sin( x
0
1
0
1
0
3、 的作用:研究 y=sin(x+ )与y=sinx 图象的关系
与 y=sinx 的图象间的关系 先观察y = sin(x+ )、y = sin(x - )
3sin(2x+π) 3
注
一、正弦型函数 y = Asin(ω x+ ) (A 0, 0) 的图象可以将 y = sinx 的图象怎样变换得到 1、沿 x 轴压缩或伸长
1
倍;
2、沿 y 轴压缩或伸长A倍; 3、向左或向右平移 个单位
二、正弦型函数 y = Asin(ωx+ ) ,A>0, ω>0 的一些主要性质:
3、 的作用:研究 y=sin(x+ )与y=sinx 图象的关系
与 y=sinx 的图象间的关系 先观察y = sin(x+ )、y = sin(x - )
3 4
y 1
y = sin(x + ) 3
y=sinx
y = sin(x - 4 )
0 -1
x
x
π
2π
x
3 0
6
跟踪练习
横坐标缩短到原来的1/4倍 横坐标伸长到原来的4倍
1、y=sinx
y=sin4x
x 2、求函数y=sin 的最大值、最小值和最小正周期。 4 解:最大值是1,最小值是-1,最小正周期 T=8π。
3、将函数y=sin2x的横坐标伸长为原来的4倍得到( C) A y=sinx B y=sin4x C=sin( x/2 ) D y=sin8x
3 4
y 1
4
3
0 -1
2
3 2
π
2π
x
的作用:使正弦函数的图象发生平移。 y=sin(x+)(0)的图象是由y=sinx的图象
向左( >0)或向右(<0)平移 ∣ ∣个单位而成.
跟踪练习
图像向左平移
1、y=sinx
图像向右平移 个单位
6
个单位
y=sin( x+ ) 6
1 f T 2
2
为周期
周期T的倒数
为 频率,
ωx+ 为相位,
x=0 时的相位为初相。
1、A的作用:研究 y=Asinx 与 y=sinx 图象的关系 1 先观察y=2sinx、y= sinx与y=sinx的图象间的关系
y 2 1 0 -1 -2
x sinx 2sinx
1 sinx 2
3 2
3、连线
2
x
1 x 2
0
x
sin
0
0
1
2
0
3
-1
4
0
2、ω的作用:研究 y=sinωx与y=sinx 图象的关系
先观察y=sin2x、y=sin x与y=sinx的图象间的关系
y 1
1 2
0 -1
π
2π
3π
4π
x
ω的作用:使正弦函数的周期发生变化。
y=sinω x(ω >0, ω 1)的图象是由y=sinx 的图象上所有点的横坐标缩小(当ω >1时)或 扩大(当0<ω <1时)到原来的ω -1倍而得到.
1
y=sin2x
π
y=sin 1 x
2
2π
y=sinx
3π
周期变换
4π
0
-1
x
y
1
3
y = sin(x+ 3 )
4
y = sin(x - 4 )
2π
y=sinx
π
相位变换
x
-1
0
作函数y=3sin( 2x+ )简图并讨论此图像是由 y=sinx图像怎样变换得到的。
y 3
3
-π o 6
跟踪练习
1、函数y=sinx
纵坐标扩大到原来的4倍 纵坐标缩小到原来的1/4
y=4sinx
2、求函数y=8sinx的最大值、最小值和最小正 周期:
解 y=8sinx的最大值是8,最小值是-8, 最小正周期T=2π
2、ω的作用:研究 y=sinωx与y=sinx 图象的关系
1 先观察y=sin2x、y=sin x与y=sinx的图象间的关系 2 y
定义域:R
值域:[-A,A],最大值是A,最小值是-A 2 周期: T
想一 想 求下列函数的最大值、最小值和周期:
1.y=5sinx
4.y= 2sin(x+ ) 6
1 2.y=sin x 4
3 5.y=2sin(3x+ 4 )
3.y=sin(x- )
思考 题
2π 已知函数y=5sin(3x) 3
复 习
正弦函数 y = sinx 的图象、定义域、值域、周期
y
1 x 0 -1 x sinx 0 0
2
π 0
2π
3 2
3π 2 0
4π
1
-1
定义域: R
值域: [-1,1]
周期: 2π
正弦型函数y =Asin(ωx + )
对于正弦型函数,我们称:
A 为 振幅, ω为 角速度, T
