2021届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
2021届江苏省淮安、宿迁、连云港、徐州苏北四市高三上学期期末化学试卷

C.对工业废水、生活污水净化处理,减少污染物的排放
D.催化处理汽车尾气,减轻氮氧化物污染和光化学烟雾
2.下列有关氮元素及其化合物的表示正确的是
A.质子数为7、中子数为8的氮原子:87N
B.溴化铵的电子式:
C.氮原子的结构示意图:
D.间硝基甲苯的结构简式:
【最新】江苏省淮安、宿迁、连云港、徐州苏北四市高三上学期期末化学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.【最新】巴黎气候变化大会召开,旨在保护环境造福人类。下列说法不正确的是
A.扩大铅蓄电池、汞锌锰干电池的生产,满足消费需求
B.向氨水中不断通入CO2,随着CO2的增加, 不断增大
C.3C(s) +CaO(s)=CaC2(s) +CO( g)在常温下不能自发进行,说明该反应的△H>0
D.合成氨时,其他条件不变升高温度,反应速率v(H2)和氢气的平衡转化率均增大
12.利用CO和H2在催化剂的作用下合成甲醇,发生的反应如下:CO(g)+2H2(g) CH3OH(g)。在体积一定的密闭容器中按物质的量之比1:2充入CO和H2,测得平衡混合物中CH3OH的体积分数在不同压强下随温度的变化如图所示下列说法正确的是( )
C.化合物X2Y,Z2Y中化学键的类型相同
D.元素Y的简单气态氢化物的热稳定性比W的弱
6.常温下,下列各组离子一定能在指定溶液中大量共存的是()
A.pH=l的溶液中:Ba2+、Fe3+、Cl-、SCN-
B.能使酚酞变红的溶液:Ca2+、K+、HCO3-、CO32-
江苏省苏北四市2021届高三上学期第一次质量检测(期末)数学(文)试题(含答案)

江苏省苏北四市2020-2021学年度高三年级第一次质量检测数学文科Ⅰ卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知集合{|02}A x x =<<,{|11}B x x =-<<,则A B =U _____. 答案:{12}x x -<<2.已知复数z 满足24z =-,且z 的虚部小于0,则z =_____. 答案:2i -3.若一组数据7,,6,8,8x 的平均数为7,则该组数据的方差是_____. 答案:454.执行如图所示的伪代码,则输出的结果为_____. 答案:205.函数2()log 2f x x =-的定义域为_____. 答案:[4,+)∞6.某学校高三年级有,A B 两个自习教室,甲、乙、丙3名学生各自随机选择其中一个教室自习,则甲、乙两人不在同一教室上自习的概率为______. 答案:127.若关于x 的不等式230x mx -+<的解集是(1,3),则实数m 的值为______. 答案:48.在平面直角坐标系xOy 中,双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px =上,则实数p 的值为______.9.已知等差数列{}n a 的前n 项和为n S ,298a a +=,55S =-,则15S 的值为_____. 答案:13510.已知函数3sin 2y x =的图象与函数cos2y x =的图象相邻的三个交点分别是,,A B C ,则ABC ∆的面积为_____.答案:3π 11.在平面直角坐标系xOy 中,已知圆22:48120M x y x y +--+=,圆N 与圆M 外切与点(0,)m ,且过点(0,2)-,则圆N 的标准方程为______. 答案:22(2)8x y ++=12.已知函数()f x 是定义在R 上的奇函数,其图象关于直线1x =对称,当(0,1]x ∈时,()ax f x e =-(其中e 是自然对数的底数),若(2020ln 2)8f -=,则实数a 的值为_____. 答案:313.如图,在ABC ∆中,,D E 是BC 上的两个三等分点,2AB AD AC AE ⋅=⋅u u u r u u u ru u u r u u u r,则cos ADE ∠的最小值为____.答案:4714.设函数3()||f x x ax b =--,[1,1]x ∈-,其中,a b R ∈.若()f x M ≤恒成立,则当M 取得最小值时,a b +的值为______.答案:34二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤15. (本小题满分14分)如图,在三棱锥P ABC -中,AP AB =,,M N 分别为棱,PB PC 的中点,平面PAB ⊥平面PBC . (1)求证:BC ∥平面AMN ; (2)求证:平面AMN ⊥平面PBC .解:(1)在PBC △中,因为M ,N 分别为棱PB ,PC 的中点,所以MN // BC . ………………………………3分 又MN ⊂平面AMN ,BC ⊄平面AMN ,所以BC //平面AMN .…………………………6分 (2)在PAB △中,因为AP AB =,M 为棱PB 的中点,所以AM PB ⊥.………………………………8分又因为平面PAB ⊥平面PBC ,平面PAB I 平面PBC PB =,AM ⊂平面PAB , 所以AM ⊥平面PBC .…………………………………………………………12分 又AM ⊂平面AMN ,所以平面AMN ⊥平面PBC . …………………………14分16. (本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且5cos A =. (1)若5a =,25c =b 的值; (2)若4B π=,求tan2C 的值.解:(1)在ABC △中,由余弦定理2222cos b c bc A a +-=得,252022525b +-⨯=,即2450b b --=, …………………………4分 解得5b =或1b =-(舍),所以5b =. ………………………………………6分 (2)由5cos A =及0A <<π得,22525sin 1cos 1()55A A =-=-=,…8分 所以210cos cos(())cos()sin )4C A B A A A π=π-+=-+=-=又因为0C <<π,所以2210310sin 1cos 1()1010C C =-=-=, 从而310sin 10tan 3cos 1010C C C ===,………………………………………………12分所以222tan 233tan 21tan 134C C C ⨯===---.………………………………………14分17. (本小题满分14分)如图,在圆锥SO 中,底面半径R 为3,母线长l 为5.用一个平行于底面的平面区截圆锥,截面圆的圆心为1O ,半径为r ,现要以截面为底面,圆锥底面圆心O 为顶点挖去一个倒立的小圆锥1OO ,记圆锥1OO 的体积为V . (1)将V 表示成r 的函数; (2)求V 得最大值.解:(1)在SAO △中,2222534SO SA AO =-=-, …………………………2分 由1SNO △∽SAO △可知,1SO r SO R =,所以143SO r =,……………………4分 所以1443OO r =-,所以223144()π(4)π(3),03339V r r r r r r =-=-<<.…7分(2)由(1)得234()π(3),039V r r r r =-<<,所以24()π(63)9V r r r '=-,令()0V r '=,得2r =,………………………9分当(0,2)r ∈时,()0V r '>,所以()V r 在(0,2)上单调递增; 当(2,3)r ∈时,()0V r '<,所以()V r 在(2,3)上单调递减.所以当2r =时,()V r 取得最大值16π(2)9V =.答:小圆锥的体积V 的最大值为16π9.………………………………………14分18. (本小题满分16分)在平面直角坐标系xOy 中,已知椭圆2222:1x y C a b +=(0)a b >>的右顶点为A ,过点A 作直线l 与圆222:O x y b +=相切,与椭圆C 交于另一点P ,与右准线交于点Q .设直线l 的斜率为k .(1)用k 表示椭圆C 的离心率;(2)若0OP OQ ⋅=u u u r u u u r,求椭圆C 的离心率.(1)直线l 的方程为)(a x k y -=,即0=--ak y kx ,因为直线l 与圆222b y x O =+:相切,所以b k ak=+-12,故2222b a b k -=. 所以椭圆C 的离心率222111b e a k =-=+4分(2)设椭圆C 的焦距为2c ,则右准线方程为2a x c=, 由⎪⎩⎪⎨⎧=-=c ax a x k y 2)(得c ac a k a c a k y -=-=22)(,所以))(,(22c ac a k c a Q -,…6分 由⎪⎩⎪⎨⎧-==+)(12222a x k y b y a x 得02)(2224232222=-+-+b a k a x k a x k a b , 解得222223k a b ab k a x p +-=,则22222222232)(k a b kab a k a b ab k a k y p +-=-+-=, 所以)2-2222222223ka b kab k a b ab k a P ++-,(,……………………………………………10分 因为0=⋅OQ OP ,所以02)(222222222232=+-⋅-++-⋅k a b kab c ac a k k a b ab k a c a ,即)(2)(22222c a k b b k a a -=-,………………………………………………12分由(1)知,2222ba b k -=,所以22422222)(2)(b a c a b b b a b a a --=--, 所以c a a 22-=,即c a 2=,所以21=a c ,故椭圆C 的离心率为21.……16分19. (本小题满分16分) 已知函数1()()ln f x a x x=-()a R ∈.(1)若曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=,求a 的值; (2)若()f x 的导函数'()f x 存在两个不相等的零点,求实数a 的取值范围; (3)当2a =时,是否存在整数λ,使得关于x 的不等式()f x λ≥恒成立?若存在, 求出λ的最大值;若不存在,说明理由.解:(1)()2111()ln f x x a x x x'=+-,因为曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=,所以(1)11f a '=-=-,得0a =.……………………………………………2分(2)因为21ln ()ax x f x x-+'=存在两个不相等的零点. 所以()1ln g x ax x =-+存在两个不相等的零点,则1()g x a x'=+.①当0a ≥时,()0g x '>,所以()g x 单调递增,至多有一个零点.……4分②当0a <时,因为当1(0)x a∈-,时,()0g x '>,()g x 单调递增, 当1(+)x a∈-∞,时,()0g x '<,()g x 单调递减, 所以1x a =-时,max 11()()ln()2g x g a a=-=--. …………………………6分因为()g x 存在两个零点,所以1ln()20a-->,解得2e 0a --<<.………7分因为2e 0a --<<,所以21e 1a->>.因为(1)10g a =-<,所以()g x 在1(0)a-,上存在一个零点. …………8分 因为2e 0a --<<,所以211()a a->-.因为22111[()]ln()1g a a a-=-+-,设1t a =-,则22ln 1(e )y t t t =-->,因为20t y t-'=<,所以22ln 1(e )y t t t =-->单调递减,所以()2222ln e e 13e 0y <--=-<,所以22111[()]ln()10g a a a-=-+-<,所以()g x 在1()a-+∞,上存在一个零点. 综上可知,实数a 的取值范围为2(e ,0)--.…………………………………10分(3)当2a =时,1()(2)ln f x x x =-,()2211121ln ()ln 2x x f x x x x x x-+'=+-=, 设()21ln g x x x =-+,则1()20g x x'=+>.所以()g x 单调递增,且11()ln 022g =<,(1)10g =>,所以存在01(1)2x ∈,使得0()0g x =,……12分 因为当0(0)x x ∈,时,()0g x <,即()0f x '<,所以()f x 单调递减;当0(+)x x ∈∞,时,()0g x >,即()0f x '>,所以()f x 单调递增,所以0x x =时,()f x 取得极小值,也是最小值,此时()0000000111()(2)ln (2)12(4)4f x x x x x x x =-=--=-++,……………14分因为01(1)2x ∈,,所以0()(10)f x ∈-,, 因为()f x λ≥,且λ为整数,所以1λ-≤,即λ的最大值为1-.………16分20. (本小题满分16分)已知数列{}n a 的首项13a =,对任意的*n N ∈,都有11n n a ka +=-(0)k ≠,数列{1}n a -是公比不为1的等比数列. (1)求实数k 的值;(2)设4,1,n n n n b a n -⎧⎪=⎨-⎪⎩为奇数为偶数,数列{}n b 的前n 项和为n S ,求所有正整数m 的值,使得221m m S S -恰好为数列{}n b 中的项.解:(1)由11n n a ka +=-,13a =可知,231a k =-,2331a k k =--,因为{1}n a -为等比数列,所以2213(1)(1)(1)a a a -=--,即22(32)2(32)k k k -=⨯--,即231080k k -+=,解得2k =或43k =,…2分 当43k =时,143(3)3n n a a +-=-,所以3n a =,则12n a -=, 所以数列{1}n a -的公比为1,不符合题意;当2k =时,112(1)n n a a +-=-,所以数列{1}n a -的公比1121n n a q a +-==-,所以实数k 的值为2. …………………………………………………………4分(2)由(1)知12n n a -=,所以4n n n n b n - , ⎧⎪=⎨2, ⎪⎩为奇数,为偶数,则22(41)4(43)4[4(21)]4m m S m =-++-+++--+L2(41)(43)[4(21)]444m m =-+-++--++++L L144(4)3m m m +-=-+,……………………………………………………6分 则212244(4)3m m m m S S b m m --=-=-+,因为22+1324m m m b b m +=-+,又222+322+1()()3420m m m m m b b b b ++-+=⨯->,且2350b b +=>,130b =>,所以210m S ->,则20m S >,设2210,m t m Sb t S -=>∈*N ,…………………………………………………………8分 则1,3t =或t 为偶数,因为31b =不可能,所以1t =或t 为偶数,①当2121=m m S b S -时,144(4)3344(4)3m m m m m m +--+=--+,化简得2624844m m m -+=--≤, 即242m m -+≤0,所以m 可取值为1,2,3,验证624135787,3,323S S S S S S ===得,当2m =时,413S b S =成立.…………………12分②当t 为偶数时,1222144(4)331443124(4)134m m m m mm m S S m m m m +---+==+--+--++, 设231244m m m m c -+-=,则211942214m m m m m c c ++-+-=, 由①知3m >,当4m =时,545304c c --=<;当4m >时,10m m c c +->,所以456c c c ><<L ,所以m c 的最小值为5191024c -=, 所以22130151911024m m S S -<<+<-+,令22214m m S b S -==,则2314312414mm m +=-+-+,即2-+-=,无整数解.m m31240综上,正整数m的值2.………………………………………………………16分。
江苏省淮安宿迁连云港徐州苏北四市2021届高三上学期期末考

江苏省淮安宿迁连云港徐州苏北四市2021届高三上学期期末考江苏省淮安、宿迁、连云港、徐州苏北四市2021届高三上学期期末考淮安等苏北四市2022-2022学年高三第二次调查测试生物试题2021.1(满分120分,考试时间100分钟)注意事项:考生在答题前,必须在答题纸的相应位置填写学校、姓名、班级和考试号,并填写相应的考试号。
回答多项选择题时,必须用2B铅笔填写;如果答案超过0.5毫米,请用黑色写在答题纸上。
如果答案无效,请用黑色写在答题纸上。
第ⅰ卷选择题(共55分)一、单选题:这部分包括20个子题,每个子题2分,共40分。
每个子问题中给出的四个选项中只有一个。
最符合问题的意思。
1.关于组成生物体化合物的叙述,正确的是a、核糖核苷酸是DNA的基本单位。
RNA是HIV的主要遗传物质。
磷脂是生物膜的基本支架。
D.脂质的所有组成元素都含有磷[解析]本题考查细胞中化合物相关知识。
核糖核苷酸是rna的基本单位,脱氧核苷酸是dna的基本单位,a错误;一种生物的遗传物质是dna或rna,hiv的遗传物质是rna,b错误;生物膜的基本支架是磷脂双分子层,c正确;脂质包括脂肪、磷脂和固醇,脂肪的元素组成为c、h、o,d错误。
[答案]c2.ATP的描述是正确的a.大肠杆菌细胞产生atp的主要场所是线粒体b、细胞的持续分裂伴随着ATP和ADP的相互转化。
T代表胸腺嘧啶,所以ATP的结构与核苷酸非常相似。
D.ATP分子由一个腺嘌呤和三个磷酸基团组成[解析]本题考查atp的结构和功能相关知识。
大肠杆菌细胞为原核细胞,无线粒体,a错误;细胞分裂过程中需要atp水解供应能量,因此伴随着atp与adp的相互转化,b 正确;atp中“t”表示三个,c错误;atp是由一个腺苷和三个磷酸基组成的,d错误。
[答案]b3.下图为P物质和Q物质移出细胞的示意图。
相关描述是正确的a.物质p可能是二氧化碳b.物质q可能表示神经递质c、 P物质和Q物质的细胞外转运都需要ATPD。
江苏省苏北四市2022-2023学年高三上学期期末考试 数学含答案

2022~2023学年高三年级模拟试卷数 学(答案在最后)(满分:150分 考试时间:120分钟)2023.1一、 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若非空且互不相等的集合M ,N ,P 满足M ∩N =M ,N ∪P =P ,则M ∪P =( ) A. M B. N C. P D. ∅2. 已知i 5=a +b i(a ,b ∈R ),则a +b 的值为( ) A. -1 B. 0 C. 1 D. 23. 设p :4x -3<1;q :x -(2a +1)<0,若p 是q 的充分不必要条件,则( ) A. a >0 B. a >1 C. a ≥0 D. a ≥14. 已知点Q 在圆C :x 2-4x +y 2+3=0上,点P 在直线y =x 上,则PQ 的最小值为( ) A. 2 -1 B. 1 C. 2 D. 25. 某次足球赛共8支球队参加,分三个阶段进行.(1) 小组赛:经抽签分成甲、乙两组,每组4队进行单循环比赛,以积分和净胜球数取前两名;(2) 半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名进行主、客场交叉淘汰赛(每两队主、客场各赛1场),决出胜者;(3) 决赛:两个胜队参加,比赛1场,决出胜负. 则全部赛程共需比赛的场数为( )A. 15B. 16C. 17D. 186. 若f (x )=sin (2x +π6 )在区间[-t ,t ]上单调递增,则实数t 的取值范围是( )A. [π6 ,π2 ]B. (0,π3 ]C. [π6 ,π3 ]D. (0,π6]7. 足球是由12个正五边形和20个正六边形组成的.如图,将足球上的一个正六边形和它相邻的正五边形展开放平,若正多边形边长为a ,A ,B ,C 分别为正多边形的顶点,则AB → ·AC →=( )A. (3+3 cos 18°)a 2B. (3 +cos 18°)a 2C. (3+2 cos 18°)a 2D. (33 +3cos 18°)a 28. 在某次数学节上,甲、乙、丙、丁四位同学分别写下了一个命题:甲:ln 3<3 ln 2;乙:ln π<πe;丙:212<12;丁:3eln 2>42 .所写为真命题的是( )A. 甲和乙B. 甲和丙C. 丙和丁 D .甲和丁二、 多选题:本题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9. 连续抛掷一枚骰子2次,记事件A 表示“2次结果中正面向上的点数之和为奇数”,事件B 表示“2次结果中至少一次正面向上的点数为偶数”,则( )A. 事件A 与事件B 不互斥B. 事件A 与事件B 相互独立C. P (AB )=34D. P (A |B )=2310. 在长方体ABCDA 1B 1C 1D 1中,AA 1=3,底面ABCD 是边长为2的正方形,底面A 1B 1C 1D 1的中心为M ,则( )A. C 1D 1∥平面ABMB. 向量AM → 在向量AC →上的投影向量为12 AC →C. 棱锥MABCD 的内切球的半径为31010D. 直线AM 与BC 所成角的余弦值为111111. 公元前6世纪,古希腊的毕达哥拉斯学派把5-12 (5-12≈0.618)称为黄金数.离心率等于黄金数的倒数的双曲线称为黄金双曲线.若黄金双曲线E :x 2a 2 -y 2=1(a >0)的左、右顶点分别为A 1,A 2,虚轴的上端点为B ,左焦点为F ,离心率为e ,则( )A. a 2e =1B. A 2B ·FB →=0C. 顶点到渐近线的距离为eD. △A 2FB 的外接圆的面积为2+54π 12. 设函数f (x )的定义域为R ,f (2x +1)为奇函数,f (x +2)为偶函数,当x ∈[0,1]时,f (x )=a x +b ,若f (0)+f (3)=-1,则( )A. b =-2B. f (2 023)=-1C. f (x )为偶函数D. f (x )的图象关于点(12,0)对称三、 填空题:本题共4小题,每小题5分,共计20分.13. 若(1-2x )5(x +2)=a 0+a 1x +…+a 6x 6,则a 3=________. 14. 某学校组织1 200名学生进行“防疫知识测试”.测试后统计分析如下:学生的平均成绩为x =80,方差为s 2=25.学校要对成绩不低于90分的学生进行表彰.假设学生的测试成绩X 近似服从正态分布N (μ,σ2),其中μ近似为平均数x ,σ2近似为方差s 2,则估计获表彰的学生人数为________.(四舍五入,保留整数)参考数据:随机变量X 服从正态分布N (μ,σ2),则P (μ-σ<X <μ+σ)=0.682 7, P (μ-2σ<X <μ+2σ)=0.954 5,P (μ-3σ<X <μ+3σ)=0.997 3.15. 已知抛物线y 2=2x 与过点T (6,0)的直线相交于A ,B 两点,且OB ⊥AB (O 为坐标原点),则△OAB 的面积为________.16. 已知函数f (x )=⎩⎪⎨⎪⎧e x -1,x ≤1,|ln (x -1)|,x >1,则函数F (x )=f (f (x ))-2f (x )-12 的零点个数为________.四、 解答题:本题共6小题,共计70分.解答时应写出必要的文字说明、证明过程或演算步骤.17. (本小题满分10分)已知△ABC 为锐角三角形,内角A ,B ,C 的对边分别为a ,b ,c ,且a cos B +b cos A =2c cos C .(1) 求角C 的大小;(2) 若c =2,求△ABC 的周长的取值范围.18.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ,S 3=14,S 6=126. (1) 求数列{a n }的通项公式;(2) 当n ∈N *时,a n b 1+a n -1b 2+…+a 1b n =4n -1,求数列{b n }的通项公式.19.(本小题满分12分)如图,在四棱锥SABCD 中,侧面SAD ⊥底面ABCD ,SA ⊥AD ,且四边形ABCD 为平行四边形,AB =1,BC =2,∠ABC =π3,SA =3.(1) 求二面角SCDA 的大小;(2) 若点P 在线段SD 上且满足SP → =λSD →,试确定实数λ的值,使得直线BP 与平面PCD 所成的角最大.20.(本小题满分12分)设椭圆E :x 2a 2 +y 2b 2 =1(a >b >0)的左、右焦点分别为F 1(-c ,0),F 2(c ,0),离心率为33 ,若椭圆E 上的点到直线l :x =a 2c的最小距离为3-3 .(1) 求椭圆E 的方程;(2) 过F 1作直线交椭圆E 于A ,B 两点,设直线AF 2,BF 2与直线l 分别交于C ,D 两点,线段AB ,CD 的中点分别为M ,N ,O 为坐标原点,若M ,O ,N 三点共线,求直线AB 的方程.21.(本小题满分12分)第22届世界杯于2022年11月21日到12月18日在卡塔尔举办.在决赛中,阿根廷队通过点球战胜法国队获得冠军.(1) 扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有23 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数X 的分布列和数学期望.(2) 好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外2人中的1人,接球者接到球后再等可能地随机传向另外2人中的1人,如此不停地传下去,假设传出的球都能接住.记第n 次传球之前球在甲脚下的概率为p n ,易知p 1=1,p 2=0.① 试证明:{p n -13}为等比数列;② 设第n 次传球之前球在乙脚下的概率为q n ,比较p 10与q 10的大小.22. (本小题满分12分)已知函数f (x )=a e x +cos x +12 x 2,其中a 为实数,e 是自然对数的底数.(1) 当a =0时,求曲线f (x )在点(π2 ,f (π2))处的切线方程;(2) 若g (x )为f (x )的导数,g (x )在(0,π)上有两个极值点,求a 的取值范围.2022~2023学年高三年级模拟试卷(苏北四市)数学参考答案及评分标准1. C2. C3. A4. A5. C6. D7. A8. B9. AD 10. ABD 11. ABD 12. AC 13. -120 14. 27 15. 152 16. 517. 解:(1) 由正弦定理,得sin A cos B +sin B cos A =2sin C cos C , 即sin (A +B )=2sin C cos C ,即sin C = 2sin C cos C .(2分) 又C ∈(0,π),所以sin C ≠0, 所以cos C =12 ,故C =π3.(4分)(2) 由正弦定理,得a =c sin A sin C =43 sin A ,b =43 sin B ,(5分)所以△ABC 的周长L =a +b +c =43 (sin A +sin B )+2=43[sin A +sin (2π3 -A )]+2=4(32 sin A +12 cos A )+2=4sin (A +π6)+2.(8分) 由△ABC 为锐角三角形可知,⎩⎨⎧0<A <π2,0<B =2π3-A <π2,得π6 <A <π2 ,所以π3 <A +π6 <2π3 ,所以sin (A +π6 )∈(32 ,1],所以△ABC 的周长的取值范围是(2+23 ,6].(10分) 18. 解:(1) 设数列{a n }的公比为q .⎩⎪⎨⎪⎧S 3=a 1+a 2+a 3=14 ①,S 6-S 3=a 4+a 5+a 6=112 ②, ②① 得q 3=8,所以q =2,(3分) 有S 3=a 1+a 2+a 3=a 1+2a 1+4a 1=14,得a 1=2, 则数列{a n }的通项公式为a n =2n .(注:若使用等比求和公式没有讨论公比q =1,扣1分)(5分)(2) 由2n b 1+2n -1b 2+…+2b n =4n -1,n =1时2b 1=3,得b 1=32 ,(6分)所以n ≥2时,2n -1b 1+2n -2b 2+…+2b n -1=4n -1-1.(8分)2n b 1+2n -1b 2+…+2b n =2(2n -1b 1+2n -2b 2+…+2b n -1)+2b n =4n -1,(10分) 有2(4n -1-1)+2b n =4n -1,得n ≥2时,b n =4n -1+12 ,(11分)又b 1=32 ,故b n =4n -1+12.(12分)19. 解:(1) 连接AC ,在△ABC 中,AB =1,BC =2,∠ABC =π3 ,由余弦定理得AC =3 ,所以∠BAC =π2.(2分)因为侧面SAD ⊥底面ABCD ,平面SAD ∩底面ABCD =AD ,SA ⊥AD , 所以SA ⊥平面ABCD ,所以SA ⊥AC .(4分)(解法1)以A 为原点建立如图所示的空间直角坐标系.则B (1,0,0),C (0,3 ,0),S (0,0,3),D (-1,3 ,0),CD → =(-1,0,0),SC →=(0,3 ,-3).设平面SCD 的法向量为n =(x ,y ,z ),由⎩⎪⎨⎪⎧n ·CD →=0,n ·SC →=0, 得⎩⎨⎧x =0,3y -3z =0, 可取n =(0,3 ,1).易知m =(0,0,1)为平面ABCD 的一个法向量.(6分)所以cos θ=n ·m |n ||m | =11+3 =12 .因为二面角SCDA 为锐角,所以θ=π3 ,即二面角SCDA 的大小为π3.(8分)(解法2)因为SA ⊥平面ABCD ,所以SA ⊥CD .因为四边形ABCD 为平行四边形,所以AC ⊥CD , 又SA ∩AC =A ,所以CD ⊥平面SAC ,所以CD ⊥SC .又平面ACD ∩平面SCD =CD ,所以∠ACS 为二面角SCDA 的平面角.(6分)因为tan ∠ACS =33 =3 ,二面角SCDA 为锐角,所以θ=π3 ,即二面角SCDA 的大小为π3.(8分)(2) 设P (x 1,y 1,z 1),SP → =λSD →, 得(x 1,y 1,z 1-3)=λ(-1,3 ,-3),x 1=-λ,y 1=3 λ,z 1=3-3λ,所以P (-λ,3 λ,3-3λ) ,所以BP →=(-λ-1,3 λ,3-3λ).(10分)由(1)知平面PCD 的一个法向量为n =(0,3 ,1).因为cos α=BP →·n |BP →||n | =3λ+3-3λ2(λ+1)2+(3λ)2+(3-3λ)2 =3213λ2-16λ+10 , 所以当λ=813 时,cos α最大, 即当λ=813时,BP 与平面PCD 所成的角最大.(12分)20. 解:(1) 由条件知⎩⎨⎧c a =33,a2c -a =3-3,解得⎩⎨⎧a =3,c =1,所以b 2=a 2-c 2=2,所以椭圆E 的方程为x 23 +y 22=1.(4分)(2) 由(1)知,F 1(-1,0),F 2(1,0),由题意知,直线AB 的斜率不为0.设直线AB 的方程为x =my -1,联立⎩⎪⎨⎪⎧x 23+y 22=1,x =my -1,消去x 并整理得(2m 2+3)y 2-4my -4=0.设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=4m2m 2+3 ,y 1y 2=-42m 2+3 .(6分)所以y M =2m2m 2+3 ,x M =my M -1=-32m 2+3 ,所以直线OM 的斜率为k OM =y M x M =-2m3. 直线AF 2的方程为y =y 1x 1-1 (x -1),直线l 的方程为x =3,则C (3,2y 1x 1-1 ).直线BF 2的方程为y =y 2x 2-1 (x -1),同理有D (3,2y 2x 2-1).(8分)所以y N =y 1x 1-1 +y 2x 2-1 =y 1my 1-2 +y 2my 2-2 =y 1(my 2-2)+y 2(my 1-2)(my 1-2)(my 2-2)=2my 1y 2-2(y 1+y 2)m 2y 1y 2-2m (y 1+y 2)+4 =2m ·-42m 2+3-2×4m2m 2+3m 2·-42m 2+3-2m ·4m2m 2+3+4 =4mm 2-3 ,(10分) 所以直线ON 的斜率为k ON =y N x N =4m3(m 2-3).由M ,O ,N 三点共线可得k OM =k ON ,即-2m 3 =4m3(m 2-3) ,所以m =0或m =±1.故直线AB 的方程为x =-1或x -y +1=0或x +y +1=0.(12分)21. (1) 解:依题意可得,门将每次可以扑到点球的概率为p =13 ×13 =19 ,(1分)门将在前三次扑到点球的个数X 可能的取值为0,1,2,3,易知X ~B (3,19 ),所以P (X =k )=C k 3 ×(19 )k ×(89 )3-k,k =0,1,2,3,(2分) 故X 的分布列为所以X 的数学期望E (X )=3×19 =13.(6分)(2) ① 证明:第n 次传球之前球在甲脚下的概率为p n ,则当n ≥2时,第n -1次传球之前球在甲脚下的概率为p n -1, 第n -1次传球之前球不在甲脚下的概率为1-p n -1, 则p n =p n -1×0+(1-p n -1)×12 =-12 p n -1+12 ,(8分)所以{p n -13 }是以23 为首项, 公比为-12的等比数列. (10分)② 解:由①可知p n =23 (-12 )n -1+13 ,所以p 10=23 (-12 )9+13 <13 ,所以q 10=12 (1-p 10)=12 [23 -23 (-12 )9]>13,故p 10<q 10.(12分)22. 解:(1) 当a =0时,f (x )=cos x +12 x 2,则f ′(x )=-sin x +x ,所以f ′(π2 )=π2 -1.(1分)又f (π2 )=π28 ,所以曲线y =f (x )在点(π2 ,f (π2 ))处的切线方程为y =(π2 -1)x -π28 +π2 .(3分)(2) 因为g (x )=a e x -sin x +x ,所以g ′(x )=a e x -cos x +1,g (x )在(0,π)上有两个极值点,即g ′(x )在(0,π)内有两个变号零点. 令g ′(x )=0得a e x -cos x +1=0,所以a -cos x -1e x=0.(5分)设h (x )=a -cos x -1e x ,则h ′(x )=sin x +cos x -1e x =2sin (x +π4)-1e x, 当x ∈(0,π2 )时,sin (x +π4 )∈(22,1],所以h ′(x )>0,所以h (x )单调递增;当x ∈(π2 ,π)时,sin (x +π4 )∈(-22 ,22),所以h ′(x )<0,所以h (x )单调递减,(7分)所以h (0)=a ,h (π2)=a +e -π2 ,h (π)=a +2e -π.当-e-π2<a <-2e-π时,h (0)<0,h (π2)>0,h (π)<0,所以∃x 1∈(0,π2 ),x 2∈(0,π),使h (x 1)=h (x 2)=0.(9分)当x ∈(0,x 1)时,h (x )<0,g ′(x )<0,g (x )单调递减; 当x ∈(x 1,x 2)时,h (x )>0,g ′(x )>0,g (x )单调递增; 当x ∈(x 2,π)时,h (x )<0,g ′(x )<0,g (x )单调递减; 即-e -π2<a <-2e-π时,g (x )在(0,π)上有两个极值点.(12分)。
2020届江苏省苏北四市(徐州、宿迁、淮安、连云港)高三上学期期末数学试题(解析版)

2020届江苏省苏北四市(徐州、宿迁、淮安、连云港)高三上学期期末数学试题一、填空题1.已知集合{}02A x x =<<,{}11B x x =-<<,则A B =U _________. 【答案】{}12x x -<<利用并集的定义可计算出集合A B U . 【详解】{}02A x x =<<Q ,{}11B x x =-<<,因此,{}12A B x x ⋃=-<<.故答案为:{}12x x -<<.本题考查并集的计算,熟悉并集的定义是关键,考查计算能力,属于基础题. 2.已知复数z 满足24z =-,且z 的虚部小于0,则z =_________. 【答案】2i -设(),z a bi a b R =+∈,可知0b <,利用复数的乘法法则可得出关于实数a 、b 的方程组,解出即可. 【详解】设(),z a bi a b R =+∈,由题意可知()()222224z a bi a babi =+=-+=-,则224200a b ab b ⎧-=-⎪=⎨⎪<⎩,解得02a b =⎧⎨=-⎩,因此,2z i =-.故答案为:2i -.本题考查复数的求解,涉及复数的乘法运算和复数相等,解题的关键就是利用复数相等列方程组求解,考查运算求解能力,属于基础题.3.若一组数据7,x ,6,8,8的平均数为7,则该组数据的方差是______. 【答案】45根据平均值计算得到6x =,再计算方差得到答案. 【详解】 平均数为768875x ++++=,故6x =,方差为()()()()()222227776767878455-+-+-+-+-=故答案为:45本题考查了平均值和方差的计算,意在考查学生的计算能力. 4.执行如图所示的伪代码,则输出的结果为_________.【答案】20根据程序伪代码,列举出程序的每一步,即可得出输出结果. 【详解】当16I =<时,112I =+=,022S =+=; 当26I =<时,213I =+=,235S =+=; 当36I =<时,314I =+=,549S =+=; 当46I =<时,415I =+=,9514S =+=; 当56I =<时,516I =+=,14620S =+=.66I =<不满足,输出S 的值为20.故答案为:20.本题考查利用程序伪代码求输出结果,只需结合程序伪代码列举出程序的每一步,计算即可,考查计算能力,属于基础题.5.函数2()log 2f x x =-的定义域是 . 【答案】[4,)+∞解:因为2log 204x x -≥∴≥,故定义域为[4,)+∞6.某学校高三年级有A 、B 两个自习教室,甲、乙、丙3名学生各自随机选择其中一个教室自习,则甲、乙两人不在同一教室上自习的概率为________. 【答案】12利用乘法计数原理可计算出甲、乙、丙3名学生各自随机选择其中一个教室自习共有32种,利用分步乘法计数原理计算出甲、乙两人不在同一教室上自习的排法种数,然后利用古典概型的概率公式可计算出所求事件的概率. 【详解】由题意可知,甲、乙、丙3名学生各自随机选择其中一个教室自习共有32种, 甲、乙两人不在同一教室上自习,可先考虑甲在A 、B 两个自习教室选一间教室自习,然后乙在另一间教室自习,则丙可在A 、B 两个自习教室随便选一间自习教室自习,由分步计数原理可知,有224⨯=种选择. 因此,甲、乙两人不在同一教室上自习的概率为4182=. 故答案为:12. 本题考查利用古典概型的概率公式计算事件的概率,同时也考查了分步计数原理的应用,考查计算能力,属于中等题.7.若关于x 的不等式230x mx -+<的解集是()1,3,则实数m 的值为_____. 【答案】4由题意知,关于x 的方程230x mx -+=的两根分别为1和3,利用韦达定理可求出实数m 的值. 【详解】由题意知,关于x 的方程230x mx -+=的两根分别为1和3,由韦达定理得134m =+=.故答案为:4.本题考查利用一元二次不等式的解求参数,考查计算能力,属于基础题.8.在平面直角坐标系xOy 中,双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px =上,则实数p 的值为________.【答案】14求出双曲线2213x y -=的右准线与渐近线的交点坐标,并将该交点代入抛物线的方程,即可求出实数p 的方程. 【详解】双曲线2213x y -=的半焦距为2,则双曲线2213x y -=的右准线方程为32x =,渐近线方程为y x =,所以,该双曲线右准线与渐近线的交点为3,2⎛ ⎝⎭.由题意得23222p ⎛⎫±=⨯ ⎪ ⎪⎝⎭,解得14p =. 故答案为:14.本题考查利用抛物线上的点求参数,涉及到双曲线的准线与渐近线方程的应用,考查计算能力,属于中等题.9.已知等差数列{}n a 的前n 项和为n S ,298a a +=,55S =-,则15S 的值为_________.【答案】135设等差数列{}n a 的公差为d ,根据题意列出关于1a 和d 的方程组,求出这两个量的值,然后利用等差数列的求和公式可计算出15S 的值. 【详解】设等差数列{}n a 的公差为d ,则291512985105a a a d S a d +=+=⎧⎨=+=-⎩,解得152a d =-⎧⎨=⎩,因此,()15115141515510521352S a d ⨯=+=⨯-+⨯=. 故答案为:135.本题考查等差数列基本量的计算,同时也考查了等差数列求和公式的应用,解题的关键就是求出等差数列的首项和公差,考查方程思想的应用与计算能力,属于基础题. 10.已知函数2y x =的图象与函数cos 2y x =的图象相邻的三个交点分别是A 、B 、C ,则ABC ∆的面积为________.设A 、B 、C 是两个函数图象在y 轴右边且靠近y 轴的三个交点,求出这三个点的坐标,即可计算出ABC ∆的面积. 【详解】设A 、B 、C 是两个函数图象在y 轴右边且靠近y 轴的三个交点, 设点()11,A x y 、()22,B x y 、()33,C x y2cos 2x x =,得tan 23x =,得()26x k k Z ππ=+∈,解得()122k x k Z ππ=+∈.由于A 、B 、C 是两个函数图象在y 轴右边且靠近y 轴的三个交点,则112x π=,2712x π=,31312x π=,可得,122A π⎛⎫ ⎪ ⎪⎝⎭、7,122B π⎛⎫- ⎪ ⎪⎝⎭、13,122C π⎛ ⎝⎭,因此,ABC ∆的面积为131211222ABC S x x y y π∆=⨯-⨯-=⨯=.. 本题考查三角函数图象交点坐标的计算,同时也涉及了三角形面积的计算,求出交点坐标是关键,考查计算能力,属于中等题.11.在平面直角坐标系xOy 中,已知圆22:48120M x y x y +--+=,圆N 与圆M 外切于点()0,m ,且过点()0,2-,则圆N 的标准方程为_________. 【答案】()2228x y ++=将圆M 的方程化为标准方程,可求出m 的值,记点()0,A m 、()0,2B -,可知圆心N 为直线AM 和线段AB 中垂线的交点,进而可求出点N 的坐标,计算出BN 为圆N 的半径,即可得出圆N 的标准方程. 【详解】记点()0,A m 、()0,2B -,圆M 的标准方程为()()22248x y -+-=,圆心()2,4M ,将点A 的坐标代入圆M 的方程得28120m m -+=,得2m =或6.①若6m =,则点()0,6A ,线段AB 的中垂线方程为2y =,直线AM 的方程为6x y +=,由题意可知,圆心N 在直线AM 上,且在线段AB 的中垂线上,联立260y x y =⎧⎨+-=⎩,解得42x y =⎧⎨=⎩,则圆心N 的坐标为()4,2,圆N 的半径为BN ==,MN =M 的半径为此时,BN MN -=,则两圆内切,不合乎题意;②若2m =,则点()0,2A ,线段AB 的中垂线方程为0y =,直线AM 的方程为20x y -+=,由题意可知,圆心N 在直线AM 上,且在线段AB 的中垂线上, 联立020y x y =⎧⎨-+=⎩,解得20x y =-⎧⎨=⎩,则圆心N 的坐标为()2,0-,圆N 的半径为BN ==,MN =M 的半径为此时,BN MN +=,则两圆外切,合乎题意. 综上所述,圆N 的标准方程为()2228x y ++=. 故答案为:()2228x y ++=.本题考查利用两圆外切求圆的标准方程,解题的关键就是确定圆心的位置和半径,考查分析问题和解决问题的能力,属于中等题.12.已知函数()f x 是定义在R 上的奇函数,其图象关于直线1x =对称,当(]0,1x ∈时,()ax f x e =-(其中e 是自然对数的底数,若()2020ln 28f -=,则实数a 的值为_____. 【答案】3先推导出函数()y f x =的周期为4,可得出()()()2020ln 2ln 2ln 28f f f -=-=-=,代值计算,即可求出实数a 的值.【详解】由于函数()y f x =是定义在R 上的奇函数,则()()f x f x -=-, 又该函数的图象关于直线1x =对称,则()()11f x f x -=+, 所以,()()()()211f x f x f x f x +=-+=-=-⎡⎤⎣⎦,则()()()42f x f x f x +=-+=,所以,函数()y f x =是周期为4的周期函数, 所以()()()()ln 2ln 22020ln 2ln 2ln 228aa a f f f e e -=-=-====,解得3a =.故答案为:3.本题考查利用函数的对称性计算函数值,解题的关键就是结合函数的奇偶性与对称轴推导出函数的周期,考查推理能力与计算能力,属于中等题.13.如图,在ABC ∆中,D 、E 是BC 上的两个三等分点,2AB AD AC AE ⋅=⋅u u u r u u u r u u u r u u u r,则cos ADE ∠的最小值为________.【答案】47利用基底DA uuu r 、DE u u u r 表示向量AB u u u r 、AC u u u r 、AE u u u r,结合等式2AB AD AC AE ⋅=⋅u u u r u u u r u u u r u u u r 可得出cos ADE ∠的表达式,然后利用基本不等式可求出cos ADE ∠的最小值.【详解】由于D 、E 是BC 上的两个三等分点,则BD DE EC ==u u u r u u u r u u u r,由图形可得AB DB DA DE DA =-=--u u u r u u u r u u u r u u u r u u u r ,2AC DC DA DE DA =-=-u u u r u u u r u u u r u u u r u u u r,AE DE DA =-u u u r u u u r u u u r,2AB AD AC AE ⋅=⋅uu u r uuu r uuu r uu u rQ ,即()()()()22DE DA DA DE DA DE DA --⋅-=-⋅-u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,整理得2274DA DE DA DE ⋅=+u u u r u u u r u u u r u u u r ,即227cos 4DA DE ADE DA DE ⋅∠=+u u u r u u u r u u u r u u u r ,由基本不等式得22222444cos 777DA DE DA DE ADE DA DE DA DE ⋅⨯+∠=≥=⋅⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r, 当且仅当2DA DE =u u u r u u u r时,等号成立,因此,cos ADE ∠的最小值为47. 故答案为:47. 本题考查由平面向量数量积的运算求最值,解题的关键就是找出合适的基底来表示向量,考查计算能力,属于中等题.14.设函数()3f x x ax b =--,[]1,1x ∈-,其中a 、b ∈R .若()f x M ≤恒成立,则当M 取得最小值时,+a b 的值为______. 【答案】34构造函数()3g x x ax b =--,可知该函数关于点()0,b -对称,然后分0a ≤、3a ≥、0<<3a 三种情况讨论,分析函数()y g x =在区间[]1,1-上的单调性,得出函数()()f x g x =在区间[]1,1-上最值的可能取值,利用绝对值三角不等式可求出当M 取得最小值时+a b 的值. 【详解】构造函数()3g x x ax b =--,则()()f x g x =,由于()()()()332g x g x x ax b x ax b b +-=--+-+-=-,所以,函数()y g x =的图象关于点()0,b -对称,且()23g x x a '=-.①当0a ≤时,()0g x '≥,函数()y g x =在区间[]1,1-上单调递增,则()()1111M f a b M f a b ⎧≥=--⎪⎨≥-=-+-⎪⎩,所以()()111111122a b a b a b a b M a a ----+---+-+-≥≥=-=-≥,此时,当0a =,11b -≤≤时,M 取最小值1;②当3a ≥时,对任意的[]1,1x ∈-,()0g x '≤,函数()y g x =在区间[]1,1-上单调递减, 则()()1111M f a b M f a b ⎧≥=--⎪⎨≥-=-+-⎪⎩,所以()()111111222a b a b a b a b M a a ----+---+-+-≥≥=-=-≥,此时,当3a =,22b -≤≤时,M 取最小值2; ③当0<<3a 时,令()0g x '=,得x =()0,1t =,列表如下:不妨设()00g b =-≥,则0b ≤,则()()()()33112211M f a b Mf t t b M f t t bMf a b⎧≥=--⎪≥=--⎪⎪⎨≥-=-⎪⎪≥-=-+-⎪⎩,()()()(){}max 1,,,1M f f t f t f ∴≥--,()()()200g t g t g -+=≥Q ,且()()g t g t <-,()()()g t g t f t ∴-≥=, ()()()11200g g g -+=≥Q ,若()()11g g -≥,则()()()111g g f -≥=,若()()11g g -<,则()10g >,但()()1g t g ->-,()()()()()()2333212*********g t g t b a b t a t t t t --=----=+-=+-=-+Q ,所以,()(){}()()11,02max ,11,12g t g t g g t t ⎧<≤⎪⎪-=⎨⎪-<<⎪⎩.当102t <≤时,()2211113134M g a b t b t ≥=--=--≥-≥,当且仅当0b =,12t ==时,即当34a =,0b =时,M 取得最小值14;当112t <<时,()33222M g t t b t ≥-=-≥>. 综上所述,当34a =,0b =时,M 取得最小值14,此时34a b +=.故答案为:34. 本题考查利用绝对值三次函数的最值求参数,解题的关键就是充分利用三次函数的单调性,找出绝对值三次函数最大值的可能值,并结合绝对值三角不等式的性质来求解,考查分析问题和解决问题的能力,属于难题.二、解答题15.如图,在三棱锥P ABC -中,PA AB =,,M N 分别为棱,PB PC 的中点,平面PAB ⊥平面PBC .求证:(1)BC ∥平面AMN ; (2)平面AMN ⊥平面PBC .【答案】(1)详见解析;(2)详见解析.(1)证得MN ∥BC ,由线面平行的判定定理证明即可;(2)证得AM ⊥平面PBC . 由面面垂直的判定定理证明即可 【详解】(1)∵,M N 分别为棱,PB PC 的中点,∴MN ∥BC 又BC ⊄平面AMN ,∴BC ∥平面AMN . (2)∵PA AB =,点M 为棱PB 的中点, ∴AM PB ⊥,又平面PAB ⊥平面PBC ,平面PAB ⋂平面PBC PB =,∴AM ⊥平面PBC . ∵AM ⊂平面AMN ,∴平面AMN ⊥平面PBC . 本题考查线面平行,面面垂直的判定,考查定理,是基础题16.在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,且5cos 5A =. (1)若5a =,25c =,求b 的值; (2)若4B π=,求tan 2C 的值.【答案】(1)5b =;(2)3tan 24C =-. (1)利用余弦定理得出关于b 的二次方程,结合0b >,可求出b 的值;(2)利用两角和的余弦公式以及诱导公式可求出()cos cos C A B =-+的值,利用同角三角函数的基本关系求出tan C 的值,然后利用二倍角的正切公式可求出tan 2C 的值. 【详解】(1)在ABC ∆中,由余弦定理2222cos b c bc A a +-=得,252022525b +-⨯=,即2450b b --=, 解得5b =或1b =-(舍),所以5b =;(2)由5cos5A=及0Aπ<<得,22525sin1cos1()5A A=-=-=,所以210 cos cos(())cos()(cos sin)4C A B A A Aπ=π-+=-+=--=,又因为0Cπ<<,所以2210310sin1cos1()10C C=-=-=,从而310sin10tan3cos1010CCC===,所以222tan233tan21tan134CCC⨯===---.本题考查利用余弦定理解三角形,同时也考查了两角和的余弦公式、同角三角函数的基本关系以及二倍角公式求值,考查计算能力,属于中等题.17.如图,在圆锥SO中,底面半径R为3,母线长l为5.用一个平行于底面的平面去截圆锥,截面圆的圆心为1O,半径为r,现要以截面为底面,圆锥底面圆心O为顶点挖去一个倒立的小圆锥1OO,记圆锥1OO体积为V.(1)将V表示成r的函数;(2)求V的最大值.【答案】(1)234()=π(3)9V r r r-,03r<<;(2)16π9.(1)求出SO,利用1SNO SAO:△△,求出1SO,可得出1443OO r=-,然后利用圆锥的体积公式可得出V关于r的函数表达式,结合实际情况求出该函数的定义域;(2)对函数234()=π(3)9V r r r-求导,求出该函数的极大值,利用极值与最值的关系可得出V的最大值.【详解】(1)在SAO∆中,2222534SO SA AO=-=-=,由1SNO SAO :△△可知,1SO r SO R =,所以143SO r =, 所以1443OO r =-,所以223144()π(4)π(3)339V r r r r r =-=-,03r <<;(2)由(1)得234()π(3)9V r r r =-,03r <<,所以24()π(63)9V r r r '=-,令()0V r '=,得2r =,当(0,2)r ∈时,()0V r '>,所以()V r 在(0,2)上单调递增; 当(2,3)r ∈时,()0V r '<,所以()V r 在(2,3)上单调递减. 所以当2r =时,()V r 取得最大值16π(2)9V =. 答:小圆锥的体积V 的最大值为16π9. 本题考查圆锥体积的计算,同时也考查了利用导数求函数的最值,解题的关键就是求出函数的解析式,考查计算能力,属于中等题.18.在平面直角坐标系xOy 中,已知椭圆2222:1(0)x y C a b a b+=>>的右顶点为A ,过点A 作直线l 与圆222:O x y b +=相切,与椭圆C 交于另一点P ,与右准线交于点Q .设直线l 的斜率为k .(1)用k 表示椭圆C 的离心率;(2)若0OP OQ ⋅=u u u r u u u r,求椭圆C 的离心率.【答案】(1)211e k =+(2)12. (1)由题意可得出直线l 的方程为0kx y ak --=,利用该直线与圆O 相切,得出圆心到直线l 的距离等于半径可得出2222b k a b=-,由此可计算出e 关于k 的关系式; (2)设椭圆C 的焦距为()20c c >,将直线l 的方程与椭圆C 的右准线方程联立,可求出点Q 的坐标,将直线l 的方程与椭圆C 的方程联立,可求出点P 的坐标,再由0OP OQ ⋅=u u u r u u u r,结合(1)中的结论,可得出关于a 、c 的齐次等式,从而求出椭圆C 的离心率. 【详解】(1)直线l 的方程为()y k x a =-,即0kx y ak --=,因为直线l 与圆222O x y b +=:b =,故2222b k a b =-. 所以椭圆C的离心率e = (2)设椭圆C 的焦距为2c ,则右准线方程为2a x c=,由2()y k x a ax c =-⎧⎪⎨=⎪⎩得22()a a ac y k a k c c -=-=,所以22()(,)a k a ac Q c c -, 由22221()x y a b y k x a ⎧+=⎪⎨⎪=-⎩得2222324222()20b a k x a k x a k a b +-+-=, 解得322222p a k ab x b a k -=+,则32222222222()p a k ab ab k y k a b a k b a k --=-=++, 所以32222222222)a k ab ab kP b a k b a k--++(,, 因为0OP OQ ⋅=u u u r u u u r ,所以232222222222()20a a k ab k a ac ab k c b a k c b a k---⋅+⋅=++, 即22222()2()a a k b b k a c -=-,由(1)知,2222b k a b =-,所以224222222()()a b b a c a b a b a b--=--, 所以22a a c =-,即2a c =,所以12c a =,故椭圆C 的离心率为12. 本题考查椭圆离心率的计算,同时也考查了椭圆中向量的数量积的计算,解题的关键就是结合题意得出关于a 、b 、c 的齐次等式,考查计算能力,属于难题. 19.已知函数1()ln ()f x a x a x ⎛⎫=-∈ ⎪⎝⎭R .(1)若曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=,求a 的值;(2)若()f x 的导函数()f x '存在两个不相等的零点,求实数a 的取值范围;(3)当2a =时,是否存在整数λ,使得关于x 的不等式()f x λ≥恒成立?若存在,求出λ的最大值;若不存在,说明理由.【答案】(1)0a =;(2)()2,0e --;(3)存在,最大值为1-.(1)求出函数()y f x =的导数()f x ',由题意得出()11f '=-从而可求出实数a 的值; (2)令()21ln 0ax xf x x -+'==,可得知函数()1ln g x ax x =-+在()0,∞+上有两个零点,分0a ≥和0a <两种情况讨论,利用导数分析函数()y g x =在区间()0,∞+上的单调性和极值,由题意转化为函数()y g x =极值相关的不等式,解出即可得出实数a 的取值范围;(3)将2a =代入函数()y f x =的解析式得出()12ln f x x x ⎛⎫=- ⎪⎝⎭,对该函数求导得出()221ln x xf x x-+'=,构造函数()21ln h x x x =-+,利用单调性结合零点存在定理找出函数()y f x =的极小值点01,12x ⎛⎫∈⎪⎝⎭,并满足00ln 12x x =-,结合此关系式计算得出()()()0min 1,0f x f x =∈-,从而可得出整数λ的最大值. 【详解】(1)()2111()ln f x x a x x x'=+-,因为曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=, 所以(1)11f a '=-=-,得0a =;(2)因为21ln ()ax xf x x -+'=存在两个不相等的零点.所以()1ln g x ax x =-+存在两个不相等的零点,则1()g x a x '=+.①当0a ≥时,()0g x '>,所以()y g x =单调递增,至多有一个零点 ②当0a <时,因为当1(0)x a ∈-,时,()0g x '>,()y g x =单调递增, 当1(+)x a∈-∞,时,()0g x '<,()y g x =单调递减,所以1x a=-时,max 11()()ln()2g x g a a =-=--.因为()g x 存在两个零点,所以1ln()20a-->,解得2e 0a --<<.因为2e 0a --<<,所以21e 1a->>.因为(1)10g a =-<,所以()y g x =在1(0)a -,上存在一个零点. 因为2e 0a --<<,所以211()a a->-.因为22111[()]ln()1g a a a -=-+-,设1t a=-,则22ln 1(e )y t t t =-->,因为20t y t-'=<,所以22ln 1(e )y t t t =-->单调递减, 所以()2222ln e e 13e 0y <--=-<,所以22111[()]ln()10g a a a-=-+-<,所以()y g x =在1()a-+∞,上存在一个零点.综上可知,实数a 的取值范围为2(e ,0)--;(3)当2a =时,1()(2)ln f x x x =-,()2211121ln ()ln 2x x f x x x x x x -+'=+-=,设()21ln h x x x =-+,则1()20h x x'=+>.所以()y h x =单调递增,且11()ln 022h =<,(1)10h =>,所以存在01(1)2x ∈,使得0()0h x =,因为当0(0)x x ∈,时,()0h x <,即()0f x '<,所以()y f x =单调递减; 当0(+)x x ∈∞,时,()0h x >,即()0f x '>,所以()y f x =单调递增, 所以0x x =时,()y f x =取得极小值,也是最小值,此时()0000000111()(2)ln (2)12(4)4f x x x x x x x =-=--=-++,因为01(1)2x ∈,,所以0()(10)f x ∈-,, 因为()f x λ≥,且λ为整数,所以1λ≤-,即λ的最大值为1-.本题考查利用切线方程求参数、利用导数研究函数的零点,同时也考考查了利用导数研究不等式恒成立问题,涉及隐零点法的应用,考查分析问题和解决问题的能力,属于难题.20.已知数列{}n a 的首项13a =,对任意的*n ∈N ,都有11(0)n n a ka k +=-≠,数列{}1n a -是公比不为1的等比数列.(1)求实数k 的值;(2)设4,,1,,n n n n b a n -⎧=⎨-⎩为奇数为偶数数列{}n b 的前n 项和为n S ,求所有正整数m 的值,使得221mm S S -恰好为数列{}n b 中的项. 【答案】(1)2;(2)2.(1)根据递推公式求出2a 、3a ,由题意得出()()()2213111a a a -=--,求出k 的值,结合数列{}1n a -公比不为1的等比数列进行检验,进而得出实数k 的值;(2)求出4,,2,,n n n n b n -⎧=⎨⎩为奇数为偶数利用奇偶分组法求出2m S 、21m S -,设()221m t m S b t N S *-=∈,可得知2210m t m Sb S -=>,从而可知1t =、3或t 为偶数,由31b =结合2211m m S S -≠可推出3t =不成立,然后分1t =和t 为偶数两种情况讨论,结合221mm S S -的取值范围可求出符合条件的正整数m 的值. 【详解】(1)由11n n a ka +=-,13a =可知,231a k =-,2331a k k =--, 因为{1}na -为等比数列,所以2213(1)(1)(1)a a a -=--,即22(32)2(32)k k k -=⨯--,即231080k k -+=,解得2k =或43k =, 当43k =时,143(3)3n n a a +-=-,所以3n a =,则12n a -=, 所以数列{1}n a -的公比为1,不符合题意;当2k=时,112(1)n n a a +-=-,所以数列{1}na -的公比1121n n a q a +-==-, 所以实数k 的值为2.(2)由(1)知12nn a -=,所以4,,2,,n nn n b n -⎧=⎨⎩为奇数为偶数 则22(41)4(43)4[4(21)]4m m S m =-++-+++--+L2(41)(43)[4(21)]444m m =-+-++--++++L L144(4)3m m m +-=-+,则212244(4)3m m m mS S b m m --=-=-+,因为22+1324m m m b b m +=-+,又222+322+1()()3420m m m m m b b b b ++-+=⨯->, 且2350b b +=>,130b =>,所以210m S ->,则20m S >,设2210,mt m S b t S -=>∈*N , 则1,3t =或t 为偶数,因为31b =不可能,所以1t =或t 为偶数,①当2121=mm S b S -时,144(4)3344(4)3m mm m m m +--+=--+,化简得2624844m m m -+=--≤, 即242m m -+≤0,所以m 可取值为1,2,3, 验证2173S S =,433S S =,658723S S =得,当2m =时,413S b S =成立.②当t 为偶数时,1222144(4)331443124(4)134m mm m mm m S S m m m m +---+==+--+--++, 设231244m m m m c -+-=,则211942214m m m m m c c ++-+-=,由①知3m >,当4m =时,545304c c --=<;当4m >时,10m m c c +->,所以456c c c ><<L ,所以m c 的最小值为5191024c -=, 所以22130151911024m m S S -<<+<-+,令22214m m S b S -==,则2314312414mm m +=-+-+, 即231240m m -+-=,无整数解. 综上,正整数m 的值为2.本题考查利用等比数列的定义求参数、数列中的存在性问题,同时也涉及了奇偶分组法求和,考查分类讨论思想的应用,属于难题.21.已知矩阵231M t ⎡⎤=⎢⎥⎣⎦的一个特征值为4.求矩阵M 的逆矩阵1M -. 【答案】113441122M -⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦由题意,先设矩阵M 的特征多项式为23()1λλλ--=--f t,由题意求出2t =,进而可求出结果. 【详解】矩阵M 的特征多项式为23()(2)(1)31f t tλλλλλ--==-----.因为矩阵M 的一个特征值为4,所以方程()0f λ=有一根为4, 即(4)630f t =-=,所以2t =.所以2321M ⎡⎤=⎢⎥⎣⎦,所以113441122M -⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦. 本题主要考查求矩阵的逆矩阵问题,熟记矩阵的特征多项式,会由特征值求出矩阵中的参数即可,属于常考题型.22.在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为(cos sin )12ρθθ+=,曲线C的参数方程为,2sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数,θ∈R )在曲线C 上求点M ,使点M 到l 的距离最小,并求出最小值. 【答案】点M 的坐标为()3,1.最小值将直线l 的方程化为普通方程,设点M的坐标为(),sin θθ,利用点到直线的距离公式结合辅助角公式求出点M 到直线l 距离的最小值,并求出对应的θ的值,进而可求出对应的点M 的坐标. 【详解】由:cos sin 120l ρθρθ+-=,及cos x ρθ=,sin y ρθ=, 所以l 的直角坐标方程为120x y +-=.在曲线C上取点()2sin M ϕϕ,,则点M 到l 的距离124sin 3d ϕπ-+===, 当6π=ϕ时,d 取最小值,此时点M 的坐标为()3,1. 本题考查利用椭圆的参数方程求点到直线距离的最值,对于这类问题,一般将椭圆上的点利用椭圆的参数方程表示,结合三角恒等变换思想以及正弦函数的有界性求解,考查计算能力,属于中等题.23.已知正数,,x y z 满足1x y z ++=,求111222x y y z z x+++++的最小值.【答案】3由题意得出()()()122213x y z x y y z z x ++=+++++=⎡⎤⎣⎦,然后将代数式()()()12223x y y z z x +++++⎡⎤⎣⎦与代数式111222x y y z z x +++++相乘,利用柯西不等式可求出111222x y y z z x+++++的最小值.【详解】因为x y z ,,都为正数,且1x y z ++=,所以由柯西不等式得, 1113()222x y y z z x +++++111()[(2)(2)(2)]222x y y z z x x y y z z x=++⋅++++++++ 2111(222)9222x y y z z x x y y z z x⋅++⋅++⋅+=+++≥,当且仅当13x y z ===时等号成立,所以111222x y y z z x +++++的最小值为3.本题考查利用柯西不等式求代数式的最值,解题的关键就是对代数式进行变形,考查计算能力,属于中等题.24.如图,在三棱柱111ABC A B C -中,侧面11AA B B 为正方形,侧面11BB C C 为菱形,1160BB C ︒∠=,平面11AA B B ⊥平面11BB C C .(1)求直线1AC 与平面11AA B B 所成角的正弦值; (2)求二面角1B AC C --的余弦值.【答案】(1)64;(2)77.(1)证明出AB ⊥平面11BB C C ,然后以点B 为坐标原点,分别以BA ,1BB 所在的直线为,x y 轴,建立空间直角坐标系B xyz -,设正方形11AA B B 的边长为2,利用空间向量法可计算出直线1AC 与平面11AA B B 所成角的正弦值;(2)计算出平面1ACC 的一个法向量1n u r ,以及平面1ABC 的一个法向量2n u u r,利用空间向量法可计算出二面角1B AC C --的余弦值. 【详解】(1)因为四边形11AA B B 为正方形,所以1AB BB ⊥,因为平面11AA B B ⊥平面11BB C C ,平面11AA B B Ç平面111BB C C BB =,AB Ì平面11AA B B ,所以AB ⊥平面11BB C C .以点B 为坐标原点,分别以BA ,1BB 所在的直线为,x y 轴,建立如图所示的空间直角坐标系B xyz -.不妨设正方形11AA B B 的边长为2,则()200A ,,,()1020B ,,. 在菱形11BB C C 中,因为1160BB C ∠=︒,所以1(013)C ,,,所以1(213)AC =-u u u u r,,. 因为平面11AA B B 的法向量为()001n =r,,,设直线1AC 与平面11AA B B 所成角为α,则1sin |cos AC α=<u u u u r ,|3|6|4221n >==⨯r , 即直线1AC 与平面11AA B B 所成角的正弦值为6;(2)由(1)可知,(0C -,,所以()1020CC =u u u u r ,,. 设平面1ACC 的一个法向量为()1111,,n x y z =u r ,因为11110,0,n AC n CC ⎧⋅=⎪⎨⋅=⎪⎩u v u u u u v u v u u u u v 即()(()()111111,,2,10,,0200x y z x y z ⎧⋅-=⎪⎨⋅=⎪⎩,,,,,取12x =,10y =,11z =,即101)n =u u r ,. 设平面1ABC 的一个法向量为()2222,,n x y z =u u r ,因为()2,0,0BA =u u u r,(1BC =u u u u r ,因为22100n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u v u u v u u u u v ,所以()()()(222222,,2,0,00,,0x y z x y z ⎧⋅=⎪⎨⋅=⎪⎩,取()21n =-u u r . 设二面角1B AC C --的平面角为θ,则121212cos cos ,n n n n n n θ⋅=-<>=-==⋅u r u u r u r u u r u r u u r , 所以二面角1B AC C --本题考查利用空间向量法计算线面角和二面角,合理建系是关键,考查计算能力,属于中等题.25.已知n 为给定的正整数,设201223nn n x a a x a x a x ⎛⎫+=++++ ⎪⎝⎭L ,x ∈R . (1)若4n =,求01,a a 的值;(2)若13x =,求0()n k k k n k a x =-∑的值. 【答案】(1)01681a =,13227a =.(2)23n (1)利用二项式定理可求出0a 和1a 的值;(2)利用组合数公式得出11k k n n kC nC --=,可得出()00121213333n k k n k kn n n k k k k n n k k k n k a x nC nC --===⎛⎫⎛⎫⎛⎫⎛⎫-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑∑∑,然后利用二项式定理即可求得答案.【详解】(1)因为4n =,所以0404216C ()381a ==,1314232C ()327a ==; (2)当13x =时,21C ()()33k kn k k k n a x -=, 又因为11!(1)!C C !()!(1)!()!k k n n n n k kn n k n k k n k ---===---, 当1n =时,011022()C ()33nk k k n k a x =-==∑; 当2n ≥时,0021()()C ()()33n n k k n k k k n k k n k a x n k -==-=-∑∑ 012121C ()()C ()()3333n n k n k k k n k k n n k k n k --===-∑∑ 1112121()C ()()3333n n k n k k n k n n ---==+-∑ 1111121C ()()333n k n k k n k n n ----==-∑ 11212()3333n n n n -=-+=,当1n =时,也符合. 所以0()n k k k n k a x =-∑的值为23n . 本题考查二项式定理求指定项的系数,同时也考查了利用二项式定理化简求值,解题的关键就是二项展开式通项和二项式定理的逆用,考查计算能力,属于中等题.。
2021年江苏省苏北七市(南通、泰州、扬州、徐州、淮安、连云港、宿迁)高考数学三调试卷(附答案详解)

2021年江苏省苏北七市(南通、泰州、扬州、徐州、淮安、连云港、宿迁)高考数学三调试卷学校:___________姓名:___________班级:___________考号:___________ 一、单选题(本大题共8小题,共40.0分)1. 设集合A ={x|log 2(x −1)≤1},B ={x|21−x ≥12},则A ∩B =( )A. (−∞,2]B. [1,2]C. (1,2]D. (1,3]2. 已知复数z =21+i +3i ,则|z|=( )A. 5B. √5C. √17D. 3+√23. 设a =314,b =log 43,c =414,则( )A. c >b >aB. a >c >bC. c >a >bD. a >b >c4. 已知点A(1,1),B(7,5),将向量AB ⃗⃗⃗⃗⃗ 绕点A 逆时针旋转π2得到AC⃗⃗⃗⃗⃗ ,则点C 的坐标为( ) A. (5,−5) B. (3,−7) C. (−5,5) D. (−3,7)5. “角谷猜想”最早流传于美国,不久传到欧洲,后来日本数学家角谷把它带到亚洲.该猜想是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,经过有限步演算,最终都能得到1.若正整数n 经过5步演算得到1,则n 的取值不可能是( )A. 32B. 16C. 5D. 46. 已知双曲线E :x 2a −y 2b =1(a >0,b >0)的左、右焦点分别为F 1、F 2,点A 在双曲线E 的左支上,且∠F 1AF 2=120°,AF 2=2AF 1,则双曲线E 的离心率为( )A. √3B. √5C. √7D. 77. 在数1和3之间插入n 个实数,使得这n +2个数构成等差数列,将这n +2个数的和记为b n ,则数列{log 3b n+1b n}的前78项的和为( )A. 3B. log 378C. 5D. log 388. 已知函数f(x)=2lnx −x 2e x +1.若存在x 0>0,使f(x 0)≥ax 0,则a 的最大值为( )A. 0B. −1C. 1−eD. 1−e 2二、多选题(本大题共4小题,共20.0分)9. 在△ABC 中,M 是BC 的中点.若AB ⃗⃗⃗⃗⃗ =a ⃗ ,AC ⃗⃗⃗⃗⃗ =b ⃗ ,则|AM ⃗⃗⃗⃗⃗⃗|=( )A. 12|a⃗−b⃗ | B. 12|a⃗+b⃗ |C. 12√2(a⃗2+b⃗ 2)−(a⃗−b⃗ )2 D. 12√a⃗2+b⃗ 210.在(2x2−1x)6的展开式中,下列说法正确的是()A. 各项系数和为1B. 第2项的二项式系数为15C. 含x3的项的系数为−160D. 不存在常数项11.2021年3月30日,小米正式开始启用具备“超椭圆”数学之美的新logo.设计师的灵感来源于曲线C:|x|n+|y|n=1.则下列说法正确的是()A. 曲线C关于原点成中心对称B. 当n=−2时,曲线C上的点到原点的距离的最小值为2C. 当n>0时,曲线C所围成图形的面积的最小值为πD. 当n>0时,曲线C所围成图形的面积小于412.已知菱形ABCD的边长为2,∠ABC=π3,将△DAC沿着对角线AC折起至△D′AC,连结BD′.设二面角D′−AC−B的大小为θ,则下列说法正确的是()A. 若四面体D′ABC为正四面体,则θ=π3B. 四面体D′ABC的体积最大值为1C. 四面体D′ABC的表面积最大值为2(√3+2)D. 当θ=2π3时,四面体D′ABC的外接球的半径为√213三、单空题(本大题共4小题,共20.0分)13.在△ABC中,角A,B,C的对边分别为a,b,c.若a=4,b=6,cosB=513,则sinA= ______ .14.为了解某小区居民的家庭年收入x(万元)与年支出y(万元)的关系,随机调查了该小区的10户家庭,根据调查数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为ŷ=b̂x+â,已知x−=20,y−=16,b̂=0.76.若该小区某家庭的年收入为30万元,则据此估计,该家庭的年支出为______ 万元.15.已知定义在R上的奇函数f(x)满足f(1+x)=f(1−x).当x∈[0,1]时,f(x)=x2,则直线y=15x与函数y=f(x)的图象的交点的个数为______ .16.若矩形ABCD满足ADAB =√5−12,则称这样的矩形为黄金矩形,现有如图1所示的黄金矩形卡片ABCD,已知AD=2x,AB=2y,E是CD的中点,EF⊥CD,FG⊥EF,且EF=FG=x,沿EF,FG剪开.用3张这样剪开的卡片,两两垂直地交又拼接,得到如图2所示的几何模型.若连结这个几何模型的各个顶点,便得到一个正______ 面体;若y=2,则该正多面体的表面积为______ .四、解答题(本大题共6小题,共70.0分)17.设各项均为正数的等差数列{a n}的前n项和为S n,S7=35,且a1,a4−1,a7成等比数列.(1)求数列{a n}的通项公式;(2)数列{b n}满足b n+b n+1=a n,求数列{b n}的前2n项的和T2n.18.已知函数f(x)=3sin(2x+φ)(−π2<φ<0)同时满足下列3个条件中的2个.3个条件依次是:①f(x)的图象关于点(π12,0)对称;②当x=5π12时,f(x)取得最大值;③0是函数y=f(x)+32的一个零点.(1)试写出满足题意的2个条件的序号,并说明理由;(2)求函数g(x)=f(x)+6cos2x的值域.19.面对新一轮科技和产业革命带来的创新机遇,某企业对现有机床进行更新换代,购进一批新机床.设机床生产的零件的直径为X(单位:mm).(1)现有旧机床生产的零件10个,其中直径大于124mm的有3个,若从中随机抽取4个,记ξ表示取出的零件中直径大于124mm的零件的个数,求ξ的概率分布及数学期望E(ξ);(2)若新机床生产的零件直径X~N(120,4),从生产的零件中随机取出10个,求至少有一个零件直径大于124mm的概率.参考数据:若X~N(μ,σ2),则P(|X−μ|≤σ)≈0.6827,P(|X−μ|≤2σ)≈0.9545,P(|X−μ|≤3σ)≈0.9974,0.9772510≈0.7944,0.954510≈0.6277.20.如图,A是以BD为直径的半圆O上一点,平面BCD⊥平面ABD,BC⊥BD.(1)求证:AD⊥平面ABC;(2)若BD=2BC=2,AD⏜=2AB⏜,求二面角A−CD−B的余弦值.21. 已知圆M :x 2+(y −52)2=4与抛物线E :x 2=my(m >0)相交于点A ,B ,C ,D ,且在四边形ABCD 中,AB//CD . (1)若OA ⃗⃗⃗⃗⃗ ⋅OD ⃗⃗⃗⃗⃗⃗ =154,求实数m 的值; (2)设AC 与BD 相交于点G ,△GAD 与△GBC 组成蝶形的面积为S ,求点G 的坐标及S 的最大值.22. 已知函数f(x)=asin 2x −√3x.(1)若x =π3是f(x)的一个极值点,试讨论f(x)在区间(0,π2)上的单调性; (2)设−2≤a ≤2,证明:当x ≠0时,xf(x)<0.答案和解析1.【答案】C【解析】解:∵A ={x|0<x −1≤2}={x|1<x ≤3},B ={x|1−x ≥−1}={x|x ≤2}, ∴A ∩B =(1,2]. 故选:C .根据指数函数和对数函数的单调性可求出集合A ,B ,然后进行交集的运算即可. 本题考查了指数函数和对数函数的单调性,对数函数的定义域,交集及其运算,考查了计算能力,属于基础题.2.【答案】B【解析】解:因为z =21+i +3i =2(1−i)(1+i)(1−i)+3i =1−i +3i =1+2i , 所以|z|=2+22=√5, 故选:B .先化简复数z 的关系式,再根据模的运算公式即可求解.本题考查了复数的运算性质,涉及到求解复数模的运算公式,属于基础题.3.【答案】C【解析】解:∵幂函数y =x 14在(0,+∞)上为增函数, ∴30<314<414,即c >a >1,∵b =log 43<log 44=1,∴b <1, ∴c >a >b . 故选:C .由幂函数的单调性得到c >a >1,再由对数函数的单调性得到b <1,即可求解. 本题考查幂函数、对数函数的单调性,属于基础题.4.【答案】D【解析】解:设C(x,y),则AB ⃗⃗⃗⃗⃗ =(6,4),AC ⃗⃗⃗⃗⃗ =(x −1,y −1), ∴AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =0,|AB ⃗⃗⃗⃗⃗ |=|AC⃗⃗⃗⃗⃗ |, 化为:6(x −1)+4(y −1)=0,2+42=√(x −1)2+(y −1)2, 联立解得:x =−3,y =7,∴C(−3,7), 故选:D .设C(x,y),则AB ⃗⃗⃗⃗⃗ =(6,4),AC ⃗⃗⃗⃗⃗ =(x −1,y −1),可得AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =0,|AB ⃗⃗⃗⃗⃗ |=|AC ⃗⃗⃗⃗⃗ |,联立解得即可得出.本题考查了向量的坐标运算性质、向量垂直于数量积的关系、数量积运算性质,考查了推理能力与计算能力,属于中档题.5.【答案】B【解析】解:对于A ,322=16,162=8,82=4,42=2,22=1,故经过5步演算得到1; 对于B ,162=8,82=4,42=2,22=1,故经过4步演算得到1,1×3+1=4,42=2,22=1,则经过7步演算得到1,故16不可能经过5步演算得到1;对于C ,5×3+1=16,162=8,82=4,42=2,22=1,故经过5步演算得到1; 对于D ,42=2,22=1,1×3+1=4,42=2,22=1,故经过5步演算得到1. 故选:B .利用题中给出的演算方法,对四个选项中的数值进行逐一的分析判断,即可得到答案. 本题考查了简单的合情推理的应用,解题的关键是正确理解题中所给的演算方法,考查了逻辑推理能力,属于基础题.6.【答案】C【解析】解:双曲线E :x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,点A 在双曲线E 的左支上,且∠F 1AF 2=120°,|AF 2|=2|AF 1|, 由双曲线的定义可知,|AF 2|=2|AF 1|=4a , 所以4c 2=16a 2+4a 2−2×2a ×4acos120°, 即4c 2=28a 2,e =ca >1, 解得e =√7, 故选:C .利用双曲线的定义,结合余弦定理,转化求解双曲线的离心率即可. 本题考查双曲线的简单性质的应用,离心率的求法,是基础题.7.【答案】A【解析】解:由题意可得b n=12(n+2)(1+3)=2(n+2),log3b n+1b n =log32(n+3)2(n+2)=log3n+3n+2,所以数列{log3b n+1b n}的前78项的和为log343+log354+...+log38180=log3(43×54×...×8180)=log3813=3.故选:A.由等差数列的求和公式和对数的运算性质,化简计算,可得所求值.本题考查等差数列的求和公式和对数的运算性质,考查转化思想和运算能力,属于中档题.8.【答案】B【解析】解:令ℎ(x)=e x−x−1,则ℎ′(x)=e x−1,则当x∈(−∞,0)时,ℎ′(x)<0,ℎ(x)单调递减,当x∈(0,+∞)时,ℎ′(x)>0,ℎ(x)单调递增,∴ℎ(x)min=ℎ(0)=0,则ℎ(x)≥ℎ(0)=0,即e x≥x+1.存在x0>0,使f(x0)≥ax0,即f(x0)x0≥a,令g(x)=f(x)x =2lnx−x2e x+1x,则g(x)max≥a,∵g(x)=2lnx−x2e x+1x =2lnx+1−e x+2lnxx,又e x+2lnx≥x+2lnx+1,∴−e x+2lnx≤−(x+2lnx+1),∴g(x)=2lnx−x2e x+1x=2lnx+1−e x+2lnxx≤2lnx+1−(x+2lnx+1)x=−1(当且仅当x+2lnx=0时取等号).∴a≤−1.故a的最大值为−1.故选:B.首先证明e x≥x+1,构造函数g(x)=f(x)x,利用导数求其最大值,即可求得a的范围,从而可得a的最大值.本题考查利用导数求函数的最值,考查化归与转化思想,考查运算求解能力,是中档题.9.【答案】BC【解析】解:根据题意,在△ABC 中,M 是BC 的中点. 则AM ⃗⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=12(a ⃗ +b ⃗ ), 故|AM ⃗⃗⃗⃗⃗⃗ |=12|a ⃗ +b ⃗ |,则A 错误,B 正确; 对于C ,12√2(a ⃗ 2+b ⃗ 2)−(a ⃗ −b ⃗ )2=12×√a ⃗ 2+2a ⃗ ⋅b ⃗ +b ⃗ 2=12|a ⃗ +b ⃗ |,C 正确, 对于D ,12√a ⃗ 2+b ⃗ 2≠12|a ⃗ +b ⃗ |,D 错误; 故选:BC .根据题意,由向量线性运算可得AM ⃗⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=12(a ⃗ +b ⃗ ),据此分析选项,即可得答案.本题考查向量模的计算,涉及向量的线性运算,属于基础题.10.【答案】AC【解析】解:在(2x 2−1x )6的展开式中,令x =1,可得各项系数和为1,故A 正确;第2项的二项式系数为C 61=6≠15,故B 错误;由于通项公式为T r+1=C 6r ⋅(−1)r ⋅26−r ⋅x 12−3r ,令12−3r =3,求得r =3, 可得含x 3的项的系数为−C 63⋅23=−160,可得C 正确;令12−3r =0,求得r =4,可得展开式中第5项为常数项,故D 错误, 故选:AC .由题意利用二项展开式的通项公式,逐一判断各个选项是否正确,从而得出结论. 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于中档题.11.【答案】ABD【解析】解:对于A ,在曲线C :|x|n +|y|n =1中,以−x 替换x ,以−y 替换y ,方程不变,则曲线C 关于原点成中心对称, 故A 正确;对于B ,当n =−2时,C :|x|n +|y|n =1化为1x 2+1y 2=1, 由(x 2+y 2)(1x 2+1y 2)=2+y 2x 2+x 2y 2≥2+2√y 2x 2⋅x 2y2=4,当且仅当x 4=y 4时等号成立,得√x 2+y 2≥2,即曲线C 上的点到原点的距离的最小值为2,故B正确;对于C,取n=1,曲线C:|x|+|y|=1,曲线C所围成图形的面积S=12×2×2=2<π,故C错误;对于D,当n>0时,取曲线C在第一象限的面积为S1,则S=4S1,又在第一象限的曲线为x n+y n=1,∴S1<1×1=1,则S<4,故D正确.故选:ABD.以−x替换x,以−y替换y,方程不变判断A;利用基本不等式求最值判断B;举例说明C错误;求得曲线在第一象限围成图形的面积的范围,结合由对称性判断D.本题考查曲线与方程,考查逻辑思维能力与运算求解能力,是中档题.12.【答案】BCD【解析】解:A.若四面体D′ABC为正四面体,则BD′=AB=2,设O是AC的中点,则BO=DO=√3=D′O,在△BOD′中,cos∠BOD′=−2×√3×√3=13≠cosπ3,故A错误,B.∵V D′−ABC=13S△ABC⋅ℎ,h为点D′到平面ABC的距离,∴体积最大时,即h最大,即点D′到平面ABC的距离最大,即平面AD′C⊥面ABC时,此时ℎ=√3,最大体积V=13×(12×2×2×sinπ3)×√3=1,故B正确,C.四面体D′ABC的表面积S D′−ABC=S△AD′C+S△ABC+S△ABD′+S△BCD′,∵S△ABC=S△AD′C=√34×22=√3,S△ABD′=S△BCD′,∴S D′−ABC=2S△ABC+2S△ABD′,则表面积最大时,即S△ABD′最大时,此时最大值为2×12×2×2×sinπ3+2×12×2×2=2√3+4,故C正确,D.设△ABC的外接圆半径为r,则r=22sinπ3=2√33,过△ABC的外心与平面ABC垂直的直线与过△D′AC的外心与平面AD′C垂直的直线的交点,即为四面体外接球的球心,设球心距离平面ABC 的高度为d ,四面体的外接球的半径为R , ∴d =tan θ2⋅rsin π6=1,∴R =√r 2+d 2=√(2√33)2+12=√213,故D 正确故选:BCD .分别根据二面角的定义,四面体的体积以及表面积公式分别进行求解判断即可. 本题主要考查命题的真假判断,涉及空间二面角的计算,空间几何体的体积与表面积的计算,涉及知识点较多,运算量较大,是个难题.13.【答案】813【解析】解:因为cosB =513, 所以B 为锐角,sinB =1213, 因为a =4,b =6, 由正弦定理得,asinA =b sinB , 故sinA =asinB b =4×12136=813.故答案为:813.由已知结合同角基本关系可求sin B ,然后结合正弦定理即可求解.本题主要考查了同角基本关系及正弦定理在求解三角形中的应用,属于基础题.14.【答案】23.6【解析】解:因为回归直线恒过样本中心点(x −,y −), 所以16=0.76×20+a ̂, 解得a ̂=0.8,所以回归直线方程为y ̂=0.76x +0.8, 当x =30时,y ̂=0.76×30+0.8=23.6, 故答案为:23.6.由回归直线恒过样本中心点(x −,y −),求得a ̂=0.8,从而得回归直线方程,再把x =30代入,求得ŷ的值,即可.本题考查回归直线方程的性质与应用,理解回归直线恒过样本中心点是解题的关键,考查运算求解能力,属于基础题.15.【答案】7【解析】解:∵f(1+x)=f(1−x),∴f(x)关于直线x=1对称,又f(x)奇函数,其图象关于(0,0)对称,∴f(x)为周期函数,且周期为4×|1−0|=4,而当x∈[0,1]时,f(x)=x2,故可作出f(x)的大致图象如下图所示,x有3个交点,由对称性可知,当x<0时,函数f(x)当x>0时,函数f(x)与直线y=15x也有3个交点,显然(0,0)也是一个交点,与直线y=15x与函数y=f(x)的图象共有7个交点.∴直线y=15故答案为:7.x,由图象观察即可得依题意,函数f(x)的图象为4,作出函数f(x)的图象及直线y=15解.本题考查函数奇偶性,对称性,周期性及函数零点与方程根的关系,考查数形结合思想,属于中档题.16.【答案】20 120√3−40√15【解析】解:如图所示:图为18上图形,则18图形中有S ,S 1,S 2,S 3四个面,S =2S 1=2S 3,即18图形中有52个面,故共有8×52=20个面;x设该正二十面体的边长为l =√x 2+(y −x)2+y 2,又因为y =2,且xy =√5−12,则x =√5−1,所以l 2=2x 2+2y 2−2xy =24−8√5, 所以该正二十面体的表面积为: S 1=20×12×l 2×√32=120√3−40√15.故答案为:20,120√3−40√15.由图分析可以看出为正二十面体,通过算出正二十面体的边长进一步建立和x ,y 的关系,从而求出此正二十面体的外接球的表面积.本题主要考查学生对新知识的探索能力,通过已有的方程思想列出对应的等式,进一步分析得到结果.17.【答案】解:(1)设等差数列{a n }的公差为d ,d >0,由S 7=35,可得7a 1+21d =35,即为a 1+3d =5,① 由a 1,a 4−1,a 7成等比数列,可得(a 4−1)2=a 1a 7, 即为(a 1+3d −1)2=a 1(a 1+6d),② 由①②可得a 1=2,d =1, 可得a n =2+n −1=n +1; (2)由b n +b n+1=a n =n +1,则T 2n =(b 1+b 2)+(b 3+b 4)+(b 5+b 6)+...+(b 2n−1+b 2n )=2+4+6+...+2n =12n(2+2n)=n 2+n .【解析】(1)设等差数列{a n }的公差为d ,d >0,运用等差数列的通项公式和求和公式,解方程可得首项和公差,可得所求;(2)求得b n +b n+1=a n =n +1,由数列的并项求和,由等差数列的求和公式,可得所求和.本题考查等差数列的通项公式和求和公式的运用,以及数列的并项求和,考查方程思想和运算能力,属于中档题.18.【答案】解:(1)满足条件为①③,由条件①,f(x)的图象关于点(π12,0)对称;故f(π12)=0,整理得3sin(π6+φ)=0,由于−π2<φ<0,故φ=−π6, 由条件②,当x =5π12时,f(x)取得最大值;故2×5π12+φ=2kπ+π2,整理得φ=2kπ−π3,由于−π2<φ<0,故φ=−π3,由条件③,0是函数y =f(x)+32的一个零点,故sinφ=−12,由于−π2<φ<0,故φ=−π6. 故满足条件的序号为①③. (2)由(1)得:f(x)=3sin(2x −π6), 故函数g(x)=3sin(2x −π6)+6cos 2x =3√32sin2x +32cos2x +3=3sin(2x +π6)+3.由于−1≤sin(2x +π6)≤1, 故g(x)∈[0,6].【解析】(1)直接利用条件①②③整理出来的结论,判断结果;(2)利用三角函数关系式的恒等变换,正弦型函数的性质的应用求出函数的值域. 本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,主要考查学生的运算能力和数学思维能力,属于基础题.19.【答案】解:(1)由题意可知:ξ的可能取值为0,1,2,3,ξ~H(4,3,10),P(ξ=0)=C 74C 104=16,P(ξ=1)=C 31C 73C 104=12,P(ξ=2)=C 32C 72C 104=310,P(ξ=3)=C 33C 71C 104=130.可得ξ的分布列为:ξ 0 1 2 3P1612310130∴E(ξ)=0×16+1×12+2×310+3×130=65.或根据:ξ~H(4,3,10),E(ξ)=4×310=65.(2)设“至少有一个零件直径大于124mm”为事件A,∵X~N(120,4),∴μ=120,σ=2,∴P(X>124)=1−P(|X−μ|≤2σ)2≈1−0.95452=0.002275,∴P(X≤124)≈1−0.002275=0.97725,∴P(A)=1−0.9772510≈1−0.7944=0.2056,答:至少有一个零件直径大于124mm的概率为0.2056.【解析】(1)由题意可知:ξ的可能取值为0,1,2,3,ξ~H(4,3,10),计算出P(ξ=k)=C3k C74−kC104,k=0,1,2,3,即可得出ξ的分布列与E(ξ).(2)设“至少有一个零件直径大于124mm”为事件A,可得X~N(120,4),可得P(X>124)=1−P(|X−μ|≤2σ)2,再利用对立事件与二项分布列的计算公式即可得出.本题考查了超几何分布列、正态分布列与二项分布列的计算公式、对立事件概率计算公式,考查了推理能力与计算能力,属于中档题.20.【答案】(1)证明:∵平面BCD⊥平面ABD,且平面BCD∩平面ABD=BD,BC⊂平面BCD,BC⊥BD,∴BC⊥平面ABD,而AD⊂平面ABD,∴BC⊥AD,又AD⊥AB,且AB∩BC=B,∴AD⊥平面ABC;(2)解:∵AD⏜=2AB⏜,∴∠AOB=60°,则△AOB为等边三角形,取OB中点E,连接AE,则AE⊥OB,又平面BCD⊥平面ABD,且平面BCD∩平面ABD=BD,AE⊂平面ABD,AE⊥BD,则AE⊥平面BCD,在平面BCD中,过E作EF⊥CD,垂足为F,连接AF,由三垂线定理可得,CD⊥AF,则∠AFE为二面角A−CD−B的平面角.∵BD =2BC =2,∴AE =√32,ED =32,CD =√5,由Rt △DBC∽Rt △DFE ,得EDEF =CDBC ,即EF =BC⋅ED CD =1×325=3√510, 在Rt △AEF 中,有AF =√AE 2+EF 2=√34+920=√305,∴cos∠AFE =EFAF =3√510√305=√64.【解析】(1)由已知证明BC ⊥AD ,又AD ⊥AB ,由直线与平面垂直的判定可得AD ⊥平面ABC ;(2)由AD⏜=2AB ⏜,得∠AOB =60°,取OB 中点E ,连接AE ,则AE ⊥OB ,再由已知证明AE ⊥平面BCD ,在平面BCD 中,过E 作EF ⊥CD ,垂足为F ,连接AF ,得CD ⊥AF ,即∠AFE 为二面角A −CD −B 的平面角,然后求解三角形得答案.本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,训练了二面角的平面角的求法,是中档题.21.【答案】解:(1)依据圆与抛物线的对称性,四边形ABCD 是以y 轴为对称轴的等腰梯形,不妨设|AB|<|CD|,A ,D 在第一象限,A(x 1,y 1),D(x 2,y 2), 则B(−x 1,y 1),C(−x 2,y 2), 联立{x 2+(y −52)2=4x 2=my,得y 2+(m −5)y +94=0.上述方程有互异两正根,则{△=(m −5)2−9>05−m >094>0,解得0<m <2.由OA ⃗⃗⃗⃗⃗ ⋅OD ⃗⃗⃗⃗⃗⃗ =154,得x 1x 2+y 1y 2=m √y 1y 2+y 1y 2=154, ∴32m +94=154,即m =1;(2)由对称性,点G 在y 轴上,可设G(0,a), 由k AG =k AC ,得y 1−a x 1=y 1−y2x 1+x 2,∴1√m⋅√y =12√m⋅(√y +√y )=√y 1−√y 2√m,则a =√y 1y 2=32,即G(0,32).S =S 梯形ABCD −(S △GAB +S △GCD )=(x 1+x 2)(y 2−y 1)−[x 1(a −y 1)+x 2(y 2−a)] =x 1y 2−x 2y 1+a(x 2−x 1)=√m ⋅√y 1y 2⋅(√y 2−√y 1)+a √m ⋅(√y 2−√y 1) =√m ⋅(√y 2−√y 1)⋅(√y 1y 2+a)=3√m ⋅√y 1+y 2−2√y 1y 2=3√m(2−m)≤3⋅m+(2−m)2=3.当且仅当m =2−m ,即m =1时,S 取最大值为3.【解析】(1)设A(x 1,y 1),D(x 2,y 2),联立圆与抛物线方程,可得关于y 的一元二次方程,由判别式大于0及方程根的情况求得m 的范围,再由OA ⃗⃗⃗⃗⃗ ⋅OD ⃗⃗⃗⃗⃗⃗ =154列式求得m 的值; (2)由对称性,点G 在y 轴上,可设G(0,a),由k AG =k AC ,结合根与系数的关系求得a 值,即可得到G 的坐标.再由S =S 梯形ABCD −(S △GAB +S △GCD ),结合根与系数的关系及基本不等式求最值.本题考查圆与抛物线位置关系的应用,考查运算求解能力,训练了利用基本不等式求最值,考查化归与转化思想,是中档题.22.【答案】解:(1)∵f(x)=asin 2x −√3x ,∴f′(x)=asin2x −√3,由f′(π3)=0,解得:a =2, 故f(x)=2sin 2x −√3x ,f′(x)=2sin2x −√3, 令f′(x)>0,解得:π6<x <π3,令f′(x)<0,解得:0<x <π6或π3<x <π2, 故f(x)在(0,π6)递减,在(π6,π3)递增,在(π3,π2)递减;(2)证明:(i)当0≤a ≤2时,f(x)≤2sin 2x −√3x ,设ℎ(x)=2sin 2x −√3x ,①当0<x <π2时,由(1)知:ℎ(x)max =ℎ(π3)=32−√33π<0,又ℎ(0)=0,故ℎ(x)<0,从而f(x)<0;②当x ≥π2时,f(x)≤ℎ(x)≤2−√32π<0,由①②知,当x >0时,f(x)<0(i 1), 当x <0时,f(x)≥−√3x >0(i 2), 由(i 1)(i 2)得:x ≠0时,xf(x)<0,故f(x)在(0,π6)递减,在(π6,π3)递增,在(π3,π2)递增, (ii)当−2≤a <0,当x <0时,f(x)≥−2sin 2x −√3x , 设g(x)=−2sin 2x −√3x ,g′(x)=−2(sin2x +√32),①当−π2<x <0时,由g′(x)=0,解得:x 1=−π6,x 2=−π3, 同理f(x)极小值=g(−π3)=−32+√33π>0,又g(−π2)>g(−π3)>0,g(0)=0,故g(x)>0,从而f(x)>0,②当x≤−π2时,f(x)≥−2+√32π>0,由①②得,当x<0时,f(x)>0(j1),当x>0时,显然f(x)<0(j2),由(j1)(j2)得,x≠0时,xf(x)<0,综上:当x≠0时,xf(x)<0.【解析】(1)求出函数的导数,根据f′(π3)=0,求出a的值,解关于导函数的不等式,求出函数的单调区间;(2)通过讨论a的取值范围,求出函数的单调区间,根据函数的单调性证明结论成立即可.本题考查了函数的单调性,极值问题,考查导数的应用以及分类讨论思想,转化思想,是难题.。
苏北四市2021届高三上学期期末统考数学试题理

苏北四市2021届高三上学期期末统考数学试题理苏北四市数学试题数学我必须做问题部分(本部分满分160分,时间120分钟)注:考生在回答问题之前,应仔细阅读笔记并回答要求。
1.本试卷共4页,均为非多项选择题(问题1~20,共20题)。
本卷满分为160分,考试时间为120分钟。
考试结束后,请将试卷和答题纸一并交回。
2.在回答问题之前,请务必用0.5毫米的黑色签字笔在试卷和答题卡的指定位置填写您的姓名和录取卡号。
3.回答问题时,必须使用0.5毫米黑色签字笔在答题纸上指定的位置作答。
其他位置的答案无效。
4.如需绘制图纸,应使用2B 铅笔清晰地绘制和书写,线条和符号应为黑色和粗体。
1参考公式:锥体体积公式:v?SH,其中s是圆锥体底部的面积,H是高度3一、填空题:本题共14小题,每小题5分,共70分.请把答案填写在答题卡上.....1.将复数设置为Z1?2.i、 z2?MI(M?R,I是虚单位),如果Z1?如果Z2是实数,那么M的值是▲. 2.已知集合a?{2?a,a},b?{1,1,3}和a?b、那么实数a的值是▲3.某林场有树苗3000棵,其中松树苗400棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的棵数为▲.4.在哪里?在ABC边ab上取一个随机点P,记得吗?帽子和帽子?CBP的面积分别是S1和S2,那么S1?2s2的概率是▲开始x2y25.已知双曲线2?2?1的一条渐近线方程为2x?y?0,防抱死制动系统?0,n?1那么双曲线的偏心率是▲6.右图是一个算法流程图,则输出s的值是▲.n?n?27.函数f(x)?lg(2x?3x)的定义域为▲.8.如果正三角形棱锥的底边长为2,边长为1,则该三角形棱锥的体积为▲9.在△abc中,已知ab?3,a?120o,且?abc的面积153,那么BC边长是▲. 410.已知函数f(x)?xx?2,然后是不等式f(2?X)≤f(1)为解决方案集是▲s?s?nn?10yn输出s结束(第6题图)11.已知函数f(x)?2英寸(2?x?)最大值(?0)与最小正周期相同,则函数f(x)为4[?1,1]上的单调增区间为▲.12.如果A4、A3和A5构成等差序列,则等比序列{an}的前n项之和为Sn,并且SK?33,sk?1.63,k在哪里?N那是SK吗?2的值是▲13.在平面四边形abcd中,已知ab?3,dc?2,点e,f分别在边ad,bc上,且公元公元前3世纪?3BF。
江苏省苏北四市(徐州、淮安、宿迁、连云港)2021-2022学年高三上学期期末考试数学试题变式题

江苏省苏北四市(徐州、淮安、宿迁、连云港)2022届高三年级第一学期期末调研考试数学试题变式题1 知识点 交并补混合运算【正确答案】D1-1(基础) 已知集合{}5A x x =<,{}17B x x =<<,则() RA B ⋂=().A.[]5,7B.[)5,7C.(]5,7D.()5,7【正确答案】 B1-2(基础) 已知集合{}310A x x =≤<,{}13516B x x =<-<,则()A B =R ()A.{}23x x <<B.{}23x x <≤C.{}710x x <<D.{}210x x <<【正确答案】 A1-3(巩固) 已知集合{}{260,1A xx x B x x =--≤=≤-∣∣或}4x >,则RA B =()A.{}21xx -≤≤-∣ B.{3xx ≤∣或}4x > C.{}24xx -≤≤∣ D.{}13xx -<≤∣ 【正确答案】 D1-4(巩固) 设全集U =R ,集合{}{}21,40M x x N x x =≤=-<,集合()U M N 等于()A.[)1,2B.()1,2C.()2,1-D.[)2,1-【正确答案】 B1-5(提升) 设全集U =R ,集合{}21A x x =-<,{}240xB x =-≥,则集合()UA B =()A.()1,2B.(]1,2C.[)1,2D.[]1,2【正确答案】 A已知全集为R ,集合{}2311,4302x A xB x x x x -⎧⎫=≥=-+≤⎨⎬-⎩⎭∣∣,则()R A B ⋂() A.3,34⎡⎤⎢⎥⎣⎦ B.3,14⎡⎤⎢⎥⎣⎦C.[]2,3D.(]2,3【正确答案】 C2 知识点 求复数的模,复数的除法运算3i+A.5C.3【正确答案】 B2-2(基础) 复平面内表示复数62i2iz +=-,则z =()A. B. C.4D.【正确答案】 A2-3(巩固) 已知i 是虚数单位,复数z 满足()2i 12i z +⋅=-+,则=z () A.iB.1C.35D.53【正确答案】 B2-4(巩固) 若()()1i 12z +-=,则=z ()A.1B.2【正确答案】 D已知复数2i1iz -=+(其中i 为虚数单位),则||z z -=() A.0B.1C.32D.3【正确答案】 D设i 为虚数单位,若复数z 满足()1i 2z +=,则i z -=()A.1D.2【正确答案】 C3 知识点 分式不等式,充分条件的判定及性质【正确答案】C3-1(基础) 若x ∈R ,则使“22x x <”成立的一个必要不充分条件为() A.01x << B.224x x >C.21x> D.0x >【正确答案】 D3-2(基础) 若p :23x -≤,则p 成立的一个充分不必要条件是() A.16x -≤≤ B.25x -≤≤ C.15x -<≤ D.06x ≤≤【正确答案】 C3-3(巩固) “a b >”的一个充分条件是() A.11a b < B.2ab b >C.110b a-<-<D.2a ab >【正确答案】 C3-4(巩固) 对于实数x ,规定[]x 表示不大于x 的最大整数,例如][1.22,1.51⎡⎤-=-=⎣⎦,那么不等式[]24[]1670x x -+<成立的充分不必要条件是()A.1722x << B.13x ≤≤ C.14x ≤<D.14x ≤≤不等式20x x m -+>在R 上恒成立的一个必要不充分条件是( ) A.14m >B.01m <<C.0m >D.1m >【正确答案】 C“ a b >”的一个充分条件是() A.e 0a b -> B.ln0ab> C.a b a b >D.110a b<< 【正确答案】 D4 知识点 不相邻排列问题【正确答案】A4-1(基础) 高中数学新教材有必修一和必修二,选择性必修有一、二、三共5本书,把这5本书放在书架上排成一排,必修一、必修二不相邻的排列方法种数是() A.72B.144C.48D.36【正确答案】 A4-2(基础) 现有10本书,其中有4本不同的英文读物,6本不同的中文读物,某学生计划一年看完这10本书,为了缓解疲劳,要求英文读物不能相邻阅读,则可以排出的阅读顺序总数为() A.7476A A B.1646A AC.4467A AD.6467A A【正确答案】 D4-3(巩固) 某学校组织6×100接力跑比赛,某班级决定派出A ,B ,C ,D ,E ,F 等6位同学参加比赛.在安排这6人的比赛顺序时要保证A 要在B 之前,D 和F 的顺序不能相邻,则符合要求的安排共有() A.240种 B.180种C.120种D.150种【正确答案】 A4-4(巩固) 自2020年“新冠”出现后,全国人民“众志成城,齐心抗疫”.许多志愿者挺身而出,现安排4名男性志愿者,3名女性志愿者站成一排将逐一进行核酸检测,要求男女相间且女性甲要在女性乙之前检测,则不同的安排方法的种数是() A.36种B.72种C.108种D.144种某人根据自己爱好,希望从{},,,W X Y Z 中选2个不同字母,从{}0,2,6,8中选3个不同数字编拟车牌号,要求前3位是数字,后两位是字母,且数字2不能排在首位,字母Z 和数字2不能相邻,那么满足要求的车牌号有() A.198个 B.180个 C.216个 D.234个【正确答案】 A援鄂医护人员A ,B ,C ,D ,E ,F 共6人(其中A 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这6名医护人员和当地的一位领导共7人站成一排拍照,则领导和队长A 相邻且不站两端,B 与C 相邻,B 与D 不相邻的排法种数为(). A.120B.240C.288D.360【正确答案】 B5 知识点 平面向量线性运算的坐标表示,由向量共线(平行)求参数,坐标计算向量的模,利用向量垂直求参数【正确答案】B5-1(基础) 已知向量()32a =-,,()1b x =,(0x >),若()()2a b a b +⊥-,则b =()【正确答案】 B5-2(基础) 已知()3,4a =,(),1b t =,()a b a -⊥,则b =()A.2B. C.1D.【正确答案】 B5-3(巩固) 已知平面向量(2,)a m =,(1,2)b =-,且|2||2|a b a b -=+,则||a b +=() A.1B.2C.3D.4已知向量,a b 满足||1,||2,(3,2)a b a b ==-=,则|2|a b -等于()A.D.【正确答案】 A已知直角梯形ABCD 中,AD ∥BC ,∠ADC =90,AD =4,BC =2,P 是腰DC 上的动点,则|2|PA PB +的最小值为()A.8B.7C.6D.4【正确答案】 A(提升) 已知e 为单位向量,向量a 满足:()()50a e e a --⋅=,则a e +的最大值为() A.4B.5C.6D.7【正确答案】 C6 题】 知识点 椭圆定义及辨析,求椭圆的离心率或离心率的取值范围,根据抛物线方程求焦点或准线,抛物线的对称性的应用22【正确答案】 B6-2(基础) 已知椭圆C :22221x y a b +=与抛物线E :()220y px p =>有公共焦点F ,椭圆C 与抛物线E 交于A ,B 两点,且A ,B ,F 三点共线,则椭圆C 的离心率为()1 【正确答案】 A已知12F F 、是椭圆22221(0)x ya b a b+=>>的左、右焦点,点P 为抛物线28(0)y ax a =->准线上一点,若12F PF △是底角为15︒的等腰三角形,则椭圆的离心率为()1 1【正确答案】 A已知椭圆22122:1(0)x y C a b a b +=>>的右焦点F 与抛物线22:2(0)C y px p =>的焦点重合,P 为椭圆1C 与抛物线2C 的公共点,且PF x ⊥轴,那么椭圆1C 的离心率为()1 C.21【正确答案】 A已知椭圆22221x y a b+=(0)a b >>的右焦点2(,0)F c ,此椭圆在第一象限交抛物线24y cx =于点P ,且232cPF =,则椭圆的离心率为( )【正确答案】 A已知椭圆()2222:10x y E a b a b+=>>的焦距为2c ,左焦点为F ,右顶点为A ,若抛物线()2158y a c x =+与椭圆交于B ,C 两点,且四边形ABFC 是菱形,则椭圆E 的离心率是()A.815B.415C.23D.12【正确答案】 D7 题】 知识点 柱体体积的有关计算,椭圆的其他应用【正确答案】 C7-1(基础) 中国古代数学的瑰宝《九章第术》中记载了一种称为“曲池”的几何体,该几何体为上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如下图所示的“曲池”,其高为3,1AA ⊥底面,底面扇环所对的圆心角为2π,AD 长度为BC 长度的3倍,且线段2AB CD ==,则该“曲池”的体积为()A.92π B.5π C.112πD.6π【正确答案】 D7-2(基础) 陀螺是中国民间最早的娱乐工具之一,也称陀罗.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中,B C 分别是上、下底面圆的圆心,且3AC AB =,则该陀螺下半部分的圆柱与上半部分的圆锥的体积的比值是()A.2B.3C.4D.6【正确答案】 D7-3(巩固) 图1中的机械设备叫做“转子发动机”,其核心零部件之一的转子形状是“曲侧面三棱柱”,图2是一个曲侧面三棱柱,它的侧棱垂直于底面,底面是“莱洛三角形”(如图3),莱洛三角形是以正三角形的三个顶点为圆心,正三角形的边长为半径画圆弧得到的,若曲侧面三棱柱的高为4,底面任意两顶点之间的距离为A.(2002π-B.(400πC. D.(4002π【正确答案】B7-4(巩固)2022年6月5日,我国三名航天员乘坐神舟十四号载入飞船成功升空.预计三名航天员在太空工作6个月,在轨期间将进行多个科学实验,任务完成后,乘返回舱返回地面.某自然科学博物馆为了青少年参观学习的需要,仿制了一个返回舱,如图所示,若仿制的返回舱的内腔轴截面曲线C近似由半椭圆:221(0)1612y xy+=>和弧:22(2)16(0)x y y+-=≤组成,曲线C内接一各边与坐标轴分别平行的矩形,满足水平方向矩形的边长为6,若由这个矩形绕y轴旋转,形成圆柱作为返回时载物及航天员座椅的空间,则这个空间的体积为()A. B. C.36π D.【正确答案】B7-5(提升)《乌鸦喝水》是《伊索寓言》中的一个寓言故事,通过讲述一只乌鸦喝水的故事,告诉人们遇到困难要运用智慧、认真思考才能让问题迎刃而解的道理.如图所示,乌鸦想喝水,发现有一个锥形瓶,已知该锥形瓶上面的部分是圆柱体,下面的部分是圆台,瓶口的直径为3cm,瓶底的直径为9cm,瓶口距瓶颈.现将1颗石子投入瓶中,发现水位,时,乌鸦就能喝到水,则乌鸦共需要投入的石子数量至少是(石子体积均视为一致)()A.2颗B.3颗C.4颗D.5颗【正确答案】 B7-6(提升) 如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120︒,腰为3的等腰三角形,则该几何体的体积为()A.23B.24C.26D.27【正确答案】 D【原卷 8 题】 知识点 分组(并项)法求和【正确答案】B8-1(基础) 已知数列{}n a 的通项公式为cos 1),(n n a n n S π=-为数列的前n 项和,2021S =() A.1008 B.1009C.1010D.1011【正确答案】 D数列()(){}121nn --的前2022项和等于() A.1010- B.2022 C.2018- D.2019【正确答案】 B设数列{}n a 的通项公式为()()121cos12nn n a n π=--⋅-,其前n 项和为n S ,则2022S =() A.4041 B.5- C.2021- D.4045-【正确答案】 D已知数列{}n a 的前n 项和为n S ,111012a =,1221012n n n n a a a +++++=,则2023S =() A.138B.674C.675D.2023【正确答案】 C高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设x ∈R ,用[]x 表示不超过x 的最大整数,则()[]f x x =称为高斯函数.已知数列{}n a 满足21a =,且121(1)2n n n n a na +++-=,若[]lg n n b a =数列{}n b 的前n 项和为n T ,则2021T =() A.3950 B.3953 C.3840 D.3845【正确答案】 D设数列{}n a 的通项公式为()()()*121cos1N 2nn n a n n π=--⋅+∈,其前n 项和为n S ,则120S =() A.60-B.120-C.180D.240【正确答案】 D9 知识点 二项式的系数和,求有理项或其系数,二项展开式各项的系数和【正确答案】 A C D9-1(基础) 已知()22nx n⎛∈ ⎝N 的展开式中各项的二项式系数之和为64,则().A.6n =B.展开式中各项的系数和为1C.展开式中第3项或第4项的二项式系数最大D.展开式中有理项只有4项 【正确答案】 ABD在nx⎛⎝的展开式中,只有第4项的二项式系数最大,下列结论正确的是()A.6n =B.各项二项式系数之和为128C.各项系数之和为0D.有理项共4项【正确答案】 ACD在72x⎛⎝的展开式中,下列说法正确的有()A.所有项的二项式系数和为128B.所有项的系数和为1C.二项式系数最大的项为第4项D.有理项共3项【正确答案】 AB已知二项式12nx ⎫⎪⎭的展开式中各项系数之和是1128,则下列说法正确的有()A.展开式共有7项B.二项式系数最大的项是第4项C.所有二项式系数和为128D.展开式的有理项共有4项【正确答案】 CD已知6112a x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2,则下列结论正确的有()A.1a =B.展开式中常数项为160C.展开式系数的绝对值的和1458D.展开式中含2x 项的系数为240【正确答案】 ACD下列结论正确的是()A.*023()nk k n n k C n N ==∈∑B.多项式621x x ⎛⎫+- ⎪⎝⎭展开式中3x 的系数为52 C.若1021001210(21),x a a x a x a x x R -=++++∈,则10012103a a a a ++++=D.012321221*22222222232()n n n n n n n n n C C C C C C n N --++++++=⋅∈ 【正确答案】 ACD10 知识点 由图象确定正(余)弦型函数解析式,求sinx 型三角函数的单调性,求正弦(型)函数的奇偶性π的是()A.为了得到()sin 2g x x =的图象,只要将()f x 的图象向右平移6π个单位长度 B.函数()f x 的图象的一条对称轴为712x π=C.函数()f x 在区间0,10π⎛⎫⎪⎝⎭上单调递增D.方程()0f x =在区间[]0,2020上有1285个实数解 【正确答案】 AB已知()sin()0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象关于点7,012π⎛⎫⎪⎝⎭对称,相邻两条对称轴的距离为2π,则下列说法正确的是() A.2ω=,6πϕ=B.将函数()f x 的图象向右平移6π个单位长度后,得到的图象关于y 轴对称C.函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的单调递减区间为,32ππ⎡⎤⎢⎥⎣⎦D.为了得到()f x 的图象,可以将函数sin 2y x =的图象向右平移6π个单位 【正确答案】 BC已知函数()()sin f x A x ωϕ=+ (A >0,ω>0,2πϕ<)的部分图象如图所示,下列说法正确的是()A.函数f (x )的图象关于点(,0)6π-对称 B.函数f (x )的图象关于直线512x π=-对称 C.函数f (x )在2,36ππ⎡⎤--⎢⎥⎣⎦单调递增 D.该图象向右平移3π个单位可得y =2sin2x 的图象【正确答案】 AB10-4(巩固) 已知函数()()πsin 20,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示,则下列结论正确的是()A.()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称B.()f x 的图象向右平移π12个单位后得到sin2y x =的图象C.()f x 在区间π,2π⎡⎤--⎢⎥⎣⎦上单调递增D.π6f x ⎛⎫+ ⎪⎝⎭为偶函数【正确答案】 BD10-5(提升) 已知函数()()()sin 0,0,0πf x A x A ωϕωϕ=+>><<的部分图象如图所示,则下列说法正确的是().A.π2f ⎛⎫= ⎪⎝⎭B.()f x 在区间5π0,12⎛⎫⎪⎝⎭单调递减C.()f x 在区间π11π,1212⎛⎫- ⎪⎝⎭上有且仅有2个零点D.将()f x 的图象向右平移π12个单位长度后,可得到一个奇函数的图象 【正确答案】 BC10-6(提升) 已知函数π()sin()0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,下列说法正确的是()A.函数()y f x =的周期为π2B.函数()y f x =的图象关于直线19π12x =对称 C.函数()y f x =在区间2ππ,36⎡⎤--⎢⎥⎣⎦上单调递增D.函数()1y f x =-在区间[]0,2π上有4个零点 【正确答案】 BD【原卷 11 题】 知识点 画出具体函数图象,垂直关系的向量表示,函数新定义【正确答案】 B D11-1(基础) 在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石,布劳威尔不动点定理得名于荷兰数学家鲁伊兹•布劳尔(L.E.J.Brouwer ),简单的讲就是对于满足一定条件的连续函数()f x 存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点函数”,下列为“不动点函数”的是()A.()23f x x x =++B.()21xf x x =+-C.()221,12,1x x f x x x ⎧-≤⎪=⎨->⎪⎩D.()1f x x =-【正确答案】 BC11-2(基础) 已知函数=()y f x 的定义域为D ,若存在区间[,]a b D ⊆,使得{=(),[,]}=[,]yy f x x a b a b ∈∣,则称区间[,]a b 为函数=()y f x 的“和谐区间”.下列说法正确的是() A.[1,0]-是函数2()2f x x x =-的一个“和谐区间” B.[1,3]-是函数2()2f x x x =-的一个“和谐区间” C.[0,2]是函数3()=12f x x -的一个“和谐区间” D.2,25⎡⎤⎢⎥⎣⎦是函数3()=12f x x -的一个“和谐区间”【正确答案】 BC对于定义在I 上的函数()y f x =,如果存在区间[,]m n I ⊆,同时满足下列两个条件:①()f x 在区间[],m n 上为增函数;②当[,]x m n ∈时,函数()f x 值域也为[,]m n ,则称[,]m n 是函数()y f x =的一个“递增黄金区间”.下列函数中存在“递增黄金区间”的是() A.1y x =+ B.222y x x -=+ C.22x y =- D.lg y x =【正确答案】 BC定义一:关于一个函数()()f x x D ∈,若存在两条距离为d 的直线1y kx m =+和2y kx m =+,使得在x D ∈时,()12kx m f x kx m +≤≤+恒成立,则称函数()f x 在D 内有一个宽度为d 的通道.定义二:若一个函数()f x ,关于任意给定的正数ε,都存在一个实数0x ,使得函数()f x 在[)0,x ∞+内有一个宽度为ε的通道,则称()f x 在正无穷处有永恒通道.则下列在正无穷处有永恒通道的函数为()A.()ln f x x =B.()sin xf x x=C.()f x =D.()e xf x -=【正确答案】 BCD对于定义域为D 的函数()y f x =,若同时满足:①()f x 在D 内单调递增或单调递减;②存在区间[,]a b D ⊆,使()f x 在[,]a b 上的值域为[,]a b ,则把()()y f x x D =∈称为闭函数.下列结论正确的是() A.函数21y x =+是闭函数 B.函数3y x =-是闭函数 C.函数1xy x =+是闭函数D.若函数y k =是闭函数,则9,24k ⎛⎤∈-- ⎥⎝⎦【正确答案】 BD设R x ∈,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,也叫取整函数.如[1.2]1=,[2]2=,[ 1.2]2-=-.令()[]f x x x =-,以下结论正确的有()A.( 1.1)0.9f -=B.1133f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭C.(1)()1f x f x +=+D.函数()f x 的值域为[0,1)【正确答案】 AD12 知识点 柱体体积的有关计算,证明面面垂直【正确答案】 B C D12-1(基础) 四面体ABCD 的每个顶点都在球O 的表面上,AB 是球O 的一条直径,且2AC =,4BC =,现有下面四个结论,其中所有正确结论的编号是() A.球O 的表面积为20πB.若3AD =,则4BD =C.AC 上存在一点M ,使得//AD BMD.四面体ABCD 【正确答案】 AD12-2(基础) 如图,在多面体EFG ABCD -中,四边形ABCD ,CFGD ,ADGE 均是边长为1的正方形,点H 在棱EF 上,则()A.该几何体的体积为23B.点D 在平面BEF 内的射影为BEF △的垂心C.GH BH +D.存在点H ,使得DH BF ⊥【正确答案】 BD12-3(巩固) 如图,平行六面体1111ABCD A B C D -中,以顶点A 为端点的三条棱长均为1,且它们彼此的夹角都是60°,则()A.1ACB.1AC BD ⊥C.四边形11BDD BD.平行六面体1111ABCD A B C D -【正确答案】 ABD12-4(巩固) 如图,直三棱柱111ABCA B C 中,12AA =,1AB BC ==,90ABC ︒∠=,侧面11AA C C 中心为O ,点E 是侧棱1BB 上的一个动点,有下列判断,正确的是()A.直三棱柱侧面积是4+ B.直三棱柱体积是13C.三棱锥1E AAO -的体积为定值D.1AE EC +的最小值为【正确答案】 ACD12-5(提升) 如图,已知三棱柱111ABCA B C 的侧棱垂直于底面,且底面ABC ∆为等腰直角三角形,2ACB π∠=,1AA =,M N ,分别是1BC BB ,的中点,P 是线段11A C 上的动点,则下列结论正确的是()A.1A P MN ⊥B.直线MN 与直线11A BC.直线MN ⊥平面1A PND.若P 是线段11A C 的中点,则三棱锥1A PMN -的体积1V 与三棱柱111ABC A B C 的体积2V 之比为18【正确答案】 ACD12-6(提升) 正方体1111ABCD A B C D -的棱长为2,E ,F ,G 分别为BC ,1CC ,1BB 的中点.则()A.正方体1111ABCD A B C D -体积是三棱锥D EFC -体积的24倍B.正方体1111ABCD A B C D -外接球的体积为C.平面DEF 截正方体所得的截面面积为32D.三棱锥C DEF -与三棱锥G DEF -的体积相等 【正确答案】 ABC【原卷 13 题】 知识点 直线与圆相交的性质——韦达定理及应用【正确答案】13-1(基础) 已知直线x y a +=与圆224x y +=交于A ,B 两点,O 为坐标原点,3OA OB OA OB +=-,则实数a 的值为___________.【正确答案】13-2(基础) 在直角坐标系xoy 中,直线122y x =-+与圆22:240C x y x y a +--+=(a R ∈)相交于A ,B 两点,且2AOB π∠=,则=a __________.1.613-3(巩固) 已知直线():0l y kx k =>与圆()22:14C x y ++=交于不同的两点A ,B ,点()2,1P ,则22PA PB +的最大值为______.【正确答案】 22或22+已知动点A 到()1,3P 的距离是到()4,0Q 的距离的2倍,记动点A 的轨迹为C ,直线l :40x ty --=与C 交于E ,F 两点,若13OQF OQE S S =△△(点O 为坐标原点,S 表示面积),则t =___________.【正确答案】 1-已知直线:l y kx =与圆222210x y x y +--+=相交于A ,B 两点,存在点()0,M b ,()0b >,使得MA MB ⊥,则实数k 的取值范围是______. 【正确答案】 [1,+∞)(提升) 已知圆22(1)9x y ++=与直线3y tx =+交于A ,B 两点,点(,)P a b 在直线2y x =上,且PA PB =,则a 的取值范围为_____【正确答案】 ()()1,00,2-⋃14 题】 知识点 求函数值【正确答案】-214-1(基础) 设函数()f x 满足(3)2()3f x f x x -+=+,则(3)f =______. 【正确答案】 314-2(基础) 已知函数()y f x =,对任意x N ∈,满足(1)()2f x f x +=+,若(l)3f =,则(3)f =___________. 【正确答案】 714-3(巩固) 已知()f x 是定义在R 上的奇函数,()13f =,且()()()+1=2,-1,0f x f x x x ≠≠,则()3f -=___________. 【正确答案】 12-14-4(巩固) 定义在()1,+∞上的函数()f x 满足下列两个条件(1)对任意的()1,x ∈+∞恒有()()22f x f x =成立;(2)当(]1,2x ∈时,()2f x x =-.则()6f 的值是__________. 【正确答案】 2定义在R 上的函数()f x 满足()()f x f x -=-,()()22f x f x -=+,且()2,0x ∈-时,()212f x x =+,则()2017f =________________.14-6(提升) 已知函数()f x 为奇函数,且当0x >时,()ln f x x =,则21e f f ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭___. 【正确答案】 ln 2-或1ln 215 题】 知识点 三角函数的化简、求值——同角三角函数基本关系,用和、差角的正切公式化简、求值sin cos 1αα⋅1【正确答案】 -115-2(基础) 已知()310,sin ,tan 253παααβ<<=-=-,则tan β=___________.15-3(巩固) 若0,2πα⎛⎫∈ ⎪⎝⎭,且sin 2cos αα+=,则tan 4πα⎛⎫+= ⎪⎝⎭________.【正确答案】 2-15-4(巩固) 设1tan 2α=,()4cos 5πβ+=-,()0,βπ∈,则()tan 2αβ-的值为____.,2πβπ⎛⎫∈ ⎪⎝⎭,sin 13β=,若()3sin 2sin αβα+=,则()tan αβ+=______.已知sin 2θ=35,0<2θ<2π,则22cos sin 12)4θθπθ--+=________.0.516 题】 知识点 棱柱的结构特征和分类,圆锥的结构特征辨析,多面体与球体内切外接问题,柱、锥、台体的轴截面【正确答案】16-1(基础) 已知圆锥的底面半径为若圆锥内某正方体的底面在圆锥的底面上,则该正方体的最大体积为______. 【正确答案】 116-2(基础) 四棱锥S ABCD -中,底面ABCD 是边长为2的正方形,侧面SAD 是以SD 为斜边的等腰直角三角形,若四棱锥S ABCD -的体积取值范围为83⎤⎥⎣⎦,则该四棱锥外接球表面积的取值范围是______.【正确答案】 28,203ππ⎡⎤⎢⎥⎣⎦.16-3(巩固) 已知四面体ABCD 的各棱长都为4,点E 是线段BD 的中点,若球O 是四面体ABCD 的外接球,过点E 作球O 的截面,则所得截面圆的面积取值范围是______. 【正确答案】 []4,6ππ16-4(巩固) 已知正三棱柱111ABCA B C 的各棱长均为2,D 为棱AB 的中点,则过点D 的平面截该三棱柱外接球所得截面面积的取值范围为___________. 【正确答案】 7,3ππ⎡⎤⎢⎥⎣⎦已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且23l ≤≤,则该正四棱锥体积的取值范围是______. 【正确答案】 12827,814⎡⎤⎢⎥⎣⎦已知球O 是正三棱锥A BCD -的外接球,3BC =,AB =点E 在线段BD 上,且6BD BE =,过点E 作球O 的截面,则所得截面圆面积的取值范围是___________. 【正确答案】 5,44ππ⎡⎤⎢⎥⎣⎦17 知识点 正弦定理边角互化的应用,三角形面积公式及其应用,求三角形中的边长或周长的最值或范围【正确答案】 (1)答案见解析 (2)(2,8)17-1(基础) 在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且()2cos cos 0b a C c B -+=请在①2b =,②c =a c =这三个条件中任选两个,将问题(1)补充完整,然后解答问题 1、已知______,计算ABC 的面积; 2、当5c =时,求ABC 的周长的最大值.注:如选择多种搭配方式分别解答,按第一个解答计分. 【正确答案】 1、答案见解析 2、1517-2(基础) 在①cos cos 2B bC a c =-+,②sin sin sin A b c B C a c+=-+,③2S BC =⋅三个条件中任选一个补充在下面的横线上,并加以解答.在ABC 中,ABC 的面积为S ,角A ,B ,C 的对边分别为a ,b ,c 且选条件:_____________.1、求B ∠;2、作AB AD ⊥,使得四边形ABCD 满足,4ACD AD π∠==BC 的取值范围.【正确答案】 1、条件选择见解析,23B π=;2、⎛ ⎝⎭.17-3(巩固) 在ABC 中,内角,,A B C 的对边分别为,,a b c ,且______.在①cos cos 2b C B π⎛⎫-= ⎪⎝⎭;②2ABC S BC =⋅△;③tan tan tan A C A C +=这三个条件中任选一个,补充在上面的问题中,并进行解答. 1、求角B 的大小;2、若角B 的内角平分线交AC 于D ,且1BD =,求4a c +的最小值. 【正确答案】 1、23B π= 2、917-4(巩固) 在①222)S a b c +-,②cos cos 2cos a B b A c C +=,请在这两个条件中任选一个,补充到下面问题中,并完成解答.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,设S 为ABC 的面积,满足______________(填写序号即可).1、求角C 的大小;2、若3c =,求ABC 周长的最大值.注:如果选择多个条件分别解答,按第一个解答计分. 【正确答案】 1、3C π=2、9在①sinsin 2A B b c B +=,②cos cos cos c a bC A B +=+,)cos sin c A b a C -=-这三个条件中任选一个,补充在下面的问题中,并解答.在锐角ABC 中,内角,,A B C 的对边分别为,,a b c ,且满足__________. 1、求角C 的大小;2、若c ,角A 与角B 的内角平分线相交于点D ,求ABD △面积的取值范围.注:如果选择多个条件分别解答,按第一个解答计分. 【正确答案】 1、3π2、⎝⎦在ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,记ABC 的面积为S .已知_________.从①2sin tan a C c A =,②2cos 2a B c b =-,③)2224S b c a =+-三个条件中选择一个填在上面的横线上,并解答下列问题.(注:如果选择多个条件分别解答,则按第一个解答计分) 1、求角A 的大小;2、若边长2a =,求ABC 的周长的取值范围. 【正确答案】 1、无论选择①②③,3A π=; 2、(]4,618 题】 知识点 累加法求数列通项,含绝对值的等差数列前n 项和,由递推关系证明等比数列【正确答案】18-1(基础) 已知在前n 项和为n S 的等差数列{}n a 中,42222a a -=,3102S =. 1、求数列{}n a 的通项公式; 2、求数列{}n a 的前20项和20T . 【正确答案】 1、403n a n =-; 2、324.18-2(基础) 已知等差数列{}n a 的前n 项和为n S ,4228S S =+,21219n n a a +=+,*n ∈N .1、求{}n a 的通项公式;2、设n n b a =,求数列{}n b 的前20项之和20T . 【正确答案】 1、217n a n =- 2、208已知n S 是数列{}n a 的前n 项和,且214n S n n =-.1、求{}n a 的通项公式;2、若123n n T a a a a =++++,求n T .【正确答案】 1、152n a n =-2、2214,171498,7n n n n T n n n ⎧-≤≤=⎨-+>⎩已知等差数列{}n a 的公差为d ,数列{}n a 的前n 项和为n S ,且2510,20a S ==. 1、求数列{}n a 的通项公式; 2、求数列2{2}n a n a +的前n 项和n T ; 3、请直接写出n A =123||||||||n a a a a ++++的结果.【正确答案】 1、226n a n =-2、11212(1)81937n n T n n -=-+3、22193,3=31960,>3n n n n A n n n -≤-⎧⎨+⎩在等比数列{}n a 中,()0,n a n +>∈N ,公比()0,1q ∈,且3546392100a a a a a a ++=,又有4是3a 和7a 的等比中项.1、求数列{}n a 的通项公式;2、设2log n n b a =,求数列{}n b 的前21项和21S .【正确答案】 1、72nn a -=2、126在数列{}n a 中,18a =,42a =,且满足212n n n a a a +++=. 1、求数列{}n a 的通项公式;2、设n S 是数列{}n a 的前n 项和,求n S . 【正确答案】 1、210n a n =-+;2、229,5940,6n n n n S n n n ⎧-+≤=⎨-+≥⎩.19 知识点 证明线面垂直,线面垂直证明线线垂直,已知面面角求其他量【正确答案】19-1(基础) 如图,在四棱锥P ABCD -中,平面PAD ⊥平面,,1,2,ABCD AD BC PA AB BC AD CD PA AD =====⊥∥,点E 在棱PC 上,设CE CP λ=.1、证明:CD AE ⊥.2、设二面角C AE D --的平面角为θ,且cos θ=,求λ的值. 【正确答案】 1、证明见解析; 2、34λ=.19-2(基础) 如图,四棱锥S ABCD -的底面ABCD 是直角梯形,且//AB CD ,AD DC ⊥,24CD AB ==,AD a =,正三角形SAD 所在平面与平面ABCD 相互垂直,E 、O 分别为SD 、AD 的中点.1、求证:SO BC ⊥;2、若二面角E AC D --,求a 的值. 【正确答案】 1、证明见解析; 2、6.19-3(巩固) 如图,在四面体ABCD 中,ABC 是正三角形,ACD 是直角三角形,,ABD CBD AB BD ∠=∠=.1、求证:AC BD ⊥;2、已知点E 在棱BD 上,且2AB =,设DE mDB =,若二面角D AC E --,求m .【正确答案】 1、证明见解析; 2、13.如图,在三棱锥D ABC -中,二面角D AB C --是直二面角,AB BD ⊥,且,AB BD AC BC ==,P 为CD 上一点,且BP ⊥平面ACD .,E F 分别为棱,DA DC 上的动点,且DE DFDA DCλ==.1、证明:AC BC ⊥;2、若平面EFB 与平面ABC λ的值. 【正确答案】 1、证明见解析 2、12λ=19-5(提升) 三棱锥-P ABC 中,PAB PAC ≅△△,2BC AB ,PA AB ⊥,直线PC 与平面ABC 所成的角为3π,点D 在线段PA 上.1、求证:BD AC ⊥;2、若点E 在PC 上,满足34PE PC =,点D 满足(01)AD AP λλ=<<,求实数λ使得二面角A BE D --的余弦值为25. 【正确答案】 1、证明见解析; 2、12λ=. 19-6(提升) 如图,四棱锥P ABCD -中,底面ABCD 是直角梯形,90AB DC BAD ∠=︒∥,,222PD DC BC PA AB =====,PD DC ⊥.1、求证:PA ⊥平面ABCD ;2、设(01)BM BD λλ=<<,当平面P AM 与平面PBD λ的值. 【正确答案】 1、证明见解析 2、12λ=【原卷 20 题】 知识点 由频率分布直方图计算频率、频数、样本容量、总体容量,由频率分布直方图估计平均数,指定区间的概率【正确答案】20-1(基础) 为了提高生产效率,某企业引进一条新的生产线,现要定期对产品进行检测.每次抽取100件产品作为样本,检测新产品中的某项质量指标数,根据测量结果得到如下频率分布直方图.1、指标数不在175.和22.5之间的产品为次等品,试估计产品为次等品的概率; 2、技术评估可以认为,这种产品的质量指标数X 服从正态分布()2,1.22N μ,其中μ近似为样本的平均数(同一组中的数据用该组区间的中点值为代表),计算μ值,并计算产品指标数落在()17.56,22.44内的概率. 参考数据:()2,XN μσ,则()0.6826P X μσμσ-<<+=,(22)0.9544P X μσμσ-<<+=.【正确答案】 1、0.04 2、20μ=,0.954420-2(基础) 2021年是“十四五”规划开局之年,也是建党100周年.为了传承红色基因,某学校开展了“学党史,担使命”的知识竞赛.现从参赛的所有学生中,随机抽取100人的成绩作为样本,得到成绩的频率分布直方图,如图.(1)求频率分布直方图中a 的值,并估计该校此次竞赛成绩的平均分x (同一组中的数据用该组区间中点值代表);(2)在该样本中,若采用分层抽样的方法,从成绩高于75分的学生中随机抽取7人查看他们的答题情况,再从这7人中随机抽取3人进行调查分析,求这3人中至少有1人成绩在[]85,95内的概率; (3)假设竞赛成绩服从正态分布()2,N μσ,已知样本数据的方差为121,用平均分x 作为μ的近似值,用样本标准差s 作为σ的估计值,求该校本次竞赛的及格率(60分及以上为及格).参考数据:()0.6827P μσξμσ-<+≈≤,()220.9545P μσξμσ-<+≈≤,()330.9973P μσξμσ-<≤+≈. 【正确答案】 (1)0.035a =;平均分为71分;(2)57;(3)0.84135.2022年北京冬季奥运会将在北京市和河北省张家口市联合举行,北京市延庆区张山营镇的2022北京冬奥森林公园于2020年4月22日正式启动了冬奥赛区的树木移植工作.本次移植的树木来自2022北京冬奥赛区树木假植区,包含暴马丁香、核桃楸、大叶白蜡等多个品种.现从冬奥赛区树木假植区中抽取300棵暴马丁香,并对树木高度H (单位:m )进行测量,将测量结果绘制为如图所示的频率分布直方图.(1)估计抽取的300棵暴马丁香树木高度的平均值(同一组中的数据可用该区间的中点值为代表); (2)北京冬奥赛区树木假植区内的暴马丁香的高度H (m )服从正态分布()2,0.122N μ,其中μ近似为样本平均数x .记X 为假植区内10000棵暴马丁香中高度位于区间()2.122,2.244的数量,求()E X ; (3)在树木移植完成后,采取施用生根粉、加挂营养液等方式确保了移植树木的成活率,经验收,单棵移植成活率达到了90%.假设各棵树木成活与否相互不影响,求移植五棵暴马丁香成活四棵及以上的概率.(保留三位小数)附:若()2~,H N μσ,则()0.6827-<<+=P H μσμσ,()220.9545-<<+=P H μσμσ.【正确答案】 (1)()2m ;(2)()1359E X =;(3)0.919.20-4(巩固) 某科技公司新研制生产一种特殊疫苗,为确保疫苗质量,定期进行质量检验.某次检验中,从产品中随机抽取100件作为样本,测量产品质量体系中某项指标值,根据测量结果得到如下频率分布直方图:。
江苏省苏北四市高三数学上册期末联考试题(有答案)

江苏省苏北四市(徐州、淮安、连云港、宿迁)高三数学上学期期末联考试题一、填空题(本大题共14小题,每小题5分,共70分)1、已知集合{}{}2,0,2,3A B =-=-,则A B =U .2、已知复数z 满足(1)2i z i -=,其中i 为虚数单位,则z 的模为 .3、某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个 分数的方差为 .4、根据如图所示的伪代码,则输出S 的值为 .5、从1,2,3,4,5,6这六个数中一次随机地取2个数,则所取2个数的和能被3整除的概率 为 .6、若抛物线28y x =的焦点恰好是双曲线2221(0)3x y a a -=>的右焦点,则实数a 的值为 .7、已知圆锥的底面直径与高都是2,则该圆锥的侧面积为 . 8、若函数()sin()(0)6f x x πωπω=->的最小正周期为15,则1()3f 的值为 .9、已知等比数列{}n a 的前n 项和为n S ,若223323,23S a S a =+=+,则公比q 的值为 .10、已知函数()f x 是定义R 在上的奇函数,当0x >时,()23xf x =-,则不等式()5f x -≤ 的解集为 .11、若实数,x y 满足133(0)2xy x x +=<<,则313x y +-的最小值为 . 12、已知非零向量,a b r r满足a b a b ==+r r r r ,则a r 与2a b -r r 夹角的余弦值为 .13、已知,A B 是圆221:1C x y +=上的动点,AB =,P 是圆222:(3)(4)1C x y -+-=上的动点,则PA PB +u u u r u u u r的取值范围为 .14、已知函数32sin ,1()925,1x x f x x x x a x <⎧=⎨-++⎩≥,若函数()f x 的图象与直线y x =有三个不同的公共点,则实数a 的取值集合为 .二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明、证明 或演算步骤)15、在ABC ∆中,角,,A B C 的对边分别为,,a b c .已知2cos (cos cos )A b C c B a +=. (1)求角A 的值; (2)若3cos 5B =,求sin()BC -的值.16、如图,在四棱锥E ABCD -中,平面EAB ⊥平面ABCD ,四边形ABCD 为矩形,EA EB ⊥,点,M N 分别是,AE CD 的中点.求证:(1)直线MN ∥平面EBC ;(2)直线EA ⊥平面EBC .17、如图,已知,A B 两镇分别位于东西湖岸MN 的A 处和湖中小岛的B 处,点C 在A 的 正西方向1km 处,3tan ,44BAN BCN π∠=∠=.现计划铺设一条电缆联通,A B 两镇,有两种铺设方案:①沿线段AB 在水下铺设;②在湖岸MN 上选一点P ,先沿线段AP 在地下铺设,再沿线段PB 在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km 、4万元∕km .(1)求,A B 两镇间的距离;(2)应该如何铺设,使总铺设费用最低?18、如图,在平面直角坐标系xOy中,已知椭圆2222:1(0)x yC a ba b+=>>的离心率为22,且右焦点F到左准线的距离为62.(1)求椭圆C的标准方程;(2)设A为椭圆C的左顶点,P为椭圆C上位于x轴上方的点,直线PA交y轴于点M,过点F作MF的垂线,交y轴于点N.(ⅰ)当直线的PA斜率为12时,求FMN∆的外接圆的方程;(ⅱ)设直线AN交椭圆C于另一点Q,求APQ∆的面积的最大值.19、已知函数2(),()ln ,2R x f x ax g x x ax a e=-=-∈. (1)解关于()R x x ∈的不等式()0f x ≤; (2)证明:()()f x g x ≥;(3)是否存在常数,a b ,使得()()f x ax b g x +≥≥对任意的0x >恒成立?若存在,求 出,a b 的值;若不存在,请说明理由.20、已知正项数列{}n a 的前n 项和为n S ,且11,(1)(1)6()n n n a a a a S n +=++=+,*∈N n .(1)求数列{}n a 的通项公式;(2)若对于N n *∀∈ ,都有(31)n S n n +≤成立,求实数a 取值范围;(3)当2a =时,将数列{}n a 中的部分项按原的顺序构成数列{}n b ,且12b a =,证明: 存在无数个满足条件的无穷等比数列{}n b .苏北四市高三年级第二次调研测试数学II(附加题)21.[选做题]本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A.【选修4-1几何证明选讲】(本小题满分10分)如图,AB 为半圆O 的直径,D 为弧BC 的中点,E 为BC 的中点, 求证:AB ·BC=2AD ·BD .B .【选修4-2矩阵与变换】(本小题满分10分)已知矩阵A= 的一个特征值为2,其对应的一个特征向量为a = ,求实数a ,b 的值.C.【选修4-4:坐标系与参数方程】(本小题满分10分)在平面直角坐标系Oy 中,以O 为极点,轴的正半轴为极轴建立极坐标系.直线 l :2ρsin (θ一4π)=m (m ∈R ),圆C 的参数方程为(t 为参数).当圆心C 到直线l 的距离为2时,求m 的值。
江苏省淮安、宿迁、连云港、徐州苏北四市高三数学上学
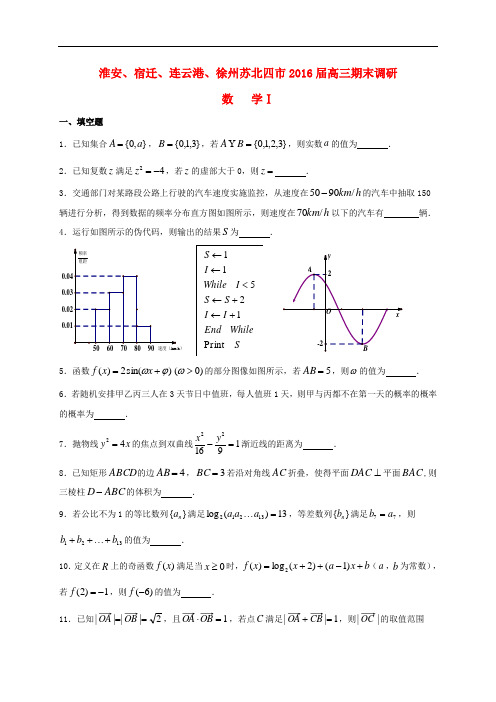
淮安、宿迁、连云港、徐州苏北四市2016届高三期末调研数 学Ⅰ一、填空题1.已知集合},0{a A =,}3,1,0{=B ,若}3,2,1,0{=B A Y ,则实数a 的值为 . 2.已知复数z 满足42-=z ,若z 的虚部大于0,则=z .3.交通部门对某路段公路上行驶的汽车速度实施监控,从速度在h km /9050-的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在h km /70以下的汽车有 辆. 4.运行如图所示的伪代码,则输出的结果S 为 .)5.函数)sin(2)(ϕω+=x x f )0(>ω的部分图像如图所示,若5=AB ,则ω的值为 . 6.若随机安排甲乙丙三人在3天节日中值班,每人值班1天,则甲与丙都不在第一天的概率的概率的概率为 .7.抛物线x y 42=的焦点到双曲线191622=-y x 渐近线的距离为 . 8.已知矩形ABCD 的边4=AB ,3=BC 若沿对角线AC 折叠,使得平面DAC ⊥平面BAC ,则三棱柱ABC D -的体积为 .9.若公比不为1的等比数列}{n a 满足13)(log 13212=⋯a a a ,等差数列}{n b 满足77a b =,则1321b b b +⋯++的值为 .10.定义在R 上的奇函数)(x f 满足当0≥x 时,b x a x x f +-++=)1()2(log )(2(a ,b 为常数),若1)2(-=f ,则)6(-f 的值为 . 11.已知2||||==OB OA ,且1=⋅OB OA ,若点C 满足1||=+CB OA ,则||OC 的取值范围是 . 12.已知函数⎩⎨⎧<-≥+=0)(0cos 2)(x x a x x x x x f ,若关于x 的不等式π<)(x f 的解集为)2,(π-∞,则实数a 的取值范围是 .13.已知)1,0(A ,)0,1(B ,)0,(t C ,点D 是直线AC 上的动点,若BD AD 2≤恒成立,则最小正整数t 的值为 .14.设c b a ,,是正实数,满足a c b ≥+,则ba cc b ++的最小值为 . 二、解答题15.在锐角三角形ABC 中,角C B A ,,的对边为c b a ,,,已知53sin =A ,21)tan(-=-B A , (1)求B tan ; (2)若5=b ,求c .16.如图,在四棱锥ABCD P -中,已知底面ABCD 为矩形,⊥PA 平面PDC ,点E 为棱PD 的中点,求证:(1)//PB 平面EAC ;(2)平面⊥PAD 平面ABCD .17.如图,OA 是南北方向的一条公路,OB 是北偏东045方向的一条公路,某风景区的一段边界为曲线C .为方便游客光,拟过曲线C 上的某点分别修建与公路OA ,OB 垂直的两条道路PN PM ,,且PN PM ,的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy ,则曲线符合函数)91(242≤≤+=x x x y 模型,设x PM =,修建两条道路PN PM ,的总造价为)(x f 万元,题中所涉及的长度单位均为百米. (1)求)(x f 解析式;(2)当x 为多少时,总造价)(x f 最低?并求出最低造价.OPABCDE18.已知各项均为正数的数列}{n a 的首项11=a ,n S 是数列}{n a 的前项和,且满足:).0(*1111N n a a a a S a S a n n n n n n n n ∈≠=-+-++++λλ.(1)若1a ,2a ,3a 成等比数列,求实数λ的值; (2)若21=λ,求n S .19. 如图,在平面直角坐标系xoy 中,已知椭圆C :)0(12222>>=+b a b y a x 的离心率21=e ,左顶点为)0,4(-A ,过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ,交y 轴于点E . (1)求椭圆C 的方程;(2)已知P 为AD 的中点,是否存在定点Q ,对于任意的)0(≠k k 都有EQ OP ⊥,若存在,求出点Q 的坐标;若不存在说明理由;(3)若过O 点作直线l 的平行线交椭圆C 于点M ,求OMAEAD +的最小值.20.已知函数]42)4(231[)(23--++-=a x a x x e x f x,其中R a ∈,e 为自然对数的底数 (1)若函数)(x f 的图像在0=x 处的切线与直线0=+y x 垂直,求a 的值. (2)关于x 的不等式xe xf 34)(-<在)2,(-∞上恒成立,求a 的取值范围. (3)讨论)(x f 极值点的个数.x附加题部分21.【选做题】A .[选修4—1:几何证明选讲](本小题满分10分)如图,PAQ ∠是直角,圆O 与射线AP 相切于点T ,与射线AQ 相交于两点,B C .求证:BT 平分OBA ∠.B .[选修4—2:矩阵与变换](本小题满分10分)已知矩阵1214A ⎡⎤=⎢⎥-⎣⎦,求矩阵A 的特征值和特征向量.C .[选修4—4:坐标系与参数方程](本小题满分10分) 在极坐标系中,圆C 的极坐标方程为28sin()1303πρρθ--+=,已知33(1,),(3,)22A B ππ,P 为圆C 上一点,求PAB ∆面积的最小值.D .[选修4—5:不等式选讲](本小题满分10分) 设,x y 均为正数,且x y >,求证:2212232x y x xy y +≥+-+.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写 出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,在直三棱柱111ABC A B C -中,底面ABC ∆是直角三角形,1AB AC ==,点P 是棱1BB 上一点,满足1(01)BP BB λλ=≤≤u u u r u u u r. (1)若13λ=,求直线PC 与平面1A BC 所成角的正弦值; (2)若二面角1P AC B --的正弦值为23,求λ的值.23.(本小题满分10分)已知数列{}n a 满足21211132,(),()()(1)n na n f n g n f n f n a a a =-=+++=--L ,*n N ∈. (1)求证:1(2)3g >;(2)求证:当3n ≥时,1()3g n >.数学I 参考答案及评分标准一、填空题1. 2;2. 2i ; 3.75; 4.9; 5.3π; 6.13; 7.35; 8. 245; 9.26; 10. 4; 11.; 12.()-∞+;13.4; 14.12.二、解答题15.(1)在锐角三角形ABC 中,由3sin 5A =,得4cos 5A , …………2分所以sin 3tan cos 4A A A ==.……………………………………………………………4分由tan tan 1tan()1tan tan 2A B A B A B --==-+⋅,得tan 2B =. ………………7分(2)在锐角三角形ABC 中,由tan 2B =,得sin B =,cos B =9分所以sin sin()sin cos cos sin 25C A B A B A B =+=+=,…………………11分由正弦定理sin sin b cB C =,得sin 11sin 2b Cc B ==. ………………14分 16.(1) 连接BD 与AC 相交于点O ,连结OE .………2分因为四边形ABCD 为矩形,所以O 为BD 中点. 因为E 为棱PD 中点,所以PB ∥OE .………4分 因为PB ⊄平面EAC ,OE ⊂平面EAC ,所以直线PB ∥平面EAC .……………………6分(2) 因为PA ⊥平面PDC ,CD ⊂平面PDC ,所以 PA ⊥CD . …………………8分因为四边形ABCD 为矩形,所以AD ⊥CD .…………………………………10分 因为 PA ∩AD =A ,PA ,AD ⊂平面PAD ,所以 CD ⊥平面PAD .…………12分 因为CD ⊂平面ABCD ,所以 平面PAD ⊥平面ABCD . …………………14分17. (1)在如图所示的直角坐标系中,因为曲线C的方程为)=19y x x ≤≤,PM x = 所以点P坐标为2,x x x ⎛+ ⎝⎭,直线OB 的方程为0x y -=, ……………………………………………………2分OPABCDE则点P 到直线0x y -=24x =,………………4分又PM 的造价为5万元/百米,PN 的造价为40万元/百米. 则两条道路总造价为()22432()540519f x x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭≤≤. …………8分 (2) 因为22432()5405f x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭, 所以 333645(64)()=51x f x x x -⎛⎫'-= ⎪⎝⎭, ………………………10分令()0f x '=,得4x =,列表如下:所以当4x =时,函数()f x 有最小值,最小值为()232454304f ⎛⎫=+= ⎪⎝⎭.……13分答:(1)两条道路PM ,PN 总造价()f x 为232()5f x x x ⎛⎫=+ ⎪⎝⎭()19x ≤≤;(2)当4x =时,总造价最低,最低造价为30万元. ……………………14分(注:利用三次均值不等式223232()5553022x x f x x x x ⎛⎫⎛⎫=+=++⨯= ⎪ ⎪⎝⎭⎝⎭≥,当且仅当23222x x x ==,即4x =时等号成立,照样给分.) 18.(1)令1n =,得221a λ=+.令2n =,得23322323a S a S a a a a λ--=+,所以()()324121a λλλ=+++.…………2分由2213a a a =,得()()22241121λλλλ⎛⎫= ⎪⎝⎭++++,因为0λ≠,所以1λ=.………4分(2)当12λ=时,111112n n n n n n n n a S a S a a a a ++++--=+, 所以11111112n n n n n n S S a a a a ++++--=+,即111112n n n n S S a a ++-=++,………………………6分 所以数列1n n S a ⎧⎫⎨⎬⎩⎭+是以2为首项,公差为12的等差数列,所以()11212n n S n a =-⋅++, ……………………………………………………8分 即3122n n n S a ⎛⎫= ⎪⎝⎭++,①当2n ≥时,113122n n n S a --⎛⎫= ⎪⎝⎭++,②①-②得,13222n n n n n a a a -=-++,……………………………………………10分 即()()112n n n a n a -=++,所以()1221n n a an n n -=++≥, ………………………12分所以2n a n ⎧⎫⎨⎬⎩⎭+是首项为13是常数列,所以()123n a n =+. ……………………14分代入①得2351226n n n n n S a +⎛⎫=-= ⎪⎝⎭+. ……………………16分19. (1)因为左顶点为(40)A -,,所以4a =,又12e =,所以2c =.…………………2分 又因为22212b a c =-=,所以椭圆C 的标准方程为2211612x y +=. ………………………………………4分(2)直线l 的方程为(4)y k x =+,由2211612(4),x y y k x ⎧+=⎪⎨⎪=+⎩,消元得,22[(4)]11612x k x ++=.化简得,22(4)[(43)1612)]0x k x k +++-=,所以14x =-,222161243k x k -+=+. ……………………………………………………6分当22161243k x k -+=+时,222161224(4)4343k k y k k k -+=+=++, 所以222161224,4343()D k k k k -+++.因为点P 为AD 的中点,所以P 的坐标为2221612,4343()k kk k -++,则3(0)4OP k k k-=≠.…………………………………………………………………………8分 直线l 的方程为(4)y k x =+,令0x =,得E 点坐标为(0,4)k , 假设存在定点(,)(0)Q m n m ≠,使得OP EQ ⊥, 则1OP EQ k k =-,即3414n k k m--⋅=-恒成立, 所以(412)30m k n +-=恒成立,所以412030m n +=⎧⎨-=⎩,,即30m n =-⎧⎨=⎩,,因此定点Q 的坐标为(3,0)-. …………………………………………10分 (3)因为OM l P ,所以OM 的方程可设为y kx =,由2211612x y y kx⎧+=⎪⎨⎪=⎩,得M点的横坐标为x =12分由OM l P ,得2D A E A D AM Mx x x x x x AD AE OM x x -+--+==22216128k -++=…………………………………………………14分≥即k =所以当k =AD AE OM+的最小值为 …………………………16分 20. (1) 由题意,321()e 3x f x x x ax a ⎛⎫'=-+- ⎪⎝⎭, …………………………………………2分因为()f x 的图象在0x =处的切线与直线0x y +=垂直,所以(0)=1f ',解得1a =-. ……………………………4分(2) 法一:由4()e 3x f x <-,得3214e 2(4)24e 33x x x x a x a ⎡⎤-++--<-⎢⎥⎣⎦,即326(312)680x x a x a -++--<对任意(2)x ∈-∞,恒成立,……………………………6分即()32636128x a x x x ->-=-对任意(2)x ∈-∞,恒成立,因为2x <,所以()()322612812323x x x a x x -++>=----, ……………………………8分记()21()23g x x =--,因为()g x 在(2)-∞,上单调递增,且(2)0g =, 所以0a ≥,即a 的取值范围是[0)+∞,. ………………………………………10分法二:由4()e 3x f x <-,得3214e 2(4)24e 33x x x x a x a ⎡⎤-++--<-⎢⎥⎣⎦,即326(312)680x x a x a -++--<在(2)-∞,上恒成立,……………………………6分因为326(312)680x x a x a -++--<等价于2(2)(434)0x x x a --++<,①当0a ≥时,22434(2)30x x a x a -++=-+≥恒成立, 所以原不等式的解集为(2)-∞,,满足题意. …………………………………………8分 ②当0a <时,记2()434g x x x a =-++,有(2)30g a =<, 所以方程24340x x a -++=必有两个根12,x x ,且122x x <<,原不等式等价于12(2)()()0x x x x x ---<,解集为12()(2)x x -∞U ,,,与题设矛盾, 所以0a <不符合题意.综合①②可知,所求a 的取值范围是[0)+∞,.…………………………………………10分(3) 因为由题意,可得321()e 3x f'x x x ax a ⎛⎫=-+- ⎪⎝⎭,所以()f x 只有一个极值点或有三个极值点. ………………………………………11分令321()3g x x x ax a =-+-,①若()f x 有且只有一个极值点,所以函数()g x 的图象必穿过x 轴且只穿过一次, 即()g x 为单调递增函数或者()g x 极值同号.ⅰ)当()g x 为单调递增函数时,2()20g'x x x a =-+≥在R 上恒成立,得1a ≥…12分 ⅱ)当()g x 极值同号时,设12,x x 为极值点,则12()()0g x g x ⋅≥,由2()20g'x x x a =-+=有解,得1a <,且21120,x x a -+=22220x x a -+=, 所以12122,x x x x a +==,所以3211111()3g x x x ax a =-+-211111(2)3x x a x ax a =--+-11111(2)33x a ax ax a =---+-[]12(1)3a x a =--,同理,[]222()(1)3g x a x a =--,所以()()[][]121222(1)(1)033g x g x a x a a x a =--⋅--≥,化简得221212(1)(1)()0a x x a a x x a ---++≥,所以22(1)2(1)0a a a a a ---+≥,即0a ≥,所以01a <≤.所以,当0a ≥时,()f x 有且仅有一个极值点; …………………14分 ②若()f x 有三个极值点,所以函数()g x 的图象必穿过x 轴且穿过三次,同理可得0a <; 综上,当0a ≥时,()f x 有且仅有一个极值点,当0a <时,()f x 有三个极值点. …………………16分数学Ⅱ(附加题)参考答案及评分标准21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两小题........,并在相应的答题区域.........内作答...,若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.21A .连结OT .因为AT 是切线,所以OT AP ⊥.………………………2分 又因为PAQ ∠是直角,即AQ AP ⊥, 所以AB OT P ,所以TBA BTO ∠=∠. ………………………………… 5分 又OT OB =,所以OTB OBT ∠=, …………………8分 所以OBT TBA ∠=∠,即BT 平分OBA ∠. …………………………………10分 21B .矩阵A 的特征多项式为()2125614f λλλλλ--==--+, ……………2分 由()0f λ=,解得12λ=,23λ=.. …………………………………………4分当12λ=时,特征方程组为20,20,x y x y -=⎧⎨-=⎩故属于特征值12λ=的一个特征向量121α⎡⎤=⎢⎥⎣⎦;………………………………7分当23λ=时,特征方程组为220,0,x y x y -=⎧⎨-=⎩故属于特征值23λ=的一个特征向量211α⎡⎤=⎢⎥⎣⎦. …………………………10分21C .圆C 的直角坐标方程为22434130x y x y ++-+=,即22(23)(2)3x y ++-=. ………………………………………………4分 又(0,1),(0,3)A B --,所以2AB =.……………………………………………6分P 到直线AB 距离的最小值为2333-=,………………………………8分所以PAB ∆面积的最小值为123=32⨯⨯.…………………………………10分21D .因为x >0,y >0,x -y >0,22211222()2()x y x y x xy y x y +-=-+-+-,…………………………………4分=21()()()x y x y x y -+-+-23213()3()x y x y -=-≥, ……………………8分所以2212232x y x xy y ++-+≥. ……………………………………………10分【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写 出文字说明、证明过程或演算步骤.22.以A 为坐标原点O ,分别以AB ,AC ,1AA 所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系O xyz -.因为=1AB AC =,12AA =,则(0,0,0)A ,(1,0,0)B ,(0,1,0)C ,1(0,0,2)A ,1(1,0,2)B ,(1,0,2)P λ.……………………………………………1分(1)由13λ=得,2(1,1,)3CP =-u u u r ,1(1,02)A B =u u u r ,-,1(0,1,2)A C =-u u u u r , 设平面1A BC 的法向量为1111(,,)x y z =n ,由11110,0A B A C ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u u r ,n n 得111120,20.x z y z -=⎧⎨-=⎩ 不妨取11z =,则112x y ==,从而平面1A BC 的一个法向量为1(2,2,1)=n .……………………………………3分 设直线PC 与平面1A BC 所成的角为θ,则111sin |cos ,|||||CP CP CP θ⋅=<>==⋅u u u r u u u r u u u r n n n , 所以直线PC 与平面1A BC所成的角的正弦值为33.…………………………5分 (2)设平面1PAC 的法向量为2222(,,)x y z =n , 1(1,022)A P λ=u u u r ,-, 由21210,0A C A P ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u r ,n n 得222220,(22)0.y z x z λ-=⎧⎨+-=⎩ 不妨取21z =,则22222x y λ=-=,,所以平面1PAC 的法向量为2(22,2,1)λ=-n .……………………………………7分则12cos ,<>=n n ,又因为二面角1P AC B --的正弦值为23,,………………………………………………………9分 化简得2+890λλ-=,解得1λ=或9λ=-(舍去),故λ的值为1. …………………………10分23.(1)由题意知,32n a n =-,2121111()n n n n g n a a a a ++=++++L , …………1分当2n =时,234111111691(2)47101403g a a a =++=++=>. ……………2分 (2)用数学归纳法加以证明: ①当3n =时,34591111(3)g a a a a =++++L 11111117101316192225=++++++1111111()()7101316192225=++++++ 1111111()()8161616323232>++++++133131181632816163=++>++>, 所以当3n =时,结论成立.………………………………………………4分②假设当n k =时,结论成立,即1()3g k >, 则1n k =+时,(1)g k +()g k =22212(1)1111()k k k k a a a a +++++++-L …………6分 22212(1)11111()3k k k k a a a a +++>++++-L 21(21)133(1)232k k k +>+-+-- 221(21)(32)[3(1)2]3[3(1)2][32]k k k k k +--+-=++--2213733[3(1)2][32]k k k k --=++--, 由3k ≥可知,23730k k -->,即1(1)3g k +>. 所以当1n k =+时,结论也成立.综合①②可得,当3n ≥时,1()3g n >. …………………10分。
2021年高三上学期期末练习(4)数学试题含答案

2021年高三上学期期末练习(4)数学试题含答案一、填空题.1. 抛物线的准线方程为,则m 的值为_____2.若函数是偶函数,则实数的值为 ________.3.若的值为4. 从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是 5.已知向量的模为2,向量为单位向量,,则向量与的夹角大小为 .6.设函数是定义在R 上的奇函数,且对任意都有,当时,,则= .7.已知直线x =a (0<a <π2)与函数f (x )=sin x 和函数g (x )=cos x 的图象分别交于M ,N 两点,若MN =15,则线段MN 的中点纵坐标为 .8. 已知双曲线(a >0)的一条渐近线为y =kx (k >0),离心率e =,则双曲线方程为9.已知函数满足对任意成立,则的取值范围是 .10.设x ∈⎝⎛⎭⎫0,π2,则函数y =2sin 2x +1sin 2x 的最小值为________11. △ABC 中,,,则的最小值是12.给出如下四个命题: ①,; ②,;③函数定义域为,且,则的图象关于直线对称; ④ 若函数的值域为,则或;其中正确的命题是 .(写出所有正确命题的题号). 13.在平面直角坐标系xOy 中,点P 是第一象限内曲线上的一个动点,以点P 为切点作切线与两个坐标轴交于A ,B 两点,则△AOB 的面积的最小值为 . 14.若关于的方程有四个实数根,则实数的取值范围是 .PA B CD EF 二、解答题15.已知,.(Ⅰ)求的值;(Ⅱ)求函数的值域16.在四棱锥P -ABCD 中,∠ABC =∠ACD =90°,∠BAC =∠CAD =60°,PA ⊥平面ABCD ,E为PD 的中点,PA =2AB =2.(Ⅰ)求四棱锥P -ABCD 的体积V ;(Ⅱ)若F 为PC 的中点,求证PC ⊥平面AEF ; (Ⅲ)求证CE ∥平面PAB .17.某企业有两个生产车间分别在、两个位置,车间有100名员工,车间有400名员工。
江苏省苏北四市2021届高三数学上学期第一次质量检测(期末)试题(含解析).doc

江苏省苏北四市2021届高三数学上学期第一次质量检测(期末)试题(含解析)一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知集合{|02}A x x =<<,{|11}B x x =-<<,则A B =_____.答案:{12}x x -<< 解:由题意直接求解即可得AB ={12}x x -<<2.已知复数z 满足24z =-,且z 的虚部小于0,则z =_____. 答案:2i -解: 24z =-,则2z i =±,又因为z 的虚部小于0,则2z i =- 3.若一组数据7,,6,8,8x 的平均数为7,则该组数据的方差是_____. 答案:45解:7++6+8+875x = 解得6x =,222222(77)(67)(67)(87)(87)455S -+-+-+-+-==4.执行如图所示的伪代码,则输出的结果为_____. 答案:205.函数2()log 2f x x =-的定义域为_____. 答案:[4,+)∞解:由题意得:2log 2x x >⎧⎨≥⎩,解得4x ≥,所以函数的定义域为[4,+)∞6.某学校高三年级有,A B 两个自习教室,甲、乙、丙3名学生各自随机选择其中一个教室自习,则甲、乙两人不在同一教室上自习的概率为______. 答案:12解:22222222212..A P A A A ==7.若关于x 的不等式230x mx -+<的解集是(1,3),则实数m 的值为______. 答案:4解:由题意得:221303330m m ⎧-+=⎪⎨-+=⎪⎩,解得4m =8.在平面直角坐标系xOy 中,双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px=上,则实数p 的值为______. 答案:14解:由题意得:双曲线右准线与渐近线的交点为33(,)2±,代入22y px =得:14p =9.已知等差数列{}n a 的前n 项和为n S ,298a a +=,55S =-,则15S 的值为_____. 答案:135解:298a a +=,55S =-,则388a a +=,355a =-,解得:31a =-,89a = 因为158********S a ==⨯=10.已知函数3sin 2y x =的图象与函数cos2y x =的图象相邻的三个交点分别是,,A B C ,则ABC ∆的面积为_____.答案:3π 11.在平面直角坐标系xOy 中,已知圆22:48120M x y x y +--+=,圆N 与圆M 外切与点(0,)m ,且过点(0,2)-,则圆N 的标准方程为______.答案:22(2)8x y ++=12.已知函数()f x 是定义在R 上的奇函数,其图象关于直线1x =对称,当(0,1]x ∈时,()ax f x e =-(其中e 是自然对数的底数),若(2020ln 2)8f -=,则实数a 的值为_____.答案:3解:由题意得:4T = ,ln 2(2020ln 2)(ln 2)(ln 2)28a a f f f e -=-=-===,解得:3a =13.如图,在ABC ∆中,,D E 是BC 上的两个三等分点,2AB AD AC AE ⋅=⋅,则cos ADE ∠的最小值为____.答案:47解:323(2)2(2)AB AD AC AE AB AB AC AC AB AC ⋅=⋅⇒⋅+=⋅+ 22222424c AB AC b AB AC c b =⋅+⇒⋅=- 222222()(2)2cos |||2|442AB AC AB AC c b AB ACADE AB AC AB AC c b AB AC b c AB AC-⋅+--⋅∠==-⋅+++⋅⋅+-⋅2222247(45)(3)b c b c b =≥--+14.设函数3()||f x x ax b =--,[1,1]x ∈-,其中,a b R ∈.若()f x M ≤恒成立,则当M 取得最小值时,a b +的值为______. 答案:34方法一:(1)|1|111()||282111()||282M f a b M f a b M f a b ⎧⎪≥=--⎪⎪≥=--⎨⎪⎪≥-=-+-⎪⎩所以111111362(1)()3()2|1|||3||2282822M f f f a b a b a b ≥+-+≥--+-+-+--≥当且仅当0b =,34a =时,上述等号成立,所以M 取最小值时,34a b +=. 方法二:由对称性可知,M 最小时,0b =,且3min ()1x ax a -=-(,(0,1))a x ∈ 所以3+1(1)x a x ≥+,即2min 3(1)4a x x =-+=,则34a b += 二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤15. (本小题满分14分)如图,在三棱锥P ABC -中,AP AB =,,M N 分别为棱,PB PC 的中点,平面PAB ⊥平面PBC .(1)求证:BC ∥平面AMN ; (2)求证:平面AMN ⊥平面PBC .解:(1)在PBC △中,因为M ,N 分别为棱PB ,PC 的中点,所以MN // BC . ………………………………3分 又MN ⊂平面AMN ,BC ⊄平面AMN ,所以BC //平面AMN .…………………………6分 (2)在PAB △中,因为AP AB =,M 为棱PB 的中点,所以AM PB ⊥.………………………………8分又因为平面PAB ⊥平面PBC ,平面PAB 平面PBC PB =,AM ⊂平面PAB , 所以AM ⊥平面PBC .…………………………………………………………12分 又AM ⊂平面AMN ,所以平面AMN ⊥平面PBC . …………………………14分16. (本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且5cos A =. (1)若5a =,25c =b 的值; (2)若4B π=,求tan2C 的值.解:(1)在ABC △中,由余弦定理2222cos b c bc A a +-=得,2202255b+-⨯=,即2450b b--=,…………………………4分解得5b=或1b=-(舍),所以5b=.………………………………………6分(2)由cos A=及0A<<π得,sin A===,…8分所以cos cos(())cos()sin)4C A B A A Aπ=π-+=-+=-=又因为0C<<π,所以sin C===,从而sintan3cosCCC===,………………………………………………12分所以222tan233tan21tan134CCC⨯===---.………………………………………14分17. (本小题满分14分)如图,在圆锥SO中,底面半径R为3,母线长l为5.用一个平行于底面的平面区截圆锥,截面圆的圆心为1O,半径为r,现要以截面为底面,圆锥底面圆心O为顶点挖去一个倒立的小圆锥1OO,记圆锥1OO的体积为V.(1)将V表示成r的函数;(2)求V 得最大值.解:(1)在SAO △中,2222534SO SA AO =--, …………………………2分由1SNO △∽SAO △可知,1SO r SO R=,所以143SO r =,……………………4分所以1443OO r =-,所以223144()π(4)π(3),03339V r r r r r r =-=-<<.…7分(2)由(1)得234()π(3),039V r r r r =-<<,所以24()π(63)9V r r r '=-,令()0V r '=,得2r =,………………………9分当(0,2)r ∈时,()0V r '>,所以()V r 在(0,2)上单调递增; 当(2,3)r ∈时,()0V r '<,所以()V r 在(2,3)上单调递减.所以当2r =时,()V r 取得最大值16π(2)9V =.答:小圆锥的体积V 的最大值为16π9.………………………………………14分18. (本小题满分16分)在平面直角坐标系xOy 中,已知椭圆2222:1x y C a b+=(0)a b >>的右顶点为A ,过点A 作直线l 与圆222:O x y b +=相切,与椭圆C 交于另一点P ,与右准线交于点Q .设直线l 的斜率为k .(1)用k 表示椭圆C 的离心率;(2)若0OP OQ ⋅=,求椭圆C 的离心率.(1)直线l 的方程为)(a x k y -=,即0=--ak y kx ,因为直线l 与圆222b y x O =+:相切,所以b k ak=+-12,故2222b a b k -=. 所以椭圆C 的离心率222111b e ak =-=+4分 (2)设椭圆C 的焦距为2c ,则右准线方程为2a x c=, 由⎪⎩⎪⎨⎧=-=c ax a x k y 2)(得c ac a k a c a k y -=-=22)(,所以))(,(22c ac a k c a Q -,…6分 由⎪⎩⎪⎨⎧-==+)(12222a x k y b y a x 得02)(2224232222=-+-+b a k a x k a x k a b , 解得222223k a b ab k a x p +-=,则22222222232)(k a b kab a k a b ab k a k y p +-=-+-=, 所以)2-2222222223k a b kab k a b ab k a P ++-,(,……………………………………………10分 因为0=⋅,所以02)(222222222232=+-⋅-++-⋅ka b kab c ac a k k a b ab k a c a , 即)(2)(22222c a k b b k a a -=-,………………………………………………12分由(1)知,2222b a b k -=,所以22422222)(2)(b a c a b b b a b a a --=--,所以c a a 22-=,即c a 2=,所以21=a c ,故椭圆C 的离心率为21.……16分19. (本小题满分16分)已知函数1()()ln f x a x x=-()a R ∈.(1)若曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=,求a 的值; (2)若()f x 的导函数'()f x 存在两个不相等的零点,求实数a 的取值范围;(3)当2a =时,是否存在整数λ,使得关于x 的不等式()f x λ≥恒成立?若存在, 求出λ的最大值;若不存在,说明理由.解:(1)()2111()ln f x x a x x x'=+-,因为曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=,所以(1)11f a '=-=-,得0a =.……………………………………………2分(2)因为21ln ()ax x f x x-+'=存在两个不相等的零点. 所以()1ln g x ax x =-+存在两个不相等的零点,则1()g x a x'=+.①当0a ≥时,()0g x '>,所以()g x 单调递增,至多有一个零点.……4分②当0a <时,因为当1(0)x a∈-,时,()0g x '>,()g x 单调递增, 当1(+)x a∈-∞,时,()0g x '<,()g x 单调递减, 所以1x a =-时,max 11()()ln()2g x g a a=-=--. …………………………6分因为()g x 存在两个零点,所以1ln()20a-->,解得2e 0a --<<.………7分因为2e 0a --<<,所以21e 1a->>.因为(1)10g a =-<,所以()g x 在1(0)a-,上存在一个零点. …………8分 因为2e 0a --<<,所以211()a a->-.因为22111[()]ln()1g a a a-=-+-,设1t a =-,则22ln 1(e )y t t t =-->,因为20t y t-'=<,所以22ln 1(e )y t t t =-->单调递减,所以()2222ln e e 13e 0y <--=-<,所以22111[()]ln()10g a a a-=-+-<,所以()g x 在1()a-+∞,上存在一个零点. 综上可知,实数a 的取值范围为2(e ,0)--.…………………………………10分(3)当2a =时,1()(2)ln f x x x =-,()2211121ln ()ln 2x x f x x x x x x-+'=+-=, 设()21ln g x x x =-+,则1()20g x x'=+>.所以()g x 单调递增,且11()ln 022g =<,(1)10g =>,所以存在01(1)2x ∈,使得0()0g x =,……12分 因为当0(0)x x ∈,时,()0g x <,即()0f x '<,所以()f x 单调递减;当0(+)x x ∈∞,时,()0g x >,即()0f x '>,所以()f x 单调递增, 所以0x x =时,()f x 取得极小值,也是最小值,此时()0000000111()(2)ln (2)12(4)4f x x x x x x x =-=--=-++,……………14分因为01(1)2x ∈,,所以0()(10)f x ∈-,, 因为()f x λ≥,且λ为整数,所以1λ-≤,即λ的最大值为1-.………16分20. (本小题满分16分)已知数列{}n a 的首项13a =,对任意的*n N ∈,都有11n n a ka +=-(0)k ≠,数列{1}n a -是公比不为1的等比数列. (1)求实数k 的值;(2)设4,1,n n n n b a n -⎧⎪=⎨-⎪⎩为奇数为偶数,数列{}n b 的前n 项和为n S ,求所有正整数m 的值,使得221mm S S -恰好为数列{}n b 中的项.解:(1)由11n n a ka +=-,13a =可知,231a k =-,2331a k k =--,因为{1}n a -为等比数列,所以2213(1)(1)(1)a a a -=--,即22(32)2(32)k k k -=⨯--,即231080k k -+=,解得2k =或43k =,…2分 当43k =时,143(3)3n n a a +-=-,所以3n a =,则12n a -=, 所以数列{1}n a -的公比为1,不符合题意;当2k =时,112(1)n n a a +-=-,所以数列{1}n a -的公比1121n n a q a +-==-,所以实数k 的值为2. …………………………………………………………4分(2)由(1)知12n n a -=,所以4n n n n b n - , ⎧⎪=⎨2, ⎪⎩为奇数,为偶数,则22(41)4(43)4[4(21)]4m m S m =-++-+++--+2(41)(43)[4(21)]444m m =-+-++--++++144(4)3m m m +-=-+,……………………………………………………6分则212244(4)3m m m m S S b m m --=-=-+,因为22+1324m m m b b m +=-+,又222+322+1()()3420m m m m m b b b b ++-+=⨯->,且2350b b +=>,130b =>,所以210m S ->,则20m S >,设2210,m t m Sb t S -=>∈*N ,…………………………………………………………8分 则1,3t =或t 为偶数,因为31b =不可能,所以1t =或t 为偶数,①当2121=m m S b S -时,144(4)3344(4)3m m m m m m +--+=--+,化简得2624844m m m -+=--≤, 即242m m -+≤0,所以m 可取值为1,2,3,验证624135787,3,323S S S S S S ===得,当2m =时,413S b S =成立.…………………12分②当t 为偶数时,1222144(4)331443124(4)134m m m m m m m S S m m m m +---+==+--+--++, 设231244m mm m c -+-=,则211942214m m m m m c c ++-+-=,由①知3m >,当4m =时,545304c c --=<; 当4m >时,10m m c c +->,所以456c c c ><<,所以m c 的最小值为5191024c -=, 所以22130151911024m m S S -<<+<-+,令22214m m S b S -==,则2314312414mm m +=-+-+, 即231240m m -+-=,无整数解.综上,正整数m 的值2.………………………………………………………16分徐州市2021-2022度高三年级第一次质量检测数学Ⅱ(附加题)21.【选做题】本题包含A 、B 、C 小题,请选定其中两题,并在答题卡相应的答题区域内作答.若多做,则按作答的前两题评分,解答应写出文字说明、证明过程或演算步骤. A .[选修4—2:矩阵与变换] (本小题满分10分)已知矩阵2M t ⎡=⎢⎣ 31⎤⎥⎦的一个特征值为4,求矩阵M 的逆矩阵1M -.解:矩阵M 的特征多项式为23()(2)(1)31f t t λλλλλ--==-----.…………2分 因为矩阵M 的一个特征值为4,所以(4)630f t =-=,所以2t =.…………5分所以2321⎡⎤=⎢⎥⎣⎦M ,所以11313213221324422112132213222--⎡⎤⎡⎤-⎢⎥⎢⎥⨯-⨯⨯-⨯==⎢⎥⎢⎥--⎢⎥⎢⎥⨯-⨯⨯-⨯⎣⎦⎣⎦M .……10分B .[选修4—4:坐标系与参数方程] (本小题满分10分)在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为(cos sin )12ρθθ+=,曲线C的参数方程为2sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数,R θ∈).在曲线C 上点M ,使点M 到l 的距离最小,并求出最小值.解:由:cos sin 120l ρθρϕ+-=,及cos x ρθ=,sin y ρθ=,所以l 的直角坐标方程为120x y +-=. ………………………………………2分在曲线C上取点()2sin M ϕϕ,,则点M 到l 的距离124sin 3d ϕπ-+===,…………6分 当6ϕπ=时,d 取最小值8分此时点M 的坐标为()3,1.………………………………………………………10分 C .[选修4—5:不等式选讲] (本小题满分10分) 已知正数,,x y z 满足1x y z ++=,求111+222x y y z z x++++的最小值. 解:因为x y z ,,都为正数,且1x y z ++=,所以由柯西不等式得,1113()222x y y z z x+++++111()[(2)(2)(2)]222x y y z z x x y y z z x=++⋅++++++++………………5分29=≥, 当且仅当13x y z ===时等号成立,所以111222x y y z z x+++++的最小值为3.…………………………………10分第22题、第23题,每题10分,共计20分,请在答题卡指定区域内作答,解答应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,在三棱柱111ABC A B C -中,侧面11AA B B 为正方形,侧面11BB C C 为菱形,1160BB C ∠=,平面11AA B B ⊥平面11BB C C .(1)求直线1AC 与平面11AA B B 所成角的正弦值;(第22题)BACxyzB 1 A 1C 1 (2)求二面角1B AC C --的余弦值.解:(1)因为四边形11AA B B 为正方形,所以1AB BB ⊥,因为平面11AA B B ⊥平面11BB C C ,平面11AA B B平面111BB C C BB =,AB ⊂平面11AA B B ,所以AB ⊥平面11BB C C . ……………………………2分以点B 为坐标原点,分别以BA ,1BB 所在的直线为x ,y 轴,建立如图所示的空间直角坐标系B xyz -.不妨设正方形11AA B B 的边长为2,则()2 0 0A ,,,()10 2 0B ,,. 在菱形11BB C C 中,因为1160BB C ∠=︒,所以1(0 1 3)C ,,,所以1( 2 1 3)AC =-,,. 因为平面11AA B B 的法向量为()0 0 1=,,n , 设直线1AC 与平面11AA B B 所成角为α, 则1|3|6sin |cos ,|221AC α=<>=⨯n ,即直线1AC 与平面11AA B B 6.………………………6分(2)由(1)可知,(0 1 3C -,,,所以()10 2 0CC =,,. 设平面1ACC 的一个法向量为()1111 x y z =,,n , 因为11110,0,AC CC ⎧⋅=⎪⎨⋅=⎪⎩n n 即()(()()111111 2 1 30 0 2 00x y z x y z ⎧⋅-=⎪⎨⋅=⎪⎩,,,,,,,,,取13x =,10y =,11z =,即13 0 1⎫=⎪⎭,,n . 设平面1ABC 的一个法向量为()2222 x y z =,,n , 因为()2 0 0BA =,,,(10 1 3BC =,,, 所以()()()(222222 2 0 00 0 1 30x y z x y z ⋅=⎧⎪⎨⋅=⎪⎩,,,,,,,,,取()20 3 1=-,,n .…………8分 设二面角1B AC C --的平面角为θ,则121212 71cos cos 31314θ⋅-=-<>=-==⋅+⋅+,n n n n n n所以二面角1B AC C --7.…………………………………10分23.(本小题满分10分)已知n 为给定的正整数,设20122()3n n n x a a x a x a x +=++++,x R ∈.(1)若4n =,求0a ,1a 的值;(2)若13x =,求0()nk k k n k a x =-∑的值.解:(1)因为4n =,所以0404216C ()=381a =,1314232C ()=327a =.……………………2分 (2)当13x =时,21C ()()33k k n k kk na x -=, 又因为11!(1)!C C !()!(1)!()!k k n n n n k k n n k n k k n k ---===---,………………………4分当1n =时,011022()C ()33nk k k n k a x =-==∑; …………………………………5分 当2n ≥时,0021()()C ()()33n nkk n k k k n k k n k a x n k -==-=-∑∑ 012121C ()()C ()()3333n nk n k k k n k k n n k k n k --===-∑∑1112121()C ()()3333n n k n k kn k n n ---==+-∑ 1111121C ()()333n k n k k n k n n ----==-∑1121()333n n n -=-+23n =,当1n =时,也符合.所以0()nk k k n k a x =-∑的值为23n .………………………………………………10分。
江苏省连云港、淮安、徐州、宿迁四市高三期末调查测试数学试卷

数学试题一、填空题:本大题共14题,每小题5分,共70分.请把答案填写在答题纸相应位置上. 1.已知集合A={x|x=2n —l ,n ∈Z},B={x |x 2一4x<0},则A ∩B= . 2.在复平面内,复数z=1ii+(i 是虚数单位)对应的点位于第 象限· 3.若命题“∃x ∈R ,x 2+a x +1<0”是真命题,则实数a 的取值范围是 . 4.已知向量a=(sinx,cosx),b =(1,一2),且a ⊥b ,则tan2x= .5.如果实数x ,y 满足不等式组110220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩,则z=x+2y 最小值为 .6.若函数f(x)=2sin ωx(ω>0)在22,33ππ⎡⎤-⎢⎥⎣⎦上单调递增,则ω的最大值为 . 7.已知一个棱长为6cm 的正方体塑料盒子(无上盖),上口放着一个半径为5cm 的钢球,则球心到盒底的距离为 cm.8.根据如图所示的伪代码,可知输出的结果T 为 .注 意 事 项考生在答题前认真阅读本注意事项及各题答题要求1.本斌卷共4页,包含填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分160分,考试时间为120分钟.考试结束后,请将本试卷和答题纸一并交回.2.答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题纸上.3.作答时必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置,在其它位;置作答一律无效.4.如有作图需要,可用2B 铅笔作答,并请加黑加粗,描写清楚. T ←1I ←3While I<50 T ←T +I I ←I +2 End While Print TABDE第10题第8题第9题9.如图,在△ABC 中,∠BAC =1200,AB =AC =2,D 为BC 边上的点,且0AD BC =,2CE EB =,则AD AE = .10.如图,已知双曲线以长方形ABCD 的顶点A ,B 为左、右焦点,且过C ,D 两顶点.若AB=4,BC=3,则此双曲线的标准方程为 .11.已知函数f(x)= ()2f π'sinx+cosx ,则()4f π= .12.如图,半径为10 cm 的圆形纸板内有一个相同圆心的半径为1 cm 的 小圆.现将半径为1 cm 的一枚硬币抛到此纸板上,使硬币整体随机 落在纸板内,则硬币落下后与小圆无公共点的概率为 .13.已知数列{a n }共有m 项,记{a n }的所有项和为s(1),第二项及以后所有项和为s(2),第三项及以后所有项和为s(3),…,第n 项及以后所有项和为s(n),若s(n)是首项为1,公差为2的等差数列的前n 项和,则当n<m 时,a n = .14.设函数12,0()(1),0x x f x f x x -⎧≤=⎨->⎩,方程f(x)=x+a 有且只有两相不等实数根,则实a 的取值范围为 .二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤 15.(本小题满分14分)(1)从x ,y 中各取一个数,求x+y ≥10的概率;(2)对于表中数据,甲、乙两同学给出的拟合直线分别为113y x =+与1122y x =+,试利 用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好. 16.(本小题满分14分)如图,四边形ABCD 为矩形,BC 上平面ABE ,F 为CE 上的点,且BF ⊥平面ACE. (1)求证:AE ⊥BE ;(2)设点M 为线段AB 的中点,点N 为线段CE 的中点.ACDFN求证:MN ∥平面DAE .17.(本小题满分14分)在直角坐标系xoy 中,若角α的始边为x 轴的非负半轴,终边为射线l :y=x ≥0). (1)求sin()6πα+的值;(2)若点P ,Q 分别是角α始边、终边上的动点,且PQ=4,求△POQ 面积最大时,点P ,Q 的坐标.18.(本小题满分16分)设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为A ,过点A 且与AF 垂直的光线经椭圆的右准线反射,反射光线与直线AF 平行. (1)求椭圆的离心率;(2)设入射光线与右准线的交点为B ,过A ,B ,F 三点的圆恰好与直线3x 一y+3=0相切,求椭圆的方程. 19.(本题满分16分)已知函数f(x)=a lnx+x 2(a 为实常数).(1)若a =-2,求证:函数f(x)在(1,+.∞)上是增函数; (2)求函数f(x)在[1,e]上的最小值及相应的x 值;(3)若存在x ∈[1,e],使得f(x )≤(a +2)x 成立,求实数a 的取值范围. 20.(本小题满分16分)已知以a 为首项的数列{}n a 满足:13,3,2, 3.n n n n n a a a a a +->⎧=⎨≤⎩(1)若0<n a ≤6,求证:0<1n a +≤6;(2)若a ,k ∈N ﹡,求使n k n a a +=对任意正整数n 都成立的k 与a ; (3)若321m a =- (m ∈N ﹡),试求数列{}n a 的前4m+2项的和42m s +.调查数学附加题21.【选做题】在A 、B 、c 、D 四道题中只能选做2题,每题10分,共计20分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. A.选修4一l :几何证明选讲在△ABC 中,已知CM 是∠ACB 的平分线,△AMC 的外接圆交BC 于点N .若AC=12AB , 注 意 事 项考生在答题前认真阅读本注意事项及各题答题要求1.本斌卷共2页,包含选做题(第21题中A 、B 、C 、D 四小题)、必做题(第22题、第23题)两部分.本试卷满分40分,考试时间为30分钟.考试结束后,请将本试卷和答题纸一并交回.2.答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题纸上.3.作答时必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置,在其它位;置作答一律无效.4.如有作图需要,可用2B 铅笔作答,并请加黑加粗,描写清楚.求证:BN=2AM.B.选修4—2:矩阵与变换设a,b∈R,若矩阵A=1ab⎡⎤⎢⎥-⎣⎦把直线l:2x+y一7=0变换为另一直线l':9x+y一91=0,试求a,b的值.C.选修4—4:坐标系与参数方程已知在直角坐标系x0y内,直线l的参数方程为22,14,x ty t=+⎧⎨=+⎩(t为参数).以Ox为极轴建立极坐标系,圆C的极坐标方程为)4πρθ=+.(1)写出直线l的普通方程和圆C的直角坐标方程;(2)判断直线l和圆C的位置关系.D.选修4—5:不等式选讲设x,y,z为正数,证明:2(x3+y3+z3)≥x2(y+z)+ y2(x+z)+ z2(x+y).【必做题】第22题、第23题,每题10分,共计20分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.在正方体ABCD—A1B1C1D1中,F是BC的中点,点E在D1C1上,且D1E=14D1C1,试求直线EF与平面D1AC所成角的正弦值.第21-A题A BC DFA1B1C1ED123.(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花. ①求恰有两个区域用红色鲜花的概率;②记花圃中红色鲜花区域的块数为S ,求拿的分布列及其数学期望E(S).参考答案及评分标准必做题部分一、填空题:本大题共14题,每小题5分,共70 分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷学校:___________姓名:___________班级:___________考号:___________一、填空题1.已知集合},0{a A =,}3,1,0{=B ,若}3,2,1,0{=B A ,则实数a 的值为 .2.已知复数z 满足42-=z ,若z 的虚部大于0,则=z .3.交通部门对某路段公路上行驶的汽车速度实施监控,从速度在的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在以下的汽车有辆.4.运行如图所示的伪代码,则输出的结果为 .5.函数)sin(2)(ϕω+=x x f )0(>ω的部分图像如图所示,若5=AB ,则ω的值为 .6.若随机安排甲乙丙三人在3天节日中值班,每人值班1天,则甲与丙都不在第一天的概率为 .7.抛物线x y 42=的焦点到双曲线191622=-y x 渐近线的距离为 . 8.已知矩形ABCD 的边4=AB ,3=BC 若沿对角线AC 折叠,使得平面DAC ⊥平面BAC ,则三棱锥ABC D -的体积为 .9.若公比不为1的等比数列}{n a 满足13)(log 13212=⋯a a a ,等差数列}{n b 满足77a b =,则1321b b b +⋯++的值为 .10.定义在R 上的奇函数)(x f 满足当0≥x 时,b x a x x f +-++=)1()2(log )(2(a ,b 为常数),若1)2(-=f ,则)6(-f 的值为 . 11.已知|OA ⃗⃗⃗⃗⃗ |=|OB ⃗⃗⃗⃗⃗ |=√2,且OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =1,若点C 满足|OA⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ |=1,则|OC ⃗⃗⃗⃗⃗ |的取值范围是 .12.已知函数⎩⎨⎧<-≥+=0)(0cos 2)(x x a x x x x x f ,若关于x 的不等式π<)(x f 的解集为)2,(π-∞,则实数a 的取值范围是 . 13.已知)1,0(A ,)0,1(B ,)0,(t C ,点D 是直线AC 上的动点,若BD AD 2≤恒成立,则最小正整数t 的值为 .14.设c b a ,,是正实数,满足a c b ≥+,则b ac c b ++的最小值为 .二、解答题15.在锐角三角形ABC 中,角C B A ,,的对边为c b a ,,,已知53sin =A ,21)tan(-=-B A , (1)求B tan ;(2)若5=b ,求c .16.如图,在四棱锥ABCD P -中,已知底面ABCD 为矩形,⊥PA 平面PDC ,点E 为棱PD 的中点,求证:O PA B C DE(1)//PB 平面EAC ;(2)平面⊥PAD 平面ABCD .17.如图,OA 是南北方向的一条公路,OB 是北偏东045方向的一条公路,某风景区的一段边界为曲线C .为方便游客光,拟过曲线C 上的某点分别修建与公路OA ,OB 垂直的两条道路PN PM ,,且PN PM ,的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy ,则曲线符合函数)91(242≤≤+=x x x y 模型,设x PM =,修建两条道路PN PM ,的总造价为)(x f 万元,题中所涉及的长度单位均为百米.(1)求)(x f 解析式;(2)当x 为多少时,总造价)(x f 最低?并求出最低造价.18.已知各项均为正数的数列}{n a 的首项11=a ,n S 是数列}{n a 的前n 项和,且满足:).0(*1111N n a a a a S a S a n n n n n n n n ∈≠=-+-++++λλ.(1)若1a ,2a ,3a 成等比数列,求实数λ的值;(2)若21=λ,求n S . 19.如图,在平面直角坐标系xoy 中,已知椭圆C :)0(12222>>=+b a by a x 的离心率21=e ,左顶点为)0,4(-A ,过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ,交y轴于点E . PD M A O xyE(1)求椭圆C 的方程;(2)已知P 为AD 的中点,是否存在定点Q ,对于任意的)0(≠k k 都有EQ OP ⊥,若存在,求出点Q 的坐标;若不存在说明理由;(3)若过O 点作直线l 的平行线交椭圆C 于点M ,求OMAE AD +的最小值. 20.已知函数]42)4(231[)(23--++-=a x a x x e x f x ,其中R a ∈,e 为自然对数的底数(1)若函数)(x f 的图像在0=x 处的切线与直线0=+y x 垂直,求a 的值.(2)关于x 的不等式x e x f 34)(-<在)2,(-∞上恒成立,求a 的取值范围.(3)讨论)(x f 极值点的个数.21.如图,PAQ ∠是直角,圆O 与射线AP 相切于点T ,与射线AQ 相交于两点,B C .求证:BT 平分OBA ∠.22.[选修4—2:矩阵与变换]已知矩阵1214A ⎡⎤=⎢⎥-⎣⎦,求矩阵A 的特征值和特征向量. 23.在极坐标系中,圆C 的极坐标方程为28sin()1303πρρθ--+=,已知33(1,),(3,)22A B ππ,P 为圆C 上一点,求PAB ∆面积的最小值. 24.设,x y 均为正数,且x y >,求证:2212232x y x xy y +≥+-+. 25.如图,在直三棱柱111ABC A B C -中,底面ABC ∆是直角三角形,1AB AC ==,点P 是棱1BB 上一点,满足1(01)BP BB λλ=≤≤.(1)若13λ=,求直线PC 与平面1A BC 所成角的正弦值;(2)若二面角1P A C B --的正弦值为23,求λ的值.26.已知数列{}n a 满足()()()()21211132,,1n na n f n g n f n f n a a a =-=+++=--,*n N ∈. (1)求证:()123g >;(2)求证:当3n ≥时, ()13g n >.参考答案1.2【解析】试题分析:由题意得,2B ∉,则2A ∈,则2a =考点:元素与集合关系2.2i【解析】试题分析:设222(,,0),24z a bi a b R b z a b abi =+∈>=-+=-则,因此 20,4,2a b b =-=-=±,又0b >则2,2b z i ==考点:复数概念3.75【解析】试题分析:由频率分布直方图得,速度在以下的汽车所占频率为(0.020.03)100.5+⨯=,则速度在以下的汽车有1500.575⨯=辆 考点:频率分布直方图4.9【解析】运行程序一次,12,2s i =+=,第二次运行后122,3s i =++=,第三次运行后1222,4s i =+++=,第四次运行后1222+2,5s i =+++=,不满足条件5i <,跳出循环,输出9s =,故填9.点睛:处理此类问题时,一般模拟程序的运行,经过几次运算即可跳出循环结束程序,注意每次循环后变量的变化情况,寻找规律即可顺利解决,对于运行次数比较多的循环结构,一般能够找到周期或规律,利用规律或周期确定和时跳出循环结构,得到问题的结果.5.3π【解析】试题分析:5AB ==,解得26,3T ππωω===考点:三角函数图像与性质6.13【解析】试题分析:随机安排甲乙丙三人在3天节日中值班,每人值班1天,共有6种不同的安排方法,其中丙在第一天的安排方法有两种,则甲与丙都不在第一天的概率为2163= 考点:古典概型概率7.35【解析】试题分析:抛物线x y 42=的焦点为(1,0),双曲线191622=-y x 渐近线为3,3404y x x y =±±=,所求距离为35d == 考点:双曲线渐近线8.245【解析】试题分析:因为平面DAC ⊥平面BAC ,所以D 到直线BC 距离为三棱柱ABC D -的高,11341211224,346,,63255355D ABC ABC ABC V S h S h V -∆∆⨯==⨯⨯====⨯⨯=考点:三棱锥体积9.26【解析】试题分析:由13)(log 13212=⋯a a a 得,131312137772,2a a a a a b ⋯====,121371326b b b b ++⋯+== 考点:等差与等比数列性质10.4【解析】试题分析:由“定义在R 上的奇函数)(x f ”,得(0)01,1f b b ==+=-,(2)22(1)11,0f a a =+--=-=,2()log (2)1(0),(6)(6)3614f x x x x f f =+--≥-=-=-++=考点:函数性质11.【解析】试题分析: OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =|OA ⃗⃗⃗⃗⃗ |×|OB ⃗⃗⃗⃗⃗ |×cos <OA ⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ >=1,cos <OA ⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ >=12,cos <OA ⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ >=π3, 以O 为坐标原点,OA 所在直线为x 轴,建立平面直角坐标系,则O(0,0),A(√2,0),B(√22,√62),令OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ =(3√22,√62),|OP⃗⃗⃗⃗⃗ |=√6, ,则点C 的运动轨迹是以点P 为圆心,1为半径的圆,而|OP⃗⃗⃗⃗⃗ |=√6,则|OC ⃗⃗⃗⃗⃗ |的取值范围为考点:向量数量积,动点轨迹 12.()-∞+【解析】 试题分析:由题意得()=()f x x a x π-<对任意0x <总成立,即a x x π>+对任意0x <总成立,而x x π+≤-x =时取“=”,则实数a 的取值范围是()-∞+ 考点:基本不等式求最值13.4【解析】试题分析:11(0,1),(,0):1,(,1)A C t l y x D x x t t ⇒=-+-+,2AD BD ≤⇒≤化简得2238(3)(8)80x x t t +-++≥对任意x 总成立,则2283(8)48(3)0t t +-⨯⨯+≤化简得2410t t -+≥,解得2t ≥+02t <≤-,因此最小正整数t 的值为4考点:不等式恒成立1412【解析】 试题分析:11,2,,22c c b c a b c a b a b b c a b b c +≥+≥+≥≥++++,2b c b c c a b c b c +≥+++,令1211111,221221222b b c t t t c c b c t t +=+=+=+-≥=+++当且仅当12t =时取“=”, 则b a c c b ++12 考点:基本不等式求最值15.(1)tan 2B =(2)112c =【解析】 试题分析:(1)由()B A A B =--得,利用两角差的正切公式求B tan ,因此先求tan A ,这可由同角三角函数关系求:由3sin 5A =,A 为锐角,得4cos 5A =, sin 3tan cos 4A A A ==,从而tan tan()tan 21tan tan()A A B B A A B --==+⋅-(2)已知三角一边求一边,应用正弦定理sin sin b c B C =,所以关键转化为利用同角三角函数关系求sin B 及由两角和的正弦公式求sin sin()sin cos cos sin 25C A B A B A B =+=+=.试题解析:(1)在锐角三角形ABC 中,由3sin 5A =,得4cos 5A ==, 所以sin 3tan cos 4A A A ==.由tan tan 1tan()1tan tan 2A B A B A B --==-+⋅,得tan 2B =.(2)在锐角三角形ABC 中,由tan 2B =,得sin B =,cos B =,所以sin sin()sin cos cos sin C A B A B A B =+=+=,由正弦定理sin sin b c B C =,得sin 11sin 2b C c B ==. 考点:两角差的正切公式,两角和的正弦公式,正弦定理,同角三角函数关系 16.(1)详见解析(2)详见解析 【解析】试题分析:(1)证明线面平行,一般利用线面平行判定定理进行论证,即从线线平行出发,而线线平行的证明一般从平面几何条件寻求,本题利用中位线性质得PB ∥OE .(2)面面垂直的证明,一般利用线面垂直给予证明,即需证明CD ⊥平面PAD .而线面垂直的证明,需多次利用线面垂直的判定及性质定理进行转化论证:先由PA ⊥平面PDC 转化为线线垂直PA ⊥CD ,再由AD ⊥CD ,转化为线面垂直CD ⊥平面PAD . 试题解析:(1)连接BD 与AC 相交于点O ,连结OE . 因为四边形ABCD 为矩形,所以O 为BD 中点. 因为E 为棱PD 中点,所以PB ∥OE . 因为PB ⊄平面EAC ,OE ⊂平面EAC , 所以直线PB ∥平面EAC .(2)因为PA ⊥平面PDC ,CD ⊂平面PDC ,所以 PA ⊥CD . 因为四边形ABCD 为矩形,所以AD ⊥CD .因为 PA∩AD=A ,PA ,AD ⊂平面PAD ,所以 CD ⊥平面PAD . 因为CD ⊂平面ABCD ,所以 平面PAD ⊥平面ABCD .考点:线面平行判定定理,线面垂直的判定及性质定理17.(1)()22432()540519f x x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭≤≤(2)当4x =时,总造价最低,最低造价为30万元 【解析】试题分析:(1)研究函数实际问题的关键在于建立函数关系式:()540f x PM PN =+,因此解题关键转化为确定PN ,即点到直线OB 距离:点P坐标为,x x ⎛ ⎝⎭,直线OB 的方程为0x y -=,则点P 到直线0x y -=24x ==,最后明确函数定义域(2)利用导数求函数最值:先确定定义区间,再求导函数,明确导函数再定义区间上的零点,最后列表分析单调趋势,确定函数最值.试题解析:(1)在如图所示的直角坐标系中,因为曲线C的方程为)=19y x x ≤≤,PM x =所以点P坐标为2,x x x ⎛+ ⎝⎭, 直线OB 的方程为0x y -=,则点P 到直线0x y -=24x ==, 又PM 的造价为5万元/百米,PN 的造价为40万元/百米.则两条道路总造价为()22432()540519f x x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭≤≤.OPAB CDE(2)因为22432()5405f x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭, 所以 333645(64)()=51x f x x x -⎛⎫'-=⎪⎝⎭, 令()0f x '=,得4x =,列表如下:所以当4x =时,函数()f x 有最小值,最小值为()232454304f ⎛⎫=+= ⎪⎝⎭. 答:(1)两条道路PM ,PN 总造价()f x 为232()5f x x x ⎛⎫=+ ⎪⎝⎭()19x ≤≤; (2)当4x =时,总造价最低,最低造价为30万元.(注:利用三次均值不等式223232()5553022x x f x x x x ⎛⎫⎛⎫=+=++⨯= ⎪ ⎪⎝⎭⎝⎭≥,当且仅当23222x x x ==,即4x =时等号成立,照样给分.)考点:函数实际问题,利用导数求函数最值18.(1)1λ=(2)2351226n n n n n S a +⎛⎫=-=⎪⎝⎭+ 【解析】试题分析:(1)因为1a ,2a ,3a 成等比数列,所以2213a a a =,因此由1111n n n n n n n n a S a S a a a a λ++++-+-=分别求出221a λ=+,()()324121a λλλ=+++,代入化简得1λ=(2)当12λ=时,111112n n n n n n n n a S a S a a a a ++++--=+,变形构造成一个特殊数列是本题关键及难点:1111(1)(1)2n n n n n n a S a S a a ++++-=+,111112n n n n S S a a ++-=++,所以数列1n n S a ⎧⎫⎨⎬⎩⎭+是以2为首项,公差为12的等差数列,解得3122n nn S a ⎛⎫= ⎪⎝⎭++,再利用n S 与n a 关系得到数列}{n a 递推关系()()112n n n a n a -=++,()1221n n a a n n n -=++≥,即数列2n a n ⎧⎫⎨⎬⎩⎭+是首项为13是常数列,所以()123n a n =+.因此2351226n n n n n S a +⎛⎫=-= ⎪⎝⎭+ 试题解析:(1)令1n =,得221a λ=+.令2n =,得23322323a S a S a a a a λ--=+,所以()()324121a λλλ=+++.由2213a a a =,得()()22241121λλλλ⎛⎫= ⎪⎝⎭++++,因为0λ≠,所以1λ=.(2)当12λ=时,111112n n n n n n n n a S a S a a a a ++++--=+,所以11111112n n n n n n S S a a a a ++++--=+,即111112n n n n S S a a ++-=++, 所以数列1n n S a⎧⎫⎨⎬⎩⎭+是以2为首项,公差为12的等差数列,所以()11212n nS n a =-⋅++, 即3122n nn S a ⎛⎫= ⎪⎝⎭++,① 当2n ≥时,113122n n n S a --⎛⎫= ⎪⎝⎭++,②①②得,13222n n n n n a a a -=-++,即()()112n n n a n a -=++,所以()1221n n a a n n n -=++≥,所以2n a n ⎧⎫⎨⎬⎩⎭+是首项为13是常数列,所以()123n a n =+. 代入①得2351226n n n n n S a +⎛⎫=-=⎪⎝⎭+. 考点:构造数列求通项,利用nS 与n a 关系求通项19.(1)2211612x y +=;(2)(3,0)-;(3)【解析】试题分析:(1)确定椭圆标准方程,只需两个独立条件即可:一个是左顶点为(40)A -,,所以4a =,另一个是12e =,所以2c =,22212b a c =-=(2)实质利用斜率k 表示点222161224,4343()D k k k k -+++,P 2221612,4343()k k k k -++,E (0,4)k ,假设存在定点(,)(0)Q m n m ≠,使得OP EQ ⊥,因此=0OP EQ ⋅,即(412)30m k n +-=恒成立,从而412030m n +=⎧⎨-=⎩,,即30m n =-⎧⎨=⎩,,(3)利用斜率k 表示点M或,因此2D A E A D AM M x x x x x x AD AE OM x x -+--+==2==≥,本题思路简单,但运算量较大.试题解析:(1)因为左顶点为(40)A -,,所以4a =,又12e =,所以2c =又因为22212b a c =-=,所以椭圆C 的标准方程为2211612x y +=.(2)直线l 的方程为(4)y k x =+,由2211612(4),x y y k x ⎧+=⎪⎨⎪=+⎩,消元得,22[(4)]11612x k x ++=.化简得,22(4)[(43)1612)]0x k x k +++-=, 所以14x =-,222161243k x k -+=+. 当22161243k x k -+=+时,222161224(4)4343k k y k k k -+=+=++, 所以222161224,4343()D k k k k -+++.因为点P 为AD 的中点,所以P 的坐标为2221612,4343()k kk k -++,则3(0)4OP k k k -=≠.直线l 的方程为(4)y k x =+,令0x =,得E 点坐标为(0,4)k , 假设存在定点(,)(0)Q m n m ≠,使得OP EQ ⊥,则1OP EQk k =-,即3414n kk m --⋅=-恒成立,所以(412)30m k n +-=恒成立,所以412030m n +=⎧⎨-=⎩,,即30m n =-⎧⎨=⎩,,因此定点Q 的坐标为(3,0)-. (3)因为OMl ,所以OM 的方程可设为y kx =,由2211612x y y kx⎧+=⎪⎨⎪=⎩,得M点的横坐标为x = 由OM l ,得2D A E A D AM Mx x x x x x AD AE OM x x -+--+==22216128k -+=+==≥,当且仅当=即k =时取等号,所以当k =时,AD AE OM +的最小值为考点:直线与椭圆位置关系20.(1)1a =-(2)[0)+∞,(3)当0a ≥时,()f x 有且仅有一个极值点,当0a <时,()f x 有三个极值点. 【解析】试题分析:(1)利用导数几何意义得(0)=1f ',而321()e 3x f x x x ax a ⎛⎫'=-+- ⎪⎝⎭,因此1a =-(2)不等式恒成立问题,一般利用变量分离,转化为对应函数最值:()()()3222max max 612811()[2203233x x x a x x x -++>=----<--],,因此0a ≥(3)先求函数导数:321()e 3x f x x x ax a ⎛⎫'=-+- ⎪⎝⎭,这是一个三次函数与指数函数的乘积,因此导函数的零点为一个或三个,即()f x 只有一个极值点或有三个极值点.再分类讨论:当321()3g x x x ax a=-+-与x 轴有且仅有一个交点时,分两种情形,一是()g x 为单调递增函数(无极值),二是()g x 极值同号.当321()3g x x x ax a=-+-与x 轴有且仅有三个交点时,()g x 极值异号.试题解析:(1)由题意,321()e 3x f x x x ax a ⎛⎫'=-+- ⎪⎝⎭, 因为()f x 的图象在0x =处的切线与直线0x y +=垂直,所以(0)=1f ',解得1a =-.(2)法一:由4()e 3xf x <-,得3214e 2(4)24e 33x x x x a x a ⎡⎤-++--<-⎢⎥⎣⎦,即326(312)680x x a x a -++--<对任意(2)x ∈-∞,恒成立,即()32636128x a x x x ->-=-对任意(2)x ∈-∞,恒成立, 因为2x <,所以()()322612812323x x x a x x -++>=----,记()21()23g x x =--,因为()g x 在(2)-∞,上单调递增,且(2)0g =, 所以0a ≥,即a 的取值范围是[0)+∞,. 法二:由4()e 3xf x <-,得3214e 2(4)24e 33x x x x a x a ⎡⎤-++--<-⎢⎥⎣⎦, 即326(312)680x x a x a -++--<在(2)-∞,上恒成立, 因为326(312)680x x a x a -++--<等价于2(2)(434)0x x x a --++<, ①当0a ≥时,22434(2)30x x a x a -++=-+≥恒成立, 所以原不等式的解集为(2)-∞,,满足题意. ②当0a <时,记2()434g x x x a =-++,有(2)30g a =<, 所以方程24340x x a -++=必有两个根12,x x ,且122x x <<,原不等式等价于12(2)()()0x x x x x ---<,解集为12()(2)x x -∞,,,与题设矛盾,所以0a <不符合题意.综合①②可知,所求a 的取值范围是[0)+∞,. (3)因为由题意,可得321()e 3x f'x x x ax a ⎛⎫=-+- ⎪⎝⎭, 所以()f x 只有一个极值点或有三个极值点.令321()3g x x x ax a=-+-,①若()f x 有且只有一个极值点,所以函数()g x 的图象必穿过x 轴且只穿过一次, 即()g x 为单调递增函数或者()g x 极值同号.ⅰ)当()g x 为单调递增函数时,2()20g'x x x a =-+≥在R 上恒成立,得1a ≥…12分ⅱ)当()g x 极值同号时,设12,x x 为极值点,则12()()0g x g x ⋅≥,由2()20g'x x x a =-+=有解,得1a <,且21120,x x a -+=22220x x a -+=, 所以12122,x x x x a +==,所以3211111()3g x x x ax a =-+-211111(2)3x x a x ax a=--+- 11111(2)33x a ax ax a =---+-[]12(1)3a x a =--,同理,[]222()(1)3g x a x a =--,所以()()[][]121222(1)(1)033g x g x a x a a x a =--⋅--≥,化简得221212(1)(1)()0a x x a a x x a ---++≥, 所以22(1)2(1)0a a a a a ---+≥,即0a ≥, 所以01a <≤.所以,当0a ≥时,()f x 有且仅有一个极值点;②若()f x 有三个极值点,所以函数()g x 的图象必穿过x 轴且穿过三次,同理可得0a <; 综上,当0a ≥时,()f x 有且仅有一个极值点, 当0a <时,()f x 有三个极值点.考点:利用导数求函数最值,利用导数研究函数极值 21.详见解析 【解析】试题分析:由AT 是切线,PAQ ∠是直角得ABOT ,因此TBA BTO ∠=∠.半径 OT OB=得OTB OBT ∠=,因此OBT TBA ∠=∠, 即BT 平分OBA ∠. 试题解析:连结OT .因为AT 是切线,所以OT AP ⊥.又因为PAQ ∠是直角,即AQ AP ⊥, 所以AB OT ∥, 所以TBA BTO ∠=∠.又OT OB =,所以OTB OBT ∠=, 所以OBT TBA ∠=∠, 即BT 平分OBA ∠. 考点:平行线内错角相等22.属于特征值12λ=的一个特征向量121α⎡⎤=⎢⎥⎣⎦属于特征值23λ=的一个特征向量211α⎡⎤=⎢⎥⎣⎦【解析】试题分析:由特征多项式为()2125614f λλλλλ--==--+=0解得两个特征值12λ=,23λ=.再代入得对应特征方程组,因此属于特征值12λ=的一个特征向量121α⎡⎤=⎢⎥⎣⎦,属于特征值23λ=的一个特征向量211α⎡⎤=⎢⎥⎣⎦. 试题解析:矩阵A 的特征多项式为()2125614f λλλλλ--==--+,由()0f λ=,解得12λ=,23λ=.当12λ=时,特征方程组为20,20,x y x y -=⎧⎨-=⎩故属于特征值12λ=的一个特征向量121α⎡⎤=⎢⎥⎣⎦;当23λ=时,特征方程组为220,0,x y x y -=⎧⎨-=⎩故属于特征值23λ=的一个特征向量211α⎡⎤=⎢⎥⎣⎦.考点:特征值及特征向量23 【解析】试题分析:利用222,cos ,sin x y x y ρρθρθ=+==将极坐标33(1,),(3,)22A B ππ及极坐标方程28sin()1303πρρθ--+=化为直角坐标及直角坐标方程(0,1),(0,3)A B --,22((2)3x y ++-=,从而直线AB 方程为y 轴,P 到直线AB 距离的最小值为2AB =,所以PAB ∆面积的最小值为122⨯试题解析:圆C 的直角坐标方程为224130x y y ++-+=,即22((2)3x y ++-=. 又(0,1),(0,3)A B --,所以2AB =.P 到直线AB 距离的最小值为=所以PAB ∆面积的最小值为122⨯考点:极坐标方程化为直角坐标方程 24.详见解析 【解析】试题分析:作差再利用均值不等式得22211222()2()x y x y x xy y x y +-=-+-+-=21()()()x y x y x y -+-+-33≥试题解析:因为x >0,y >0,x -y >0, 22211222()2()x y x y x xy y x y +-=-+-+-,=21()()()x y x y x y -+-+-3≥,所以2212232x y x xy y ++-+≥.考点:均值不等式 25.(1)33(2)λ的值为1 【解析】试题分析:(1)利用空间向量求线面角,先建立恰当的空间直角坐标系,设出各点坐标,从而有2(1,1,)3CP =-,再利用方程组求出平面1A BC 的一个法向量1(2,2,1)=n ,根据向量数量积求两向量夹角余弦值,最后根据线面角与向量夹角的关系得结论(2)同上利用方程组求出平面1PA C 的法向量2(22,2,1)n λ=-,再根据向量数量积求两向量夹角余弦值,根据二面角与向量夹角的关系得等量关系,解出1λ=试题解析:以A 为坐标原点O ,分别以AB ,AC ,1AA 所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系O xyz -.因为=1AB AC =,12AA =,则(0,0,0)A ,(1,0,0)B ,(0,1,0)C ,1(0,0,2)A ,1(1,0,2)B ,(1,0,2)P λ.(1)由13λ=得,2(1,1,)3CP =-,1(1,02)A B =-,,1(0,1,2)AC =-, 设平面1A BC 的法向量为1111(,,)x y z =n ,由11110,{0n A B n A C ⋅=⋅=,得111120,{20.x z y z -=-= 不妨取11z =,则112x y ==,从而平面1A BC 的一个法向量为1(2,2,1)=n . 设直线PC 与平面1A BC 所成的角为θ,则111sin cos ,33CP n CP n CP n θ⋅===⋅, 所以直线PC 与平面1A BC . (2)设平面1PA C 的法向量为2222(,,)x y z =n ,1(1,022)A P λ=-,,由21210,{0n AC n A P ⋅=⋅=,得222220,{(22)0.y z x z λ-=+-= 不妨取21z =,则22222x y λ=-=,, 所以平面1PA C 的法向量为2(22,2,1)n λ=-.则12cos ,n n =,又因为二面角1P A C B --的正弦值为23,=3化简得2+890λλ-=,解得1λ=或9λ=-(舍去), 故λ的值为1.考点:利用空间向量求线面角,利用空间向量研究二面角, 26.(1)详见解析(2)详见解析【解析】试题分析:(1)由题意得()2121111n n n n g n a a a a ++=++++,因此()234111111691247101403g a a a =++=++=>(2)利用数学归纳法证明,先找出n k =与1n k =+相互关系: ()1g k + ()g k = ()2221211111kk k k a a a a +++⎛⎫⎪++++- ⎪⎝⎭,再根据1n a 递减放缩得()()222212111111211k kk k k k k a a a a a a ++++++++->-,最后通分化简得()()[]()()()[]()2222132332113730,33123231232k k k k k k k k a a k k k k ++-++---==>≥⎡⎤⎡⎤+--+--⎣⎦⎣⎦试题解析:(1)由题意知, 32n a n =-, ()2121111n n n n g n a a a a ++=++++, 当2n =时, ()234111111691247101403g a a a =++=++=>. (2)用数学归纳法加以证明:①当3n =时, ()345911113g a a a a =++++11111117101316192225=++++++ 11111117101316192225⎛⎫⎛⎫=++++++ ⎪ ⎪⎝⎭⎝⎭ 11111118161616323232⎛⎫⎛⎫>++++++ ⎪ ⎪⎝⎭⎝⎭ 133131181632816163=++>++>, 所以当3n =时,结论成立.②假设当n k =时,结论成立,即()13g k >, 则1n k =+时, ()1g k + ()g k = ()2221211111k k k k a a a a +++⎛⎫⎪++++- ⎪⎝⎭()222121111113kk k k a a a a +++⎛⎫ ⎪>++++- ⎪⎝⎭()()22111332312k k k +>+--+- ()()()()[]2221323121331232k k k k k ⎡⎤+--+-⎣⎦=+⎡⎤+--⎣⎦ ()[]221373331232k k k k --=+⎡⎤+--⎣⎦, 由3k ≥可知,,即()113g k +>. 所以当1n k =+时,结论也成立. 综合①②可得,当3n ≥时, ()13g n >. 考点:数学归纳法。
