2方--6方关系设计

合集下载

5升6奥数拓展：数与形(试题)-小学数学六年级上册人教版

5升6奥数拓展：数与形（试题）-小学数学六年级上册人教版一、选择题1．用小木棒按下图方式摆放图形，第⑧个图形需要（）根小木棒。

A．33B．30C．36D．272．如下图，第5个图形是由（）个小正方形拼成的。

A．16B．20C．25D．363．观察下面的点子图，如果按图中的规律画下去，第⑧个方框里应画（）个点。

A．29B．31C．334．古希腊著名的毕达哥拉斯学派把1、3、6、10、15、21…这样的数称为“三角形数”，而把1、4、9、16、25、36…这样的数称为“正方形数”。

从下图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和。

下列等式中，不符合这一规律的是（）。

A．25＝9＋16B．36＝15＋21C．49＝21＋28D．64＝28＋365．如下图，等边三角形的边长是1cm，第n个图形的周长是（）cm。

A ．nB ．21nC ．2n +D ．31n +6．下图能够大概描述汽车由静止开始发动，加速到一定速度匀速行驶一段距离后减速上坡，再加速下坡，然后逐渐减速到匀速行驶的过程是（）。

A ．B ．C ．D ．二、填空题7．按照下图所示的规律继续摆，第5个图案需要( )枚棋子；第n 个图案需要( )个枚棋子。

8．如下图，用小棒摆一个正六边形，摆4个正六边形需要( )根小棒；摆51个小正六边形需要( )根小棒；用1001根小棒，可以摆( )个小正六边形。

9．按照下面图形的规律可知，第6个图形中有( )个小正方形，第n 个图形中有( )个小正方形。

……10．根据图形中各个数的关系，★＝( )，★＝( )。

11．观察下图，找到规律，第4个图案中有白色正方形( )个，第n个图案中有白色正方形( )个。

12．某校园文化长廊里设计了长方形步道，该步道由相同的棕色正方形瓷砖和相同的白色等腰直角三角形瓷砖排列而成。

当只需要用1块正方形瓷砖时，步道铺设如图1；当需要用2块正方形瓷砖时，步道铺设如图2，……按照这样的规律铺设，当需要100块正方形瓷砖时，则需要用( )块等腰直角三角形瓷砖。

六方最密堆积教育-2022年学习资料

金属晶体熔点变化规律-1、金属晶体熔点变化较大，-与金属晶体紧密堆积方式、金属阳离子与自由电子间的金-属键的强弱有密切关系-2、一般情况下，金属晶体熔点由金属键强弱决定：-金属阳离子半径越，所带电荷越多，自由电子越多，-金属键越强，熔点就相应越高，硬度也越大。但金属性越弱-如：K< a<Mg<Al-Li>Na K Rb Cs-熔点最低的金属：汞（常温时成液态-熔点很高的金属： 3410℃-铁的熔点：1535℃
3-简单立方晶胞平均占有的原子数目：
2体心立方堆积IA,B,VIB-体心立方晶胞
①配位数：-8-上下层各4-5-0-7-2-3
2金属原子半径"与正方体边长a的关系：-8-V2 a-b=V3a-b=4r-V3a=4r
锋-x100%=68.02%-3
3-体心立方晶胞平均占有的原子数目：-X8-1=2
资料-金属之最-熔点最低的金属是---汞-熔点最高的金属是-„钨-密度最小的金属是--锂-密度大的金属是--锇-硬度最小的金属是--铯-硬度最大的金属是---一-铬-延性最好的金属是-一-展性最好的金属是-一-最活泼的金属是--最稳定的金属是-
3、金属晶体的基本堆积模型-1紧密堆积：微粒之间的作用力使微-粒间尽可能的相互接近，使它们占有小-的空间。-2空间利用率：-晶体的空间被微粒占-满的体积百分数，用它来表示紧密堆积-的程度。 3配位数：在晶体中与每个微粒紧密-相邻的微粒个数。-一紧密堆积
活动与探究1：-平面上金属原子紧密排列的方式-·从蓝色盒子里取出：-4组乒乓球（3个排成一条直的-将乒乓球放置在平面上，排成4排，使球面-紧密接触，有哪些排列方式？
平面上金属原子紧密排列的两种方式-2-配位数为4-配位数为6
·4个小球形成一个四边形空隙，一种空隙。-见“0”。

正规s_n_p_部分因子设计最优区组和折叠反转方案_雷轶菊

ｎ－ｐ摘要：讨论了同时应用区组方案和折叠反转技巧时在ｓ正规部分因子设计中选择最优设计的ｎ－ｐ问题，其中ｓ是一个素数或素数幂．以分区组ｓ正规部分因子设计折叠反转的一般结构为基础，
给出了组合区组设计的处理和区组裂区字长型的定义．该文证明了，对于已分区组的初始设计，它的组合区组设计的处理和区组裂区字长型与区组折叠反转方案无关．对于一个未分区组的初始设计，其组合区组设计定义的区组和折叠反转方案有最小混杂的充分必要条件是在不考虑区组方案时折叠反转方案有最小混杂，在不考虑折叠反转方案时区组方案有最小混杂．关键词：最优区组方案；最优折叠反转方案；最小混杂；裂区字长型中图分类号：Ｏ２１２．６文献标识码：Ａ
ｎｓ一个全面的因子设计要求ｓ次试验来安ｎ个水平的因子，出于试验次数方面的考虑，当ｎ很大
意义的问题．对一个给定的分区组的正规２－水平］通过代数计算搜索了在提出的两个设计，文献［７最优性准则下的最优处理折叠反转方案，但是没］有给出理论证明．文献［给出了在同时应用分区８组和折叠反转技巧时对正规２－水平设计的一些理论性质．所有以前的文献结果都仅限于２－水平设计的情形．但是在实际中，较高水平数可能被使］研用，因此这是一个令人感兴趣的领域．文献［９究了在考虑或不考虑区组因子的情况下正规ｓ－水平部分因子设计的初始设计和其组合设计之间的］关系，其中ｓ是一个素数或素数幂．但是，文献［９仅仅研究了含有隐含区组因子的情形．本文将文］献［的结论推广到了ｓ８－水平的情形，得到了与文］类似的结果．献［８

北师版九年级上册数学精品教学课件第二章一元二次方程第2课时利用一元二次方程解决面积问题

4
故左右边衬的宽为 7 6 3 3 1.4.
4
21 cm
试一试：如果换一种设未知数的方法，是否可以更简单
地解决上面的问题？
例2 如图，在 Rt△ABC 中，∠C = 90°，AC = 6 cm，BC
= 8 cm. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s 的速度移
动；同时点 Q 沿 CB 边从点 C 向终点 B 以 2 cm/s 的速度
解得
x1= 17 3 229
10.71(舍)，x2=
17 229 3
0.62.
∴x≈0.62，则 3x≈1.86，2x≈1.24.
答：横、竖小路的宽度分别为 1.86 米、1.24 米.
方法点拨
我们利用“图形经过平移，它的面积大小不会改变”的性质，把纵、横两条路平移，使列方程容易些（目的是求出小路的宽，至于实际施工，仍可按原图的位置修路）.
整理，得 x2 − 15x − 250 = 0.
解得 x1 = −10(舍)，x2 = 25，所以 2x = 50. 答：铁板的长 50 cm，宽为 25 cm.
3.如图，要设计一个宽 20 cm，长为 30 cm 的矩形图案，
其中有两横两竖彩条，横竖彩条的宽度之比为 2∶3 ，
若使所有彩条的面积是原来矩形图案面积的三分之一，
上个花园，并使花园所占面积为荒地面积的一半.
16 m
想一想，你会怎么设计这片荒地？
看一看：下面几位同学的设计方法是否合理？
12 m
小明设计：如右图所示，其中花园四周小路的宽都相等.
通过解方程，得到小路的宽为 2 m 或 12 m.
问题：他的结果对吗？你能将小明的解答过程重现吗？
解：设小路的宽为 x m，根据题意得：

用字母表示数教学设计6篇

用字母表示数教学设计6篇用字母表示数教学设计1教学目标1、使学生进一步理解用字母表示数的意义和作用。

2、能正确运用字母表示常用数量关系。

3、能较熟练地利用公式、常用数量关系求值知识重点、难点能正确运用字母表示常用数量关系教学过程一、复习。

1、用字母表示数，有哪些好处？但要注意什么？2、用字母a、b、c表示加法结合律、乘法交换律、乘法分配律等。

请学生结合字母表示的运算定律说说其含义。

3、用S表示面积，C表示周长，a表示边长，b表示宽，写出长方形、正方形的面积和周长公式。

4、下面各式中，哪些运算符号可以省略？能省略的就省略写出来。

2×3a×714＋ba÷7a×a5－x0.6×0.6二、新授。

1、教学：（1）引导学生看书提问：从图、表中你了解到哪些信息？A、爸爸比小红大30岁。

B、当小红1岁时，爸爸（）岁，......师：这些式子，每个只能表示某一年爸爸的年龄。

（2）启发学生：你能用一个式子表示出任何一年爸爸的年龄吗？（可让同桌的两个同学小声讨论）结合讨论情况师适时板书：法1：小红的年龄＋30岁＝爸爸的年龄法2：a＋30提问：比一比，你比较喜欢哪一种表示方法，为什么？让学生发表各自意见。

在式子a＋30中，a表示什么？30表示什么？a＋30表示什么？（a表示小红的年龄，30表示爸爸比小红大的年龄，a＋30即表示爸爸的年龄）想一想：a可以是哪些数？a能是200吗？为什么？（3）结合关系式解答：当a＝11时，爸爸的年龄是多少？学生把算式和结果填在书上。

2、小结：用含有字母的式子不仅可以表示运算定律、公式，也可以表示数量。

引导学生看书讨论：（可分成四人小组进行讨论）（1）从图、表中你了解到哪些信息？（2）你能用含有字母的式子表示出人在月球上能举起的质量吗？（3）式子中的字母可以表示哪些数？（4）图中小朋友在月球上能举起的质量是多少？请小组派代表回答以上问题。

4、总结：今天你学会了什么？有哪些收获？课堂练习1、独立完成P48做一做集体评议。

《简易方程》教学设计6篇

《简易方程》教学设计6篇《简易方程》教学设计1【教学内容】教材第78页例4，“做一做”和练习十七5~10题。

【教学目标】1.学生通过自主探索、交流互助学会根据两个未知量之间的关系，列方程解答含有两个未知数的实际问题。

2.学会用检验答案是否符合已知条件的方法，提高学生求解验证的能力。

3.培养学生的主体意识、创新意识、合作意识,以及分析、观察能力和表达能力。

4.让学生体验到生活中处处是数学，体验数学的应用价值和数学学习的乐趣。

【重点难点】正确设未知数，找出等量关系列方程解决问题。

【教学准备】教具：地球仪多媒体课件【复习导入】1.填空。

（1）学校科技组的`男同学人数是女同学的3倍。

设女同学有x 人，则男同学有（）人；设男同学有x人，则女同学有（）人。

（2）学校书法组有女同学x人，男同学人数是女同学的2.5倍。

男同学有（）人，一共有（）人，男同学比女同学多（）人。

2.看图列方程，并求出方程的解。

3.导入新课：这节课我们继续学习列稍复杂的方程解决实际问题。

（出示课题）【新课讲授】1.情景导入。

课件出示：转动着的地球。

师：同学们，这就是我们人类赖以生存的地球，地球表面大部分的地方都被海洋所覆盖，海洋的面积要远远超出陆地的面积。

因此，也有人把地球称为“水球”，所以，地球看上去是漂亮的深蓝色。

那么你们想知道地球上的陆地面积、海洋面积究竟有多大吗？好，下面老师给你们提供一些信息。

2.出示例4。

地球的表面积为5.1亿平方千米，其中，海洋面积约为陆地面积的2.4倍。

海洋面积和陆地面积分别是多少亿平方千米？3.分析，理解题意，找等量关系，列方程。

师：请同学们先思考下面的问题：（1）题中有几个未知量？（2）设谁为x比较合适？为什么？（3）问题中包含有怎样的等量关系？（4）怎样列方程？汇报交流，总结：（1）题中有两个未知量，陆地面积和海洋面积。

海洋面积约为陆地面积的2.4倍。

（2）根据“海洋面积约为陆地面积的2.4倍”设未知数，陆地面积是x，海洋面积是2.4x。

人教版-第6章平方根教学设计(共8课时).

6.1平方根〔1〕〔第一课时〕学习目标：了解数的算术平方根，并会用符号表示；重点：了解数的算术平方根，会求某些非负数的算术平方根，会用根号表示一个数的算术平方根难点：a 是非负数；一、学习准备1、什么样的运算是平方运算？2、你还记得1～20之间整数的平方吗？二自主学习1 、学校要举行美术作品比赛，小鸥想裁出一块面积为25平方分米的正方形画布，画上自己的得意之作参比赛，这块正方形画布的边长应取多少一般地，如果一个的平方等于a,即_____ =a,那么这个叫做a 的_____,a 的算术平方根记为_____,读作“根号a ”，a 叫做被开方数。

特殊：0的算术平方根是_____,记作：_____,3．你能根据等式：212 =144说出144的算术平方根是多少吗？并用等式表示出来。

4．以下式子表示什么意思？你能求出它们的值吗；5．例1 求以下各数的算术平方根：〔1〕100 〔2〕〔3〕0.0001 思考：1. －4有算术平方根吗？2..以下各式哪些有意义，哪些没有意义？(1〕- 〔2 〔3〕2 〔4小结：算术平方根具有非负双重性.〔1〕任何非负实数的算术平方根都为______数64494123252(81)1(22）　（））（　方根，：求下列各数的算术平例-2222764165864232592113）（）　（）　（）　（）　（）　（）　（：求下列各式的值，例-+25081.0〔2〕被开方数都为_______数三课堂跟踪反馈练习；1 ：P41练习 1、22：判断：〔1〕5是25的算术平方根；〔2〕-6是 36 的算术平方根；〔3〕0的算术平方根是0；〔4〕0.01是0.1的算术平方根；〔5〕-5是-25的算术平方根。

3．填空〔1 〕非负数a 的算术平方根表示为___，225的算术平方根是____，0的算术平方根是____〔2〕____,_____===_____, 0.64-的算术平方根____〔3〕假设x 是49的算术平方根，则x =_____,4 。

人教版六年级上册第五单元《圆》单元作业设计

8
4.我尝试：用一根绳子在操场上围出一块地，你有几种围法？怎样围面积最大？（1）你觉得选择多长的绳子方便操作，说说你的想法。
（2）你学过哪些平面图形，有几种围法？分别画出示意图，并计算每种图形的面积，说说你的理由。
（3）如果在这块地上，摆放直径为1m的圆形桌子，最多可以放几张，请你结合生活实际画图说理。
2.我能行：体育课上，同学们正在进行抢球比赛。老师把球筐放在操场中间，要求同学们围在一起比赛，想一想，要如何站位才公平呢？说说你的想法，并试着在方框里画出示意图。
示意图
3，我尝试：（1）怎样才能画出一个半径2米的圆，你有什么好办法？先试着画个示意图，再实践体验，并与大家分享你的收获。
示意图
（2）
减去
得到
外圆面积 —
内圆面积 = 圆环面积
用字母表示（
）— （
）=（
）
2.我善思：
在研究圆环面积的计算方法时，我们学会运用“外圆面积-内圆面积=圆环面积”的方法。观
察上图，你能借助研究圆的面积计算公式的方法，把圆环也平均分成若干份吗？试着拼成一
个近似的平行四边形，这时平行四边形的底是（），平行四边形的面积是（
示意图
3.收获乐园: 收获乐园
用你喜欢的方式（如画图、列表、写提纲等），把当天的学习内容整理记录下来。
4.成长乐园:
我勤学
能基本完成 ☆
有实践精神 ☆☆
有突破和协作 ☆☆☆
精神
自评
○ 满意
他评
○ 满意
师评
○ 满意
送给自己一句话:
我反思我善思 ☆ ☆☆ ☆☆☆
我成长我能行 ☆ ☆☆ ☆☆☆
我尝试 ☆ ☆☆ ☆☆☆

国开《建筑工程项目管理》4次形考作业-(1、2、3、4)及答案.doc

成绩：建筑工程项目管理形成性考核册专业：户口·子亏．姓名：河北广播电视大学开放教育学院（请按照顺序打印，并左侧装订）《建筑工程项目管理》作业一一、单项选择题（每小题2分，共20分）1. 以下说法正确的是(C)。

A. 项目管理的对象就是建设工程B. 建设工程一－定要有明确的目标C. 没有明确目标的建设工程不是项目管理的对象D. 无论目标是否明确，建设工程都是项目管理的对彖2.投资方提供的项目管理服务属千cc)方的项目管理。

A. 政府B承包商C业主D.工程师3.供货方的项目管理工作主要在CB)阶段进行。

A. 设计B设计前准备C施工D动用前准备4.项目管理的三大目标是c B)。

A. 范围、费用、进度C·投资、进度、质量B. 费用、进度、质量D范围、投资、质量5.开发方提供的项目管理服务属于CC)方的项目管理。

A. 政府B承包商C·业主D.工程师6.施工方的项目管理工作涉及CA)全过程。

A. 设计前的准备阶段至保修期B. 设计阶段至动用前准备阶段C. 设计前的准备阶段至动用前准备阶段D. 设计阶段至保修期7. C B)组织机构每一个部门只有一个指令源。

A. 职能B线性C矩阵D事业部）组织机构。

8.每一个工作部门可能有多个矛盾的指令源的组织机构是CAA. 职能B.线性C矩阵D事业部9. 建设工程项目管理规划的编制应由c A)负责。

A. 项目经理B设计方C施工方D总承包方10. 施工企业根据监理企业制订的旁站监理方案，在需要实施旁站监理的关键部位施工前CA)小时，应当书面通知监理企业派驻工地的项目监理机构。

A. 24B. 36C. 48D. 12二、多项选择题（每小题3分，共18分）1.施工方项目管理的目标包括(A BC)。

A. 施工的成本目标C·施工的质晕目标B. 施工的进度目标D项目的投资目标E.项目的质量目标2.以下对施工企业项目经理的工作性质的说明，正确的是(A BDE)A. 建筑业企业项目经理资质管理制度向建造师执业资格制度过渡的时间定为5年B. 过渡期内，凡持有项目经理资质证书或者建造师注册证书的人员均可受聘担任施工项目经理C. 过渡期满后，所有工程项目施工的项目经理必须由取得建造师注册证书的人员担任D. 项目经理是建筑施工企业法定代表入在工程项目上的代表人E. 项目经理对工程项目施工过程全面负责3.供货方项目管理的目标包括(A BC)A. 供货的成本目标D.项目的投资目标C. 供货的质量目标B供货的进度H标E. 项目的质量目标4.下列有关建设工程监理的工作方法的说明，正确的是(A BDE)。

平方根优秀教案设计

平方根优秀教案设计平方根优秀教案设计作为一位优秀的人民教师，可能需要进行教案编写工作，教案有助于顺利而有效地开展教学活动。

那么大家知道正规的教案是怎么写的吗？下面是店铺精心整理的平方根优秀教案设计，仅供参考，欢迎大家阅读。

平方根优秀教案设计篇1教学目标：【知识与技能】了解平方根与算术平方根的概念，理解负数没有平方根及非负数开平方的意义。

【过程与方法】理解开平方与平方是一对互逆的运算，会用平方根的概念求某些数的平方根，并能用根号加以表示，能用科学计算器求平方根及其近似值。

【情感、态度与价值观】体会平方与开平方这一对互逆运算的辩证关系，感受平方根在现实世界中的客观存在，增强数学知识的应用意识。

【教学重点】理解开平方与平方是一对互逆的运算，会用平方根的概念求某些数的平方根，并能用根号加以表示。

【教学难点】会用平方根的概念求某些数的平方根，并能用根号加以表示。

【教具准备】小黑板科学计算器【教学过程】一、导入1、通过七年级的学习，相信同学们都对数学这门课程有了更深入的认识，这个学期，我们将一起来学习八年级的数学知识，这个学期的知识将会更加有趣。

2、板书：实数 1.1 平方根二、新授（一）探求新知1、探讨：有面积为8平方厘米的正方形吗？如果有，那它的边长是多少？（少数学习超前的学生可能能答上来）这个边长是个怎样的数？你以前见过吗？2、引入“无理数”的概念：像（2.82842712……）这样无限不循环的小数就叫做无理数。

3、你还能举出哪些无理数？（，）、、1/3是无理数吗？4、有理数和无理数统称为实数。

（二）知识归纳：1、板书：1.1平方根2、李老师家装修厨房，铺地砖10.8平方米，用去正方形的地砖120块，你能算出所用地砖的边长是多少吗？（0.3米）3、怎么算？每块地砖的面积是：10.8 120=0.09平方米。

由于0.32=0.09，因此面积为0.09平方米的正方形，它的边长为0.3米。

4、练习：由于（）=400，因此面积为400平方厘米的正方形，它的边长为（）厘米。

1.2《长方体和正方体的展开图》(教案)-六年级上册数学苏教版

1.2《长方体和正方体的展开图》（教案）六年级上册数学苏教版作为一名经验丰富的教师，我深知教学的重要性。

为了让学生更好地掌握知识，我需要精心设计每一堂课。

下面是我对1.2《长方体和正方体的展开图》这一课的教学设计和思考。

一、教学内容本节课的教学内容主要包括教材中关于长方体和正方体展开图的章节。

我会向学生介绍长方体和正方体的展开图的特点，以及如何通过展开图来理解长方体和正方体的结构。

二、教学目标通过本节课的学习，我希望学生能够掌握长方体和正方体的展开图的特点，能够自己画出长方体和正方体的展开图，并能够通过展开图来理解长方体和正方体的结构。

三、教学难点与重点本节课的重点是让学生掌握长方体和正方体的展开图的特点，难点是让学生能够自己画出长方体和正方体的展开图。

四、教具与学具准备为了更好地进行教学，我准备了长方体和正方体的模型，以及相关的展开图的图片。

五、教学过程1. 实践情景引入：我会让学生观察教室里的长方体和正方体物体，引导他们发现这些物体的展开图。

2. 知识点讲解：我会利用长方体和正方体的模型，向学生讲解长方体和正方体的展开图的特点。

3. 例题讲解：我会给学生展示一些长方体和正方体的展开图，让学生通过观察，理解展开图是如何体现长方体和正方体的结构的。

4. 随堂练习：我会让学生自己画出一些长方体和正方体的展开图，并通过展开图来理解长方体和正方体的结构。

六、板书设计我会利用板书，将长方体和正方体的展开图的特点进行直观的展示，帮助学生更好地理解和记忆。

七、作业设计1. 请学生画出自己的文具盒的展开图，并描述文具盒的结构。

答案：文具盒的展开图应该包括上盖、下底和侧壁。

通过展开图，我们可以看到文具盒的结构。

2. 请学生画出一个长方体的展开图，并描述长方体的结构。

答案：长方体的展开图应该包括上盖、下底和四个侧面。

通过展开图，我们可以看到长方体的结构。

八、课后反思及拓展延伸本节课的教学达到了预期的目标，大部分学生能够掌握长方体和正方体的展开图的特点，并能够自己画出长方体和正方体的展开图。

五年级上册第五单元《简易方程》(作业设计)-五年级上册数学人教版

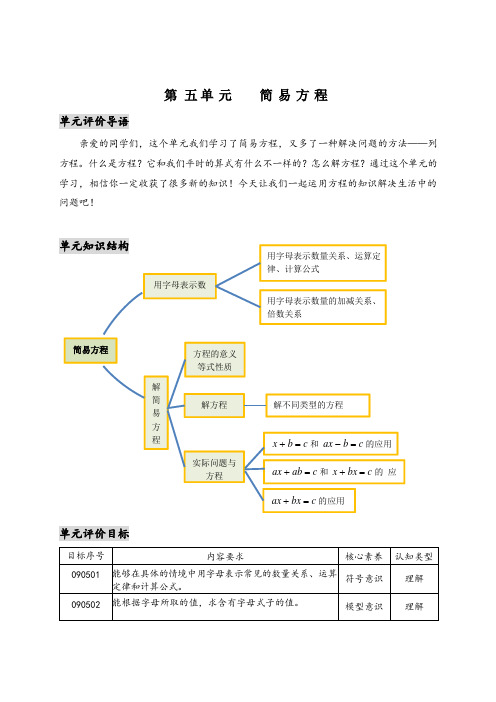
简易方程方程的意义等式性质第五单元简易方程单元评价导语亲爱的同学们，这个单元我们学习了简易方程，又多了一种解决问题的方法——列方程。

什么是方程？它和我们平时的算式有什么不一样的？怎么解方程？通过这个单元的学习，相信你一定收获了很多新的知识！今天让我们一起运用方程的知识解决生活中的问题吧！单元知识结构用字母表示数量关系、运算定律、计算公式用字母表示数量的加减关系、倍数关系解不同类型的方程x + b = c 和 ax - b = c 的应用ax + ab = c 和 x + bx = c 的应ax + bx = c 的应用单元评价目标实际问题与方程解方程解简易方程用字母表示数当自行车行驶 2000 米、3000米 ..... 时，车队汽车行驶的路程是多少呢？n 可以是哪些数呢？说说你是怎么想的？当 n=8000 时，车队汽车行驶（）米。

单元评价内容第一课时用字母表示数（一）✭ 基础素养 ✭【题 1】2023“环广西公路自行车世界巡回赛”在柳州完美落幕，在比赛中规定车队汽车跟随距离为 15 米（汽车与车手保持 15 米距离）。

根据题目回答下面问题。

（1）完善表格。

自行车行驶的路程 2000 3000 4000 5000…车队汽车行驶的路程（2）当自行车行驶 n 米时，车队汽车行驶的路程是（）米。

（3）在比赛中第一名选手骑行速度大约是车队汽车速度的 1.5 倍，你能表示出第一名选手的速度吗？请说一说你的想法。

目标序号 090501 090502 核心素养符号意识（水平二）认知维度理解预估难度易预估时长5 分钟设计方式创编设计意图在学生的生活经验和认知的基础上设计用字母来表示一个具体的数，初步学会根据字母所取的值进行求值，并体会字母在具体情境中所表示的含义。

当自行车行驶 1000 米时，车队汽车行驶（）米。

★能力素养★【题 2】柳州作为新晋网红城市，水上公交颇受网友喜爱，周末小思从东堤码头乘坐水上公交到东门，途中经过壶东大桥和文昌大桥。

小学六年级下学期数学《问题解决(找等量关系列方程解决问题》教学设计

问题解决（列方程解决问题）【教学目标】1、会根据问题的特点，总结找等量关系的方法，会列方程解决实际问题，会灵活运用不同的方法解决生活中的简单问题，提高分析、解决实际问题的能力。

2、经历与他人交流各自算法的过程，培养画图分析问题的意识，体验解决问题策略的多样化，强化数形结合的思想。

3、在解决实际问题的过程中进一步体会数学与现实生活的密切联系。

【教学重、难点】能灵活运用不同的方法解决生活中的简单问题，重点掌握用【教学准备】多媒体课件【教学过程】（主要环节）一、课堂引入1、回顾列方程解决问题的解题步骤和关键师：同学们，我们已经是六年级了，学了不少知识，孩子们，能尝试解释一下“列方程解决问题”吗?请自己说一说。

对，列方程解决问题是一种解题方法。

解题时要用字母表示未知数，根据等量关系列出方程，然后解方程求出问题的答案。

（1）设未知数（2）找等量关系（关键）（3）列方程（4）解方程（5）检验写答语以上就是列方程解决问题有5个步骤?哪一步最关键呢?接下来我们就一起来复习一下。

2、多媒体出示一.请列出每题的等量关系，不解答。

(1)将一个棱长6分米的立方体钢材熔铸成一个底面积是48平方分米的圆锥形模具，这个模具的高是多少分米？(2)一条裤子48元，是上衣的三分之二，一件上衣多少元？(3)一列快车和一列慢车同时分别从相距630千米的两地相对开出，4.5小时相遇，快车每小时行78千米，慢车每小时行多少千米？师边读题边讲解,多媒体出示等量关系与算式。

3、小结方法。

通过刚刚的复习，想一想：有哪些常用的方法可以找等量关系?（1）是的我们可以：根据常用公式找，例如面积、体积、周长等公式（2）还可以从关键句中找，可以是题目中关键句的文字描述等（3）也可以按常用数量关系找.例如：行程问题、工程问题基本数量关系，时间×速度=路程等.······师：同学们真是厉害！今天我们就以此为基础一起来复习列方程解决问题。

苏教版五年级数学下册第一单元《简易方程》教案设计

方程的意义。

(教材第1~2页)1.使学生在自主探究的学习过程中,理解并掌握方程的意义,弄清方程与等式间的联系与区别。

2.帮助学生初步建立分类思想,进一步感受数学与生活之间的密切联系。

3.培养学生认真观察的良好习惯。

重点:理解方程的意义。

难点:理解方程的意义。

天平、不同质量的砝码。

师:同学们,今天老师上课带来了一件重要的称量工具。

(出示天平)同学们认识吗?它是什么呢?对,它是天平。

同学们对天平有哪些了解呢?天平由天平秤与砝码组成,当放在两端托盘的物体的质量相等时,天平就会平衡,根据这个原理,可以称出物体的质量。

其实,在天平中蕴含着很多有关数学方面的知识,同学们想知道吗?让我们一起走进天平的世界来学习天平里的数学知识。

【设计意图:引导学生认识天平,导入新课,激发学生探究的兴趣,为新课教学做准备】1.学习方程的意义。

这节课我们共同研究方程的意义。

(板书:方程的意义)(1)介绍天平。

教师出示天平。

提问:同学们,你们认识这个物体吗?(认识,这是天平)天平是用来干什么的?(测量物体的质量)当天平两边不放物体的时候,指针指向中点,这时天平是平衡的。

如果我们在天平两边分别放上物体,在什么情况下天平才能平衡?(当天平两边的物体质量相等时,天平才能平衡)(2)观察。

在天平的左盘放两个50g的砝码,右盘放一个100g的砝码,观察这时的天平怎么样?(天平平衡)天平平衡说明天平两边所放物体的质量怎么样?(质量相等)你能用一个数学式子表示这时候的现象吗?(50+50=100或者50×2=100)为什么用等号连接?(因为等号两边的数相等)你能给这个式子起个名字吗?(等式)你能再举出一个等式的例子吗?把天平左盘中50g的砝码拿走一个,提问:这时天平出现了什么现象?(天平失去平衡)你能用一个数学式子来表示这时的现象吗?(50<100)这是一个等式吗?(不是)提问:如果我们在左盘上放一个重x克的砝码,猜猜看,会出现什么情况?学生猜测:天平可能平衡;也可能左边重,右边轻;还可能左边轻,右边重。

组织诊断工具方法及实操-6个盒子

组织诊断工具方法及实操：六个盒子一、六个盒子的价值阿里这么推崇六个盒子，主要是因为它能够为组织中的问题诊断提供全方位的视角。

一个组织如果出现问题，原因通常不止一个，而且相互关联，你必须从不同的视角切入，才能看清楚问题的本质所在，从而发现每个关联部分的内在关系。

它相当于一面镜子，帮助我们去看到组织所存在的问题。

六个盒子，还是非常好的沟通工具，不同的人对组织状态，大家开诚布公的讨论、分享，让每个人最后对组织的状况、状态了然于心。

分享完六个盒子最重要的两个价值后，接下来是我们的重点内容：六个盒子包括哪些内容？怎么应用呢？相信这都是大家非常感兴趣的问题。

二、六个盒子内容和应用六个盒子对应组织的六个维度，包括使命/目标、结构/组织、关系/流程、回报/激励、支持/帮助、领导/管理，而组织诊断也正是基于这六个维度出发的。

盒子一：使命与目标使命与目标是组织的根基，没有这两者，就没有组织。

在这个盒子里，我们要回答的核心问题是：我们为什么而存在？为谁提供什么样的产品或服务？关于使命，我们在之前的课分享过了，不再赘述。

目标，就是一个阶段要实现什么样的工作成果。

好目标可以帮助我们指引方向、激发每个人的斗志、热情。

不好的目标是什么样的呢？定了和没定差不多，甚至比没定还糟糕。

比如目标不清晰、与团队关联不高、超出能力太多，甚至大家根本看不懂目标，不理解目标，不认同目标。

所以，一个好的目标需要清晰、明确，上下达成共识，具有挑战性，并对人有激励。

使命与目标是组织诊断的基础，只有明确了这两个，我们的诊断才能保持正确的方向。

盒子二：结构/组织组织、结构是为了看组织的效能、运转是否高效？是否有助于战略、业务的成功？内容包括我们上文提到的战略和组织结构的关系是什么样的？目标是如何被分配的？组织之间的职责、流程、衔接是否清晰？是否有遗漏？是否有重复的工作？工作关系是什么样的？人才分配是否合理?人的能力够不够？数量是否合理？等等盒子三：关系与流程盒子三的关键在于公司各部门关系、流程是否顺畅，只有顺畅的关系、流程，才能让大家齐心协力、共同为了一个目标努力。

5.3-应用一元一次方程示范课-——-水箱变高了

§5.3 应用一元一次方程——水箱变高了学习目标：1、通过分析图形问题中的基本等量关系，建立方程解决问题。

2、进一步了解一元一次方程在解决实际问题中的应用。

3、认识方程模型的重要性学习重点：列出一元一次方程解有关形积变化的问题学习难点：依题意准确把握形积问题中的相等关系学法指导：阅读教材，完成自学检测和合作探究部分自学提示：阅读课本P141-142内容，完成书中提出的问题。

1．列方程解应用题应注意哪些事项？2．列方程解应用题的步骤是什么？自学检测：1.填空：长方形的周长= 面积= 长方体的体积=正方形的周长面积正方体的体积=圆的周长= 面积 = 圆柱的体积=合作探究：2、将一块橡皮泥由一个瘦长的圆柱捏成一个短胖的圆柱，其中的变量是，不变量是3、在较高的玻璃杯中倒入半杯水，再将水倒入较矮的玻璃杯中，不变的是。

4、将一根12cm长的细绳围成一个长为3cm的正方形，再改成一个长为4cm，宽为2cm的长方形，不变的是5、某居民楼顶有一个底面直径和高均为4米的圆柱形储水箱，为减少楼顶原储水箱的占地面积，将它的底面直径减少为3.2米，那么在容积不变的前提下，水箱的高度变为多少米？等量关系：旧水箱的容积=新水箱的容积解：设新水箱的高为x 米，填写下表旧水箱新水箱底面半径/米高/米容积/米3 根据等量关系，列出方程：解得：因此，高变为米。

展示解疑，点拨提升6、用一根长为10米的铁丝围成一个长方形，（1）使得该长方形的长比宽多1.4米，此时长方形的长和宽各为多少米？（2）使得该长方形的长比宽多0.8米，此时长方形的长和宽各为多少米？（3）使得该长方形的长与宽相等，及围成一个正方形，此时正方形的边长是多少米？分享成功7、课本142页随堂练习8、将一块棱长为30厘米的正方形钢坯锻造成长为25厘米，宽为20厘米长方体钢材，则锻造成的钢材的高是多少厘米？小结：本节课我们通过建立方程模型，学习了形积变化，解决了生活中的实际问题，使数学应用于生活，学完以后你有什么收获？列方程时，关键是找出问题中的等量关系3应用一元一次方程——水箱变高了【教学目标】知识与技能：1.通过计算进一步思考量与量的关系,从中获得有用的信息.2.学会通过分析图形问题中的基本等量关系,并由此关系列方程解相关的应用题.过程与方法：在老师的指导下,经历分析具体问题中的等量关系的过程,列方程进行求解.通过比较不同状态下方程的解的情况,从中探索出规律.情感、态度价值观:1.在观察中思考问题,并选择适当的数学工具解决问题,初步培养分析问题、解决问题的意识和能力.2.了解方程模型对于解决实际问题的有效性,并增强学生学习数学的信心和决心.【教学重难点】【重点】根据实际问题中等量关系列出一元一次方程,利用方程解决实际问题.【难点】在具体实例中准确地找出等量关系,设出适当的未知数,列方程进行求解.【教学准备】【教师准备】教材引例(课件1)和例题(课件2).【学生准备】预习教材.【教学过程】【1 新课导入】导入一:成语“朝三暮四”的故事.从前有个叫狙公的人养了一群猴子.每一天他都拿足够的栗子给猴子吃,猴子高兴他也快乐.有一天他发现如果再这样喂猴子的话,等不到下一个栗子的收获季节,他和猴子都会饿死,于是他想了一个办法,并且把这个办法说给猴子听,当猴子听到只能早上吃四个,晚上吃三个栗子的时候很是生气,龇牙咧嘴的.没办法狙公只好说早上三个,晚上四个,没想到猴子一听高兴得直打筋斗.请回答:猴子为什么高兴了?事实又是怎样的呢?【师生活动】学生先思考,后回答.教师给予积极的评价.[设计意图]通过故事引入,激发学生的兴趣,也为本节课后面“寻找不变的量”做铺垫.导入二:教师从讲台下拿出了两瓶矿泉水(容量一样,一个短且粗,另一个长且细).请大家说一说哪瓶矿泉水多,为什么?【师生活动】让学生亲自动手操作,在动手操作的过程中,体会哪些量发生了变化,哪些量没有变化?教师对基础差的同学可适当引导.导入三:用一块橡皮泥先捏出一个“瘦长”的圆柱体,然后再让这个“瘦长”的圆柱“变矮”,变成一个又矮又粗的圆柱,请思考下列几个问题:(1)在你操作的过程中,圆柱由“高”变“矮”,圆柱的底面直径是否变化?还有哪些量改变了?(2)在这个变化过程中,什么量没有变化呢?[设计意图]让学生在愉快地玩的过程中体会等体积变化的现象中蕴涵的不变量.同时分析出不变量与变量间的等量关系.【2 构建新知】探究活动1体积相等问题[过渡语]本节课我们将利用一元一次方程知识解决与体积变化有关的问题.(教师板书课题)【课件1】某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的前提下,水箱的高度将由原先的4 m变为多少米?思路一列方程解决实际问题的关键是找等量关系,请大家根据提示完成下面的知识.问题1在这个问题中水箱的不变.根据题意,可以找出如下的等量关系:.问题2设水箱的高变为x m,试填写下表:旧水箱新水箱底面半径4 3.2(m)高(m) 4 x体积(m3)问题3根据等量关系,列出方程:.解得x=.因此,水箱的高变成了m.【师生活动】让学生独立读题并思考,然后再根据分析完成填空内容,教师适时点拨引导,并给予肯定性评价.思路二小组活动,共同探究,思考:(1)分析题意,水箱在改造前后有何变化?哪些量变了?(2)分析题意,不变的量是什么?从题中哪句话可以看出?(3)在这个问题中有如下的等量关系:.(4)如何设未知数?根据题中等量关系怎样列方程?【师生活动】教师在巡视过程中及时解决疑难问题,学生讨论后小组展示讨论结果,教师及时补充.[设计意图]利用生活中熟知的情境,使学生感受到数学与生活的紧密联系,让学生经历从实际问题中抽象出方程的过程,激发学生的学习热情.同时利用表格法培养学生分析问题的方法,提高解决问题的能力.探究活动2周长相等问题【课件2】用一根长为10 m的铁丝围成一个长方形.(1)若该长方形的长比宽多1.4 m,此时长方形的长、宽各为多少米?(2)使得该长方形的长比宽多0.8 m,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围长方形相比,面积有什么变化?(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它围成的正方形的面积与(2)中相比又有什么变化?【师生活动】学生分组完成前面三个小题.小组讨论解题过程中,教师巡视课堂,指导、参与学生的讨论制作,帮助有学习困难的个人或小组.在讨论解答完成后,让小组选代表阐述解题的步骤、思路,并展示自己小组所做的长方形(或正方形).通过猜测、验证说明三个长方形面积变化的规律.同时用多媒体展示解题步骤,进一步规范学生的解题格式.解:(1)设此时长方形的宽为x m,则它的长为(x+1.4)m.根据题意,得x+x+1.4=10×.解这个方程,得x=1.8.1.8+1.4=3.2.此时长方形的长为3.2 m,宽为1.8 m.问题:本题还有其他方法吗?生:设长为x m,则宽为(x - 1.4)m.(2)此时长方形的宽为x m,则它的长为(x+0.8)m.根据题意,得x+x+0.8=10×.解这个方程,得x=2.1.2.1+0.8=2.9.此时长方形的长为2.9 m,宽为2.1 m,面积为2.9×2.1=6.09(m2),(1)中长方形的面积为3.2×1.8=5.76(m2).此时长方形的面积比(1)中长方形的面积增大6.09 - 5.76=0.33(m2).(3)设正方形的边长为x m.根据题意,得x+x=10×.解这个方程,得x=2.5.正方形的边长为2.5 m,正方形的面积为2.5×2.5=6.25(m2),比(2)中面积增大6.25 - 6.09=0.16(m2).【思考】解决这道题的关键是什么?从解这道题中你有何收获和体验?[设计意图]鼓励学生通过独立思考发现:围成的长方形的长和宽在发生变化,但在围的过程中,长方形的周长不变,由此建立“等量关系”.通过分组解决问题,提高学生解决问题的能力,发展同学合作意识,提高课堂效率,并培养学生做好解题反思的能力和习惯.【探究总结】通过探究活动,我们知道了如何去解决生活中的实际问题:(1)物体锻压或液体更换容器题,体积(或容积)不变.(2)固定长度,虽然围成的图形形状及面积不同,但是应抓住图形的周长不变.(3)图形的拼接、割补、平移、旋转等类型题,应抓住图形的面积或体积不变.即时演练把一块长、宽、高分别为5 cm,3 cm,3 cm的长方体铁块,浸入半径为4 cm的圆柱形玻璃杯中(盛有水),水面将增高多少?(不外溢)【师生活动】独立思考,解决问题,积极发言,阐述自己的解题思路,计算后说出答案.相等关系:水面增高体积=长方体体积.解:设水面增高x cm,由题意,得5×3×3=π×42·x.解得x=≈0.9.因此,水面增高约0.9 cm.[设计意图]通过分析、演示、观察、思考,让学生直观地感受图形的变化过程中各个量的变与不变,从而逐步地领悟到寻找等量关系是列方程解决应用型问题的关键.[知识拓展]1.通过对“水箱变高了”的了解,我们知道:物体锻压或液体更换容器题,体积(或容积)不变.固定长度,虽然围成的图形形状及面积不同,但是应抓住图形的周长不变.图形的拼接、割补、平移、旋转等类型题,应抓住图形的面积或体积不变,这是解决此类问题的关键,即变的是什么,不变的是什么.2.遇到较为复杂的实际问题时,我们可以借助表格分析问题中的等量关系,借此列出方程.3.解出的数学问题要联系生活实际问题来检验它的结果的合理性.【3 课堂小结】本节课通过分析一些几何图形,如圆柱、长方形的变化,寻找不变的量作为列方程中的等量关系做依据,从而用方程解决实际问题.列方程解决实际问题的关键是找等量关系,认识方程是解决实际问题的有效数学模型.【4 检测反馈】1.有一块长、宽、高分别为4 cm,3 cm,5 cm的长方体橡皮泥,要用它来捏一个底面半径为1.5 cm的圆柱,若设它的高为x cm,则可列方程为.解析:由题意列方程为3×4×5=π×1.52·x.故填3×4×5=π×1.52x.2.直径为30 cm,高为50 cm的圆柱形瓶里存满了饮料,现将饮料倒入底面直径为10 cm的圆柱形水杯,刚好倒满30杯.则水杯的高度是多少?解:设水杯的高度是x cm,根据题意,列方程得152×50π=52×30πx,解方程,得x=15.所以水杯的高度是15 cm.3.一块长、宽、高分别为4 cm、3 cm、2 cm的长方体橡皮泥,要用它来捏一个底面半径为1.5 cm的圆柱,圆柱的高是多少?解:设圆柱的高是x cm,根据题意,得4×3×2=π×1.52x,解得x=.答:圆柱的高是cm.4.将一个底面直径是10 cm、高为36 cm的“瘦长”形圆柱锻压成底面直径为20 cm的“矮胖”形圆柱,高变成了多少?解:设锻压后圆柱的高为x cm,根据题意,列方程为π×(10÷2)2×36=π×(20÷2)2×x,解得x=9.答:高变成了9 cm.【5 板书设计】3应用一元一次方程——水箱变高了1.体积相等问题引例2.周长相等问题例题【6 作业布置】一、教材作业【必做题】教材第144页习题5.6的1,2题.【选做题】教材第144页习题5.6的3题.二、课后作业【基础巩固】1.一个底面半径为10 cm,高为30 cm的圆柱形大杯中存满了水,把水倒入一个底面直径为10 cm的圆柱形小杯中,刚好倒满12杯,则小杯的高为()A.6 cmB.8 cmC.10 cmD.12 cm2.一个长方形的周长是40 cm,若将长减少8 cm,宽增加2 cm,长方形就变成了正方形,则正方形的边长为()A.6 cmB.7 cmC.8 cmD.9 cm3.用7.8米长的铁丝做成一个长方形框架,使长比宽多1.2米,求这个长方形框架的宽是多少米.设长方形的宽是x米,可列方程为()A.x+(x+1.2)=7.8B.x+(x - 1.2)=7.8C.2[x+(x+1.2)]=7.8D.2[x+(x - 1.2)]=7.84.锻造直径为70 mm,高为25 mm的圆柱形零件毛坯,应取直径为50 mm的圆钢多长?设应取直径为50 mm的圆钢长x mm,则根据题意可列出方程:.解得x=.因此应取直径为50 mm的圆钢长mm.【能力提升】5.在底面直径为12 cm,高为20 cm的圆柱形容器中注满水,倒入底面是边长为10 cm 的正方形的长方体容器,正好注满.这个长方体容器的高是多少?【拓展探究】6.地面上钉着用一根彩绳围成的直角三角形,如果将直角三角形锐角顶点的一个钉子去掉,并将这条彩绳钉成一个长方形,则所钉长方形的长、宽各是多少?面积是多少?【答案与解析】1.C(解析:设小杯的高为x cm,大杯中水的体积为π×102×30 cm3,小杯的底面积为π×52 cm2,根据题意,列方程得π×102×30=π×52×12x,解得x=10,故选C.)2.B(解析:设正方形的边长为x cm,根据题意,列方程为2×(x+8+x - 2)=40,解得x=7,故选B.)3.C(解析:长方形框架的宽为x米,则长是(x+1.2)米,根据题意,列方程得2[x+(x+1.2)]=7.8,故选C.)4.(70÷2)2×π×25=(50÷2)2×π×x4949(解析:根据题意,列方程得(70÷2)2×π×25=(50÷2)2×π×x,解得x=49.)5.解:设长方体容器的高为x cm,根据题意,得π×(12÷2)2×20=102x.解得x≈22.6.答:这个长方体容器的高约是22.6 cm.6.解:设长方形的另一边长为x.当去掉∠A顶点的钉子时,6+8+10=6×2+2x,解得x=6,所以当长方形的长为6,宽为6时,面积为S1=6×6=36.当去掉∠B顶点的钉子时,6+8+10=8×2+2x,解得x=4,所以当长方形的长为8,宽为4时,面积为S2=8×4=32.答:所钉长方形的长为6,宽为6,面积为36,或长方形的长为8,宽为4,面积为32.【教学反思】【成功之处】通过引导学生进行探索,使学生确实是在旧知识的基础上探求新内容,探索的过程是任何学生都会动手操作,每个学生都有体会的过程,都有感悟的可能,这种形式让学生切身去体验问题的情景,从而进一步帮助学生理解比较复杂的问题,再把实际问题抽象成数学问题.【不足之处】学生在完成课本上的表格时,部分同学把半径与直径混淆,方程中直接用3.14代替π,圆柱体的体积公式遗忘等,教学时只是随时加以纠正.如果做题之前就把这些问题加以复习或强调,那么效果会好得多.【再教设计】让学生更好地体会建模思想在数学中的应用,对于学生的发言,给予充分的肯定,激发学生学习数学的激情,真正让学生在课堂上动起来.。

二次根式教学设计6篇

二次根式教学设计6篇（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如讲话致辞、报告体会、合同协议、策划方案、职业规划、规章制度、应急预案、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as speeches, report experiences, contract agreements, planning plans, career planning, rules and regulations, emergency plans, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!二次根式教学设计6篇下面是本店铺收集的二次根式教学设计6篇，供大家参阅。

沪教版(五四制)六年级下册数学第八章长方体的再认识同步讲义

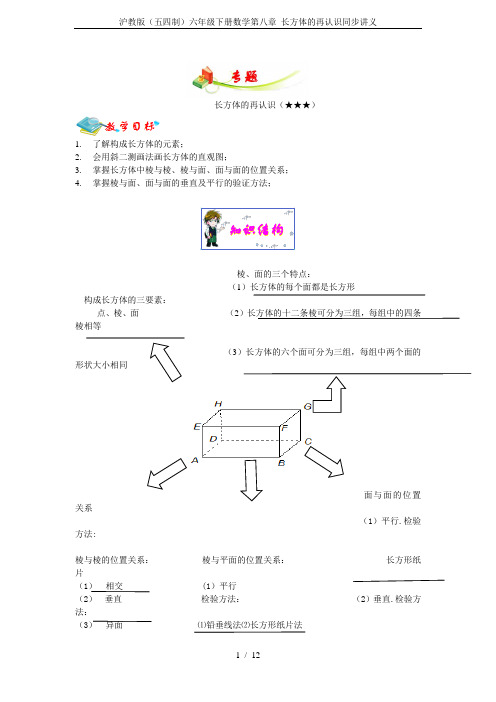
-------------长方体的再认识（★★★）1.了解构成长方体的元素；2.会用斜二测画法画长方体的直观图；3.掌握长方体中棱与棱、棱与面、面与面的位置关系；4.掌握棱与面、面与面的垂直及平行的验证方法；知识结构棱、面的三个特点：（1）长方体的每个面都是长方形构成长方体的三要素：点、棱、面（2）长方体的十二条棱可分为三组，每组中的四条棱相等（3）长方体的六个面可分为三组，每组中两个面的形状大小相同面与面的位置关系（1）平行.检验方法:棱与棱的位置关系：棱与平面的位置关系：长方形纸片（1）相交 (1）平行（2）垂直检验方法：（2）垂直.检验方法：（3）异面⑴铅垂线法⑵长方形纸片法（1）铅垂线（2）三角板法（3）合页型折纸（2）垂直检验方法：⑴铅垂线法⑵三角板法⑶合页型折纸1.本部分建议时长5分钟.2.请学生先试着自行补全上图，发现学生有遗忘时教师帮助学生完成.1.本部分建议时长20分钟.2.进行例题讲解时，教师宜先请学生试着自行解答.若学生能正确解答，则不必做过多的讲解；若学生不能正确解答，教师应对相关概念、公式进行进一步辨析后再讲解例题.3.在每一道例题之后设置了变式训练题，应在例题讲解后鼓励学生独立完成，以判断学生是否真正掌握了相关考点和题型.4.教师应正确处理好例题与变式训练题之间的关系，宜采用讲练结合的方式，切不可将所有例题都讲完后再让学生做变式训练题.例题1一个长方体中，有公共点的三条棱的长度的比为2：3：4，最小的一个面的面积为2162cm ，（1）求这个长方体的所有棱长的总和；“典例精讲”这一部分的教学，可采用下面的策略：“知识结构”这一部分的教学，可采用下面的策略：（2）求这个长方体的表面积；（3）求这个长方体的体积。

（★★）答案：（1）216cm ；（2）18722cm ；（3）51843cm两条较短的棱为长和宽的长方形的面积，是最小的面积，又知三棱长之比，故可求得三棱长，进而可得其他所求。