特征标121
3-2 特征标表

对于绕主轴 对于绕主轴 Cn 转动 2π/n 对称(特征标等于 +1 )的一维表示用 π 对称( A ,反对称(特征标等于 -1 )的用 B。 反对称( 。
附加到 A 或 B 上的下标 1 和 2 ,用来分别标记它们对于副轴 C2 上的下标 用来分别标记它们对于副轴 是对称的还是反对称的。 轴时, 是对称的还是反对称的。如果没有这种 C2 轴时,标记对于 σv 是对 称的或是反对称的。 称的或是反对称的。
3.5 特征标表
群论和分子对称性的全部应用, 群论和分子对称性的全部应用,都要不断用到点群的不可约表 示的特征标。所以将它们组合在一起,称为特征标表。 示的特征标。所以将它们组合在一起,称为特征标表。如:
C3v 点群的特征标表
C3v A1 A2 E
ˆ ˆ E 2C 3 1 1 1 2 1 −1
ˆ 3σ v 1 −1 0
一维表示(或称非简并表示) 一维表示(或称非简并表示)标记为 A(a) 或 B(b)。如果 ( ) ( ) 与原子轨道联系的话(即以原子轨道作为表示的基),一维表示就 与原子轨道联系的话(即以原子轨道作为表示的基),一维表示就 ), 意味着只有一个轨道,且不可约表示与该轨道的对称性相同。 意味着只有一个轨道,且不可约表示与该轨道的对称性相同。 二维表示(或称二重简并表示) 二维表示(或称二重简并表示)标记为 E(e)。如果与原子轨 ( ) 道联系的话(即以原子轨道作为基),二维表示就意味着只有二个 道联系的话(即以原子轨道作为基),二维表示就意味着只有二个 ), 能量相同的轨道,且不可约表示与轨道的对称性相同。 能量相同的轨道,且不可约表示与轨道的对称性相同。 三维表示(或称三重简并表示) 三维表示(或称三重简并表示)标记为 T(t)。如果与原子轨 () 道联系的话(即以原子轨道作为基),三维表示就意味着只有三个 道联系的话(即以原子轨道作为基),三维表示就意味着只有三个 ), 能量相同的轨道,且不可约表示与轨道的对称性相同。 能量相同的轨道,且不可约表示与轨道的对称性相同。
gb12311—90

GB 12311—90本标准参照采用国际标准ISO 4120—1983《感官分析方法学──三点检验》。
1 主题内容和适用范围本标准规定了用三点比较的方法来鉴别二个样品之间的差别。
本标准适用于鉴别样品间的细微差别,也可以用于选择和培训评价员或者检查评价员的能力。
2 引用标准GB 10220 感官分析方法总论GB 10221.1~10221.4 感官分析术语GB 3358 统计学名词术语及符号3 方法提要同时向评价员提供一组三个样品,其中二个是完全相同的,评价员挑出单个的样品。
4 设备检验负责人根据产品性质和样品数量等选择设备。
使用的设备不应影响检验结果。
应优先使用符合检验需要的标准化设备。
5 抽样应按被检产品的抽样标准进行抽样。
如果没有这样的标准或抽样标准不完全适用时,则由有关各方协商议定抽样方法。
6 检验的一般条件6.1 环境应满足GB 10220所需条件。
6.2 评价员6.2.1 条件应符合GB 10220规定的条件,所有评价员应该具有同等的资格和检验能力。
6.2.2 评价员数评价员数是根据检验目的与显著水平而定。
通常是6个以上专家;或15个以上优选评价员;或25个以上初级评价员。
在0.1%显著水平上需7个以上专家。
6.2.3 检验负责人检验负责人一般不应参加检验,如果参加,也不应知道样品编号。
6.3 准备检验负责人可就有关问题和样品性质进行不影响评价的初步介绍,当涉及检验玷染物时,应准备一个非玷染物样品和一个与之对照的玷染物样品。
7 检验步骤7.1 被检样品的制备7.1.1 提供足够量的样品A和B,每三个检验样品为一组。
7.1.2 按下述六种组合:ABB AAB ABA BAA BBA BAB,从实验室样品中制备数目相等的样品组。
7.1.3 不能使评价员从样品提供的方式中对样品的性质作出结论。
应以同一方式〔相同设备、相同容器、相同数量产品和相同排列形式(三角形,直线等)〕制备各种检验样品组。
有限可解群的Brauer特征标表的一个注记

2 0 1 3年 9月
有 限可 解 群 的 B r a u e r 特 征 标 表 的 一 个 注 记
王 坚 , 曾 吉 文 , 范 娟 娟
( 1 . 厦 门 大学 数 学 科 学 学 院 , 福建 厦门 3 6 1 0 0 5 ; 2 . 福 建 江 夏 学 院经 济 贸易 学 院 , 福建 福 州 3 5 0 1 0 8 )
取一个 本 原 q次单 位根 . 根 据文献 [ 4 ] 中的定 理 1 , 集
关键词 : 可解群 ; B r a u e r 特征标 ; P正则元 .
中 图分 类 号 : O 1 5 2 . 6
文 献标 志码 : A
文章编 号 : 0 4 3 8 — 0 4 7 9 ( 2 0 1 3 ) 0 5 — 0 5 9 0 — 0 2
G O 一{ gE Gl p f 0 ( g ) } . I B r ( G ) 是 G 的不可 约 P — B r a u e r
正规 的西 罗 q 一 子 群 Q, 那 么 Z( Q) 所 有 的元 素 都 是 G
群( q ≠ ) , 那 么 Z( Q) NO q ( G ) 中所有 q阶元都 是 G 的
非零化 正 则元. 证明 假 设 ∈I B r ( G) . 那 么 有
的非 零化元 . 在文献[ 4 ] 中, Ma s a h i k o Mi y a mo t o推 广
受文献 I - 4 ] 的启 发 , 本 文 讨 论 G 的非 零 化 P 一 正则 元. 下 面我 们 引进 一些 记 号 , G 总是 指 代一 个 有 限群 , P是 一 个 固 定 素 数 . G 。是 正 则 元 的 集 合 , 也 就 是
是 — EI r r ( Z( ( G) ) ) 在 G 的 共 轭 作 用 下 的 共 轭
一d轨道在配位场中的能级分裂电子光谱的基础和来源

HS
HS
二. O大小的表征―电子光谱(或电子光谱,紫 外可见光谱)
1.单电子的近似的配合物光谱
定性判断:
ligand 显色
吸收颜色
O
excitation
Cu(NH3)42+ Cu(OH2)42+
强场 弱场
紫色 蓝色
黄色
大
橙色
小
Cr(NH3)63+ 强场
橙色
蓝色
大
Cr(OH2)63+ 弱场
紫色
黄色
小
HS
d5
Mn2+ 25,500 H2O 7,800
HS
HS
Fe3+ 30,000 H2O 13,700 HS
HS
d6
Fe2+ 17,600 H2O 10,400 HS
HS
CN 33,000 LS
LS
Co3+ 21,000 F 13,000 HS
HS
NH3 23,000 LS
LS
d7
Co2+ 22,500 H2O 9,300
ML= 0 MS =0 (2S+1)(2L+1)=1
能量相同的微状态归为一组,得到自由离子的5个光谱项:
L=4, ML= 4, 3, 2, 1 0, S=0 MS= 0
1G
L=3, ML= 3, 2, 1 0,
S=1 MS= 1, 0 3F
L=2, ML= 2, 1 0,
S=0 MS= 0
1D
L=1, ML= 1, 0,
d1
3
P
3T1g
三重简并
2 Eg
2D 2T2g
d1
特征标表

对任意 a, b ∈V ,有
并且
∑ a = α ju j j
∑ b = βkuk k
∑ ∑ ⎛
a⋅b = ⎜ ⎝
j
α
j
u
j
⎞ ⎟ ⎠
⋅
⎛ ⎜⎝
k
β k uk
⎞ ⎟⎠
∑ = α j βku j ⋅ uk jk
∑ ∑ =
jk
α jβk
⎛ ⎜⎝
A
ν
A jk
uA
⎞ ⎟⎠
∑ ∑ =
⎛ ⎜
α
j βkν
A jk
⎞ ⎟uA
6
4)第一正交关系(行正交关系)
∑ 1
|G|
ν
nν Χ(α ) (Kν )Χ(β ) (Kν ) = δαβ
(α , β = 1, 2,", q)
α =1 时 Χ(1) (Kν ) = 1 (Kν ∈ KG )
故
(第一行)
∑ nν Χ(β ) (Kν ) = 0
ν
5)第二正交关系(列正交关系)
(β = 2,3,", q)
14
由 12 + s22 + s32 + s42 + s52 = 8
解得 s2 = s3 = s4 = 1
s5 = 2
故 C4v 的类特征标表示及第一行第一列就求出来了
剩下 16 个未知数,由第一,第二正交关系可以建立 16 个方程,只有 8 个 是线性的,
1)τ (2) ,τ (3) ,τ (4) 都是一维的, 特征标就是矩阵元
11
1)τ (2) 是 1 维的, χ (2) (g) 就是矩阵元, 故
所以
(χ (2) (c2′))2 = χ (2) (c2′ ⋅ c2′) = χ (2) (e) ,
二氟一氯一溴甲烷灭火剂

中华人民共和国国家标准UDC 661.715.21:614.84GB 4065-83二氟一氯一溴甲烷灭火剂Fire extinguishing agent-Bromochlorodifluoromethane本标准适用于二氟一氯一溴甲烷(简称1211)灭火剂,用于扑灭B类(系指液体或可融化的固体)、C类(系指气体)火灾。
1211在常温下为略带芋香味、化学性质稳定的气体。
其液体应为无色透明。
分子式:CF2C1Br分子量:165.381技术要求1211灭火剂须符合下列要求:指标名称指标1211含量(重量计),%≥99.0水分,mg/kg ≤20酸性物(以HBr计),mg/kg ≤ 3卤离子合格蒸发残留物,mg/kg ≤80色度不深于15号2检验方法2.1 1211含量测定――气相色谱分析法2.1.1 仪器102G型气相色谱仪或灵敏度与102G型相当的其他气相色谱仪。
2.1.1.1 载气:氢气。
入口压:2.5kg/cm2;流量:40~45ml/min(用皂膜流量计实测)。
2.1.1.2 色谱柱:不锈钢管,长4m,内径3mm,外径5mm,盘形绕制,曲率半径为8cm。
2.1.1.3 柱填充物a. 载体:6201红色载体,60~80目。
b. 固定液:邻苯二甲酸二壬酯(DNP),聚乙二醇400(PEG400)。
c. 涂渍度及涂渍方法:将DNP:PEG400:6201红色载体按20:5:100(重量比)的比例称好后,用丙酮(分析纯)为溶剂溶解固定液,倒入载体,搅拌均匀,置于红外灯下蒸除溶剂至干,装柱。
装填好的色谱柱在氢气流量为40~45ml/min,柱温为70℃老化2~4h。
2.1.1.4检测器:热导池检测器。
桥电流为220~240mΑ(根据杂质含量高低可适当增减);衰减比:杂质用1/1;1211用1/128。
国家标准局1983-12-22发布1984-11-01实施940)/(54.5221≥=Y tR n2.1.1.5 记录仪:满标量程为5m ⅴ;满标长为250mm ;纸速为10mm/min 。
MS121-04(中文)
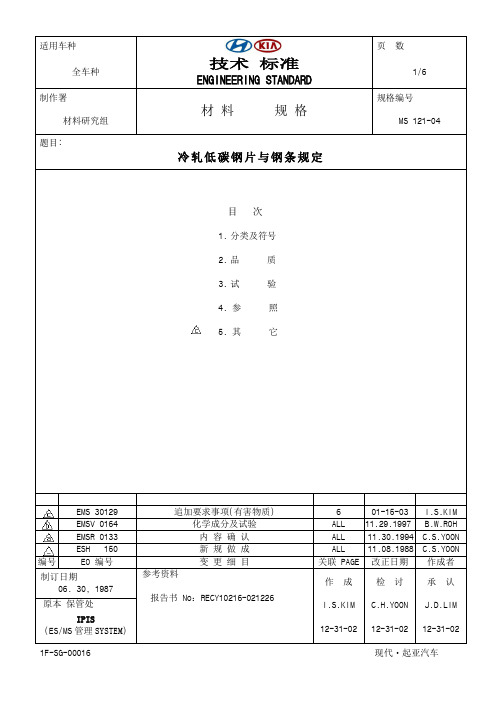
适用车种技术标准ENGINEERING STANDARD 页数全车种1/6制作署材料规格规格编号材料研究组MS 121-04题目:冷轧低碳钢片与钢条规定目次1.分类及符号2.品质3.试验4. 参照5. 其它EMS 30129 追加要求事项(有害物质) 6 01-15-03 I.S.KIM EMSV 0164 化学成分及试验ALL 11.29.1997 B.W.ROH EMSR 0133 内容确认ALL 11.30.1994 C.S.YOON ESH 150 新规做成ALL 11.08.1988 C.S.YOON 编号EO 编号变更细目关联 PAGE 改正日期作成者制订日期06. 30, 1987参考资料报告书No:RECY10216-021226作成I.S.KIM12-31-02检讨C.H.YOON12-31-02承认J.D.LIM12-31-02原本保管处IPIS(ES/MS管理SYSTEM)1. 分类及符号1.1 冷轧低碳钢片及钢条分类及符号冷轧低碳钢片及钢条 (以下钢片及钢条)应依据表 1.分为五类.表 1. 符号分类符号备 注Class 1SPCC商业等级钢(拉伸试验值不完全适用于该等级)SPCCT冲压品质(对满足拉伸试验及/或Erichsen 试验的情况, 应在标号后标记T) Class 2SPCD 冲压品质 Class 3SPCE深度冲压品质SPCEN深度冲压品质(对保证非失效性的情况下, 应在标号后标记N)1.2 淬火程度区分及符号淬火程度区分应遵照表2. 分为6类,其符号见下表表 2. 淬火程度区分淬火程度区分符 号 备 注退火 NS 结构疲劳很容易出现标准淬火 S SKIN PASS (如无特别规定应遵照本规定施行.)1/8 硬度 1/4 硬度 1/2 硬度 全硬度 8 4 2 1添加化学成份或增加表面光轧机减速比提高硬度1.3 表面抛光度区分及符号表面抛光等级应分为两级并且标记符号参照表 3.表 3. 表面抛光度区分表面抛光度区分符号备注亚光处理 D 使用经机械或化学处理的滚轴进行表面亚光处理.(如无特别规定应遵照本规定施行.)光洁处理 B 使用经光洁处理的滚轴进行表面光洁处理.备注) 本规定不适用于退火处理的钢片及钢条.2. 种类及编号2.1 化学成分钢片及钢板的化学成分(LADLE 分析)不应超过表4所示数值.表 4. 化学成分(wt%)分类标号 C Mn P SClass 1 SPCC最大0.12. 最大0.50. 最大0.040.最大0.023. SPCCTClass 2 SPCD 最大0.10. 最大0.45. 最大0.035.Class 3 SPCE最大0.08. 最大0.40. 最大0.030. SPCEN3. 试验3.1 化学分析试验成分分析的一般事项及试样的制造方法参见JIS G 0303(钢材检查通则)第3项.4. 参考4.1 类别编号, 淬火程度及表面抛光&部件的机械特性应遵照表5.表 5. 机械特性应用事项分类淬火程度表面抛光标记拉伸试验 &Erichsen 值非失效性弯曲性硬度Class 1退火处理- SPCC-NS - - ○- 退火处理(设计确保机械性能)- SPCCT-NS ○- ○- 标准淬火等级亚光SPCC-SD- - ○-光洁SPCC-SB标准淬火等级(设计确保机械性能)亚光SPCCT-SD○- ○-光洁SPCCT-SB1/8 硬度亚光SPCC-8D- - ●○光洁SPCC-8B1/4硬度亚光SPCC-4D- - ●○光洁SPCC-4B1/2硬度亚光SPCC-2D- - ●○光洁SPCC-2B全硬度亚光SPCC-1D- - ○光洁SPCC-1BClass 2退火处理- SPCD-NS ○- ○- 标准淬火等级亚光SPCD-SD○- ○-光洁SPCD-SBClass 3退火处理- SPCE-NS ○- ○- 标准淬火等级亚光SPCE-SD○- ○-光洁SPCE-SB标准淬火等级(设计确保机械性能)亚光SPCEN-SD○○○-光洁SPCEN-SB标注) 1) 拉伸及Erichsen试验测定值①拉伸及Erichsen试验值应在表5中标记‘○’, 并且在没有特别要求的情况下只有拉伸试验值适用. 对以下情况, HMC应特别注明:‘E’ : 当使用Erichsen试验值替代拉伸试验值时‘B’ : 当同时使用拉伸试验值和Erichsen试验值时.②厚度从0.25 mm 变化到0.6 mm的钢片与钢条的拉伸试验通常被忽略,如进行试验应在HMC担当者指导下进行.2) 非失效性非失效性应在表5中使用项目标号‘○’.3) 弯曲试验①即使弯曲试验应在表5中使用项目标号‘○’, 试验也有可能被忽略.②HMC提出要求的情况,完成的弯曲试验在表5中使用项目标号‘●’.4) 硬度硬度应在表5中使用项目标号‘○’.5) 其它①此外对于表 5, 1/8, 1/4, 1/2 及全硬度也可能单独应用于第2类及第3 类.在此情况下机械性能适用项目应同分类1相同.②应用其他表5中未规定的试验项目, 如锥形杯深冲试验,应与HMC 当事人进行协议.4.2 退火及标准淬火等级的钢片及钢条退火及标准淬火等级钢片及钢条的硬度, 和1/8, 1/4, 1/2 及全硬度应在表 6 与 7 中分别标出.表6.退火处理及标准淬火等级钢片及钢条的硬度淬火程度区分标记硬度H R B Hv退火处理NS 最大57. 最大105.标准淬火S 最大65. 最大115.表7. 1/8, 1/4, 1/2及全硬度拉伸试验值淬火程度区分标记拉伸试验抗张强度kgf/㎟(N/㎟)延长率 (%) 试样1/8 硬度830 to 42(290 to 410)25 min.No. 5 alongrolling1/4 硬度 4 38 to 50 (370 to 490) 10 min.direction1/2 硬度 2 45 to 60 (440 to 590) - 全硬度156 min. (550 min.)-5. 图面标识方法5.1 重金属禁用事项: 在部件及材料中不应含有铅, 镉, 汞及六价铬.但是, 依照MS 201-02以上元素可以部分的存在于材料及部件中.5.2 其余事项遵照 JIS G 3141. 对本规定的全部内容如有疑问请向现代·起亚研究开发本部非金属材料研究组询问.c c。
特征标

第一部分群论基础第三章群表示特征标理论(1)(一) 群表示的特征标及其性质 2 一, 特征标的定义群表示的特征标是群表示矩阵的迹 ( 对角矩阵元之和 )χ ( R ) = tr D ( R ) = ∑αDαα ( R ) ------------- (1)二, 特征标的性质(1) 同类群元的特征标相同证明: R 和 S 同类, 则有 T 使 S = T-1 R T因此, χ ( S ) = tr D ( S ) = tr D ( T-1 R T )= tr [ D ( T-1 ) D ( R ) D ( T ) ]= tr [ D -1( T ) D ( R ) D ( T ) ]= tr D ( R ) = χ ( R )即特征标是类的函数 *(2) [ 提问: 等价表示的特征标是否相同? 为什么? ] 3 [ 答案: 相同, 矩阵作相似变换其迹不变 ](3) [ 提问: 可约表示与所含不可约表示的特征标有什么关系? ] [答案: 可约表示的特征标是所含不可约表示特征标之和]三, 对特征标的评价1, 以3 × 3 的表示矩阵为例, 一个特征标比九个矩阵元简单得多, 可使问题大大简化;2, 特征标保留了群的重要信息. 不少情况下, 利用特征标就能解决问题;3, 与表示矩阵相比, 特征标丢掉了一些信息.[ 提问: 丢掉了什么信息? ][ 答案: 丢掉了类里的信息, 即类中群元间关系的信息. ][ 提问: 为什么 ? ][ 答案: 同类元的特征标相同, 特征标是类的函数. ]*(二)可约表示的约化 ( 简捷有效的约化途径 ) 4 1, 群的不可约表示的(矩阵)形式一般说来不是唯一的。
通过相似变换, 可以得到许多不同的彼此等价的不可约表示,但它们的特征标相同,是确定的。
2, 群的任何一个可约表示都可以通过相似变换将其(准)对角化,这就是可约表示约化的过程。
如果该表示不能再进一步对角化, 则该表示就可写成其对角线上的不可约表示的直和。
31241标准

31241标准31241标准是指一种技术评估和测试标准,广泛用于各个行业。
本文将详细介绍31241标准的背景、内容、应用及其优势。
一、背景31241标准起源于20世纪90年代,随着信息技术的快速发展,市场上出现了大量的产品和服务,但由于缺乏统一的评估和测试标准,导致产品质量无法保证,用户无法满意。
为了解决这一问题,31241标准应运而生。
二、内容31241标准主要包括以下几个方面的内容:1. 产品评估: 31241标准提供了一套全面的评估指标和方法,用于评估产品的性能、可靠性、安全性和易用性等。
通过这些评估,可以对产品的质量进行客观的判断。
2. 测试方法: 31241标准规定了一系列的测试方法和流程,用于验证产品是否符合规范要求。
这些测试方法旨在发现产品的潜在问题并进行修复,以确保产品的可靠性和性能。
3. 数据分析: 31241标准提供了一套数据分析的方法和工具,用于对评估和测试结果进行统计和分析。
通过这些数据分析,可以得出产品的质量水平和改进措施。
4. 文档要求: 31241标准规定了产品评估和测试的相关文档要求,包括实施计划、测试报告、评估结果等。
这些文档是评估和测试过程的重要记录,对于产品的质量控制和追溯具有重要意义。
三、应用31241标准适用于各个行业和领域,特别是那些需要保证产品质量和性能的领域。
以下是几个典型的应用场景:1. 信息技术行业: 在软件开发和测试过程中,31241标准可以用于评估和测试软件的功能和性能。
它可以帮助开发团队发现和解决软件中的潜在问题,提高软件的质量和可靠性。
2. 电子产品行业: 在电子产品的设计和生产过程中,31241标准可以用于评估和测试产品的可靠性和安全性。
它可以帮助制造商提前发现产品的缺陷,降低产品质量问题的风险。
3. 汽车行业: 在汽车的研发和生产过程中,31241标准可以用于评估和测试汽车的性能和安全性。
它可以帮助汽车制造商提高车辆的质量和可靠性,减少事故和故障的发生。
c3v点群的特征标表

c3v点群的特征标表
C3v点群是一种具有三个C3旋转轴和三个垂直于旋转轴的镜面
的点群。
特征标表是用于描述该点群下不同表示的矩阵的工具,它
可以帮助我们理解分子的对称性和分子轨道的对称性。
C3v点群的
特征标表如下所示:
首先,C3v点群有3个一维不可约表示和1个二维不可约表示。
这些表示可以用特征标表示,特征标是对称操作对应的矩阵的特征值。
对于C3v点群的一维表示,它们的特征标可以表示为:
A1: (1, 1, 1)。
A2: (1, 1, -1)。
E: (2, -1, 0)。
这里,括号里的数字表示C3、C3^2和σv的特征标,按顺序对
应这些操作的特征值。
对于C3v点群的二维表示,它的特征标可以表示为:
E: (0, 0, 2)。
这里的数字表示C3、C3^2和σv的特征标。
特征标表的编制是根据点群的对称操作和它们在不同表示下的作用方式来完成的。
特征标表的应用可以帮助化学家理解分子的振动、光谱和化学键的性质,对于分子对称性的分析和预测具有重要意义。
以上就是关于C3v点群的特征标表的基本介绍,希望能够对你有所帮助。
如果你对此还有其他问题,欢迎继续提问。
特征数字的含义
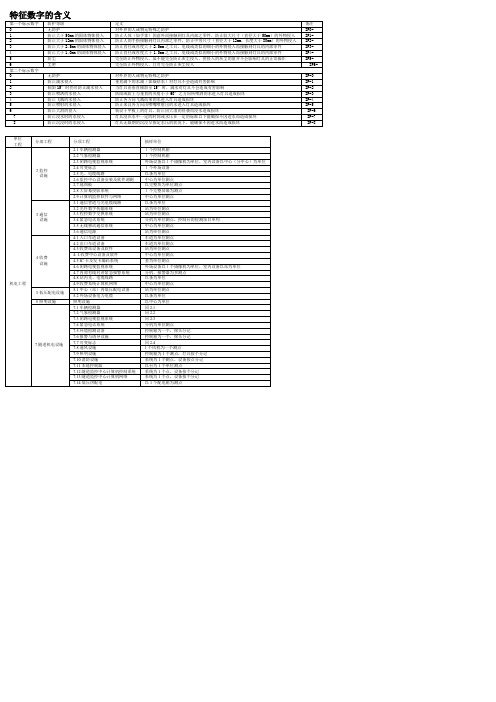
3
防止大于2.5mm的固体物体侵入
防止直径或厚度大于2.5mm之工具、电线或类似的细小的外物侵入而接触到灯具的内部零件
IP3-
4
防止大于1.0mm的固体物体侵入
防止直径或厚度大于1.0mm之工具、电线或类似的细小的外物侵入而接触到灯具的内部零件
IP4-
5
防尘
完全防止外物侵入。虽不能完全防止灰尘侵入,但侵入的灰尘的量并不会影响灯具的正常操作
IP5-
6
尘密
完全防止外物侵入,且可完全防止灰尘侵入
IP6-
第二个标示数字
0
无防护
对外界的人或物无特殊之防护
IP-0
1
防止滴水侵入
垂直滴下的水滴(如凝结水)对灯具不会造成有害影响
IP-1
2
倾斜15°时仍可防止滴水侵入
当灯具由垂直倾斜至15°时,滴水对灯具不会造成有害影响
IP-2
3
防止喷洒的水侵入
防雨或防上与垂直的夹角小于60°之方向所喷洒的水进入灯具造成损坏
分机为单位测点,控制台的检测项目单列
3.5无线移动通信系统
中心为单位测点
3.6通信电源
站为单位测点
4收费
设施
4.1入口车道设备
车道为单位测点
4.2出口车道设备
车道为单位测点
4.3收费站设备及软件
站为单位测点
4.4收费中心设备及软件
中心为单位测点
4.5 IC卡及发卡编码系统
套为单位测点
4.6闭路电视监视系统
外场设备以1个摄像机为单位,室内设备以站为单位
4.7内部有线对讲紧急报警系统
分机、报警器为多测点
4.8站内光、电缆线路
特殊特性清单

产品/过程
图号
产品/过程
名称
序号
特殊特性符号
设计要求
特殊特性
符号说明
⊕—重要特性:①间接影响产品的配合/功能/安装/外观特性;
②间接影响产品的安全/排放/节能/法规/防盗特性;
③用户对产品质量缺陷有较大抱怨的。
▽—法规特性:①直接影响产品的燃烧特性/车内人员保护/转向控制/制动特性的;
②直接影响产品的安全/排放/节能/法规/防盗特性的。
△—关键特性:①对产生的质量缺陷用户不能容忍的;
②对配合/功能/外观/装配等要求必须保证的。
编制/日期:审批/日期:
【国家自然科学基金】_种群统计_基金支持热词逐年推荐_【万方软件创新助手】_20140731
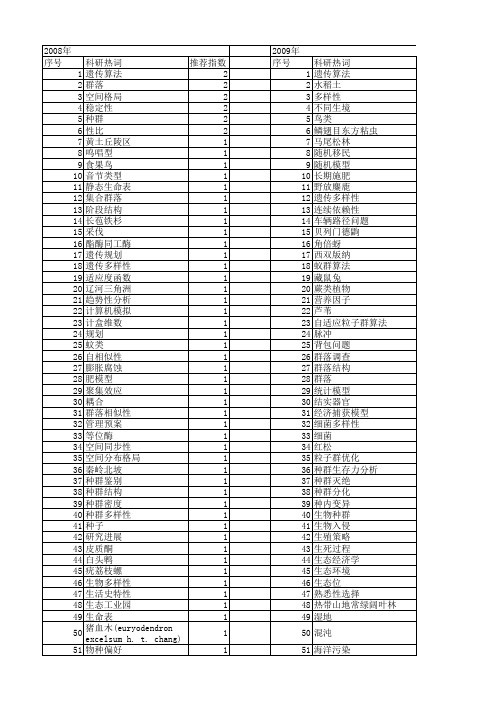
水生植物 水温 水层深度 气候事件 棕色田鼠 杂色山雀 机器人足球比赛 有限差分 早更新世早期 数量特征 数量 数学模型 持久 情绪 性别鉴定 性二型 微卫星 开花物候 平衡点 差异 山系 居群水平 宏观分类 安徽繁昌 季节变化 存在唯一性 头骨 大小结构种群模型 大坝安全预警评价 多智能体 多态性 基因分型 地理隔离 土壤理化性质 四合木种群 周期倍减 可解群 古田山 变异度 反应-扩散模型 华北驼绒藜 半知菌群体 升金湖 区系地理 北柴胡资源量 北京地区 动态进化算法 动态网络 动态复杂性 分岔图 内源激素 典型对应分析(cca) 全局渐近稳定 入侵预测
2009年 科研热词 推荐指数 序号 遗传算法 2 1 群落 2 2 空间格局 2 3 稳定性 2 4 种群 2 5 性比 2 6 黄土丘陵区 1 7 鸣唱型 1 8 食果鸟 1 9 音节类型 1 10 静态生命表 1 11 集合群落 1 12 阶段结构 1 13 长苞铁杉 1 14 采伐 1 15 酯酶同工酶 1 16 遗传规划 1 17 遗传多样性 1 18 适应度函数 1 19 辽河三角洲 1 20 趋势性分析 1 21 计算机模拟 1 22 计盒维数 1 23 规划 1 24 蚊类 1 25 自相似性 1 26 膨胀腐蚀 1 27 肥模型 1 28 聚集效应 1 29 耦合 1 30 群落相似性 1 31 管理预案 1 32 等位酶 1 33 空间同步性 1 34 空间分布格局 1 35 秦岭北坡 1 36 种群鉴别 1 37 种群结构 1 38 种群密度 1 39 种群多样性 1 40 种子 1 41 研究进展 1 42 皮质酮 1 43 白头鹎 1 44 疣荔枝螺 1 45 生物多样性 1 46 生活史特性 1 47 生态工业园 1 48 生命表 1 49 猪血木(euryodendron excelsum h. 1 t. chang) 50 物种偏好 1 51 濒危植物 1 52
ECE R121控制件标识认证法规知识介绍

Roland Berger Strategy Consultants
标识符号
表1 标识符及其照明和颜色
Roland Berger Strategy Consultants
标识符号
Roland Berger Strategy Consultants
标识符号
Roland Berger Strategy Consultants
Roland Berger Strategy Consultants
认证一般要求说明
3、颜色
(1)表1中每一个信号装置的发光都应该是该表第5栏中所介绍的颜色。 (2)表1中未包括的指示器、信号装置以及指示器和控制装置的标识可以是制 造商所选择的任何颜色;但是,这种颜色不可干扰或遮盖表 1中规定的任 何信号装置、控制装置或指示器的标识。所选定的颜色应符合标准 ISO 2575:2000段落5 中规定的说明。 (3)所有标识信号装置、控制装置或指示器的标识在背景的衬托下应十分清 楚醒目。 (4)任何标识符上的暗色部分都可换上其外形轮廓(即从标识符上的深色部 分就可以勾画出标识符的轮廓)。
标识符号
Roland Berger Strategy Consultants
标识符号
Roland Berger Strategy Consultants
标识符号
Roland Berger Strategy Consultants
控制装置、信号装置及指示器实例图
灯:控制装置及其信号装置
Roland Berger Strategy Consultants
Roland Berger Strategy Consultants
认证一般列中的控制装置、信号装置及指示器,则应使用表 1 第2列中为其指定的符号加以标识。如果要用符号来标识未在表 1中列出 的信号装置或指示器,则建议使用标准ISO 2575:2000中已存在的、适 用于相关应用的为此情况指定的符号。 (2)为了标识表1或标准中ISO 2575:2000未包括的控制装置或信号装置, 制造商可以使用其自己设计的符号。这些符号可以包括国际上都认可字 母或数字标示。所使用的全部符号都应符合ISO 2575:2000段落4中规定 的设计原则。 附:如果使用彩色编码标识温度功能的调整幅度限制,则应使用红色来识 别热限制,而用蓝色标识冷限制。
【国家自然科学基金】_矩阵代数_基金支持热词逐年推荐_【万方软件创新助手】_20140801
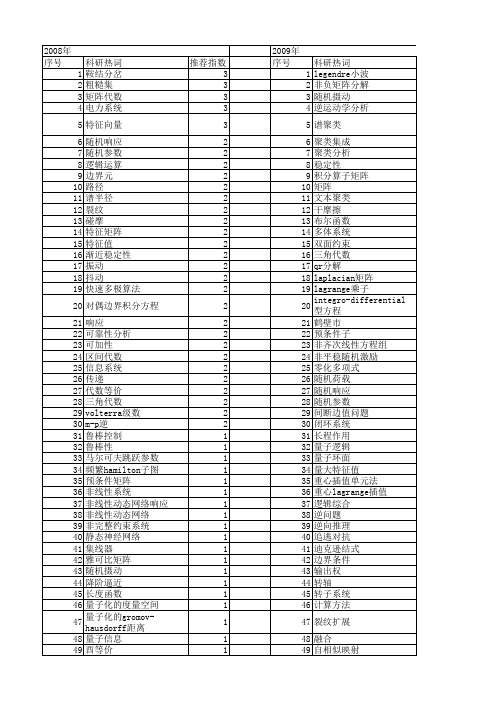
科研热词 推荐指数 鞍结分岔 3 粗糙集 3 矩阵代数 3 电力系统 3 特征向量 3 随机响应 2 随机参数 2 逻辑运算 2 边界元 2 路径 2 谱半径 2 裂纹 2 碰摩 2 特征矩阵 2 特征值 2 渐近稳定性 2 振动 2 抖动 2 快速多极算法 2 对偶边界积分方程 2 响应 2 可靠性分析 2 可加性 2 区间代数 2 信息系统 2 传递 2 代数等价 2 三角代数 2 volterra级数 2 m-p逆 2 鲁棒控制 1 鲁棒性 1 马尔可夫跳跃参数 1 频繁hamilton子图 1 预条件矩阵 1 非线性系统 1 非线性动态网络响应 1 非线性动态网络 1 非完整约束系统 1 静态神经网络 1 集线器 1 雅可比矩阵 1 随机摄动 1 降阶逼近 1 长度函数 1 量子化的度量空间 1 量子化的gromov-hausdorff距离 1 量子信息 1 酉等价 1 遍历作用 1 逻辑综合 1 速度逆解 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
联合对角化 联合代数重建算法 群环 网络模型 结块 线性系统 线性矩阵不等式(lmi) 线性矩阵不等式 线性保持 线性代数 线性 纯无限单c*-代数 约束最小二乘解 系数矩阵 粗糙集 算子矩阵 简单图 立方幂等阵 空间自相关 积分方程 积分-微分方程 离散广义系统 离散对数问题 离散余弦变换 离散事件动态系统 碰摩 矩阵蕴涵运算 矩阵的群逆 矩阵的一个正定形式 矩阵广义逆 矩阵对角化问题 矩阵右半张量积 矩阵余代数 矩阵低秩近似 相似性 直流电场 盲信源分离 盖尔圆定理 电网络 理想拓扑 独立成份分析 特征矢量 特征标 特征多项式 特征值 灵敏度分析 灵敏度 流密码 法方程 正则化 正交阵 正交投影 正交化 欧几里德若当代数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正交性定理
设D(i)(R)和D( j)(R)是群G的两个ni,nj维的不等价不可 约表示(R代表群G中的任一元),则有
AP 可约 (gi )
L(gi ) S P AP (gi )
p 1
Hale Waihona Puke q正则表示含不等价不可约酉表示的次数,等于该表示的 维数。
群表示的特征标
1.定义:设群G={E,A,B,C,…},它的一个表示 D={D(E),D(A),D(B),D(C),…},则群元R的特征标为 D(R)的对角元之和(迹) X(R)=TrD(R)=
i
a A ( g )
p
p
p, v
v
v
i
av S p ( Av | )
p
p
推论:
1、勃恩赛德(Burside)定理 有限群的所有不等价不可约酉表示维数的平方和, 等于群的阶。即
2 2 S12 S2 ... S q n
2、正则表示L(gi)按不等价不可约酉表示 化为
i
2,...,q) A ( p 1,是有限群
p
G 的所有不等价不可 g ,..., g ,...g
生成的群函数
1
i
n
A
p
在群
1 p ( ) 函数集{ A }是 的完备基。 是群函数空 ( ) A v g i g s v R G i 间的正交归一基。群G的任意复函数可展为:
p
p
(g )
亦即( i ,
j ) = ij
此正交关系也称为特征标的第一正交关系 注:若将一个群的所有不等价不可约表示的特征标列成表,并 以群元类作为行编号而以不等价不可约表示作为列编号的话, 则不同行的特征标是正交的
推论: 1、群G的所有不等价不可约表示的个数r≤C (G中共轭类的个数)
例:验证正交性
(2) : 同一不可约(幺正)表示的基函数彼此正交
ij
正交
┌ 1 i ┐ ∣ 2i ∣ ┌ 1j ┐ ∣ 2j ∣ ∣ ∣ └ njj ┘
正交∣ ∣
∣ ∣ └ nii ┘
∣ ∣ 正交
完备性定理
设 约酉(幺正)表示,则 p 函数中间是完备的。 Av ( g )
X ( R) X j ( R)a j
j
(5)不可约表示特征标的正交性定理
定理:一个群G的两个不等价不可约表示D(i)和D( j)的特征 标X(i)和X( j)满足关系式
(i ) ( j )* X ( R ) X ( R) g ij R
其中,g是群阶,R是群G中的任一元,X(i),X( j)代 表第i和第j个不可约表示的特征标。
(3)属于同一共轭类的群元在同一表示中有相同的特征标, 因此特征标是类的函数,独立的特征标个数等于类的个数
证明:Ri与Rj共轭,则有 R-1RiR=Rj
所以D(R-1)D(Ri)D(R)=D(Rj)
D-1(R)D(Ri)D(R)=D(Rj) 得:X(Ri)=X(Rj)(相似矩阵有相同的迹)
(4)一个可约表示的特征标,等于约化后各不可约表示的特 征标之和
D
a 1
n
aa
( R)
式中,R表示G的任一元 Daa是对角元,n是表示空间的维数。 特征标系:群G中所有的g个群元在D中的特征标 注:对可约表示和不可约表示同样适用, 第a个不可约表示Da(R)的特征标写成Xa(R)
2.特征标的性质
(1)单位矩阵的特征标等于它的阶,若表示是一维的,则特 征标就是表示自身 (2)等价表示有相同的特征标 (由于相似变换并不改变矩阵的迹)
当我们寻找一个群的全部表示是,只须考虑那 些互不等价的表示。
可约表示和不可约表示
可约表示:设A是群G在表示空间V上的一个表示。如果V 存在一个G不变的真子空间W(即W既不是空集或V本身) 则称表示A是可约表示。亦即对任意y ∈W,任意g ∈G,有 A(g )y ∈W。 A(g )不把W中的向量变到W以外去。
A1~A2:1×1×1+2×1×1+3×1×(-1)=0 A2~E:1×1×2+2×1×(-1)+3×(-1)×0=0 E~E:1×2×2+ 2×(-1)×(-1)+ 3×0×0=6
2、有限群不可约表示的特征标内积等于1即:
( p , p ) 1
3、可约表示A的特征标
A 的内积大于1
q p 1
p A (gi ) mp ( gi )
mp为不可约表示Ap在可约表示A的等价幺正表示 A’中的重复度。
( A , A ) m2 p 1
P 1
可约表示的约化: 只要知道群的所有不可约表示的特征标 ( 即 不可约表示特征标表 ), 就可对该群任一表示的 可约性作出判断。 1.如该表示的特征标和某一不可约表示的特 征表完全相同, 则与这一不可约表示等价,亦为不 可约表示。
content
1、相关概念热身 2、特征标基本性质 3、特征标正交性与完备性 4、特征标表的构造
等价表示和非等价表示
等价表示:群G存在两个表示 D1={D1(E),D1(A),D1(B),…} D2={D2(E),D2(A),D2(B),…} 若存在一个非奇异矩阵S,使得每个元素都能满足 D1(A)=S-1D2(A)S,D1(B)=S-1D2(B)S,…等,即 D1=S-1D2S (相似变换) 则称两个表示D1和D2等价。记作D1∽D2
证明:
( i )* ( j) ( i )* ( j) X ( R ) X ( R ) D ( R ) D uu aa ( R) R R u a ( i )* ( j) Duu ( R)Daa ( R) ua R
g g ij ua ij ua ni ua ni ua g ij 1 g ij ni ua
(i ) ( j )* D ( R ) D ap q ( R) g ij a pq / ni R
用内积表示即: (D( j)p (R)|D(i)ßq (R))= ij ij /ni
其中,g是群G的阶,求和对一切群元进行。 ni是不 可约表示D(i)(R)的维数。
注:为什么叫正交性定理? (1) i j: 两个不等价不可约(幺正)表示的基函数彼此正 交;
