人教版高中数学必修二平面与平面平行的性质课件

合集下载

人教版高中数学必修2 2.2.4 平面与平面平行的性质课件(共20张PPT)

变式探究:将本例中的三棱锥改为长方体,如图是长方体被一平面所截得到
的几何体,四边形EFGH为截面,则四边形EFGH的形状为
.
解析:因为平面ABFE∥平面CDHG,平面EFGH与两平面分别交于EF,GH. 由面面平行的性质定理得EF∥GH,同理可得EH∥FG,所以四边形EFGH为平行四边形. 答案:平行四边形
D)
3.下列说法正确的是( B ) (A)平行于同一条直线的两个平面平行 (B)平行于同一个平面的两个平面平行 (C)一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行 (D)若三直线a,b,c两两平行,则在过直线a的平面中,有且只有一个平面与 b,c均平行
4.已知α∥β,a⊂α,B∈β,则在β内过点B的所有直线中( D ) (A)不一定存在与a平行的直线 (B)只有两条与a平行的直线 (C)存在无数条与a平行的直线 (D)存在唯一一条与a平行的直线
方法技巧面面平行的性质定理是由面面平行得到线线平行.证明线线平行的关键是把要证明的直线看作是平面的交线,所以构造三个平面:即两个平行平面,一个经过两直线的平面,有时需要添加辅助面.
训练1:已知如图所示,三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的点.
若平面BC1D∥平面AB1D1,求

又 BE
1 B1C1,所以 BE 2
FO1. ……………………………………………9 分
所以四边形 BEFO1 为平行四边形, 所以 EF∥BO1, …………………………………………………………………10 分又 EF⊄ 平面 BB1D1D,BO1⊂ 平面 BB1D1D, 所以 EF∥平面 BB1D1D. ………………………………………………………12 分

高中数学必修二《平面与平面平行的判定》PPT

问题与探究
三角板的一边所在直线与桌面平行，这个三角板所在平面与桌面平行吗？三角板的两条边所在直线分别与桌面平行，情况又如何？
根据平面与平面平行的定义可知，判定面面平行的关键在于判定它们有没有公共点。若一个平面内的所有直线都与另一平面平行，那么这两个平面一定平行。否则，这两个平面就会有公共点，这样在一个平面内通过这个公共点的直线就不平行另一平面了。
对于③：一个平面内任何直线都与另外一个平面平行，则这两个平面平行．这是两个平面平行的定义．
对于④：一个平面内有两条相交直线都与另外一个平面平行，则这两个平面平行．这是两个平面平行的判定定理．
所以只有③④正确，选择D.
规律总结：
判断两个平面平行的方法有四种：
（1）利用定义；（2）利用面面平行的判定定理；（3）利用面面平行判定定理的推论；（4）利用面面平行的传递性。对于考查定义的问题，只需要找出一个反例就行，没必要把每个选项都正面推导一次。
直线与平面平行来证明平面与平面平行．通常我们将其记为：线面平行，则面面平行。因此处理面面平行(即空间问题) 转化为处理线面平行，进一步转化为处理线线问题(即平面问题)来解决，以后证明平面与平面平行，只要在一个平面内找到两条相交直线和另一个平面平行即可．面面平行判定定理的推论：若一个平面内的两条相交直线与另一个平面内的两条相交直线对应平行，则这两个平面平行．
【例2】如图,已知正方体ABCD—A1B1C1D1，
求证：平面AB1D1//平面C1BD。 .
【分析】
只要证一个平面内有两条相交直线和另一个平面平行即可
跟踪练习2
棱长为a的正方体AC1中,设M、N、E、F分别为棱 A1B1、A1D1、 C1D1、 B1C1的中点.

人教A版高中数学必修二课件第五讲直线与平面、平面与平面平行的性质.pptx

a

思考：教室内的日光灯管所在的直线与地面平行，如何在地面上作一条直线与灯管所在的直线平行？
Aa B

思考：教室内的日光灯管所在的直线与地面平行，如何在地面上作一条直线与灯管所在的直线平行？
Aa B

思考：教室内的日光灯管所在的直线与地面平行，如何在地面上作一条直线与灯管所在的直线平行？
∴a与b无公共点．又∵ a , b ,
解决问题
已知：直线a∥平面, a , b.
求证：a∥b．

a

b
证明： b, b , 又a //
∴a与b无公共点．又∵ a , b , 即a与b共面．
解决问题
已知：直线a∥平面, a , b.
BC 面BC' 面BC' 面A'C' B'C'
BC//B'C'
EF//B'C'
BC//EF
D'
A'
P E
D
F B'
C' C
EF、BE、CF共面． A
B
则EF、BE、CF为应画的线．
直线与平面平行的性质定理的运用：例1 如图所示的一块木料中, 棱BC平行于面A'C'．
⑴要经过面内的一点P和棱BC将木料锯开，应怎

a

b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行，则过这条直线的任一个平面与此平面的交线和该直线平行．
符号语言：

a

b
讲授新课
直线与平面平行的性质定理

人教版2017高中数学(必修二)2.2.4 平面与平面平行的性质PPT课件

α∥β,α∩γ=a,β∩ γ=b⇒a∥ b 证明两条直线平行
首页
课前预习案
课堂探究案
首页
课前预习案
课堂探究案
做一做若α∥β,a⊂α,b⊂β,下列几种说法中正确的是 ( ) ①a∥b;②a与β内无数条直线平行;③a与β内的任何一条直线都不垂直;④a∥β. A.①② B.②④ C.②③ D.①③④ 答案:B
首页探究一探究二思想方法当堂检测
课前预习案
课堂探究案
首页探究一探究二思想方法当堂检测
课前预习案
课堂探究案
变式训练2 如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.
证明:因为D,E分别是PA,PB的中点,所以DE∥AB. 又DE⊄平面ABC,AB⊂平面ABC, 所以DE∥平面ABC, 同理DF∥平面ABC,且DE∩DF=D, 所以平面DEF∥平面ABC. 又平面PCM∩平面DEF=NF,平面PCM∩平面ABC=CM, 所以NF∥CM.
首页探究一探究二思想方法当堂检测
课前预习案
课堂探究案
的一点(不在α与β之间), 直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD; (2)已知PA=4,AB=5,PC=3,求PD的长. 思路分析:(1)由面面平行的性质定理直接推证;(2)先由三角形相似得对应线段成比例,再求值.
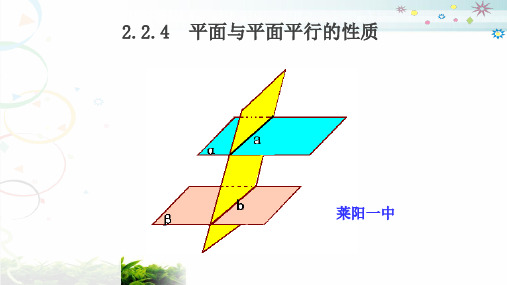
2.2.4 平面与平面平行的性质
-1-
首页
课前预习案
课堂探究案
学习目标思维脉络 1.理解并能证明平面与平面平行的性质定理. 2.能利用平面与平面平行的性质定理解决有关的平行问题.

平面与平面平行的性质【新教材】人教A版高中数学必修第二册课件

8平.面5 .与3 平第面二平行课的时性平质面【与新平教面材平】行人的教性A版质高-【中数新学教必材修】第人二教册A版课（件2019）高中数学必修第二册课件(共 23张P PT)
2．[变条件，变结论]将本例改为：已知平面 α∥β∥γ，两条直线 l， m 分别与平面 α，β，γ 相交于点 A，B，C 与 D，E，F.已知 AB＝6，DDEF＝25，则 AC＝________.
利用面面平行的性质判断位置关系 [例 2] 如图，平面四边形 ABCD 的四个顶点 A，B，C，D 均在▱A′B′C′D′所确定的平面 α 外，且 AA′，BB′，CC′，DD′ 互相平行．求证：四边形 ABCD 是平行四边形．
8平.面5 .与3 平第面二平行课的时性平质面【与新平教面材平】行人的教性A版质高-【中数新学教必材修】第人二教册A版课（件2019）高中数学必修第二册课件(共 23张P PT)
2．已知平面 α∥平面 β，直线 l∥α，则
A．l∥β
B．l⊂β
C．l∥β 或 l⊂β
D．l，β 相交
()
解析：假设 l 与 β 相交，又 α∥β，则 l 与 α 相交，与 l∥α 矛盾，则假设不成立，则 l∥β 或 l⊂β.故选 C.
答案：C
3．六棱柱的两底面为 α，β，且 A∈α，B∈α，C∈β，D∈β，AD ∥BC，则 AB 与 CD 的位置关系是______．解析：因为 AD∥BC，且平面 ABCD∩α＝AB，平面 ABCD∩β ＝CD，又 α∥β，所以 AB∥CD.
8平.面5 .与3 平第面二平行课的时性平质面【与新平教面材平】行人的教性A版质高-【中数新学教必材修】第人二教册A版课（件2019）高中数学必修第二册课件(共 23张P PT)

人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18

例2: P是长方形ABCD所在平面外的一点，AB、
PD上两点M、N满足AM：MB=ND：NP。
求证：MN∥平面PBC。
P
N
D
C
E
A
B
M
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18 人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18
四、课内练习：
1、已知α∥β，AB交α、β于A、B，CD交
α、β于C、D，AB∩CD=S，
AC
α
S
AC
α
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18
βD
B
B
D
β
16或272
探究2
若两个平面平行则一个平面内的直线与另一个平
面的位置关系如何？
l α
平行
β
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18
性质1：
两个平面平行，其中一个平面内的直线必平行于另一个平面
面面平行转化为线面平行
求证： AB=CD
证明：因为AB∥CD,所以过AB,CD可
A
C
作平面γ，且平面γ与平面α和β α
分别相交于AC和BD.
因为α∥β，所以BD∥AC
γ
βB
D
因此，四边形ABDC是平行四边形.
所以AB=CD.
人教版高中数学必修二2.2.4 平面与平面平行的性质教学课件 18

8.5.3 平面与平面平行课件ppt

∴PM∥AB1.
又AB1∥C1D,∴PM∥C1D.
又PM⊄平面C1BD,C1D⊂平面C1BD,
∴PM∥平面C1BD.
同理MN∥平面C1BD.
又PM∩MN=M,
∴平面PMN∥平面C1BD.
探究二
面面平行性质定理的应用
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线
PB,PD分别与α,β相交于点A,B和C,D.
D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行
或相交
答案 CD
解析如图①,在平面α内作α,β交线的无数条平行线,可知A,B错误;
对C,由题意可知AB∥β,BC∥β,AB∩BC=B,由面面平行的判定定理可知
α∥β,C正确;
对D,参考选项C的解析,假设α内有一个点位于点A处,而其余点均位于直线
所以PQ∥平面CBE.
(方法二)如图②,连接AC,则Q∈AC,且Q是AC的中点.
因为P是AE的中点,所以PQ∥EC.
因为PQ⊄平面CBE,EC⊂平面CBE,
所以PQ∥平面CBE.
方法点睛 (1)线线、线面、面面间的平行关系的判定和性质,常常是通过
线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问

4
3
15
∴ = ,∴5 = ,∴CD= 4 ,
15 27
∴PD=PC+CD=3+ 4 = 4 .
反思感悟证明线线平行的方法
(1)定义法:在同一个平面内没有公共点的两条直线平行.
(2)平行线的传递性:平行于同一条直线的两条直线平行.
∥
(3)线面平行的性质定理: ⊂
⇒a∥b,应用时题目条件中需有线面平行.

高中数学课件两个平面平行的判定与性质ppt课件.优秀文档PPT

（2）重学生学习体验。 (1)判定两个平面平行的主要途径有那些.
定义
如果两个平面有公共点，它们就相交于一条过该公共点的直线，就称这两个平面相交．
提问：能否加上某些条件，从而由“线线平行”推出“面面平行”。
形式：讲述、提问、讨论
返回
过程分析 ——设计思路
问题：（1）若两条直线平行，则分别经过这两条直线的
(2)平面 BC CB内的直 BC 和线 BC有什么关系？为
(3)若AA12，直A线 A和平A面 B所 C 成 NhomakorabeaC
3
的角6是 0，则两个平A行 B和 C平面A 2
B
ABC的距离是多少？
4C
1
A
B
课时小结
a
1.两个平面平行的性质
（1）一个结论 / /,a a/ /
面面平行
线面平行
（2）性质定理a/,/ba//b
②一条直线和两个平行平面相交,则此直线和两个平
面成等角;
③一条直线和两个平面成等角,则此两个平面平行;
④夹在两个平行平面间的两条线段长相等,那么这两
条线段平行.
A1 B2 C3 D4
巩固与拓展
3且.一不个为平零面,则上这不两同个的平三面点到另一个平面的距离( B相等)
A. 平行
B. 相交
C. 平行或重合
9.5.2两个平面平行的判定和性质
珲春一中崔星
复习与引入
1.两个平面的位置关系
两个平面的位置关系只有两种 (1)两个平面平行——没有公共点 (2)两个平面相交——有一条公共直线．
l
符号表示 //
l
2.两个平面平行的判定
（1）判定定理：如果一
个平面内有两条相交直线

人教版高中数学必修二课件：线面平行的性质

03 探究三
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
线面平行性质定理的应用
01
如图，四面体A-BCD被一平面所截，截面EFGH是一个矩形。求证：CD∥平面EFGH.
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
该直线与此平面平行.
a
符号语言：b
a
/
/
a / /b
直线与平面平行有哪些性质呢？
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
01 探究一
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
01
如果一条直线和一个平面平行，那么这条直线和这个平面内的直线有怎样的位置关系？
线线平行
βa αb
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
02 探究二
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
线面平行的性质定理的理解
1 直线a ∥平面α，平面α内有n条互相平行的直线，
那么这n条直线和直线a( C )
（2）若直线a，b都与平面α平行，则a与b平行（ × ）
（3）若直线a与平面α， β平行，则α与β平行
（×）
人教版高中数学必修二课件：线面平行的性质
人教版高中数学必修二课件：线面平行的性质
02 线面平行的性质定理的理解
3 已知平面外的两条平行直线中的一条平行于这个平面, 求证:另一条也平行于这个平面.

8.5.1空间直线、平面的平行课件(人教版)

那么该直线与交线平行.
符号表示 // , ⊂ ， ∩ = //.
简记：线面平行，则线线平行.
作用：判定线线平行的重要依据.
关键：寻找面面交线.
β
α
a
b
应用举例
如图所示的一块木料中，棱平行于面A′C′.
（1）要经过面A′C′内的一点和棱将木料锯开，在木料表面应该怎样画线？
动.在转动的过程中（离开桌面），的对边与桌面有公共点吗？
边与桌面平行吗？
无论门扇转动到什么位置，因为
转动的一边与固定的一边总是平
行的，所以它与墙面是平行的；
（1）
（2）
硬纸板的边与平行，只要
边紧贴着桌面，边转动时
就不可能与桌面有公共点，所以
它与桌面平行.
新知探究
直线与平面平行的判定定理
如果平面外一条直线与此平面内的一条直线平行，那么该直线与
a
此平面平行.
符号表示

⊄α， ⸦，且//
//.
处理空间位置关系常用方法：
直线间的平行
空间几何问题
转
化
转
化
直线与平面的平行
平面几何问题
α
b
新知探究
求证：空间四边形相邻两边中点的连线平行于经过另外两边的平面.
求证：过直线的平面与平面相交于，则//.
已知： // , ⊂ ， ∩ = .
求证： //.
证明：∵ ∩ = ，
β
a
∴ ⊂ .
又//，
∴ 与无公共点.
又 ⊂ ， ⊂ ，
∴//.
α
b
新知探究
直线与平面平行的性质定理
一条直线与一个平面平行，如果过该直线的平面与此平面相交，

高中数学人必修二课件平面与平面平行的判定

高中数学人必修二课件平面与平面平行的判定
汇报人：
目录
01
添加目录标题
04
平面与平面平行的判定定理的应用
02
平面与平面平行的判定方法
05
平面与平面平行的判定定理的证明方法
03
平面与平面平行的性质
定义法
两个平面平行的定义：如果两个平面没有公共点，那么这两个平面平行。
两个平面平行的判定方法：如果两个平面的法向量平行，那么这两个平面平行。
应用场景：在几何、物理等领域中，常常需要判定一个点是否与平面共面。
判定定理：如果一个点在平面内，且与平面内其他三个点构成的向量共面，则该点与平面共面。
判定方法：利用向量叉积为零的性质，判断该点与平面内任意两
向量构成的向量是否共线。
注意事项：在三维空间中，点与平面的位置关系有三种：点在平面内、
添加标题
添加标题
添加标题
平行公理的推论
如果一个平面内的一条直线与另一个平面平行，那么这两个平面平行。如果两个平面都与第三个平面平行，那么这两个平面平行。如果两个平面都与第三个平面垂直，那么这两个平面平行。如果两个平面都与第三个平面相交，那么这两个平面不平行。
判定两平面是否平行
定理：如果两个平面的法向量平行，那么这两个平面平行
平行公理的应用：平行公理是平面几何中的基本公理之一，可以用来证明其他几何命题。平行公理的局限性：平行公理在非欧几何中并不成立，因此需要引入其他公理来代替。
反证法
单击此处输入你的项正文，文字是您思想的提炼，请尽量言简意赅的阐述观点；
a. 假设两个平面不平行 b. 推导出矛盾 c. 得出结论：两个平面平行
例子：在几何图形中，如果已知一条直线与一个平面内的两条相交直线都平行，

高中数学人教A版必修第二册《平面与平面平行---平面与平面平行的性质》名师课件

解：法一：(1)证明：因为BC∥AD,BC
⊄平面PAD,AD⊂平面
法二：(1)证明：由于AD∥BC,AD ⊄平面PBC,BC⊂平面PBC,所以AD∥平面
PAD,所以BC∥平面PAD.
PBC.
又因为平面PBC∩平面PAD＝l,所以BC∥l.
又因为平面PBC∩平面PAD＝l,所以 l ∥AD ,l∥BC.
求证：N为AC的中点.
证明：因为平面AB1M∥平面BC1N,平面ACC1A1∩平面AB1M＝AM,平面
BC1N∩平面ACC1A1＝C1N,所以C1N∥AM.
又AC∥A1C1,所以四边形ANC1M为平行四边形,所以AN∥C1M且AN＝C1M,

又C1M＝ A1C1,A1C1＝AC,所以AN＝ AC,所以N为AC的中点．
证明:因为//,所以过, 可作平面,且平
面与平面和分别相交于和.
因为//,所以//.
因此,四边形是平行四边形. 所以 = .
典例讲授
例2、如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β
相交于点A、B和C、D.
置关系？
借助长方体模型探究
结论:异面直线或平行直线.
探究新知
探究3:当第三个平面和两个
平行平面都相交时,两条交线
有什么关系？为什么？
答:两条交线平行.
下面我们来证明这个结论
β
a
α
b
探究新知
结论:当第三个平面和两个平行平面都相交时,两条交线平行
如图,平面, , 满足//, ∩ = , ∩ = ,求证：//.
(2)平行．
(2)平行．证明如下：设Q是CD的中点,连接NQ,MQ,则MQ∥AD,NQ∥PD,而

人教版高中数学必修二课件 2.2.4 平面与平面平行的性质

a
②判定直线与直线平行的重要依据.
关键：寻找两平行平面与第三个平面的交线.
11
三种平行关系的转化
线
线
线线面平行判定面
平
平
行线面平行性质行
面面面平行判定面
平
面面平行性质
行
面面平行性质
12
【即时训练】
下列命题正确的是（ D ） A.两个平面有无数个公共点，则这两个平面重合 B.若一个平面内有两条直线平行于另一个平面，则这两个平面平行 C.若一个平面内有无数条直线平行于另一个平面，则这两个平面平行 D.若两个平面平行，则其中的一个平面与另一个平面内的无数条直线平行
2.2.4 平面与平面平行的性质
1
一块长方体木料，将木料按虚线锯开，如图所示，那么，所得的截面有什么特点？
2
1.理解平面与平面平行的性质定理.（重点） 2.会用平面与平面平行的性质定理分析解决有关
问题.（难点） 3.培养空间想象能力与转化化归的思想.
3
问题1：若两个平面平行，则一个平面内的直线a与另一个平面内的直线有什么位置关系?
证明：
如图，取CD的中点E，连接NE、ME， ∵M、N分别是AB、PC的中点， ∴NE∥PD，ME∥AD
∴NE∥平面PAD，ME∥平面PAD 又NE∩ME＝E， ∴平面MNE∥平面PAD，又MN⊂平面MNE， ∴MN∥平面PAD.
22
平面与平面平行的性质
性质定理
应用：判定线线平行
面面平行线线平行
23
不轻易献出成功的皇冠乃是困难的天性。
24
b，求证：a / /b.
证明: a
γ
b

高中数学人教A版必修二.2平面与平面平行的性质PPT课件

a
c b
异面、平行
问题2：平面ABCD内哪些直线会与直线
B'D'平行？怎么样找到这些直线？
D′
C′
A′
性质探究
B′
D
C
A
B
平面ABCD内的直线只要与B'D'共面即可
平面与平面平行性质
若 // ，且 a,则与的位置关系如何？
设 b，则直线a、b的位置关系如何？为什么？
已知平面，，， // , a, b
推论：
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线，那么这两个平面平行
面面平行性质定理: 面面平行线面平行
如果两个平行平面同时与第三个平面相交，那么它们的交线平行。
求证：a // b
证明
a
b
a
b
//
a, b没有公共点
a, b都在平面内
a // b
平面与平面平行的性质定理
如果两个平行平面同时与第三个平面相交，那么它们的交线平行。
α
a
b
β
面面平行的几条性质：
1．性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．
β
b
α
a
r
练习
面、之间的线段,且直线AB、CD为异
面直线,M、P 分别为AB、CD 的中点，
A
求证:直线MP // 平面 .
C
NP
M
D
B
举例
例5. 设平面α、β、γ两两相交,且
a， b, c
若a∥b，求证：b∥c .
a
c
b
α
β
γ

《平面与平面平行的性质》人教版高中数学必修二PPT课件(第2.2.4课时)

a ＋2b ＝(2,1)＋2(3，－4)＝(2,1)＋(6，－8)＝(8，－7)，
∵(λa －b )∥(a ＋2b )，
1 ∴8(λ＋4)＋7(2λ－3)＝0⇒22λ＋11＝0⇒λ＝－2.
1
1
1
7
∴－2a －b＝(－2×2－3，－2＋4)＝(－4，2)，
1
即 λa－b＝－2(a＋2b)．
1
故当 λ＝－2时，λa－b 与 a＋2b 平行；平行时它们反向．
典例 1
已知a＝(2,1)，b＝(3，－4)，当λ为何值时，λa－b与a＋2b平
行？平行时，它们是同向还是反向？
根据平行条
判断
[思路分析] 求λa－b与a＋2b的坐标 → 件构造方程 → 求λ → 方向 .
第二章平面向量
[解析] λa－b＝λ(2,1)－(3，－4)
＝(2λ，λ)－(3，－4)＝(2λ－3，λ＋4)，
求证:AB=CD
证明:∵AB//CD ∴过AB，CD可以作平面γ,
且平面γ与平面α和β分别相较于过AD和BC, ∵α//β
∴AD//BC
因此，四边形ABCD是平行四边形.
β
∴ AB=CD
D αA
γ C
B
新知探究
已知三个平行平面 , ,与两条直线 l, m 分别相并于点A, B,C和点D, E, F.
人教版高中数学必修二
第2章关系点、直线、平面之间的位置关系
2.2.4平面与平面平行的性质
MENTAL HEALTH COUNSELING PPT
讲解人：时间：2020.6.1
复习回顾
1.空间两平面有哪些位置关系？
相交
平行
有公共点
无公共点

人教A版数学必修二平面与平面平行的判定课件

又AB∥
所以D1C1∥AB，D1C1 =AB，
A所1B以1,DA1BC=1BAA1B为1平，行四边形，
D1
所以D1A∥ C1B.
A1
由直线与平面平行的判定定理得
D1A∥平面C1BD，同理D1B1 ∥平面C1BD， D
② a，b 相交，即 a b P；
ba
③ 平行，即 a / /,b / / .
P
人教A版数学必修二2.2.2平面与平面平行的判定课件(共34 张PPT)
人教A版数学必修二2.2.2平面与平面平行的判定课件(共34 张PPT)
思考交流下列命题正确的是( ) ①一个平面内有两条直线都与另外一个平面平行，则这两个平面平行； ②一个平面内有无数条直线都与另外一个平面平行，则这两个平面平行； ③一个平面内任何直线都与另外一个平面平行，则这两个平面平行；
这两个平面相交也能够找得到这样的直线存在．对于②：一个平面内有无数条直线都与另外一个平面平行，同①. 对于③：一个平面内任何直线都与另外一个平面平行，则这两个平面平行．这是两个平面平行的定义．对于④：一个平面内有两条相交直线都与另外一个平面平行，则这两个平面平行．这是两个平面平行的判定定理．所以只有③④正确，选择D.
人教A版数学必修二2.2.2平面与平面平行的判定课件(共34 张PPT)
人教A版数学必修二2.2.2平面与平面平行的判定课件(共34 张PPT)
例1 已知正方体ABCD - A1B1C1D1，
求证：平面AB1D1 ∥平面C1BD.
证明:因为ABCD-A1B1C1D1为正方体，
所以D1C1∥ A1B1，D1C1 =A1B1
人教A版数学必修二2.2.2平面与平面平行的判定课件(共34 张PPT)

【人教版】高中数学必修二：《平面与平面平行的性质》ppt课件

第二章空间点、直线、平面之间的位置关系
2.2.4平面与平面平行的性质
2020/6/26
1
复习1：两个平面的位置关系 ①两个平面平行——没有公共点 ②两个平面相交——有一条公共直线．
复习2：面面平行的判定方法
1、定义法：若两平面无公共点，则两平面平行.
2、判定定理：如果一个平面内有两条相交直线分别平行于
// 即： a a // b
b
2020/6/26
4
例1 如图，已知平面，，，满足 // 且 I a, I b, 求证：a // b 。
证明 Q I a, I b, a ,b .
Q //
所以a,b没有公共点
Q a,b
a//b
2020/6/26
5
例2 求证：夹在两个平行平面同时和第三个平面相交，那么它们的交线平行。
已知:如图 // ,AB//CD,且A,C , B , D
求证:AB=CD. 证明：因为AB//CD，所以过
AB,CD可作平面，
且平面与平面和
分别相交AC和BD.
因为 //
所以BD//AC.
因此，四边形ABCD是平行四边形。
2所020/以6/26 AB=CD.
6
课堂练习
1、课本P67练习 2、课本P67习题2.2：A组1、2；
2020/6/26
7
课堂小结
2020/6/26
8
布置作业
课本P69习题：B组第2、3
2020/6/26
9
另一个平面，那么这两个平面平行.
2020/6/26
2
思考：
1、两个平面平行，那么其中一个平面内的直线与另一平面有什么样的关系？

人教课标版高中数学必修2《平面与平面平行的性质》名师课件

【解题过程】分两种情况： ①当AB，CD在同一平面内时，由α∥β，α∩ 平面ABDC＝AC，β∩平面ABDC＝BD， ∴AC∥BD，∵AE∶EB＝CF∶FD， ∴EF∥BD，∴EF∥AC，
又EF β，BD⊂β，∴EF∥β.
同理可证，EF∥平面α.
知识回顾问题探究课堂小结随堂检测
②当AB与CD异面时，设平面ACD∩β＝l，在l上取一
知识回顾问题探究课堂小结随堂检测探究二平面与平面平行的性质定理的证明活动① 证明平面与平面平行的性质定理
如图，平面α、β、γ满足α∥β，α∩γ＝a，β∩γ＝b. 求证a∥b.
证明 ∵α∩γ＝a，β∩γ＝b， ∴a⊂α，b⊂β. 又∵α∥β， ∴a，b没有公共点，又∵a，b同在平面γ内，∴ a∥b.
知识回顾问题探究课堂小结随堂检测
（3）若平面α∥平面β，P∈α，PQ∥β，则PQ⊂α. 此说法正确吗？答案：正确．如图，过直线PQ作平面γ， γ∩α＝a，γ∩β＝b，由α∥β得a∥b. 因为PQ∥β，PQ⊂γ，所以PQ∥b. 因为过直线外一点有且只有一条直线与已知直线平行，所以直线a与直线PQ重合．因为a⊂α，所以PQ⊂α. （4）若直线a∥平面β，直线b∥平面α，且α∥β，则a∥b. 此说法正确吗？答案：错误．若直线a∥平面β，直线b∥平面α，且α∥β，则a与b平行、相交和异面都有可能．
【解题过程】因为AB∥CD，所以过AB、CD可作平面γ，
且平面γ与平面α和β分别相交于AC和BD.因为α∥β，所以 BD∥AC.因此，四边形ABDC是平行四边形. 所以AB＝CD. 【思路点拨】由面面平行得线线平行，得四边形ABDC是平行四边形．
知识回顾问题探究课堂小结随堂检测
活动③ 灵活应用，突破思维例3 如图，平面四边形ABCD的四个顶点A、B、C、D均在平行四边形A′B′C′D′所确定一个平面α外，且AA′、BB′、 CC′、DD′互相平行. 求证：四边形ABCD是平行四边形.