最新华南理工大学网络教育2017线性代数与概率统计平时作业资料
华南理工大学网络教育学院2017统计学原理作业主观题
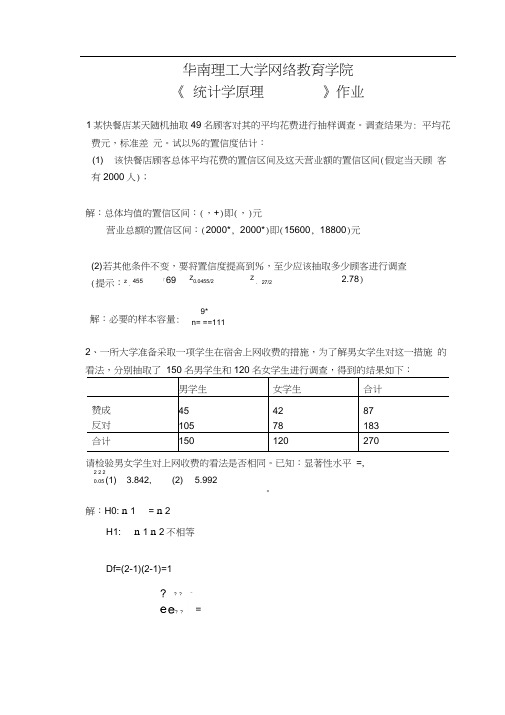
华南理工大学网络教育学院 《 统计学原理》作业1某快餐店某天随机抽取49名顾客对其的平均花费进行抽样调查。
调查结果为: 平均花费元,标准差 元。
试以%的置信度估计:(1) 该快餐店顾客总体平均花费的置信区间及这天营业额的置信区间(假定当天顾 客有2000人);解:总体均值的置信区间:(,+)即(,)元营业总额的置信区间:(2000*, 2000*)即(15600, 18800)元(2) 若其他条件不变,要将置信度提高到%,至少应该抽取多少顾客进行调查2、一所大学准备采取一项学生在宿舍上网收费的措施,为了解男女学生对这一措施 的看法,分别抽取了 150名男学生和120名女学生进行调查,得到的结果如下:男学生女学生 合计 赞成 45 42 87 反对 105 78 183 合计150120270请检验男女学生对上网收费的看法是否相同。
已知:显著性水平 =,2 2 2 0.05(1) 3.842,(2)5.992。
解:H0: n 1= n 2H1:n 1 n 2不相等Df=(2-1)(2-1)=1(提示:z °.°455「69 Z 0.0455/2 Z °.°°27/2 2.78) 解:必要的样本容量:9*n= ==111决策:在二的水平上不能拒绝H0结论:可以认为男女学生对上网收费的看法相同3、一家管理咨询公司为不同的客户举办人力资源管理讲座。
每次讲座的内容基本上是一样的,但讲座的听课者,有时是中级管理者,有时是低级管理者。
该咨询公司认为,不同层次的管理者对讲座的满意度是不同的,对听完讲座后随机抽取的不同层次管理者的满意度评分如下(评分标准从 1 10,10代表非常满意)高级管理者中级管理者低级管理者78579688571079941088经计算得到下面的方差分析表:差异源SS df MS F P-value F crit组间组内总计17(1)请计算方差分析表中的F值。
2017线性代数与概率统计随堂练习答案(精编文档).doc

【最新整理,下载后即可编辑】1.(单选题) 计算?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:A2.(单选题) 行列式?A.3;B.4;C.5;D.6.答题: A. B. C. D. (已提交)参考答案:B3.(单选题) 计算行列式.A.12;B.18;C.24;D.26.答题: A. B. C. D. (已提交)参考答案:B问题解析:4.(单选题) 利用行列式定义计算n阶行列式:=?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:C问题解析:5.(单选题) 计算行列式展开式中,的系数。
A.1, 4;B.1,-4;C.-1,4;D.-1,-4.答题: A. B. C. D. (已提交)参考答案:B问题解析:6.(单选题) 计算行列式=?A.-8;B.-7;C.-6;D.-5.答题: A. B. C. D. (已提交)参考答案:B问题解析:7.(单选题) 计算行列式=?A.130 ;B.140;C.150;D.160.答题: A. B. C. D. (已提交)参考答案:D问题解析:8.(单选题) 四阶行列式的值等于多少?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:D问题解析:9.(单选题) 行列式=?A.;B.;C.;D..10.(单选题) 已知,则?A.6m;B.-6m;C.12m;D.-12m.答题: A. B. C. D. (已提交)参考答案:A问题解析:11.(单选题) 设=,则?A.15|A|;B.16|A|;C.17|A|;D.18|A|.答题: A. B. C. D. (已提交)12.(单选题) 设矩阵,求=?A.-1;B.0;C.1;D.2.答题: A. B. C. D. (已提交)参考答案:B问题解析:13.(单选题) 计算行列式=? A.-1500;B.0;C.-1800;D.-1200.答题: A. B. C. D. (已提交)参考答案:C问题解析:14.(单选题) 齐次线性方程组有非零解,则=?A.-1;15.(单选题) 齐次线性方程组有非零解的条件是=?A.1或-3;B.1或3;C.-1或3;D.-1或-3.答题: A. B. C. D. (已提交)参考答案:A问题解析:16.(单选题) 如果非线性方程组系数行列式,那么,下列正确的结论是哪个?A.无解;B.唯一解;C.一个零解和一个非零解;D.无穷多个解.17.(单选题) 如果齐次线性方程组的系数行列式,那么,下列正确的结论是哪个?A.只有零解;B.只有非零解;C.既有零解,也有非零解;D.有无穷多个解.答题: A. B. C. D. (已提交)参考答案:A问题解析:18.(单选题) 齐次线性方程组总有___解;当它所含方程的个数小于未知量的个数时,它一定有___解。
华南理工大学网络教育线性代数与概率统计作业

一.问答题1.叙述n 阶行列式的余子式和代数余子式的定义,并写出二者之间的关系。
答:定义:在n 阶行列式D 中划去a ij 所在的第i 行和带j 列的元素后,剩下的元素按原来相对位置所组成的(n-1)阶行式,称为a ij 的余子式,记为M ij ;即M ij =aaaaaaaaa a a a a a a annnj nj n Lni j L i j L i L i Ln i j L i j L i L i nj j1111,1,11,1,11111111+-+++-++-+----+-(-1)i+j ×M ij 称为a ij 的代数余子式,记为A ij ,即A ij =(-1)i+j ×M ij 。
2.叙述矩阵的秩的定义。
答:定义:设A 为m ×n 矩阵。
如果A 中不为零的子式最高阶为r ,即存在r 阶子式不为零,而任何r+1阶子式皆为零,则称r 为矩阵A 的秩,记作(秩)=r 或R (A )=r 。
3.齐次线性方程组的基础解系是什么?答:定义:设T 是⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++000221122221211212111n nn n n nn n n x a x a x a x a x a x a x a x a x a 的所有解的集合,若T 中存在一组非零解V 1,V 2,…Vs ,满足(1)V 1,V 2,……Vs ,线性无关;(2)任意V ∈T,都可用V 1,V 2,…Vs ,线性表出; 则称V 1,V 2,…Vs ,是此方程组的一个基础解系。
4.试写出条件概率的定义。
答:条件概率定义:在事件B 发生的条件下事件A 发生的概率定义为P ()B A =()()B P AB P ()()0>B P 。
5.试写出全概率公式和贝叶斯公式这两个定理。
答:定理1(全概率公式)设事件A A A n ,,,21 构成完备事件组,且()()().1Ai B P P B P ni i A ∑==特别地,当n=2时,全概率公式为()()()()()A B P A P A B P A P B P +=. 定理2(贝叶斯公式)设事件AA A n,,,21构成完备事件组,()()n i P A i ,2,10=>,则对任意事件()()0>B P B ,有()()()()()()n k A B P A P A B P A P B A P ni iik k k ,2,11==∑=二.填空题1.行列式111111111D =-=-- 4 .2.设,A B 均为3阶矩阵,且||||3A B ==-,则2T AB -= -72 。
华南理工网络教育 线性代数与概率统计》作业题(题目)

华南理工网络教育线性代数与概率统计》作业题(题目)《线性代数与概率统计》作业题第一部分单项选择题xx,,12111(计算,( A) ,xx,,1222A( xx,12B( xx,12C( xx,21D( 2xx,21111(2行列式, B D,,,111,,111A(3B(4C(5D(6231123,,,,,,,,,AB3(设矩阵,求=,B AB,,111,112,,,,,,,,011011,,,,,A(-1B(0C(1D(2,xxx,,,0,123,,4(齐次线性方程组有非零解,则=,( C) xxx,,,0,,123,xxx,,,0123,A(-11B(0C(1D(200,,,,197636,,,,,,B,5(设,,求=,(D ) ABA,,,,,530905,,,,,,76,, 104110,,A( ,,6084,,104111,, B( ,,6280,,104111,, C( ,,6084,,104111,, D(,,6284,,0A,,Aa,Bb,C6(设为m阶方阵,为n阶方阵,且,,,则=,( D) ABC,,,B0,, mA( (1),abn B( (1),abnm, C( (1),abnmD( (1),ab123,,,,,1A,221,,A7(设,求=,( D),,343,,2132,,,,35,,A( ,,3,,22,,111,,,132,,,,,35,, B( ,3,,22,,111,,,132,,,,,35,, C( ,3,,22,,111,,,132,,,,,35,,D( ,,3,,22,,111,,,AB,8(设均为n阶可逆矩阵,则下列结论中不正确的是(B )TTT,,,111A( [()]()()ABAB,,,,111 B( ()ABAB,,,kk,,11 C((k为正整数) ()()AA,,1n,,1D( (k为正整数) ()(0)kAkAk,,9(设矩阵的秩为r,则下述结论正确的是( D) Amn,A(A中有一个r+1阶子式不等于零B(A中任意一个r阶子式不等于零C(A中任意一个r-1阶子式不等于零 D(A中有一个r阶子式不等于零3213,,,,,,10(初等变换下求下列矩阵的秩,的秩为,(C ) A,,2131,,,,7051,,,3A(0B(1C(2D(311(写出下列随机试验的样本空间及下列事件的集合表示:掷一颗骰子,出现奇数点。
2017的线性代数与概率统计随堂练习题目答案详解

1.(单选题) 计算?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:A2.(单选题) 行列式?A.3;B.4;C.5;D.6.答题: A. B. C. D. (已提交)参考答案:B3.(单选题) 计算行列式. A.12;B.18;C.24;D.26.答题: A. B. C. D. (已提交)参考答案:B问题解析:4.(单选题) 利用行列式定义计算n阶行列式:=?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:C问题解析:5.(单选题) 计算行列式展开式中,的系数。
A.1, 4;B.1,-4;C.-1,4;D.-1,-4.答题: A. B. C. D. (已提交)参考答案:B问题解析:6.(单选题) 计算行列式=?A.-8;B.-7;C.-6;D.-5.答题: A. B. C. D. (已提交)参考答案:B问题解析:7.(单选题) 计算行列式=?A.130 ;B.140;A. B. D.参考答案:D8.(单选题) 四阶行列式的值等于多少?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:D问题解析:9.(单选题) 行列式=?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:B问题解析:10.(单选题) 已知,则?A.6m;B.-6m;C.12m;D.-12m.答题: A. B. C. D. (已提交)参考答案:A问题解析:11.(单选题) 设=,则?A.15|A|;B.16|A|;C.17|A|;D.18|A|.答题: A. B. C. D. (已提交)参考答案:D问题解析:12.(单选题) 设矩阵,求=?A.-1;B.0;C.1;A. B. C. D.参考答案:B13.(单选题) 计算行列式=?A.-1500;B.0;C.-1800;D.-1200.答题: A. B. C. D. (已提交)参考答案:C问题解析:14.(单选题) 齐次线性方程组有非零解,则=?A.-1;B.0;C.1;D.2.答题: A. B. C. D. (已提交)参考答案:C问题解析:15.(单选题) 齐次线性方程组有非零解的条件是=?A.1或-3;A. C.参考答案:A16.(单选题) 如果非线性方程组系数行列式,那么,下列正确的结论是哪个?A.无解;B.唯一解;C.一个零解和一个非零解;D.无穷多个解.答题: A. B. C. D. (已提交)参考答案:B问题解析:17.(单选题) 如果齐次线性方程组的系数行列式,那么,下列正确的结论是哪个?A.只有零解;B.只有非零解;C.既有零解,也有非零解;D.有无穷多个解.答题: A. B. C. D. (已提交)参考答案:A问题解析:18.(单选题) 齐次线性方程组总有___解;当它所含方程的个数小于未知量的个数时,它一定有___解。
华南理工大学网络教育2017-线性代数与概率统计-平时作业

华南理工大学网络教育2017-线性代数与概率统计-平时作业《线性代数与概率统计》作业题第一部分 单项选择题 1.计算11221212x x xx ++=++?(A )A .12x x - B .12x x +C .21x x - D .212xx -2.行列式111111111D =-=-- BA .3B .4C .5D .63.设矩阵231123111,112011011A B -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求AB =B A .-1 B .06.设A 为m 阶方阵,B 为n 阶方阵,且A a =,B b =,0A C B⎛⎫=⎪⎝⎭,则C =?( D )A .(1)mab-B .(1)nab - C .(1)n mab+-D .(1)nmab-7.设⎪⎪⎪⎭⎫ ⎝⎛=343122321A ,求1-A =?( D )A .13235322111⎛⎫ ⎪ ⎪-- ⎪ ⎪-⎝⎭B .132********-⎛⎫ ⎪ ⎪- ⎪ ⎪-⎝⎭C .13235322111-⎛⎫ ⎪ ⎪- ⎪ ⎪-⎝⎭D .13235322111-⎛⎫⎪ ⎪-- ⎪ ⎪-⎝⎭8.设,A B 均为n 阶可逆矩阵,则下列结论中不正确的是(B ) A .111[()]()()T T TAB A B ---=B .111()A B A B ---+=+C .11()()k kA A --=(k 为正整数)D .11()(0)n kA k A k ---=≠ (k 为正整数)9.设矩阵m nA ⨯的秩为r ,则下述结论正确的是( D )A .A 中有一个r+1阶子式不等于零B .A 中任意一个r 阶子式不等于零C .A 中任意一个r-1阶子式不等于零D .A 中有一个r 阶子式不等于零10.初等变换下求下列矩阵的秩,321321317051A --⎛⎫⎪=- ⎪ ⎪-⎝⎭的秩为?(C ) A .0 B .1 C .2 D .311.写出下列随机试验的样本空间及下列事件的集合表示:掷一颗骰子,出现奇数点。
2017年度下半年华工继续教育提高线性代数与概率统计随堂理解练习参备考资料答案解析

1.(单选题)计算B .参考答案:A 问题解析:5;6.参考答案:B 问题解析:1 2 3 D=31 22 3 13.(单选题)计算行列式 A. 12 ; B. 18 ; C. 24 ; D . 26.(已提交)答题:.——D.(已提交)-12.(单选题)行列式-13;B . 4;答题:A. *B.C.D.(已提交)参考答案:C问题解析:A. 1,4;B. 1 , -4;C. -1 , 4;-1 , -4.参考答案:B 问题解析:1 2 1 40 -1 2 1D =]0 136.(单选题) 计算行列式131 =?A . -8;B . -7;C . -6;D .-5.r f g nc答题: A. BCD. (已提4.(单选题)利用行列式定义计算 n 阶行列式: B . ;心…心. 答题:A. C.曬D.(已提交)=?"1 4 3 12 x- 2 317 9 X 05.(单选题)计算行列式 5311-1 展开式中的系数答题: A. (已提交)B . D.1 2 3 42 3 4 1D =3 4127.(单选题) 计算行列式4 1 2 ?=?A . 130 ;B . 140;C . 150;D .160.答题:A 「 B.「C.ri- D. (已提交) 参考答案:D问题解析:B .(.叩汀呵昭■鸟Q ).答题:A. B. C. * D.(已提交) 参考答案:D 问题解析:yXA +jryy9.(单选题)行列式=?A .B.・2(戸+戸);C.农-b).8.(单选题)四阶行列式%0 04毎% 0的值等于多少?参考答案:B 问题解析:10.(单选题)已知6m ; -6m ;12m ; -12m.参考答案:A11.(单选题)设占=角1 山22,则-如兔21-%一务A . 15|A|;B . 16|A|;C . 17|A|;D .18|A|.答题:'A.B.C. ! *D.(已提交)参考答案:D问题解析:答题:A. B . D. (已提交)12.(单选题)设矩阵 B . -1; 0;1; 2. A- C. 』=D.(已提交),则B . 答题:A. B. C.D. (已提交)13.(单选题)计算行列式-1500;-1800; -1200.参考答案:C 问题解析:陆十无十巧=0E +乂乜+也=0L 1 2有非零解,则丸=?眄一亏一令十心4 = ° _画 +Xj- 0-Xj + 蛛-I ■召一召二 °一口一站 + 屁二0卜L有非零解的条件是J ?-1201 102B . 0;答题:A.B.C. D.(已提交)-1; B . 0; 1; 2. 答题:A .也B. C. D.(已提交)参考答案:C 问题解析:A .1或一3 ; B.1或3 ; C .—1或3 ; D .—1或一3 . 答题:A. B. C. — D.(已提交)=?14.(单选题)齐次线性方程组15.(单选题)齐次线性方程组巧的十毛©十…+%兀7色Mi+0打花+…十的击兀=b2确的结论是哪个?A .无解;B.唯一解;C.一个零解和一个非零解;D •无穷多个解.答题:二A.去B. I■-」C. 口D.(已提交)参考答案:B问题解析:「九无+用弓十…十务兀=0 禺]巧4^22%亠…+角工耳=°18.(单选题)齐次线性方程组且^三。
《线性代数与概率统计》-平时作业

《线性代数与概率统计》作业题及其解答一、计算题1.答案:原式=18.2.计算行列式133353664x x x ---+---. 答案:原式=31216x x --.3.计算行列式1214012110130131D -=. 答案:原式= -7.4.设1213A ⎛⎫= ⎪⎝⎭,1012B ⎛⎫= ⎪⎝⎭,求AB 与BA .答案:1213AB ⎛⎫= ⎪⎝⎭1012⎛⎫⎪⎝⎭3446⎛⎫= ⎪⎝⎭, 1012BA ⎛⎫= ⎪⎝⎭1213⎛⎫ ⎪⎝⎭1238⎛⎫= ⎪⎝⎭.5.设2()21f x x x =-+,1101A ⎛⎫= ⎪⎝⎭,求矩阵A 的多项式()f A .(密封线内不答题)解:因为 2111112010101A AA ⎛⎫⎛⎫⎛⎫=== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,所以,2121110()22010101f A A A E ⎛⎫⎛⎫⎛⎫=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=2302⎛⎫⎪⎝⎭.6.设矩阵263113111,112011011A B ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求AB .解:AB =A B ⋅=(5)15-⋅=-.7.设101111211A ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,求逆矩阵1-A .解:因为 ()101100111010211001A E ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭23132100211010312001111r r r r --⎛--⎫⎪−−−→-- ⎪ ⎪-⎝⎭.所以 1211312111A ---⎛⎫⎪=-- ⎪⎪-⎝⎭.8.求224114113021121113312211422608A ⎛⎫ ⎪---- ⎪⎪= ⎪--- ⎪ ⎪---⎝⎭的秩.答案:原式=5.9.解线性方程组 123123123214254225x x x x x x x x x -+=⎧⎪++=⎨⎪++=⎩.解 :12323321246x x x x x x -+=⎧⎪+=⎨⎪=-⎩.这样,就容易求出方程组的解为123656x x x =⎧⎪=⎨⎪=-⎩.10.解线性方程组 ⎪⎩⎪⎨⎧=+=++=+-622452413231321321x x x x x x x x .解用初等行变换将增广矩阵(,)A b 化为行阶梯形矩阵,2131(,)42542026A b -⎛⎫⎪= ⎪ ⎪⎝⎭1323r r r r -+−−−→100901010016⎛⎫ ⎪- ⎪ ⎪-⎝⎭. 这个行最简形矩阵对应的线性方程组为⎪⎩⎪⎨⎧-=++-=++=++610010109001321321321x x x x x x x x x , 所以此线性方程组的唯一解为 ⎪⎩⎪⎨⎧-=-==619321x x x .11.甲、乙二人依次从装有7个白球,3个红球的袋中随机地摸1个球,求甲、乙摸到不同颜色球的概率.解:11732107()15C C P A C ==.12. 一箱中有50件产品,其中有5件次品,从箱中任取10件产品,求恰有两件次品的概率.解 由概率的古典定义,事件A 的概率为2854510505!45!50!()/0.20982!3!8!37!10!40!C C P A C ==⋅=.13.设有甲、乙两批种子,发芽率分别为0.9和0.8,在两批种子中各随机取一粒,求:(1)两粒都发芽的概率; (2)至少有一粒发芽的概率; (3)恰有一粒发芽的概率.解: (1)()P AB =()()P A P B =0.9⨯0.8=0.72(2)()()()()()P A B P A P B P A P B +=+-=0.9+0.8-0.72=0.98 (3)()()()()()P AB AB P A P B P A P B +=+0.90.20.10.80.26=⨯+⨯=14.某工厂生产一批商品,其中一等品点12,每件一等品获利3元;二等品占13,每件二等品获利1元;次品占16,每件次品亏损2元。
华南理工大学网络教育学院《统计学原理》作业

精选文档华南理工大学网络教育学院《统计学原理》作业1、某快餐店某天随机抽取 49 名顾客对其的均匀花销进行抽样检查。
检查结果为: 均匀花销 8.6 元,标准差 2.8 元。
试以%的置信度预计:(1)该快餐店顾客整体均匀花销的置信区间及这日营业额的置信区间(假定当日顾客有 2000 人);(2)若其余条件不变,要将置信度提升到%,起码应当抽取多少顾客进行调查? (提示:z,z0.0455 / 22;z0.0027 / 23, z2.78)解:( 1)、 x0.4 , x 249整体均值的置信区间:( , 8.6+0.8 )即( 7.8 ,9.4 )元营业总数的置信区间:( 2000*7.8 ,2000*9.4 )即( 15600,18800)元。
(2)必需的样本容量:2 n2110.25 1112、一所大学准备采纳一项学生在宿舍上网收费的举措,为认识男女学生对这一举措的见解,分别抽取了 150 名男学生和 120 名女学生进行检查,获得的结果以下:男学生 女学生 共计 同意 45 42 87 反对105 78 183 共计150120270请检 验男 女学 生对 上网 收费 的 见解 能否 同样 。
已 知: 明显 性水 平 =0.05,02.05 (1) 3.842, 02.05 (2) 5.992, 02.05 ( 4) 9.487 。
解:H0: μ1 =μ2H1:μ1μ2 不相等Df=(2-1)(2-1)=1决议:在 = 0.05 的水平上不可以拒绝 H0,结论:.3、一家管理咨询公司为不一样的客户举办人力资源管理讲座。
每次讲座的内容基本上是同样的,但讲座的听课者,有时是中级管理者,有时是初级管理者。
该咨询公司以为,不一样层次的管理者对讲座的满意度是不一样的,对听完讲座后随机抽取的不一样层次管理者的满意度评分以下(评分标准从1—— 10, 10 代表特别满意):高级管理者中级管理者初级管理者78579688571079941088经计算获得下边的方差剖析表:差别源SS df MS F P-value F crit组间组内总计17(1)请计算方差剖析表中的F值。
2017年度下半年华工继续教育提高线性代数与概率统计随堂理解练习参备考资料答案解析

1.(单选题) 计算?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:A问题解析:2.(单选题) 行列式?A.3;B.4;C.5;D.6.答题: A. B. C. D. (已提交)参考答案:B问题解析:3.(单选题) 计算行列式. A.12;B.18;C.24;D.26.答题: A. B. C. D. (已提交)参考答案:B问题解析:4.(单选题) 利用行列式定义计算n阶行列式:=? A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:C问题解析:5.(单选题) 计算行列式展开式中,的系数。
A.1, 4;B.1,-4;C.-1,4;D.-1,-4.答题: A. B. C. D. (已提交)参考答案:B问题解析:6.(单选题) 计算行列式=?A.-8;B.-7;C.-6;D.-5.答题: A. B. C. D. (已提交)问题解析:7.(单选题) 计算行列式=?A.130 ;B.140;C.150;D.160.答题: A. B. C. D. (已提交)参考答案:D问题解析:8.(单选题) 四阶行列式的值等于多少?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:D问题解析:9.(单选题) 行列式=?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:B问题解析:10.(单选题) 已知,则?A.6m;B.-6m;C.12m;D.-12m.答题: A. B. C. D. (已提交)参考答案:A11.(单选题) 设=,则?A.15|A|;B.16|A|;C.17|A|;D.18|A|.答题: A. B. C. D. (已提交)参考答案:D问题解析:12.(单选题) 设矩阵,求=?A.-1;B.0;C.1;D.2.答题: A. B. C. D. (已提交)参考答案:B问题解析:13.(单选题) 计算行列式=?A.-1500;B.0;C.-1800;D.-1200.答题: A. B. C. D. (已提交)参考答案:C问题解析:14.(单选题) 齐次线性方程组有非零解,则=?A.-1;B.0;C.1;D.2.答题: A. B. C. D. (已提交)参考答案:C问题解析:15.(单选题) 齐次线性方程组有非零解的条件是=?A.1或-3;B.1或3;C.-1或3;D.-1或-3.答题: A. B. C. D. (已提交)参考答案:A问题解析:16.(单选题) 如果非线性方程组系数行列式,那么,下列正确的结论是哪个?A.无解;B.唯一解;C.一个零解和一个非零解;D.无穷多个解.答题: A. B. C. D. (已提交)参考答案:B问题解析:17.(单选题) 如果齐次线性方程组的系数行列式,那么,下列正确的结论是哪个?A.只有零解;B.只有非零解;C.既有零解,也有非零解;D.有无穷多个解.答题: A. B. C. D. (已提交)参考答案:A问题解析:18.(单选题) 齐次线性方程组总有___解;当它所含方程的个数小于未知量的个数时,它一定有___解。
2017线性代数与概率统计随堂练习答案

1、(单选题) 计算?A.;B.;C.;D.、答题: A、B、C、D、(已提交)参考答案:A2、(单选题) 行列式?A.3;B.4;C.5;D.6、答题: A、B、C、D、(已提交)参考答案:B3、(单选题) 计算行列式、A.12;B.18;C.24;D.26、答题: A、B、C、D、(已提交)参考答案:B问题解析:4、(单选题) 利用行列式定义计算n阶行列式:=?A.;B.;C.;D.、答题: A、B、C、D、(已提交)参考答案:C问题解析:5、(单选题) 计算行列式展开式中,的系数。
A.1, 4;B.1,-4;C.-1,4;D.-1,-4、答题: A、B、C、D、(已提交)参考答案:B问题解析:6、(单选题) 计算行列式=?A.-8;B.-7;C.-6;D.-5、答题: A、B、C、D、(已提交)参考答案:B问题解析:7、(单选题) 计算行列式=?A.130 ;B.140;C.150;D.160、答题: A、B、C、D、(已提交)参考答案:D问题解析:8、(单选题) 四阶行列式的值等于多少?A.;B.;C.;D.、答题: A、B、C、D、(已提交)参考答案:D问题解析:9、(单选题) 行列式=?A.;B.;C.;D.、答题: A、B、C、D、(已提交)参考答案:B问题解析:10、(单选题) 已知,则?A.6m;B.-6m;C.12m;D.-12m、答题: A、B、C、D、(已提交)参考答案:A问题解析:11、(单选题) 设=,则?A.15|A|;B.16|A|;C.17|A|;D.18|A|、答题: A、B、C、D、(已提交)参考答案:D问题解析:12、(单选题) 设矩阵,求=?A.-1;B.0;C.1;D.2、答题: A、B、C、D、(已提交)参考答案:B问题解析:13、(单选题) 计算行列式=?A.-1500;B.0;C.-1800;D.-1200、答题: A、B、C、D、(已提交)参考答案:C问题解析:14、(单选题) 齐次线性方程组有非零解,则=?A.-1;B.0;C.1;D.2、答题: A、B、C、D、(已提交)参考答案:C问题解析:15、(单选题) 齐次线性方程组有非零解的条件就是=?A.1或-3;B.1或3;C.-1或3;D.-1或-3、答题: A、B、C、D、(已提交)参考答案:A问题解析:16、(单选题) 如果非线性方程组系数行列式,那么,下列正确的结论就是哪个?A.无解;B.唯一解;C.一个零解与一个非零解;D.无穷多个解、答题: A、B、C、D、(已提交)参考答案:B问题解析:17、(单选题) 如果齐次线性方程组的系数行列式,那么,下列正确的结论就是哪个?A.只有零解;B.只有非零解;C.既有零解,也有非零解;D.有无穷多个解、答题: A、B、C、D、(已提交)参考答案:A问题解析:18、(单选题) 齐次线性方程组总有___解;当它所含方程的个数小于未知量的个数时,它一定有___解。
2017线性代数与概率统计随堂练习答案

1.(单选题) 计算?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:A2.(单选题) 行列式?A.3;B.4;C.5;D.6.答题: A. B. C. D. (已提交)参考答案:B3.(单选题) 计算行列式. A.12;B.18;C.24;D.26.答题: A. B. C. D. (已提交)参考答案:B问题解析:4.(单选题) 利用行列式定义计算n阶行列式:=?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:C问题解析:5.(单选题) 计算行列式展开式中,的系数。
A.1, 4;B.1,-4;C.-1,4;D.-1,-4.答题: A. B. C. D. (已提交)参考答案:B问题解析:6.(单选题) 计算行列式=?A.-8;B.-7;C.-6;D.-5.答题: A. B. C. D. (已提交)参考答案:B7.(单选题) 计算行列式=?A.130 ;B.140;C.150;D.160.答题: A. B. C. D. (已提交)参考答案:D问题解析:8.(单选题) 四阶行列式的值等于多少?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:D问题解析:9.(单选题) 行列式=?A.;B.;C.;D..答题: A. B. C. D. (已提交)参考答案:B问题解析:10.(单选题) 已知,则?A.6m;B.-6m;C.12m;D.-12m.答题: A. B. C. D. (已提交)参考答案:A问题解析:11.(单选题) 设=,则?A.15|A|;B.16|A|;C.17|A|;A. C.12.(单选题) 设矩阵,求=?A.-1;B.0;C.1;D.2.答题: A. B. C. D. (已提交)参考答案:B问题解析:13.(单选题) 计算行列式=?A.-1500;B.0;C.-1800;D.-1200.答题: A. B. C. D. (已提交)参考答案:C问题解析:14.(单选题) 齐次线性方程组有非零解,则=?A. B. C. D.15.(单选题) 齐次线性方程组有非零解的条件是=?A.1或-3;B.1或3;C.-1或3;D.-1或-3.答题: A. B. C. D. (已提交)参考答案:A问题解析:16.(单选题) 如果非线性方程组系数行列式,那么,下列正确的结论是哪个?A.无解;B.唯一解;C.一个零解和一个非零解;D.无穷多个解.A. B. C. D.17.(单选题) 如果齐次线性方程组的系数行列式,那么,下列正确的结论是哪个?A.只有零解;B.只有非零解;C.既有零解,也有非零解;D.有无穷多个解.答题: A. B. C. D. (已提交)参考答案:A问题解析:18.(单选题) 齐次线性方程组总有___解;当它所含方程的个数小于未知量的个数时,它一定有___解。
华南理工大学 2017概率论试卷

诚信应考,考试作弊将带来严重后果!华南理工大学本科生期末考试2016-2017学年第二学期《概率论与数理统计》A 卷注意事项:1. 开考前请将密封线内各项信息填写清楚; 2. 所有答案请直接答在试卷上; 3.考试形式:闭卷;4. 本试卷共八大题,满分100分,考试时间120分钟。
一、 填空题(每小题3分,共18分)1. 设随机变量X 服从参数为λ的Poisson 分布,且已知[](1)(2)1E X X --=,则λ=。
2.随机变量X 的概率密度函数1221)(-+-=x xe xf π,则E (X )= 。
3. 设随机变量X 服从以n , p 为参数的二项分布,且EX =15,DX =10,则n = 。
4. 甲乙二人独立地同时破译密码,甲破译的概率为21,乙破译的概率为31,则该密码被破译的概率为_______。
5. 321,,Y Y Y 独立且均服从分布)(2n χ,则3212Y Y Y +服从_____________分布。
6. 设总体),(~2σμN X ,123,,X X X 为来自X 的样本,则当常数a =_________时,12311ˆ42X aX X μ=++是未知参数μ的无偏估计。
二、单项选择题(每小题3分,共18分)1. 设随机变量X 服从参数为3的泊松分布,1~8,3Y B ⎛⎫⎪⎝⎭,且Y X ,相互独立,则)43(--Y X D =()。
(A )13- (B )15(C )19(D )232. 有m 个球,随机地放在n 个盒子中(m n ≤),则某指定的m 个盒子中各有一球的概率为( ). A.!mm nB.!mn mC m n C.!n n m D. !nm nC n m3. 设0()1,0()1,()()1P A P B P A B P A B <<<<+=,则事件A 与B ( ) A. 互不相容 B. 互相对立 C. 互不独立 D. 相互独立4. 随机变量X 的概率密度函数为21(),(1)X f x x R x π=∈+,则3Y X =的密度函数()Y f y =( )A. 21,(1)y R y π∈+ B.23,(9)y R y π∈+C.21,(1)9y R y π∈+D.21,(19)∈+y R y π5. 设随机变量服从正态分布,对给定的,数满足.若,则等于( ).(A) (B) (C) (D)6. 设),,,(21n X X X 为总体)2,1(2N 的一个样本,X 为样本均值,则下列结论中正确的是( )。
华南理工线性代数与概率统计

1. 行列式?A.3B.4C.5D.6参考答案:B2. 用行列式的定义计算行列式中展开式,的系数。
A.1, 4B.1,-4C.-1,4D.-1,-4参考答案:B3. 计算行列式=()A.-8B.-7C.-6D.-5参考答案:B4. 行列式=()A.B.C.D.参考答案:B5. 设=,则?A.15|A|B.16|A|C.17|A|D.18|A|参考答案:D6. 齐次线性方程组有非零解,则=()A.-1B.0C.1D.2参考答案:C7. 设,,求=()A.B.C.D.参考答案:D8. 利用初等变化,求的逆=()A.B.C.D.参考答案:D9. 设,是其伴随矩阵,则=()A.B.C.D.参考答案:A10. 求的秩为()A.2B.3C.4D.5参考答案:D线性代数与概率统计·第二次作业1.用消元法解线性方程组,方程的解为:A.B.C.D.错误!未找到引用源。
参考答案:A2.齐次线性方程组有非零解,则必须满足()A.B.C.D.错误!未找到引用源。
参考答案:D3.非齐次线性方程组中未知量个数为n,方程个数为m,系数矩阵的秩为r,则()A.r=m时,方程组有解B.r=n时,方程组有唯一解C.m=n时,方程组有唯一解D.r<n时,方程组有无穷多个解错误!未找到引用源。
参考答案:A4.线性方程组:有解的充分必要条件是=()A.B.-1C.D.1错误!未找到引用源。
参考答案:A5.求齐次线性方程组的基础解系为()A.B.C.D.错误!未找到引用源。
参考答案:A6.设n元非齐次方程组的导出组仅有零解,则()A.仅有唯一解B.必有无穷多解C.必无解D.未必有解错误!未找到引用源。
参考答案:D7.设为矩阵,线性方程组的对应导出组为,则下面结论正确的是()A.若仅有零解,则有唯一解B.若有非零解,则有无穷多解C.若有无穷多解,则有非零解D.若有无穷多解,则仅有零解错误!未找到引用源。
参考答案:C8.写出下列随机试验的样本空间及下列事件的集合表示:从0,1,2三个数字中有放回的抽取两次,每次取一个,A:第一次取出的数字是0。
华南理工大学网路教育 线性代数与概率统计随堂练习作业

1.(单选题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403答题: A. B. C. D.4.(单选题)ff80808170a403答题: A. B. C. D.5.(单选题)ff80808170a403答题: A. B. C. D.6.(单选题)ff80808170a403答题: A. B. C. D.7.(单选题)ff80808170a403答题: A. B. C. D.8.(单选题)ff80808170a403答题: A. B. C. D.9.(单选题)ff80808170a403A. B. C.10.(单选题)ff80808170a403答题: A. B. C. D.1.(单选题)A. B. C.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403答题: A. B. C. D.4.(单选ff80808170a403答题: A. B. C. D.5.(单选题)ff80808170a403答题: A. B. C. D.随堂练习提交截止时间:2020-06-14 23:59:59当前页有3题,你已做0题,已提交0题,其中答对0题。
*提示:点击底部【保存我的答案】按钮,保存本页已答练习答案。
点击【提交当前页】按钮,提交当前页随堂练习。
点击【提交已做的题目】按钮,提交本练习所有已做随堂练习,题目不再允许修改。
1.(单选题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403答题: A. B. C. D.1.(单选题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403答题: A. B. C. D.4.(单选ff80808170a403答题: A. B. C. D.5.(单选题)ff80808170a403答题: A. B. C. D.6.(单选题)A. B. C.7.(单选题)ff80808170a403答题: A. B. C. D.第二章矩阵·2.3 逆矩阵1.(单选题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403答题: A. B. C. D.4.(单选题)ff80808170a403答题: A. B. C. D.5.(单选题)ff80808170a403答题: A. B. C. D.6.(单选题)ff80808170a403答题: A. B. C. D.7.(单选题)ff80808170a403答题: A. B. C. D.8.(单选题)ff80808170a403答题: A. B. C. D.9.(单选题)ff80808170a403答题: A. B. C. D.10.(单选题)ff80808170a403答题: A. B. C. D.第二章矩阵·2.4 矩阵的初等变换与矩阵的秩1.(单选题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403B.4.(单选题)ff80808170a403答题: A. B. C. D.5.(单选题)ff80808170a403答题: A. B. C. D.6.(单选题)ff80808170a403B.7.(单选题)ff80808170a403答题: A. B. C. D.8.(单选题)ff80808170a403答题: A. B. C. D.9.(单选题)B.10.(单选题)ff80808170a403答题: A. B. C. D.第三章线性方程组·3.1 线性方程组的解1.(单选题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.1.(单选题)ff80808170a403B.2.(单选题)ff80808170a403答题: A. B. C. D.3.(单选题)ff80808170a403答题: A. B. C. D.4.(单选题)ff80808170a403B.5.(单选题)ff80808170a403答题: A. B. C. D.6.(单选题)ff80808170a403答题: A. B. C. D.7.(单选题)ff80808170a403答题: A. B. C. D.8.(单选题)ff80808170a403答题: A. B. C. D.9.(单选题)ff80808170a403答题: A. B. C. D.第四章随机事件及其概率·4.1 随机事件题)ff80808170a403答题: A. B. C. D.2.(单选题)ff80808170a403答题: A. B. C. D.随堂练习提交截止时间:2020-06-14 23:59:59当前页有3题,你已做0题,已提交0题,其中答对0题。
华南理工大学网络教育学院作业主观题(统计学原理)完成

华南理工大学网络教育学院 《 统计学原理 》作业1、某快餐店某天随机抽取49名顾客对其的平均花费进行抽样调查。
调查结果为:平均花费8.6元,标准差2.8 元。
试以95.45%的置信度估计:(1)该快餐店顾客总体平均花费的置信区间及这天营业额的置信区间(假定当天顾客有2000人);(2)若其他条件不变,要将置信度提高到99.73%,至少应该抽取多少顾客进行调查? (提示:69.10455.0=z ,22/0455.0=z ;32/0027.0=z ,78.20027.0=z )答:4.0498.2==x μ,8.04.02=⨯=∆x总体均值的置信区间:(8.6-0.8,8.6+0.8)即(7.8,9.4)元 营业总额的置信区间:(2000*7.8,2000*9.4)即(15600,18800)元。
必要的样本容量: 11125.1108.08.2*922===n2、一所大学准备采取一项学生在宿舍上网收费的措施,为了解男女学生对这一措施请检验男女学生对上网收费的看法是否相同。
已知:显著性水平α=0.05, 487.9)4(,992.5)2(,842.3)1(205.0205.0205.0===χχχ。
答:H0: π1 = π2 H1: π1π2不相等α = 0.05 Df=(2-1)(2-1)=16176.011=-=∑∑==ijij ij ej ri e e f t决策:在α = 0.05的水平上不能拒绝H0结论:可以认为男女学生对上网收费的看法相同3、一家管理咨询公司为不同的客户举办人力资源管理讲座。
每次讲座的内容基本上是一样的,但讲座的听课者,有时是中级管理者,有时是低级管理者。
该咨询公司认为,不同层次的管理者对讲座的满意度是不同的,对听完讲座后随机抽取的不同层次管理者的满意度评分如下(评分标准从1——10,10代表非常满意):7 9 68 8 57 10 79 9 410 88经计算得到下面的方差分析表:差异源SS df MS F P-value F crit 组间0.0008 3.68组内18.9 1.26总计48.5 17(1)(2)请用α = 0.05的显著性水平进行方差分析。
华南理工大学《线性代数与概率统计》随堂练习及答案

第一章行列式·1.1 行列式概念1.(单选题)答题: A. B. C. D. (已提交)参考答案:A2.(单选题)答题: A. B. C. D. (已提交)参考答案:B3.(单选题)答题: A. B. C. D. (已提交)参考答案:B4.(单选题)答题: A. B. C. D. (已提交)参考答案:C5.(单选题)答题: A. B. C. D. (已提交)参考答案:C6.(单选题)答题: A. B. C. D. (已提交)参考答案:D7.(单选题)答题: A. B. C. D. (已提交)参考答案:C8.(单选题)答题: A. B. C. D. (已提交)参考答案:B第一章行列式·1.2 行列式的性质与计算1.(单选题)答题: A. B. C. D. (已提交)参考答案:B2.(单选题)答题: A. B. C. D. (已提交)参考答案:D3.(单选题)答题: A. B. C. D. (已提交)参考答案:C4.(单选题)答题: A. B. C. D. (已提交)参考答案:D5.(单选题)答题: A. B. C. D. (已提交)参考答案:D6.(单选题)答题: A. B. C. D. (已提交)参考答案:B7.(单选题)答题: A. B. C. D. (已提交)参考答案:A8.(单选题)答题: A. B. C. D. (已提交)参考答案:D9.(单选题)答题: A. B. C. D. (已提交)参考答案:B10.(单选题)答题: A. B. C. D. (已提交)参考答案:C第一章行列式·1.3 克拉姆法则1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:A3.(单选题)答题: A. B. C. D. (已提交)参考答案:B4.(单选题)答题: A. B. C. D. (已提交)参考答案:A5.(单选题)答题: A. B. C. D. (已提交)参考答案:B.(单选题)答题: A. B. C. D. (已提交)参考答案:D2.(单选题)答题: A. B. C. D. (已提交)参考答案:A3.(单选题)答题: A. B. C. D. (已提交)参考答案:C第二章矩阵·2.2 矩阵的基本运算1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:D3.(单选题)答题: A. B. C. D. (已提交)参考答案:B4.(单选题)答题: A. B. C. D. (已提交)参考答案:B5.(单选题)答题: A. B. C. D. (已提交)参考答案:D6.(单选题)答题: A. B. C. D. (已提交)参考答案:C7.(单选题)答题: A. B. C. D. (已提交)参考答案:D第二章矩阵·2.3 逆矩阵1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:B3.(单选题)答题: A. B. C. D. (已提交)参考答案:D4.(单选题)答题: A. B. C. D. (已提交)参考答案:C5.(单选题)答题: A. B. C. D. (已提交)参考答案:C6.(单选题)答题: A. B. C. D. (已提交)参考答案:D7.(单选题)答题: A. B. C. D. (已提交)参考答案:B8.(单选题)答题: A. B. C. D. (已提交)参考答案:C9.(单选题)答题: A. B. C. D. (已提交)参考答案:D10.(单选题)答题: A. B. C. D. (已提交)参考答案:B第二章矩阵·2.4 矩阵的初等变换与矩阵的秩1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:D3.(单选题)答题: A. B. C. D. (已提交)参考答案:B4.(单选题)答题: A. B. C. D. (已提交)参考答案:A5.(单选题)答题: A. B. C. D. (已提交)参考答案:A6.(单选题)答题: A. B. C. D. (已提交)参考答案:D7.(单选题)答题: A. B. C. D. (已提交)参考答案:C8.(单选题)答题: A. B. C. D. (已提交)参考答案:C9.(单选题)答题: A. B. C. D. (已提交)参考答案:C10.(单选题)答题: A. B. C. D. (已提交)参考答案:D11.(单选题)答题: A. B. C. D. (已提交)参考答案:B12.(单选题)答题: A. B. C. D. (已提交)参考答案:A13.(单选题)答题: A. B. C. D. (已提交)参考答案:B第三章线性方程组·3.1 线性方程组的解1.(单选题)答题: A. B. C. D. (已提交)参考答案:D2.(单选题)答题: A. B. C. D. (已提交)参考答案:A第三章线性方程组·3.2 线性方程组解的结构1.(单选题)答题: A. B. C. D. (已提交)参考答案:D2.(单选题)答题: A. B. C. D. (已提交)参考答案:A3.(单选题)答题: A. B. C. D. (已提交)参考答案:A4.(单选题)答题: A. B. C. D. (已提交)参考答案:B5.(单选题)答题: A. B. C. D. (已提交)参考答案:A6.(单选题)答题: A. B. C. D. (已提交)参考答案:C7.(单选题)答题: A. B. C. D. (已提交)参考答案:A8.(单选题)答题: A. B. C. D. (已提交)参考答案:D9.(单选题)答题: A. B. C. D. (已提交)参考答案:C第四章随机事件及其概率·4.1 随机事件1.(单选题)答题: A. B. C. D. (已提交)参考答案:D2.(单选题)答题: A. B. C. D. (已提交)参考答案:B第四章随机事件及其概率·4.2 随机事件的运算1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:A3.(单选题)答题: A. B. C. D. (已提交)参考答案:B1.(单选题)答题: A. B. C. D. (已提交)参考答案:B2.(单选题)答题: A. B. C. D. (已提交)参考答案:C3.(单选题)答题: A. B. C. D. (已提交)参考答案:B4.(单选题)甲乙两人同时向目标射击,甲射中目标的概率为0.8,乙射中目标的概率是0.85,两人同时射中目标的概率为0.68,则目标被射中的概率为()A.0.8 ;B.0.85;C.0.97;D.0.96.答题: A. B. C. D. (已提交)参考答案:C5.(单选题)答题: A. B. C. D. (已提交)参考答案:D第四章随机事件及其概率·4.4 条件概率与事件的独立性1.(单选题)答题: A. B. C. D. (已提交)参考答案:D2.(单选题)答题: A. B. C. D. (已提交)参考答案:B3.(单选题)答题: A. B. C. D. (已提交)参考答案:AA4.(单选题)设有甲、乙两批种子,发芽率分别为0.9和0.8,在两批种子中各随机取一粒,则两粒都发芽的概率为()A.0.8 ; B.0.72 ; C.0.9 ; D.0.27 .答题: A. B. C. D. (已提交)参考答案:B5.(单选题)设有甲、乙两批种子,发芽率分别为0.9和0.8,在两批种子中各随机取一粒,则至少有一粒发芽的概率为()A.0.9 ; B.0.72 ; C.0.98 ; D.0.7答题: A. B. C. D. (已提交)参考答案:C6.(单选题)设有甲、乙两批种子,发芽率分别为0.9和0.8,在两批种子中各随机取一粒,则恰有一粒发芽的概率为()A.0.1 ; B.0.3 ; C.0.27 ; D.0.26答题: A. B. C. D. (已提交)参考答案:D第四章随机事件及其概率·4.5 全概率公式与贝叶斯公式1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:D3.(单选题)答题: A. B. C. D. (已提交)参考答案:A4.(单选题)答题: A. B. C. D. (已提交)参考答案:B5.(单选题)答题: A. B. C. D. (已提交)参考答案:C1.(单选题)答题: A. B. C. D. (已提交)参考答案:A2.(单选题)答题: A. B. C. D. (已提交)参考答案:C3.(单选题)答题: A. B. C. D. (已提交)参考答案:B第五章随机变量及其分布·5.2 离散型随机变量1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:C3.(单选答题: A. B. C. D. (已提交)参考答案:B4.(单选题)答题: A. B. C. D. (已提交)参考答案:A5.(单选题)从一副扑克牌(52张)中任意取出5张,求抽到2张红桃的概率?A 0.1743;B 0.2743;C 0.3743;D 0.4743答题: A. B. C. D. (已提交)参考答案:B第五章随机变量及其分布·5.3 连续型随机变量1.(单选题)答题: A. B. C. D. (已提交)参考答案:C2.(单选题)答题: A. B. C. D. (已提交)参考答案:C3.(单选题)答题: A. B. C. D. (已提交)参考答案:A4.(单选题)答题: A. B. C. D. (已提交)参考答案:B5.(单选题)答题: A. B. C. D. (已提交)参考答案:A第五章随机变量及其分布·5.4 正态分布1.(单选题)答题: A. B. C. D. (已提交)参考答案:B2.(单选题)答题: A. B. C. D. (已提交)参考答案:C3.(单选题)答题: A. B. C. D. (已提交)参考答案:B4.(单选题)答题: A. B. C. D. (已提交)参考答案:C5.(单选题)答题: A. B. C. D. (已提交)参考答案:C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《线性代数与概率统计》作业题第一部分 单项选择题 1.计算11221212x x x x ++=++?(A )A .12x x -B .12x x +C .21x x -D .212x x -2.行列式111111111D =-=-- BA .3B .4C .5D .63.设矩阵231123111,112011011A B -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求AB =B A .-1B .0C .1D .24.齐次线性方程组123123123000x x x x x x x x x λλ++=⎧⎪++=⎨⎪++=⎩有非零解,则λ=?(C )A .-1B .0C .1D .25.设⎪⎪⎭⎫ ⎝⎛=50906791A ,⎪⎪⎪⎪⎪⎭⎫⎝⎛=67356300B ,求AB =?(D ) A .1041106084⎛⎫⎪⎝⎭B .1041116280⎛⎫⎪⎝⎭C .1041116084⎛⎫ ⎪⎝⎭D .1041116284⎛⎫⎪⎝⎭6.设A 为m 阶方阵,B 为n 阶方阵,且A a =,B b =,00A C B⎛⎫=⎪⎝⎭,则C =?( D ) A .(1)mab - B .(1)n ab - C .(1)n m ab +-D .(1)nmab -7.设⎪⎪⎪⎭⎫⎝⎛=343122321A ,求1-A =?( D )A .13235322111⎛⎫ ⎪ ⎪-- ⎪ ⎪-⎝⎭B .132********-⎛⎫⎪ ⎪- ⎪ ⎪-⎝⎭ C .13235322111-⎛⎫ ⎪⎪- ⎪ ⎪-⎝⎭ D .13235322111-⎛⎫⎪ ⎪-- ⎪ ⎪-⎝⎭8.设,A B 均为n 阶可逆矩阵,则下列结论中不正确的是(B )A .111[()]()()T TTAB A B ---= B .111()A B A B ---+=+C .11()()k k A A --=(k 为正整数)D .11()(0)n kA k A k ---=≠ (k 为正整数)9.设矩阵m n A ⨯的秩为r ,则下述结论正确的是( D ) A .A 中有一个r+1阶子式不等于零B .A 中任意一个r 阶子式不等于零C .A 中任意一个r-1阶子式不等于零D .A 中有一个r 阶子式不等于零10.初等变换下求下列矩阵的秩,321321317051A --⎛⎫⎪=- ⎪ ⎪-⎝⎭的秩为?(C )B .1C .2D .311.写出下列随机试验的样本空间及下列事件的集合表示:掷一颗骰子,出现奇数点。
DA .样本空间为{1,2,3,4,5,6}Ω=,事件“出现奇数点”为{2,4,6}B .样本空间为{1,3,5}Ω=,事件“出现奇数点”为{1,3,5}C .样本空间为{2,4,6}Ω=,事件“出现奇数点”为{1,3,5}D .样本空间为{1,2,3,4,5,6}Ω=,事件“出现奇数点”为{1,3,5}12.向指定的目标连续射击四枪,用i A 表示“第i 次射中目标”,试用i A 表示四枪中至少有一枪击中目标(C ):A .1234A A A AB .12341A A A A -C .1234A A A A +++D .113.一批产品由8件正品和2件次品组成,从中任取3件,则这三件产品中至少有一件不是正品的概率为(B )A .25 B .715C .815D .3514.甲乙两人同时向目标射击,甲射中目标的概率为0.8,乙射中目标的概率是0.85,两人同时射中目标的概率为0.68,则目标被射中的概率为(C )B .0.85C .0.97D .0.9615.袋中装有4个黑球和1个白球,每次从袋中随机的摸出一个球,并换入一个黑球,继续进行,求第三次摸到黑球的概率是( D )A .16125B .17125C .108125D .10912516.设A ,B 为随机事件,()0.2P A =,()0.45P B =,()0.15P AB =,(|)P A B =BA .16B .13C .12D .2317.市场供应的热水瓶中,甲厂的产品占50%,乙厂的产品占30%,丙厂的产品占20%,甲厂产品的合格率为90%,乙厂产品的合格率为85%,丙厂产品的合格率为80%,从市场上任意买一个热水瓶,则买到合格品的概率为(D )A .0.725B .0.5C .0.825D .0.86518.有三个盒子,在第一个盒子中有2个白球和1个黑球,在第二个盒子中有3个白球和1个黑球,在第三个盒子中有2个白球和2个黑球,某人任意取一个盒子,再从中任意取一个球,则取到白球的概率为(C )A .3136B .3236C .2336D .343619.观察一次投篮,有两种可能结果:投中与未投中。
令1,;0,X ⎧=⎨⎩投中未投中.试求X 的分布函数()F x 。
CA .0,01(),0121,1x F x x x <⎧⎪⎪=≤<⎨⎪>⎪⎩B .0,01(),0121,1x F x x x ≤⎧⎪⎪=<<⎨⎪≥⎪⎩C .0,01(),0121,1<⎧⎪⎪=≤<⎨⎪≥⎪⎩x F x x xD .0,01(),0121,1x F x x x <⎧⎪⎪=≤≤⎨⎪>⎪⎩20.设随机变量X 的分布列为===(),1,2,3,4,515kP X k k ,则或===(12)PX X ?(C )A .115B .215C .15D .415第二部分 计算题1.设矩阵231123111,112011011A B -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求AB .解:AB == ==- +(-1)=0 2.已知行列式2512371446125927-----,写出元素43a 的代数余子式43A ,并求43A 的值.解:43A =(-1)4+3M 43=-=(2 -(-5)+2 )=543.设1100010000100021A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥-⎣⎦,求. 解: A 2=4.求矩阵25321585431742041123A -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦的秩. 解:A=→→→所以,矩阵的秩为25.解线性方程组12312312331331590x x x x x x x x x +-=⎧⎪--=⎨⎪+-=⎩.解:对增广矩阵施以初等行变换: A=→ →2A所以,原方程组无解。
6..解齐次线性方程组1234123412341234240 23450413140750x x x xx x x xx x x xx x x x--++=⎧⎪+--=⎪⎨--+=⎪⎪--+=⎩.解:对系数矩阵施以初等变换:A=→→→→与原方程组同解得方程组为:所以,方程组一般解为:(其中,为自由未知量)7.袋中有10个球,分别编有号码1到10,从中任取一球,设A={取得球的号码是偶数},B={取得球的号码是奇数},C={取得球的号码小于5},问下列运算表示什么事件:(1)A+B;(2)AB;(3)AC;(4)AC;(5)B C+;(6)A-C.解:(1)A和B互斥事件且是对立事件,Ω;(2)AB是相互独立事件,ø;(3)AC是相互独立事件,,;(4)是相互独立的,,,,,,,,(5)是互斥时间,也是对立事件,,,(6)(A-C)表示的是互斥时间也是对立事件,,,8.一批产品有10件,其中4件为次品,现从中任取3件,求取出的3件产品中有次品的概率。
解:样本点总数=设A={取出的3件产品中有次品}P(A)=1﹣P(A)=1﹣=9.设A,B,C为三个事件,1P(A)=P(B)=P(C)=4,()()0P AB P BC==,1()8P AC=,求事件A,B,C至少有一个发生的概率。
解:同概率的一般加法公式相类似,有单由于,而所以即,这样,使得10.一袋中有m个白球,n个黑球,无放回地抽取两次,每次取一球,求:(1)在第一次取到白球的条件下,第二次取到白球的条件概率;(2)在第一次取到黑球的条件下,第二次取到白球的条件概率。
解:用A表示“第一次取到白球”,B表示“第二次取到白球”。
(1)带中原有m+n个球,其中m个白球。
第一次取到白球后,袋中还有m+n-1个球,其中m-1个为白球。
故;(2)袋中原有m+n个球,其中m个白球,第一次取到黑球后,袋中还有m+n-1个球,其中m个为白球。
故11.设A,B是两个事件,已知()0.5P A=,()0.7P B=,()0.8P A B+=,试求:()P A B-与()P B A-。
解:由于,则有所以,12.某工厂生产一批商品,其中一等品点12,每件一等品获利3元;二等品占13,每件二等品获利1元;次品占16,每件次品亏损2元。
求任取1件商品获利X的数学期望()E X与方差()D X。
解:()()()()13.某工厂采用三种方法生产甲乙丙丁四种产品,各种方案生产每种产品的数量如下列矩阵所示:5 9 7 47 8 9 646 5 7A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦甲乙丙丁方法一方法二方法三若甲乙丙丁四种产品的单位成本分别为10、12、8、15(万元),销售单位价格分别为15、16、14、17(万元),试用矩阵运算计算用何种方法进行生产获利最大?解:设单位成本矩阵 ,销售单价矩阵为,则单位利润矩阵为,从而获利矩阵为,于是可知,采用第二种方法进行生产,工厂获利最大14.某市场零售某蔬菜,进货后第一天售出的概率为0.7,每500g 售价为10元;进货后第二天售出的概率为0.2,每500g 售价为8元;进货后第三天售出的概率为0.1,每500g 售价为4元,求任取500g 蔬菜售价X 元的数学期望()E X 与方差()D X 。
解:。
