琼海市2013-2014学年度第二学期初三模拟测试(三)数学科试题

合集下载

2013年海南省中考数学科模拟试题(4)(含答案)

2013年初中毕业生学业考试模拟试题数学试卷一、选择题（每小题3分，共42分）1．－5的绝对值是（）A ．5B ．5-C ．15 D ． 15-2．下列图形中既是中心对称图形又是轴对称图形的是（）3．2008年爆发了世界金融危机，中国工商银行年度税后利润却比上一年增加了人民币28 900 000 000元．用科学记数法表示这个数字为（）（A ）9109.28⨯．（B ）91089.2⨯．（C ）101089.2⨯．（D ）1110289.0⨯．4．图1中几何体的主视图是（）5．下列运算正确的是（）A ．4222a a a =+ B ．832)(a a -=- C ．（-ab ）2=2ab 2 D ．a a a 4)2(2=÷6．某班七个合作学习小组人数为：5，5，6，x ，7，7，8，已知这组数据的平均数是6，则这组数据的中位数是（） A ．7 B ．6C ．5D ．47．若21-x 没有意义，则x 的取值范围（）A ． x ＞2B ．x ≥ 2C ．x ＜2D ．x ≤2 8．方程220x x -=的解是（）A ．2x =．B ．0x =．C ．10x =，22x =-．D ．10x =，22x =．9. 已知⊙1O 的半径为3㎝, ⊙2O 的半径为4㎝,且圆心距125O O cm =，则⊙1O 与⊙2O 的位置关系是（）A.外离B.外切C.相交D.内含B ACD正面A Ｂ C D图110．一次函数2y x =-+的图象是（）11．如图2，D 、E 为△ABC 边上的点，DE ∥BC ，AB AD 31=，△ADE 的面积等于2，则四边形DBCE 的面积等于（）A ．8B ．9C ．16D ．2512．下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小明从中抽出一张，则抽到偶数的概率是（）A ．13B ．12C ．34D ．2313．如图3，∠AOB ＝90°，∠B ＝30°，△A’OB’可以看作是由△AOB 绕点O 顺时针旋转α角度得到的，若点A’在AB 上，则旋转角α的大小可以是（）A ．30°B ．45°C ．60°D ．90°14．如图4，在⊙O 中，AB 为弦，OC ⊥AB 于C ，若AO =5，OC =3，则弦AB 的长为（） A ．4 B ．6 C ．8 D ．10 二、填空题（每小题3分，共12分）15．分解因式：29a -= ．16．如图5，四边形ABCD 的对角线互相平分，要使它变为菱形，需要添加的条件是__________．（只填一个你认为正确的即可）．17．如图6，PA 是O ⊙的切线，切点为A ，36APO ∠=°，则AOP ∠的度数为．y xO 2-2 A yxO 2 -2 By xO -2 C- 2 y x O 2 D2OABC 图4BA /A OB /图3图218．观察下面的一列单项式：x ，22x -，34x ，48x -，…根据你发现的规律，第7个单项式为；第n 个单项式为．三、解答题（共56分）19．（1）计算: 01132(π1)4sin 45()3--+++° （2）解方程：113-+=-x x x x ． 20．为了整治环境卫生，某地区需要一种消毒药水3250瓶，药业公司接到通知后马上采购两种专用包装箱，将药水包装后送往该地区．已知一个大包装箱价格为5元，可装药水10瓶；一个小包装箱价格为3元，可以装药水5瓶．该公司采购的大小包装箱共用了1700元，刚好能装完所需药水．求该药业公司采购的大小包装箱各是多少个？ 21．在大课间活动中，同学们积极参加体育锻炼，小明就本班同学“我最喜爱的体育项目”进行了一次调查统计，下面是他通过收集数据后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：（1）该班共有名学生；（2）请补全条形统计图和扇形统计图．（3）在扇形统计图中，“乒乓球”部分所对应的圆心角度数为；（4）若全校有1830名学生，请计算出“其他”部分的学生人数．22．（10分）如图，已知O 是坐标原点，B 、C 两点的坐标分别为（3，–1）、（2，1）.（1）以O 为位似中心，在y 轴的左侧将 △OBC 放大到两倍（即新图与原图的相似△比为2），画出图形；（2）分别写出B 、C 两点的对应点B ′、 C ′的坐标;（3）如果△OBC 内部一点M 的坐标为（x , y ）,写出M 的对应点M ′的坐标.ADCBOOA P-5-22y xCBO 16 14 12 10 8 6 4 2 0人数篮球足球乒乓球其他项目其他篮球 30%足球 18% 乒乓球图5图623．如图7，在梯形ABCD 中，AB DC ∥，90BCD ∠=，且1AB =，2BC =，tan 2ADC ∠=．（1）求证：DC BC =；（2）E 是梯形内一点，F 是梯形外一点，且EDC FBC ∠=∠，DE BF =，试判断ECF △的形状，并证明你的结论；（3）在（2）的条件下，当:1:2BE CE =，135BEC ∠=时，求sin BFE ∠的值．24．已知：如图8，抛物线2y ax bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ．其中点A 在x 轴的负半轴上，点C 在y 轴的负半轴上，线段OA 、OC 的长（OA <OC ）是方程2540x x -+=的两个根，且抛物线的对称轴是直线1x =．（1）求A 、B 、C 三点的坐标；（2）求此抛物线的表达式；（3）若点D 是线段AB 上的一个动点（与点A 、B 不重合），过点D 作DE ∥BC 交AC 于点E ，连结CD ，设BD 的长为m ，△CDE 的面积为S ，求S 与m 的函数关系式，并写出自变量m 的取值范围．S 是否存在最大值？若存在，求出最大值并求此时D 点坐标；若不存在，请说明理由．EBFCDA图7yxBD O A EC图82013年初中毕业生学业考试模拟试题数学试卷参考答案一、选择题1．A 2．B 3．C 4．C 5．D 6．B 7．C 8．D 9．C 10．D 11．C 12．C 13．C 14．C二、填空题15．（a ＋3）(a －3) 16．AC BD ⊥或AB BC =，或BC CD =，或CD DA =，或AB AD = 17．540 18．64x 7 (－2)n-1x n 三、解答题19．（１）1132(π1)4sin 453-⎛⎫-++ ⎪⎝⎭+° 2421432=-++⨯ 421223=-++ 622=+（２）方程两边同乘以(x －3)(x －1)，得 x （x －1）＝(x ＋1)（x －3）解这个方程，得x ＝－3．检验：把x ＝－3代入最简公分母，得(x －3)(x －1)≠0．∴原方程的解是x ＝－3．20．设公司采购了x 个大包装箱，y 个小包装箱.根据题意得：⎩⎨⎧=+=+1700353250510y x y x 解之得：⎩⎨⎧==150250y x 答：公司采购了250个大包装箱，150个小包装箱． 21．（1）50 （2）略（3）115．２０（4）366名． 22．（1）如图，△O B ′C ′即为所求. （2）点B ′的坐标为（–6，2），点C ′的坐标为（–4，–2）. （3）M ′的坐标为（–2 x , –2 y ）.23．（1）过A 作DC 的垂线AM 交DC 于M ．则2AM BC ==．又tan 2ADC =∠，所以212DM ==．因为1M C AB ==，所以2DC DM M C =+=．即DC BC =．（2）等腰直角三角形．证明：因为DE BF =，EDC FBC =∠∠，DC BC =，所以，DEC BFC △≌△．所以CE CF =，ECD BCF =∠∠．所以90ECF BCF BCE ECD BCE BCD =+=+==∠∠∠∠∠∠．即ECF △为等腰直角三角形．B'C'-5-22y x CBOABEFCMD（3）设BE k =，则2CE CF k ==．所以22EF k =．因为135BEC =∠，又45CEF =∠，所以90BEF =∠．所以()22223BF k k k =+=．所以1sin 33k BFE k ==∠． 24．（1）∵OA 、OC 的长是x 2－5x +4=0的根，OA <OC ∴OA =1，OC =4∵点A 在x 轴的负半轴，点C 在y 轴的负半轴 ∴A （－1，0） C （0，－4） ∵抛物线2y ax bx c =++的对称轴为1x = ∴由对称性可得B 点坐标为（3，0）∴A 、B 、C 三点坐标分别是：A （－1，0），B （3，0），C （0，－4）（2）∵点C （0，－4）在抛物线2y ax bx c =++图象上 ∴4c =-将A （－1，0），B （3，0）代入24y ax bx =+-得 ⎩⎨⎧=-+=--043904b a b a 解之得⎪⎪⎩⎪⎪⎨⎧-==3834b a∴ 所求抛物线表达式为：438342--=x x y （3）根据题意，BD m =，则4AD m =- 在Rt △OBC 中，BC =22OC OB +=5∵DE BC ∥，∴△ADE ∽△ABC AB AD BC DE =∴5(4)20544AD BC m mDE AB --===· 过点E 作EF ⊥AB 于点F ，则sin ∠EDF =sin ∠CBA =54=BC OC ∴54=DE EF ∴EF =54DE =452054m-⨯=4－m ∴S △CDE =S △ADC －S △ADE=21（4－m ）×421-（4－m ）（ 4－m ） =21-m 2+2m （0<m <4）∵S =21-（m －2）2+2， a =21-<0∴当m =2时，S 有最大值2. ∴点D 的坐标为（1，0）.yxA F O DBE C。

2013年中考数学模拟试卷(三)+答题卡+答案A3版

2013年中考数学模拟试卷（三）（满分120分，考试时间100分钟）一、选择题（每小题3分，共24分） 1. |-3|的倒数是【】A ．-3B ．13-C ．3D ．132. 已知：如图，BD 平分∠ABC ，点E 在BC 上，EF ∥AB ．若∠CEF =100°，则∠ABD 的度数为【】 A ．60° B ．50° C ．40° D ．30° C E FD A B 50321-1-2 -3-4 4-5 11231第2题图第3题图第5题图 3. 如图，数轴上表示的是某不等式组的解集，则这个不等式组可能是【】A ．1020x x +⎧⎨-⎩≥≥B ．1020x x +⎧⎨-⎩≤≥C ．1020x x +⎧⎨-⎩≤≥D ．1020x x +⎧⎨-⎩≥≥4. 2如下表所示：甲乙丙丁 x8.3 9.2 9.2 8.5 S 2111.11.7A ．甲B ．乙C ．丙D ．丁5. 如图是一个由多个正方体堆积而成的几何体的俯视图．图中所示数字为该位置上小正方体的个数，则这个几何体的左视图是【】A ．B ．C ．D ． 6. 如图，A ，B ，C 是⊙O 上的点，∠CAB =20°，过点C 作⊙O 的切线交OB 的延长线于点D ，则∠D =【】 A ．40° B ．50° C ．60° D ．70° 7. 已知二次函数y =12-x 2-7x +152，若自变量x 分别取x 1，x 2，x 3，且0<x 1<x 2<x 3，则对应的函数值y 1，y 2，y 3的大小关系正确的是【】 A ．y 1>y 2>y 3 B ．y 1<y 2<y 3 C ．y 2>y 3>y 1D ．y 2<y 3<y 1 8. 如图，OA ⊥OB ，等腰直角三角形CDE 的腰CD 在OB 上，∠ECD =45°，将△CDE 绕点C 逆时针旋转75°，点E 的对应点N 恰好落在OA 上，则OC CD的值为【】 A ．12 B ．13 C ．22 D 3二、填空题（每小题3分，共21分）9. 分解因式：269mn mn m ++=____________________． 10. 用反证法证明命题“三角形中至少有一个内角大于或等于60°”，首先应假设__________．11. 如图，直线x =t （t >0）与反比例函数2y x =，1y x=-的图象分别交于B ，C 两点，A 为y轴上的任意一点，则△ABC 的面积为____________．30°D CBE A第11题图第13题图第14题图12. 实验中学安排四辆车组织九年级学生团员去敬老院参加学雷锋活动，这四辆车的编号分别是1，2，3，4．小王和小李都可以从这四辆车中任选一辆搭乘，那么小王和小李搭乘的车编号相邻的概率是_______． 13. 如图，在□ABCD 中，AD =2，AB =4，∠A =30°，以点A 为圆心，AD 的长为半径画弧交AB于点E ，连接CE ，则阴影部分的面积是____________（结果保留π）．14. 如图，矩形纸片ABCD 中，AB =5cm ，BC =10cm ，CD 上有一点E ，EC =3cm ，AD 上有一点P ，P A =7cm ，过点P 作PF ⊥BC 交BC 于点F ，将纸片折叠，使点P 与点E 重合，折痕与PF 交于点Q ，则线段PQ 的长是___________cm ． 15. 如图，梯形ABCD 中，AD ∥BC ，点E 在BC 上，AE =BE ，点F 是CD 的中点，且AF ⊥AB ，若AD =2.7，AF =4，AB =6，则CE 的长为_________．三、解答题（本大题共8小题，满分75分）16. （8分）（1）计算：123(2)|1|3--π+-；（2）先化简，再求值：221111x x x x x ÷--+-，其中o2tan 45x =．CD B OAx =tyxO C B17. （9分）如图1，有一张矩形纸片，将它沿对角线AC 剪开，得到△ACD 和△A ′BC ′．（1）如图2，将△ACD 沿A ′C ′边向上平移，使点A 与点C ′重合，连接A ′D ，BC ，四边形A ′BCD 是形．（2）如图3，将△ACD 的顶点A 与A ′点重合，然后绕点A 沿逆时针方向旋转，使点D ，A ，B 在同一直线上，则旋转角为度；连接CC ′，四边形CDBC ′是形．（3）如图4，将AC 边与A ′C ′边重合，并使顶点B 和D 在AC 边的同一侧，设AB ，CD 相交于点E ，连接BD ，四边形ADBC 是什么特殊四边形？请说明你的理由．C C'B A'ADC D B A (C')A'C A (A')B C'C (C')B D E A (A')图1 图2 图3 图418. （9分）为增强环保意识，某社区计划开展一次“减碳环保，减少用车时间”的宣传活动，对部分家庭五月份的平均每天用车时间进行了一次抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图．请根据图中提供的信息，解答下列问题：（1）本次抽样调查了多少个家庭？（2）将图1中的条形图补充完整，直接写出用车时间的中位数落在哪个时间段内；（3）求用车时间在1~1.5小时的部分对应的扇形圆心角的度数；（4）若该社区有车家庭有1 600个，请你估计该社区用车时间不超过1.5小时的约有多少个家庭．19. （9分）小强在教学楼的点P 处观察对面的办公大楼．为了测量点P 到对面办公大楼上部AD 的距离，小强测得办公大楼顶部点A 的仰角为45°，底部点B 的俯角为60°，已知办公大楼高 46米，CD =10米．求点P 到AD 的距离（用含根号的式子表示）．20. （9分）如图，一次函数y =ax -1的图象与反比例函数k y x =的图象交于A ，B 两点，与x 轴交于点C ，与y 轴交于点D ，已知 OA 10tan ∠AOC 13=．（1）求a ，k 的值及点B 的坐标；（2）观察图象，请直接写出不等式1ax -≥kx 的解集；（3）在y 轴上存在一点P ，使得△PDC 与△ODC 相似（不包括全等），请你求出点P 的坐标． 21. （10分）某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y （万件）与销售单价x （元）之间的关系可以近似地看作一次函数y =-2x +100．（利润=售价-制造成本）（1）写出每月的利润z （万元）与销售单价x （元）之间的函数关系式．（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？（3）根据相关部门规定，这种电子产品的销售单价不能高于32元，如果厂商要获得每月不低于350万元的利润，那么这种产品每月的最低制造成本需要多少万元？ 22. （10分）如图1，在平面直角坐标系中，点A 的坐标为(1，0)，以OA 为边在第一象限内作正方形OABC ，点D 是x 轴正半轴上一动点（OD >1），连接BD ，以BD 为边在第一象限内作正方形DBFE ，设M 为正方形DBFE 的中心，直线MA 交y 轴于点N ．如果定义：只有一组对角是直角的四边形叫做损矩形．（1）试找出图1中的一个损矩形并说明这个损矩形的四个顶点在同一个圆上．（2）随着点D 位置的变化，点N 的位置是否会发生变化？若没有发生变化，求出点N 的坐标；若发生变化，请说明理由．（3）在图2中，过点M 作MG ⊥y 轴于点G ，连接DN ，若四边形DMGN 为损矩形，求点D 的坐标． 23. （11分）如图，在平面直角坐标系中，点A ，B ，C 在x 轴上，点D ，E 在y 轴上，OA =OD =2，OC =OE =4，DB ⊥DC ，直线AD 与经过B ，E ，C 三点的抛物线交于F ，G 两点，与其对称轴交于点M ．点P 为线段FG 上一个动点（不与F ，G 重合），PQ ∥y 轴与抛物线交于点Q ．（1）求经过B ，E ，C 三点的抛物线的解析式．（2）是否存在点P ，使得以P ，Q ，M 为顶点的三角形为等腰直角三角形？若存在，求出满足条件的点P 的坐标；若不存在，请说明理由．（3）若抛物线的顶点为N ，连接QN ，探究四边形PMNQ 的形状：①能否成为菱形；②能否成为等腰梯形．若能，请直接写出点P 的坐标；若不能，请说明理由．P B D C MA 0图1图2108°54°0.5~1小时2~2.5小时1.5~2小时1~1.5小时903010080604020 2.521.510.5 小时家庭数/个2013年中考数学模拟试卷（三）答题卡一、选择题（每小题3分，共24分）1．[A ] [B ] [C ] [D ] 2．[A ] [B ] [C ] [D ] 3．[A ] [B ] [C ] [D ] 4．[A ] [B ] [C ] [D ]5．[A ] [B ] [C ] [D ] 6．[A ] [B ] [C ] [D ] 7．[A ] [B ] [C ] [D ] 8．[A ] [B ] [C ] [D ]二、填空题（每小题3分，共21分）9._______________ 10.____________________________________11.______________ 12.________________ 13.________________ 14.______________ 15.________________三、解答题（本大题共8小题，满分75分） 16.（8分）注意事项1.答题前，考生务必先认真核对条形码上的姓名、准考证号、考场号、座位号，无误后将本人姓名、准考证号填在相应位置。

海南省2013届中考模拟卷(数学)

海南省2013届中考模拟卷（数学） (总分：120分，时间：100分钟)一、选择题(本大题满分42分，每小题3分)1、下列四个数中，其相反数是正整数的是A ．3B ．13C ．2-D ．12- 2、下列运算正确的是A.()222b a b a -=-B.()62342a a =-C.5232a a a =+D.()11--=--a a3、2012年一季度，全国城镇新增就业人数为2890000人，用科学记数法表示2890000是A ．71089.2⨯ B. 6109.2⨯ C. 61089.2⨯ D. 7109.28⨯4、函数2y x =+中，自变量x 的取值范围是A.2x >-B.2x -≥C.2x ≠-D.2x -≤5、我省五个旅游景区门票票价如下表所示（单位：元），关于这五个景区门票票价，下列说法中错误的是景区名称南山旅游区天涯海角亚龙湾热带森林公园呀诺达热带雨林大小洞天票价（元） 135 100 175 178 135A ．极差是78B ．中位数是135C ．众数是135D ．平均数是1456、已知关于x 的方程260x kx --=的一个根为3x =，则实数k 的值为（）A ．1B ．1-C ．2D ．2-7、如图,是某几何体的三视图及相关数据，下列判断正确的是A ．a ＞c B. b ＞cC ．2224c b a =+ D. 222c b a =+8、如图1所示，DE 是△ABC 的中位线，FG 为梯形BCED 的中位线，若BC=8，则FG 等于（）A.2B.3C.49、如图2，在 ABCD 中，已知AD=5cm ，AB=3cm ，AE 平分∠BAD 交BC 边于点E ，则EC 等于10、一个不透明的盒子中装有2个红球和1个白球，它们除颜色外都相同．若从中任意摸出一个球，则下列叙述正确的是（）A ．摸到红球是必然事件B ．摸到白球是不可能事件C ．摸到红球与摸到白球的可能性相等D ．摸到红球比摸到白球的可能性大图1 图2 图3 图411、洗衣机在洗涤衣服时，每浆洗一遍都经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水）．在这三个过程中，洗衣机内的水量y （升）与浆洗一遍的时间x （分）之间函数关系的图象大致为A. B . C . D. 12、如图3，△ABC 中，AB=AC ，∠BAC=90°，P 为BC 边的中点，∠EPF=90°，给出四个结论： ①∠B=∠BAP ；②AE=CF ；③PE=PF ；④ABC AEPF S S ∆=21四边形，其中正确的有 A ．4个 B ．3个 C ．2个 D ．1个13、如图4，梯形ABCD 中，∠ABC 和∠DCB 的平分线相交于梯形中位线EF 上的一点P ，若EF=3，则梯形ABCD 的周长为A ．9B ．10.5C ．12D ．1514、如图5，在平面直角坐标系中，点A 在第一象限，⊙A 与x 轴相切于点B （2， 0），与y 轴交于C （0，1），D （0，4）两点，则点A 的坐标是A.⎪⎭⎫ ⎝⎛2,25B. ⎪⎭⎫ ⎝⎛2,23C. ⎪⎭⎫ ⎝⎛25,2D. ⎪⎭⎫ ⎝⎛23,2 图5 二、填空题（本大题满分16分，每小题4分）15、当a=3，a-b=1时，代数式ab a -2的值是___ ____．16、已知一元二次方程0342=+-x x 的两根是1x 、2x ，则()()=--1121x x .17、如图6，⊙O 的半径为1，直线AB 是⊙O 的切线，切点为点B ，x y x y xyx y x y CD A B OD EPO A C B 弦BC ∥AO ，若∠A=30°，则劣弧⋂BC 的长为 .图618、如图7所示，∠AOP=∠BOP=15°，PC ∥OA 交OB 于C ，PE ⊥OB于E ，PD ⊥OA 于D,若PC=4，则PD 等于 . 三、解答题（本大题满分62分） 19、计算(满分10分，每小题5分) 图7（1） 30tan 33120092310+⎪⎭⎫ ⎝⎛--+-- （2）()()()422--+-a a a a 20、（满分8分）某中学学生会为考察该校学生参加课外体育活动的情况，采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名学生的兴趣爱好（每人只能选其中一项），并将调查结果绘制成如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：（1）在这次考察中一共调查了名学生。

海南省2013年中考数学科试题参考答案与评分标准

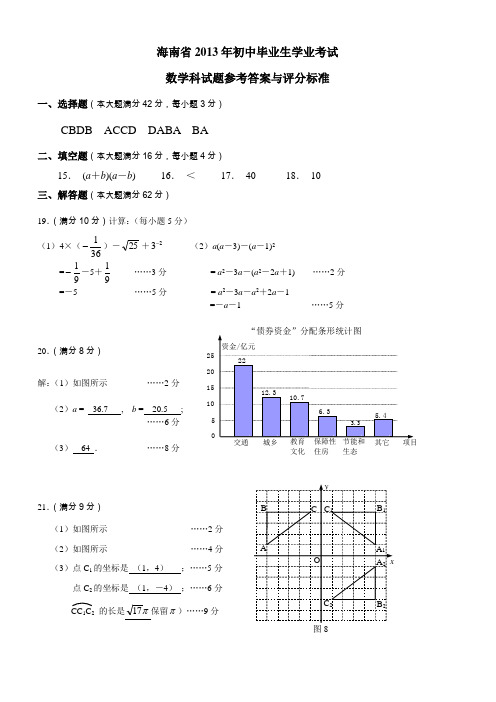
海南省2013年初中毕业生学业考试数学科试题参考答案与评分标准一、选择题（本大题满分42分，每小题3分）CBDB ACCD DABA BA二、填空题（本大题满分16分，每小题4分）15． (a ＋b )(a －b ) 16．＜ 17． 40 18． 10 三、解答题（本大题满分62分）19．（满分10分）计算：（每小题5分）（1）4×（361-）－25＋23- （2）a (a －3)－(a －1)2 =91-－5＋91……3分 = a 2－3a －(a 2－2a ＋1) ……2分=－5 ……5分 = a 2－3a －a 2＋2a －1=－a －1 ……5分20．（满分8分）解：（1）如图所示 ……2分（2）a = 36.7 , b = 20.5 ;……6分（3） 64 ． ……8分 21．（满分9分）（1）如图所示 ……2分（2）如图所示 ……4分（3）点C 1的坐标是（1，4）；……5分点C 2的坐标是（1，－4）；……6分的长是π17保留π）……9分22．（满分8分）解：七（1）班和七（2）班参加“光盘行动”的人数和为：128－38=90（人）设七（1）班参加“光盘行动”的人数为x ，七（2）班参加“光盘行动”的人数为y ，依题意得：⎩⎨⎧=-=+1090y x y x 解得：⎩⎨⎧==4050x x 答：七（1）班参加“光盘行动”的人数有50，七（2）班参加“光盘行动”的人数有40人．510152025文化住房生态CC 1C 223．（满分13分）（1）证明：∵四边形ABCD 是正方形 ∴BC=DC ， ∠BCP=∠DCE=90° 又CE=CP∴△BCP≌△DCE (SAS) ……4分（2） ①当CD=2PC 时，DP=CP ， ∵正方形ABCD 中，AD ∥BC ∴∠FDP=∠ECP=90° 又∠DPF=∠CPE∴△DPF ≌△CPE (ASA) ∴PF=PE∴四边形CEDF 是平行四边形 ∴FC ∥DE ，∠1=∠2 由（1）知△BCP≌△DCE (SAS) ∴∠3=∠1 ∴∠2=∠3∵∠3+∠BPC=90° ∴∠BPC+∠2=90° ∴∠PGC=90°∴BP ⊥CF ……8分②∵四边形ABCD 是正方形， ∴AD ∥BC ，CD=BC设PC=x ，则CE = CP=x ，又∵CD=n ·PC∴CD=BC=nx ， ∴BE=（n ＋1）x ∴PD=（n -1）x过点F 作FH ⊥BC 于点H ，则FH=CD=nx 则S 1=S △B FE －S △B PE=12（n ＋1）x ·nx －12（n ＋1）x ·x =12（n ＋1）（n -1）x 2 S 2=12（n -1）x ·x =12（n -1）x 212s s =221(1)(1)21(1)2n n x n x+--= n ＋1 ∴S 1=(n +1)S 2 ……13分24．（满分14分）（1）解：∵二次函数的图象过点A (－3，0)、B (－1，0) ∴设该函数的函数关系式为y =a (x +3)(x +1) 又∵函数的图象过点C (0，3)∴3a =3， a =1 ∴二次函数的函数关系式为y =(x +3)(x +1)即y =x 2+4x +3 ……3分（2）∵点P 的坐标为(－4，m )∴(－4)2+4×(－4)+3=m ，得m =3 则点P 的坐标为（－4，3）又点C 的坐标为（0，3） ∴PC ∥OQ PC =4∵Q 是一次函数y =kx －4k 的图象与x 轴的交点 ∴当y =0时，kx －4k =0，即k (x －4)=0 ∵k ≠0， ∴x =4∴点Q 的坐标为(4，0) ∵PC =OQ =4∴四边形POQC 是平行四边形∴∠OPC =∠AQC ……6分（3）①连结AN ，则有AM =3t ，CN =t∵点C 的坐标为C (0，3)， ∴OC =3 由（2）得OQ =4， ∴CQ =5∴QN =5－t过点N 作NG ⊥AQ 于点G ，则△QGN ∽△QOC ∴OC NG CQ NQ =，355NGt =-即图9(1) A D B C EP G1 23图9(2) A D B E F P∴NG =t 533-∴△AMN 的面积为S 与时间t 的函数关系式为)533(321t t S -⨯⨯=即845)25(1092+--=t S ∵点M 从点A 运动到点Q 需37秒，点N 从点C 运动到点Q 需5秒 ∴点M 先到达点Q ，即25370<≤≤t ∵当25≤t 时，S 随着t 的增大而增大∴当△AMN 的面积最大时， 37=t ……10分②直线PQ 能垂直平分线段MN当NQ =MQ ，且PQ 与MN 的交点H 是MN 的中点时，PQ 垂直平分线段MN ，∵QN =5－t ，MQ =7－3t ，则5－t =7－3t ， ∴t =1 即t =1，且PQ 与MN 的交点H 是MN 的中点时，直线PQ 垂直平分线段MN ，此时NQ =MQ =4，点M 的坐标为(0，0) 由①可得OQQGOC NG CQ NQ == 4354QG NG ==即，516512==，QG NG 则∴54=OG ， ∴点N 的坐标为(54，512)∴线段MN 的中点H 的坐标为(52，56)∴31,56452-==-k k k 则 ∴线段MN 的垂直平分线段PQ 的函数关系式为3431+-=x y∵点P 是直线PQ 与抛物线y =x 2+4x +3的公共点 ∴3431342+-=++x x x 解得⎪⎪⎩⎪⎪⎨⎧-=+-=181093761091311y x ，⎪⎪⎩⎪⎪⎨⎧+=--=181093761091322y x ∴点P 的坐标为)1810937,610913(-+-或)1810937,610913(+-- ……14分。

海南省中考数学模拟试题（3）(1)

海南省2014年初中毕业生学业模拟考试数学科试题（全卷满分120分，考试时间100分钟）一、选择题（本大题满分42分，每小题3分）在下列各题的四个备选答案中，有且只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求．．．用2B 铅笔涂黑． 1．3-的绝对值是A ．3B ．3-C ．13D ．13-2．下列运算正确的是A ．a 4•a 2=a 6B ．22532a b a b -=C ．325()a a -=D ．2336(3)9ab a b =3．当2x =-时，代数式x 2+1的值是A ．3B ．-3C ．5D ．5-4．在下面的四个几何体中，它们各自的左视图与主视图不相同的是（）5．一个三角形的两边长分别为3cm 和7cm ，则此三角形的第三边的长可能是 A ．3cm B ．4cm C ．7cm D ．11cm6．据中国之声《新闻纵横》2014年4月17日报道，澳大利亚海事安全局根据当地时间16日获得的最新消息，已经对搜索MH370的范围进行了修正，目前划定的搜索区域约为55151平方公里，用科学计数法表示55151为A ．5.5151x104B ．55.151x103C ．551.51x102D ．0.55151x1057．计算：)21(22x xx -÷-的正确结果为 . A.x B.x1C.-x 1D. -x x 2-8.一次函数12+=x y 的图像经过A. 第二、三、四象限B. 第一、三、四象限C. 第一、二、四象限D. 第一、二、三象限 9.不等式组⎩⎨⎧<>-31x x 的解集是 A. 1>x B. 31<<x C. 1->x D. 3<x10.下列图形中，既是轴对称图形又是中心对称图形的是正方体长方体圆柱圆锥 A B C DCBAE12DMCANB11.在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：跳高成绩(m) 1.50 1.55 1.60 1.65 1.70 1.75 跳高人数132351这些运动员跳高成绩的中位数和众数分别是A ．1.70，1.65B ． 1.65，1.70C ．1.70，1.70D ．3，5 12..如图3，已知21∠=∠，那么添加下列一个条件后，仍无法．．判定ABC ∆∽ADE ∆的是 A.AE AC AD AB = B. AED C ∠=∠ C.D B ∠=∠ D. DEBCAD AB =图3 图4 13.如图4，⊙B 的半径为4cm ， 60=∠MBN ，点A 、C 分别是射线BM 、BN 上的动点，且直线BN AC ⊥.当AC 平移到与⊙B 相切时，AB 的长度是A. cm 2B. cm 4C. cm 6D. cm 814.如图5，将□ABCD 折叠，使顶点D 恰落在AB 边上的点M 处，折痕为AN ，那么对于结论 ①MN ∥BC ，②MN AM =，下列说法正确的是A. ①②都错B. ①②都对C. ①对②错D. ①错②对二、填空题（本大题满分16分，每小题4分） 15．分解因式：a 2b -4b=_________．16．某工厂计划a 天生产60件产品，则平均每天生产该产品__________件．17．如图6，在平行四边形ABCD 中，AB = 6cm ，∠BCD 的平分线交AD 于点E ，则线段DE 的长度是____ cm ．18．如图7，将半径为4cm 的圆形纸片折叠后，圆弧恰好经过圆心的长度为_________cm ．三、解答题（本大题满分62分）19．（满分8分）（1）计算：11824()3-÷+-- （2）解方程：0111=--xABCD MN 图5A B CED 图6 图7 A O B20．（满分10分）在当地农业技术部门指导下，小明家增加种植菠萝的投资，使今年的菠萝喜获丰收. 下面是小明爸爸、妈妈的一段对话.请用学过的知识帮助小明算出他们家今年菠萝的收入。

九年级数学中考模拟考试检测试题3

海南省琼海市中考模拟考试数学科试题（3）（全卷满分110分，考试时间100分钟）特别提醒：1.选择题用2B 铅笔填涂，其余答案一律用黑色笔填写在答题卡上，写在试题卷上无效.2.答题前请认真阅读试题及有关说明.3.请合理安排好答题时间.一、选择题（本大题满分20分，每小题2分）在下列各题的四个备选答案中，只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求．．．用2B 铅笔涂黑. 1．化简－（－2）的结果是（）A ．－2B ．C ．D ．22．5月12日四川汶川发生8.0级大地震，给当地群众造成生命、财产重大损失，全国人民团结一心，帮助灾区人民渡过难关．中央电视台举办了《爱的奉献》抗震救灾募捐活动，募捐到救灾款15.14亿元．将15.14亿用科学记数法表示为（） A ．B ．C ．D ．3．下列计算中正确的是（）A ．B ．C ．D ．4．下列四个几何体中，已知某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆，则该几何体是（）Ａ．球体Ｂ．长方体Ｃ．圆锥体Ｄ．圆柱体5．如图1，直线，分别与相交，如果，那么的度数是（） A ．30°B ．45°C ．120°D ．75°6．下列四个选项中的三角形，与图2中的三角形相似的是（）7．不等式组的解集在数轴上表示正确的是（）21-21100.151410⨯9151410⨯91.51410⨯101.51410⨯336x x x +=339x x x =235()x x =32(3)()3x x x -÷-=12l l ∥l 12l l ，160∠=2∠2133x x +⎧⎨>-⎩≤ll 1 l 212图1A B DC 图28．如图3，利用标杆BE测量建筑物DC的高度，如果标杆BE长为1.5米，测得AB=2米，BC=10米．则楼高CD是（）A．8米 B．7.5米 C．9米 D．9.5米9．如图4，⊙O的直径AB垂直于弦CD，垂足为E，∠BAD=20°，则∠DOC等于（）A．60°B．50°C．40°D．20°10. 某商场对上周女装的销售情况进行了统计，销售情况如下表所示：颜色黄色绿色白色紫色红色数量（件）100 180 220 80 550 经理决定本周进女装时多进一些红色的，可用来解释这一现象的统计知识是（）Ａ．平均数Ｂ．中位数Ｃ．众数Ｄ．方差二、填空题（本大题满分24分，每小题3分）11.计算： .12.方程的解是 .13.写出图象经过点的反比例函数的表达式．14. 在盒子里放有三张分别写有整式x+3, 2x-3, 3的卡片，从中随机抽取两张卡片，把两张卡片上的整式分别作为分子和分母，则能组成分式的概率是．15．如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个的正方形图案，则其中完整的圆共有个．=(y+2)(y-2)2690x x-+=(13)-，22⨯33⨯44⨯1010⨯-3 1A．-3 1B．-3 1C．-3 1D．CAB图4ODEA BDC图316.如图5，在等腰梯形ABCD 中，AD ∥BC ，AE ∥DC ，∠B=60° AB =8cm ，则△AB E 的周长 cm .17. 如图6，将一副三角板叠放在一起,使直角的顶点重合于点O ，并能绕O 点自由旋转，若∠DOB =65°，则∠AOC+∠DOB = °.18．如图7，在矩形中，分别是边的中点，点在边上，且．若，，则图中阴影部分的面积为．三、解答题（本大题满分66分） 19.（本题满分10分，每小题5分）（1）计算: . （2）解方程： .20.（本题满分10分）5月12日，四川汶川发生了里氏8.0级大地震，给当地人民造成了巨大的损失．“一方有难，八方支援”，我省某中学全体师生积极捐款，其中九年级的3个班学生的捐款金额如下表：班级（1）班（2）班（3）班金额（元）1800吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上，但他知道下面三条信息：信息一：这三个班的捐款总金额是6800元；信息二：（2）班的捐款金额比（3）班的捐款金额多200元；请根据以上信息，帮助吴老师解决下列问题，求出（2）班与（3）班的捐款金额各是多少元；ABCD E F ，AD BC ，G H ，DC 12GH DC =10AB =12BC =121(4)16(8)4-⎛⎫-+÷- ⎪⎝⎭21321-=---x x x 图6A BDCOAB C图5ED图7FEC21. （本题满分10分）某市推行新型农村医疗合作，村民只要每人每年交10元钱，就可以加入合作医疗，每年先由自己支付医疗费，年终时可得到按一定比例返回的返回款.这一举措极大地增强了农民抵御大病风险的能力.小明与同学随机调查了他们乡的一些农民，根据收集到的数据绘制了以下的统计图.根据以上信息，解答以下问题：（1）本次调查了多少村民，被调查的村民中，有多少人参加合作医疗得到了返回款？（2）该乡若有10000村民，请你估计有多少人参加了合作医疗？要使两年后参加合作医疗的人数增加到9680人，假设这两年的年增长率相同，求这个年增长率.图9人数类别合作医疗参加合作医疗24060参加合作医疗得到了返回款占2.5%参加合作医疗但没得到返回款占97.5%22. （本题满分10分）如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（1）图形与图形关于直线成轴对称，请在图中画出对称轴并标注上相应字母、；（2）以图中点为位似中心，将图形放大，得到放大后的图形，则图形与图形的对应边的比是多少？（注：只要写出对应边的比即可）（3）求图形的面积．23．（本题满分12分）如图，在Rt △ABC 中，AB ＝AC ，P 是边AB （含端点）上的动点．过P 作BC 的垂线PR ，R 为垂足，∠PRB 的平分线与AB 相交于点S ，在线段RS 上存在一点T ，若以线段PT 为一边作正方形PTEF ，其顶点E ，F 恰好分别在边BC ，AC 上．（1）△ABC 与△SBR 是否相似，说明理由；（2）请你探索线段TS 与PA 的长度之间的关系；（3）设边AB ＝1，当P 在边AB （含端点）上运动时，请你探索正方形PTEF 的面积y的最小值和最大值．ABCD 1111A B C D MN M N O ABCD 2222A B C D ABCD 2222A B C D 2222A B C D TSR EB24. （本题满分14分）已知，在Rt △OAB 中，∠OAB ＝900，∠BOA ＝300，AB ＝2。

2014年海南省琼海市中考数学二模试卷(解析版)

2014年海南省琼海市中考数学二模试卷一、选择题（本大题满分42分，每小题3分）1．（3分）﹣4的绝对值是（）A．B．C．4D．﹣42．（3分）下列各式计算正确的是（）A．2a3﹣a3＝2B．a3•a2＝a6C．a6÷a3＝a3D．（a3）2＝a9 3．（3分）从不同方向看一只茶壶，你认为是俯视效果图的是（）A．B．C．D．4．（3分）海南省2010人口普查数据显示，全省总人口约为8670000，数据8670000用科学记数法表示应是（）A．8.67×106B．86.7×105C．8.67×105D．8.67×107 5．（3分）若式子在实数范围内有意义，则x的取值范围是（）A．x＞1B．x＜1C．x≥1D．x≤16．（3分）在一次歌咏比赛中，某选手的得分情况如下：92，88，95，93，96，95，94．这组数据的众数和中位数分别是（）A．94，94B．95，95C．94，95D．95，947．（3分）一元二次方程x2+3x＝0的解是（）A．x＝﹣3B．x1＝0，x2＝3C．x1＝0，x2＝﹣3D．x＝38．（3分）如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1＝28°，那么∠2的度数是（）A．60°B．62°C．68°D．72°9．（3分）如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为（）A．14B．15C．16D．1710．（3分）一条排水管的截面如图所示．已知排水管的截面圆半径OB＝10，截面圆圆心O 到水面的距离OC是6，则水面宽AB是（）A．16B．10C．8D．611．（3分）若从长度分别为3、5、6、9的四条线段中任取三条，则能组成三角形的概率为（）A．B．C．D．12．（3分）甲队修路120m与乙队修路100m所用天数相同，已知甲队比乙队每天多修10m．设甲队每天修路xm，依题意，下面所列方程正确的是（）A．＝B．＝C．＝D．＝13．（3分）如图，已知AE＝CF，∠AFD＝∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A．∠A＝∠C B．AD＝CB C．BE＝DF D．AD∥BC 14．（3分）如图，D是△ABC的边BC上一点，已知AB＝4，AD＝2．∠DAC＝∠B，若△ABD的面积为a，则△ACD的面积为（）A．a B．C．D．a二、填空题（本大题满分12分，每小题3分）15．（3分）分解因式：m2﹣6m+9＝．16．（3分）已知反比例函数y＝的图象经过点A（﹣3，﹣6），则k的值是．17．（3分）如图，梯形ABCD中，AD∥BC，AB＝DC＝3，AD＝5，∠C＝60°，则下底BC 的长为．18．（3分）如图，矩形纸片ABCD，AB＝6，点E在BC上，且AE＝EC．若将纸片沿AE 折叠，点B的对应点B′恰好落在AC上，则AC的长是．三、解答题（本大题满分62分）19．（10分）（1）计算：4×（﹣）﹣2cos60°+（2+π）0+2﹣2；（2）解不等式组：．20．（9分）苏州某旅行社组织甲、乙两个旅游团分别到西安、北京旅行，已知这两旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人．问甲、乙两个旅游团各有多少人？21．（8分）海桂学校青年志愿者协会对报名参加海南省大学生沙滩排球锦标赛的志愿者进行了一次与沙滩排球知识有关的测试，他们对测试的成绩作了适当的处理，将成绩分成三个等级：一般，良好，优秀，并将统计结果绘成了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：（1）请将两幅统计图补充完整；（2）一共有名学生参加了这次测试，如果青年志愿者协会决定让成绩为“优秀”的学生参加下一轮选拔测试，那么有人将参加下轮测试；（3）初三某班的小亮也参加了这次测试，并且获得了参加下一轮测试的资格．若学校最终只能从参加下一轮测试的人中推荐50人参加志愿者活动，则小亮被选中的概率是多少？（4）你最喜欢的体育运动项目是．22．（8分）在正方形网格中建立如图的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标是（4，4），请解答下列问题：（1）将△ABC向下平移5单位长度，画出平移后的△A1B1C1并写出点A对应点A1的坐标；（2）画出△A1B1C1关于y轴对称的△A2B2C2并写出A2的坐标；（3）S△ABC＝．23．（13分）如图，正方形ABCD中，点E从点A出发沿着AD向D运动，（点E不与点A，点D重合）同时点F从点D出发沿着线段DC向C运动，（点F不与点D，点C重合）点E与F点运动速度相同，当点E停止运动时，另一动点F随之停止运动，设BE与AF 相交于点P，连接PC请研究：（1）AF＝BE，AF⊥BE；（2）当点E运动到AD中点位置时：①P A：PB的值是多少？②PC和BC又怎样的数量关系？并证明你的结论．24．（14分）如图所示，在平面直角坐标中，抛物线经过原点O与点M（﹣4，0），顶点N 的纵坐标为4，以线段OM上的一个动点C为一个顶点，构造矩形ABCD，使边CD在线段OM上，点D在点C的左侧，点A、B在抛物线上（1）连接MN、ON，求△MON的面积；（2）求抛物线的解析式；（3）探究：当拖动点C时，矩形ABCD的形状会发生变化①当矩形ABCD为正方形时，求出点A的坐标；②设矩形ABCD的周长为l，请问l是否存在一个最大值？如果存在，求出这个最大值；如果不存在，请说明理由．2014年海南省琼海市中考数学二模试卷参考答案与试题解析一、选择题（本大题满分42分，每小题3分）1．（3分）﹣4的绝对值是（）A．B．C．4D．﹣4【解答】解：|﹣4|＝4．故选：C．2．（3分）下列各式计算正确的是（）A．2a3﹣a3＝2B．a3•a2＝a6C．a6÷a3＝a3D．（a3）2＝a9【解答】解：A、2a3﹣a3＝a3，故本选项错误；B、a3•a2＝a3+2＝a5，故本选项错误；C、a6÷a3＝a6﹣3＝a3，故本选项正确；D、（a3）2＝a3×2＝a6，故本选项错误．故选：C．3．（3分）从不同方向看一只茶壶，你认为是俯视效果图的是（）A．B．C．D．【解答】解：选项A的图形是从茶壶上面看得到的图形．故选：A．4．（3分）海南省2010人口普查数据显示，全省总人口约为8670000，数据8670000用科学记数法表示应是（）A．8.67×106B．86.7×105C．8.67×105D．8.67×107【解答】解：8670000＝8.67×106．故选：A．5．（3分）若式子在实数范围内有意义，则x的取值范围是（）A．x＞1B．x＜1C．x≥1D．x≤1【解答】解：由题意得：x﹣1≥0，解得：x≥1，故选：C．6．（3分）在一次歌咏比赛中，某选手的得分情况如下：92，88，95，93，96，95，94．这组数据的众数和中位数分别是（）A．94，94B．95，95C．94，95D．95，94【解答】解：这组数据按顺序排列为：88，92，93，94，95，95，96，故众数为：95，中位数为：94．故选：D．7．（3分）一元二次方程x2+3x＝0的解是（）A．x＝﹣3B．x1＝0，x2＝3C．x1＝0，x2＝﹣3D．x＝3【解答】解：x2+3x＝0，x（x+3）＝0，x＝0，x+3＝0，x1＝0，x2＝﹣3，故选：C．8．（3分）如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1＝28°，那么∠2的度数是（）A．60°B．62°C．68°D．72°【解答】解：如图，∵∠1＝28°，∴∠3＝90°﹣∠1＝90°﹣28°＝62°，∵直尺的两边互相平行，∴∠2＝∠3＝62°．故选：B．9．（3分）如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为（）A．14B．15C．16D．17【解答】解：∵四边形ABCD是菱形，∴AB＝BC，∵∠B＝60°，∴△ABC是等边三角形，∴AC＝AB＝4，∴正方形ACEF的周长是AC+CE+EF+AF＝4×4＝16，故选：C．10．（3分）一条排水管的截面如图所示．已知排水管的截面圆半径OB＝10，截面圆圆心O 到水面的距离OC是6，则水面宽AB是（）A．16B．10C．8D．6【解答】解：∵截面圆圆心O到水面的距离OC是6，∴OC⊥AB，∴AB＝2BC，在Rt△BOC中，OB＝10，OC＝6，∴BC＝＝＝8，∴AB＝2BC＝2×8＝16．故选：A．11．（3分）若从长度分别为3、5、6、9的四条线段中任取三条，则能组成三角形的概率为（）A．B．C．D．【解答】解：∵从长度分别为3、5、6、9的四条线段中任取三条的可能结果有：3、5、6；3、5、9；3、6、9；5、6、9；能组成三角形的有：3、5、6；5、6、9；∴能组成三角形的概率为：＝．故选：A．12．（3分）甲队修路120m与乙队修路100m所用天数相同，已知甲队比乙队每天多修10m．设甲队每天修路xm，依题意，下面所列方程正确的是（）A．＝B．＝C．＝D．＝【解答】解：设甲队每天修路xm，依题意得：＝，故选：A．13．（3分）如图，已知AE＝CF，∠AFD＝∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A．∠A＝∠C B．AD＝CB C．BE＝DF D．AD∥BC【解答】解：∵AE＝CF，∴AE+EF＝CF+EF，∴AF＝CE，A、∵在△ADF和△CBE中∴△ADF≌△CBE（ASA），正确，故本选项错误；B、根据AD＝CB，AF＝CE，∠AFD＝∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；C、∵在△ADF和△CBE中∴△ADF≌△CBE（SAS），正确，故本选项错误；D、∵AD∥BC，∴∠A＝∠C，∵在△ADF和△CBE中∴△ADF≌△CBE（ASA），正确，故本选项错误；故选：B．14．（3分）如图，D是△ABC的边BC上一点，已知AB＝4，AD＝2．∠DAC＝∠B，若△ABD的面积为a，则△ACD的面积为（）A．a B．C．D．a【解答】解：∵∠DAC＝∠B，∠C＝∠C，∴△ACD∽△BCA，∵AB＝4，AD＝2，∴△ACD的面积：△ABC的面积为1：4，∴△ACD的面积：△ABD的面积＝1：3，∵△ABD的面积为a，∴△ACD的面积为a，故选：C．二、填空题（本大题满分12分，每小题3分）15．（3分）分解因式：m2﹣6m+9＝（m﹣3）2．【解答】解：m2﹣6m+9＝（m﹣3）2，故答案为：（m﹣3）2．16．（3分）已知反比例函数y＝的图象经过点A（﹣3，﹣6），则k的值是18．【解答】解：根据题意得k＝﹣3×（﹣6）＝18．故答案为18．17．（3分）如图，梯形ABCD中，AD∥BC，AB＝DC＝3，AD＝5，∠C＝60°，则下底BC 的长为8．【解答】解：过D作DE∥AB交CB于E，∵AD∥BC，∴四边形ABED是平行四边形，∴DE＝AB＝3，BE＝AD＝5，∵AB＝DC＝3，∠C＝60°，∴DC＝DE＝3，∴△CDE是等边三角形，∴EC＝DC＝3，∴BC＝BE＝EC＝8，故答案为：8．18．（3分）如图，矩形纸片ABCD，AB＝6，点E在BC上，且AE＝EC．若将纸片沿AE折叠，点B的对应点B′恰好落在AC上，则AC的长是12．【解答】解：∵四边形ABCD是矩形，∴∠B＝90°，根据题意得：∠BAE＝∠EAB′，∠AB′E＝∠B＝90°，∴EB′⊥AC，∵AE＝EC，∴AB′＝CB′＝AB＝6，∴AC＝12．故答案为：12．三、解答题（本大题满分62分）19．（10分）（1）计算：4×（﹣）﹣2cos60°+（2+π）0+2﹣2；（2）解不等式组：．【解答】解：（1）原式＝﹣＝0；（2）由①得：x＜4由②得：x＞﹣3∴此不等式组的解集为﹣3＜x＜4．20．（9分）苏州某旅行社组织甲、乙两个旅游团分别到西安、北京旅行，已知这两旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人．问甲、乙两个旅游团各有多少人？【解答】解：设甲、乙两个旅游团各有x人、y人，由题意得：，解得，答：甲、乙两个旅游团各有35人、20人．21．（8分）海桂学校青年志愿者协会对报名参加海南省大学生沙滩排球锦标赛的志愿者进行了一次与沙滩排球知识有关的测试，他们对测试的成绩作了适当的处理，将成绩分成三个等级：一般，良好，优秀，并将统计结果绘成了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：（1）请将两幅统计图补充完整；（2）一共有500名学生参加了这次测试，如果青年志愿者协会决定让成绩为“优秀”的学生参加下一轮选拔测试，那么有250人将参加下轮测试；（3）初三某班的小亮也参加了这次测试，并且获得了参加下一轮测试的资格．若学校最终只能从参加下一轮测试的人中推荐50人参加志愿者活动，则小亮被选中的概率是多少？（4）你最喜欢的体育运动项目是跳高．【解答】解：（1）表现良好所占百分比为1﹣50%﹣20%＝30%，全班总人数：100÷20%＝500人，表现优秀人数为500×50%＝250人；（2）全班人数为100÷20%＝500（人），优秀人数为500×50%＝250（人）．故答案为500，250．（3）因为该校学生测试成绩为优秀的人数为500×50%＝250人，又因为参加下一轮测试中推荐50人参加志愿者活动，所以小亮被选中的概率是＝．（4）我最喜欢的体育运动项目是跳高；故答案为：跳高．22．（8分）在正方形网格中建立如图的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标是（4，4），请解答下列问题：（1）将△ABC向下平移5单位长度，画出平移后的△A1B1C1并写出点A对应点A1的坐标；（2）画出△A1B1C1关于y轴对称的△A2B2C2并写出A2的坐标；（3）S△ABC＝2．【解答】解：（1）如图所示，△A1B1C1即为所求作的三角形，点A1的坐标（4，﹣1）；（2）如图所示，△A2B2C2即为所求作的三角形；A2（﹣4，﹣1）；（3）S△ABC＝×2×2＝2．23．（13分）如图，正方形ABCD中，点E从点A出发沿着AD向D运动，（点E不与点A，点D重合）同时点F从点D出发沿着线段DC向C运动，（点F不与点D，点C重合）点E与F点运动速度相同，当点E停止运动时，另一动点F随之停止运动，设BE与AF 相交于点P，连接PC请研究：（1）AF＝BE，AF⊥BE；（2）当点E运动到AD中点位置时：①P A：PB的值是多少？②PC和BC又怎样的数量关系？并证明你的结论．【解答】（1）证明：∵E在AD边上（不与A、D重合），点F在DC边上（不与D、C重合）．又∵点E、F分别同时从A、D出发以相同的速度运动，∴AE＝DF，∵四边形ABCD是正方形，∴AB＝DA，∠BAE＝∠D＝90°，在△BAE和△ADF中，，∴△BAE≌△ADF（SAS），∴∠1＝∠2，∵∠2+∠3＝90°∴∠1+∠3＝90°即∠APB＝90°∴AF⊥BE．（2）解：由（1）知当点E运动到AD中点时，点F也运动到DC中点，此时就有AF⊥BE．∵F是CD的中点，∴DF＝CD，∵AD＝CD，∴DF＝AD，∵∠1＝∠2，∴tan∠1＝tan∠2在Rt△ADF中，tan∠2＝，∴在Rt△APB中，tan∠1＝∴P A：PB的值是1：2．（3）PC＝BC．证明：延长AF交BC的延长线于点G，在△ADF和△GCF中，∴△ADF≌△GCF（ASA），∴CG＝AD，∵BC＝AD，∴CG＝BC＝BG，由（1）知AF⊥BE，∴∠BPG＝90°，∴△BPG为直角三角形∴PC＝BG，∵BC＝BG，∴PC＝BC．24．（14分）如图所示，在平面直角坐标中，抛物线经过原点O与点M（﹣4，0），顶点N 的纵坐标为4，以线段OM上的一个动点C为一个顶点，构造矩形ABCD，使边CD在线段OM上，点D在点C的左侧，点A、B在抛物线上（1）连接MN、ON，求△MON的面积；（2）求抛物线的解析式；（3）探究：当拖动点C时，矩形ABCD的形状会发生变化①当矩形ABCD为正方形时，求出点A的坐标；②设矩形ABCD的周长为l，请问l是否存在一个最大值？如果存在，求出这个最大值；如果不存在，请说明理由．【解答】解：（1）∵点M的坐标为（﹣4，0）∴OM＝4作NE⊥y轴于点E，又顶点N的纵坐标为4∴NE＝4∴S△MON＝MO•NE＝×4×4＝8（平方单位）（3分）（2）抛物线的顶点N的纵坐标为4，且又经过原点O与点M（﹣4，0），所以顶点N的坐标为（﹣2，4）所以可设抛物线的解析式为y＝a（x+2）2+4（4分）∵抛物线y＝a（x+2）2+4过原点（0，0），∴0＝a（0+2）2+4∴a＝﹣1（5分）抛物线的解析式为y＝﹣（x+2）2+4即y＝﹣x2﹣4x（6分）（3）①设点D的坐标为（x，0），因为点A在抛物线y＝﹣x2﹣4x上，所以点A的坐标为（x，﹣x2﹣4x）（7分）D的坐标为（x，0），所以OD＝|X|＝﹣X，MD＝OC＝4+x∴CD＝OM﹣MD﹣OC＝﹣4﹣2x∴AD＝﹣x2﹣4x当矩形ABCD为正方形时有CD＝AD所以有﹣4﹣2x＝x2﹣4x即x2+2x﹣4＝0（8分）解得x1＝﹣1﹣，x2＝﹣1+﹣1+＞0时，点D不在OM上，不符合舍去．（9分）所以x＝﹣1﹣，所以﹣x2﹣4x＝﹣2+2当矩形ABCD为正方形时点A的坐标为（﹣1﹣，﹣2+2）（10分）②存在设点D的坐标为（x，0）则由①知：CD＝﹣4﹣2x，AD＝﹣X2﹣4X则l＝2（﹣4﹣2x）+2（﹣x2﹣4x）＝﹣2x2﹣12x﹣8＝﹣2（x+3）2+10（12分）所以当x＝﹣3时l存在最大值，最大值为10（13分）。

2014年琼海市度第一学期初中教学质量监测(期考)九年级数学科试题

琼海市2013-2014学年度第一学期初中教学质量监测（期考）九年级数学科试题（考试时间：100分钟满分：120分）一、单项选择题（每小题3分，共42分）1. 下列二次根式中，最简二次根式是（） A B C D2. 在等边三角形、平行四边形、矩形和圆这四个图形中，即是轴对称图形，又是中心对称图形的有（）个A ．1B ．2C ．3D ．43. 有一批型号相同的杯子，其中一等品7只，二等品3只，三等品2只，从中任意取一只杯子，是二等品的概率是（） A ．112B ．16C ．14 D．7124. 如果4x =是一元二次方程223x x a -=的一个根，则常数a 的值是（）A ．2B ．2-C ．2±D ．4± 5. ）A B ．2 C D ．1.4 6.下列计算正确的是（） A = B = C = D 3=-7. 二次函数2y x =的图像向右平移3个单位，得到新图像的函数表达式为（） A ．23y x =+ B ．23y x =- C ．()23y x =+D ．()23y x =-8. 如图，AB 是⊙O 的弦，BC 与⊙O 相切于点B ，连接OA 、OB ．若∠ABC =70°，则∠A 等于（） A ．15° B ．20°C ．30°D ．70°9. 若两圆的半径分别是1cm 和5cm ，圆心距为6cm ，则这两圆的位置关系是（） A ．内切 B ．相交 C ．外切 D ．外离 10. 二次函数()212y x =++的最小值是（）第8题第12题A ．2B ．1C ．-3D ．2311. 二次函数222y x x =-+的图像与x 轴的交点个数是 ( ) A ．0个 B ．1个 C ．2个 D ．3个 12.二次函数2y ax bx c =++图像如图所示，下列结论错误．．的是( ) A ．0a > B ．0b > C ．0c < D ．0abc >13. 将二次函数223y x x =-+化为()2y x h k =-+的形式，结果是（） A ．()214y x =++ B ．()214y x =-+ C ．()212y x =++ D ．()212y x =-+14. 如图所示，⊙O 的直径CD 过弦EF 的中点G ，∠EOD =40°，则 ∠DCF 等于（） A ．80° B ．50° C ．40° D ．20° 二、填空题（每小题4分，共16分） 15.函数y =x 的取值范围是 .16.方程22530x x ++=的解是．17. 某个房间的地板用如图所示的黑白瓷砖铺满，每块瓷砖都是边长相等的正方形，阴影部分是黑瓷砖，小华随意向其内部抛一三、解答题（本大题共62分） 19.计算：（每小题5分，共10分）（1）（2）(44+-20.（本题8分）某中学准备建一个面积375平方米的矩形游泳池，且游泳池的宽比长短10米，求游泳池的长与宽。

【初中数学】海南省2013年初中毕业升学模拟考试数学科试卷人教版

海南省2013年初中毕业升学模拟考试数学科试卷满分120分, 考试时间100分钟. （命题人：府城中学数学组）一、选择题（本大题满分42分，每小题3分） 1. 8-的倒数是（） A ．8B ．8-C ．18D ．18-2. 在等式()82a aa =⋅⋅中，括号内所填的代数式应当是（）A. 6a B. 5a C. 4a D. 3a3. 第29届北京奥运会火炬接力活动历时130天,传递行程约为137000km ．用科学记数法表示137000km 是（）A ．1.37×105km B ．13.7×104km C ．1.37×104km D ．1.37×103km 4. 函数21-=x y 中自变量x 的取值范围是（）A. 2+≠xB. 2<xC. 2≥xD. 2>x5. 下图是五个相同的小正方体搭成的几何体，其左视图．．．是（）6. 如图1所示，扇形AOB 的圆心角为120°，半径为2，则图中阴影部分的面积为（）（A ）43π（B ）43π-（C ）43π（D ）43π 图17. 如图2，是一个正方体的平面展开图，原正方体中“祝”的对面是（）图3（A ）考（B ）试（C ）顺（D ）利8. 在一个不透明的盒子里有3个分别标有数字5，6，7的小球，它们除数字外其他均相同．充DC B A……图①图②图③图④分摇匀后，先摸出1个球不放回，再摸出1个球，那么这两个球上的数字之和为奇数的概率为（） A ．23 B ．59 C ．49 D ．139．在平面直角坐标系中，点P(-4,3)与点Q 关于原点对称，则点Q 的坐标是( )A ．(4,3)B ．(-4,-3)C ．(4,-3)D ．(3,-4)10.如图3，点E(0,4)，O(0,0)，C(5,0)在⊙A 上，BE 是⊙A 上的一条弦．则tan ∠OBE 的值为（）A ．54B ． 34C ． 45D ．3511. 若等腰三角形中有一个角等于50，则这个等腰三角形的顶角的度数为（A ．50B ．80C ．65或50D ．50或8012．小龙和小刚两人玩“打弹珠”游戏，小龙对小刚说：“把你珠子的一半给我，我就有10颗珠子”.小刚却说：“只要把你的31给我，我就有10颗”，如果设小刚的弹珠数为x 颗，小龙的弹珠数为y 颗，则列出的方程组是（）A.⎩⎨⎧=+=+303202y x y x B .⎩⎨⎧=+=+103102y x y x C.⎩⎨⎧=+=+103202y x y x D ．⎩⎨⎧=+=+303102y x y x 13．如图4，//AB ED ， ︒=∠70ECF ，则BAF ∠的度数为( )A ．︒130B ．︒110C ．︒70D ．︒2014．下列图形都是由同样大小的矩形按一定的规律组成，其中，第①个图形中一共有6个矩形，第②个图形中一共有11个矩形，……，按此规律，第⑥个图形中矩形的个数为( )A ．30B ．25C ．28D ．31 二、填空题（本大题满分16分，每小题4分）15．因式分解：a ab 252-＝．16．已知反比例函数()0≠=k xk y 的图象经过点P(1,3)，若点(-3,b )在该图象上，则b = .ABC DEF 图417．如图5，在□ ABCD 中，对角线AC 、BD 交于点O ，E 是BC 边上的中点，若OE=2，AD=5，则□ ABCD 的周长为 .18．如图6，在△ABD 和△ACE 中，有下列四个论断：①AB=AC ；②AD=AE ；③∠B=∠C ；④BD=CE. 请以其中三个论断作为条件，余下一个论断作为结论，写出一个真命题是 . 三、解答题（本大题满分62分）19.（本题满分13分,第1小题6分、第2小题7分）（1）21(2)tan 452012⎛⎫+-+ ⎪⎝⎭⑵ 先化简，再求值：aa a -+-+12112，其中21-=a20. （本题满分8分）某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件。

2013～2014学年度第二学期初三第三次模拟考试数学试卷

新世纪教育网精选资料版权全部@新世纪教育网
附件 1. 考试命题双向详目表
(_2013 学年第二学期期中考试数学学科九年级)
2014年 3月20 日
题号知识点题型学习水平分数希望难度1相反数的观点选择题认识40.95 2整式的运算选择题运用40.90 3三视图选择题认识40.95 4图形的平移选择题理解40.85 5解直角三角形选择题理解40.80 6众数的观点选择题认识40.80 7一次函数的分析式选择题运用40.75 8垂径定理选择题理解40.75 9相像三角形及勾股定理选择题运用40.70 10勾股定理与正方形的性质选择题综合运用40.60 11因式分解填空题理解50.90 12分式的值填空题理解50.90 13平行线的性质填空题理解50.85 14圆周角定理及直角三角形的性质填空题理解50.80 15概率的计算填空题认识50.85 16反比率函数与平行四边形的性质应用填空题综合运用50.60 17实数的运算与解一元二次方程解答题理解100.75 18全等三角形的判断绘图题理解80.80 19作图 --- 图形的平移与等积变形解答题认识80.90 20统计图与概率的应用解答题运用100.70 21圆的切线及相像三角形的综合运用解答题综合运用100.65 22二元一次方程组及一元一次不等式的应用解答题运用100.60 23二次函数的综合运用解答题理解100.70 24相像三角形、特别四边形的综合应用解答题综合运用140.55
新世纪教育网精选资料版权全部@新世纪教育网
明：
1、型：、填空、解答、⋯⋯
2、学水平：认识（）、理解、运用、合运用；
3、目度散布基：中等：＝7：2：1；
得分率在 0.7 以上属基，得分率在 0.4-0.7 之属中等 , 得分率在 0.4 以部下。

2013届九年级第三次模拟考试数学试题(附答案)

2013届九年级第三次模拟考试数学试题一、选择题（每小题4分，共40分） 1.反比例函数xy 2-=的图象在 ……………………………( ) A. 第一、三象限 B. 第二、四象限 C. 第一、二象限 D. 第一、四象限2. 如图1，在直角△ABC 中，∠C ＝90°，若AB ＝5，AC ＝4，则tan ∠B ＝（）（A ）35（B ）45（C ）34 （D ）433. 已知：如图2，在△ABC 中，∠ADE ＝∠C ，则下列等式成立的是（）（A ）AD AB ＝AEAC（B ）AE BC ＝AD BD（C ）DE BC ＝AE AB （D ）DE BC ＝AD AB4. 袋中有3个红球，2个白球，若从袋中任意摸出1个球，则摸出白球的概率是（） A ．15 B ．25 C ．23 D ．135. 如图3，AB 是⊙O 的直径，弧BC=弧BD ，∠A =25°，则∠BOD 的度数为（） A. 25° B. 50° C. 12.5° D. 30°6.已知⊙O 1与⊙O 2内切，它们的半径分别为2和3，则这两圆的圆心距d 满足（）（A ）d=1 （B ）d=5 （C ）1＜d ＜5 （D ）d ＞57. 把抛物线y =3x 2向右平移一个单位, 则所得抛物线的解析式为…………… ( ) A. y =3(x +1)2 B. y =3(x -1)2 C. y =3x 2+1 D. y =3x 2-18. 如图4，身高为1.6m 的某学生想测量一棵大树的高度，她沿着树影BA 由B 到A 走去，当走到C 点时，她的影子顶端正好与树的影子顶端重合，测得BC =3.2m , CA =0.8m, 则树的高度为…（）A. 4.8mB. 6.4mC. 8mD. 10m9. 抛物线y =ax 2+bx +c 的图角如图3，则下列结论： ①abc >0；②a +b +c =2；③a >21；④b <1．其中正确的结论是（）（A ）①② （B ）②④ （C ） ②③ （D ）③④10. 小明、小亮、小梅、小花四人共同探究代数式x 2-4x +5的值的情况，他们作了如下分工：小明负责找值为1时的x 值，小亮负责找值为0时的x 值，小梅负责找最小值，小花负责找最大值。

2013年海南省中考数学科模拟试题(3)(无答案)

新世纪教育网精选资料版权全部 @新世纪教育网2013 年琼山二中九年级数学科中考模拟试题（一）（时间： 100 分钟满分： 120 分）一、选择题（每题3 分 . 本大题满分 42 分）在以下各题的四个备选答案中，只有一个是正确的，请把你以为正确的答案的字母代号填写在答题卡表格相应题号的方格内.1、 3 的绝对值是 ( )A． 3B ． 3 C．1 13D ．32. 把 1 枚质地平均的昔通硬币重复掷两次，落地后两次都是正面向上的概率是（）A ．1B ．1C ．1D ．12343. 以下计算正确的选项是（）A ．23 42 65B ．8 4 2C ．2733D ．( 3)234．某市总人口数约373 万，这人口数用科学记数法可表示为（）A. 3.73 104B. 3.73105C. 3.73 106D.3.73 1075．在以下图形中，既是轴对称图形又是中心对称图形的是A .BC.D6．方程组x y 4,的解是 ()x y2A ．x 2B ．x 2C ．x 1D ．x3 y2 y 0 y 3y 17. 如图，是由 5 个大小同样的小正方体摆成的立体图形，它的左视图．．．是 ( )正面AB. C. D.8. 将直线 y=2x 向下平移两个单位，所获取的直线为( )A ． y=2(x-2)B ． y=2(x+2)C ． y=2x+2 D． y=2x-29. 一组数据 2，- 1 ， 0， 2， -3 ， 3 的中位数和众数分别是 ( )A ．1，2B ．1，3 C． -1 ，2D ．0，2 10. 不等式 x 2 0 的解集是 ( )A. x 2 B． x 2 C． x 2 D ． x 211. 如图，已知∠ 1 = 70o ，假如 CD ∥ BE ，那么∠ B 的度数为（）新世纪教育网精选资料版权全部 @新世纪教育网12．如图，正比率函数y k 1x 与反比率函数 yk 2的图象订交于 A 、 B 两点，若点 A 的坐x标为（2， 1），则点 B 的坐标是 ( )A ．（1，2）B ．（-2，1）C ．（ -1 ，-2 ）D ．（-2，-1）3 13．如图，在菱形 ABCD 中， DEAB ， cos A ，则 tan DBE5A ．1B ．2C ．5 D ．5 22514．如图，△ ABC 是面积为 18cm 的等边三角形，被一平行于BC 的矩形所截， AB 被截成三平分，则图中暗影部分的面积为A ． 4cm 2 B． 6cm 2C ． 8 cm 2D． 10 cm 2ADyCA A EH1DOxFCB(EAEBBB第 14题图第 11 题图第 12题图第 13题图二、填空题（每题 4 分，本大题满分16 分）15. 若 2a - b= -3 ，则代数式 3-2a+b的值为．16．若 x ＝ 1 是一元二次方程 x 2＋ x ＋ c ＝ 0 的一个解，则 c 2．17．如图，将矩形 ABCD 沿 EF 、 EC 折叠，点 B 恰巧落在 EA上，已知 CD=4，BC=2， BE=1，则 EF 的长为.18．如图，已知⊙ P 的半径为 2，圆心 P 在抛物线 y1 x2 1 上运动，当⊙ P 与 x 轴相切时，2圆心 P 的坐标为.yACDPFBOxE第 18题图第 17题图三、解答题（本大题满分62 分）19. （此题满分 10 分，每题 5 分）1（1）计算：1183 26sin603GC新世纪教育网精选资料版权全部@新世纪教育网（2）化简求值：x21x 22x 2 1. 22x 1xx, 此中x=x220. ( 此题满分8 分 ) 某学校为 22 名“希望杯”数学比赛获奖学生买奖品，共用了2000 元，一等奖每人获取 200 元的奖品，二等奖每人获取 50 元的奖品，求获取一等奖和二等奖的学生疏别是多少人？21．（本小题满分8 分）为活跃校园文化氛围，某校举行以“看我家乡”为主题的图片制作比赛，赛后整理参赛同学的成绩，并制作成图表以下：分数段频数频次频数60≤x＜ 70300.1512070≤x＜ 80m0.459080≤x＜ 9060n6090≤x＜ 100200.13080 90 10060 70分数（分）请依据以上图表供给的信息，解答以下问题：（ 1）表中 m和 n 所表示的数分别为： m=,n=；（2 分）（ 2）请在图中，补全频数散布直方图；（ 2 分）（ 3）比赛成绩的中位数落在哪个分数段？（ 2 分）（ 4）假如比赛成绩80 分以上（含 80 分）能够获取奖赏，那么获奖率是多少？（ 2 分）22．( 此题满分 10 分 ) 以下图，正方形网格中，△ABC为格点三角形（即三角形的极点都在格点上）．（ 1）把△ABC沿BA方向平移后，点 A 移到点A1，在网格中画出平移后获取的△ A1B1C1；（3分）（ 2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△ A1 B2C2；（3分）（ 3）假如网格中小正方形的边长为1，求点 B 经过（1）、（2）变换的路径总长．（ 4 分）新世纪教育网精选资料版权全部 @新世纪教育网23．（此题满分 12 分）已知 E 是边长为 7 的正方形 ABCD 对角线 BD 上一点，过点MN 平行于 DC ，交 AD 于 M ，交 BC 于 N ， EF ⊥ AE 于 E ，交 CB 于 F ， MD=3.．．（ 1）求证：△ AME ≌△ ENF ；（ 4 分） M（ 2）求 AF 的长；（ 4 分）（ 3）求 tan ∠ BEF 的值 . （4 分）AEBFNE 的直线DC24．（本小题满分 14 分）已知：抛物线的极点坐标为 C(1,4) ，抛物线交 x 轴于点 A ，交 y 轴于点 B （ 0,3 ）． (1) 求抛物线分析式和线段AB 的长度；（ 3 分）(2) 连接 CA ， CB ，求△ ABC 的面积；（ 4 分） (3) 点 P 是在第一象限内的抛物线上的一个动点，过点P 作 y 轴的平行线，交AB 于点 D.①求线段 PD 的最大值，并求出此时P 点的坐标 . （3 分）②能否存在点P ，使 S △PAB = 5S △CAB ，若存在，求出 P 点的坐标；若不存在，请说明原因．（ 34分）yCPBDAxO2013 年琼山二中九年级数学科中考模拟试题（一）（答题卡）班别： ___________姓名： ______________座号： _________得分 ______________一、选择题（每题 3 分，共 42 分）题号1234567891011121314答案二、填空题（每题4分，共16分）15、 ______________； 16、 ______________； 17、 ______________ ；18、 ______________。