详解matlab如何将两组不同数量级的数据画在同一个y轴上
matlab对数曲线拟合

matlab对数曲线拟合Matlab是科学计算中非常流行的工具,在处理数据分析和数学模型方面有着广泛的应用。
其中,对数拟合是一种常用的数据拟合方法,可以在处理数据时起到非常重要的作用。
下面将分步骤阐述如何使用Matlab进行对数拟合。
第一步,导入数据。
对于需要拟合的数据,可以先将其保存为csv格式的文件,然后使用Matlab中的readmatrix函数将数据导入到工作区中。
例如:```data = readmatrix('data.csv');```其中,data代表导入的数据矩阵,data.csv为数据的文件名。
第二步,对数转换。
因为对数拟合是作用于对数函数(如y=log(x))上的,因此需要将原始数据进行对数转换。
可以使用Matlab中的log10函数进行转换。
例如,将x和y两列数据进行对数转换:```x = log10(data(:,1));y = log10(data(:,2));```第三步,进行拟合。
在将数据进行对数转换之后,可以使用Matlab中的polyfit函数进行拟合。
polyfit函数可以拟合一组多项式系数,其调用方式如下:```p = polyfit(x,y,n);```其中,x和y为对数转换后的数据矩阵,n为要拟合的多项式次数,p为拟合得到的多项式系数。
例如,对于一次对数拟合:```p = polyfit(x,y,1);```第四步,绘制拟合曲线。
拟合得到的多项式系数可以用于绘制对数拟合曲线。
可以使用Matlab中的polyval函数计算多项式函数在给定x点上的值。
例如,对于一次对数拟合:```fit_y = polyval(p,x);```然后可以使用Matlab中的plot函数将原始数据和拟合曲线进行绘制。
例如:```plot(x,y,'o');hold on;plot(x,fit_y);```其中,'o'表示绘制点,hold on表示保留画图区域,以便绘制多条曲线。
双变量联合概率分布matlab copula

双变量联合概率分布是指两个随机变量X和Y的联合分布。
在统计学和概率论中,联合概率分布描述了两个或多个随机变量同时取某些值的可能性。
matlab是一种功能强大的数学软件,它可以用来计算和可视化双变量联合概率分布。
copula是用来描述两个或多个随机变量之间依赖关系的数学工具,它可以将变量的边缘分布和联合概率分布分离开来,从而更好地描述变量之间的关系。
在matlab中,我们可以使用copulatoolbox来处理copula。
对于双变量联合概率分布,我们首先要定义两个边缘分布,然后再用copula 来描述它们之间的依赖关系。
接下来,我将介绍如何在matlab中使用copulatoolbox来计算和可视化双变量联合概率分布。
1. 定义边缘分布在matlab中,我们可以使用normpdf函数来定义正态分布。
我们可以定义X和Y的边缘分布为标准正态分布,代码如下:```matlabX = -3:0.1:3;Y = -3:0.1:3;mu = 0;sigma = 1;pdfX = normpdf(X, mu, sigma);pdfY = normpdf(Y, mu, sigma);```2. 定义copula在matlab中,我们可以使用copulaparam函数来定义copula的参数。
我们可以使用二元t分布来定义copula,代码如下:```matlabrho = 0.5; %相关系数df = 5; %自由度family = 't'; %分布类型param = copulaparam('t', [rho, df]);```3. 计算联合分布在matlab中,我们可以使用copulacdf函数来计算联合概率分布。
代码如下:```matlab[u, v] = meshgrid(0:0.1:1, 0:0.1:1); %设置横纵坐标C = copulacdf('t', [u(:), v(:)], param); %计算联合概率分布C = reshape(C, length(u), length(v)); %重塑C的维度```4. 可视化联合分布在matlab中,我们可以使用surf函数来可视化联合概率分布。
matlab 多组数据拟合曲线

matlab 多组数据拟合曲线在MATLAB中,可以使用多种方法对多组数据进行拟合。
其中,一种常用的方法是使用fit函数,它允许用户拟合多个数据集到一条或多条曲线。
下面是一个简单的例子来说明如何对多组数据进行拟合。
假设你有三组数据,分别存储在三个数组中:x1, y1, x2, y2, x3, y3。
% 创建数据x1 = 0:0.1:10; % x1的数据点y1 = 2*x1 + 1 + randn(size(x1)); % y1是x1的函数,加入一些随机噪声x2 = 5:0.5:20; % x2的数据点y2 = 3*x2 - 5 + randn(size(x2)); % y2是x2的函数,加入一些随机噪声x3 = 1:0.2:15; % x3的数据点y3 = 4*x3 + 3 + randn(size(x3)); % y3是x3的函数,加入一些随机噪声% 将数据组合到一起X = [x1; x2; x3]; % 所有x的数据组合到一起Y = [y1; y2; y3]; % 所有y的数据组合到一起% 使用fit函数拟合数据fitresult = fit(X,Y,'poly1'); % 使用一次多项式进行拟合% 绘制原始数据和拟合曲线figure;hold on;plot(X,Y,'o'); % 原始数据plot(fitresult); % 拟合曲线legend('Data','Fitted Polynomial');在上面的代码中,我们首先创建了三组数据,每组数据都是一些函数的值,其中包含一些随机噪声。
然后,我们将所有数据组合到一起,并使用fit函数对数据进行拟合。
在这个例子中,我们使用了一次多项式进行拟合,也就是'poly1'。
最后,我们将原始数据和拟合曲线一起绘制出来。
注意,如果你的数据适合更复杂的模型,你可以选择其他的拟合类型。
plotyy在matlab中的用法

plotyy在matlab中的用法plotyy是Matlab中的一个函数,用于在同一图中绘制两个不同的y 轴的曲线。
它可以帮助我们更清晰地展示两个不同变量之间的关系,提高数据可视化的效果。
在Matlab中,我们经常需要绘制多个变量之间的关系,但是如果这些变量的取值范围相差较大,那么在同一张图上绘制可能会导致其中一个变量的曲线被另一个变量的曲线所掩盖,从而无法准确观察到两者之间的关系。
这时,plotyy函数就派上了用场。
plotyy函数的基本用法如下:```[hAx, hLine1, hLine2] = plotyy(x1, y1, x2, y2, 'plot1', 'plot2')```其中,x1和y1是第一个曲线的横坐标和纵坐标数据,x2和y2是第二个曲线的横坐标和纵坐标数据。
'plot1'和'plot2'是可选参数,用于指定第一个曲线和第二个曲线的样式。
通过plotyy函数绘制的图形中,左侧的y轴对应第一个曲线,右侧的y轴对应第二个曲线。
我们可以通过设置不同的y轴范围,使得两个曲线在同一张图上都能够清晰地展示出来。
下面我们以一个简单的例子来说明plotyy函数的用法。
假设我们要绘制一个月份和温度之间的关系图,同时还要展示降雨量的变化。
我们可以先生成一些随机的数据作为示例数据:```x = 1:12; % 月份y1 = randi([0, 30], 1, 12); % 温度y2 = randi([0, 100], 1, 12); % 降雨量```然后,我们可以使用plotyy函数将这两个变量的曲线绘制在同一张图上:```[hAx, hLine1, hLine2] = plotyy(x, y1, x, y2, 'plot', 'plot');```接下来,我们可以对图形进行一些个性化的设置,比如设置y轴的范围、曲线的颜色和线型等:```set(hAx(1), 'YLim', [0, 30]); % 设置第一个y轴的范围set(hAx(2), 'YLim', [0, 100]); % 设置第二个y轴的范围set(hLine1, 'Color', 'r', 'LineStyle', '-'); % 设置第一个曲线的颜色和线型set(hLine2, 'Color', 'b', 'LineStyle', '--'); % 设置第二个曲线的颜色和线型```最后,我们可以添加一些标签和标题,使得图形更加清晰易懂:```xlabel('月份');ylabel(hAx(1), '温度');ylabel(hAx(2), '降雨量');title('月份、温度和降雨量关系图');```通过以上步骤,我们就可以得到一张包含两个y轴的关系图,清晰地展示了月份、温度和降雨量之间的关系。
教你如何用matlab绘图(全面)

强大的绘图功能是Matlab的特点之一,Matlab提供了一系列的绘图函数,用户不需要过多的考虑绘图的细节,只需要给出一些基本参数就能得到所需图形,这类函数称为高层绘图函数。
此外,Matlab还提供了直接对图形句柄进行操作的低层绘图操作。
这类操作将图形的每个图形元素(如坐标轴、曲线、文字等)看做一个独立的对象,系统给每个对象分配一个句柄,可以通过句柄对该图形元素进行操作,而不影响其他部分。
本章介绍绘制二维和三维图形的高层绘图函数以及其他图形控制函数的使用方法,在此基础上,再介绍可以操作和控制各种图形对象的低层绘图操作。
一.二维绘图二维图形是将平面坐标上的数据点连接起来的平面图形。
可以采用不同的坐标系,如直角坐标、对数坐标、极坐标等。
二维图形的绘制是其他绘图操作的基础。
一.绘制二维曲线的基本函数在Matlab中,最基本而且应用最为广泛的绘图函数为plot,利用它可以在二维平面上绘制出不同的曲线。
1.plot函数的基本用法plot函数用于绘制二维平面上的线性坐标曲线图,要提供一组x坐标和对应的y坐标,可以绘制分别以x和y为横、纵坐标的二维曲线。
plot函数的应用格式plot(x,y) 其中x,y为长度相同的向量,存储x坐标和y坐标。
例51 在[0 , 2pi]区间,绘制曲线程序如下:在命令窗口中输入以下命令>> x=0:pi/100:2*pi;>> y=2*exp(-0.5*x).*sin(2*pi*x);>> plot(x,y)程序执行后,打开一个图形窗口,在其中绘制出如下曲线注意:指数函数和正弦函数之间要用点乘运算,因为二者是向量。
例52 绘制曲线这是以参数形式给出的曲线方程,只要给定参数向量,再分别求出x,y向量即可输出曲线:>> t=-pi:pi/100:pi;>> x=t.*cos(3*t);>> y=t.*sin(t).*sin(t);>> plot(x,y)程序执行后,打开一个图形窗口,在其中绘制出如下曲线以上提到plot函数的自变量x,y为长度相同的向量,这是最常见、最基本的用法。
最全的MATLAB绘图命令

Matlab绘图强大的绘图功能是Matlab的特点之一,Matlab提供了一系列的绘图函数,用户不需要过多的考虑绘图的细节,只需要给出一些基本参数就能得到所需图形,这类函数称为高层绘图函数。
此外,Matlab还提供了直接对图形句柄进行操作的低层绘图操作。
这类操作将图形的每个图形元素(如坐标轴、曲线、文字等)看做一个独立的对象,系统给每个对象分配一个句柄,可以通过句柄对该图形元素进行操作,而不影响其他部分。
本章介绍绘制二维和三维图形的高层绘图函数以及其他图形控制函数的使用方法,在此基础上,再介绍可以操作和控制各种图形对象的低层绘图操作。
一.二维绘图二维图形是将平面坐标上的数据点连接起来的平面图形。
可以采用不同的坐标系,如直角坐标、对数坐标、极坐标等。
二维图形的绘制是其他绘图操作的基础。
一.绘制二维曲线的基本函数在Matlab中,最基本而且应用最为广泛的绘图函数为plot,利用它可以在二维平面上绘制出不同的曲线。
1. plot函数的基本用法plot函数用于绘制二维平面上的线性坐标曲线图,要提供一组x坐标和对应的y 坐标,可以绘制分别以x和y为横、纵坐标的二维曲线。
plot函数的应用格式plot(x,y) 其中x,y为长度相同的向量,存储x坐标和y坐标。
例51 在[0 , 2pi]区间,绘制曲线程序如下:在命令窗口中输入以下命令>> x=0:pi/100:2*pi;>> y=2*exp(-0.5*x).*sin(2*pi*x);>> plot(x,y)程序执行后,打开一个图形窗口,在其中绘制出如下曲线注意:指数函数和正弦函数之间要用点乘运算,因为二者是向量。
例52 绘制曲线这是以参数形式给出的曲线方程,只要给定参数向量,再分别求出x,y向量即可输出曲线:>> t=-pi:pi/100:pi;>> x=t.*cos(3*t);>> y=t.*sin(t).*sin(t);>> plot(x,y)程序执行后,打开一个图形窗口,在其中绘制出如下曲线以上提到plot函数的自变量x,y为长度相同的向量,这是最常见、最基本的用法。
matlab中plotyy的用法

matlab中plotyy的用法
plotyy 是MATLAB 中用于绘制双Y 轴图的一个函数。
它允许你在一个图上显示两个或更多具有不同量级或单位的Y 轴数据。
以下是plotyy 的基本用法:
plotyy(X1,Y1,X2,Y2)
其中:
X1 和X2 是用于第一个和第二个Y 轴的数据的X 坐标。
Y1 和Y2 是与X1 和X2 对应的Y 坐标。
例如,考虑以下数据:
X1 是年份,范围从1980 到2020。
Y1 是每年的人数,范围从1000 到10000。
X2 是年份,范围与X1 相同。
Y2 是每年的销售额,范围从100000 到500000。
使用plotyy 来绘制这两个数据集的方法如下:
X1 = 1980:2020;
Y1 = rand(51,1) * 10000 + 1000; % 随机生成的人数数据
Y2 = rand(51,1) * 500000 + 100000; % 随机生成的销售额数据plotyy(X1,Y1,X1,Y2)
此命令将在同一图上为Y1 和Y2 创建两个不同的Y 轴。
默认情况下,plotyy 会自动调整Y 轴的范围以适应数据。
您还可以使用其他函数来自定义Y 轴的外观和格式,例如更改标签、添加刻度等。
matlab多个坐标轴实现技巧

matlab多个坐标轴实现技巧摘要:一、Matlab多个坐标轴的基本概念二、Matlab多个坐标轴的实现方法1.创建多个坐标轴2.调整坐标轴属性3.添加轴标签和图例4.设置坐标轴比例尺三、实例演示1.绘制三维散点图2.绘制等高线图3.绘制双坐标轴图四、坐标轴的交互操作1.轴切换2.轴旋转3.轴缩放五、总结与拓展正文:一、Matlab多个坐标轴的基本概念在Matlab中,坐标轴是图形的重要组成部分,用于展示数据的分布和变化。
在某些情况下,单个坐标轴无法满足展示需求,此时需要使用多个坐标轴。
多个坐标轴可以使得数据展示更加丰富和直观,有助于分析数据之间的关系。
二、Matlab多个坐标轴的实现方法1.创建多个坐标轴在Matlab中,可以使用`axes`函数创建多个坐标轴。
例如,创建一个二维坐标轴:```matlabax1 = axes("Position", [0.1, 0.1, 0.8, 0.8]);```2.调整坐标轴属性创建坐标轴后,可以利用`set`函数调整坐标轴的属性,如颜色、线型等。
例如:```matlabax1.Color = "blue";ax1.LineWidth = 2;```3.添加轴标签和图例为了让图形更加清晰易懂,可以添加轴标签和图例。
使用`xlabel`、`ylabel`函数添加轴标签,使用`legend`函数添加图例。
例如:```matlabxlabel("X轴标签");ylabel("Y轴标签");legend("图例1", "图例2", "位置");```4.设置坐标轴比例尺坐标轴比例尺用于设置坐标轴的刻度间隔和范围。
可以使用`axes("XScale", "log");`设置横坐标轴比例尺为对数刻度。
axis equal在matlab中的用法

axis equal在matlab中的用法在MATLAB中,axisequal是一个非常重要的命令,它用于确保图形中的所有轴具有相同的比例。
这对于绘制不同类型的图表,例如面积图、条形图和散点图等非常有用,因为这样可以确保在不同轴上的数据能够以正确的方式进行比较。
本文将详细介绍axisequal在MATLAB中的用法,以及如何根据不同的情况使用它。
一、基本用法在MATLAB中,要使用axisequal命令,只需在绘图命令中加入该命令即可。
例如,要在绘制散点图时使用axisequal命令,可以这样写:```matlabx=[12345];y=[23456];plot(x,y,'o');%原代码:plot(x,y)axisequal;%在这里加入axisequal命令```这样,图形中的x轴和y轴就会具有相同的比例,使得我们可以比较不同点之间的距离。
二、其他用法除了基本用法之外,axisequal还有很多其他的使用方法。
例如,我们可以在绘制其他类型的图形时使用该命令,以确保图形中的所有轴具有相同的比例。
下面是一些示例:1.绘制面积图时使用axisequal命令:```matlabx=0:0.1:2*pi;y=sin(x);plot(x,y,'o');%原代码:plot(x,y)axisequaltight;%在这里加入axisequal和tight命令```通过使用axisequal和tight命令,我们可以确保面积图中的横纵坐标比例相等,并且图形不会被压缩或拉伸。
2.在绘制多条曲线时使用axisequal命令:```matlabx=[01234];y1=[12345];y2=[23456];plot(x,y1,'-o');%原代码:plot(x,y1,'-o')holdon;%加入holdon命令以在同一图形中绘制其他曲线plot(x,y2,'--o');%原代码:plot(x,y2,'--o')axisequal;%在这里加入axisequal命令holdoff;%最后加入holdoff命令以结束当前图形的绘制```通过使用holdon和holdoff命令,我们可以将多个曲线绘制在同一图形中,并确保它们之间的比较是正确的。
matlab中多组变量绘图:plot

matlab中多组变量绘图:plot2.plot(x,y)------ 绘制由x,y所确定的曲线.1)x,y是两组向量,且它们的长度相等,则plot(x,y)可以直观地绘出以x为横坐标,y为纵坐标的图形.如:画正弦曲线:t=0:0.1:2*pi;y=sin(t);plot(t,y)2)当plot(x,y)中,x是向量,y是矩阵时,则绘制y矩阵中各行或列对应于30向量x的曲线.如果y阵中行的长度与x向量的长度相同,则以y的行数据作为一组绘图数据;如果y阵中列的长度与x向量的长度相同,则以y的列数据作为一组绘图数据;如果y阵中行, 列均与x向量的长度相同,则以y的每列数据作为一组绘图数据.例:下面的程序可同时绘出三条曲线.MATLAB在绘制多条曲线时,会按照一定的规律自动变化每条曲线的的颜色.x=0:pi/50:2*pi;y(1,:)=sin(x);y(2,:)=0.6*sin(x);y(2,:)=0.3*sin(x);plot(x,y)或者还可以这样用:x=0:pi/50:2*pi;y=[ sin(x); 0.6*sin(x); 0.3*sin(x)];plot(x,y)01234567-1-0.8-0.6-0.4-0.20.20.40.60.813) 如果x,y是同样大小的矩阵,则plot(x,y)绘出y中各列相应于x 中各列的图形.例:x(1,:)=0:pi/50:2*pi;x(2,:)=pi/4:pi/50:2*pi+pi/4;x(3,:)=pi/2:pi/50:2*pi+pi/2;y(1,:)=sin(x(1,:));y(2,:)=0.6*sin(x(2,:));y(3,:)=0.3*sin(x(3,:));plot(x,y)x=x';y=y';figure31plot(x,y)在这个例子中,x------ 3x101,y------3x101,所以第一个plot按列画出101条曲线,每条3个点;而x'------101x3,y'------ 101x3,所以第二个plot按列画出3条曲线,每条101个点.012345678-1-0.8-0.6-0.4-0.20.20.40.60.81012345678-1-0.8-0.6-0.4-0.20.20.40.60.813. 多组变量绘图:plot(x1, y1, 选项1, x2, y2, 选项2, ……)上面的plot格式中,选项是指为了区分多条画出曲线的颜色,线型及标记点而设定的曲线的属性.MATLAB在多组变量绘图时,可将曲线以不同的颜色,不同的线型及标记点表示出来.这些选项如下表所示:各种颜色属性选项选项意义选项意义'r' 红色 'm' 粉红'g' 绿色 'c' 青色32'b' 兰色 'w' 白色'y' 黄色 'k' 黑色各种线型属性选项选项意义选项意义'-' 实线 '--' 虚线':' 点线 '-.' 点划线各种标记点属性选项选项意义选项意义'.' 用点号绘制各数据点 '^' 用上三角绘制各数据点'+' 用'+'号绘制各数据点 'v' 用下三角绘制各数据点'*' 用'*'号绘制各数据点 '>' 用右三角绘制各数据点' .' 用'.'号绘制各数据点 '<' 用左三角绘制各数据点's'或squar 用正方形绘制各数据点'p' 用五角星绘制各数据点'd'或diamond用菱形绘制各数据点 'h' 用六角星绘制各数据点这些选项可以连在一起用,如:'-.g'表示绘制绿色的点划线,'g+'表示用绿色的 '+'号绘制曲线.注意:1)表示属性的符号必须放在同一个字符串中;2)可同时指定2~3个属性;3) 与先后顺序无关;4)指定的属性中,同一种属性不能有两个以上.例:t=0:0.1:2*pi;y1=sin(t);y2=cos(t);y3=sin(t).*cos(t);plot(t,y1, '-r',t,y2, ':g',t,y3, '*b')该程序还可以按下面的方式写:t=0:0.1:2*pi;y1=sin(t);y2=cos(t);y3=sin(t).*cos(t);plot(t,y1, '-r')hold onplot(t,y2, ':g')plot(t,y3, '*b')hold off注:在MATLAB中,如画图前已有打开的图形窗口,则再画图系统将自动擦掉坐标系中已有的图形对象,但设置了hold on后,可以保持坐标系中已绘出的图形.。
matlab中plotyyy的用法

matlab中plotyyy的用法Matlab是一款广泛应用于数学计算、数据分析、图形绘制等领域的软件,它提供了丰富的函数和工具,方便用户进行各种数据处理和可视化操作。
在Matlab 中,plotyyy函数是一种用于绘制两个二维图形组合图形的函数,可以方便地展示两个变量之间的关系。
本文将介绍plotyyy函数的用法和实例。
一、概述plotyyy函数用于绘制两个y轴坐标系上的图形组合,它可以同时显示两个变量之间的关系。
该函数的基本语法为:plotyyy(x,y1,z1,xlabel,y1label,z1label,xsubs,y1subs,z1subs);其中x为数据x坐标,y1为第一个变量的数据,z1为第二个变量的数据,其他参数分别为x坐标轴的标签、y1轴的标签和z1轴的标签。
二、使用方法在使用plotyyy函数之前,需要先准备好数据。
通常,数据可以是数值型或矩阵型,需要根据实际情况进行选择。
下面是一个简单的例子:假设我们有两个变量x和y,它们之间的关系可以用散点图来表示。
我们可以使用plotyyy函数将它们组合在一起,如下所示:x=[12345];y=[23456];z=sin(x)+randn(size(x));plotyyy(x,y,z,'Xlabel','X-axisLabel','Y1label','Y1-axisLabel','Zlabel','Z-axisLabel');在这个例子中,我们首先定义了三个变量x、y和z,其中x是横坐标数据,y是第一个变量的数据,z是第二个变量的数据。
然后我们使用plotyyy函数将它们组合在一起,并指定了x坐标轴的标签、y1轴的标签和z轴的标签。
最后,我们使用x、y和z的值绘制出图形。
三、实例分析下面是一个更复杂的例子,展示如何使用plotyyy函数绘制两个三维图形组合:假设我们有两个变量x和y,它们之间的关系可以用三维曲面图来表示。
如何将两个不同坐标系的不同图形合并到一张图上

. 如何将两个不同坐标系的不同图形合并到一张图上1. 在两个图上选择两个公共点A和B(两点的距离尽量长一下,以保证转换的相对精度)。
在甲图中查询并记录下AB两点的XY坐标值,作为转换的目标坐标系的坐标值。
2. 打开另一张乙图,命令行输入Align对齐命令并回车,命令行提示如下:
选择对象: 鼠标框选中乙图中所有图形对象。
指定第一个源点: 鼠标拾取乙图面上公共点A,获取其坐标。
指定第一个目标点: 输入在甲图中查询并记录下来的点A的坐标值
指定第二个源点: 鼠标拾取乙图面上个公共点B,获取其坐标。
指定第二个目标点: 输入在甲图中查询并记录下来的点B的坐标值
指定第三个源点或<继续>: 回车
是否基于对齐点缩放对象?[是(Y)/否(N)] <否>: 输入Y。
命令结束,乙图就平移旋转到与甲图相同的坐标系上了。
3. 鼠标框选乙图的所有图形,输入CopyClip 复制命令回车。
4. 打开甲图,并输入PasteOrig命令回车,可将乙图的所有图形粘贴到甲图中,完成甲乙两图的合并。
;.。
matlab在两个数据点之间插值一条曲线的方法

一、插值的定义在数学和计算机科学中,插值是指在已知数据点的基础上,利用插值算法来估算出在这些数据点之间未知位置上的数值。
插值可以用于生成平滑的曲线、曲面或者函数,以便于数据的分析和预测。
二、matlab中的插值方法在matlab中,有多种插值方法可以用来在两个数据点之间插值一条曲线。
这些方法包括线性插值、多项式插值、样条插值等。
下面我们将逐一介绍这些方法及其使用场景。
1. 线性插值线性插值是最简单的插值方法之一。
它的原理是通过已知的两个数据点之间的直线来估算未知位置上的数值。
在matlab中,可以使用interp1函数来进行线性插值。
该函数的调用格式为:Y = interp1(X, Y, Xq, 'linear')其中X和Y分别是已知的数据点的横纵坐标,Xq是待估算数值的位置,'linear'表示使用线性插值方法。
使用线性插值可以快速地生成一条近似直线,但是对于非线性的数据分布效果可能不佳。
2. 多项式插值多项式插值是利用多项式函数来逼近已知数据点之间的曲线。
在matlab中,可以使用polyfit和polyval函数来进行多项式插值。
polyfit函数用于拟合多项式曲线的系数,polyval函数用于计算多项式函数在给定点的数值。
多项式插值的优点是可以精确地通过已知数据点,并且可以适用于非线性的数据分布。
3. 样条插值样条插值是一种比较常用的插值方法,它通过在每两个相邻的数据点之间拟合一个低阶多项式,从而保证整条曲线平滑且具有良好的拟合效果。
在matlab中,可以使用splinetool函数来进行样条插值。
样条插值的优点是对于非线性的数据分布可以有较好的拟合效果,且能够避免多项式插值过拟合的问题。
4. 三角函数插值三角函数插值是一种常用的周期性数据插值方法,它利用三角函数(如sin和cos)来逼近已知数据点之间的曲线。
在matlab中,可以使用interpft函数来进行三角函数插值。
matlab 多条曲线拟合公式

MATLAB是一种非常强大的数学软件,它可以用来进行数值计算、数据分析、图形展示等多种功能。
在MATLAB中,拟合多条曲线是一个常见的需求,它可以用来分析多种因素对某一变量的影响,也可以用来预测未来的趋势。
在本文中,我们将讨论MATLAB中拟合多条曲线的公式及其实现方法。
1. 多条曲线拟合的常见公式在MATLAB中,拟合多条曲线的常见公式包括多项式拟合、曲线拟合、曲线拟合等。
其中,多项式拟合是一种最常见的方法,它可以用来拟合多项式函数,一般形式为:y = a0 + a1*x + a2*x^2 + ... + an*x^n其中,y是因变量,x是自变量,a0、a1、a2等是多项式的系数,n是多项式的阶数。
使用MATLAB的polyfit函数可以实现多项式拟合。
2. 多条曲线拟合的实现方法在MATLAB中,拟合多条曲线的实现方法主要包括使用polyfit函数进行多项式拟合、使用curve fitting工具箱进行曲线拟合等。
下面我们将分别介绍这两种方法的具体实现步骤。
2.1 使用polyfit函数进行多项式拟合polyfit函数是MATLAB中用来进行多项式拟合的函数,它的基本用法是:p = polyfit(x, y, n)其中,x和y是要拟合的数据点的自变量和因变量,n是多项式的阶数。
p是多项式的系数,它可以通过polyval函数来计算拟合后的曲线。
以下是一个具体的例子:x = [1, 2, 3, 4, 5];y = [2, 3, 5, 7, 11];p = polyfit(x, y, 2);f = polyval(p, x);plot(x, y, 'o', x, f, '-');2.2 使用curve fitting工具箱进行曲线拟合除了polyfit函数,MATLAB还提供了curve fitting工具箱,它可以用来进行更加复杂的曲线拟合。
使用curve fitting工具箱进行曲线拟合的基本步骤如下:(1) 导入数据:使用importdata函数导入要拟合的数据。
matlab坐标轴刻度科学计数法

【文章标题:深度解析 MATLAB 坐标轴刻度科学计数法】一、MATLAB 坐标轴刻度科学计数法简介在 MATLAB 中,坐标轴的刻度科学计数法是指当数据非常大或者非常小的时候,坐标轴上的刻度会显示为科学计数法,以便更好地展示数据的大小范围和变化趋势。
科学计数法的形式为a × 10^n,其中 a 为系数,n 为次方数,通常是一个整数。
二、MATLAB 坐标轴刻度科学计数法的设置方法在 MATLAB 中,可以通过以下步骤来设置坐标轴的刻度科学计数法:1. 使用 set 函数设置坐标轴的刻度格式为科学计数法。
2. 调整刻度的系数和次方数的显示精度,以便更清晰地表达数据的大小。
关于第二步的调整,可以通过对坐标轴属性 TickLabelFormat 进行设置,以控制刻度的显示精度。
三、MATLAB 坐标轴刻度科学计数法的深入理解科学计数法的使用可以有效地展示出数据的规模和趋势,但是在实际应用中,我们需要根据具体的数据特点和展示要求来灵活调整科学计数法的设置。
比如对于工程领域的数据,可能需要显示更精确的小数位数;对于科学实验的数据,可能需要更直观地展示数据的数量级等。
设置坐标轴刻度科学计数法时,需要综合考虑数据的特点、观察者的需求以及图表的整体布局等因素。
四、对 MATLAB 坐标轴刻度科学计数法的个人理解与观点在我的理解中,MATLAB 坐标轴刻度科学计数法是一种非常重要的数据展示方式,在处理大数据和小数据时都能够有效地展现出数据的规模和变化趋势。
但是在实际使用中,需要根据具体情况做出合理的调整,以满足观察者对数据的全面理解。
在编写 MATLAB 图表时,我通常会根据数据的大小范围和分布特点来设置坐标轴刻度的科学计数法,并且会根据图表的整体风格和展示要求来调整刻度的显示精度和格式,以达到最佳的展示效果。
总结回顾:MATLAB 坐标轴刻度科学计数法是一种重要的数据展示方式,在实际使用中需要根据数据特点和展示需求进行灵活设置,以达到最佳的展示效果。
在Matlab软件包中画多个函数的图形
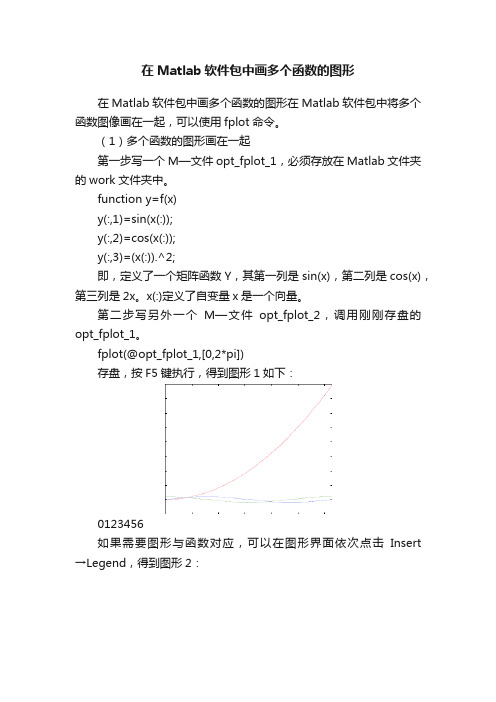
在Matlab软件包中画多个函数的图形在Matlab软件包中画多个函数的图形在Matlab软件包中将多个函数图像画在一起,可以使用fplot命令。
(1)多个函数的图形画在一起第一步写一个M—文件opt_fplot_1,必须存放在Matlab文件夹的work文件夹中。
function y=f(x)y(:,1)=sin(x(:));y(:,2)=cos(x(:));y(:,3)=(x(:)).^2;即,定义了一个矩阵函数Y,其第一列是sin(x),第二列是cos(x),第三列是2x。
x(:)定义了自变量x是一个向量。
第二步写另外一个M—文件opt_fplot_2,调用刚刚存盘的opt_fplot_1。
fplot(@opt_fplot_1,[0,2*pi])存盘,按F5键执行,得到图形1如下:0123456如果需要图形与函数对应,可以在图形界面依次点击Insert →Legend,得到图形2:图形2中,蓝色曲线对应data1,即,蓝色曲线是第一个函数sin(x);绿色曲线对应data2,即,绿色曲线是第二个函数cos(x);红色曲线对应data3,即,红色曲线是第三个函数2x。
(2)在图形中增加格子线在第二个M—文件opt_fplot_2中增加一条命令即可:fplot(@opt_fplot_1,[0,2*pi])grid on执行后得到图形3:(3)在图形中标记曲线与格子线交点的坐标在图形3界面点击这个键然后点击图形中需要坐标的点如果还需要其他点的坐标,按住CTRL 键,点击需要坐标的点,画面如下:选择第三项:“Creat New Datatip ”选项,然后,再一次点击相应的点,即可。
这个点的坐标来啦fplot('0.008+0.002*x+0.0005*x^2',[1930,1980])fplot('0.08+0.002*x+0.00005*x^2',[1930,1980])fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[1930,1980]) fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[1980,2200]) fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[2300,2500]) fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[2250,2300])fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[2275,2285])fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[2280,2285])fplot('0.08+0.002*(x-1930)+0.00005*(x-1930)^2',[1930,1980])。
matlab多副图使用同一标尺例子

matlab中如何使不同图片的colorbar范围相同以及刻度显示极值1:请问matlab中画多张图如何使用同一范围的colorbar?例如生成了图1,2,3生成图1时,使用temp1=caxis;将图1的z值的取值范围(即colorbar的取值范围)取出。
生成图2,3时使用caxis(temp1)命令将图2,3的z值的取值范围设为同1相同。
然后对各个同使用colorbar命令便可以了。
解释:matlab将z值映射到colormap,colorbar通过z值和colormap的映射关系生成的,所以需要将不同的figure,z值映射相同的colormap索引。
命令:caxiscaxis([cmin cmax])caxis controls the mapping of data values to thecolormap.2:colorbar的刻度经常达不到极值,可以使用下面的方法达到极值figure[x,y,z]=peaks(20);subplot(2,1,1),contourf(x,y,z),colorbarsubplot(2,1,2),contourf(x,y,z)t1=caxis;t1=linspace(t1(1),t1(2),6);my_handle=colorbar('ytick',t1);再比如:load toposubplot('position',[0 0.5 1 0.45 ])axesm robinsonmeshm(topo,topolegend)demcmap(caxis)h=colorbar('northoutside');t=get(h,'xtick');subplot('position',[0 0.05 1 0.45 ])axesm robinsonmeshm(topo,topolegend)a=caxis;demcmap(caxis)colorbar('northoutside','xtick',[a(1),t,a(2)]) 其结果如下:下面程序给出地形和大地水煮面的结果:load topoload geoidload coastsubplot('position',[0 0.5 1 0.45 ])axesm robinsonmeshm(topo,topolegend)plotm(lat,long)a=caxis;demcmap(caxis)colorbar('northoutside','xtick',[a(1),-6000:2000:4000,a(2)])subplot('position',[0 0.05 1 0.45 ])axesm robinsonmeshm(geoid,geoidlegend)plotm(lat,long)demcmap(caxis)a=caxis;h=colorbar('northoutside','xtick',[ceil(a(1)),-80:20:60,floor(a(2))]);。
横坐标程序设计

横坐标程序设计绘制出具有不同纵坐标标刻度的两个图形——plotyy() 两个函数绘制在同一个坐标中(横坐标的标度相同,纵坐标有两个——不同量纲不同数量级)。
MATLAB作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给MATLAB......双纵坐标函数plotyy 在Matlab中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy函数,它能把具有不同量纲。
... 'MarkerSize',10) xlabel('x'); ylabel('y'); ·用Matlab 画图时,有时候需要对各种图标进行标注,例如,用“+”代表A 的运动情况,“*”代表B 的运动情况。
[x1;x2;x3]'; y=[y1;y2;y3]'; plot(x,y,x1,y1-1) 3.具有两个纵坐标标度的图形在MATLAB中。
('横坐标x') ylabel('纵坐标y') title('描点绘制曲线') legend('描点坐标','绘制的曲线') grid off 实例2: matlab 如何画图时将数据点的值在图中......MATLAB作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给MATLAB......... 'MarkerSize',10) xlabel('x'); ylabel('y'); ·用Matlab 画图时,有时候需要对各种图标进行标注,例如,用“+”代表A 的运动情况,“*”代表B的运动情况。
[x1;x2;x3]'; y=[y1;y2;y3]'; plot(x,y,x1,y1-1) 8 3.具有两个纵坐标标度的图形在MATLAB中。
