[吉林大学]《计算方法》期末试题
吉大18秋学期《计算方法》在线作业一-2答案

[奥鹏]吉大18秋学期《计算方法》在线作业一-2
18秋作业试卷参考答案
一、单选题共15题,60分
1、秦九韶算法的特点在于,它通过一次式的反复计算,逐步得出高次多项式的值,具体地说就是将一个n次多项式的求值问题,归结为重复计算()个一次式来实现。
An
Bn-1
Cn+1
Dn*n
这门答案选择:A
2、若 x = 1.345678,|x*-x|=0.00041... ,则x*的近似数x 具有( )位有效数字.
A1
B2
C3
D4
这门答案选择:D
3、题面如下所示,正确的是:
AA
BB
CC
DD
这门答案选择:C
4、差商形式插值公式称为()
A牛顿插值公式
B拉格朗日插值公式
C分段插值公式
D埃尔米特插值公式
这门答案选择:A
5、题面如下图所示,正确的是()
AA
BB
CC
DD
这门答案选择:B。
吉林大学网络教育作业考试练习题-计算方法

计算方法交卷时间:2018-10-15 14:46:52一、单选题1.(4分)当A ( )时,线性方程组的迭代解一定收敛• A. >=6• B. =6• C. <6• D. >6得分:0知识点:计算方法作业题展开解析答案D解析2.(4分)4.3490是4.3490287…的近似值,有( )位有效数字• A. 6• B. 5• C. 4• D. 7得分:0知识点:计算方法作业题展开解析答案B解析3.(4分)以下各值,当间隔分段n为()时,牛顿-柯斯特求积公式稳定性不好• A. 1• B. 4• C. 6• D. 12得分:0知识点:计算方法作业题展开解析答案D解析4.(4分)应用二分法求方程在区间[0, 1]上误差不超过的近似根,需要二分()次• A. 14• B. 15• C. 16• D. 17得分:0知识点:计算方法作业题展开解析答案D解析5.(4分)用简单迭代法求方程的近似根,下列迭代格式收敛的是( )• A. ex-x-1=0,[1,1.5],令xk+1 =In(xk+1)• B. x3-x2-1=0,[1.4,1.5],令x k+1=1+• C. x3-x2-1=0,[1.3,1.6],令xk+1</sup>=• D. 4-2x=x,[1,2],令xk+1=得分:0知识点:计算方法作业题展开解析答案D解析6.(4分)应用二分法求方程在区间[0, 1]上误差不超过的近似根,需要二分()次• A. 12• B. 15• C. 19• D. 20得分:0知识点:计算方法作业题展开解析答案C解析7.(4分)关于列主元高斯-约当消去法,以下说法正确的是()• A. 通常用来求解正定矩阵• B. 不能同时求解系数矩阵相同的多个方程组• C. 能够判断矩阵是否非奇异• D. 能够避免零主元或小主元得分:0知识点:计算方法作业题展开解析答案D解析8.(4分)假设矩阵是正定对称矩阵,并且,在矩阵的Cholesky分解中,下三角矩阵()• A.• B.• C.• D.得分:0知识点:计算方法作业题展开解析答案A解析9.(4分)用选主元方法解方程组,是为了()• A. 提高运算速度• B. 减少舍入误差• C. 增加有效数字• D. 方便计算得分:0知识点:计算方法作业题展开解析答案B解析10.(4分)应用二分法求方程在区间[0, 1]上误差不超过的近似根,需要二分()次• A. 4• B. 5• C. 6• D. 7得分:0知识点:计算方法作业题展开解析答案B解析11.(4分)设是对称正定矩阵,经过高斯消元法第一步后,变为,则有性质()• A.• B. 是对称正定矩阵• C. 是对称矩阵• D. 是正定矩阵得分:0知识点:计算方法作业题展开解析答案B解析12.(4分)关于预测-校正公式,以下描述正确的是()• A. 步长h较大• B. 进行多次迭代• C. 比龙格-库塔法精度高• D. 局部阶段误差为O(h3)得分:0知识点:计算方法作业题展开解析答案D解析(4分)以下方法中,哪个方法不能求解一元非线性方程的根?()• A. 逐步搜索法• B. 迭代法• C. 欧拉法• D. 区间二分法得分:0知识点:计算方法作业题展开解析答案C解析14.(4分)以下对欧拉法描述错误的是()• A. 用差商代替导数求常微分方程初值问题• B. 不能由数值微分方法推导得到• C. 用一条初始点重合的折线来近似表示曲线• D. 可用泰勒展开法导出得分:0知识点:计算方法作业题展开解析解析15.(4分)为使两点数值求积公式具有最高阶代数精度,则求积结点应为()• A. 任意• B.• C.• D.得分:0知识点:计算方法作业题展开解析答案C解析16.(4分)设方程f(x)=0的有根区间为[1, 2],使用二分法时,误差限为|xk+1-x*|≤(),其中• A. 1/2• B. 1/2 k• C. 1/2 k+1• D. 1得分:0知识点:计算方法作业题展开解析答案C解析17.(4分)用高斯―赛德尔迭代法解方程组收敛的充分必要条件是()• A.• B.• C.• D.得分:0知识点:计算方法作业题展开解析答案A解析18.(4分)满足插值条件的LAgrAnge插值多项式的次数()• A. 等于• B. 小于• C. 大于• D. 不超过得分:0知识点:计算方法作业题展开解析答案D解析(4分)用牛顿迭代法计算,取=10-3,正确结果为()• A. 5.55• B. 5.56• C. 5.57• D. 5.58得分:0知识点:计算方法作业题展开解析答案C解析20.(4分)拟合三点A(0,1),B(1,3),C(2,2)的直线是()• A. 2x-y+1=0• B. 2x-y+3=0• C. x-2y+5=0• D. x-2y+3=0得分:0知识点:计算方法作业题展开解析解析二、判断题1.(2分)算式在ALGOL中写为••得分:0知识点:计算方法作业题展开解析答案对解析2.(2分)解方程的牛顿迭代公式••得分:0知识点:计算方法作业题展开解析答案对解析3.(2分)源程序由开始部分、说明部分、语句部分、结束部分组成••得分:0知识点:计算方法作业题展开解析答案对解析4.(2分)浮点数的加法满足结合律••得分:0知识点:计算方法作业题展开解析答案对解析5.(2分)数值计算中,误差主要来源于模型误差••得分:0知识点:计算方法作业题展开解析答案错解析6.(2分)求解f(x)=0的牛顿法,误差具有平方收敛性••得分:0知识点:计算方法作业题展开解析答案对解析7.(2分)在实际进行插值时插值时,将插值范围分为若干段,然后在每个分段上使用低阶插值――――如线性插值和抛物插值,这就是所谓分段插值法•得分:0知识点:计算方法作业题展开解析答案对解析8.(2分)导数有三种差商,其中称为向前差商,称为向后差商,而则称为中心差商••得分:0知识点:计算方法作业题展开解析答案对解析9.(2分)对给定的数据点,插值函数必须要经过这些点,而拟合函数不一定经过•得分:0知识点:计算方法作业题展开解析答案对解析10.(2分)已知函数表,则一次差商0.8()算法是指解题方案的准确而完整的描述••得分:0知识点:计算方法作业题展开解析答案错解析考试成绩0 分用时: -2分-17秒交卷的时候提示提示关闭计算方法交卷时间:2018-10-15 14:47:09一、单选题1.(4分)用1+近似表示所产生的误差是( )误差• A. 舍入• B. 观测• C. 模型• D. 截断得分:0知识点:计算方法作业题展开解析答案D解析2.(4分)下列求积公式中用到外推技术的是()• A. 梯形公式• B. 复合抛物线公式• C. 龙贝格公式• D. 高斯型求积公式得分:0知识点:计算方法作业题展开解析答案B解析3.(4分)顺序高斯消去法的计算量近似为()• A.。
计算方法期末考试试卷(7)及解答

计算方法期末考试试卷(7)及解答一.(20分)给定代数方程01.21.12=--x x(1) 证明该方程只有唯一正根,并取步长1h = 搜索含有该正根的区间。
(2) 适当选定初值,用Newton 迭代法求该正根(精度要求210ε-= )二.(20分)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡8117152362205321x x x(1) 用全主元约当消去法求上述方程组。
(2) 建立收敛的Gauss-Seidel 迭代格式,并用此迭代格式求解上述方程组,取初值T x )0,0,0()0(=,计算到)3(x ,(保留小数点后三位数)。
三.(20分)(1(2)求解矛盾方程组 ⎪⎪⎩⎪⎪⎨⎧=+-=-=+-=-4332222121212121x x x x x x x x四.(20分)试利用函数x xe x f -=)(在节点kh x x k +=0,其中00=x ,h =1/8,k =0,1,2,3,4,5,6,7,8上的值,分别用复化Simpson 公式和复化梯形公式计算定积分⎰-10dx xe x ,(保留小数点后三位数).五.(20分)(1)取步长0.1h =,用改进的Euler 公式求解常微分方程初值问题⎩⎨⎧=='+-0)0()(y e y y x在0.3x =处的近似值。
(计算结果保留三位小数) (10分)(2)试分析改进欧拉法的局部截断误差。
参考答案及评分标准一.(20分)(1)证明:由1200x x ∆>⎧⎨<⎩ ⇒该方程只有唯一正根 (5分)由 f(0)=-2.1 f(1)<0 f(2)<0 f(3)<0可知 f(2)f(3)<0 推得 正根区间为 (2,3) (5分)(2)计算公式为)()(1k k k k x f x f x x '-=+ (4分) (3)建立计算结果表格,判断达到计算精度要求的迭代结果21010.2-± (6分)。
吉林大学智慧树知到“计算机科学与技术”《计算方法》网课测试题答案卷3

吉林大学智慧树知到“计算机科学与技术”《计算方法》网课测试题答案(图片大小可自由调整)第1卷一.综合考核(共10题)1.用数值微分公式中求导数值时,步长越小计算就越精确。
()A、错误B、正确2.若线性代数方程组AX=b的系数矩阵A为严格对角占优阵,则雅可比迭代和高斯-塞德尔迭代都不收敛。
()A、错误B、正确3.利用克莱姆法则求解行列式时,求解一个n阶方程组,需要()个n阶行列式。
A、nB、n+1C、n-1D、n*n4.常用的阶梯函数是简单的()次样条函数。
A、零B、一C、二D、三5.截断误差也称为插值余项。
()A、错误B、正确6.对于代数插值,插值多项式的次数随着节点个数的增加而升高。
()A、错误B、正确7.以下近似值中,保留四位有效数字,()。
A、0.01234B、-12.34C、-2.20D、0.22008.3.142和3.141分别作为π的近似数具有()位有效数字。
A、4和3B、3和2C、3和4D、4和49.数值3.1416的有效位数为()。
A、3B、4C、5D、610.设x*=1.234是真值x=1.23445的近似值,则x*有()位有效数字。
A、1B、2C、3D、4第1卷参考答案一.综合考核1.参考答案:A2.参考答案:A3.参考答案:C4.参考答案:A5.参考答案:B6.参考答案:B7.参考答案:D8.参考答案:A9.参考答案:C10.参考答案:D。
吉大18年9月《计算方法》作业考核试题

吉大18年9月《计算方法》作业考核试题------------------------------------------------------------------------------------------------------------------------------ (单选题) 1: 题面如下,正确的是()A: AB: BC: CD: D正确答案:(单选题) 2: 常用的阶梯函数是简单的()次样条函数。
A: 零B: 一C: 二D: 三正确答案:(单选题) 3: 所谓松弛法,实质上是()的一种加速方法。
A: 雅可比迭代B: 高斯-赛得尔迭代C: 变分迭代D: 牛顿迭代正确答案:(单选题) 4: 辛普生求积公式具有()次代数精度A: 1B: 2C: 3D: 4正确答案:(单选题) 5: 以下近似值中,保留四位有效数字,A: 0.01234B: –12.34C: –2.20D: 0.2200正确答案:(单选题) 6: 秦九韶算法的特点在于,它通过一次式的反复计算,逐步得出高次多项式的值,具体地说就是将一个n次多项式的求值问题,归结为重复计算()个一次式来实现。
A: nB: n-1C: n+1D: n*n正确答案:(单选题) 7: 为了保证插值函数能更好地密合原来的函数,不但要求“过点”,即两者在节点上具有相同的函数值,而且要求“相切”,即在节点上还具有相同的导数值,这类插值称为()A: 牛顿插值B: 埃尔米特插值C: 分段插值------------------------------------------------------------------------------------------------------------------------------ D: 拉格朗日插值正确答案:(单选题) 8: 差商形式插值公式称为()A: 牛顿插值公式B: 拉格朗日插值公式C: 分段插值公式D: 埃尔米特插值公式正确答案:(单选题) 9: 题面如下,正确的是()A: 1B: 2C: 3D: 4正确答案:(单选题) 10: 构造拟合曲线不可以采用下列哪种准则()A: 使残差的最大绝对值为最小B: 使残差的绝对值之和为最小C: 使残差的平方和为最小D: 是残差的绝对值之差为最小正确答案:(单选题) 11: 设求方程f(x)=0的根的牛顿法收敛,则它具有()敛速。
【奥鹏】吉大19秋学期《计算方法》在线作业二[3]答案
![【奥鹏】吉大19秋学期《计算方法》在线作业二[3]答案](https://img.taocdn.com/s3/m/6f35aa7e964bcf84b9d57bdb.png)
【奥鹏】吉大19秋学期《计算方法》在线作业二
试卷总分:100 得分:100
一、单选题(共15题,60分)
1、题面如下所示,正确的是:
AA
BB
CC
DD
[仔细分析以上题目,运用所学知识完成作答]
参考选择:C
2、题面如下图所示,正确的是()
AA
BB
CC
DD
[仔细分析以上题目,运用所学知识完成作答]
参考选择:D
3、设x=2.40315是真值2.40194的近似值,则x具有()为有效数字
A2
B3
C4
D5
[仔细分析以上题目,运用所学知识完成作答]
参考选择:B
4、利用克莱姆法则求解行列式时,求解一个n阶方程组,需要()个n阶行列式。
An
Bn+1
Cn
Dn*n
[仔细分析以上题目,运用所学知识完成作答]
参考选择:C
5、()的优点是收敛的速度快,缺点是需要提供导数值。
A牛顿法
B下山法
C弦截法
D迭代法
[仔细分析以上题目,运用所学知识完成作答]
参考选择:A。
2019-2020学年第一学期期末考试《计算方法》大作业答案

吉林大学网络教育学院2019-2020学年第一学期期末考试《计算方法》大作业答案学生姓名专业层次年级学号学习中心成绩年月日作业完成要求:大作业要求学生手写,提供手写文档的清晰扫描图片,并将图片添加到word文档内,最终wod文档上传平台,不允许学生提交其他格式文件(如JPG,RAR等非word文档格式),如有雷同、抄袭成绩按不及格处理。
一、解线性方程(每小题8分,共80分)1、用矩阵的LU分解算法求解线性方程组X1+2X2+3X3= 02X1+2X2+8X3= -4-3X1-10X2-2X3= -11答:2、用矩阵的Doolittle分解算法求解线性方程组X1+2X2+3X3= 12X1– X2+9X3= 0-3X1+ 4X2+9X3= 1答:3、用矩阵的Doolittle分解算法求解线性方程组2X1+X2+X3= 46X1+4X2+5X3=154X1+3X2+6X3= 13答:4、用高斯消去法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:5、用无回代过程消元法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:6、用主元素消元法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:7、用高斯消去法求解线性方程组1231231232344272266x x x x x x x x x -+=++=-++=答:8、利用Doolittle 分解法解方程组Ax=b ,即解方程组12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 答:9、利用Doolittle 分解法解方程组Ax=b ,即解方程组123421111443306776081011112x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 答:10、用高斯消元法解方程组1237811351341231x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦答案:二、计算(每小题10分,共20分)1、已知节点x1,x2及节点处函数值f(x1),f(x2),构造线性插值多项式p1(x). 答:2、设f(xi)=i(i=0,1,2),构造二次式p2(x),使满足: p2(xi)=f(xi)(i=0,1,2)答:。
吉大16秋学期《计算方法》在线作业一答案

吉大16秋学期《计算方法》在线作业一
一、单选题(共 15 道试题,共 60 分。
)
1. 所谓松弛法,实质上是()的一种加速方法。
A. 雅可比迭代
B. 高斯-赛得尔迭代
C. 变分迭代
D. 牛顿迭代
正确答案:B
2. 为了防止迭代发散,通常对迭代过程再附加一项要求,即保证函数值单调下降,满足这项要求的算法称为()
A. 快速弦截法
B. 弦截法
C. 下山法
D. 牛顿法
正确答案:C
3. 常用的阶梯函数是简单的()次样条函数。
A. 零
B. 一
C. 二
D. 三
正确答案:A
4. 差商形式插值公式称为()
A. 牛顿插值公式
B. 拉格朗日插值公式
C. 分段插值公式
D. 埃尔米特插值公式
正确答案:A
吉大16秋学期《计算方法》在线作业一
一、单选题(共 15 道试题,共 60 分。
)
1. 所谓松弛法,实质上是()的一种加速方法。
A. 雅可比迭代
B. 高斯-赛得尔迭代
C. 变分迭代
D. 牛顿迭代
正确答案:B
2. 为了防止迭代发散,通常对迭代过程再附加一项要求,即保证函数值单调下降,满足这。
吉大19秋学期《计算方法》在线作业二-0001参考答案

答案:D
辛普生求积公式具有()次代数精度
A.4
B.3
C.2
D.1
答案:B
二、判断题(共10道试题,共40分)
递推法的基本思路是将一个复杂的计算过程归结为简Βιβλιοθήκη 过程的多次重复。答案:正确
在数值分析中,经常用矩形框和圆边框来描述算法。
答案:正确
复化求积法就是利用低阶的求积公式求得每个子段上的积分值,然后将他们累加求和。
伴随着我国资本市场的逐步开放,部分外资银行也进入我国金融业,给中国传统商业银行带来巨大冲击。面对资本市场开放带来的重重挑战,民生银行应该积极应对。首先,商业银行要积极学习外资银行业务方面的先进经验,取长补短,弥补自己的不足。其次,民生银行要提升自己参与资本市场的程度。民生银行投资业务占总资产的比例 2016 年达 37.43%,比上年提高 17.22%,但仍有进一步提高的空间。银行在参与资本市场在获得资本收益的同时,拓宽了银行收入来源丰富了资产管理业务,可谓实现多方面共赢。
A.高斯-赛得尔迭代
B.雅可比迭代
C.牛顿迭代
D.变分迭代
答案:A
题面如下图所示,正确的是()
{图}
A.D
B.C
2018-2019学年第二学期期末考试《计算方法》大作业参考答案

吉林大学网络教育学院2018-2019学年第二学期期末考试《计算方法》大作业学生姓名专业层次年级学号学习中心成绩年月日一、构造次数不超过三次的多项式P3(X),使满足:(10分)P3(0)= 1;P3(1)=0;P3′(0)=P3′(1)=0。
二、设f(x i)=i(i=0,1,2),构造二次式p2(x),使满足:(10分) p2(x i)=f(x i)(i=0,1,2)三、设节点x i=i(i=0,1,2,3),f(0)=1,f(1)=0,f(2)=-7,f(3)=26,构造次数不超过3次的多项式p3(x),满足p3(x i)=f(x i),i=0,1,2,3 (10分)四、对于上题的问题,构造Newton插值多项式。
(10分)五、构造三次多项式P 3(X )满足:P 3(0)= P 3(1)=0,P 3′(0)=P 3′(1)=1。
(10分)六、利用Doolittle 分解法解方程组Ax=b 即解方程组 (15分) 12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦解:用公式七、基于迭代原理证明(10分)+++=22 (22)八、构造二次多项式2()x p 满足: (10分)'010222()1;()0;()1p p p x x x ===九、构造一个收敛的迭代法求解方程3210x x --=在[1.3,1.6]内的实根。
合理选择一个初值,迭代一步,求出1x 。
(15分)作业完成要求:大作业要求学生手写,提供手写文档的清晰扫描图片,并将图片添加到word 文档内,最终word文档上传平台,不允许学生提交其他格式文件(如JPG,RAR等非word 文档格式),如有雷同、抄袭成绩按不及格处理。
[吉林大学]《计算方法》期末试题
![[吉林大学]《计算方法》期末试题](https://img.taocdn.com/s3/m/c4aef23502d276a201292e54.png)
吉林大学2019-2020学年第二学期期末考试《计算方法》试题
学生姓名专业
层次年级学号
学习中心成绩
一计算题 (共10题,总分值100分 )
1. 应用迭代法求解方程并讨论迭代过程的收敛性。
(10 分)
2. 用矩阵的Doolittle分解算法求解线性方程组
X1+2X2+3X3 = 1
2X1– X2+9X3 = 0
-3X1+ 4X2+9X3 = 1 (10 分)
3. 构造一个收敛的迭代法求解方程X3-X-1=0的唯一正根。
合理选择一个初值,迭代两步,求出x2。
(10 分)
4. 用高斯消去法求解线性方程组
2X1- X2+3X3 = 2
4X1+2X2+5X3 = 4
-3X1+4X2-3X3 = -3 (10 分)
5. 用高斯—赛德尔迭代法求解方程组
(10 分)
6. 设方程组
迭代公式为
求证:由上述迭代公式产生的向量序列收敛的充要条件是
(10 分)
7. 并说明其几何意义。
(10 分)
8. 对于给定的方阵A,若,则矩阵I-A是非奇异的。
(10 分)
9. 基于迭代原理证明(10 分)
10. 用迭代法求方程
x3-x2-1=0
在[1.3,1.6]内的一个实根,选初值x0 =1.3,迭代一步。
(10 分)。
《计算方法》期末考试试题

《计算方法》期末考试试题一选择(每题3分,合计42分)1.x* =1。
732050808,取x=1。
7320,则x具有位有效数字。
A、3B、4C、5D、62.取(三位有效数字),则 .A、B、C、D、0.53.下面_ _不是数值计算应注意的问题。
A、注意简化计算步骤,减少运算次数B、要避免相近两数相减C、要防止大数吃掉小数D、要尽量消灭误差4.对任意初始向量及常向量,迭代过程收敛的充分必要条件是_ _。
A、B、C、D、5.用列主元消去法解线性方程组,消元的第k步,选列主元,使得=。
A、B、C、D、6.用选列主元的方法解线性方程组AX=b,是为了A、提高计算速度B、简化计算步骤C、降低舍入误差D、方便计算7.用简单迭代法求方程f(x)=0的实根,把方程f(x)=0转化为x=ϕ(x),则f(x)=0的根是:。
A、y=x与y=ϕ(x)的交点B、y=x与y=ϕ(x)交点的横坐标C、y=x与x轴的交点的横坐标D、y=ϕ(x)与x轴交点的横坐标8.已知x0=2,f(x0)=46,x1=4,f(x1)=88,则一阶差商f [x0, x1]为。
A、7B、20C、21D、429.已知等距节点的插值型求积公式,那么_____。
A、0B、2C、3D、910.用高斯消去法解线性方程组,消元过程中要求____。
A、B、C、D、11.如果对不超过m次的多项式,求积公式精确成立,则该求积公式具有次代数精度。
A、至少mB、mC、不足mD、多于m12.计算积分,用梯形公式计算求得的值为。
A、0.75B、1C、1.5D、2.513.设函数f(x)在区间[a,b]上连续,若满足,则方程f(x)=0在区间[a,b]内一定有实根。
A、f(a)+f(b)〈0B、f(a)+f(b)>0C、f(a)f(b)<0D、f(a)f(b)>014.由4个互异的数据点所构造的插值多项式的次数至多是____。
A、2次B、3次C、4次D、5次二、计算(共58分)1.将方程写成以下两种不同的等价形式:①;②试在区间[1.40,1。
最新国家开放大学电大本科《计算方法》期末试题标准题库及答案(试卷号:1084)

最新国家开放大学电大本科《计算方法》期末试题标准题库及答案(试卷号:1084)
考试说明:本人汇总了历年来该科的试题及答案,形成了一个完整的标准考试题库,对考生的复习和考试起着非常重要的作用,会给您节省大量的时间。
内容包含:单选题、填空题、计算题、证明题。
做考题时,利用本文档中的查找工具(Ctrl+F),把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他网核、机考及教学考一体化试题答案,敬请查看。
《计算方法》题库一
试题答案及评分标准(仅供参考)
《计算方法》题库二
试题答案及评分标准(仅供参考)
《计算方法》题库三
试题答案及评分标准(仅供参考)
《计算方法》题库四
试题答案及评分标准(仅供参考)
《计算方法》题库五一、单项选择题(每小题5分,共15分)
二、填空题(每小题5分,共15分)
三、计算题(每小题15分,共60分)
四、证明题(本题10分)
试题答案及评分标准
(仅供参考)
《计算方法》题库六
试题答案及评分标准(仅供参考)。
吉林大学 研究生 数值计算方法期末考试 样卷
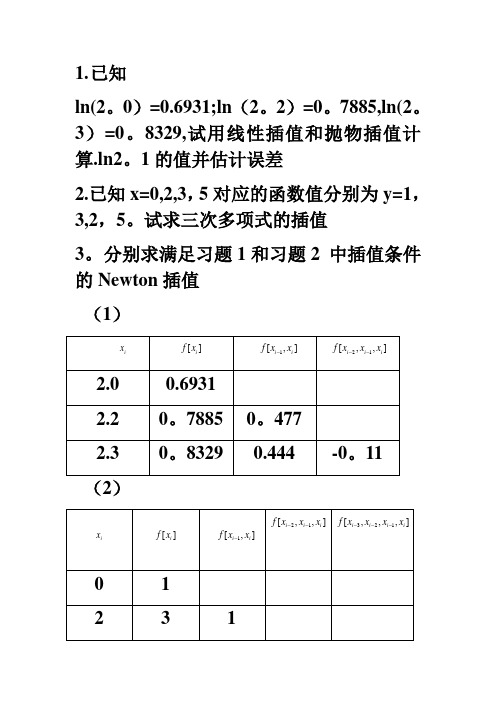
1.已知ln(2。
0)=0.6931;ln(2。
2)=0。
7885,ln(2。
3)=0。
8329,试用线性插值和抛物插值计算.ln2。
1的值并估计误差2.已知x=0,2,3,5对应的函数值分别为y=1,3,2,5。
试求三次多项式的插值3。
分别求满足习题1和习题2 中插值条件的Newton插值(1)(2)3()1(2)(2)(3)310N x x x x x x x=+--+--4.给出函数f(x)的数表如下,求四次Newton 插值多项式,并由此计算f(0。
596)的值解:5。
已知函数y=sinx的数表如下,分别用前插和后插公式计算sin0.57891的值6。
求最小二乘拟合一次、二次和三次多项式,拟合如下数据并画出数据点以及拟合函数的图形。
(a)(b)7。
试分别确定用复化梯形、辛浦生和中矩形求积公式计算积分214dxx+⎰所需的步长h,使得精度达到5 10-。
8。
求A、B使求积公式⎰-+-++-≈11)]21()21([)]1()1([)(f f B f f A dx x f 的代数精度尽量高,并求其代数精度;利用此公式求⎰=211dxx I (保留四位小数)。
9.已知分别用拉格朗日插值法和牛顿插值法求)(x f 的三次插值多项式)(3x P ,并求)2(f 的近似值(保留四位小数)。
10.已知求)(x f 的二次拟合曲线)(2x p ,并求)0(f '的近似值。
11.已知x sin 区间[0.4,0。
8]的函数表如用二次插值求63891.0sin 的近似值,如何选择节点才能使误差最小?并求该近似值。
12。
利用矩阵的LU 分解法解方程组⎪⎩⎪⎨⎧=++=++=++2053182521432321321321x x x x x x x x x 。
13。
已知下列实验数据 试按最小二乘原理求一次多项式拟合以上数据。
14。
取节点1,5.0,021===x x x ,求函数xx f -=e )(在区间[0,1]上的二次插值多项式)(2x P ,并估计误差。
吉林大学工程数学计算方法习题答案

第三章习题答案1.分别用梯形公式、Simpson公式、Cotes公式计算积分1,I=⎰并估计误差。
解:1)用梯形公式有:()()110.51[10.5]10.42678242f f⎛-≈+=+≈⎝⎭⎰()()()333333220.512.6042107.36571012124Tb aE f fηηη-----⎛⎫''=-=--=⨯≤⨯⎪⎝⎭事实上,()()()()()()110.430964410.50.510.4267767210.50.510.00418772Tf x II f fE f f f===-≈+=⎡⎤⎣⎦-∴=-+=⎡⎤⎣⎦⎰⎰2)Simpson公式()110.53111410.43093 64212f f f⎛-⎡⎤⎛⎫⎛⎫≈++=+=⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭⎰[]()()44744211111522 1.1837710180218028Sb a b aE f fηη--⎛⎫--⎪⎛⎫--⎛⎫=-=--≤⨯⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭()312()''()48T f fb aE h=?--事实上,()()()110.50.510.5410.000030462SE f f f f-⎡+⎤⎛⎫=-++=⎪⎢⎥⎝⎭⎣⎦⎰3)由Cotes公式有:()() ()111537270.5321232719084814.9497525.2982210.3923029.9332670.43096180f f f f f-⎡⎤⎛⎫⎛⎫⎛⎫≈++++⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=++++=⎰17)180+++()6116211294522 2.697410945464C E f η--⎛⎫⨯ ⎪⎛⎫=-⨯-≤⨯ ⎪ ⎪⎝⎭⎪⎝⎭()7(6)945*4()()82Cf b a E f h =?-- 事实上,()0.0000003C E f =2.证明Simpson 公式()2.8具有三次代数精度。
吉林大学计算方法作业答案1

第一章作业答案(习题一P28)1. 解:由已知可得所求二次插值函数为解:由已知可得所求二次插值函数为()()()()()()()()()()()()()1121211121112122111212´-+-++´-+-++´------=x x x x x x x L()83612+-=x x3. 解:解:()()()()()()()()()()()()925.694925.674725.6925.6425.6974749425.649725.677´----+´----+´----»6484848.2»误差估计误差估计()()()()9725.67471617252---×==-xR , ()9,4Îx()()()9725.6747416125---×=£-00879.0< 5. 解:(1)Lagrange 插值多项式:插值多项式:()()()()()()()()()()()()()941210142014020104213´------+´------=x x x x x x x L()()()()()()()()()()()()324140421023421202410´------++´------+x x x x x x12144541123+-+-=x x x (2)Newton 插值多项式(解法同P13例2.1)先作差商表先作差商表k k x ()k x f ()1,+k k x x f ()21,,++k k k x x x f ()321,,,+++k k k k x x x x f 0 0 1 1 1 9 8 2 2 23 14 3343-10- 8-11/4 则有则有()()()()()()()2104111030813------+-+=x x x x x x x N12144541123+-+-=x x x 此题此题 Lagrange 插值多项式和Newton 插值多项式是相等的,故其插值多项式是唯一的。
1084计算方法(本)-国家开放大学2021春(2021年7月)期末统一考试试卷真题及答案

试卷代号:1084国家开放大学2021年春季学期期末统一考试计算方法(本) 试题(开卷)2021年7月一、单项选择题(每小题5分,共15分)1.已知近似值a =1.47,b =0.6564,则a +b 的误差限为( ). A.12×10-4B. 12×10-3C. 12×10-2D. 12×10-12.已知函数f (x )=x 2+2x +3,则二阶差商f [0,1,2]=( ). A.1 B.6C.3D.53.求解方程f (x )=0的根的迭代公式是x n +l =x n 一f(x n )f ′(x n)(n =0,1,2,…),则它是( ). A.一般迭代法 B.单点弦法C.切线法D.双点弦法二、填空题(每小题5分,共15分) 4.用n =2的复化梯形公式计算积分∫1x 21d x ≈ .5.若X =(3,-4,1)T,则∥X ∥∞= .6.欧拉法的局部截断误差为 .三、计算题(每小题15分,共60分) 7.求矛盾方程组{x 1+x 2=4x 1−x 2=22x 1−x 2=3的最小二乘解.8.用直接三角分解法解方程组:[2−1−1−120−103][x 1x 2x 3]=[121].9.用雅可比迭代法解方程组:{8x 1+2x 2+x 3=22x 1+8x 2+2x 3=5x 1+2x 2+8x 3=1取初始值X (0)=(O ,0,O)T,求出X (1).10.用预估一校正法求初值问题:{y ′=x +yy (0)=1在x =0(0.2)0.4处的解.四、证明题(本题10分)11.设l k (x )(k =0,1,…,n )为n 次插值基函数,证明当n ≥3时,有∑l k (x )x k 3n k=0=x 3.试卷代号:1084国家开放大学2 0 2 1年春季学期期末统一考试 计算方法(本) 试题答案及评分标准(开卷)(供参考)2021年7月一、单项选择题(每小题5分,共15分) 1.D 2.A 3.C二、填空题(每小题5分,共15分) 4. 1724 5.4 6.O (h 2)三、计算题(每题15分,共60分)7.解:φ(x 1, x 2)=( x 1+ x 2 -4)2 +( x 1 – x 2 -2)2 +(2 x 1 – x 2 -3)2 6分 由{ðφðx 1=4(3x 1−x 2−6)=0ðφðx 2=2(−2x 1+3x 2+1)=0得法方程组 {3x 1−x 2=6−2x 1+3x 2=−1由此求得最小二乘解为x 1=177,x 2=97 15分 8.解:对系数矩阵直接分解得: A =[2−1−1−120−103]=[1−121−12−131][2−1−132−1273] 8分解方程LY =b 即解[1−121−12−131][y 1y 2y 3]=[121],得Y =(1,52,73)T再解方程RX =Y 即解[2−1−132−1273][x1x 2x 3]=[15273],得X =(2,2,1)T 15分 9.解:因为A 是严格对角占优矩阵,所以雅可比迭代法收敛 4分雅可比迭代公式为{ x 1(m+1)=18(2−2x 2(m )−x 3(m ))x 2(m+1)=18(5−2x 1(m )−2x 3(m ))x 3(m+1)=18(1−2x 1(m )−2x 2(m )) m =0,1,…… 10分 取X (0)一=(0,0,0)T ,计算得X (1)=(14,58,18)T 15分 10.解:因为 h =0.2,f (x ,y )=x +y ,x 0 =0,y 0=1,n =0,1 则预估一校正公式为 {y n+1(0)=0.2x n +1.2y ny n+1=y n +0.1×(x n +y n+x n+1+y n+1(0)10分计算得y 1=1. 24,y 2 =1. 5768 15分 四、证明题(本题10分)11.证明:由拉格朗日插值法可知f(x )=L n (x )+R n (x ) 令f(x )=x 3,由n ≥3,R n (x )=f (n+1)(ξ)(n+1)!ω(x )=0所以,∑l k (x )x k 3=f (x )=x 3,n k=0 (n ≥3) 10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林大学2019-2020学年第二学期期末考试《计算方法》试题
学生姓名专业
层次年级学号
学习中心成绩
一计算题 (共10题,总分值100分 )
1. 应用迭代法求解方程并讨论迭代过程的收敛性。
(10 分)
2. 用矩阵的Doolittle分解算法求解线性方程组
X1+2X2+3X3 = 1
2X1– X2+9X3 = 0
-3X1+ 4X2+9X3 = 1 (10 分)
3. 构造一个收敛的迭代法求解方程X3-X-1=0的唯一正根。
合理选择一个初值,迭代两步,求出x2。
(10 分)
4. 用高斯消去法求解线性方程组
2X1- X2+3X3 = 2
4X1+2X2+5X3 = 4
-3X1+4X2-3X3 = -3 (10 分)
5. 用高斯—赛德尔迭代法求解方程组
(10 分)
6. 设方程组
迭代公式为
求证:由上述迭代公式产生的向量序列收敛的充要条件是
(10 分)
7. 并说明其几何意义。
(10 分)
8. 对于给定的方阵A,若,则矩阵I-A是非奇异的。
(10 分)
9. 基于迭代原理证明(10 分)
10. 用迭代法求方程
x3-x2-1=0
在[1.3,1.6]内的一个实根,选初值x0 =1.3,迭代一步。
(10 分)。
