数学镶嵌课件
合集下载
数学人教版八年级上册平面图形的镶嵌课件

60° 60° 60 ° 60° 60 ° 60°
n=3 n=4 n=5 n=6
的 平 面 镶 嵌
正 方 形
90° 90° 90° 90°
n=3 n=4 n=5 n=6
正 六 边 形 的 平 面 镶 嵌
n=3 n=4 n=5 n=6
正五边形可以镶嵌吗?
1 2
原来拼不了! 为什么?
3
∠1+∠2+∠3=?
形镶嵌问题的资料
让我们放飞理想, 翱翔于种形状、大小相同的平 面图形进行拼接,彼此之间不留缝隙, 也不重叠地铺成一片,叫做平面图形 的镶嵌.也叫平面图形的密铺。
上一页
判断:下列图形是平面图形的镶嵌吗?
图1
图2
图3
图4
小试牛刀1
试着用一种正多边形拼平面镶嵌图。
n=3 n=4 n=5 n=6
正 三 角 形 的 平 面 镶 嵌
正五边形不能镶嵌!
n=3 n=4 n=5 n=6
小试牛刀2
试着用两种或两种以上正多边形拼 平面镶嵌图。
自己动手制作一幅美丽的平面镶嵌
图,并说出其寓意。
小结
• • • • 平面图形镶嵌的概念及其特点 数学在生活中的应用 数学的美 学生创造力的培养
、
选择你喜欢的题目
1.身体力行:完成学习探究里的习题二 2.挑战自我:设计镶嵌图案,为本班设 计班徽,并说明设计理想 3.开拓视野:到网站上查询有关平面图
镶嵌(1)课件1

结 n=6
1200
3
能拼好 1200 ×3=3600
果
n =8
1350
不能拼好
2
0有缺口 0
135 ×2<360
不能拼好
3
0有重叠 0
135 ×3>360
规律:当这种正多边形的每个内角的度数恰好是360 0的
约数时,这种正多边形就能镶嵌.
练一练
1. 仅用正十边形能进行镶嵌吗? 为什么?
2. 只用一种正多边形能进行镶嵌的有 _正__三_角__形_、__正_方__形__、_正__六__边_形_.
当围绕一点拼在一起的几种正多边形的内角加在 一起恰好组成一个周角时,这几种正多边形就能镶嵌.
请你创造美
这是某公园的呈正六 边形的花坛,现要在其周 围用正多边形铺地,请你 设计出一种铺法,并画出 草图?
收获与体会 ● 你学到了什么知识? ● 你是怎样获得这些数学知识的?
欢 迎 指 正
拼拼看
拼拼看
想一想
如果选择其中的两 种平面图形进行镶嵌, 你又会选择哪两种呢 ?
正三角形
正方形
正六边形
正八边形
拼拼看
用两种正多边 形进行镶嵌应满足 什么条件 ?
规律:当围绕一点拼在一起的两种正多边形的内角加在
一起恰好组成一个周角时,这两种正多边形就能镶嵌.
用三种或多种 正多边形进行镶嵌 应满足什么条件 ?
拼拼看
拼拼看
拼拼看Biblioteka 正三角形正方形正六边形
正八边形
拼拼看
拼拼看
拼拼看
拼拼看
拼拼看
议一议
为什么有的正多 边形可以镶嵌,而 有的却不能镶嵌?
理一理
正n边形 拼图
平面图形的镶嵌-ppt课件

设在一个顶点周围有个m正四边形的角、n个正八边形 的角,那么有
。
。。
m·90 +n· =360
2m+3n=8
∵m、n为正整数
m=1
∴解为
n=2
形 的 平 面 镶 嵌
正 八 边 形 与 正 方
正十二边形与正三角形 的平面镶嵌
正十边形与正五边 形的平面镶嵌
〔05山东〕9.用两种正多边形镶嵌,不能与正三 角形匹配的正多边形是
用两种正多边形镶嵌不能与正三角形匹配的正多边形是角形匹配的正多边形是aa正方形正方形bb正六边形正六边形cc正十二边形正十二边形dd正十八边形正十八边形当围绕一点拼在一起的几个正多边形的内角和加在一起恰好组成一个周角时就能镶嵌成一个平面图形
新课标北师大版课件系列
<初中数学> 八年级 上册
7.4 平面镶嵌
请他欣赏
察看以以下图案,阐它们都 是由哪些几何图形组成?
察看以以下图案,阐明它们都 是由哪些几何图形组成?
第一页 第二页 第三页 第四页
定 义
用一些不重叠摆放的多边形把平面 的一部分全部覆盖,在几何里叫做用
多边形覆盖平面(或平面镶嵌)。
例如:
察看以以下图形并思索在镶嵌 时如何做到既无缝隙又不重叠?
用四边形也可以作平面镶嵌
D
C
那么四边形如何
镶嵌呢? 请看!
A
B
练习一:
(2019年中考题〕商店出卖以下外形的地砖:①正方形; ②长方形; ③正五边形;④正六边形。假设只选择其 中某一种地砖镶嵌地面,可供选择的地砖共有〔 〕
A.1种C B.2种 C.3种 D.4种
边长为a的正方形与以下边长为a的正多边形组合起来,
《﹡数学活动 平面镶嵌》PPT课件(县级优课)
单独使用正三角形、正方形、正六边形可以镶嵌。
如果用边长相等的正三角形、正方形、正 五边形、正六边形其中的两种组合呢?
3×60°+2×90°=360°
不能镶嵌
2×120°+2×60° =360°
不能镶嵌
不能镶嵌
不能镶嵌
探究2:用几个全等的任意三角形能镶嵌吗? 任意四边形呢?
2
1
3
3 2
1
4
谈一谈:通过本课的学习有哪些收获和体会?
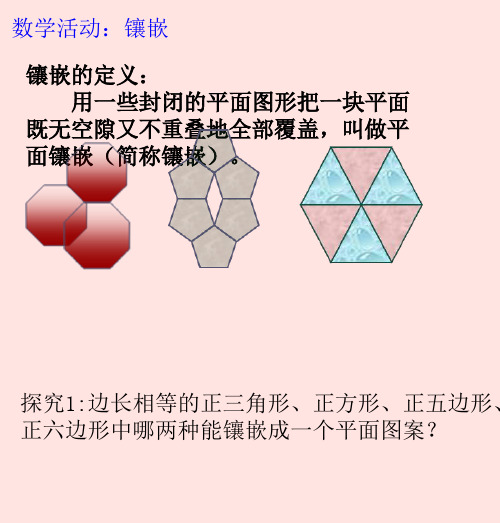
数学活动:镶嵌 镶嵌的定义: 用一些封闭的平面图形把一块平面 既无空隙又不重叠地全部覆盖,叫做平 面镶嵌(简称镶嵌)。
探究1:边长相等的正三角形、正方形、正五边形、 正六边形中哪两种能镶嵌成一个平面图案?
平面镶嵌的条件:
1、拼接处顶点公用、边长相等。 2、拼接处角度和为360度。
探究1:仅用一种正多边形,哪些能单独镶嵌 成嵌调查表.docx
如果用边长相等的正三角形、正方形、正 五边形、正六边形其中的两种组合呢?
3×60°+2×90°=360°
不能镶嵌
2×120°+2×60° =360°
不能镶嵌
不能镶嵌
不能镶嵌
探究2:用几个全等的任意三角形能镶嵌吗? 任意四边形呢?
2
1
3
3 2
1
4
谈一谈:通过本课的学习有哪些收获和体会?
数学活动:镶嵌 镶嵌的定义: 用一些封闭的平面图形把一块平面 既无空隙又不重叠地全部覆盖,叫做平 面镶嵌(简称镶嵌)。
探究1:边长相等的正三角形、正方形、正五边形、 正六边形中哪两种能镶嵌成一个平面图案?
平面镶嵌的条件:
1、拼接处顶点公用、边长相等。 2、拼接处角度和为360度。
探究1:仅用一种正多边形,哪些能单独镶嵌 成嵌调查表.docx
人教版八年级数学上册数学活动——平面镶嵌(用多边形覆盖平面)课件

6n =__3_和__5_,___n__=__4_和__5_,___n__=__4_和__6_,___n__=__5_和_不6
能镶嵌.
在边长相等的正三角形、正方形、正五边形、正六边 形中取两种正多边形镶嵌,哪两种正多边形可以进行平面 镶嵌?
用 n 表示正多边形的边数.
(2)用两种正多边形进行镶嵌的条件是:
ax _+__b_y__=_3_6_0_,__其__中__a,__b_表__示__正__多__边__形__的__个__数__,___ x°__,__y_°__表__示__正__多__边__形__每__个__内__角__的__度__数________.
任意用一些形状、大小相同的三角形能否进行
平面镶嵌?四边形呢?
1.从课后习题中选取; 2.完成练习册本课时的习题。
教学反思
本课时通过探索平面图形的镶嵌,让学生 知道任意形状的三角形、四边形或正六边形可 以镶嵌设计,提高了学生对三角形以及多边形 内角和与外角和等知识的综合运用能力与实际 操作中的动手能力.
镶(嵌2).用两种正多边形进行镶嵌的条件是:
ax _+__b_y__=_3_6_0_,__其__中__a,__b_表__示__正__多__边__形__的__个__数__,___ x°__,__y_°__表__示__正__多__边__形__每__个__内__角__的__度__数________.
课后作业
角形恰好无缝隙、无重叠嵌入,则 n 的值是(
)
A.3A
B.4
C.5
D.6
4.试用边长相等的一个正六边形、6个正方形、6 个正三角形镶嵌成一个平面图案,画出草图.
解:如图所示:
综合应用 5.如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,
能镶嵌.
在边长相等的正三角形、正方形、正五边形、正六边 形中取两种正多边形镶嵌,哪两种正多边形可以进行平面 镶嵌?
用 n 表示正多边形的边数.
(2)用两种正多边形进行镶嵌的条件是:
ax _+__b_y__=_3_6_0_,__其__中__a,__b_表__示__正__多__边__形__的__个__数__,___ x°__,__y_°__表__示__正__多__边__形__每__个__内__角__的__度__数________.
任意用一些形状、大小相同的三角形能否进行
平面镶嵌?四边形呢?
1.从课后习题中选取; 2.完成练习册本课时的习题。
教学反思
本课时通过探索平面图形的镶嵌,让学生 知道任意形状的三角形、四边形或正六边形可 以镶嵌设计,提高了学生对三角形以及多边形 内角和与外角和等知识的综合运用能力与实际 操作中的动手能力.
镶(嵌2).用两种正多边形进行镶嵌的条件是:
ax _+__b_y__=_3_6_0_,__其__中__a,__b_表__示__正__多__边__形__的__个__数__,___ x°__,__y_°__表__示__正__多__边__形__每__个__内__角__的__度__数________.
课后作业
角形恰好无缝隙、无重叠嵌入,则 n 的值是(
)
A.3A
B.4
C.5
D.6
4.试用边长相等的一个正六边形、6个正方形、6 个正三角形镶嵌成一个平面图案,画出草图.
解:如图所示:
综合应用 5.如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,
人教版数学八年级上册 11.4 数学活动 -平面图形的镶嵌 课件(共45张PPT)

作镶嵌 ( 能 )
6 4. 用任意三角形镶嵌平面时,同一顶点处应摆放 ( )个 4 三角形;用任意四边形镶嵌平面时,同一顶点处应摆放( )
个四边形. 5、下面四种正多边形中,用同一种图形不能平面镶嵌的是
( C ).
A
B
C
D
六、升华知识 深化认识
说说你的 收获
通过这节课的学习你有哪些收获? 你还有什么体会吗?
我们都来做个有心人,多 思考、多研究,把学过的数学 知识应用于生活,解决生活中 的实际问题,使我们的生活更 加美好!
❖
本 课 到 此 结 束
教学后记
90°
4. 正六边形
用边长相同的正五边形不能镶嵌
你正五能边说形的说内角道不理能 吗?
组成360°的角。
13 2
∠1+∠2+∠3=?
活动一实验结论:
1.能镶嵌的图形在一个拼接点处的特点: 各角之和等于360º
2.要用正多边形镶嵌成一个平面的关键
是看:这种正多边形的一个内角的倍数 是否是360°,在正多边形里,正三角 形的每个内角都是60°,正四边形的每 个内角都是90°,正六边形的每个内角 都是120°,这三种多边形的一个内角 的倍数都是360°,而其他的正多边的 每个内角的倍数都不是360°
某一种地砖镶嵌地面,可供选择的地砖共有( )C
A.1种 B.2种 C.3种 D.4种
边长为a的正方形与下列边长为a的正多边形组合起来,
不能镶嵌成平面的是( )B
①正三角形;②正五边形;③正六边形;④正八边形
A. ① ②
B. ② ③
C. ① ③
D. ① ④
课堂练习
3、形状、大小完全相同的任意三角形、四边形 能否单独
6 4. 用任意三角形镶嵌平面时,同一顶点处应摆放 ( )个 4 三角形;用任意四边形镶嵌平面时,同一顶点处应摆放( )
个四边形. 5、下面四种正多边形中,用同一种图形不能平面镶嵌的是
( C ).
A
B
C
D
六、升华知识 深化认识
说说你的 收获
通过这节课的学习你有哪些收获? 你还有什么体会吗?
我们都来做个有心人,多 思考、多研究,把学过的数学 知识应用于生活,解决生活中 的实际问题,使我们的生活更 加美好!
❖
本 课 到 此 结 束
教学后记
90°
4. 正六边形
用边长相同的正五边形不能镶嵌
你正五能边说形的说内角道不理能 吗?
组成360°的角。
13 2
∠1+∠2+∠3=?
活动一实验结论:
1.能镶嵌的图形在一个拼接点处的特点: 各角之和等于360º
2.要用正多边形镶嵌成一个平面的关键
是看:这种正多边形的一个内角的倍数 是否是360°,在正多边形里,正三角 形的每个内角都是60°,正四边形的每 个内角都是90°,正六边形的每个内角 都是120°,这三种多边形的一个内角 的倍数都是360°,而其他的正多边的 每个内角的倍数都不是360°
某一种地砖镶嵌地面,可供选择的地砖共有( )C
A.1种 B.2种 C.3种 D.4种
边长为a的正方形与下列边长为a的正多边形组合起来,
不能镶嵌成平面的是( )B
①正三角形;②正五边形;③正六边形;④正八边形
A. ① ②
B. ② ③
C. ① ③
D. ① ④
课堂练习
3、形状、大小完全相同的任意三角形、四边形 能否单独
人教版数学八年级上册镶嵌-课件

镶嵌
平面镶嵌:
用一些不重叠摆放的多 边形把平面的一部分完全覆 盖,通常把这类问题叫做用 多边形覆盖平面(或平面镶 嵌)的问题.
探究1: 如果只允许选择 一种正多边形进行平 面镶嵌,有哪些正多 边形肯定能做到呢?
活动1:
请你用准备好 的正多边形进行试 验探究吧.
探究3:
如果只用一种多边形进行平面 镶嵌,有哪些多边形肯定能够做到?
活动3:
请用准备好的三 角形、四边形等进行 试验.
2
1
3
2
131ຫໍສະໝຸດ 32131
3
2
2
2
1
3
4 1
2 3
结论3:
如果只用一种多边形进 行平面镶嵌,肯定能够做到 的有 : 任意三角形
任意四边形
正六边形
课堂小结
多边形能覆盖平面 应满足 什么条件?
⑴拼接在同一个点的各个角 的和恰好等于360°;
⑵相邻的多边形有公共边.
请你用课上所学知识,设 计一幅镶嵌艺术画.
正多边形 能否
平面
图形
镶嵌
正三角形
能
正四边形 能
正五边形 不能
正六边形
能
一个顶点周围正 多边形的个数
6 4
3
360°
思考1:用m个相同的正n边形进行 平面镶嵌,n的可能值是多少?
设m个相同的正n边形镶嵌成平面.
(n2)1800 m3600 n
(n-2)m=2n
m
2n n2
2n 4 4 n2
活动2:
用边长相等的正三角形和 正六边形进行平面镶嵌,你能 拼出几种不同的图案?
正三角形与正方形
还有没有其他的两种多边形组合镶嵌的形式 呢?
平面镶嵌:
用一些不重叠摆放的多 边形把平面的一部分完全覆 盖,通常把这类问题叫做用 多边形覆盖平面(或平面镶 嵌)的问题.
探究1: 如果只允许选择 一种正多边形进行平 面镶嵌,有哪些正多 边形肯定能做到呢?
活动1:
请你用准备好 的正多边形进行试 验探究吧.
探究3:
如果只用一种多边形进行平面 镶嵌,有哪些多边形肯定能够做到?
活动3:
请用准备好的三 角形、四边形等进行 试验.
2
1
3
2
131ຫໍສະໝຸດ 32131
3
2
2
2
1
3
4 1
2 3
结论3:
如果只用一种多边形进 行平面镶嵌,肯定能够做到 的有 : 任意三角形
任意四边形
正六边形
课堂小结
多边形能覆盖平面 应满足 什么条件?
⑴拼接在同一个点的各个角 的和恰好等于360°;
⑵相邻的多边形有公共边.
请你用课上所学知识,设 计一幅镶嵌艺术画.
正多边形 能否
平面
图形
镶嵌
正三角形
能
正四边形 能
正五边形 不能
正六边形
能
一个顶点周围正 多边形的个数
6 4
3
360°
思考1:用m个相同的正n边形进行 平面镶嵌,n的可能值是多少?
设m个相同的正n边形镶嵌成平面.
(n2)1800 m3600 n
(n-2)m=2n
m
2n n2
2n 4 4 n2
活动2:
用边长相等的正三角形和 正六边形进行平面镶嵌,你能 拼出几种不同的图案?
正三角形与正方形
还有没有其他的两种多边形组合镶嵌的形式 呢?
八年级数学下册《平面图形的镶嵌》参考课件

m=6,n=3; m=4,n=4 ; m=3,n=6。
实践之窗
问题
动手操作 同桌合作拼拼摆摆
用形状、大小完全相同的三角形能否镶嵌平面? 如果能,观察每个拼接点处有几个角,它们与这 种三角形的三个内角有什么关系。如果不能,说明 为什么。
用同一种四边形能否镶嵌平面呢?
任意三角形的镶嵌
实践之窗
任意四边形的镶嵌
实践之窗
实践小结
用同一种三角形可以镶嵌平面 用同一种四边形可以镶嵌平面 平面图形能镶嵌平面的条件是,每个拼接点处 的多边形各内角之和能组合成 180°或360°
思考时空
在一个正方形的内部按图示1的方式剪去 一个正三角形,并平移,形成如图2所示的新 图案。以这个图案为“基本单位”能否镶嵌平面? 说说你的理由。
(1) (2)
交流乐园
如何以下图中的(1)、(2)为拼图的“基本单 位”,拼出图(3)、(4)、(5)、(6)?如果允 许图形作轴对称变换,那么还可以拼出怎样的图案?
(1)
(3)
(5)
(7)
(9)
(2)
(4)
(6)
(8)
(10 )
收获与评价
• 本节课你有什么收获和感受?
• 本节课你有什么疑惑和问题? • 你能给自己和同伴在本节课的学习
小组合作实践作业
同时用边长相同的正八边形和正方形能 否镶嵌平面?说明为什么。请用硬纸板为材 料进行实验验证。你能设计一个用边长相同 的其它两种正多边形进行镶嵌的方案吗 ? (各小组写出实践总结报告,两周后周二交)
2. 用大小相同的 正三角形、正四边形、 正六边形都可以镶嵌平 面,其他正多边形都不 可以镶嵌平面。
对于正n边形,其内角都为 (n-2)×180°, n
实践之窗
问题
动手操作 同桌合作拼拼摆摆
用形状、大小完全相同的三角形能否镶嵌平面? 如果能,观察每个拼接点处有几个角,它们与这 种三角形的三个内角有什么关系。如果不能,说明 为什么。
用同一种四边形能否镶嵌平面呢?
任意三角形的镶嵌
实践之窗
任意四边形的镶嵌
实践之窗
实践小结
用同一种三角形可以镶嵌平面 用同一种四边形可以镶嵌平面 平面图形能镶嵌平面的条件是,每个拼接点处 的多边形各内角之和能组合成 180°或360°
思考时空
在一个正方形的内部按图示1的方式剪去 一个正三角形,并平移,形成如图2所示的新 图案。以这个图案为“基本单位”能否镶嵌平面? 说说你的理由。
(1) (2)
交流乐园
如何以下图中的(1)、(2)为拼图的“基本单 位”,拼出图(3)、(4)、(5)、(6)?如果允 许图形作轴对称变换,那么还可以拼出怎样的图案?
(1)
(3)
(5)
(7)
(9)
(2)
(4)
(6)
(8)
(10 )
收获与评价
• 本节课你有什么收获和感受?
• 本节课你有什么疑惑和问题? • 你能给自己和同伴在本节课的学习
小组合作实践作业
同时用边长相同的正八边形和正方形能 否镶嵌平面?说明为什么。请用硬纸板为材 料进行实验验证。你能设计一个用边长相同 的其它两种正多边形进行镶嵌的方案吗 ? (各小组写出实践总结报告,两周后周二交)
2. 用大小相同的 正三角形、正四边形、 正六边形都可以镶嵌平 面,其他正多边形都不 可以镶嵌平面。
对于正n边形,其内角都为 (n-2)×180°, n
北师大版八下数学《平面图形的镶嵌》参考课件

m=6,n=3; m=4,n=4 ; m=3,n=6。
实践之窗
问题
动手操作 同桌合作拼拼摆摆
用形状、大小完全相同的三角形能否镶嵌平面? 如果能,观察每个拼接点处有几个角,它们与这 种三角形的三个内角有什么关系。如果不能,说明 为什么。
用同一种四边形能否镶嵌平面呢?
任意三角形的镶嵌
实践之窗
任意四边形的镶嵌
问 题:
用大小相同的正三角形、正六边形能否镶嵌平面? 简述你的理由。能否用正五边形镶嵌平面?
正三角形的镶嵌
正六边形的镶嵌
思考 探究
除正三角形、正四边形、正六边 形能镶嵌平面外,还能找到其他能镶嵌 平面的正多边形吗?
合作议论归纳
1. 同一种正多边形 是否可以镶嵌平面的关 键是:一种正多边形的 一个内角的倍数是否 360°。
综合与实践
平面图形的镶嵌
观察在线
观察在线
观察小结
平面图形的镶嵌
用形状、大小完全相同的一种或几种平面图形进行 拼接,彼此之间不留空隙、不重叠地铺成一片,这就是 平面图形的镶嵌。
ห้องสมุดไป่ตู้
探索活动
四人小组合作、讨论
知识介绍:
在平面内,各角相等,各边也都相等的多边形 叫做正多边形。
边数为n的多边形的内角和等于(n-2)·180°
小组合作实践作业
同时用边长相同的正八边形和正方形能 否镶嵌平面?说明为什么。请用硬纸板为材 料进行实验验证。你能设计一个用边长相同 的其它两种正多边形进行镶嵌的方案吗 ? (各小组写出实践总结报告,两周后周二交)
(1) (2)
交流乐园
如何以下图中的(1)、(2)为拼图的“基本单 位”,拼出图(3)、(4)、(5)、(6)?如果允 许图形作轴对称变换,那么还可以拼出怎样的图案?
实践之窗
问题
动手操作 同桌合作拼拼摆摆
用形状、大小完全相同的三角形能否镶嵌平面? 如果能,观察每个拼接点处有几个角,它们与这 种三角形的三个内角有什么关系。如果不能,说明 为什么。
用同一种四边形能否镶嵌平面呢?
任意三角形的镶嵌
实践之窗
任意四边形的镶嵌
问 题:
用大小相同的正三角形、正六边形能否镶嵌平面? 简述你的理由。能否用正五边形镶嵌平面?
正三角形的镶嵌
正六边形的镶嵌
思考 探究
除正三角形、正四边形、正六边 形能镶嵌平面外,还能找到其他能镶嵌 平面的正多边形吗?
合作议论归纳
1. 同一种正多边形 是否可以镶嵌平面的关 键是:一种正多边形的 一个内角的倍数是否 360°。
综合与实践
平面图形的镶嵌
观察在线
观察在线
观察小结
平面图形的镶嵌
用形状、大小完全相同的一种或几种平面图形进行 拼接,彼此之间不留空隙、不重叠地铺成一片,这就是 平面图形的镶嵌。
ห้องสมุดไป่ตู้
探索活动
四人小组合作、讨论
知识介绍:
在平面内,各角相等,各边也都相等的多边形 叫做正多边形。
边数为n的多边形的内角和等于(n-2)·180°
小组合作实践作业
同时用边长相同的正八边形和正方形能 否镶嵌平面?说明为什么。请用硬纸板为材 料进行实验验证。你能设计一个用边长相同 的其它两种正多边形进行镶嵌的方案吗 ? (各小组写出实践总结报告,两周后周二交)
(1) (2)
交流乐园
如何以下图中的(1)、(2)为拼图的“基本单 位”,拼出图(3)、(4)、(5)、(6)?如果允 许图形作轴对称变换,那么还可以拼出怎样的图案?
【数学课件】平面镶嵌(人教新课标)

想做一做
剪出一些形状、大小完全相同 的任意三角形纸板,拼拼看,它们 能否镶嵌成平面图案?
问题 剪出一些形状、大小完全相同 的任意四边形纸板,拼拼看,它 们能否镶嵌成平面图案?
问题
如果用其中两种正多变形镶嵌,哪 两种正多变形能镶嵌成平面图案?
我们可以利用多边形设计一些美丽的 图案.
2
1
3
3
4 13
想一想
镶嵌平面图案需要的什么条件?
拼接在同一个点的同的图形不留空隙、不重叠 地镶嵌一个平面,需使得拼 接点处的各角之和为 360°.
你还能找到能镶嵌的其他正多边形吗?
要用正多边形镶嵌成一个平面的关键是看:这 种正多边形的一个内角的倍数是否是360°, 在正多边形里,正三角形的每个内角都是 60°,正四边形的每个内角都是90°,正六 边形的每个内角都是120°,这三种多边形的 一个内角的倍数都是360°,而其他的正多边 形的每个内角的倍数都不是360°,所以说: 在正多边形里只有正三角形、正四边形、正六 边形可以镶嵌,而其他的正多边形不可镶嵌.
心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
好漂亮的地板!这 是怎么铺设的?一点空 隙也没有.
我们经常能见到各种建筑物的地 板,观察地板,就能发现地板常用各 种正多边形地砖铺砌成美丽的图案
用一些形状、大小完全相 同的一种或几种平面图形进行 拼接,彼此之间不留空隙,不 重叠地把平面的一部分完全覆 盖,这就是平面图形的镶嵌.
注意:各种图形拼接后要既 无缝隙,又不重叠
上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探究活动:只用一种正多边形, 哪几种正多边形能够进行镶嵌?
收 正n边形 集 n =3 整 n =4
拼图
每个内角 使用正多边 的度数 形的个数k
60°
K= 6
90°
K= 4
结论
能镶嵌 能镶嵌
理
n =5
数
108° 108°
K= 3 不能镶嵌 K= 4 不能镶嵌
据 n =6
120°
K= 3
能镶嵌
正n边形 拼图
想一想
有你 什能 么归 规纳 律出 吗其
中
正三角形和正六 边形能否镶嵌?
正三角形和正五 边形能否镶嵌?
正方形和正八边 形能否镶嵌?
得出结论:
拓展延伸
现在用三种正多边形:正 三角形、正方形、正六边 形能否进行平面镶嵌?如 果不能镶嵌,为什么?如 果能,你能把它画出来吗 (草图)?
收获与启示
课后作业:
设在一个顶(点n周-2围)×有k1个8正0。n边形的角,。则有
k·
= 360
n
n2 4 k 2
k=6
k=4
k=3
∴解为
n=3
n=4
n=6
思考:用下列正多边形能镶嵌吗?
正7边 形?
正十边 形?
正100 边形?
小颖家正在为新房子 装修,在他的房间里, 他想用正三角形和另 一种正多边形镶嵌成 地板,他有哪些选择? 你能帮他出出注意吗?
1. 用一种正多边形镶嵌,哪些可 以,分别是哪些正多边形?
2. 你能找到用两种正多边形镶 嵌,还有哪些吗?请你设计一个 用两个正多边形镶嵌的图形。
2019 SUCCESS
POWERPOINT
2019/5/25
2019 SUCCESS
THANK YOU
2019/鸟分割的平面
通过观察上面的图片,你发现 它们有哪些共同特征?
【1】不重叠 【2】完全覆盖
从数学角度看,用一些不重 叠摆放的图形把平面的一部分完 全覆盖,通常把这类问题叫做覆 盖平面(或平面镶嵌)的问题
本课只探究正多边形的镶嵌
请同学们观察用于镶嵌的基本图形有哪些?
如果用两种 正多边形进 行镶嵌需要 满足什么条 件?
正多边形
拼
图
和 它们的内角度 和360°的关系:
和 它们的内角度 和360°的关系:
正多边形
拼
图
正三角形
和
正四边形
3×60°+ 2 ×90°= 360°
正三角形
和
正六角形
3×60°+2 ×90°=360° 4×60°+1 ×120°=360°
?
分
n=3
每个内角的度数 与360°的关系
6×60°= 360°
结论
能镶嵌
析 n=4
4×90°= 360° 能镶嵌
数 n=5
据
n=6
3×108°< 360° 不能镶嵌
4×108°> 360°不能镶嵌
3×120°= 360° 能镶嵌
得出结论:
如果一个正多边形可以进行镶 嵌,那么内角一定是360°的约数 (或360°一定是这个多边形内角 的整数倍)!
