相似三角形总复习
相似三角形中考复习

相似三角形中考复习相似三角形是初中数学中的重要内容,在中考中占据着相当重要的地位。
为了帮助同学们更好地复习相似三角形,提高解题能力,我们来一起系统地梳理一下这部分知识。
一、相似三角形的定义如果两个三角形的对应角相等,对应边成比例,那么这两个三角形就叫做相似三角形。
相似三角形的对应边的比叫做相似比。
二、相似三角形的判定1、两角分别相等的两个三角形相似。
2、两边成比例且夹角相等的两个三角形相似。
3、三边成比例的两个三角形相似。
在实际解题中,我们要根据题目所给的条件,灵活选择合适的判定方法。
三、相似三角形的性质1、相似三角形的对应角相等,对应边成比例。
2、相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比,面积的比等于相似比的平方。
这些性质在求解边长、角度、面积等问题时经常用到。
四、常见的相似三角形模型1、“A”字型在平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
2、“8”字型与“A”字型类似,只不过图形的形状像数字“8”。
3、母子相似型直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
4、一线三等角型在一条直线上有三个相等的角,往往可以通过角的相等关系证明三角形相似。
五、相似三角形的应用相似三角形在实际生活中有广泛的应用,比如测量建筑物的高度、河流的宽度等。
例如,要测量一座塔的高度,我们可以在塔的旁边立一根已知长度的标杆,然后分别测量出标杆的影长和塔的影长。
由于在同一时刻,太阳光线是平行的,所以标杆和塔与地面形成的三角形是相似的。
根据相似三角形的性质,我们就可以求出塔的高度。
六、中考真题解析例 1:如图,在△ABC 中,D、E 分别是 AB、AC 边上的点,且DE∥BC,如果 AD:AB = 2:3,AE = 4,那么 AC 的长是多少?解:因为 DE∥BC,所以△ADE∽△ABC。
所以 AD:AB = AE:AC因为 AD:AB = 2:3,AE = 4所以 2:3 = 4:AC解得 AC = 6例 2:如图,在△ABC 中,∠ABC = 90°,BD⊥AC 于点 D,若AB = 3,BC = 4,求 BD 的长。
相似三角形总复习

分析:要在三角形内裁出面积最大的正方形,那么这个正方形所有顶点 应落在△ABC 的边上,先画出不同方案,把每种方案中的正方形边长求出.
15
网络构建 一 二 三 四 五
专题归纳
真题集粹
解:如图甲,设正方形 EFGH 的边长为 x cm,由勾股定理得 AC=4 cm. 而 CD×AB=AC×BC=2S△ABC,得 CD= 又△CEH∽△CAB,得
网络构建 1 2 3
专题归纳 4 5 6
真题集粹 7 8
2.(2013 山东聊城中考)如图,点 D 是△ABC 的边 BC 上任一点,已知 AB=4,AD=2,∠DAC=∠B.若△ABD 的面积为 a,则△ACD 的面积为( )
关闭
A.a ∠DAC=∠B,∠ACD= B. a 由已知 ∠BCA,
∴ △ABC∽△DAC,
=
2 2 3
= .∴ 2 = .∴ S1∶ S2∶ S3=1∶ 3∶ 5.
4 9
������ ������3
3 5
答案:1∶ 3∶ 5
12
网络构建 一 二 三 四 五
专题归纳
真题集粹
跟踪训练 3.已知△ABC 的三边长分别为 5,12,13,与其相似的△A'B'C'的最大边长 为 26,求△A'B'C'的面积 S.
由 GH∥AC,得 即 =
������������ ������������
=
������������ , ������������
������ 3-������ 12 ,解得 y= . 4 3 7 60 12 60 ∵ x= ,y= = ,∴ y>x. 37 7 35
即应如图乙那样裁剪,这时正方形的面积最大,它的边长为
相似三角形专题复习
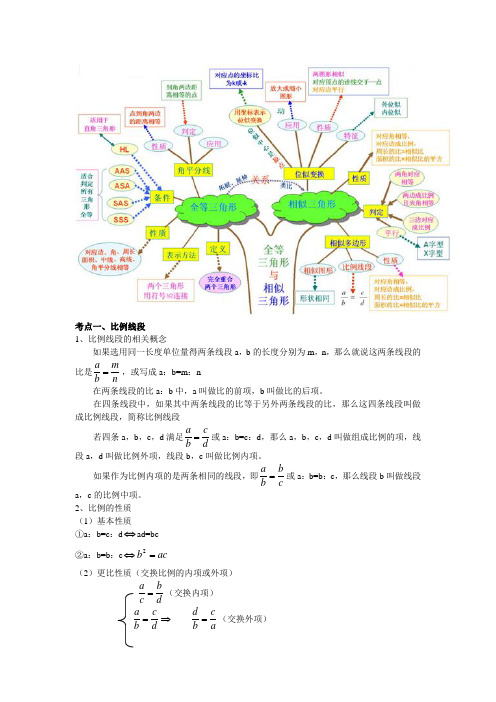
考点一、比例线段 1、比例线段的相关概念如果选用同一长度单位量得两条线段a ,b 的长度分别为m ,n ,那么就说这两条线段的比是a mb n=,或写成a :b=m :n 在两条线段的比a :b 中,a 叫做比的前项,b 叫做比的后项。
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段若四条a ,b ,c ,d 满足a cb d=或a :b=c :d ,那么a ,b ,c ,d 叫做组成比例的项,线段a ,d 叫做比例外项,线段b ,c 叫做比例内项。
如果作为比例内项的是两条相同的线段,即cbb a =或a :b=b :c ,那么线段b 叫做线段a ,c 的比例中项。
2、比例的性质 (1)基本性质①a :b=c :d ⇔ad=bc ②a :b=b :c ac b =⇔2(2)更比性质(交换比例的内项或外项)dbc a =(交换内项) ⇒=dcb a ac bd =(交换外项)abc d =(同时交换内项和外项) (3)反比性质(交换比的前项、后项):cda b d c b a =⇒= (4)合比性质:dd c b b a d c b a ±=±⇒= (5)等比性质:ba n f db m ec a n fd b n m fe d c b a =++++++++⇒≠++++==== )0( 3、黄金分割把线段AB 分成两条线段AC ,BC (AC>BC ),并且使AC 是AB 和BC 的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AC=215-AB ≈0.618AB 考点二、平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
推论:(1)平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
相似三角形性质和判定复习

相似三角形复习【知识要点】1、相似三角形的定义三边对应成_________,三个角对应________的两个三角形叫做相似三角形. 2、相似三角形的判定方法1.两个三角形相似,一般说来必须具备下列六种图形之一:2. 两个角对应相等的两个三角形__________.3. 两边对应成_________且夹角相等的两个三角形相似.4. 三边对应成比例的两个三角形___________.性质:⎪⎪⎩⎪⎪⎨⎧比的平方、对应面积比等于相似比、对应周长比等于相似、对应边成比例、对应角相等4321判定:⎪⎩⎪⎨⎧、三边对应成比例夹角相等、两边对应成比例,且、两角对应相等3211.相似比:相似三角形对应边的比叫做相似比。
当相似比等于1时,这两个三角形不仅形状相同,而且大小也 相同,这样的三角形我们就称为全等三角形。
全等三角形是相似三角形的特例。
2. 相似三角形的判定:①两角对应相等,两三角形相似。
②两边对应成比例,且夹角相等,两三角形相似。
③三边对应成比例,两三角形相似。
3. 相似三角形的性质:①相似三角形的对应角相等。
②相似三角形的对应线段(边、高、中线、角平分线)成比例。
③相似三角形的周长比等于相似比,面积比等于相似比的平方。
FEC【典型例题】1、如图在4×4的正方形方格中,△ABC 和△DEF 的顶点都在长为1的小正方形顶点上. (1)填空:∠ABC=______,BC=_______. (2)判定△ABC 与△DEF 是否相似?2、如图所示,D 、E 两点分别在△ABC 两条边上,且DE 与BC 不平行,请填上一个你认为适合的条件_________,使得△ADE ∽△ABC .并证明3、如图,在△ABC 中,AB =AC ,点D 、E 、F 分别在AB 、BC 、AC 边上,DE=DF ,∠EDF =∠A .(1)求证:BCABEF DE =.(2)证明:BDE ∆与EFC ∆相似。
4、已知,如图,CD 是Rt ABC ∆斜边上的中线,DE AB ⊥交BC 于F ,交AC 的延长线于E , 说明:⑴ ADE ∆∽FDB ∆; ⑵DF DE CD ∙=2.5、已知:如图,□AB C D 中E 为AD 的中点,AF :AB =1:6,EF 与AC 交于M 。
相似三角形复习

相似三角形复习关键信息项:1、相似三角形的定义及性质定义:____________________________性质:____________________________2、相似三角形的判定方法方法:____________________________示例:____________________________3、相似三角形的应用应用场景:____________________________解题思路:____________________________11 相似三角形的定义相似三角形是指三角分别相等,三边成比例的两个三角形。
两个三角形相似用符号“∽”表示。
111 相似比相似三角形对应边的比称为相似比。
相似比为 1 时,两个三角形全等。
112 相似三角形的性质1、相似三角形的对应角相等,对应边成比例。
2、相似三角形的对应高的比、对应中线的比与对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比。
4、相似三角形面积的比等于相似比的平方。
12 相似三角形的判定方法1、两角分别相等的两个三角形相似。
2、两边成比例且夹角相等的两个三角形相似。
3、三边成比例的两个三角形相似。
121 直角三角形相似的判定1、一个锐角相等的两个直角三角形相似。
2、两条直角边成比例的两个直角三角形相似。
3、斜边和一条直角边成比例的两个直角三角形相似。
122 判定方法示例例如,在三角形 ABC 和三角形 A'B'C'中,如果∠A =∠A',∠B =∠B',那么三角形 ABC ∽三角形 A'B'C'。
又比如,在三角形 ABC 和三角形 A'B'C'中,如果 AB / A'B' = AC / A'C' 且∠A =∠A',那么这两个三角形相似。
13 相似三角形的应用131 应用场景1、测量物体的高度,如测量旗杆、大树等的高度。
相似三角形复习

相似三角形【基础知识回顾】1、相似三角形的定义:对应角相等,对应边的比相等的两个三角形。
对应边的比叫做相似比。
2、相似三角形的判定:①平行法②三组对应边的比相等(类似于三角形全等判定“SSS ”)③两组对应边的比相等,且夹角相等(类似于三角形全等判定“SAS ”)④两角对应相等(AA) 直角三角形中斜边、直角边对应比相等(类似于直角三角形全等判定“HL ”)。
相似三角形的基本图形:判断三角形相似,若已知一角对应相等,可先考虑另一角对应相等,注意公共角或对顶角或同角(等角)的余角(或补角)相等,若找不到第二对角相等,就考虑夹这个角的两对应边的比相等;若无法得到角相等,就考虑三组对应边的比相等。
3、相似三角形的性质:①对应角相等②对应边的比相等③对应的高、中线、角平分线、周长之比等于相似比④对应的面积之比等于相似比的平方。
4、相似三角形的应用:求物体的长或宽或高;求有关面积等。
考点一:相似三角形的判定1、下列各组三角形一定相似的是( ) A .两个直角三角形 B .两个钝角三角形 C .两个等腰三角形 D .两个等边三角形2、已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB 、CD 交于O 点,对于各图中的两个的两个三角形而言,下列说法正确的是( )A.都相似B.都不相似C.只有(1)相似D.只有(2)相似3、如图,点D 在△ABC 的边AC 上,要判定△ADB 与△ABC 相似,添加一个条件,不正确的是( ) A. ∠ABD=∠CB. ∠ADB=∠ABCC. D .考点二:相似三角形的性质1、如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为_____,面积的比为_____ 。
2、两个相似三角形的面积比为4∶25,则它们的周长比为_________。
3、顺次连结三角形三边中点所构成的三角形与原三角形,的(1)ABCD O4 3 6 8 (2)AB CBBDCD =AD ABAB AC=周长比等于______,面积比等于_________。
第二十四章-相似三角形-复习ppt课件

1
一、本章知识结构图
放缩与相似形
比例线段
相
比例线段
似
三角形一边的平行线
相似三角形
判定 性质
平面向量
实数与向量相乘
向量的线性运算
2
回顾与思考
一、相似形
1. 各角对应相等,各边对应成比例的两个多边形叫相 似多边形. 2. 三个角对应相等,三条边对应成比例的两个三角形 叫相似三角形.两个相似三角形用“∽”表示,读做 “相似于”.
(2) 以连接后的这两个向量为邻边向量 构造平行四边形
(3) 这个平行四边形的对角线向量就是 这两个向量的和向量与差向量
3.向量加法和减法的三角形法则 加法: 一终二起,一起二终 减法: 共起点指向被减
9
五、典例精析,复习新知
2.如图,在△ABC中,AB=AC=27,D在AC上,且 BD=BC=18,DE//BC交AB于E,则DE= 分析:由△ABC∽△BCD,列出比例式,求出CD,再用 △ABC∽△AED A答案:10
称比例线段.此时也称这四条线段成比例.
4
➢ 线段的比要注意以下几点: • 线段的比是正数 • 单位要统一 • 线段的比与线段的长度无关
如果 (b=d=f≠0),
那么
如果,
,那么ad=bc.
如果ad=bc(a、b、c、d都不等于0),那么
.
5
三、相似三角形的判定与性质 方法1:通过定义(不常用)
方法2:平行于三角形一边的直线与其他两边(或延 长线)相交,所构成的三角形与原三角形相似; 方法3:两对应角相等的,两三角形相似. 方法4:两边对应成比例且夹角相等,两三角形相似. 方法5:三边对应成比例的,两三角形相似.
27.2.1_相似三角形的判定(复习)

D E 3 1
4 C O
2 F
A
B
例2:已知如图,AB∥A'B',BC∥B'C' 求证:△ABC∽△A'B'C’
A A’ 2 O 4 1 B’ 3
C’
B
c
证明: ∵AB∥A’B’ ∴∠1=∠2, A’B’/AB=OB’/OB ∵BC∥B’C’ ∴∠3=∠4, B’C’/BC = OB’/OB ∴∠ABC=∠A’B’C ∴ A’B’/AB =B’C’/BC ∴△ABC∽△A'B'C'
AB BC DE
AB AD BC DE AC
,求证:∠BAD=∠CAE。 AE A E
D
AC AE
∴△ABC∽△ADE
B
∴∠BAC=∠DAE ∴∠BAC-∠DAC =∠DAE-∠DAC 即 ∠BAD=∠CAE
C
例题教学:
2.如图,在□ABCD中,E、F分别是AB、 BC的中点,连接AC、EF.求证: △BEF∽△ACD.
A D E B F C
1、已知如图,DC∥AB,AC、BD相交于点 O,AO=BO,DF=FB 求证:DE2=EC· EO 证明: ∵OA=OB ∴∠3=∠2 ∵DF=FB ∴∠1=∠2 ∵DC∥AB ∴∠3=∠4 ∴∠1=∠4 又∵∠DEO=∠DEC ∴△DEO∽ △CED ∴ DE/CE = EO/DE ∴DE2=EC· EO
牛刀小试:
8..如图,在△ABC中,DE//BC,AD:CD=1:3, BE=6cm,则AE= cm.
A E D
B
C
9.如图,E是平行四边形ABCD的边BC的延 长线上的一点,连结AE交CD于F,则图中共 有相似三角形( ) A.1对B.2对C.3对D.4对
相似三角形复习(较全)

相似三角形知识点汇总【知识要点】1. 比例线段的有关概念: 在比例式::中,、叫外项,、叫内项,、叫前项,a b cda b c d a d b c a c ==()b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。
把线段AB 分成两条线段AC 和BC ,使AC 2=AB ²BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。
2. 比例性质: ①基本性质:a b c dad bc =⇔= ②合比性质:±±a b c d a b b c dd =⇒= ③等比性质:……≠……a b c d m n b d n a c m b d n ab===+++⇒++++++=()03. 平行线分线段成比例定理:①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3。
则,,,…AB BC DE EF AB AC DE DF BC AC EFDF=== ②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
二、有关知识点:1.相似三角形定义:对应角相等,对应边成比例的三角形,叫做相似三角形。
2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。
3.相似三角形的相似比:相似三角形的对应边的比叫做相似比。
4.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
5.相似三角形的判定定理:(1)三角形相似的判定方法与全等的判定方法的联系列表如下:从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理,这就是我们数学中的用类比的方法,在旧知识的基础上找出新知识并从中探究新知识掌握的方法。
中考总复习 相似三角形

【名师提醒】解相似三角形问题时,要注意相似三角形中 的对应关系,可根据相似三角形对应的字母写对应边,这 样可避免对应关系混乱.
命题点3 相似三角形的实际应用
例(’15兰州24题8分)如图,在一面 与地面垂直的围墙的同侧有一根高10 米的旗杆AB和一根高度未知的电线杆 CD,它们都与地面垂直,为了测得电 线杆的高度,一个小组的同学进行了 如下测量:某一时刻,在太阳光照射 下,旗杆落在围墙上的影子EF的长度 为2米,落在地面上的影子BF的长为10米,而电线杆落 在围墙上的影子GH的长度为3米,落在地面上的影子DH 的长为5米.依据这些数据,该小组的同学计算出了电线 杆的高度. (1)该小组的同学在这里利用的是_____投影的有关知识 进行计算的; (2)试计算出电线杆的高度,并写出计算的过程.
【解析】∵两个相似三角形的面积比是1:4,∴这两个相 似三角形的相似比是1:2, ∴它们的周长比是1:2.
3. 如图,在 △ABC中,DE∥BC,AD=6,DB=3,AE=4, 则EC的长为( B )
A. 1
B. 2
C. 3
D. 4
【解析】本题考查平行线分线段成比例定理
AD AE = , 又∵AD=6, DB=3, DB EC AE=4,∴ 6 = 4 ,解得EC=2. 3 EC
6.某一时刻,身高1.6m的小明在阳光下的影长是0.4m, 同一时刻同一地点,测得某旗杆的影长是5m,则该旗 杆的高度是____m. 20
【解析】根据题意可得
1.6 = 0.4 ,解得h=20m. h 5
7. 如图, 在△ABC中,∠C=90°,AD是 ∠CAB的角平分线,BE⊥AE,垂足为点E. 求证: △BDE~ △ABE. 证明:∵AD是∠CAB的角平分线, ∴ ∠CAD= ∠BAD , ∵∠C=90°, ∴∠CAD+∠ADC=90°, ∵ BE⊥AE, ∴∠E=90°, ∴∠DBE+∠BDE=90°, ∵∠ADC= ∠BDE, ∴∠CAD= ∠BAD = ∠DBE , ∴ △BDE~ △ABE.
相似三角形专题复习(共66张PPT)

3.右图中, DE∥BC,S△ADE:S四边形DBCE = 1:8,则AE:AC=_____
1:3
课堂训练:
E
B
D
C
4. 在△ABCAC=4,AB=5.D是AC上一动点,且∠ADE=∠B,设AD=x,AE=y,写出y与x之间的函数关系式.试确定x的取值范围.
A
解: ∵∠A=∠A ∵∠ADE=∠B ∴△ADE∽△ABC ( ) ∴AD:AB=AE:AC ∴x:5=y:4 ∴y=0.8x
相似三角形
DE∥BC
△ ADE∽ △ ABC
∠DAE= ∠CAB
△ ADE∽ △ ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
△ADE∽ △ ABC
对应角相等;
性质定理
对应边成比例;
周长的比 等于相似比;
面积的比等于 相似比的平方;
三边对应成比例的 两个三角形相似.
灵感 智慧
M1
A
B
C
P
Q
A
B
C
P
Q
M2
例:如图,在ABC中,∠C=90°,AC=4,BC=3,PQ∥AB,点P在AC上(与点A、C不重合),点Q在BC上。试问:在AB上是否存在点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长。
灵感 智慧
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E重合,若AD=10, AB= 8, 则EF=______
善于在复杂图形中寻找基本型
5
A
D
B
C
E
F
A
B
C
F
E
E
E
相似三角形中考复习(知识点+题型分类练习)

相似三角形一、知识概述1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
3.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形.4.相似三角形的基本性质①相似三角形的对应边成比例、对应角相等.②相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示:①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例.②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC的相似比,当且仅当它们全等时,才有k=k′=1.③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出.5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。
温馨提示:(1)判定三角形相似的几条思路:①条件中若有平行,可采用判定定理1;②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例;③条件中若有两边对应成比例,可找夹角相等;但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等.④条件中若有等腰关系,可找顶角相等或底角相等,也可找腰和底对应成比例。
(2)在综合题中,注意相似知识的灵活运用,并熟练掌握线段代换、等比代换、等量代换技巧的应用,培养综合运用知识的能力。
(3)运用相似的知识解决一些实际问题,要能够在理解题意的基础上,把它转化为纯数学知识的问题,要注意培养当数学建模的思想。
三角形相似中考总复习原创课件

3.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,求证:△ABC∽ADE.
2.如图,点P是▱ABCD的边AB上一点,射线CP交DA的延长线于点E,则图中相似的三角形有________对.
解:(1)∵∠ACB=90°,AC=8,BC=6,∴AB=10. ∵CD⊥AB,∴S△ABC= BC·AC= AB·CD. ∴CD= . ∴线段CD的长为4.8.
【变式2】如图,四边形ABCD为平行四边形,以 CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的 切线DE与边AB相交于点E. 求证:△ADE∽△CDF.
证明:∵CD是⊙O的直径, ∴∠DFC=90°. ∵四边形ABCD是平行四边形, ∴∠A=∠C,AD∥BC. ∴∠ADF=∠DFC=90°, ∵DE为⊙O的切线,∴DE⊥DC. ∴∠EDC=90°. ∴∠ADF=∠EDC=90°. ∴∠ADE=∠CDF. ∵∠A=∠C, ∴△ADE∽△CDF.
第四章 三角形第18课 三角形相似
1.相似三角形的判定:(1)如图,若DE∥BC(A型和X型)则 △ADE∽__________.(2)两个角对应相等的两个三角形__________.(3)两边对应成__________且夹角________的两个三角形 相似.(4)三边对应成比例的两个三角形__________.
相似三角形的复习

.D
B E
.D
B E C
C
A
6.如图,DE∥BC,D是AB的中点, DC、BE相交于点G。
求
D
E
DE ⑴ BC =1:2
G
B C
S GED ⑵ =1:4 S GBC
7、已知:如图在这两个直角三角形中, ∠ACB =∠ADC= 90°,∠1=∠B, AC= 4 ,CD=2. 则AB的长为 。
A
P
P
5、如图 ABCD ,E为DC边上的一点, 连接AE并延长交BC的延长线于F,在这个 图形中,有几对相似三角形?若CF:CB= 1:2, S⊿CEF=4,求S⊿AED 和S再见!!
C C Q B A
P
A
P
Q M2 B
M1
(6.已知如图AB DB于B点,CD DB于D点,AB=6, CD=4,BD=14,问:在DB上是否存在P点,使以C,D, P为顶点的三角形与以P,B,A为顶点的三角形相似? 如果存在,请算出P点的位置;若不存在,请说明理由?
A C
D
B
8.如图,在ABC中,∠C=90°,AC=4,BC=3, PQ∥AB,点P在AC上(与点A、C不重合),点 Q在BC上。试问:在AB上是否存在点M,使得 △PQM为等腰直角三角形?若不存在,请简要说 明理由;若存在,请求出PQ的长。
A
D O B
E
C
2、下列命题: ①所有的等腰三角形都相似。 ②所有的等边三角形都相似; ③所有的等腰直角三角形都相似; ④所有的直角三角形都相似。 ⑤有一个钝角相等的两等腰三角形相似 ⑥有一个(锐)角相等的两等腰三角形相似 其中是真命题的有 。
3.AD、BC相交于点O,添加一个条件, 使△AOB∽ △ DOC
相似三角形复习

.
F1 F2
C
B
相似三角形应用的复习
6.如图,正方形ABCD的边长为 ,E是AB的中 如图,正方形 的边长为8, 是 的中 如图 的边长为 分别在BC, 上 点,点M,N分别在 ,CD上,且CM=2,则 , 分别在 , 当CN=_________时,△CMN与△ADE的形状 时 与 的形状 相同。 相同。
M
A D E
B
C
3.如图,P是△ABC中AB边上的一点,要使△ACP和△ABC相似,则需 如图,P ,P是 ABC中AB边上的一点 边上的一点, ACP和 ABC相似 相似,
∠ACP=∠B; ∠ 或∠APC=∠ACB; ∠ 添加一个条件: 添加一个条件:_____________________________________ 或AP:AC=AC:AB即AC2=AP·AB。 即
1 cm 比例中项是____ .
3.黄金分割:A 黄金分割: 黄金分割
C
B
把一条线段( AB )分成两条线段,使其 中较长线段( AC )是 原线段( AB )与较短线段( BC )的比例中项,就叫做 把这条 线段黄金分割。
5 −1 即:AC = AB ⋅ BC , AC = AB 2
2
4 C是线段 AB 的黄金分割点,较长线 段AC = 2 5 − 1 , 则AB = ____ .
(
)
1.相似三角形的定义: 相似三角形的定义: 相似三角形的定义
对应角相等、对应边成比例的三角形叫做相似三角形。 对应角相等、对应边成比例的三角形叫做相似三角形。
2.相似比: 相似比: 相似比
相似三角形的对应边的比,叫做相似三角形的相似比。 相似三角形的对应边的比,叫做相似三角形的相似比。
三角形相似的判定复习

全等三角形 的判定方法
•定义 定义 •边角边公理 边角边公理 边角边 •角边角公理 角边角公理 角边角 •角角边定理 角角边定理 角角边 •边边边公理 边边边公理 边边边 •斜边、直角 斜边、 斜边 边公理
相似三角形 的判定方法
•定义 定义 •定理 定理 •两角对应相等,两 两角对应相等, 两角对应相等 个三角形相似 •两边对应成比例且 两边对应成比例且 夹角相等,两三角 形相似. 形相似 •三边对应成比例 , 三边对应成比例, 三边对应成比例 两三角形相似. 两三角形相似.
图 形
挑战自我
一个边长为a的正方形 一个边长为 的正方形ABEG,对角线 的正方形 , AE的长是 的长是 ;
挑战自我
一个边长为a的正方形 一个边长为 的正方形ABEG,对角线 的正方形 , AE的长是 的长是 ;
挑战自我
两个边长为a的正方形 两个边长为 的正方形ABEG和GEFH, 的正方形 和 , 矩形对角线AF的长是 矩形对角线 的长是 ;
相似三角形 的判定方法
思 想 方 法
思 想 方 法
思 想 方 法
思 想 方 法
如图, a、b、c 分别表示△ABC 中 如图, 、 、 分别表示△ ∠A、∠B、∠C 的 对 边 , a´、b´、c´ 分 、 、 别 表 示 △ A´B´C´ 中 ∠A´、∠B´、∠C´ 的对边. 的对边
c a
证法1: 正方形 的边长为a, 证法 :∵正方形ABEG的边长为 , 的边长为 ∴AE= a.
在△AEF和△CEA中, 和 中 AE∶EF= ∶ a∶a= ∶ a= . .
EC∶EA=2a∶ ∶ ∶
证法1: 正方形 的边长为a, 证法 :∵正方形ABEG的边长为 , 的边长为 ∴AE= a.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23章:相似形知识点强化记忆知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)在四条线段dc b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:a d c b =.②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c叫比例内项, a 、c 叫比例前项,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d=::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
(3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB.即12AC BC AB AC ==简记为:12长短==全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0) (1) 基本性质:①bc ad d c b a =⇔=::;②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项(3)反比性质(把比的前项、后项交换): a c b d b d a c=⇔=.(4)合、分比性质:a c abcd b d b d±±=⇔=.注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=dc d c b a b a ccd a a b d c b a 等等.(5)等比性质:如果)0(≠++++====n f d b n m f e d c b a ,那么ban f d b m e c a =++++++++ .注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零. ③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:ba f db ec a f ed c b a fe d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b .知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE ∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边......与原三角形三.....边.对应成比例. ②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等.注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
知识点5 相似三角形的概念B对应角相等,对应边成比例的三角形,叫做相似三角形.相似用符号“∽”表示,读作“相似于” .相似三角形对应边的比叫做相似比(或相似系数).相似三角形对应角相等,对应边成比例. 注:①对应性:即两个三角形相似时,一定要把表示对应顶点的字母写在对应位置上,这样写比较容易找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的.③两个三角形形状一样,但大小不一定一样.④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对应边成比例.知识点6 三角形相似的等价关系与三角形相似的判定定理的预备定理 (1)相似三角形的等价关系:①反身性:对于任一ABC ∆有ABC ∆∽ABC ∆.②对称性:若ABC ∆∽'''C B A ∆,则'''C B A ∆∽ABC ∆.③传递性:若ABC ∆∽C B A '∆'',且C B A '∆''∽C B A ''''''∆,则ABC ∆∽C B A ''''''∆(2) 三角形相似的判定定理的预备定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:用数学语言表述是:BC DE // , ∴ADE ∆∽ABC ∆.知识点7 三角形相似的判定方法1、定义法:三个对应角相等,三条对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.6、判定直角三角形相似的方法: (1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.注:射影定理:在直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则AD 2=BD·DC ,AB 2=BD·BC ,AC 2=CD·BC 。
(1)B (3)D B (2)D BC知识点8 相似三角形常见的图形1、下面我们来看一看相似三角形的几种基本图形:(1)如图:称为“平行线型”的相似三角形(有“A型”与“X型”图)(2) 如图:其中∠1=∠2,则△ADE∽△ABC称为“斜交型”的相似三角形。
(有“反A共角型”、“反A共角共边型”、“蝶型”)(3)如图:称为“垂直型”(有“双垂直共角型”、“双垂直共角共边型(也称“射影定理型”)”、“三垂直型”)ABCDE12AABB C CDDEE12412BC(D)B(3)DB(2)D(4)如图:∠1=∠2,∠B=∠D,则△ADE∽△ABC,称为“旋转型”的相似三角形。
2、几种基本图形的具体应用:(1)若DE∥BC(A型和X型)则△ADE∽△ABC(2)射影定理若CD为Rt△ABC斜边上的高(双直角图形)则Rt△ABC∽Rt△ACD∽Rt△CBD且AC2=AD·AB,CD2=AD·BD,BC2=BD·AB;(3)满足1、AC2=AD·AB,2、∠ACD=∠B,3、∠ACB=∠ADC,都可判定△ADC∽△ACB.(4)当AD AEAC或AD·AB=AC·AE时,△ADE∽△ACB.知识点8:全等与相似的比较:知识点9 相似三角形的性质(1)相似三角形对应角相等,对应边成比例.(2)相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.(3)相似三角形周长的比等于相似比.(4)相似三角形面积的比等于相似比的平方.BEACD12注:相似三角形性质可用来证明线段成比例、角相等,也可用来计算周长、边长等.知识点10 相似三角形中有关证(解)题规律与辅助线作法 1、证明四条线段成比例的常用方法: (1)线段成比例的定义 (2)三角形相似的预备定理 (3)利用相似三角形的性质 (4)利用中间比等量代换 (5)利用面积关系证明题常用方法归纳:(1)总体思路:“等积”变“比例”,“比例”找“相似”(2)找相似:通过“横找”“竖看”寻找三角形,即横向看或纵向寻找的时候一共各有三个不同的字母,并且这几个字母不在同一条直线上,能够组成三角形,并且有可能是相似的, 则可证明这两个三角形相似,然后由相似三角形对应边成比例即可证的所需的结论.(3)找中间比:若没有三角形(即横向看或纵向寻找的时候一共有四个字母或者三个字母,但这几个字母在同一条直线上),则需要进行“转移”(或“替换”),常用的“替换”方法有这样的三种:等线段代换、等比代换、等积代换.即:找相似找不到,找中间比。
方法:将等式左右两边的比表示出来。
①)(,为中间比n mn m d c n m b a == ②'',,n n nm d c n m b a === ③),(,''''''nm n m n n m m n m d c n m b a =====或(4) 添加辅助线:若上述方法还不能奏效的话,可以考虑添加辅助线(通常是添加平行线)构成比例.以上步骤可以不断的重复使用,直到被证结论证出为止.注:添加辅助平行线是获得成比例线段和相似三角形的重要途径。
