特殊的平行四边形菱形精品PPT课件
合集下载
19.2 特殊平行四边形 (第3课时)19.2.2菱形(菱形的性质)

∠ADC 。
证明:因为四边形ABCD是菱形, 证明:因为四边形ABCD是菱形, ABCD是菱形 所以AB=AD 菱形的四条边都相等)。 AB=AD( 所以AB=AD(菱形的四条边都相等)。 ABD中 在△ABD中, 又因为BO=DO BO=DO, 又因为BO=DO, B 所以AC⊥BD AC平分 BAD。 AC⊥BD, 平分∠ 所以AC⊥BD,AC平分∠BAD。 同理: AC平分 BCD; 平分∠ 同理: AC平分∠BCD; BD平分 ABC和 ADC。 平分∠ BD平分∠ABC和∠ADC。
矩形
两组对边 分别平行 平行 四边形
菱形
有一组邻边相等的平行四边形叫做菱形。 有一组邻边相等的平行四边形叫做菱形。 邻边相等 叫做菱形
AB=BC 四边形ABCD是菱形 是菱形 四边形 ABCD
如何利用折纸、剪切的方法,既快又准 如何利用折纸、剪切的方法, 确地剪出一个菱形的纸片? 确地剪出一个菱形的纸片?
他是这样做的: 他是这样做的:将一张长方形的纸 对折、再对折,然后沿图中的虚线剪下, 对折、再对折,然后沿图中的虚线剪下, 打开即可.你知道其中的道理吗? 打开即可 你知道其中的道理吗? 你知道其中的道理吗
D O A C B
菱形的性质Leabharlann 菱形的性质:(1)菱形具有平行四边形的一切性质; )菱形具有平行四边形的一切性质; (2)菱形的四条边都相等; )菱形的四条边都相等; (3)菱形的两条对角线互相垂直, )菱形的两条对角线互相垂直, 并且每一条对角线平分一组对角; 并且每一条对角线平分一组对角; (4)菱形是轴对对称图形;也是中心对称图形。 )菱形是轴对对称图形;也是中心对称图形。
?
1.已知菱形的周长是12cm, 1.已知菱形的周长是12cm,那 已知菱形的周长是12cm 3cm 么它的边长是______. 么它的边长是______. 2.菱形ABCD中 ABC=60度 2.菱形ABCD中∠ABC=60度, 菱形ABCD 60度 BAC= 60度 则∠BAC=_______. B
证明:因为四边形ABCD是菱形, 证明:因为四边形ABCD是菱形, ABCD是菱形 所以AB=AD 菱形的四条边都相等)。 AB=AD( 所以AB=AD(菱形的四条边都相等)。 ABD中 在△ABD中, 又因为BO=DO BO=DO, 又因为BO=DO, B 所以AC⊥BD AC平分 BAD。 AC⊥BD, 平分∠ 所以AC⊥BD,AC平分∠BAD。 同理: AC平分 BCD; 平分∠ 同理: AC平分∠BCD; BD平分 ABC和 ADC。 平分∠ BD平分∠ABC和∠ADC。
矩形
两组对边 分别平行 平行 四边形
菱形
有一组邻边相等的平行四边形叫做菱形。 有一组邻边相等的平行四边形叫做菱形。 邻边相等 叫做菱形
AB=BC 四边形ABCD是菱形 是菱形 四边形 ABCD
如何利用折纸、剪切的方法,既快又准 如何利用折纸、剪切的方法, 确地剪出一个菱形的纸片? 确地剪出一个菱形的纸片?
他是这样做的: 他是这样做的:将一张长方形的纸 对折、再对折,然后沿图中的虚线剪下, 对折、再对折,然后沿图中的虚线剪下, 打开即可.你知道其中的道理吗? 打开即可 你知道其中的道理吗? 你知道其中的道理吗
D O A C B
菱形的性质Leabharlann 菱形的性质:(1)菱形具有平行四边形的一切性质; )菱形具有平行四边形的一切性质; (2)菱形的四条边都相等; )菱形的四条边都相等; (3)菱形的两条对角线互相垂直, )菱形的两条对角线互相垂直, 并且每一条对角线平分一组对角; 并且每一条对角线平分一组对角; (4)菱形是轴对对称图形;也是中心对称图形。 )菱形是轴对对称图形;也是中心对称图形。
?
1.已知菱形的周长是12cm, 1.已知菱形的周长是12cm,那 已知菱形的周长是12cm 3cm 么它的边长是______. 么它的边长是______. 2.菱形ABCD中 ABC=60度 2.菱形ABCD中∠ABC=60度, 菱形ABCD 60度 BAC= 60度 则∠BAC=_______. B
北师大版九年级上册数学《菱形的性质与判定》特殊平行四边形说课教学复习课件

(二)预习反馈 1. 下列四个几何体中,左视图为圆的是( D )
2. 如图所示的几何体的主视图为( B )
3. 如图是一个正方体被截去一个直三棱柱得到的几何 体,则该几何体的俯视图是( D )
4. 一座楼房的三种视图中, 主主视视图图和和左左视视 图可以反映 出楼房的高度, 俯俯视视 图可以反映出楼房的建筑面积.
∴∠CEF=∠EFG,∴∠CEF=∠CFE,
∴CE=CF,∴CE=FG,
∵CE∥FG,∴四边形CEGF是平行四边形,
∵CE=CF,∴平行四边形CEGF菱形
课堂小结
定义 有一组邻边相等的平行四边形叫做菱形.
菱形的判定
定理1:对角线互相垂直的平行四边形是菱形.
定理 定理2:四边相等的四边形是菱形.
第五章 投影与视图
合作探究
已知:如图,在□ABCD中,对角线AC与BD相较于点O,AC⊥BD.
求证:□ABCD是菱形.
证明:∵四边形ABCD是平行四边形,
B
∴OA=OC. 又∵AC⊥BD,
A
O
C
∴直线BD是线段AC的垂直平分线.
D
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
新课讲授
菱形的判定
B
定理:对角线互相垂直的平行四边形是菱形.
合作探究
什么样的四边形是菱形? 有一组邻边相等的平行四边形.
我们还可以从哪 些角度考虑?
合作探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成 一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动 木条,这个四边形什么时候变成菱形?
你能证明它吗?
可以发现: 对角线互相垂直的平行四边形是菱形.
北师版九年级数学上册课件 第一章 特殊平行四边形 菱形的性质与判定 第3课时 菱形的性质和判定的应用

∴四边形 AECF 的面积为12 AC·EF=12 ×8×6=24
17.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°, 则四边形ABCD的面积为__6__3___.
18.(教材 P10 习题 5 变式)(2020·广州)如图,在△ABD 中,∠ABD=∠ADB. (1)作点 A 关于 BD 的对称点 C; (要求:尺规作图,不写作法,保留作图痕迹) (2)在(1)所作的图中,连接 BC,DC,连接 AC,交 BD 于点 O. ①求证:四边形 ABCD 是菱形;
北师版
第一章 特殊平行四边形
1.1 菱形的性质与判定
第3课时 菱形的性质和判定的应用
1.菱形的两条对角线的长为 a 和 b,且 a,b 满足(a-1)2+ b-4 =0, 那么菱形的面积为__2__.
2.(2020·营口)如图,在菱形 ABCD 中,对角线 AC,BD 交于点 O, 其中 OA=1,OB=2,则菱形 ABCD 的面积为_4__.
7.(2020·遵义)如图,在菱形 ABCD 中,AB=5,AC=6,
过点 D 作 DE⊥BA,交 BA 的延长线于点 E,则线段 DE 的长为(D )
A.152
B.158
C.4 D.254
8.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6, 24
OE⊥AD于点E,交BC于点F,则EF的长为____5___.
B.52 C.3 D.4
13.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一 个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( D)
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
14.如图,菱形 ABCD 的周长为 8 cm,高 AE 长为 3 cm, 则对角线 AC 和 BD 的长之比为 __1_∶___3_____ .
17.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°, 则四边形ABCD的面积为__6__3___.
18.(教材 P10 习题 5 变式)(2020·广州)如图,在△ABD 中,∠ABD=∠ADB. (1)作点 A 关于 BD 的对称点 C; (要求:尺规作图,不写作法,保留作图痕迹) (2)在(1)所作的图中,连接 BC,DC,连接 AC,交 BD 于点 O. ①求证:四边形 ABCD 是菱形;
北师版
第一章 特殊平行四边形
1.1 菱形的性质与判定
第3课时 菱形的性质和判定的应用
1.菱形的两条对角线的长为 a 和 b,且 a,b 满足(a-1)2+ b-4 =0, 那么菱形的面积为__2__.
2.(2020·营口)如图,在菱形 ABCD 中,对角线 AC,BD 交于点 O, 其中 OA=1,OB=2,则菱形 ABCD 的面积为_4__.
7.(2020·遵义)如图,在菱形 ABCD 中,AB=5,AC=6,
过点 D 作 DE⊥BA,交 BA 的延长线于点 E,则线段 DE 的长为(D )
A.152
B.158
C.4 D.254
8.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6, 24
OE⊥AD于点E,交BC于点F,则EF的长为____5___.
B.52 C.3 D.4
13.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一 个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( D)
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
14.如图,菱形 ABCD 的周长为 8 cm,高 AE 长为 3 cm, 则对角线 AC 和 BD 的长之比为 __1_∶___3_____ .
菱形性质与判定课件ppt

面积计算
菱形面积的计算公式为
面积 = (对角线1 × 对角线2) / 2。由于菱形的对角线互相垂直且平分,因此可以使用此公式来计算面积。
另一种计算菱形面积的方法是
面积 = 底 × 高。在这里,底是菱形的一条边,高是从这条边到对角顶点的垂直距离。
周长计算
01
菱形的周长计算公式为:周长 = 4 × 边长。由于菱形的四条边都相等, 因此可以使用此公式来计算周长。
建筑学中的应用
建筑设计
菱形结构在建筑设计中常被用作装饰元素,如菱形窗格、菱形图案的墙面等,增加建筑物的美感和独特性。
空间划分
菱形地砖、菱形玻璃等可以用于室内空间划分,创造出独特视觉效果,同时起到引导人流、划分功能区域的作用。
工程学中的应用
结构工程
菱形结构具有较好的稳定性和承重能力,在桥梁、道路、隧道等工程建设中,菱形结构 常被用于增强结构的稳定性和承载能力。
邻边互相垂直且相等判定
邻边互相垂直
菱形的任意一组邻边互相垂直,因此 可以通过测量任意一组邻边的夹角是 否为90度来判断一个四边形是否为菱 形。
邻边长度相等
除了互相垂直外,菱形的任意一组邻 边的长度还相等。这也是菱形的一个 基本性质。
03
菱形与其他四边形的比较
与矩形的关系
01
02
03
边的性质
菱形的对边相等,与矩形 相同;但菱形的邻边也相 等,这是矩形不具备的性 质。
角度关系
两组对角相等,即∠A=∠C,∠B=∠D;邻角互补,即∠A+∠B=180°, ∠B+∠C=180°。
对角线性质
对角线互相垂直: AC⊥BD。
对角线长度关系:对 角线长度不一定相等 ,但满足 AC²+BD²=4AB²。
菱形(第二课时 菱形的判定)(课件)

故选:C.
)
菱形的判定
如图,、、、分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,则四边形
ABCD应具备的条件是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.一组对边平行而另一组对边不平行
【详解】
解:连接AC,BD,
∵四边形ABCD中,E、F、G、H分别是四条边的中点,要使四边形EFGH为菱形,
D
1
2
做法:分别以A、C为圆心,以大于 AC
的长为半径作弧,两条弧分别相交于点B ,
D,依次连接A、B、C、D四点.
A
C
[思考]得到的这个四边形是菱形吗?
B
探索与证明
四条边都相等的四边形是菱形
A
D
B
C
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵AB=BC=CD=AD
∴AB=CD,BC=AD
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形
判定1:四条边都相等的四边形是菱形
探索与证明
对角线互相垂直的的平行四边形是菱形
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:▱ABCD是菱形.
B
证明: ∵四边形ABCD是平行四边形
A.3个
B.4个
C.1个
D.2个
【详解】
解:∵四边形ABCD是平行四边形,
∴①当AB=BC时,四边形ABCD是菱形;故符合题意;
②当AC⊥BD时,四边形ABCD是菱形;故符合题意;
③当∠ABC=90°时,四边形ABCD是矩形;故不符合题意;
)
菱形的判定
如图,、、、分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,则四边形
ABCD应具备的条件是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.一组对边平行而另一组对边不平行
【详解】
解:连接AC,BD,
∵四边形ABCD中,E、F、G、H分别是四条边的中点,要使四边形EFGH为菱形,
D
1
2
做法:分别以A、C为圆心,以大于 AC
的长为半径作弧,两条弧分别相交于点B ,
D,依次连接A、B、C、D四点.
A
C
[思考]得到的这个四边形是菱形吗?
B
探索与证明
四条边都相等的四边形是菱形
A
D
B
C
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵AB=BC=CD=AD
∴AB=CD,BC=AD
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形
判定1:四条边都相等的四边形是菱形
探索与证明
对角线互相垂直的的平行四边形是菱形
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:▱ABCD是菱形.
B
证明: ∵四边形ABCD是平行四边形
A.3个
B.4个
C.1个
D.2个
【详解】
解:∵四边形ABCD是平行四边形,
∴①当AB=BC时,四边形ABCD是菱形;故符合题意;
②当AC⊥BD时,四边形ABCD是菱形;故符合题意;
③当∠ABC=90°时,四边形ABCD是矩形;故不符合题意;
特殊的平行四边形——菱形的定义与性质
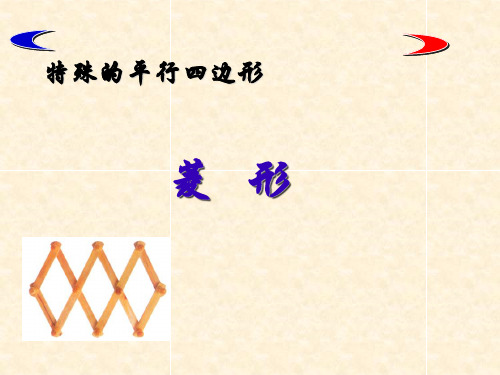
6.已知菱形的周长是12cm,那么它的 3cm 边长是 ______. 7.如下图:菱形ABCD中∠BAD=60度, 若BD=6cm,则菱形的周长是( ) D
C
A A.3cm B.12cm C. 6cm D.4cm B
O
C
7、已知,菱形对角线长分别为12cm和 16cm,求菱形的高。 8、如图,E为菱形ABCD边BC上一点, 且AB=AE,AE交BD于O,且 A ∠DAE=2∠BAE, D 求证:EB=OA; O
= AC×BD
C 思考:计算菱形的面积除了上式方法外,利用对 角线能 计算菱形的面积公式吗?
面积:S菱形=底×高=对角线乘积的一半
2
1、菱形ABCD两条对角线BD、AC长分别 是6cm和8cm,求菱形的面积。
D A O B C
S菱形ABCD
1 AC BD 2
24
D O
A
C
B
如图,在菱形ABCD中,对角线AC、BD相交于点O
已知:在
ABCD 中,AC ⊥ BD B
A
∟
求证: ABCD 是菱形
证明:
O C
D
∵四边形ABCD是平行四边形
∴OA=OC 又∵AC⊥BD;
∴BA=BC ∴ ABCD是菱形
判定方法3:
对角线互相垂直的平行四边形是菱形
A
D AC⊥BD B C B C A D
□ABCD
菱形ABCD
数学语言
∵在□ABCD中,AC⊥BD ∴ □ABCD是菱形
∥ ∴ AD BC ∴ ∠ ∴ DAB+ ∠ DAC= ∠ ABC= ∠BAC 180° ∴ AB=BC=CD=DA ∴OA=OC;OB=OD ∠DAB= ∠ DCB ∴ =
1.菱形的性质与判定第2课时 菱形的判定PPT课件(北师大版)

第2课时 菱形的判定
新知导航
变式训练 1.如图,CE是△ABC外角∠ACD的平分线,AF∥CD 交CE于点F,FG∥AC交CD于点G. 求证:四边形ACGF是菱形. 证明:∵AF∥CD,FG∥AC, ∴四边形ACGF是平行四边形,∠2=∠3, ∵CE平分∠ACD,∴∠1=∠2, ∴∠1=∠3,∴AC=AF, ∴四边形ACGF是菱形.
,
∠EOD=∠FOB
∴△DOE≌△BOF(ASA);∴OE=OF,又∵OB=OD,
∴四边形EBFD是平行四边形, ∵EF⊥BD,∴四边形BFDE为菱形.
第2课时 菱形的判定
新知导航
3.将Rt△ACB沿直角边AC所在直线翻折180°,得到Rt△ACE
(如图所示),点D与点F分别是斜边AB,AE的中点,连接
第2课时 菱形的判定
轻松过招
6.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE 垂直平分BC,垂足为D,交AB于点E. 点F在DE的延长线上,且AF=CE. 求证:四边形ACEF是菱形. 证明:∵AC⊥BC,DE垂直平分BC, ∴DE∥AC∴点E是BA中点,∴在Rt△ACB中,CE=AE 又∵∠BAC=60°,∴△ACE是等边三角形 ∴AC=CE=AE,又∵AF=CE,∴AF=AE 又∵DF∥AC,∴∠FEA=∠CAE=60° ∴△AEF为等边三角形,∴EF=AF. ∴CE=AC=AF=EF,∴四边形ACEF是菱形
第2课时 菱形的判定
轻松件是( B )
A. AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
第2课时 菱形的判定
轻松过招
2.(202X·宁夏)如1题图,四边形ABCD的两条对
角线相交于点O,且互相平分.添加下列条件,仍不
八下第六章《特殊平行四边形复习课》ppt课件-(共42张PPT)-(1)

的有 _______________________(组合序号)
4.若平行四边形一边长为8cm,一条对角线长为6cm,则另一条
对角线长X的取值范围是_____________
5.M为□ABCD 的边AD上一点,若▲MBC的面积为8cm2,□ABCD
的面积为_______
A
D
6.如图,□ABCD中,AE⊥BC,AF⊥CD,E,
(1)求证:EO=FO (2)当点O运动到何处时,四边形AECF是 矩形?并证明你的结论.
A
M E
B
O FN
D C
(1)证明 ∵ CE 平分∠ ACB ∴ ∠ ACE= ∠ ECB ∵ MN // BC ∴ ∠ ECB= ∠ OEC ∴ ∠ OEC= ∠ ECO ∴ OE=OC
同理OF=OC ∴ OE=OF
A、对角相等
B、对角线相 C、对边相等 D、对角线互相平分
2、菱形有而一般的平行四边形不具有的性质是( )
A、对角相等 B、对角线互相平分C、对边平行且相等 D、对角线互相垂直
3.下列性质中,平行四边形不一定具备的是( )
(A)对角相等
(B)邻角互补 (C )对角互补
(D)内角和是360°
(4).下面判定四边形是平行四边形的方法中,错误的是( )。
(B)两条对角线互相平分。
(C )两条对角线互相垂直。 (D)一对邻角的和为180°。
5.不能判定四边形ABCD是平行四边形的条件是( ) (A) AB =CD, AD =BC。(B) BC // AD。 (C ) AB//DC, AD//BC。 (D) AB =CD,AD//BC。
1、矩形具有而一般的平行四边形不具有的性质是( )
O
人教版八年级数学下册第十八章 平行四边形18.2.2菱形 课件(2课时共64张)

A∴S△AOFra bibliotek=1 2
OA·OB=
1 2
×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
B
O
D
∵ AB AO2 BO2 52 122 13,
C
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,∴13h=120,得h= 11230.
课堂检测
能力提升题
求证:∠AFD=∠CBE. 证明:∵四边形ABCD是菱形, ∴CB=CD, CA平分∠BCD. ∴∠BCE=∠DCE.
B
F
C
EA
又 CE=CE,∴△BCE≌△DCE(SAS).
D
∴∠CBE=∠CDE.
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠EDC.∴∠AFD=∠CBE.
课堂小结
边
菱
形 的
角
性
O
C
形
的
菱形的两组对角分别相等 角
性
菱形的邻角互补
质
B
怎样判断一 个四边形是 菱形?
菱形的两条对角线互相平分
对角线 菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角。
素养目标
2. 经历菱形判定定理的探究过程,渗透类比 思想,体会研究图形判定的一般思路. 1. 掌握菱形的三种判定方法,能根据不同的已 知条件,选择适当的判定定理进行推理和计算 .
B
O
D
C
= AC(BO+DO)
= AC·BD. 菱形的面积 = 底×高 = 对角线乘积的一半
探究新知 素养考点 1 利用菱形的面积公式解答问题
例3 如图,菱形花坛ABCD的边长为20m,∠ABC=60°, 沿着菱形的对角线修建了两条小路AC和BD,求两条小路的 长和花坛的面积(结果分别精确到0.01m和0.1m2).
OA·OB=
1 2
×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
B
O
D
∵ AB AO2 BO2 52 122 13,
C
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,∴13h=120,得h= 11230.
课堂检测
能力提升题
求证:∠AFD=∠CBE. 证明:∵四边形ABCD是菱形, ∴CB=CD, CA平分∠BCD. ∴∠BCE=∠DCE.
B
F
C
EA
又 CE=CE,∴△BCE≌△DCE(SAS).
D
∴∠CBE=∠CDE.
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠EDC.∴∠AFD=∠CBE.
课堂小结
边
菱
形 的
角
性
O
C
形
的
菱形的两组对角分别相等 角
性
菱形的邻角互补
质
B
怎样判断一 个四边形是 菱形?
菱形的两条对角线互相平分
对角线 菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角。
素养目标
2. 经历菱形判定定理的探究过程,渗透类比 思想,体会研究图形判定的一般思路. 1. 掌握菱形的三种判定方法,能根据不同的已 知条件,选择适当的判定定理进行推理和计算 .
B
O
D
C
= AC(BO+DO)
= AC·BD. 菱形的面积 = 底×高 = 对角线乘积的一半
探究新知 素养考点 1 利用菱形的面积公式解答问题
例3 如图,菱形花坛ABCD的边长为20m,∠ABC=60°, 沿着菱形的对角线修建了两条小路AC和BD,求两条小路的 长和花坛的面积(结果分别精确到0.01m和0.1m2).
《菱形》平行四边形

《菱形》平行四边形
2023-11-08
contents
目录
• 定义与性质 • 菱形的基本性质 • 菱形与平行四边形的联系与区别 • 菱形和平行四边形是一种四 边形,其中两组对边 分别平行。
平行四边形是轴对称 图形,其对称轴是两 条对角线所在的直线 。
四边形。
中点法
根据中点法,连接平行四边形的一 条对角线,如果与这条对角线平行 的直线与另一条对角线平行,则这 个四边形是平行四边形。
角平分线法
根据角平分线法,如果一个四边形 的一条对角线平分另一条对角线, 则这个四边形是平行四边形。
02
菱形的基本性质
菱形的定义
菱形是四边相等的平行四边形。
定义中的“四边相等”是菱形的本质属性,它使得菱形区别于其他平行四边形。
平行四边形属于中心 对称图形,其对称中 心是两条对角线的交 点。
平行四边形的性质
对边平行
平行四边形的两组对边分别平行。
对角相等
平行四边形的对角分别相等。
对边相等
平行四边形的两组对边分别相等。
邻角互补
平行四边形的邻角互补。
平行四边形的判别方法
定义法
根据平行四边形的定义,两组 对边分别平行的四边形是平行
菱形与平行四边形的联系
菱形属于平行四边形的一种特殊 形式。
菱形的对边平行且相等,这符合 平行四边形的定义。
菱形的对角线互相垂直平分,这 也是平行四边形的一种属性。
菱形与平行四边形的区别
平行四边形的对角线不一定互相垂直,而菱形的对角线 是互相垂直的。
平行四边形的对边可以相等也可以不相等,而菱形的对 边是相等的。
菱形还常出现在组合几何中, 作为构建复杂图形的基本单元 。
2023-11-08
contents
目录
• 定义与性质 • 菱形的基本性质 • 菱形与平行四边形的联系与区别 • 菱形和平行四边形是一种四 边形,其中两组对边 分别平行。
平行四边形是轴对称 图形,其对称轴是两 条对角线所在的直线 。
四边形。
中点法
根据中点法,连接平行四边形的一 条对角线,如果与这条对角线平行 的直线与另一条对角线平行,则这 个四边形是平行四边形。
角平分线法
根据角平分线法,如果一个四边形 的一条对角线平分另一条对角线, 则这个四边形是平行四边形。
02
菱形的基本性质
菱形的定义
菱形是四边相等的平行四边形。
定义中的“四边相等”是菱形的本质属性,它使得菱形区别于其他平行四边形。
平行四边形属于中心 对称图形,其对称中 心是两条对角线的交 点。
平行四边形的性质
对边平行
平行四边形的两组对边分别平行。
对角相等
平行四边形的对角分别相等。
对边相等
平行四边形的两组对边分别相等。
邻角互补
平行四边形的邻角互补。
平行四边形的判别方法
定义法
根据平行四边形的定义,两组 对边分别平行的四边形是平行
菱形与平行四边形的联系
菱形属于平行四边形的一种特殊 形式。
菱形的对边平行且相等,这符合 平行四边形的定义。
菱形的对角线互相垂直平分,这 也是平行四边形的一种属性。
菱形与平行四边形的区别
平行四边形的对角线不一定互相垂直,而菱形的对角线 是互相垂直的。
平行四边形的对边可以相等也可以不相等,而菱形的对 边是相等的。
菱形还常出现在组合几何中, 作为构建复杂图形的基本单元 。
北师大版九年级数学上册第一章 特殊的平行四边形 菱形的判定

相交于点 O,AB = 5 ,OA=2,OB=1.
求证:□ABCD 是菱形.
证明:在△AOB 中,
B
∵AB = 5 ,OA=2,OB=1, ∴AB2 = AO2 + OB2.
A
O
C
∴△AOB 是直角三角形,∠AOB 是直角. D
∴AC⊥BD.
∴□ABCD 是菱形(对角线垂直的平行四边形是菱形).
练一练
第一章 特殊的平行四边形
1.1 菱形的性质与判定
第2课时 菱形的判定
问题 上节课我们已经知道“菱形的对角线相互垂直”, 反过来,小明猜想对角线垂直的四边形是菱形, 你觉得对吗?
不对,菱形是特殊 的平行四边形,所 以它的对角线不仅 垂直且平分.
不对, 如图.
1 对角线互相垂直的平行四边形是菱形
我们用一长一短两根细木条,在它们的中点处固定 一个小钉,做成一个可以转动的十字,四周围上一根橡 皮筋,可得到一个平行四边形. 那么转动木条,这个平 行四边形什么时候变成菱形? 对此你有什么猜想?
╳
(2) 对角线互相垂直且平分的四边形是菱形; √
(3) 对角线互相垂直,且有一组邻边相等的 ╳ 四边形是菱形;
(4) 两条邻边相等,且一条对角线平分一组 ╳ 对角的四边形是菱形.
2. 一边长为 13 cm 的平行四边形的两条对角线的长分别
为 24 cm 和 10 cm,则其周长为 52 cm .
3. 如图,将△ABC 沿 BC 方向平移得到 △DCE,连接
B
小刚:分别以 A、C 为圆心,
A
C
以大于 1 AC 的长为半径作弧, 两条弧分2 别相交于点 B,D,
D
依次连接 A、B、C、D 四点.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
具有平行四边形的所有性质 形
四条边都相等
四条边都相等的四边形是菱形
对角线互相垂直
对角线互相垂直的平行四边形是菱形
每条对角线平分一组对角 猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
文字语言
判定方法一
一组邻边相等的平 行四边形是菱形
归
纳
判定方法二
四边相等的四边形是 菱形
师生小结,归纳提升
练习1:一个平行四边形的一条边长是9,两条对角线 的长分别是12和 6 5,这是一个特殊的平行四边形吗? 为什么?求出它的面积.
A
B
Hale Waihona Puke ODC复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
练习2:如图,两张等宽的纸条交叉叠放在一起,重合部分构成 的四边形ABCD是一个菱形吗?为什么?
师生小结,归纳提升
根据菱形的定义,可得菱形的第一个判定的方法 有一组邻边相等的平行四边形叫做菱形
符号语言:
A
D
O
∵四边形ABCD是平行四边形且AB=AD ∴四边形ABCD是菱形
B
C
还有其他方法吗?
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质
一组邻边相等的平行四边形是菱 形
四条边都相等
猜想1:四条边相等的四边形是菱形
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质 四条边都相等 对角线互相垂直
一组邻边相等的平行四边形是菱 形
猜想1:四四条条边边都都相相等等的的四平边行形四是边菱形形是菱形
猜想2:
每条对角线平分一组对角 猜想3:
复习回顾,引入新知
图形语言
A
D
B
C
符号语言
∵四边形ABCD是平行四边形 AB=AD
∴四边形ABCD是菱形
A
D
∵AB=BC=CD=DA
B
C
∴四边形ABCD是菱形
判定方法三
对角线互相垂直的平 行四边形是菱形
A
D
O
B
C
∵四边形ABCD是平行四边形 AC⊥BD
∴四边形ABCD是菱形
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质
一组邻边相等的平行四边形是菱 形
四条边都相等 对角线互相垂直 每条对角线平分一组对角
四条边相等的四边形是菱形
师生小结,归纳提升
归纳
四边形
平行 四边形
菱形
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
1、填空 (1)如图,若AD=8cm, 那么当
A
D
AB=___8___ cm,BC= _8____cm,
B
CD= __8_ cm时,四边形ABCD是菱形.
C
(2)如图,若AO=8cm, OD=6cm,
菱形的判定
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
活动1 你能用两个全等的等腰(不等边)三角形纸片 拼成一个平行四边形吗?
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
你有几种拼法?
重合底
重合腰
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
A
D
F
∟
B
C
E
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
1.知识总结
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 一组邻边相等的平行四边形是菱形
具有平行四边形的所有性质
一组邻边相等的平行四边形是菱 形
四条边都相等
四条边相等的四边形是菱形
对角线互相垂直
猜想2:对角线互相垂直的平行四边形是菱形
每条对角线平分一组对角
猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
命题:对角线互相垂直的平行四边形是菱形.
已知:在四边形ABCD中,对角线AC、
猜想2:对角线互相垂直的四边形是菱形
对角线互相垂直的平行四边形是菱形
猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质
对角线互相垂直
猜想2:
每条对角线平分一组对角 猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
命题:四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
D
C
A
B
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
18.2特殊的平行四边形
18.2.2菱形(2)
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题1:通过之前的学习,我们对菱形已经有了一些了 解,请你说说你都知道了哪些知识?
菱形的定义
有一组邻边相 等的平行四边 形是菱形
菱形的性质
一组邻边相等的平行四边形 具有平行四边形的所有性质 四条边都相等 对角线互相垂直 每条对角线平分一组对角
BD交于点O,AC⊥BD.
A
求证:四边形ABCD是菱形.
∟
B
O
D
C
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 一组邻边相等的平行四边形是菱
则当AD=_1_0 _cm,则□ABCD是菱形.
B
A
O
D
C
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
例1 如图,□ABCD的对角线AC,BD相交于点O, 且AB=5,AO=4,BO=3,求证:□ABCD是菱形.
A
D
O
C
B
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
四条边都相等
四条边都相等的四边形是菱形
对角线互相垂直
对角线互相垂直的平行四边形是菱形
每条对角线平分一组对角 猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
文字语言
判定方法一
一组邻边相等的平 行四边形是菱形
归
纳
判定方法二
四边相等的四边形是 菱形
师生小结,归纳提升
练习1:一个平行四边形的一条边长是9,两条对角线 的长分别是12和 6 5,这是一个特殊的平行四边形吗? 为什么?求出它的面积.
A
B
Hale Waihona Puke ODC复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
练习2:如图,两张等宽的纸条交叉叠放在一起,重合部分构成 的四边形ABCD是一个菱形吗?为什么?
师生小结,归纳提升
根据菱形的定义,可得菱形的第一个判定的方法 有一组邻边相等的平行四边形叫做菱形
符号语言:
A
D
O
∵四边形ABCD是平行四边形且AB=AD ∴四边形ABCD是菱形
B
C
还有其他方法吗?
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质
一组邻边相等的平行四边形是菱 形
四条边都相等
猜想1:四条边相等的四边形是菱形
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质 四条边都相等 对角线互相垂直
一组邻边相等的平行四边形是菱 形
猜想1:四四条条边边都都相相等等的的四平边行形四是边菱形形是菱形
猜想2:
每条对角线平分一组对角 猜想3:
复习回顾,引入新知
图形语言
A
D
B
C
符号语言
∵四边形ABCD是平行四边形 AB=AD
∴四边形ABCD是菱形
A
D
∵AB=BC=CD=DA
B
C
∴四边形ABCD是菱形
判定方法三
对角线互相垂直的平 行四边形是菱形
A
D
O
B
C
∵四边形ABCD是平行四边形 AC⊥BD
∴四边形ABCD是菱形
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质
一组邻边相等的平行四边形是菱 形
四条边都相等 对角线互相垂直 每条对角线平分一组对角
四条边相等的四边形是菱形
师生小结,归纳提升
归纳
四边形
平行 四边形
菱形
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
1、填空 (1)如图,若AD=8cm, 那么当
A
D
AB=___8___ cm,BC= _8____cm,
B
CD= __8_ cm时,四边形ABCD是菱形.
C
(2)如图,若AO=8cm, OD=6cm,
菱形的判定
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
活动1 你能用两个全等的等腰(不等边)三角形纸片 拼成一个平行四边形吗?
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
你有几种拼法?
重合底
重合腰
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
A
D
F
∟
B
C
E
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
1.知识总结
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 一组邻边相等的平行四边形是菱形
具有平行四边形的所有性质
一组邻边相等的平行四边形是菱 形
四条边都相等
四条边相等的四边形是菱形
对角线互相垂直
猜想2:对角线互相垂直的平行四边形是菱形
每条对角线平分一组对角
猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
命题:对角线互相垂直的平行四边形是菱形.
已知:在四边形ABCD中,对角线AC、
猜想2:对角线互相垂直的四边形是菱形
对角线互相垂直的平行四边形是菱形
猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 具有平行四边形的所有性质
对角线互相垂直
猜想2:
每条对角线平分一组对角 猜想3:
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
命题:四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
D
C
A
B
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
18.2特殊的平行四边形
18.2.2菱形(2)
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题1:通过之前的学习,我们对菱形已经有了一些了 解,请你说说你都知道了哪些知识?
菱形的定义
有一组邻边相 等的平行四边 形是菱形
菱形的性质
一组邻边相等的平行四边形 具有平行四边形的所有性质 四条边都相等 对角线互相垂直 每条对角线平分一组对角
BD交于点O,AC⊥BD.
A
求证:四边形ABCD是菱形.
∟
B
O
D
C
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
问题2 回忆平行四边形和矩形的判定方法的探究, 我们是怎么做的?
菱形的定义
菱形的性质
菱形的判定
有一组邻边相 等的平行四边 形是菱形
一组邻边相等的平行四边形 一组邻边相等的平行四边形是菱
则当AD=_1_0 _cm,则□ABCD是菱形.
B
A
O
D
C
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
师生小结,归纳提升
例1 如图,□ABCD的对角线AC,BD相交于点O, 且AB=5,AO=4,BO=3,求证:□ABCD是菱形.
A
D
O
C
B
复习回顾,引入新知
类比经验,探究方法
运用定理,解决问题
