4计量经济学一元线性回归模型——统计检验修改
线性回归模型的经典假定及检验修正

线性回归模型的经典假定及检验、修正一、线性回归模型的基本假定1、一元线性回归模型一元线性回归模型是最简单的计量经济学模型,在模型中只有一个解释变量,其一般形式是Y =β0+β1X 1+μ其中,Y 为被解释变量,X 为解释变量,β0与β1为待估参数,μ为随机干扰项。
回归分析的主要目的是要通过样本回归函数(模型)尽可能准确地估计总体回归函数(模型)。
为保证函数估计量具有良好的性质,通常对模型提出若干基本假设。
假设1:回归模型是正确设定的。
模型的正确设定主要包括两个方面的内容:(1)模型选择了正确的变量,即未遗漏重要变量,也不含无关变量;(2)模型选择了正确的函数形式,即当被解释变量与解释变量间呈现某种函数形式时,我们所设定的总体回归方程恰为该函数形式。
假设2:解释变量X 是确定性变量,而不是随机变量,在重复抽样中取固定值。
这里假定解释变量为非随机的,可以简化对参数估计性质的讨论。
假设3:解释变量X 在所抽取的样本中具有变异性,而且随着样本容量的无限增加,解释变量X 的样本方差趋于一个非零的有限常数,即∑(X i −X ̅)2n i=1n→Q,n →∞ 在以因果关系为基础的回归分析中,往往就是通过解释变量X 的变化来解释被解释变量Y 的变化的,因此,解释变量X 要有足够的变异性。
对其样本方差的极限为非零有限常数的假设,旨在排除时间序列数据出现持续上升或下降的变量作为解释变量,因为这类数据不仅使大样本统计推断变得无效,而且往往产生伪回归问题。
假设4:随机误差项μ具有给定X 条件下的零均值、同方差以及无序列相关性,即E(μi|X i)=0Var(μi|X i)=σ2Cov(μi,μj|X i,X j)=0, i≠j随机误差项μ的条件零均值假设意味着μ的期望不依赖于X的变化而变化,且总为常数零。
该假设表明μ与X不存在任何形式的相关性,因此该假设成立时也往往称X为外生性解释变量随机误差项μ的条件同方差假设意味着μ的方差不依赖于X的变化而变化,且总为常数σ2。
第四章计量经济学答案

第四章一元线性回归第一部分学习目的和要求本章主要介绍一元线性回归模型、回归系数的确定和回归方程的有效性检验方法。
回归方程的有效性检验方法包括方差分析法、t检验方法和相关性系数检验方法。
本章还介绍了如何应用线性模型来建立预测和控制。
需要掌握和理解以下问题:1 一元线性回归模型2 最小二乘方法3 一元线性回归的假设条件4 方差分析方法5 t检验方法6 相关系数检验方法7 参数的区间估计8 应用线性回归方程控制与预测9 线性回归方程的经济解释第二部分练习题一、术语解释1 解释变量2 被解释变量3 线性回归模型4 最小二乘法5 方差分析6 参数估计7 控制8 预测二、填空ξ,目的在于使模型更1 在经济计量模型中引入反映()因素影响的随机扰动项t符合()活动。
2 在经济计量模型中引入随机扰动项的理由可以归纳为如下几条:(1)因为人的行为的()、社会环境与自然环境的()决定了经济变量本身的();(2)建立模型时其他被省略的经济因素的影响都归入了()中;(3)在模型估计时,()与归并误差也归入随机扰动项中;(4)由于我们认识的不足,错误的设定了()与()之间的数学形式,例如将非线性的函数形式设定为线性的函数形式,由此产生的误差也包含在随机扰动项中了。
3 ()是因变量离差平方和,它度量因变量的总变动。
就因变量总变动的变异来源看,它由两部分因素所组成。
一个是自变量,另一个是除自变量以外的其他因素。
()是拟合值的离散程度的度量。
它是由自变量的变化引起的因变量的变化,或称自变量对因变量变化的贡献。
()是度量实际值与拟合值之间的差异,它是由自变量以外的其他因素所致,它又叫残差或剩余。
4 回归方程中的回归系数是自变量对因变量的()。
某自变量回归系数β的意义,指的是该自变量变化一个单位引起因变量平均变化( )个单位。
5 模型线性的含义,就变量而言,指的是回归模型中变量的( );就参数而言,指的是回归模型中的参数的( );通常线性回归模型的线性含义是就( )而言的。
一元线性回归模型(计量经济学)

总体回归函数说明被解释变量Y的平均状 态(总体条件期望)随解释变量X变化的 规律。至于具体的函数形式,则由所考 察的总体的特征和经济理论来决定。
在例2.1中,将居民消费支出看成是其可 支配收入的线性函数时,该总体回归函
数为: E (Y |X i)01 X i
它是一个线性函数。其中,0,1是未知
第二章 经典单方程计量经济学模型: 一元线性回归模型
§2.1 回归分析概述 §2.2 一元线性回归模型的基本假设 §2.3 一元线性回归模型的参数估计 §2.4 一元线性回归模型的统计检验 §2.5 一元线性回归模型的预测 §2.6 一元线性回归建模实例
§2.1 回归分析概述
一、变量间的关系及回归分析的基本概念 二、总体回归函数 三、随机扰动项 四、样本回归函数
1430 1650 1870 2112
1485 1716 1947 2200
2002
2420 4950 11495 16445 19305 23870 25025 21450 21285 15510
一个抽样
由于调查的完备性,给定收入水平X的消费 支出Y的分布是确定的。即以X的给定值为条 件的Y的分布是已知的,如 P(Y=561 | X = 800) =1/4。 进而,给定某收入Xi,可得消费支出Y的条 件均值,如 E(Y | X = 800) =605。 这样,可依次求出所有不同可支配收入水平 下相应家庭消费支出的条件概率和条件均值 ,见表2.1.2.
相关分析主要研究随机变量间的相关形式 及相关程度。变量间的相关程度可通过计 算相关系数来考察。
具有相关关系的变量有时存在因果关系,
这时,我们可以通过回归分析来研究它们
之间的具体依存关系。
课堂思考题
一元线性回归模型的统计检验

3. 怎样进行拟合优度检验 (1)总离差平方和的分解 已知有一组样本观测值( Xi ,Yi )(i 1, 2, , n),得到 如下样本回归直线:
Yˆi ˆ0 ˆ1Xi
Y的第i个观测值与样本均值的离差yi Yi Y 可分 解为两部分之和:
yi Yi Y Yi Yˆi Yˆi Y ei yˆi (1)
规则:p值越小,越能拒绝原假设H0.
三、回归系数的置信区间
对参数作出的点估计虽然是无偏估计,但一 次抽样它并不一定等于真实值,所以需要找到包 含真实参数的一个范围,并确定这个范围包含参 数真实值的可靠程度。
在变量的显著性检验中已经知道:
t ˆi i ~ t(n 2) i=0,1
Sˆi
给出置信度1,查自由度为(n 2)的t分布表,
假设检验的步骤: (1)提出原假设和备择假设; (2)根据已知条件选择检验统计量; (3)根据显著性水平确定拒绝域或临界值; (4)计算出统计量的样本值并作出判断。
(2)变量的显著性检验
对于最小二乘估计量ˆ1,已经知道它服从正态分布
ˆ1 ~ N(1,
2
xi2 )
由于真实的 2未知,在用它的无偏估计量ˆ 2
在上述收入——消费支出的例子中,如果给定
=0.01,查表得:
t 2 (n 2) t0.005 (8) 3.355
由于
Sˆ1 0.042
Sˆ0 98.41
于是,计算得到1、0的置信区间分别为:
(0.6345,0.9195)
(-433.32,226.98)
则
TSS RSS ESS
Y的观测值围绕其均值的总离差可分解为两部 分:一部分来自回归线(RSS),另一部分则来自随 机势力(ESS)。因此,我们可以用回归平方和RSS 占Y的总离差平方和TSS的比例来度量样本回归线 与样本观测值的拟合优度。
计量经济学重点知识整理

计量经济学重点知识整理1一般性定义计量经济学是以经济理论和经济数据的事实为依据,运用数学和统计学的方法,通过建立数学模型来研究经济数量关系和规律的一门经济学科。
研究的主体(出发点、归宿、核心):经济现象及数量变化规律研究的工具(手段):模型数学和统计方法必须明确:方法手段要服从研究对象的本质特征(与数学不同),方法是为经济问题服务2注意:计量经济研究的三个方面理论:即说明所研究对象经济行为的经济理论——计量经济研究的基础数据:对所研究对象经济行为观测所得到的信息——计量经济研究的原料或依据方法:模型的方法与估计、检验、分析的方法——计量经济研究的工具与手段三者缺一不可3计量经济学的学科类型●理论计量经济学研究经济计量的理论和方法●应用计量经济学:应用计量经济方法研究某些领域的具体经济问题4区别:●经济理论重在定性分析,并不对经济关系提供数量上的具体度量●计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容5计量经济学与经济统计学的关系联系:●经济统计侧重于对社会经济现象的描述性计量●经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据●经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据6计量经济学与数理统计学的关系联系:●数理统计学是计量经济学的方法论基础区别:●数理统计学是在标准假定条件下抽象地研究一般的随机变量的统计规律性;●计量经济学是从经济模型出发,研究模型参数的估计和推断,参数有特定的经济意义,标准假定条件经常不能满足,需要建立一些专门的经济计量方法3、计量经济学的特点:计量经济学的一个重要特点是:它自身并没有固定的经济理论,而是根据其它经济理论,应用计量经济方法将这些理论数量化。
4、计量经济学为什么是一门单独的学科计量经济学是经济理论、数理经济、经济统计与数理统计的混合物。
1、经济理论所作的陈述或假说大多数是定性性质的,计量经济学对大多数经济理论赋予经验内容。
计量经济学课件4

方法G有i*良好的统计性质。
2.3 一元线性回归模型的参数估计 2.3.1普通最小二乘法
由(2.3.2)、(2.3.3)式得:
(2.3.4)
(2.3.5)
这样我们就定义了变量x和y之间的一个简单线性回归模型,也称为两变 量或一元线性回归模型。其线性的含义表示无论变量x的取值如何,它 的任何一单位变化都对变量y产生相同的影响。
2.2 一元线性回归模型的基本假设 2.2.1对回归模型设定的假设
假设1:回归模型是正确设定的。 模型的正确设定主要包括两方面的内容:(1)模型选择了正确的变量 ;(2)模型选择了正确的函数形式。 计量经济模型应用于现实经济问题时,因果关系必须有经济理论为其依 据,函数关系也必须要有可靠的依据。 模型选择了正确的变量指既没有遗漏重要的相关变量,也没有多选无关 变量且有经济理论支持该因果关系。当假设1满足时,称模型没有设定 偏误,否则模型存在设定偏误。 假设1‘:线性回归模型 回归模型对变量不一定是线性的,但对参数是线性的。在计量经济学里 说到的线性回归都是指关于参数是线性的。要注意的是回归模型的估计 原理不依赖于y和x的定义,但系数的解释依赖于它们的定义。
xi(yi y ) (xi x )xi
x(y i x(xi
y) x)
(xi x )(yi y ) (xi x )2
2.3 一元线性回归模型的参数估计 2.3.2最小二乘估计量的统计性质
(1)线性性
这里指 ˆ0和 ˆ1分别是 y1, y2 , , yn 的线性函数。
令 ki
(xi x ) ,代入上式得
计量经济学-第4章

TSS ESS RSS
4
4.1.1 总离差平方和旳分解
已知由一组样本观察值(Xi,Yi),i=1,2…,n 得到如下样本回归直线
Yˆi ˆ0 ˆ1 X i
yi Yi Y (Yi Yˆi ) (Yˆi Y ) ei yˆi
2
即
P(i
t s t s ) P(t 2
i i
si
t ) 1
2
2
i
i
i
2
i
1
21
于是得到:(1-)旳置信度下, i旳置信区间是
(i
t
2
si , i
t
2
si )
在上述收入-消费支出例中,假如给定 =0.01,
查表得:
因为
t (n 2) t0.005 (8) 3.355 2
▪判断成果合理是否,是基于“小概率事件不易 发生”旳原理
➢ 一次抽样中,尽然不能支持原假设,也就是举反 例否决。
13
4.2.2 变量旳明显性检验
ˆ1 ~ N (1,
2
) xi2
t ˆ1 1 ˆ1 1 ~ t(n 2)
ˆ 2 xi2
S ˆ1
14
检验环节:
(1)对总体参数提出假设
H0: 1=0,
18
4.3 参ห้องสมุดไป่ตู้旳置信区间检验法
假设检验能够经过一次抽样旳成果检验总体参数 假设值旳范围(如是否为零),但它并没有指出 在一次抽样中样本参数值究竟离总体参数旳真值 有多“近”。
要判断样本参数旳估计值在多大程度上能够“近 似”地替代总体参数旳真值,往往需要经过构造 一种以样本参数旳估计值为中心旳“区间”,来 考察它以多大旳可能性(概率)包括着真实旳参 数值。这种措施就是参数检验旳置信区间估计。
计量经济学第二篇一元线性回归模型

第二章 一元线性回归模型2.1 一元线性回归模型的基本假定有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略,(2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。
2.1.3 一元线性回归模型的基本假定通常线性回归函数E(y t ) = β0 + β1 x t 是观察不到的,利用样本得到的只是对E(y t ) =β0 + β1 x t 的估计,即对β0和β1的估计。
计量经济学实验二-一元线性回归模型的估计、检验和预测

目录一、加载工作文件 (7)二、选择方程 (7)1.作散点图 (7)2.进行因果关系检验 (9)三、一元线性回归 (10)四、经济检验 (12)五、统计检验 (13)六、回归结果的报告 (15)七、得到解释变量的值 (15)八、预测应变量的值 (17)实验二一元线形回归模型的估计、检验和预测实验目的:掌握一元线性回归模型的估计、检验和预测方法。
实验要求:选择方程进行一元线性回归,进行经济、拟合优度、参数显著性和方程显著性等检验,预测解释变量和应变量。
实验原理:普通最小二乘法,拟合优度的判定系数R2检验和参数显著性t检验等,计量经济学预测原理。
实验步骤:已知广东省宏观经济部分数据如表2-1所示,要根据这些数据研究和分析广东省宏观经济,建立宏观计量经济模型,从而进行经济预测、经济分析和政策评价。
实验二~实验十二主要都是用这些数据来完成一系列工作。
表2-1 广东省宏观经济数据续上表续上表一、加载工作文件广东省宏观经济数据已经制成工作文件存在盘中,命名为GD01.WF1,进入EViews后选择File/Open打开GD01.WF1。
二、选择方程根据广东数据(GD01.WF1)选择收入法国国内生产总值(GDPS)、财政收入(CS)、财政支出(CZ)和社会消费品零售额(SLC),分别把①CS作为应变量,GDPS作为解释变量;②CZ作为应变量,CS作为解释变量;③SLC作为应变量,GDPS作为解释变量进行一元线性回归分析。
1.作散点图从三个散点图(图2-1~图2~3)可以看出,三对变量都呈现线性关系。
图2-1 图2-2图2-3 2.进行因果关系检验从三个因果关系检验可以看出,GDPS是CS的因;CS不是CZ 的因;GDPS不是SLC的因。
但根据理论CS是CZ的因,GDPS是SLC的因,可能是由于指标设置问题。
所以还是把CS作为应变量,GDPS作为解释变量;CZ作为应变量,CS作为解释变量;SLC作为应变量,GDPD作为解释变量进行一元线性回归分析。
第二章 一元线性回归模型

∂Q ˆ ˆ = −2∑ (Yi − β 0 − β1 X i ) = 0 ∂β ˆ0 ˆ ˆ ∂Q = −2∑ (Y − β − β X )X = 0 i 0 1 i i ˆ ∂β1
化简得: 化简得:
ˆ ˆ ∑ (Yi − β 0 − β1 X i ) = 0 ˆ ˆ ∑ (Yi − β 0 − β1 X i )X i = 0
2.总体回归方程(线)或回归函数 总体回归方程( 总体回归方程 即对( )式两端取数学期望: 即对(2.8)式两端取数学期望:
E y i)= β 0 + β 1 x i (
(2.9)
(2.9)为总体回归方程。由于随机项的影响,所 )为总体回归方程。由于随机项的影响, 有的点( )一般不在一条直线上; 有的点(x,y)一般不在一条直线上;但所有的点 (x,Ey)在一条直线上。总体回归线描述了 与y )在一条直线上。总体回归线描述了x与 之间近似的线性关系。 之间近似的线性关系。
Yi = β X i + ui
需要估计, 这个模型只有一个参数 需要估计,其最 小二乘估计量的表达式为: 小二乘估计量的表达式为:
∑XY ˆ β= ∑X
i i 2 i
例2.2.1:在上述家庭可支配收入-消费支出例中,对 :在上述家庭可支配收入-消费支出例中, 于所抽出的一组样本数据, 于所抽出的一组样本数据,参数估计的计算可通过下面 的表2.2.1进行。 进行。 的表 进行
二、一元线性回归模型 上述模型中, 为线性的, 上述模型中, 若f(Xi)为线性的,这时的模型 为线性的 一元线性回归模型: 即为 一元线性回归模型:
yi = β 0 + β1 xi + ui 其中:yi为被解释变量,xi为解释变量,ui为随机误 差项,β 0、β1为回归系数。
计量经济学的2.3 一元线性回归模型的统计检验

ˆ ˆ P( ) 1
如果存在这样一个区间,称之为置信区间 (confidence interval); 1-称为置信系数(置信度) (confidence coefficient), 称为显著性水平(level of significance)(或犯第I类错误的概率,即拒真的概 率);置信区间的端点称为置信限(confidence limit) 或临界值(critical values)。置信区间以外的区间称 4 为临界域
由于置信区间一定程度地给出了样本参数估计 值与总体参数真值的“接近”程度,因此置信区间 越小越好。 (i t s , i t s )
2 i 2 i
要缩小置信区间,需要减小 (1)增大样本容量n,因为在同样的置信水平 下, n越大,t分布表中的临界值越小;同时,增大样本 容量,还可使样本参数估计量的标准差减小;
5
如何构造参数值的估计区间? 通过构造已知分布的统计量
6
构造统计量(1)
回顾: 在正态性假定下
以上统计量服从自由度为n-2的x2分布,n为样本量
7
构造统计量(2)
ˆ ˆ 0 和 1 服从正态分布
ˆ E ( 0 )= 0
ˆ E ( 1 )=1
Var 0) (ˆ
X
i 1 n i 1
§2.3 一元线性回归模型的统 计检验
一、参数的区间估计 二、拟合优度检验 三、参数的假设检验 (对教材内容作了扩充)
1
一、参数的区间估计
参数的两种估计:点估计和区间估计
点估计
通过样本数据得到参数的一个估计值。
(如:最小二乘估计、最大似然估计)
点估计不足:
(1)点估计给出在给定样本下估计出的参数的可能取值,但 它并没有指出在一次抽样中样本参数值到底离总体参数的真 值有多“近”。 (2)虽然在重复抽样中估计值的均值可能会等于真值,但由 于抽样波动,单一估计值很可能不同于真值。 2
计量经济学实验报告一元线性回归模型实验

2013-2014第1学期计量经济学实验报告实验(一):一元线性回归模型实验学号姓名:专业:国际经济与贸易选课班级:实验日期:2013年12月2日实验地点:K306实验名称:一元线性回归模型实验【教学目标】《计量经济学》是实践性很强的学科,各种模型的估计通过借助计算机能很方便地实现,上机实习操作是《计量经济学》教学过程重要环节。
目的是使学生们能够很好地将书本中的理论应用到实践中,提高学生动手能力,掌握专业计量经济学软件EViews的基本操作与应用。
利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
【实验目的】使学生掌握1.Eviews基本操作:(1)数据的输入、编辑与序列生成;(2)散点图分析与描述统计分析;(3)数据文件的存贮、调用与转换。
2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测【实验内容】1.Eviews基本操作:(1)数据的输入、编辑与序列生成;(2)散点图分析与描述统计分析;(3)数据文件的存贮、调用与转换;2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
实验内容以下面1、2题为例进行操作。
1、为了研究深圳地方预算中财政收入与国内生产总值关系,运用以下数据:(1)建立深圳的预算内财政收入对GDP的回归;(2)估计模型的参数,解释斜率系数的意义;(3)对回归结果进行检验;(4)若2002年的国内生产总值为3600亿元,试确定2002年财政收入的预测值和预α=)。
测区间(0.052、在《华尔街日报1999年年鉴》(The Wall Street Journal Almanac 1999)上,公布有美国各航空公司业绩的统计数据。
航班正点准时到达的正点率和此公司每10万名乘客中投诉1(1)做出上表数据的散点图(2)依据散点图,说明二变量之间存在什么关系?(3)描述投诉率是如何根据航班正点率变化,并求回归方程。
计量经济学中的各种检验

需要说明的问题
在实际应用中,我们往往希望所建立模型的决定 系数或修正的决定系数越大越好。但应注意,决 定系数只是对模型拟合优度的度量,决定系数或 修正的决定系数越大,只能说明列入模型的解释 变量对被解释变量整体的影响程度很大,并不能 说明模型中各个解释变量对被解释变量的影响程 度显著。因此在选择模型时,不能单纯地凭决定 系数的高低来断定模型的优劣,有时从模型的经 济意义和整体可靠程度的角度出发,可以适当降 低对决定系数的要求。
拟合优度检验和F检验的关系
F检验和拟合优度检验都是把总变差TSS分 解为回归平方和与残差平方和,并在这一 分解的基础上构造统计量进行的检验。区 别在于前者有精确的分布而后者没有。一 般来说,模型对观测值的拟合程度越高, 模型总体线性关系的显著性越强。
拟合优度检验和F检验的关系
F显著==>拟合优度必然显著
这两准则均要求仅当所增n 加n的解释变量能够减少 AIC值或SC值时才在原模型中增加该解释变量。
回归模型的总体显著性检验
拟合优度检验可以说明模型对样本数据的 近似情况。模型的总体显著性检验则一般 用来检验全部解释变量对被解释变量的共 同影响是否显著。
回归模型的总体显著性检验
检验全部解释变量对被解释变量的共同影响是否显著,或者说,检验回
TSS=RSS+ESS 被解释变量Y总的变动(差异)=解释变量
X引起的变动(差异)+除X以外的因素引 起的变动(差异) 如果X引起的变动在Y的总变动中占很大比 例,那么X很好地解释了Y;否则,X不能 很好地解释Y。
计量经济学EVIEWS自相关检验与修正
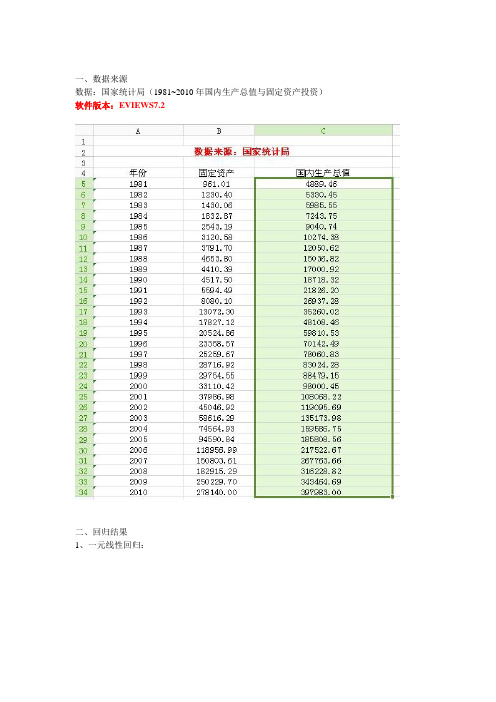
一、数据来源
数据:国家统计局(1981~2010年国内生产总值与固定资产投资)软件版本:EVIEWS7.2
二、回归结果
1、一元线性回归:
三、模型诊断与修正
DW检验:相关系数δ=0.8546,查表得,
1.35
1.49
L
U
d
d
=
=
经检验,DW<1.35,自变量呈一阶正自
相关
四、广义差分法修正后的结果
对E 进行滞后一期的自回归,可得回归方程:E=0.9337E(-1)
对原模型进行广义差分,输出结果为:
**ˆˆ6981.723 1.002749t t y x =+
由于使用广义差分数据,样本容量减少了1个,为29个。
查5%的显著性水平的DW
统计表可知, 1.341.48
L U d d ==,模型中的4-DU>DW>DU ,所以广义差分模型已无序列相关。
根据()1ˆˆ16981.723βρ-=,可得1
ˆ=105305.023β。
因此,原回归模型应为 105305.023 1.002749t t y x =+
采用普莱斯-文斯滕变换后第一个观测值变为211y δ-为1750.7019和211x δ-为344.1377,变换后普通最小二乘结果为**ˆˆ7555.503 1.0611t t y
x =+,根据()1ˆˆ17555.503βρ-=,得1
ˆ=113959.321β,由此,最终模型是 ˆ113959.321 1.0611t t y
x =+。
计量经济学复习重点10

计量经济学复习(48学时)
第二章 回归模型
2022年9月29日星期四 Page 13 of 74
4.误差项的假设
设 Yi b0 b1 X i ei
i 1,, n
(1) Xi是互不相关的确定型变量 (2) E(ei)=0
(3) D(ei)= 2 , 2 为总体方差
(4) E( ei ej)=0 (5) COV(X,e)=0
计量经济学复习(48学时)
第一章 绪论
2022年9月29日星期四 Page 6 of 74
1.4 计量经济学与数理经济学、数理统计学和经济统计学的关系
1.5 建立计量经济学模型的步骤
1.5.1 设定模型(Specification) 1. 模型设定 2.研究有关经济理论
3.确定变量和函数形式 (1)方程
当样本较大时(n>30)常用 Z 统计量(Z~N(0,1)), 当样本较小时(n≤30)常用 t 统计量。
构造零假设:H0:b0 0及H0:b1 0
或备择假设 H1:b0 0及H1:b1 0
对bˆ0 :T
bˆ0
~ t(n 2) 对bˆ1 :T
n
X
2 i
xi2
ˆ
2
bˆ1 ~ t(n 2)
计量经济学复习(48学时)
第一章 绪论
2022年9月29日星期四 Page 9 of 74
变量
按取值划分:离散型变量、 连续性变量 按时间划分:本期变量 滞后变量
按其地位分
在单一方程中:解释变量 被解释变量
在联立方程中: 外生变量、 内生变量、 工具变量、目标变量
计量经济学复习(48学时)
第一章 绪论
yˆi=bˆ1 ( X i X ) bˆ1xi
计量经济学eviews一元线性回归模型实验指导

第二章 一元线性回归模型一、 实验目的掌握EViews 软件的基本功能,理解一元线性回归模型及最小二乘估计的基本原理。
二、 基本知识点:样本回归方程与总体回归方程的联系与区别;满足古典假设的前提,一元线性回归模型的最小二乘法参数估计,一元线性回归模型的检验以及均值与个值预测。
三、 实验内容及要求:依据经济学理论,以实际数据为基础,建立经济数学模型,分析经济变量之间的数量关系。
以本章所学内容,研究2012年中国各地区农村家庭人均生活消费支出与人均纯收入之间关系,数据来源于《2013年中国统计年鉴》。
要求:在认真理解本章内容的基础上,通过实验掌握一元线性回归模型的实际应用方法,并熟悉EViews 软件的基本使用方法。
四、 实验指导:由经济学理论知,收入是影响消费的主要因素,二者之间有密切关系。
二者之间关系的散点图如图2.4.1所示。
图2.4.1说明,各地区农村居民家庭人均生活消费支出与家庭人均纯收入大致呈现出线性相关关系。
(CD 表示农村居民家庭人均生活消费支出,RD 农村居民家庭人均纯收入)图2.4.1 RD —CD 散点图故假设二者之间关系设定为一元线性回归模型:i i i rd cd μββ++=10,其中cd i 各地区农村居民家庭人均生活消费支出,rd i 为各地区农村居民家庭人均纯收入,μi 为随机误差项,即除人均收入外,影响农村居民家庭人均生活消费支出的其他因素。
假设该模型满足古典假设,可运用OLS 方法估计模型的参数。
利用计量经济学软件EViews5.0。
建立工作文件STEP1:进入EViews 目录,然后双击EViews 程序图标,进入EViews 主页见图2.4.2。
图2.4.2 EViews工作界面STEP2:点击Eviews主页面菜单\Workfile见图2.4.3,弹出work对话框(图2.4.4)。
在work type中选择Unsteuctured/Undated【由于本例是截面数据】,并在observation中输入观察值得个数,本例为31(图2.4.4),点击OK出现数据编辑窗口(图2.4.5)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 ESS RSS TSS TSS
或者:
1
(Yˆi (Yi
Y Y
)2 )2
ei 2 (Yi Y )2
我们定义回归平方和 ESS (Yˆi Y )2 在总离差平 方和 TSS (Yi Y )2 中所占的比重为可决系数(也
称决定系数或判定系数),用 R2 表示,即:
得到一条样本回归直线:Yˆi ˆ0 ˆ1Xi 其模型形式:Yi ˆ0 ˆ1Xi ei Yˆi ei
如果以 Y 的样本均值 Y 为基准,说明 Yi 和 Yˆi 对样本 均值 Y 的偏离程度,如下页图所示:
因变量 Y的离差分解示意图
Y
Y
Yˆi ˆ0 ˆ1Xi
R2 ESS TSS
(Yˆi Y )2 (Yi Y )2
一、模型的拟合优度检验
(2)可决系数 R2(判定系数 R2)
或者: R2 ESS 1 RSS 1
ei 2
TSS
TSS
(Yi Y )2
可决系数 R2 的取值范围是:0 R2 1 ;
R2 越大, ei2越小,模型的拟合优度越高;当 R2 1
第三节: 一元线性回归模型的统计检验
一、模型的拟合优度检验 ( R2 检验) 二、变量(参数) 的显著性检验 ( t 检验) 三、模型总体的显著性检验 (F 检验) 四、参数的置信区间(参数的区间估计)
一、模型的拟合优度检验
所谓“拟合优度”就是模型对样本数据的拟合程度; 检验方法是构造一个可以表征拟合程度的指标——判 定系数又称为样本可决系数; (1)总离差平方和的分解 为了说明可决系数的意义,回顾前面已经讨论过的 样本回归函数,即已知由一组样本观测值 (Xi,Yi ),(i 1, 2,L n)
假H 0
H0
设 备
成H立1 ”是错误的,从而拒绝原假设
,接受
择假设 ;如H果0 该小概率事件没有出现,就没有理
由拒绝原假设 ,这时候应该接受原假设。
概率论知识:
在介绍变量的显著性检验(t 检验)之前,补充一
些概率论的知识:
(1)如果随机变量 X1, X 2,K , X n彼此独立,且服从
N (0, 1) ,则: 2
RSS
ei2
(Yi
Yˆi
2
)
称为残差平方和(RSS:Residual Sum of Squares)。 这样上式就可写为:
TSS ESS RSS
一、模型的拟合优度检验
(2)可决系数 R2(判定系数 R2)
如果将式 TSS ESS RSS 两边同除以 TSS,得:
二、变量(参数) 的显著性检验 ( t 检验)
变量的显著性检验所应用的方法是数理统计学中
的“假设检验”。
假设检验的基本思想是:是在某种原假设 H0 成立 的条件下,利用适当的统计量和给定的显著性水
平,构造一个小概率事件(小概率事件原理认为:
小概率事件在一次观察中几乎是不可能发生的),
如果小概率事件在一次观察中发生了,就认为“原
(1)总离差平方和的分解
推导出这个式子: (Yi Y )2 (Yˆi Y )2 ei2
其中:
TSS (Yi Y )2
称为总离差平方和或总平方和(TSS: Total Sum of
Squares);
ESS (Yˆi Y )2
称为回归平方和(ESS:Explained Sum of Squares);
X
2 1
X
2 2
L
X
2 n
~ 2 (n) ;
(2)如果 X ~ N(0,1), 2 ~ 2 (n) ,且它们相互独 立,则:t X ~ t(n) ;
2 n
(3)
如果
12
~
2
(m)
,
2 2
~
12 m ~ F(m, n) 22 n
前面已经介绍过:在 i ~ N (0, 2 ) 的基本假定的条
件下,参数最小二乘估计量 ˆ1 和 ˆ0 的概率分布表
示为:
ˆ1 ~ N(1,
2
(Xi
X )2 )
;ˆ0
~
N(0, n
2
(Xi
X
2 i
X
)2
)
由于随机误差项的总体方差 2未知,用无偏估计量
由于: ei (Yˆi Y ) ei (ˆ0 ˆ1Xi Y ) ei (ˆ0 Y ) ˆ1 ei Xi
由前面的正规方程:
ei 0; ei Xi 0
得到: ei (Yˆi Y ) 0
所以有: (Yi Y )2 (Yˆi Y )2 ei2
计量经济学
——单方程计量经济学模型 理论与方法
第二章 经典单方程计量经济学模型: 一元线性回归模型
第一节 第二节 第三节 第四节
回归分析概述 一元线性回归模型的参数估计 一元线性回归模型的统计检验 一元线性回归模型的预测
模型估计式检验的必要性
用最小二乘法计算出估计结果以后,也就是 得到了模型估计式以后,需要对模型估计式 进行具体的评估: 1、模型解释变量选择的正确性需要证明; 2、模型函数形式的正确性需要验证; 3、模型估计的可靠性需要评价;
.(Xi ,Yi )
. 来自残差
ei Yi Yˆi
SRF
Yi Y
. . (Xi,Yˆi )
. 来自回归线 Yˆi Y
.
0
X
Xi
X
(1)总离差平方和的分解
Y 的离差 Yi Y 可分解为两部分: Yi Y Yˆi Y ei
则: (Yi Y )2 (Yˆi Y ei )2 (Yˆi Y )2 ei2 2 ei (Yˆi Y )
时, ei2 0 ;经济含义:R2 定量地描述了被解释变
量的变化中可以用解释变量的变化来说明的部分,即
模型的可解释程度。
我们有: (1) 0 R2 1; (2) R2 越大,越接近于 1,模型的拟合优度越高;
(3) R2 1: ei2 0 ,完全拟合,这种情况很少发生;
(4) R2 0: ei2 (Yi Y )2,X 与 Y 完全不存在线性关系。
