线性规划试题(含答案)
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于在给定的约束条件下,寻找一个线性目标函数的最优解。
在实际应用中,线性规划可以用于解决各种决策问题,如生产计划、资源分配、投资组合等。
以下是一个线性规划问题的示例:问题描述:某工厂生产两种产品A和B,每天的生产时间为8小时。
产品A每件需要2小时的加工时间,产品B每件需要3小时的加工时间。
每天的加工时间总共有16个小时。
产品A的利润为100元/件,产品B的利润为150元/件。
工厂的目标是最大化每天的总利润。
解决步骤:1. 定义变量:设产品A的生产数量为x,产品B的生产数量为y。
2. 建立目标函数:目标函数是每天的总利润,即:Z = 100x + 150y。
3. 建立约束条件:a) 加工时间约束:2x + 3y ≤ 16,表示每天的加工时间不能超过16小时。
b) 非负约束:x ≥ 0,y ≥ 0,表示产品的生产数量不能为负数。
4. 求解最优解:将目标函数和约束条件带入线性规划模型,使用线性规划算法求解最优解。
最优解及分析:经过计算,得到最优解为x = 4,y = 4,此时总利润最大为100 * 4 + 150 * 4 = 1000元。
通过最优解的分析可知,工厂每天应生产4件产品A和4件产品B,才能达到每天最大利润1000元。
同时,由于加工时间约束,每天的加工时间不能超过16小时,这也是生产数量的限制条件。
此外,也可以通过灵敏度分析来了解生产数量的变化对最优解的影响。
例如,如果产品A的利润提高到120元/件,而产品B的利润保持不变,那么最优解会发生变化。
在这种情况下,最优解为x = 6,y = 2,总利润为120 * 6 + 150 * 2 = 960元。
这表明,产品A的利润提高会促使工厂增加产品A的生产数量,减少产品B 的生产数量,以获得更高的总利润。
总结:线性规划是一种重要的数学优化方法,可以用于解决各种实际问题。
通过建立目标函数和约束条件,可以将实际问题转化为数学模型,并通过线性规划算法求解最优解。
高二数学线性规划试题

高二数学线性规划试题1.若x、y满足约束条件,则z=x+2y的取值范围()A.[2,6]B.[2,5]C.[3,6]D.(3,5]【答案】A【解析】作出可行域如图:,并作出,然后平移到过点A(2,0)时z取最小值为:,平移到过点C(2,2)时z取最大值为:,所以z的取值范围为:[2,6];故选A.【考点】线性规划.2.已知点P(x,y)在不等式组表示的平面区域上运动,则x-y的取值范围是( ). A.[-2,-1]B.[-2,1]C.[-1,2]D.[1,2]【答案】C【解析】设,即,作出可行域和目标函数基准线;当直线过点时,最大,即取得最小值为-1;当直线过点时,最小,即取得最大值为2;即x-y的取值范围是.【考点】简单的线性规划.3.设变量x,y满足约束条件,则目标函数z=2x+y的最大值为.【答案】5【解析】约束条件表示一个三角形ABC及其内部,其中因此直线过点时,目标函数z=2x+y取最大值为5.【考点】线性规划4.已知实数满足条件,则的最大值为.【答案】10【解析】作出满足约束条件下的平面区域,如图所示.由图可知点目标函数经过点时取得最大值,且最大值为.【考点】简单的线性规划.5.若实数满足不等式组,则的最小值为。
【答案】【解析】由不等式组作可行域如图,可行域内点的横纵坐标均为非负值,且不同时为0,可知在点C(0,1)处去最小值,将点C 代入,可知最小值为-1.【考点】简单线性规划..6.若变量、满足约束条件,则的最大值为 .【答案】1【解析】可行域为如图所示三角形内部(包括边界)则【考点】线性规划问题7.某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?【答案】该厂每天安排生产甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产值为124万元.【解析】根据已知条件列出线性约束条件,和目标函数。
高二数学线性规划 测试题

高二数学线性规划 测试题一、选择题(本大题共8小题,每小题6分,共48分)1.设直线l 的方程为:)0(0≠=++b c by ax ,则点集{0|),(>++c by ax y x }的图形是 ( )A .l 上方的平面区域B .l 下方的平面区域C .b>0时是l 上方的平面区域,b<0时是l 下方的平面区域D .b>0时是l 下方的平面区域,b<0时是l 上方的平面区域2.已知x ,y 满足约束条件y x z x y x y x 42,3005+=⎪⎪⎩⎪⎪⎨⎧≤≥+≥+-则的最小值为( )A .5B .-6C .10D .-10 3.不等式0)3)(12(<-++-y x y x 表示的平面区域是( )A B C D4.图中的平面区域(包括边界)可用不等式组表示为 ( )A .22≤≤-xB .⎩⎨⎧≤≤≤≤-1022y xC .⎪⎪⎩⎪⎪⎨⎧-≥-≤+121121y x y xD .⎩⎨⎧≥-≤≤--0)1(2)1(2y y x y 5.目标函数y x z -=3,将其看成直线方程时z 的意义是( )A .该直线的纵截距B .该直线纵截距的相反数C .该直线的横截距D .该直线横截距的相反数6.在约束条件⎪⎩⎪⎨⎧≥-+≤-≥+0220401y x x x 下,目标函数y x z-=( )A .有最小值,也有最大值B .有最小值,无最大值C .无最小值,有最大值D .无最小值,也无最大值 7.在△ABC 中,三个顶点的坐为A (2,5)B (-1,2),C (1,0)点P (x ,y )在△ABC33内部及其边界上运动,则使z =x +y 取得最大值和最小值的x ,y 值分别有 ( )A .一组和一组B .一组和无数组C .无数组和一组D .无数值和无数组8.已知点A (5,2),B (1,1),C (1,522),P (x ,y )在△ABC 表示的区域内(包括边界)且目标函数)0(>+=a y ax z 取得最大值的最优解有无穷多个,则a 值为 ( )A .41 B .53 C .4 D .35 二、填空题(本题共4小题,每小题6分,共24分)9.已知点集)0,0(},052,2,012|),{(O y x x y y x y x A 则点≤-++≤≥-+=与集合A 的关系为 ,点M (1,1)与集合A 的关系为 .10.已知点P (-1,2)及其关于原点的对称点均在不等式012>+-ky x 表示的平面区域内,则k 的取值范围是 .11.已知点(x ,y )在不等式组⎪⎩⎪⎨⎧≥+≤≤222y x y x 表示的平面区域内,则y x +-2的取值范围为.12.用不等式组表示图中的平行四边形区域为 . 三、解答题(本大题共6题,共78分)13.画出不等式组⎪⎩⎪⎨⎧≥++≤-≥+-020022y x y x y x 所表示的平面区域.(12分)14.设R 为平面上以A (4,1) B (-1,-6) C (-3,2)三点为顶点的三角形区域(包括边界及内部)试求(x ,y )在R 上变动时函数y x z 34-=的最大值和最小值.(12分)15.求y x z 2+=的最小值及取得最小值时y x ,的值,使式中y x ,的值满足⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥636300y x y x y x(12分)16.某化工厂生产A 、B 两种产品,按订单要求每天生产A 、B 产品均不少于5t ,已知生产1tA 产品需要用煤9t ,用电4kw ·h ,用工3个;生产1tB 产品需要用煤4t ,用电5kw ·h ,用工10个,已知1tA 产品价值为7万元,1tB 产品价值为12万元,但该厂有关资源均有一定限度,每天用煤不可超过300t ,用电不可超过200kw ·h ,用工不可超过300个,则该厂每天生产A 、B 产品各多少,才能既保证完成生产任务;又能让产值最高?(14分)17.如图,在坐标平面上有两个区域M 和N ,M 是由不等式组⎪⎩⎪⎨⎧-≤≤≥x y x y y 20确定,N 是随t变化的区域,它由不等式1+≤≤t x t 所确定,t 的取值范围是10≤≤t ,设M 和N 的公共面积是)(t f .求证:21)(2++-=t t t f .(14分)18.某厂用甲、乙两种原料生产A 、B 两种产品,已知生产1tA 产品,1tB 产品分别需要的甲、乙原料数,可获得的利润数及该厂现有原料数如下表所示。
高三数学线性规划试题答案及解析

高三数学线性规划试题答案及解析1.,满足约束条件,若取得最大值的最优解不唯一,则实数的值为()A.或B.或C.或D.或【答案】D.【解析】如图,画出线性约束条件所表示的可行域,坐出直线,因此要使线性目标函数取得最大值的最优解不唯一,直线的斜率,要与直线或的斜率相等,∴或.【考点】线性规划.2.已知最小值是5,则z的最大值是()A.10B.12C.14D.15【答案】A【解析】首先作出不等式组所表示的平面区域,如图中黄色区域,则直线-2x+y+c=0必过点B(2,-1),从而c=5,进而就可作出不等式组所表示的平面区域,如图部的蓝色区域:故知只有当直线经过点C(3,1)时,z取最大值为:,故选A.【考点】线性规划.3.执行如图1所示的程序框图,如果输入的,则输出的的最大值为()A.B.C.D.【答案】C【解析】该程序执行以下运算:已知,求的最大值.作出表示的区域如图所示,由图可知,当时,最大,最大值为.选C.【考点】程序框图与线性规划.4.执行如图1所示的程序框图,如果输入的,则输出的的最大值为()A.B.C.D.【答案】C【解析】该程序执行以下运算:已知,求的最大值.作出表示的区域如图所示,由图可知,当时,最大,最大值为.选C.【考点】程序框图与线性规划.5.设变量满足约束条件则目标函数的最小值为()A.2B.3C.4D.5【答案】B【解析】作出可行域:oyxA(1,1)由图可知,当直线过点时,目标函数取最小值为3,选B.【考点】线性规划6.已知x,y满足条件,则目标函数的最大值为 .【答案】【解析】画出可行域,如下图所示,将目标函数变形为,当取到最大值时,直线的纵截距最大,故将直线向上平移到过点C时,目标函数取到最大值,,得,故.【考点】线性规划.7.若变量满足约束条件,则的最大值为_________.【答案】【解析】作出不等式组表示的区域如下,则根据线性规划的知识可得目标函数在点处取得最大值,故填.【考点】线性规划8.设x,y满足约束条件,则z=(x+1)2+y2的最大值为()A.80B.4C.25D.【答案】A【解析】作出不等式组表示的平面区域,如图中阴影部分所示.(x+1)2+y2可看作点(x,y)到点P(-1,0)的距离的平方,由图可知可行域内的点A到点P(-1,0)的距离最大.解方程=(3+1)2+82=80.组,得A点的坐标为(3,8),代入z=(x+1)2+y2,得zmax9.已知实数满足,则目标函数的取值范围是.【答案】【解析】可行域表示一个三角形ABC,其中当直线过点A时取最大值4,过点B时取最小值2,因此的取值范围是.【考点】线性规划求取值范围10.设变量满足,则的最大值和最小值分别为()A.1,-1B.2,-2C.1,-2D.2,-1【答案】B【解析】由约束条件,作出可行域如图,设,则,平移直线,当经过点时,取得最大值,当经过点时,取得最小值,故选.【考点】线性规划.11.(2011•浙江)设实数x、y满足不等式组,若x、y为整数,则3x+4y的最小值是()A.14B.16C.17D.19【答案】B【解析】依题意作出可行性区域如图,目标函数z=3x+4y在点(4,1)处取到最小值z=16.故选B.12.若点(x,y)位于曲线y = |x|与y = 2所围成的封闭区域, 则2x-y的最小值为A.-6B.-2C.0D.2【答案】A【解析】的图像围成一个三角形区域,3个顶点的坐标分别是 (0,0),(-2,2),(2,2). 且当取点(-2,2)时,2x – y =" -" 6取最小值。
高三数学线性规划试题
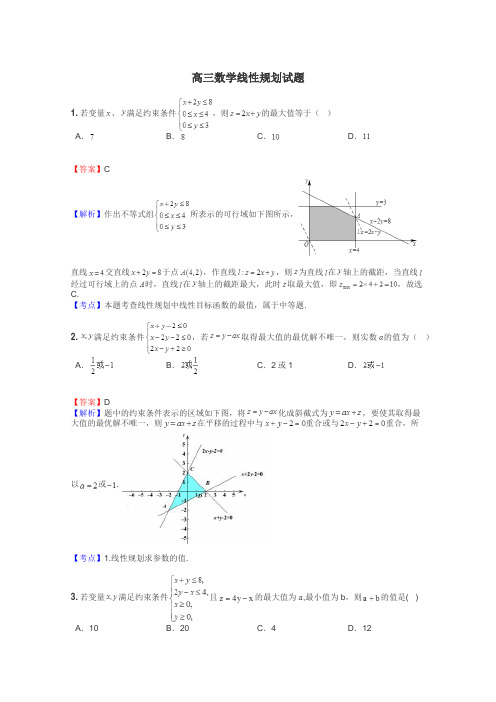
高三数学线性规划试题1.若变量、满足约束条件,则的最大值等于()A.B.C.D.【答案】C【解析】作出不等式组所表示的可行域如下图所示,直线交直线于点,作直线,则为直线在轴上的截距,当直线经过可行域上的点时,直线在轴上的截距最大,此时取最大值,即,故选C.【考点】本题考查线性规划中线性目标函数的最值,属于中等题.2.满足约束条件,若取得最大值的最优解不唯一,则实数的值为()A.B.C.2或1D.【答案】D【解析】题中的约束条件表示的区域如下图,将化成斜截式为,要使其取得最大值的最优解不唯一,则在平移的过程中与重合或与重合,所以或.【考点】1.线性规划求参数的值.3.若变量满足约束条件且的最大值为,最小值为b,则的值是( ) A.10B.20C.4D.12【答案】C【解析】变量满足约束条件,如图所示,目标函数过点A时z最小,目标函数过点B时z取最大.所以.故选C.【考点】1.线性规划.2.数形结合.4.若,则点必在()A.直线的左下方B.直线的右上方C.直线的右上方D.直线的左下方【答案】A【解析】由基本不等式得,即,因此有,因此点在直线的左下方,故选A.【考点】1.基本不等式;2.线性规划5.已知向量,是平面区域内的动点,是坐标原点,则的最小值是 .【答案】【解析】设,则,所以.令.画出点所在的平面区域及目标函数线如图所示:平移目标函数线使之经过可行域,当目标函数线经过点时,取得最小值为.【考点】1平面向量数量积公式;2线性规划.6. [2014·德州模拟]在平面直角坐标系中,若不等式组 (a为常数)所表示的平面区域的面积等于2,则a的值为()A.-5B.1C.2D.3【答案】D【解析】由题意知不等式组所表示的平面区域为一个三角形区域,设为△ABC,其中A(1,0),=2,所以×(1+a)×1=2,解得a=3.B(0,1),C(1,1+a)且a>-1,因为S△ABC7.(5分)(2011•陕西)如图,点(x,y)在四边形ABCD内部和边界上运动,那么2x﹣y的最小值为.【答案】1【解析】由已知中点(x,y)在四边形ABCD内部和边界上运动,那么2x﹣y取最小值时,点(x,y)一定落在A、B、C、D四个点的某一个点上,我们将四个点的坐标依次代入目标函数的解析式,比较分析后,即可得到答案.解:结合已知的四边形ABCD的图形,我们将四边形的各个顶点坐标依次代入可得:当x=1,y=1时,2x﹣y=1当x=,y=时,2x﹣y=当x=,y=1时,2x﹣y=2﹣1>1当x=1,y=0时,2x﹣y=2>1故2x﹣y的最小值为 1故答案为:1点评:本题考查的知识点是简单线性规划,其中利用角点法是解答线性规划问题的最优解问题是解答线性规划问题最常用,最快捷,最有效的方法,希望大家熟练掌握.8.(3分)(2011•重庆)设m,k为整数,方程mx2﹣kx+2=0在区间(0,1)内有两个不同的根,则m+k的最小值为()A.﹣8B.8C.12D.13【答案】D【解析】将一元二次方程的根的分布转化为确定相应的二次函数的图象来处理,根据图象可得到关于m和k的不等式组,此时不妨考虑利用不等式所表示的平面区域来解决,但须注意这不是线性规划问题,同时注意取整点.解:设f(x)=mx2﹣kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),因此要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点即由题意可以得到:必有,即,在直角坐标系mok中作出满足不等式平面区域,如图所示,设z=m+k,则直线m+k﹣z=0经过图中的阴影中的整点(6,7)时,z=m+k取得最小值,即z=13.min故选D.点评:此题考查了二次函数与二次方程之间的联系,解答要注意几个关键点:(1)将一元二次方程根的分布转化一元二次函数的图象与x轴的交点来处理;(2)将根据不等式组求两个变量的最值问题处理为规划问题;(3)作出不等式表示的平面区域时注意各个不等式表示的公共区域;(4)不可忽视求得最优解是整点.9.已知,若恒成立, 则的取值范围是 .【答案】【解析】要使不等式成立,则有,即,设,则.作出不等式组对应的平面区域如图,平移直线,由图象可知当直线经过点B时,直线的截距最小,此时最大,由,解得,代入得,所以要使恒成立,则的取值范围是,即,【考点】线性规划.10.设变量x,y满足约束条件,则目标函数z=2x+3y+1的最大值为( )A.11B.10C.9D.8.5【答案】B【解析】作出不等式组表示的可行域,如图阴影部分所示.又z=2x+3y+1可化为y=-x+-,结合图形可知z=2x+3y+1在点A处取得最大值.由得,故A(3,1).此时z=2×3+3×1+1=10.11.若实数、满足条件,则的最大值为_______.【答案】.【解析】作出不等式组所表示的平面区域如下图所示,直线与直线交于点,作直线,则为直线在轴上的截距,当直线经过可行域上的点时,此时直线在轴上的截距最大,取最大值,即.【考点】线性规划12.设z=kx+y,其中实数x、y满足,若z的最大值为12,则实数k= .【答案】2【解析】由得.作出不等式组表示的区域如图所示.由图可知,若,则当或时最大,且最大值不超过4. 若,则当时最大,由得.【考点】线性规划.13.已知实数满足,则的最小值是.【答案】4【解析】因为实数满足,如图所示,令=k,所以.由于当k<0时抛物线的开口向下,所以不合条件.所以k>0,有两种情况当k取最小值即抛物线过点.所以的最小值是.当抛物线与直线相切的情况,,即的最小值是4.【考点】1.线性规划问题.2.抛物线的问题.3.分类归纳的思想.4.构建数形结合解题的思想.14.已知点、,直线与线段相交,则的最小值为( )A.B.C.D.【答案】B【解析】由已知有,作出可行域,令,则的最小值为点到直线的距离,此时,所以的最小值为,选B.【考点】线性规划.15.若目标函数在约束条件下仅在点处取得最小值,则实数的取值范围是 .【答案】【解析】约束条件表示一个三角形及其内部.因此直线的斜率在内,即【考点】线性规划16.设变量x,y满足约束条件,则目标函数的最小值为。
高三数学线性规划试题

高三数学线性规划试题1.在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则直线OM斜率的最小值为()A.2B.1C.D.【答案】C【解析】不等式组为如图所表示的阴影区域.由图可知当M与C重合时,直线OM 斜率最小.解不等式组得C(3,-1),∴直线OM斜率的最小值为2.已知点满足,则的最小值是.【答案】【解析】根据线性规划的知识画出不等式的可行域如图所示,则目标函数在交点处取得最小值为,故填.【考点】线性规划3.设实数满足则的最大值等于________.【答案】2 【解析】实数满足所以x,y 的可行域如图所示.的最大值即为目标函数在y 轴的截距最小.即过点A (2,0),所以的最大值为2. 【考点】1.线性规划.2.截距最大对应的目标函数的最小值. 4. 已知满足不等式设,则的最大值与最小值的差为( )A .4B .3C .2D .1【答案】A【解析】作出不等式组所表示的区域,,由图可知,在点取得最小值,在点取得最大值,故的最大值与最小值的差为.【考点】线性规划.5. 已知实数x ,y 满足若z =ax +y 的最大值为3a +9,最小值为3a -3,则实数a 的取值范围为__________. 【答案】[-1,1]【解析】作出可行域如图中阴影部分所示,则z 在点A 处取得最大值,在点C 处取得最小值.又k BC =-1,k AB =1,∴-1≤-a≤1,即-1≤a≤1.6. 某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A 原料1kg 、B 原料2kg ;生产乙产品1桶需耗A 原料2kg ,B 原料1kg.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A 、B 原料都不超过12kg.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是多少? 【答案】2800元【解析】设公司每天生产甲种产品x 桶,乙种产品y 桶,公司共可获得利润为z 元/天,则由已知,得z=300x+400y,且画可行域如图所示,目标函数z=300x+400y可变形为y=-x+,这是随z变化的一簇平行直线,解方程组∴即A(4,4),∴z=1200+1600=2800(元).max故公司每天生产甲产品4桶、生产乙产品4桶时,可获得最大利润为2800元.7.设变量x.y满足约束条件则目标函数的最大值和最小值分别为()A.3,一11B.-3,一11C.11,—3D.11,3【答案】A【解析】线性约束条件表示三角形及其内部,当目标函数经过点时,取最小值,经过点时取最大值.【考点】线性规划求最值8.若关于的不等式组表示的平面区域是一个三角形,则的取值范围是.【答案】.【解析】当时,,因此根据图象可知,要使得不等式组所表示的平面区域是一个三角形,那么的取值范围是.【考点】线性规划.9.已知x,y满足则z=2x+4y的最小值为().A.5B.-5C.6D.-6【答案】D【解析】画出线性约束条件下的平面区域.由,得点P(3,-3).此时z=2x+4y达到最小值,最小值为-6.10.已知实数满足约束条件,则的最小值是____________.【答案】【解析】因为实数满足约束条件,x,y的可行域如图为三角形ABC围成的区域.又因为目标函数.所以要求z的最小值即为求出的最小值,即过原点直线的斜率的最小值.通过图形可知过点A的最小,由题意得A(3,1).所以z的最小值为.故填.【考点】1.线性规划问题.2.构造的思想.3数形结合的思想.11.已知O是坐标原点,点M的坐标为(2,1),若点N(x,y)为平面区域上的一个动点,则的最大值是________.【答案】3【解析】=2x+y,设z=2x+y,则y=-2x+z,不等式组对应的区域为BCD.平移直线y=-2x+z,由图可知当直线y=-2x+z经过点C时,直线y=-2x+z的截距最大,此时z最大,由,解得,即C(1,1),代入z=2x+y得z=2x+y=3,所以的最大值为3. 12.已知实数,满足约束条件则的最大值为.【答案】【解析】解线性规划问题,不仅要正确确定可行域,本题是直角三角形及其内部,而且要挖出目标函数的几何意义,本题中可理解为坐标原点到可行域中点的距离的平方.要求目标函数最大值,就是求的最小值,即坐标原点到直线的距离的平方,为.【考点】线性规划求最值13.若变量满足线性约束条件,则的最大值为________.【答案】5【解析】由约束条件,得如下图所示的三角形区域,由得直线过点时,取得最大值为5.【考点】线性规划.14.已知变量x,y满足约束条件则z=4x·2y的最大值为。
高一数学线性规划试题答案及解析

高一数学线性规划试题答案及解析1.若实数、满足约束条件则的最大值是_________【答案】3【解析】画出可行域如下图所示,为目标函数在轴上的截距,画出的图像如图中虚线部分,平移直线过点时有最大值3.故答案为3.【考点】线性规划的应用.2.在直角坐标系中,已知点,,,点在三边围成的区域(含边界)上,且.(Ⅰ)若,求;(Ⅱ)用表示,并求的最小值.【答案】(1),(2)的最小值-1.【解析】(1)向量的坐标运算主要是利用加、减、数乘运算法则进行的.若已知有向线段两端点的的坐标,则应先求出向量的坐标,解题过程中要注意方程的思想的运用及运算法则的正确使用;(2)利用线性规划求目标函数的最值一般步骤:一画、二移、三求,其关键是准确的作出可行域,理解目标函数的意义;(3)在线性约束条件下,线性目标函数只有在可行域的顶点或者边界上取得最值.在解答选择题和填空题时可以根据可行域的顶点直接进行检验.试题解析:解(Ⅰ),∴....................5分由,,,8分设,直线过点时,取得最小值-1,即的最小值-1【考点】(1)向量的坐标表示;(2)线性目标函数的最值.3.已知点(3,1)和(- 4,6)在直线3x-2y+a=0的两侧,则a的取值范围是()A.a<-7或 a>24B.a="7" 或 a=24C.-7<a<24D.-24<a<7【答案】C【解析】由线性规划相关知识:两点位于直线的两侧,则一侧使得直线方程大于零,一侧使得直线方程小于零.即有,故选C.【考点】线性规划.4.实数满足,如果目标函数的最小值为,则实数b的值为_____ .【答案】8【解析】绘制平面区域可得:要使由最小值-2,则直线,在轴上有最大截距为2,且经过点B,由,又因B也在上,故有.【考点】线性规划.5.已知变量满足约束条件,若的最大值为,则实数.【答案】-1或.【解析】作出约束条件所对应的可行域:,由于的最大值为,所以直线必过点A(-2,3)或点B(4,3),因此有解得或,故应填入:-1或.【考点】线性规划.6.设动点满足,则的最大值是.【答案】100【解析】先画出可行域,根据目标函数可知最优解为C(20,0),带入目标函数得最大者为100【考点】线性规划问题7.已知变量,满足约束条件,则的最小值为()A.B.C.D.【答案】B.【解析】依题意可画出不等式组所表示的的可行域,可知直线与的交点,作出直线:,平移直线,则可知当,时,的最小值为.【考点】线性规划.8.设变量、满足约束条件,则z=2x+3y的最大值为【答案】18【解析】变量x,y满足约束条件,表示的可行域为如图,所以z=2x+3y的最大值就是经过M即的交点(3,4)时,所以最大值为:3×2+4×3=18.故答案为:18.【考点】线性规划的应用.9.不等式组表示的平面区域的面积为 .【答案】9【解析】由题意得:平面区域为一个三角形及其内部,其中因此面积为【考点】线性规划求面积10.某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.求该公司从每天生产的甲、乙两种产品中,可获得的最大利润.【答案】该公司从每天生产的甲、乙两种产品中,可获得的最大利润为2800元.【解析】设公司每天生产甲种产品x桶,乙种产品y桶,公司共可获得利润为z元/天,则由已知,得z=300x+400y.且画可行域如图所示,目标函数z=300x+400y可变形为解方程组得,即A(4,4).所以,Z=1200+1600=2800.所以,该公司从每天生产的甲、乙两种产品中,可获得的最大利润为2800元. 9分【考点】简单线性规划的应用点评:中档题,作为应用问题,解简单线性规划问题,要遵循“审清题意,设出变量,布列不等式组,画,移,解,答”等步骤。
线性规划期末试题及答案

《线性规划》试题一.单项选择题(每小题2分,共20分)1.在有两个变量的线性规划问题中,若问题有唯一最优解,则( )A 、此最优解一定在可行域的一个顶点上达到。
B 、此最优解一定在可行域的内部达到。
C 、此最优解一定在可行域的一条直线段边界上达到。
D 、此时可行域只有一个点。
2.设有两个变量的线性规划模型的可行域的图如下,若目标函数只在点处达到最优值,则此目标函数可能就是( )A 、212x x z +=B 、2x z =C 、215x x z +=D 、218x x z +=3、若线性规划模型有可行解,则此线性规划( )基可行解必唯一。
基可行解有无穷多个。
基可行解个数必有限。
基可行解都就是最优解。
4.任何一个线性规划模型的可行解就是( )A. 一个无界集合。
B 、就是一个闭多面凸集。
C 、就是一个空集。
D 、就是一个无边界的集合5.设有下面线性规划问题有最优解,则( )..min ≥==X b AX t s CX f A. 此目标函数在可行域上必有下界 B 、此目标函数在可行域上必有上界 C 、 此目标函数在可行域上必有上界与下界 D 、此目标函数在可行域上必无下界 6.设有线性规划模型3213min x x x f ++=s 、t 、4,3,2,1,07436326213214321=≥=+=++=+++i x x x x x x x x x x i则( )就是一组对应于基的基变量A 、21,x xB 、321,,x x xC 、31,x xD 、432,,x x x 7.设有线性规划模型..max ≥==X b AX t s CX f则它的对偶线性规划的目标函数就是( )A 、CX g =maxB 、 Cb g =minC 、Ub g =minD 、CX g =max 8.设有两个对偶的线性规划问题的模型,下面说法正确的就是( )A 、一个模型有可行解且目标函数在可行集上无界,另一个模型有可行解。
线性规划高考试题精选

线性规划高考试题精选一一.选择题共15小题1.设x,y满足约束条件,则z=2x+y的最小值是A.﹣15 B.﹣9 C.1 D.92.若x,y满足,则x+2y的最大值为A.1 B.3 C.5 D.93.设x,y满足约束条件,则z=x+y的最大值为A.0 B.1 C.2 D.34.已知x,y满足约束条件则z=x+2y的最大值是A.﹣3 B.﹣1 C.1 D.35.若x、y满足约束条件,则z=x+2y的取值范围是A.0,6 B.0,4 C.6,+∞D.4,+∞6.设x,y满足约束条件则z=x﹣y的取值范围是A.﹣3,0 B.﹣3,2 C.0,2 D.0,37.已知x,y满足约束条件,则z=x+2y的最大值是A.0 B.2 C.5 D.68.设变量x,y满足约束条件,则目标函数z=x+y的最大值为A.B.1 C.D.39.已知变量x,y满足约束条件,则4x+2y的取值范围是A.0,10 B.0,12 C.2,10 D.2,1210.不等式组,表示的平面区域的面积为A.48 B.24 C.16 D.1211.变量x、y满足条件,则x﹣22+y2的最小值为A.B.C.5 D.12.若变量x,y满足约束条件且z=2x+y的最大值和最小值分别为m和n,则m﹣n等于A.8 B.7 C.6 D.513.设x,y满足约束条件,当且仅当x=y=4时,z=ax﹣y取得最小值,则实数a的取值范围是A.﹣1,1 B.﹣∞,1 C.0,1 D.﹣∞,1∪1,+∞14.实数x,y满足,若z=2x+y的最大值为9,则实数m的值为A.1 B.2 C.3 D.415.平面区域的面积是A.B.C.D.二.选择题共25小题16.设x,y满足约束条件,则z=3x﹣2y的最小值为.17.若x,y满足约束条件,则z=3x﹣4y的最小值为.18.已知x,y满足约束条件,则z=5x+3y的最大值为.19.若实数x,y满足,如果目标函数z=x﹣y的最小值为﹣2,则实数m= .20.已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a= .21.设z=x+y其中x,y满足,若z的最大值为6,则z的最小值为.22.已知点x,y满足不等式组,若ax+y≤3恒成立,则实数a的取值范围是.23.设实数x,y满足约束条件,若目标函数z=ax+bya>0,b>0的最大值为10,则a2+b2的最小值为.24.已知实数x,y满足,则的最小值为.25.若变量x,y满足,则x2+y2的最大值是.26.设变量x,y满足约束条件,则的取值范围是.27.在平面直角坐标系xOy上的区域D由不等式组给定,若Mx,y为D上的动点,点A的坐标为2,1,则的最大值为.28.已知动点Px,y满足:,则x2+y2﹣6x的最小值为.29.已知实数x,y满足,则的最小值是.30.设实数x,y满足,则2y﹣x的最大值为.31.设x、y满足约束条件,则目标函数z=x2+y2的最大值为.32.已知x,y满足约束条件,若z=ax+y的最大值为4,则a= .33.若x,y满足约束条件,则的最小值是.34.若x,y满足约束条件,则的范围是.35.已知实数x,y满足:,z=2x﹣2y﹣1,则z的取值范围是.36.若实数x,y满足不等式组,目标函数z=kx﹣y的最大值为12,最小值为0,则实数k= .37.若实数x、y满足不等式组,且z=y﹣2x的最小值等于﹣2,则实数m的值等于.38.设x,y满足不等式组,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为.39.已知不等式组表示的平面区域的面积为,则实数k= .40.已知变量x,y满足的约束条件,若x+2y≥﹣5恒成立,则实数a的取值范围为.线性规划高考试题精选一参考答案与试题解析一.选择题共15小题1.2017新课标Ⅱ设x,y满足约束条件,则z=2x+y的最小值是A.﹣15 B.﹣9 C.1 D.9解答解:x、y满足约束条件的可行域如图:z=2x+y 经过可行域的A时,目标函数取得最小值,由解得A﹣6,﹣3,则z=2x+y 的最小值是:﹣15.故选:A.2.2017北京若x,y满足,则x+2y的最大值为A.1 B.3 C.5 D.9解答解:x,y满足的可行域如图:由可行域可知目标函数z=x+2y经过可行域的A时,取得最大值,由,可得A3,3,目标函数的最大值为:3+2×3=9.故选:D.3.2017新课标Ⅰ设x,y满足约束条件,则z=x+y的最大值为A.0 B.1 C.2 D.3解答解:x,y满足约束条件的可行域如图:,则z=x+y经过可行域的A时,目标函数取得最大值,由解得A3,0,所以z=x+y 的最大值为:3.故选:D.4.2017山东已知x,y满足约束条件则z=x+2y的最大值是A.﹣3 B.﹣1 C.1 D.3解答解:x,y满足约束条件的可行域如图:目标函数z=x+2y经过可行域的A 时,目标函数取得最大值,由:解得A﹣1,2,目标函数的最大值为:﹣1+2×2=3.故选:D.5.2017浙江若x、y满足约束条件,则z=x+2y的取值范围是A.0,6 B.0,4 C.6,+∞D.4,+∞解答解:x、y满足约束条件,表示的可行域如图:目标函数z=x+2y经过C点时,函数取得最小值,由解得C2,1,目标函数的最小值为:4目标函数的范围是4,+∞.故选:D.6.2017新课标Ⅲ设x,y满足约束条件则z=x﹣y的取值范围是A.﹣3,0 B.﹣3,2 C.0,2 D.0,3解答解:x,y满足约束条件的可行域如图:目标函数z=x﹣y,经过可行域的A,B时,目标函数取得最值,由解得A0,3,由解得B2,0,目标函数的最大值为:2,最小值为:﹣3,目标函数的取值范围:﹣3,2.故选:B.7.2017山东已知x,y满足约束条件,则z=x+2y的最大值是A.0 B.2 C.5 D.6解答解:画出约束条件表示的平面区域,如图所示;由解得A﹣3,4,此时直线y=﹣x+z在y轴上的截距最大,所以目标函数z=x+2y的最大值为=﹣3+2×4=5.zmax故选:C.8.2017天津设变量x,y满足约束条件,则目标函数z=x+y的最大值为A.B.1 C.D.3解答解:变量x,y满足约束条件的可行域如图:目标函数z=x+y结果可行域的A点时,目标函数取得最大值,由可得A0,3,目标函数z=x+y的最大值为:3.故选:D.9.2017大庆三模已知变量x,y满足约束条件,则4x+2y的取值范围是A.0,10 B.0,12 C.2,10 D.2,12解答解:法1:作出不等式组表示的平面区域,得到如图的四边形及其内部,其中A2,1,B0,1,设z=Fx,y=4x+2y,将直线l:z=4x+2y进行平移,可得当l经过点A时,目标函数z达到最大值,z=F2,1=10,最大值=F0,1=2当l经过点B时,目标函数z达到最小值,z最小值因此,z=4x+2y的取值范围是2,10.法2:令4x+2y=μx+y+λx﹣y,则,解得μ=3,λ=1,故4x+2y=3x+y+x﹣y,又1≤x+y≤3,故3≤3x+y≤10,又﹣1≤x﹣y≤1,所以4x+2y∈2,10.故选C.10.2017潮州二模不等式组,表示的平面区域的面积为A.48 B.24 C.16 D.12解答解:画出不等式组表示的平面区域如图阴影所示,则点A﹣2,2、B2,﹣2、C2,10,所以平面区域面积为S=|BC|h=×10+2×2+2=24.△ABC故选:B.11.2017汉中二模变量x、y满足条件,则x﹣22+y2的最小值为A.B.C.5 D.解答解:作出不等式组对应的平面区域,设z=x﹣22+y2,则z的几何意义为区域内的点到定点D2,0的距离的平方,由图象知CD的距离最小,此时z最小.由得,即C0,1,此时z=x﹣22+y2=4+1=5,故选:C.12.2017林芝县校级三模若变量x,y满足约束条件且z=2x+y的最大值和最小值分别为m和n,则m﹣n等于A.8 B.7 C.6 D.5解答解:作出不等式组对应的平面区域如图:由z=2x+y,得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点C时,直线y=﹣2x+z的截距最大,此时z最大,由,解得,即C2,﹣1,此时最大值z=2×2﹣1=3,当直线y=﹣2x+z经过点B时,直线y=﹣2x+z的截距最小,此时z最小,由,解得,即B﹣1,﹣1,最小值为z=﹣2﹣1=﹣3,故最大值m=3,最小值为n=﹣3,则m﹣n=3﹣﹣3=6,故选:C13.2017瑞安市校级模拟设x,y满足约束条件,当且仅当x=y=4时,z=ax﹣y取得最小值,则实数a的取值范围是A.﹣1,1 B.﹣∞,1 C.0,1 D.﹣∞,1∪1,+∞解答解:作出约束条件所对应的可行域如图阴影,变形目标函数可得y=ax﹣z,其中直线斜率为a,截距为﹣z,∵z=ax﹣y取得最小值的最优解仅为点A4,4,∴直线的斜率a<1,即实数a的取值范围为﹣∞,1故选:B.14.2017肇庆一模实数x,y满足,若z=2x+y的最大值为9,则实数m的值为A.1 B.2 C.3 D.4解答解:作出不等式组对应的平面区域如图:阴影部分.由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点B时,直线y=﹣2x+z的截距最大,此时z最大,此时2x+y=9.由,解得,即B4,1,∵B在直线y=m上,∴m=1,故选:A15.2017五模拟平面区域的面积是A.B.C.D.解答解:作出不等式组对应的平面区域如图,则区域是圆心角是是扇形,故面积是.故选:A.二.选择题共25小题16.2017新课标Ⅰ设x,y满足约束条件,则z=3x﹣2y的最小值为﹣5 .解答解:由x,y满足约束条件作出可行域如图,由图可知,目标函数的最优解为A,联立,解得A﹣1,1.∴z=3x﹣2y的最小值为﹣3×1﹣2×1=﹣5.故答案为:﹣5.17.2017新课标Ⅲ若x,y满足约束条件,则z=3x﹣4y的最小值为﹣1 .解答解:由z=3x﹣4y,得y=x﹣,作出不等式对应的可行域阴影部分,平移直线y=x﹣,由平移可知当直线y=x﹣,经过点B1,1时,直线y=x﹣的截距最大,此时z取得最小值,将B的坐标代入z=3x﹣4y=3﹣4=﹣1,即目标函数z=3x﹣4y的最小值为﹣1.故答案为:﹣1.18.2017明山区校级学业考试已知x,y满足约束条件,则z=5x+3y的最大值为35 .解答解:不等式组对应的平面区域如图:由z=5x+3y得y=﹣,平移直线y=﹣,则由图象可知当直线y=﹣经过点B时直线y=﹣的截距最大,此时z最大,由,解得,即B4,5,此时M=z=5×4+3×5=35,故答案为:3519.2017重庆模拟若实数x,y满足,如果目标函数z=x﹣y的最小值为﹣2,则实数m= 8 .解答解:画出x,y满足的可行域如下图:可得直线y=2x﹣1与直线x+y=m的交点使目标函数z=x﹣y取得最小值,故,解得x=,y=,代入x﹣y=﹣2得﹣=﹣2m=8故答案为:8.20.2017湖南三模已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a= .解答解:先根据约束条件画出可行域,设z=2x+y,将最大值转化为y轴上的截距,当直线z=2x+y经过点B时,z最小,由得:,代入直线y=ax﹣3得,a=;故答案为:21.2017山东模拟设z=x+y其中x,y满足,若z的最大值为6,则z的最小值为﹣3 .解答解:作出可行域如图:直线x+y=6过点Ak,k时,z=x+y取最大,∴k=3,z=x+y过点B处取得最小值,B点在直线x+2y=0上,∴B﹣6,3,∴z的最小值为=﹣6+3=﹣3.故填:﹣3.22.2017黄冈模拟已知点x,y满足不等式组,若ax+y≤3恒成立,则实数a的取值范围是﹣∞,3 .解答解:满足不等式组的平面区域如右图所示,由于对任意的实数x、y,不等式ax+y≤3恒成立,==﹣3,根据图形,可得斜率﹣a≥0或﹣a>kAB解得:a≤3,则实数a的取值范围是﹣∞,3.故答案为:﹣∞,3.23.2017惠州模拟设实数x,y满足约束条件,若目标函数z=ax+bya>0,b>0的最大值为10,则a2+b2的最小值为.解答解:由z=ax+bya>0,b>0得y=,作出可行域如图:∵a>0,b>0,∴直线y=的斜率为负,且截距最大时,z也最大.平移直线y=,由图象可知当y=经过点A时,直线的截距最大,此时z也最大.由,解得,即A4,6.此时z=4a+6b=10,即2a+3b﹣5=0,即a,b在直线2x+3y﹣5=0上,a2+b2的几何意义为直线上点到原点的距离的平方,则原点到直线的距离d=,则a2+b2的最小值为d2=,故答案为:.24.2017历下区校级三模已知实数x,y满足,则的最小值为.解答解:作出不等式组对应的平面区域如图,的几何意义是区域内的点与点E3,0的斜率,由图象知AE的斜率最小,由得,即A0,1,此时的最小值为=,故答案为:.25.2017平遥县模拟若变量x,y满足,则x2+y2的最大值是10 .解答解:由约束条件作出可行域如图,联立,解得B3,﹣1,x2+y2的几何意义为可行域内动点与原点距离的平方,其最大值|OB|2=32+﹣12=10,故答案为:10.26.2017遂宁模拟设变量x,y满足约束条件,则的取值范围是.解答解:不等式组表示的区域如图,的几何意义是可行域内的点与点﹣1,﹣1构成的直线的斜率问题.当取得点A0,1时,取值为2,当取得点C1,0时,取值为,故答案为:27.2017渭南一模在平面直角坐标系xOy上的区域D由不等式组给定,若Mx,y 为D上的动点,点A的坐标为2,1,则的最大值为7 .解答解:由约束条件作出可行域如图,令z==2x+y,化为y=﹣2x+z,由图可知,当直线y=﹣2x+z过B2,3时,z有最大值为2×2+3=7.故答案为:7.28.2017湖北二模已知动点Px,y满足:,则x2+y2﹣6x的最小值为.解答解:由,∵y+>y+|y|≥0,∴,∵函数fx=是减函数,∴x≤y,∴原不等式组化为.该不等式组表示的平面区域如下图:∵x2+y2﹣6x=x﹣32+y2﹣9.由点到直线的距离公式可得,P3,0区域中A的距离最小,所以x2+y2﹣6x的最小值为.故答案为:﹣.29.2017盐城一模已知实数x,y满足,则的最小值是.解答解:作出不等式组所表示的平面区域如图所示:由于可以看做平面区域内的点与原点的连线的斜率,结合图形可知,当直线过OA时斜率最小.由于可得A4,3,此时k=.故答案为:.30.2017和平区校级模拟设实数x,y满足,则2y﹣x的最大值为 5 .解答解:画出,的可行域如图:将z=2y﹣x变形为y=x+z作直线y=x将其平移至A时,直线的纵截距最大,z最大,由可得A﹣1,2,z的最大值为:5.故答案为:5.31.2017德州二模设x、y满足约束条件,则目标函数z=x2+y2的最大值为52 .解答解:作出不等式组表示的平面区域,得到如图的四边形OABC,其中A0,2,B4,6,C2,0,O为原点设Px,y为区域内一个动点,则|OP|=表示点P到原点O的距离∴z=x2+y2=|OP|2,可得当P到原点距离最远时z达到最大值因此,运动点P使它与点B重合时,z达到最大值∴z=42+62=52最大值故答案为:5232.2017镇江模拟已知x,y满足约束条件,若z=ax+y的最大值为4,则a= 2 .解答解:作出不等式组对应的平面区域如图:阴影部分.则A2,0,B1,1,若z=ax+y过A时取得最大值为4,则2a=4,解得a=2,此时,目标函数为z=2x+y,即y=﹣2x+z,平移直线y=﹣2x+z,当直线经过A2,0时,截距最大,此时z最大为4,满足条件,若z=ax+y过B时取得最大值为4,则a+1=4,解得a=3,此时,目标函数为z=3x+y,即y=﹣3x+z,平移直线y=﹣3x+z,当直线经过A2,0时,截距最大,此时z最大为6,不满足条件,故a=2;故答案为:2.33.2017南雄市二模若x,y满足约束条件,则的最小值是.解答解:x,y满足约束条件的可行域如图:则的几何意义是可行域的点到坐标原点距离,由图形可知OP的距离最小,直线x+y﹣2=0的斜率为1,所以|OP|=.故答案为:.34.2017清城区校级一模若x,y满足约束条件,则的范围是.解答解:作出不等式组对应的平面区域如图:的几何意义是区域内的点到定点D﹣1,0的斜率,由图象知CD的斜率最小,由得C,,则CD的斜率z==,即z=的取值范围是0,,故答案为:.35.2017梅河口市校级一模已知实数x,y满足:,z=2x﹣2y﹣1,则z的取值范围是﹣,5 .解答解:不等式对应的平面区域如图:阴影部分.由z=2x﹣2y﹣1得y=x﹣,平移直线y=x﹣,由平移可知当直线y=x﹣,经过点C时,直线y=x﹣的截距最小,此时z取得最大值,由,解得,即C2,﹣1,此时z=2x﹣2y﹣1=4+2﹣1=5,可知当直线y=x﹣,经过点A时,直线y=y=x﹣的截距最大,此时z取得最小值,由,得,即A,代入z=2x﹣2y﹣1得z=2×﹣2×﹣1=﹣,故z∈﹣,5.故答案为:﹣,5.36.2017深圳一模若实数x,y满足不等式组,目标函数z=kx﹣y的最大值为12,最小值为0,则实数k= 3 .解答解:实数x,y满足不等式组的可行域如图:得:A1,3,B1,﹣2,C4,0.①当k=0时,目标函数z=kx﹣y的最大值为12,最小值为0,不满足题意.②当k>0时,目标函数z=kx﹣y的最大值为12,最小值为0,当直线z=kx﹣y过C4,0时,Z 取得最大值12.当直线z=kx﹣y过A1,3时,Z取得最小值0.可得k=3,满足题意.③当k<0时,目标函数z=kx﹣y的最大值为12,最小值为0,当直线z=kx﹣y过C4,0时,Z 取得最大值12.可得k=﹣3,当直线z=kx﹣y过,B1,﹣2时,Z取得最小值0.可得k=﹣2,无解.综上k=3故答案为:3.37.2017夏邑县校级模拟若实数x、y满足不等式组,且z=y﹣2x的最小值等于﹣2,则实数m的值等于﹣1 .解答﹣1解:由z=y﹣2x,得y=2x+z,作出不等式对应的可行域,平移直线y=2x+z,由平移可知当直线y=2x+z经过点A1,0时,直线y=2x+z的截距最小,此时z取得最小值为﹣2,即y﹣2x=﹣2,点A也在直线x+y+m=0上,则m=﹣1,故答案为:﹣138.2017阳山县校级一模设x,y满足不等式组,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为﹣2,1 .解答解:由z=ax+y得y=﹣ax+z,直线y=﹣ax+z是斜率为﹣a,y轴上的截距为z的直线,作出不等式组对应的平面区域如图:则A1,1,B2,4,∵z=ax+y的最大值为2a+4,最小值为a+1,∴直线z=ax+y过点B时,取得最大值为2a+4,经过点A时取得最小值为a+1,若a=0,则y=z,此时满足条件,若a>0,则目标函数斜率k=﹣a<0,要使目标函数在A处取得最小值,在B处取得最大值,=﹣1,则目标函数的斜率满足﹣a≥kBC即0<a≤1,若a<0,则目标函数斜率k=﹣a>0,要使目标函数在A处取得最小值,在B处取得最大值,则目标函数的斜率满足﹣a≤k=2,AC即﹣2≤a<0,综上﹣2≤a≤1,故答案为:﹣2,1.39.2017许昌三模已知不等式组表示的平面区域的面积为,则实数k= 4 .解答解:画出不等式组表示的平面区域,如图所示,由题意可知k>0,可行域的三个顶点为A0,0,B,,C,,∵AB⊥BC,|AB|=k,点C到直线AB的距离为k,=ABBC=×k×k=,∴S△ABC解得k=4,故答案为:4.40.2017白银区校级一模已知变量x,y满足的约束条件,若x+2y≥﹣5恒成立,则实数a的取值范围为﹣1,1 .解答解:由题意作出其平面区域,则x+2y≥﹣5恒成立可化为图象中的阴影部分在直线x+2y=﹣5的上方,则实数a的取值范围为﹣1,1.故答案为:﹣1,1.。
高一数学线性规划试题

高一数学线性规划试题1.若,满足约束条件,则的最大值是( ).A.B.C.D.【答案】C【解析】作出可行域和目标函数基准线(如图),将化为;当直线向右下方平移时,直线在轴上的截距减小,即增大;当直线过点B时,取到最大值;联立,得,此时.【考点】简单的线性规划.2.已知点在不等式组表示的平面区域上运动,则的取值范围是()A.B.C.D.【答案】B【解析】作出不等式组表示的平面区域,得到如图的及其内部,其中.设,将直线进行平移,观察轴上的截距变换,可得当经过点时,达到最小值;当经过点时,达到最大值.∴,,即的取值范围是.【考点】1、简单线性规划;2、二元一次不等式组表示的平面区域.3.设实数满足约束条件,则的最大值为()A.10B.8C.3D.2【答案】B.【解析】作出不等式组所表示的平面区域,即可行域,则直线与直线的交点.,作直线:,平移直线,则可知,当,时,【考点】线性规划.4.设x,y满足约束条件,若目标函数z=ax+by(a>0,b>0)的最大值为12,则+的最小值为_____________.【答案】4【解析】作出可行域(如图),,当目标直线过点A时 ,目标函数取得最大值,联立,得即;则(当且仅当,即时取等号).【考点】线性规划、基本不等式.5.目标函数,变量满足,则有()A.B.无最小值C.D.既无最大值,也无最小值【答案】C【解析】由题意知线性区域为:,当目标函数经过点时,有最小值;当目标函数经过点时,有最大值为.【考点】线性规划问题.6.若点在直线的下方,则的取值范围是_____________.【答案】.【解析】∵点在直线的下方,∴,∴的取值范围是.【考点】二元一次不等式与平面区域.7.已知,求的取值范围【答案】【解析】设,则,,又①②则①+②,故答案为【考点】简单的线性规划8.已知x,y满足约束条件,则的最小值为______________.【答案】—12.5【解析】作出不等式组表示的平面区域,得到如图的三角形及其内部,由,联立得A(-2.5,2.5),设z=F(x,y)=4x-y,将直线l:进行平移,可得当l经过点A时,目标函数z达到最小值∴z=F(-2.5,2.5)=—12.5.故答案为:—最小值12.5.【考点】二元一次不等式组表示的平面区域;简单的线性规划等知识.9.设=(1,1),=(3,1),O为坐标原点,动点P(x,y)满足0≤·≤1,0≤·≤1,则的最大值是()A.B.0C.D.1【答案】B【解析】,,,即,画出可行域如图平移目标函数线,使之经过可行域当过时纵截距最小此时最大为0。
高三数学线性规划试题

高三数学线性规划试题1.若点满足线性约束条件,则的取值范围是.【答案】【解析】作出不等式组所表示的平面区域,如图:作出直线x-y=0,对该直线进行平移,可以发现当直线经过点(0,0)时,Z取得最大值0,当直线经过点(-2,0)时,Z取得最小值-2,所以Z的取值范围为[-2,0).故答案为:[-2,0).【考点】简单线性规划.2.已知点、的坐标满足不等式组,若,则的取值范围是()A.B.C.D.【答案】D【解析】作出不等式组所表示的可行域如下图所示,假设点为上的一点,过点作直线的垂线,需使得垂线与与可行域有公共点,结合图象知,当点,时,在方向上的投影最大,此时,且取最大值,此时;同理当点,,此时,此时取最小值,,故的取值范围是,故选D.【考点】线性规划3.已知变数满足约束条件目标函数仅在点处取得最大值,则的取值范围为_____________.【答案】【解析】由题意知满足条件的线性区域如图所示:,点,而目标函数仅在点处取得最大值,【考点】线性规划、最值问题.4.已知实数满足:,,则的取值范围是( )A.B.C.D.【答案】C【解析】画出约束条件限定的可行域为如图阴影区域,令,则,先画出直线,再平移直线,当经过点,时,代入,可知,∴,故选.【考点】线性规划.5.设是定义在上的增函数,且对于任意的都有恒成立.如果实数满足不等式,那么的取值范围是【答案】(9,49)【解析】是定义在上的增函数,且对于任意的都有恒成立.所以可得函数为奇函数.由可得,..满足m,n如图所示.令.所以的取值范围表示以原点O为圆心,半径平方的范围,即过点A,B两点分别为最小值,最大值,即9和49.【考点】1.线性规划的问题.2.函数的单调性.3.函数的奇偶性.4.恒成立的问题.6.已知实数满足,则的取值范围是【答案】【解析】由不等式,得,在平面直角坐标系中用虚线画出圆,再作出虚线,则的可行域是由虚线与此虚线的右半圆围成的区域(不包括边界),又目标函数可化为,则当直线过可行域的上顶点时,有,当直线与半圆相切于点时,目标函数有最大值,将目标函数化为,则此时有,解得,如图所示,所以正确答案为.【考点】直线与圆、线性规划.7.已知点满足约束条件,为坐标原点,则的最大值为_______________.【答案】5【解析】作出可行域,得到当位于时,最大,其值为5.【考点】线性规划.8.设实数x、y满足,则的取值范围是( ) A.B.C.D.【答案】B【解析】作出可行域如图,当平行直线系在直线BC与点A间运动时,,此时,平行直线线在点O与BC之间运动时,,此时,. .选B【考点】线性规划9.不等式组所表示的平面区域的面积是________.【答案】25【解析】直线x-y+4=0与直线x+y=0的交点为A(-2,2),直线x-y+4=0与直线x=3的交点为B(3,7),直线x+y=0与直线x=3的交点为C(3,-3),则不等式组表示的平面区域是=×5×10=25.一个以点A(-2,2)、B(3,7)、C(3,-3)为顶点的三角形,所以其面积为S△ABC10.已知点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,给出下列说法:①3a-4b+10>0;②当a>0时,a+b有最小值,无最大值;③>2;④当a>0且a≠1,b>0时,的取值范围为∪.其中正确的个数是( )A.1B.2C.3D.4【答案】B【解析】因为点A(a,b),B(1,0)在直线3x-4y+10=0的两侧,所以(3a-4b+10)(3-0+10)<0,即3a-4b+10<0,故①错误;因为a>0时,点(a,b)对应的平面区域如图(不含边界),所以a+b既没有最小值,也没有最大值,故②错误;因为原点到直线3x-4y+10=0的距离为=2,而点(a,b)在直线3x-4y+10=0的左上方,所以>2,故③正确;的几何意义是点(a,b)与(1,0)的连线的斜率,由图可知,取值范围是∪,故④正确.11.若x,y满足条件当且仅当x=y=3时,z=ax-y取最小值,则实数a的取值范围是________.【答案】【解析】画出可行域,如图所示,得到最优解(3,3).把z=ax-y变为y=ax-z,即研究-z的最大值.当a∈时,y=ax -z均过(3,3)时截距-z最大.12.若满足,则的最小值为 .【答案】3【解析】由已知不等式得出区域如图所示,目标函数在点处取得最小值,且最小值为3.【考点】线性规划.13.设实数满足约束条件,若目标函数的最大值为9,则的最小值为__ ___.【答案】【解析】有可行域与目标函数形式可知,只能在点取得最大值,即,整理得:,所以,故.【考点】1、线性规划, 2、基本不等式.14.若,满足约束条件,则的最大值是.【答案】1【解析】根据题意,作出,满足约束条件的平面区域,那么结合三角形区域可知当过点(1,1)点时,则目标函数平移过程中截距最小,此时函数值最大,故答案为1.【考点】线性规划知识点评:本题主要考查了利用线性规划知识的简单应用,属于基础试题,解题的关键是明确目标函数的几何意义15.已知变量x、y,满足的最大值为【答案】3【解析】由复合对数函数的性质,欲使函数最大,即最大。
线性规划试题

第一章线性规划1、写出下列运输问题的模型(1)一家玩具公司制造三种桌上高尔夫玩具,每一种要求不同的制造技术。
高级的一种需要17小时加工装配劳动力,8小时检验,每台利润300元。
中级的需要10小时劳动力,4小时检验,利润200元。
低级的需要2小时劳动力,2小时检验,利润100元。
可供利用的加工劳动力为1000小时,检验500小时。
其次,有市场预测表明,对高级的需求量不超过50台,中级的不超过80台,低级的不超过150台。
制造商决定采用一个能使总利润为最大的最优生产计划。
(2)某建筑材料预制厂生产、两种产品,现有两种原料,第一种有72立方米,第二种有56平方米,,假设生产每种产品都需要两种原材料。
生产每件产品所需原料如表1-1所示。
每生产一件可获得利润60元,生产一件可获得利润1000元,预制厂在现有原料的条件下,、各应生产多少,才能使获得利润最大。
(3)用长度为500厘米的条材,截成长度分别为98厘米和78厘米的两种毛坯,要求共截出长98厘米的毛坯10000根,78厘米的20000根,问怎样截取,才能使用料最少?(4)某商店制定某商品7-12月的进货收货计划,已知商店仓库容量不得超过500件,六月底已存货200件,以后每月初进货一次,假设各月份某商品买进、售出单位如下表1-2所示,问各月进货售货各多少,才能使总收入最多?(5)某厂生产、、三种产品。
每单位产品需要1小时技术准备(指设针、试验等)、10小时直接劳动和3公斤材料。
每单位产品需要2小时技术准备、4小时劳动和2千克材料。
每单位产品需要1小时技术准备、5小时劳动和1千克材料。
可利用的技术准备时间为100小时,劳动时间为700小时,材料为400千克。
公司对大量购买提供较大的折扣,利润数字如下表1-3所示。
试列出使利润最大的数模。
(6)某一市政建设工程项目在随后的四年中需分别拨款200万元、400万元、800万和500万元,要求拨款在该年年初提供,市政府拟以卖长期公债的方法筹款。
高二数学线性规划试题

高二数学线性规划试题1.若实数满足则的最大值为;【答案】9【解析】先在平面直角坐标系中画出实数的可行解范围,将目标函数化为,在直角坐标系中作出函数的图像,考虑到前的符号是“”,所以将函数的图像向上平移至可行解范围的最上顶点,此时函数的图像在轴上的截距为所求的最大值(另解:可将可行解范围的最上顶点的坐标代入目标函数可得解).如下图所示.【考点】简单线性规划问题.2.设变量满足约束条件,则目标函数的取值范围是()A.B.C.D.【答案】A【解析】由约束条件在直角坐标系中画出目标函数的可行域,如图所包围的阴影部分(包括边界):因为,所以,故选A.【考点】简单线性规划问题(用平面区域表示二元一次不等式组)3.已知实数x,y满足条件,则z=x+3y的最小值是()A.B.C.12D.-12【答案】B【解析】画出不等式表示的平面区域,作直线,将平移过点时取得最小值.【考点】线性规划求最值.4.已知平面区域如图,,,,在平面区域内取得最大值时的最优解有无数多个,则.【答案】.【解析】由得,故是直线的纵截距,因此当直线向上平移时增加,要使得最优解有无数个,从图可知必有直线平移到与直线AC重合,因此,.【考点】线性规划.5.设,满足若目标函数的最大值为14,则()A.1B.2C.23D.【答案】B【解析】根据题意作出可行域如图所示,目标函数z=ax+y(a>0)最大值为14,即目标函数z=ax+y(a>0)在3x-y-6≤0与x-y+2≥0的交点M(4,6)处,目标函数z最大值为14,所以4a+6=14,所以a=2.故选B【考点】本试题主要是考查了线性规划区域的最优解的问题。
研究二元一次目标函数的最大值问题。
点评:解决这类问题的核心就是准确作图,表示出目标区域,并利用直线的截距的平移得到过哪个点时,得到最优解的问题。
6.设满足则()A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最小值D.既无最小值,也无最大值【答案】B【解析】作出不等式表示的可行域可知当直线z=x+y经过直线2x+y=4与直线x-2y=2的交点(2,0)时,z取得最小值2.无最大值.7.某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?【答案】投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大【解析】先设投资人分别用x万元、y万元投资甲、乙两个项目得到x,y满足的约束条件为,目标函数,再作出不等式组表示的可行域,找出最优解,求出z的最大值.解:设投资人分别用x万元、y万元投资甲、乙两个项目,由题意:,目标函数,上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域.作直线,并作平行于直线的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线的距离最大,其中M点是直线和直线的交点,解方程组得,此时(万元),,当时,最得最大值.答:投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大.8.已知, 则的最大值是 .【答案】10【解析】作出不等组表示的可行域,当直线经过直线x+y=3与直线x-y=1的交点(2,1)时,z取得最大值10.9.某工厂计划生产A.B两种涂料,生产A种涂料1t需要甲种原料1t.乙种原料2t,可获利润3千元;生产B种涂料1t需要甲种原料2t,乙种原料1t,可获利润2千元,又知该工厂甲种原料的用量不超过400t,乙种原料的用量不超过500t,问如何安排生产才能获得最大利润?(注:t表示重量单位“吨”)【答案】应分别生产A、B两种涂料各200t、100t才能获得最大利润【解析】本试题主要是考查了线性规划的最优解问题在实际生活中的运用。
线性规划期末试题及答案

线性规划期末试题及答案一、选择题1. 在线性规划中,以下哪个是目标函数?(A) 约束条件(B) 决策变量(C) 目标变量(D) 限制条件答案:(C) 目标变量2. 在线性规划模型中,以下哪个是限制条件?(A) 目标函数(B) 决策变量(C) 目标变量(D) 约束条件答案:(D) 约束条件3. 在线性规划中,如果目标函数系数有变动,但其它条件保持不变,对最优解的影响是:(A) 没有影响(B) 无法确定(C) 会改变最优解(D) 不确定,需要重新求解线性规划模型答案:(A) 没有影响4. 在线性规划中,如果某个约束条件右侧的常数项发生变动,但其它条件保持不变,对最优解的影响是:(A) 没有影响(B) 无法确定(C) 会改变最优解(D) 不确定,需要重新求解线性规划模型答案:(C) 会改变最优解5. 在线性规划中,以下哪个方法可以确定解的有界性?(A) 单纯形法(B) 对偶法(C) 整数规划(D) 罚函数法答案:(A) 单纯形法二、简答题1. 什么是线性规划?请简要描述线性规划的基本思想和应用领域。
答:线性规划是一种数学优化方法,用于解决在一定约束条件下,目标函数为线性的最优化问题。
其基本思想是通过线性规划模型的建立,将实际问题转化为数学问题,并利用数学方法求解最优解。
线性规划的应用领域非常广泛,包括生产调度、资源分配、投资组合、运输问题等。
2. 简述线性规划模型的一般形式,并解释模型中各要素的含义。
答:线性规划模型的一般形式如下:Max/Min Z = c₁x₁ + c₂x₂ + ... + cₙxₙsubject to:a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ ≤ b₁a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ ≤ b₂...aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ ≤ bₙx₁, x₂, ..., xₙ ≥ 0其中,Z为目标函数的值,c₁, c₂, ..., cₙ为目标函数的系数;x₁, x₂, ..., xₙ为决策变量;a₁₁, a₁₂, ..., aₙₙ为约束条件的系数;b₁,b₂, ..., bₙ为约束条件的常数项。
《线性与非线性规划》试题A及其标准答案

《线性与非线性规划》试题A及其标准答案一、选择题(每题5分,共25分)1. 以下哪个问题是线性规划问题?A. 最小化目标函数 f(x) = x^2 + 2x + 1,约束条件为x ≥ 0B. 最大化目标函数 f(x) = 3x + 4y,约束条件为x + 2y ≤ 8,x ≥ 0,y ≥ 0C. 最小化目标函数 f(x) = 2x + 3y,约束条件为 x^2 + y^2 ≤ 4D. 最大化目标函数 f(x) = e^x,约束条件为x + y ≤ 5,x ≥ 0,y ≥ 02. 在线性规划中,以下哪个条件不是线性规划的基本假设?A. 目标函数是线性函数B. 约束条件是线性不等式C. 变量可以取负值D. 约束条件是线性方程3. 以下哪个非线性规划问题是凸规划问题?A. 最小化目标函数 f(x) = x^3 - 3x^2 + 2x,约束条件为 x ∈ [0, 3]B. 最小化目标函数 f(x) = sin(x),约束条件为x ∈ [0, π]C. 最小化目标函数 f(x) = x^2 + y^2,约束条件为 x^2 +y^2 ≤ 1D. 最小化目标函数 f(x) = -x^2,约束条件为x ≤ 04. 在非线性规划中,以下哪个方法属于无约束优化方法?A. 拉格朗日乘数法B. KKT条件C. 梯度下降法D. 罚函数法5. 以下哪个非线性规划问题有唯一极值点?A. 最小化目标函数 f(x) = x^3 - 3x^2 + 2x,约束条件为 x ∈ [0, 3]B. 最小化目标函数 f(x) = sin(x),约束条件为x ∈ [0, π]C. 最小化目标函数 f(x) = x^2 + y^2,约束条件为 x^2 +y^2 ≤ 1D. 最小化目标函数 f(x) = -x^2,约束条件为x ≤ 0二、填空题(每题10分,共30分)6. 线性规划问题的标准形式为:______。
7. 在非线性规划中,梯度下降法的基本思想是:______。
线性规划试题

线性规划试题一、题目描述某家具制造公司生产两种类型的桌子:A型和B型。
生产A型桌子每个需要2个小时的加工时间,生产B型桌子每个需要3个小时的加工时间。
公司每天总共有10个小时的加工时间可用。
A型桌子售价为1000元,B型桌子售价为1500元。
每天销售的A型桌子不超过5个,销售的B型桌子不超过4个。
制造一张A型桌子的成本为450元,制造一张B型桌子的成本为600元。
请问,该公司每天应该制造多少张A型桌子和多少张B型桌子,才能使利润最大化?二、问题分析本问题属于线性规划问题,即在满足一定约束条件下,使目标函数达到最大(或最小)值。
该问题涉及两个变量:A型桌子的生产数量和B型桌子的生产数量。
目标是使利润最大化。
我们可以设A型桌子的生产数量为x,B型桌子的生产数量为y。
根据题目要求,我们可以列出以下约束条件:1. 加工时间约束条件:2x + 3y ≤ 102. 销售数量约束条件:x ≤ 5,y ≤ 43. 非负约束条件:x ≥ 0,y ≥ 0利润最大化目标函数为:1000x + 1500y - 450x - 600y。
我们可以通过求解以上线性规划问题,找到最优解,即生产多少张A型桌子和B型桌子时可以使利润最大化。
三、线性规划求解使用线性规划求解方法,可以求得最优解。
根据约束条件和目标函数,我们可以得到线性规划模型:```Maximize 1000x + 1500y - 450x - 600ySubject to:2x + 3y ≤ 10x ≤ 5, y ≤ 4x ≥ 0, y ≥ 0```将上述模型输入线性规划求解器进行计算,得到最优解为:A型桌子的生产数量(x)为4张,B型桌子的生产数量(y)为2张。
四、结论根据线性规划求解结果,该公司每天应该生产4张A型桌子和2张B型桌子,才能使利润最大化。
通过优化生产数量,公司将获得的利润为:利润 = (售价 - 成本) * 数量= [(1000 - 450) * 4] + [(1500 - 600) * 2]= 2,800元因此,该公司每天生产4张A型桌子和2张B型桌子时,可以获得最大利润2800元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(2009山东卷理)不等式0212<---x x 的解集为 . 2.若直线0ax by c ++=在第一、二、三象限,则 ( ) (A )0,0ab bc >> (B )0,0ab bc ><(C )0,0ab bc <> (D )0,0ab bc <<
3、在约束条件:x+2y ≤5,2x+y ≤4,x ≥0,y ≥0下,z=3x+4y 的最大值是 ( )
A 、9
B 、10
C 、11
D 、12
4、设R 为平面上以A (4,1),B (-1,-6),C (-3,2)为顶点的三角形区域(包括边界),则z=4x -3y 的最大值与最小值分别为: ( )
A 、最大值14,最小值-18
B 、最大值-14,最小值-18
C 、最大值18,最小值14
D 、最大值18,最小值-14
5、曲线x=y 2与y=x 2的交点个数是: ( )
A 、1
B 、2
C 、3
D 、4
6. (全国卷Ⅰ)在坐标平面上,不等式组⎩
⎨⎧+-≤-≥131x y x y 所表示的平面区域的面积为( ) (A )2 (B )23
(C )22
3 (D )2
7.(山东卷)设x 、y 满足约束条件5,
3212,03,0 4.
x y x y x y +≤⎧⎪+≤⎪⎨≤≤⎪
⎪≤≤⎩则使得目标函数65z x y =+的最大的点(,)x y 是 .
8.不等式组3,
0,20x x y x y ≤⎧⎪+≥⎨⎪-+≥⎩
表示的平面区域的面积等于 ( )
A.28
B.16
C.439
D.121
9、(山东省乐陵一中2009届高三考前练习)
已知变量230
,330.10x y x y x y y +-≤⎧⎪+-≥⎨⎪-≤⎩
满足约束条件若目标函数
z ax y =+(其中a>0)仅在点(3,0)处取得最大值,则a 的取值范围为 。
10、(广东省深圳市2008年高三年级第一次调研考试)已知点P
是边长为的等边三角形内一点,它到三边的距离分别为x 、y 、z ,则x 、y 、z 所满足的关系式为 ,222
x y z ++的最小值是 .
线性规划
知识要点
1、二元一次不等式表示平面区域
(1)一般地,二元一次不等式
0>++C By Ax 在平面直角坐标系中表示直线0=++C By Ax 某一侧的所有点组成的平面区域(半平面)不含边界线.
不等式0≥++C By Ax 所表示的平面区域(半平面)包括边界线.
(2)对于直线0=++C By Ax 同一侧的所有点(x,y ),使得C By Ax
++的值符号相同。
因此,如果直线0=++C By Ax 一侧的点使0>++C By Ax
,另一侧的点就使0<++C By Ax 。
所以判定不等式0>++C By Ax (或0
<++C By Ax )所表示的平面区域时,只要在直线0=++C By Ax 的一侧任意取一点),(00y x ,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域。
(3) 由几个不等式组成的不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
2、线性规划
⑴ 基本概念
①、设出所求的未知数
②、列出约束条件(即不等式组)
③、建立目标函数
④、作出可行域
⑤、运用图解法求出最优解
答案 3x y z ++=,3。
