粒子群算法在概率积分法沉陷预计模型参数反演中的应用
粒子群优化算法理论及应用ppt课件

学报》、《分析化学》等
15
PSO的研究与应用现状概述
截至2010年3月
• 在《科学引文索引扩展版SCI Expanded》的“Science
Citation Index Expanded (SCI-EXPANDED)--1999-present” 数据库中以“General Search,TOPIC,Title only”为检索 方式,以“Particle Swarm Optimization”为检索词,进行 检索,可以检索到1075篇相关文章;
进化计算是模拟自然界生物进化过程与机理求解优化 问题的人工智能技术,其形式是迭代算法,从选定的初始群 体(一组初始解)出发,对群体中的每个个体进行评价,并 利用进化产生机制产生后代个体,通过不断迭代,直至搜索 到优化问题的最优解或者满意解。
6
开始
群体初始化
算
对群体中的每个个体进行评价
法
流
利用进化产生机制产生后代个体
11
PSO算法起源
• 模拟鸟类飞行的Boid模型
群体行为可以用几条简单行为规则在计算机
中建模,Reynolds使用以下规则作为行为规则:
向背离最近同伴的方向移动;
向目的移动;
向群体的中心移动。
12
PSO算法起源
• 假设在一个区域里只有一块食物,一群鸟进行随机
搜索,所有鸟都不知道食物具体在哪里,但知道它 们当前位置离食物还有多远,那么一种简单有效的 觅食策略是搜索目前离食物最近的鸟的周围区域。
过程中,个体适应度和群体中所有个体的平均适应度不断得到
改进,最终可以得到具有较高适应度的个体,对应于问题的最
粒子群算法及其应用

粒子群算法是一种基于计算机的优化算法,它可以用来解决复杂的优化问题,如最优化,最小化或最大化目标函数。
它是一种基于群体智能的算法,它的概念来自于生物学中的群体行为,如鸟群的飞行,蚁群的聚集等。
粒子群算法是一种迭代搜索算法,它通过不断更新粒子的位置来搜索最优解。
粒子群算法的基本思想是,在搜索空间中模拟一群粒子,每个粒子有一个位置和一个速度,它们遵循一定的算法进行移动,移动的目的是最大限度地改善粒子的位置,以达到最优解。
算法的每一步都是基于粒子的位置和速度计算出新的粒子位置,并将其计算结果与原来的粒子位置进行比较,如果新位置更优,则更新粒子的位置,如果不是,则保持原位置。
每次迭代后,粒子群算法都会更新粒子的位置,以达到最优解。
粒子群算法在优化问题中有着广泛的应用,它可以用来解决最小化或最大化目标函数的问题,也可以用来求解约束优化问题。
它的优势在于它可以快速地搜索最优解,而且它可以处理复杂的优化问题,比如多维度和非凸优化问题。
粒子群算法在实际应用中也有很多。
例如,它可以用来解决机器学习中的优化问题,比如神经网络的训练,支持向量机的训练,以及模式识别问题。
它也可以用来解决工程设计中的优化问题,如机械设计,汽车设计,航空航天设计等。
此外,它还可以用来解决经济学中的优化问题,比如资源分配,货币政策等。
粒子群算法是一种有效的优化算法,它可以有效地解决复杂的优化问题,并且具有良好的收敛性。
由于它的优势,粒子群算法在实际应用中被广泛应用,它可以用来解决机器学习,工程设计和经济学中的优化问题。
粒子群算法及应用解析

A brief description of how the algorithm works is as follow
Initially, some particle is identified as the best particle in a neighborhood of particles, based on its fitness.
The Origination of the PSO
Particle Swarm Optimization (PSO) is a population based stochastic optimization technique developed by Kennedy and Eberhart in 1995
粒子群算法及其应用
朱汉洪 上海财经大学
2010.07
内容
粒子群优化算法背景 粒子群算法思想 粒子群算法 案例——积极投资决策与被动投资决策优化 未来可以研究的方向
Dumb parts, properly connected into a swarm, yield smart results.
Various population topologies on the PSO performance
Reference: Ajith Abraham, He Guo, and Hongbo Liu,Swarm Intelligence: Foundations, perspectives and Applications
All the particles are then accelerated in the direction of this particle, but also in direction of their own best solutions that they have discovered previously.
粒子群算法原理及在函数优化中的应用(附程序)

粒子群算法原理及其在函数优化中的应用1 粒子群优化(PSO )算法基本原理1.1 标准粒子群算法假设在一个D 维的目标搜索空间中,有m 个代表问题潜在解的粒子组成一个种群12[,,...,]m =x x x x ,第i 个粒子的信息可用D 维向量表示为12[,,...,]T i i i iD x x x =x ,其速度为12[,,...,]T i i i iD v v v =v 。
算法首先初始化m 个随机粒子,然后通过迭代找到最优解。
每一次迭代中,粒子通过跟踪2个极值进行信息交流,一个是第i 个粒子本身找到的最优解,称之为个体极值,即12[,,...,]T i i i iD p p p =p ;另一个是所有粒子目前找到的最优解,称之为群体极值,即12[,,...,]T g g g gD p p p =p 。
粒子在更新上述2个极值后,根据式(1)和式(2)更新自己的速度和位置。
11122()()t t t t t t i i i i g i w c r c r +=+-+-v v p x p x (1)11t t t i i i ++=+x x v (2)式中,t 代表当前迭代次数,12,r r 是在[0,1]之间服从均匀分布的随机数,12,c c 称为学习因子,分别调节粒子向个体极值和群体极值方向飞行的步长,w 为惯性权重,一般在0.1~0.9之间取值。
在标准的PSO 算法中,惯性权重w 被设为常数,通常取0.5w =。
在实际应用中,x 需保证在一定的围,即x 的每一维的变化围均为min max [,]X X ,这在函数优化问题中相当于自变量的定义域。
1.2 算法实现步骤步骤1:表示出PSO 算法中的适应度函数()fitness x ;(编程时最好以函数的形式保存,便于多次调用。
)步骤2:初始化PSO 算法中各个参数(如粒子个数,惯性权重,学习因子,最大迭代次数等),在自变量x 定义域随机初始化x ,代入()fitness x 求得适应度值,通过比较确定起始个体极值i p 和全局极值g p 。
利用果蝇算法反演概率积分法开采沉陷预计参数

概率积分法在开采沉陷预计中的应用

关键 词 : 沉 陷预 计 ; 概 率 积分 法 ; “ 三 下” 开采 中图分 类号 : T D 8 2 3 . 8 3 文献标 志码 : B
华 润天 能徐 州煤 电有 限公 司龙 固煤 矿地处 微 山 湖畔 . 紧邻京 杭 大运河 , 在河 堤 下赋存 的大量优 质煤
) 2 / r 2 )
分 可 采 的薄煤层 : 2 1 煤厚 0 . 2 4 3 . 1 5 / 1 . 2 3 m, 为 全
区可 采 高硫 分 的 薄煤 层 .占矿井 资 源储 量 的 7 0 %, 为矿 井主要 可 采煤层 .受 底板 高压 岩溶 灰岩 水 的影 响 .深部 区域 开 采 突水 系数 大于 0 . 1 .突 水威 胁 较
t a n J B为 影 响 角 p之 正 切 ; Z i = ・ c o t 0 , 0为最 大 下 沉
角, ( 。 ) 。
地 表任 一点 的下 沉为 W( x , y ) = Wd f W ( x , y ) d x d y
煤开 采 , 降低矿 井 原煤 硫 分 。 提 高 原煤 发 热 量 。 提 高 经济 效益 .龙 固煤矿 对解 放微 山湖 大堤 压覆 的 7煤 可采 资源进 行论 证
仅会产生细小的裂纹不会发生大型的1一水平变形2一水平变形3f沉深切裂缝沿堤方向垂直堤方向图1开采后湖堤地表变形剖面343湖堤防洪标准分析区域最大下沉23m
2 0 1 4年第 4期
No .4 2 01 4
煤
炭
科
技
C0AL S CI ENCE & TECHNOL 0GY MAGAZI NE
式中 : r 为 影 响半 径 , r =H Jt a n / 3 ; Ho 为 平均 采 深 , m;
直观理解粒子群算法

直观理解粒子群算法1.引言1.1 概述粒子群算法是一种模拟自然界群体行为的优化算法。
它最早由Eberhart和Kennedy于1995年提出,受到了鸟群觅食和鱼群游动行为的启发。
粒子群算法模拟了一个由许多粒子组成的群体,每个粒子代表一个潜在的解,并通过不断地调整自身的位置和速度来寻找最优解。
粒子群算法的基本原理是通过粒子之间的合作与竞争来达到全局最优解。
在算法开始时,每个粒子都会随机地在问题的解空间内选择一个初始位置和速度。
然后,根据粒子的当前位置和速度以及历史最优解的信息,每个粒子会更新自己的速度和位置。
更新的过程中,粒子会根据个体历史最优解和群体历史最优解两方面的信息进行权衡,从而平衡个体探索和群体协作的需求。
通过不断地迭代更新,粒子群算法能够逐渐收敛到全局最优解。
粒子群算法被广泛应用于优化问题的求解。
它在函数优化、组合优化、神经网络训练等领域取得了显著的成果。
由于其简单而直观的思想,粒子群算法易于理解和实现,同时具有较快的收敛速度和较好的全局搜索能力。
与其他优化算法相比,粒子群算法在处理高维、非线性、多模态等复杂问题时具有一定的优势。
综上所述,粒子群算法是一种基于群体行为的优化算法,通过模拟粒子之间的合作与竞争来寻找最优解。
它具有简单直观、易于实现和较好的全局搜索能力等优势。
在实际应用中,粒子群算法已经取得了一些显著的成果,并且有着较大的发展潜力。
文章结构部分的内容如下:文章结构部分旨在介绍本文的组织框架和内容安排,让读者能够清晰地了解整篇文章的结构和逻辑顺序。
本文分为三个主要部分:引言、正文和结论。
接下来将对每个部分的内容进行简要介绍。
首先是引言部分(Section 1),它主要用于引入本文的主题和背景。
在引言的第一部分(1.1 概述),我们将简要概括粒子群算法的基本概念和特点,为读者提供一个整体的认识。
接着,在第二部分(1.2 文章结构),我们将详细说明本文的组织结构和每个部分的内容安排,以便读者能够清晰地了解整个文章的构成。
概率积分法用于开采沉陷预计时参数求取方法研究现状

概率积分法用于开采沉陷预计时参数求取方法研究现状引言XX对一个计划进行的开采,在开采进行以前,根据其地质采矿条件和选用的预计函数、参数,预先计算出受此开采影响的岩层和(或)地表的移动和变形的工作,称为开采沉陷预计,也称岩层和(或)地表移动预计(或预算),简称“预计”.XX 我国开采沉陷工建立的沉陷预计方法主要有概率积分法、负指数函数法、典型曲线法、积分格网法、威布尔分布法、样条函数法、双曲函数法、皮尔森函数法、山区地表移动变形预计法、三维层状介质理论预计法和基于托板理论的条带开采预计法。
在这些预计方法中,积分格网法已很少使用,双曲函数法是基于**XX区具有巨厚冲积层时的开采预计方法,皮尔森函数法是基于**XX区急倾斜煤层开采时的预计方法,一般仅限于该XX区使用;三维层状介质理论和托板理论是针对条带开采提出的新方法,还有待于进一步的检验和完善;概率积分法以其理论基础坚实、易于计算机实现、应用效果好而成为我国开采沉陷预计的主要方法。
1 概率积分法基本原理XX概率积分法是因其所用的移动和变形预计公式中含有概率积分(或其倒数)而得名。
由于此方法的理论基础是随机介质理论,所以又叫随机介质理论方法。
随机介质理论首先由波兰学者李特威尼申与50 年代引入岩层移动研究,后由我国学者刘宝琛、廖国华等为概率积分法。
经过我国开采沉陷工不断的研究,目前以成为我国较成熟的、应用最为预计方法之一。
该方法认为开采引起的岩层和地表移动的规律与作为随机介质的颗粒体介质模型所描述的规律在宏观上相似。
XX概率积分法属于影响函数法,通过对单元开采下沉盆地进行积分即可求取工作面开采地表移动与变形值,中给出了详细的推导过程。
在计算机实现过程中,可以将工作面剖分成0.1H 0。
1H(H 为工作面平均采深)的矩形网格进行积分。
具体实现过程可参见文献。
2 概率积分法应用于开采沉陷预计时的误差分析XX概率积分法应用于开采沉陷预计主要有两种误差来源,即模型误差和参数误差.其中,模型误差又分为“第一类模型误差"、“第二类模型误差”和“第三类模型误差”。
粒子群算法简介优缺点及其应用.

——Calculate particle velocity according equation (1) ——Update particle position according equation (2) — End
While maximum iterations or minimum error criteria is not attained
2019/2/18
2
粒子群算法的基本原理
PSO的基本概念源于对鸟群捕食行为的研究:
一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有鸟 都不知道食物在哪里。但是他们知道当前的位置离食物还有多 远。
那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目 前离食物最近的鸟的周围区域。
2019/2/18
2019/2/18
7
粒子群优化算法的一般数学模型
假设在一个N维空间进行搜索,粒子i的信息可用两个N维向量 来表示:
第i个粒子的位置可表示为 xi xi1 , xi 2 , xiN
速度为 vi vi1, vi 2 ,viN
T
T
在找到两个最优解后,粒子即可根据下式来更新自己的速度和 位置:
2019/2/18
5
每个粒子使用下列信息改变自己的当前位置: (1)当前位置; (2)当前速度; (3)当前位置与自己最好位置之间的距离; (4)当前位置与群体最好位置之间的距离。
2019/2/18
6
粒子群算法的基本思想
用随机解初始化一群随机粒子,然后通过迭代找到最优解。在 每一次迭代中,粒子通过跟踪两个“极值”来更新自己:
2019/2/18
11
参数意义
(1)粒子的长度N:问题解空间的维数。 (2)粒子种群大小M:粒子种群大小的选择视具体问题而定,但 是一般设置粒子数为20-50。对于大部分的问题10个粒子已经可 以取得很好的结果,不过对于比较难的问题或者特定类型的问 题,粒子的数量可以取到100或200。另外,粒子数目越多,算 法搜索的空间范围就越大,也就更容易发现全局最优解。当然, 算法运行的时间也较长。 (3)加速常数c1和 c2:分别调节向Pbest和Gbest方向飞行的最大 步长,决定粒子个体经验和群体经验对粒子运行轨迹的影响, 反映粒子群之间的信息交流。 如果c1=0,则粒子只有群体经验,它的收敛速度较快,但容易 陷入局部最优;
基于Matlab的概率积分法开采沉陷预计参数解算

基于Matlab的概率积分法开采沉陷预计参数解算沈震;徐良骥;刘哲;秦长才【期刊名称】《金属矿山》【年(卷),期】2015(000)009【摘要】通过在开采工作面地表建立观测站获取地表变形数据解算概率积分法开采沉陷预计参数,从而预计工作面周边或相似开采条件下工作面的开采沉陷并评估和指导开采作业,其前提是精确获取概率积分法开采沉陷预计参数.为此,基于Matlab软件,采用最小二乘法拟合观测点变形数据解算概率积分法开采沉陷预计参数,并结合Mat-lab软件绘图工具开发了集数据载入、坐标转换、参数解算、结果输出、开采沉陷预计及反演为一体的可视化开采沉陷预计系统.以淮南谢桥煤矿11316工作面为例,根据地表移动观测点位移数据解算开采沉陷预计参数并与实测值进行对比分析,结果表明,该系统解算出的开采沉陷预计参数符合两淮矿区开采沉陷的基本规律,反演结果与实测值基本吻合,该系统对于实现矿区开采沉陷高精度预计和反演具有一定的参考价值.【总页数】5页(P170-174)【作者】沈震;徐良骥;刘哲;秦长才【作者单位】安徽理工大学测绘学院,安徽淮南232000;安徽理工大学测绘学院,安徽淮南232000;安徽理工大学测绘学院,安徽淮南232000;安徽理工大学测绘学院,安徽淮南232000【正文语种】中文【中图分类】TD325【相关文献】1.利用果蝇算法反演概率积分法开采沉陷预计参数 [J], 陈涛;郭广礼;朱晓峻;郭庆彪;方齐2.基于FLAC3D的煤矿开采沉陷预计及与概率积分法的对比分析 [J], 秦世界;张和生;李国栋3.基于松散层厚影响的概率积分法开采沉陷预计模型 [J], 王宁;吴侃;秦志峰4.基于概率积分法的开采沉陷预计研究 [J], 顾叶;宋振柏;张胜伟5.开采沉陷预计概率积分法动态参数研究 [J], 葛家新;于丰德因版权原因,仅展示原文概要,查看原文内容请购买。
概率积分法在某煤矿项目开采沉陷预测分析中的应用
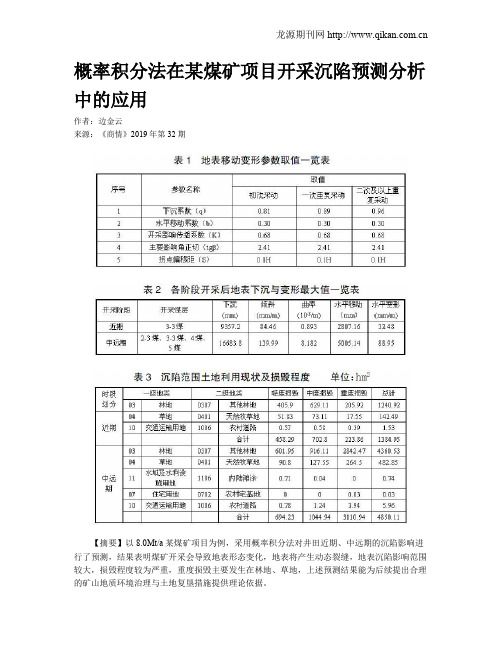
概率积分法在某煤矿项目开采沉陷预测分析中的应用作者:边金云来源:《商情》2019年第32期【摘要】以8.0Mt/a 某煤矿项目为例,采用概率积分法对井田近期、中远期的沉陷影响进行了预测,结果表明煤矿开采会导致地表形态变化,地表将产生动态裂缝,地表沉陷影响范围较大,损毁程度较为严重,重度损毁主要发生在林地、草地,上述预测结果能为后续提出合理的矿山地质环境治理与土地复垦措施提供理论依据。
【关键词】煤矿项目 ;沉陷预测一、项目概况某煤矿设计规模8.0Mt/a,服务年限74.4年,开采方式为井工开采。
全井田范围内共含可采煤层6层,不可采煤层5层。
井田范围内无文物古迹、重大设施及其他需特殊保护的敏感目标,井下保护煤柱类型主要包括井田境界煤柱、工业场地保护煤柱、主要井巷保护煤柱、断层煤柱等。
二、预测模式本预测采用的是根据概率积分法编制的“地表移动与变形计算”程序,输入相关参数,程序自动计算各种变形数据。
预测模式采用国家煤炭局《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》中所推荐的模式。
三、地表移动变形参数的选取地表移动变形计算的主要参数有下沉系数q、主要影响角正切tgβ,水平移动系数b,拐点偏移距S和开采影响传播系数k等。
这些参数的取值主要与煤层开采方法、顶板管理方法、上覆岩层性质、工作面宽度、重复采动次数以及采深采厚比等因素有关。
本矿区为新建矿区,基本尚未开发,矿区无岩移观测资料。
因此本预测根据井田勘探报告,参考《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》确定地表沉陷预测参数,见表1。
四、预测与影响分析(一)地表形态变化预测结果为了体现远粗近细、边生产边复垦的思想,并为工程量计算提供基础,根据开采工作面接续情况,结合复垦时序要求,将开采时间划分为近期、中远期,各阶段的开采最大变形值见表2。
(二)地裂缝分析开采前30年内预计工作面最大水平变形为88.95mm/m,结合岩性特征,一般地表水平变形拉伸值大于4mm/m将可能出现裂缝,矿区煤层开采时,地表将会产生动态裂缝。
基于概率积分法的矿区地表沉陷预计分析

,
合 理 的 解 决政 区 划 归 兖 州 市 管 辖
。
,
区 内 公路 四通 八达
,
,
交通
,
三下
”
采 煤 问题 显得尤 为重 要
、
但 由 于 煤 矿 地 十 分 便 利
.
区 内 为 第 四 系 冲 积平原 地 形 平坦
,
下 开采 范 围 大 采 的影响 地表的
一 一
开 采 层 数多 而 开采 深 度 有 限
单 元 盆 地 叠
,
”
1
0 303
作面 位于 大施 村 东 水 源井 家属 区
,
加 构 成总 的 地 表 移 动 盆 地
]
。
这 个 过 程 的 叠 加西 汶 邹 公 路 从
。 、
工
作 面 上方通 过
1
。
大施 村的村庄
。
与 计 算 可 以 用 概 率 分 布 密 度 曲 线 的 积 分 来 完 成 人 口
2 4
北 京 测绘
.
.
2 0
1
7
年第
1
期
表
丨
大 施 村 人 口 建 筑 物 统计
、
压 煤 建筑 物 情 况
(
预计 方法
1
2
…
n
。
地 下 管 网
、
文物 等
)
?
目
前均没有 受到 开 采影响
。
[
收 稿日 期] 作 者简 介 ]
2 0
—
1
6
07
—
1
4
[
刘欣
粒子群算法在薄膜参数反演中的参数选择

粒子裙算法(Particle Swarm Optimization, PSO)是一种优化算法,它模拟了鸟裙或鱼裙觅食的行为,通过不断地调整粒子的位置来寻找最优解。
在薄膜参数反演中,选择合适的参数对于算法的有效性至关重要。
本篇文章将从深度和广度两个方面探讨粒子裙算法在薄膜参数反演中的参数选择。
**一、粒子裙算法简介**粒子裙算法是一种裙体智能算法,它模拟了鸟裙或鱼裙寻找食物的行为。
在算法中,每个粒子代表一个潜在的解,这些粒子通过不断地调整自身的位置和速度来搜索最优解。
粒子裙算法具有快速收敛、全局寻优能力强等优点,因此在薄膜参数反演中得到了广泛的应用。
**二、参数选择的重要性**在粒子裙算法中,参数的选择对算法的性能和效果有着直接的影响。
常见的参数包括惯性权重、个体和社会学习因子等,这些参数的选择直接关系到算法的搜索能力、收敛速度和最终结果的质量。
合理地选择这些参数对于算法的性能至关重要。
**三、深度探讨参数选择的影响**1. **惯性权重的选择**惯性权重控制了粒子的更新速度,它在个体最优解和全局最优解之间进行权衡。
当惯性权重较大时,粒子更倾向于继续沿其原来的移动方向前进;当惯性权重较小时,粒子更倾向于朝着个体最优或全局最优的方向前进。
在薄膜参数反演中,合理地选择惯性权重可以加快算法的收敛速度,同时避免陷入局部最优解。
2. **个体和社会学习因子的选择**个体学习因子和社会学习因子分别控制了粒子根据个体最优和全局最优来进行位置更新的程度。
在薄膜参数反演中,这两个因子的选择直接关系到算法的搜索范围和精度,合理地选择可以使算法更快地收敛到最优解。
**四、广度探讨参数选择的实践操作**在实际的薄膜参数反演中,如何根据实际情况选择合适的参数也是至关重要的。
需要根据具体的问题和目标来确定参数的范围和初始值。
可以通过观察算法的收敛情况和结果的稳定性来调整参数的值。
可以通过对比不同参数取值下的算法性能来确定最佳的参数组合。
利用果蝇算法反演概率积分法开采沉陷预计参数

利用果蝇算法反演概率积分法开采沉陷预计参数陈涛;郭广礼;朱晓峻;郭庆彪;方齐【摘要】针对概率积分法开采沉陷预计参数反演时存在算法复杂、计算量大等问题,将具有算法简单、计算量小、精度高等特点的果蝇算法引入到概率积分法开采沉陷预计参数反演中,研究了利用果蝇算法反演概率积分法开采沉陷预计参数的基本原理,构造了下沉拟合值与实测值均方差最小的适应度函数模型。
结合安徽省某煤矿的实测数据,分别采用果蝇算法、遗传算法以及粒子群算法反演概率积分法开采沉陷预计参数,并以下沉拟合值与实测值的均方差为各算法反演精度的评价标准进行对比分析,结果表明:利用果蝇算法反演出的下沉拟合值与实测值的均方差(33.7 mm)以及相对中误差(1.4%)均小于同类条件下遗传算法、粒子群算法的反演结果,说明果蝇算法适用于反演概率积分法开采沉陷预计参数,对于提高概率积分法开采沉陷预计的精度有一定的参考价值。
%In order to solve the problems of complexity,large amount of calculating the mining subsidence prediction pa-ramters inversion of the probability integral method,the fruit flies algorithm with the characteristics of simple,low computational complexity and high precision is introduced to the mining subsidence prediction parameters inversion of the probability integral method. The basic principle of the mining subsidence prediction parameters inversion of the probability integral method based on fruit flies algorithm is studied in depth. The fitness function model of minimum mean square of the subsidence fitting values and measured values is established. Based on the mining subsidence measured data of a coal mine in Anhui province,the min-ing subsidence prediction parameters inversion of the probabilityintegral method are conducted by using the fruit flies algo-rithm,genetic algorithm and particle swarm algorithm respectively,the mean square error of the subsidence fitting values and measured values is taken as the evaluation criteria of the above three algorithms,the comparison results show that the mean square error of the subsidence fitting values and measured values is 33. 7 mm,the relative mean error is 1. 4%,which are lower than that of the genetic algorithm and particle swarm algorithm,therefore,it is further indicated that the fruit flies algorithm is suitable to conduct mining subsidence prediction parameters inversion of the probability integral method,it has some reference for improving the mining subsidence prediction precision of the probability integral method.【期刊名称】《金属矿山》【年(卷),期】2016(000)006【总页数】4页(P185-188)【关键词】开采沉陷;果蝇算法;概率积分法;参数反演;遗传算法;粒子群算法【作者】陈涛;郭广礼;朱晓峻;郭庆彪;方齐【作者单位】中国矿业大学环境与测绘学院,江苏徐州221116; 国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116; 江苏省资源环境信息工程重点实验室,江苏徐州221116;中国矿业大学环境与测绘学院,江苏徐州221116; 国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116; 江苏省资源环境信息工程重点实验室,江苏徐州221116;中国矿业大学环境与测绘学院,江苏徐州221116; 国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116; 江苏省资源环境信息工程重点实验室,江苏徐州221116;中国矿业大学环境与测绘学院,江苏徐州221116; 国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116; 江苏省资源环境信息工程重点实验室,江苏徐州221116;中国矿业大学环境与测绘学院,江苏徐州221116; 国土环境与灾害监测国家测绘地理信息局重点实验室,江苏徐州221116; 江苏省资源环境信息工程重点实验室,江苏徐州221116【正文语种】中文【中图分类】TD325现阶段,开采沉陷的预计方法主要有基于实测资料的经验公式法、影响函数法和理论模拟法,其中,应用较广泛的是概率积分法,该方法是一种基于非连续介质理论的理论模拟法,其开采沉陷预计参数主要有下沉系数q、主要影响角正切tanβ、开采影响传播角θ和拐点偏移距s[1],该类参数主要根据工作面上方地表移动观测站的实测沉陷变形值经反演得出。
量子粒子群算法在测井反演解释中的应用

量子粒子群算法在测井反演解释中的应用刘建军;卢以水;王全洲;王慧颖【摘要】量子粒子群算法是在粒子群算法的基础上,结合了量子运动原理提出的新算法,在数值试验中与其它的优化算法(如粒子群算法,蚁群算法,拟牛顿法,遗传算法,模拟退火算法)相比较有着收敛快,精度高的优点.粒子群算法,蚁群算法,拟牛顿法等都是测井反演问题中应用较为广泛的优化算法.本文用量子粒子群优化算法来确定侧向测井几何因子表达式,并且与粒子群算法在该问题上的运算结果进行了比较,结果表明量子粒子群具有运算速度快,需要资源少等优点,在现实测井中有应用价值.【期刊名称】《工程地球物理学报》【年(卷),期】2012(009)002【总页数】4页(P151-154)【关键词】测井反演解释;量子粒子群;深浅侧向测井;几何因子【作者】刘建军;卢以水;王全洲;王慧颖【作者单位】中国石油大学理学院,北京102249;中国石油大学理学院,北京102249;中国石油大学理学院,北京102249;中国石油大学理学院,北京102249【正文语种】中文【中图分类】P631.81 引言量子粒子群优化算法是2004年提出的智能随机优化算法[1],它在一些连续的优化问题上与粒子群算法,遗传算法、蚁群算法、模拟退火算法和拟牛顿法等算法相比较,具有收敛速度快、精度高、调节参数少等优点。
最优化测井解释是根据地球物理学中的广义反演理论,以经过校正后的、较为真实的测井值为基础,以储层参数和矿物相对体积为自变量,采用适当的解释模型和测井响应方程,通过合理选择的参数初始值,反演出响应的理论测井值,并将它们与实际测井值相比较,根据最小二乘法原理,结合某些地区地质经验来建立数学模型,应用最优化方法不断调整储层参数,使计算的理论测井值不断逼近相应的实际测井值。
一旦两者充分接近,则此时用以计算理论测井值所采用的自变量就是最充分反映实际底层原貌的储层参数及矿物相对含量值,即最优化测井解释结果[2]。
改进粒子群优化算法在边坡工程力学参数反演中的应用的开题报告

改进粒子群优化算法在边坡工程力学参数反演中的应用的开题报告1.选题背景和意义边坡工程是土木工程中最为重要的分支之一,其在地质灾害防治、山区基础设施建设等方面扮演着至关重要的角色。
由于边坡在长期的自然作用下,其力学性质会发生相应的变化,因此需要对边坡的力学参数进行反演,以便更好地评估工程的稳定性。
粒子群优化算法是一种常用于求解最优化问题的算法,其在求解非线性优化问题方面具有独特的优势。
因此,将粒子群优化算法应用于边坡工程力学参数反演中,不仅可以有效地提高反演精度和效率,还可以为相关科研和工程实践提供有力的帮助。
2.研究内容和方法本文旨在基于粒子群优化算法,研究其在边坡工程力学参数反演中的应用,并进一步改进算法以提高其性能。
具体的研究内容和方法包括:(1) 综述边坡工程力学参数反演的研究现状和发展趋势,分析粒子群优化算法的基本原理和在参数反演中的应用情况,提出研究的具体问题和目标。
(2) 改进粒子群优化算法的表现形式和优化策略,使其更适合于边坡工程力学参数反演中的问题求解,并通过数值计算和仿真实验验证其性能和效果。
(3) 将改进后的粒子群优化算法应用于边坡工程力学参数反演中的具体问题,探究算法求解的有效性和可行性,并提出相关的优化建议和改进方案。
3.预期结果和意义预计本研究将获得以下结果和意义:(1) 针对边坡工程力学参数反演中存在的问题和挑战,提出基于粒子群优化算法的求解方法,为相关科研与工程实践提供有效的支持和参考。
(2) 在改进算法的过程中,提高其搜索能力和收敛速度,在复杂优化问题中具有更强的适应性,进一步拓展了算法的应用领域。
(3) 通过数值仿真和实验验证,在边坡工程力学参数反演中具有较高的精确度和稳定性,可为预测边坡工程的稳定性提供重要的基础数据和分析方法。
基于狮群算法的概率积分预计参数反演方法

基于狮群算法的概率积分预计参数反演方法黄金中;李忠;李世保【期刊名称】《北京测绘》【年(卷),期】2022(36)2【摘要】针对传统的开采沉陷预计方法,在求取预计参数时存在计算量烦琐、精度低、速度慢等缺陷,本文开展了基于狮群算法(LSO)的概率积分预计参数反演方法研究。
LSO是一种群体智能算法,该算法已在光伏最大功率跟踪中方面得到广泛的应用,至今尚未发现应用于矿山开采沉陷预计领域中。
为了准确获取预计参数,本文将LSO应用于概率积分参数反演中,以此构建基于LSO的概率积分预计参数反演方法。
研究结果表明:①仿真实验:反演参数q、tanβ、b、θ的反演参数中误差分别为0.0325、0.1188、0.0285、1.0678且4个反演参数相对误差最大值均小于4.90%;拐点偏移距S_(a)、S_(b)、S_(c)、S_(d)反演参数中误差均小于6.8,反演参数相对误差均小于2.90%。
②应用实例:利用基于LSO的概率积分预计参数反演方法求解淮南矿区顾桥矿1414(1)工作面的概率积分预计参数,求取参数结果分别为:q=1.10;tanβ=1.82;b=0.35;θ=86.62°;S_(a)=-3.20 m;S_(b)=-5.12m;S_(c)=59.28 m;S_(d)=43.45 m;下沉值与水平移动值拟合中误差为122.76 mm,满足工程要求。
【总页数】8页(P101-108)【作者】黄金中;李忠;李世保【作者单位】安徽理工大学空间信息与测绘工程学院【正文语种】中文【中图分类】P258【相关文献】1.基于PSO算法的概率积分法预计参数反演2.基于改进果蝇算法的概率积分法预计参数反演3.基于实测数据的概率积分法预计参数反演方法研究4.基于Matlab 的概率积分法预计参数反演方法比较5.基于蝙蝠算法的概率积分预计参数反演方法因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
, ) , ( Z h a n i a k o u 0 7 5 0 0 0, C h i n a h e T h i r d G e o l o i c a l B r i a d e H e b e i P r o v i n c i a l B u r e a u o f G e o l o T g j g g g y
粒子群北省地矿局第三地质大队 , 河北 张家口 0 7 5 0 0 0 摘 要: 针对开采沉陷预计模型参数反演所存 在 的 算 法 复 杂 、 计 算 量 大 等 缺 陷, 将粒子群算法引入到概率积分法开 采沉陷预计模型参数反演中 。 研究粒子群算法 反 演 概 率 积 分 法 预 计 模 型 参 数 的 基 本 原 理 、 编码方法及适应度函数 的构造方法 , 同时结合河北省某煤矿的实测数据 , 以下沉拟合值与实测 值 的 中 误 差 作 为 反 演 精 度 的 评 价 标 准 对 算 法 进行实例验证 , 对提高开采沉陷预计的精度有一定的参考实用价值 。 关键词 : 开采沉陷预计 ; 概率积分法 ; 粒子群算法 ; 适应度函数 ( ) 中图分类号 : 7 0 0 P 2 5 8 文献标识码 : 0 0 6 9 4 9 2 0 1 7 1 0 0 3 6 4 A 文章编号 : 1 - - -
第2 6 卷第 1 0期 2 0 1 7年1 0月
测 绘 工 程 E n i n e e r i n o f S u r v e i n a n d M a i n g g y g p p g
o l . 2 6, N o . 1 0 V , c t . 0 1 7 O 2
] ( ) : 魏宗海 . 粒子群算法在概率积分法沉陷预计模型参数反演中的应用 [ 引用著录 : 测绘工程 , J . 0 1 7, 2 6 1 0 3 6 9. 2 3 - : / D O I 1 0 . 1 9 3 4 9 . c n k i . i s s n 1 0 0 6 7 9 4 9 . 2 0 1 7 . 1 0 . 0 0 7 - j
, : A a r a m e t e r a r t i c l e s w a r m o t i m i z a t i o n( P S O) a l o r i t h m i s i n t r o d u c e d i n t o t h e a e r t h e b s t r a c t I n t h i s p p p g p p ,w r o b a b i l i s t i c i n t e r a t i o n m e t h o d h i c h i s u s e d t o e s t i m a t e t h e e s t i m a t i o n o f t h e m i n i n m o d e l o f t h e p g g , a r a m e t e r t h e c o d i n m e t h o d a n d t h e c o n s t r u c t i o n r i n c i l e o f t h e r o b a b i l i t i n t e r a l m e t h o d . T h e b a s i c p g p p p y g , m e t h o d o f t h e f i t n e s s f u n c t i o n a r e c o m b i n e d .A t t h e s a m e t i m e t h e a l o r i t h m i s v a l i d a t e d b u s i n t h e g y g m e a s u r e d v a l u e o f t h e s e t t l e m e n t v a l u e a n d t h e m e a s u r e d v a l u e o f t h e c o a l m i n e i n H e b e i P r o v i n c e a s t h e e v a l u a t i o n c r i t e r i o n o f t h e i n v e r s i o n a c c u r a c . I m r o v i n t h e a c c u r a c o f m i n i n s u b s i d e n c e w i l l h a v e a y p g y g c e r t a i n r e f e r e n c e v a l u e . :m ;p ;p K e w o r d s i n i n u b s i d e n c e r e d i c t i o n r o b a b i l i t n t e r a l e t h o d a r t i c l e s w a r m a l o r i t h m; m g p y g g y s i f i t n e s s f u n c t i o n 地下 煤 层 开 采 引 起 的 地 表 沉 陷 使 矿 区 的 生 态 环境 、 地表 建 筑 物 等 遭 到 破 坏 , 在地下煤层开采前 对其进 行 沉 陷 预 计 , 可以提前评估开采对地表公 路、 建筑物 造 成 的 破 坏 程 度 , 科学地制定保护煤柱 的留设范围或压 煤 村 庄 的 搬 迁 计 划 。 另 外 , 开采沉 陷预计在矿区土地 复 垦 、 采煤塌陷地治理规划设计 等领域也有着广泛的应用 。 作为当前矿山 开 采 沉 陷 预 计 的 重 要 手 段 , 其概 率积分法预测的精 度 受 参 数 与 模 型 精 度 影 响 显 著 ,
A l i c a t i o n o f a r t i c l e s w a r m o t i m i z a t i o n i n a r a m e t e r i n v e r s i o n o f p p p p p r o b a b i l i s t i c i n t e r a l s u b s i d e n c e r e d i c t i o n m o d e l p g p
