二面角课件
合集下载
二面角PPT课件

于是,人们又把狼“请”了回来。狼还是吃
鹿,为了避免让狼捉到,狼一来鹿就跑,在这 种相互竞争中,鹿的数目不但没有减少,反而 更强壮了。
自然界就是这样的奇妙,狼成了鹿的医生了。
问题 为什么动物的数量不能无限增长呢?
生物与生物之间是相互依赖的,相 互制约的关系。
草
兔
问题1 兔子为什么要吃草
问题2 草(植物)中的营养物质从哪而来
麻雀啄食和糟蹋农作物,曾被 列为主要害鸟。20世纪50~60 年代,我国开展了一场轰轰烈 烈的“剿灭麻雀”的全民运动。
“成果”:
仅一天,上海就消灭麻雀194432只! 据不完全报道:从3月到11月上旬, 8个月的时间中全国捕杀麻雀19.6亿 只!
通过以上资料的分析,你认为人类能否 随意灭杀某种动物吗?为什么? 人为的破坏动物的种类和数量,会导致 整个生态系统失去平衡
2、在300二面角的一个面内有一点,它到另 一个面的距离是10cm,求它到棱的距离。
解:如图所示,过点A作AH⊥β,垂足为H, 由题意AH=10cm.
过点H作HO⊥EF,垂足为O,连OA,
则OA⊥EF,OA就是点A到棱EF的距离。
所以
A
∠ AOH 就 是 二 面 角 αEF-β的一个
α
F
β 平 面 角 ,
二氧化碳
光 合 作 用
有机物
光 合 作 用
有机物
动物促进生态系统中的物质循环
据估计:在开花植物中,约有84% 的植物是通过昆虫来帮助它们授粉 的
动物和植物的关系
自然界中的动物和植物在长期生存与发 展的过程中,形成了相互适应、相互依存 的关系
植物: 为各种动物制造营养物质, 并提供栖息场所
动物: 帮助植物更好地繁衍 给植物的生长提供肥料 对植物造成危害
二面角课件

二、二面角的表示方法:
二 面 角 -AB- 二 面 角 C-AB- D
二 面 角 - l-
三、二面角的平面角: 1、二面角的平面角必须满足
三个条件
四、二面角的平面角的作法2:、二面角的平面角的大小与
其顶点在棱上的位置无关 3、二面角的大小用它的平面
五、二面角一的“计作算”:二“123、 、 、证找 证计”到 明算角三所或1123的、、、中求作“大的的出定三垂小计角二角义垂面来就面算度法线法是角量”(所的求逆平的面)角角定理法
解:①在PB上取不同于P 的一点O,
在内过O作OC⊥AB交PM 于C,
C M
在 内作OD⊥AB交PN于D, A PD是二面角 AB 的平面角
D N
③设PO = a ,∵∠BPM =∠BPN = 45º
∴CO=a,DO=a, PC 2 a , PD 2a
又∵∠MPN=60º
∵BD⊥l ∴ AO∥BD,∴四边形ABDO为矩形,
∴ DO∥ l , AO=BD ∵ AC⊥l , AO⊥l ,
∴ l ⊥平面CAO ∴ AO⊥l ∴ CO⊥DO
∵ BD=1 ∴ AO=1,在△OAC中,AC=2,
∴CO2 AC 2 AO2 2AO AC COS120 7
在Rt △COD中,DO=AB=3
且PA=5,PB=8,AB =7,求这二面角的度数。
解: 设过PA、PB 的平面PAB
与棱l 交于O 点
P
∵PA⊥ ∴PA⊥ l
B
∵PB⊥ ∴PB⊥ l
lO
A
∴ l ⊥平面PAB
∴∠AOB为二面角 l 的平面角 又∵PA=5,PB=8,AB=7
由余弦定理得 cosP AP 2 BP 2 AB 2 1
二面角的有关概念-PPT课件

β
棱
面
l
α
10
知识探究(二):二面角的平面角
思考1:把门打开,门和墙构成二面角; 把书打开,相邻两页书也构成二面角 .随着打开的程度不同,可得到不同 的二面角,这些二面角的区别在哪里?
11
思考2:我们设想用一个平面角来反映 二面角的两个半平面的相对倾斜度, 那么平面角的顶点应选在何处?角的 两边在如何分布?
2.3.2 平面与平面垂直的判定 第一课时
二面角的有关概念
1
问题提出
1.空间两个平面有平行、相交两 种位置关系,对于两个平面平行, 我们已作了全面的研究,对于两个 平面相交,我们应从理论上有进一 步的认识.坡, 常用石块修筑护坡斜面,并使护坡斜面 与水平面成适当的角度;修筑水坝时, 为了使水坝坚固耐用,必须使水坝面与 水平面成适当的角度,如何从数学的观 点认识这种现象?
β
l
α
12
思考3:在二面角α-l-β的棱上取一 点O,过点O分别在二面角的两个面内 任作两条射线OA,OB,能否用∠AOB 来刻画二面角的张开程度?
β
B
O
lA
α
13
思考4:在上图中如何调整OA、OB的位 置,使∠AOB被二面角α-l-β唯一确 定?这个角的大小是否与顶点O在棱 上的位置有关?
β
B
O
lA
α β
B
lO
A
α
14
思考5:上面所作的角叫做二面角的平
面角,你能给二面角的平面角下个定
义吗?
Bβ
lO
A
α
以二面角的棱上任意一点为顶点,
在两个面内分别作垂直于棱的两条
射线,这两条射线所成的角叫做二
面角的平面角.
课件1:1.2.4 二面角

2.用空间向量求二面角的大小 如果 n1,n2 分别是平面 α1,α2 的一个法向量,设 α1 与 α2 所成角的 大小为 θ.则 θ=〈n1,n2〉或 θ=π-〈n1,n2〉,sin θ=_s_in_〈__n_1_,__n_2_〉.
【初试身手】
1.思考辨析(正确的打“√”,错误的打“×”)
(1)二面角的范围是0,π2.(
则nn11··AA→→BE1==00,,
x1+z1=0, 即x1+12y1=0,
令 y1=2,则 x1=-1,z1=1,所以 n1=(-1,2,1). 设平面 AD1F 的法向量为 n2=(x2,y2,z2),
则nn22··AA→→DF=1=00,,
y2+z2=0, 即12x2+y2=0.
令 x2=2,则 y2=-1,z2=1.所以 n2=(2,-1,1).
【合作探究】
类型一 用定义法求二面角 【例 1】 如图,设 AB 为圆锥 PO 的底面直径,PA 为母线,点 C 在底面圆周上,若△PAB 是边长为 2 的正三角形,且 CO⊥AB, 求二面角 P-AC-B 的正弦值.
[解] 如图,取 AC 的中点 D,连接 OD,PD, ∵PO⊥底面,∴PO⊥AC, ∵OA=OC,D 为 AC 的中点, ∴OD⊥AC,又 PO∩OD=O, ∴AC⊥平面 POD,则 AC⊥PD, ∴∠PDO 为二面角 P-AC-B 的平面角.
1 3
[如图,建立空间直角坐标系,设正方体的棱长为 1,
则 D(0,0,0),B(1,1,0),A1(1,0,1),D→A1=(1,0,1),D→B=(1,1,0).
设 n=(x,y,z)是平面 A1BD 的一个法向量, 则nn··DD→→BA1==00,, 即xx++zy==00,, 令 x=1,则 y=-1,z=-1,∴n=(1,-1,-1). 同理,求得平面 BC1D 的一个法向量 m=(1,-1,1), 则 cos〈m,n〉=|mm|·|nn|=13, 所以二面角 A1-BD-C1 的余弦值为13.]
1.2.4二面角(课件)高二数学(人教B版2019选择性必修第一册)

=(-2,1,1).所以1 · =0×(-2)-1×1+1×1=0,
所以1 ⊥ ,所以 EF⊥A1E.
(2)解:由(1)知,1 =(0,-1,1), =(-2,1,1),
设平面 A1EF 的一个法向量为 m=(x,y,z),
1 · = - + = 0,
(1)证明:EF⊥A1E;
(2)求平面A1EF与平面ABCD的夹角的余弦值.
【典型例题三】
(1)证明:以 C1 为坐标原点,C1D1,C1B1,C1C 所在直线分别为 x 轴、y
轴、z 轴,建立如图所示的空间直角坐标系,
则 A1(2,1,0),E(2,0,1),F(0,1,2),所以1 = (0,-1,1),
AD 中点 F,连接 OE,OF.设 PA=AB=a,AC=b,
则 A(0,0,0),C(b,0,0),B(0,a,0),D(b,-a,0),P(0,0,a),
E
,- ,
2 2 2
,O ,0,0 ,
2
所以 = 0,- 2 , 2
, =(b,0,0),=(0,-a,0),
例2. 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,
PA⊥平面ABCD , 且PA=AB , E是PD的中点 , 求平面EAC与平
面ABCD的夹角.
解: 方法一 如图,以 A 为坐标原点,AC,AB,AP 所在直线分别为
x 轴、y 轴、z 轴,建立空间直角坐标系,连接 BD,与 AC 交于点 O,取
则
令 z=1,则 m=(1,1,1).
· = -2 + + = 0,
由题意得 C1C⊥平面 ABCD,所以1 是平面 ABCD 的一个法向
所以1 ⊥ ,所以 EF⊥A1E.
(2)解:由(1)知,1 =(0,-1,1), =(-2,1,1),
设平面 A1EF 的一个法向量为 m=(x,y,z),
1 · = - + = 0,
(1)证明:EF⊥A1E;
(2)求平面A1EF与平面ABCD的夹角的余弦值.
【典型例题三】
(1)证明:以 C1 为坐标原点,C1D1,C1B1,C1C 所在直线分别为 x 轴、y
轴、z 轴,建立如图所示的空间直角坐标系,
则 A1(2,1,0),E(2,0,1),F(0,1,2),所以1 = (0,-1,1),
AD 中点 F,连接 OE,OF.设 PA=AB=a,AC=b,
则 A(0,0,0),C(b,0,0),B(0,a,0),D(b,-a,0),P(0,0,a),
E
,- ,
2 2 2
,O ,0,0 ,
2
所以 = 0,- 2 , 2
, =(b,0,0),=(0,-a,0),
例2. 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,
PA⊥平面ABCD , 且PA=AB , E是PD的中点 , 求平面EAC与平
面ABCD的夹角.
解: 方法一 如图,以 A 为坐标原点,AC,AB,AP 所在直线分别为
x 轴、y 轴、z 轴,建立空间直角坐标系,连接 BD,与 AC 交于点 O,取
则
令 z=1,则 m=(1,1,1).
· = -2 + + = 0,
由题意得 C1C⊥平面 ABCD,所以1 是平面 ABCD 的一个法向
二面角优质课课件市公开课一等奖省优质课获奖课件
第9页
二面角平面角作法:
1、定义法
2、三垂线定理法
3、垂面法
B
O
l
P
A
第10页
练习:指出以下各图中二面角平面角:
A, B l, AC , BD ,
AC l, BD l.
二面角--l--
Bl
C
D
AO
D’
C’
A’
D
B’
O C
A
B
二面角B--B’C--A
A
B
D
O
E
C
二面角A--BC--D
一个平面内一条直线把这个平面分成两个部分,其中每一 部分都叫做半平面。
l
A
l
第5页
从一条直线出发两个半平面所组成图形叫做二面角。 这条直线叫做二面角棱。 这两个半平面叫做二面角面。
B
O
A
平面角由射线--点--射线组成。
二面角表示
二面角 l 二面角 AB
Q B
l
P
A 二面角由半平面--线--半平面组成。
A
∴AO=2 3 ,AD=4
在Rt △ADO中,
∵sin∠ADO=
AO AD
2 3 4
3 2
D
O
∴ ∠ADO=60°
l
∴二面角 - l- 大小为60 °
第12页
二面角计算:
1、找到或作出二面角平面角 2、证实 1中角就是所求角 3、计算出此角大小
一“作”二“证”三“计算”
第13页
例 2 如图: 河堤斜面与水平面所成的二面角为60,堤面
上有一条直道CD, 它与堤脚的水平线AB的夹角为 30, 沿这条直道从堤脚向上行走到10m时人升高了 多少(精确到0.1m) ?
二面角平面角作法:
1、定义法
2、三垂线定理法
3、垂面法
B
O
l
P
A
第10页
练习:指出以下各图中二面角平面角:
A, B l, AC , BD ,
AC l, BD l.
二面角--l--
Bl
C
D
AO
D’
C’
A’
D
B’
O C
A
B
二面角B--B’C--A
A
B
D
O
E
C
二面角A--BC--D
一个平面内一条直线把这个平面分成两个部分,其中每一 部分都叫做半平面。
l
A
l
第5页
从一条直线出发两个半平面所组成图形叫做二面角。 这条直线叫做二面角棱。 这两个半平面叫做二面角面。
B
O
A
平面角由射线--点--射线组成。
二面角表示
二面角 l 二面角 AB
Q B
l
P
A 二面角由半平面--线--半平面组成。
A
∴AO=2 3 ,AD=4
在Rt △ADO中,
∵sin∠ADO=
AO AD
2 3 4
3 2
D
O
∴ ∠ADO=60°
l
∴二面角 - l- 大小为60 °
第12页
二面角计算:
1、找到或作出二面角平面角 2、证实 1中角就是所求角 3、计算出此角大小
一“作”二“证”三“计算”
第13页
例 2 如图: 河堤斜面与水平面所成的二面角为60,堤面
上有一条直道CD, 它与堤脚的水平线AB的夹角为 30, 沿这条直道从堤脚向上行走到10m时人升高了 多少(精确到0.1m) ?
《二面角》课件

在本节中,我们将介绍二面角在日常生活中的应用,并分享二面角在各学科领域中的应用案例。
二面角的计算方法
在本节中,我们将介绍如何计算二面角的方法,并分步骤演示如何计算二面角。
二面角的性质和定理
在本节中,我们将介绍二面角的基本性质和相关定理,并分享二面角性质和 定理的应用案例。
结论
在本节中,我们将总结本次课程的主要内பைடு நூலகம்,并提出下一步需要深入研究的 问题。
《二面角最新》PPT课件
在这个《二面角最新》PPT课件中,我们将全面介绍二面角的定义、性质、计 算方法以及应用案例。让我们一起深入了解二面角的奥秘吧!
引言
在本节中,我们将介绍什么是二面角,并简述本次课件的主题。
重温二面角定义
在本节中,我们将回顾二面角的定义和性质,通过图形解释二面角的概念。
二面角的应用
参考资料
在本节中,我们将列出本次课件使用的参考资料和网站。
二面角的计算方法
在本节中,我们将介绍如何计算二面角的方法,并分步骤演示如何计算二面角。
二面角的性质和定理
在本节中,我们将介绍二面角的基本性质和相关定理,并分享二面角性质和 定理的应用案例。
结论
在本节中,我们将总结本次课程的主要内பைடு நூலகம்,并提出下一步需要深入研究的 问题。
《二面角最新》PPT课件
在这个《二面角最新》PPT课件中,我们将全面介绍二面角的定义、性质、计 算方法以及应用案例。让我们一起深入了解二面角的奥秘吧!
引言
在本节中,我们将介绍什么是二面角,并简述本次课件的主题。
重温二面角定义
在本节中,我们将回顾二面角的定义和性质,通过图形解释二面角的概念。
二面角的应用
参考资料
在本节中,我们将列出本次课件使用的参考资料和网站。
二面角及其平面角 课件

有时为了方便,也可在α,β内(棱以外的半平 面部分)分别取点P,Q,将这个二面角记作二面 角P-AB-Q。
如右图,在三棱锥A-BCD中,面 ABC与面BCD所成的二面角可以记 作二面角A-BC-D.
3. 画法
⑴ 平卧式:
l
A
B
A
l
B
⑵ 直立式: A
l
B
三、二面角的平面角
1.定义 在二面角-l-的棱l上任取一点O,以点O
(1)二面角C'-BD-C;(2)二面角C'-BD-A;
(3)二面角D'-DC-A;(4)二面角D'-AB-D.
D'
C'
A'Βιβλιοθήκη B'D A
C B
例: 在正方体ABCD-A'B'C'D'中,找出下列二面角 的平面角:
(1)二面角C'-BD-C;(2)二面角C'-BD-A;
(3)二面角D'-DC-A;(4)二面角D'-AB-D.
① 二面角的两个面重合: 0o ② 二面角的两个面合成一个平面: 180o ③ 平面角是直角的二面角叫直二面角. 90o
二面角的范围: [ 0o, 180o ]
例: 在正方体ABCD-A'B'C'D'中,找出下列二面角 的平面角:
(1)二面角C'-BD-C;(2)二面角C'-BD-A;
(3)二面角D'-DC-A;(4)二面角D'-AB-D.
二面角及其平面角
一、半平面的定义
平面内的一条直线把平面分为两部分,其中的每
一部分都叫做半平面.
二、二面角
如右图,在三棱锥A-BCD中,面 ABC与面BCD所成的二面角可以记 作二面角A-BC-D.
3. 画法
⑴ 平卧式:
l
A
B
A
l
B
⑵ 直立式: A
l
B
三、二面角的平面角
1.定义 在二面角-l-的棱l上任取一点O,以点O
(1)二面角C'-BD-C;(2)二面角C'-BD-A;
(3)二面角D'-DC-A;(4)二面角D'-AB-D.
D'
C'
A'Βιβλιοθήκη B'D A
C B
例: 在正方体ABCD-A'B'C'D'中,找出下列二面角 的平面角:
(1)二面角C'-BD-C;(2)二面角C'-BD-A;
(3)二面角D'-DC-A;(4)二面角D'-AB-D.
① 二面角的两个面重合: 0o ② 二面角的两个面合成一个平面: 180o ③ 平面角是直角的二面角叫直二面角. 90o
二面角的范围: [ 0o, 180o ]
例: 在正方体ABCD-A'B'C'D'中,找出下列二面角 的平面角:
(1)二面角C'-BD-C;(2)二面角C'-BD-A;
(3)二面角D'-DC-A;(4)二面角D'-AB-D.
二面角及其平面角
一、半平面的定义
平面内的一条直线把平面分为两部分,其中的每
一部分都叫做半平面.
二、二面角
高中数学人教B版 选择性必修第一册 二面角 课件

―A→E =1,12,0 ,―AB→1 =(1,0,1),―A→F =12,1,0 ,―AD→1=(0,1,1).
设平面AB1E的法向量为n
n 1=(x1,y1,z1),则
n
1·―AB→1 =0, 1·―A→E =0,
x1+z1=0, 即x1+12y1=0,
令y1=2,则x1=-1,z1=1,所以n 1=(-1,2,1).
答案:45° 45°
来个随堂小测试,比比谁更快!!
1.在正方体ABCDA1B1C1D1中,设E,F分别是棱BC,CD的中点,求平 面AB1E与平面AD1F所成的角的大小.
解:以A为坐标原点建立空间直角坐标系,如图所示,设正方体的棱长为
1,则A(0,0,0),B1(1,0,1),E1,12,0 ,D1(0,1,1),F12,1,0 ,
6
=12
.
所以平面AB1E与平面AD1F所成的角为60°.
2.如图,已知△ABC和△BCD均为边长为a的等边三角形,且AD=
3 2
a,则二面角
A-BC-D的大小为
()
A.30°
B.45°
C.60°
解析:如图,取BC的中点为E,连接AE,DE,
由题意得AE⊥BC,DE⊥BC,
且AE=DE=
3 2
a,又AD=
设平面AD1F的法向量为n 2=(x2,y2,z2).
n 则
n
2·―AD→1 =0, 2·―A→F =0,
y2+z2=0, 即12x2+y2=0.
令x2=2,则y2=-1,z2=1.所以n 2=(2,-1,1).
|n 所以平面AB1E与平面AD1F所成的角的余弦值为
1·n
2|
|n 1||n 2|
高考中的二面角问题课件

详细描述
二面角的大小可以通过角的度量来衡 量,通常使用角度制或弧度制来表示。 角度制是以度为单位,而弧度制是以 弧长与半径之比来衡量。
二面角的性 质
总结词
详细描述
CATALOGUE
二面角的计算方法
定义法
定义法
根据二面角的定义,通过测量两个平 面的夹角来计算二面角的大小。这种 方法需要使用量角器等工具,适用于 一些简单的二面角问题。
高考中二面角问题的备考建议
熟悉题型,掌握解题思路
掌握二面角的基本概念 掌握解题思路 掌握常见题型解法
多做练习,提高解题能力
大量练习
举一反三
学会总结
注重总结,积累经验
总结解题经验 归纳题型 形成知识体系
THANKS
感谢观看
详细描述 总结词 详细描述
立体几何中的二面角问题
总结词
详细描述
。
总结词
详细描述 总结词 详细描述
CATALOGUE
高考中二面角的常见题型及解析
求二面角的度数
求二面角的平面角
。
求二面角的余弦 值
CATALOGUE
二面角问题的解题策略与技巧
掌握基础知识,理解概念
理解二面角的定义
二面角是两个半平面形成的角,通常用符号“θ”表示。二面角的大小确性,避免误差。
适用于二面角容易测量的简单几何体, 如三角形、矩形等。
垂线法
01
垂线法
02 适用范围
03 注意事项
射影面积法
射影面积法
适用范围 注意事项
向量法
向量法
利用向量的数量积、向量的外积 等性质来计算二面角的大小。这 种方法需要掌握向量的基本性质
和运算规则。
二面角的大小可以通过角的度量来衡 量,通常使用角度制或弧度制来表示。 角度制是以度为单位,而弧度制是以 弧长与半径之比来衡量。
二面角的性 质
总结词
详细描述
CATALOGUE
二面角的计算方法
定义法
定义法
根据二面角的定义,通过测量两个平 面的夹角来计算二面角的大小。这种 方法需要使用量角器等工具,适用于 一些简单的二面角问题。
高考中二面角问题的备考建议
熟悉题型,掌握解题思路
掌握二面角的基本概念 掌握解题思路 掌握常见题型解法
多做练习,提高解题能力
大量练习
举一反三
学会总结
注重总结,积累经验
总结解题经验 归纳题型 形成知识体系
THANKS
感谢观看
详细描述 总结词 详细描述
立体几何中的二面角问题
总结词
详细描述
。
总结词
详细描述 总结词 详细描述
CATALOGUE
高考中二面角的常见题型及解析
求二面角的度数
求二面角的平面角
。
求二面角的余弦 值
CATALOGUE
二面角问题的解题策略与技巧
掌握基础知识,理解概念
理解二面角的定义
二面角是两个半平面形成的角,通常用符号“θ”表示。二面角的大小确性,避免误差。
适用于二面角容易测量的简单几何体, 如三角形、矩形等。
垂线法
01
垂线法
02 适用范围
03 注意事项
射影面积法
射影面积法
适用范围 注意事项
向量法
向量法
利用向量的数量积、向量的外积 等性质来计算二面角的大小。这 种方法需要掌握向量的基本性质
和运算规则。
高二立体几何第九章(二面角)课件(PPT 18页)

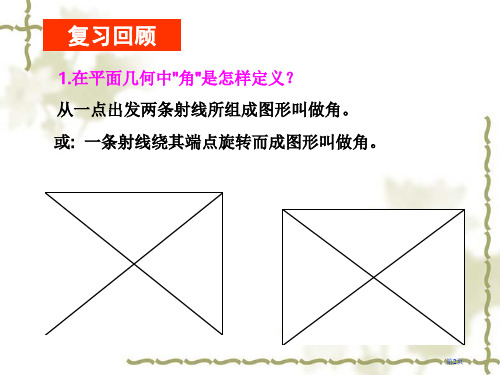
复习回顾
1.在平面几何中"角"是怎样定义的? 1.在平面几何中" 是怎样定义的? 在平面几何中 从一点出发的两条射线所组成的图形叫做角。 从一点出发的两条射线所组成的图形叫做角。 或: 一条射线绕其端点旋转而成的图形叫做角。 一条射线绕其端点旋转而成的图形叫做角。
2.在立体几何中,"异面直线所成的角"是怎样定义的? 2.在立体几何中,"异面直线所成的角"是怎样定义的? 在立体几何中,"异面直线所成的角 直线a、b是异面直线,经过空间任意一点O,分别引直线a' //a, 直线a 是异面直线,经过空间任意一点O,分别引直线a' O,分别引直线 b'// b,我们把相交直线a' 和 b'所成的锐角 (或直角)叫做异 b,我们把相交直线a' b'所成的锐角 或直角) 我们把相交直线 面直线所成的角。 面直线所成的角。 3.在立体几何中,"直线和平面所成的角"是怎样定义的? 3.在立体几何中,"直线和平面所成的角"是怎样定义的? 在立体几何中,"直线和平面所成的角 平面的一条斜线和它在平面上的射影所成的锐角, 叫 平面的一条斜线和它在平面上的射影所成的锐角, 做这条直线和这个平面所成的角。 做这条直线和这个平面所成的角。
l
A
l
从一条直线出发的两个半平面所组成的图形叫做二面角。 从一条直线出发的两个半平面所组成的图形叫做二面角。 二面角 这条直线叫做二面角的棱。 二面角的面。 这两个半平面叫做二面角的面 这条直线叫做二面角的棱。 二面角的棱 这两个半平面叫做二面角的面。
B
β
Q
B PαlOAA平面角由射线--点--射线构成。 射线构成。
1.在平面几何中"角"是怎样定义的? 1.在平面几何中" 是怎样定义的? 在平面几何中 从一点出发的两条射线所组成的图形叫做角。 从一点出发的两条射线所组成的图形叫做角。 或: 一条射线绕其端点旋转而成的图形叫做角。 一条射线绕其端点旋转而成的图形叫做角。
2.在立体几何中,"异面直线所成的角"是怎样定义的? 2.在立体几何中,"异面直线所成的角"是怎样定义的? 在立体几何中,"异面直线所成的角 直线a、b是异面直线,经过空间任意一点O,分别引直线a' //a, 直线a 是异面直线,经过空间任意一点O,分别引直线a' O,分别引直线 b'// b,我们把相交直线a' 和 b'所成的锐角 (或直角)叫做异 b,我们把相交直线a' b'所成的锐角 或直角) 我们把相交直线 面直线所成的角。 面直线所成的角。 3.在立体几何中,"直线和平面所成的角"是怎样定义的? 3.在立体几何中,"直线和平面所成的角"是怎样定义的? 在立体几何中,"直线和平面所成的角 平面的一条斜线和它在平面上的射影所成的锐角, 叫 平面的一条斜线和它在平面上的射影所成的锐角, 做这条直线和这个平面所成的角。 做这条直线和这个平面所成的角。
l
A
l
从一条直线出发的两个半平面所组成的图形叫做二面角。 从一条直线出发的两个半平面所组成的图形叫做二面角。 二面角 这条直线叫做二面角的棱。 二面角的面。 这两个半平面叫做二面角的面 这条直线叫做二面角的棱。 二面角的棱 这两个半平面叫做二面角的面。
B
β
Q
B PαlOAA平面角由射线--点--射线构成。 射线构成。
《二面角》课件

上一张 下一张
C
B
β
B
p α A
O O
ι
例1、已知锐二面角α- l- β ,A为面α内一点,A到β 、 的距离为 2 3 ,到 l 的距离为 4;求二面角 α- l- β ; 的大小。 的大小。 解: 过 A作 AO⊥α于O,过 O作 OD⊥ l 于D, 作 ⊥ , 作 ⊥ , 连AD则由三垂线定理得 AD⊥ l 则由三垂线定理得 ⊥
如图, 是二面角α棱上一点, 例 2.如图, 已知 P是二面角 AB-β棱上一点, 过 P分 如图 棱上一点 别 在 α 、 β 内 引 射 线 PM 、 PN , 且 ∠ MPN=60º 求此二面角的度数。 ∠BPM=∠BPN=45º ,求此二面角的度数。 ∠ 在 解: PB上取不同于P 的一点O, 在α内过O作OC⊥AB交PM于C, P A 在β内作OD⊥AB交PN于D, 连CD,可得 ∠COD是二面角α-AB-β的平面角 设PO = a ,∵∠BPM =∠BPN = 45º ∴CO=a, DO=a, PC= 2 a , PD = 又∵∠MPN=60º ∴CD=PC = 2 a
上一张 下一张
C M O D N
α
B β
2a
C
∴∠COD=90º 因此,二面角的度数为90º 因此,二面角的度数为
a
P O
一、二面角的定义 二面角的定义
从空间一直线出发的两个半 平面所组成的图形叫做二面角
α
ι
β
二、二面角的平面角 二面角的平面角
二 面 角 小 结
1、定义 、 2 、画法
γ
ι
P
α
β
B
构成
上一张 下一张
表示法
或二面角α 或二面角α—AB—β β
C
B
β
B
p α A
O O
ι
例1、已知锐二面角α- l- β ,A为面α内一点,A到β 、 的距离为 2 3 ,到 l 的距离为 4;求二面角 α- l- β ; 的大小。 的大小。 解: 过 A作 AO⊥α于O,过 O作 OD⊥ l 于D, 作 ⊥ , 作 ⊥ , 连AD则由三垂线定理得 AD⊥ l 则由三垂线定理得 ⊥
如图, 是二面角α棱上一点, 例 2.如图, 已知 P是二面角 AB-β棱上一点, 过 P分 如图 棱上一点 别 在 α 、 β 内 引 射 线 PM 、 PN , 且 ∠ MPN=60º 求此二面角的度数。 ∠BPM=∠BPN=45º ,求此二面角的度数。 ∠ 在 解: PB上取不同于P 的一点O, 在α内过O作OC⊥AB交PM于C, P A 在β内作OD⊥AB交PN于D, 连CD,可得 ∠COD是二面角α-AB-β的平面角 设PO = a ,∵∠BPM =∠BPN = 45º ∴CO=a, DO=a, PC= 2 a , PD = 又∵∠MPN=60º ∴CD=PC = 2 a
上一张 下一张
C M O D N
α
B β
2a
C
∴∠COD=90º 因此,二面角的度数为90º 因此,二面角的度数为
a
P O
一、二面角的定义 二面角的定义
从空间一直线出发的两个半 平面所组成的图形叫做二面角
α
ι
β
二、二面角的平面角 二面角的平面角
二 面 角 小 结
1、定义 、 2 、画法
γ
ι
P
α
β
B
构成
上一张 下一张
表示法
或二面角α 或二面角α—AB—β β
二面角的定义课件

二面角的定义课件
目录
• 二面角的定义 • 二面角的性质 • 二面角的计算方法 • 二面角的应用
01
二面角的定义
平面角与二面角的区别
平面角
平面内两条射线或线段在平面内 相交所形成的角,其大小由两条 射线的夹角决定。
二面角
两个半平面在三维空间中相交所 形成的角,其大小由两个半平面 的夹角决定。
二面角的几何意义
时。
04
二面角的应用
立体几何中的二面角
总结词
描述二面角在立体几何中的具体应用, 如空间几何体的表面积和体积计算等。
VS
详细描述
在立体几何中,二面角是描述两个平面相 交的夹角大小的量,对于计算空间几何体 的表面积和体积等具有重要意义。例如, 在计算圆锥体的侧面积时,需要用到二面 角的大小来计算。
解析几何中的二面角
特殊情况
当两个半平面平行或重合时,二面角的大小为0或180度。当两个半平面垂直时 ,二面角的大小为90度。
02
二面角的性质
二面角的度量性质
定义
二面角是两个半平面之间的夹角,通常用θ表示。它是一个标量,其取值范围是 [0,π]。
性质
二面角的度量性质包括其大小和方向。大小可以通过测量或计算得出,方向可以 通过半平面的法向量来确定。
01
二面角的大小反映了两个半平面 的相对位置关系,是三维空间中 两个半平面相互旋转的角度。
02
二面角的度量可以通过测量两个 半平面的夹角来得出,也可以通 过测量与二面角相关的平面角来 得出。
二面角的度量
度量方法
通过测量与二面角相关的平面角来得出二面角的度量值。具体来说,可以在二 面角的棱上选择一点,分别在两个半平面上作垂直于棱的射线,这两条射线所 形成的平面角的大小就是二面角的度量值。
目录
• 二面角的定义 • 二面角的性质 • 二面角的计算方法 • 二面角的应用
01
二面角的定义
平面角与二面角的区别
平面角
平面内两条射线或线段在平面内 相交所形成的角,其大小由两条 射线的夹角决定。
二面角
两个半平面在三维空间中相交所 形成的角,其大小由两个半平面 的夹角决定。
二面角的几何意义
时。
04
二面角的应用
立体几何中的二面角
总结词
描述二面角在立体几何中的具体应用, 如空间几何体的表面积和体积计算等。
VS
详细描述
在立体几何中,二面角是描述两个平面相 交的夹角大小的量,对于计算空间几何体 的表面积和体积等具有重要意义。例如, 在计算圆锥体的侧面积时,需要用到二面 角的大小来计算。
解析几何中的二面角
特殊情况
当两个半平面平行或重合时,二面角的大小为0或180度。当两个半平面垂直时 ,二面角的大小为90度。
02
二面角的性质
二面角的度量性质
定义
二面角是两个半平面之间的夹角,通常用θ表示。它是一个标量,其取值范围是 [0,π]。
性质
二面角的度量性质包括其大小和方向。大小可以通过测量或计算得出,方向可以 通过半平面的法向量来确定。
01
二面角的大小反映了两个半平面 的相对位置关系,是三维空间中 两个半平面相互旋转的角度。
02
二面角的度量可以通过测量两个 半平面的夹角来得出,也可以通 过测量与二面角相关的平面角来 得出。
二面角的度量
度量方法
通过测量与二面角相关的平面角来得出二面角的度量值。具体来说,可以在二 面角的棱上选择一点,分别在两个半平面上作垂直于棱的射线,这两条射线所 形成的平面角的大小就是二面角的度量值。
二面角课件

作法:B1B 面ABC, 作B1O AC, 连BO
由三垂线定理得, 二面角B1 AC B的平面角 B1OB
A1
B1
D
C
O
A B
自主总结
二面角的定义、画法、表示、 今天学了什么? 找二面角的平面角:定义法、三垂线法
角类比到二面角 它如何得到? 具体上升到抽象
用定义法和三垂线法 它又有何用? 求作二面角的平面角 以度量二面角的大小
适应性练习
判断下列哪些是二面角的平面角 (并请说出原因)
l
B
√
B
A
×
l
× ×
A
×
l
√
l
方法训练
1.求作水平面与拦洪坝平面所成二面角的平面角
B A
作二面角的平面角
问题1:棱l与平面ABO垂直吗 ? 为什么?
A
l
l AB且l OB l 面ABO
问题2:已知AO , OB 棱l 求证:ABO是二面角a, 则AO 2a
即二面角的度数是30
sin AOB a 1 AOB 3O 2a 2
l
a
O
?
解
B
题后记:
作
证
点
解 Rt
三垂线法作证二面角的平面角 找二面角的平面角
实践体验
3.如图正方体 ABCD A1B1C1D1
(1)求作侧面D1C与底面AC所成二面角的平面角 (2)求作对角面A1 ACC1与底面AC所成二面角的平面角
PDA
A
D
C
B
由三垂线定理得, 二面角B1 AC B的平面角 B1OB
A1
B1
D
C
O
A B
自主总结
二面角的定义、画法、表示、 今天学了什么? 找二面角的平面角:定义法、三垂线法
角类比到二面角 它如何得到? 具体上升到抽象
用定义法和三垂线法 它又有何用? 求作二面角的平面角 以度量二面角的大小
适应性练习
判断下列哪些是二面角的平面角 (并请说出原因)
l
B
√
B
A
×
l
× ×
A
×
l
√
l
方法训练
1.求作水平面与拦洪坝平面所成二面角的平面角
B A
作二面角的平面角
问题1:棱l与平面ABO垂直吗 ? 为什么?
A
l
l AB且l OB l 面ABO
问题2:已知AO , OB 棱l 求证:ABO是二面角a, 则AO 2a
即二面角的度数是30
sin AOB a 1 AOB 3O 2a 2
l
a
O
?
解
B
题后记:
作
证
点
解 Rt
三垂线法作证二面角的平面角 找二面角的平面角
实践体验
3.如图正方体 ABCD A1B1C1D1
(1)求作侧面D1C与底面AC所成二面角的平面角 (2)求作对角面A1 ACC1与底面AC所成二面角的平面角
PDA
A
D
C
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 、 A 为二面角 -CD- 的棱 CD 上一点, AB 在平 面 内且与棱CD 成45º 角,又 AB 与平面 成30º ,求二 面角-CD- 的大小。
B
C
A
O C
D
所求二面角的大小为45º
练 习
2、已知Rt△ABC在平面内,斜边AB在30º 的二 面角-AB- 的棱上,若AC=5,BC=12,求点C 到 平面 的距离CO。
C O A D B
3、如图,PA⊥平面ABC,二面角P-BC-A的平面角 为 ,求证: S△ABC=S△PBC×cos
P
C A
B
4、如图,AB是圆的直径,PA垂直圆所在的平面, C是圆上任一点,则二面角P-BC-A的平面角为: A.∠ABP B.∠ACP C.都不是
小 结
一、二面角的定义 二、二面角的表示法
三、二面角的平面角
四、二面角的平面角的作法
五、二面角的计算
A、B ,则 PA=2 ,PB=4,试分析 下列解法那一个正确?
例4.在平面四边形ABCD中,AB=BC=2,AD=CD= 15 , ∠B=120º ;将三角形ADC沿四边形ABCD的对角线AC 折起,使BD′= 19,求二面角D′-AC-B大小。
D′ D D
C O A B
C O
A
B
练 习
思
考:异面直线所成的角、直线和平面所成
的角有什么共同的特征?
它们的共同特征都是将三维空间的角转化 为二维空间的角,即平面角。
讲授新课
一条直线上的一个点把这条直线分成两部分, 其中的每一部分都叫做射线。
平面内的一条直线把平面分成两部分,其中的 每一部分都叫做半平面。
l
A
l
二面角的定义
从一条直线出发的两个半平面所组成的图形叫做 二面角, 这条直线叫做二面角的棱, 这两个半平面叫做 二面角的面。
2、证明 1中的角就是所求的角 3、计算出此角的大小
一“作”二“证”三“计算”
1、作出下列各图中的二面角的平面角
B D′ l A C′ B′ O
A′
P
D A
B
C
过棱上一点P作二 面角--l--的平面 角
过A点作二面角B--B′C—A
的平面角
2、如图,正方体ABCD—A1B1C1D1中,二面角B1-AA1-C1
二面角的平面角的三个特征:
3. 1.点在棱上,2.线在面内, 与棱垂直
二面角的大小的范围:
0 180
B
平面角是直角的二面角叫做直二面角. 相交成直二面角的两个平面,叫做互相垂 直的平面。
O
B
l
O
A
A
二面角的平面角的作法:
1、定义法
2、三垂线定理法
二面角的计算:
1、找到或作出二面角的平面角
构成
表示法
二面角的画法 (1) 半卧式 α
l F E B D
β l
A
C
二面角- l-
C B D
二面角F-AB- C
β
A
(2) 直立式
l α α
l
β
二面角C-AB- D
二面角的度量
以二面角的棱上任意一点为端 点,在两个面内分别作垂直于棱的 两条射线,这两条射线所成的角叫 做二面角的平面角。
Q
B P
l
A
二面角由: 二面角的表示
半平面--线--半平面
二面角 l
二面角 P l Q
二面角 P AB Q
二面角 AB
角
二面角
A
图形
A
a O
B B
定义
从平面内一点出发 的两条射线所组成的图 形叫做角。
由射线—点—射线 (顶点) ∠AOB
从空间一直线出发 的两个半平面所组成的 图形叫做二面角。 由半平面—线—半平面 (棱) 二面角—a— 或二面角—AB—
45° 的大小为_____,二面角B-AA1-D的大小为 90° 2 ______,二面角C1-BD-C的正切值是_______.
D1 A1 D A B B1
C1
A1 C A
D1 B1 D
B
C1 A1 C A
D1 B1
C1
D
O B
C
例题精讲
例1、已知二面角- l - ,A为面内一点,A到 的
距离为 2
3
,到 l 的距离为 4。求二面角 - l - 的大小。
A.
O
D
l
例2、山坡的倾斜度(坡面与水平面所成的二面角的
度数)是60度,山坡上有一条直道CD,它和坡脚 的水平线AB的夹角是30度,沿这条山路上山,行 走100米后升高多少米?
山坡α
D
水平面β
30
60
H B
A
C
G
设点 P 在平面α、 β的射影分别是
