NOIP复赛复习12STL算法与树结构模板
模板_备战noip

备战NOIP2012(一)作者:纪焘输入:崔善尧编排:李孜旭第一轮复习:巩固与提升1、RQNOJ2、回顾基础算法3、自学《数学与程序设计》基础算法提纲(第一轮)1、Mr算法2、高精度运算3、平面凸包算法4、二项式定理5、卡兰特数列6、排列生成算法7、组合生成算法8、背包九大问题9、卡鲁思卡尔算法10、SPFA算法11、弗洛伊德算法12、前向星链表13、拓扑排序14、二叉树相关内容15.其它一、Miller Rabin 算法Const a:array[1..4]od integer=(2,3,5,7);V ar p,i:longint;T:boolean;Function ksm(a,p,q:longint):qword;V ar s:qword;BeginIf p=1 then exit(a);S:=ksm(a,p div 2,q) mod q;If odd(p) then ksm:=s*s*a mod qElse ksm:=s*s mod q;End;beginread(p);if (p=2) or (p=3) or (p=5) oe (p=7)then writeln('yes')elsebegint:=true;for i:=1 to 4 doif ksm(a[i],p-1,p)<>1 then begint:=false;break;end;if t then writeln('yes')else writeln('no');end.二、高精度加法var len1,len2,len,i,x:longint;a,b,c:array[1..20000] of integer;st1,st2:ansistring;beginreadln(st1);readln(st2);len1:=length(st1);len2:=length(st2);for i:=len1 downto 1 do val(st1[i],a[len1-i+1]);for i:=len2 downto 1 do val(st2[2],b[len2-i+1]);if len1>len2 then len:=len1else len:=len2;for i:=1 to len dobeginx:=a[i]+b[i]+c[i];c[i]:=x mod 10;inc(c[i+1],x div 10);end;if c[i+1]<>0 then inc(len);for i:=len downto 1 do writel(c[i]);writeln;end.三、高精度减法var len1,len2,i,x:longint;a,b,c:array[1..20000]of longint;st1,st2:ansistring;beginreadln(st1);readln(st2);len1:=length(st1);len2:=length(st1);for i:=len1 downto 1 do val(st1[i],a[len1-i+1]);for i:=len2 downto 1 do val(st2[i],b[len2-i+1]);for i:=1 to len1 dobegindec(a[i+1]);x:=a[i]-b[i]+x+10;c[i]:=x mod 10;x:=x div 10;end;while (c[len1]=0) and (len1>1) do dec(len1);for i:=len1 downto 1 do write(c[i]);writeln;end.四、高精度乘法var len1,len2,i,j,len,x:longint;a,b,c:array[1..20000]of longint;st1,st2:ansistring;beginreadln(st1);readln(st2);len1:=length(st1);len2:=length(st2);for i:=len1 downto 1 do val(st1[i],a[len1-i+1]);for i:=len2 downto 1 do val(st2[i],b[len2-i+1]);for i:=1 to len1 dofor j:=1 to len2 dobeginc[i+j-1]:=c[i+j-1]+a[i]*b[j];c[i+j]:=c[i+j-1] div 10 +c[i+j];c[i+j-1]:=c[i+j-1] mod 10;end;len:=len1+len2;while (c[len]=0) and (len>1) do dec(len);for i:=len downto 1 dowrite(c[i]);writeln;end.五、求C n rvar f:array[0..1000000]of longint;n,r,i,j:longint;beginread(n,r);f[0]:=1;for i:=1 to n dobeginf[i]:=1;for j:=i-1 downto 1 dof[j]:=f[j]+f[j-1];end;writeln;end.六、求Catalan数var n,i,s:longint;beginread(n);s:=1;for i:=1 to n dos:=s*(s*n-i+1) div i;s:=s div (n+1);writeln(s);end.七、生成组合var i,j,n,r:longint;a:aray[1.100]of longint;beginread(n,r);for i:=1 to r do a[i]:=i;while a[0]=0 dobeginfor i:=1 to r-1 do write(a[i],'_');writeln(a[r]);i:=r;while a[i]=n-r+i do dec(i);inc(a[i]);for j:=i+1 to r doa[j]:=a[j-1]+1;end;end.八、生成排列var n,i,j:longint;a:array[0.100]of longint;beginread(n);for i:=1 to n do a[i]:=i;while i=1 dobeginprint;i:=n-1;while a[i]>a[i+1] do dec(i);if i=0 then break;j:=n;while a[j]<a[i] do dec[j];swap(a[i],a[j]);inc(i);j:=n;while i<j dobeginswap(a[i],a[j]);inc(i);dec(j);end;end;end.九、Kruskal+并查集type jt=recordf,r,w:longint;end;var a:array[1..100000]of jt;bcj:array[1.1000]of longint;n,i,j,e,ans:longint;function find(x:longint):longint;beginif x<>bcj[x] then bcj[x]:=find(bcj[x]);exit(bcj[x]);end;beginread(n,e);for i:=1 to e do read(a[i].f,a[i].r,a[i].w);qsort(1,e);for i:=1 to n do bcj[i]:=i;i:=1;j:=1;while i<=n-1 dobeginwhile find(a[j].f)=find(a[j].r) do inc(j);inc(i);bcj[find[a[j].f]]:=find(a[j].r);inc(ans,a[j].w);end;writeln(ans);end.十、Floyed算法var a:array[1..100,1..100]of longint;beginfillchar(a,sizeof(a),63);read(n,m);for i:=1 to m dobegin //无向图read(x,y,z);a[x][y]:=z;a[y][x]:=z;end;for i:=1 to n dofor j:=1 to n doif i<j thenfor k:=1 to n doif (i<>k) and (j<>k) and (a[j][i]+a[i][k]<a[i][j]) thena[j][k]:=a[j][i]+a[i][k];for i:=1 to n do beginfor j:=1 to n-1 dowrite(a[i][j],'_');writeln(a[i][n]);end;end.十一、SPFA+前向星var n,m,i,j,now,f,r,k,x,y,z:longint;v:array[1..1000]of boolean;head,dist:array[1..1000]of longint;q,e,w,next:array[1..1000000]of longint;beginread(n,m);for i:=1 to m do //有向图beginread(x,y,z);e[i]:=y;w[i]:=z;next[i]:=head[x];head[x]:=i;end;fillchar(dist,sizeof(dist),63);fillchar(v,sizeof(v),0);q[1]:=1;v[1]:=0;dist[1]:=0;f:=1;r:=1;while f<=r dobeginnow:=q[f];k:=head[now];while k<>0 dobeginif dist[e[k]]>dist[now]+w[k] thenbegindist[e[k]]:=dist[now]+w[k];if not v[e[k]] thenbegininc(r);q[r]:=e[k];v[e[k]]:=true;end;end;k:=next[k];end;inc(f);r[now]:=false;end;writeln(dist[n]);end.十二、二项式定理varprocedure make(n,m:longint);var i:longint;beginfor i:=1 to n-m doans:=ans*(i+m) div i;end;beginread(n,m);ans:=1;make(n,min(n-m,m));writeln(ans);c[0]:=1;for i:=1 to n doc[i]:=c[i-1]*(n-i+1) div i;for i:=0 to n-1 do write(c[i],' ');writeln(c[n]);end.十三、二项式定理varprocedure make(n,m:longint);var i:longint;beginfor i:=1 to n-m doans:=ans*(i+m) div i;end;beginread(n,m);ans:=1;make(n,min(n-m,m));writeln(ans);c[0]:=1;for i:=1 to n doc[i]:=c[i-1]*(n-i+1)div i;for i:=0 to n-1 do write(c[i],' ');writeln(c[n]);end.十三、背包九讲归纳,有n件物品,每件物品有一定的代价和价值,在这几件物品中选择若干件,使得总代价不超过给定值的条件下总价值最大。
NOIP高中信息技术竞赛资料数据结构

第1章绪论程序设计就是使用计算机解决现实世界中的实际问题。
对于给定的一个实际问题,在进行程序设计时,首先要把实际问题中用到的信息抽象为能够用计算机表示的数据;第二要把抽象出来的这些数据建立一个数据模型,这个数据模型也称为逻辑结构,即建立数据的逻辑结构;第三要把逻辑结构中的数据及数据之间的关系存放到计算机中,即建立数据的存储结构;最后在所建立的存储结构上实现对数据元素的各种操作,即算法的实现。
本章就是要使大家了解计算机中的数据表示,理解数据元素、逻辑结构、存储结构和算法的有关概念;掌握基本逻辑结构和常用的存储方法,能够选择合适的数据的逻辑结构和存储结构;掌握算法及算法的五个重要特性,能够对算法进行时间复杂度分析,从而选择一个好的算法,为后面的学习打下良好的基础。
1.1基本概念和术语1.数据(data):是对客观事物的符号的表示,是所有能输入到计算机中并被计算机程序处理的符号的总称。
2.数据元素(data element):是数据的基本单位,在计算机程序中通常作为一个整体来处理。
一个数据元素由多个数据项(data item)组成,数据项是数据不可分割的最小单位。
3.数据结构(data structure):是相互之间存在一种或多种特定关系的数据元素的集合。
数据结构是一个二元组,记为:data_structure=(D,S).其中D为数据元素的集合,S是D上关系的集合。
数据元素相互之间的关系称为结构(structure)。
根据数据元素之间关系的不同特性,通常由下列四类基本结构:(1)集合:数据元素间的关系是同属一个集合。
(图1)(2)线性结构:数据元素间存在一对一的关系。
(图2)(3)树形结构:结构中的元素间的关系是一对多的关系。
(图3)(4)图(网)状结构:结构中的元素间的关系是多对多的关系。
(图4)图1 图2图3 图41.2 数据的逻辑结构和物理结构1.逻辑结构:数据元素之间存在的关系(逻辑关系)叫数据的逻辑结构。
NOIP知识点总结

1时间复杂度
时间复杂度的分析方法
2排序算法
(1)平方排序算法(冒泡,插入,选择)
shell排序算法
(2)nlogn排序算法
快速排序(qsort,sort)
归并排序(求逆序对个数)
*
外部排序(堆排序)
3 数论
模运算
集合论
素数(Eratosthenes筛法)
进位制
欧几里德算法(辗转相除法)
扩展欧几里德算法(同余)ax + by = gcd(a,b)解线性同余方程ax ≡b(mod n)
*
中国剩余定理
高斯消元(线性代数)
4 数据结构
广度/ 宽度优先搜索及剪枝
表达式计算
Hash表
并查集
Tarjan算法(LCA最近公共祖先)
树状数组
*
线段树
5 动态规划(DP)
背包问题(背包九讲)
LIS(最长上升子序列)的二分优化
DP的队列优化(LCIS,单调队列)
区间的DP
树上的DP(记忆化搜索)
6 图论
单源最短路(dijkstra,floyd,spfa)
最小生成树(prim,kruskal)
拓扑排序
floyd求最小环
求图的强连通分量
判断图中是否有环
差分约束系统(就是求最长路,用spfa)
others:
指针(链表,搜索判重,邻接表,散列表,二叉树的表示,多叉树的表示)位运算
高精度的加减乘除开方(开方直接二分)
乘法转加法神器:log。
信息学竞赛中的算法与数据结构讲解模板

信息学竞赛中的算法与数据结构讲解模板在信息学竞赛中,算法和数据结构是解决问题的关键。
掌握了合适的算法和数据结构,可以更高效地解决问题,并取得更好的成绩。
本文将介绍信息学竞赛中常用的算法和数据结构,并提供相应的讲解模板。
一、算法1.贪心算法(Greedy Algorithm)贪心算法是一种基于贪心策略的算法,即在每一步选择中都选择当前状态下最优的选择,最终得到全局最优解。
贪心算法的关键是确定贪心策略,以及证明该策略的正确性。
以下是贪心算法的讲解模板:【算法名称】贪心算法【输入】输入参数及其含义【输出】输出结果及其含义【算法步骤】详细描述算法的步骤【算法分析】分析算法的时间复杂度和空间复杂度【代码示例】给出算法的代码实现2.动态规划(Dynamic Programming)动态规划是一种将问题划分为子问题,并通过求解子问题的最优解来求解原问题的算法。
动态规划一般需要使用一个数组来记录已经解决过的子问题的最优解,以避免重复计算。
以下是动态规划的讲解模板:【算法名称】动态规划【输入】输入参数及其含义【输出】输出结果及其含义【算法步骤】详细描述算法的步骤,包括状态转移方程的推导【算法分析】分析算法的时间复杂度和空间复杂度【代码示例】给出算法的代码实现二、数据结构1.线性表线性表是一种简单且常用的数据结构,可以通过数组或链表来实现。
线性表中的元素按照顺序存储,可以进行插入、删除、查找等操作。
以下是线性表的讲解模板:【数据结构名称】线性表【定义】定义线性表的结构和属性【操作】列出线性表的基本操作,包括插入、删除、查找等【应用】介绍线性表的常见应用场景【代码示例】给出线性表的代码实现2.树树是一种分层存储数据的数据结构,具有层次性和递归性。
树由节点和边组成,每个节点可以有多个子节点。
常见的树结构包括二叉树、二叉搜索树、堆等。
以下是树的讲解模板:【数据结构名称】树【定义】定义树的结构和属性【遍历】介绍树的遍历方式,包括前序遍历、中序遍历、后序遍历等【应用】介绍树的常见应用场景【代码示例】给出树的代码实现,如二叉搜索树的插入、删除等操作三、总结算法和数据结构是信息学竞赛中必须要掌握的核心内容。
NOIP复赛复习7STL算法与树结构模板

if(left == right) { scanf("%d",&segment[root]); return; } int mid = (left + right) / 2; buildTree(root * 2, left, mid); buildTree(root * 2 + 1, mid + 1, right); pushUp(root); } voidupdate(int root, int pos, int add_num, int left, int right) { if (left == right) { segment[root] += add_num; return; } int mid = (left + right) / 2; if (pos <= mid) update(root * 2, pos, add_num, left,mid); else update(root * 2 + 1, pos, add_num, mid+ 1, right); pushUp(root); } intgetSum(int root, int left, int right, int L, int R) { if(left == L && right == R) { return segment[root]; } int mid = (L + R) / 2; int res = 0; if(left > mid) { res += getSum(root * 2 + 1, left,right, mid + 1, R); }
树结构模板 1、树状数组 例:HDU 1166 #include<stdio.h> #include<math.h> const intMAX = 50010 * 4; intsegment[MAX]; voidpushUp(int root) { segment[root] = segment[root * 2] + segment[root* 2 + 1]; } voidbuildTree(int root, int left, int right) {
信息学奥赛NOIP标准模板库入门

STL
• 在C++标准中,STL被组织为下面的13个头文件: <algorithm>、<deque>、<functional>、<iterator>、 <vector>、<list>、<map>、<memory>、<numeric>、 <queue>、<set>、<stack>和<utility>。
Vector应用——谁的孙子最多
【输出要求】一行两个整数,表示孙子节点最多的节点,以及其 孙子节点的个数,如果有多个,输出编号最小的。 【输入样例】 5 223 14 【输出样例】 11
0
15 0
Vector的Insert操作
• Insert(x, y)是Vector的成员函数,其中,x是一个迭代器,y是 一个具体的值。 • Insert(x, y)在x对应的元素之前插入了一个值为y的元素。
Vector元素的遍历
结合实例,我们可以进一步理解iterator的使用方式。 下面的循环中i++也可以改写为i+=1或i=i+1,可以理解为将i指 向下一个位置。
Vector应用——存图
N个点,M条边,点数不超过100000,边数不超过1000000,再求 图上的一些东西。 如何存这幅图?
邻接矩阵,空间复杂度O(n2),遍历时间复杂度O(n2),BOOM!
vector应用——链表操作
给定一个N个数的数组,M次操作,每次操作为下列操作之一。 求最后的数组。 操作1:在第X个数之后插入一个数Y。 操作2:删除第X个数。 【输入要求】 第一行两个整数N,M(N,M≤100000)含义见试题描述。
4、NOIP提高组竞赛复试中需要用到的算法或涉及到知识点

NOIP提高组竞赛复试中需要用到的算法或涉及到知识点具体内容如下:(一)数论1.最大公约数,最小公倍数2.筛法求素数3.mod规律公式4.排列组合数5.Catalan数6.康拓展开7.负进制(二)高精度算法1.朴素加法减法2.亿进制加法减法3.乘法4.除法5.亿进制读入处理6.综合应用(三)排序算法1.冒泡排序2.快速排序3.堆排排序4.归并排序5.选择排序(四)DP(动态规划)1.概念2.解题步骤3.背包类DP4.线性DP5.区间动态规划6.坐标型动态规划(规则类DP)7.资源分配型动态规划8.树型动态规划9.状态压缩的动态规划10.动态规划的一般优化方法(五)图论1.Floyd-Warshall2.Bellman-ford3.SPFA4.dijkstra5.prim6.kruskal7.欧拉回路8.哈密顿环9.flood fill(求图的强连通分量)10.最小环问题(基于floyd)11.Topological sort12.次短路13.次小生成树(六)树1.堆2.二叉排序树3.最优二叉树(哈夫曼树)4.求树的后序遍历5.并查集及应用(七)分治1.二分查找2.二分逼近(注意精度问题)3.二分答案4.快排(见排序算法)5.归并排序(见排序算法)(八)贪心(九)搜索1.BFS2.DFS(十)回溯1.八皇后2.剪枝技巧(十一)其它1.离散化2.KMP3.字符串哈希4.常用字符串函数过程5.位运算6.快速幂。
noip提高组复赛知识点

Noip提高组复赛知识点1. 简介NOIP(National Olympiad in Informatics in Provinces)是中国计算机学会主办的全国性计算机竞赛。
它分为初赛和复赛两个阶段,复赛则进一步分为提高组和普及组。
本文将重点介绍NOIP提高组复赛的知识点。
2. 复赛知识点2.1 数据结构在NOIP提高组复赛中,对数据结构的理解和应用是非常重要的。
以下是一些常见的数据结构及其应用:2.1.1 数组数组是一种线性数据结构,可以在O(1)的时间复杂度内访问任意位置的元素。
在复赛中,经常需要使用数组来解决一些简单的问题,如统计字符出现次数、记录中间结果等。
2.1.2 链表链表是一种动态数据结构,它通过指针将多个节点连接起来。
在复赛中,链表常常用于实现一些特定的数据结构,如队列、栈等。
2.1.3 栈和队列栈和队列是两种基本的数据结构。
栈是一种后进先出(LIFO)的数据结构,而队列是一种先进先出(FIFO)的数据结构。
它们在复赛中的应用非常广泛,如深度优先搜索(DFS)和广度优先搜索(BFS)等算法中常常使用栈和队列来辅助实现。
2.1.4 树和图树和图是两种重要的非线性数据结构。
树是一种层次结构,图是一种由节点和边组成的网络结构。
在复赛中,树和图常常用于解决一些复杂的问题,如最短路径、最小生成树等。
2.2 算法和技巧在NOIP提高组复赛中,算法和技巧的掌握是至关重要的。
以下是一些常见的算法和技巧:2.2.1 动态规划动态规划是一种将复杂问题分解成简单子问题的方法,通过保存子问题的解来避免重复计算。
在复赛中,动态规划常常用于解决一些涉及最优化问题的算法。
2.2.2 贪心算法贪心算法是一种每一步都选择当前最优解的算法。
在复赛中,贪心算法常常用于解决一些涉及最优解问题的算法,如最小生成树问题、最短路径问题等。
2.2.3 搜索算法搜索算法是一种通过遍历问题的所有可能解空间来寻找解的方法。
在复赛中,搜索算法常常用于解决一些复杂的问题,如深度优先搜索(DFS)、广度优先搜索(BFS)等。
NOIP初赛辅导教材数据结构算法.doc

数据:对客观事物的符号的表示,是所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素:数据的基本单位,在计算机程序中通常作为一个整体来处理。
一个数据元素由多个数据项组成,数据项是数据不可分割的最小单位。
数据结构:相互之间存在一种或多种特定关系的数据元素的集合。
根据数据元素之间关系的不同特性,通常由下列四类基本结构:(1)集合:数据元素间的关系是同属一个集合。
(2)线性结构:数据元素间存在一对一的关系。
(3)树形结构:结构中的元素间的关系是一对多的关系。
(4)图(网状结构):结构中的元素间的关系是多对多的关系。
逻辑结构:数据元素之间存在的关系(逻辑关系)叫数据的逻辑结构。
物理结构:数据结构在计算机中的表示(映象)叫数据的物理结构。
一种逻辑结构可映象成不同的存储结构(物理结构):顺序存储结构和非顺序存储结构(链式存储结构和散列结构)。
1、线性表:n个数据元素的的有限序列。
其特点是除了表头和表尾外,表中的每一个元素有且仅有唯一的前驱和唯一的后继,表头有且只有一个后继,表尾有且只有一个前驱。
线性表的顺序存储结构:用一组地址连续的存储单元依次存储线性表中的元素。
线性表的链式存储结构:用指针将存储表元素的那些单元依次串联在一起。
这种方法避免了在数组中用连续的单元存储元素的缺点,因而在执行插入或删除运算时,不再需要移动元素来腾出空间或填补空缺。
然而我们为此付出的代价是,需要在每个单元中设置指针来表示表中元素之间的逻辑关系,因而增加了额外的存储空间的开销。
单链表循环链表双向链表2、栈:一种特殊的表。
这种表只在表头进行插入和删除操作。
因此,表头对于栈来说具有特殊的意义,称为栈顶。
相应地,表尾称为栈底。
不含任何元素的栈称为空栈。
栈的修改是按后进先出的原则进行的。
(1)遇到操作数,进操作数栈;(2)遇到运算符时,则需将此运算符的优先级与栈顶运算符的优先级比较,若高于栈顶元素则进栈,继续扫描下一符号,否则,将运算符栈的栈顶元素退栈,形成一个操作码Q,同时操作数栈的栈顶元素两次退栈,形成两个操作数a、b,让计算机对操作数与操作码完成一次运算操作,即aQb,并将其运算结果存放在操作数栈中。
NOIP复习资料(C++版)精编版

NOIP复习资料(C++版)主编葫芦岛市一高中李思洋完成日期2012年8月27日……………………………………………………………最新资料推荐…………………………………………………前言有一天,我整理了NOIP的笔记,并收集了一些经典算法。
不过我感觉到笔记比较凌乱,并且有很多需要修改和补充的内容,于是我又搜集一些资料,包括一些经典习题,在几个月的时间内编写出了《NOIP复习资料》。
由于急于在假期之前打印出来并分发给同校同学(我们学校既没有竞赛班,又没有懂竞赛的老师。
我们大家都是自学党),《NOIP复习资料》有很多的错误,还有一些想收录而未收录的内容。
在“减负”的背景下,暑期放了四十多天的假。
于是我又有机会认真地修订《NOIP复习资料》。
我编写资料的目的有两个:总结我学过(包括没学会)的算法、数据结构等知识;与同学共享NOIP知识,同时使我和大家的RP++。
大家要清醒地认识到,《NOIP复习资料》页数多,是因为程序代码占了很大篇幅。
这里的内容只是信息学的皮毛。
对于我们来说,未来学习的路还很漫长。
基本假设作为自学党,大家应该具有以下知识和能力:①能够熟练地运用C++语言编写程序(或熟练地把C++语言“翻译”成Pascal语言);②能够阅读代码,理解代码含义,并尝试运用;③对各种算法和数据结构有一定了解,熟悉相关的概念;④学习了高中数学的算法、数列、计数原理,对初等数论有一些了解;⑤有较强的自学能力。
代码约定N、M、MAX、INF是事先定义好的常数(不会在代码中再次定义,除非代码是完整的程序)。
N、M、MAX 针对数据规模而言,比实际最大数据规模大;INF针对取值而言,是一个非常大,但又与int的最大值有一定差距的数,如100000000。
对于不同程序,数组下标的下限也是不同的,有的程序是0,有的程序是1。
阅读程序时要注意。
阅读顺序和方法没听说过NOIP,或对NOIP不甚了解的同学,应该先阅读附录E,以加强对竞赛的了解。
noip知识点

noip知识点NOIP(全国青少年信息学奥林匹克竞赛)是中国信息学竞赛中最重要的赛事之一,也是许多计算机爱好者所瞩目的目标。
对于参加NOIP的选手来说,掌握一些基础的知识点是非常必要的。
本文将从准备阶段、算法设计、数据结构、编程语言和调试技巧等方面来谈谈NOIP的一些重要知识点。
在准备阶段,一个好的准备是成功的一半。
首先,选手要熟悉并掌握编程语言(如C++)的基础知识,能够完成常见的输入输出操作、常见的数据类型和运算符的使用。
其次,选手要了解算法的基本概念和思想,掌握一些常见的算法模板,如贪心算法、动态规划等。
此外,选手还需要刷一些NOIP历年真题,熟悉考试的题型和难度。
通过反复练习,选手可以提高自己的解题能力和编程速度。
在算法设计方面,选手需要学会分析问题,找出问题的规律和特点。
常见的算法设计思想有:贪心算法、分治算法和动态规划。
贪心算法是指每一步都选择当前状况下最优的解,但不能保证一定能得到全局最优解;分治算法是将问题分解成若干个相似的子问题,通过解决子问题来解决原问题;动态规划是通过维护中间状态,避免重复计算,从而提高效率。
选手需要熟练运用这些算法思想,灵活应用于不同的问题场景。
数据结构也是NOIP中一个重要的考点。
常见的数据结构有:数组、链表、栈、队列、树和图等。
选手需要了解不同数据结构的特点和应用场景,能够根据问题需求选择合适的数据结构并进行操作。
例如,对于查找问题,可以使用二分查找;对于维护顺序的问题,可以使用排序算法等。
选手还需要了解常见的数据结构算法,如快速排序、堆排序等,以及这些算法的时间复杂度和空间复杂度。
对于编程语言的掌握,选手需要熟悉编程语言的语法和特性。
C++是NOIP常用的编程语言,具有强大的功能和高效的执行速度。
选手需要掌握C++的基本语法、函数的定义和调用、类的使用等。
此外,选手还应该了解一些C++的高级特性,如模板、STL(标准模板库)等,以便在解题过程中能够灵活运用。
stl 常用算法

stl 常用算法摘要:1.STL 简介2.STL 常用算法分类3.排序算法4.查找算法5.图算法6.字符串匹配算法7.容器和迭代器正文:一、STL 简介STL(Standard Template Library,标准模板库)是C++编程语言中的一个重要组成部分,它包含了一系列通用、高效的模板类和函数,为程序员提供了对数据结构和算法的高级抽象。
STL 的目的是提高代码的可重用性、可移植性和效率。
二、STL 常用算法分类STL 中的算法主要可以分为以下几类:1.排序算法:用于对数据进行排序。
2.查找算法:用于在数据集合中查找特定元素。
3.图算法:用于处理图结构数据。
4.字符串匹配算法:用于在文本中查找子字符串。
5.容器和迭代器:用于存储和管理数据。
三、排序算法STL 中提供了一系列排序算法,如冒泡排序、选择排序、插入排序、快速排序、归并排序等。
这些算法可以根据数据类型和排序需求进行选择。
四、查找算法STL 中的查找算法包括顺序查找、二分查找、哈希查找等。
顺序查找适用于有序或无序数据,二分查找适用于有序数据,哈希查找则适用于快速查找。
五、图算法STL 中的图算法主要包括深度优先搜索(DFS)、广度优先搜索(BFS)、最短路径算法(如Dijkstra 算法、Floyd-Warshall 算法等)、最小生成树算法(如Prim 算法、Kruskal 算法等)。
这些算法可以处理各种图结构问题。
六、字符串匹配算法STL 中的字符串匹配算法主要有KMP 算法、Boyer-Moore 算法等。
这些算法可以在文本中高效地查找子字符串。
七、容器和迭代器STL 中的容器包括数组、链表、栈、队列、映射(如红黑树、哈希表等)、集合(如红黑树、哈希表等)等。
迭代器则是用于在容器中进行遍历的抽象概念,如输入迭代器、输出迭代器、前缀迭代器、后缀迭代器等。
总之,STL 中的常用算法为程序员提供了丰富的工具,可以帮助我们高效地实现各种数据结构和算法。
NOIP考点
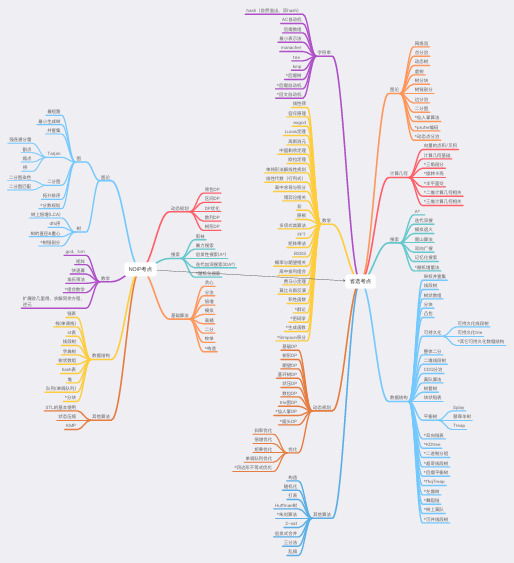
NOIP考点动态规划背包DP 区间DP DP优化数列列DP 树形DP搜索剪枝暴暴⼒力力搜索启发性搜索(A*)迭代加深搜索(IDA*)*随机化搜索基础算法贪⼼心分治倍增模拟⾼高精⼆二分枚举*构造其他算法STL的基本使⽤用状态压缩KMP数据结构链表栈(单调栈)st表线段树字典树树状数组hash表堆队列列(单调队列列)*分块数学gcd,lcm矩阵快速幂埃⽒氏筛法*组合数学扩展欧⼏几⾥里里得,求解同余⽅方程,逆元图论图最短路路最⼩小⽣生成树并查集Tarjan强连通分量量割点缩点桥⼆二分图⼆二分图染⾊色⼆二分图匹配拓拓扑排序*分数规划树树上倍增(LCA)dfs序树的直径&重⼼心*树链剖分省选考点图论⽹网络流点分治动态树虚树树分块树链剖分边分治⼆二分图*仙⼈人掌算法*prufer编码*动态点分治计算⼏几何向量量的点积/叉积计算⼏几何基础*三⻆角剖分*旋转卡壳*半平⾯面交*⼆二维计算⼏几何相关*三维计算⼏几何相关搜索A*迭代深搜模拟退⽕火爬⼭山算法双向⼴广搜记忆化搜索*随机增量量法数据结构带权并查集线段树树状数组分块凸包可持久化可持久化线段树可持久化trie*其它可持久化数据结构整体⼆二分⼆二维线段树CDQ分治莫队算法树套树块状链表平衡树Splay 替罪⽺羊树Treap*双向链表*KDtree *⼆二进制分组*超哥线段树*后缀平衡树*fhqTreap *左偏树*舞蹈链*树上莫队*可并线段树其他算法构造随机化打表Huffman树*朱刘算法2-sat 启发式合并三分法乱搞动态规划基础DP 树形DP 期望DP 基环树DP 状压DP 数位DP trie图DP *仙⼈人掌DP *插头DP优化斜率优化倍增优化矩乘优化单调队列列优化*四边形不不等式优化数学线性筛容斥原理理exgcd Lucas定理理⾼高斯消元中国剩余定理理欧拉定理理单纯形法解线性规划线性代数(⾏行行列列式)⾼高中求导与积分博弈论相关阶原根多项式类算法FFT 矩阵乘法BSGS概率与期望相关⾼高中排列列组合费⻢马⼩小定理理莫⽐比乌斯反演积性函数*群论*密码学*⽣生成函数*Simpson积分字符串串hash(⾃自然溢出,双hash)AC⾃自动机后缀数组最⼩小表示法manachertrie kmp *后缀树*后缀⾃自动机*回⽂文⾃自动机。
NOIP复习资料(C++版)精编版

NOIP复习资料(C++版)主编葫芦岛市一高中李思洋完成日期2012年8月27日……………………………………………………………最新资料推荐…………………………………………………前言有一天,我整理了NOIP的笔记,并收集了一些经典算法。
不过我感觉到笔记比较凌乱,并且有很多需要修改和补充的内容,于是我又搜集一些资料,包括一些经典习题,在几个月的时间内编写出了《NOIP复习资料》。
由于急于在假期之前打印出来并分发给同校同学(我们学校既没有竞赛班,又没有懂竞赛的老师。
我们大家都是自学党),《NOIP复习资料》有很多的错误,还有一些想收录而未收录的内容。
在“减负”的背景下,暑期放了四十多天的假。
于是我又有机会认真地修订《NOIP复习资料》。
我编写资料的目的有两个:总结我学过(包括没学会)的算法、数据结构等知识;与同学共享NOIP知识,同时使我和大家的RP++。
大家要清醒地认识到,《NOIP复习资料》页数多,是因为程序代码占了很大篇幅。
这里的内容只是信息学的皮毛。
对于我们来说,未来学习的路还很漫长。
基本假设作为自学党,大家应该具有以下知识和能力:①能够熟练地运用C++语言编写程序(或熟练地把C++语言“翻译”成Pascal语言);②能够阅读代码,理解代码含义,并尝试运用;③对各种算法和数据结构有一定了解,熟悉相关的概念;④学习了高中数学的算法、数列、计数原理,对初等数论有一些了解;⑤有较强的自学能力。
代码约定N、M、MAX、INF是事先定义好的常数(不会在代码中再次定义,除非代码是完整的程序)。
N、M、MAX 针对数据规模而言,比实际最大数据规模大;INF针对取值而言,是一个非常大,但又与int的最大值有一定差距的数,如100000000。
对于不同程序,数组下标的下限也是不同的,有的程序是0,有的程序是1。
阅读程序时要注意。
阅读顺序和方法没听说过NOIP,或对NOIP不甚了解的同学,应该先阅读附录E,以加强对竞赛的了解。
高三数学复习 第十二章 复数、算法、推理与证明 第二节 算法与程序框图夯基提能作业本 理(2021

2018届高三数学一轮复习第十二章复数、算法、推理与证明第二节算法与程序框图夯基提能作业本理2018届高三数学一轮复习第十二章复数、算法、推理与证明第二节算法与程序框图夯基提能作业本理编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018届高三数学一轮复习第十二章复数、算法、推理与证明第二节算法与程序框图夯基提能作业本理)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018届高三数学一轮复习第十二章复数、算法、推理与证明第二节算法与程序框图夯基提能作业本理的全部内容。
2018届高三数学一轮复习第十二章复数、算法、推理与证明第二节算法与程序框图夯基提能作业本理第二节算法与程序框图A组基础题组1。
(2016山西四校二联)阅读如图所示的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为( )A。
64 B.73 C。
512 D.5852.定义运算a⊗b的结果为执行如图所示的程序框图输出的S,则⊗的值为()A。
4 B。
3 C.2 D.-13.阅读下面的程序框图,运行相应的程序,则输出S的值为()A。
10 B。
-15 C。
21 D.-284.从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为()A。
B。
C.D。
5。
阅读下面的程序框图,运行相应的程序,如果输入a=(1,-3),b=(4,-2),则输出的λ的值是()A。
-4 B.-3 C.—2 D.—16。
(2016四川,6,5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法。
树算法题模板

树算法题通常可以使用递归或迭代的方式来解决。
下面是一个常见的树算法题的模板:1. 树的遍历:- 前序遍历(Preorder Traversal):根节点 -> 左子树 -> 右子树- 中序遍历(Inorder Traversal):左子树 -> 根节点 -> 右子树- 后序遍历(Postorder Traversal):左子树 -> 右子树 -> 根节点```python# 递归方式def traverse(root):if root is None:return# 前序遍历代码位置traverse(root.left)# 中序遍历代码位置traverse(root.right)# 后序遍历代码位置# 迭代方式(使用栈)def traverse(root):if root is None:returnstack = []node = rootwhile stack or node:while node:# 前序遍历代码位置stack.append(node)node = node.leftnode = stack.pop()# 中序遍历代码位置node = node.right# 后序遍历代码位置```2. 树的深度优先搜索(DFS):- 通常使用递归的方式进行深度优先搜索,可以通过传递参数记录当前节点的深度等信息。
```pythondef dfs(node, depth):if node is None:return# 处理当前节点的逻辑# ...dfs(node.left, depth + 1) # 左子节点的深度为当前节点深度加一dfs(node.right, depth + 1) # 右子节点的深度为当前节点深度加一```3. 树的广度优先搜索(BFS):- 使用队列进行广度优先搜索,首先将根节点入队,然后循环遍历队列中的节点,并将其子节点入队,直到队列为空。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP复赛复习12STL算法与树结构模板STL算法STL 算法是一些模板函数,提供了相当多的有用算法和操作,从简单如for_each(遍历)到复杂如stable_sort(稳定排序),头文件是:#include <algorithm>。
常用STL 算法库包括:sort快速排序算法、二分查找算法、枚举排列算法等。
1、 sort排序系列sort:对给定区间所有元素进行排序(全排)stable_sort:对给定区间所有元素进行稳定排序,就是相等的元素位置不变,原来在前面的还在前面。
partial_sort:对给定区间所有元素部分排序,就是找出你指定的数目最小或最大的值放在最前面或最后面,比如说我只要找到1000000个数中最大的五个数,那你用这个函数是最好的,排序后最大的五个数就在最前面的五个位置,其他的元素位置分布不确定。
partial_sort_copy:对给定区间复制并排序,和上面的一样,只是这是指定区间进行复制然后排序的。
nth_element:找出给定区间的某个位置对应的元素,根据比较函数找到第n个最大(小)元素,适用于寻找“第n个元素”。
is_sorted:判断一个区间是否已经排好序(返回bool值判断是否已排序)partition:使得符合某个条件的元素放在前面,划分区间函数,将 [first, last]中所有满足的元素置于不满足的元素前面,这个函数会返回迭代器,设返回的迭代器为 i,则对 [first, i]中的任意迭代器 j,*j满足给定的判断,对 [i, last] 中的任意迭代器 k,*k不满足。
stable_partition:相对稳定的使得符合某个条件的元素放在前面(和上面的一样,只是位置不变)使用时根据需要选择合理的排序函数即可,所有的排序函数默认从小到大排序,可以定义自己的比较方式。
2、二分系列二分检索,复杂度O(log(last-first))itr =upper_bound(first, last, value, cmp);//itr 指向大于value 的第一个值(或容器末尾)itr = lower_bound(first, last, value, cmp);//itr 指向不小于valude 的第一个值(或容器末尾)pairequal_range(first, last, value, cmp);//找出等于value的值的范围O(2*log(last–first))Binary_search(first,last, value)返回bool值,找到则true,否则false。
二分经常会与其他算法结合。
例:HDU 1496#include <iostream>#include <algorithm>#include <cstring>using namespace std;int val[40010];int main() {pair <int*, int*> p;int a, b, c, d;while (cin >> a >> b >> c >> d) {if( (a > 0 && b > 0 && c > 0 && d > 0) || (a < 0 && b < 0 && c < 0 && d < 0)){ cout << 0 << endl;continue;}memset(val, 0, sizeof(val));int k = 0;for (int i = -100; i <= 100; i++){if (i == 0) continue;for (int j = -100; j <= 100; j++) {if (j == 0) continue;val[k++] = a*i*i + b*j*j;}}sort(val, val+k);int cnt = 0;for (int j = -100; j <= 100; j++) {if (j == 0) continue;for (int i = -100; i <= 100; i++) {if (i == 0) continue;int sum = c*j*j + d*i*i;p = equal_range(val, val+k, -sum);cnt += p.second - p.first;}}cout << cnt << endl;}return 0;}3、排列系列next_permutation是一个求一个排序的下一个排列的函数,可以遍历全排列,要包含头文件<algorithm>,与之完全相反的函数还有prev_permutation。
int 类型的next_permutationint main(){int a[3];a[0]=1;a[1]=2;a[2]=3;do{cout<<a[0]<<""<<a[1]<<""<<a[2]<<endl;} while (next_permutation(a,a+3));}输出:1 2 31 3 22 1 32 3 13 1 23 2 1char 类型的next_permutationint main(){char ch[205];cin >> ch;sort(ch, ch + strlen(ch) );char *first = ch;char *last = ch + strlen(ch);do {cout<< ch << endl;}while(next_permutation(first, last));return 0;}string 类型的next_permutationint main(){string line;while(cin>>line&&line!="#"){if(next_permutation(line.begin(),line.end()))cout<<line<<endl;else cout<<"Nosuccesor\n";}}int main(){string line;while(cin>>line&&line!="#"){sort(line.begin(),line.end());cout<<line<<endl;while(next_permutation(line.begin(),line.end()))cout<<line<<endl;}}4、常用函数copy、copy_if:copy直接拷贝,比for循环高效,最坏为线性复杂度,而且这个可以说是一个copy族函数,还有类似的满足一定条件的copy_if等。
find、find_i:查找第一个匹配的值或第一个满足函数使其为true的值位置,没有返回指定区间的末尾,线性复杂度,还有一些不怎么常用的find族函数就不多介绍了。
count、count_if:返回匹配或使函数为true的值的个数,线性复杂度。
search:这是寻找序列是否存在于另一个序列中的函数,挺好用的,某些简单的寻找公共子串的题就可以这样写,时间复杂度二次。
reverse:翻转一个区间的值,我经常遇到需要这种题,直接reverse了,不需要for循环了,主要是方便。
for_each:直接对一个区间内的每个元素执行后面的函数操作,写起来简单。
max、min、max_element、min_element:寻找两个数或者一个区间的最大最小值,都可以添加比较函数参数。
集合操作函数:includes、set_union、set_difference、set_intersection、set_symmetric_difference、前面这些函数的最差复杂度为线性,另外附加一个序列的操作函数merge,相当于归并排序中的合并函数,时间复杂度为线性,注意这些函数的操作对象都必须是升序的。
例:#include<cstdio>#include<algorithm>using namespace std;void out(int a) { if (a != -1) printf("%d ",a); }int main() {int a[5] = {1, 8, 10, 52, 100};int b[5] = {6, 8, 9, 10, 1000};int c[20];printf("a集合为:");for_each(a, a+5, out);puts("");printf("b集合为:");for_each(b, b+5, out);puts("");//判断b是否是a的子集。
if(includes(a, a+5, b, b+5)) printf("bis a sub set of a\n");//合并两个有序序列,必须为合并后的序列分配空间,否则程序会崩溃。
printf("两个集合的合并序列为:");merge(a, a+5, b, b+5, c);for_each(c, c+10, out);puts("");//求两个集合的并集。
fill(c, c+20, -1);set_union(a, a+5, b, b+5, c);printf("两个集合的并集为:");for_each(c, c+10, out);puts("");//求两个集合的交集。
fill(c, c+20, -1);set_intersection(a, a+5, b, b+5, c);printf("两个集合的交集为:");for_each(c, c+10, out);puts("");//求两个集合的差集,这里为a-b。
fill(c, c+20, -1);set_difference(a, a+5, b, b+5, c);printf("a-b的差集为:");for_each(c, c+10, out);puts("");//求两个集合的差集,这里为b-a。
