浙教版2021年中考数学总复习《圆》(含答案)
2021年浙江中考数学真题精编精练——专题7圆
2021年浙江中考数学真题汇编——专题7圆一.选择题〔共7小题〕1.〔2021•衢州〕扇形的半径为6,圆心角为150°,那么它的面积是〔 〕 A .32πB .3πC .5πD .15π2.〔2021•金华〕如图,在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向形外作正方形,正方形的顶点E ,F ,G ,H ,M ,N 都在同一个圆上.记该圆面积为S 1,△ABC 面积为S 2,那么S 1S 2的值是〔 〕A .5π2B .3πC .5πD .11π23.〔2021•绍兴〕如图,正方形ABCD 内接于⊙O ,点P 在AB ̂上,那么∠BPC 的度数为〔 〕A .30°B .45°C .60°D .90°4.〔2021•嘉兴〕平面内有⊙O 和点A ,B ,假设⊙O 半径为2cm ,线段OA =3cm ,OB =2cm ,那么直线AB 与⊙O 的位置关系为〔 〕 A .相离B .相交C .相切D .相交或相切5.〔2021•丽水〕如图,AB 是⊙O 的直径,弦CD ⊥OA 于点E ,连结OC ,OD .假设⊙O 的半径为m ,∠AOD =∠α,那么以下结论一定成立的是〔 〕A.OE=m•tanαB.CD=2m•sinαC.AE=m•cosαD.S△COD=12m2•sinα6.〔2021•湖州〕如图,在矩形ABCD中,AB=1,BC=√3,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1,当点P运动时,点C1也随之运动.假设点P从点A运动到点D,那么线段CC1扫过的区域的面积是〔〕A.πB.π+3√34C.3√32D.2π7.〔2021•湖州〕如图,点O是△ABC的外心,∠A=40°,连结BO,CO,那么∠BOC的度数是〔〕A.60°B.70°C.80°D.90°二.填空题〔共5小题〕8.〔2021•杭州〕如图,⊙O的半径为1,点P是⊙O外一点,且OP=2.假设PT是⊙O的切线,T为切点,连结OT,那么PT=.9.〔2021•宁波〕抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.假设∠P=120°,⊙O的̂的长为cm.〔结果保存π〕半径为6cm,那么图中CD10.〔2021•台州〕如图,将线段AB绕点A顺时针旋转30°,得到线段AC.假设AB=12,̂长度为.〔结果保存π〕那么点B经过的路径BC11.〔2021•温州〕假设扇形的圆心角为30°,半径为17,那么扇形的弧长为.12.〔2021•温州〕如图,⊙O与△OAB的边AB相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B,使点O′落在⊙O上,边A′B交线段AO于点C.假设∠A′=25°,那么∠OCB=度.三.解答题〔共8小题〕13.〔2021•衢州〕如图,在△ABC中,CA=CB,BC与⊙A相切于点D,过点A作AC的垂线交CB的延长线于点E,交⊙A于点F,连结BF.〔1〕求证:BF是⊙A的切线.〔2〕假设BE=5,AC=20,求EF的长.14.〔2021•衢州〕如图1,点C是半圆O的直径AB上一动点〔不包括端点〕,AB=6cm,过点C作CD⊥AB交半圆于点D,连结AD,过点C作CE∥AD交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记AC=xcm,EC=y1cm,EB=y2cm.请你一起参与探究函数y1、y2随自变量x变化的规律.通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.x……y1……y2……〔1〕当x=3时,y1=.〔2〕在图2中画出函数y2的图象,并结合图象判断函数值y1与y2的大小关系.〔3〕由〔2〕知“AC取某值时,有EC=EB〞.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.̂上存在点E,满足AÊ=CD̂,15.〔2021•宁波〕如图1,四边形ABCD内接于⊙O,BD为直径,AD连结BE并延长交CD的延长线于点F,BE与AD交于点G.〔1〕假设∠DBC=α,请用含α的代数式表示∠AGB.〔2〕如图2,连结CE,CE=BG.求证:EF=DG.〔3〕如图3,在〔2〕的条件下,连结CG,AD=2.①假设tan∠ADB=√32,求△FGD的周长.②求CG的最小值.16.〔2021•台州〕如图,BD是半径为3的⊙O的一条弦,BD=4√2,点A是⊙O上的一个动点〔不与点B,D重合〕,以A,B,D为顶点作▱ABCD.〔1〕如图2,假设点A是劣弧BD̂的中点.①求证:▱ABCD是菱形;②求▱ABCD的面积.〔2〕假设点A运动到优弧BD̂上,且▱ABCD有一边与⊙O相切.①求AB的长;②直接写出▱ABCD对角线所夹锐角的正切值.17.〔2021•温州〕如图,在平面直角坐标系中,⊙M经过原点O,分别交x轴、y轴于点A 〔2,0〕,B〔0,8〕,连结AB.直线CM分别交⊙M于点D,E〔点D在左侧〕,交x轴于点C〔17,0〕,连结AE.〔1〕求⊙M的半径和直线CM的函数表达式;〔2〕求点D,E的坐标;〔3〕点P在线段AC上,连结PE.当∠AEP与△OBD的一个内角相等时,求所有满足条件的OP的长.18.〔2021•金华〕在扇形AOB中,半径OA=6,点P在OA上,连结PB,将△OBP沿PB折叠得到△O′BP.̂所在的圆相切于点B.〔1〕如图1,假设∠O=75°,且BO′与AB①求∠APO′的度数.②求AP的长.̂相交于点D,假设点D为AB̂的中点,且PD∥OB,求AB̂的长.〔2〕如图2,BO′与AB19.〔2021•丽水〕如图,在△ABC中,AC=BC,以BC为直径的半圆O交AB于点D,过点D作半圆O的切线,交AC于点E.〔1〕求证:∠ACB=2∠ADE;̂的长.〔2〕假设DE=3,AE=√3,求CD̂所对的圆周角,∠ACD=30°.20.〔2021•湖州〕如图,AB是⊙O的直径,∠ACD是AD〔1〕求∠DAB的度数;〔2〕过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.假设AB=4,求DF的长.2021年浙江中考数学真题汇编——专题7圆参考答案与试题解析一.选择题〔共7小题〕1.【解答】解:扇形面积=150π×62360=15π,应选:D . 2.【解答】解:如图,设AB =c ,AC =b ,BC =a , 那么a 2+b 2=c 2,① 取AB 的中点为O , ∵△ABC 是直角三角形, ∴OA =OB =OC ,∵圆心在MN 和HG 的垂直平分线上, ∴O 为圆心,连接OG ,OE ,那么OG ,OE 为半径, 由勾股定理得:r 2=(a +b 2)2+(a 2)2=c 2+(c 2)2,② 由①②得a =b , ∴a 2=c 22, ∴S 1=54πc 2,∴S 2=12ab =c 24,∴S 1S 2=54πc 2÷c 24=5π,应选:C .3.【解答】解:连接OB 、OC ,如图,∵正方形ABCD内接于⊙O,∴BC弧所对的圆心角为90°,∴∠BOC=90°,∴∠BPC=12∠BOC=45°.应选:B.4.【解答】解:⊙O的半径为2cm,线段OA=3cm,OB=2cm,即点A到圆心O的距离大于圆的半径,点B到圆心O的距离等于圆的半径,∴点A在⊙O外,点B在⊙O上,∴直线AB与⊙O的位置关系为相交或相切,应选:D.5.【解答】解:∵AB是⊙O的直径,CD⊥OA,∴CD=2DE,∵⊙O的半径为m,∠AOD=∠α,∴DE=OD•sinα=m•sinα,∴CD=2DE=2m•sinα,应选:B.6.【解答】解:如图,当P与A重合时,点C关于BP的对称点为C′,当P与D重合时,点C关于BP的对称点为C″,∴点P从点A运动到点D,那么线段CC1扫过的区域为:扇形BC'C''和△BCC'',在△BCD中,∵∠BCD=90°,BC=√3,CD=1,∴tan∠DBC=√3=√33,∴∠DBC=30°,∴∠CBC″=60°,∵BC=BC''∴△BCC''为等边三角形,∴S扇形BC′C″=120×π×(√3)2360=π,作C''F⊥BC于F,∵△BCC''为等边三角形,∴BF=12BC=√32,∴C''F=tan60°×√32=32,∴S△BCC''=12×√3×32=3√34,∴线段CC1扫过的区域的面积为:π+3√3 4.应选:B.7.【解答】解:∵点O为△ABC的外心,∠A=40°,∴∠A=12∠BOC,∴∠BOC=2∠A=80°,应选:C.二.填空题〔共5小题〕8.【解答】解:∵PT是⊙O的切线,T为切点,∴OT⊥PT,在Rt△OPT中,OT═1,OP═2,∴PT═√OP2−OT2═√22−12═√3,故:PT═√3.9.【解答】解:如下图,连接OC,OD,OP,∵AC,BD分别与⊙O相切于点C,D,故∠OCP =∠ODP =90°,又OC =OD ,OP =OP ,那么Rt △OCP ≌Rt △ODP 〔HL 〕.∵∠CPD =120°,∴∠OPC =∠OPD =60°,∴∠COP =∠DOP =30°,∴∠COD =60°.∴CD ̂的长为l CD ̂=nπr 180=60°×π×6180=2π. 故答案为:2π.10.【解答】解:BC ̂长度=30π⋅12180=2π, 故答案为:2π.11.【解答】解:根据弧长公式可得:l =nπr 180=30⋅π⋅17180=176π. 故答案为:176π.12.【解答】解:∵⊙O 与△OAB 的边AB 相切,∴OB ⊥AB ,∴∠OBA =90°,连接OO ′,如图,∵△OAB 绕点B 按顺时针方向旋转得到△O ′A ′B ,∴∠A =∠A ′=25°,∠ABA ′=∠OBO ′,BO =BO ′,∵OB =OO ′,∴△OO ′B 为等边三角形,∴∠OBO ′=60°,∴∠ABA ′=60°,∴∠OCB =∠A +∠ABC =25°+60°=85°.故答案为85.三.解答题〔共8小题〕13.【解答】解:〔1〕证明:连接AD ,如图,∵CA =CB ,∴∠CAB =∠ABC .∵AE ⊥AC ,∴∠CAB +∠EAB =90°.∵BC 与⊙A 相切于点D ,∴∠ADB =90°.∴∠ABD +∠BAD =90°.∴∠BAE =∠BAD .在△ABF 和△ABD 中,{AB =AB ∠BAE =∠BAD AF =AD,∴△ABF ≌△ABD 〔SAS 〕.∴∠AFB =∠ADB =90°.∴BF 是⊙A 的切线.〔2〕由〔1〕得:BF ⊥AE ,∵AC ⊥AE ,∴BF ∥AC .∴△EFB ∽△EAC .∴BE CE =BF CA ,∵BE =5,CB =AC =20,∴CE =EB +CB =20+5=25,∴525=BF 20.∴BF =4.在Rt △BEF 中,EF =√BE 2−BF 2=√52−42=3.14.【解答】解:〔1〕当x =3时,点C 和圆心O 重合,此时CE 为半圆O 的半径,∵AB =6,∴EC =y 1cm =3cm ,∴y 1=3,故答案为:3;〔2〕函数y 的图象如图:由图象得:当0<x <2时,y 1<y 2,当x =2时,y 1=y 2,当2<x <6时,y 1>y 2;〔3〕〕连接OD ,作EH ⊥AB 于H ,由〔2〕知时,有EC =EB ,∵AC =2,AB =6cm ,∴OA =OD =OE =OB =3cm ,OC =1cm ,∵CD ⊥AB ,∴CD =√OD 2−OC 2=2√2,设OH =m ,那么CH =1+m ,∵EH ⊥AB ,∴EH =√32−m 2=√9−m 2,∵CE ∥AD ,∴∠DAC =∠ECH ,∵∠DCA =∠EHC =90°,∴△DAC ∽△ECH ,∴CD AC =EH CH ,即2√22=√9−m 21+m , ∴m 1=1,m 2=−73〔不合题意,舍去〕,∴HB =3﹣1=2,EH =√OE 2−OH 2=2√2,∴EC =√EH 2+CH 2=√8+4=2√3,EB =√EH 2+HB 2=√8+4=2√3, ∴EC =EB .15.【解答】解:〔1〕∵BD 为⊙O 的直径,∴∠BAD =90°,∵AÊ=CD ̂, ∴∠ABG =∠DBC =α,∴∠AGB =90°﹣α;〔2〕∵BD 为⊙O 的直径,∴∠BCD=90°,∴∠BEC=∠BDC=90°﹣α,∴∠BEC=∠AGB,∵∠CEF=180°﹣∠BEC,∠BGD=180°﹣∠AGB,∴∠CEF=∠BGD,又∵CE=BG,∠ECF=∠GBD,∴△CFE≌△BDG(ASA),∴EF=DG;〔3〕①如图,连接DE,∵BD为⊙O的直径,∴∠A=∠BED=90°,在Rt△ABD中,tan∠ADB=√32,AD=2,∴AB=√32,AD=√3,∵AÊ=CD̂,∴AÊ+DÊ=CD̂+DÊ,即AD̂=CÊ,∴AD=CE,∵CE=BG,∴BG=AD=2,∵在Rt△ABG中,sin∠AGB=ABBG=√32,∴∠AGB=60°,AG=12BG=1,∴EF=DG=AD﹣AG=1,∵在Rt △DEG 中,∠EGD =60°,∴EG =12DG =12,DE =√32DG =√32,在Rt △FED 中,DF =√EF 2+DE 2=√72,∴FG +DG +EF =5+√72, ∴△FGD 的周长为5+√72; ②如图,过点C 作CH ⊥BF 于H ,∵△BDG ≌△CFE ,∴BD =CF ,∠CFH =∠BDA ,∵∠BAD =∠CHF =90°,∴△BAD ≌△CHF (AAS ),∴FH =AD ,∵AD =BG ,∴FH =BG ,∵∠BCF =90°,∴∠BCH +∠HCF =90°,∵∠BCH +∠HBC =90°,∴∠HCF =∠HBC ,∵∠BHC =∠CHF =90°,∴△BHC ∽△CHF ,∴BH CH =CH FH ,设GH =x ,∴BH =2﹣x ,∴CH2=2(2﹣x),在Rt△GHC中,CG2=GH2+CH2,∴CG2=x2+2(2﹣x)=(x﹣1)2+3,当x=1时,CG2的最小值为3,∴CG的最小值为√3.16.【解答】〔1〕①证明:∵AD̂=AB̂,∴AD=AB,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.②解:连接OA交BD于J,连接OC.∵AD̂=AB̂,∴OA⊥BD,∵四边形ABCD是菱形,∴AC⊥BD,∴A,O,C共线,在Rt△OJD中,DJ=BJ=2√2,OD=3,∴OJ=√OD2−DJ2=√32−(2√2)2=1,∴AJ=OA=OJ=3﹣1=2,∵四边形ABCD是菱形,∴AJ=CJ=2,∴S菱形ABCD=12•AC•BD=12×4×4√2=8√2.〔2〕①解:当CD与⊙O相切时,连接AC交BD于H,连接OH,OD,延长DO交AB于P ,过点A 作AJ ⊥BD 于J .∵CD 是⊙O 的切线,∴OD ⊥CD ,∵CD ∥AB ,∴DP ⊥AB ,∴P A =PB ,∴DB =AD =4√2,∵四边形ABCD 是平行四边形,∴DH =BH =2√2,∴OH ⊥BD ,∴∠DHO =∠DPB =90°,∵∠ODH =∠BDP ,∴△DHO ∽△DPB ,∴DH DP =DO DB =OH PB ,∴2√2DP =4√2=1PB, ∴DP =163,PB =4√23, ∴AB =2PB =8√23,当BC 与⊙O 相切时,同法可证AB =BD =4√2.综上所述,AB 的长为4√2或8√23. ②解:如图3﹣1中,过点A 作AJ ⊥BD 于J .∵12•AB •DP =12•BD •AJ , ∴AJ =329,∴BJ =√AB 2−AJ 2=(8√23)2−(329)2=8√29, ∴JH =BH =BJ =2√2−8√29=10√29, ∴tan ∠AHJ =AJ HJ =32910√29=8√25, 如图3﹣2中,同法可得▱ABCD 对角线所夹锐角的正切值为8√25,综上所述,▱ABCD 对角线所夹锐角的正切值为8√25, 17.【解答】解:〔1〕∵点M 是AB 的中点,那么点M 〔1,4〕, 那么圆的半径为AM =√(2−1)2+42=√17,设直线CM 的表达式为y =kx +b ,那么{17k +b =0k +b =4,解得{k =−14b =174, 故直线CM 的表达式为y =−14x +174;〔2〕设点D 的坐标为〔x ,−14x +174〕,由AM =√17得:〔x ﹣1〕2+〔−14x +174−4〕2=〔√17〕2,解得x =5或﹣3,故点D 、E 的坐标分别为〔﹣3,5〕、〔5,3〕;〔3〕过点D 作DH ⊥OB 于点H ,那么DH =3,BH =8﹣5=3=DH , 故∠DBO =45°,由点A 、E 的坐标,同理可得∠EAP =45°;由点A 、E 、B 、D 的坐标得,AE =√(5−2)2+(0−3)2=3√2, 同理可得:BD =3√2,OB =8,①当∠AEP =∠DBO =45°时,那么△AEP 为等腰直角三角形,EP ⊥AC ,故点P 的坐标为〔5,0〕,故OP =5;②∠AEP =∠BDO 时,∵∠EAP =∠DBO ,∴△EAP ∽△DBO ,∴AE BD =AP BO ,即√23√2=APBO =AP8,解得AP =8,故PO =10;③∠AEP =∠BOD 时,∵∠EAP =∠DBO , ∴△EAP ∽△OBD ,∴AE OB =APBD ,即3√28=3√2,解得AP =94, 那么PO =2+94=174, 综上,OP 为5或10或174.18.【解答】解:〔1〕①如图1中,∵BO′是⊙O的切线,∴∠OBO′=90°,由翻折的性质可知,∠OBP=∠PBO′=45°,∠OPB=∠BPO′,∵∠AOB=75°,∴∠OPB=∠BPO′=180°﹣75°﹣45°=60°,∴∠OPO′=120°,∴∠APO′=180°﹣∠OPO′=180°﹣120°=60°.②如图1中,过点B作BH⊥OA于H,在BH上取一点F,使得OF=FB,连接OF.∵∠BHO=90°,∴∠OBH=90°﹣∠BOH=15°,∵FO=FB,∴∠FOB=∠FBO=15°,∴∠OFH=∠FOB+∠FBO=30°,设OH=m,那么HF=√3m,OF=FB=2m,∵OB2=OH2+BH2,∴62=m2+(√3m+2m)2,∴m=3√6−3√22或−3√6−3√22〔舍弃〕,∴OH=3√6−3√22,BH=3√2+3√62,在Rt△PBH中,PH=BHtan60°=√6+3√22,∴P A=OA﹣OH﹣PH=6−3√6−3√22−√6+3√22=6﹣2√6.(2)如图2中,连接AD,OD.∵AD̂=BD̂,∴AD=BD,∠AOD=∠BOD,由翻折的旋转可知,∠OBP=∠PBD,∵PD∥OB,∴∠DPB=∠OBP,∴∠DPB =∠PBD ,∴DP =DB =AD ,∴∠DAP =∠APD =∠AOB ,∵AO =OD =OB ,AD =DB ,∴△AOD ≌△BOD ,∴∠OBD =∠OAD =∠AOB =2∠BOD ,∵OB =OD ,∴∠OBD =∠ODB =2∠DOB ,∴∠DOB =36°,∴∠AOB =72°,∴AB ̂的长=72π⋅6180=12π5。
专题14圆(解答题)--浙江省2019-2021年3年中考真题数学分项汇编(解析版)

三年(2019-2021)中考真题数学分项汇编(浙江专用)专题14圆(解答题)一.解答题(共20小题)1.(2021•丽水)如图,在△ABC中,AC=BC,以BC为直径的半圆O交AB于点D,过点D作半圆O的切线,交AC于点E.(1)求证:∠ACB=2∠ADE;̂的长.(2)若DE=3,AE=√3,求CD【分析】(1)连接OD,CD,根据切线的性质得到∠ODE=90°,根据圆周角定理得到∠BDC=90°,求得∠ADE=∠ODC,根据等腰三角形的性质即可得到结论;(2)根据勾股定理得到AD=√32+(√3)2=2√3,tan A=√3,求得∠A=60°,推出△ABC是等边三角形,得到∠B=60°,BC=AB=2AD=4√3,根据弧长公式即可得到结论.【详解】(1)证明:连接OD,CD,∵DE是⊙O的切线,∴∠ODE=90°,∴∠ODC+∠EDC=90°,∵BC为⊙O直径,∴∠BDC=90°,∴∠ADC=90°,∴∠ADE+∠EDC=90°,∴∠ADE=∠ODC,∵AC=BC,∴∠ACB=2∠DCE=2∠OCD,∵OD=OC,∴∠ODC =∠OCD ,∴∠ACB =2∠ADE ;(2)解:由(1)知,∠ADE +∠EDC =90°,∠ADE =∠DCE ,∴∠AED =90°,∵DE =3,AE =√3,∴AD =√32+(√3)2=2√3,tan A =√3,∴∠A =60°,∵AC =BC ,∴△ABC 是等边三角形,∴∠B =60°,BC =AB =2AD =4√3,∴∠COD =2∠B =120°,OC =2√3,∴CD ̂ 的长为nπr 180=120⋅π×2√3180=4√3π3.2.(2021•湖州)如图,已知AB 是⊙O 的直径,∠ACD 是AD̂所对的圆周角,∠ACD =30°. (1)求∠DAB 的度数;(2)过点D 作DE ⊥AB ,垂足为E ,DE 的延长线交⊙O 于点F .若AB =4,求DF 的长.【分析】(1)连接BD ,根据AB 是⊙O 的直径,可得∠ADB =90°,进而可以求∠DAB 的度数;(2)根据直角三角形30度角所对直角边等于斜边的一半可得AD 的长,再根据垂径定理和特殊角三角函数值可得EF =DE 的值,进而可得DF 的长.【详解】解:(1)如图,连接BD ,∵∠ACD=30°,∴∠B=∠ACD=30°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠DAB=90°﹣∠B=60°;(2)∵∠ADB=90°,∠B=30°,AB=4,∴AD=12AB=2,∵∠DAB=60°,DE⊥AB,且AB是直径,∴EF=DE=AD sin60°=√3,∴DF=2DE=2√3.3.(2021•金华)在扇形AOB中,半径OA=6,点P在OA上,连结PB,将△OBP沿PB折叠得到△O′BP.(1)如图1,若∠O=75°,且BO′与AB̂所在的圆相切于点B.①求∠APO′的度数.②求AP的长.(2)如图2,BO′与AB̂相交于点D,若点D为AB̂的中点,且PD∥OB,求AB̂的长.【分析】(1)①利用三角形内角和定理求解即可。
2021年中考数学第三轮专题冲刺复习:圆的综合(含答案)

2021年中考数学第三轮专题冲刺复习:圆的综合1、如图,AB 是⊙O 的直径,点C 在AB 的延长线上,AD 平分∠CAE 交⊙O 于点D ,且AE ⊥CD ,垂足为点E .(1)求证:直线CE 是⊙O 的切线.(2)若BC=3,CD=3,求弦AD 的长.2、如图,AN 是M 的直径,//NB x 轴,AB 交M 于点C .(1)若点()()00,6,0,2,30A N ABN ∠=,求点B 的坐标; (2)若D 为线段NB 的中点,求证:直线CD 是M 的切线.3、如图,⊙O 与Rt △ABC 的直角边AC 和斜边AB 分别相切于点C 、D ,与边BC 相交于点F ,OA 与CD 相交于点E ,连接FE 并延长交AC 边于点G .(1)求证:DF ∥AO ;(2)若AC=6,AB=10,求CG 的长.4、如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且PA=.∠ACP,PD=60(1)试判断PD与⊙O的位置关系,并说明理由;(2)若点C是弧AB的中点,已知4CE⋅的值.AB=,求CP5、如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为6,BC=8,求弦BD的长.6、如图,AB是⊙O的直径,点E是上的一点,∠DBC=∠BED.(1)求证:BC是⊙O的切线;(2)已知AD=3,CD=2,求BC的长.7、如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.(1)求证:直线DE是⊙O的切线;(2)若 BF=10,sin∠BDE=,求DE的长.8、如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC 的中点,连接DE、OE.(1)判断DE与⊙O的位置关系并说明理由;(2)若ta n C=,DE=2,求AD的长.9、如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.(1)求证:AD是⊙O的切线;(2)若⊙O的半径为5,CE=2,求EF的长.10、如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.(1)求证:CF是⊙O的切线.(2)若∠A=22.5°,求证:AC=DC.11、如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.(1)求证:DC为⊙O的切线;(2)线段DF分别交AC,BC于点E,F且∠CEF=45°,⊙O的半径为5,sinB=,求CF的长.12、如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD,连接AF.(1)判断直线AF与⊙O的位置关系,并说明理由.(2)若AC=10,tan∠CAE=,求AE的长.13、(1)如图1,有一个残缺圆,请作出残缺圆的圆心O(保留作图痕迹,不写作法).(2)如图2,设AB是该残缺圆⊙O的直径,C是圆上一点,∠CAB的角平分线AD交⊙O于点D,过D作⊙O的切线交AC的延长线于点E.①求证:AE⊥DE;②若DE=3,AC=2,求残缺圆的半圆面积.14、如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△PBD∽△DCA;(3)当AB=6,AC=8时,求线段PB的长.15、如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,于点F,连结CB.(1)求证:CB是的平分线;(2)求证:CF=CE;(3)当时,求劣弧BC的长度(结果保留π).16、如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;(2)求sin∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.17、如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.(1)求证:PQ是⊙O的切线;(2)求证:BD2=ACBQ;(3)若AC、BQ的长是关于x的方程x+=m的两实根,且tan∠PCD=,求⊙O的半径.18、(1)方法选择如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN=AD…请你选择一种方法证明.(2)类比探究【探究1】如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.【探究2】如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是BD=CD+2AD.(3)拓展猜想如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是BD=CD+ AD.参考答案2021年中考数学第三轮专题冲刺复习:圆的综合1、如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.(1)求证:直线CE是⊙O的切线.(2)若BC=3,CD=3,求弦AD的长.【解答】(1)证明:连结OC,如图,∵AD平分∠EAC,∴∠1=∠3,∵OA=OD,∴∠1=∠2,∴∠3=∠2,∴OD∥AE,∵AE⊥DC,∴OD⊥CE,∴CE是⊙O的切线;(2)∵∠CDO=∠ADB=90°,∴∠2=∠CDB=∠1,∵∠C=∠C,∴△CDB∽△CAD,∴==,∴CD 2=CB •CA ,∴(3)2=3CA ,∴CA=6,∴AB=CA ﹣BC=3, ==,设BD=K ,AD=2K ,在Rt △ADB 中,2k 2+4k 2=5,∴k=, ∴AD=.2、如图,AN 是M 的直径,//NB x 轴,AB 交M 于点C .(1)若点()()00,6,0,2,30A N ABN ∠=,求点B 的坐标; (2)若D 为线段NB 的中点,求证:直线CD 是M 的切线.解:(1)∵A 的坐标为(0,6),N (0,2)∴AN =4,∵∠ABN =30°,∠ANB =90°,∴AB =2AN =8,∴由勾股定理可知:NB =,∴B (,2)(2)连接MC ,NC ∵AN 是⊙M 的直径,∴∠ACN =90°,∴∠NCB =90°在Rt △NCB 中,D 为NB 的中点,∴CD =12NB =ND ,∴∠CND=∠NCD,∵MC=MN,∴∠MCN=∠MNC.∵∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,即MC⊥CD.∴直线CD是⊙M的切线.3、如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC 相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.(1)求证:DF∥AO;(2)若AC=6,AB=10,求CG的长.【解答】(1)证明:连接OD.∵AB与⊙O相切与点D,又AC与⊙O相切与点,∴AC=AD,∵OC=OD,∴OA⊥CD,∴CD⊥OA,∵CF是直径,∴∠CDF=90°,∴DF⊥CD,∴DF ∥AO .(2)过点作EM ⊥OC 于M ,∵AC=6,AB=10,∴BC==8,∴AD=AC=6,∴BD=AB ﹣AD=4,∵BD 2=BF •BC ,∴BF=2,∴CF=BC ﹣BF=6.OC=CF=3,∴OA==3, ∵OC 2=OE •OA ,∴OE=, ∵EM ∥AC ,∴===,∴OM=,EM=,FM=OF+OM=, ∴===,∴CG=EM=2.4、如图,以AB 边为直径的⊙O 经过点P ,C 是⊙O 上一点,连结PC 交AB 于点E ,且 60=∠ACP ,PD PA =.(1)试判断PD 与⊙O 的位置关系,并说明理由;(2)若点C 是弧AB 的中点,已知4AB =,求CP CE ⋅的值.解:(1)如图,PD 是⊙O 的切线.证明如下:连结OP , 60=∠ACP ,∴ 120=∠AOP ,OP OA = ,∴ 30=∠=∠OPA OAP ,PD PA =,∴ 30=∠=∠D PAO ,∴ 90=∠OPD ,∴PD 是⊙O 的切线. (2)连结BC ,AB 是⊙O 的直径, ∴ 90=∠ACB ,又C 为弧AB 的中点, ∴ 45=∠=∠=∠APC ABC CAB ,4=AB ,2245== sin AB AC .APC CAB C C ∠=∠∠=∠, ,∴CAE ∆∽CPA ∆, ∴CACE CP CA =,∴82222===⋅)(CA CE CP .5、如图,△ABD 是⊙O 的内接三角形,E 是弦BD 的中点,点C 是⊙O 外一点且∠DBC=∠A ,连接OE 延长与圆相交于点F ,与BC 相交于点C .(1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径为6,BC=8,求弦BD 的长.【解答】(1)证明:连接OB,如图所示:∵E是弦BD的中点,∴BE=DE,OE⊥BD, =,∴∠BOE=∠A,∠OBE+∠BOE=90°,∵∠DBC=∠A,∴∠BOE=∠DBC,∴∠OBE+∠DBC=90°,∴∠OBC=90°,即BC⊥OB,∴BC是⊙O的切线;(2)解:∵OB=6,BC=8,BC⊥OB,∴OC==10,∵△OBC的面积=OC•BE=OB•BC,∴BE===4.8,∴BD=2BE=9.6,即弦BD的长为9.6.6、如图,AB是⊙O的直径,点E是上的一点,∠DBC=∠BED.(1)求证:BC是⊙O的切线;(2)已知AD=3,CD=2,求BC的长.解:(1)证明:∵AB是⊙O的切直径,∴∠ADB=90°,又∵∠BAD=∠BED,∠BED=∠DBC,∴∠BAD=∠DBC,∴∠BAD+∠ABD=∠DBC+ABD=90°,∴∠ABC=90°,∴BC是⊙O的切线;(2)解:∵∠BAD=∠DBC,∠C=∠C,∴△ABC∽△BDC,∴=,即BC2=AC•CD=(AD+CD)•CD=10,∴BC=.7、如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.(1)求证:直线DE是⊙O的切线;(2)若 BF=10,sin∠BDE=,求DE的长.【解答】解:(1)如图所示,连接OD,∵OD=OB,∴∠ODB=∠OBD,∵BD平分∠OBC,∴∠OBD=∠DBE,∴∠ODB=∠DBE,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∵OD是⊙O的半径,∴直线DE是⊙O的切线;(2)如图,连接DF,∵BF是⊙O的直径,∴∠FDB=90°,∴∠F+∠OBD=90°,∵∠OBD=∠DBE,∠BDE+∠DBE=90°,∴∠F=∠BDE,在Rt△BDF中,=sinF=sin∠BDE=,∴BD=10×=2,∴在Rt△BDE中,sin∠BDE==,∴BE=2×=2,∴在Rt△BDE中,DE===4.8、如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC 的中点,连接DE、OE.(1)判断DE与⊙O的位置关系并说明理由;(2)若ta n C=,DE=2,求AD的长.解:(1)DE与⊙O相切,理由如下:连接OD,BD,∵AB是直径,∴∠ADB=∠BDC=90°,∵E是BC的中点,∴DE=BE=CE,∴∠EDB=∠EBD,∵OD=OB,∴∠OBD=∠ODB.∴∠EDO=∠EBO=90°,(用三角形全等也可得到)∴DE与⊙O相切.(2)∵ta n C=,可设BD=x,CD=2x,∵在Rt△BCD中,BC=2DE=4,BD2+CD2=BC2∴(x)2+(2x)2=16,解得:x=±(负值舍去)∴BD=x=,∵∠ABD=∠C,∴ta n∠ABD=ta n CAD=BD=×=.答:AD的长是.9、如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.(1)求证:AD是⊙O的切线;(2)若⊙O的半径为5,CE=2,求EF的长.【解答】解:(1)∵BC是⊙O的直径,∴∠BAF+∠FAC=90°,∵∠D=∠BAF,∠AOD=∠FAC,∴∠D+∠AOD=90°,∴∠OAD=90°,∴AD是⊙O的切线;(2)连接BF,∴∠FAC=∠AOD,∴△ACE∽△OCA,∴,∴,∴AC=AE=,∵∠CAE=∠CBF,∴△ACE∽△BFE,∴,∴=,∴EF=.10、如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.(1)求证:CF是⊙O的切线.(2)若∠A=22.5°,求证:AC=DC.【解答】(1)证明:∵AB是⊙O的直径,∴∠ACB=∠ACD=90°,∵点F是ED的中点,∴CF=EF=DF,∴∠AEO=∠FEC=∠FCE,∵OA=OC,∴∠OCA=∠OAC,∵OD⊥AB,∴∠OAC+∠AEO=90°,∴∠OCA+∠FCE=90°,即OC⊥FC,∴CF与⊙O相切;(2)解:∵OD⊥AB,AC⊥BD,∴∠AOE=∠ACD=90°,∵∠AEO=∠DEC,∴∠OAE=∠CDE=22.5°,∵AO=BO,∴AD=BD,∴∠ADO=∠BDO=22.5°,∴∠ADB=45°,∴∠CAD=∠ADC=45°,∴AC=CD.11、如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.(1)求证:DC为⊙O的切线;(2)线段DF分别交AC,BC于点E,F且∠CEF=45°,⊙O的半径为5,sinB=,求CF的长.【解答】(1)证明:连接OC,∵AB为⊙O的直径,∴∠ACB=∠BCO+∠OCA=90°,∵OB=OC,∴∠B=∠BCO,∵∠ACD=∠B,∴∠ACD=∠BCO,∴∠ACD+∠OCA=90°,即∠OCD=90°,∴DC为⊙O的切线;(2)解:Rt△ACB中,AB=10,sinB=,∴AC=6,BC=8,∵∠ACD=∠B,∠ADC=∠CDB,∴△CAD∽△BCD,∴,设AD=3x,CD=4x,Rt△OCD中,OC2+CD2=OD2,52+(4x)2=(5+3x)2,x=0(舍)或,∵∠CEF=45°,∠ACB=90°,∴CE=CF,设CF=a,∵∠CEF=∠ACD+∠CDE,∠CFE=∠B+∠BDF,∴∠CDE=∠BDF,∵∠ACD=∠B,∴△CED∽△BFD,∴,∴,a=,∴CF=.12、如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD,连接AF.(1)判断直线AF与⊙O的位置关系,并说明理由.(2)若AC=10,tan∠CAE=,求AE的长.【解答】解:(1)直线AF是⊙O的切线,理由是:连接AC,∵AB为⊙O直径,∴∠ACB=90°,∴AC⊥BC,∵CF=CD,∴∠CAF=∠EAC,∵AC=CE,∴∠E=∠EAC,∵∠B=∠E,∴∠B=∠FAC,∵∠B+∠BAC=90°,∴∠FAC+∠BAC=90°,∴OA⊥AF,又∵点A在⊙O上,∴直线AF是⊙O的切线;(2)过点C作CM⊥AE,∵tan∠CAE=,∴=,∵AC=10,∴设CM=3x,则AM=4x,在Rt△ACM中,根据勾股定理,CM2+AM2=AC2,∴(3x)2+(4x)2=100,解得x=2,∴AM=8,∵AC=CE,∴AE=2AE=2×8=16.13、(1)如图1,有一个残缺圆,请作出残缺圆的圆心O(保留作图痕迹,不写作法).(2)如图2,设AB是该残缺圆⊙O的直径,C是圆上一点,∠CAB的角平分线AD交⊙O于点D,过D作⊙O的切线交AC的延长线于点E.①求证:AE⊥DE;②若DE=3,AC=2,求残缺圆的半圆面积.【解答】(1)解:如图1:点O即为所求.(2)①证明:如图2中,连接OD交BC于F.∵AD平分∠BAC,∴∠DAC=∠DAB,∴=,∴OD⊥BC,∴CF=BF,∠CFD=90°,∵DE是切线,∴DE⊥OD,∴∠EDF=90°,∵AB是直径,∴∠ACB=∠BCE=90°,∴四边形DECF是矩形,∴∠E=90°,∴AE⊥DE.②∵四边形DECF是矩形,∴DE=CF=BF=3,在Rt△ACB中,AB==2,∴残缺圆的半圆面积=•π•(2)2=20π.14、如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△PBD∽△DCA;(3)当AB=6,AC=8时,求线段PB的长.【解答】(1)证明:∵圆心O在BC上,∴BC是圆O的直径,∴∠BAC=90°,连接OD,∵AD平分∠BAC,∴∠BAC=2∠DAC,∵∠DOC=2∠DAC,∴∠DOC=∠BAC=90°,即OD⊥BC,∵PD∥BC,∴OD⊥PD,∵OD为圆O的半径,∴PD是圆O的切线;(2)证明:∵PD∥BC,∴∠P=∠ABC,∵∠ABC=∠ADC,∴∠P=∠ADC,∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,∴∠PBD=∠ACD,∴△PBD∽△DCA;(3)解:∵△ABC为直角三角形,∴BC2=AB2+AC2=62+82=100,∴BC=10,∵OD垂直平分BC,∴DB=DC,∵BC为圆O的直径,∴∠BDC=90°,在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,∴DC=DB=5,∵△PBD∽△DCA,∴=,则PB===.15、如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,于点F,连结CB.(1)求证:CB是的平分线;(2)求证:CF=CE;(3)当时,求劣弧BC的长度(结果保留π).证明:连接AC,∵AB为直径,∴∠ACB=90°∴∠1+∠2=90°,∠2+∠3=90°∴∠1=∠3又∵CP为切线∴∠OCP=90°∵DC为直径∴∠DBC=90°∴∠4+∠DCB=90°,∠DCB+∠D=90°∴∠4=∠D又∵弧BC=弧BC∴∠3=∠D∴∠1=∠4即:CB 是∠ECP 的平分线(2)∵∠ACB =90°∴∠5+∠4=90°,∠ACE +∠1=90°由(1)得∠1=∠4∴∠5=∠ACE在Rt △AFC 和Rt △AEC 中AEC AFC AC AC ECA FCA AEC F ≌△△∴⎪⎩⎪⎨⎧=∠=∠︒=∠=∠90 ∴CF =CE(3)延长CE 交DB 于Qx x x EQ xCQ CP PQCB QCB CB xCE CF xCP x CF CP CF =-=∴==∴⊥∠=====344324343的角平分线是∵)得由(,设: ππ332321806032346060-60-18060333tan 33290219019022=⨯∴=∴=︒=︒︒︒=∠∴︒=∠∴===∠=∴=⋅⋅=∴=∴∴∠=∠∴︒=∠+∠︒=∠+∠︒=∠⊥的长度为:弧∵中,在△即∽△△,,,BC OB AB CBE CBE x x EB CE CBE CEB xEB EB x x EQ CE EB EQEB EB CE BEQCEB CQBCQB CBQ EB CE16、如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;(2)求sin∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.【解答】解:(1)如图1中,连接OC.∵AB⊥CD,∴∠CHO=90°,在Rt△COH中,∵OC=r,OH=r﹣2,CH=4,∴r2=42+(r﹣2)2,∴r=5.(2)如图1中,连接OD.∵AB⊥CD,AB是直径,∴==,∴∠AOC=∠COD,∵∠CMD=∠COD,∴∠CMD=∠COA,∴sin∠CMD=sin∠COA==.(3)如图2中,连接AM.∵AB是直径,∴∠AMB=90°,∴∠MAB+∠ABM=90°,∵∠E+∠ABM=90°,∴∠E=∠MAB,∴∠MAB=∠MNB=∠E,∵∠EHM=∠NHFM∴△EHM∽△NHF,∴=,∴HE•HF=HM•HN,∵HM•HN=AH•HB,∴HE•HF=AH•HB=2•(10﹣2)=16.17、如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.(1)求证:PQ是⊙O的切线;(2)求证:BD2=ACBQ;(3)若AC、BQ的长是关于x的方程x+=m的两实根,且tan∠PCD=,求⊙O 的半径.【解答】(1)证明:∵PQ∥AB,∴∠ABD=∠BDQ=∠ACD,∵∠ACD=∠BCD,∴∠BDQ=∠ACD,如图1,连接OB,OD,交AB于E,则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,在△OBD中,∠OBD+∠ODB+∠O=180°,∴2∠ODB+2∠O=180°,∴∠ODB+∠O=90°,∴PQ是⊙O的切线;(2)证明:如图2,连接AD,由(1)知PQ是⊙O的切线,∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,∴AD=BD,∵∠DBQ=∠ACD,∴△BDQ∽△ACD,∴=,∴BD2=ACBQ;(3)解:方程x+=m可化为x2﹣mx+4=0,∵AC、BQ的长是关于x的方程x+=m的两实根,∴ACBQ=4,由(2)得BD2=ACBQ,∴BD2=4,∴BD=2,由(1)知PQ是⊙O的切线,∴OD⊥PQ,∵PQ∥AB,∴OD⊥AB,由(1)得∠PCD=∠ABD,∵tan∠PCD=,∴tan∠ABD=,∴BE=3DE,∴DE2+(3DE)2=BD2=4,∴DE=,∴BE=,设OB=OD=R,∴OE=R﹣,∵OB2=OE2+BE2,∴R2=(R﹣)2+()2,解得:R=2,∴⊙O的半径为2.18、(1)方法选择如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN=AD…请你选择一种方法证明.(2)类比探究【探究1】如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.【探究2】如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是BD=CD+2AD.(3)拓展猜想如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是BD=CD+ AD.【解答】解:(1)方法选择:∵AB=BC=AC,∴∠ACB=∠ABC=60°,如图①,在BD上截取DEMAD,连接AM,∵∠ADB=∠ACB=60°,∴△ADM是等边三角形,∴AM=AD,∵∠ABM=∠ACD,∵∠AMB=∠ADC=120°,∴△ABM≌△ACD(AAS),∴BM=CD,∴BD=BM+DM=CD+AD;(2)类比探究:如图②,∵BC是⊙O的直径,∴∠BAC=90°,∵AB=AC,∴∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,∵∠ADB=∠ACB=45°,∴△ADM是等腰直角三角形,∴AM=AD,∠AMD=45°,∴DM=AD,∴∠AMB=∠ADC=135°,∵∠ABM=∠ACD,∴△ABM≌△ACD(AAS),∴BM=CD,∴BD=BM+DM=CD+AD;【探究2】如图③,∵若BC是⊙O的直径,∠ABC=30°,∴∠BAC=90°,∠ACB=60°,过A作AM⊥AD交BD于M,∵∠ADB=∠ACB=60°,∴∠AMD=30°,∴MD=2AD,∵∠ABD=∠ACD,∠AMB=∠ADC=150°,∴△ABM∽△ACD,∴=,∴BM=CD,∴BD=BM+DM=CD+2AD;故答案为:BD=CD+2AD;(3)拓展猜想:BD=BM+DM=CD+AD;理由:如图④,∵若BC是⊙O的直径,∴∠BAC=90°,过A作AM⊥AD交BD于M,∴∠MAD=90°,∴∠BAM=∠DAC,∴△ABM∽△ACD,∴=,∴BM=CD,∵∠ADB=∠ACB,∠BAC=∠NAD=90°,∴△ADM∽△ACB,∴==,∴DM=AD,∴BD=BM+DM=CD+AD.故答案为:BD=CD+AD。
2021年九年级数学中考一轮复习知识点中考真题演练27:圆(附答案)

2021年九年级数学中考一轮复习知识点中考真题演练27:圆(附答案)2021年九年级数学中考一轮复习知识点中考真题演练:圆(附答案)1.在平面直角坐标系xOy中,直线l经过点A(﹣3,0),点B (0,),点P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P 沿x轴向左平移,平移后得到⊙P′(点P 的对应点为点P′),当⊙P′与直线l相交时,横坐标为整数的点P′共有()A.1个B.2个C.3个D.4个2.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是()A.B.C.D.3.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是()A.2B.2C.2D.44.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是()A.10°B.20°C.30°D.40°5.如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是()A.125°B.130°C.135°D.140°6.如图,点A,B的坐标分别为A(2,0),B(0,2),点C 为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为()A.+1B.+C.2+1D.2﹣7.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为()A.4B.4C.D.28.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是()A.65°B.60°C.58°D.50°9.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为()A.2πB.4πC.D.π10.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM 中有一个角是30°,OM =2,则弦AB的长为.11.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2=°.12.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD =50°,则∠ADB =.13.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP=.14.有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN=4,E为MN的中点,点D到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为.15.如图,⊙O是△ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则DE的长是.16.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP 的长为.17.如图,已知直线y=﹣x+4与x、y轴交于A、B两点,⊙O 的半径为1,P为AB上一动点,PQ切⊙O于Q点.当线段PQ长取最小值时,直线PQ交y轴于M点,a为过点M的一条直线,则点P 到直线a的距离的最大值为.18.如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P 是线段AD上一动点,当半径为6的⊙P与△ABC的一边相切时,AP的长为.19.如图所示的网格由边长为1个单位长度的小正方形组成,点A、B、C在直角坐标系中的坐标分别为(3,6),(﹣3,3),(7,﹣2),则△ABC内心的坐标为.20.如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC 于点E,F是OE上的一点,使CF∥BD.(1)求证:BE=CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.21.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.22.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:(1)=;(2)AE=CE.23.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.(1)求证:△BFG≌△CDG;(2)若AD=BE=2,求BF的长.24.如图,在⊙O中,点P为的中点,弦AD、PC互相垂直,垂足为M,BC分别与AD、PD相交于点E、N,连接BD、MN.(1)求证:N为BE的中点.(2)若⊙O的半径为8,的度数为90°,求线段MN的长.25.如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是上一点,∠ADC=∠G.(1)求证:∠1=∠2.(2)点C关于DG的对称点为F,连结CF.当点F落在直径AB 上时,CF=10,tan∠1=,求⊙O的半径.26.如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC.(1)求证:△ABC是等边三角形;(2)过点B作BE∥CD交DA的延长线于点E,若AD=2,DC=3,求△BDE的面积.27.如图,四边形ABCD内接于⊙O,AC与BD为对角线,∠BCA=∠BAD,过点A作AE ∥BC交CD的延长线于点E.(1)求证:EC=AC.(2)若cos∠ADB=,BC=10,求DE的长.28.如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE 并延长交AB于点G,连结CD,CF.(1)求证:四边形DCFG是平行四边形.(2)当BE=4,CD=AB时,求⊙O的直径长.参考答案1.解:如图所示,∵点P的坐标为(1,0),⊙P与y轴相切于点O,∴⊙P的半径是1,若⊙P与AB相切时,设切点为D,由点A(﹣3,0),点B (0,),∴OA=3,OB=,由勾股定理得:AB=2,∠DAM=30°,设平移后圆与直线AB第一次相切时圆心为M(即对应的P′),∴MD⊥AB,MD=1,又因为∠DAM=30°,∴AM=2,M点的坐标为(﹣1,0),即对应的P′点的坐标为(﹣1,0),同理可得圆与直线第二次相切时圆心N的坐标为(﹣5,0),所以当⊙P′与直线l相交时,横坐标为整数的点P′的横坐标可以是﹣2,﹣3,﹣4共三个.故选:C.2.解:∵AB=4,AC=2,∴S1+S3=2π,S2+S4=,∵S 1﹣S2=,∴(S1+S3)﹣(S2+S4)=(S1﹣S2)+(S3﹣S4)=π∴S3﹣S4=π,故选:D.3.解:过点O作OF⊥CD于点F,OG⊥AB于G,连接OB、OD、OE,如图所示:则DF=CF,AG=BG=AB=3,∴EG=AG﹣AE=2,在Rt△BOG中,OG===2,∴EG=OG,∴△EOG是等腰直角三角形,∴∠OEG=45°,OE=OG=2,∵∠DEB=75°,∴∠OEF=30°,∴OF=OE=,在Rt△ODF中,DF===,∴CD=2DF=2;故选:C.4.解:连接OD、OE,∵OC=OA,∴△OAC是等腰三角形,∵点D为弦AC的中点,∴∠DOC=40°,∠BOC=100°,设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,∵OC=OE,∠COE=100°﹣x,∴∠OEC=∠OCE=40°+x,∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,∴∠OED<20°+x,∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,∵∠CED<∠ABC=40°,∴20°<∠CED<40°故选:C.5.解:连接OA,OB,OC,∵∠BDC=50°,∴∠BOC=2∠BDC=100°,∵,∴∠BOC=∠AOC=100°,∴∠ABC=∠AOC=50°,∴∠ADC=180°﹣∠ABC=130°.故选:B.6.解:如图,∵点C为坐标平面内一点,BC=1,∴C在⊙B上,且半径为1,取OD=OA=2,连接CD,∵AM=CM,OD=OA,∴OM是△ACD的中位线,∴OM=CD,当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM 最大,∵OB=OD=2,∠BOD=90°,∴BD=2,∴CD=2+1,∴OM=CD=,即OM的最大值为+;故选:B.7.解:连接CD,∵AB=BC,∠BAC=30°,∴∠ACB=∠BAC=30°,∴∠B=180°﹣30°﹣30°=120°,∴∠D=180°﹣∠B=60°,∵AD是直径,∴∠ACD=90°,∵∠CAD=30°,AD=8,∴CD=AD=4,∴AC===4,故选:B.8.解:如图,连接OE,OF.∵⊙O是△ABC的内切圆,E,F是切点,∴OE⊥AB,OF⊥BC,∴∠OEB=∠OFB=90°,∵△ABC是等边三角形,∴∠B=60°,∴∠EOF=120°,∴∠EPF=∠EOF=60°,故选:B.9.解:∵∠AOC:∠AOD:∠DOB=2:7:11,∠AOD+∠DOB =180°,∴∠AOD=×180°=70°,∠DOB=110°,∠COA=20°,∴∠COD=∠COA+∠AOD=90°,∵OD=OC,CD=4,∴2OD2=42,∴OD=2,∴的长是==,故选:D.10.解:∵OM⊥AB,∴AM=BM,若∠OAM=30°,则tan∠OAM=,∴AM=6,∴AB=2AM=12;若∠AOM=30°,则tan∠AOM=,∴AM=2,故答案为:12或4.11.解:如图,连接AD.∵AB是直径,∴∠ADB=90°,∵∠1=∠ADE,∴∠1+∠2=90°,∵∠1=55°,∴∠2=35°,故答案为35.12.解:∵=,∠CAD=30°,∴∠CAD=∠CAB=30°,∴∠DBC=∠DAC=30°,∵∠ACD=50°,∴∠ADB=∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.故答案为:70°.13.解:根据相交弦定理,得:AP?PB=CP?DP∵AB=11∴AP(11﹣AP)=CP?DP∴AP2﹣11AP+18=0∴AP=2或9.14.解:如图,连接BE,BD.由题意BD==2,∵∠MBN=90°,MN=4,EM=NE,∴BE=MN=2,∴点E的运动轨迹是以B为圆心,2为半径的弧,∴当点E落在线段BD上时,DE的值最小,∴DE的最小值为2﹣2.(也可以用DE≥BD﹣BE,即DE≥2﹣2确定最小值)故答案为2﹣2.15.解:连结OB,OC,OA,过O点作OF⊥BC于F,作OG⊥AE于G,∵⊙O是△ABC的外接圆,∠BAC=45°,∴∠BOC=90°,∵BD=4,CD=1,∴BC=4+1=5,∴OB=OC=,∴OA=,OF=BF=,∴DF=BD﹣BF=,∴OG=,GD=,在Rt△AGO中,AG==,∴GE=,∴DE=GE﹣GD=.16.解:∵直线a⊥b,O为直线b上一动点,∴⊙O与直线a相切时,切点为H,∴OH=1cm,当点O在点H的左侧,⊙O与直线a相切时,如图1所示:OP=PH﹣OH=4﹣1=3(cm);当点O在点H的右侧,⊙O与直线a相切时,如图2所示:OP=PH+OH=4+1=5(cm);∴⊙O与直线a相切,OP的长为3cm或5cm,故答案为:3cm或5cm.17.解:如图,在直线y=﹣x+4上,x=0时,y=4,当y=0时,x=,∴OB=4,OA=,∴tan∠OBA==,∴∠OBA=30°,由PQ切⊙O于Q点可知:OQ⊥PQ,∴PQ=,由于OQ=1,因此当OP最小时PQ长取最小值,此时OP⊥AB,∴OP=OB=2,此时PQ==,BP==2,∴OQ=OP,即∠OPQ=30°,若使点P到直线a的距离最大,则最大值为PM,且M位于x轴下方,过点P作PE⊥y轴于点E,∴EP=BP=,∴BE==3,∴OE=4﹣3=1,∵OE=OP,∴∠OPE=30°,∴∠EPM=30°+30°=60°,。
2022-2023 数学浙教版新中考 考点23圆的有关性质(解析版)

考点23圆的有关性质考点总结1.圆的有关概念(1)圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆,定点叫做圆心,定长叫做圆的半径.以点O为圆心的圆,记做⊙O.(2)弧和弦:圆上任意两点间的部分叫做圆弧,简称弧.连结圆上任意两点的线段叫做弦.经过圆心的弦叫做直径,直径是圆中最长的弦.(3)与圆有关的角:①圆心角:顶点在圆心的角叫做圆心角,圆心角的度数等于它所对的弧的度数.②圆周角:顶点在圆上,两边分别和圆相交的角叫做圆周角.圆周角的度数等于它所对弧上的圆心角度数的一半.(4)三角形的外心:三角形外接圆的圆心叫做三角形的外心.外心也是三角形三边中垂线的交点.(5)圆的内接四边形:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.2.圆的有关性质:(1)圆是轴对称图形,其对称轴是任意一条过圆心的直线.圆是中心对称图形,对称中心为圆心,圆绕着它的圆心旋转任意一个角度都能和原来的圆重合.(2)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.推论2:平分弧的直径垂直平分弧所对的弦.(3)在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各组量都相等.(4)圆心角与圆周角的关系:一条弧所对的圆周角等于它所对的圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.(5)确定圆的条件:①已知圆心、半径;②已知直径;③不在同一条直线上的三点.真题演练一、单选题1.(2021·浙江衢州·中考真题)已知扇形的半径为6,圆心角为150︒.则它的面积是( )A .32π B .3π C .5π D .15π【答案】D【分析】 已知扇形的半径和圆心角度数求扇形的面积,选择公式2360n R S π=直接计算即可. 【详解】 解:2150615360S ππ⨯==. 故选:D2.(2021·浙江嘉兴·中考真题)如图,在ABC ∆中,90BAC ∠=︒,AB =AC =5,点D 在AC 上,且2AD =,点E 是AB 上的动点,连结DE ,点F ,G 分别是BC ,DE 的中点,连接AG ,FG ,当AG =FG 时,线段DE 长为( )A B C D .4【答案】A【分析】连接DF ,EF ,过点F 作FN ⊥AC ,FM ⊥AB ,结合直角三角形斜边中线等于斜边的一半求得点A ,D ,F ,E 四点共圆,⊥DFE =90°,然后根据勾股定理及正方形的判定和性质求得AE 的长度,从而求解.【详解】解:连接DF ,EF ,过点F 作FN ⊥AC ,FM ⊥AB⊥在ABC ∆中,90BAC ∠=︒,点G 是DE 的中点,⊥AG =DG =EG又⊥AG =FG⊥点A ,D ,F ,E 四点共圆,且DE 是圆的直径⊥⊥DFE =90°⊥在Rt ⊥ABC 中,AB =AC =5,点F 是BC 的中点,⊥CF =BF =122BC =,FN =FM =52 又⊥FN ⊥AC ,FM ⊥AB ,90BAC ∠=︒⊥四边形NAMF 是正方形⊥AN =AM =FN =52又⊥90NFD DFM ∠+∠=︒,90DFM MFE ∠+∠=︒⊥NFD MFE ∠=∠⊥⊥NFD ⊥⊥MFE⊥ME =DN =AN -AD =12⊥AE =AM +ME =3⊥在Rt ⊥DAE 中,DE故选:A .3.(2021·浙江·中考真题)如图,已知点O 是ABC 的外心,∠40A =︒,连结BO ,CO ,则BOC ∠的度数是( ).A .60︒B .70︒C .80︒D .90︒【答案】C【分析】 结合题意,根据三角形外接圆的性质,作O ;再根据圆周角和圆心角的性质分析,即可得到答案.【详解】 ABC 的外接圆如下图⊥⊥40A =︒⊥280BOC A ∠=∠=︒故选:C .4.(2021·浙江·中考真题)如图,已知在矩形ABCD 中,1,AB BC ==P 是AD 边上的一个动点,连结BP ,点C 关于直线BP 的对称点为1C ,当点P 运动时,点1C 也随之运动.若点P 从点A 运动到点D ,则线段1CC 扫过的区域的面积是( )A .πB .π+CD .2π【答案】B【分析】先判断出点Q 在以BC 为直径的圆弧上运动,再判断出点C 1在以B 为圆心,BC 为直径的圆弧上运动,找到当点P 与点A 重合时,点P 与点D 重合时,点C 1运动的位置,利用扇形的面积公式及三角形的面积公式求解即可.【详解】解:设BP 与CC 1相交于Q ,则⊥BQC =90°,⊥当点P 在线段AD 运动时,点Q 在以BC 为直径的圆弧上运动,延长CB 到E ,使BE =BC ,连接EC ,⊥C 、C 1关于PB 对称,⊥⊥EC 1C =⊥BQC =90°,⊥点C 1在以B 为圆心,BC 为直径的圆弧上运动,当点P 与点A 重合时,点C 1与点E 重合,当点P 与点D 重合时,点C 1与点F 重合,此时,tanPC AB PBC BC BC ∠=== ⊥⊥PBC =30°,⊥⊥FBP =⊥PBC =30°,CQ =12BC =BQ 32=,⊥⊥FBE =180°-30°-30°=120°,11322BCF S CC BQ =⨯==线段1CC 扫过的区域的面积是2120360BCF S ππ⨯+= 故选:B . 5.(2021·浙江丽水·中考真题)如图,AB 是O 的直径,弦CD OA ⊥于点E ,连结,OC OD .若O 的半径为,m AOD α∠=∠,则下列结论一定成立的是( )A .tan OE m α=⋅B .2sin CD m α=⋅C .cos AE m α=⋅D .2sin COD S m α=⋅【答案】B【分析】 根据垂径定理、锐角三角函数的定义进行判断即可解答.【详解】解:⊥AB 是O 的直径,弦CD OA ⊥于点E , ⊥12DE CD = 在Rt EDO ∆中,OD m =,AOD α∠=∠ ⊥tan =DE OE α ⊥=tan 2tan DE CD OE αα=,故选项A 错误,不符合题意; 又sin DE OD α=⊥sin DE OD α=⊥22sin CD DE m α==,故选项B 正确,符合题意; 又cos OE ODα= ⊥cos cos OE OD m αα==⊥AO DO m ==⊥cos AE AO OE m m α=-=-,故选项C 错误,不符合题意;⊥2sin CD m α=,cos OE m α=⊥2112sin cos sin cos 22COD S CD OE m m m αααα∆=⨯=⨯⨯=,故选项D 错误,不符合题意;故选B .6.(2021·浙江金华·中考真题)如图,在Rt ABC 中,90ACB ∠=︒,以该三角形的三条边为边向形外作正方形,正方形的顶点,,,,,E F G H M N 都在同一个圆上.记该圆面积为1S ,ABC 面积为2S ,则12S S 的值是( )A .52πB .3πC .5πD .112π 【答案】C【分析】先确定圆的圆心在直角三角形斜边的中点,然后利用全等三角形的判定和性质确定⊥ABC 是等腰直角三角形,再根据直角三角形斜边中线的性质得到2214S AB =,再由勾股定理解得2254OF AB =,解得2154S AB π=⋅,据此解题即可. 【详解】 解:如图所示,正方形的顶点,,,,,E F G H M N 都在同一个圆上,∴圆心O 在线段,EF MN 的中垂线的交点上,即在Rt ABC 斜边AB 的中点,且AC =MC ,BC =CG ,⊥AG =AC +CG =AC +BC ,BM =BC +CM =BC +AC ,⊥AG =BM ,又⊥OG =OM ,OA =OB ,⊥⊥AOG ⊥⊥BOM ,⊥⊥CAB =⊥CBA ,⊥⊥ACB =90°,⊥⊥CAB =⊥CBA =45°,12OC AB ∴=, 2211112224S AB OC AB AB AB ∴=⋅=⋅= 22222215()24OF AO AF AB AB AB =+=+= 22154S OF AB ππ∴==⋅, 212254514AB S S AB ππ⋅∴==.故选:C .7.(2021·浙江绍兴·中考真题)如图,正方形ABCD 内接于O ,点P 在AB 上,则P ∠的度数为( )A .30B .45︒C .60︒D .90︒【答案】B【分析】 连接OB ,OC ,由正方形ABCD 的性质得90BOC ∠=°,再根据圆周角与圆心角的关系即可得出结论.【详解】解:连接OB ,OC ,如图,⊥正方形ABCD 内接于O ,⊥90BOC ∠=° ⊥11904522BPC BOC ∠=∠=⨯︒=︒ 故选:B .8.(2021·浙江嘉兴·中考真题)已知平面内有O 和点A ,B ,若O 半径为2cm ,线段3cm OA =,2cm OB =,则直线AB 与O 的位置关系为( )A .相离B .相交C .相切D .相交或相切【答案】D【分析】根据点与圆的位置关系的判定方法进行判断.【详解】解:⊥⊥O 的半径为2cm ,线段OA =3cm ,线段OB =2cm ,即点A 到圆心O 的距离大于圆的半径,点B 到圆心O 的距离等于圆的半径, ⊥点A 在⊥O 外.点B 在⊥O 上,⊥直线AB 与⊥O 的位置关系为相交或相切,故选:D .9.(2021·浙江·杭州市丰潭中学二模)如图,已知平面直角坐标系中,点A ,B 坐标分别为A (4,0),B (﹣6,0).点C 是y 轴正半轴上的一点,且满足∠ACB =45°,圆圆得到了以下4个结论:∠∠ABC 的外接圆的圆心在OC 上;∠∠ABC =60°;∠∠ABC的外接圆的半径等于∠OC =12.其中正确的是( )A .∠∠B .∠∠C .∠∠D .∠∠【答案】C【分析】 如图,作出ABC 的外接圆,以AB 为斜边在x 轴上方作等腰Rt ABE △,过点E 作ED x ⊥轴于D ,连接EC ,过点E 作EF y ⊥轴于F ,由圆心必然在弦的垂直平分线上可判断⊥;再证明E 为ABC 外接圆圆心,求出半径,可判断⊥;再在ECF △中由勾股定理求出CF ,可求得OC 和1tan 2OC ABC OB ∠==,即可判断⊥⊥. 【详解】解:如图,作出ABC 的外接圆,以AB 为斜边在x 轴上方作等腰Rt ABE △, 过点E 作ED x ⊥轴于D ,连接EC ,过点E 作EF y ⊥轴于F ,⊥ABC 的外接圆的圆心必在弦AB 的垂直平分线上,⊥圆心肯定不在OC 上,故⊥错误;⊥⊥ACB =45°,⊥由圆周角定理得:AB 所对的圆心角必为90°,⊥EB =EA ,⊥在弦AB 的垂直平分线上,⊥⊥AEB =90°,⊥E 必为圆心,即AE 、BE 为半径, ⊥AE =⊥正确;⊥BD =5,OB =6,⊥OD =1,⊥⊥EDO =⊥DOF =⊥OFE =90°,⊥OD =EF =1,ED =FO =5,⊥7CF ==,⊥OC =OF +FC =12,故⊥正确;⊥1 tan2OCABCOB∠==,⊥⊥ABC≠60°,故⊥错误;故选:C.10.(2021·浙江·杭州市丰潭中学二模)如图,点A的坐标为(﹣3,2),∠A的半径为1,P为坐标轴上一动点,PQ切∠A于点Q,在所有P点中,使得PQ长最小时,点P 的坐标为()A.(0,2)B.(0,3)C.(﹣2,0)D.(﹣3,0)【答案】D【分析】连接AQ、P A,如图,利用切线的性质得到⊥AQP=90°,再根据勾股定理得到PQ=AP⊥x轴时,AP的长度最小,利用垂线段最短可确定P点坐标.【详解】解:连接AQ、P A,如图,⊥PQ切⊥A于点Q,⊥AQ⊥PQ,⊥⊥AQP=90°,⊥PQ当AP的长度最小时,PQ的长度最小,⊥AP⊥x轴时,AP的长度最小,⊥AP⊥x轴时,PQ的长度最小,二、填空题11.(2021·浙江杭州·中考真题)如图,已知O 的半径为1,点P 是O 外一点,且2OP =.若PT 是O 的切线,T 为切点,连接OT ,则PT =_____.【分析】根据圆的切线的性质,得90OTP ∠=︒,根据圆的性质,得1OT =,再通过勾股定理计算,即可得到答案.【详解】⊥PT 是O 的切线,T 为切点⊥90OTP ∠=︒⊥PT⊥O 的半径为1⊥1OT =⊥PT12.(2021·浙江台州·中考真题)如图,将线段AB 绕点A 顺时针旋转30°,得到线段AC .若AB =12,则点B 经过的路径BC 长度为_____.(结果保留π)直接利用弧长公式即可求解.【详解】 解:30122180BC l ππ⋅==, 故答案为:2π.13.(2021·浙江温州·中考真题)图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的d 的值为______;记图1中小正方形的中心为点A ,B ,C ,图2中的对应点为点A ',B ',C '.以大正方形的中心O 为圆心作圆,则当点A ',B ',C '在圆内或圆上时,圆的最小面积为______.【答案】6- (16π-【分析】(1)先求出剪拼后大正方形的面积,得到其边长,再结合图2,求出图1中长方形的长边除去长为d 部分的线段后,剩下的线段长刚好为大正方形的边长,最后用图1中的长方形的长减去图2中大正方形的边长即可完成求解;(2)结合两图分别求出对应线段的长,通过作辅助线构造直角三角形,利用勾股定理求出O 点到'B 、'A 、'C 之间的距离即可确定最小圆的半径,即可完成求解.【详解】解:⊥图1是邻边长为2和6的矩形,它由三个小正方形组成,⊥每个小正方形边长为2,图1和图2中整个图形的面积为2612=⨯,所以图2中正方形的边长''M N =如下图3所示;分别连接'OB 、'OA 、'OC ,并分别过点'B 、'A 、'C 向大正方形的对边作垂线,得到如图所示辅助线,综合两图可知,'1LA =,LJ ='1MA =,O⊥'1JA =,1OJ =,⊥)'1OA ===综合两图可知:'1B E =,6'32B D d =-=,DF =⊥()''33B F DF B D =-==1OF =,⊥'OB =;继续综合两图可知:''1C H C G ==,⊥'1C I OI =,⊥'OC =⊥2816=-<-⊥'B 距离O 点最远,⊥⊥圆的面积为(16π-;故答案为:6-(16π-.14.(2021·浙江宁波·中考真题)抖空竹在我国有着悠久的历史,是国家级的非物质文P .若120P ∠=︒,O 的半径为6cm ,则图中CD 的长为________cm .(结果保留π)【答案】2π【分析】连接OC 、OD ,利用切线的性质得到90OCP ODP ∠=∠=︒,根据四边形的内角和求得60COD ∠=︒,再利用弧长公式求得答案.【详解】连接OC 、OD ,⊥,AC BD 分别与O 相切于点C ,D ,⊥90OCP ODP ∠=∠=︒,⊥120P ∠=︒,360OCP ODP P COD ∠+∠+∠+∠=︒,⊥60COD ∠=︒,⊥CD 的长=6062180(cm ),故答案为:2π..15.(2021·浙江温州·中考真题)如图,O 与OAB 的边AB 相切,切点为B .将OAB 绕点B 按顺时针方向旋转得到O A B '''△,使点O '落在O 上,边A B '交线段AO 于点C .若25A '∠=︒,则OCB ∠=______度.【答案】85AB 相切,可求⊥CBO ==30°,利用三角形内角和公式即可求解.【详解】解:连结OO′,⊥将OAB 绕点B 按顺时针方向旋转得到O A B '''△,⊥BO′=BO =OO′,⊥⊥BOO′为等边三角形,⊥⊥OBO′=60°,⊥O 与OAB 的边AB 相切,⊥⊥OBA =⊥O′BA′=90°,⊥⊥CBO =90°-⊥OBO′=90°-60°=30°,⊥⊥A′=25°⊥⊥A′O′B =90°-⊥A′=90°-25°=65°⊥⊥AOB =⊥A′O′B =65°,⊥⊥OCB =180°-⊥COB -⊥OBC =180°-65°-30°=85°.故答案为85.三、解答题16.(2021·浙江衢州·中考真题)如图,在ABC 中,CA CB =,BC 与A 相切于点D ,过点A 作AC 的垂线交CB 的延长线于点E ,交A 于点F ,连结BF .(1)求证:BF 是A 的切线.【答案】(1)见解析;(2)3【分析】(1)连接AD ,根据题意证明ABF ABD △△≌,即可证明BF 是A 的切线;(2)根据题意即(1)的结论可得BEF CEA △∽△,列比例求出FB 的长,根据勾股定理求EF 即可.【详解】(1)证明如图,连接AD ,CA CB =,CAB ABC ∴∠=∠,AE AC ⊥,90CAB EAB ∴∠+∠=︒又A 切BC 于点D ,=90ADB ∴∠︒,90ABD BAD ∴∠+∠=︒,BAE BAD ∴∠=∠.又AB AB ,AF AD =,()ABF ABD SAS ∴△△≌,90AFB ADB ∴∠=∠=︒,BF ∴是A 的切线.(2)由(1)得:90AFB FAC ∠=∠=︒,//BF AC ∴,BEF CEA ∴△∽△,BE BF CE CA∴=, 20CB CA ==,5BE =,∴=.EF317.(2021·浙江台州·中考真题)如图,BD是半径为3的∠O的一条弦,BD=点A是∠O上的一个动点(不与点B,D重合),以A,B,D为顶点作平行四边形ABCD.(1)如图2,若点A是劣弧BD的中点.∠求证:平行四边形ABCD是菱形;∠求平行四边形ABCD的面积.(2)若点A运动到优弧BD上,且平行四边形ABCD有一边与∠O相切.∠求AB的长;∠直接写出平行四边形ABCD对角线所夹锐角的正切值.【答案】⊥证明见解析;⊥(2)⊥AB【分析】(1)⊥利用等弧所对的弦相等可得AD AB=,根据一组邻边相等的平行四边形是菱形可得证;⊥连接AO,交BD于点E,连接OD,根据垂径定理可得DE BE==用勾股定理求出OE的长,即可求解;(2)⊥分情况讨论当CD与O相切时、当BC与O相切时,利用垂径定理即可求解;⊥根据等面积法求出AH的长度,利用勾股定理求出DH的长度,根据正切的定义即可求解.【详解】解:(1)⊥⊥点A是劣弧BD的中点,⊥四边形ABCD 是平行四边形,⊥平行四边形ABCD 是菱形;⊥连接AO ,交BD 于点E ,连接OD ,,⊥点A 是劣弧BD 的中点,OA 为半径,⊥OA BD ⊥,OA 平分BD , ⊥DE BE ==⊥平行四边形ABCD 是菱形,⊥E 为两对角线的交点,在Rt ODE △中,1OE ,⊥2AE =,⊥122ABCD S BD AE =⋅⨯= (2)⊥如图,当CD 与O 相切时,连接DO 并延长,交AB 于点F ,⊥CD 与O 相切,⊥DF CD ⊥,⊥四边形ABCD 是平行四边形,⊥//AB CD ,⊥DF AB ⊥,在Rt BDF △中,()2222323BF BD DF OF =-=-+, 在Rt BOF △中,22229BF BO OF OF =-=-,⊥()223239OF OF -+=-,解得73OF =,⊥BF =⊥2AB BF = 如图,当BC 与O 相切时,连接BO 并延长,交AD 于点G ,同理可得AG DG =73OG =,所以AB综上所述,AB ⊥过点A 作AH BD ⊥,,由(2)得:7163,33BD AD BG ==+= 根据等面积法可得1122BD AH AD BG ⋅=⋅, 解得329AH =,在在Rt ADH 中,DH ==⊥HI =⊥tan AH AIH HI ∠== 18.(2021·浙江金华·中考真题)在扇形AOB 中,半径6OA =,点P 在OA 上,连结PB ,将OBP 沿PB 折叠得到O BP '.(1)如图1,若75O ∠=︒,且BO '与AB 所在的圆相切于点B .∠求APO ∠'的度数.∠求AP 的长.(2)如图2,BO '与AB 相交于点D ,若点D 为AB 的中点,且//PD OB ,求AB 的长.【答案】(1)⊥60°;⊥6-(2)125π 【分析】(1)根据图像折叠的性质,确定角之间的关系,通过已知的角度来间接求所求角的角度;求AP 的长,先连接'OO ,先在Rt OBQ △中,求出OQ ;再在Rt OPQ 中,求出OP 即可得到答案;(2)要求AB 的长,扇形的半径已知,就转化成求AOB ∠的度数,连接'OO ,通过条件找到角之间的等量关系,再根据三角形内角和为180︒,建立等式求出AOB ∠,最后利用弧长的计算公式进行计算.【详解】解:(1)⊥如图1,'BO 为圆的切线'90OBO ∴∠=︒.由题意可得,'45O BP OBP ∠=∠=︒,'O PB OPB ∠=∠.180180754560OPB BOP OBP ∴∠=︒-∠-∠=︒-︒-︒=︒ '60O PB OPB ∴∠=∠=︒'60APO ∴∠=︒,⊥如图1,连结'OO ,交BP 于点Q .则有'BP OO ⊥.在Rt OBQ △中,sin 45OQ OB =⨯︒=在Rt OPQ △中,sin 60OQ OP ==︒6AP OA OP ∴=-=-(2)如图2.连结OD .设1a ∠=.⊥点D 为AB 的中点.BD AD ∴=21a ∴∠=∠=//PD OB321a ∴∠=∠=∠=.PD PO ∴=由题意可得,','PO PO O BOP =∠=∠.'PD PO ∴=''2PDO O BOP a ∴∠=∠=∠=又//,''2PD OB OBO PDO a ∴∠=∠=,4'2OB OD OBO a =∴∠=∠=43'180PDO ∠+∠+∠=︒,22180a a a ∴++=︒,解得36a =︒. 72AOB ∴∠=︒726121801805n R AB πππ⨯∴===.。
2021年九年级数学中考复习专题之圆:切线长定理综合运用(一)
2021年九年级数学中考复习专题之圆:切线长定理综合运用(一)一.选择题1.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为()A.12 B.6 C.8 D.42.如图,△MBC中,∠B=90°,∠C=60°,MB=,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为()A.B.C.2 D.33.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确()A.AB>CE>CD B.AB=CE>CD C.AB>CD>CE D.AB=CD=CE4.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°5.如图,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC、CD、DA相切,若BC=2,DA=3,则AB的长()A.等于4 B.等于5 C.等于6 D.不能确定6.如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是()A.4 B.8 C.4D.87.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()A.PA=PB B.∠APO=20°C.∠OBP=70°D.∠AOP=70°8.如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7 B.8 C.9 D.169.如图,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若AB=10,BC=4,则AD的长()A.4 B.5 C.6 D.710.已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:①S四边形ABCD=AB•CD;②AD=AB;③AD=ON;④AB为过O、C、D三点的圆的切线.其中正确的个数有()A.1个B.2个C.3个D.4个二.填空题11.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是.12.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是cm.13.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,则∠CPD=.14.如图,已知:PA、PB、EF分别切⊙O于A、B、D,若PA=10cm,那么△PEF周长是cm.若∠P=35°,那么∠AOB=,∠EOF=.15.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E,若△PDE的周长是10,则PA=.三.解答题16.已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求△PEF的周长.17.如图,AC是⊙O的直径,∠ACB=60°,连接AB,分别过A、B作圆O的切线,两切线交于点P,若已知⊙O的半径为1,求△PAB的周长.18.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.19.如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6.(1)求边AD、BC的长;(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.20.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E.(1)若PA=4,求△PED的周长;(2)若∠P=40°,求∠AFB的度数.参考答案一.选择题1.解:∵PA,PB分别和⊙O切于A,B两点,∴PA=PB,∵DE是⊙O的切线,∴DA=DC,EB=EC,∵△PDE的周长为12,即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,∴PA=6.故选:B.2.解:在直角△BCM中,tan60°==,得到BC==2,∵AB为圆O的直径,且AB⊥BC,∴BC为圆O的切线,又CD也为圆O的切线,∴CD=BC=2.故选:C.3.解:∵∠1=60°,∠2=65°,∴∠ABC=180°﹣∠1﹣∠2=180°﹣60°﹣65°=55°,∴∠2>∠1>∠ABC,∴AB>BC>AC,∵CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,∴AC=CD,BC=CE,∴AB>CE>CD.故选:A.4.解:如图,连接OB、OC,∵AB、AC是⊙O的切线,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=130°,∵∠BOC=2∠P,∴∠BPC=65°;故选:C.5.解:如图,连接OC,OD,设⊙O的半径为r,∵BC、CD、DA与半⊙O相切,∴AD边上的高和AO边上的高都为r,∴AO=AD,同理BO=BC,∴AB=AO+BO=AD+BC=2+3=5.故选:B.6.解:∵PA,PB分别切⊙O于点A、B,∴PA=PB,又∠P=60°,∴△APB是等边三角形,∴AB=PA=8.故选:B.7.解:∵PA,PB是⊙O的切线,且∠APB=40°,∴PA=PB,∠APO=∠BPO,∠A=∠B=90°,∴∠OBP=∠OAP,∴C是错误的.故选:C.8.解:∵AB、AC、BC、DE都和⊙O相切,∴BI=BG,CI=CH,DG=DF,EF=EH.∴BG+CH=BI+CI=BC=9,∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC)=25﹣2×9=7.故选:A.9.解:连接OC,OD,设⊙O的半径为r,∵BC、CD、DA与半⊙O相切,∴AD和AO的高为r,∴AO=AD,同理BO=BC,∴AB=AO+BO=AD+BC,又知AB=10,BC=4,故知AD=6,故选:C.10.解:连接OD、AP,∵DA、DP、BC分别是圆的切线,切点分别是A、P、B,∴DA=DP,CP=CB,∠A=90°=∠B=∠DPO,∴AD+BC=DP+CP=CD,∴S四边形ABCD=(AD+BC)•AB=AB•CD,∴①正确;∵AD=DP<OD,∵四边形ODPN是平行四边形,得到OD=NP<BP<AB,则AD<AB,∴②错误;∵AB是圆的直径,∴∠APB=90°,∵DP=AD,AO=OP,∴D、O在AP的垂直平分线上,∴OD⊥AP,∵∠DPO=∠APB=90°,∴∠OPB=∠DPA=∠DOP,∵OM∥CD,∴∠POM=∠DPO=90°,在△DPO和△NOP中∠PON=∠DPO,OP=OP,∠DOP=∠OPN,∴△DPO≌△NOP,∴ON=DP=AD,∴③正确;∵AP⊥OD,OA=OP,∴∠AOD=∠POD,同理∠BOC=∠POC,∴∠DOC=×180°=90°,∴△CDO的外接圆的直径是CD,∵∠A=∠B=90°,取CD的中点Q,连接OQ,∵OA=OB,∴AD∥OQ∥BC,∴∠AOQ=90°,∴④正确.故选:C.二.填空题(共5小题)11.解:如图所示:连接圆心与各切点,在Rt△DEO和Rt△DFO中,∴Rt△DEO≌Rt△DFO(HL),∴∠1=∠2,同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,∴∠3=∠4,∠5=∠7,∠6=∠8,∴∠5+∠6=∠7+∠8=108°,∴2∠2+2∠3=360°﹣2×108°,∴∠2+∠3=∠DOC=72°.故答案为:72°.12.解:如图所示:菱形ABCD,对角线AC,BD,可得菱形内切圆的圆心即为对角线交点,设AB与圆相切于点E,可得OE⊥AB,∵一个菱形的周长是20cm,两对角线之比是4:3,∴AB=5cm,设BO=4x,则AO=3x,故(4x)2+(3x)2=25,解得:x=1,则AO=3,BO=4,故EO•AB=AO•BO,解得:EO=.故答案为:.13.解:∵PA=6,⊙O的半径为2,∴PB=PA﹣AB=6﹣4=2,∴OP=4,∵PC、PD切⊙O于点C、D.∴∠OPC=∠OPD,∴CO⊥PC,∴sin∠OPC==,∴∠OPC=30°,∴∠CPD=60°,故答案为:60°.14.解:∵PA、PB、EF分别切⊙O于A、B、D.∴AE=ED,DF=FR∴△PEF周长是PE+PF+EF=PE+EA+PF+FR=PA+PR=2PA=20cm;∵PA、PB、EF分别切⊙O于A、B∴∠PAO=∠PRO=90°∴∠AOB=360°=90°﹣90°﹣35°=145°;∴∠EOF=∠AOB=72.5°故答案是:20,145°,72.5°.15.解:∵DA,DC都是圆O的切线,∴DC=DA,同理EC=EB,PA=PB,∴△PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=10,∴PA=5;故答案为5.三.解答题(共5小题)16.解:∵PA、PB是⊙O的切线,切点分别是A、B,∴PA=PB=12,∵过Q点作⊙O的切线,交PA、PB于E、F点,∴EB=EQ,FQ=FA,∴△PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,=PE+EB+PF+FA=PB+PA=12+12=24,答:△PEF的周长是24.17.解:∵PA,PB是圆O的切线.∴PA=PB,∠PAB=60°∴△PAB是等边三角形.在直角△ABC中,AB=AC•sin60°=2×=∴△PAB的周长为PA+PB+AB=3.18.解:连接OC、OD.∵OA是⊙B的直径,∴∠OCA=∠ODA=90°,∴AC、AD都是⊙O的切线.∴AD=AC=5.19.解:(1)方法1:过D作DF⊥BC于F,在Rt△DFC中,DF=AB=8,FC=BC﹣AD=6,∴DC2=62+82=100,即DC=10.(1分)设AD=x,则DE=AD=x,EC=BC=x+6,∴x+(x+6)=10.∴x=2.∴AD=2,BC=2+6=8.(4分)方法2:连OD、OE、OC,由切线长定理可知∠DOC=90°,AD=DE,CB=CE,设AD=x,则BC=x+6,由射影定理可得:OE2=DE•EC.(2分)即:x(x+6)=16,解得x1=2,x2=﹣8,(舍去)∴AD=2,BC=2+6=8.(4分)(2)存在符合条件的P点.设AP=y,则BP=8﹣y,△ADP与△BCP相似,有两种情况:①△ADP∽△BCP时,∴y=;(6分)②△ADP∽△BPC时,∴y=4.(7分)故存在符合条件的点P,此时AP=或4.(8分)20.解:(1)∵DA,DC都是圆O的切线,∴DC=DA,同理EC=EB,∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B∴PA=PB,∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,即三角形PDE的周长是8;(2)连接AB,∵PA=PB,∴∠PAB=∠PBA,∵∠P=40°,∴∠PAB=∠PBA=(180﹣40)=70°,∵BF⊥PB,BF为圆直径∴∠ABF=∠PBF=90°﹣70°=20°∴∠AFB=90°﹣20°=70°.答:(1)若PA=4,△PED的周长为8;(2)若∠P=40°,∠AFB的度数为70°.。
中考数学复习《圆》经典题型及测试题(含答案)
中考数学复习《圆》经典题型及测试题(含答案)【专题分析】圆在中考中的常见考点有圆的性质及定理,圆周角定理及其推论,圆心角、圆周角、弧、弦之间的“等推”关系;切线的判定,切线的性质,切线长定理,弧长及扇形面积的计算,求阴影部分的面积等.对圆的考查在中考中以客观题为主,考查题型多样,关于圆的基本性质一般以选择题或填空题的形式进行考查,切线的判定等综合性强的问题一般以解答题的形式进行考查;圆在中考中的比重约为10%~15%.【解题方法】解决圆的有关问题常用的数学思想就是转化思想,方程思想和数形结合思想;常用的数学方法有分类讨论法,设参数法等.【知识结构】【典例精选】如图,⊙O的半径是3,点P是弦AB延长线上的一点,连结OP,若OP =4,∠APO=30°,则弦AB的长为( )A.2 5 B. 5C.213 D. 13【思路点拨】先过点O作OC⊥AP,连结OB,根据OP=4,∠APO=30°,求出OC的值,在Rt△BCO中,根据勾股定理求出BC的值,进而得出AB的值.【解析】如图,过点O作OC⊥AP于点C,连结OB,∵OP=4,∠APO=30°,∴OC=4×sin 30°=2.∵OB=3,∴BC=OB2-OC2=32-22=5,∴AB=2 5.故选A.答案:A规律方法:利用垂径定理进行证明或计算,通常是在半径、圆心距和弦的一半所组成的直角三角形中,利用勾股定理构建方程求出未知线段的长.如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )A.4 2 m B.5 m C. 30 m D.215 m【思路点拨】首先连结AO,求出AB,然后求出扇形的弧长BC,进而求出扇形围成的圆锥的底面半径,最后应用勾股定理求出圆锥的高即可.【解析】如图,连结AO,∵AB=AC,点O是BC的中点,∴AO⊥BC.又∵∠BAC=90°,∴∠ABO=∠ACO=45°,∴AB=2OB=2×(8÷2)=42(m).∴l BC=90π×42180=22π(m).∴将剪下的扇形围成的圆锥形的半径是22π÷2π=2(m).∴圆锥的高是422-22=30(m).故选C.答案:C规律方法:解决圆锥的相关问题,可以利用圆的周长等于扇形的弧长建立方程,利用方程解决问题.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心、ED 为半径作半圆,交A,B所在的直线于M,N两点,分别以MD,ND为直径作半圆,则阴影部分的面积为( )A.9 5 B.18 5 C.36 5 D.72 5【思路点拨】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN 的面积-大半圆的面积,MN为半圆的直径,从而可知∠MDN=90°,在Rt△MDN 中,由勾股定理可知MN2=MD2+DN2,从而可得到两个小半圆的面积=大半圆的面积,故此阴影部分的面积=△DMN的面积,在Rt△AED中,ED=AD2+AE2=62+32=35,所以MN=65,然后利用三角形的面积公式求解即可.【解析】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积.∵MN为大半圆的直径,∴∠MDN=90°.在Rt△MDN中,MN2=MD2+DN2,∴两个小半圆的面积和=大半圆的面积.∴阴影部分的面积=△DMN 的面积.在Rt△AED中,ED=AD2+AE2=62+32=35,∴阴影部分的面积=△DMN的面积=12MN·AD=12×65×6=18 5.故选B.答案:B规律方法:求阴影部分的面积,一般是将所求阴影部分进行分割组合,转化为规则图形的和或差.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连结CD.(1)求证:∠A=∠BCD.(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.【思路点拨】(1)根据圆周角定理可得∠ADC=90°,根据直角三角形的性质可得∠A+∠ACD=90°,再由∠DCB+∠ACD=90°,可得∠A=∠BCD;(2)当点M是BC的中点时,直线DM与⊙O相切.连结DO,证明∠ODM =90°,进而证得直线DM与⊙O相切.【自主解答】(1)证明:∵AC为直径,∴∠ADC=90°,∴∠A+∠ACD=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°,∴∠A=∠BCD.(2)解:当点M是BC的中点时,直线DM与⊙O相切.理由如下:如图,连结DO,∵DO=CO,∴∠1=∠2.∵∠BDC=90°,点M是BC的中点,∴DM=CM,∴∠4=∠3.∵∠2+∠4=90°,∴∠1+∠3=90°,∴直线DM与⊙O相切.规律方法:在判定一条直线是圆的切线时,如果这条直线和圆有公共点,常作出经过公共点的半径,证明这条直线与经过公共点的半径垂直,概括为“连半径,证垂直,得切线”.【能力评估检测】一、选择题1.如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连结BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( B )A.40° B.50° C.60° D.20°2.如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( C )A. 3 B.3 C.2 3 D.43.如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( A )A.25° B.50° C.60° D.30°4.如图,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP 的度数为( B )A.15° B.30° C.60° D.90°5.如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB长为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( D )A.6 B.7 C.8 D.96.如图,已知AB为⊙O的直径,AD切⊙O于点A,EC=CB.则下列结论中不一定正确的是( D )A.BA⊥DA B.OC∥AEC.∠COE=2∠CAE D.OD⊥AC7.如图,菱形ABCD的对角线BD,AC分别为2,23,以B为圆心的弧与AD,DC相切,则阴影部分的面积是( D )A.23-33π B.43-33πC.43-π D.23-π8.如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( B )A .13π cmB .14π cmC .15π cmD .16π cm9.如图,在矩形ABCD 中,AB =4,AD =5,AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A. 133B. 92C. 4313 D .2 5 解:如图,连接OE ,OF ,ON ,OG .∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°.∴四边形AFOE ,FBGO 都是正方形.∴AF =BF =AE =BG =2.∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG . ∴CM =5-2-MN =3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=(3-MN )2+42.∴NM =43.∴DM =3+43=133.故选A. 答案:A二、填空题10.在平面直角坐标系中,O 为坐标原点,则直线y =x +2与以O 点为圆心,1为半径的圆的位置关系为 相切.11.如图,圆内接四边形ABCD 两组对边的延长线分别相交于点E ,F ,且∠A =55°,∠E =30°,则∠F =40° .12.如图,正三角形ABC 的边长为2,点A ,B 在半径为2的圆上,点C 在圆内,将正三角形ABC 绕点A 逆时针旋转,当点C 第一次落在圆上时,点C 运动的路线长为 .【解析】设点C 落在圆上的点为C ′,连结OA ,OB ,OC ′,则OA =OB = 2.又∵AB =2,∴OA 2+OB 2=AB 2,∴∠AOB =90°,∴∠OAB =45°,同理∠OAC ′=45°,∴∠BAC ′=90°.∵△ABC 为等边三角形,∴∠CAB =60°,∴∠CAC ′=30°,∴点C 运动的路线长为30π×2180=π3.故答案为π3. 答案:π3 13.如图,在△ABC 中,∠BAC =90°,AB =5 cm ,AC =2 cm ,将△ABC 绕顶点C按顺时针方向旋转45°至△A 1B 1C 的位置,则线段AB 扫过区域(图中的阴影部分)的面积为 cm 2.【解析】在Rt△ABC 中,BC =AC 2+AB 2=29(cm),S 扇形BCB 1=45π×292360=29π8(cm 2),S △CB 1A 1=12×5×2=5(cm 2),S 扇形CAA 1=45π×22360=π2(cm 2),故S 阴影部分=S 扇形BCB 1+S △CB 1A 1-S △ABC -S 扇形CAA 1=29π8+5-5-π2=25π8(cm 2). 答案:25π8三、解答题14.如图,AB 是⊙O 的直径,BC 切⊙O于点B ,OC 平行于弦AD ,过点D 作DE ⊥AB 于点E ,连结AC ,与DE 交于点P .求证:(1)PE =PD ;(2)AC ·PD =AP ·BC .证明:(1)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴EP BC =AE AB .又∵AD ∥OC ,∴∠DAE =∠COB ,∴△AED ∽△OBC ,∴ED BC =AE OB =AE 12AB =2AE AB .∴ED =2EP ,∴PE =PD . (2)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴AP AC =PE BC .∵PE =PD ,∴AP AC =PD BC,∴AC ·PD =AP ·BC . 15.如图,在△OAB 中,OA =OB =10,∠AOB =80°,以点O 为圆心,6为半径的优弧MN 分别交OA ,OB 于点M ,N .(1)点P 在右半弧上(∠BOP 是锐角),将OP 绕点O 逆时针旋转80°得OP ′,求证:AP =BP ′;(2)点T 在左半弧上,若AT 与弧相切,求点T 到OA 的距离;(3)设点Q 在优弧MN 上,当△AOQ 的面积最大时,直接写出∠BOQ 的度数.(1)证明:如图,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,∠BOP′=∠POP′+∠BOP=80°+∠BOP,∴∠AOP=∠BOP′.又∵OA=OB,OP=OP′,∴△AOP≌△BOP′.∴AP=BP′.(2)解:如图,连结OT,过点T作TH⊥OA于点H.∵AT与MN相切,∴∠ATO=90°.∴AT=OA2-OT2=102-62=8.∵12OA·TH=12AT·OT,即12×10×TH=12×8×6,∴TH=245,即点T到OA的距离为245.(3)10°,170°.16.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°.①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).解:(1)直线BC与⊙O相切.理由如下:如图,连结OD,∵OA=OD,∴∠OAD=∠ODA,∵∠BAC的角平分线AD交BC边于点D,∴∠CAD=∠OAD,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.∴直线BC与⊙O相切.(2)①设OA=OD=r,∵在Rt△BDO中,∠B=30°,∴OB=2r,∴在Rt△ACB中,∠B=30°,∴AB=2AC=6,∴3r=6,解得r=2.②∵在Rt△ODB中,∠B=30°,∴∠BOD=60°,∴S扇形ODE=60π×22360=23π,∴阴影部分面积为S△BOD-S扇形ODE=23-23π.11。
浙教版2021年中考数学总复习《图形与坐标》(含答案)

浙教版2021年中考数学总复习《图形与坐标》一、选择题1.如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)2.如图,半径为1圆,在x轴上从原点O开始向右滚动一周后,落定点M的坐标为( )A.(0,2π)B.(2π,0)C.(π,0)D.(0,π)3.在平面直角坐标系中,点(-1,m2+1)一定在( )A.第一象限B.第二象限C.第三象限D.第四象限4.在平面直角坐标系中,点P(m-3,4-2m)不可能在( )A.第一象限B.第二象限C.第三象限D.第四象限5.在坐标平面内,若点P(x﹣3,x+2)在第二象限,则x的取值范围是()A.x>3B.x<3C.x>﹣2D.﹣2<x<36.如图,线段AB经过平移得到线段A1B1,其中点A,B的对应点分别为点A1,B1,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P'在A1B1上的对应点P的坐标为()A.(a-2,b+3)B.(a-2,b-3)C.(a+2,b+3)D.(a+2,b-3)7.如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()A.(﹣3,1) B.(4,1) C.(﹣2,1) D.(2,﹣1)8.在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n),如g(2,1)=(-2,-1).按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(-3,2)]等于()A.(3,2)B.(3,-2)C.(-3,2)D.(-3,-2)二、填空题9.已知点M(a,3-a)是第四象限的点,则a的取值范围是__________.10.若点A(x,2)在第二象限,则x的取值范围是.11.坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍.若A 点在第二象限,则A点坐标是___________.12.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则C n的坐标是 .三、解答题13.如图,已知四边形ABCD(网格中每个小正方形的边长均为1).(1)写出点A,B,C,D的坐标;(2)求四边形ABCD的面积.14.如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.(1)写出A,B,C,D,E的坐标;(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?15.如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐为(﹣4,3);(3)在(2)的条件下,直接写出点A1的坐标.16.如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D.(1)点C的坐标为;(2)①设△BCD的面积为S,用含m的式子表示S,并写出m的取值范围;②当S=6时,求点B的坐标(直接写出结果即可).参考答案1.答案为:C.2.答案为:B.3.答案为:B;4.答案为:A.5.D6.A7.A8.A.9.答案为:0<a<3;10.答案为:x<0.11.答案为:(-9,3);12.答案为:(﹣×4n﹣1,4n)13.解:(1)由图象可知A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);(2)S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF=0.5×1×3+0.5×1×3+0.5×2×4+3×3=16。
中考数学专题复习《圆的阅读理解题》测试卷(附带参考答案)

中考数学专题复习《圆的阅读理解题》测试卷(附带参考答案)学校:___________班级:___________姓名:___________考号:___________1.请阅读下列材料 并完成相应的任务:斯库顿定理:如图1.在ABC 中 AD 为BAC ∠的平分线 则2··AD BD DC AB AC +=.下面是该定理的证明过程: 证明:如图2O 是ABC 的外接圆 延长AD 交O 于点E 连接BE .∵AD 为BAC ∠的平分线 ∵BAE DAC ∠=∠.∵E C ∠=∠ (依据∵__________________________) ABE ADC ∴△∽△.(依据∵_________________________) AB ADAE AC∴= AD AE AB AC ∴⋅=⋅又AE AD DE =+()AD AD DE AB AC ∴⋅+=⋅.2AD AD DE AB AC ∴+⋅=⋅.……任务:(1)证明过程中的依据是:∵__________________________________. ∵__________________________________. (2)将证明过程补充完整:(3)如图3.在圆内接四边形ACEB 中 对角线AE BC 相交于点D .若BE CE = 4AC =6AB=2BD=请利用斯库顿定理直接写出线段AE的长.CD=32.如图1 正五边形ABCDE内接于∵O阅读以下作图过程并回答下列问题作法:如图2 ∵作直径AF∵以F为圆心FO为半径作圆弧与∵O交于点M N∵连接AM MN NA.,,∠的度数.(1)求ABC(2)AMN是正三角形吗?请说明理由.(3)从点A开始以DN长为半径在∵O上依次截取点再依次连接这些分点得到正n边形求n的值.3.阅读与应用请阅读下列材料完成相应的任务:托勒密是“地心说”的集大成者著名的天文学家地理学家占星学家和光学家.后人从托勒密的书中发现一个命题:圆内接四边形对边乘积的和等于对角线的乘积.下面是对这个命题的证明过程.如图1 四边形ABCD 内接于O .求证:AB DC AD BC AC BD ⋅+⋅=⋅.证明:如图2 作BAE CAD ∠=∠交BD 于点E .∵AD AD = ∵ABE ACD ∠=∠.(依据) ∵ABE ACD ∽△△.∵AB BEAC CD=.AB DC AC BE ⋅=⋅. …∵ABC AED ∽△△. ∵AC BCAD ED=.∵AD BC AC ED ⋅=⋅. ∵AB DC AC BE ⋅=⋅∵()AB DC AD BC AC BE AC ED AC BE ED AC BD ⋅+⋅=⋅+⋅=+=⋅. ∵AB DC AD BC AC BD ⋅+⋅=⋅. 任务:(1)证明过程中的“依据”是______ (2)补全证明过程(3)如图3 O的内接五边形ABCDE的边长都为2 求对角线BD的长.4.阅读与思考请阅读下列材料,并按要求完成相应的任务.阿基米德是伟大的古希腊数学家哲学家物理学家他与牛顿高斯并称为三大数学王子.他的著作《阿基米德全集》的《引理集》中记述了有关圆的15个引理其中第三个引⊥于点C点D在弦AB上且理是:如图1 AB是O的弦点P在O上PC AB=.小明思考后给出如=在PB上取一点Q使PQ PAAC CD=连接BQ则BQ BD下证明:任务:(1)写出小明证明过程中的依据: 依据1:________ 依据2:________(2)请你将小明的证明过程补充完整(3)小亮想到了不同的证明方法:如图3 连接AP PD PQ DQ .请你按照小亮的证明思路 写出证明过程.5.阅读资料:我们把顶点在圆上 一边和圆相交 另一边和圆相切的角叫做弦切角 如图1中CBD ∠即为弦切角.同学们研究发现:A 为圆上任意一点 当弦AB 经过圆心O 且DB 切O 于点B 时 易证:弦切角CBD A ∠=∠.问题拓展:如图2 点A 是优弧BC 上任意一点 DB 切O 于点B 求证:CBD A ∠=∠. 证明:连接BO 并延长交O 于点A ' 连接A C ' 如图2所示. ∵DB 与O 相切于点B ∵A BD ∠'=________ ∵90A BC CBD ∠'+∠=︒. ∵A B '是直径∵90ACB ∠'=︒_____________(依据). ∵90A A BC ∠'+∠'=︒.∵CBD A ∠=∠'________________(依据).又∵A A ∠'=∠________________(依据) ∵CBD A ∠=∠.(1)将上述证明过程及依据补充完整.(2)如图3 ABC 的顶点C 在O 上 AC 和O 相交于点D 且AB 是O 的切线 切点为B 连接BD .若2,6,3AD CD BD === 求BC 的长.6.阅读:如图1所示 四边形ABCD 是∵O 的内接四边形 连接AC BD .BC 是∵O 的直径 AB =AC .请说明线段AD BD CD 之间的数量关系.下面是王林解答该问题的部分解答过程 请补充完整:+CD =BD .理由如下:∵BC 是∵O 的直径 ∵∵BAC =90°. ∵AB =AC ∵∵ABC =∵ACB =45°.如图2所示 过点A 作AM ∵AD 交BD 于点M …(1)补全王林的解答过程(2)如图3所示 四边形ABCD 中∵ABC =30° 连接AC BD .若∵BAC =∵BDC =90° 直接写出线段AD BD CD 之间的关系式是 . 7.阅读下列材料 并按要求完成相应的任务. 黄金三角形与五角星当等腰三角形的顶角为36°(或108°)时 我们把这样的三角形叫做黄金三角形. 按下面的步骤画一个五角星(如图):∵作一个以AB 为直径的圆 圆心为O ∵过圆心O 作半径OC ∵AB ∵取OC 的中点D 连接AD∵以D 为圆心OD 为半径画弧交AD 于点E ∵从点A 开始以AE 为半径顺时针依次画弧正好把∵O 十等分(其中点F G B H I 为五等分点) ∵以点F G B H I 为顶点画出五角星. 任务: (1)求出AEOA的值为 (2)如图 GH 与BF BI 分别交于点M N 求证:△BMN 是黄金三角形. 8.阅读下面材料 并按要求完成相应的任务.阿基米德是古希腊的数学家 物理学家.在《阿基米德全集》里 他关于圆的引理的论证如下:命题:设AB 是一个半圆的直径 并且过点B 的切线与过该半圆上的任意一点D 的切线交于点T 如果作DE 垂直AB 于点E 且与AT 交于点F 则DF EF =. 证明:如图1 延长AD 与BT 交于点H 连接OD OT . ∵DT BT 与半圆O 相切 ∵……∵ ∵BT DT =. ∵AB 是半圆O 的直径 ∵90ADB ︒∠=.∵在BDH △中 由BT DT = 可得TDB TBD ∠=∠ ∵H TDH ∠=∠.∵BT DT HT ==. 又∵//DE BH ∵DF AFHT AT = EF AF BT AT=∵EF DFBT HT=. 又∵BT HT = ∵DF EF =任务:(1)请将∵处的证明过程补充完整. (2)证明过程中∵的证明依据是 .(3)如图2 AB 为∵O 的直径 ∵BED 是等边三角形 BE 是∵O 的切线 切点是B 点D 在∵O 上 CD ∵AB 垂足为C 连接AE 交CD 于点F .若∵O 的半径为2 求CF 的长. 9.阅读材料 某个学习小组成员发现:在等腰ABC 中 AD 平分BAC ∠ ∵AB AC =BD CD = ∵AB BDAC CD= 他们猜想:在任意ABC 中 一个内角角平分线分对边所成的两条线段与这个内角的两边对应成比例.【证明猜想】如图1所示 在ABC 中 AD 平分BAC ∠ 求证:AB BDAC CD=. 丹丹认为 可以通过构造相似三角形的方法来证明△和ACD面积的角度来证明.思思认为可以通过比较ABD(1)请你从上面的方法中选择一种进行证明.(2)【尝试应用】如图2O是Rt ABC的外接圆点E是O上一点(与B不重合且=连结AE并延长AE BC交于点D H为AE的中点连结BH交AC于点G求AB AEHG的值.GB(3)【拓展提高】如图3在(2)的条件下延长BH交O于点F若BE EF=求=GH xO的直径(用x的代数式表示).10.请阅读下面材料并完成相应的任务阿基米德折弦定理阿基米德(Arehimedes 公元前287—公元前212年古希腊)是有史以来最伟大的数学家之一他与牛顿高斯并称为三大数学王子.阿拉伯Al-Biruni(973年—1050年)的译文中保存了阿基米德折弦定理的内容苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》第一题就是阿基米德的折弦定理.阿基米德折弦定理:如图1 AB和BC是O的两条弦(即折线ABC是圆的一条折弦)>M是ABC的中点则从点M向BC所作垂线的垂足D是折弦ABC的中点即BC ABCD AB BD=+.=+的部分证明过程.这个定理有很多证明方法下面是运用“垂线法”证明CD AB BD证明:如图2 过点M作MH⊥射线AB垂足为点H连接MA MB MC.∵M 是ABC 的中点 ∵MA MC =. … 任务:(1)请按照上面的证明思路 写出该证明的剩余部分(2)如图3 已知等边三角形ABC 内接于O D 为AC 上一点 15ABD ∠=︒ CE BD ⊥于点E 2CE = 连接AD 则DAB 的周长是______.11.阅读与思考请阅读下列材料 并完成相应的任务:任务:(1)材料中划横线部分应填写的内容为 .(2)如图2 正五边形ABCDE 内接于∵O AB =2 求对角线BD 的长.12.阅读下列材料 完成相应任务:如图∵ ABC 是∵O 的内接三角形 AB 是∵O 的直径AD 平分BAC ∠交∵O 于点D 连接BD 过点D 作∵O 的切线 交AB 的延长线于点E .则CAD BDE ∠=∠.下面是证明CAD BDE ∠=∠的部分过程:证明:如图∵ 连接DO AB 是∵O 的直径 90ADB ∴∠=︒ODA ∴∠+∵________90=︒.(1) DE 为∵O 的切线 90ODE ∴∠=︒90ODB BDE ∴∠+∠=︒ (2)由(1)(2)得 ∵________________. AD 平分,BAC CAD OAD ∠∴∠=∠.,OA OD OAD ODA =∴∠=∠CAD ∴∠=∵________CAD BDE ∴∠=∠.任务:(1)请按照上面的证明思路 补全证明过程:∵________ ∵________ ∵________ (2)若5,2OA BE == 求DE 的长.13.阅读下列材料:平面上两点P 1(x 1 y 1) P 2(x 2 y 2)之间的距离表示为()()22121212PP x x y y =-+- 称为平面内两点间的距离公式 根据该公式 如图 设P (x y )是圆心坐标为C (a b )半径为r 的圆上任意一点 则点P ()()22x a y b r -+-= 变形可得:(x ﹣a )2+(y ﹣b )2=r 2 我们称其为圆心为C (a b ) 半径为r 的圆的标准方程.例如:由圆的标准方程(x ﹣1)2+(y ﹣2)2=25可得它的圆心为(1 2) 半径为5.根据上述材料 结合你所学的知识 完成下列各题.(1)圆心为C (3 4) 半径为2的圆的标准方程为:(2)若已知∵C 的标准方程为:(x ﹣2)2+y 2=22 圆心为C 请判断点A (3 ﹣1)与∵C的位置关系.14.阅读以下材料 并按要求完成相应的任务:几何定论 是指变化的图形中某些几何元素的几何量保持不变(如定长 定角 定比 定积等) 或几何元素间的某些性质或位置关系不变(如定点 定线 定方向等)如图∵ 点A 为O 外一点 过点A 为O 作直线与O 相交于点B C 点B '为点B 关于OA 的对称点 连接B C '交OA 于点M 设O 的半径为R .如图∵ 当过点A 的直线与O 相切时 点B C 重合 可得2R OA OM =⋅.如图∵ 当过点A 的直线与O 相交时 证明2R OA OM =⋅.证明:如图∵ 连接OC CD .∵B ' B 关于OA 对称∵BD BD '=.∵∵1=∵2 .(依据)…任务:(1)上述证明过程中的依据是____________________(2)根据以上的证明提示 完成上述证明过程(3)如图∵ 若5OA = 1OM = 求O 的半径.15.阅读下列相关材料 并完成相应的任务.婆罗摩笈多是古印度著名的数学家 天文学家他编著了《婆罗摩修正体系》 他曾经提出了“婆罗摩笈多定理” 也称“布拉美古塔定理”.定理的内容是:“若圆内接四边形的对角线互相垂直 则垂直于一边且过对角线交点的直线平分对边”.任务:(1)按图(1)写出了这个定理的已知和求证 并完成这个定理的证明过程已知:__________________求证:_________________证明:(2)如图(2) 在O 中 弦AB CD ⊥于M 连接,,,,,AC CB BD DA E F 分别是,AC BC 上的点 EM BD ⊥于,G FM AD ⊥于H 当M 是AB 中点时 直接写出四边形EMFC 是怎样的特殊四边形:__________.参考答案:1.解:(1)∵同弧或等弧所对的圆周角相等∵E ∠和C ∠所对的弧是同一条弧∵∵应填:同弧或等弧所对的圆周角相等∵两角分别相等的两个三角形相似∵题目中的结论是两个三角形相似 用的方式是三角形的两个角分别相等∵∵应填两角分别相等的两个三角形相似(2)∵BDE ADC ∠=∠ E C ∠=∠.BDE ADC ∽△∴△.BD DE AD DC∴= AD DE BD DC ∴⋅=⋅2AD BD DC AB AC ∴+⋅=⋅(3)42AE =∵BE CE =.∵弧BE =弧CE∵BAE CAE ∠=∠∵AE 平分BAC ∠.由斯库顿定理 得2AD BD DC AB AC +⋅=⋅又∵4AC = 6AB = 2CD = 3BD =∵23264AD +⨯=⨯.解得=AD AD =-。
2023年中考数学复习---圆综合知识点总结与专项练习题(含答案解析)

2023年中考数学复习---圆综合知识点总结与专项练习题(含答案解析)知识点总结1.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
2.垂径定理的推论:推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题。
3.圆心角、弦以及弧之间的关系:①定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
②推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧。
4.圆周角定理:5.圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
6.圆的内接四边形:①定义:四个顶点都在圆上的四边形叫做圆的内接四边形。
②性质:I:圆内接四边形的对角互补。
II:圆内接四边形的任意一个外角等于它的内对角。
7.三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆。
圆心是三角形三条边垂直平分线的交点,叫做三角形的外心。
8.切线的性质:①圆的切线垂直于经过切点的半径。
②经过圆心且垂直于切线的直线必经过切点。
③经过切点且垂直于切线的直线必经过圆心。
运用切线的性质进行计算或证明时,常常作的辅助线是连接圆心和切点,通过构造直角三角形或相似三角形解决问题。
9. 切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线。
在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径,可简单的说成“无交点,作垂线段,证半径”;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,可简单地说成“有交点,作半径,证垂直”。
2020-2021中考数学圆的综合的综合复习含详细答案

2020-2021中考数学圆的综合的综合复习含详细答案一、圆的综合1.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣33,O),C(3,O).(1)求⊙M的半径;(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.(3)在(2)的条件下求AF的长.【答案】(1)4;(2)见解析;(3)4.【解析】【分析】(1)过M作MT⊥BC于T连BM,由垂径定理可求出BT的长,再由勾股定理即可求出BM的长;(2)连接AE,由圆周角定理可得出∠AEC=∠ABC,再由AAS定理得出△AEH≌△AFH,进而可得出结论;(3)先由(1)中△BMT的边长确定出∠BMT的度数,再由直角三角形的性质可求出CG 的长,由平行四边形的判定定理判断出四边形AFCG为平行四边形,进而可求出答案.【详解】(1)如图(一),过M作MT⊥BC于T连BM,∵BC是⊙O的一条弦,MT是垂直于BC的直径,∴BT=TC=123∴124;(2)如图(二),连接AE,则∠AEC=∠ABC,∵CE⊥AB,∴∠HBC+∠BCH=90°在△COF中,∵∠OFC+∠OCF=90°,∴∠HBC=∠OFC=∠AFH,在△AEH和△AFH中,∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEH≌△AFH(AAS),∴EH=FH;(3)由(1)易知,∠BMT=∠BAC=60°,作直径BG,连CG,则∠BGC=∠BAC=60°,∵⊙O的半径为4,∴CG=4,连AG,∵∠BCG=90°,∴CG⊥x轴,∴CG∥AF,∵∠BAG=90°,∴AG⊥AB,∵CE⊥AB,∴AG∥CE,∴四边形AFCG为平行四边形,∴AF=CG=4.【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质,根据题意作出辅助线是解答此题的关键.2.如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.(1)OC的长为;(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ=;(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t (秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.【答案】(1)4;(2)35;(3)点E的坐标为(1,2)、(53,103)、(4,2).【解析】分析:(1)过点B作BH⊥OA于H,如图1(1),易证四边形OCBH是矩形,从而有OC=BH,只需在△AHB中运用三角函数求出BH即可.(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2),则有OH=2,BH=4,MN⊥OC.设圆的半径为r,则MN=MB=MD=r.在Rt△BHD中运用勾股定理可求出r=2,从而得到点D与点H重合.易证△AFG∽△ADB,从而可求出AF、GF、OF、OG、OB、AB、BG.设OR=x,利用BR2=OB2﹣OR2=BG2﹣RG2可求出x,进而可求出BR.在Rt△ORB中运用三角函数就可解决问题.(3)由于△BDE的直角不确定,故需分情况讨论,可分三种情况(①∠BDE=90°,②∠BED=90°,③∠DBE=90°)讨论,然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题.详解:(1)过点B作BH⊥OA于H,如图1(1),则有∠BHA=90°=∠COA,∴OC∥BH.∵BC∥OA,∴四边形OCBH是矩形,∴OC=BH,BC=OH.∵OA=6,BC=2,∴AH=0A﹣OH=OA﹣BC=6﹣2=4.∵∠BHA=90°,∠BAO=45°,∴tan∠BAH=BHHA=1,∴BH=HA=4,∴OC=BH=4.故答案为4.(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2).由(1)得:OH=2,BH=4.∵OC与⊙M相切于N,∴MN⊥OC.设圆的半径为r,则MN=MB=MD=r.∵BC ⊥OC ,OA ⊥OC ,∴BC ∥MN ∥OA .∵BM =DM ,∴CN =ON ,∴MN =12(BC +OD ),∴OD =2r ﹣2,∴DH =OD OH -=24r -.在Rt △BHD 中,∵∠BHD =90°,∴BD 2=BH 2+DH 2,∴(2r )2=42+(2r ﹣4)2.解得:r =2,∴DH =0,即点D 与点H 重合,∴BD ⊥0A ,BD =AD .∵BD 是⊙M 的直径,∴∠BGD =90°,即DG ⊥AB ,∴BG =AG .∵GF ⊥OA ,BD ⊥OA ,∴GF ∥BD ,∴△AFG ∽△ADB , ∴AF AD =GF BD =AG AB =12,∴AF =12AD =2,GF =12BD =2,∴OF =4,∴OG同理可得:OB AB ,∴BG =12AB .设OR =x ,则RG x .∵BR ⊥OG ,∴∠BRO =∠BRG =90°,∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2,∴(2﹣x 2=()2﹣(x )2.解得:x ,∴BR 2=OB 2﹣OR 2=(2)2=365,∴BR在Rt △ORB 中,sin ∠BOR =BR OB35. 故答案为35. (3)①当∠BDE =90°时,点D 在直线PE 上,如图2.此时DP =OC =4,BD +OP =BD +CD =BC =2,BD =t ,OP =t . 则有2t =2.解得:t =1.则OP =CD =DB =1.∵DE ∥OC ,∴△BDE ∽△BCO ,∴DE OC =BD BC =12,∴DE =2,∴EP =2, ∴点E 的坐标为(1,2).②当∠BED =90°时,如图3.∵∠DBE =OBC ,∠DEB =∠BCO =90°,∴△DBE ∽△OBC ,∴BEBC =2DB BE OB ∴,∴BE . ∵PE ∥OC ,∴∠OEP =∠BOC .∵∠OPE =∠BCO =90°,∴△OPE ∽△BCO , ∴OEOB =OP BC,2t ,∴OE .∵OE+BE=OB=255,∴t+55t=25.解得:t=53,∴OP=53,OE=55,∴PE=22OE OP-=103,∴点E的坐标为(51033,).③当∠DBE=90°时,如图4.此时PE=PA=6﹣t,OD=OC+BC﹣t=6﹣t.则有OD=PE,EA=22PE PA+=2(6﹣t)=62﹣2?t,∴BE=BA﹣EA=42﹣(62﹣2t)=2t﹣22.∵PE∥OD,OD=PE,∠DOP=90°,∴四边形ODEP是矩形,∴DE=OP=t,DE∥OP,∴∠BED=∠BAO=45°.在Rt△DBE中,cos∠BED=BEDE=22,∴DE=2BE,∴t=22(t﹣22)=2t﹣4.解得:t=4,∴OP=4,PE=6﹣4=2,∴点E的坐标为(4,2).综上所述:当以B、D、E为顶点的三角形是直角三角形时点E的坐标为(1,2)、(51033,)、(4,2).点睛:本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识,还考查了分类讨论的数学思想,有一定的综合性.3.如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.(1)求证:AC∥OD;(2)如果DE⊥BC,求»AC的长度.【答案】(1)证明见解析;(2)2π.【解析】试题分析:(1)由OC=OD,CD平分∠ACO,易证得∠ACD=∠ODC,即可证得AC∥OD;(2)BC切⊙O于点C,DE⊥BC,易证得平行四边形ADOC是菱形,继而可证得△AOC是等边三角形,则可得:∠AOC=60°,继而求得弧AC的长度.试题解析:(1)证明:∵OC=OD,∴∠OCD=∠ODC.∵CD平分∠ACO,∴∠OCD=∠ACD,∴∠ACD=∠ODC,∴AC∥OD;(2)∵BC切⊙O于点C,∴BC⊥OC.∵DE⊥BC,∴OC∥DE.∵AC∥OD,∴四边形ADOC 是平行四边形.∵OC=OD,∴平行四边形ADOC是菱形,∴OC=AC=OA,∴△AOC是等边三角形,∴∠AOC=60°,∴弧AC的长度=606180π⨯=2π.点睛:本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式.此题难度适中,注意掌握数形结合思想的应用.4.定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;(2)在(1)的条件下,⊙O半径为5.①若AD为直径,且sinA=45,求BC的长;②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是;(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.【答案】(1)见解析;(2)①BC=6,②7534或754;(3)见解析【解析】【分析】(1)先判断出∠ADC=180°﹣2∠A.进而判断出∠ABC=2∠A,即可得出结论;(2)①先用锐角三角函数求出BD,进而得出AB,由(1)得出∠ADB=∠BDC,即可得出结论;②分两种情况:利用面积和差即可得出结论;(3)先得出BE=BC=b,DE=DA=b,进而得出CE=d﹣c,再判断出△EBC∽△EDA,即可得出结论.【详解】(1)设∠A=α,则∠DCB=180°﹣α.∵∠DCB﹣∠ADC=∠A,∴∠ADC=∠DCB﹣∠A=180°﹣α﹣α=180°﹣2α,∴∠ABC=180°﹣∠ADC=2α=2∠A,∴四边形ABCD是⊙O内接倍角四边形;(2)①连接BD.∵AD是⊙O的直径,∴∠ABD=90°.在Rt△ABD中,AD=2×5=10,sin∠A=45,∴BD=8,根据勾股定理得:AB=6,设∠A=α,∴∠ADB=90°﹣α.由(1)知,∠ADC=180°﹣2α,∴∠BDC=90°﹣α,∴∠ADB=∠BDC,∴BC=AB=6;②若∠ADC=60°时.∵四边形ABCD是圆内接倍角四边形,∴∠BCD=120°或∠BAD=30°.Ⅰ、当∠BCD=120°时,如图3,连接OA,OB,OC,OD.∵BC=CD,∴∠BOC=∠COD,∴∠OCD=∠OCB=12∠BCD=60°,∴∠CDO=60°,∴AD是⊙O 的直径,(为了说明AD是直径,点O没有画在AD上)∴∠ADC+∠BCD=180°,∴BC∥AD,∴AB=CD.∵BC=CD,∴AB=BC=CD,∴△OAB,△BOC,△COD是全等的等边三角形,∴S四边形ABCD=3S△AOB 32753.Ⅱ、当∠BAD=30°时,如图4,连接OA,OB,OC,OD.∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠BAD=150°.∵BC =CD ,∴∠BOC =∠COD ,∴∠BCO =∠DCO =12∠BCD =75°,∴∠BOC =∠DOC =30°,∴∠OBA =45°,∴∠AOB =90°.连接AC ,∴∠DAC =12∠BAD =15°. ∵∠ADO =∠OAB ﹣∠BAD =15°,∴∠DAC =∠ADO ,∴OD ∥AC ,∴S △OAD =S △OCD . 过点C 作CH ⊥OB 于H .在Rt △OCH 中,CH =12OC =52,∴S 四边形ABCD =S △COD +S △BOC +S △AOB ﹣S △AOD =S △BOC +S △AOB =1522⨯×5+12×5×5=754. 故答案为:7534或754;(3)延长DC ,AB 交于点E .∵四边形ABCD 是⊙O 的内接四边形,∴∠BCE =∠A =12∠ABC . ∵∠ABC =∠BCE +∠A ,∴∠E =∠BCE =∠A ,∴BE =BC =b ,DE =DA =b ,∴CE =d ﹣c . ∵∠BCE =∠A ,∠E =∠E ,∴△EBC ∽△EDA ,∴CE BC AE AD =,∴d c b a b d-=+,∴d 2﹣b 2=ab +cd .【点睛】本题是圆的综合题,主要考查了圆的内接四边形的性质,新定义,相似三角形的判定和性质,等边三角形的判定和性质,正确作出辅助线是解答本题的关键.5.如图,已知在△ABC中,AB=15,AC=20,tanA=12,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.(1)求⊙P的半径;(2)当AP=65时,试探究△APM与△PCN是否相似,并说明理由.【答案】(1)半径为35;(2)相似,理由见解析.【解析】【分析】(1)如图,作BD⊥AC,垂足为点D,⊙P与边AC相切,则BD就是⊙P的半径,利用解直角三角形得出BD与AD的关系,再利用勾股定理可求得BD的长;(2)如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,根据垂径定理得出MN=2MH,PM=PN,再利用勾股定理求出PH、AH、MH、MN的长,从而求出AM、NC的长,然后求出AMMP、PNNC的值,得出AMMP=PNNC,利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】(1)如图,作BD⊥AC,垂足为点D,∵⊙P与边AC相切,∴BD就是⊙P的半径,在Rt△ABD中,tanA= 1BD2AD ,设BD=x,则AD=2x,∴x2+(2x)2=152,解得:5∴半径为5(2)相似,理由见解析,如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,∴PH垂直平分MN,∴PM=PN ,在Rt △AHP 中,tanA=12PH AH =, 设PH=y ,AH=2y ,y 2+(2y )2=(65)2解得:y=6(取正数),∴PH=6,AH=12,在Rt △MPH 中,MH=()22356-=3,∴MN=2MH=6,∴AM=AH-MH=12-3=9,NC=AC-MN-AM=20-6-9=5,∴3535AM MP ==,35PN NC =, ∴AM MP =PN NC, 又∵PM=PN ,∴∠PMN=∠PNM ,∴∠AMP=∠PNC ,∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等,综合性较强,有一定的难度,正确添加辅助线、灵活应用相关的性质与定理是解题的关键.6.如图,已知四边形ABCD 是矩形,点P 在BC 边的延长线上,且PD=BC ,⊙A 经过点B ,与AD 边交于点E ,连接CE .(1)求证:直线PD 是⊙A 的切线;(2)若5sin ∠P=23,求图中阴影部份的面积(结果保留无理数).【答案】(1)见解析;(2)20-4π.【解析】分析:(1)过点A作AH⊥PD,垂足为H,只要证明AH为半径即可.(2)分别算出Rt△CED的面积,扇形ABE的面积,矩形ABCD的面积即可.详解:(1)证明:如图,过A作AH⊥PD,垂足为H,∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∠PCD=∠BCD=90°,∴∠ADH=∠P,∠AHD=∠PCD=90°,又PD=BC,∴AD=PD,∴△ADH≌△DPC,∴AH=CD,∵CD=AB,且AB是⊙A的半径,∴AH=AB,即AH是⊙A的半径,∴PD是⊙A的切线.(2)如图,在Rt△PDC中,∵sin∠P=23CDPD,5,令CD=2x,PD=3x,由由勾股定理得:(3x)2-(2x)252,解得:x=2,∴CD=4,PD=6,∴AB=AE=CD=4,AD=BC=PD=6,DE=2,∵矩形ABCD的面积为6×4=24,Rt△CED的面积为12×4×2=4,扇形ABE的面积为12π×42=4π,∴图中阴影部份的面积为24-4-4π=20-4π.点睛:本题考查了全等三角形的判定,圆的切线证明,三角形的面积,扇形的面积,矩形的面积.7.如图,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点,…,最后一个△A n B n C n 的顶点B n 、C n 在圆上.如图1,当n=1时,正三角形的边长a 1=_____;如图2,当n=2时,正三角形的边长a 2=_____;如图3,正三角形的边长a n =_____(用含n 的代数式表示).3831343n 【解析】 分析:(1)设PQ 与11B C 交于点D ,连接1B O ,得出OD=1A D -O 1A ,用含1a 的代数式表示OD ,在△O 1B D 中,根据勾股定理求出正三角形的边长1a ;(2)设PQ 与2B 2C 交于点E ,连接2B O ,得出OE=1A E-O 1A ,用含2a 的代数式表示OE ,在△O 2B E 中,根据勾股定理求出正三角形的边长2a ;(3)设PQ 与n B n C 交于点F ,连接n B O ,得出OF=1A F-O 1A ,用含an 的代数式表示OF ,在△O n B F 中,根据勾股定理求出正三角形的边长an . 本题解析:(1)易知△A 1B 1C 1的高为323 ∴a 13.(2)设△A 1B 1C 1的高为h ,则A 2O =1-h ,连结B 2O ,设B 2C 2与PQ 交于点F ,则有OF =2h -1. ∵B 2O 2=OF 2+B 2F 2,∴1=(2h -1)2+2212a ⎛⎫ ⎪⎝⎭ . ∵h =32a 2,∴1=32-1)2+14a 22, 解得a 2=8313. (3)同(2),连结B n O ,设B n C n 与PQ 交于点F ,则有B n O 2=OF 2+B n F 2, 即1=(nh -1)2+212n a ⎛⎫ ⎪⎝⎭. ∵h 3a n ,∴1=14a n 2+2312n na ⎛⎫- ⎪ ⎪⎝⎭ ,解得a n =24331n n + .8.如图,在⊙O 中,直径AB ⊥弦CD 于点E ,连接AC ,BC ,点F 是BA 延长线上的一点,且∠FCA =∠B .(1)求证:CF 是⊙O 的切线;(2)若AE =4,tan ∠ACD =3,求FC 的长.【答案】(1)见解析【解析】分析:(1)利用圆周角定理以及等腰三角形的性质得出∠OCF=90°,进而得出答案; (2)根据正切的性质求出EC 的长,然后利用垂径定理求出圆的半径,再根据等边三角形的性质,利用勾股定理求出即可.详解:(1)证明:连接OC.∵AB 是⊙O 的直径,∴∠ACB =90°,∴∠OCB +∠ACO =90°.∵OB =OC ,∴∠B =∠OCB.又∵∠FCA =∠B ,∴∠FCA =∠OCB ,∴∠FCA +∠ACO =90°,即∠FCO =90°,∴FC ⊥OC ,∴FC 是⊙O 切线.(2)解:∵AB ⊥CD ,∴∠AEC =90°,∴EC=AE 43tan ACE 3∠== 设OA =OC =r ,则OE =OA -AE =r -4.在Rt △OEC 中,OC 2=OE 2+CE 2,即r 2=(r -4)2+32,解得r =8.∴OE =r -4=4=AE.∵CE ⊥OA ,∴CA =CO =8,∴△AOC 是等边三角形,∴∠FOC =60°,∴∠F =30°.在Rt △FOC 中,∵∠OCF =90°,OC =8,∠F =30°,∴OF =2OC =16,∴FC 22OF OC 83-=.点睛:此题主要考查了切线的判定、垂径定理的推论以及勾股定理等知识,得出BC的长是解题关键.9.四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.(1)如图1,求证:CE=CD;(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= 53,EG=2,求AE的长.【答案】(1)见解析;(2)60°;(3)7.【解析】试题分析:(1)利用圆的内接四边形定理得到∠CED=∠CDE.(2) 作CH⊥DE于H, 设∠ECH=α,由(1)CE=CD,用α表示∠CAE,∠BAC,而∠BAD=∠BAC+∠CAE.(3)连接AG,作GN⊥AC,AM⊥EG,先证明∠CAG=∠BAC,设NG=3m,可得AN=11m,利用直角n AGM,n AEM,勾股定理可以算出m的值并求出AE长.试题解析:(1)解:证明:∵四边形ABCD内接于⊙O.∴∠B+∠D=180°,∵∠B=∠AEC,∴∠AEC+∠D=180°,∵∠AEC+∠CED=180°,∴∠D=∠CED,∴CE=CD.(2)解:作CH⊥DE于H.设∠ECH=α,由(1)CE=CD,∴∠ECD=2α,∵∠B=∠AEC,∠B+∠CAE=120°,∴∠CAE+∠AEC=120°,∴∠ACE=180°﹣∠AEC﹣∠ACE=60°,∴∠CAE=90°﹣∠ACH=90°﹣(60°+α)=30°﹣α,∠ACD=∠ACH+∠HCD=60°+2α,∵∠ACD=2∠BAC,∴∠BAC=30°+α,∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°.(3)解:连接AG,作GN⊥AC,AM⊥EG,∵∠CED=∠AEG,∠CDE=∠AGE,∠CED=∠CDE,∴∠AEG=∠AGE,∴AE=AG,∴EM=MG=1EG=1,2∴∠EAG=∠ECD=2α,∴∠CAG=∠CAD+∠DAG=30°﹣α+2α=∠BAC,∵tan ∠BAC =5311, ∴设NG=53m ,可得AN =11m ,AG =22AG AM -=14m , ∵∠ACG =60°,∴CN=5m ,AM =83m ,MG =22AG AM -=2m =1, ∴m =12, ∴CE=CD =CG ﹣EG =10m ﹣2=3, ∴AE =22AM EM +=221+43()=7.10.已知:如图1,∠ACG=90°,AC=2,点B 为CG 边上的一个动点,连接AB ,将△ACB 沿AB 边所在的直线翻折得到△ADB ,过点D 作DF ⊥CG 于点F .(1)当BC=23 时,判断直线FD 与以AB 为直径的⊙O 的位置关系,并加以证明; (2)如图2,点B 在CG 上向点C 运动,直线FD 与以AB 为直径的⊙O 交于D 、H 两点,连接AH ,当∠CAB=∠BAD=∠DAH 时,求BC 的长.【答案】(1)直线FD 与以AB 为直径的⊙O 相切,理由见解析;(2)22 .【解析】试题分析:(1)根据已知及切线的判定证明得,直线FD 与以AB 为直径的⊙O 相切; (2)根据圆内接四边形的性质及直角三角形的性质进行分析,从而求得BC 的长. 试题解析:(1)判断:直线FD 与以AB 为直径的⊙O 相切.证明:如图,作以AB 为直径的⊙O ;∵△ADB 是将△ACB 沿AB 边所在的直线翻折得到的,∴△ADB ≌△ACB ,∴∠ADB=∠ACB=90°.∵O 为AB 的中点,连接DO ,∴OD=OB=AB,∴点D在⊙O上.在Rt△ACB中,BC=,AC=2;∴tan∠CAB==,∴∠CAB=∠BAD=30°,∴∠ABC=∠ABD=60°,∴△BOD是等边三角形.∴∠BOD=60°.∴∠ABC=∠BOD,∴FC∥DO.∵DF⊥CG,∴∠ODF=∠BFD=90°,∴OD⊥FD,∴FD为⊙O的切线.(2)延长AD交CG于点E,同(1)中的方法,可证点C在⊙O上;∴四边形ADBC是圆内接四边形.∴∠FBD=∠1+∠2.同理∠FDB=∠2+∠3.∵∠1=∠2=∠3,∴∠FBD=∠FDB,又∠DFB=90°.∴EC=AC=2.设BC=x,则BD=BC=x,∵∠EDB=90°,∴EB=x.∵EB+BC=EC,∴x+x=2,解得x=2﹣2,∴BC=2﹣2.11.如图所示,AB 是半圆O 的直径,AC 是弦,点P 沿BA 方向,从点B 运动到点A ,速度为1cm/s ,若10AB cm ,点O 到AC 的距离为4cm .(1)求弦AC 的长;(2)问经过多长时间后,△APC 是等腰三角形.【答案】(1)AC=6;(2)t=4或5或145s 时,△APC 是等腰三角形; 【解析】 【分析】(1)过O 作OD ⊥AC 于D ,根据勾股定理求得AD 的长,再利用垂径定理即可求得AC 的长;(2)分AC=PC 、AP=AC 、AP=CP 三种情况求t 值即可.【详解】(1)如图1,过O 作OD ⊥AC 于D ,易知AO=5,OD=4,从而AD==3,∴AC=2AD=6;(2)设经过t 秒△APC 是等腰三角形,则AP=10﹣t①如图2,若AC=PC ,过点C 作CH ⊥AB 于H ,∵∠A=∠A ,∠AHC=∠ODA=90°,∴△AHC ∽△ADO ,∴AC :AH=OA :AD ,即AC :=5:3,解得t=s , ∴经过s 后△APC 是等腰三角形; ②如图3,若AP=AC ,由PB=x ,AB=10,得到AP=10﹣x ,又∵AC=6,则10﹣t=6,解得t=4s ,∴经过4s 后△APC 是等腰三角形;③如图4,若AP=CP ,P 与O 重合,则AP=BP=5,∴经过5s 后△APC 是等腰三角形.综上可知当t=4或5或s 时,△APC 是等腰三角形.【点睛】本题是圆的综合题,解决问题利用了垂径定理,勾股定理等知识点,解题时要注意当△BPC 是等腰三角形时,点P 的位置有三种情况.12.如图所示,ABC ∆内接于圆O ,CD AB ⊥于D ;(1)如图1,当AB 为直径,求证:OBC ACD ∠=∠;(2)如图2,当AB 为非直径的弦,连接OB ,则(1)的结论是否成立?若成立请证明,不成立说明由;(3)如图3,在(2)的条件下,作AE BC ⊥于E ,交CD 于点F ,连接ED ,且2AD BD ED =+,若3DE =,5OB =,求CF 的长度.【答案】(1)见解析;(2)成立;(3)145【解析】【分析】 (1)根据圆周角定理求出∠ACB=90°,求出∠ADC=90°,再根据三角形内角和定理求出即可;(2)根据圆周角定理求出∠BOC=2∠A ,求出∠OBC=90°-∠A 和∠ACD=90°-∠A 即可; (3)分别延长AE 、CD 交⊙O 于H 、K ,连接HK 、CH 、AK ,在AD 上取DG=BD ,延长CG 交AK 于M ,延长KO 交⊙O 于N ,连接CN 、AN ,求出关于a 的方程,再求出a 即可.【详解】(1)证明:∵AB 为直径,∴ACB 90∠=︒, ∵CD AB ⊥于D , ∴ADC 90∠=︒,∴OBC A 90∠∠+=︒,A ACD 90∠∠+=︒,∴OBC ACD ∠∠=;(2)成立,证明:连接OC ,由圆周角定理得:BOC 2A ∠∠=,∵OC OB =,∴()()11OBC 180BOC 1802A 90A 22∠∠∠∠=︒-=︒-=︒-, ∵ADC 90∠=︒,∴ACD 90A ∠∠=︒-,∴OBC ACD ∠∠=;(3)分别延长AE 、CD 交⊙O 于H 、K ,连接HK 、CH 、AK ,∵AE BC ⊥,CD BA ⊥,∴AEC ADC 90∠∠==︒,∴BCD CFE 90∠∠+=︒,BAH DFA 90∠∠+=︒,∵CFE DFA ∠∠=,∴BCD BAH ∠∠=,∵根据圆周角定理得:BAH BCH ∠∠=,∴BCD BAH BCH ∠∠∠==,∴由三角形内角和定理得:CHE CFE ∠∠=, ∴CH CF =,∴EH EF =,同理DF DK =,∵DE 3=,∴HK 2DE 6==,在AD 上取DG BD =,延长CG 交AK 于M ,则AG AD BD 2DE 6=-==,BC GC =,∴MCK BCK BAK ∠∠∠==,∴CMK 90∠=︒,延长KO 交⊙O 于N ,连接CN 、AN ,则NAK 90CMK ∠∠=︒=,∴CM //AN ,∵NCK ADK 90∠∠==︒,∴CN //AG ,∴四边形CGAN 是平行四边形,∴AG CN 6==,作OT CK ⊥于T ,则T 为CK 的中点,∵O 为KN 的中点, ∴1OT CN 32==, ∵OTC 90∠=︒,OC 5=,∴由勾股定理得:CT 4=,∴CK 2CT 8==,作直径HS ,连接KS ,∵HK 6=,HS 10=,∴由勾股定理得:KS 8=, ∴3tan HSK tan HAK 4∠∠==, ∴1tan EAB tan BCD 3∠∠==, 设BD a =,CD 3a =, ∴AD BD 2ED a 6=+=+,11DK AD a 233==+, ∵CD DK CK +=, ∴13a a 283++=, 解得:9a 5=, ∴113DK a 235=+=, ∴2614CF CK 2DK 855=-=-=. 【点睛】本题考查了垂径定理、解直角三角形、等腰三角形的性质、圆周角定理、勾股定理等知识点,能综合运用知识点进行推理是解此题的关键,综合性比较强,难度偏大.13.如图,AB 是O e 的直径,DF 切O e 于点D ,BF DF ⊥于F ,过点A 作AC //BF 交BD 的延长线于点C .(1)求证:ABC C ∠∠=;(2)设CA 的延长线交O e 于E BF ,交O e 于G ,若¼DG的度数等于60o ,试简要说明点D 和点E 关于直线AB 对称的理由.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)作辅助线,连接OD,由DF为⊙O的切线,可得OD⊥DF,又BF⊥DF,AC∥BF,所以OD∥AC,∠ODB=∠C,由OB=OD得∠ABD=∠ODB,从而可证∠ABC=∠C;(2)连接OG,OD,AD,由BF∥OD,»GD=60°,可求证»BG=»»==60°,由平行线GD AD的性质及三角形的内角和定理可求出∠OHD=90°,由垂径定理便可得出结论.【详解】(1)连接OD,∵DF为⊙O的切线,∴OD⊥DF.∵BF⊥DF,AC∥BF,∴OD∥AC∥BF.∴∠ODB=∠C.∵OB=OD,∴∠ABD=∠ODB.∴∠ABC=∠C.(2)连接OG,OD,AD,DE,DE交AB于H,∵BF∥OD,∴∠OBG=∠AOD,∠OGB=∠DOG,∴»»GD AD==»BG.∵»GD=60°,∴»BG=»»GD AD==60°,∴∠ABC=∠C=∠E=30°,∵OD//CE∴∠ODE=∠E=30°.在△ODH 中,∠ODE=30°,∠AOD=60°,∴∠OHD=90°,∴AB ⊥DE .∴点D 和点E 关于直线AB 对称.【点睛】本题考查的是切线的性质、圆周角定理及垂径定理,解答此题的关键是作出辅助线,利用数形结合解答.14.如图,已知AB 是⊙O 的直径,直线CD 与⊙O 相切于C 点,AC 平分∠DAB . (1)求证:AD ⊥CD ;(2)若AD =2,AC=6,求⊙O 的半径R 的长.【答案】(1)证明见解析(2)32【解析】试题分析:(1)连接OC ,由题意得OC ⊥CD .又因为AC 平分∠DAB ,则∠1=∠2=12∠DAB .即可得出AD ∥OC ,则AD ⊥CD ; (2)连接BC ,则∠ACB =90°,可证明△ADC ∽△ACB .则2AD AC AC R ,从而求得R . 试题解析:(1)证明:连接OC ,∵直线CD 与⊙O 相切于C 点,AB 是⊙O 的直径,∴OC ⊥CD .又∵AC 平分∠DAB ,∴∠1=∠2=12∠DAB . 又∠COB =2∠1=∠DAB ,∴AD ∥OC ,∴AD ⊥CD .(2)连接BC ,则∠ACB =90°,在△ADC 和△ACB 中∵∠1=∠2,∠3=∠ACB =90°,∴△ADC ∽△ACB .∴2AD AC AC R= ∴R =2322AC AD = 15.如图,已知四边形ABCD 内接于⊙O ,点E 在CB 的延长线上,连结AC 、AE ,∠ACB =∠BAE =45°.(1)求证:AE 是⊙O 的切线;(2)若AB=AD ,AC =32,tan ∠ADC=3,求BE 的长.【答案】(1)证明见解析;(2)52BE = 【解析】试题分析:(1)连接OA 、OB ,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A 作AF ⊥CD 于点F,由AB=AD ,得到∠ACD =∠ACB =45°,在Rt △AFC 中可求得AF =3,在Rt △AFD 中求得DF =1,所以AB =AD =10 ,CD = CF +DF =4,再证明△ABE ∽△CDA ,得出BE AB DA CD=,即可求出BE 的长度; 试题解析: (1)证明:连结OA ,OB ,∵∠ACB =45°,∴∠AOB =2∠ACB = 90°,∵OA=OB ,∴∠OAB =∠OBA =45°,∵∠BAE =45°,∴∠OAE =∠OAB +∠BAE =90°,∴OA ⊥AE .∵点A 在⊙O 上,∴AE 是⊙O 的切线.(2)解:过点A 作AF ⊥CD 于点F ,则∠AFC =∠AFD =90°. ∵AB=AD , ∴AB u u u r =AD u u u r∴∠ACD =∠ACB =45°,在Rt △AFC 中,∵AC =∠ACF =45°,∴AF=CF=AC ·sin ∠ACF =3,∵在Rt △AFD 中, tan ∠ADC=3AF DF =, ∴DF =1,∴AB AD ==且CD = CF +DF =4,∵四边形ABCD 内接于⊙O ,∴∠ABE =∠CDA ,∵∠BAE =∠DCA ,∴△ABE ∽△CDA , ∴BE AB DA CD =,∴=∴5 BE .2。
2020-2021中考数学圆的综合的综合复习含答案解析

2020-2021中考数学圆的综合的综合复习含答案解析一、圆的综合1.(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系猜想结论:(要求用文字语言叙述)写出证明过程(利用图1,写出已知、求证、证明)(性质应用)①初中学过的下列四边形中哪些是圆外切四边形(填序号)A:平行四边形:B:菱形:C:矩形;D:正方形②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是.③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.【答案】见解析.【解析】【分析】(1)根据切线长定理即可得出结论;(2)①圆外切四边形是内心到四边的距离相等,即可得出结论;②根据圆外切四边形的对边和相等,即可求出结论;③根据圆外切四边形的性质求出第四边,利用周长建立方程求解即可得出结论.【详解】性质探讨:圆外切四边形的对边和相等,理由:如图1,已知:四边形ABCD的四边AB,BC,CD,DA都于⊙O相切于G,F,E,H.求证:AD+BC=AB+CD.证明:∵AB,AD和⊙O相切,∴AG=AH,同理:BG=BF,CE=CF,DE=DH,∴AD+BC=AH+DH+BF+CF=AG+BG+CE+DE=AB+CD,即:圆外切四边形的对边和相等.故答案为:圆外切四边形的对边和相等;性质应用:①∵根据圆外切四边形的定义得:圆心到四边的距离相等.∵平行四边形和矩形不存在一点到四边的距离相等,而菱形和正方形对角线的交点到四边的距离相等.故答案为:B,D;②∵圆外切四边形ABCD ,∴AB +CD =AD +BC .∵AB =12,CD =8,∴AD +BC =12+8=20,∴四边形的周长是AB +CD +AD +BC =20+20=40. 故答案为:40;③∵相邻的三条边的比为5:4:7,∴设此三边为5x ,4x ,7x ,根据圆外切四边形的性质得:第四边为5x +7x ﹣4x =8x .∵圆外切四边形的周长为48cm ,∴4x +5x +7x +8x =24x =48,∴x =2,∴此四边形的四边为4x =8cm ,5x =10cm ,7x =14cm ,8x =16cm .【点睛】本题是圆的综合题,主要考查了新定义圆的外切的性质,四边形的周长,平行四边形,矩形,菱形,正方形的性质,切线长定理,理解和掌握圆外切四边形的定义是解答本题的关键.2.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC (1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30. 【解析】 【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案. 【详解】(1)证明:∵CD 与⊙O 相切于点E , ∴OE CD ⊥,∴90CEO ∠=︒, 又∵OC BE P ,∴COE OEB ∠=∠,∠OBE=∠COA ∵OE=OB ,∴OEB OBE ∠=∠, ∴COE COA ∠=∠, 又∵OC=OC ,OA=OE , ∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒, 又∵AB 为⊙O 的直径, ∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形, ∴OF=OB=BF=EF , ∴OE=OB=BE ,∴OBE ∆为等边三角形, ∴60BOE ∠=︒, 而OE CD ⊥, ∴30D ∠=︒. 故答案为30. 【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.3.如图,在平面直角坐标系xoy 中,E (8,0),F(0 , 6). (1)当G(4,8)时,则∠FGE= °(2)在图中的网格区域内找一点P ,使∠FPE=90°且四边形OEPF 被过P 点的一条直线分割成两部分后,可以拼成一个正方形.要求:写出点P 点坐标,画出过P 点的分割线并指出分割线(不必说明理由,不写画法).【答案】(1)90;(2)作图见解析,P (7,7),PH 是分割线. 【解析】试题分析:(1)根据勾股定理求出△FEG 的三边长,根据勾股定理逆定理可判定△FEG 是直角三角形,且∠FGE="90" °.(2)一方面,由于∠FPE=90°,从而根据直径所对圆周角直角的性质,点P在以EF为直径的圆上;另一方面,由于四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形,从而OP是正方形的对角线,即点P在∠FOE的角平分线上,因此可得P(7,7),PH是分割线.试题解析:(1)连接FE,∵E(8,0),F(0 , 6),G(4,8),∴根据勾股定理,得FG=,EG=,FE=10.∵,即.∴△FEG是直角三角形,且∠FGE=90 °.(2)作图如下:P(7,7),PH是分割线.考点:1.网格问题;2.勾股定理和逆定理;3.作图(设计);4.圆周角定理.4.如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交OD于E,连接AD、AE、CE.(1)求证:∠ACE=∠DCE;(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;(3)若AC=4,23CDFCOESS∆∆=,求CF的长.【答案】(1)证明见解析,(2)60°;(3)43【解析】 【分析】(1)易证∠OEC =∠OCE ,∠OEC =∠ECD ,从而可知∠OCE =∠ECD ,即∠ACE =∠DCE ; (2)延长AE 交BC 于点G ,易证∠AGC =∠B +∠BAG =60°,由于OE ∥BC ,所以∠AEO =∠AGC =60°,所以∠EAO =∠AEO =60°; (3)易证12COE CAE S S =V V ,由于23CDF COE S S =V V ,所以CDF CAE S S V V =13,由圆周角定理可知∠AEC =∠FDC =90°,从而可证明△CDF ∽△CEA ,利用三角形相似的性质即可求出答案. 【详解】(1)∵OC =OE ,∴∠OEC =∠OCE .∵OE ∥BC ,∴∠OEC =∠ECD ,∴∠OCE =∠ECD ,即∠ACE =∠DCE ; (2)延长AE 交BC 于点G .∵∠AGC 是△ABG 的外角,∴∠AGC =∠B +∠BAG =60°. ∵OE ∥BC ,∴∠AEO =∠AGC =60°. ∵OA =OE ,∴∠EAO =∠AEO =60°.(3)∵O 是AC 中点,∴12COE CAE S S =V V . 23CDF COE S S =V V Q,∴CDF CAE SS V V =13. ∵AC 是直径,∴∠AEC =∠FDC =90°. ∵∠ACE =∠FCD ,∴△CDF ∽△CEA ,∴CF CA =3,∴CF =3CA =43.【点睛】本题考查了圆的综合问题,涉及平行线的性质,三角形的外角的性质,三角形中线的性质,圆周角定理,相似三角形的判定与性质等知识,需要学生灵活运用所学知识.5.如图,△ABC中,∠A=45°,D是AC边上一点,⊙O经过D、A、B三点,OD∥BC.(1)求证:BC与⊙O相切;(2)若OD=15,AE=7,求BE的长.【答案】(1)见解析;(2)18.【解析】分析:(1)连接OB,求出∠DOB度数,根据平行线性质求出∠CBO=90°,根据切线判定得出即可;(2)延长BO交⊙O于点F,连接AF,求出∠ABF,解直角三角形求出BE.详解:(1)证明:连接OB.∵∠A=45°,∴∠DOB=90°.∵OD∥BC,∴∠DOB+∠CBO=180°.∴∠CBO=90°.∴直线BC是⊙O的切线.(2)解:连接BD.则△ODB是等腰直角三角形,∴∠ODB=45°,BD=OD=15,∵∠ODB=∠A,∠DBE=∠DBA,∴△DBE∽△ABD,∴BD2=BE•BA,∴(15)2=(7+BE)BE,∴BE=18或﹣25(舍弃),∴BE=18.点睛:本题考查了切线的判定,圆周角定理,解直角三角形等知识点,能综合运用定理进行推理和计算是解此题的关键,题目综合性比较强,难度偏大.6.函数是描述客观世界运动变化的重要模型,理解函数的本质是重要的任务。
2021年浙江省中考数学知识点复习 圆----填空题
浙江中考复习----圆(填空题)1.如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是cm.2.如图所示,已知C为的中点,OA⊥CD于M,CN⊥OB于N,若OA=r,ON=a,则CD=.3.如图,MN为⊙O的直径,MN=10,AB为⊙O的弦,已知MN⊥AB于点P,AB=8,现要作⊙O的另一条弦CD,使得CD=6且CD∥AB,则PC的长度为.4.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=________.5.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为(计算结果保留π)6.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2018的坐标为.7.如图,已知点E为圆外的一点,EA交圆于点B,EC交圆于点D,若=80°,=30°,则∠BED=度.8.如图,点A、B、C是半径为4的⊙O上的三个点,若∠BAC=45°,则弦BC的长等于.9.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是.10.如图,四边形ABCD内接于⊙O,连接AC,若AC=AD,且∠DAC=50°,则∠B的度数为.11.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.12.如图,点A,B,C都在⨀O上,tan∠ABC=,将圆O沿BC翻折后恰好经过弦AB的中点D,则的值是.13.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,D为弧AC的中点,E为BA延长线上一点,若∠DAE=108°,则∠CAD=度.14.如图,在△ABC中,BA,BC分别为⊙O的切线,点E和点C为切线点,线段AC经过圆心O且与⊙O相交于D、C两点,若tan A=,AD=2,则BO的长为.15.如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=2,以C为圆心,r为半径作圆.若该圆与线段AB只有一个交点,则r的取值范围为.16.如图将母线长为9的圆锥侧面展开后得到扇形的圆心角为120°,若将该扇形剪成两个同样的扇形再围成2个同样的圆锥,则新圆锥的底面半径是.17.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB=.18.如图,矩形ABCD中,AB=7cm,BC=6cm,⊙O与矩形的边AB、BC、CD分别相切于点E、F、G,点P是⊙O上任意一点,则线段AP长度的最小值为.19.已知王星记的一款折扇打开后是一个圆心角为120的扇形,半径为30厘米,则打开后折扇的弧长是.20.如图,曲线AMNB和MON是两个半圆,MN∥AB,大半圆半径为2,则阴影部分的面积是.21.如图,直线AB与⊙O相切于点C,AO交⊙O于点D,连接CD,OC.若∠AOC=60°,则∠ACD=°.22.如图,已知AD是∠BAC的平分线,以线段AB为直径作圆,交∠BAC和角平分线于C,D两点.过D向AC作垂线DE垂足为点E.若DE=2CE=4,则直径AB=.23.如图,P A,PB分别切⊙O于A,B两点,CD切⊙O于点E.若P A=10,则△PCD的周长为.24.如图1,是某隧道的入口,它的截面如图2所示,是由和Rt∠ACB围成,且点C也在所在的圆上,已知AC=4m,隧道的最高点P离路面BC的距离DP=7m,则该道路的路面宽BC=m;在上,离地面相同高度的两点E,F装有两排照明灯,若E是的中点,则这两排照明灯离地面的高度是m.25.如图,在圆心角为90°的扇形ACB中,半径CA=6,以AC为直径作半圆O.过点O作BC的平行线交两弧于点D、E,则图中阴影部分的面积是.26.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为(,0)、(3,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为.。
2021年浙江省中考数学知识点复习圆-----选择题
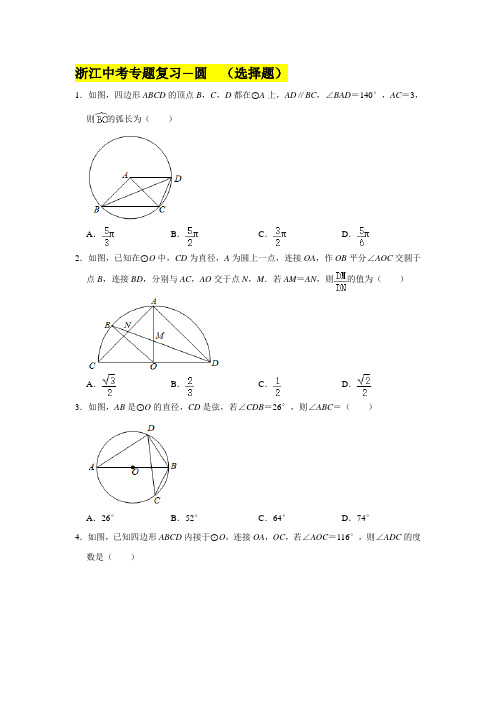
浙江中考专题复习—圆(选择题)1.如图,四边形ABCD的顶点B,C,D都在⊙A上,AD∥BC,∠BAD=140°,AC=3,则的弧长为()A.πB.πC.πD.π2.如图,已知在⊙O中,CD为直径,A为圆上一点,连接OA,作OB平分∠AOC交圆于点B,连接BD,分别与AC,AO交于点N,M.若AM=AN,则的值为()A.B.C.D.3.如图,AB是⊙O的直径,CD是弦,若∠CDB=26°,则∠ABC=()A.26°B.52°C.64°D.74°4.如图,已知四边形ABCD内接于⊙O,连接OA,OC,若∠AOC=116°,则∠ADC的度数是()A.122°B.120°C.117°D.116°5.已知,如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若AE=2,CD=6,则OB的长度为()A.B.C.D.56.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD分别与⊙O相切于点A,点D,连接BD,AD.若∠ACD=50°,则∠DBA的度数是()A.15°B.35°C.65°D.75°7.如图,⊙O的半径为5,点P在⊙O上,点A在⊙O内,且AP=3,过点A作AP的垂线交⊙O于点B、C.设PB=x,PC=y,则y与x的函数表达式()A.y=B.y=C.y=2x D.y=3x8.如图,⊙O的半径为2,弦AB平移得到CD(AB与CD位于点O两侧),且CD与⊙O相切于点E.若的度数为120°,则AD的长为()A.4B.2C.D.39.如图,BC与⊙O相切于点B,CO连接并延长后交⊙O于点A,连接AB,若∠BAC=36°,则∠C的度数为()A.36°B.24°C.18°D.15°10.如图,⊙O的半径OD⊥AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则cos∠OCE为()A.B.C.D.11.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=()A.10°B.15°C.20°D.25°12.如图,AD是半圆的直径,点C是弧BD的中点,∠ADC=55°,则∠BAD等于()A .50°B .55°C .65°D .70°13.圆内接正三角形、正方形、正六边形的边长之比为( )A.321::B.321::C.3123::D.无法确定 14.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( )A.()54+cm B .9cm C .54cm D .26cm15.如图,四边形ABCD 内接于O ,AE CB ⊥交CB 的延长线于点E ,若BA 平分DBE ∠,5AD =,13CE =,则(AE = )A .3B .32C .43D .2316.已知O 的半径为10cm ,弦//MN EF ,且12MN cm =,16EF cm =,则弦MN 和EF 之间的距离为( )cm .A .14或2B .14C .2D .617.如图,扇形AOB 中,OA =2,C 为上的一点,连接AC ,BC ,如果四边形 AOBC 为菱形,则图中阴影部分的面积为( )A .﹣B .﹣2C .﹣D .﹣218.如图,一个半径为1的⊙O1经过一个半径为2的⊙O的圆心,则图中阴影部分的面积为( )A.1 B.12 C. 2 D.2219.如图,在边长为2的正方形ABCD中,点E是边CD的中点,以A为圆心,AB为半径作弧,交BE于点F.记图中分割部分的面积为S1,S2,则S1﹣S2的值为()A.4﹣πB.2π﹣4 C.6﹣2πD.π﹣320.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是()A.2B.2C.2D.421.如图,A、B、C三点在⊙O上,若∠ACB=∠AOB,则∠AOB的度数是()A.60°B.90°C.100°D.120°22.若四边形ABCD是圆内接四边形,则它的内角∠A,∠B,∠C,∠D的度数之比可能是()A.3:1:2:5 B.1:2:2:3 C.2:7:3:6 D.1:2:4:3 23.如图,弦CD与直径AB相交,连接BC、BD,若∠ABC=50°,则∠BDC=()A.20°B.30°C.40°D.50°24.下列各说法中:①圆的每一条直径都是它的对称轴;②长度相等的两条弧是等弧;③相等的弦所对的弧也相等;④同弧所对的圆周角相等;⑤90°的圆周角所对的弦是直径;⑥任何一个三角形都有唯一的外接圆;其中正确的有()A.3个B.4个C.5个D.6个25.如图,半圆O的直径AB为15,弦BC为9,弦BD平分∠ABC,则BD的长是()A.12 B.5C.6D.26.已知,点A、B是CD为直径的⊙O上两点,分别在直径的两侧.其中点A是弧的中点,若tan∠ACB=2,则sin∠BCD的值为()A.B.C.D.27.如图,AB是⊙O的直径,C为⊙O上的点,把△AOC沿OC对折,点A的对应点D恰好落在⊙O上,且C、D均在直径AB上方,连接AD、BD,若AC=4,BD=4,则AD的长度应是()A.12 B.10 C.8D.628.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠OFE的度数是()A.30°B.20°C.40°D.35°29.如图,已知△ABC,O为AC上一点,以OB为半径的圆经过点A,且与BC、OC交于点E、D,设∠C=α,∠A=β,则()A.若α+β=70°,则弧DE的度数为20°B.若α+β=70°,则弧DE的度数为40°C.若α﹣β=70°,则弧DE的度数为20°D.若α﹣β=70°,则弧DE的度数为40°30.如图,锐角三角形ABC内接于⊙O,连接AO并延长,交BC于点D,OE⊥BC于点E.设∠B=α,∠C=β,∠DOE=γ,α<β,则α,β,γ的关系正确的是()A.β+γ=2αB.α+β﹣γ=90°C.α+β+γ=180°D.α+γ=β。
2021年浙江省中考一轮复习数学知识点圆---解答题

浙江中考知识点复习圆(解答题)1如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.(1)求证:∠CBE=∠BAE;(2)求证:BG=2PB;(3)若AB=,BC=3,直接写出BG的长.2.已知⊙O的圆心为点O,半径为3,点M为⊙O内的一个定点,OM=5,AB、CD是圆O的两条相互垂直的弦,垂足为M.(1)当AB=4时,求四边形ADBC的面积;(2)当AB变化时,求四边形ADBC的面积的最大值.3.如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.(1)判断△ABC的形状并证明你的结论;(2)当点P位于什么位置时,四边形PBOA是菱形?并说明理由.(3)求证:PA+PB=PC.4.如图,在扇形AOB 中,圆心角∠AOB =150°,D ,C 是AB ︵上的两点,∠DAB=30°,C 是DB ︵的中点.(1)连结OD ,求证:△AOD 是等腰直角三角形;(2)若扇形的半径为2.①求AB 的长度;②求四边形ABCD 的面积.5.如图,AB 为⊙O 的直径,弦CD ⊥AB 于E ,∠CDB =15°,OE =2. (1)求⊙O 的半径;(2)将△OBD 绕O 点旋转,使弦BD 的一个端点与弦AC 的一个端点重合,则弦BD 与弦AC 的夹角为 .6.如图,∠AOB =120°,OC 平分∠AOB ,∠MCN =60°,CM 与射线OA 相交于M 点,CN 与直线BO 相交于N 点.把∠MCN 绕着点C 旋转.(1)如图1,当点N 在射线OB 上时,求证:OC =OM +ON ;(2)如图2,当点N 在射线OB 的反向延长线上时,OC 与OM ,ON 之间的数量关系是 (直接写出结论,不必证明)7.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.8.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连接ED交AB于点F.(1)求证:△CDE是等腰三角形.(2)当CD:AC=2:时,求的值.9.已知四边形ABCD内接于⊙O,∠DAB=90°.(Ⅰ)如图1,连接BD,若⊙O的半径为6,,求AB的长;(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.10.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF;(2)若CD=6,AC=8,求⊙O的半径及CE的长.11.如图,AB是⊙O的直径,点C和点D分别在AB和⊙O上,且AC=AD,DC的延长线交⊙O于点E,过E作AC的平行线交⊙O于点F,连接AF,DF.(1)求证:四边形ACEF是平行四边形;(2)当sin∠EDF=,BC=4时,求⊙O的半径.12.如图,已知AC,BD为⊙O的两条直径,连接AB,BC,OE⊥AB于点E,点F是半径OC 的中点,连接EF.(1)设⊙O的半径为1,若∠BAC=30°,求线段EF的长.(2)连接BF,DF,设OB与EF交于点P,①求证:PE=PF.②若DF=EF,求∠BAC的度数.13.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E,DE与OB交于点F.(1)求证:BE=CE.(2)若∠A=45°,求的值.14.如图,在△ABC中,AC=4,BC=20,∠C=90°,点O为AB边上一点,⊙O切边AC于点D,设CD=x,⊙O的半径为y.(1)求y关于x的函数解析式;(2)当y=5时,求⊙O在BC边上截得的线段EF的长.15.如图,Rt△ABC中,∠ABC=90°,以BC为直径作⊙O交AC于点H,E为AC上一点,且AB=AE,BE交⊙O于点D,OD交AC于点F.(1)求证:DO⊥AC.(2)若CE=4,BC=8,求DE的长.16.如图,AB是⊙O的直径,点C为圆上一点,点D为的中点,连接AD,作DE⊥AB交BC的延长线于点E.(1)求证:DE=EB.(2)连接DO并延长交BC于点F.若CF=2CE,BD=5,求⊙O的半径.17.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连接AD,GD,AG.(1)找出图中和∠ADC相等的角,并给出证明;(2)已知BE=2,AE=8,求CD的长.18.如图,在Rt△ACB中,∠ACB=90°,点D为BC延长线上一点,以BD为直径作半圆O分别交AB,AC于点G,E,点E为的中点,过点E作⊙O的切线交AB于点F.(1)求证:∠AEF=∠ABC.(2)若sin A=,FG=1,求AC的长.19.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是弧BD上不与B、D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC 于点G.(1)求证:△ADF≌△BDG.(2)若AB=4,且点E是弧BD的中点,求阴影部分面积.(结果保留π)20.如图所示,⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D,(1)求证:△ABD是等腰三角形;(2)求CD的长.。
备战中考数学(浙教版)巩固复习圆的基本性质(含解析)

备战中考数学(浙教版)巩固复习圆的基本性质(含解析)A. cmB.C.D. 1cm4.如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为( )A.B. 1C. 或1D. 或1或5.若正多边形的一个外角为60°,则这个正多边形的中心角的度数是()A. 30°B. 60°C. 90°D. 120°6.下列结论错误的是()A. 圆是轴对称图形B. 圆是中心对称图形C. 半圆不是弧 D. 同圆中,等弧所对的圆心角相等7.如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是()A. C1>C2B. C1<C2C. C1=C2D. 不能确定8.如图,三角形ABC内接于圆O,AH BC于点H,若AC=8,AH=6,圆O的半径OC=5,则AB的值为().A. 5B.C. 7D.9.下列结论正确的是()A. 经过圆心的直线是圆的对称轴B. 直径是圆的对称轴C. 与圆相交的直线是圆的对称轴D. 与直径相交的直线是圆的对称轴10.如图,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A. 4个B. 3个C. 2个D. 1个11.如图,AB为⊙O的直径,点C在⊙O上,若∠C=15°,则∠BOC =().A. 60°B. 45°C. 30°D. 15°二、填空题12.如图,在半径为4cm的⊙O中,劣弧AB的长为2πcm,则∠C=________ 度.13.如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则点B转过的路径长为________ (结果保留π).14.已知扇形的半径为3,扇形的圆心角是120°,则该扇形面积为________.15.如图,A、B、C、D是圆上的点,∠1=70°,∠A=40°则∠C=________度.16.已知扇形的圆心角为120°,弧长等于一个半径为5cm的圆的周长,则扇形的面积为________.17.如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是________.18.如图,点A、B、C在⊙O上,∠A=50°,则∠BOC度数为________ .19.已知正六边形的边心距为,则这个正六边形的边长为________ .三、解答题20.“不在同一直线上的三点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.21如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上的点,DC⊥AN,与AN交于点C,己知AC=15,⊙O的半径为30,求的长.四、综合题22.已知点在⊙ 上,,仅使用无刻度的直尺作图(保留痕迹)(1)在图①中画一个含的直角三角形;(2)点在弦上,在图②中画一个含的直角三角形.答案解析部分一、单选题1.【答案】A【考点】弧长的计算【解析】【解答】解:∵l=,∴r==18,故选A.【分析】根据弧长公式l=进行计算即可.2.【答案】D【考点】点与圆的位置关系【解析】【解答】设以QP为直径的圆为⊙O,则⊙O的半径为QP,如果OA>QP,那么点A在⊙O外;如果OA=QP,那么点A在⊙O上;如果OA<QP,那么点A在⊙O内;∵题目没有告诉OA与QP的大小关系,∴以上三种情况都有可能.故选D.【分析】设以QP为直径的圆为⊙O,要判断点A 与此圆的位置关系,只需比较OA与⊙O的半径大小即可.3.【答案】A【考点】正多边形和圆【解析】【解答】连接AC ,过B作BD⊥AC于D;∵AB=BC,∴△ABC是等腰三角形,∴AD=CD;∵此多边形为正六边形,∴∴∠ABD= =60°∴∠BAD=30°,AD=AB·cos30°=∴a= cm故选A【分析】连接AC,作BD⊥AC于D;根据正六边形的特点求出∠ABC的度数,再由等腰三角形的性质求出∠BAD的度数,由特殊角的三角函数值求出AD的长,进而可求出AC的长.4.【答案】D【考点】圆周角定理【解析】【分析】若△BEF是直角三角形,则有两种情况:①∠BFE=90°,②∠BEF=90°;在上述两种情况所得到的直角三角形中,已知了BC边和∠B的度数,即可求得BE的长;AB的长易求得,由AE=AB-BE即可求出AE的长,也就能得出E点运动的距离,根据时间=路程÷速度即可求得t的值.【解答】∵AB是⊙O的直径,∴∠ACB=90°;Rt△ABC中,BC=2,∠ABC=60°;∴AB=2BC=4cm;①当∠BFE=90°时;Rt△BEF中,∠ABC=60°,则BE=2BF=2cm;故此时AE=AB-BE=2cm;∴E点运动的距离为:2cm,故t=1s;所以当∠BFE=90°时,t=1s;②当∠BEF=90°时;同①可求得BE=0.5cm,此时AE=AB-BE=3.5cm;∴E点运动的距离为:3.5cm,故t=1.75s;③当E从B回到O的过程中,在运动的距离是:2(4-3.5)=1cm,则时间是:1.75+=.综上所述,当t的值为1s或1.75s和s时,△BEF是直角三角形.故选:D.【点评】此题主要考查了圆周角定理以及直角三角形的判定和性质,同时还考查了分类讨论的数学思想5.【答案】B【考点】正多边形和圆【解析】【解答】解:∵正多边形的一个外角为60°,∴正多边形的边数为=6,其中心角为=60°.故选B.【分析】根据正多边形的外角和是360°求出正多边形的边数,再求出其中心角.6.【答案】C【考点】圆的认识【解析】【解答】A、圆是轴对称图形,说法正确;B、圆是中心对称图形,说法正确;C、半圆不是弧,说法错误;D、同圆中,等弧所对的圆心角相等,说法正确;故选:C【分析】根据圆既是轴对称图形,也是中心对称图形,圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,进行分析.7.【答案】B【考点】圆的认识【解析】【解答】解:设半圆的直径为a,则半圆周长C1为:aπ+a,4个正三角形的周长和C2为:3a,∵aπ+a<3a,∴C1<C2故选B.【分析】首先设出圆的直径,然后表示出半圆的周长与三个正三角形的周长和,比较后即可得到答案.8.【答案】D【考点】三角形的外接圆与外心【解析】试题分析:作直径AE,连接CE,∴∠ACE=90°,∵AH⊥BC,∴∠AHB=90°,∴∠ACE=∠ADB,∵∠B=∠E,∴△ABH∽△AEC,∴ ,∴AB= ,∵AC=24,AH=18,AE=2OC=26,∴AB=故选:D.9.【答案】A【考点】圆的认识【解析】【解答】A、经过圆心的直线是圆的对称轴,所以A正确;B、直径所在的直线为圆的对称轴,所以B错误;C、与圆相交的直线不一定是圆的对称轴,所以C错误;D、与直径相交的圆心的直线是圆的对称轴,所以D错误.故选A.【分析】利用直径所在的直线为圆的对称轴对各选项进行判断.10.【答案】B【考点】圆周角定理【解析】【分析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半。
浙江省2021—2021年中考数学真题汇编专题11:圆(原卷)

浙江省2021—2021年中考数学真题汇编专题11:圆姓名:__________班级:__________考号:__________一、、选择题(本大题共10小题,每小题3分,共30分)1.(2019年浙江省温州市)若扇形的圆心角为90°,半径为6,则该扇形的弧长为()A.πB.2πC.3πD.6π2.(2019年浙江省湖州市)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是()A.60πcm2B.65πcm2C.120πcm2D.130πcm23.(2019年浙江省台州市)如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为()A.2B.3 C.4 D.4﹣4.(2019年浙江省绍兴市)如图,△ABC内接于⊙O,∠B=65°,∠C=70°.若BC=2,则的长为()A.πB.πC.2πD.2π5.(2019年浙江省宁波市)如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为()A.3.5cm B.4cm C.4.5cm D.5cm6.(2019年浙江省嘉兴市)如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为()A.2 B.C.D.7.(2019年浙江省湖州市)如图,已知正五边形ABCDE内接于⊙O,连结BD,则∠ABD的度数是()A.60°B.70°C.72°D.144°8.(2019年浙江省杭州市)如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB=()A.2 B.3 C.4 D.59.(2019年浙江省衢州市)如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为()A.1 B.C.D.210.(2019年浙江省金华市、丽水市)如图物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为()A.2 B.C.D.二、、填空题(本大题共6小题,每小题4分,共24分)11.(2019年浙江省杭州市)如图是一个圆锥形冰淇淋外壳(不计厚度),已知其母线长为12cm,底面圆半径为3cm,则这个冰淇淋外壳的侧面积等于cm2(结果精确到个位).12.(2019年浙江省湖州市)已知一条弧所对的圆周角的度数是15°,则它所对的圆心角的度数是.13.(2019年浙江省温州市)如图,⊙O分别切∠BAC的两边AB,AC于点E,F,点P在优弧()上,若∠BAC=66°,则∠EPF等于度.14.(2019年浙江省台州市)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连接AE.若∠ABC=64°,则∠BAE的度数为.15.(2019年浙江省嘉兴市)如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.16.(2018年浙江省温州市)小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为cm2,则该圆的半径为cm.三、、解答题(本大题共8小题,共66分)17.(2019年浙江省绍兴市)在屏幕上有如下内容:如图,△ABC内接于⊙O,直径AB的长为2,过点C的切线交AB的延长线于点D.张老师要求添加条件后,编制一道题目,并解答.(1)在屏幕内容中添加条件∠D=30°,求AD的长.请你解答.(2)以下是小明、小聪的对话:小明:我加的条件是BD=1,就可以求出AD的长小聪:你这样太简单了,我加的是∠A=30°,连结OC,就可以证明△ACB与△DCO全等.参考此对话,在屏幕内容中添加条件,编制一道题目(可以添线添字母),并解答.18.(2019年浙江省衢州市)如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.(1)求证:DE是⊙O的切线.(2)若DE=,∠C=30°,求的长.19.(2019年浙江省金华市、丽水市)如图,在▱OABC中,以O为圆心,OA为半径的圆与BC相切于点B,与OC相交于点D.(1)求的度数.(2)如图,点E在⊙O上,连结CE与⊙O交于点F,若EF=AB,求∠OCE的度数.20.(2019年浙江省湖州市)已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3).(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长,(2)如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2为半径画圆.①当点Q与点C重合时,求证:直线l1与⊙Q相切,②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标,若不存在,请说明理由.21.(2019年浙江省杭州市)如图,已知锐角三角形ABC内接于圆O,OD⊥BC于点D,连接OA.(1)若∠BAC=60°,①求证:OD=OA.②当OA=1时,求△ABC面积的最大值.(2)点E在线段OA上,OE=OD,连接DE,设∠ABC=m∠OED,∠ACB=n∠OED(m,n是正数),若∠ABC<∠ACB,求证:m﹣n+2=0.22.(2019年浙江省宁波市)如图1,⊙O经过等边△ABC的顶点A,C(圆心O在△ABC内),分别与AB,CB的延长线交于点D,E,连结DE,BF⊥EC交AE于点F.(1)求证:BD=BE.(2)当AF:EF=3:2,AC=6时,求AE的长.(3)设=x,tan∠DAE=y.①求y关于x的函数表达式,②如图2,连结OF,OB,若△AEC的面积是△OFB面积的10倍,求y的值.23.(2018年浙江省温州市)如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.(1)求证:∠BPD=∠BAC.(2)连接EB,ED,当tan∠MAN=2,AB=2时,在点P的整个运动过程中.①若∠BDE=45°,求PD的长.②若△BED为等腰三角形,求所有满足条件的BD的长.(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记△OFP的面积为S1,△CFE 的面积为S2,请写出的值.24.(2018年浙江省台州市)如图,△ABC是⊙O的内接三角形,点D在上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.(1)求证:AC=CE;(2)求证:BC2﹣AC2=AB•AC;(3)已知⊙O的半径为3.①若=,求BC的长;②当为何值时,AB•AC的值最大?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙教版2021年中考数学总复习
《圆》
一、选择题
1.如图,在⊙O中与∠1一定相等的角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数为()
A.60°
B.50°
C.40°
D.30°
3.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是()
A.110°
B.70°
C.55°
D.125°
4.如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是()
A.40°
B.60°
C.70°
D.80°
5.如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为()
A.20° B.25° C.40° D.50°
6.阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为()
A.(60°,4)B.(45°,4)C.(60°,2)D.(50°,2)
7.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c值为
()
A.1:2:3
B.3:2:1
C.1::
D.::1
8.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为()
A.45° B.50° C.55° D.60°
二、填空题
9.将面积为32π的半圆围成一个圆锥的侧面,则这个圆锥的底面半径为.
10.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD
为的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”。
(1尺=10寸)则
CD=____________
11.如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7,则∠A4A1A7= °.
12.如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP=_______.
三、解答题
13.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠
ABC.
(1)求证:直线BF是⊙O的切线.
(2)若CD=2,OP=1,求线段BF的长.
14.如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交
AB延长线于点C.
(1)求⊙O的半径;
(2)求证:CE是⊙O的切线;
(3)若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.
15.已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接
AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
16.如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接
CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
参考答案
1.答案为:A.
2.B
3.D
4.答案为:D
5.B
6.A
7.C.
8.答案为:B.
9.答案为:4.
10.答案为:2尺6寸
11.答案为:54°;
12.答案为:40°或100°或20°.
13.(1)证明:∵∠AFB=∠ABC,∠ABC=∠ADC,∴∠AFB=∠ADC,
∴CD∥BF,∴∠AFD=∠ABF,
∵CD⊥AB,∴AB⊥BF,∴直线BF是⊙O的切线.
(2)解:连接OD,∵CD⊥AB,∴PD=0.5CD=,
∵OP=1,∴OD=2,∵∠PAD=∠BAF,∠APO=∠ABF,∴△APD∽△ABF,∴=,∴=,∴BF=.
14.
15.(1)证明:连接OD,
∴OD=OA,
∴∠1=∠2,
∵BC为⊙O的切线,
∴∠ODB=90°,
∵∠C=90°,
∴∠ODB=∠C,
∴OD∥AC,
∴∠3=∠2,
∴∠1=∠3,
∴AD是∠BAC的平分线;
(2)解:连接DF,
∵∠B=30°,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠3=30°,
∵BC是⊙O的切线,
∴∠FDC=∠3=30°,
∴CD=CF=,
∴AC=CD=3,
∴AF=2,
过O作OG⊥AF于G,∴GF=AF=1,四边形ODCG是矩形,
∴CG=2,OG=CD=,∴OC==.
16.(1)证明:如图连接OD.
∵四边形OBEC是平行四边形,∴OC∥BE,∴∠AOC=∠OBE,∠COD=∠ODB,∵OB=OD,∴∠OBD=∠ODB,∴∠DOC=∠AOC,
在△COD和△COA中,,∴△COD≌△COA,
∴∠CAO=∠CDO=90°,∴CF⊥OD,
∴CF是⊙O的切线.
(2)解:∵∠F=30°,∠ODF=90°,
∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠DBO=60°,
∵∠DBO=∠F+∠FDB,
∴∠FDB=∠EDC=30°,
∵EC∥OB,
∴∠E=180°﹣∠OBD=120°,
∴∠ECD=180°﹣∠E﹣∠EDC=30°,
∴EC=ED=BO=DB,
∵EB=4,∴OB=OD═OA=2,
在RT△AOC中,
∵∠OAC=90°,OA=2,∠AOC=60°,
∴AC=OA•tan60°=2,
∴S阴=2•S△AOC﹣S扇形OAD=2××2×2﹣=2﹣.。
