初三圆测试题222打印
初三数学圆测试题及答案

初三数学圆测试题及答案一、选择题(每题3分,共30分)1. 下列说法正确的是()。
A. 圆的直径是半径的2倍B. 圆的周长是直径的π倍C. 圆的面积是半径的平方乘以πD. 圆的周长是半径的2π倍答案:D2. 圆的面积公式为()。
A. S = πrB. S = πr²C. S = πdD. S = πd²答案:B3. 圆的周长公式为()。
A. C = 2πrB. C = 2πdC. C = πrD. C = πd答案:A4. 圆心角为60°的扇形面积是()。
A. πr²/6B. πr²/3C. πr²/2D. πr²答案:A5. 一个圆的半径为3cm,其面积为()。
A. 9π cm²B. 18π cm²C. 27π cm²D. 36π cm²答案:C6. 圆的直径增加1倍,其面积增加()。
A. 1倍B. 2倍C. 4倍D. 8倍答案:C7. 圆的半径增加1倍,其周长增加()。
A. 1倍B. 2倍C. 3倍D. 4倍答案:B8. 一个圆的周长为12.56cm,其直径为()。
A. 2cmB. 4cmC. 6cmD. 8cm答案:B9. 圆的半径为4cm,其直径为()。
A. 2cmB. 4cmC. 8cmD. 16cm答案:C10. 圆的半径为2cm,其周长为()。
A. 4π cmB. 8π cmC. 12π cmD. 16π cm答案:B二、填空题(每题3分,共30分)1. 圆的周长公式为______。
答案:C = 2πr2. 圆的面积公式为______。
答案:S = πr²3. 圆的直径是半径的______倍。
答案:24. 圆的周长是直径的______倍。
答案:π5. 圆的面积是半径的平方乘以______。
答案:π6. 圆心角为90°的扇形面积是圆面积的______。
答案:1/47. 圆心角为180°的扇形面积是圆面积的______。
初三数学圆的测试卷

一、选择题(每题5分,共20分)1. 下列说法正确的是()A. 圆的直径是圆的最长弦B. 圆的半径是圆的最短弦C. 圆的周长与直径的比值是常数πD. 圆的面积与半径的平方成线性关系2. 已知圆的半径为5cm,则其直径的长度是()A. 10cmB. 15cmC. 20cmD. 25cm3. 在一个圆中,若圆心角是直角,则对应的弧长与半径的比值是()A. πB. π/2C. 1/2πD. 1/4π4. 下列图形中,不属于圆的是()A. 圆形B. 矩形C. 正方形D. 椭圆5. 已知圆的周长是31.4cm,则其面积是()A. 78.5cm²B. 50.24cm²C. 157cm²D. 314cm²二、填空题(每题5分,共20分)6. 圆的半径为r,则其直径长度为______。
7. 圆的周长公式为______。
8. 圆的面积公式为______。
9. 若一个圆的半径增加了1cm,则其面积增加了______平方厘米。
10. 一个圆的周长是62.8cm,则其半径是______cm。
三、解答题(每题10分,共30分)11. 已知一个圆的直径为10cm,求这个圆的周长和面积。
12. 在一个圆中,一个圆心角的度数是90°,求这个圆心角对应的弧长和它所对的圆周角。
13. 一个圆的半径是6cm,如果将这个圆的半径扩大到原来的两倍,求扩大后的圆的周长和面积。
四、应用题(每题10分,共20分)14. 一条绳子围成一个圆形,绳子长40cm,求这个圆的直径和面积。
15. 在一个圆形花坛中,直径为8m,若在花坛周围铺设宽2m的小路,求小路的面积。
答案:一、选择题1. C2. A3. A4. B5. B二、填空题6. 2r7. C = 2πr8. S = πr²9. 12π10. 10cm三、解答题11. 周长:C = 2πr = 2π × 5 = 31.4cm;面积:S = πr² = π × 5² = 78.5cm²。
九年级圆 几何综合检测题(WORD版含答案)

九年级圆 几何综合检测题(WORD 版含答案)一、初三数学 圆易错题压轴题(难)1.如图,以A (0,3)为圆心的圆与x 轴相切于坐标原点O ,与y 轴相交于点B ,弦BD的延长线交x 轴的负半轴于点E ,且∠BEO =60°,AD 的延长线交x 轴于点C .(1)分别求点E 、C 的坐标;(2)求经过A 、C 两点,且以过E 而平行于y 轴的直线为对称轴的抛物线的函数解析式; (3)设抛物线的对称轴与AC 的交点为M ,试判断以M 点为圆心,ME 为半径的圆与⊙A 的位置关系,并说明理由.【答案】(1)点C 的坐标为(-3,0)(2)2343333y x x =++3)⊙M 与⊙A 外切 【解析】试题分析:(1)已知了A 点的坐标,即可得出圆的半径和直径,可在直角三角形BOE 中,根据∠BEO 和OB 的长求出OE 的长进而可求出E 点的坐标,同理可在直角三角形OAC 中求出C 点的坐标;(2)已知了对称轴的解析式,可据此求出C 点关于对称轴对称的点的坐标,然后根据此点坐标以及C ,A 的坐标用待定系数法即可求出抛物线的解析式;(3)两圆应该外切,由于直线DE ∥OB ,因此∠MED=∠ABD ,由于AB=AD ,那么∠ADB=∠ABD ,将相等的角进行置换后可得出∠MED=∠MDE ,即ME=MD ,因此两圆的圆心距AM=ME+AD ,即两圆的半径和,因此两圆外切.试题解析:(1)在Rt△EOB 中,3cot60232EO OB =⋅︒==, ∴点E 的坐标为(-2,0).在Rt△COA 中,tan tan60333OC OA CAO OA =⋅∠=⋅︒==, ∴点C 的坐标为(-3,0).(2)∵点C 关于对称轴2x =-对称的点的坐标为F (-1,0), 点C 与点F (-1,0)都在抛物线上. 设()()13y a x x =++,用(03A ,代入得()()30103a =++,∴33a =. ∴()()313y x x =++,即 2343333y x x =++. (3)⊙M 与⊙A 外切,证明如下: ∵ME ∥y 轴,∴MED B ∠=∠.∵B BDA MDE ∠=∠=∠, ∴MED MDE ∠=∠. ∴ME MD =.∵MA MD AD ME AD =+=+, ∴⊙M 与⊙A 外切.2.如图①,已知Rt △ABC 中,∠ACB =90°,AC =8,AB =10,点D 是AC 边上一点(不与C 重合),以AD 为直径作⊙O ,过C 作CE 切⊙O 于E ,交AB 于F . (1)若⊙O 半径为2,求线段CE 的长; (2)若AF =BF ,求⊙O 的半径;(3)如图②,若CE =CB ,点B 关于AC 的对称点为点G ,试求G 、E 两点之间的距离.【答案】(1)CE =2;(2)⊙O 的半径为3;(3)G 、E 两点之间的距离为9.6 【解析】 【分析】(1)根据切线的性质得出∠OEC=90°,然后根据勾股定理即可求得; (2)由勾股定理求得BC ,然后通过证得△OEC ∽△BCA ,得到OE OC BC BA =,即8610r r-= 解得即可;(3)证得D 和M 重合,E 和F 重合后,通过证得△GBE ∽△ABC ,GB GEAB AC=,即12108GE =,解得即可.【详解】解:(1)如图①,连接OE,∵CE切⊙O于E,∴∠OEC=90°,∵AC=8,⊙O的半径为2,∴OC=6,OE=2,∴CE=2242OC OE-=;(2)设⊙O的半径为r,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,∴BC22AB A C-=6,∵AF=BF,∴AF=CF=BF,∴∠ACF=∠CAF,∵CE切⊙O于E,∴∠OEC=90°,∴∠OEC=∠ACB,∴△OEC∽△BCA,∴OE OCBC BA=,即8610r r-=解得r=3,∴⊙O的半径为3;(3)如图②,连接BG,OE,设EG交AC于点M,由对称性可知,CB=CG,∵CE=CG,∴∠EGC=∠GEC,∵CE切⊙O于E,∴∠GEC+∠OEG=90°,∵∠EGC+∠GMC=90°,∴∠OEG=∠GMC,∵∠GMC=∠OME,∴∠OEG=∠OME,∴OM=OE,∴点M和点D重合,∴G、D、E三点在同一直线上,连接AE、BE,∵AD是直径,∴∠AED=90°,即∠AEG=90°,又CE=CB=CG,∴∠BEG=90°,∴∠AEB=∠AEG+∠BEG=180°,∴A、E、B三点在同一条直线上,∴E、F两点重合,∵∠GEB=∠ACB=90°,∠B=∠B,∴△GBE∽△ABC,∴GB GEAB AC=,即12108GE=∴GE=9.6,故G、E两点之间的距离为9.6.【点睛】本题考查了切线的判定,轴的性质,勾股定理的应用以及三角形相似的判定和性质,证得G、D、E三点共线以及A、E、B三点在同一条直线上是解题的关3.已知:在△ABC中,AB=6,BC=8,AC=10,O为AB边上的一点,以O为圆心,OA长为半径作圆交AC于D点,过D作⊙O的切线交BC于E.(1)若O为AB的中点(如图1),则ED与EC的大小关系为:ED EC(填“”“”或“”)(2)若OA<3时(如图2),(1)中的关系是否还成立?为什么?(3)当⊙O过BC中点时(如图3),求CE长.【答案】(1)ED=EC;(2)成立;(3)3【解析】试题分析:(1)连接OD,根据切线的性质可得∠ODE=90°,则∠CDE+∠ADO=90°,由AB=6,BC=8,AC=10根据勾股定理的逆定理可证得∠ABC=90°,则∠A+∠C=90°,根据圆的基本性质可得∠A=∠ADO,即可得到∠CDE=∠C,从而证得结论;(2)证法同(1);(3)根据直角三角形的性质结合圆的基本性质求解即可.(1)连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6,BC=8,AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC;(2)连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6,BC=8,AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC;(3)CE=3.考点:圆的综合题点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.4.如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q 以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC﹣CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.(1)当2<m≤8时,AP=,AQ=.(用m的代数式表示)(2)当线段FG长度达到最大时,求m的值;(3)在点P,Q整个运动过程中,①当m为何值时,⊙O与△ABC的一边相切?②直接写出点F所经过的路径长是.(结果保留根号)【答案】(1)2+m ,m ﹣2;(2)m=5.5;(3)①当m=1或4或10﹣433时,⊙O 与△ABC 的边相切.②点F 的运动路径的长为1136+572. 【解析】试题分析:(1)根据题意可得AP =2+m ,AQ =m −2.(2)如图1中在Rt △EFG 中, 30,90EFG A EGF ∠=∠=∠=, 推出3cos30cos30FG EF PE EP =⋅=⋅=,所以当点E 与点C 重合时,PE 的值最大,求出此时EP 的长即可解决问题.(3)①当02t <≤ (Q 在往A 运动)时,如图2中,设O 切AC 于H ,连接OH .当28m <≤(Q 从A 向B 运动)时,则PQ =(2+m )−(m −2)=4,如图3中,设O 切AC 于H .连接OH .如图4中,设O 切BC 于N ,连接ON .分别求解即可.②如图5中,点F 的运动轨迹是F 1→F 2→B .分别求出122F F F B ,即可解决问题. 试题解析:(1)当28m <≤时,AP =2+m ,AQ =m −2. 故答案为2+m ,m −2. (2)如图1中,在Rt △EFG 中, 30,90EFG A EGF ∠=∠=∠=,3cos30cos30FG EF PE EP ∴=⋅=⋅=, ∴当点E 与点C 重合时,PE 的值最大, 易知此时53553AC BC EP AB ⨯⨯===3tan30(2)3EP AP m =⋅=+⋅, 533(2)m ∴=+⋅,∴m =5.5(3)①当02t <≤ (Q 在往A 运动)时,如图2中,设O 切AC 于H ,连接OH .则有AD =2DH =2, ∴DH =DQ =1,即m =1.当28m <≤(Q 从A 向B 运动)时,则PQ =(2+m )−(m −2)=4, 如图3中,设O 切AC 于H .连接OH .则AO =2OH =4,AP =4+2=6, ∴2+m =6, ∴m =4. 如图4中,设O 切BC 于N ,连接ON .在Rt △OBN 中, 43sin603OB ON ==, 4310AO ∴=-, 43123AP ∴=-, 432123m ∴+=-, 4310m ∴=-, 综上所述,当m =1或4或4310-时,O 与△ABC 的边相切。
初三圆测试题及答案

初三圆测试题及答案一、选择题(每题3分,共30分)1. 圆的半径为r,圆的周长为()。
A. 2πrB. πrC. 2rD. πr²2. 圆的直径为d,圆的面积为()。
A. πd²/4B. πd²C. πr²D. πr²/23. 点P在圆O的内部,则点P到圆心O的距离()。
A. 大于半径B. 等于半径C. 小于半径D. 不确定4. 圆的切线与过切点的半径垂直,切线的长度等于()。
A. 半径B. 直径C. 半径的一半D. 无法确定5. 已知圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是()。
A. 相离B. 相切C. 相交D. 内切6. 圆的内接四边形的对角互补,即()。
A. 对角和为180°B. 对角和为90°C. 对角和为360°D. 对角差为180°7. 圆的外接圆的半径等于()。
A. 边长B. 对角线的一半C. 对角线D. 无法确定8. 圆的内切圆的半径等于()。
A. 边长的一半B. 对角线的一半C. 对边之和的一半D. 无法确定9. 圆的弧长公式为()。
A. L = 2πrθ/360B. L = πrθC. L = rθD. L = 2πr10. 圆的扇形面积公式为()。
A. S = 1/2r²θB. S = r²θC. S = 1/2LD. S = 1/2rL二、填空题(每题2分,共20分)11. 圆的周长公式为C = ____________。
12. 若圆的半径为4,则圆的面积为___________。
13. 圆的切线与半径的关系是___________。
14. 圆的内接正六边形的边长等于___________。
15. 圆的外接正三角形的边长等于___________。
16. 圆的内切圆的半径等于圆的内接正六边形的边长的___________。
17. 圆的弧长公式中θ表示的是___________。
初三圆园测试题及答案

初三圆园测试题及答案一、选择题(每题2分,共10分)1. 圆的周长公式是()A. C = πdB. C = 2πrC. C = πrD. C = 2d2. 圆的面积公式是()A. S = πr²B. S = 2πrC. S = πdD. S = πd²3. 圆的直径是半径的()A. 1倍B. 2倍C. 4倍D. 不确定4. 半径为3的圆的面积是()A. 28.26B. 9C. 18.84D. 365. 如果一个圆的半径增加1,那么它的面积将增加多少?()A. πB. 2πC. π(2r+1)D. π(r+1)²二、填空题(每题2分,共10分)6. 一个圆的半径为5厘米,那么它的直径是________厘米。
7. 圆的周长是它直径的________倍。
8. 如果一个圆的半径为2,那么它的周长是________π。
9. 圆心到圆上任意一点的距离叫做________。
10. 半径为1的圆的面积是________π。
三、解答题(每题5分,共20分)11. 已知一个圆的半径为4厘米,求它的周长和面积。
12. 如果一个圆的周长为12π厘米,求它的半径。
13. 一个圆的面积为28.26平方厘米,求它的半径。
14. 一个圆的半径从2厘米增加到3厘米,它的面积增加了多少?四、应用题(每题10分,共20分)15. 一个车轮的直径是50厘米,如果车轮每分钟转100圈,求车轮每分钟行驶的距离。
16. 一个圆形花坛的半径是10米,如果花坛的周围要围上一圈篱笆,篱笆的长度至少是多少?答案:一、选择题1. B2. A3. B4. C5. C二、填空题6. 107. π8. 49. 半径10. 1三、解答题11. 周长:2πr = 2 × 3.14 × 4 = 25.12厘米;面积:πr² = 3.14 × 4² = 50.24平方厘米。
12. 半径:C/d = 12π / (2 × 3.14) = 6厘米。
九年级数学圆测试题及答案

九年级数学圆测试题一、选择题1.若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a,最小距离为ba>b,则此圆的半径为A .2b a +B .2b a - C .22b a b a -+或 D .b a b a -+或 2.如图24—A —1,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长是A .4B .6C .7D .83.已知点O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为A .40°B .80°C .160°D .120°4.如图24—A —2,△ABC 内接于⊙O,若∠A=40°,则∠OBC 的度数为A .20°B .40°C .50°D .70°5.如图24—A—3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为A .12个单位B .10个单位C .1个单位D .15个单位6.如图24—A —4,AB 为⊙O 的直径,点C 在⊙O 上,若∠B=60°,则∠A 等于A .80°B .50°C .40°D .30°7.如图24—A —5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B,CD 切⊙O 于点E,分别交PA 、PB 于点C 、D,若PA=5,则△PCD 的周长为A .5B .7C .8D .108.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m,母线长为3m,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是A .26mB .26m πC .212mD .212m π9.如图24—A —6,两个同心圆,大圆的弦AB 与小圆相切于点P,大圆的弦CD 经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是A .16πB .36πC .52πD .81π10.已知在△ABC 中,AB=AC=13,BC=10,那么△ABC 的内切圆的半径为A .310B .512 C .2 D .3 11.如图24—A —7,两个半径都是4cm 的圆外切于点C,一只蚂蚁由点图24—A 图24—A 图24—A 图24—A —2 图24—A 图24—A 图24—AA 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm 后才停下来,则蚂蚁停的那一个点为A .D 点B .E 点C .F 点D .G 点二、填空题12.如图24—A —8,在⊙O 中,弦AB 等于⊙O 的半径,OC ⊥AB 交⊙O 于点C,则∠AOC= ; 13.如图24—A —9,AB 、AC 与⊙O 相切于点B 、C,∠A=50゜,P 为⊙O 上异于B 、C 的一个动点,则∠BPC 的度数为 ;14.已知⊙O 的半径为2,点P为⊙O 外一点,OP 长为3,那么以P 为圆心且与⊙O 相切的圆的半径为 ;15.一个圆锥的底面半径为3,高为4,则圆锥的侧面积是 ;16.扇形的弧长为20πcm,面积为240πcm 2,则扇形的半径为 cm;17.如图24—A —10,半径为2的圆形纸片,沿半径OA 、OB 裁成1:3两部分,用得到的扇形围成圆锥的侧面,则圆锥的底面半径分别为 ;18.在Rt △ABC 中,∠C=90゜,AC=5,BC=12,以C 为圆心,R 为半径作圆与斜边AB 相切,则R 的值为 ;19.已知等腰△ABC 的三个顶点都在半径为5的⊙O 上,如果底边BC 的长为8,那么BC 边上的高为 ;20.已知扇形的周长为20cm,面积为16cm 2,那么扇形的半径为 ;21.如图24—A —11,AB 为半圆直径,O 为圆心,C 为半圆上一点,E 是弧AC 的中点,OE 交弦AC 于点D;若AC=8cm,DE=2cm,则OD 的长为cm;三.解答题 22.如图24—A —13,AD 、BC 是⊙O 的两条弦,且AD=BC,求证:AB=CD;23.如图24—A —14,已知⊙O 的半径为8cm,点A 为半径OB 的延长线上一点,射线AC 切⊙O 于点C,BC 的长为cm 38,求线段AB 的长;24.已知:△ABC 内接于⊙O,过点A 作直线EF;1如图24—A —15,AB 为直径,要使EF 为⊙O 的切线,还需添加的条件是只需写出三种情况: ① ;② ;③ ;2如图24—A —16,AB 是非直径的弦,∠CAE=∠B,求证:EF 是⊙O 的切线;答案一、选择题1.D 2.D 3.C 4.C 5.B 6.D 7. D 8.B 9.B 10.A 11.A 图24—A 图24—A图24—A —图24—A —⌒ 图24—A —图24—A —图24—A —15 图24—A二、填空题12.30゜ 13.65゜或115゜ 14.1或5 15.15π 16.2417.2321或 18.1360 19.8 20.2或8 21.3 22.证明:∵AD=BC,∴AD=BC,∴AD+BD=BC+BD,即AB=CD,∴AB=CD;23.解:设∠AOC=︒n ,∵BC 的长为cm π38,∴180838⨯=ππn ,解得︒=60n ; ∵AC 为⊙O 的切线,∴△AOC 为直角三角形,∴OA=2OC=16cm,∴AB=OA-OB=8cm; 24.1①BA ⊥EF ;②∠CAE=∠B ;③∠BAF=90°;2连接AO 并延长交⊙O 于点D,连接CD,则AD 为⊙O 的直径,∴∠D+∠DAC=90°;∵∠D 与∠B 同对弧AC,∴∠D=∠B,又∵∠CAE=∠B,∴∠D=∠CAE,∴∠DAC+∠EAC=90°,∴EF 是⊙O 的切线; ⌒。
九年级数学圆的测试题和答案解析(两套)

圆圆的有关概念与性质1.圆上各点到圆心的距离都等于半径。
2.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;圆又是中心对称图形,圆心是它的对称中心。
3.垂直于弦的直径平分这条弦,并且平分弦所对的弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量相等,那么它们所对应的其余各组量都分别相等。
5.同弧或等弧所对的圆周角相等,都等于它所对的圆心角的一半。
6.直径所对的圆周角是 90°,90°所对的弦是直径。
7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫外心,是三角形三边垂直平分线的交点。
8.与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点的交点,叫做三角形的内心。
9.圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角与圆有关的位置关系1.点与圆的位置关系共有三种:①点在圆外,②点在圆上,③点在圆内;对应的点到圆心的距离d和半径r之间的数量关系分别为:①d > r,②d = r,③d < r.2.直线与圆的位置关系共有三种:①相交,②相切,③相离;对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为:①d < r,②d = r,③d > r.3.圆与圆的位置关系共有五种:① 内含 ,② 相内切 ,③ 相交 ,④ 相外切 ,⑤ 外离 ; 两圆的圆心距d 和两圆的半径R 、r (R ≥r )之间的数量关系分别为:①d < R-r ,②d = R-r ,③ R-r < d < R+ r ,④d = R+r ,⑤d > R+r. 4.圆的切线 垂直于 过切点的半径;经过 直径 的一端,并且 垂直于 这条 直径 的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
初三中考圆的试题及答案

初三中考圆的试题及答案一、选择题(每题3分,共30分)1. 若圆的半径为5,圆心为坐标原点,则圆的方程为()A. (x-0)^2 + (y-0)^2 = 25B. (x-5)^2 + (y-5)^2 = 25C. (x+5)^2 + (y+5)^2 = 25D. (x-5)^2 + (y+5)^2 = 25答案:A2. 圆与直线相切的条件是()A. 圆心到直线的距离等于半径B. 圆心到直线的距离小于半径C. 圆心到直线的距离大于半径D. 圆心到直线的距离等于直径答案:A3. 已知圆的半径为3,圆心坐标为(-2, 3),求圆上的点(1, 4)与圆心的距离为()A. 2B. 3C. 4D. 5答案:D4. 圆的直径是()A. 圆上任意两点间最长的线段B. 圆上任意两点间最短的线段C. 圆上任意两点间距离的两倍D. 圆上任意两点间距离的一半答案:A5. 圆的周长公式为()A. C = 2πrB. C = πrC. C = 4πrD. C = πr^2答案:A6. 圆的面积公式为()A. S = πr^2B. S = 2πrC. S = πrD. S = 4πr^2答案:A7. 圆内接四边形的对角线()A. 相等B. 不相等C. 垂直D. 平行答案:A8. 圆的切线与半径的关系是()A. 切线与半径垂直B. 切线与半径平行C. 切线与半径相交D. 切线与半径重合答案:A9. 圆的内切圆与外切圆的半径之和等于()A. 圆的直径B. 圆的半径C. 圆的周长D. 圆的面积答案:A10. 圆的内接三角形的面积公式为()A. S = 1/2 * a * b * sin(C)B. S = 1/2 * a * b * cos(C)C. S = 1/2 * r * (a + b + c)D. S = 1/2 * r * (a - b + c)答案:C二、填空题(每题3分,共30分)1. 圆的方程为(x-2)^2 + (y+3)^2 = 16,则圆心坐标为______。
九年级数学圆测试题及答案

九年级数学圆测试题一、选择题1.若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ,最小距离为b (a>b ),则此圆的半径为( )A .2b a +B .2b a - C .22b a b a -+或 D .b a b a -+或 2.如图24—A —1,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长是( )A .4B .6C .7D .83.已知点O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为( )A .40°B .80°C .160°D .120°4.如图24—A —2,△ABC 内接于⊙O ,若∠A=40°,则∠OBC 的度数为( )A .20°B .40°C .50°D .70°5.如图24—A —3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )A .12个单位B .10个单位C .1个单位D .15个单位图24—A —5 图24—A —1图24—A —2 图24—A —3 图24—A —46.如图24—A —4,AB 为⊙O 的直径,点C 在⊙O 上,若∠B=60°,则∠A 等于( )A .80°B .50°C .40°D .30°7.如图24—A —5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA=5,则△PCD 的周长为( )A .5B .7C .8D .108.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m ,母线长为3m ,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( )A .26mB .26m πC .212mD .212m π9.如图24—A —6,两个同心圆,大圆的弦AB 及小圆相切于点P ,大圆的弦CD 经过点P ,且CD=13,PC=4,则两圆组成的圆环的面积是( )A .16πB .36πC .52πD .81π10.已知在△ABC 中,AB=AC=13,BC=10,则△ABC 的内切圆的半径为( )A .310B .512C .2D .3 11.如图24—A —7,两个半径都是4cm 的圆外切于点C ,一只蚂蚁由点A 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm 后才停下来,则蚂蚁停的那一个点为( )A .D 点B .E 点C .F 点D .G 点图24—A —6图24—A —7二、填空题12.如图24—A —8,在⊙O 中,弦AB 等于⊙O 的半径,OC ⊥AB 交⊙O 于点C ,则∠AOC=。
人教版初三圆测试题及答案

人教版初三圆测试题及答案一、选择题(每题2分,共10分)1. 半径为2的圆的面积是多少?A. 4πB. 6πC. 8πD. 12π2. 圆的周长公式是:A. C = πrB. C = 2πrC. C = 4πrD. C = 8πr3. 若圆的半径是3,圆心角为60°,那么这个弧长是多少?A. πB. 3πC. 6πD. 9π4. 点P到圆心O的距离是5,圆的半径是3,那么点P与圆的位置关系是:A. 在圆上B. 在圆内C. 在圆外D. 无法确定5. 圆的切线与半径垂直,且切点到圆心的距离等于:A. 半径B. 直径C. 周长的一半D. 面积的平方根二、填空题(每题2分,共10分)6. 半径为4的圆的面积是_________。
7. 若圆的周长为12π,那么圆的半径是_________。
8. 圆心角为120°的弧所对的圆心角是_________。
9. 点P到圆心O的距离是2,圆的半径是4,点P与圆的位置关系是_________。
10. 圆的切线与半径垂直,切点到圆心的距离是_________。
三、计算题(每题5分,共20分)11. 已知圆的半径为5,求圆的周长和面积。
12. 已知圆的周长为16π,求圆的半径。
13. 若圆的半径为7,圆心角为45°,求该弧长。
14. 已知点P到圆心O的距离为10,圆的半径为8,求点P与圆的位置关系。
四、解答题(每题10分,共20分)15. 某圆的半径为6,圆心角为30°,求该弧所对的圆心角和弧长。
16. 已知圆的切线在点M处与圆相切,OM=6,半径为4,求切线PM的长度。
五、综合题(15分)17. 某工厂需要在一块半径为10米的圆形场地上安装一个直径为4米的圆形水池,水池的中心与场地的中心重合。
求水池的半径占场地半径的比例,以及水池的面积占整个场地面积的比例。
六、结束语本测试题覆盖了圆的基本概念、公式和计算方法,旨在帮助学生巩固和检验对圆的相关知识的掌握。
初中九年级数学圆测试题及答案(两套题)整理版

圆基础知识+两套题附参考答案与圆有关的位置关系1.点与圆的位置关系共有三种:① 点在圆外 ,② 点在圆上 ,③ 点在圆内 ;对应的点到圆心的距离d 和半径r 之间的数量关系分别为: ①d > r ,②d = r ,③d < r.2.直线与圆的位置关系共有三种:① 相交 ,② 相切 ,③ 相离 ; 对应的圆心到直线的距离d 和圆的半径r 之间的数量关系分别为: ①d < r ,②d = r ,③d > r.3.圆与圆的位置关系共有五种:① 内含 ,② 相内切 ,③ 相交 ,④ 相外切 ,⑤ 外离 ; 两圆的圆心距d 和两圆的半径R 、r (R ≥r )之间的数量关系分别为:①d < R-r ,②d = R-r ,③ R-r < d < R+ r ,④d = R+r ,⑤d > R+r. 4.圆的切线 垂直于 过切点的半径;经过 直径 的一端,并且 垂直于 这条 直径 的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
与圆有关的计算1.圆的周长为 2πr ,1°的圆心角所对的弧长为 180rπ ,n °的圆心角所对的弧长为 180r n π ,弧长公式为180rn l π=n 为圆心角的度数上为圆半径) .2. 圆的面积为 πr 2,1°的圆心角所在的扇形面积为 3602r π ,n °的圆心角所在的扇形面积为S= 360n 2R π⨯ = r l 21(n 为圆心角的度数,R 为圆的半径). 3.圆柱的侧面积公式:S= 2 πr l (其中r 为 底面圆 的半径 ,l 为 圆柱 的高.) 4. 圆锥的侧面积公式:S=πr l (其中r 为 底面 的半径 ,l 为 母线 的长.) 圆锥的侧面积与底面积之和称为圆锥的全面积A 组一、选择题(每小题3分,共45分)1.在△ABC 中,∠C=90°,AB =3cm ,BC =2cm,以点A 为圆心,以2.5cm 为半径作圆,则点C 和⊙A 的位置关系是( )。
初三数学圆测试题和答案

、选择题1.下列命题:①长度相等的弧是等弧②任意三点确定一个圆 在三角形的一条边上的三角形是直角三角形,其中真命题共有A. 0个B. 1个C. 2个D. 3个3. 如图,四边形 ABCD 内接于O O 若它的一个外角/ DCE=704. 如图,O O 的直径为10,弦AB 的长为8, M 是弦AB 上的动点,贝U OM 的长的取值范围() A.3 < OMS 5B.4 < OMC 5C.3 V OM k 5D.4 V OM k 55. 如图,O O 的直径 AB 与弦CD 的延长线交于点 E ,若DE=OB / AOC=84,则/ E 等于()&已知O O 与O Q 外切于点 A , O O 的半径R=2, O O 的半径r=1 ,若半径为 4的O C 与O O 、O O 都相 切,则满足条件的O C 有() A.2个B.4个C.5个D.6个9•设O O 的半径为2,圆心O 到直线的距离OP=m 且m 使得关于x 的方程「丄 - ■:-" - '■有实数根,则直线「与O O 的位置关系为()圆练习2.同一平面内两圆的半径是R 和r ,圆心距是d ,若以R 、r 、d 为边长,能围成一个三角形,则这两个圆A.外离 的位置关系是()B.相切C.相交D.内含 A.35C.110OOB.70(3题图) (4题图) ③相等的圆心角所对的弦相等 ④外心,则/ BOD=()A.42B.28C.216.如图, O, AD 丄 BC 于点 D, AD=2cm AB=4cm AC=3cm 则 O O 的直径是() A.2cmB.4cmC.6cmD.8cm7.如图, 影部分的面积为圆心角都是 90 的扇形OAB 与扇形OCD 叠放在一起,OA=3 OC=1分别连结 AC BD,则图中阴1— JIA. 1C.--D.-ox J D△ ABC 内接于O (5题图) (6题图)10 .如图,把直角厶ABC 的斜边AC 放在定直线上,按顺时针的方向在直线 J 上转动两次,使它转到△ A 2B 2C 2的位置,设AB= -,BC=1,则顶点A 运动到点 A 的位置时,点 A 所经过的路线为()、填空题11. 某圆柱形网球筒,其底面直径是 10cm,长为80cm,将七个这样的网球筒如图所示放置并包装侧面,则需 _________________ 液'的包装膜(不计接缝,洱取3).12.如图,在“世界杯”足球比赛中,甲带球向对方球门 PQ 进攻,当他带球冲到 A 点时,同样乙已经助攻冲到B 点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门 •仅从射门角度考虑,应选择 _________种射门方式•13. 如果圆的内接正六边形的边长为 __________ 6cm,则其外接圆的半径为14如图,直角坐标系中一条圆弧经过网格点在圆的圆心坐标为 _______________.15•如图,两条互相垂直的弦将O O 分成四部分,相对的两部分面积之和分别记为S 、S 2,若圆心到两弦的距离分别为 2和3,则|S 1-S 2|= _____________ .A.相离或相切B.相切或相交C.相离或相交D.无法确定£回A.I 八丿71C."A 、B 、C,其中,B 点坐标为(4 , 4),则该圆弧所(15题图)(11题图)... .... 」..亠,: 丄—L —■ (14 题图)、解答题16.为了探究三角形的内切圆半径r与周长■'、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究• O O 是厶ABC 的内切圆,切点分别为点D E 、F.(1)用刻度尺分别量出表中未度量的△ ABC 的长,填入空格处,并计算出周长」和面积S.(结果精确到0.1厘米)ACBCAB rIS图甲0.6图乙1.0(2)观察图形,利用上表实验数据分析.猜测特殊三角形的r 与.、S 之间关系,并证明这种关系对任意三角形 (图 丙)是否也成立17•如图,以等腰三角形」二匚的一腰-兀为直径的O O 交底边占二于点匸,交于点了,连结-迄,并过 点丄-作二匸丄…-,垂足为三.根据以上条件写出三个正确结论 (除-匸—丄-----_-- -- __-外)是:(1) ____________ ;⑵ _________________ ;⑶ _________________19•如图是一纸杯,它的母线AC 和 EF 延长后形成的立体图形是圆锥, 该圆锥的侧面展开图形是扇形 OAB 经测 量,纸杯上开口圆的直径是 6cm,下底面直径为4cm 母线长为EF=8cm.求扇形OAB 的圆心角及这个纸杯的表面积 (面 积计算结果用 表示).18•如图,要在直径为 50厘米的圆形木板上截出四个大小相同的圆形凳面 .问怎样才能截出直径最大的凳面,最大直径是多少厘米? C20. 如图,在△ ABC 中,/ BCA =90°,以BC 为直径的O 位置关系,并说明理由•21. 有这样一道习题:如图 1,已知OA 和OB 是O O 的半径,并且 OAL OB P 是OA 上任一点(不与O A 重合), BP 的延长线交O O 于Q,过Q 点作O O 的切线交OA 的延长线于 R.说明:RP=RQ.请探究下列变化:变化一:交换题设与结论•已知:如图1, OA 和 OB 是O O 的半径,并且 OALOB P 是OA 上任一点(不与 O A 重合),BP 的延长线交O O 于Q R 是OA 的延长线上一点,且 RP=RQ.说明:RQ 为O O 的切线•变化二:运动探求•⑴ 如图2,若0A 向上平移,变化一中的结论还成立吗?(只需交待判断)答: ___________ .⑵如图3,如果P 在0A 的延长线上时,BP 交O 0于Q,过点Q 作O 0的切线交0A 的延长线于R,原题中的结 论还成立吗?为什么?PQ 与O O的22. (深圳南山区)如图,在平面直角坐标系中,矩形A BC0的面积为15,边0A比0C大2.E为BC的中点,以0E为直径的O 0'交芒轴于D点,过点D作DF丄AE于点F.(1) 求0A 0C的长;(2) 求证:DF为O 0'的切线;(3) 小明在解答本题时,发现△ A0E是等腰三角形•由此,他断定:“直线BC上一定存在除点E以外的点卩,使厶A0P也是等腰三角形,且点P一定在O 0'夕卜”.你同意他的看法吗?请充分说明理由•答案与解析:一、选择题1.B2.C3.D4.A5.B6.C7.C提示:易证得△ AOC^A BOD屯~^QA£ +儿创-_^aoco =鴻如-徭OCT =Q次(F 1 八)二2酒8.D 9.B 10.B、填空题11.12000 12.第二种13.6cm 14.(2 , 0)4X 6=24)ED二DC , (2) / BAD2 CAD ⑶ DE是°° 的切线(以及ADL BC,弧BD=M DG等).18. 设计方案如左图所示,在右图中,易证四边形OAO C为正方形,00 +0' B=25,所以圆形凳面的最大直径为25^ -1)厘米.15.24(提示:如图,由圆的对称性可知'一•「一'- L等于e的面积,即为三、解答题16.(1) I 略;由图表信息猜测,得并且对一般三角形都成立•连接OA OB OC运用面积法证明:亡~ £」处十十脸丄胆OD十十丄AB~OF2 2 217.(1)19. 扇形OAB的圆心角为45°,纸杯的表面积为44打. 解:设扇形OAB的圆心角为n°弧长AB等于纸杯上开口圆周长:弧长CD等于纸杯下底面圆周长: MT OF180=2TV -12丿可列方程组180珂■ OF *------- =4L 180,解得(9F = 16所以扇形OAB的圆心角为45°, OF等于16cm纸杯表面积=纸杯侧面积+纸杯底面积=扇形OAB的面积-扇形OCD的面积+纸杯底面积即S纸杯表面积=-x 6TT x 0^4 — x OF2 21 1 <4— x67rx(8 + 16) — x4zrxl6 + 7T 一2v 2 1220.连接OR CP 则/ OPC M OCP.由题意知厶ACR是直角三角形,又Q是AC的中点,因此QP=QC / QPC M QCR. 而/ OCP y QCP=90,所以/ OPC+/ QPC=90 即OPL PQ PQ与O O相切.21.解:连接OQ•/ OQ=OB •••/ OBP2 OQP 为O O的切线,• OQL QROQP/ PQR=90OBP+Z OPB=90PQR/ OPB/ OPB与/ QPR为对顶角OPB2 QPR PQR/ QPRRP=RQ一、连接OQ证明OQL QR •/ QR 即/ 而/ 故/ 又•••• /变化变化、(1)结论成立(2)结论成立,连接OQ 证明/ B=/ OQB则/ P=/ PQR所以RQ=PR.22.(1)在矩形OAB(中,设OC=x则OA=x+2依题意得x(x+2) = 15解得:叫二巧(不合题意,舍去)•••0C=3 0A=55(2) 连结O D,在矩形OABC中,OC=AB / 0CB2 ABC=90 , CE=BE=••• △ OCE^A ABE • EA=EO「./ 仁/2在O O'中,•/ O ' O= O' D 1 = / 3•••/ 3= / 2 • O' D// AE, •/ DF丄AE • DF 丄O' D又•••点D在O O'上,O' D为O O'的半径,• DF为O O'切线.(3) 不同意.理由如下:①当AO=AF时,以点A为圆心,以AO为半径画弧交BC于P i和P4两点过P i 点作P i H丄OA于点H, P i H=OC=3 T AP=OA=5• AH=4, • OH =1求得点P i(1 , 3)同理可得:F4(9 , 3)②当OA=OP寸,同上可求得:P2(4 , 3) , P3( 4, 3)因此,在直线BC上,除了E点外,既存在O O'内的点P i,又存在O O'外的点P2、P3、P4, 它们分别使△ AOP为等腰三角形.。
初三圆园测试题及答案

初三圆园测试题及答案一、选择题(每题3分,共30分)1. 圆的周长公式是()。
A. C = 2πrB. C = πr²C. C = 2πdD. C = πd2. 圆的面积公式是()。
A. A = πrB. A = 2πrC. A = πr²D. A = 2πd3. 圆的直径是半径的()倍。
A. 2B. 3C. 4D. 14. 圆的半径增加一倍,面积增加()倍。
A. 1B. 2C. 4D. 85. 圆的周长与直径的比值称为()。
A. 圆周率C. 半径率D. 面积率6. 圆的内接四边形的对角线()。
A. 相等B. 不相等C. 垂直D. 平行7. 圆的外切四边形的对角线()。
A. 相等B. 不相等C. 垂直D. 平行8. 圆的切线与半径()。
A. 垂直B. 平行C. 相交D. 重合9. 圆的内接三角形的角平分线()。
A. 相等B. 不相等C. 垂直D. 平行10. 圆的外接三角形的边()。
A. 相等B. 不相等D. 平行二、填空题(每题2分,共20分)1. 圆的周长公式为 C = ________。
2. 圆的面积公式为 A = ________。
3. 圆的直径是半径的 ________ 倍。
4. 圆的半径增加一倍,面积增加 ________ 倍。
5. 圆的周长与直径的比值称为 ________。
6. 圆的内接四边形的对角线 ________。
7. 圆的外切四边形的对角线 ________。
8. 圆的切线与半径 ________。
9. 圆的内接三角形的角平分线 ________。
10. 圆的外接三角形的边 ________。
三、解答题(每题10分,共50分)1. 已知一个圆的半径为5cm,请计算该圆的周长和面积。
2. 一个圆的直径是10cm,求该圆的半径和面积。
3. 一个圆的周长是31.4cm,求该圆的直径和半径。
4. 一个圆的面积是78.5平方厘米,求该圆的半径。
5. 已知一个圆的半径是4cm,求该圆的直径和周长。
(完整)九年级数学圆测试题及(两套),文档

圆圆的有关看法与性质1.圆上各点到圆心的距离都等于半径。
2.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;圆又是中心对称图形,圆心是它的对称中心。
3.垂直于弦的直径均分这条弦,并且均分弦所对的弧;均分弦〔不是直径〕的直径垂直于弦,并且均分弦所对的弧。
4.在同圆或等圆中,若是两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量相等,那么它们所对应的其余各组量都分别相等。
5.同弧或等弧所对的圆周角相等,都等于它所对的圆心角的一半。
6.直径所对的圆周角是 90°,90°所对的弦是直径。
7.三角形的三个极点确定1个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫外心,是三角形三边垂直均分线的交点。
8.与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角均分线的交点的交点,叫做三角形的内心。
9.圆内接四边形:极点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角与圆有关的地址关系1. 点与圆的地址关系共有三种:①点在圆外,②点在圆上,③点在圆内;对应的点到圆心的距离 d 和半径 r 之间的数量关系分别为:① d > r,② d =r,③ d <r.2. 直线与圆的地址关系共有三种:①订交,②相切,③相离;对应的圆心到直线的距离 d 和圆的半径r 之间的数量关系分别为:① d < r,② d =r,③ d >r.3.圆与圆的地址关系共有五种:①内含,②相内切,③订交,④相外切,⑤外离;两圆的圆心距 d 和两圆的半径R、 r 〔 R≥r 〕之间的数量关系分别为:① d < R-r,② d = R-r,③R-r < d < R+ r,④ d = R+r,⑤ d > R+r.4. 圆的切线垂直于过切点的半径;经过直径的一端,并且垂直于这条直径的直线是圆的切线.5. 从圆外一点能够向圆引2条切线,切线长相等,这点与圆心之间的连线平分这两条切线的夹角。
九年级数学圆的测试题及答案[1]
![九年级数学圆的测试题及答案[1]](https://img.taocdn.com/s3/m/ae438a2758f5f61fb636668c.png)
九年级数学圆的测试题及答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学圆的测试题及答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学圆的测试题及答案(word版可编辑修改)的全部内容。
1.如图,直角三角形ABC 中,∠C =90°,AC =2,AB =4,分别以AC 、BC 为直径作半圆,则图中阴影的面积为( ) A 2π-3B 4π-43C 5π-4D 2π-232.半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )A 1∶2∶3B 1∶2∶3C 3∶2∶1D 3∶2∶13.在直角坐标系中,以O(0,0)为圆心,以5为半径画圆,则点A(3 ,4)的位置在 ( )A ⊙O 内B ⊙O 上C ⊙O 外D 不能确定4.如图,两个等圆⊙O 和⊙O ′外切,过O OA 、OB ,A 、B 是切点,则∠AOB 等于( )A. 30°B 。
45°C 。
60°D 。
90°5.在Rt △ABC 中,已知AB =6,AC =8,∠A =90°,如果把此直角三角形绕直线AC旋转一周得到一个圆锥,其表面积为S 1;把此直角三角形绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于OO'AB 第4题图BCA( )A 2∶3B 3∶4C 4∶9D 5∶126.若圆锥的底面半径为 3,母线长为5,则它的侧面展开图的圆心角等于 ( )A . 108°B . 144°C . 180°D . 216°7.已知两圆的圆心距d = 3 cm ,两圆的半径分别为方程0352=+-x x 的两根,则两圆的位置关系( ) A 相交 B 相离 C 相切 D 内含8.四边形中,有内切圆的是 ( )A 平行四边形B 菱形C 矩形D 以上答案都不对9.如图,以等腰三角形的腰为直径作圆,交底边于D ,连结AD ,那么 ( )A ∠BAD +∠CAD= 90°B ∠BAD >∠CADC ∠BAD =∠CAD D ∠BAD <∠CAD 10.下面命题中,是真命题的有( )①平分弦的直径垂直于弦;②如果两个三角形的周长之比为3∶2,则其面积之比为3∶4;③圆的半径垂直于这个圆的切线;④在同一圆中,等弧所对的圆心角相等;⑤过三点有且只有一个圆。
(完整word版)初三数学圆测试题及,文档
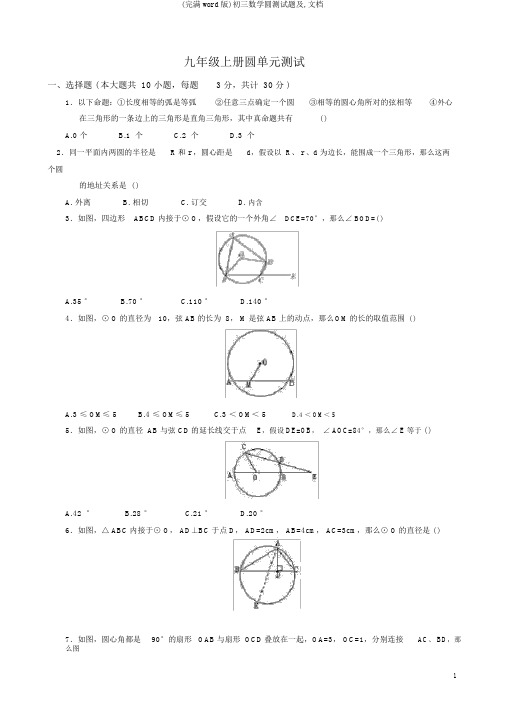
九年级上册圆单元测试一、选择题 ( 本大题共 10 小题,每题 3 分,共计 30 分 )1.以下命题:①长度相等的弧是等弧②任意三点确定一个圆③相等的圆心角所对的弦相等④外心在三角形的一条边上的三角形是直角三角形,其中真命题共有( )A.0 个B.1 个C.2 个D.3 个2.同一平面内两圆的半径是R和 r ,圆心距是d,假设以 R、 r 、d 为边长,能围成一个三角形,那么这两个圆的地址关系是 ( )A. 外离B. 相切C. 订交D. 内含3.如图,四边形ABCD内接于⊙ O,假设它的一个外角∠DCE=70°,那么∠ BOD=( )A.35 °B.70 °C.110 °D.140 °4.如图,⊙ O的直径为10,弦 AB的长为 8, M是弦 AB上的动点,那么OM的长的取值范围( )A.3 ≤ OM≤ 5B.4 ≤ OM≤ 5C.3 < OM< 5D.4 < OM< 55.如图,⊙ O的直径 AB与弦 CD的延长线交于点E,假设 DE=OB,∠ AOC=84°,那么∠ E 等于 ( )A.42 °B.28 °C.21 °D.20 °6.如图,△ ABC内接于⊙ O, AD⊥BC于点 D, AD=2cm, AB=4cm, AC=3cm,那么⊙ O的直径是 ( ) 7.如图,圆心角都是90°的扇形OAB与扇形 OCD叠放在一起,O A=3, OC=1,分别连接AC、 BD,那中阴影局部的面积为( )A. B. C. D.8.⊙ O1与⊙ O2外切于点A,⊙ O1的半径 R=2,⊙ O2的半径 r=1 ,假设半径为 4 的⊙ C与⊙ O1、⊙ O2都相切,那么满足条件的⊙C有( )A.2 个B.4 个C.5 个D.6 个9.设⊙ O的半径为 2,圆心 O到直线的距离OP=m,且m使得关于x的方程有实数根,那么直线与⊙ O的地址关系为 ( )A. 相离或相切B. 相切或订交C. 相离或订交D. 无法确定10.如图,把直角△ABC的斜边 AC放在定直线上,按顺时针的方向在直线上转动两次,使它转到△A2B2C2的地址,设AB=,BC=1,那么极点 A 运动到点A2的地址时,点 A 所经过的路线为( )A. B. C. D.二、填空题 ( 本大题共 5 小题,每小 4 分,共计 20 分 )11. ( 山西 ) 某圆柱形网球筒,其底面直径是10cm,长为 80cm,将七个这样的网球筒以以下图放置并包装侧面,那么需 ________________的包装膜(不计接缝,取3).2从射门角度考虑,应选择________种射门方式 .13. 若是圆的内接正六边形的边长为6cm,那么其外接圆的半径为___________.14. ( 北京 ) 如图,直角坐标系中一条圆弧经过网格点A、 B、 C,其中, B 点坐标为 (4 , 4) ,那么该圆弧所在圆的圆心坐标为_____________.15.如图,两条互相垂直的弦将⊙O分成四局部,相对的两局部面积之和分别记为S1、S2,假设圆心到两弦的距离分别为 2 和 3,那么 |S 1-S 2|=__________.三、解答题 (16 ~21 题,每题 7 分, 22 题 8 分,共计 50 分 )16. ( 丽水 ) 为了研究三角形的内切圆半径r 与周长、面积S之间的关系,在数学实验活动中,采用等边三角形 ( 图甲 ) 和直角三角形 ( 图乙 ) 进行研究 . ⊙ O是△ ABC的内切圆,切点分别为点D、 E、F.(1) 用刻度尺分别量出表中未胸襟的△ABC的长,填入空格处,并计算出周长和面积S.(结果精确到0.1 厘米 )AC BC AB r S图甲图乙(2)观察图形,利用上表实验数据解析 . 猜想特别三角形的 r 与、S 之间关系,并证明这种关系对任意三角形 ( 图丙 ) 可否也成立 ?17. ( 成都 ) 如图,以等腰三角形的一腰为直径的⊙ O交底边于点,交于点,连接,并过点作,垂足为.依照以上条件写出三个正确结论(除外) 是:(1)________________ ;(2)________________ ; (3)________________.18.( 黄冈 ) 如图,要在直径为50 厘米的圆形木板上截出四个大小相同的圆形凳面. 问怎样才能截出直径最大的凳面,最大直径是多少厘米?19.( 山西 ) 如图是一纸杯,它的母线AC和 EF 延长后形成的立体图形是圆锥,该圆锥的侧面张开图形是扇形 OAB.经测量,纸杯上张口圆的直径是6cm,下底面直径为4cm,母线长为EF=8cm.求扇形 OAB的圆心角及这个纸杯的表面积( 面积计算结果用表示) .20.如图,在△ ABC中,∠ BCA =90°,以 BC为直径的⊙ O交 AB于点 P, Q是 AC的中点 . 判断直线 PQ 与⊙ O的地址关系,并说明原由 .21.( 武汉 ) 有这样一道习题:如图1,OA和OB是⊙ O的半径,并且OA⊥ OB,P是OA上任一点(不与 O、 A 重合 ) , BP的延长线交⊙O于 Q,过 Q点作⊙ O的切线交OA的延长线于R. 说明: RP=RQ.请研究以下变化:变化一:交换题设与结论.:如图 1, OA和 OB是⊙ O的半径,并且 OA⊥ OB,P 是 OA上任一点 ( 不与 O、 A 重合 ) , BP 的延长线交⊙ O于 Q, R 是 OA的延长线上一点,且 RP=RQ.说明: RQ为⊙ O的切线 .变化二:运动研究 .(1) 如图 2,假设 OA向上平移,变化一中的结论还成立吗?( 只需交待判断 )答:_________.(2)如图 3,若是 P 在 OA的延长线上时, BP 交⊙ O 于 Q,过点 Q作⊙ O的切线交 OA的延长线于 R,原题中的结论还成立吗?为什么?22.( 深圳南山区 ) 如图,在平面直角坐标系中,矩形ABCO的面积为 15,边 OA比 OC大 2.E 为 BC的中点,以 OE为直径的⊙ O′交轴于D点,过点D作 DF⊥AE 于点 F.(1)求 OA、 OC的长;(2)求证: DF 为⊙ O′的切线;(3)小明在解答此题时,发现△ AOE是等腰三角形 . 由此,他判断:“直线 BC上必然存在除点 E 以外的点P,使△ AOP也是等腰三角形,且点P 必然在⊙ O′外〞 . 你赞成他的看法吗?请充分说明原由.答案与解析:一、选择题提示:易证得△ AOC≌△ BOD,二、填空题11.1200012. 第二种14.(2 ,0) 15.24( 提示:如图,由圆的对称性可知,等于 e 的面积,即为 4× 6=24)三、解答题16.(1) 略;(2) 由图表信息猜想,得,并且对一般三角形都成立. 连接 OA、OB、OC,运用面积法证明:17.(1),(2)∠ BAD=∠ CAD,(3)是的切线(以及AD⊥ BC,弧BD=弧DG等).18.设计方案如左图所示,在右图中,易证四边形OAO′ C 为正方形, OO′+O′ B=25,因此圆形凳面的最大直径为25(-1) 厘米 .19.扇形 OAB的圆心角为 45°,纸杯的表面积为 44 .解:设扇形OAB的圆心角为n°弧长 AB等于纸杯上张口圆周长:可列方程组,解得因此扇形OAB的圆心角为45°, OF等于 16cm纸杯表面积 =纸杯侧面积 +纸杯底面积 =扇形 OAB的面积 - 扇形 OCD的面积 +纸杯底面积即 S 纸杯表面积 ==20.连接 OP、 CP,那么∠ OPC=∠ OCP.由题意知△ ACP是直角三角形,又 Q是 AC的中点,因此 QP=QC,∠ QPC=∠ QCP.而∠ OCP+∠ QCP=90°,因此∠ OPC+∠ QPC=90°即 OP⊥ PQ, PQ与⊙ O相切 .21.解:连接 OQ,∵OQ=OB,∴∠ OBP=∠ OQP又∵ QR为⊙ O的切线,∴ OQ⊥ QR即∠ OQP+∠PQR=90°而∠ OBP+∠OPB=90°故∠ PQR=∠OPB又∵∠ OPB与∠ QPR为对顶角∴∠ OPB=∠QPR,∴∠ PQR=∠QPR∴ RP=RQ变化一、连接OQ,证明 OQ⊥QR;变化二、 (1)结论成立 (2) 结论成立,连接OQ,证明∠ B=∠OQB,那么∠ P=∠ PQR,因此RQ=PR.22.(1) 在矩形 OABC中,设 OC=x 那么 OA=x+2,依题意得解得:( 不合题意,舍去)∴ OC=3,OA=5(2) 连接 O′D,在矩形OABC中, OC=AB,∠ OCB=∠ ABC=90°, CE=BE=∴ △ OCE≌△ ABE ∴ EA=EO∴∠ 1=∠2在⊙ O′中,∵ O′O= O′ D∴∠ 1=∠3∴∠ 3=∠2 ∴ O′D∥ AE,∵ DF⊥ AE ∴ DF⊥O′ D又∵点 D在⊙ O′上, O′ D为⊙ O′的半径,∴ DF为⊙ O′切线.(3) 不相同意 .原由以下:①当AO=AP时,以点A为圆心,以AO为半径画弧交BC于 P1和 P4两点过 P1点作 P1H⊥ OA于点 H, P1H=OC=3,∵ AP1=OA=5∴AH=4,∴ OH =1 求得点 P1(1 , 3) 同理可得: P4(9 , 3)②当 OA=OP时,同上可求得:P(4,3),P(4, 3)23因此,在直线BC上,除了 E 点外,既存在⊙ O′内的点 P1,又存在⊙ O′外的点 P2、 P3、 P4,它们分别使△ AOP为等腰三角形 .。
初三数学圆测试题及答案-

圆圆的有关概念与性质1.圆上各点到圆心的距离都等于 半径 。
2.圆是 轴 对称图形,任何一条直径所在的直线都是它的 对称轴 ;圆又是 中心 对称图形, 圆心 是它的对称中心。
3.垂直于弦的直径平分 这条弦 ,并且平分 弦所对的弧 ;平分弦(不是直径)的 直径 垂直于弦,并且平分 弦所对的弧 。
4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量 相等 ,那么它们所对应的其余各组量都分别 相等 。
5.同弧或等弧所对的圆周角 相等 ,都等于它所对的圆心角的 一半 。
6.直径所对的圆周角是 90° ,90°所对的弦是 直径 。
7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫 外 心,是三角形 三边垂直平分线 的交点。
8.与三角形各边都相切的圆叫做三角形的 内切圆 ,内切圆的圆心是三角形 三条角平分线的交点 的交点,叫做三角形的 内心 。
9.圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角与圆有关的位置关系1.点与圆的位置关系共有三种:① 点在圆外 ,② 点在圆上 ,③ 点在圆内 ;对应的点到圆心的距离d 和半径r 之间的数量关系分别为:①d > r ,②d = r ,③d < r.2.直线与圆的位置关系共有三种:① 相交 ,② 相切 ,③ 相离 ; 对应的圆心到直线的距离d 和圆的半径r 之间的数量关系分别为: ①d < r ,②d = r ,③d > r.3.圆与圆的位置关系共有五种:① 内含 ,② 相内切 ,③ 相交 ,④ 相外切 ,⑤ 外离 ; 两圆的圆心距d 和两圆的半径R 、r (R ≥r )之间的数量关系分别为:①d < R-r ,②d = R-r ,③ R-r < d < R+ r ,④d = R+r ,⑤d > R+r. 4.圆的切线 垂直于 过切点的半径;经过 直径 的一端,并且 垂直于 这条 直径 的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
B C
初三数学圆检测题200班
一、选择题(每小题4分,共48分)
1.⊙O的半径r=10cm,圆心到直线a的距离OM=8cm,在直线a上有一点P,且PM=6cm,则点P()
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.可能⊙O内也可能在外
2.有4个命题:①直径相等的两圆是等圆;②长度相等的两条弧是等弧;③圆中最大的弦是通过圆
心的弦;④一条弦把圆分为两条弧,这两条弧不可能是等弧,其中真命题是()
A.①③B.①③④C.①④D.①
3.如图,A、B、C、D在同一个圆上,则圆中相等的圆周角有()对
A.1 B.2 C.3 D.4
4.有下列命题:①直径是圆的对称轴;②垂直于弦的直线必经过圆心;③平分弦的直径必平分弦所
对的两条弧;④相等的圆周角所对的弧相等,其中假命题的个数为()
A.1 B.2 C.3 D.4
5. 如图,△ABC 内接于⊙O ,∠B = 45º, AC =4 ,则⊙O的半径为
A . 22
B . 4
C . 23
D . 5
6. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不一定
...成立的是
A.CM=DM
B.弧AC=弧AD
C.AD=2BD
D.∠BCD=∠BDC
7.已知⊙O的半径为3cm,直线l上有一点P,OP=3cm,则直线l与⊙O的位置关系为()
A.相交 B.相离 C.相切 D.相交或相切
8.如图4,在直角坐标系中,圆O的半径为
1,则直线
y x
=-+与圆O的位置关系是()
A.相离B.相交
C.相切D.以上三种情形都有可能
9. 已知⊙O的半径为5mm,弦mm
AB8
=,则圆心O到AB的距离是
A.1 mm B.2 mm C.3 mm D.4 mm
10、在圆O中,圆O的半径为6厘米,弦AB的长为6厘米,则弦AB所对的圆周角是
(A)30°或150°(B)45°或135°(C)60°或120°(D)以上答案都不对
11、在平面直角坐标系中,A(0,3)、B(1,0),以A为圆心,以5为半径作圆A,以B为圆心,
以3为半径作圆B,判断圆A、圆B的位置关系
(A)外切(B)内切(C)相交(D)内含
12、点A到圆O的最近点的距离为10厘米,点A到圆上最远点的距离为6厘米,则圆O的半径是
(A)8厘米(B)2厘米(C)8厘米或2厘米(D)以上答案都不对
二、填空题:(每题3分,共18分)
13、如图,PA是⊙O的切线,切点为A,
PA=,∠APO=30°,
则⊙O的半径长为.
14如图,在⊙O中,∠ACB=∠D=60°,AC=3,则△ABC的周长为_________。
15.Rt△ABC中,∠C=90°,AC=6,BC=8,则Rt△ABC外接圆半径为,内切圆半径为。
16.在△ABC中,∠A=80°,若O为外心,则∠BOC= ,若I为内心,则∠BIC= 。
17.相切两圆的圆心距为18cm,其中小圆半径为7cm,则大圆半径为。
18.已知⊙O内两弦AB⊥AC,它们的中点分别为D、E,若OD=3cm,OE=4cm,则弦AB= cm,
弦AC= cm,半径OA= cm.
三、解答题:
19、(6分)在三角形ABC中,∠ACB=90°,AC=6,BC=8,以C为圆心,以AC为半径作圆C,交AB
于点D,求BD的长
20、(6分)等边三角形ABC的边长为2,尺规作图,作三角形ABC的外接圆O,
求圆O的半径
A
D
14题
图4
P
C D
- 1 -
- 2 -
21、(6分)在圆O 中,点A 、B 、C 、D 在圆O 上,若∠ADB=∠ADC=60°,判断三角形ABC 的形状
22、(7分)如图,已知Rt △ABC 中,BC =9, AB =12.过点A 作AE ⊥AB ,且AE =16,连接BE 交AC 于点P .
⑴求PA 的长;
⑵以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;
23、(8分)如图,⊙O 的直径34,30,4=︒=∠=BC ABC AB ,D 时线段BC 的中点, (1)试判断点D 与⊙O 的位置关系,并说明理由;
(2)过点D 作AC DE ⊥,垂足为点E ,求证直线DE 是⊙O 的切线。
23、(7分)如图所示,AB 是⊙O 的弦,半径OC 、OD 分别交AB 于点E 、F ,且AE=BF ,请你找出线段OE 与OF 的数量关系,并给予证明.
25、(8分)如图的两个圆是以O 为圆心的同心圆,大圆的弦AB 是小圆的切线,C 为切点,且AB=10cm,求圆环的面积.
26、(9分)如图,以等腰△ABC 的腰AB 为⊙O 的直径交底边BC 于D ,DE ⊥AC 于E 。
求证:(1)DB=DC (2)DE 为⊙O 的切线
第23题图
A。
