安徽省巢湖市柘皋中学2018届高三上学期第三次月考数学(理)试题 Word版含解析
安徽省六安市高三数学上学期第三次月考试题理(new)
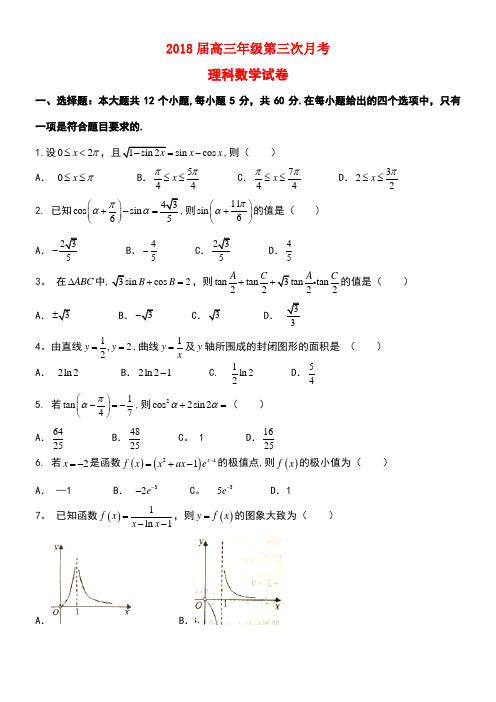
2018届高三年级第三次月考理科数学试卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设02x π≤<,且1sin 2sin cos x x x -=-,则( ) A . 0x π≤≤ B .544x ππ≤≤C .744x ππ≤≤D .322x π≤≤ 2. 已知43cos sin 65παα⎛⎫+-= ⎪⎝⎭,则11sin 6πα⎛⎫+⎪⎝⎭的值是( ) A .23-B .45-C .23D .453。
在ABC ∆中,3sin cos 2B B +=,则tantan 3tan tan 2222A C A C++的值是( ) A .3± B .3- C .3 D .34。
由直线1,22y y ==,曲线1y x=及y 轴所围成的封闭图形的面积是 ( )A . 2ln 2B .2ln 21- C. 1ln 22 D .545. 若1tan 47πα⎛⎫-=- ⎪⎝⎭,则2cos 2sin αα+2=( )A .6425 B .4825 C 。
1 D .16256. 若2x =-是函数()()211x f x x ax e -=+-的极值点,则()f x 的极小值为( ) A . —1 B . 32e -- C 。
35e - D .1 7。
已知函数()1ln 1f x x x =--,则()y f x =的图象大致为( )A .B .C. D .8.若函数()()3log a f x x ax =-(0a >且1a ≠)在区间102⎛⎫- ⎪⎝⎭,内单调递增,则a 的取值范围是 ( )A . 1,14⎡⎫⎪⎢⎣⎭B . 3,14⎡⎫⎪⎢⎣⎭C 。
9,4⎡⎫+∞⎪⎢⎣⎭D .91,4⎛⎫ ⎪⎝⎭9. 设偶函数()()f x x R ∈的导函数是函数()(),20f x f '=,当0x <时,()()0xf x f x '->,则使得()0f x >成立的x 的取值范围是( ) A .()(),20,2-∞- B .()(),22,-∞-+∞ C 。
安徽省巢湖市柘皋中学高三上学期第一次月考数学(理)试题Word版含答案

柘皋中学2018届高三第一次月考数学(理)试卷一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求. )1、已知集合A ={x |x <1},B ={x |31x <},则()A C R B ⋂=( ) A .}{0x x <B .}{01x x <<C .}{01x x ≤<D .∅2、设集合{}1,2,4A =,{}240x x x m B =-+=。
若{}1A B =,则B =( ) A.{}1,3 B.{}1,0 C.{}1,-3 D.{}1,53、已知函数1()()33x x f x =-,则()f x(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数4、设函数A ,函数y=ln(1-x)的定义域为B ,则A B ⋂= (A )(1,2) (B )⎤⎦(1,2 (C )(-2,1) (D )[-2,1) 5、已知命题p:()x x ∀+>0,ln 1>0;命题q :若a >b ,则a b 22>,下列命题为真命题的是(A ) ∧p q (B )⌝∧p q (C ) ⌝∧p q (D )⌝⌝∧p q 6、设x ∈R ,则“20x -≥”是“|1|1x -≤”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件 (D )既不充分也不必要条件7、设()()121,1x f x x x <<=-≥⎪⎩,若()()1f a f a =+,则1f a ⎛⎫= ⎪⎝⎭A. 2B. 4C. 6D. 88、有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为(A )15(B )25(C )35(D )459、为了研究某班学生的脚长x (单位:厘米)和身高y (单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y 与x 之间有线性相关关系,设其回归直线方程为ˆˆˆybx a =+.已知101225i i x ==∑,1011600i i y ==∑,ˆ4b=.该班某学生的脚长为24,据此估计其身高为 (A )160 (B )170 (C )163 (D )16610、若函数f (x )=x 2-2x +m 在[3,+∞)上的最小值为1,则实数m 的值为( )A .-3B .-2C .-1D .111、设随机变量X ~N (100,σ),p (80<X≤120)=,则p (X >120)=( ) 1.8A 1B.4 1C.16 1D.212、已知函数()y f x =是定义在R 上的偶函数,对任意()12,0,x x ∈+∞,都有()()()()2121210ln,ln ,x x f x f x a b c ππ--<===⎡⎤⎣⎦,设则( )A .()()()f a f b f c >>B .()()()f b f a f c >>C .()()()f c f b f a >>D .()()()f c f a f b >>二、填空题:本大题共4小题,每小题5分,共20分13、已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+, 则(3)f = ________.14、函数y =log 2|x +1|的单调递减区间为________ 15、设随机变量X 的分布列为则a = ______ ;E (X )= ______ 16、已知函数31()2e e x xf x x x =++-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,则实数a 的取值范围是 .三、解答题(本大题共5小题,共70分.解答应写出必要的文字说明或推理、验算过程. )17、已知集合A={x |x <-1,或x >2},B={x |2p -1≤x ≤p +3}. (1)若p =,求A∩B ;(2)若A∩B=B ,求实数p 的取值范围.18、已知函数.(1)求f (f (5))的值; (2)画出函数的图象.19、已知p :∀x ∈R ,mx 2+1>0,q :∃x ∈R ,x 2+mx +1≤0. (1)写出命题p 的否定¬p ,命题q 的否定¬q ; (2)若¬p ∨¬q 为真命题,求实数m 的取值范围.20、为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X(单位:元),求X的分布列和数学期望;21、已知函数f(x)=log a(x+1)-log a(1-x),a>0且a≠1.(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明;(3)当a>1时,求使f(x)>0的x的解集.22、海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg)某频率分布直方图如下:(1) 设两种养殖方法的箱产量相互独立,记A 表示事件:“旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg”,估计A 的概率;(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:(3) 根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01) 附:22()()()()()n ad bc K a b c d a c b d -=++++柘皋中学2018届高三第一次月考理科数学答案一、选择题1-5CACDB 6 -10BCBDB 11-12AD二、填空题三解答题17、(1)当p=时,B={x|0≤x≤},∴A∩B={x|2<x≤};(2)当A∩B=B时,B⊆A;令2p-1>p+3,解得p>4,此时B=∅,满足题意;当p≤4时,应满足,解得p不存在;综上,实数p的取值范围p>4.18、.解:(1)函数.f(f(5))=f(-5+2)=f(-3)=-3+4=1.(2)函数.的图象如图:19、解:(1)¬p:∃x∈R,mx2+1≤0;¬q:∀x∈R,x2+mx+1>0;(2)由题意知,¬p真或¬q真,当¬p真时,m<0,当¬q真时,△=m2-4<0,解得-2<m<2,因此,当¬p∨¬q为真命题时,m<0或-2<m<2,即m<2.20、(1)36 33(2)E(x)=165.521、(1))1,1(- (2)奇函数(2))1,0( 22、()0.0680.0460.0100.00850.66+++⨯=,故()P C 的估计值为0。
2018届安徽省巢湖市柘皋中学高三上学期第一次月考数学(理)试题

柘皋中学2017—2018学年高三第一次月考数学(理)试卷一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求. )1、已知集合A ={x |x <1},B ={x |31x <},则()A C R B ⋂=( ) A .}{0x x <B .}{01x x <<C .}{01x x ≤<D .∅2、设集合{}1,2,4A =,{}240x x x m B =-+=。
若{}1A B =,则B =( ) A.{}1,3 B.{}1,0 C.{}1,-3 D.{}1,53、已知函数1()()33x x f x =-,则()f x(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数4、设函数A ,函数y=ln(1-x)的定义域为B ,则A B ⋂= (A )(1,2) (B )⎤⎦(1,2 (C )(-2,1) (D )[-2,1) 5、已知命题p:()x x ∀+>0,ln 1>0;命题q :若a >b ,则a b 22>,下列命题为真命题的是(A ) ∧p q (B )⌝∧p q (C ) ⌝∧p q (D )⌝⌝∧p q 6、设x ∈R ,则“20x -≥”是“|1|1x -≤”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件 (D )既不充分也不必要条件7、设()()121,1x f x x x <<=-≥⎪⎩,若()()1f a f a =+,则1f a ⎛⎫= ⎪⎝⎭A. 2B. 4C. 6D. 88、有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为(A )15(B )25(C )35(D )459、为了研究某班学生的脚长x (单位:厘米)和身高y (单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y 与x 之间有线性相关关系,设其回归直线方程为ˆˆˆybx a =+.已知101225i i x ==∑,1011600i i y ==∑,ˆ4b=.该班某学生的脚长为24,据此估计其身高为 (A )160 (B )170 (C )163 (D )16610、若函数f (x )=x 2-2x +m 在[3,+∞)上的最小值为1,则实数m 的值为( )A .-3B .-2C .-1D .111、设随机变量X ~N (100,σ),p (80<X≤120)=,则p (X >120)=( ) 1.8A 1B.4 1C.16 1D.212、已知函数()y f x =是定义在R 上的偶函数,对任意()12,0,x x ∈+∞,都有()()()()2121210ln,ln ,x x f x f x a b c ππ--<===⎡⎤⎣⎦,设则( )A .()()()f a f b f c >>B .()()()f b f a f c >>C .()()()f c f b f a >>D .()()()f c f a f b >>二、填空题:本大题共4小题,每小题5分,共20分13、已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+, 则(3)f = ________.14、函数y =log 2|x +1|的单调递减区间为________ 15、设随机变量X 的分布列为则a = ______ ;E (X )= ______ 16、已知函数31()2e e x xf x x x =++-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,则实数a 的取值范围是 .三、解答题(本大题共5小题,共70分.解答应写出必要的文字说明或推理、验算过程. )17、已知集合A={x |x <-1,或x >2},B={x |2p -1≤x ≤p +3}. (1)若p =,求A∩B ;(2)若A∩B=B ,求实数p 的取值范围.18、已知函数.(1)求f (f (5))的值; (2)画出函数的图象.19、已知p :∀x ∈R ,mx 2+1>0,q :∃x ∈R ,x 2+mx +1≤0. (1)写出命题p 的否定¬p ,命题q 的否定¬q ; (2)若¬p ∨¬q 为真命题,求实数m 的取值范围.20、为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X(单位:元),求X的分布列和数学期望;21、已知函数f(x)=log a(x+1)-log a(1-x),a>0且a≠1.(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明;(3)当a>1时,求使f(x)>0的x的解集.22、海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg)某频率分布直方图如下:(1) 设两种养殖方法的箱产量相互独立,记A 表示事件:“旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg”,估计A 的概率;(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:(3) 根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01) 附:22()()()()()n ad bc K a b c d a c b d -=++++柘皋中学2018届高三第一次月考理科数学答案一、选择题1-5CACDB 6 -10BCBDB 11-12AD二、填空题三解答题17、(1)当p=时,B={x|0≤x≤},∴A∩B={x|2<x≤};(2)当A∩B=B时,B⊆A;令2p-1>p+3,解得p>4,此时B=∅,满足题意;当p≤4时,应满足,解得p不存在;综上,实数p的取值范围p>4.18、.解:(1)函数.f(f(5))=f(-5+2)=f(-3)=-3+4=1.(2)函数.的图象如图:19、解:(1)¬p:∃x∈R,mx2+1≤0;¬q:∀x∈R,x2+mx+1>0;(2)由题意知,¬p真或¬q真,当¬p真时,m<0,当¬q真时,△=m2-4<0,解得-2<m<2,因此,当¬p∨¬q为真命题时,m<0或-2<m<2,即m<2.20、(1)36 33(2)E(x)=165.521、(1))1,1(- (2)奇函数(2))1,0( 22、()0.0680.0460.0100.00850.66+++⨯=,故()P C 的估计值为0。
安徽省六安市2018届高三数学上学期第三次月考试题理 Word版 含答案

2018届高三年级第三次月考理科数学试卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设02x π≤<sin cos x x =-,则( ) A . 0x π≤≤ B .544x ππ≤≤C .744x ππ≤≤D .322x π≤≤2. 已知cos sin 65παα⎛⎫+-= ⎪⎝⎭,则11sin 6πα⎛⎫+ ⎪⎝⎭的值是( )A ..45- C .453. 在ABC ∆cos 2B B +=,则tantan tan 2222A C A C++ 的值是( )A ... 4.由直线1,22y y ==,曲线1y x=及y 轴所围成的封闭图形的面积是 ( ) A . 2ln 2 B .2ln 21- C. 1ln 22 D .545. 若1tan 47πα⎛⎫-=- ⎪⎝⎭,则2cos 2sin αα+2=( ) A .6425 B .4825 C. 1 D .16256. 若2x =-是函数()()211x f x x ax e -=+-的极值点,则()f x 的极小值为( )A . -1B . 32e -- C. 35e - D .1 7. 已知函数()1ln 1f x x x =--,则()y f x =的图象大致为( )A .B .C. D .8.若函数()()3log a f x x ax =-(0a >且1a ≠)在区间102⎛⎫- ⎪⎝⎭,内单调递增,则a 的取值范围是 ( )A . 1,14⎡⎫⎪⎢⎣⎭B . 3,14⎡⎫⎪⎢⎣⎭ C. 9,4⎡⎫+∞⎪⎢⎣⎭ D .91,4⎛⎫ ⎪⎝⎭9. 设偶函数()()f x x R ∈的导函数是函数()(),20f x f '=,当0x <时,()()0xf x f x '->,则使得()0f x >成立的x 的取值范围是( )A .()(),20,2-∞-B .()(),22,-∞-+∞ C. ()()2,02,-+∞ D .()()0,22,0-10.已知,2sin cos 2a R αα∈-=,则tan 2α= ( ) A .43 B .34 C. 34- D .43- 11. 过点(),A m n 与曲线()ln f x x x =相切的直线有且只有两条,则实数m 的取值范围是( )A .(),e -∞B . (),e +∞ C. 10,e ⎛⎫ ⎪⎝⎭D .()1,+∞12.已知函数()2ln 2,03,02x x x x f x x x x ->⎧⎪=⎨+≤⎪⎩的图象有且仅有四个不同的点关于直线1y =-的对称点在1y kx =-的图象上,则实数k 的取值范围是 ( )A .1,12⎛⎫⎪⎝⎭ B . 13,24⎛⎫⎪⎝⎭ C. 1,13⎛⎫ ⎪⎝⎭ D .1,22⎛⎫ ⎪⎝⎭二、填空题:本大题共4小题,每小题5分,满分20分,将答案填在答题纸上 13.曲线()ln 21y x =-上的点到直线280x y -+=的最短距离是 .14.(222sin x x dx -=⎰.15. 0001cos 202cos80tan802sin 20+-= . 16.若实数,x y 满足方程组332cos 2082cos 230x x x y y y ⎧++-=⎨-++=⎩,则()cos 2x y += . 三、解答题 :本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.已知1cos cos ,,63432ππππααα⎛⎫⎛⎫⎛⎫+-=-∈⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(1)求sin 2α的值; (2)求1tan tan αα-的值. 18.已知函数()()1ln ,2f x xg x ax b ==+. (1)若曲线()f x 与曲线()g x 在它们的公共点()()1,1P f 处具有公共切线,求()g x 的表达式;(2)若()()()11m x x f x x ϕ-=-+在[)1,+∞上是减函数,求实数m 的取值范围.19.现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥1111P A BC D -,下部的形状是正四棱柱1111ABCD A BC D -(如图所示),并要求正四棱柱的高1O O 是正四棱锥的高1PO 的4倍.(1)若16,2AB m PO m ==,则仓库的容积是多少?。
高三数学上学期第三次月考试题文(扫描版)(2021学年)

安徽省六安市2018届高三数学上学期第三次月考试题文(扫描版)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(安徽省六安市2018届高三数学上学期第三次月考试题文(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为安徽省六安市2018届高三数学上学期第三次月考试题文(扫描版)的全部内容。
安徽省六安市2018届高三数学上学期第三次月考试题文(扫描版)以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The above is the whole content of this article, Gorky said:"thebook is the ladder ofhuman progress." I hope you can make progresswith the help of this ladder. Material life is extremely rich, science and technologyare developing rapidly, all of which gradually change the way of people's study and leisure.Many people are no longer eager topursuea document, but as long as you still have such a small persistence, you will continue to grow and progress. When thecomplex world leads us to chaseout, reading anarticle or doing a problem makes us calm downand return to ourselve s.With learning,we can activate our imagination andthin king, establish ourbelief, keep our purespiritualworld and resist the attackof the external world.。
高三上学期第三次月考数学试卷(附答案解析)

高三上学期第三次月考数学试卷(附答案解析)考试时间:120分钟;总分:150分学校:___________姓名:___________班级:___________第I卷(选择题)一、单选题(本大题共8小题,共40分。
在每小题列出的选项中,选出符合题目的一项)1. 已知集合A={−1,0,1,2,},B={x∈Z|x−2x≤0},则A∩B=( )A. {0,1}B. {1,2}C. {−1,1,2}D. {0,1,2}2. 若复数z=a+2i2−i(a∈R)为纯虚数,则a=( )A. −4B. −2C. −1D. 13. 已知向量a=(1,−1),b=(1,t),若〈a,b〉=π3,则t=( )A. 2−3B. 2+3C. 2+3或2−3D. −14. 若函数f(x)=1−cosxsinx(x∈[π3,π2]),则f(x)的值域为( )A. [3,+∞)B. [33,+∞)C. [1,3]D. [33,1]5. 正四面体S−ABC内接于一个半径为R的球,则该正四面体的棱长与这个球的半径的比值为( )A. 64B. 33C. 263D. 36. 在给某小区的花园绿化时,绿化工人需要将6棵高矮不同的小树在花园中栽成前后两排,每排3棵,则后排的每棵小树都对应比它前排每棵小树高的概率是( )A. 13B. 16C. 18D. 1127. 如图,圆内接四边形ABCD中,DA⊥AB,∠D=45°,AB=2,BC=22,AD=6.现将该四边形沿AD旋转一周,则旋转形成的几何体的体积为( )A. 84π3B. 30πC. 92π3D. 40π8. 函数f(x)的定义域为R,且f(x)−f(x+4)=0,当−2≤x<0时,f(x)=(x+1)2,当0≤x<2时,f(x)=1−x,则n=12022f(n)=( )A. 1010B. 1011C. 1012D. 1013二、多选题(本大题共4小题,共20分。
安徽省巢湖市柘皋中学2018届高三上学期第二次月考数学(理)试题 Word版含解析

巢湖市柘皋中学2017-2018学年第一学期高三第二次月考理科数学一.选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,,则A. (3,4)B.C. D.【答案】D【解析】由,得:,,故,故选D.2. 已知i是虚数单位、复数,则的虚部为A. B. C. D.【答案】C【解析】由题意可得,选C.3. 下列说法正确的是A. 命题“,则”的否命题是“若”B. 是函数在定义域上单调递增的充分不必要条件C.D. 若命题则【答案】D【解析】“若p则q”的否命题是“若则”,所以A错。
在定义上并不是单调递增函数,所以B错。
不存在,C错。
全称性命题的否定是特称性命题,D对,选D.4. 《九章算术》是中国古代的数学专著,其中的一段话“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
”用程序框图表示如图,那么这个程序的作用是A. 求两个正数,的最小公倍数B. 求两个正数,的最大公约数C. 判断其中一个正数是否能被另一个正数整除D. 判断两个正数,是否相等【答案】B【解析】这是更相减损术,是用来求两个正数的最大公约数,选B.5. 在中,分别是角的对应边,若,则下列式子正确的是A. B.C. D.【答案】C【解析】由题意可知,由余弦定理,所以,即,选C.6. 在中,,,是的中点,在上,且,则A. 16B. 12C. 8D. -4【答案】A【解析】如下图,以B为原点,BA,BC分别为x,y轴建立平面坐标系A(4,0),B(0,0),C(0,6),D(2,3),设E(0,t),,即,。
选A.7. 学校为了奖励数学竞赛中获奖的优秀学生,将梅、兰、竹、菊四幅名画送给获奖的甲、乙、丙三位同学,每隔学生至少获得一幅,则在所有送法中甲得到名画“竹”的概率是A. B. C. D.【答案】C【解析】由题意可知总方法数,先分3组,,再分配=6,由分步计数原理可知总方法数,满足条件方法数,概率。
安徽省巢湖市柘皋中学2018届高三上学期第三次月考数学(文)试题

巢湖市柘皋中学2017-2018学年第一学期高三第三次月考试卷数学(文科) 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有 一项是符合题目要求的.1.已知全集U R =,集合{|ln(1)}A x y x ==-,2{|20}B x x x =-<,则A B ⋂=( ) A .()0,1 B .()0,2 C .()1,2 D .[)1,22.若向量a 、b 满足||5a =,()1,3b =-,5a b ⋅=,则a 与b 的夹角为( ) A .90 B .60 C .45 D .303.已知:|1|1p m +<,:q 幂函数2(1)m y m m x =--在()0,+∞上单调递减,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.已知等差数列{}n a 的前n 项和为n S ,若2469123()2()12a a a a a ++++=,则11S =( ) A .6 B .11 C .33 D .485.下列命题中正确的是( )A .命题“[]0,1x ∃∈,使210x -≥”的否定为“[]0,1x ∀∈,都有210x -≤”B .若命题p 为假命题,命题q 为真命题,则()()p q ⌝∨⌝为假命题C .命题“若0a b ⋅>,则a 与b 的夹角为锐角”及它的逆命题均为真命题D .命题“若20x x +=,则0x =或1x =-”的逆否命题为“若0x ≠且1x ≠-,则20x x +≠”6.已知函数()()sin 0f x x x ωωω=>的图像与x 轴交点的横坐标依次构成一个公差为2π的等差数列,把函数()f x 的图像沿x 轴向右平移6π个单位,得到函数()g x 的图像,则下列叙述不正确...的是( ) A .()g x 的图像关于点(),02π-对称B .()g x 的图像关于直线4x π=对称C .()g x 在[42]ππ,上是增函数D .()g x 是奇函数7.函数()222xe x xf x +=的大致图像是( )A .B .C .D .8.在AOB 中,G 为AB 边上一点,OG 是AOB ∠的平分线,且25OG OA mOB =+,m R ∈,则||||OA OB =( ) A .12 B .1 C .32D .2 9.已知ABC ,角A B C 、、的对边分别为a b c 、、,2b =,6B π=,sin 211cos 2CC=+,则ABC 的面积为( )A .2B .2C 1D 110.在ABC 中,a b c 、、分别为角A B C 、、对边的长,若4230aBC bCA cAB ++=,则cos B =( )A .1124-B .1124C .2936D .2936- 11.奇函数()f x 定义域为()(),00,ππ-⋃,其导函数是()f x ',当0x π<<时,有()()sin cos 0f x x f x x '->,则关于x 的不等式()2()sin 6f x f x π<的解集为( )A .(,0)(,)66πππ-⋃B .(,0)(0,)66ππ-⋃C .(,)(,)66ππππ--⋃D .(,)(0,)66πππ--⋃12.已知数列{}n a 的前n 项和为n S ,定义11ni i S n =∑为数列{}n a 前n 项的叠加和,若2016项数列1232016,,,a a a a 的叠加和为2017,则2017项数列1220161,,,a a a 的叠加和为( )A .2017B .2018C .22017 D .22018第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.函数()f x =的定义域是 .14.已知奇函数()f x 对于任意实数x 满足条件()()2f x f x +=-,若()13f -=-,则()2017f = .15.tan10tan 50tan 60tan10tan 50+-= .16.在OAB 中,3OA OC =,2OB OD =,AD 与BC 的交点为M ,过M 作动直线l 分别交线段AC 、BD 于E F 、两点,若OE OA λ=,OF OB μ=,(0λμ>、),则λμ+的最小值为_ .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知数列{}n a 的前n 项和为n S ,且237(22)n S n n n N *=∈-. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设()132n nb n a =-⋅,求数列{}n b 的前n 项和n T .18.已知向量(3cos ,0)a x =,(0,sin )b x =,记函数2()()3sin 2f x a b x =++. (Ⅰ)求函数()f x 的最大值及取得最大值时x 的取值集合; (Ⅱ)求函数()f x 在区间[,]22ππ-上的单调递减区间. 19.已知函数()232xf x e x ax =-+. (Ⅰ)若函数()f x 的图像在(1,(1))f 处的切线方程为()1y e x b =-+,求a b 、的值; (Ⅱ)若函数()f x 在R 上是增函数,求实数a 的最小值.20.已知ABC 中,角A B C 、、所对的边分别为a b c 、、,2A C =.(Ⅰ)若a =,求角C 的大小;(Ⅱ)若a b c 、、为三个相邻的正偶数,且A B C >>,求ABC 的面积.21.设正项数列{}n a 的前n 项和为n S ,且满足37a =,21691n n a S n +=++,*n N ∈,各项均为正数的等比数列{}n b 满足1132,b a b a ==. (Ⅰ)求数列{}n a 和{}n b 的通项公式;(Ⅱ)若n n n c a b =⋅,数列{}n c 的前n 项和为n T .若对任意2n ≥,*n N ∈,均有2(5)63135n T m n n -≥-+恒成立,求实数m 的取值范围.22.设函数()ln 2f x x ax =-+. (Ⅰ)讨论()f x 的单调性;(Ⅱ)当0a >时,()1af x e -≤恒成立,求实数a 的取值范围.试卷答案一、选择题1-5: ACBBD 6-10: CBCDA 11、12:DA 二、填空题13. 2(,1]3 14. 3 15. 35+ 三、解答题17. 解析:(Ⅰ)当1n =时,1137222a S ==-=-, 当2n ≥时,213722n n n a S S n n -=-=--237[(1)(1)]3522n n n ---=-将1n =代入上式验证显然适合,∴*35()n a n n N =-∈ (Ⅱ)()()13235n b n n =-⋅-111()33532n n =--- ∴12n n T b b b =+++1111(1)(1)3234=--+-++111()33532n n --- 111()323264n n n =--=---. 18. 解析:(Ⅰ)由(3cos ,sin )a b x x +=,22()||a b a b +=+=22)(sin )x x +=223cos sin x x +,∴()223cos sin 2f x x x x =++212cos 2x x =+2cos22x x =++22sin(2)6x π=++当2262x k πππ+=+,即()6x k k Z ππ=+∈时,()f x 取得最大值.此时sin(2)16x π+=,()f x 最大值2214=+⨯=,且取得最大值时x 的集合为{|,}6x x k k Z ππ=+∈.(Ⅱ)由题意:3222262k x k πππππ+≤+≤+,k Z ∈,即263k x k ππππ+≤≤+,k Z ∈.于是,()f x 在[,]22ππ-的单调递减区间是[,]23ππ--和[,]62ππ.19. 解析:(Ⅰ) ∵()3xf x e x a '=-+,∴()131f e a e '=-+=-,2a =当1x =时,1y e b =-+,()3112f e a e b =-+=-+,解得:32b = (Ⅱ)由题意知()30x f x e x a '=-+≥恒成立,∴3xa e x -≤-, 设()3x g x e x =-,()3x g x e '=-,当(),ln3x ∈-∞,()0g x '<;当()ln3,x ∈+∞,()0g x '> ∴()()min ln333ln3g x g ==-,∴33ln 3a -≤-, 所以a 的最小值是33ln 3-+.20.解析:(Ⅰ) ∵a =,∴由正弦定理有sin A C =,又2A C =,即sin 2C C =,于是2sin cos C C C ,在ABC 中,sin 0C ≠,于是cos C =,6C π=.(Ⅱ) ∵A B C >>,故a b c >>,且a b c 、、为三个连续相邻的正偶数, 故可设4,2,a n b n c n =+=+=,其中n 为偶数, 由2A C =,得sin sin 22sin cos A C C C ==,∴sin cos 2sin 2A aC C c==.由余弦定理得:22222a b c aab c+-=,代入a b c 、、可得: ()()()()2224242422n n n n n n n+++-+=++,解得:8n =, ∴12,10,8a b c ===故3cos 24a C c ==,故sin C =,故ABC 的面积为11sin 1210224ab C =⨯⨯⨯= 21. 解:(Ⅰ) 21691n n a S n +=++,()()2169112n n a S n n -=+-+≥,∴()221692n n n a a a n +-=+≥,∴221(3n n a a +=+)且各项为正,∴()132n n a a n +=+≥又37a =,所以24a =,再由221691a S =++得11a =,所以213a a -=∴{}n a 是首项为1,公差为3的等差数列,∴32n a n =-131,4b b ==∴12n n b -=.(Ⅱ) ()1322n n n n c a b n -=⋅=-⋅()0111242322n n T n -=⋅+⋅++-⋅ ()1221242322n n T n =⋅+⋅++-⋅∴12113(222)n n T --=++++(32)2n n --⋅()3525n n T n =-⋅+()352n n m -⋅⋅≥2*63135(2,)n n n n N -+≥∈恒成立∴()263135352n n n m n -+≥=-⋅()()()3527273522n nn n n n ---=-⋅,即272n n m -≥恒成立. 设272n n n k -=,111252792222n n n nn n n nk k +++----=-= 当4n ≤时,1n n k k +>;5n ≥时,1n n k k +< ∴max 5533()232n k k ===,∴332m ≥. 22. 解析:(Ⅰ)由定义域为()0,+∞,()1f x a x'=-, 当0a ≤时,()0f x '>,()f x 在()0,+∞单调增.当0a >时,()0f x '>,110a x x a >⇒<<;()10f x x a'<⇒> ()f x 在1(0,)a 单调增,()f x 在1(,)a+∞单调减.(Ⅱ)由(Ⅰ)可知0a >,max 1()()1ln f x f a a==-,则11ln aa e --≤恒成立.令()1ln 1ag a ea -=+-,显然()10g =,()11111a a a e ag a e a ae----'=-+= 再令()1a h a ea -=-,()11a h a e -'=-,当()01h a a '>⇒>,当()001h a a '<⇒<<.()h a 在()0,1单调减,()1,+∞单调增.()()min 10h a h ==,()0h a ≥,∴()0g a '≥, ()g a 在()0,+∞单调增,()()01g a g ≥=,∴1a ≥.。
安徽省巢湖市柘皋中学高三数学上学期第三次月考试题理(含解析)

巢湖市柘皋中学2017-2018学年第一学期高三第三次月考试卷数学(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,则的子集的个数为()A. 1B. 2C. 3D. 4【答案】B【解析】由题意,令,得,所以,其子集的个数为,故选B.2. 的内角的对边分别为,则“”是“”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】C【解析】在中,则,即,若,则,即,所以是成立的充要条件,故选C.3. ()A. B. C. D.【答案】D【解析】由,故选D.4. 下列命题中正确的是()A. 命题“,使”的否定为“,都有”B. 若命题为假命题,命题为真命题,则为假命题C. 命题“若,则与的夹角为锐角”及它的逆命题均为真命题D. 命题“若,则或”的逆否命题为“若且,则”【答案】D【解析】选择A:命题“,使”的否定为“,都有”;选项B:为真命题;选项C:“若,则与的夹角为锐角”原命题为假命题,逆命题为真命题,故选D5. 中,角的对边分别为,,,,则为()A. B. C. D.【答案】A..................由正弦定理,可得,进而得到,故选A.6. 已知数阵中,每行的三个数依次成等差数列,每列的三个数也依次成等差数列,若,则所有九个数的和为()A. 18B. 27C. 45D. 54【答案】C【解析】由题意得,这九个数的和根据等差数列的性质,得,又因为各列也构成等差数列,则,所以,故选C.7. 已知函数(),且导函数的部分图象如图所示,则函数的解析式为()A. B.C. D.【答案】B【解析】因为,所以,由图象可得,函数的最大值,又因为,所以,可得,所以,将代入,得,即,即,因为,所以,所以所以,故选B.8. 如图,设是平面内相交成角的两条数轴,、分别是与轴、轴正方向同向的单位向量,若向量,则把有序数对叫做向量在仿射坐标系中的坐标.若在此仿射坐标系下,的坐标为,的坐标为,则()A. B. C. D.【答案】A【解析】在平面直角坐标系可得:,则,所以,故选A.9. 函数()的图象大致是()A. B.C. D.【答案】B【解析】由题意可知,所以函数是奇函数,依据图象排除A和C选项,由于,即,排除D选项,故选B.10. 将向量组成的系列称为向量列,并定义向量列的前项和.若,则下列说法中一定正确的是()A. B. 不存在,使得C. 对,且,都有D. 以上说法都不对【答案】C【解析】由,则,所以数列构成首项为,公比为的等比数列,所以,又当时,,所以当,且时,是成立的,故选C.11. 已知,,,则函数()的各极大值之和为()A. B. C. D.【答案】A【解析】由题意得,,所以,则,所以的极大值点为,的各极大值之和为,故选A.点睛:本题主要考查了导数在函数中的应用以及等比数列的求和问题,其中解答中涉及到归纳推理、利用导数研究函数的极值,以及等比数列求和公式等知识点的综合应用,试题有一定的综合性,属于中档试题,解答中认真审题,利用导数判定出函数在定义域上的极大值点是解答的关键.12. 如图,点为的边上一点,,为边上的一列点,满足,若,则()A. B.C. D.【答案】B【解析】因为,所以,所以,因为,且,所以,得,所以,又,所以数列表示首项为,公差为的等差数列,所以,故选B.点睛:本题主要考查了向量的运算和数列的通项公式的求解问题,其中解答中涉及到向量的线性运算,共线向量的表示和等差数列的判定和等差数列的通项公式的应用,试题综合性强,属于中档试题,解答中根据向量的运算和共线向量的表示,得出数列和的关系是解答的关键.二、填空题(每题5分,满分20分,将答案填在答题纸上)13. __________.【答案】【解析】由,及,可得,所以.14. 已知函数,若,则实数的值是__________.【答案】0或或【解析】由题意得,①当时,,符合题意;②当时,,解得,符合题意;③当时,,解得,符合题意,综上所述,或或.15. 若直线为函数图象的一条切线,则的最小值为__________.【答案】0【解析】设切点,则,所以方程为,即,所以,,可得在上单调递减,在单调递增,所以当时,取得最小值.点睛:本题主要考查了导致在函数中的应用,其中解答中涉及到导数的几何意义求解切线的方程,利用导数研究函数的单调性,以及利用导数研究函数的最值等知识点的综合应用,试题有一定的综合性,属于中档试题,解答中根据导数的几何意义,得出切线方程,求得的解析式是解答的关键.16. 点为所在平面内的一点且满足,,动点满足,,则的最小值为__________.【答案】【解析】因为,即点是外接圆的圆心,即外心,又因为,即点是外接圆的重心,所以是等边三角形,由,解得,即三角形的边长为,以点为原点建立坐标系,并且做单位元,点是圆上任意一点,则,点是的中点,所以,,当时,函数取得最小值,即的最小值为.点睛:本题主要考查了三角函数的综合应用问题,其中解答中涉及到三角形的性质,正弦定理解三角形,以及三角函数的恒等变换和三角函数的性质,试题综合性强,属于难题,解答中根据三角形的形式和正弦定理得到三角形为等边三角形,建立坐标系,利用坐标法求解是解答的关键.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知向量,,记函数.(1)求函数的最大值及取得最大值时的取值集合;(2)求函数在区间内的单调递减区间.【答案】(1)最大值,且取得最大值时的集合为;(2)和【解析】试题分析:(Ⅰ)由题意,化简得,即可求解函数的最值,及其相应的的值.(Ⅱ)由题意:根据三角函数的图象与性质,即可求解在的单调递减区间.试题解析:当,即时,取得最大值.此时,最大值.且取得最大值时的集合为.(2)由题意: ,即,.于是,在的单调递减区间是和.18. 在等差数列中,,.记数列的前项和为.(1)求;(2)设数列的前项和为,若成等比数列,求.【答案】(1);(2)【解析】试题分析:(Ⅰ)由题意,求得等差数列的公差,进而得到数列的通项公式,即可求解数列的前项和.(Ⅱ)由成等比数列,求解,进而得到数列通项公式,再猜裂项相消求和即可.试题解析:(1)由得,∵,∴,∴,∴,∴,.(2)若成等比数列,则,即,∴,∵∴ .19. 设分别为三个内角的对边,若向量,,且. (1)求的值; (2)求的最小值(其中表示的面积).【答案】(1);(2)【解析】试题分析:(Ⅰ)由题意得,得出向量的坐标,根据,利用,化简即可到结论;(Ⅱ)由三角形的面积公式及余弦定理,得,在中,得出,再利用正切的两角和公式和基本不等式,即可求解结论.试题解析: (1) ∵ ,,且,∴即,, 因此.(2)由及余弦定理,得在中,∵,易知,∴即当且仅当时,.20. 设函数.(1)讨论的单调性;(2)当时,恒成立,求实数的取值范围.【答案】(1)见解析;(2)【解析】试题分析:(Ⅰ)由定义域为,求得,分,两种情况讨论,即可得出函数的单调性;(Ⅱ)由(Ⅰ)可知得到,则恒成立,转化为函数,得出,令令,利用导数得出的单调性和最值,即可求解实数的取值范围.试题解析:(1)由定义域为,,当时,,在单调增.当时,,;在单调增,在单调减.综上所述:当时,在单调增;当时,在单调增,在单调减.(2)由(Ⅰ)可知,,则恒成立.令,显然,再令,,当,当.在单调减,单调增.,,∴,在单调增,,∴.21. 设正项数列的前项和为,且满足,,.(1)求数列的通项公式;(2)若正项等比数列满足,且,数列的前项和为.①求;②若对任意,,均有恒成立,求实数的取值范围.【答案】(1);(2)【解析】试题分析:(Ⅰ) 由题意,可化简得,进而求得,所以,利用等差数列的通项公式,即可求解数列的通项公式;(Ⅱ)由(1)得出,利用乘公比错位相减法,求解数列的和,在利用恒成立,分类参数转化为恒成立,即可求解结论.试题解析:(1) ,,∴,∴且各项为正,∴又,所以,再由得,所以∴是首项为1,公差为3的等差数列,∴(2)∴,①,②∴,恒成立∴,即恒成立.设,当时,;时,∴,∴.点睛:本题主要考查了数列的综合应用问题,其中解答中涉及到等差数列的通项公式的求解,数列的乘公比错位相减法求和,数列的恒成立的求解等知识点的综合运用,试题有一定的综合性,属于中档试题,解答中准确运算和合理转化恒成立问题是解答的关键.22. 已知函数.(1)若,试判断函数的零点个数;(2)若函数在上为增函数,求整数的最大值,(可能要用的数据:;).【答案】(1)1个;(2)6【解析】试题分析:(Ⅰ)根据导数求解函数的单调性,利用零点的存在定理,即可判定函数在上的零点的个数.(Ⅱ)由题意,把在上恒成立,在上恒成立,进而转化为在上恒成立,令,即,利用导数求解函数的单调性和最小值,即可求解实数的取值范围.试题解析:(1)因为,易知在上为增函数,则,故在上为增函数,又,,所以函数在上的零点有且只有1个.(2)因为,由题意在上恒成立,因为显然成立,故只需在上恒成立,令,则因为由(1)可知: 在上为增函数,故在上有唯一零点记为,,,则,,则在为减函数,在为增函数,故时,有最小值.令,则最小值有,因,则的最小值大约在之间,故整数的最大值为6.点睛:本题主要考查了导数在函数中的综合应用问题,其中解答中涉及到利用导数研究函数的单调性,利用导数研究函数的极值与最值,以及恒成立问题的求解,试题综合性强,属于难题,此类问题的解答中,根据题意合理利用分离参数转化为新函数的性质是解答的关键.。
安徽省巢湖市柘皋中学2018届高三上学期第三次月考数学(理)试题含答案

巢湖市柘皋中学2017-2018学年第一学期高三第三次月考试卷数学(理科) 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有 一项是符合题目要求的。
1。
已知集合{|ln(2)}P x y e x ==-,则*P N ⋂的子集的个数为( )A .1B .2C .3D .4 2.ABC 的内角A B C 、、的对边分别为,,a b c ,则“a b >”是“cos cos A B <”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 3。
222(4)x x dx --=⎰( )A .πB .4πC .3πD .2π 4。
下列命题中正确的是( ) A .命题“[]0,1x ∃∈,使210x -≥”的否定为“[]0,1x ∀∈,都有210x -≤”B .若命题p 为假命题,命题q 为真命题,则()()p q ⌝∨⌝为假命题C 。
命题“若0a b ⋅>,则a 与b 的夹角为锐角”及它的逆命题均为真命题D .命题“若20x x +=,则0x =或1x =-”的逆否命题为“若0x ≠且1x ≠-,则20xx +≠”5。
ABC 中,角A B C、、的对边分别为a b c 、、,2b =,6B π=,sin 211cos 2CC =+,则a 为( )A .62+B .232+ C 。
31- D .232-6.已知数阵111213212223313233a a a a a a aa a ⎛⎫ ⎪ ⎪ ⎪⎝⎭中,每行的三个数依次成等差数列,每列的三个数也依次成等差数列,若225a =,则所有九个数的和为( )A .18B .27C 。
45D .54 7.已知函数()sin()f x A x ωϕ=+(0,0,||2A πωϕ>><),且导函数()f x '的部分图象如图所示,则函数()f x 的解析式为( )A .()cos(2)6f x x π=-B .()sin(2)6f x x π=-C.1()cos(2)26f x x π=+D .1()sin(2)26f x x π=+8.如图,设,Ox Oy 是平面内相交成45角的两条数轴,1e 、2e 分别是与x 轴、y 轴正方向同向的单位向量,若向量12OP xe ye =+,则把有序数对(),x y 叫做向量OP 在仿射坐标系xOy 中的坐标。
安徽省巢湖市柘皋中学2018届高三数学上学期第二次月考试题 理(含解析)

巢湖市柘皋中学2017-2018学年第一学期高三第二次月考理科数学一.选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,,则A. (3,4)B.C. D.【答案】D【解析】由,得:,,故,故选D.2. 已知i是虚数单位、复数,则的虚部为A. B. C. D.【答案】C【解析】由题意可得,选C.3. 下列说法正确的是A. 命题“,则”的否命题是“若”B. 是函数在定义域上单调递增的充分不必要条件C.D. 若命题则【答案】D【解析】“若p则q”的否命题是“若则”,所以A错。
在定义上并不是单调递增函数,所以B错。
不存在,C错。
全称性命题的否定是特称性命题,D对,选D.4. 《九章算术》是中国古代的数学专著,其中的一段话“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
”用程序框图表示如图,那么这个程序的作用是A. 求两个正数,的最小公倍数B. 求两个正数,的最大公约数C. 判断其中一个正数是否能被另一个正数整除D. 判断两个正数,是否相等【答案】B【解析】这是更相减损术,是用来求两个正数的最大公约数,选B.5. 在中,分别是角的对应边,若,则下列式子正确的是A. B.C. D.【答案】C【解析】由题意可知,由余弦定理,所以,即,选C.6. 在中,,,是的中点,在上,且,则A. 16B. 12C. 8D. -4【答案】A【解析】如下图,以B为原点,BA,BC分别为x,y轴建立平面坐标系A(4,0),B(0,0),C(0,6),D(2,3),设E(0,t),,即,。
选A.7. 学校为了奖励数学竞赛中获奖的优秀学生,将梅、兰、竹、菊四幅名画送给获奖的甲、乙、丙三位同学,每隔学生至少获得一幅,则在所有送法中甲得到名画“竹”的概率是A. B. C. D.【答案】C【解析】由题意可知总方法数,先分3组,,再分配=6,由分步计数原理可知总方法数,满足条件方法数,概率。
安徽省六安市高三数学上学期第三次月考试题理(扫描版)(new)

安徽省六安市2018届高三数学上学期第三次月考试题理(扫描版)
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
【新】安徽省巢湖市柘皋中学2018届高三数学上学期第三次月考试题文(含解析)

巢湖市柘皋中学2017-2018学年第一学期高三第三次月考试卷数学(文科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集,集合,,则( )A. B. C. D.【答案】A【解析】故选A2. 若向量、满足,,,则与的夹角为( )A. B. C. D.【答案】C【解析】由已知故选C3. 已知,幂函数在上单调递减,则是的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】等价于,∵幂函数在上单调递减,且,解得,∴是的的必要不充分条件,故选B4. 已知等差数列的前项和为,若,则( )A. 6B. 11C. 33D. 48【答案】B【解析】由,得,即,故选B.5. 下列命题中正确的是( )A. 命题“,使”的否定为“,都有”B. 若命题为假命题,命题为真命题,则为假命题C. 命题“若,则与的夹角为锐角”及它的逆命题均为真命题D. 命题“若,则或”的逆否命题为“若且,则”【答案】D【解析】选择A:命题“,使”的否定为“,都有”;...............6. 已知函数的图像与轴交点的横坐标依次构成一个公差为的等差数列,把函数的图像沿轴向右平移个单位,得到函数的图像,则下列叙述不正确...的是( )A. 的图像关于点对称B. 的图像关于直线对称C. 在上是增函数D. 是奇函数【答案】C【解析】由已知由题意可知,,则的图象关于点对称,故A正确;的图象关于直线对称,故B 正确;由得可知在上是减函数,故C错误;由,可得是奇函数,故D正确.故选C.7. 函数的大致图像是( )A. B.C. D.【答案】B【解析】函数的定义域为,又函数有两个零点,排除选项A,又,可知函数由两个极值点,排除C,D;故选B.8. 在中,为边上一点,是的平分线,且,,则( )A. B. 1 C. D. 2【答案】C【解析】如图所示,中,由平面向量的基本定理得,解得又是的平分线,故选C.9. 已知,角的对边分别为,,,,则的面积为( )A. B. C. D.【答案】D【解析】由,化简可得,得,即由正弦定理:可得的面积故选D.10. 在中,分别为角对边的长,若,则( )A. B. C. D.【答案】A【解析】解:,11. 奇函数定义域为,其导函数是,当时,有,则关于的不等式的解集为( )A. B.C. D.【答案】D【解析】根据题意,可构造函数其导数当时,有,其导数在上为增函数,又由为奇函数,即,则,即函数为偶函数,当时,,不等式又由函数为偶函数且在上激增,则解得此时的取值范围为;当时,,不等式同理解得此时的取值范围为;综合可得:不等式的解集为故选D.【点睛】本题考查函数的导数与函数单调性的关系,解题的关键是根据题意构造新函数,并利用导数分析的单调性.12. 已知数列的前项和为,定义为数列前项的叠加和,若2016项数列的叠加和为2017,则2017项数列的叠加和为( )A. 2017B. 2018C.D.【答案】A【解析】由则.则2017项数列的叠加和故选A.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 函数的定义域是__________.【答案】【解析】由知,,又因为,所以解得,函数的定义域为即答案为14. 已知奇函数对于任意实数满足条件,若,则__________.【答案】3【解析】根据题意,函数满足条件,则,即函数为周期为4的函数,又由函数为奇函数,则,则;故答案为3.【点睛】本题考查抽象函数的求值,涉及函数的周期性与奇偶性,解题的关键是根据条件求出函数的周期.15. __________.【答案】【解析】故答案为16. 在中,,,与的交点为,过作动直线分别交线段、于两点,若,,(),则的最小值为__________.【答案】【解析】由三点共线可得存在实数,使得同理由三点共线可得存在实数,使得,解得,设,可得三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知数列的前项和为,且.(Ⅰ)求数列的通项公式;(Ⅱ)设,求数列的前项和.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(1)首先当时,,然后当时,,在验证当代入仍然适合;(2),再由列相消法求得.试题解析:(1)当时,,当时,将代入上式验证显然然适合,(2)18. 已知向量,,记函数.(Ⅰ)求函数的最大值及取得最大值时的取值集合;(Ⅱ)求函数在区间上的单调递减区间.【答案】(Ⅰ)最大值为,取得最大值时的集合为.(Ⅱ)和.【解析】试题分析:(Ⅰ)由题意,化简得,即可求解函数的最值,及其相应的的值.(Ⅱ)由题意:根据三角函数的图象与性质,即可求解在的单调递减区间.试题解析:(1)由,,当,即时,取得最大值.此时,最大值.且取得最大值时的集合为.(2)由题意: ,即,.于是,在的单调递减区间是和.19. 已知函数.(Ⅰ)若函数的图像在处的切线方程为,求的值;(Ⅱ)若函数在上是增函数,求实数的最小值.【答案】(Ⅰ),;(Ⅱ).【解析】试题分析:(1),,.根据函数f(x)的图象在处的切线方程为,可得,,.联立解.(2)由函数在上是增函数,可得在上恒成立,,令,利用导数研究其单调性极值与最值即可得出.试题解析:(Ⅰ) ∵,∴,当时,,,解得:(Ⅱ)由题意知恒成立,∴,设,,当,;当,∴,∴,所以的最小值是.20. 已知中,角所对的边分别为,.(Ⅰ)若,求角的大小;(Ⅱ)若为三个相邻的正偶数,且,求的面积.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(1)直接利用三角函数关系式的恒等变换和正弦定理求出C的值.(2)利用正弦定理和余弦定理求出边长,进一步求出三角形的面积试题解析:(Ⅰ) ∵,∴由正弦定理有,又,即,于是,在中,,于是,.(Ⅱ) ∵,故,且为三个连续相邻的正偶数,故可设,其中为偶数,由,得,∴.由余弦定理得: ,代入可得:,解得:,∴故,故,故的面积为.21. 设正项数列的前项和为,且满足,,,各项均为正数的等比数列满足.(Ⅰ)求数列和的通项公式;(Ⅱ)若,数列的前项和为.若对任意,,均有恒成立,求实数的取值范围.【答案】(Ⅰ),;(Ⅱ).【解析】试题分析:(1),可得时,,两式相减得,根据数列的各项均为正数,可得,根据,解得.利用等差数列的通项公式即可得出.进而利用等比数列的通项公式可得.(2)由(1)可知.利用错位相减法可得.可知若对任意均有恒成立,等价于恒成立,即恒成立,利用数列单调性即可得出.试题解析:(Ⅰ) ,,∴,∴且各项为正,∴又,所以,再由得,所以∴是首项为1,公差为3的等差数列,∴∴.(Ⅱ)∴恒成立∴,即恒成立.设,当时,;时,∴,∴.【点睛】本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、错位相减法、等价转化方法、不等式的性质,对学生推理能力与计算能力有较高要求.22. 设函数.(Ⅰ)讨论的单调性;(Ⅱ)当时,恒成立,求实数的取值范围.【答案】(Ⅰ)答案见解析;(Ⅱ).【解析】试题分析:(Ⅰ)由定义域为,求得,分,两种情况讨论,即可得出函数的单调性;(Ⅱ)由(Ⅰ)可知得到,则恒成立,转化为函数,得出,令令,利用导数得出的单调性和最值,即可求解实数的取值范围.试题解析:(1)由定义域为,,当时,,在单调增.当时,,;在单调增,在单调减.综上所述:当时,在单调增;当时,在单调增,在单调减.(2)由(Ⅰ)可知,,则恒成立.令,显然,再令,,当,当.在单调减,单调增.,,∴,在单调增,,∴.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巢湖市柘皋中学2017-2018学年第一学期高三第三次月考试卷数学(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,则的子集的个数为()A. 1B. 2C. 3D. 4【答案】B【解析】由题意,令,得,所以,其子集的个数为,故选B.2. 的内角的对边分别为,则“”是“”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】C【解析】在中,则,即,若,则,即,所以是成立的充要条件,故选C.3. ()A. B. C. D.【答案】D【解析】由,故选D.4. 下列命题中正确的是()A. 命题“,使”的否定为“,都有”B. 若命题为假命题,命题为真命题,则为假命题C. 命题“若,则与的夹角为锐角”及它的逆命题均为真命题D. 命题“若,则或”的逆否命题为“若且,则”【答案】D【解析】选择A:命题“,使”的否定为“,都有”;选项B:为真命题;选项C:“若,则与的夹角为锐角”原命题为假命题,逆命题为真命题,故选D5. 中,角的对边分别为,,,,则为()A. B. C. D.【答案】A..................由正弦定理,可得,进而得到,故选A.6. 已知数阵中,每行的三个数依次成等差数列,每列的三个数也依次成等差数列,若,则所有九个数的和为()A. 18B. 27C. 45D. 54【答案】C【解析】由题意得,这九个数的和根据等差数列的性质,得,又因为各列也构成等差数列,则,所以,故选C.7. 已知函数(),且导函数的部分图象如图所示,则函数的解析式为()A. B.C. D.【答案】B【解析】因为,所以,由图象可得,函数的最大值,又因为,所以,可得,所以,将代入,得,即,即,因为,所以,所以所以,故选B.8. 如图,设是平面内相交成角的两条数轴,、分别是与轴、轴正方向同向的单位向量,若向量,则把有序数对叫做向量在仿射坐标系中的坐标.若在此仿射坐标系下,的坐标为,的坐标为,则()A. B. C. D.【答案】A【解析】在平面直角坐标系可得:,则,所以,故选A.9. 函数()的图象大致是()A. B.C. D.【答案】B【解析】由题意可知,所以函数是奇函数,依据图象排除A和C选项,由于,即,排除D选项,故选B.10. 将向量组成的系列称为向量列,并定义向量列的前项和.若,则下列说法中一定正确的是()A. B. 不存在,使得C. 对,且,都有D. 以上说法都不对【答案】C【解析】由,则,所以数列构成首项为,公比为的等比数列,所以,又当时,,所以当,且时,是成立的,故选C.11. 已知,,,则函数()的各极大值之和为()A. B. C. D.【答案】A【解析】由题意得,,所以,则,所以的极大值点为,的各极大值之和为,故选A.点睛:本题主要考查了导数在函数中的应用以及等比数列的求和问题,其中解答中涉及到归纳推理、利用导数研究函数的极值,以及等比数列求和公式等知识点的综合应用,试题有一定的综合性,属于中档试题,解答中认真审题,利用导数判定出函数在定义域上的极大值点是解答的关键.12. 如图,点为的边上一点,,为边上的一列点,满足,若,则()A. B.C. D.【答案】B【解析】因为,所以,所以,因为,且,所以,得,所以,又,所以数列表示首项为,公差为的等差数列,所以,故选B.点睛:本题主要考查了向量的运算和数列的通项公式的求解问题,其中解答中涉及到向量的线性运算,共线向量的表示和等差数列的判定和等差数列的通项公式的应用,试题综合性强,属于中档试题,解答中根据向量的运算和共线向量的表示,得出数列和的关系是解答的关键.二、填空题(每题5分,满分20分,将答案填在答题纸上)13. __________.【答案】【解析】由,及,可得,所以.14. 已知函数,若,则实数的值是__________.【答案】0或或【解析】由题意得,①当时,,符合题意;②当时,,解得,符合题意;③当时,,解得,符合题意,综上所述,或或.15. 若直线为函数图象的一条切线,则的最小值为__________.【答案】0【解析】设切点,则,所以方程为,即,所以,,可得在上单调递减,在单调递增,所以当时,取得最小值.点睛:本题主要考查了导致在函数中的应用,其中解答中涉及到导数的几何意义求解切线的方程,利用导数研究函数的单调性,以及利用导数研究函数的最值等知识点的综合应用,试题有一定的综合性,属于中档试题,解答中根据导数的几何意义,得出切线方程,求得的解析式是解答的关键.16. 点为所在平面内的一点且满足,,动点满足,,则的最小值为__________.【答案】【解析】因为,即点是外接圆的圆心,即外心,又因为,即点是外接圆的重心,所以是等边三角形,由,解得,即三角形的边长为,以点为原点建立坐标系,并且做单位元,点是圆上任意一点,则,点是的中点,所以,,当时,函数取得最小值,即的最小值为.点睛:本题主要考查了三角函数的综合应用问题,其中解答中涉及到三角形的性质,正弦定理解三角形,以及三角函数的恒等变换和三角函数的性质,试题综合性强,属于难题,解答中根据三角形的形式和正弦定理得到三角形为等边三角形,建立坐标系,利用坐标法求解是解答的关键.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知向量,,记函数.(1)求函数的最大值及取得最大值时的取值集合;(2)求函数在区间内的单调递减区间.【答案】(1)最大值,且取得最大值时的集合为;(2)和【解析】试题分析:(Ⅰ)由题意,化简得,即可求解函数的最值,及其相应的的值.(Ⅱ)由题意:根据三角函数的图象与性质,即可求解在的单调递减区间.试题解析:当,即时,取得最大值.此时,最大值.且取得最大值时的集合为.(2)由题意: ,即,.于是,在的单调递减区间是和.18. 在等差数列中,,.记数列的前项和为.(1)求;(2)设数列的前项和为,若成等比数列,求.【答案】(1);(2)【解析】试题分析:(Ⅰ)由题意,求得等差数列的公差,进而得到数列的通项公式,即可求解数列的前项和.(Ⅱ)由成等比数列,求解,进而得到数列通项公式,再猜裂项相消求和即可.试题解析:(1)由得,∵,∴,∴,∴,∴,.(2)若成等比数列,则,即,∴,∵∴ .19. 设分别为三个内角的对边,若向量,,且. (1)求的值; (2)求的最小值(其中表示的面积).【答案】(1);(2)【解析】试题分析:(Ⅰ)由题意得,得出向量的坐标,根据,利用,化简即可到结论;(Ⅱ)由三角形的面积公式及余弦定理,得,在中,得出,再利用正切的两角和公式和基本不等式,即可求解结论.试题解析: (1) ∵ ,,且,∴即,, 因此.(2)由及余弦定理,得在中,∵,易知,∴即当且仅当时,.20. 设函数.(1)讨论的单调性;(2)当时,恒成立,求实数的取值范围.【答案】(1)见解析;(2)【解析】试题分析:(Ⅰ)由定义域为,求得,分,两种情况讨论,即可得出函数的单调性;(Ⅱ)由(Ⅰ)可知得到,则恒成立,转化为函数,得出,令令,利用导数得出的单调性和最值,即可求解实数的取值范围.试题解析:(1)由定义域为,,当时,,在单调增.当时,,;在单调增,在单调减.综上所述:当时,在单调增;当时,在单调增,在单调减.(2)由(Ⅰ)可知,,则恒成立.令,显然,再令,,当,当.在单调减,单调增.,,∴,在单调增,,∴.21. 设正项数列的前项和为,且满足,,.(1)求数列的通项公式;(2)若正项等比数列满足,且,数列的前项和为.①求;②若对任意,,均有恒成立,求实数的取值范围.【答案】(1);(2)【解析】试题分析:(Ⅰ) 由题意,可化简得,进而求得,所以,利用等差数列的通项公式,即可求解数列的通项公式;(Ⅱ)由(1)得出,利用乘公比错位相减法,求解数列的和,在利用恒成立,分类参数转化为恒成立,即可求解结论.试题解析:(1) ,,∴,∴且各项为正,∴又,所以,再由得,所以∴是首项为1,公差为3的等差数列,∴(2)∴,①,②∴,恒成立∴,即恒成立.设,当时,;时,∴,∴.点睛:本题主要考查了数列的综合应用问题,其中解答中涉及到等差数列的通项公式的求解,数列的乘公比错位相减法求和,数列的恒成立的求解等知识点的综合运用,试题有一定的综合性,属于中档试题,解答中准确运算和合理转化恒成立问题是解答的关键.22. 已知函数.(1)若,试判断函数的零点个数;(2)若函数在上为增函数,求整数的最大值,(可能要用的数据:;).【答案】(1)1个;(2)6【解析】试题分析:(Ⅰ)根据导数求解函数的单调性,利用零点的存在定理,即可判定函数在上的零点的个数.(Ⅱ)由题意,把在上恒成立,在上恒成立,进而转化为在上恒成立,令,即,利用导数求解函数的单调性和最小值,即可求解实数的取值范围.试题解析:(1)因为,易知在上为增函数,则,故在上为增函数,又,,所以函数在上的零点有且只有1个.(2)因为,由题意在上恒成立,因为显然成立,故只需在上恒成立,令,则因为由(1)可知: 在上为增函数,故在上有唯一零点记为,,,则,,则在为减函数,在为增函数,故时,有最小值.令,则最小值有,因,则的最小值大约在之间,故整数的最大值为6.点睛:本题主要考查了导数在函数中的综合应用问题,其中解答中涉及到利用导数研究函数的单调性,利用导数研究函数的极值与最值,以及恒成立问题的求解,试题综合性强,属于难题,此类问题的解答中,根据题意合理利用分离参数转化为新函数的性质是解答的关键.。
