专题1.2相交线与平行线(精讲精练)(解析版)【北师大版】
压轴题02:相交线与平行线综合专练20题(解析版)-年七年级数学下学期期末精选题汇编(北师大版)
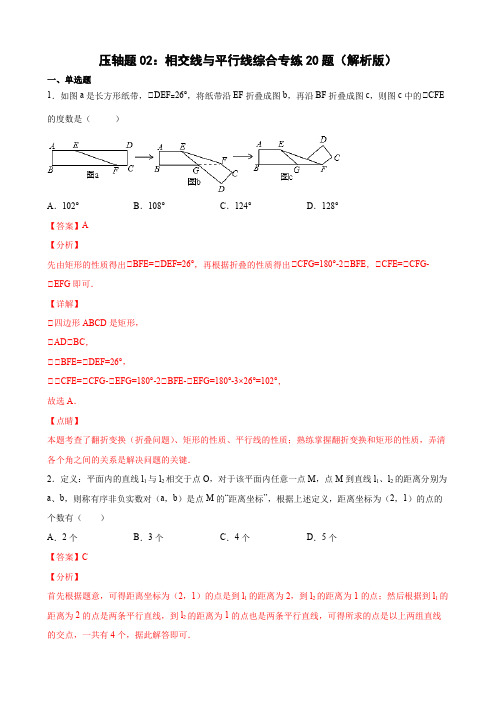
压轴题02:相交线与平行线综合专练20题(解析版)一、单选题1.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE 的度数是()A.102°B.108°C.124°D.128°【答案】A【分析】先由矩形的性质得出∠BFE=∠DEF=26°,再根据折叠的性质得出∠CFG=180°-2∠BFE,∠CFE=∠CFG-∠EFG即可.【详解】∠四边形ABCD是矩形,∠AD∠BC,∠∠BFE=∠DEF=26°,∠∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,故选A.【点睛】本题考查了翻折变换(折叠问题)、矩形的性质、平行线的性质;熟练掌握翻折变换和矩形的性质,弄清各个角之间的关系是解决问题的关键.2.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有()A.2个B.3个C.4个D.5个【答案】C【分析】首先根据题意,可得距离坐标为(2,1)的点是到l1的距离为2,到l2的距离为1的点;然后根据到l1的距离为2的点是两条平行直线,到l2的距离为1的点也是两条平行直线,可得所求的点是以上两组直线的交点,一共有4个,据此解答即可.【详解】解:如图1,,到l 1的距离为2的点是两条平行直线l 3、l 4,到l 2的距离为1的点也是两条平行直线l 5、l 6,∠两组直线的交点一共有4个:A 、B 、C 、D ,∠距离坐标为(2,1)的点的个数有4个.故选C .【点睛】此题主要考查了点的坐标,以及对“距离坐标”的含义的理解和掌握,解答此题的关键是要明确:到l 1的距离为2的点是两条平行直线,到l 2的距离为1的点也是两条平行直线.3.如图1n //AB CB ,则∠1+∠2+∠3+…+∠n=( )A .540°B .180°nC .180°(n-1)D .180°(n+1)【答案】C【分析】 根据题意,作21//DB AB ,31//EB AB ,41//FB AB ,由两直线平行,同旁内角互补,即可求出答案.【详解】解:根据题意,作21//DB AB ,31//EB AB ,41//FB AB ,∠1n //AB CB ,∠121180B B D ∠+∠=︒,2323180DB B B B E ∠+∠=︒,3434180EB B B B F ∠+∠=︒,……∠122323343411803B B D DB B B B E EB B B B F ∠+∠+∠+∠+∠+∠=︒⨯,……∠123180(1)n n ∠+∠+∠++∠=︒⨯-;故选:C .【点睛】本题考查了平行线的性质,解题的关键是正确作出辅助线,熟练运用两直线平行同旁内角互补进行证明.4.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( ) A .50°、130°B .都是10°C .50°、130°或10°、10°D .以上都不对 【答案】C【分析】首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x °,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.【详解】解:∠两个角的两边分别平行,∠这两个角相等或互补.设其中一角为x °,若这两个角相等,则x =3x ﹣20,解得:x =10,∠这两个角的度数是10°和10°;若这两个角互补,则180﹣x =3x ﹣20,解得:x =50,∠这两个角的度数是50°和130°.∠这两个角的度数是50°、130°或10°、10°.故选:C .【点睛】此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.5.如图,已知//AB CD ,M 为平行线之间一点连接AM ,CM ,N 为AB 上方一点,连接AN ,CN ,E 为NA 延长线上一点.若AM ,CM 分别平分BAE ∠,DCN ∠,则M ∠与N ∠的数量关系为( ).A .90M N ∠-∠=︒B .2180M N ∠-∠=︒C .180M N ∠+∠=︒D .2180M N ∠+∠=︒【答案】B【分析】 过点M 作//MO AB ,过点N 作//NP AB ,则//////MO AB CD NP ,根据平行线的性质可得12AMC ∠=∠+∠,223CNE ∠=∠-∠,318021∠=︒-∠,即可得出结论.【详解】解:过点M 作//MO AB ,过点N 作//NP AB ,//AB CD ,//////MO AB CD NP ∴,1AMO ∴∠=∠,OMC MCD ∠=∠, AM ,CM 分别平分BAE ∠,DCN ∠,21BAE ∴∠=∠,22NCD ∠=∠,2MCD ∠=∠,12AMC ∴∠=∠+∠,//CD NP ,22PNC NCD ∴∠=∠=∠,223CNE ∴∠=∠-∠,//NP AB ,∴∠=∠=︒-∠,NAB31802122(18021)2(12)1802180CNE AMC ∴∠=∠-︒-∠=∠+∠-︒=∠-︒,2180AMC CNE ∴∠-∠=︒,故选:B .【点睛】本题考查了平行线的性质,邻补角的定义,解题的关键是熟练掌握平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6.如图,△ABC 中,∠ACB =90°,AC =3,BC =4,AB =5,P 为直线AB 上一动点,连接PC ,则线段PC 的最小值是( )A .3B .2.5C .2.4D .2【答案】C【分析】 当PC ∠AB 时,PC 的值最小,利用面积法求解即可.【详解】解:在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,AB =5,∠当PC ∠AB 时,PC 的值最小,此时:△ABC 的面积=12•AB •PC =12•AC •BC ,∠5PC =3×4,∠PC =2.4,故选:C .【点睛】本题主要考查了垂线段最短和三角形的面积公式,解题的关键是学会利用面积法求高.7.如图,已知直线AB 、CD 被直线AC 所截,//AB CD ,E 是平面内任意一点(点E 不在直线AB 、CD 、AC 上),设BAE α∠=,DCE β∠=.下列各式:∠αβ+,∠αβ-,∠a β-,∠360αβ︒--,AEC ∠的度数可能是( )A.∠∠B.∠∠C.∠∠∠D.∠∠∠∠【答案】D【分析】由题意根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.【详解】解:(1)如图1,由AB∠CD,可得∠AOC=∠DCE1=β,∠∠AOC=∠BAE1+∠AE1C,∠∠AE1C=β-α.(2)如图2,过E2作AB平行线,则由AB∠CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∠∠AE2C=α+β.(3)如图3,由AB∠CD,可得∠BOE3=∠DCE3=β,∠∠BAE3=∠BOE3+∠AE3C,∠∠AE3C=α-β.(4)如图4,由AB∠CD,可得∠BAE4+∠AE4C+∠DCE4=360°,∠∠AE4C=360°-α-β.(5)(6)当点E在CD的下方时,同理可得∠AEC=α-β或β-α.综上所述,∠AEC的度数可能为β-α,α+β,α-β,360°-α-β,即∠∠∠∠.故选:D.【点睛】本题主要考查平行线的性质的运用,解题时注意两直线平行,同位角相等;两直线平行,内错角相等以及分类讨论.8.∠如图1,AB∥CD,则∠A+∠E+∠C=180°;∠如图2,AB∥CD,则∠E=∠A+∠C;∠如图3,AB ∥CD,则∠A+∠E-∠1=180°;∠如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是()A.∠∠∠∠B.∠∠∠C.∠∠∠D.∠∠∠【答案】C【分析】∠过点E作直线EF AB∥,由平行线的性质即可得出结论;∠过点E作直线EF AB∥,由平行线的性质即可得出结论;∠过点E作直线EF AB∥,由平行线的性质可得出∠A+∠E-∠1=180°;∠先过点P作直线PF AB∥,再根据两直线平行,内错角相等和同位角相等即可作出判断.【详解】∥,解:∠过点E作直线EF AB∥∥,∠∠A+∠1=180°,∠2+∠C=180°,∠AB CD∥,∠AB CD EF∠∠A+∠C+∠AEC=360°,故∠错误;∠过点E作直线EF AB∥,∠AB CD∥,∥∥,∠∠A=∠1,∠2=∠C,∠AB CD EF∠∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故∠正确;∠过点E作直线EF AB∥,∥∥,∠∠A+∠3=180°,∠1=∠2,∠AB CD∥,∠AB CD EF∠∠A+∠AEC-∠2=180°,即∠A+∠AEC-∠1=180°,故∠正确;∠如图,过点P作直线PF AB∥,∠AB CD∥∥,∥,∠AB CD PF∠∠1=∠FP A,∠C=∠FPC,∠∠FP A=∠FPC+∠CP A,∠∠1=∠C+∠CP A,∠AB ∠CD ,∠∠A =∠1,即∠A =∠C+∠C P A ,故∠正确.综上所述,正确的小题有∠∠∠.故选:C .【点睛】本题考查的是平行线的性质及平行公理的推论,根据题意作出辅助线是解答此题的关键. 9.如图,//,AD BC D ABC ∠=∠,点E 是边DC 上一点,连接AE 交BC 的延长线于点H ,点F 是边AB 上一点,使得FBE FEB ∠=∠,作FEH ∠的角平分线EG 交BH 于点G ,若100DEH ︒∠=,则BEG ∠的度数是( ).A .30︒B .40︒C .50︒D .60︒【答案】B【分析】 AD ∠BC ,∠D =∠ABC ,则AB ∠CD ,则∠AEF =180°-∠AED -∠BEG =180°-2β,在△AEF 中,100°+2α+180°-2β=180°,故β-α=40°,即可求解.【详解】解:设FBE =∠FEB =α,则∠AFE =2α,∠FEH 的角平分线为EG ,设∠GEH =∠GEF =β,∠AD ∠BC ,∠∠ABC +∠BAD =180°,而∠D =∠ABC ,∠∠D +∠BAD =180°,∠AB ∠CD ,∠DEH=100°,则∠CEH=∠F AE=80°,∠AEF=180°-∠FEG-∠BEG=180°-2β,在∠AEF中,在∠AEF中,80°+2α+180-2β=180°,故β-α=40°,而∠BEG=∠FEG-∠FEB=β-α=40°,故选:B.【点睛】此题考查平行线的性质,解题关键是落脚于∠AEF内角和为180°,即100°+2α+180°-2β=180°,题目难度较大.10.如图,直线AB MN∥,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC 的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令ECMα∠=,用含α的式子表示∠EBC为().A.52αB.10α︒-C.1102α︒-D.1102α-︒【答案】D【分析】先求出∠ABC,再延长CE,交AB于点G,结合平行线的性质表示出∠BCE,然后根据三角形内角和定理表示∠CED,再根据角平分线得定义表示出∠CEB,最后根据三角形内角和定理得出答案.【详解】在∠ABC中,∠CAB=40°,∠ACB=90°,∠∠ABC=50°.延长CE,交AB于点G,∠MN BA∥,∠EGBα∠=,∠ACM=∠BAC=40°,∠∠ACE=α-40°,∠∠BCE=90°-(α-40°)=130°-α.∠∠CEA=180°-∠CAE-∠ACE,∠∠CED=180°-∠CEA=∠CAE+∠ACE=20°+(α-40°)=α-20°.∠EF平分∠CED,∠∠CEF=111022CEDα∠=-︒,∠∠CEB=1110706022αα-︒+︒=+︒,∠∠EBC=11180(60)(130)10 22ααα︒-+︒-︒-=-︒.故选:D.【点睛】本题主要考查了角平分线的定义,三角形内角和定理,平行线的性质,将待求角转化到适合的三角形是解题的关键.二、填空题11.如图,已知,∠ABG为锐角,AH∠BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∠AB交直线AH于点D,CE∠CD交AB于点E,CF∠AD,垂足为F(F不与A重合),若∠ECF =n°,则∠BAF的度数为_____度.(用n来表示)【答案】n或180﹣n【分析】分两种情况讨论:当点M在线段BC上;点C在BM延长线上,根据平行线的性质,即可得到结论.【详解】解:过A作AM∠BC于M,如图1,当点C在BM延长线上时,点F在线段AD上,∠AD∠BC,CF∠AD,∠CF∠BG,∠∠BCF=90°,∠∠BCE+∠ECF=90°,∠CE∠AB,∠∠BEC=90°,∠∠B+∠BCE=90°,∠∠B=∠ECF=n°,∠AD∠BC,∠∠BAF=180°﹣∠B=180°﹣n°,过A作AM∠BC于M,如图2,当点C在线段BM上时,点F在DA延长线上,∠AD∠BC,CF∠AD,∠CF∠BG,∠∠BCF=90°,∠∠BCE+∠ECF=90°,∠CE∠AB,∠∠BEC=90°,∠∠B+∠BCE=90°,∠∠B=∠ECF=n°,∠AD∠BC,∠∠BAF=∠B=n°,综上所述,∠BAF的度数为n°或180°﹣n°,故答案为:n或180﹣n.【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.12.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是.【答案】6秒或19.5秒【分析】设A灯旋转t秒,两灯光束平行,B灯光束第一次到达BQ需要180÷4=45(秒),推出t≤45−12,即t≤33.利用平行线的性质,结合角度间关系,构建方程即可解答.【详解】解:设A灯旋转t秒,两灯的光束平行,B灯光束第一次到达BQ需要180÷4=45(秒),∠t≤45﹣12,即t≤33.由题意,满足以下条件时,两灯的光束能互相平行:∠如图,∠MAM'=∠PBP',12t=4(12+t),解得t=6;∠如图,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;综上所述,满足条件的t的值为6秒或19.5秒.故答案为:6秒或19.5秒.【点睛】本题主要考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠B 的补角,则∠BAH的度数是_____.【答案】60°##60度【分析】首先设∠BAF=x°,∠BCF=y°,过点B作BM AD,过点F作FN AD,根据平行线的性质,可得∠AFC =(x+2y)°,∠ABC=(2x+y)°,又由∠F的余角等于2∠B的补角,可得方程:90﹣(x+2y)=180﹣2(2x+y),继而求得答案.【详解】解:设∠BAF=x°,∠BCF=y°,∠∠BCF=∠BCG,CF与∠BAH的平分线交于点F,∠∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,过点B作BM AD,过点F作FN AD,如图所示:∠AD CE,∠AD FN BM CE ,∠∠AFN =∠HAF =x °,∠CFN =∠GCF =2y °,∠ABM =∠BAH =2x °,∠CBM =∠GCB =y °,∠∠AFC =(x +2y )°,∠ABC =(2x +y )°,∠∠F 的余角等于2∠B 的补角,∠90﹣(x +2y )=180﹣2(2x +y ),解得:x =30,∠∠BAH =60°.故答案为:60°【点睛】此题考查了平行线的性质与判定以及余角、补角的定义.此题难度适中,注意掌握辅助线的作法,掌握数形结合思想与方程思想的应用.14.如图,已知AB //CD ,BE 、DE 的交点为E ,现作如下操作:第一次操作,分别作∠ABE 和∠CDE 的平分线,交点为E 1,第二次操作,分别作∠ABE 1和∠CDE 1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠CDE 2的平分线,交点为E 3,...第n (n ≥2)次操作,分别作∠ABEn ﹣1和∠CDEn ﹣1的平分线,交点为En ,若∠En =α度,则∠BED =___度.【答案】2n a【分析】先过E 作//EF AB ,确定BED ABE CDE ∠=∠+∠,再根据角平分线的性质确定n E ∠与BED ∠的关系,即可求解.【详解】解:如下图,过E 作//EF AB ,∠//AB CD ,∠////AB EF CD ,∠B BEF D DEF ∠=∠∠=∠,,∠BED BEF DEF ∠=∠+∠,∠BED ABE CDE ∠=∠+∠;如下图,∠ABE ∠和CDE ∠的平分线交点为1E ∠111111222DE B ABE CDE ABE CDE BED ∠=∠+∠=∠+∠=∠ ∠1ABE ∠和1CDE ∠的平分线交点为2E , ∠22211111122412BE ABE CDE ABE CD E D E DE B B D ∠=∠+∠=∠+∠∠=∠=; ∠2ABE ∠和2CDE ∠的平分线交点为3E , ∠33322211122812BE ABE CDE ABE CD E D E DE B B D ∠=∠+∠=∠+∠∠=∠=; … 以此类推,12n n E BED ∠=∠ ∠当n E α∠=度时,2n BED α∠=度.故答案为2n α .【点睛】本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,找到角之间的关系.15.如图,直线,,AB CD EF 与直线,,GH IJ KL 分别相交,图中的同位角共有__________对.【答案】156【分析】观察图形,直线 GH,IJ,KL 上,每条直线有5个交点,直线AB,CD,EF 上,每条直线有3个交点,每个交点存在4个角,根据每2个交点可以构成4对同位角,分别求得直线GH,IJ,KL 和AB,CD,EF 上的同位角的对数即可.【详解】观察图形,直线,,GH IJ KL 上,每条直线有5个交点,直线,,AB CD EF 上,每条直线有3个交点,每个交点存在4个角,则直线,,GH IJ KL 上存在的同位角的个数是:5(51)4310434031202-⨯⨯=⨯⨯=⨯=对,同理直线,,AB CD EF 上存在的同位角的个数是:3(31)43362-⨯⨯=对, 则总数是12036156+=对.故答案为:156.【点睛】 本题考查了找同位角,分类讨论是解题的关键.三、解答题16.探究并尝试归纳:(1)如图1,已知直线a 与直线b 平行,夹在平行线间的一条折线形成一个角∠A ,试求∠1+∠2+∠A 的度数,请加以说明.(2)如图2,已知直线a 与直线b 平行,夹在平行线间的一条折线增加一个折,形成两个角∠A 和∠B,请直接写出∠1+∠2+∠A +∠B = 度.(3)如图3,已知直线a 与直线b 平行,夹在平行线间的一条折线每增加一个折,就增加一个角.当形成n 个折时,请归纳并写出所有角与∠1、∠2的总和: 【结果用含有n 的代数式表示,n 是正整数,不用证明】【答案】(1)360°(2)540(3)180(1)n ⋅+︒【分析】(1)过A 作AB //直线a ,再根据平行线的性质即可得到结论;(2)过A 作AC //直线a ,BD //直线a ,则AC//BD //直线b ,根据平行线的性质即可得到结论; (3)根据平行线的性质即可得到结论.(1)解:过A 作AB //直线a ,则AB //直线b ,1342180∴∠+∠=∠+∠=︒,12360MAN ∴∠+∠+∠=︒;(2)解:过A 作AC //直线a ,BD //直线a ,则AC //BD //直线b ,135642180∴∠+∠=∠+∠=∠+∠=︒,12540MAB ABN ∴∠+∠+∠+∠=︒,故答案为:540;(3)解:由(1),(2)知,当形成1个折时,所有角与1∠、2∠的总和180(11)360=⋅+︒=︒,当形成2个折时,所有角与1∠、2∠的总和180(21)540=⋅+︒=︒,当形成n 个折时,所有角与1∠、2∠的总和180(1)n =⋅+︒,故答案为:180(1)n ⋅+︒.【点睛】本题考查了平行线的性质,正确的作出图形是解题的关键.17.如图,已知AB CD ∥,E 、F 分别在AB CD 、上,点G 在AB 、CD 之间,连接GE GF 、.(1)当40BEG ∠=︒时,EP 平分,BEG FP ∠平分DFG ∠;∠如图1,当EG FG ⊥时,则P ∠=______°;∠如图2,在CD 的下方有一点Q ,若EG 恰好平分,BEQ FD ∠恰好平分GFQ ∠,求2Q P ∠+∠的度数;(2)在AB 的上方有一点O ,若FO 平分GFC ∠.线段GE 的延长线平分OEA ∠,则当100EOF EGF ∠+∠=︒时,直接写出OEA ∠与OFC ∠的关系.【答案】(1)∠45;∠140︒(2)3160OEA OFC ∠-∠=︒【分析】(1)根据平行线的性质,以及角平分线的定义即可求解;(2)过点O 作OT AB ∥,则OT CD ∥设OFC OFG ∠=∠β=,OEH HEA α∠=∠=,1802G BEG GFD αβ∠=∠+∠=+︒-,根据平行线的性质求得80αβ+=︒,进而根据()33222160OEA OFC ββαβα∠-∠=--=+=︒即可求解.(1)∠如图,分别过点,G P 作,GN AB PM AB ∥∥,BEG EGN ∴∠=∠,AB CD ∥,NGF GFD ∴∠=∠,EGF BEG GFD ∴∠=∠+∠,同理可得EPF BEP PFD ∠=∠+∠,EG FG ⊥,90EGF ∴∠=︒,EP 平分,BEG FP ∠平分DFG ∠;11,22BEP BEG PFD GFD ∴∠=∠∠=∠, ∴()114522EPP BEG GFD EGF ∠=∠+∠=∠=︒, 故答案为:45,∠如图,过点Q 作QR CD ∥,40BEG ∠=︒,EG 恰好平分,BEQ FD ∠恰好平分GFQ ∠,40GEQ BEG ∴∠=∠=︒,GFQ QFD ∠=∠,设GFQ QFD ∠=∠α=,QR CD ∥,AB CD ∥,1801802100EQR QEB QEG ∴∠=︒-∠=︒-∠=︒,CD QR ∥,180DFQ FQR ∴∠+∠=︒,180FQR α∴+∠=︒,100FQE α∴+∠=︒,100FQE α∴∠=︒-,由(1)可知240G P BEG EFD α∠=∠=∠+∠=︒+,210040140FQE P αα∴∠+∠=︒-+︒+=︒;(2)如图,在AB 的上方有一点O ,若FO 平分GFC ∠,线段GE 的延长线平分OEA ∠,设H 为线段GE 的延长线上一点,则OFC OFG ∠=∠,OEH HEA ∠=∠设OFC OFG ∠=∠β=,OEH HEA α∠=∠=如图,过点O 作OT AB ∥,则OT CD ∥TOF OFC β∴∠=∠=,2TOE OEA α∠=∠=2EOF βα∴∠=-HEA BEG α∠=∠=,1802GFD β∠=︒-由(1)可知1802G BEG GFD αβ∠=∠+∠=+︒-100EOF EGF ∠+∠=︒∴2βα-+1802αβ+︒-100=︒80αβ∴+=︒2,OFC OEA βα∠=-∠=β()33222160OEA OFC ββαβα∴∠-∠=--=+=︒即3160OEA OFC ∠-∠=︒【点睛】本题考查了平行线的性质,以及角平分线的定义,掌握平行线的性质是解题的关键.18.点O 是直线AB 上的一点,射线OC 从OA 出发绕点O 顺时针方向旋转,旋转到OB 停止,设AOC α∠=(0180α︒≤≤︒),射线OD OC ⊥,作射线OE 平分BOD ∠.(1)如图1,若40α=︒,且OD 在直线AB 的上方,求DOE ∠的度数(要求写出简单的几何推理过程).(2)射线OC 顺时针旋转一定的角度得到图2,当射线OD 在直线AB 的下方时,其他条件不变,请你用含α的代数式表示DOE ∠的度数,(要求写出简单的几何推理过程).(3)射线OC 从OA 出发绕点O 顺时针方向旋转到OB ,在旋转过程中你发现DOE ∠与AOC∠(01800180AOC DOB ︒≤∠≤︒︒≤∠≤︒,)之间有怎样的数量关系?请你直接用含α的代数式表示DOE ∠的度数.【答案】(1)25DOE ∠=︒ (2)1452DOE α∠=-︒ (3)1452DOE AOC ∠=︒-∠即1452DOE α∠=︒-或1452DOE AOC ∠=︒+∠即1452DOE α∠=︒+或11352DOE AOC ∠=︒-∠即11352DOE α∠=︒-或1452DOE AOC ∠=∠-︒即1452DOE α∠=-︒ 【分析】(1)根据40α=︒,∠COD =90°,求出∠BOD =50°,根据OE 平分∠BOD ,即可得出结果;(2)先用α表示出∠BOC ,再根据∠COD =90°表示出∠BOD ,根据OE 平分∠BOD ,即可得出结果; (3)分四种情况进行讨论,分别求出∠DOE 与∠AOC 的关系,用含α的代数式表示∠DOE 的度数即可.(1)解:∠OD ∠OC ,∠∠COD =90°,∠40α=︒,即40AOC ∠=︒,∠18050BOD COD AOC ∠=︒-∠-∠=︒,∠OE 平分∠BOD , ∠1252DOE BOD ∠=∠=︒. (2)AOC α∠=,180BOC α∴∠=︒-,∠OD ∠OC ,∠∠COD =90°,∠BOD COD BOC ∠=∠-∠()90180α=︒-︒-90α=-︒∠OE 平分∠BOD , ∠114522DOE BOD α∠=∠=-︒. (3)∠当090AOC ︒≤∠≤︒,OD 在直线AB 的上方时,如图所示:180BOD COD AOC ∠=︒-∠-∠18090AOC =︒-︒-∠90AOC =︒-∠,∠OE 平分∠BOD , ∠114522DOE BOD AOC ∠=∠=︒-∠, 即1452DOE α∠=︒-. ∠当090AOC ︒≤∠≤︒,OD 在直线AB 的下方时,如图所示:∠90AOD COD AOC AOC ∠=∠-∠=︒-∠,∠18090BOD AOD AOC∠=︒-∠=︒+∠,∠OE平分∠BOD,∠114522DOE BOD AOC ∠=∠=︒+∠,即1452 DOEα∠=︒+.∠当90180AOC︒∠≤︒<,OD在直线AB的上方时,如图所示:180BOC AOC∠=︒-∠,BOD DOC BOC∴∠=∠+∠90180AOC=︒+︒-∠270AOC=︒-∠,∠OE平分∠BOD,∠1113522DOE BOD AOC ∠=∠=︒-∠,即11352 DOEα∠=︒-.∠当90180AOC︒∠≤︒<,OD在直线AB的下方时,如图所示:∠180BOC AOC ∠=︒-∠,BOD COD BOC ∴∠=∠-∠()90180AOC =︒-︒-∠90AOC =∠-︒,∠OE 平分∠BOD , ∠114522DOE BOD AOC ∠=∠=∠-︒, 即1452DOE α∠=-︒. 综上分析可知,1452DOE AOC ∠=︒-∠即1452DOE α∠=︒-或1452DOE AOC ∠=︒+∠即1452DOE α∠=︒+或11352DOE AOC ∠=︒-∠即11352DOE α∠=︒-或1452DOE AOC ∠=∠-︒即1452DOE α∠=-︒. 【点睛】本题主要考查了角平分线的定义,垂直的定义,根据α的大小和OD 的位置分类讨论,是解决本题的关键.19.如图,AD //BC ,127DAC ∠=︒,15ACF ∠=︒,142EFC ∠=︒.(1)求证:EF //AD ;(2)连接CE ,若CE 平分∠BCF ,求∠FEC 的度数.【答案】(1)证明见解析(2)19FEC ∠=︒【分析】(1)先根据平行线的性质,得到∠ACB 的度数,进而得出∠FCB 的度数,再根据∠EFC =140°,即可得到∠EFC =142°,即可得到EF ∠BC ,进而得出EF ∠AD ;(2)先根据CE 平分∠BCF ,可得∠BCE =19°,再根据EF ∠BC ,即可得到∠FEC =19°.(1)证明:∠AD BC ∥∠180ACB DAC ∠+∠=︒∠127DAC ∠=︒∠53ACB ∠=︒又∠15ACF ∠=︒∠38FCB ACB ACF ∠=∠-∠=︒∠142EFC ∠=︒∠180FCB EFC ∠+∠=︒∠EF BC ∥又∠AD BC ∥∠EF AD ∥(2)解:∠CF 平分∠BCF ∠1192BCE FCB ∠=∠=︒ ∠EF BC ∥∠19FEC ECB ∠=∠=︒答:∠FEC 的度数19°.【点睛】本题考查平行线的判定,三角形内角和定理,角平分线定义,三角形的外角性质,邻补角定义,能综合运用定理运行推理是解此题的关键,难度适中.20.已知点B ,D 分别在AK 和CF 上,且∥CF AK .(1)如图1,若25CDE ∠=︒,80DEB ∠=︒,则ABE ∠的度数为________;(2)如图2,BG 平分ABE ∠,GB 的延长线与EDF ∠的平分线交于H 点,若DEB ∠比DHB ∠大60︒,求DEB ∠的度数;(3)保持(2)中所求的DEB ∠的度数不变,如图3,BM 平分EBK ∠,DN 平分CDE ∠,作∥BP DN ,则PBM ∠的度数是否改变?若不变,请求值;若改变,请说明理由.【答案】(1)55°(2)100°(3)不变,40°【分析】(1)过点E 作ES CF ,根据∥CF AK ,则ES CF AK ,运用平行线的性质计算即可.(2) 延长DE ,交AB 于点M ,则∠DEB =∠EMB +∠EBM ,利用平行线的性质,角平分线的定义,三角形外角的性质计算即可.(3) 过点E 作EQ DN ,则EQ DN BP ,利用前面的结论和方法,进行等量代换并推理计算即可.(1)解:如图1,过点E 作ES CF ,∠∥CF AK ,∠ES CF AK ,∠∠CDE =∠DES ,∠SEB =∠ABE ,∠∠CDE +∠ABE =∠DES +∠SEB =∠DEB ,∠∠CDE =25°,∠DEB =80°,∠∠ABE =∠DEB -∠CDE =80°-25°=55°.故答案为:55°.(2)解:如图2,延长DE ,交AB 于点M ,则∠DEB =∠EMB +∠EBM ,∠∥CF AK ,BG 平分ABE ∠,∠∠EMB =180°-∠MDF ,∠EBM =2∠ABG =2∠HBN ,∠MDH =∠HDF =∠HNK =12∠MDF ,∠∠HBN +∠DHB =∠HNK ,∠∠DEB =(180°-∠MDF ) +2∠HBN =180°-∠MDF +122MDF DHB ⎛⎫⨯∠-∠ ⎪⎝⎭, ∠∠DEB =180°-∠MDF +∠MDF -2∠DHB =180°-2∠DHB ,∠DEB ∠60DHB -∠=︒,∠∠DEB =180°-2(∠DEB -60°),∠3∠DEB =300°,解得∠DEB =100°.(3)解:过点E作EQ DN,则EQ DN BP,根据(1)得,∠DEB=∠CDE+∠ABE,∠BM平分EBK∠,∠,DN平分CDE∠∠DEB=2∠NDE+180°-2∠EBM,∠∠DEB=100°,∠∠EBM-∠NDE=40°,∠EQ DN,∠∠DEQ=∠NDE,∠∠EBM =40°+∠DEQ,,,∠EQ DN DN BP∠EQ BP,∠∠EBM+∠PBM +∠BEQ =180°,∠40°+∠DEQ+∠PBM +∠BEQ =180°,∠40°+∠DEB+∠PBM =180°,∠∠PBM =180°-100°-40°=40°,∠∠PBM 的度数不变,值为40°.【点睛】本题考查了平行线的判定和性质,三角形外角的性质,角的平分线定义,熟练掌握平行线的判定和性质是解题的关键.。
北师大版七年级数学下册第二章 :相交线与平行线培优讲义(含解析)
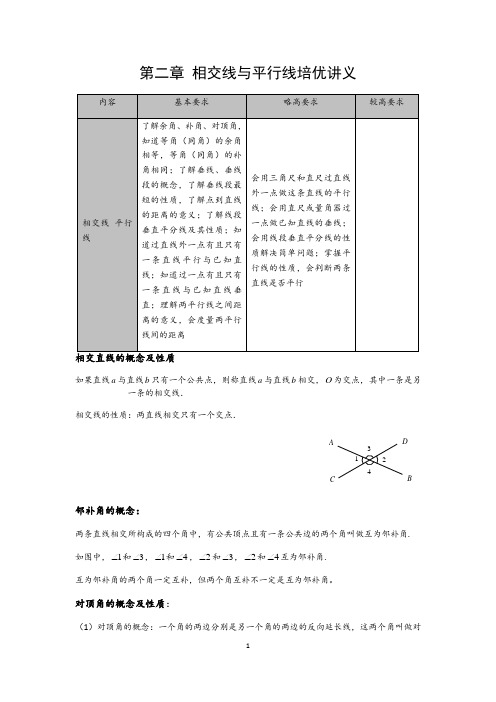
第二章 相交线与平行线培优讲义如果直线a 与直线b 只有一个公共点,则称直线a 与直线b 相交,O 为交点,其中一条是另一条的相交线. 相交线的性质:两直线相交只有一个交点.邻补角的概念:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角叫做互为邻补角. 如图中,1∠和3∠,1∠和4∠,2∠和3∠,2∠和4∠互为邻补角. 互为邻补角的两个角一定互补,但两个角互补不一定是互为邻补角。
对顶角的概念及性质:(1)对顶角的概念:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对4321D CBA顶角. 我们也可以说,两条直线相交成四个角,其中有公共顶点而没有公共边的两个角叫做对顶角.如图中,1∠和2∠,3∠和4∠是对顶角.(2)对顶角的性质:对顶角相等。
垂线的概念及性质:(1)垂线的概念:垂直是相交的一种特殊情况,两条直线互相垂直,其中一条叫另一条直线的垂线,它们的交点叫垂足.如图所示,可以记作“AB CD ⊥于O ”(2)垂线的性质:①过直线外一点有且只有一条直线与已知直线垂直;②连接直线外一点与直线上各点的所有线段中,垂线段最短,简单说成:垂线段最短.5.同位角、内错角、同旁内角的概念:①同位角:两条直线被第三条直线所截,位置相同的一对角(两个角分别在两条直线的相同一侧,并且在第三条直线的同旁)叫做同位角如图所示,∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8都是同位角.②内错角:两条直线被第三条直线所截,两个角都在两条直线之间,并且位置交错,(即分别在第三条直线的两旁),这样的一对角 叫做内错角,如图中,∠3与∠5,∠4与∠6都是内错角③同旁内角:两条直线被第三条直线所截,两个角都在两条直线之间,并且在第三条直线的同旁,这样的一对角叫做同旁内角,如图中,∠3与∠6,∠4与∠5都是同旁内角.DCBA看图识角:(1)“F ”型中的同位角.如图.(2)“Z ”字型中的内错角,如图.(3)“U”字型中的同旁内角.如图.平行线的概念:在同一平面内,不相交的两条直线叫做平行线,直线a 与直线b 互相平行,记作a ∥b 。
北师大版七年级数学下册第二章《相交线与平行线》考试卷附解析版)
(3)利用上述结论解决问题:如图已知 , 和 的平分线相交于 , ,求 的度数.
22.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线 射到平面镜 上,被 反射到平面镜 上,又被 反射,若被 反射出的光线 与光线 平行,且 ,则 _________, ________.
4.如图, , ,则图中与 相等 角(不含 )有______个;若 ,则 ________.
5.在 、 两座工厂之间要修建一条笔直的公路,从 地测得 地的走向是南偏东 ,现 、 两地要同时开工,若干天后,公路准确对接,则 地所修公路的走向应该是( )
A.北偏西 B.南偏东 C.西偏北 D.北偏西
6.如图,直线l//m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为()
【答案】95°
【解析】
【详解】如图,作EF∥AB,则EF∥CD,
∴∠ABE+∠BEF=180°,∵∠ABE=120°,∴∠BEF=60°,
∵∠DCE=∠FEC=35°,∴∠BEC=∠BEF+∠FEC=95°.
故答案为95°.
点睛:本题关键在于构造平行线,再利用平行线的性质解题.
13.某人在练车场上练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则这两次拐弯的角度可能是________.①第一次向左拐 ,第二次向右拐 ;②第一次向右拐 ,第二次向左拐 ;③第一次向右拐 ,第二次向左拐 ;④第一次向左拐 ,第二次向左拐 .
A. 20°B. 25°C. 30°D. 35°
【答案】A
【解析】
【详解】如图,过点B作BD//l,
北师大版初一(下)数学第二章相交线与平行线教案:相交线与平行线讲义(含解析)

北师大版初一(下)数学第二章相交线与平行线教案:相交线与平行线讲义(含解析)把握对顶角和邻补角的概念;把握垂线段的定义及其画法;3.把握三线八角的定义和找法;4.把握平行线的性质与判定.相交线在同一平面内,两条直线的位置关系有_________和________。
(2)相交:在同一平面内,有__________的两条直线称为相交线。
(3)邻补角:①定义:有公共顶点,且有一条公共边,另一条边互为反向延长线,具有这种位置关系的两个角,互为邻补角。
②性质:位置——互为邻角数量——互为补角(两角之和为180°)(4)对顶角:①定义:有一个公共顶点,同时有一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角②性质:对顶角相等几何语言:∵∠1+∠2=180°∠2+∠3=180°∴∠1=∠3(同角的补角相等)两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:注意点:⑴对顶角是成对显现的,对顶角是具有专门位置关系的两个角;⑵假如∠α与∠β是对顶角,那么一定有∠α=∠β;反之假如∠α=∠β,那么∠α与∠β不一定是对顶角⑶假如∠α与∠β互为邻补角,则一定有_____________;反之假如∠α+∠β=180°,则∠α与∠β不一定是邻补角。
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2.垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做_______。
符号语言记作:如图所示:AB⊥CD,垂足为O垂线性质1:过一点_______________一条直线与已知直线垂直。
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:_______________。
3.垂线的画法:(1)过直线上一点画已知直线的垂线;(2)过直线外一点画已知直线的垂线。
北师大版七年级数学下册第二章 :相交线与平行线培优讲义(含解析)

第二章 相交线与平行线培优讲义如果直线a 与直线b 只有一个公共点,则称直线a 与直线b 相交,O 为交点,其中一条是另一条的相交线. 相交线的性质:两直线相交只有一个交点.邻补角的概念:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角叫做互为邻补角. 如图中,1∠和3∠,1∠和4∠,2∠和3∠,2∠和4∠互为邻补角. 互为邻补角的两个角一定互补,但两个角互补不一定是互为邻补角。
对顶角的概念及性质:(1)对顶角的概念:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对4321D CBA顶角. 我们也可以说,两条直线相交成四个角,其中有公共顶点而没有公共边的两个角叫做对顶角.如图中,1∠和2∠,3∠和4∠是对顶角.(2)对顶角的性质:对顶角相等。
垂线的概念及性质:(1)垂线的概念:垂直是相交的一种特殊情况,两条直线互相垂直,其中一条叫另一条直线的垂线,它们的交点叫垂足.如图所示,可以记作“AB CD ⊥于O ”(2)垂线的性质:①过直线外一点有且只有一条直线与已知直线垂直;②连接直线外一点与直线上各点的所有线段中,垂线段最短,简单说成:垂线段最短.5.同位角、内错角、同旁内角的概念:①同位角:两条直线被第三条直线所截,位置相同的一对角(两个角分别在两条直线的相同一侧,并且在第三条直线的同旁)叫做同位角如图所示,∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8都是同位角.②内错角:两条直线被第三条直线所截,两个角都在两条直线之间,并且位置交错,(即分别在第三条直线的两旁),这样的一对角 叫做内错角,如图中,∠3与∠5,∠4与∠6都是内错角③同旁内角:两条直线被第三条直线所截,两个角都在两条直线之间,并且在第三条直线的同旁,这样的一对角叫做同旁内角,如图中,∠3与∠6,∠4与∠5都是同旁内角.DCBA看图识角:(1)“F ”型中的同位角.如图.(2)“Z ”字型中的内错角,如图.(3)“U”字型中的同旁内角.如图.平行线的概念:在同一平面内,不相交的两条直线叫做平行线,直线a 与直线b 互相平行,记作a ∥b 。
北师大版七年级数学下册第二章相交线与平行线复习课件

因为S△ABC = 1/2 AB×CD 所=以C1D=/2.24cmAC×BC
4.你能求出点C到AB的距离吗?你是
怎样做的?小组合作交流.
等面积法
三线八角:
C
两条直线AB与CD被第三条
3
E 1
直线EF所截,形成:
75
D
(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
A1
D
4
(两直线平行,同旁内角互补) 2
3
又∵∠1=∠4(对顶角相等)
B
C
∴∠1+∠2=180°(等量代换)
已知AB∥CD,E为平面内一点(E不在AB和CD
上),连接AE,CE,探索∠AEC与∠A,∠C之间
的关系。
情况1
E在AB与CD之间且向内凹
的度数。
DC
1 25 7
3 46 AE B
16.如图,两平面镜所成的角为 ∠1,一束光线由点P发出,经 OB,OA两次反
后(,1∠)1=P1Q2与0°R∠CP平Q行B吗=4?0° B
变式 P
(2)要使 PQ与RC平行 Q
C
必须改变∠1和∠PQB任何一个角的度
数,问要改变哪一个角?这个角改变
后度数是多少?
EB与AD一定平行吗?”。 ❖小王说“一定平行”;
D
E1
❖而小李说“不一定平行”。
❖你更赞同谁的观点?
❖为什么?
A
B
C
E2
操作与解释
二、强化知识、技能训练
1.(1)若∠1=50 °,
则∠2 =___5_0_°__
ED
∠BOC=__1_3_0_°__
七年级数学下册 第2章 相交线与平行线 2.3 平行线的性质精练 (新版)北师大版-(新版)北师大版

3 平行线的性质测试时间:25分钟一、选择题1.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,那么∠2的度数是( )A.20°B.30°C.35°D.50°1.答案 C 如图,∵AB⊥BC,∴∠ABC=90°,∴∠3=180°-90°-∠1=35°,∵a∥b,∴∠2=∠3=35°.故选C.2.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )A.65°B.55°C.45°D.35°2.答案 B ∵DA⊥AC,垂足为A,∴∠CAD=90°,又∵∠ADC=35°,∴∠ACD=180°-90°-35°=55°,∵AB∥CD,∴∠1=∠ACD=55°,故选B.3.如图,直线a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )A.20°B.25°C.30°D.40°3.答案 A 如图,∵a∥b,∴∠3=∠1=70°,∴∠2=90°-∠3=20°.故选A.4.将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为( )A.10°B.15°C.20°D.25°4.答案 B ∵BC∥DE,∴∠BCE=∠E=30°,∴∠ACE=∠ACB-∠BCE=45°-30°=15°,故选B.二、填空题5.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于.5.答案70°解析∵∠1+∠2+∠3=180°,∠3=40°,∴∠1+∠2=140°.∵∠1=∠2,∴∠1=70°.∵a∥b,∴∠4=∠1=70°.6.图①是我们常用的折叠式小刀,图②中刀柄外形是一个直角梯形挖去一个小半圆,刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图②所示的∠1与∠2,则∠1与∠2的度数和是度.6.答案90解析如图,AB∥CD,∠AEC=90°,作EF∥AB,则EF∥CD,所以∠1=∠AEF,∠2=∠CEF,所以∠1+∠2=∠AEF+∠CEF=∠AEC=90°.7.如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=°.7.答案105解析如图,过点C作CD∥AE,则∠DCA=∠CAE=60°.∵CD∥AE,BF∥AE,∴CD∥BF,∴∠DCB=∠CBF=45°.∴∠ACB=∠DCA+∠DCB=105°.8.如图,l∥m,点A在直线m上,若∠ABC=60°,∠1=40°,则∠2=.8.答案20°解析如图,延长CB交直线m于点D,∵∠ABC=60°,∴∠ABD=120°.∵l∥m,∴∠BDA=∠1=40°.∴∠2=180°-∠ABD-∠BDA=180°-120°-40°=20°.9.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=.9.答案46°解析如图,因为a∥b,所以∠3=∠1=34°.因为∠3+∠BAC+∠2=180°,∠BAC=100°,所以∠2=180°-34°-100°=46°.10.如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为.10.答案35°解析如图,∠3=180°-∠1=180°-55°=125°,∵直尺两边互相平行,∴∠2+90°=∠3,∴∠2=125°-90°=35°.三、解答题11.如图,已知AB∥CD,EF交AB于点E,交CD于点F,FG平分∠EFD,交AB于点G.若∠1=50°,求∠BGF的度数.11.解析∵AB∥CD,∠1=50°,∴∠CFE=∠1=50°.∵∠CFE+∠EFD=180°,∴∠EFD=180°-∠CFE=130°.∵FG平分∠EFD,∠EFD=65°.∴∠DFG=12∵AB∥CD,∴∠BGF+∠DFG=180°,∴∠BGF=180°-∠DFG=180°-65°=115°.12.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.12.解析∠AED=∠ACB.理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知),∴∠2=∠4(同角的补角相等).∴EF∥AB(内错角相等,两直线平行).∴∠3=∠ADE(两直线平行,内错角相等).∵∠3=∠B(已知),∴∠B=∠ADE(等量代换).∴DE∥BC(同位角相等,两直线平行).∴∠AED=∠ACB(两直线平行,同位角相等).。
北师大版七年级下册第二单元相交线与平行线单元——探索直线平行的条件(知识梳理与考点分类讲解)

北师大版七年级下册第二单元相交线与平行线单元——探索直线平行的条件(全章知识梳理与考点分类讲解)【知识点一】平行线的定义及画法1.定义:在同一平面内,不相交的两条直线叫做平行线,如果直线a与b平行,记作a∥b.特别提醒:(1)平行线的定义有三个特征:一是在同一个平面内;二是两条直线;三是不相交,三者缺一不可;(2)有时说两条射线平行或线段平行,实际是指它们所在的直线平行,两条线段不相交并不意味着它们就平行.(3)在同一平面内,两条直线的位置关系只有相交和平行两种.特别地,重合的直线视为一条直线,不属于上述任何一种位置关系.2.平行线的画法:用直尺和三角板作平行线的步骤:①落:用三角板的一条直角边与已知直线重合.②靠:用直尺紧靠三角板另一条直角边.③推:沿着直尺平移三角板,使与已知直线重合的直角边通过已知点.④画:沿着这条直角边画一条直线,所画直线与已知直线平行.【知识点二】平行公理及推论1.平行公理:经过直线外一点,有且只有一条直线与这条直线平行.2.推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.特别提醒:(1)平行公理特别强调“经过直线外一点”,而非直线上的点,要区别于垂线的第一性质.(2)公理中“有”说明存在;“只有”说明唯一.(3)“平行公理的推论”也叫平行线的传递性.【知识点三】两直线平行的判定方法1判定方法1:同位角相等,两直线平行.如图1,几何语言:∵∠3=∠2∴AB∥CD(同位角相等,两直线平行)图1【知识点二】两直线平行的判定方法2判定方法2:内错角相等,两直线平行.如图2,几何语言:∵∠1=∠2∴AB∥CD(内错角相等,两直线平行)图2【知识点三】两直线平行的判定方法3判定方法3:同旁内角互补,两直线平行.如图3,几何语言:∵∠4+∠2=180°∴AB∥CD(同旁内角互补,两直线平行)图3特别提醒:平行线的判定是由角相等或互补,得出平行,即由数推形.【考点目录】【考点1】平行线的画法;【考点2】平行公理及推论的应用;【考点3】同位角相等,两直线平行;【考点4】内错角相等,两直线平行;【考点5】同旁内角互补,两直线平行;【考点6】垂直于同一直线的两直线平行;【考点7】判定两直线平行综合应用.【考点目录】【考点1】平行线的画法;【答案】(1)见分析;(2)见分析;(3)见分析【分析】本题考查了射线、线段的作法,画平行线,掌握平行线画法是解题关键.(1)根据射线及线段的定义作图即可;(2)过点B作AC的垂线BD,垂足为D即可;(3)将C点向右移3个单位得到点E,作直线BE即可;(1)解:射线AC,线段AB即为所求;(2)解:垂线段BD即为所求;(3)解:直线BE即为所求.【变式1】(2022下·辽宁辽阳·七年级统考期末)下列说法正确的是()A.相等的角是对顶角B.在同一平面内,两直线的位置关系有三种:平行,垂直,相交C.过一点有且只有一条直线与已知直线平行D.平面内,过一点有且只有一条直线与已知直线垂直【答案】D【分析】由对顶角的概念可判断A,由平面内直线与直线的位置关系可判断B,由过直线外一点画已知直线的平行线可判断C,由过一点画已知直线的垂线可判断D,从而可得答案.解:相等的角不一定是对顶角,故A不符合题意;在同一平面内,两直线的位置关系有二种:平行,相交,故B不符合题意;过直线外一点有且只有一条直线与已知直线平行,故C不符合题意;平面内,过一点有且只有一条直线与已知直线垂直,描述正确,故D符合题意;故选D【点拨】本题考查的是对顶角的性质,平面内,直线与直线的位置关系,平行线的含义,垂直的性质,掌握以上基础的概念是解本题的关键.【变式2】(2020·四川达州·校考一模)如图,利用三角尺和直尺可以准确的画出直线AB∥CD,下面是某位同学弄乱了顺序的操作步骤:①沿三角尺的边作出直线CD;②用直尺紧靠三角尺的另一条边;③作直线AB,并用三角尺的一条边贴住直线AB;④沿直尺下移三角尺;正确的操作顺序应是:.【答案】③②④①【分析】根据同位角相等两直线平行判断即可.解:根据同位角相等两直线平行则正确的操作步骤是③②④①,故答案我③②④①.【点拨】此题主要考查了复杂作图,关键是掌握同位角相等,两直线平行.【考点2】平行公理及推论的应用;【例2】(2022上·河南南阳·七年级校考期末)【操作】在如图的方格纸中(网格线的交点叫格点),按要求画图、填空.(1)过点A 作BC 的垂线,垂足为点D ,该垂线经过的一个格点记为点E .(2)过点E 作AC 的平行线EF ,该平行线经过的一个格点记为F ;过点B 作AC 的平行线BG ,该平行线经过的一个格点记为G .【发现】EF 与BG 的位置关系为______.【概括】根据你的发现,概括一条事实或结论:______.【答案】(1)画图见分析;(2)画图见分析;发现:平行;概括:平行于同一条直线的两条直线平行.【分析】(1)根据网格结构作出BC 的垂线AD 即可;(2)根据网格结构的特征构造相等的同位角再画图,然后标注即可.再根据平行线的判定可得EF 与BG 的位置关系以及结论.解:(1)如图,AD BC ,D 为垂足;(2)如图,EF AC ∥,BG AC ∥,EF 与BG 的位置关系为平行;结论:平行于同一条直线的两条直线平行.【点拨】本题考查了这题-应用与设计作图,利用网格结构作垂线,作平行线,熟练掌握网格结构的特征,准确找出对应点的位置是解题的关键.【变式1】(2022下·湖南长沙·七年级校考阶段练习)下列说法错误的是()A .在同一平面内,没有公共点的两条直线是平行线B .如果两条直线都与第三条直线平行,那么这两条直线也互相平行C .经过直线外一点有且只有一条直线与该直线平行D .在同一平面内,不相交的两条线段是平行线【答案】D【分析】根据平行公理等即可逐一进行判断.解:A 、在同一平面内,没有公共点的两条直线是平行线.正确,本选项不符合题意;B 、如果两条直线都与第三条直线平行,那么这两条直线也互相平行.平行线具有“传递性”,正确,本选项不符合题意;C 、经过直线外一点有且只有一条直线与该直线平行.正确,本选项不符合题意;D 、在同一平面内,不相交的两条直线是平行线.原说法错误,本选项符合题意.故选:D .【点拨】本题考查了平行公理等知识点.掌握相关结论是解题的关键.【变式2】(2022上·上海·九年级开学考试)如图,点E 、F 分别是梯形ABCD 两腰的中点,联结EF 、DE ,如果图中DEF △的面积为1.5,那么梯形ABCD 的面积等于.【答案】6【分析】过点A 作AH BC ⊥于H ,交EF 于G ,根据梯形中位线定理得到AD BC ∥EF ∥,根据三角形的面积公式、梯形的面积公式计算,得到答案.解:过点A 作AH BC ⊥于H ,交EF 于G ,如图,∵点E 、F 分别是梯形ABCD 两腰的中点,∴EF 是梯形ABCD 的中位线,∴AD BC ∥EF ∥,∴AG EF ⊥,AG GH =,∵ 1.5DEF S = ,∴1 1.52EF AG ⋅=,∴• 1.546EF AH =⨯=,∴•6ABCD S EFAH 梯形==,故答案为:6.【点拨】本题考查的是梯形的中位线、三角形的面积计算,掌握梯形中位线定理是解题的关键.【考点3】同位角相等,两直线平行;【例3】(2022上·黑龙江绥化·七年级统考期末)AB BC ⊥,12=90∠+∠︒,23∠∠=.BE 与DF 平行吗?为什么?解:BE DF ∥.AB BC ⊥ ,ABC \Ð=︒,即34∠+∠=︒.又1290∠+∠=︒ ,且23∠∠=,∴=.理由是:.BE DF ∴∥.理由是:.【答案】90;90;1∠,4∠;等角的余角相等;同位角相等,两直线平行【分析】由AB 垂直于BC ,利用垂直的定义得到ABC ∠为直角,进而得到3∠与4∠互余,再由1∠与2∠互余,根据23∠∠=,利用等角的余角相等得到14∠=∠,利用同位角相等两直线平行即可得证.解:BE DF ∥.AB BC ⊥ ,90ABC ∴∠=︒,即3490∠+∠=°.又1290∠+∠=︒ ,且23∠∠=,14∴∠=∠.理由是:等角的余角相等.BE DF ∴∥.理由是:同位角相等,两直线平行.故答案为:90;90;1∠,4∠;等角的余角相等;同位角相等,两直线平行.【点拨】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键【变式1】(2022下·福建宁德·七年级校联考期中)如图,若12∠=∠,则下列选项中,能直接利用“同位角相等,两直线平行”判定a b )A .B .C .D .【答案】B【分析】先判断出1∠与2∠是同位角,然后根据平行线的判定即可得出答案.解:A 、1∠与2∠是内错角,故该选项错误;B 、1∠与2∠是同位角,∵12∠=∠,∴a b ,故该选项正确;C 、1∠与2∠不是内错角、同位角,同旁内角,故该选项错误;D 、1∠与2∠是对顶角,故该选项错误;故选:B .【点拨】本题考查了平行线的判定,内错角相等、同位角相等,同旁内角互补两直线平行,是需要同学们熟练记忆的内容.【变式2】(2023上·七年级课时练习)如图,若12∠=∠,则 ;若23∠∠=,则 .【答案】AB DE BC EF【分析】根据12∠=∠,利用同位角相等两直线平行推出AB DE ∥;由23∠∠=,利用同位角相等两直线平行推出BC EF ∥.解:∵12∠=∠,∴AB DE ∥,∵23∠∠=,∴BC EF ∥,故答案为:AB ,DE ,BC ,EF .【点拨】此题考查平行线的判定定理,熟练掌握同位角相等两直线平行是解题的关键.【考点4【例4】(2023上·七年级课时练习)如图,已知CD AD ⊥于点,D DA AB ⊥于点,12A ∠=∠.试说明:DF AE ∥.解:CD AD ⊥ (已知),90CDA ∴∠=︒(__________).同理,90DAB ∠=︒.90CDA DAB ∴∠=∠=︒(__________),即132490∠+∠=∠+∠=︒.12∠=∠ (已知)3∴∠=_______(___________).∴_____∥_____(____________).【答案】垂直的定义,等量代换,4∠,等量代换,DF ,AE ,内错角相等,两直线平行【分析】根据垂直的定义得到90CDA DAB ∠=∠=︒,推出132490∠+∠=∠+∠=︒,得到3=4∠∠,由此证得DF AE ∥.解:CD AD ⊥ (已知),90CDA ∴∠=︒(垂直的定义).同理,90DAB ∠=︒.90CDA DAB ∴∠=∠=︒(等量代换),即132490∠+∠=∠+∠=︒.12∠=∠ (已知)3∴∠=4∠(等量代换).∴DF AE ∥(内错角相等,两直线平行).【点拨】此题考查了垂直的定义,平行线的判定,熟练掌握平行线的判定定理是解题的关键.【变式1】(2022·广东深圳·蛇口育才二中校考三模)如图,能判定EB AC ∥的条件是()A .C ABE∠∠=B .A EBD ∠∠=C .C ABC ∠∠=D .A ABE∠∠=【答案】D 【分析】通过角相等判定两直线平行,则判断两角是否能推出同位角或内错角相等即可.解:∵只有同位角相等,内错角相等,同旁内角互补才能判断两直线平行,选项D 中A ABE ∠∠=是内错角相等,故能判定两直线平行,其他选项不符合判定定理,无法判断.故选:D .【点拨】本题考查了平行线的判定,掌握平行线的判定是解题的关键.【变式2】(2023下·陕西宝鸡·七年级统考期中)三个完全相同的含30︒角的三角板如图摆放,可以判断AB 与EC 平行的理由是.【答案】BAC ACE =∠∠,内错角相等,两直线平行(答案不唯一)【分析】根据平行线的判定定理求解.解:由题意知90BAC ACE ∠=∠=︒,由内错角相等,两直线平行,可判断AB 与EC 平行.故答案为:BAC ACE =∠∠,内错角相等,两直线平行.【点拨】本题考查平行线的判定,解题的关键是掌握平行线的判定定理,即内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.【考点5】同旁内角互补,两直线平行;【例5】(2023下·山东青岛·七年级统考期中)如图,EF BC ∥,CE 平分BCF ∠,111DAC ∠=︒,23ACF FEC ∠=∠=︒,则AD 与BC 平行吗?请说明理由.【答案】AD 与BC 平行.理由见分析【分析】根据角平分线的定义可得246BCF FEC ∠=∠=︒,进而得出69ACB ∠=︒,结合题意可得69111180ACB DAC ∠+∠=︒+︒=︒,即可得证.解:AD 与BC 平行.理由如下:∵CE 平分BCF ∠,23ACF FEC ∠=∠=︒,∴246BCF FEC ∠=∠=︒,∴462369ACB BCF ACF ∠=∠+∠=︒+︒=︒,又∵111DAC ∠=︒,∴69111180ACB DAC ∠+∠=︒+︒=︒,∴AD BC ∥.【点拨】本题考查了平行线的判定,角平分线的定义,熟练掌握平行线的判定定是解题的关键.【变式1】(2023下·山东济南·七年级统考期末)如图,将一纸条ABCD 沿折痕MG 折叠,MA 时对应线段MA '与CD 相交于点N 则下列条件中,不足以证明AB CD ∥的是()A .180BMN CNM ∠+∠=︒B .2AMN MGN ∠=∠C .MN NG=D .MN MG=【答案】D 【分析】根据翻折的性质和平行线的判定逐一进行判断即可.解:A.180BMN CNM ∠+∠=︒ ,∴AB CD ∥;B .由翻折可知:2AMN AMG ∠=∠,2AMN MGN ∠=∠ ,AMG MGN ∴∠=∠,∴AB CD ∥,故B 选项不符合题意;C .由翻折可知:AMG NMG ∠=∠,MN NG = ,NMG MGN ∴∠=∠,AMG MGN ∴∠=∠,∴AB CD ∥,故C 选项不符合题意;MN MG = ,MGN MNG ∴∠=∠,AMG MGN ∴∠≠∠,AB ∴不平行CD ,故D 选项符合题意;故选:D .【点拨】本题考查了折叠的性质,平行线的判定,熟练掌握平行线的判定定理是解题的关键.【变式2】(2019下·七年级课时练习)如图,某工件要求AB ∥ED ,质检员小李量得∠ABC =146°,∠BCD =60°,∠EDC =154°,则此工件.(填“合格”或“不合格”)【答案】合格【分析】作CF ∥AB ,由平行线的性质得出∠ABC+∠1=180°,求出∠1,得出∠2,由∠2+∠EDC=180°,得出CF ∥ED ,证出AB ∥ED ,即可得出结论.解:作CF ∥AB ,如图所示:则∠ABC+∠1=180°,∴∠1=180°-146°=34°,∴∠2=∠BCD-∠1=60°-34°=26°,∵∠2+∠EDC=26°+154°=180°,∴CF ∥ED ,∴AB ∥ED ;故答案为合格.【点拨】本题考查了平行线的性质与判定;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键【考点6】垂直于同一直线的两直线平行.【例6】(2023下·七年级课时练习)探索与发现(在同一平面内):(1)若直线12a a ⊥,23a a ∥,判断直线1a 与3a 的位置关系,请说明理由;(2)若直线12a a ⊥,23a a ∥,34a a ⊥,则直线1a 与4a 的位置关系是______;(直接填结论,不需要证明)(3)现在有2023条直线1a ,2a ,3a ,…,2023a ,且有12a a ⊥,23a a ∥,34a a ⊥,45a a ∥,…,请你探索直线1a 与2023a 的位置关系.【答案】(1)13⊥a a .理由见分析;(2)14a a ∥;(3)直线1a 与2023a 的位置关系是12023a a ⊥【分析】(1)根据垂直定义和平行线的性质求解即可;(2)根据垂直定义和平行线的性质求解即可;(3)根据垂直定义和平行线的性质,找到变化规律即可求解.(1)解:13⊥a a .理由如下:如图,∵12a a ⊥,∴190∠=︒,∵23a a ∥,∴2190∠=∠=︒,∴13⊥a a .(2)解:由(1)知13⊥a a ,又34a a ⊥,根据垂直于同一条直线的两条直线平行可得14a a ∥,故答案为:14a a ∥;(3)解:直线1a 与2a ,3a 的位置关系分别是12a a ⊥,13⊥a a ,直线1a 与4a ,5a 的位置关系分别是14a a ∥,15a a ∥,从2a 开始,直线2a ,3a ,…,2023a 与直线1a 的位置关系以⊥,⊥,∥,∥为一次循环,∴12022a a ⊥,12023a a ⊥,∴直线1a 与2023a 的位置关系是12023a a ⊥.【点拨】本题考查垂直定义和平行线的性质,熟练掌握平行线的性质,得到变化规律是解答的关键.【变式1】(2018下·七年级单元测试)在同一平面内,a 、b 、c 是直线,下列说法正确的是()A .若a b ∥,b c ∥则a c∥B .若a b ⊥r r ,b c ⊥,则a c ⊥C .若a b ∥,b c ⊥,则a c∥D .若a b ∥,b c ∥,则a c ⊥【答案】A【分析】根据平行公理、平行线的性质对各选项分析判断即可解答.解:A.在同一平面内,若a b ∥,b c ∥则a c ∥正确,故本选项正确;B.在同一平面内,若a b ⊥r r ,b c ⊥则a c ∥,故本选项错误;C.在同一平面内,若a b ∥,b c ⊥则a c ⊥,故本选项错误;D.在同一平面内,若a b ∥,b c ∥则a c ∥,故本选项错误.故选:A .【点拨】本题主要考查了平行公理、平行线的性质等知识点,灵活运用相关性质是解答本题的关键.【变式2】(2018下·七年级课时练习)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线.(1)它的理由如下:(如图1)∵b ⊥a ,c ⊥a ,∴∠1=∠2=90°,∴b ∥c(2)如图2是木工师傅使用角尺画平行线,有什么道理?.【答案】平行同位角相等,两条直线平行垂直于同一条直线的两条直线平行解:∵在同一平面内,两条直线都垂直于同一条直线,∴这两条直线互相平行.故答案为平行;(1)∵b ⊥a ,c ⊥a ,∴∠1=∠2=90°,∴b ∥c (同位角相等,两条直线平行).故答案为同位角相等,两条直线平行;(2)垂直于同一条直线的两条直线平行,故答案为垂直于同一条直线的两条直线平行.【考点7】判定两直线平行的综合应用.【例7】(2024下·七年级课时练习)如图,AK 与BC 相交于点B ,BC 与CD 相交于点C ,如果160∠=︒,2120∠=︒,60D ∠=︒,那么AB 与CD 平行吗?BC 与DE 呢?并说明理由.【答案】AB CD ∥,BC DE ∥.理由见分析【分析】根据对顶角相等得出60ABC ∠=︒,进而可得2180ABC ∠+∠=︒,则AB CD ∥,进而得出BCD D ∠=∠,即可得证.解:AB CD ∥,BC DE ∥.理由如下:∵160∠=︒,1ABC ∠=∠∴60ABC ∠=︒.又∵2120∠=︒,∴2180ABC ∠+∠=︒.∴AB CD ∥.又∵2180BCD ∠+∠=︒,∴60BCD ∠=︒.∵60D ∠=︒,∴BCD D ∠=∠.∴BC DE ∥.【点拨】本题考查了对顶角相等,平行线的判定,熟练掌握平行线的判定定理是解题的关键.【变式1】(2024下·全国·七年级假期作业)如图,将一副三角尺如图放置,DE 、BC 交于点F ,(45C ∠=︒,30D ∠=︒)则下列结论不正确...的是()A .13∠=∠B .2180CAD ∠+∠=︒C .若230∠=︒,则BC AD∥D .若230∠=︒,则AC DF∥【答案】C 【分析】由余角的性质,得到13∠=∠,由 3 21802CAD CAB CAB EAD ∠=∠+∠=∠+∠-∠=︒-∠,得到2180CAD ∠+∠=︒,因为3B ∠≠∠,故BC 和DA 不平行,由160E ∠=∠=︒,得到AC DF ∥.解:1∠ +23∠=∠+290∠=︒,13∴∠=∠,故A 正确;3 21802CAD CAB CAB EAD ∠=∠+∠=∠+∠-∠=︒-∠ ,2180CAD ∴∠+∠=︒,故B 正确;230∠=︒ ,390260∴∠=︒-∠=︒,45B ∠=︒ ,3B ∴∠≠∠,BC ∴和DA 不平行,故C 错误;230∠=︒ ,190260∴∠=︒-∠=︒,60E ∠=︒ ,1E ∴∠=∠,∴AC DF ∥,故D 正确.故选:C .【点拨】本题考查平行线的判定,关键是掌握平行线的判定方法.【变式2】(2024下·全国·七年级假期作业)如图,有下列说法:①若12∠=∠,则AB CD ∥;②若3=4∠∠,则AD BC ∥;③若180ABC BCD ∠+∠=︒,则AD BC ∥;④若13180ABC ∠+∠+∠=︒,则AD BC ∥.其中说法正确的有个.【答案】1【解析】略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年七年级下学期期中考试高分直通车(北师大版)专题1.2相交线与平行线【目标导航】【知识梳理】1.对顶角与邻补角(1)对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.(2)邻补角:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.(3)对顶角的性质:对顶角相等.(4)邻补角的性质:邻补角互补,即和为180°.(5)邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.2.垂线及其性质:(1)垂线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.(2)垂线的性质在平面内,过一点有且只有一条直线与已知直线垂直.注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”“过一点”的点在直线上或直线外都可以.(3)垂线段:从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.(4)垂线段的性质:垂线段最短.正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.3.同位角、内错角、同旁内角(1)同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.(2)内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.(3)同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.(4)三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.4.平行线的判定:(1)定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.(2)定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.(3)定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.5.平行线性质定理定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.6.平行线的性质与判定综合题解题方法:(1)平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.(2)应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.(3)平行线的判定与性质的联系与区别区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.(4)辅助线规律,经常作出两平行线平行的直线或作出联系两直线的截线,构造出三类角.【典例剖析】【考点1】余角和补角【例1】.如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠EOD=67.5°的度数.(1)求∠BOD的度数;(2)∠AOE与∠BOC互余吗?请说明理由.【分析】(1)根据角平分线的定义可求∠AOE与∠BOE,再根据角的和差关系可求∠BOD的度数;(2)根据角平分线的定义可求∠BOC,再根据角的和差关系可求∠AOE与∠BOC是否互余.【解析】(1)∵OE是∠AOB的平分线,∠AOB=90°,∴∠AOE=∠BOE=45°,∴∠BOD=∠EOD﹣∠BOE=22.5°;(2)∵OD是∠BOC的平分线,∴∠BOC=45°,∴∠AOE+∠BOC=45°+45°=90°,∴∠AOE与∠BOC互余.点评:考查了余角和补角,角平分线的定义,首先确定各角之间的关系,利用角平分线的定义来求.【变式1-1】如图,将一副三角板的直角顶点重合,摆放在桌面上,∠AOD=130°,则∠BOC=()A.20°B.30°C.40°D.50°【分析】从图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解.【解析】∵∠AOB=∠COD=90°,∠AOD=130°∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣130°=50°.故选:D.点评:此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.【变式1-2】一个角的补角比这个角的余角的3倍少20°,这个角的度数是()A.30°B.35°C.40°D.45°【分析】设这个角为α,根据余角的和等于90°,补角的和等于180°表示出这个角的补角与余角,然后根据题意列出方程求解即可.【解析】设这个角为α,则它的补角为180°﹣α,余角为90°﹣α,根据题意得,180°﹣α=3(90°﹣α)﹣20°,解得α=35°.故选:B.点评:本题考查了余角与补角的定义,熟记“余角的和等于90°,补角的和等于180°”是解题的关键.【变式1-3】已知∠AOB+∠COD=180°.(1)如图1,若∠AOB=90°,∠AOD=68°,求∠BOC的度数;(2)如图2,指出∠AOD的补角并说明理由.【分析】(1)根据角的和差关系解答即可;(2)根据如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角,据此解答即可.【解析】(1)∵∠AOB+∠COD=180°,∠AOB=90°,∴∠COD=180°﹣∠AOB=90°,∵∠AOC=∠COD﹣∠AOD,∠AOD=68°,∴∠AOD=90°﹣68°=22°,∵∠BOC=∠AOB+∠AOC,∴∠BOC=90°+22°=112°;答:∠BOC=112°.(2)∵∠BOC+∠AOD=180°﹣∠AOD+∠AOD=180°,∴∠BOC是∠AOD的补角.点评:本题考查了补角邻补角的定义,解题的关键是了解有关的定义,属于基础题,难度不大.【考点2】对顶角与邻补角【例2】如图,直线AB与CD相交于点O,∠AOE=90°.(1)如图1,若OC平分∠AOE,求∠AOD的度数;(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.【分析】(1)依据角平分线的定义,即可得到∠AOC的度数,进而得出∠AOD的度数;(2)设∠BOF=α,则∠BOC=4α,∠COF=3α,依据∠BOE=90°,即可得到α的值,进而得出∠EOF的度数.【解析】(1)∵∠AOE=90°,OC平分∠AOE,∴∠AOC=45°,∴∠AOD=180°﹣∠AOC=135°;(2)设∠BOF=α,则∠BOC=4α,∠COF=3α,∵OE平分∠FOC,∴∠EOF=1.5α,∵∠BOE=90°,∴1.5α+α=90°,∴α=36°,∴∠EOF=54°.点评:本题主要考查了角的计算,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.【变式2-1】如图,直线AB、CD相交于点O,∠AOE=2∠AOC,若∠1=38°,则∠DOE等于()A.66°B.76°C.90°D.144°【分析】根据条件∠AOE=2∠AOC、对顶角相等和补角的定义可得答案.【解析】如图,∠1=∠AOC=38°.∵∠AOE=2∠AOC,∴∠AOE=76°.∴∠DOE=180°﹣∠AOC﹣∠AOE=180°﹣38°﹣76°=66°.故选:A点评:此题主要考查了邻补角和对顶角,关键是掌握对顶角相等.【变式2-2】如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠MOC=35°,则∠BON的度数为()A.35°B.45°C.55°D.64°【分析】根据角平分线的定义求出∠MOA的度数,根据邻补角的性质计算即可.【解析】∵射线OM平分∠AOC,∠MOC=35°,∴∠MOA=35°,又∠MON=90°,∴∠BON=55°,故选:C.点评:本题考查的是邻补角的概念以及角平分线的定义,掌握邻补角的性质是邻补角互补是解题的关键.【变式2-3】下列各图中,∠1与∠2是对顶角的是()【分析】根据对顶角的定义对各选项分析判断后利用排除法求解.【解析】A、∠1与∠2不是对顶角,故A选项不符合题意;B、∠1与∠2不是对顶角,故B选项不符合题意;C、∠1与∠2是对顶角,故C选项符合题意;D、∠1与∠2不是对顶角,故D选项不符合题意.故选:C.点评:本题主要考查了对顶角的定义,熟记对顶角的图形是解题的关键.【变式2-4】如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE:∠DOE=2:3.(1)求∠BOE的度数;(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.【解析】(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠AOC=∠AOF.点评:本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.【例1】如图直线AB,CD被EF所截,图中标注的角中为同旁内角的是()A.∠1与∠7B.∠2与∠8C.∠3与∠5D.∠4与∠7【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.【解析】A.∠1与∠7不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;B.∠2与∠8不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;C.∠3与∠5是直线AB,CD被EF所截而成的同旁内角,故本选项正确;D.∠4与∠7不是直线AB,CD被EF所截而成的同旁内角,故本选项错误;故选:C.点评:此题考查了同位角,内错角,同旁内角的概念,同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.【变式3-1】下列所示的四个图形中,∠1和∠2是同位角的是()A.①②B.②③C.①③D.②④【分析】根据同位角,内错角,同旁内角的概念解答即可.【解析】∠1和∠2是同位角的是①②,故选:A.点评:此题考查同位角,内错角,同旁内角的概念,关键是根据同位角,内错角,同旁内角的概念解答.【变式3-2】已知∠1与∠2是同旁内角,则()A.∠1=∠2B.∠1+∠2=180°C.∠1<∠2D.以上都有可能【分析】同旁内角在两直线平行时互补,也可能相等,不平行时,∠1<∠2,也可能∠1>∠2,进而可得答案.【解析】∠1与∠2是同旁内角,则可能∠1=∠2,∠1+∠2=180°,∠1<∠2,故选:D.点评:此题主要考查了同旁内角,关键是掌握同旁内角的边构成“U”形.【考点44】平行线【例2】若P,Q是直线AB外不重合的两点,则下列说法不正确的是()A.直线PQ可能与直线AB垂直B.直线PQ可能与直线AB平行C.过点P的直线一定能与直线AB相交D.过点Q只能画出一条直线与直线AB平行【分析】根据过直线外一点有且只有一条直线与已知直线平行以及两直线的位置关系即可回答.【解析】PQ与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、D均正确,故C错误;故选:C.点评:本题考查了平行线、相交线、垂线的性质,掌握相关定义和性质是解题的关键.【变式4-1】下列语句正确的有()个①任意两条直线的位置关系不是相交就是平行②过一点有且只有一条直线和已知直线平行③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b④若直线a∥b,b∥c,则c∥a.A.4B.3C.2D.1【分析】根据同一平面内,任意两条直线的位置关系是相交、平行;过直线外一点有且只有一条直线和已知直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行进行分析即可.【解析】①任意两条直线的位置关系不是相交就是平行,说法错误,应为根据同一平面内,任意两条直线的位置关系不是相交就是平行;②过一点有且只有一条直线和已知直线平行,说法错误,应为过直线外一点有且只有一条直线和已知直线平行;③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b,说法错误;④若直线a∥b,b∥c,则c∥a,说法正确;故选:D.点评:此题主要考查了平行线,关键是掌握平行公理:过直线外一点有且只有一条直线和已知直线平行;推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.【变式4-2】在同一平面内,不重合的两条直线的位置关系可能是()A.相交或平行B.相交或垂直C.平行或垂直D.不能确定【分析】同一平面内,直线的位置关系通常有两种:平行或相交;垂直不属于直线的位置关系,它是特殊的相交.【解析】平面内的直线有平行或相交两种位置关系.故选:A.点评:本题主要考查了在同一平面内的两条直线的位置关系.【考点5】平行线的判定条件【例5】如图,能判定EB∥AC的条件是()A.∠C=∠ABE B.∠BAC=∠EBD C.∠ABC=∠BAE D.∠BAC=∠ABE【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.【解析】A、∠C=∠ABE不能判断出EB∥AC,故本选项错误;B、∠BAC=∠EBD不能判断出EB∥AC,故本选项错误;C、∠ABC=∠BAE只能判断出EA∥CD,不能判断出EB∥AC,故本选项错误;D、∠BAC=∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确.故选:D.点评:本题考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.【变式5-1】如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是()A.B.C.D.【分析】根据两条直线被第三条所截,如果内错角相等,那么这两条直线平行可得只有D答案中∠1,∠2是AB和DC是被AC所截而成的内错角.【解析】若∠1=∠2,则下列四个选项中,能够判定AB∥CD的是D,故选:D.点评:此题主要考查了平行线的判定,关键是掌握同位角相等,两直线平行.【变式5-2】如图,下列条件能判定AD∥BC的是()A.∠C=∠CBE B.∠FDC=∠CC.∠FDC=∠A D.∠C+∠ABC=180°【分析】根据平行线的判断对每一项分别进行分析即可得出答案.【解析】A、∵∠C=∠CBE,∴DC∥AB,故本选项错误,不符合题意;B、∵∠FDC=∠C,∴AD∥BC,故本选项正确,符合题意;C、∵∠FDC=∠A,∴DC∥AB,故本选项错误,不符合题意;D、∵∠C+∠ABC=180°,∴DC∥AB,故本选项错误,不符合题意;故选:B.点评:本题考查的是平行线的判定,熟练掌握内错角相等,两直线平行;同旁内角互补,两直线平行;同位角相等,两直线平行是本题的关键.【变式5-3】以下四种沿AB折叠的方法中,由相应条件不一定能判定纸带两条边线a,b互相平行的是()A.展开后测得∠1=∠2B.展开后测得∠1=∠2且∠3=∠4C.测得∠1=∠2D.测得∠1=∠2【分析】根据平行线的判定定理,进行分析,即可解答.【解析】A、∠1=∠2,根据内错角相等,两直线平行进行判定,故正确;B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,∴∠1=∠2=∠3=∠4=90°,∴a∥b(内错角相等,两直线平行),故正确;C、测得∠1=∠2,∵∠1与∠2即不是内错角也不是同位角,∴不一定能判定两直线平行,故错误;D、∠1=∠2,根据同位角相等,两直线平行进行判定,故正确.故选:C.点评:本题考查了平行线的判定,解决本题的关键是熟记平行线的判定定理.【例6】如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC.若∠ABC=54°,则∠1的度数为()A.36°B.54°C.60°D.72°【分析】根据题意和平行线的性质,可以得到∠1+∠ACB+∠ABC=180°,再根据AC=BC,∠ABC=54°,即可求得∠1的度数.【解析】∵直线l1∥l2,∴∠1+∠ACB+∠ABC=180°,∵∠ABC=54°,AC=AB,∴∠ABC=∠ACB=54°,∴∠1=72°,故选:D.点评:本题考查平行线的性质,解答本题的关键是明确题意,利用平行线的性质和数形结合的思想解答.【变式6-1】如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为()A.45°B.55°C.35°D.不能确定【分析】利用平行线的性质以及三角形的外角的性质解决问题即可.【解析】∵AE∥DF,∴∠3+∠4=180°,∵∠ABC=∠1+∠3=120°,∠DCB=∠2+∠4=95°,∴∠1+∠3+∠2+∠4=120°+95°,∴∠1+∠2=215°﹣180°=35°,故选:C.点评:本题考查平行线的性质,三角形的外角等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.【变式6-2】如图,已知AB∥CD,BE和DF分别平分∠ABF和∠CDE,2∠E﹣∠F=48°,则∠CDE的度数为()A.16°B.32°C.48°D.64°【分析】利用基本结论:∠E=∠ABE+∠CDE,∠F=∠CDF+∠ABF,构建方程组解决问题即可.【解析】设∠ABE=∠EBF=x,∠FDE=∠FDC=y,∵AB∥CD,∴易知∠E=∠ABE+∠CDE=x+2y,∠F=∠CDF+∠ABF=2x+y,∵2∠E﹣∠F=48°,∴2(x+2y)﹣(2x+y)=48°,∴y=16°,∴∠CDE=2y=32°,故选:B.点评:本题考查平行线的性质,解题的关键是掌握基本结论,学会构建方程组解决问题.【例7】如图,△ABC中,∠B=∠ACB,D在BC的延长线,CD平分∠ECF,求证:AB∥CE.【分析】根据角平分线及对顶角相等可得∠ACB=∠EDC,再借助已知可得∠B=∠DEC,根据同位角相等两直线平行可得结论.【解答】证明:∵CD平分∠ECF,∴∠DCF=∠DCE.又∵∠DCF=∠ACB,∴∠ACB=∠DCE.又∵∠B=∠ACB,∴∠B=∠EDC.∴AB∥CE.点评:本题主要考查了平行线的判定,解决这类问题关键是熟知平行线的判定方法以及对角的转化.【变式7-1】如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.【分析】首先证明AD∥EF,再根据平行线的性质可得∠1=∠BAD,再由∠1=∠2,可得∠2=∠BAD,根据内错角相等,两直线平行可得DG∥BA.【解答】证明:∵AD⊥BC,EF⊥BC,∴∠EFB=∠ADB=90°,∴AD∥EF,∴∠1=∠BAD,∵∠1=∠2,∴∠2=∠BAD,∴AB∥DG.点评:此题主要考查了平行线的判定和性质,关键是掌握内错角相等,两直线平行;两直线平行,同位角相等.【变式7-2】已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)【分析】结合图形,利用平行线的性质及判定逐步分析解答.【解答】证明:∵∠1与∠CGD是对顶角,∴∠1=∠CGD(对顶角相等),∵∠1+∠2=180°(已知),∴∠CGD+∠2=180°(等量代换),∴AE∥FD(同旁内角互补,两直线平行),∴∠A=∠BFD(两直线平行,同位角相等),又∵∠A=∠D(已知),∴∠BFD=∠D(等量代换),∴AB∥CD(内错角相等,两直线平行).点评:本题利用了平行线的判定和性质,还利用了对顶角相等,等量代换等知识.【变式7-3】如图,已知∠1=∠2,∠C=∠D,证明AC∥DF.【分析】利用平行线的判定与性质证明即可.【解答】证明:如图,∵∠1=∠2(已知),∠2=∠3(对顶角相等)∴∠1=∠3(等量代换)∴BD∥CE(同位角相等,两直线平行)∴∠C=∠ABD(两直线平行,同位角相等)又∵∠C=∠D(已知)∴∠D=∠ABD(等量代换)∴DF∥AC(内错角相等,两直线平行).点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.【例8】已知如图,CD是△ABC的高,∠1=∠ACB,∠2=∠3.(1)∠2与∠DCB相等吗?为什么?(2)判断FH与AB的位置关系并说明理由.【分析】(1)由同位角∠1=∠ACB证出DE∥BC,由平行线的性质即可得出∠2=∠DCB;(2)证出∠3=∠DCB,得出CD∥FH,由平行线的性质得出∠BDC=∠BHF,即可得出结论.【解析】(1)∠2=∠DCB;理由如下:∵∠1=∠ACB,∴DE∥BC,∴∠2=∠DCB;(2)FH⊥AB;理由如下;∵∠2=∠3,∠2=∠DCB,∴∠3=∠DCB,∴CD∥FH,∴∠BDC=∠BHF,又∵CD是△ABC的高,∴CD⊥AB,∴∠BDC=∠BHF=90°,∴FH⊥AB.点评:本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解题的关键.【变式8-1】已知如图,CD是△ABC的高,∠1=∠ACB,∠2=∠3.(1)∠2与∠DCB相等吗?为什么?(2)判断FH与AB的位置关系并说明理由.【分析】(1)由同位角∠1=∠ACB证出DE∥BC,由平行线的性质即可得出∠2=∠DCB;(2)证出∠3=∠DCB,得出CD∥FH,由平行线的性质得出∠BDC=∠BHF,即可得出结论.【解析】(1)∠2=∠DCB;理由如下:∵∠1=∠ACB,∴DE∥BC,∴∠2=∠DCB;(2)FH⊥AB;理由如下;∵∠2=∠3,∠2=∠DCB,∴∠3=∠DCB,∴CD∥FH,∴∠BDC=∠BHF,又∵CD是△ABC的高,∴CD⊥AB,∴∠BDC=∠BHF=90°,∴FH⊥AB.点评:本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解题的关键.【变式8-2】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,∠1+∠2=180°,∠3=∠4.求证:EF∥GH.【分析】由对顶角相等得出∠AEG=∠1,得出∠AEG+∠2=180°,证出AB∥CD,由平行线的性质得出∠AEG=∠DGE,证出∠FEG=∠HGE,即可得出结论.【解析】∵∠1+∠2=180°(已知),∠AEG=∠1(对顶角相等)∴∠AEG+∠2=180°,∴AB∥CD(同旁内角互补,两直线平行),∴∠AEG=∠DGE(两直线平行,内错角相等),∵∠3=∠4(已知),∴∠3+∠AEG=∠4+∠DGE,(等式性质)∴∠FEG=∠HGE,∴EF∥GH.点评:本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解题的关键.。
