自动控制原理实验一
自动控制原理实验资料

自动控制原理实验实验1 控制系统典型环节的模拟利用运算放大器的基本特性,如:开环增益高,输入阻抗大、输出阻抗小等,通过设置不同的反馈网络,可以模拟各种典型环节。
一.实验目的● 掌握用运算放大器组成控制系统典型环节的电子电路原理。
● 观察几种典型环节的阶跃响应曲线。
● 了解参数变化对典型环节输出动态性能(即阶跃响应)的影响。
二.实验仪器● THSCC-1实验箱一台。
● 示波器一台。
三.实验内容 1.比例环节比例(P )环节的方框图如图1-1所示。
图1-1比例环节方框图K Z Z S u S u S G i o ==-=12)()()(当输入为单位阶跃信号,即u i =-1V 时,u i (s )=s 1,则u o (s )=K s1,所以输出响应为:u o (t )=K (t ≥0)。
比例环节实验原理图如图1-2所示。
选择:K=R2/R1=2,例如选择R2=820k ,R1=410k ,或选择R2=100k ,R1=51k 。
R2图1-2 比例环节实验原理图和输出波形实验步骤:(1)调整示波器:● 选择输入通道CH1或CH2。
● 逆时针调节示波器的时间旋钮“TIME/DIV ”到底,使光标为一点,并调节上下“位移”旋钮使光标位于0线上。
● 调整示波器的输入幅度档位选择开关,选择合适的档位使信号幅度便于观察,例如选择档位为1V 档。
● 将输入幅度档位选择开关中心的微调旋钮顺时针旋到底。
● 将信号选择开关打到DC 档。
(2)顺时针调节实验箱的旋钮,使阶跃信号为负(绿灯亮)。
(3)阶跃信号接到示波器上,调节实验箱的幅度旋钮。
使负跳变幅度为一格(即Ui=-1V )。
(4)接好实验线路,按下阶跃信号按钮,观察示波器的波形。
预习思考:输出幅度跳变应为……? 2.惯性环节惯性环节实验原理图如图1-3所示。
其传递函数为:11)()()(+==TS Ks u s u S G i o , K= R2/R1,T=R2*C 当输入为单位阶跃信号,即u i (t )=-1V 时,u i (s )=S 1,则u o (s )=S11TS 1⋅+ 所以输出响应为u o (t )=)e1(K Tt--。
自动控制原理 实验一 控制系统的电子模拟实验
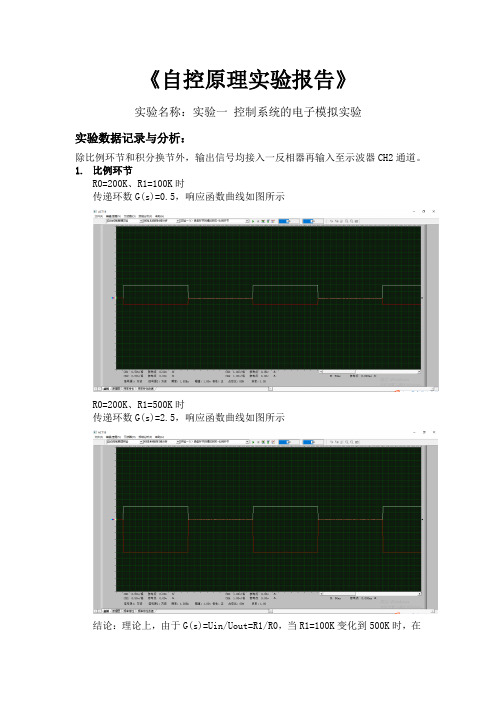
《自控原理实验报告》实验名称:实验一控制系统的电子模拟实验实验数据记录与分析:除比例环节和积分换节外,输出信号均接入一反相器再输入至示波器CH2通道。
1.比例环节R0=200K、R1=100K时传递环数G(s)=0.5,响应函数曲线如图所示R0=200K、R1=500K时传递环数G(s)=2.5,响应函数曲线如图所示结论:理论上,由于G(s)=Uin/Uout=R1/R0,当R1=100K变化到500K时,在输入信号不变的情况下,输出信号幅值应当变为原来的5倍。
由虚拟示波器图像可知输出红线(CH2)代表Uout,当R1=100K变化到500K时,其幅值变为原来的5倍。
这一结果符合理论分析结果。
2.积分环节R0=500K、C=1uF时传递环数G(s)=2/s,响应函数曲线如图所示R0=500K、C=2uF时传递环数G(s)=1/s,响应函数曲线如图所示R0=500K、C=3uF时传递环数G(s)=2/3s,响应函数曲线如图所示结论:理论上,由于G(s)分别为2/s、1/s、2/3s,可知响应曲线图像为斜率分别为2、1、1.5的直线,在输入信号为1V、1Hz的方波时,在有信号输入的阶段响应曲线上升但是斜率不相同,在无信号输入的阶段响应曲线保持不变。
由虚拟示波器图像可知输出红线(CH2)代表Uout。
结果符合理论分析结果。
3.惯性环节R0=200K、R1=200K、C=1uF时测量所得时间常数T=201.667ms理论上,传递环数G(s)=1/(0.2s+1),时间常数理论值为0.2s,响应函数曲线如图所示R0=200K、R1=200K、C=2uF时测量所得时间常数T=416.667ms理论上,传递环数G(s)=1/(0.4s+1),时间常数理论值为0.4s,响应函数曲线如图所示R0=200K、R1=100K、C=1uF时测量所得时间常数T=120ms理论上,传递环数G(s)=0.5/(0.1s+1),时间常数理论值为0.1s,响应函数曲线如图所示结论:实验测得时间常数与理论值基本符合。
自动控制原理实验一 典型系统的时域响应和稳定性分析

实验一典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图1-1所示。
图1-1(2)图1-2(3) 理论分析系统开环传递函数为:G(s)=K1T0⁄s(T1s+1)开环增益:K= K1T0⁄先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中由图1-2,可以确地1-1中的参数。
T0= 1s , T1= 0.1s ,K1= 200R , K= 200R系统闭环传递函数为:W(s)=5Ks2+5s+5K其中自然振荡角频率:?n ω= 10√10R;阻尼比:?ζ= √10R402.典型的三阶系统稳定性分析(1) 结构框图:如图1-3所示。
图1-3(2) 模拟电路图:如图1-4所示。
图1-4(3) 理论分析系统的开环传函为: G(s)H(s)=20K s 3+12s 2+20s系统的特征方程为:1()()0G s H s += : s 3+12s 2+20s+20K=0 (4) 实验内容实验前由Routh 判断得Routh 行列式为:S 3 1 20 S 2 12 20K S 1 20-5/3*K 0 S 0 20K为了保证系统稳定,第一列各值应为正数,因此可以确定系统稳定 K 值的范围 : 0<K <12 R >41.7k系统临界稳定K: K=12 R =41.7k 系统不稳定K 值的范围: K >12 R <41.7k四、实验步骤1)将信号源单元的“ST ”端插针与“S ”端插针用“短路块”短接。
自动控制原理实验一

自动控制理论实验报告姓名学号班级同组人实验一典型系统的阶跃响应分析一、实验目的1. 熟悉一阶系统、二阶系统的阶跃响应特性及模拟电路;2. 测量一阶系统、二阶系统的阶跃响应曲线,并了解参数变化对其动态特性的影响;3. 掌握系统动态性能的测试方法。
二、实验内容1. 设计并搭建一阶系统、二阶系统的模拟电路;2. 观测一阶系统的阶跃响应,并研究参数变化对其输出响应的影响;σ、3. 观测二阶系统的阻尼比0<ξ<1时的单位阶跃响应曲线;并求取系统的超调量%调节时间t s(Δ= ±0.05);并研究参数变化对其输出响应的影响。
三、实验结果(一)一阶系统阶跃响应研究1. 一阶系统模拟电路如图1-1所示,推导其传递函数G(s)=K/(Ts+1),其中R0=200K。
图1-1 一阶系统模拟电路2. 将阶跃信号发生器的输出端接至系统的输入端。
3. 若K=1、T=1s时,取:R1=100K,R2=100K,C=10uF(K= R2/ R1=1,T=R2C=100K×10uF=1)。
当T=1,光标为起点和终值:光标为起点和0.95的终值:传递函数为:(R2/R1)/(R2CS+1)4 若K=1、T=0.1s时,重复上述步骤(R1=100K,R2=100K,C=1uF(K= R2/ R1=1,T=R2C=100K×1uF=0.1))。
当T=0.1时,光标为起点和终值;光标为起点和0.95终值:6. 保存实验过程中的波形,记录相关的实验数据.,参数变化对系统动态特性的影响分析。
传递函数为:(R2/R1)/(R2CS+1), t=3T ,当T 减小需要达到稳定的时间也会减少,(二)二阶系统阶跃响应研究二阶系统模拟电路如图1-2所示,Rx 阻值可调范围为0~470K 。
图1-2 二阶系统模拟电路传递函数为1. n ω值一定(取10n ω=)时:1.1 当ξ=0.2时,各元件取值:C=1uF ,R=100K , R X =250K (实际操作时可用200k+51k=251k 代替),理论计算系统的%σ,t s (Δ= ±0.05),记录此时系统的阶跃响应曲线(阶跃信号的幅值自定),在曲线上求取系统的%σ,t s (Δ= ±0.05),并与理论值进行比较。
自动控制原理实验.doc
实验一 典型环节的模拟研究一、实验目的:1. 了解并掌握XG2003自控理论教学实验系统模拟电路的使用方法,掌握典型环节模拟电路的构成方法,培养学生实验技能。
2. 熟悉各种典型环节的阶跃响应曲线。
3. 了解参数变化对典型环节动态特性的影响。
二、实验要求:1. 观测各种典型环节的阶跃响应曲线。
2. 观测参数变化对典型环节阶跃响应的影响。
三、实验仪器:1. XG2003教学实验板 一台 2. 示波器一台 3. 万用表一块四、实验原理和电路:本实验是利用运算放大器的基本特性(开环增益高、输入阻抗大、输出阻抗小等),设置不同的反馈网络来模拟各种典型环节。
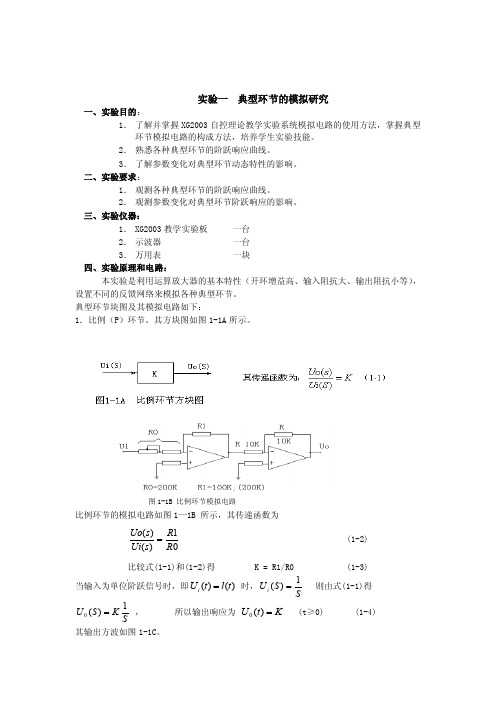
典型环节块图及其模拟电路如下:1.比例(P )环节。
其方块图如图1-1A 所示。
图1-1B 比例环节模拟电路比例环节的模拟电路如图1—1B 所示,其传递函数为1)()(R R s Ui s Uo = (1-2)比较式(1-1)和(1-2)得 K = R1/R0 (1-3)当输入为单位阶跃信号时,即)()(t l t U i = 时,SS U i 1)(=则由式(1-1)得 SKS U 1)(0= , 所以输出响应为 K t U =)(0 (t ≥0) (1-4) 其输出方波如图1-1C 。
2.积输分(I )环节。
其方块图如图1—2A 所示。
图1-1C 比例环节输出波形图 图1-2A 积分环节方块图 其传递函数为TSs Ui s Uo 1)()(=(1-5) 积分环节的模拟电路如图1—2B 所示。
图1-2B 积分环节模拟电路 积分环节模拟电路的传递函数为RoCSs Ui s Uo 1)()(=(1-6) 比较式(1-5)和(1-6)得C R T 0= 当输入为单位阶跃信号,即)()(t l t U i =时,S S U i 1)(=,则由式(1-5)得到TS S U 1)(0=·S 1=21TS 所以输出响应为:t T t U 1)(0=其输出波形如图1-2C 所示。
自动控制原理实验报告 (1)

实验1 控制系统典型环节的模拟实验(一)实验目的:1.掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2.测量典型环节的阶跃响应曲线,了解参数变化对环节输出性能的影响。
实验原理:控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
实验内容及步骤实验内容:观测比例、惯性和积分环节的阶跃响应曲线。
实验步骤:分别按比例,惯性和积分实验电路原理图连线,完成相关参数设置,运行。
①按各典型环节的模拟电路图将线接好(先接比例)。
(PID先不接)②将模拟电路输入端(U i)与阶跃信号的输出端Y相连接;模拟电路的输出端(Uo)接至示波器。
③按下按钮(或松开按钮)SP时,用示波器观测输出端的实际响应曲线Uo(t),且将结果记下。
改变比例参数,重新观测结果。
④同理得积分和惯性环节的实际响应曲线,它们的理想曲线和实际响应曲线。
实验数据实验二控制系统典型环节的模拟实验(二)实验目的1.掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2.测量典型环节的阶跃响应曲线,了解参数变化对环节输出性能的影响。
实验仪器1.自动控制系统实验箱一台2.计算机一台实验原理控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
实验内容及步骤内容:观测PI,PD和PID环节的阶跃响应曲线。
步骤:分别按PI,PD和PID实验电路原理图连线,完成相关参数设置,运行①按各典型环节的模拟电路图将线接好。
自动控制原理(实验指导书)

⾃动控制原理(实验指导书)⽬录实验⼀典型环节的模拟研究(验证型)(2)实验⼆典型系统的瞬态响应和稳定性(设计型)(9)实验三动态系统的数值模拟(验证型)(15)实验三动态系统的频率特性研究(综合型)(16)实验四动态系统的校正研究(设计型)(18)附录XMN—2学习机使⽤⽅法简介(20)实验⼀典型环节的模拟研究⼀、实验⽬的:1、了解并掌握XMN-2型《⾃动控制原理》学习机的使⽤⽅法,掌握典型环节模拟电路的构成⽅法,培养学⽣实验技能。
2、熟悉各种典型线性环节的阶跃响应曲线。
3、了解参数变化对典型环节动态特性的影响。
⼆、实验设备Uo(S)=(K+TS 1)S1?)1()()(21210210CS R R RR R R R S U S U i +++≈(1-19)⽐较式(1-17)和(1-19)得K=21R R R +T=C R R R R ?+2121 (1-20)当输⼊为单位阶跃信号,即Ui(t)=1(t)时,Ui(S)=1/S 。
则由式(1-17)得到111)()(23111022100210++?+++=S C R S C R C R C R S C R R R R S U S U i (1-24) 考虑到R 1》R 2》R 3,则式(1-24)可近似为S C R R R S C R R R S U S U i 2021100101)()(++≈(1-25)⽐较式(1-23)和(1-25)得K P =1R R , T 1=R 0C 1T D =2021C R R R ? (1-26)当输⼊为单位阶跃信号,即Ui(t)=1(t)时,Ui(S)=1/S 。
则由式(1-23)得到U o (S)=(K P +ST 11+T D S )S 1?五、实验报告要求:1、实验前计算确定典型环节模拟电路的元件参数各⼀组,并推导环节传递函数参数与模拟电路电阻、电容值的关系以及画出理想阶跃响应曲线。
2、实验观测记录。
自动控制原理实验(1)

实验一 典型环节的电路模拟一、实验目的1.熟悉THKKL-5型 控制理论·计算机控制技术实验箱及“THKKL-5”软件的使用; 2.熟悉各典型环节的阶跃响应特性及其电路模拟;3.测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二、实验设备1.THKKL-5型 控制理论·计算机控制技术实验箱;2.PC 机一台(含“THKKL-5”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应,将对系统的设计和分析十分有益。
本实验中的典型环节都是以运放为核心元件构成,其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1.比例(P )环节比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
图1-1 它的传递函数与方框图分别为:KS U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号,且比例系数为K 时的响应曲线如图1-2所示。
2.积分(I )环节 图1-2积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为:设U i (S)为一单位阶跃信号,当积分系数为T 时的响应曲线如图1-3所示。
TsS U S U s G i O 1)()()(==图1-33.比例积分(PI)环节比例积分环节的传递函数与方框图分别为:)11(11)()()(21211212CS R R R CS R R R CS R CS R S U S U s G i O +=+=+==其中T=R 2C ,K=R 2/R 1设U i (S)为一单位阶跃信号,图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。
自动控制原理实验

返回
实验二 典型环节的模拟研究(2学时) 实验三 典型二阶系统实验(2学时)
1、 实验目的:(1)学习系统(或环节)频率特 性的测量方法;(2)学习用频率特性确定数学模型的 方法 。 2、 实验要求:(1)测量并绘制一阶和二阶典型 环节的频率特性;(2)根据一阶和二阶典型环节的频 率特性确定其传递函数;(3)测量并绘制一个闭环系 统的频率特性
返回
实验六 系统的串联校正(2学时)
返回
实验四 根轨迹曲线的计算机绘制(2学时)
1、实验目的(1)训练学生应用计算机进行根轨迹 辅助分析;(2)让学生进一步加深系统零极点分布 对根轨迹形状的影响。 2、实验要求:(1)教师提供辅助分析软件,让学 生尽快学会使用;(2)每个学生做十例以上,并记 录各种根轨迹图。
返回
实验五 频率特性的研究 (2学时)
1、 实验目的:(1)学习正确选择校正装置的 种类及参数;(2)学习系统的调试方法。 2、 实验要求:(1)学生必须根据给定的条件及 指标要求确定校正装置的传递函数;(2)测出系统 的开环频率特性和闭环频率特性;(3)根据频率特 性求取系统的性能指标。
返回
1、 实验目的:(1)学习用阻容元件及线性组件 组成一个二阶系统进行各种实验的方法;(2)研 究阻尼比ξ和无阻尼自然振荡频率ω 对阶跃响应的
n
影响。 2、 实验要求:(1)要求学生画出实验电路图, 选择元器件并按照原理图连接成控制系统;(2) 改变参数,用长余辉示波器观察系统阶跃响应的变 化并记录。
自动控制原理实验(全面)

自动控制原理实验实验一 典型环节的电模拟及其阶跃响应分析一、实验目的⑴ 熟悉典型环节的电模拟方法。
⑵ 掌握参数变化对动态性能的影响。
二、实验设备⑴ CAE2000系统(主要使用模拟机,模/数转换,微机,打印机等)。
⑵ 数字万用表。
三、实验内容1.比例环节的模拟及其阶跃响应微分方程 )()(t Kr t c -= 传递函数 =)(s G )()(s R s C K -= 负号表示比例器的反相作用。
模拟机排题图如图9-1所示,分别求取K=1,K=2时的阶跃响应曲线,并打印曲线。
图9-1 比例环节排题图 图9-2 积分环节排题图 2.积分环节的模拟及其阶跃响应微分方程 )()(t r dtt dc T= 传递函数 sKTs s G ==1)(模拟机排题图如图9-2所示,分别求取K=1,K=0.5时的阶跃响应曲线,并打印曲线。
3.一阶惯性环节的模拟及其阶跃响应微分方程 )()()(t Kr t c dtt dc T=+ 传递函数 1)(+=TS KS G模拟机排题图如图3所示,分别求取K=1, T=1; K=1, T=2; K=2, T=2 时的阶跃响应曲线,并打印曲线。
4.二阶系统的模拟及其阶跃响应微分方程 )()()(2)(222t r t c dt t dc T dt t c d T =++ξ传递函数 121)(22++=Ts s T s G ξ2222nn n s s ωξωω++= 画出二阶环节模拟机排题图,并分别求取打印: ⑴ T=1,ξ=0.1、0.5、1时的阶跃响应曲线。
⑵ T=2,ξ=0.5 时的阶跃响应曲线。
四、实验步骤⑴ 接通电源,用万用表将输入阶跃信号调整为2V 。
⑵ 调整相应系数器;按排题图接线,不用的放大器切勿断开反馈回路(接线时,阶跃开关处于关断状态);将输出信号接至数/模转换通道。
⑶ 检查接线无误后,开启微机、打印机电源;进入CAE2000软件,组态A/D ,运行实时仿真;开启阶跃输入信号开关,显示、打印曲线。
自动控制原理实验(1)

实验一 典型环节的电路模拟一、实验目的1.熟悉THKKL-5型 控制理论·计算机控制技术实验箱及“THKKL-5”软件的使用; 2.熟悉各典型环节的阶跃响应特性及其电路模拟;3.测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二、实验设备1.THKKL-5型 控制理论·计算机控制技术实验箱;2.PC 机一台(含“THKKL-5”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应,将对系统的设计和分析十分有益。
本实验中的典型环节都是以运放为核心元件构成,其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1.比例(P )环节比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
图1-1 它的传递函数与方框图分别为:KS U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号,且比例系数为K 时的响应曲线如图1-2所示。
2.积分(I )环节 图1-2积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为:设U i (S)为一单位阶跃信号,当积分系数为T 时的响应曲线如图1-3所示。
TsS U S Us G i O1)()()(==图1-33.比例积分(PI)环节比例积分环节的传递函数与方框图分别为:)11(11)()()(21211212CSR R R CSR R R CSR CS R S U S U s G i O +=+=+==其中T=R 2C ,K=R 2/R 1设U i (S)为一单位阶跃信号,图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。
自动控制原理实验一:二阶系统阶跃响应
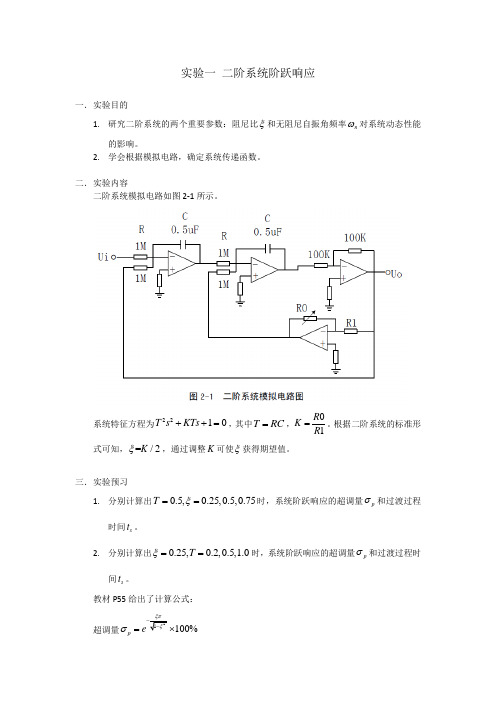
实验一 二阶系统阶跃响应一. 实验目的1. 研究二阶系统的两个重要参数:阻尼比ξ和无阻尼自振角频率n ω对系统动态性能的影响。
2. 学会根据模拟电路,确定系统传递函数。
二. 实验内容二阶系统模拟电路如图2-1所示。
系统特征方程为2210T s KTs ++=,其中T RC =,01R K R =。
根据二阶系统的标准形式可知,=/2K ξ,通过调整K 可使ξ获得期望值。
三. 实验预习1. 分别计算出0.5,0.25,0.5,0.75T ξ==时,系统阶跃响应的超调量p σ和过渡过程时间s t 。
2. 分别计算出0.25,0.2,0.5,1.0T ξ==时,系统阶跃响应的超调量p σ和过渡过程时间s t 。
教材P55给出了计算公式:超调量100%p eσ=⨯过渡过程时间44s nTt ξωξ==(近似值,只适合二阶系统的欠阻尼状态)。
另外,为对实验结果做误差分析,还需计算0.5,1T ξ==时的p σ和s t 。
此时系统为临界阻尼状态,0p σ=,s t 若再用上面给出的式子计算则会使得误差较大。
我们将根据定义采用数值计算的方法计算出s t 。
临界阻尼状态下,二阶系统的单位阶跃响应为()1(1)n tn y t t eωω-=-+,令1()0.98,2n y t Tω===,计算得 2.917()t s =。
根据以上公式计算,将计算结果整理成下表:四. 实验步骤1. 通过改变K ,使ξ获得0,0.25,0.5,0.75,1.0等值,在输入端加同样幅值的阶跃信号,观察过渡过程曲线,记下超调量p σ和过渡过程时间s t ,将实验值和理论值进行比较。
2. 当0.25ξ=时,令0.2,0.5,1.0T =秒秒秒(T RC =,改变两个C ),分别测出超调量p σ和过渡过程时间s t ,比较三条阶跃响应曲线的异同。
五. 数据处理1. 数据整理与计算(1)0.5T =,ξ取不同值其中,记录(0)V 是为了矫正系统误差,因为理论上(0)V 应该等于0。
自动控制原理实验报告

自动控制原理实验报告姓 名班 级学 号指导教师1自动控制原理实验报告(一)一.实验目的1.了解掌握各典型环节模拟电路的构成方法、传递函数表达式及输出时域函数表达式。
2.观察分析各典型环节的阶跃响应曲线,了解各项电路参数对典型环节动态特性的影响。
3.了解掌握典型二阶系统模拟电路的构成方法及Ⅰ型二阶闭环系统的传递函数标准式。
4.研究Ⅰ型二阶闭环系统的结构参数--无阻尼振荡频率ωn 、阻尼比ξ对过渡过程的影响。
5.掌握欠阻尼Ⅰ型二阶闭环系统在阶跃信号输入时的动态性能指标σ%、t p 、t s 的计算。
6.观察和分析Ⅰ型二阶闭环系统在欠阻尼、临界阻尼、过阻尼的瞬态响应曲线,及在阶跃信号输入时的动态性能指标σ%、t p 值,并与理论计算值作比对。
二.实验过程与结果1.观察比例环节的阶跃响应曲线1.1模拟电路图1.2传递函数(s)G(s)()o i U K U s == 10R K R =1.3单位阶跃响应U(t)K 1.4实验结果1.5实验截图2342.观察惯性环节的阶跃响应曲线2.1模拟电路图2.2传递函数(s)G(s)()1o i U KU s TS ==+10R K R =1T R C =2.3单位阶跃响应0(t)K(1e)tTU-=-2.4实验结果2.5 实验截图5673.观察积分环节的阶跃响应曲线3.1模拟电路图3.2传递函数(s)1G(s)()TS o i U U s ==i 0T =R C3.3单位阶跃响应01(t)i U t T =3.4 实验结果3.5 实验截图89104.观察比例积分环节的阶跃响应曲线4.1模拟电路图4.2传递函数0(s)1(s)(1)(s)i i U G K U T S ==+10K R R =1i T R C=4.3单位阶跃响应1 (t)(1)U K tT=+ 4.4实验结果4.5实验截图1112135.观察比例微分环节的阶跃响应曲线5.1模拟电路图5.2传递函数0(s)1(s)()(s)1i U TSG K U S τ+==+12312(R )D R R T CR R =++3R C τ=120R R K R +=141233(R //R )R D K R +=0.06D D T K sτ=⨯=5.3单位阶跃响应0(t)()U KT t Kδ=+5.4实验结果截图6.观察比例积分微分(PID )环节的响应曲线6.1模拟电路图156.2传递函数0(s)(s)(s)p p p d i i K U G K K T S U T S ==++123212(R )C d R R T R R =++i 121(R R )C T =+120p R R K R +=1233(R //R )R D K R +=32R C τ= D D T K τ=⨯6.3单位阶跃响应0(t)()p p D p K U K T t K tTδ=++6.4实验观察结果截图16三.实验心得这个实验,收获最多的一点:就是合作。
自动控制原理实验

唐山学院实验中心
自动控制原理实验室
自动控制原理实验
一. 典型线性环节 二. 二阶系统阶跃响应 三. 二阶系统频率响应 四. 线性系统稳定性研究
实验一
• • • 一 实验目的:
典型线性环节
• •
1.学习典型线性环节的模拟方法; 2.研究阻、容参数对典型性环节阶跃响应的 影响 二、实验设备: XMN-2型机;
实验四
线性系统稳定性研究
2.系统的开环放大系数K对稳定性的影响。 (1)适当调整Rw,观察K增大;K减小时的系统响应 曲线。 (2)记录当K=0.5Kj1时的系统响应曲线。 (3)记录当K=1.25Kj1时的系统响应曲线。 3.验证时间常数错开原理。 取T=0.47秒,T1=T/n;T2=T;T3=nT。 (1) 求取该系统在n=2时的临界开环放大系数Kj2,记录 此时的系统响应曲线。 (2) 记录该系统在n=5;K=Kj2时的系统响应曲线。 (3) 记录该系统在n=1;K=Kj2时的系统响应曲线。
• • CAE98; 万用表。
实验一
•
•
典型线性环节
三 实验内容:
1、比例(P)环节:其方块图如图1-1A所 示。 Ui(S) Uo(S)
K
图1-1A 比例环节方块图
实验一 典型线性环节
其传递函数为:
U 0 (S ) K U i (S )
(1-1)
其中: K=R1/R0 当输入为单位阶跃信号,即Ui(t)=1(t)时,Ui(s)=1/S。则由式(1-1) 得到 Uo(S)=K 所以输出响应为 Uo(t)=K (t≥0) (1-2)
三 实验内容
典型二阶系统方块图如下:
•
其闭环传递函数: WB(s)=
自动控制原理实验

⾃动控制原理实验实验⼀典型系统动态性能和稳定性分析⼀.实验⽬的1.学习和掌握动态性能指标的测试⽅法。
2.研究典型系统参数对系统动态性能和稳定性的影响。
⼆.实验内容观测⼆阶系统的阶跃响应,测出其超调量和调节时间,并研究其参数变化对动态性能和稳定性的影响。
三.实验步骤1.熟悉实验箱,利⽤实验箱上的模拟电路单元,参考本实验附录中的图2.1.1和图2.1.2,设计并连接由⼀个积分环节和⼀个惯性环节组成的⼆阶闭环系统的模拟电路(如⽤U9、U15、U11和U8连成)。
注意实验接线前必须对运放仔细调零(出⼚已调好,⽆需调节)。
信号输出采⽤U3单元的O1、信号检测采⽤U3单元的I1、锁零接U3单元的G1。
2.利⽤实验设备观测该⼆阶系统模拟电路的阶跃特性,并测出其超调量和调节时间。
3.改变该⼆阶系统模拟电路的参数,观测参数对系统动态性能的影响。
4.分析实验结果,完成实验报告。
软件界⾯上的操作步骤如下:①按通道接线情况:通过上位机界⾯中“通道选择”选择I1、I2路A/D通道作为被测环节的检测端⼝,选择D/A通道的O1(“测试信号1”)作为被测对象的信号发⽣端⼝.不同的通道,图形显⽰控件中波形的颜⾊将不同。
②硬件接线完毕后,检查USB⼝通讯连线和实验箱电源后,运⾏上位机软件程序,如果有问题请求指导教师帮助。
③进⼊实验模式后,先对显⽰模式进⾏设置:选择“X-t模式”;选择“T/DIV”为1s/1HZ。
④完成上述实验设置,然后设置实验参数,在界⾯的右边可以设置系统测试信号参数,选择“测试信号”为“周期阶跃信号”,选择“占空⽐”为50%,选择“T/DIV ”为“1000ms ”,选择“幅值”为“3V ”,可以根据实验需要调整幅值,以得到较好的实验曲线,将“偏移”设为“0”。
以上除必须选择“周期阶跃信号”外,其余的选择都不是唯⼀的。
要特别注意,除单个⽐例环节外,对其它环节和系统都必须考虑环节或系统的时间常数,如仍选择“输⼊波形占空⽐”为50%,那么“T/DIV ”⾄少是环节或系统中最⼤时间常数的6~8倍。
自动控制原理实验一控制系统的阶跃响应

自动控制原理实验一控制系统的阶跃响应实验目的:通过实验,掌握控制系统的阶跃响应的测量方法,了解控制系统的响应特性,并研究控制系统的参数对阶跃响应的影响。
实验原理:阶跃响应是指当控制系统输入信号突然从零变为常数时,系统的输出信号的响应过程。
通过观察阶跃响应可以了解控制系统的稳态误差、超调量、调节时间等参数,从而评估和改善控制系统的性能。
在实验中,常用的控制系统模型是一阶惯性环节,其传递函数为:G(s)=K/(Ts+1)其中,K为系统的增益,T为系统的时间常数。
通过改变K和T的值,可以观察到控制系统阶跃响应的变化。
实验仪器和材料:1.控制系统阶跃响应实验台2.配套的实验软件3.电脑实验步骤:1.打开实验软件,并连接实验台和电脑。
2.在软件中选择阶跃响应实验,并设置初始参数。
3.点击开始实验按钮,系统开始运行,记录实验数据。
4.观察实验数据的变化,并绘制出阶跃响应曲线。
5.改变控制系统的参数,如增益K和时间常数T的值,重新进行实验测量。
6.比较不同参数下的阶跃响应曲线,分析参数对响应的影响。
7.根据实验结果,评估系统的性能,并提出改进措施。
实验注意事项:1.实验过程中要保持实验台和电脑的连接良好,确保数据的准确性。
2.实验中应注意安全防护,避免操作中发生意外。
3.实验前要熟悉实验仪器的操作方法和实验原理,确保能够正确进行实验。
4.实验结束后,要及时清理实验台和关闭相关设备。
实验结果:通过实验测量得到的阶跃响应曲线,可以用于评估控制系统的性能。
通常,我们关注的参数包括稳态误差、超调量、调节时间等。
稳态误差是指系统在稳定状态下的输出值与期望值之间的差值。
通过观察阶跃响应曲线的稳态值,可以评估系统的稳态误差。
稳态误差越小,系统的控制性能越好。
超调量是指系统响应过程中最大超过期望值的幅值,通常以百分比形式表示。
通过观察阶跃响应曲线的峰值,可以评估系统的超调量。
超调量越小,系统的控制性能越好。
调节时间是指控制系统从初始状态到稳态所需的时间。
自动控制原理实验

二、实验方法
器仪表或软件对系统输入端加入不同的 激励信号(由信号发生器、计算机本 身产生,如时域特性——阶跃信号,频 率特性——正弦波信号),在系统的某 一环节或输出端利用相应的测试仪器 (如示波器、记录仪、打印机等),观 测和记录系统输出响应曲线,用以分析
8Байду номын сангаас
二、实验方法
系统的动态特性和稳态特性,验证和体 会理论教学的内容。 为了分析和研究系统的内部运动过程, 先建立系统的模型,然后在模型上进行 试验分析,这一过程称为仿真。 在自动控制原理实验中,仿真就是用物 理模型或数学模型代替实际控制系统进 行分析研究的过程。
20
自动控制原理实验室
21
模拟仿真实验所用实验仪器:控制理论实验平台; 慢扫描示波器;数字万用表。
22
4
二、实验方法
数学模型一般用微分方程来表示,由于微分方 程求解比较复杂,因此常用拉氏变换将微分方 程变为传递函数,然后进行分析和求解。 传递函数不仅可以表征系统性能,而且可以用 来研究系统的结构参数对系统性能的影响 。 从一定意义上来说,做实验就是用实验方法来 求解系统的传递函数,对系统进行分析和综合。
自动控制原理实验 (一)
1
一、实验目的
自动控制原理是研究自动控制系统共同
规律的一门学科,是分析、设计和研究自 动控制系统的理论基础。因此,自动控制 原理是一门理论性强,其中许多内容实践 性又较强,具有一定的实际工程背景的课 程,也比较难“教”与难“学”。
2
一、实验目的
自动控制原理实验是自动控制原理课程 教学的一个组成部分。
•
例如:
G(s) K Ts 1
不可以模拟;
G(s) 10 s 1
自动控制原理实验.
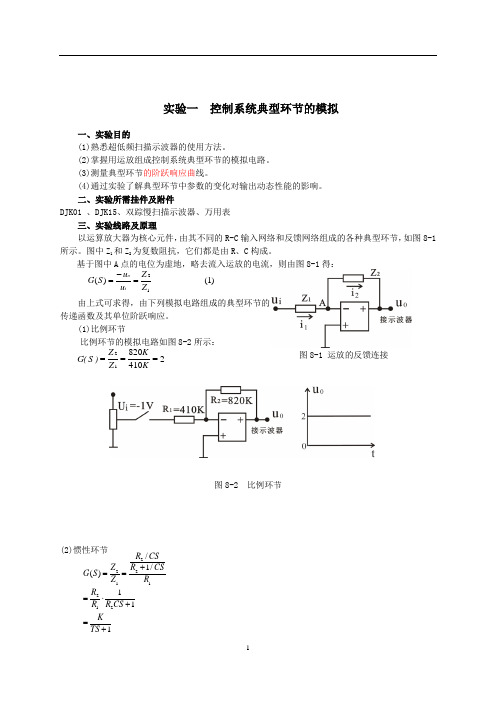
实验一控制系统典型环节的模拟 一、实验目的 (1)熟悉超低频扫描示波器的使用方法。
(2)掌握用运放组成控制系统典型环节的模拟电路。
(3)测量典型环节的阶跃响应曲线。
(4)通过实验了解典型环节中参数的变化对输出动态性能的影响。
二、实验所需挂件及附件DJK01 、DJK15、双踪慢扫描示波器、万用表三、实验线路及原理以运算放大器为核心元件,由其不同的R-C 输入网络和反馈网络组成的各种典型环节,如图8-1所示。
图中Z 1和Z 2为复数阻抗,它们都是由R 、C 构成。
基于图中A 点的电位为虚地,略去流入运放的电流,则由图8-1得:由上式可求得,由下列模拟电路组成的典型环节的传递函数及其单位阶跃响应。
(1)比例环节比例环节的模拟电路如图8-2所示:图8-1 运放的反馈连接图8-2 比例环节(2)惯性环节 (1) )(12Z Z u u S G i o =-=2=410820==12K K Z Z )S (G 111/1/)(21212212+=+⋅=+==TS K CS R R R R CS R CS R Z Z S G取参考值R1=100K,R2=100K,C=1uF图8-3 惯性环节(3)积分环节式中积分时间常数T=RC,取参考值R=200K,C=1uF图8-4 积分环节(4)比例微分环节(PD),其接线图如图及阶跃响应如图8-5所示。
参考值R1=200K,R2=410K,C=0.1uF)(311/1)(12TSRCSRCSZZSG====CR=T,=K(4)1+=1+•=1+==1D1211211212RR)ST(K)CSR(RRCS/RCS/RRZZ)S(GD其中图8-5 比例微分环节(5)比例积分环节,其接线图单位阶跃响应如图8-6所示。
参考值R1=100K R2=200K C=0.1uF图8-6 比例积分环节(6)振荡环节,其原理框图、接线图及单位阶跃响应波形分别如图8-7、8-8所示。
图8-8为振荡环节的模拟线路图,它是由惯性环节,积分环节和一个反号器组成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
KTδ(t)+K
实测:μo(t)=
+
e-t/R3C
Ro=
100K R2=
100K
C=1uF
R3=
10K
R1=
100K
R1=
200K
典型
环节
传递函数参数与模拟电路参数
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
PID
KP=
TI=Ro C1
TD=
理想:μo(t)= TDδ(t)+Kp+
答:传递函数的相角始终大于零,a>1。
3.你能解释校正后系统的瞬态响应变快的原因吗?
答:由于实际控制系统具有惯性、摩擦、阻尼等原因。
表3-1
参数
项目
Mp(%)
Ts(s)
阶 跃 响 应 曲 线
未校正
0.6
4
校正后
0.125
0.42
实验四 控制系统的频率特性
一、被测系统的方块图及原理:
图4—1 被测系统方块图
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
惯性
K=
T=R1C
μo(t)=
K(1-e-t/T)
R1=
250K
Ro=
250K
C=
1μF
C=
2μF
I
T=RoC
μo(t)=
Ro=
200K
C=
1μF
C=
2μF
PI
K=
T=RoC
μo(t)=K+
R1=
100K
Ro=
200K
C=
1uF
C=
2uF
PD
K=
T=
实测:μo(t)=
+
[1+
( )e-t/R3C2
Ro=
100K
R2=10K
R3=
10K
C1=
C2=
1μF
R1=
100K
R1=
200K
四、实验思考题:
1.为什么PI和PID在阶跃信号作用下,输出的终值为一常量?
答:按理论来说,只要输入的阶跃信号一直保持,PI和PID的响应曲线就不会是常量,因为这两个环节中I作为积分器是会随着时间的改变而逐渐累积的,所以不可能为常量的。估计有两个原因,①过早的把阶跃信号置零了②输入没有置零,但是显示窗口限制了显示,所以看起来像是常量!
2.为什么PD和PID在单位阶跃信号作用下,在t=0时的输出为一有限值?
答:在一个闭环系统中,即使是一个阶跃信号,由于存在积分器和微分器的作用,T=0时输出也是一个有限值。
五、实验总结:
阶跃信号
PID控制
惯性环节
比例环节
实验二 线性定常系统的瞬态响应和稳定性分析
一、实验目的
1.通过二阶、三阶系统的模拟电路实验,掌握线性定常系统动、静态性能的一般测试方法。
2.研究二阶、三阶系统的参数与其动、静态性能间的关系。
二、实验原理
1.二阶系统
图2-1为二阶系统的方块图。由图可知,系统的开环传递函数
G(S)= ,式中K=
相应的闭环传递函数为
………………பைடு நூலகம்……①
二阶系统闭环传递函数的标准形式为
= ………………………②
比较式①、②得:ωn= ………………………③
ξ= = ………………………④
表一:
一种情况
各参数
0<ξ<1
ξ=1
ξ>1
K
K=K1/τ=K1
ωn
ωn= =
ξ
ξ =
C(tp)
C(tp)=1+e—ξπ/
C(∞)
1
Mp%
Mp= e—ξπ/
tp(s)
tp=
ts(s)
ts=
表二:二阶系统不同ξ值时的单位阶跃响应
R值
ξ
单位阶跃响应曲线
10K
0.5
R值
ξ
单位阶跃响应曲线
20K
40K
1
100K
一、实验目的
1.掌握串联校正装置设计的一般方法。
2.设计一个有源串联超前校正装置,使之满足实验系统动、静态性能的要求。
二、实验内容
1.未校正系统的方块图如图3—1所示,设计相应的模拟电路图,参见图3—2。
图3—1 未校正系统的方块图
图3—2 未校正系统的模拟电路图
ωn=6.32 Mp=60%
2.由闭环传递函数G(S)= ts=4s
实验步骤:
①按表二中的各典型环节的模拟电路图将线接好(先接比例)。(PID先不接)
②将模拟电路输入端(Ui)与阶跃信号的输出端Y相连接;模拟电路的输出端(Uo)接至示波器。
③按下按钮(或松开按钮)SP时,用示波器观测输出端的实际响应曲线Uo(t),且将结果记下。改变比例参数,重新观测结果。
④同理得积分、比例积分、比例微分和惯性环节的实际响应曲线,它们的理想曲线和实际响应曲线参见表三。
图中τ=1s,T1=0.1s
图2-1
表一列出了有关二阶系统在三种情况(欠阻尼,临界阻尼、过阻尼)下具体参数的表达式,以便计算理论值。
图2-2为图2-1的模拟电路,其中τ=1s,T1=0.1s,K1分别为10、5、2.5、1,即当电路中的电阻R值分别为10K、20K、40K、100K时系统相应的阻尼比ξ为0.5、 、1、1.58,它们的单位阶跃响应曲线为表二所示。
表一:典型环节的方块图及传递函数
典型环节名称
方 块 图
传递函数
比例
(P)
积分
(I)
比例积分
(PI)
比例微分
(PD)
惯性环节
(T)
比例积分
微分(PID)
表二:典型环节的模拟电路图
各典型环节名称
模拟电路图
比例
(P)
积分
(I)
比例积分
(PI)
比例微分
(PD)
惯性环节
(T)
各典型环节名称
模拟电路图
比例积分
微分(PID)
答:二阶没送。
2.通过改变三阶系统的开环增益K和第一个惯性环节的时间常数,讨论得出它们的变化对系统的动态性能产生什么影响?
答::G(S)=K/ [S(T1 S+1)( T2 S+2)],通过改变开环增益K和T1改变G(S)的大小,从而影响动态性能的变化。
六、
R=10K
R=20K
R=40K
R
实验三 自动控制系统的校正
②阶跃信号的产生:
电路可采用图1-1所示电路,它由“阶跃信号单元”(U3)及“给定单元”(U4)组成。
具体线路形成:在U3单元中,将H1与+5V端用1号实验导线连接,H2端用1号实验导线接至U4单元的X端;在U4单元中,将Z端和GND端用1号实验导线连接,最后由插座的Y端输出信号。
以后实验若再用阶跃信号时,方法同上,不再赘述。
4
——
——
1.0
0.94
ξ>1
过阻尼
响应
100
1
3.16
1.58
——
4
——
——
3.6
3.55
注意:临界状态时(即ξ=1) ts=4.7/ωn
表四:
R(KΩ)
K
输出波形
稳定性
30
17
不稳定(发散)
42.6
11.96
临界稳定(等幅振荡)
100
5.1
稳定(衰减振荡)
五、实验思考题
1.为什么图2-1所示的二阶系统不论K增至多大,该系统总是稳定的?
③将①中产生的周期性方波信号加到PID环节的输入端(Ui),用示波器观测PID输出端(Uo),改变电路参数,重新观察并记录。
表三:
典型
环节
传递函数参数与模拟电路参数
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
比例
K=
μo(t)=K
Ro=
250K
R1=
100K
R1=
250K
典型
环节
传递函数参数与模拟电路参数
系统(或环节)的频率特性G(jω)是一个复变量,可以表示成以角频率ω为参数的幅值和相角。
G(jω)=|G(jω)|G(jω)(4—1)
本实验应用频率特性测试仪测量系统或环节的频率特性。
图4—1所示系统的开环频率特性为:
G1(jω) G2(jω)H(jω)= (4—2)
采用对数幅频特性和相频特性表示,则式(4—2)表示为:
由Routh稳定判据可知K≈12 (系统稳定的临界值)系统产生等幅振荡,K>12,系统不稳定,K<12,系统稳定。
图2—3 三阶系统方块图
图2—3 三阶系统方块图
三、实验内容
1.通过对二阶系统开环增益的调节,使系统分别呈现为欠阻尼0<ξ<1(R=10K,K=10),临界阻尼ξ=1(R=40K,K=2.5)和过阻尼ξ>1(R=100K,K=1)三种状态,并用示波器记录它们的阶跃响应曲线。
R
KΩ
K
(1/s)
ωn
(1/s)
ξ
C
(tp)
C
(OO)
Mp(%)
Tp(s)
ts(s)
阶跃响应曲线
测量
计算
测量
计算
测量
计算
0<ξ<1
欠阻尼
响应
10
10
10
0.5
4.6
4
15
16
0.4
0.36
0.75
0.8
20
5
7.07
0.707
