2014立体几何训练题001
2014届高三理数立体几何综合训练题

12014届高三理数《立体几何》综合训练题一.选择题:本大题共8小题,每小题5分,满分40分. 1. 在下列命题中,不是公理..的是( ) A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 2. 设γβα,,是三个不重合的平面,l 是直线,给出下列命题 ①若γββα⊥⊥,,则γα⊥;②若l 上两点到α的距离相等,则α//l ; ③若βαβα⊥⊥则,//,l l ; ④若.//,//,,//βαββαl l l 则且⊄其中正确的命题是( ) A .①② B .②③ C .②④ D .③④3. 在正四面体P -ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,下面四个结论中不成立...的是( ) A .//BC 平面PDF B .DF ⊥平面PA EC .平面PDF ⊥平面ABCD .平面PAE ⊥平面 ABC4. 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的体积是( )A.16πB.14πC.12πD.8π5. 若正四棱柱ABCD -A 1B 1C 1D 1的底面边长为1,AB 1与底面ABCD 成60°角,则A 1C 1到底面ABCD 的距离为( )A.33B .1 C. 2 D. 3 6. 如图,在直三棱柱111ABC A B C -中,若已知12CACC CB ==, 则异面直线1BC 与直线1AB 夹角的余弦值为()A.C. D. 35 7. 如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A.35003cm π B.38663cm π C.313723cm π D.320483cm π 8. 如图:正方体1111ABCD A B C D -,棱长为1,黑白二蚁都从点A 出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是111,AA A D →→黑蚁爬行的路线是1.AB BB →→它们都遵循如下规则:所爬行的第2i +段所在直线与第i 段所在直线必须是异面直线(其中*i N ∈).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是( )A.1 D.0正视图俯视图左视图2 31正视图侧视图二、填空题:本大题共6小题,每小题5分,满分30分.9. 一个三棱锥的正视图和侧视图及其尺寸如图3所示(均为直角三角形),则该三棱锥的俯视图的面积为.10. 设,,x y z是空间中不同的直线或不同的平面,且直线不在平面内,则下列结论中能保证“若x⊥z,且y⊥z,则//x y”为真命题的是____________(把你认为正确的结论的代号都填上).①x为直线,y,z为平面;②x,y,z为平面;③x,y为直线,z为平面;④x,y为平面,z为直线;⑤x,y,z为直线.11. 右图是一个几何体的三视图,根据图中数据可得该几何体的表面积是.12. 我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)13. 已知圆锥底面半径与球的半径都是1cm,如果圆锥的体积恰好也与球的体积相等,那么这个圆锥的母线长为cm.14. 若正四棱柱1111ABCD A B C D-中,12AA AB=,则CD与平面1BDC所成角的正弦值等于.三、解答题:本大题共6小题,前两道各12分,后4道各14分,满分80分,解答应写出文字说明、证明过程或演算步骤)。
2014年高考数学试题分类汇编 立体几何 word版含答案
2014年高考数学试题汇编立体几何一.选择题1. (2014福建)某空间几何体的正视图是三角形,则该几何体不可能是()圆柱圆锥四面体三棱柱A2. (2014新课标I)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为...6 .4【答案】:C【解析】:如图所示,原几何体为三棱锥,其中,,故最长的棱的长度为,选C3. (2014新课标II)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A. B. C. D.【答案】C4(2014浙江)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是A. 90B. 129C. 132D. 138D5. (2014江西)一几何体的直观图如右图,下列给出的四个俯视图中正确的是()【答案】B【解析】俯视图为在底面上的投影,易知选:B6(2014重庆)某几何体的三视图如图所示,则该几何体的表面积为()A.54B.60C.66D.72【答案】B【解析】7.(2014辽宁)某几何体三视图如图所示,则该几何体的体积为()A. B. C. D.【答案】B【解析】8(2014湖南)一块石材表示的几何体的三视图如图2所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.49(2014安徽)一个多面体的三视图如图所示,则该多面体的表面积为(A)(B)(C)21 (D)187 A10. (2014湖北)在如图所示的空间直角坐标系中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C. ④和③D.④和②点评:本题考查空间由已知条件,在空间坐标系中作出几何体的形状,再正视图与俯视图,容易题。
2014年高考立体几何(解析版)

2014年高考真题立体几何汇编解析版16.(2014江苏)(本小题满分14 分)如图,在三棱锥P ABC -中,D E F ,,分别为棱PC AC AB ,,的中点.已知6PA AC PA ⊥=,,8BC =,5DF =.(1)求证:直线P A ∥平面DEF ; (2)平面BDE ⊥平面ABC .【答案】本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系, 考查空间想象能力和推理论证能力.满分14分. (1)∵D E ,为PC AC ,中点 ∴DE ∥P A ∵PA ⊄平面DEF ,DE ⊂平面DEF ∴P A ∥平面DEF (2)∵D E ,为PC AC ,中点 ∴13DE PA == ∵E F ,为AC AB ,中点 ∴142EF BC == ∴222DE EF DF += ∴90DEF ∠=°,∴DE ⊥EF∵//DE PA PA AC ⊥,,∴DE AC ⊥ ∵AC EF E = ∴DE ⊥平面ABC∵DE ⊂平面BDE , ∴平面BDE ⊥平面ABC .17.(2014山东)(本小题满分12分)如图,在四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,60,DAB ∠=22AB CD ==,M 是线段AB 的中点.(I )求证:111//C M A ADD 平面;B 1C 1D 1A 1DCBMA(II )若1CD 垂直于平面ABCD且1CD 平面11C D M 和平面ABCD 所成的角(锐角)的余弦值. 解:(Ⅰ)连接1AD1111D C B A ABCD - 为四棱柱,11//D C CD ∴ 11D C CD =又M 为AB 的中点,1=∴AM AM CD //∴,AM CD =11//D C AM ∴,11D C AM =11D AMC ∴为平行四边形 11//MC AD ∴又111ADD A M C 平面⊄ 111A D D A AD 平面⊂111//ADD A AD 平面∴(Ⅱ)方法一:11//B A AB 1111//D C B A共面与面1111D ABC M C D ∴作AB CN ⊥,连接N D 1 则NC D 1∠即为所求二面角在ABCD 中, 60,2,1=∠==DAB AB DC 23=∴CN 在CN D Rt 1∆中,31=CD ,23=CN 2151=∴N D 方法二:作AB CP ⊥于p 点以C 为原点,CD 为x 轴,CP 为y 轴,1CD 为z 轴建立空间坐标系,)0,23,21(),3,0,0(),3,0,1(11M D C -∴)3,23,21(),0,0,1(111-==∴M D D C设平面M D C 11的法向量为),,(111z y x =⎪⎩⎪⎨⎧=-+=∴03232101111z y x x )1,2,0(1=∴n 显然平面ABCD 的法向量为)0,0,1(2=n5551,cos 21==<∴n n 显然二面角为锐角,所以平面M D C 11和平面ABCD 所成角的余弦值为555515321523cos 11====∠∴N D NC CN D18.三棱锥A BCD -及其侧视图、俯视图如图所示。
立体几何练习题(含答案)

立几测001试一、选择题:1.a 、b 是两条异面直线,下列结论正确的是( )A .过不在a 、b 上的任一点,可作一个平面与a 、b 都平行B .过不在a 、b 上的任一点,可作一条直线与a 、b 都相交C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行D .过a 可以且只可以作一个平面与b 平行2.空间不共线的四点,可以确定平面的个数为 ( )A.0 B.1 C.1或4 D.无法确定3.在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 、1BB 的中点,则异面直线CM 和1D N 所成角的正弦值为 ( )A.19 B.23C.9 D.94.已知平面α⊥平面β,m 是α内的一直线,n 是β内的一直线,且m n ⊥,则:①m β⊥;②n α⊥;③m β⊥或n α⊥;④m β⊥且n α⊥。
这四个结论中,不正确...的三个是 ( )A.①②③ B.①②④ C.①③④ D.②③④5.一个简单多面体的各个面都是三角形,它有6个顶点,则这个简单多面体的面数是( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球半径为R )( ) A.R π42 B. R 3π C. R 2π D. 3R7. 直线l ⊥平面α,直线m ⊂平面β,有下列四个命题(1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形,侧面与底面所成角为α,则下列不等式成立的是( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9.ABC ∆中,9AB =,15AC =,120BAC ∠=︒,ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14,则P 到平面α的距离为( )A.7 B.9 C.11 D.1310.在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒,则此直线与二面角的另一个平面所成角的大小为 ( )A.30︒ B.45︒ C.60︒ D.90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出下列位置关系:①SD ⊥面DEF; ②SE ⊥面DEF;③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )A. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,则地球仪的表面积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2二、填空题(本大题共4小题,每小题4分,共16分)13. 直二面角α—MN —β中,等腰直角三角形ABC 的斜边BC ⊂α,一直角边AC ⊂β,BC 与β所成角的正弦值是46,则AB 与β所成角大小为__________。
立体几何典型例题精选(含答案)
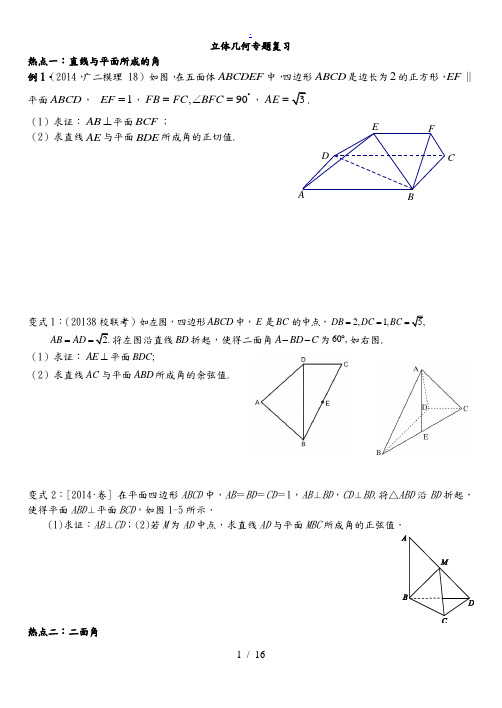
FEDCBA立体几何专题复习热点一:直线与平面所成的角例1.(2014,广二模理 18) 如图,在五面体ABCDEF 中,四边形ABCD 是边长为2的正方形,EF ∥平面ABCD , 1EF =,,90FB FC BFC ︒=∠=,3AE =.(1)求证:AB ⊥平面BCF ;(2)求直线AE 与平面BDE 所成角的正切值.变式1:(20138校联考)如左图,四边形ABCD 中,E 是BC 的中点,2,1,5,DB DC BC ===2.AB AD ==将左图沿直线BD 折起,使得二面角A BD C --为60,︒如右图.(1)求证:AE ⊥平面;BDC(2)求直线AC 与平面ABD 所成角的余弦值.变式2:[2014·卷] 在平面四边形ABCD 中,AB =BD =CD =1,AB ⊥BD ,CD ⊥BD .将△ABD 沿BD 折起,使得平面ABD ⊥平面BCD ,如图15所示.(1)求证:AB ⊥CD ;(2)若M 为AD 中点,求直线AD 与平面MBC 所成角的正弦值.热点二:二面角例2.[2014·卷] 如图14,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.(1)证明:CF⊥平面ADF;(2)求二面角D AF E的余弦值.变式3:[2014·卷] 如图15,在四棱锥ABCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= 2.(1)证明:DE⊥平面ACD;(2)求二面角B AD E的大小.变式4:[2014·全国19] 如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B; (2)设直线AA1与平面BCC1B1的距离为3,求二面角A1 -AB -C的大小.热点三:无棱二面角例3.如图三角形BCD 与三角形MCD 都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥平面BCD ,23AB =(1)求点A 到平面MBC 的距离;(2)求平面ACM 与平面BCD 所成二面角的正弦值.变式5:在正方体1111ABCD A B C D -中,1K BB ∈,1M CC ∈,且114BK BB =,134CM CC =. 求:平面AKM 与ABCD 所成角的余弦值.变式6:如图1111ABCD A B C D -是长方体,AB =2,11AA AD ==,求二平面1AB C 与1111A B C D 所成二面角的正切值.高考试题精选1.[2014·,18] 三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.(1)证明:P是线段BC的中点;(2)求二面角A NP M的余弦值.2.[2014·卷] 如图所示,四棱柱ABCDA1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.(1)证明:O1O⊥底面ABCD;(2)若∠CBA=60°,求二面角C1OB1D的余弦值.3.[2014·19] 如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.(1)求证:AB⊥PD.(2)若∠BPC=90°,PB=2,PC=2,问AB为何值时,四棱锥P ABCD的体MO HFEDCBA 积最大?并求此时平面BPC 与平面DPC 夹角的余弦值.立体几何专题复习 答案例1.(2014,广二模)(1)证明:取AB 的中点M ,连接EM ,则1AM MB ==,∵EF ∥平面ABCD ,EF ⊂平面ABFE ,平面ABCD 平面ABFE AB =, ∴EF ∥AB ,即EF ∥MB .……………1分 ∵EF =MB 1=∴四边形EMBF 是平行四边形.……………2分 ∴EM ∥FB ,EM FB =.在Rt△BFC 中,2224FB FC BC +==,又FB FC =,得FB =∴EM =……………3分在△AME中,AE =1AM =,EM =∴2223AM EM AE +==,∴AM EM ⊥.……………4分 ∴AM FB ⊥,即AB FB ⊥. ∵四边形ABCD 是正方形, ∴AB BC ⊥.……………5分∵FB BC B =,FB ⊂平面BCF ,BC ⊂平面BCF , ∴AB ⊥平面BCF .……………6分(2)证法1:连接AC ,AC 与BD 相交于点O ,则点O 是AC 的中点, 取BC 的中点H ,连接,OH EO ,FH ,则OH ∥AB ,112OH AB ==. 由(1)知EF ∥AB ,且12EF AB =,∴EF ∥OH ,且EF OH =.∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==.……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥. ……………8分∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD . ……………9分 ∴EO ⊥平面ABCD . ∵AO ⊂平面ABCD ,∴EO ⊥AO .……………10分 ∵AO BD ⊥,,EOBD O EO =⊂平面EBD ,BD ⊂平面EBD ,∴AO ⊥平面EBD .……………11分∴AEO ∠是直线AE 与平面BDE 所成的角.……………12分 在Rt △AOE中,tan AOAEO EO∠==……………13分 ∴直线AE 与平面BDE……………14分 证法2:连接AC ,AC 与BD 相交于点O ,则点O 取BC 的中点H ,连接,OH EO ,FH ,则OH ∥AB ,112OH AB ==.由(1)知EF ∥AB ,且12EF AB =,∴EF ∥OH ,且EF OH =. ∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==.……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥.∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD .∴EO ⊥平面ABCD .……………8分以H 为坐标原点,BC 所在直线为x 轴,OH 所在直线为y 轴,HF 所在直线为z 轴, 建立空间直角坐标系H xyz -,则()1,2,0A -,()1,0,0B ,()1,2,0D --,()0,1,1E -. ∴()1,1,1AE =-,()2,2,0BD =--,()1,1,1BE =--.……………9分 设平面BDE 的法向量为=n (),,x y z ,由n 0BD ⋅=,n 0BE ⋅=, 得220x y --=,0x y z --+=,得0,z x y ==-.令1x =,则平面BDE 的一个法向量为=n ()1,1,0-.……………10分 设直线AE 与平面BDE 所成角为θ, 则sin θ=cos ,n AE⋅=n AE n AE63=.……………11分 ∴23cos 1sin 3θθ=-=,sin tan 2cos θθθ==……………13分 ∴直线AE 与平面BDE 2……………14分 变式1:(20138校联考)(1)取BD 中点F ,连结,EF AF ,则11,,60,2AF EF AFE ==∠=……………2分由余弦定理知22222113121cos 60,22AE AF EF AE AE EF ⎛⎫=+-⋅⋅=+=∴⊥ ⎪⎝⎭………4分又BD ⊥平面AEF ,,BD AE AE ∴⊥⊥平面BDC ………6分(2)以E 为原点建立如图示的空间直角坐标系,则31),(1,,0)2A C -,11(1,,0),(1,,0)22B D ---………8分设平面ABD 的法向量为n (,,)x y z =,由00n DB n DA ⎧⋅=⎪⎨⋅=⎪⎩得201302x x y =⎧⎪⎨+=⎪⎩,取3z =,则3,(0,3)y =-∴=-n . 136(1,,),cos ,2||||AC AC AC AC =--∴<>==-n n n 11分故直线AC 与平面ABD 10. …………12分变式2:(2014卷)解:(1)证明:∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AB ⊂平面ABD ,AB ⊥BD ,∴AB ⊥平面BCD .…………3分 又CD ⊂平面BCD ,∴AB ⊥CD .…………4分 (2)过点B 在平面BCD 作BE ⊥BD . 由(1)知AB ⊥平面BCD ,BE ⊂平面BCD ,BD ⊂平面BCD ,∴AB ⊥BE ,AB ⊥BD .……6分以B 为坐标原点,分别以BE →,BD →,BA →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图所示).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝ ⎛⎭⎪⎫0,12,12. 则BC →=(1,1,0),BM →=⎝ ⎛⎭⎪⎫0,12,12,AD →=(0,1,-1).…………7分设平面MBC 的法向量n =(x 0,y 0,z 0),则⎩⎪⎨⎪⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0, 取z 0=1,得平面MBC 的一个法向量n =(1,-1,1).…………9分设直线AD 与平面MBC 所成角为θ,则sin θ=||cos 〈n ,AD →〉=|n ·AD →||n |·|AD →|=63. …………11分 即直线AD 与平面MBC 所成角的正弦值为63. …………12分例2.(2014,卷):(1):,,,,A ,,,,,,,,,,.(2):E EG//CF DF G,,,G GH AF H,EH,PD ABCD PD PCD PCD ABCD PCD ABCD CD D ABCD AD CD AD PCD CF PCD CF AD AF PC CF AF AD AF ADF ADAF A CF ADF CF DF EG DF ⊥⊂∴⊥=⊂⊥∴⊥⊂∴⊥⊥∴⊥⊂=∴⊥⊥∴⊥⊥∠解证明平面平面平面平面平面平面平面平面又平面平面解法一过作交于平面A 平面A 过作于连则00,CD 2,30,130,==1,21324,,,,,22333EG .,423EHG D AF E DPC CDF CF CD DECF CP EF DC DEDF DP CP DE EF AE AF EF DF AE EF EH HG AF --=∠=∴∠==∴=∴⋅=====⋅∴====为二面角的平面角设从而∥还易求得EF=从而易得故cos GH EHG EH ∴∠===12:,,,,,2,1(0,0,2),C(0,2,0),,(23,22,0),,,431,0),ADF CP (3,1,0),22AEF (x DP DC DA x y z DC A CF CP F DFCF F E n n λλλλ==-⊥===-=解法二分别以为轴建立空间直角坐标系设则设则可得从而易得取面的一个法向量为设面的一个法向量为2212212,y,z),0,0,||||2n AE n AF n n n n n ⋅=⋅=⋅==⋅⨯利用且得可以是从而所求二面角的余弦值为变式3:(2014卷)解:(1)证明:在直角梯形BCDE 中,由DE =BE =1,CD =2,得BD =BC =2, 由AC =2,AB =2,得AB 2=AC 2+BC 2,即AC ⊥BC .…………2分 又平面ABC ⊥平面BCDE ,从而AC ⊥平面BCDE ,所以AC ⊥DE .又DE ⊥DC ,从而DE ⊥平面ACD .…………4分 (2)方法一:过B 作BF ⊥AD ,与AD 交于点F ,过点F 作FG ∥DE ,与AE 交于点G ,连接BG .由(1)知DE ⊥AD ,则FG ⊥AD .所以∠BFG 是二面角B AD E 的平面角.…………6分在直角梯形BCDE 中,由CD 2=BC 2+BD 2,得BD ⊥BC .又平面ABC ⊥平面BCDE ,得BD ⊥平面ABC ,从而BD ⊥AB .由AC ⊥平面BCDE ,得AC ⊥CD . 在Rt △ACD 中,由DC =2,AC =2,得AD = 6.在Rt △AED 中,由ED =1,AD =6,得AE =7.…………7分在Rt △ABD 中,由BD =2,AB =2,AD =6,得BF =2 33,AF =23AD .从而GF =23ED =23.…………9分在△ABE ,△ABG 中,利用余弦定理分别可得cos ∠BAE =5 714,BG =23.…………11分在△BFG 中,cos ∠BFG =GF 2+BF 2-BG 22BF ·GF =32.…………13分所以,∠BFG =π6,即二面角B AD E 的大小是π6.…………14分方法二:以D 为原点,分别以射线DE ,DC 为x ,y 轴的正半轴, 建立空间直角坐标系D xyz ,如图所示.由题意知各点坐标如下:D (0,0,0),E (1,0,0),C (0,2,0),A (0,2,2),B (1,1,0).设平面ADE 的法向量为m =(x 1,y 1,z 1),平面ABD 的法向量为n =(x 2,y 2,z 2).可算得AD =(0,-2,-2),AE =(1,-2,-2),DB →=(1,1,0).…………7分由⎩⎨⎧m ·AD =0,m ·AE →=0,即⎩⎨⎧-2y 1-2z 1=0,x 1-2y 1-2z 1=0,可取m =(0,1,-2).…………9分 由⎩⎪⎨⎪⎧n ·AD →=0,n ·DB →=0,即⎩⎨⎧-2y 2-2z 2=0,x 2+y 2=0,可取n =(1,-1,2).…………11分于是|cos 〈m ,n 〉|=|m ·n ||m |·|n |=33×2=32.…………13分由题意可知,所求二面角是锐角,故二面角B AD E 的大小是π6.…………14分变式4:(2014全国卷)19.解:方法一:(1)证明:因为A 1D ⊥平面ABC ,A 1D ⊂平面AA 1C 1C ,故平面AA 1C ⊥平面ABC . 又BC ⊥AC ,所以BC ⊥平面AA 1C 1C .…………2分连接A 1C ,因为侧面AA 1C 1C 为菱形,故AC 1⊥A 1C .由三垂线定理得AC 1⊥A 1B .……4分(注意:这个定理我们不能用) (2)BC ⊥平面AA 1C 1C ,BC ⊂平面BCC 1B 1,故平面AA 1C 1C ⊥平面BCC 1B 1.作A 1E ⊥CC 1,E 为垂足,则A 1E ⊥平面BCC 1B 1.…………6分又直线AA 1∥平面BCC 1B 1,因而A 1E 为直线AA 1与平面BCC 1B 1的距离,即A 1E = 3. 因为A 1C 为∠ACC 1的平分线,所以A 1D =A 1E = 3.…………8分 作DF ⊥AB ,F 为垂足,连接A 1F .由三垂线定理得A 1F ⊥AB ,故∠A 1FD 为二面角A 1AB C 的平面角.…………10分 由AD =AA 21-A 1D 2=1,得D 为AC 中点,DF =55,tan ∠A 1FD =A 1DDF=15,……12分 所以cos ∠A 1FD =14.…………13分所以二面角A 1AB C 的大小为arccos 14.…………14分方法二:以C 为坐标原点,射线CA 为x 轴的正半轴,以CB 的长为单位长,建立如图所示的空间直角坐标系C xyz .由题设知A 1D 与z 轴平行,z 轴在平面AA 1C 1C .(1)证明:设A 1(a ,0,c ).由题设有a ≤2,A (2,0,0),B (0,1,0),则AB →=(-2,1,0),AC →=(-2,0,0),AA 1→=(a -2,0,c ),AC 1→=AC →+AA 1→=(a -4,0,c ),BA 1→=(a ,-c ).由|AA 1→|=2,得(a -2)2+c 2=2,即a 2-4a +c 2=0.①又AC 1→·BA 1→=a 2-4a +c 2=0,所以AC 1⊥A 1B .…………4分(2)设平面BCC 1B 1的法向量m =(x ,y ,z ),则m ⊥CB →,m ⊥BB 1→,即m ·CB →=0,m ·BB 1→为CB →=(0,1,0),BB 1→=AA 1→=(a -2,0,c ),所以y =0且(a -2)x +cz =0.令x =c ,则z =2-a ,所以m =(c ,0,2-a ),故点A 到平面BCC 1B 1的距离为 |CA →|·|cos 〈m ,CA →〉|=|CA →·m ||m |=2c c 2+(2-a )2=c .…………6分又依题设,A 到平面BCC 1B 1的距离为3,所以c =3,代入①,解得a =3(舍去)或a =1, 于是AA 1→=(-1,0,3).…………8分 设平面ABA 1的法向量n =(p ,q ,r ), 则n ⊥AA 1→,n ⊥AB →,即n ·AA 1→=0,n ·AB →=0,-p +3r =0,且-2p +q =0.令p =3,则q =2 3,r =1,所以n =(3,2 3,1).…………10分 又p =(0,0,1)为平面ABC 的法向量,…………11分故cos 〈n ,p 〉=n ·p |n ||p |=14.…………13分所以二面角A 1AB C 的大小为arccos 14.…………14分例3. 无棱二面角(2010年卷)解法一:(1)取CD 中点O ,连OB ,OM ,则OB ⊥CD ,OM ⊥CD .又平面MCD ⊥平面BCD ,则MO ⊥平面BCD ,所以MO ∥AB ,A 、B 、O 、M 共面.延长AM 、BO 相交于E ,则∠AEB 就是AM 与平面BCD 所成的角.OB =MO 3MO ∥AB ,MO//面ABC ,M 、O 到平面ABC 的距离相等,作OH ⊥BC 于H ,连MH ,则MH ⊥BC ,求得:OH=OCsin600=32,MH=152,利用体积相等得:155A MBC M ABC V V d --=⇒=。
高中数学立体几何测试题(10套)

∴ BD ∥平面 PMN ,
位置关系为
平行
。
∴ O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。
11 、a,b 为异面直线,且 a,b 所成角为 40 °,直线 c 与 a,b 均异面,且所成角均为
∵ BD ⊥ AC , MN ∥ BD
∵ PA⊥面 ABCD
θ,若这样的 c 共有四条,则 θ的范围为 (70 °, 90° ) 。
D
C
A
B
D1 A1
C1 B1
17 、 已知异面直线 a, b 的公垂线段 AB 的中点为 O,平面 满足 a∥ , b∥ , 且 O , M 、 N 是 a, b 上的任意两点, MN ∩ = P,求证: P 是 MN 的中
点
A aM
O
P
BN b
.
立几面测试 001
参考答 案
一、 1- 8 ACDDBDBA
2、已知 m, n 为异面直线, m∥平面 , n∥平面 , ∩ =l ,则 l( ) ( A)与 m, n 都相交 ( B)与 m,n 中至少一条相交 ( C)与 m, n 都不相交 ( D )与 m, n 中一条相交
3、已知 a, b 是两条相交直线, a∥ ,则 b 与 的位置关系是 ( )
A 、 b∥
PAM
∵ AB=2 , BM=1 , CM=1
∴ AM= 5 ,
P
A H
O
.
B
F M
B
D N C
立几面测试 003
一、选择题
1.异面直线是指
(A) 在空间内不能相交的两条直线
(B) 分别位于两个不同平面的两条直线
(C) 某一个平面内的一条直线和这个平面外的一条直线
考数学文科2014立体几何高考题[1]
![考数学文科2014立体几何高考题[1]](https://img.taocdn.com/s3/m/b3a138e2f61fb7360b4c6578.png)
立体几何高考专题题精选1.某四棱锥的三视图如图所示,该四棱锥的表面积是A.32B.C.48D.2.如图,正方体ABCD-A1B1C1D1中,AB=2。
,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于_____________.3.一个空间几何体的三视图如图所示,则该几何体的表面积为(A)48 (B)(C)(D)80 4.几何体的三视图如图所示,则这个几何体的直观图可以是∉,则5.若直线l不平行于平面a,且l aA.a内的所有直线与异面B.a内不存在与l平行的直线C.a内存在唯一的直线与l平行D.a内的直线与l都相交8.1l ,2l ,3l 是空间三条不同的直线,则下列命题正确的是(A )12l l ⊥,23l l ⊥13//l l ⇒(B )12l l ⊥,23//l l ⇒13l l ⊥(C )233////l l l ⇒1l ,2l ,3l 共面(D )1l ,2l ,3l 共点⇒1l ,2l ,3l 共面9.若一个圆锥的主视图(如图所示)是边长为3,3,2的三角形,则该圆锥的侧面积是 。
10.某几何体的三视图如图所示,则它的体积是【 】 (A)283π- (B)83π-(C)8-2π (D)23π11.下图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯 视图如下图;③存在圆柱,其正(主)视图、俯视图如下图.其中真命 题的个数是 A .3 B .2 C .1 D .012.已知直二面角l αβ--,点A ∈α,AC l ⊥,C 为垂足,点B ∈β,BD l ⊥,D 为垂足.若AB =2,AC =BD =1,则CD =(A ) 2 (B(C(D )113. 已知平面α截一球面得圆M ,过圆心M 且与α成060二面角的平面β截该球面得圆N.若该球面的半径为4,圆M 的面积为4π,则圆N 的面积为 (A)7π (B)9π (C)11π (D)13π14.已知正方体ABCD-A 1B 1C 1D 1中,E 为C 1D 1的中点,则异面直线AE 与BC所成角的余弦值为 .15.一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是A .4B .32C .2D .316.已知球的直径SC=4,A ,B 是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC 的体积为ABCD17.将长方体截去一个四棱锥,得到的几何体如右图所示,则该几何体的左视图为( )18.设图1是某几何体的三视图,则该几何体的体积为 A .942π+ B.3618π+ C.9122π+ D.9182π+19.设球的体积为V ,它的内接正方体的体积为V ,下列说法中最合适的是 A. V 比V 大约多一半B. V 比V 大约多两倍半 C. V 比V大约多一倍D. V 比V大约多一杯半20.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有 A .20 B .15 C .12 D .10正视图侧视图俯视图 图122.如图,在四面体PABC 中,PC ⊥AB ,PA ⊥BC,点D,E,F,G 分别是棱AP,AC,BC,PB 的中点.(Ⅰ)求证:DE ∥平面BCP ;(Ⅱ)求证:四边形DEFG 为矩形; (Ⅲ)是否存在点Q ,到四面体PABC 六条棱的中点的距离相等?说明理由.23.(本小题满分12分)如图,四棱锥P-ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB 。
立体几何试题(2014)

立体几何试题 G 单元 立体几何G1 空间几何体的结构 20.、、[2014·安徽卷] 如图1-5,四棱柱ABCD - A 1B 1C 1D 1中,A 1A ⊥底面ABCD ,四边形ABCD 为梯形,AD ∥BC ,且AD =2BC .过A 1,C ,D 三点的平面记为α,BB 1与α的交点为Q .图1-5(1)证明:Q 为BB 1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA 1=4,CD =2,梯形ABCD 的面积为6,求平面α与底面ABCD 所成二面角的大小.20.解: (1)证明:因为BQ ∥AA 1,BC ∥AD , BC ∩BQ =B ,AD ∩AA 1=A , 所以平面QBC ∥平面A 1AD ,从而平面A 1CD 与这两个平面的交线相互平行, 即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行, 于是△QBC ∽△A 1AD ,所以BQ BB 1=BQ AA 1=BC AD =12,即Q 为BB 1的中点.(2)如图1所示,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .图1V 三棱锥Q -A 1AD =13×12·2a ·h ·d =13ahd ,V 四棱锥Q -ABCD=13·a +2a 2·d ·⎝⎛⎭⎫12h =14ahd , 所以V 下=V 三棱锥Q -A 1AD +V 四棱锥Q -ABCD =712ahd . 又V 四棱柱A 1B 1C 1D 1 ABCD =32ahd ,所以V 上=V 四棱柱A 1B 1C 1D 1 ABCD -V 下=32ahd -712ahd =1112ahd ,故V 上V 下=117.(3)方法一:如图1所示,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E .又DE ⊥AA 1,且AA 1∩AE =A ,所以DE ⊥平面AEA 1,所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA . 又因为梯形ABCD 的面积为6,DC =2, 所以S △ADC =4,AE =4.于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4.故平面α与底面ABCD 所成二面角的大小为π4.方法二:如图2所示,以D 为原点,DA ,DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系.设∠CDA =θ,BC =a ,则AD =2a .因为S 四边形ABCD =a +2a2·2sin θ=6, 所以a =2sin θ.图2从而可得C (2cos θ,2sin θ,0),A 1⎝⎛⎭⎫4sin θ,0,4, 所以DC =(2cos θ,2sin θ,0),DA 1→=⎝⎛⎭⎫4sin θ,0,4.设平面A 1DC 的法向量n =(x ,y ,1),由⎩⎨⎧DA 1→·n =4sin θx +4=0,DC →·n =2x cos θ+2y sin θ=0,得⎩⎪⎨⎪⎧x =-sin θ,y =cos θ, 所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1), 所以cos 〈n ,m 〉=n·m|n||m|=22,故平面α与底面ABCD 所成二面角的大小为π4.7.、[2014·辽宁卷] 某几何体三视图如图1-1所示,则该几何体的体积为( )A .8-2πB .8-πC .8-π2D .8-π4图1-17.BG2 空间几何体的三视图和直观图 7.[2014·安徽卷] 一个多面体的三视图如图1-2所示,则该多面体的表面积为( ) A .21+ 3 B .8+ 2 C .21 D .18图1-27.A 7.、[2014·湖南卷] 一块石材表示的几何体的三视图如图1-2所示,将该石材切削、打( )图1-2A .1B .2C .3D .4 7.B 7.、[2014·辽宁卷] 某几何体三视图如图1-1所示,则该几何体的体积为( )A .8-2πB .8-πC .8-π2D .8-π4图1-17.B3.[2014·浙江卷] 几何体的三视图(单位:cm)如图1-1所示,则此几何体的表面积是( )1-1A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 2 3.D10.[2014·天津卷] 一个儿何体的三视图如图1-3所示(单位:m),则该几何体的体积为________m 3.图1-310.20π37.[2014·重庆卷] ( )1-2A .54B .60C .66D .72 7.BG4 空间中的平行关系 20.、、[2014·安徽卷] 如图1-5,四棱柱ABCD - A 1B 1C 1D 1中,A 1A ⊥底面ABCD ,四边形ABCD 为梯形,AD ∥BC ,且AD =2BC .过A 1,C ,D 三点的平面记为α,BB 1与α的交点为Q .图1-5(1)证明:Q 为BB 1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA 1=4,CD =2,梯形ABCD 的面积为6,求平面α与底面ABCD 所成二面角的20.解: (1)证明:因为BQ ∥AA 1,BC ∥AD , BC ∩BQ =B ,AD ∩AA 1=A , 所以平面QBC ∥平面A 1AD ,从而平面A 1CD 与这两个平面的交线相互平行, 即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行, 于是△QBC ∽△A 1AD ,所以BQ BB 1=BQ AA 1=BC AD =12,即Q 为BB 1的中点.(2)如图1所示,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .图1V 三棱锥Q -A 1AD =13×12·2a ·h ·d =13ahd ,V 四棱锥Q -ABCD =13·a +2a2·d ·⎝⎛⎭⎫12h =14ahd , 所以V 下=V 三棱锥Q -A 1AD +V 四棱锥Q -ABCD =712ahd . 又V 四棱柱A 1B 1C 1D 1 ABCD =32ahd ,所以V 上=V 四棱柱A 1B 1C 1D 1 ABCD -V 下=32ahd -712ahd =1112ahd ,故V 上V 下=117.(3)方法一:如图1所示,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E .又DE ⊥AA 1,且AA 1∩AE =A ,所以DE ⊥平面AEA 1,所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA . 又因为梯形ABCD 的面积为6,DC =2, 所以S △ADC =4,AE =4.于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4.故平面α与底面ABCD 所成二面角的大小为π4.方法二:如图2所示,以D 为原点,DA ,DD 1→分别为x 轴和z 轴正方向建立空间直角设∠CDA =θ,BC =a ,则AD =2a .因为S 四边形ABCD =a +2a2·2sin θ=6, 所以a =2sin θ.图2从而可得C (2cos θ,2sin θ,0),A 1⎝⎛⎭⎫4sin θ,0,4,所以DC =(2cos θ,2sin θ,0),DA 1→=⎝⎛⎭⎫4sin θ,0,4.设平面A 1DC 的法向量n =(x ,y ,1),由⎩⎨⎧DA 1→·n =4sin θx +4=0,DC →·n =2x cos θ+2y sin θ=0,得⎩⎪⎨⎪⎧x =-sin θ,y =cos θ, 所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1), 所以cos 〈n ,m 〉=n·m|n||m|=22,故平面α与底面ABCD 所成二面角的大小为π4.18.、[2014·新课标全国卷Ⅱ] 如图1-3,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB ∥平面AEC ;(2)设二面角D -AE -C 为60-ACD 的体积.图1-318.解:(1)证明:连接BD 交AC 于点O ,连接EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB . 因为EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .(2)因为P A ⊥平面ABCD ,ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB →,AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|AP →|为单位长,建立空间直角坐标系A -xyz ,则D ()0,3,0,E ⎝⎛⎭⎫0,32,12,AE →=⎝⎛⎭⎫0,32,12.设B (m ,0,0)(m >0),则C (m ,3,0),AC =(m ,3,0). 设n 1=(x ,y ,z )为平面ACE 的法向量,则⎩⎪⎨⎪⎧n 1·AC →=0,n 1·AE →=0,即⎩⎪⎨⎪⎧mx +3y =0,32y +12z =0,可取n 1=⎝⎛⎭⎫3m ,-1,3.又n 2=(1,0,0)为平面DAE 的法向量,由题设易知|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32. 因为E 为PD 的中点,所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V =13×12×3×32×12=38. G8 多面体与球 7.、[2014·湖南卷] 一块石材表示的几何体的三视图如图1-2所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )图1-2A .1B .2C .3D .4 7.B 8.、[2014·全国卷] 正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π48.A5.[2014·陕西卷] 已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A.32π3 B .4π C .2π D.4π35.DG10 空间向量解决线面位置关系 18.、[2014·新课标全国卷Ⅱ] 如图1-3,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB ∥平面AEC ;(2)设二面角D -AE -C 为60-ACD 的体积.18.解:(1)证明:连接BD 交AC 于点O ,连接EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB . 因为EO ⊂平面AEC ,PB ⊄平面AEC ,所以PB ∥平面AEC .(2)因为P A ⊥平面ABCD ,ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB →,AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|AP →|为单位长,建立空间直角坐标系A -xyz ,则D ()0,3,0,E ⎝⎛⎭⎫0,32,12,AE →=⎝⎛⎭⎫0,32,12.设B (m ,0,0)(m >0),则C (m ,3,0),AC =(m ,3,0). 设n 1=(x ,y ,z )为平面ACE 的法向量,则⎩⎪⎨⎪⎧n 1·AC →=0,n 1·AE →=0,即⎩⎪⎨⎪⎧mx +3y =0,32y +12z =0,可取n 1=⎝⎛⎭⎫3m ,-1,3.又n 2=(1,0,0)为平面DAE 的法向量,由题设易知|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32. 因为E 为PD 的中点,所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V =13×12×3×32×12=38.。
十四、立体几何(答案)

十四、立体几何(逐题详解)第I 部分1.【2014年陕西卷】已知底面边长为1,侧棱长为2则正四棱柱的各顶点均在同一个球面上,则该球的体积为( )32.3A π .4B π .2C π 4.3D π【解】D r r r r 选解得设球的半径为.π3434V ∴,1,4)2(11)2(,32222====++=π 2.【2014年重庆卷(理07)】某几何体的三视图如下图所示,则该几何体的表面积为( )A.54B.60C.66D.72【答案】B【解析】在长方体中构造几何体'''ABC A B C -,如右图所示,4,'5,'2,3AB A A B B AC ====,经检验该几何体的三视图满足题设条件。
其表面积'''''''''ABC ACC A ABB A BCC B A B C S S S S S S ∆∆=++++,3515615146022=++++=,故选择B 3.【2014年安徽卷(理07)】一个多面体的三视图如图所示,则该多面体的表面积为 (A )321+ (B )318+(C )21 (D )18 【答案】A【解此多面体的直观图如下图所示 表面积为61121622⨯⨯⨯-⨯⨯第(3)题图俯视图左视图正视图3245C'B'A'C BA正(主)视图侧(左)视图俯视图1111111111113212)2(432+=⨯⨯+4.【2014年福建卷】某空间几何体的正视图是三角形,则该几何体不可能是( )A . 圆柱B .圆锥C .四面体D .三棱柱 【答案】A【解析】圆柱的正视图为矩形,故选:A5.【2014年湖南卷】一块石材表示的几何体的三视图如图2所示. 将该石材切割、打磨,加工成球,则能得到最大球的半径等于A. 1B. 2C. 3D. 4【答案】B【解析】由图可得该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r ,则2286862r r r -+-=+⇒=,故选B6.【2014年辽宁卷】已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是( )A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥【解析】A .若m ∥α,n ∥α,则m ,n 相交或平行或异面,故A 错;B .若m ⊥α,n ⊂α,则m ⊥n ,故B 正确;C .若m ⊥α,m ⊥n ,则n ∥α或n ⊂α,故C 错;D .若m ∥α,m ⊥n ,则n ∥α或n ⊂α或n ⊥α,故D 错.故选B7.【2014年全国大纲卷】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A .814π B .16π C .9π D .274π【答案】A【解析】设球的半径为R ,则∵棱锥的高为4,底面边长为2, ∴R 2=(4﹣R )2+()2,∴R=,∴球的表面积为4π•()2=.故选:A8.【2014年四川卷(理08)】如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点。
2014高考立体几何解答题及答案

2014高考立体几何解答题及答案一.解答题(共17小题)1.(2014•山东)如图,四棱锥P﹣ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=AD,E,F分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.BC=2.(2014•四川)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形(Ⅰ)若AC⊥BC,证明:直线BC⊥平面ACC1A1;(Ⅱ)设D、E分别是线段BC、CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.MD=AC3.(2014•湖北)在四棱锥P﹣ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.(Ⅰ)求证:BE∥平面PAD;(Ⅱ)求证:BC⊥平面PBD;(Ⅲ)设Q为侧棱PC上一点,,试确定λ的值,使得二面角Q﹣BD﹣P为45°.的法向量,利用的法向量的坐标,由两个法向量的数量积运算表示二面角的余弦值,化简后求出,且,,=,,4.(2014•江苏)如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.PA=3EF=BC=45.(2014•黄山一模)如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2,E、F分别是AB、PD的中点.(1)求证:AF∥平面PCE;(2)求证:平面PCE⊥平面PCD;(3)求四面体PEFC的体积.AECD AE CDCD=,=V=6.(2014•南海区模拟)如图,四棱锥P﹣ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.(Ⅰ)求证:PO⊥平面ABCD;(Ⅱ)求证:OE∥平面PDC;(Ⅲ)求直线CB与平面PDC所成角的正弦值.的法向量为,∴=,,,的法向量为,即,解得,又所成角的正弦值为7.(2014•天津模拟)如图,在四棱台ABCD﹣A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.(1)求证:B1B∥平面D1AC;(2)求证:平面D1AC⊥平面B1BDD1.8.(2013•北京)如图,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E 和F分别是CD和PC的中点,求证:(Ⅰ)PA⊥底面ABCD;(Ⅱ)BE∥平面PAD;(Ⅲ)平面BEF⊥平面PCD.9.(2013•天津)如图,三棱柱ABC﹣A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.(Ⅰ)证明:EF∥平面A1CD;(Ⅱ)证明:平面A1CD⊥平面A1ABB1;(Ⅲ)求直线BC与平面A1CD所成角的正弦值.ACD=BG==,所成角的正弦值10.(2013•浙江)如图,在四棱锥P﹣ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=,PA=,∠ABC=120°,G为线段PC上的点.(Ⅰ)证明:BD⊥平面PAC;(Ⅱ)若G是PC的中点,求DG与PAC所成的角的正切值;(Ⅲ)若G满足PC⊥面BGD,求的值.PC=AD=CD=PAPA=,.OD=DGO==,可得,解得GC=﹣,∴=11.(2013•湖南)如图.在直棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=,AA1=3,D是BC的中点,点E 在棱BB1上运动.(1)证明:AD⊥C1E;(2)当异面直线AC,C1E 所成的角为60°时,求三棱锥C1﹣A1B1E的体积.面积为,由此结合锥体体积公式即可算出三棱锥=E=S××12.(2012•山东)如图,几何体E﹣ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(Ⅰ)求证:BE=DE;(Ⅱ)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.AB=AF13.(2012•江苏)如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.14.(2011•天津)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC 中点,PO⊥平面ABCD,PO=2,M为PD中点.(Ⅰ)证明:PB∥平面ACM;(Ⅱ)证明:AD⊥平面PAC;(Ⅲ)求直线AM与平面ABCD所成角的正切值.MN=PO=1中,,所以,中,=所成的正切值为15.(2011•北京)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC垂直时,求PA的长.,则,代入公式可求的法向量的法向量,,﹣,,,=|)知,设的法向量令,的法向量所以的法向量=0t=PA=16.(2010•深圳模拟)如图,在四棱锥S﹣ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点(1)求证:EF∥平面SAD(2)设SD=2CD,求二面角A﹣EF﹣D的大小.法二:建立空间直角坐标系,和,利用,又的平面角的大小为,的中点.,,,所以向量的夹角等于二面角的平面角.的大小为17.(2010•重庆)如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.(1)求证:AB⊥平面PCB;(2)求二面角C﹣PA﹣B的大小的余弦值.,PB=COD=。
2014高考立体几何真题汇编

CC1 上,直线 OP 与平面 A1BD 所成的角为 ,则 sin 的取值范围是()
A. [
3 ,1] 3 6 2 2 , ] 3 3
B. [
6 ,1] 3 2 2 ,1] 3
C. [
D. [
立体大题
1. (2014 安徽理 20)如图,四棱柱
ABCD A1B1C1D1 中, A1 A 底面 ABCD .四边形 ABCD 为梯形,
7.(2014 江西理 19)如图,四棱锥 P ABCD 中, ABCD 为矩形,平面 PAD 平面 ABCD . (1)求证: AB PD; (2)若 BPC 90 , PB 2, PC 2, 问 AB 为何值时, 四棱锥 P ABCD 的体积最大?并求此时平面
PBC 与平面 DPC 夹角的余弦值.
ABCD A1B1C1D1 中, AB =11, AD =7, AA1 =12,一质点从顶
E 4, 312 ,
,
,遇长方体的面反射(反射服从光的反射原理) ,将 i 1 次到第 i 次反射点之间的线
Li i 2,3,4
L1 AE ,将线段 L1 , L2 , L3 , L4 竖直放置在同一水平线上,则大致的图形是()
13.(2014 全国理 19)如图,三棱柱 ABC A1B1C1 中,点 A1 在平面 ABC 内的射影学科网 D 在 AC 上,
ACB 900 , BC 1, AC CC1 2 .
(1)证明: AC1 A 1B ; (2)设直线 AA1 与平面 BCC1B1 的距离为 3 ,求二面角 A1 AB C 的大小.
14.(2014 湖北理 5)在如图所示的空间直角坐标系 O xyz 中,一个四面体的顶点坐标分别是(0,0,2) , (2,2,0) , (1,2,1) , (2,2,2) ,给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()
2014年高考立体几何证明题精选

立体几何证明解答 (共10道题)1.(2014四川,18,12分) (本小题满分12分)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(Ⅰ)若AC⊥BC,证明:直线BC⊥平面ACC1A1;(Ⅱ)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.2.(2014湖北,20,13分) (本小题满分13分)如图,在正方体ABCD-A1B1C1D1中,E,F,P,Q,M,N分别是棱AB,AD,DD1,BB1,A1B1,A1D1的中点.求证:(Ⅰ)直线BC1∥平面EFPQ;(Ⅱ)直线AC1⊥平面PQMN.3.(2014陕西,17,12分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(Ⅰ)求四面体ABCD的体积;(Ⅱ)证明:四边形EFGH是矩形.4.(2014安徽,19,13分) 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.(Ⅰ)证明:GH∥EF;(Ⅱ)若EB=2,求四边形GEFH的面积.5.(2014江苏,16,14分)如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.6.(2014山东,18,12分) 如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=AD,E,F 分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.7.(2014天津,17,13分) 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=,AD=2,PA=PD=,E,F分别是棱AD,PC的中点.(Ⅰ)证明EF∥平面PAB;(Ⅱ)若二面角P-AD-B为60°,(i)证明平面PBC⊥平面ABCD;(ii)求直线EF与平面PBC所成角的正弦值.8.(2014北京,17,14分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(Ⅰ)求证:平面ABE⊥平面B1BCC1;(Ⅱ)求证:C1F∥平面ABE;(Ⅲ)求三棱锥E-ABC的体积.9.(2014课标Ⅱ,18,12分)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD 的中点.(Ⅰ)证明:PB∥平面AEC;(Ⅱ)设AP=1,AD=,三棱锥P-ABD的体积V=,求A到平面PBC的距离.10.(河北省衡水中学2014届高三下学期二调) 如图,在四棱锥中,, ,平面, 为的中点,.(I ) 求证:∥平面;( II ) 求四面体的体积.。
江苏2014高考数学-立体几何专题
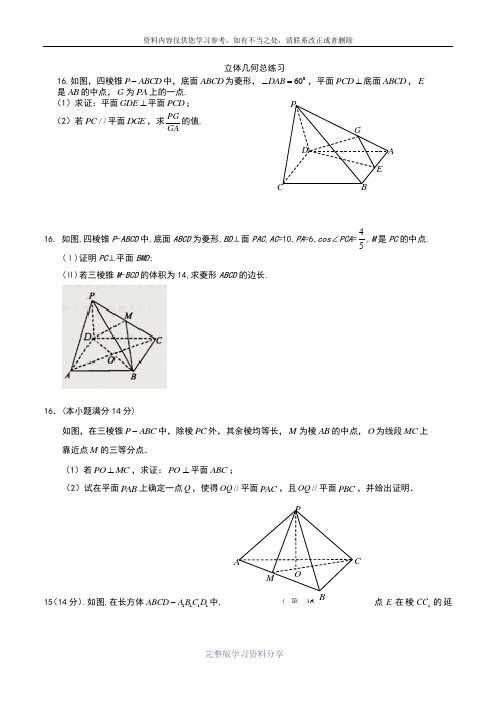
PABCOM(第16立体几何总练习16.如图,四棱锥P ABCD -中,底面ABCD 为菱形,060DAB ∠=,平面PCD ⊥底面ABCD ,E 是AB 的中点,G 为PA 上的一点. (1)求证:平面GDE ⊥平面PCD ; (2)若//PC 平面DGE ,求PGGA 的值.16. 如图,四棱锥P -ABCD 中,底面ABCD 为菱形,BD ⊥面PAC ,AC =10,PA =6,cos ∠PCA =45,M 是PC 的中点. (Ⅰ)证明PC ⊥平面BMD ;(Ⅱ)若三棱锥M -BCD 的体积为14,求菱形ABCD 的边长.16.(本小题满分14分)如图,在三棱锥P ABC -中,除棱PC 外,其余棱均等长,M 为棱AB 的中点,O 为线段MC 上 靠近点M 的三等分点.(1)若PO MC ⊥,求证:PO ⊥平面ABC ;(2)试在平面PAB 上确定一点Q ,使得//OQ 平面PAC ,且//OQ 平面PBC ,并给出证明.点E 在棱1CC 的延15(14分).如图,在长方体1111ABCD A B C D -中,PB CD E G长线上,且11112CC C E BC AB ====. (Ⅰ)求证:1D E ∥平面1ACB ; (Ⅱ)求证:平面11D B E ⊥平面1DCB ; (Ⅲ)求四面体11D B AC 的体积.16.、如图,已知E ,F 分别是正方形ABCD 边BC 、CD 的中点,EF 与AC 交于点O ,PA 、NC 都垂直于平面ABCD ,且4PA AB ==, 2NC =,M 是线段PA 上一动点.(Ⅰ)求证:平面PAC ⊥平面NEF ;(Ⅱ)若//PC 平面MEF ,试求:PM MA 的值;16.在四棱柱ABCD -A 1B 1C 1D 1中,AA 1⊥平面ABCD ,底面ABCD 为菱形,∠BAD =60°,P 为AB 的中点,Q 为CD 1的中点.(1)求证:DP ⊥平面A 1ABB 1; (2)求证:PQ ∥平面ADD 1A 1.BEADC1A1B 1C 1D 第16题图17、(本题满分14分)如图,长方体1111D C B A ABCD -中,a AA AB ==1,a BC 2=,M 是AD 中点,N 是11C B 中点.(1)求证:1A 、M 、C 、N 四点共面; (2)求证:MC BD ⊥1;(3)求证:平面MCN A 1⊥平面11BD A ;16.(本小题满分14分)如图,在四棱锥P ABCD -中,AB ∥DC ,2DC AB =,AP AD =,PB ⊥AC ,BD ⊥AC ,E 为PD 的中点. 求证:(1)AE ∥平面PBC ;(2)PD ⊥平面ACE .16.如图,在四面体ABCD 中,AB AC DB DC ===,点E 是BC 的中点,点F 在线段AC 上,且AF AC λ=.(1)若EF ∥平面ABD ,求实数λ的值;(2)求证:平面BCD ⊥平面AED .B 1 ABCD QPA 1C 1D 1ABCD A 1B 1C 1D 1MN(第16题图)EABDF。
2014年高考数学立体几何试题汇编

2014年高考数学立体几何试题汇编—选择题1.(四川理)如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点。
设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是 A. B.D. 2、(四川文)某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( )(锥体体积公式:13V Sh =,其中S 为底面面积,h 为高) A 、3B 、2CD 、13.(大纲文)已知正四面体ABCD 中,E 是AB 的 中点,则异面直线CE 与BD 所成角的余弦值为( )A .16 B.6 C .13D.34.(广东理)已知向量()1,0,1a =-,则下列向量中与a 成60︒夹角的是A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)5.(广东理)若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是A.14l l ⊥B.14//l lC.14,l l 既不垂直也不平行D.14,l l 的位置关系不确定 6. (广东文) 若空间中四条两两不相同的直线1l ,2l ,3l ,4l ,满足12l l ⊥,23//l l ,34l l ⊥,则下列结论一定正确的是A.14l l ⊥B.14//l lC.1l 与4l 既不平行也不垂直D.14l l 与位置关系不确定7.(课标1文)如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( )A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱侧视图俯视图112222118.(大纲理)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A .814πB .16πC .9πD .274π9.(大纲理)已知二面角l αβ--为060,AB α⊂,AB l ⊥,A 为垂足,CD β⊂,C l ∈,0135ACD ∠=,则异面直线AB 与CD 所成角的余弦值为( )A .14 B .4 C .4 D .1210、(湖北理)在如图所示的空间直角坐标系xyz O -中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )A. ①和②B.③和①C. ④和③D.④和②11(北京理)在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的面积,则( )(A )123S S S == B )12S S =且 31S S ≠(C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠12(江西理)一几何体的直观图如右图,下列给出的四个俯视图中正确的是( )13(全国文)如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为(A )1727 (B ) 59 (C )1027 (D) 1314(新课标理)直三棱柱ABC-A 1B 1C 1中,∠BCA=90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC=CA=CC 1,则BM 与AN 所成的角的余弦值为( )A. 110B. 25C.D.15(全国文)正三棱柱111ABC A B C -的底面边长为2D 为BC 终点,则三棱锥111A A B C -的体积为( ) (A )3 (B )32 (C )1 (D )216.(新课标理)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A .B .C .6D .417(重庆理)某几何体的三视图如图所示, 则该几何体的表面积为( )A.54B.60C.66D.7218(重庆文)某几何体的三视图如图所示,则该几何体的体积为( )A.12B.18C.24D.302014年高考数学立体几何试题汇编—填空题1(天津理)已知一个几何体的三视图如图所示(单位:m ),则该几何体的体积为_______3m . 2.(北京文)某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为.侧(左)视图正(主)视图3(课标1文)如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得 M 点的仰角60MAN ∠=︒,C 点的仰角45CAB ∠=︒以及75MAC ∠=︒;从C 点测得60MCA ∠=︒.已知山高100BC m =,则山高MN =________m.4(山东文)一个六棱锥的体积为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为 。
2014年全国高考真题分类——立体几何答案

数 学 一、选择题1.A [解析] 由题意可知,该正方形旋转一周后所得的圆柱的底面半径r =1,高h =1,则该圆柱的侧面积S =2πrh =2π,故选A.2.B [解析] 设圆锥的底面圆半径为r ,底面积为S ,则L =2πr .由题意得136L 2h ≈13Sh ,代入S =πr 2化简得π≈3.类比推理,若V ≈275L 2h 时,π≈258.故选B.3.C [解析] 因为D 为BC 的中点,所以AD ⊥BC ,故AD ⊥平面BCC 1B 1,且AD =3,所以V 三棱锥A - B 1DC 1=13S △B 1DC 1×AD =13×12B 1C 1×BB 1×AD =13×12×2×3×3=1.4.A [解析] 如图所示,由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分,其体积V =8-2×13×12×1×1×1=233.图1-35.D [解析] 由三视图可知,该几何体的正视图显然是一个直角三角形(三个顶点坐标分别是(0,0,2),(0,2,0),(0,2,2))且内有一虚线(一锐角顶点与一直角边中点的连线),故正视图是④;俯视图是一个斜三角形,三个顶点坐标分别是(0,0,0),(2,2,0),(1,2,0),故俯视图是②.故选D.6.B [解析] 由三视图可知,石材为一个三棱柱(相对应的长方体的一半),故可知能得到的最大球为三棱柱的内切球.由题意可知正视图三角形的内切圆的半径即为球的半径,可得R =6+8-102=2.7.C [解析] 根据三视图可知,该几何体是正方体切去两个体积相等的圆柱的四分之一后余下的部分,故该几何体体积V =23-12×π×12×2=8-π.8.B [解析] 此几何体是由长方体与三棱柱组合而成的,其体积为6×4×3+12×3×4×3=90 cm 3,故选B.9.C [解析] 该零件是一个由两个圆柱组成的组合体,其体积V =π×32×2+π×22×4=34π(cm 3),原毛坯的体积V 毛坯=π×32×6=54π(cm 3),被切部分的体积V 切=V 毛坯-V =54π-34π=20π(cm 3),所以V 切V 毛坯=20π54π=1027.10.B [解析] 从俯视图为矩形可以看出,此几何体不可能是三棱锥或四棱锥,其直观图如图,是一个三棱柱.11、D [解析] 由图可知,三棱锥的底面为边长为2的正三角形,左侧面垂直于底面,且为边长为2的正三角形,所以该三棱锥的底面积S =12×2×3,高h =3,所以其体积V=13Sh =13×3×3=1,故选D.12.C [解析] 由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥得到的.三棱柱的底面是一个两直角边长分别为3和4的直角三角形,高为5;截去的锥体的底面是两直角边的长分别为3和4的直角三角形,高为3,所以该几何体的体积为V =12×3×4×5-13×12×3×4×3=24.13.B [解析] 由题可知,若m ∥α,n ∥α,则m 与n 平行、相交或异面,所以A 错误;若m ⊥α,n ⊂α,则m ⊥n ,故B 正确;若m ⊥α,m ⊥n ,则n ∥α或n ⊂α,故C 错误;若m ∥α,m ⊥n ,则n ∥α或n ⊥α或n 与α相交,故D 错误.14.C [解析] A ,B ,D 中m 与平面α可能平行、相交或m 在平面内α;对于C ,若m ⊥β,n ⊥β,则m ∥n ,而n ⊥α,所以m ⊥α.故选C.15.B [解析] 由三视图可知,石材为一个三棱柱(相对应的长方体的一半),故可知能得到的最大球为三棱柱的内切球.由题意可知正视图三角形的内切圆的半径即为球的半径,可得R =6+8-102=2.16.C [解析] 由题意可知,旋转体是一个底面半径为1,高为1的圆柱,故其侧面积为2π×1×1=2π.17.A [解析] 如图所示,因为正四棱锥的底面边长为2,所以AE =12AC = 2.设球心为O ,球的半径为R ,则OE =4-R ,OA =R .又因为△AOE 为直角三角形,所以OA 2=OE 2+AE 2,即R 2=(4-R )2+2,解得R =94,所以该球的表面积S =4πR 2=4π⎝⎛⎭⎫942=81π4.18.D [解析] 由勾股定理得BC =20 m .如图,过P 点作PD ⊥BC 于D ,连接AD ,则由点A 观察点P 的仰角θ=∠P AD ,tan θ=PDAD.设PD =x ,则DC =3x ,BD =20-3x ,在Rt △ABD 中,AD =152+(20-3x )2=625-403x +3x 2,所以tan θ=x625-403x +3x 2=1625x 2-403x+3=1625⎝⎛⎭⎫1x -2036252+2725≤539,故tan θ的最大值为539,故选D.19.B [解析] 如图所示,取CF ,则EF ∥BD ,故EF 与CE 所成的角即为异面直线CE 与BD 所成的角.设正四面体的棱长为2,则CE =CF =3,EF=1.在△CEF 中,cos ∠CEF =CE 2+EF 2-CF 22CE ·EF =3+1-32×3×1=36,所以异面直线CE 与BD所成角的余弦值为36.图1-1二、填空题1、22 [解析] 该三棱锥的直观图如图所示,并且PB ⊥平面ABC ,PB =2,AB =2,AC =BC =2,P A =22+22=22,PC =22+(2)2=6,故P A 最长.2、.20π3[解析] 由三视图可知,该几何体为圆柱与圆锥的组合体,其体积V =π×12×4+13π×22×2=20π3.3、.32 [解析] 因为S 1S 2=πr 21πr 22=r 21r 22=94,所以r 1r 2=32.又圆柱的侧面积S 侧=2πrh ,所以S 侧1=2πr 1h 1=S 侧2=2πr 2h 2,则h 1h 2=r 2r 1=23,故V 1V 2=S 1h 1S 2h 2=94×23=32.4.12 [解析] 设该六棱锥的高是h .根据体积公式得,V =13×12×2×3×6×h ,解得h=1,则侧面三角形的高为1+(3)2=2,所以侧面积S =12×2×2×6=12.三、综合题1、(安徽)解析:(1)证明:因为BC ∥平面GEFH ,BC ⊂平面PBC ,且平面PBC ∩平面GEFH =GH ,所以GH ∥BC .同理可证EF ∥BC ,因此GH ∥EF .(2)连接AC ,BD 交于点O ,BD 交EF 于点K ,连接OP ,GK .因为P A =PC ,O 是AC 的中点,所以PO ⊥AC ,同理可得PO ⊥BD .又BD ∩AC =O ,且AC ,BD 都在平面ABCD 内,所以PO ⊥平面ABCD .又因为平面GEFH ⊥平面ABCD ,且PO ⊄平面GEFH ,所以PO ∥平面GEFH . 因为平面PBD ∩平面GEFH =GK , 所以PO ∥GK ,所以GK ⊥平面ABCD . 又EF ⊂平面ABCD ,所以GK ⊥EF , 所以GK 是梯形GEFH 的高.由AB =8,EB =2得EB ∶AB =KB ∶DB =1∶4,从而KB =14DB =12OB ,即K 是OB 的中点.再由PO ∥GK 得GK =12PO ,所以G 是PB 的中点,且GH =12BC =4.由已知可得OB =42,PO =PB 2-OB 2=68-32=6,所以GK =3,故四边形GEFH 的面积S =GH +EF 2·GK =4+82×3=18.2、(重庆)解析:(1)证明:如图所示,因为四边形ABCD 为菱形,O 为菱形的中心,连接OB ,则AO ⊥OB .因为∠BAD =π3,所以OB =AB ·sin ∠OAB =2sin π6=1.又因为BM =12,且∠OBM =π3,在△OBM 中,OM 2=OB 2+BM 2-2OB ·BM ·cos ∠OBM=12+⎝⎛⎭⎫122-2×1×12×cos π3=34,所以OB 2=OM 2+BM 2,故OM ⊥BM .又PO ⊥底面ABCD ,所以PO ⊥BC .从而BC 与平面POM 内的两条相交直线OM ,PO 都垂直,所以BC ⊥平面POM .(2)由(1)可得,OA =AB ·cos ∠OAB =2×cos 6= 3.设PO =a ,由PO ⊥底面ABCD ,知△POA 为直角三角形,故P A 2=PO 2+OA 2=a 2+3.又△POM 也是直角三角形,故PM 2=PO 2+OM 2=a 2+34.连接AM ,在△ABM 中,AM 2=AB 2+BM 2-2AB ·BM ·cos ∠ABM =22+⎝⎛⎭⎫122-2×2×12×cos 2π3=214. 由已知MP ⊥AP ,故△APM 为直角三角形,则P A 2+PM 2=AM 2,即a 2+3+a 2+34=214,解得a =32或a =-32(舍去),即PO =32.此时S 四边形ABMO =S △AOB +S △OMB =12·AO ·OB +12·BM ·OM =12×3×1+12×12×32 =5 38.所以四棱锥P -ABMO 的体积V 四棱锥P -ABMO =13·S 四边形ABMO·PO =13×5 38×32=516.3、(陕西)解析:(1)由该四面体的三视图可知,BD ⊥DC ,BD ⊥AD ,AD ⊥DC ,BD =DC =2,AD =1, ∴AD ⊥平面BDC ,∴四面体ABCD 的体积V =13×12×2×2×1=23.(2)证明:∵BC ∥平面EFGH ,平面EFGH ∩平面BDC =FG ,平面EFGH ∩ 平面ABC=EH ,∴BC ∥FG ,BC ∥EH ,∴FG ∥EH .同理EF ∥AD ,HG ∥AD ,∴EF ∥HG , ∴四边形EFGH 是平行四边形.又∵AD ⊥平面BDC ,∴AD ⊥BC ,∴EF ⊥FG , ∴四边形EFGH 是矩形.4(湖南)解析、连接BD ,由题设知,△ABD 是正三角形,又E 是AB 的中点,所以DE ⊥AB .而DO ∩DE =D(2)因为BC ∥AD ,所以ADO 是BC 与OD 所成的角.由(1)知,AB ⊥平面ODE ,所以AB ⊥OE .又DE ⊥AB ,于是∠DEO 是二面角α-MN -β的平面角,从而∠DEO =60°.不妨设AB =2,则AD =2,易知DE = 3.在Rt △DOE 中,DO =DE ·sin 60°=32.连接AO ,在Rt △AOD 中,cos ∠ADO =DO AD =322=34.故异面直线BC 与OD 所成角的余弦值为34.5、(新课标全国II)解析:(1)证明:设BD 与AC 的交点为O ,连接EO .因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB . EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .(2)V =13×12×P A ×AB ×AD =36AB ,由V =34,可得AB =32. 作AH ⊥PB 交PB 于点H .由题设知BC ⊥平面P AB ,所以BC ⊥AH , 因为PB ∩BC =B ,所以AH ⊥平面PBC . 又AH =P A ·AB PB =31313,所以点A 到平面PBC 的距离为31313.6、(北京)解析:(1)证明:在三棱柱ABC - A 1B 1C 1中,BB 1⊥底面ABC ,所以BB 1⊥AB . 又因为AB ⊥BC ,所以AB ⊥平面B 1BCC 1.所以平面ABE ⊥平面B 1BCC 1.(2)证明:取AB 的中点G ,连接EG ,FG .因为E ,F ,G 分别是A 1C 1,BC ,AB 的中点, 所以FG ∥AC ,且FG =12AC ,EC 1=12A 1C 1.因为AC ∥A 1C 1,且AC =A 1C 1,所以FG ∥EC 1,且FG =EC 1, 所以四边形FGEC 1为平行四边形, 所以C 1F ∥EG .又因为EG ⊂平面ABE ,C 1F ⊄平面ABE , 所以C 1F ∥平面ABE .(3)因为AA 1=AC =2,BC =1,AB ⊥BC , 所以AB =AC 2-BC 2= 3. 所以三棱锥E - ABC 的体积V =13S △ABC ·AA 1=13×12×3×1×2=33.图1-67、(福建)解析:方法一:(1)证明:∵AB ⊥平面BCD ,CD ⊂平面BCD , ∴AB ⊥CD .又∵CD ⊥BD ,AB ∩BD =B ,AB ⊂平面ABD ,BD ⊂平面ABD , ∴CD ⊥平面ABD .(2)由AB ⊥平面BCD ,得AB ⊥BD .∵AB =BD =1,∴S △ABD =12.∵M 是AD 的中点, ∴S △ABM =12S △ABD =14.由(1)知,CD ⊥平面ABD ,∴三棱锥C - ABM 的高h =CD =1,因此三棱锥A - MBC 的体积 V A - MBC =V C ABM=13S △ABM ·h =112.方法二:(1)同方法一.(2)由AB ⊥平面BCD ,得平面ABD ⊥平面BCD .且平面ABD ∩平面BCD =BD .如图所示,过点M 作MN ⊥BD 交BD 于点N , 则MN ⊥平面BCD ,且MN =12AB =12.又CD ⊥BD ,BD =CD =1,∴S △BCD =12.∴三棱锥A - MBC 的体积V A MBC =V A BCD -V M BCD =13AB ·S △BCD -13MN ·S △BCD =112. 8、(广东)解析:9、(湖北)解析:证明:(1)连接AD 1,由ABCD - A 1B 1C 1D 1是正方体,知AD 1∥BC 1.因为F ,P 分别是AD ,DD 1的中点,所以FP ∥AD 1. 从而BC 1∥FP .而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ , 故直线BC 1∥平面EFPQ .(2)如图,连接AC ,BD ,A 1C 1,则AC ⊥BD . 由CC 1⊥平面ABCD ,BD ⊂平面ABCD , 可得CC 1⊥BD .又AC ∩CC 1=C ,所以BD ⊥平面ACC 1A 1. 而AC 1⊂平面ACC 1A 1,所以BD ⊥AC 1.因为M ,N 分别是A 1B 1,A 1D 1的中点,所以MN ∥同理可证PN ⊥AC 1.又PN ∩MN =N ,所以直线AC 1⊥平面PQMN.00:(1):,,,,,,,,,,,,,.11(2),,60,30,==,22,PD ABCD PD PCD PCD ABCD PCD ABCD CD MD ABCD MD CD MD PCD CF PCD CF MD CF MF MD MF MDF MD MF M CF MDF CF MDF CF DF PCD CDF CF CD DE EF DC D ⊥⊂∴⊥=⊂⊥∴⊥⊂∴⊥⊥⊂=∴⊥⊥∴⊥∠=∴∠=∴解证明平面平面平面平面平面平面平面平面又平面平面平面又易知从而∥2112,,2211.33CDE M CDE CDE CF DE PE S CD DE P CP MD VS MD ∆-∆=∴=∴==⋅=====∴=⋅==10、(上海)解析:11、(江苏)解析:证明: (1)因为D ,E 分别为棱PC ,AC 的中点, 所以DE ∥P A .又因为P A ⊄平面DEF ,DE ⊂平面DEF , 所以直线P A ∥平面DEF .(2)因为D ,E ,F 分别为棱PC ,AC ,AB 的中点,P A =6,BC =8,所以DE ∥P A ,DE =12P A =3,EF =12BC =4.又因为DF =5,所以DF 2=DE 2+EF 2,所以∠DEF =90°,即DE ⊥EF .又P A ⊥AC ,DE ∥P A , 所以DE ⊥AC .因为AC ∩EF =E ,AC ⊂平面ABC ,EF ⊂平面ABC , 所以DE ⊥平面ABC . 又DE ⊂平面BDE ,所以平面BDE ⊥平面ABC .12、(山东)解析:证明:(1)设AC ∩BE =O ,连接OF ,EC .由于E 为AD 的中点,AB =BC =12AD ,AD ∥BC ,所以AE ∥BC ,AE =AB =BC , 所以O 为AC 的中点.又在△P AC 中,F 为PC 的中点,所以AP ∥OF . 又OF ⊂平面BEF ,AP ⊄平面BEF , 所以AP ∥平面BEF .(2)由题意知,ED ∥BC ,ED =BC ,所以四边形BCDE 为平行四边形, 所以BE ∥CD .又AP ⊥平面PCD ,所以AP ⊥CD ,所以AP ⊥BE . 因为四边形ABCE 为菱形, 所以BE ⊥AC .又AP ∩AC =A ,AP ,AC ⊂平面P AC , 所以BE ⊥平面P AC .13、(江西)解析:(1)证明:由AA 1⊥BC 知BB 1⊥BC .又BB 1⊥A 1B ,故BB 1⊥平面BCA 1,所以BB 1⊥A 1C .又BB 1∥CC 1,所以A 1C ⊥CC 1. (2)方法一:设AA 1=x .在Rt △A 1BB 1中,A 1B =A 1B 21-BB 21=4-x 2.同理,A 1C =A 1C 21-CC 21=3-x 2. 在△A 1BC 中,cos ∠BA 1C =A 1B 2+A 1C 2-BC 22A 1B ·A 1C =-x 2(4-x 2)(3-x 2),sin ∠BA 1C =12-7x 2(4-x 2)(3-x 2),所以S △A 1BC =12A 1B ·A 1C ·sin ∠BA 1C =12-7x 22.从而三棱柱ABC - A 1B 1C 1的体积V =S 直·l =S △A 1BC ·AA 1=x 12-7x 22.因为x 12-7x 2=12x 2-7x 4=-7⎝⎛⎭⎫x 2-672+367,所以当x =67=427,即AA 1=427时,体积V 取到最大值377.(2)方法二:过A 1作BC 的垂线,垂足为D ,连接AD .由AA 1⊥BC ,A 1D ⊥BC ,得BC ⊥平面AA 1D ,故BC ⊥AD .又∠BAC =90°,所以S △ABC =12AD ·BC =12AB ·AC ,得AD =2217.设AA 1=x .在Rt △AA 1D 中,A 1D =AD 2-AA 21=127-x 2,S △A 1BC =12A 1D ·BC =12-7x 22.从而三棱柱ABC - A 1B 1C 1的体积V =S 直·l =S △A 1BC ·AA 1=x 12-7x 22.因为x 12-7x 2=12x 2-7x 4=-7⎝⎛⎭⎫x 2-672+367,所以当x =67=427,即AA 1=427时,体积V 取到最大值377.14、(辽宁)解析解:(1)证明:由已知得△ABC ≌△DBC ,因此AC =DC .又G 为AD 的中点,所以CG ⊥AD ,同理BG ⊥AD .又BG ∩CG =G ,所以AD ⊥平面BGC . 又EF ∥AD ,所以EF ⊥平面BCG .(2)在平面ABC 内,作AO ⊥CB ,交CB 延长线于点O . 由平面ABC ⊥平面BCD ,知AO ⊥平面BDC .又G 为AD 的中点,所以G 到平面BDC 的距离h 是AO 在△AOB 中,AO =AB ·sin 60°=3,所以V 三棱锥D -BCG =V 三棱锥G -BCD =13·S △DBC ·h =13×12·BD ·BC ·sin 120°·32=12.15、(全国新课标I)解析:解:(1)证明:由已知得△ABC ≌△DBC ,因此AC =DC .又G 为AD 的中点,所以CG ⊥AD ,同理BG ⊥AD .又BG ∩CG =G ,所以AD ⊥平面BGC . 又EF ∥AD ,所以EF ⊥平面BCG .(2)在平面ABC 内,作AO ⊥CB ,交CB 延长线于点O . 由平面ABC ⊥平面BCD ,知AO ⊥平面BDC .又G 为AD 的中点,所以G 到平面BDC 的距离h 是AO 在△AOB 中,AO =AB ·sin 60°=3,所以V 三棱锥D -BCG =V 三棱锥G -BCD =13·S △DBC ·h =13×12·BD ·BC ·sin 120°·32=12. .因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1. 又AO ⊥平面BB 1C 1C ,所以B 1C ⊥AO , 由于BC 1∩AO =O ,故B 1C ⊥平面ABO . 由于AB ⊂平面ABO ,故B 1C ⊥AB .(2)作OD ⊥BC ,垂足为D ,连接AD .作OH ⊥AD ,垂足为H . 由于BC ⊥AO ,BC ⊥OD ,且AO ∩OD =O , 故BC ⊥平面AOD ,所以OH ⊥BC . 又OH ⊥AD ,且AD ∩BC =D , 所以OH ⊥平面ABC .因为∠CBB 1=60°,所以△CBB 1为等边三角形,又BC =1,可得OD =34. 因为AC ⊥AB 1,所以OA =12B 1C =12.由OH ·AD =OD ·OA ,且AD =OD 2+OA 2=74,得OH =2114. 又O 为B 1C 的中点,所以点B 1到平面ABC 的距离为217.故三棱柱ABC - A 1B 1C 1的高为217.16、(四川)解析:(1)证明:因为四边形ABB 1A 1和ACC 1A 1都是矩形,所以AA 1⊥AB ,AA 1⊥AC .因为AB ,AC 为平面ABC 内的两条相交直线, 所以AA 1⊥平面ABC .因为直线BC ⊂平面ABC ,所以AA 1⊥BC .又由已知,AC ⊥BC ,AA 1,AC 为平面ACC 1A 1内的两条相交直线, 所以BC ⊥平面ACC 1A 1.(2)取线段AB 的中点M ,连接A 11,设O 为A 1C ,AC 1的交点.由已知,O 为AC 1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC 1的中位线,所以MD 綊12AC ,OE 綊12AC ,因此MD 綊OE .连接OM ,从而四边形MDEO 为平行四边形,所以DE ∥MO . 因为直线DE ⊄平面A 1MC ,MO ⊂平面A 1MC . 所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点),使直线DE ∥平面A 1MC .17、(天津)解析:(1)证明:如图所示,取PB 中点M ,连接MF ,AM .因为F 为PC 中点,所以MF ∥BC ,且MF =12BC .由已知有BC ∥AD ,BC =AD ,又由于E 为AD 中点,因而MF ∥AE 且MF =AE , 故四边形AMFE 为平行四边形,所以EF ∥AM .又AM ⊂平面P AB ,而EF ⊄平面P AB , 所以EF ∥平面P AB .(2)(i)证明:连接PE ,BE.因为P A =PD ,BA =BD ,而E 为AD 中点,所以PE ⊥AD ,BE ⊥AD ,所以∠PEB 为二面角P - AD -B 的平面角.在△P AD 中,由P A =PD =5,AD =2,可解得PE =2. 在△ABD 中,由BA =BD =2,AD =2,可解得BE =1. 在△PEB 中,PE =2,BE =1,∠PEB =60˚,由余弦定理,可解得PB =3,从而∠PBE =90˚,即BE ⊥PB .又BC ∥AD ,BE ⊥AD , 从而BE ⊥BC,因此BE ⊥平面PBC .又BE ⊂平面ABCD , 所以平面PBC ⊥平面ABCD .(ii)连接BF ,由(i)知,BE ⊥平面PBC ,所以∠EFB 为直线EF 与平面PBC 所成的角.由PB =3及已知,得∠ABP 为直角,而MB =12PB =32,可得AM =112,故EF =112.又BE =1,故在直角三角形EBF 中,sin ∠EFB =BE EF =21111.所以直线EF 与平面PBC 所成角的正弦值为21111.18、(浙江)解析:(1)证明:连接BD ,在直角梯形BCDE 中,由DE =BE =1,CD =2,得BD =BC =2,由AC =2,AB =2,得AB 2=AC 2+BC 2,即AC ⊥BC .又平面ABC ⊥平面BCDE ,从而AC ⊥平面BCDE .(2)在直角梯形BCDE 中,由BD =BC =2,DC =2,得BD ⊥BC .又平面ABC ⊥平面BCDE ,所以BD ⊥平面ABC .作EF ∥BD ,与CB 的延长线交于点F ,连接AF ,则EF ⊥平面ABC . 所以∠EAF 是直线AE 与平面ABC 所成的角.在Rt △BEF 中,由EB =1,∠EBF =π4,得EF =22,BF =22;在Rt △ACF 中,由AC =2,CF =322,得AF =262. 在Rt △AEF 中,由EF =22,AF =262, 得tan ∠EAF =1313. 所以,直线AE 与平面ABC 所成的角的正切值是1313.19.(全国券)解析:.解:方法一:(1)证明:因为A 1D ⊥平面ABC ,A 1D ⊂平面AA 1C 1C ,故平面AA 1C 1C ⊥平面ABC .又BC ⊥AC ,平面AA 1C 1C ∩平面ABC =AC ,所以BC ⊥平面AA 1C 1C .连接A 1C ,因为侧面AA 1C 1C 为菱形,故AC 1⊥A 1C . 由三垂线定理得AC 1⊥A 1B .(2)BC ⊥平面AA 1C 1C ,BC ⊂平面BCC 1B 1, 故平面AA 1C 1C ⊥平面BCC 1B 1.作A 1E ⊥CC 1,E 为垂足,则A 1E ⊥平面BCC 1B 1.又直线AA 1∥平面BCC 1B 1,因而A 1E 为直线AA 1与平面BCC 1B 1的距离,即A 1E = 3. 因为A 1C 为∠ACC 1的平分线,故A 1D =A 1E = 3.作DF ⊥AB ,F 为垂足,连接A 1F .由三垂线定理得A 1F ⊥AB , 故∠A 1FD 为二面角A 1 AB C 的平面角.由AD =AA 21-A 1D 2=1,得D 为AC 中点,所以DF =55,tan ∠A 1FD =A 1DDF=15, 所以cos ∠A 1FD =14.所以二面角A 1 AB C 的大小为arccos 14.。
立体几何2014年高考

立体几何1.在如图所示的多面体中,底面BCFE 是梯形,EF//BC ,又EF ⊥平面AEB ,,//.24AE EB AD EF BC AD ⊥==,3,2,EF AE BE G BC ===为的中点.(I )求证:AB//平面DEG ; (2)求证:BD EG ⊥;(3)求二面角C —DF —E 的正弦值. 解:(1)证明://,//,//AD EF EF BC AD BC ∴,2,//,BC AD G BC AD BG AD BG =∴=为的中点,且.//.ABGD AB DG ∴∴四边形是平行四边形, …………2分 ,,//.AB DEG DG DEG AB DEG ⊄⊂∴平面平面平面…………4分(2)证明:EF AEB AE AEB BE AEB ∴⊥⊂⊂平面,平面,平面,,,,,,EF AE EF BE AE EB EB EF EA ∴⊥⊥⊥∴两两垂直.……6分以点E 为坐标原点,,,,,EB EF EA x y z 分别为轴,建立空间直角坐标系如图所示,由已知得(002),(200),(240),(022),(030),(220).A B C D F G ,,,,,,,,,,,,(220),(22,2),=-2222200.EG BD EG BD ∴==-⋅⨯+⨯+⨯=,,,故BD EG ∴⊥ ………………………8分(3)由已知可得(2,0,0)EB =是平面EFDA 的一个法向量. 设平面DCF 的一个法向量为()=x,y,z n ,(0-1,2(210)FD FC ==,),,,,20,11, 2.(1,2,1).20y z z x y x y -+=⎧∴==-==-⎨+=⎩n 令得即……………10分设二面角C FD E --的大小为θ,则cos cos ,66n EB θθ=<>==-=…………11分C DF E ∴--二面角………………………12分 2.如图1,在3090Rt ABC ACB ABC ∆∠=∠=中,,,D 为AC 中点,AE BD ⊥于E ,延长AE 交于BC 于F ,将ABD ∆沿BD 折起,使平面ABD ⊥平面BCD ,如图2所示. (I )求证:AE ⊥平面BCD ;(II )求二面角A DC B --的余弦值;(III )已知点M 在线段AF 上,且EM//平面ADC ,求AMAF的值.3.如图,四棱锥E ABCD -中,平面EAD ⊥平面ABCD ,DC // AB ,BC CD ⊥,EA ED ⊥,且4AB =,2BC CD EA ED ====.(I )求证:BD ⊥平面ADE ;(II )求BE 和平面CDE 所成角的正弦值;(III )在线段CE 上是否存在一点F 使得平面BDF ⊥平面CDE ,请说明理由. 解:(I )由BC CD ⊥,2BC CD ==.,可得BD =.由EA ED ⊥,且2EA ED ==可得AD = 又4AB =. 所以BD AD ⊥.又平面EAD ⊥平面ABCD , 平面ADE平面ABCD =BD ⊂平面ABCD ,所以BD ⊥平面ADE . (II )如图建立空间直角坐标系D xyz -,则(0,0,0)D ,(0,B ,(C ,E ,(2,BE =-,(2,0,DE =,(DC =.x设(,,)x y z =n 是平面CDE 的一个法向量,则0DE ⋅=n ,0DC ⋅=n , 即0,0.x z x y +=⎧⎨-+=⎩令1x =,则(1,1,1)=-n .设直线BE 与平面CDE 所成的角为α,则||sin |cos ,|3||||BE BE BE ⋅=<>===⋅αn n n .所以BE 和平面CDE 所成的角的正弦值3. ……………10分 (III )设CF CE =λ,[0,1]λ∈.(DC =,CE =,(0,DB =.则2(21,1,)DF DC CF DC CE =+=+=--+λλλλ.设(,,)x'y'z'=m 是平面BEF 一个法向量,则0EB ⋅=n ,0EF ⋅=n , 即0,(21)(1)0.y'x'y'z'=⎧⎨-+-++=⎩λλλ令1x'=,则21(1,0,)λλ-=-m .若平面BEF ⊥平面CDE ,则0⋅=m n ,即2110λλ-+=,1[0,1]3λ=∈.所以,在线段CE 上存在一点F 使得平面BEF ⊥平面CDE .……………14分4. 如图,在底面是正方形的四棱锥P ABCD PA -⊥中,面ABCD ,BD 交AC 于点E ,F 是PC 中点,G 为AC 上一点.(I )求证:BD FG ⊥;(II )确定点G 在线段AC 上的位置,使FG//平面PBD ,并说明理由;(III )当二面角B PC D --的大小为23π时,求PC 与底面ABCD 所成角的正切值.。
2014年立体几何大题
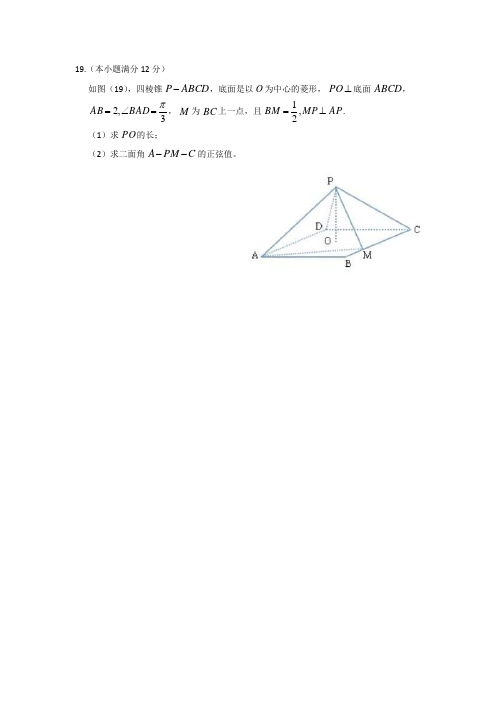
19.(本小题满分12分)如图(19),四棱锥,底面是以为中心的菱形,底面, ,为上一点,且. (1)求的长;(2)求二面角的正弦值。
ABCD P -O ⊥PO ABCD 3,2π=∠=BAD AB M BC AP MP BM ⊥=,21PO C PM A --EA20.(本题满分15分)如图,在四棱锥中,平面平面.(1)证明:平面; (2)求二面角的大小BCDE A -⊥ABC ======∠=∠AC BE DE CD AB BED CDE BCDE ,1,2,90,02⊥DE ACD E AD B --17.(本小题满分13分)如图,在四棱锥中,底面,,,,,点为棱的中点.⑴证明:;⑵求直线与平面所成角的正弦值;⑶若为棱上一点,满足,求二面角的余弦值.P ABCD -PA ⊥ABCD AD AB ⊥//AB DC 2AD DC AP ===1AB =E PC BE DC ⊥BE PBD F PC BF AC ⊥F AB P --18.三棱锥及其侧视图、俯视图如图所示。
设,分别为线段,的中点,为线段上的点,且。
(1)证明:为线段的中点; (2)求二面角的余弦值。
CABD M NP17. (本小题满分12分)四面体及其三视图如图所示,过棱的中点作平行于,的平面分别交四面体的棱于点.(1)证明:四边形是矩形;(2)求直线与平面夹角的正弦值.ABCD AB E AD BC CA DC BD ,,H G F ,,221俯左 主ABCDEFGHEFGH AB EFGH17.(本小题满分12分)如图,在四棱柱中,底面是等腰梯形,,是线段的中点.(I )求证:;(II )若垂直于平面且求平面和平面所成的角(锐角)的余弦值.1111ABCD A B C D -ABCD 60,DAB ∠=22AB CD ==M AB 111//C M A ADD 平面B 1C 1D 1A 1DCBMA1CD ABCD 1CD 11C D M ABCD20.(本题满分13分)如图,四棱柱中,底面.四边形为梯形,,且.过三点的平面记为,与的交点为。
