北科大matlab数学实验第四次实验报告

MATLAB实验报告(1-4)

信号与系统MATLAB第一次实验报告一、实验目的1.熟悉MATLAB软件并会简单的使用运算和简单二维图的绘制。

2.学会运用MATLAB表示常用连续时间信号的方法3.观察并熟悉一些信号的波形和特性。

4.学会运用MATLAB进行连续信号时移、反折和尺度变换。

5.学会运用MATLAB进行连续时间微分、积分运算。

6.学会运用MATLAB进行连续信号相加、相乘运算。

7.学会运用MATLAB进行连续信号的奇偶分解。

二、实验任务将实验书中的例题和解析看懂，并在MATLAB软件中练习例题，最终将作业完成。

三、实验内容1.MATLAB软件基本运算入门。

1). MATLAB软件的数值计算：算数运算向量运算：1.向量元素要用”[ ]”括起来，元素之间可用空格、逗号分隔生成行向量，用分号分隔生成列向量。

2.x=x0:step:xn.其中x0位初始值，step表示步长或者增量，xn为结束值。

矩阵运算：1.矩阵”[ ]”括起来；矩阵每一行的各个元素必须用”,”或者空格分开；矩阵的不同行之间必须用分号”;”或者ENTER分开。

2.矩阵的加法或者减法运算是将矩阵的对应元素分别进行加法或者减法的运算。

3.常用的点运算包括”.*”、”./”、”.\”、”.^”等等。

举例：计算一个函数并绘制出在对应区间上对应的值。

2).MATLAB软件的符号运算：定义符号变量的语句格式为”syms 变量名”2.MATLAB软件简单二维图形绘制1).函数y=f(x)关于变量x的曲线绘制用语：>>plot(x,y)2).输出多个图像表顺序：例如m和n表示在一个窗口中显示m行n列个图像，p表示第p个区域，表达为subplot(mnp)或者subplot(m,n,p)3).表示输出表格横轴纵轴表达范围：axis([xmax,xmin,ymax,ymin])4).标上横轴纵轴的字母：xlabel(‘x’),ylabel(‘y’)5).命名图像就在subplot写在同一行或者在下一个subplot前：title(‘……’)6).输出：grid on举例1：举例2：3.matlab程序流程控制1).for循环：for循环变量=初值:增量:终值循环体End2).while循环结构：while 逻辑表达式循环体End3).If分支：(单分支表达式)if 逻辑表达式程序模块End(多分支结构的语法格式)if 逻辑表达式1程序模块1Else if 逻辑表达式2程序模块2…else 程序模块nEnd4).switch分支结构Switch 表达式Case 常量1程序模块1Case 常量2程序模块2……Otherwise 程序模块nEnd4.典型信号的MATLAB表示1).实指数信号：y=k*exp(a*t)举例：2).正弦信号：y=k*sin(w*t+phi)3).复指数信号：举例：4).抽样信号5).矩形脉冲信号:y=square(t,DUTY) (width默认为1)6).三角波脉冲信号：y=tripuls(t,width,skew)(skew的取值在-1~+1之间，若skew取值为0则对称)周期三角波信号或锯齿波:Y=sawtooth(t,width)5.单位阶跃信号的MATLAB表示6.信号的时移、反折和尺度变换:Xl=fliplr(x)实现信号的反折7.连续时间信号的微分和积分运算1).连续时间信号的微分运算：语句格式：d iff(function,’variable’,n)Function:需要进行求导运算的函数，variable:求导运算的独立变量，n：求导阶数2).连续时间信号的积分运算：语句格式：int(function,’variable’,a,b)Function:被积函数variable:积分变量a:积分下限b:积分上限(a&b默认是不定积分)8.信号的相加与相乘运算9.信号的奇偶分解四、小结这一次实验让我能够教熟悉的使用这个软件，并且能够输入简单的语句并输出相应的结果和波形图，也在一定程度上巩固了c语言的一些语法。

MATLAB实验报告(四份!!!)

0380160815880001449451490168779983287916534749293454515731] >> double(x) ans = -33.5325 60.6078 -54.7098 27.3192 实验三 MATLAB 绘图
一实验环境计算机 MATLAB 软件二实验目的 1. 掌握 MATLAB 的基本绘命令。 2. 掌握运用 MATLAB 绘制一维、二维、三维的图形方法。 3. 给图形加以修饰。三预备知识特殊的二维图形函数有：直方图、柄图、阶梯图、饼图、频数累计柱状图、极坐标图四实验内容和步骤
3.创建一个 3x3 矩阵，并求其转置，逆矩阵。 >> A=magic(3) A= 8 3 4 >> A' ans = 8 1 6 >> inv(A) 3 5 7 4 9 2 1 5 9 6 7 2
ans = 0.1472 -0.0611 -0.0194 -0.1444 0.0222 0.1889 0.0639 0.1056 -0.1028
3. 画出 y=的曲线（x(-5,5)）。在这曲线上加入相同区间里的 y=的曲线，并且采用绿色折线标识。 >> x=linspace(-5,5,100); >> y=x.^2; >> plot(x,y) >> hold on >> z=x.^(1/3); >> plot(x,z,'g--')
4. 在同一窗口不同坐标系里分别绘出 y1=sinx,y2=cosx,y3=cinh(x),y4=cosh(x)4 个图形。 >> x=linspace(0,2*pi,30); >> subplot(2,2,1);plot(x,sin(x)); >> subplot(2,2,2);plot(x,cos(x)); >> subplot(2,2,3);plot(x,sinh(x)); >> subplot(2,2,4);plot(x,cosh(x));

MATLAB实验报告(1-4)

信号与系统MATLAB第一次实验报告一、实验目的1.熟悉MATLAB软件并会简单的使用运算和简单二维图的绘制。

2.学会运用MATLAB表示常用连续时间信号的方法3.观察并熟悉一些信号的波形和特性。

4.学会运用MATLAB进行连续信号时移、反折和尺度变换。

5.学会运用MATLAB进行连续时间微分、积分运算。

6.学会运用MATLAB进行连续信号相加、相乘运算。

7.学会运用MATLAB进行连续信号的奇偶分解。

二、实验任务将实验书中的例题和解析看懂，并在MATLAB软件中练习例题，最终将作业完成。

三、实验内容1.MATLAB软件基本运算入门。

1). MATLAB软件的数值计算：算数运算向量运算：1.向量元素要用”[ ]”括起来，元素之间可用空格、逗号分隔生成行向量，用分号分隔生成列向量。

2.x=x0:step:xn.其中x0位初始值，step表示步长或者增量，xn为结束值。

矩阵运算：1.矩阵”[ ]”括起来；矩阵每一行的各个元素必须用”,”或者空格分开；矩阵的不同行之间必须用分号”;”或者ENTER分开。

2.矩阵的加法或者减法运算是将矩阵的对应元素分别进行加法或者减法的运算。

3.常用的点运算包括”.*”、”./”、”.\”、”.^”等等。

举例：计算一个函数并绘制出在对应区间上对应的值。

2).MATLAB软件的符号运算：定义符号变量的语句格式为”syms 变量名”2.MATLAB软件简单二维图形绘制1).函数y=f(x)关于变量x的曲线绘制用语：>>plot(x,y)2).输出多个图像表顺序：例如m和n表示在一个窗口中显示m行n列个图像，p表示第p个区域，表达为subplot(mnp)或者subplot(m,n,p)3).表示输出表格横轴纵轴表达范围：axis([xmax,xmin,ymax,ymin])4).标上横轴纵轴的字母：xlabel(‘x’),ylabel(‘y’)5).命名图像就在subplot写在同一行或者在下一个subplot前：title(‘……’)6).输出：grid on举例1：举例2：3.matlab程序流程控制1).for循环：for循环变量=初值:增量:终值循环体End2).while循环结构：while 逻辑表达式循环体End3).If分支：(单分支表达式)if 逻辑表达式程序模块End(多分支结构的语法格式)if 逻辑表达式1程序模块1Else if 逻辑表达式2程序模块2…else 程序模块nEnd4).switch分支结构Switch 表达式Case 常量1程序模块1Case 常量2程序模块2……Otherwise 程序模块nEnd4.典型信号的MATLAB表示1).实指数信号：y=k*exp(a*t)举例：2).正弦信号：y=k*sin(w*t+phi)3).复指数信号：举例：4).抽样信号5).矩形脉冲信号:y=square(t,DUTY) (width默认为1)6).三角波脉冲信号：y=tripuls(t,width,skew)(skew的取值在-1~+1之间，若skew取值为0则对称)周期三角波信号或锯齿波:Y=sawtooth(t,width)5.单位阶跃信号的MATLAB表示6.信号的时移、反折和尺度变换:Xl=fliplr(x)实现信号的反折7.连续时间信号的微分和积分运算1).连续时间信号的微分运算：语句格式：d iff(function,’variable’,n)Function:需要进行求导运算的函数，variable:求导运算的独立变量，n：求导阶数2).连续时间信号的积分运算：语句格式：int(function,’variable’,a,b)Function:被积函数variable:积分变量a:积分下限b:积分上限(a&b默认是不定积分)8.信号的相加与相乘运算9.信号的奇偶分解四、小结这一次实验让我能够教熟悉的使用这个软件，并且能够输入简单的语句并输出相应的结果和波形图，也在一定程度上巩固了c语言的一些语法。

数学软件MATLAB实验报告实验四

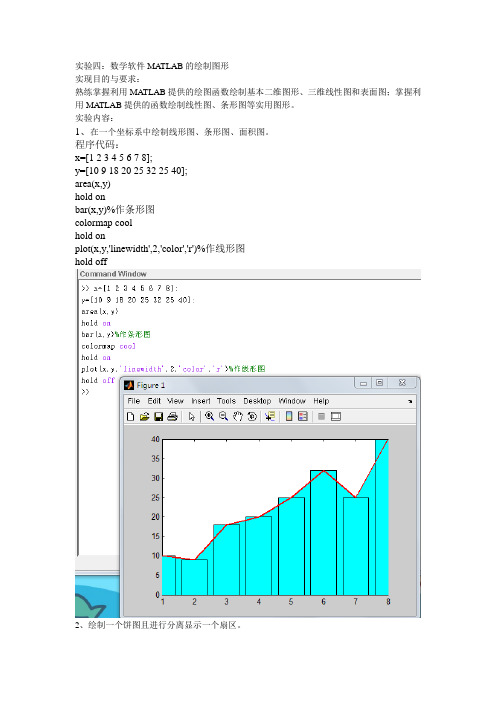
实验四：数学软件MATLAB的绘制图形实现目的与要求：熟练掌握利用MATLAB提供的绘图函数绘制基本二维图形、三维线性图和表面图；掌握利用MA TLAB提供的函数绘制线性图、条形图等实用图形。

实验内容：1、在一个坐标系中绘制线形图、条形图、面积图。

程序代码：x=[1 2 3 4 5 6 7 8];y=[10 9 18 20 25 32 25 40];area(x,y)hold onbar(x,y)%作条形图colormap coolhold onplot(x,y,'linewidth',2,'color','r')%作线形图hold off2、绘制一个饼图且进行分离显示一个扇区。

程序代码：x=[10 33 55 15];explode=[0 1 0 0];pie3(x,explode)%3、绘制一个误差条图。

程序代码：x=1:7;y=[10 6 17 13 20 15 25]; e=[2.5 1.5 1 3 1 2 1.6]; errorbar(x,y,e)%4、绘制一个散点图。

程序代码：x=[1:80];y=rand(size(x)); scatter(x,y,'filled','b')%5、绘制一个直方图。

程序代码:y=randn(888,3);hist(y,20)%6、创建一个M文件，它返回一个两列矩阵。

在创建一个函数句柄，并作图先创建一个M文件：Function y=example4_6(x)y(:,1)=200*sin(x(:))./x(:);y(:,2)=x(:)^2;再用fplot函数作图命令：fplot('example4_6',[-20 20])7、做122=-y x 的曲线图。

程序代码：ezplot('x^2-y^2-1',[-4,4,-4,4])8、做下面参数方程的曲线图⎪⎪⎩⎪⎪⎨⎧===t z t t y e x t cos sin 10程序：ezplot3('exp(t/10)','sin(t)*cos(t)','t',[0,16*pi],'animate')9、用ezmesh 函数绘制下列函数的曲面图223y-=z+xxy程序代码：ezmesh('x^2-3*x*y+y^2')。

MATLAB实验报告四

实验四文件操作一、实验目的掌握MATLAB文件操作的各个函数。

二、实验内容1. 验证本章所举的例子例 5.1>> Fid=fopen('std.dat','w');>> Fid=fopen('std.dat','r')Fid =3>> A=fread(Fid);>> Sat=fclose(Fid)Sat =例 5.2>> magic=[1 2 3 4;5 6 7 8]magic =123 45678>> Fid=fopen('magic5.bin','w') Fid =3>> fwrite(Fid,magic,'int32') ans =8>> Sat=fclose(Fid)Sat =>> A=[-0.6515 -0.2727 -0.4354 -0.3190 -0.9047;-0.7534 -0.4567 -0.3212 -0.4132 -0.3583;-0.9264 -0.8173 -0.7823 -0.3265 -0.0631;-0.1735 -0.7373 -0.0972 -0.3267 -0.6298;-0.4768 -0.6773 -0.6574 -0.1923 -0.4389]A =-0.6515-0.2727-0.4354-0.3190-0.9047-0.7534-0.4567-0.3212-0.4132-0.3583-0.9264-0.8173-0.7823-0.3265-0.0631-0.1735-0.7373-0.0972-0.3267-0.6298-0.4768-0.6773-0.6574-0.1923-0.4389>> Fid=fopen('test.dat','w')Fid =3>> cnt=fwrite(Fid,A,'float')25>> fclose(Fid)ans =程序段将矩阵A的数据以二进制浮点数格式写入文件test.dat 中。

matlab实验报告总结

matlab实验报告总结Matlab实验报告总结引言：Matlab是一种广泛应用于科学计算和工程领域的高级编程语言和环境。

在这个实验报告总结中，我将回顾我在使用Matlab进行实验时的经验和收获。

通过这些实验，我学到了很多关于Matlab的功能和应用，同时也提高了自己的编程和数据分析能力。

一、Matlab基础知识的学习和应用在实验中，我首先学习了Matlab的基础知识，包括变量的定义、矩阵和数组的操作、函数的使用等。

通过这些基础知识的学习，我能够更加熟练地使用Matlab进行数值计算和数据处理。

例如，我学会了如何定义一个矩阵，并进行矩阵的加减乘除运算，这对于解决线性方程组或者进行矩阵变换非常有帮助。

二、数据可视化与图像处理Matlab具有强大的数据可视化功能，通过使用Matlab的绘图函数，我可以将数据以图表的形式直观地展示出来。

在实验中，我使用Matlab绘制了各种类型的图表，包括折线图、柱状图、散点图等。

这些图表不仅美观，而且能够更好地帮助我理解和分析数据。

此外，我还学习了Matlab的图像处理工具箱，通过使用这些工具，我可以对图像进行滤波、增强、分割等操作，从而得到更好的图像效果。

三、数值计算和优化算法Matlab提供了丰富的数值计算和优化算法，通过使用这些算法，我可以解决各种数学问题和优化问题。

在实验中，我学习了如何使用Matlab进行数值积分、数值微分、方程求解等操作。

同时，我还学习了一些常用的优化算法，如遗传算法、粒子群算法等。

这些算法在实际问题中具有广泛的应用，通过使用Matlab，我能够更加高效地解决这些问题。

四、信号处理与模拟仿真Matlab在信号处理和模拟仿真方面也有很强的功能。

通过使用Matlab的信号处理工具箱，我可以对信号进行滤波、降噪、频谱分析等操作。

这对于处理实际采集到的信号数据非常有帮助。

同时，我还学习了如何使用Matlab进行模拟仿真，通过建立数学模型和仿真算法，我可以模拟和分析各种实际系统的行为。

matlab实验报告

matlab实验报告《matlab 实验报告》一、实验目的通过本次实验，熟悉 MATLAB 软件的基本操作和功能，掌握使用MATLAB 进行数学计算、数据处理、图形绘制等方面的方法和技巧，提高运用 MATLAB 解决实际问题的能力。

二、实验环境1、计算机：＿____2、操作系统：＿____3、 MATLAB 版本：＿____三、实验内容及步骤（一）矩阵运算1、创建矩阵在 MATLAB 中，可以通过直接输入元素的方式创建矩阵，例如：｀A ＝ 1 2 3; 4 5 6; 7 8 9`，创建了一个 3 行 3 列的矩阵 A。

还可以使用函数来创建特定类型的矩阵，如全零矩阵`zeros(m,n)｀、全 1 矩阵`ones(m,n)｀、单位矩阵`eye(n)｀等。

2、矩阵的基本运算加法和减法：两个矩阵相加或相减，要求它们的维度相同，对应元素进行运算。

乘法：矩阵乘法需要满足前一个矩阵的列数等于后一个矩阵的行数。

转置：使用`A'｀来获取矩阵 A 的转置。

（二）函数的使用1、自定义函数可以在 MATLAB 中自定义函数，例如定义一个计算两个数之和的函数：｀｀｀matlabfunction s ＝ add_numbers(a,b)s ＝ a ＋ b;end｀｀｀2、调用函数在命令窗口中输入`add_numbers(3,5)｀即可得到结果 8。

（三）数据的读取和写入1、读取数据使用`load`函数可以读取数据文件，例如`load(＇datatxt'）｀。

2、写入数据使用`save`函数可以将数据保存到文件中，例如`save(＇resulttxt'，A)｀，将矩阵 A 保存到`resulttxt`文件中。

（四）图形绘制1、二维图形绘制折线图：使用`plot(x,y)｀函数，其中 x 和 y 分别是横坐标和纵坐标的数据。

绘制柱状图：使用`bar(x,y)｀函数。

2、三维图形绘制三维曲线：使用`plot3(x,y,z)｀函数。

北科大matlab第4次实验报告

《数学实验》报告实验名称数学实验学院自动化专业班级姓名学号2015年4月一、【实验目的】使用MATLAB 进行线性代数相关运算及求数值积分二、【实验任务】1、求下列线性方程组的通解: (1)1234123123420302340x x x x x x x x x x x ++-=⎧⎪-++=⎨⎪-+-=⎩ (2)123412341234031231/2x x x x x x x x x x x x --+=⎧⎪-+-=⎨⎪--+=-⎩2、用三种方法求积分的数值解:20sin 1cos x xdx xπ+⎰3、用多种数值方法计算定积分411sin dx xπ-⎰,,观察不同方法相应的误差.三、【实验程序】1、 (1)A = [1 1 2 -1; -1 1 3 0; 2 -3 4 -1]; rref(A)(2)A = [1 -1 -1 1 0; 1 -1 1 -1 1; 1 -1 -2 3 -1/2]; rref(A)2、建立函数文件integration.m function y = integration(x) y = x.*sin(x)./(1+cos(x).^2); 编程如下：x = 0:pi/100:pi;y = x.*sin(x)./(1+cos(x).^2); t = length(x);s1 = sum(y(1:(t-1)))*pi/100 %矩形公式7-1 s2 = sum(y(2:t))*pi/100 %矩形公式7-2 s3 = trapz(x,y) %梯形公式7-5 s4 = quad('integration',0,pi) %辛普生公式7-63、建立函数文件integration.mfunction y = integration(x) y = 1./(1-sin(x)); 编程如下：x = 0 : pi/400 : pi/4; y = 1./(1-sin(x)); t = length(x);s1 = sum(y(1 : (t - 1)))*pi/400 %矩形公式7-1 s2 = sum(y(2 : t))*pi/400 %矩形公式7-2 s3 = trapz(x,y) %梯形法7-5 s4 = quad('integration',0,pi/4) %辛普生法7-6 vpa(sqrt(2))四、【实验结果】 1、（1）ans =1 0 0 -14/25 0 1 0 -1/5 0 0 1 -3/25A 的秩为3，方程组有无穷多解同解方程组：⎪⎪⎪⎩⎪⎪⎪⎨⎧===425351251434241x x x x x x取1x 4=，解得方程组的基础解系为：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1253512514ξ所以方程组的通解为：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡12535125144321k x x x x ，其中k 为任意实数（2）ans =1 -1 0 0 1/2 0 0 1 0 1/2 0 0 0 1 0增广矩阵的秩为3，等于系数矩阵的秩，而小于未知量的个数4，所以方程组有无穷多解，原方程组对应的同解方程组为：⎪⎪⎪⎩⎪⎪⎪⎨⎧==+=021221431x x x x 可找到其中一个特解为：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=*021021η再求解对应的齐次方程组⎪⎩⎪⎨⎧===002431x x xx ，可得到一个基础解系：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0011ξ因此，此方程组的通解为：()R k k x x x x ∈⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡021021001143212、s1 =2.4673 s2 =2.4673 s3 =2.4673 s4 =2.4674矩形公式以及梯形法计算结果都是2.4673，辛普生法计算结果是2.46743、s1 =1.4048 s2 =1.4237s3 =1.4143s4 =1.4142ans =1.4142135623730950488016887242097矩形公式7-1计算，结果是1.4048；矩形公式7-2计算，结果是1.4237；梯形法计算，结果是1.4143；辛普生法计算结果是1.4142。

北科大Matlab_数学实验报告1~6次(全)

《数学实验》报告实验名称 Matlab 基础知识学院专业班级姓名学号2014年 6月一、【实验目的】1.认识熟悉Matlab这一软件，并在此基础上学会基本操作。

2.掌握Matlab基本操作和常用命令。

3.了解Matlab常用函数，运算符和表达式。

4.掌握Matlab工作方式和M文件的相关知识。

5.学会Matlab中矩阵和数组的运算。

二、【实验任务】P16 第4题编写函数文件，计算1!nkk =∑，并求出当k=20时表达式的值。

P27第2题矩阵A=123456789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，B=468556322⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，计算A*B,A.*B,并比较两者的区别。

P27第3题已知矩阵A=5291⎡⎤⎢⎥⎣⎦，B=1292⎡⎤⎢⎥⎣⎦，做简单的关系运算A>B,A==B,A<B,并做逻辑运算(A==B)&(A<B),(A==B)&(A>B)。

P34 第1题用11114357π=-+-+……公式求π的近似值，直到某一项的绝对值小于-610为止。

三、【实验程序】P16 第4题function sum=jiecheng(n) sum=0;y=1;for k=1:nfor i=1:ky=y*i;endsum=sum+y;endsumP27第2题>>A=[1 2 3;4 5 6;7 8 9]>>B=[4 6 8;5 5 6;3 2 2]>>A*BP27第3题>> A=[5 2;9 1];B=[1 2;9 2];>>A>B>>A==B>>A<B>> (A==B)&(A<B)>> (A==B)&(A>B)P34 第1题t=1;pi=0;n=1;s=1;while abs(t)>=1e-6pi=pi+t;n=n+2;s=-s;t=s/n;endpi=4*pi;四、【实验结果】P16 第4题P27第2题两者的区别：A*B是按正规算法进行矩阵的计算, A.*B是对应元素相乘。

MATLAB 第四次实验

subplot(2,2,2),plot(x,y,'*'),hold on,plot(scalar_x,y_linear),title('method=linear');
subplot(2,2,3),plot(x,y,'*'),hold on,plot(scalar_x,y_spline),title('method=spline');
Exiting: Maximum number of function evaluations has been exceeded
- increase MaxFunEvals option.
Current function value: -359212266339440800000000000000000000000000000000000000000000000000000000000000000000.000000
x =
1.0e+041 *
0.9523 -6.0686
fvalue =-3.5921e+083
flag =0
output =
iterations: 200
funcCount: 401
algorithm: 'Nelder-Mead simplex direct search'
message: [1x233 char]
scalar_x=[x(1):0.05:x(length_of_x)];
length_of_sx=length(scalar_x)
for
i=1:length_of_sx y_nearest(i)=interp1(x,y,scalar_x(i),'nearest');

MATLAB 实验报告

学号姓名班级指导教师王朋飞《MATLAB编程技术》实验报告实验一：熟悉MATLAB 及其工具箱实验目的和要求：实验目的是熟悉MA TLAB界面和help功能。

打开MATLAB软件，查看窗口布局，命令窗口的使用方法，help命令的使用方法，查看help文档。

上机实验代码：打开MATLAB软件，使用help命令查看abs的说明，进入Help浏览器查看工具箱。

有很多Toolbox上机实验讨论和总结：点击Reference page in Help browser doc abs 可以进一步进入MA TLAB的Help浏览器，可以进一步搜索和链接相关的函数。

列出MA TLAB常用的基本数学函数：abs(x)：纯量的绝对值或向量的长度angle(z)：复数z的相角(Phase angle)sqrt(x)：开平方real(z)：复数z的实部imag(z)：复数z的虚部conj(z)：复数z的共轭复数round(x)：四舍五入至最近整数fix(x)：无论正负，舍去小数至最近整数floor(x)：地板函数，即舍去正小数至最近整数ceil(x)：天花板函数，即加入正小数至最近整数rat(x)：将实数x化为分数表示rats(x)：将实数x化为多项分数展开sign(x)：符号函数(Signum function)。

当x<0时，sign(x)=-1；当x=0时，sign(x)=0;当x>0时，sign(x)=1。

rem(x,y)：求x除以y的馀数gcd(x,y)：整数x和y的最大公因数lcm(x,y)：整数x和y的最小公倍数exp(x) ：自然指数pow2(x)：2的指数log(x)：以e为底的对数，即自然对数或log2(x)：以2为底的对数log10(x)：以10为底的对数实验二：M文件的写法实验目的和要求：实验目的是掌握如何编写M文件，有哪几种M文件。

实际编写2个M文件实现函数调用，完成找1000以内的素数的功能。

MATLAB基础性实验报告4

学生实验报告一、实验目的1. 归纳和学习求解常微分方程(组)的基本原理和方法；2. 掌握解析、数值解法，并学会用图形观察解的形态和进行解的定性分析；3. 熟悉MATLAB软件关于微分方程求解的各种命令；4. 通过范例学习建立微分方程方面的数学模型以及求解全过程；通过该实验的学习，使学生掌握微分方程(组)求解方法（解析法、欧拉法、梯度法、改进欧拉法等），对常微分方程的数值解法有一个初步了解，同时学会使用MATLAB软件求解微分方程的基本命令，学会建立微分方程方面的数学模型。

这对于学生深入理解微分、积分的数学概念，掌握数学的分析思维方法，熟悉处理大量的工程计算问题的方法是十分必要的。

二、实验仪器、设备或软件：电脑,MATLAB软件三、实验内容1．微分方程及方程组的解析求解法；2．微分方程及方程组的数值求解法——欧拉、欧拉改进算法；3．直接使用MATLAB命令对微分方程(组)进行求解(包括解析解、数值解)；4．利用图形对解的特征作定性分析；5．建立微分方程方面的数学模型，并了解建立数学模型的全过程。

四、实验步骤1．开启软件平台——MATLAB，开启MATLAB编辑窗口；2．根据微分方程求解步骤编写M文件3．保存文件并运行；4．观察运行结果(数值或图形)；5．根据观察到的结果和体会写出实验报告。

五、实验要求与任务1．求微分方程的解析解，并画出它们的图形。

y '= y + 2 x, y (0) = 1, 0< x <1；解：命令为：dsolve('Dy=y+2*x','y(0)=0','x') 结果为：ans =2*exp(x) - 2*x – 2绘制图形程序：x=linspace(0,1,50);y=2*exp(x) - 2*x - 2;plot(x,y)图形如下：2．求微分方程⎪⎩⎪⎨⎧====-+]100[0)0(;0)0(01.03t uu u u u 的数值解，要求编写求解程序。

MATLAB第四次实验报告

MATLAB 第四次实验报告1. 选用复合Simpson 公式，计算()()11ln 1ln 1x x dx -+-⎰并用Matlab 的符号运算工具箱计算其精确值。

比较结果，找出问题原理，提出解决问题的方法。

程序：主程序：clcclearf=inline('log(1+x).*log(1-x)','x')y=simpson(f,-0.9999,0.9999,100)Simpson 函数：function s=simpson(f,a,b,n)h=(b-a)/(2*n);s1=0;s2=0;for k=1:nx=a+h*(2*k-1);s1=s1+feval(f,x);endfor k=1:(n-1)x=a+h*k*2;s2=s2+feval(f,x);ends=h*(feval(f,a)+feval(f,b)+4*s1+2*s2)/3;运行结果：y =-1.11042. 求积分方程()()1021t t y t e y s ds e e =--⎰ 的数值解和精确解，分析二者的差异。

程序：主程序：clcclearf=inline(dsolve('Dy=y','y(0)=1','x'));F=inline('y','x','y')y=euler(F,0,1,5,500);hold onX=linspace(0,5);Y=f(X);plot(X,Y,'r')legend('Euler 近似','y=e^t',0)Euler 函数：function [x,y]=euler(fun,x0,y0,xN,N)y(1)=y0;h=(xN-x0)/N;x=x0:h:xN;for n=1:Nx(n+1)=x(n)+h;y(n+1)=y(n)+h*feval(fun,x(n),y(n));endplot(x,y,'b')3. 利用Euler 法对不同的步长求下面初值问题的数值解：()()()'20010y t y t y ⎧=-⎪⎨=⎪⎩ 并通过绘图，与方程的解析解进行比较。

MATLAB实验报告_4

《数学实验》综合实验报告报告成员（2人）:李庆超自动化1301 41321038陈吉采矿理留1401 614020152015年 6月运用MATLAB求解电路问题电路问题主要分为稳态电路与动态电路, 这里结合电路原理中的节点电压法, 通过MATLAB求解稳态电路；结合电路原理中的状态方程, 通过MATLAB求解动态电路。

§1运用MATLAB求解稳态电路一、问题提出:求解如图所示的稳态电路, 求出各电阻、电感、电容两端的电压及流过他们的电流和有功功率和功率因数。

（w=100rad/s;Is3=1A;Is4=2A;L1=10mH;L2=50mH;R3=5Ώ;R4=2Ώ;R5=10Ώ;C6=0.1mF）模型建立:本题首先可以运用电路原理的知识, 列出节点电压方程, 将电路结构及其参数用矩阵形式表达出来, 然后运用MATLAB 的知识对其进行求解。

根据电路原理知识, 任何稳态电路的求解可以根据以下公式列节点电压方程：s n TI A U AYA ..=其中, A 为电路的关联矩阵, Y 为支路导纳矩阵, 为节点电压, 为电源列向量。

对本题而言:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=011100001010011101A ⎥⎦⎤⎢⎣⎡=65432111111jwC R R R jwL jwL diag Y⎥⎦⎤⎢⎣⎡=0000.4.3.s s s I I I因此, 在根据 , 可以运用MATLAB 求解出本题的节点电压矩阵: , 进而得到各处节点相对于参考节点的电压。

问题求解:程序代码:w=100;Is3=1;Is4=2;L1=0.01;L2=0.05;R3=5;R4=2;R5=10;C6=0.0001;A=[1 0 1 1 0 0;-1 1 0 0 0 1;0 -1 0 -1 1 0];Is=[0;0;Is3;Is4;0;0];y=[1/(j*w*L1),1/(j*w*L2),1/R3,1/R4,1/R5,1/(j*w*C6)];Y=diag(y,0)Un=inv(A*Y*A')*A*IsIR3=Un(1)/R3IR4=(Un(1)-Un(3))/R4IR5=Un(3)/R5IC6=Un(2)*j*w*C6IL1=(Un(1)-Un(2))/(j*w*L1)IL2=(Un(3)-Un(2))/(j*w*L2)求解结果:Un =0.7705 + 1.1223i0.0023 + 0.0112i-2.6991 + 0.0347iIR3 =0.1541 + 0.2245iIR4 =1.7348 + 0.5438iIR5 =-0.2699 + 0.0035iIC6 =-1.1158e-04 + 2.2793e-05iIL1 =1.1111 - 0.7682iIL2 =0.0047 + 0.5403i结论:通过MATLAB求解得：相对于参考节点4, 节点1、2、3的节点电压分别为（0.7705+j1.223）V,（0.0023+j0.0112）V, （-2.6991+j0.0347）V。

MATLAB实验报告

MATLAB实验报告实验报告课程名称 MATLAB基础及应用专业班级电子xxxx姓名学号电气与信息学院实验二 MATLAB 数值计算（一）一实验目的：1．掌握数组的创建与运算方法；2. 掌握矩阵的创建与运算方法；3. 掌握数组的运算方法和矩阵运算方法的区别；4．掌握线性方程的求解方法二实验装置：计算机三实验内容：1．数组的创建和运算创建两个含5个元素的一维数组，并求这两个数组的四则运算。

2．矩阵的创建和运算（1）创建两个3×3的矩阵，并求这两个矩阵的四则运算。

（2）创建一个4×4的矩阵，并求这个矩阵的行列式值。

（3）线性方程的求解解方程组=6613753467294x 。

四实验要求:写出实验程序与仿真结果。

1. >> a=linspace(2,10,5) a =2 4 6 8 10>> b=linspace(1,9,5) b =1 3 5 7 9>> a+bans =3 7 11 15 19>> a-bans =1 1 1 1 1>> a.*bans =2 12 30 56 90>> a./bans =2.0000 1.3333 1.2000 1.1429 1.1111 >> a.\b ans =0.5000 0.7500 0.8333 0.8750 0.9000 2.(1) >> a=[1 1 1;2 2 2;3 3 3];>> b=[4 4 4;5 5 5;6 6 6];>> a+bans =5 5 57 7 79 9 9>> a-bans =-3 -3 -3-3 -3 -3-3 -3 -3>> a*bans =15 15 1530 30 3045 45 45>> a/bWarning: Matrix is singular to working precision. ans =NaN NaN NaNNaN NaN NaNNaN NaN NaN>> a\bWarning: Matrix is singular to working precision. ans =NaN NaN NaNNaN NaN NaNInf Inf Inf(2).>> a=[1 1 1 1;2 2 2 2;3 3 3 3;4 4 4 4];>> det(a)ans =(3).>> a=[4 9 2;7 6 4;3 5 7];>> b=[13;6;6];>> x=inv(a)*bx =-0.53081.7109-0.1374实验三 MATLAB数值计算（二）一实验目的：1．掌握多项式的创建与运算方法；2. 掌握基本的数据分析方法；二实验装置：计算机三实验内容：1．多项式创建输入系数矢量，创建多项式x^3-2*x^2+5*x+3。

MATLAB实验报告次次

M A T L A B数学实验报告姓名：李犁学号：1304120724指导老师：易昆南专业班级：统计1203目录1学生管理程序 (3)2自测题 (8)3动画函数的生成 (10)4MATLAB在高等数学中的应用 (12)5利用MATLAB求π的值 (14)6零件的参数设计储 (16)7油罐的变位识别与罐容表标定 (21)一.学生管理程序7：实验总结在学习MATLAB过程中我们要多动脑，多动手写程序、调试，看程序时候多想几个为什么，理解别人程序中精华的东西，多自己调调程序，可以改改程序，把知识转成自己的，弄懂一两个经典例子比粗粗的看一大书要好，值得一提是不是一下子就能看懂相对比较长，比较复杂的程序的，要做的是自己慢慢去分析，利用已经有的资料和帮助，等慢慢搞懂它，要多看几遍，相信多看一遍你就会有一些新的认识，一直到你已经掌握里例子的精华。

MATLAB是一款功能强大的软件，在这次实践中，我也是收获颇丰，刚开始面对这个问题，不知道该如何设计，但是努力着回忆老师每节课讲的内容，再加上对课本的查阅，渐渐有了思路，设计出了大概的框架。

但是在具体编程过程中的确遇到了好多麻烦，自身原因还是因为对MATLAB的不熟悉，经过一番努力，终于设计出了一项相对简单的学生成绩管理系统。

今后还有继续听老师认真讲课，在下次课题实践中设计更好的程序。

最后多读matlab高手写的程序，帖子，找到一个高手，在几个大的论坛可以搜索出一大堆的帖子，然后慢慢去看吧，从中可以学到很多东西,也许你会发现很多你都看不懂，这很正常，别人写程序考虑的是能实现这样的功能，运行效率等问题，而不是考虑是不是很容易能让别人理解，你就看你现在能看懂，再看些通过你断点调试，查help能看明白的，看不懂的就先放下，遇到好的和看不懂，你又很挺感兴趣的话题，你先收藏起来，过段时间你再回头看看，你会发现，每看一遍，你就会多懂一些东西，当你第三遍甚至第四遍看同一个程序的时候，也许你就会有豁然开朗的感觉。

MATLAB第四章实验报告

MATLAB 图形基础班级：11电信一班姓名：何得中学号：实验目的：1.掌握MATLAB图形绘制功能；2.学会使用MATLAB提供的绘图函数；3.了解MATLAB对图形线性、色彩、光线、视角等的制定和处理。

实验仪器：MA TLAB软件，电脑实验数据：绘制fracreturnl变量同一图轴下绘制两条曲线增加子图分割子图删除图轴后仍保留两个子图效果添加图轴信息设定曲线样式在交互式绘图工具中增加图例>> rand('state',27)>> startprice=50;>>fracreturns1=0.0015*randn(200,1)+0.0003; >> x1=[startprice;1+fracreturns1];>> prices1=cumprod(x1);>> t=(1:length(prices1))';>> randn('state',7)>>fracreturns2=0.0015*randn(200,1)+0.0003; >> x2=[startprice;1+fracreturns2];>> prices2=cumprod(x2);>> whosName Size Bytes ClassL 51x51 20808 double arrayfracreturns1 200x1 1600 double arrayfracreturns2 200x1 1600 double arrayl1 1x1 8 double arrayl2 1x1 8 double arrayprices1 201x1 1608 double arrayprices2 201x1 1608 double arrays 1x1 8 double arraystartprice 1x1 8 double arrayt 201x1 1608 double arrayx1 201x1 1608 double arrayx2 201x1 1608 double arrayGrand total is 4010 elements using 32080 bytes>> plot (prices2, 'DisplayName', 'prices2', 'YDataSource', 'prices2'); figure(gcf) >> x=0:pi/1000:2*pi;>> y=exp(-0.5*x).*sin(2*pi*x+pi/4);>> plot(x,y)plot(x,y,x,y+1,x,y-1)>> B=pascal(6)B = 1 1 1 1 1 11 2 3 4 5 61 3 6 10 15 211 4 10 20 35 561 5 15 35 70 1261 6 21 56 126 252 >> plot(B)>> x=(0:pi/100:2*pi)';>> y1=2*exp(-0.5*x)*[1,-1];>> y2=2*exp(-0.5*x).*sin(2*pi*x);>> x1=(0:12)/2;>> y3=2*exp(-0.5*x1).*sin(2*pi*x1);>> plot(x,y1,'g:',x,y2,'b--',x1,y3,'rp');>> x1=0:pi/100:2*pi;>> x2=0:pi/100:3*pi;>> y1=exp(-0.5*x1).*sin(2*pi*x1);>> y2=1.5*exp(-0.1*x2).*sin(x2);>> plotyy(x1,y1,x2,y2);>> x=(0:pi/100:2*pi)';y1=2*exp(-0.5*x)*[1,-1];y2=2*exp(-0.5*x).*sin(2*pi*x);x1=(0:12)/2;y3=2*exp(-0.5*x1).*sin(2*pi*x1);plot(x,y1,'g:',x,y2,'b--',x1,y3,'rp');>> title('曲线及其包络线'); %加图形标题>> xlabel('independent variable X'); %加X轴说明>> ylabel('independent variable Y'); %加y轴说明>> text(2.8,0.5,'包络线'); %在指定位置添加图形说明>> text(0.5,0.5,'曲线y');>> text(1.4,0.1,'离散数据点');>> legend('包络线','包络线','曲线y','离散数据点') %加图例>> x=(0:pi/100:2*pi)';>> y1=2*exp(-0.5*x)*[1,-1];>>y2=2*exp(-0.5*x).*sin(2*pi*x);>> plot(x,y1,'b:');>> axis([0,2*pi,-2,2]);>> hold on;>> plot(x,y2,'k');>> grid on;>> box off;>> hold off; >> x=(0:pi/100:2*pi)';>> y1=2*exp(-0.5*x)*[1,-1];>> y2=2*exp(-0.5*x).*sin(2*pi*x);>> plot(x,y1,'b:');>> hold on;>> plot(x,y2,'k');>> grid on;>> box off;>> hold off>>alpha=-0.5;>>beta=3;>>A=50;>>t=0:0.01:10;>>y=A*exp(alpha*t).*sin(beta*t);>>plot(t,y);>>title('\fontname{隶书}\fontsize{16}{隶书}\fontname{Impact}{Impact}')>>xlabel('^{上标}and_{下标}')>>ylabel('Some\bf粗体\rm and some\it{斜体}')>>txt={'y={\itAe}^{\alphax}sin(\beta\itt)',... >> ['\itA\rm','='.num2str(A)],...>> ['\alpha='num2str(alpha)],...>> ['\beta=',num2str(beta)];>> text(2,22,txt)x=linspace(0,2*pi,60);y=sin(x);z=cos(x);t=sin(x)./(cos(x)+eps);ct=cos(x)./(sin(x)+eps); subplot(2,2,1);plot(x,y);title('sin(x)');axis([0,2*pi,-1,1]); subplot(2,2,2);plot(x,z);title('cos(x)');axis([0,2*pi,-1,1]);subplot(2,2,3);plot(x,t);title('tangent(x)');axis([0,2*pi,-40,40] );subplot(2,2,4);plot(x,ct);title('cotangent(x)');axis([0,2*pi,-40,40]);x=linspace(0,2*pi,60);y=sin(x);z=cos(x);t=sin(x)./(cos(x)+eps);ct=cos(x)./(sin(x)+eps); subplot(2,2,1);stairs(x,y);title('sin(x)-1');axis([0,2*pi,-1,1]); subplot(2,1,2);stem(x,y);title('sin(x)-2');axis([0,2*pi,-1,1]); subplot(4,4,3);plot(x,y);title('sin(x)');axis([0,2*pi,-1,1]); subplot(4,4,4);plot(x,z);title('cos(x)');axis([0,2*pi,-1,1]); subplot(4,4,7);plot(x,t);title('tangent(x)');axis([0,2*pi,-40,40] );subplot(4,4,8);plot(x,ct);title('cotangent(x)');axis([0,2*pi,-40, 40]);x=0:0.35:7;y=2*exp(-0.4*x);subplot(2,2,1);bar(x,y,'g');title('bar(x,y,''g'')');axis([0,7,0,2]);subplot(2,2,2);fill(x,y,'r');title('fill(x,y,''r'')');axis([0,7,0,2]);subplot(2,3,4);stairs(x,y,'b');title('stairs(x,y,''b'')');axis([0,7,0,2]); subplot(2,3,5);stem(x,y,'k');title('stem(x,y,k'')');axis([0,7,0,2]);subplot(2,3,6);area(x,y);title('area(x,y)');axis([0,7,0,2]);theta=0:0.01:2*pi;rho=sin(3*theta).*cos(3*theta);polar(theta,rho,'r');x=0:0.1:10;y=12*x.*x;subplot(2,2,1);plot(x,y);title('plot(x,y)');grid on;subplot(2,2,2);semilogx(x,y);title('semilogx(x, y)');grid on;subplot(2,2,3);semilogx(x,y);title('semipogx(x ,y)');grid on;subplot(2,2,4);loglog(x,y);title('loglog(x,y)');grid on;function y=myf(x);y=cos(tan(pi*x));fplot('myf',[-0.2,1.2],1e-4);subplot(1,2,1);pie([7,17,23,19,5]);title('饼图');legend('优秀','良好','中等','及格','不及格');subplot(1,2,2);compass([3+2i,4.5-i,-1.5+5i]);title('相量图');t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*si n(t);plot3(x,y,z,'p');title('Line in 3-D space');text(0,0,0,'origin'); xlabel('X'),ylabel('Y'),zlabel('Z');grid;x=5:29;y=14:35;[x,y]=meshgrid(x,y);z=2*x+5*y;k=find(z==126);x(k)',y(k)'>> bans =8 13 18 23 28ans =22 20 18 16 14x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos (x);mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zla bel('z-axis');title('mesh');x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos (x);surf(x,y,z);xlabel('x-asis'),ylabel('y-axis'),zlabe l('z-axis');title('surf');x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos (x);plot3(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zla bel('z-axis');title('plot3');grid;[x,y]=meshgrid(-10:0.5:10);z=sin(sqrt(x.^3+y.^2))./sqrt(x.^2+y.^2+eps); subplot(2,2,1);meshc(x,y,z);title('meshc(x,y,x)');subplot(2,2,2);meshz(x,y,z);title('meshz(x,y,x)');subplot(2,2,3);surfc(x,y,z);title('surfc(x,y,z)');subplot(2,2,4);surfl(x,y,z);title('surfl(x,y,z)');t=0:pi/20:2*pi;[x,y,z]=cylinder(2+sin(t),30);subplot(1,3,1);surf(x,y,z);subplot(1,3,2);[x,y,z]=sphere;surf(x,y,z);subplot(1,3,3);[x,y,z]=peaks(300);meshz(x,y,z);subplot(2,2,1);bar3(magic(5));subplot(2,2,2);y=3*sin(0:pi/10:2*pi);stem3(y);subplot(2,2,3);pie3([2347,1827,2043,3025]);subplot(2,2,4);fill3(rand(3,6),rand(3,6),rand(3,6),'r');subplot(1,2,1);[x,y,z]=peaks;waterfall(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis'); title('waterfall of peaks');subplot(1,2,2);contour3(x,y,z,12,'k');xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('contour3 of peaks');subplot(2,2,1);mesh(peaks);view(-37.5,30);title('azimuth=-37.5,elevation=30')subplot(2,2,2);mesh(peaks);view(0,90);title('azimuth=0,elevation=90')subplot(2,2,3);mesh(peaks);view(90,0);title('azimuth=90,elevation=0')subplot(2,2,4);mesh(peaks);view(-7,-10);title('azimuth=-7,elevation=-10')z=peaks(20);colormap(copper);subplot(1,3,1);surf(z);subplot(1,3,2);surf(z);shading flat;subplot(1,3,3);surf(z);shading interp;x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x);[I,J]=find(z>0.2);for ii=1:length(I)z(I(ii),J(ii))=NaN;endsurf(x,y,z);。

北科大matlab数学实验第四次实验报告

MATLAB实验报告(1-4)

MATLAB实验报告(四份!!!)

MATLAB实验报告(1-4)

数学软件MATLAB实验报告 实验四

MATLAB实验报告四

matlab实验报告总结

matlab实验报告

北科大matlab第4次实验报告

北科大Matlab_数学实验报告1~6次(全)

MATLAB 第四次实验

MATLAB 实验报告

MATLAB基础性实验报告4

MATLAB第四次实验报告

MATLAB实验报告_4

MATLAB实验报告

MATLAB实验报告次次

MATLAB第四章实验报告

数学软件MATLAB实验报告实验四