数学建模练习题
数学建模练习题

数学建模练习题数学建模是运用数学工具和方法来解决实际问题的一种综合能力。
它不仅培养了学生的逻辑思维能力,还提高了他们的问题解决能力和实践操作能力。
为了巩固数学建模的理论知识和应用能力,以下是一系列数学建模练习题,帮助大家提升数学建模水平。
题目一: 财务规划假设你是一家公司的财务经理,现需要为公司制定一份财务规划报告。
请根据以下信息,回答相应问题:1. 公司现有资金500万元,年利率为2%;2. 公司每月开支为30万元;3. 公司每季度向银行贷款100万元,年利率为3%;4. 公司每年收入为800万元。
请回答以下问题:1. 请计算公司一年的利润是多少?2. 如果公司每年的开支增加到40万元,一年的利润会有何变化?3. 如果公司每个季度向银行贷款300万元,一年的利润会有何变化?4. 请提出一些建议,如何优化财务规划,提高公司的利润。
题目二: 交通流量某城市的交通局需要对城市道路的交通流量进行研究和预测。
请根据以下信息,回答相应问题:1. 城市拥有5条主要道路,分别为A、B、C、D、E;2. 每条道路的通行能力为100辆/小时;3. 每条道路的通行时间为8小时/天;4. 城市每天的交通流量为3000辆。
请回答以下问题:1. 请计算城市每条道路的日平均通行量是多少?2. 如果城市每天的交通流量增加到5000辆,每条道路的通行能力是否足够?3. 如果城市每条道路的通行时间减少到6小时/天,每天的交通流量不变,城市每条道路的日平均通行量会有何变化?4. 请提出一些建议,如何应对城市交通流量的持续增加。
题目三: 人口预测某国家正进行人口统计和预测工作。
请根据以下信息,回答相应问题:1. 该国家近年来人口增长率为2%;2. 该国家现有人口为1亿;3. 该国家每年有200万人出生,80万人死亡;4. 该国家每年有30万人移民。
请回答以下问题:1. 请计算该国家5年后的预计人口数量是多少?2. 如果该国家每年有150万人出生,100万人死亡,预计人口增长率会有何变化?3. 如果该国家每年有50万人移民,预计人口增长率会有何变化?4. 请提出一些建议,如何应对人口增长带来的社会问题。
数学建模活动(1)-练习题

课后练习
请同学们仿照上述过程开展一次建立模型解决实际问题的活动,可以继续研究不同室温下泡制一杯最佳口感茶水所需的时间,也可以从下列选题中选择一个:
1、应在炒菜之前多长时间将冰箱里的肉拿出来解冻?
2、根据某一同学的身高和体重,判断该同学是否超重.
3、用微波炉或电磁炉烧一壶开水,找到最省电的功率设定方法.
4估计阅读一本书所需要的时间.
也可以根据自己的兴趣成3—5人的研究小组,每位同学参加其中一个小组。在小组内,要确定一个课题负责人,使每位成员都有明确的分工.拟定研究课题、确定研究方案、规划研究步骤、编制研究手册,然后在班里进行一次开题报告。
数学建模练习题

数学建模练习题一、基础数学知识类某企业生产两种产品,生产每吨产品A需耗用原料1吨、工时4小时,生产每吨产品B需耗用原料2吨、工时3小时。
若企业每月原料供应量为10吨,工时供应量为36小时,求该企业每月生产产品A和产品B的数量。
某湖泊污染问题,已知污染物的降解速度与污染物浓度成正比,求污染物浓度随时间的变化规律。
计算由曲线y=x^2和直线x=2、y=0所围成的图形的面积。
二、统计分析类2, 4, 6, 8, 10, 12, 14, 16, 18, 20某地区居民消费水平(y)与收入(x)之间的关系,数据如下表所示,求出线性回归方程。
| 收入(x) | 消费水平(y) || | || 1000 | 800 || 1500 | 1200 || 2000 | 1600 || 2500 | 2000 || 3000 | 2400 |三、优化方法类某企业生产三种产品,产品A、B、C的单件利润分别为5元、4元、3元。
生产每吨产品A、B、C所需的原料分别为2吨、1吨、1吨。
若企业每月原料供应量为10吨,求该企业每月生产产品A、B、C的数量,使得总利润最大。
某企业生产两种产品,产品A、B的单件利润分别为10元、8元。
生产每吨产品A、B所需的工时分别为4小时、3小时。
若企业每月工时供应量为120小时,求该企业每月生产产品A、B的数量,使得总利润最大。
四、离散数学类关系矩阵为:| 1 0 1 0 || 0 1 0 1 || 1 0 1 0 || 0 1 0 1 |A (3)>B (4)> D\ |\ (2)\ /C (1)>五、实际问题建模类某城市交通拥堵问题,分析道路宽度、车辆数量、交通信号等因素对交通拥堵的影响,建立数学模型。
某地区水资源分配问题,考虑农业、工业、生活用水等因素,建立数学模型,并提出合理的水资源分配方案。
六、运筹学方法类一位背包客有最大负重为50公斤的背包,现有五种物品,每种物品的重量和价值如下表所示。
大学生数学建模练习题

大学生数学建模练习题一、线性规划问题假设你是一家制造公司的经理,公司生产两种产品A和B。
生产一个产品A需要3小时的机器时间和2小时的人工时间,产品B需要2小时的机器时间和4小时的人工时间。
公司每天有24小时的机器时间和40小时的人工时间可用。
如果产品A的销售价格是50元,产品B是80元,如何安排生产计划以最大化利润?二、排队论问题一家银行有3个服务窗口,平均每天接待200名顾客。
每名顾客的平均服务时间是5分钟。
假设顾客到达银行是随机的,服从泊松分布,服务时间服从指数分布。
请计算银行的平均排队长度和顾客的平均等待时间。
三、库存管理问题一家零售商销售一种季节性产品,该产品的需求量在一年中波动很大。
产品的成本是每个20元,存储成本是每个每年2元,缺货成本是每个10元。
如果零售商希望在一年内保持至少95%的服务水平,应该如何确定最优的订货量和订货频率?四、网络流问题在一个供水系统中,有四个水库和五个城市。
水库1和2可以向城市A 供水,水库2和3可以向城市B供水,水库3和4可以向城市C和D供水。
每个水库的供水能力不同,每个城市的需求也不同。
如果需要确保所有城市的需求都得到满足,如何确定最优的供水方案?五、预测问题给定一个公司过去5年的季度销售额数据,使用时间序列分析方法预测下个季度的销售额。
请考虑季节性因素和趋势,并给出预测的置信区间。
六、优化问题一个农场主有一块矩形土地,打算围成一个矩形的牧场。
如果围栏的总长度是固定的,比如400米,如何确定牧场的长和宽,使得牧场的面积最大?七、多目标决策问题一家公司需要在多个项目中做出选择,每个项目都有不同的预期收益、风险和实施时间。
如果公司需要在风险和收益之间做出权衡,并且希望项目尽快完成,如何使用多目标决策方法来选择最合适的项目组合?通过解决这些练习题,大学生可以加深对数学建模的理解,提高分析和解决实际问题的能力。
希望这些练习题能够帮助学生在数学建模的道路上更进一步。
数学建模练习试题

1、放射性废料的处理问题美国原子能委员会以往处理浓缩的放射性废料的方法,一直是把它们装入密封的圆桶里,然后扔到水深为90多米的海底。
生态学家和科学家们表示担心,怕圆桶下沉到海底时与海底碰撞而发生破裂,从而造成核污染。
原子能委员会分辨说这是不可能的。
为此工程师们进行了碰撞实验。
发现当圆桶下沉速度超过12.2 m/s 与海底相撞时,圆桶就可能发生碰裂。
这样为避免圆桶碰裂,需要计算一下圆桶沉到海底时速度是多少? 这时已知圆桶重量为239.46 kg,体积为0.2058m3,海水密度为1035.71kg/m3,如果圆桶速度小于12.2m/s就说明这种方法是安全可靠的,否则就要禁止使用这种方法来处理放射性废料。
假设水的阻力与速度大小成正比例,其正比例常数k=0.6。
现要求建立合理的数学模型,解决如下实际问题:1.判断这种处理废料的方法是否合理?2.一般情况下,v大,k也大;v小,k也小。
当v很大时,常用kv来代替k,那么这时速度与时间关系如何? 并求出当速度不超过12.2 m/s,圆桶的运动时间和位移应不超过多少? (的值仍设为0.6)鱼雷攻击问题在一场战争中,甲方一潜艇在乙方领海进行秘密侦察活动。
当甲方潜艇位于乙方一潜艇的正西100千米处,两方潜艇士兵同时发现对方。
甲方潜艇开始向正北60千米处的营地逃跑,在甲方潜艇开始逃跑的同时,乙方潜艇发射了鱼雷进行追踪攻击。
假设甲方潜艇与乙方鱼雷是在同一平面上进行运动。
已知甲方潜艇和乙方鱼雷的速度均匀且鱼雷的速度是甲方潜艇速度的两倍。
试建立合理的数学模型解决以下问题:1) 求鱼雷在追踪攻击过程中的运动轨迹;2) 确定甲方潜艇能否安全的回到营地而不会被乙方鱼雷击中3、贷款买房问题某居民买房向银行贷款6万元,利息为月利率1%,贷款期为25年,要求建立数学模型解决如下问题:1)问该居民每月应定额偿还多少钱?2)假设此居民每月可节余700元,是否可以去买房?4、养老保险问题养老保险是保险中的一种重要险种,保险公司将提供不同的保险方案以供选择,分析保险品种的实际投资价值。
小学数学建模练习题

小学数学建模练习题在小学数学教学中,数学建模是一种培养学生综合应用数学解决实际问题的能力的有效方法。
通过数学建模,学生可以运用所学的数学知识和技能,将数学运用到生活实际中,培养他们的创新思维和问题解决能力。
为了提高学生的数学建模能力,以下是一些小学数学建模练习题,供大家练习和思考。
题目一:小明放风筝小明想放风筝,他站在一个长方形草坪的一角,正北方向有一面墙,南边是一条宽为10米的小溪,他希望风筝飞向墙上方,但是又不希望风筝落入小溪中。
现在假设整个草坪的长和宽分别是100米和50米,请问小明站在哪个位置放风筝比较好呢?题目二:水果销售某水果店的负责人想要通过一些促销活动提高水果的销量。
经过分析,他发现在夏季,顾客特别喜欢购买西瓜和橙子。
为了促进销售,他决定对这两种水果进行优惠。
西瓜的售价为每斤2元,而橙子的售价为每斤1元。
他希望考虑到顾客的购买力和需求情况,从而设置一个合理的促销策略,使得总销售额最大化。
请帮助他确定西瓜和橙子的最佳促销比例。
题目三:花坛设计小学的花坛设计已经老旧不堪,学校决定对花坛进行翻新。
花坛的形状为一个等腰梯形,底边长为4米,上底边长为2米,高为3米。
学校希望设计一个新的花坛,使得花坛内尽可能多地摆放花朵。
已知每平方米花坛能够容纳8朵花,请计算这个新花坛最多可以摆放多少朵花。
题目四:学校跑步比赛学校要举办一场跑步比赛,共有4个年级的学生参加,每个年级的学生人数分别为100人、150人、120人和80人,比赛规则是每个年级选择3名参赛选手代表该年级参加比赛。
为了公平起见,学校希望每个年级参加比赛的总成绩最好的选手之和尽可能接近。
请帮助学校确定每个年级的3名代表选手。
题目五:果园采摘小明去果园采摘水果,他发现果园里有苹果、橘子和桃子,他看到的苹果数是橘子数的2倍,橘子数又是桃子数的3倍。
小明准备采摘苹果和橘子,但是由于时间有限,他只能采摘400个水果,请问他应该采摘多少个苹果和多少个橘子才能使得采摘的水果总重量最大?以上是五道小学数学建模练习题,通过这些练习题,学生可以锻炼他们的数学思维和解决问题的能力。
数学建模习题

数学建模练习题1.1.线性规划题目问题1:毛坯切割问题用长度为500厘米的材料,分别截成长度为98厘米和78厘米的两种毛坯,要求截出长度98厘米的毛坯1000根,78厘米的毛坯2000根,问怎样去截,才能是所用的原材料最少,试建立数学模型。
问题2:进货收获问题某商店你制定某种商品7-12月的进货、售货计划,已知商品仓库最大容量为1500件,6月底已经库存300件,年底不少于300件为宜,以后每月初进货一次,假设各月份该商品买进和售出的价格如下表所示,若每件每月库存费为0.5元,问各月进货,售货多少件,才能是净收益最多。
试建立数学模型。
问题3:货船装货问题某货船的载重量为12000吨,总容积为45000立方米,冷藏容积为3000立方米,可燃性指数的总和不得超过7500,准备装6中货物,每种货物的单价、重量、体积和可燃性指数如下表:1.2.微分方程题目问题1. 什么时候开始下雪?早晨开始下雪,整天稳降不停。
正午一辆扫雪车开始扫雪,每小时扫雪量按体积计为一常数。
到下午2时它清扫了两公里,到下午4时又清扫了1公里,问雪是什么时候开始下的?问题2. 谁喝的咖啡热一些?总统与首相面前同时送上同温度的热咖啡。
总统在送到咖啡后立即加上一点冷奶油,等了10分钟才喝;首相则等了10分钟后添加等量的冷奶油开始喝,问谁喝的咖啡热一些?问题3. 需冷却多久?一位稀里糊涂的咖啡泡煮师,想让水达到185o F,可他几乎总是忘记这一点而把水煮开。
温度计又坏了,他要你计算一下,从212o F冷却到185o F要等多少时间,你能解决他的问题吗?问题4. 纽约的人口如果不考虑移民与高杀人率,纽约城的人口将满足方程,其中t 以年度量。
(1)事实上,每年有6000人从该城迁出,又有4000人被杀,试修正上面方程。
(2)已知1970年纽约城人口为800万,求未来任何时刻的人口,且求时的极限。
问题5.开火的最优距离A 方反坦克导弹与B 方坦克之间进行战斗。
2023全国数学建模题目

2023全国数学建模题目一、选择题(每题3分,共15分)下列哪个数不是质数?A. 2B. 3C. 9D. 13若一个圆的半径是5cm,则它的面积是多少平方厘米?A. 25πB. 50πC. 75πD. 100π下列哪个方程表示的是一条直线?A. y = x²B. y = 2x + 1C. y = 1/xD. xy = 1下列哪个数最接近√10?A. 2B. 3C. 4D. 5一个三角形的两边长分别为3和4,第三边的取值范围是多少?A. 1 < x < 7B. 2 < x < 8C. 3 < x < 9D. 4 < x < 10二、填空题(每题4分,共20分)绝对值等于5的数是_______。
已知|a - 3| + (b + 2)² = 0,则 a + b = _______。
已知一个正方体的棱长是6cm,则它的体积是_______ cm³。
方程2x - 3 = 5 的解是x = _______。
已知扇形的圆心角为120°,半径为3cm,则扇形的面积是_______ cm²。
三、计算题(每题10分,共30分)计算:√27 - | - 2| + (1/2)^(-1) - (π - 3)^0。
解方程组:{x + 2y = 5,3x - y = 8.}已知一个矩形的面积是48cm²,一边长为6cm,求另一边长。
四、应用题(每题15分,共30分)某商店购进一批苹果,进价为每千克5元,售价为每千克8元。
若商店想要获得至少300元的利润,则至少需要售出多少千克的苹果?一辆汽车从A地开往B地,前两小时行驶了120km,后三小时行驶了180km。
求这辆汽车的平均速度。
精品《数学建模》练习题

《数学建模》作业一、计算题1. 求差分方程 ⎩⎨⎧===++++0)1(,1)0(0)(6)1(5)2(x x k x k x k x 的初值解。
2. 求差分方程 (2)3(1)2()0(0)1, (1)2x k x k x k x x ++++=⎧⎨==⎩的初值解。
二、1.某储蓄所每天的营业时间是上午9:00到下午5:00。
根据经验,每天不同时间段所需要的服务员数量如下:储蓄所可以雇佣全时和半时两类服务员。
全时服务员每天报酬100元,从上午9:00到下午5:00工作,但中午12:00到下午2:00之间必须安排1小时的午餐时间。
储蓄所每天可以雇佣不超过3名的半时服务员,每个半时服务员必须连续工作4小时,报酬40元。
问该储蓄所应如何雇佣全时和半时两类服务员?如果不能雇佣半时服务员,每天至少增加多少费用?如果雇佣半时服务员的数量没有限制,每天可以减少多少费用?2. 已知某人有债务25000元,月利率为1%,计划在未来12个月用分期付款的方式付清债务,每月要偿还多少元?(利息按照复利计算,即把利息加入本金后一起计算利息的算法)。
三.与Logistic 模型不同的另一种描述种群增长规律的是Gompertz 模型:xNn rx t x1)(= ,其中r 和N 的意义与Logistic 模型相同。
设渔场鱼量的自然增长服从这个模型,且单位时间捕捞量为Ex h =。
讨论渔场鱼量的平衡点及其稳定性,求最大持续产量m h 及获得最大产量的捕捞强度m E 和渔场鱼量水平*0x 。
四. 在鱼塘中投放0n 尾鱼苗。
随着时间的增长,尾数将减少而每尾的重量将增加。
(1)设尾数)(t n 的(相对)减少率为常数;由于喂养引起的每尾鱼重量的增加率与鱼表面积成正比,由于消耗引起的每尾鱼重量的减少率与重量本身成正比。
分别建立尾数和每尾鱼重的微分方程,并求解。
(2)用控制网眼的办法不捕小鱼,到时刻T 才开始捕捞,捕捞能力用尾数的相对减少量()n ϕ表示,记作E ,单位时间捕获量是)(t En 。
数学建模练习题作业

1、马青公式 π=16arctan1/5-4arctan1/239 这个公式由英国天文学教授约翰·马青于 1706 年发现。他利用这个公式计
算到了 100 位的圆周率。马青公式每计算一项可以得到 1.4 位的十进制精度。因 为它的计算过程中被乘数和被除数都不大于长整数,所以可以很容易地在计算机 上编程实现。
练习题 6:兄弟三人戴帽子问题 解放前,在一个村子里住着聪明的三兄弟,他们除恶杀了财主的儿子,犯了人命案。县太爷有意想免他们
一死,决意出一个难题测测他们是否真的聪明,如果他们能在一个时辰内回答出来,就免他们一死,否则就被 处死。题目如下:
兄弟三人站成一路纵队(老三选择了站在最前面,他后面是老二,老大站在了最后面 ),并分别被蒙住了眼 睛,县太爷说我这里有两顶黑帽子和三顶红帽子,接着分别给他们头上各带了一顶帽子,然后又分别把被蒙住 的眼睛解开。
还有很多类似于马青公式的反正切公式。在所有这些公式中,马青公式似乎是 最快的了。虽然如此,如果要计算更多的位数,比如几千万位,马青公式就力不 从心了。
2、拉马努金公式 1914 年,印度天才数学家拉马努金在他的论文里发表了一系列共 14 条圆周
率的计算公式。这个公式每计算一项可以得到 8 位的十进制精度。1985 年 Gosper 用这个公式计算到了圆周率的 17,500,000 位。
此时,老大只可以看见老三和老二头上的帽子,老二只可以看见老三头上的帽子,老三看不见帽子。 只有一个时辰的时间,看谁能说出自己头上帽子的颜色,第一句声音有效。现在开始! (县太爷有多少种带帽子的方案,那一种最难?你能回答吗?)
解答:
县太爷一共有 7 种戴帽子方案:
1 黑黑红 2 黑红黑 3 黑红红 4 红红红 5 红红黑 6 红黑红 7 红黑黑
数学建模练习题

数学建模练习题
1. 某城市中心有一家商场,由于道路狭窄,经常造成交通堵塞,当地政府决定解决这个问题,经有关专家会商研究,制定出3个可行方案:
1A :在商场附近修建一座环形天桥;
2A :在商场附近修建地下人行通道;
3A :搬迁商场。
根据当地实际情况,专家组拟定了4个评议准则:1u 通车能力,2u 基建费用,3u 方便群众,4u 市容美观。
专家组经过决策比较, 得到了1u ,2u ,3u ,4u 这四个方面的两两比较矩阵
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡=12/14/17/1212/13/14212/17321A ; 同时, 对于方案321,,A A A , 专家组也分别就4321,,,u u u u 四个准则进行了比较,得到了以下4个两两比较矩阵:
⎪⎪⎪⎭⎫ ⎝⎛=12/13/1212/13211B ;⎪⎪⎪⎭
⎫ ⎝⎛=13/13/13113112B ;
⎪⎪⎪⎭⎫ ⎝⎛=1313/11313/113B ;⎪⎪⎪⎭
⎫ ⎝⎛=12/132143/14/114B 。
(注:矩阵1B ,2B ,3B ,4B 全部元素的和分别为11.3,11.7,11.7,13.1)
试建立层次结构模型,对上述矩阵进行一致性检验,并通过已有的比较矩阵,对3个可行方案进行评估, 从而为当地政府提出改善城市中心交通环境的决策建议(精确到0.01)。
数学建模习题

数学建模习题景德镇陶瓷学院信息工程学院习题一1.在1.3节“椅子能在不平的地面上放稳吗”的假设条件中,将四脚的连线呈正方形改为呈长方形,其余不变。
试构造模型并求解。
2.模仿1.4节商过河问题中的状态转移模型,作下面这个众所周知的智力游戏:人带着猫、鸡、米过河,船除需要人划之外,至多能载猫、鸡、米三者之一,而当人不在场时猫要吃鸡、鸡要吃米。
试设计一个安全过河方案,并使渡河次数尽量地少。
3.利用1.5节表1和表3给出的1790-2000年的美国实际人口资料建立下列模型:(1)分段的指数增长模型。
将时间分为若干段,分别确定增长率r 。
(2)阻滞增长模型。
换一种方法确定固有增长率r 和最大容量m x 。
4.说明1.5节中Logistic 模型(9)可以表为)(01)(t t r m ex t x --+=,其中0t 是人口增长出现拐点的时刻,并说明0t 与r, m x 的关系.5.假定人口的增长服从这样的规律:时刻t 的人口为)(t x ,t 到t+∆t 时间内人口的增长与m x -)(t x 成正比例(其中m x 为最大容量).试建立模型并求解.作出解的图形并与指数增长模型、阻滞增长模型的结果进行比较。
6.某甲早8:00从山下旅店出发,沿一条路径上山,下午5:00到达山顶并留宿。
次日早8:00沿同一条路径下山,下午5:00回旅店。
某乙说,甲必在二天中的同一时刻经过路径中的同一地点。
为什么?7.37支球队进行冠军争夺赛,每轮比赛中出场的每两支球队中的胜者及轮空者进入下一轮,直至比赛结束。
问共需进行多少场比赛,共需进行多少轮比赛。
如果是n支球队比赛呢?8.甲乙两站之间有电车相通,每隔10分钟甲乙两站相互发一趟车,但发车时刻不一定相同。
甲乙之间有一中间站丙,某人每天在随机的时刻到达丙站,并搭乘最先经过丙站的那趟车,结果发现100天中约有90天到达甲站,约有10天到达乙站。
问开往甲乙两站的电车经过丙站的时刻表是如何安排的。
数学建模练习题汇编
数学建模习题题目11.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。
比如洁银牙膏50g装的每支1.5元,120g装的每支3.00元,二者单位重量的价格比是1.2:1.试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
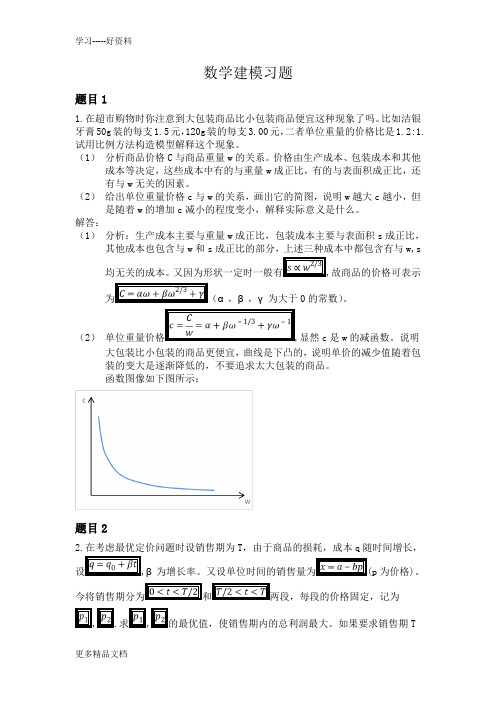
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w的增加c减小的程度变小,解释实际意义是什么。
解答:(1)分析:生产成本主要与重量w成正比,包装成本主要与表面积s成正比,其他成本也包含与w和s成正比的部分,上述三种成本中都包含有与w,s均无关的成本。
故商品的价格可表示α,β,γ为大于0的常数)。
(2)显然c是w的减函数。
说明大包装比小包装的商品更便宜,曲线是下凸的,说明单价的减少值随着包装的变大是逐渐降低的,不要追求太大包装的商品。
函数图像如下图所示:题目22.在考虑最优定价问题时设销售期为T,由于商品的损耗,成本q随时间增长,β为价格)。
T解答:由题意得:总利润为在此约束条件下的最大值点为题目33.某商店要订购一批商品零售,订购费c(与数量无关),随机需求量r的概率密度为p(r),与时间无关)。
问如何确定订购量才能使商店的平均利润最大,这个平均利润是多少。
为使这个平均加什么限制?利润为正值,需要对订购费c解答:设订购量为u,则平均利润为u为使这个利润为正值,应有题目44.雨滴匀速下降,空气阻力与雨滴表面积和速度平方的乘积成正比,试确定雨速与雨滴质量的关系。
解答:雨滴质量m,体积V,表面积S与某特征尺寸lv降落,题目55.某银行经理计划啊用一笔资金进行有价证券的投资,可供购进的证券以及其信用等级、到期年限、收益如表1所示。
按照规定,市政证券的收益可以免税,其他证券的收益需按50%的税率纳税。
此外还有以下限制:1)政府及代办机构的证券总共至少要购进400万元;2)所购证券的平均信用等级不超过1.4(信用等级数字越小,信用程度越高);(2)如果能够以2.75%的利率借到不超过100万元资金,该经理如何操作?(3)在1000万元资金情况下,若证券A的税前收益增加为4.5%,投资应否改变?若证券C的税前收益减少为4.8%,投资应否改变?解答:(1)设投资证券A,B,C,D,E,按照规定、限制和1000万元资金约束,列出模型用LINGO求解得到:证券A,C,E分别投资2.182百万元,7.364百万元,0.454百万元,最大税后收益为0.298百万元。
数学建模课程及答案

《数学建模课程》练习题一一、填空题一、填空题1.1. 设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若人口增长率是常数r ,那麽人口增长问题的马尔萨斯模型应为长问题的马尔萨斯模型应为 。
2.2. 设某种商品的需求量函数是,1200)(25)(+-=t p t Q 而供给量函数是3600)1(35)(--=t p t G ,其中)(t p 为该商品的价格函数,那麽该商品的均衡价格是 。
3. 3. 某服装店经营的某种服装平均每天卖出某服装店经营的某种服装平均每天卖出110件,进货一次的手续费为200元,存储费用为每件0.01元/天,店主不希望出现缺货现象,则最优进货周期与最优进货量分别为 。
4. 4. 一个连通图能够一笔画出的充分必要条件是一个连通图能够一笔画出的充分必要条件是一个连通图能够一笔画出的充分必要条件是 .5.5.设开始时的人口数为设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若允许的最大人口数为m x ,人口增长率由sx r x r -=)(表示,则人口增长问题的罗捷斯蒂克模型为表示,则人口增长问题的罗捷斯蒂克模型为 . 6. 在夏季博览会上,商人预测每天冰淇淋销量N 将和下列因素有关:将和下列因素有关:(1)参加展览会的人数n ; (2)气温T 超过C10; (3)冰淇淋的售价p .由此建立的冰淇淋销量的比例模型应为由此建立的冰淇淋销量的比例模型应为 . 7、若银行的年利率是x %,则需要则需要 时间,存入的钱才可翻番存入的钱才可翻番.. 若每个小长方形街路的路的8. . 如图是一个邮路,邮递员从邮局如图是一个邮路,邮递员从邮局A 出发走遍所有长方形街路后再返回邮局出发走遍所有长方形街路后再返回邮局.. 边长横向均为1km ,纵向均为2km ,则他至少要走,则他至少要走 km.. A9. 设某种新产品的社会需求量为无限,开始时的生产量为100件,且设产品生产的增长率控制在0.1,t 时刻产品量为)(t x ,则)(t x = . 10. 商店以10元/件的进价购进衬衫,若衬衫的需求量模型是802,Q p p =-是销售单价(元(元//件),为获得最大利润,商店的出售价是,为获得最大利润,商店的出售价是 . 二、分析判断题二、分析判断题1.从下面不太明确的叙述中确定要研究的问题,需要哪些数据资料.从下面不太明确的叙述中确定要研究的问题,需要哪些数据资料(至少列举(至少列举3个),要做些甚麽建模的具体的前期工作(至少列举3个)个) ,建立何种数学模型:一座高层办公楼有四部电梯,早晨上班时间非常拥挤,该如何解决。
数学建模练习题
数学建模练习题数学建模习题题⽬11. 在超市购物时你注意到⼤包装商品⽐⼩包装商品便宜这种现象了吗。
⽐如洁银⽛膏50g装的每⽀元,120g装的每⽀元,⼆者单位重量的价格⽐是:1.试⽤⽐例⽅法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由⽣产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正⽐,有的与表⾯积成正⽐,还有与w⽆关的因素。
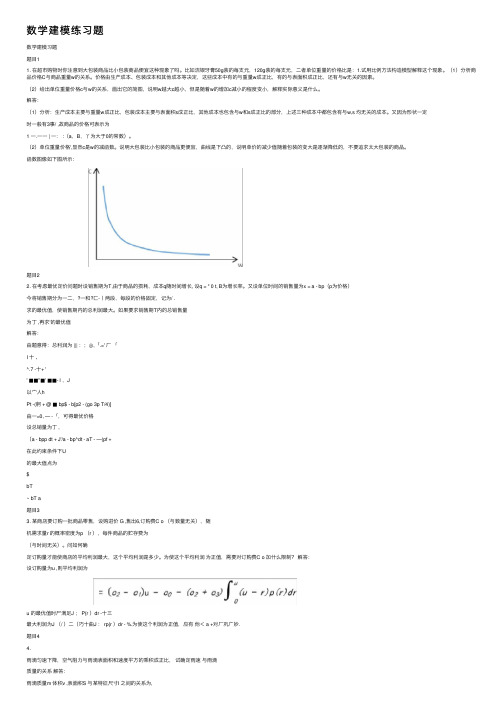
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越⼤c越⼩,但是随着w的增加c减⼩的程度变⼩,解释实际意义是什么。
解答:(1)分析:⽣产成本主要与重量w成正⽐,包装成本主要与表⾯积s成正⽐,其他成本也包含与w和s成正⽐的部分,上述三种成本中都包含有与w,s 均⽆关的成本。
⼜因为形状⼀定时⼀般有3事/ ,故商品的价格可表⽰为1 ⼀.⼀⼀ | ⼀: :(a,B,丫为⼤于0的常数)。
(2)单位重量价格',显然c是w的减函数。
说明⼤包装⽐⼩包装的商品更便宜,曲线是下凸的,说明单价的减少值随着包装的变⼤是逐渐降低的,不要追求太⼤包装的商品。
函数图像如下图所⽰:题⽬22. 在考虑最优定价问题时设销售期为T,由于商品的损耗,成本q随时间增长, 设q = * 0 t, B为增长率。
⼜设单位时间的销售量为x = a - bp(p为价格)今将销售期分为⼀⼆,?⼀和?⼕-⼁两段,每段的价格固定,记为/ .求的最优值,使销售期内的总利润最⼤。
如果要求销售期T内的总销售量为丁 ,再求'的最优值解答:由题意得:总利润为 ||| :;◎,「.=' ⼚「I ⼗、^.7 -⼗+ '' ■■''■' ■■- l ,J以⼧⼈hPt -(舸 + @ ■ bp$ - b[p2 - (go 3p T/4)]由⼀=0, — -「,可得最优价格设总销量为丁 ,〔a - bpp dt + J'/a - bp^dt - aT - —(pf +在此约束条件下U的最⼤值点为$bT~ bT a题⽬33. 某商店要订购⼀批商品零售,设购进价 G ,售出6,订购费C o (与数量⽆关),随机需求量r 的概率密度为p (r ),每件商品的贮存费为(与时间⽆关)。
简单数学建模100例

实用标准
分析与假设
①将 243 颗珠子平均分成 3 份,每份 81 颗,任取其 2 份放置在天平两边,若平衡则稍重的一颗在另 1 份中;若不平衡则
稍重的一颗在天平下沉的 1 份中.
②在找出含有稍重珠子的一份中(含 81 颗),再将其 81 颗珠子平均分成 3 份,每份 27 颗,任取其 2 份放置在天平两边,若 平衡则稍重的一颗在另 1 份中;若不平衡则稍重的一颗在天平下沉的 1 份中.
③在找出含有稍重珠子的一份中(含 27 颗),再将其 27 颗珠子平均分成 3 份,每份 3 颗,任取其 2 份放置在天平两边, 若平衡则稍重的一颗在另 1 份中;若不平衡则稍重的一颗在天平下沉的 1 份中.
④在找出含有稍重珠子的一份中(含 1 颗),再将其 3 颗珠子平均分成 3 份,每份 1 颗,任取其 2 颗放置在天平两边,若 平衡则另 1 颗稍重的一颗;若不平衡则稍重的一颗为天平下沉的 1 颗.
【8】甲、乙两人去沙漠中探险,他们每天向沙漠深处走 20 千米,已知每人最多可带一个人 4 天的食物和水。如果允许将部分食物存放于途 中,其中 1 人最远可深入沙漠多少千米?(要求最后两人返回出发点)
分析与假设 要使其中一位探险者尽可能走得远,另一位须先回,留下食物和水给另一位,所以必须分头行动.问题是在何处留下食物和 水?
练习题
文档大全
实用标准
小敏把 100 只彩色小灯泡串联起彩灯,用来布置教室,可是其中有只小灯泡坏了,这可急坏了小敏。你能用最速捷的方法很快地找出了 那只损坏的小灯泡吗?
【7】水果店进了十筐苹果,每筐
10 个,共 100 个,每筐里的苹果重 量都一样,其中有九筐每个苹果的 重量都是 1 斤,另一筐中每个苹果 的重量都是 0.9 斤,但是外表完全 一样,用眼看或用手摸无法分辨。 现在要你用一台普通的大秤一次把 这筐重量轻的找出来。你可以办到么?
数学建模练习题

5.一个身高为153cm,下肢92cm的女士穿高跟鞋,她的鞋跟高度为_______cm看起来最美。
6.某女士身高为165cm,下肢100cm的女士穿高跟鞋,她的鞋跟高度为_______cm看起来最美。
7某人的身高为175cm,他的下肢长度应该_________cm身材比例才协调。
8.欧拉在建立七桥问题数学模型时把桥假设为________,把岛与岸假设为_____9.欧拉通过巧妙的假设,把原来的七桥问题能否不重复走遍问题转化为一个图能否_______问题。
nchester战争数学模型判断战争的结局主要根据双方的_________.11.根据混合战争模型分析美国与越南战争的结局,美国最后失败是因为________________。
12. 商人过河数学模型中用状态变量表示某岸________情况;用决策变量表示_______情况;最后找出状态变量随________变化的规律。
13.兔子出生以后两个月就能生小兔子,假设每次不多不少恰好生一对〔一雌一雄〕。
某人买了初生的小兔子一对,那么一年后共有______对兔子。
〔假设生下来的小兔子都正常活着〕14.拳击冠军的争夺赛中共有63人参加,每轮比赛中出场的两人中的胜者及轮空者进入下一轮,直至比赛完毕,问共需要进展______场比赛,共需要_____轮比赛。
15.在个人围棋冠军的争夺赛中共有67人参加,,每轮比赛中出场的两人中的胜者及轮空者进入下一轮,直至比赛完毕,问共需要进展______场比赛,共需要____ 轮比赛。
16在层次分析法中,当一致性比率小于_______时,通过一致性检验。
17决策按照方案与条件可分为确定型决策、不确定型决策与_______。
18在层次分析法中,当一致性比率大于_______时,认为没有通过一致性检验。
20线性规划问题中根本可行解与可行解域的________等价。
21.在线性规划问题中,根本可行解的非基变量取值应该是_______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模试题
1、新工人的学习曲线
在电冰箱、电视机、汽车等行业中,装配工人的工作是一种重复性的熟练劳动。
在这些行业中,新工人的学习过程如下:刚开始时由于技术不熟练,生产单位产品需要较多的劳动时间,随着不断的工作,新工人的熟练程度逐步提高,生产单位产品所需的劳动时间越来越短;当工人达到完全熟练程度以后,生产单位产品所需要的劳动时间就会稳定在一个定值。
纺织厂招收一批新工人学习1511型织布机的操作。
观察工人的学习过程发现,当累计织完25匹布以后,工人织每匹布需要用16小时;当累计织完64匹布时,工人织每匹布用10小时.已知熟练工人织每匹布用8小时,是确定出新工人的学习曲线,并计算新工人用多少时间才能达到熟练工人的程度。
2、乙酸回收的最好效果
在,A B 两种物质的溶液中,我们想提取出物质A ,可以采取这样的方法:在,A B 的溶液中加入第三种物质C ,而C 与B 不互溶,利用A 在C 中的溶解度较大的特点,将A 提取出来。
这种方法就是化工中的萃取过程。
现有稀水溶液的乙酸,利用苯作为溶剂,设苯的总体积为m 。
进行3次萃取来回收乙酸.问每次应取多少苯量,方使从水溶液中萃取的乙酸最多?
3、陈酒出售的最佳时机
某酒厂有批新酿的好酒,如果现在就出售,可得总收入050R =万元,如果窖
藏起来待来日(第n 年)按陈旧价格出售,第n 年末可得总收入为0R R =元。
而银行利率为0.05r =。
试分析这批好酒窖藏多少年后出售可使总收入的现值最大。
4、电子游戏中的数学
近年来,随着电子游戏的日益普及,电子游戏业已成为横跨信息技术和文化的重要产业。
对电子游戏中的一些数学问题进行研究,成为数学界和相关人士的一个热门话题。
在某电子游戏中,玩家每次下注一元,由机器随机分配给玩家五张扑克牌,然后允许玩家有一次换牌的机会,即可以放弃其中的某几张牌,放弃的牌留下的空缺由机器在剩下的47张牌中再次随机分配。
玩家的奖金依据其最后所持有的牌型而定。
下面是一份典型的奖金分配表:
牌型 奖金(元)
同花大顺(10到A ) 800
同花顺 50
四张相同点数的牌 25
满堂红(三张同点加一对) 8
同花 5
顺子 4
三张相同点数的牌 3
两对 2
一对高分对(J及以上) 1
其它0
在上表中,玩家的牌型属于某一类型且不属于任何更高的类型,则赢得该牌型相应的奖金。
1、若某玩家采取以下策略,当原始的牌型构成一个顺子或更高的牌型时,则放弃换牌的机会;否则,除保留对子或三张相同点数的牌外,将手中其余的牌放弃,由机器再次随机分配。
根据上述游戏规则和策略,分析各类牌型出现的可能性,计算采取该策略能获得的期望奖金金额。
2、对上述策略进行评价。
3、是否存在更好的策略。
若有,请与上述策略进行比较。
5、选址问题
许多学校都建有新校区,常常需要将老校区的教师和工作人员用校车送到新校区。
由于每天到新校区的教师和工作人员很多,往往需要安排许多车辆。
如何有效的安排车辆及让教师和工作人员尽量满意是个十分重要的问题。
现有如下问题请你设计解决。
假设老校区的教师和工作人员分布在50个区,各区的距离见表1。
各区人员分布见表2。
问题1:如果要建立n个乘车点,为使各区人员到最近乘车点的距离最小,应该将校车乘车点建立在哪n个点。
建立一般模型,并给出n=2,3时的结果。
问题2:若考虑每个区的乘车人数,为使教师和工作人员满意度最大,应该将校车乘车点应建立在哪n个点。
建立一般模型,并给出n=2,3时的结果。
