第十届新枝杯
初中数学竞赛列表

目录一、【(全国)数学:初一、初二、初三】全国初中数学联赛 (2)二、【(全国)数学:六年级、初一、初二、初三】全国中学生数理化学科能力竞赛 (5)三、【(全国)数学:初三】全国初中数学竞赛 (7)四、【(全国)数学:六年级、初一、初二】华罗庚金杯少年数学邀请赛 (8)五、【(全国)数学:初一、初二】“希望杯”全国数学邀请赛 (11)六、【(上海)数学:初一、初二、初三】上海市初三数学竞赛(新知杯) (14)一、全国初中数学联赛【竞赛简介】1981年,中国数学会开始举办“全国高中数学联赛”,经过1981、1982、1983三年的实践,这一群众性的数学竞赛活动得到了广大中学师生欢迎,也得到教育行政部门、各级科学技术协会、以及社会各阶层人士的肯定和支持。
“试题所涉及的知识范围不超出现行教学大纲”这一命题原则,得到了更多的理解和拥护,由此“全国高中数学联赛”形成制度。
同时,各地都提出了举行“全国初中数学联赛”的要求。
1984年,中国数学会普及工作委员会商定,委托天津市数学会举办一次初中数学邀请赛,有14个省、市、自治区参加,当时条件较简陋,准备时间也较仓促,天津数学会在南开大学数学系和天津师范大学数学系的大力支持下,极其认真负责地把这次活动搞得很成功,为后来举办“全国初中数学联赛”摸索了很多经验。
当年11月,在宁波召开的中国数学会第三次普及工作会议时,一致通过了举办“全国初中数学联赛”的决定,并详细商定了一些具体办法,规定每年四月的第一个星期天举行“全国初中数学联赛”。
会上湖北省数学会、山西省数学会、黑龙江省数学会分别主动承担了1985年、1986年、1987年的“全国初中数学联赛”承办单位,从此,“全国初中数学联赛”也形成了制度。
“全国初中数学联赛”原来不分一试、二试。
为了更好地贯彻“在普及的基础上不断提高”的方针,1989年7月,在济南召开的“数学竞赛命题研讨会”上,各地的代表商定,初中联赛也分两试进行,并对一、二试各种题型的数目,以及评分标准作出明确的规定,使初中联赛的试卷走向规范化。
最新上海新知杯高中数学竞赛试卷及答案资料

ODCBA2012上海市高中数学竞赛(新知杯)试卷【说明】解答本试卷不得使用计算器一、填空题(本题满分60分,前4题每小题7分,后4小题每小题8分)1.如图,正六边形111111A B C D E F 的边长为1,它的6条对角线又围成一个正六边 形222222A B C D E F ,如此继续下去,则所有这些六边形的面积和是 .2.已知正整数1210,,,a a a 满足:3,1102>≤<≤ji a i j a ,则10a 的最小可能值是 . 3.若17tan tan tan 6αβγ++=,4cot cot cot 5αβγ++=-,cot cot αβγβcot cot +αγcot cot +517-=,则()tan αβγ++= .4.已知关于x 的方程()()lg 2lg 1=+kx x 仅有一个实数解,则实数k 的取值范围是 .5.如图,∆AEF 是边长为x 的正方形ABCD 的内接三角形,已知90∠=︒AEF , ,,==>AE a EF b a b ,则=x . 6.方程1233213+⋅-+=mnn m 的非负整数解(),=m n .7.一个口袋里有5个大小一样的小球,其中两个是红色的,两个是白色的,一个是黑色的,依次从中摸出5个小球,相邻两个小球的颜色均不相同的概率是 .(用数字作答) 8.数列{}n a 定义如下:()1221211,2,,1,2,22+++===-=++n n n n na a a a a n n n .若201122012>+m a ,则正整数m 的最小值为 . 二、解答题 9.(本题满分14分)如图,在平行四边形ABCD 中,AB x =,1BC =, 对角线AC 与BD 的夹角45BOC ∠=︒,记直线AB 与CD 的距离为()h x . 求()h x 的表达式,并写出x 的取值范围.10.(本题满分14分)给定实数1a >,求函数(sin )(4sin )()1sin a x x f x x++=+的最小值.11.(本题满分16分)正实数,,x y z 满足94xyz xy yz zx +++=; 求证:(1)43xy yz zx ++≥;(2)2x y z ++≥.12.(本题满分16分)给定整数(3)n ≥,记()f n 为集合{}1,2,,21n -的满足如下两个条件的子集A 的元素个数的最小值:①1,21nA A ∈-∈;②A 中的元素(除1外)均为A 中的另两个(可以相同)元素的和.(1)求(3)f 的值;(2)求证:(100)108f ≤.2012上海市高中数学竞赛(新知杯)参考答案12、923、114、(){},04-∞ 52 6、()()3,0,2,2 7、25 8、40259.解 由平行四边形对角线平方和等于四条边的平方和得2222211()(1)22OB OC AB BC x +=+=+. ① …………………(2分)在△OBC 中,由余弦定理2222cos BC OB OC OB OC BOC =+-⋅∠,所以221OB OC OC +⋅=, ②由①,②得2OB OC ⋅= ③ …………………(5分)所以:144sin 2ABCD OBC S S OB OC BOC ∆==⋅⋅∠OC =⋅212x -=,故:()AB h x ⋅212x -=, 所以 :21()2x h x x -=. …………………(10分)由③可得,210x ->,故1x >.因为222OB OC OB OC +≥⋅,结合②,③可得:221(1)22x +≥解得(结合1x >)11x <≤.综上所述,21()2x h x x-=,11x <≤. …………………(14分)10.解 (sin )(4sin )3(1)()1sin 21sin 1sin a x x a f x x a x x ++-==++++++.当71a <≤时,02≤,此时:3(1)()1sin 221sin a f x x a a x-=++++≥++,且当(]()sin 11,1x =∈-时不等式等号成立,故min ()2f x a =+. ………(6分)当73a >2>,此时“耐克”函数3(1)a y t t-=+在(内是递减,故此时min 3(1)5(1)()(1)2222a a f x f a -+==+++=.综上所述,min 72,1;3()5(1)7,.23a a f x a a ⎧+<≤⎪⎪=⎨+⎪>⎪⎩ …………………(14分) 11.证 (1)记t =33223xy yz zx xyz ++⎛⎫=≤ ⎪⎝⎭.…………………(4分)于是 324993xyz xy yz zx t t =+++≤+, 所以 ()()2323320t t t -++≥,而23320t t ++>,所以320t -≥,即23t ≥,从而43xy yz zx ++≥. …………………(10分) (2)又因为:2()3()x y z xy yz zx ++≥++,所以 2()4x y z ++≥,故 2x y z ++≥. …………………(16分) 12.解 (1)设集合{}31,2,,21A ⊆-,且A 满足(a ),(b ).则1,7A A ∈∈.由于{}()1,,72,3,,6m m =不满足(b ),故3A >.又 {}{}{}{}{}{}{}1,2,3,7,1,2,4,7,1,2,5,7,1,2,6,7,1,3,4,7,1,3,5,7,1,3,6,7, {}{}{}1,4,5,7,1,4,6,7,1,5,6,7都不满足 (b ),故4A >.而集合{}1,2,4,6,7满足(a ),(b ),所以(3)5f =. …………………(6分) (2)首先证明:(1)()2,3,4,f n f n n +≤+=. ①事实上,若{}1,2,,21n A ⊆-,满足(a ),(b ),且A 的元素个数为()f n . 令{}1122,21n n B A ++=--,由于12221n n +->-,故()2B f n =+.又111222(21),211(22)n n n n +++-=--=+-,所以,集合{}11,2,,21n B +⊆-,且B 满足(a ),(b ).从而:(1)()2f n B f n +≤=+. …………………(10分)其次证明: (2)()1,3,4,f n f n n n ≤++=. ②事实上,设{}1,2,,21n A ⊆-满足(a ),(b ),且A 的元素个数为()f n . 令{}222(21),2(21),,2(21),21nn n n n B A=----,由于 222(21)2(21)2(21)21nnn n n -<-<<-<-,所以{}21,2,,21n B ⊆-,且()1B f n n =++.而12(21)2(21)2(21),0,1,,1k nknknk n +-=-+-=-, 2212(21)(21)nnnn-=-+-,从而B 满足(a ),(b ),于是:(2)()1f n B f n n ≤=++. …………………(14分)由①,②得 (21)()3f n f n n +≤++. ③反复利用②,③可得(100)(50)501(25)25151f f f ≤++≤+++(12)12377(6)6192f f ≤+++≤+++(3)3199108f ≤+++=. …………………(16分)。
浙江省强基联盟2024-2025学年高二上学期10月联考数学试卷含答案

浙江强基联盟2024年10月高二联考数学试题(答案在最后)浙江强基联盟研究院命制考生注意:1.本试卷满分150分,考试时间120分钟.2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效.............,在试题卷....、草稿纸上作答无效.........一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在空间直角坐标系中,已知点(2,1,2),(1,2,2)A B --,则AB =()A.(1,3,4)-B.(2,6,8)-C.(1,3,1)--D.(2,6,2)--【答案】A 【解析】【分析】根据题意,结合向量减法运算的运算法则,即可求解.【详解】由向量减法运算的运算法则,因为(2,1,2),(1,2,2)A B --,可得(1,3,4)AB =-。
故选:A.2.直线10x y -+=的倾斜角为()A.1B.6π C.4π D.34π【答案】C 【解析】【分析】先求出斜率,然后根据倾斜角与斜率的关系,即可得到结果.【详解】由方程得直线斜率111k =-=-,所以倾斜角4πα=.故选:C .3.已知α,β是两个不重合的平面,且直线l α⊥,则“ αβ⊥”是“//l β”的()A .充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】由线面、面面关系,结合平面的基本性质判断线面关系,根据面面垂直的判定判断线面是否平行,再由充分、必要性定义判断条件间的充分、必要关系.【详解】解:由l α⊥,若αβ⊥,则,l β可能平行或l β⊂,充分性不成立;由l α⊥,//l β,由面面垂直的判定知αβ⊥,必要性成立.所以“ αβ⊥”是“//l β”的必要不充分条件.故选:B.4.在平面直角坐标系中,直线:123x yl -=,则直线l 过()A.一、二、三象限B.一、二、四象限C.二、三、四象限D.一、三、四象限【答案】D 【解析】【分析】用坐标轴上的截距得到大致草图可解.【详解】直线在x 轴上截距为2,y 轴上截距为3-,画出直线l ,发现直线l 过一、三、四象限,故选:D.5.设复数z 满足1z i +=,z 在复平面内对应的点为(),P x y ,则点P 的轨迹方程为()A.()2211x y ++= B.()2211x y -+=C.()2211x y +-= D.()2211x y ++=【答案】D 【解析】【分析】复数z 满足1z i +=,由复数的模的几何意义可得:z 在复平面内对应的点(),P x y 到复数i -在复平面内对应的点()0,1A -的距离为1,再求解即可.【详解】解:由z 在复平面内对应的点为(),P x y ,且复数z 满足1z i +=,由复数的模的几何意义可得:z 在复平面内对应的点(),P x y 到复数i -在复平面内对应的点()0,1A -的距离为11=,则点P 的轨迹方程为()2211x y ++=,故选:D.【点睛】本题考查了复数的模的几何意义,重点考查了运算能力,属基础题.6.已知点(1,2,3)Q ,平面{|0}P n PQ α=⋅= ,其中(2,1,2)=-n ,则点(1,0,1)A -到平面α的距离是()A.53B.73C.2D.3【答案】C 【解析】【分析】根据题意,求得(2,2,2)QA =---和平面α的法向量,结合向量的距离公式,即可求解.【详解】由点(1,2,3),,(1,01)A Q -,可得(2,2,2)QA =---,又由{|0}P n PQ α=⋅= ,可得向量n为平面α的法向量,且3n = ,则4246QA n =-+-⋅=-uu r r ,所以点A 到平面α的距离为||623||QA n d n ⋅===.故选:C.7.正八面体结构(正八面体每个面都是正三角形)作为一种对称稳定的几何结构,在物质世界中具有广泛的应用.从晶体材料到生物分子,正八面体结构都发挥着重要作用,影响着物质的性质.如六氟化硫(化学式为6SF )分子结构为正八面体结构,在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.则在如图所示的正八面体E ABCD F --中,二面角E AB F --的正弦值为()A.13B.223C.33D.63【答案】B 【解析】【分析】由图可得EGF ∠为所求的二面角的平面角,后由余弦定理可得答案.【详解】取AB 中点G ,连结EG ,GF ,EF ,由正八面体定义可知,EGF ∠为所求的二面角的平面角,不妨设2AB =,则3EG FG ==22EF =,在EFG 中,由余弦定理,得222(3)(3)(22)1cos 3233EGF ∠+-=-⨯⨯,所以22sin 3EGF ∠=.故选:B.8.已知正三角形ABC 的边长为1,D 在平面ABC 内,若向量AD 满足2430AD AD AB -⋅+=,则||CD 的最大值为()A.31+B.31-C.2 D.3【答案】A 【解析】【分析】利用平面向量的坐标运算,确定出点D 的轨迹为圆,即可求解.【详解】以A 为坐标原点,AB 为x 轴建立平面直角坐标系,如图,设(,)D x y ,则(,)AD x y = ,(1,0)AB =,所以,满足2430AD AD AB -⋅+=的点D 坐标满足:22430x y x +-+=,即D 在以(2,0)E 为圆心,1为半径的圆上,当C ,E ,D 三点共线,且D 在如图所示位置时,||CD最大,因为1(,22C ,所以CE ==,,所以max ||1CD =.故选:A.二、多项选择题:本大题共3小题,每小题,共1.在每小题给出的选项中,有多项符合题目要求.全部选对的得,部分选对的得部分分,有选错的得0分.9.在空间直角坐标系O xyz -中,已知(1,2,1)A -,(0,1,1)B ,下列结论正确的有()A.||4AB = B.1OA OB ⋅= C.若(4,2,)n t = ,且n AB ⊥,则3t = D.若(1,1,)m k = 且//m AB,则2k =【答案】BC 【解析】【分析】根据题意,得到向量(1,2,1)OA =- ,(0,1,1)OB =,(1,1,2)AB =-- ,结合空间向量的坐标运算法则,逐项判定,即可求解.【详解】对于A ,因为(1,2,1)A -,(0,1,1)B ,所以(1,1,2)AB =-- ,可得||AB ==A 错误;对于B ,因为(1,2,1)OA =- ,(0,1,1)OB = ,所以0211OA OB ⋅=+-=,所以B 正确;对于C ,若(4,2,)n t = ,且n AB ⊥ ,则4(1)2(1)20n AB t =⨯-+⨯-+⋅⨯=,解得3t =,所以C 正确,对于D ,若(1,1,)m k = 且//m AB ,因为(1,1,2)AB =-- ,可得112k=-,解得2k =-,所以D 错误.故选:BC.10.已知曲线22:x y x y Ω+=+,点(,)P a b 在曲线Ω上,则下列结论正确的是()A.曲线Ω有4条对称轴B.3a b ++的最小值是C.曲线Ω围成的图形面积为π2+ D.2ba -的最大值是1【答案】ACD 【解析】【分析】当0,0x y >>时,化简方程为22111()()222x y -+-=,结合曲线Ω的对称性,画出曲线Ω的图象,结合图象,可得判定A 正确,把3a b ++表示曲线Ω上的点P 到直线30x y ++=倍,可判定B 错误;结合圆的面积公式和正方形的面积公式,可判定以C 正确;设2bk a =-表示点(2,0)与点P 确定的直线的斜率,结合图象,利用点到直线的距离公式,列出方程,可得判定D 正确.【详解】当0,0x y >>时,原方程化为22x y x y +=+,即22111()()222x y -+-=,所以曲线是以圆心为11,22⎛⎫⎪⎝⎭,半径为2的圆在第一象限的部分,又由22||||x y x y +=+图象关于x 轴,y 轴对称,所以曲线Ω,如图所示.,对于A 中,由图象可得,该曲线Ω关于x 轴,y 轴,y x =和y x =-对称,所以该曲线Ω有4条对称轴,所以A 正确,对于B 中,由3a b ++表示曲线Ω上的点P 到直线30x y ++=倍,结合图象得,当(,)P a b 是(1,1)--2=,所以3a b ++最小值为12=,所以B 错误;对于C 中,曲线Ω的正方形组成,所以面积为22(π24π22⨯+=+,所以C 正确;对于D 中,设2bk a =-表示点(2,0)与点P 确定的直线的斜率,设该直线方程为(2)y k x =-,结合图象,当0,0x y ><,即22x y x y +=-,则圆心为11,22⎛⎫-⎪⎝⎭,半径为2的圆在第四象限的部分与直线相切时,该切线的斜率是k 的最大值,由d r =,可得2=,解得1k =或17k =-(舍),则k 的最大值为1,所以D 正确.故选:ACD.11.正方体1111ABCD A B C D -的棱长为1,E ,F 分别是11B C ,11C D 的中点,点P 在正方体表面上运动,且(0PA x x =<<,记点P 的轨迹长度为()f x ,则下列结论正确的是()A.3π(1)2f =B.3πf =C.若//PA 平面BEF ,且点P ∈平面11A C ,则x的最小值为3D.若(,)BP BE BF λμλμ=+∈ R,则()2f x =+【答案】AD 【解析】【分析】A 选项,得到点P 的轨迹为以A 为球心,1为半径的球与正方体表面的交线,从而求出轨迹长度;B 选项,与A 同理可得;C 选项,作出辅助线,得到点P 的轨迹是线段HI ,则当AP HI ⊥时,AP 最小,由勾股定理求出答案;D 选项,作出辅助线,得到P 的轨迹为等腰梯形EFDB ,求出轨迹总长()f x .【详解】对于A 、B ,如图,(1)f 等于以A 为球心,1为半径的球与正方体表面的交线总长,所以(1)2π3f =,故A 正确;(2)f 等于以A 2为半径的球与正方体表面的交线总长,21>,所以球A 与过A 的三个正方体表面没有交线,与另外三个面的交线长为2π3π3(2)122⨯-=,故B 错误;对于C ,如图,取11A D 的中点H ,11A B 的中点I ,连接,,,,,EF BE BF HI AH AI ,可知//,//HI AH BE EF ,因为EF ⊂平面EFB ,HI ⊄平面EFB ,所以//HI 平面EFB ,同理可得//AH 平面EFB ,又AH HI H = ,,AH HI ⊂平面AHI ,故平面//AHI 平面EFB ,则当点P ∈平面AHI 时,//PA 平面EFB ,又点P ∈平面11A C ,所以点P 的轨迹是线段HI ,则当AP HI ⊥时,AP 最小,由勾股定理得22232144AP ⎛⎫=+= ⎪ ⎪⎝⎭,即x 的最小值为324,故C 错误;对于D ,因为(,)BP BE BF λμλμ=+∈R ,所以点P 与点B ,E ,F 共面,从而点P 的轨迹为平面BEF 与正方体表面的交线,连接BD ,则//EF BD ,故,,,B D E F 四点共面,画出交线如图,所以P 的轨迹为等腰梯形EFDB (如图),故轨迹总长2532()225f x =,故D 正确.故选:AD.【点睛】思路点睛:(1)直接连接法:有两点在几何体的同一个平面上,连接该两点即为几何体与截面的交线,找截面就是找交线的过程;(2)作平行线法:过直线与直线外一点作截面,若直线所在的平面与点所在的平面平行,可以通过过点找直线的平行线找到几何体与截面的交线;(3)作延长线找交点法:若直线相交但在立体几何中未体现,可通过作延长线的方法先找到交点,然后借助交点找到截面形成的交线;(4)辅助平面法:若三个点两两都不在一个侧面或者底面中,则在作截面时需要作一个辅助平面.三、填空题:本大题共3小题,每小题5分,共15分.12.已知直线1:22l y x =+,直线:m y kx =,若l m ⊥,则实数k 的值为________.【答案】−2【解析】【分析】根据垂直关系得到直线的斜率之积为1-,得到方程,求出2k =-.【详解】因为l m ⊥,所以两直线的斜率之积为1-,即112k =-,所以2k =-.故答案为:−2.13.已知在直三棱柱111ABC A B C -中,90ABC ∠= ,1CB =,2CA =,M 是1CC 的中点,若1AM BA ⊥,则1AA =________.【答案】6【解析】【分析】建立空间直角坐标系,设1AA t =,再利用空间向量求解即可.【详解】以B 为坐标原点,分别以BA ,BC ,1BB 所在直线为x ,y ,z 轴建立空间直角坐标系,设1AA t =,则由题意:A ,0,1,2t M ⎛⎫⎪⎝⎭,1)A t ,则2t AM ⎛⎫= ⎪⎝⎭,1)BA t =,又1AM BA ⊥所以21302t BA AM ⋅=-+= ,解得t =,即1AA =..14.在平面直角坐标系中,已知圆22:21M x y x ++=,直线:230l x y --=,过l 上一点P 作圆M 的切线,切点为A ,则PA PM ⋅的最小值为________.【答案】3【解析】【分析】利用直线与圆的位置关系,结合平面向量数量积的几何意义将PA PM ⋅ 化为22PM - ,计算minPM 即可.【详解】由题意()2212x y ++=,则圆M的半径()1,0AM M =-,根据向量数量积的几何意义,得2222PA PM PA PM MA PM ⋅==-= 2-.所以只要PM 最小即可,当PM l ⊥时,min ||PM ==,所以PA PM⋅的最小值为223-=.故答案为:3四、解答题:本大题共5小题,共7.解答应写出必要的文字说明、证明过程及演算步骤.15.已知空间三点(0,2,3)A ,(2,1,6)B -,(1,1,5)D -,以向量AB ,AD为一组邻边组成平行四边形ABCD ,(1)求C 点坐标;(2)求平行四边形ABCD 的面积S .【答案】(1)(1,2,8)--(2)【解析】【分析】(1)设(,,)C x y z ,根据空间向量的线性运算及平行四边形法则求解即可;(2)先根据空间向量求出,AB AD,进而结合面积公式求解即可.【小问1详解】设(,,)C x y z ,则(2,1,3)AB =-- ,(1,3,2)AD =- ,(,2,3)AC x y z =--,由平行四边形法则:(1,4,5)(,2,3)AC AB AD x y z =+=--=--,所以1x =-,2y =-,8z =,即C 点坐标为(1,2,8)--.【小问2详解】由题意,||AB ==,||AD ==,1cos ,2AB AD AB AD AB AD ⋅==⋅,所以π,3AB AD = ,所以πsin3S AB AD =⋅⋅==.16.如图,在直三棱柱111ABC A B C -中,底面是等腰三角形,120ACB ∠= ,1AC BC AA ==,D ,E 分别是棱AB ,11B C 的中点.(1)求证://DE 平面11ACC A ;(2)求直线DE 与平面11A B C 所成的角的正弦值.【答案】(1)证明见解析;(2)35.【解析】【分析】(1)取AB 中点D ,以点D 为原点建立空间直角坐标系,利用空间位置关系的向量证明推理即得.(2)求出平面11A B C 的法向量,利用线面角的向量求法求解即得.【小问1详解】在直三棱柱111ABC A B C -中,AC BC =,120ACB ∠= ,取AB 中点D ,连接CD ,则CD AB ⊥,过点D 作1//Dz AA ,由1AA ⊥平面ABC ,得Dz ⊥平面ABC ,则直线,,DB DC Dz 两两垂直,以点D 为原点,直线,,DB DC Dz 分别为,,x y z轴建立空间直角坐标系,设2AC =,则1(0,0,0),(0,1,)1((0,0),,1,2)(,,222D C A CE ,则1(,,2)22DE =,0)AC =,1AC = ,设平面11ACC A 的法向量(,,)n x y z =,则1020n AC y n AC y z ⎧⋅=+=⎪⎨⋅=++=⎪⎩,取1x =,得(1,n =,于是0022DE ⋅=-+=n ,即DE n ⊥ ,//DE 平面11ACC A ,又DE ⊄平面11ACC A ,所以//DE 平面11ACC A .【小问2详解】由(1)知(0,1,0)C,1)2(0,A,1B,则1(1,2)CA =-,11A B =,设平面11CA B 的法向量为(,,)m a b c =,则11120m CA b c m A B ⎧⋅=-+=⎪⎨⋅==⎪⎩,取1c =得(0,2,1)m = ,又31(,,2)22DE = ,设直线DE 与平面11A B C 所成的角为θ,则|3sin |cos ,|5|||||DE m DE m DE m θ⋅=〈〉===,所以直线DE 与平面11A B C 所成的角的正弦值为35.17.已知平面直角坐标系中,圆22:8O x y +=,点(4,2)P -,(1)若A 是圆O 上的动点,线段AP 的中点为M ,求M 的轨迹方程;(2)以OP 为直径的圆交圆O 于C ,D 两点,求CD .【答案】(1)22(2)(1)2x y ++-=(2)5CD =【解析】【分析】(1)利用轨迹方程求法设(,)M x y ,可求得M 的轨迹方程为22(2)(1)2x y ++-=;(2)求出公共弦CD 的方程240x y -+=,利用点到直线距离以及弦长公式可得5CD =.【小问1详解】设(,)M x y ,00(,)A x y ,则根据题意可得()004,22,2x x y y ⎧+-=⎪⎪⎨+⎪=⎪⎩所以可得002422x x y y =+⎧⎨=-⎩,代入圆22:8O x y +=,得()()2224228x y ++-=,化简得()()22212x y ++-=,M 的轨迹方程为()()22212x y ++-=.【小问2详解】如下图所示:因为OP 的中点坐标为()2,1-,OP ==,所以以OP 为直径的圆的方程为22(2)(1)5++-=x y ,即22420x y x y ++-=.圆22420x y x y ++-=的圆心为()2,1-,半径为圆228x y +=的圆心为()0,0,半径为+-<<,两圆相交,由22228420x y x y x y ⎧+=⎨++-=⎩得直线CD 的方程240x y -+=.圆心O 到直线CD 的距离d =O 的半径R =,可得CD ===,4305CD ==,所以4305CD =.18.如图,三棱锥P ABC -中,底面ABC 是边长为2的等边三角形,PA PC ==.(1)若PB =,求三棱锥P ABC -的外接球的表面积;(2)若异面直线PC 和AB 所成角的余弦值为4,点F 是线段PB (不含端点)上的一个动点,平面ACF 与平面PBC 的夹角为α,求cos α的取值范围.【答案】(1)6π(2)7⎡⎢⎣⎭【解析】【分析】(1)根据题意可知PA ,PB ,PC 两两垂直,所以可将其补成正方体,正方体对角线就是外接球的直径,再根据外接球的表面积计算公式可求解;(2)根据异面直线所称的角的关系求出OB OP ⊥,构建空间坐标系,分别求出平面ACF 的一个法向量m,平面PBC 的一个法向量为n,再利用空间向量法求出二面角的余弦值取值范围.【小问1详解】当PB =时,PA ,PB ,PC 两两垂直,可将其补成正方体,正方体的体对角线即为外接球的直径.所以三棱锥P ABC -的外接球直径为:2R =,两边平方得246R =,所以24π6πS R ==.【小问2详解】如图,取AC 中点O ,由题意,1OP =,OB =,设POB θ∠=,OC a =,OB b = ,OP c =.则0a b ⋅=,0a c ⋅= ,θ⋅=b c ,因为PC ,AB 所成角的余弦值为24,所以cos ,4PC AB PC AB PC AB⋅=〈〉== ,得1PC AB ⋅=±.又PC =-a c ,AB =+b a ,2()()11PC AB θ⋅=-+=⋅+-⋅-⋅=-=±a c b a a b a c b c a,解得cos 0θ=或cos 13θ=>(舍去).所以cos 0θ=,此时,90〈〉=︒b c ,这样,可以以OA ,OB ,OP分别为x ,y ,z 轴正方向,建立空间直角坐标系(如图).则(1,0,0)A ,3,0)B ,(1,0,0)C -,(0,0,1)P ,设(,,)F x y z ,因为点F PB ∈,所以设((0,1))PF tPB t =∈,3,1)PB =- ,(,,1)PF x y z =-,所以(,,1)3,1)x y z t -=-.所以0,3,1,x y t z t =⎧⎪=⎨⎪=-⎩得3,1)F t t -.因为(2,0,0)AC =- ,3,1)OF t t =-,设平面ACF 的一个法向量000(,,)m x y z =,则00020,3(1)0,AC m x OF m ty t z ⎧⋅=-=⎪⎨⋅=+-=⎪⎩ 取(0,1,3)m t t =- ,又(1,0,1)PC =--,3,1)PB =- ,同理可求得平面PBC 的一个法向量为(3,1,3)n =-.因为平面ACF 与平面PBC 的夹角为α,所以2222||71681cos 7421||||(1)37m n t t t t m n t t α⋅-+===-+-+⋅ 设242x t t =-,(0,1)t ∈,1,24x ⎡⎫∈-⎪⎢⎣⎭,则221681414211t t x t t x -++=-++,记()413411x f x x x +==-++,1,24x ⎡⎫∈-⎪⎢⎣⎭,显然()f x 在1,24x ⎡⎫∈-⎪⎢⎣⎭上单调递增,所以min 1()04f x f ⎛⎫=-= ⎪⎝⎭,当2x →时,()3f x →,所以21cos 0,7α⎡⎫∈⎪⎢⎪⎣⎭.即cos α的取值范围是210,7⎡⎫⎪⎢⎪⎣⎭.19.古希腊亚历山大时期最后一位重要的几何学家帕普斯(Pappus ,公元3世纪末)在其代表作《数学汇编》中研究了“三线轨迹”问题:平面上,到两条已知直线距离的乘积是到第三条直线距离的平方的k 倍的动点轨迹为二次曲线(在平面上,由二元二次方程所表示的曲线,叫做二次曲线).常数k 的大小和直线的位置等决定了曲线的形状.为了研究方便,我们设平面内三条给定的直线为(1,2,3)i l i =,当三条直线中有相交直线时,记12l l A ⋂=,23l l B ⋂=,31l l C ⋂=,动点P 到直线i l 的距离为(1,2,3)i d i =,且满足2123d d kd =.阅读上述材料,完成下列问题:(1)当12l l //,31l l ⊥时,若1k =,且1l 与2l 的距离为2,点P 在1l 与2l 之间运动时,求动点P 的轨迹所围成的面积.(2)若ABC V 是等腰直角三角形,BAC ∠是直角,点P 在BAC ∠内(包括两边)运动,试探求k 为何值时,P 的轨迹是圆?(3)若ABC V 是等腰三角形,AB AC =,点P 在BAC ∠内(包括两边)任意运动,当1k =时,问在此等腰三角形对称轴上是否存在一点D ,使PAPD为大于1的定值.若存在,求出点D 的位置,若不存在,请说明理由.【答案】(1)π(2)当1k =时,P 的轨迹是圆(3)存在,点D 为BC 中点【解析】【分析】(1)适当建系,以1l 为y 轴,3l 为x 轴,同时2:2l x =,再结合新定义确定轨迹方程即可求解;(2)适当建系,以A 为坐标原点,1l 为y 轴,2l 为x 轴,同时3:0(0)l x y c c +-=>.再结合新定义即可求解;(3)适当建系,以A 为坐标原点,CAB ∠的角平分线为x 轴,设1:l y tx =,2:(0)l y tx t =->,3:(0)l x a a =>,结合新定义列出等式即可求解.【小问1详解】以1l 为y 轴,3l 为x 轴,建立平面直角坐标系,2:2l x =,设(,)P x y ,因为P 在1l ,2l 之间,所以1d x =,22d x =-,3||d y =,由定义得2123d d d =,所以2(2)x x y -=,化简得22(1)1x y -+=,表示以(1,0)为圆心,1为半径的圆.所以动点P 的轨迹围成的图形面积2ππS r ==.【小问2详解】以A 为坐标原点,1l (AB )为y 轴,2l (AC )为x 轴,建立平面直角坐标系.设()3:0(0)l BC x y c c +-=>,点(,)(00)P x y x y ≥≥且,则1d x =,2d y =,3d =,2123d d kd =,代入坐标得:2222222x y c xy cx cyxy k +++--=.化简整理:222(22)220kx ky k xy kcx kcy kc ++---+=①当1k =时,方程①没有xy 项,此时方程①为:222220x y cx cy c +--+=.即222()()x c y c c -+-=,此方程表示圆心为(,)c c ,半径为c 的圆,所以当1k =时,P 的轨迹是圆.【小问3详解】以A 为坐标原点,CAB ∠的角平分线为x 轴,建立平面直角坐标系,设()1:l AB y tx =,()2:(0)l AC y tx t =->,()3:(0)l BC x a a =>,点(,)P x y ,先求点P 的轨迹方程:由1d =P 在CAB ∠内部,所以0tx y ->,得1d =同理:2d =3||d x a =-.由题意,当1k =时,得2||x a =-.化简整理得:222222(1)(1)0x y a t x a t +-+++=.②假设存在点(,0)(0)D m m >,满足条件,则PA PD =③由②得:222222(1)(1)x y a t x a t +=+-+.代入③得PAPD=要使此式为定值,则22222()2(1)at a m a t m a+-=+-,化简得m a =,故存在点(a,0)D ,即点D 为3l 与CAB ∠的角平分线的交点,即点D 为BC 中点,此时1PA PD t=>.【点睛】关键点点睛:这类新定义的关键是适当建系,简化计算过程,减少计算量是关键点.。
2009年上海市高中数学竞赛(新知杯)试题及答案

2009年上海市高中数学竞赛(新知杯)试卷(2009年3月22日 星期日 上午8:30~10:30)【说明】解答本试卷不得使用计算器一、填空题(本题满分60分,前4小题每小题7分,后4小题每小题8分) 1. 设1210,,,(1,)a a a ∈+∞L ,则121012102009200920092009log log log loga a a a a a +++L L 的最小值是 。
2. 已知,*x y N ∈,且12121999x y -+++=++++L L ,则将y 表示成x 的函数,其解析式是y = 。
3. 已知函数2()|2|f x x =-,若()()f a f b =,且0a b <<,则ab 的取值范围是 。
4. 满足方程222213log [2cos ()]2cos ()4xy y y xy +=-++的所有实数对(,)x y = 。
5. 若 []a 表示不超过实数 a 的最大整数,则方程 2[tan ]2sin x x =的解是 。
6.不等式223242xx ≤⋅+⋅的解集是 。
7. 设A 是由不超过2009的所有正整数构成的集合,即{1,2,,2009}A =L ,集合L A ⊆,且L 中任意两个不同元素之差都不等于4,则集合L 元素个数的最大可能值是 。
8. 给出一个凸10边形及其所有对角线,在以该凸10边形的顶点及所有对角线的交点为顶点的三角形中,至少有两个顶点是该凸10边形顶点的三角形有 个。
二、解答题9.(本题满分14分)设函数()f x 定义于闭区间[0,1],满足(0)0,(1)1f f ==,且对任意,[0,1],x y x y ∈≤,都有22()(1)()()2x yf a f x a f y +=-+,其中常数a 满足01a <<,求a 的值。
10. (本题满分14分)如图,A 是双曲线2214x y -=的右顶点,过点A 的两条互相垂直的直线分别与双曲线的右支交于点,M N ,问直线MN这样的定点,请说明理由;如果存在这样的定点P11. (本题满分16分)设,A B 是集合12345{,,,,}a a a a a 的两个不同子集,使得A 不是B 的子集,B 也不是A 的子集,求不同的有序集合对(,)A B 的组数。
中数学各类竞赛获奖一览表

王圣仕
第九届全国“华罗庚金杯”少年数学邀请赛决赛三等奖
王进敬
2003、12
04届4班
徐磊
2003年上海市数学竞赛二等奖
梁国胜
2003、12
05届5班
俞若诚
2003年上海市数学竞赛三等奖
涂斌祖
吕尤
第五届小学希望杯全国数学邀请赛六年级三等奖
王进敬
10届7班
左淳诚
第五届小学希望杯全国数学邀请赛六年级三等奖
王进敬
2007
10届6班
毛雁
2007年第七届“中环杯”中小学生思维能力训练活动(市级)决赛二等奖
王进敬
2007
10届6班
王诗伟
2007年第七届“中环杯”中小学生思维能力训练活动(市级)决赛三等奖
涂斌祖
徐驰
华中师范大学数统学院第九届全国中学生数学奥林匹克活动二等奖
涂斌祖
俞若诚
华中师范大学数统学院第九届全国中学生数学奥林匹克活动一等奖
涂斌祖
朱志尧
华中师范大学数统学院第九届全国中学生数学奥林匹克活动一等奖
涂斌祖
2004、12
05届5班
俞若诚
2004年上海初三数学竞赛二等奖
涂斌祖
朱志尧
2004年上海初三数学竞赛二等奖
11届6班
陈晓轩
第二十届“五羊杯”初中数学竞赛预备年一等奖
但水平
2009.2
11届6班
戎欣
第二十届“五羊杯”初中数学竞赛预备年三等奖
但水平
2009.2
11届6班
马大任
第二十届“五羊杯”初中数学竞赛预备年三等奖
但水平
2009.2
11届6班
刘唯楚
最新上海市新知杯初中数学竞赛试题及答案(1)
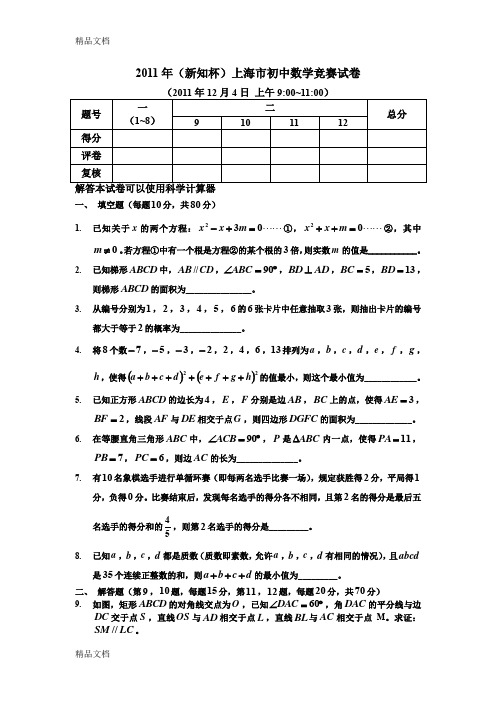
2011年(新知杯)上海市初中数学竞赛试卷一、 填空题(每题10分,共80分)1. 已知关于x 的两个方程: 032=+-m x x ①, 02=++m x x ②,其中0≠m 。
若方程①中有一个根是方程②的某个根的3倍,则实数m 的值是___________。
2. 已知梯形ABCD 中,AB //CD ,︒=∠90ABC ,AD BD ⊥,5=BC ,13=BD ,则梯形ABCD 的面积为_______________。
3. 从编号分别为1,2,3,4,5,6的6张卡片中任意抽取3张,则抽出卡片的编号都大于等于2的概率为______________。
4. 将8个数7-,5-,3-,2-,2,4,6,13排列为a ,b ,c ,d ,e ,f ,g ,h ,使得()()22h g f e d c b a +++++++的值最小,则这个最小值为____________。
5. 已知正方形ABCD 的边长为4,E ,F 分别是边AB ,BC 上的点,使得3=AE ,2=BF ,线段AF 与DE 相交于点G ,则四边形DGFC 的面积为_____________。
6. 在等腰直角三角形ABC 中,︒=∠90ACB ,P 是ABC ∆内一点,使得11=PA ,7=PB ,6=PC ,则边AC 的长为______________。
7. 有10名象棋选手进行单循环赛(即每两名选手比赛一场),规定获胜得2分,平局得1分,负得0分。
比赛结束后,发现每名选手的得分各不相同,且第2名的得分是最后五名选手的得分和的54,则第2名选手的得分是_________。
8. 已知a ,b ,c ,d 都是质数(质数即素数,允许a ,b ,c ,d 有相同的情况),且abcd是35个连续正整数的和,则d c b a +++的最小值为_________。
二、 解答题(第9,10题,每题15分,第11,12题,每题20分,共70分)9. 如图,矩形ABCD 的对角线交点为O ,已知︒=∠60DAC ,角DAC 的平分线与边DC 交于点S ,直线OS 与AD 相交于点L ,直线BL 与AC 相交于点M 。
2011上海市高中数学竞赛(新知杯)

2011上海市高中数学竞赛(新知杯)试卷【说明】解答本试卷不得使用计算器一、填空题(本题满分60分,前4题每小题7分,后4小题每小题8分)1.方程组271211x x y x y ++⎧=⎪⎨+=⎪⎩的解集是 。
2.在平面直角坐标系中,长度为1的线段AB 在x 轴上移动(点A 在点B 的左边),点(0,1)P 与点A 连成直线,点(1,2)Q 与点B 连成直线,则直线PA 与直线QB 的交点R 轨迹的普通方程是 。
3.已知M 是椭圆221169x y +=在第一象限的弧上一动点,MN y ⊥轴,垂足为N ,当OMN ∆面积最大时,它的内切圆半径r = 。
4.已知ABC ∆的外接圆半径为1,角A B C 、、的平分线分别交ABC ∆的外接圆于点111A B C 、、,则111coscos cos 222sin sin sin A B C AA BB CC A B C++++的值为 。
5.设()sin[(1)]2f x a x π=++,其中,a b 为实常数,若(lg5)5f =,则(lg 20)f 的值为 。
6.在平面直角坐标系中,O 为坐标原点,点(3,),(3,)A a B b 使45AOB ∠= ,其中,a b 为整数,且a b >,则满足条件的数对(,)a b 共有 组。
7.已知圆C 的方程为224210x y x y +--+=(圆心为点O ),直线(tan10)y x = C 交于A B 、两点,则直线AC BC ,的倾斜角之和为 。
8.甲、乙两运动员乒乓比赛在进行中,甲必须再胜2局才最后获胜;乙必须再胜3局才最后获胜,若甲、乙两人每局取胜的概率都是12,则甲最后获胜的概率是 。
(用最简分数作答) 二、解答题(共60分)9.(本题满分14分)对于两个实数,a b ,min{,}a b 表示,a b 中的较小数,求所有的非零实数x ,使41min{,4}8min{,}x x x x+≥⋅。
2010年新知杯上海市高中数学竞赛

丽
< <
。
求 这 种 n的最 小值.
中 等 数 学
参 考 答 案
一
、[ ,, ,】 1_6 【 . . 2]詈
=
1
一
=
一
【一)(—】 2t t) 了一t ) 詈 4= 3 一 2 -)一(2+ . £ ) 3
.
由 1 4 /0 得 一 ≤ 2+ x— > , 2 ≤6 此 时 , .
故g = ( )g ) () Ⅱ — . , (
21 第 5 0 1年 期
3 1
其 中 , ( 为 整 系数多项 式. q ) 于是 ,
gO ( 、=1 20 0: 一1 9 1— 1 9 9
=
由平均 不等 式及 积化 和差 得
A ≥6 B
Ⅱ ( X go. 一 i () )
Q
图4
当 34 a 0 , 都有 1 0 3  ̄ ≤l 0时 b < 0 0种取法. 0
故 (>) P 了 詈1
2 (+) (+ ) …+2 3 )6 0 +2 3+2 2 3+ (+3x + 7 l0 x 2 3 6x 0
ቤተ መጻሕፍቲ ባይዱ一
设 B Q=O 则 A 1 . A Q= 0 一 . B 6 。
反之 , 当 , =… = =1时 , = 已知 等 式显然 成立.
故 (
一
)
) 五五 翌 : !
+
f 2 : !
3_ . }.
一
4 +2 +2  ̄4 / x4—4 2+ 1
8
注 意到
:
2 一1
—2 一1。
詈 考= 0 3 + l≤≤) ( ,
试题:2011年新知杯上海市初中数学竞赛试题(含答案解析)

2011年新知杯上海市初中数学竞赛试题一、填空题(每题10分,共80分)1.已知关于x的两个方程:错误!未找到引用源。
-x+3m=0……①,错误!未找到引用源。
+x+m=0……②,其中m≠0.若方程①有一个根是方程②的一个根的3倍,则实数m的值是_________。
2.已知梯形ABCD中AB‖CD,∠ABC=90°,BD⊥AD,BC=5,BD=13,则梯形ABCD的面积为______。
3.从编号为1、2、3、4、5、6的六张卡片中任意抽取三张,则抽出的卡片编号都大于2的概率为________.4.将8个数,-7,-5,-3,-2,2,4,6,13排列为a,b,c,d,e,f,g,h,使得+的值最小,则这个最小值为________.5.已知正方形ABCD边长为4,E、F分别在AB,BC上,AE=3,BF=2,AF,DE交于G,则四边形DGFC的面积为。
6.在等腰直角三角形ABC中,∠ACB=90°,P是△ABC内一点,使得PA=11,PB=7,PC=6,则AC边长为____________。
7.有10名象棋选手进行单循环赛,规定每场比赛胜方得2分,负方得0分,平局各得1分,比赛结束后发现每位选手得分各不同,且第二名的得分是最后五名选手得分之和的,则第二名选手得分是_______。
8.已知a,b,c,d都是素数(可以相同),并且abcd是35个连续正整数之和,则a+b+c+d 的最小值为_________.二、解答题(第9、10题每题15分,第11、12题每题20分,共70分)9.如图,矩形ABCD的对角线交于O,已知∠DAC=60°,∠DAC的平分线与DC交于S,直线OS,AD相交于L,直线BL与AC交于M。
求证:SM‖LC.10.求所有正整数组a ≥b ≥c ≥d ≥e ≥f ,使得a !=b !+c !+d !+e !+f !。
11.①求证:存在整数x ,y ,满足+4xy+=2022②是否存在整数x ,y ,满足+4xy+=2011?请证明你的结论。
2013年新知杯上海市初中数学竞赛试题及参考答案

当且仅当 BD FC 时等号成立,此时
1 1 1 1 2 1 2 1 1 + + , + + 的最大值是 1 . 1 1 4 AB AC BC AB 4 AC BC 2 2
10.已知是不为 0 的实数,求解方程组: x (1) xy a y xy y 1 (2) x a 分析:可考虑两式相减,得:
=
1 4 1 , ab = , 3 3 (2 7 )(2 7 )
∴ a 3 a b 3 b = (a b)(a 2 ab b 2 ) (a b) = (a b)[(a b) 2 3ab) (a b) 4 4 64 1 4 = ( )[( ) 2 3( )] ( ) = . 3 3 27 3 3
11.已知 n 1 , a1 , a 2 , a 3 ,…, a n 为整数且 a1 + a 2 + a 3 +…+ a n = a1 a 2 a 3 … a n =2013,求 n 的最小值. 分析:既然 n 1 且 a1 , a 2 , a 3 ,…, a n 为整数,那么我们就从 n 2,3,4 试起,没有发现适合的.当 n 5 时,取 a1 = a 2 =-1, a 3 = a 4 =1, a5 2013 , 则有 a1 + a 2 + a 3 + a 4 + a 5 =-1+(-1)+1+1+2013=2013, a1 a 2 a 3 a 4 a 5 =(-1)×(-1) ×1×1×2013=2013, 以下证明 n 4 时没有适合条件的.不妨设 a1 ≤ a 2 ≤ a 3 ≤…≤ a n , 分两种情况: ⑴当 a1 , a 2 , a 3 ,…, a n 均为正整数时: 由 a1 a 2 a 3 … a n =2013 知, a1 , a 2 , a 3 ,…, a n 均为 2013 的正约数,注意到 2013=3×11×61,欲 a1 + a 2 + a 3 +…+ a n =2013 且 n 4 ,则 a n ≥671,所以 a n =671 或 2013,经验算,n=2,3,4 均不可能; ⑵当 a1 , a 2 , a 3 ,…, a n 中有负整数时:
2010年上海市新知杯详解

(6 2 y) 2 8(2 y 2 6) 12( y 1) 2 0
故 y 2 y 1 0
2
y 1
可得 x 2
3 已知直角三角形 ABC 中, C 90 ,BC 6,CA 3 , CD 为 C 的角平分线,则
CD= 2 2 解:令 CD=x 由面积正弦定理可知
2
数,则 p -2278 解:令 p=67a, q=67b, 可知 a+b=30
p x1 x 2 a 67 由根与系数的关系可知, x x q b 1 2 67
x1 x 2 x1 x 2 a b 30 ( x1 1)( x 2 1) 31
a 2 b 2 a b (a b) 2 16
即 a b 4 2 当且仅当 a b 2 2 成立
所以 a b c 4 2 4 12 这是一道技巧题 显然11 (a c b d f e g i h)
11[(a b c d e f g h i 2(b e h)] 11[45 2(b e h)]
B
1 1 S abc 9 3 x sin 45 6 x sin 45 2 2
故 x= 2 2
D
C
A
4 若前 2011 个正整数的乘积 1 2 2011 能被 2010 k 整除,则正整数 k 的最大值为 30 解: 2010 2 3 5 67
1 2
10 设 a,b,c 是整数,1 a b c 9 ,且 abc bca cab 1 能被 9 整除,则 a b c 的最小值
是 8 ,最大值是 23 解:易知 a+b+c 被 9 除余 2 或 5 或 8 所以(a+b+c)min= 1+2+5=8 (a+b+c)max= 9+8+6=23
2011年新知杯上海市高中数学竞赛

车 戈 一 2 一 4 . ( l + 3 ) ≥0
十3 ・= _口西 0
C
() 6 乙胜 , 乙胜 , 甲胜 , 甲胜.
P
其概 率依次 为 1
寺1 . 、 1 、 故 求概 是 + + = . 所 的率{ 詈 31 1
、
1
1
、
、
图3
由B O:O 知 C,
二 、. 9 当 > 0时
4≥2
・ : 4;
B ,A .P= N= . P/ C B C 3 / 因点 M 在 N P的垂直平分 线上 , 以 , 所
§
:i C+s i A, n
=s +sn B iA n i .
X 3= - ’
4,
故 原式 = . 2
;
5. 一 1 .
设 A( ,) B( a0 , 口+10 , 线 P , )直 A与 Q 8 的交 点为 R( ,) x) . ,
.
显然 ,
AM = 6, B = 4, M AN = 4, NC = 3, M ON =
曰 D C
A
3 知 是 圆 分 l第 象 . 肘 椭 十 =在 一 限 已
的弧 上 一 动 点 , MN 上 Y轴 , 足 为 垂 当
A M O N面 积 最 大 时 , 内切 圆 半 径 r 其 =
t1 + )=ai £ b + g t 2 s n + 2= ()+ , + 是奇 函数 . 6
由 ①② 得 =+, 一 式 、解 口2 詈・ y
2000-2022年(新知杯)历年上海市初中数学竞赛试卷及答案(试题全与答案分开)

2022上海市初中数学竞赛(新知杯)一、填空题(每题10分) 1.721,721-=+=b a ,那么.________33=-+-b b a a2.43214321//////,//////m m m m l l l l ,._______,20,100===EFGH ILKJ ABCD S S S 则3.F E AC AB A 、,,8,690==︒=∠在AB 上且3,2==BF AE 过点E 作AC 的平行线交BC 于D ,FD 的延长线交AC 的延长线于G ,那么.__________=GF4.凸五边形的边长为)(,,,,,54321x f a a a a a 为二次三项式;当1a x =或者5432a a a a x +++=时,5)(=x f ,当21a a x +=时,,)(p x f =当543a a a x ++=时,q x f =)(,那么.________=-q p 5.一个三位数是35的倍数且各个数位上数字之和为15,那么这个三位数为___________.6.关于x 的一元二次方程0)2)(1(2=++++m m ax x 对于任意的实数a 都有实数根,那么m 的取值范围是_________________.7.四边形ABCD 的面积为2022,E 为AD 上一点,CDE ABE BCE ∆∆∆,,的重心分别为321,,G G G ,那么321G G G ∆的面积为________________.8.直角三角形斜边AB 上的高3=CD ,延长DC 到P 使得2=CP ,过B 作AP BF ⊥交CD 于E ,交AP 于F ,那么._________=DE二、解答题〔第9题、第10题15分,第11题、第12题20分〕 9.︒=∠90BAC ,四边形ADEF 是正方形且边长为1,求CABC AB 111++的最大值. 10.a 是不为0的实数,求解方程组:⎪⎪⎩⎪⎪⎨⎧=-=-ax y xy a yxxy 111.:,1>n n a a a a ,,,,321 为整数且2013321321=⋅⋅⋅⋅=++++n n a a a a a a a a ,求n 的最小值.12.正整数d c a 、、、b 满足),13(),13(22-=+=d c b d c a 求所有满足条件的d 的值. 答案:1.27102- 2.60 3.265 4.0 5.735 6.12-≤≤-m 7.36718.599.CA BC AB 111++4221+≤ 10.经检验原方程组的解为:⎪⎩⎪⎨⎧+=+=1122a y a a x ,⎪⎩⎪⎨⎧+-=+-=1122a y a a x .11.【解析】2013,1,1,554321===-===a a a a a n 当满足题设等式,下证当4≤n 时,不存在满足等式要求的整数,不妨设n a a a a ≤≤≤≤ 321,(1)当4=n 时,611132013⨯⨯=,当4321,,,a a a a 中有负整数时,必为⎩⎨⎧==+⇒-==20132015,1434321a a a a a a ,假设2013,143==a a 不满足条件,当20152671,344343<≤+⇒≤⇒≥a a a a a 无解.不可能,当4321,,,a a a a 中无负整数时,显然20134≠a ,6714≤a ,容易验证等式不可能成立.(2)当3=n 时,当321,,a a a 中有负整数时,必为,121-==a a 显然等式不成立,当321,,a a a 中无负整数时,同上容易验证等式不可能成立.(3)当2=n 时,21,a a 均为正整数,同上易验证等式不可能成立. 综上所述,n 的最小值为5. 12.85=d2022上海新知杯初中数学竞赛答案2022年〔新知杯〕上海市初中数学竞赛试卷〔2022年12月9日 上午9:00~11:00〕一、填空题〔每题10分,共80分〕1. 的边上的高为,与边平行的两条直线将的面积三等分,那么直线与之间的距离为_____________。
上海市历届高中数学竞赛(新知杯)试卷及答案(1980-2012)

【说明】解答本试卷不得使用计算器 一、填空题(本题满分 60 分,前 4 题每小题 7 分,后 4 小题每小题 8 分)
1.如图,正六边形 A1B1C1D1E1F1 的边长为 1,它的 6 条对角线又围成一个正六边
形 A2B2C2D2E2F2 ,如此继续下去,则所有这些六边形的面积和是
.
6.在平面直角坐标系中,O 为坐标原点,点 A(3, a) , B (3, b) 使 ∠AOB = 450 ,其中 a 、b 均为整数,且
a > b ,则满足条件的数对 (a,b) 共有
组.
( ) 7.已知圆 C 的方程为 x2 + y2 − 4x − 2 y +1 = 0(圆心为 C ),直线 y = tan100 x + 2 与圆 C 交于 A 、B
2
22
解得(结合 x > 1 )
1< x ≤ 2 +1.
综上所述, h(x) = x2 −1 ,1 < x ≤ 2 +1 . 2x
…………………(14 分)
10.解 f (x) = (a + sin x)(4 + sin x) = 1+ sin x + 3(a −1) + a + 2 .
1+ sin x
6
5
= − 17 ,则 tan (α + β + γ ) =
.
5
4.已知关于 x 的方程 lg (kx) = 2 lg ( x +1) 仅有一个实数解,则实数 k 的取值
范围是
.
5.如图, ΔAEF 是边长为 x 的正方形 ABCD 的内接三角形,已知 ∠AEF = 90° ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 2、黄金与其它金属混合可以制成五颜六色 的色金首饰,当黄金与铜按比例混合,能 制成: • A、白色金 B、红色金 • C、紫色金 D、黄色金
• 3、哈雷慧星的最早记录是哪国人留下的? • • A、英国人 B、法国人 • C、中国人 D、埃及人
• 4、世界上第一架实用直升机在哪个国家诞 生? • A、美国 B、英国 • C、俄国 D、法国
C.地球、水星、金星、火星、木星、土星、海王星、天王星
D.水星、金星、土星、地球、火星、木星、天王星、海王星
• 6、在写作业时,用何种灯具照明较好? • A、白炽灯 D、LED灯 B、荧光灯 C、蜡烛
第二组
每小题200分
• 1、儿童夜间磨牙有多种原因,其中最主要 的原因是由于 • A、白天受惊 B、牙齿疾病 C、消化不良 D、肠道寄生虫病
• 1、两根蜡烛:将两根长短不一的蜡烛竖立 在托盘上并点燃,往托盘里注入适当的水 ,然后将透明的钟罩把两根蜡烛罩住, 钟罩 内的水面上升,钟罩外的水面下降。长蜡 烛先熄灭,为什么?
00 01 59 4 3 1 2 0 1 2 3 4 5 6 7 8 20
Hours Minutes Seconds
Insert Text Here
00 00 59 4 3 1 2 0 1 2 3 4 5 6 7 8 10
Hours Minutes Seconds
Insert Text Here
答:日全食,小孔成像
• 4、人眨眼的作用是什么?
00 01 59 4 3 1 2 0 1 2 3 4 5 6 7 8 20
抢答题环节——我们都是快枪手
• 规则:共18道题,选手通过按抢答器争夺 答题资格,各队成员不分顺序都可回答, 答对加100分,答错扣掉100分。在主持人 宣布“开始”之前有抢答者,取消该队该 题的答题资格,由其他队重新抢答。
• 1、轮船发出六声短笛,这是表示什么呢? • A、倒退 险 B、避让 C、转弯 D、遇
2、激光,由于具有方向性强的特 性,它几乎是一束理想的
A交叉光束 B.发射光束 C、平 行光束 D.环行光束
•3、自然科学中最早出现的学科是 •A、数学
B、天文学
C、医学
D
化学
• 4、在第二次工业革命中,首先制成发电机 的是: • A.迈克尔•法拉第 B.爱迪生 C.贝尔 D 西门子
5、九大行星距离太阳由近及远的顺序依次是: A.水星、金星、地球、火星、木星、土星、天王星、海王星 B.火星、水星、金星、地球、木星、天王星、土星、海王星
• 2、从单纯的逻辑上来讲,荒谬的假设可以 推论出任何荒谬的结论 。那么如何从 “2+2=5”推出“我是奥巴马”? • (此题仅限奥巴马以外的人回答)
00 01 59 4 3 1 2 0 1 2 3 4 5 6 7 8 20
Hours Minutes Seconds
Insert Text Here
“
第十届 ”科技知识竞 赛
机电工程学院科技创新中心
总则
• 每队在比赛开始前先抽取本队的号码。每 组起始分值为1000分。每次得分后由计分 员计分,并在环节结束后公布场上得分。 总分无上限,最低分为零分。
第一环节
第二环节 第六环节
第三环节
第七环节
第四环节
第五环节
第八环节
第一环节
必答题环节——步步为营
• 1、诗经中的“七月流火’是指秋天到了么? • 是
2.打油诗中的“打油”是指人名么? 是
• 3.世界上第一个发现氧气的是中国人么? • 是
• 4.东北林业大学是亚洲占地面积最大的大学 么?
• 5.睡不着觉的时候数数会有利于入睡对吗? • 否
• 6.常听音乐有益于身体健康么? • 是
第五环节
Insert Text Here
00 00 59 4 3 1 2 0 1 2 3 4 5 6 7 8 10
Hours Minutes Seconds
Insert Text Here
• 答: 原因是:燃烧产生的二氧化碳温度很高 ,密度比钟罩内的空气轻,聚集在钟罩上 端。二氧化碳不助燃,所以长蜡烛先熄灭.
D
• 2、下列关于基因工程应用的叙述,正确的是
B
• • • • •
A.基因治疗就是把缺陷基因诱变成正常基因 B.基因诊断的基本原理是DNA分子杂交 C.一种基因探针能检测水体中的各种病毒 D.原核基因不能用来进行真核生物的遗传改良
• 3、上世纪80年代初中国提出了“蓝色革命”的新 构想,其科学含义是: • A.围海造田 B.利用海水提炼食盐 C.利用现代科学技术向蓝色海洋乃至内陆水域索 取人们所需要的众多优质水产品 D.利用现代科学技术使海洋和内陆河水变得更蓝
00 00 59 4 3 1 2 0 1 2 3 4 5 6 7 8 10
Hours Minutes Seconds
Insert Text Here
• • • • •
答案: 1.由于2+2=5,等式两边同时减去2 2.得出2=3,两边同时再减去1 3.得出2=1 4.由于我与奥巴马是2个人,既然2=1,那么 我与奥巴马是1个人,所以我是奥巴马。
Hours Minutes Seconds
Insert Text Here
00 00 59 4 3 1 2 0 1 2 3 4 5 6 7 8 10
Hours Minutes Seconds
Insert Text Here
C
• 17、石油生成的物质来源是? • A、古生物遗体 B、原始森林 C、 岩石
A
• 18、第一个公开向神学挑战并宣告自然科 学的独立的科学家是: A.亚里斯多德 B.哥白尼 C.伽利略
B
第三环节
抢答题环节——顺藤摸瓜
• 规则:由大屏幕给出提示,每题共有4个提示,在 给出第一个提示后,每组选一个选手,选手想出 答案后即可抢答,每题为400分,从第二个提示开 始,每给出一个提示分值减少100分,最低为100 分,答错不扣分,选手答错后,由主大屏幕继续 给出提示,所有选手可以继续抢答。本环节共6道 题。
D
• 11、太阳光是由三部分组成,下面哪种不 是太阳光的组成之一? • A、可见光 B、紫外线 C、不可见光 D 、红外线
C
• 12、短距离通信技术能有效不简化掌上电 脑、笔记本电脑和移动电话等移动通信终 端设备之间的通信,使其更加迅速高效, 这种技术又叫 • A、光通信技术 B、蓝牙技术 • C、宽带技术
• 5、在夜晚天空晴朗的情况下,我们用肉眼 能看到的星星大约有几颗? • A、 3000 B、2000 • C、2500 D、3500
• 6、DNA的双螺旋结构在哪年提出? • A、1951 • C、1953 B、1952 D、1954
第四组
每题400分
• 1、谁发明了E—MAIL? • A、雷托 B、美国BBN公司的技术人员 • C、ARPA的工作人员 D有关 量子理论、狭义相对论和什么等五篇论文,从根 本上改变了物理学的面貌。 • A、α粒子散射 • B、布朗运动 • C、放射性元素的嬗变理论 • D、物体惯性和能量的关系
6、我国南方的梅雨属于: A.地形雨 D.雷阵雨 B.对流雨 C.锋面雨
第二环节
• 规则:共4轮,4组题目,每组题目共6道小 题,4组每组题目的分值分别为100分,200 分,300和400分,每组参赛队轮流选题, 从100分的题目选起,答对加上相应分数, 答错不扣分。每次由每队一名选手作答。 由抽签决定答题顺序。
每题100分
• 1、南极和北极最大的不同在于什么? • A 、有无居民 B、生物多样性 C、永久性 冻土带的存在
• 5、地球磁力线是从南到北吗? • A、是 B、不是 C、从南到北从北 到南都有
• (TRIZ题)1.俄罗斯套娃,运用了TRIZ 40个原理中 的哪个?() • A分解原理 B多用性原理
•
•
•
C等势原理
D嵌套原理
第三组
每题300分
• 1、世界天气的推动力是: • 地球 B、太阳 C、月亮 D、宇宙
简答题环节——王者之战
• 规则:共6道题,每题400分,在主持人念 完题目后,选手有2分钟的时间整理思路, 并将关键语句写在答题板上,2分钟后,依 照分数由高到底的顺序,每组选出一名选 手进行解释,由评委团负责打分,根据解 释的情况,评委团有权给予选手100分, 200分,300分或400分不等的分值。
• •
2、全球第一个蓝牙产品---采用蓝牙技术 的耳机是下列哪个厂商的产品? A、爱立信 B、摩托罗拉 C、诺基亚 D、三星
• 3、电报最早起源于 A、英国 C、法国
B、美国 D、日本
• 4、MP3在不降低音质的前提之下,是以多 少比例压缩CD中的音乐? • A、12:1 B、13:1 • C、11:1 D、14:1
A • 4、下列哪一种茶属于发酵茶 • A红茶 B绿茶 C菊花茶 龙茶
D乌
• 5、奥运五环旗中的绿色环代表哪里? • A、美洲 B、欧洲 C、澳洲 D、亚洲
C
• 6、长度单位中的“码”是多少厘米? A、30厘米 B、60厘米 C、90厘米 D、100厘米
C
• 7、中国最大的淡水湖在哪里? • A、青海湖 B、洞庭湖 C、鄱阳湖 太湖
B
• 13、第一位两次荣获诺贝尔奖的科学家是: • A、爱因斯坦 B、爱迪生 C、居里夫 人
C
• 14、摆钟的发明要归功于伟大的科学家 • A、亚里士多德 B、爱迪生 C、伽利 略
C
• 15、原子核中没有哪种微粒? • A、质子 B、中子 C、电子
C
• 16、核能发电厂内的核反应堆里发生的是 : • A、核聚变 B、核裂变 C、可控 核裂变
提示二:
提示三:
答案不可能是C
